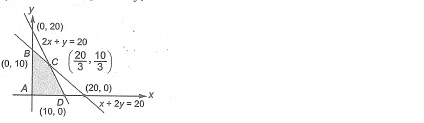MCQ Questions for Class 12 Commerce Maths Linear Programming Quiz 2

Q.1.

Study the graph carefully and answer the question given below it.

The import in

$1976$ was approximately how many times that of the year

$1971$ ?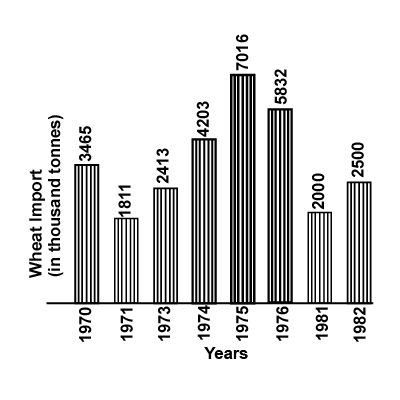

0%
$0.31$
0%
$1.68$
0%
$2.41$
0%
$3.22$

Explanation

Import in

$1976=5832$ tonnes

Import in

$1971=1811$ tonnes

So, import in

$1976/$ import in

$1971=\dfrac{5832}{1811}=3.22$

It is approximately more than three i.e

$3.22$
So,

$Answer (D) \Rightarrow 3.22$

Q.2.

Evaluate

$\displaystyle \frac{(a-b)^{2}}{(b-c)(c-a)}+\frac{(b-c)^{2}}{(a-b)(c-a)}+\frac{(c-a)^{2}}{(a-b)(b-c)}$

0%
0
0%
1
0%
2
0%
3

Explanation

Given,

$\displaystyle \frac{(a-b)^{2}}{(b-c)(c-a)}+\frac{(b-c)^{2}}{(a-b)(c-a)}+\frac{(c-a)^{2}}{(a-b)(b-c)}$

$=\displaystyle \frac{(a-b)^{3}+(b-c)^{3}+(c-a)^{3}}{(a-b)(b-c)(c-a)}$

$=\displaystyle \frac{(a^3-b^3+3b^2a-3a^2b)+(b^3-c^3-3b^2c+3c^2b)+(c^3-a^3-3c^2a+3a^2c)}{(a-b)(b-c)(c-a)}$

$=\displaystyle \frac{3b^2a-3a^2b+3c^2b-3b^2c+3a^2c-3c^2a}{(a-b)(b-c)(c-a)}$

$=\displaystyle \frac{3(b^2a-a^2b+c^2b-b^2c+a^2c-c^2a)}{(a-b)(b-c)(c-a)}$

$=\displaystyle \frac{3(a-b)(b-c)(c-a)}{(a-b)(b-c)(c-a)}$

$= 3$
Option D is correct.

Q.3.

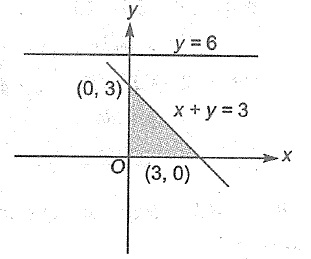
The region represented by the inequation system

$x, y\ge 0, y\le 6, x+y\le 3$ is

0%
Unbounded in first quadrant
0%
Unbounded in first and second quadrants
0%
Bounded in first quadrant
0%
None of the above

Explanation

Q.4.

$z=30x+20y,x+y\le 8,x+2y\ge 4,6x+4y\ge 12,x\ge 0,y\ge 0$ has

0%
Unique solution
0%
Infinitely many solution
0%
Minimum at $\left( 4,0 \right)$
0%
Minimum 60 at point $\left( 0,3 \right)$

Explanation

Since,

$x+y=8$ ....(i)
This line meets axes at

$\left( 8,0 \right)$ and

$\left( 0,8 \right)$ respectively.

$x+2y=4$ .....(ii)

$\Rightarrow \dfrac { x }{ 4 } +\dfrac { y }{ 2 } =1$
This line meet axes at

$\left( 4,0 \right)$ and

$\left( 0,2 \right)$ .
And

$6x+4y=12$ ......(iii)

$\Rightarrow \dfrac { x }{ 2 } +\dfrac { y }{ 3 } =1$
This line meets axes at

$\left( 2,0 \right)$ and

$\left( 0,3 \right)$
The point of intersection of equations (ii) and (iii) is

$F\left( 1,\dfrac { 3 }{ 2 } \right)$
Now, at

$A\left( 4,0 \right) ,z=30\times 4=120$

$B\left( 8,0 \right) ,z=30\times 8=240$

$C\left( 0,8 \right) ,z=20\times 8=160$

$D\left( 0,3 \right) ,z=20\times 3=60$
and

$F\left( 1,\dfrac { 3 }{ 2 } \right) ,z=30\times 1+20\times \dfrac { 3 }{ 2 } =60$
It is clear that

$z$ is minimum 60 at points

$D\left( 0,3 \right)$ and

$F\left( 1,\dfrac { 3 }{ 2 } \right)$
Hence, option (D) is correct.
1039426_460398_ans_79d33e1f75e7494489e3fa20aa46b71f.jpg

Q.5.

An aeroplane can carry a maximum of

$200$ passengers. A profit of Rs.

$1000$ is made on each executive class ticket and a profit of Rs.

$600$ is made on each economy class ticket. The airline reserves at least

$20$ seats for executive class. However, at least

$4$ times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximize the profit for the airline. What is the maximum profit?

0%
$136000$
0%
$1360000$
0%
$13600$
0%
$1360$

Explanation

Let the airline sell

$x$ tickets of executive class and

$y$ tickets of economy class.
The mathematical formulation of the given problem is as follows.
Maximize

$z=1000x+600y .......(1)$
subject to the constraints,

$x+y\le 200 ......(2)$

$x\ge 20 ..........(3)$

$y-4x\ge 0 .......(4)$

$x,y\ge 0 ..........(5)$
The feasible region determined by the constraints is as shown
The corner points of the feasible region are

$A(20,80), B(40,160)$ and

$C(20,180)$
The values of

$z$ at these corner points are as follows.
The maximum value of

$z$ is

$136000$ at

$(40,160)$
Thus,

$40$ tickets of executive class and

$160$ tickets of economy class should be sold to maximize the profit and the maximum profit is Rs.

$136000$ .
1027779_423254_ans_1039e6477de94f20839ba85ff6ad695a.PNG

Q.6.

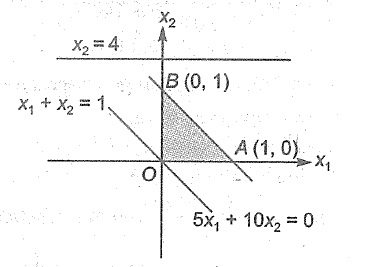
For the LPP

$Minz={ x }_{ 1 }+{ x }_{ 2 }$ such that inequalities

$5{ x }_{ 1 }+10{ x }_{ 2 }\ge 0, { x }_{ 1 }+{ x }_{ 2 }\le 1, { x }_{ 2 }\le 4$ and

${ x }_{ 1 },{ x }_{ 2 }\ge 0$

0%
There is a bounded solution
0%
There is no solution
0%
There are infinite solutions
0%
None of the above

Explanation

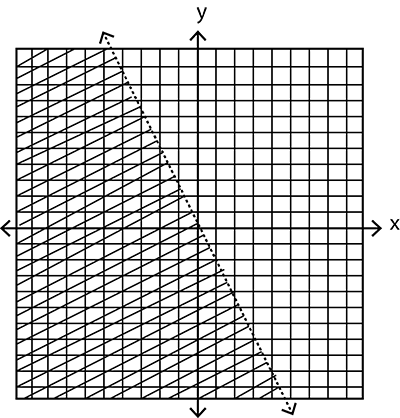
Q.7.

Which inequality is represented by the graph at the right?

0%
$y< 2x+1$
0%
$y< -2x+1$
0%
$y<\cfrac{1}{2}x+1$
0%
$y< -\cfrac{1}{2}x+1$

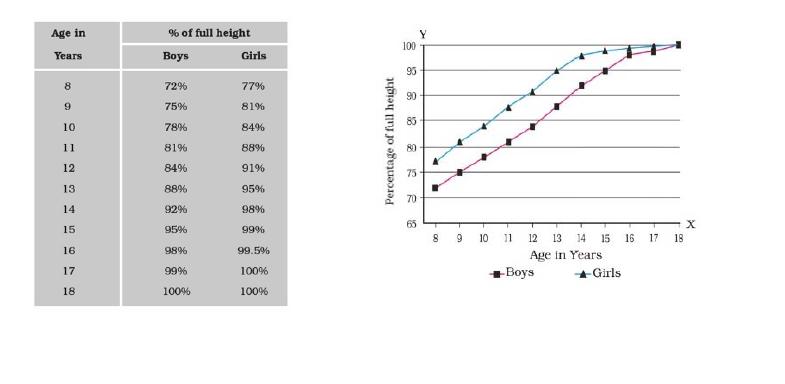
Q.8.

Observe the given chart and graph and answer the following: a girl is

$17$ years old and

$160$ cms tall. At the end of the growth period she is likely to be how tall

0%
$160$ cm
0%
$151$ cm
0%
$160$ m
0%
$151$ m

Explanation

According to given chart 17 years is the end of the growth period of girls.

$\therefore$ answer is 160 cm

Q.9.

A wholesale merchant wants to start the business of cereal with Rs.

$24000$ . Wheat is Rs.

$400$ per quintal and rice is Rs.

$600$ per quintal. He has capacity to store

$200$ quintal cereal. He earns the profit Rs.

$25$ per quintal on wheat and Rs.

$40$ per quintal on rice. If he stores

$x$ quintal rice and

$y$ quintal wheat, then for maximum profit the objective function is

0%
$25x+40y$
0%
$40x+25y$
0%
$400x+600y$
0%
$\dfrac{400}{40}x + \dfrac{600}{25}y$

Q.10.

The fessible region of LPP is a convex polygon and its two consecutive vertices gives optimum solution the LPP has

0%
Only one and finite solution
0%
No solution
0%
Two solutions
0%
None of the above

Explanation

The feasible religion of PP convex polygon

The feasible region of LLP is convex pa polygon and its two consecutive verities gives optimum solution the LLP has infinity many solutions,

For examples,

If points P and Q gives optimum solution then all the points on the line segments OQ also give optimum solution.

so is has infinity many solutions.

$\therefore D is correct.$

2105478_460452_ans_c4691d4f1c884192bdf25ba7cd80b07d.png

Q.11.

A LPP means

0%
Only objective function is linear
0%
Only constraints are linear
0%
Either objective function or constraints are linear
0%
All objective function and constraints are linear

Q.12.

Vikas printing company takes fee of Rs.

$28$ to print a oversized poster and Rs.

$7$ for each colour of ink used. Raaj printing company does the same work and charges poster for Rs.

$34$ and Rs.

$5.50$ for each colour of ink used. If

$z$ is the colours of ink used, find the values of

$z$ such that Vikas printing company would charge more to print a poster than Raaj printing company.

0%
$z < 4$
0%
$2 \leq z \leq 4$
0%
$4 \leq z \leq 7$
0%
$z > 4$

Explanation

$28+7z>34+5.50z$

$\rightarrow 1.50z>6$

$\rightarrow z>6/1.5$

$z>4$

Q.13.

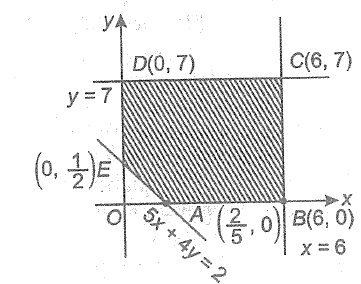
If given constraints are

$5x + 4y \geq 2, x \leq 6, y \leq 7$ , then the maximum value of the function

$z = x + 2y$ is

0%
$13$
0%
$14$
0%
$15$
0%
$20$

Explanation

Given,

$z = x + 2y$
and

$5x + 4y = 2$

$\Rightarrow \dfrac {x}{\dfrac 25} + \dfrac {y}{\dfrac 12} = 1$
At point

$A \left (\dfrac {2}{5}, 0\right ), z = \dfrac {2}{5} + 0 = \dfrac {2}{5}$
At point

$B (6, 0), z = 6 + 0 = 6$
At point

$C (6, 7), z = 6 + 14 = 20$
At point

$D (0, 7), z = 0 + 2(7) = 14$
At point

$E \left (0, \dfrac {1}{2}\right ), z = 0 + 2\left (\dfrac {1}{2}\right ) = 1$

$\therefore$ The maximum value of

$z$ is

$20$ .

1047034_462252_ans_e2bf80a8871d483ca9a7ed7c0e27d29b.png

Q.14.

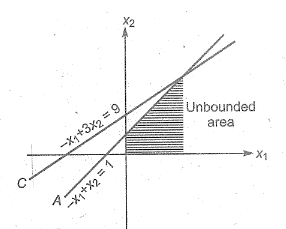
The constraints

$-{ x }_{ 1 }+{ x }_{ 2 }\le 1,\quad -{ x }_{ 1 }+3{ x }_{ 2 }\le 9$ and

${ x }_{ 1 },{ x }_{ 2 }\ge 0$ defines on

0%
bounded feasible space
0%
unbounded feasible space
0%
both unbounded and bounded feasible space
0%
None of the above

Explanation

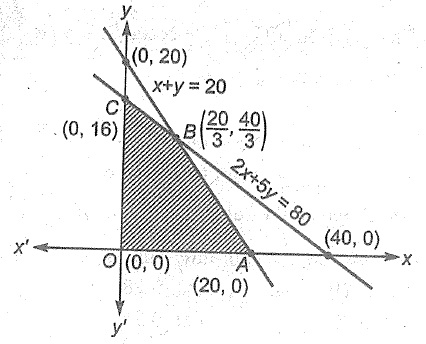
Q.15.

Shaded region is represented by

0%
$2x+5y\ge 80,x+y\le 20,x\ge 0,y\le 0$
0%
$2x+5y\ge 80,x+y\ge 20,x\ge 0,y\ge 0$
0%
$2x+5y\le 80,x+y\le 20,x\ge 0,y\ge 0$
0%
$2x+5y\le 80,x+y\le 20,x\le 0,y\le 0$

Explanation

Shaded region is represented by the inequalities

$2x+5y\le 80,x+y\le 20,x\ge 0,y\ge 0$

Q.16.

$\displaystyle z=10x+25y$ subject to

$\displaystyle 0\le x\le 3$ and

$\displaystyle 0\le y\le 3,x+y\le 5$ then the maximum value of z is

0%
$80$
0%
$95$
0%
$30$
0%
$75$

Explanation

The end points of the figure which forms as per the given condition are

$(0,0), (3,0), (0,3), (3,2), (2,3)$

We check the value of z at these points.

At

$(0,3), z = 0 + 75 = 75$

At

$(3,0), z = 30 + 0 = 30$

At

$(0,0), z = 0$

At

$(3,2), z = 30 + 50 = 80$

At

$(2,3), z = 20 + 75 = 95$

Therefore, the maximum value of z turns out to be 95.

Q.17.

A dealer wishes to purchase toys

$A$ and

$B$ . He has Rs.

$580$ and has space to store

$40$ items.

$A$ costs Rs.

$75$ and

$B$ costs Rs.

$90$ . He can make profit of Rs.

$10$ and Rs.

$15$ by selling

$A$ and

$B$ respectively assuming that he can sell all the items that he can buy formulation of this as L.P.P. is

0%
Maximize $\displaystyle z=10x+15y$

Subject to $\displaystyle x+y\le 40,75x+90y\le 580,x\ge 0,y\ge 0$
0%
Maximize $\displaystyle z=10x+15y$

Subject to $\displaystyle x+y\ge 40,x\ge 0,y\ge 0,75x+90y\ge 580$
0%
Maximize $\displaystyle z=15x+10y$

Subject to $\displaystyle x+y\le 40,75x+90y\le 580,x\ge 0,y\ge 0$
0%
Maximize $\displaystyle z=10x+15y$

Subject to $\displaystyle x+y\ge 40,75x+90y\le 580,x\ge 0,y\ge 0$

Explanation

Let the dealer have

$x$ items of

$A$ and

$y$ items of

$B$ .

Clearly,

$x \geq 0, y \geq 0$

The total number of items must not exceed

$40$ , and so

$x + y \leq 40$

Also, since he has only Rs.

$580$ with him, the total cost must not exceed that.

$\Rightarrow 75x + 90y \leq 580$

Since we need to maximize the profit, which can be written as

$z = 10x + 15y$ since by selling

$1$ item of

$A$ , the profit earned is Rs.

$10$ and Rs.

$15$ for

$B.$

Q.18.

Given a system of inequation:

$\displaystyle 2y-x\le 4$

$\displaystyle -2x+y\ge -4$

Find the value of

$s$ , which is the greatest possible sum of the

$x$ and

$y$ co-ordinates of the point which satisfies the following inequalities as graphed in the

$xy$ plane.

0%
$8$
0%
$12$
0%
$2$
0%
$4$

Explanation

First, rewrite each equation, so that it is in the slope-intercept form of a line, which is

$y = mx + b$ , where

$m$ is the slope and

$b$ is the

$y$ -intercept of the line.

The first equation becomes

$2y< x+4$ or

$y\leq \dfrac{1}{2}x+2$ .

The second equation becomes

$y\geq 2x-4$ .

The greatest

$x + y$ is the point at which the two lines intersect.

Set the equations of the two lines,

$y=\dfrac{1}{2}x+2$ and

$y=2x-4$ , equal to each other and solve for

$x$ .

The resulting equation is

$y=\dfrac{1}{2}x+2$ and

$y=2x-4$ .

Solve for

$x$ to get

$y=\dfrac{3}{-2}x+2=-4$ or

$\dfrac{3}{-2}x=-6$ ,

$\Rightarrow x = 4$

Next, plug

$4$ into one of the two equations to solve for

$y$ .

Therefore,

$y = 2(4) - 4 = 4$ and

$x + y = 4 + 4 = 8$ .

The correct answer is

$8$ .

Q.19.

The maximum value of

$P=x+3y$ such that

$2x+y\leq 20, x+2y\leq 20, x\geq 0, y\geq 0,$ is.

0%
$50$
0%
$40$
0%
$30$
0%
None of these

Explanation

The points in the feasible region are

$A(0, 0), B(0, 10), C\left(\displaystyle\frac{20}{3}, \frac{10}{3}\right)$ and

$D(10, 0)$ .
Objective function is

$(P=x+3y)$
At point A,

$P=0+3(0)=0$
At point B,

$P=0+3(10)=30$
At point C,

$P=\displaystyle\frac{20}{3}+\frac{3(10)}{3}=\frac{50}{3}$
At point D,

$P=10+3(0)=10$

$\therefore$ Maximum value of

$P=30$ at

$B(0, 10)$ .
1169100_461401_ans_5e041d8f551f47ccb93cf229ca6e4146.jpg

Q.20.

For a linear programming equations, convex set of equations is included in region of

0%
feasible solutions
0%
disposed solutions
0%
profit solutions
0%
loss solutions

Explanation

Q.21.

In linear programming, oil companies used to implement resources available is classified as

0%
implementation modeling
0%
transportation models
0%
oil model
0%
resources modeling

Explanation

In linear programming,

$\text{transportation model}$ are applied to problems related to the study of efficient transportation routes.

For oil companies, how effectively the available resources are transported to different destinations with minimum cost.

Q.22.

Linear programming used to optimize mathematical procedure and is

0%
subset of mathematical programming
0%
dimension of mathematical programming
0%
linear mathematical programming
0%
all of above

Explanation

Q.23.

In transportation models designed in linear programming, points of demand is classified as

0%
ordination
0%
transportation
0%
destinations
0%
origins

Explanation

Q.24.

Which of the following is a property of all linear programming problems?

0%
alternate courses of action to choose from
0%
minimization of some objective
0%
a computer program
0%
usage of graphs in the solution
0%
usage of linear and nonlinear equations and inequalities

Explanation

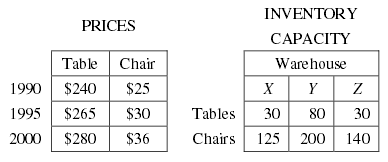
Q.25.

A furniture company makes one style of tables and chairs. The chart on the left above gives the prices of these tables and chairs in three different years. The chart on the right gives the maximum number of tables and chairs that can be stocked in each of three ware-houses,

$X, Y$ , and

$Z$ . Based on the prices shown, what was the maximum possible value of the table and chair inventory in warehouse

$Y$ in 1995 ?

0%
$\$23,950$
0%
$\$26,500$
0%
$\$27,200$
0%
$\$28,400$
0%
$\$29,500$

Explanation

In

$1995$ ,

Price of each table

$=$

$$265$

Price of each chair

$=$

$$30$

In warehouse

$'Y'$ ,

Maximum Number of tables that can be stocked

$=$

$80$

Maximum Number of chairs that can be stocked

$=$

$200$

Price of

$80$ tables

$=$

$80$

$\times$ Price of each table

$=$

$80$

$\times$

$$265$

$=$

$$21,200$

Price of

$200$ chairs

$=$

$200$

$\times$ Price of each chair

$=$

$200$

$\times$

$$30$

$=$

$$6,000$

Maximum possible value of the table and chair inventory in

$'Y'$ in

$1995$

$=$ Price of

$80$ tables

$+$ Price of

$200$ chairs

$=$

$$21,200$

$+$

$$6,000$

$=$

$$27,200$

Therefore, Maximum possible value of the table and chair inventory in

$'Y'$ in

$1995$ is

$'27,200'$ .

Q.26.

In graphical solutions of linear inequalities, solution can be divided into

0%
one subset
0%
two subsets
0%
three subsets
0%
four subsets

Explanation

In graphical solutions of linear inequalities, solution can be divided into two subsets.

for example,

$2x+y\leq 4$

One subset includes all values (x,y) that satisfy the equation

$2x+y = 4$

and the other subset includes all the values (x,y) that satisfy

$2x+y < 4$

Q.27.

Linear programming model which involves funds allocation of limited investment is classified as

0%
ordination budgeting model
0%
capital budgeting models
0%
funds investment models
0%
funds origin models

Explanation

In linear programming,

$\text{Capital budgeting models}$ to minimize the total capital cost.

The solutions from the model are used to decide the best combination of capital resources and best times to start and finish projects and to determine the net capital cost.

Q.28.

In linear programming, objective function and objective constraints are

0%
solved
0%
linear
0%
quadratic
0%
adjacent

Explanation

Q.29.

In order for a linear programming problem to have a unique solution, the solution must exist

0%
at the intersection of the nonnegativity constraints.
0%
at the intersection of a nonnegativity constraint and a resource constraint.
0%
at the intersection of the objective function and a constraint.
0%
at the intersection of two or more constraints.
0%
none of the above

Explanation

Q.30.

The first step in formulating an LP problem is

0%
graph the problem.
0%
perform a sensitivity analysis.
0%
identify the objective and the constraints.
0%
define the decision variables.
0%
understand the managerial problem being faced.

Explanation

Support mcqexams.com by disabling your adblocker.