MCQ Questions for Class 11 Commerce Maths Quiz with Answers Chapter Wise PDF Download
CBSE Multiple Choice Type Questions for 11th Class Commerce Maths PDF formatted study resources are available for free download. These Grade 11 Commerce Maths CBSE MCQ Mock Test helps you learn & practice the concepts in a fun learning way.
Class 11 Commerce Maths MCQs Multiple Choice Questions with Answers
Here are the chapterwise CBSE MCQ Quiz Test Questions for Class 11th Commerce Maths in pdf format that helps you access & download so that you can practice online/offline easily.
- Binomial Theorem Class 11 Commerce Maths MCQ Questions
- Complex Numbers And Quadratic Equations Class 11 Commerce Maths MCQ Questions
- Conic Sections Class 11 Commerce Maths MCQ Questions
- Introduction To Three Dimensional Geometry Class 11 Commerce Maths MCQ Questions
- Limits And Derivatives Class 11 Commerce Maths MCQ Questions
- Linear Inequalities Class 11 Commerce Maths MCQ Questions
- Mathematical Reasoning Class 11 Commerce Maths MCQ Questions
- Permutations And Combinations Class 11 Commerce Maths MCQ Questions
- Principle Of Mathematical Induction Class 11 Commerce Maths MCQ Questions
- Probability Class 11 Commerce Maths MCQ Questions
- Relations And Functions Class 11 Commerce Maths MCQ Questions
- Sequences And Series Class 11 Commerce Maths MCQ Questions
- Sets Class 11 Commerce Maths MCQ Questions
- Statistics Class 11 Commerce Maths MCQ Questions
- Straight Lines Class 11 Commerce Maths MCQ Questions
- Trigonometric Functions Class 11 Commerce Maths MCQ Questions
Binomial Theorem Class 11 Commerce Maths MCQ Quiz
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16
Binomial Theorem Questions and Answers
| Binomial Theorem Quiz Question | Answer |
|---|---|
| The constant term in the expansion of $${ (1+x) }^{ n }{ (1+\frac { 1 }{ x } ) }^{ n }$$ is | $${ C }_{ 0 }^{ 2 }+{ C }_{ 1 }^{ 2 }+.....+{ C }_{ n }^{ 2 }$$ |
| The coefficient of $${ x }^{ 4 }$$ in $${ \left( \dfrac { x }{ 2 } -\dfrac { 3 }{ { x }^{ 2 } } \right) }^{ 10 }$$ is | $$\dfrac { 405 }{ 256 } $$ |
| the coefficient of $$x ^ { 5 }$$ in the expansion of $$( 1 + x ) ^ { 10 }.( 1 + \cfrac { 1 } { x }) ^ { 20 }$$ is | $$^ { 10 }{ C } _ { 5 }$$ |
| The general term in the expansion of $$(x + a)^n$$ |
$$\,^nC_r\,x^{n-r} .a^r$$ |
| If the 4th term in the expansion of $$\left( ax+\frac { 1 }{ x } \right) ^{ n }\quad is\quad \frac { 5 }{ 2 } ,$$ then the values of a and n are- | 1/2, 6 |
| In the expansion of $$\left( \dfrac { x+1 }{ { x }^{ 2/3 }-{ x }^{ 1/3 }+1 } -\dfrac { x-1 }{ x-x^{ -1/2 } } \right) ^{ 10 },$$ the term which does not contain x is | $$^{ 10 }{ { C }_{ 4 } }$$ |
| The coefficient of $$x^2$$ in expansion of the product (2 $$x^2$$).($$(1 + 2x + 3x^2)^6$$ + $$(1 4x^2)^6$$) is : |
108 |
| The first integral term in the expansion of $$(\sqrt{3}+\sqrt[3]{2})^{9}$$, is its | 4th term |
| $$\left (5^{\dfrac {1}{2}} + 7^{\dfrac {1}{6}}\right )^{642}$$ contains $$n$$ integral terms then $$n$$ is | $$108$$ |
| The sum of the coefficients in the expansion of $${ (1+x-{ 3x }^{ 2 }) }^{ 171 }$$ is | 0 |
Complex Numbers And Quadratic Equations Class 11 Commerce Maths MCQ Quiz
Complex Numbers And Quadratic Equations Questions and Answers
| Complex Numbers And Quadratic Equations Quiz Question | Answer |
|---|---|
| The principal amplitude of ($$sin40^o + i cos40^o)^5$$ is | $$-110^o$$ |
| If $$z=\dfrac { \sqrt { 3 } +i }{ \sqrt { 3 } -i } $$, then the fundamental amplitude of z is | $$\dfrac { \pi }{ 3 } $$ |
| If z= $$\dfrac { 1 }{ { \left( 2+3i \right) }^{ 2 } } ,\quad then\left| z \right| $$= | $$\dfrac { 1 }{ 13 } $$ |
| Argument of the complex number $$\left( \dfrac { -1-3i }{ 2+i } \right) $$ | $$225^{ 0 }$$ |
| If $${ z }_{ 1 },{ z }_{ 2 },{ z }_{ 3 },{ z }_{ 4 }$$ be the vertices of a square in Argand plane , then | `$${ 2z }_{ 2 }=\left( 1-i \right) { z }_{ 1 }+\left( 1+i \right) { z }_{ 3 }$$ |
| The complex numbers $${ z }_{ 1 },{ z }_{ 2 },{ z }_{ 2 }$$ satisfying $$\dfrac { { z }_{ 1 }+{ z }_{ 3 } }{ { z }_{ 2 }-{ z }_{ 3 } } =\dfrac { 1-i\sqrt { 3 } }{ 2 } $$ | If area zero |
| If $$z$$ is a complex number such that $$| z | = 1 , z \neq 1 ,$$ then the real part of $$\frac { z - 1 } { z + 1 }$$ is | 0 |
| In which quadrant of the complex , the point $$\dfrac { 1+2i }{ 1-i } $$ kies? | Fourth |
| The amplitude of $$\sin \dfrac { \pi }{ 5 } +i\left( 1-cos\dfrac { \pi }{ 5 } \right) $$ is | $$\dfrac { \pi }{ 10 } $$ |
| The complex number $$z$$ satisfies $$z+|z|=2+8i$$. The value of $$|z|$$ is | 17 |
Conic Sections Class 11 Commerce Maths MCQ Quiz
Conic Sections Questions and Answers
| Conic Sections Quiz Question | Answer |
|---|---|
| The graph of the conic $$x ^ { 2 } - ( y - 1 ) ^ { 2 } = 1$$ has one tangent line with positive slope that passes through the origin, the point of tangency being (a, b). Then Length of the latus rectum of the conic is | $$2$$ |
| If S be the focus of a parabola and PQ be the focal chord,such that SP=3 and SQ = 6,then the length of latus rectum of the parabola is | 8 |
| If eccentricity of the hyperbola $$\dfrac {x^{2}}{\cos^{2}\theta}-\dfrac {y^{2}}{\sin^{2}\theta}=1$$ is more then $$2$$ when $$\theta\ \in \ \left(0,\dfrac {\pi}{2}\right)$$. Find the possible values of length of latus rectum | $$(3,\infty)$$ |
| The graph of the equation $$x^2+\dfrac{y^2}{4}=1$$ is | an ellipse |
| Let$$0<\theta <\dfrac { \pi }{ 2 } .$$ If the eccentricity of the hyperbola $$\dfrac { { x }^{ 2 } }{ { cos }^{ 2 }\theta } -\dfrac { { y }^{ 2 } }{ { sin }^{ 2 }\theta } =1$$ is greater than 2, then the length of its latus rectum lies in the interval: | $$\left( 3,\infty \right) $$ |
| If the radius of the circle $$ x ^ { 2 } + y ^ { 2 } $$ - 18 x - 12 y + k = 0 be 11 then k = |
-4 |
| The latus rectum of a parabola whose focal chord is PSQ such that SP=3 and SQ=2 is given by | 24/5 |
| The value of $$\alpha $$ for which three distinct chords drawn from $$(\alpha ,0)$$ to the ellipse $${ x }^{ 2 }+2{ y }^{ 2 }=1$$ are bisected by the parabola $${ y }^{ 2 }=4x$$ is | $$9$$ |
| The equation $$\dfrac{x^2}{10 - a} + \dfrac{y^2}{4 - a} = 1$$ , represents an ellipse , if | $$a < 4$$ |
| Let PQ be the latus rectum of the parabola $$y^2=4x$$ with vertex A. Minimum length of the projection of PQ on a tangent drawn in portion of parabola PAQ is : | $$2 \sqrt{2}$$ |
Introduction To Three Dimensional Geometry Class 11 Commerce Maths MCQ Quiz
Introduction To Three Dimensional Geometry Questions and Answers
| Introduction To Three Dimensional Geometry Quiz Question | Answer |
|---|---|
| The shortest distance between the lines $$\dfrac {x - 3}{2} = \dfrac {y + 15}{-7} = \dfrac {z - 9}{5}$$ and $$\dfrac {x + 1}{2} = \dfrac {y - 1}{1} = \dfrac {z - 9}{-3}$$ is | $$4 \sqrt 3$$ |
| If $$a,b$$ and $$c$$ are non coplanar vectors then $$-\bar {a}+4\bar {b}-3\bar {c},3\bar {a}+2\bar {b}-5\bar {c},-3\bar {a}+8\bar {b}-5\bar {c},-3\bar {a}+2\bar {b}+\bar {c}$$ are collinear. | True |
Let $$A(2,3,5),B(-1,3,2)$$ and $$C(\lambda ,5,\mu )$$ are the vertices of a triangle and its median through A meets side BC at D. AD is equally inclined with the axes. If E is the point on BC such that $$BE:EC=1:2.$$ Equation of plane containing triangle ABC |
$$x+y+3=0$$ |
Point $$D$$ has coordinates as $$(3,4,5)$$. Referring to the given figure, find the coordinates of point $$C$$. |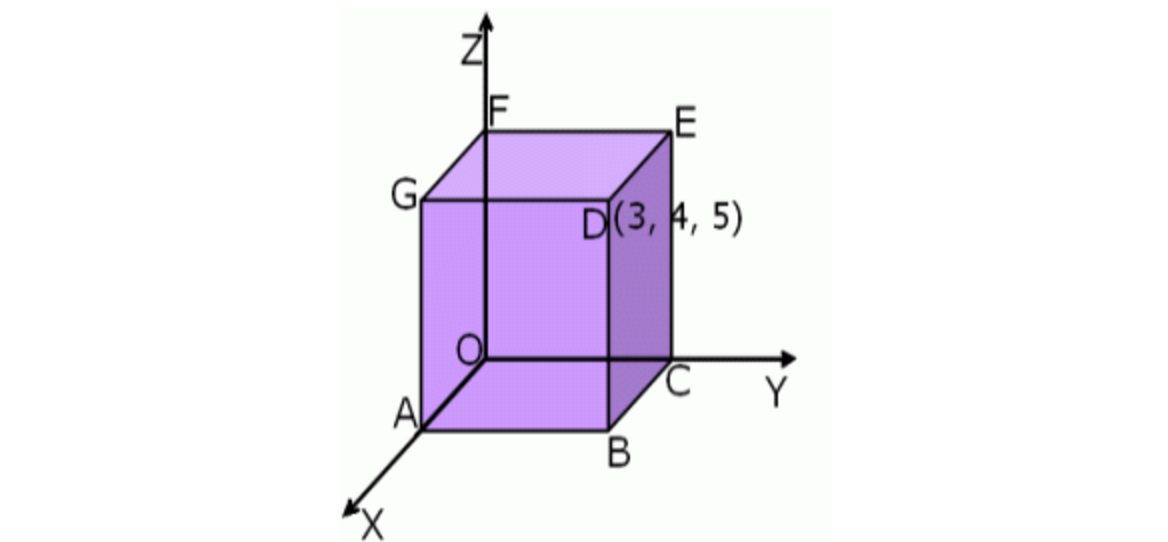
$$(0,4,0)$$ |
| The locus of a point, which is equidistant from the points $$(1, 1)$$ and $$(3, 3)$$, is | $$x + y = 4$$ |
| Perpendicular distance from the origin to the line joining the points $$(a\cos{\theta},a\sin{\theta})(a\cos{\theta},a\sin{\theta})$$ is | $$2a\cos{(\theta-\phi)}$$ |
| Distance between $$A(4,5,6)$$ from origin $$O$$ is | $$\sqrt {77}$$ |
In the given figure, co-ordinates of the midpoint of $$AB$$ are  |
$$(3,1)$$ |
| Name three undefined terms. |
All of the above |
State the following statement is True or False If two distinct lines are intersecting each other in a plane then they cannot have more than one point in common. |
True |
Limits And Derivatives Class 11 Commerce Maths MCQ Quiz
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16
Quiz 17
Limits And Derivatives Questions and Answers
| Limits And Derivatives Quiz Question | Answer |
|---|---|
| $$\mathop {\lim }\limits_{x \to \infty } \left( {\dfrac{{{x^2}\sin \left( {\dfrac{1}{x}} \right) - x}}{{1 - \left| x \right|}}} \right) = $$ | 0 |
| $$\begin{matrix} lim \\ x\rightarrow 0 \end{matrix}(cos\quad +\quad sinx{ ) }^{ 1/x }$$ is equal to | e |
| $$ \lim _{x \rightarrow a}\left(2-\frac{a}{x}\right)^{\tan \left(\frac{\pi x}{2 a}\right)} $$ |
$$ e^{-\frac{a}{\pi}} $$ |
| $$\displaystyle \lim _{ \theta \rightarrow 0 }{ \frac { 4\theta \left( \tan { \theta -2\theta \tan { \theta } } \right) }{ { \left( 1-\cos { 2\theta } \right) }^{ 2 } } } $$ is | $$2$$ |
| $$\displaystyle \lim_{x\rightarrow0 }{\dfrac{(\cos\alpha)^{x}-(\sin\alpha)^{x}-\cos 2\alpha}{(x-4)}}, \alpha\in \left(0, \dfrac{\pi}{2}\right)$$ is equal to | $$\cos^{4}\alpha.\log(\cos\alpha)-\sin^{4}\alpha.\log(\sin\alpha)$$ |
| evaluate$$ \underset { x\rightarrow 0 }{ lim } \frac { x-\int _{ 0 }^{ x }{ { cost }^{ 2 }dt } }{ { x }^{ 3 }-6x } $$ | $$0$$ |
| $$\lim _ { x \rightarrow 0 } \left\{ \tan \left( \frac { \pi } { 4 } + x \right) \right\} ^ { \frac { 1 } { x } } =$$ | $$e ^ { 2 }$$ |
| $$\displaystyle\lim_{x\rightarrow \infty}\left(\dfrac{x+1}{2x+1}\right)^{x^2}$$ equals? | $$0$$ |
| $$\lim_{x\rightarrow 0}\frac{ln(sin 3x)}{ln(sin x)}$$ is equal to | 1 |
| If $$\displaystyle \lim_{x\rightarrow 0}\dfrac {ae^{-x}-b\cos x-\dfrac {1}{2}cx}{x\cos x}=2$$ then the value of $$a+b+c$$ is- | $$-4$$ |
Linear Inequalities Class 11 Commerce Maths MCQ Quiz
Linear Inequalities Questions and Answers
| Linear Inequalities Quiz Question | Answer |
|---|---|
Which equation has the solution shown on the number line? |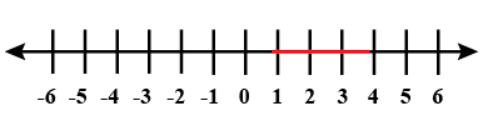
$$1\leq x < 4$$. |
| Ordered pair that satisfy the equation $$x + y + 1 < 0$$ is: | Both (B) and (C) |
| Which of the following number line represents the solution of the inequality $$15 < 4x + 3 \le 31$$ ?  |
|
Which equation has the solution shown on the number line? |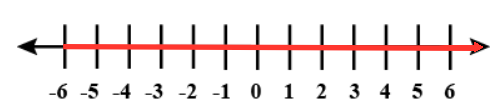
$$x \geq -6$$ |
Which equation has the solution shown on the number line? |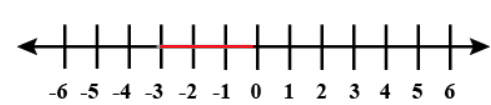
$$-3\leq x < 0 $$. |
| If you multiply an inequality by a negative number, when should you reverse the inequality symbol? | Always |
| Find solution of following inequality also show it graphically. $$x<5,x\in W$$. |
|
| Solve the following inequality and show it graphically: $$-2<x+3<5,x\in Z$$ |
|
| Which of the following number line represents the solution of the inequality $$2x+1 \ge 9$$? | |
| Find the solution of following inequality, also show it graphically: $$x<4,x\in R$$ |
Mathematical Reasoning Class 11 Commerce Maths MCQ Quiz
Mathematical Reasoning Questions and Answers
| Mathematical Reasoning Quiz Question | Answer |
|---|---|
| If $$(p\wedge \sim q)\wedge (p\wedge r)\rightarrow \vee \sim p \vee q$$ is false then the truth values of $$p,q$$ and $$r$$ are respectively | $$T,F,T$$ |
| Rohith makes a statements p,q about future.If it is Known that p$$\rightarrow $$q and probability of occurance of p is $$\frac { 3 }{ 5 } $$. what is the probability that q doesn't happen. | $$\dfrac { 3 }{ 5 } $$ |
| The contrapositive of the following statement, "If the side of a square doubles, then its area increases four times"' is: | If the area of a square does not increase four times, then its side is not doubled |
| Consider the following two statements: P: If $$7$$ is an odd number, then $$7$$ is divisible by $$2$$. Q: If $$7$$ is a prime number, then $$7$$ is an odd number. If $$V_{1}$$ is the truth value of the contrapositive of P and $$V_{2}$$ is the truth value of contrapositive of Q, then the ordered pair $$(V_{1}, V_{2})$$ equals: |
$$(F, T)$$ |
| The Boolean expression $$( ( p \wedge q ) \vee ( p \vee \sim q ) ) \wedge ( \sim p \wedge \sim q )$$ is equivalent to : | $$(\sim { p })\wedge (\sim { q })$$ |
| The negation of $$\sim s \vee (\sim r\wedge s)$$ is equivalent to | $$S\wedge\ r$$ |
| State true or false. A rhombus is a parallelogram. |
True |
| The contrapositive of the statement 'If I am not feeling well, then I will go to the doctor' is: | If I will not go to the doctor, then I am feeling well |
| The contrapositive of the statement 'I go to school if it does not rain' is: | If I do not go to school, it rains. |
| The contrapositive of the statement "If it is raining, then I will not come", is : | If I will come, then it is not raining. |
Permutations And Combinations Class 11 Commerce Maths MCQ Quiz
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Permutations And Combinations Questions and Answers
| Permutations And Combinations Quiz Question | Answer |
|---|---|
| If $$^nC_{10}={^{n}C_{14}}$$, then $$n=?$$ | $$24$$ |
| There are infinite, alike, blue, red, green and yellow balls. Find the number of ways to select $$10$$ balls. | $$286$$ |
| Let $$(1+x)^n=C_0+C_1x+C_2x^2+.....+C_nX^n$$. (where $$C_r=^nC_r$$) On the basis of given information, answer the following question. $$C_1-3(C_3)+5(C_5)-7(C_7)+$$_______ is? |
$$n.2^{\left(\dfrac{n-1}{2}\right)}$$ |
| The no .of ways of selecting a prime numbers from First 10 natural numbers is | $$^{10}C_4$$ |
| $$^n$$C$$_0$$ + 2$$^2$$ . $$\dfrac{^nC_1}{2}$$ + 2$$^3$$ . $$\dfrac{^nC_2}{3}$$ +.......+ 2$${n + 1}$$ . $$\dfrac{^nC_n}{n + 1}$$ = | $$\dfrac{3^{n+1} - 1}{n + 1}$$ |
| If $$(1+x)^{n}=C_{0}+C_{1}x+C_{2}x^{2}+...+C_{n}x^{n}$$, then the value of $$C_{0}^{2}+\dfrac{C_{1}^{2}}{2}+\dfrac{C_{2}^{2}}{2}+.........+\dfrac{C_{n}^{2}}{n+1}$$ is | $$\dfrac{(2n+1)!}{\left\{(n+1)!\right\}^{2}}$$ |
| The number of ways in which three girls and ten boys can be seated in two vans, each having numbered seats, three in the front and four at the back is | $$14!$$ |
| The sum $$\sum _{ r=1 }^{ n }{ r.{ }^{ 2n }{ C }_{ r } } $$ is equal to. | $$n.2^{2n-1}$$ |
| The total no. of six digit numbers $${ x }_{ 1 }{ x }_{ 2 }{ x }_{ 3 }{ x }_{ 4 }{ x }_{ 5 }{ x }_{ 6 }$$ having the property $${ x }_{ 1 }<{ x }_{ 2 }\le { x }_{ 3 }<{ x }_{ 4 }<{ x }_{ 5 }\le { x }_{ 6 }$$, is equal to | $$_{ }^{ 11 }{ C }_{ 6 }$$ |
| If $$^nC_r$$ denotes the number of combinations of n things taken r things at a time, then the expression $$^nC_{r+1} + ^nC_{r-1}+2 ^nC_r is$$ |
$$^{n+2}C_{r+1}$$ |
Principle Of Mathematical Induction Class 11 Commerce Maths MCQ Quiz
Principle Of Mathematical Induction Questions and Answers
| Principle Of Mathematical Induction Quiz Question | Answer |
|---|---|
| Statement-l: For every natural number $$n\geq 2,\ \displaystyle \frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\ldots\ldots+\frac{1}{\sqrt{n}}>\sqrt{n}$$. Statement-2: For every natural number $$n\geq 2,\ \sqrt{n(n+1)}<n+1$$. |
Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1. |
| Let $$S(k) = 1 + 3 + 5 + .... + (2k - 1) = 3 + k^2$$. Then which of the following is true? | $$S (k)$$ $$\Rightarrow$$ $$S (k + 1)$$ |
| Mathematical Induction is the principle containing the set |
N |
| Let $$P(n)$$ be a statement and $$P(n)=P(n+1) \forall n\in N$$, then $$P(n)$$ is true for what values of $$n$$? |
For all $$n$$ |
| State whether the following statement is true or false. cos x + cos 2x + .... + cos nx = $$\dfrac{cos\left (\dfrac{n \, + \, 1 }{2} \right )x sin \dfrac{nx}{2}}{sin\dfrac{x}{2}}$$ |
True |
| $$1+3+5+....+(2n-1)=n^2$$. | True |
A bag contains $$3$$ red and $$2$$ black balls. One ball is drawn from it at random. Find the probability of drawing red ball is $$\dfrac 35$$ |
True |
| Let $$P(n)$$ be the statement $$"3^n>n"$$. If $$P(n)$$ is true, $$P(n+1)$$ is true. | True |
| Let $$P(n)= 5^{n}-2^{n}$$. $$P(n)$$ is divisible by $$ 3\lambda$$ where $$\lambda$$ and $${n}$$ both are odd positive integers, then the least value of $$n$$ and $$\lambda$$ will be |
$$1$$ |
| For every integer $$n\geq 1, (3^{2^{n}}-1)$$ is always divisible by |
$$2^{n+2}$$ |
Probability Class 11 Commerce Maths MCQ Quiz
Probability Questions and Answers
| Probability Quiz Question | Answer |
|---|---|
| Let A and B are two events such that $$P(A)>0$$ and $$P(B)\neq 1$$, then $$P(\overset { - }{ A } /\overset { - }{ B } )$$ is not equal to - | $$\cfrac { 1-P(A\cup B) }{ P(\overset { - }{ B) } } $$ |
| If $$P\left( B \right) = \frac{3}{5},P\left( {A/B} \right) = \frac{1}{2}$$ and $$P\left( {A \cup B} \right) = \frac{4}{5},$$ then $$P\left( {\left( {A \cup B'} \right)} \right) + P\left( {A' \cup B} \right) = $$ | $$1$$ |
| Which of the following are impossible events ? |
Sun rising in the West |
| Probability of an event $$E\, +$$ Probability of the event 'not $$E$$'$$=$$_____ | $$1$$ |
| Suppose six coins are flipped. Then the probability of getting at least one tail is: | $$\dfrac {63}{64}$$ |
| If $$P(A) = P(B)$$, then the two events $$A$$ and $$B$$ are - |
Equally likely |
| The probability of an impossible event is ____ | $$0$$ |
| The probability of an event that cannot happen is ____? | $$0$$ |
A student appears for tests, I, II and III. The student is successful if he passes in tests I, II or I, III. The probabilities of the student passing in tests I, II and III are respectively p, q and $$\dfrac{1}{2}$$. If the probability of the student to be successful is $$\dfrac{1}{2}$$ then |
p(1 + q) $$=$$ 1 |
| The probability of an event that is certain to happen is ____? | $$1$$ |
Relations And Functions Class 11 Commerce Maths MCQ Quiz
Relations And Functions Questions and Answers
| Relations And Functions Quiz Question | Answer |
|---|---|
| Let $$X$$ be a family of sets and $$R$$ be a relation on $$X$$ defined by $$'A$$ is disjoint from $$B ^ { \prime }$$ . Then $$R$$ is _________. |
Symmetric |
| If $$ \int f(x) \, cos x \, dx = \dfrac{1}{2} f^2(x) + c$$ then f(x) is | sin x |
| The complete set of values of $$x$$ for which the function $$f(x)=2\tan^{-1}x+\sin^{-1} \dfrac{2x}{1+x^{2}}$$ behaves like a constant function with positive output is equal to |
$$x \in [-1,1]$$ |
| Find the second component of an ordered pair $$(2, -3)$$ |
$$-3$$ |
| Which of the ordered pair satisfies the relation $$x<y$$? | $$(1,2)$$ |
| Let $$f:(-1, 1)\rightarrow R$$ be such that $$f\left(\cos 4\theta\right)=\dfrac {2}{2-\sec^{2}\theta}$$ for $$\theta \in \left(0, \dfrac {\pi}{4}\right)\cup \left(\dfrac {\pi}{4},\dfrac {\pi}{2}\right)$$. Then the value(s) of $$f\left(\dfrac {1}{3}\right)$$ is/are | $$1-\sqrt {\dfrac {3}{2}}$$ |
| The domain of the relation R = $$\displaystyle \left \{ \left ( x,y \right ):x,y\epsilon N \ and\ x+y\leq 3 \right \}$$ is____ | {1,2} |
| If A= {0, 1} and B ={1, 0}, then what is A x B equal to ? | A X A |
| The ______ product of two sets is the set of all possible ordered pairs whose first component is a member of the first set and whose second component is a member of the second set. |
cartesian |
| Identify the first component of an ordered pair $$(2, 1)$$. |
$$2$$ |
Sequences And Series Class 11 Commerce Maths MCQ Quiz
Sequences And Series Questions and Answers
| Sequences And Series Quiz Question | Answer |
|---|---|
| Let $$N=\{1,2,3,.......,10\},$$ then sum of product of number taken two at a time from the set $$N$$ is |
$$55 \times 24$$ |
| 2, 7, 24, 77, 238, .... | 723 |
| The geometric sequence is also called as |
geometric progression |
| Find the wrong term in sequence :1, 3, 7, 15, 27, 63, 127 | 27 |
| Find the wrong term in sequence :24, 27, 31, 33, 36, 39 | 31 |
| The value of $$\displaystyle \sum_{r = 16}^{30}{ (r + 2)(r - 3) } $$ is equal to : | $$7780$$ |
Let $$\mathrm{a}_{1},\ \mathrm{a}_{2},\ \mathrm{a}_{3},\ \ldots,\ \mathrm{a}_{11}$$ be real numbers satisfying $$\mathrm{a}_{1}=15,27-2\mathrm{a}_{2}>0$$ and $$\mathrm{a}_{\mathrm{k}}=2\mathrm{a}_{\mathrm{k}-1}-\mathrm{a}_{\mathrm{k}-2}$$ for $$\mathrm{k}=3,4,\ \ldots, 11.$$ If $$\displaystyle \frac{a_{1}^{2}+a_{2}^{2}+\ldots+a_{11}^{2}}{11}=90$$, then the value of $$\displaystyle \frac{a_{1}+a_{2}+\ldots+a_{11}}{11}$$ is equal to |
$$0$$ |
| $$x\left (x + \dfrac {1}{x}\right )^{2} + \left (x^{2} + \dfrac {1}{x^{2}}\right )^{2} + \left (x^{3} + \dfrac {1}{x^{3}}\right )^{2}$$ .... upto $$n$$ terms is | $$\dfrac {x^{2n} - 1}{x^{2} - 1}\times \dfrac {x^{2n + 2} + n}{x^{2n}} + 2n$$ |
| Which letter will be the fifth from the right if the first and second, the third and fourth and so on are interchanged among each other in the word "COMPANIONATE"? | I |
| If the sum of the first n natural numbers is 1/5 times the sum of the their squares, then the value of n is | 7 |
Sets Class 11 Commerce Maths MCQ Quiz
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Sets Questions and Answers
| Sets Quiz Question | Answer |
|---|---|
| Let $$S={1,2,3,.....10}$$ and $$P={1,2,3,4,5}$$ The number of subsets $$'Q'$$ of $$S$$ such that $$p \cup Q=S$$, are..... | $$128$$ |
| For two sets $$A$$ and $$B$$, $$A^c-B^c=B-A$$. | True |
| The statement that is true among the following is | $$p\Longrightarrow q$$ is equivalent to $$p\wedge -q$$ |
| Which of the following statements is true (if N, W and I are sets of Natural, Whole and Integer numbers respectively ? | $$N\, \subset \, W\, \subset \, I$$ |
| S = {1, 2, 3, 5, 8, 13, 21, 34 }. Find $$\displaystyle \sum $$ max (A), where the sum is taken over all 28 elements subsets A to S. | 484 |
| If two sets $$A$$ and $$B$$ are having $$80$$ elements in common, then the number of element common to each of the sets $$A\times B$$ and $$B\times A$$ are | $${2}^{80}$$ |
| Examine whether the following statements are true or false: $$(1,2,3)\subset (1,3,5)$$ |
False |
| If P is true and Q is false, then Bi-implication of p and q is | False |
| For any two sets $$ A$$ and $$B, A = B$$ is equivalent to |
$$A \cup C = B \cup C$$ and $$A \cap C = B \cap C $$ for any set $$C$$ |
| If A = {1, 2, 3, 4, 5, 6, 7, 8} and B = {1, 3, 5, 7}, then find $$A - B$$ and $$A \cap B$$ |
{2, 4, 6, 8} and {1, 3, 5, 7} |
Statistics Class 11 Commerce Maths MCQ Quiz
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Statistics Questions and Answers
| Statistics Quiz Question | Answer |
|---|---|
| $$\sum _{ i=1 }^{ 10 }{ { \left( { X }_{ i }-10 \right) }^{ 2 }=2000 } \sum _{ i=1 }^{ 10 }{ { X }_{ i }-10 } =100$$ then the standard deviation of data set $${X}_{i}$$. | $$1$$ |
| Find the standard deviation of 10 observation 111, 211, 311,.......,1011. | 100$$\sqrt { 3 } $$ |
| The mean and standard deviation of $$1,2,3,4,5,6$$ are | $$\dfrac{7}{2},\sqrt{\dfrac{35}{12}}$$ |
| Which one of the following is a measure of dispersion? | Standard deviation |
| Two sets each of $$20$$ observations, have the same standard deviation $$'5'$$. The first set has a mean $$'17'$$ and the second set mean $$'22'$$ then standard deviation of the combining the given two sets is | $$5.59$$ |
| The mean deviation from mean of the observation $$a,\ a+d,\ a+2d,....,a+2nd$$ is | $$None\ of\ these$$ |
| The standard deviation of a varibale x is$$\sigma $$. The standard devaition of the varibale $$\frac { ax+b }{ c } $$ where a, b, c are constant is _____________________. | $$\left( \frac { a }{ b } \right) \sigma $$ |
| The average marks of 10 students in a class is 60 with standard deviation 4 while the average marks of other 10 students is 40 with standard deviationIf all the 20 students are taken together, their standard deviation will be | $$\sqrt {109}$$ |
| Ina a class of 20 students, each student can score 10 or 0 marks in a certain examination. The maximum possible variance in the marks of the students in the class is | 25 |
| Consider the first $$10$$ positive integers. If we multiply each number by $$-1$$ and then add $$1$$ to each number, the variance of the numbers so obtained is | $$8.25$$ |
Straight Lines Class 11 Commerce Maths MCQ Quiz
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Straight Lines Questions and Answers
| Straight Lines Quiz Question | Answer |
|---|---|
| The angle at which the circle $$x^2$$ + $$y^2$$ = 16 can be seen from the point (8 , 0) is | $$\dfrac{\pi}{6}$$ |
| Area of a triangle whose vertices are $$(a\cos \theta ,b\sin \theta ),(-a\sin \theta ,b\cos \theta)$$ and $$(-a\cos \theta ,-b\sin \theta )$$ is- | ab |
| If A+B=C and A=B=C then what should be the angle between A and B ? | $$2\pi /3$$ |
| Two sides of a rhombus are along the lines, $$x-y+1=0$$ and $$7x-y-5=0$$. If its diagonals intersect at (-1, -2), then which one of the following is a vertex of this rhombus? | $$(\frac 13,\frac 83)$$ |
| If $$m_1$$ and $$m_2$$ are the roots of the equation $$x^2 +(\sqrt 3 +2) x + \sqrt 3 - 1 = 0 $$, then the area of the triangle formed by the lines $$y=m_1x,y=-m_2x$$ and $$y=1$$ is: | $$\dfrac{1}{2} \Bigg ( \dfrac{-\sqrt 3 + 2}{\sqrt 3 -1} \Bigg )$$ |
| If $$ (\sqrt{2x}+\sqrt{3y}^{2} -36(\sqrt{3x}-\sqrt{2y})^{2}=0$$ and $$\sqrt{2x}-\sqrt{3y}+4\sqrt{5}=0$$ represents an Issosceles traiangle with base angle $$tan^{-1}6$$ then its area is | 8/3 |
| If $$A ( 3 , - 1 ) , B ( 2,3 )$$ and $$= ( 5,1 ) ,$$ then $$m \angle A =$$ | $$\sin ^ { - 1 } \cfrac { 5 } { \sqrt { 34 } }$$ |
| Area of the triangle formed by $${ (x }_{ 1 },{ y }_{ 1 })$$,$${ (x }_{ 2 },{ y }_{ 2 })$$, $${ (3x }_{ 2 }-{ 2x }_{ 1 },{ 3y }_{ 2 }-{ 2y }_{ 1 })$$ is |
0 sq.units |
| Find the inclination of a line with slope $$\sqrt { 3 } $$ |
$${ 30 }^{ o }$$ |
| The area of a triangle whose sides are $$ a , b $$ and $$ c $$ is | $$ \sqrt { s ( s - a ) ( s - b ) ( s - c ) } $$ sq. units |
Trigonometric Functions Class 11 Commerce Maths MCQ Quiz
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16
Quiz 17
Trigonometric Functions Questions and Answers
| Trigonometric Functions Quiz Question | Answer |
|---|---|
| If $$sin \alpha + sin \beta = \dfrac{1}{2} $$ and $$cos \alpha + cos \beta = \dfrac{\sqrt{3}}{2}$$ then $$3 \beta + \alpha = $$ | $$0^o$$ |
| The value of $$\sin \dfrac {2\pi}{7}+\sin \dfrac {4\pi}{7}+\sin \dfrac {8\pi}{7}$$ is | $$\dfrac {\sqrt {15}}{4}$$ |
| The value of $$\tan\theta+\sec\theta$$ is equal to | $$3t$$ |
| If $$\tan^{2}\alpha-\tan^{2}\beta-\dfrac{1}{2}\sin(\alpha-\beta)\sec^{2}\alpha\sec^{2}\beta$$ is zero then value of $$\sin(\alpha+\beta)$$ is $$(\alpha\neq\beta)$$ | $$\dfrac{1}{2}$$ |
| The value of $$\sin{\left(\alpha+\beta\right)}$$ is | $$\dfrac{24}{25}$$ |
| If $$\alpha + \beta = 90^{\small\circ}$$ and $$\alpha = 2\beta$$, then $$\cos^2\alpha + \sin^2\beta$$ equal | $$\displaystyle\frac{1}{2}$$ |
| $$\displaystyle \frac { \tan ^{ 2 }{ \theta } }{ \tan ^{ 2 }{ \theta } -1 } +\frac { \csc ^{ 2 }{ \theta } }{ \sec ^{ 2 }{ \theta } -\csc ^{ 2 }{ \theta } } =\frac { 1 }{ \sin ^{ 2 }{ \theta } -\cos ^{ 2 }{ \theta } } $$. | True |
| In a $$\triangle ABC, \sum a \cos A=4 \sin A \sin B \sin C$$, then value of $$\left(\dfrac{\sum \sin A}{\sum a}\right)^{2}$$ is- | $$\dfrac{1}{4}$$ |
| The number of $$x\epsilon [0, 2\pi]$$ for which $$|\sqrt {2\sin^{4} x + 18\cos^{2}x} - \sqrt {2\cos^{4} x + 18\sin^{2} x}| = 1$$ is: | $$8$$ |
| For $$x \in (0, \pi)$$, the equation $$\sin x + 2 \sin 2 x - \sin 3x =3$$, has | no solution |
Commerce Maths MCQ Questions for Class 11 - Practice Test with Solutions
Do you want to overcome your drawbacks while attempting the quizzes or MCQ tests like time consumption, approaching questions, etc.? Take the advantage of practicing with MCQExams.com MCQ Questions for Standard 11 Commerce Maths Test. As it is a time-based approach and also provides answers to all questions.
One should practice the MCQs in this way for a better assessment of their preparation level. All chapters CBSE Class 11 Commerce Maths MCQ Quiz Questions with Solutions PDF free download links are available for easy access & quick reference.
How to Use MCQExams.com Chapterwise 11th Commerce Maths MCQ Interactive Quiz?
Guys do you love to share your practice hacks and tips with your friends? If yes, then our 11tth standard CBSE Commerce Maths MCQ interactive quiz help you do the same. Excited to know the process then jump into the below steps right away:
- Go with the respective chapter class 11 Commerce Maths MCQ quiz link from the above
- Now, you will find the MCQ quiz boxes for the Limits And Derivatives chapter along with the interactive quiz windows.
- Click on the CBSE 11th Class Limits And Derivatives MCQ Interactive Quiz and it will redirect you to another window where it displays the questions with options in stories format.
- Answer the question one after another and learn the answers right away this helps you to do a quick assessment of your knowledge.
- You can also share this cool MCQ Interactive Quiz Questions of Plus One Commerce Maths topicwise with your friends by just tapping on the send arrow located at the top left corner of the story.
- After clicking the button, you can opt for the copy link option and easily paste the link on your friend's chat or else in your whatsapp story too. Isn’t it cool!!
- Keep passing this interesting approach of practicing Plus One CBSE Commerce Maths Limits And Derivatives MCQ Questions to your co-students and help them in attempting the entrance exams like JEE & NEET.