MCQ Questions for Class 11 Physics Quiz with Answers Chapter Wise PDF Download

CBSE Multiple Choice Type Questions for 11th Class Physics PDF formatted study resources are available for free download. These Grade 11 Physics CBSE MCQ Mock Test helps you learn & practice the concepts in a fun learning way.

Class 11 Physics MCQs Multiple Choice Questions with Answers

Here are the chapterwise CBSE MCQ Quiz Test Questions for Class 11th Physics in pdf format that helps you access & download so that you can practice online/offline easily.

• Gravitation Class 11 Engineering Physics MCQ Questions
• Kinetic Theory Class 11 Engineering Physics MCQ Questions
• Laws Of Motion Class 11 Engineering Physics MCQ Questions
• Mechanical Properties Of Fluids Class 11 Engineering Physics MCQ Questions
• Mechanical Properties Of Solids Class 11 Engineering Physics MCQ Questions
• Motion In A Plane Class 11 Engineering Physics MCQ Questions
• Motion In A Straight Line Class 11 Engineering Physics MCQ Questions
• Oscillations Class 11 Engineering Physics MCQ Questions
• Physical World Class 11 Engineering Physics MCQ Questions
• Systems Of Particles And Rotational Motion Class 11 Engineering Physics MCQ Questions
• Thermal Properties Of Matter Class 11 Engineering Physics MCQ Questions
• Units And Measurement Class 11 Engineering Physics MCQ Questions
• Waves Class 11 Engineering Physics MCQ Questions
• Work,Energy And Power Class 11 Engineering Physics MCQ Questions

Gravitation Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15 Quiz 16

Gravitation Questions and Answers

Gravitation Quiz Question	Answer
A planet in a distant solar system is $$10$$ times more massive than the earth and its radius is $$10$$ times smaller. Given that the escape velocity from the earth is $$11 km$$ $$\mathrm{s}^{-1}$$ , the escape velocity from the surface ofthe planet would be	$$110 km \mathrm{s}^{-1}$$
The mass of a spaceship is $$1000\  kg$$ . It is to be launched from the earths surface out into free space. The value of $$g$$ and $$R$$ (radius of earth) are $$10\  m/s$$ and $$6400\ km$$ respectively. The required energy for this work will be :	$$6.4\times 10^{10}\ J$$
If g is the acceleration due to gravity on the earth's surface, the gain in the potential energy of an object of mass m raised from the surface of the earth to a height equal to the radius R of the earth, is:	$$\displaystyle \dfrac{1}{2}\mathrm{m}\mathrm{g}\mathrm{R}$$
A body weighs $$72 N$$ on the surface of the earth. What is the gravitational force on it due to the earth at a height equal to half the radius of the earth?	32 N
A satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth. Then,	the acceleration of S is always directed towards the centre of the earth.
A body of mass ' $$m$$ ' taken from the earth's surface to the height equal to twice the radius ( $$R$$ ) of the earth. The change in potential energy of body will be	$$\displaystyle \frac{2}{3}mgR$$
A body weighs 200 N on the surface of the earth. How much it weigh half way down to the centre of the earth ?	$$100 N$$
The ratio of escape velocity at earth $$(v_e)$$ to the escape velocity at a planet $$(v_p)$$ whose radius and mean density are twice as that of earth is:	$$1:2\sqrt 2$$
The acceleration due to gravity at a height 1 km above the earth is the same as at a depth d below the surface of earth. Then:	$$d=2km$$
If $${v}_{e}$$ is escape velocity and $${v}_{o}$$ is orbital velocity of a satellite for orbit close to the earth's surface, then these are related by :	$${v}_{e}=\sqrt {2}{v}_{o}$$

Kinetic Theory Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15 Quiz 16 Quiz 17

Kinetic Theory Questions and Answers

Kinetic Theory Quiz Question	Answer
An ideal gas goes through a reversible cycle  $$a\rightarrow b\rightarrow c\rightarrow d$$ has the V- T diagram shown below. Process  $$d\rightarrow a$$ and $$b\rightarrow c$$ are adiabatic. The corresponding P-V diagram for the process is ( all figure are schematic and not drawn to scale).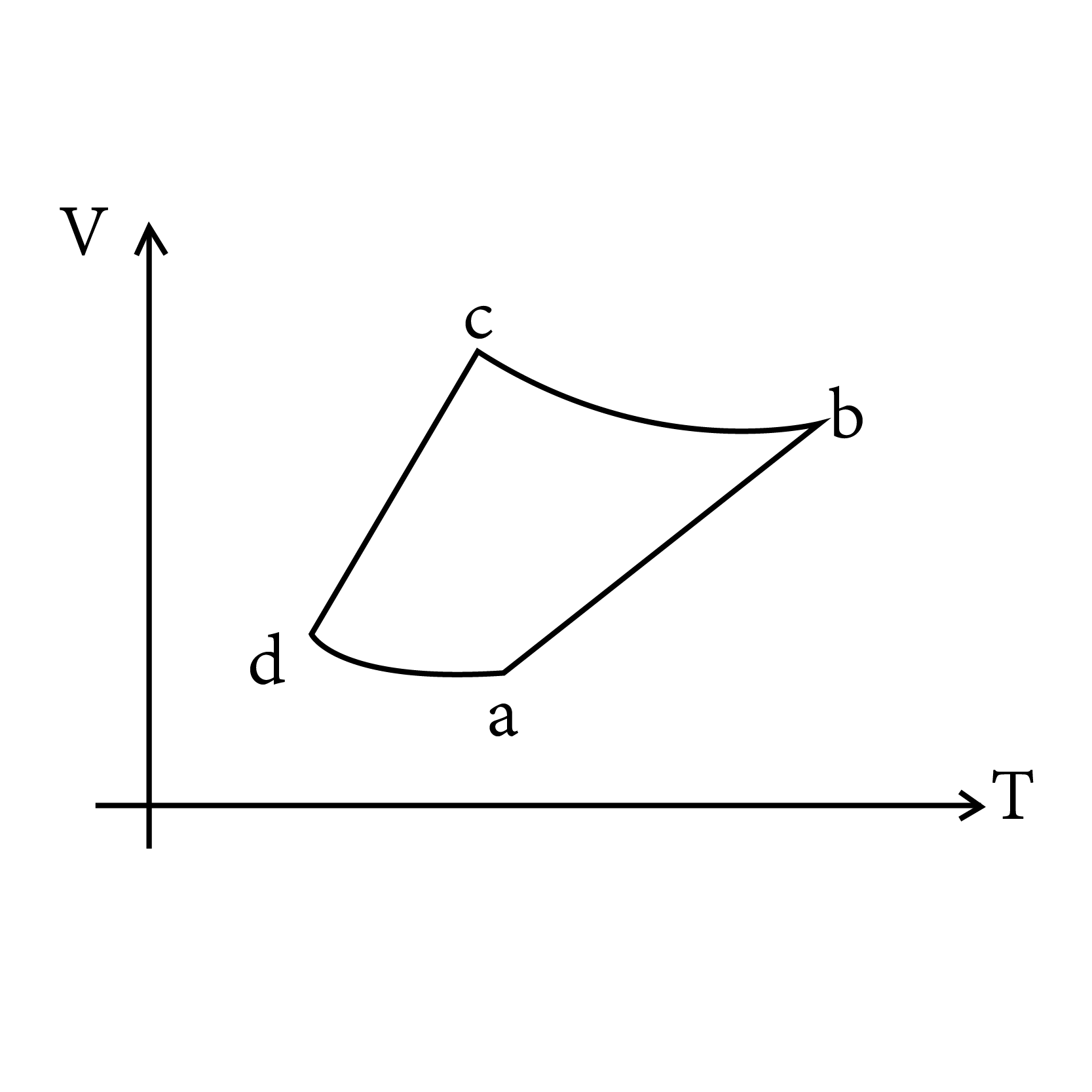
In the nuclear fusion reaction,  $$_{1}^{2}\mathrm{H}+_{1}^{3}\mathrm{H}\rightarrow_2^4{He}$$ $$+\ {n}$$ given that the repulsive potential energy between the two nuclei is $$7.7\times 10^{-14}\ {J}$$ , the temperature at which the gases must be heated to initiate the reaction is nearly [Boltzmann's constant $$\mathrm{k}=1.38\times 10^{-23}\mathrm{J}/\mathrm{K}$$ ]	$$10^{9}\ {K}$$
An ideal gas is enclosed in a cylinder at pressure of $$2 \,atm$$ and temperature, $$300 \,K$$ . The mean time between two successive collisions is $$6 \times 10^{-8} \,s$$ . If the pressure is doubled and temperature is increased to $$500 \,K$$ , the mean time between two successive collisions will be close to:	$$4 \times 10^{-8} \,s$$
$$'N'$$ moles of a diatomic gas in a cylinder are at a temperature $$'T'$$ . Heat is supplied to the cylinder such that the temperature remains constant but n moles of the diatomic gas gets converted into monatomic gas. What is the change in the total kinetic energy of the gas ?	$$\dfrac{3}{2}nRT$$
Which of the following shows the correct relationship between the pressure $$'P'$$ and density $$\rho$$  of an ideal gas at constant temperature ?
Two non-reactive monoatomic ideal gases have their atomic masses in the ratio 2:The ratio of their partial pressures, when enclosed in a vessel kept at a constant temperature, is 4:The ratio of their densities is	8 : 9
A gas molecule of mass $$M$$ at the surface of the Earth has kinetic energy equivalent to $$0^oC$$ . If it were to go up straight without colliding with any other molecules, how high it would rise? Assume that the height attained is much less than radius of the earth. ( $$k_B$$ is Boltzmann constant)	$$\dfrac {819 k_B}{2 Mg}$$
	Statement -1 is True, Statement-2 is True; Statement -2 is NOT a correct explanation for Statement-1.
The ratio of the specific heats $$\dfrac {C_p}{C_v}=\gamma$$ in terms of degree of freedom (n) is given by:	$$\left (1+\dfrac {2}{n}\right )$$
A given sample of an ideal gas occupies a volume V at a pressure P and absolute temperature T. The mass of each molecule of the gas is m. which of the following gives the density of the gas?	Pm/(kT)

Laws Of Motion Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15

Laws Of Motion Questions and Answers

Laws Of Motion Quiz Question	Answer
A uniform rod $$AB$$ is suspended from a point $$X$$ , at a variable distance $$x$$ from $$A$$ , as shown. To make the rod horizontal, a mass $$m$$ is suspended from its end $$A$$ . A set of $$(m,x)$$ values is recorded. The appropriate variables that give a straight line, when plotted, are:	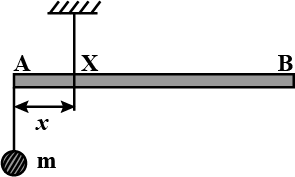$$m,\cfrac { 1 }{ x }$$
A beaker of radius r is filled with water (refractive index $$\dfrac{4}{3}$$ ) up to a height H as shown in the figure on the left. The beaker is kept on a horizontal table rotating with angular speed $$\omega$$ . This This makes the water surface curved so that the difference in the height of water level at the center and at the circumference of the beaker is $$h (h << H, h << r)$$ , as shown in the figure on the right. Take this surface to be approximately spherical with a radius of curvature R. Which of the following is/are correct? (g is the acceleration due to gravity)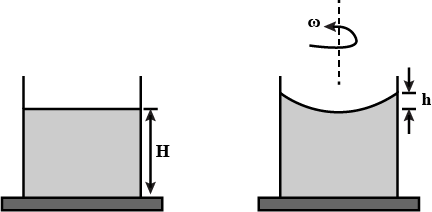	Apparent depth of the bottom of the beaker is close to $$\dfrac{3H}{4} \left(1 + \dfrac{\omega^2 H}{4g} \right)^{-1}$$
What is the minimum velocity with which a body of mass $$m$$ must enter a vertical loop of radius $$R$$ so that it can complete the loop?	$$\sqrt{5gR}$$
	Both Assertion and Reason are correct but Reason is not the correct explanation for Assertion
A ball is suspended by a thread of length L at the point O on a wall which is inclined to the vertical by $$\alpha$$ . The thread with the ball is displaced by a small angle $$\beta$$ away from the vertical and also away from the wall. If the ball is released, the period of oscillation of the pendulum when $$\beta > \alpha$$ will be	$$\displaystyle \sqrt{\frac{L}{g}}\left[\pi+2sin^{-1}\frac{\alpha}{\beta}\right]$$
An object placed on a ground is in stable equilibrium. If the objects is given a slight push, then initially the position of centre of gravity:	rises higher above the ground
Cleaning of dust from carpet is due to _____.	Inertia of rest
A ball of mass 'm' moves normal to a wall with a velocity 'u' and rebounds with the same speed. The change in momentum of the ball during the rebounding is	2mu away from the wall
When an athlete takes part in a long jump he runs for a while and then jumps. This is because:	inertia of motion helps him to take a longer jump.
Statement A: If the force varies with time then the net force is measured by the total change in momentum of the body. Statement B: Change in momentum and impulsive force are numerically equal.	A is wrong and B is correct

Mechanical Properties Of Fluids Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14

Mechanical Properties Of Fluids Questions and Answers

Mechanical Properties Of Fluids Quiz Question	Answer
The top of a water tank is open to air and its water level is maintained. It is giving out $$0.74 m^3$$ water per minute through a circular opening of 2 cm radius in its wall. The depth of the centre of the opening from the level of water in the tank is close to :	$$4.8 m$$
Two liquids of densities $${ \rho  }_{ 1 }$$ and $${ \rho  }_{ 2 }\left( { \rho  }_{ 2 }=2{ \rho  }_{ 1 } \right)$$ are filled up behind a square wall of side $$10m$$ as shown in figure. Each liquid has a height of $$5m$$ . The ratio of the forces due to these liquids exerted on upper part $$MN$$ to that at the lower part $$NO$$ is (Assume that the liquids are not mixing)	$$1/4$$
A capillary tube (A) is dipped in water. Another identical tube (B) is dipped in a soap-water solution. Which of the following shows the relative nature of the liquid columns in the two tubes?
A glass capillary tube is of the shape of truncated cone with an apex angle $$\alpha$$ so that its two ends have cross sections of different radii. When dipped in water vertically, water rises in it to a height $$h$$ , where the radius of its cross section is $$b$$ . If the surface tension of water is $$S$$ , its density is $$\rho$$ , and its contact angle with glass is $$\theta$$ , the value of $$h$$ will be ( $$g$$ is the acceleration due to gravity)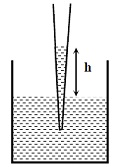	$$\dfrac{2S}{b \rho g} \cos (\theta + \alpha /2)$$
If the density of air is $$\rho_a$$ and that of the liquid $$\rho_l$$ , then for a given piston speed the rate (volume per unit time) at which the liquid is sprayed will be proportional to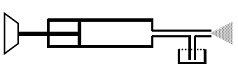	$$\displaystyle \sqrt{\dfrac{\rho_a}{\rho_l}}$$
A person in a lift is holding a water jar, which has a small hole at the lower end of its side. When the lift is at rest, the water jet coming out of the hole hits the floor of the lift at a distance $$d$$ of $$1.2 m$$ from the person. In the following, state of the lift's motion is given in List I and the distance where the water jet hits the floor of the lift is given in List II. Match the statements from List I with those in List II and select the correct answer using the code given below the lists. List I List II P. Lift is accelerating vertically up. 1. $$d= 1.2 m$$ Q. Lift is accelerating vertically down with an acceleration less than the gravitational acceleration. 2. $$d > 1.2 m$$ R. Lift is moving vertically up with constant speed. 3. $$d < 1.2 m$$ S. Lift is falling freely. 4. No water leaks out of the jar	P-1, Q-1, R-1, S-4
A wind with speed $$40$$ m/s blows parallel to the roof of a house. The area of the roof is $$250\ m^2$$ . Assuming that the pressure inside the house is atmospheric pressure, the force exerted by the wind on the roof and the direction of the force will be $$(\rho_{air}=1.2 \ kg/m^3)$$	$$2.4\times 10^5N$$ , upward
A small hole of an area of cross-section $$2 mm^2$$ is present near the bottom of a fully filled open tank of height 2 m. Taking $$g = 10 m/s^2$$ ,  the rate of flow of water through the open hole would be nearly	$$12.6 \times 10^{-6} m^3/s$$
	Both Assertion and Reason are correct but Reason is not the correct explanation for Assertion.
A spherical body of diameter D is falling in viscous medium. Its terminal velocity is proportional to:	$${ V }_{ 1 }\propto { D }^{ 2 }$$

Mechanical Properties Of Solids Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15 Quiz 16

Mechanical Properties Of Solids Questions and Answers

Mechanical Properties Of Solids Quiz Question	Answer
Two wires are made of the same material and have the same volume. However wire 1 has cross-sectional area $$A$$ and wire 2 has cross- sectional area $$3A$$ . If the length of wire 1 increases by $$\Delta \mathrm{x}$$ on applying force $$\mathrm{F}$$ , how much force is needed to stretch wire 2 by the same amount  ?	$$9\mathrm{F}$$
Two steel wires having same length are suspended from a ceiling under the same load. If the ratio of their energy stored of their unit volume is $$1:4$$ , the ratio of their diameters is:	$$\sqrt 2 :1$$
At $$40^oC$$ , a brass wire of $$1 mm$$ radius is hung from the ceiling. A small mass, $$M$$ is hung from the free end of the wire. When the wire is cooled down from $$40^oC$$ to $$20^oC$$ it regains its original length of $$0.2 m$$ . The value of $$M$$ is close to : (Coefficient of linear expansion and Young's modulus of brass are $$10^{-5} / ^oC$$ and $$10^{11} \ N/m^2$$ , respectively; $$g = 10 ms^{-2}$$ )	$$9 \ kg$$
A uniformly tapering conical wire is made from a material of Young's modulus $$Y$$ and has a normal, unextended length $$L$$ . The radii, at the upper and lower ends of this conical wire, have values $$R$$ and $$3R$$ , respectively. The upper end of the wire is fixed to a rigid support and a mass $$M$$ is suspended from its lower end. The equilibrium extended length, of this wire, would equal to:	$$L\left( 1+\dfrac { 1 }{ 3 } \dfrac { Mg }{ \pi \Upsilon { R }^{ 2 } } \right)$$
A thin 1 m long rod has a radius of 5 mm.1 A force of 50 $$\pi kN$$ is applied at one end to determine its Young's modulus. Assume that the force is exactly known. If the least count in the measurement of all lengths is 0.01 mm, which of the following statements is false ?	The maximum value of Y that can be determined is $$10^{14} N/m^2$$ .
If speed(V), acceleration(A) and force(F) are considered as fundamental units, the dimension of Young's modulus will be?	$$V^{-4}A^2F$$
A bottle has an opening of radius $$a$$ and length $$b$$ . A cork of length $$b$$ and radius $$(a+ \Delta a)$$ where $$(\Delta a << a)$$ is compressed to fit into the opening completely (See figure). If the bulk modulus of cork is B and the frictional coefficient between the bottle and cork is $$\mu$$  then the force needed to push the cork into the bottle is :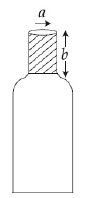	$$(4\pi \mu B b)\Delta a$$
Temperature of a gas is $$20^{0}\mathrm{C}$$ and pressure is changed from $$1.01\times 10^{5}$$ Pa to $$1.165\times 10^5\mathrm{P}\mathrm{a}$$ . If volume is decreased isothermally by 10%. The bulk modulus of gas is (in $$Pa$$ ):	$$1.55\times 10^{5}$$
$$\mathrm{A}$$ student performs an experiment to determine the Young's modulus of a wire, exactly 2 $$\mathrm{m}$$ long, by Searle's method. In a particular reading, the student measures the extension in the length of the wire to be $$0.8 mm$$ with an uncertainty of $$\pm 0.05$$ mm at a load of exactly $$1.0 kg$$ . The student also measures the diameter of the wire to be $$0.4 mm$$ with an uncertainty of $$\pm 0.01$$ mm. Take $$\mathrm{g}=9.8\mathrm{m}/\mathrm{s}^{2}$$ (exact). The Young's modulus obtained from the reading is	$$(2.0\pm 0.2)\times 10^{11}\mathrm{N}/\mathrm{m}^{2}$$
Dimensions of stress are :	$$[ML^{-1}T^{-2}]$$

Motion In A Plane Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15

Motion In A Plane Questions and Answers

Motion In A Plane Quiz Question	Answer
A water fountain on the ground sprinkles water all around it. If the speed of water coming out of the fountain is $$v$$ , the total area around the fountain that gets wet is :	$$\displaystyle \pi\dfrac{\mathrm{v}^{4}}{\mathrm{g}^{2}}$$
A particle starts from the origin at $$t=0$$ with an initial velocity of $$3.0\ \hat i\ m/s$$ and moves in the $$x-y$$ plane with a constant acceleration $$(6.0\ \hat i +4.0\ \hat j) m/s^2$$ . The $$x-$$ coordinates of the particle at the instant when its $$y-$$ coordinates is $$32\ m$$ is $$D$$ meters. The value of $$D$$ is:	$$60$$
For a particle in uniform circular motion the acceleration $$\vec{\mathrm{a}}$$ at a point $$\mathrm{P}(\mathrm{R}, \theta)$$ on the circle of radius $$\mathrm{R}$$ is (here 'v' is the speed of the particle and $$\theta$$ is measured from the x-axis)	$$-\displaystyle \frac{\mathrm{v}^{2}}{\mathrm{R}}\cos\theta\hat{\mathrm{i}}-\frac{\mathrm{v}^{2}}{\mathrm{R}}\sin\theta\hat{j}$$
A uniform circular disc of radius $$50\  cm$$ at rest is free to turn about an axis which is perpendicular to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of $$2.0\  rad {s}^{-2}$$ . Its net acceleration in  $${ms}^{-2}$$ at the end of $$2.0 \ s$$ is approximately:	$$8.0$$
The position vector of a particle $$\overrightarrow { R}$$ as a function of time is given by: $$\overrightarrow { R}  = 4\, sin(2\pi t)\hat{i}+4 cos (2\pi t)\hat{j}$$ , where $$R$$ is in meters, $$t$$ is in seconds and $$\hat{i}$$ and $$\hat{j}$$ denote unit vectors along x-and y- directions, respectively. Which one of the following statements is wrong for the motion of particle?	Magnitude of the velocity of particle is $$8\ m/s$$
The angular displacement of a particle is given by $$\theta =t^{3}+t^{2}+t+1$$ then, its angular velocity at $$t = 2$$ sec is _____ $$rads^{-1}$$ :	$$17$$
The pair containing a scalar and a vector quantity is:	electromotive force and force
Which of the following is a scalar quantity?	Work
(1) In uniform circular motion, tangential acceleration is zero.  (2) In uniform circular motion, velocity is constant.	1 is true and 2 is false
	Both Assertion and Reason are correct and Reason is the correct explanation for Assertion

Motion In A Straight Line Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15

Motion In A Straight Line Questions and Answers

Motion In A Straight Line Quiz Question	Answer
A lizard, at an initial distance of $$21$$ cm behind an insect, moves from rest with an acceleration of $$2 cm/s^{2}$$ and pursues the insect which is crawling uniformly along a straight line at a speed of $$20$$ cm/s. Then the lizard will catch the insect after	$$21$$ s
Two points $$A$$ and $$B$$ move from rest along a straight line with same acceleration $$f$$  and $$f'$$ respectively. If   $$A$$ takes $$m\ \text{sec}$$ more than $$B$$ and describes $$n$$ units more than $$B$$  in acquiring the same speed then	$$(f^{'}-f)n=\frac{1}{2}ff^{'}m^{2}$$
Two stones are thrown up simultaneously from the edge of a cliff $$240\ m$$  high with initial speed $$10\ m/s$$  and $$40\ m/s$$  respectively.  Which of the following graph best represents the time variation of relative position of the second stone with respect to the first ? (Assume stones do not rebound after hitting the ground and neglect air resistance, take $$g = 10\ m /s^2$$ ) (The figures are schematic and not drawn to scale.)
STATEMENT-1: For an observer looking out through the window of a fast moving train, the nearby objects appear to move in the opposite direction to the train, while the distant objects appear to be stationary. STATEMENT-2: If the observer and the object are moving at velocities $$\vec{\mathrm{V}}_{1}$$ and $$\vec{\mathrm{V}}_{2}$$ respectively with reference to a laboratory frame, the velocity of the object with respect to the observer is $$\vec{\mathrm{V}}_{2}-\vec{\mathrm{V}}_{1}$$ .	STATEMENT-1 is True, STATEMENT-2 is True; STATEMENT-2 is NOT a correct explanation for STATEMENT-1
A toy car with charge q moves on a frictionless horizontal plane surface under the influence of a uniform electric field $$\overrightarrow{E}$$ . Due to the force $$q\overrightarrow{E}$$ , its velocity increases from $$0$$ to $$6\ m/s$$  in one-second duration. At that instant, the direction of the field is reversed. The car continues to move for two more seconds under the influence of this field. The average velocity and the average speed of the toy car between $$0$$ to $$3$$ seconds are respectively:	$$1$$ m/s, $$3$$ m/s
A ball is dropped from a bridge $$122.5 m$$ high. After the first ball has fallen for $$2 seconds$$ , a second ball is thrown straight down after it, what must be the initial velocity of the second ball be, so that both the balls hit the surface of water at the same time?	$$26.1 {m}/{s}$$
If a car at rest accelerated uniformly to a speed of $$144  {km}/{hour}$$ in $$20 second$$  it covers a distance:	$$400 m$$
A ball is thrown vertically upwards with a given velocity such that it rises for T seconds (T > 1). What is the distance traversed by the ball during the last one second of ascent (in meters) ? (Acceleration due to gravity is g $$m/s^{2}$$ ) .	$$\dfrac {g}{2}$$
The accelerated motion of a body can occur :	Due to change in both speed and direction of motion.
Unit for the rate of change of velocity is	$$m / s^2$$

Oscillations Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15 Quiz 16

Oscillations Questions and Answers

Oscillations Quiz Question	Answer
A particle performs simple harmonic motion with amplitude A. Its speed is tripled at the instant that it is at a distance $$\displaystyle\frac{2A}{3}$$ from equilibrium position. The new amplitude of the motion is.	$$\displaystyle\frac{7A}{3}$$
A $$1\, kg$$ block attached to a spring vibrates with a frequency of $$1\,Hz$$ on a frictionless horizontal table. Two springs identical to the original spring are attached in a parallel to an $$8\,kg$$ block placed on the same table. So, the frequency of vibration of the $$8\, kg$$ block is ;	$$\dfrac{1}{2} Hz$$
A small block is connected to one end of a massless spring of unstretched length 4.9 m. The other end of the spring (see the figure) is fixed. The system lies on a horizontal frictionless surface. The block is stretched by 0.2 m and released from rest at t=lt then executes simple harmonic motion with angular frequency  $$\omega =\frac { \pi }{ 3 } rad/s$$ . Simultaneously at t=0, a small pebble is projected with speed v from point P at an angle of 45 as shown in the figure. Point P is at a horizontal distance of 10 m from O. If the pebble hits the block at t = 1 s, the value of v is (take $$g = 10 m/{ s }^{ 2 }$$ 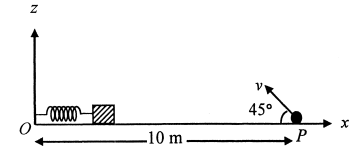)	$$\sqrt { 50 } m/s$$
A particle is executing SHM along a straight line. Its velocities at distances $$x_1$$ and $$x_2$$ from the mean position are $$V_1$$ and $$V_2$$ , respectively. Its time period is:	$$2\pi \sqrt {\cfrac {x_2^2-x_1^2}{V_1^2-V_2^2}}$$
Average velocity of a particle executing SHM in one complete vibration is :	zero
Two particle are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is:	$${2\pi}/{3}$$
A particle is describing simple harmonic motion. If its velocities are $$v_{1}$$ and $$v_{2}$$ when the displacements from the mean position are $$y_{1}$$ and $$y_{2}$$ respectively, then its time period is	$$2\pi \sqrt {\dfrac {y_{1}^{2} - y_{2}^{2}}{v_{1}^{2} - v_{2}^{2}}}$$
If maximum speed of a particular in SHM is given by  $$\displaystyle { V }_{ m }$$ . What is its average speed?	$$\displaystyle \frac { 2 V_m}{ \pi }$$
The velocity vector v and displacement vector x of a particle executing SHM are related as $$\dfrac{vdv}{dx}=-\omega^2x$$ with the initial condition $$V=v_0$$ at $$x=0$$ . The velocity v, when displacement is x, is?	$$v=\sqrt{v^2_0-\omega^2x^2}$$
If $$K_i$$ and $$K_p$$ respectively are effective spring constant in series and parallel combination of springs as shown in figure, find $$\displaystyle\frac{K_i}{K_p}$$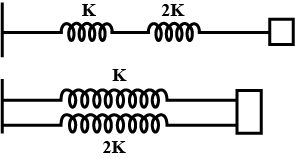	$$\displaystyle\frac{2}{9}$$

Physical World Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9

Physical World Questions and Answers

Physical World Quiz Question	Answer
The man who has won Nobel Prize twice in physics is	Bardeen
Earth pulls every object towards it with a force called:	Gravity
Which of the following is true regarding the physical science?	Both a and b
_____ suggested that the ships should be marked with load lines.	Samuel plimsoll
Earth has no gravitational force:	False
The person who has been awarded the title of the Father of Physics of $$20^{th}$$ century is	Albert Einstein
Gravity is defined  as:	The pull of the earth
The man who is known as the Father of Experimental Physics is	Galileo
Gravity is :	Down wardly directed force
A scientific way of doing things involve	All of the above

Systems Of Particles And Rotational Motion Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15

Systems Of Particles And Rotational Motion Questions and Answers

Systems Of Particles And Rotational Motion Quiz Question	Answer
A rigid massless rod of length 3 $$l$$ has two masses attached art each end as shown in the figure. The rod is pivoted at point P on the horizontal position, its instantaneous angular acceleration will be:	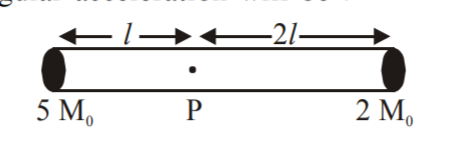$$\dfrac{g}{13l}$$
A rod of length 50 cm is pivoted at one end. It is raised such that if makes an angle of $$30^o$$ from the horizontal as shown and released from rest. Its angular speed when it passes through the horizontal (in rad $$s^{-1}$$ ) will be ( $$g = 10 ms^{-2}$$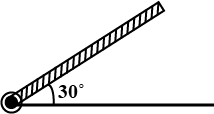 )	$$\sqrt{30}$$
The phase space diagram for a ball thrown vertically up from ground is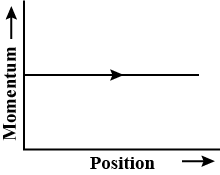
The force 'F' acting on a particle of mass 'm' is indicated by the force-time graph shown below. The change in momentum of the particle over the time interval from zero to 8 s is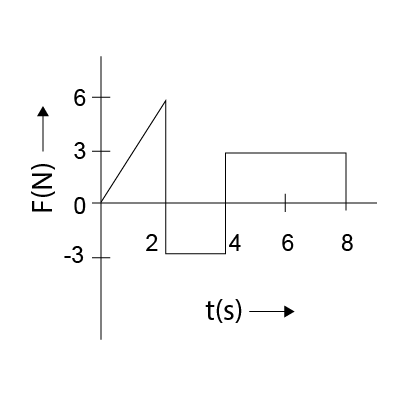	12 Ns
The reading of a spring balance corresponds to $$100$$ N while situated at the north pole and a body is kept on it. The weight record on the same scale if it is shifted to the equator, is(take, $$g=10m/s^2$$ ) and radius of the earth, $$(R=6.4\times 10^3m$$ ).	$$99.66$$ N
Two spheres of same size one of mass $$2 kg$$ and another of mass $$4 kg$$ are dropped simultaneously from the top of Qutab Minar (height  $$= 72   m$$ ). When they are $$1 m$$  above the ground, the two spheres have the same:	acceleration
	Both Assertion and Reason are correct and Reason is the correct explanation for Assertion
A thin rod of length $$4l$$ and $$4m$$ is bent at the points as shown in figure. What is the moment of inertia of the rod about the axis passes through point $$O$$ and perpendicular to the plane of paper?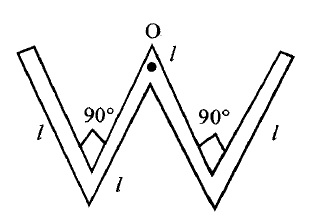	$$\dfrac {10Ml^{2}}{3}$$
Two rings of radius $$R$$ and $$nR$$ made of same material have the ratio of moment of inertia about an axis passing through centre in $$1 : 8$$ . The value of $$n$$ is	$$2$$
Consider the following two statements A and B and identify the correct choice A) The torques produced by two forces of couple are opposite to each other B) The direction of torque is always perpendicular to plane of rotation of body	A is false but B is true

Thermal Properties Of Matter Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15

Thermal Properties Of Matter Questions and Answers

Thermal Properties Of Matter Quiz Question	Answer
An ideal gas goes through a reversible cycle  $$a\rightarrow b\rightarrow c\rightarrow d$$ has the V- T diagram shown below. Process  $$d\rightarrow a$$ and $$b\rightarrow c$$ are adiabatic. The corresponding P-V diagram for the process is ( all figure are schematic and not drawn to scale).
A leak proof cylinder of length $$1m$$ , made of a metal which has low coefficient of expansion is floating vertically in water at $$0^oC$$ such that its height above the water surface is $$20cm$$ . When the temperature of water is increased to $$4^oC$$ , the height of the cylinder above the water surface becomes $$21cm$$ . The density of water at $$T = 4^oC$$ , relative to the density at $$T = 0^oC$$ is close to:	$$1.01$$
Which of the following shows the correct relationship between the pressure $$'P'$$ and density $$\rho$$  of an ideal gas at constant temperature ?
Two non-reactive monoatomic ideal gases have their atomic masses in the ratio 2:The ratio of their partial pressures, when enclosed in a vessel kept at a constant temperature, is 4:The ratio of their densities is	8 : 9
A given sample of an ideal gas occupies a volume V at a pressure P and absolute temperature T. The mass of each molecule of the gas is m. which of the following gives the density of the gas?	Pm/(kT)
A vessel of volume $$20\ L$$ contains a mixture of hydrogen and helium at temperature of $$27^{\circ}C$$ and pressure $$2\ atm$$ . The mass of mixture is $$5\ g$$ . Assuming the gases to be ideal, the ratio of mass of hydrogen to that of the helium in the given mixture will be	$$2 : 5$$
A hot and a cold body are kept in vacuum separated from each other. Which of the following causes decrease in temperature of the hot body?	Radiation
$$0.5$$ moles of an ideal gas at constant temperature $$27^{\circ}C$$ kept inside a cylinder of length $$L$$ and cross-section area $$A$$ closed by a massless piston. The cylinder is attached with a conducting rod of length $$L$$ , cross-section area $$(\dfrac{1}{9})m^{2}$$ and thermal conductivity $$k$$ , whose other end is maintained at $$0^{\circ}C$$ . If piston is moved such that rate of heat flow through the conducing rod is constant then velocity of piston when it is at height $$\dfrac{L}{2}$$ from the bottom of cylinder is: [Neglect any kind of heat loss from system]	$$\left (\dfrac {k}{100R}\right )m/sec$$
The difference between volume and pressure coefficients of an ideal gas is :	Zero
A sealed glass jar is full of water. When it is kept in a freezing mixture, it is broken because :	water expands from $$4^{o}C$$ to $$0^{o}C$$

Units And Measurement Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15 Quiz 16

Units And Measurement Questions and Answers

Units And Measurement Quiz Question	Answer
Dimensions of $$\displaystyle \frac{1}{\mu_{0}{\varepsilon_{0}}}$$ , where symbols have their usual meaning, are :	$$[\mathrm{L}^{2}\mathrm{T}^{-2}]$$
In the following $$I$$ refers to current and other symbols have their usual meaning. Choose the option that corresponds to the dimensions of electrical conductivity:	$${M}^{-1}{L}^{-3}{T}^{3}{I}^{2}$$
The physical quantities not having same dimensions are:	momentum and Plancks constant
The dimension of magnetic field in $$\mathrm{M},\ \mathrm{L},\ \mathrm{T}$$ and $$\mathrm{C}$$ (Coulomb) is given as :	$$\mathrm{M}\mathrm{T}^{-1}\mathrm{C}^{-1}$$
Which of the following does not have the same dimension?	Electric flux, Electric field, Electric dipole moment
The relation between $$[\in_0]$$ and $$[\mu_0]$$ is	$$[\mu_0] = [\in_0]^{-1} [L]^{-2}[T]^{2}$$
The dimensions of $${ \left( { \mu }_{ 0 }{ \varepsilon }_{ 0 } \right)  }^{ -1/2 }$$ are :	$$[L{T}^{-1}]$$
The work done to raise a mass m from the surface of the earth to a height h, which is equal to the radius of the earth, is :	$$\dfrac{1}{2} mgR$$
If force $$(F)$$ , velocity $$(V)$$ and time $$(T)$$ are taken as fundamental units, the dimensions of mass are	$$[FV^{-1}T]$$
Planck's constant ( $$h$$ ), speed of light in vacuum ( $$c$$ ) and Newton's gravitational constant ( $$G$$ ) are three fundamental constants. Which of the following combinations of these has the dimension of length?	$$\dfrac{\sqrt{hG}}{c^{3/2}}$$

Waves Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15 Quiz 16

Waves Questions and Answers

Waves Quiz Question	Answer
A transverse wave travels on a taut steel wire with a velocity of $$v$$ when the tension in it is $$2.06\times { 10 }^{ 4 }N$$ . When the tension is changed to $$T$$ , the velocity changed to $$v/2$$ . The value of $$T$$ is closet to:	$$5.15\times { 10 }^{ 3 }N$$
The displacement of a particle varies according to the relation $$x = 4(\cos \pi t + \sin \pi t)$$ . The amplitude of the particle is	$$4\sqrt{2}$$
Amplitude of a wave is represented by $$A = \dfrac {c}{a + b - c}$$ . Then resonance will occur when	$$b = 0$$ and $$a = c$$
A simple wave motion represented by $$y=5(\sin 4\pi t+\sqrt 3 \cos 4\pi t)$$ . Its amplitude is:	$$10$$
The phase change between incident and reflected sound wave from a free end is	$$0$$
Which of the following is conserved when light waves interfere?	energy
Phase difference between a particle at a compression and a particle at the next rarefaction is	$$\pi$$
Thickness of very thin films can be found by the technique of	Interference
Two light waves are represented by $$y_{1}=4\sin  \omega t$$ and  $$y_{2}= 3\sin(\omega t+\frac{\pi }{2} )$$ . The resultant amplitude due to interference will be	$$5cm$$
For the sustained interference of light, the necessary condition is that the two sources should	of same amplitude with constant phase difference

Work,Energy And Power Class 11 Engineering Physics MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15

Work,Energy And Power Questions and Answers

Work,Energy And Power Quiz Question	Answer
This question has statement 1 and statementOf the four choices given after the statements, choose the one that best describes the two statements. If two springs $$\mathrm{S}_{1}$$ and $$\mathrm{S}_{2}$$ of the force constants $$\mathrm{k}_{1}$$ and $$\mathrm{k}_{2}$$ , respectively, are stretched by the same force, it is found that more work is done on spring $$\mathrm{S}_{1}$$ than on spring $$\mathrm{S}_{2}$$ . Statement-l : When stretched by the same amount, work done on $$\mathrm{S}_{1}$$ , will be more than that of $$\mathrm{S}_{2}$$ Statement-2: $$\mathrm{k}_{1}<\mathrm{k}_{2}$$ .	Statement-1 is false, statement-2 is true
When a rubber-band is stretched by a distance $$x$$ , it exerts a restoring force of magnitude $$F = ax + bx^2$$ where $$a$$ and $$b$$ are constants. The work done in stretching the unstretched rubber band by $$L$$ is	$$\displaystyle \dfrac{aL^2}{2} + \dfrac{bL^3}{3}$$
If collision between the block and the incline is completely elastic, then the vertical (upward) component of the velocity of the block at point B, immediately after it strikes the second incline is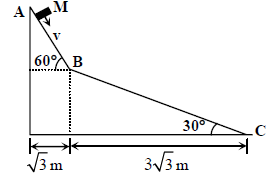	0
The balls, having linear momenta $$\vec{\mathrm{p}}_{1}=\mathrm{p}\hat{i}$$ and $$\vec{\mathrm{p}}_{2}=-\mathrm{p}\hat{\mathrm{i}}$$ , undergo a collision in free space. There is no extemal force acting on the balls. Let $$\vec{\mathrm{p}}_{1}$$ and $$\vec{\mathrm{p}}_{2}$$ be their final momenta. The following option(s) is (are) NOT ALLOWED for any non-zero value of $$\mathrm{p},\ \mathrm{a}_{1},\ \mathrm{a}_{2},\ \mathrm{b}_{1},\ \mathrm{b}_{2},\ \mathrm{c}_{1}$$ and $$\mathrm{c}_{2}$$ .	$$\vec{\mathrm{p}}_{1}=\mathrm{a}_{1}\hat{\mathrm{i}}+\mathrm{b}_{1}\hat{\mathrm{j}}$$ ; $$\vec{\mathrm{p}}_{2}=\mathrm{a}_{2}\mathrm{i}+\mathrm{b}_{1}\hat{\mathrm{j}}$$
What is the minimum velocity with which a body of mass $$m$$ must enter a vertical loop of radius $$R$$ so that it can complete the loop?	$$\sqrt{5gR}$$
Two similar spring P and Q have spring constants $$K_P$$ and $$K_Q$$ , such that $$K_P > K_Q$$ . They are stretched, first by the same amount (case a), then by the same force (case b). The work done by the spring $$W_P$$ and $$W_Q$$ are related as, in case (a) and case (b), respectively:	$$W_P > W_Q; W_Q > W_P$$
The force on a particle as the function of displacement x(in x-direction) is given by $$F=10+0.5x$$ The work done corresponding to displacement of particle from $$x=0$$ to $$x=2$$ unit is?	$$21$$ J
A ball is suspended by a thread of length L at the point O on a wall which is inclined to the vertical by $$\alpha$$ . The thread with the ball is displaced by a small angle $$\beta$$ away from the vertical and also away from the wall. If the ball is released, the period of oscillation of the pendulum when $$\beta > \alpha$$ will be	$$\displaystyle \sqrt{\frac{L}{g}}\left[\pi+2sin^{-1}\frac{\alpha}{\beta}\right]$$
How much work must be done by a force on $$50\ $$ $$kg$$ body in order to accelerate it from rest to $$20\ m/s$$   in $$10\ $$ $$s$$ ?	$$10^4\ $$ $$J$$
The amount of work done in stretching a spring from a stretched length of 10 cm to a stretched length of 20 cm is-	Less than the work done in stretching it from 20 cm to 30 cm.

Physics MCQ Questions for Class 11 - Practice Test with Solutions 

Do you want to overcome your drawbacks while attempting the quizzes or MCQ tests like time consumption, approaching questions, etc.? Take the advantage of practicing with MCQExams.com MCQ Questions for Standard 11 Physics Test. As it is a time-based approach and also provides answers to all questions.

One should practice the MCQs in this way for a better assessment of their preparation level. All chapters CBSE Class 11 Physics MCQ Quiz Questions with Solutions PDF free download links are available for easy access & quick reference.

How to Use MCQExams.com Chapterwise 11th Physics MCQ Interactive Quiz?

Guys do you love to share your practice hacks and tips with your friends? If yes, then our 11tth standard CBSE Physics MCQ interactive quiz help you do the same. Excited to know the process then jump into the below steps right away: 

• Go with the respective chapter class 11 Physics MCQ quiz link from the above
• Now, you will find the MCQ quiz boxes for the Gravitation chapter along with the interactive quiz windows.
• Click on the CBSE 11th Class Gravitation MCQ Interactive Quiz and it will redirect you to another window where it displays the questions with options in stories format.
• Answer the question one after another and learn the answers right away this helps you to do a quick assessment of your knowledge.
• You can also share this cool MCQ Interactive Quiz Questions of Plus One Physics topicwise with your friends by just tapping on the send arrow located at the top left corner of the story.
• After clicking the button, you can opt for the copy link option and easily paste the link on your friend's chat or else in your whatsapp story too. Isn’t it cool!!
• Keep passing this interesting approach of practicing Plus One CBSE Physics gravitation MCQ Questions to your co-students and help them in attempting the entrance exams like JEE & NEET.