MCQ Questions for Class 12 Commerce Maths Quiz with Answers Chapter Wise PDF Download
CBSE Multiple Choice Type Questions for 12th Class Commerce Maths PDF formatted study resources are available for free download. These Grade 12 Commerce Maths CBSE MCQ Mock Test helps you learn & practice the concepts in a fun learning way.
Class 12 Commerce Maths MCQs Multiple Choice Questions with Answers
Here are the chapterwise CBSE MCQ Quiz Test Questions for Class 12th Commerce Maths in pdf format that helps you access & download so that you can practice online/offline easily.
- Application Of Derivatives Class 12 Commerce Maths MCQ Questions
- Application Of Integrals Class 12 Commerce Maths MCQ Questions
- Continuity And Differentiability Class 12 Commerce Maths MCQ Questions
- Determinants Class 12 Commerce Maths MCQ Questions
- Differential Equations Class 12 Commerce Maths MCQ Questions
- Integrals Class 12 Commerce Maths MCQ Questions
- Inverse Trigonometric Functions Class 12 Commerce Maths MCQ Questions
- Linear Programming Class 12 Commerce Maths MCQ Questions
- Matrices Class 12 Commerce Maths MCQ Questions
- Probability Class 12 Commerce Maths MCQ Questions
- Relations And Functions Class 12 Commerce Maths MCQ Questions
- Three Dimensional Geometry Class 12 Commerce Maths MCQ Questions
- Vector Algebra Class 12 Commerce Maths MCQ Questions
Application Of Derivatives Class 12 Commerce Maths MCQ Quiz

Application Of Derivatives Questions and Answers
| Application Of Derivatives Quiz Question | Answer |
|---|---|
| The tangent at the point $$(2, -2)$$ to the curve, $$x^2y^2-2x=4(1-y)$$ does not pass through the point. | $$(-2, -7)$$ |
| If the tangent to the conic, $$y - 6 = x^2$$ at (2, 10) touches the circle, $$x^2 + y^2 + 8x - 2y = k$$ (for some fixed k) at a point $$(\alpha, \beta)$$; then $$(\alpha, \beta)$$ is; | $$\displaystyle \left( -\frac{8}{17}, \frac{2}{17} \right)$$ |
| Let b be a nonzero real number. Suppose $$f : R \rightarrow R$$ is a differentiable function such that $$f(0) = 1$$. If the derivative f' of f satisfies the equation $$f'(x) = \dfrac{f(x)}{b^2 + x^2}$$ for all $$x \in R$$, then which of the following statements is/are TRUE? |
$$f\left( x \right) f\left( -x \right) =1$$ for all $$x\in R$$ |
| What is the $$x$$-coordinate of the point on the curve $$f(x) = \sqrt {x}(7x - 6)$$, where the tangent is parallel to $$x$$-axis? | $$\dfrac {2}{7}$$ |
| Consider the following statements in respect of the function $$f(x) = x^{3} - 1, \quad x\epsilon [-1, 1]$$ I. $$f(x)$$ is increasing in $$[-1, 1]$$ II. $$f'(x)$$ has no root in $$(-1, 1)$$. Which of the statements given above is/ are correct? |
Only I |
| If $$\dfrac{x^2}{f(4a)}=\dfrac{y^2}{f(a^2-5)}$$ respresents and ellipse with major axis as y-axis and $$f$$ is a decreasing function, then | $$a \in (-1, 5)$$ |
| The values of $$\mathrm{x}$$ at which $$\mathrm{f}(\mathrm{x})=\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{x}$$ is stationary are given by |
$$(2\displaystyle \mathrm{n}+1)\frac{\pi}{2},\ \forall n\in Z$$ |
The number of stationary points of $$\mathrm{f}(\mathrm{x})=\mathrm{s}\mathrm{i}\mathrm{n} \mathrm{x}$$ in $$[0, 2{\pi}]$$ are |
2 |
| Find the equation of a line passing through $$(-2,3)$$ and parallel to tangent at origin for the circle $$\displaystyle x^{2}+y^{2}+x-y=0$$ | $$x - y + 5 = 0$$ |
Stationary point of $$\displaystyle \mathrm{y}=\frac{\log \mathrm{x}}{\mathrm{x}}(\mathrm{x}>0)$$ is |
$$(\displaystyle \mathrm{e},\frac{1}{\mathrm{e}})$$ |
Application Of Integrals Class 12 Commerce Maths MCQ Quiz

Application Of Integrals Questions and Answers
| Application Of Integrals Quiz Question | Answer |
|---|---|
| The area of the region bounded by the parabola $$(\mathrm{y}-2)^{2}=\mathrm{x}-1$$, the tangent to the parabola at the point $$(2,\ 3)$$ and the $$\mathrm{x}$$-axis is |
$$9$$ |
| The area (in square units) of the region bounded by the curves $$y + 2x^2 = 0$$ and $$y + 3x^2 = 1$$, is equal to | $$\displaystyle \frac{4}{3}$$ |
| The area (in sq. units) of the region $$\{(x, y):x \geq 0, x+y \leq 3, x^2 \leq 4y$$ and $$y\leq 1+\sqrt{x}\}$$ is. | $$\displaystyle\frac{5}{2}$$ |
| The area of the region described by $$ A= (x,y):x^{2}+y^{2}\leq 1$$ and $$ y^{2}\leq 1-x$$ is: | $$ \displaystyle \frac{\pi }{2}+\displaystyle \frac{4}{3}$$ |
| The parabolas $$y^{2}=4x$$ and $$x^{2}=4y$$ divide the square region bounded by the lines x = 4, y = 4 and the coordinate axes. If $$S_{1},S_{2},S_{3}$$ are respectively the areas of these parts numbered from top to bottom(Example: $$S_1$$ is the area bounded by $$y=4$$ and $$x^{2}=4y$$ ); then $$S_{1},S_{2},S_{3}$$ is |
$$1 : 1 : 1$$ |
| The area of the region bounded by the curves $$x+2y^{2}=0$$ and $$x+3y^{2}=1$$ is equal to |
$$\displaystyle \frac{4}{3}$$ |
| The area bounded by the curves $$\mathrm{y}=$$ cosx and $$\mathrm{y}=$$ sinx between the ordinates $$\mathrm{x}=0$$ and $$\displaystyle \mathrm{x}=\frac{3\pi}{2}$$: |
$$4\sqrt{2}-2$$ |
| The area(in sq. units) of the smaller portion enclosed between the curves, $$x^2+y^2=4$$ and $$y^2=3x$$, is. | $$\displaystyle\frac{1}{\sqrt{3}}+\frac{4\pi}{3}$$ |
| The area bounded between the parabolas $$4 x^{2}=y$$ and $$x^{2}=9y$$, and the straight line $$\mathrm{y}=2$$ is: |
$$\displaystyle \frac{20\sqrt{2}}{3}$$ |
| The area enclosed between the curves $$\mathrm{y}=\mathrm{a}\mathrm{x}^{2}$$ and $$\mathrm{x}=\mathrm{a}\mathrm{y}^{2} (\mathrm{a}>0)$$ is 1 sq. unit, then the value of a is |
$$1/\sqrt{3}$$ |
Continuity And Differentiability Class 12 Commerce Maths MCQ Quiz

Continuity And Differentiability Questions and Answers
| Continuity And Differentiability Quiz Question | Answer |
|---|---|
| If $$\mathrm{f}(\mathrm{x})$$ is a differentiable function and $$\mathrm{g}(\mathrm{x})$$ is a double differentiable function such that $$|\mathrm{f}(\mathrm{x})|\leq 1$$ and $$\mathrm{f}'(\mathrm{x})=\mathrm{g}(\mathrm{x})$$. If $$\mathrm{f}^{2}(0)+\mathrm{g}^{2}(0)=9$$such that there exists some $$\mathrm{c}\in(-3, 3)$$ such that $$\mathrm{g}(\mathrm{c}).\ \mathrm{g}''(\mathrm{c})<0$$, True or false |
True |
| Let f be a polynomial function such that $$f(3x)=f'(x)\cdot f''(x)$$, for all $$x\in R$$. Then. | $$f''(2)-f'(2)=0$$ |
| If $$y=\left[\displaystyle x+\sqrt{x^2-1}\right]^{15}+\left[\displaystyle x-\sqrt{x^2-1}\right]^{15}$$, then $$(x^2-1)\displaystyle\dfrac{d^2y}{dx^2}+x\dfrac{dy}{dx}$$ is equal to. | $$225y$$ |
| Let $$f : R \rightarrow R$$ and $$g : R \rightarrow R$$ be functions satisfying $$f(x + y) = f(x) + f(y) + f(x)f(y)$$ and $$f(x) = xg(x)$$ for all $$x, y \in R$$. If $$\underset{x \rightarrow 0}{\lim} g(x) = 1$$, then which of the following statements is/are TRUE? | The derivative $${ f }^{ \prime }\left( 0 \right) $$ is equal to $$1$$ |
| For the curve $$x = t^2 - 1, y = t^2 - t$$, tangent is parallel to $$x$$ - axis where, |
$$t=\dfrac{1}{2}$$ |
| $$\displaystyle \frac{d}{dx}(\tan ^{-1}x)$$ | $$ \displaystyle \frac{1}{1+x^{2}}.$$ |
| Say true or false. Every continuous function is always differentiable. |
False |
| $$\displaystyle \frac{d(sin^{-1}x)}{dx}$$ |
$$\displaystyle \frac{1}{\sqrt{\left ( 1-x^{2} \right )}}$$ |
| If $$y$$ is expressed in terms of a variable $$x$$ as $$y = f(x)$$, then $$y$$ is called | Explicit function |
| The function $$f(x)=\dfrac{1-\sin x+\cos x}{1+\sin x+\cos x}$$ is not defined at $$x=\pi$$. The value of $$f(\pi)$$ so that $$f(x)$$ is continuous at $$x=\pi$$ is | $$-1$$ |
Determinants Class 12 Commerce Maths MCQ Quiz

Determinants Questions and Answers
| Determinants Quiz Question | Answer |
|---|---|
| The number of distinct real roots of the equation, $$\begin{vmatrix} \cos x& \sin x & \sin x\\ \sin x & \cos x & \sin x\\ \sin x & \sin x & \cos x\end{vmatrix} = 0$$ in the interval $$\left [-\dfrac {\pi}{4}, \dfrac {\pi}{4}\right ]$$ is/are : |
$$2$$ |
| The points $$\displaystyle \left( 0, \frac{8}{3} \right), (1, 3)$$ and $$(82, 30)$$ : | lie on a straight line. |
| If $$A=\begin {bmatrix} 2 & -3\\ -4 & 1\end{bmatrix}$$, then adj $$(3A^2+12A)$$ is equal to. | $$\begin{bmatrix} 51 & 63\\ 84 & 72\end{bmatrix}$$ |
| Let $$P = [a_{ij}]$$ be a 3 $$\times$$ 3 matrix and let $$Q = [b_{ij}]$$, where $$b_{ij} = 2^{i + j} a_{ij}$$ for $$1 \leq i, j \leq 3$$. If the determinant of P is 2, then the determinant of the matrix Q is | $$2^{13}$$ |
| Consider three points $${P}=(-\sin(\beta-\alpha), -\cos\beta) , {Q}=(\cos(\beta-\alpha), \sin\beta)$$ and $${R}=(\cos(\beta-\alpha +\theta), \sin(\beta-\theta))$$ , where $$0< \alpha,\ \beta,\ \theta <\displaystyle \frac{\pi}{4}$$. Then |
$$P, Q, R$$ are non-collinear |
| The number of $$A$$ in $$T_p$$ such that $$A$$ is either symmetric or skew-symmetric or both, and det $$(A)$$ divisible by $$p$$, is | $$2 p - 1$$ |
| Let k be a positive real number and let $$A = \begin{bmatrix}2k-1 & 2\sqrt{k} & 2\sqrt{k}\\ 2\sqrt{k} & 1 & -2k\\ -2\sqrt{k} & 2k & -1\end{bmatrix}$$ and $$B=\begin{bmatrix}0 & 2k-1 & \sqrt{k}\\ 1-2k & 0 & 2\sqrt{k}\\ -\sqrt{k} & -2\sqrt{k} & 0\end{bmatrix}$$ . If det $$(adj A) + det (adj B) = 10^{6}, then [k]$$ is equal to [Note: adj M denotes the adjoint of a square matrix M and [k] denotes the largest integer less than or equal to k]. |
$$4$$ |
| The value of $$|\mathrm{U}|$$ is |
3 |
| $$A = \begin{bmatrix}1&2\\3&4\end{bmatrix}, B = \begin{bmatrix}2&1\\3&4\end{bmatrix}$$ then $$\left|(B^TA^T)^{-1}\right|$$ is equal to | $$1$$ |
| If three points $$(k, 2k), (2k, 3k), (3, 1)$$ are collinear, then $$k$$ is equal to: |
$$-2$$ |
Differential Equations Class 12 Commerce Maths MCQ Quiz

Differential Equations Questions and Answers
| Differential Equations Quiz Question | Answer |
|---|---|
| For $$x\epsilon R, x\neq 0$$, if $$y(x)$$ is a differentiable function such that $$x\int_{1}^{x}y (t) dt = (x + 1) \int_{1}^{x} t y (t) dt$$, then $$y (x)$$ equals: (Where C is a constant) |
$$\dfrac {C}{x^{3}} e^{-\dfrac {1}{x}}$$ |
| The differential equation $$\displaystyle \frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{x}}=\frac{\sqrt{1-\mathrm{y}^{2}}}{\mathrm{y}}$$ determines a family of circles with: |
fixed radius 1 and variable centres along the x-axis |
| Check whether the function is homogenous or not. If yes then find the degree of the function $$g(x)=x^2-8x^3$$. |
Not homogenous |
| Solution of differential equation $$\displaystyle \frac{dy}{dx} = sin x + 2x$$, is | $$y = x^2 - cos x + c$$ |
| Which of the following is/are correct regarding homogenous functions? |
Denoted by: $$f(kx)= k^n f(v)$$, where $$n$$ is the degree |
| The solution of $$\dfrac{dy}{dx}=e^{logx}$$ is: | $$2y=x^{2}+c$$ |
| The solution of $$\dfrac{dy}{dx}=\dfrac{2x}{3y^{2}}$$ is: | $$y^{3}-x^{2}=c$$ |
| The solution of $$\dfrac{dy}{dx}-\dfrac{2xy}{1+x^{2}}=0$$ is | $$y=c\left ( 1+x^{2} \right )$$ |
| The solution of $$x^{2} \cfrac{dy}{dx}=2$$ is |
$$y=-\cfrac{2}{x}+c$$ |
| Check whether the function is homogenous or not. If yes then find the degree of the function $$g(x)=8x^4$$. |
Homogenous with degree 4 |
Integrals Class 12 Commerce Maths MCQ Quiz
Integrals Questions and Answers
| Integrals Quiz Question | Answer |
|---|---|
| Let $$F(x)=f(x)+f\left ( \dfrac{1}{x} \right )$$, where $$f(x)=\int_{l}^{x}\dfrac{logt}{l+t}dt$$. Then $$F(e)$$ equals | $$\dfrac{1}{2}$$ |
| The following integral $$\displaystyle \int_{\pi/4}^{\pi/2} (2 cosec x)^{17}dx$$ is equal to | $$\displaystyle \int_{0}^{log(1+\sqrt{2})} 2(e^u + e^{-u})^{16} du$$ |
| The value of $$g\displaystyle \left ( \frac{1}{2} \right )$$ is? | $$\pi$$ |
| $$\int x log x dx $$ is equal to | $$\displaystyle\frac{x^2}{4}(2log x-1)+c$$ |
| $$\int \dfrac {dx}{\sqrt {x^{10} - x^{2}}}; x > 1=$$ ______ $$+ C$$. | $$\dfrac {1}{4}\sec^{-1} (x^{4})$$ |
| Evaluate the integral $$\displaystyle \int_{0}^{1}\frac{1}{1+x^{2}}dx$$ |
$$\pi/4$$ |
| The value of $$\int { { e }^{ \tan { \theta } } } \left( \sec { \theta } -\sin { \theta } \right) d\theta$$ is equal to ? |
$${ e }^{ \tan { \theta } }\cos { \theta } +C$$ |
| Find $$\displaystyle\int_0^\dfrac{\pi}{2}{cos^3}{x}\ dx$$ = | $$\dfrac{2}{3}$$ |
| $$\displaystyle \int _{ 0 }^{ 1 }{ \tan ^{ -1 }{ \left( \dfrac { x }{ \sqrt { 1-{ x }^{ 2 } } } \right) } dx }$$ | $$\dfrac{\pi}{2}-1$$ |
| $$\int _{ 0 }^{ 1 }{ \dfrac { { e }^{ x }.x }{ { \left( x+1 \right) }^{ 2 } } dx= }$$ | $$\dfrac{e}{2}-1$$ |
Inverse Trigonometric Functions Class 12 Commerce Maths MCQ Quiz

Inverse Trigonometric Functions Questions and Answers
| Inverse Trigonometric Functions Quiz Question | Answer |
|---|---|
| Statement I : The equation $$(sin^{-1}x)^3+(cos^{-1}x)^3-a\pi^3=0$$ has a solution for all $$a\geqslant \dfrac {1}{32}.$$ Statement II : For any $$x\epsilon R, sin^{-1}x+cos^{-1}x=\dfrac {\pi}{2}$$ and $$0\leq (sin^{-1}x-\dfrac {\pi}{4})^2\leq \dfrac {9\pi^2}{16}$$. |
Statement I is false and statement II is true. |
| If $$\cos ^{ -1 }{ x } -\cos ^{ -1 }{ \cfrac { y }{ 2 } } =\alpha $$, then $$4{ x }^{ 2 }-4xy\cos { \alpha } +{ y }^{ 2 }\quad $$ is equal to | $$4\sin ^{ 2 }{ \alpha } $$ |
| If $$\sin^{-1}\left (\dfrac {2a}{1 + a^{2}}\right ) - \cos^{1}\left (\dfrac {1 - b^{2}}{1 + b^{2}}\right ) = \tan^{-1}\left (\dfrac {2x}{1 - x^{2}}\right )$$, then what is the value of $$x$$? | $$\dfrac {a - b}{1 + ab}$$ |
| The value of $$\tan^{-1}(1)+\cos^{-1}\left(\dfrac{-1}{2}\right)+\sin^{-1}\left(\dfrac{-1}{2}\right)$$ is equal to | $$\dfrac{3\pi}{4}$$ |
| $${cos}^{-1}\left \{ \frac{1}{2}x^2+\sqrt{1-x^2}.\sqrt{1-\frac{x^2}{4}} \right \}={cos}^{-1}\frac{x}{2}-{cos}^{-1}x$$ holds for | $$0\leq x\leq 1$$ |
| Solve: $$\displaystyle { \tan }^{ -1 }\left( \frac { x }{ y } \right) -{ \tan }^{ -1 }\frac { x-y }{ x+y } $$ is equal to | $$\displaystyle \frac { \pi }{ 4 } $$ |
| Value of $$\tan^{-1}\begin{Bmatrix}\dfrac{\sin\,2-1}{\cos\,2}\end{Bmatrix}$$ is | $$1-\dfrac{\pi}{4}$$ |
| The number of triplets $$\left ( x,y,z \right )$$ satisfies the equation $$\displaystyle f\left ( x,y,z \right )= \sin ^{-1}x+\sin ^{-1}y+\sin ^{-1}z= \dfrac{3\pi }{2}$$ is | $$1$$ |
| Sin-1 $$(\displaystyle \frac{3}{5})+\mathrm{S}\mathrm{i}\mathrm{n}^{-1}(\frac{5}{13})=\sin_{X}^{-1}$$ then$$\mathrm{x}=$$ |
$$\displaystyle \frac{56}{65}$$ |
| If $$\sec^{-1} x+ \sec^{-1}y + \sec^{-1}z = 3\pi$$, then $$xy + yz + zx =$$ _______. | $$3$$ |
Linear Programming Class 12 Commerce Maths MCQ Quiz



Linear Programming Questions and Answers
| Linear Programming Quiz Question | Answer |
|---|---|
| Minimise $$Z=\sum _{ j=1 }^{ n }{ \sum _{ i=1 }^{ m }{ { c }_{ ij }.{ x }_{ ij } } } $$ Subject to $$\sum _{ i=1 }^{ m }{ { x }_{ ij } } ={ b }_{ j },j=1,2,......n$$ $$\sum _{ j=1 }^{ n }{ { x }_{ ij } } ={ b }_{ j },j=1,2,......,m$$ is a LPP with number of constraints |
$$m+n$$ |
| The solution of the set of constraints of a linear programming problem is a convex (open or closed) is called ______ region. | feasible |
| Solving an integer programming problem by rounding off answers obtained by solving it as a linear programming problem (using simplex), we find that | The value of the objective function for a maximization problem will likely be less than that for the simplex solution. |
| If a = b then ax = ........... | bx |
| The bar graph shows the grades obtained by a group of pupils in a test. If grade C is the passing mark, how many pupils passed the test? 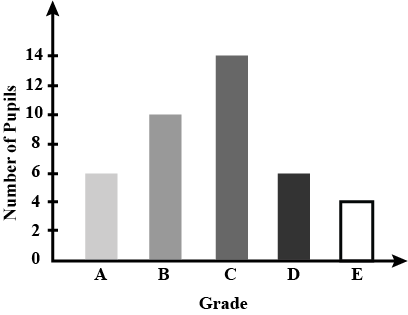 |
30 |
| An iso-profit line represents | An infinite number of solutions all of which yield the same profit |
| In linear programming, lack of points for a solution set is said to | have no feasible solution |
| If x + y = 3 and xy = 2, then the value of $$\displaystyle x^{3}-y^{3}$$ is equal to | 7 |
| If the constraints in linear programming problem are changed | the problem is to be re-evaluated |
| The bar graph shows the number of cakes sold at a shop in four days. What is the difference in number of cakes between the highest and the lowest daily sale? 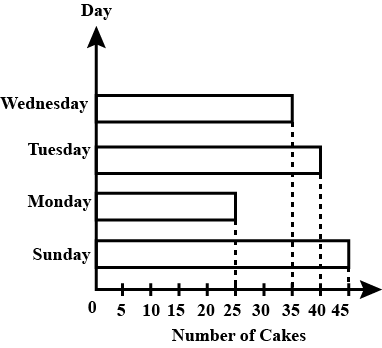 |
20 |
Matrices Class 12 Commerce Maths MCQ Quiz

Matrices Questions and Answers
| Matrices Quiz Question | Answer |
|---|---|
| Let $$X$$ and $$Y$$ be two arbitrary, $$3\times 3$$, non-zero, skew-symmetric matrices and $$Z$$ be an arbitrary $$3\times 3$$, non-zero, symmetric matrix. Then which of the following matrices is (are) skew symmetric? | $$X^{23}+Y^{23}$$ |
| If $$\displaystyle A=\left[ \begin{matrix} 3 & 1 \\ -1 & 2 \end{matrix} \right] $$ and $$\displaystyle I=\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right] $$, then the correct statement is: | $$\displaystyle { A }^{ 2 }-5A+7I=O$$ |
| If AB = AC then | B need not be equal to C |
| If $$\mathrm{A}^{2}=\mathrm{A},\ \mathrm{B}^{2}=\mathrm{B},\ \mathrm{A}\mathrm{B}=\mathrm{B}\mathrm{A}=O$$ (Null Matrix), then $$(\mathrm{A}+\mathrm{B})^{2}=$$ |
$$\mathrm{A}+\mathrm{B}$$ |
| $$I$$ $$A=\left[\begin{array}{ll} 0 & 1\\ 1 & 0 \end{array}\right]$$, $$A^{4}=$$ ($$I$$ is an identity matrix.) |
$$I$$ |
| lf $$\mathrm{A}= \left[\begin{array}{lll} o & c & -b\\ -c & o & a\\ b & -a & o \end{array}\right]\mathrm{a}\mathrm{n}\mathrm{d}$$ $$ \mathrm{B}=\left[\begin{array}{lll} a^{2} & ab & ac\\ ab & b^{2} & bc\\ ac & bc & c^{2} \end{array}\right],$$ then $$\mathrm{A}\mathrm{B}=$$ |
$$\mathrm{O}$$ |
| lIf $$\mathrm{A} =\left[\begin{array}{ll} a & 0\\ a & 0 \end{array}\right],\ \mathrm{B}=\left[\begin{array}{ll} 0 & 0\\ b & b \end{array}\right],$$ then $$\mathrm{A}\mathrm{B}=$$ |
$$O$$ |
| If $$A=\left[\begin{array}{lll} 1 & -2 & 3\\ -4 & 2 & 5 \end{array}\right]$$ and $$B=\left[\begin{array}{ll} 2 & 3\\ 4 & 5\\ 2 & 1 \end{array}\right],$$ then |
$$\mathrm{A}\mathrm{B},\ \mathrm{B}\mathrm{A}$$ exist and are not equal |
| $$\left[\begin{array}{ll} x & 0\\ 0 & y \end{array}\right]\left[\begin{array}{ll} a & b\\ c & d \end{array}\right]=$$ |
$$\left[\begin{array}{ll} ax & b_{X}\\ yc & dy \end{array}\right]$$ |
| If $$\mathrm{A}=\left[\begin{array}{lll} 1 & -3 & -4\\ -1 & 3 & 4\\ 1 & -3 & -4 \end{array}\right]$$, then $$\mathrm{A}^{2}=$$ |
Null matrix |
Probability Class 12 Commerce Maths MCQ Quiz


Probability Questions and Answers
| Probability Quiz Question | Answer |
|---|---|
| Let A and E be any two events with positive probabilities : Statement - 1 : $$P \left (\displaystyle \frac{E}{A} \right) \geq P \left (\displaystyle \frac{A}{E} \right ) P(E)$$ Statement - 2 : $$P \left (\displaystyle \frac{A}{E}\right ) \geq P(A\cap E)$$ |
Both the statement are true |
| If $$\mathrm{C}$$ and $$\mathrm{D}$$ are two events such that $$\mathrm{C}\subset \mathrm{D}$$ and $$\mathrm{P}(\mathrm{D})\neq 0$$, then the correct statement among the following is |
$$P\left(\dfrac{C}{D}\right) \geq \mathrm{P}(\mathrm{C})$$ |
| If $$A$$ and $$B$$ are any two events such that $$P(A) = \dfrac {2}{5}$$ and $$P(A\cap B) = \dfrac {3}{20}$$, then the conditional probability, $$P(A|(A'\cup B'))$$, where A' denotes the complement of $$A$$, is equal to: | $$\dfrac {5}{17}$$ |
| It is given that the events A and $$B$$ are such that $$P(A)=\displaystyle \frac{1}{4},\ P(A|B)=\displaystyle \frac{1}{2}$$ and $$P(B|A)=\displaystyle \frac{2}{3}$$. Then $$P(B)$$ is |
$$\displaystyle \frac{1}{3}$$ |
| Assertion is False, Reason is True | |
| A computer producing factory has only two plants $${ T }_{ 1 }$$ and $$ { T }_{ 2 }$$. Plant $$ { T }_{ 1 }$$ produces $$20\%$$ and plant $${ T }_{ 2 }$$ produces $$80\%$$ of total computers produced. $$7\%$$ of computers produced in the factory turn out to be defective. It is known that $$P$$ (computer turns out to be defective given that it is produced in plant $${ T }_{ 1 }$$) $$=10P$$ (computer turns out to be defective given that it is produced in plant $$\displaystyle { T }_{ 2 }$$). where $$P(E)$$ denotes the probability of an event $$E$$. A computer produced in the factory is randomly selected and it does not turn out to be defective. Then the probability that it is produced in plant $$ { T }_{ 2 }$$ is |
$$\displaystyle \frac { 78 }{ 93 } $$ |
| One of the two boxes, box $$I$$ and box $$II$$, was selected at random and balls are drawn randomly out of this box. The ball was found to be red.If the probability that this red ball was drawn from box $$II$$ is $$\dfrac{1}{3}$$, then the correct option options with the possible values of $$n_1,n_2,n_3$$ and $$n_4$$ is (are) |
$$n_1 = 3, n_2=6,n_3=10,n_4=50$$ |
A fair die is rolled repeatedly until a six is obtained. Let X denote the number of rolls required. The conditional probability that $$X \geq 6$$ given $$X > 3$$ equals |
$$\displaystyle \frac{25}{36}$$ |
| Let $$\mathrm{E}^{\mathrm{c}}$$ denote the complement of an event $$\mathrm{E}$$. Let $$\mathrm{E},\ \mathrm{F},\ \mathrm{G}$$ be pairwise independent events with $$\mathrm{P}(\mathrm{G})>0$$ and $$\mathrm{P}(\mathrm{E}\,\mathrm{\cap}\,\mathrm{F}\,\mathrm{\cap}\,\mathrm{G}) =0$$. Then $$\mathrm{P}(\mathrm{E}^{\mathrm{c}}\,\mathrm{\cap}\,\mathrm{F}^{\mathrm{c}}|\mathrm{G})$$ equals |
$$\mathrm{P}(\mathrm{E}^{\mathrm{c}})-\mathrm{P}(\mathrm{F})$$ |
| Let $$X$$ and $$Y$$ be two events such that $$P(X) = \dfrac {1}{3}, P(X/Y) = \dfrac {1}{2}$$ and $$P(Y/X)= \dfrac {2}{5}$$. Then | $$P(X'|Y) = \dfrac {1}{2}$$ |
Relations And Functions Class 12 Commerce Maths MCQ Quiz


Relations And Functions Questions and Answers
| Relations And Functions Quiz Question | Answer |
|---|---|
| If $$f(x) =x+\tan x$$ and $$f$$ is inverse of $$g$$, then $$g'(x)$$ is equal to | $$\dfrac{1}{2+(x-g(x))^2}$$ |
| $$f:R\rightarrow R$$ is a function defined by $$f(x)=10x-7$$. If $$g=f^{-1}$$ then $$g(x)=$$ |
$$\dfrac{x+7}{10}$$ |
| A constant function $$f:A\rightarrow B$$ will be one-one if | $$n(A) = 1$$ |
| If $$f:\mathbb{N} \rightarrow \mathbb{N}$$ and $$f(x) = x^{2}$$ then the function is |
one to one function |
| $$f(x)=1$$, if $$x$$ is rational and $$f(x)=0$$, if $$x$$ is irrational then $$(fof) (\sqrt{5})=$$ |
$$1$$ |
| If $$f(x) = 3x + 2, g(x) = x^2 + 1$$, then the value of $$(fog) (x^2 +1)$$ is | $$3x^4 + 6x^2 + 8$$ |
| If $$f:A\rightarrow B $$ is surjective then | every element of $$B$$ has at least one pre-image in $$A$$ |
| If $$f:(0,\infty )\rightarrow (0,\infty )$$ is defined by $$f(x)=x^{2}$$, then $$f^{-1}(x)=$$ |
$$\sqrt{x}$$ |
| $$f:R\rightarrow R , g:R\rightarrow R$$ and $$f(x)= \sin x$$, $$g(x)=x^{2}$$ then $$fog(x)=$$ |
$$\sin x^{2}$$ |
| Find the value of $$\displaystyle \left( g\circ f \right) \left( 6 \right) $$ if $$\displaystyle g\left( x \right) ={ x }^{ 2 }+\frac { 5 }{ 2 } $$ and $$\displaystyle f\left( x \right) =\frac { x }{ 4 } -1$$. |
2.75 |
Three Dimensional Geometry Class 12 Commerce Maths MCQ Quiz

Three Dimensional Geometry Questions and Answers
| Three Dimensional Geometry Quiz Question | Answer |
|---|---|
| If a line makes an angle of $${\pi }/{4}$$ with the positive direction of each of $$x$$-axis and $$y$$-axis, then the angle that the line makes with the positive direction of the $$z$$-axis is | $$\dfrac{\pi}{2}$$ |
| A line $$AB$$ in three-dimensional space makes angles $$45^{\mathrm{o}}$$ and $$120^{\mathrm{o}}$$ with the positive $$\mathrm{x}$$-axis and the positive $$\mathrm{y}$$-axis respectively. lf $$AB$$ makes an acute angle $$e$$ with the positive $$\mathrm{z}$$-axis, then $$e$$ equals |
$$60^{\mathrm{o}}$$ |
| A line makes the same angle $$\Theta$$, with each of the $$\mathrm{x}$$ and $$\mathrm{z}$$ axis. If the angle $$\beta$$, which it makes with $$\mathrm{y}$$-axis, is such that $$\sin^{2}\beta=3\sin_{\Theta}^{2}$$, then $$\cos^{2}\Theta$$ equals: |
$$\displaystyle \frac{3}{5}$$ |
| A line in the 3-dimensional space makes an angle $$\theta \left(0 < \theta \leq \dfrac {\pi}{2}\right)$$ with both the x and y axes, then the set of all values of $$\theta$$ is the interval : | $$\left[\dfrac {\pi}{4}, \dfrac {\pi}{2}\right]$$ |
| The points with position vectors $$60 \widehat{i} + 3 \widehat{j}$$, $$40 \widehat{i} - 8 \widehat{j}$$, $$a\widehat{i} -52\widehat{j}$$ are collinear if | $$a = -40$$ |
| The vector equation $$r=i-2j-k+t(6j-k)$$ represents a straight line passing through the points: | $$(1, -2, -1)$$ and $$(1, 4, -2)$$ |
| A line makes the same angle $$\theta$$ with each of the $$X$$ and $$Z$$-axes. If the angle $$\beta$$, which it makes with $$Y$$-axis, is such that $$\sin ^{ 2 }{ \beta } =3\sin ^{ 2 }{ \theta } $$, then $$\cos ^{ 2 }{ \theta } $$ equals | $$\dfrac {3}{5}$$ |
| The points with position vectors $$ 60i + 3j, 40i -8j$$ and $$ ai -52j $$ are collinear if |
$$a = -40$$ |
| Equation to a line parallel to the vector $$2\hat{i}-\hat{j}{+}\hat{k}$$ and passing through the point $$\hat{i}+\hat{j}{+\hat{k}}$$ |
$$(x-1)\hat{i}+(y-1)\hat{j}+(z -1)\hat{k}=\lambda(2\hat{i}-\hat{j}+\hat{k})$$ |
| The direction ratios of the diagonal of the cube joining the origin to the opposite corner are (when the $$3$$ concurrent edges of the cube are coordinate axes) |
$$1,1,1$$ |
Vector Algebra Class 12 Commerce Maths MCQ Quiz

Vector Algebra Questions and Answers
| Vector Algebra Quiz Question | Answer |
|---|---|
| If $$|\overrightarrow{C}|^2=60$$ and $$\overrightarrow{C} \times (\widehat{i}+2\widehat{j}+5\widehat{k})=\overrightarrow{0}$$, then a value of $$\overrightarrow{C}\cdot (-7 \widehat{i}+2\widehat{j}+3\widehat{k})$$ is : |
$$12\sqrt{2}$$ |
| In a parallelogram ABCD, $$|\overrightarrow{AB}| = a, |\overrightarrow{AD}| = b$$ and $$|\overrightarrow{AC}| = c$$, then $$\overrightarrow{DB}.\overrightarrow{AB}$$ has the value | $$\displaystyle \frac{1}{2} (a^2 + b^2 - c^2)$$ |
| Let $$P,\ Q,\ R$$ and $$S$$ be the points on the plane with position vectors $$-2\hat{i}-\hat{j},\ 4\hat{i},\ 3\hat{i}+3\hat{j}$$ and $$-3\hat{i}+2\hat{j}$$ respectively. The quadrilateral $$PQRS$$ must be a |
parallelogram, which is neither a rhombus nor a rectangle |
| Statement -$$1$$ is True, Statement -$$2$$ is False | |
| $$ABCD$$ is a parallelogram and $$AC, BD$$ be its diagonals Then $$ \vec{AC} +\vec{BD}$$ is |
$$2\vec{BC} $$ |
| The triangle $$ABC$$ is defined by the vertices $$A= (0,7,10)$$ , $$B=(-1,6,6)$$ and $$C=(-4,9,6)$$. Let $$D$$ be the foot of the attitude from $$B$$ to the side $$AC$$ then $$BD$$ is |
$$-\overline{i}+2\overline{j}+2\overline{k}$$ |
| The point $$C=(\dfrac{12}{5}, \dfrac{-1}{5},\dfrac{4}{5})$$ divides the line segment $$AB$$ in the ratio $$3:2$$. If $$B=(2,-1,2)$$ then $$A$$ is |
$$(3, 1,-1)$$ |
| Let $$\vec{A}= \hat{i}+6\mathrm{i}+6\mathrm{k},\vec{B}=-4\hat{i}+9\hat{i}+6\hat{k},\vec{G}=\displaystyle \dfrac{-5}{3}\hat{i}+\dfrac{22}{3}\hat{j}+\dfrac{22}{3}\hat{k}$$. If $$\mathrm{G}$$ is the centroid then the triangle $$ABC$$ is |
A right angled isosceles triangle |
| If $$A(\overline{a})$$ , $$B(\overline{b})$$ and $$C(\overline{c})$$ be the vertices of a triangle $$ABC$$ whose circumcentre is the origin then orthocentre is given by |
$$\overline{ a}+\overline{b}+\overline{c}$$ |
| Let $$a,b,c,d $$ be the position vectors of the points $$\mathrm{A},\mathrm{B},\mathrm{C},\mathrm{D}$$ respectively. The condition for the figure $$ABCD$$ to be a parallelogram is |
$${ \hat { a } }+{ \hat { c } }={ \hat { b } }+\hat { d } $$ |
Commerce Maths MCQ Questions for Class 12 - Practice Test with Solutions
Do you want to overcome your drawbacks while attempting the quizzes or MCQ tests like time consumption, approaching questions, etc.? Take the advantage of practicing with MCQExams.com MCQ Questions for Standard 12 Commerce Maths Test. As it is a time-based approach and also provides answers to all questions.
One should practice the MCQs in this way for a better assessment of their preparation level. All chapters CBSE Class 12 Commerce Maths MCQ Quiz Questions with Solutions PDF free download links are available for easy access & quick reference.
How to Use MCQExams.com Chapterwise 12th Commerce Maths MCQ Interactive Quiz?
Guys do you love to share your practice hacks and tips with your friends? If yes, then our 12tth standard CBSE Commerce Maths MCQ interactive quiz help you do the same. Excited to know the process then jump into the below steps right away:
- Go with the respective chapter class 12 Commerce Maths MCQ quiz link from the above
- Now, you will find the MCQ quiz boxes for the Application Of Derivatives chapter along with the interactive quiz windows.
- Click on the CBSE 12th Class Application Of Derivatives MCQ Interactive Quiz and it will redirect you to another window where it displays the questions with options in stories format.
- Answer the question one after another and learn the answers right away this helps you to do a quick assessment of your knowledge.
- You can also share this cool MCQ Interactive Quiz Questions of Plus Two Commerce Maths topicwise with your friends by just tapping on the send arrow located at the top left corner of the story.
- After clicking the button, you can opt for the copy link option and easily paste the link on your friend's chat or else in your whatsapp story too. Isn’t it cool!!
- Keep passing this interesting approach of practicing Plus Two CBSE Commerce Maths Application Of Derivatives MCQ Questions to your co-students and help them in attempting the entrance exams like JEE & NEET.