Basic Science - Class 7 General Knowledge - Extra Questions

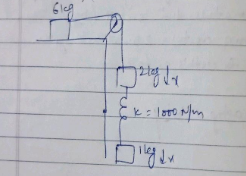
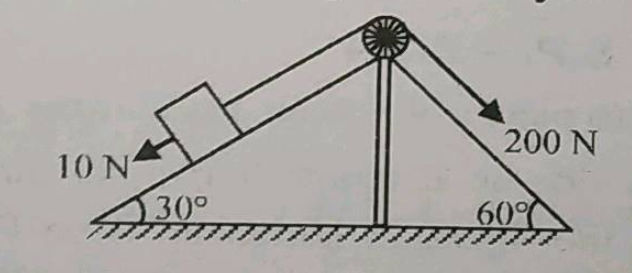
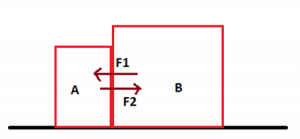
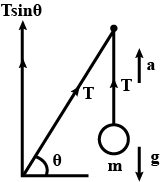
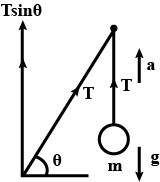
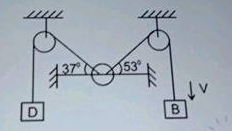
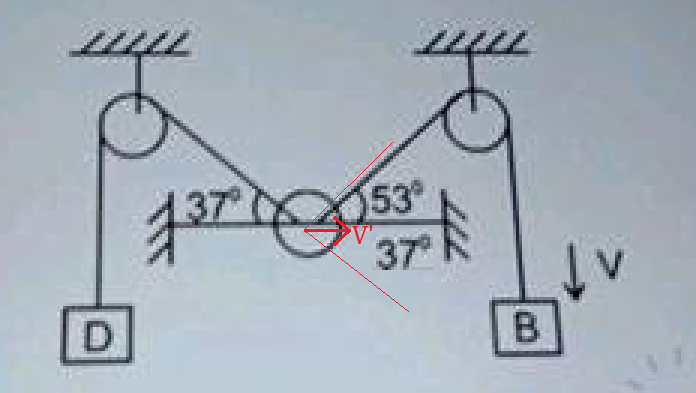
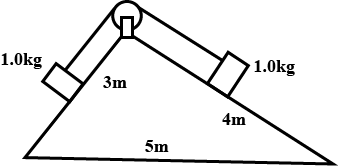
Consider the situation shown in figure. All the surfaces are frictionless and the string and the pulley are light. Find the magnitude of the acceleration of the two blocks.
1889429_dd1eea8e761c45c6816099adb1b14d36.png

$$\tan {\theta}_{1}=\cfrac{4}{3}={53}^{o}$$
$$\tan {\theta}_{2}=\cfrac{3}{4}={37}^{o}$$
let acceleration of the blocks be towards left along the inclined planes.
From the FBD of the two blocks
$$ma=mg\sin {\theta}_{1}-T$$ and $$Ma=T-mg\sin {\theta}_{2}$$
$$a=\cfrac{g}{10}$$
1854958_1889429_ans_42f30d109f544d95bcc86c48fb0cd178.png


Force $$F$$ and density $$d$$ are related as $$F=\frac{\alpha}{\beta+\sqrt{d}}$$ then find the diamention of $$\alpha$$ and $$\beta$$

Diamension of $$\beta$$ = Diamension of $$\sqrt{d}$$
$$=1^{1/2}$$
$$F=\frac{\alpha}{\beta+\sqrt{d}}$$
$$MLT^{-2}=\frac{{\alpha}}{L^{1/2}}$$
$$[\alpha]=ML^{3/2}T^{-2}$$


$$Mass M = 1$$ unit is divided into two parts $$X$$ and $$( 1 - x)$$. For a given separation the value of $$X$$ for which the gravitational force between them becomes maximum is 

$$F = [\frac{g(m_1 .m_2)}{r^2}]$$
i .e$$ F \times m_1 .m_2$$
$$F \times mx (1 - x) m$$
$$F \times m^2 . x (1  -x)$$
For maximum force 
$$\Rightarrow \dfrac{df}{dx} = 0$$
$$\Rightarrow \dfrac{df}{dx} = \dfrac{d}{dx} [ x (1  -x) m^2] = 0$$
 $$\dfrac{d}{dx} [(x - x^2)m^2]$$
$$\Rightarrow m^2 ( - 2x + 1) = 0$$
$$2x = 1$$
$$\Rightarrow x = \dfrac{1}{2}$$


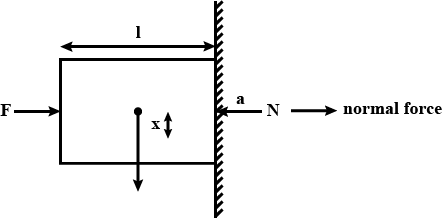
A cube of mass $$2\ kg$$ is held stationary against a rough wall by a force $$F = 40\ N$$ passing through centre $$C$$. Find perpendicular distance of normal reaction between wall and cube from point $$C$$. Side of the cube is $$20\ cm$$. Take $$g = 10\ m/s^{2}$$.
1602707_60b12998153a4d11a821f0b81c556047.png

Point $$(a)$$ torque
$$F\cdot x = mg \dfrac {l}{2}$$.
$$x=\dfrac{2×10×0.1}{40}$$
$$x=0.05$$m

1852167_1602707_ans_dbb6174d81244a2ba34bf129697ea652.png


What is a force?

Explanation :
  • Force is defined as an external cause that changes or tends to change the state of the body once applied, if the body is in motion it comes to rest and if at rest then will come to motion. It can also cause a change in the direction, shape, and size of the body.
  • Example: Pushing or pulling a door by applying force.


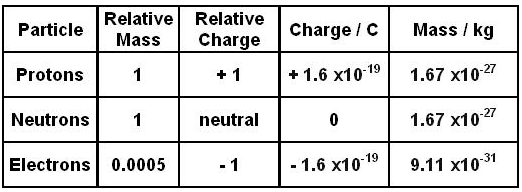
How does the mass of an electron compare to the mass of a proton?

Neutrons have the largest mass, but protons are approximately $$99.9\%$$ of a neutron's size. They're very close in size, but an electron is so much smaller.
1842008_1883972_ans_0cdfc316dcad45aa8810eb64461d0ff5.png


How does one Coulomb of charge compare with the charge of a single electron?

One electron is equal to $$-1.6 \times 10^{-19} C$$ of charge. So it takes $$6.25 \times 10^{18}$$ electrons to have a charge of $$-1$$ Coulomb.


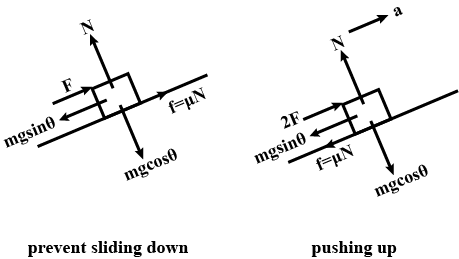
How does static friction differ from kinetic friction?


1843534_1884042_ans_e4d4162d1189440bbbf3021a4af957e8.png


How does the acceleration of an object depend on the net force acting on it if the total mass is constant?

When $$M$$ is Constant

$$a_{Net}= \dfrac{F_{Net}}{M_{Net}}$$


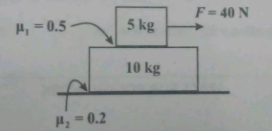
How does the roughness of surfaces that are touching affect the friction between the surfaces?

Friction is caused when two surfaces move against each other in opposing directions.

The resistance offered by friction depends directly on the force applied to move the two surfaces (calculated as vertical or normal force) and the roughness of the surfaces.

The smoother the surfaces, the less the resistance; the rougher the surface, the more the resistance.


A 50 cm long straight piece of thread is kept on the surface of water. Find the force with which the surface on one side of the thread pulls it. Surface tension of water $$-0.076 N/m $$. 

$$F = l \times T$$
$$= \frac{5}{100} \times 0.076$$
$$3.8 \times 10^{-3}N$$


Match column-I with cohimn-II and select the correct answer using the codes given below:

Cell body is broad, rounded, pyriform part of the neuron that contains a central nucleus, abundant cytoplasm and various cell organelles except centrioles. Dendrites are fine short and branched protoplasmic processes of cell body that pick up sensations and transmit the same to the cell body. Axon is a long fibre like cytoplasmic process that carries impulses away from cell body. Myelin sheath covers the axon of nerve cell.


Why does a boatman push the bank with his pole to make the boat move?

When he pushes the bank, the bank pushes him - action and reaction are equal and opposite. The bank cannot move but the boat moves.


Why does a train stop when you pull the chain?

As soon as the chain is pulled, vacuum breaks, air rushes in and brakes are applied.


Why does the gun kick back when a bullet is fired?

For every action there is equal and opposite reaction.


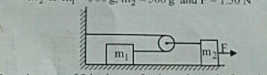
The acceleration of the $$2\ kg$$ block if the free end of string is pulled with a force of $$20\ N$$ as shown is
1030815_950db6c15ee043dbbfa97d3c5f456632.png

For the given situation
$$T=F$$
$$T=20\,N$$
So,
$$ma=2T-mg$$
$$2 \times a=2 \times 20 -2 \times 10$$
$$2 \times a=40 -20$$
$$2 \times a=20$$
$$a=10\,m/s^2$$
1852083_1030815_ans_20eab774dd4a4f28b07e0d7c9008bb2e.png


A block is shot with an initial velocity $$5 ms^{-1} $$ on a rough horizontal plane. Find the distance covered by the blocks toll it comes to rest. The coefficient of kinetic friction between the block and plane is $$0.1$$.

Given : $$\mu=0.1$$      $$u=5\ m/s$$
Retardation of the block $$a=-\mu g=-0.1\times 10=-1\ m/s^{2}$$
Final velocity $$v=0$$
Using $$v^{2}-u^{2}=2aS$$
Or $$0-5^{2}=2\times (-1)\times S$$
Finally we get S = 12.5 m


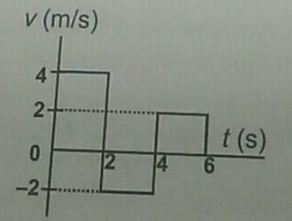
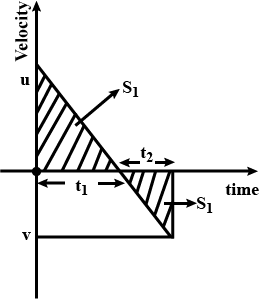
What is the acceleration of the body moving with uniform acceleration at the midpoint of two points on a straight line, where the speeds are $$u$$ and $$v$$ respectively?


1943893_1214878_ans_b64cfd1bbed749f09d21eef6f05f78c2.jpg


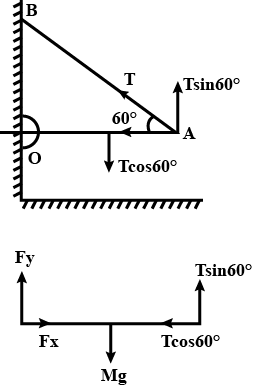
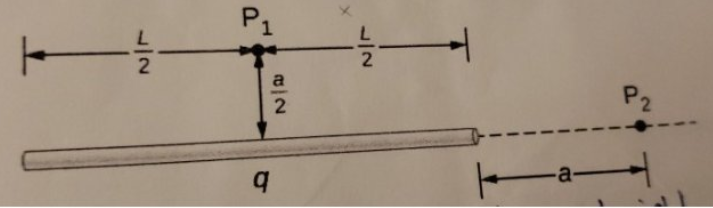
A rod $$OA$$ of mass $$4\ kg$$ is held in horizontal position by a massless string $$AB$$ as shown in figure. Length of the rod is $$2\ m$$. Find
(a) tension in the string.
(b) net force exerted by hinge on the rod. $$(g = 10\ m/s^{2})$$.
1405222_aeaad29ddbf649728e932735fcd4e1d1.png

For equilibrium condition
$$F_{y} + T\sin 60^{\circ} = mg ... (i)$$
$$F_{x} = T\cos 60^{\circ} ... (ii)$$
Torque about point $$A$$
$$mg \dfrac {l}{2} = F_{y} \times l$$
$$F_{y} = \dfrac {mg}{2} = \dfrac {9\times 10}{2}$$
$$= 20\ N$$
1852127_1405222_ans_7f22d18431074b0c82ca5b86dd5f3df6.png


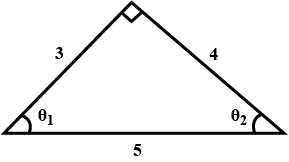
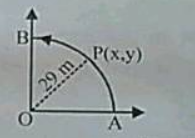
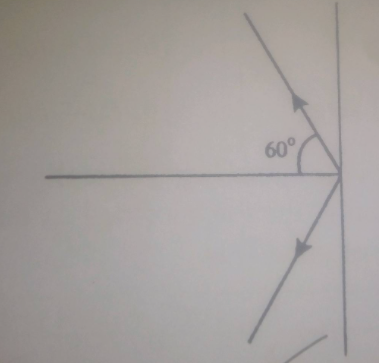
Two vectors having magnitude 12 and 13 are inclined at an angle $${45^0}$$ to each other. find their resultant vector.


1978287_1373394_ans_84cbfe50304543f69dab4017fe2c69cc.jpg


A force of $$5N$$ acting on a body $$A$$ produces an acceleration of $$2m{s}^{-2}$$. The same force acting on the body $$B$$ produces an acceleration of $$5m{s}^{-2}$$. Find the mass of the bodies $$A$$ and $$B$$. What will be the acceleration produced if both the bodies are tied together and same force (ie $$5N$$) acts on it.

$$F=ma$$
$${m}_{2}=\cfrac{F}{{a}_{2}}=\cfrac{5}{5}=1kg$$
$${m}_{2}=\cfrac{F}{a}=\cfrac{5}{2}=2.5kg$$
Total mass $$=\cfrac{5}{2}+1=3.5kg$$
Acceleration $$=\cfrac{}{m}=\cfrac{10}{7}m/{s}^{2}$$


How does the Bohr's model of the atom differ from the quantum mechanical model?

In the Bohr Model, the electron is treated as a particle in fixed orbits around the nucleus. In the Quantum Mechanical Model, the electron is treated mathematically as a wave. The electron has properties of both particles and waves.

The Bohr model was a one-dimensional model that used one quantum number to describe the distribution of electrons in the atom. The only information that was important was the size of the orbit, which was described by “n” the principle quantum number.

Schrodinger's model (Quantum Mechanical Model) allowed the electron to occupy three-dimensional space. It therefore required three coordinates, or three quantum numbers, to describe the distribution of electrons in the atom.


How does oxygen has mass?

Balanced equation:

$$2Mg(s) + O_2(g) \overset{\Delta}{\rightarrow} 2 MgO(s)$$

The product, magnesium oxide, contains the magnesium you started with chemically combined with oxygen gas from the air in your classroom. If you subtract the amount of magnesium that you started with from the mass of the magnesium oxide you obtained, you will get the mass of oxygen that reacted.

One thing to keep in mind is that you may also get some magnesium nitride because of nitrogen gas in the air, so your product may not have the mass you expect if just oxygen gas reacted with the magnesium.


What is the mass number of an atom?

The mass number (represented by the letter A) is defined as the total number of protons and neutrons in an atom.


A  thin uniform rod of length 1 m and mass 1 kg is roasting an axis passing through its centre and perpendicular to its length . Calculate the moment of inertia and radius of gyration of the rod about an axis passing through a point midway between the centre and its edge, perpendicular to its length . 

Answer 
By parallel axis theorem we have
 $$ I = I_{cm} + ma^2$$
$$ I = I_{cm} + m \left ( \dfrac{L}{4} \right )^{2} $$
$$= \dfrac{mL^{2}}{12} + \dfrac{mL^{2}}{16} $$
$$= \dfrac{12 mL  + 9mL^{2}}{144} = \dfrac{21 mL^{2}}{144}$$
$$mR^{2} = \dfrac{21 mL^{2}}{144}  = \dfrac{21}{144} \times 1 \times 1^{2} $$ $$= 0.14583$$
$$R = \dfrac{\sqrt{2}}{12} L $$
$$ = \dfrac{\sqrt{21}}{12} \times 0.3818$$


A disc with linear velocity $$ v $$ and angular velocity $$ \omega $$ is placed on rough ground. Suppose $$ a $$ and $$ \alpha $$ be the magnitudes of linear and angular acceleration due to friction. Then:
Column IColumn II
(A) When $$ v = R \omega $$ (p) $$ a = R \alpha (a \neq 0) $$
(B) When $$ v = \frac{R \omega}{2} $$(q) $$ a > R \alpha $$
(C) When $$ v = 2 R |omega $$(r)  $$ a > R \alpha $$
(s) None

(1) When $$ v = R \omega \rightarrow $$ No friction factor $$ a = 0, \alpha = 0 $$
(2) $$ v = \frac{r \omega}{2} $$
      $$ 2v = R \omega $$ it mean $$ R \omega > v $$
                                         So $$ R \alpha > a $$
(3) $$ v = 2 R \omega $$ its mean R \omega < v $$
                                          So $$ R \alpha < a $$


$$v=at+\cfrac{b}{t+c}$$ is a dimensionally valid equation. Obtain the dimensional formula for $$a,b$$ and $$c$$ where $$v$$ is velocity, $$t$$ is time and $${v}_{0}$$ is initial velocity

$$\left[ c \right] =\left[ t \right] =\left[ { M }^{ 0 }{ L }^{ -1 }T \right] $$
$$\left[ v \right] =\cfrac { b }{ \left[ t+c \right]  } \Rightarrow \left[ { M }^{ 0 }{ L }^{ -1 }T \right] =\cfrac { b }{ \left[ T \right]  } \Rightarrow b=\left[ { M }^{ 0 }{ L }^{  }{ T }^{ 0 } \right] $$


A particle describes a horizontal circle of radius  r on a smooth surface of an inverted  cone . The height of the plane of the circle above the vertex is h . Then the speed of the particle will be  

Answer
$$ N \cos \theta  = \dfrac{m v^{3}}{Y} $$
$$ N  \sin \theta  =  m g $$
$$ \dfrac{\cos \theta }{\sin \theta} = \dfrac{v^{2}}{r{g}} $$
$$ \cot\theta  = \dfrac{\cos \theta}{\sin \theta} = \dfrac{h}{r} $$
$$  \dfrac{h}{r} = \dfrac{v^{2}}{r{g}} $$
$$ V  = g\sqrt{h} $$


A total charge $$q$$ is distributed uniformly along a thin straight rod of length $$l$$. Choose the positive $$y$$ direction as up and the positive x-direction as up and the positive x direction as right and calculate and express in unit vector notation.
a. the electric field at point $$P_{1} $$ in terms of the given variables
b. the electric field at point $$P_{2} $$ in terms of the given variables
[See integral given on formula page.]
1889389_fd818a64ca3d483abaff32c53acf6bf6.png

Take an element of length $$dx$$ at  distance $$x$$ from point P.
Charge on this element $$ = dq = \lambda dx $$

Field at P due to this element of charge
$$ dE = \dfrac{kdq}{x^2} $$ 

$$ \Rightarrow dE = \dfrac{k \lambda dx}{x^2} $$ 

$$\displaystyle \Rightarrow E = \int^{l + a}{a} \dfrac{k \lambda}{x^2} dx $$ 

$$\displaystyle \Rightarrow E = k \lambda \left  [\dfrac{-1}{x}  \right  ]^{l + a}{a} $$ 

$$\displaystyle \Rightarrow E = k \lambda \left  (\dfrac{1}{a} - \dfrac{1}{l + a}  \right  ) $$ 

$$\displaystyle \Rightarrow E = \dfrac{k \lambda l}{a (a + l)} $$ 

Total charge on the rod = $$Q = \lambda l $$ 

Hence $$ E = \dfrac{kQ}{a (a + l)} $$


A uniform solid cylinder of mass $$M = 2\,kg$$ and radius $$R = 10\,cm$$ is connected about an axis through the centre of the cylinder to a horizontal spring with spring constant $$4\,N/m$$. The cylinder is pulled back, stretching the spring $$1\,m$$ from equilibrium. When released, the cylinder rolls without slipping. What is the speed of the center of the cylinder when it returns to equilibrium?


1992143_1889378_ans_cd400b988f3d4da58e36638d1f18cc6c.jpg


Find the angle it makes with one of the rectangular components of a force of $$40\,N$$ is $$20\,N.$$ Find the angle it makes with this component.

from torque
$$cos\theta = \dfrac{20}{40} = \dfrac{1}{2}$$
$$cos\theta = \dfrac{1}{2}$$
$$\theta = 60$$

1856349_1890621_ans_418e348a4b0b4c0a9a4049f71a796d66.png


A heavy ball of mass $$M$$ is suspended from the ceiling of a car by a light string of mass $$m(M<<M)$$. When the car is at rest, the speed of transverse waves in the string is $$60m{s}^{-1}$$. When the car has an acceleration $$a$$, the wave-speed increases to $$60.5m{s}^{-1}$$. The value of $$a$$, in terms of gravitational acceleration $$a$$ is closest to:

We know that when two identical object collide elastically then their velocities are interchanged
$$T=mg$$
$$\mu =\cfrac{M}{L}$$
$$V=\sqrt { \cfrac { T }{ \mu  }  } $$
$$\cfrac{V}{V'}=\sqrt { \cfrac { m\left( { a }^{ 2 }+{ g }^{ 2 } \right)  }{ m{ g }^{ 2 } }  } \Rightarrow { \left( \cfrac { 60.5 }{ 60 }  \right)  }^{ 2 }=\cfrac { \sqrt { { a }^{ 2 }+{ g }^{ 2 } }  }{ g } $$
$$\Rightarrow { \left( \cfrac { 60.5 }{ 60 }  \right)  }^{ 4 }=\cfrac { { a }^{ 2 }+{ g }^{ 2 } }{ { g }^{ 2 } } \Rightarrow { a }^{ 2 }={ g }^{ 2 }{ \left( \cfrac { 60.5 }{ 60 }  \right)  }^{ 4 }-{ g }^{ 2 }=g\sqrt { { \left( \cfrac { 60.5 }{ 60 }  \right)  }^{ 4 }-1 } =g\times 0.1837=\cfrac { g }{ 5.44 } \Rightarrow a\approx \cfrac { g }{ 5 } $$


Derive the formula for the range and maximum height achieved by a projectile thrown from thee origin with initial velocity u at an angle $$\theta$$ to the horizontal.

Answer
$$\tan$$ height
$$v^{2} - u^{2} = 2as$$
$$o - (usin)2 = 2(-g) H$$
$$h = \dfrac{u^{2} \sin^{2} Q}{2g}$$
Time to go and came in
S = ut + $$+ \dfrac{1}{2}$$ at $$2$$
$$ 0 = u \sin t \dfrac{-1}{2} g t^{2}$$
$$t = \dfrac{2 u \sin q}{g}$$


In the figure shown masses of the blocks A, B and C are 6 kg , 2Kg and 1 Kg respectively . Masses of the spring is negligibly small and its stiffiness is 100 N/m . The co-efficient of friction between the block A and the table is $$\mu  = 0.8 $$ . Initially block C is held such that spring is i n relaxed position . The block is released from rest Find the maximum distance moved by the block C in cm 

Answer 
$$ \dfrac{1}{2} kx^{2} = 2g cx - 1g x $$
$$ x = \dfrac{2g}{k} \Rightarrow  x = \dfrac{20}{100} \times 100 = 2 cm $$

1844889_1889515_ans_e7907413848a4bf0be23bffd89629764.PNG


Example 2.12 The periodic of oscillation of a simple pendulum  is T  =  21 . /L /g . Measured value of Lis 20.0 cm known to 1 mm accuracy and time for 100 oscillation  of the pendulum is found to be 90 s using a wrist watch of 1 s resolution  . What is the accuracy in the determination of g ?

Answer
$$ T  =  2 \pi \sqrt{\dfrac{L}{g}} $$
$$  g = 4\pi^{2} \dfrac{L}{T^{2}} $$
$$ \dfrac{\Delta g}{g} = \dfrac{\Delta L}{L} + 2 \dfrac{\Delta T}{T} $$
$$ \dfrac{\Delta g}{g} = \dfrac{10^{-3}}{0.2} + \dfrac{2 \times 1}{90} $$
$$ \dfrac{\Delta g}{g} \times 100 = \dfrac{1}{2} + \dfrac{20}{9} =  2.7 $$ %


A block of wood of mass 0.5 kg is placed on a plane making $$30^{\circ}$$  with the horizontal . If the co-efficient of friction between the surfaces of contact of the body and the plane is 0.5 . What force is required to keep the body sliding down ?

Answer 
By balancing the force we get
$$F = (m \sin 30^{\circ} + Nmg \cos 30^{\circ}) $$
$$= \dfrac{5}{2} + \dfrac{5}{2} $$
$$ = 3.2 N $$


Prove that angle of friction is equal to angle of repose.

The maximum value of static friction up to which body does
not move is called limiting friction. Angle of repose is defined as the angle
of the inclined plane with horizontal such that a body placed on it is just
begins to slide. In limiting condition, F=mgsinαF=mgsin⁡α


In this problem, we will use mechanical similarity to find the period T of simple pendulum ($$\theta$$ is very small).
If gravitational acceleration is changed by a factor $$\alpha$$ and time by a factor $$\beta : g \rightarrow g' = \alpha g, t \rightarrow t' = \beta t,$$ find the relation between $$t' / t$$ and $$g' / g$$
(hint: L' = constant $$\times$$ L)
1889580_075b9c1ec8ed4dc5962fecdb852ea2a7.png

$$t' = \sqrt{\dfrac{2\pi}{l^1g^1}}$$
$$t = \sqrt{\dfrac{2\pi}{lg}}$$
$$\dfrac{t'}{t} = \sqrt{\dfrac{lg}{l' g' }} = \sqrt{\dfrac{l}{l'}} \dfrac{g}{g'}$$
$$\beta = \sqrt{\dfrac{l}{l'}}a$$
$$\beta$$ = constant a


The speed of a motor increases from $$1200 rpm $$to $$1800 rpm$$ in $$205$$. How many revolutions does it make in this period of time?

$$w_o = 1200 \frac{rev}{min} = \frac{1200 \times 2\pi rad}{60 sec} = 40\pi $$
$$w = \frac{8200 \times 2\pi rad}{60 sec} =60\pi $$
$$\alpha = \frac{w - w_o}{20} = \frac{20\pi }{20} = \pi $$
$$\theta = w_ot + \frac{1}{2} \times t^2 = 40\pi \times 20 + \frac{1}{2} \pi (20)^2$$
$$= 800\pi + 20\pi = 1000\pi $$


What do you mean by projectile motion? A point object is projected at an angle $$\theta $$ with the horizontal with velocity u from the ground and the object strikes the ground on the same level as that of projection after some time. Prove that - The trajectory of the projectile is parabolic.

Motion experienced by a obseat or particle that is thrown near the earth's
surface and moves along a curved path under the action of gravity only. 


The angular frequency of a fa increases from $$30 rpm$$ to $$60 rpm$$ in $$\pi s$$. A dust particle is present at a distance of $$20 cm$$ from axis of rotation. The tangential acceleration of the particle in $$\pi s$$ is 


1946858_1890494_ans_32c24839b07a4bc0b7a35552ff691ae0.jpg


Two identical balls of mass $$2 kg$$ each are kept in contact with a compressed spring, on either side of it. When the spring is released, the balls move with a velocity $$10 m s^{-1}$$. Find the acceleration produced in each ball if the spring constant is $$4 N m^{-1}$$

All the elastic potential energy of spring goes into kinetic energy of balls
$$\Rightarrow \frac{1}{2} . k . x^2 = \frac{1}{2} . m . y^2$$
$$\Rightarrow \frac{1}{2} \times 4 \times x^2 = \frac{1}{2} \times 4 \times 100$$
$$\Rightarrow x = 10m$$
acceleration of each ball = $$\frac{f}{m} = \frac{kx}{m} = \frac{10 \times 4}{2} \frac{m}{b^2}$$
$$a = 20 \frac{m}{b^2}$$



Calculate the height of the communication satellite. $$\left [ Given G = 6.67 \times 10^{-11} Nm^2/kg^2, M = 6 \times 10^{24} kg, R = 6400 km \right ]$$

$$G = 6.67 \times 10^{-11} N/m^2/kg^2$$
$$M = 6 \times 10^{24} kg$$
$$R = 6400 km$$
$$T = 2 \times \sqrt{\frac{\mu ^3}{Gm}}$$
$$T^2 = \left ( \frac{4x}{Gm} \right ) x^3 \therefore \mu^3 = \frac{T^2 Gm}{4\pi^2 }$$
$$\therefore (R + h)^3 = \frac{T^2 Gm}{4\pi^2 } [\because (\pi )^3 = (R + h)^3]$$
Putting the values we geb:
$$R + h = 3\sqrt{75.74 \times 10^{21}}$$
$$R + h = 4.231 \times 10^6 m$$
$$h = 4.231 \times 10^6 m - R$$
$$h = 4.231 \times 10^6 m - 6.4 \times 10^6 [\because R = 6.4  \times 10^6]$$
$$h = 35.9 \times 10^6 m $$ or $$ 35910 km$$


A ball is thrown from ground such that it just crosses two poles of equal height kept $$ 80 \mathrm{m} $$ apart. The maximum height attained by the ball is $$ 80 \mathrm{m} $$. When the ball passes the first pole, its velocity makes $$ 45^{\circ} $$ with horizontal. The correct alternatives is/are :- $$ \left(g=10 \mathrm{m} / \mathrm{s}^{2}\right) $$
(A) Time interval between the two poles is $$ 4 \mathrm{s} $$(B)Height of the pole is $$ 60 \mathrm{m} $$.
(C) Range of the ball is $$ 160 \mathrm{m} $$.
(D) Angle of projection is $$ \tan ^{-1}(2) $$ with horizontal.

Here,we can assume projectile motion from A to B as an independent projectile motion with range as 80m(given)
Now, we know that,
$$R=\dfrac{2 \mu^2\sin \theta \cos \theta}{g}$$
$$80=\dfrac{2 \times V^2 \times 1/2}{10}$$
$$V^2=800$$
$$V=20\sqrt{2}$$
$$(20)^2-V_y^2=2 \times 80 \times (-10)$$
$$V_y^2=2000 \implies V_y=10 \sqrt{20}$$
$$=20\sqrt{5}$$
$$\tan\theta=\dfrac{20\sqrt{5}}{20}=\sqrt{5}$$

1856403_1890730_ans_41c79da808d747b294e35ad9efc92896.png


Two balls of equal masses are projected upward simultaneously one from the ground with speed 50 m/s and other from a 40 m high tower initial speed 30 m/s. Find the maximum height attained by their center of mass.

$$Vcm =  \dfrac{m_{1}v_{1} + m_{2}v_{2}}{m_{1} + m_{2}} = (v_{1} + v_{2})/2$$
Initially, $$U_{cm} = 40 m/s$$
$$X_{CM} = 40 / 2 = 20 m$$ above ground.
Maximum height means $$V_{CM} = 0$$
That is, $$0^{2} - 40^{2} = 2 \times (-10) \times (H - 20)$$
Thus $$H = 100m$$


A 4m long ladder weighing 25 kg rests with its upper end against a smooth wall and lower end on rough ground What should be the minimum coefficient of friction between the ground and the ladder for it to be inclined at $$60^{\circ}$$ with the horizontal without slipping ? (Take $$g = 10 ms^{-2}$$)


In the figure, AB is a ladder of weight W which acts at its centre of gravity G.

$$ABC=60^{}$$

$$BAC=30^{}$$

Let


$$N_1$$ be the reaction of the wall, and


$$N_2$$ the reaction of the ground. Force of friction $$f$$


between the ladder and the ground acts along $$BC$$. For horizontal


equilibrium,

$$f=N_1$$ ... (i)

For vertical equilibrium,

$$N_2=W$$... (ii)

Taking moments about $$B$$, we get for equilibrium,

$$N_1(4cos30^{})W(2cos60^{})=0$$...(iii)

Here,  $$W=250N$$

Solving these three equations, we get

$$f=72.17N \ and \ N_2=250N$$

$$\mu=\dfrac{f}{N_2}=\dfrac{72.17}{250}=0.288$$



1865922_1899761_ans_50ed48d1d3744b00990da9e1e8290e86.png


A  10  kg block kept on an inclined plane is pulled by a string applying 200  N force . A  10 N force is also applied  on 10 kg block as shown in fig Find (a) tension in  the string .
acceleration of 10 kg block
net force on pulley exerted by string .
1899770_191c62ccd1084125bd0f24d6a088643c.PNG


1978329_1899770_ans_ab9c5aaa3915479aaf99f9e3d9e77086.jpg


Two forces $$ F_{1} $$ and $$F_{2} (F_{1}- F_{2}) $$ are applied at the free ends of uniform rod kept on a horizontal frictionless surface . The rod has length L and total mass M , Find tension in rod at distance x from end 'A'
1899811_2b87bebbe16e40adb79c1cbfc46b9c60.PNG

In the figure, AB is a ladder of weight W which acts at its centre of gravity G.
∠ABC=60∘
∠BAC=30∘
Let
N1 be the reaction of the wall, and
N2 the reaction of the ground. Force of friction f
between the ladder and the ground acts along BC. For horizontal
equilibrium,
f=N1 ... (i)
For vertical equilibrium,
N2=W ... (ii)
Taking moments about B, we get for equilibrium,
N1(4cos30∘)−W(2cos60∘)=0 ...(iii)
Here,  W=250N
Solving these three equations, we get
f=72.17NandN2=250N
∴μ=N2f=25072.17=0.288
mass of both parts of rods are :
m1=(LM)l,m2=(LM)(L−l)
Also F2−F=m2a……………………….(1)
F−F1=m1a………………………..(2)
and a=MF2−F1
Acceleration of rod =MF2−F1
This will be acceleration of 'l' part
F1+LMl×MF2−F1=F
⇒F=F1+L(F2−F1)l



In the system shown below , function and mass  of the pulley are neglibible . Find the acceleration of $$ m_{2}$$ if $$ m_{1} =  300 g , m_{2} =  500 g $$ and F  =  1.50 N
1899822_4fe5fea2d4b4445e98db3402e55a5f0d.PNG

Let , Tension in the string connecting pulley and block of mass m2 be T,

therefore tension on string connecting pulley and block of mass m1 will be T/2.let acceleration of block of mass m2 be a2 and that of m1 be a1.

Now,

from F.B.D. of block of mass m2,

we get,

F−T=m2(a2) .....(1)

also, from F.B.D. of block of mass m1,

we get,

T/2=m1(a1) .....(2)

Using constraint equation,

we get,

(a2)(−T)+(a1)(T/2)=0

a1=2(a2) .....(3)

On solving eqn1 , 2 , and 3;

we've

Ans:

a2 = 0.37s2m

and T = 0.296N








A point $$P$$ moves in counter-clockwise direction on a circular path as shown in the figure. The movement of $$P$$ is such that it sweeps out a length $$s= t^3 + 5$$, where $$s$$ is in metre and $$t$$ is in second. The radius of the path is $$29 \ m$$. The acceleration of $$P$$ when $$t= 2s$$ is nearly.
1899851_976d8780340c4cf386bebf1e5e796318.png


Here, s=t3+5,v=dsdt=3t2,r=20ms=t3+5,v=dsdt=3t2,r=20m
Tangential acceleration,
aT=dvdt=ddt(3t2)=6taT=dvdt=ddt(3t2)=6t
at t=2sec,aT=6×2=12m/s2t=2sec,aT=6×2=12m/s2
Centripetal acceleration
ac=v2r=(12)220=14420m/s2ac=v2r=(12)220=14420m/s2
Total acceleration,
a=a2T+a2C−−−−−−−√=(2)2+(14420)2−−−−−−−−−−−−√≈14m/s2            



A man is running on a hill with velocity (2i+3j)m/s with respect to ground he feels that trained drops are falling vertically with velocity 4m/s. if man is running on heel in a new direction with same speed find velocity of rain with respect to man. 


1978394_1899860_ans_ca932fa2bd89406eb15840b22923bc00.jpg


Find the value of g at a height of 400 km above the surface of the earth. Given radius of the earth, R = 6400 km and value of g at the surface of the earth = $$9.8 ms^{-2}.$$


2154372_1899902_ans_7abfdc5f731442439448f06f8977816a.jpg


A particle A moves along a circle of radius R = 50 cm so that its radius vector r relative to the point O (Fig. 1.5) rotates with the constant angular velocity $$\omega = 0.40 rad s^{-1}.$$ Find the modulus of the velocity of the particle, and the modulus and direction of its total acceleration.
1899920_029cf1d353514ddcbf0462dca1773a40.PNG

Particle is rotating $$\omega$$ with point O so it will rotate with $$2\omega$$ with centre.
Acceleration = $$\dfrac{V^2}{R}$$
$$= \dfrac{0.16}{0.5}$$
$$= 0.32 m/s^2$$


State Newton's $$ 3^{rd} $$ law of motion. Explain any two examples based on this law.

Statement: To every action, there is an equal and opposite reaction.

It means that if a body A exerts a force F1 on a body B, and the body B exerts a force F2 on body A, then:

Newton’s Third Law

F1=F2

That is, they are equal in magnitude but opposite in direction.

Whenever two bodies interact, they will exert equal and opposite forces on each other.

This law can be observed anywhere and everywhere in the surroundings. Some examples of action-reaction pairs are mentioned below:

A swimmer pushes the water backward by his/her hands and in return the water pushes the swimmer forwards, thus enabling him to go forward during swimming.



A $$100\,g$$ ball is coming towards a bat with a velocity of $$10\,m/s.$$ It strikes that bat at $$60^\circ$$ and rebounds. If the ball remains in contact with the bat for $$0.1\,s,$$ what is the force applied on the bat.
1902026_cae3cbeb35c84bbcb06c5ac66327d11e.png

$$\Delta P = 2mv \,cos60^\circ$$
$$= 2 \times \dfrac{mv}{2} = mv$$
$$= (0.1)(10) = 1$$
$$F = \dfrac{\Delta P}{t} = \dfrac{1}{0.1} = 10$$


The velocity(v) versus time (t) graph of a body moving on a straight line is shown in figure. The average speed of body in the interval of $$6$$ s is
1902578_1816b3fb729a4412925c5b13c04cf6ff.png

We know that
$$V_{avg} = \dfrac{\text{Total distance}}{\text{Total time}}$$
Are under the graph is total distance therefore
$$= \dfrac{4 \times 2 - 2 \times 2 + 2 \times 2}{6}$$
$$= \dfrac{8}{6} = \dfrac{4}{3}$$


The frictional force acting on $$10\,kg$$ block by the ground is $$\left ( \dfrac{2n + 65}{3} \right )N.$$ Find the value of n.
1902612_b0c8db8524c44396abeede81da1a827b.png

From figure we have 
On $$5$$ kg block
$$40 = \mu mg + ma$$  (Let $$g = 10$$)
$$40 = 0.5 \times 5 \times 10 + 5 \times 10$$
$$\dfrac{40 - 25}{5} = a$$
$$a = 3$$
$$5 \times 3 = \mu mg$$
$$15 = \left ( \dfrac{2n \times 65}{3} \right ) \times 15 \times 10$$ [as now whole block solve as single system]
$$\dfrac{3}{2 \times 10 \times 15} = 8n$$
On solving we get 
$$n = 0.0023$$


For a particle undergoing rectilinear motion with uniform acceleration, the magnitude displacement is one third the distance covered in some time interval. The magnitude of final velocities is less than the magnitude of initial velocity for this time interval. The ratio of initial speed to final speed for this time interval is $$\dfrac{4\sqrt{2}}{n}$$, Find the value of $$n$$.

$$S_{1}+S_{2}=$$ distance 
$$S_{1}-S_{2}$$ displacement
If distance $$=3$$ (displacement)
then $$S_{1}=2S_{2}$$
$$\dfrac{1}{2}t_{1}\times u=2\left(\dfrac{1}{2}t_{2}\times v\right)$$
& for slope
$$\dfrac{u}{t_{1}}=\dfrac{v}{t_{2}}$$
Slope of graph a value 
$$\dfrac{u}{t_{1}}=\dfrac{v}{t_{2}}$$
$$\left(\dfrac{1}{2}\times t_{1}\times u\right)=2\left(\dfrac{1}{2}\times t_{2}\times v\right)$$
$$\dfrac{t_{1}}{t_{2}}=\dfrac{2v}{u}$$
But
$$\dfrac{t_{1}}{t_{2}}=\dfrac{u}{v}$$
$$\dfrac{u}{v}=\dfrac{2v}{u}$$
$$\dfrac{u^{2}}{v^{2}}=2$$
$$\dfrac{u}{v}=\sqrt{2}$$........(1)
$$\dfrac{4\sqrt{2}}{n}$$...........(2)
On comparing above two equation 
$$n=2$$

1882800_1903099_ans_74632f9da1a542e0bd338942df639479.png


A light straight fixed at one end to a wooden clamp on a ground passes over a pulley and hangs at the other side. It makes an angle $$30^o$$ with the ground. A body weighing $$60\ kg$$ climbs up the rope. The wooden clamp and tolerate up to vertical force $$360\ N$$. Find the maximum acceleration in the upward direction with which the boy can climb safely. The friction of pulley and wooden clamp may be ignored $$(g=10\ m/s^2)$$

1903066_4841f36b6dc64a5bb585898fd9de3f1b.png

$$\theta=30^o$$
$$T=m (g+a)$$
$$T=60(10+a)$$
$$T \sin \theta =360 \ N$$
$$T=360 \times 2 =m (g+a)$$
$$720=60 (10+a)$$
$$10+a=12$$
$$a=2 m/s^2$$
1882648_1903066_ans_bb5a59ebd7134bfa9226c2033384e5a6.png


A wooden plank of mass 20 kg is resting on a smooth horizontal floor. A man of mass 60 kg starts moving from one end of the plank to the other end. The length of the plank is 10 m. Find the displacement of the plank over the floor when the man reaches the other end of the plank,
1903169_baab35df3aa34121aaabf8eca92003c8.png

When it moved let displacement of plank be $$v$$
But since there is no external force so can will be same
$$\therefore \dfrac{50 \times 0+ 30 \times \dfrac{L}{2}}{50 +30}= \dfrac{50 (L+x) +30 \left( \dfrac{1}{2}+ x \right)}{50+30}$$
$$30 \times \dfrac{L}{2} =50L+ 50x+ 30 \times \dfrac{L}{2}+30x$$
$$-50L=80x$$
$$x=-\dfrac{5}{8}L$$
so its displacement will be $$\dfrac{5}{8}L$$ in backward direction.

2008542_1903169_ans_7a48eb40517744fa918f2874341ae9e1.png


A bead can freely move on a horizontal rod. The bead is connected by block $$B$$ and $$D$$ by a string as shown in the figure. If the velocity of $$B$$ is $$V$$. Find the velocity of Block $$D$$.
1903378_0bd01a631a7f465aa3a0eefb41dd41b6.png

$$V' \cos 53^o =v$$
$$V'  = 5v/3$$
$$\dfrac{5v}{3} \times \cos 37 = v_d$$
$$v_d =\dfrac{5v}{3} \times 4/5 =4v/3$$

2008570_1903378_ans_bf61103bf1a144bdab8e4d426faf409b.png


The force required just to move a body up an inclined plane is double the force required just to prevent the body sliding down it. If the coefficient of friction is $$0.333$$, angle of inclination of the plane is ....

Prevent sliding down:
$$F+f=mg \sin \theta $$
$$F=mg\sin \theta -\mu mg \cos \theta $$
$$F=mf[\sin \theta -\mu \cos \theta]$$
Pushing :
$$2F-mg \sin \theta -f=ma$$
$$2F-mg\sin \theta -\mu mg \cos \theta =ma$$
$$a=0$$
$$2F=mg \sin \theta +\mu mg\cos \theta$$
$$2mg[\sin \theta -\mu \cos \theta ]=mg[\sin \theta +\mu \cos \theta )$$
$$2\sin \theta -2\mu \cos \theta =\sin \theta +\mu \cos \theta $$
$$\sin \theta =3\mu \cos \theta$$
$$\tan \theta =3\mu$$
$$\tan \theta \approx 1$$
$$\theta =45^o$$
1878951_1903260_ans_662a96e7b02a4cc9a4313d33a8ff684b.png


How much force is needed to accelerate a 66 kg skier at $$ 2 m/s^{2}$$

Answer:
By Newton's second law
F = ma
Plug in the numbers:
$$F = 66kg(2ms^{2})$$
$$F = 132 N$$


Why action and reaction forces are not balanced forces?

Although action and reaction forces are always equal and opposite to each other, they are acting on two different objects. Saying that the forces balance each other implies that they are adding up to equal zero. Forces are only added when they are acting on the same object, not on different objects. If you are looking at the motion of a car, you are interested in the forces that are acting ON the car, but not on any forces that the car is exerting on other objects. That would affect the motion of the other objects, but not the motion of the car.


Why $$MgSO_4$$ soluble in water whereas $$BaSO_4$$ is insoluble in water?

Solubility is a relative term. There are no compounds (or hardly any compound) that is completely insoluble in water. Thus in our question, we are assuming the fact that $$MgSO_4$$ is more soluble than $$BaSO_4$$. 
Generally, solubility is related with lattice energy. More the lattice energy, less the solubility. Thus compounds containing ions with a $$-2$$ charge are normally not soluble in water. $$BaSO_4$$ has $$B{a}_{2}^{+}$$ and $$S{O}_{4}^{2-}$$. If the salt is composed of highly charged ions, it is insoluble in water. 

Anhydrous form of $$MgSO_4$$ is hygroscopic and thus highly soluble in water. $$MgSO_4$$ is composed $$f$$ relatively low charged ions and thus it is very soluble in water. 


What does a skydiver achieve terminal velocity?

Answer
Terminal velocity is the highest velocity which an object can reach as it falls through a fluid. In this case, the air is the fluid.
Here the sum of the drag force and the buoyancy is directly proportional to the downward force of gravity acting on the skydiver. Here the net force on the skydiver is zero and resultant zero acceleration.
Here the skydiver can reach the terminal velocity by falling freely under acceleration due to gravity through air.


Describe any five man-made sources of water?

Five man-made sources of water are:

• Water well – This is a structure that is created by drilling, driving, or boring. The water from the well is pumped out using a pump.

• Dam – A dam is a structure that obstructs the flow of water. It ensures that the water is used when there is scarcity of water.

• Underground tanks – This is another source that is used to store water. They are built below the surface.

• Canals – These are man-made channels that are primarily used for transportation.

• Tube well – This is a long well that is connected to an underground aquifer.


Two trains start from $$p$$ and $$q$$ respectively and travel towards each other at a speed of $$50\ km/hr$$ and $$40\ km/hr$$ respectively. By the time they meet, the first train has travelled $$100\ km$$ more than the second. The distance between $$p$$ and $$q$$ is:

Let the distance covered by the second train be $$dm$$ then the distance covered by the first train will be $$(100+d)m$$.
Speed of the first train $$=50\ km/hr$$
Speed of the second train $$=40\ km/hr$$
Time taken by the first train $$=\dfrac{50}{100+d}$$
Time taken by the second train $$=\dfrac{40}{d}$$
When both trains meet each other, they have travelled for the same time duration.
$$\Rightarrow \dfrac{50}{100+d}=\dfrac{40}{d}$$
$$\Rightarrow 50d=4000+40d$$
$$\Rightarrow 10d=4000$$
$$\Rightarrow d=400$$
$$\Rightarrow$$\Distance covered by second train $$=400\ Km$$
$$\Rightarrow$$ Distance covered by first train $$=(400+100)Km=500\ Km$$
$$\therefore$$ Distance between $$P$$ and $$Q=400Km+500Km=900Km$$


Examples of static inertia and dynamic inertia

Answer 
static inertia refers to the inertia of a body at rest . The inertia of a book on the table is static inertia. Dynamic inertia refers to the inertia of a body in uniform motion. The inertia of a ball moving in a frictionless floor is dynamic inertia.



A ball is thrown vertically upwards with a velocity of $$20m/s$$ 
from the top of a multi storey building.The height of the point where the ball is thrown 25 m from the ground.How high will the ball rises.( b) How long it will be before hits the ground.$$g=10m/s^{2}$$

a) we know that 
  $$H=\dfrac{u^2}{2g}$$
 $$H=\dfrac{20^2}{2×10}$$
$$H=20m$$

b) let $$t_1$$ be time to come back at initial position of throwing.
So, $$t_1=\dfrac{2u}{g}$$
$$t_1=\dfrac{2×20}{10}$$
$$t_1=4sec$$

Now, v is the velocity with which it hits the ground.
So, $$v=\sqrt{u^2+2as}$$
$$v=\sqrt{20^2+2×10×25}$$
$$v=30m$$

Now , $$t_2=\dfrac{v-u}{g}$$
    $$t_2=\dfrac{30-20}{10}$$
$$t_2=1sec$$

So, $$time taken to hit the ground is 
    $$t_1+t_2=1+4=5$$sec



How does the atomic number change when an element emits an alpha particle?

Alpha decay involves the ejection of an alpha particle from the nucleus. Since an alpha particle is a helium $$(^4_2He)$$ nucleus having $$2$$ protons and $$2$$ neutrons, alpha decay involves the loss of $$2$$ protons and $$2$$ neutrons from an element.

As a result, the atom that loses an alpha particle has its mass number decreased by four ($$2$$ protons and $$2$$ neutrons) and its atomic number decreased by $$2$$ ( as it loses two protons). Consequently, the identity of the element is changed to a new element.

When uranium$$-238$$ undergoes alpha decay, it emits an alpha particle and the uranium atom is changed to a thorium atom a follows:

$$_{92}^{238} U\ \rightarrow\ _{90}^{234}Th\ +\  _2^4 He$$


Class 7 General Knowledge Extra Questions