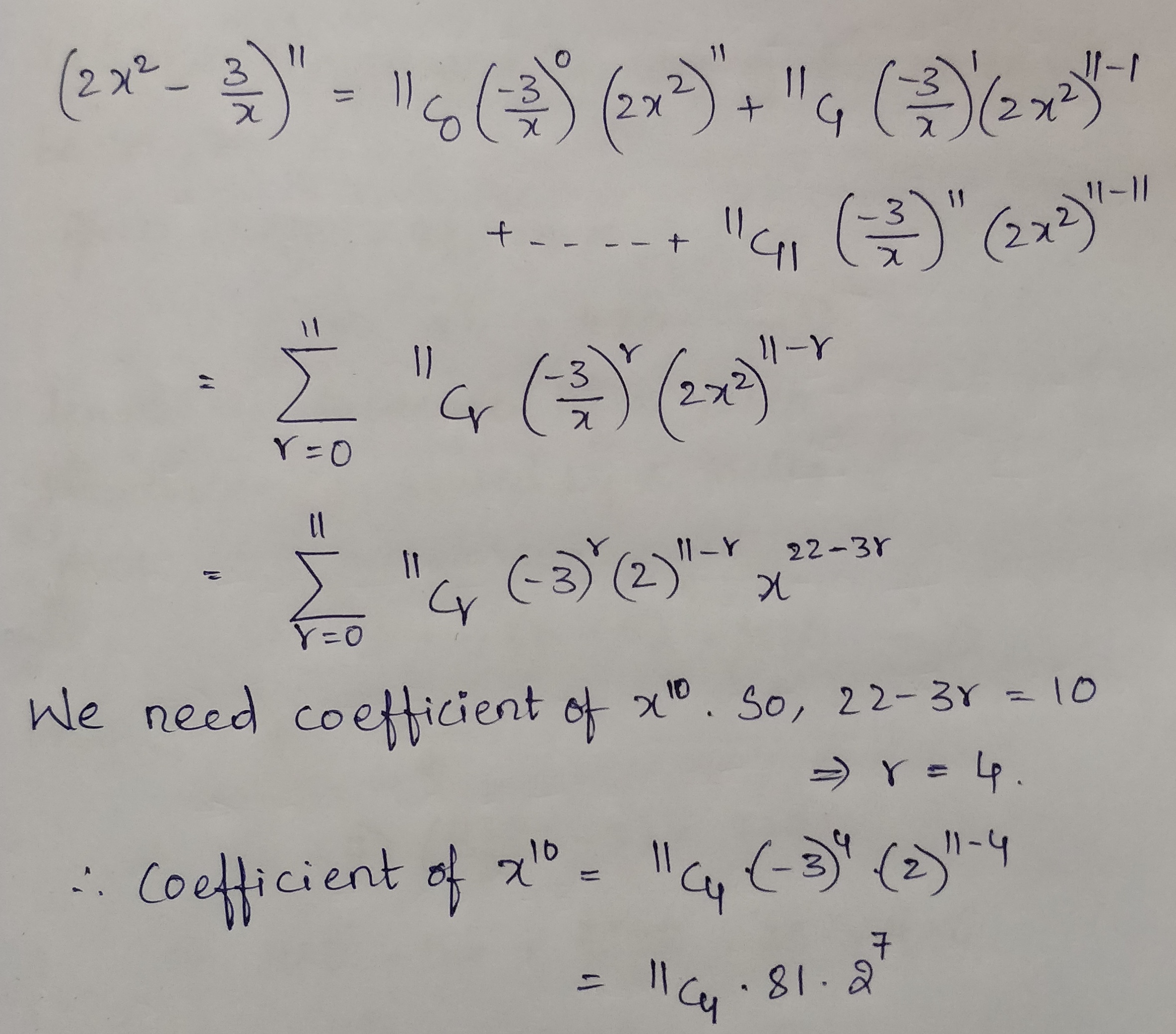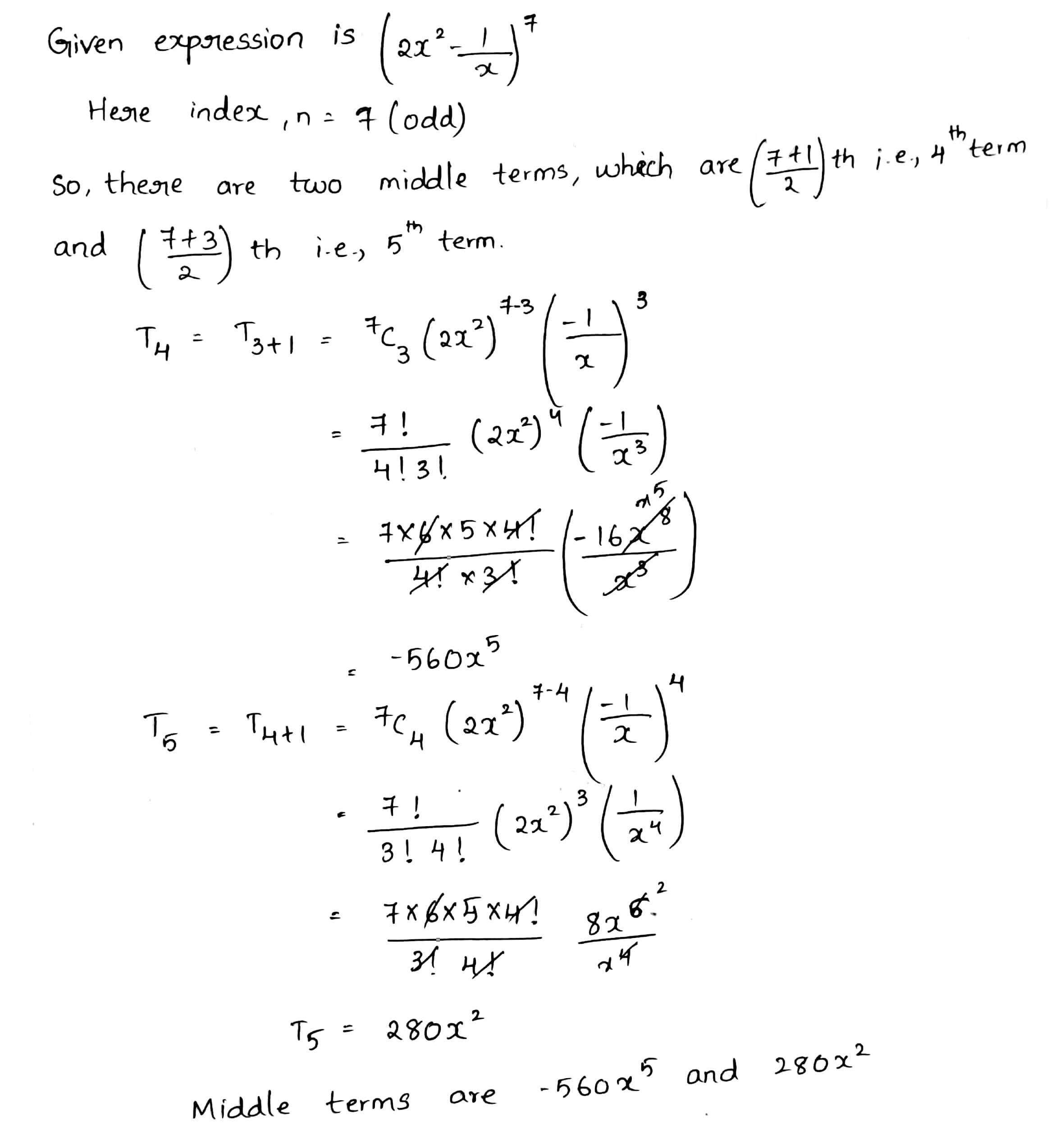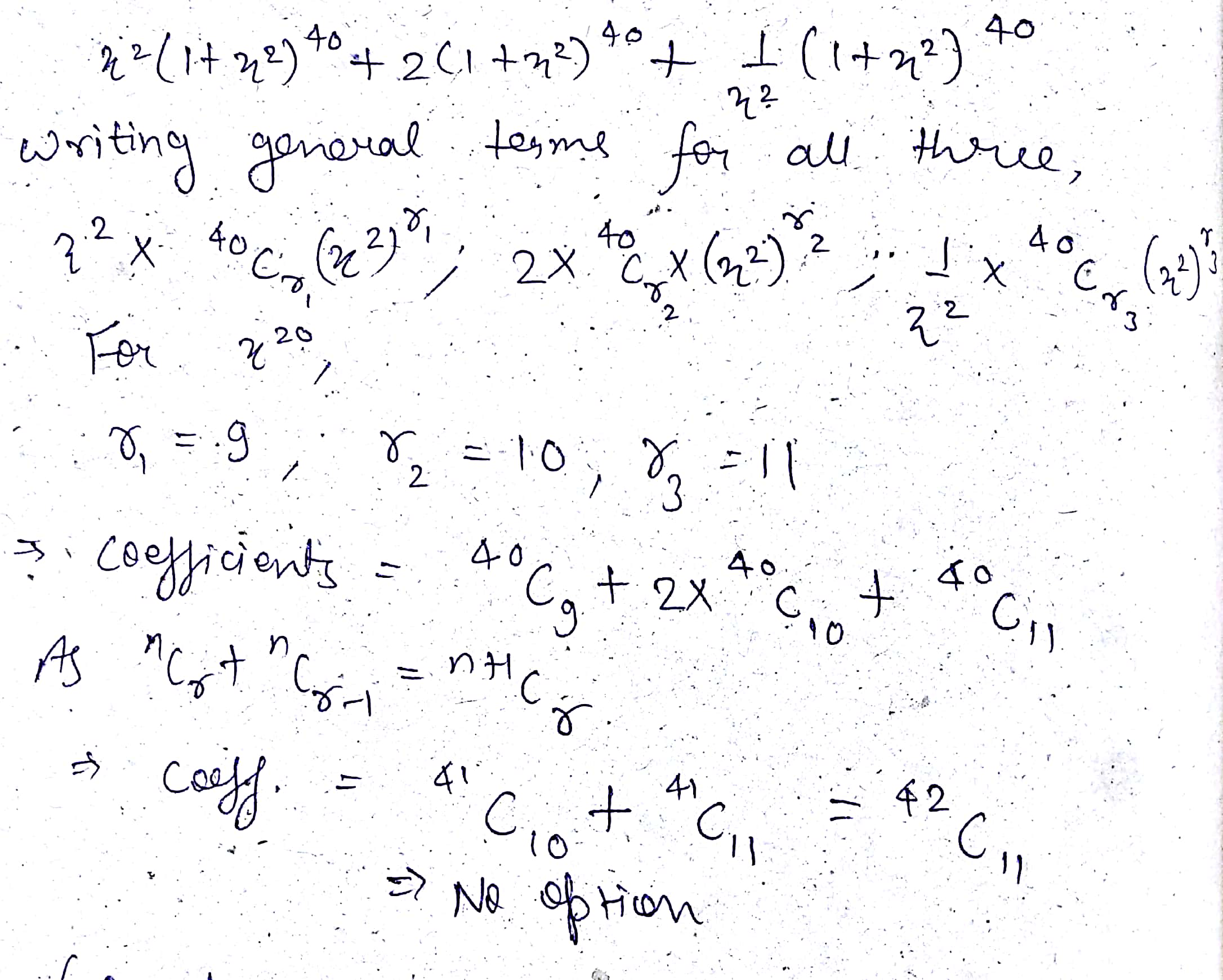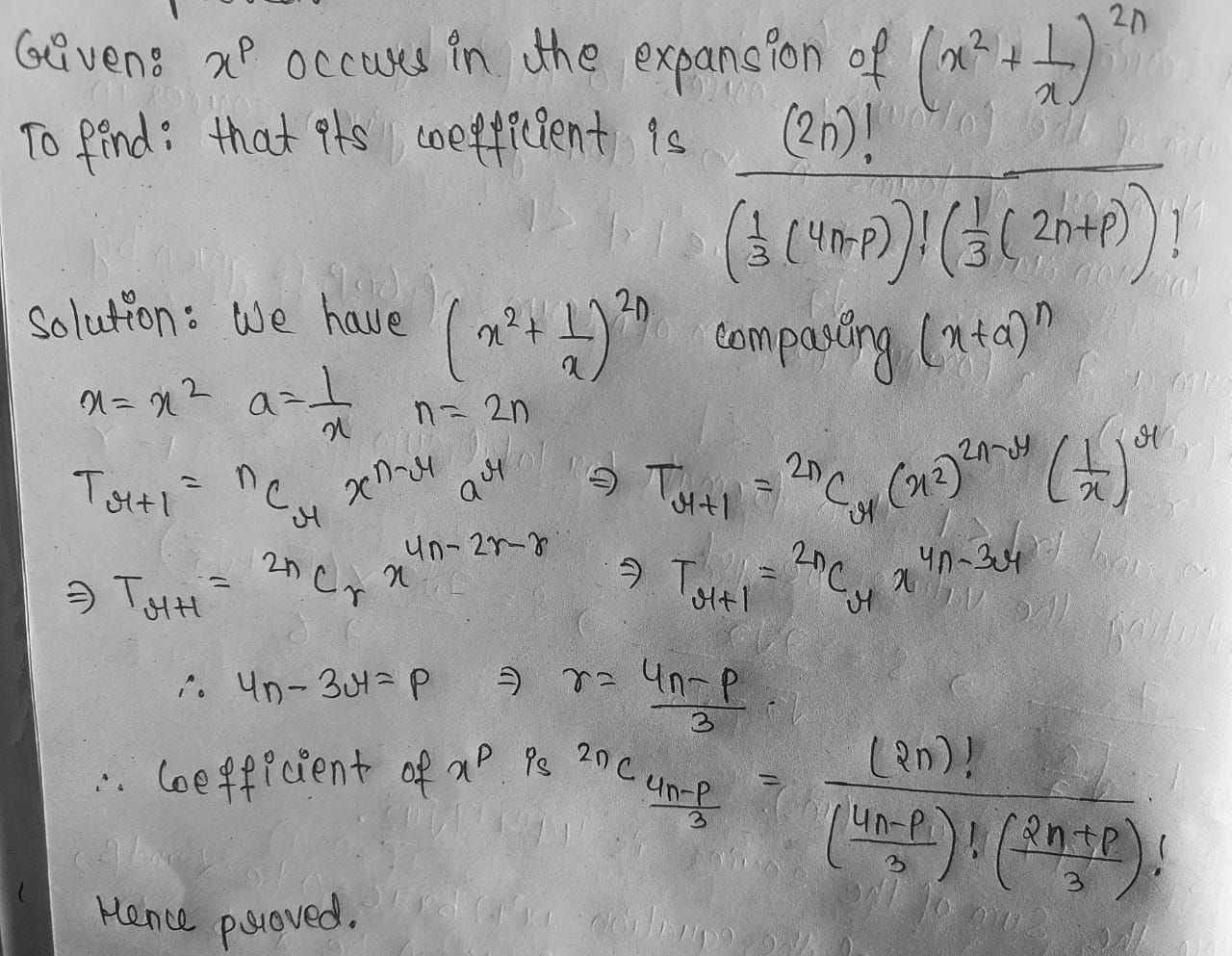Binomial Theorem - Class 11 Commerce Maths - Extra Questions

Find the sum of all rational terms in the expansion of $${ \left( { 3 }^{ 1/5 }+{ 2 }^{ 1/3 } \right)  }^{ 15 }$$.

$$\displaystyle T_{r+1}=\:^{15}C_{r}3^{3-\dfrac{r}{5}}2^{\dfrac{r}{3}}$$
Hence only $$T_{1}$$ and $$T_{16}$$ will be the rational terms.
$$T_{0+1}=\:^{15}C_{0}3^{3}$$
$$=27$$ $$...(a)$$
$$T_{15+1}=\:^{15}C_{15}2^{5}$$
$$=32$$ $$...(b)$$
Hence, $$a+b$$ implies
$$27+32$$
$$=59$$


Find the number of terms in the expansion of $${ \left( \sqrt [ 4 ]{ 9 } +\sqrt [ 6 ]{ 8 }  \right)  }^{ 500 }$$ which are integers.

$$\therefore$$ General term $${ _{  }^{  }{ T } }_{ r+1 }$$ $$={ _{  }^{ 500 }{ C } }_{ r }{ \left( { 3 }^{ 1/2 } \right)  }^{ 500-r }{ \left( { 2 }^{ 1/2 } \right)  }^{ r } $$   $$ ={ _{  }^{ 500 }{ C } }_{ r }{ 3 }^{ 250-r/2 }.{ 2 }^{ r/2 }$$ 
For $$r=0,2,4,6,8,10,12,.....500,$$ 
Powers of  $$3$$ and  $$   2  $$  are integers.
Hence, the integers terms $$=251$$

Alternative:
$$(9^{1/4}+8^{1/6})^{500}$$
$$=(3^{1/2}+2^{1/2})^{500}$$
Now, the total number of integral terms will be
$$1+\dfrac{500}{L.C.M(2,2)}$$

$$=1+\dfrac{500}{2}$$
$$=1+250$$
$$=251$$


Find the coefficient of $$x^5$$ in $$(x+3)^8$$

It is known that $$(r+1)$$th term $$ (T_{r+1})$$ in the binomial expansion of
$$ (a+b)^n$$ is given by $$T_{r+1} = ^nC_r a^{a-r}b^r$$
Assuming that $$x^5$$ occurs in the $$(r+1)$$th term of expansion $$(x+3)^8$$ we obtain 
 $$T_{r+1} = ^8C_r(x) ^{8-r} (3)^r$$
Comparing the indices of $$x$$ in $$x^5$$ and in $$T_{r+1} $$, we obtain $$r= 3$$
Thus, the coefficient of $$x^5$$ is 
$$\displaystyle ^8C_3(3)^3 = \frac{8!}{3!5!}x 3^3 = \frac{8.7.6.5!}{3.2.5!}.3^3 = 1512$$


The coefficient of three consecutive terms in the expansion of $${ \left( 1+a \right)  }^{ n }$$ are in ratio $$1:7:21$$, then find the value of $$n$$.

First term =$$^nC_r$$ 
Second term =$$^nC_{r+1}$$
Third term =$$^nC_{r+2}$$
$$\dfrac{1}{7}=\dfrac{^nC_r}{^nC_{r+1}}=\dfrac{n!}{r!|n-r|!}=\dfrac{|r+1|(n-r-1)1}{n!}($$
$$\dfrac{1}{7}=\dfrac{r+1}{n-r}$$
$$n-r=7r+7$$......(1)
$$\dfrac{7}{21}=\dfrac{1}{3}=\dfrac{n!}{(r+1)!(n-r-1)!}\times \dfrac{(r+2)!(n-r-2)}{n!}$$
$$\dfrac{1}{3}=\dfrac{r+2}{n-r-1}$$
$$n-r-1=3r+6$$
$$n=4r+7$$...........(2)
$$n=8r+7$$........(1)
$$r=0$$
$$\therefore n=7$$



$$\dfrac { { C }_{ 1 } }{ 2 } +\dfrac { { C }_{ 3 } }{ 4 } +\dfrac { { C }_{ 5 } }{ 6 } +...=\dfrac { { 2 }^{ n }-1 }{ n+1 }$$

The $$r_{th}$$ term in the given expansion is
$$T_{r}=\dfrac{\displaystyle^{n}C_{2r-1}}{2r}$$

Since $$\dfrac{1}{r+1}\cdot \displaystyle^nC_{r}=\dfrac{1}{n+1}\cdot \displaystyle^{n+1}C_{r+1}$$

$$\therefore T_{r}=\dfrac{\displaystyle^n C_{2r-1}}{2r}=\dfrac{1}{n+1}\cdot \displaystyle^{n+1}C_{2r}$$

$$\therefore \dfrac{\displaystyle^nC_{1}}{2}+\dfrac{\displaystyle^nC_{3}}{4}+\dfrac{\displaystyle^nC_{5}}{6}+......=\dfrac{1}{n+1}[\displaystyle^{n+1}C_{2}+\displaystyle^{n+1}C_{4}+.....]$$

$$=\dfrac{1}{n+1}[2^{n+1-1}-\displaystyle^nC_{0}]=\dfrac{2^n-1}{n+1}$$


Find the term of the expansion of $$(a + b)^{50}$$ which is the greatest in absolute value if $$\displaystyle\, \left | a \right | = \sqrt{3}\left | b \right |$$

Given 
$$(a+b)^{50}$$
General term of given expansion is
$$T_{r+1}=\sum_{r=0}^{50}\displaystyle^{50}C_{r}(a)^{50-r}(b)^r$$
Here $$a=\sqrt{3}b$$
$$T_{r+1}=\sum_{r=0}^{50}\displaystyle^{50}C_{r}(\sqrt{3}b)^{50-r}(b)^r$$
$$T_{r+1}=\sum_{r=0}^{50}\displaystyle^{50}C_{r}(\sqrt{3})^{50-r}(b)^{r+50-r}$$
$$T_{r+1}=\sum_{r=0}^{50}\displaystyle^{50}C_{r}(\sqrt{3})^{50-r}(b)^{50}$$
Middle term $$25^{th}$$ has maximum value of binomial coefficient 
$$T_{25}=\displaystyle^{50}C_{24}(\sqrt{3})^{26}(b)^{50}$$
But we should compare it with $$26^{th}$$ term
$$T_{26}=\displaystyle^{50}C_{25}(\sqrt{3})^{25}(b)^{50}$$
Hence comaparing $$T_{25},T_{26}$$ 
we get $$T_{25}$$ is greatest term


Prove that the following equations hold for any natural n.
Prove that $$\displaystyle (C_{n}^{o})^2 \, + \, (C_{n}^{1})^2 \, + \, ... \, + \, (C_{n}^{n})^2 \, = \, C_{2n}^{n}.$$

For deriving our expression 
we have to first simplyfy this
$$\quad \quad ({ ^nC }_{ 0 })^{ 2 }+9^n{ C }_{ 1 })^{ 2 }+(^n{ C }_{ 3 })^{ 2 }+(^n{ C }_{ 4 })^{ 2 }+.......+({ ^nC }_{ n })^{ 2 }\\ =({ C }_{ 0 }{ C }_{ n }+{ C }_{ 2 }{ C }_{ n-1 }+.........+{ C }_{ n }{ C }_{ 0 })(\therefore\ ^nC_0=^nC_n)$$

$$ =Cofficient\quad of\quad { x }^{ n }\quad in\quad { (1+x) }^{ n }{ (1+x) }^{ n }\\ =Cofficient\quad of\quad { x }^{ n }\quad in\quad { (1+x) }^{ 2n }\\ =^{ 2n }C_{ n }$$


Find the power $$n$$ of the binomial $$\displaystyle\, \left ( \frac{x}{5} + \frac{2}{5} \right )^n$$, if the ninth term of the expansion has the greatest coefficient.

Given:
$$ \left ( \dfrac{x}{5} + \dfrac{2}{5} \right )^n$$
General term of given expansion is 
$$T_{r+1}=\sum_{r=0}^{n}\displaystyle^{n}C_{r}\left ( \dfrac{x}{5} \right )^{n-r}\left ( \dfrac{2}{5} \right )^r$$
$$9^{th }$$ term When $$r=8$$
$$T_{8+1}=\displaystyle^{n}C_{8}\left ( \dfrac{x}{5} \right )^{n-8}\left ( \dfrac{2}{5} \right )^8$$
$$T_{9}=\displaystyle^{n}C_{8}x^{n-8}2^8\left( \dfrac{1}{5} \right )^{8+n-8}$$
$$T_{9}=\displaystyle^{n}C_{8} x^{n-8}2^8\left( \dfrac{1}{5^n} \right )$$
As we know that in the binomial expansion the middle term has the greatest value
So if n is even ,then $$\dfrac{n}{2}=9\Rightarrow n=18$$
Hence 
$$T_{9}=\displaystyle^{18}C_{8} x^{10}2^8\left( \dfrac{1}{5^{18}} \right )$$
Coefficient of above term is $$\displaystyle^{18}C_{8}2^8\left( \dfrac{1}{5^{18}} \right )$$ ..... $$(1)$$
When n is odd then $$9^{th}$$ term can be middle term of $$\dfrac{n+1}{2}=9$$ and $$\dfrac{n+3}{2}=9$$
$$9^{th}$$ term can be middle term of $$n=17$$ and $$n=15$$
When $$n=17$$
$$T_{9}=\displaystyle^{17}C_{8} x^{9}2^8\left( \dfrac{1}{5^{17}} \right )$$
Coefficient $$\displaystyle^{17}C_{8} 2^8\left( \dfrac{1}{5^{17}} \right )$$ ...... $$(2)$$
When $$n=15$$
$$T_{9}=\displaystyle^{15}C_{8} x^{7}2^8\left( \dfrac{1}{5^{15}} \right )$$
Coefficient $$\displaystyle^{15}C_{8} 2^8\left( \dfrac{1}{5^{15}} \right )$$ ..... $$(3)$$
Comparing equations $$(2)$$ and $$(3),$$ we get 
$$\displaystyle^{15}C_{8} 2^8\left( \dfrac{1}{5^{15}} \right )$$ is greatest 
But we should also compare eq (3) and (1) ,we get 
$$\displaystyle^{15}C_{8} 2^8\left( \dfrac{1}{5^{15}} \right )$$ is greatest
Hence $$n=15$$ 


Evaluate :
$$\left( {\dfrac{{{C_0} + {C_1}}}{{{C_0}}}} \right)\left( {\dfrac{{{C_1} + {C_2}}}{{{C_1}}}} \right)\left( {\dfrac{{{C_2} + {C_3}}}{{{C_2}}}} \right)\left( {\dfrac{{{C_3} + {C_4}}}{{{C_3}}}} \right)........\left( {\dfrac{{{C_{n - 1}} + {C_n}}}{{{C_{n - 1}}}}} \right)$$

We know, for any $$k < n$$ ,$${{{C_{k + 1}}} \over {{C_k}}}$$

$$ = {{n!\,\,\left( {n - k} \right)!k!} \over {\left( {k + 1} \right)!\left( {n - k - 1} \right)!n!}}$$

$$ = {{\left( {n - k} \right)\left( {n - k - 1} \right)!k!} \over {\left( {k + 1} \right)k!\left( {n - k - 1} \right)!}} = {{n - k} \over {k + 1}}$$

Now, $${{{C_k} + {C_{k + 1}}} \over {{C_k}}} = 1 + {{{C_{k + 1}}} \over {{C_k}}} = 1 + {{n - k} \over {k + 1}} = {{n - k + k + 1} \over {k + 1}} = {{n + 1} \over {k + 1}}$$

Then, $$\left( {{{{C_0} + {C_1}} \over {{C_0}}}} \right)\left( {{{{C_1} + {C_2}} \over {{C_1}}}} \right).....\left( {{{{C_n} + {C_n}} \over {{C_{n - 1}}}}} \right)$$

$$ = {{n + 1} \over {0 + 1}}.{{n + 1} \over {1 + 1}}.....{{n + 1} \over {\left( {n - 1} \right) + 1}} = {{{{\left( {n + 1} \right)}^n}} \over {1.2......n}} = {{{{\left( {n + 1} \right)}^n}} \over {n!}}$$

$$\left( {{{{C_0} + {C_1}} \over {{C_0}}}} \right)\left( {{{{C_1} + {C_2}} \over {{C_1}}}} \right)....\left( {{{{C_{n - 1}} + {C_n}} \over {{C_{n - 1}}}}} \right) = {{{{\left( {n + 1} \right)}^n}} \over {n!}}$$



If in the expansion of $$(1+x)^{20}$$, the coefficients of $$r^{th}$$ and $$(r+4)^{th}$$ terms are equal, then r is equal to?

We are given In the expansion of $$(1+x)^{20}$$, the coefficients of $$r^{th}$$ and $$(r+4)^{th}$$ terms are equal.
here the any $$r^{th}$$ term will be
$$Tr=\left (\dfrac {n}{r-1}\right) (a)^{n-r+1} (b)^{r-1}$$
now, here $$a=1$$ & $$b=x$$
so, the coefficient of $$r^{th}$$ term is $$=\left (\dfrac {n}{r-1}\right) (1)^{n-r+1}, \boxed {n=20}$$
$$=\left (\dfrac {20}{r-1}\right)$$
& the co-efficient of $$(r+4)^{th}$$ term is $$=\left (\dfrac {n}{r+4-1}\right) (1)^{n-r-4+1}, \boxed {n=20}$$
$$=\left (\dfrac {20}{r+3}\right)$$
so, $$\left (\dfrac {20}{r-1}\right)=\left (\dfrac {20}{r+3}\right)$$
now, it $$\left (\dfrac {n}{r_1}\right)=\left (\dfrac {n}{r_2}\right)\Rightarrow \ n=r_1+r_2$$
so, $$20=r-1+r+3$$
$$2r+2=20$$
$$2r=18$$
$$r=9$$
The $$r$$ is equal to $$9$$


If $$n> 2$$ then prove that $${C}_{1}(a-1)-{C}_{2}\times(a-2)+.....+{(-1)}^{n-1}{C}_{n}(a-n)=a$$,where $${C}_{r}={ _{  }^{ n }{ C } }_{ r }$$

$$(1-x)^{n}=C_{0}+C_{1}(-x)+C_{2}(-x)^{2}+.......+C_{n}(-x)^{n}.........(1)$$
Differentiating on both sides 
$$-n(1-x)^{n-1}=0-C_{1}+2{C_{2}}(x)-3{C_{3}}(x)^{2}+......+n(-1)^{n}(x)^{n-1}......(2)$$
When $$x=1 $$
$$(1)$$ becomes $$0=C_{0}-C_{1}+C_{2}-........+(-1)^{n-1}C_{n}$$
                          $$\implies C_{1}-C_{2}+C_{3}-.....+(-1)^{n-1}C_{n}=C_{0}=1$$
$$(2)$$ becomes $$0=-C_{1}+{2}C_{2}-{3}C_{3}+....+(-1)^{n}{n}C_{n}$$
$$LHS=C_{1}(a-1)-C_{2}(a-2)+.......+(-1)^{n-1}C_{n}(a-n)$$
           $$=a(C_{1}-C_{2}+C_{3}-....+(-1)^{n-1}C_{n})+(-C_{1}+2{C_2}-3{C_{3}}+....+(-1)^{n}{n}C_{n})=a(1)+0=a=RHS$$
$$LHS=RHS$$
Hence Proved 


Coefficient of $$x^{10}$$ in the expansion of $$\left(2x^2-\dfrac{3}{x}\right)^{11}, x\neq 0$$.


1084468_1113413_ans_1d90de945eb945859ff7715432763fb0.jpg


Find the middle term in expansion of $$\left (2x^{2} - \dfrac {1}{x}\right )^{7}$$.


1407614_1138925_ans_be1494be73d14bf4abbde1c928c5d1da.jpg


Find a positivevalue of m for which the confficient of $$x^{2}$$ in the expansion $$\left ( 1+x \right )^{m}$$ is $$6$$

Consider the problem

It is know that $${\left( {r + 1} \right)^{th}}$$ term, $$\left( {{T_{r + 1}}} \right)$$, in the binomial expansion of $${\left( {a + b} \right)^n}$$ is given by

$${T_{r + 1}}{ = ^n}{C_r}{a^{n - r}}{b^r}$$

Assuming that $${x^2}$$ occurs in the $${\left( {r + 1} \right)^{th}}$$ term of expansion $${\left( {1 + x} \right)^m}$$ we obtain

$${T_{r + 1}}{ = ^m}{C_r}{\left( 1 \right)^{m - r}}{\left( x \right)^r}{ = ^m}{C_r}{\left( x \right)^r}$$

Now comparing the indices of $$x$$ in $${x^2}$$ and in $${T_{r + 1}}$$ we obtain 
$$r=2$$

Therefore, the coefficient of $${x^2}$$ is $$^m{C_2}$$

It is given that the coefficient of $${x^2}$$ in the expansion $${\left( {1 + x} \right)^m}$$ is $$6$$

$$\begin{array}{l} \therefore \, { \, ^{ m } }{ C_{ 2 } }=6 \\ \Rightarrow \dfrac { { m! } }{ { 2!\left( { m-2 } \right) ! } } =6 \\ \Rightarrow \dfrac { { m\left( { m-1 } \right) \left( { m-2 } \right) ! } }{ { 2\times \left( { m-2 } \right) ! } } =6 \\ \Rightarrow m\left( { m-1 } \right) =12 \\ \Rightarrow { m^{ 2 } }-m-12=0 \\ \Rightarrow { m^{ 2 } }-4m+3m-12=0 \\ \Rightarrow m\left( { m-4 } \right) +3\left( { m-4 } \right) =0 \\ \Rightarrow \left( { m-4 } \right) \left( { m-3 } \right) =0 \\ \Rightarrow \left( { m-4 } \right) =0\, or\left( { m+3 } \right) =0 \\ \Rightarrow m=4\, or\, m=-3 \end{array}$$

Thus, the positive value of $$m$$ for which the coefficient of  $${x^2}$$ in the expansion $${\left( {1 + x} \right)^m}$$ is $$6$$ is $$4$$.


The coefficient of $${x}^{20}$$ in the expansion of $${(1+{x}^{2})}^{40}({x}^{2}+2+\cfrac{1}{{x}^{2}})$$ is

$$ x^{2}(1+x^{2})^{40}+2(1+x^{2})^{40}+\frac{1}{x^{2}}(1+x^{2})^{40} $$
writing general tence for all three,
$$ x^{2}\times ^{40}C_{r_{1}}(x^{2})^{r_{1}},2\times ^{40}C_{2}\times (x^{2})^{r_{2}},\frac{1}{^{2}}\times ^{40}C_{3}(x^{2})^{r_{3}} $$
For $$x ^{20}, $$
$$ r_{1} = 9,r_{2} = 10, r_{3} = 11 $$
$$ \Rightarrow $$ cofficients $$ = ^{40}C_{9}+2\times ^{40}C_{10}+^{40}C_{11} $$
As $$ ^{n}C_{r}+^{n}C_{r-1} = ^{n+1}C_{r} $$
$$ \Rightarrow $$ coeff. $$ = ^{41}C_{10}+^{41}C_{11} = ^{42}C_{11} $$
$$ \Rightarrow $$ No option 

1124067_1204045_ans_9b861085102f454da1e12ba58810b0dd.jpg


The $$2^{nd}$$, $$3^{rd}$$, $$4^{th}$$ terms in the expansion of $$(x+y)^n$$ are $$240$$, $$720$$, $$1080$$ respectively; find $$x, y, n$$.

The general term,
$$T_{r+1}=\,^nC_rx^{n-r}y^r$$
$$\Rightarrow$$  $$T_2=\,^nC_1.x^{n-1}.y=240$$          ---- ( 1 )

$$\Rightarrow$$  $$T_3=\,^nC_2.x^{n-2}.y^2=720$$       

$$\Rightarrow$$  $$T_4=\,^nC_3.x^{n-3}.y^3=1080$$

$$\Rightarrow$$  $$\dfrac{T_3}{T_2}=\dfrac{(n-1)}{2}\times \dfrac{y}{x}=3$$            ---- ( 2 )

$$\Rightarrow$$  $$\dfrac{T_4}{T_2}=\dfrac{(n-1)(n-2)}{3\times 2}\times\dfrac{x^2}{y^2}=\dfrac{9}{2}$$               ---- ( 3 )

$$\Rightarrow$$  $$\dfrac{T_4}{T_3}=\dfrac{(n-2)}{3}\times\dfrac{y}{x}=\dfrac{3}{2}$$           ---- ( 4 )
Dividing equation ( 2 ) by ( 4 ) we get,
$$\Rightarrow$$  $$\dfrac{n-1}{2}\times\dfrac{3}{n-2}=2$$

$$\Rightarrow$$  $$3n-3=4n-8$$
$$\Rightarrow$$  $$5=n$$
Substituting value of $$n$$ in ( 4 ) we get,
$$\Rightarrow$$  $$\dfrac{y}{x}=\dfrac{3}{2}$$                
Putting $$y=\dfrac{3}{2}x$$ and $$n=5$$ in equation ( 1 ) we get,
$$\Rightarrow$$  $$5x^5\times\dfrac{3}{2}=240$$
$$\Rightarrow$$  $$x^5=32$$
$$\Rightarrow$$  $$x=2$$
Now, substituting value of $$x$$ in $$y=\dfrac{3}{2}x$$ we get,
$$\Rightarrow$$  $$y=3$$
$$\therefore$$  $$x=,2,\,y=3,\,n=5$$



In the expansion of $$(1+x)^{43}$$ the coefficients of the $$(2r+1)^{th}$$ and the $$(r+2)^{th}$$ terms are equal; find $$r$$.

In the expansion of $$(1+x)^{43}$$
$$T_{2r+1}=\,^{43}C_{2r}1^{43-2r}x^{2r}=\,^{43}C_{2r}x^{2r}$$
$$T_{r+2}=\,^{43}C_{r+1}1^{43-(r+1)}x^{r+1}=\,^{43}C_{r+1}x^{r+1}$$
According to the question,
$$\Rightarrow$$  $$^{43}C_{2r}=\,^{43}C_{r+1}$$
So, either $$2r=r+1$$ or $$2r+(r+1)=43$$
$$\Rightarrow$$  $$r=1$$  or $$3r=42$$
$$\therefore$$  $$r=1$$ or $$r=14$$


Find the coefficient of $$x^{5}$$ in $$\left( x + 3 \right)^{n}$$

It is known that $$(r + 1)^{th}$$ term, $$(T_{r+1})$$, in the binomial expansion of $$(a+b)6n$$ is given by 
$$T_{r+1} =\ ^nC_r a^{n-r}b^r$$
Assuming that $$x^5$$ occurs in the $$(r+1)^{th}$$ term of the expansion $$(x+3)^8$$, we obtain
$$T_{r+2} = \ ^nC_r (x)^{8-r}(3)^r$$

Comparing the indices of $$x$$ in $$x^5$$ in $$T_{r+1}$$.

we obtain $$r=3$$

thus, the coefficient of $$x^5$$ is $$^8C_3 (3)^3 = \dfrac{8!}{3!5!} 3^3 = \dfrac{8.7.6.5!}{3.25!} . 3^3 = 1512$$.


Find the coefficient of $$a^{5} b^{7}$$ in $$\left (a - 2b  \right )^{12}$$

It is known that $$\left (r + 1  \right )^{th}$$ term, $$\left ( T_{r-2} \right )$$, in the binomial expansion of $$\left (a + b  \right )^{n}$$ is given by
$$T_{r+1} = {^n}C_r a^{n-r} b^{r}$$
Assuming that $$a^{5} b^{7}$$ occurs in the $$\left ( r + 1 \right )^{12}$$ term of the expansion $$\left ( a - 2b \right )^{12}$$, we obtain
$$T_{r+1} = {^12}C_2 (a)^{12-r} (-2b)^{r} = {^12}C_2 (-2)^{r} (a)^{12-r} (b)^{r}$$
Comparing the indices of a and b in $$a^{5} b^{7}$$ in $$T_{2*}$$
We obtain r = 7
Thus, the coefficient of $$a^{5} b^{7}$$ is
$${^12}C_r (-2)^{7} = \frac{12!} {7!5!} \cdot 2^{7} = \frac{12 \cdot 11.10 \cdot 9 \cdot 8 \cdot 7!} {5 \cdot 4.3 \cdot 2 \cdot 7!} \cdot(-2)^{7} = - (792) (128) = -101376$$


Find the number of term in the expansion of $$(x + a)^{200}+ (x - a)^{200}$$ after simplification.

$$\because (x + a)^n + (x – a)^n$$
$$= 2[\,^nC_0 x^na^0 + \,^nC_0 x^{n-2} - a^2 + \,^nC_4x^{n-4} .a^4 +…]$$
where n is an even number then
[Number of terms in the expansion of $$(x + a)^n + (x – a)^n$$]
will be $$\bigg(\dfrac{n}{2}+1\bigg)$$
Here, $$n = 200$$
Hence, number of terms in the expansion
Will be
$$=\bigg(\dfrac{200}{2}+1\bigg)=101$$

Hence, the number of terms is $$101$$ in the expansion.


Find the coefficient of $$x^{256}$$ in $$(1 - x)^{101} (x^{2} + x + 1)^{100}$$

$$(1 - x)^{101} (x^{2} + x + 1)^{100}$$
$$= (1 - x)(1 - x)^{100} (x^{2} + x + 1)^{100}$$
$$= (1 - x)(1 - x^{3})^{100}$$
$$= (1 - x^{3})^{100} - x(1 - x^{3})^{100}$$
First term will not have $$x^{256}$$.
Coefficient of $$x^{256}$$ is $$-1\times$$ coefficient of $$x^{255}$$ in $$(1 - x^{3})^{100}$$       $$[\because\,x^{255}=(x^3)^{85}]$$
$$= -1(-^{100}C_{85}) = ^{100}C_{85}$$


If $$a_n$$ denotes the coefficient of $$x^n$$ in $$P(x)=(1+x+2x^2+....+25x^{25})^2$$, find $$\dfrac {a_5}{5}$$.

$$\displaystyle P(x)=(1+x+2x^2+3x^3+....+25x^{25})(1+x+2x^2+3x^3+....+25x^{25})$$
Looking at the terms that can have $$x^5$$, we get
$$\displaystyle a_5=\text{coeff of}\: x^5=1.5+1.4+2.3+3.2+4.1+5=30$$
$$\Rightarrow \dfrac {a_5}{5}=6$$


If the sixth term in the expansion of $${ \left( \cfrac { 1 }{ { x }^{ 8/3 } } +{ x }^{ 2 }\log _{ 10 }{ x }  \right)  }^{ 8 }$$ is $$5600$$, find $$x.$$

Step 1:Apply formula of general term

Given :$$(\dfrac { 1 }{ { x }^{ 8/3  } } +{ x }^{ 2 }\log { x)^{ 8 } }$$  

we know that general term of expansion of $$(a+b)^n$$ is $$ T_{ r+1 }=^nC_{ r } (a )^{ n-r }b^{ r} $$

so  $$ T_{ r+1 }=^nC_{ r } (\dfrac { 1 }{ { x }^{ 8/3  } } )^{ 8-r }(x^{ 2 }\log { x)^{ r } }$$   

Step2: Simplify to evaluate required unknown 

 $$ T_{ 6}=$$ $$\quad ^{ 8 }C_{ 5 }[\dfrac { 1 }{ { x }^{ \tfrac { 8 }{ 3 }  } } ]^{ 3 }({ x }^{ 2 }\log { x)^{ 5 } } =5600$$

$$\Rightarrow  { x }^{ -8+10 }{ (\log { x } ) }^{ 5 }\times 8\times 7=5600$$

$$\Rightarrow  { x }^{ 2 }(\log { x } )^{ 5 }=100$$

$$\Rightarrow  x=10$$

Hence value of x is 10


The value of $$p$$, for which coefficient of $$x^{50}$$ in the expression $$(1 + x)^{1000} + 2x (1 + x)^{999} + 3x^{2} (1 + x)^{998} + .... + 1001 x^{1000}$$ is equal to $$^{1002}C_{p}$$, is

Let $$S=\sum^{1000}_{r=0}{(1+r)x^r(1+x)^{1000-r}}$$

So, $$S-\dfrac x{(1+x)}S=(\sum^{1000}_{r=0}{x^r(1+x)^{1000-r})-1001\dfrac {x^{1001}}{(1+x)}}=(\dfrac {(1+x)^{1000}(1-(\dfrac x{1+x})^{1001})}{1-\dfrac x{1+x}})-1001\dfrac {x^{1001}}{1+x}$$

$$\Rightarrow S(1-\dfrac x{1+x})=((1+x)^{1001}-x^{1001})-1001\dfrac {x^{1001}}{1+x}$$
$$\Rightarrow S=(1+x)((1+x)^{1001}-x^{1001})-1001x^{1001}=(1+x)^{1002}-1002x^{1001}-x^{1002}$$

So, $$S=(\sum^{1002}_{r=0}{^{1002}C_rx^r})-1002x^{1001}-x^{1002}$$

So, coefficient of $$x^{50}$$ in the expansion will be, $$^{1002}C_{50}$$

So, $$p=50$$ or $$p=1002-50=952$$ ($$\because ^nC_r=^nC_{n-r}$$).


Find $$n$$, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of $${ \left( \sqrt [ 4 ]{ 2 } +\cfrac { 1 }{ \sqrt [ 4 ]{ 3 }  }  \right)  }^{ n }$$ is $$\sqrt { 6 } :1$$

$$T_5$$ in $$\left[\sqrt[4]{2}+\dfrac{1}{\sqrt[4]{3}}\right]^n=nC_4(\sqrt[4]{2})^{n-4}\cdot \left(\dfrac{1}{\sqrt[4]{3}}\right)^4=nC_42^{\dfrac{n-4}{4}}\cdot \dfrac{1}{3}\quad ...(1)$$ 

Total number of terms $$=n+1$$

Fifth term from the end $$=[(n+1)-5+1]^{th}$$ term from the beginning.

$$\Rightarrow (n-3)^{th}$$ term from the beginning.

$$\Rightarrow T_{n-3}=nC_{n-4}\left(\sqrt[4]{2}\right)^{n-(n-4)}\left(\dfrac{1}{\sqrt[4]{3}}\right)^{n-4}=nC_{n-4}\cdot 2\left(\dfrac{1}{3}\right)^{\dfrac{n-4}{4}}\quad ...(2)$$

Given $$\dfrac{T_5}{T_{n-3}}=\dfrac{\sqrt{6}}{1}$$

$$\dfrac{nC_42^{\dfrac{n-4}{4}}\cdot \dfrac{1}{3}}{nC_{n-4}\cdot 2\left(\dfrac{1}{3}\right)^{\dfrac{n-4}{4}}}=\dfrac{\sqrt{6}}{1}$$

$$\Rightarrow \dfrac{nC_4}{nC_{n-4}}(2)^{\dfrac{n-4}{4}-1}\cdot \left(\dfrac{1}{3}\right)^{1-\dfrac{n-4}{4}}=\sqrt{6}$$

$$\Rightarrow \dfrac{nC_4}{nC_{n-4}}(2)^{\dfrac{n-8}{4}}\cdot \left(\dfrac{1}{3}\right)^{\dfrac{8-n}{4}}=\sqrt{6}$$

$$\Rightarrow \dfrac{nC_4}{nC_{n-4}}(2)^{\dfrac{n-8}{4}}\cdot (3)^{-\dfrac{8-n}{4}}=\sqrt{6}$$

$$\Rightarrow \dfrac{nC_4}{nC_{n-4}}(2)^{\dfrac{n-8}{4}}\cdot (3)^{\dfrac{n-8}{4}}=\sqrt{6}$$

$$\Rightarrow \dfrac{nC_4}{nC_{n-4}}(6)^{\dfrac{n-8}{4}}=\sqrt{6}$$

Comparing powers of $$6$$

$$\Rightarrow \dfrac{n-8}{4}=\dfrac{1}{2}$$

$$\Rightarrow \dfrac{n-8}{4}=\dfrac{1}{2}$$

$$\Rightarrow n-8=2$$

$$\therefore n=10$$




Let $$X = (^{10}C_{1})^{2} + (^{10}C_{2})^{2} + 3(^{10}C_{3})^{2} + .... + 10 (^{10}C_{10})^{2}$$, where $$^{10}C_{r}, r\epsilon \left \{1, 2, ..., 10\right \}$$ denote binomial coefficients. Then, the value of $$\dfrac {1}{1430}X$$ is 

$$X = \displaystyle \sum_{r = 0}^{n} r. (^{n}C_{r})^{2}; n = 10$$
$$\Rightarrow X = n. \displaystyle \sum_{r = 0}^{n} \ ^{n}C_{r} . ^{n - 1}C_{r - 1}$$

$$\Rightarrow X = n. \displaystyle \sum_{r = 0}^{n}\ ^{n}C_{n - r}. ^{n - 1}C_{r - 1}$$

$$\Rightarrow X = n . ^{2n - 1}C_{n - 1}; n = 10$$

$$\Rightarrow X = 10 . ^{19}C_{9}$$

$$\Rightarrow \dfrac {X}{1430} = \dfrac {1}{143} . ^{19}C_{9}$$

$$= 646$$.


Evaluate $$\sum_{r = 0 }^{n } \, (r \, + \, 1)^3 \, C_r  \, whee C_r  \, = \, ^nC_r$$

$$\sum_{r=0}^{n} \, (C_r) \, = \, C_0 \, + \, 2^3c_1 \, + \,2^3c_2 \, + \, ....+ \, (n+1)^3\,C_n$$ 
Now $$(1+x)^n \, = \, C_0 \, + \, C_1x \, + \, C_2x^2 \, + \, ....$$
We have the term $$C_2x^2$$ whereas we want the term of $$C_2\cdot\, 3^3$$. Hence multiply by x to make it $$3C_2x^3$$ . Again differentiate to make $$3^2C_2x^2$$. Again multiply by x to make $$3^2C_2x^2$$ and differentiate it to get $$3^2C_2x^2$$ and finally put $$x \, = \, 1$$. The above procedure is shown below.
Multiple by x
$$x(1+x)^n \, = \, C_0x \, + \, C_1x^2 \, + \, C_3x^3 \, + \, ....$$
Differentiate w.r.t.x.
$$(1+x)^n \, + \, x.n(1+x)^{n-1} \, = \, C_0 \, + \, 2C_1x \, + \, 3C_2x^2 \, + \, ....$$
or $$(1+x)^{n-1} \, [1\, + \,(n+1)x] \, = \,C_0 \, + \, 2C_1x \, + \, 3C_2x^2 \, + \, ....$$
Again multiply by x
$$(1+x)^{n-1} \, [1\, + \,(n+1)x] \, = \,C_0 \, + \, 2C_1x \, + \, 3C_2x^2 \, + \, ....$$
differentiate w.r.t.x.
$$(n-1)\,(1+x)^{n-2}\,[x\,+\,(n+1)x^2] \, + \, (1+x)^{n-1}\,[1\, + \, 2\, (n+1)x]$$
$$= \, C_0 \, + \, 2^2C_1x \, + \, 3^2C_2x^2 \, + ....$$
$$L.H.S. \, = \, (1+x)^{n-2}\,[(n-1)x \, + \, (n^2-1) \, + \, (1+x) \, + \, 2(n+1)\,(x+x^2)]$$
$$ = \, (1+x)^{n-2}\,[1 \, + \, (3n+2)x \, + \, (n^2 + 2n +1)x^2]$$
$$R.H.S. \, = \, C_0 \, + \, 2^2C_1x \, + \, 3^2C_2x^2 \, + ....$$
Again multiply both sides by x and differentiate and lastly put $$x \, = \, 1$$
$$\sum_{r=0}^{n} \, (r+1)^3 \,C_r \, = \, (n-2)2^{n-3} \, (4+5n+n^2) \, + \, 2^{n-2}\,(8+12n+3n^2)$$

   


If $$x^p$$ occurs in the expansion of $$\left(x^2+\dfrac{1}{x}\right)^{2n}$$, prove that its cofficient is $$\dfrac{(2n)!}{\left(\dfrac{1}{3}(4n-p)\right)!\left(\dfrac{1}{3}(2n+p)\right)!}$$.


1973839_1743511_ans_81421dbbdb2649fd8a9920b952303a3c.jpg


Class 11 Commerce Maths Extra Questions