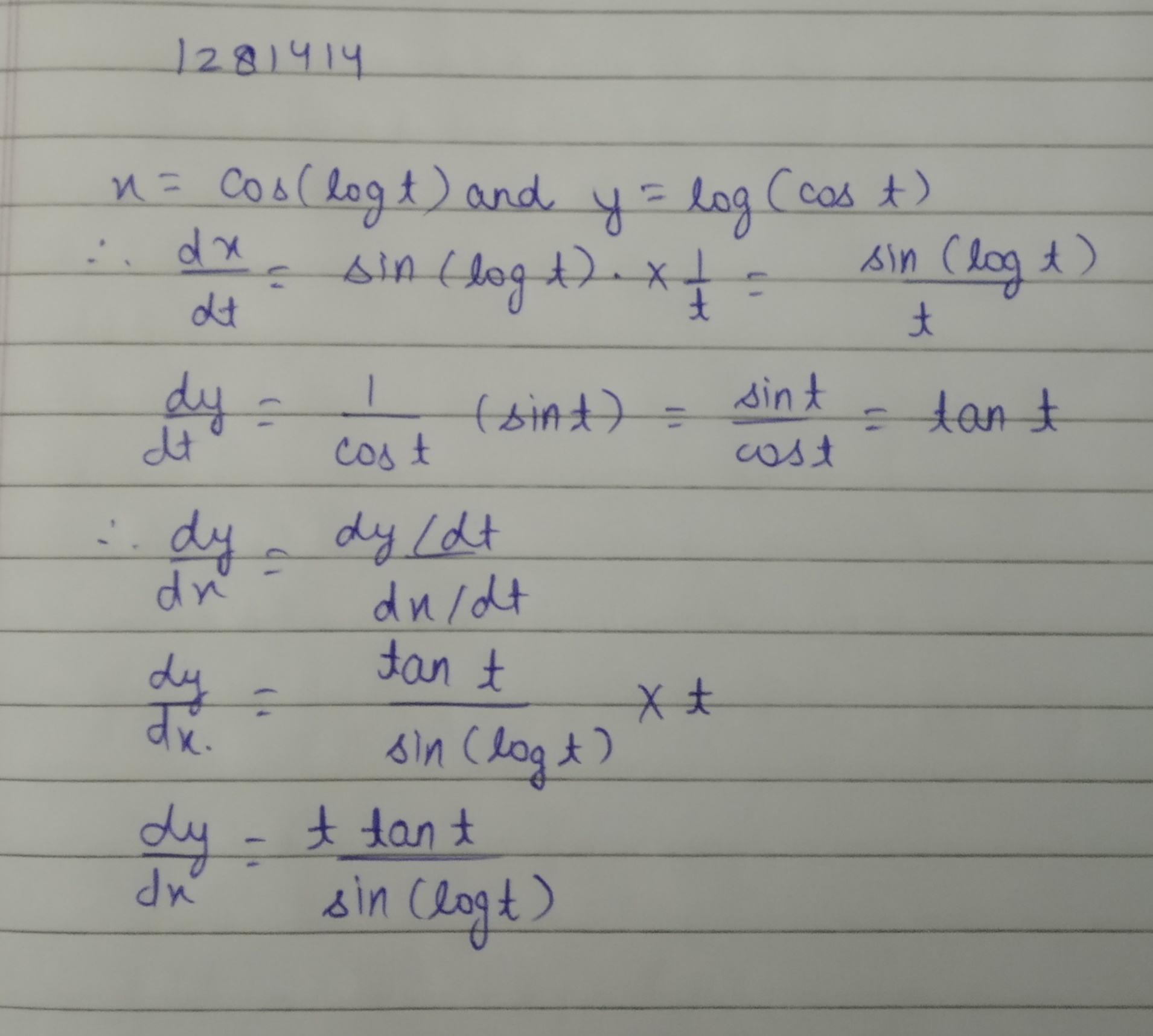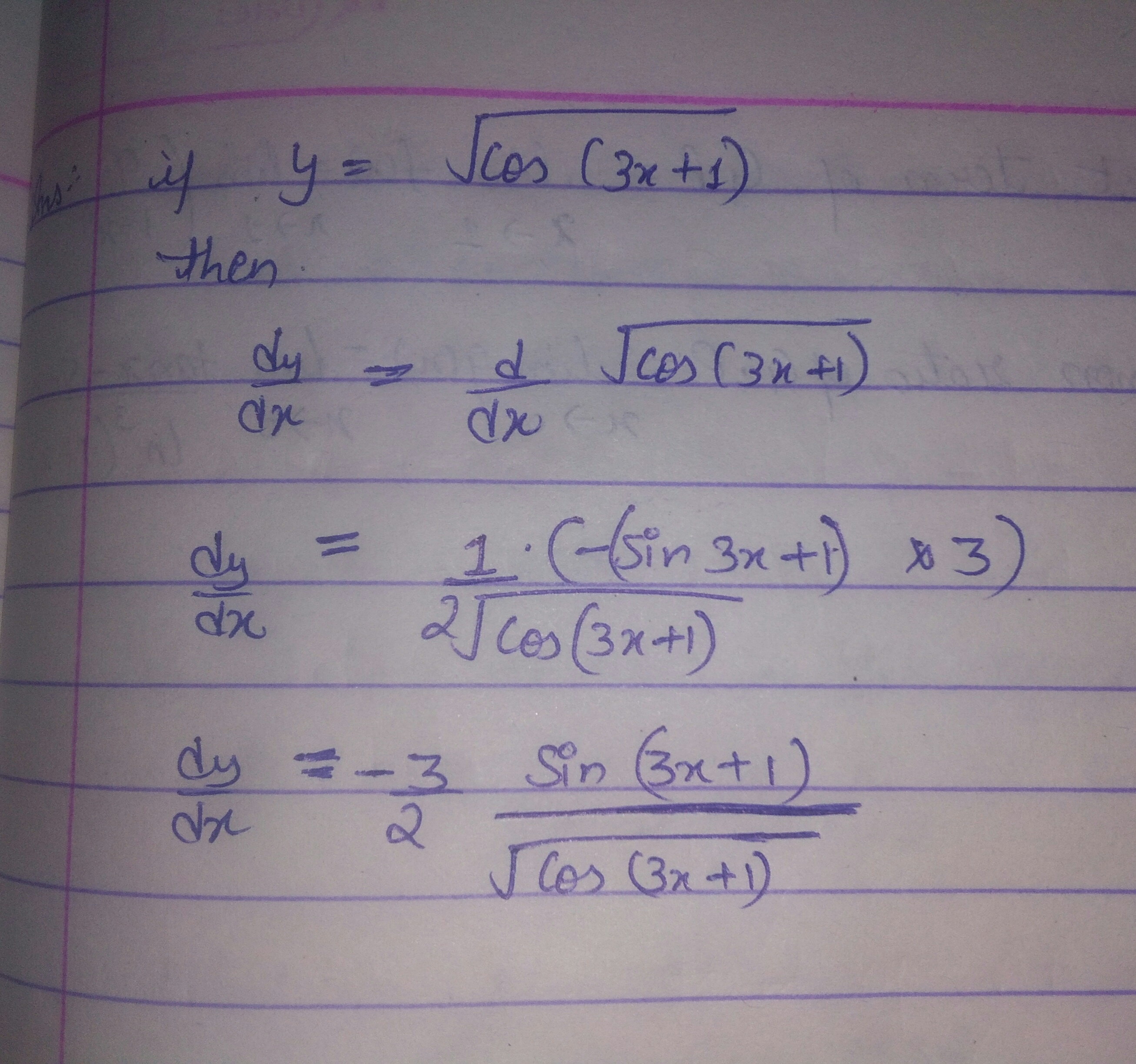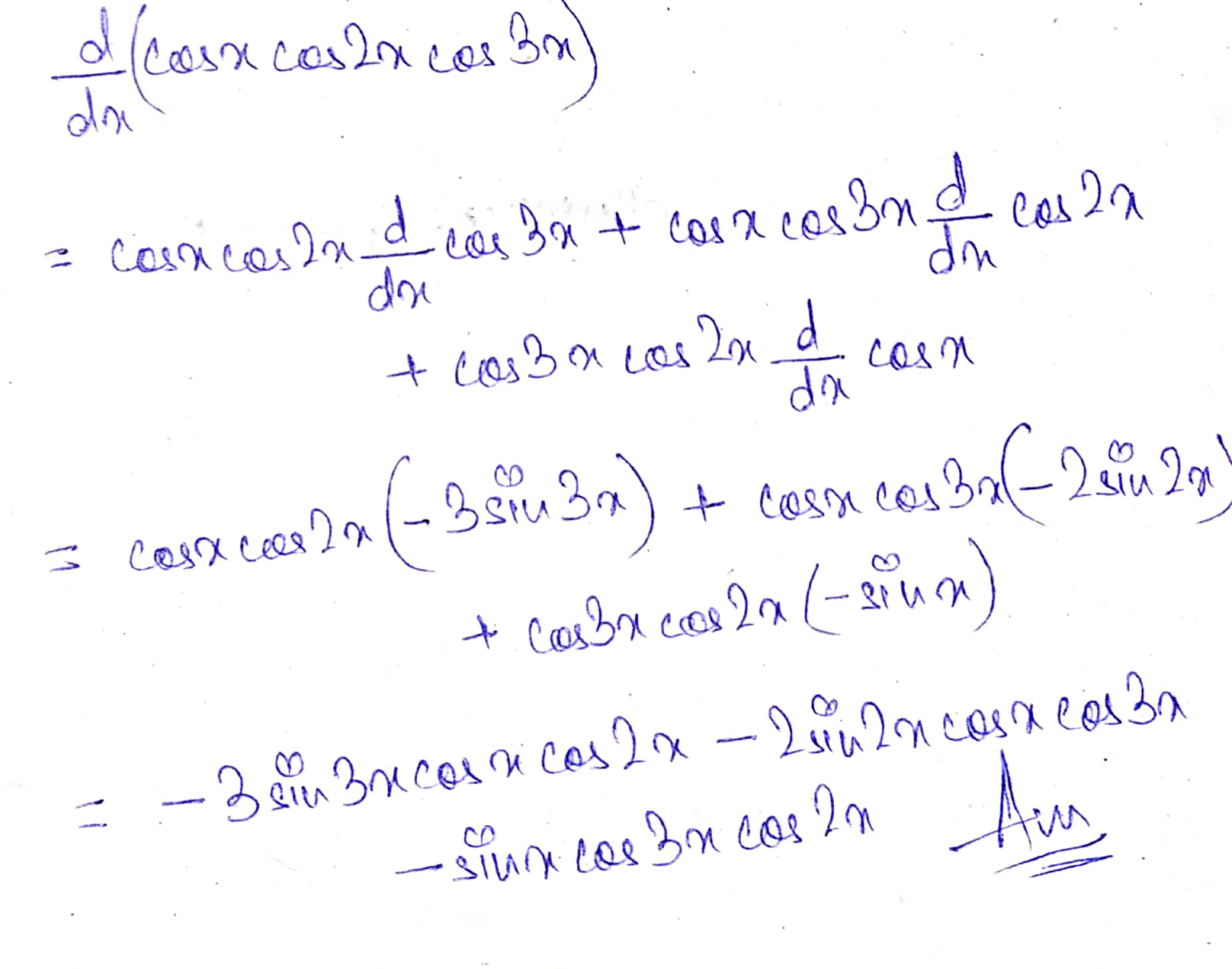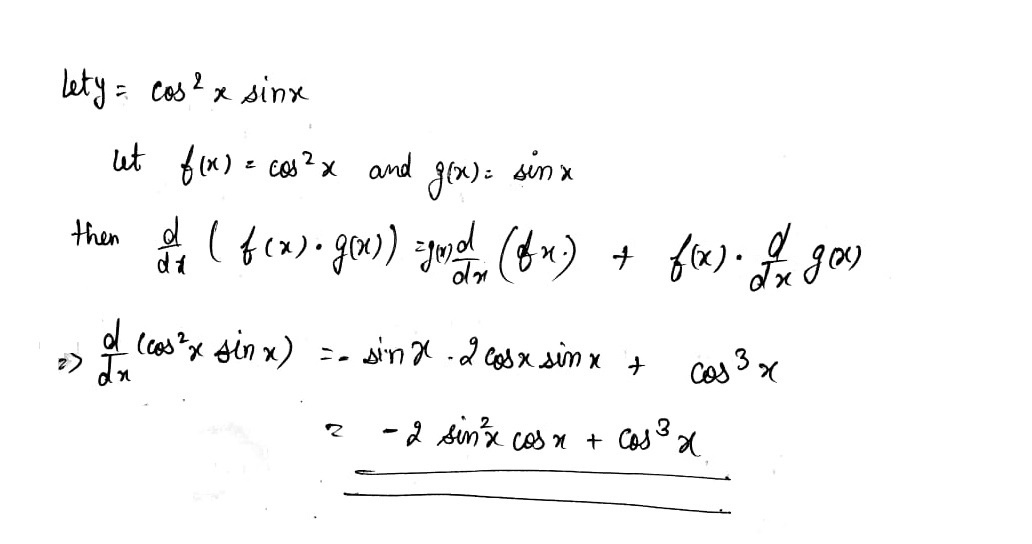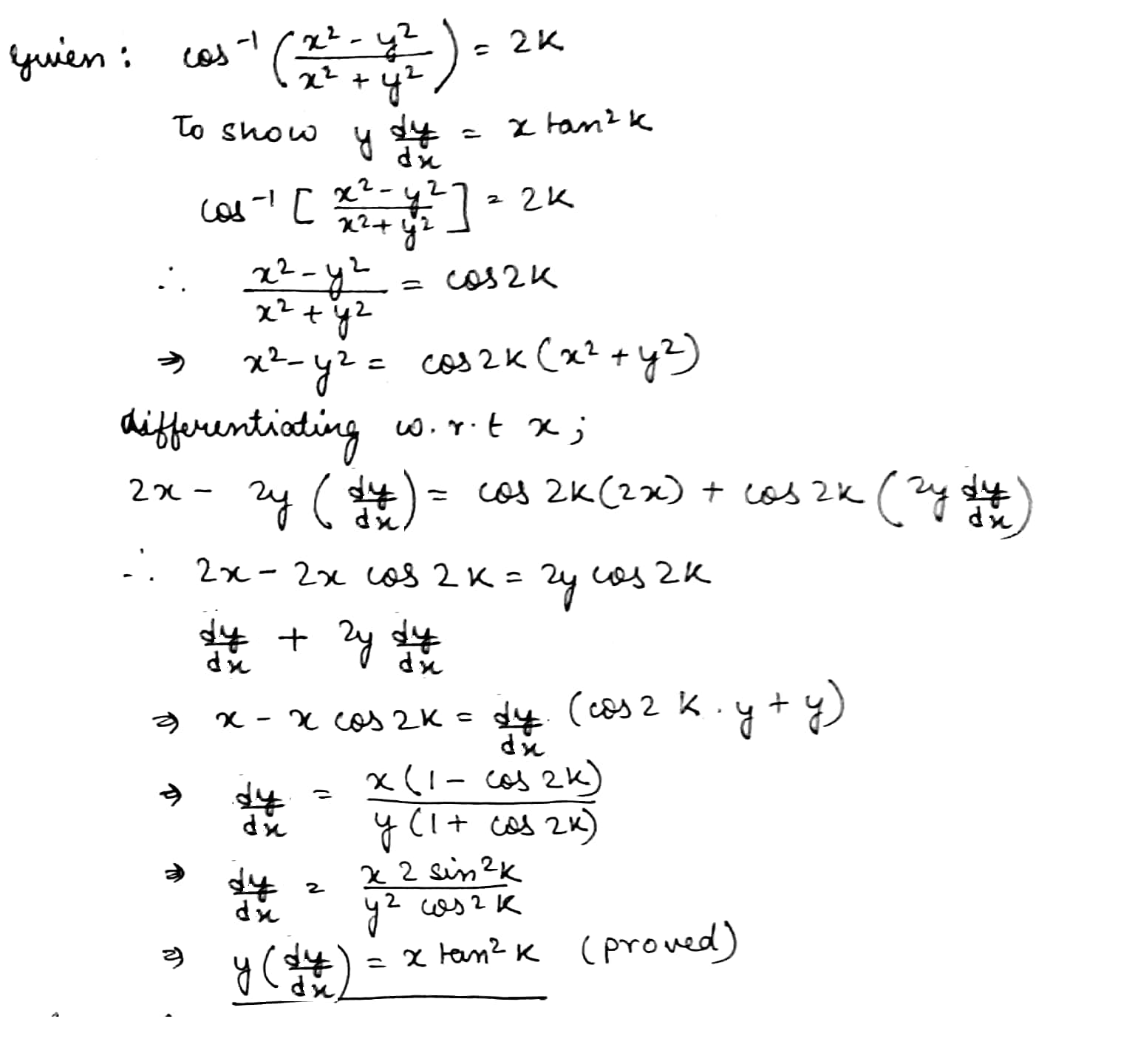Limits And Derivatives - Class 11 Commerce Maths - Extra Questions

Find the derivative of the following functions (it is to be understood that $$a, b, c, d, p, q, r$$ and $$s$$ are fixed non-zero constants and $$m$$ and $$n$$ are integers) : $$\sin (x + a)$$

Let  $$f (x) = \displaystyle \sin (x +a)$$
Thus using first principle
$$f'(x) = \displaystyle \lim_{x\rightarrow 0}\frac{f\left ( x+h \right )-f\left ( x \right )}{h}$$
$$=\displaystyle \lim_{x\rightarrow 0}\frac{\sin \left ( x+h+a \right )-\sin \left ( x+a \right )}{h}$$
 $$=\displaystyle

\lim_{x\rightarrow 0}\frac{1}{h}\left [ 2 \cos \left (

\frac{x+h+a+x+a}{2} \right )\sin \left ( \frac{x+h+a-x-a}{2} \right )

\right ]$$
$$=\displaystyle \lim_{x\rightarrow 0}\frac{1}{h}\left [ 2

\cos \left ( \frac{2x +2a + h}{2} \right )\sin \left ( \frac{h}{2}

\right ) \right ]$$
$$=\displaystyle \lim_{x\rightarrow 0}\left [

\cos \left ( \frac{2x+2a+h}{2} \right )\left \{ \frac{\sin \left (

\frac{h}{2} \right )}{\left ( \frac{h}{2} \right )} \right \} \right ]$$
$$=\displaystyle

\lim_{x\rightarrow 0}\cos \left ( \frac{2x+2a+h}{2} \right

)\lim_{x\rightarrow 0}\left \{ \frac{\sin \left ( \frac{h}{2} \right

)}{\left ( \frac{h}{2} \right )} \right \}$$
$$=\displaystyle

\cos \left ( \frac{2x+2a}{2} \right )\times 1$$    
$$=\displaystyle \cos \left ( x + a \right )$$


$$\dfrac{d}{dx}\left\{\cos x^0\right\}=?$$

$$=-\sin x^0 \times (0) \times x^{0-1}$$
$$=0$$


Find dy/dx=? If, x=$$\cos(\log t )$$ and y=$$\log(\cos t)$$


1339971_1281414_ans_7c0c6dc768a94951b4cf915421b332a6.jpg


Find the derivatives of $$x \cos x$$

$$y=x\cos{x}$$

By using product rule of differentiation,

$$\dfrac{d(u \ . v)}{dx}=v\dfrac{du}{dx}+u\dfrac{dv}{dx}$$

$$\dfrac{dy}{dx}=x\dfrac{d}{dx}\left(\cos{x}\right)+\cos{x}\dfrac{d}{dx}\left(x\right)$$

$$\dfrac{dy}{dx}=-x\sin{x}+\cos{x}$$


Find the differentiation of $$\sec \left( {{{\tan }^{ - 1}}{\rm{x}}} \right)$$ w.r.t. $$x$$.

Let $$y=\sec (\tan^{-1}x)$$

On differentiating w.r.t $$x$$, we get
$$\dfrac{dy}{dx}=\dfrac{d}{dx}(\sec (\tan^{-1}x))$$

$$\dfrac{dy}{dx}=\sec (\tan^{-1}x). \tan (\tan^{-1}x)\times \dfrac{d}{dx}(\tan^{-1} x)$$

$$\dfrac{dy}{dx}=\sec (\tan^{-1}x).(x)\times \dfrac{1}{1+x^2}$$

$$\dfrac{dy}{dx}=\dfrac{x\sec (\tan^{-1}x)}{1+x^2}$$

Hence, this is the answer.


Find the derivative of the following functions:
$$\displaystyle 5\sec x+4\cos x$$

Let $$\displaystyle f\left ( x \right )=5\sec x+4\cos x$$
Thus using first principle,
$$\displaystyle f^{'}\left ( x \right )=\lim_{h\rightarrow 0}\frac{f\left ( x+h \right )-f\left ( x \right )}{h}$$
= $$\displaystyle

\lim_{h\rightarrow 0}\frac{5\sec \left ( x+h \right )+4\cos \left ( x+h

\right )-\left [ 5\sec x+4\cos x \right ]}{h}$$
= $$\displaystyle

5\lim_{h\rightarrow 0}\frac{\left [ \sec \left ( x+h \right ) -\sec

x\right ]}{h}+4\lim_{h\rightarrow 0}\frac{\left [ \cos \left ( x+h

\right ) -\cos x\right ]}{h}$$
= $$\displaystyle 5\lim_{h\rightarrow

0}\frac{1}{h}\left [ \frac{1}{\cos \left ( x+h \right )}-\frac{1}{\cos

x} \right ]+4\lim_{h\rightarrow 0}\frac{1}{h}\left [ \cos \left ( x+h

\right )-\cos x \right ]$$
= $$\displaystyle 5\lim_{h\rightarrow

0}\left [ \frac{\cos x-\cos \left ( x+h \right )}{\cos x\cos \left ( x+h

\right )} \right ]+4\lim_{h\rightarrow 0}\frac{1}{h}\left [ \cos x\cos

h-\sin x\sin h-\cos x \right ]$$
= $$\displaystyle \frac{5}{\cos

x}\cdot \lim_{h\rightarrow 0}\frac{1}{h}\left [ \frac{-2\sin \left (

\frac{2x+h}{2} \right )\sin \left ( -\frac{h}{2} \right )}{\cos \left (

x+h \right )} \right ]+4\left [ -\cos x\lim_{h\rightarrow 0}\frac{\left (

1-\cos h \right )}{h}-\sin x\lim_{h\rightarrow 0}\frac{\sin h}{h}

\right ]$$
= $$\displaystyle \frac{5}{\cos x}\cdot \lim_{h\rightarrow

0}\left [ \frac{\sin \left ( \frac{2x+h}{2} \right )\cdot\frac{\sin

\left ( \frac{h}{2} \right )}{\frac{h}{2}} }{\cos \left ( x+h \right )}

\right ]+4\left [ \left ( -\cos x \right ) \cdot \left ( 0 \right

)-\left ( \sin x \right )\cdot 1\right ]$$
= $$\displaystyle

\frac{5}{\cos x}\cdot \left [ \lim_{h\rightarrow 0} \frac{\sin \left (

\frac{2x+h}{2} \right )}{\cos \left ( x+h \right )}\cdot

\lim_{h\rightarrow 0}\frac{\sin \left ( \frac{h}{2} \right

)}{\frac{h}{2}}\right ]-4\sin x$$
= $$\displaystyle \frac{5}{\cos x}\cdot \frac{\sin x}{\cos x}\cdot 1-4\sin x$$
= $$\displaystyle 5\sec x\tan x\cdot -4\sin x$$


Find the derivative of the following functions: $$\displaystyle \cos ec\,x$$

Let $$\displaystyle f\left ( x \right )=\cos ec\,x$$
Thus using first principle,
$$\displaystyle f^{'}\left ( x \right )=\lim_{h\rightarrow 0}\frac{f\left ( x+h \right )-f\left ( x \right )}{h}$$
$$\displaystyle f^{'}\left ( x \right )=\lim_{h\rightarrow 0}\frac{1}{h}\left [ \cos ec\left ( x+h \right )-\cos ecx \right ]$$
= $$\displaystyle \lim_{h\rightarrow 0}\frac{1}{h}\left [ \frac{1}{\sin \left ( x+h \right )}-\frac{1}{\sin x} \right ]$$
= $$\displaystyle

\lim_{h\rightarrow 0}\frac{1}{h}$$$$\displaystyle \left [ \frac{\sin

x-\sin \left ( x+h \right )}{\sin \left ( x+h \right )\sin x} \right ]$$
= $$\displaystyle

\lim_{h\rightarrow 0}\frac{1}{h}\left [ \frac{2\cos \left (

\frac{x+x+h}{2} \right )\cdot \sin \left ( \frac{x-x-h}{2} \right

)}{\sin \left ( x+h \right )\sin x} \right ]$$
= $$\displaystyle

\lim_{h\rightarrow 0}\frac{1}{h}\left [ \frac{2\cos \left (

\frac{2x+h}{2} \right )\sin \left ( -\frac{h}{2} \right )}{\sin \left (

x+h \right )\sin x} \right ]$$
=$$\displaystyle \lim_{h\rightarrow

0}\frac{-\cos \left ( \frac{2x+h}{2} \right ),\frac{\sin \left (

\frac{h}{2} \right )}{\left ( \frac{h}{2} \right )}}{\sin \left ( x+h

\right )\sin x}$$
= $$\displaystyle \lim_{h\rightarrow 0}\left (

\frac{-\cos \left ( \frac{2x+h}{2} \right )}{\sin \left ( x+h \right

)\sin x} \right ).\lim_{\frac{h}{2}\rightarrow 0}\frac{\sin \left (

\frac{h}{2} \right )}{\left ( \frac{h}{2} \right )}$$
= $$\displaystyle \left ( \frac{-\cos x}{\sin x\sin x} \right ).1= - \cos ec x\cot x$$


Find the derivative of the following functions (it is to be understood that $$a, b, c, d, p, q, r$$ and $$s$$ are fixed non-zero constants and $$m$$ and $$n$$ are integers) : $$\displaystyle \sin ^{n}x$$

Let $$y = \displaystyle \sin ^{n}x$$
$$\displaystyle \frac{dy}{dx}=\frac{d}{dx}$$$$\displaystyle

\left ( \sin ^{n} x\right )=n\,\sin ^{\left ( n-1 \right )}x\,\cos

\,x$$


Find the differential coefficient of $$\sin x$$ by first principle.

Find the differential coefficient of $$\sin x$$ by first principle. Suppose that
$$f(x) = \sin x$$
$$\therefore f(x + h) = \sin (x + h)$$
$$\therefore f(x + h) - f(x) = \sin (x + h) - \sin x$$
$$\Rightarrow \dfrac {f(x + h) - f(x)}{h} = \dfrac {\sin (x + h) - \sin x}{h}$$
$$\Rightarrow \displaystyle \lim_{h\rightarrow 0} \dfrac {f(x + h) - f(x)}{h} = \displaystyle \lim_{h\rightarrow 0} \dfrac {\sin (x + h) - \sin x}{h}$$
$$\Rightarrow \dfrac {d}{dx}f(x) = {\displaystyle \lim_{h\rightarrow 0}} \left [\dfrac {2\cos \left (x + \dfrac {h}{2}\right ). \sin \dfrac {h}{2}}{h}\right ]$$
$$\Rightarrow \dfrac {d}{dx}\sin x = \displaystyle \lim_{h\rightarrow 0}\cos \left (x + \dfrac {h}{2}\right ) . \displaystyle \lim_{h\rightarrow 0} \left (\dfrac {\sin \dfrac {h}{2}}{\dfrac {h}{2}}\right )$$
$$= \cos (x + 0) . \displaystyle \lim_{\tfrac {h}{2}\rightarrow 0}\left (\dfrac {\sin \dfrac {h}{2}}{\dfrac {h}{2}}\right ) \because h\rightarrow 0$$
$$\therefore \dfrac {h}{2}\rightarrow 0$$
$$= \cos x . 1$$
$$\Rightarrow \dfrac {d}{dx}\sin x = \cos x$$.


Prove that the following functions are increasing.
$$y \, = \, 2x \, + \, sin \, x \, for \, x \, \epsilon \, R$$

$$y=2x+\sin x$$

$$\implies \dfrac{dy}{dx}=y'=2+\cos x$$

Since for all $$x\in R$$, we have $$-1\leq \cos x\leq 1$$

$$1\leq 2+\cos x\leq 3$$

Hence, we see that $$y'>0 \forall x\in R$$

And, hence $$y=2x+\sin x$$ is increasing for $$x\in R$$


Find the derivative of the following functions from the first principals w.r.t to $$x$$.
$$\tan 2x$$

We know, first principal is,
$$f'(x)=\lim\limits_{h\to0}\dfrac{f(x+h)-f(x)}{h}$$
So with $$f(x)=\tan\,2x$$ we have

$$f'(x)=\lim\limits_{h\to0}\dfrac{\tan(2x+2h)-\tan\,2x}{h}$$

          $$=\lim\limits_{h\to0}\dfrac{\dfrac{\sin(2x+2h)}{\cos(2x+2h)}-\dfrac{\sin\,2x}{\cos\,2x}}{h}$$                       [ $$\tan\,A=\dfrac{\sin\,A}{\cos\,A}$$]
         
          $$=\lim\limits_{h\to0}\dfrac{1}{h}\left[\dfrac{\sin(2x+2h)}{\cos(2x+2h)}-\dfrac{\sin\,2x}{\cos\,2x}\right]$$
   
          $$=\lim\limits_{h\to0}\dfrac{1}{h}\left[\dfrac{\sin(2x+2h)\cos\,2x-\cos(2x+2h)\sin\,2x}{\cos(2x+2h)\cos\,2x}\right]$$

          $$=\lim\limits_{h\to0}\dfrac{1}{h}\left[\dfrac{\sin(2x+2h-2x)}{\cos(2x+2h)\cos\,2x}\right]$$                         [ $$\sin(A-B)=\sin\,A.\cos\,B-\cos\,B.\sin\,A$$]

          $$=\lim\limits_{h\to0}\dfrac{1}{h}\left[\dfrac{\sin(2h)}{\cos(2x+2h)\cos\,2x}\right]$$

          $$=\lim\limits_{h\to0}\dfrac{1}{\cos(2x+2h)\cos\,2x}.\dfrac{\sin\,2h}{h}$$

           $$=\lim\limits_{h\to0}\dfrac{2}{\cos(2x+2h)\cos\,2x}.\dfrac{\sin\,2h}{2h}$$

           $$=\lim\limits_{h\to0}\dfrac{2}{\cos(2x+2h)\cos\,2x}.\lim\limits_{h\to0}\dfrac{\sin\,2h}{2h}$$

We know, $$\lim\limits{h\to0}\dfrac{\sin\,h}{h}=1\Rightarrow \lim\limits_{h\to 0}\dfrac{\sin\,2h}{2h}=1$$

$$f'(x)=\dfrac{2}{\cos\,2x.\cos\,2x}.1$$

          $$=\dfrac{2}{\cos^22x}$$

          $$=2\sec^22x$$




Solve : $$I_n=\displaystyle \int_{0}^{\dfrac{\pi}{2}}e^{-x}\sin ^nxdx$$  

$$I_n=\int_{0}^{\frac{\pi}{2}}e^{-x}\sin ^nxdx$$  

show that $$I_n=-e^{\frac{-\pi}{2}}+n\int_{0}^{\frac{\pi}{2}}e^{-x}\sin ^{n-1}xdx$$

$$I_n=\int_{0}^{\frac{\pi}{2}}e^{-x}\sin ^nxdx$$

substitute $$u=\sin ^nx,\dfrac{dv}{dx}=e^{-x}\Rightarrow v=-e^{-x}$$

$$I_n=[-e^{-x}\sin ^nx]_{0}^{\frac{\pi}{2}}-\int_{0}^{\frac{\pi}{2}}-e^{-x}n\sin ^{n-1}x\cos xdx$$

$$I_n=-e^{\frac{-\pi}{2}}+n\int_{0}^{\frac{\pi}{2}}-e^{-x}\cos x\sin ^{n-1}xdx$$

--------------------------------------------------
$$\int_{0}^{\frac{\pi}{2}}e^{-x}\cos x\sin ^{n-1}xdx$$

$$=[-e^{-x}\cos x\sin ^{n-1}x]_{0}^{\frac{\pi}{2}}+\int_{0}^{\frac{\pi}{2}}e^{-x}((n-1)\sin ^{n-2}x-n\sin ^nx)dx$$

$$=(n-1)\int_{0}^{\frac{\pi}{2}}e^{-x}\sin ^{n-2}xdx-n\int_{0}^{\frac{\pi}{2}}e^{-x}\sin ^nxdx$$

$$=(n-1)I_{n-2}-nI_n$$

$$\therefore I_n=-e^{\frac{-\pi}{2}}+n(n-1)I_{n-2}-n^2I_n$$

$$\Rightarrow (n^2+1)I_n=-e^{\frac{-\pi}{2}}+n(n-1)I_{n-2}$$


Solve:$$\dfrac{d}{dx}(cosec x)=?$$

Given, 
$$\dfrac { d }{ dx } (cosecx)\\ =\dfrac { d }{ dx } (\dfrac { 1 }{ \sin { x }  } )$$
We know the quotient rule of differentiation,
$$\dfrac { d }{ dx } (\dfrac { u }{ v } )=\dfrac { v\dfrac { du }{ dx } -u\dfrac { dv }{ dx }  }{ { v }^{ 2 } } $$
Now, let $$u=1,\sin { x } =v$$
$$\therefore \dfrac { d }{ dx } (\dfrac { 1 }{ \sin { x }  } )\\ =\dfrac { \sin { x } \dfrac { d }{ dx } (1)-1\dfrac { d }{ dx } (\sin { x } ) }{ { (\sin { x } ) }^{ 2 } } \\ =\dfrac { \sin { x } (0)-\cos { x }  }{ { (\sin { x } ) }^{ 2 } } \\ =\dfrac { -\cos { x }  }{ { (\sin { x } ) }^{ 2 } } \\ =\dfrac { -\cos { x }  }{ \sin { x }  } \cdot \dfrac { 1 }{ \sin { x }  } \\ =-\cot { x } cosecx\\ \therefore \dfrac { d }{ dx } (cosecx)=-\cot { x } cosecx.$$ 


Find the derivative of tan x using  first principle of derivatives

From the first principle of derivatives,

$$f'(x)=\overset{lim}{h\rightarrow 0} \dfrac{f(x+h)-f(x)}{h}$$

           $$=\overset{lim}{h\rightarrow 0} \dfrac{tan(x+h)-tanx}{h}$$

           $$=\overset{lim}{h\rightarrow 0} \dfrac{\dfrac{sin(x+h)}{cos(x+h)}-\dfrac{sinx}{cosx}}{h}$$

           $$=\overset{lim}{h\rightarrow 0} \dfrac{cos\:x\:sin(x+h)-sin\:x\:cos(x+h)}{hcos\:x\:cos(x+h)}$$

           $$=\overset{lim}{h\rightarrow 0} \dfrac{\dfrac{sin(2x+h)+sin\:h}{2}-\dfrac{sin(2x+h)-sin\:h}{2}}{hcos\:x\:cos(x+h)}$$

           $$=\overset{lim}{h\rightarrow 0} \dfrac{sin\:h}{hcos\:x\:cos(x+h)}$$

           $$=\overset{lim}{h\rightarrow 0}\dfrac{sin\:h}{h} \times \overset{lim}{h\rightarrow 0} \dfrac{1}{cos\:x\:cos(x+h)}$$

           $$=1\times \dfrac{1}{cos\:x \times cos\:x}$$

           $$=\dfrac{1}{cos^2x}$$

$$f'(x)=sec^2x$$


Find the derivative of $$cos^2\:x$$, by using first principle of derivatives.
1227860_0461f42ba1d243fa9f8e7a1dbb26eae8.JPG

Increase from $$y$$ to $$y+\delta y$$ correspondingly $$x$$ to $$x+\delta x$$ in the above equation$$\left(1\right)$$
$$\Rightarrow y+\delta y={\cos}^{2}{\left(x+\delta x\right)}$$       .....$$\left(2\right)$$
Eqn$$\left(2\right)$$-Eqn$$\left(1\right)$$
$$\Rightarrow y+\delta y-y={\cos}^{2}{\left(x+\delta x\right)}-{\cos}^{2}{x}$$
$$\Rightarrow \delta y={\cos}^{2}{\left(x+\delta x\right)}-{\cos}^{2}{x}$$
Divide both sides by $$\delta x$$ we get
$$\Rightarrow \dfrac{\delta y}{\delta x}=\dfrac{{\cos}^{2}{\left(x+\delta x\right)}-{\cos}^{2}{x}}{\delta x}$$
$$\Rightarrow \dfrac{\delta y}{\delta x}=-\dfrac{\sin{\left(2x+\delta x\right)}\sin{\delta x}}{\delta x}$$ by using $${\cos}^{2}{B}-{\cos}^{2}{A}=\sin{\left(A+B\right)}\sin{\left(A-B\right)}$$
$$\Rightarrow {\lim}_{x\rightarrow 0}\dfrac{\delta y}{\delta x}={\lim}_{x\rightarrow 0}-\dfrac{\sin{\left(2x+\delta x\right)}\sin{\delta x}}{\delta x}$$
$$\Rightarrow \dfrac{dy}{dx}={\lim}_{x\rightarrow 0}-\dfrac{\sin{\left(2x+\delta x\right)}\sin{\delta x}}{\delta x}$$
$$\Rightarrow \dfrac{dy}{dx}=-\dfrac{\sin{\left(2x+0\right)}\times 1$$ since $${\lim}_{x\rightarrow 0}\sin{\delta x}}{\delta x}=1$$
$$\therefore \dfrac{dy}{dx}=-\sin{2x}=-2\cos{x}\sin{x}$$


Dfferentiate w.r.t x:
$$tan^2\, 7x$$

Consider the given expression,

$$\Rightarrow {{\tan }^{2}}7x$$

Differentiate with respect to x,

$$ \Rightarrow \dfrac{d}{dx}{{\tan }^{2}}7x $$

$$ \Rightarrow 2\tan 7x\dfrac{d}{dx}7x $$

$$ \Rightarrow 2\left( \tan 7x \right).7 $$

$$ \Rightarrow \Rightarrow 14\tan 7x $$


Hence, this is the answer.



Find the derivation of $$\sqrt{tan x}$$ with respect to x using first principle.

$$a \rightarrow f'(a)=\underset{h\rightarrow 0}{lim}\dfrac{f(a+h)-f(a)}{h}=\underset{h\rightarrow 0}{lim}\dfrac{\sqrt{\tan(a+h)}-\sqrt{\tan a}}{h}\times \dfrac{\sqrt{\tan(a+h)}+\sqrt{\tan a}}{\sqrt{\tan(a+h)}+\sqrt{\tan a}}$$
$$=\underset{h \rightarrow 0}{lim}\dfrac{\tan(a+h)-\tan a}{h(2\sqrt{\tan a})}=\underset{h\rightarrow 0}{lim}\left(\dfrac{\tan a+\tan h-\tan a}{1-\tan a\tan h}\right)\dfrac{1}{2h\sqrt{\tan a}}$$
$$=\underset{h\rightarrow 0}{lim}\dfrac{\tan h+\tan^2a\tan h}{2h\sqrt{\tan a}}=\underset{h\rightarrow 0}{\lim}\dfrac{\tan h(1+\tan^2a)}{4\, 2\sqrt{\tan a}}=\dfrac{\sec^2a}{2\sqrt{\tan a}}$$


If $$y=x^{ \cos x }+{ \left( \tan x \right)  }^{ \cot x },find\dfrac { dy }{ dx } $$

We have,

$$y={{x}^{\cos x}}+{{\left( \tan x \right)}^{\cot x}}$$


Taking log both side and we get,

$$ \log y=\log {{\left( x \right)}^{\cos x}}+\log {{\left( \tan x \right)}^{\cot x}} $$

$$ \log y=\cos x\log x+\cot x\log \tan x $$


On differentiating with respect to x and we get,

$$ \dfrac{d}{dx}\log y=\cos x\dfrac{d}{dx}\log x+\log x\dfrac{d}{dx}\cos x+\cot x \dfrac{d}{dx}\log \tan x+\operatorname{logtan}x\dfrac{d}{dx}\cot x $$

$$ \Rightarrow \dfrac{1}{y}\dfrac{dy}{dx}=\cos x\dfrac{1}{x}+\log x\left( -\sin x \right)+\cot x\dfrac{1}{\tan x}\left( {{\sec }^{2}}x \right)+\log \tan x\left( -{{\csc }^{2}}x \right) $$

$$ \Rightarrow \dfrac{1}{y}\dfrac{dy}{dx}=\dfrac{\cos x}{x}-\sin x\log x-\dfrac{\cot x}{\tan x}{{\sec }^{2}}x-{{\csc }^{2}}x\cos x\log \tan x $$

$$ \Rightarrow \dfrac{1}{y}\dfrac{dy}{dx}=\dfrac{\cos x}{x}-{{\csc }^{2}}x-\sin x\log x-{{\csc }^{2}}x\cos x\log \tan x $$

$$ \Rightarrow \dfrac{dy}{dx}=y\left[ \dfrac{\cos x}{x}-{{\csc }^{2}}x-\sin x\log x-{{\csc }^{2}}x\cos x\log \tan x \right] $$

$$ \Rightarrow \dfrac{dy}{dx}={{x}^{\cos x}}+{{\left( \tan x \right)}^{\cot x}}\left[ \dfrac{\cos x}{x}-{{\csc }^{2}}x-\sin x\log x-{{\csc }^{2}}x\cos x\log \tan x \right] $$


Hence, this is the answer.



Find $$\frac{dy}{dx},$$  if $$y=\sqrt{cos(3x+1)}$$  

If $$y=\sqrt{\cos (3x+1)}$$
then
$$\dfrac{dy}{dx}=\dfrac{d}{dx}\sqrt{\cos (3x+1)}$$
$$\dfrac{dy}{dx}=\dfrac{1.(-(\sin 3x+1)\times 3)}{2\sqrt{\cos (3x+1)}}$$
$$\dfrac{dy}{dx}=-\dfrac{3}{2}\dfrac{\sin (3x+1)}{\sqrt{\cos (3x+1)}}$$.

1179641_1351821_ans_c9083a1212b54c4ebe26c3eddbd49623.JPG


If $$y = \tan \left( {2x + 3} \right)$$ . Find $$\dfrac{{dy}}{{dx}}$$.

We have,
$$y=\tan(2x+3)$$

On differentiating w.r.t $$x$$, we get
$$\dfrac{dy}{dx}=\dfrac{d}{dx}\tan(2x+3)$$

$$\dfrac{dy}{dx}=\sec^2(2x+3)\dfrac{d}{dx}(2x+3)$$

$$\dfrac{dy}{dx}=\sec^2(2x+3)\times (2+0)$$

$$\dfrac{dy}{dx}=2\sec^2(2x+3)$$

Hence, this is the answer.


$$2\dfrac{dy}{dx}-y\sec x=y^3\tan x$$.

$$2\dfrac{dy}{dx}-y\sec x=y^3\tan x$$.

$$ 2 \dfrac{dy}{dx} = y^{3} \tan x + y \sec x $$ 

$$ 2\dfrac{dy}{dx} = y(y^{2} \tan x + \sec x) $$ 

$$ 2 \dfrac{dy}{y} = (y^{2} \tan x + \sec x) dx $$ 

$$ 2 \log y = y^{2} \sec^{2} x + \ln |\sec x +  \tan x|+ C $$

$$ \dfrac{2}{y^2} \cdot \log y = \sec^{2} x + \ln |\sec x + \tan x| $$ 

$$ \dfrac{2}{y^2} \cdot \log y = \log e^{\sec^2 x} + \ln |\sec x + \tan x| $$ 

$$  \dfrac{-2}{y^2} = -1 + (\pi + x) \cot \left  (\dfrac{\pi}{4} + \dfrac{x}{2}  \right  ) $$ 


Differentiate:$$y=\sin{\left(2x+3\right)}$$ w.r.t $$x$$

$$y=\sin{\left(2x+3\right)}$$
$$\Rightarrow\,\dfrac{dy}{dx}=\cos{\left(2x+3\right)}\dfrac{d}{dx}\left(2x+3\right)$$
$$\therefore\,\dfrac{dy}{dx}=2\cos{\left(2x+3\right)}$$


$$f\left( x \right) =\left( \sin x+\cos x \right) $$ Find $$f^{\prime} (x)$$

$$f\left( x \right) =\left( \sin x+\cos x \right) \\f^{\prime}(x)=\dfrac d{dx}(\sin x+\cos x)\\f^{\prime}(x)=\cos x-\sin x$$


Find the derivative of  $$\dfrac { x ^ { 5 } - \cos x } { \sin x } $$   with respect to  $$x.$$


1894583_1487447_ans_a2e19b54d5fc4810b965d3735b3af1b0.jpg


Differentiate the function with respect to x.
$$\cos x\cdot \cos 2x\cdot \cos 3x$$.


1315517_1584923_ans_26afa66a2b114e029f8328abface6e7a.jpg


Differentiate the following from first principle.
$$\sin(x+1)$$.


1445498_1666119_ans_b330502d0f8d4752a007d0d1222d8eff.jpg


Differentiate the following from first principle.
$$f(x)=\cos\left(x-\dfrac{\pi}{8}\right)$$

We have, $$f(x)=\cos\left(x-\dfrac{\pi}{8}\right)$$

$$\therefore f(x+h)=\cos\left(x+h-\dfrac{\pi}{8}\right)=\cos\left\{\left(x-\dfrac{\pi}{8}\right)+h\right\}$$

So, $$f'(x)=\displaystyle\lim_{h\rightarrow 0}\dfrac{f(x+h)-f(x)}{h}$$

$$\Rightarrow f'(x)=\displaystyle\lim_{h\rightarrow 0}\dfrac{\cos\left\{\left(x-\dfrac{\pi}{8}\right)+h\right\}-\cos\left(x-\dfrac{\pi}{8}\right)}{h}$$  

$$\Rightarrow f'(x)=\displaystyle\lim_{h\rightarrow 0}\dfrac{-2\sin\left\{\left(x-\dfrac{\pi}{8}\right)+\dfrac{h}{2}\right\}\sin\left(\dfrac{h}{2}\right)}{h}$$ [$$\because \cos (a)-\cos(b)=-2\sin\dfrac{a+b}{2} \sin\dfrac{a-b}{2} $$]

$$\Rightarrow f'(x)=-\displaystyle\lim_{h\rightarrow 0}\sin\left\{\left(x-\dfrac{\pi}{8}\right)+\dfrac{h}{2}\right\}\dfrac{\sin\left(\dfrac{h}{2}\right)}{\left(\dfrac{h}{2}\right)}$$     As $$\displaystyle \lim_{x\rightarrow0}\dfrac{sinx}x=1$$

$$=-\sin\left(x-\dfrac{\pi}{8}\right)$$.


Differentiate the following 
$$\cos \sqrt{x}$$.


1422602_1668954_ans_25678de4af82451585f038756f74569a.jpg


Differentiate: $$2\sqrt{\cot (x^{2})}$$ w.e.t.X

Let $$y = 2\sqrt{\cot (x^{2})}$$Differentiating w.r.t.x both sides, we get 

$$\dfrac{dy}{dx} = 2 \times \dfrac{1}{2\sqrt{\cot (x^{2})}} \times -\ cosec^{2} (x^{2}) \times 2x$$

$$= \dfrac{-2x \ cosec^{2}x^{2}}{\sqrt{\cot (x^{2})}}$$


Find $$\dfrac{dy}{dx}$$ if $$y + \sin y = \cos x.$$

Given, $$y + \sin y = \cos x.$$

Differentiating w.r.t. x, we get 

$$\dfrac{dy}{dx} + \cos y. \dfrac{dy}{dx} =- \sin x$$

$$\Rightarrow \dfrac{dy}{dx} (1 + \cos y) = -\sin x$$

$$\Rightarrow \dfrac{dy}{dx} = \dfrac{-\sin x}{1 + \cos y}\left [ \because y \neq (2n + 1) \pi \right ]$$


If $$y = f \left (\frac{2x - 1} {x^{2} + 1}  \right )$$ and $$f^{'}(x) = \sin x^{2}$$, then $$\frac{dy} {dx} = $$ ___________.                                 (IIT-JEE, 1982)

$$y = f \left (\frac{2x - 1} {x^{2} + 1}  \right )$$; 

$$f^{'}(x) = \sin x^{2}$$

$$\dfrac{dy} {dx} = f^{'} \left (\frac{2x - 1} {x^{2} + 1}  \right ) \frac{d} {dx} \left ( \frac{2x - 1} {x^{2} + 1} \right )$$

$$= \sin \left (\dfrac{2x _ 1} {x^{2} + 1}  \right )^{2} \left (\dfrac{2\left (x^{2} + 1  \right ) - 2x\left (2x - 1 \right )} {\left (x^{2} + 1  \right )^{2}}  \right )$$

$$= \dfrac{2 + 2x - 2x^{2}} {\left ( x^{2} + 1 \right )^{2}} \sin\left ( \dfrac{2x - 1} {x^{2} + 1} \right )^{2}$$


Differentiable the function w.r.t .x.
$$ x ^{\sin x} + (\sin x) ^{\cos x} $$

Let $$  y =  x^{\sin x} + (\sin x)^{\cos x} $$ $$ = u + v , $$ 
where u and v $$ u = x^{\sin x} and  v = (\sin x)^{\cos x} $$
$$ \log u = \sin x (\log x) $$
$$ v = (\sin x)^{\cos x} $$
$$ \log v = \cos x  \log (sin x ) $$
$$ \dfrac{1}{v} \times \dfrac{dv}{dx} = \cos x \times \dfrac{1}{\sin x} \cos x + \log (\sin x) $$
$$ \dfrac{dv}{dx} = (\sin x)^{\cos x} \left \{ \cos x \cot x - \sin x \log (\sin x) \right \} $$


If $$  y = (\tan ^{-1} x)^{2} $$ show that $$ (x ^{2} +  1)^{2} y_{2} +  2x (x^{2}+ 1)^{2} y_{2} +  2x ( x^{2} +  1) y_{1} =  2 $$where$$y_{1},y_{2}$$ have their usual meaning.

$$  y = (\tan ^{-1} x)^{2} $$
$$Differentiating \space wrt \space x$$
$$ \dfrac{dy}{dx} =  2 \tan^{-1} x \times \dfrac{1}{(1 + x^{2})} $$
$$ (x^{2} + 1) \dfrac{dy}{dx} =  2 \tan^{-1} x $$
$$ ( x^{2} + 1) y_{1} = 2\tan^{-1} x $$
$$(x^{2}+  1) y_{2} + y_{1} \times 2x =  2 \times \dfrac{1}{(x^{2} +  1)}$$
$$ (x^{2}+ 1)^{2} y_{2} + 2x (x^{2}+ 1) y_{1} = 2 $$


prove that , $$ \dfrac{dy}{dx} = \dfrac{(1 + y) \cos x + y \sin x}{1 + 2y + \cos x  - \sin x} $$
1860299_b8d9ebf9384144c28d89b7f79ef6c71a.png

$$y$$ can be rewritten as
$$  y = 1 + \dfrac{\cos x}{1 + y}$$
$$ y = \dfrac{(1+ y)\sin x}{1 +y + \cos x} $$
$$ y ^{2} + y + y \cos x = \sin x + y  \sin x $$
 $$ \dfrac{dy}{dx} = \dfrac{(1 + y)\cos x + y \sin x}{1 + 2y + \cos x - \sin x}$$


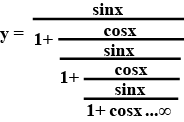
Find whether function is increasing or decreasing in given domain
$$f (x) = sin^4 X + cos^4 x, x \epsilon (0, \frac{\pi }{4})$$

$$f (x) = sin^4 X + cos^4 x$$
Diff. w.r.t. x,
$$f'(x) = 4 sin^3 \times cos X + 4 cos^3 X (-sin X)$$
$$\Rightarrow f'(x) = 4 sin X cos  X (sin^2 X - cos^2 X)$$
$$\Rightarrow f'(x) = -2.2 sin X cos X (cos^2 x - sin^2 X)$$
$$\Rightarrow f' (x) = -2 sin 2x cos 2x$$
$$ f' (x) = - sin 4 x$$
In Interval $$(0, \frac{\pi }{4}), - sin 4x < 0$$
or $$ f' (x) < 0$$
Hence, function is decreasing in internal $$(0, \frac{\pi }{4})$$.


If $$y=(\sin x - \cos x)^{(\sin x- \cos x)}$$ then find $$\dfrac{dy}{dx}$$

Let $$y-(\sin x - \cos x){(\sin x- \cos )}$$
Taking $$\log$$ on both sides,
$$\log y= (\sin x - \cos x) \log{(\sin x- \cos x)}$$
Diff.w.r.t.$$x$$ of both sides,
$$\dfrac{1}{y}\dfrac{dy}{dx}=(\sin x- \cos x) \times \dfrac{d}{dx} [\log (\sin x- \cos x)]+ \log (\sin x - \cos x) \times \dfrac{d}{dx} (\sin x - \cos x)$$
$$\Rightarrow \dfrac{1}{y}\dfrac{dy}{dx}=(\sin x- \cos x) \dfrac{1}{(\sin x- \cos x) } \times \dfrac{d}{dx} (\sin x- \cos x) +\log (\sin x- \cos x) \left\{ (\cos x -(- \sin x))\right\}$$
$$\Rightarrow \dfrac{1}{y}\dfrac{dy}{dx}=\left\{ (\cos x -(- \sin x))\right\} + (\cos x+ \sin x) \log (\sin x - \cos x)$$
$$\Rightarrow \dfrac{1}{y}\dfrac{dy}{dx}=(\cos x+ \sin x)+\log (\sin x - \cos x)$$
$$\Rightarrow \dfrac{dy}{dx}=y (\cos x+ \sin x) \times [1+ \log (\sin x - \cos x)]$$
Hence, $$\dfrac{dy}{dx} (\sin x - \cos x)^{(\sin x- \cos x)} \times (\cos x+ \sin x) \times [1+ \log (\sin x - \cos x)]$$


Differentiate given functions w.r.t. $$x$$:
$$x^3e^x \sin x$$

Let $$y=x^3e^x\sin x$$
Diff.w.r.t.$$x$$ of both sides,
$$\dfrac{dy}{dx}=\dfrac{d}{dx} (x^3 e^x \sin x)$$
$$\Rightarrow \dfrac{dy}{dx}=x^3 \dfrac{d}{dx} (e^x \sin x)+e^x \sin x \dfrac{d}{dx} (x^3)$$
$$\Rightarrow \dfrac{dy}{dx}=x^2 [e^x \cos x+ \sin x e^x]+e^x \sin 3x^2 $$
Hence, $$\dfrac{dy}{dx}=x^3 e^x \cos x+x^3 e^x \sin x +3 x^2 e^x \sin x$$


Find the derivatives of the following:
$$cosec x$$.

Let $$f(x) = cosec (x)$$
Then, derivative of $$f(x)$$
$$\dfrac {d}{dx} f(x) = \dfrac {d}{dx} (cosec x)$$
$$= \dfrac {d}{dx} \left (\dfrac {1}{\sin x}\right )$$
$$= \dfrac {\sin x \times \dfrac {d}{dx} (1) - 1\times \dfrac {d}{dx} (\sin x)}{(\sin x)^{2}}$$
[From the formula of derivative of quotient of two functions]
$$= \dfrac {\sin x\times 0 - 1\times \cos x}{(\sin x)^{2}} \left (\because \dfrac {d}{dx} \sin x = \cos x\right )$$
$$= -\dfrac {\cos x}{\sin^{2}x}$$
$$= -\dfrac {\cos x}{\sin x}\times \dfrac {1}{\sin x}$$
$$= -\cot x\times cosec x$$
$$= -cosec x \cot x$$
Hence, derivative of the given function $$cosec x$$
$$= -cosec x \cot x$$.


$$\dfrac{d}{dx}$$(cos$$^2$$ x sin x)


2040757_1285874_ans_5ad828f367a34aec8fd5e79e68c6dc01.jpeg


If $$cos^{-1}{(\dfrac{x^2-y^2}{x^2+y^2})}=2k$$, show that $$y\dfrac{dy}{dx}=x tan^2k$$


2042784_1533963_ans_3dd791c43549468983cfd3d2bb94bb02.png


$$\sum _{ 0 }^{ \pi  }{ \dfrac { (ax+b) \sec x \tan x }{ 4+{ tan }^{ 2 }x }  } dx(a,b>0)$$


2044527_1565752_ans_e6059096bdba4b89b6f43a3eddf93e97.jpg


Class 11 Commerce Maths Extra Questions