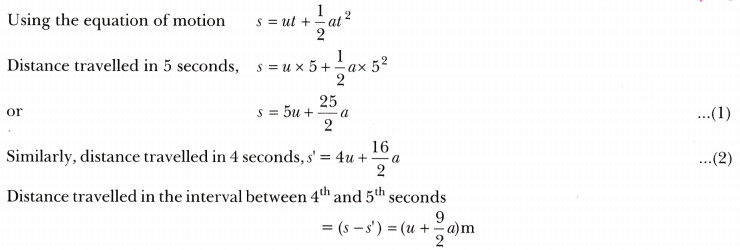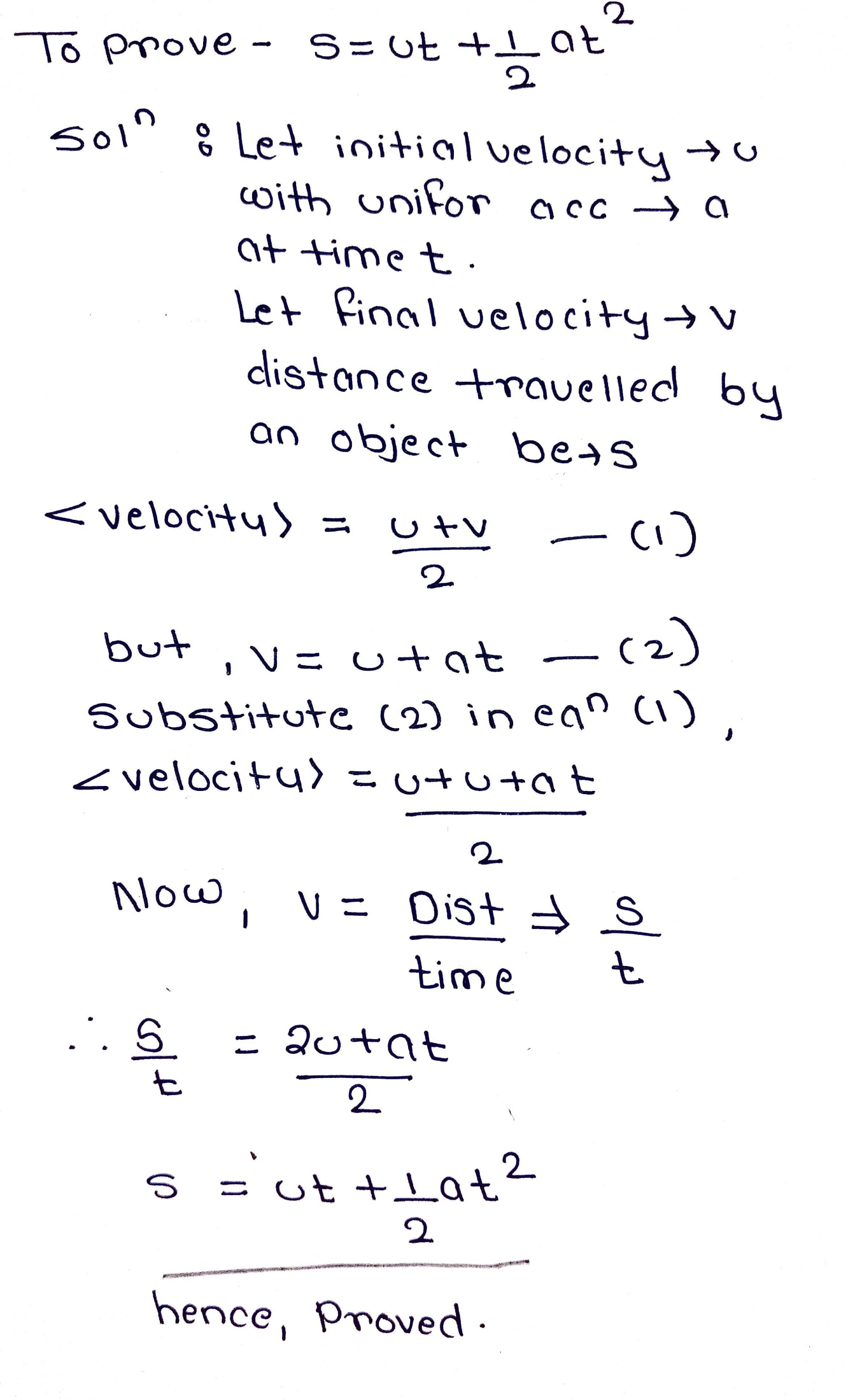Motion - Class 9 Physics - Extra Questions
A motorboat starting from rest on a lake accelerates in a straight line at a constant rate of $$3.0m/s^{2}$$ for $$8.0$$s. How far does the boat travel during this time?
What is the unit of acceleration?
An object starts from rest and has a uniform acceleration of $$4 m s^{-2}$$. What will be its velocity at the end of half a meter?
What is the speed of an apple dropped from a tree after $$1.5$$ second? What distance will it cover during this time? Take $$g=10m/s^2$$.
Velocity has both magnitude and ___________ .
An object at rest starts moving with uniform acceleration of 1ms$$^{-2}$$. Calculate the distance travelled by it in 4 seconds.
Name the two quantities, the slope of whose graph gives :
(a) speed, and
(b) acceleration
A car of mass 2400 kg moving with a velocity of $$20 m/s^{-1}$$ is applied stopped in 10 seconds on applying brakes.Calculate the retardation and the retarding force.
A cyclist is travelling at $$15 ms^{-1}$$. She applies brakes so that she does not collide with a wall $$18 m$$ away. What deceleration must she have?
A jumbo jet must reach a speed of 360 km/h on the runway for takeoff. What is the lowest constant acceleration needed for take off from a 1.80 km runway?
A car moving with a uniform velocity $$54\ kmph$$ is brought to rest in traveling a distance $$5m$$ What is the retardation produced by brake?
A car is moving in a straight line with speed $$18\ km\ h^{-1}$$. It is stopped in $$5s$$ by applying the brakes. Find the initial speed of car in $$m/s$$
Define average speed.
Define Displacement.
Is acceleration a scalar or a vector quantity?
Motion of wheel of a bicycle is _________(projectile, circular) motion.
A bus decreases its speed from 60 km/hr to 30 km/hr in 5 sec. Find the acceleration of the bus.
An object drop from a with a constant acceleration of $$10m/{s^{ 2}}$$ . Find its speed 2 sec after it was dropped.
What is the other name of negative acceleration ?
What is rotatory motion?
A boy standing on the roof of a building $$45\ m$$ high, throws a stone up in the air. If the stone reached its highest point and fell $$63\ m$$ below to the ground, how high was the stone thrown form the roof?
Are the following motions same or different?
(1) Motion of tip of second hand of a clock.
(2) Motion of entire second hand of a clock.
What is the SI unit of retardation ?
A train moving with a velocity of $$20\ ms$$ is brought to rest by applying brakes in $$5s$$.
Calculate the retradation.
Give one example of the following type of the motion:
Uniform retardation
How to calculate velocity?
Given$$v=0$$ $$m/s$$
$$u=15m/s$$
$$a=-2.5$$ $$ms^{-2}$$
$$t=?$$
$$u=15m/s$$
$$a=-2.5$$ $$ms^{-2}$$
$$t=?$$
(a) What remains constant in uniform circular motion?
(b) What changes continuously in uniform circular motion?
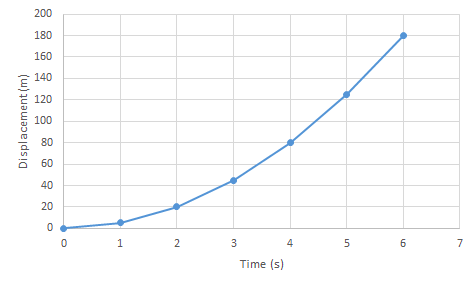
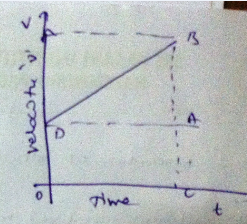
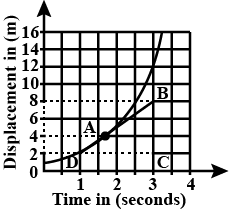
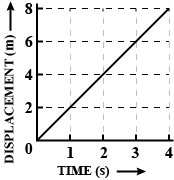
What conclusion can you draw about the velocity of a body from the displacement-time graph shown above :
What does the slope of a distance-time graph indicate?
A car is moving in a straight line with speed $$18\ km\ h^{-1}$$. It is stopped in $$5s$$ by applying the brakes. Find the retardation
The acceleration due to gravity on the planet $$A$$ is $$8$$ times the acceleration due to gravity on the planet $$B$$. A man jumps to a height of $$1.5 m$$ on the surface of $$A$$. What is the height of the jump by the same person on the planet $$B$$?
Rewrite the following equation in terms of $$a$$:$$s\, = \, ut + \dfrac{1}{2}at^2\,$$
What do you mean by retardation? What is its SI unit?
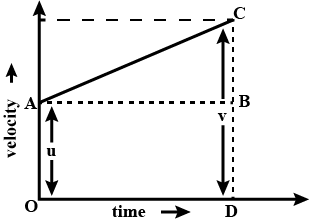
The graph given alongside shows the positions of a body at different times. Calculate the speed of the body as it moves from :
(i) $$A$$ to $$B$$.
(ii) $$B$$ to $$C$$, and
(iii) $$C$$ to $$D$$
What conclusion can you draw about the speed of a body from the following distance-time graph?
If a bus travelling at 20 m/s is subjected to a steady deceleration of 5 m/s2, how long will it take to come to rest ?
A car starting from rest travels $$ 100 m $$ in $$ 5 s $$ with uniform acceleration. Find the acceleration of the car.
Define centripetal acceleration.
A stone is dropped from a height of 125 m. If g $$=$$ 10 m s$$^{-2}$$, what is the ratio of the distances travelled by it during the first and the last second of its motion?
The displacement - time graph is shown in the figure above. What does this graph represent? Find velocity at point A.
A car moving at a certain speed stops on applying brakes within 16 m. If the speed of the car is doubled, maintaining the same retardation. Then at what distance does it stop? Also calculate the percentage change in this distance.
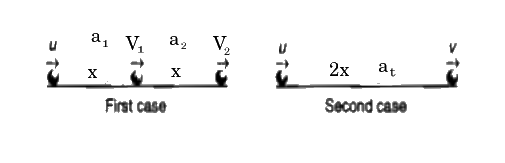
Two bodies, initially separated by $$'x'$$ m and having an initial velocity $$2 m s^{-1}$$ each, are moving towards each other along a straight line. If the rate of increase in their speeds is $$3 \ m s^{-2}$$ and $$2 \ m s^{-2}$$ respectively and the two meet after 4 seconds, find $$x.$$
A freely falling body crosses points $$P, Q$$ and $$R$$ with velocities $$v, 2v$$ and $$3v$$ respectively. Find the ratio of the distances $$PQ$$ to $$QR$$.
Determine the acceleration if a car maintained a uniform acceleration in the first second and the distance traveled is $$100\ m$$. The velocity at the end of the first second is $$75\ m s^{-1}$$.
What is the condition for which the average velocity and average speed of a body are equal?
Distinguish between acceleration and retardation.
A body at rest is dropped from the top of a tower. Draw a displacement-time graph of its free fall under gravity during the first 06 seconds. Show table for displacement and time starting from t = 0 with an interval of 01 second. Take $$g=10 \,m\, s^{-2}.$$
The body is at rest before it is being dropped from the tower. So the displacement of the body at any point is given by the equation
$$s=ut+\dfrac{1}{2}gt^2$$
where,
u = initial velocity, g = acceleration due to gravity and t = time taken.
u = initial velocity, g = acceleration due to gravity and t = time taken.
Initial velocity $$u = 0,$$ Acceleration $$a =10 \ m/{ s }^{ 2 }$$
Therefore, when the body is at rest, t = 0, then
$$s_0=0$$
Therefore, when the body is at rest, t = 0, then
$$s_0=0$$
The displacement covered is calculated for every increase of 1 second.
At $$t = 1s$$, $$s_1 = 0 + \dfrac{1}{2}(10)(1)^2 = 5 m$$
At $$t = 2s$$, $$s_2 = 0 + \dfrac{1}{2}(10)(2)^2 = 20 m$$
At $$t = 3s$$, $$s_3 = 0 + \dfrac{1}{2}(10)(3)^2 = 45 m$$
At $$t = 4s$$, $$s_4 = 0 + \dfrac{1}{2}(10)(4)^2 = 80 m$$
At $$t = 5s$$, $$s_5 = 0 + \dfrac{1}{2}(10)(5)^2 = 125 m$$
At $$t = 6s$$, $$s_6 = 0 + \dfrac{1}{2}(10)(6)^2 = 180 m$$
At $$t = 1s$$, $$s_1 = 0 + \dfrac{1}{2}(10)(1)^2 = 5 m$$
At $$t = 2s$$, $$s_2 = 0 + \dfrac{1}{2}(10)(2)^2 = 20 m$$
At $$t = 3s$$, $$s_3 = 0 + \dfrac{1}{2}(10)(3)^2 = 45 m$$
At $$t = 4s$$, $$s_4 = 0 + \dfrac{1}{2}(10)(4)^2 = 80 m$$
At $$t = 5s$$, $$s_5 = 0 + \dfrac{1}{2}(10)(5)^2 = 125 m$$
At $$t = 6s$$, $$s_6 = 0 + \dfrac{1}{2}(10)(6)^2 = 180 m$$
Therefore, the points corresponding to displacement $$s$$ every second $$t$$ are as follows:
$$t=0, s= 0 m$$
$$t=1, s= 5 m$$
$$t=2, s= 20 m$$
$$t=3, s= 45 m$$
$$t=4, s= 80 m$$
$$t=5, s= 125 m$$
$$t=6, s= 180 m$$
These points have been plotted as a displacement-time graph of free fall under gravity during the first 06 seconds.
Is a body in uniform circular motion in equilibrium?
Fill in the blanks.Retardation means _________ acceleration.
A particle is rotating in a circle of radius $$\displaystyle R= \frac{2}{\pi }m,$$ with constant speed $$\displaystyle 1 ms^{-1}.$$ Match the following two columns for the time interval when it completes $$\displaystyle \frac{1}{4}th$$ of the circle.
(A) Since speed is constant therefore average speed is going to be same
A $$\rightarrow $$ 4
(B) Average velocity $$=\dfrac{\text{total displacement}}{\text{total time}} $$
A $$\rightarrow $$ 4
(B) Average velocity $$=\dfrac{\text{total displacement}}{\text{total time}} $$
Displacement is equal to the hypotenuse made by the two radii at $$90^o$$
Displacement $$AB=\sqrt{(OA)^2+(OB)^2}=\sqrt{R^2+R^2}=\sqrt{2R^2}$$
$$\Rightarrow AB=\sqrt 2 R$$
Time for $$\dfrac{1}{4}th$$ of circle $$t_{1/4}=\dfrac{1}{4} \times Time \ period \ T$$
Time period = $$\dfrac{circumference}{speed}=\dfrac{2\pi R}{v}$$
$$t_{1/4}=\dfrac{1}{4} \times \dfrac{2 \pi R}{v}=\dfrac{\pi R}{2v}$$
Average velocity $$=\dfrac{\sqrt2 R}{\left( \dfrac{\pi R}{2v}\right) }=\dfrac{2\sqrt2v}{\pi}$$
$$v=1 \ m/s$$
So average velocity $$=\dfrac{2\sqrt2}{\pi}$$
B $$\rightarrow$$ 2
(C) Average acceleration = Centripetal acceleration= $$\dfrac{v^2}{R}=\dfrac{1}{R}=\dfrac{\pi}{2}$$
C $$\rightarrow $$ 3
(D) Displacement is $$\sqrt 2R=\dfrac{2\sqrt2}{\pi}$$
D $$\rightarrow$$ 2
C $$\rightarrow $$ 3
(D) Displacement is $$\sqrt 2R=\dfrac{2\sqrt2}{\pi}$$
D $$\rightarrow$$ 2
Fill in the blanks:The reference point from which the distance of a body is measured is called _______.
Fill in the blanks:Distance is the _______ path followed by a body between two points
A stone dropped from the top of a tower of height 300 m high splashes into
the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 m $$ \displaystyle s^{-1} $$? (g = 9.8 m$$ \displaystyle s^{-2} $$)
Differentiate between Speed and Velocity.
A man is $$48 m$$ behind a bus which is at rest. The bus starts accelerating at the rate of $$1 {m}/{{s}^{2}}$$, at the same time the man starts running with uniform velocity of $$10 {m}/{s}$$. What is the minimum time in which the man catches the bus?
Find the displacement of a car which increases its speed from 20 m/s to 80 m/s in 12 seconds.
A $$5\ N$$ force acts on a $$2.5\ kg$$ mass at rest, making it accelerate in a straight line.
i) What is the acceleration of the mass?
ii) How long will it take to move the mass through $$20 m$$?
iii) Find its velocity after $$3\ seconds$$
Consider the motions in the following cases.
(i) A moving car
(ii) A man climbing up a ladder to the terrace and coming down
(iii) A ball that has completed one rotation.
a) In which of the above cases the displacement of the object may be zero. Justify your answer.
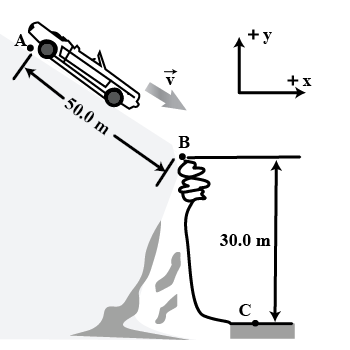
A car travelling at $$72\ km/h$$ decelerates uniformly at $$2m/s^{2}$$. Calculate (a) the distance it goes before it stops, (b) the time it takes to stop, and (c) the distance it travels during the first and third seconds.
Which of the following are not correct?
(i) The basic unit of time is second.
(ii) Every object moves with a constant speed.
(iii) Distances between two cities are measured in kilometers.
(iv) The time period of a given pendulum is not constant.
(v) The speed of a train is expressed in m$$/$$h.
The relation between $$t$$ and distance $$x$$ is $$t=a{x}^{2}+bx$$ where $$a$$ and $$b$$ are constants. Express the instantaneous acceleration in terms of instantaneous velocity.
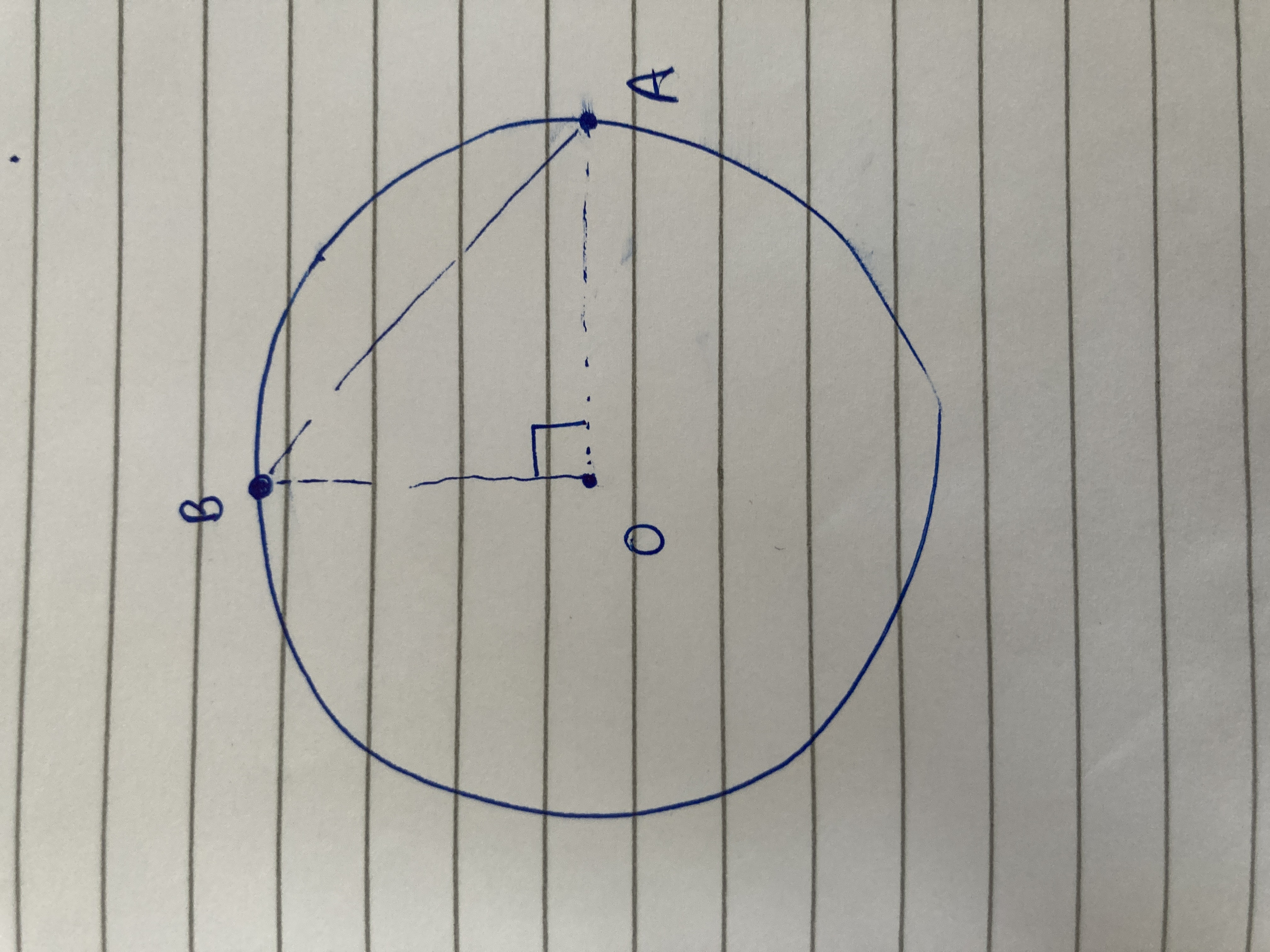
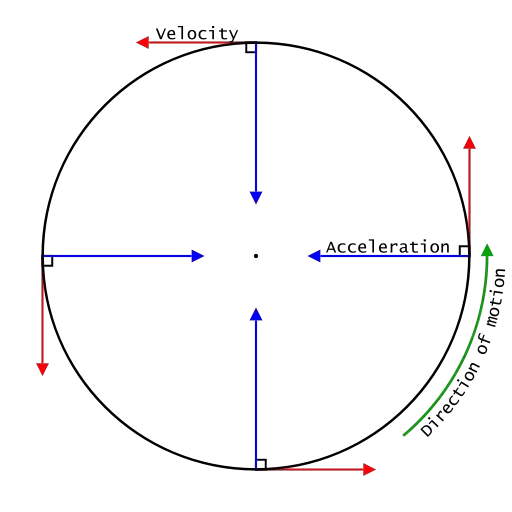
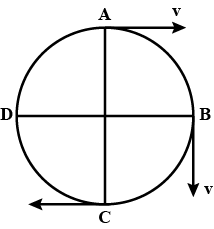
A car is moving round a circular track with a constant speed $$v$$ of $$20 m s^{-1}$$ (as shown in figure). At different times, the car is at $$A,B,C$$ and $$D$$, respectively. Find the velocity change(a) from $$A$$ to $$C$$, and(b) from $$A$$ to $$B$$
(a). Change in velocity, as the particle moves from $$A$$ to $$C$$, is the difference of final velocity vector and initial velocity vector.
$$\Delta\overrightarrow{v}_{AC}= \overrightarrow{v}_{C}$$ - $$\overrightarrow{v}_{A}$$ = $$\overrightarrow{v}_{C} +(- \overrightarrow{v}_{A})$$
(If we take left direction as positive, the right direction will be negative.)
$$\Delta\overrightarrow{v}_{AC} = 20 +20 =40\,ms^{-1}$$
As $$\Delta\overrightarrow{v}_{AC}$$ is positive, hence, change in the velocity should be in the direction of left, i.e., in the direction of $$\overrightarrow{v}_{C}$$
$$\Delta\overrightarrow{v}_{AC} = 40 \,ms^{-1}$$ in the direction of $$\overrightarrow{v}_{C}$$
(b). Change in velocity, as the particle moves from $$A$$ to $$B$$,
$$\Delta \overrightarrow{v}_{AB} = \overline{v}_B-\overrightarrow{v}_A = \overrightarrow{v}_B + (-\overrightarrow{v}_A)$$
Since velocities at A and B are perpendicular to each other so
$$\Delta{v}_{AB}= \sqrt{20^{2} + 20^{2}} = \sqrt{800}ms^{-1}$$
$$\tan \theta = \dfrac{20}{20}= 1$$; $$\theta = 45^{\circ}$$
So this change in velocity will be parallel to line joining BC
The SI unit of displacement is _______.
Can force determine the direction of motion? Direction of acceleration?
When brakes are applied to a bus, the retardation produced is $$25\ cm\ {s^{ - 2}}$$ and the bus takes 20 sec to stop. Calculate the initial velocity of the bus.
An object undergoes an acceleration of $$10m/{\sec ^2}$$ starting from rest. Find the distance traveled in 5 sec?
A body starts with an initial velocity of 10 $$m{s^{ - 1}}$$ and accelerates with 5 $$m{s^{ - 2}}$$. Find the distance covered by it in 5 sec.
Two paper screens $$A$$ and $$B$$ are separated by a distance of $$100$$ m. $$A$$ bullet pierces $$A$$ and then $$B$$. The hole in $$B$$ is $$10$$ cm below the hole in $$A$$. If the bullet is travelling horizontally at the time of hitting the screen $$A$$, calculate the velocity of the bullet when it hits the screen $$A$$. Neglect the resistance of paper and air.
An object moves along a straight line with an acceleration of $$2\ m/s^2$$. If its initial speed is $$10\ m/s$$ what will be its speed $$5\ s$$ later?
The position-time graph of an object is given below. What is the velocity of the object?
at $$t=0$$,
Initial position $$x_1=20$$
at $$t=4$$
Final position $$x_2=50$$
velocity $$ = \dfrac{ displacement }{ time }$$
$$v=\dfrac{dx}{dt}=\dfrac{x_2-x_1}{t_2-t_1}=\dfrac{50-20}{4-0}=\dfrac{30}{4}=7.5\ ms^{-1}$$
$$\boxed{v=7.5ms^{-1}}$$
An elevator is accelerating upward at a rate of $$6\ ft/{sec}^{2}$$ when a bolt from its ceiling falls to the floor of the lift (Distance=$$9.5$$ feet). The time (in seconds) taken by the falling bolt to hit the floor is (take $$g=32\ ft/{sec}^{2}$$)
A mass of $$5$$ kg is acted upon by a force of $$1 N$$ Starting from rest , how much distance covered by the mass in $$10s$$?
On an object of mass $$1 kg$$ moving along the x-axis with a constant speed of $$ 8\ m/s$$, a constant force of $$2\ N$$ is applied in positive y-direction. Find it's speed after $$4$$ seconds.
A particle is moving with uniform acceleration. Its displacement at any instant t is given as $$s=10t+49{ t }^{ 2 }$$. What is the initial velocity, velocity at $$t= 3 \ sec$$ and uniform acceleration?
A body is projected downwards at an angle of $${30}^{o}$$ to the horizontal with a velocity of $$9.8m/s$$ from the top of a tower $$29.4m$$ high. How long will it take before striking the ground?
$$\textbf{Step 1: Resolving velocity in x and y direction [Refer Fig.]}$$
$$s_{y} = h;$$ $$a_{y} = g$$
$$\textbf{Step 2: Solving equation}$$
Since acceleration is constant, therefore applying equation of motion in $$y$$ direction (Taking downward as positive)
$$s_{y} = u_{y}t + \dfrac {1}{2} a_{y}t^{2}$$
$$\Rightarrow$$ $$29.4 (m) = 9.8\sin 30^o (m/s) \times t (s) + \dfrac {1}{2} 9.80 (m/s^2) \times t^{2} (s^2)$$
Solving quadratic equation
$$t = 2, -3$$
$$t = -3$$ (Not possible)
$$\therefore t = 2s$$
Hence time taken to strike the ground is $$2\ seconds$$.
What is the magnitude of the total force on a driver by the racing car he operates, as it accelerates horizontally along a straight line from rest to $$60m/s$$ in $$8.0s$$ (mass of the driver $$=80kg$$)
An object of mass $$1\ kg$$ moving on a horizontal surface with initial velocity $$8\ m/s$$ comes to rest after $$10\ s$$. If one wants to keep the object moving on the same surface with velocity $$8\ m/s$$ the force required is
A body starts slipping down an incline and moves half meter in half second. How long will it take to move the next half meter?
What force will change the velocity of a body of mass $$1kg$$ from $$20{ms}^{-1}$$ to $$30{ms}^{-1}$$ in two seconds.
An automobile travelling with speed of $$60\ {kmh}^{-1}$$ can brake to stop within a distance of $$20\ m$$. If the car is going twice, i.e., $$120\ {kmh}^{-1}$$, the stopping distance will be
A particle starts from rest, moves with constant acceleration for $$15s$$. If it covers $${s}_{1}$$ distance in first $$5s$$ their distance $${s}_{2}$$ in next $$10s$$, then find the relation between $${s}_{1}$$ and $${s}_{2}$$.
How can you say circular motion of an object is said to be an accelerated motion.
A force of $$1000N$$ on a particle parallel to its direction of motion which is horizontal.Its velocity increase from $$1ms^{-1}$$ to $$10ms^{-1}$$,when the force acts through a distance of $$4 m $$.calculate the mass of the particle, given a force of $$10$$ newton is necessary for overcoming friction.
A bus decreases its speed from $$80 \ km \ h^{-1}$$ to $$60 \ km \ h^{-1}$$ in 5 s. Find the acceleration of the bus.
A submersible is lowered into the sea at a speed of $$4m/s$$ and comes to rest with uniform retardation at a distance of $$10 m$$ below the surface, calculate (a) Its retardation and (b) the time it takes to come to rest.
R.E.F image
(I) using $$ v^{2}-u^{2} = 2as $$
$$ 0^{2}-4^{2} = 2\times a\times 10 $$
$$ -16 = 20\times a $$
$$ a = -0.8\,m/s^{2} $$
retardation $$ 0.8m/s^{2} $$
(II) using $$ v = u+at $$
$$ 0 = 4+0.8\times t $$
$$ t = \dfrac{40}{8} = 5 $$
time taken $$ = 5\,sec $$
A ball thrown vertically upwards with a speed of 19.6 m/s from the top of a tower return to the earth in 6 s. What is the height of the tower?
state and prove work-Energy Theorem
A car moving along straight road with a speed of 126 $$kmh^{-1}$$ ( kmph) is brought to rest within a distance of 200 m. What is its retardation ? (assumed to be uniform) and also calculate the time taken for the car to stop.
A shot travelling at the rate of $$100ms^{-1}$$ is just able to piece a plank $$4cm$$ thick.What velocity is required to just pierce a planks $$9cm$$ thick?
Write two differences between speed and velocity.
A car of mass $$2000\ Kg$$ moving with a velocity of $$72\ km/h$$ is brought to rest by the application of brakes within a distance of $$20\ m$$. Find the average braking force and the time taken for the car to come to rest.
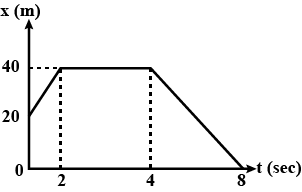
A particle is moving along x-axis. It $$x - t$$ graph is given below-
Find:
(i) Displacement in $$8\ sec $$
(ii) Distance in $$8\ sec$$
(iii) Average velocity in $$8\ sec$$
(iv) Velocity at $$t=1\ sec$$
Georgia is jogging with a velocity of $$4\ m/s$$ when she accelerate at $$2\ m/s^{2}$$ for $$3$$ seconds. How fast is Georgia running now?
A bullet traveling with a velocity of $$16\ m/s$$ penetrates a tree trunk and comes to rest in $$0.4\ m$$. Find the time taken during the retardation.
An object is moving with constant acceleration. Its velocity is $$48m\ s^{-1}$$ at the end of $$10$$ second and becomes $$68m\ s^{-1}$$ at the end of the $$15$$ second. What would be the distance travelled by the object in $$15$$ second?
A block is kept on the floor of an elevator at rest. The elevator starts descending with an acceleration of $$12m/s^2$$ Find the displacement of the block during the first $$0.2sec$$ after the starts.
A motor vehicle left point $$A$$ and reached the point $$B$$ by travelling in a straight line for $$2$$ hours. The vehicle travelled half of the distance at a speed of $$v$$. The distance between A and B is:
An object takes $$5\ sec$$ to reach the ground from a height of $$5\ m$$ on a planet. What is the value of $$g$$ on the planet?
A scooter acquires a velocity of 36 km per hour in 10 seconds just after the start. Calculate the acceleration of the scooter.
A bus accelerates uniformly from 54 km/h to 72 km/h in 10 seconds. Calculate the acceleration in $$m/s^2$$.
Following is the distance time table of a body of mass 100g in motion starting from rest.
$$ \dfrac { time \ (sec) }{ \dfrac { 1 }{ 2 } } \quad \dfrac { distance(m) }{ \dfrac { 1 }{ 8 } } $$
Calculate the force acting it?
$$ \dfrac { time \ (sec) }{ \dfrac { 1 }{ 2 } } \quad \dfrac { distance(m) }{ \dfrac { 1 }{ 8 } } $$
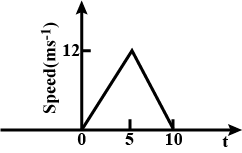
The speed-time graph of a particle moving along a fixed direction is shown in Fig. Obtain the distance traversed by the particle between (a) $$t = 0\ s$$ to $$10\ s$$, (b) $$t = 2\ s$$ to $$6\ s$$.
A block is kept on the floor of an elevator at rest. The elevator starts descending with an acceleration of $$12 \, m/{s^2}$$. Find the displacement of the block during the first $$0.2\, s$$ after the start. Take $$g = 10 \,m/{s^2}$$
Since the elevator is moving downward with an acceleration $$12\ m/s^{2}(>g)$$,
the body gets separated
So, body moves with acceleration $$g=10\ m/s^{2}$$[freely falling body]
and the elevator move with acceleration $$12\ m/s^{2}$$
Ths displacement of the body can be obtained as:
$$s=ut+\dfrac { 1 }{ 2 } at²$$
$$s=\dfrac { 1 }{ 2 } \times 10\times 0.2\times 0.2(u=0)$$
$$s=0.2m=20cm$$
Why is the work done on an object moving with uniform circular motion zero?
Define average speed?
Velocity and acceleration of a particle at some instant are $$v=(3\hat{i}-4\hat{j}+2\hat{k})m/s$$ and $$a=(2\hat{i}+\hat{j}-2\hat{k})m/s^2$$. What is the angle between $$v$$ and $$a$$ - acute, obtuse or $$90^o$$?
Why do the passengers fall forward when a fast moving bus stops suddenly?
Derive the equation of uniformly acceleration motion by graphical.
Let on object on moving in uniform acceleration
$$u=$$ initial velocity of object
$$v=$$ final velocity of object
$$a=$$ uniform velocity of object
Let object reach point $$B$$ other time $$(t)$$
Slope =Acceleration (a) $$=\dfrac {change\ in\ velocity}{time}$$
Change in velocity $$AB=\bar {v}-\bar {u}$$
time $$AD=t$$
$$\therefore \ a=\dfrac {v-u}{t},$$ or $$v=u+at$$
On the earth, a stone is thrown from a height in a direction parallel to the earth's surface while another stone is simultaneously dropped from the same height. which stone would reach the ground first and why?
A bus starts from rest with a constant acceleration of $$5\ m/s^{2}$$. At the same time a car travelling with a constant velocity $$50\ m/s$$ over takes and passes the bus. How fast is the bus travelling when they side by side?
An object is thrown vertically upwards to a height of $$10$$ m. Calculate its
(a) velocity with which it was thrown upward.
(b) time taken by the object to reach the highest point.
A racing car has a uniform acceleration of $$4\ m\ s^{-2}.$$ How much distance will it cover in $$10\ s$$ after start?
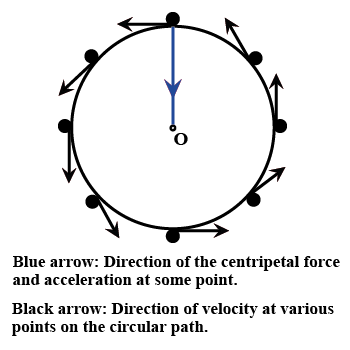
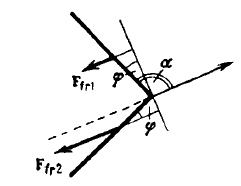
What is uniform circular motion?
A stone is dropped from a cliff. Its speed after it has fallen $$100\mathrm { m } .$$ is:
Define uniform circular motion.
What name is given to the speed in a specified direction ?
Find the initial velocity of a car which is stopped in $$10$$ seconds by applying brakes. The retardation due to brakes is $$2.5 m/s^2$$.
Explain why, the motion of a body which is moving with constant speed in a circular path is said to be accelerated.
The motion of a body which is moving with constant speed in a circular path is said to be accelerated because its velocity changes continuously due to the continuous change in the direction of motion.
State an important characteristic of uniform circular motion. Name the force which brings about uniform circular motion.
A bus running at a speed of $$18 km/h$$ is stopped in $$2.5$$ seconds by applying brakes. Calculate the retardation produced.
Is the uniform circular motion accelerated ? Give reasons for your answer
Give one example of a motion where an object does not change its speed but its direction of motion changes continuously.
What is the difference between uniform linear motion and uniform circular motion? Explain with examples.
Fill in the following blanks with suitable words :
The slope of a distance-time graph indicates _______ of a moving body.
On a dry road, a car with good tires may be able to apply brakes with a constant deceleration of $$4.92\,m/s^{2}$$. How long does such a car, initially travelling at $$24.6\,m/s$$, take to stop?
A certain elevator cab has a total run of $$190\,m$$ and a maximum speed of $$305\,m/min$$, and it accelerates from rest and then back to rest at $$1.22\,m/s^{2}$$. What is the total time duration of this run?
(a) What is meant by uniform circular motion? Give two examples of uniform circular motion.
(b) The tip of seconds' hand of a dock takes $$60$$ seconds to move once on the circular dial of the clock If the radius of the dial of the clock be $$10.5 cm$$, calculate the speed of the tip of the seconds' hand of the clock. $$\left(\text{Given} \, \pi = \dfrac{22}{7}\right).$$
A car is travelling at $$20 m/s$$ along a road. A child runs out into the road $$50 m$$ ahead and the car driver steps on the brake pedal. What must the car's deceleration be if the car is to stop just before it reaches the child?
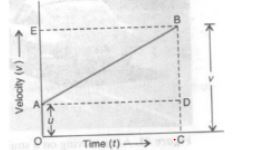
Show by means of graphical method that: $$v = u + at$$, where the symbols have their usual meanings.
The body has an initial velocity $$u$$ at a point $$A$$ and then its velocity changes at a uniform rate from $$A$$ to $$B$$ in time $$t$$. In other words, there is a uniform acceleration a from $$A$$ to $$B$$, and after time $$t$$ its final velocity becomes $$v$$ which is equal to $$BC$$ in the graph. The time $$t$$ is represented by $$OC$$.
To complete the figure, we draw the perpendicular $$CB$$ from point $$C$$, and draw $$AD$$ parallel to $$OC$$. $$BE$$ is the perpendicular from point $$B$$ to $$OE$$.
Now, Initial velocity of the body, $$u= OA$$ ...(1)
And, Final velocity of the body, $$v=BC$$ ...(2)
But from the graph $$BC =BD + DC$$
Therefore, $$v=BD + DC$$ ...(3)
Again $$DC = OA$$
So, $$v =BD + OA$$
Now, from equation (1), $$OA =u$$
So, $$v=BD + u$$ ...(4)
So, $$v=BD + u$$ ...(4)
We should find out the value of $$BD$$ now. We know the slope of a velocity-time graph is equal to the acceleration, $$a$$.
Thus, Acceleration, $$a=$$ slope of line $$AB$$
or $$a = \dfrac{BD}{AD}$$
But $$AD =OC= t$$, so putting $$t$$ in place of $$AD$$ in the above relation, we get:
$$a = \dfrac{BD}{t}$$
or $$BD=at$$
Now, putting this value of $$BD$$ in equation(4), we get:
$$v= u+ at$$
$$a = \dfrac{BD}{t}$$
or $$BD=at$$
Now, putting this value of $$BD$$ in equation(4), we get:
$$v= u+ at$$
An electric vehicle starts from rest and accelerates at a rate of $$2.0\,m/s^{2}$$ in a straight line until it reaches a speed of $$20\,m/s$$. The vehicle then slows at a constant rate of $$1.0\,m/s^{2}$$ until it stops. How much time elapses from start to stop?
The brakes on your car can slow you at a rate of $$ 5.2\,m/s^{2}$$. If you are going $$137\,km/h$$ and suddenly see a state trooper, what is the minimum time in which you can get your car under the $$90\,km/h$$ speed limit? (The answer reveals the futility of braking to keep the high speed from being detected with a radar or laser gun.)
A stone thrown vertically upwards takes $$3$$ seconds to attain maximum height , calculate
(i) initial velocity of stone
(ii) maximum height attained by the stone
When a force of $$40 \,N$$ is applied on a body it moves with an acceleration of $$5 \,m \,s^{-2}.$$ Calculate the mass of the body.
If the maximum acceleration that is tolerable for passengers in a subway train is $$1.34\,m/s^{2}$$ and subway stations are located $$806\,m$$ apart, what is the maximum average speed of the train, from one start-up to the next? Given the "dead time" at a station is $$20\,s$$.
What is meant by uniform circular motion ? Why do we need a force to keep a body moving uniformly along a circular path ? Name this force.
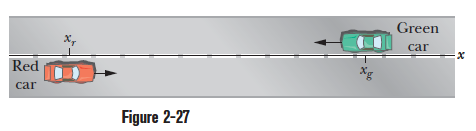
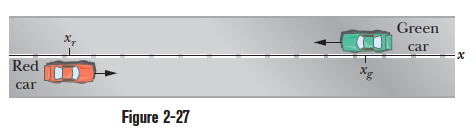
In the figure, a red car and a green car, identical except for the colour, move toward each other in adjacent lanes and parallel to the $$x-$$axis. At time $$ t = 0$$, the red car is at $$x_{r}=0$$, and the green car is at $$x_{g} =220\,m$$. If the red car has a constant velocity of $$20\,km/h$$, the cars pass each other at $$x = 44.5\,m$$, and if it has a constant velocity of $$40\, km/h$$, they pass each other at $$x = 76.6\, m$$. What is the constant acceleration of the green car?
Suppose a rocket ship in deep space moves with a constant acceleration equal to $$9.8\,m/s^{2}$$, which gives the illusion of normal gravity during the flight. If it starts from rest, how long will it take to acquire a speed one-tenth that of light, which travels at $$3.0 \times 10^{8} m/s$$? How far will it travel in doing so?
If the maximum acceleration that is tolerable for passengers in a subway train is $$1.34\,m/s^{2}$$ and subway stations are located $$806\,m$$ apart, what is the maximum speed a subway train can attain between stations?
Prove that is a body is thrown vertically upwards , then the time of ascent is equal to the time of descent .
An object undergoes an acceleration of $$8 \,m \,s^{-2}$$ starting from rest. Find the distance travelled in 1 second.
A stone is dropped into a river from a bridge $$43.9\, m$$ above the water. Another stone is thrown vertically down $$1.00\, s$$ after the first is dropped. The stones strike the water at the same time. What is the initial speed of the second stone?
In the figure, a red car and a green car, identical except for the colour, move toward each other in adjacent lanes and parallel to the $$x-$$axis. At time $$ t = 0$$, the red car is at $$x_{r}=0$$, and the green car is at $$x_{g} =220\,m$$. If the red car has a constant velocity of $$20\,km/h$$, the cars pass each other at $$x = 44.5\,m$$, and if it has a constant velocity of $$40\, km/h$$, they pass each other at $$x = 76.6\, m$$. What is the green car's initial velocity?
Give an example of negative acceleration from daily life situations.
Two trains $$A$$ and $$B$$ of length $$400m$$ each are moving on two parallel tracks with uniform speed of $$72km$$ $${h}^{-1}$$ in the same direction with $$A$$ ahead of $$B$$. The driver of $$B$$ decides to overtake $$A$$ and accelerated by $$1m{s}^{-2}$$. If after $$50s$$, the guard of $$B$$ just passes the driver of $$A$$, what was the original distance between them?
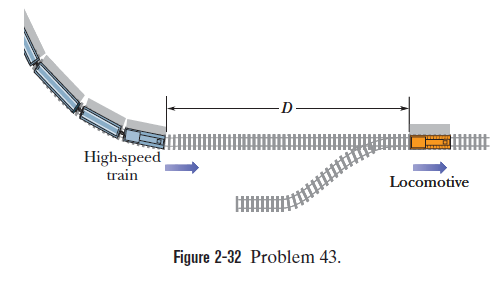
When a high-speed passenger train travelling at $$161\, km/h$$ rounds a bend, the engineer is shocked to see that a locomotive has improperly entered onto the track from a siding and is a distance $$D = 676\, m$$ ahead. The locomotive is moving at $$29.0\, km/h$$. The engineer of the high-speed train immediately applies the brakes. What must be the magnitude of the resulting constant deceleration if a collision is to be just avoided?
A girl running a race accelerates at $$2.5m{s}^{-2}$$ for the first $$4s$$ of the race. How far does she travel in this time?
When you apply brakes to a car, in which direction is its acceleration?
A ball is thrown vertically upwards with a velocity u. Calculate the velocity with which it falls to the earth again.
$$ u$$ = Initial velocity
Ball is thrown up
Ball goes up and attains a maximum height H and then again comes down.
Let
$$u$$ = Initial Speed
$$v$$ = Final Speed
$$t$$ = time
$$a$$ = acceleration
s = distance
Case – I
Ball is going upward
$$ a = -g $$
$$ u = u $$
$$ v = 0 $$
$$ s = H $$
Since , $$ v^2 = u^2 + 2as $$
$$ 0 = u^2 - 2gH $$
$$ H = \dfrac{u^2}{2g} $$ ...... 1
Case II
Ball comes downward
So , $$ u = 0 $$
$$ v $$ = Final speed
$$ a = g $$
Since , $$ v^2 = u^2 + 2as $$
$$ v^2 = 0 + 2gH $$
$$ H = \dfrac{u^2}{2g} $$ ........2
From equation $$1$$ and $$2$$ , we see that ,
$$ v = u $$
An automobile driver increases the speed at a constant rate from $$25 \ km/h$$ to $$55 \ km/h$$ in $$0.50 \ min$$. A bicycle rider speeds up at a constant rate from rest to $$30 \ km/h$$ in $$0.50 \ min$$. What are the magnitudes of (a) the driver’s acceleration and (b) the rider’s acceleration?
A car can accelerate from 0 to 60 m/s in 5.4 s. From rest, how much time would it require to go a distance of 0.25 m if its acceleration could be maintained at the value?
On average, an eye blink lasts about $$100 \ ms$$. How far does aMiG-$$25$$ “Foxbat” fighter travel during a pilot’s blink if the plane’s average velocity is $$3400 \ km/h$$?
A train started from rest and moved with constant acceleration. At one time it was traveling $$30 \ m/s$$, and $$160 \ m$$ farther on, it was traveling $$50 \ m/s.$$ Calculate the time required to travel the $$160 \ m$$ mentioned. Given the acceleration of the train is $$5 \ m/s^2$$.
A car can accelerate from 0 to 60 m/s in 5.4 s. How far will it travel during the 5.4 s,
assuming its acceleration is constant?
Raindrops fall $$1700\, m$$ from a cloud to the ground. If they were not slowed by air resistance, how fast would the drops be moving when they hit the ground?
The head of a rattlesnake can accelerate at 50 m/s$$^{2}$$ in striking a victim. If a car could do as well, how long would it take to reach a speed of 100 km/h from rest?
A car travels with a uniform velocity of $$25\ m/s$$ for $$5\ s$$. The brakes are then applied and the car is uniformly retarded and comes to rest in further $$10\ s$$. Find the retardation
An object is dropped from rest at a height of $$150\ m$$ and simultaneously another object is dropped from rest at a height $$100\ m$$. What is the difference in their heights after $$2\ s$$ if both the object drop with same acceleration? How does the difference in heights vary with time?
An electron moving with a velocity of $$5\times 10^{4}\ ms^{-1}$$ enters into a uniform electric field and acquires a uniform acceleration of $$10^{4}\ ms^{-2}$$ in the direction of its initial motion.
Calculate the time in which the electron would acquire a velocity double of its initial velocity.
Obtain a relation for the distance travelled by an object moving with a uniform acceleration in the interval between $$4^{th}$$ and $$5^{th}$$ seconds.
Two stones are thrown vertically upwards simultaneously with their initial velocities $$u_{1}$$ and $$u_{2}$$ respectively. Prove that the heights reached by them would be in the ratio of $$u_{1}^{2}.u_{1}^{2}$$ (Assume upward acceleration is $$-g$$ and downward acceleration to be $$+g$$.
A lead bullet of mass $$20g$$. travelling with a velocity of $$350$$ ms. comes to rest after penetrating $$40$$ cm in a still target. Find the retardation caused by it.
A uniform car of mass $$500g$$ travels with a uniform velocity of $$25 m\ s^{-1}$$ for $$5$$ s. The brakes are then applied and the car is uniformly retarded and comes to rest in further $$10$$ s calculate the retardation.
A motor car moving at a speed of $$ 72 \mathrm{km} / \mathrm{h} $$ cannot come to stop in less than 3.0second while for a truck this time interval is 5.0 second. On a highway, the car is behind the truck both moving $$ 72 \mathrm{km} / \mathrm{h} $$. The truck gives a signal that it is going to stop at an emergency. At what distance the car should be from the truck so that it does not bump onto (collide with) the truck? Human response time is 0.5 s. (Comment: This is to illustrate why vehicles carry the message on the rear side. "Keep safe distance").
What is meant by the term retardation? Name its S.I. unit.
Explain the meaning of uniform circular motion. Give one example of such a motion.
Uniform circular motion is an accelerated motion explain it.
What does the slope of a displacement-time graph represent?
Define velocity. State its unit.
The velocity-times graph for a uniformly retarded body is a straight line inclined to the time axis with an obtuse angle. How is retardation calculated from the velocity-time graph?
The retardation is nothing but the negative acceleration. For acceleration, we find the slope of the velocity-time graph. Similarly, in order to calculate the retardation from the velocity-time graph, a negative slope should be obtained. The graph makes an obtuse angle $$\theta$$ with the time axis.
The slope can be obtained by marking two points on the graph and finding the corresponding values of velocity $$v_1, v_2$$ and time $$t_1, t_2$$.
Then the retardation can be found by the relation:
$$a=\dfrac{\Delta v}{\Delta t}=\dfrac{v_2-v_1}{t_2-t_1}$$
This quantity $$a$$ will be negative because $$v_1>v_2.$$
Alternatively, the retardation $$a=tan \ \theta=negative$$ because $$\theta>90^o.$$
A body initially moving with a velocity $$20\ ms^{-1}$$ strikes a target and comes to rest after penetrating a distance $$10\ cm$$ in the target. Calculate the retardation caused by the target.
A toy car initially moving with a uniform velocity of $$18\ km\ h^{-1}$$ comes to stops in $$2 \ s$$. Find the retardation of the car in S.I. units.
The figure show displacement-times graph of two vehicles $$A$$ and $$B$$ along a straight road. Which vehicle is moving faster? Give reason.
Complete the sentence and explain them .
Deceleration is .......... acceleration .
A pebble is thrown vertically upwards with a speed of $$20\ ms^{-1}$$. How high will it be after $$2\ s$$? (Take $$g = 10\ m s^{-2}$$)
A train starts from rest and accelerates uniformly at a rate of $$2\ m/s^{2}$$ for $$10\ s$$. It then maintains a constant speed for $$200\ s$$. The brakes are then applied and the train is uniformly retarded and comes to rest in $$50s$$. Find: the retardation in the last $$50s$$
Answer the following question:What is centripetal force?
The force required to keep an object under circular motion is known as the centripetal force. This force always acts towards the centre of the circular path.
Give S.I. unit of retardation.
What is negative acceleration called ?
Give S.I. unit of velocity
Define velocity.
State differences: Acceleration and Retardation.
What will be the rate of decrease in the velocity of an object thrown upwards?
Derive an expression for the velocity of the particle after covering distance s OR Derive the equation $$v^2 = u^2 + 2as$$ using the velocity-time graph.
particle moving along a straight line with a constant acceleration ‘a’. Let u be its velocity at time t = 0 and ‘v’ be the velocity after ‘t’ seconds. The velocity-time graph AC of this particle is shown in the figure.
Distance travelled by the particle is given by,
s = area under v-t graph
= area of the trapezium OACD
$$= 1/2 (OA+CD) \times OD$$
But OA = u, CD = v and OD = t
∴ $$s = 1/2 (u + v) t$$ or
$$2s = (u+v) t$$ ………(1)
But, a = slope of the graph = v−ut
∴ t = v−ua
On substituting in (1),
$$2s = (u+v)(v−ua)$$
i.e., $$v^2 – u^2 = 2as$$
or $$v^2 = u^2 + 2as.$$
Distance travelled by the particle is given by,
s = area under v-t graph
= area of the trapezium OACD
$$= 1/2 (OA+CD) \times OD$$
But OA = u, CD = v and OD = t
∴ $$s = 1/2 (u + v) t$$ or
$$2s = (u+v) t$$ ………(1)
But, a = slope of the graph = v−ut
∴ t = v−ua
On substituting in (1),
$$2s = (u+v)(v−ua)$$
i.e., $$v^2 – u^2 = 2as$$
or $$v^2 = u^2 + 2as.$$
Can the displacement of a moving body be zero?
The displacement of a moving object in a given time interval can be $$0$$ if the object comes back to its initial position in the given time.
Derive the equation of motion $$v^2=u^2+2as$$.
If a body undergoes equal displacements in equal intervals of time, however small intervals of time may be then velocity is said to be uniform velocity.
Particle moving along a straight line with a constant acceleration ‘a’. Let u be its velocity at time t= 0 and ‘v’ be the velocity after ‘t’ seconds. The velocity-time graph AC of this particle is shown in the figure.
Distance travelles by the particle is given by,
s = area under v-t graph
= area of the trapezium OACD
$$= 1/2 (OA+CD) \times OD$$
But OA = u, CD = v and OD = t
∴ $$s = 1/2 (u + v) t$$ or $$2s = (u+v) t$$ ………(1)
But, a = slope of the graph $$=\dfrac{v−u}{t}$$
∴ t = v−ua
On substituting in (1), $$2s = (u+v)\dfrac{v−u}{a}$$
i.e., $$v^2 – u^2 = 2as$$
or $$v^2 = u^2 + 2as$$.
Particle moving along a straight line with a constant acceleration ‘a’. Let u be its velocity at time t= 0 and ‘v’ be the velocity after ‘t’ seconds. The velocity-time graph AC of this particle is shown in the figure.
Distance travelles by the particle is given by,
s = area under v-t graph
= area of the trapezium OACD
$$= 1/2 (OA+CD) \times OD$$
But OA = u, CD = v and OD = t
∴ $$s = 1/2 (u + v) t$$ or $$2s = (u+v) t$$ ………(1)
But, a = slope of the graph $$=\dfrac{v−u}{t}$$
∴ t = v−ua
On substituting in (1), $$2s = (u+v)\dfrac{v−u}{a}$$
i.e., $$v^2 – u^2 = 2as$$
or $$v^2 = u^2 + 2as$$.
Define negative acceleration ?
An object of mass $$20\,kg$$ is moving with an initial velocity of $$2\,ms^{-1} $$. If its velocity changes to $$4\,ms^{-1} $$ in one second. What should be the force acting on it? What will be the direction of the motion?
If the velocity of a car moving with uniform velocity changes from $$ 20 m/s $$ to $$ 40 m/s $$ in $$ 5 s $$
a) What is the acceleration of the car?
b) What is the displacement by the car during this interval?
An automobile vehicle has a mass of $$1500 Kg$$. what must be the force between the vehicle and road if the vehicle is to be stopped with a negative acceleration of $$1.7 ms^{-2}$$.
Define circular motion and uniform circular motion.
How does velocity change?
When an object moves in a circular path with uniform speed, its motion is called ________.
A car came to rest when brake was applied for $$ 4s $$ to get a retardation of $$ 3 m/s^2$$. Calculate how far the car would have traveled after applying the brake.
What are the SI units of mass and acceleration.
If the velocity of a training string from rest becomes $$ 72 km/h $$ in $$10 $$ minutes.
a) What is the acceleration?
b) Calculate the distance traveled by train within this time interval
A car attains a velocity of $$ 54 km/h (15m/s) $$ within $$ 5 $$ second from an initial velocity of $$ 18km/h(5m/s).$$ Calculate its acceleration and displacement
Write the equations of motion. What does each letter indicate?
A truck covers $$40.0 m$$ in $$8\ s$$ while smoothly slowing down to a final speed of $$2 m/s$$. Find its acceleration if it starts with a speed $$10\ m/s$$.
Brakes are applied suddenly to a racing car travelling at $$50\ m/s$$. If the car stops after $$20$$ seconds, calculate the retardation of the car.
An object starting from rest travels with an acceleration of $$ 5\ m/s^2 $$. What will be its velocity after $$ 3\ s$$?
The driver of a car slams on the brakes when he sees a tree blocking the road. The car slows uniformly with an acceleration of $$-5.60 m/s^{2}$$ for $$4.20 s$$, making straight skid marks $$62.4 m$$ long, all the way to the tree. With what speed does the car then strike the tree?
The gravitational force exerted on a baseball is $$2.21 N$$ down. A pitcher throws the ball horizontally with velocity $$18.0 m/s$$ by uniformly accelerating it along a straight horizontal line for a time interval of $$170 m/s$$. The ball starts from rest. (a) Through what distance does it move before its release? (b) What are the magnitude and direction of the force the pitcher exerts on the ball?
A car acquires a velocity of 72 km/h in 10 sec starting from rest. Calculate.
The acceleration
A proton is projected in the positive $$x$$ direction into a region of a uniform electric field $$\overrightarrow{E}=(-6.00\times 10^5)\hat{i} N/C$$ at $$t=0$$. The proton travels $$7.00 cm$$ as it comes to rest. Determine (a) the acceleration of the proton, (b) its initial speed, and (c) the time interval over which the proton comes to rest.
A helicopter takes off along the vertical with an acceleration $$a=3m /s^2$$ and zero initial velocity. In a certain time $$t_1$$ the pilot switches off the engine. At the point of take-off the sound dies away in a time $$t_s=30\ s$$
Determine the velocity $$\nu$$ of the helicopter at the moment when its engine is switched off assuming that the velocity $$c$$ of sound is $$320\ m/s$$
An object moving with uniform acceleration has a velocity of $$12.0 cm/s$$ in the positive $$x$$ direction when its $$x$$ coordinate is $$3.00 cm$$. If its $$x$$ coordinate $$2.00 s$$ later is $$25.00 cm$$, what is its acceleration?
$$t = 0$$ to $$t = 2\ s$$.
Fig. shows the displacement-time graph for the motion of a body. Use it to calculate the velocity of body at $$t = 1 s, 2 s$$ and $$3 s$$, then draw the velocity-time graph for the body.
Slope of displacement-time graph represents the velocity. Since slope of displacement-time graph has a uniform value of $$2 m/s$$, velocity at $$t=1 s, 2 s$$ and $$3 s$$ will be $$2 m/s$$.
Show that the rate of change of the speed is $$\displaystyle \frac{dv}{dt}=\frac{\left ( v_{x}a_{x}+v_{y}a_{y} \right )}{\sqrt{v_{x}^{2}+v_{y}^{2}}}.$$
its y-coordinate.
t= 2 s to t = 4s.
A particle starts with an initial velocity and passes successively over the two halves of a given distance with accelerations $$\displaystyle a_{1}$$ and $$\displaystyle a_{2}$$ respectively. Show that the final velocity is the same as if the whole distance is covered with a uniform acceleration $$\displaystyle \frac{\left ( a_{1}+a_{2} \right )}{2}.$$
Let the initial velocity in both cases be $$u$$
First case :
For first half,
Apply 3rd equation of motion-
$$v^2 = u^2 + 2aS$$
$$v$$ : Final velocity of the particle
$$u$$ : Initial velocity of the particle
$$a$$ : Acceleration of the particle
$$S$$ : Displacement of the oarticle
$$v_1^2 - u^2 = 2a_1 x$$ ..........(1)
For another half,
$$v^2_2 - v^2_1 = 2a_2 x$$ ...............(2)
Adding (1) and (2) we get
$$v_2^2 - u^2 =2 (a_1 + a_2) x$$
$$\implies v_2 = \sqrt{u^2 + 2 (a_1 + a_2)x}$$ ............(a)
Second case :
$$a_t = \dfrac{a_1 + a_2}{2}$$
$$S = 2x$$
$$\therefore V^2 - u^2 = 2 \bigg(\dfrac{a_1+ a_2}{2} \bigg) 2x $$
$$\implies$$ $$V = \sqrt{u^2 + 2(a_1 + a_2)x}$$ ..................(b)
Thus from (a) and (b), the final velocity is same in both cases.
A train accelerates from rest for time $$t_{1}$$ at a constant rate $$a$$ and then it retards at the constant rate $$b$$ for time $$t_{2}$$ and comes to rest. Find the ratio $$\dfrac{t_1}{t_2}$$.
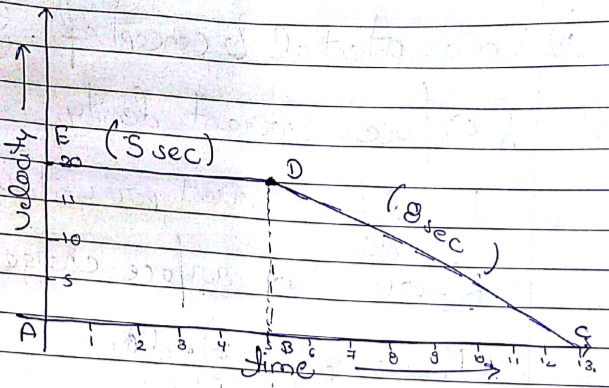
Acar travels with a uniform velocity of $$20m{s^{ - 1}}$$ for 5 sec. The brakes are then applied and the car is uniformly retarded. It comes to rest in further 8 sec. by drawing a graph between velocity and time-find.
- The distance traveled in the first 5 sec.
- The distance traveled after the brakes are applied.
- Total distance traveled.
- Acceleration during the first 5 sec.
- Acceleration during the last 8 sec.
$$t_1= 5s$$
$$t_2= 8s$$
Graph: (Refer to Image)
(1) Distance travelled in first $$5$$ sec= area of ABDE= $$20 \times s= 80m$$
(2) Distance travelled after the brakes are applied (area of BCD)= $$\cfrac {1}{2}\times 8 \times 5= 20m$$
(3) Total distance travelled= $$Area\quad of\quad ABCDE+ Area\quad of\quad BCD=80+20=100m $$
(4) Acceleration during the first $$5$$ sec= $$0$$, because uniform velocity.
(5) Acceleration during the last $$8$$ sec= $$v=0,u=20m/s, t=8sec$$
$$\Rightarrow v= u+at \Rightarrow 0=20+a(8)$$
$$\Rightarrow a= -2.5m/s^2$$ (slope of the line DC)
Define uniform circular motion. A particle is travelling in a circle of diameter $$15 m $$ . Calculate the distance covered and the displacement when it completes two rounds.
When the engine is switched off a vehicle of mass $$'M'$$ is moving in a rough horizontal road with momentum $$P$$. If the coefficient of friction between the road and tires of the vehicle is $${\mu}_{k}$$, the distance traveled by the vehicle before it comes to rest is:
A balloon is rising with constant acceleration $$2m/{\sec ^2}$$.Two stones are released from the balloon at the interval of $$2$$ sec. Find out the distance between the two stones $$1$$ sec after the release of second stone.
A bullet losses $$1/n$$ of its velocity in passing through a plank. What is the least number of planks required to stop the bullet? (Assuming constant retardation)
Can a body have constant speed as well as variable velocity? If yes, give one example.
Define following :
Displacement vector
A body is moving with initial speed of $$5\ m/s$$ by application of uniform retardation, it comes to rest in a distance of $$20\ m$$. If same body is moving with speed $$15\ m/s$$ and retardation is same then after how much distance it will comes to rest.
A ball is dropped from a height of $$5\ m$$ onto a sandy floor and penetrates the sand up to $$10\ cm$$ before coming to rest. Find the retardation of the ball in sand assuming it to be uniform.
A car is moving with speed $$100\ m/s$$ by applying brakes it comes to rest in $$10\ seconds$$, if same car is moving with speed $$400\ m/s$$ then what will stopping time if same brakes are applied.
How will the equation of motion $$ s = ut + \dfrac{1}{2}at^{2} $$, change this equation when the object is moving with a moving constant velocity?
Derive :-
$$S=Ut+\dfrac { 1 }{ 2 } { at }^{ 2 }$$
Derive first equation of motion by graphical method.
Let us consider an object moving in a straight line with a constant acceleration. For such a situation the first equation of motion gives the final velocity (v) after time t given that the object is having an initial velocity of u and constant acceleration of a. Now for deriving it, let us consider the following velocity-time graph:
The initial velocity of the body, $$u = OA.................(1)$$
The final velocity of the body, $$v = BC....................(2)$$
From the graph $$BC = BD + DC$$
Therefore, $$v = BD + DC..............................(3)$$
Again $$DC = OA$$
So, $$v = BD + OA$$
Now from equation (1), $$OA = u$$
So, $$v = BD + u......................................(4)$$
We should find the value of BD now
Now, from the velocity-time graph, if we calculate the change in velocity to change in time, then we can find the acceleration, a. This is nothing but the slope of the graph.
Thus,
Acceleration, a = Slope of line AB
$$a = \dfrac{BD}{AD}$$
But $$AC = OC = t$$
Hence we get
$$ a = \dfrac{BD}{t}$$
$$BD = at$$
Now putting this in equation (4) we get
$$v = u + at$$
The initial velocity of the body, $$u = OA.................(1)$$
The final velocity of the body, $$v = BC....................(2)$$
From the graph $$BC = BD + DC$$
Therefore, $$v = BD + DC..............................(3)$$
Again $$DC = OA$$
So, $$v = BD + OA$$
Now from equation (1), $$OA = u$$
So, $$v = BD + u......................................(4)$$
We should find the value of BD now
Now, from the velocity-time graph, if we calculate the change in velocity to change in time, then we can find the acceleration, a. This is nothing but the slope of the graph.
Thus,
Acceleration, a = Slope of line AB
$$a = \dfrac{BD}{AD}$$
But $$AC = OC = t$$
Hence we get
$$ a = \dfrac{BD}{t}$$
$$BD = at$$
Now putting this in equation (4) we get
$$v = u + at$$
Catapulting mushrooms.Certain mushrooms launch their spores by a catapult mechanism. As water condenses from the air onto a spore that is attached to the mushroom, a drop grows on one side of the spore and a film grows on the other side.The spore is bent over by the drops weight,but when the film reaches the drop, the drops water suddenly spreads into the film and the spore springs upward so rapidly that it is slung off into the air. Typically, the spore reaches a speed of 1.6m/s in a 5.0 $$\mu$$ m launch; its speed is then reduced to zero in 1.0 mm by the air. Using those data and assuming constant accelerations, find the acceleration
in terms of $$g$$ during the speed reduction?
Define motion. What do you understand by the terms 'uniform motion' and 'non-uniform motion' ?Explain with examples. (a) Define speed. What is the SI unit of speed ? (b) What is meant by (i) average speed, and (ii) uniform speed.
A ball moving at a velocity $$v=10\ m/s$$ hits the foot of a football player.
Determine the velocity $$u$$ with which the foot should move for the ball impinging on it to come to a halt, assuming that the mass of the ball is much smaller than the mass of the foot and that the impact is perfectly elastic.
If the foot of the football player moves at a velocity $$u$$ at the moment of kick, the velocity of the ball is $$v+u$$ ( the axis of motion is directed along the motion of the ball) in the reference frame fixed to the foot of the player. After the perfectly elastic impact, the velocity of the ball in the same reference frame will be $$-(v+u)$$, and its velocity relative to the ground will be $$-( v+u)-u$$. If the ball comes to a halt after the impact, $$v+2u=0$$, where $$u=-v/2=-5\ m/s$$. The minus sign indicates that the foot of the sportsman must move in the same direction as that of the ball before the impact.
Two bodies move in a straight line towards each other at initial velocities $$\nu_1$$ and $$\nu_2$$ and with constant accelerations $$a_1$$ and $$a_2$$ directed against the corresponding velocities at the initial instant.
What must be the maximum initial separation $$l_{max}$$ between the bodies for which they meet during the motion?
In an arcade video game, a spot is programmed to move across the screen according to $$x = 9.00t - 0.750t^{3}$$, where $$x$$ is distance in centimeters measured from the left edge of the screen and $$t$$ is time in seconds. When the spot reaches a screen edge, at either $$x$$ = 0 or $$x$$ = 15.0 cm, $$t$$ is reset to 0 and the spot starts moving again according to $$x(t)$$. At what time t> 0 does it first reach an edge of the screen?
All objects having uniform speed need not have uniform velocity. Describe with the help of examples.
Consider a car moving with constant speed on a straight road.Velocity is speed+direction so it is moving with uniform velocity as both speed and direction are constant.But it is not necessary everytime.
For example.
In figure the object in uniform circular motion has uniform speed as speed is constant. But it does not have uniform velocity as velocity is speed + direction and direction in circular motion keeps changing with time. 
An electron in a cathode-ray tube accelerates uniformly from $$2.00 * 10^{4} m/s$$ to $$6.00 * 10^{6} m/s$$ over $$1.50 cm$$. (a) In what time interval does the electron travel this $$1.50 cm$$? (b) What is its acceleration?
A race car is moving on a straight road with a speed of $$180\,km\,h^{-1}$$. If the driver stops the car in $$25$$ s by applying the brakes, calculate the distance covered by the car during the time brakes are applied. Assume the acceleration of the car is uniform throughout the retarding motion.
A car is parked on a steep incline, making an angle of $$37.0^{0}$$ below the horizontal and overlooking the ocean, when its brakes fail and it begins to roll. Starting from rest at $$t = 0$$, the car rolls down the incline with a constant acceleration of $$4.00 m/s^{2}$$, traveling $$50.0 m$$ to the edge of a vertical cliff. The cliff is $$30.0 m$$ above the ocean. Find (a) the speed of the car when it reaches the edge of the cliff, (b) the time interval elapsed when it arrives there, (c) the velocity of the car when it lands in the ocean, (d) the total time interval the car is in motion, and (e) the position of the car when it lands in the ocean, relative to the base of the cliff.
The car has one acceleration while it is on the slope and a different acceleration when it is falling, so we must take the motion apart into two different sections. Our standard equations only describe a chunk of motion during which acceleration stays constant. We imagine the acceleration to change instantaneously at the brink of the cliff, but the velocity and the position must be the same just before point $$B$$ and just after point $$B$$.
(a) From point $$A$$ to point $$B$$ (along the incline), the car can be modeled as a particle under constant acceleration in one dimension, starting from rest $$(v_{i} = 0)$$. Therefore, taking $$\Delta x$$ to be the position along the incline,
$$v_{f}^{2} − v_{i}^{2} = 2a\Delta x$$
$$v_{f}^{2} − 0 = 2(4.00 m/s^{2} )(50.0 m)$$
$$v_{f} = 20.0 m/s$$
(b) We can find the elapsed time interval from
$$v_{f} = v_{i} + at$$
$$20.0 m/s = 0 + (4.00 m/s^{2} )t$$
$$t = 5.00 s$$
(c) Initial free-fall conditions give us $$v_{xi} = 20.0 \cos 37.0^{0} = 16.0 m/s$$
and $$v_{yi}=-20.0\sin37.0^{0}=-12.0m/s$$. Since $$a_{x}=0,v_{xf}=v_{xi}$$ and
$$v_{yf}=-\sqrt{2a_{y}\Delta y+v_{yi}^{2}}$$
$$-\sqrt{2(-9.80m/s^{2})(-30.0m)+(-12.0m/s)^{2}}$$
$$=-27.1m/s$$
$$v_{f}=\sqrt{v_{xf}^{2}+v_{yf}^{2}}=\sqrt{(16.0m/s)^{2}+(-27.1m/s)^{2}}$$
$$=31.5m/s$$ at $$59.4^{0}$$ below the horizontal.
(d) From the point $$B$$ to $$C$$ the time is
$$t_{i}=5s$$; $$t_{2}=\frac{v_{yt}-v_{yi}}{a_{y}}=\frac{-27.1m/s+12.0m/s}{-9.80m/s^{2}}=1.53s$$
The total elapsed time interval is
$$t=t_{1}+t_{2}=6.53s$$
(e) The horizontal distance covered is
$$\Delta x=v_{xi}t_{2}=(16.0m/s)(1.53s)=24.5m$$
(a) From point $$A$$ to point $$B$$ (along the incline), the car can be modeled as a particle under constant acceleration in one dimension, starting from rest $$(v_{i} = 0)$$. Therefore, taking $$\Delta x$$ to be the position along the incline,
$$v_{f}^{2} − v_{i}^{2} = 2a\Delta x$$
$$v_{f}^{2} − 0 = 2(4.00 m/s^{2} )(50.0 m)$$
$$v_{f} = 20.0 m/s$$
(b) We can find the elapsed time interval from
$$v_{f} = v_{i} + at$$
$$20.0 m/s = 0 + (4.00 m/s^{2} )t$$
$$t = 5.00 s$$
(c) Initial free-fall conditions give us $$v_{xi} = 20.0 \cos 37.0^{0} = 16.0 m/s$$
and $$v_{yi}=-20.0\sin37.0^{0}=-12.0m/s$$. Since $$a_{x}=0,v_{xf}=v_{xi}$$ and
$$v_{yf}=-\sqrt{2a_{y}\Delta y+v_{yi}^{2}}$$
$$-\sqrt{2(-9.80m/s^{2})(-30.0m)+(-12.0m/s)^{2}}$$
$$=-27.1m/s$$
$$v_{f}=\sqrt{v_{xf}^{2}+v_{yf}^{2}}=\sqrt{(16.0m/s)^{2}+(-27.1m/s)^{2}}$$
$$=31.5m/s$$ at $$59.4^{0}$$ below the horizontal.
(d) From the point $$B$$ to $$C$$ the time is
$$t_{i}=5s$$; $$t_{2}=\frac{v_{yt}-v_{yi}}{a_{y}}=\frac{-27.1m/s+12.0m/s}{-9.80m/s^{2}}=1.53s$$
The total elapsed time interval is
$$t=t_{1}+t_{2}=6.53s$$
(e) The horizontal distance covered is
$$\Delta x=v_{xi}t_{2}=(16.0m/s)(1.53s)=24.5m$$
Two objects move with initial velocity $$-8.00\ m/s$$, final velocity $$16.0\ m/s$$, and constant accelerations.$$(a)$$ The first object has displacement $$20.0\ m$$. Find its acceleration.$$(b)$$ The second object travels a total distance of $$22.0\ m$$. Find its acceleration.
A $$10\ g$$ bullet is fired into a stationary block of wood having mass $$m= 5\ kg$$. The bullet embeds into the block. The speed of the bullet-plus-wood combination immediately after the collision is $$0.600\ m/s$$. What was the original speed of the bullet?
When you jump straight up as high as you can, what is the order of magnitude of the maximum recoil speed that you give to the Earth? Model the Earth as a perfectly solid object. In your solution, state the physical quantities you take as data and the values you measure or estimate for them.
A racing car travels on a circular track of radius $$250\ m$$. Assuming the car moves with a constant speed of $$45.0\ m/s$$, find the magnitude and direction of its acceleration.
