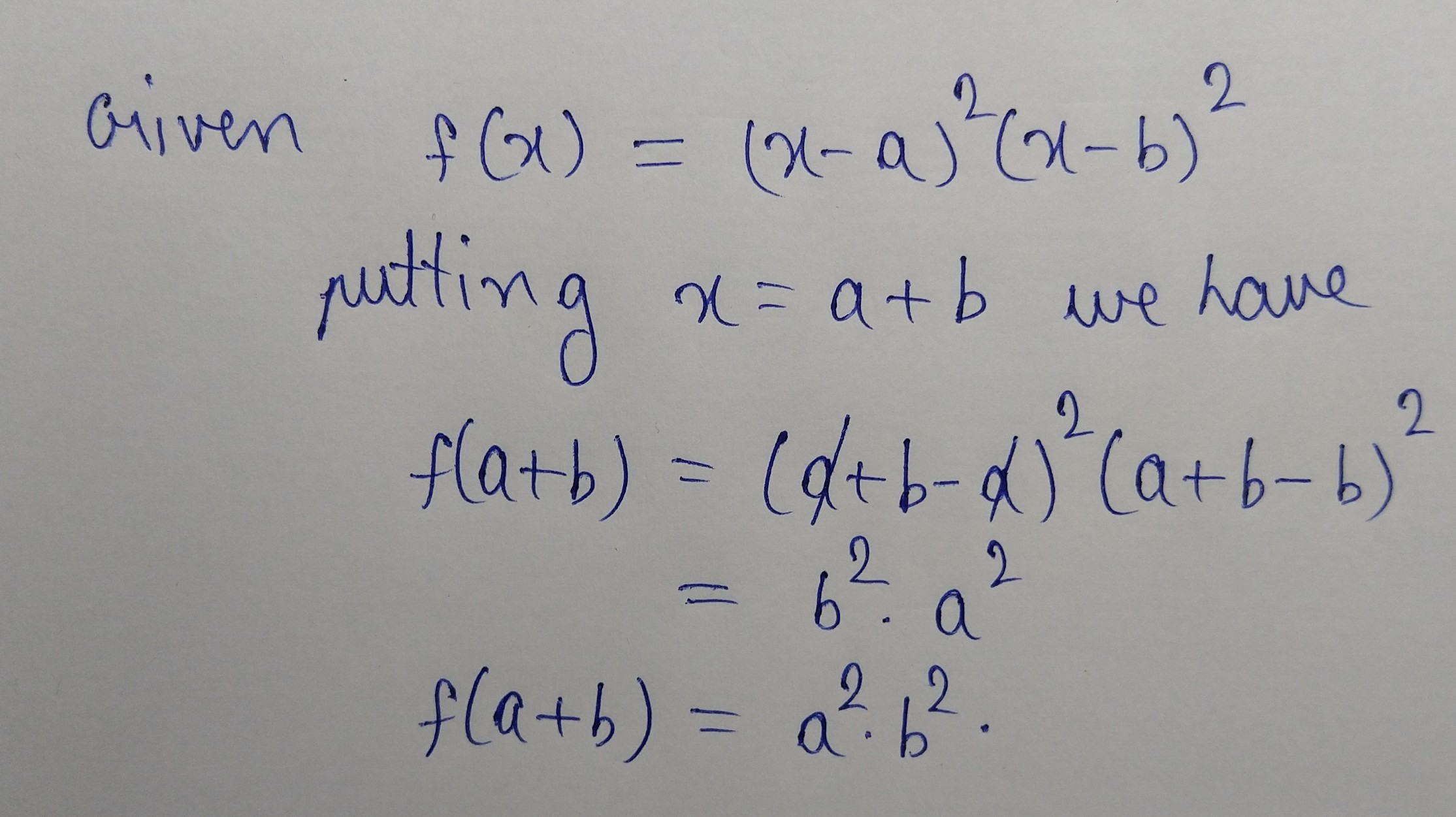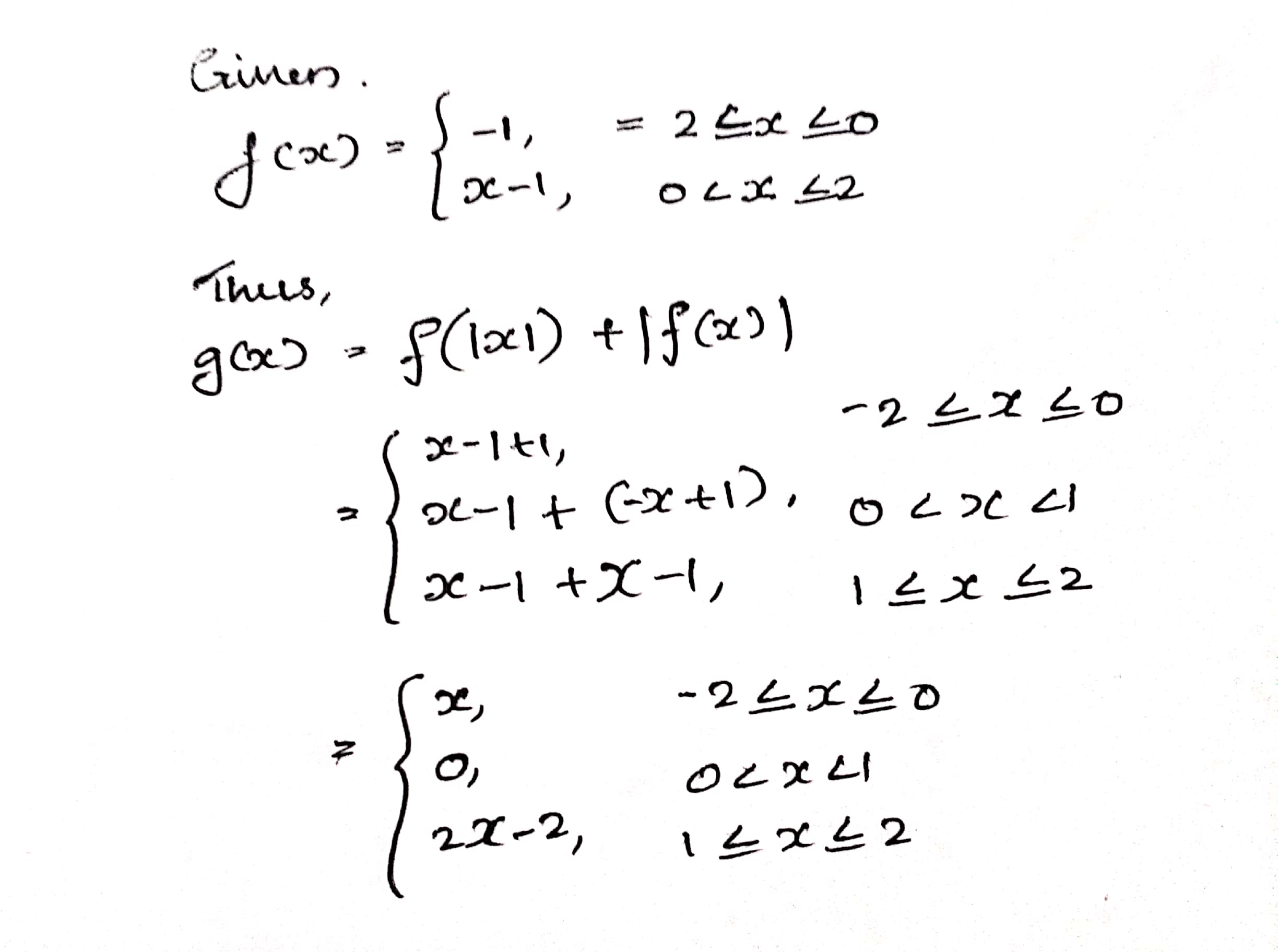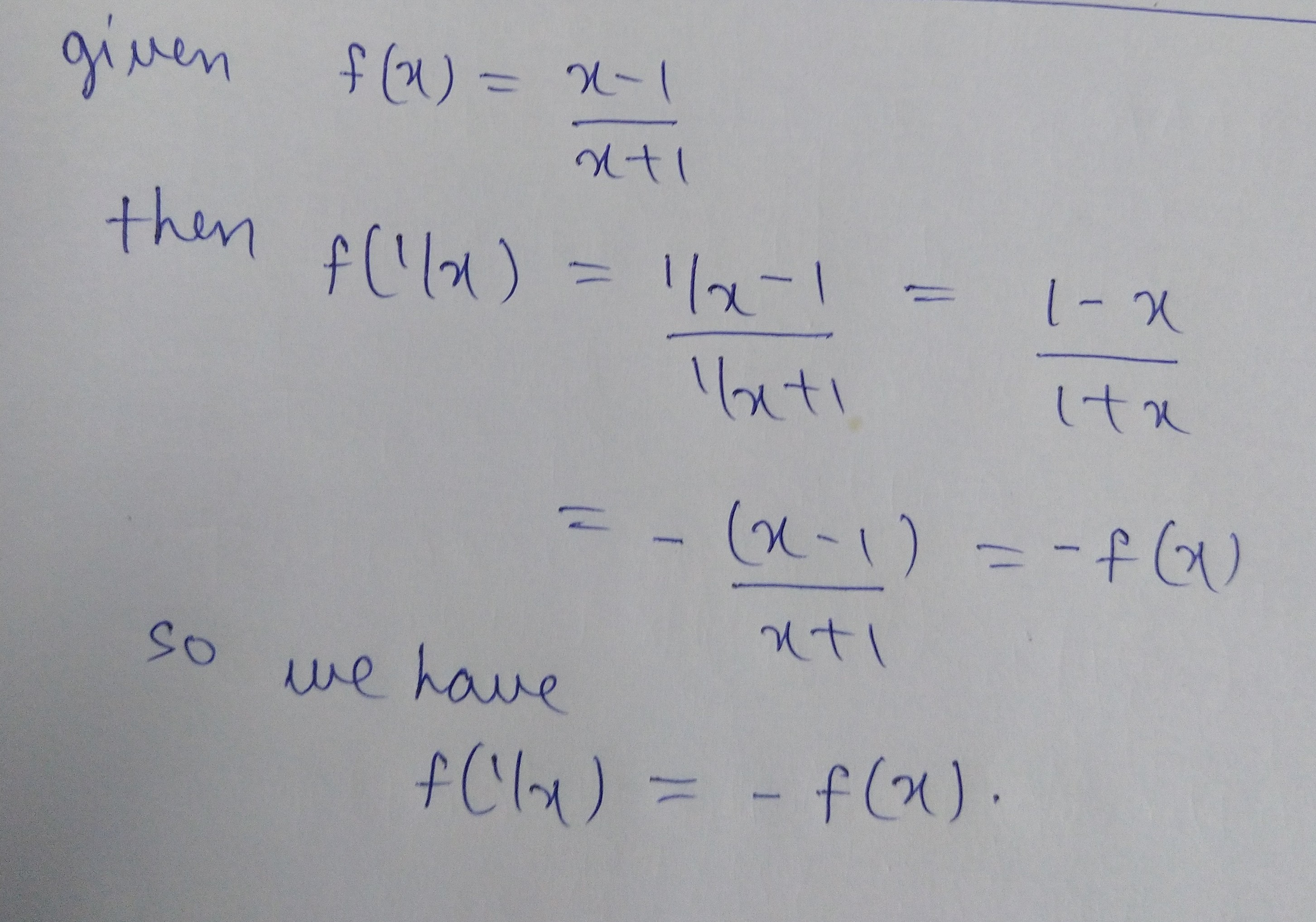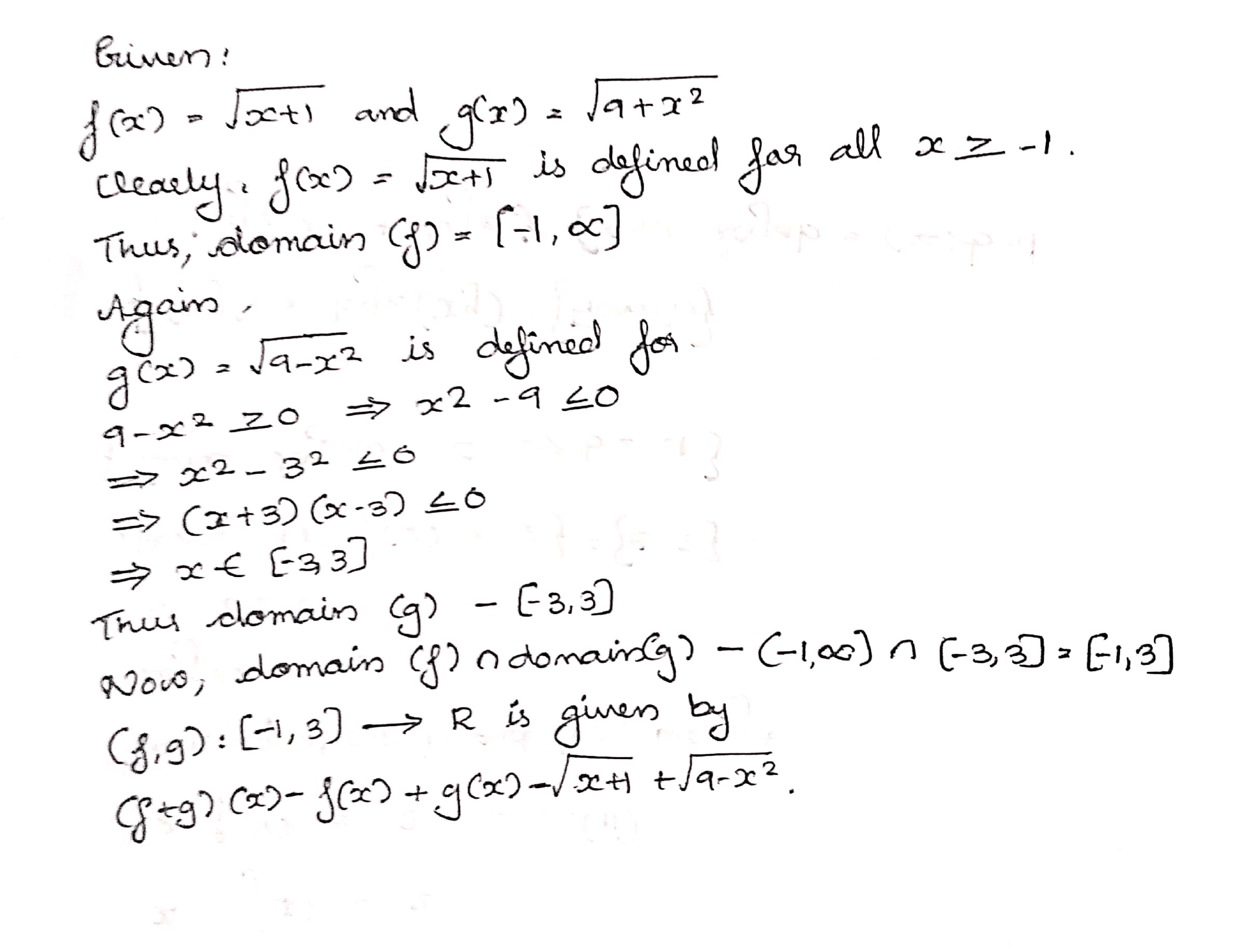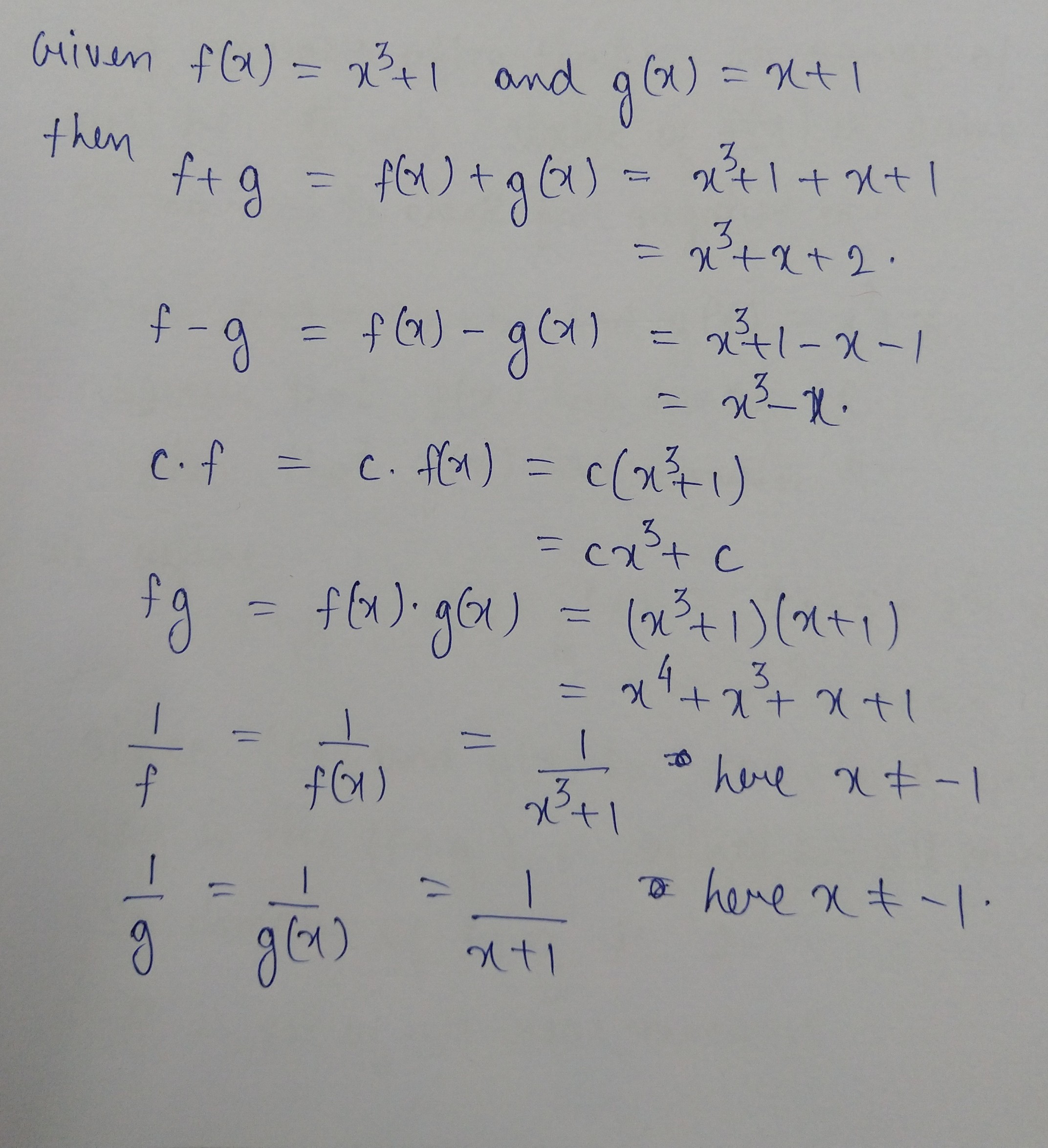Relations And Functions - Class 11 Commerce Maths - Extra Questions

Find an explicit formula (in terms of n$$\epsilon $$ N)for $$f(n)= (n - 1)+ 2n -1$$

$$f(n)=(n-1)+2n-1$$
$$f(n)=n+2n-1-1$$
$$f(n)=3n-2$$
$$f(n)=-2+3n$$
where $$n\in N$$


If f is a real function defined by $$f(x) = \dfrac{x - 1}{x + 1}$$, then prove that
$$f(2x) = \dfrac{3f(x) + 1}{f(x) + 3}$$

$$3f(x) + 1 = \dfrac{3(x-1)}{x+1} +1 = \dfrac{4x-2}{x+1}$$

$$f(x) +3 = \dfrac{x-1}{x+1}+3=\dfrac{4x+2}{x+1}$$

Dividing we get

$$\dfrac{4x-2}{4x+2}=\dfrac{2x-1}{2x+1}=f(2x)$$


Find the least value of $$x$$ when $$-5\le 2x-7$$.

Given,
$$-5\le 2x-7$$
or, $$2x\ge 7-5$$
or, $$2x\ge 2$$
or, $$x\ge 1$$
From this we get the least value of $$x$$ is $$1$$.


If $$f(x)=x$$, then which of the following must be true?
(a) $$f(a+b)=f(a)+f(b)$$
(b) $$f(2a)=2f(a)$$
(c) $$f(-a)=-f(a)$$

$$(i)$$ $$f(a+b)=f(a)+f(b)$$ acn be possible because.
$$f(a+b)=(a+b)$$
$$f(a)+f(b)$$
$$(ii)$$ $$f(2a)=2a[\because f(x)=x]$$
$$f(2a)=2f(a)$$
$$(iii)$$$$ f(-a)=-a$$
$$f(a)=-f(a)$$
Three conditions are true.


If $$f(x)=x+7$$ and $$g(x)=x-7, x\in R$$, find $$fog(6)$$.

Given,
$$f(x)=x+7$$ and $$g(x)=x-7$$
Now, $$fog(x)=f(g(x))=f(x-7)=x-7+7=x$$
Therefore,
$$fog(6)=6$$


In  eq  $$x^{2}+y=6x-14$$
if $$x=0 ,1,2 $$
then the values of $$y$$ are

Consider given the equation,

$$ {{x}^{2}}+y=6x-14 $$

$$ {{x}^{2}}-6x+y=-14 $$


Put, $$x=0$$

$$ {{0}^{2}}-6\times 0+y=-14 $$

$$ y=-14 $$


Again put, x=1

$$ {{1}^{2}}-6\times 1+y=-14 $$

$$ y=-14+6-1=-9 $$


Again put, x=2

$$ {{2}^{2}}-6\times 2+y=-14 $$

$$y=-2-4$$

$$ y=-6$$


Hence, this is the answer.


The length, l metres, of a garden is $$78.5$$ metres, correct to the nearest half metre. Complete this statement about the value of l.
________$$\leq$$ l $$<$$ _______.

The length is $$78.5m$$ which is correct upto half meter
So it can be given as $$78.25m \leq l < 78.75m$$


If $$y=f(x)=\dfrac {ax-b}{bx-a}$$, show that $$x=f(y)$$


1417170_1664586_ans_1ed14b27475641b5899b72a626108480.jpg


Prove that $$\displaystyle f' \, (1) \, + \, f \, (-1) \, = \, -\, f \, (0) $$, if $$ f \, (x) \, = \, x^5 \, +\, x^3 \, - \, 2x\, -\, 3$$

$$f(x) = x^{5} + x^{3} - 2x - 3$$
So $$f'(x) = 5x^{4} + 3x^{2} - 2$$

$$\therefore f'(1) = 5(1)^{4} + 3(1)^{2} - 2$$
$$= 5 + 3 - 2$$
$$= 6$$

$$Also\  f(1) = (1)^{5} + (1)^{3} - 2(1) -3$$
$$= 1 + 1 - 2 - 3$$
$$= 2 - 2 - 3$$
$$= -3$$

$$\therefore f(0) = -3$$

and $$f(-1) = (-1)^{5} + (-1)^{3} - 2(-1) - 3$$
$$= -1 - 1 + 2 - 3$$
$$\Rightarrow -3$$
So $$f'(1) + f(-1) = 6 - 3 = 3=-f(0)$$.


Discuss the commutativity and associativity of binary operation $$\ast$$. defined on $$A=Q-\left\{ 1 \right\} $$ by the rule $$a\ast b=a-b+ab$$ fo all $$a,b\in A$$. Also find the identity element of $$\ast$$ in $$A$$ and hence find the invertible elements of $$A$$.

Given # is a binary operation on $$Q-\left\{ 1 \right\} $$
defined by $$a*b=a-b+ab$$
Commutativity:
for any $$a,b \in A$$
We have $$a*b=a-b+ab$$ and $$b*a=b-a+ba$$
Since, $$a-b+ab \neq b-a+ab$$
$$\therefore a*b \neq b*a$$
So, $$*$$ is not commutative on $$A$$
Associativity:
Let $$a,b,c \in A(a*b)*c=(a-b+ab)*c$$
$$\Rightarrow (a*b)*c=(a-b+ab)-c+(a-b+ab)c$$
$$\Rightarrow (a*b)*c=a-b+ab-c+ac-bc+abc$$
$$a*(b*c)=a*(b-c+bc)$$
$$\Rightarrow a*(b*c)=a-(b-c+bc)+a(b-c+bc)$$
$$\Rightarrow a*(b*c)=a-b+c-bc+ab-ac+abc$$
$$\Rightarrow (a*b)*c\neq a*(b*c)$$
so $$*$$ is not associative on $$A$$
Identity Element:
Let $$e$$ be the identity elements in $$A$$ 
the $$a*e=a=e*a  a\in Q-\left\{ 1 \right\} $$
$$a-e+ae=a$$
$$(a-1)e=0$$
$$e=0$$ $$($$ as $$a\neq 1)$$[so $$'0' $$ si identity element in $$A]$$
Inverse of an Element:
Let $$a$$ be an arbitary element of $$A$$ as $$b$$ be the inverse of $$a$$.
$$\because$$ $$a*b=e=b*a$$
$$\Rightarrow a*b=e$$
$$\Rightarrow a-b+ab=0[\because e=0]$$
$$a=b(1-a)$$
$$b=a/1-a$$
since $$b\in Q-1$$
So, every elements of $$A$$ is invertible.


If $$f (x)=a+bx+cx^2$$, show that
$$\displaystyle \underset{0}{\overset{1}{\int}} f(x)dx=\dfrac{1}{6} \left[f(0)+4f \left(\dfrac{1}{2}\right)+f(1)\right]$$ 

$$f(x) = a + bx + cx^2$$
$$\therefore f(0) = a$$
$$\therefore f(1/2) = a + \dfrac{b}{2} + \dfrac{c}{4}$$
$$\therefore f(1) = a + b + c$$
$$\therefore \displaystyle \int_0^1 f(x) dx = \int_0^1 (a + bx + cx^2) dx$$
$$= ax + \dfrac{bx^2}{2} + \dfrac{cx^3}{3} |_0^1$$
$$= a(1-0) + \dfrac{b}{2} (1 - 0) + \dfrac{c}{3} (1 - 0)$$
$$= a + \dfrac{b}{2} + \dfrac{c}{3} \,\,\, ......(1) \, \rightarrow LHS$$
$$\therefore RHS = \dfrac{1}{6} [f(0) + 4f (1/2) + f(1)]$$
$$= \dfrac{1}{6} \left[a + 4 \left(a + \dfrac{b}{2} + \dfrac{c}{4} \right) + a + b + c \right]$$
$$= \dfrac{1}{6} (a + 4a + a + 2b + c + b + c)$$
$$= a + \dfrac{3b}{6} + \dfrac{2c}{6}$$
$$= a + \dfrac{b}{2} + \dfrac{c}{3} \rightarrow RHS$$
$$\therefore LHS = RHS$$
Hence proved.


Divide polynomial  $$P(x) = x^{4} + 4x^{3} + 5x^{2} - 7x - 3, by \ S(x) = x^{2} - 1$$.


1372804_1127027_ans_a9f7d945fced4412840eaaa2a1971c19.jpg


Let $$f(x)=x^2$$ and $$g(x)=2x+1$$ be two real functions. Find $$(f+g)(x),(f-g)(x),(fg)(x), \left(\dfrac{f}{g}\right)(x).$$

$$(f+g)(x)=f(x)+g(x)$$

$$=x^{2}+2x+1$$

$$(f-g)(x)=f(x)-g(x)$$

$$=x^{2}-(2x+1)$$

$$=x^{2}-2x-1$$

$$(fg)(x)=f(x).g(x)$$

$$=x^{2}\left ( 2x+1 \right )$$

$$=2x^{3}+x^{2}$$

$$\left ( \cfrac{f}{g} \right )(x)=\cfrac{f(x)}{g(x)}$$          $$\left ( \; g(x)\neq 0 \right )$$

$$=\cfrac{x^{2}}{2x+1}$$                         $$\left ( \; x\neq -\cfrac{1}{2} \right )$$



$$f=\{ (3,4),(4,3)\}\ \ g=\{(3,7),(4,8)\}$$  Find $$f-g$$

$$f=\{(3,4),(4,3)\}$$
$$g=\{(3,7),(4,8)\}$$
$$f-g=\{ (3,-3),(4,-5)\}$$


If $$f(x)=\dfrac {x-1}{x+1}$$ then show that

$$f\left (\dfrac {1}{x}\right)=-f(x)$$


1417189_1664621_ans_360578f4ddd9436eadd8ab624824c1ee.jpg


If $$f(x)=(x-a)^2 (x-b)^2$$, find $$f(a+b)$$


1417171_1664585_ans_9a3dc08ad84d4591919499f3b2b3252c.jpg


If $$f(x)$$ be defined on $$[-2, 2]$$ and is given by $$f\left( x \right)=\begin{cases} -1,\quad -2\le x\le 0 \\ x-1,\quad 0<x\le 2 \end{cases}$$ and $$g(x)=f(|x|)+|f(x)|$$. Find $$g(x)$$


1418889_1664716_ans_b537ebee5e3b4870a5dbc91a4a13054b.jpg


If $$f(x)=\dfrac {x-1}{x+1}$$ then show that $$f\left (\dfrac {1}{x}\right) =-{f(x)}$$


1428677_1664624_ans_dc94712124dc42fbb798f8396f0ae2c6.jpg


Let $$f, g$$ be two real functions defined by $$f(x)=\sqrt {x+1}$$ and $$g(x)=\sqrt {9-x^2}$$. Then, described each of the following functions:
$$f+g$$


1419018_1664722_ans_104de14c6b8846d89424248053e8ac41.jpg


Find $$f+g, f-g, cf (c \in R, c\neq 0), \ fg, \dfrac {1}{f}$$ and $$\dfrac {1}{g}$$ in each of the following:
$$f(x)=x^3+1$$ and $$g(x)=x+1$$


1418661_1664705_ans_bc72bb250f5e4133b6c3b335ecf22315.jpg


If $$f:R\rightarrow R,$$ defined as
$$f(x)=x^3+5$$
Find $$f^{-1}(x) $$

According to question,
$$f:R\rightarrow R,f(x)=x^3+5$$
One-one/onto: Let $$a,b\epsilon R$$
$$f(a)=f(b)$$
$$\Rightarrow a^3+5=b^3+5$$
$$\Rightarrow a^3=b^3$$
$$a=b$$
So, $$f(a)=f(b)$$
$$\Rightarrow a=b,\forall a,b \epsilon R$$
$$\therefore f$$ is one-one function.
Onto/into:
Let $$y\epsilon R$$(co-domain)
$$f(x)=y$$
$$\\Rightarrow x^3+5=y$$
$$\Rightarrow x^3=y-5$$
$$\Rightarrow x=(y-5)^{1/3}\epsilon R, \forall x\epsilon R$$
So pre-image for each value of $$y$$ exists in domain $$R$$.
Thus, range of $$f=$$ co-domain of $$f$$.
So, function $$'f'$$ is onto function.
Hence, we can say that $$f$$ is one-one onto function.
So, $$f^{-1}:R\rightarrow R$$ defined as
$$f^{-1}(y)=x\Leftrightarrow f(x)=y$$..........(i)
$$\Rightarrow f(x)=y$$
$$\Rightarrow x^3+5=y$$
$$x^3=y-5$$
$$\Rightarrow x=(y-5)^{1/3}$$
$$\Rightarrow f^{-1}(y)=(y-5)^{1/3}$$ [from(i)]
$$\Rightarrow f^{-1}(x)=(x-5)^{1/3}$$





If $$f:R\rightarrow R,$$ defined as
$$f(x)=2x-3$$
Find $$f^{-1}(x) $$

Given function,
$$f:R\rightarrow R, f(x)=2x-3$$
One-one/many-one:
Let $$a,b\epsilon R$$
$$f(a)=f(b)$$
$$\Rightarrow 2a-3=2b-3$$
$$\Rightarrow 2a=2b$$
$$\Rightarrow a=b$$
So, $$f(a)=f(b)\Rightarrow a=b,\forall a,b \epsilon R$$
$$\therefore f$$ is one-one function.
onto/into:
Let $$y\epsilon R$$(co-domain)
$$f(x)=y$$
$$\Rightarrow 2x-3=y$$
$$\Rightarrow x=\dfrac{y+3}{2}\epsilon R,\forall y\epsilon R$$
So, pre-image for each value of $$y$$ exists in domain $$R$$. Thus, function $$'f'$$ is onto function.
It is clear that $$'f'$$ is one-one into function.
Hence $$f^{-1}:R\rightarrow R$$ exists.
Let $$x\epsilon R$$(domain of $$f$$)
and $$y\epsilon R$$(co-domain of $$f$$)
Let $$f(x)=y,$$ then $$f^{-1}(y)=x$$
$$\Rightarrow f(x)=y$$
$$\Rightarrow 2x-3=y$$
$$\Rightarrow x=\dfrac{y+3}{2}\epsilon R$$
$$\Rightarrow f^{-1}(y)=\dfrac{y+3}{2}$$
$$\Rightarrow f^{-1}(x)=\dfrac{x+3}{2},\forall x\epsilon R$$





If statement

$$P(n) : 1^2 + 3^2 + 5^2 + ...+ (2n-1)^2 = \dfrac{n(2n-1)(2n+1)}{3}$$,

then test the authenticity of $$P(4)$$.

Let the given statement is $$P(n)$$, where $$n \epsilon N$$
So, $$P(n) = 1^2 + 3^2 + 5^2 + ...+ (2n-1)^2$$

                            $$= \dfrac{n(2n-1)(2n+1)}{3}$$

Putting $$n=4$$

              $$L.H.S. = P(4) : = 1^2 + 3^2 + 5^2 + ...+ (2 \times 4 -1)^2$$
                             $$= 1^2 + 3^2 + 5^2 + 7^2$$
                             $$= 1+ 9 + 25 + 49$$
                             $$=84$$
               
                $$R.H.S= \dfrac{4(2 \times 4 -1)(2 \times 4 + 1)}{3} = \dfrac{(4(8-1)(8+1)}{3}$$

                               $$= \dfrac{4 \times 7 \times 9}{3} = 84$$

$$L.H.S. = R.H.S.$$
Hence, $$P(4)$$ is true.


Find a, b, c when $$f(x) = ax^2 + bx + c$$ and $$f(0) = 6, f(2) = 11, f(-3) = 6$$ Determine the value of $$f(1)$$.

Given $$f(x) = ax^2 + bx + c$$
$$\therefore f(0) = a.0^2 + b.0 + c = 6$$
or $$0.a + 0.b + 1.c = 6$$              (i)
and $$f(2) = a(2)^2 + b(2) + c = 11$$
$$\Rightarrow 4.a + 2.b + 1.c = 11$$         (ii)
and $$f(-3) = a(-3)^2 + b(-3) + c = 6$$ 
$$\Rightarrow 9.a - 3.b + c = 6$$              (iii)
Since (i), (ii) and (iii) are three equations in a, b, c solving these by Cramer's rule
$$\therefore D = \begin{vmatrix} 0& 0 & 1\\ 4 & 2 & 1\\ 9 & -3 & 1\end{vmatrix} = 1. (-12 - 18) = - 30$$
$$D_1 = \begin{vmatrix}6 & 0 & 1\\ 11 & 2 & 1\\ 6 & -3 & 1\end{vmatrix} = 6(2 + 3) - 0 + 1 (-33 - 12)$$ $$= - 15$$
$$D_2 = \begin{vmatrix}0 & 6 & 1\\ 4 & 11 & 1\\ 9 & 6 & 1\end{vmatrix}$$ $$= 0 - 6 (4 - 9) + 1 (24 - 99)$$ $$= 20 - 75$$ $$= - 45$$
$$D_3 = \begin{vmatrix}0 & 0 & 6\\ 4 & 2 & 11\\ 9 & -3 & 6\end{vmatrix} $$ $$= 6 (-12 - 18)$$ $$= - 180$$
Hence by Cramer's rule
$$\displaystyle a = \frac{D_1}{D} = \frac{- 15}{-30} = \frac{1}{2}$$
$$\displaystyle b = \frac{D_2}{D} = \frac{-45}{-30} = \frac{3}{2}$$
and $$\displaystyle c = \frac{D_3}{D } = \frac{- 180}{-30} = 6$$
Hence $$a = \dfrac{1}{2} , b = \dfrac{3}{2} , c = 6$$
$$\therefore f(x) = \dfrac{1}{2} x^2 + \dfrac{3}{2} x + 6$$
and $$f(1) = \dfrac{1}{2} (1)^2 +\dfrac{3}{2} (1) + 6$$ $$= 8$$


 If $$f(x)$$ be a function such that $$ f(x-1)+f(x+1)=\sqrt{3} f(x) $$ and $$f(5) =10,$$ then the sum of digits of the value of $$ \displaystyle \sum_{r=0}^{19} f(5+12r)$$ is ......

$$f(x-1)+f(x+1)=\sqrt{3}f(x)$$
$$\Rightarrow f(x)+f(x+2)=\sqrt{3}f(x+1)$$
Putting, $$x=x+2$$,
$$f(x+1)+f(x+3)=\sqrt{3}f(x+2)$$
$$f(x-1)+2f(x+2)+f(x+3)=\sqrt{3}\left [\sqrt{3}f(x+1)  \right ]$$
$$f(x-1)+f(x+3)=f(x+1)$$
Putting, $$x=x+2$$, again
$$f(x+1)+f(x+5)=f(x+3)$$
$$f(x-1)+f(x+5)=0$$
$$f(x+5)=-f(x-1)$$
$$f(x)=-f(x+6)$$
$$f(x+12)=f(x)$$
$$\sum_{r-0}^{19}f(5+12r)=20f(5)=20\times 10=200$$
Hence, sum of digits $$=2+0+0=2$$


If $$ f(x) \varepsilon [1, 2]$$ when $$x\varepsilon R$$ and for a fixed positive real number p, $$f(x+p)=1+\sqrt{2f(x)-{f(x)}^2}$$ for all $$x \varepsilon R$$ then prove that f(x) is a periodic function .

$$f(x+p)=1+\sqrt{2f(x)-f(x)^2}$$
put $$x=x+p$$
$$f(x+2p)=1+\sqrt{2f(x+p)-f(x+p)^2}$$
$$f(x+2p)=1+\sqrt{(1+\sqrt{2f(x)-f(x)^2}(1-\sqrt{2f(x)-f(x)^2}})$$
$$f(x+2p)=1+\sqrt{1-2f(x)+f(x)^2}=1+f(x)-1$$
$$f(x+2p)=f(x)$$
hence $$f(x)$$ is a periodic function with period $$=2p$$


Class 11 Commerce Maths Extra Questions