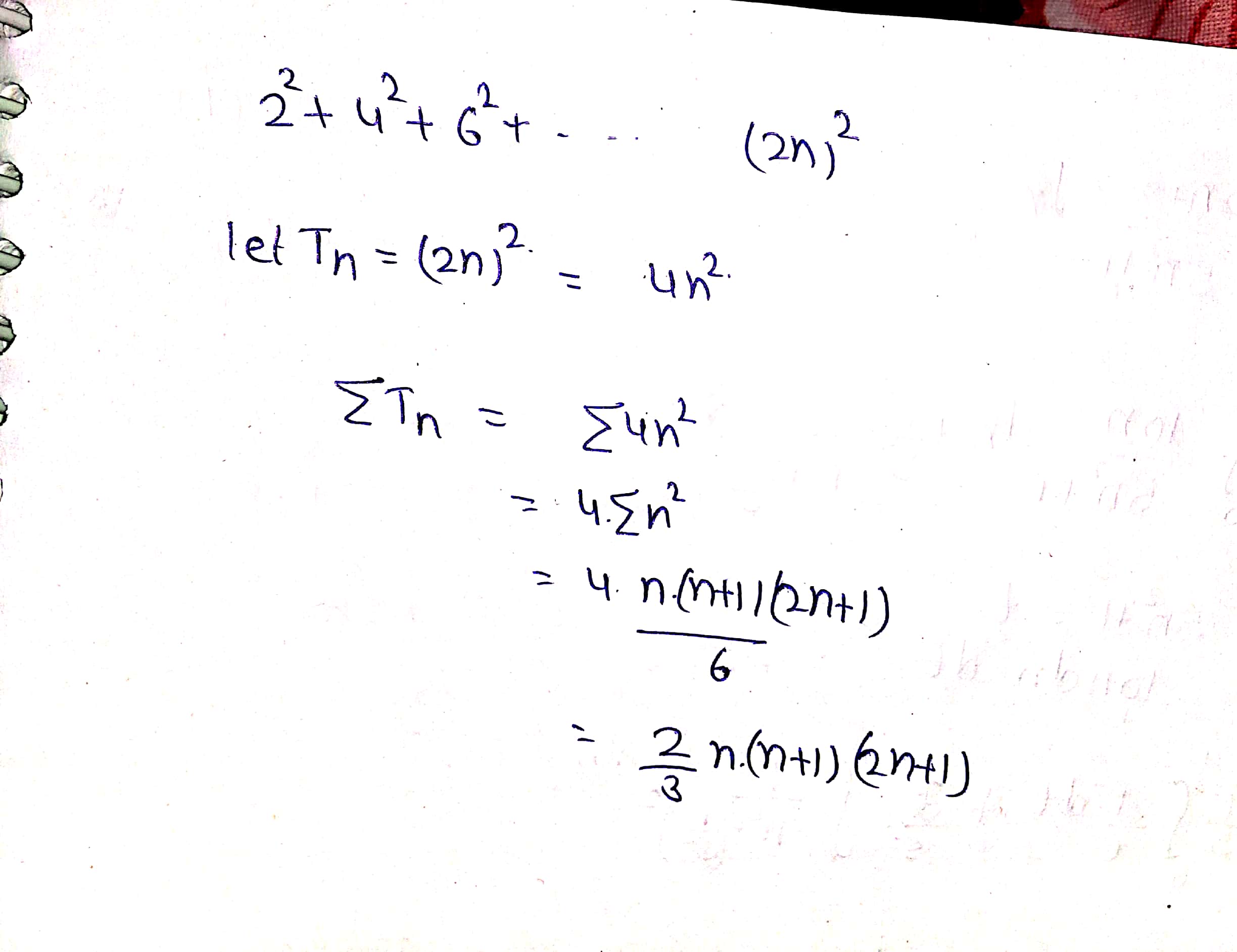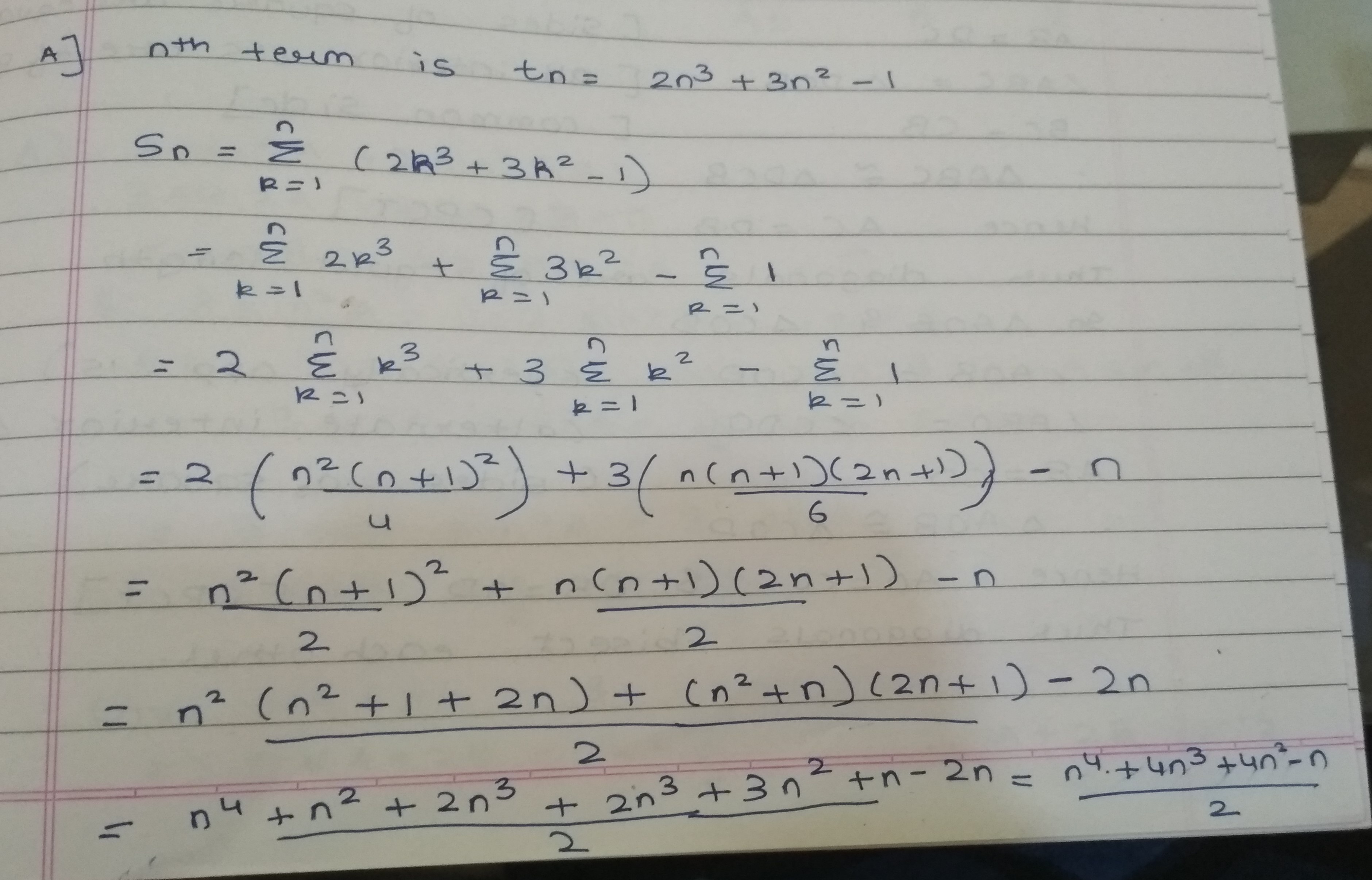Class 11 Commerce Maths - Sequences And Series

Find the following sum.
$$\sum\limits_{r = 1}^n {\left( {6{r^2} - 2r + 6} \right)} $$

$$\begin{array}{l}\sum\limits_{r = 1}^n {\left( {6{r^2} - 2r + 6} \right)} \\ = 6\sum {{r^2}} - 2\sum r + 6\sum 1 \\ = 6\dfrac{{n\left( {n - 1} \right)\left( {2n + 1} \right)}}{6} - 2\dfrac{{n\left( {n + 1} \right)}}{2} + 6n\\ = n\left[ {\left( {n + 1} \right)\left( {2n + 1} \right) - \left( {n + 1} \right) + 6} \right]\\ = n\left[ {2{n^2} + 3n + 1 - n - 1 + 6} \right]\\ = n\left( {2{n^2} + 2n + 6} \right)\\ = 2n\left( {{n^2} + n + 3} \right)\end{array}$$

$$1.2 + 2.3x + 3.4x^{2} + ....\infty (|x| < 1)$$.

1521166_1153875_ans_961d610b0fb240ef9232e8dc83ba7b76.jpg

Write the general term for the given series $$\frac{1}{(n-1)},\frac{1}{3(n-3)},\frac{1}{5(n-5)},....$$

General term can be observed as $$\dfrac{1}{(2r-1)(n-(2r-1))}$$ for r to be some natural number

Solve:

$$\displaystyle\sum\limits_{r = 1}^n {\left( {6{r^2} - 2r + 6} \right)} $$

$$\displaystyle\int^n_{r=}(6r^2-2r+6)$$

$$\Rightarrow 2\displaystyle\sum^n_{r=1}[3r^2-r+3]$$

$$\Rightarrow 2\left[3\displaystyle\sum^n_{r=1}r^2-\displaystyle\sum^n_{r=1}r+3\displaystyle\sum^n_{r=1}(1)\right]$$

$$\Rightarrow 2\left[3\left[\dfrac{n(n+1)(2n+1)}{6}\right]-\dfrac{n(n+1)}{2}+3n\right]$$

$$\Rightarrow 2\left[\dfrac{n(n+1)(2n+1)}{2}-\dfrac{n(n+1)}{2}+3n\right]$$

$$\Rightarrow 2\left[\dfrac{n(n+1)}{2}\left[2n+1-1\right]+3n\right]$$

$$\Rightarrow 2\left[n^2(n+1)+3n\right]$$

$$\Rightarrow 2n[n^2+n+3]$$

$$\therefore \displaystyle\sum^n_{r=1}6r^2-2r+6$$

$$=2n[n^2+n+3]$$.

1123619_1197135_ans_0aa92c313fc44c12ae6cb47f1ce630bd.jpeg

The product of two consecutive positive numbers is $$182$$. Find the numbers.

A] Let two numbers be x , x + 1

given , x (x + 1) = 182

$$ = x^{2}+x-182 = 0$$

$$ = x^{2}+14x-13x-182 = 0$$

$$= x (x + 14) - 13 (x + 14) = 0$$

= (x + 14) (x - 13) = 0

as x is positive

so x = 13

Two numbers are 13 , 14

1177886_1292279_ans_902baba0409e417a918a156e805b95a8.jpg

Evaluate $$1+i^{2}+i^{4}+i^{6}+...+i^{2n}$$.

$$1+i^{2}+i^{4}+i^{6}+ ...+i^{2n}$$

If n is odd.

$$\Rightarrow 1-1+1-1+1-1=0$$

If n is even

$$\Rightarrow 1-1+1 ...+1=1$$

What is the sum of first 20 odd natural numbers?

$$\begin{array}{l} The\, first\, 20\, odd\, natural\, number\, is\, given\, by \\ 1,3,5,7,9,.....37,39. \\ here, \\ a=1 \\ d=2 \\ and \\ n=20 \\ Now, \\ { S_{ n } }=\dfrac { n }{ 2 } \left[ { 2{ a_{ 1 } }+\left( { n-1 } \right) d } \right] \\ { S_{ 20 } }=\dfrac { { 20 } }{ 2 } \left[ { 2\left( 1 \right) +\left( { 20-1 } \right) 2 } \right] \\ =10\left[ { 2+\left( { 19 } \right) 2 } \right] \\ =10\left[ { 2+38 } \right] \\ =10\left[ { 400 } \right] \\ =400 \\ Hence,\, the\, sum\, of\, first\, 20\, odd\, natural\, number\, is\, 400. \end{array}$$

Sum the following series
$$1 + \dfrac {3}{4} + \dfrac {7}{16} + \dfrac {15}{64} + \dfrac {31}{256} + ....$$ to infinity.

We have

$$S=1+\dfrac{3}{4}+\dfrac{7}{16}+\dfrac{15}{64}+\dfrac{31}{256}\dots\dots(1)$$

Multiplying $$S$$ by $$4$$, we get

$$4S=4+3+\dfrac{7}{4}+\dfrac{15}{16}+\dfrac{31}{64}\dots\dots(2)$$

$$(2)-(1)$$

$$\Rightarrow 3S=6+1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}\dots\dots=6+2=8$$

$$\Rightarrow S=\dfrac{8}{3}$$

Find value of the sum $$\displaystyle \frac{1}{sin45^o sin 46^o} + \frac{1}{sin47^o sin 48^o} + \frac{1}{sin49^o sin 50^o} + ....... + \frac{1}{sin133^o sin 134^o}$$

$$\dfrac {1}{\sin 45 \sin 46}+\dfrac {1}{\sin 46 \sin 47}+....+\dfrac {1}{\sin 133 \sin 134}$$

$$\Rightarrow \ $$ Multiply and divide by $$\sin 1$$ we get

$$=\dfrac {1}{\sin 1} \left [\dfrac {\sin (46-45)}{\sin 45 \sin 46}+\dfrac {\sin (48-47)}{\sin 47 \sin 48}+...+ \dfrac {\sin (134 -133)}{\sin 133 \sin 134}\right]$$

$$\Rightarrow \ \dfrac {1}{\sin 1} [\cot 45 -\cot 46+\cot 47-\cot 48+....+\cot 133-\cot 134]$$

= we know that $$\cot (\pi -\theta)=-\cot \theta$$

using this we get

$$\Rightarrow \ \dfrac {1}{\sin 1} [\cot 45 -\cot 46 +\cot 47 -\cot 48..... +\cot 48-\cot 47+\cot 46]$$

All terms cancel out except first one

$$\Rightarrow \ \dfrac {\cot 45}{\sin 1}=\dfrac {1}{\sin 1}$$.

Let $$a_{1},a_{2},..., a_{n}$$ be fixed real numbers and define a function $$f(x)=(x-a_{1})(x-a_{2})....(x-a_{n})$$.
What is $$\displaystyle \lim _{ x\rightarrow a_{1} }f(x)$$? For some $$a\neq a_{1},a_{2},..., a_{n}$$, compute $$\displaystyle \lim _{ x\rightarrow a }f(x)$$.

$$\begin{array}{l} f\left( x \right) =\left( { X-{ a_{ 1 } } } \right) \left( { X-{ a_{ 2 } } } \right) ..........\left( { X-{ a_{ n } } } \right) \\ { \lim }_{ x\to a }f\left( x \right) =\left( { { a_{ 1 } }-{ a_{ 1 } } } \right) \left( { { a_{ 1 } }-{ a_{ 2 } } } \right) ..........\left( { { a_{ 1 } }-{ a_{ n } } } \right) \\ 0.\left( { { a_{ 1 } }-{ a_{ 2 } } } \right) ......... \\ =0 \\ { \lim }_{ x\to a }f\left( x \right) =\left( { { a_{ 1 } }-{ a_{ 1 } } } \right) \left( { { a_{ 1 } }-{ a_{ 2 } } } \right) ..........\left( { { a_{ 1 } }-{ a_{ n } } } \right) =0 \end{array}$$

Hence, this is the answer.

If $$\displaystyle\frac{1}{1!10!}+\frac{1}{2!9!}+\frac{1}{3!10!}+...+\frac{1}{1!10!}=\frac{2}{k!}(2^{k-1}-1)$$ then find the value of k.

Multiplying and dividing by $$11!$$ we get

$$\left\{ \dfrac { 1 }{ 11! } \right\} \{ \dfrac { 11! }{ 1!10! } +\dfrac { 11! }{ 2!9! } +\dfrac { 11! }{ 3!8! } +............+\dfrac { 11! }{ 10!1! } \} $$

$$\Rightarrow\left\{ \dfrac { 1 }{ 11! } \right\} \left\{ { 11 }_{ { C }_{ 1 } }+{ 11 }_{ { C }_{ 2 } }+{ 11 }_{ { C }_{ 3 }.................... }+{ 11 }_{ { C }_{ 10 } } \right\} $$

$$\Rightarrow \left\{ \dfrac { 1 }{ 11! } \right\} \left\{ { 2 }^{ 11 }-2 \right\}=\left\{ \dfrac { 2 }{ 11! } \right\} \left\{ { 2 }^{ 10 }-1 \right\} $$

by comparing we get $$\Rightarrow k=11$$

If $$\beta \, \neq \, 1$$ be any nth root of unity then prove that $$1 \, + \, 3\beta \, + \, 5\beta^2 \, + \, ..... \, + \, n \, terms \, = \, -\dfrac{2n}{1 \, - \, \beta}$$

$$\beta \, = \, (1)^{1/n}\Rightarrow \beta^n \, = \, 1$$ ...(1)
If S be the sum of the given series which is arithmetico-geometric series ,then
$$S \, = \, 1 \, + \, 3\beta \, + \, 5\beta^2 \, + \,...(2n \, - \, 1)\beta^{n \, - \, 1}$$
$$\beta S \, = \, \beta \, + \, 3\beta^2 \, + \, ...(2n \, - \, 3)\beta^{n \, - \, 1} \, + \, (2n \, - \, 1)\beta^n$$
$$S(1 \, - \, \beta) \, = \, 1 \, + \, [2\beta \, + \, \beta^2 \, + \, ...(n \, - \, 1)\, \,terms] \, - \,(2n \, - \,1) \, , \,by(1)$$
$$ = \, 2 \, + \, 2\beta \, + \, 2\beta^2 \, + \, ...n \, \, terms \, \, \, - \, 2n$$
$$ = \, 2\dfrac{(1 \, - \,\beta^n)}{1 \, - \,\beta} \, - \, 2n \, = \, 0 \, - \, 2n\, , \,by \,(1) $$
$$\therefore \, \, \, S \, = \, \dfrac{- \,2n}{1 \, - \, \beta}$$

Let a sequence be defined by $$a_1 = 1, a_2 = 1$$ and, $$a_n=a_{n-1} + a_{n - 2}$$ for all $$n > 2$$,
find $$\dfrac{a_{n + 1}}{a_n}$$ for $$n = 1, 2, 3, 4$$.

We have, $$a_1 = 1, a_2 = 1$$
and, $$a_n = a_{n - 1} + a_{n -2}$$ for all $$n > 2$$

Putting $$n = 3, 4$$ and $$5$$, we get

$$a_3 = a_2 + a_1 = 1 + 1 = 2$$
$$a_4 = a_3 + a_2 = 2 + 1 = 3$$
and, $$a_5 = a_4 + a_3 = 2 + 1 = 5$$

Thus, we have
$$a_1 = 1, a_2 = 1, a_3 = 2, a_4 = 3$$ and $$a_5 = 5$$

Now, putting $$n = 1, 2, 3$$ and $$4$$ in $$\dfrac{a_{n + 1}}{a_n}$$, we get

$$\dfrac{a_2}{a_1} = \dfrac{1}{1} = 1$$ $$[\because a_1 = a_2 = 1]$$

$$\dfrac{a_3}{a_2} = \dfrac{2}{1} = 2$$ $$[\because a_2 = 1$$and $$a_3 = 2]$$

$$\dfrac{a_4}{a_3} = \dfrac{3}{2}$$ $$[\because a_4 =3$$ and $$a_3 = 2]$$

$$\dfrac{a_5}{a_4} = \dfrac{5}{3} $$ $$[\because a_4 =3$$ and $$a_5 = 5]$$

A sequence is defined by $$a_n = n^3 - 6n^2 + 11n - 6$$. Show that the first three terms of the sequence are zero and all other terms are positive.

We have, $$a_n = n^3 - 6n^2 + 11n - 6$$

Putting $$n = 1, 2, 3$$ we get

$$a_1 = (1)^3 - 6 \times 1^2 + 11 \times 1 - 6 = 1 - 6 + 11 - 6 = 12 - 12 = 0$$

$$a_2 = 2^3 - 6 \times 2^2 + 11 \times 2 - 6 = 8 - 24 + 22 - 6 = 30 - 30 = 0$$

and, $$a_3 = 3^3 - 6 \times 3^2 + 11 \times 3 - 6 = 27 - 54 + 33 - 6 = 60 - 60 = 0$$

Thus, we have
$$a_1 = a_2 = a_3 = 0$$

We observe that $$a_n = n^3 - 6n^2 + 11n - 6$$ is a cubic polynominal in $$n$$ and it vanished for $$n = 1, 2$$ and $$3$$.

Therefore, by factor theorem $$(n - 1), (n - 2)$$ and $$(n - 3)$$ are factors of $$a_n$$.

Thus, we have
$$a_n = (n - 1)(n - 2)(n - 3)$$

In this expression, if we substitute any value of $$n$$ which is greater than $$3$$, then each factor on the $$RHS$$ is positive.

Therefore,
$$a_n > 0$$ for all $$n > 3$$.

Hence, first three of them sequence are zero and all other terms are positive.

$$\underset{n \rightarrow \infty}{lim} \dfrac{1^P + 2^P + 3^P + ....+ n^P}{n^{P+ 1}}$$ equals-

$$\underset{n \rightarrow \infty}{lim} \dfrac{1^P + 2^P + 3^P + .... +n^P}{n^{P+ 1}}$$

$$=\underset{n \rightarrow \infty}{lim}\dfrac{1}{n} \dfrac{1^P + 2^P + 3^P + .... +n^P}{n^{P}}$$

$$=\underset{n \rightarrow \infty}{lim}\dfrac{1}{n}\left( \dfrac{1^P}{n^p} + \dfrac{2^P}{n^p} + \dfrac{3^P}{n^P} + .... +\dfrac{n^P}{n^{P}}\right)$$

$$=\underset{n \rightarrow \infty}{lim}\dfrac{1}{n}\sum\limits_{r=1}^{n}\left(\dfrac{r}{n}\right)^P$$

$$=\displaystyle\int\limits_{0}^{1}x^Pdx$$ [ From the definition of the definite integral]

$$=\dfrac{1}{P+1}$$.

Evaluate: $$\sum_\limits{r=1}^n (3r-1)(r+1)$$

$$\sum_{r=1}^{n}(3r-1)(r+1)$$

$$=\sum_{r=1}^{n}(3r^2+2r-1)$$

$$=\sum_{r=1}^{n}3r^2+\sum_{r=1}^{n}2r-\sum_{r=1}^{n}1$$

$$=3\sum_{r=1}^{n}r^2+2\sum_{r=1}^{n}r-1\sum_{r=1}^{n}1$$

$$=3\left ( \dfrac{n(n+1)(2n+1)}{6} \right )+2\left ( \dfrac{n(n+1)}{2} \right )-n$$

$$=\dfrac{n(n+1)(2n+1)}{2}+n(n+1)-n$$

$$=\dfrac{(n^2+n)(2n+1)}{2}+n^2$$

$$=\dfrac{2n^3+n^2+2n^2+n+2n^2}{2}$$

$$=\dfrac{2n^3+5n^2+n}{2}$$

Evaluate $$\sum _{ k=1 }^{ 11 }{ \left( 2+{ 3 }^{ k } \right) } $$

$$ \displaystyle \sum_{K=1}^{11}(2+3^{K})$$

$$= \displaystyle \sum_{K=1}^{11}2+\sum_{K=1}^{11}3^{K}$$

$$=11\times 2+\dfrac{(3)(3^{11}-1)}{(3-1)}$$

$$=22+\dfrac{3}{2}(3^{11}-1)$$

Solve :
$$ \dfrac {1}{1.2} + \dfrac {1}{2.3} + ...... + \dfrac {1}{n(n+1)} = ? $$

Consider $$n^{th}$$ term=$$\dfrac{1}{n(n+1)}$$

$$=\dfrac{(n+1)-{n}}{(n+1)n}$$

$$\boxed{n^{th}term=\dfrac{1}{n}-\dfrac{1}{(n+1)}}$$

$$\Rightarrow \dfrac{1}{1.2}=\dfrac{1}{1}-\dfrac{1}{2}$$

$$\dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}$$

$$\dfrac{1}{3.4}=\dfrac{1}{3}-\dfrac{1}{4}$$

$$\dfrac{1}{(n+1)}=\dfrac{1}{n}-\dfrac{1}{(n+1)}$$

On adding all terms we gen

$$\dfrac{1}{1.2}+\dfrac{1}{2.3}+.....\dfrac{1}{n(n+1)}=\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+.....\dfrac{1}{n}+\dfrac{1}{n}-\dfrac{1}{(n+1)}$$

$$\Rightarrow \left [\dfrac{1}{1.2}+\dfrac{1}{2.3}+.....\dfrac{1}{n.(n+1)}\right]=1-\dfrac{1}{n+1}$$

$$\boxed{\left[\dfrac{1}{1.2}+\dfrac{1}{2.3}+....\dfrac{1}{n.(nh)}\right]=\dfrac{(n+1)-1}{(n+1)}=\left (\dfrac{n}{n+1}\right)}$$

Obtain $$\sum\limits_{r = 2}^{10} {\left( {4{r^2} - 28r + 4a} \right)} $$

$$\displaystyle\sum^{10}_{r=2}(4r^2-28r+4a)$$

$$=4(2^2+3^2+.....+10^2)-28(2+3+...….+10)+(4a+4a+....9 times)$$

$$=4[(1^2+2^2+3^2+.....+10^2)-1]-28[(1+2+3+.....+10)-1]+36a$$

$$=4\left[\dfrac{10\times (10+1)\times (2\times 10+1)}{6}-1\right]-28\left(\dfrac{10\times 11}{2}-1\right)+36a$$

$$=4\times 384-28\times 54+36a$$

$$=1536-1512+36a$$

$$=36a+24$$.

Find the sum to $$n$$ terms of the series
$$1.2^{2}+2.3^{2}+3.4^{2}+...$$

$$1,2^{2}+2,3^{2}+3,4^{2}+$$….

$$Tn \Rightarrow n \left(n+1\right)^{2}$$ (General Term of this series)

$$=n \left(n^{2}+1+2n\right)$$

$$Tn=n^{3}+2n^{2}+n$$

$$Sn= \sum Tn= \sum n^{3}+\sum 2n^{2}+\sum n$$

$$=\left(\dfrac{n\left(n+1\right)}{2}\right)^{2}+2\left(\dfrac{n\left(n+1\right) \left(2n+1\right)}{6}\right)+ \dfrac{n\left(n+1\right)}{2}$$

$$\Rightarrow \dfrac{n\left(n+1\right)}{2} \left[\dfrac{n\left(n+1\right)}{2}\dfrac{2\left(2n+1\right)}{3}+1\right]$$

$$Sn\Rightarrow \dfrac{n\left(n+1\right)}{2} \left[\dfrac{3\left( n\left(n+1\right)\right)+4\left(2n+1\right)+6}{6}\right)$$

Find the sum to n terms of the sequence, $$8, 88, 888, 8888,....$$.

$$ 8+88+888+8888........... \\ 8\left[ { 1+11+111+1111+..... } \right] \\ \frac { 8 }{ 9 } \left[ { 9+99+999+..... } \right] \\ \frac { 8 }{ 9 } \left[ { \left( { 10-1 } \right) +\left( { 100-1 } \right) +\left( { 1000-1 } \right) +........to\, \, n\, \, term } \right] \\ \frac { 8 }{ 9 } \left[ { \left\{ { 10+100+1000+.......to\, \, n\, \, term } \right\} -n } \right] \\ \frac { 8 }{ 9 } \left[ { \left( { 10+{ { 10 }^{ 2 } }+{ { 10 }^{ 3 } }+.......+to\, \, n\, \, term } \right) -n } \right] \\ \frac { 8 }{ 9 } \left\{ { \frac { { 10\left( { { { 10 }^{ n-1 } } } \right) } }{ { \left( { 10-1 } \right) } } -n } \right\} \, \, =\, \, \frac { 8 }{ 9 } \, \, \left( { \frac { { { { 10 }^{ (n+1) } }-10-9n } }{ 9 } } \right) \, \, =\, \, \frac { 8 }{ { 81 } } \left( { { { 10 }^{ \left( { n+1 } \right) } }-9n-10 } \right) \, \, Ans. \\ $$

$$\cfrac{1}{1.3.5}+\cfrac{1}{3.5.7}+....$$ to $$n$$ terms.

This is

$$\sum _{ r=1 }^{ n }{ \cfrac { 1 }{ \left( 2r-1 \right) \left( 2r+1 \right) \left( 2r+3 \right) } } $$

$$=\sum { \cfrac { 1 }{ 2 } } \times \cfrac { \left( 2r+3 \right) -\left( 2r-1 \right) }{ \left( 2r-1 \right) \left( 2r+1 \right) \left( 2r+1 \right) } =\cfrac { 1 }{ 2 } \times \left[ \sum { \cfrac { 1 }{ \left( 2r-1 \right) \left( 2r+1 \right) } } -\sum { \cfrac { 1 }{ \left( 2r+1 \right) \left( 2r+3 \right) } } \right] $$

$$=\cfrac { 1 }{ 2 } \times \begin{bmatrix} \cfrac { 1 }{ 1.3 } -\cfrac { 1 }{ 3.5 } \\ \cfrac { 1 }{ 3.5 } -\cfrac { 1 }{ 5.7 } \\ --- \\ --- \\ -\cfrac { 1 }{ \left( 2n+1 \right) \left( 2n+3 \right) } \end{bmatrix}=\cfrac { 1 }{ 2 } \left[ \cfrac { 1 }{ 3 } -\cfrac { 1 }{ \left( 2n+1 \right) \left( 2n+3 \right) } \right] $$

Find the sum to $$n$$ terms of the series, whose $$n$$th term is given by $${(2n-1)}^{2}$$.

Given

$$a_n=(2n-1)^2$$

$$=4n^2-4n+1$$

Sum of n terms is

$$S_n=\sum_{n=1}^{n}{a_n}$$

$$=\sum_{n=1}^{n}{4n^2-4n+1}$$

$$=\sum_{n=1}^{n}{4n^2}-\sum_{n=1}^{n}{4n}+\sum_{n=1}^{n}{1}$$

$$=4\left(\dfrac{n(n+1)(2n+1)}{6}\right)-4\left(\dfrac{n(n+1)}{2}\right)+n$$

$$=2\left(\dfrac{2(n+1)(2n+1)-6(n+1)+3}{3}\right)$$

$$=\dfrac{n}{3}[(2n+2)(2n+1)-6n-6+3$$

$$=\dfrac{n}{3}[4n^2+2n+4n+2-6n-3]$$

$$=\dfrac{n}{3}[4n^2-1]$$

$$=\dfrac{n}{3}[(2n)^2-(1)^2]$$

$$=\dfrac{n}{3}[(2n-1)(2n+1)]$$

Find the sum of series upto $$n$$ terms whose $${ n }^{ th }$$ term is $${\left( {2n - 1} \right)^2}$$

Consider the problem

Given

$$\begin{array}{l} { a_{ n } }={ \left( { 2n-1 } \right) ^{ 2 } } \\ ={ \left( { 2n } \right) ^{ 2 } }+{ \left( 1 \right) ^{ 2 } }-2\left( { 2n } \right) \left( 1 \right) \\ =4{ n^{ 2 } }+1-4n \\ =4{ n^{ 2 } }-4n+1 \end{array}$$

Sum of $$n$$ term is

$$\begin{array}{l} { s_{ n } }=\sum _{ n=1 }^{ n }{ { a_{ n } } } \\ =\sum _{ n=1 }^{ n }{ 4{ n^{ 2 } }-4n+1 } \\ =\sum _{ n=1 }^{ n }{ 4{ n^{ 2 } }-\sum _{ n=1 }^{ n }{ 4n+\sum _{ n=1 }^{ n } 1 } } \\ =4\sum _{ n=1 }^{ n }{ { n^{ 2 } }-4\sum _{ n=1 }^{ n }{ n+\sum _{ n=1 }^{ n } 1 } } \\ =4\left( { \frac { { n\left( { n+1 } \right) \left( { 2n+1 } \right) } }{ 6 } } \right) -4\left( { \frac { { n\left( { n+1 } \right) } }{ 2 } } \right) +n \\ =n\left( { \frac { { n\left( { n+1 } \right) \left( { 2n+1 } \right) } }{ 6 } } \right) -4\left( { \frac { { n\left( { n+1 } \right) } }{ 2 } +1 } \right) \\ =n\left( { \frac { 2 }{ 3 } \left( { n+1 } \right) \left( { 2n+1 } \right) -2\left( { n+1 } \right) +1 } \right) \\ =n\left( { \frac { { 2\left( { n+1 } \right) \left( { 2n+1 } \right) -6\left( { n+1 } \right) +3 } }{ 3 } } \right) \\ =\frac { n }{ 3 } \left[ { \left( { 2n+2 } \right) \left( { 2n+1 } \right) -6n-6+3 } \right] \\ =\frac { n }{ 3 } \left[ { 4{ n^{ 2 } }+2n+4n+2-6n-3 } \right] \\ =\frac { n }{ 3 } \left[ { 4{ n^{ 2 } }+6n-6n-1 } \right] \\ =\frac { n }{ 3 } \left[ { 4{ n^{ 2 } }-1 } \right] \\ =\frac { n }{ 3 } \left[ { { { \left( { 2n } \right) }^{ 2 } }-{ { \left( 1 \right) }^{ 2 } } } \right] \\ =\frac { n }{ 3 } \left[ { \left( { 2n-1 } \right) \left( { 2n+1 } \right) } \right] \end{array}$$

Hence, the required sum is $$\frac { n }{ 3 } \left[ { \left( { 2n-1 } \right) \left( { 2n+1 } \right) } \right]$$

Find the sum of $$1 + 5 + {5^2} + ....$$ upto 8 terms.

$$\begin{array}{l} sum\, \, of1+5+{ 5^{ 2 } }+{ 5^{ 3 } }\, \, ...\, \, up\, \, 8th\, \, terms \\ \left( a \right) First\, \, term=1 \\ common\, \, ratio\left( r \right) =5 \\ Sum\, \, of\, \, 8th\, \, term=\frac { { a\left( { { r^{ n } }-1 } \right) } }{ { r-1 } } =\frac { { 1\left( { { 5^{ 8 } }-1 } \right) } }{ { 5-1 } } =\frac { { { 5^{ 8 } }-1 } }{ 4 } \end{array}$$

Find the sum of the series $$2 ^ { 2 } + 4 ^ { 2 } + 6 ^ { 2 } + \ldots + ( 2 n ) ^ { 2 }$$

$$ 2^{2}+4^{2}+6^{2}+...(2n)^{2}$$

let $$Tn=(2n)^{2}=4n^{2}$$

$$ \sum Tn = \sum 4n^{2}$$

$$ = 4\sum n^{2}$$

$$ = \frac{4n(n+1)(2n+1)}{6}$$

$$ = \frac{2}{3}n(n+1)(2n+1)$$

1141738_1246910_ans_bc5b3bafb08f44349cd60148d6ee1b28.jpg

Show that $$1^{2}+(1^{2}+2^{2})+(1^{2}+2^{2}+3^{2})+........$$ upto $$n$$ terms $$=\dfrac{n(n+1)^{2}(n+2)}{12}, \forall n \in N$$

Formuale being used:

$$\sum_{i=1}^{n}i=\dfrac{n(n+1)}{2}$$

$$\sum_{i=1}^{n}i^2=\dfrac{n(n+1)(2n+1)}{6}$$

$$\sum_{i=1}^{n}i^3=\dfrac{n^2(n+1)^2}{4}$$

Given,

$$1^2+(1^2+2^2)+(1^2+2^2+3^2)+..............+(1^2+2^2+3^2+........+n^2)$$

$$=\sum_{i=1}^{n}(1^2+2^2+3^2+........+i^2)$$

$$=\sum_{i=1}^{n}\sum_{j=1}^{i}j^2$$

$$=\sum_{i=1}^{n}\dfrac{i(i+1)(2i+1)}{6}$$

$$=\sum_{i=1}^{n}\dfrac{2i^3+3i^2+i}{6}$$

$$=\sum_{i=1}^{n}\dfrac{1}{3}i^3+\sum_{j=1}^{n}\dfrac{1}{2}j^2+\sum_{k=1}^{n}\dfrac{1}{6}k$$

$$=\dfrac{1}{3}\left ( \dfrac{n^2(n+1)^2}{4} \right )+\dfrac{1}{2}\left ( \dfrac{n(n+1)(2n+1)}{6} \right )+\dfrac{1}{6}\left (\dfrac{n(n+1)}{2} \right )$$

$$=\dfrac{n^2(n+1)^2+n(n+1)(2n+1)+n(n+1)}{12}$$

$$=\dfrac{n(n+1)[n(n+1)+(2n+1)+1]}{12}$$

$$=\dfrac{n(n+1)(n^2+3n+2)}{12}$$

$$=\dfrac{n(n+1)^2(n+2)}{12}$$

Find the sum of the series whose $$n^{th}$$ term is :
$$2n^{3}+3n^{2}-1$$

$$n^{th}$$ term is $$t_{n}=2n^{3}+3n^{2}-1$$

$$S_{n}=\sum_{k=1}^{n}(2k^{3}+3k^{2}-1)$$

$$=\sum_{k=1}^{n}2k^{3}+\sum_{k=1}^{n}3k^{2}-\sum_{k=1}^{n}1$$

$$=2\sum_{k=1}^{n}k^{3}+3\sum_{k=1}^{n}k^{2}-\sum_{k=1}^{n}1$$

$$=2(\frac{n^{2}(n+1)^{2}}{4})+3(\frac{n(n+1)(2n+1)}{6})-n$$

$$=\frac{n^{2}(n+1)^{2}}{2}+\frac{n(n+1)(2n+1)}{2}-n$$

$$=\frac{n^{2}(n^{2}+1+2n)+(n^{2}+n)(2n+1)-2n}{2}$$

$$=\frac{n^{4}+n^{2}+2n^{3}+2n^{3}+3n^{2}+n-2n}{2}=\frac{n^{4}+4n^{3}+4n^{2}-n}{2}$$

1186827_1292317_ans_014a1721b30d41aabbc00b6bef156d31.jpg

$$\left( r+1 \right) ^{ 2 }+\left( r+2 \right) ^{ 2 }+....+{ n }^{ 2 }$$

We have,

$${{\left( r+1 \right)}^{2}}+{{\left( r+2 \right)}^{2}}+......+{{n}^{2}}$$

Let $$r+1=m$$

So,

$$ {{m}^{2}}+{{\left( m+1 \right)}^{2}}+{{\left( m+2 \right)}^{2}}+......+{{n}^{2}} $$

$$ \Rightarrow \sum\limits_{1}^{n}{{{m}^{2}}} $$

$$ \Rightarrow \sum\limits_{1}^{n}{{{\left( r+1 \right)}^{2}}} $$

Hence, this is the answer.

Find sum of $$n$$ terms of following series ?
$$1 + 3 x + 5 x ^ { 2 } + 7 x ^ { 3 } + \dots$$

$$S=1+3x+{ 5x }^{ 2 }+{ 7x }^{ 3 }+......+\left( 2n+1 \right) { x }^{ n }$$

$$\underline { xS=x+{ 3x }^{ 2 }+{ 5x }^{ 3 }+......+\left( 2n-1 \right) { x }^{ n }+{ \left( 2n+1 \right) }^{ n+1 }x } $$

$$\Rightarrow S\left( 1-x \right) =1+2x+{ 2x }^{ 2 }+{ 2x }^{ 3 }+......+{ 2x }^{ n }+\left( 2n+1 \right) { x }^{ n+1 }$$

$$=\left[ 1+\left( 2n+1 \right) { x }^{ n+1 } \right] +2x\left( 1+x+{ x }^{ 2 }+......{ x }^{ n } \right) $$

$$\Rightarrow S=\left\{ \left[ 1+\left( 2n+1 \right) { x }^{ n+1 } \right] +\dfrac { 2x\left( { x }^{ n }-1 \right) }{ \left( x-1 \right) } \right\} \dfrac { 1 }{ \left( 1-x \right) } $$

For all real numbers $$a, b$$ and positive integer $$n$$ prove that:
$$(a+b)^{n}=^{n}C_{0}a^{n}+^{n}C_{1}a^{n-1}b+^{n}C_{1}a^{n-2}b^{2}+..........+^{n}C_{n}b^{n}$$.

$$\begin{array}{l} { \left( { a+b } \right) ^{ n } }{ =^{ n } }{ c_{ 0 } }{ a^{ n } }{ =^{ n } }{ c_{ 1 } }{ a^{ n-1 } }b{ +^{ n } }{ c_{ 2 } }{ a^{ n-2 } }{ b^{ 2 } }+.......{ +^{ n } }{ c_{ n } }{ b^{ n } } \\ \Rightarrow { \left( { a+b } \right) ^{ 1 } }{ =^{ 1 } }{ c_{ 0 } }{ a^{ 1 } }{ +^{ 1 } }{ c_{ 1 } }{ a^{ 0 } }b=\left( { a+b } \right) \\ \Rightarrow \left( { a+{ b^{ 2 } } } \right) { =^{ 2 } }{ c_{ 0 } }{ a^{ 2 } }{ +^{ 2 } }{ c_{ 1 } }ab{ +^{ 2 } }{ c_{ 2 } }{ b^{ 2 } }={ a^{ 2 } }+2ab+{ b^{ 2 } } \\ \Rightarrow { \left( { a+b } \right) ^{ 3 } }=3{ c_{ 0 } }{ a^{ 3 } }{ +^{ 3 } }{ c_{ 1 } }{ a^{ 2 } }b{ +^{ 3 } }{ c_{ 2 } }a{ b^{ 2 } }+3{ c_{ 3 } }{ a^{ 0 } }{ b^{ 3 } }={ a^{ 3 } }+3{ a^{ 2 } }b+3a{ b^{ 2 } }+{ b^{ 3 } } \\ \Rightarrow \therefore { \left( { a+b } \right) ^{ n } }{ =^{ n } }{ c_{ 0 } }{ a^{ n } }{ =^{ n } }{ c_{ 1 } }{ a^{ \left( { n-1 } \right) } }b{ +^{ n } }{ c_{ 2 } }{ a^{ \left( { n-2 } \right) } }{ b^{ 2 } }+......{ +^{ n } }{ c_{ n } }{ b^{ n } }. \end{array}$$

Prove that
$$\dfrac {C_{1}}{C_{0}}+\dfrac {2C_{2}}{C_{1}}+\dfrac {3C_{3}}{C_{2}}+....+\dfrac {n.C_{n}}{C_{n-1}}=\dfrac {n(n+1)}{2}$$

We have,

$$\dfrac{kC_k}{C_{k-1}}=\dfrac{k \binom {n}{k}} {\binom{n}{k-1}}$$

$$=k\cdot \dfrac{n!}{k!(n-k)!}\dfrac{(k-1)!(n-k+1)!}{n!}$$

$$=k\cdot \dfrac{(n-k+1)}{k}$$

$$=n-k+1$$

$$k=1\rightarrow \dfrac{C_1}{C_0}=n$$

$$k=2\rightarrow \dfrac{2C_2}{C_1}=n-1$$

$$k=3\rightarrow \dfrac{3C_3}{C_2}=n-2$$

$$k=n\rightarrow \dfrac{nC_n}{C_{n-1}}=1$$

On adding all the above terms, we get,

$$\dfrac{C_1}{C_0}+\dfrac{2C_2}{C_1}+\dfrac{3C_3}{C_2}+.........+\dfrac{nC_n}{C_{n-1}}=n+(n-1)+(n-2)+......+1$$

$$=\dfrac {n(n+1)}{2}$$

Hence proved.

Write the first five terms of the sequence and obtain the corresponding series:
$$a_{1}=a_{2}=2,a_{n}=a_{n-1}-1,n > 2$$

Given,

$$a_1=a_2=2$$

Formula,

$$a_n=a_{n-1}-1$$

$$a_3=a_{3-1}-1$$

$$=a_2-1=2-1=1$$

$$a_4=a_{4-1}-1$$

$$=a_3-1=1-1=0$$

$$a_5=a_{5-1}-1$$

$$=a_4-1=0-1=-1$$

Hence the first five terms of the series are:

$$2,2,1,0,-1$$

Evaluate:
$$\dfrac{1+\dfrac{1}{2!}+\dfrac{1}{3!}+.......}{1+\dfrac{1}{3!}+\dfrac{1}{5!}+.......}$$.

We've,

$$e=1+\dfrac{1}{1!}+\dfrac{1}{2!}+.......$$.

And,

$$e^{-1}=1-\dfrac{1}{1!}+\dfrac{1}{2!}-......$$.

Then $$e+e^{-1}=2(1+\dfrac{1}{2!}+\dfrac{1}{4!}+......)$$.....(1) and $$e-e^{-1}=2(1+\dfrac{1}{3!}+\dfrac{1}{5!}+......)$$.....(2).

Now,

$$\dfrac{1+\dfrac{1}{2!}+\dfrac{1}{3!}+.......}{1+\dfrac{1}{3!}+\dfrac{1}{5!}+.......}$$

$$=\dfrac{\dfrac{1}{2}(e+e^{-1})}{\dfrac{1}{2}(e-e^{-1})}$$

$$=\dfrac{e^2+1}{e^2-1}$$.

Find the coefficient of $$x$$ in the expansion of $$\left( 1+\dfrac { x }{ 1! } +\dfrac { x^2 }{ 2! } +\dfrac { x^3 }{ 3! } +...+\dfrac { x^n }{ n! } \right) $$

$$1 + \cfrac{x}{1!} + \cfrac{{x}^{2}}{2!} + \cfrac{{x}^{3}}{3!} + ..... + \cfrac{{x}^{n}}{n!}$$

Therefore,

Coefficient of $$x = \cfrac{1}{1!} = \cfrac{1}{1} = 1$$

Hence the coefficient of $$x$$ in the given expression is $$1$$.

The sum, $$\sum _{ n=1 }^{ 7 }{ \cfrac { n\left( n+1 \right) \left( 2n+1 \right) }{ 4 } } $$ is equal to ________

$$= \sum_{n = 1}^7 \dfrac{n (n + 1) (2n + 1)}{4}$$

$$=\dfrac{1}{4} \sum_{n = 1}^7 (2n^3 + 3n^2 + n)$$
$$=\dfrac{1}{4} \left[2 . \left(\dfrac{n. (n + 1)}{2}\right)^2 + 3 \dfrac{n (n + 1)(2n + 1)}{6} + \dfrac{n(n + 1)}{2} \right]$$

$$=\dfrac{1}{4} \left[2 . \left(\dfrac{7. (7 + 1)}{2}\right)^2 + 3 \dfrac{7 (7 + 1)(2.7 + 1)}{6} + \dfrac{7(7 + 1)}{2} \right]$$

$$=\dfrac{1}{4} \left[2 \times \dfrac{7^2 . 8^2}{4} + \dfrac{7 \times 8 \times 15}{2} + \dfrac{7 \times 8}{2}\right)$$

$$=\dfrac{1}{4} (1568 + 420 + 28)$$

$$= 504$$

Determine whether the following series is convergent or divergent
$$\displaystyle \frac {1}{1^p}+\frac {1}{3^p}+\frac {1}{5^p}+\frac {1}{7^p}+.....$$

We have to find the given series is convergent or not

$$\dfrac{1}{1^p}+\dfrac{1}{3^p}+\dfrac{1}{5^p}+\dfrac{1}{7^p}+....+\dfrac{1}{(2n-1)^p}$$

$$u_n=\dfrac{1}{(2n-1)^p};$$ $$u_{n+1}=\dfrac{1}{(2n+1)^p}$$

$$\Rightarrow$$ $$\dfrac{u_{n+1}}{u_n}=\dfrac{(2n-1)^p}{2n+1)^p}=\dfrac{2^pn^p\left(1-\dfrac{1}{2n}\right)^p}{2^pn^p\left(1+\dfrac{1}{2n}\right)^p}$$

$$\displaystyle\lim_{n\rightarrow\infty}\dfrac{u_{n+1}}{u_n}=\dfrac{1-0}{1+0}=1$$

$$\therefore$$ Ratio test fails.

Now, take $$v_n=\dfrac{1}{n^p}$$

$$\dfrac{u_n}{v_n}=\dfrac{n^p}{(2n-1)^p}=\dfrac{1}{2^p\left(1-\dfrac{1}{2n}\right)^p}$$

$$\Rightarrow$$ $$\displaystyle\lim_{n\rightarrow\infty}\dfrac{u_n}{v_n}=\dfrac{1}{2^p}$$

Which is non-zero and finite.

$$\therefore$$ By comparison test, $$\sum u_n$$ and $$\sum v_n$$ both converge or both diverge.

But by $$p-$$ series test,

$$\sum v_n=\sum\dfrac{1}{n^p}$$ converges, when $$p>1$$ and diverges when $$p\le 1$$

$$\therefore$$ $$\sum u_n$$ is convergent if $$p>1$$ and divergent if $$p\le 1.$$

Find the general term and the sum of $$n$$ terms of the series:
$$2,5,12,31,86,......$$

1979060_1744873_ans_0d3fdf033bb245dea90372b4db15e5d4.jpg

Determine whether the following series is convergent or divergent
$$\displaystyle 1+ \frac {1}{2^2}+\frac {2^2}{3^3}+\frac {3^3}{4^4}+\frac {4^4}{5^5}....$$

Neglecting the first term, the series is $$\dfrac{1}{2^2}+\dfrac{2^2}{3^3}+\dfrac{3^3}{4^4}+...\dfrac{n^n}{(n+1)^{n+1}}$$

$$u_n=\dfrac{n^n}{(n+1)^{n+1}}=\dfrac{n^n}{(n+1)(n+1)}n=\dfrac{n^n}{n\left(1+\dfrac{1}{n}\right)n^n\left(1+\dfrac{1}{n}\right)^n}$$

$$u_n=\dfrac{1}{n\left(1+\dfrac{1}{n}\right)\left(1+\dfrac{1}{n}\right)^n}$$

Take $$v_n=\dfrac{1}{n}$$

$$\therefore$$ $$\displaystyle\lim_{n\rightarrow\infty}\dfrac{u_n}{v_n}=\lim_{n\rightarrow \infty}\dfrac{1}{\left(1+\dfrac{1}{n}\right)\left(1+\dfrac{1}{n}\right)^n}=\lim_{n\rightarrow \infty}\dfrac{1}{\left(1+\dfrac{1}{n}\right)^n.1}=\dfrac{1}{e}$$

Which is finite and $$\sum v_n=\sum\dfrac{1}{n}$$ is divergent by $$p-$$ series test $$(p=1)$$

$$\therefore$$ $$\sum u_n$$ is divergent.

Determine whether the following series is convergent or divergent
$$\displaystyle1 + \frac {2}{5}x+\frac {6}{9}x^2+\frac {14}{17}x^3+....+\frac {2^n-2}{2^n+1}x^{n-1}+....$$

Neglecting the first term,

$$u_n=\left(\dfrac{2^n-2}{2^n+1}\right)x^{n-1},\,(n\ge 2)$$ and $$u_n$$ are all positive.

$$u_{n+1}=\dfrac{(2^{n+1}-2)}{(2^{n+1}+1)}x^{n-1}$$

$$\displaystyle\lim_{n\rightarrow\infty}\dfrac{u_{n+1}}{u_n}=\lim_{n\rightarrow \infty}\left(\dfrac{2^{n+1}-2}{2^{n+1}+1}\right)\times\left(\dfrac{2^n+1}{2^n-2}\right)x$$

$$=\displaystyle\lim_{n\rightarrow \infty}\left[\dfrac{2^{n+1}(1-1/2^n)}{2^{n+1}(1+1/2^{n+1})}\times \dfrac{2^(1+1/2^n)}{2^n(1-2/2^n)}.x\right]$$

$$=x$$

Hence, by ratio test, $$\sum u_n$$ converges if $$x<1$$ and diverges if $$x>1$$.

When $$x=1,$$ the test fails.

Then, $$u_n=\dfrac{2^n-2}{2^n+1}$$

$$\Rightarrow$$ $$\displaystyle\lim_{n\rightarrow\infty}u_n=1\ne 0$$

$$\therefore$$ $$\sum u_n$$ diverges.

Hence, $$\sum u_n$$ is convergent when $$x<1$$ and divergent $$x>1$$

If $$y=x+ x^2 + x^3 + ...\infty$$, where $$|x| < 1$$, then prove that

$$x= \left( \dfrac{y}{1+y} \right)$$

$$y= x(1+x+x^2 + ...\infty)$$
$$\implies y(1-x) = x$$
$$x= \left( \dfrac{y}{1+y} \right)$$

Prove that $$\left(\displaystyle a+\frac{1}{b+}\frac{1}{a+}\frac{1}{b+}\frac{1}{a+}....\right)\left(\displaystyle\frac{1}{b+}\frac{1}{a+}\frac{1}{b+}\frac{1}{a+}....\right)=\displaystyle \frac{a}{b}$$.

Let $$x=a+\cfrac { 1 }{ b+ } \cfrac { 1 }{ a+ } \cfrac { 1 }{ b+ } \cfrac { 1 }{ a+ } .....$$

$$=a+\cfrac { 1 }{ b+\cfrac { 1 }{ a+x-a } } =a+\cfrac { x }{ bx+1 } $$

Thus $$b{ x }^{ 2 }+x=abx+x+a$$

$$\Rightarrow b{ x }^{ 2 }-abx-a=0$$

$$\Rightarrow x=\cfrac { ab+\sqrt { { a }^{ 2 }{ b }^{ 2 }+4ab } }{ 2b } $$

$$\Rightarrow y=\cfrac { 1 }{ b+\cfrac { 1 }{ a+y } } =\cfrac { a+y }{ ab+by+1 } $$

$$\Rightarrow aby+b{ y }^{ 2 }+y=a+y$$

$$\Rightarrow b{ y }^{ 2 }+aby-a=0$$

$$\Rightarrow y=\cfrac { -ab+\sqrt { { a }^{ 2 }{ b }^{ 2 }+4ab } }{ 2b } $$

$$\Rightarrow xy=\cfrac { { a }^{ 2 }{ b }^{ 2 }+4ab-{ a }^{ 2 }{ b }^{ 2 } }{ 4{ b }^{ 2 } } $$

$$=\cfrac { a }{ b } $$

Hence, proved.

Find the sum of the infinite series $$1 + \dfrac{2}{3}.\dfrac{1}{2} + \dfrac{2.5}{3.6}(\dfrac{1}{2})^{2} + \dfrac{2.5.8}{3.6.9}(\dfrac{1}{2})^{3} + ....\infty$$

The given infinite series is,

$$S=1+\frac { 2 }{ 3 } .\frac { 1 }{ 2 } +\frac { 2 }{ 3 } .\frac { 5 }{ 6 } .{ \left( \frac { 1 }{ 2 } \right) }^{ 2 }+\frac { 2 }{ 3 } .\frac { 5 }{ 6 } .\frac { 8 }{ 9 } .{ \left( \frac { 1 }{ 2 } \right) }^{ 3 }------------$$ (1)

Now, expansion of binomial series $${ \left( 1+x \right) }^{ n }$$ is given by,

$${ \left( 1+x \right) }^{ n }=1+nx+\frac { n\left( n-1 \right) }{ 2! } { x }^{ 2 }+\frac { n\left( n-1 \right) \left( n-2 \right) }{ 3! } { x }^{ 2 }+----------$$ (2)

Comparing equation (1) and (2), first term of both equations is same.

Thus, comparing second term of both equations, we get,

$$nx=\frac { 2 }{ 3 } \times \frac { 1 }{ 2 } $$

$$\therefore nx=\frac { 1 }{ 3 } $$

Squaring both sides, we get,

$$\therefore { n }^{ 2 }{ x }^{ 2 }=\frac { 1 }{ 9 } $$

$$\therefore { x }^{ 2 }=\frac { 1 }{ 9{ n }^{ 2 } } $$ (3)

Comparing third term of both series, we get,

$$\frac { n\left( n-1 \right) }{ 2! } { x }^{ 2 }=\frac { 2 }{ 3 } .\frac { 5 }{ 6 } .{ \left( \frac { 1 }{ 2 } \right) }^{ 2 }$$

$$\therefore \frac { n\left( n-1 \right) }{ 2 } { x }^{ 2 }=\frac { 5 }{ 9 } .\frac { 1 }{ 4 } $$

$$\therefore \frac { n\left( n-1 \right) }{ 2 } { x }^{ 2 }=\frac { 5 }{ 36 } $$

From equation (3),

$$\therefore \frac { n\left( n-1 \right) }{ 2 } .\frac { 1 }{ 9{ n }^{ 2 } } =\frac { 5 }{ 36 } $$

$$\therefore n\left( n-1 \right) \times \frac { 1 }{ { n }^{ 2 } } =\frac { 5\times 18 }{ 36 } $$

$$\therefore \frac { \left( n-1 \right) }{ { n } } =\frac { 5 }{ 2 } $$

$$\therefore \left( n-1 \right) =\frac { 5 }{ 2 } n$$

$$\therefore \frac { 5 }{ 2 } n-n=-1$$

$$\therefore \frac { 3 }{ 2 } n=-1$$

$$\therefore n=\frac { -2 }{ 3 } $$

From equation (1),

$$\frac { -2 }{ 3 } x=\frac { 1 }{ 3 } $$

$$\therefore x=\frac { -1 }{ 2 } $$

Thus, sum of series is given by,

$$S={ \left( 1+x \right) }^{ n }$$

$$S={ \left( 1-\frac { 1 }{ 2 } \right) }^{ \frac { -2 }{ 3 } }$$

$$S={ \left( \frac { 1 }{ 2 } \right) }^{ \frac { -2 }{ 3 } }$$

$$\therefore S=\frac { 1 }{ { \left( 2 \right) }^{ \frac { -2 }{ 3 } } } $$

$$\therefore S={ \left( 2 \right) }^{ \frac { 2 }{ 3 } }$$

$$\therefore S={ \left( 4 \right) }^{ \frac { 1 }{ 3 } }$$

Find sum of $$3+33+333+3333+$$....... up to n terms.

From the given series, take common factor 3

Thus

$$S=3(1+11+111+1111+...............nth term)$$

$$S=3\left\{ 1+\left( 1+10 \right) +\left( 1+10+100 \right) +\left( 1+10+100+1000 \right) +...to\quad n\quad terms \right\}$$

Thus the nth term.

$${ t }_{ n }=1+10+100+..............+{ 10 }^{ n-1 }$$

This is a G.P. where first term is 1 and common ratio is 10 ,

Thus sum of n terms is

$${ t }_{ n }=\dfrac { 1\left( 1-{ 10 }^{ n } \right) }{ 1-10 } \\ { t }_{ n }=\dfrac { \left( { 10 }^{ n }-1 \right) }{ 9 }$$

Thus

$$S=3\sum _{ i=1 }^{ n }{ { t }_{ n } } =3\sum _{ i=1 }^{ n }{ \dfrac { { 10 }^{ n }-1 }{ 9 } } $$

Hence the sum,

$$S=3\sum { \dfrac { { 10 }^{ n } }{ 9 } - } 3\sum { \dfrac { 1 }{ 9 } } $$

$$S=3\left\{ \dfrac { 10\left( 1-{ 10 }^{ n } \right) }{ \left( 1-10 \right) .9 } -\left( \dfrac { 1 }{ 9 } \right) .n \right\} $$

$$S=3\left\{ 10.\dfrac { \left( { 10 }^{ n }-1 \right) }{ 81 } -\dfrac { n }{ 9 } \right\} $$

Thus,

$$S=\left\{ 10.\dfrac { \left( { 10 }^{ n }-1 \right) }{ 27 } -\dfrac { n }{ 3 } \right\} \\ =\dfrac { { 10 }^{ n+1 }-10-9n }{ 27 } $$

Find the sum of the series $$(1^2+1)1!+(2^2+1)2!+(3^2+1)3!+......(n^2+1)n!$$

$$n!=1\times2\dots n$$
$$(n+1)n! = 1\times2\dots n\times(n+1)=(n+1)!$$         $$(P)$$
------------------------------------------------------------------------

$$S=\displaystyle\sum_{k=1}^{n}(k^2+1)k!$$

$$=\displaystyle\sum_{k=1}^{n}(k^2+2k+1-2k)k!$$

$$=\displaystyle\sum_{k=1}^{n}((k+1)^2-2k)k!$$

$$=\displaystyle\sum_{k=1}^{n}(k+1)^2k!-2k\cdot k!$$

$$=\displaystyle\sum_{k=1}^{n}(k+1)\cdot(k+1)!-2k\cdot k!$$         (using $$(P)$$)

$$=\displaystyle\sum_{k=1}^{n}[(k+1)\cdot(k+1)!-k\cdot k!] - \displaystyle\sum_{k=1}^{n}k\cdot k!$$

$$=(n+1)(n+1)!-1\cdot1! -\displaystyle\sum_{k=1}^{n}(k+1-1)k!$$

$$=(n+1)(n+1)!-1 -\left[\displaystyle\sum_{k=1}^{n}(k+1)k!-k!\right]$$

$$=(n+1)(n+1)!-1 -\left[\displaystyle\sum_{k=1}^{n}(k+1)!-k!\right]$$         (using $$(P)$$)

$$=(n+1)(n+1)!-1 -\left[(n+1)!-1!\right]$$

$$=(n+1)(n+1)!-(n+1)!$$

$$=\boxed{n(n+1)!}$$

$$3+33+333+.....+$$n terms.

$$\begin{array}{l} S=3+33+333+.....+n\, \, term\, \, is \\ S=3\left( { 1+11+111+.....+n } \right) \\ S=\frac { { 3\times 9 } }{ 9 } \left( { 1+11+111+.......n } \right) \\ S=\frac { 3 }{ 9 } \left( { 9+99+999+.....+n } \right) \\ S=\frac { 3 }{ 9 } \left( { 10-1 } \right) +\left( { 100-1 } \right) +\left( { { { 10 }^{ 2 } }-1 } \right) +...+n \\ S=\frac { 3 }{ 9 } \left[ { \left( { 10+{ { 10 }^{ 2 } }+{ { 10 }^{ 3 } }+{ { .....10 }^{ n } } } \right) -\left( n \right) } \right] \\ The\, \, sense\, \, in\, GP,\, \, then \\ S=\frac { 1 }{ 3 } \left( { \frac { { 10\left( { { { 10 }^{ n } }-1 } \right) } }{ { 10-1 } } -n } \right) \\ S=\frac { 1 }{ 3 } \left( { \frac { { { { 10 }^{ n+1 } }-10 } }{ 9 } -n } \right) \\ S=\frac { 1 }{ 3 } \left( { \frac { { { { 10 }^{ n+1 } }10-9n } }{ 9 } } \right) \\ S=\frac { 1 }{ { 27 } } \left[ { { { 10 }^{ n+1 } }-9n-10 } \right] \end{array}$$

The sum of the series $$\displaystyle \sum _{ k=1 }^{ 62 }{ \frac { 1 }{ \left( k+2 \right) \sqrt { k+1 } +\left( k+1 \right) \sqrt { k+2 } } } $$.

$$\sum_{k =1}^{62} \dfrac{1}{(k+2) \sqrt{k+1}+ (k+1) \sqrt{k+2}}$$

$$\sum_{k=1}^{62} \dfrac{(k+2)-(k+1)}{(k+2) \sqrt{k+1}+ (k+1) \sqrt{k+2}}$$

$$S_{n} = \sum_{k=1}^{62} \left[ \dfrac{1}{\sqrt{k+1}}- \dfrac{1}{\sqrt{k+2}} \right]$$

$$S_{1}= \dfrac{1}{\sqrt{2}}- \dfrac{1}{\sqrt{3}}$$

$$S_{2}= \dfrac{1}{\sqrt{3}}- \dfrac{1}{\sqrt{4}}$$

$$S_{3}= \dfrac{1}{\sqrt{4}}- \dfrac{1}{\sqrt{5}}$$

$$S_{62}=\dfrac{1}{\sqrt{63}}- \dfrac{1}{\sqrt{64}}$$

Adding the above sums, we get

$$S_{62} = \sum_{k=1}^{62} = \dfrac{1}{\sqrt{2}}- \dfrac{1}{\sqrt{64}} = \dfrac{1}{\sqrt{2}}- \dfrac{1}{8}= \dfrac{8- \sqrt{2}}{8 \sqrt{2}}= \dfrac{8 \sqrt{2}-2}{8.2}$$

$$=\dfrac{2 (4 \sqrt{2}-1)}{8 \times 2} = \dfrac{4 \sqrt{2}-1}{8} = S_{62}$$

How many three-digit numbers are there with no digit repeated?

$$\begin{array}{l} Digits\, \, \, we\, \, have \\ 0,1,2,3,4,5,6,7,8,9 \\ 9=1-9 \\ 9=0-9 \\ 8= \\ (i)\, \, for\, I\, we\, \, have\, \, 9\, \, choices\, \, 1-9 \\ (ii)\, \, for\, \, II\, \, we\, \, have\, \, \, 9\, \, choices\, \, except\, I \\ (iii)\, \, for\, \, III\, \, we\, \, have\, \, 8\, \, choices \end{array}$$

Find the sum of the series $$1.3^{2}+2.5^{2}+3.7^{2}+$$ to $$n$$ terms.

$$\begin{array}{l} S={ 1.3^{ 2 } }+{ 2.5^{ 2 } }+{ 3.7^{ 2 } }+...... \\ S=\sum _{ r=1 }^{ n }{ r{ { \left( { 2r+1 } \right) }^{ 2 } } } \\ =\sum { r\left( { 4{ r^{ 2 } }+1+4r } \right) } =4\sum { { r^{ 3 } } } +\sum r+4\sum { { r^{ 2 } } } \\ =\frac { { 4{ { \left[ { n\left( { n+1 } \right) } \right] }^{ 2 } } } }{ 4 } +\frac { { n\left( { n+1 } \right) } }{ 2 } +4\frac { { n\left( { n+1 } \right) \left( { 2n+1 } \right) } }{ 6 } \\ ={ n^{ 2 } }{ \left( { n+1 } \right) ^{ 2 } }+\frac { { n\left( { n+1 } \right) } }{ 2 } +\frac { 2 }{ 3 } \left( n \right) \left( { n+1 } \right) \left( { 2n+1 } \right) \\ =n\left( { n+1 } \right) \left[ { n\left( { n+1 } \right) +\frac { 1 }{ 2 } +\frac { 2 }{ 3 } \left( { 2n+1 } \right) } \right] \\ =n\left( { n+1 } \right) \left[ { { n^{ 2 } }+\frac { { 7n } }{ 3 } +\frac { 7 }{ 6 } } \right] \\ \end{array}$$

Solve:
$$\frac{1}{{2.5}} + \frac{1}{{5.8}} + \frac{1}{{8.11}} + ...\frac{1}{{(3n - 1)(3n + 2)}}$$

1213639_1438144_ans_9453d8612050407bad0cd1c55cd61dd0.jpg

Sequences And Series - Class 11 Commerce Maths - Extra Questions

Find the following sum.$$\sum\limits_{r = 1}^n {\left( {6{r^2} - 2r + 6} \right)} $$