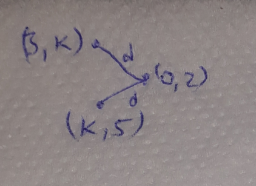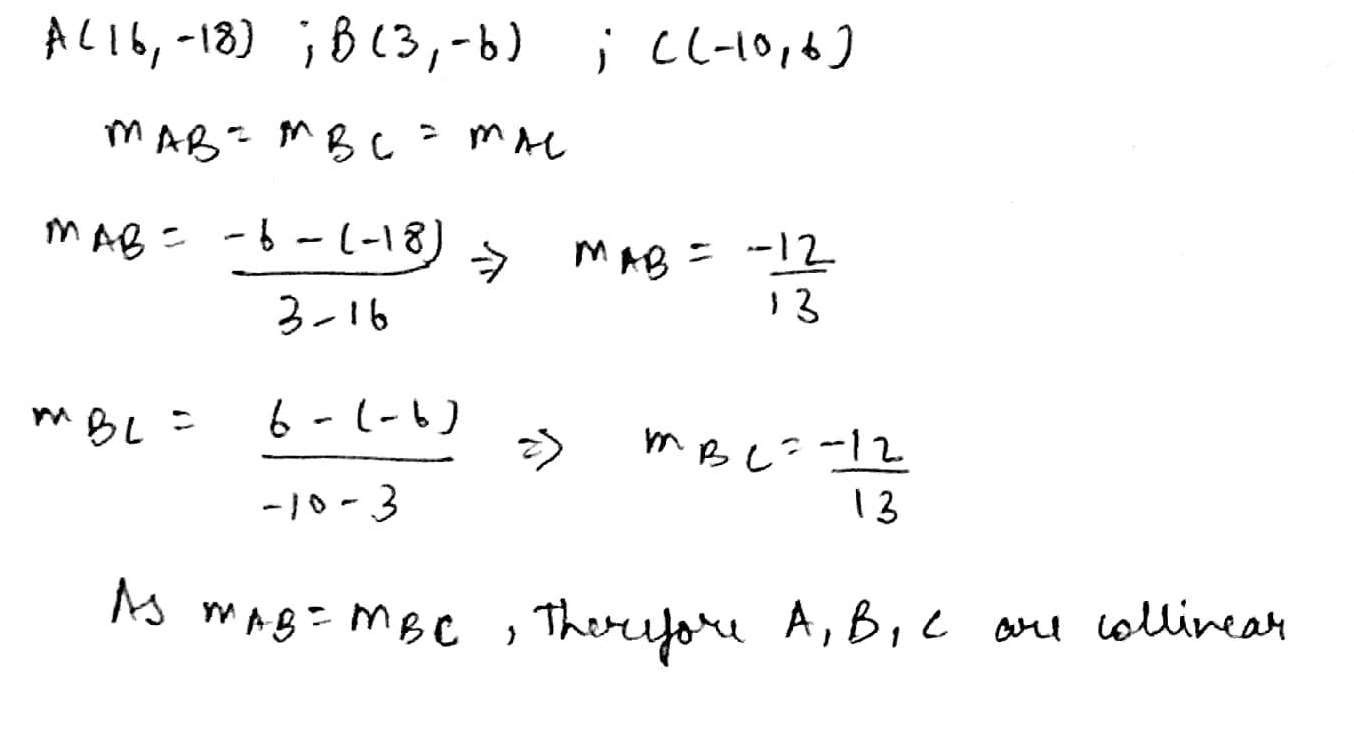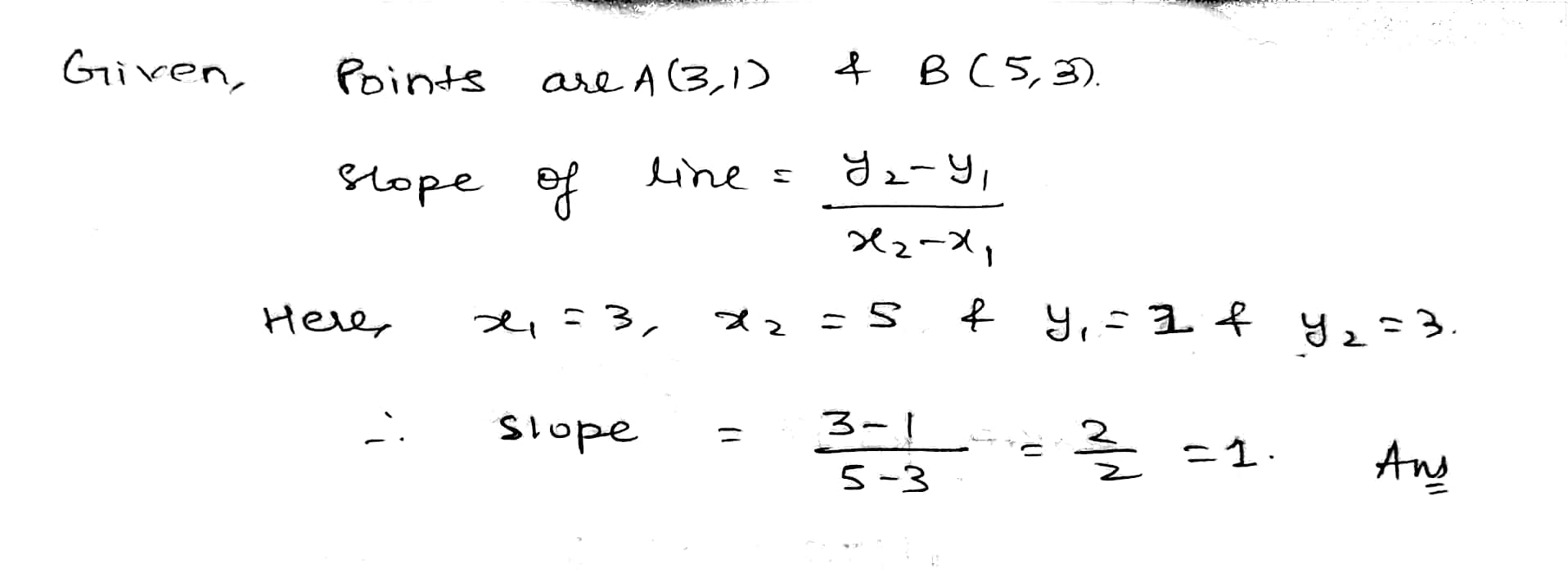Straight Lines - Class 11 Commerce Maths - Extra Questions

Find the slope of the line passing through the points $$A(2, 3)$$ and $$B(4, 7)$$.

Fact:  Slope of line passing through the points $$(x_1,y_1)$$ and $$(x_2,y_2)$$ is given by,  $$m = \dfrac{y_2-y_1}{x_2-x_1}$$

Therefore slope of line passing through the points $$A(2,3)$$ and $$B(4,7)$$ is $$=\dfrac{7-3}{4-2}=\dfrac{4}{2}=2$$


Find the slope of line having inclination $${60}^{o}$$.

Inclination of the line is $${60}^{o}$$.
$$\therefore \theta = {60}^{o}$$
Now, the slope of the line $$= \tan{\theta} = \tan{{60}^{o}}=\sqrt{3}$$.


Find the slope of the line passing through the points $$C(3, 5)$$ and $$D(-2, -3)$$

$$C \equiv (3, 5) = (x_{1}, y_{1})$$
and $$D \equiv (-2, -3) = (x_{2}, y_{2})$$
Then, Slope of line $$CD = \dfrac {y_{1} - y_{2}}{x_{1} - x_{2}}$$
$$= \dfrac {5 - (-3)}{3 - (-2)}$$
$$= \dfrac {5 + 3}{3 + 2} = \dfrac {8}{5}$$


If the straight line joining two points $$P(5,8)$$ and $$Q (8,k)$$ is parallel to $$x-axis$$, then write the value of $$ k$$.

As we know that slope $$\left( m \right)$$ of the line joining the two points $$\left( {x}_{1}, {y}_{1} \right)$$ and $$\left( {x}_{2}, {y}_{2} \right)$$, is given as-
$$m = \cfrac{\left( {y}_{2} - {y}_{1} \right)}{\left( {x}_{2} - {x}_{1} \right)}$$
Therefore, slope of line joining the points $$\left( 5, 8 \right)$$ and $$\left( 8, k \right)$$ is-
$$m = \cfrac{k - 8}{8 - 5} = \cfrac{\left( k - 8 \right)}{3}$$
Now,
Slope of $$x$$-axis $$= 0$$
As we know that if lines are parallel then they have the same slope.
$$\therefore \cfrac{\left( k - 8 \right)}{3} = 0$$
$$\Rightarrow k - 8 = 0$$
$$\Rightarrow k = 8$$
Thus the value of $$k$$ is $$8$$.
Hence the correct answer is $$8$$.


If the distance between the points $$(4,\,p)$$ and $$(1,\,0)$$ is $$5$$, then the find the value of $$p$$. 


1338028_1275888_ans_b209d11891cf4500abd6496a49981aed.PNG


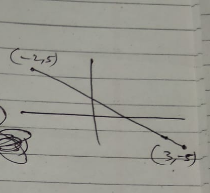
The points $$(-2,5)$$ and $$(3,-5)$$ are plotted in xy planes. Find the slope and y intercept of the line joining the points.

Slope(m)$$ = \frac{{5 + 5}}{{ - 2 - 3}} =  - 2$$
$$\begin{array}{l} y-5=-2\left( { x+2 } \right)  \\ y-5=-2x-4 \\ y+2x=1 \end{array}$$
$$(0,1)$$                Slope $$=-2$$
$$y$$ intercept $$=1[(0,1)]$$

1212536_1305957_ans_6e27ee6437064096bba1292f22c3a87c.PNG


Find the distance between $$\left(-4,5\right)$$ from the origin.

Distance between $$\left(-4,5\right)$$ from the origin

$$=$$Distance between $$\left(-4,5\right)$$ from $$\left(0,0\right)$$

$$=\sqrt{ { \left( {x_2}-{ { x_1 } } \right)  }^{ 2}+{ \left( {y_2 }-{ y_1  } \right)  }^{ 2 } } $$

$$=\sqrt{{\left(-4-0\right)}^{2}+{\left(5-0\right)}^{2}}$$ 

$$=\sqrt{16+25}$$

$$=\sqrt{41}$$ units.


Solve the following question:
Find the slope of the line passing through the points $$A(2, 3)$$ and $$B(4, 7)$$.

Given $$A(2,3)$$ and $$B(4,7)$$

Slope of the line passing through $$(x_1,y_2)$$ and $$(x_2,y_2)$$ is $$m=\dfrac {y_{2} - y_{1}}{x_{2} - x_{1}}$$

Here $$(x_1,y_2)=A(2,3)$$ and $$(x_2,y_2)=(4,7)$$

$$m=\dfrac {7-3}{4-2}=\dfrac 42=2$$

$$\therefore$$  the slope of the line passing through the points $$A(2,3)$$ and $$B(4,7)$$ is $$2$$


The type of triangle formed by the points A (5, 6), B (4, 2) and C (7, 5) is Scalene triangle
If true then enter $$1$$ and if false then enter $$0$$

$$ Let\quad the\quad points\quad A\left( { x }_{ 1 },{ y }_{ 1 } \right) =\left( 5,6 \right) ,\quad B\left( { x }_{ 2 },{ y }_{ 2 } \right) =\left( 4,2 \right) ,\quad C\left( { x }_{ 3 },{ y }_{ 3 } \right) =\left( 7,5 \right) \\ be\quad the\quad vertices\quad of\quad the\quad \Delta ABC.\\ AB=\sqrt { { \left( { x }_{ 2 }-{ x }_{ 1 } \right)  }^{ 2 }+{ \left( { y }_{ 2 }-{ y }_{ 1 } \right)  }^{ 2 } } =\sqrt { { \left( 4-5 \right)  }^{ 2 }+{ \left( 2-6 \right)  }^{ 2 } } units=\sqrt { 17 } units.\\ BC=\sqrt { { \left( { x }_{ 3 }-{ x }_{ 2 } \right)  }^{ 2 }+{ \left( { y }_{ 3 }-{ y }_{ 2 } \right)  }^{ 2 } } =\sqrt { { \left( 7-4 \right)  }^{ 2 }+{ \left( 5-2 \right)  }^{ 2 } } units=\sqrt { 18 } units.\\ CA=\sqrt { { \left( { x }_{ 3 }-{ x }_{ 1 } \right)  }^{ 2 }+{ \left( { y }_{ 3 }-{ y }_{ 1 } \right)  }^{ 2 } } =\sqrt { { \left( 5-7 \right)  }^{ 2 }+{ \left( 5-6 \right)  }^{ 2 } } units=\sqrt { 5 } units.\\ AB\neq BC\neq CA.\\ So\quad \Delta ABC\quad is\quad a\quad scalene\quad one.\\ Ans-\quad ABC\quad is\quad a\quad scalene\quad \Delta \quad . $$


Let the vertices of a triangle ABC be (4, 4), (3, 5), $$ (-1,  -1)$$, then show that $$\Delta  ABC$$ is right angled.

Let $$A\equiv (4, 4), B\equiv (3, 5), C\equiv (-1, -1)$$
$$AB=\sqrt{(3-4)^{2}+(5-4)^{2}}=\sqrt{2}$$
$$BC=\sqrt{(-1-3)^{2}+(-1-5)^{2}}=\sqrt{52}$$
$$AC=\sqrt{(-1-4)^{2}+(-1-4)^{2}}=\sqrt{50}$$
$$\therefore   AB^{2}+AC^{2}=BC^{2}$$
Hence by the Pythagoras Theorem, ABC is a right angled triangle.


Show that three points $$A (1,  -2),   B   (3,   4)   and   C (4,   7)$$ are lie an a straight line.

$$m_{1}=slope   of  AB=\frac{4-(-2)}{3-1}=3$$
$$m_{2}=slope   of  BC=\frac{7-4}{4-3}=3$$
$$\therefore  m_{1}=m_{2}$$
$$\therefore $$ AB is parallel to BC and B is common to both AB and BC. Hence, the points. A
$$(1,   -2), B(3,   4)      and    C(4,   7)$$   are collinear.
i.e., A, B, C lie on a straight line.


Name the quadrilateral formed, if any by the following points, and give reaons for your answer.
(i) $$(-1, -2)$$, $$(1, 0)$$, $$(-1, 2)$$, $$(-3, 0)$$
(ii)$$(-3, 5)$$, $$(3, 1)$$, $$(0, 3)$$, $$(-1, -4)$$
(iii)$$(4,5)$$, $$(7, 6)$$, $$(4, 3)$$, $$(1, 2)$$

 Given, $$A(-1, -2)$$, $$B(1, 0)$$, $$C(-1, 2)$$, $$D(-3, 0)$$ Determine distances: $$AB$$, $$BC$$, $$CD$$, $$DA$$, $$AC$$ and $$BD$$.
$$AB=\sqrt { (1+1)^{ 2 }+(0+2)^{ 2 } } =\sqrt { 4+4 } =\sqrt { 8 } =2\sqrt { 2 } $$
$$BC=\sqrt { (-1-1)^{ 2 }+(2-0)^{ 2 } } =\sqrt { 4+4 } =\sqrt { 8 } =2\sqrt { 2 }$$
$$CD=\sqrt { (-3+1)^{ 2 }+(0-2)^{ 2 } } =\sqrt { 4+4 } =\sqrt { 8 } =2\sqrt { 2 } $$
 $$DA=\sqrt { (-1+3)^{ 2 }+(-2-0)^{ 2 } } =\sqrt { 4+4 } =\sqrt { 8 } =2\sqrt { 2 } $$ $$AB = BC = CD = DA$$
Since, the sides of the quadrilateral are equal.
 $$AC=\sqrt { (-1+1)^{ 2 }+(2+2)^{ 2 } } =\sqrt { 0+16 } =4$$ $$BD=\sqrt { (-3-1)^{ 2 }+(0-0)^{ 2 } } =\sqrt { 16+0 } =4$$
Diagonals of the quadrilateral are also equal.
$$\therefore $$
  we conclude that $$ABCD$$ is a square.



Find the distance of the point $$(-1, 1)$$ from the line $$\displaystyle  12(x+6)= 5(y-2)$$

The given equation of the line is $$\displaystyle  12(x+6)= 5(y-2)$$
$$\displaystyle \Rightarrow 12x+72= 5y-10$$
$$\displaystyle \Rightarrow 12x-5y+82= 0$$
Therefore, the distance of point $$(-1,1)$$ from the given line
$$\displaystyle

= \frac{\left | 12(-1)+(-5)(1)+82 \right

|}{\sqrt{(12)^{2}+(-5)^{2}}}$$ units $$\displaystyle = \frac{\left |

-12-5+82 \right |}{\sqrt{169}}$$ units $$\displaystyle = \frac{\left | 65

\right |}{13}$$ units $$\displaystyle = 5$$ units


Find the value of x such that the distance between the points $$(2, 5)$$ and $$(x, -7)$$ is $$13$$.

$$d=13, (x_1, y_1)=(2, 5)$$ and $$(x_2, y_2)=(x, 7)$$
$$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
$$13=\sqrt{(x-2)^2+(-7-5^2)^2}=\sqrt{(x-2)^2+144}$$
Squaring both sides, $$13^2=x^2-4x+148$$
$$169=x^2-4x+148$$
$$x^2-4x+148-169=0$$
$$x^2-4x-21=0$$
$$(x-7)(x+3)=0$$
$$\therefore x=7$$ or $$x=-3$$.


Find the co-ordinate of points on x-axis which are at a distance of $$5$$ units form the point $$(6, -3)$$.

Any point on X-axis has co-ordinates of form $$(x, 0)$$
$$\therefore (x_1, y_1)=(6, -3)$$ and $$(x_2, y_2)=(x, 0)$$ and $$d=5$$
$$\therefore d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
$$5=\sqrt{(x-6)^2+[0-(-3)]^2}=\sqrt{(x-6)^2+3^2}$$
Squaring on both sides $$5^2(\sqrt{(x-6)^2+9})^2$$
$$25=x^2-12x+36+9$$
$$x^2-12x+45-25=0\Rightarrow x^2-12x+20=0\Rightarrow (x-10)(x-2)=0$$
$$\therefore x-10=0$$ or $$x-2=0\Rightarrow x=10$$ or $$x=2$$
$$\therefore$$ Required points on X-axis are $$(10, 0)$$ and $$(2, 0)$$


Show that the triangle whose vertices are $$(8, -4), (9, 5)$$ and $$(0, 4)$$ is an isosceles triangle.

We know that the distance between the two points $$(x_1,y_1)$$ and $$(x_2,y_2)$$ is 
$$d=\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-{ y }_{ 1 }) }^{ 2 } }$$ 

Let the given vertices be $$A=(8,-4)$$, $$B=(9,5)$$ and $$C=(0,4)$$

We first find the distance between $$A=(8,-4)$$ and $$B=(9,5)$$ as follows:

$$AB=\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-{ y }_{ 1 }) }^{ 2 } } =\sqrt { { (10-2) }^{ 2 }+{ (1-1) }^{ 2 } } =\sqrt { { 8 }^{ 2 }+{ 0 }^{ 2 } } =\sqrt { 64 } =8$$

Similarly, the distance between $$B=(9,5)$$ and $$C=(0,4)$$ is:

$$BC=\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-{ y }_{ 1 }) }^{ 2 } } =\sqrt { { (6-10) }^{ 2 }+{ (9-1) }^{ 2 } } =\sqrt { { (-4) }^{ 2 }+{ 8 }^{ 2 } } =\sqrt { 16+64 } =\sqrt { 80 } =\sqrt { 4^{ 2 }\times 5 } =4\sqrt { 5 }$$ 

Now, the distance between $$C=(0,4)$$ and $$A=(8,-4)$$ is:

$$CA=\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-{ y }_{ 1 }) }^{ 2 } } =\sqrt { { (6-2) }^{ 2 }+{ (9-1) }^{ 2 } } =\sqrt { { 4 }^{ 2 }+{ 8 }^{ 2 } } =\sqrt { 16+64 } =\sqrt { 80 } =\sqrt { 4^{ 2 }\times 5 } =4\sqrt { 5 }$$

We also know that If any two sides have equal side lengths, then the triangle is isosceles.

Here, since the lengths of the two sides are equal that is $$BC=CA=4\sqrt {5}$$

Hence, the given vertices are the vertices of an isosceles triangle.


Prove that the points $$A(-3, -2), B(5, -2), C(9, 3)$$ and $$D(1, 3)$$ are the vertices of a parallelogram.

We know that the distance between the two points $$(x_1,y_1)$$ and $$(x_2,y_2)$$ is 
$$d=\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-{ y }_{ 1 }) }^{ 2 } }$$ 

Let the given vertices be $$A=(-3,-2)$$, $$B=(5,-2)$$, $$C=(9,3)$$ and $$D=(1,3)$$

We first find the distance between $$A=(-3,-2)$$ and $$B=(5,-2)$$ as follows:

$$AB=\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-{ y }_{ 1 }) }^{ 2 } } =\sqrt { { (1-(-5)) }^{ 2 }+{ (-11-(-3)) }^{ 2 } } =\sqrt { { (1+5) }^{ 2 }+{ (-11+3) }^{ 2 } } =\sqrt { { 6 }^{ 2 }+{ (-8) }^{ 2 } }$$
$$=\sqrt { 36+64 } =\sqrt { 100 } =\sqrt { 10^{ 2 } } =10$$

Similarly, the distance between $$B=(5,-2)$$ and $$C=(9,3)$$ is:

$$BC=\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-{ y }_{ 1 }) }^{ 2 } } =\sqrt { { (7-1) }^{ 2 }+{ (-6-(-11)) }^{ 2 } } =\sqrt { { 6 }^{ 2 }+{ (-6+11) }^{ 2 } } =\sqrt { { 6 }^{ 2 }+{ 5 }^{ 2 } } =\sqrt { 36+25 }$$
$$=\sqrt { 61 }$$  

Now, the distance between $$C=(9,3)$$ and $$D=(1,3)$$ is:

$$CD=\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-{ y }_{ 1 }) }^{ 2 } } =\sqrt { { (1-7) }^{ 2 }+{ (2-(-6)) }^{ 2 } } =\sqrt { { (-6) }^{ 2 }+{ (2+6) }^{ 2 } } =\sqrt { { (-6) }^{ 2 }+{ 8 }^{ 2 } } =\sqrt { 36+64 }$$
$$=\sqrt { 100 } =\sqrt { 10^{ 2 } } =10$$

Now, the distance between $$D=(1,3)$$ and $$A=(-3,-2)$$ is:

$$DA=\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-{ y }_{ 1 }) }^{ 2 } } =\sqrt { { (1-(-5)) }^{ 2 }+{ (2-(-3)) }^{ 2 } } =\sqrt { { (1+5) }^{ 2 }+{ (2+3) }^{ 2 } } =\sqrt { { 6 }^{ 2 }+{ 5 }^{ 2 } } =\sqrt { 36+25 }$$
$$=\sqrt { 61 }$$ 

We also know that if the opposite sides have equal side lengths, then $$ABCD$$ is a parallelogram.

Here, since the lengths of the opposite sides are equal that is:

$$AB=CD=10$$ and $$BC=DA=\sqrt {61}$$

Hence, the given vertices are the vertices of parallelogram.


Find the distance between the points $$P(3, 4, -7)$$ and $$Q(-2, 5, 10)$$

Distance between two points
$$\sqrt { { (x2-x1) }^{ 2 }+{ (y2-y1) }^{ 2 }+{ (z2-z1) }^{ 2 } } $$
$$=\sqrt { { (5) }^{ 2 }+{ (-1) }^{ 2 }+{ (-17) }^{ 2 } } $$
$$=\sqrt {{25}+{1}+{289}}$$
$$=\sqrt {315} \quad Ans$$




The center of a circle is $$(2a-1,7)$$ and it passes through the point $$(-3,-1)$$. If the diameter of the circle is $$20$$ units, then find the value of $$a$$.

Centre: $$C(2a-1,7)$$
Point: $$P(-3,-1)$$
Radius=$$\cfrac { 1 }{ 2 } (20)=10$$
As circle passes through P, distance between p and centre is equal to radius.
=>$${ (PC) }^{ 2 }={ (10 })^{ 2 }\\ =>(2a-1+3)^{ 2 }+\left( 7+1 \right) ^{ 2 }=(10)^{ 2 }\\ =>({ a+1 })^{ 2 }=\cfrac { 36 }{ 4 } \\ =>({ a+1 })^{ 2 }=9\\ =>a=2,-4$$


The point $$(1, 2.5)$$ divides the line in two equal parts,  joining the points $$(a, 1)$$ and $$(11, 4)$$. Find the value of $$\mid a \mid$$.

Mid point formula $$\left ( \dfrac{x_{1}+x_{2}}{2},\dfrac{y_{1}+y_{2}}{2} \right )$$
 $$1=\dfrac{a+11}{2}$$
$$a=-9$$
$$\mid a \mid = 9$$


Find the circumcentre and circumradius of the triangle whose vertices are $$(1,1), (2,-1)$$ and $$(3,2)$$

Let the coordinates of the vertices of the triangle are $$A(1,1), B(2,-1)$$ and $$C(3,2)$$
Now, Lets find the distance between each of the three points.
We will use the distance formula to find the distance between $$AB, BC$$ and $$AC$$
Thus $$ AB= \sqrt{(2-1)^2+ (-1-1)^2}=\sqrt{5}$$
$$BC= \sqrt{(3-2)^2+ (2+1)^2}=\sqrt{10}$$
$$AC=\sqrt{(3-1)^2+ (2-1)^2}=\sqrt{5}$$
Now$$ AB^2+AC^2= 10 =BC^2$$
Thus it form a right angled triangle, right angled at $$ A.$$
Now the circumcentre will be the mid-point of the hypotenuse $$BC.$$
Thus mid-point of $$BC $$ is $$\left (\dfrac{2+3}{2},\dfrac{-1+2}{2}  \right ) = \left (\dfrac{5}{2},\dfrac{1}{2}  \right ).$$
And the circumradius is the half the length of $$BC $$
$$\Rightarrow$$ Circumradius $$= \dfrac{\sqrt{10}}{2}$$


The vertices of a triangle are $$A(1,1), B(4,5)$$ and $$C(6,13)$$. Find $$\cos{A}$$

Using law of cosines, we have, $$a^2=b^2+c^2-2bccosA$$
From the given points, $$a^2=BC^2=68$$, $$b^2=AC^2=169$$, $$c^2=AB^2=25$$
Substituting these values, we have $$cosA=\dfrac{b^2+c^2-a^2}{2bc}$$
$$cosA=\dfrac{169+25-68}{2 \times 13 \times 5}$$=$$\dfrac{126}{130}$$
$$=\dfrac{63}{65}$$


If points $$(3,K)$$ and $$(K,5)$$ are equidistant from a point $$(0,2)$$, then find the value of $$K$$.

$$d=[(3-0)^2+(k-2)^2]^{1/2}$$ ……..$$(1)$$
$$d=[(k-0)^2+(5-2)^2]^{1/2}$$ ………..$$(2)$$
$$(1) = (2)$$
Squaring both sides
$$3^2+(k-2)^2=k^2+3^2$$
Take square root both sides
$$k-2=\pm k$$
$$(+)$$ $$k-2=k$$
$$k-2=0$$ not possible
$$(-)$$ $$k-2=-k$$
$$k=1$$.

1381387_1211209_ans_e7aa1a8fb4604be8866d6e50dcd3a7fb.PNG


Find the angles between the lines
$$x-\sqrt{3}y=1$$

Consider the given equations,

$$x-\sqrt{3}y=1$$       …..(1)

$$\sqrt{3}x-y=1$$     …..(2)


From equation 1st,

$$y=\dfrac{1}{\sqrt{3}}x-\dfrac{1}{\sqrt{3}}$$

Compare with, $$y={{m}_{1}}x+C$$

$${{m}_{1}}=\dfrac{1}{\sqrt{3}}$$


From equation 2nd ,

$$y=\sqrt{3}x-1$$

Compare with $$y={{m}_{2}}x+C$$

$${{m}_{2}}=\sqrt{3}$$


Now,let the angle between line 1st and 2nd$$=\theta $$,

Using the formula,$$\tan \theta =\dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}}$$


$$ \tan \theta =\dfrac{\sqrt{3}-\dfrac{1}{\sqrt{3}}}{1+\sqrt{3}\times \dfrac{1}{\sqrt{3}}}=\dfrac{\sqrt{3}\times \sqrt{3}-1}{1+1} $$

$$ \tan \theta =\dfrac{3-1}{2}=1 $$

$$ \tan \theta =1 $$

$$ \tan \theta =\tan \dfrac{\pi }{4} $$

$$ \theta =\dfrac{\pi }{4} $$


Hence, this is the answer.



The corner point of the feasible region determined by the system of Iinear constraints are $$( 0,10 )$$,$$( 5,5 ) , ( 15,15 )$$ and $$( 0,20 )$$.Let $$Z = p x + q y ,$$ where $$p , q > 0$$.Find the condition on $$p$$ and $$q$$ so that the maximum of $$Z$$ occurs at both the points $$( 15,15 )$$ and $$( 0,20 )$$.

Given $$Z=p{x}+q{y}$$
 $$Z$$ is maximum at both points
$$\implies Z$$ at $$(15,15)$$ is equal to $$Z$$ at $$(0,20)$$ 
 $$\implies 15{p}+15{q}=20{q}\implies 3{p}=q$$


If the points $$A(4, 3)$$ and $$B(x, 5)$$ are on the circle with the centre $$O(2, 3)$$. Find the value of $$x$$. 

Let equation of circle be

$$x^2+y^2+2gx+2fy+c=0$$

$$(-g,-f)\rightarrow $$ centre is $$(2,3)$$

$$x^2+y^2+2(-2)(x)+2(-3)y+c=0$$

$$A(4,3)$$ lies on circle.

$$(4)^2+(3)^3-4(4)-6(3)+c=0$$

                $$c=9$$

$$\therefore x^2+y^2-4x-6y+9=0$$ is equation of circle.

$$B(x,5)$$

$$x^2+25-4x-6(5)+9=0$$

$$x^2-4x+4=0$$

$$(x-2)^2=0\Rightarrow x=2$$


Find the point on the $$x-$$axis which is equidistant from the points $$\left(-3,4\right)$$ and $$\left(2,5\right)$$


1338031_1276082_ans_ab36789e760c4aa8a422642b15d69b5f.PNG


$$AD$$ is the median of $$\triangle ABC$$ and bisectors of $$\angle ADB$$ and$$\angle ADC$$ are $$DE$$ and $$DF$$, which meet $$AB$$ at $$E$$ and $$AC$$ at $$F$$. Prove that $$EF\parallel BC$$.

In $$\Delta DAE, \, DE$$ bisect angle $$ADB$$

So we have 

$$\dfrac{DA}{DB} = \dfrac{AE }{EB}$$ ... (1)

Similarly in $$\Delta DAC, \, DE$$ bisect angle $$ADC$$ 

we get

$$\dfrac{DA}{DC} = \dfrac{AF}{AC}$$

$$(DC = DB)$$

$$\dfrac{DA}{DB} = \dfrac{AF}{FC}$$ ... (2)

from eq (1) and eq (2)

$$\dfrac{AE}{EB} = \dfrac{AF}{FC}$$

ln $$\Delta ABC$$

$$EF || BE (... BPT)$$


The equation of the straight line passing through the point  of intersection of the straight lines$$\dfrac{x}{a} =\dfrac{y}{b} = 1$$ and $$\dfrac{x}{b} + \dfrac{y}{a} = 1$$ and having infinite slopes is

Let $$L_{1}:\dfrac{x}{a}+\dfrac{y}{b}-1=0$$ & $$L_{2}=\dfrac{x}{b}+\dfrac{y}{a}-1=0$$

the required line would be of the form $$L_{1}-\lambda L_{2}=0$$

$$\Rightarrow (\dfrac{x}{a}+\dfrac{y}{b}-1)-\lambda (\dfrac{x}{b}+\dfrac{y}{a}-1)=0$$

$$\Rightarrow x(\dfrac{1}{a}-\dfrac{\lambda }{b})+y(\dfrac{1}{b}-\dfrac{\lambda }{a})-1+\lambda =0$$

As slope = $$\infty \Rightarrow $$ line is parallel to y-axis

$$\Rightarrow $$ coeff. of $$y=0\Rightarrow \dfrac{\lambda }{a}=\dfrac{1}{b}\Rightarrow \lambda =\dfrac ab$$

$$\Rightarrow Eq^{n}$$ of line : $$x(\dfrac{1}{a}-\dfrac{a}{b^{2}})+y(\dfrac{1}{b}-\dfrac{1}{b})-1+\dfrac{a}{b}=0$$

$$\Rightarrow x(\dfrac{b^{2}-a^{2}}{ab^{2}})+\dfrac{a}{b}-1=0$$


Given the points $$A\left(0,\,4\right)$$ and $$B\left(0,\,-4\right)$$, find the locus of $$P\left(x,y\right)$$ such that $$\left|AP-BP\right|=6$$


1338047_1276691_ans_355d56cf004547b0ada9a70ced638e17.PNG


If $$\angle B$$ and $$\angle Q$$ are acute angels such that $$\sin B-\sin Q$$, then prove that $$\angle B=\angle Q$$.

We have,

In $$\Delta ABC\,\,and\,\,\Delta PQR$$

Given that, $$\angle B\,\,and\,\,\angle Q$$ are acute angles

$$\therefore AC=k\times PR\,\,and\,\,AB=k\times PQ$$

From $$\Delta ACB\,$$

By Pythagoras theorem,

$$ A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}} $$

$$ \Rightarrow {{\left( k\times PR \right)}^{2}}={{\left( k\times PQ \right)}^{2}}+B{{C}^{2}} $$

$$ \Rightarrow {{k}^{2}}\times P{{R}^{2}}={{k}^{2}}\times P{{Q}^{2}}+B{{C}^{2}} $$

$$ \Rightarrow B{{C}^{2}}={{k}^{2}}\times P{{R}^{2}}-{{k}^{2}}\times P{{Q}^{2}} $$

$$ \Rightarrow B{{C}^{2}}={{k}^{2}}\left[ P{{R}^{2}}-P{{Q}^{2}} \right] $$

$$ \Rightarrow BC=k\sqrt{P{{R}^{2}}-P{{Q}^{2}}} $$

From right angle triangle PRQ,

Using Pythagoras theorem,

We have,

$$ P{{Q}^{2}}=P{{R}^{2}}+Q{{R}^{2}} $$

$$ \Rightarrow Q{{R}^{2}}=P{{Q}^{2}}-P{{R}^{2}} $$

Hence,

$$ \Delta ACB\sim \Delta PRQ\,\,\left( S.S.S.\,\,similarity\,triangle \right) $$

$$ \therefore \,\,\angle B=\angle Q $$

Hence, this is the answer.



Reduce the equation in to slope intercept from $$6x+3y-5=$$

$$6x+3y-5=0$$

$$3y=-6x+5$$

$$y=\dfrac{-6}{3}x+\dfrac{5}{3}$$

$$\Rightarrow y=-2x+\dfrac{5}{3}$$

This is the slope intercept form $$(y=mx+c)$$

where slope $$=-2$$ & intercept$$=\dfrac{5}{3}$$.


Show that the points 
A(2,-2), B(8,4) , C(5,7) ,D(-1,1) are the vertices of a rectangle .

We know the distance between the two points is given by,
$$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$

Here $$AB=\sqrt{(8-2)^2+(4+2)^2}$$
$$=\sqrt{36+36}$$
$$=6\sqrt{2},$$

$$BC=\sqrt{(5-8)^2+(7-4)^2}=\sqrt{9+9}$$
$$=3\sqrt{2},$$

$$CD=\sqrt{(-1-5)^2+(1-7)^2}=\sqrt{36+36}$$
$$=6\sqrt{2}$$ and

$$AD=\sqrt{(2+1)^2+(-2-1)^2}=\sqrt{9+9}$$
$$=3\sqrt{2}$$

$$AC=\sqrt{(5-2)^2+(7+2)^2}=\sqrt{90}$$ and
$$BD=\sqrt{(-1-8)^2+(1-4)^2}=\sqrt{90}$$

Here$$AB=CD,BC=AD,AC=BD$$

i.e.,opposite sides are equal and diagonal are equal.
Hence it is a rectangle


Find the value of $$y$$ for which the distance between the points $$P(2, -3)$$ and $$Q(10, y)$$ is $$10$$ units.

Given points are  $$P(2,-3)$$ and $$Q(10,y)$$

Distance between two point $$(x_1,y_1) $$ and $$ (x_2,y_2)$$ is given by,

$$=\sqrt{ { \left( {x_2}-{ { x_1 } } \right)  }^{ 2}+{ \left( {y_2 }-{ y_1  } \right)  }^{ 2 } } $$

$$PQ = \sqrt{8^{2}+(y+3)^{2}} =10$$

$$\Rightarrow \sqrt{64+y^{2}+9+6y} = 10$$

$$\Rightarrow y^{2}+6y+73=100$$

$$\Rightarrow y^{2}+6y-27=0$$

$$\Rightarrow y^{2}+9y-3y-27=0$$

$$\Rightarrow y(y+9)-3(y+9)=0$$

$$\Rightarrow (y+9)(y-3)=0$$

$$\Rightarrow y=-9,3$$


Prove that the points $$A(1,-3),B(-3,0)$$ and $$C(4,1)$$ are the vertices of a right angled Isosceles triangle

$$AB=\sqrt{(1-(-3))^2+(-3-0)^2}=\sqrt{4^2+3^2}=\sqrt{16+9}=\sqrt{25}=5$$

$$BC=\sqrt{(-3-4)^2+(0-1)^2}=\sqrt{49+1}=\sqrt{50}=5\sqrt{2}$$

$$AC=\sqrt{(1-4)^2+(-3-1)^2}=\sqrt{9+16}=\sqrt{25}=5$$

$$AB^2+AC^2=5^2+5^2=50=BC^2$$

By Pythagoras theorem 

$$\angle A=90^0$$

and $$AC=AB$$

$$\therefore ABC$$ is right isosceles $$\Delta$$

2040490_1481731_ans_7755eb7e1d1f4aa8832a500b5bdad53d.png


Using the method of slope, show that the following points are collinear:
$$A(16, -18), B(3,-6), C(-10,6)$$


1414166_1667226_ans_7eef954a3b8a4a3389e1ab4e728f7142.jpg


Find the slope of a line whose inclination is 
(i)   $$45^o$$
(ii)  $$30^o$$

The slope of a line inclination : 
(i)  $$45^o$$
$$Slope = tan \,45^o = 1$$
(ii) $$30^o$$
$$Slope = tan\,30^o = 1/\sqrt{3}$$


Prove that the line through $$\left(0,0\right)$$ and $$\left(2,3\right)$$ is parallel to the line through $$\left(2, -2 \right)$$ and $$\left(6,4\right)$$. 

Let the slope of the line through $$\left(2,-2\right)$$ and $$\left(6,4\right)$$ be $$m_1$$
So, $$m_1 = \dfrac{\left(y_2 - y_1\right)}{\left (x_2 - x_1\right)}$$
$$=\dfrac{\left(4 + 2\right)}{\left (6 - 2\right)}$$
$$=\dfrac{6}{4} = \dfrac{3}{2}$$

Let the slope of the line through $$\left(0,0\right)$$ and $$\left(2,3\right)$$ be $$m_2$$
So, $$m_2 = \dfrac{\left(y_2 - y_1\right)}{\left (x_2 - x_1\right)}$$
$$=\dfrac{\left(3 -0\right)}{\left (2 - 0\right)}$$
$$= \dfrac{3}{2}$$

It's clearly seen that the slopes $$m_1 = m_2$$
Thus, the lines are parallel to each other.


Show that the triangle formed by the point $$A \left(1,3\right) \, B  \left(3, -1\right)\, and \, C \left(-5, -5 \right)$$ is a right  - angled triangle by using slopes.

Given, points $$A \left(1,3\right) , B \left(3,-1\right) \, and \, C \left(-5, -5\right)$$ form a triangle
Now, 
Slope of the line $$AB = m_1 = \dfrac{\left(-1 - 3\right)}{\left (3 - 1\right)} = \dfrac{-4}{2} = -2$$
And,
Slope of the line $$BC = m_2 = \dfrac{\left(-5 + 1\right)}{\left (-5 - 3\right)} = \dfrac{-4}{-8} = \dfrac{1}{2}$$
Hence,
$$m_1 \times m_2 = \left(-2\right) \times \left(\dfrac{1}{2}\right) = -1$$
So, the line AB and BC are perpendicular to each other .
Therefore, $$\triangle ABC $$ is a right - angled triangle.


Prove that the line through $$\left(-2,6\right)$$ and $$\left(4, 8 \right)$$ is perpendicular to the line through $$\left(8,12\right)$$ and $$\left(4,24\right)$$

Let the slope of the line through points $$\left (-2,6\right)$$ and $$\left(4,8\right)$$ be $$m_1$$

So, $$m_1 = \dfrac{\left(y_2 - y_1\right)}{\left (x_2 - x_1\right)}$$
$$ = \dfrac{\left(8 - 6\right)}{\left (4 + 2\right)}$$
$$ = \dfrac{2}{6}$$
$$ = \dfrac{1}{3}$$

And, let the slope of the line through $$\left(8,2\right)$$ and $$\left(4,24\right)$$ be $$m_2$$
So, $$m_2 = \dfrac{\left(y_2 - y_1\right)}{\left (x_2 - x_1\right)}$$
$$ = \dfrac{\left(24 - 12\right)}{\left (4 - 8\right)}$$
$$= \dfrac{12}{\left(-4\right)}$$
$$= -3$$

Now, product of slopes is
$$m_1 \times m_2 = \dfrac{1}{3} \times \left(-3\right) = -1$$
Thus, the lines are perpendicular to each other.


Prove that the line through $$\left(0,0\right)$$ and $$\left(2,3\right)$$ is parallel to the line through $$\left(2, -2 \right)$$ and $$\left(6,4\right)$$.

Let the slope of the line through $$\left(0,0\right)$$ and $$\left(2,3\right)$$ be $$m_1$$
So, $$m_1 = \dfrac{\left(y_2 - y_1\right)}{\left (x_2 - x_1\right)}$$
$$=\dfrac{\left(3-0\right)}{\left (2-0\right)}=\dfrac{3}{2}$$
Similarly $$m_{2}$$$$=\dfrac{\left(4 + 2\right)}{\left (6 - 2\right)}$$$$=\dfrac{6}{4} = \dfrac{3}{2}$$
It's clearly seen that the slopes $$m_1 = m_2$$
Thus, the lines are parallel to each other.


The lien through the point (h,3) and (4,1) intersects the line $$7 x = 9y = 19 $$ at right angle. Find the value of h 

Given line is  $$7 x - 9y = 19 $$ which is perpendicular to the our line
given point are (h,3),(4,1) 
For perpendicular lines $$m_1m_2=-1$$ where $$m_1,m_2$$ are slope of perpendicular lines
$$\therefore m_1=\frac{-1}{\frac{-7}{-9}}\Rightarrow m_1=\frac{9}{7}$$
Therefore,Required equations is of the form 
$$ y - y_{1} = m_1 ( x - x_{1})$$ 
$$y-1=\frac{9}{7}(x-4)$$
$$7y-7=9x-36$$
$$9x-7y-29=0$$
Required equation,For h
$$\Rightarrow 9\times h -7\times 3-29=0$$
$$h=\frac{50}{3}$$
Answer


Find slope of a line passing through the points $$A(3, 1)$$ and $$B(5, 3).$$


1895683_1911511_ans_84fe5d780bc5412cbe41b542a292afd6.jpeg


Show that the line given by $$x(a+2b)+y(a+3b)=a+b$$ for different values of $$a$$ and $$b$$ pass through a fixed point.

$$\begin{array}{l} x\left( { a+zb } \right) +y\left( { a+zb } \right) =a+b \\ a\left( { x+y } \right) +b\left( { 2x+3y } \right) =a+b \\ x+y=1\to (i) \\ 2x+3y=1\to (ii) \\ Multiply\, \, 2\, \, in\, \, eq.\, \, (i) \\ 2x+2y=2 \\ 2x+3y=1 \\ -\, \, \, \, \, -\, \, \, \, \, \, \, - \\ \overline { \, \, \, \, \, \, \, \, -y=1 }  \\ y=-1 \\ put\, \, y\, \, in\, \, eq\, (i) \\ x-1=1 \\ x=2 \\ fixed\, \, po{ { int } }\, \, \left( { 2,-1 } \right)  \end{array}$$


Class 11 Commerce Maths Extra Questions