Trigonometric Functions - Class 11 Commerce Maths - Extra Questions

$$\sin \theta =\cos \theta $$ for all values of $$\theta$$
Enter $$1$$ for true and $$0$$ for false

$$\sin { { 30 }^{ \circ  }=\frac { 1 }{ 2 }  } ,\cos { { 30 }^{ \circ  }=\frac { \sqrt { 3 }  }{ 2 }  } \\ \therefore \sin { \theta \neq \cos { \theta  }  } $$
for all values of $$\theta$$. 


$$\cos{(A-B)}=$$

From Trignnometric equations,
$$\cos(A-B)=\cos A\cos B+\sin A\sin B$$


Convert $${ 25 }^{ 0 }$$ into Radian measure.

We know that $${ \pi  }^{ c }={ 180 }^{ 0 }\\ \Longrightarrow { 1 }^{ 0 }={ \left( \frac { \pi  }{ 180 }  \right)  }^{ c }\\ \Longrightarrow { 25 }^{ 0 }={ \left( \frac { 5\pi  }{ 36 }  \right)  }^{ c }\\ $$


If $$7\sin ^{ 2 }{ x } +3\cos ^{ 2 }{ x } =4$$, show that $$\tan { x } =\dfrac { 1 }{ \sqrt { 3 }  }$$

$$7\sin^{2}x+3\cos^{2}x=4$$
$$4\sin^{2}x+3\sin^{2}x+3\cos^{2}x=4$$
$$4\sin^{2}x+3=4$$
$$4\sin^{2}x=1$$
$$\sin^{2}x=\dfrac{1}{4}$$
$$\sin x=\dfrac{1}{2}$$ or $$\sin x=-\dfrac{1}{2}$$ 
Taking the positive root
$$x=\dfrac{\pi}{6}$$
$$\tan (\dfrac{\pi}{6})=\dfrac{1}{\sqrt{3}}$$
Hence proved.


Solve
$$\cos (A - B) - \cos (180 - (A + B)=0$$

$$\cos (A-B)-\cos (180-(A+B))=-2\sin \bigg(\dfrac{A-B+180-A-B}{2}\bigg)\sin \bigg(\dfrac{A-B-180+A+B}{2}\bigg)$$
                                                              $$=-2\sin (90-B)\sin (A-90)=2\cos A\cos B$$
$$\cos (A-B)-\cos(180-(A+B))=0\implies \cos A=0$$ or $$\cos B=0\implies A=90$$ or $$B=90$$


The value of $$\cos \theta $$ increases as $$\theta $$ increases.
Enter $$1$$ for true and $$0$$ for false

$$\cos { { 45 }^{ \circ  }=\frac { 1 }{ \sqrt { 2 }  }  },\cos { { 90 }^{ \circ  }=0 } $$
Here, as $$\theta$$ increases from 45 to 90, value of $$cos\theta$$ decreases from $$1/\sqrt2$$ to 0. Thus, given statement is not correct.


Find the value of $$\theta$$ laying between 0 and $$\displaystyle \frac{\pi}{2}$$ and satisfying the equation

 $$\begin{vmatrix}1 + \cos^2 \theta & \sin^2 \theta & 4 \sin  4 \theta \\ \cos^2 \theta & 1 + \sin^2 \theta & 4 \sin 4 \theta\\ \cos^2 \theta & \sin^2 \theta & 1 + 4 \sin 4 \theta\end{vmatrix} = 0$$.

If the value of $$\theta = \displaystyle \frac{a \pi}{b}$$, then find the value of $$\dfrac{(b-3)}a$$

$$\begin{vmatrix}1 + \cos^2 \theta & \sin^2 \theta & 4 \sin  4 \theta \\ \cos^2 \theta & 1 + \sin^2 \theta & 4\sin 4 \theta\\ \cos^2 \theta & \sin^2 \theta & 1 + 4\sin 4 \theta\end{vmatrix} = 0$$

$${ R }_{ 1 }\rightarrow { R }_{ 1 }-{ R }_{ 2 },{ R }_{ 3 }\rightarrow { R }_{ 3 }-{ R }_{ 2 }$$

$$\begin{vmatrix} 1 & -1 & 0 \\ cos^{ 2 }\theta  & 1+sin^{ 2 }\theta  & 4sin4\theta  \\ 0 & -1 & 1 \end{vmatrix}=0$$

$${ C }_{ 2 }\rightarrow { C }_{ 2 }+{ C }_{ 1 }$$

$$\begin{vmatrix} 1 & 0 & 0 \\ cos^{ 2 }\theta  & 2 & 4sin4\theta  \\ 0 & -1 & 1 \end{vmatrix}=0$$

$$\Rightarrow 2+4\sin\theta=0$$
$$\Rightarrow \sin4\theta=-\dfrac{1}{2}$$
$$\Rightarrow \sin4\theta=-\sin (\dfrac{\pi}{6})$$
$$\Rightarrow \sin4\theta=\sin (\pi+\dfrac{\pi}{6})$$
$$\Rightarrow 4\theta=\dfrac{7\pi}{6}$$
$$\Rightarrow \theta=\dfrac{7\pi}{24}$$

Comparing with the given value of $$\theta$$, we get

$$a=7,b=24$$

Value of $$\dfrac{b-3}{a}=3$$


If $$ \Delta = \begin{vmatrix}1 & sin  \theta & 1\\ - sin  \theta & 1 & sin  \theta\\ -1 & -sin  \theta & 1\end{vmatrix} ; 0 \leq \theta < 2 \pi$$ then $$\Delta \in [a,b]$$ Find $$\dfrac{b}{a}?$$

$$ \Delta = \begin{vmatrix}1 & sin  \theta & 1\\ - sin  \theta & 1 & sin  \theta\\ -1 & -sin  \theta & 1\end{vmatrix}$$
$$\Rightarrow \Delta =(1+\sin^2 \theta)-\sin\theta(-\sin\theta+\sin\theta)+(\sin^2\theta+1)$$
$$\Rightarrow \Delta=2+2\sin^2\theta$$
$$\sin^2\theta \in [0,1]$$
$$\Rightarrow \Delta \in [2,4]$$
$$\Rightarrow a=2$$ and $$b=4$$
$$\therefore \displaystyle\frac{b}{a}=2$$



The general solution of $$\displaystyle 4\tan^{2}\theta=3\sec^{2}\theta$$  is $$\theta = n\pi\pm\dfrac{\pi}{m}$$. Then, find the value of $$m$$.

$$\displaystyle \because 4\tan^{2}\theta=3\sec^{2}\theta$$
$$\displaystyle \frac{4\sin^{2}\theta}{\cos^{2}\theta}=\frac{3}{\cos^{2}\theta}$$
$$ \cos^{2}\theta\neq 0 \therefore \theta\neq \left ( 2n+1 \right )\frac{\pi }{2},n\in I$$

Hence, $$4\sin^{2}\theta=3$$
$$\Rightarrow \sin^{2}\theta=\left ( \frac{\sqrt{3}}{2} \right )^{2}$$
$$\Rightarrow \sin^{2}\theta=\sin^{2}\frac{\pi }{3}$$
$$\Rightarrow \theta=n\pi \pm \frac{\pi }{3},n\in I$$


Solve $$\displaystyle \sin5x.\cos3x=\sin6x.\cos2x$$. then $$\displaystyle \frac{n\pi }{2},n\in I$$ or $$\displaystyle n\pi \pm \frac{\pi }{6},n\in I$$
If true then enter $$1$$ and if false then enter $$0$$

$$\displaystyle \because \sin5x.\cos3x=\sin6x.\cos2x$$
$$\Rightarrow 2\sin5x.\cos3x=2\sin6x.\cos2x$$
$$\Rightarrow \sin8x+\sin2x=\sin8x+\sin4x$$
$$\Rightarrow \sin4x-\sin2x=0$$
$$\Rightarrow 2\sin2x.\cos2x-\sin2x=0$$
$$\Rightarrow \sin2x\left ( 2\cos2x-1 \right )=0$$
$$\Rightarrow \sin2x=0$$ or $$\displaystyle 2 cos 2x-1=0$$
$$\Rightarrow 2x=n\pi \in I$$ or $$\displaystyle \cos2x=\frac{1}{2}$$
$$\Rightarrow x=\frac{n\pi }{2},n\in I$$
$$\Rightarrow x=n\pi \pm \frac{\pi }{6},n\pi I$$
$$\therefore $$ Solution of given equation is $$\displaystyle \frac{n\pi }{2},n\in I$$ or $$\displaystyle n\pi \pm \frac{\pi }{6},n\in I$$


Solve $$\displaystyle \sin x+\cos x=\sqrt{2}$$, then  $$x=\displaystyle 2n\pi +\frac{\pi }{4},n\in I$$
If true then enter $$1$$ and if false then enter $$0$$

$$\displaystyle \because \sin x +\cos x=\sqrt{2}$$
$$\displaystyle \therefore $$ divide both sides of equation (i) by $$\displaystyle \sqrt{2},$$ we get,
$$\displaystyle \sin x \frac{1}{\sqrt{2}}+\cos x \frac{1}{\sqrt{2}}=1$$
$$\Rightarrow \sin x\sin\frac{\pi }{4}+\cos x.\cos\frac{\pi}{4}=1$$
$$\Rightarrow \cos\left ( x-\frac{\pi }{4} \right )=1$$ (Since, $$\sin A \sin B + \cos A \cos B =\cos (A- B) $$)
$$\Rightarrow x-\frac{\pi }{4}=2n\pi ,n\in I$$
$$\Rightarrow x=2n\pi +\frac{\pi }{4},n\in I$$
$$\therefore $$ Solution of given equation is $$\displaystyle 2n\pi +\frac{\pi }{4},n\in I$$


Solve $$\displaystyle \sin x+\cos x=1+\sin x.\cos x$$, then $$2n\pi \pm \frac{\pi }{4}$$ 
If true then enter $$1$$ and if false then enter $$0$$

$$\displaystyle \because \sin x\cos x=1\sin x.\cos x$$
Let $$\displaystyle \sin x+\cos x=t\Rightarrow \sin^{2}x+\cos^{2}x+2\sin x.\cos x=t^{2}\Rightarrow \sin x.\cos s=\frac{t^{2}-1}{2}$$
Now Put $$\displaystyle \sin x +cos x=t$$ and $$\displaystyle \sin x.\cos x=\frac{t^{2}-1}{2}$$ in (i), we get $$\displaystyle t=1+\frac{t^{2}-1}{2}\Rightarrow t^{2}2t+1=0\Rightarrow t=1\Rightarrow \sin x\cos x=1\because t=\sin x+\cos x\Rightarrow \sin x +\cos x=1$$
divide both sides of equation (ii) by $$\displaystyle \sqrt{2},$$ we get
$$\displaystyle \Rightarrow \sin x\frac{1}{\sqrt{2}}+\cos x.\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}}\Rightarrow \cos\left ( x-\frac{\pi }{4} \right )=\cos\frac{\pi }{4}\Rightarrow x-\frac{\pi }{4}\Rightarrow x-\frac{\pi }{4}=2n\pi \pm \frac{\pi }{4}$$


Find the general solution of the equation $$4\cos^{2} x = 1$$

The given equation is
$$4\cos^{2}x = 1$$
$$\Rightarrow \cos^{2} x = \dfrac {1}{4}$$
$$\Rightarrow \cos^{2}x = \left (\dfrac {1}{2}\right )^{2}$$
$$\cos^{2} x = \left (\cos \dfrac {\pi}{3}\right )^{2}$$
$$\Rightarrow \cos^{2}x = \cos^{2}\dfrac {\pi}{3}$$
$$x = \dfrac {\pi}{3}$$
$$\therefore$$ The general solution, $$x = n\pi \pm \dfrac {\pi}{3}$$. where $$n\epsilon I$$.


Find the general solution of $$\cos x + \sin x = 1$$

We have,
$$\cos x + \sin x = 1$$

$$\Rightarrow \cfrac {1}{\sqrt {2}} \cos x + \cfrac {1}{\sqrt {2}} \sin x = \cfrac {1}{\sqrt {2}}$$ ....[Dividing both sides by $$\sqrt {2}$$]

$$\Rightarrow \cos \cfrac {\pi}{4}\cos x + \sin \cfrac {\pi}{4}\sin x = \cfrac {1}{\sqrt {2}}$$

$$\Rightarrow \cos \left (x - \cfrac {\pi}{4}\right ) = \cos \cfrac {\pi}{4}$$

$$\therefore x - \cfrac {\pi}{4} = 2n\pi \pm \cfrac {\pi}{4}$$, where $$n \in I$$

$$\Rightarrow x = 2n\pi \pm \cfrac {\pi}{4} + \cfrac {\pi}{4}$$, where $$n \in I$$

$$\Rightarrow x = 2n \pi + \cfrac {\pi}{4} + \cfrac {\pi}{4}, 2n\pi - \cfrac {\pi}{4} + \cfrac {\pi}{4}$$, where $$n \in I$$

$$\Rightarrow x = 2n\pi + \cfrac {\pi}{2}, 2n \pi$$, where $$n \in I$$

$$\Rightarrow x = (4n + 1) \cfrac {\pi}{2}, 2n\pi$$, where $$n \in I$$

This is the required general solution.


If $$\alpha + \beta - \gamma = \pi$$, and $$\sin^{2} \alpha + \sin^{2}\beta - \sin^{2}\gamma = \lambda \sin \alpha \sin \beta \cos \gamma$$, then write the value of $$\lambda$$.

Identity
$$\sin^{2}A-\sin^{2}B$$
$$=\sin\left(A+B\right)\sin\left(A-B\right)$$
$$=\left(\sin\left(A \right )+\sin\left(B\right)\right)\left(\sin\left(A \right )-\sin\left(B \right )\right)$$
$$=2\sin\left ( \dfrac{A+B}{2} \right )\cos\left ( \dfrac{A-B}{2} \right ).2\cos\left ( \dfrac{A+B}{2} \right )\sin\left ( \dfrac{A+B}{2} \right )$$
$$=2\sin\left ( \dfrac{A+B}{2} \right )\cos\left ( \dfrac{A+B}{2} \right ).2\sin\left ( \dfrac{A-B}{2} \right )\cos\left ( \dfrac{A-B}{2} \right )$$
$$=\sin\left ( A+B \right )\sin\left ( A-B \right )$$

Given equation
$$\sin^{2}\alpha +\left [ \sin^{2}\beta  -\sin^{2}\gamma  \right ]$$

$$=\sin^{2}\alpha + \sin\left( \beta-\gamma\right)\sin\left(\beta + \gamma\right)$$

$$=\sin^{2}\alpha+\sin\left(\pi - \alpha\right) \sin\left(\beta + \gamma\right)$$

$$=\sin^{2} \alpha + \sin \alpha \sin\left(\beta + \gamma\right)$$

$$=\sin \alpha \left[\sin \alpha +\sin\left(\beta + \gamma\right)\right]$$

$$=\sin \alpha\left [\sin \left(\pi-\left(\beta-\gamma\right)\right)+\sin\left(\beta+\gamma\right)\right]$$

$$=\sin\alpha\left [\sin\left(\beta-\gamma\right)+\sin\left(\beta +\gamma\right)\right]$$

$$=\sin \alpha\left[2\sin \beta \cos \gamma\right]$$

$$=2\sin \alpha \sin \beta \cos \gamma$$

$$\therefore  \lambda=2$$


Find the domain of definition of the following function:
$$\displaystyle y \, = \, arc\cos \, \frac{2x \, + \, 1}{2 \, \sqrt{2x}}$$

$$y= \text{arc }\cos(\cfrac { 2x+1 }{ 2\sqrt { 2x }  } )$$
$$-1\le \cfrac { 2x+1 }{ 2\sqrt { 2x }  }\le 1$$
$$-2\sqrt { 2x }  \le 2x+1,$$
$$\Longrightarrow 8x\le 4{x}^{2}+4x+1,$$
$$\Longrightarrow 4{x}^{2}-4x+1\ge 0,$$
$$\Longrightarrow {(2x-1)}^{2}\ge 0$$
This verifies for all $$x.$$
$${(2x-1)}^{2}\le { (2\sqrt { 2x } ) }^{ 2 }$$
$$\Longrightarrow 4{x}^{2}+4x+1\le 8x,$$
$$\Longrightarrow{(2x-1)}^{2}\le 0,$$
$$\Longrightarrow 2x-1=0,$$
$$\Longrightarrow x=\cfrac{1}{2},$$
$$\therefore$$ So, domain will be $$\cfrac{1}{2}.$$


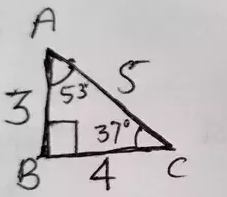
How to calculate $$\sin { 37 } $$

We know that $${37}^{\circ}<{90}^{\circ}$$

Hence $${37}^{\circ}$$ is acute.

From $$\triangle{ABC},\,\,\angle{C}$$ is acute.

$$\therefore\,\angle{B}={90}^{\circ}$$

$$\therefore\,\,\angle{A}+\angle{B}+\angle{C}={180}^{\circ}$$

$$\Rightarrow\,\angle{C}={180}^{\circ}-\left(\angle{A}+\angle{B}\right)$$

$$\Rightarrow\,\angle{C}={180}^{\circ}-\left({37}^{\circ}+{90}^{\circ}\right)$$

$$\Rightarrow\,\angle{C}={180}^{\circ}-{127}^{\circ}={53}^{\circ}$$

Let $$AB=3$$ units,$$BC=4$$ units then

By Pythagoras theorem,$${AC}^{2}={AB}^{2}+{BC}^{2}$$

$${AC}^{2}={3}^{2}+{4}^{2}=9+16=25$$

$$\Rightarrow\,AC=5$$ units

$$\therefore\,\sin{{37}^{\circ}}=\dfrac{AB}{AC}=\dfrac{3}{5}$$

1452824_862880_ans_0a32cf62826d4a33a3f0f121a8c397d4.PNG


Solve the following equation:
$$\displaystyle \tan \, x \, + \, \tan \, 2x \, + \, \tan \, 3x \, = \, 0$$

$$ tanx + tan2x +tan3x = 0...(1)$$
we have $$ tan 3x = tan (x+2x) = (tanx + tan2x)(1-tanx .tan2x)$$
$$ \Rightarrow tanx + tan2x = tan3x - tanx . tan2x. tanx3x $$
using the above realation equation (1) can written as
$$ \Rightarrow tan3x - tan x. tan 2x .tan3x + tan 3x = 0$$
$$ \Rightarrow  tan 3x (2-tanx . tan2x)= 0$$
$$ \therefore tan 3x = 0 $$
$$ x = x\pi/ 3 ; x\epsilon $$ integers.
and, $$ 2- tanx . tan2x = 0$$
$$ \Rightarrow  tanx . tan 2x = 2 $$
$$ \Rightarrow  tanx \dfrac{2tanx}{1-tan^2x} = x $$
$$ \Rightarrow tan^2x = 1-tan^2x $$
$$ \Rightarrow 2tan^2 x = 1 $$
$$ \Rightarrow  tanx = \pm1/\sqrt{2}$$
$$ x = n\pi\pm tan^{-1}(\pm 1/\sqrt{2})$$

1137948_887981_ans_c113e0b53ba04cf9afdce42b91b7a262.jpg


Prove that $$\cfrac { \sin { 9x } +\sin { 7x } +\sin { 5x } +\sin { 3x }  }{ \cos { 9x } +\cos { 7x } +\cos { 5x } +\cos { 3x }  } =\tan { 6x } $$

Formulas :

$$1)\sin(C+D)=2\sin(\dfrac {C+D} {2})\cos(\dfrac {C-D} {2})$$

$$2)\cos(C+D)=2\cos(\dfrac {C+D} {2})\cos(\dfrac {C-D} {2})$$

Rewriting the above equation ;

$$\dfrac {(\sin9x+\sin3x) +(\sin7x+\sin5x)} {(\cos9x+\cos3x) +(\cos7x+\cos5x)} $$

$$\Rightarrow \dfrac {2\sin(6x)\cos(2x)+2\sin(6x)\cos(x)}{2\cos(6x)\cos(2x)+2\cos(6x)\cos(x)} $$

$$\Rightarrow \dfrac {\sin6x} {\cos6x} =\tan6x$$


Prove that $$\sin(A-B)=\sin A \cos B-\cos A \sin B$$

We can prove this by using euler’s identity : $$e^{ix} = cosx + i\ sinx$$

therefore we have $$e^{iA} = cosA + i\ sinA$$,

and $$e^{iB} = cosB + isinB$$

now

$$e^{iA}*e^{iB} = e^{i(A+B)}$$

$$\Rightarrow (cosA + i\ sinA)(cosB + i\ sinB) = (cos(A+B) + i\ sin(A+B))$$

$$\Rightarrow (cosA*cosB - sinA*sinB) + i(sinA*cosB + cosA*sinB) = (cos(A+B) + i\ sin(A+B))$$

On equating the imaginary parts on both sides of the equation we get the required result

$$i.e. sin(A+B) = sinA*cosB + cosA*sinB$$



Find the general solution of the following  questions
$$ \cos x= 2x$$
$$ \sin 2x + \cos x=0$$.

$$\sin2x+cosx=0$$
$$\because \quad \sin2x=2sinxcosx$$
$$\Rightarrow \quad 2sinxcosx+cosx=0$$
$$\Rightarrow \quad cosx\left( 2sinx+1 \right) =0$$
                    $$\swarrow $$$$\searrow $$
     $$cosx=0$$       $$2sinx=-1$$
                               $$sinx=-1/2$$
General solution for $$cosx=0$$
$$x=\left( 2n+1 \right) \pi /2\quad ,\quad n\in z$$
$$\Rightarrow \quad x=2n\pi \pm \pi /2\quad ,\quad n\in z$$
General solution for $$sinx=-1/2$$
let  $$sinx=siny\quad \rightarrow \left( 1 \right) $$
      $$sinx=-1/2\quad \rightarrow \left( 2 \right) $$
From $$(1)$$ & $$(2)$$
$$siny=-1/2$$
$$siny=\sin\dfrac { 7\pi  }{ 6 } $$
      $$y=\dfrac { 7\pi  }{ 6 } $$
General solution $$=x=n\pi +{ \left( -1 \right)  }^{ n }y\quad ,\quad n\in z$$
put  $$y=\dfrac { 7\pi  }{ 6 } $$
$$x=n\pi +{ \left( -1 \right)  }^{ n }\dfrac { 7\pi  }{ 6 } \quad ,\quad n\in z$$
Hence for  $$cosx=0,\quad x=\left( 2n+1 \right) \pi /2\quad ,\quad n\in z$$
            for  $$sinx=-1/2,\quad x=n\pi +{ \left( -1 \right)  }^{ n }\dfrac { 7\pi  }{ 6 } \quad ,\quad n\in z$$


Find the general solution for each of the following equation:
$$\sin 2x + \cos x = 0$$

Given $$\sin 2x+\cos x=0$$

$$\implies 2\sin x\cos x+\cos x=0$$

$$\implies (2\sin x+1)\cos x=0$$

$$\implies (2\sin x+1)=0$$ or $$\cos x=0$$

$$\implies \sin x=-\dfrac 12$$ or $$\cos x=0$$

$$\implies x=\dfrac{7\pi}{6}+2n\pi, x=\dfrac{11\pi}{6}+2n\pi$$ or $$x=\pm\dfrac{\pi}{2}+2n\pi$$ (Since, $$\sin$$ is negative in third and fourth quadrant)


Solve $$ \sin x+ \sqrt3 \cos x = \sqrt2$$

Solution:-
$$\sin{x} + \sqrt{3}\cos{x} = \sqrt{2}$$
$$\sqrt{3} \cos{x} = \sqrt{2} - \sin{x}$$
Squaring both sides, we have
$${\left( \sqrt{3} \cos{x} \right)}^{2} = {\left( \sqrt{2} - \sin{x} \right)}^{2}$$
$$3\cos^{2}{x} = 2 + \sin^{2}{x} - 2\sqrt{2}\sin{x}$$
$$\Rightarrow \; 3 \left( 1 - \sin^{2}{x} \right) = 2 + \sin^{2}{x} - 2 \sqrt{2} \sin{x} \; \left( \because \sin^{2}{x} + \cos^{2}{x} = 1 \right)$$
$$3 - 3 \sin^{2}{x} = 2 + \sin^{2}{x} - 2 \sqrt{2} \sin{x}$$
$$\Rightarrow 4 \sin^{2}{x} - 2\sqrt{2} \sin{x} - 1 = 0$$
The above equation is in the quadratic form, i.e. $$a{x}^{2} + bx + c$$.
Now, by using quadratic formula, i.e., $$x = \cfrac{ -b \pm \sqrt{{b}^{2} - 4ac}}{2a}$$, we have
$$\sin{x} = \cfrac{- \left(-2 \sqrt{2} \right) \pm \sqrt{ {\left( -2 \sqrt{2} \right)}^{2} - \left( 4 \times 4 \times \left( -1 \right) \right)}}{2 \times 4}$$
$$\Rightarrow \; \sin{x} = \cfrac{2 \sqrt{2} \pm \sqrt{8 + 16}}{8}$$
$$\Rightarrow \; \sin{x} = \cfrac{\sqrt{2} \pm \sqrt{6}}{4}$$
$$\therefore \; x = \sin^{-1}{\left( \cfrac{\sqrt{2} + \sqrt{6}}{4} \right)} + 2n\pi \; \text{ Or } \; x = \sin^{-1}{\left( \cfrac{\sqrt{2} - \sqrt{6}}{4} \right)} + 2n\pi \; \text{ For all n} \in \text{integer}$$


Prove that
If $$2 \, \sin \, \left(\theta + \dfrac{\pi}{3} \right) = \cos \left(\theta - \dfrac{\pi}{6} \right) \, then , \, \tan \theta + \sqrt{3} = 0$$

$$\sin(A+B)=\sin A\cos B+\sin B\cos A$$
$$\cos(A-B)=\cos A\cos B-\sin A\sin B$$


$$2\sin(\theta+\dfrac\pi3)=\cos(\theta-\dfrac\pi6)$$

$$\rightarrow 2(\sin\theta \cos\dfrac\pi3+\cos\theta \sin\dfrac\pi3)=\cos\theta \cos\dfrac\pi6+\sin\theta \sin\dfrac\pi6$$

$$\rightarrow 2(\dfrac {\sin\theta}2+\dfrac{\sqrt3 \cos\theta}2)=\dfrac{\sqrt3 \cos\theta}2+\dfrac{\sin\theta}2$$

$$\rightarrow 2(\sin\theta+\sqrt3 \cos\theta)= \sqrt3 \cos\theta+\sin\theta$$

$$\rightarrow \sin\theta=-\sqrt3\cos\theta$$

$$\rightarrow \dfrac{\sin\theta}{\cos\theta}=-\sqrt3$$

$$\rightarrow \tan\theta+\sqrt3=0$$


Prove: $$\dfrac{1 + sec \, A}{sec \, A } = \dfrac{sin^2 A}{1 - cos \, A}$$

$$L.H.S. =\dfrac{1+secA}{secA}$$

$$=\dfrac{1+\dfrac{1}{cosA}}{\dfrac{1}{cosA}}$$     ...............  $$\sec{x}=\dfrac{1}{\cos{x}}$$

$$=\dfrac{\dfrac{1+cosA}{cosA}}{\dfrac{1}{cosA}}$$

$$=\dfrac{1+cosA}{1}$$

Now multiply the numerator and denominator with $$1-cosA$$

$$=\dfrac{(1+cosA)(1-cosA)}{1-cosA}$$

$$=\dfrac{1-cos^{2}A}{1-cosA}$$   ...........  $$a^2-b^2=(a-b)(a+b)$$

$$=\dfrac{sin^{2}A}{1-cosA}$$     ..............  $$ [sin²θ+cos²θ=1]$$

$$=R.H.S.$$


If $$\cos (65^0-A)\cos(25^0+B)- \sin(65^0-A) \sin( 25^0+B)= \sin (m+A-B)$$.Find $$m$$

$$cos(65^\circ-A)cos(25^\circ+B)-sin(65^\circ-A)sin(25^\circ+B)\\=cos[(65^\circ-A)+(25^\circ+B)]\\=cos[90^\circ-(A-B)]\\=sin(A-B)\\now\>compare\>it\>with\>given\>value\>sin(m+A-B)\>we\>get\>m\>=\>0$$



Convert the angles:
a) $$4.4^{c}$$
b) $$-\frac{9\pi}{2}^{c}$$
into degree.

(a) $$2\pi^{c}=360^{\circ}$$
$$\Rightarrow 1^{c}=(\cfrac{180}{\pi})^{\circ}$$
$$\Rightarrow 4.4^{c}=\cfrac{180\times 7}{22} \times 4.4$$
$$=252^{\circ}$$
$$\therefore 4.4^{c}=252^{\circ}$$

(b) $$2\pi^{c}=360^{\circ}$$
$$\Rightarrow \pi^{c}=180^{\circ}$$
$$\Rightarrow \cfrac{-9\pi^{c}}{2}=(\cfrac{-9}{2}\times 180)^{\circ}$$
$$=810^{\circ}$$
$$\therefore \cfrac{-9\pi^{c}}{2}=-810^{\circ}$$



$$ifsec\theta +tan\theta =p\quad then\quad the\quad value\quad of\quad cosec\theta $$


2040926_1454762_ans_66a9b2be8fcd4161b6756cf44818b244.jpeg


Class 11 Commerce Maths Extra Questions