MCQ Questions for CBSE Class 10 Maths Quiz with Answers

Students can practice the MCQ Questions for Class 10 Maths to test their conceptual knowledge and improve in weak areas accordingly. CBSE Class 10th Maths Mock Test over here will improve your overall skills in the subject.

Multiple Choice Questions for Class 10th Maths Quiz with Answers

Practice using the Maths Grade 10 MCQ Questions Quiz by simply clicking on the conceptwise links mentioned below.

• Areas Related To Cricles Class 10 Maths MCQ Questions
• Arithmetic Progressions Class 10 Maths MCQ Questions
• Circles Class 10 Maths MCQ Questions
• Constructions Class 10 Maths MCQ Questions
• Coordinate Geometry Class 10 Maths MCQ Questions
• Introduction To Trigonometry Class 10 Maths MCQ Questions
• Pair Of Linear Equations In Two Variables Class 10 Maths MCQ Questions
• Polynomials Class 10 Maths MCQ Questions
• Probability Class 10 Maths MCQ Questions
• Quadratic Equations Class 10 Maths MCQ Questions
• Real Numbers Class 10 Maths MCQ Questions
• Some Applications Of Trigonometry Class 10 Maths MCQ Questions
• Statistics Class 10 Maths MCQ Questions
• Surface Areas And Volumes Class 10 Maths MCQ Questions
• Triangles Class 10 Maths MCQ Questions

Areas Related To Cricles Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5

Areas Related To Cricles Questions and Answers

Areas Related To Cricles Quiz Question	Answer
Identify the center of the circle.	$$O$$
What is the length of arc AB making angle of $$126^0$$ at center of radius $$8$$ ?	$$5.6\displaystyle \pi$$
Two concentric circles intersect at _____ number of points.	$$0$$
The diameter of a circle is $$10 cm$$ . Find the length of the arc, when the corresponding central angle is $$270^o$$ .   $$(\pi =3.14)$$	$$23.55 cm$$
The length of an arc of a sector of a circle of radius r units and of centre angle $$\theta$$ is $$\displaystyle \frac{\theta}{360^{\circ}} \times \pi r^2$$ .	False
The area of a sector of angle p (in degrees) of a circle with radius R is	$$\displaystyle \frac{p}{720} \times 2 \pi R^2$$
If an arc of a circle of radius $$14\ cm$$ subtends an angle of $$60^{\circ}$$ at the centre, then the length of the arc is $$\displaystyle \dfrac{44}{3}\ cm$$ .	True
In a circle of radius 21 cm, an arc subtends an angle of $$60^{\circ}$$ at the centre the length of the arc is 22 cm.	True
Identify which among the pieces given below will not be requires to complete the square.	J
From the figure, identify the center of the circle.	$$C$$

Arithmetic Progressions Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15 Quiz 16 Quiz 17

Arithmetic Progressions Questions and Answers

Arithmetic Progressions Quiz Question	Answer
In an arithmetic series, $$a_1 = -14$$ and $$a_{5}=50$$ . Find the sum of the first 5 terms.	$$90$$
$$-20, -16, -12, -8.....$$ is the sequence and each term is increased by $$4$$ . Then which of the following could not be a term in the sequence?	$$762$$
The sum of first $$20$$ natural numbers is	$$210$$
Find first term 'a' and common difference 'd' for the following AP. $$\sqrt{2}$$ ,  $$\sqrt{8}$$ ,  $$\sqrt{18}$$ ,  $$\sqrt{32}$$ ,.....	$$a =$$ $$\sqrt{2}$$ $$, d=$$ $$\sqrt{2}$$
The sum of the first $$1000$$ positive integer is	$$500500$$
State the following statement is true or false: Progression means increment of quantity in a particular pattern.	True
Which term of the sequence $$-7, -2, 3, 8,.........$$ is $$73$$ ?	$$17$$
Find the $$11$$ th term of the sequence $$5,2,-1,-4,......$$	$$-25$$
The nth term of the sequence $$2, 4, 6, 8....$$ is	$$2n$$
Find the A.P. whose sum to $$n$$ terms is $$2n$$ $$^2$$ $$+ n$$	The required A.P. is $$3, 7, 11, 15,...$$

Circles Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4

Circles Questions and Answers

Circles Quiz Question	Answer
How many parallel tangents can a circle have?	2
The length of tangent drawn from a point $$8\  cm$$ away from centre of circle of radius $$6\  cm$$ is :	$$2\sqrt{7} cm$$
The tangent to a circle is a special case of the secant. It is:	True
There are exactly two tangents to a circle passing through a point lying ____ the circle.	Outside
There cannot be more than two tangents to a circle parallel to a given secant.	True
From an external point, if  $$K$$ tangents can be drawn to a  circle, then $$K$$ is equal to	$$2$$
Which of the following is point of contact?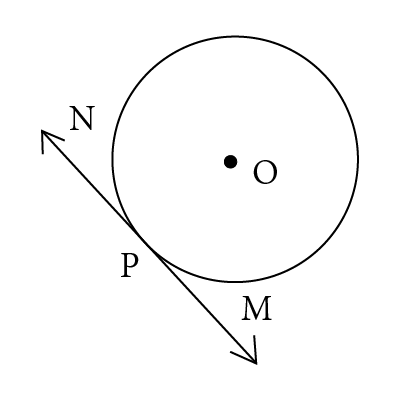	$$P$$
The maximum number of common tangents drawn to two intersecting circles at two points is	$$2$$
There is no tangent to a circle passing through a point lying ..... the circle.	inside
A tangent to a circle is a line that intersects the circle in only one point.	True

Constructions Class 10 Maths MCQ Quiz

Quiz 1

Constructions Questions and Answers

Constructions Quiz Question	Answer
To construct a triangle similar to a given ABC with its sides $$\cfrac{3}{7}$$ of the corresponding sides of $$\Delta$$ ABC, first draw a ray BX such that $$\angle$$ CBX is an acute angle and X lies on the opposite side of A with respect to BC. Then locate points $$B_1, B_2, B_3,$$ ... on BX at equal distances and next step is to join	$$B_{7}$$ to C
Which is $$2^{nd}$$ step?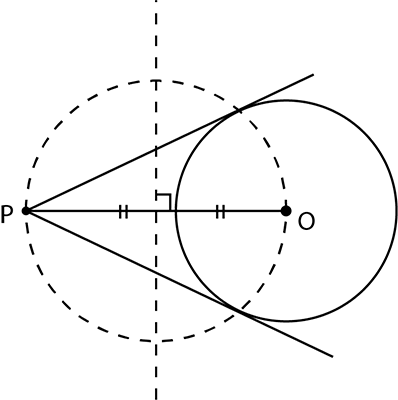	$$(d)$$
To construct a triangle similar to given $$\triangle ABC$$ with its sides $$\dfrac23$$ of that of $$\displaystyle \Delta ABC$$ , locate points on ray $$BX$$ at equal distances as $$\displaystyle { B }_{ 1 },{ B }_{ 2 },{ B }_{ 3 },....$$ such that $$\displaystyle \angle CBX$$ is acute. The points to be joined in the next step are:	$$\displaystyle { B }_{ 3 },C$$
To construct a triangle similar to given $$\displaystyle \Delta ABC$$ with its sides $$\dfrac35$$ of that of  $$\displaystyle \Delta ABC$$ , a ray $$BX$$ is drawn at acute angle with $$BC$$ . How many minimum no. of points should be marked on $$BX$$ ?	$$5$$
To construct a triangle similar to given $$\displaystyle \Delta ABC$$ with its sides $$\dfrac45$$ of that of  $$\displaystyle \Delta ABC$$ , locate points $$\displaystyle { X }_{ 1 },{ X }_{ 2 },{ X }_{ 3 },....$$ . on ray $$BX$$ at equal distances such that $$\displaystyle \angle ABX$$ is acute. The points to be joined in the next step are:	$$\displaystyle { X }_{ 5 },A$$
If two tangents are drawn at the end points of two radii that are inclined at an angle of $$\displaystyle { 110 }^{ \circ  }$$ . Find the angle between the tangents.	$$\displaystyle { 70 }^{ \circ }$$
To construct a triangle similar to given $$\displaystyle \Delta ABC$$ with sides equal to $$\dfrac75$$ of the sides of  $$\displaystyle \Delta ABC$$ , a ray $$BX$$ is drawn such that $$\displaystyle \angle CBX$$ is acute angle and $$\displaystyle { B }_{ 1 },{ B }_{ 2 },{ B }_{ 3 },...$$ are marked at equal distances on $$BX$$ . The points to be joined in the next step are:	$$\displaystyle { B }_{ 5 },C$$ and  $$\displaystyle { B }_{ 7 },Q$$
To draw a pair of tangents to a circle which are at right angles to each other, it is required to draw tangents at end points of two radii which are inclined at an angle of?	$$\displaystyle { 90 }^{ \circ }$$
What should be the angle between corresponding radii such that the tangents don't intersect?	$$\displaystyle { 180 }^{ \circ }$$
If tangents are drawn from the end points of $$2$$ radii that are inclined at an angle $$\displaystyle { 125 }^{ \circ  }$$ , what is the angle between the tangents?	$$\displaystyle { 55 }^{ \circ }$$

Coordinate Geometry Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11

Coordinate Geometry Questions and Answers

Coordinate Geometry Quiz Question	Answer
If (5, 7, 10), (1, 9, 6) are the extremities of the hypotenuse of a right angled isosceles triangle, then the third vertex is	(4, 6, 6)
The arrangement of the areas of the triangles formed by the following points in ascending order is  i) P(0,0), Q(4,0), R(0,3) ii) P(0,0), Q(5,0), R(0,2) iii) P(0,0), Q(0,5), R(6,0) iv) p(3,0), Q(0,6), R(0,0)	ii,i,iv,iii
two medians drawn from the acute angles of a right angled  triangle interect at the angle $$\pi /6$$ if thelength the hypotenuse of the triangle is 3 units then the area of the triangle is	$$\sqrt { 3 }$$
The area inside the parabola $$5x^2 - y = 0$$ but outside the parabola $$2x^2 - y + 9 = 0$$ is	$$6\sqrt{3}$$ sq.units
Area of the triangle formed by co-ordinate axes and the line x + y = 5 is	$$\dfrac { 5 }{ 2 }$$
The centre of the circle which passes through A ( $$\alpha, 0$$ ), B (0, $$\beta$$ ), C (0, 0) is	( $$\frac{\alpha}{2},\frac{\beta}{2}$$ )
The centroid and two vertices of a triangles are (4,-8), (-9,7), (1,4) then the area of the triangle is	333 sq.units
The centre of a circle passing through the points (0 , 0), (1 , 0) and touching the circle $$x^2 + y^2$$ = 9	( $$\frac{3}{2} , \frac{1}{2}$$ )
If the points (3, -8), (4, -11) and (5, -k) are collinear them, the value of k is	14
The centers of the passing through (0,0) and (1,0) and touching the circle $${ x }^{ 2 }+{ y }^{ 2 }=9$$ is	$$\left( \dfrac { 1 }{ 2 } ,\dfrac { 1 }{ 2 } \right)$$

Introduction To Trigonometry Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13

Introduction To Trigonometry Questions and Answers

Introduction To Trigonometry Quiz Question	Answer
The value of $$\displaystyle\,\frac{2}{tan\,30^{\circ}}$$ is ________	3.46
The value of $$\tan\theta \times \cot\theta =$$ _____	$$1$$
Which of the following is equal to $$\sin x \sec x$$ ?	$$\tan x$$
The value of $$\sin\theta\times  \text{cosec}\,\theta =$$ _____	$$1$$
Who published the trigonometry in 1595?	Bartholomaeus Pitiscus
Choose the correct alternative answer for the following question. $$cosec \ 45^\circ= ?$$	$$\sqrt{2}$$
If $$\sqrt{3} \cos A = \sin A$$ , then the value of $$\cot A$$ is:	$$\dfrac{1}{\sqrt{3}}$$
$$\tan {45^ \circ } =?$$	$$1$$
The value of $$\cos 1^o.\cos 2^o.\cos 3^o.....\cos 179^o$$ is equal to	$$0$$
In $$\triangle ABC$$ , $$\angle B= {90}^{\circ}$$ , $$\sin{C} = \dfrac{3}{5}$$ , then $$\cos{A} =$$ ______	$$\dfrac{3}{5}$$

Pair Of Linear Equations In Two Variables Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15 Quiz 16

Pair Of Linear Equations In Two Variables Questions and Answers

Pair Of Linear Equations In Two Variables Quiz Question	Answer
The condition for the pair of equations $$a_1x+b_1y+c_1=0$$ and $$a_2x+b_2y+c_2 = 0$$ to have a unique solution is -	$$a_1b_2-a_2b_1 \neq 0$$
If $$\cfrac { a }{ x+y } =\cfrac { b }{ y+z } =\cfrac { c }{ z-x }$$ , then which of the following equations is true?	$$b=a+c$$
The point of intersection of the lines $$y=3x$$ and $$x=3y$$ is :	(0, 0)
If, $$\displaystyle \frac{1}{x}+\frac{1}{y}=k$$ and $$\displaystyle \frac{1}{x}-\frac{1}{y}=k$$ , then the value of y .................	Does not exist.
If the pair of equations has no solution, then the pair of equations is :	inconsistent
Which of the following pairs of equations represent inconsistent system?	$$3x - y = - 8$$ $$3x - y = 24$$
If the lines are parallel, then the pair of equations has no solution. In this case, the pair of equations is ...................	inconsistent.
State whether the given statement is true or false: A pair of linear equations is given by $$a_1x+b_1y+c_1=0$$ and $$a_2x+b_2y +c_2=0$$ also $$\displaystyle \frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$$ .  In this case, the pair of linear equations is consistent.	True
State whether the given statement is true or false: A pair of linear equations is given by $$a_1x + b_1y+c_1=0$$ and $$a_2x+b_2y+c_2=0$$ and $$\displaystyle \frac{a_1}{a_2}=\frac{b_1}{b_2}\neq \frac{c_1}{c_2}$$ .  In this case, the pair of linear equations is inconsistent.	True
State true\false: A pair of linear equations is given by $$a_1x+b_1y+{ c }_{ 1 }=0$$ and $$a_2x+b_2y+c_2=0$$ and $$\displaystyle \frac{a_1}{a_2} \neq \frac{b_1}{b_2}$$ . In this case, the pair of linear equations is consistent.	True

Polynomials Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10

Polynomials Questions and Answers

Polynomials Quiz Question	Answer
The degree of the polynomial $$2x-1$$ is	$$1$$
The polynomials in which the highest power of the variable is two are known as .................. polynomials.	Quadratic
State True Or False, whether the following expression is a quadratic polynomial or not: $$x^2+x$$	True
For what value of $$k$$ , $$-2$$ is a zero of the polynomial  $$3x^2 + 4x + 2k$$ ?	$$-2$$
Find the degree of the polynomial  $$4-y^2$$ .	$$2$$
Find the variable of the linear polynomial $$t+5$$ .	$$t$$
Which one of the following can be an example of cubic polynomial?	$$x^3=0$$
Which of the following graphs is the graph of linear polynomial?
A cubic polynomial is a polynomial of degree:	$$3$$
Find the zeroes of the linear polynomial from the graph.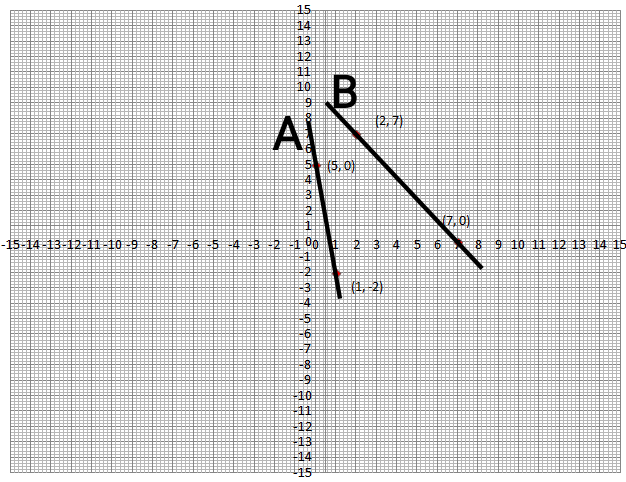	$$A- (1.8, 0), B- (7, 0)$$

Probability Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5

Probability Questions and Answers

Probability Quiz Question	Answer
A die is thrown then find the probability of getting an odd number.	$$\displaystyle \frac{1}{2}$$
In tossing a coin, the chance of throwing head and tail alternatively in $$3$$ successive trials is	$$\dfrac{1}{4}$$
A die is thrown then find the probability of getting a perfect square.	$$\displaystyle \frac{1}{3}$$
What is number of outcomes when tossing two coins together?	$$4$$
If two coins are tossed then find the probability of the event that at least one tail turns up is:	$$\displaystyle \frac{3}{4}$$
If two coins are tossed then find the probability of the event that no head turns up.	$$\displaystyle \frac{1}{4}$$
A box contains $$3$$ red, $$3$$ white and $$3$$ green balls. A ball is selected at random. Find the probability that the ball picked up is neither a white nor a red ball:	$$\displaystyle \frac{1}{3}$$
If two coins are tossed then find the probability of the events that at the most one tail turns up	$$\displaystyle \frac{3}{4}$$
Two coins are tossed. Find the probability that a head does not appear:	$$\displaystyle \frac{1}{4}$$
In a sample study of $$642$$ people, it was found that $$514$$ people have a high school certificate. If a person is selected at random, the probability that the person has a high school certificate is :	$$0.8$$

Quadratic Equations Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11

Quadratic Equations Questions and Answers

Quadratic Equations Quiz Question	Answer
Solve the following equations. $$x^4\,-\,3x^2\,+\,2\,=\,0$$ , roots are	$$x\,=\,\pm\,\sqrt2,\,\pm\,1$$
Which of the following methods is used to derive the Standard Quadratic Formula for the Quadratic Equation $$ax^2+bx+c=0$$ ?	Completing Square Method
Let $$\alpha(a)$$ and $$\beta(a)$$ be the roots of the equation $$\\ \left( \sqrt [ 3 ]{ 1+a } -1 \right) x^{ 2 }+\left( \sqrt { 1+a } -1 \right) x+\left( \sqrt [ 6 ]{ 1+a } -1 \right) =0$$ $$\displaystyle \lim _{ a\rightarrow 0 }{ \alpha  } \left( a \right)$$ and $$\displaystyle \lim _{ a\rightarrow 0 }{ \beta  } \left( a \right)$$ are	$$-\dfrac{11}{2}$$ and $$-1$$
The roots of the equation $$\sqrt{3y + 1} = \sqrt{y - 1}$$   are?	None of these
A quadratic equation in $$x$$ is $$ax^2 + bx + c = 0$$ , where $$a, b, c$$ are real numbers and the other condition is	$$a \neq 0$$
Find the roots of following quadratic equation  $$x^2\,+\,3x\,-\,2\,=\,0$$	$$\displaystyle\,x\,=\,\frac{-3\,\pm\,\sqrt{17}}{2}$$
Find the discriminant for the given quadratic equation: $$\sqrt{3}x^2\,+\,2\sqrt{2}x\,-\,2\sqrt{3}\,=\,0$$	$$32$$
Find the discriminant for the given equation: $$3x^2\,+\,2x\,-\,1\,=\,0$$	$$16$$
Find the discriminant for the given quadratic equation: $$x^2\,+\,4x\,+\,k\,=\,0$$	$$16\,-\,4k$$
Find the value of discriminant for the following equation. $$x^{2}\, +\, 4x\, +\, k\, =\, 0$$	$$\Delta\, =\, 16\, -4k$$

Real Numbers Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7

Real Numbers Questions and Answers

Real Numbers Quiz Question	Answer
The non-terminating non-recurring decimal cannot be represented as:	rational numbers
Euclids division lemma can be used to find the $$...........$$ of any two positive integers and to show the common properties of numbers.	Highest common factor
$$m$$ is not a perfect square, then $$\sqrt {m}$$  is	An irrational number
What is the square of $$(2 + \sqrt {2})$$ ?	An irrational number
What is the HCF of $$13$$ and $$22$$ ?	$$1$$
The decimal expansion of the rational number $$\dfrac {33}{2^2\cdot 5}$$ will terminate after:	two decimal places
The decimal representation of $$\dfrac { 93 }{ 1500 }$$   will be	Terminating
The fact that $$3+2\sqrt{5}$$ is irrational is because	Sum of a rational and an irrational number is irrational
$$HCF$$ of $$(10224, 1608)$$ is _________.	$$24$$
State true or false: $$\dfrac {\sqrt 2}{3}$$ is an irrational number.	True

Some Applications Of Trigonometry Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14 Quiz 15

Some Applications Of Trigonometry Questions and Answers

Some Applications Of Trigonometry Quiz Question	Answer
Let $$10$$ vertical poles standing at equal distances on a straight line, subtend the same angle of elevation $$\alpha$$ at a point $$O$$ on this line and all the poles are on the same side of $$O$$ . If the height of the longest pole is $$h$$ and the distance of the foot of the smallest pole from $$O$$ is $$a$$ ; then the distance between two consecutive poles, is	$$\displaystyle \frac{h \cos \alpha - a \sin \alpha}{9 \sin \alpha}$$
A kite is flying at an inclination of $$60^\circ$$ with the horizontal. If the length of the thread is $$120\text{ m},$$ then the height at which kite is:	$$60\sqrt 3\text{ m}$$
A vertical pole of height $$10$$ meters stands at one corner of a rectangular field. The angle of elevation of its top from the farthest corner is $$30^{\circ}$$ , while that from another corner is $$60^{\circ}$$ . The area (in $$m^{2})$$ of rectangular field is	$$\dfrac {200\sqrt {2}}{3}$$
A pole $$15$$ m long rests against a vertical wall at an angle of  $$\displaystyle 30^{\circ}$$ with the ground How high up the wall does the pole reach?	$$7.5$$ m
the shadow cast by a tower is 30 m long when the elevation of sum is  $$\displaystyle 30^{\circ}$$ If the elevation of sum is  $$\displaystyle 60^{\circ}$$  then the length of the shadow is	10 m
The angle of depression of  a boat from the top of a cliff 300 m high is  $$\displaystyle 60^{\circ}$$  The distance of the boat from the foot of the cliff is	$$\displaystyle 100 \sqrt{3}$$
If the length of the shadow of a pole is equal to the height , of the pole, then the angle of the elevation of the sun is	$$\displaystyle 45^{\circ}$$
The angle of elevation of an object viewed is the angle formed by the line of sight with the horizontal when it is	Above the horizontal level
From the point B a perpendicular BD is drawn on AC. If $$\cos 30^o=0.8$$ , find the length of AD.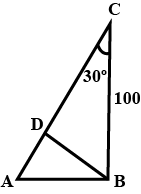	$$45$$
The length of the shadow of a pole is $$\displaystyle \sqrt{3}$$  times its height  The elevation of the sum must be	$$\displaystyle 30^{\circ}$$

Statistics Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12 Quiz 13 Quiz 14

Statistics Questions and Answers

Statistics Quiz Question	Answer
A cricket player scored the following runs in $$11$$ one-day international matches: $$65$$ , $$30$$ , $$7$$ , $$60$$ , $$65$$ , $$65$$ , $$30$$ , $$28$$ , $$30$$ , $$15$$ , $$30$$ Find the modal runs.	$$30$$ runs
Mode of a set of observations is the value which	occurs most frequently
To find mean, we use the formula	$$\frac {1}{N}\displaystyle \sum_{i=1}^{n}f_ix_i$$
Find mode from the following grouped frequency distribution table: Number of Trees Planted Number of Students $$0-10$$ $$30$$ $$10-20$$ $$60$$ $$20-30$$ $$50$$ $$30-40$$ $$70$$ $$40-50$$ $$40$$	$$34$$ trees
Variable   $$4$$ $$8$$     $$9$$   $$10$$ $$11$$   $$12$$   $$13$$    Frequency   $$3$$ $$4$$ $$5$$   $$8$$   $$4$$   $$3$$   $$2$$   Mode of the distribution	$$10$$
Calculate the median for the following data. Marks (out of 60.) $$32$$ $$27$$ $$26$$ $$24$$ $$23$$ $$21$$ Number of students   $$6$$ $$4$$ $$7$$ $$9$$ $$16$$ $$2$$	$$24$$
The mean of the following frequency distribution is $$16.6$$ $$x_{ i }$$ $$8$$ $$12$$ $$15$$ $$18$$ $$20$$ $$25$$ $$30$$ Total $$f_{ i }$$ $$12$$ $$16$$ $$p$$ $$24$$ $$16$$ $$q$$ $$4$$ $$100$$	$$q=8$$
Frequency distribution of daily commission received by 100 salesmen is given. Daily commission (in Rs.) $$100 - 120$$ $$120 - 140$$ $$140 - 160$$ $$160 - 180$$ $$180 - 200$$ No. of salesman $$20$$ $$45$$ $$22$$ $$9$$ $$4$$ Find mean daily commission received by a salesman.	$$136.4$$
The median for the following frequency distribution is: $$x:$$ 1 2 3 4 5 6 7 8 9 $$f:$$ 8 10 11 16 20 25 15 9 6	$$5$$
Determine the mode of the following data. Marks 10 16 12 19 13 20 11 14 Number of Students 3 3 4 2 6 1 5 2	$$13$$

Surface Areas And Volumes Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9 Quiz 10 Quiz 11 Quiz 12

Surface Areas And Volumes Questions and Answers

Surface Areas And Volumes Quiz Question	Answer
Calculate the total surface area of frustum cone given below: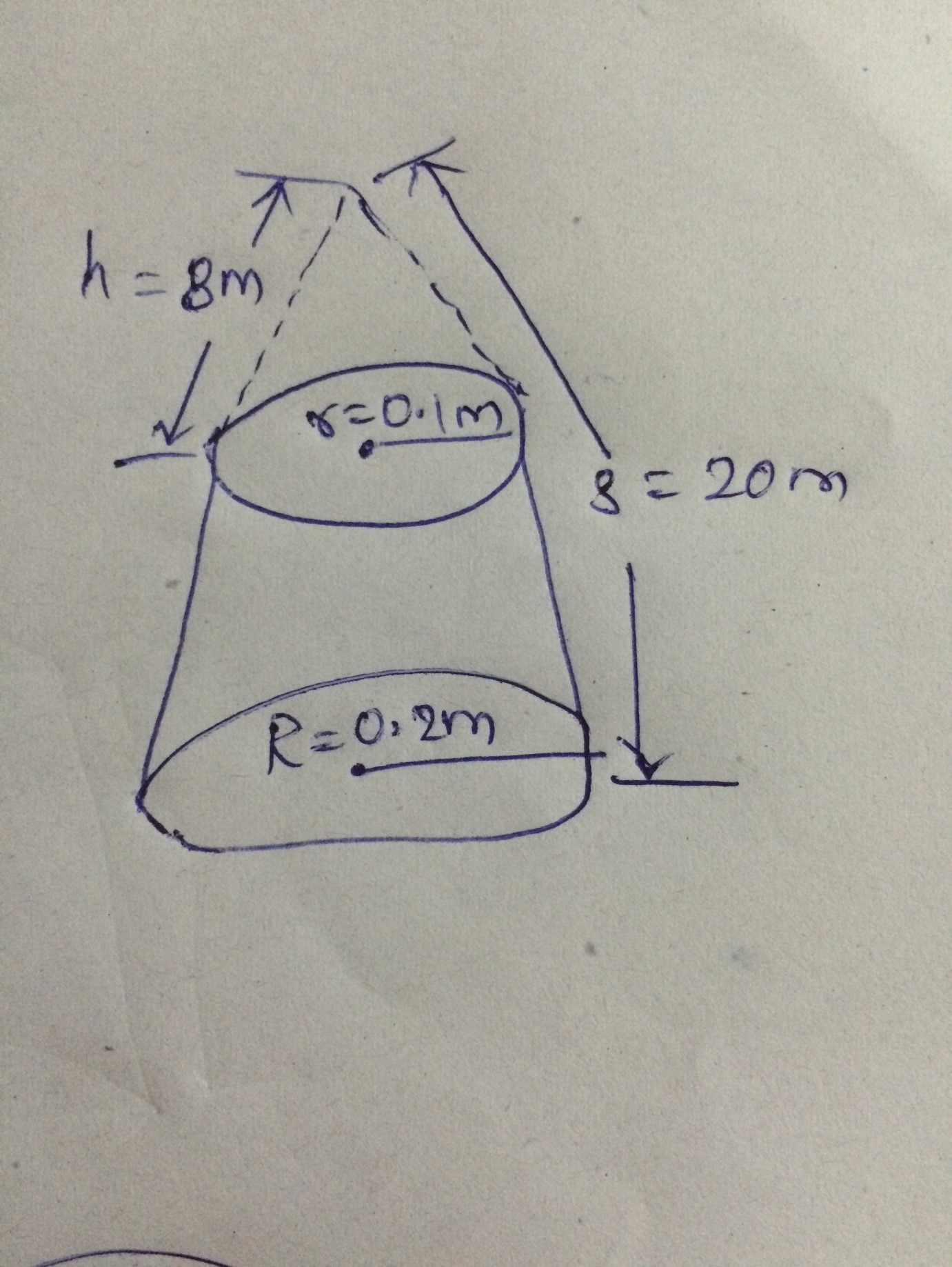	6.05 $$\pi m^2$$
A conical flask of base radius r and height h is full of milk. The milk is now poured into a cylindrical flask of radius 2r. What is the height to which the milk will rise in the flask?	$$\displaystyle\frac{h}{12}$$
A bucket is in the shape of the frustum of a right circular cone, whose radii are 5 and 10 mm. The curved surface area is $$210$$ mm. Find the slant height. (Use $$\pi$$ = $$3$$ )	$$4.66$$ mm
Say true or false: The volume of the largest right circular cone that can be fitted in a cube whose edge is $$2r$$ equals to the volume of a hemisphere of radius $$r$$ .	True
A medicine-capsule is in the shape of a cylinder of diameter $$0.5$$ cm with two hemispheres stuck to each of its ends. The length of entire capsule is $$2$$ cm. The capacity of the capsule is	$$0.36 cm^{3}$$
The surface area of the frustum cone is given its base radius, R = 6 cm and top radius, r = 3 cm. The height of the cone is 4 cm. Find the slant height of the cone.	5 cm
Find the volume of a frustum cone, whose base and upper area of a circle is 6 and 6  $$cm^2$$ . The height of the cone is 100 cm.	600 $$cm^3$$
A solid in shape of a frustum is 21 cm high. Its radius of top is 10 cm and diameter of bottom is 30 cm. The volume of the solid is	10450 $$\displaystyle cm^{3}$$
If the ratio of the radii of the circular ends of a conical bucket whose height is $$60$$ cm is $$2:1$$ and addition of the areas is $$770$$ sq.cm. Find the capacity of the bucket in litres.	$$21.56$$ litres
A shuttle cock used for playing badminton has the shape of the combination of	frustum of a cone and a hemisphere

Triangles Class 10 Maths MCQ Quiz

Quiz 1 Quiz 2 Quiz 3 Quiz 4 Quiz 5 Quiz 6 Quiz 7 Quiz 8 Quiz 9

Triangles Questions and Answers

Triangles Quiz Question	Answer
Fill in the blank All .............. triangles are similar	equilateral
Fill in the blank All squares are ............... (similar, congruent)	similar
In the given figure of $$\triangle ABC,\bar { XY } ||\bar { BC } ,AX=1cm,XB=3cm\quad and\quad BC=6cm.ThenXY=........cm.$$	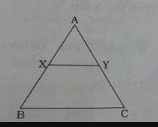1.5
In $$\triangle{ABC}$$ , $$\angle{B}=90$$ , $$AB=8\:cm$$ and $$BC=6\:cm$$ . The length of the median BM is	5 cm
In the given figure of $$\triangle ABC,\overline { XY } ||\overline { BC } ,AX=1cm,XB=3cm\quad and\quad BC=6\quad cm.\quad Then\quad ,XY......cm$$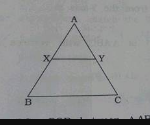	1.5
In an equilateral $$\Delta ABC$$ ,D is the midpoint of AB and E is the midpoint of AC then $$ar\left( \Delta ABC \right) :a\left( \Delta ADE \right) =?$$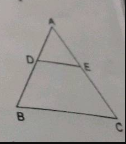	4:1
If the ratio of the corresponding sides of the two similar triangles is 2 : 3, then the ratio of their corresponding altitudes is	$$2 : 3$$
If ABC and DEF are similar triangles such that  $$\displaystyle \angle A=47^{\circ}$$ and  $$\displaystyle \angle B=83^{\circ}$$ then  $$\displaystyle \angle F$$ is	$$\displaystyle 50^{\circ}$$
Which of the following cannot be the sides a right angle triangle?	9 cm, 5 cm, 7 cm
In the above figure, if DE || BC, then x equals :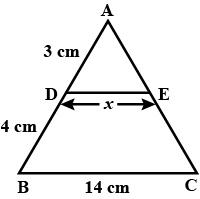	6 cm

CBSE Class 10th Maths Sample Paper MCQ Questions with Answers

Free CBSE 10th Standard Maths Exam Mock Test will be of great help with all the concepts and subtopics in the subject. Identify your strengths and weaknesses by attempting the Math Grade 10 Practice Questions and improve your scores in final exams. Get to know the Pattern of Questions that is being asked by solving the CBSE Class 10th Maths MCQ Quiz and build a stronger understanding of the subject.

Importance of MCQExams.com Provided CBSE Class 10 Maths MCQ Quiz with Answers

Below is the information stating why you should opt the CBSE Grade 10 Math Practice Questions given by us. They are along the lines

• With ample practice using the MCQs for Class 10th Math you will slowly and steadily develop a deeper understanding of the concepts.
• Class 10 Maths MCQ Quiz with Answers will boost the self esteem and thus help you face the actual exams with confidence.
• You will no longer feel difficulty in finding the perfect resources for your study plan with our Chapterwise 10th Standard Maths Multiple Choice Question and Answers.
• The CBSE Grade 10 Math Question Bank will definitely be of help to you in your journey of preparing for academic or competitive exams.

conclusion

We as a team wish the information shared regarding the MCQ Questions for Class 10th Math has enlightened you. Please refer to the other subjects MCQs as well on our site and study to score. Stay tuned for more updates on all Preparation Related Resources such as Study Material, Revision Notes, homework Help, etc. Downloading Multiple type choice questions of all subjects for cbse classes 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, and 1 is very easy from MCQExams.com