MCQ Questions for Class 12 Applied Mathematics Quiz with Answers Chapter Wise PDF Download
CBSE Multiple Choice Type Questions for 12th Class Applied Mathematics PDF formatted study resources are available for free download. These Grade 12 Applied Mathematics CBSE MCQ Mock Test helps you learn & practice the concepts in a fun learning way.
Class 12 Applied Mathematics MCQs Multiple Choice Questions with Answers
Here are the chapterwise CBSE MCQ Quiz Test Questions for Class 12th Applied Mathematics in pdf format that helps you access & download so that you can practice online/offline easily.
- Application Of Derivatives Class 12 Commerce Applied Mathematics MCQ Questions
- Applications Of Integrals Class 12 Commerce Applied Mathematics MCQ Questions
- Definite Integrals Class 12 Commerce Applied Mathematics MCQ Questions
- Determinants Class 12 Commerce Applied Mathematics MCQ Questions
- Differential Equations Class 12 Commerce Applied Mathematics MCQ Questions
- Indefinite Integrals Class 12 Commerce Applied Mathematics MCQ Questions
- Linear Equations Class 12 Commerce Applied Mathematics MCQ Questions
- Matrices Class 12 Commerce Applied Mathematics MCQ Questions
- Probability Distribution And Its Mean And Variance Class 12 Commerce Applied Mathematics MCQ Questions
- Quantification And Numerical Applications Class 12 Commerce Applied Mathematics MCQ Questions
- Standard Probability Distributions Class 12 Commerce Applied Mathematics MCQ Questions
Application Of Derivatives Class 12 Commerce Applied Mathematics MCQ Quiz
Application Of Derivatives Questions and Answers
| Application Of Derivatives Quiz Question | Answer |
|---|---|
| $$f(x) = x^3- 6x^2 + 12x- 16$$ is strictly decreasing for | $$x\in \phi$$ |
| $$\displaystyle f:(0, \infty) \rightarrow (-\frac {\pi}{2}, \frac {\pi}{2})$$ be defined as, $$\displaystyle f(x) = arc \: \tan( \: x)$$ The above function can be classified as |
both injective as well as surjective |
The graph a function $$f$$ is given. On what interval is $$f$$ increasing ? |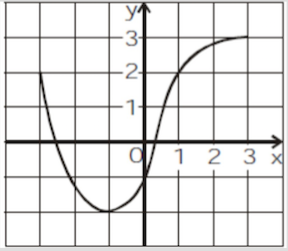
$$(-1, 3]$$ |
| Let $$f(x)$$ be a non-zero polynomial of degree $$4$$. Extreme points of $$f(x)$$ are $$0, -1, 1$$. If $$f(k)=f(0)$$ then? | k has one rational & two irrational roots |
$$\displaystyle \mathrm{f}(\mathrm{x})=\frac{\mathrm{a}\sin \mathrm{x}+\mathrm{b}\cos \mathrm{x}}{\mathrm{a}\cos \mathrm{x}-\mathrm{b}\sin \mathrm{x}} \ \ \ \ \ (\tan \mathrm{x}\neq\frac{\mathrm{a}}{\mathrm{b}})$$ is |
increasing in domain $$\mathrm{f}$$ |
| The curve $$y = xe^{x}$$ has minimum value equal to | $$-\dfrac {1}{e}$$ |
| The sum of two +ve numbers isIf the sum of their square is minimum then one of the number is | $$10$$ |
| If the volume of a spherical ball is increasing at the rate of $$4\pi\ cc/sec$$, then the rate of increase of its radius (in cm/sec), when the volume is $$288\pi\ cc$$, is | $$\dfrac {1}{36}$$ |
| A spherical balloon is filled with $$4500\ \pi$$ cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of $$72\ \pi$$ cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases $$49\ minutes$$ after the leakage began is: |
$$2/9$$ |
| Let b be a nonzero real number. Suppose $$f : R \rightarrow R$$ is a differentiable function such that $$f(0) = 1$$. If the derivative f' of f satisfies the equation $$f'(x) = \dfrac{f(x)}{b^2 + x^2}$$ for all $$x \in R$$, then which of the following statements is/are TRUE? |
$$f\left( x \right) f\left( -x \right) =1$$ for all $$x\in R$$ |
Applications Of Integrals Class 12 Commerce Applied Mathematics MCQ Quiz
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Applications Of Integrals Questions and Answers
| Applications Of Integrals Quiz Question | Answer |
|---|---|
| The area of the region bounded by the curves $$y = x^2$$ and $$y = |x|$$ is | $$\dfrac{1}{3}$$ |
| Area bounded by the curves $$y = \sin x ,$$ tangent drawn to it at $$x = 0$$ and the line $$x = \frac { \pi } { 2 }$$ is equal to | $$\frac { \pi ^ { 2 } - 2 } { 2 }$$ sq.units |
| The area enclosed by the line y = x + 1, X- axis and the lines x = -3 and x = 3 is | 10 |
| Area bounded by curve $$y = (x - 1)(x - 2)(x - 3)$$ and x-axis between lines $$x = 0, x = 3$$ | $$5/2$$ |
| As shown in the figure of an ellipse $$\frac{x^{2}}{16}+\frac{y^{2}}{9}=1$$. The area of shaded region is ....... .  |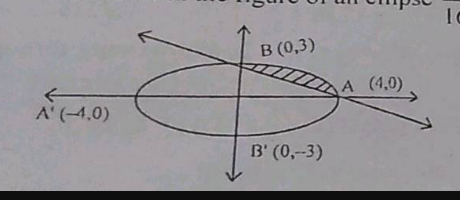
$$12\pi $$ |
| The area bounded by the curves $$x+2|y|=1$$ and $$x=0$$ is? | $$\dfrac{1}{2}$$ |
| Area included between $${ y }=\dfrac { { x }^{ { 2 } } }{ 4{ a } } $$ and $$y = \dfrac { 8 a ^ { 3 } } { x ^ { 2 } + 4 a ^ { 2 } }$$ is | $$\dfrac { a ^ { 2 } } { 3 } ( 6 \pi - 4 )$$ |
| The area of the figure formed by $$a|x|+b|y|+c=0$$, is | $$\dfrac{2c^{2}}{|ab|}$$ |
| Find the area of bounded by $$y=\sin x $$ from $$x=\dfrac{\pi}{4} $$ to $$x=\dfrac{\pi}{2}$$ | $$\dfrac{\sqrt 2-1}{\sqrt2}$$ |
| The area of the region by curves $$y=x\log x$$ and $$y=2x-2x^{2}=$$ | $$7/12$$ |
Definite Integrals Class 12 Commerce Applied Mathematics MCQ Quiz
Definite Integrals Questions and Answers
| Definite Integrals Quiz Question | Answer |
|---|---|
| Evaluate : $$\displaystyle\int^a_{-a}\sqrt{\dfrac{a-x}{a+x}}dx$$ | $$a\pi$$ |
| The value of the definite integral $$\displaystyle\int^1_0\dfrac{xdx}{(x^2+16)}$$ lies in the interval $$[a, b]$$. Then smallest such interval is? | $$\left[0, \dfrac{1}{17}\right]$$ |
| Let $$F(x)=f(x)+f\left ( \dfrac{1}{x} \right )$$, where $$f(x)=\int_{l}^{x}\dfrac{logt}{l+t}dt$$. Then $$F(e)$$ equals | $$\dfrac{1}{2}$$ |
| The integral $$\displaystyle\int^{{\pi}/{4}}_{{\pi}/{12}}\frac{8\cos 2x}{(\tan x+\cot x)^3}dx$$ equals? | $$\displaystyle\frac{15}{128}$$ |
| The value of $$\displaystyle \int_{0}^{1}\frac{8\log(1+\mathrm{x})}{1+\mathrm{x}^{2}}$$ dx is |
$$\pi \log 2$$ |
| The following integral $$\displaystyle \int_{\pi/4}^{\pi/2} (2 cosec x)^{17}dx$$ is equal to | $$\displaystyle \int_{0}^{log(1+\sqrt{2})} 2(e^u + e^{-u})^{16} du$$ |
| The value of $$g\displaystyle \left ( \frac{1}{2} \right )$$ is? | $$\pi$$ |
| $$\int _{ 0 }^{ \pi }{ \cfrac { xdx }{ 4\cos ^{ 2 }{ x } +9\sin ^{ 2 }{ x } } } =$$ | $$\cfrac { { \pi }^{ 2 } }{ 12 } $$ |
| Evaluate the integral $$\displaystyle \int_{0}^{1}\frac{1}{1+x^{2}}dx$$ |
$$\pi/4$$ |
| $$\displaystyle \int _{ 0 }^{ 1 }{ \tan ^{ -1 }{ \left( \dfrac { 2x }{ 1-{ x }^{ 2 } } \right) dx } } =\dfrac{\pi}{a}-\ln a$$. Find $$a$$. | $$2$$ |
Determinants Class 12 Commerce Applied Mathematics MCQ Quiz
Determinants Questions and Answers
| Determinants Quiz Question | Answer |
|---|---|
| The coefficient of $$x$$ in the determinant $$\begin{vmatrix}(1+x)^{a_1b_1}& (1+x)^{a_1b_2} & (1+x)^{a_1b_3}\\ (1+x)^{a_2b_1}& (1+x)^{a_2b^2} & (1+x)^{a_2b_3}\\ (1+x)^{a_3b_1}& (1+x)^{a_3b_2} & (1+x)^{a_3b_3}\end{vmatrix}$$ is |
$$0$$ |
| Which of the following is/are true ? (i) Adjoint of a symmetric matrix is symmetric (ii) Adjoint of a unit matrix is a unit matrix (iii) A(adj A)=(adj A) A= [A]f and (iv) Adjoint of a diagonal matrix is a diagonal matrix |
$$None$$ $$of$$ $$these$$ |
| If $$A$$ is a $$2\times 2$$ matrix such that $$A^{2}-4A+3I=0$$, then the inverse of $$A+3I$$ is equal to | $$\dfrac{7}{24}I+\dfrac{1}{24}A$$ |
| Let A be a $$3\times 3$$ matrix such that $$A\left[ \begin{matrix} 1 & 2 & 3 \\ 0 & 2 & 3 \\ 0 & 1 & 1 \end{matrix} \right] =\left[ \begin{matrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{matrix} \right] $$ Then $${ A }^{ -1 }$$. |
$$\left[ \begin{matrix} 1 & 2 & 3 \\ 0 & 1 & 1 \\ 0 & 2 & 3 \end{matrix} \right] $$ |
| Let A be a $$3\times 3$$ matrix such that $$A^{2} - 5A + 7I = O$$ Statement I: $$A^{-1} = \dfrac {1}{7} (5I - A)$$ Statement II: The polynomial $$A^{3} - 2A^{2} - 3A + I$$ can be reduced to $$5(A - 4I)$$ Then: |
Both the statements are true |
| The system of equation $$(a\alpha +b)x+ay+bz=0, (b\alpha +c)x+by+cz=0, (a\alpha +b)y+(b\alpha +c)z=0$$ has non-trivial solution, if | a,b,c are in G.P |
| $$A=\begin{bmatrix} 1 & 1 \\ 3 & 4 \end{bmatrix}$$ and A (adj A)=KI, then the value of 'K' is ... | 2 |
| The points $$\displaystyle \left( 0, \frac{8}{3} \right), (1, 3)$$ and $$(82, 30)$$ : | lie on a straight line. |
| $$A=\begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta\end{bmatrix}$$ and $$AB=BA=I$$, then B is equal to | $$\begin{bmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta\end{bmatrix}$$ |
| $$Adj \begin{bmatrix} 1 & 0 & 2 \\ -1 & 1 & -2 \\ 0 & 2 & 1 \end{bmatrix}=\begin{bmatrix} 5 & a & -2 \\ 1 & 1 & 0 \\ -2 & -2 & b \end{bmatrix}\Rightarrow \left [ a\ b\ \right ]=$$ ____ |
$$\begin{bmatrix} 4 & 1 \end{bmatrix}$$ |
Differential Equations Class 12 Commerce Applied Mathematics MCQ Quiz
Differential Equations Questions and Answers
| Differential Equations Quiz Question | Answer |
|---|---|
| Solve $$(1+\cos x)dy=(1-\cos x)dx$$. | $$y = \displaystyle \tan \cfrac{x}{2} - x +C$$ |
| The solution of $$\displaystyle \dfrac{dy}{dx}=2y\tanh x $$ is | $$cy=\cosh^{2}x$$ |
| The solution of $$\dfrac{dy}{dx}=2^{x-y}$$ is: | $$2^{x}-2^{y}=c$$ |
| The solution of $$(x^{2}+x)\frac{dy}{dx}=1+2x$$ is: | $$e^{y}=c(x^{2}+x)$$ |
| $$\displaystyle ydx-x dy=xy\:dx$$ Then the solution is: |
$$\displaystyle x=ky\:e^{x}.$$ |
| The order of differential equation of family of all concentric circles centered at $$(h,k)$$ is | 1 |
| The solution of $$\dfrac { dx }{ dy } -\dfrac { 2 }{ 3 } xy={ x }^{ 4 }{ y }^{ 3 }$$ is | $$\dfrac { 1 }{ { x }^{ 3 } } =\dfrac { 3 }{ 2 } \left( 1-{ y }^{ 2 } \right) +c{ e }^{ -{ y }^{ 2 } }$$ |
| The solution of the differential equation $$( x \cot y + \log \cos x ) d y$$ $$+ ( \log \sin y - y \tan x ) d x = 0$$ is:- |
$$( \sin y ) ^ { x } ( \cos x ) ^ { y } = c$$ |
| Check whether the function is homogenous or not. If yes then find the degree of the function $$g(x)=x^2-8x^3$$. |
Not homogenous |
| The number of arbitrary constants in the particular solution of the differential equation of order $$3$$ is ______. | $$0$$ |
Indefinite Integrals Class 12 Commerce Applied Mathematics MCQ Quiz
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Indefinite Integrals Questions and Answers
| Indefinite Integrals Quiz Question | Answer |
|---|---|
| $$\displaystyle \int_{0}^{1}\tan ^{-1}x\:dx.$$ | $$\displaystyle \frac{\pi }{4}-\frac{1}{2}\log 2.$$ |
| $$\int \dfrac {dx}{\sqrt {x^{10} - x^{2}}}; x > 1=$$ ______ $$+ C$$. | $$\dfrac {1}{4}\sec^{-1} (x^{4})$$ |
| The value of $$\int log x dx$$ is | $$\displaystyle x log \left ( \frac{x}{e} \right ) + c$$ |
| $$\displaystyle \int x.e^{x}dx=$$ |
$$ e^{x}(x-1)+c$$ |
| $$\displaystyle \int x^{3}e^{x}dx=$$ |
$$e^{x}(x^{3}- 3x^{2}+6x-6)+c$$ |
| $$\displaystyle \int\log\sqrt{x+1}dx=$$ |
$$\displaystyle \frac{1}{2}[(x+1)\log (x+1)-x]+c$$ |
| $$\displaystyle \int[\sin(\log x)+\cos(\log x)]dx=$$ |
$$\displaystyle x\sin (\log x)+c$$ |
| The integral $$\displaystyle \int (1+x-\displaystyle \frac{1}{x})e^{x+\frac{1}{x}} dx $$ is equal to | $$ xe^{x+\frac{1}{x}} +c $$ |
| The integral $$\displaystyle \int x { \cos^{ -1 }\left(\displaystyle \frac { 1-x^{ 2 } }{ 1+x^{ 2 } } \right) dx } $$ is equal to : (Note : $$(x>0)$$) |
$$-x+(1+x^{2})\tan^{-1}x+c$$ |
| If $$\int f(x)\ dx $$ $$=\Psi(x)$$ , then $$\int x^{5}f(x^{3})\ dx $$ is equal to |
$$\dfrac{1}{3}x^{3}\Psi(x^{3})-\int x^{2}\Psi(x^{3})dx+C$$ |
Linear Equations Class 12 Commerce Applied Mathematics MCQ Quiz
Linear Equations Questions and Answers
| Linear Equations Quiz Question | Answer |
|---|---|
| Solve the following equations by substitution method. $$2x-3y=14; \, \, 5x+2y=16$$ |
$$x = 4, y= -2$$ |
| IF $$x - 2y = -1$$, $$y=-\dfrac { 1 }{ 2 } $$, then find the value of $$x$$ | $$-2$$ |
| Giri is 20 year older than his son. If the sum of their ages ishow old is his son? | 25 years |
| If $$\cfrac { a }{ x+y } =\cfrac { b }{ y+z } =\cfrac { c }{ z-x } $$, then which of the following equations is true? | $$b=a+c$$ |
| Given that $$3x-y=-11$$ and $$4x+y=4$$. Calculate the value of $$x$$. | $$-1$$ |
| The cost of 9 chairs and 3 tables is Rs. 306, while the cost of 6 chairs and 3 tables is Rs.Then the cost of 6 chairs and 1 table is | Rs. 162 |
| If, $$\displaystyle \frac{1}{x}+\frac{1}{y}=k$$ and $$\displaystyle \frac{1}{x}-\frac{1}{y}=k$$, then the value of y ................. | Does not exist. |
| Given that $$4x-3y=6$$ and $$x-3y=-3$$, the value of $$y$$ is | $$2$$ |
| The sum of two numbers is equal to $$20$$ and their difference is $$2.5$$. Find the ratio of the numbers | $$9 : 7$$ |
| Solve the following pair of simultaneous equations: $$a\, =\, b\, +\, 2$$ $$2a\, -\, b\, =\, 7$$ |
$$a = 5, b = 3$$ |
Matrices Class 12 Commerce Applied Mathematics MCQ Quiz
Matrices Questions and Answers
| Matrices Quiz Question | Answer |
|---|---|
| If $$A \times \bigl(\begin{smallmatrix} 1& 1\\0 & 2\end{smallmatrix}\bigr) = \bigl(\begin{smallmatrix}1 & 2 \end{smallmatrix}\bigr)$$, then the order of A is |
$$2 \times 1$$ |
| If $$ AB = A $$ and $$ BA =B, $$ then | $$ BAB = B $$ |
| X is a matrix then $$X- X' $$ is _______________. | skew symmetric matrix |
| If $$A=[1\ \ 2\ \ 3\ \ 4]$$ and $$AB = [3 \ \ 4\ \ -1],$$ then the order of matrix $$B$$ is |
$$4 \times 3$$ |
| $$A=\begin{bmatrix}x& -7\\ 7& y\end{bmatrix}$$ is a skew-symmetric matrix, then (x,y) = |
(0,0) |
| If $$A$$ and $$B$$ are symmetric matrices of order $$\displaystyle n,\left( A\neq B \right) $$, then |
$$A+B$$ is symmetric |
| If $$A$$ is a skew symmetric matrix then $$ \displaystyle A^{T} $$ | $$-A$$ |
| Let $$X$$ and $$Y$$ be two arbitrary, $$3\times 3$$, non-zero, skew-symmetric matrices and $$Z$$ be an arbitrary $$3\times 3$$, non-zero, symmetric matrix. Then which of the following matrices is (are) skew symmetric? | $$X^{23}+Y^{23}$$ |
| If $$\displaystyle A=\left[ \begin{matrix} 3 & 1 \\ -1 & 2 \end{matrix} \right] $$ and $$\displaystyle I=\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right] $$, then the correct statement is: | $$\displaystyle { A }^{ 2 }-5A+7I=O$$ |
| If $$\mathrm{A}^{2}=\mathrm{A},\ \mathrm{B}^{2}=\mathrm{B},\ \mathrm{A}\mathrm{B}=\mathrm{B}\mathrm{A}=O$$ (Null Matrix), then $$(\mathrm{A}+\mathrm{B})^{2}=$$ |
$$\mathrm{A}+\mathrm{B}$$ |
Probability Distribution And Its Mean And Variance Class 12 Commerce Applied Mathematics MCQ Quiz
Probability Distribution And Its Mean And Variance Questions and Answers
| Probability Distribution And Its Mean And Variance Quiz Question | Answer |
|---|---|
| The p.m.f.of a r.v. X is as follows ; $$P(X=0)=3{ K }^{ 3 }\quad ,\quad P(X=1)=4K-10{ K }^{ 2 },\quad P(X=2)=5K-1,\quad P(X-x)=0$$ for any other value of x. then k is equal to |
$$\frac { 1 }{ 3 } $$ |
| Variance of the random variable $$X$$ is $$4$$. Its mean is $$2$$. Then $$E(X^{2})$$ is: | $$8$$ |
| Another name for the mean of a probability distribution is expected value. | True |
| The variance of the random variable $$x$$ whose probability distribution is given by $$X=x_{i}: \quad-1 \quad, 0, \quad +1$$ $$p(X=x_{i}): 0.4, \ 0.2, \ \ \ 0.4 $$ is |
$$0.8$$ |
| To define probability disribution function we assign to each variable | the respective probabilities |
| Out of following which are random variables | $$x=$$ "Raining" |
| Given $$E(X + c) = 8$$ and $$E(X - c) = 12$$ then the value of $$c$$ is | $$-2$$ |
| Which of the following is an example of a random experiment? | Throwing two coins together. |
| To verify Pythagoras theorem is a random experiment. | False |
| The mathematical expectation of sum of points when we throw n symmetrical dice is |
$$7\displaystyle \times\frac{n}{2}$$ |
Quantification And Numerical Applications Class 12 Commerce Applied Mathematics MCQ Quiz
Quiz 1
Quiz 2
Quiz 3
Quiz 4
Quiz 5
Quiz 6
Quiz 7
Quiz 8
Quiz 9
Quiz 10
Quiz 11
Quiz 12
Quiz 13
Quiz 14
Quiz 15
Quiz 16
Quantification And Numerical Applications Questions and Answers
| Quantification And Numerical Applications Quiz Question | Answer |
|---|---|
| $$5$$ mangoes and $$4$$ oranges cost as much as $$3$$ mangoes and $$7$$ oranges. What is the ratio of the cost of one mango to that of one orange? | $$\;3\,\colon\,2$$ |
State whether True or False The ratio of the following. $$5$$ m to $$10$$ km ratio is $$1:2000$$ |
True |
State whether the given statement is True or False. The ratio of 50 paise to Rs. 5 ratio is 1: 10 |
True |
| Ordered pair that satisfy the equation $$x + y + 1 < 0$$ is: | Both (B) and (C) |
| What must be subtracted from each term of the ratio $$4 : 7$$ so that the ratio becomes $$2 : 5$$ ? | $$2$$ |
| True | |
| Find the order relation between the following pairs of ratios. a, b are integers. $$\displaystyle \frac{a-1}{b-1}, \frac{a+1}{b+1}$$ where $$a > b$$ and $$b \neq \pm 1$$. |
$$\displaystyle \frac{a-1}{b-1} > \frac{a+1}{b+1}$$ |
| The ratio of the two areas of two triangles with the common base is $$6:5$$. Height of the larger triangle is $$9\, cm$$. Then find the corresponding height of the smaller triangle. | Height of the smaller triangle is $$7.5\, \, cm$$. |
| Solve the inequality: $$3-2x\leq 9$$ | $$x\geq -3$$ |
| The ratio of the velocities of the hour hand and minute hand of a clock is: | $$\;1\,\colon\,12$$ |
Standard Probability Distributions Class 12 Commerce Applied Mathematics MCQ Quiz
Standard Probability Distributions Questions and Answers
| Standard Probability Distributions Quiz Question | Answer |
|---|---|
| Consider 5 independent bernoulli's trials each with probability p of success. If the probability of one failure is greater than or equal to $${{31} \over {32}}$$, then p lies in the interval | $$\left[ {0,{1 \over 2}} \right]$$ |
| If the mean of Poisson distribution is $$\displaystyle \frac{1}{2}$$, then the ratio of $$P(X=3)$$ to $$P(X=2)$$ is | 1:6 |
| Mean and variance of binomial variable X are 2 and 1 respectively, then $$ \displaystyle P\left ( X\geq 1 \right ) $$ is |
$$ \displaystyle \frac{15}{16} $$ |
| If for a $$BD$$ the mean is $$6$$ and standard deviation is $$\dfrac{1}{\sqrt{2}}$$, then the probability of success is |
$$\dfrac{11}{12}$$ |
| In a $$B.D.$$ $$n = 400, P=\displaystyle \frac{1}{5}$$. Its standard deviation is |
$$8$$ |
| In $$15$$ throws of a die $$4$$ or $$5$$ is considered to be a success. The mean number of success is |
$$5$$ |
| Suppose $$X$$ follows binomial distribution with parameters $$n = 100$$ and $$p=\dfrac{1}{3}$$ then $$P(x=r)$$ is maximum when $$r =$$ |
$$33$$ |
| If the mean of binomial distribution is $$\mu $$, then the variance lies in the interval |
$$\left [ 0,\mu \right ]$$ |
| If the first two terms of a Poisson distribution are equal to $$k$$, find $$k$$. | $$\displaystyle \frac{1}{e}$$ |
| If the probability of selecting a bolt from $$400$$ bolts is $$0.1$$, then the mean for the distribution is ________ | $$40$$ |
Applied Mathematics MCQ Questions for Class 12 - Practice Test with Solutions
Do you want to overcome your drawbacks while attempting the quizzes or MCQ tests like time consumption, approaching questions, etc.? Take the advantage of practicing with MCQExams.com MCQ Questions for Standard 12 Applied Mathematics Test. As it is a time-based approach and also provides answers to all questions.
One should practice the MCQs in this way for a better assessment of their preparation level. All chapters CBSE Class 12 Applied Mathematics MCQ Quiz Questions with Solutions PDF free download links are available for easy access & quick reference.
How to Use MCQExams.com Chapterwise 12th Applied Mathematics MCQ Interactive Quiz?
Guys do you love to share your practice hacks and tips with your friends? If yes, then our 12tth standard CBSE Applied Mathematics MCQ interactive quiz help you do the same. Excited to know the process then jump into the below steps right away:
- Go with the respective chapter class 12 Applied Mathematics MCQ quiz link from the above
- Now, you will find the MCQ quiz boxes for the Application Of Derivatives chapter along with the interactive quiz windows.
- Click on the CBSE 12th Class Application Of Derivatives MCQ Interactive Quiz and it will redirect you to another window where it displays the questions with options in stories format.
- Answer the question one after another and learn the answers right away this helps you to do a quick assessment of your knowledge.
- You can also share this cool MCQ Interactive Quiz Questions of Plus Two Applied Mathematics topicwise with your friends by just tapping on the send arrow located at the top left corner of the story.
- After clicking the button, you can opt for the copy link option and easily paste the link on your friend's chat or else in your whatsapp story too. Isn’t it cool!!
- Keep passing this interesting approach of practicing Plus Two CBSE Applied Mathematics Application Of Derivatives MCQ Questions to your co-students and help them in attempting the entrance exams like JEE & NEET.