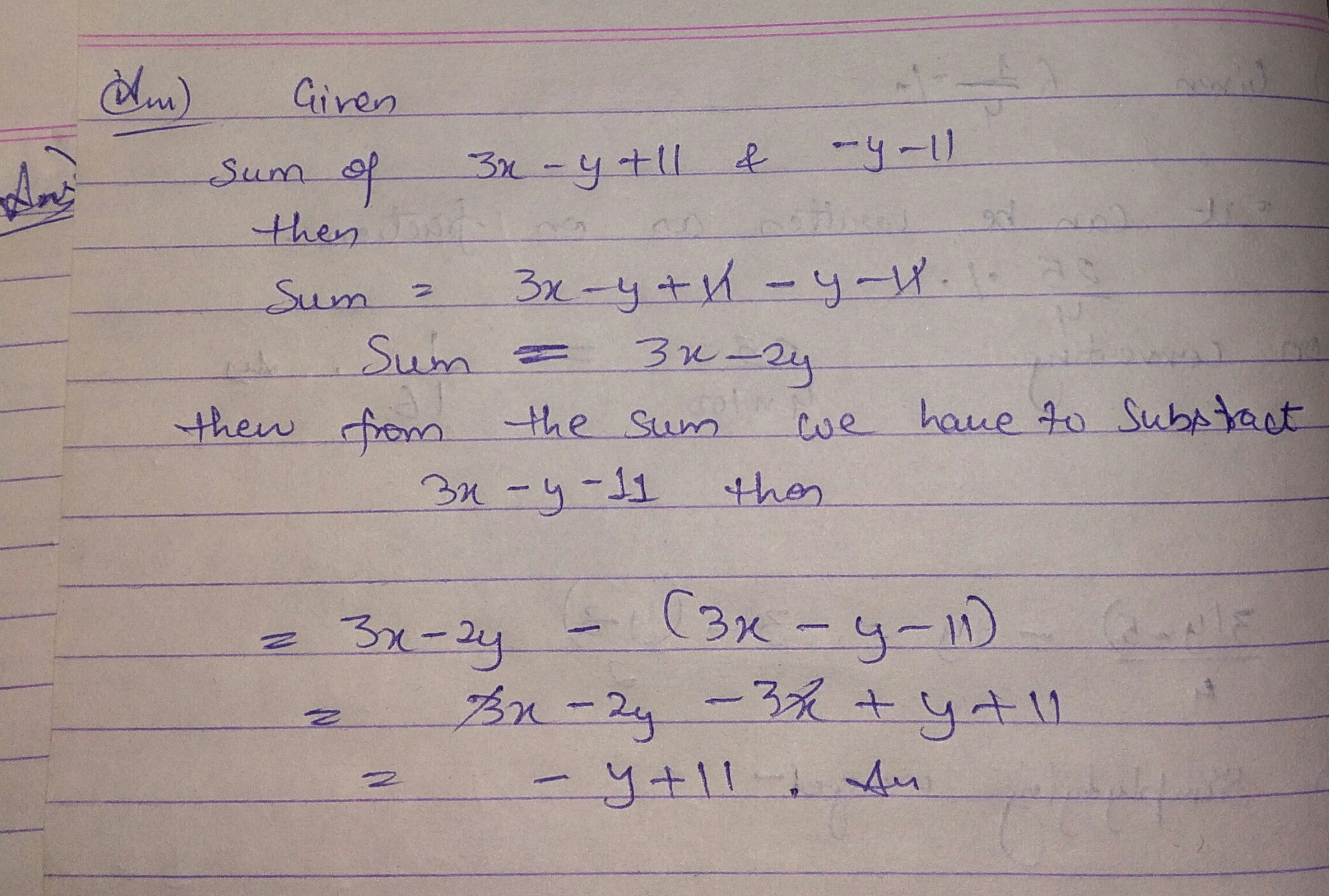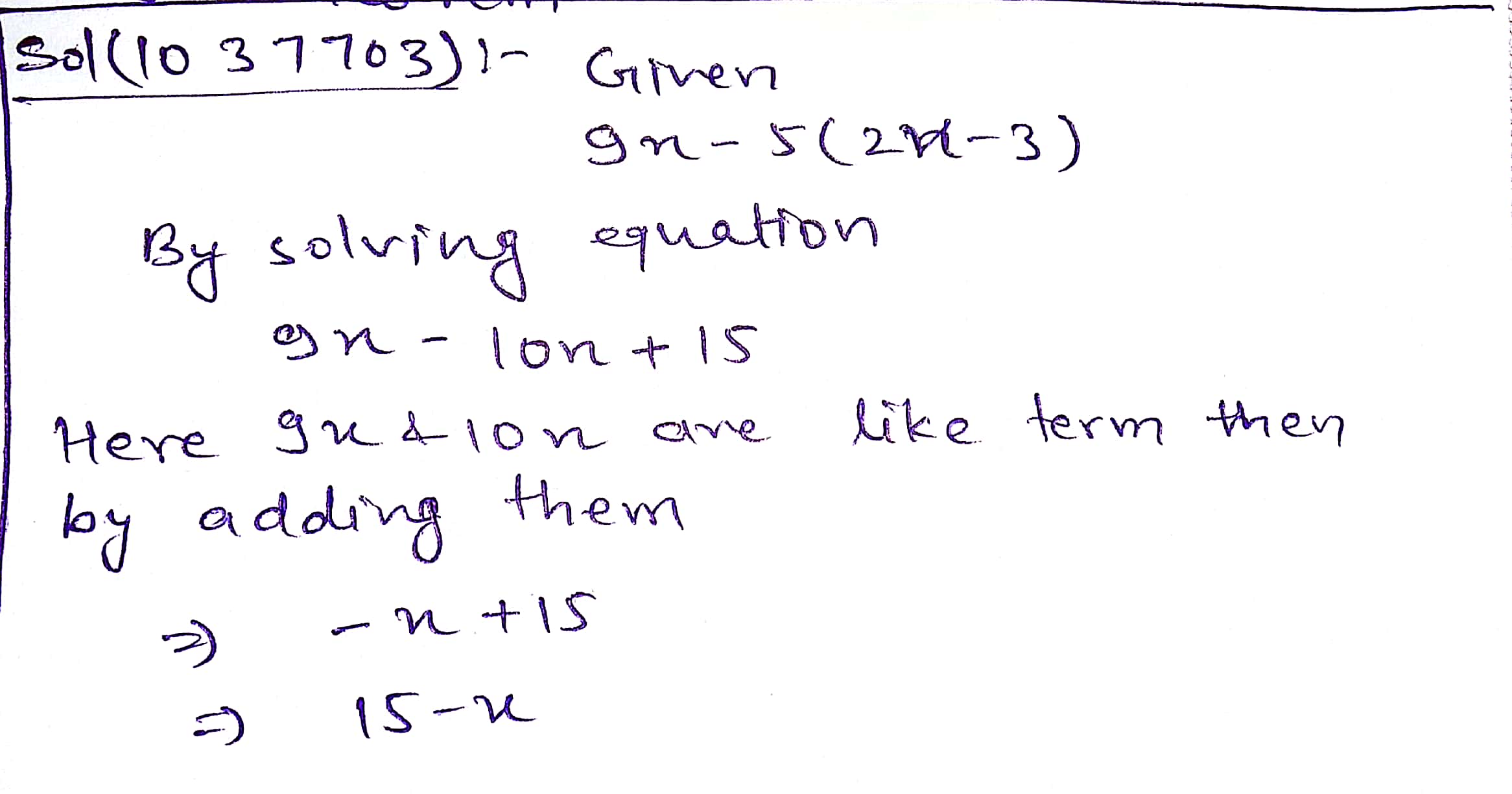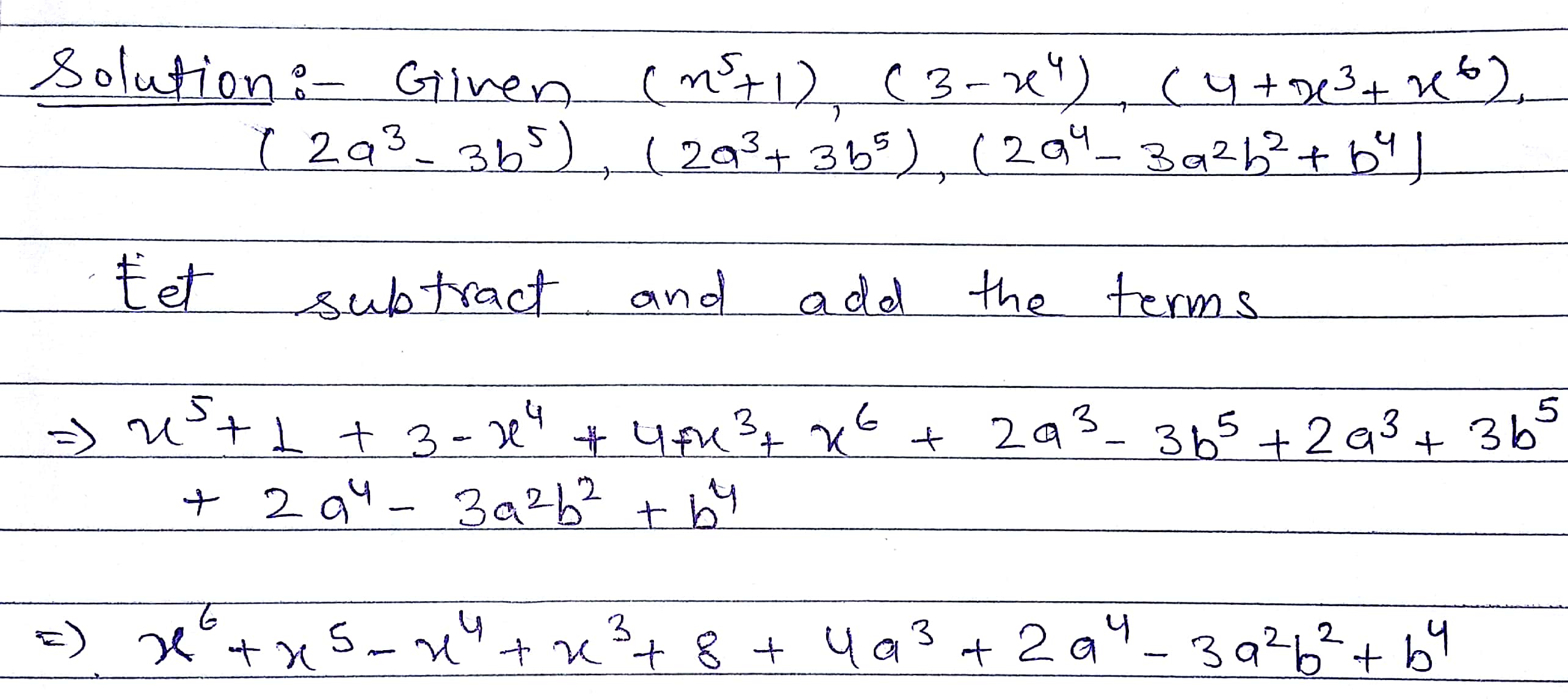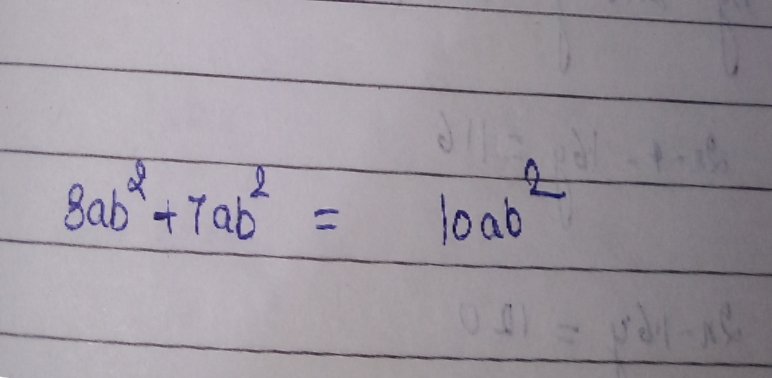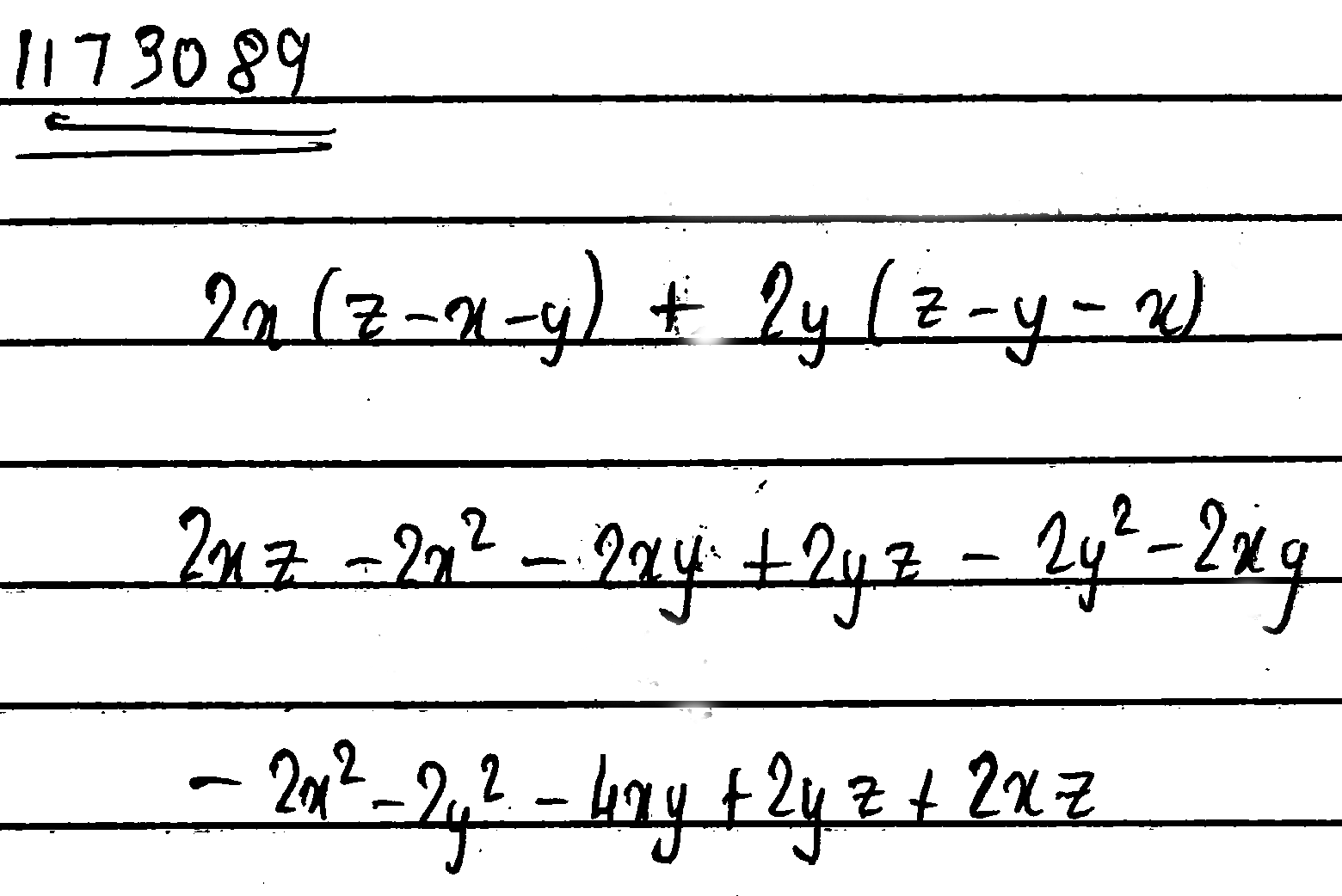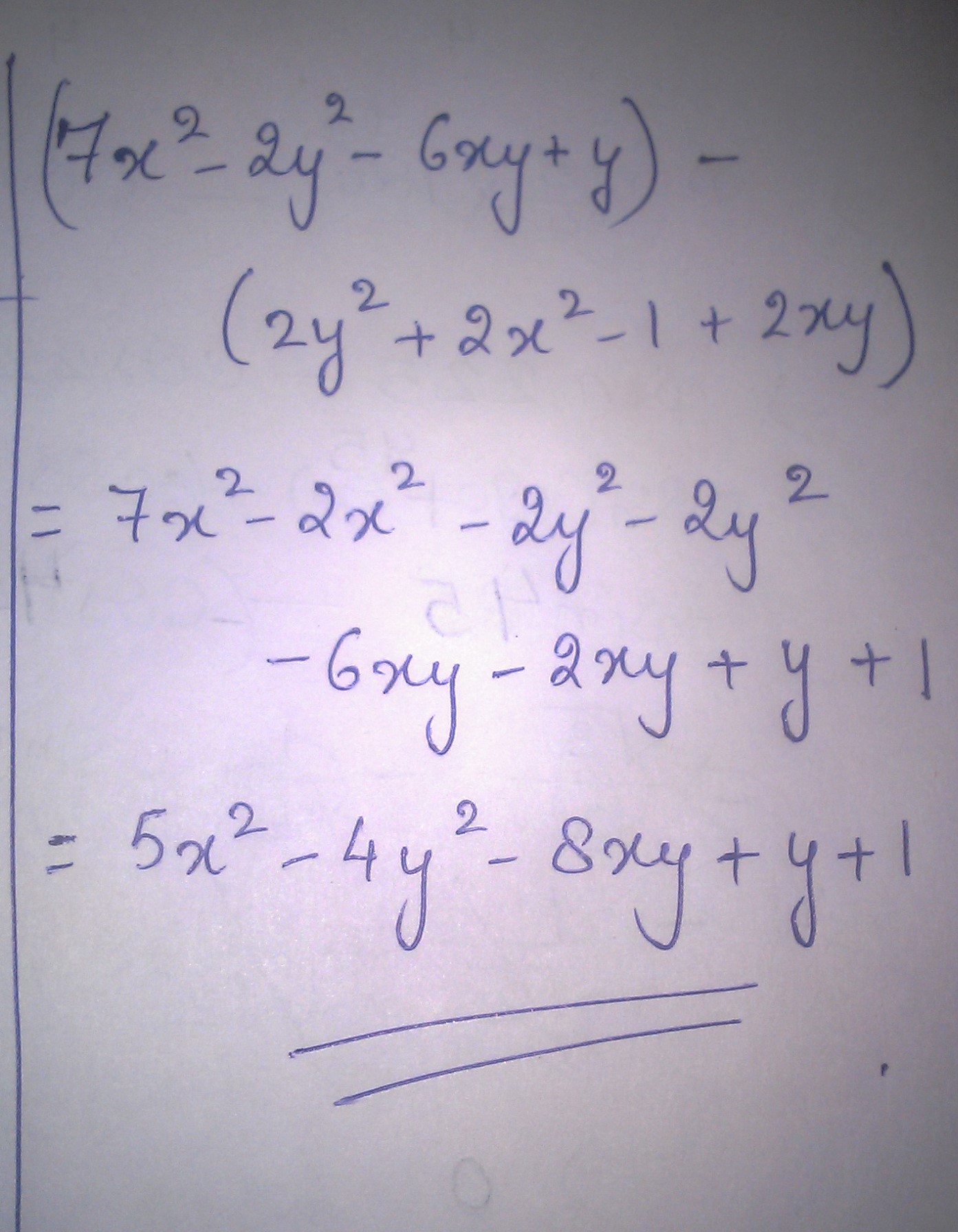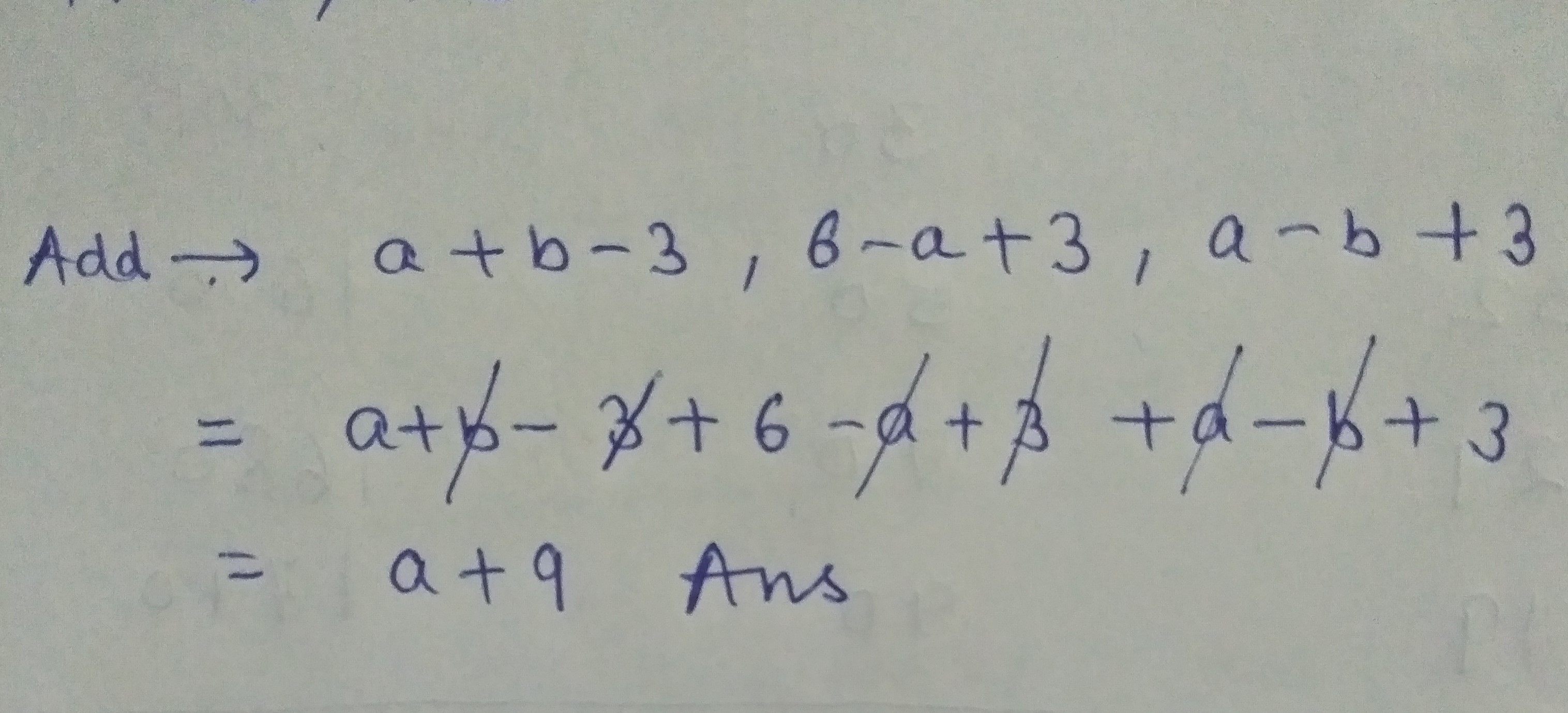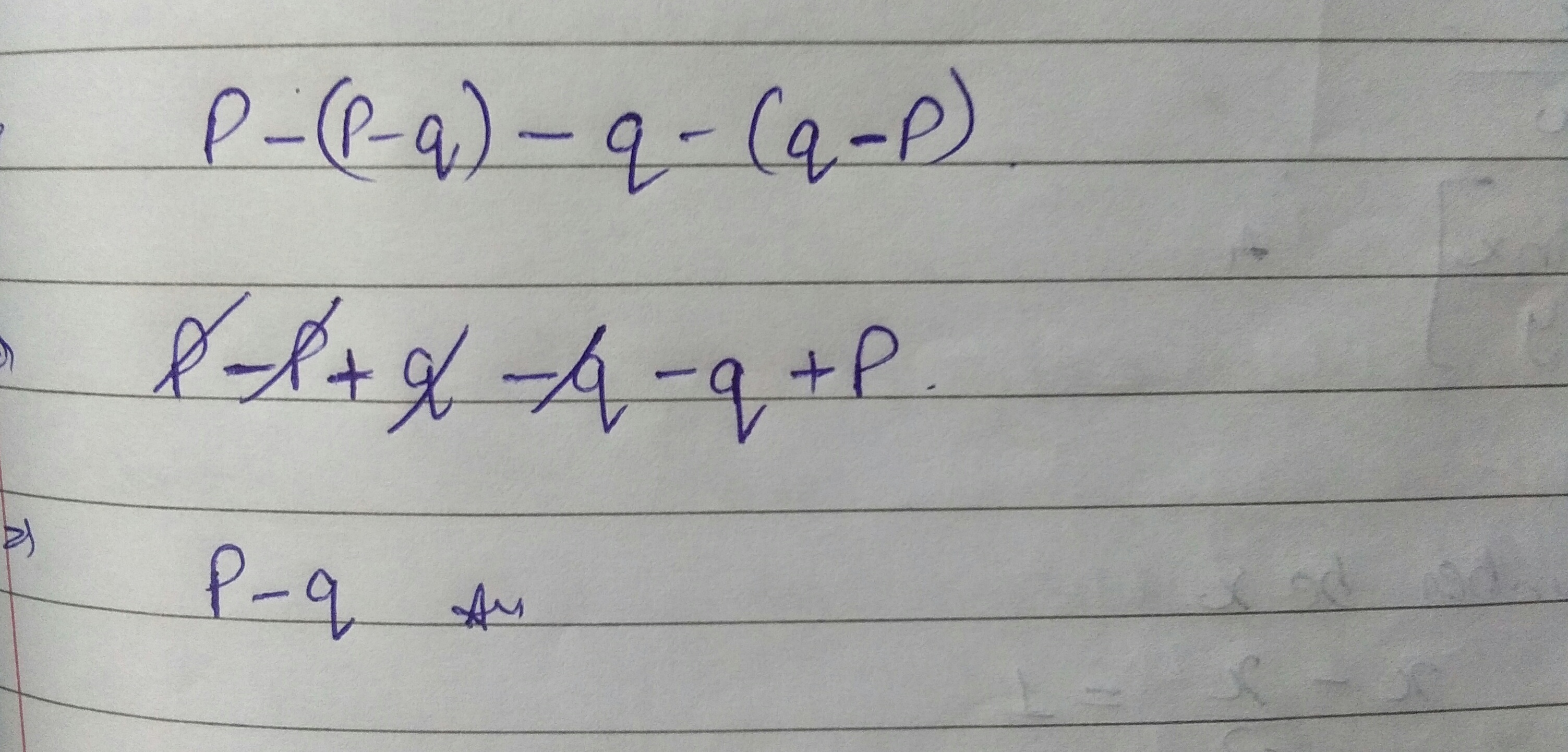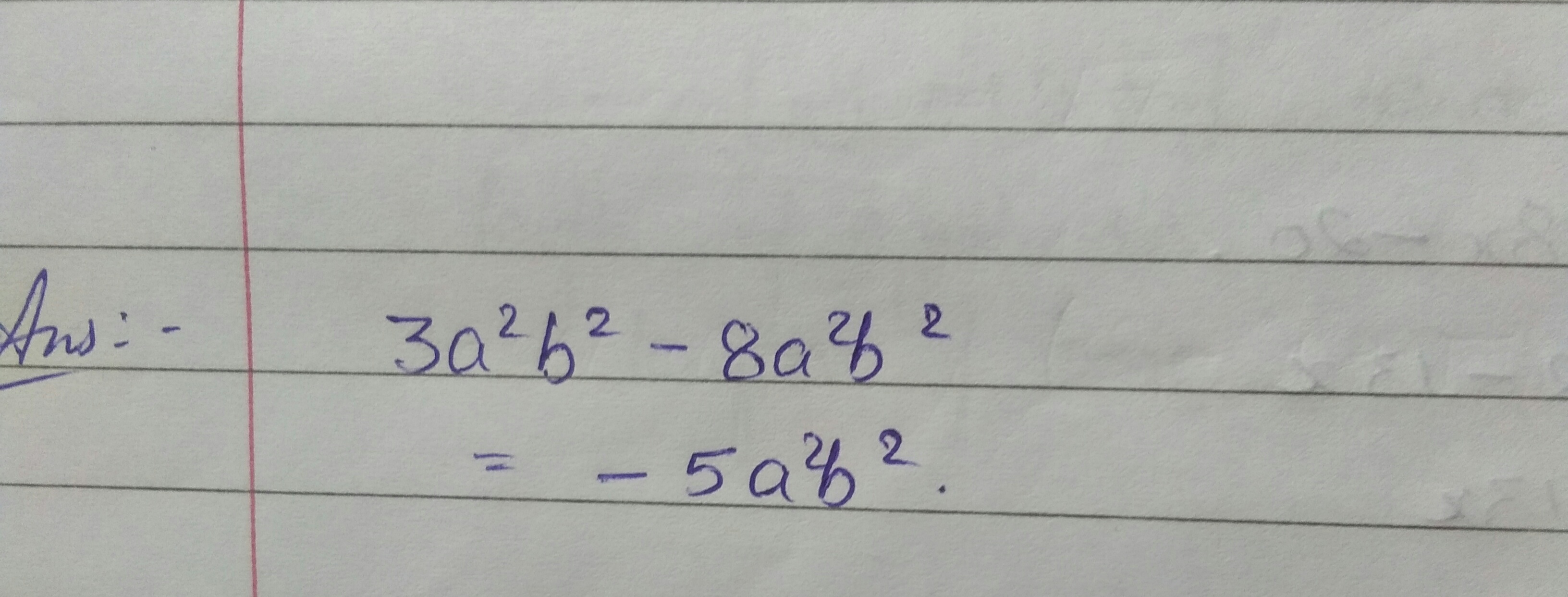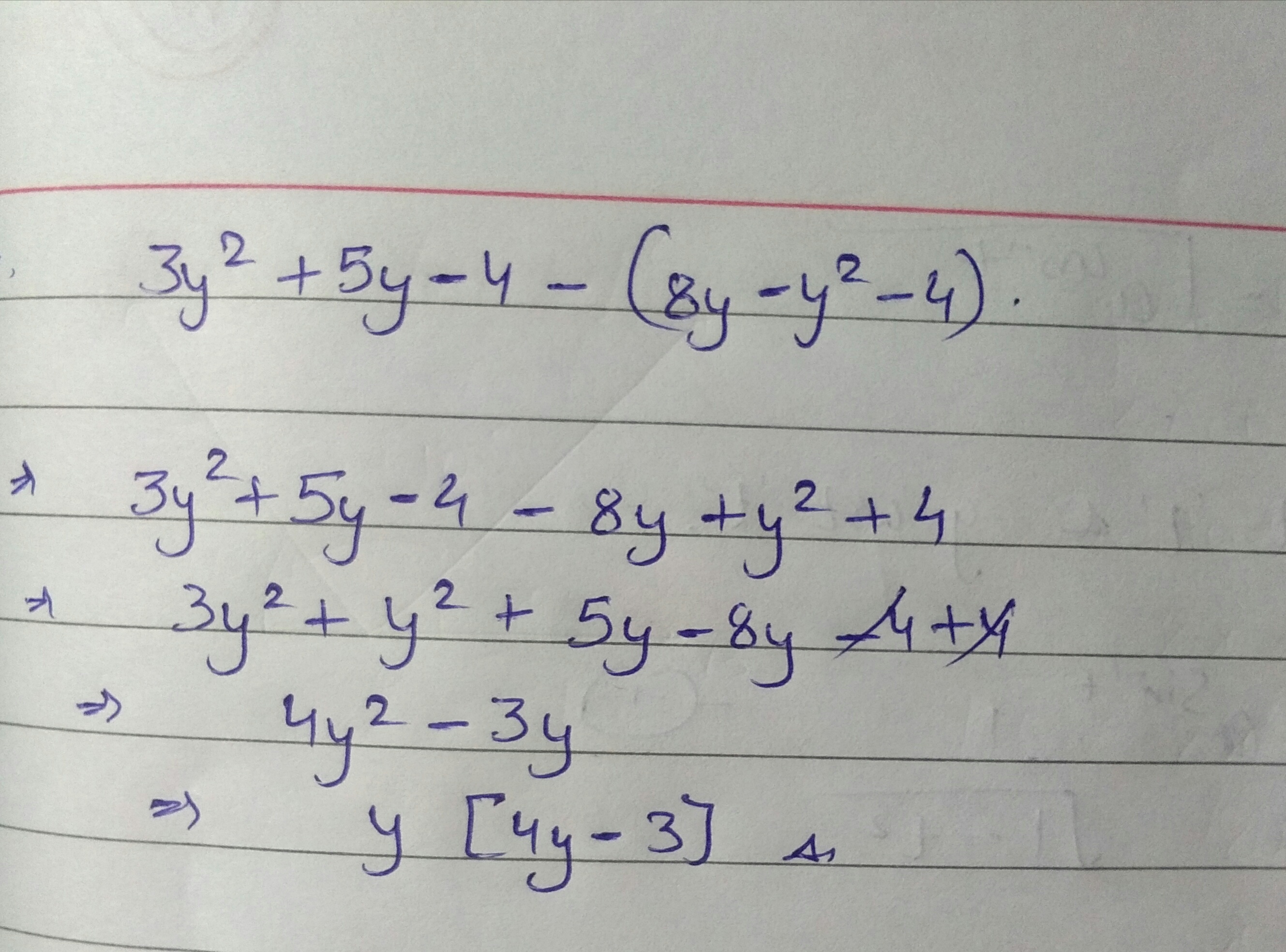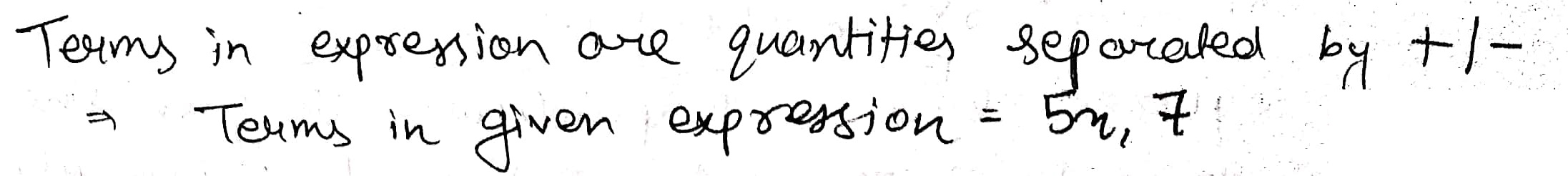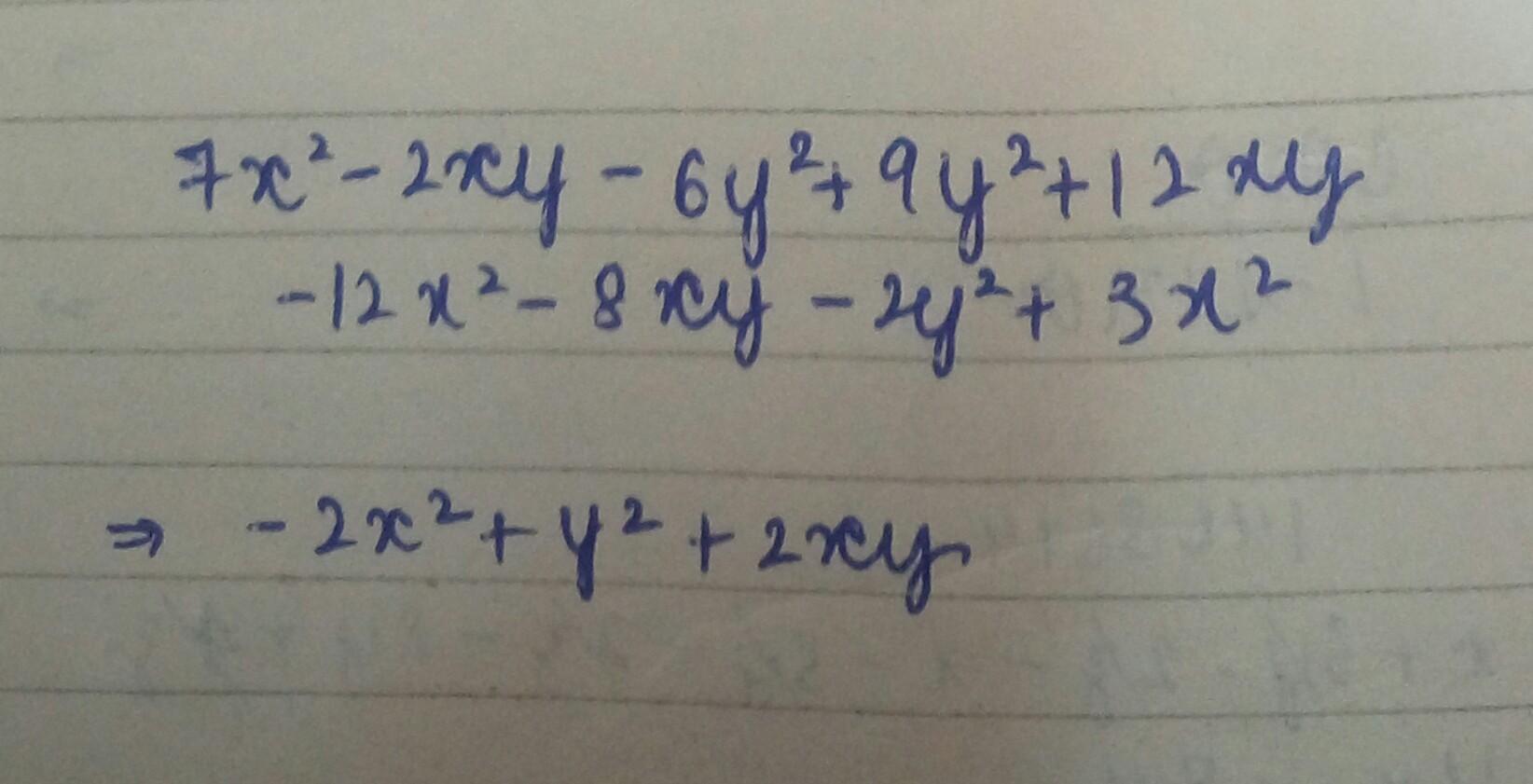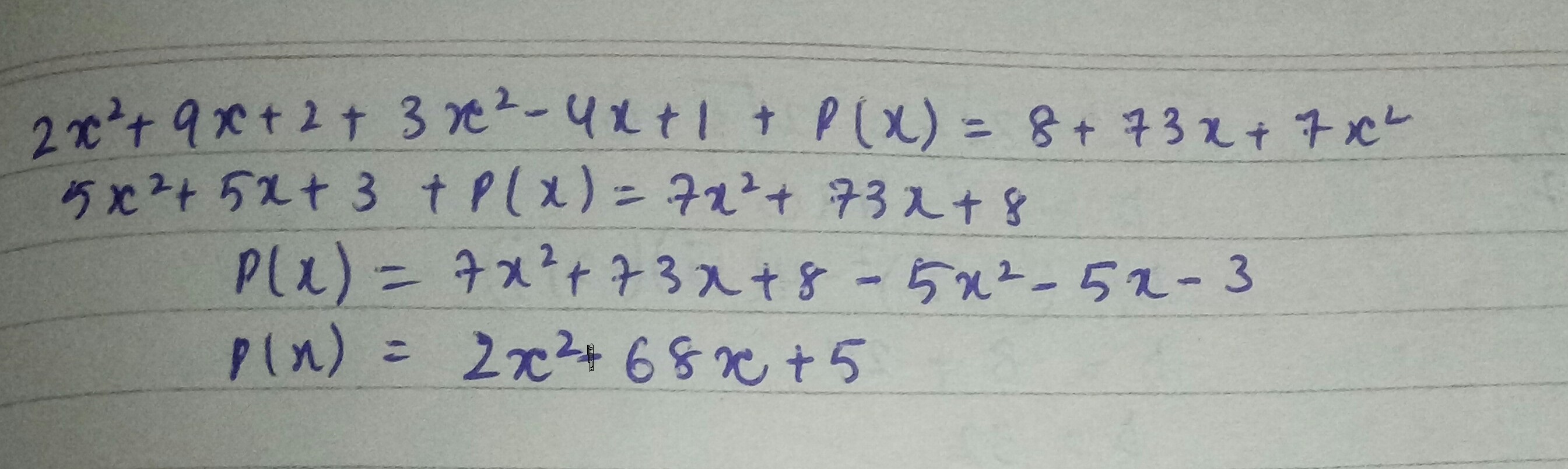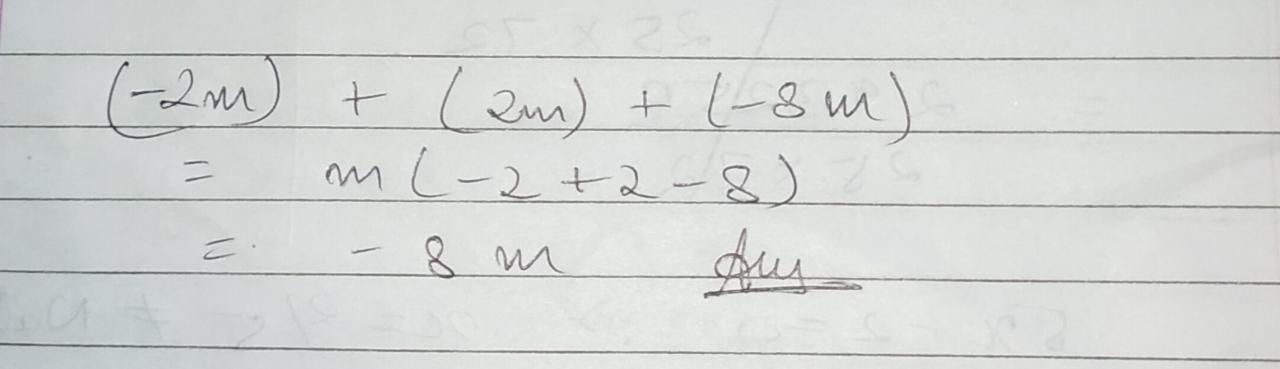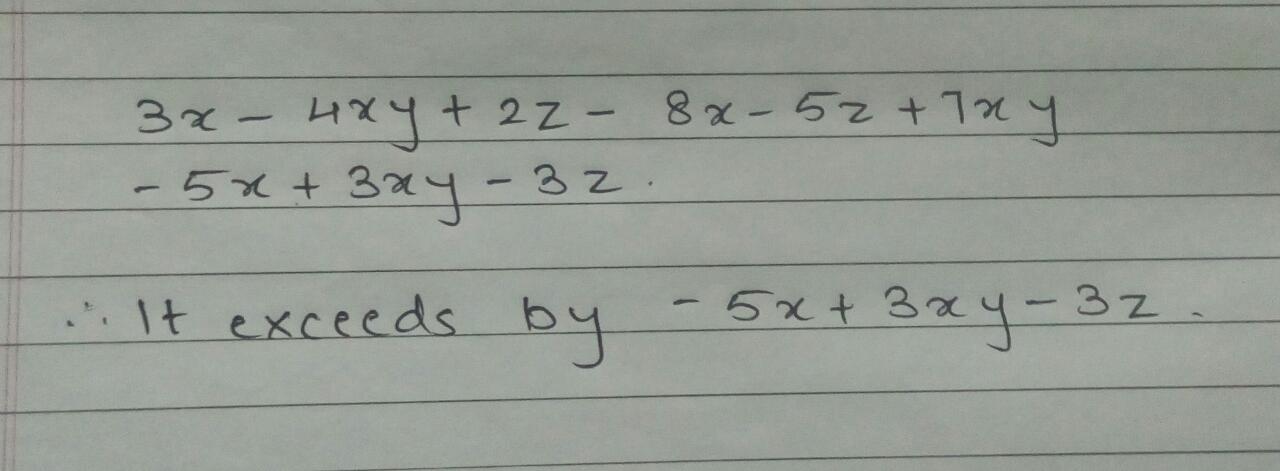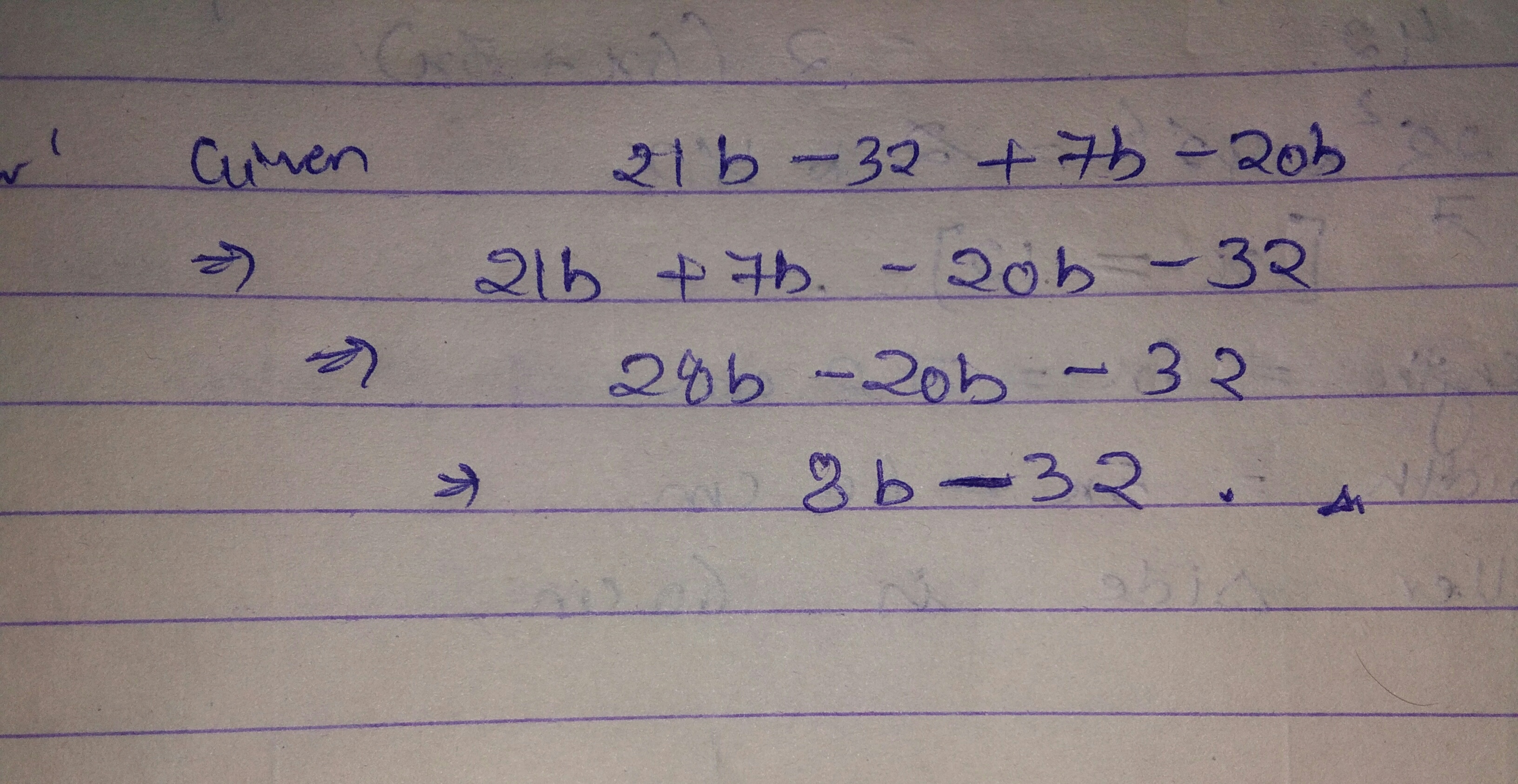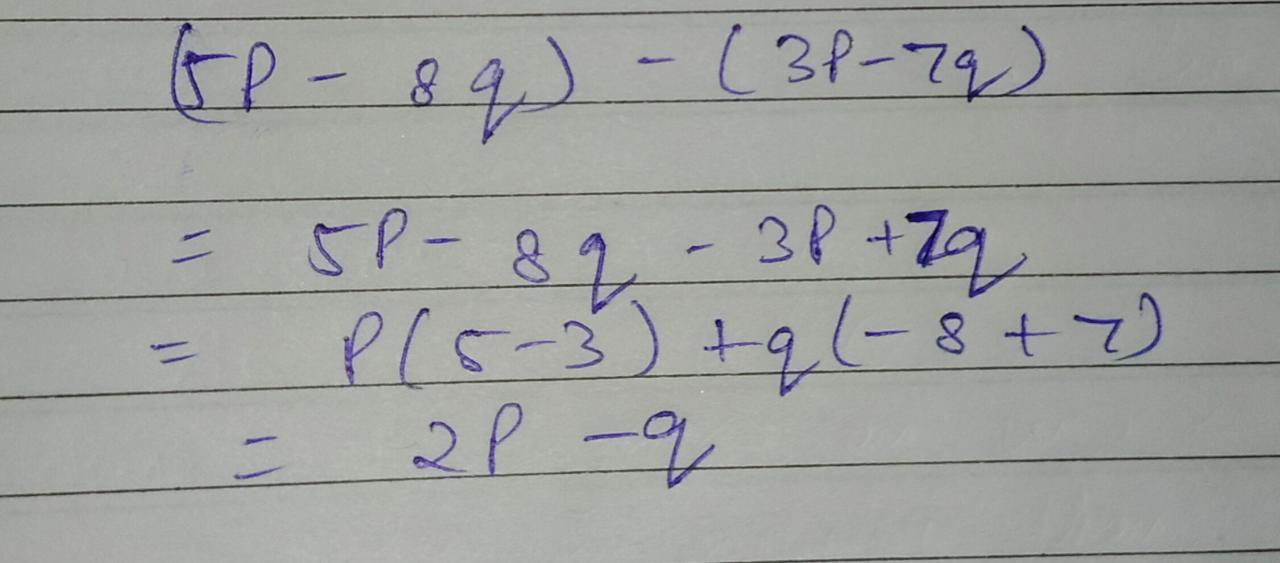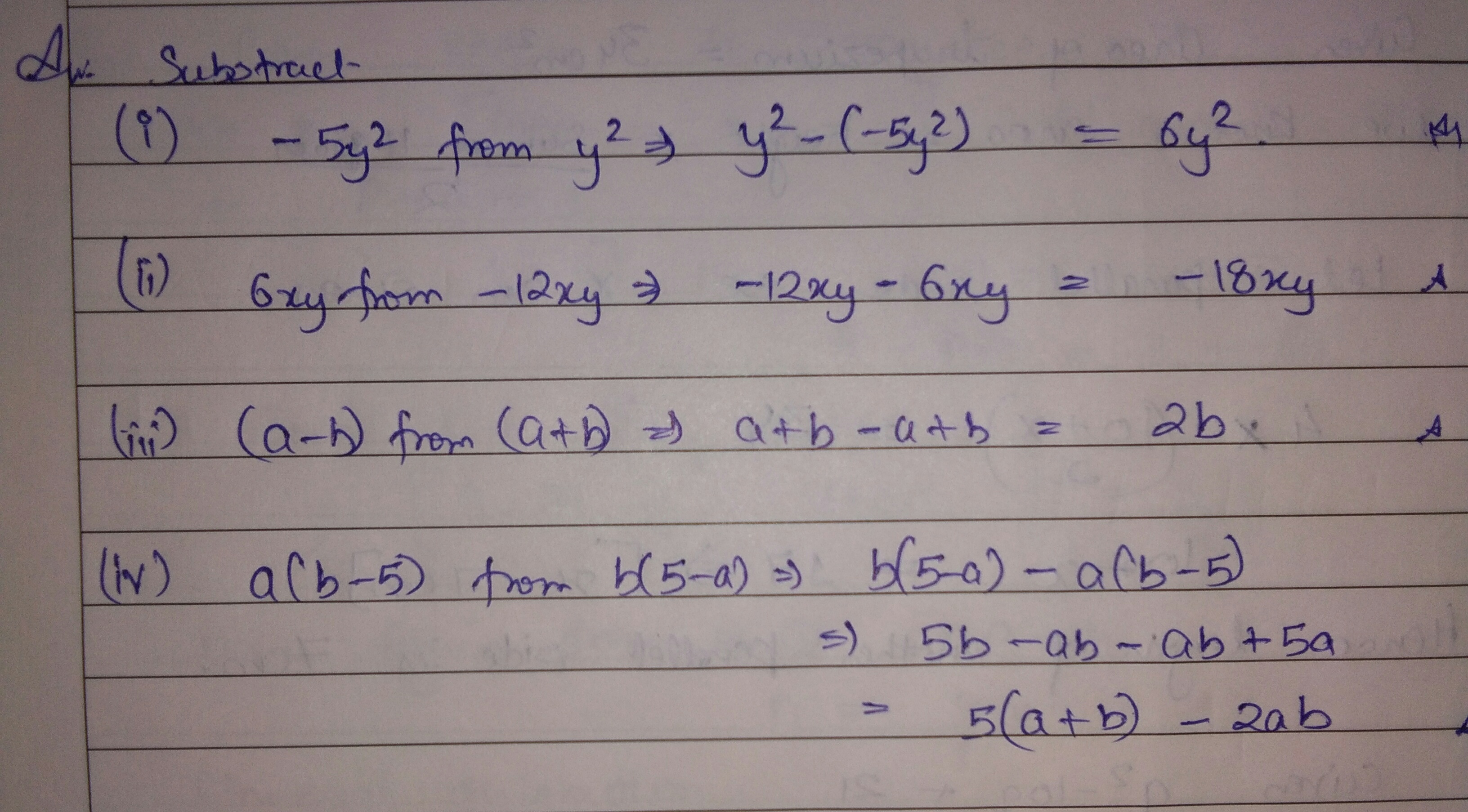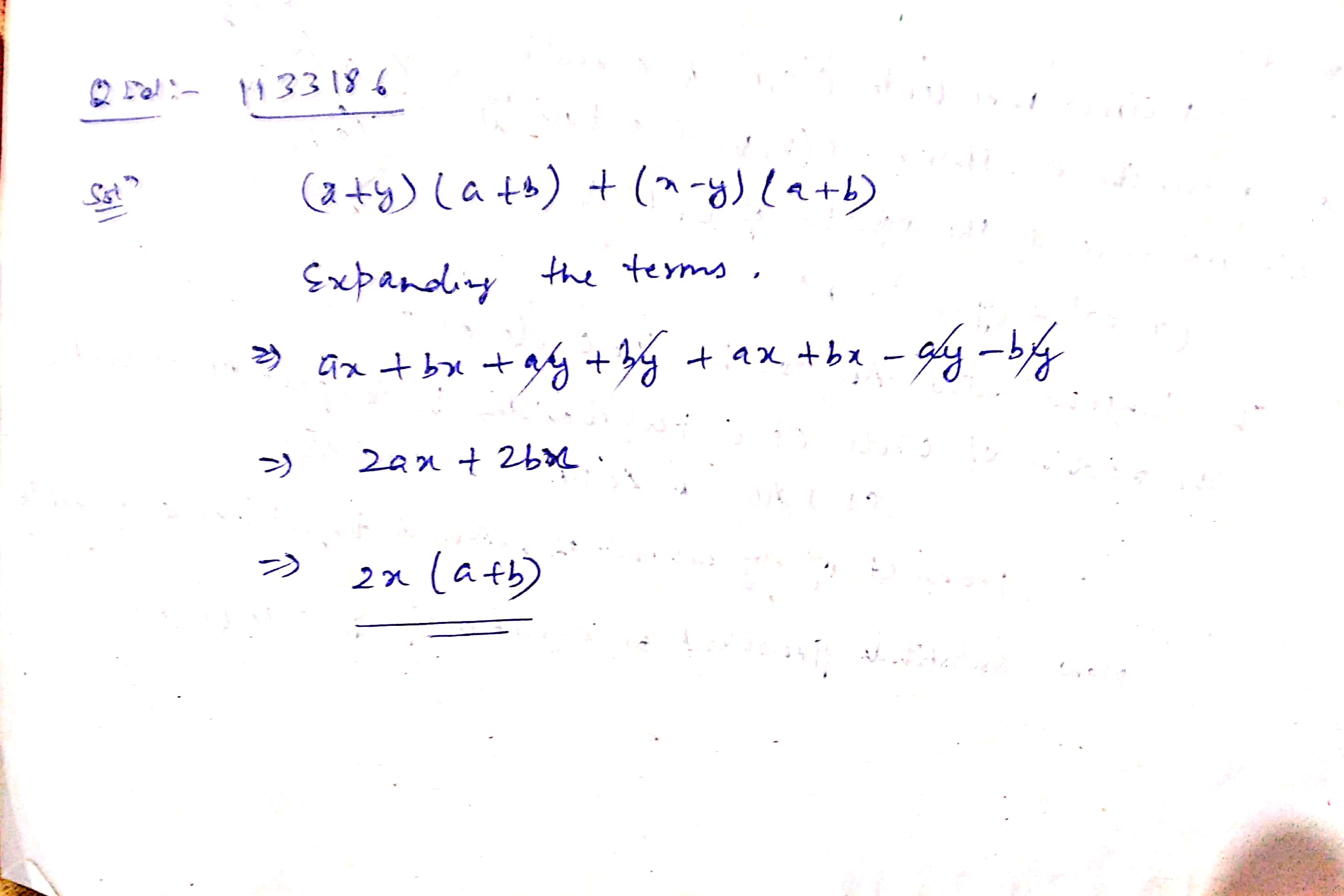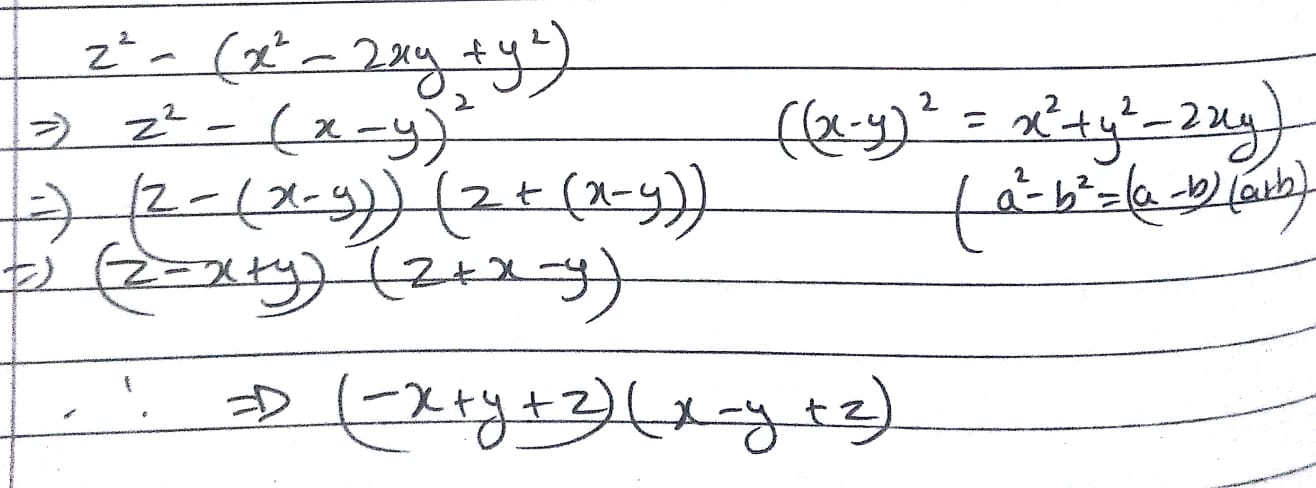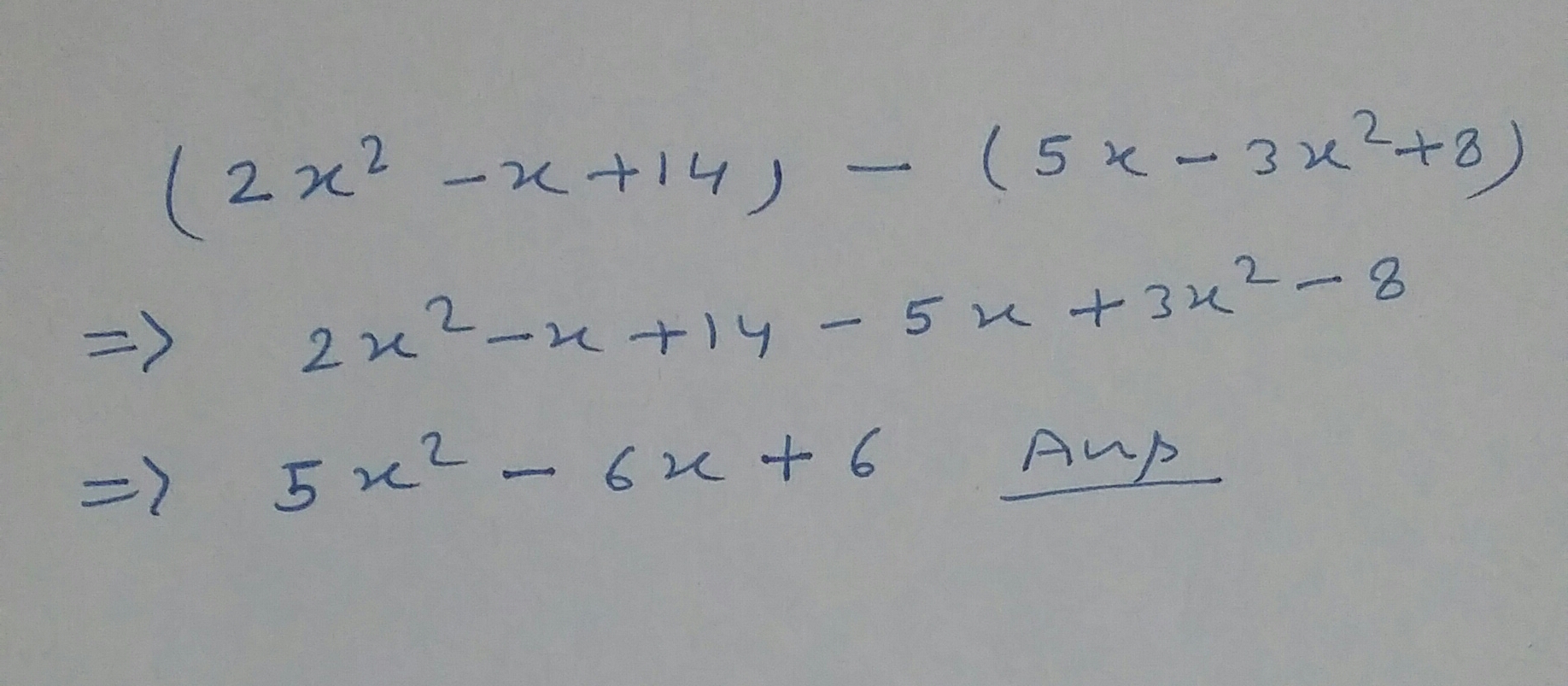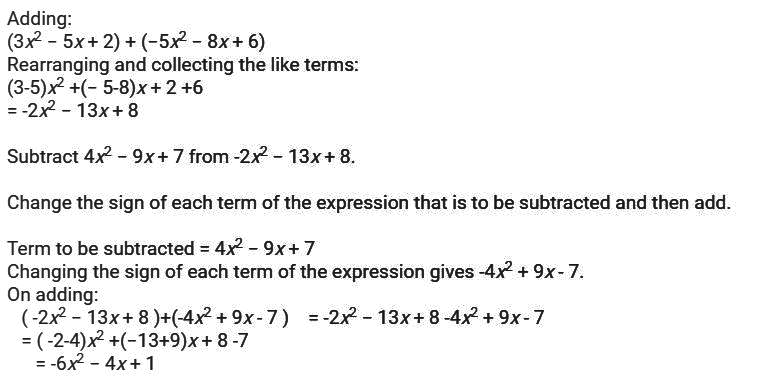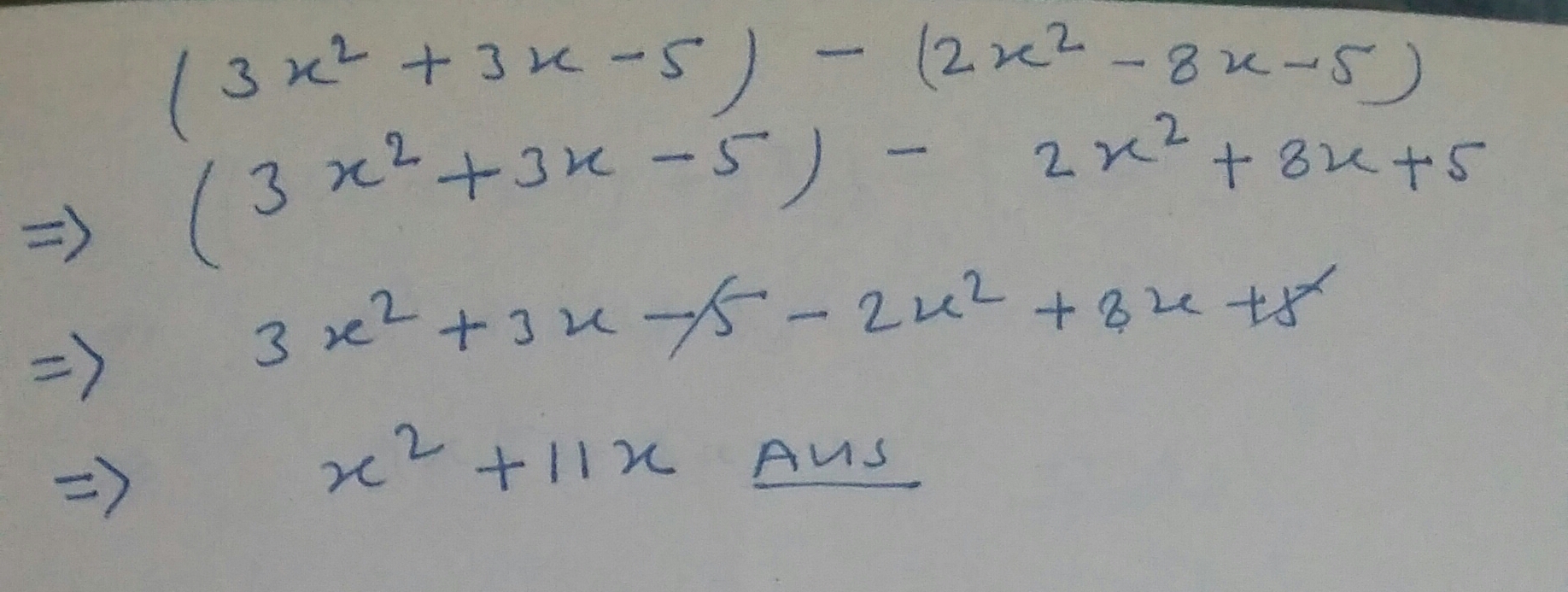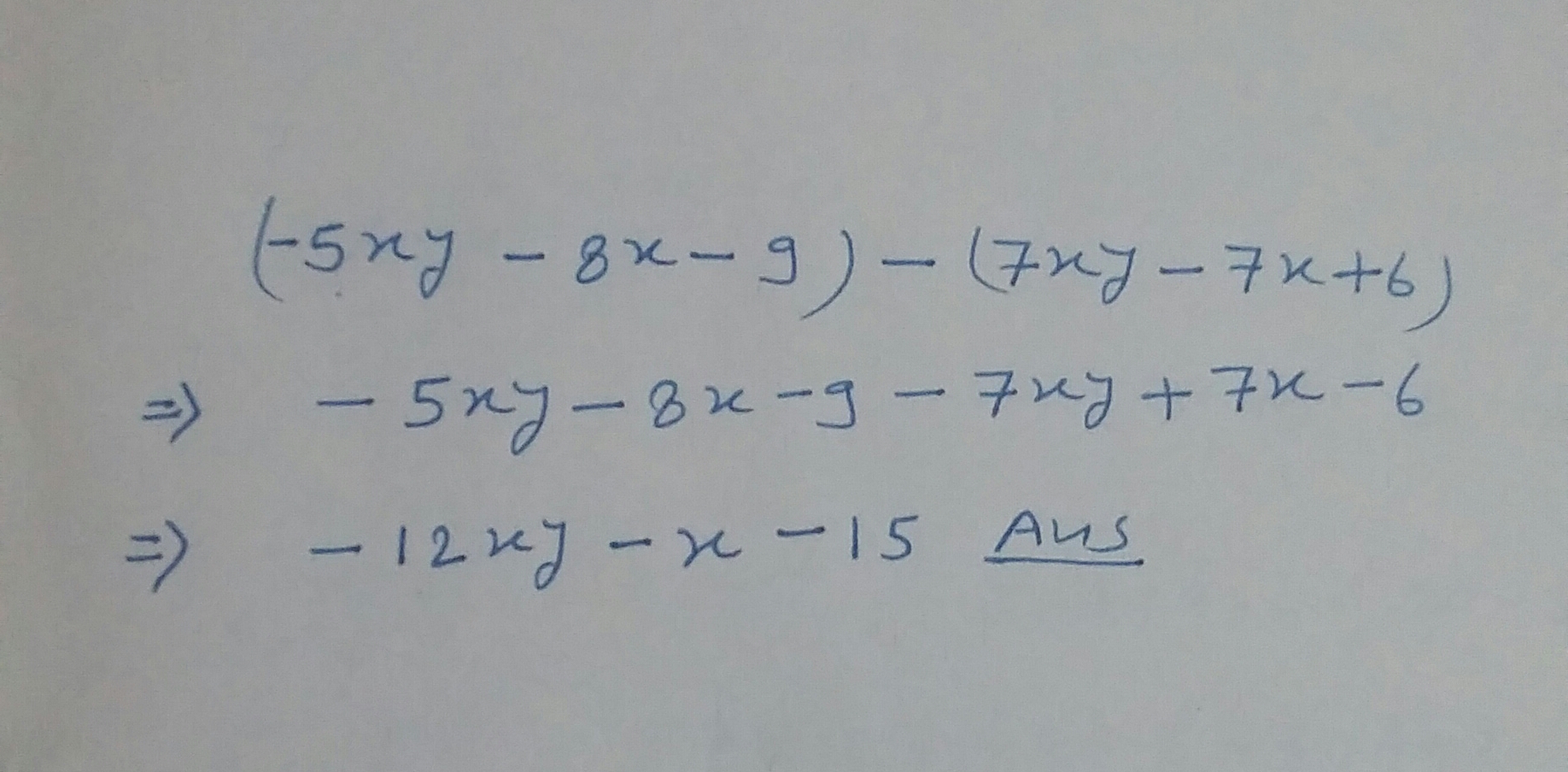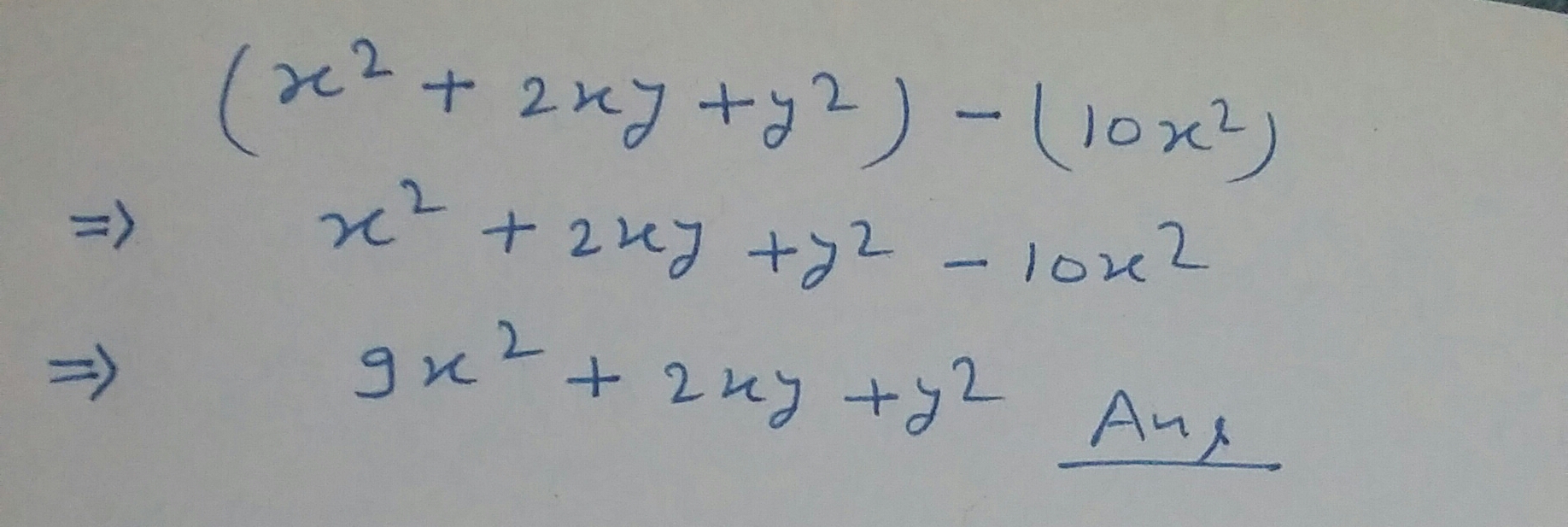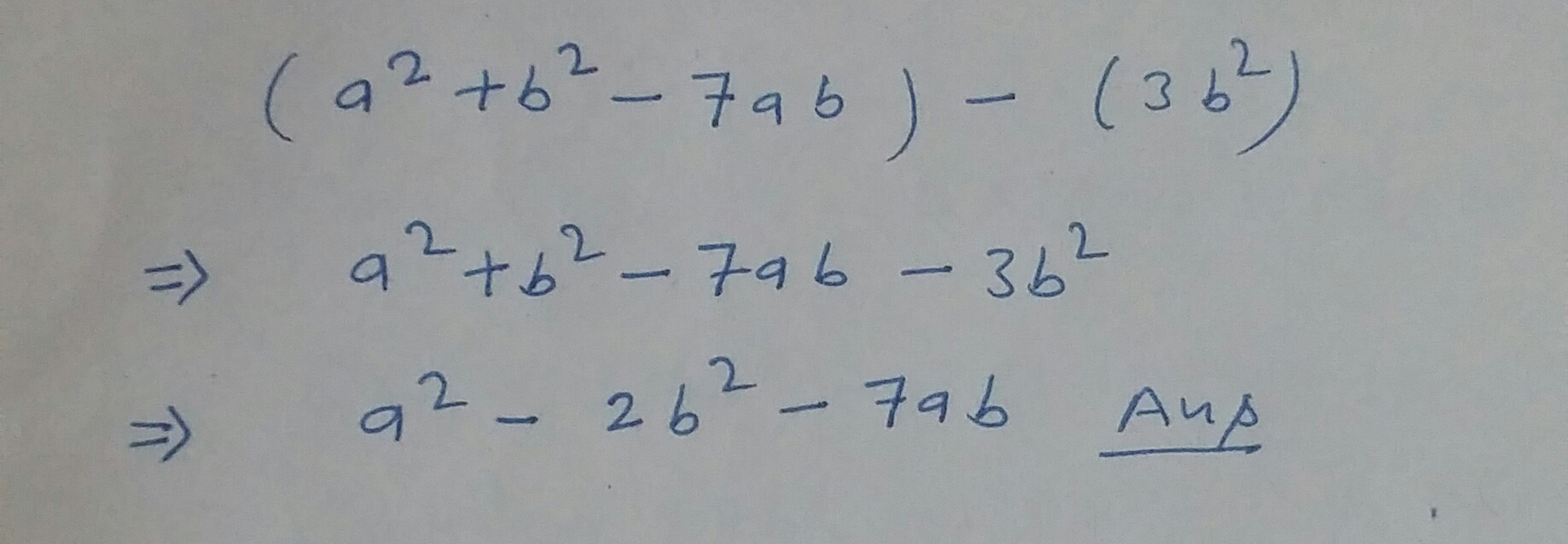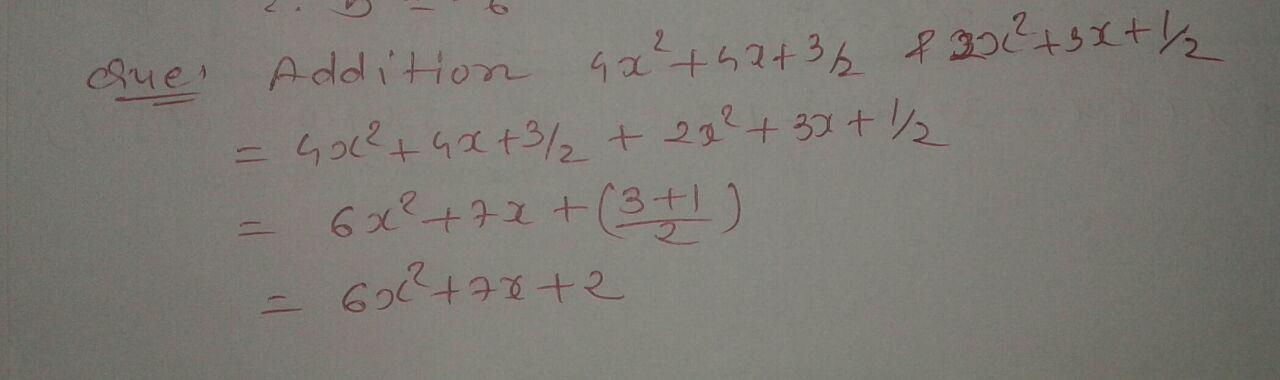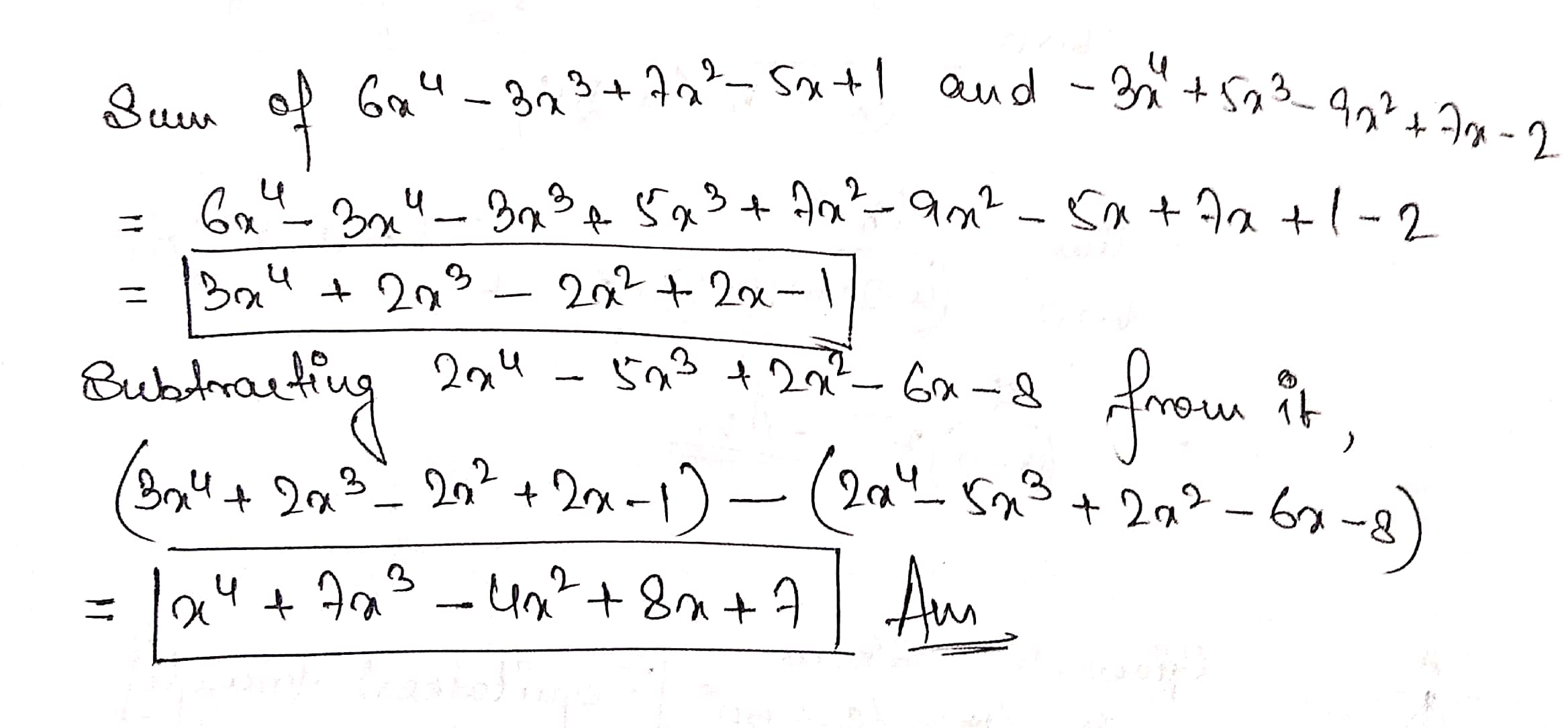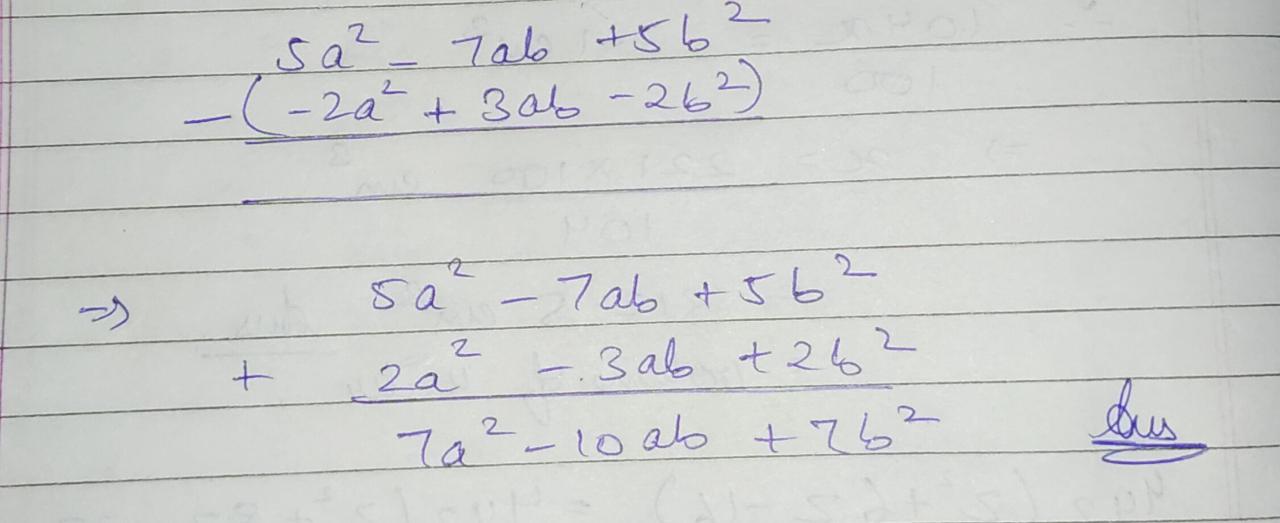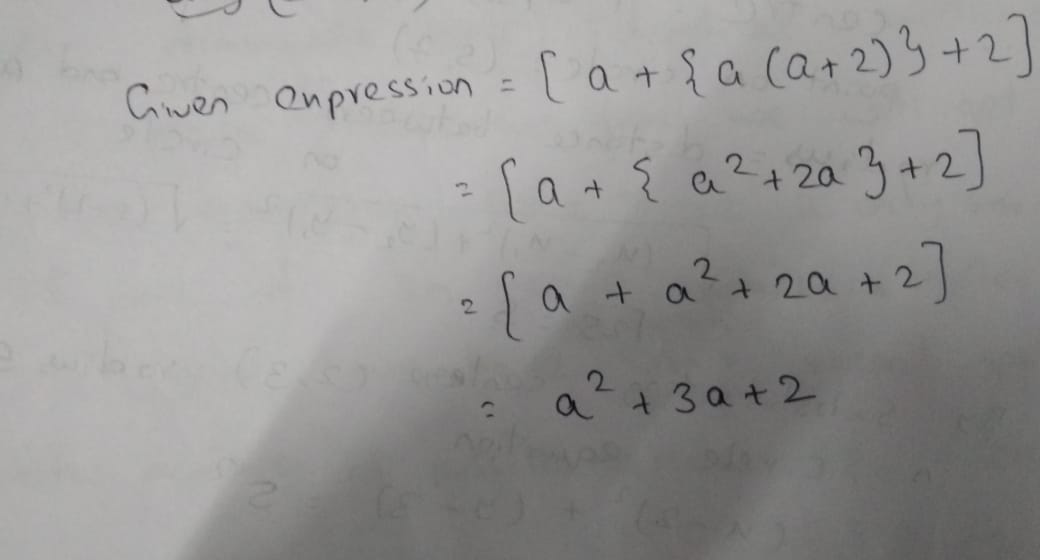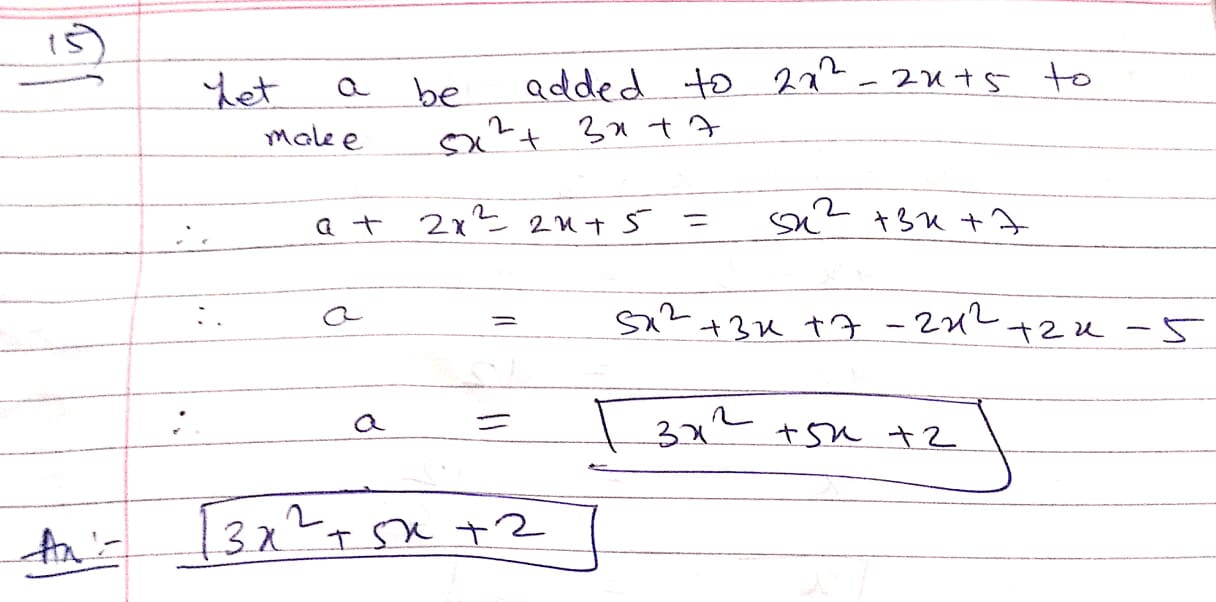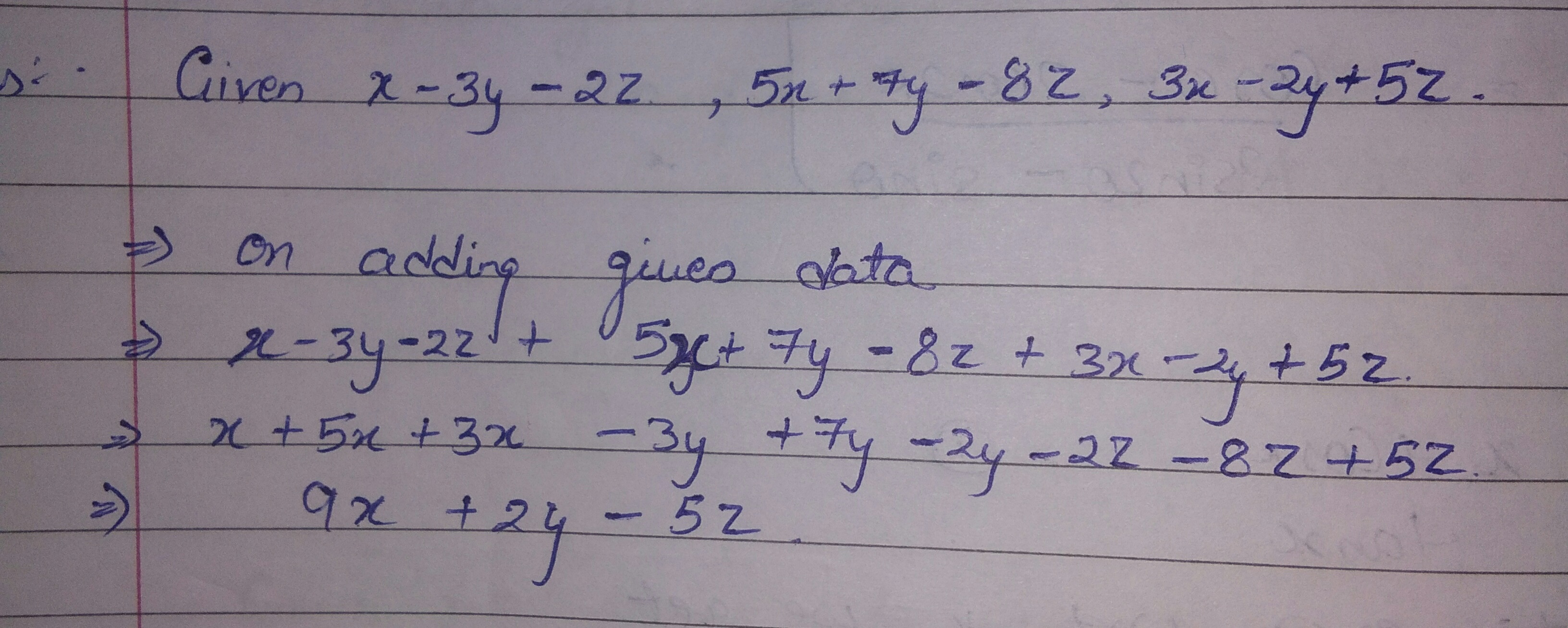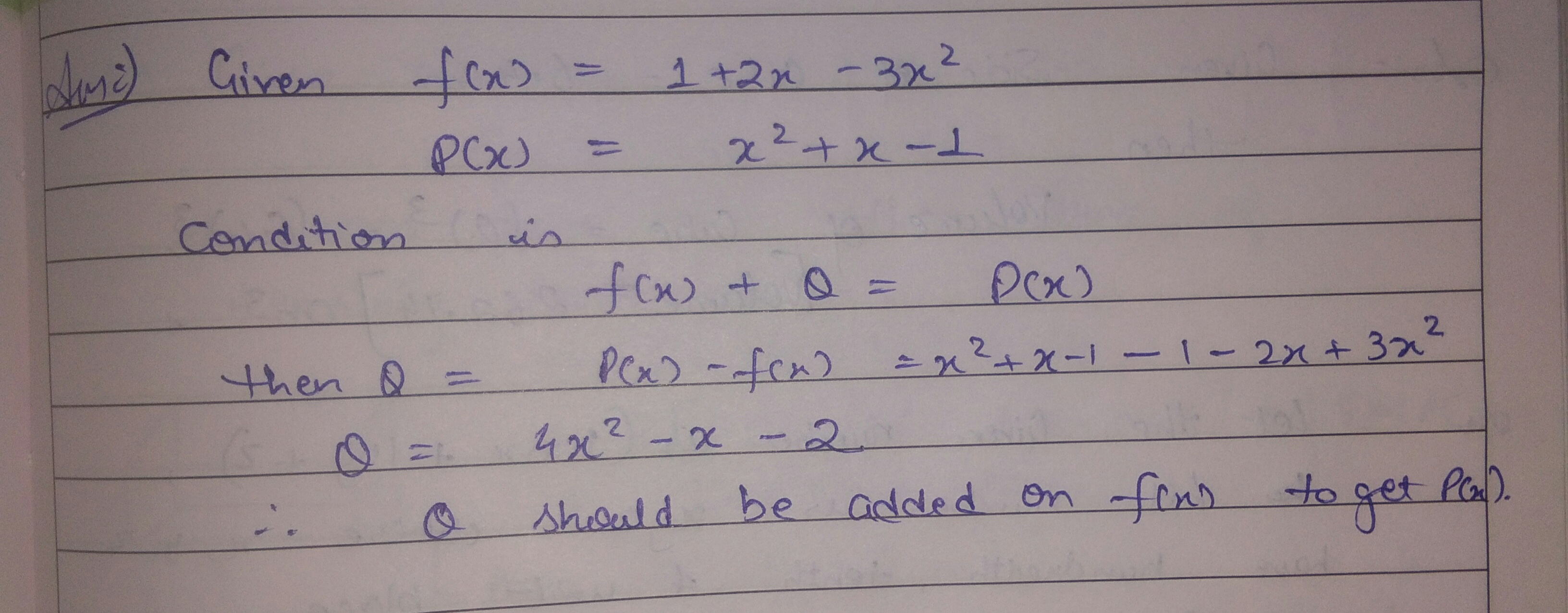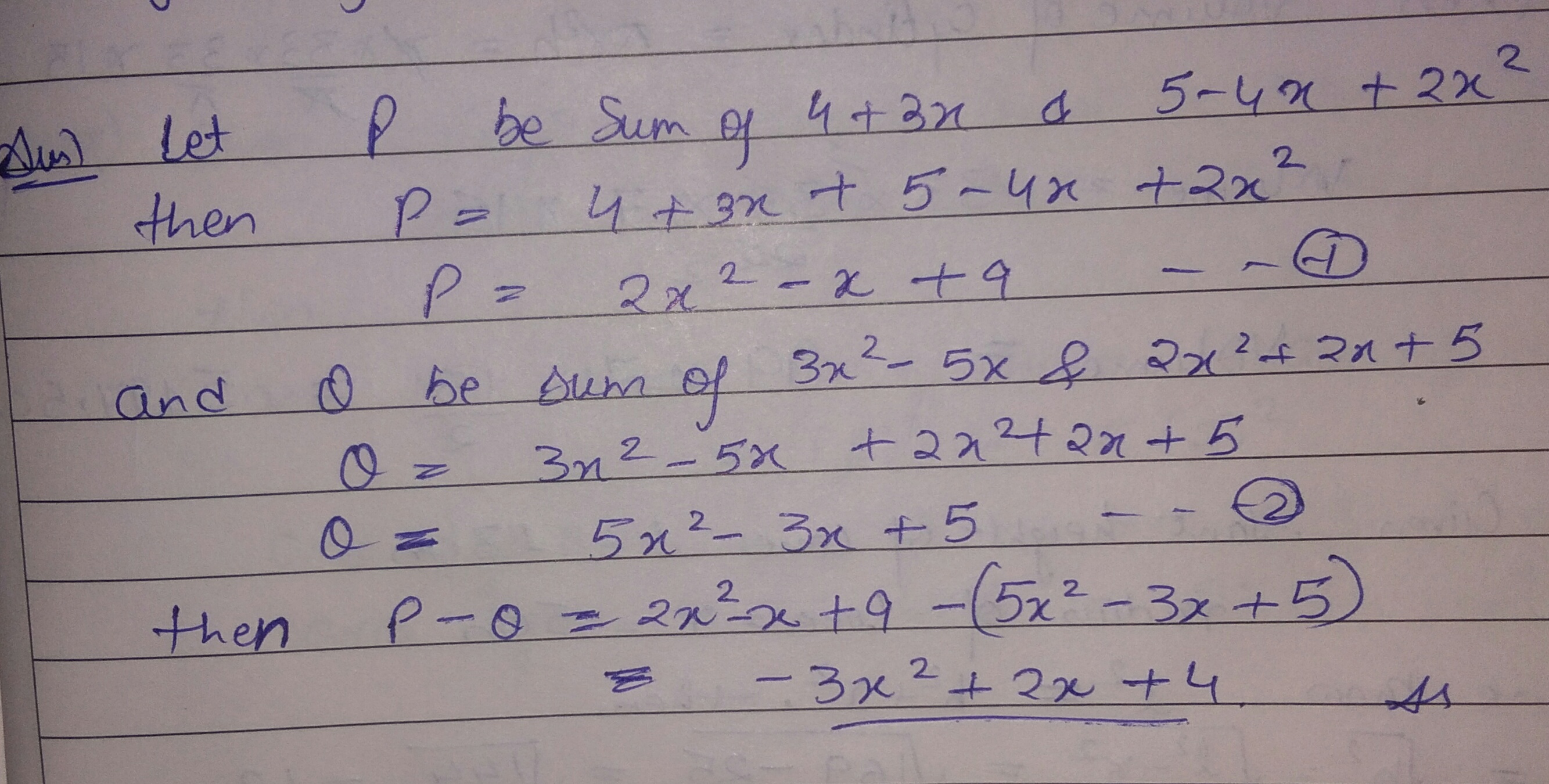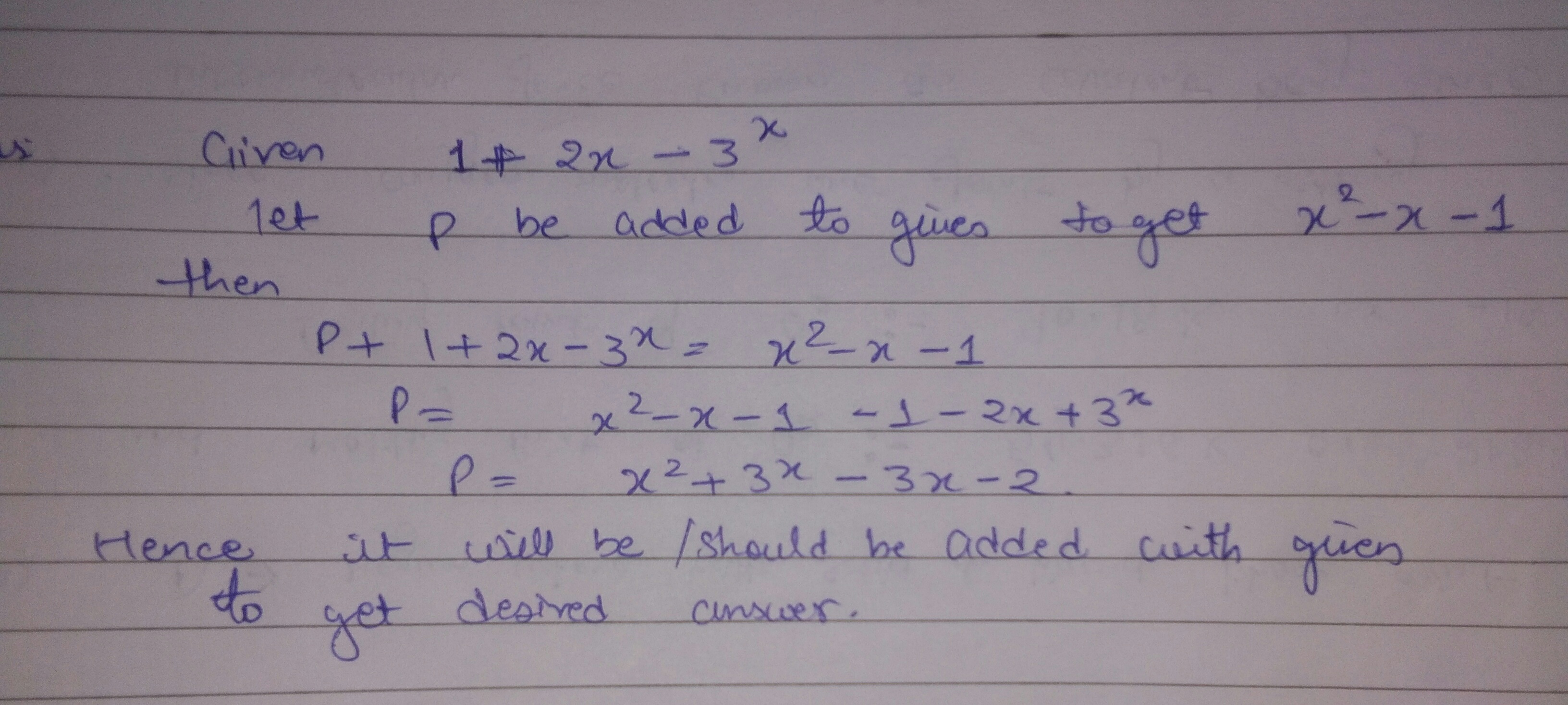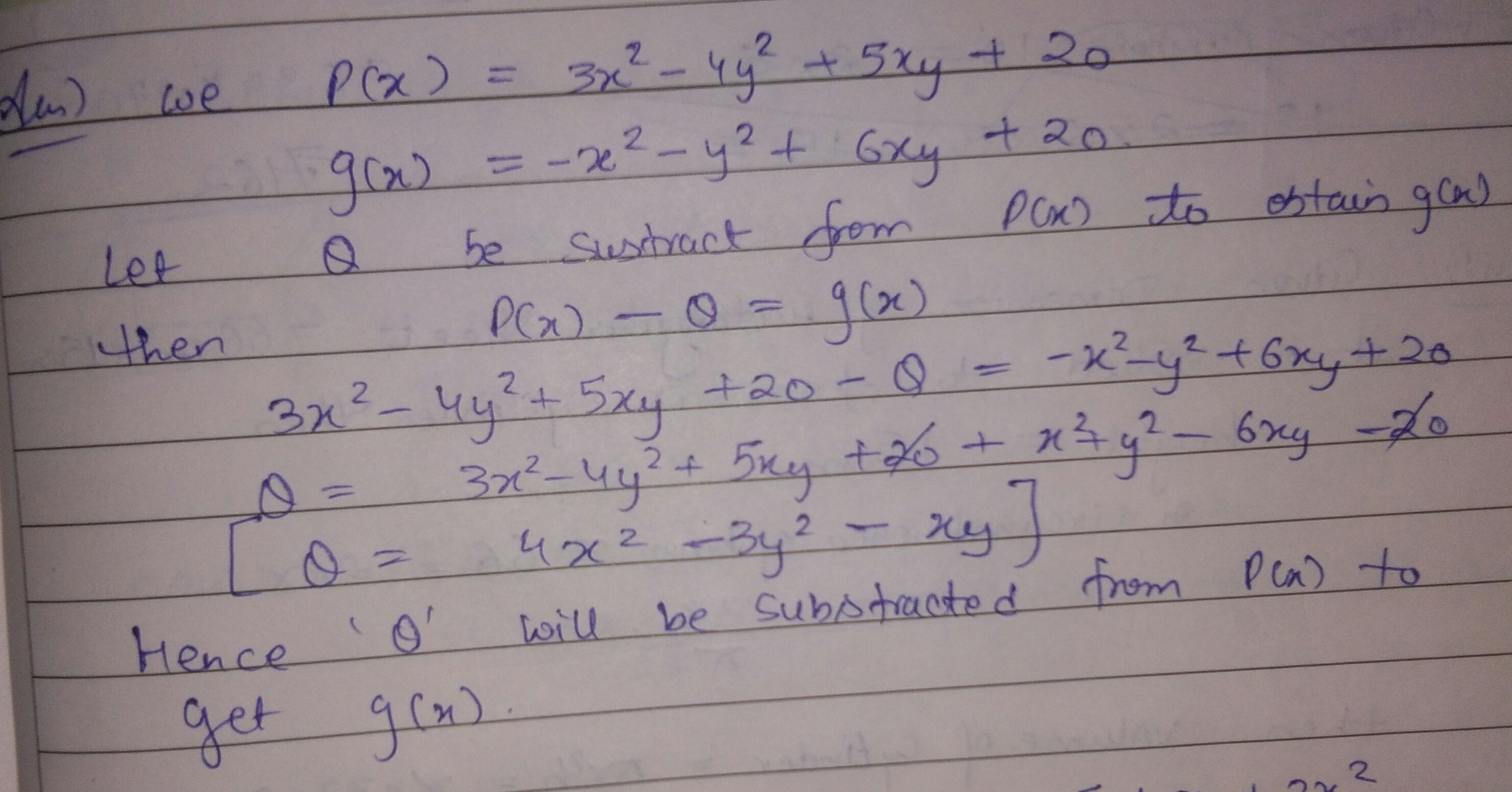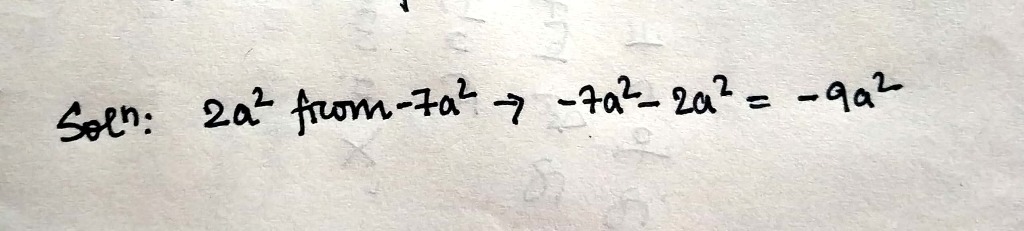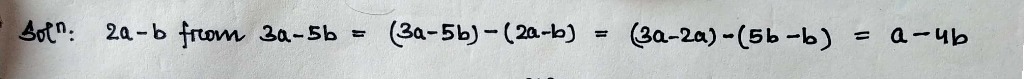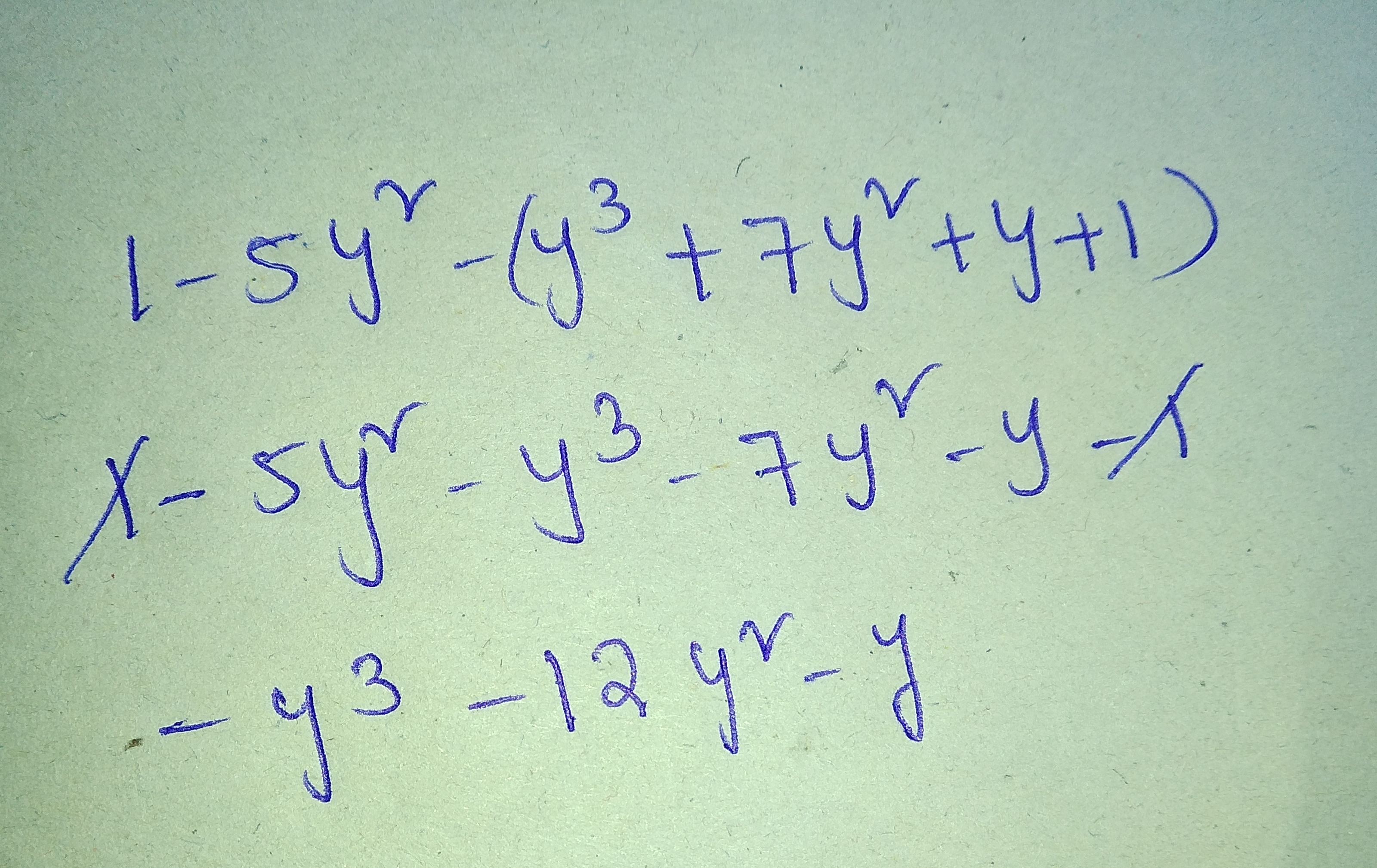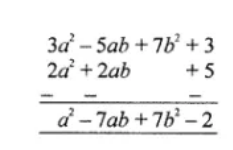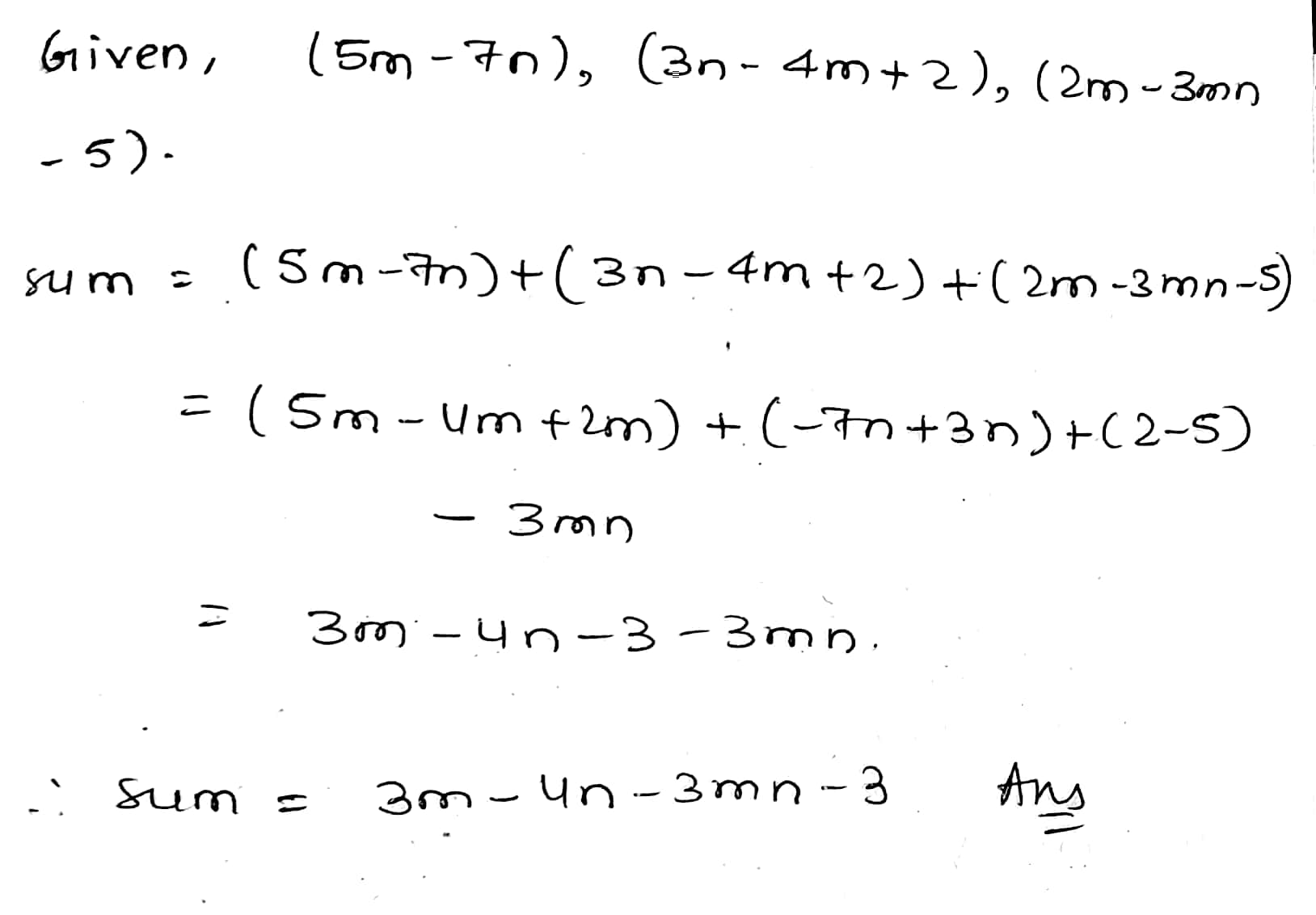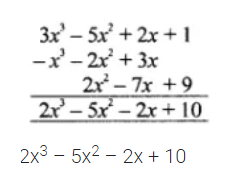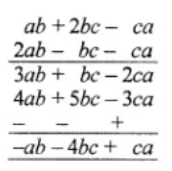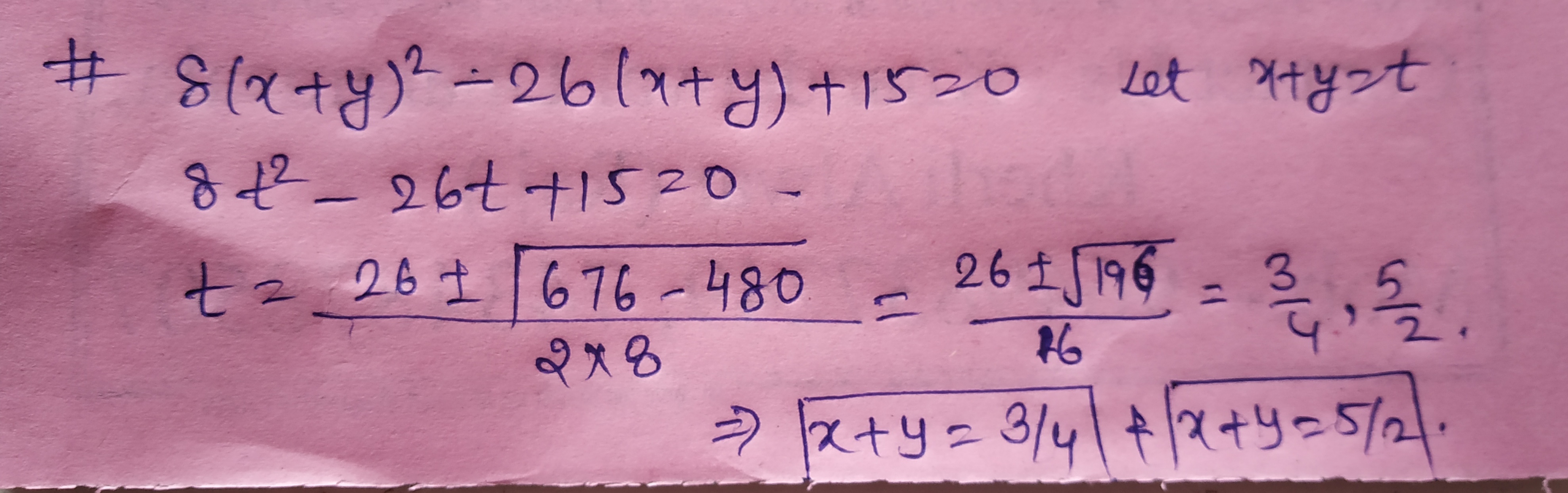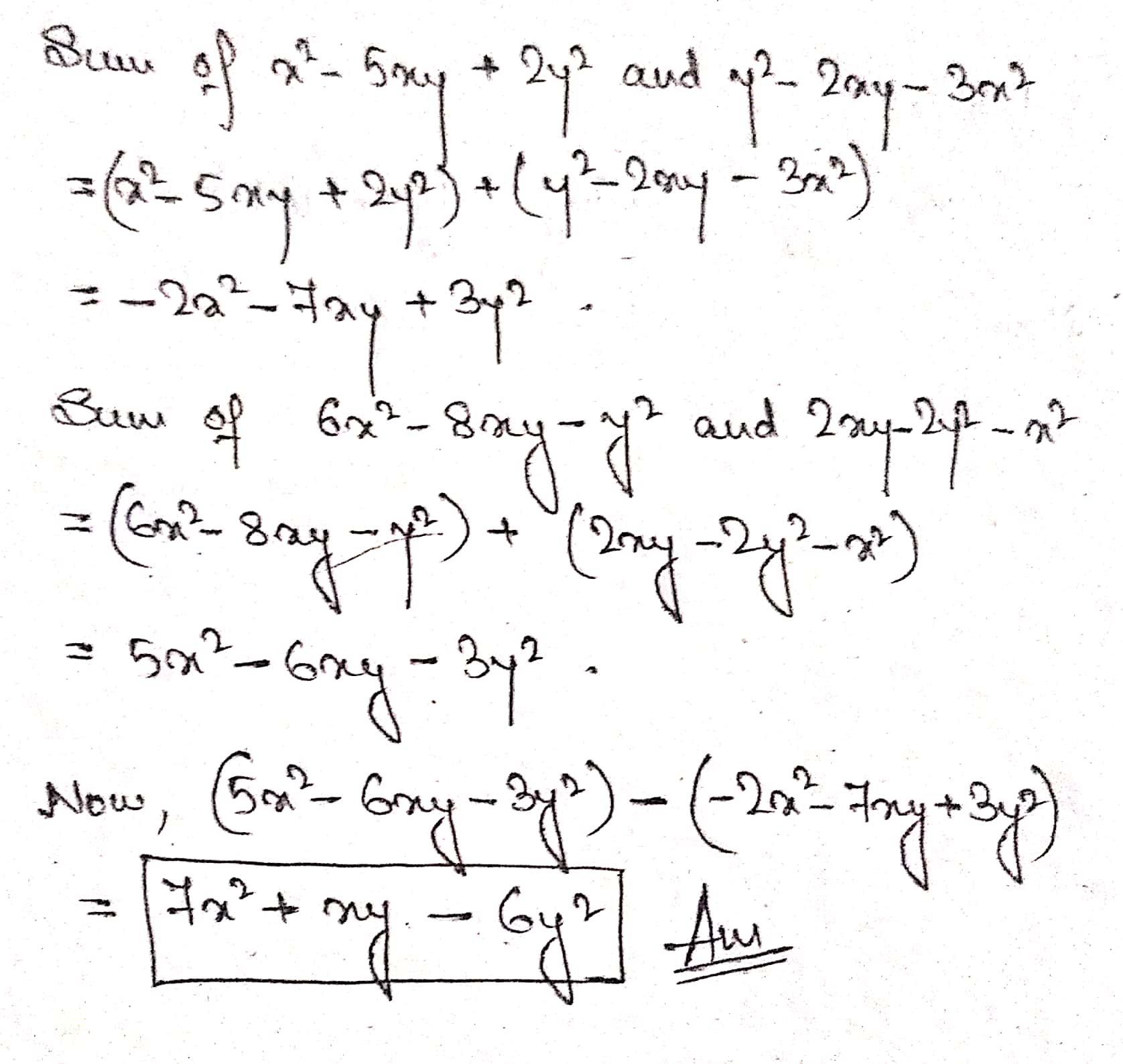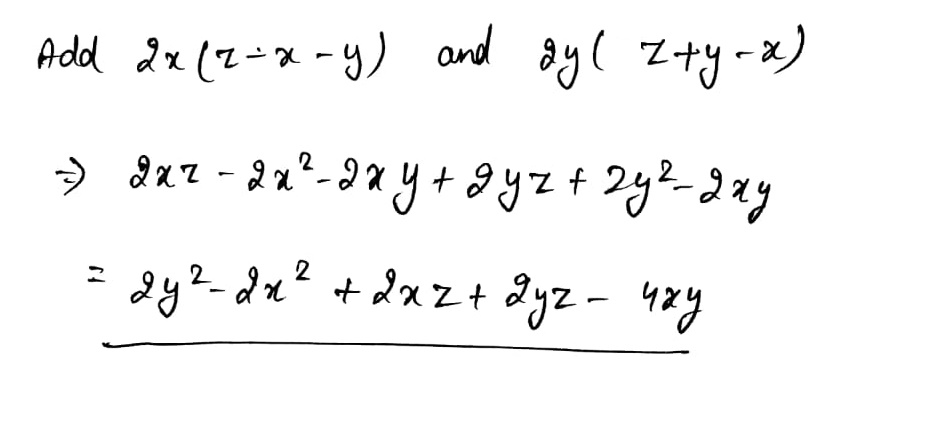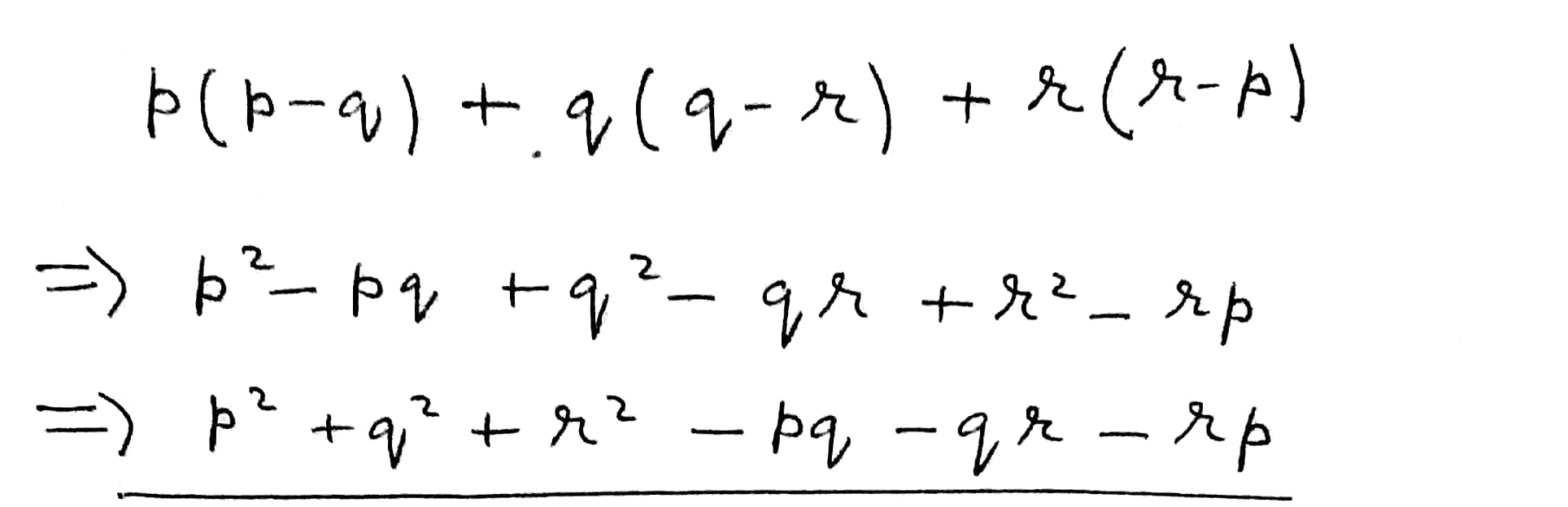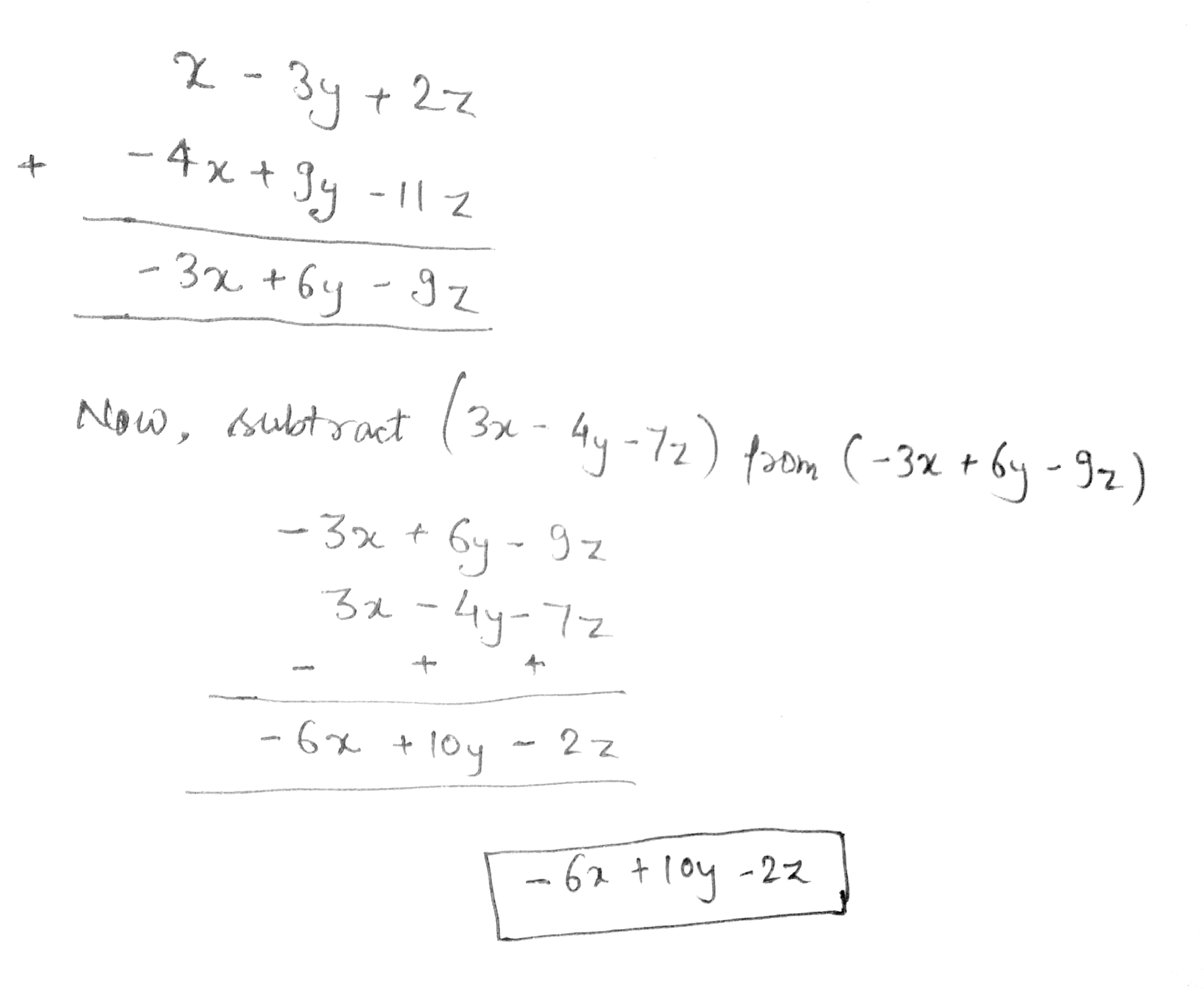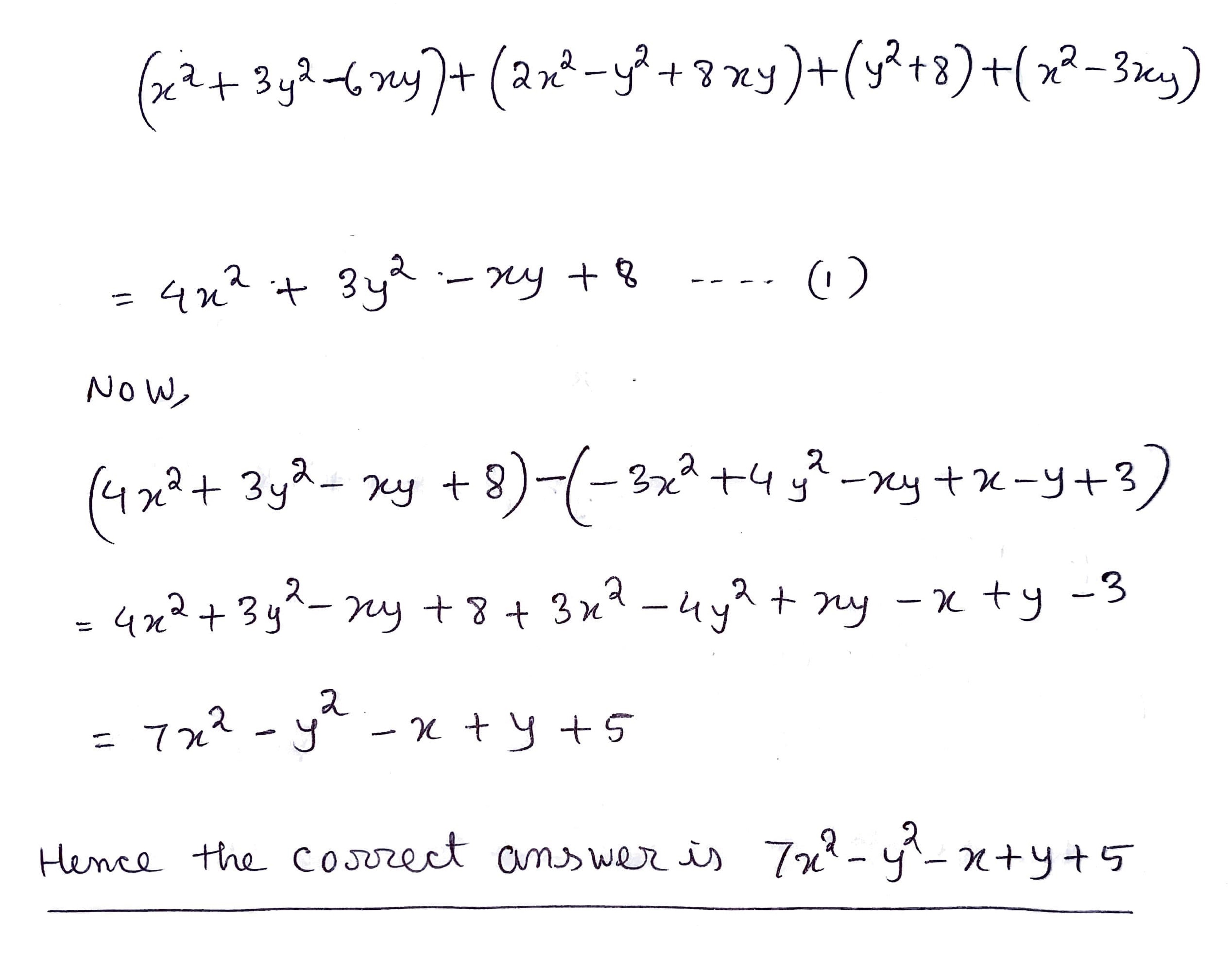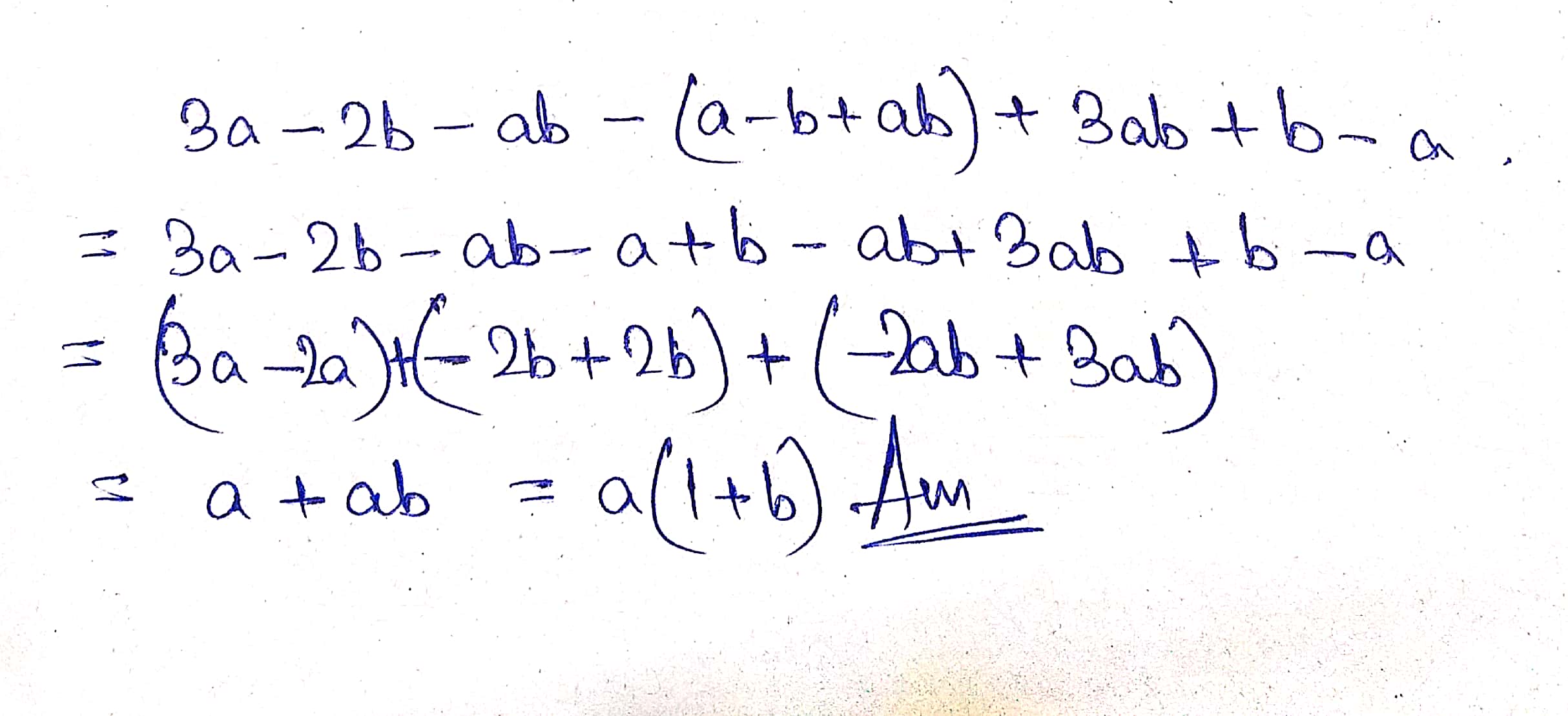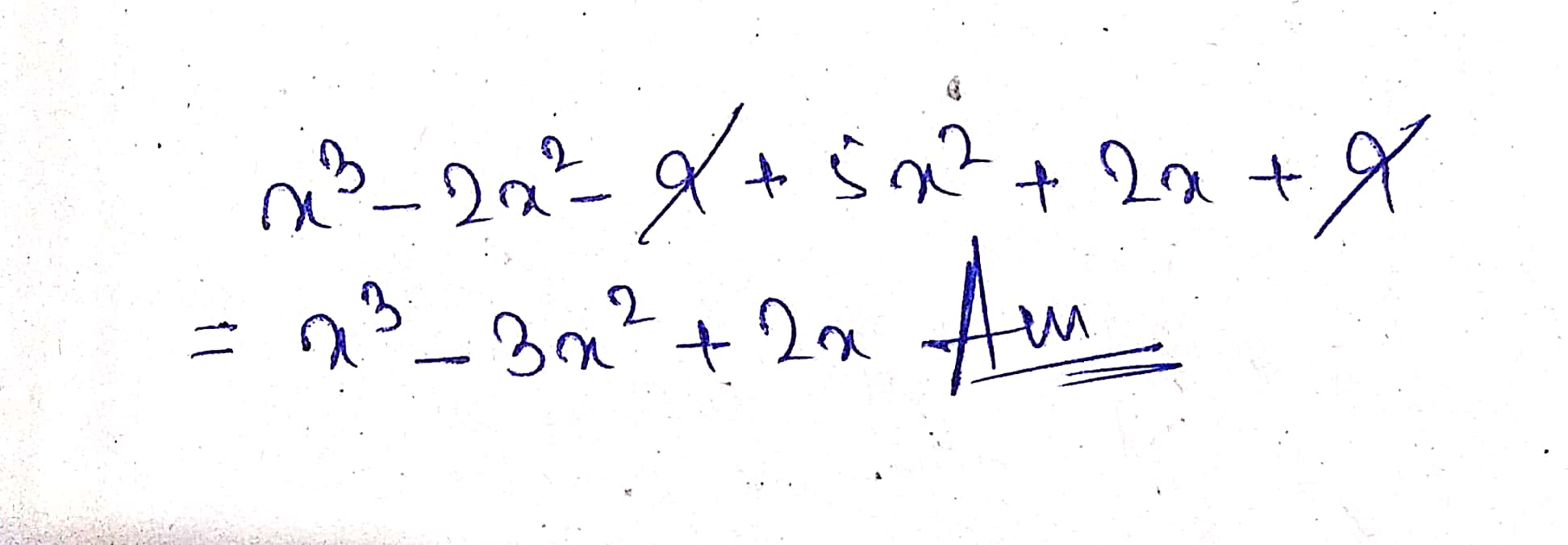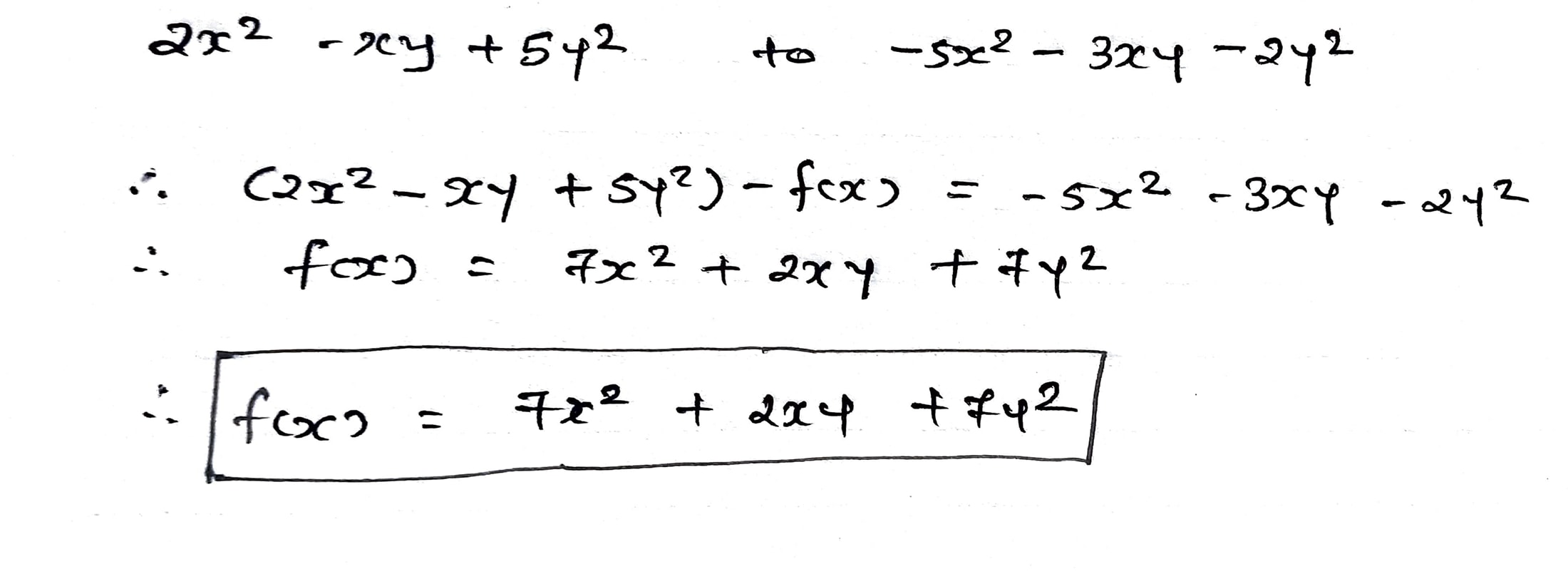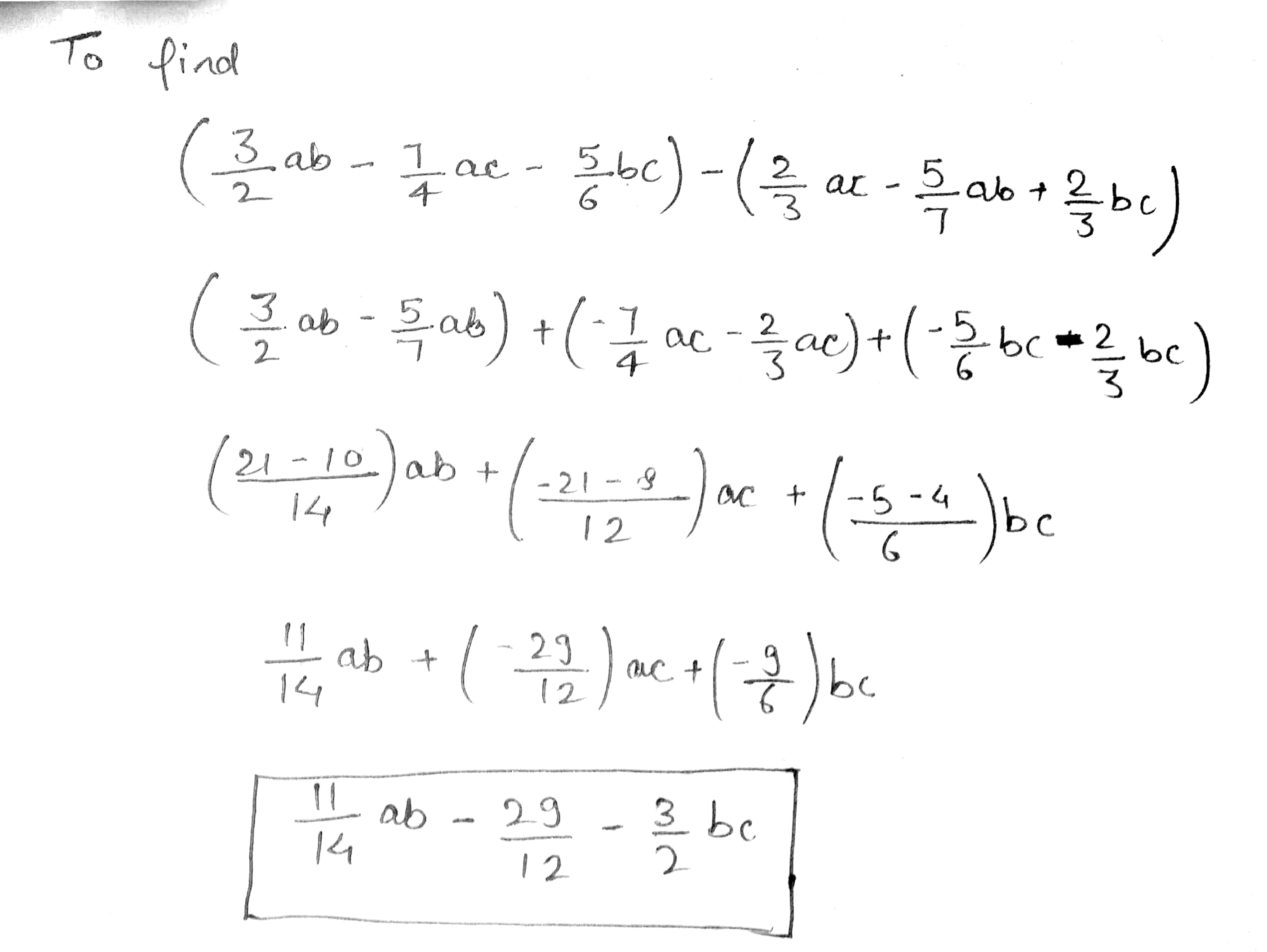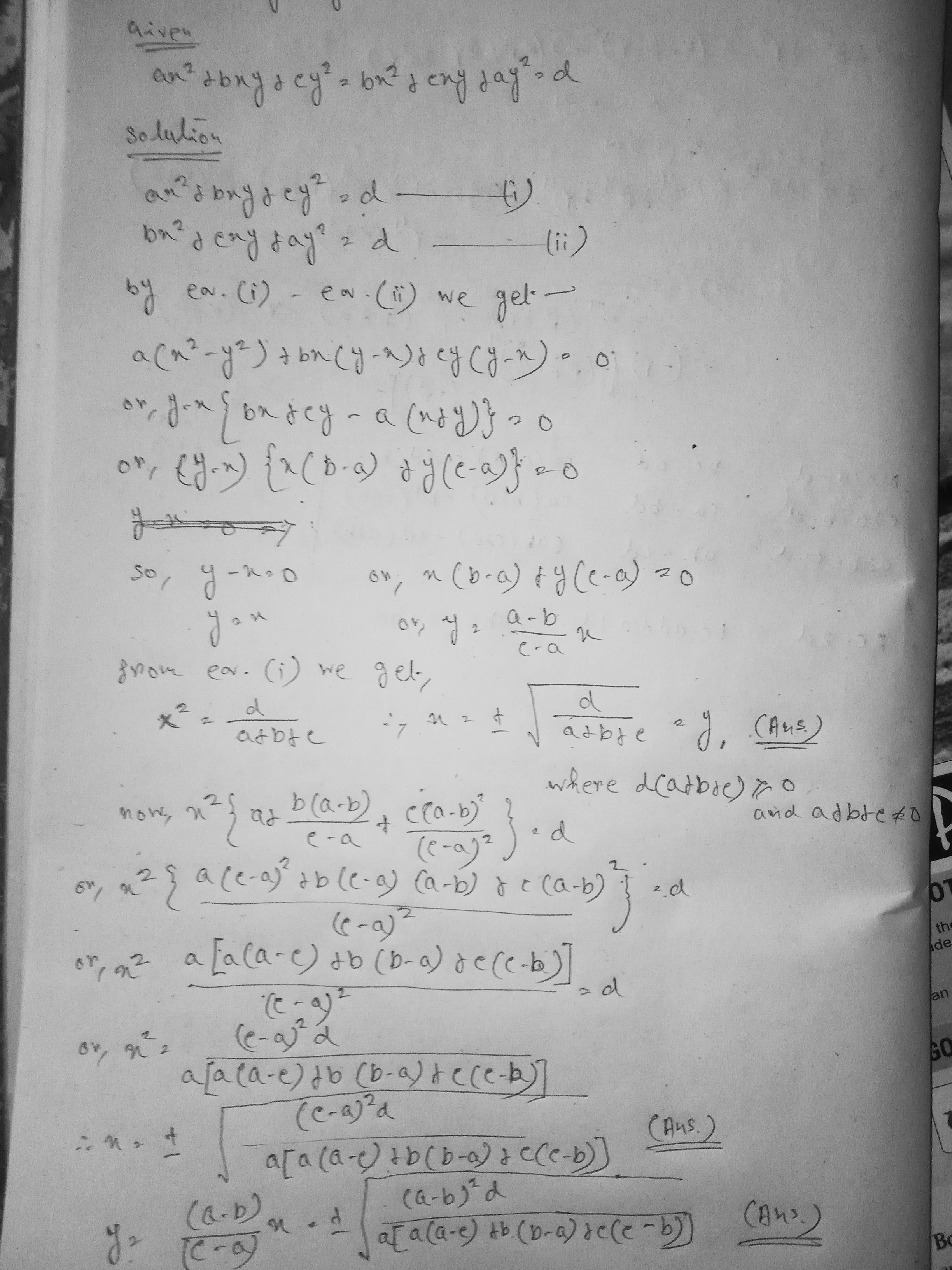Algebraic Expressions - Class 7 Maths - Extra Questions
Add:
$$6ax-2by+3cz, 6by-11ax-cz$$ and $$10cz-2ax-3by$$
Add:
$$6p+4q-r+3, 2r-5p-6, 11q-7p+2r-1$$ and $$2q-3r+4$$
Subtract :
$$-2a + b + 6d$$ from $$5a -2b -3c$$
Subtract
$$ 5x^2 -3xy + y^2$$ from $$7x^2 - 2xy -4y^2$$
Subtract :
$$a - 2b -3c $$ from $$-2a + 5b -4c$$
Subtract
$$ -11 x^2y^2 + 7xy - 6$$ from $$9x^2y^2 -6xy +9$$
Simplify :
$$ x^4 - 6x^3 + 2x - 7 + 7x^3 - x + 5x^2 + 2 - x^4$$
Add :
$$2x^3–3x^2+7x–8,\ \ –5x^3+2x^2–4x+1,\ \ 3–6x+5x2–x^3$$
Add
$$2 + x -x^2+6x^3,\ -6-2x+4x^2-3x^3,\ \ 2 +x^2,\ \ 3-x^3+4x-2x^2$$
Subtract :
$$6x^3 - 7x^2 + 5x - 3$$ from $$4 - 5x + 6x^2 -8x^3$$
Subtract:
$$-8xy$$ from $$7xy$$
Subtract $$x - 2y - z$$ from the sum of $$3x - y + z$$ and $$x + y - 3 z$$.
Enclose the given terms in brackets as required:
$$x^{2}- y^{2} + z^{2} + 3x - 2y = x^{2} - (..............)$$
Enclose the given terms in brackets as required:
$$x^{2} - xy^{2} - 2xy - y^{2} = x^{2} - (..........)$$
Simplify :
$$k / 2 + k / 3 + 2k / 5$$
Simplify :
$$2p / 3 - 3p / 5$$
Simplify :
$$y / 5 + y - 19y / 15$$
Simplify :
$$x + x / 2 + x / 3$$
Simplify :
$$3y / 4 - y / 5$$
Simplify :
$$y / 4 + 3y / 5$$
Simplify:
$$\dfrac{2x}{5} +\dfrac{3x}{4} - \dfrac{3x}{5}$$
$$\dfrac{2x}{5} +\dfrac{3x}{4} - \dfrac{3x}{5}$$
Simplify :
$$6k / 7 - (8k / 9 - k / 3)$$
Simplify :
$$4a / 7 - 2a / 3 + a / 7$$
Simplify :
$$x / 2 - x / 8$$
Simplify :
$$x / 5 + (x + 1)/ 2$$
Write the number of terms in following polynomial: $$ ax-by+y \times z $$
If $$a = 3x - 5y, b = 6x + 3y$$ and $$c = 2y - 4x$$, then $$ 2a - 3b + 4c.$$ $$=$$
Subtract: $$8x - 7y - 8p + 10q$$ from $$10x + 10y - 7p + 9q$$.
Subtract: $$a- b - 2c$$ from $$4a + 6b - 2c$$.
If $$a = 3x - 5y, b = 6x + 3y$$ and $$c = 2y - 4x$$, then $$ a + b - c$$ $$=$$
Subtract the sum of $$2x-{x}^{2}+5$$ and $$-4x-3+7{x}^{2}$$ from $$5$$ is
How much does $$-5a^{2}+3a-5b^{2}$$ exceed $$7a^{2}+4a-9b^{2}$$?
Simplify:$$4x+3-(2x-5y)$$
$$(n-10)^2 + (10-n)$$
Factorize $$\left( 1+\dfrac { 1 }{ x } +\dfrac { 1 }{ { x }^{ 2 } } +\dfrac { 1 }{ { x }^{ 3 } } \right)$$
$$-3{x}^{2}y+4{x}^{2}y-5{x}^{2}{y}^{2}$$What is a coficient of $$x$$
Subtract the sum of $$a+2b-3c$$ and $$2c-3b-4a$$ from the sum of $$5b-4c+a$$ and $$2c-3b-4a$$.
Simplify
$$\left( a+b \right) \left( c-d \right) +\left( a-b \right) \left( c+d \right) $$
Simplify : $${ (4m+5n) }^{ 2 }-{ (4m-5n) }^{ 2 }$$
What is the result when $$2x^2+5x-6$$ is subtracted from $$4x^2-9x+6$$
Enclose the given terms in brackets as required:
$$4a - 9 + 2b - 6 = 4a - (..........)$$
Simplify :
$$a/10 + 2a/5$$
Enclose the given terms in brackets as required:
$$-2a^{2} + 4ab - 6a^{2}b^{2} + 8ab^{2} = -2a (...........)$$
Simplify :
$$2x - (x + 2y - z)$$
Simplify :
$$x / 2 + x / 4$$
Simplify :
$$8 (2a + 3b - c) - 10 (a + 2b + 3c)$$
Add the following:
$$2x^3-9x^2+8,3x^2-6x-5,7x^3-10x+1$$ and $$3+2x-5x^2-4x^3$$
Add:$$8ab, -5ab, 3ab, -ab$$
Simplify:$$p+2(q- \overline { r+p } )$$
Add: $$p(p-q),q(q-r)$$ and $$r(r-p)$$
Combine the following : $$( x - 3 ) ( x + 3 ) \left( x ^ { 2 } + 9 \right)$$
Simplify: $$(3.5e-4.5f)(1.5e+4f+ef)-4.5e+10f$$.
Identify terms and factors in the expression given.
$$-4x+5y$$.
Identify the numerical coefficients of terms (other than constants) in the following expression
$$(5-3t)$$
Simplify :$$a^{2}+4a^{2}-3a+6-10+5a$$
Solve:
$$z+z=?$$
Simplify the following expression.
$$6xy+13x-2yx-5x$$.
Subtract: {$$4(2p - 3q)$$} - {$$4(2p - 3q)$$}
Simplify: $$9{\left( {x - 2y} \right)^2} - 13 + 4\left( {x - 2} \right)$$
Find and correct errors of the following mathematical expressions:
$$2x+3y =5xy$$
Find and correct errors of the following mathematical expressions:
$$x+2x+3x = 5x$$
Find and correct errors of the following mathematical expressions:
$$5y+2y+y-7y =0$$
Simplify the polynomial and write it in standard form:
$$2(x+3)-(-3x+7)$$
The length and breadth a rectangular field are $$( 2 x + 3 y )$$ units and $$( 3 x - y )$$ respectively. Find the perimeter of the field in the form of an algebraic expression .
Solve :
$$2a - 3b - [4a - 3b - \{ a - 2c - (a - 2b - c)\} ]]$$
Add:-$$(4x^2-12xy+9y^2)+(25x^2+4xy-32y^2)$$
Evaluate:$$(l+m) -4m\quad $$
From the sum of $$3x-y+11$$ and $$-y-11$$ subtract $$3x-y-11$$
Find the difference between $$P\left( x \right) ={ x }^{ 4 }-{ 3x }^{ 2 }+4x+5,g\left( x \right) ={ x }^{ 2 }+1-x$$
Identify the terms and factors in the expression given.
$$\dfrac{3}{4}x+\dfrac{1}{4}$$.
Add $$14x+10y-12xy-13, 18-7x-10y+8xy, 4xy$$.
Add $$-7mn+5, 12mn+2, 9mn-8, -2mn-3$$.
Add $$4x^2y, -3xy^2, -5xy^2, 5x^2y$$.
Simplify combining like terms.
$$5x^2y-5x^2+3yx^2-3y^2+x^2-y^2+8xy^2-3y^2$$.
Add $$5m-7n, 3n-4m+2, 2m-3mn-5$$.
Add $$x^2-y^2-1, y^2-1-x^2, 1-x^2-y^2$$.
Simplify combining like terms.
$$(3y^2+5y-4)-(8y-y^2-4)$$.
Identify the terms and factors in the expression given.
$$0.1p^2+0.2q^2$$.
Add $$a+b-3, b-a+3, a-b+3$$.
Subtract $$6xy$$ from $$-12xy$$.
Subtract $$5a^2-7ab+5b^2$$ from $$3ab-2a^2-2b^2$$.
Add:
$$x^2 - a^2, - 5x^2 + 2a^2, -4x^2 + 4a^2$$
Subtract:
$$8a + 3ab - 2b + 7$$ from $$14a - 5ab + 7b - 5$$
Subtract: $$4p^2q-3pq +5pq^2-8p+7q-10 $$ from $$18 -3p-11q+5pq -2pq^2 + 5p^2q$$
Add $$ab- bc, bc- ca, ca -ab$$.
Write the number of terms in following polynomial: $$ 5x^2+3 \times ax $$
Write the number of terms in following polynomial: $$ ax\div 4 -7$$
Write the number of terms in following polynomial: $$23+ a\times b \div{2} $$
$$x^3-x-4$$ added to $$ x^4-x^3-x^2+x+3 $$ to obtain $$x^4+x^2-1$$ ?
If true then enter $$1$$ and if false then enter $$0$$
Simplify the polynomial and write it in standard form:
$$-4(8x-10)-3(7x-1)+3(4x)+12$$
Simplify the polynomial and write it in standard form:
$$(-2x-5)(2x-8)-(2x-5)(3x+7)$$
Simplify the polynomial and write it in standard form:
$$(-{x}^{3}+4)(x+2)-(2x-1)(5x)$$
Simplify the polynomial and write it in standard form:
$$2({x}^{2}-3x-2)-(-3{x}^{2}+7x-1)$$
Subtract the following:
$$p\left( y \right) =3{ y }^{ 7 }-2{ y }^{ 2 }+3$$ and $$q\left( y \right) ={ y }^{ 7 }+{ y }^{ 2 }+y$$
Simplify : $$3x^2 + 5xy - 4y^2 + x^2 - 8xy - 5y^2$$
Add the given polynomials: $$x^3 - x^2y + 5xy^2 +y^3, x^3 - 9xy^2 +y^3$$ and $$3x^2y + 9xy^2$$.
Add the given polynomials: $$5a+ 3b, a - 2b$$ and $$3a+ 5b$$
Simplify: $$7x - 9y+3 -3x -5y+8$$
Add $$7x^2- 4x + 5$$ and $$9x-10$$.
Add $$8xy + 4yz -7zx, 6yz + 11zx -6y$$ and $$-5xz + 6x -2yx$$
Add: $$5x^2y, -7x^2y$$, $$9x^2y$$.
Subtract $$2a - b$$ from $$3a - b$$.
Add $$5{x}^{2}+3xy+2{y}^{2}$$ and $$2{y}^{2}-xy+4{x}^{2}$$
Add the following algebraic expressions:
(i) $$2x^{2} + 3x + 5, 3x^{2} - 4x - 7$$
(ii) $$x^{2} - 2x - 3, x^{2} + 3x + 1$$
(iii) $$2t^{2} + t - 4, 1 - 3t - 5t^{2}$$
(iv) $$xy - yz, yz - xz, zx - xy$$
(v) $$a^{2} + b^{2}, b^{2} + c^{2}, c^{2} + a^{2}, 2ab + 2bc + 2ca$$
substract $$4{p^2}q - 3pq + 5p{q^2} - 8p + 7q - 10$$ from $$18 - 3p - 11q - 2p{q^2} + 5{p^2}q$$
The two adjacent sides of a rectangle are $$2x^2- 5xy+3z^2$$ and $$4xy-x^2-z^2$$. Find its perimeter
Subtract $$3x^{2}y - 2xy + 2xy^{2} + 5x - 7y - 10$$ from $$15 - 2x + 5y - 11xy + 2xy^{2} + 8x^{2}y$$
Add the polynomials $$2x (x - y - z)$$ and $$2y(z - y - x)$$
Subtract the polynomial $$2ab + 5bc - 3ca$$ from the polynomial $$7ab - 2bc + 10ca$$
Subtract $$-3x + 8y$$ from $$-7x - 10y.$$
Subtract: $$-2x^2y + 3xy^2$$ from $$8x^2y$$ .
Subtract the polynomial : $$x^{5} - 2x^{2} - 3x$$ from $$x^{3} + 3x^{2} + 1$$
Find out the sum of the polynomials $$3x - y, 2y - 2x$$ and $$x + y$$
What should be added to $$(3x^3-2x^2+3x-1)$$ to get $$(x^3+2x^2-6x+5)?$$.
Subtract the second term from first term.
$$8x , 5x $$
Find the length of the line segment $$PR$$ in the following figure in terms of $$'a'$$.
Subtract $$5xy$$ from $$8xy$$
Subtract $$3c + 7d^{2}$$ from $$5c - d^{2}$$
Simplify $$3x^{2}+5xy-4y^{2}+x^{2}-8xy-5y^{2}$$
Add : $$9p+16q+13p+2q$$
Simplify:$$3x-[5y-\left\{{6y+2(10y-x)} \right\}]$$
Subtract:
- $$5x$$ from $$2x$$
- $$-7x$$ from $$9y$$
Add: $$ 3{ x }^{ 2 }y-5x{ y }^{ 2 }-6xy$$, $$ -7x{ y }^{ 2 }+4{ x }^{ 2 }y$$ and $$ -5xy-6{ x }^{ 2 }y+7{ y }^{ 2 }x$$
Simplify $$9x-5(2x-3)$$
Given
$$ 9x - 5(2x-3)$$
By solving equation
$$ 9x -10x + 15 $$
Here $$ 9x+10x$$ are like term then by adding then
$$ \Rightarrow -x +15 $$
$$ \Rightarrow 15 -x $$
Solve:-
$$ar+br+at+bt$$
$$(x^{5}+1),(3-x^{4}),(4+x^{3}+x^{6})$$ $$-$$
$$(2a^{3}-3b^{5}),(2a^{3}+3b^{5}),(2a^{4}-3a^{2}b^{2}+b^{4})$$
Solution :- Given $$ (x^{5}+1), (3-x^{4}), (4+x^{3}+x^{6}), $$
$$ (2a^{3}-3b^{5}), (2a^{3}+3b^{5}), (2a^{4}-3a^{2}b^{2}+b^{4}) $$
Let subtract and add the terms
$$ \Rightarrow x^{5}+1+3-x^{4}+4+x^{3}+x^{6}+2a^{3}-3b^{5}+2a^{3}+3b^{5}$$
$$ +2a^{4}-3a^{2}b^{2}+b^{4} $$
$$ \Rightarrow x^{6}+x^{5}-x^{4}+x^{3}+8+4a^{3}+2a^{4}-3a^{2}b^{2}+b^{4} $$
Simplify:$$x-(y-z)+x+(y-z)+y-(z+x)$$
Evaluate $${a^2} - {b^2} - {(a + b)^2}$$
Solve : $$5a - 9b - 7a + 10b$$
Simplify:
$$(4x^{2} + 7x^{3}y^{2}) -(-6x^{2} - 7x^{3}y^{2} -4x) - (10x + 2x^{2})$$
Subtract
i) $$4a - 2b - c$$ from $$-a + 2b + 3c$$
ii) $$-3x^2 + 7y^2 - z^2 \,$$ from $$\, 2x^2 - 5y^2 - 7z^2$$
Simplify:
$$-4x\left(5x^{2}-12\right)+ 7(x+5)$$
Subtract : $$9b\left(-2a^{2}b^{2}+2b^{2}+3a\right)$$ from $$2a\left(7a^{2}b^{2}+ab^{2}+5b\right)$$
Add the expressions in each of the following.
i) $$2l + 3m - 6n + 4p, \, 3l - 5m + 16n - 4p , \, 12l - 6m - 4n - 2p \, and \, l - 2m + 3n - 4p$$
ii) $$7x^3 + 3x + 9 , \, -2x^3 -3x^2 - 15, \, 3x^3 - 6x^2 + 4x - 6 \, and \, 12x^2 - 6$$
iii) $$5a^2 - 7ab + 9b^2 , \, 4a^2 - 2b^2 - 9ab - 6, \, 4 - 3b^2 + 2ab + 6a^2 \, and \, 12 ab - 3a^2 - 9b^2$$
Subtract $$(7 pqr-8q+6)$$ from $$(10-4pqr+3q)$$
Express the polynomial $$(1, 2, 3)$$ in index form.
What must be subtracted from $$2{x^4} + 4{x^2} - 3x + 7$$ to get $$3{x^3} - {x^2} + 2x + 1$$?
Relation between $$m_{1}$$ and $$m_{2}$$: $$-4m_{1}-4m_{2}=3m_{1}-6m_{2}$$
Simplify $$(5p^{2}-3)+(2p^{2}-3p^{3})$$
Simplify $$4{x^2} + 7 - \left( {{x^2}y + 3 - \overline {2{x^2}y + 2} } \right)$$
Add $$(6ab^{3}-5ab)(2a^{2}+b-5),\ ab(a^{2}+1)$$ and $$ab^{3}(3a^{3}+2b+1).$$
Add all of them $$x-8y, 3xy-y$$ and $$y+1$$
Subtract $$a^{3}-4a^{2}+5a-6$$ from the sum of $$3a^{3}+a^{2}+1$$ and $$a^{2}-2$$
Subtract $$(x-y)$$ from $$(4y-5x)$$
If $$(3a^{2}+1)-(4+2a^{2})=0$$, find the value of $$a$$.
Simplify $$x + y - \left[ {x + y - \left\{ {x + y - \left( {\overline {x + y} } \right)} \right\}} \right]$$
Subtract the following :
$$4z^2xy+x^2zy-5xyz+2xy^2z$$ from $$ x^2zy+xyz+xy^2z-z^2xy$$
Add : $$3x - 5y - 5z $$ and $$-5x - 2y - 3$$
Subtract the following :
$$3m^2-2+1m$$ from $$m^3-9$$
Subtract $$2p - 2q + 2 pq$$ from $$7p - 8q - pq$$.
Add the followings: $$3ab,-4ab,7ab,-5ab$$.
Subtract the following :
$$3r+2t$$ from $$2r-3t$$
Add : $$3a + 4b - 2c $$ and $$-6a - 2b + 3c$$
Find $$3a{ b }^{ 2 }$$ + $$7a{ b }^{ 2 }$$
$$8ab^{2}+7ab^{2}= 10ab^{2}$$
Add: $${2x^2}-{4y^2}-{z^2},\,{8x^2}+{5y^2}+{4z^2},\,{5x^2}-{5y^2}+{2z^2}$$
Solve: $$\dfrac{11a^2 + 9ac}{11b^2 + 9bd} = \dfrac{a^2 + 3ac}{b^2 + 3bd}$$
Identify terms and factors in the expression given.
$$pq+q$$.
Identify terms and factors in the expression given.
$$xy+2x^2y^2$$.
Identify the terms in the expression given below:
$$2x - 3$$.
Identify terms and factors in the expression given.
$$-4x+5$$.
If $$x = 1, y = 2$$ and $$z = 5$$, find the value of $$x^{2} + y^{2} + z^{2}$$.
Simplify:$$15pq + 15 + 9q + 25p$$.
Subtract $$3x (x - 4y + 5z)$$ from $$4x (2x - 3y + 10z)$$
$$\left(x-6\right)$$ + $$\left(3x-4\right)$$ + $$\left(x-1\right)$$
Leo bought a shit for $$Rs(5x+20)$$ and a belt for $$Rs(2x-10)$$. How much did he spend?
Identify the terms in the expression $$ab+2b^{2}-3a^{2}$$.
Simplify $$x(a-3)+y(3-a)$$
$$\dfrac{3+5x}{2x}-\dfrac{36}{x}+\dfrac{5}{2x}$$
Add the following like terms
$$13x,\ -27x$$ and $$-39x$$
Add the following like terms
$$7xyz$$ and $$-4xyz$$
$$\dfrac{2}{3x}+\dfrac{4}{3x(2x)}$$
Add the following like terms
$$19x,\ -55x$$ and $$\dfrac{2}{3}x$$
Identify terms and factors in the expressions given.
$$1.2ab-2.4b+3.6a$$.
Subtract :
$$-x^{2}+y^{2}-x^{2}y+5xy^{2}$$ from $$x^{2}+x^{2}y-5xy^{2}-y^{2}$$
Substract $$x^{3}+2y^{2}$$ from $$2y^{3}+x^{2}$$.
From the sum of $$4 + 3x$$ and $$5 - 4x + 2{x^2}$$, subtract the sum of $$3{x^2} - 5x$$ and $$ - {x^2} + 2x + 5$$.
Add the following like terms
$$-15pq,\ 12qp,\ -23pq$$ and $$7pq$$
(i)Subtract $$4 a - 7 a b + 3 b + 12$$ from $$12 a - 9 a b + 5 b - 3$$.
(ii)Subtract $$3 x y + 5 y z - 7 z x$$ from $$5 x y - 2 y z - 2 z x + 10 x y z$$.
(iii)Subtract $$4 p ^ { 2 } q - 3 p q + 5 p q ^ { 2 } - 8 p + 7 q - 10$$ from $$18 - 3 p - 11 q + 5 p q - 2 p q ^ { 2 } + 5 p ^ { 2 } q$$.
Add $$p^{2}-5pq-q^{2}$$ and $$-3p^{2}+2pq-2p^{2}$$
Solve $${ ab }^{ 2 }+\left( a-1 \right) b-1$$
Add $$-10v+6v$$
Substract $$xyz+2xy$$ from $$3zxy-5yx$$.
Substract $$x^{2}$$ from $$x^{2}+y^{2}-3y$$
Add: $$2x(z-x-y)$$ and $$2y(z-y-x)$$
$$2x(z-x-y)+2y(z-y-x)$$
$$2xz-2x^2-2xy+2yz-2y^2-2xy$$
$$2xz-2x^2-2xy+2yz-2y^2-2xy$$
$$-2x^2-2y^2-4xy+2yz+2xz$$
Add $$a - b + ab,b - c + bc,c - a + ac$$
Subtract $$3a(a+b+c)-2b(a-b+c)$$ from $$4c(-a+b+c)$$
Solve the following:$$2\left(5x^{2}+7x+8\right)-\left(4x^{2}-7x+3\right) = $$
Add the following:
$$ab-bc,bc-ca,ca-ab$$
Add the following :-
$$ab-ba,bc-ca,ca-ab$$
Add:
$$2{p^4} - 3{p^3} + {p^2} - 5p + 7, - 3{p^4} - 7{p^3} - 3{p^2} - p - 12$$
Subtract $$4a-7ab+3b+12$$ from $$12a-9ab+5b-3$$.
Subtract $$3xy+5yz-7zx$$ from $$5xy-2yz-2zx+10xyz$$.
Solve :
$$1 + x y - x - y$$
Add $$x+3,-3x^{2}-x-4,1+3$$
Simplify: $$(-10{a}^{3}b+12{a}^{2}{b}^{2}-6a{b}^{3})-(8{a}^{3}b+6{a}^{2}{b}^{2}-9a{b}^{3})$$
Subtract:
$$a+2b-c$$ from $$3a-b+2c$$
Subtract $$(2x - 4y + 3z)$$ from the sum of $$(x + 3y - 4z), (2x + y - z)$$ and $$(-2x + 3y - z)$$.
Solve:
$$ - [3{a^2} - 2{a^2} + 9{a^2} - \{ 6{a^2} - ( - 2{a^2} + 3{a^2})\} ]$$
Find the sum of $$-3ab+7cd-5qr;\,\,2ry+8qr-cd;\,\,2cd-3qr+ab-2ry$$
Simplify $$(3x-11y)-(17x+13y)$$
Group the like terms together from the following : $$12x,12,-25x,-25,-25y,1,x,12y,y$$
Add
$$7{x^3} + 2{x^2} - 5x - 7\,\& \, - 5{x^2} + {x^3} + 4x - 5$$
Subtract $$2x-3y+4z$$ from $$4x-6y-z$$.
Factorize:$$16a^4-9b^4$$
$$(7x^{2}-2y^{2}-6xy+y)-(2y^{2}+2x^{2}-1+2xy)$$
$$(7x^2-2y^2-6xy+y)-(2y^2+2x^2-1+2xy)$$
$$=7x^2-2x^2-2y^2-2y^2-6xy-2xy+y+1$$
$$=5x^2-4y^2-8xy+y+1$$.
$$ (x^{3}+ x^{2}-3x +5)+(x-1)$$
$$ (x^{3}+x^{2}-3x+5)+(x-1)$$
$$ = x^{3}+x^{2}-3x+x+5-1$$
$$ = x^{3}+x^{2}-2x+4$$
$$A=\dfrac { { 3x }^{ 4 } }{ 4 } -\dfrac { { x }^{ 4 } }{ 2 } +5x-7;B=\dfrac { { 2x }^{ 3 } }{ 3 } +\dfrac { { 3x }^{ 3 } }{ 2 } -\dfrac { x }{ 6 } ;C=\dfrac { { 2x }^{ 4 } }{ 3 } -\dfrac { { 3x }^{ 4 } }{ 4 } +5$$ find
$$A+B+C$$ ?
$$(4x-5y)-(2x-3y)$$
Add and subtract
$$(i)m-n,m+n$$
$$(ii)mn+5-2,mn+3$$
If $$\frac { a } { b } = \frac { c } { d }$$ prove that
$$( 5 a + 7 b ) ( 2 c - 3 d ) = ( 5 c + 7 d ) ( 2 a - 3 b )$$
$$A=\dfrac { { 3x }^{ 4 } }{ 4 } -\dfrac { { x }^{ 4 } }{ 2 } +5x-7;b=\dfrac { { 2x }^{ 3 } }{ 3 } +\dfrac { { 3x }^{ 3 } }{ 2 } -\dfrac { x }{ 6 } ;C=\dfrac { { 2x }^{ 4 } }{ 3 } -\dfrac { { 3x }^{ 4 } }{ 4 } +5$$ find
$$-A+B-C$$
Addition of $$(x^{2}+y^{2})$$ and $$(x^{2}-y^{2})$$ is______________
Subtract $$-a-b-9c$$ from $$-a+b-9c$$
The sum of two expressions is $$3 a^2 + 2 ab - b^2$$. If one of them is $$2 a^2 + 3 b^2$$, find the other.
multiple$$A=\dfrac { { 3x }^{ 4 } }{ 4 } -\dfrac { { x }^{ 4 } }{ 2 } +5x-7;B=\dfrac { { 2x }^{ 3 } }{ 3 } +\dfrac { { 3x }^{ 3 } }{ 2 } -\dfrac { x }{ 6 } ;C=\dfrac { { 2x }^{ 4 } }{ 3 } -\dfrac { { 3x }^{ 4 } }{ 4 } +5$$ find
$$3A-2B-C$$
Add the given expressions:
$$a + b - 3, 6 - a + 3, a - b + 3$$
Find sum $$a(b-c)+b(c-d)+c(a-b)$$
From the sum of $$4+3x$$ and $$5-4x+2x^{2}$$, subtract the sum of $$3x^{3}-5x$$ and $$-x^{2}+2x+5$$
Subtract: $$-5y^2$$ from $$y^2$$.
Subtract $$-6x^{2}+4a^{2}-1$$ from $$25x^2+16xy-3b^2-2$$
What should be added to $${x^2} + \dfrac{1}{{25}}{x^2}{y^2}$$ make it a perfect square
If $$P = 7 x ^ { 2 } + 5 x y - 9 y ^ { 2 } , Q = 4 y ^ { 2 } - 3 x ^ { 2 }$$ and $$R = 4 x ^ { 2 } + x y + 5 y ^ { 2 }$$ show that $$P + Q + R = 8x^2+6xy$$
Simplify:$$1\dfrac{3}{5}+5\dfrac{4}{7}$$
Solve:-$$(5x^2+2y)+(7x^2-y)$$
Add: $$3x$$ and $$7x$$
$$2x^2+4xy-3x$$ subtracted from $$3x - xy + 8{y^2}$$
Simplify combining like terms:
$$p-(p-q)-q-(q-p)$$
p-(p-q)-q-(q-p)
p-p+q-q-q+p
p-q
Subtract $$8a^{2}b^{2}$$ from $$3a^{2}b^{2}$$
$$3a^{2}b^{2}-8a^{2}b^{2}$$
$$=-5a^{2}b^{2}$$
Simplify combining like terms:
$$(3y^{2}+5y-4)-(8y-y^{2}-4)$$
$$3y^{2}+5y-4-(8y-y^{2}-4)$$
$$\Rightarrow 3y^{2}+5y-4-8y+y^{2}+4$$
$$\Rightarrow 3y^{2}+y^{2}+5y-8y-4+4$$
$$\Rightarrow 4y^{2}-3y$$
$$\Rightarrow y[4y-3]$$
Simplify :$$(a-3b+2c)-(a+3b-2c)$$
Find the value of -$$({ x }^{ 2 }-3x+5)+(2{ x }^{ 2 }-x-2)-(3{ x }^{ 2 }+7x-3)$$
Add:
$$5 x ^ { 2 } y , - 7 x ^ { 2 } y , 9 x ^ { 2 } y$$
Add the product: $$x ( x + y - r ) , y ( x - y + r ) , z ( x - y - z )$$
Subtract $$4abc$$ from $$-6abc$$
Simplify:$$12m-\left(-7m\right)$$
simplify :-
$$3(x+y)+3(x-y)$$
Find the sum of $${x}^{2}+2xy+3{y}^{2},\,\,3{z}^{2}+2yz+{y}^{2},\,\,{x}^{2}+3{z}^{2}+2xz,\,\,{z}^{2}-3xy-3yz$$
Solve:$$11\left(5-4x\right)=7\left(5-6x\right)$$
In the expression given below identify all the terms.
$$5x-7$$
Terms in expression are quantities separated by $$+1 -$$
$$\Rightarrow$$ Terms in given expression $$= 5x, 1$$
Simplify
$$\left( { 7x }^{ 2 }-2xy-{ 6y }^{ 2 } \right) +\left( { 9y }^{ 2 }+12xy-{ 12x }^{ 2 } \right) -\left( 8xy+{ 2y }^{ 2 }-{ 3x }^{ 2 } \right) $$
$$7x^2-2xy-6y^2+9y^2+12xy-12x^2-8xy-2y^2+3x^2$$
$$\Rightarrow -2x^2+y^2+2xy$$.
Subtract the second expression from the first expression
$$2a + b, a + b$$
Simplify :$$x^{3}(a-2b)+x^{2}(a-2b)$$
Simplify :$$a(a+b)+8a+8b$$
Solve $$(4{ x }^{ 4 }-5{ x }^{ 3 }-7x+1)+(4x-1)$$.
Simplify: $$12x^3-3(2x^3+4x-1)-5x+7$$
$$\text{Subtract } a(b - 5) \text{ from } b(5 - a).$$
The sum of three expression is $$8 + 73x+{ 7x }^{ 2 }$$ and two of then are $${ 2x }^{ 2 }+9x+2$$ and $${ 3x }^{ 2 }-4x+1$$
$$2x^2+9x+2+3x^2-4x+1+p(x)=8+73x+7x^2$$
$$5x^2+5x+3+p(x)=7x^2+73x+8$$
$$p(x)=7x^2+73x+8-5x^2-5x-3$$
$$p(x)=2x^2+68x+5$$.
Subtract the second expression form the first expression
$$2a+b,a+b$$
What is the sum of $$-2 m, +2 m ,-8 m$$.
By how much does 3x-4xy+2z exceed 8x+5z-7xy?
$$3x-4xy+2z-8x-5z+7xy-5x+3xy-3z$$
$$\therefore$$ It exceeds by $$-5x+3xy-3z$$.
Simplify combining like terms.
$$3a-2b-ab-(a-b+ab)+3ab+b-a$$.
Simplify combining like terms:
$$-z^2+13z^2-5x+7z^2-15z$$.
Simplify combining like terms.
$$21b-32+7b-20b$$.
Simplify:
$$(24m^{4} - 15 m^{3} +10 m +8) + (5m^{3}+4)$$
Simplify combining like terms:
21 b - 32 + 7 b - 20 b
Simplify combining like terms.
$$p-(p-q)-q-(q-p)$$.
Solve:
(5p-8q)-(3p-7q)=?
Subtract:$$ \begin{array} { l } { \text { (i) } - 5 y ^ { 2 } \text { from } y ^ { 2 } } \\ { \text { (ii) } 6 x y \text { from } - 12 x y } \\ { \text { (ii) } ( a - b ) \text { from } ( a + b ) } \\ { \text { (iv) } a ( b - 5 ) \text { from } b ( 5 - a ) } \end{array} $$
Add $$3mn, -5mn, 8mn-4mn$$.
Subtract:
$$-8pq$$ from $$6pq$$
Add $$t-8tz, 3tz-z, z-t$$.
Add $$3p^2q^2-4pq+5, -10p^2q^2, 15+9pq+7p^2q^2$$.
What should be added to $$3x^2-4y^2+5xy+20$$ to obtain $$-x^2-y^2+6xy+20$$?
Add $$ab-4a, 4b-ab, 4a-4b$$.
Subtract:
$$3a^2b$$ from $$-5a^2b$$
Subtract $$-5y^2$$ from $$y^2$$.
From the sum of $$3x-y+11$$ and $$-y-11$$, subtract the sum of $$3x^2-5x$$ and $$-x^2+2x+5$$.
Subtract $$(a-b)$$ from $$(a+b)$$.
Add
$$2x^2,\ -3x^2,\ 7x^2$$
Subtract:
$$-2abc$$ from $$-8bac$$
Subtract :
$$5x$$ from $$2x$$
Add
$$7xyz,\ -5xyz,\ 9xyz,\ -8xyz$$
Add
$$7y$$, $$-9y$$
Subtract:
$$-16p$$ from $$-11p$$
Subtract:
$$ xy$$ from $$6xy$$
Subtract
$$ 7x$$ from $$9y$$
Add
$$3x$$, $$7x$$
Add
$$2xy,\ 5xy,\ -xy$$
Add the following expressions:
$$(3/5)x, (2/3)x, (-4/5)x$$
Subtract:
$$10x^2$$ from $$-7x^2$$
Simplify
$$a - (b -2a)$$
Subtract :
$$5a + 7b - 2c$$ from $$3a -7b + 4c$$
How much is 3p-4q+r less than 4p+3q-5r?
Using the horizontal method:
Subtract $$-x^2+y^2+2xy$$ from $$2x^2-3y^2$$
Subtract:
$$- 8 x - 12 y + 17 z$$ from $$x - y - z$$
Simplify the following by combining the like terms and then write whether the expression is a monomial, a binomial or a trinomial.
$$2a+2b+2c-2a-2b-2c-2b+2c+2a$$
Subtract :
$$a^2 - b^2$$ from $$b^2 - a^2$$
Add:$$5x^2,-9x^2$$
Add: $$3ab^2,-5ab^2$$
Add: $$7x,-3x $$
Verify the following: $$(a + b + c) (a^{2} + b^{2} +c^{2} - ab- bc - ca) = a^{2} + b^{2}+ c^{2} - 3abc$$
Subtract: $$5a^{2}b^{2}c^{2}$$ from $$-7a^{2}b^{2}c^{2}$$
Add: $$\dfrac{1}{2}pq,\dfrac{-1}{3}pq$$
Add: $$6x,-11 x $$
Subtract: $$7xy+5x^2-7y^2+3$$ from $$7x^2-8xy+3y^2-5$$
Add: $$5x^3y,\dfrac{-2}{3}x^3y$$
Add:$$2x^3,3x^3,-4x^3,-5x^3$$
Find the sum of the following algebraic expressions:$$5xy,-7xy,3x^2$$
Add: $$7xy,2xy,-8xy$$
Add: $$3x,-5x,7x$$
Subtract:$$-m^2+5mn$$ from $$4m^2-3mn+8$$
Add: $$-2abc,3abc,abc$$
Subtract:
$$7xy(x^2 - 2xy + 3y^2) - 8x(x^2y - 4xy + 7xy^2)$$ from $$3y(4x^2y - 5xy + 8xy^2)$$
Evaluate: $$(23 15) + 4$$.
Take $$- ab + bc - ca\,\, from\,\, bc - ca + ab$$
Take $$(-3 / 2) p + q - r\,\, from\,\, (1 / 2)p - (1 / 3)q - (3 / 2) r$$
Fill in the blanks:
$$5 + 4 =$$ .. and $$5x + 4x
=$$
Add the following expressions:
$$ab - bv, bv - ca, ca - ab$$
Subtract
(i) $$4a-7ab+3b+12$$ from $$12a-9ab+5b-3$$
(ii) $$3xy+5yz-7zx$$ from $$5xy-2yz-2zx+10xyz$$
(iii) $$4p^2q-3pq+5pq^2-8p+7q-10$$ from $$18-3p-11q+5pq-2pq^2+5p^2q$$
Add following.
(i) $$ab-bc,\,bc-ca,\,ca-ab$$
(ii) $$a-b+ab,\,b-c+bc,\,c-a+ac$$
(iii) $$2p^2q^2-3pq+4,\,5+7pq-3p^2q^2$$
(iv) $$l^2+m^2,\,m^2+n^2,\,n^2+l^2,\,2lm+2mn+2nl$$
Identify the terms, their coefficients for each of the following expressions.
(i) $$5xyz^2-3zy$$
(ii) $$1+x+x^2$$
(iii) $$4x^2y^2-4x^2y^2z^2+z^2$$
(iv) $$3-pq+qr-rp$$
(v) $$\dfrac{x}{2}+\dfrac{y}{2}-xy$$
(vi) $$0.3a-0.6ab+0.5b$$
(a) What should be added to $$2{ x }^{ 2 }+6x-5$$ to get $$3{ x }^{ 2 }-2x+6$$?
(b) What must be subtracted from $${ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 }-3abc$$ to get $$2{ a }^{ 2 }-{ b }^{ 2 }-3{ c }^{ 2 }+abc$$
Find the sum of the following:
(a) $$P\left( x \right) ={ x }^{ 2 }-2x+1$$ and $$Q\left( x \right) ={ x }^{ 3 }+3{ x }^{ 2 }+2x-1$$
(b) $$P\left( t \right) =4{ t }^{ 3 }-3{ t }^{ 2 }+2$$, $$Q\left( t \right) ={ t }^{ 4 }-2{ t }^{ 3 }+6$$ and $$R\left( t \right) ={ t }^{ 3 }+4{ t }^{ 2 }+4$$
(a) Add $$p(p-q),\,q(q-r)$$ and $$r(r-p)$$
(b) Add $$2x(z-x-y)$$ and $$27(z-y-x)$$
(c) Subtract $$3l(l-4m+5n)$$ from $$4l(10n-3m+2l)$$
(d) Subtract $$3a(a+b+c)-2b(a-b+c)$$ from $$4c(-a+b+c)$$
(b) Add $$2x(z-x-y)$$ and $$27(z-y-x)$$
Simplify the polynomial and write it in standard form:
$$({x}^{4}-3)(3x-4)+2{x}^{3}(2{x}^{2}-2)$$
Subtract $$2x^3- x^2 + 4x- 6$$ from $$x^3 + 5x^2 -4x + 6$$.
The perimeter of a triangle is $$15x^2 - 23x + 9$$ and two of its sides are $$5x^2+8x-1$$ and $$6x^2-9x+4$$. Find the third side
Subtract $$2x^{2} + 2y^{2} - 6$$ from $$3x^{2} - 7y^{2} + 9$$
If $$ A=4x^2+y^2-6xy$$ ;
$$ B=3y^2+12x^2+8xy$$;
$$ C=6x^2+8y^2+6xy$$
Find the (i) $$A+B+C$$(ii) $$(A-B)-C$$
Add the product: $$x(x+y-r), y(x-y+r), z(x-y-z)$$
Subtract $$2xy+9{x}^{2}$$ from $$12xy+4{x}^{2}-3{y}^{2}$$.
The additive inverse of $$x+\displaystyle\frac{1}{x}$$ will be ________.
Subtract $$3a(a - 2b + 3c)$$ from $$4a(5a + 2b - 3c)$$
Prove that :
$$\large{\frac{1}{1+x^{a-b}}}+\large{\frac{1}{1+x^{b-a}}}=1$$
solve: $$ab\left( {{x^2} + 1} \right) + x\left( {{a^2} + {b^2}} \right)$$
Simplify: $$\{(3x^2-6x+5)+(2x-2x^2+5)\}-(x^2-4x+10)$$
Subtract the following:
(1) $$16x^3$$ from $$15x^3 + 3x^2 - 25$$
(2) $$5m^2 + 3mn + n^2$$ from $$m^2 + 6mn - 7n^2$$
Add the following:
(1) $$a - b + ab, b - c + bc, c - a + ac$$
(2) $$2lm + 2mn, -7lm + 2nl$$
simplify$$(\cfrac { 1 }{ 3 } { y }^{ 2 }-\cfrac { 4 }{ 7 } y+5)-(\cfrac { 2 }{ 7 } { y }-\cfrac { 2 }{ 3 } { y }^{ 2 }+2)-(\cfrac { 1 }{ 7 } { y }-3+2{ y }^{ 2 })$$
ExampleAdd $$(2{x}^{2}+6y+3xy),(3{x}^{2}-5xy-x)$$ and $$(6xy+5)$$.
Add $$(a + 1) (a^2 - a + 1) \, and \, (a - 1) (a^2 + a + 1) $$
$$\sqrt [ 3 ]{ \left( x+1 \right) \left( y+2 \right) \left( z+3 \right) } =7$$ the find $$xyz$$
What should be added to $$6x +y$$ to get $$ -6x + 4y$$?
Subtract $$\dfrac{7}{4}y^3+\dfrac{3}{5}y^2+\dfrac{1}{2}y+\dfrac{7}{2}$$ from $$\dfrac{9}{2}-\dfrac{y}{3}-\dfrac{y^2}{5}$$.
Simplify: $$(a + b) (c - d) + (a - b) (c + d) + 2(ac + bd)$$
Subtract $$3xy + 2z^2$$ from $$5xy + 3z^2 - xz$$
Add:$$2, \dfrac{2}{3}x -\dfrac{5}{3}x^2+\dfrac{5}{2}x^3, \dfrac{-4}{3}+\dfrac{2x^2}{3}-\dfrac{x}{2}, \dfrac{5x^3}{3}+3x^2+3x+\dfrac{6}{5}$$.
Subtract $$(4x^2+2x+3)$$ from $$(x^3+5x^2+3x+5)$$.
Add $$6x^2 + 3y - 2z$$ and $$3x^2 - y$$.
Add the following expressions:$$6ax-2by+3cz,\ 6by-11ax-cz$$ and $$10cz-2ax-3by$$.
By how much must $$2{p^2}{q^2} - 3{p^2}q + 4pq$$ be increased to get $$8{p^2}{q^2} + 4{p^2}q - 3{p^2}q - 2pq + 4?$$
Find sum of : $$8ab, -5ab, 3ab, -ab$$.
If a, b , c, d are positive real numbers such that $$a^2 + b^2 = c^2 + d^2$$ and $$a^2 + d^2 - ad = b^2 + c^2 + bc$$, find the value of $$\dfrac{ab + cd}{ad + bc}$$
A rope of length $$(2x+5)$$ metre. It is cut into two parts, one measuring $$(6x-4)$$ metre, what will be the length of the other part?
Add: $$3a-4b+4c, 2a+3b-8c, a-6b+c$$.
To expression to be subtracted from :
$$x^3 + x-1 $$ to get $$ 2x^3 - x^2 + 3x - 7 $$ is :
Subtract $${2ab + 5bc + 3ca}$$ from $$(7ab+ 2bc + 10ca)$$
Subtract:
$$ - {c^2} + 5c$$
$$\underline { - 4{c^2} + 8c} $$
Identify the terms and factors in the expression given below:
$$-2x + 3$$.
Subtract : $$3l (l - 4m + 5n)$$ from $$4l (10n - 3m + 2l)$$.
Subtract the sum of $$\left( 8m-7n+6 \right)$$ and $$\left( -3m-4n-{ p }^{ 2 } \right)$$ from the sum of $$\left( 2m+4n-3{ p }^{ 2 } \right)$$ and $$\left( -m-n-{ p }^{ 2 } \right) $$?
What polynomial added to $$x^{2}+4x-5$$ gives $$2x^{2}-3x+1$$?
Solve:
$$\left\{ {\left( {3{x^2} - 6x + 5} \right) + \left( {2x - 2{x^2} + 5} \right)} \right\} - \left( {{x^2} - 4x + 10} \right)$$
Simplify :
$$12a - 4a - 9 ab + 7 ab + 5b - 3b - 3 - 12 $$
Find the sum:
(i) $$7x-4y,2x+6y$$
(ii) $$9{x^2} + 5x,6{x^2} - 2x$$
(iii) $$2a +b,6{a^2} -7a-b$$
Find the sum of the following.
$$-b-4a$$, $$7b-6a$$.
Solve:$$a\left( x-2y+1 \right) ^{ 2 }+9\left( 2x+y+2 \right) ^{ 2 }=25$$
what should be taken away from $$3x^2+4x+1$$ to get $$2x^2-4x+35$$?
Add the following terms:
$$ 5xy , \;-2xy \;, -11xy , \;8xy $$
Simplify: $$(m+n)(3m+n)+(m+2n)(m-n)$$.
Simplify the following
$$(2x-3y)(3x+y)+(x+2y)(x-y)$$.
Solve the following expression:
$$(x+y)(a+b)+(x-y)(a+b)$$
$$\left( a+2b \right) \left( 3a+b \right) -\left( a+b \right) \left( a+2b \right) +{ \left( a+2b \right) }^{ 2 }$$
Subtract.
$$5a^{2} - 7ab + 5b^{2}$$ from $$3ab - 2a^{2} - 2b^{2}$$.
Simplify:$$15xy - 6x + 5y - 2$$.
Subtract $$(-x^{2})+10x-5$$ from $$5x-10$$
Factorise :
$$z^{2}-(x^{2}-2xy+y^{2})$$
$$z^{2}(x^{2}-2xy+y^{2})$$
$$\Rightarrow z^{2}-(x-y)^{2}$$
$$((x-y)^{2}=x^{2}+y^{2}-2xy) \: (a^{2}-b^{2}=(a-b)(a+b))$$
$$\Rightarrow (z-(x-y))(z+(x-y))$$
$$\Rightarrow (z-x+y)(z+x-y)$$
$$\therefore \Rightarrow (-x+y+z)(x-y+z)$$
Prove:$$(a+b)^3=a^3+3a^2b+3ab^2+b^3$$.
$${5}^{2}-{a}^{2}$$, $${7x}^{2}-{8a}^{2}$$, $${-7x}^{2}-{9a}^{2}$$
Subtract $$x^{5}-2x^{2}-3x$$ form $$x^{3}+3x^{2}+1$$
Evaluate:
$$2a+6b-3(a+3b)^{2}$$
Evaluate
$$12(2x-3y)^{2}-16(3y-2x)$$
Find the sum of the following.
$$6d-4c$$, $$-7c+6d$$.
$$-3(a+b)+4(2a-3b)-(2a-b)$$
If $$\sqrt{3}[\sqrt{7}-\sqrt{3}]=\sqrt{a}+b$$, then find the values of $$a$$ and $$b$$.
$${9x}^{2}-{y}^{2}+4y-4$$
$${x}^{2}-{y}^{2}-2y-1$$
Solve the following:$$ a-\left( 2a- 4a- 3a \right)$$
Simplify: $$\left(\dfrac{x^2}{3} - \dfrac{4x}{7} + 11\right) - \left(\dfrac{x}{7} - 3 + 2x^2\right) - \left(\dfrac{2x}{7} - \dfrac{2x^2}{3} + 2\right)$$
If $$A = (16x + 8) + 4$$ and $$B = (15x - 10) + -5$$ then $$A - B$$ is ____.
Factorise $$x - 1 - ( x - 1 ) ^ { 2 } + a x - a$$
The perimeter of a triangle is $$8 + 13a + 7a^{2}$$ and two of its sides are $$2a^{2} + 3a + 2$$ and $$3a^{2} - 4a - 1$$. Find the third side of the triangle.
From the sum of $$3y^{2}-5x^{2}-3yx$$ and $$3x^{2}-3y^{2}+4xy-1$$ subtract the sum of $$11x^{2}-2y^{2}-3xy.$$ Write the expression one below the corner for adding and subtracting.
Simplify the expression and find its value, when $$x=-1$$ and $$y=2$$.
$${ 2x }^{ 2 }-3y+{ 3x }^{ 2 }+{ 5x }^{ 2 }+5x-7-7x+2y$$
Find the coefficient of $$x^{2}$$ in $$-15x^{2}y^{2}$$.
Subtract the first term from the second term:
$$2 x y , 7 x y$$
Find the value of the addition of $$(x - 3y + 4z), (y - 2x - 8z), (5x - 2y - 3z)$$
Show that :
$$n ^ { 2 } + ( n + 1 ) ^ { 2 } + \left( n ^ { 2 } + n \right) ^ { 2 } = \left( n ^ { 2 } + n + 1 \right) ^ { 2 }$$
Subtract $$4x-2y+z$$ from the sum of $$3x+4y+z$$ and $$-6x+7y-8z$$
Add the following expressions :$$m - 7mn + 6, 2m + 9mn - 4$$ and $$-11m - 8mn - 5$$
$$m - 7mn + 6, 2m + 9mn - 4$$ and $$-11m - 8mn - 5$$
Subtract :
$$3xy+5yz-7zx$$ from $$4xy-yz+zx-9xyz$$
Subtract $$24ab-10b-18a$$ from $$30ab+12b+14a$$
The value of $$\left(\dfrac{8}{5}x^3 - \dfrac{3}{2}x^2 - 1\right) - \left(\dfrac{3}{5}x^3 + \dfrac{1}{2}x^2 - 3x + 2\right)$$ is
Subtract :
$$-3x^{3}-4x+1$$ from $$-5x^{3}-x-9$$
Subtract :
$$4x^{2}-5x+9$$ from $$7x^{2}+x-3$$
Subtract:$$2x^2-x+14,5x-3x^2+8$$
Simplify:
$$2p^3 - 3p^2 + 4p - 5 - 6p^3 + 2p^2 - 8p - 2 + 6p + 8$$
From the sum of $$3 x ^ { 2 } - 5 x + 2$$ and $$- 5 x ^ { 2 } - 8 x + 9$$ subtract $$4 x ^ { 2 } - 7 x + 9.$$
Adding:
$$ (3x^{2}-5x+2)+(-5x^{2}-8x+6) $$
Rearranging and collecting the like terms:
$$ (3-5)x^{2}+(-5-8)x+2+6 $$
$$ = -2x^{2}-13x+8 $$
Subtract $$ 4x^{2}-9x+7 $$ from $$ -2x^{2}-13x+8 $$
Change the sign of each term of the expression that is to be subtracted and then add.
Term to be subtracted $$ = 4x^{2}-9x+7 $$
Changing the sign of each term of the expression gives $$ -4x^{2}+9x-7 $$
On adding:
$$ (-2x^{2}-13x+8)+(-4x^{2}+9x-7) = -2x^{2}-13+8-4x^{2}+9x-7 $$
$$ = (-2-4)x^{2}+(-13+9)x+8-7 $$
$$ = -6x^{2}-4x+1 $$
Solve:
Add $$3a(a - b + c),2b(a - b + c)$$
Subtract:$$3x^2+3x-5,2x^2-8x-5$$
Subtract:$$-5xy-8x-9,7xy-7x+6$$
Subtract:$$x^2+2xy+y^2,10x^2$$
Enter 1 if it is true else enter 0.$$(3x+4y)+(5x+7y)$$ $$=8x+11y$$
Subtract:
(i) $$-5y^2$$ from $$y^2$$
(ii) $$6xy$$ from $$-12xy$$
(iii) $$(a-b)$$ from $$(a+b)$$
(iv) $$a(b-5)$$ from $$b(5-a)$$
(v) $$-m^2+5mn$$ from $$4m^2-3mn+8$$
(vi) $$-x^2+10x-5$$ from $$5x-10$$
(vii) $$5a^2-7ab+5b^2$$ from $$3ab-2a^2-2b^2$$
(viii) $$4pq-5q^2-3p^2$$ from $$5p^2+3q^2-pq$$
Subtract:$$a^2+b^2-7ab,3b^2$$
Simplify the given expression:$$4\left( {a + b} \right) - 6\left( {a + b} \right)$$
Solve : $$3$$x, - $$3$$x, $$5$$y, $$7$$y
Solve:
$$ - [3{a^2} - 2{a^2} + 9{a^2} - (6{a^2} - ( - 2{a^2} + 3{a^2})]]$$
Simplify $$10a(2x+y)^3-15b(2x+y)^2+35(2x+y)$$
If A=$$10W^{3}+20W^{2}-55W+60,$$
$$B=-25W^{2}+15W-10$$ and $$C=5W^{2}-10W+20,$$ then A+B-C is equal to -
Subtract the sum of $$2x^2-4x+11$$ and $$7x^2-4x+1$$ from the sum of $$8x^2-7x-7$$ and $$6x^2+4x-6.$$
Simplify :
$$(x^{2}-x)-\dfrac{1}{2}(x-3+3x^{2})$$
Subtract by horizontal method:
$$2x-4y$$ from $$-4x+3y$$
Subtract $$2x-5y$$ from the sum of the binomials $$x+7y$$ and $$3x-6y$$.
Subtract $$4 p ^ { 2 } q - 3 p q + 5 p q ^ { 2 } - 8 p + 7 q - 10$$ from
$$18 - 3 p - 11 q + 5 p q - 2 p q ^ { 2 } + 5 p ^ { 2 } q$$
Simplify: $$y{\left( {x - 2y} \right)^2} - 13 + 4\left( {x - 1} \right)$$
Simplify: $$9{\left( {x - 2y} \right)^2} - 13 + 4\left( {x - 2y} \right)$$
$$6 p - 12 q$$
Add $$2x^2-8xy+7y^2-8xy^2, 2y^2, 6xy^2-y^2+3x^2, 4y^2-xy-x^2+xy^2$$.
Solve :
$$(x^2+4xy)+(4y^2-9z^2)$$
$$\begin{array} { l } { \text { Add: } x ( x + y ) ; y ( y + z ) : z ( z + x ) } \\ { \text { Add } : 3 m ( 1 - m - n ) \text { and } 2 n ( m - n - 1 ) } \\ { \text { Subtract: } 2 x ( x - 3 y + 4 z ) \text { from } x ( 7 x - y + 9 z ) } \\ { \text { Subtract: } ( a - b + c ) - 2 ( - a + b - c ) \text { from } 5 ( a + 2 b - c ) } \end{array}$$
$$-7p+20p-3$$ is a binomial or trinomial.
Evaluate:
$$( x + 4 y + 7 x ) - ( x + 2 y )$$
Simplify : $$({a^3} - 2{a^2} + 4a - 5) - ( - {a^3} - 8a + 2{a^2} + 5)$$
Add the following expressions:
$$a + b - 3, b - a + 3, a - b + 3$$
Subtract $$4{y^4} - 2{y^3} - 6y - y + 5$$ from $$5{y^4} - 3{y^3} + 2{y^2} + y - 1$$
Add: $$6a^3, -4a^3, 10a^3, -8a^3$$.
Addition
$$4x^{2}+4x+\dfrac{3}{2}$$ and $$2x^{2}+3x+\dfrac{1}{2}$$
Addition $$ 4x^{2}+4x+\frac{3}{2} $$ & $$ 2x^{2}+3x+\frac{1}{2} $$
$$ = 4x^{2}+4x+\frac{3}{2}+2x^{2}+3x+\frac{1}{2} $$
$$ = 6x^{2}+7x+(\frac{3+1}{2}) $$
$$ = 6x^{2}+7x+2 $$
If $$A=4x^2+y^2-6xy,\, B=3y^2+12x^2+8xy$$ and $$C=6x^2+y^2+6xy$$, find $$A+B+C$$.
From the sum of $$6x^{4}-3x^{3}+7x^{2}-5x+1$$ and $$-3x^{4}+5x^{3}-9x^{2}+7x-2$$ subtract $$2x^{4}-5x^{3}+2x^{2}-6x-8$$
$$\sqrt { 2 x - 3 } + \sqrt { 7 - 3 x }$$
Solve : $$(5a^2 - 7ab + 5b^2) - (3ab - 2a^2 -2b^2)$$
What would be subtracted from $$x^{2}-xy+y^{2}-x+y+3$$ to obtain $$-x^{2}+3y^{2}-4xy+1$$?
Let m should be subtracted from $$ x^{2}-xy+y^{2}-x+y+3 $$ to obtain $$ -x^{2}+3y^{2}-4xy+1 $$
$$ x^{2}-xy+y^{2}-x+y+3-m = -x^{2}+3y^{2}-4xy+1$$
$$ m = x^{2}-xy+y^{2}-x+y+3+x^{2}-3y^{2}+4xy-1 $$
$$ m = 2x^{2}-2y^{2}+3xy-x+y+2 $$
If $$A=2y^{2}+3x-x^{2},\ B=3x^{2}-y^{2}$$ and $$C=5x^{2}-3xy$$ then find
$$A-B$$
[a + {a (a+2)} + 2]
Given expression$$=[a+\{a(a+2)\}+2]$$
$$=[a+\{a^2+2a\}+2]$$
$$=[a+a^2+2a+2]$$
$$=a^2+3a+2$$.
If $$A = 4 x - 6 y$$ $$B = 5 x + 4 y$$ $$C = 3 y - 3 c$$ , then find the value of i) $$A + B - C$$ ii) $$2 A - 3 B + 4 C$$
How much smaller is $$2x^2-2x+5$$ than $$7+5x^2+3x$$
What should be added to $$7x^{2}-5x+1$$ to get $$3x^{2}+4x+7$$.
What should be taken away from $$3x^2 - 4y^2 + 5xy + 20 \ get \ -x^2-y^2 + 6xy + 20$$.
If $$\Delta = 2 x ^ { 2 } + 3 y$$
$$\square = 8 y ^ { 2 } - 3 x ^ { 4 } + 2 x + 3 y$$
$$O = 5 x ^ { 2 } + 3 x$$
Then $$\Delta - 0 - \square$$ represents
Add the following algebraic expression using both horizontal and vertical methods. Did you get the same answer with both methods.
$$2x^{2}-6x+3;\ -3x^{2}-x-4;\ 1+2x-3x^{2}$$
Substract second expression from the first expression $$x+2y+z,-x-y-33$$
Subtract:-
$$2a\left( a-3b+5c \right) $$ from $$5a\ \left( 2a-3c+b \right) $$
Subtract $$a\left( {b - 5} \right)from\;b\;\left( {5 - a} \right)$$
Add the following algebraic expression using both horizontal and vertical methods. Did you get the same answer with both methods
$$2x+9y-7z;3y+z+3x;2x-4y-z$$
Add
$$3a-2b+5c, 2a+5b-7c, -a-b+c$$
What must be added to $$5x^{3}-3x+1$$ to get $$3x^{3}-7x^{2}+8?$$
Add
(a) 7x+3y and -4x-2y
(b) 3a-2b+c+3 and a+3b-2c-4
Subtract : $$4pq-3pq+5pq^{2}-8p+7q-10$$ from $$18-3p-11q+5pq-2pq^{2}+5p^{2}q$$
If the land owner gives one forth of his yield of rice of charity, how much yield is left with him. What value is exhibited by the owner?
Simplify $${\left( {a + 2b} \right)^2}\, - {\left( {a - 2b} \right)^2}$$.
Solve:
$$(24m^{4}-16m^{2})+8m^{2}$$
Add:
$$2x\ (y-2x+z)$$ and $$3y\ (2z+x+x^{2})$$
Solve
$$xy-[yz-zx-yx-(3y-xz)-(x-y-2y)].$$
Subtract $$4x^2+5y^2$$ from $$3x - 8{y^2}$$.
Evaluate: $$8\left( {{x^3}{y^2}{z^2} + {x^2}{y^3}{z^2} + {x^2}{y^2}{z^3}}+x^2y^2z^2 \right) + 4{x^2}{y^2}{z^2}$$
Simplify
$$20x - \left[ {15{x^3} + 5{x^2} - \{ 8{x^2} - (4 - 2x - {x^3}) - 5{x^3}\} - 2x} \right]$$
Add: $$a,\,\,c,\,\,-a+b-2c$$
subtract: $$3a(a+b+c)-2b(a-b+c)$$ from $$4c(-a+b+c)$$
Solve:$$\dfrac{x+20}{9}+\dfrac{3x}{7}=6$$
Let $$P={a}^{2}-{b}^{2}-2ab,\,Q={a}^{2}+4{b}^{2}-6ab,\,R={b}^{2}+6,\,S={a}^{2}-4ab$$ and $$T=-2{a}^{2}+{b}^{2}-ab+a$$.Find the value of $$P+Q+R+S+T$$?
Solve: $$\dfrac{4\left(x+2\right)}{5}=\dfrac{7+5x}{13}$$
Add: $$x-3y-2z,\,\,5x+7y-z,\,\,-7x-2y+4z$$
Add:$$3x+4y,\,\,x-2y$$
If $$A=5{p}^{2}-3{q}^{2}+{r}^{2},\,\,B=-2{q}^{2}+3{p}^{2}-4{r}^{2}$$ and $$C=-7{r}^{2}+3{p}^{2}+2{q}^{2}$$.Find $$A+B-C$$
Simplify:$$\left({x}^{2}-{y}^{2}+2xy+1\right)-\left({x}^{2}+{y}^{2}+4xy-5\right)$$
Find the sum of $$-xyz,\,-2xyz,\,7xyz,\,-xyz$$
what must be added to $$2{x}^{2}{y}^{2} - 5x +7$$ to get the sum $$-5{x}^{2}{y}^{2} +7x-9$$?
Subtract $$1-{p}^{3}$$ from $$2{p}^{3}-3p{q}^{2}-2{q}^{3}$$
Divide and Simplify:
$$4a^{2}+12ab+9b^{2}-25c^{2}$$ by $$2a+3b+5c$$.
Solve: $$5\left(x-3\right)-7\left(6-x\right)+3=24-3\left(8-x\right)$$
Find the value of $$13pqx-5xpq-19qpx$$
Solve: $$\left(x+1\right)\left(2x-1\right)-5x=\left(2x-3\right)\left(x-5\right)+47$$
From the sum of $$5{a}^{2} - 3a +2$$ and $$-8{a}^{2} + 5a +6$$, subtract $${a}^{2} + 7a -4$$
By how much does $${x}^{2}-2ax+5$$ exceed $$3{x}^{2} - 5x+6$$?
From the sum $${ 2y }^{ 2 }+3yz,-{ y }^{ 2 }yz-{ z }^{ 2 }$$ and $$yz+{ 2z }^{ 2 }$$ subtract the sum $$3y^{ 2 }+{ z }^{ 2 }$$ and $$y^{ 2 }+yz+{ z }^{ 2 }.$$
Add the following
(i) $$x-3y-2z$$
$$5x+7y-8z$$
$$3x-2y+5z$$
Given $$x-3y-2z, 5x+7y-8z, 3x-2y+5z$$
$$\Rightarrow$$ On adding given data
$$\Rightarrow x-3y-2z+5x+7y-8z+3x-2y+5z$$
$$\Rightarrow x+5x+3x-3y+7y-2y-2z-8z+5z$$
$$\Rightarrow 9x+2y-5z$$.
If $$A=4x^ {2}+y^ {2}-6xy;B=3y^ {2}+12x^ {2}+8xy$$ $$C=6x^ {2}+8y^ {2}+6xy$$ find $$A+B-C$$
Add : $$-7mn+5,12mn+2,9mn-8,-2mn-3$$
Subtract:
$$(x^{2}-2xy+3y^{2})$$ from $$(4x^{2}-5xy+8y^{2})$$
Add :$$2x(z-x-y)$$ and $$2y(z-y-x)$$
Solve the following
$$15a(2p-3q)-10b(2p-3q)$$
If $$A=x+2,$$ and $$B=2x$$ then,find $$A+2B=$$
What should be added to $$1+2x-3x^ {2}$$ to get $$x^ {2}+x-1$$
Subtract: $$(a-b)$$ from $$(a+b)$$
If $$\dfrac{a}{b} = \dfrac{5}{3},$$ then find the value of $$\dfrac{{{a^3} - {b^3}}}{{{b^3}}}.$$
Simplify :-
$$\left( m+n \right) ^{ 2 }-\left( m-n \right) ^{ 2 }$$
Subtract: $$5{x^2} - 9xy - 3{y^2}$$ from $$3{x^2} - 5xy - 2{y^2}$$
Subtract the second polynominal from the first polynomial:
$${ 5x }^{ 2 }-2y+9;{ 3x }^{ 2 }+5y-7$$
Simplify
Subtract 3 kg (p - q) from 2 kg (p + q)
Simplify : Subtract $$3pq ( p-q )$$ from $$2pq ( p+q )$$
Write the degree of the following polynomial:
$$3xy+7{ xy }^{ 2 }-8{ xy }^{ 3 }+7{ y }^{ 2 }{ x }^{ 2 }$$
Subtract $$\dfrac { 7x+14 }{ 3 } -6x$$ from $$\dfrac { 17-3x }{ 5 } -\dfrac { 4x+2 }{ 3 } $$
Subract $$ 5 a^{2}-7 a b+5 b^{2} $$ from $$ 3 a b-2 a^{2}-2 b^{2} $$
Solve : $$\left( \dfrac { 1 }{ 4{ ab }^{ 2 }c } \right) ^{ 2 }\div \left( \dfrac { 3 }{ 2{ a }^{ 2 }{ bc }^{ 2 } } \right) ^{ 4 }$$
From the sum of 4 + 3x and 5 - 4x +$${ 2x }^{ 2 },$$ subtract the sum of $${ 3x }^{ 2 }-5x$$ and $$ { 2x }^{ 2 }+2x+5.$$
Subtract the second expression from the first expression
$$6m^{ 3 } + 4m^{ 2 } + 7m+ 3, 3m^{ 3 } + 4$$
What should be added to $$1+2x-{ 3 }^{ x }\quad to\quad get\quad { x }^{ 2 }-x-1\quad $$
Solve : $$(ax+by)^2+(bx-ay)^2$$
Subtract the second expression from the first expression
$$x + 2y + z, -x -y -3z$$
Subtract $$a \left(b-5\right)$$ from $$b \left(5-a\right)$$
Subtract the second expression from the first expression
$$x + 2y + z, -x-y-3z$$
What should be taken away from $${ 3x }^{ 2 }-{ 4y }^{ 2 }+5xy+20$$ to obtain $$-{ x }^{ 2 }-{ y }^{ 2 }+6xy+20?$$
What should be added to $${ x }^{ 2 }-{ y }^{ 2 }+2xy\quad to\quad obtain\quad { x }^{ 2 }+{ y }^{ 2 }+5xy?$$
Solve : $$2x^2-xy+6y-4y+5xy-4x+6x^2+3y$$.
Evaluate:$$\left( 4{ x }^{ 2 }-\dfrac { 1 }{ 5 } x+7 \right) -\left( -2{ x }^{ 2 }-\dfrac { 1 }{ 2 } x+\dfrac { 1 }{ 3 } \right) $$
For $$x=\dfrac { 1 }{ 5 } $$and $$y=\dfrac { 3 }{ 7 } $$, verify that $$ \left( x+y \right) =\left( -x \right) +\left( -y \right) .$$
Add :$$\displaystyle \left( 3 x ^ { 2 } - \frac { y } { 3 } - 4 \right) + \left( 2 y ^ { 2 } - 4 x ^ { 2 } + \frac { y } { 4 } + 8 \right) $$
Add $$-5p^2, 3p^2, 2p^2$$.
Subtract $$-x^{ 2 }+10x-5 \,\,from \,\,5x-10$$
What should be subtracted from $$(6a+7b-10)$$ to get $$(2a-5b)?$$
Add the following equations: $$4 a ^ { 2 } + 5 b ^ { 2 } + 6 a b ; 3 a b ; 6 a ^ { 2 } - 2 b ^ { 2 } ; 4 b ^ { 2 } - 5 a b$$
Solve: From the sum the of $$3x^{2}-5x+26$$ and $$-5x^{2}-8x+1$$ subtract $$4x^{2}+7x+1$$.
Simplify: $$(m+l)+m+1$$.
Subtract : $$4pq-5q^{ 2 }-3p^{ 2 } $$ from $$5p^{ 2 }+3q^{ 2 }-pq$$
$$(a^{2}+b^{2}+2ab)-(a^{2}+b^{2}-2ab)$$
Add:
$$(a+b-3),(b-a+3),(a-b+3)$$
If both x + 1 and x - 1 are factors of $${ ax }^{ 3 }+{ x }^{ 2 }-2x+b$$, find the values of a and b.
Give expressions in the following cases.
$$y$$ is multiplied by $$-8$$ and then $$5$$ is added to the result.
Give expressions in the following cases.
$$y$$ is multiplied by $$5$$ and results is subtracted from $$16$$.
Give expressions in the following cases.
$$11$$ added to $$2m$$.
Give expressions in the following cases.
$$y$$ is multiplied by $$-8$$.
Give expressions in the following cases.
$$5$$ times $$y$$ from which $$3$$ is subtracted.
Give expressions in the following cases.
$$5$$ times $$y$$ to which $$3$$ is added.
Give expressions in the following cases.
$$y$$ is multiplied by $$-5$$ and results is added from $$16$$.
Give expressions in the following cases.
$$11$$ subtracted from $$2m$$.
Identify the terms and factors in the expression given.
$$1.2ab-2.4b+3.6a$$.
Show that
$$ \left ( \dfrac{x^{a^{2}+b^{2}}}{x^{ab}} \right )^{a+b}\left ( \dfrac{x^{b^{2}+c^{2}}}{x^{bc}} \right )^{b+c}\left ( \dfrac{x^{c^{2}+a^{2}}}{x^{ac}} \right )^{a+c} = x^{2(a^{3}+b^{3}+c^{3})} $$
Subtract $$4pq-5q^2-3p^2$$ from $$5p^2+3q^2-pq$$.
Subtract $$-m^2+5mn$$ from $$4m^2-3mn+8$$.
Subtract $$a(b-5)$$ from $$b(5-a)$$.
Classify the following polynomials as polynomials in one-variable, two variables etc.:
$$x^{2} - xy + 7y^{2}$$.
Add the following algebraic expressions.
$$3a^2b, -4a^2b, 9a^2b$$.
What should be added to $$x^2+xy+y^2$$ to obtain $$2x^2+3xy$$?
Subtract $$-x^2+10x-5$$ from $$5x-10$$.
What should be subtracted from $$2a+8b+10$$ to get $$-3a+7b+16$$?
Subtract $$-5xy$$ from $$12xy$$.
Subtract $$2a^2$$ from $$-7a^2$$.
Subtract $$2a-b$$ from $$3a-5b$$.
Write all the terms of the following algebraic expressions: $$3x$$
Add the following: $$2x^{2}y, -4x^{2}y, 6x^{2}y, -5x^{2}y$$
Add the following:$$ -5xy $$ and $$ 9xy $$
Add the following: $$ 3x $$ and $$ 7x $$
Simplify each of the following:$$ 7x^{3}y+9yx^{3} $$
Add the following: $$7abc, -5abc, 9abc, -8abc$$
Add $$2x^{2}-3x+1$$ to the sum of $$3x^{2}-2x$$ and $$3x+7$$.
Subtract: $$4xy$$ from $$-3xy$$
Add the following expressions: $$5x^{3}+7+6x-5x^{2},2x^{2}-8-9x, 4x-2x^{2}+3x^{3},3x^{3}-9x-x^{2}$$ and $$x-x^{2}-x^{3}-4$$
Subtract: $$7a^{2}b$$ from $$3a^{2}b$$
Add the following expressions: $$a^{4}-2a^{3}b+3ab^{3}+4a^{2}b^{2}+3b^{4}\ , \ -2a^{4}-5ab^{3}+7a^{3}b-6a^{2}b^{2}+b^{4}$$
Add the following expressions: $$x^{3}-2x^{2}y+3xy^{2}-y^{3}\ ,\ 2x^{3}-5xy^{2}+3x^{2}y-4y^{3}$$
Subtract: $$-2x$$ from $$-5y$$
Add $$x^{2}+2xy+y^{2}$$ to the sum of $$x^{2}-3y^{2}$$ and $$2x^{2}-y^{2}+9$$.
Add the following:
$$4ab-5bc+7ca$$
$$-3ab+2bc-3ca$$
$$5ab-3bc+4ca$$
Add the following expressions: $$8a-6ab+5b, -6a-ab-8b$$ and $$-4a+2ab+3b$$
What should be added to $$xy-3yz+4zx$$ to get $$4xy-3zx+4yz+7$$?
From $$p^{3}-4+3p^{2}$$, subtract $$5p^{2}-3p^{3}+p-6$$
From $$1-5y^{2}$$, take away $$y^{3}+7y^{2}+y+1$$
Subtract: $$x^{3}+2x^{2}y+6xy^{2}-y^{3}$$ from $$y^{3}-3xy^{2}-4x^{2}y$$
What should be subtracted from $$x^{2}-xy+y^{2}-x+y+3$$ to obtain $$-x^{2}+3y^{2}-4xy+1$$?
From $$x^{3}-5x^{2}+3x+1$$, take away $$6x^{2}-4x^{3}+5+3x$$
From the sum of $$3x^{2} - 5x + 2$$ and $$-5x^{2} - 8x + 9$$ subtract $$4x^{2} - 7x + 9$$.
Subtract the sum of $$13x-4y+7z$$ and $$-6z+6x+3y$$ from the sum of $$6x-4y-4z$$ and $$2x+4y-7$$
Subtract: $$6x^{3}-7x^{2}+5x-3$$ from $$4-5x+6x^{2}-8x^{3}$$
From $$7+x-x^{2}$$, take away $$9+x+3x^{2}+7x^{3}$$
Add:
$$4x^2-4xy+4y^2-3, 5+6y^2-8xy+x^2$$ and $$6-2xy+2x^2-5y^2$$
Write the constant term in $$\dfrac{\pi}{2}x^2+7x-\dfrac{2}{5}\pi$$.
Add:
$$3a-3b+4c, 2a+3b-8c, a+6b+c$$
Add:
$$2x^3-9x^2+8, 3x^2-6x-5, 7x^3-10x+1$$ and $$3+2x-5x^2-4x^3$$
Add:
$$5x-8y+2z, 3z-4y-2x, 6y-z-x $$, and $$3x-2z-3y$$.
If $$P=a^{2}-b^{2}+2ab, Q=a^{2}+4b^{2}-6ab,\ R=b^{2}+b,\ S=a^{2}-4ab$$ and $$T=-2a^{2}+b^{2}-ab+a$$. Find $$P+Q+R+S-T$$.
How much is $$x-2y+3z$$ greater than $$3x+5y-7$$?
If $$P=7x^{2}+5xy-9y^{2}\ ,\ Q=4y^{2}-3x^{2}-6xy$$ and $$R=-4x^{2}+xy+5y^{2}$$, show that $$P+Q+R=0$$.
How much is $$x^{2}-2xy+3y^{2}$$ less than $$2x^{2}-3y^{2}+xy$$?
Add:
$$7x, -3x, 5x, -x, -3x$$
Add:
$$8ab, -5ab, 3ab, -ab$$
Add the following:
$$2x^2 - 3xy + y^2$$
$$ -7x^2 -5xy - 2y^2$$
$$ 4x^2 + xy -6y^2$$
-------------------------------
Subtract:
$$2a-5b+2c-9$$ from $$3a-4b-c+6$$
Add the following:
$$x 3y 2z$$
$$5x + 7y z$$
$$-7x 2y + 4z$$
--------------------------
Add the following:
$$\ \ 4xy - 5yz - 7z$$
$$– 5xy +2yz + zx$$
$$– 2xy -3yz +3zx$$
------------------------------
Add the following:
$$ m^2 -4m +5$$
$$-2m^2 + 6m -6$$
$$ -m^2 - 2m -7 $$
--------------------------
From the sum of $$3x^2 - 5x + 2$$ and $$-5x^2 -8x + 6,$$ subtract $$ 4x^2 -9x + 7.$$
Add:
$$x^3+y^3-z^3+3xyz,\ \ -x^3+y^3+z^3 -6xyz,\ \ x^3-y^3-z^3-8xyz$$
Add the following expressions:
$$5x, 7x, -6x$$
Add the following expressions:
$$x-3y+4z, y-2x-8z, 5x-2y-3z$$
If $$A = 7x^2 + 5xy -9y^2, B = -4x^2 + xy + 5y^2$$ and $$C = 4y^2 - 3x^2 - 6xy$$ then show that $$A +B+C= 0.$$
Add the following expressions:
$$\dfrac34 x^{2}, \ 5x^{2}, \ -3x^{2}, -\dfrac14 x^{2}$$
Add the following expressions:
$$2x^{2}-3y^{2}, 5x^{2}+6y^{2}, -3x^{2}-4y^{2}$$
Add the following expressions:
$$5a^{2}b, -8a^{2}b, 7a^{2}b$$
Add the following expressions:
$$\dfrac32x^{3}-\dfrac14x^{2}+\dfrac53,\hspace{2mm} \dfrac{-5}4x^{3}+ \dfrac35x^{2}-x+\dfrac15,\hspace{2mm} -x^{2}+\dfrac38x-\dfrac8{15}$$
Add the following expressions:
$$\dfrac85x+\dfrac{11}7y+\dfrac94xy,\hspace{2mm} \dfrac{-3}2x-\dfrac53y-\dfrac95xy$$
Add the following expressions:
$$5x-2x^{2}-8, 8x^{2}-7x-9, 3+7x^{2}-2x$$
Add the following expressions:
$$(2/3)a-(4/5)v+(3/5)c, -(3/4)a-(5/2)b+(2/3)c, (5/2)a+(7/4)b-(5/6)c$$
Identify the terms and their factors in the algebraic expressions given below: $$xy+2x^2y^2$$
Subtract:
$$(x^{2}-y^{2})$$ from $$(2x^{2}-3y^{2}+6xy)$$.
Subtract:
$$(a^{2}+b^{2}-2ab)$$ from $$(a^{2}+b^{2}+2ab)$$
Subtract:
$$(x-y)$$ from $$(4y-5x)$$
Subtract $$(2a-3b+4c)$$ from the sum of $$(a+3b-4c), \hspace{1mm}(4a-b+9c)$$ and $$(-2b+3c-a)$$.
Subtract:
$$(x-y+3z)$$ from $$(2z-x-3y)$$
Subtract:
$$x^{2}$$ from $$-3x^{2}$$
Simplify the following by combining the like terms and then write whether the expression is a monomial, a binomial or a trinomial.
$${x}^{4}+3{x}^{3}y+3{x}^{2}{y}^{2}-3{x}^{3}y-3x{y}^{3}+{y}^{4}-3{x}^{2}{y}^{2}$$
Sum or difference of two like terms is _____
If $$({ x }^{ 2 }{ y }+{y}^{2}+3)$$ is subtracted from $$(3{ x }^{ 2 }{ y }+2{y}^{2}+5)$$, then coefficient of $$y$$ in the result is _____
How much is $$3a^2-5ab+7b^2+3$$ greater than $$2a^2+2ab+5$$?
Required expression
Simplify the following by combining the like terms and then write whether the expression is a monomial, a binomial or a trinomial.
$$3{ x }^{ 2 }{ y }{z}^{2}-3x{ y }^{ 2 }{ z }+{ x }^{ 2 }{ y }{ z }^{ 2 }+7x^{ 2 }{ y }^{ 2 }{ z }$$
Add the following expressions:
$${p}^{2}-7pq-{q}^{2}$$ and $$-3{p}^{2}-2pq+7{q}^{2}$$
Simplify the following by combining the like terms and then write whether the expression is a monomial, a binomial or a trinomial.
$$50{x}^{3}-21x+107+41{x}^{3}-x+1-93+71x-31{x}^{3}$$
Simplify the following by combining the like terms and then write whether the expression is a monomial, a binomial or a trinomial.
$${p}^{3}{q}^{2}r+p{q}^{2}{r}^{3}+3{p}^{2}q{r}^{2}-9{p}^{2}q{r}^{2}$$
Add the following expressions:
$${a}^{2}+3ab-bc,{b}^{2}+3bc-ca$$ and $${c}^{2}+3ca-ab$$
Subtract :
$$-{a}^{2}-ab$$ from $${b}^{2}+ab$$
Add the following expressions:
$${p}^{2}qr+p{q}^{2}r+pq{r}^{2}$$ and $$-3p{q}^{2}r-2pq{r}^{2}$$
Add the following expressions:
$$ab+bc+ca$$ and $$-bc-ca-ab$$
Add the following expressions:
$${x}^{3}-{x}^{2}y-x{y}^{2}-{y}^{3}$$ and $${x}^{3}-2{x}^{2}y+3x{y}^{2}+4y$$
Add the following expressions:
$${x}^{3}{y}^{2}+{x}^{2}{y}^{3}+3{y}^{4}$$ and $${x}^{4}+3{x}^{2}{y}^{3}+4{y}^{4}$$
Add the following expressions:
$$uv-vw,vw-wu$$ and $$wu-uv$$
Add the following expressions:
$$t-{t}^{2}-{t}^{3}-14$$, $$15{t}^{3}+13+9t-8{t}^{2}$$, $$12{t}^{2}-19-24t$$ and $$4t-9{t}^{2}+19{t}^{3}$$
How much should $$5x^3+3x^2-2x+1$$ be increased to get $$6x^2+7$$?
Add the following expressions:
$${p}^{2}-q+r$$, $${q}^{2}-r+p$$ and $${r}^{2}-p+q$$
Subtract:
$$-7{p}^{2}qr$$ from $$-3{p}^{2}qr$$
Subtract :
$$-2{a}^{2}-2{b}^{2}$$ from $$-{a}^{2}-{b}^{2}+2ab$$.
Subtract:
$$ab-bc-ca$$ from $$-ab+bc+ca$$
Subtract:
$$-4{x}^{2}y-{y}^{3}$$ from $${x}^{3}+3x{y}^{2}-{x}^{2}y$$
Subtract:
$${x}^{4}+3{x}^{3}{y}^{3}+5{y}^{4}$$ from $$2{x}^{4}-{x}^{3}{y}^{3}+7{y}^{4}$$
What should be added to $${x}^{3}+3{x}^{2}y+3x{y}^{2}+{y}^{3}$$ to get $${x}^{3}+{y}^{3}$$
Subtract:
$$2(ab+bc+ca)$$ from $$-ab-bc-ca$$
What should be added to $$3pq+5{p}^{2}{q}^{2}+{p}^{3}$$ to get $${p}^{3}+2{p}^{2}{q}^{2}+4pq$$
Subtract:
$${x}^{3}{y}^{2}+3{x}^{2}{y}^{2}-7x{y}^{3}$$ from $${x}^{4}+{y}^{4}+3{x}^{2}{y}^{2}-x{y}^{3}$$
Subtract:
$$4.5{x}^{5}-3.4{x}^{2}+5.7$$ from $$5{x}^{4}-3.2{x}^{2}-7.3x$$
Subtract:
$$11-15{y}^{2}$$ from $${y}^{3}-15{y}^{2}-y-11$$
What should be subtracted from $$-7mn+2{m}^{2}+3{n}^{2}$$ to get $${m}^{2}+2mn+{n}^{2}$$
Simplify the following expression.
$$5x+22-6x=23$$.
How much is $${y}^{4}-12{y}^{2}+y+14$$ greater than $$17{y}^{3}+34{y}^{2}-51y+68$$.
How much is $$21{a}^{3}-17{a}^{2}$$ less than $$89{a}^{3}-64{a}^{2}+6a+16$$
What should be subtracted from $$2{x}^{3}-3{x}^{2}y+2x{y}^{2}+3{y}^{3}$$ to get $${x}^{3}-2{x}^{2}y+3x{y}^{2}+4{y}^{3}$$
From the sum of $${x}^{2}-{y}^{2}-1$$, $${y}^{2}-{x}^{2}-1$$ and $$1-{x}^{2}-{y}^{2}$$ subtract $$-(1+{y}^{2})$$
How much does $$93{p}^{2}-55p+4$$ exceed $$13{p}^{3}-5{p}^{2}+17p-90$$
Each symbol given below represents an algebraic expression: (first figure)
The symbol are then represented in the expression: (second figure)
Find the expression which is represented by the given symbols.
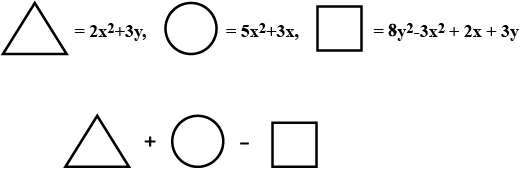
Subtract the sum of $$12ab-10{b}^{2}-18{a}^{2}$$ and $$9ab+12{b}^{2}+14{a}^{2}$$ from the sum of $$ab+2{b}^{2}$$ and $$3{b}^{2}-{a}^{2}$$
Subtract $$9{a}^{2}-15a+3$$ from unity
To what expression must $$99x^3-33x^2-13x-41$$ be added to make the sum zero.
Observe the following nutritional chart carefully:
| Food Item | Carbohydrates |
| Rajma | $$60\text{g}$$ |
| Cabbage | $$5\text{g}$$ |
| Potato | $$22\text{g}$$ |
| Carrot | $$11\text{g}$$ |
| Tomato | $$4\text{g}$$ |
| Apples | $$14\text{g}$$ |
(a) $$y$$ units of potatoes and $$2$$ units of rajma
(b) $$2x$$ units tomatoes and $$y$$ units apples
Add: $$9ax$$, $$+ 3by - cz$$, $$— 5by + ax + 3cz$$
Number of terms in the expression $$a^{2} + bc \times d$$ is __________ .
Add: $$xy^{2}z^{2} + 3x^{2}y^{2}z - 4x^{2}yz^{2}$$, $$-9x^{2}y^{2}z + 3xy^{2}z^{2} + x^{2}yz^{2}$$
Add: $$7a^{2}bc\ , -3abc^{2}\ ,\ 3a^{2}bc\ ,\ 2abc^{2}$$
Add: $$5x^{2}-3xy+4y^{2}-9$$,$$7y^{2}+5xy-2x^{2}+13$$
Subtract $$6x^{2} - 4xy + 5y^{2}$$ from $$8y^{2} + 6xy - 3x^{2}$$
Subtract $$2ab^{2}c^{2} + 4a^{2}b^{2}c - 5a^{2}bc^{2}$$ from $$-10a^{2}b^{2}c + 4ab^{2}c^{2} +2a^{2}bc^{2}$$
Subtract $$3t^{4} - 4t^{3} + 2t^{2}- 6t + 6$$ from $$-4t^{4} + 8t^{3}-4t^{2} - 2t+ 11$$
Simplify: $$(3x + 2y)^{2} - (3x - 2y)^{2}$$
Simplify: $$(3x + 2y)^{2} + (3x - 2y)^{2}$$
Simplify: $$(1.5p + 1.2q)^{2} - (1.5p - 1.2q)^{2}$$
Find the value of $$a$$, if $$pqa = (3p + q)^{2} - (3p - q)^{2}$$
Identify the terms and their factors in the algebraic expressions given below:
$$1.2 ab-2.4 b+3.6 a$$
Simplify: $$(2.5m + 1.5q)^{2} + (2.5m - 1.5q)^{2}$$
Find the sum of the following algebraic expressions:$$7a^2-5a +2,3a^2-7,2a+9,1+2a-5a^2$$
Find the sum of the following algebraic expressions: $$5m-7n,3n-4m+2,2m-3mn-5$$
Find the sum of the following algebraic expressions:$$4x^2y,-3xy^2,-5xy^2,5x^2y$$
Simplify the following:$$3xy^2-5x^2y+7xy-8xy^2-4xy+6x^2y$$
Find the sum of the following algebraic expressions: $$3x^3-5x^2+2x+1,3x-2x^2-x^3,2x^2-7x+9$$
$$3x^3-5x^2+2x+1,3x-2x^2-x^3,2x^2-7x+9$$
$$2x^3-5x^2-2x+10$$
$$2x^3-5x^2-2x+10$$
Simplify the following:$$2x^2+3y^2-5xy+5x^2-y^2+6xy-3x^2$$
Find the sum of the following algebraic expressions: $$14x+10y-12xy-13,18-7x-10y+8xy,4xy$$
Find the sum of the following algebraic expressions: $$-7mn + 5, 12 mn+2,8mn-8,-2mn-3$$
Find the sum of the following algebraic expressions:$$a+b-3,b-a+3,a-b+3$$
Subtract:-7xy from -2xy
Using the horizontal method:
Add $$x^2+y^2-2xy,-2x^2-y^2-2xy$$ and $$3x^2+y^2+xy$$
Using column method, add $$ab+2bc-ca$$ and $$2ab-bc-ca$$ and subtract $$4ab+5bc-3ca$$
Subtract:$$2x^4-7x^2+5x+3$$ from $$x^4-3x^3-2x^2+3$$
Subtract p-2q+r from the sum of 10p-r and 5p+2q.
Simplify the following:$$5x^4-7x^2+8x-1+3x^3-9x^2+7-3x^4+11x-2+8x^2$$
Subtract the sum of $$3x^2 + 5xy + 7y^2 + 3$$ and $$2x^2 - 4xy - 3y^2 + 7$$ from $$9x^2 - 8xy + 11y^2$$
What must be added to $$5x^3-2x^2+3x+7$$ to get $$7x^3+7x-5$$?
What must be subtracted from $$3a^2 - 5ab - 2b^2 - 3$$ to get $$5a^2 - 7ab - 3b^2 + 3a$$?
Subtract the sum of $$3x^2+2xy-2y^2$$ and $$5y^2-7xy$$ from $$5x^2+2y^2-3xy$$
Simplify:
$$(x + 5) (x + 6) (x + 7)$$
Add the following expressions:
$$5p^2q^2 + 4pq + 7, 3 + 9pq - 2p^2q$$
Subtract:
$$8xy + 4yz + 5zx$$ from $$12xy - 3yz - 4zx + 5xyz$$
Add the following:
$$4p(2 - p^2)$$ and $$8p^3 - 3p$$
Add the following expressions:
$$I^2 + m^2 + n^2, Im + mn, mn + nI + Im$$
Subtract:
$$6x(x - y + z) - 3y(x + y - z)$$ from $$2z(-x + y + z)$$
Subtract:
$$4p^2q - 3pq + 5pq^2 - 8p + 7q - 10$$ from $$18 - 3p - 11q + 5pq - 2pq^2 + 5p^2q$$
Add the following expressions:
$$4x^3 - 7x^2 + 9, 3x^2 - 5x + 4, 7x^3 - 11x + 1, 6x^2 - 13x$$
Add the following:
$$7xy(8x + 2y - 3)$$ and $$4xy^2(3y - 7x + 8)$$
Show that:
$$(3p/7 - 7q/6)^2 + pq = 9p^2/49 + 49q^2/36$$
Simplify:
$$(p + q) (r + s) + (p - q)(r - s) - 2(pr + qs)$$
Show that:
$$(p-q)(p+q)+ (q-r)(q+r)+(r-p)(r+p) = 0$$
$$2a + b c = 2a + ()$$
Simplify the following:
$$(2x + 5y)^2 + (2x - 5y)^2$$
Simplify:
$$(x + y + z) (x - y + z) + (x + y - z) (- x + y + z) - 4zx$$
Simplify:
$$(p + q - 2r) (2p - q + r) - 4qr$$
Simplify the following expression.
$$6x-20y+7z-8x+25y-11z$$.
Show that:
$$(4x + 7y)^2 - (4x - 7y)^2 = 112 xy$$
Evaluate: $$(9a 3a) + 4a$$.
Subtract:
$$5 a - 3 b + 2 c$$ from $$a - 4 b - 2 c$$
$$a 3b + 5c = a (..)$$
$$a + 4b 4c = a + (..)$$
$$a + b c + d = a + (..)$$
$$5a + 4b + 4x 2c = 4x ()$$.
Subtract:
$$4 x - 6 y + 3 z$$ from $$12 x + 7 y - 21 z$$
$$m + n p = - (..)$$.
$$x^{2} y^{2} + z^{2} = x^{2} ()$$
$$3x z + y = 3x (...)$$
Subtract:
$$5 - a - 4 b + 4 c$$ from $$5 a - 7 b + 2 c$$
Subtract the sum of $$x + y$$ and $$x - z$$ from the sum of $$x - 2 z$$ and $$x + y + z.$$
Subtract ($$ 5x + 6y - 3z$$) from ($$3x + 5y - 4z$$)
Subtract:
$$2 ab + cd - ac - 2 bd$$ from $$ab - 2 cd + 2 ac + bd$$
The sum of two expressions is $$5 x^2 - 3 y^2$$. If one of them is $$3 x^2 + 4 xy - y^2$$, find the other.
From the sum of $$x + y - 2 z$$ and $$2x - y + z$$, subtract $$x + y + z$$.
By how much should $$x + 2y - 3 z$$ be increased to get $$3x$$?
From the sum of $$3 a - 2 b + 4 c$$ and $$3 b - 2 c$$ subtract $$a - b - c$$.
Solve: $$2x^{2}+5x-1+8x+x^{2}+7-6x+3-3x^{2}$$
Take $$1 - a + a^2\,\, from \,\,a^2 + a + 1$$
Separate constant terms and variable terms from the following :
$$ 8 , x , 6 + x,- 5xy^{2},15az^{2} ,32 z/ xy ,y^{2} / 3x $$
Enclose the given terms in brackets as required:
$$x - y - z = z - (..........)$$
Simplify :
$$9x - (-4x + 5)$$
Simplify :
$$3a / 8 + 4a / 5 - (a / 2 + 2a / 5)$$
Simplify :
$$- 2x (x + y) + x^{2}$$
Add:
$$x^3-x^2y+5xy^2 +y^3; -x^3 -9xy^2 +y^3; 3x^2y+9xy^2$$
Simplify :
$$(p - 2q) - (3q - r)$$
Simplify :
$$p + q - (p - q) + (2p - 3q)$$
Simplify :
$$6a - (-5a - 8b) + (3a + b)$$
Simplify :
$$2b / 5 - 7b / 15 + 13b/ 3$$
Simplify :
$$b (2b - 1/b) - 2b (b - 1/b)$$
Solve x $$\dfrac{10x^2+12x+36x}{x}=\dfrac{120+x^2}{x}$$
$$\text { Take away } 8 x-7 y-8 p+10 q \text { from } 10 x+10 y-7 p+9 q$$
What must be added
$$x^4 -x^3 +x^2 +x+3$$ to obtain $$x^4+x^2-1$$?
Subtract:
$$abc -4cad- bcd$$ form $$3abc+5bcd -cad$$
How much more than
$$2x^2 +4xy+2y^2$$ is $$5x^2 +10xy-y^2$$?
Take $$m^2+m+4$$ from $$-m^2+3m+6$$ and the results from $$m^2+m+1$$
Take away $$3a^3 +4x^2-5x+6$$ from $$3x-4x^2 +5x-6$$
Subtract the sum of
$$5y^2+y-3$$ and $$y^2-3y+7$$ from $$6y^2+y-2$$
How much less $$2a^2+1$$ is than $$3a^2-6$$?
Subtract:
$$a^2 +ab+b^2$$ from $$4a^2-3ab +2b^2$$
Two adjacent sides of a rectangle are $$ 2 x^{2}-5 x y+3 z^{2} $$ and $$ 4 x y-x^{2}-z^{2} $$. Find its perimeter.
Add :
$$5(x+y),\ 3(x+2y),\ 5(2x-y)$$
What should be added to $$2xy+3yz+4zx+5xyz$$ to get $$x+y+z+2xy+3yz+4zx-xyz$$?
The perimeter of a triangle is $$ 15 -23 x+9 $$ and two of its sides are $$ 5 \times 2+8 x-1 $$ and $$ 6 \times 2-9 x+ 4.$$ Find the third side
Add: $$5x-8y+2z, 3z-4y-2x, 6y-z-x$$ and $$3x-2z-3y$$.
Simpllify $$:\ 2x^{2}+5x-1+8x+x^{2}+7-6x+3-3x^{2}$$
Add: $$(4x^2-7xy+4y^2-3), (5+6y^2-8xy+x^2)$$ and $$(6-2xy+2x^2-5y^2)$$.
Subtract$$4a+3b$$ from $$2a+2b-4$$.
Simplify $$4x-(3y-x+2z)$$
Add: $$2x^3-9x^2+8, 3x^2-6x-5, 7x^3-10x+1$$ and $$3+2x-5x^2-4x^3$$.
Simplify $$2(3b-5a)-7[9-6{2-5(a-6)}]$$
Find what must be subtracted from the polynomial $$4y^{4} + 12y^{3} + 6y^{2} + 50y + 26$$ so that the obtained polynomial is exactly divisible by $$y^{2} +4y+2$$.
Polynomial is $$4y^4+12y^3+6y^2+50y+26$$
Divisor $$=y^2+4y+2$$
Divisor -
So, remainder $$=2y-2$$
so $$2y-2$$ must be subtracted from the polynomial so that the obtained polynomial is exactly divisible by $$y^2+4y+2.$$
Hence, the answer is $$2y-2.$$
Add: $$6p+4q-r+2r-5p-6, 11q-7p+2r-1$$ and $$2q-3r+4$$.
$$\dfrac{a}{a-c}+\dfrac{b}{b-c}$$.
Find the sum of the following.
$$2x+4y, -5y$$.
$$-2\left( { x }^{ 2 }-{ y }^{ 2 }+xy \right) -3\left( { x }^{ 2 }+{ y }^{ 2 }-xy \right)$$
Find the sum of the following.
$$3pq-6hk$$, $$-3qp+14kh$$.
Simplify the following expression.
$$x+3y+6x+4y$$.
Subtract $$(20-3x+4x^2-x^3)$$ from $$(x^3-x^2+2x-19)$$.
Add the following algebraic expression using both horizontal and vertical methods. Did you get the same answer with both methods
$$2x^ {2}-6xy+3;-3x^ {2}-x-4;1+2x-3x^ {2}$$
Evaluate : $$8 ( x + y ) ^ { 2 } - 26 ( x + y ) + 15$$=$$0$$
# $$8(x+y)^{2}-2b(x+y)+15=0$$ Let $$x+y=t$$
$$8t^{2}-26t+15=0$$
$$t=\frac{26\pm \sqrt{676-480}}{2\times 8}=\frac{26\pm \sqrt{196}}{16}=\frac{3}{4},\frac{5}{2}$$.
$$\Rightarrow x+y= 3/4$$ & $$x+= 5/2$$.
Solve: $$8 ( p - q ) ^ { 2 } - 12 ( p - q ) ^ { 2 }$$
Verify: $$(6x^{3}y-3xy-7)-2(-2xy-1)=(9x^{3}y-2xy-13)-(3x^{3}y-3xy-8).$$
Add the following algebraic expression using both horizontal and vertical methods. Did you get the same answer with both methods
$$x^ {2}-2xy+3y^ {2};5y^ {2}+3xy-6x^ {2}$$
Simplify:
$$(pq-qr+pr)(pq+qr)-(pr+pq)(p+q-r)$$
Subtract the sum of $${ x }^{ 2 }-5xy+2{ y }^{ 2 }$$ and $${ y }^{ 2 }-2xy-3{ x }^{ 2 }$$ from the sum of $$6{ x }^{ 2 }-8xy-{ y }^{ 2 }$$ and $$2xy-2{ y }^{ 2 }-{ x }^{ 2 }$$.
Add : $$2x(z-x-y)$$ and $$2y(z+y-x)$$
What should be added to $$3x^{2}-2x+8$$ to get $$4x^{2}-x+2?$$
$${ x }^{ 2 }-2xy+{ 3 }y^{ 2 };{ 5y }^{ 2 }+3xy-{ 6x }^{ 2 }$$
Add the following : $$- 3 m n , - 2 m n , 6 m n$$
Add the following :
$$3 x ^ { 2 } ; - 7 x ^ { 2 } ; 5 x ^ { 2 }$$
Add : $$x ^ { 2 } + y ^ { 2 } + 3 x y - 6$$ and $$2 x ^ { 2 } - 4 y ^ { 2 } $$
Solve:
$$Add-2p^{2}+7p^{2}$$
$$add:p\left( p-q \right) ,q\left( q-r \right) and\quad r\left( r-p \right)$$
How much does $$a^{2}-3ab+2b^{2}$$ exceed $$2a^{2}-7ab+9b^{2}$$?
Simplify $$\dfrac{36t^{-3}}{6^{-3}\times t^{-5}}(t\neq 0)$$
Add $$a^{3}+b^{3}-3$$ to the sum of $$2a^{3}-3b^{3}-3ab+7$$ and $$-a^{3}+b^{3}+3ab-9$$.
Subtract $$3x-4y-7z$$ from the sum of $$x-3y+2z$$ and $$-4x+9y-11z$$.
Subtract: $$-4x$$ from $$3y$$
From the sum of $$x^{2}+3y^{2}-6xy, 2x^{2}-y^{2}+8xy, y^{2}+8$$ and $$x^{2}-3xy$$ subtract $$-3x^{2}+4y^{2}-xy+x-y+3$$.
Simplify combining like terms:
3a-2b-ab-(a-b+ab)+3ab+b-a
Add the polynomials $$x^{3}-2x^{2}-9$$ and $$5x^{2}+2x+9$$
What must be subtracted from $$2x^{2}-xy+5y^{2}$$ to make it $$-5x^{2}-3xy-2y^{2}$$?
Take away $$\dfrac{2}{3}ac-\dfrac{5}{7}ab+\dfrac{2}{3}bc$$ from $$\dfrac{3}{2}ab-\dfrac{7}{4}ac-\dfrac{5}{6}bc$$.
Solve the equations:
$$ax^{2}+bxy+cy^{2}=bx^{2}+cxy+ay^{2}=d$$
What must be added to $$12x^{3}-4x^{2}+3x-7$$ to make the sum $$x^{3}+2x^{2}-3x+2$$?
Solve the following equations:
$$\dfrac{x^3 + 1}{x^2 -1} = x + \sqrt{\dfrac{6}{x}}$$.
Class 7 Maths Extra Questions
- Algebraic Expressions Extra Questions
- Comparing Quantities Extra Questions
- Data Handling Extra Questions
- Exponents And Powers Extra Questions
- Fractions And Decimals Extra Questions
- Integers Extra Questions
- Lines And Angles Extra Questions
- Perimeter And Area Extra Questions
- Practical Geometry Extra Questions
- Rational Numbers Extra Questions
- Simple Equations Extra Questions
- Symmetry Extra Questions
- The Triangle And Its Properties Extra Questions
- Visualising Solid Shapes Extra Questions