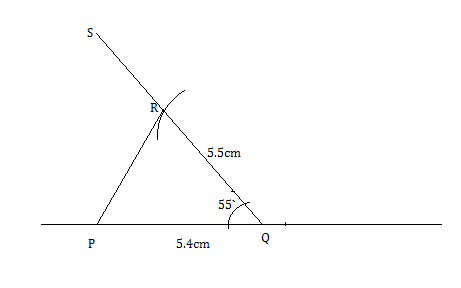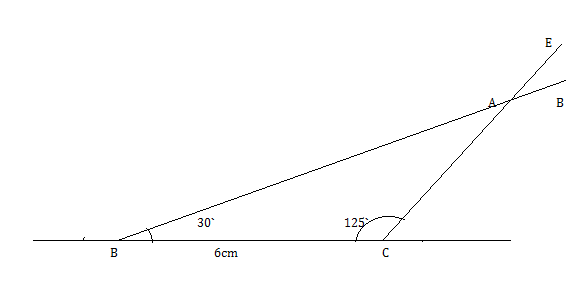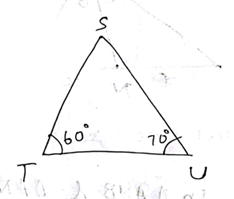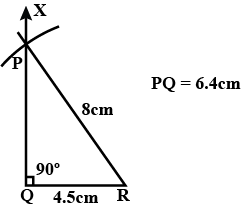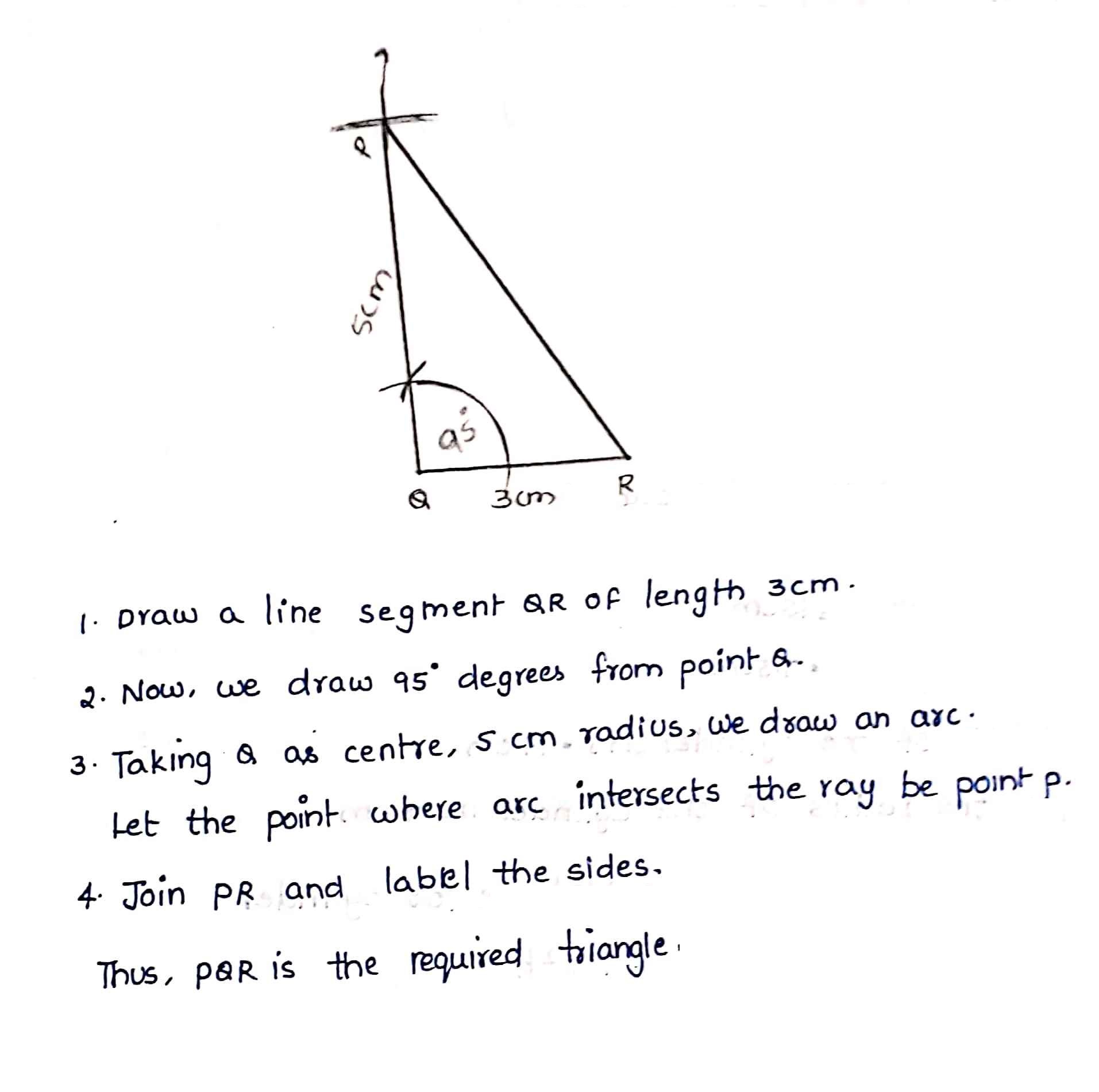Class 7 Maths - Practical Geometry

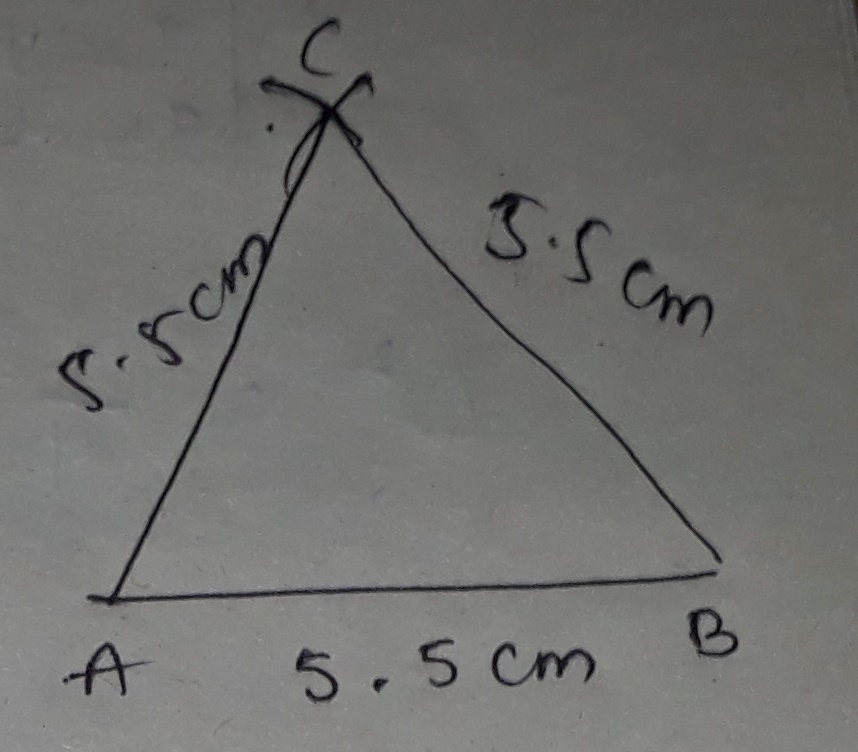
Write down the procedure of constructing of a $\triangle ABC$ with $BC=7.5\ cm, AC=5\ cm$ and $\angle C=60^{o}$

1. Draw

$BC=7.5cm$ as base

2. Take

$'C'$ as centre draw an angle of

$60^{o}$ with

protractor.

3. Take a compass cut an arc of

$5cm$ and

mark it as

$A$ .

4. Join

$AB$

$\therefore \triangle ABC$ is formed.

Is it possible to have a triangle with the following sides $2\ cm,3\ cm,5\ cm$

$\begin{array}{l} 2\, \, cm,\, \, 3\, \, cm,\, \, 5\, \, cm \\ Not\, \, possible\, \, to\, \, construct\, \, at\, \, triangle\, \, because, \\ the\, \, sum\, \, of\, \, two\, \, sides\, \, is\, \, greater\, \, than\, \, { 3^{ rd } }\, \, side.\, \, \, \, \, \, \, \, \, \end{array}$

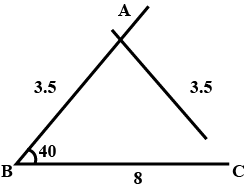
Is it possible to construct a triangle $ABC$ in which $BC=8\ cm,\angle B=40^\circ$ and $AB=AC=3.5\ cm\ ?$

$\begin{array}{l} Given\, \, data\, \, are\, \, wrong \\ such\, \, \Delta \, \, is\, \, not\, \, possible\, \, because \\ AB+AC<BC \end{array}$
1380851_1315379_ans_bd9a35cc121144368e1ed47c097e9f3a.png

1380851_1315379_ans_bd9a35cc121144368e1ed47c097e9f3a.png

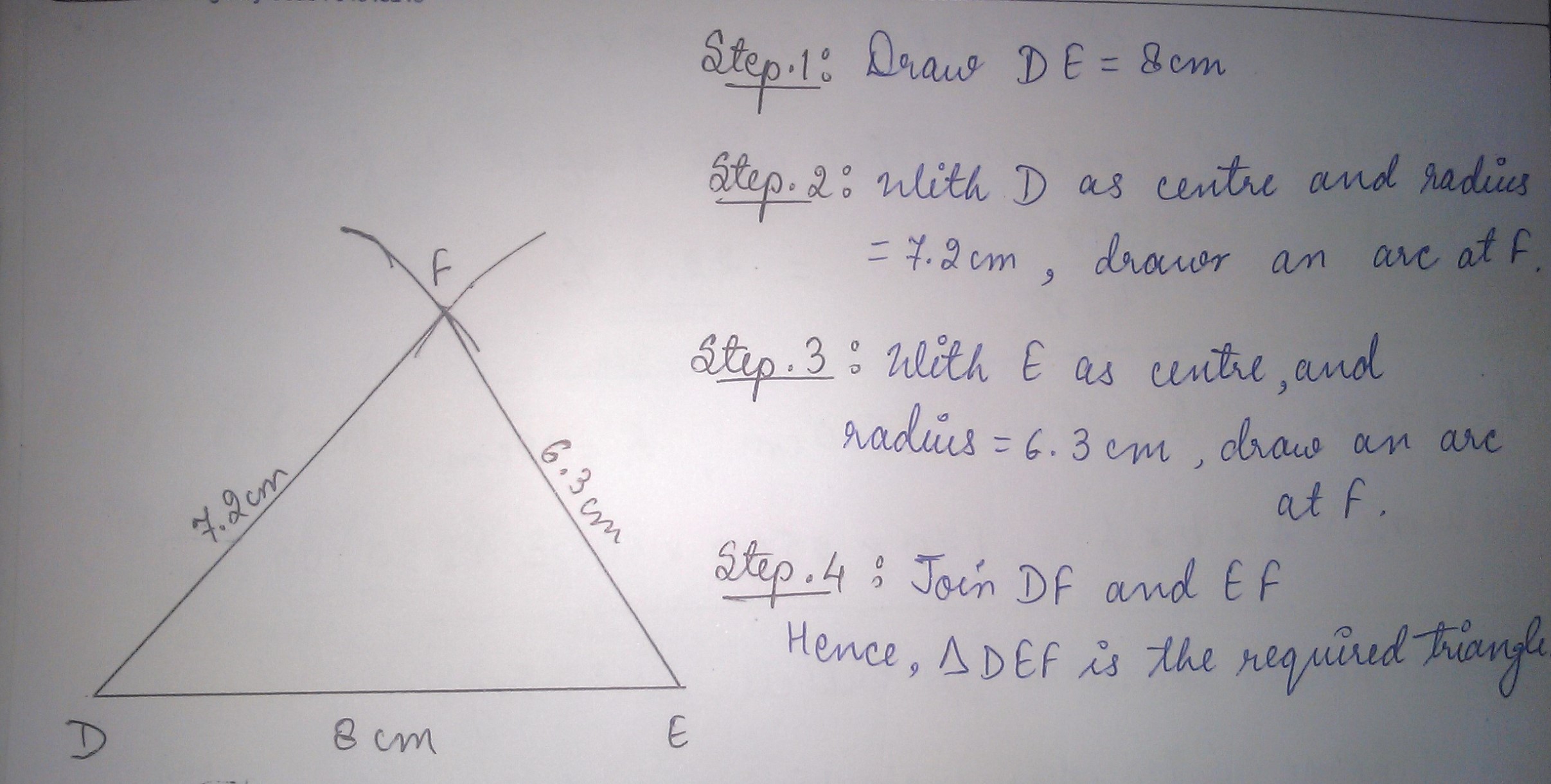
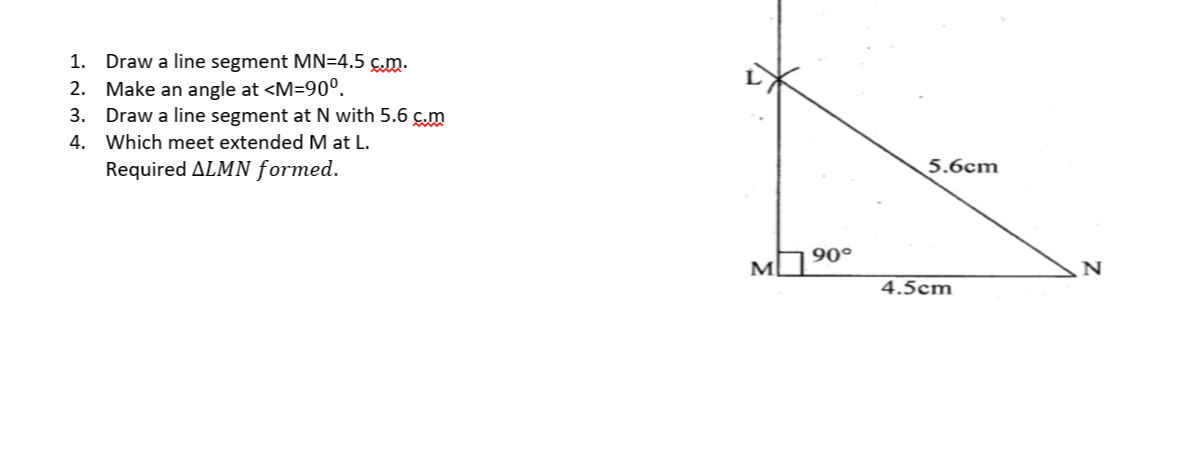
Construct $\Delta DEF$ in which DE=8 cm, DF=7.2 cm, EF=6.3 cm.

Step

$1$ : Draw DE

$=8$ cm

Step

$2$ : With D as centre and radius

$=7.2$ cm, draw an arc at F.

Step

$3$ : With E as centre, and radius

$=6.3$ cm, draw an arc at F.

Step

$4$ : Join DF and EF.

Hence,

$\Delta$ DEF is the required triangle.

1169499_1281543_ans_0f92556fff8c410b86b7ade024b2545e.jpg

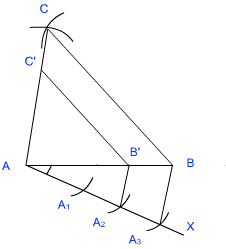
Construct a triangle $PQR$ with side $QR=7cm,$ $PQ=6cm$ and angle $PQR={60^0}$ then construct another triangle whose side are $3/5$ of the corresponding sides of triangle $PQR?$

1914476_1282771_ans_7d1d603a960c43adadafd9d9a5c726b8.jpeg

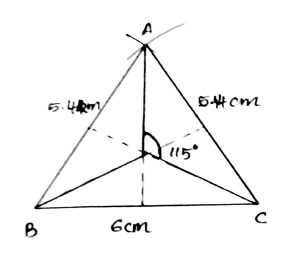
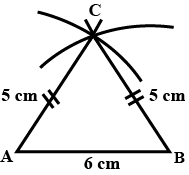
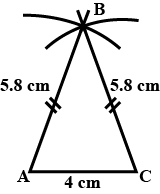
Construct a triangle ABC in which $AB= AC=5.44\ cm\ and\$ BC=6 cm. Draw all its lines of symmetry.

First draw line segment 6 cm BC

After that open compass 5.44 cm and draw curve from point B

There after an another curve is drawn from point C, these curve cut the

Curve from point B at point A

Join A to B and A to C

The figure ABC is the given triangle.

Draw perpendicular bisector of line BC this go from vertex A and Cut BC at point D join to A

Then AD is the line of symmetry.

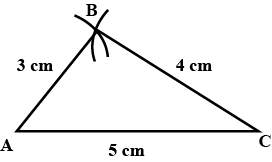
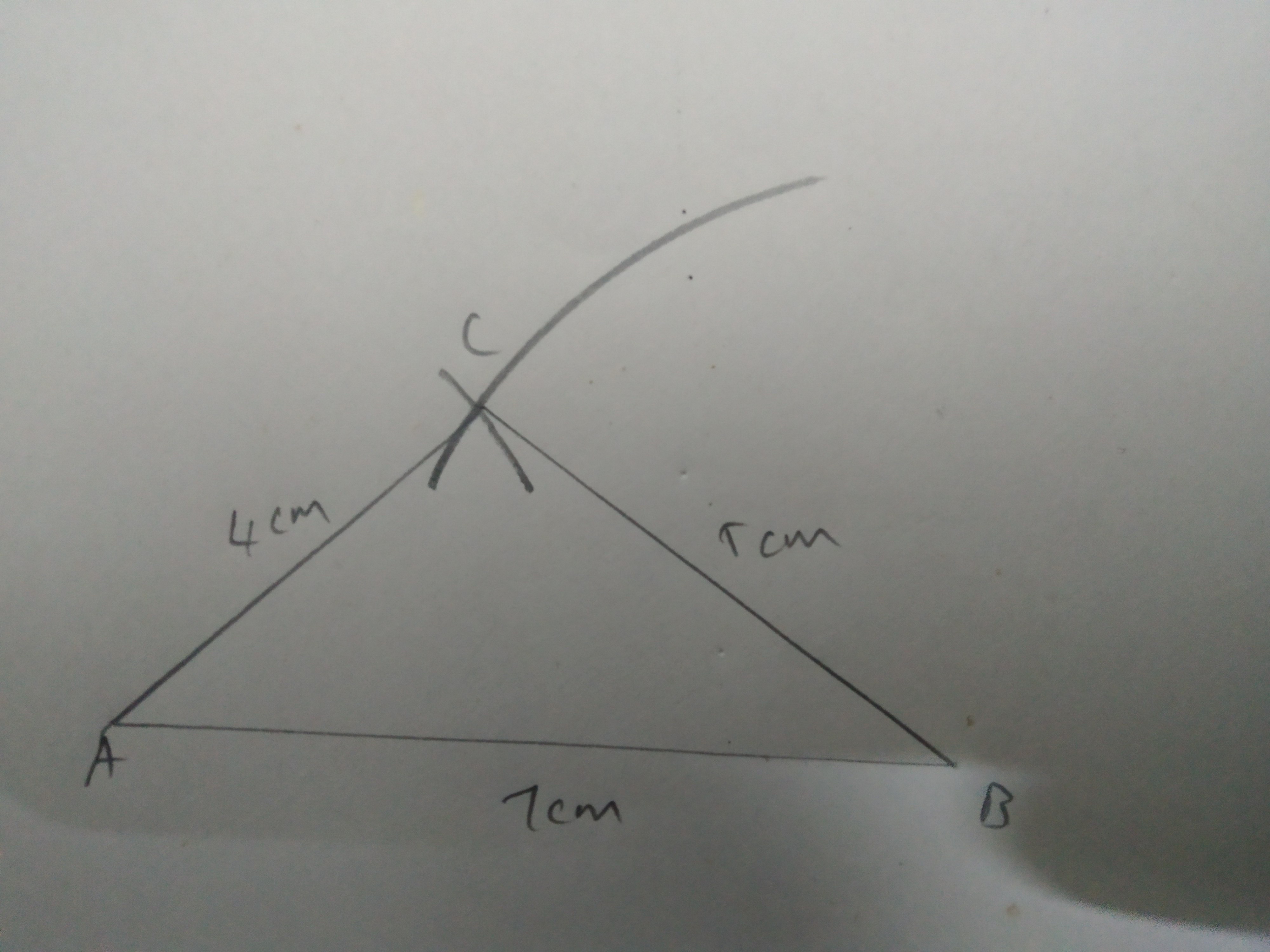
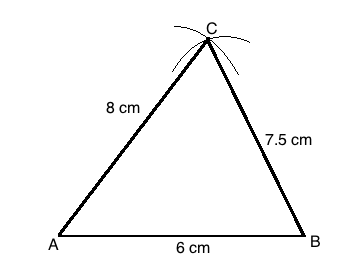
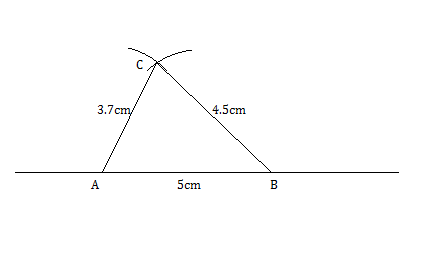
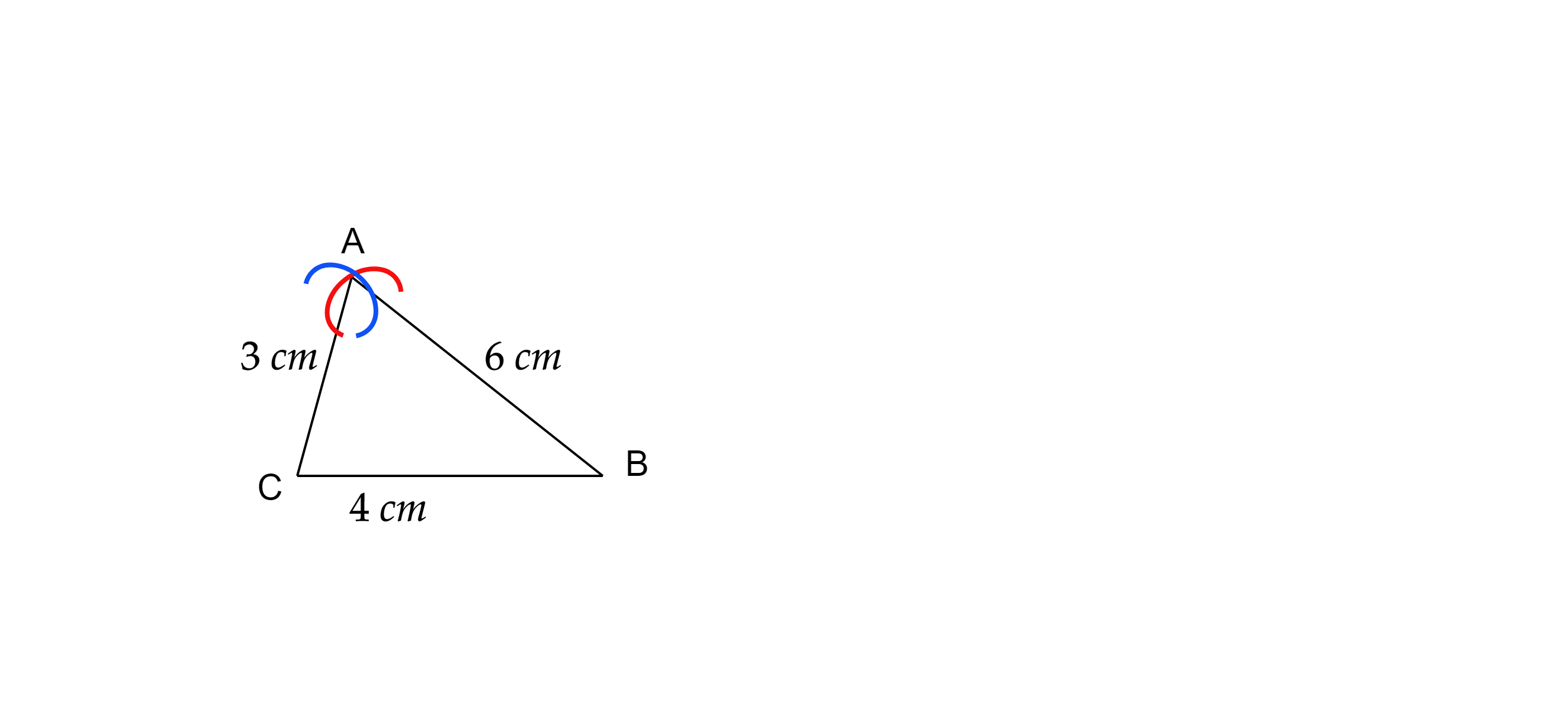
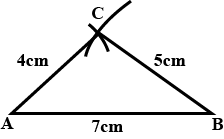
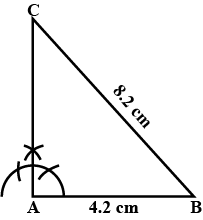
Construct a scalene triangle $ABC$ , given $AB=3$ cm, $AC =5$ cm and $BC =4$ cm.

Step 1: Draw the base as

$AC=5cm$ .

Step 2: Take

$3cm$ on the compass and cut an arc from

$A$ .

Step 3: Take

$4cm$ on the compass and cut an arc from

$C$ which intersects the previous arc at

$B$ .

Step 4: Join

$AB$ and

$AC$ . We get

$\triangle ABC$

Given a line segment SR of 2.5 cm. Construct a line segment PT of 2 cm parallel to SR.

$Steps$

$of$

$construction:$

$Step 1:$ Draw the Base line

$SR$ of

$2.5 cm$

$Step 2:$ With S as center Draw a perpendicular Ray of

$6 cm$

$Step 3:$ Join the end point of ray (say

$X$ ) and

$R$

$Step 4:$ With

$S$ as center and radius

$1.2cm$ draw an arc on the ray .Mark the point as

$P$

$Step5:$ With

$R$ as radius Draw an arc of radius

$1.3 cm$ on the line

$RX$ .Mark it as

$T$

$Step6:$ Join

$P,T$

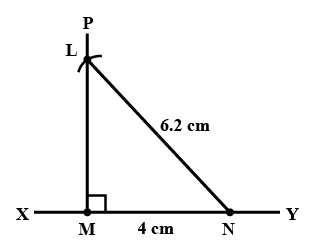
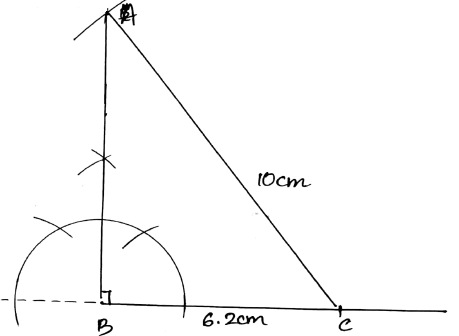
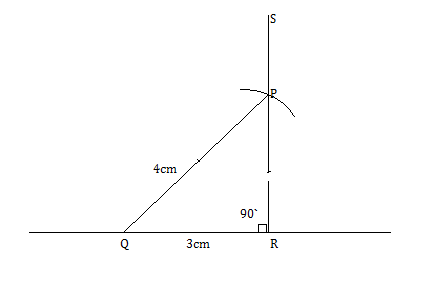
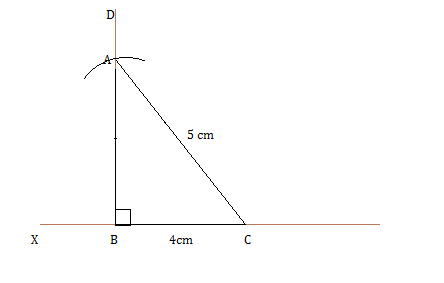
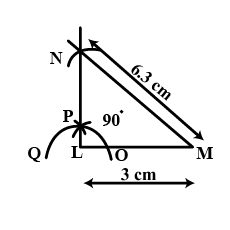
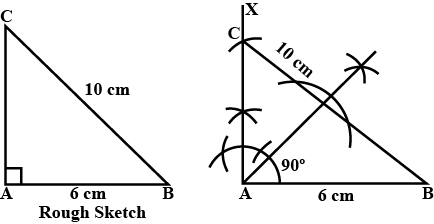
Construct a right triangle $LMN$ in which $\angle M = 90^{\circ}, MN = 4 cm$ and $LN = 6.2\ cm$

Steps of construction

$1$ . Draw a line segment

$XY$ .

$2$ . Locate

$M, N$ on

$XY$ such that

$MN = 4\ cm$ .

$3$ . Construct a line segment

$MP$ , sufficiently large, such that

$\angle NMP = 90^{\circ}$ .

$4$ . With

$N$ as centre and radius

$6.2\ cm$ draw an arc, cutting

$MP$ at

$L$ ; join

$NL$ .
Then,

$LMN$ is the required triangle.

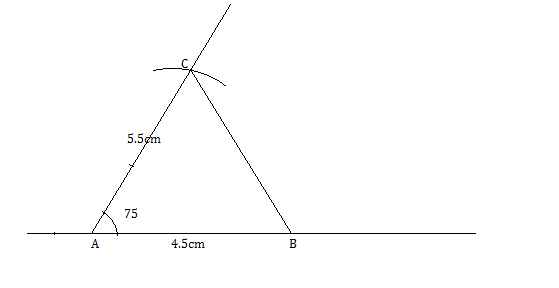
Construct a triangle $ABC$ , in which $AB = 4.5 cm, AC = 5.5 cm$ and $\angle BAC = 75^{\circ}$

Steps of Construction:
(i) Draw a line segment which is sufficiently long using ruler.
(ii) Locate points

$A$ and

$B$ on it such that

$AB = 4.5cm$ .
(iii) At A, construct a line segment

$AE$ , sufficiently large, such that

$\angle BAC$ at

$60^\circ$ , use protractor to measure

$60^\circ$
(iv) With

$A$ as centre and radius

$5.5cm$ , draw the line cutting

$AE$ at C, join

$BC$ .
Then

$ABC$ is the required triangle.

Two sides of a triangle are $12\ cm$ and $14\ cm$ . The perimeter of the triangle is $36\ cm$ . What is the length of third side

Given two sides of the triangle are

$12cm$ and

$14cm$

the perimeter of triangle

$=36cm$

Let the length of the third side

$=a cm$

the perimeter of triangle = sum of the length of sides of the triangle.

Accoreding to problem,

$12+14+a=36$

$\Rightarrow 26+a=36$

$\Rightarrow a=36-26$

$\Rightarrow a=10$

$\therefore$ length of the third side of triangle

$=10cm$

Construct $\Delta TEN$ such that TE = 3 cm, $\angle E = 90^o$ and NE = 4 cm.

Step:

$1$ : Draw a line NE

$=4$ cm

Step:

$2$ : Then construct a

$90^o$ angle using compass.

Step:

$3$ : Measuring

$3$ cm length from the tip of compass mark an arc at point T.

Step:

$4$ : Join the points N and T.

Step:

$5$ : Hence

$\Delta$ TEN is the required triangle, TN

$=5$ cm.

1119295_705208_ans_a2d2ff39c3ac4d59b1283aea0bf55ba8.jpg

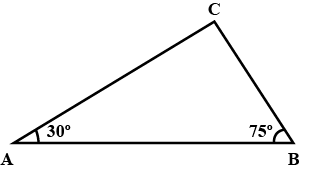
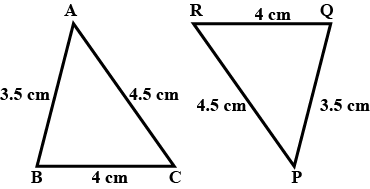
Are the triangle shown in Fig congruent?why?

Yes they are congruent

AB=QP

AC=RP

BC=QR

By SSS congruence, the triangles ABC and PQR are congruent

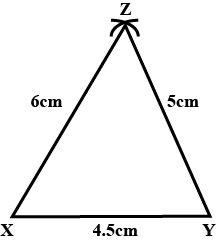
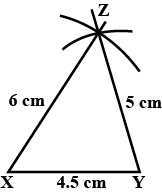
Construct $\triangle XYZ$ in which $XY=4.5\ cm,YZ=5\ cm$ and $ZX=6\ cm$ .

(i) Draw a line segment of

$4.5$ cm and name it as

$XY.$

(ii) Taking X as centre and scale

$6$ cm, draw an arc.

(iii) Similarly, Taking

$Y$ as centre and scale

$5$ cm, draw another arc. Name the point of intersection of two arc as

$Z$ .

(iv) Join

$YZ \ and \ XZ.$

1117414_1039804_ans_e57a7177787d451d9901012665c5d375.png

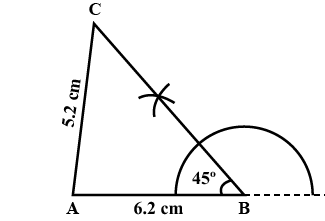
Draw a triangle ABC in which AB = 5 cm, BC = 7 cm, and $\angle B = 75^{o}$ .

Steps of construction :

1) Draw a line segment AB = 5 cm.

2) Make

$\angle ABC = 75^{o}$ .

3) Cut off BC = 7 cm.

4) Join AC.

Therefore,

$\triangle ABC$ is the required triangle.

1326333_1052946_ans_99e7d65433024db88df88d3860aa9e0d.png

Try to construct a triangle with $5\ cm, 8\ cm$ and $1\ cm$ . Is it possible or not? Why?Give your justification?

Given

$a=5\ cm$

$b=8\ cm$

$c= 1\ cm$

The concept behind this is sum of two sides is always greater than 3rd side.

Then

$a+b > c=5+8 > 1$

$b+c > a = 8+1 > 5$

$c+a > b=1+5 > 8$ (This is not right )

Then we do not construct a triangle with sides

$5\ cm$ ,8 cm

$~and~$ 1

$cm$

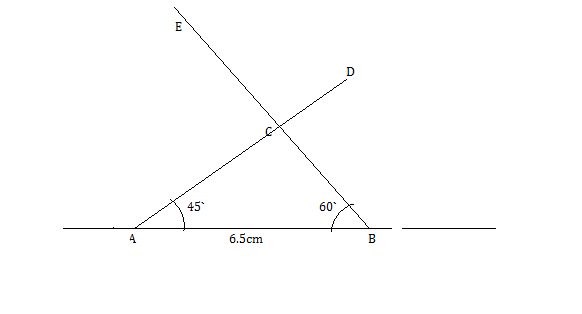
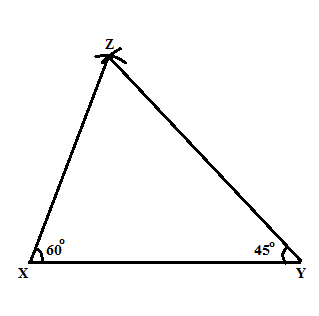
Construct a triangle $\Delta ABC$ in which BC= 6 cm, $\angle B=60^{\circ},\angle C=45^{\circ}$

Steps of construction:

1)Draw a line segment BC=6 cm.

2)Draw

$60^o$ angle at B and

$45^o$ angle at C.

3) Mark the point where the rays of both the angles meet as A.

4)ABC is the triangle required.

1299806_1373335_ans_a85fe77a68e340179b87bcb8bac97421.png

Construct a $\Delta ABC$ whose sides are $4\ cm,\ 5\ cm$ and $7\ cm$ respectively

1305513_1402638_ans_3f582eddd74a4f92aae24e6ca80ad068.jpg

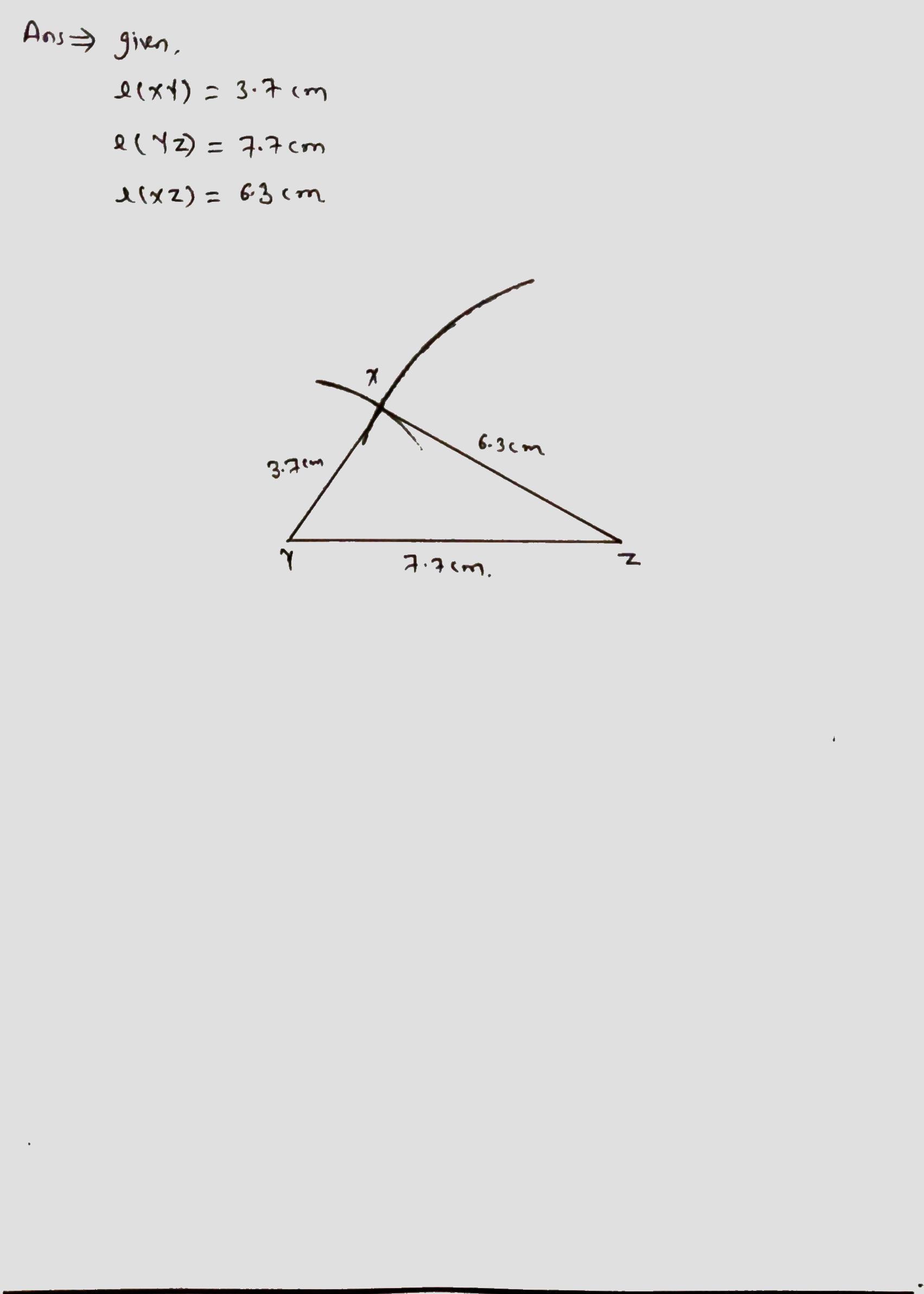
Construct $\Delta$ XYZ such that, $l(XY)=3.7cm$ , $l(YZ)=7.7cm$ , $l(XZ)=6.3cm$ .

1917944_1124555_ans_e89258b62aae49a6ab62e04b87f37e6d.jpg

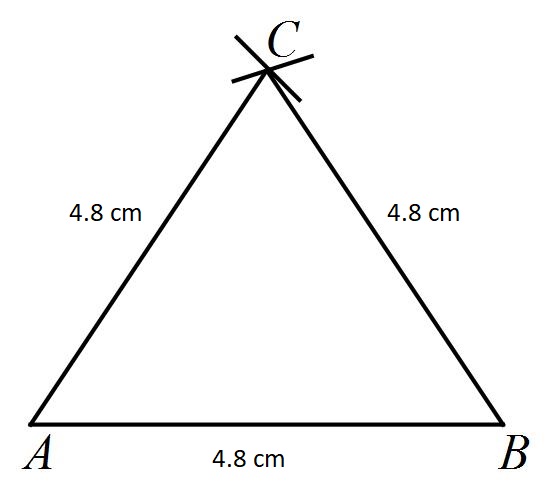
Draw an equilateral triangle whose sides are $4.8\,\, cm$ each .

Construction:

(1) Draw a line

$AB=4.8\ cm$ .

(2) Draw two arcs of the same length as

$AB$ from point

$A$ and another from point

$B$ using the compass.

(3) Mark the point as

$C$ where these arcs intersect. Then draw lines

$AC$ and

$BC.$

The

$\triangle ABC$ is an equilateral triangle of each side

$4.8\ cm$ .

1035604_1098848_ans_6d89edebadfb40599650cffb169db42c.jpg

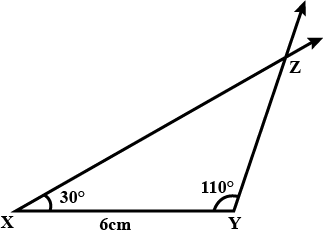
Construct $\Delta$ PQR if PQ $=5$ cm, m $\angle$ PQR $=105^o$ and m $\angle$ QRP $=40^o$ .

$\angle PQR + \angle QRP+ \angle RPQ=180$

$105+ 40+ \angle RPQ=180$

$145+ \angle RPQ=180$

$\angle RPQ= 180-145$

$\angle RPQ= 35$

Draw

$PQ = 5 cm$

Draw angle

$P = 35°$

Draw angle

$Q = 105°$

They intersect at point

$R= 40°$

1060495_1072611_ans_58ae445feefa4567ba553fcce32deb7e.png

Construct a $\triangle{XYZ}$ in which $XY=4.5$ cm, $YZ=5$ cm and $ZX=6$ cm

$1.$ Draw a line segment

$XY$ of length

$4.5$ cm

$2.$ Taking

$6$ cm as radius, and

$X$ as center, draw an arc.

$3.$ Taking

$5$ cm as radius, and

$Y$ as center, draw another arc.

$4.$ Let

$Z$ be the point where the two arcs intersect.

Join

$XZ$ and

$YZ$ and label the sides.

Thus,

$\triangle{XYZ}$ is the required triangle.

1347314_1113944_ans_785505a4d20e41c7b66c0c2568816867.png

What is the side included between the angles M and N of $\triangle MNP$ ?

Given that,

The angles $M$ and $N$ of triangle MNP.

We need to draw a triangle

Using given data

Firstly, we draw a line $MN$ .

Now we draw the angles with $M$ and $N$ .

The angle $M$ and angle $N$ meet at the point $P$ .

Here is a triangle $MNP$ created.

Hence, $MN$ is the side include between the angles $M$ and $N$ of triangle.

1263950_1328161_ans_594b4ac18a124fe785dde17e8c0e798a.png

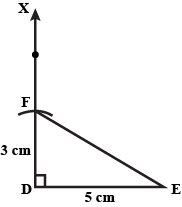
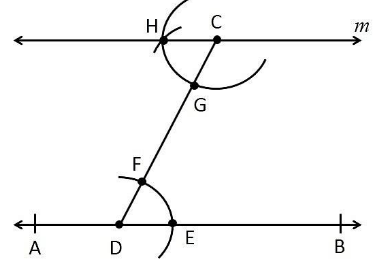
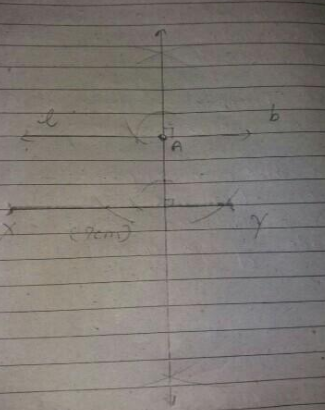
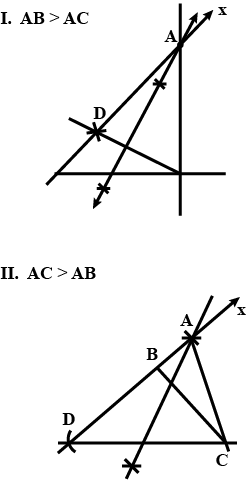
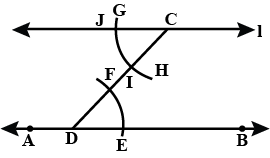
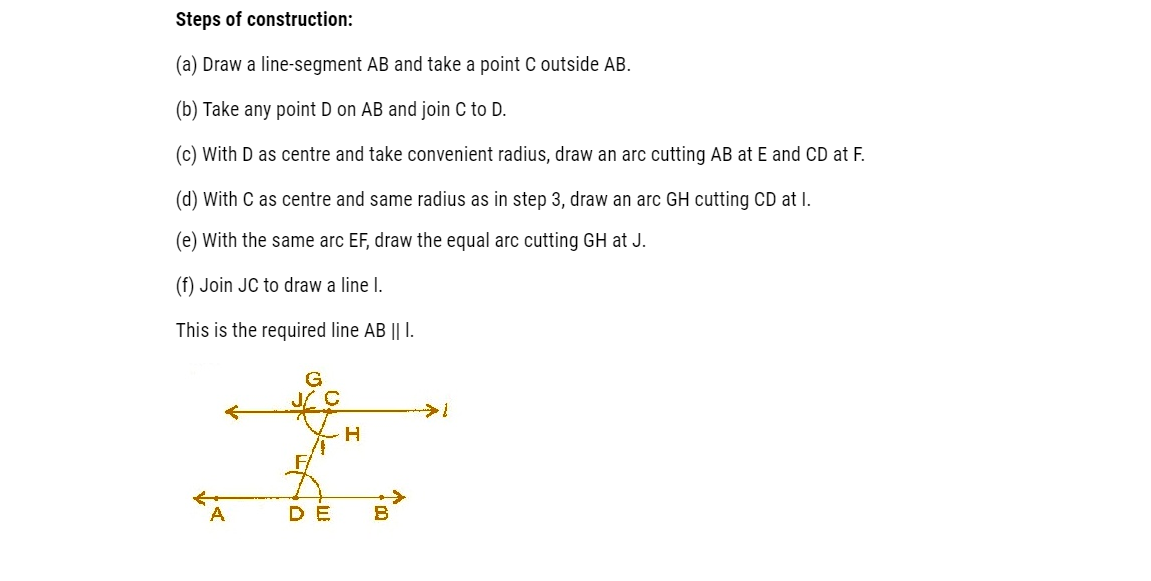
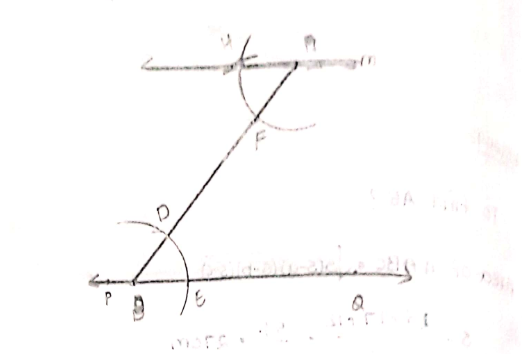
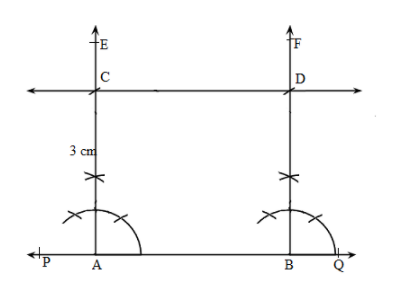
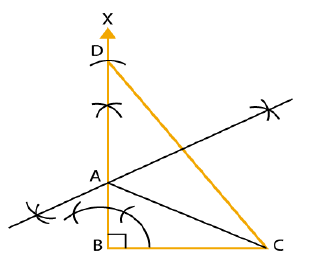
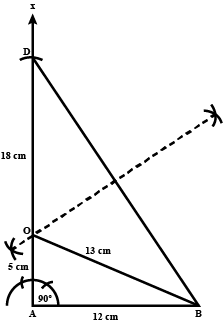
Draw a line, say $AB$ , take a point $C$ outside it. Through $C$ , draw a line parallel to $AB$ using ruler and compasses only.

Draw a line

$AB$ and then plot a point

$C$ which is outside the line

$AB$ .

From the point

$A$ , draw another line which passes through

$C$ .

With

$A$ as centre, draw a semi-circle on

$AB$ .

With

$C$ as centre, draw a semi-circle on the line which passes through

$C$ .

With the same radius as in above circles, and point

$Q$ as centre draw an arc which intersects the semi-circle drawn above.

Draw the line

$MN$ which is parallel to

$AB$ .

1297478_1426920_ans_2b96e0f3413b490f9a7eb01f431d469c.png

Draw $\Delta ABC$ with $AB=6$ cm, $AC=5$ cm and $\angle A = {85^ \circ }$

1335862_1266445_ans_dfc3757de1834daf94eba71fd971610a.PNG

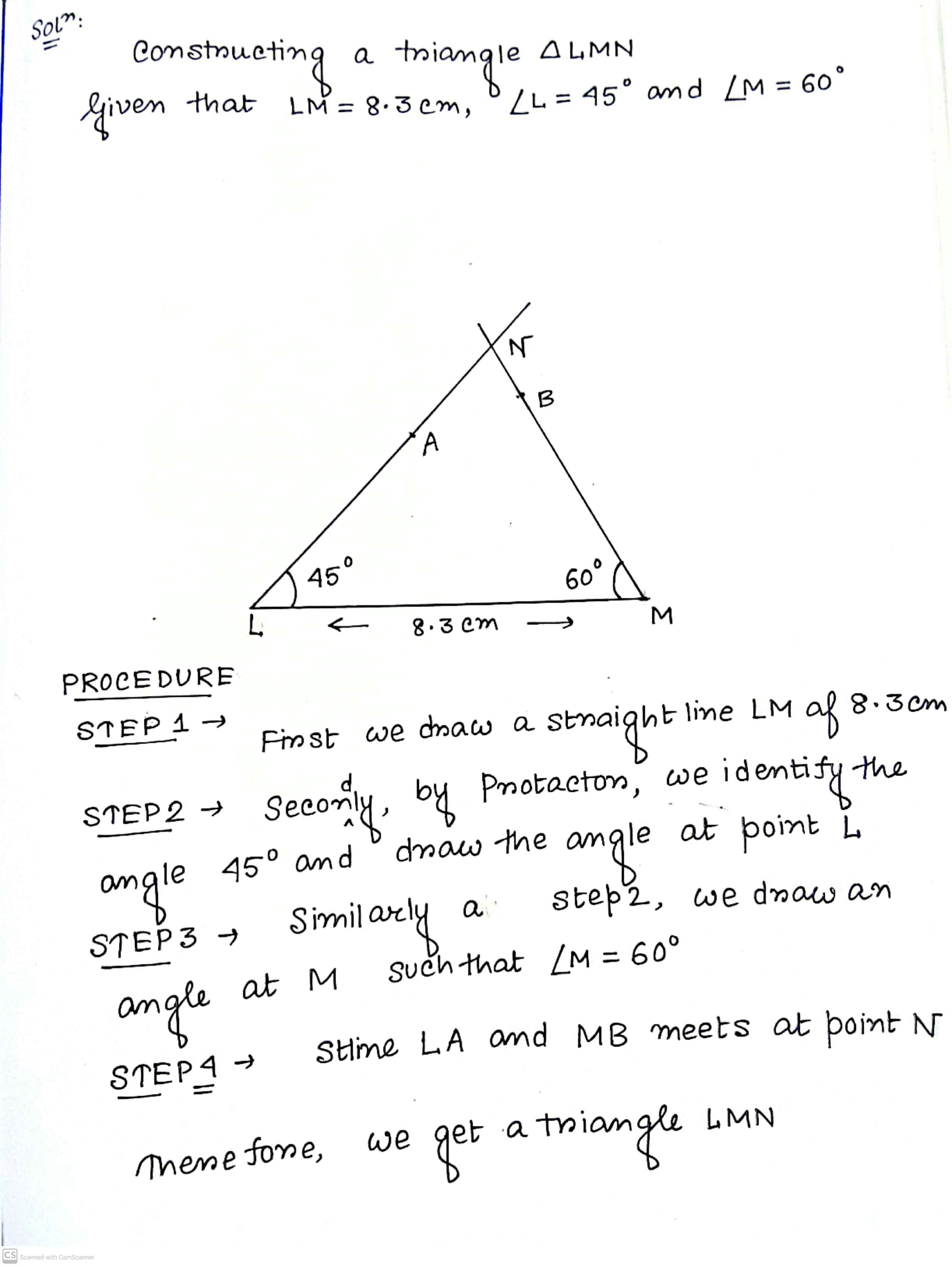
Construct a $\triangle LMN$ in which $LM=8.3\ cm, \angle L=45^{o}$ and $\angle M=60^{o}$ .

1912926_1313262_ans_267dafb459954446acb28419170041cf.jpg

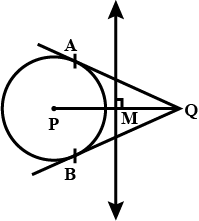
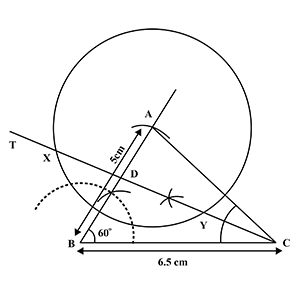
Draw a circle with centre $P$ and radius $2.1 cm$ . Take point $Q$ at a distance $5.2 cm$ from the centre. Draw tangents to the circle from point $Q$ . Measure and write the length of a tangent segment.

Draw a circle with centre

$P$ and radius

$2.1$ cm.Take a point

$Q$ at a distance

$5.2$ cm from the centre.Draw tangents to the circle from point

$Q$ .Measure and write the length of a tangent segment.

Length of tangent segment

$=4.8$ cm

$\pm 0.2$ cm

$=5$ cm,

$4.6$ cm

1297490_1426923_ans_5dc1514f797d4c25b48382e8315dc921.png

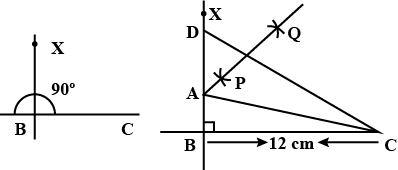
Construct a right angled triangle $PQR$ , in which $\angle Q={90}^{o}$ , hypotenuse $PR=8cm$ and $QR=4.5cm$ . Draw a bisector of angle $PQR$ and let it meet $PR$ at point $T$ . Prove that $T$ is equidistant from $PQ$ and $QR$ .

Steps of Construction:
(i) Draw a line segment

$QR=4.5cm$
(ii) At

$Q$ , draw a ray

$QX$ making an angle of

${ 90 }^{ o }$
(iii) With centre

$R$ and radius

$8cm$ , draw an arc which intersects

$QX$ at

$P$ .
(iv) Join

$RP$

$\triangle PQR$ is the required triangle
(v) Draw the bisector of

$\angle PQR$ which meets

$PR$ in

$T$
(vi) From

$T$ , draw perpendicular

$PL$ and

$PM$ respectively on

$PQ$ and

$QR$ .
Proof:
In

$\triangle LTQ$ and

$\triangle MTQ$

$\angle TLQ=\angle TMQ$ (Each

${ 90 }^{ o }$ )

$\angle LQT =\angle TQM$ (

$QT$ is angle bisector)

$QT=QT$ (Common)
Thus, by AAS criterion of congrence

$\triangle LTQ \cong \triangle MTQ$
And, by Corresponding Parts of Congruent Triangle (CPCT)

$TL=TM$
Therefore,

$T$ is equidistant from

$PQ$ and

$QR$

1796970_1832762_ans_735f021b7e2d4cee90fa3d68c821ecf7.png

Construct a $\triangle ABC$ , when:
$\displaystyle AB=6.0\ cm,AC=8.0\ cm$ and $BC=7.5\ cm.$

To construct a triangle with three given sides,
1. First draw the base , say

$AB = 6 cm$
2. Set the width of the compass as the second side

$AC = 8.0 cm$ and draw an arc from

$A$ on any one side of the line segment

$AB$
3. Similarly, set the width of the compass as the third side

$BC = 7.5 cm$ and draw an arc from

$B$ on the same side of the line segment

$AB$ as done in Step 2
4. Mark the intersection of the two arcs as

$C$
5. Join points

$A,C$ and

$B,C$ using a ruler.
6.

$ABC$ is a required triangle.

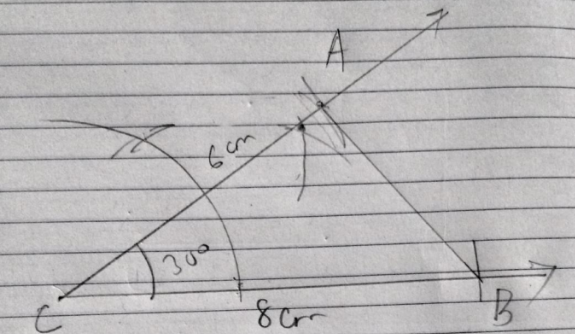
Construct a $\triangle PQR$ such that $\angle P = 30^\circ, \angle Q = 60^\circ$ and $PQ = 10\ cm$ .
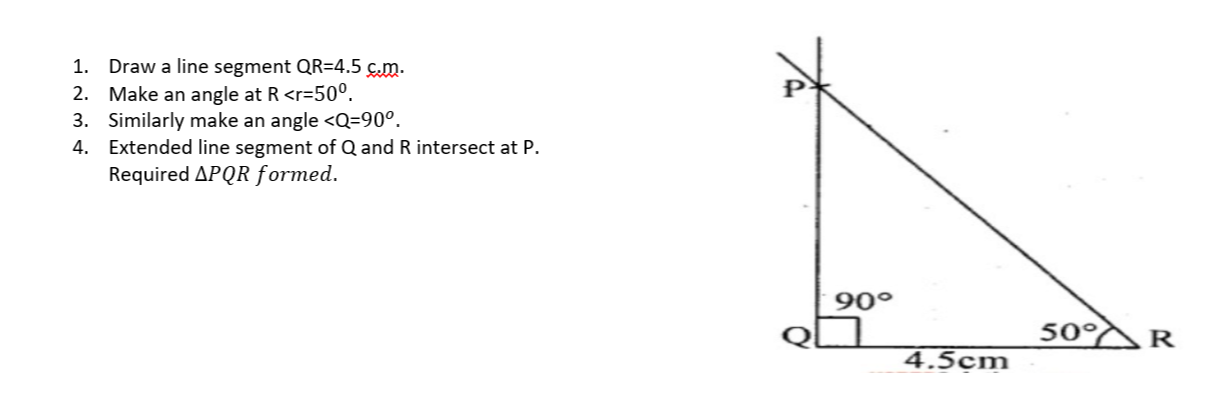
Type 1 if following are the steps of construction and type 0 if following are not tue steps of construction.
Steps of Construction:
(i) Draw a line segment $PQ = 10\space\mathrm{cm}$ .
(ii) At $P$ , draw a ray making an angle of $30^{\circ}$ .
(iii) At $Q$ , draw another ray making an angle of $60^{\circ}$ which intersects the first ray at $R$ .
$\triangle PQR$ is the required triangle.

Steps of Construction:

(i) Draw a line segment

$PQ = 10\space\mathrm{cm}$ .

(ii) At

$P$ , draw a ray making an angle of

$30^{\circ}$ .

(iii) At

$Q$ , draw another ray making an angle of

$60^{\circ}$ which intersects the first ray at

$R$ .

$\triangle PQR$ is the required triangle.

Hence answer will be 1.

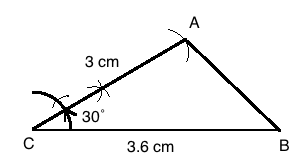
Construct a $\triangle ABC$ , when $\displaystyle BC= 3.6\ cm, CA=3.0\ cm$ and $\angle C=30^{\circ}.$

1. Draw the base side

$BC = 3.6\ cm$
2. At point

$C$ , draw an angle of

${30}^{\circ}$
3. From

$C$ cut an arc of length

$AC = 3.0\ cm$ using a compass
4. Name the point of intersection of the arm of the angle

${30}^{\circ}$ and the arc drawn in step 3, as

$A$
5. Join

$A$ to

$B$
6.

$ABC$ is the required triangle.

If $\displaystyle A= 30^{\circ},a= 7$ and $\displaystyle b=8$ in $\displaystyle \Delta ABC$ then find the number of triangles that can be constructed.

Given,

$A=30^o, a=7, b=8$

We have

$\displaystyle \frac{a}{\sin A}= \frac{b}{\sin B}$ or

$\displaystyle \sin B= \frac{b\sin A}{a}= \frac{8\sin 30^{\circ}}{7}=\frac{4}{7}$
Thus,we have,

$\displaystyle b> a > b\sin A$

Hence, angle B has two values given by

$\displaystyle \sin B =4/7$
Thus two triangles are possible with the given information.

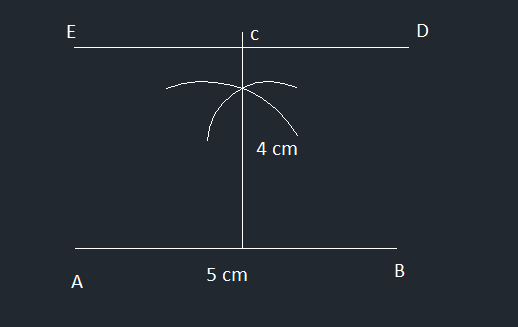
Construct a line segment AB =5cm . Construct a line segment ED parallel to AB at a distance of 4 cm from it.

draw a line segment of length

$AB=4cm$

draw a line perpendicular to AB by drawing two arcs from A , B and joining the points of intersection and mid point

on tne perpendicular line at a distance of

$4cm$ draw a line perpendicular to that line

1133438_178984_ans_3e2aca883fb74099a615f56669755791.png

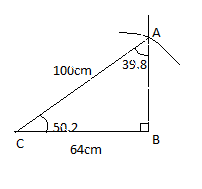
Construct a right angle $\triangle ABC$ , right angled at $B$ , when $CA = 100,\:BC = 64\ cm$ . Measure the remaining angles of the triangle.

1122337_178993_ans_e2116d3f0711427f98e9d9688c588850.png

side $AB= 4.3$ cm, side $BC= 4.9$ cm and altitude $BD= 3.3$ cm.

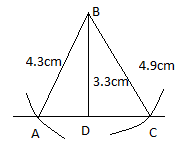
1122386_179030_ans_440a2718957a4a37a14b2606bc1da1dc.png

Construct a $\triangle ABC$ , when $\displaystyle BC=6.2\ cm, CA=9.0\ cm$ and $\angle B=90^{\circ}$

Step 1: Draw line

$BC$ of

$6.2cm$

Step 2: Construct

$90^o$ at

$B$

Step 3: Given

$AC=10cm$ . Cut

$10cm$ at line

$AB$

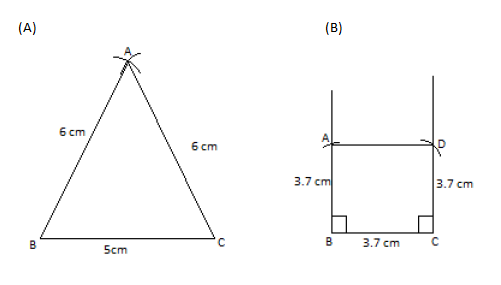
Construct $ABC$ , an isosceles triangle with $AB= AC= 13$ cm and $BC=10$ cm. Calculate the length of perpendicular from $A$ to $BC$ .

To construct a triangle with these three given sides,
1. First draw the base , say

$BC = 10 cm$
2. Set the width of the compass as one side

$AB = 13 cm$ and draw an arc from

$B$ on any one side of the line segment

$BC$
3. Similarly, set the width of the compass as the other side

$AC = 13 cm$ and draw an arc from

$C$ on the same side of the line segment

$BC$ as done in Step 2
4. Mark the intersection of the two arcs as

$A$
5. Join points

$A;B$ and

$A; C$ using a ruler.
6.

$ABC$ is a required triangle.

To find the length of the perpendicular from

$A$ to

$BC$ , join the mid point of

$BC$ that is

$D$ to

$A$

On measuring

$AD = 12 cm$

Construct the parallel lines with steps.

Step 1: Start with a line

$PQ$ and a point

$R$ off the line.
Step 2: Draw a transverse line through

$R$ and across the line

$PQ$ at an angle, forming the point J where it intersects the line

$PQ$ . The exact angle is not important.
Step 3: With the compasses' width set to about half the distance between

$R$ and

$J,$ place the point on

$J,$ and draw an arc across both lines.
Step 4: Without adjusting the compasses' width, move the compasses to

$R$ and draw a similar arc to the one in step 2
Step 5: Set compasses' width to the distance where the lower arc crosses the two lines.
Step 6: Move the compasses to where the upper arc crosses the transverse line and draw an arc across the upper arc, forming point

$S$ .
Step 7: Draw a straight line through points

$R$ and

$S$ .
Step 8: Finished. The line

$RS$ is parallel to the line

$PQ$ .

Construct a line segment LM of 10 cm.Draw a line parallel to LM at a distance of 1 cm from it.

First draw a line segment 10 cm LM

Draw right angle at point L an M by compass

Open compass 1 cm and marked curve froim right angle at point L and M

These cut at point P and Q

Join P and Q then the line segment PQ is the parallel line at a distance 1 cm from LM

Solve the right triangle $ABC$ if angle $A$ is $60$ , and the hypotenuse is $6$ m.

Using

$30-60-90$ degree triangle theorem, the sides are in the ratio

$1 : 2 : \sqrt{3}$
Shortest side

$=$

$\dfrac{1}{2} \times$ hypotenuse
Longest side

$=$

$\dfrac{1}{2}\sqrt{3}\times$ hypotenuse
So, the shortest side or adjacent side

$60$ degree

$=$

$\dfrac{1}{2} \times 6$

$= 3$ m
Longest side

$=$

$\dfrac{3}{2}\sqrt{3}$

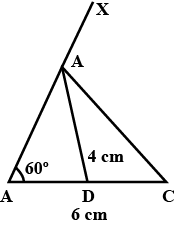
Construct a triangle $ABC,$ whose base $\displaystyle BC=6\ cm, \displaystyle \angle B=60^{o}$ and altitude $\displaystyle AD= 4$ cm.

Follow these steps for construction:

1. Draw the base

$BC=6cm$ .

2. Construct

$\angle B= 60^o$ and extend the line

$BX$ .

3. With radius as

$4\ cm,$ cut arcs at various points from

$BC$ . The line joining these arcs is parallel to

$BC$ at a distance of

$4\ cm$ .

4. Name the point of intersection of

$BX$ and the parallel line to

$BC$ as

$A$ and join

$AC$ .

$\triangle ABC$ is the required triangle

Construct a triangle with sides $5$ cm, $5.5$ cm and $6.5$ cm. Now construct another triangle, whose sides are $\dfrac {5}{3}$ times the corresponding sides of the given triangle.

Steps to follow:

Step 1. At first drawn a base line BC of length 5.5 cm with the help of scale.

Step 2. Taking B as center draw an arc of radius 5 cm with the help of compass. Similarly taking C as center draw a arc of radius 6.5 cm with the help of compass.

Join AB and AC thus completing the triangle ABC.

Step 3. A ray BX is drawn making an acute angle with BC opposite to vertex A. Five points B1 , B2 , B3, B4, and B5 at equal distance is marked on BX.

Step 4. B3 is joined with C to form B3 C as 3 point is smaller. B5 C1 is drawn parallel to B3 C as 5 point is greater.

Step 5:C1A1is drawn parallel to CA.

Thus, A1BC1 is the required triangle.

1431482_261076_ans_60d815df97c94a30a5a91173e5d8fa2a.png

Solve the right triangle $ABC$ if angle $A$ is $30$ , and the hypotenuse is $4$ m.

Using

$30-60-90$ degree triangle theorem, the sides are in the ratio

$1 : 2 : \sqrt{3}$
Shortest side

$=$

$\dfrac{1}{2} \times$ hypotenuse
Longest side

$=$

$\dfrac{1}{2}\sqrt{3}\times$ hypotenuse
So, the shortest side or adjacent side

$60$ degree

$=$

$\dfrac{1}{2} \times 4$

$= 2$ m
Longest side

$=$

$\dfrac{1}{2}\times4\sqrt{3}= 2\sqrt{3}$ m

Construct an parallel lines with an angle 45.

Step 1: Draw a line

$l$ , mark a point

$A$ on the line. Mark a point

$P$ as shown in the figure.

Step 2: Join

$A$ and

$P$ , extend the line. Cut an arc

$XX'$ from

$A$ and

$y$ from

$P$ .

Step 3: Now measure

$X'X$ and cut an arc from

$y$ . By joining the new point

$y'$ and

$P$ , we get a line parallel to

$l$ and they are at

$45^o$

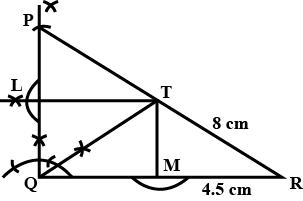
Using ruler and compasses only, construct a $\Delta ABC$ having $AB = 47 \text{ cm}$ , $AC = 34 \text{ cm}$ and $\angle BAC = 75^{\circ}$ . Draw the perpendicular bisector of $BC$ and the bisector of $\angle BAC$ . If the perpendicular bisector and the angle bisector meet at a point $M$ , measure $\angle BMC.$

1. Draw a line segment measuring 47 cm and name it as AB.

2. To Construct 75 deg:

Start with two angles, ∠RPQ and ∠DAB.

The goal is to add ∠RPQ to ∠DAB.

Set the compasses on A, and adjust to any convenient width.

Make an arc across both legs of the angle, creating points J and K.

Set the compasses on A and make an arc to the left of, and across BC.

Set the compasses on K and adjust the width to point J.

Set the compasses on L and make an arc across the previous one, creating point E.

Draw a line from A, through E. Measure 34cm on the compass and cut on the line segment AE

The angle CAB which now measures 75 deg. Join B and C and triangle CAB is formed.

3. To draw a perpendicular bisector:

Measure more than half of BC on the compass and cut arcs on either side of BC keeping the compass at B.

Similarly, with the same radius, keeping the compass at C cut the arc drawn in the previous step.

The line joining the intersection of these arcs is the perpendicular bisector of BC.

4. Construct the bisector of 75 deg.

5. The point where the angular bisector and perpendicular bisector meet is the point M.

6. BMC is 106 deg.

Construct a triangle $XYZ$ in which $XY = 5 cm, YZ = 5.5 cm$ and $\angle XYZ = 100^{\circ}$

(i) Draw a line segment which is sufficiently long using ruler.

(ii) Locate points

$X$ and

$Y$ on it such that

$XY = 5cm$ .

(iii) At Y, construct a line segment YW, sufficiently large, such that

$∠XYZ = 100˚$ ; use protractor to measure

$100˚$

(iv) With Y as centre and radius 5.5 cm, draw the line cutting YW at Z; join

$XZ$ .

$\Rightarrow$ Then

$XYZ$ is the required triangle.

Construct a triangle $ABC$ in which $AB = 5 cm$ and $BC = 4.6 cm$ and $AC = 3.7 cm$

(i) Draw a line segment which is sufficiently long using ruler.
(ii) Locate points

$A$ and

$B$ on it such that

$AB = 5cm$ .
(iii) With

$A$ as centre and radius

$4.6cm$ , draw an arc(see figure)
(iv) With

$B$ as centre and radius

$3.7cm$ , draw another arc cutting the previous arc at

$C$ .
(v) Join

$AC$ and

$BC$
Then

$ABC$ is the required triangle.

Construct a right-angled triangle whose base is $12cm$ and the sum of its hypotenuse and another side is $18cm$ .

Let triangle be

$\triangle ABC$ base

$BC = 12 cm, CB = 90^o$ and

$AB+BC=18cm$

draw base

$BC = 12 cm$ and at point B make a ray

$BX$ such that

$\angle B = 90^o$

Cut a line segment

$BD$ equal to

$AB+AC$ from ray

$BX$ .

Join

$DC$ draw perpendicular bisector

$PQ$ of the line

$DC$ .

Let

$PQ$ intersect

$BD$ a point

$A$ . Join

$AC$

Construct an isosceles triangle whose perimeter is $12\ \text{cm}$ and altitude $4\ \text{cm}$ and the sides of the triangle are in ratio $3:4:5.$

Let the triangle be $ABC$ with base $BC$ and sides $AB$ and $AC$ .

Data:

Perimeter of a triangle is $12\ \text{cm}$
Ratio is $3:4:5$
We know, Perimeter, $P$ = sum of three sides of a triangle

$P=AB + BC + AC$

Therefore, $12 = 3 + 4 + 5$

$AB =\dfrac{ 3}{12} \times 12 = 4\ \text{cm}$

$BC = \dfrac{4}{12} \times 12 = 3\ \text{cm}$

$AC = \dfrac{5}{12} \times 12 = 5\ \text{cm}$

(i) Draw a line segment which is sufficiently long using ruler.

(ii) Locate points $B$ and $C$ on it such that $BC = 3\ \text{cm}.$

(iii) With $B$ as centre and radius $4\ \text{cm}$ , draw an arc(see figure).

(iv) With $C$ as centre and radius $5\ \text{cm}$ , draw another arc cutting the previous arc at $C$ .

(v) Join $AC$ and $AB$ .

Then

$\triangle ABC$ is the required triangle.

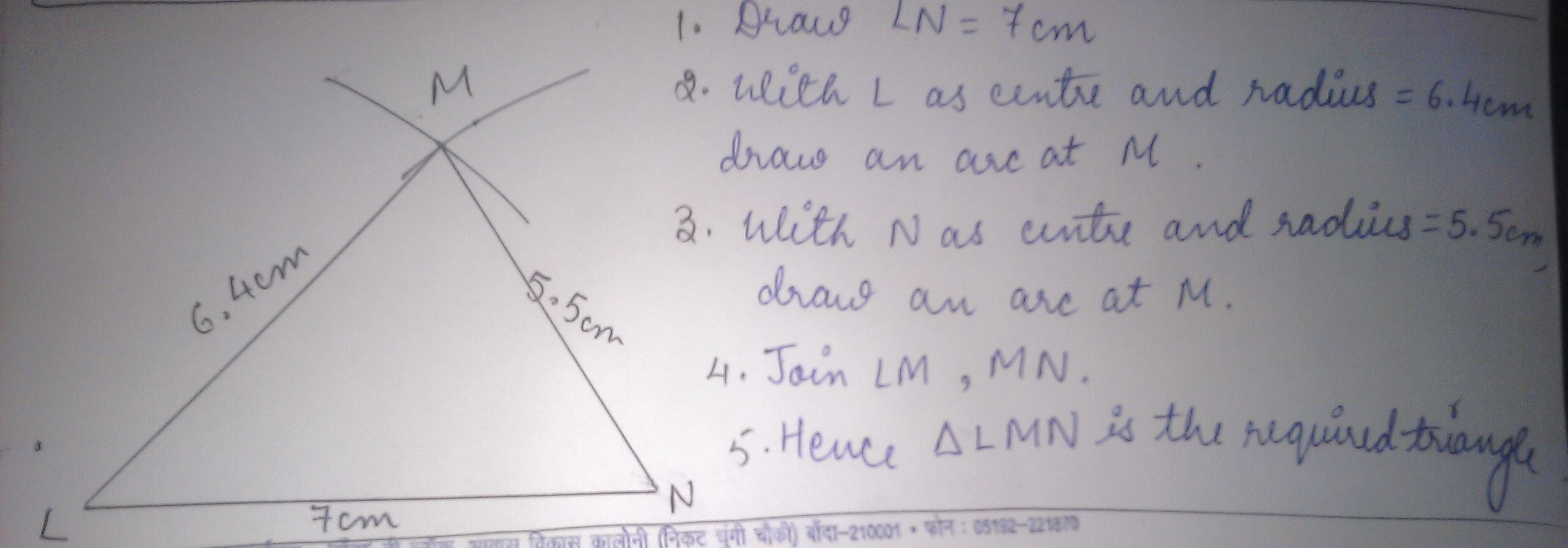
Construct $\Delta LMN$ in which LN=7 cm, NM=5.5 cm, LM=6.4 cm.

$1$ . Draw LN

$=7$ cm.

$2$ . With L as centre and radius

$=6.4$ cm, draw an arc at M.

$3$ . With N as centre and radius

$=5.5$ cm, draw an arc at M.

$4$ . Join LM, MN.

$5$ . Hence

$\Delta$ LMN is the required triangle.

1169502_1281548_ans_b17b694efc5d4018899f7734eacf736b.jpg

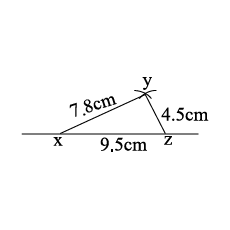
Construct a triangle $XYZ$ in which $XY = 7.8 \text{ cm}, YZ = 4.5 \text{ cm}$ and $XZ = 9.5 \text{ cm}$

Draw a line segment that is sufficiently long using a ruler.
Locate points $X$ and $Z$ on it such that $XZ = 9.5\text{ cm}$ .
With $X$ as center and radius $7.8\text{ cm}$ , draw an arc.
With $Z$ as centre and radius $4.5\text{ cm}$ , draw another arc cutting the previous arc at $C$ .
Join $XY$ and $YZ$

Then

$\triangle XYZ$ is the required triangle.

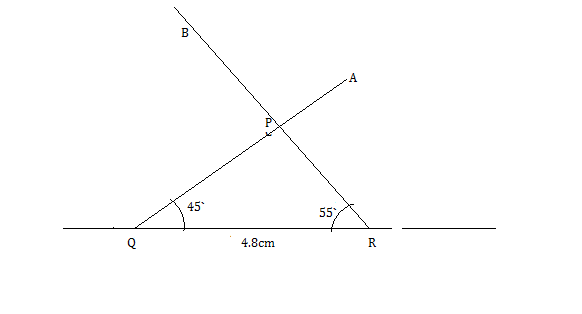
Construct a triangle $PQR$ in which $QR = 4.8 cm, \angle Q = 45^{\circ}$ and $\angle R = 55^{\circ}$

Steps of Construction:
(i) Draw a line segment which is sufficiently long using ruler.
(ii) Locate points

$Q$ and

$R$ on it such that

$QR = 4.8 cm$ .
(iii) Construct a line segment

$QA$ , sufficiently large, such that

$∠Q = 45˚$ ;Construct a line segment

$RB$ , sufficiently large, such that

$∠R = 55˚$ , use protractor to measure
(iv) Extend

$QA$ and

$RB$ to intersect at

$P$ .
Then

$PQR$ is the required triangle

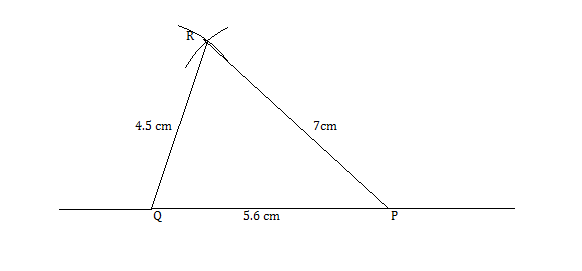
Construct a triangle $PQR$ , given that $PQ = 5.6 \text{ cm, PR = 7 cm}$ and $QR = 4.5 \text{ cm}$

(i) Draw a line segment that is sufficiently long using a ruler.

(ii) Locate points

$P$ and

$Q$ on it such that

$PQ = 5.6\text{ cm}$ .

(iii) With P as centre and radius

$7\text{ cm}$ , draw an arc(see figure)

(iv) With Q as centre and radius

$4.5\text{ cm}$ , draw another arc cutting the previous arc at

$R$ .

(v) Join

$PR$ and

$QR$

Then

$PQR$ is the required triangle

Construct a triangle $PQR$ in which $PQ = 5.4 cm, QR = 5.5 cm$ and $\angle PQR = 55^{\circ}$

Steps of Construction:

(i) Draw a line segment which is sufficiently long using ruler.

(ii) Locate points

$P$ and

$Q$ on it such that

$PQ = 5.4cm$ .

(iii) At

$Q$ , construct an angle

$55^{o}$ using protractor.

(iv) With

$Q$ as centre and radius

$5.5\;\text{cm}$ , draw an arc cutting

$QS$ at

$R$ ; join

$PR$ .

Thus

$PQR$ is the required triangle.

Construct a triangle $LMN$ in which $LM = 7.8 cm, MN = 6.3 cm$ and $\angle LMN = 45^{\circ}$ .

Steps of Construction:

(i) Draw a line segment that is sufficiently long using a ruler.
(ii) Locate points M and N on it such that

$MN = 6.3 cm$ .
(iii) At M, construct a line segment MO, sufficiently large, such that

$∠OMN = 45˚$ using ruler and protractor.
(iv) With

$M$ as centre and radius

$7.8 cm$ , draw the arc cutting

$MO$ at

$L$ and join

$LN$ .

$\therefore$

$\triangle LMN$ the required triangle

Construct a triangle $ABC$ in which $AB = 6.5 cm, \angle A = 45^{\circ}$ and $\angle B = 60^{\circ}$

Steps of Construction:
i) Draw a line segment that is sufficiently long using a ruler.

(ii) Locate points A and B on it such that

$AB = 6.5 cm$ .

(iii) Construct a line segment AD, sufficiently large, such that

$\angle A = 45˚$
Construct a line segment BE, sufficiently large, such that

$∠B= 60˚$ use a protractor to measure

(iv) Extend

$AD$ and

$BE$ to intersect at

$C$ .

$\Rightarrow$

$ABC$ is the required triangle

Construct a right angle triangle $PQR$ in which $\angle R = 90^{\circ}, PQ = 4 cm$ and $QR = 3 cm$

Steps of construction:
1.Draw a line segment

$XY$
2.Locate

$Q, R$ on

$XY$ such that

$QR = 3 cm$
3.Construct a line segment

$SR$ , sufficiently large, such that

$\angle R = 90^\circ$
4.With

$Q$ as centre and radius

$4 cm$ draw an arc, cutting

$RS$ at

$P$ ; join PR.
Then,

$PQR$ is the required triangle.

Construct a triangle $ABC$ in which $AB = 5cm, BC = 4.3 cm$ and $AC = 4 cm$

We follow several steps in the construction:
1. Draw a ling segment which is sufficiently long using ruler.

2. Locate points A and B on it such that

$AB = 5 cm$ .

3. With A as centre and radius

$4 cm$ , draw an arc.

4. With B as centre and radius

$4.3 cm$ , draw another arc cutting the previous arc at C.

5. Join

$AC$ and

$BC$

Then

$ABC$ is the required triangle.

Construct a right angle triangle $ABC$ in which $\angle B = 90^{\circ}, BC = 4 cm$ and $AC = 5 cm$

Steps of construction:
(1) Draw a line segment

$XY$ .

(2) Locate

$B$ ,

$C$ on

$XY$ such that

$BC = 4 cm$

(3)Construct a line segment

$BD$ , sufficiently large, such that

$∠B = 90°$

(4)With

$C$ as centre and radius

$5 cm$ draw an arc, cutting

$BD$ at

$A$ ; join

$AC$ .

Then,

$ABC$ is the required triangle.

Construct a triangle $ABC$ in which $AB + AC = 5.6\ cm, BC = 4.5\ cm$ and $\angle B = 45^{\circ}$

1. Construct a line segment

$BC$ of

$4.5cm$

2. Construct a

$45^o$ angle at

$B$

3. Take the length of

$PB$ as

$5.6cm$ .

4. Join

$PC$

5. Construct a bisector at

$PC$ . The line will meet

$BP$ at point

$A$ . Join

$AC$

We get the required triangle.

Examine whether you can construct $\Delta D E F$ such that $\mathrm { EF } = 7.2\ \mathrm { cm } ,\ \mathrm { m } \angle \mathrm { E } = 110 ^ { \circ }$ and $\mathrm{m} \angle F = 80 ^ { \circ } .$ Justify your answer.

$\triangle DEF:$

$\angle E=110^{\circ},\angle F=80^{\circ},\angle EF=7.2\ \text{cm}$

$\angle E+\angle F+\angle D=180^{\circ}$

$\angle D=180^{\circ}-110^{\circ}-80^{\circ}$

$=-10^{\circ}$

As angle cannot be negative, so this

$\triangle$ can not be constructed.

Construct a triangle $XYZ$ in which $XY = 4.5 cm$ and $\angle X = 100^{\circ}$ and $\angle Y = 50^{\circ}$ using ruler and protractor.

Steps of construction
1. Draw a line segment that is sufficiently long enough using a ruler.

2. Locate the points

$X$ and

$Y$ on it such that

$XY = 4.5 cm$ .

3. Construct a ling segment

$XP$ such that

$\angle PXY = 100^{\circ}$ using protractor and ruler.

4. Similarly, construct a line segment

$YQ$ such that

$\angle XYQ = 50^{\circ}$ .

5. Extend

$XP$ and

$YQ$ to intersect at

$Z$ .

Then

$XYZ$ is the required triangle.

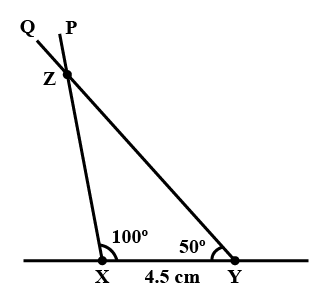
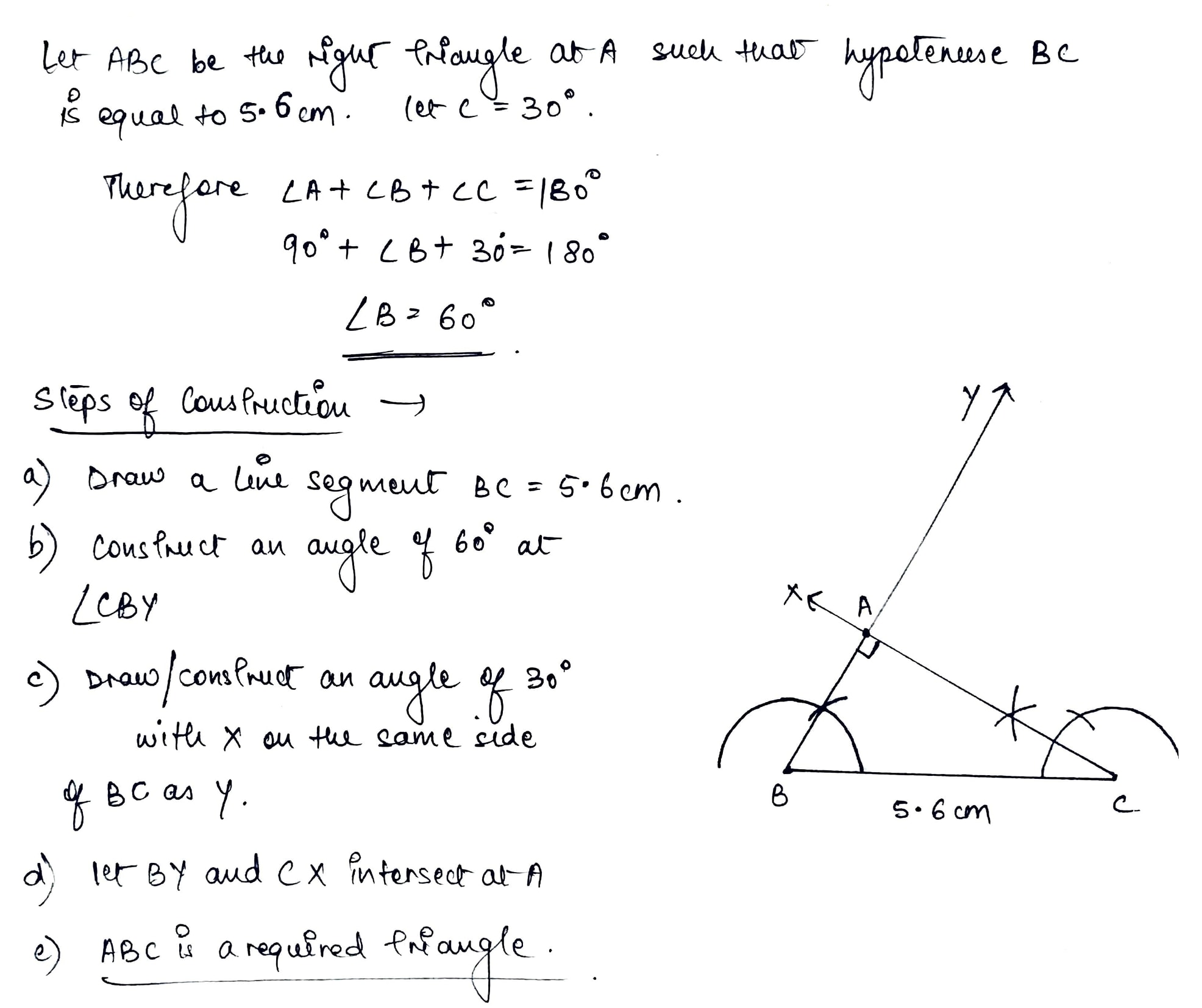
Construct a triangle $ABC$ in which $BC = 5.2\ cm, \ \angle B = 35^{\circ}$ and $\angle C = 80^{\circ}$ .

Steps of Construction:
(i) Draw a line segment which is sufficiently long using ruler.
(ii) Locate points

$B$ and

$C$ on it such that

$BC = 5.2 \ cm$ .
(iii) Construct a line segment

$BD$ , sufficiently large, such that

$∠B = 35^o$ ;
Construct a line segment

$CE$ , sufficiently large, such that

$∠C = 80^o$ , use protractor to measure the angles.
(iv) Extend

$BD$ and

$CE$ to intersect at

$A$ .

Hence,

$\Delta ABC$ is the required triangle.

Construct a right angled triangle $ABC$ in which $\angle B = 90^{\circ}, AB = 5 cm$ and $AC = 7 cm$

Steps Of Construction:
1. Locate

$A, B$ on a straight line such that

$AB = 5 cm$

3. Construct a line segment

$BD$ , sufficiently large, such that

$\angle B$ =

$90^\circ$

4. With

$A$ as centre and radius

$7 cm$ draw an arc, cutting

$BD$ at

$C$ ; join

$AC$ .

Then,

$ABC$ is the required right angled triangle.

Construct a triangle $PQR$ , given that $PQ = 4 cm, QR = 5.2 cm$ and $\angle Q = 60^{\circ}$

Steps of Construction:

(i) Draw a line segment that is sufficiently long using a ruler.

(ii) Locate points

$Q$ and

$R$ on it such that

$QR = 5.2cm$ .

(iii) At

$Q$ , construct a line segment

$QM$ , sufficiently large, such that

$\angle MQR$ at

$60^\circ$ use protractor to measure

$60^\circ$

(iv) With

$Q$ as centre and radius

$4cm$ , draw the line cutting

$QM$ at

$P$ , join

$PR$ .

Then

$PQR$ is the required triangle.

Construct a triangle $ABC$ in which $BC = 6 cm, \angle{B} = 30^{\circ}$ and $\angle C = 125^{\circ}$

Steps of Construction:
(i) Draw a line segment which is sufficiently long using ruler.
(ii) Locate points

$B$ and

$C$ on it such that

$BC = 6 cm$ .
(iii) Construct a line segment

$BD$ , sufficiently large, such that

$∠B = 30˚$ ;
Construct a line segment

$CE$ , sufficiently large, such that

$∠R = 125˚$ , use protractor to measure
(iv) Extend

$BD$ and

$CE$ to intersect at

$A$ .
Then

$ABC$ is the required triangle.

Draw a triangle with sides 5 cm, 6 cm and 6 cm. Draw a square having the same area as the triangle.

(A)
Steps of Construction for triangle:
1. Draw a line segment BC of length 5cm.
2. Measure distance of 6 cm in compass. Taking B as centre draw an arc.
3. Taking C as centre with same distance and draw another arc.
4. Both the arcs intersect each other; name that point of intersection as A.
5. Required triangle ABC is drawn.

Area of

$\Delta$ ABC can be calculated using Heron's formula.

$s=\dfrac{5+6+6}{2}$

$=\dfrac{17}{2}cm$

Therefore, Area

$\triangle ABC=\sqrt{\dfrac{17}{2}(\dfrac{17}{2}-5)(\dfrac{17}{2}-6)(\dfrac{17}{2}-6)}$

$=\sqrt{{\dfrac{17}{2}\times \dfrac{7}{2}}\times \dfrac{5}{2}\times \dfrac{5}{2}}$

$=13.6 \,cm^2$

Therefore, Area of Square

$=(side)^2$

$\Rightarrow 13.63 = (side)^2$

$\therefore side = 3.7 cm$

(B)
Now, Steps of Construction for square:

1.Draw segment BC of length 3.7cm.
2.Draw a line perpendicular to BC through B.
Measure a distance of 3.7 cm in compass and cut this line at point A.
3.Draw a line perpendicular to BC through C.
Measure a distance of 3.7 cm in compass and cut this line at point D.
4.Join AB, CD, and AD.
5.Required square ABCD is drawn.

Draw an equilateral triangle of sides 5 cm. Construct a square having the same area as that of this triangle.

Steps of construction:
1. Draw equilateral

$\Delta$ ABC according to the given measures.
2. Draw the perpendicular CD from C to AB.
Now CD is the height

$h = \sqrt{5^2 - \left(\cfrac52\right)^2} = \cfrac{5\sqrt3}2 = 4.3\ cm$ of the triangle. Draw perpendicular bisector of CD to get DE = h/2.
Area of

$\Delta ABC = \dfrac{1}{2} \times AB \times h = AB \times \dfrac{h}{2}$
To draw a square of area

$AB \times (h/2)$ , the side of the square should be

$\sqrt{AB \times \dfrac{h}{2}} = \cfrac{5(3)^{\frac14}}{2} = 3.3\ cm$ .

Steps of construction:
1. Draw

$PQ = AB + \cfrac h2 = 3.3\ cm$ .

2. At the point

$Q$ and

$P$ , draw angles of

$90˚$ on the same side of

$PQ$ .

3. Cut those perpendicular lines at

$3.3 \ cm$ at

$R$ and

$S$ .

4. Join

$RS$ .

5. Area of square

$PQ\times QR = 3.3\times3.3\ {cm}^2 \approx 10.89\ {cm}^2$

Use ruler and compass only for the following question. All construction lines and arcs must be clearly shown.
Construct a $\triangle ABC$ in which $BC = 6.5\ cm, \angle ABC = 60^{\circ}, AB = 5\ cm$ . Construct a locus of points $l_1$ at a distance of $3.5\ cm$ from $A$ . Also, construct a locus of points $l_2$ which is equidistant from $AC$ and $BC$ . Let $l_1$ intersect $l_2$ in two points $X$ and $Y$ . Measure $XY$ .

1. Draw base

$BC$ of length

$6.5\ cm$ . Make an angle of

$60^\circ$ from

$B$ .

2. Mark an arc of radius

$5\ cm$ from

$B$ on the

$60^\circ$ angle created and name it as

$A$ . Join

$A-C$ .

$\triangle ABC$ is the required triangle.

3. Draw a circle with centre as

$A$ and radius

$3.5\ cm$ . This is the locus of the points equidistant from

$A$ at a distance of

$3.5\ cm$ .

4. Draw the angle bisector of

$\angle ACB$ which will be the locus of points equidistant from

$AC$ and

$BC$ ,

5. Measure the length of

$XY$ which comes out to be

$5\ cm$ .

Construct a $\triangle ABC$ in which $BC=3.6\ cm, AB=5\ cm$ and $AC=5.4\ cm$ . Draw the perpendicular bisector of the side $BC$ .

1152579_1143885_ans_702bd850fd554bfc916083632a725076.png

Draw the right triangle whose sides are $3\ cm, 4\ cm$ and $5\ cm$ and construct its centroid

$\text{Step }1$ : Draw line

$BC$ of

$4cm$ .

$\text{Step }2$ : Draw

$90°$ at B.

$\text{Step }3$ : Cut

$3cm$ on line of

$90°$ from

$B$ .

$\text{Step }4$ : Name it as A.join a with C.where

$AC=5cm$

$\text{Step }4$ : Take midpoint of all sides

$AB,BC,CA$

$\text{Step }5$ : Draw line from

$A,B,C$ to mid point of opposite line .

$\text{Step }6$ : Cutting point of all

$three$ lines are known a centroid.

1014601_619514_ans_d6ae7ea58d7548d7b2d769041c83b833.png

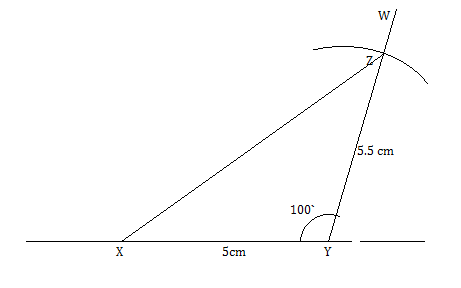
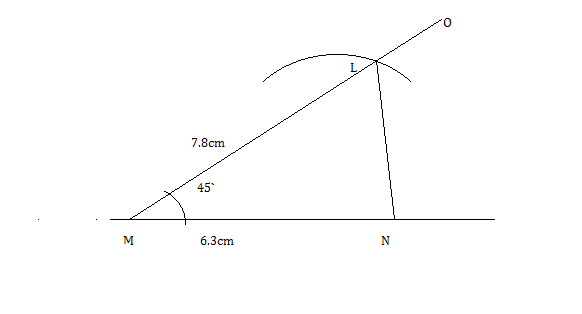
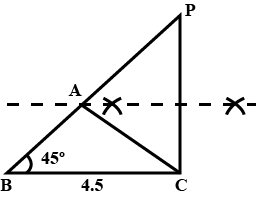
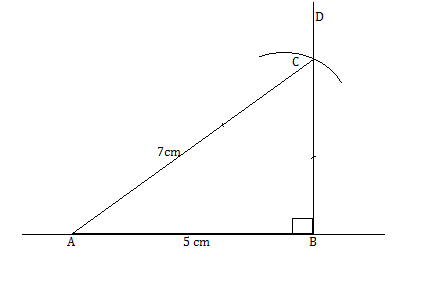
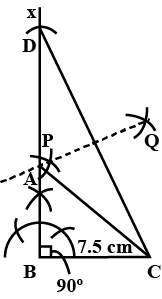
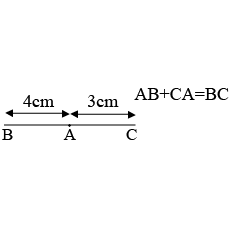
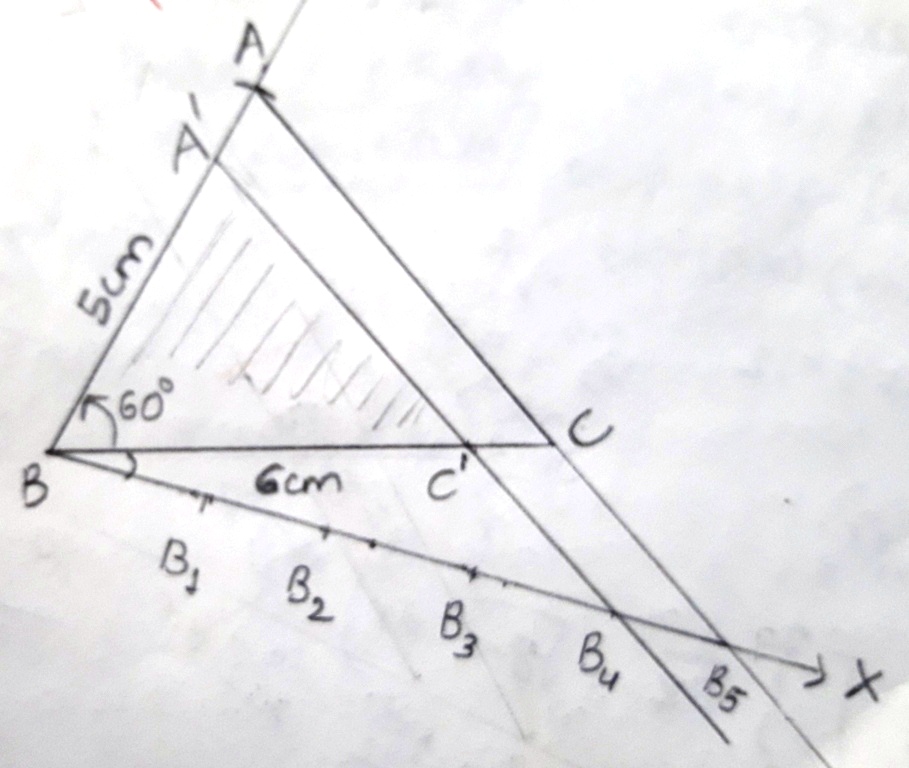
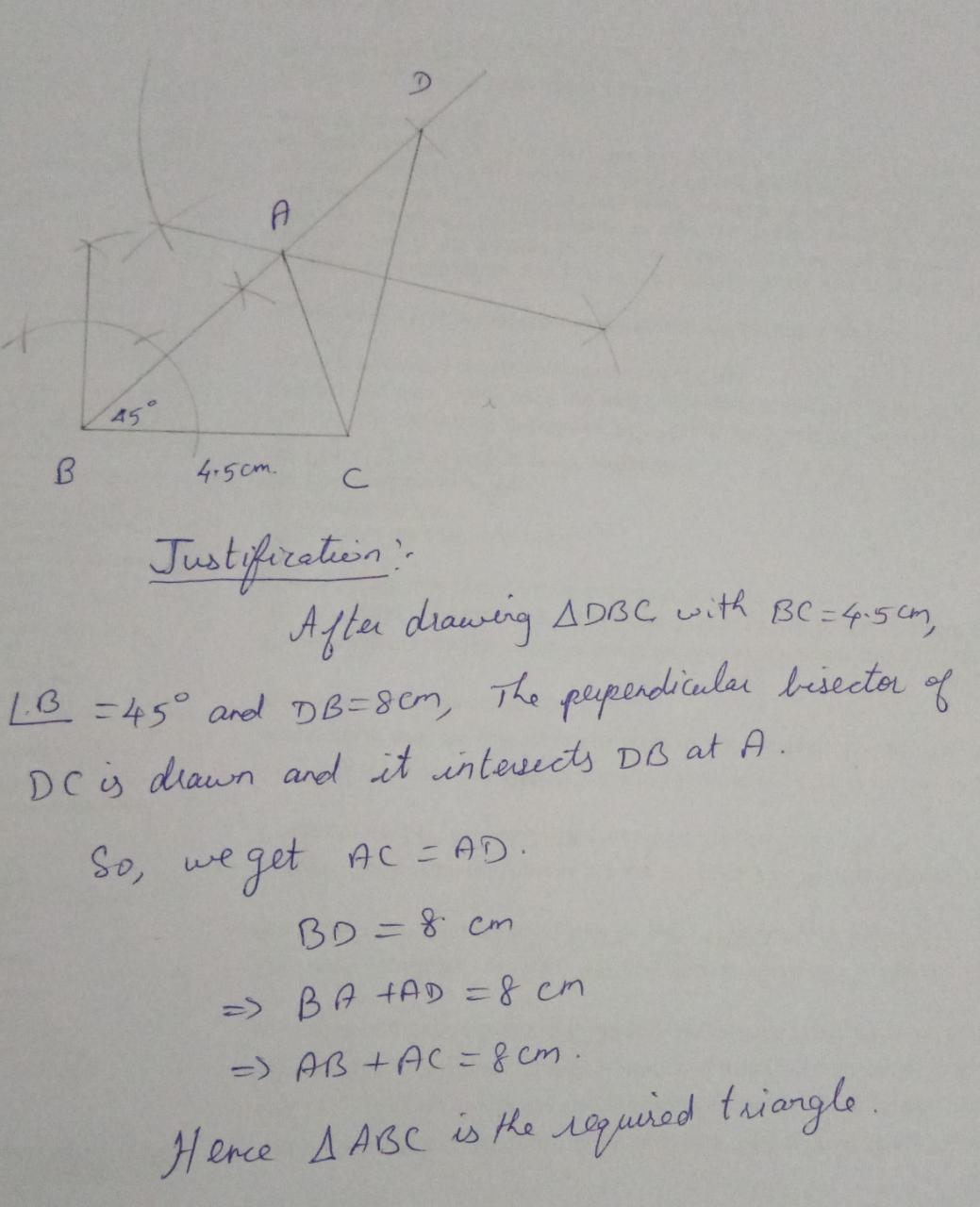
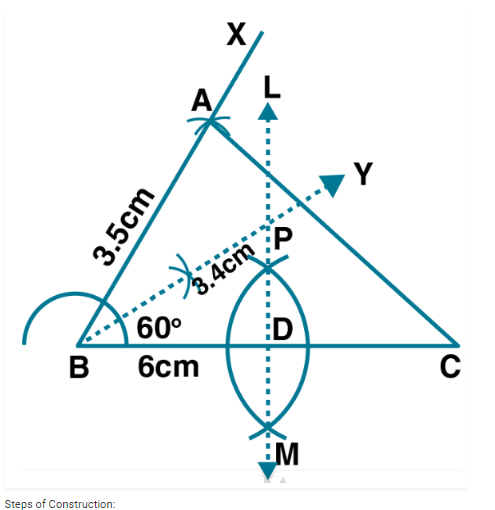
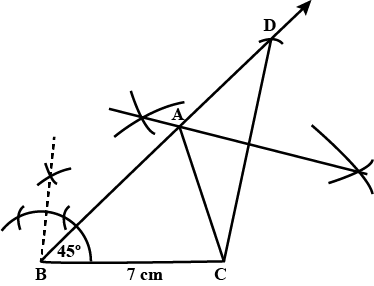
Construct $\Delta ABC$ in which $BC = 8cm$ , $\angle B=45^o$ and $AB -AC=3.5$ cm.

R.E.F image

Construct a triangle ABC in Which

$BC = 8\,cm,\angle B = 45^{\circ}$ and

$AB-AC = 3.5$

cm.

Solution:

Given: In

$\angle ABC, BC = 8\,cm, \angle B = 45^{\circ}$ and

$AB -AC = 3.5\,cm$ .

Required: To construct the triangle ABC.

Steps of construction:

1. Draw the base

$BC = 8\,cm.$

2. At the point B make an angle

$CBX = 45^{\circ}.$

2. At the point B make an angle

$CBX = 45^{\circ}.$

3. Cut the line segment BD equal to

$3.5\,cm$ from the ray BX.

4. Join DC.

5. Draw the perpendicular bisector, say

$PQ$ of

$DC$ .

6. Let in intersect BX at a point A.

7. Join AC.

Then ABC is the required triangle.

729757_569002_ans_af700b0ae38647748a1398dd3c9c9222.jfif

Construct a right triangle whose base is 7.5 cm. and sum of its hypotenuse and other side is 15 cm.

Cinstruction :

Step 1 : Draw the base

$BC$ of length

$7.5$ cms.

Step 2 : At the point B make an angle of

$90$ degrees.

Step 3 : Cut a line segment

$BD$ of length

$15$ cms from the ray

$BX$ .

Step 4 : Join

$DC$

Step 5 : Draw perpendicular bisector

$PQ$ of

$CD$ to intersect

$BD$ at point A.

Step 6: Join

$AC$ .

Thus, triangle

$ABC$ is the required triangle.

1065650_569004_ans_ed6111b137e847c1b733b1e405916a28.png

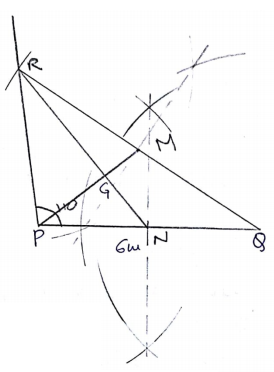
Draw the $\triangle PQR$ , where $PQ = 6\ cm, \angle P = 110^{\circ}$ and $QR = 8\ cm$ and construct its centroid

$1)$ Draw a line

$PQ=6\ cm$

$2)$ Male angle of

$110°$ at

$P$ .

$3)$ Take an arc of

$8cm$ from

$Q$ & cut at

$R$ .

$4)$ Draw

$RQ$ , then we get

$PQR$ triangle.

$5)$ Find medians of triangle from all vertices.

$6)$ Cutting point of medians is centroid.

1015463_619516_ans_6c64ba9699964fd5acac52b0eedb40fa.png

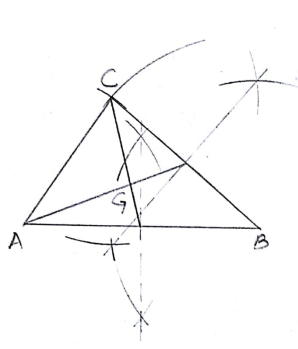
Construct the $\triangle ABC$ such that $AB = 6\ cm, BC = 5\ cm$ and $AC = 4\ cm$ and locate its centroid

$\text{Step }1$ : Draw triangle of

$AB=6cm, BC=5cm, AC=4cm$

$\text{Step }2$ : Find mid-point of all side. Draw line vertex of the mid[point of all side.

$\text{Step }3$ : Cutting point all line is known as centroid of triangle.

1014493_619506_ans_cb9ef664eb914403b769ef55710c48b6.png

Construct a $\triangle{ABC}$ such that $AB=6$ cm, $\angle{C}={40}^{o}$ and the altitude from $C$ to $AB$ is of length $4.2$ cm.

Construction:
(1) Draw a line segment

$AB=6$ cm
(2) Draw

$AX$ such that

$\angle{BAX}={40}^{o}$
(3) Draw the perpendicular bisector of

$AB$ intersections

$AY$ at

$O$ and

$AB$ at

$M$ .
(5) Draw a circle with centre as

$O$ and radius as

$OA$ .
(6) Mark a point

$H$ on

$OM$ such that

$MH=4.2$ cm
(7) Draw

$CH{C}^{1}$ parallel to

$AB$ meeting the circle at

$C$ and

${C}^{1}$ .
(8) Complete the triangle

$ABC$ which is required triangle.

Construct $\Delta ABC$ in which AB = 4 cm, BC = 7 cm and CA = 3 cm. Which type of triangle is this?

Given data

$AB=4$ cm,

$BC=7$ cm,

$CA=3$ cm

It is clear that

$AB+CA=BC$

So,

$B$ ,

$A$ and

$C$ form a straight line.

1180035_705203_ans_8cd5ad4e642c4081883877d9085896fa.png

Construct a triangle $ABC$ , in which $AB = 5.5 cm, AC = 6.5 cm$ and $\angle BAC = 70^{\circ}$ .
If the stpes of construction are given as below the answer the following question:
Which is the last step of construction?
1) At $A$ , construct a line segment $AE$ , sufficiently large, such that $\angle BAC$ at $70^\circ$ , use protractor to measure $70^\circ$
2) Draw a line segment which is sufficiently long using ruler.
3) With $A$ as centre and radius $6.5cm$ , draw the line cutting $AE$ at C, join $BC$ , then $ABC$ is the required triangle.
4) Locate points $A$ and $B$ on it such that $AB = 5.5cm$ .

Below are the correct steps.

1. Draw a line segment which is sufficiently long using ruler.
2.Locate points

$A$ and

$B$ on it such that

$AB=5.5 \ cm$

3.At

$A$ construct a line segment

$AE$ , sufficiently large, such that

$\angle BAC=70^\circ$ , use protractor to measure 70°.

4. With

$A$ as centre and radius

$6.5 \ cm$ draw the line cutting

$AE$ at

$C$ , join

$BC$ then

$ABC$ is the required triangle.

Hence the answer is 3.

Draw a line $EF$ take a point $G$ above $EF$ , draw a line $AB$ through $G$ such that $AB || EF$ .

1470858_1189235_ans_2f41814ed7ed4928b581519ca422a00b.jpg

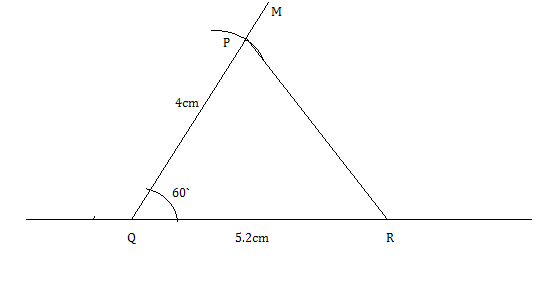
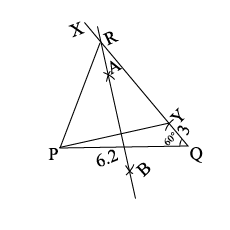
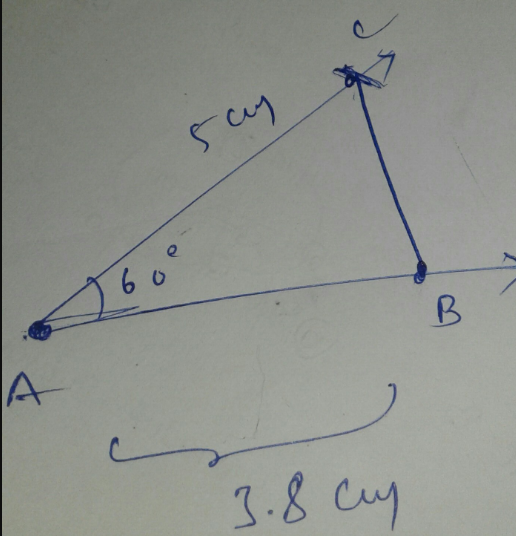
Construct a $\triangle PQR$ in which $PQ = 6.2$ cm, $\angle Q = 60^{o}$ and $RQ - PR = 3$ cm.

Given

$PQ=6.2 \text{ cm}$ ,

$\angle Q={ 60 }^{ \circ }$ &

$RQ-PR=3 \text{ cm}$

1) Draw

$PQ$ of length

$6.2 \text{ cm}$ using scale.

2) At point

$Q$ , draw

$\angle Q={ 60 }^{ \circ }$ using protractor. Let the ray be

$QX$ .

3) Cut the line segment

$QY = 3 \text{ cm}$ (equal to

$RQ-PR=3\text{ cm}$ ) on line

$QX$ .

5) Join

$PY$ and draw a perpendicular bisector

$AB$ of

$PY$ which cuts the line

$QX$ at point

$R$ .

6) Join

$P$ and

$R$

Now,

$\triangle PQR$ is the required triangle.

1013349_880391_ans_9e547f97c6134c11a7d372399a5dadcf.png

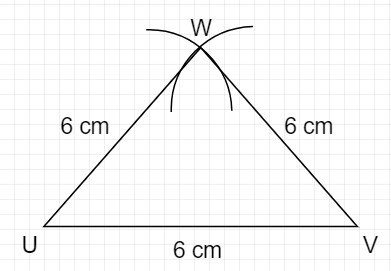
Construct $\triangle UVW$ with $UV =6\ cm, \, VW =6\,cm$ and $UW=6\,cm.$

Given:

$UV=6\ cm,$

$VW=6\ cm$ and,

$UW=6\ cm$

Steps of construction of a triangle whose lengths of three sides are given:

(i) Draw a line segment

$UV=6\,cm$

(ii) With

$V$ as centre and radius

$6\,cm$ draw an arc.

(iii) With

$U$ as centre and radius

$6\,cm$ draw an arc cutting the previous arc at

$W$

(iv) join

$VW$ and

$UW$ then

$\Delta WUV$ is the required equilateral triangle.

1081228_721339_ans_21b20985390f4aefb8402c8ea6c37b64.jpg

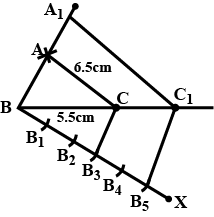
Draw a triangle ABC with $BC=6$ cm, AB $=5$ cm and $\angle$ ABC $=60^o$ . Then construct a triangle whose sides are $\displaystyle\frac{3}{4}$ of the corresponding sides of the $\Delta$ ABC.

The

$\Delta A'BC'$ whose sides are

$\dfrac{3}{4}$ of the corresponding sides of

$\Delta ABC$ can be drawn as follows:

Step 1: Draw a

$\Delta ABC$ with side

$BC=6cm,AB=5cm,\angle ABC=60^\circ$

Step 2: Draw a ray

$BX$ making an acute angle with

$BC$ on the opposite side of vertex

$A$ .

Step 3: Locate

$4$ points,

$B_1,B_2,B_3,B_4$ on line segment

$BX$ .

Step 4: Join

$B_4C$ and draw a line through

$B_3$ , parallel to

$B_4C$ intersecting

$BC$ at

$C'$ .

Step 5: Draw a line through

$C'$ parallel to

$AC$ intersecting

$AB$ at

$A'$ .

The triangle

$A'BC'$ is the required triangle.

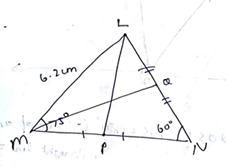
Construct a $\Delta LMN \, MN = 6.2$ cm, $\angle LMN = 75^o \, \angle LNM = 60^o$ and construct any $2$ medias.

Draw a line LM=6.2cm,then take an angle of

${ 75 }^{ \circ }$ and draw a line from M,then take an angle of

$(180-(75+62)={ 45 }^{ \circ })$ from LM and draw a line from L,the point of intersection will be point N.Then simply mark mid points of any two sides and join it with the opposite vertex to get the medians.
1005011_1036468_ans_52ab9718992c4b2b850d966993f332ec.png

1005011_1036468_ans_52ab9718992c4b2b850d966993f332ec.png

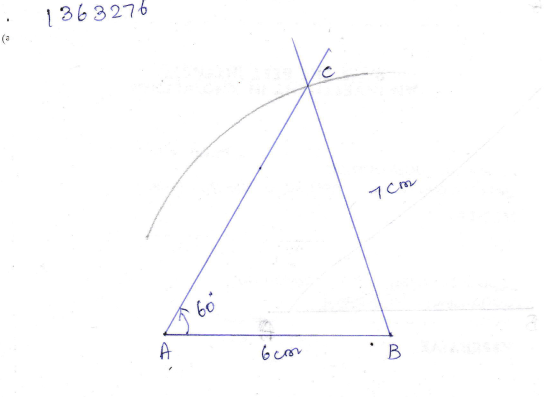
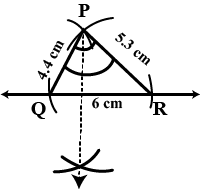
Construct $\triangle ABC$ with $BC=7.5\ cm$ , $AC=5\ cm$ and $m\angle C={60}^{o}$ .

Steps of construction:

(a) Draw a line segment

$BC=7.5cm$

(b) At poin C, draw an angle of 60 with the help of protractor, i.e.

$\angle XCB=60$ .

$C$ as centre and radius

$5cm$ , draw an arc, which cuts

$XC$ at a point

$A$ .

(d) Join

$AB$

It is the required

$\triangle ABC$ .

1026531_1039956_ans_09b35f423ec049e39d58117c07ab4400.png

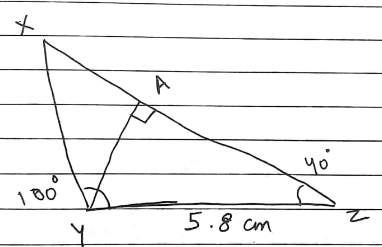
Construct $\triangle ABC$ , given $m\angle A={60}^{o}, m\angle B={30}^{o}$ and $AB=5.8\ cm$ .

1154702_1051632_ans_3d6aa2dabd394af2b96704756cb00f56.jpg

Draw a triangle of 3 , 4 and 6 cm .

Steps of construction:

$(1)$ .Draw

$BC=4cm$ .

$(2)$ . Taking

$B$ as centre cut an arc of length

$6cm$ .

$(3)$ .Again taking

$C$ as centre cut an arc of length

$3cm$ , meeting other arc at

$A$ .

$(4)$ .Join

$AC$ and

$AB$ . Hence

$\Delta ABC$ is required triangle.

1370928_1016959_ans_b32e14a2ef2b4d429f24c97660c80e8d.png

Construct $\triangle DEF$ such that $DE=5\ cm,DF=3\ cm$ and $m\angle EDF=90^{o}$ .

Draw a line segment $DE$ of length $5\ cm.$
Make a perpendicular at point $D$ and extend the line $DX.$
Make an arc at a distance $3\ cm$ from point $D$ intersecting $DX$ at $F.$
Join $F$ to $E.$

$\triangle DEF$ is the required triangle.

990470_1039361_ans_8a3ae8131825433c8dae596ff5d129ad.png

Construct an equilateral triangle of side $5.5\ cm$ .

REF.Image.

Given Side = 5.5 cm

$\rightarrow$ Draw a line segment

$\bar{AB} = 5.5$

$\rightarrow$ Take a as centre and radius

5.5 cm draw an are

$\rightarrow$ take B as centre and radius

5.5 cm draw another are which cuts

first are and mark it as C

$\rightarrow$ Now join AC & BC.

$\therefore$ The required

$\triangle ABC$ is formed

1118012_1039806_ans_e59305c8c25a4ba18ee4ba07b7dc5513.jpg

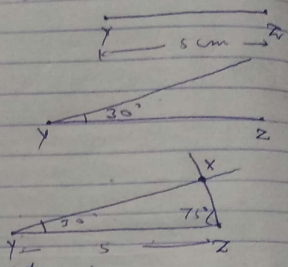
Construct a $\triangle$ STU in which $T = 60^o$ , $U = 70^o$ and $TU = 7.5 cm$ .

$\angle S={ 180 }^{ \circ }-({ 60 }^{ \circ }+{ 70 }^{ \circ })$

$\quad \quad ={ 180 }^{ \circ }-({ 130 }^{ \circ })$

$\quad \quad ={ 50 }^{ \circ }$

For construction:

Draw TU=7.5cm make from T with respect to TU,make from U with respect to

TU,the point where the two lines meet is S.

1004664_1042137_ans_8d9d623a31dd474b8d9424bfc1f0ec8f.png

Construct a $\Delta XYZ$ such that:
$XY=4.5\ \text{cm}$ , $\angle X={60 }^ { \circ }$ and $\angle Y={45 }^ { \circ }$ .

STEPS OF CONTRUCTION:

1. Draw a line $XY$ of $4.5\;{\rm{cm}}$ .

2. Draw a ray $ZX$ making an angle of $60^\circ$ with the line $XY$ .

3. Join $XZ$ .

4. Draw an angle of $45^\circ$ at $Y$ to the point $Z$ . Join $YZ$ .

5. $XYZ$ is the required triangle.

983168_1056892_ans_d4462440d9984fe5977644a842805f2e.PNG

Construct $\triangle LMN$ in which $LM=6\ cm$ , $MN=5\ cm$ and $M=75^ {o}$

1914213_1316205_ans_3c7b554be89f4de99713f032a5e1bbe0.jpeg

Draw a triangle $ABC$ with $BC=6\ cm, AB=5cm$ and $\angle ABC=60^{o}$ then construct a triangle whose sides are $4/5$ of the sides of the $\triangle ABC$ . Justify.

Draw base BC with scale 6cm.

Draw $\angle B=60^{\circ}$

Draw an arc with scale 5cm from B and mark it as A.

Join AC.

$\triangle ABC$ is the required triangle.

Draw any ray BX making an acute angle with BC on the opposite side of vertex A.

Mark 5 points (the greater of 4 and 5 in $\frac{4}{5})$ $B_1,B_2,B_3,B_4,B_5$ on BX so that $B_1B_2=B_2B_3=B_3B_4= B_4B_5$

Join $B_5 C$ and draw another line parallel to $B_5 C$ from $B_4$ to C'

Take it to A and mark it A'.

By construction,

$\dfrac{BC'}{BC}=\dfrac{BB_4}{BB_5}$

SO, $\dfrac{A'B}{AB}=\dfrac{A'C'}{AC}=\dfrac{BC'}{BC}=\dfrac{4}{5}$

Thus, construction is justified.

1121769_1042459_ans_3140d1a22e414690815c474383d3246e.jpg

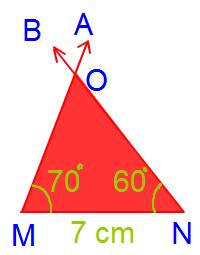
Construct a triangle $\triangle MNO$ where $\angle M =70^{o}, \angle N = 60^{o}$ and side $MN=7 \ cm$ .

Steps of construction :

1) Draw a line segment

$MN = 7 cm$ .

2) Make

$\angle AMN = 70^{o}$ .

3) Make

$\angle BNM = 60^{o}$ .

4) Let

$AM$ and

$BN$ intersect at

$O$ .

Then,

$\triangle MNO$ is the required triangle.

1326328_1052948_ans_370489ad3f7942edac7e3322cc69716d.jpg

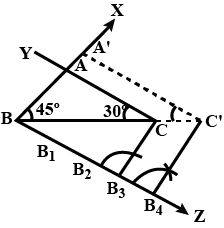
Draw a triangle $ABC$ with side $BC = 7\ cm,\ \angle B = 45^{o},\ \angle A = 105^{o}.$ Then construct a triangle whose side are $\dfrac{4}{3}$ times the corresponding sides of $\triangle ABC.$ Write the construction.

In order to construct

$\triangle ABC$ , we follow the following steps :

$STEP \ I$ Draw

$BC=7\ cm$ .

$STEP \ II$ At

$B$ construct

$\angle CBX=45^{o}$ and at

$C$ construct

$\angle BCY=180^{o}-(45^{o}-105^{o})=30^{o}$

Suppose

$BX$ and

$CY$ intersect at

$A. \triangle ABC$ so obtained is the given triangle.

To construct a triangle similar to

$\triangle ABC$ , we follow the following steps.

$STEP \ I$ Construct an acute angle

$\angle CBZ$ at

$B$ on opposite side of vertex

$A$ of

$\triangle ABC$ .

$STEP \ II$ Mark-off four (greater

$4$ of and

$3$ in

$\dfrac{4}{3}$ ) points

$B_{1},B_{2},B_{3},B_{4}$ on

$BZ$ such that

$BB_{1}=B_{1}B_{2}=B_{2}B_{3}=B_{3}B_{4}$ .

$STEP \ III$ Join

$B_{3}$ (the third point) to

$C$ and draw a line through

$B_{4}C$ parallel to

$B_{3}C$ , intersecting the extended line segment

$BC$ at

$C$ .

$STEP \ IV$ Draw a line through

$C$ parallel to

$CA$ intersecting the extended line segment

$BA$ at

$A$ .

Triangle

$ABC$ so obtained is the required triangle such that

$\dfrac{AB}{AB}=\dfrac{BC}{BC}=\dfrac{AC}{AC}=\dfrac{4}{3}$

1035200_1009828_ans_32c3f408178f4f1f883a7011214fe7fa.png

Try to construct a triangle with $5$ cm, $8$ cm and $1$ cm. Is it possible or not? Why? Give your justification?

$\begin{matrix} AB=5cm \\ BC=8cm \\ CA=1cm \\ If\, \, triangle\, possible, \\ AB+BC>CA \\ BC+CA>AB \\ CA+AB>BC \\ but\, \, here\, \\ CA+AB>BC\, \left[ { \because not\, following\, \, rules\, } \right] \\ 1+5>8\, \, \, \, \, \left[ { \because not\, following\, triangle\, rules\, for\, fermation } \right] \\ \because triangle\, \, not\, possible\, here. \\ \end{matrix}$

$\triangle XYZ$ in which $YZ=5.8cm$ , $\angle={100}^{o}$ , $\angle={40}^{o}$ Draw the perpendicular from $Y$ to $XZ$ .

$\triangle xyz, yz=5.8\ cm,\ \angle y=100^o , \angle z=40^o$

To draw

$y$

$xz$

1379433_1140792_ans_f00a1cb596cc4c118ae2cc9c263439c1.png

A ladder is placed against a vertical tower. If the ladder makes an angle of $30^{\circ}$ with the ground and reaches upto a height of $15 m$ of the tower; find length of the ladder.

${\textbf{Step 1: Draw a rough diagram from the given data.}}$

${\text{Let length of a ladder be}}$ $AB.$

$\angle ABC = {30^\circ }$ ${\text{and length of }}$ $AC = 15\text{ cm}$

${\textbf{Step 2: Use the sine formula to find height of a tower}}{\text{.}}$

${\text{As we know that,}}$

$Sin\theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}}$

$\Rightarrow Sin{30^\circ } = \dfrac{{AC}}{{{\text{AB}}}}$

$\Rightarrow \dfrac{1}{2} = \dfrac{{15}}{{AB}}$

$\Rightarrow AB = 30 \text{ cm}$

${\textbf{Hence, length of a ladder is 30}}$ $\mathbf{cm.}$

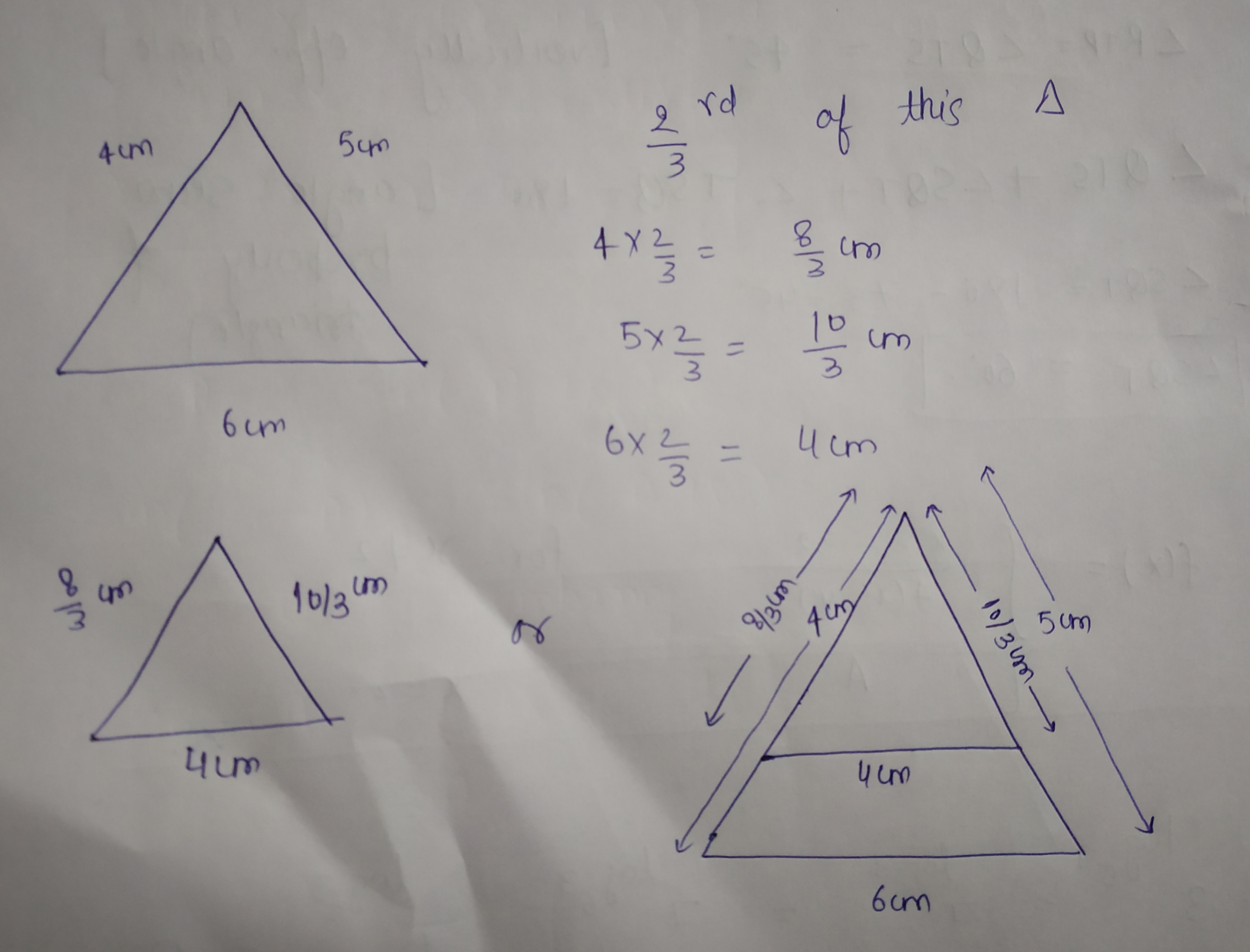
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are $\frac{2}{3}$ of the corresponding sides of the first triangle.

Let's first construct

$\triangle ABC$ with sides

$4cm, 5cm, 6cm$

Steps to draw

$\triangle ABC$

1. Draw base AB of side

$4cm.$

2. With A as centre , and

$5cm$ as radius, draw an arc.

3. With B as centre , and

$6cm$ as radius ,draw an arc.

4. Let C be the point where two points intersect.

5. Join AC and BC

Thus

$\triangle ABC$ is the required triangle

Now, lets make the triangle similar to this named as

$\triangle PQR$ whose sides are

$\dfrac{2}{3}$ of the corresponding sides so the sides will become

$\dfrac{8}{3}cm, \dfrac{10}{3}cm,4cm$

Steps to draw

$\triangle PQR$

1. Draw base PQ of side

$\dfrac{8}{3}cm.$

2. With P as centre , and

$\dfrac{10}{3}cm.$ as radius, draw an arc.

3. With Q as centre , and 4cm as radius ,draw an arc.

4. Let R be the point where two points intersect.

5. Join PQ and PR

Thus

$\triangle PQR$ is the required triangle

1035577_1058318_ans_6a5a1856edb54ff893ea1ebc55506d57.png

Draw a triangle $ABC$ in which $AB = 6\ cm, BC = 4.5\ cm$ and $AC = 5\ cm$ . Draw and label:
(i) the locus of the centres of all circles which touch $AB$ and $AC$ ,
(ii) the locus of the centres of all the circles of radius $2\ cm$ which touch $AB$ .
Hence, construct the circle of radius $2\ cm$ which touches $AB$ and $AC$ .

Steps of Construction:

i) Draw a line segment BC = 4.5 cm

ii) With B as centre and radius 6 cm and C as centre and radius 5 cm, draw arcs which intersect each other at A.

iii) Join AB and AC.

ABC is the required triangle.

iv) Draw the angle bisector of ∠BAC

v) Draw lines parallel to AB and AC at a distance of 2 cm, which intersect each other and AD at O.

vi) With centre O and radius 2 cm, draw a circle which touches AB and AC.

1138890_1136082_ans_65c1afbef4024ca185cb2abc9391f6c3.PNG

Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are $\frac{2}{3}$ of the corresponding sides of the first triangle.

1317501_1063635_ans_71034bbea55d4bc88ab9126e7133cb0b.jpg

The Sides of a triangle are $24cm$ , $18cm$ and $30cm$ . Find:
$1.$ Area of triangle
$2.$ Height of the triangle corresponding to the smallest side.
$3.$ Height of the triangle corresponding to the longest side.

REF. Image.

Consider,

$18^2+24^2$

$=324+576=900=30^2$

i.e.

$18^2+24^2=30^2$

Hence the given triangle is a right-angled triangle.

Hence,

(a) Area of

$\triangle ABC=\dfrac{1}{2}\times 18\times 24cm^2=216cm^2$

(b) Since

$AB\bot BC$ , height corresponding to shortest side

$AB$ , is

$BC=24cm$

$h$ we know, Area of

$\triangle =\dfrac{1}{2}\times base\times height$

$\Rightarrow ar(\triangle ABC)\dfrac{1}{2}\times 30\times h\,\,cm^2$

$\Rightarrow 216cm^2=15h\,\,cm$

$\Rightarrow h=14.4cm$

1054478_1068876_ans_02873927fc634f36be518f8a355fb6ce.png

Is it possible to construct a triangle with lengths of its sides as $4$ cm. $3$ cm and $7$ cm? Give reason for your answer.

Given

$3$ sides are

$4, 3, 7$ cm

We know sum of

$2$ sides of triangle are greater than

$3^{rd}$ side.

But given sides

$4+3=7$

It's not possible to construct a triangle with the given lengths

$(4, 3, 7)$ .

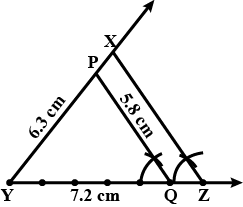
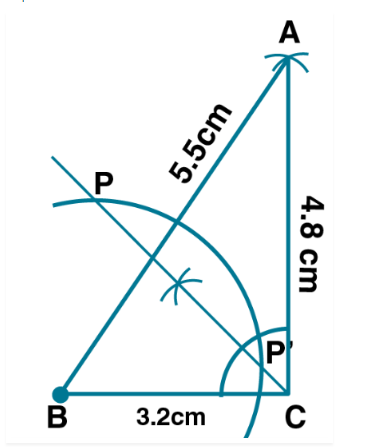
Construct $\Delta \,PYQ$ such that, $PY=6.3$ cm, $YQ = 7.2$ cm, $PQ = 5.8$ cm. If $\dfrac{{YZ}}{{YQ}}\, = \,\dfrac{6}{5}$ , then construct $\Delta \,XYZ$ similar to $\Delta \,PYQ$ .

Step 1 : Draw

$\Delta PYQ$ such that

$PY = 6.3 cm , YQ = 7.2 cm ,$ and

$PQ = 5.8 cm$

Step 2 : Divide segment YQ into

$5$ equal parts

Step 3 : Mark point Z on ray YW such that length of YX is six times of each part of segment YQ.

Step 4 : draw a line parallel to side QP through Z. name the point where the parallel line intersects ray YP as X.

Here,

$\Delta PYQ \sim \Delta XYZ$

1814626_1056522_ans_dbed85458f4944cf9a7ecc8fb2e382b0.png

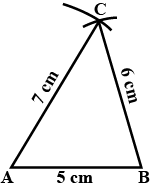
Construct a $\Delta ABC$ in which $AB=5cm,AC=7cm,BC=6cm$ .

Steps for construction:-

Draw a line segment $AB$ of $5 \; cm$ .
Taking $A$ and $B$ as centre, draw arcs of $7 \; cm$ and $6 \; cm$ radius respectively.
Let these arcs intersect each other at point $C$ .
Join $AB$ and $AC$ .
$\triangle{ABC}$ is the required triangle having length of sides as $5 \; cm, \; 7 \; cm$ and $6 \; cm$ respectively.

1163094_1162642_ans_1752f3ed04ce40659983c3f64993da14.png

If we construct a triangle $\Delta ABC$ such that $\angle C=90^o$ and $\angle A=\dfrac{2}{3}\angle B$ . Then find the measures of $\angle A, \angle B$ .

Given for the

$\Delta ABC$ we've

$\angle C=90^o$ .

Then

$\angle A+\angle B=90^o$

or,

$\cfrac{2}{3}\angle B+\angle B=90^o$

or,

$\cfrac{5}{3} \angle B=90^o$

or,

$\angle B=54^o$ .

Then

$\angle A=36^o$ .

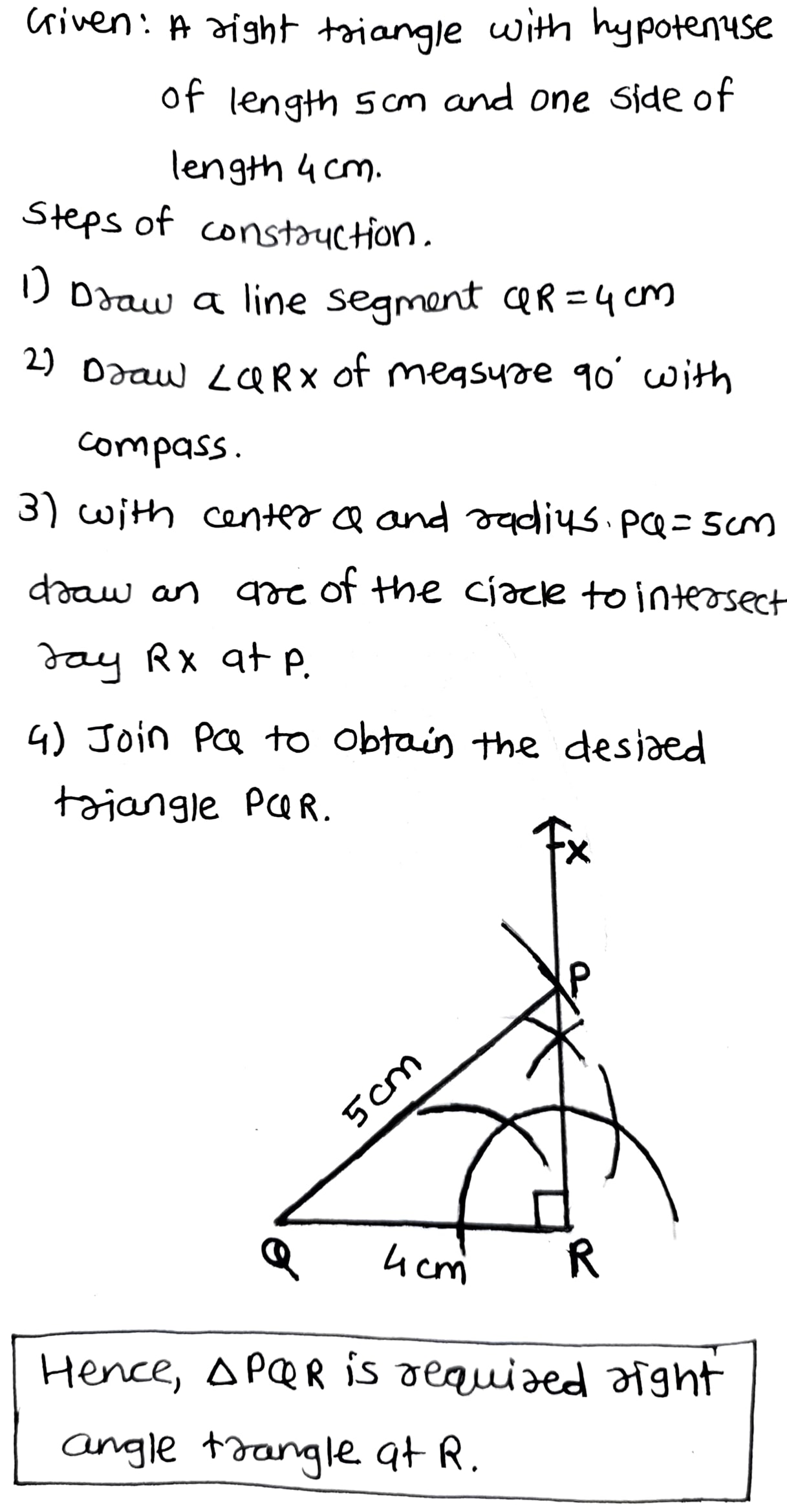
Construct a right-angled triangle $PQR$ in which $QR=4.5\ cm$ and hypotenuse $PR=6\ cm$ .

Steps

i) Draw

$QR=4.5㎝$

ii) From point Q, draw a perpendicular to QR

iii) From R, taking a radius of

$6㎝$ , cut an arc.

iv) Point of intersection of perpendicular line and the arc is P. Join PQ and PR

1166740_1184947_ans_829ef3c9c669456e9fc537c8881e5a84.JPG

Draw a line, say $AB$ take a point $C$ outside it through $C$ , draw a line parallel to $AB$ using ruler and compasses only.

Steps of construction

Given a line AB with Point C outside it.
Mark point D on the line AB. Join CD
With D as center, and any radius, draw an arc intersecting AB at E, and CD at F.
With C as center, and same radius as before, draw an arc intersecting CD at G.
Open a compass to length EF
Now,with G as center, and compass opened the same radius as before, draw an arc intersecting the previous arc at H.
Draw a line m passing through C and H.

Thus m is the line parallel to AB, and passing through point C

$\therefore m||AB$

1090992_1193253_ans_93fadf3825be45e7972440dd1e20b976.png

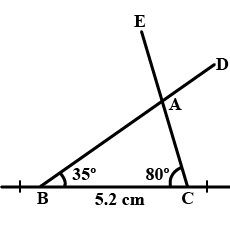
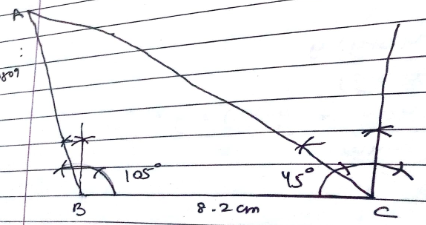
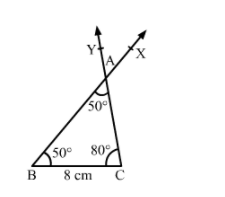
$\triangle BCD$ in which $\angle B={ 105 }^{ o },BC=8.2cm,\angle C={ 45 }^{ o }$ .

1379484_1140809_ans_8f666f7b873c4149a8fb16b48f4ba23a.png

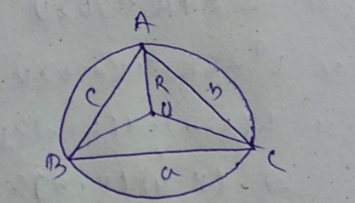
Find the circumradius of $\triangle {ABC}$ , given that $AB=6cm, BC=5.4cm, AC=7cm$ .

$R=\cfrac{abc}{4\Delta}$

$=\cfrac { 6\times 5.4\times 7 }{ 4\sqrt { 9.2(9.2-6)(9.2-5.4)(9.2-7) } }$

$R=3.61cm$

$a=5.4,b=7,c=6cm$

1355471_1197933_ans_eec3a768a1e044f7962a873687926745.PNG

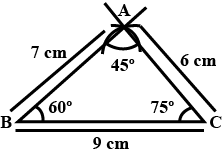
Construct a $\bigtriangleup ABC$ such that AB= 7 cm , AC = 6 cm , BC = 9 cm measure $\angle A, \angle B and \angle C$

We have,

$AB=7\,cm.$

$BC=9\,cm.$

$AC=6\,cm.$

$\angle A,\angle B,\angle C=?$

Construct triangle steps:-

(1):-First draw a line $BC=9\,cm.$

(2):-To the compass, draw an arc $7cm.$ from point $B$ . Then $AB=7\,cm.$

(3):- To the compass, draw an arc $6cm.$ from point $C$ . Then $AC=6{\ }\,cm.$

(4):-Meat the point $A$ to $B$ and $C$ respectively

(5):- measure the angles:

Above diagram

$\angle A = 45^o,\angle B=60^o,\angle C=75^o$

Hence, this is the answer.

1172160_1159076_ans_83544e08892f4a39a3c982817f02d92a.png

Draw a line segment of length $6.3\ cm$ . Draw another line parallel to it at a distance $3\ cm$ from it.

Given that,

Draw a line segment

$=AB=6.3cm$

take compass and take radius

$=3cm$

place the compass at

$F$ and cut it at

$D$ .

place the compass at

$E$ and cut it at

$C$ .

and join

$ABCD$

1198736_1308298_ans_0cf52890797f4ff7a6678e6ef4918eef.png

Construct a right angled triangle whose hypotenuse measure $6.5\ cm$ and one of its acute angle measure $60^{o}$

Steps to construct a right angle triangle whose hypotenuse and an angle are given:

1. Draw a line

$AB=6.5\ cm$

$\Rightarrow AB$ is the hypotenuse.
Hence Let

$\angle C=90^\circ$

2. Take

$B$ as a centre, draw an angle of

$\angle B={60}^{\circ}$ with ruler and compass

We know that

$\angle A+\angle B+\angle C=180^\circ$ [Angle sum property]

$\Rightarrow \angle A=180-60^\circ -90^\circ$

$\Rightarrow \angle A=30^\circ$

4. Take

$A$ as a centre, draw an angle of

$\angle C={30}^{\circ}$ with ruler and compass.

5. Join the angle lines to meet each other at point

$B.$

Thus

$\triangle ABC$ is the required triangle with

$\angle C=90^\circ,\ AB=6.5\ cm$ and

$\angle B=60^\circ$

1349789_1219962_ans_8d3f73fd985f4f449d5ac74847c3dcee.png

Fill in the blank.
The longest side of a right angled triangle is called as ___________.

The longest side of a right angled triangle is called hypotenuse.

Draw a line segment $XY=7\ cm$ . Take a point $A$ outside $XY$ . Draw a line parallel to $XY$ and passing through $A$ .

1. Draw a line

$XY$ of

$7cm$ and then plot a point

$A$ which is outside the line

$XY$ .

2. From the point

$A$ , draw another line which is perpendicular to

$XY$ .

3. Now with

$A$ as centre, draw an arc on

$XY$ as shown in figure.

4. Now by keeping a point on the arc draw another arc as shown fig. and repeat the procedure from another arc also.

5. Now we will get one intersection point, now draw a line parallel to

$XY$ through that intersection point.

1227277_1204887_ans_8a0704fcd0dc4d88a1c36f93703912ff.PNG

Using a ruler and pair of compasses only construct :
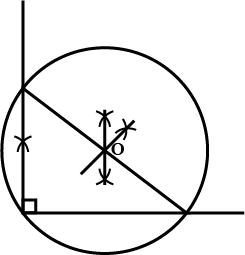
(i)a triangle ABC ,given AB =4 cm, BC=6 CM AND $\angle ABC = {90^ \circ }$
(II)a circle which passes through the points a,b,and c and mark its centre
as o.

Step 1 : Draw a line segment AB = 4 cm and extend till X

Step 2 : Using Compass Draw arc taking B as center intersecting at P & Q on AB & BX

Step 3 : Increasing compass width slightlytaking P as center Draw an arc

Step 4 : Keeping compass width same as in step 3 , draw arcs taking Q as center such that it intersects arc drawn in step 3 at R

Step 5 : Draw a line from B passing through R and taking length = 3 cm and label other end as C

Step 6 : join AC

Step 7 : Cosntrcu perpendicular Bisector of AC at O

Step 8 : Taking O as center and radius = OA = OB = OC , draw an circle

1871338_1205706_ans_3232c8a144a34b079aa06ef6e6fe4d65.png

Construct a $\triangle LMN$ , if $MN=6.3\ cm$ , $LM=3\ cm$ and $\angle L=90^{o}$ .

We need to construct a

$\triangle LMN$ with

$MN=6.3\ cm,\ LM=3\ cm\ and\ \angle L=90^0$

The following are the steps of construction:-

1) Draw a line segment

$LM=3\ cm$ .

2) Draw an arc of any suitable radius taking

$L$ as centre intersecting extended line segment

$LM$ at

$O$ and

$Q$ .

3) Draw arcs taking same radius and

$O,Q$ as centres to intersect at

$P$ . Join and extend

$LP$ to get a line at

${ 90 }^{ \circ }$ to

$LM$ .

4) Now, taking

$M$ as centre and

$6.3\ cm$ radius, draw an arc intersecting line through

$L$ at

$N$ .

Hence,

$\triangle LMN$ is the required triangle, as shown in the figure above.

1145003_1202560_ans_41c695414d454b659711b72cc8956624.png

(a) Construct a right angled $\triangle ABC$ where $\angle ACB={30}^{o}, AC=6\ cm$ and $BC=8\ cm$ .

1379474_1204946_ans_d585880ec3c948f7a99c3794990402f7.png

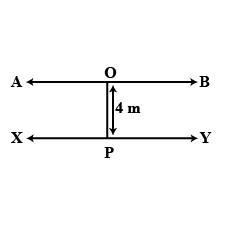
Draw a line $XY$ . Draw a line parallel to $\overline { X Y }$ at a distance of $4$ $m$ from it. (clue: Draw a a perpendicular to $\vec { X Y }$ through a point and continue).

$\begin{array}{l} AB\parallel XY \\ and\, \, OP\bot XY \end{array}$
1380750_1211797_ans_990f0f4c21a84f3a9c2cb158bb003283.png

Write down the method of constructing $\triangle ABC$ in which $AB=3\ cm$ and $BC=4\ cm,CA=3.5\ cm$

1. Draw a line from

$A$ to

$B$

$(AB=3\ cm$ ) using scale.

2. Now take a compass place it at

$B$ extend it with

$4\ cm$ and draw an arc.

3. Similarly place the compass at

$A$ and extend it till

$3.5\ cm$ and draw another arc which cuts previous arc.

4. Mark that point as

$'C'$ .

5. Now join the points

$BC$ and

$AC$ .

$\triangle ABC$ is formed.

Construct $\triangle ABC$ such that $AB=2.5\ cm,BC=6\ cm$ and $AC=6.5\ cm$ . Measure $\angle B$ .

$\rightarrow$ Draw a line segment

$BC = 6 cm$

$\rightarrow$ with 'B' as centre and

$2.5cm$ as radius draw an arc with compass.

$\rightarrow$ with 'C' as centre and radius

$6.5 cm$ radius, draw another arc.

$\rightarrow$ mark it as A wherever it intersects.

$\rightarrow$ Join

$AB \, \& \, AC$

$\therefore \Delta ABC$ is formed

On measuring,

$\angle B = 90^o$

1347818_1233059_ans_9bf670653987435c95af799b11ab4616.png

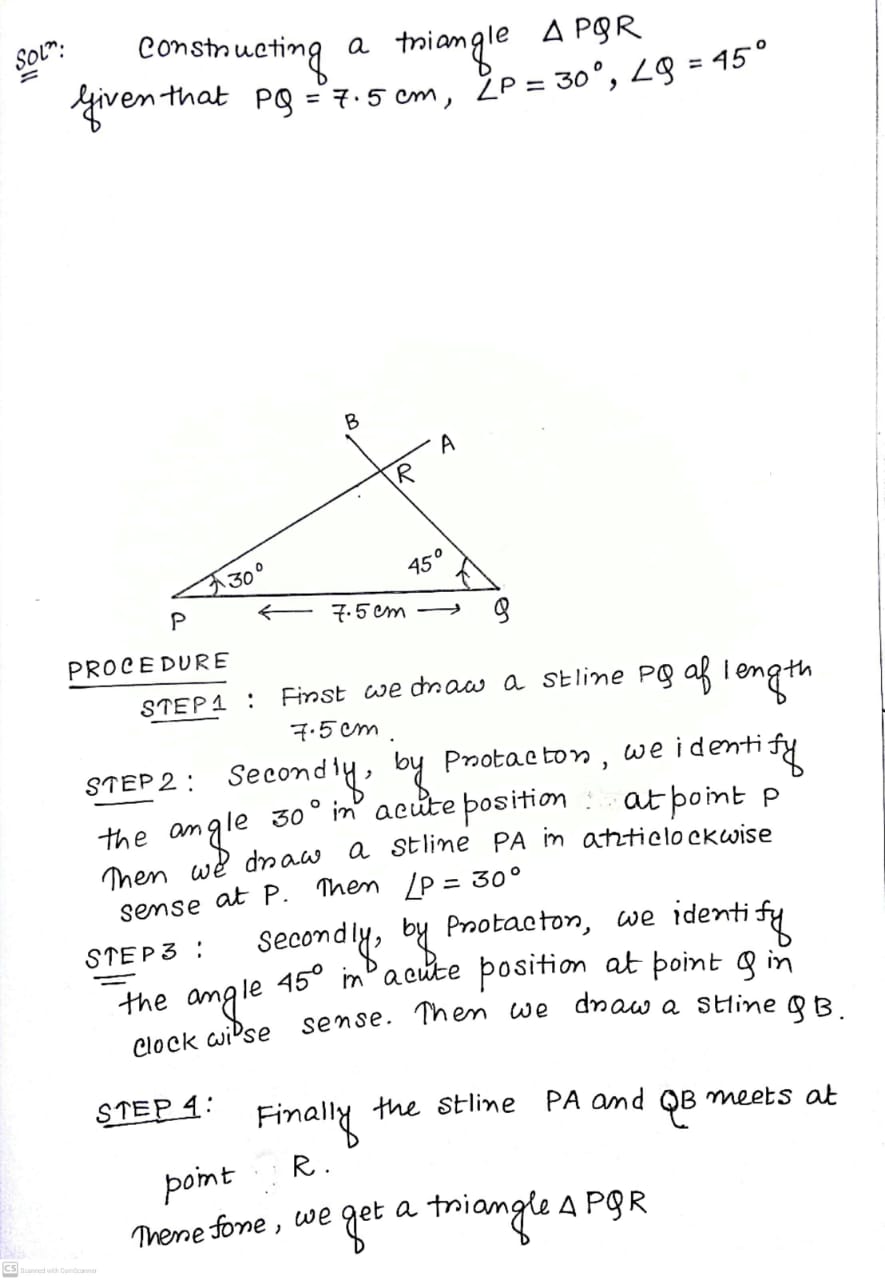
Construct a $\triangle PQR$ in which $PQ=7.5\ cm, \angle P=30^{o}$ and $\angle Q=45^{o}$ .

1914522_1313267_ans_9d88f76bdc224f51915721acfb1b142d.jpg

Construct a $\triangle XYZ$ such that:
$YZ=5\,cm,\angle ZYX=30^{o}$ and $\angle YZX=75^{o}$ .

$\begin{array}{l} Steps\, \, of\, \, construction:- \\ \left( i \right) Draw\, \, a\, \, line.\, \, YZ=5\, \, cm \\ \left( { ii } \right) Make\, \, angle.\, \, \, 30^{ \circ }\, \, at\, \, Y. \\ \left( { iii } \right) Make\, \, angle.\, \, 75^{ \circ }\, \, at\, \, Z. \\ So,\, \, XYZ\, \, is\, \, required\, \, \Delta \end{array}$
1204266_1314692_ans_34089320930b4c3d807655a583ff671f.PNG

1204266_1314692_ans_34089320930b4c3d807655a583ff671f.PNG

Construct a $\triangle A B C$ in which $B C = 4.5 \mathrm { cm } , \angle B = 45 ^ { \circ }$ and $A B + A C = 8 \mathrm { cm }$ Justify your construction.

Justification:-

After drawing

$\Delta DBC$ with

$BC=4.5$ cm,

$\angle B=45^o$ and

$DB=8$ cm. The perpendicular bisector of DC is drawn and it intersects DB at A.

So, we get AC

$=$ AD

$=8$ cm

$\Rightarrow BA+AD=8$ cm

$\Rightarrow AB+AC=8$ cm

Hence

$\Delta ABC$ is the required triangle.

1205962_1301664_ans_021b5d4ac28c4893a9306e4a3f0693c5.jpg

Construct triangle $XYZ$ if its given that $XY=6\ cm, \angle X=30^{o}$ and $\angle Y=110^{o}$ .

$\Rightarrow$ Draw a line segment

$XY=6\,cm$

$\Rightarrow$ At point

$X$ draw an angle of

$30^o$

$\Rightarrow$ At point

$Y$ draw an angle of

$110^o$

$\Rightarrow$ Join

$\angle X$ and

$\angle Y$ , give name

$Z$

$\therefore$

$\triangle XYZ$ is required triangle.

1458128_1316213_ans_2b6c3836ace543b986a39e0fd4c17a11.png

Construct a triangle $ABC$ , given the following
$AB=5.4$ cm, $AC=5$ cm and $\angle A=45^{o}$ .

$1.$ Draw a straight line

$AC=5$ cm

$2.$ Using Protractor from

$A$ mark a point

$\angle{A}={45}^{\circ}$

$3.$ Using compass of draw an arc of length

$AB=5.4$ cm

$4.$ Join

$BC$

Result:

$\triangle{ABC}$ is the required triangle.

1305279_1368554_ans_5d3ecd1497d44387adf53cba7f347c58.png

Construct a $\triangle ABC$ in which $AB=3.8\ cm. \angle A=60^{o}$ and $AC=5\ cm$ .

$\Delta ABC ,AB=3.8cm,AC=5cm$ and

$\angle A=60^0$ .

Required :To construct

$\Delta ABC$ .

1381092_1328021_ans_d5d384ad5608495084931f5d15e8f59b.png

Construct $\Delta \,ABC\,$ such that $\angle B = {100^0},\,\,BC = \,6.4\,cm,\,\,\angle C = \,{50^0}$ and construct is incircle.

1309781_1350516_ans_8c5f28e197f44be3ba22f90422cf7a0e.jpg

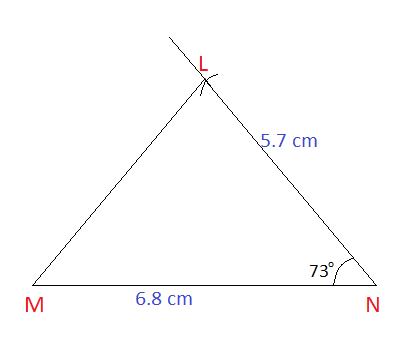
Construct $\Delta L M N$ in which $\angle N = 73 ^ { o} , L N = 5.7 \ { cm } , M { N } = 6.8 \ { cm }.$

Steps of construction-

Draw a line segment $MN$ of length $6.8\ cm.$
With the help of a protractor construct an $\angle LNM$ measure $73^o.$
From the point, $N$ and radius $5.7\ cm$ make an arc intersection the ray of angle $73^o$ at point $L.$
Join $L$ and $M .$

$LMN$ is the triangle formed.

1280101_1321810_ans_d32ac3006be34594a99ffffaa11c3453.png

Construct a $\triangle ABC, AB=6\ cm,BC=7\ cm$ and $\angle A=60^{o}$ .

$1.$ Draw a straight line

$AB=5.7$ cm

$2.$ Using Protractor from

$A$ mark a point

$\angle{A}={60}^{\circ}$

$3.$ Using compass of draw an arc of length

$BC=7$ cm

$4.$ Name the point of intersection of the arc of

$7$ cm and the line making an angle with

$A$ as

$C$

Result:

$\triangle{ABC}$ is the required triangle.

1306545_1363276_ans_9b310c10611d4b40ae5a9d79e1431e34.PNG

Construct a triangle $ABC$ , given the following
$AB=6\ cm,BC=5\ cm$ and $CA=5\ cm$

$1.$ Draw a straight line

$AB=6$ cm

$2.$ Using compass from

$A$ draw an arc of length

$5$ cm

$3.$ Using compass from

$B$ draw an arc of length

$5$ cm

$4.$ Name the point of intersection of both the arcs as

$C$

$5.$ Join

$AC$ and

$BC$

Result:

$\triangle{ABC}$ is the required triangle.

1305289_1368577_ans_a8c623976eb240bbb2ee51d14a160a03.png

Construct an equilateral triangle each of whose sides measures $6.2\ cm$ Measure each one of its angles.

In an equilateral triangle all the sides as well as well as angles are equal if one of its side is

$6.2cm$ then ,

obviously all the sides are also equal and as we know that all the angles are also equal then

Let us take the angles be

$x$

$x+x+x=180$ (angle sum property of a triangle)

Also,

$x+x+x=180$

$\Rightarrow 3x=180$

$\Rightarrow x=\dfrac { { 180 } }{ 3 } ={ 60^{ 0 } }$

$\therefore x=60^0$

Hence we get that the angle are

$60^0$ .

Construct a triangle $ABC$ , given the following
$BC=4.8\ cm,AB=5.7\ cm$ and $\angle A=45^o$ .

$1.$ Draw a straight line

$AB=5.7$ cm

$2.$ Using Protractor draw the line from

$A$ such that

$\angle{A}={45}^{\circ}$

$3.$ Using compass of draw an arc of length

$BC=4.8$ cm

$4.$ Name the point of intersection of the arc of

$4.8$ cm and the line making an angle of

${45}^{\circ}$

$5.$ Join

$AC$ and

$BC$

Result:

$\triangle{ABC}$ is the required triangle.

1305288_1368558_ans_7441b07538de49e98184172addb46273.png

To construct a triangle, given its base angle and the difference of the other two slides.

Let

triangleABCtriangleABC is the required triangle.

1299818_1362970_ans_d59fbacf7f204336ac49ebb150550959.png

Construct a triangle $PQR$ in which $QR=7cm, \angle Q=75^{o}$ and $PQ+PR=13 cm$

$1.$ Draw base

$BC=7$ cm

$2.$ Let's draw

$\angle{B}={75}^{\circ}$ .Let the ray be

$BX$

$3.$ Open the compass to length

$AB+AC=13$ cm.From point

$B$ as center, cut an arc on ray

$BX$ .Let the arc intersect

$BX$ at

$D$

$4.$ Join $$CD$

$5.$ Now, we will draw perpendicular bisector of

$CD$

$6.$ Mark point

$A$ where perpendicular bisector intersects

$BD$

$7.$ Join

$AC$

Result:

$\triangle{ABC}$ is the required triangle.

1302343_1377979_ans_d571f1014d304a469f8e46144900c543.PNG

The length of the sides of a triangle are 5 cm, 12 cm and 13 cm. Find the length of perpendicular from the opposite vertex to the side whose length is 13 cm.

Here,

$a=5, b=12, c=13$

$s=\dfrac{1}{2}(a+b+c)=15$

Area of the triangle, A =

$\sqrt{s(s-a)(s-b)(s-c)}$

$A=\sqrt{15(15-5)(15-12)(15-13)}$

$A=30$

$cm^{2}$

Let p be the length of perpendicular. Then,

$A=\dfrac{1}{2} \times 13 \times p$

Therefore,

$\dfrac{1}{2} \times 13 \times p =30$

$p=\dfrac{60}{13}$

$cm$

Construct a triangle $ABC$ using the following lengths:
$AB=BC=5.8\ cm,$ and $AC=4\ cm$

$1.$ Draw a straight line

$AC=4$ cm.

$2.$ Using compass from

$A$ draw an arc of length

$5.8$ cm.

$3.$ Using compass from

$C$ draw an arc of length

$5.8$ cm.

$4.$ Name the point of intersection of both the arcs as

$B$ .

$5.$ Join

$AB$ and

$BC$ .

Result:

$\triangle{ABC}$ is the required triangle.

1305291_1368583_ans_9d3ef446640a4c13bde436efcf115528.png

Construct a triangle of whose side lengths are $4\text{ cm},\;5\text{ cm},\;7\text{ cm}.$

To draw the required triangle follow the following steps:-

Draw a line segment $AC = 7 \text{ cm}.$
With $B$ as center and radius $5 \text{ cm},$ draw an arc.
With $A$ as center and radius $4 \text{ cm},$ draw another arc cutting the previous arc at $A.$
Join $BC$ and $AC$ .

Therefore,

$\triangle ABC$ is the required triangle.

1310109_1405425_ans_94d6bd4333234af58b3a8b97c30b8a08.png

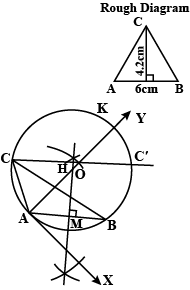
Construct $\triangle{ABC}$ , $AB=9$ cm , $BC=9$ cm and $\angle{ABC}={45}^{\circ}$ .
Also draw a circle of radius $2$ cm to touch the arms of $\angle{ACB}$

Steps:

$1)$ Draw

$BC = 9$ cm

$2)$ From

$B$ , draw

$\angle{B}={45}^{\circ}$

$3)$ From

$B$ cut arc

$BA = 9$ cm.

$4)$ Join

$AC$ ,

$\triangle{ABC}$ is required triangle.

$5)$ Draw angle bisector of

$\angle{C}$ .

$6)$ At a distance of

$2$ cm from

$BC$ , draw a line parallel to

$BC$ which intersects angle bisector at

$D$ .

$7)$ Draw a circle with centre

$D$ which touches the arms of

$\angle{ACB}$ .

Construct a triangle with perimeter $12 cm$ and the ratio of their angles is $3:4:5$

Let the angles of the given triangle be

$3x, 4x$ and

$5x$

Then,

$3x + 4x + 5x ={180}^{\circ}$

$\Rightarrow 12x={180}^{\circ}$

$\Rightarrow x=\dfrac{{180}^{\circ}}{12}$

$\therefore, x = {45}^{\circ}$ ,

${60}^{\circ}$ and

${75}^{\circ}$

Steps of construction.

Let

$\angle{A}={45}^{\circ},\angle{B}={60}^{\circ}$ and

$\angle{C}={75}^{\circ}$

$\therefore$ Perimeter

$=12$ cm and base angles are

${60}^{\circ}$ and

${75}^{\circ}$

$1.$ Draw a line segment

$PQ=12$ cm

$2.$ Construct

$\angle{QPR}={60}^{\circ}$ ad

$\angle{PQS}={75}^{\circ}$

$3.$ Draw the bisectors of

$\angle{QPR}$ and

$\angle{PQS}$ to meet at

$A$

$4.$ Draw the perpendicular bisectors of

$PA$ and

$QA$ to meet

$PQ$ at

$B$ and

$C$ respectively.

$5.$ Join

$AB$ and

$AC$

Result:

$\triangle{ABC}$ is the required triangle.

1302126_1377652_ans_a5bd925a1a624e678a2c1ba9ad1a3788.PNG

Draw a line, say $AB$ , take a point $C$ outside it. Through $C$ , draw a line parallel to $AB$ using ruler and compasses only.

$(a)$ Draw a line-segment

$AB$ and take a point

$C$ outside

$AB$ .

$(b)$ Take any point

$D$ on

$AB$ and join

$C$ to

$D$ .

$(c)$ With

$D$ as centre and take convenient radius, draw an arc cutting

$AB$ at

$E$ and

$CD$ at

$F$ .

$(d)$ With

$C$ as centre and same radius as in step

$3$ , draw an arc

$GH$ cutting

$CD$ at

$I$ .

$(e)$ With the same arc

$EF$ , draw the equal arc cutting

$GH$ at

$J$ .

$(f)$ Join

$JC$ to draw a line

$l$ .

This is the required line

$AB \parallel l$

1327191_1381792_ans_8a4744f6b0e24473b8e890a2918865f5.png

Construct a right angled $\triangle{PQR}$ , in which $\angle{Q}={90}^{\circ}$ , hypotenuse $PR = 8$ cm and $QR = 4.5$ cm.

Steps of Construction:

$i)$ Draw a line segment

$QR = 4.5$ cm

$ii)$ At

$Q$ , draw a ray

$QX$ making an angle of

${90}^{\circ}$

$iii)$ With centre

$R$ and radius

$8$ cm, draw an arc which intersects

$QX$ at

$P$ .

$iv)$ Join

$RP$ .

$\triangle{PQR}$ is the required triangle.

1327194_1383007_ans_e456a9d367e74686a58d479e4a642b8f.png

Construct $\triangle ABC$ such that $AB=2.5cm, BC=6cm$ and $AC=6.5cm$ . Measure $\angle B$ .

$1.$ Draw

$AB=2.5$ cm

$2.$ Taking

$A$ and

$B$ as centers, radius

$=BC=6$ cm and

$AC=6.5$ cm,draw two arcs intersecting each other at

$C$

$3.$ Join

$AC$ and

$BC$

Thus,

$\triangle{ABC}$ is our required triangle.

$\angle{B}={90}^{\circ}$

1306556_1369830_ans_97aa49ad3f3c44d4ad4b45116064d21f.PNG

Construct a $\Delta ABC$ with $AB = 4.2$ cm, $BC = 3.1$ cm and $CA = 5$ cm. What type of triangle in this ?

Steps of construction:

1)Draw a line segment

$AB$ of

$4.2$ cm.

2)From point

$A$ cut an arc of

$5$ cm.

3) From point

$B$ cut an arc of

$3.1$ cm.

4)Join the point on which both the arcs meet.

$\triangle ABC$ is the required triangle.

It is Scalene triangle.

1301771_1381616_ans_9e50452973774ceb83e2f633ae7a4cf9.png

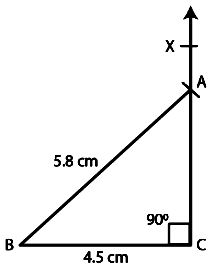
In right $\Delta ABC$ , the lengths of the legs are given. Find the length of the hypotenuse.
$a=6$ cm, $b=8$ cm.

By Pythagoras theorem, we know

$(\text{Hypotenuse})^2=(\text{Base})^2+(\text{Height})^2$

Here, Base

$=6\space\mathrm{cm}$ and Height

$=8\space\mathrm{cm}$

So,

$c^2=a^2+b^2$

$\Rightarrow c^2=6^2+8^2$

$\Rightarrow c^2=36+64$

$\Rightarrow c^2=100$

$\Rightarrow c=\sqrt {100}$

$\Rightarrow c=10$

$\therefore$ Hypotenuse

$=10\space\mathrm{cm}$

Construct the right angled $\triangle {PQR}$ where $m\angle {Q}={90}^{o}$ , $QR=8cm$ and $PR=10cm$ .

To construct: A right angled

$\triangle {PQR}$ where

$m\angle {Q}={90}^{o}$ ,

$QR=8cm$ and

$PR=10cm$ .
Steps of construction:
(a) Draw a line segment

$QR=8cm$
(b) At point

$Q$ , draw

$QX\bot QR$
(c) Taking

$R$ as centre, draw an arc of radius

$10cm$
(d) This arc cuts

$QX$ at point

$P$
(e) Join

$PQ$
It is the required right angled triangle

$PQR$

1346133_1645983_ans_cbafa7974cda422fa502b6cac260eaca.png

Construct a right angle triangle whose hypotenuse is $6cm$ long and one of the legs is $4cm$ long.

To construct: A right angle triangle

$DEF$ where

$DF=6cm$ and

$EF=4cm$
Steps of construction:
(a) Draw a line segment

$EF=4cm$
(b) At point

$Q$ , draw

$EX \bot EF$
(c) Taking

$F$ as centre and radius

$6cm$ , draw an arc (Hypotenuse)
(d) This arc cuts the

$EX$ at point

$D$
(e) Join

$DF$
It is the right angled triangle

$DEF$

1346135_1645984_ans_47dcbd62006f459eaa6e7cecd23f6308.png

Draw a line, say $AB$ take a point $C$ outside it. Through $C$ , draw a line parallel to $AB$ using ruler and compasses only.

1230534_1464084_ans_bbad3f588a324537b0369bb5587140dd.PNG

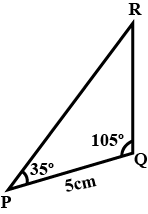
Construct $\Delta PQR$ if PQ=5 cm, $m\angle PQR=105^o$ and $m\angle QRP=40^o$ .
(Hint : Recall angle-sum property of a triangle),

PQR +QRP+RPQ=180
105+ 40+ RPQ=180
145+ RPQ=180
RPQ= 180-145
RPQ= 35
LET DRAW A LINE PQ = 5CM
DRAW ANGLE P = 35°
DRAW ANGLE Q = 105°
FINALLY THEY INTERSECT EACH OTHER AT POINT R= 40°

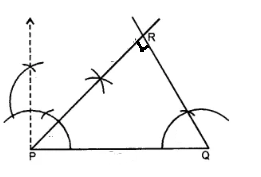
Draw a line PQ and take a point A outside it. Through A draw a line parallel to PQ. using rural and compass only

$1$ . Given a line PQ with point A outside it.

$2$ . Mark point B on the lie PQ join AB.

$3$ . Taking B as centre, and any radius, draw an arc intersecting PQ at E, and AB at D.

$4$ . With A as centre, and same radius before, draw an arc intersecting AB at F.

$5$ . Open compass to length DE.

$6$ . Now, with F as centre, and compass opened the same radius as before, draw an arc intersecting the previous arc at H.

$7$ . Draw a line m passing through A and H.

Thus m is parallel to PQ, and passing through point A.

$\therefore m||PQ$ .

1221367_1451023_ans_376c220f305d4121836b57c3f5ce51c8.PNG

Construct $\triangle {PQR}$ if $PQ=5cm$ , $m\angle {PQR}={105}^{o}$ and $m\angle {QRP}={40}^{o}$

$\textbf{Step 1:}$

We need to make the constructions according to the information given.

$\textbf{Step 2:}$

Let's first calculate

$m\angle QPR$

$m\angle{PQR}={105}^{o}$ and

$m\angle {QRP}={40}^{o}$

We know that sum of angles of a triangle is

${180}^{o}$

$\therefore$

$m\angle {PQR}+m\angle {QRP}+m\angle {QPR}={180}^{o}$

$\Rightarrow$

${105}^{o}+{40}^{o}+m\angle {QPR}={180}^{o}$

$\Rightarrow$

${145}^{o}+m\angle {QPR}={180}^{o}$

$\Rightarrow$

$m\angle {QPR}={180}^{o}-{145}^{o}$

$\Rightarrow$

$m\angle {QPR}={35}^{o}$

$\textbf{Step 3:}$

Now, to construct

$\triangle {PQR}$ where

$m\angle {P}={35}^{o},m\angle {Q}={105}^{o}$ and

$PQ=5cm$

$\bullet$ We will follow these steps of construction :

$(a)$ Draw a line segment

$PQ=5cm$

$(b)$ At point

$P$ draw

$\angle {XPQ}={35}^{o}$ with the help of protractor

$(c)$ At point

$Q$ , draw

$\angle {YQP}={105}^{o}$ with the help of protractor

$(d)$

$XP$ and

$YQ$ intersect at point

$R$

It is the required triangle

$\triangle PQR$ .

2133633_1645978_ans_17a10357f21441c1a69de30e629e7f50.png

Construct $\triangle PQR$ such that $PQ=5$ cm, $QR=3$ cm and $\angle Q =95^ \circ$ .

$1$ . Draw a line segment QR of length

$3$ cm.

$2$ . Now, we draw

$95^o$ degrees from point Q.

$3$ . Taking Q as centre,

$5$ cm radius, we draw an arc. Let the point where arc intersects the ray be point p.

$4$ . Joint PR and label the sides.

Thus, PQR is the required triangle.

1221422_1449262_ans_37ba313c51054fa3b50327eaa55075d8.jpg

Construct a $\triangle ABC$ , when $\displaystyle AB=6.2\ cm, AC=5.2\ cm$ and $\angle B=45^{\circ}$

Step 1: Draw a line

$AB=6.2cm$

Step 2: Construct

$45^o$ at

$B$

Step 3: Extend the line from

$BX$ so that

$AC$ meets

$BX$ at

$5.2cm$ at

$C$ .

$\triangle ABC$ is the required triangle.

Construct $\triangle {ABC}$ given $m\angle {A}={60}^{o}$ , $m\angle {B}={30}^{o}$ and $AB=5.8cm$

$\textbf{Step 1:}$

We need to make the constructions according to the information given.

$\textbf{Step 2:}$

We will follow the following steps of construction.

$(a)$ Draw a line segment

$AB=5.8cm$

$(b)$ AT point

$A$ draw an angle

$\angle {YAB}={60}^{o}$ with the help of a compass

$(c)$ At point

$B$ , draw

$\angle {XBA}={30}^{o}$ with the help of a compass

$(d)$

$AY$ and

$BX$ intersect at the point

$C$

It is the required triangle

$\triangle ABC$

2133632_1645976_ans_f38de78bbfef4254904fe03eeefeaafd.png

The perimeter of a right angled triangle is 70units and its hypotenuse is 29 the units. Find the length of the other sides.

2043990_1553316_ans_7d215165e6b446a58094fca34f2eda6d.jpg

In right $\Delta ABC$ , the lengths of the legs are given. Find the length of the hypotenuse.
$a=3$ cm, $b=4$ cm.

By Pythagoras theorem, we know

$(\text{Hypotenuse})^2=(\text{Base})^2+(\text{Height})^2$

Here, Base

$=3\space\mathrm{cm}$ and Height

$=4\space\mathrm{cm}$

So,

$c^2=a^2+b^2$

$\Rightarrow c^2=3^2+4^2$

$\Rightarrow c^2=9+16$

$\Rightarrow c^2=25$

$\Rightarrow c=\sqrt {25}$

$\Rightarrow c=5$

$\therefore$ Hypotenuse

$=5\space\mathrm{cm}$

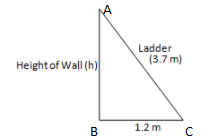
A ladder $3.7$ m long is placed against a wall in such a way that the foot of the ladder is $1.2$ m away from the wall. Find the height of the wall to which the ladder reaches.

Given:

$AC=3.7\space\mathrm{m}$ and

$BC=1.2\space\mathrm{m}$

Using the Pythagoras theorem, we get

$(AB)^2=(AC)^2-(BC)^2$

$\Rightarrow (AB)^2=(3.7)^2-(1.2)^2$

$\Rightarrow (AB)^2=13.69-1.44$

$\Rightarrow (AB)^2=12.25$

$\Rightarrow (AB)=\sqrt {12.25}$

$\Rightarrow AB=3.5$

$\therefore$ Height of the wall

$=3.5\space\mathrm{m}$

1910397_1677881_ans_18f1993722c8409281dc25e58ab1c5e5.png

Draw a line PQ. Draw another line parallel to PQ at a distance of $3$ cm from it.

Steps of Construction:

1) Draw a line

$\text{PQ}$ .

2) Take any two points

$\text{A}$ and

$\text{B}$ on the line.

3) With the help of compass construct

$\angle PBF=90^{\circ}$ and

$\angle QAE=90^{\circ}$

4) With

$\text{A}$ as centre and radius equal to

$3\space\mathrm{cm}$ cut

$\text{AE}$ at

$\text{C}$ .

5) With

$\text{B}$ as centre and radius equal to

$3\space\mathrm{cm}$ cut

$\text{BF}$ at

$\text{D}$ .

6) Join

$\text{CD}$ and produce it on either side to get the required line parallel to

$\text{AB}$ and at a distance of

$5\space\mathrm{cm}$ from it.

1913564_1678132_ans_75b647fc0ff145b4a21e95b593a3f86b.png

Draw $\Delta ABC$ in which $BC=8$ cm, $\angle B=50^o$ and $\angle A=50^o$ .

Given,

$\angle ABC=50^o$ and

$\angle CAB=50^o$

Clearly,

$\angle A B C+\angle B C A+\angle C A B=180^{\circ}\quad$ [By angle sum property of triangle]

$\Rightarrow \angle B C A=180^{\circ}-\angle A B C-\angle C A B$

$\Rightarrow \angle B C A=180^{\circ}-50^{\circ}-50^{\circ}$

$\Rightarrow \angle B C A=180^{\circ}-100^{\circ}$

$\Rightarrow \angle BCA=80^{\circ}$

Steps of construction:

1) Draw a line segment

$BC$ of length

$8 \space\mathrm{cm}$ .

2) Draw

$\angle CBX$ such that

$\angle CBX=50^{\circ}$ .

3) Draw

$\angle BCY$ with

$Y$ on the same side of

$BC$ as

$X$ such that

$\angle BCY=80^{\circ}$ .

4) Let

$CY$ and

$BX$ intersect at

$A$ .

Thus, the required triangle

$\Delta ABC$ is obtained.

1913658_1678151_ans_a978e512bf3e419e83271e503c86603f.png

The hypotenuse of a triangle is $2.5$ cm. If one of the sides is $1.5$ cm, find the length of the other side.

By Pythagoras theorem, we know

$(\text{Hypotenuse})^2=(\text{Base})^2+(\text{Height})^2$

Here, Hypotenuse

$=2.5\space\mathrm{cm}$ and Base

$=1.5\space\mathrm{cm}$

So,

$c^2=a^2+b^2$

$\Rightarrow 2.5^2=1.5^2+b^2$

$\Rightarrow 6.25=2.25+b^2$

$\Rightarrow b^2=6.25-2.25$

$\Rightarrow b^2=4$

$\Rightarrow b=\sqrt 4$

$\Rightarrow b=2$

$\therefore$ Length of the other side

$=2\space\mathrm{cm}$

In right $\Delta ABC$ , the lengths of the legs are given. Find the length of the hypotenuse.
$a=2$ cm, $b=1.5$ cm.

By Pythagoras theorem, we know

$(\text{Hypotenuse})^2=(\text{Base})^2+(\text{Height})^2$

Here, Base

$=2\space\mathrm{cm}$ and Height

$=1.5\space\mathrm{cm}$

So,

$c^2=a^2+b^2$

$\Rightarrow c^2=2^2+1.5^2$

$\Rightarrow c^2=4+2.25$

$\Rightarrow c^2=6.25$

$\Rightarrow c=\sqrt {6.25}$

$\Rightarrow c=2.5$

$\therefore$ Hypotenuse

$=2.5\space\mathrm{cm}$

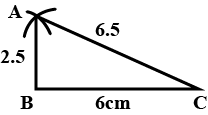
Construct a right triangle whose one side is $3.5\ cm$ and the sum of the other side and the hypotenuse is $5.5\ cm$ .

Step of Construction:

Construct

$BC=3.5\ cm$

Construct

$\angle CBX =90^o$

From

$BX$ cut off line segment

$BD=AB+AC=5.5\ cm$

Join the points

$CD$

Construct the perpendicular bisector of

$CD$ which meets the line

$BD$ at point

$A$

Join

$AC$

Therefore,

$\triangle ABC$ is the required triangle.

1565124_1715825_ans_b1ec32e1ec0445b1894eee56bda5c8ab.png

Draw a line AB and take a point P outside it. Draw a line CD parallel to AB and passing through the point P.

Steps for construction,
1. Draw a line AB.
2. Take any point Q on AB and a point P outside AB and join PQ,
3. With Q as center and any radius draw an arc to cut AB at E and PQ at F.
4. With P as center and same radius draw an arc to cut QP at G.
5. With G as center and radius equal to EF, draw an arc to cut the previous arc at H.
6. Join PH and produce it on both sides to get the required line CD parallel to AB.

In right $\Delta ABC$ , the lengths of the legs are given. Find the length of the hypotenuse.
$a=8$ cm, $b=15$ cm.

By Pythagoras theorem, we know

$(\text{Hypotenuse})^2=(\text{Base})^2+(\text{Height})^2$

Here, Base

$=8\space\mathrm{cm}$ and Height

$=15\space\mathrm{cm}$

So,

$c^2=a^2+b^2$

$\Rightarrow c^2=8^2+15^2$

$\Rightarrow c^2=64+225$

$\Rightarrow c^2=289$

$\Rightarrow c=\sqrt 289$

$\Rightarrow c=17$

$\therefore$ Hypotenuse

$=17\space\mathrm{cm}$

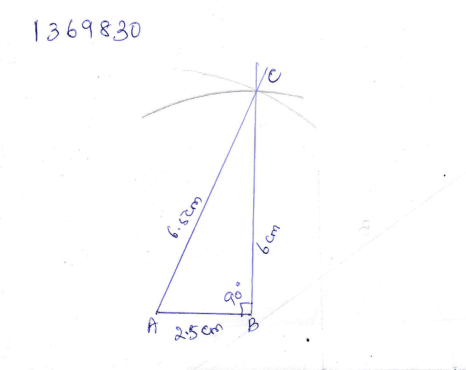
Construct a right angled triangle $ABC$ in which $AB$ $=5.8\ cm$ , $BC$ $=4.5\ cm$ and $\angle C=90^o$ .

It is given that,

$AB$

$=5.8\ cm$ ,

$BC$

$=4.5\ cm$ and

$\angle C=90^o$

$Steps\,of\,construction:$
1. Draw a line segment

$BC=4.5\ cm$ .
2. At point

$C$ , draw an angle

$BCX=90^o$ .
3. With center

$B$ and radius

$5.8\ cm$ , draw an arc which intersect ray

$CX$ at

$A$ .
4. Join

$AB$ to obtain the desired triangle

$ABC$ .

Hence,

$\triangle ABC$ is the required triangle.

1878299_1678158_ans_c4cd711c803d4820ac303897eb0d634d.JPG

Use ruler and compasses only for this question.
Construct $\Delta ABC$ where AB = 3.5 cm, BC = 6 cm and $\angle ABC=60^{\circ }$

We know that

$\Delta ABC$

$AB = 3.5 cm, BC = 6$ cm and

$\angle ABC=60^{\circ }$
Steps of Construction:
(i) Construct a line segment

$BC = 6$ cm.
At the point

$B$ construct a ray

$BX$ which makes an angle

$60^{\circ }$ and cut off

$BA = 3.5$ cm.
Now join

$AC$ .
Therefore,

$\Delta ABC$ is the required triangle.
1706258_1783550_ans_c104a28dc1d9414982ba31123c44e547.PNG

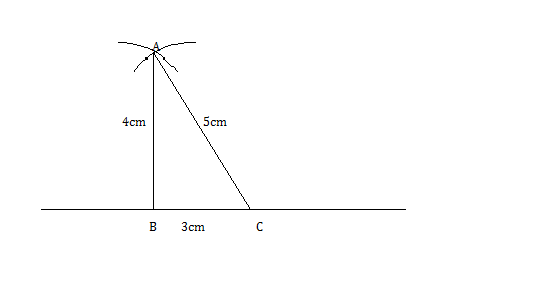
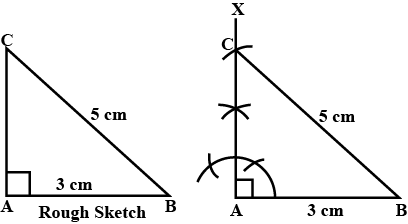
Construct a right-angled triangle the length of whose hypotenuse is $5$ cm and one of the remaining side is $3$ cm long.

Steps of construction :
1. Draw a line segment

$AB = 3$ cm.
2. Take

$A$ as a centre, draw an angle of

$90^{\circ}$ by ruler and compass.
3. Join angle line.
4. Take

$B$ as centre, draw an arc of radius

$5$ cm which cuts the angle line at the point

$C$ . Join

$BC$ .
Hence,

$\Delta ABC$ is required right-angled triangle.

1870036_1878879_ans_db537568d9884c6995e029954664884d.png

Construct a right triangle when one side is $3.5\,cm$ and sum of other side and the hypotenuse is $5.5\,cm$ .

$\Delta$ ABC , base BC =

$3.5 \,cm$ , the sum of the other side and hypotenuse i.e., AB + AC =

$5.5\,cm$ and

$\angle$ ABC =

$90^{\circ}$ .

To construct : An

$\Delta$ ABC.

Steps of construction :

$1$ . Draw a ray BX and cut off a line segment BC =

$3.5 \,cm$ from it.

$2$ . Construct

$\angle$ XBY =

$90^{\circ}$ . With the help of a ruler and compass.

To make this angle take suitable radius in compass and make arc with

$B$ as center.

Now with same radius make arcs point of intersection of arc with line

$BC$ from both sides, which will cut original arc at two points.

Now from these two points make an arcs with same radius which will meet at some point. Join this point with

$B$ to get

$90{\circ}$ at point

$B$ .

$3$ . From BY cut off a line segment BD =

$5.5\,cm$ .

$4$ . Join CD.

$5$ . Draw the perpendicular bisector of CD intersecting BD at A.

$6$ . Join AC.

Then , ABC is the required triangle.

1660349_1795048_ans_be82981465fa4228a4d05e9e2a668ebb.png

Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm.

Constructing a right angled triangle ABC with base, AB =12 cm and sum of hypotenuse BC and another side AC, AC + BC = 18 cm. x
Steps of Construction
1. Draw a line segment AB = 12 cm.
2. With the help of protractor construct

$\angle A = 90^0$ and produce upto AX.
3. Mark 'D' on AX such that AD = 18 cm.
4. Join BD.
5. Let the perpendicular bisector BD intersects AD at C. Join BC.
6. Now required triangle ABC is constructed with Base AB = 12cm, Side AC = 5 cm, Hypotenuse BC = 13 cm and

$\angle A = 90^0$ .
1830890_1869355_ans_6317f75b0dbd40c5995b201c16e7f1c1.png

Construct right angle triangle PQR in which $Q = 9^\circ$ , $QR = 4.5\,cm$ and $R = 50^\circ$ .

1972380_1871322_ans_1d8b0197d2e44f1eba3420a4d174e94e.png

Construct a right angled triangle $ABC$ whose $\angle A = 90^{\circ}$ and $a = 10$ cm and $c = 6$ cm, from the vertex $A$ draw a perpendicular on the hypotenuse.

Steps of construction :
1. Draw a line segment

$AB = 6$ cm as base.
2. With

$A$ as centre, draw an angle of

$90^{\circ}$ .
3. With

$B$ as centre, draw an arc of radius

$10$ cm which intersects the angle line at

$C$ .
4. Again

$A$ as centre, draw perpendicular bisector of

$BC$ .
Hence,

$\Delta ABC$ is the required right angled triangle.
1870039_1878893_ans_19669f07156d4dfd99d58658bad75920.png

Construct right angle triangle LMN in which $M = 90^\circ$ , $MN = 4.5\,cm$ and $LN = 5.6cm$ .

1972381_1871319_ans_5dedbcbc56a74eddae3099f0efe6f746.png

Construct a right angle triangle $ABC$ in which hypotenuse $BC = 8.2$ cm and one side $= 4.2$ cm.

Steps of construction :
1. Draw a line segment

$AB = 4.2$ cm.
2. At

$A$ , draw an angle of

$90^{\circ}$ .
3. From

$B$ , draw an arc of radius

$8.2$ cm which cuts the line segment at

$C$ .
Hence,

$\Delta ABC$ is the required triangle.
1870063_1878982_ans_b68fa0df5b984aba8a3a4d0ca1ac84cf.png

Without using set-squares or protractor construct:
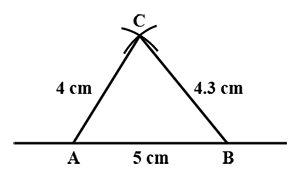
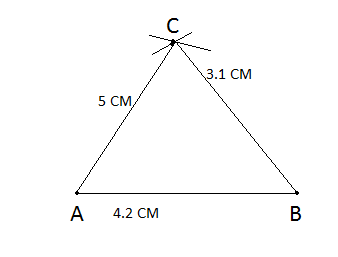
Triangle $ABC$ , in which $AB = 5.5$ cm, $BC = 3.2$ cm and $CA = 4.8$ cm.

Steps of construction
1. Construct

$BC = 3.2$ cm long.
2. draw an arc taking

$B$ as centre and

$radius=5.5cm$
3. draw another arc taking

$C$ as centre and

$radius=4.8cm$ to cut the previous arc at

$A$
4. Join

$AB$ and

$AC$

Hence,

$\triangle ABC$ is the required triangle
1708233_1783584_ans_72cb7183d3ae41d3ab5fbfea8b20c0bf.PNG

Using ruler and compasses construct:
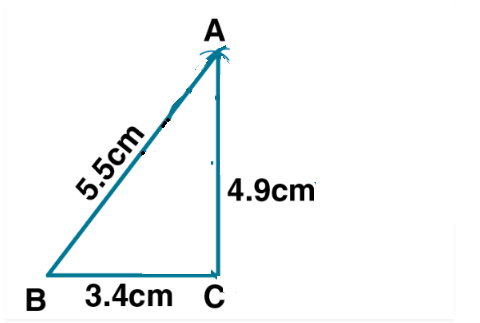
a triangle $ABC$ in which $AB = 5.5$ cm, $BC = 3.4$ cm and $CA = 4.9$ cm.

Steps of construction
1. Construct

$BC = 3.4$ cm
2. and mark the arcs

$5.5cm$ and

$4.9$ cm from the points

$B$ and

$C$ which intersects at

$A$
3. Now join

$A, B$ and

$C$ where

$ABC$ is the required triangle..
1705903_1783539_ans_637efcc6ab5c4094ae1d27277ce23a51.PNG

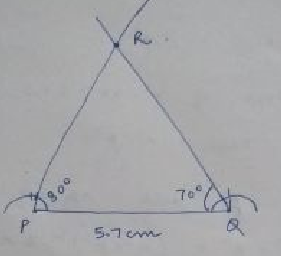
Construct $\Delta PQR$ such that, $m\angle P=80^o$ , $m\angle Q=70^o$ , $l(QR)=5.7\ cm$ .

$\angle P=80^o\quad \angle Q=70^o\quad PQ=5.7\ cm$

Hence, to draw a sealene triangle when

$2$ angles and included side

is given,

Step

$1$ draw the line

Step

$2$ draw angle at

$1$ side

Step

$3$ draw angle at another side

Step

$4$ join the lines as intersection points

the triangle is ready,

1403981_1124557_ans_8e0da1952d9a474c8c5364d70f88ea9b.png

Construct a right angle $\triangle ABC$ , right angled at $B$ , when hypotenuse $CA=7.0\ cm$ and $AB=4.3\ cm$ . Measure the length of $BC$ .

1. Draw the base side

$AB = 4.3\ cm$
2. At point

$B$ , draw an angle of

${90}^{\circ}$
3. From

$A$ cut an arc of length

$AC = 7.0\ cm$ using a compass
4. Name the point of intersection of the arm of the angle

${90}^{\circ}$ and the arc drawn in step 3, as

$C$
5. Join

$A$ to

$C$
6.

$ABC$ is the required triangle.

On measuring

$BC = 5.5 \ cm$

Construct a $\triangle ABC$ , when $\displaystyle AB=5.2\ cm, \angle A=30^{\circ}$ and $\angle B=75^{\circ}$ .

Step 1: Draw a line

$AB$ given

$5.2cm$

Step 2: Construct

$\angle 30^o$ at

$A$ . Similarly construct

$75^o$ at

$B$ .

Step 3: Join the point

$C$ with

$AC$ and

$BC$ .

Construct a $\triangle PQR$ in which $QR=6\ cm, PQ=4.4\ cm$ and $PR=5.3\ cm$ . Draw the bisector of $\angle P$ .

Given, to construct a

$\Delta PQR$

in which

$QR=6\ cm,\ PQ=4.4\ cm\ and\ PR=53\ cm$

Also given to draw the bisector of

$\angle P$ .

Construction steps:

$(1)$ Firstly, draw a line segment

$QR=6\ cm$ .

$(2)$ Now, taking

$Q$ as the centre, draw an arc of

$4.4\ cm$ radius.

$(3)$ Similarly, taking

$R$ as the centre and

$5.3\ cm$ radius, draw another arc that intersects the previous arc at

$P$ .

$(4)$ Join

$PQ$ and

$PR$ . Thus,

$\Delta PQR$ is the required triangle.

$(5)$ From point

$P$ draw an arc such that it intersects line segment

$QR$ .

$(6)$ Now from

$Q$ or

$R$ cut the arc.

$(8)$ Now joint the intersection point of arc to

$P$ .

$(9)$ Having joined the intersection point, angle bisector of

$P$ is obtained.

$(10)$ Thus, required figure is obtained.

1379351_1216190_ans_aac14e5820244e239581a6730dd6b0c4.png

Construct a triangle of sides $4\ cm, 5\ cm$ and $6\ cm$ and then a triangle similar to it whose sides are $\dfrac{2}{3}$ of the corresponding sides of the first triangle.

Making the triangle.

Draw a line segment AB = $4$ cm
Draw an arc at 5 cm from point A.
Draw an arc at 6 cm from point B so that it intersects the previous arc.
Joint the point of intersection from A and B.
This gives the required triangle ABC.

Dividing the base in $2 : 3$ ratio:

Draw a ray AX at an acute angle from AB.
Plot three points on AX so that; AA1 = A1A2 = A2A3
Join A3 to B.
Draw a line from point A2 so that this line is parallel to A3B and intersects AB at point B’.
Draw a line from point B’ parallel to BC so that this line intersects AC at point C’.

Triangle AB’C’ is the required triangle.

1072901_1063524_ans_77d3665d486d4a6bb2009df038430ff6.png

Construct an isosceles $\triangle ABC$ when base $BC=5.4\ cm$ and side $AB=6.8\ cm$

Since the triangle is isosceles, then the third side

$AC = AB = 6.8 \ cm$

To construct a triangle with these three given sides,
1. First draw the base, say

$BC = 5.4\ cm$
2. Set the width of the compass as one side

$AB = 6.8\ cm$ and draw an arc from

$B$ on any one side of the line segment

$BC$
3. Similarly, set the width of the compass as the other side

$AC = 6.8\ cm$ and draw an arc from

$C$ on the same side of the line segment

$BC$ as done in Step 2
4. Mark the intersection of the two arcs as

$A$
5. Join points

$A,B$ and

$A, C$ using a ruler.
6.

$ABC$ is the required triangle.

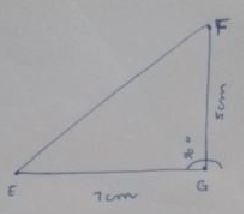
Construct $\Delta EFG$ from the given measures. $l(FG)=5\ cm$ , $m\angle EFG=90^o$ , $l(EG)=7\ cm$ .

$FG=5\ cm\quad EG=7\ cm\quad \angle EGF=90^o$

To Draw a between triangle when

$2$ sides and on included

$\angle$ is given

Step

$1$ Draw

$1$ side

Step

$2$ Make the angle at the common

$pc$

Step

$3$ Draw entire side

$w.t$ angle and recruitment as specified

Step $$4$ Draw remaining side the triangle is ready.

1403923_1124594_ans_6645e453f3c244e088273f112b352ebb.png

Draw a triangle $ABC$ with side $BC = 6cm$ , $AB = 5cm$ and $\angle ABC={ 60 }^{ o }$ , Then construct a triangle whose sides are $\ \dfrac { 3 }{ 4 }$ of the corresponding sides of the triangle $ABC$ .

$Following\quad steps\quad will\quad be\quad followed\quad to\quad draw\quad a\quad \quad triangle\quad A'BC'\quad whose\quad sides\quad are\quad of\quad corresponding\quad sides\quad of\quad ABC.$

$1.Draw\quad a\quad line\quad segment\quad BC\quad of\quad 6cm.Draw\quad an\quad arc\quad of\quad any\quad radius\quad while\quad taking\quad B\quad as\quad centre.Let\quad it\quad intersect\quad line\quad BC\quad at\quad point\quad O.Now\quad taking\quad O\quad as\quad centre\quad draw\quad another\quad arc\quad to\quad cut\quad the\quad previous\quad arc\quad at\quad point\quad O'.Joint\quad BO'\quad which\quad is\quad the\quad ray\quad making\quad 60°\quad with\quad line\quad BC.$

$2.Now\quad draw\quad an\quad arc\quad of\quad 5cm.radius,while\quad taking,B\quad as\quad centre,intersecting\quad extended\quad line\quad segment\quad BO'\quad at\quad point\quad A.Join\quad AC.DABC\quad is\quad having\quad AB=5cm.BC=6cm\quad and\quad ABC=60°.$

$3.Draw\quad a\quad ray\quad BX\quad making\quad an\quad acute\quad angle\quad with\quad BC\quad on\quad opposite\quad side\quad of\quad vertex\quad A.$

$4.Locate\quad 4\quad points\quad (as\quad 4\quad is\quad greater\quad in\quad 3\quad and\quad 4).B1,B2,B3,B4\quad on\quad line\quad segment\quad BX.$

$5.Join\quad B\quad to\quad C\quad and\quad draw\quad a\quad line\quad through\quad B3,parallel\quad to\quad B4\quad intersecting\quad BC\quad at\quad C'.$

$6.Draw\quad a\quad line\quad through\quad C'\quad parallel\quad to\quad AC\quad intersecting\quad AB\quad at\quad A'.DA'BC'\quad is\quad the\quad required\quad triangle.$

Draw a right triangle whose hypotenuse is of length $4$ cm and one side is of length $2.5$ cm.

2039904_1678156_ans_11e76376802642699a0a9289b0b7cbb0.jpg

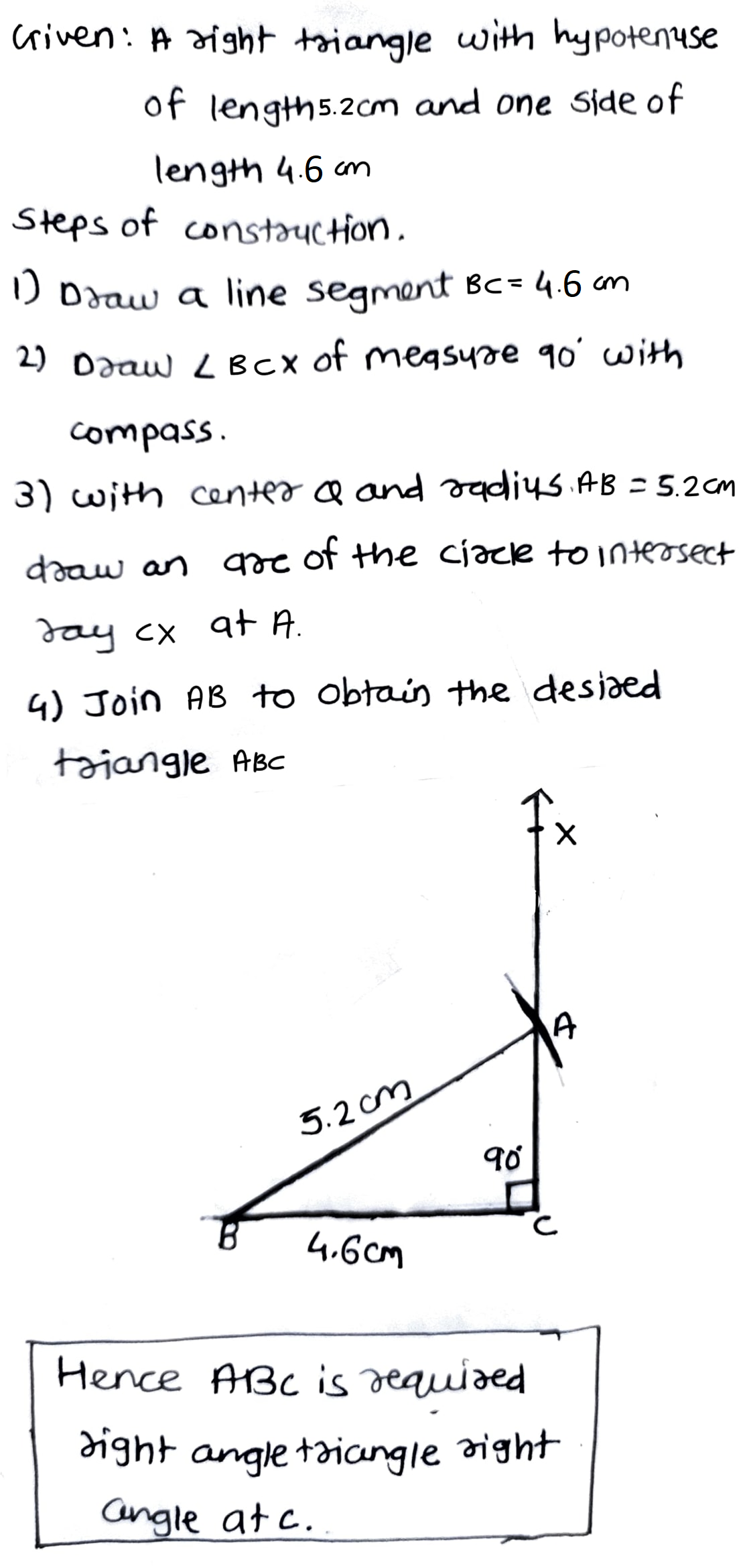
Construct a right triangle, right angled at C in which AB $=5.2$ cm and BC $=4.6$ cm.

2039905_1678159_ans_45de6ca32d904b479de31143dc0c74f1.png

A man goes $15$ m due west and then $8$ m due north. How far is he from the starting point?

1961084_1677886_ans_ac163d16f87848ceb8c3e0b3c213f0be.jpg

Draw a right triangle with hypotenuse of length $5$ cm and one side of length $4$ cm.

2039903_1678155_ans_b3b7039c02e0438db00528e9e55a7db7.jpg

Construct a right triangle having hypotenuse of length 5.6 $\mathrm { cm }$ . and one of whose acute angle measures $30 ^ { \circ }$ .

2042713_1432690_ans_004d73c7638944a7928d652d3415d80d.jpg

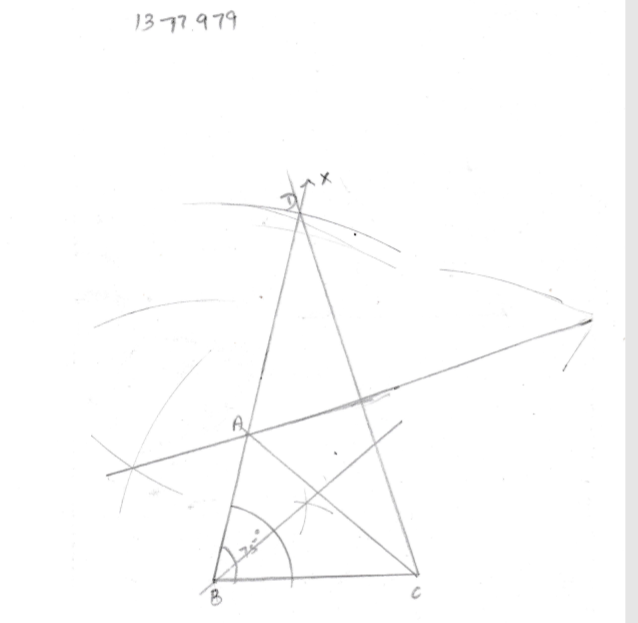
Construct a $\triangle ABC$ in which $BC = 7$ cm, $\angle B = {75^0}$ and $AB + BC = 13$ cm.

Steps of construction,

i) Draw BC=7cm

ii) Construct ∠YBC = 45°

iii) From Ray BY, cut off line segment BD=AB+AC=13cm

iv) Join CD

v) Draw the perpendicular bisector of CD meeting BY at A.

vi) Join AC to obtain the required triangle ABC.

Justification,

Since A lies on the perpendicular bisector of CD.

Therefore AC=AD

Now, BD = 13cm

=> BA+AD = 13cm

=> BA+AC = 13cm

Hence, ABC is the required triangle.

1316602_1440536_ans_8888ccd1ea004d85af3658e089eddcff.png

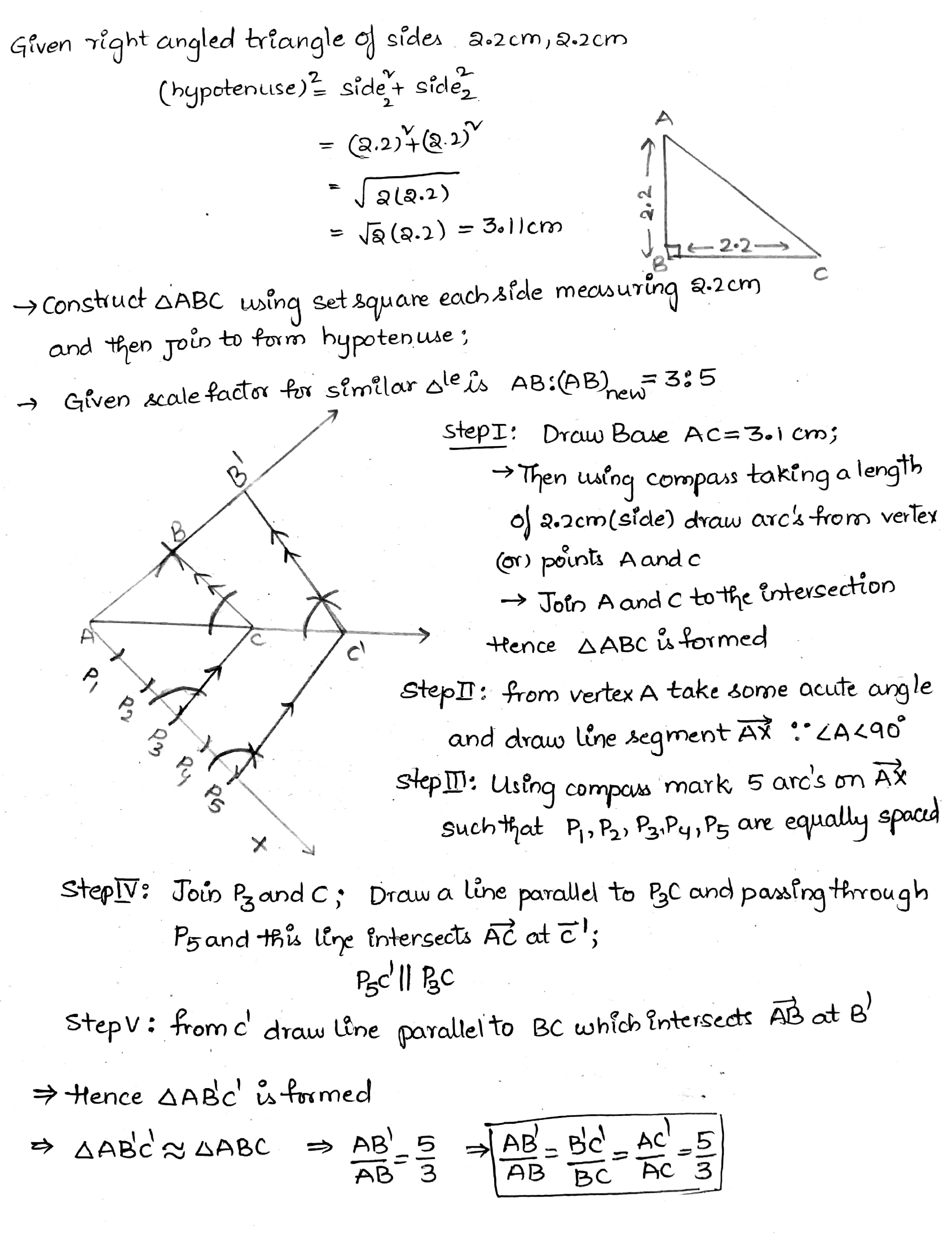
Draw a right triangle in which sides (other than hypotenuse) are of lengths $2.2 \,cm$ and $2.2\,cm$ . Then construct another triangle whose sides are $\dfrac{5}{3}$ times the corresponding sides of the given triangle.

1960974_1814991_ans_8cced08f7d994bd8abe41bb1ed9fdf84.jpg

Practical Geometry - Class 7 Maths - Extra Questions

Write down the procedure of constructing of a △ABC\triangle ABC with BC=7.5 cm,AC=5 cmBC=7.5\ cm, AC=5\ cm and ∠C=60o\angle C=60^{o}

Is it possible to have a triangle with the following sides 2 cm,3 cm,5 cm2\ cm,3\ cm,5\ cm

Is it possible to construct a triangle ABCABC in which BC=8 cm,∠B=40∘BC=8\ cm,\angle B=40^\circ and AB=AC=3.5 cm ?AB=AC=3.5\ cm\ ?

Construct ΔDEF\Delta DEF in which DE=8 cm, DF=7.2 cm, EF=6.3 cm.

Construct a triangle PQRPQR with side QR=7cm,QR=7cm, PQ=6cmPQ=6cm and angle PQR=600PQR={60^0} then construct another triangle whose side are 3/53/5 of the corresponding sides of triangle PQR?PQR?

Construct a triangle ABC in which AB=AC=5.44 cm and AB= AC=5.44\ cm\ and\ BC=6 cm. Draw all its lines of symmetry.

Construct a scalene triangle ABCABC, given AB=3AB=3 cm, AC=5AC =5 cm and BC=4BC =4 cm.

Given a line segment SR of 2.5 cm. Construct a line segment PT of 2 cm parallel to SR.

Construct a right triangle LMNLMN in which ∠M=90∘,MN=4cm\angle M = 90^{\circ}, MN = 4 cm and LN=6.2 cmLN = 6.2\ cm

Construct a triangle ABCABC, in which AB=4.5cm,AC=5.5cmAB = 4.5 cm, AC = 5.5 cm and ∠BAC=75∘\angle BAC = 75^{\circ}

Two sides of a triangle are 12 cm12\ cm and 14 cm14\ cm. The perimeter of the triangle is 36 cm36\ cm. What is the length of third side

Construct ΔTEN\Delta TEN such that TE = 3 cm, ∠E=90o\angle E = 90^o and NE = 4 cm.

Are the triangle shown in Fig congruent?why?

Construct △XYZ\triangle XYZ in which XY=4.5 cm,YZ=5 cmXY=4.5\ cm,YZ=5\ cm and ZX=6 cmZX=6\ cm.

Draw a triangle ABC in which AB = 5 cm, BC = 7 cm, and ∠B=75o\angle B = 75^{o}.

Try to construct a triangle with 5 cm,8 cm5\ cm, 8\ cm and 1 cm1\ cm. Is it possible or not? Why?Give your justification?

Construct a triangle ΔABC\Delta ABC in which BC= 6 cm, ∠B=60∘,∠C=45∘\angle B=60^{\circ},\angle C=45^{\circ}

Construct a ΔABC\Delta ABC whose sides are 4 cm, 5 cm4\ cm,\ 5\ cm and 7 cm7\ cm respectively

Construct Δ\DeltaXYZ such that, l(XY)=3.7cml(XY)=3.7cm, l(YZ)=7.7cml(YZ)=7.7cm, l(XZ)=6.3cml(XZ)=6.3cm.

Draw an equilateral triangle whose sides are 4.8cm4.8\,\, cm each .

Construct Δ\DeltaPQR if PQ=5=5 cm, m∠\anglePQR =105o=105^o and m∠\angleQRP=40o=40^o.

Construct a \triangle{XYZ}\triangle{XYZ} in which XY=4.5XY=4.5cm,YZ=5YZ=5cm and ZX=6ZX=6cm

What is the side included between the angles M and N of \triangle MNP\triangle MNP?

Draw a line, say ABAB, take a point CC outside it. Through CC, draw a line parallel to ABAB using ruler and compasses only.

Draw \Delta ABC\Delta ABC with AB=6AB=6 cm, AC=5AC=5 cm and \angle A = {85^ \circ }\angle A = {85^ \circ }

Construct a \triangle LMN\triangle LMN in which LM=8.3\ cm, \angle L=45^{o}LM=8.3\ cm, \angle L=45^{o} and \angle M=60^{o}\angle M=60^{o}.

Draw a circle with centre PP and radius 2.1 cm2.1 cm. Take point QQ at a distance 5.2 cm5.2 cm from the centre. Draw tangents to the circle from point QQ. Measure and write the length of a tangent segment.

Construct a right angled triangle PQRPQR, in which \angle Q={90}^{o}\angle Q={90}^{o}, hypotenuse PR=8cmPR=8cm and QR=4.5cmQR=4.5cm. Draw a bisector of angle PQRPQR and let it meet PRPR at point TT. Prove that TT is equidistant from PQPQ and QRQR.

Construct a \triangle ABC\triangle ABC, when:\displaystyle AB=6.0\ cm,AC=8.0\ cm\displaystyle AB=6.0\ cm,AC=8.0\ cm and BC=7.5\ cm.BC=7.5\ cm.

Construct a \triangle ABC\triangle ABC, when \displaystyle BC= 3.6\ cm, CA=3.0\ cm\displaystyle BC= 3.6\ cm, CA=3.0\ cm and \angle C=30^{\circ}.\angle C=30^{\circ}.

If \displaystyle A= 30^{\circ},a= 7 \displaystyle A= 30^{\circ},a= 7 and \displaystyle b=8 \displaystyle b=8 in \displaystyle \Delta ABC \displaystyle \Delta ABC then find the number of triangles that can be constructed.

Construct a line segment AB =5cm . Construct a line segment ED parallel to AB at a distance of 4 cm from it.

Construct a right angle \triangle ABC\triangle ABC, right angled at BB, when CA = 100,\:BC = 64\ cmCA = 100,\:BC = 64\ cm. Measure the remaining angles of the triangle.

Construct a \triangle ABC\triangle ABC in which: side AB= 4.3AB= 4.3 cm, side BC= 4.9BC= 4.9 cm and altitude BD= 3.3BD= 3.3 cm.

Construct a \triangle ABC\triangle ABC, when \displaystyle BC=6.2\ cm, CA=9.0\ cm\displaystyle BC=6.2\ cm, CA=9.0\ cm and \angle B=90^{\circ}\angle B=90^{\circ}

Construct ABCABC, an isosceles triangle with AB= AC= 13AB= AC= 13 cm and BC=10BC=10 cm. Calculate the length of perpendicular from AA to BCBC.

Construct the parallel lines with steps.

Construct a line segment LM of 10 cm.Draw a line parallel to LM at a distance of 1 cm from it.

Solve the right triangle ABCABC if angle AA is 6060, and the hypotenuse is 66 m.

Construct a triangle ABC,ABC, whose base \displaystyle BC=6\ cm, \displaystyle \angle B=60^{o} \displaystyle BC=6\ cm, \displaystyle \angle B=60^{o} and altitude \displaystyle AD= 4 \displaystyle AD= 4cm.

Construct a triangle with sides 55 cm, 5.55.5 cm and 6.56.5 cm. Now construct another triangle, whose sides are \dfrac {5}{3}\dfrac {5}{3} times the corresponding sides of the given triangle.

Solve the right triangle ABCABC if angle AA is 3030, and the hypotenuse is 44 m.

Construct an parallel lines with an angle 45.

Construct a triangle XYZXYZ in which XY = 5 cm, YZ = 5.5 cmXY = 5 cm, YZ = 5.5 cm and \angle XYZ = 100^{\circ}\angle XYZ = 100^{\circ}

Construct a triangle ABCABC in which AB = 5 cmAB = 5 cm and BC = 4.6 cmBC = 4.6 cm and AC = 3.7 cmAC = 3.7 cm

Construct a right-angled triangle whose base is 12cm12cm and the sum of its hypotenuse and another side is 18cm18cm.

Construct an isosceles triangle whose perimeter is 12\ \text{cm}12\ \text{cm} and altitude 4\ \text{cm}4\ \text{cm} and the sides of the triangle are in ratio 3:4:5.3:4:5.

Construct \Delta LMN\Delta LMN in which LN=7 cm, NM=5.5 cm, LM=6.4 cm.

Construct a triangle XYZXYZ in which XY = 7.8 \text{ cm}, YZ = 4.5 \text{ cm}XY = 7.8 \text{ cm}, YZ = 4.5 \text{ cm} and XZ = 9.5 \text{ cm}XZ = 9.5 \text{ cm}

Construct a triangle PQRPQR in which QR = 4.8 cm, \angle Q = 45^{\circ}QR = 4.8 cm, \angle Q = 45^{\circ} and \angle R = 55^{\circ}\angle R = 55^{\circ}

Construct a triangle PQRPQR, given that PQ = 5.6 \text{ cm, PR = 7 cm}PQ = 5.6 \text{ cm, PR = 7 cm} and QR = 4.5 \text{ cm}QR = 4.5 \text{ cm}

Construct a triangle PQRPQR in which PQ = 5.4 cm, QR = 5.5 cmPQ = 5.4 cm, QR = 5.5 cm and \angle PQR = 55^{\circ}\angle PQR = 55^{\circ}

Construct a triangle LMNLMN in which LM = 7.8 cm, MN = 6.3 cmLM = 7.8 cm, MN = 6.3 cm and \angle LMN = 45^{\circ}\angle LMN = 45^{\circ}.

Construct a triangle ABCABC in which AB = 6.5 cm, \angle A = 45^{\circ}AB = 6.5 cm, \angle A = 45^{\circ} and \angle B = 60^{\circ}\angle B = 60^{\circ}

Construct a right angle triangle PQRPQR in which \angle R = 90^{\circ}, PQ = 4 cm\angle R = 90^{\circ}, PQ = 4 cm and QR = 3 cmQR = 3 cm

Construct a triangle ABCABC in which AB = 5cm, BC = 4.3 cmAB = 5cm, BC = 4.3 cm and AC = 4 cmAC = 4 cm

Construct a right angle triangle ABCABC in which \angle B = 90^{\circ}, BC = 4 cm\angle B = 90^{\circ}, BC = 4 cm and AC = 5 cmAC = 5 cm

Construct a triangle ABCABC in which AB + AC = 5.6\ cm, BC = 4.5\ cmAB + AC = 5.6\ cm, BC = 4.5\ cm and \angle B = 45^{\circ}\angle B = 45^{\circ}

Construct a triangle XYZXYZ in which XY = 4.5 cmXY = 4.5 cm and \angle X = 100^{\circ}\angle X = 100^{\circ} and \angle Y = 50^{\circ}\angle Y = 50^{\circ} using ruler and protractor.

Construct a triangle ABCABC in which BC = 5.2\ cm, \ \angle B = 35^{\circ}BC = 5.2\ cm, \ \angle B = 35^{\circ} and \angle C = 80^{\circ}\angle C = 80^{\circ}.

Construct a right angled triangle ABCABC in which \angle B = 90^{\circ}, AB = 5 cm\angle B = 90^{\circ}, AB = 5 cm and AC = 7 cmAC = 7 cm

Construct a triangle PQRPQR, given that PQ = 4 cm, QR = 5.2 cmPQ = 4 cm, QR = 5.2 cm and \angle Q = 60^{\circ}\angle Q = 60^{\circ}

Construct a triangle ABCABC in which BC = 6 cm, \angle{B} = 30^{\circ}BC = 6 cm, \angle{B} = 30^{\circ} and \angle C = 125^{\circ}\angle C = 125^{\circ}

Draw a triangle with sides 5 cm, 6 cm and 6 cm. Draw a square having the same area as the triangle.

Draw an equilateral triangle of sides 5 cm. Construct a square having the same area as that of this triangle.

Construct a \triangle ABC\triangle ABC in which BC=3.6\ cm, AB=5\ cmBC=3.6\ cm, AB=5\ cm and AC=5.4\ cmAC=5.4\ cm. Draw the perpendicular bisector of the side BCBC.

Draw the right triangle whose sides are 3\ cm, 4\ cm3\ cm, 4\ cm and 5\ cm5\ cm and construct its centroid

Construct \Delta ABC\Delta ABC in which BC = 8cmBC = 8cm, \angle B=45^o\angle B=45^o and AB -AC=3.5AB -AC=3.5 cm.

Construct a right triangle whose base is 7.5 cm. and sum of its hypotenuse and other side is 15 cm.

Draw the \triangle PQR\triangle PQR, where PQ = 6\ cm, \angle P = 110^{\circ}PQ = 6\ cm, \angle P = 110^{\circ} and QR = 8\ cmQR = 8\ cm and construct its centroid

Construct the \triangle ABC\triangle ABC such that AB = 6\ cm, BC = 5\ cmAB = 6\ cm, BC = 5\ cm and AC = 4\ cmAC = 4\ cm and locate its centroid

Construct a \triangle{ABC}\triangle{ABC} such that AB=6AB=6 cm, \angle{C}={40}^{o}\angle{C}={40}^{o} and the altitude from CC to ABAB is of length 4.24.2cm.

Construct \Delta ABC\Delta ABC in which AB = 4 cm, BC = 7 cm and CA = 3 cm. Which type of triangle is this?

Draw a line EFEF take a point GG above EFEF, draw a line ABAB through GG such that AB || EFAB || EF.

Construct a \triangle PQR\triangle PQR in which PQ = 6.2PQ = 6.2 cm, \angle Q = 60^{o}\angle Q = 60^{o} and RQ - PR = 3RQ - PR = 3 cm.

Construct \triangle UVW\triangle UVW with UV =6\ cm, \, VW =6\,cmUV =6\ cm, \, VW =6\,cm and UW=6\,cm.UW=6\,cm.

Draw a triangle ABC with BC=6BC=6cm, AB=5=5cm and \angle\angleABC =60^o=60^o. Then construct a triangle whose sides are \displaystyle\frac{3}{4}\displaystyle\frac{3}{4} of the corresponding sides of the \Delta\Delta ABC.

Construct a \Delta LMN \, MN = 6.2 \Delta LMN \, MN = 6.2 cm, \angle LMN = 75^o \, \angle LNM = 60^o \angle LMN = 75^o \, \angle LNM = 60^o and construct any 22 medias.

Construct \triangle ABC\triangle ABC with BC=7.5\ cmBC=7.5\ cm, AC=5\ cmAC=5\ cm and m\angle C={60}^{o}m\angle C={60}^{o}.

Write down the procedure of constructing of a $\triangle ABC$ with $BC=7.5\ cm, AC=5\ cm$ and $\angle C=60^{o}$

Is it possible to have a triangle with the following sides $2\ cm,3\ cm,5\ cm$

Is it possible to construct a triangle $ABC$ in which $BC=8\ cm,\angle B=40^\circ$ and $AB=AC=3.5\ cm\ ?$

Construct $\Delta DEF$ in which DE=8 cm, DF=7.2 cm, EF=6.3 cm.

Construct a triangle $PQR$ with side $QR=7cm,$ $PQ=6cm$ and angle $PQR={60^0}$ then construct another triangle whose side are $3/5$ of the corresponding sides of triangle $PQR?$

Construct a triangle ABC in which $AB= AC=5.44\ cm\ and\$ BC=6 cm. Draw all its lines of symmetry.

Construct a scalene triangle $ABC$ , given $AB=3$ cm, $AC =5$ cm and $BC =4$ cm.

Construct a right triangle $LMN$ in which $\angle M = 90^{\circ}, MN = 4 cm$ and $LN = 6.2\ cm$

Construct a triangle $ABC$ , in which $AB = 4.5 cm, AC = 5.5 cm$ and $\angle BAC = 75^{\circ}$

Two sides of a triangle are $12\ cm$ and $14\ cm$ . The perimeter of the triangle is $36\ cm$ . What is the length of third side

Construct $\Delta TEN$ such that TE = 3 cm, $\angle E = 90^o$ and NE = 4 cm.

Construct $\triangle XYZ$ in which $XY=4.5\ cm,YZ=5\ cm$ and $ZX=6\ cm$ .

Draw a triangle ABC in which AB = 5 cm, BC = 7 cm, and $\angle B = 75^{o}$ .

Try to construct a triangle with $5\ cm, 8\ cm$ and $1\ cm$ . Is it possible or not? Why?Give your justification?

Construct a triangle $\Delta ABC$ in which BC= 6 cm, $\angle B=60^{\circ},\angle C=45^{\circ}$

Construct a $\Delta ABC$ whose sides are $4\ cm,\ 5\ cm$ and $7\ cm$ respectively

Construct $\Delta$ XYZ such that, $l(XY)=3.7cm$ , $l(YZ)=7.7cm$ , $l(XZ)=6.3cm$ .

Draw an equilateral triangle whose sides are $4.8\,\, cm$ each .

Construct $\Delta$ PQR if PQ $=5$ cm, m $\angle$ PQR $=105^o$ and m $\angle$ QRP $=40^o$ .

Construct a $\triangle{XYZ}$ in which $XY=4.5$ cm, $YZ=5$ cm and $ZX=6$ cm

What is the side included between the angles M and N of $\triangle MNP$ ?

Draw a line, say $AB$ , take a point $C$ outside it. Through $C$ , draw a line parallel to $AB$ using ruler and compasses only.

Draw $\Delta ABC$ with $AB=6$ cm, $AC=5$ cm and $\angle A = {85^ \circ }$

Construct a $\triangle LMN$ in which $LM=8.3\ cm, \angle L=45^{o}$ and $\angle M=60^{o}$ .

Draw a circle with centre $P$ and radius $2.1 cm$ . Take point $Q$ at a distance $5.2 cm$ from the centre. Draw tangents to the circle from point $Q$ . Measure and write the length of a tangent segment.

Construct a right angled triangle $PQR$ , in which $\angle Q={90}^{o}$ , hypotenuse $PR=8cm$ and $QR=4.5cm$ . Draw a bisector of angle $PQR$ and let it meet $PR$ at point $T$ . Prove that $T$ is equidistant from $PQ$ and $QR$ .

Construct a $\triangle ABC$ , when:
$\displaystyle AB=6.0\ cm,AC=8.0\ cm$ and $BC=7.5\ cm.$

Construct a $\triangle ABC$ , when $\displaystyle BC= 3.6\ cm, CA=3.0\ cm$ and $\angle C=30^{\circ}.$

If $\displaystyle A= 30^{\circ},a= 7$ and $\displaystyle b=8$ in $\displaystyle \Delta ABC$ then find the number of triangles that can be constructed.

Construct a right angle $\triangle ABC$ , right angled at $B$ , when $CA = 100,\:BC = 64\ cm$ . Measure the remaining angles of the triangle.

side $AB= 4.3$ cm, side $BC= 4.9$ cm and altitude $BD= 3.3$ cm.

Construct a $\triangle ABC$ , when $\displaystyle BC=6.2\ cm, CA=9.0\ cm$ and $\angle B=90^{\circ}$

Construct $ABC$ , an isosceles triangle with $AB= AC= 13$ cm and $BC=10$ cm. Calculate the length of perpendicular from $A$ to $BC$ .

Solve the right triangle $ABC$ if angle $A$ is $60$ , and the hypotenuse is $6$ m.

Construct a triangle $ABC,$ whose base $\displaystyle BC=6\ cm, \displaystyle \angle B=60^{o}$ and altitude $\displaystyle AD= 4$ cm.

Construct a triangle with sides $5$ cm, $5.5$ cm and $6.5$ cm. Now construct another triangle, whose sides are $\dfrac {5}{3}$ times the corresponding sides of the given triangle.

Solve the right triangle $ABC$ if angle $A$ is $30$ , and the hypotenuse is $4$ m.

Construct a triangle $XYZ$ in which $XY = 5 cm, YZ = 5.5 cm$ and $\angle XYZ = 100^{\circ}$

Construct a triangle $ABC$ in which $AB = 5 cm$ and $BC = 4.6 cm$ and $AC = 3.7 cm$

Construct a right-angled triangle whose base is $12cm$ and the sum of its hypotenuse and another side is $18cm$ .

Construct an isosceles triangle whose perimeter is $12\ \text{cm}$ and altitude $4\ \text{cm}$ and the sides of the triangle are in ratio $3:4:5.$

Construct $\Delta LMN$ in which LN=7 cm, NM=5.5 cm, LM=6.4 cm.

Construct a triangle $XYZ$ in which $XY = 7.8 \text{ cm}, YZ = 4.5 \text{ cm}$ and $XZ = 9.5 \text{ cm}$

Construct a triangle $PQR$ in which $QR = 4.8 cm, \angle Q = 45^{\circ}$ and $\angle R = 55^{\circ}$

Construct a triangle $PQR$ , given that $PQ = 5.6 \text{ cm, PR = 7 cm}$ and $QR = 4.5 \text{ cm}$

Construct a triangle $PQR$ in which $PQ = 5.4 cm, QR = 5.5 cm$ and $\angle PQR = 55^{\circ}$

Construct a triangle $LMN$ in which $LM = 7.8 cm, MN = 6.3 cm$ and $\angle LMN = 45^{\circ}$ .

Construct a triangle $ABC$ in which $AB = 6.5 cm, \angle A = 45^{\circ}$ and $\angle B = 60^{\circ}$

Construct a right angle triangle $PQR$ in which $\angle R = 90^{\circ}, PQ = 4 cm$ and $QR = 3 cm$

Construct a triangle $ABC$ in which $AB = 5cm, BC = 4.3 cm$ and $AC = 4 cm$

Construct a right angle triangle $ABC$ in which $\angle B = 90^{\circ}, BC = 4 cm$ and $AC = 5 cm$

Construct a triangle $ABC$ in which $AB + AC = 5.6\ cm, BC = 4.5\ cm$ and $\angle B = 45^{\circ}$

Construct a triangle $XYZ$ in which $XY = 4.5 cm$ and $\angle X = 100^{\circ}$ and $\angle Y = 50^{\circ}$ using ruler and protractor.

Construct a triangle $ABC$ in which $BC = 5.2\ cm, \ \angle B = 35^{\circ}$ and $\angle C = 80^{\circ}$ .

Construct a right angled triangle $ABC$ in which $\angle B = 90^{\circ}, AB = 5 cm$ and $AC = 7 cm$

Construct a triangle $PQR$ , given that $PQ = 4 cm, QR = 5.2 cm$ and $\angle Q = 60^{\circ}$

Construct a triangle $ABC$ in which $BC = 6 cm, \angle{B} = 30^{\circ}$ and $\angle C = 125^{\circ}$

Construct a $\triangle ABC$ in which $BC=3.6\ cm, AB=5\ cm$ and $AC=5.4\ cm$ . Draw the perpendicular bisector of the side $BC$ .

Draw the right triangle whose sides are $3\ cm, 4\ cm$ and $5\ cm$ and construct its centroid

Construct $\Delta ABC$ in which $BC = 8cm$ , $\angle B=45^o$ and $AB -AC=3.5$ cm.

Draw the $\triangle PQR$ , where $PQ = 6\ cm, \angle P = 110^{\circ}$ and $QR = 8\ cm$ and construct its centroid

Construct the $\triangle ABC$ such that $AB = 6\ cm, BC = 5\ cm$ and $AC = 4\ cm$ and locate its centroid

Construct a $\triangle{ABC}$ such that $AB=6$ cm, $\angle{C}={40}^{o}$ and the altitude from $C$ to $AB$ is of length $4.2$ cm.

Construct $\Delta ABC$ in which AB = 4 cm, BC = 7 cm and CA = 3 cm. Which type of triangle is this?

Draw a line $EF$ take a point $G$ above $EF$ , draw a line $AB$ through $G$ such that $AB || EF$ .

Construct a $\triangle PQR$ in which $PQ = 6.2$ cm, $\angle Q = 60^{o}$ and $RQ - PR = 3$ cm.

Construct $\triangle UVW$ with $UV =6\ cm, \, VW =6\,cm$ and $UW=6\,cm.$

Draw a triangle ABC with $BC=6$ cm, AB $=5$ cm and $\angle$ ABC $=60^o$ . Then construct a triangle whose sides are $\displaystyle\frac{3}{4}$ of the corresponding sides of the $\Delta$ ABC.

Construct a $\Delta LMN \, MN = 6.2$ cm, $\angle LMN = 75^o \, \angle LNM = 60^o$ and construct any $2$ medias.

Construct $\triangle ABC$ with $BC=7.5\ cm$ , $AC=5\ cm$ and $m\angle C={60}^{o}$ .

Construct $\triangle ABC$ , given $m\angle A={60}^{o}, m\angle B={30}^{o}$ and $AB=5.8\ cm$ .

Construct $\triangle DEF$ such that $DE=5\ cm,DF=3\ cm$ and $m\angle EDF=90^{o}$ .

Construct an equilateral triangle of side $5.5\ cm$ .

Construct a $\triangle$ STU in which $T = 60^o$ , $U = 70^o$ and $TU = 7.5 cm$ .

Construct a $\Delta XYZ$ such that:
$XY=4.5\ \text{cm}$ , $\angle X={60 }^ { \circ }$ and $\angle Y={45 }^ { \circ }$ .

Construct $\triangle LMN$ in which $LM=6\ cm$ , $MN=5\ cm$ and $M=75^ {o}$

Draw a triangle $ABC$ with $BC=6\ cm, AB=5cm$ and $\angle ABC=60^{o}$ then construct a triangle whose sides are $4/5$ of the sides of the $\triangle ABC$ . Justify.

Construct a triangle $\triangle MNO$ where $\angle M =70^{o}, \angle N = 60^{o}$ and side $MN=7 \ cm$ .

Draw a triangle $ABC$ with side $BC = 7\ cm,\ \angle B = 45^{o},\ \angle A = 105^{o}.$ Then construct a triangle whose side are $\dfrac{4}{3}$ times the corresponding sides of $\triangle ABC.$ Write the construction.

Try to construct a triangle with $5$ cm, $8$ cm and $1$ cm. Is it possible or not? Why? Give your justification?