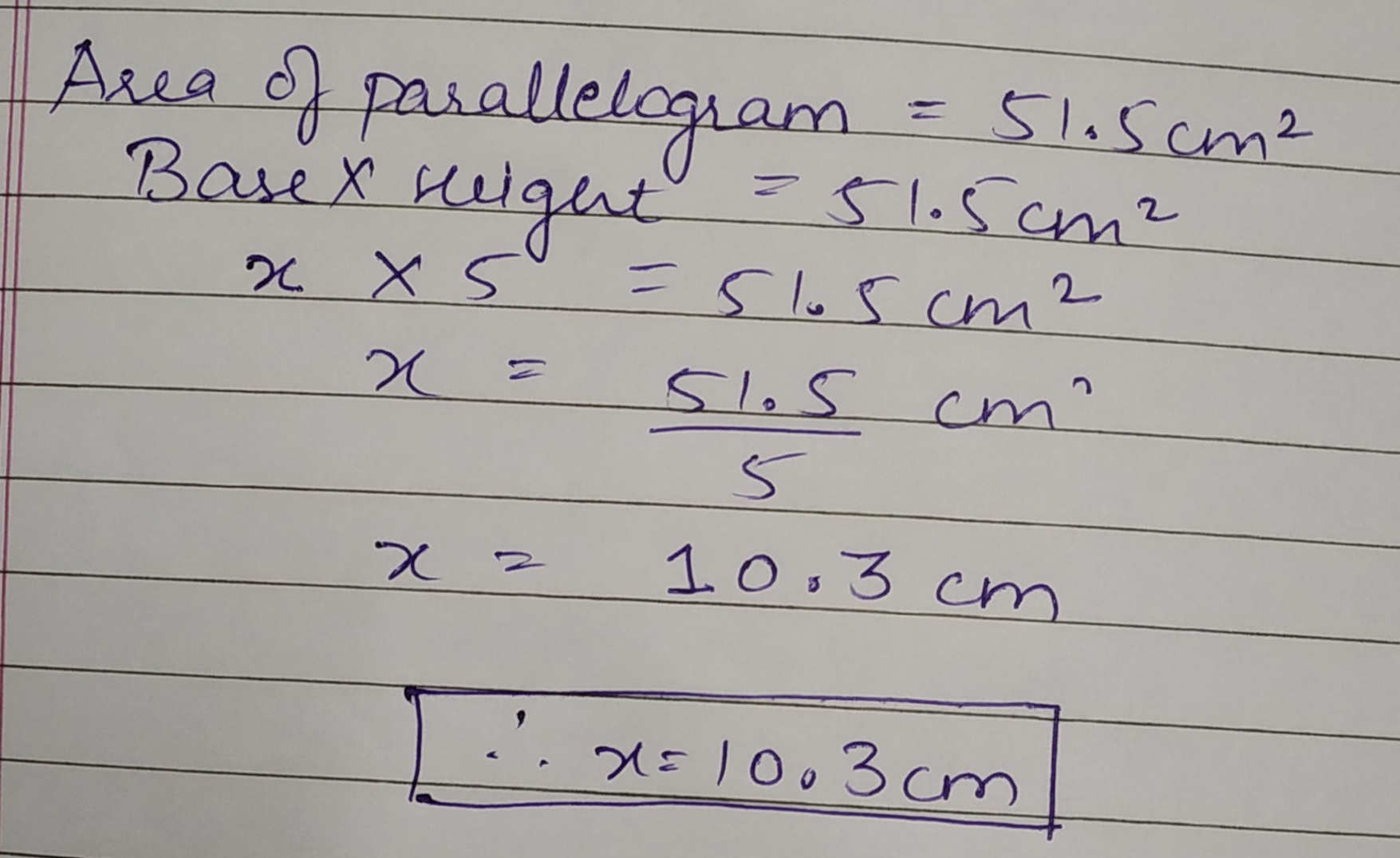Areas Of Parallelograms And Triangles - Class 9 Maths - Extra Questions
The area of parallelogram ABCD is 36 cm$$^2$$. Calculate the height of parallelogram ABEF if AB = 4.2 cm.
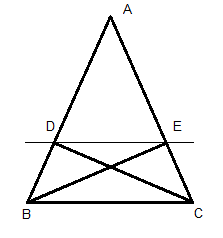
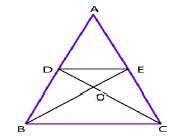
In the given figure, $$DE \parallel BC$$ and $$DE: BC= 4:5$$. Calculate the ratio of the areas of $$\triangle ADE$$ and the trapezium $$\triangle CEDB$$.
The area of this parallelogram is $$51.5 \,cm^2$$.
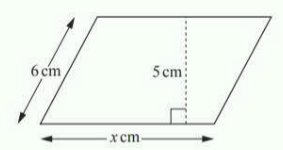
Work out the value of $$x$$.
In the given figure, $$DE \parallel BC$$. If $$DE= 5 \ cm, BC= 10 \ cm$$ and $$ar ( \triangle ADE)= 20 \ cm^2$$, find the area of $$\triangle ABC$$.
Find the area of following parallelograms:

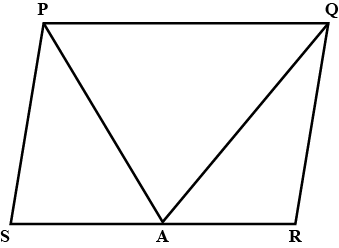
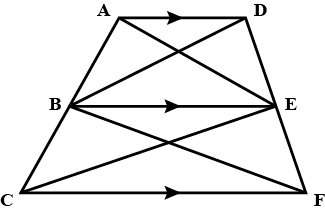
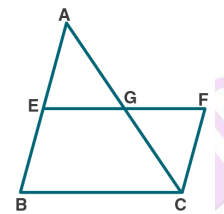
In the given figure,
$$AD || BE || CF.$$
Prove that :
$$Area \: \left ( \bigtriangleup \: AEC \right ) \: = \: Area \left ( \bigtriangleup \: DBF \right )$$
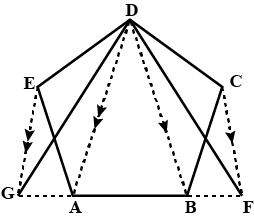
The given figure shows a pentagon $$ABCDE$$ .$$EG$$ drawn parallel to $$DA$$ meets $$BA$$ producedat G and $$CF$$ drawn parallel to $$DB$$ meets $$AB$$ produced at $$F$$ .
Prove that the area of pentagon $$ABCDE$$ is equal to the area of triangle $$GDF$$ .
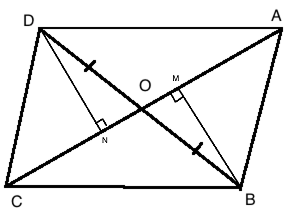
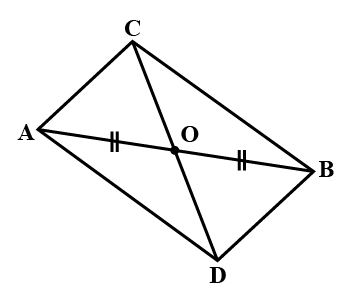
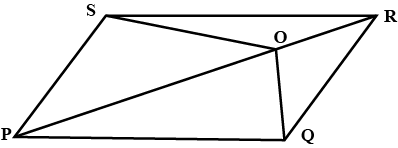
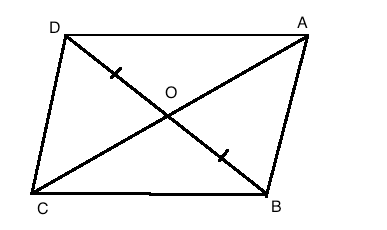
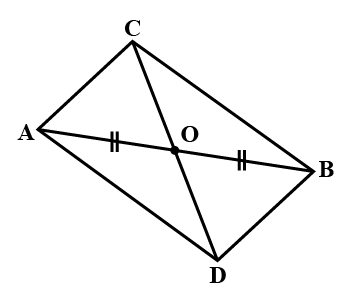
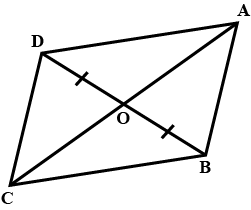
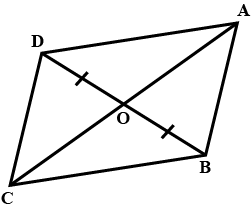
In the given figure, the diagonals AC and BD intersect at point O. If OB = OD and AB//DC, show that :$$Area (\Delta DCB)= \,Area (\Delta ACB)$$.
$$P$$ and $$Q$$ are any two points lying on the sides $$DC$$ and $$AD$$ respectively of a parallelogram $$ABCD$$. Show that $$area\ (\Delta APB) = area(\Delta BQC)$$
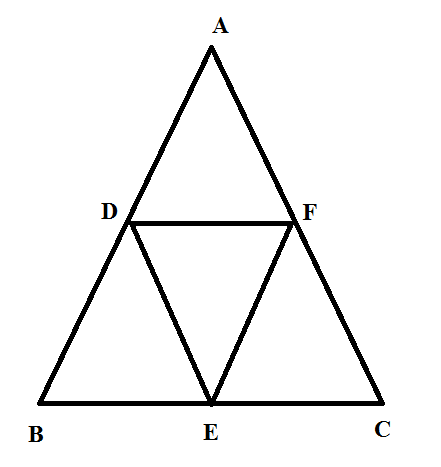
$$D$$, $$E$$ and $$F$$ are the mid-points of the sides $$BC$$, $$CA$$ and $$AB$$ respectively of triangle $$ABC$$. Prove that area of $$BDEF$$ is half the area of $$\displaystyle \Delta ABC$$.
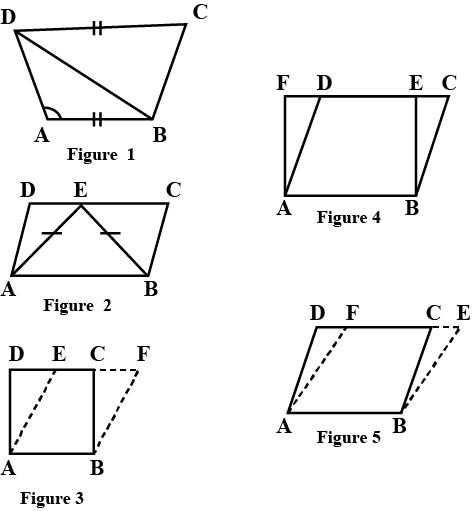
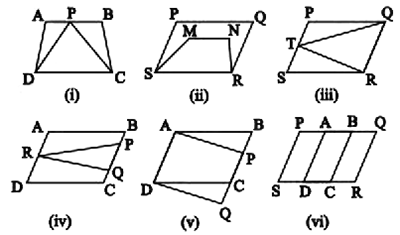
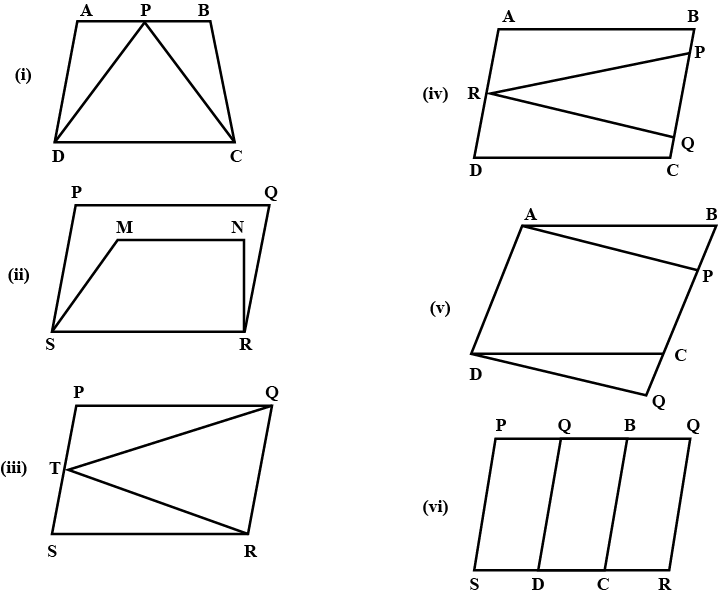
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels
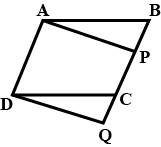
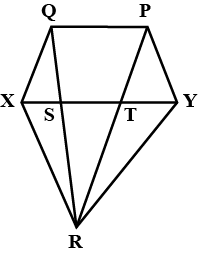
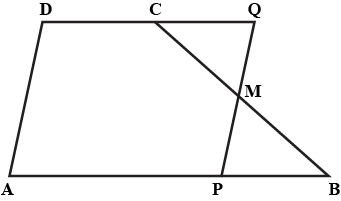
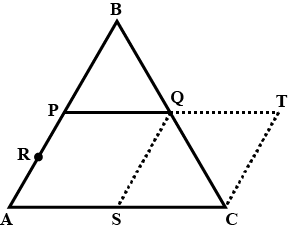
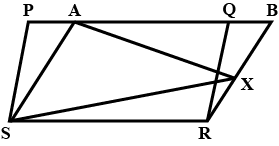
In fig, $$PQRS$$ and $$ABRS$$ are parallelogram and $$X$$ is any point on side $$BR$$. Show that
(i) $$area(PQRS) = area (ABRS)$$
(ii) $$area(AXS) = \dfrac {1}{2} area (PQRS)$$
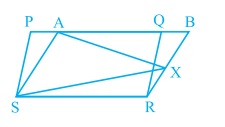
(i) $$area(PQRS) = area (ABRS)$$
(ii) $$area(AXS) = \dfrac {1}{2} area (PQRS)$$
In the given figure, DE is parallel BC.
Show that :Area ($$\Delta\,BOD$$) = Area ($$\Delta\,COE$$)
If E, F, G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that $$ar(EFGH) = \dfrac{1}{2} ar(ABCD)$$

Parallelogram $$ABCD$$ and rectangle $$ABEF$$ are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
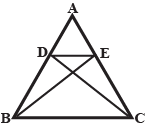
$$D$$ and $$E$$ are points on sides $$AB$$ and $$AC$$ respectively of $$\triangle ABC$$ such that $$area(DBC) = area(EBC)$$. Prove that $$DE\parallel BC$$
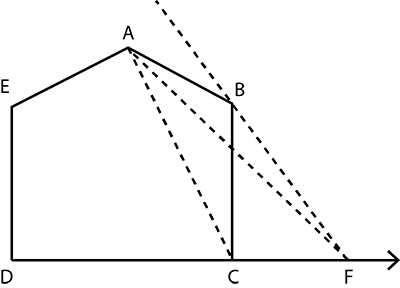
A villager Itwarri has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwarri agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented
In fig, $$ABCDE$$ is a pentagon. A line through $$B$$ parallel to $$AC$$ meets $$DC$$ produced at $$F$$. Show that
(i) $$ar(ACB) = ar(ACF)$$
(ii) $$ar(AEDF) = ar(ABCDE)$$
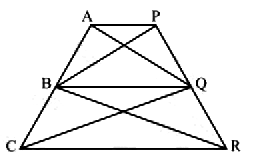
In Fig, $$AP\parallel BQ\parallel CR$$. Prove that $$ar(AQC) = ar(PBR)$$
In the figure, $$ABCD$$ is a quadrilateral. $$AC$$ is the diagonal and $$DE || AC$$ and also $$DE$$ meets $$BC$$ produced at $$E$$. Show that $$ar (ABCD) = ar (\triangle ABE)$$.
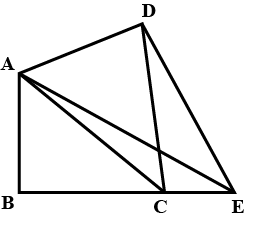
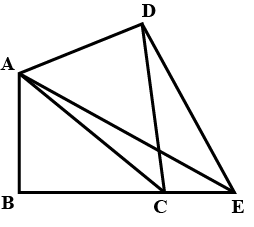
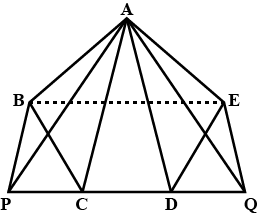
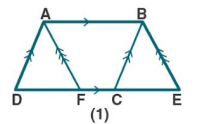
In fig, $$ABC$$ and $$BDE$$ are two equilateral triangles such that $$D$$ is the mid-point of $$BC$$. If $$AE$$ intersects $$BC$$ at $$F$$, show that:
(i) $$ar(BDE) = \dfrac {1}{4} ar(ABC)$$
(ii) $$ar(BDE) = \dfrac {1}{2} ar(BAE)$$
(iii) $$ar(ABC) = 2ar (BEC)$$
(iv) $$ar(BFE) = ar(AFD)$$
(v) $$ar(BFE) = 2 ar(FED)$$
(vi) $$ar(FED) = \dfrac {1}{8} ar(AFC)$$
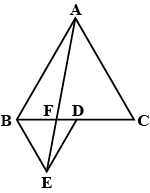
A farmer was having a field in the form of a parallelogram $$PQRS$$. She took any point A on $$RS$$ and joined it to points $$P$$ and $$Q$$. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
In the figure, diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that $$area(\triangle AOD) = area (\triangle BOC)$$.
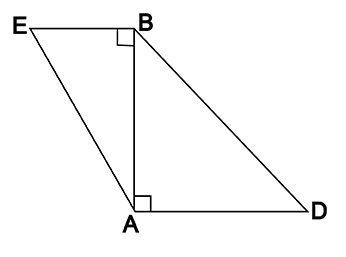
In the given figure drawn, seg $$BE \perp$$ seg $$AB$$ and seg $$BA \perp$$ seg $$AD$$. If $$BE=8$$ and $$AD=12$$, find $$\dfrac { A\left( \Delta ABE \right) }{ A\left( \Delta BAD \right) } $$.
The ratio of the areas of two triangles with common base in $$4 : 3$$. Height of the larger triangle is $$20$$ $$cm$$, then find the corresponding height of the smaller triangle
In the figure, $$\triangle ABC$$ and $$\triangle ABD$$ are two triangles on the same base $$AB$$. If line segment $$CD$$ is bisected by $$\overline{AB}$$ at $$O$$, show that $$area(\triangle ABC) = area (\triangle ABD)$$.
A villager Ramayya has a plot of land in the shape of a quadrilateral. The grampanchayat of the village decided to take over some portion of his plot from one of the corners to construct a school. Ramayya agrees to the above proposal with the condition that he should be given equal amount of land in exchange of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Find the number of shot in an incomplete square pile of $$16$$ courses when the number of shot in the upper course is $$1005$$ less than in the lowest course.
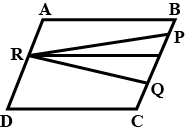
In the given figure , QP || XY, QX || PR and PY || QR. prove that ar($$\bigtriangleup$$QXR) = ar($$\bigtriangleup$$PQR)
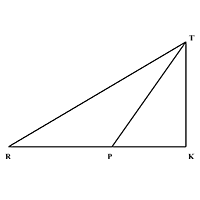
In the following figure $$RP : PK = 3 : 2$$, then find the value of $$A(\Delta TRP) : A(\Delta TPK)$$.
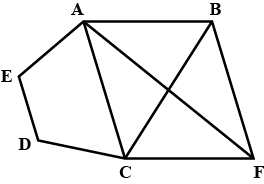
$$ar(\triangle ACB) = ar (\triangle ACF)$$
In a parallelogram $$ABCD, AB = 8$$ cm. The altitudes corresponding to sides $$AB$$ and $$AD$$ are respectively $$4$$ m and $$5$$ cm. Find $$AD$$.

In a parallelogram $$ABCD$$, $$AB = 10 cm$$. The altitudes corresponding to the sides $$AB$$ and $$AD$$ are respectively $$7 cm$$ and $$8 cm$$. Find $$AD$$.
$$A$$ point $$E$$ is taken on the side $$BC$$ of a parallelogram $$ABCD, AE$$ and $$DC$$ produced to meet at $$F$$. Prove that area $$(\Delta ADF) =$$ Area $$(ll^m \,ABFC)$$.
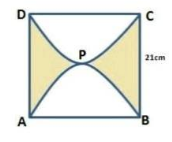
Find the permeter of the shaded region if ABCD is a square if sides 21cm and APB & CPD are semicircles.
In$$\Delta ABC$$, D E,F, are mid point of side AB, BC and AC reaspectively. If area($$CEDF$$)=$$24cm^{2}$$, find $$area (BEFD)$$:
If base a parallelogram is 8 cm and height is 5 cm then find its area.
In a figure $$X$$ and $$Y$$ are the mid point of $$AC$$ and $$AB$$ respectively, $$QP \parallel BC$$ and $$CYQ$$ and $$BXP$$ are straight lines. Prove that $$ar (\triangle ABP)=ar(\triangle ACQ)$$.

How wc can find the area of
Parallelogram = ?
Rhombus = ?
Trapezium = ?
Solve for p: $$ p ^ {2} - 10 p + 25=0 $$
The height of a parallelogram is one-third of its base. If the area of the parallelogram is $$108\ cm^2$$ then find its base and height.
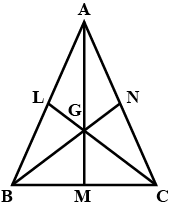
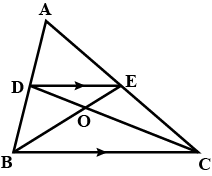
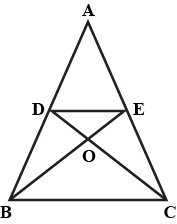
If the medians of a triangle $$ABC$$ intersect at $$G,$$ prove that:
$$ar.\left( {\Delta AGB} \right) = ar.\left( {\Delta AGC} \right) = ar\left( {\Delta BGC} \right) = \dfrac{1}{3}ar\left( {\Delta ABC} \right)$$
Find the area of rhombus with diagonals $$4cm,6cm$$
Find the area of the quadrilateral whose Base is $$5m$$ and Height is $$4m$$
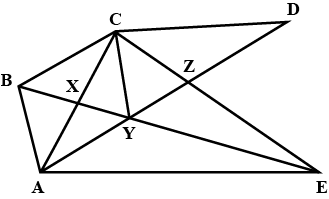
In figure , $$ABCDE$$ is any pentagon . $$BP$$ drawn parallel to $$AC$$ meets $$DC$$ produced at $$P$$ and $$EQ$$ drawn parallel to $$AD$$ meets $$CD$$ produced at $$Q$$ .
Prove that $$ar(ABCDE) = ar(APQ)$$ .
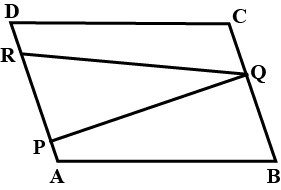
$$O$$ is any point on the diagonal $$PR$$ of parallelogram $$PQRS$$. Prove that $$ar(\triangle PSO)=ar(\triangle PQO)$$
Does the following figure lie on the same base and between the same parallels? In such a case, write the common base and two parallels.
Can the following figures be parallelograms. Justify your answer.
Does the following figure lie on the same base and between the same parallels? In such a case, write the common base and two parallels.
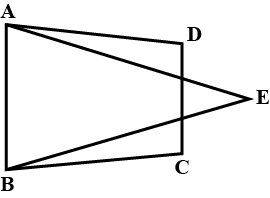
Can the following figures be parallelograms. Justify your answer.
ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively intersecting at P,Q and R. Prove that the perimeter of $$\Delta PQR$$ is double the perimeter of $$\Delta ABC$$.
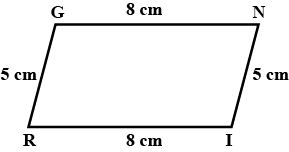
Does the following figure lie on the same base and between the same parallels? In such a case, write the common base and two parallels.
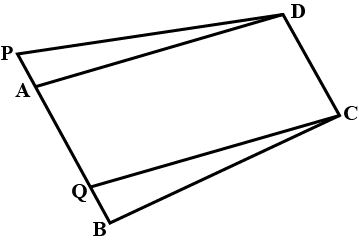
Does the following figure lie on the same base and between the same parallels? In such a case, write the common base and two parallels.
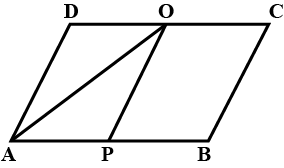
Does the following figure lie on the same base and between the same parallels? In such a case, write the common base and two parallels.
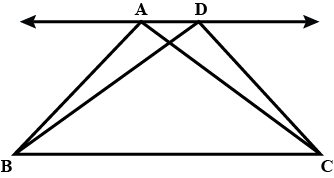
In a $$\triangle ABC$$, if $$L$$ and $$M$$ are points on $$AB$$ and $$AC$$ respectively such that $$LM||BC$$.Prove that:
$$ar(\triangle LOB)=ar (\triangle MOC)$$
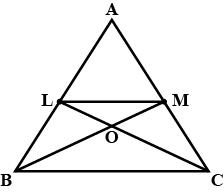
Does the following figure lie on the same base and between the same parallels? In such a case, write the common base and two parallels.
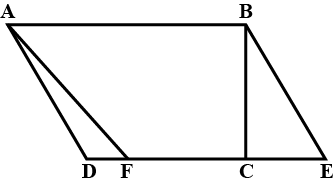
In the adjoining figure, $$ABCD$$ is a quadrilateral. A line through $$D$$, parallel to $$AC$$, meets $$BC$$ produced in $$P$$. Prove that $$ar(\triangle ABP)=ar(quad\ ABCD)$$.
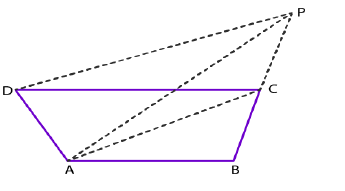
In the adjoining figure, $$DE||BC$$. Prove that
$$ar(\triangle ACD)=ar (\triangle ABE)$$
In the adjoining figure, $$ABCD$$ is a trapezium in which $$AB||DC$$ and its diagonals $$AC$$ and $$BD$$ intersect at $$O$$. Prove that $$ar(\triangle AOD)=ar(\triangle BOC)$$.

In a trapezium $$ABCD,\ AB||DC$$ and $$M$$ is the midpoint of $$BC$$. Through $$M$$ a line $$PQ|| AD$$ has been drawn meets $$AB$$ in $$P$$ and $$DC$$ produced in $$Q$$, as shown in the adjoining figure. Prove that $$ar(ABCD)=ar(APQD)$$.
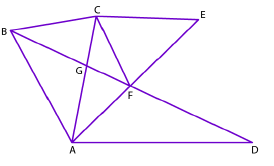
In a triangle $$ABC$$, the medians $$BE$$ and $$CF$$ intersect at $$G$$. Prove that $$ar(\triangle BCG)=ar(AFGE)$$.
In the adjoining figure, $$CE || AD$$ and $$CF || BA$$. Prove that $$ar(\triangle CBG)=ar(\triangle AFG)$$.
In the adjoining figure, $$\triangle ABC$$ and $$\triangle DBC$$ are on the same base $$BC$$ with $$A$$ and $$D$$ on opposite sides of $$BC$$ such that $$ar(\triangle ABC)=ar(\triangle DBC)$$. Show that $$BC$$ bisects $$AD$$.
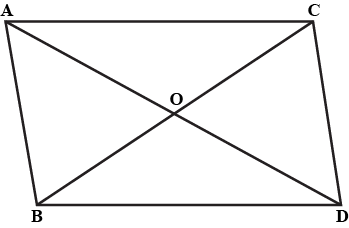
In the adjoining figure, the diagonals $$AC$$ and $$BD$$ of a quadrilateral $$ABCD$$ intersect at $$O$$. If $$BO=OD$$, prove that $$ar(\triangle ABC)=ar(\triangle ADC)$$

In Fig. 9.24, $$CD \parallel AE$$ and $$CY \parallel BA.$$ Prove that $$ar (\Delta CBX) = ar (\Delta AXY)$$
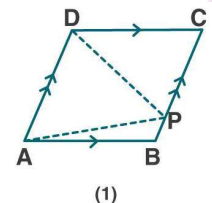
In the figure ( 1 ) given below, $$ A B C D $$ is a parallelogram and $$ P $$ is any point in BC.
Prove that: Area of $$ \triangle \mathrm{ABP}+ $$ area of $$ \Delta \mathrm{DPC}= $$ Area of $$ \triangle \mathrm{APD} $$.
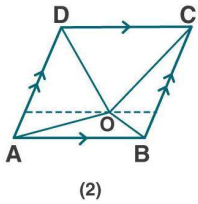
In the figure ( 2 ) given below, $$ O $$ is any point inside a parallelogram ABCD.
Prove that:
(i) area of $$ \Delta \mathrm{OAB}+ $$ area of $$ \Delta \mathrm{OCD}=1 / 2 $$ area of $$ \| \mathrm{gm} \mathrm{ABCD} $$
(ii) area of $$ \Delta \mathbf{O B C}+ $$ area of $$ \Delta \mathbf{O A D}=1 / 2 $$ area of $$ \| \mathbf{g m} \mathbf{A B C D} $$
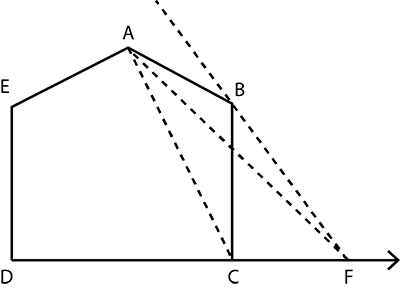
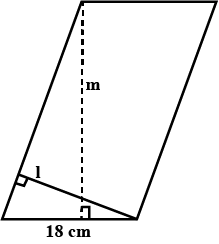
Perimeter of a parallelogram shaped land is $$96 \, \text{cm}$$ and its area is $$270\ \text{cm}^2$$. If one of the sides of this parallelogram is $$18\, \text{cm}$$, find the length of the other side. Also, find the lengths of altitudes $$l$$ and $$m$$ (Fig).
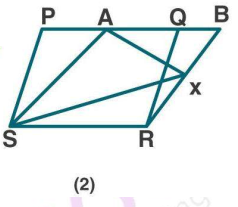
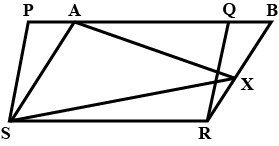
In the figure ( 2 ) given below, PQRS and ABRS are parallelograms and $$ X $$ is any point on the side BR. Show that area of $$ \Delta \mathrm{AXS}=1 / 2 $$ area of $$ \| \mathrm{gm} $$ PQRS.
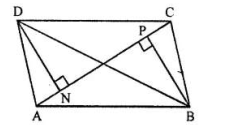
In the given figure, $$ A B C D $$ is a parallelogram. Perpendiculars DN and BP are drawn on diagonal AC. Prove that:
(i) $$ \Delta \mathrm{DCN} \cong \Delta \mathrm{BAP} $$
(ii) $$ \mathrm{AN}=\mathrm{CP} $$
In the figure ( 1 ) given below, area of parallelogram $$ A B C D $$ is $$ 29 \mathrm{cm}^{2} $$. Calculate the height of parallelogram ABEF if $$ \mathrm{AB}=5.8 \mathrm{cm} $$
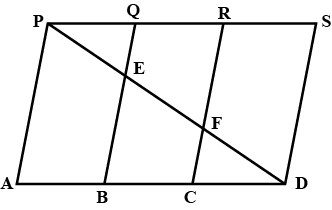
In Fig.9.11, PSDA is a parallelogram. Points Q and R are taken as PS such that $$PQ = QR = RS$$ and $$PA \parallel QB \parallel RC.$$ Prove that $$ar(PQE) = ar (CFD).$$
PQRS is a parallelogram whose area is $$180\,cm^2$$ and A is any point on the diagonal QS. The area of $$\Delta ASR = 90 \,cm^2.$$ Write True or False and justify your answer:
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
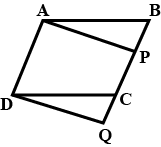
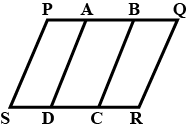
In the figure given, ABCD and AEFG are two parallelograms. Prove that area of $$ \| \mathrm{gm} \mathrm{ABCD}= $$ area of $$ \| \mathrm{gm} $$ AEFG.
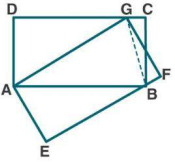
In the fig. (3) Given below, ABCD is a parallelogram. P is a point on DC such that area of $$ \Delta \mathbf{D A P}=25 \mathrm{cm}^{2} $$ and area of $$ \Delta \mathbf{B C P}=15 \mathrm{cm}^{2} . $$ Find
(i) area of $$ \| $$ gm $$ A B C D $$
(ii) DP: PC.
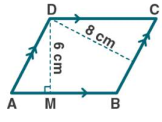
In the fig. ( 2) Given below, the side $$ A B $$ of the parallelogram ABCD is produced toE. A straight line through $$ A $$ is drawn parallel to $$ C E $$ to meet $$ C B $$ produced at $$ F $$ and parallelogram BFGE is Completed prove that area of $$ \| $$ gm $$ \mathrm{BFGE}= $$ Area of $$ \| \mathrm{gm} $$ ABCD.
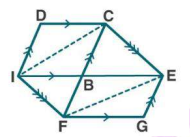
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
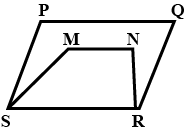
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
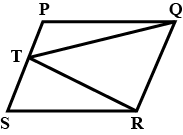
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
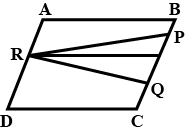
Show that:
A diagonal divides a parallelogram into two triangles of equal area.
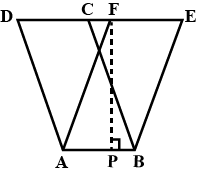
$$ABCD$$ and $$BCEF$$ are parallelograms. If area of triangle $$EBC =480\ cm^1, AB=30cm$$ and $$BC=40cm$$;
Calculate:
Area of parallelogram $$ABCD$$
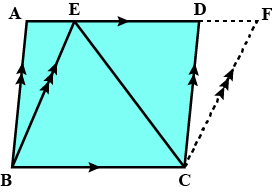
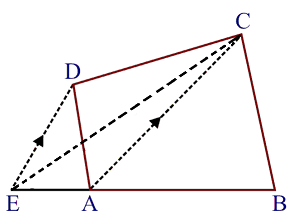
In the adjoining figure, $$ \mathbf{E} $$ is mid-point of the side $$ A B $$ of a triangle $$ A B C $$ and EBCF is a parallelogram. If the area of $$ \Delta \mathrm{ABC} $$ is $$ 25 \mathrm{sq} . $$ units, find the area of $$ \| \mathrm{gm} $$ EBCF.
In figure, $$PQRS$$ and $$ABRS$$ are parallelograms and $$X$$ is any point on side $$BR$$. Show that
$$ar. (PQRS)=ar. ( \square ABRS)$$
$$P$$ and $$Q$$ are any two points lying on the sides $$DC$$ and $$AD$$ respectively of a parallelogram $$ABCD$$. Show that $$ar(PAB)=ar (BQC)$$.

Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
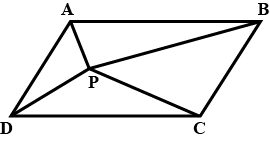
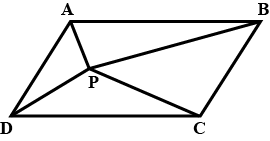
In figure, $$P$$ is a point in the interior of a parallelogram $$ABCD$$, Show that
$$ar. (ABP)=ar(PCD)=\dfrac 12 ar ( \square ABCD)$$
In Fig, diagonals $$AC$$ and $$BD$$ of quadrilateral $$ABCD$$ intersect at $$O$$ such that $$OB=OD$$. If $$AB=CD$$, then show that:
$$ar.(\triangle DOC)=ar.(\triangle AOB)$$
[Hint: From $$D$$ and $$B$$, draw perpendiculars to $$AC$$.]
$$P$$ and $$Q$$ are respectively the mid points of sides $$AB$$ and $$BC$$ of a triangle $$AABC$$ and $$R$$ is the mid point of $$AP$$, show that
$$ar. (\triangle PBQ)= ar. (\triangle ARC)$$
In figure, $$P$$ is a point in the interior of a parallelogram $$ABCD$$, Show that
$$ar. (ABD)=ar(PBC)=ar (APB)+ar(PCD)$$
(Hint: Through $$P$$, draw a line parallel to $$AB$$).
In figure, $$PQRS$$ and $$ABRS$$ are parallelograms and $$X$$ is any point on side $$BR$$. Show that
$$ar. (AXS)+=\dfrac 12ar. ( \square PQRS)$$
Show that the diagonals of a parallelogram divide it into four triangles of equal area.

In Fig, diagonals $$AC$$ and $$BD$$ of quadrilateral $$ABCD$$ intersect at $$O$$ such that $$OB=OD$$. If $$AB=CD$$, then show that:
$$ar.(\triangle DCB)=ar.(\triangle ACB)$$
[Hint: From $$D$$ and $$B$$, draw perpendiculars to $$AC$$.]
If the ratio of the altitude and the area of the parallelogram is $$2:11$$, then find the length of the base of the parallelogram.
Draw the following figure which is on the same base and in between the pair of parallel lines in your notebook.
(i) One obtuse angled triangle and a trapezium.
(ii) A parallelogram and an isosceles triangle.
(iii) A square and a parallelogram.
(iv) A rectangle and a rhombus.
(v) A rhombus and a parallelogram.
If heights of two triangles are in the ratio $$4:9$$ then find the ratio of their areas.
The side $$AB$$ of a parallelogram $$ABCD$$ is produced to any point $$P$$. A line through $$A$$ and parallel to $$CP$$ meets $$CB$$ produced at $$Q$$ and then parallelogram $$PBQR$$ is completed. Show that $$ar.(ABCD)=ar(PBQR)$$.
[Hint: Join $$AC$$ and $$PQ$$. Now compare $$ar. (\triangle ACQ)$$ and $$ar.(\triangle APQ)$$]
In the following figure, $$CD \parallel AE$$ and $$CY \parallel BA$$. Prove that $$ar (\triangle CBX)= ar ( \triangle AXY)$$.
Which of the following figures lie on the same base and between the same parallels? In such a case, write the common base and two parallels.
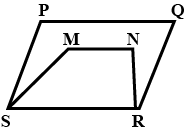
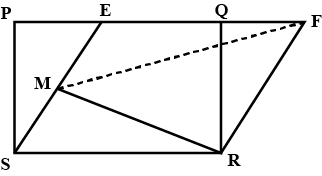
In a figure, $$PQRS$$ and $$EFRS$$ are two parallelograms then, prove that $$ar (MFR)= \dfrac12 ar (PQRS)$$.
Solve the following questions:
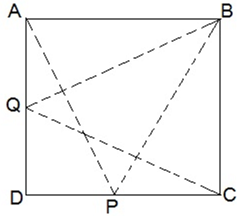
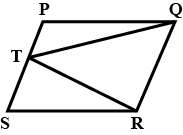
$$PB$$ and $$QA$$ are perpendicular at $$A$$ and $$B$$ of line segment $$AB$$. If $$P$$ and $$Q$$ lies on two sides $$AB$$ and by joining $$P$$ and $$Q$$. It intersects $$AB$$ at $$O$$ and $$PO=5cm,QO=7cm$$, $$ar(\triangle POB)=150{cm}^{2}$$ then find $$ar(\triangle QOA)$$
In the following figure, two triangles $$ABC$$ and $$DBC$$ are formed on same base $$BC$$. If $$AD,BC$$ intersect at point $$O$$ then show that
$$\cfrac { ar.\left( ABC \right) }{ ar.\left( DBC \right) } =\cfrac { AO }{ DO } $$
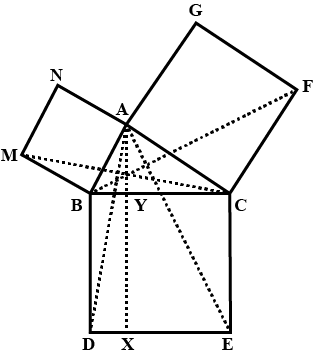
In figure $$ABC$$ is a right triangle right angled at $$A, BCED, ACFG$$ and $$ABMN$$ are square on the sides $$BC, CA$$ and $$AB$$ respectively. Line segment $$AX\bot DE$$ meets $$BC$$ at $$Y$$. Show that:
$$ar.(BCED)=ar.(ABMN)+ar.(ACFG)$$
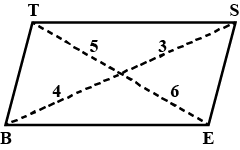
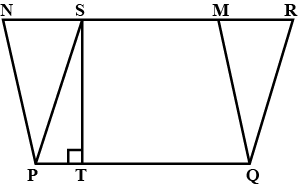
Two parallelograms $$PQRS$$ and $$PQMN$$ have common base $$PQ$$ as shown in figure. $$PQ= 9 \ cm, SM= 3 \ cm$$ and $$ST= 5 \ cm$$. Find the area of $$PQRN$$.
$$ABCD$$ is a parallelogram, $$E$$ and $$F$$ are the mid-points of $$BC$$ and $$CD$$ respectively.
Prove that: $$ar(\triangle AEF)= \dfrac38 ar(||gm \ ABCD)$$.
In the adjoining figure, $$DE||BC$$. Prove that
$$ar(\triangle OCE)=ar (\triangle OBD)$$
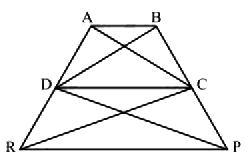
In the given fig, $$ar(DRC) = ar(DPC)$$ and $$ar(BDP) = ar(ARC)$$. Show that both the quadrilaterals $$ABCD$$ and $$DCPR$$ are trapeziums.
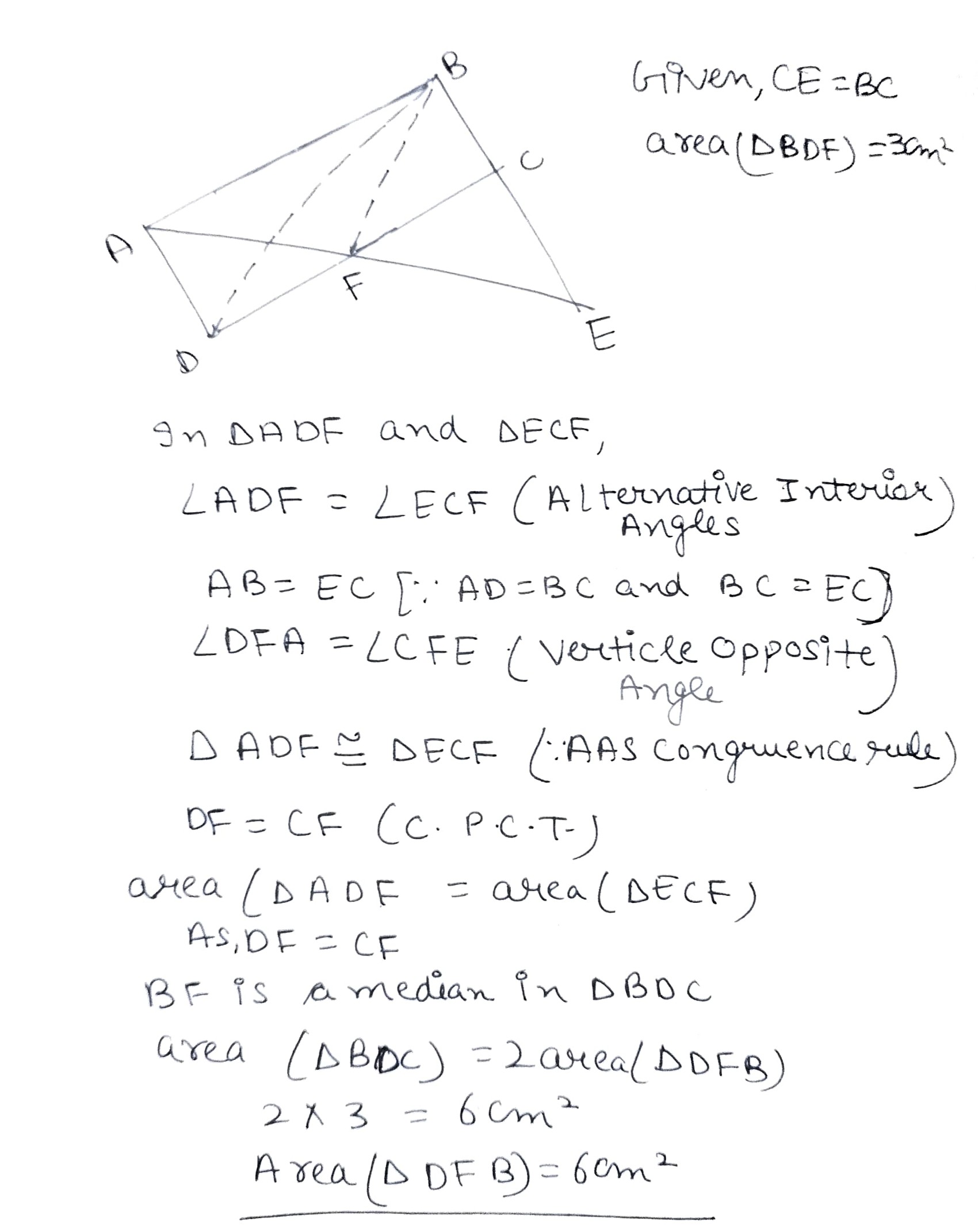
In fig. $$2$$, ABCD is a parallelogram in which BC is produced to E such that $$CE= BC$$. AE intersects CD at F. If area of $$\triangle BDF= 3 cm^2$$, find the area of parallelogram ABCD.
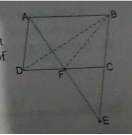
$$D$$ and $$E$$ are points on sides $$AB$$ and $$AC$$ respectively of $$\triangle ABC$$ such that $$ar(\triangle BCD)=ar(\triangle BCE)$$. Prove that $$DE || BC$$.
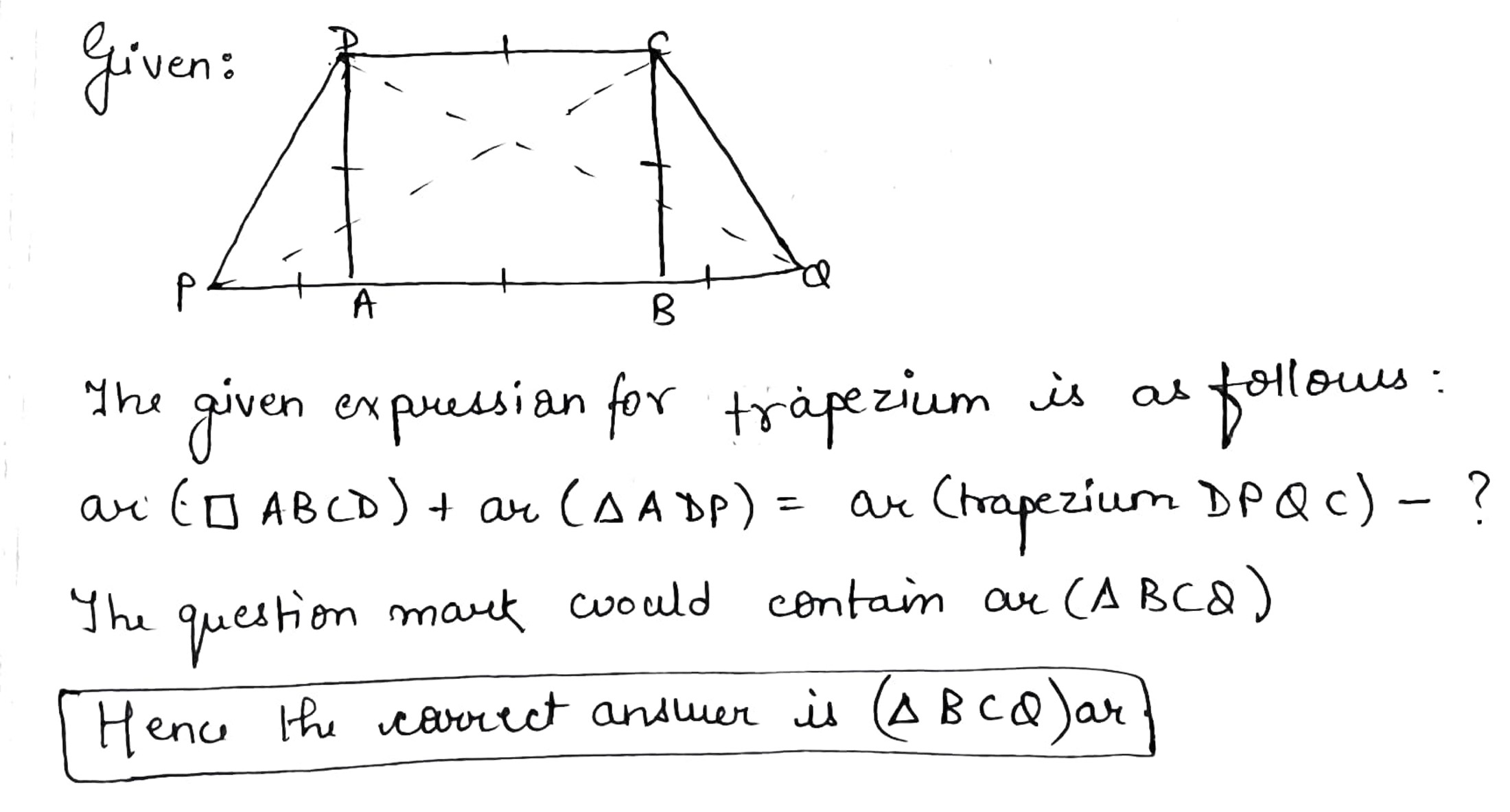
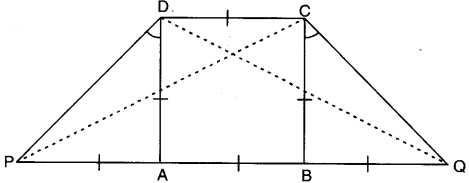
Find the missing term in the following on the basis of given diagram.
$$ ar(\square ABCD) + ar(\triangle ADP) = ar(\trapezium DPQC) - ? $$
Class 9 Maths Extra Questions
- Areas Of Parallelograms And Triangles Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Heron'S Formula Extra Questions
- Introduction To Euclid'S Geometry Extra Questions
- Linear Equations In Two Variable Extra Questions
- Lines And Angles Extra Questions
- Number Systems Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadrilaterals Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions