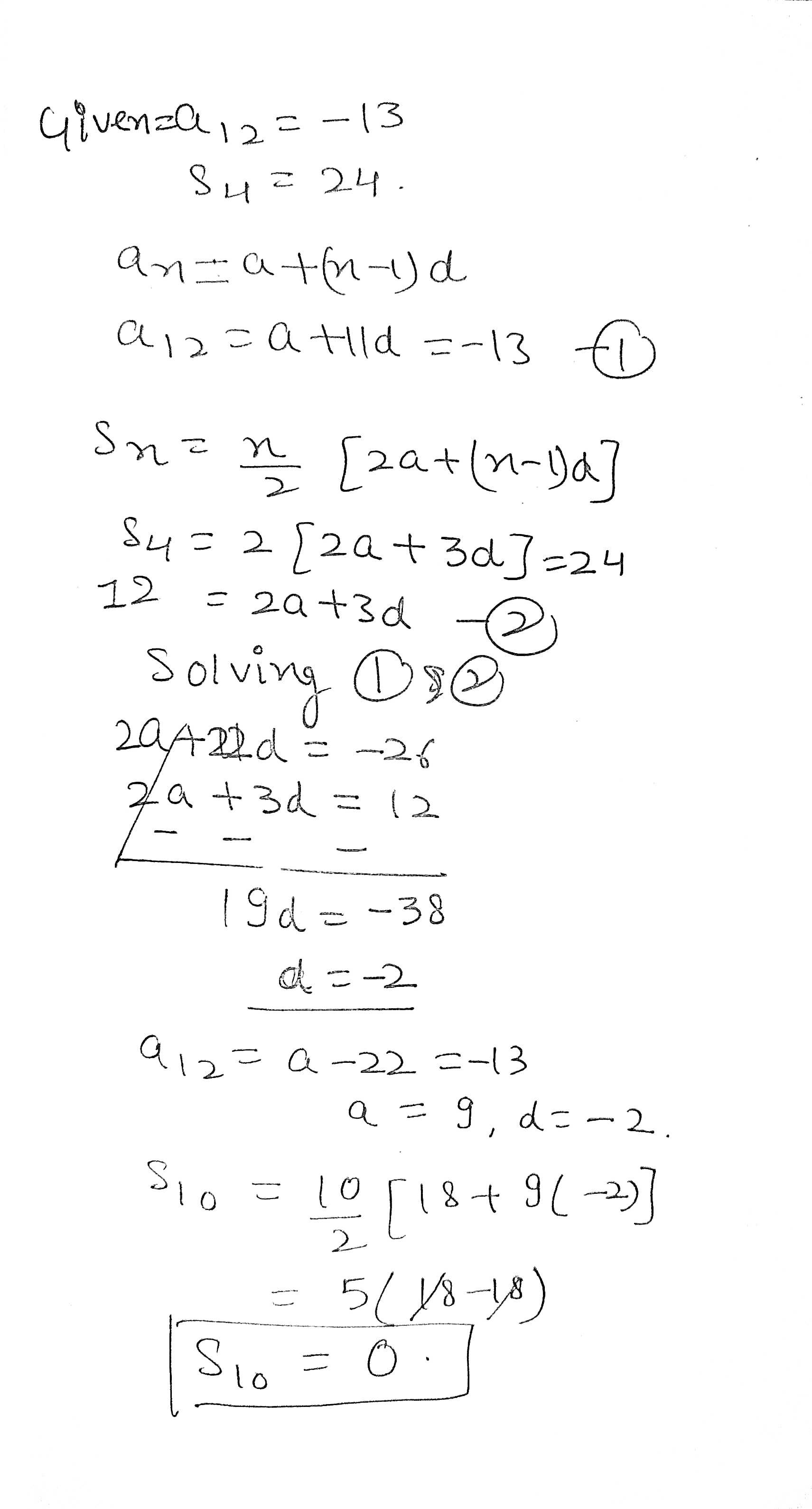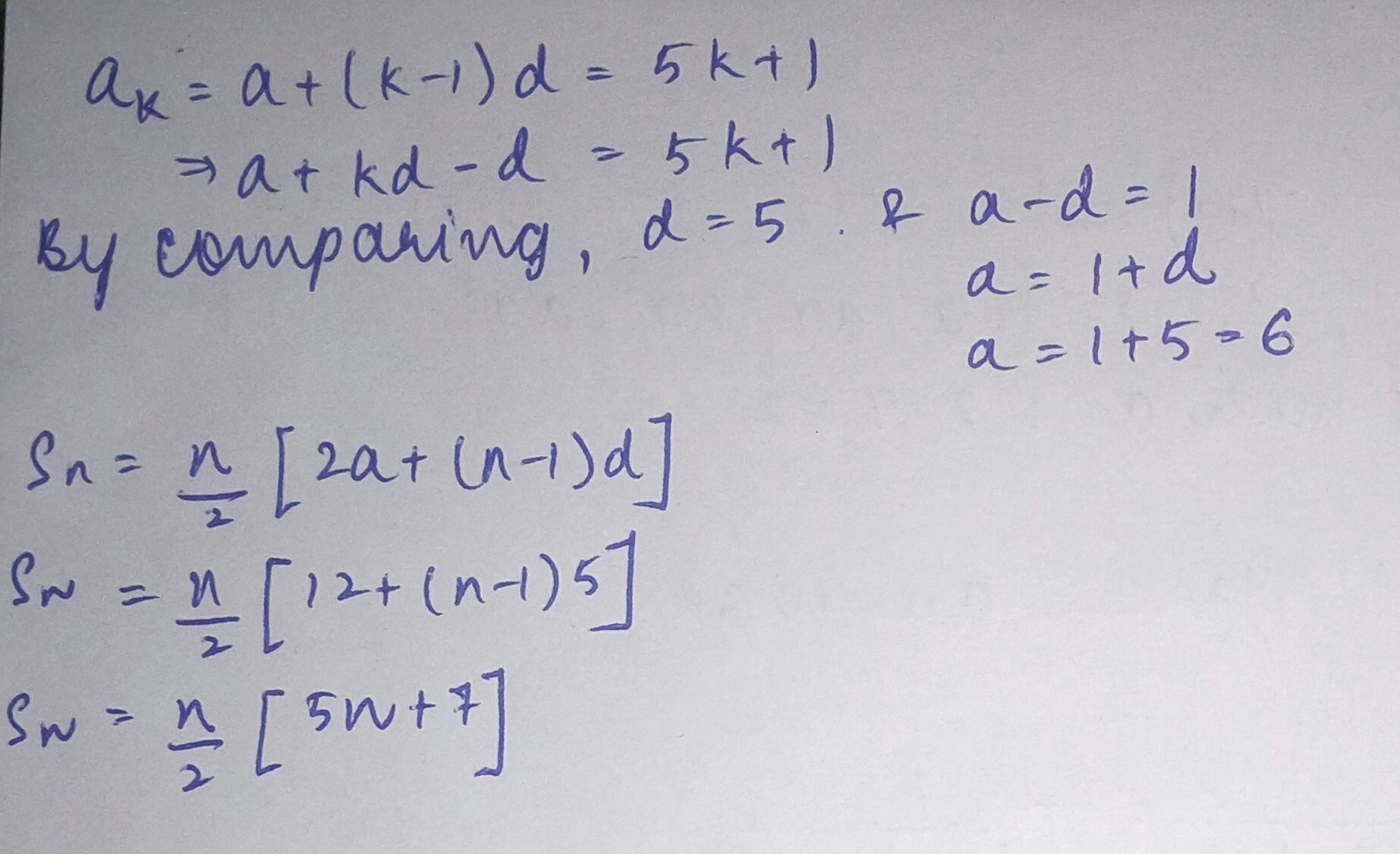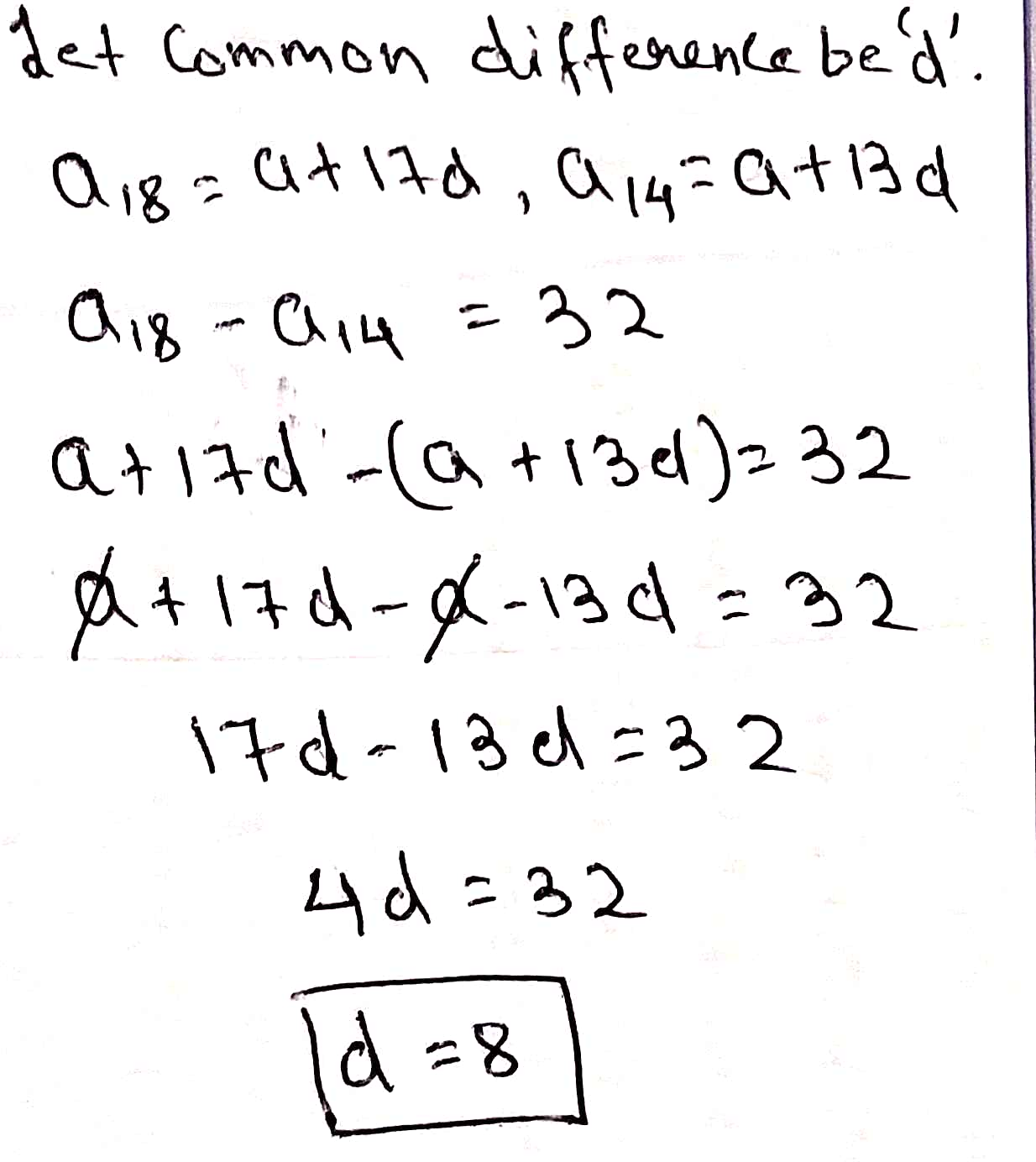Class 10 Maths - Arithmetic Progressions

Find the $20^{th}$ term of the AP whose $7^{th}$ term is 24 less than the $11^{th}$ term, first term being 12.

From the question, it is given that,

First-term

$a=12$

$7$ th term is

$24$ less than the

$11$ th term

$=T_{11}-T_{7}=24$

$\begin{array}{l}\mathrm{T}_{11}-\mathrm{T}_{7}=(\mathrm{a}+1 \mathrm{0d})-(\mathrm{a}+6 \mathrm{d})=24 \\24=\mathrm{a}+1 \mathrm{0d}-\mathrm{a}-6 \mathrm{d} \\24=4 \mathrm{d} \\\mathrm{d}=24 / 4 \\\mathrm{d}=6\end{array}\\$

$\mathrm{Now}, \mathrm{T}_{20}=\mathrm{a}+19 \mathrm{d}$

Substitute the values of

$a$ and

$d$

$\begin{array}{l}\mathrm{T}_{20}=12+19(6) \\\mathrm{T}_{20}=12+114 \\\mathrm{T}_{20}=126\end{array}\\$

Is 0 a term of the AP: 31, 28, 25, ...?
If true then enter $1$ and if false then enter $0$

The given sequence is an AP with first term

$a=31$ and common difference

$d=-3$

Let us consider that

$0$ is a term of the AP

Let

${a}_{n}=0$

$\Rightarrow a+(n-1)d=0$

$\Rightarrow 31+(n-1)\times-3=0$

$\Rightarrow n=\dfrac{31}{3}+1$

$=\dfrac{34}{3}$

$=11\dfrac{1}{3}$

Since

$n$ is a fraction which is not possible.

Hence

$0$ is not a term of an AP.

Find the eighteenth term of the A.P. $1, 7, 13, 19, ..........$

Let

$a$ be the first term and

$d$ be the common difference of given AP.
Hence

$a=1$ and

$d=7-1=6$ .

$t_n=a+(n-1)d$

$\Rightarrow t_{18}=1+17\times6$

$\Rightarrow t_{18}=1+102$

$\Rightarrow t_{18}=103$

Find the sum of all three digit natural numbers which are divisible by $7.$

The three-digit numbers that are divisible by

$7$ will be

$105, 112, 119,.........994$

These numbers will be in an Arithmetic progression with a common difference

$7$

The first number of the series is

$105$ and the last number is

$994$

The

$n^{th}$ term of an AP will be

$a_n=a+(n-1)d$

$\Rightarrow 994 = 105 + (n - 1)7$

$\Rightarrow (n-1)\times 7=889$

$\Rightarrow n-1=127$

$\Rightarrow n = 128$

Sum of

$n$ terms of the AP

$\Rightarrow S_n =\dfrac{n}{2} [2a+(n-1)d]$

$\Rightarrow S_{128}=\dfrac{128}{2} [2\times 105+(128-1)\times 7]$

$\Rightarrow S_{128}=64\times [210+127\times 7]$

$\Rightarrow S_{128}=64\times [210+889]$

$\Rightarrow S_{128}=64\times 1099$

$\Rightarrow S_{128}=70336$

Hence the sum of all the three-digit natural numbers that are divisible by

$7$ is

$70336$

Find the common difference the following A.P
$1, 4, 7, 10, 13, 16,..$

Given series is

$1,4,7,10,13,16,.......$

Common difference can be found out as :

$c.d.=a_2-a_1=a_3-a_2=a_4-a_3=...$

Let's check, therefore,

$a_2-a_1=$

$4 - 1 =3$

Also,

$a_3-a_2=$

$7 - 4 =3$

And,

$a_4-a_3=$

$10 - 7 = 3$

$\therefore$ common difference

$(d) = 3$

The difference between any two consecutive interior angles of a polygon is $\displaystyle {5} ^ {o}$ . If the smallest angle is $\displaystyle {120} ^ {o}$ , find the number of the sides of the polygon.

The angles of the polygon will form an A.P. with common difference

$d$ as

$\displaystyle {5} ^ {o}$ , and first term

$a$ is

$\displaystyle {120} ^ {o}$ .
It is known that the sum of all angles of a polygon with

$n$ sides is

$\displaystyle {180} ^ {o} \quad (n - 2 )$

$\therefore { S }_{ n }={ 180 }^{ 0 }(n-2)\\ \Rightarrow \dfrac { n }{ 2 } \left[ 2a+(n-1)d \right] ={ 180 }^{ 0 }(n-2)\\ \Rightarrow \dfrac { n }{ 2 } \left[ { 240 }^{ 0 }+(n-1){ 5 }^{ 0 } \right] ={ 180 }(n-2)\\ \Rightarrow n\left[ { 240 }+(n-1){ 5 } \right] =360(n-2)\\ \\ \Rightarrow 240n+{ 5n }^{ 2 }-5n=360n-720\\ \Rightarrow { 5n }^{ 2 }-125n+720=0\\ \Rightarrow { n }^{ 2 }-25n+144=0\\ \Rightarrow { n }^{ 2 }-16n-9n+144=0\\ \Rightarrow n(n-16)-9(n-16)=0\\ \Rightarrow (n-9)(n-16)=0\\ \Rightarrow { n=9\quad or\quad 16 }$

A man starts repaying a loan as first installment of Rs. $100$ . If he increases the installment by Rs $5$ every month. what amount he will pay in the $30^{th}$ installment?

The first installment of the loan is Rs.

$100$ .
The second installment of the loan is Rs.

$105$ and so on.
The amount that the man repays every month forms an A.P.
The A.P is

$100, 105, 110, ...$
First term,

$a=100$ , common difference

$d=5$

$\therefore \displaystyle{a}_{30} =a+(30-1)d=100+(29)(5)=100+145=245$
Thus, the amount to be paid in the

$30^{th}$ installment is Rs.

$245$ .

Find the sum of the first $40$ positive integers divisible by $6$

$6 + 12 + 18 + 24 + 40$ term
Here

$a = 6, d = a_{2} - a_{1} = 12 - 6 = 6$

$n = 40, S_{40} = ?$

$S_{n} = \dfrac{n}{2} [2a + (n - 1)d]$

$S_{40} = \dfrac{40}{2} [2 \times 6 + (40 - 1)6]$

$= 20[12 + 39 \times 6]$

$= 20 [12 + 234]$

$= 20 \times 246$

$\therefore S_{40} = 4920.$

The $17^{th}$ term of an $AP$ exceeds its $10^{th}$ term by $7$ . Find the common difference.

We know that,

For an A.P

$n^{th}$ term is given as

$a_{n}=a+(n-1)d$

$a_{17}=a+(17-1)d$

$a_{17}=a+16d$

Similarly,

$a_{10}=a+9d$

It is given that

$a_{17}-a_{10}=7$

$(a+16d)-(a+9d)=7$

$7d=7$

$\therefore d=1$

Therefore, the common difference is

$1$ .

Obtain the sum of the first $56$ terms of an A.P whose $18^{th}$ and $39^{th}$ terms are $52$ and $148$ respectively.

Given

${t}_{18}=52$ and

${t}_{39}=148$
We know that,

${t}_{n}=a+(n-1)d$
Here,

${t}_{18}=52$

$\therefore$

$a+(18-1)d=52$

$\therefore$

$a+17d=52..........(i)$
Also,

${t}_{39}=148$

$\therefore$

$a+(39-1)d=148$

$\therefore$

$a+38d=148.......(ii)$
Adding equation

$(i)$ and

$(ii)$ we get

$a+17d=52$

$a+38d=148$
-----------------------

$2a+55d=200.........(iii)$
We know that

${ S }_{ n }=\cfrac { n }{ 2 } \left[ 2a+(n-1)d \right]$

${ S }_{ 56 }=\cfrac { 56 }{ 2 } \left[ 2\times a+(56-1)d \right]$

$\therefore { S }_{ 56 }==28(2a+55d)$

$\therefore { S }_{ 56 }=28\times 200$

$\therefore { S }_{ 56 }=5600$ [From

$iii)$ ]

$\therefore$ The sum of the

$56$ term of an A.P is

$5600$

Find the eleventh term of the A.P.
$7,13,19,25,........$

We have

${t}_{1}=7,{t}_{2}=13,{t}_{3}=19$ and

${t}_{4}=25,.......$

$d={t}_{2}-{t}_{1}=13-7=6$

The common difference

$d=6$ and first term

$a=7$
We know that,

${t}_{n}=a+(n-1)d$

${t}_{11}=7+(11-1)\times 6$

$\therefore$

${t}_{11}=7+10\times 6$

$\therefore$

${t}_{11}=7+60$

$\therefore$

${t}_{11}=67$

$\therefore$ The eleventh term of the A.P is

$67$ .

Check whether the following sequence is an A.P. or not.
$1,3,6,10,....$

The given sequence is

$1,3,6,10,....$

Let

${ t }_{ 1 }=1,{ t }_{ 2 }=3,{ t }_{ 3 }=6,{ t }_{ 4 }=10....$
We can see that,

${ t }_{ 2 }-{ t }_{ 1 }=3-1=2$

${ t }_{ 3 }-{ t }_{ 2 }=6-3=3$

${ t }_{ 4 }- { t }_{ 3 }=10-6=4$
The difference between any two consecutive terms is not constant.

Hence, the given sequence is not an A.P.

Check whether the following sequence is an A.P. or not?
$1, 4, 7, 10, ...$

Here, in the series

$1,4,7,10,...$

If we observe, we find that the given sequence is an A.P.

First term:

$1$

Common Difference:

$4-1 = 7-4 = 10-7 = 3$

Check whether 13, 19, 25, 31, ............ form an A.P.

Here,

$T_1 = 13, T_2 = 19, T_3 = 25, T_4 = 31$ and so on

$d = T_2 - T_1 = 19 - 13 = 6$

$d = T_3 - T_2 = 25 - 19 = 6$

$d = T_4 - T_3 = 31 - 25 = 6$
Since the difference is common, so common difference exist.

Hence, the given sequence form an A.P.

The $11^{th}$ term and the $21^{st}$ term of an A.P. are $16$ and $29$ respectively, then find the first term and common difference.

Given,

$t_{11} = 16$ and

$t_{21} = 29$ .
We know that,

$t_{n} = a + (n - 1)d$

$\therefore t_{11} = a + (11 - 1)d$
and

$t_{21} = a + (21 - 1)d$

$\therefore 16 = a + 10d ...(i)$
and

$29 = a + 20d ...(ii)$
Subtracting equation (i) from (ii), we get

$10d = 13\Rightarrow d = 1.3$
Putting the value of

$d$ in equation (i), we get

$16 = a + 10(1.3)\Rightarrow a = 3$ .

Find the ninth term of the A.P.: $3, 7, 11, 15$ ...... .

Here,

$a=3, d=7-3=4, n=9$

$t_n=a+(n-1)d$

$t_9=3+(9-1)4$

$=3+8\times 4$

$=3+32$

$=35$

$\therefore$ The

$9^{th}$ term of the A.P. is

$35$ .

Find the term $t_{15}$ of an A.P.:
$4, 9, 14, .....$

The given A.P. is

$4,9,14,....$
We have,

$a =$ First term

$= 4$

$d =$ Common difference

$= 5$
We know that the

$n^{th}$ term of an A.P. with first term

$a$ and common difference

$d$ is given by

$t_n = a + (n - 1) d$

$t_{15} = a + (15 - 1) d$

$= 4 + (14) 5$

$= 4 + 70$

$t_{15} = 74$

Hence, the term

$t_{15}$ is

$74$

For the given A.P. 5, 10, 15, 20 ____
Find the common difference (d).

Common difference,

$d = T_2 - T_1$

$d = 10 - 5$

$d = 5$

Check whether the following sequence is an A.P. or not:
$2, 6, 10, 14, .....$

The given sequence is,

$2, 6, 10, 14, .....$

$\therefore\$ Difference,

$d = 6 - 2 = 10 - 6 = 14 - 10 = 4$

Any two consecutive terms of the given sequence have the same difference.

$\therefore\$ The given sequence is an A.P.

Write any two arithmetic progressions with common difference $5$ .

Given common difference is

$d=5$

Therefore, the two arithmetic progressions are:
Taking

$a=2$ ; the A.P. is

$2, 7, 12, 17,$ ...........
and taking

$a=-4$ ; the A.P. is

$1, 6, 11, 16,$ ...........

Write any two arithmetic progressions with common difference $3$ .

Here given common difference is

$d=3$
Taking

$a=1$ ; the A.P. is

$1, 4, 7, 10,$ ...........
and taking

$a=-3$ ; the A.P. is

$-3, 0, 3, 6,$ ...........

Write any two arithmetic progressions with common difference $2$ .

Given, the common difference

$d=2$

Therefore, the two arithmetic progression series are:
Taking

$a=-1$ ; the A.P. is

$-1,1,3,5,$ ..........
and taking

$a=3$ ; the A.P. is

$3,5,7,9,$ .........

Find the term $t_{13}$ of an A.P.
$4, 9, 14, ....$

We have

$a =$ First term

$= 4$

$d =$ Common difference

$=9-4= 5$
We know that,

$t_n = a + (n - 1) d$

$t_{13} = 4 + (13 - 1) \times 5$

$= 4 + 12 \times 5$

$= 4 + 60$

$t_{13} = 64$

There is an auditorium with $35$ rows of seats. There are $20$ seats in the first row, $22$ seats in the second row, $24$ seats in the third row and so on. Find the number of seats in the twenty-third row.

Seats are to be arranged as

$20$ in the first row,

$22$ in the second row,

$24$ in the third row, and so on.

$\therefore$ Here

$a = 20, d = 22 - 20 = 2$
We have to find

$a_{23}$ .
We know that

$a_n = a (n - 1) d$

$a_{23} = 20 + (23 - 1) \times 2$

$= 20 + 22 \times 2$

$= 20 + 44$

$= 64$

For an A.P., $t_{3} = 8$ and $t_{4} = 12$ . Find the common difference $d$ .

Given,

$t_{3} = 8, t_{4} = 12$
We know that, the common difference of an A.P. is the difference between any two consecutive terms.

The given terms

$t_3$ and

$t_4$ are consecutive.

$\therefore d = t_{4} - t_{3}$

$\Rightarrow d=12 - 8$

$\Rightarrow d = 4$

Hence, the common difference is

$4$ .

For the given A. P. $10, 15, 20, 25,$ ......., find the common difference ' $d$ '.

The given A.P. is

$10, 15, 20, 25$ .........
Here, constant term

$a=10$
Therefore,

$d=15-10$

$=20-15$

$=25-20=5$
Therefore, common difference

$d$ is

$5$ .

In a given A.P. $a=8,{T}_{n}=33,{S}_{n}=123$ . Find $d$ and $n$ .

Assuming

${T}_{n}$ as the last term

$l$
For the given A.P

$a={T}_{1}=8,l={T}_{n}=33$ and

${S}_{n}=123$
Now,

${ S }_{ n }=\cfrac { 1 }{ 2 } n\left[ a+l \right]$

$123=\cfrac { n }{ 2 } (8+33)$

$123 = \cfrac { 41 }{ 2 } n$

$123\times \cfrac { 2 }{ 41 } =n$

$\implies n=6$

Now,

${T}_{n}=a+(n-1)d$

${T}_{6}=a+5d$

$33=8+5d$

$25=5d$

$d=5$

Check whether the following sequence is an AP or not:
$3m - 1, 3m - 3, 3m - 5, ....$

Given,

$3m - 1, 3m - 3, 3m - 5, .....$
Here

$t_{1} = 3m - 1, t_{2} = 3m - 3, t_{3} = 3m - 5, ....$

$\therefore t_{2} - t_{1} = (3m - 3) - (3m - 1) = -2$
Also,

$t_{3} - t_{2} = (3m - 5) - (3m - 3) = -2$
Hence, the given sequence is an A.P. with first term

$3m - 1$ and the common difference

$-2$ .

If $t_{n} = 3n + 5$ , then find A.P.

Given,

$t_{n} = 3n + 5$
On putting

$n = 1, 2, 3, .....,$ we get

$t_{1} = 3(1) + 5 = 8$

$t_{2} = 3(2) + 5 = 6 + 5 = 11$

$t_{3} = 3(3) + 5 = 9 + 5 = 14$
The required A.P. is

$8, 11, 14, ......$

Find the first term and common difference of the following APsv
(i) $5, 2, -1, -4, ....$
(ii) $\dfrac {1}{2}, \dfrac {5}{6}, \dfrac {7}{6}, \dfrac {3}{6}, ...., \dfrac {17}{6}$

(i) First term

$a = 5$ , and the common difference

$d = 2 - 5 = -3$ .
(ii)

$a = \dfrac {1}{2}$ and the common difference

$d = \dfrac {5}{6} - \dfrac {1}{2} = \dfrac {5 - 3}{6} = \dfrac {1}{3}$ .

Write the common difference of the A.P. 7, 5, 3, 1, -1, -3, .........

Common difference of an AP is difference between two consecutive terms.

$\therefore \text{Common difference}$

$=$ second term-first term

$=5-7$

$=-2$

Write any two arithmetic progressions with common difference $4$ .

Here,

$d=4$
Taking

$a=-2$ ; the A.P. is

$2, 6, 10, 14,$ ...........
and taking

$a=4$ ; the A.P. is

$4, 8, 12, 16,$ ...........

In an A.P. the first term is $2$ , the last term is $29$ , and the sum is $155$ , then find the common difference.

Given

$a=2,l=9$ and

$S=155$

$S=\dfrac { n }{ 2 } (a+l)\\ 155=\dfrac { n }{ 2 } (2+29)\\ \Rightarrow n=10\\ l=a+(n-1)d\\ 29=2+(10-1)d\\ \Rightarrow d=3$

So the common difference is

$3$

Find the common difference of an AP: ${ 1 }^{ 2 },{ 5 }^{ 2 },{ 7 }^{ 2 },73,....$

Given sequence is,

$1^{2},5^{2},7^{2},73,...…$

first term of this A.P is

$a_{1}=1^{2}=1$

second term of this A.P is

$a_{2}=5^{2}=25$

third term of this A.P is

$a_{3}=7^{2}=49$

fourth term of this A.P is

$a_{4}=73$

the condition for an sequence to be an A.P is their must be a common difference

$(i.e., d=a_{n+1}-a_{n})$

putting n=1 in above equation

$d=a_{2}-a_{1}=25-1=24$

putting n=2 in above equation

$d=a_{3}-a_{2}=49-25=24$

putting n=3 in above equation

$d=a_{4}-a_{3}=73-49=24$ as we can see we get a common difference

$d=24$ for this sequence hence this sequence forms an A.P with first term

$a_{1}=1$ and common difference

$d=24$

For the following arithmetic progressions write the first term $a$ and the common difference $d$ :
$0.3,0.55,0.80,1.05,....$

Given Arithmetic progression (A.P) is

$0.3 ,0.55,0.80,1.05,........$

Hence the first term of the A.P is given by

$a_{1}=0.3$

And the common difference of an A.P is given by the difference of two successive terms .

$(i.e., d= a_{n+1}-a_{n})$

By putting n=1 in above expression we get

$d=a_{2}-a_{1}$

$Put \ a_{1}=0.3 \ and \ a_{2}=0.55$

$d=(0.55)-(0.3)$

$d=0.25$

For the following arithmetic progressions write the first term $a$ and the common difference $d$ :
$\cfrac { 1 }{ 5 } ,\cfrac { 3 }{ 5 } ,\cfrac { 5 }{ 5 } ,\cfrac { 7 }{ 5 } ,.....$

Ans.

given Arithmetic progression (A.P) is

$\dfrac{1}{5},\dfrac{3}{5},\dfrac{5}{5},\dfrac{7}{5},........$

Hence the first term of the A.P is

$a_{1}=\dfrac{1}{5}$

And the common difference of an A.P is given by the difference of two successive terms .

$(i.e., d= a_{n+1}-a_{n})$

Hence by putting

$n=1$ in above expression we get

$d=a_{2}-a_{1}$

According to the given condition

$\ a_{1}=\dfrac{1}{5} \ and \ a_{2}=\dfrac{3}{5}$

$d=\left(\dfrac{3}{5}\right)-\left(\dfrac{1}{5}\right)$

$d=\left(\dfrac{3-1}{5}\right)$

$d=\dfrac{2}{5}$

Find the common difference of the A.P.: $1.,2.0,2.2,2.4,.....$

Given A.P is,

$1.8,2.0,2.2,2.4,...…$

first term of this A.P is

$a_{1}=1.8$

second term of this A.P is

$a_{2}=2.0$

third term of this A.P is

$a_{3}=2.2$

fourth term of this A.P is

$a_{4}=2.4$

common difference of an A.P is

$(i.e., d=a_{n+1}-a_{n})$

putting n=1 in above equation

$d=a_{2}-a_{1}=2.0-1.8=0.2$

hence,

common difference

$d=0.2$

Find the common difference of am AP: $-225,-425,-625,-825,.....$

Given sequence is,

$-225,-425,-625,-825,...…$

first term of this A.P is

$a_{1}=-225$

second term of this A.P is

$a_{2}=-425$

third term of this A.P is

$a_{3}=-625$

fourth term of this A.P is

$a_{4}=-825$

the condition for an sequence to be an A.P is their must be a common difference

$(i.e., d=a_{n+1}-a_{n})$

putting n=1 in above equation

$d=a_{2}-a_{1}=(-425)-(-225)=-200$

putting n=2 in above equation

$d=a_{3}-a_{2}=(-625)-(-425)=-200$

putting n=3 in above equation

$d=a_{4}-a_{3}=(-825)-(-625)=-200$

as we can see we get a common difference

$d=-200$ for this sequence

hence this sequence forms an A.P

with first term

$a_{1}=-225$ and

common difference

$d=-200$

Find the common difference of the A.P. and write the next two terms: $75,67,59,51,.....$

Given A.P is,

$75,67,59,51,...…$

first term of this A.P is

$a_{1}=75$

second term of this A.P is

$a_{2}=67$

third term of this A.P is

$a_{3}=59$

fourth term of this A.P is

$a_{4}=51$

common difference of an A.P is

$(i.e., d=a_{n+1}-a_{n})$

putting n=1 in above equation

$d=a_{2}-a_{1}=67-75=-8$

hence,common difference

$d=-8$

we know that nth term of an A.P is given by

$a_{n}=a_{1}+(n-1)d$

$\implies a_{n}=75+(n-1)(-8)$

$\implies a_{n}=75-8n+8$

$\implies a_{n}=83+8n …..eq(1)$

for finding next two terms

for 5th term

$a_{5}$ put n=5 in eq(1)

$\implies a_{5}=83-8\times 5$

$\implies a_{5}=83-40$

$\implies a_{5}=43$

for 6th term

$a_{6}$ put n=6 in eq(1)

$\implies a_{6}=83-8\times 6$

$\implies a_{6}=83-48$

$\implies a_{6}=35$

For the following arithmetic progressions write the first term $a$ and the common difference: $-5,-1,3,7,....$

Given Arithmetic progression (A.P) is

$-5,-1,3,7,........$

Hence the first term of the A.P is given by

$a=-5$

And the common difference of an A.P is given by the difference of two successive terms .

$(i.e., d= a_{n+1}-a_{n})$

Hence by putting n=1 in above expression we get

$d=a_{2}-a_{1}$

$Put \ a_{1}=-5 \ and \ a_{2}=-1$

$d=(-1)-(-5)$

$d=(-1+5)$

$d=4$

For the following arithmetic progressions write the first term $a$ and the common difference $d$ :
$-1.1,-3.1,-5.1,-7.1,.....$

Given Arithmetic progression (A.P) is

$-1.1 ,-3.1,-5.1,-7.1,........$

Hence the first term of the A.P is given by

$a_{1}=-1.1$

And the common difference of an A.P is given by the difference of two successive terms .

$(i.e., d= a_{n+1}-a_{n})$

By putting n=1 in above expression we get

$d=a_{2}-a_{1}$

$put \ a_{1}=-1.1 \ and \ a_{2}=-3.1$

$d=(-3.1)-(-1.1)$

$d=(-3.1+1.1)$

$d=-2.0$

Find the common difference of the A.P.: $119,136,153,170,.....$

Given A.P is,

$119,136,153,170,...…$

first term of this A.P is

$a_{1}=119$

second term of this A.P is

$a_{2}=136$

third term of this A.P is

$a_{3}=153$

fourth term of this A.P is

$a_{4}=170$

common difference of an A.P is

$(i.e., d=a_{n+1}-a_{n})$

putting n=1 in above equation

$d=a_{2}-a_{1}=136-119=17$

hence,

common difference

$d=17$

The $n$ th term of an A.P is $6n+2$ . Find the common difference.

Ans.

given the sequence which is defined by.

$a_{n}=6n+2 .....eq(1)$

and we know that nth term of an A.p is given by

$a_{n}=a_{1}+(n-1)d$

which can also be written as

$a_{n}=a_{1}-d+nd .....eq(2)$

comparing eq(1) and eq(2) we get

common difference is

$d=6 \ (by \ comparing \ coefficients \ of \ n )$

and

$a_{1}-d=2$

by putting value of d=b in above equation we get

$a_{1}-6=2$

$\implies a_{1}=8$ (first term of A.P)

hence if a and b are real numbers this sequence form an A.P with first term

$a_{1}=8$

and have a common difference

$d=6$

The first and the last terms of an A.P are $7$ and $49$ respectively. If the sum of all its terms is $420$ , find its common difference.

Given:

$a=7, a_n=49, S_n=420$

For AP,

$S_n=\dfrac{n}{2}\times[a+a_n]$

$420=\dfrac{n}{2}\times[7+49]$

$420=\dfrac{n}{2}\times[56]$

$n=15$ .

As we know

$a_n=a+(n-1)d$

$49=7+(15-1)d$

$42=14d$

$d=3$ .

So, the common difference is

$3$ .

Find the common difference and write the next three terms of the A.P. $3, -2, -7, -12,....$

Second term - First term

$= -2 - (3) = -5$

Third term - Second term

$= -7 - (-2) = -5$

So, the given sequence is an A.P. with a common difference of

$-5$ .

Since each term of an A.P. is obtained by adding common difference to the preceding term.

$\therefore a_5 = a_4 + (-5) = -12 + (-5) = -17$

$a_6 = a_5 + (-5) = -17 + (-5) = -22$

and,

$a_7 = a_6 + (-5) = -22 + (-5) = -27$

Find the value of $x$ for which $\left( {5x + 2} \right),\left( {4x - 1} \right)\;and\;(x + 2)$ are in A.P

given,

$5x+2,4x-1,x+2$ are in A.P.

$\Rightarrow 4x-1-5x-2=x+2-4x+1$

$-x-3=-3x+3$

$3x-x=3+3$

$2x=6$

$\therefore x=3$

State whether the given list of numbers is an arithmetic progression or not.
$a) 13,20,27,34,...$
$b) 6,16,26,35,...$

In the first list of numbers

$13,20,27,34,...$

It can be noted that there is a fixed difference between each of its consecutive terms and that difference is

$7$ . Thus the list of numbers in '

$a$ ' is an arithmetic progression.

In the second list of numbers,the difference between

$6$ and

$16$ is

$10$ and so is the difference between

$16$ and

$26$ . But the difference between

$26$ and

$35$ is not

$10$ and is

$9$ . Thus, there is no fixed difference between the consecutive numbers of the list and thus '

$b$ ' is not an arithmetic progression.

Find the value of $k$ , for which $2k + 7 , 6k - 2$ and $8k + 4$ are $3$ consecutive terms of an AP.

If three numbers

$a,b,c$ are in A.P.

Then

$b=\dfrac{a+c}{2}$ (

$b$ is arithmetic mean of

$a$ and

$c$ )

$2k+7 , 6k-2$ and

$8k+4$ are in A.P.

then,

$6k-2=\dfrac{2k+7+8k+4}{2}$

$12k-4=10k+11$

$2k=15$

$k=\dfrac{15}{2}$

Find the sum of the following $AP$ .
$-37,-33,-29,.....,$ to $12$ terms

Given that ,

$a=-37,d=-33-(-37)=4,n=12$

Sum of A.P.

$=\dfrac{n}{2}(2a+(n-1)d)$

$sum=\dfrac{12}{2}[2 \times (-37)+(12-1) \times 4]$

$=-180$

If in an AP, the sum of first 10 terms is -150 and the sum of its next 10 terms is -550. Find the AP.

Given,

${S_{10}} = - 150$

${S_{20}} - {S_{10}} =$ Next 10 term

${S_{20}} - {S_{10}} = - 550$

${S_{20}} = - 550 + {S_{10}}$

${S_{20}} = - 550 - 150$

${S_{20}} = - 700$

$S_{n}=\dfrac{n}{2}\left [ 2a+(n-1)d \right ]$

${S_{10}} = \dfrac{{10}}{2}\left[ {2a + \left( {10 - 1} \right)d} \right] = - 150$

$2a + 9d = - 30$ (i)

${S_{20}} = - 700$

$\dfrac{{20}}{2}\left[ {2a + 19d} \right] = - 700$

$2a + 19d = - 70$ (ii)

eq(i)-eq(ii)

$\left( {2a + 9d = - 30} \right) - \left( {2a + 19d = - 70} \right)$

$-10d=40$

$d=-4$

$2a+9d=-30$

$2a=-30+36$

$\Rightarrow a = 3$

So the A.P. will be as:-
a, (a+d), (a+2d), ...

3, (-1), (-5) & so on

For the A.P. $-1.1,\ -3.1,\ -5.1,\ -7.1,......$ write the first term and the common difference.

Given: A.P

$-1.1,-3.1,-5.1,-7.1......$

First term

$a=-1.1$

Common difference

$d=-3.1-(-1.1)=-5.1-(-3.1)=-2$

In an A.P., if $t_7=13$ and ${S_{14}} = 203$ , find $S_8$ .

$\because t_n=a+(n-1)d$

$\Rightarrow t_7=13\Rightarrow a+(7-1)d=13$

$\Rightarrow a+6d=13.......(1)$

$\because S_n=\dfrac{n}{2}[2a+(n-1)d]$

$S_{14}=203$

$\dfrac{14}{2}[2a+(14-1)d]=203$

$7(2a+13d)=203$

$2a+13d=\dfrac{203}{7}$

$2a+13d=29......(2)$

Multiplying equation

$(1)$ , subtracting from equation

$(2)$

$2a+13d=29$

$\underline{-2a-12d=-26}$

$\quad\quad d=\quad3$

Putting the value of

$d$ in equation

$(1), a+6\times3=13$

$a=13-18=-5$

Thus,

$S_8=\dfrac{8}{2}[2\times(-5)+(8-1)\times3]$

$=4[-10+7\times3]$

$=4[-10+21]$

$=4\times11$

$=44$

Write the expression for the common difference of an $A.P$ whose first term is $a$ and $nth$ term is $b$ .

We have,

first term $A=a$

Common difference $D=?$

And ${{n}^{th}}$ term ${{A}_{n}}=b$

Then,

We know that,

${{A}_{n}}=A+\left( n-1 \right)D$

$\Rightarrow b=a+\left( n-1 \right)D$

$\Rightarrow \left( b-a \right)=\left( n-1 \right)D$

$\Rightarrow D=\dfrac{\left( b-a \right)}{\left( n-1 \right)}$

Hence, this is the answer.

If $a=2$ and $d=4$ , then $S_{20} =$ _______.

As we know that the sum of first

$n$ terms is given by

$S_n = \dfrac{n}{2} (2a+(n-1)d)$ , where

$a$ &

$d$ are the first term & common difference of an AP.

Since,

$a=2,d=4,S_{20}=?$

$\therefore S_{20}=\cfrac{20}{10}[2a+(20-1)4]$

$S_{20}=10[4+76]$

$S_{20}=800$

If sum of first $p$ terms of an AP is equal to the sum of first $q$ terms, then find the sum of the first $(p+q)$ terms.

Formula:

$S_n=\dfrac{n}{2}[2a+(n-1)d]$

Sum of first p terms,

$S_p=\dfrac{p}{2}[2a+(p-1)d]$

Sum of first q terms,

$S_q=\dfrac{q}{2}[2a+(q-1)d]$

given,

$S_p=S_q$

$\dfrac{p}{2}[2a+(p-1)d]=\dfrac{q}{2}[2a+(q-1)d]$

$p[2a+(p-1)d]=q[2a+(q-1)d]$

$2a(p-q)=-d(p-q)[p+q-1]$

$2a(p-q)+d(p-q)[p+q-1]=0$

$(p-q)[2a+d(p+q-1)]=0$

$p-q\neq 0\Rightarrow [2a+d(p+q-1)]=0$

Now,

$S_{p+q}=\dfrac{p+q}{2}[2a+(p+q-1)d]$

$=\dfrac{p+q}{2}\times 0$

$=0$

Therefore the sum of

$(p+q)$ terms is

$0$ .

Find the common difference $d$ and write three more terms if the following sequence is an AP:
$2, 4, 8, 16,.$

$2,\,4,\,8,\,16,....$

$\Rightarrow$ Difference of second and first term

$=4-2=2$

$\Rightarrow$ Difference of third and second term

$=8-4=4$

$\Rightarrow$ Since,

$2\neq 4$

$\Rightarrow$ Difference is not same.

Hence, it is not an

$AP$

In an arithmetic progression of which $a$ is the first term. If the sum of the first ten terms is zero and the sum of next ten terms is $-200$ then find the value of $a$ .

First term=a

Let the common difference

$=$ d

Sum of first ten terms

$=$ 0

Sum of first n term of an AP

$=$

$\cfrac{n}{2}(2a+(n-1)d)$

By given

$S_{10} = 0$

$\cfrac{10}{2}(2a+(10-1)d)=0$

$\cfrac{10}{2}(2a+9d)=0$

$2a+9d=0$ ----- (Equation 1)

Sum of next ten terms

$=-200$

Sum of first ten terms+Sum of next ten terms

$=0-200$

Sum of first ten terms+Sum of next ten terms

$=-200$

So,

Sum of first twenty terms

$S_{20}$

$=-200$

$\cfrac{20}{2}(2a+(20-1)d)=-200$

$\cfrac{20}{2}(2a+19d)=-200$

$2a+19d=-20$ ------ (Equation 2)

From equation 1,

$2a=-9d$

Put the value of

$2a$ in equation 2,

$-9d+19d=-20$

$10d=-20$

$d=-2$

Put the value of "

$d$ " in equation 1,

$2a-18=0$

$2a=18$

$a=9$

The ${25^{th}}$ term of $AP$ $- 5,\dfrac{{ - 5}}{2},0,\dfrac{5}{2}............ \ \$ is $-b$ ,
then what is the value of $b?$

First term of

$A.P = -5$

Common difference

$=\dfrac{-5}{2}-(-5)=\dfrac{5}{2}$

We know that,

${{a}_{n}}=a+\left( n-1 \right)d$

25th term

$=-5+ (25-1) \times \dfrac{5}{2}$

$=-5+(24)\times \dfrac{5}{2}$

$=-5+60$

$=-55$

Comparing with

$-b=-55 \Rightarrow b=55$

Show that sequence of following $n^{th}$ terms ,are not in A.P.
$\dfrac{n}{n+1}$

The first three terms can be calculated by substituting

$n=1,2,3$
Let them be denoted by

$a,b,c$ respectively.

$a=\dfrac{1}{2}$

$b=\dfrac{2}{3}$

$c=\dfrac{3}{4}$

$a+c=\dfrac{5}{4}$

$2b=\dfrac{4}{3}$

If

$a, b, c$ actually were in an A.P., then

$a+c$ would be equal to

$2b$ which is not the case here. Hence, the given sequence in not an A.P.

Find the sum of n terms of the series $(a^2+b)+({ a }^{ 2 }+2b)+({ a }^{ 2 }+3b)+....$

We have,

A.P. is

$\left( a^2+b \right)+\left( {{a}^{2}}+2b \right)+\left( {{a}^{2}}+3b \right)........$

First term $A=\left( a^2+b \right)$

Common difference

$d=b$

Then,

Sum of n terms

${{S}_{n}}=\dfrac{n}{2}\left( 2A+\left( n-1 \right)d \right)$

$=\dfrac{n}{2}\left[ 2\times \left( a^2+b \right)+\left( n-1 \right)b \right]$

$=\dfrac{n}{2}\left[ 2a^2+2b+nb-b \right]$

Hence, this is the answer.

The first term and the last term of an A.P are $17$ and $350$ respectively. If the common difference is $9$ . How many terms are there and what is their sum.

$a_1=17,a_n=350,d=9$

$a_n=a+(n-1)d$

$350=17+9(n-1)$

$333=9(n-1)$

$n-1=37$

$n=38$

So, sum,

$S_n=\dfrac{n}{2}(a+l)\Rightarrow S_{38} = \dfrac{38}{2}(17+350)$

$=19\times 367$

$=6973$

Find the common difference in the following pattern:
(a) 4,7,10,13
(b) 5,9,13,17,21,25

(a)

common difference.

$=7-4=10-7=3$

(b)

common difference

$=9-5=13-9=4$

Find the 20th term of the progression.
$-12,-5,2,9,16,23,30,....$

Let

$-12,-5,2,9,16,23,30....$

Here

$-5+12=7$

$2+5=7$

$9-2=7$

$\therefore d=7$

$\therefore$ given sequence is in

$AP$ with

$a=-12, \, d=7\,\, and\,\, n=20$

$nth$ term of the

$AP$ is given by

$a_{n} = a+(n-1)d$

$a_{20} = a+(20-1)d$

$=a+19d$

$=-12+19(7)$

$=-12+133$

$a_{20}=121$

Find the common difference of the following A.P.:
i) $3,1,-1,-3,......$
ii) $-5,-1,3,7,.....$

Given the A.P. are

$3,1,-1,-3,......$

ii)

$-5,-1,3,7,.....$ .

Common difference is the difference between the consecutive term of the A.P.

Now for the first A.P. the common difference is

$1-3=-2$ .

And for the second A.P. the common difference is

$-1-(-5)=-1+5=4$ .

The ratio of the sums of m and n terms of an A.P. is ${ m }^{ 2 }:{ n }^{ 2 }$ . Show that the ratio of ${ m }^{ th }$ and ${ n }^{ th }$ term is (2m - 1) : (2n - 1).

Let a be the first term and d be the common difference of the given A.P. Then, the sum of m and n terms are given by

$S_{m} = \dfrac{m}{2}[2a+(m-1)d]$ , and

$S_{n} = \dfrac{n}{2}[2a+(n-1)d]$

Then,

$\dfrac{S_{m}}{S_{n}} = \dfrac{m^{2}}{n^{2}}$

$\dfrac{\dfrac{m}{2}[2a+(m-1)d]}{\dfrac{n}{2}[2a+(n-1)d]} = \dfrac{m^{2}}{n^{2}}$

$\dfrac{2a+(m-1)d}{2a+(n-1)d} =\dfrac{m}{n}$

$[2a+(m-1)d]n=[2a+(n-1)d]m$

$2a(n-m)=d[(n-1)m-(m-1)n]$

$2a(n-m)=d(n-m)$

$d=2a$

Therefore,

$\dfrac{T_{m}}{T_{n}} = \dfrac{a+(m-1)d}{a+(n-1)d} =\dfrac{a+(m-1)2a}{a+(n-1)2a} =\dfrac{2m-1}{2n-1}$

Hence proved

Check whether the following sequence is an AP or not:
$-1.2,-3.2,-5.2,-7.2$ ...

$-3.2 - ( -1.2 ) = -2$

$-5.2 - ( 3.2 ) = -2$

$-7.2 - ( -5.2) = -2$

Since the difference between consecutive terms is constant,

Therefore, the given sequence is in

$A.P.$

Is the given Progression arithmetic progression?
$2, 6, 7, 10, 12, 15,.........$

Given sequence

$2, 6, 7, 10, 12, 15$ …

Difference between consecutive number in a sequence must be same to be an AP

Here

$6-2=4$

$7-6=1$

$10-7=3$

$4\neq 1\neq 3$

$\therefore$ It is not an AP.

Is the given progression arithmetic progression?
$-1, -3, -5, -7,.........$

Given sequence

$-1, -3, -5, -7$ ….

Difference between consecutive numbers/terms in a sequence must be same to be an AP

Here

$=-3+1=-2$

$-5+3=-2$

$-7+5=-2$

It is same equal to

$-2$ (common difference)

It is an AP.

What is the common difference of an A.P. in which $a_{24}-a_{17}=-28$ ?

General

$n^{th}$ term in AP,

$a_n=a+(n-1)d$

$a=$ first term,

$d=$ common difference.

Given,

$a_{24}-a_{17}=-28$

$\Rightarrow (a+23d)-(a+16d)=-28$

$\Rightarrow 23d-16d=-28$

$\Rightarrow 7d=-28$

$\Rightarrow d=-4$ .

$2, 3, 5, 7, 8, 10, 15,.........$

Given sequence

$2, 3, 5, 7, 8, 10, 15,....$

Difference between consecutive number must in a sequence be equal to be an AP

Here

$3-2=1$

$5-3=2$

$1\neq 2$

$\therefore$ It is not an AP.

Is the given sequence an A.P. If it forms an AP, find the common difference $d$

$4 - 2 = 2$

$8 - 4 = 4$

$16 - 8 = 8$

Since difference between

$2$ consecutive terms is not constant.

Therefore the given sequence is

$not$ in

$A.P.$

Find the common difference of the following AP:
$3.3 + \sqrt { 2, } 3+2\sqrt { 2 } ,3+3\sqrt { 2 }$

The given sequence is an A.P.

Common difference

$=$ second term

$-$ First term

$=3+\sqrt 2-3$

$=\sqrt 2$

Find the first term $a$ and the common difference $d$ of A.P. : $-5, -1, 3, 7, .....$

Given A.P.-

$-5, -1, 3, 7, .....$

From the given A.P.

First term

$a = -5$

Common difference

$d = {a}_{2} - {a}_{1} = \left( -1 \right) - \left( -5 \right) = 4$

Hence the first term and common difference of the given A.P. is

$-5$ and

$4$ respectively.

Which term of the sequence $72, 70, 68, 66$ , ... is $40$ ?

$a=72, d=70-72=68-70=66-68=-2$

So the given sequence is in AP

Let

$a_{n}=40$

General term :

$a_n=a+(n-1)d$

$a+(n-1)d=40$

$72+(n-1)(-2)=40$

$72-2n+2=40$

$2n=34$

$n=17$

Hence, the 17th term of the given sequence is 40.

Is the sequence $\sqrt{3},\sqrt{6},\sqrt{9},\sqrt{12},......$ from an Arithmetic Progression?Give reason.

$\sqrt{3}, \sqrt{6}, \sqrt{9}, .....$

$\sqrt{6} - \sqrt{3} = \sqrt{3} \left( \sqrt{2} - 1 \right)$

$\sqrt{9} - \sqrt{6} = \sqrt{3} \left( \sqrt{3} - \sqrt{2} \right)$

Since the difference between the two consecutive terms of the given series is not same, thus the given series is not an arithmetic progression.

Check whether the following sequence is an AP or not:
$1,3,9,27,....$

We have,

$a_2 - a_1 = 3 - 1 = 2$

$a_3 - a_2 = 9 - 3 = 6$

$a_4 - a_3 =27 - 9 = 18$

i.e.

$a_{k + 1} - a_k$ is not same every time.

So, the given list of numbers do not forms an AP.

Is the given sequence an AP? If it forms an AP, find the common difference $d$ and write the next three terms.
$0,-4, -8 ,-12$ ....

Common difference is equal to the difference between two consecutive terms

$-4 - ( 0 ) = -4$

$-8 - ( -4 ) = -4$

$-12 - ( -8 ) = -4$

Since the difference between two consecutive terms is constant which is equal to

$-4$

Therefore, the given sequence is in A.P.

Next term

$=$ previous term

$+$ common difference

$-12 + ( -4 ) = -16$

$-16 + ( -4 ) = -20$

$-20 + ( -4 ) = -24$

For the following A.P's write the first term and common difference: $\dfrac{3}{2},\dfrac{1}{2},-\dfrac{1}{2},-\dfrac{3}{2},......$

In general,for an AP

$a_1,a_2,....,a_n,$ we have

$d = a_{k + 1} - a_k$

where

$a_{k + 1}$ and

$a_k$ are the

$(k + 1)^{th}$ and

$k_{th}$ terms respectively

For the list of numbers:

$\dfrac{3}{2},\dfrac{1}{2},-\dfrac{1}{2},-\dfrac{3}{2},.....$

$a_2 - a_1 = \dfrac{1}{2} - \dfrac{3}{2} = -\dfrac{2}{2} = -1$

$a_3 - a_2 = \dfrac{-1}{2} - \dfrac{1}{2} = \dfrac{-2}{2} = -1$

$a_4 - a_3 = -\dfrac{3}{2} - \left(\dfrac{-1}{2}\right) = \dfrac{-3 + 1}{2} = \dfrac{-2}{2} = -1$

Here,the difference of any two consecutive terms in each case is

$-1$

So,the given list is an AP whose first term

$a$ is

$\dfrac{3}{2}$ and common difference

$d$ is

$-1$

Is the given sequence form an APs? If it forms an AP, find the common difference $d$ and write the next three terms.

$t_{1}=3$

$t_{2}=3+\sqrt{2}$

$t_{3}=3+3\sqrt{2}$

$t_{4}=3+3\sqrt{2}$

$t_{2}-t_{1}=\sqrt{2}$

$t_{3}-t_{2}=3+2\sqrt{2}-(3+\sqrt{2})=\sqrt{2}$

$t_{4}-t_{3}=3+3\sqrt{2}-(3+2\sqrt{2})=\sqrt{2}$

Since, the difference between two consecutive terms is constant.

$\therefore$ sequences is in A.P.

And, the next three terms are

$t_{5}=3+3\sqrt{2}+\sqrt{2}=3+4\sqrt{2}$

$t_{6}=3+4\sqrt{2}+\sqrt{2}=3+5\sqrt{2}$

$t_{7}=3+5\sqrt{2}+\sqrt{2}=3+6\sqrt{2}$

Check whether the following the sequence is an AP or not:
$-10, -6, -2, 2$ ....

Common difference

$=$ difference between two consecutive terms

$-6 - ( -10 ) = 4$

$-2 - ( -6 ) = 4$

$2 - ( -2 ) = 4$

Since difference between two consecutive terms is constant

$= 4$

Therefore , the given sequence is in A.P.

How many terms of the A.P. $-6, - \frac{11}{2}, -5, .....$ are needed to give the sum $-25$ ??

Let the sum of n terms of the given A.P. be - 25.

$S_n = \frac{n}{2}[2a + (n - 1)d]$
Where n = number of terms, a = first term, and d - common difference
Here, a = -6
d

$= - \frac{11}{2} + 6 = \frac{-11 + 12}{2} + \frac{1}{2}$
Therefore, we obtain

$- 25 = \frac{n}{2} \left [ 2 \times (-6) + (n - 1) \left ( \frac{1}{2} \right ) \right ]$

$\Rightarrow - 50 = n \left [ -12 + \frac{n}{2} + \frac{1}{2} \right ]$

$\Rightarrow -50 = n \left [ - \frac{25}{2} + \frac{1}{2} \right ]$

$\Rightarrow -100 = n(-25 + n)$

$\Rightarrow n^2 - 25n + 100 = 0$

$\Rightarrow n^2 - 5n - 20n + 100 = 0$

$\Rightarrow n(n - 5) - 20(n - 5) = 0$

$n = 20$ or 5

$0.2,0.22,0.222...$

Given series

$0.2,0.22,0.222...$
Here

$a-1=0.2, a_2=0.22, a_3=0.222, a_4=0.2222$
Difference between two consecutive terms

$(d)$ :

$=a_2-a_1 =0.22-0.2=0.02$

$=a_3-a_2=0.222-0.22=0.002$

$=a_4-a_3=0.2222-0.222=0.0002$
Difference is not the same
i.e

$a_2-a_1 \ne a_3 -a_2$
Hence, given series is not A.P

$5, 9, 12, 18, ….$

$15, 12, 9, 6$ , ….

Finding the difference between the terms,

$d_1 = 12 – 15 = -3$

$d_2 = 9 – 12 = -3$

$d_3 = 6 – 9 = -3$

As $d_1 = d_2 = d_3$ , the given sequence is in arithmetic progression.

For the following AP, write the first term and the common difference :
$-5, -1, 3, 7, ....$

$-5, -1, 3, 7,.........$

First term,

$a = -5,$

Common difference,

$d = a_{2} - a_{1} = -1 - (-5)$

$d = -1 + 5=3-(-1)=4$

$d = 4.$

The sum of the $5^{th}$ and the $7^{th}$ terms of an AP is 52 and the $10^{th}$ term is 46
then the AP is 1, 6, 11, 16.......
If true then enter $1$ and if false then enter $0$

Let

$a$ be the first term and

$d$ be the common difference of the given A.P.
Then,

${a}_{5}+{a}_{7}=52$

${a}_{10}=46$

$a+4d+a+6d=52$ and

$a+9d=46$

$\Rightarrow 2a+10d=52 ....(1)$

$a+9d=46 ....(2)$
multiplying (2) equation by 2 and we get,

$2a+18d=92 ....(3)$
now subtract (1) from (3) then we get,

$8d=40$

$\Rightarrow d=5$
now put d in (1) equation we get

$a=1$
There for the given series is

$a,a+d,a+2d,a+3d...$
i.e.

$1,6,11,16...$

The 26th, 11th and the last term of an AP are 0, 3 and $-\frac{1}{5}$ , respectively. Find the number of terms.

Let a,d and n be the first term,common difference and number of terms of an AP respectively.
Now,

${a}_{26}=a+25d=0$ ...(1)

${a}_{11}=a+10d=3$ ...(2)
on doing (1)-(2) , we get

$15d=-3$

$\Rightarrow d=\frac{-1}{5}$
On substituting the value of d in (1), we get

$a+25\times\frac{-1}{5}=0$

$\Rightarrow a=5$
Again,

${a}_{n}=a+(n-1)d=\frac{-1}{5}$
On substituting the values of a and d, we get

$5+(n-1)\times\frac{-1}{5}=\frac{-1}{5}$

$\Rightarrow(n-1)\times\frac{-1}{5}=\frac{-1}{5}-5=\frac{-26}{5}$

$\Rightarrow(n-1)=26$

$\Rightarrow n=27$
Therefore,

$d=\frac{-1}{5},n=27$

Find the $12^{th}$ term from the end of the A.P.
$2, 4, 6,..., 100.$

We have to find out the

$12^{th}$ term of an A.P. from the end.

So, we have to assume that the last term is the first term and the last term in this A.P. is

$100.$

let the first term be

$100$ and

$d =- 2$

$a_{12} = {a + (n-1)d}$

$= {100 + (12-1)(-2)}$

$= (100 - 11 × 2)$

$= 100 -22$

$= 78$

So, the

$12^{th}$ term of the A.P. from the end will be

$78$

If $a_n = 3 4n$ , find $S_{20}$ .

Since

${a}_{n}=34n$

$\therefore a_1=34\times1=34$

$a_2=34\times2=68$

$a_3=34\times3=102$
and so on..
Therefore the sequence becomes

$34,68,102,.....$
Clearly it is an AP with first term

$a=34$ and common difference

$d=34.$
Now

${S}_{20}=\dfrac{20}{2}(2a+(20-1)d)=10(2a+19d)$

$\Rightarrow{S}_{20}=10(2\times34+19\times34)=7140$

Find whether 55 is a term of the AP: 7, 10, 13,--- or not. If yes, find which term it is.

Let

${a}_{n}=a+(n-1)d=55$

$\Rightarrow 7+(n-1)\times3=55$

$\Rightarrow (n-1)\times3=48$

$\Rightarrow n-1=16$

$\Rightarrow n=17$
Clearly

$55$ is the

${17}^{th}$ term of given AP

If sum of the $3^{rd}$ and the $8^{th}$ terms of an AP is 7 and the sum of the $7^{th}$ and the $14^{th}$ terms is 3, find the $10^{th}$ term to closest integer.

Let

$a$ and

$d$ be the first term and common difference of AP respectively & nth term is given as

$a+(n-1)d$
Since

${a}_{3}+{a}_{8}=7\Rightarrow(a+2d)+(a+7d)=2a+9d=7$ ...(1)

${a}_{7}+{a}_{14}=3\Rightarrow(a+6d)+(a+13d)=2a+19d=3$ ...(2)
Subtracting (1)from(2),we get

$10d=-4$

$\Rightarrow d=\frac{-2}{5}$
putting

$d=\frac{-2}{5}$ in (1),we get

$2a+9\times\frac{-2}{5}=7$

$\Rightarrow 2a=\frac{53}{5}$

$\Rightarrow a=\frac{53}{10}$
Now,

${a}_{10}=a+9d=\frac{53}{10}+9\times\frac{-2}{5}$

$\Rightarrow {a}_{10}=\frac{17}{10} = 1.7 = 2$

If the nth terms of the two APs: 9, 7, 5, ... and 24, 21, 18,... are the same, find the value of n.

Clearly

$9,7,5,...$ is an AP with first term

$a=9$ and common difference

$d=-2$ and

$24,21,18,....$ is an AP with first term

$A=24$ and common difference

$D=-3$ .
Let

${a}_{n} and {A}_{n}$ be the

$n^{th}$ term of first and second AP respectively.
Therefore according to question,

${a}_{n}={A}_{n}$

$\Rightarrow a+(n-1)d=A+(n-1)D$

$\Rightarrow 9+(n-1)\times-2=24+(n-1)\times-3$

$\Rightarrow-2n+11=-3n+27$

$\Rightarrow n=16$

Find $a + b + c$ such that the following numbers are in AP: a, 7, b, 23, c.

Since

$a,7,b,23,c$ are in AP.

$\therefore 7-a=b-7=23-b=c-23$ ....(1)

On taking

$2^{nd}$ and

$3^{rd}$ expression, we get,

$b-7=23-b$

$\Rightarrow 2b=30\Rightarrow b=15$

On taking

$1^{st}$ and

$2^{nd}$ expression, we get,

$7-a=b-7$

$\Rightarrow 7-a=15-7\Rightarrow a=-1$

Again, on taking

$3^{rd}$ and

$4^{th}$ expression, we get,

$23-b=c-23$

$\Rightarrow 23-15=c-23\Rightarrow c=31$

Hence

$a=-1,b=15,c=31$

$\therefore a+b+c= -1+15+31=45$

Which term of the AP: 2, 7, 12,... will be 77?

Here, first term

$a=2$ and common difference

$d=5$ .
Let 77 be the nth term of given AP. Therefore,

$a_n=77$

$\Rightarrow a+(n-1)d=77$

$\Rightarrow 2+(n-1)5=77$

$\Rightarrow n-1=15\Rightarrow n=16$
Hence, 77 is the

${16}^{th}$ term of AP.

Column II give common difference for A.P. given in column I, match them correctly.

(A) Common difference

$=d=\frac {3}{2}-1=\frac {1}{2}$
(B)

$d=\frac {5}{3}-\frac {1}{3}=\frac {4}{3}$
(C)

$d=2-1.8=0.2$
(D)

$d=-4-0=-4$

If the sum of first 8 and 19 terms of an A.P. are 64 and 361 respectively, find the common difference.

$S_{ 8 }=64$

$S_{ n }=\dfrac { n }{ 2 } (2a+(n-1)d)$

$2a+7d=16$

$S_{ 19 }=361$

$2a+18d=38$

Solving,

$a=1,d=2$

The sum of first n terms of A.P. is $3n\, +\, n^{2}$ then
Find sum of first two terms.

Here

$S_n=3n+n^2$

Now, first term

$a=S_1\Rightarrow a=3\times1+1^2=4$ and

Sum of first two terms

$=S_2=3\times2+2^2=10$

Any odd square i.e $\displaystyle \left [ 2n+1 \right ]^{2}$ is equal to sum of n terms of an A.P. in increased by unity. Find the first term of that A.P ?

Let

$a$ be the first term and

$d$ be the common difference of the A.P
Given

$\displaystyle (2n+1)^2 = \frac{n}{2}[2a+(n-1)d] +1$

$\Rightarrow \displaystyle 4n^2+4n+1 = \frac{d}{2}n^2+\frac{2a-d}{2}n +1$
Comparing coefficient of

$n$ and

$n^2$ we get

$d = 8, \cfrac{2a-d}{2}=4\Rightarrow a = 8$
Hence first term of the A.P is 8.

The nth term of a series is given to be $\displaystyle \frac{3+n}{4},$ find the sum of 105 term of this series.

nth term of

$+ve$ series

$=\dfrac{3+n}{4}$

So, the series becomes,

$1,\dfrac{5}{4},\dfrac{6}{4},\dfrac{7}{4}$ .......

$\therefore a=1,d=\dfrac{5}{4}-1=\dfrac{1}{4}=\dfrac{6}{4}-\dfrac{5}{4}$

$\therefore S_{105}=\dfrac{105}{2}[2\times 1+(105-1)\dfrac{1}{4}]$

$=\dfrac{105}{2}[2+104\times \dfrac{1}{4}]$

$=\dfrac{105}{2}[\dfrac{8+104}{4}]$

$=\dfrac{105}{2}\times \dfrac{112}{4}$

$=105\times 14$

$=1470$

$\therefore \boxed{S_{105=1470}}$

Find sum of all odd integers between $2$ and $100$ divisible by $3$ .

${\textbf{Step - 1: Finding first term and common difference of A}}{\textbf{.P}}{\textbf{.}}$

${\text{Let a be the first term, d be the common difference of the A}}{\text{.P}}{\text{. and n be the number}}$

$\text{of terms in the sequence}{\text{.}}$

${\text{Numbers which are odd and also divisible by 3, between 2 and 100 = \{ 3, 9, 15, 21, }}....{\text{99\} }}$

${\text{It forms an A}}{\text{.P}}{\text{. with }}$

${\text{first term, a = 3, }}$

${\text{common difference, d = 9 - 3 = 6 }}$

${\text{and last term, }}{{\text{T}}_{\text{n}}}{\text{ = 99}}$

${\textbf{Step - 2: Finding number of terms in sequence}}$

${\text{We know that, nth term of an A}}{\text{.P}}{\text{. is given by, }}{{\text{T}}_{\text{n}}}{\text{ = a + (n - 1)d }}$

${\text{where a is first term and d is common difference}}$

${\text{Last term, }}{{\text{T}}_{\text{n}}}{\text{ = 99}}$

$\Rightarrow {\text{ a + (n - 1)d = 99}}$

$\Rightarrow {\text{ 3 + (n - 1)6 = 99}}$

$\Rightarrow {\text{ n = 17}}$

${\textbf{Step - 3: Calculating sum of sequence}}$

${\text{We know that, sum of n terms of an A}}{\text{.P}}{\text{., }}{{\text{S}}_{\text{n}}}{\text{ = }}\dfrac{{\text{n}}}{{\text{2}}}\left[ {{\text{2a + (n - 1)d}}} \right]$

$\Rightarrow {\text{ }}{{\text{S}}_{{\text{17}}}}{\text{ = }}\dfrac{{{\text{17}}}}{{\text{2}}}\left[ {{\text{2(3) + 16(6)}}} \right]$

$\Rightarrow {\text{ }}{{\text{S}}_{{\text{17}}}}{\text{ = 17 }}\left[ {{\text{3 + 8(6)}}} \right]$

$\Rightarrow {\text{ }}{{\text{S}}_{{\text{17}}}}{\text{ = 17 }}\left[ {{\text{3 + 48}}} \right]$

$\Rightarrow {\text{ }}{{\text{S}}_{{\text{17}}}}{\text{ = 17 }}\left[ {{\text{51}}} \right]$

$\Rightarrow {\text{ }}{{\text{S}}_{{\text{17}}}}{\text{ = 867}}$

${\textbf{Hence, The sum of all odd integers between 2 and 100 divisible by 3 is 867}}{\textbf{.}}$

If $t_{54}$ of an A.P. is $-61$ and $t_{4}=64,$ find $t_{10}.$

Let

$a$ be the first term and

$d$ be the common difference
so

$t_{54}=a+53d=-61$ (i)
and

$t_{4}=a+3d=64$ (ii)
equation (i)

$-$ (ii),

$\Rightarrow$

$50d=-125$

$\implies \displaystyle d=-\frac{5}{2}$

On putting value of

$d$ in equation (ii)

$\implies a-\dfrac{3\times 5}{2}=64$

$\implies a=64+\dfrac{15}{2}$

$\Rightarrow$

$\displaystyle a=\frac{143}{2}$
so,

$t_{10}=a+9d$

$\implies \displaystyle t_{10}=\frac{143}{2}+9\left ( -\frac{5}{2} \right )=49$

Find the number of terms in the sequence $4, 12, 20, ...,108.$

From the given sequence, we can derive that

$a=4, d=8$ ,

$a_n = 108$

We know the formula for

$n^{th}$ term of an AP i.e.,

$a_n=a+\left ( n-1 \right )d$

$108 = 4+(n-1)8$

$108=4+8n-8$

$108=8n-4$

$8n=108+4$

$8n=112$
So,

$n=14$

The sum 'S' of first n natural numbers is given by the relation $\displaystyle S=\frac{n(n+1)}{2}$ . Find n if the sum is 276.

We have

$\displaystyle S=\frac{n(n+1)}{2}=276$ or

$\displaystyle n^{2}+n-552=0$
This gives

$\displaystyle n=\frac{-1+\sqrt{1+2208}}{2},\frac{-1-\sqrt{1+2208}}{2}$
or

$\displaystyle n=\frac{-1+\sqrt{2209}}{2},\frac{-1-\sqrt{2209}}{2}$ or

$\displaystyle n=\frac{-1+47}{2},\frac{-1-47}{2}$
or n = 23, - 24 . We reject n = - 24 since - 24 is not a natural number Therefore n = 23

Find the sum of all three digit natural numbers which are divisible by 7.

$\textbf{Step -1: Forming an Arithmetic Progression}$

$\text{Three digit numbers divisible by 7 are, }$

$105, 112, 119..., 994.$

$\text{This series forms an AP with, }$

$\text{First term }a = 105,$

$\text{Common difference }d = 7,$

$n^{th}\text{ term } a_n = 994$

$\textbf{Step -2: Finding the number of terms in AP}$

$a_n = a + (n-1)d$

$994 = 105 + (n-1)\times 7$

$n = \dfrac{994 - 105}{7} + 1$

$n = 128$

$\textbf{Step -3: Finding the sum of all terms.}$

$\text{Sum of n terms }S_n = \dfrac{n}{2}(2a + (n-1)d)$

$S_{128} = \dfrac{128}{2} (2\times 105 +(128-1)\times 7)$

$S_{128} = 64 \times (210 +127 \times 7)$

$S_{128} = 64 \times (210 + 889)$

$S_{128} = 64 \times 1099$

$S_{128} = 70336$

$\textbf{Hence, Sum of all three digit natural numbers which are divisible by 7 is 70336.}$

Find $\displaystyle 20^{th}$ term from the end of an $AP\ 3, 7, 11, ......, 407$

$a_n=a+(n-1)d$
Here

$a_n=407,a=3,d=4$

$407 = 3 + (n - 1) 4$

$407=3+4n-4$

$408=4n$

$\Rightarrow n=102$

$\therefore 20^{th}$ term from end

$\Rightarrow m=20$

$a_{102-\left ( 20-1 \right )}=a_{102-19}=a_{83}$ from the beginning

$a_{83}=3+\left ( 83-1 \right )4=331$

Find the first term and the common difference of an AP, if the $3^{rd}$ term is $6$ and the $17^{th}$ term is $34$ .

$a$ is the first term and

$d$ is the common difference, then

$n^{th}$ term is given by

$a_n =a+(n-1)d$

Since,

$a_3=6$ &

$a_{17} = 34$

$\therefore a + 2d = 6$ ...(1)

$a + 16d = 34$ ...(2)
On subtracting equation (1) from equation (2), we get

$a+16d - a- 2d = 34-6$

$14d = 28$

$\Rightarrow$

$d = 2$
Substituting the value of

$d$ in equation (1), we get

$a +2(2)= 6$

$\Rightarrow a = 6-4=2$

$\therefore$

$a= 2$ and

$d = 2$ .

Find the sum of the first $22$ terms of an AP, whose first term is $4$ and the common difference is $\dfrac {4}{3}$ .

Given that,

$a = 4$ and

$d = \dfrac{4}{3}$
We have

$S_n = \displaystyle \frac{n}{2} [2a + (n - 1)d]$

$S_{22} = \left(\displaystyle \frac{22}{2} \right) \left[(2)(4) + (22 - 1) \left(\displaystyle \frac{4}{3} \right) \right]$

$= (11) (8 + 28) = 396$

Find the sum of first 100 natural numbers.
Or
$\displaystyle\sum_{x=1}^{100}{x}=?$

$\sum _{ x=1 }^{ 100 }{ x } = 1 + 2 + 3 +... + 100$
Clearly, it is an AP with

$a= 1, d = 1, n = 100$
Sum of first

$n$ natural numbers

$= \dfrac {n(n+1)}{2}$

So, sum from

$1$ to

$100 = \dfrac {100 \times 101}{2} = 5050$

The $\displaystyle { p }^{ th },{ q }^{ th }$ and ${ r }^{ th }$ terms of an A.P. are $a,b,c$ respectively. Show that $(q - r)a + (r - p)b + (p - q)c = 0$

Let

$t$ and

$d$ be the first term and the common difference of the A.P. respectively,
The

$n^{th}$ term of an A.P. is given by

$\displaystyle{ a }_{ n }=t+(n-1)d$ Therefore,

${ a }_{ p }=t+(p-1)d=a\quad ...(1)\\ { a }_{ q }=t+(q-1)d=b\quad \quad ...(2)\\ { a }_{ r }=t+(r-1)d=c\quad \quad ...(3)$
Subtracting equation (2) from (1), we obtain

$(p-1-q+1)d=a-b\\ \Rightarrow (p-q)d=a-b\\ \therefore d=\cfrac { a-b }{ p-q } \quad \quad \quad ...(4)$
Subtracting equation (4) from (3), we obtain

$(q-1-r+1)d=b-c\\ \Rightarrow (q-r)d=b-c\\ \Rightarrow d=\cfrac { b-c }{ q-r } \quad \quad \quad ...(5)$
Equating both the values of

$d$ obtained in (4) and (5), we obtain

$\displaystyle \frac { a-b }{ p-q } =\frac { b-c }{ q-r } \\ \Rightarrow (a-b)(q-r)=(b-c)(p-q)\\ \Rightarrow aq-bq-ar+br=bp-bq-cp+cq\\ \Rightarrow (-aq+ar)+(bp-br)+(-cp+cq)=0\quad \quad \quad \quad \\ \Rightarrow -a(q-r)-b(r-p)-c(p-q)=0\\ \Rightarrow a(q-r)+b(r-p)+c(p-q)=0$
Thus, the given result is proved.

How many terms are needed in the series $-15$ , $-12$ , $-9$ , $\dots\dots$ so that their sum is 18?

Let

$a$ be the first term and

$d$ be their common difference of the AP.

Then, Sum to

$n$ terms of an AP

$= \dfrac { n }{ 2 } (2a+(n-1)d)$

Here, in the given AP,.

$a = -15; d = -12 +15 = 3$

So,

$S_n = 18$

$=> \dfrac { n }{ 2 } (2(-15)+(n-1)(3)) = 18$

$=> \dfrac { n }{ 2 } (-30+3n-3) = 18$

$=> \dfrac { n }{ 2 } (3n-33) = 18$

$=> \dfrac { n }{ 2 } (n-11) = 6$

$=> n(n-11) = 12 \times 1$

$=> n = 12$

A man deposited $Rs\ 10000$ in a bank with interest rate of $5\%$ simple interest annually. Find the amount in $15 th$ year since he deposited the amount and also calculate the total amount after $20$ years.

It is given that the man deposited Rs 10000 in a bank at the rate of 5% simple interest annually. Since, the simple interest is added every year, the amount in every year is a term in arithmetic progression.

Formula for Simple Interest

$\displaystyle I= \frac{P\cdot T\cdot R}{100}$

$\displaystyle\therefore$ Interest for each year

$=\cfrac { 5 }{ 100 } \times Rs \ 10000=Rs\ 500$

Interest for each year is the common difference.

Formula for

$n^{th}$ term in an AP

$t_n= a+(n-1)d$

Amount in

$15^{th}$ year

$=10000+14(500)$

$=17000$

Amount after 20 years, which is amount in

$21^{st}$ year

$=10000+20(500)$

$=20000$

Find the sum of terms given below.
$34+32+30+.....+10$

We know,

$n^{th}$ term

$a_{n}= a+(n-1)d$

$a =$ First term

$d =$ Common difference

$n =$ number of terms

$a_n = n^{th}$ term

Sum formula

$S_{n}=\dfrac{n}{2}\left [ 2a+(n-1)d \right ]$

Here

$a=34, d=-2, a_n=10$

So,

$10=34-2(n-1)$

$\Rightarrow 2(n-1)=24$

$\Rightarrow n-1=12$

$\Rightarrow n=13$

So,

$S_{n}=\dfrac{n}{2}\left [ 2a+(n-1)d \right ]$

$S=\dfrac {13}{2}(68-24)=286$

In an AP: Given $a=3, n=8, S=192$ , find d

Given

$a=3, n=8, S=192$

By using

$S_{n}=\dfrac{n}{2}\left [ 2a+(n-1)d \right ]$ we have,

$S_8=\dfrac {8}{2}(6+d(8-1)=4(6+7d)$

$\Rightarrow \dfrac{192} {4}=48=6+7d$

$\Rightarrow 7d=42$

$\Rightarrow d=6$

Ramkali saved Rs. $5$ in the first week of a year and then increased her weekly savings by $Rs.\ 1.75$ . If in the $n^{ th}$ week, her weekly savings become Rs. $20.75$ . Find $n$ .

According to the question,

$a=5$ ,

$d=1.75$ ,

$a_n=20.75$

$a_n=a+(n-1)d$

Subsituting the values in above equation,

$20.75=5+(n-1)\times 1.75$

$15.75=(n-1)(1.75)$

$\Rightarrow n-1=\dfrac{15.75}{1.75}$

$\Rightarrow n-1=9$

$\Rightarrow n=10$

$n=10$ .

How many three-digit numbers are divisible by $7$ ?

The first three-digit number which is divisible by

$7$ is

$105$ and the last three-digit number which is divisible by

$7$ is

$994$

This is an A.P in which

$a=105, d=7$ and

$l=994$

Let the number of terms be

$n$ Then

${t}_{n}=994$

${n}^{th}$ term of A.P

$={t}_{n}=a+\left(n-1\right)d$

$\Rightarrow 994=105+\left(n-1\right)7$

$\Rightarrow 994-105=\left(n-1\right)7$

$\Rightarrow n-1=\dfrac{889}{7}=127$

$\Rightarrow n=127+1=128$

$\therefore$ There are

$128$ three-digit numbers which are divisible by

$7$ .

Which term of the AP : $3, 15, 27, 39, . .$ . will be $132$ more than its $54^{th}$ term.

Given A.P. is

$3, 15, 27, 39, …$

$a=3$

$d=a_2-a_1=15-3=12$

$a_{54}=a+(54-1)d$

$= 3 + (53) (12)$

$= 3 + 636 = 639$

Then,

$132$ more than its

$54^{th}$ term is

$132 + 639 = 771$

We have to find the term of this A.P. which is

$771$ .

Let

$n^{th}$ term be

$771$ .

$\Rightarrow a_n=a+(n-1)d$

$\Rightarrow 771=3+(n-1)12$

$\Rightarrow 768=(n-1)12$

$\Rightarrow (n-1) = 64$

$\therefore n=65$

Therefore,

$65^{th}$ term was

$132$ more than

$54^{th}$ term.

Determine the $AP$ whose third term is $16$ and the $7^{th}$ term exceeds the $5^{th}$ term by $12$

By using nth term

$t_{n}= a+(n-1)d$ we have

As given

$a+2d=16$ .......

$2^{nd}$ term

And

$a+6d-(a+4d)=12$

By using abovee equations,

$\Rightarrow d=6$

$\therefore a+2(6)=16$ , then

$a=4$

Then A.P is

$a, a+d ,a+2d,a+3d...............$

So,

$4,4+6,4+2(6),4+3(6) ,4+4(6)..............$

$4,10,16,22,28,34............$

Subba Rao started work in $1995$ at an annual salary of Rs. $5000$ and received an increment of Rs. $200$ each year. In which year did his income reach Rs. $7000$

It can be observed that the incomes that Subba Rao obtained in various years are in A.P. as every year, his salary is increased by Rs

$200$ .

Therefore, the salaries of each year after

$1995$ are

$5000, 5200, 5400, …$

Here,

$a=5000$

$d=200$

Let after

$n^{th}$ year, his salary be Rs

$7000$ .

Therefore,

$a_n=a+(n-1)d$

$\Rightarrow 7000=5000+(n-1)200$

$\Rightarrow 200(n-1)=2000$

$\Rightarrow (n-1)=10$

$\therefore n=11$

Therefore, in

$11^{th}$ year, his salary will be Rs

$7000$ .

Which of the following are APs ? If they form an AP, find the common difference $d$ and write three more terms.
(i) $2, 4, 8, 16, ....$
(ii) $\displaystyle 2,\frac { 5 }{ 2 } ,3,\frac { 7 }{ 2 } ,...$
(iii) $\displaystyle -1.2,-3.2,-5.2,-7.2,...$
(iv) $\displaystyle -10,-6,-2,2,...$
(v) $\displaystyle 3,3+\sqrt { 2 } ,3+2\sqrt { 2 } ,3+3\sqrt { 2 }$
(vi) $\displaystyle 0.2,0.22,0.222,0.2222,....$
(vii) $\displaystyle 0,-4,-8,-12,...$
(viii) $\displaystyle -\frac { 1 }{ 2 } ,-\frac { 1 }{ 2 } ,-\frac { 1 }{ 2 } ,-\frac { 1 }{ 2 } ,...$
(ix) $\displaystyle 1,3,9,27$
(x) $\displaystyle a,2a,3a,4a,...$
(xi) $\displaystyle a,{ a }^{ 2 },{ a }^{ 3 },{ a }^{ 4 },...$
(xii) $\displaystyle \sqrt { 2 } ,\sqrt { 8 } ,\sqrt { 18 } ,\sqrt { 32 } ,...$
(xiii) $\displaystyle \sqrt { 3 } ,\sqrt { 6 } ,\sqrt { 9 } ,\sqrt { 12 } ,...$
(xiv) $\displaystyle { 1 }^{ 2 },{ 3 }^{ 2 },{ 5 }^{ 2 },{ 7 }^{ 2 },..$
(xv) $\displaystyle { 1 }^{ 2 },{ 5 }^{ 2 },{ 7 }^{ 2 },73,..$

$a,b,c$ are said to be in AP if the common difference between any two consecutive number of the series is same ie

$b-a=c-b \Rightarrow 2b=a+c$

$(i)$ It is not in AP, as the difference between consecutive terms is different.

$(ii)$ It is in AP with common difference

$d= \dfrac{5}{2}-2= \dfrac{1}{2}$ ,

$t_n=a+(n-1)d$

$a=2$

$t_5 = 2+(5-1)\dfrac{1}{2}$
Next three terms are

$4,\dfrac{9}{2},5$

$(iii)$ It is in AP with common difference

$d=-3.2+1.2=-2$ ,and

$a=-1.2$

Next three terms are

$a+(5-1)d=-9.2,$

$a+(6-1)d=-11.2,$

$a+(7-1)d=-13.2$

$(iv)$ It is in AP with common difference

$d=-6+10=4$ , and

$a=-10$

Next three terms are

$a+(5-1)d=6,$

$a+(6-1)d=10,$

$a+(7-1)d=14$

$(v)$ It is in AP with common difference

$d=3+\sqrt{2}-3=\sqrt{2}$ , and

$a=3$

Next three terms are

$a+(5-1)d=3+4\sqrt{2},$

$a+(6-1)d= 3+5\sqrt{2},$

$a+(7-1)d=3+6\sqrt{2}$

$(vi)$ It is not in AP since

$0.22-0.2 \neq 0.222-0.22$

$(vii)$ It is in AP with common difference

$d=-4-0=-4$ and

$a=0$ ,

Next three terms are

$a+(5-1)d=-16,$

$a+(6-1)d=-20,$

$a+(7-1)d=-24$

$(viii)$ It is in AP, with common difference

$0$ , therefore next three terms will also be same as previous ones, i.e.,

$-\dfrac12$

$(ix)$ It is not in AP since

$3-1 \neq 9-3$

$(x)$ It is in AP with common difference

$d=2a-a=a$ and first term is

$a$ ,

Next three terms are

$a+(5-1)d=5a,$

$a+(6-1)d=6a,$

$a+(7-1)d=7a$

$(xi)$ It is not in AP, as the difference is not constant.

$(xii)$ It is in AP with common difference

$d=\sqrt{2}$ and

$a=\sqrt{2}$ ,

Next three terms are

$a+(5-1)d=5\sqrt{2}=\sqrt{50},$

$a+(6-1)d=\sqrt{72},$

$a+(7-1)d=\sqrt{98}$

$(xiii)$ It is not in AP as difference is not constant.

$(xiv)$ It is not in AP as difference is not constant.

$(xv)$ It is in AP with common difference

$d=5^2-1=24$ and

$a=1$ ,

Next three terms are

$a+(5-1)d=97,$

$a+(6-1)d=121,$

$a+(7-1)d=145$

Write first four terms of the AP, when the first term $a$ and the common difference $d$ are given as follows:
(i) $a=10, d=10$
(ii) $a=-2, d=0$
(iii) $a=4, d=-3$
(iv) $a=-1, d=$ $\displaystyle \frac { 1 }{ 2 }$
(v) $a=-1.25, d=-0.25$

An arithmetic progression is given by

$a, (a + d), (a + 2d), (a + 3d)$ , .
where

$a =$ the first term,

$d =$ the common difference

(i)

$10,10+10,10+2(10)$ and

$10+3(10)=10,20,30$ and

$40$

(ii)

$-2,-2+(0),-2+2(0)$ and

$-2+3(0)=-2,-2,-2$ and

$-2$ (this is not an A.P)

(iii)

$4,4+(-3),4+2(-3)$ and

$4+3(-3)=4,4-3,4-6$ and

$4-9=4,1,-2$ and

$-5$

(iv)

$-1,-1+\left (\dfrac{1}{2}\right ),-1+2\left ( \dfrac{1}{2} \right )$ and

$-1+3\left ( \dfrac{1}{2} \right )=-1,-\dfrac{1}{2},0$ and

$\dfrac{1}{2}$

(v)

$-1.25,-1.25+(-0.25),-1.25+2(-0.25)$ and

$-1.25+3(-0.25)=-1.25,-1.50,-1.75$ and

$-2.0$

For the following APs, write the first term and the common difference:
(i) $3, 1, -1, -3, ....$
(ii) $-5, -1, 3, 7, .....$
(iii) $\displaystyle \frac { 1 }{ 3 } ,\frac { 5 }{ 3 } ,\frac { 9 }{ 3 } ,\frac { 13 }{ 3 } ,....$
(iv) $0.6, 1.7, 2.8, 3.9, ...$

(i)

$3, 1, - 1, - 3 …$
Here, first term,

$a=3$
Common difference,

$d=$ Second term

$-$ First term

$d= 1 - 3 = - 2$

(ii)

$- 5, - 1, 3, 7 …$
Here, first term,

$a=-5$
Common difference,

$d=$ Second term

$-$ First term

$d= ( - 1) - ( - 5) = - 1 + 5 = 4$

(iii)

$\dfrac{1}{3},\dfrac{5}{3},\dfrac{9}{3},\dfrac{13}{3}$
Here, first term,

$a=\dfrac {1}{3}$

Common difference,

$d=$ Second term

$-$ First term

$d=\dfrac{5}{3}-\dfrac{1}{3}=\dfrac{4}{3}$

(iv)

$0.6, 1.7, 2.8, 3.9 …$
Here, first term,

$a=0.6$
Common difference,

$d=$ Second term

$-$ First term

$d= 1.7 - 0.6$

$= 1.1$

For what value of $n$ , are the $nth$ terms of two $APs : 63, 65, 67, ...$ and $3, 10, 17$ , .... equal?

2151369_466099_ans_deb2f0671de54c6b90e874321dc9c962.jpeg

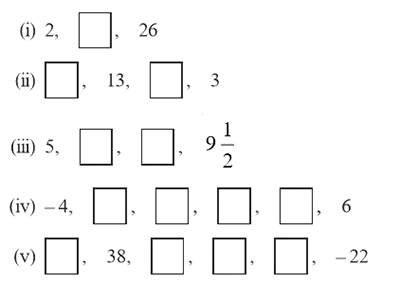
In the following APs, find the missing terms in the boxes :

(i) For this A.P.,

$a=2$

$a_3=26$

We know that,

$a_n=a+(n-1)d$

$a_3=2+(3-1)d$

$26 = 2 + 2d$

$24 = 2d$

$d=12$

$a_2=2+(2-1)12$

$= 14$

Therefore,

$14$ is the missing term.

(ii) For this A.P.,

$a_{2} = 13$ and

$a_{4} = 3$

We know that,

$a_{n}=a+(n-1)d$

$a_{2} = a + (2 - 1) d$

$13 = a + d$ ... (i)

$a_{4} = a + (4 - 1) d$

$3 = a + 3d$ ... (ii)

On subtracting (i) from (ii), we get,

$- 10 = 2d$

$d = - 5$

From equation (i), we get,

$13 = a + (-5)$

$a = 18$

$a_{3} = 18 + (3 - 1) (-5)$

$= 18 + 2 (-5) = 18 - 10 = 8$

Therefore, the missing terms are

$18$ and

$8$ respectively.

(iii) For this A.P.,

$a_1= 5$ and

$a_4=9\dfrac{1}{2}$

We know that,

$a_n=a+(n-1)d$

$a_{4} = 5 + (4 - 1) d$

$9\dfrac{1}{2} = 5 + 3d$

$d =\dfrac{3}{2}$

$a_2 = a + d$

$a_2 = 5 + \dfrac{3}{2}$

$a_2 = \dfrac{13}{2}$

$a_{3} = a_2 + \dfrac{3}{2}$

$a_{3} = 8$

Therefore, the missing terms are

$6\dfrac{1}{2}$ and

$8$ respectively.

(iv) For this A.P.,

$a = −4$ and

$a_{6} = 6$

We know that,

$a_{n}=a+(n-1)d$

$a_{6} = a + (6 − 1) d$

$6 = − 4 + 5d$

$10 = 5d$

$d = 2$

$a_{2} = a + d = − 4 + 2 = −2$

$a_{3} = a + 2d = − 4 + 2 (2) = 0$

$a_{4} = a + 3d = − 4 + 3 (2) = 2$

$a_{5} = a + 4d = − 4 + 4 (2) = 4$

Therefore, the missing terms are

$−2, 0, 2,$ and

$4$ respectively.

(v) For this A.P.,

$a_{2} = 38$

$a_{6} = −22$

We know that

$a_{n}=a+(n-1)d$

$a_{2} = a + (2 − 1) d$

$38 = a + d$ ... (i)

$a_{6}= a + (6 − 1) d$

$−22 = a + 5d$ ... (ii)

On subtracting equation (i) from (ii), we get

$− 22 − 38 = 4d$

$−60 = 4d$

$d = −15$

$a = a_{2}-a = 38 − (−15) = 53$

$a_{3} = a + 2d = 53 + 2 (−15) = 23$

$a_{4} = a + 3d = 53 + 3 (−15) = 8$

$a_{5} = a + 4d = 53 + 4 (−15) = −7$

Therefore, the missing terms are

$53, 23, 8$ and

$−7$ respectively.

A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs. $200$ for the first day, Rs. $250$ for the second day, Rs. $300$ for the third day, etc., the penalty for each succeeding day being Rs. $50$ more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work by $30$ days.

It can be observed that these penalties are in an A.P. having first term as

$200$ and common difference as

$50$ .

$a=200, d=50$

$Sum \ upto \ n \ terms$

$(S_{n})=\dfrac{n}{2}\left [ 2a+(n-1)d \right ]$

Penalty that has to be paid if he has delayed the work by

$30$ days

$=S_{30}$

$=$

$S_{30}=\dfrac{30}{2}\left [ 2(200)+(30-1)50 \right ]$

$=15[400+1450]$

$= 15 (1850)$

$= 27750$

Therefore, the contractor has to pay Rs

$27750$ as penalty.

In a potato race, a bucket is placed at the starting point, which is $5$ m from the first potato, and the other potatoes are placed $3$ m apart in a straight line. There are ten potatoes in the line (see Fig.).
A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?
[Hint : To pick up the first potato and the second potato, the total distance (in metres) run by a competitor is $\displaystyle 2\times 5+2\times \left( 5+3 \right)$ ]

The distances of potatoes from the bucket are

$5, 8, 11, 14…$
Distance run by the competitor for collecting these potatoes are two times of the distance at which the potatoes have been kept. Therefore, distances to be run are

$10, 16, 22, 28, 34,……….$

$a=10, d=16-10=6$

To find:

$S_{10}$

$S_{10}= \dfrac {10}{2}[2(10)+(10-1)6]$

$= 5[20 + 54]$

$= 5 (74)$

$= 370$
Therefore, the competitor will run a total distance of

$370$ m.

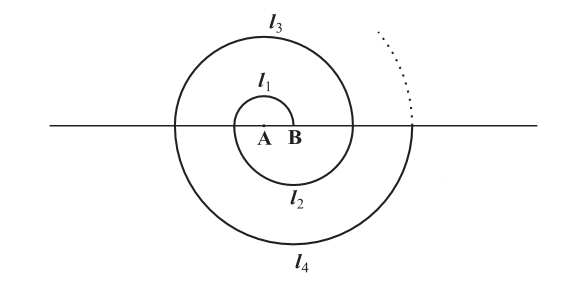
A spiral is made up of successive semicircles, with centers alternately at $A$ and $B$ , starting with center at $A$ , of radii $0.5\ cm, 1.0\ cm,1.5\ cm,2.0\ cm$ , . . . as shown in Fig. What is the total length of such a spiral made up of thirteen consecutive semicircles

Circumference of first semicircle

$=$

$\pi r=0.5\pi$

Circumference of second semicircle

$=$

$\pi r=\pi$

Circumference of third semicircle

$=$

$\pi r=1.5\pi$

It is clear that

$a=0.5\pi$ ,

$d=0.5\pi$ and

$n = 13$

Hence, length of spiral can be calculated as follows:

$S=\dfrac{n}{2}\left [ 2a+(n-1)d \right ]$

$=$

$\dfrac{13}{2}(2\times 0.5\pi +12\times 0.5\pi )$

$=$

$\dfrac{13}{2}\times 7\pi$

$=$

$\dfrac{13}{2}\times 7\times \dfrac{22}{7}$

$=143$ cm

A sum of Rs. $700$ is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is Rs. $20$ less than its preceding prize, find the value of each of the prizes.

$\textbf{Step -1: Applying formula of arithmetic progression to find the value of a}$

$\text{Total sum is Rs.}700$

$\therefore \text{ Sum of terms, }S_n=700$

$\text{Let the amount of the first prize be }a$

$\text{Number of prizes, }n=7$

$\text{Common difference, }d=-20$

$\text{We know that sum of terms of an AP }(S_n)=\dfrac{n}{2}[2a+(n-1)d]$

$\therefore\;700=\dfrac{7}{2}[2a+(7-1)(-20)]$

$\Rightarrow\;200=2a+6\times(-20)$

$\Rightarrow\;200=2a-120$

$\Rightarrow\;2a=320$

$\Rightarrow\;a=160$

$\textbf{Step -2: Finding amount of all the prizes}$

$\text{All the terms of the arithmetic progression are,}$

$a_1=160$

$a_2=a_1+(2-1)d=160-20=140$

$a_3=a_1+(3-1)d=160-40=120$

$a_4=a_1+(4-1)d=160-60=100$

$a_5=a_1+(5-1)d=160-80=80$

$a_6=a_1+(6-1)d=160-100=60$

$a_7=a_1+(7-1)d=160-120=40$

$\textbf{Hence, the value of each of the prizes are }\mathbf{Rs.160,Rs.140,Rs.120,Rs.100,Rs.80,Rs.60\textbf{ and }Rs.40. }$

In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of Class $I$ will plant $1$ tree, a section of Class $II$ will plant $2$ trees and so on till Class $XII$ . There are three sections of each class. How many trees will be planted by the students?

It can be observed that the number of trees planted by the students is in an AP.

$1, 2, 3, 4, 5………………..12$

First term,

$a=1$

Common difference,

$d=2-1=1$

$S_{n}=\dfrac{n}{2}\left [ 2a+(n-1)d \right ]$

$S_{12}=\dfrac{12}{2}\left [ 2(1)+(12-1)(1) \right ]$

$= 6 (2 + 11)$

$= 6 (13)$

$= 78$

Therefore, number of trees planted by

$1$ section of the classes

$= 78$

Number of trees planted by

$3$ sections of the classes

$=$

$3\times 78=234$

Therefore,

$234$ trees will be planted by the students.

$200$ logs are stacked in the following manner: $20$ logs in the bottom row, $19$ in the next row, 18 in the row next to it and so on. In how many rows are the $200$ logs placed and how many logs are in the top row.

It can be observed that the numbers of logs in rows are in an A.P.

$20, 19, 18…$

For this A.P.,

$a = 20$ ,

$d=19-20=-1$

Let a total of

$200$ logs be placed in n rows.

$S_n=200$

$S_{n}=\dfrac{n}{2}(a+(n-1)d$

$\Rightarrow 200=\dfrac{n}{2}\left [ 2(20)+(n-1)(-1) \right ]$

$\Rightarrow 400 = n (40 − n + 1)$

$\Rightarrow 400 = n (41 − n)$

$\Rightarrow 400=41n-n^{2}$

$\Rightarrow n^{2}-16n-25n+400$

$\Rightarrow n (n − 16) −25 (n − 16) = 0$

$\Rightarrow (n − 16) (n − 25) = 0$

Either

$(n − 16) = 0$ or

$(n − 25) = 0$

$n = 16$ or

$n = 25$

$\Rightarrow a_n = a + (n − 1)d$

$\Rightarrow a_{16}$

$= 20 + (16 − 1) (−1)$

$\Rightarrow a_{16}$

$20-15$

$a_{16}$

$= 5$

Similarly,

$a_{25}$

$= 20 + (25 − 1) (−1)$

$a_{25}$

$= 20 − 24$

$= −4$

Clearly, the number of logs in

$16^{th}$ row is

$5$ . However, the number of logs in

$25^{th}$ row is negative, which is not possible.

Therefore,

$200$ logs can be placed in

$16$ rows and the number of logs in the

$16^{t}$ h row is

$5$ .

The houses of a row are numbered consecutively from $1$ to $49$ . Show that there is a value of $x$ such that the sum of the numbers of the houses preceding the house numbered $x$ is equal to the sum of the numbers of the houses following it. Find this value of $x$ .

Here

$a=1, d=1$ and

$a_{49}=49$

As per question,

$S_{x-1}=S_{49}-S_{x}$ ............(i)$$

$S_{x}=\dfrac{x}{2}\left [ 2+(x-1)\times 1 \right ]$

$=$

$\dfrac{x}{2}(x+1)=\dfrac{x^{2}+x}{2}$

Similarly,

$S_{x-1}=\dfrac{x-1}{2}\left [ 2+(x-1-1)\times 1 \right ]$

$=$

$\dfrac{x-1}{2}(2+x-2)=\dfrac{(x-1)x}{x}\dfrac{x^{2}-x}{2}$

Similarly,

$S_{49}=\dfrac{49}{2}\left[ 2+48\times 1 \right ]=\dfrac{49}{2}\times 50=1225$

After substituting the values of

$S_{x-1}, S_{49}$ and

$S_x$ in equation (1), we get

$S_{x-1}==S_{49}-S_{x}$

$\dfrac{x^{2}-x}{2}=1225-\dfrac{x^{2}+x}{2}$

$\dfrac{x^{2}-x}{2}+\dfrac{x^{2}+x}{2}=1225$

$\dfrac{x^{2}-x+x^{2}-x}{2}=1225$

$x^{2}=1225$

$x=35$

A ladder has rungs $25$ cm apart. The rungs decrease uniformly in length from $45$ cm at the bottom to $25$ cm at the top. If the top and the bottom rungs are $\displaystyle 2\dfrac { 1 }{ 2 } m$ apart, what is the length of the wood required for the rungs

It is given that the rungs are

$25$ cm apart and the top and bottom rungs are

$2\dfrac{1}{2}$ m apart.

$\therefore$ the total number of rungs.

$\dfrac{2\dfrac{1}{2}\times 100}{25}+1$

$=$

$\dfrac{250}{25}+1=11$

Now, as the lengths of the rungs decrease uniformly, they will be in an A.P.

The length of the wood required for the rungs equals the sum of all the terms of this A.P.

First term,

$a = 45$

Last term,

$l = 25$

$n = 11$

$S_{n}=\dfrac{n}{2}(a+l)$

$S_{10}=\dfrac{11}{2}(45+25)=\dfrac{11}{2}\times 70=385$ cm

Therefore, the length of wood is

$385$ cm

Find the sum of the first $50$ even positive integers.

Sum of first

$n$ terms,

$S_n = \dfrac{n}{2} (2a+(n-1)d)$ , where

$a$ &

$d$ are the first term & common difference of an AP.

The sequence of the first

$50$ even positive integers is given by

$2 , 4 , 6 , ...$

The above sequence has a first term

$a=2$ and a common difference

$d = 2$ .

And

$n=50$

So,the sum of the first

$50$ terms

$S_{50} = \dfrac{50}{2} (2\times 2+(50-1)\times2)$

$\Rightarrow S_{50} = 25 (4+49\times2)$

$\Rightarrow S_{50} = 25 (4+98)$

$\Rightarrow S_{50} = 2550$

Find ${s}_{30}$ for an AP, where ${a}_{10}=20$ and ${a}_{20}=58$ .

As we know nth term,

$a_n = a+(n-1)d$

& Sum of first

$n$ terms,

$S_n = \dfrac{n}{2} (2a+(n-1)d)$ , where

$a$ &

$d$ are the first term & common difference of an AP.

Let

$a$ be the first term and

$d$ be the common difference of the AP

Given,

$a_{10}= 20=a+9d$

and

$a_{20}=58=a+19d$

Solving above, we get

$d=3.8$

Hence,

$S_{30}=\dfrac{30}{2}(2a+29d)$

$=15(a_{10}+a_{20}+d)$

$=15(20+58+3.8)$

$=1227$

Define arithmetic progression with one example.

An arithmetic progression is a sequence of numbers such that the difference of any two successive members is a constant.
Example: the sequence

$2, 4, 6, 8, ...$ is an arithmetic progression with common difference

$2$ .

Find the common difference $d$ for an AP, where ${a}_{1}=10$ and ${a}_{20}=466$

In a arithmetic series

${ a }_{ n }=a+(n-1)d$ where

$a$ is the first term of the sequence,

$d$ is the common difference, and

$n$ is the number of the term to find.

Since the first term is

$10$ , therefore,

${ a }_{ 20 }=10+(20-1)d=10+19d$

$466=10+19d$

$466-10=19d$

$19d=456$

$d=24$

Find the sum of all of the odd integers between $200$ and $400$

$201+203+......+399$ [It is an A.P. with

$d=2$ ]

$a=201$ ;

$a_n=399$

$\Rightarrow a_n=a+(n-1)d\Rightarrow (n-1)=\dfrac{399-201}{2}\Rightarrow n=100$

$\Rightarrow S_n=\dfrac{n}{2}[a+a_n]=50[201+399]=30000$ .

$T_n = 2n - 1$

The given sequence is

$t_n=2n-1$ .

The first term

$t_1$ can be determined by substituting

$n=1$ in the sequence

$t_n=2n-1$ as follows:

$t_1=(2\times 1)-1=2-1=1$

The second term

$t_2$ can be determined by substituting

$n=2$ in the sequence

$t_n=2n-1$ as follows:

$t_2=(2\times 2)-1=4-1=3$

The third term

$t_3$ can be determined by substituting

$n=3$ in the sequence

$t_n=2n-1$ as follows:

$t_3=(2\times 3)-1=6-1=5$

Hence, the sequence is

$1,3,5,.......$ .

f $a = 13$ , $T_{15} = 55$ , find $d$ .

We know that the formula for the nth term is

$t_n=a+(n-1)d$ , where

$a$ is the first term,

$d$ is the common difference.

It is given that the nth term is

${t}_{15}=55$ and the first term is

$a=13$ , therefore,

${ t }_{ n }=a+(n-1)d\\ \Rightarrow 55=13+(15-1)d\quad \quad \quad \quad \quad \quad \quad \quad \\ \Rightarrow 55=13+14d\\ \Rightarrow 14d=55-13\\ \Rightarrow 14d=42\\ \Rightarrow d=\frac { 42 }{ 14 } =3$

Hence,

$d=3$

$T_n = 5n + 1$

The given sequence is

$t_n=5n+1$ .

The first term

$t_1$ can be determined by substituting

$n=1$ in the sequence

$t_n=5n+1$ as follows:

$t_1=(5\times 1)+1=5+1=6$

The second term

$t_2$ can be determined by substituting

$n=2$ in the sequence

$t_n=5n+1$ as follows:

$t_2=(5\times 2)+1=10+1=11$

The third term

$t_3$ can be determined by substituting

$n=3$ in the sequence

$t_n=5n+1$ as follows:

$t_3=(5\times 3)+1=15+1=16$

Hence, the sequence is

$6,11,16,\dots\dots$ .

Obtain the sum of the first $56$ terms of an A.P whose $25^{th}$ and $32^{nd}$ terms are $52$ and $148$ respectively.

Given 25th and 32nd terms of an A.P are

$52$ and

$148$ respectively.
We have to find

${S}_{56}$ .
We know that

${t}_{n}=a+(n-1)d$

${t}_{25}=52$ and

${t}_{32}=148$
Here,

${t}_{25}=a+(25-1)d$

$\therefore$

${t}_{25}=a+(25-1)d$

$\therefore$

$52=a+24d..........(i)$
Also,

${t}_{32}=a+(32-1)d$

$\therefore$

$148=a+31d.........(ii)$
Adding equations

$(i)$ and

$(ii)$ we get

$a+24d=52$

$a+31d=148$
-----------------------

$2a+55d=200...............(iii)$
We know that

${ S }_{ n }=\cfrac { n }{ 2 } \left[ 2a+(n-1)d \right]$

${ S }_{ 56 }=\cfrac { 56 }{ 2 } \left[ 2\times a+(56-1)d \right]$

${S}_{56}=28(2a+55d)$

${S}_{56}=28\times 200$ (from

$(iii)$ )

${S}_{56}=5600$

$\therefore$ The sum of the

$56$ terms of an AP is

$5600$ .

If the sum of the first $12$ terms of an A.P. is $468$ and its common difference is $6$ , find the $10^{th}$ term

We know

$d=6$ and sum of

$12$ terms is

$468$

Using the formula for sum of

$n$ terms of an A.P.

$S_{12}=\dfrac {12}{2}[2a+(12-1)(6)]$

$468=6[2a+66]$

$468=12a+396$

$a=6$

Using the formula for

$n^{th}$ term to find

$a_{10}$ :

$a_n=a+(n-1)d$

So, the

$10^{th}$ term is:

$a_{10}=a+(10-1)d=6+9\times 6=60$ .

Find the fifteenth term of the A.P.: $7,13,19,25,...$

We have

${ t }_{ 1 }=7,{ t }_{ 2 }=13,{ t }_{ 3 }=19,{ t }_{ 4 }=25...$
The common difference

$d={t}_{2}-{t}_{1}=13-7=6$

It can be observed that difference between every consecutive terms is constant. Thus given terms are in arithmetic progression.
First term

$a=7,{t}_{15}=?$
We know that

${t}_{n}=a+(n-1)d$

${t}_{15}=7+(15-1)\times 6$

$\therefore$

${t}_{15}=7+14\times 6$

$\therefore$

${t}_{15}=7+84$

$\therefore$

${t}_{15}=91$

$\therefore$

${t}_{15}=91$

$\therefore$ The fifteenth term of the A.P is

$91$ .

Find the sum of first 15 terms of an A.P. whose 5th and 9th terms are 26 and 42 respectively

Given an AP with :

Fifth term,

$a_5 = 26$

Ninth term,

$a_9 = 42$

We know that

$n^{th}$ term of AP is given by:

$a_n = a + (n-1)d$

$a_5 = 26 = a + (5-1)d .........(i)$

$a_9 = 42 = a + (9-1)d ...........(ii)$

Subtracting (i) from (ii), we get

$16 = 4d$

$d = 4$

Substituting value of

$d$ in (i), we get

$26 = a + 4 \times 4$

$a =10$

Now, sum of first

$n$ terms is given by:

$S_{n} = \cfrac{n}{2} (2 a + (n-1)d)$

Substituting values, we get sum of fifteen terms as

$S_{15} = \cfrac{15}{2} (2 \times 10 + (15-1) \times 4)$

$S_{15}=\cfrac{15}{2}(20+56)$

$S_{15}=15\times 38$

$S_{15} = 570$

How many terms of the A.P. 17, 15, 13, ...... must be taken, so that their sum is 81?

Given:

$a_1 = 17, \ a_2 = 15, \ a_3 = 13$

Sum of

$n$ terms :

$S_n = 81$

To find

$n$

Common difference is given by:

$d = a_n - a_{n-1}$

Using above,

$d = a_2-a_1$

$d = 15-17=-2$

Sum of

$n$ -terms of an AP with first terms

$a_1$ and common difference

$d$ is given by:

$S_n = \cfrac{n}{2} (2a_1+(n-1)d)$

$81 = \cfrac{n}{2} [2 \times 17 + (n-1) \times (-2)]$

$162 = -2n^2 + 36n$

$n^2 - 18n +81 = 0$

$(n-9)^2 = 0$

$n=9$

Find the eighteenth term of the A.P
$7,13,19,25,....$

We have

${ t }_{ 1 }=7,{ t }_{ 2 }=13,{ t }_{ 3 }=19,{ t }_{ 4 }=25....$

$d={t}_{2}-{t}_{1}=13-7=6$
The common difference,

$d=6$ and first term,

$a=7$
We know that,

${t}_{n}=a+(n-1)d$

$\therefore$

${t}_{18}=7+(18-1)\times 6$

$\therefore$

${t}_{18}=7+17\times 6$ .

$\therefore$

${t}_{18}=7+102$

$\therefore$

${t}_{18}=109$

$\therefore$ the eighteenth term of the A.P is

$109$

What is the common difference of an A.P., in which $a_{21} - a_7 = 644$ .

We know that,

$a_n=a+(n-1)d$

Now, by using the above defination,

$\begin{aligned}{}{a_{21}} - {a_7} &= 644\\a + \left( {21 - 1} \right)d - \left[ {a + \left( {7 - 1} \right)d} \right] &= 644\\a + 20d - a - 6d &= 644\\14d &= 644\\d &= 46\end{aligned}$

So, the difference of A.P is

$46.$

For an A, P, $\dfrac{1}{3}, \dfrac{4}{3}, \dfrac{7}{3}, \dfrac{10}{3} ..........,$ Find $T_{18^o}$
For an A, P, 3, 9, 15, 21 ............, Find $S_{10^o}$

Given A.P.:

$\dfrac{1}{3}, \dfrac{4}{3}, \dfrac{7}{3}, \dfrac{10}{3}, ..........$
Here,

$a = \dfrac{1}{3}$
And,

$d = \dfrac{4}{3} - \dfrac{1}{3} = 1$
Now,

$T_n = a + (n - 1) d$

$\therefore T_{18} = \dfrac{1}{3} + 17 (1) = \dfrac{1}{3} = \dfrac{11 + 51}{3} = \dfrac{52}{3}$

Also, given A. P. : 3, 9, 15, 21, .............
Here, a = 3
And, d = 9 - 3 = 6
Now,

$S_n = \dfrac{n}{2} [2a + (n - 1)]d$

$\therefore S_{10} = \dfrac{10}{2} [2(3) + 9(6)] = 5[6 + 54] = 5 \times 60 = 300$

Find the sum of the following numbers without actually adding the numbers.
(i) $1 + 3 + 5 + 7 + 9 + 11 + 13 + 15$
(ii) $1 + 3 + 5 + 7$
(iii) $1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17$

Given

$S=1+3+5+7+....+(2n-1)$

This is an arithmetic progression

Sum of AP:

$S_n=\cfrac{n}{2}[2a+(n-1)d]=\cfrac{n}{2}[2+(n-1)2]=n^2$

$(i)$

$1+3+5+7+9+11+13+15$

$n=8 \quad S_n=n^2=8^2=64$

$(ii)$

$1+3+5+7$

$n=4 \quad S_n=n^2=4^2=16$

$(iii)$

$1+3+5+7+9+11+13+15+17$

$n=9 \quad S_n=n^2=9^2=81$

In an A.P., prove that $d=S_n -2S_{n-1}+S_{n-2}$ .

For an Arithmetic Progression,

$S_n=\dfrac{n}{2}.\left[2a+(n-1)d\right]$

$S_{n-1}=\dfrac{n-1}{2}.\left[2a+(n-2)d\right]$

$S_{n-2}=\dfrac{n-2}{2}\left[2a+(n-3)d\right]$

Now, let's take the

$RHS$ :

$RHS=\ \ \ S_n-2S_{n-1}+S_{n-2}\\=an+\dfrac{n(n-1)}{2}.d-2a(n-1)-(n-1)(n-2)d+a(n-2)+\dfrac{(n-2)(n-3)}{2}.d\\=a\left[n-2(n-1)+n-2\right]+d\left[\dfrac{n(n-1)}{2}-(n-1)(n-2)+\dfrac{(n-2)(n-3)}{2}\right]\\=0+\dfrac{d}{2}\left[(n^2-n)-2(n^2-3n+2)+(n^2-5n+6)\right]\\=\dfrac{d}{2}\left(-4+6\right)=\dfrac{d}{2}\times2=d\ \ \ =LHS$

$LHS=RHS$

Thus it is proved.

Find the common difference and $15^{th}$ term of the A.P. $125, 120, 115, 110,$ ______

The given arithmetic progression is

$125,120,115,110,......$ where the first term is

$a_1=125$ , second term is

$a_2=120$ and so on.

We find the common difference

$d$ by subtracting the first term from the second term as shown below:

$d=a_2-a_1=120-125=-5$

We know that the general term of an arithmetic progression with first term

$a$ and common difference

$d$ is

$T_n=a+(n-1)d$

To find the

$15^{15}$ term of the A.P, substitute

$n=15,a=125$ and

$d=-5$ in

$T_n=a+(n-1)d$ as follows:

$T_{15}=125+(15-1)(-5)=125+(14\times (-5))=125-70=55$

Hence, the

$15$ th term of the given A.P is

$55$ .

The product of the third by the sixth term of an arithmetic progression is $406$ . The division of the ninth term of the progression by the fourth term gives a quotient $2$ and a remainderFind the first term and the difference of the progression.

Let

$a$ be the first term and

$d$ be the common difference and we know that

$n$ th term,

$T_n = a+(n-1)d$

$\therefore { T }_{ 3 }=a+2d\quad \& \quad { T }_{ 6 }=a+5d\\ { T }_{ 3 }\times { T }_{ 6 }=406$

$(a+2d)(a+5d)=406$

${ a }^{ 2 }+2ad+5ad+10{ a }^{ 2 }=406$

${ a }^{ 2 }+7ad+10{ d }^{ 2 }=406\quad -(i)\\ Now,{ T }_{ 9 }={ T }_{ 4 }\times 2+6$

$a+8d=(a+3d)2+6$

$a+8d=2a+6d+6$

$a-2d+6=0$

$=2d-6\quad -(ii)$

Replacing

$a$ from

$(ii)$ in

$(i)$ .

${ (2d-6) }^{ 2 }+7(2d-6)d+10{ d }^{ 2 }=406$

${ 4 }d^{ 2 }-24d+36+{ 14d }^{ 2 }-42d+10{ d }^{ 2 }=406$

${ 28d }^{ 2 }-66d+36=406$

${ 14 }d^{ 2 }-33d+18=203$

${ 14d }^{ 2 }-33d-185=0$

Using quadratic equation:

$d=\cfrac { -(-33)\pm \sqrt { { (-33) }^{ 2 }-4\times 14\times (-185) } }{ 2\times 14 } \\ =\cfrac { 33\pm \sqrt { { (33) }^{ 2 }+4\times 14\times 185 } }{ 28 } \\ =\cfrac { 33\pm \sqrt { 1089+10360 } }{ 28 } \\ =\cfrac { 33\pm 107 }{ 28 } \\ d=\cfrac { 33+107 }{ 28 } ,\cfrac { 33-107 }{ 28 } \\ =\cfrac { 140 }{ 28 } ,\cfrac { -74 }{ 28 } \\ =5,\cfrac { -37 }{ 28 }$

But common difference cannot be negative in this case.

$\therefore$ Common difference

$=5$ .

From

$(ii)$

$a=2d-6=2\times 5-6=10-6=4$

$\therefore$ The first term is

$4$ .

If $t_{n}$ , represents $n^{th}$ term of an A.P., $t_{2}+ t_{5}-t_{3}=10$ and $t_{2} + t_{9}=17$ , then find its first term and its common difference.

$t_2+t_5-t_3=10$

Let the first term be

$a$ and common difference

$=d$

$\Rightarrow t_n=a+\left(n-1\right)d$

$t_2+t_5-t_3=10$

$\left(a+d\right) +\left(a+4d\right)-\left(a+2d\right)=10$

$a+3d=10.............\left(1\right)$

also,

$\Rightarrow t_2+t_9=17$

$a+d+a+8d=17$

$2a+9d=17............\left(2\right)$

Now by multiply eq. (1) by 2 and subtract eq. (2) from it we got:

$\Rightarrow -3d=3$

$d=-1$

From eq. (1):

$a-3=10$

$\Rightarrow a=13$

$\therefore$ First term

$=13$ Common difference

$=-1.$

Hence, the answer is

$13,-1.$

Find the first term $a$ and the common difference $d$ of the arithmetic progression in which $\displaystyle\, a_2\, +\, a_5 - a_3 = 10$ , $\displaystyle\, a_2 + a_9 = 17$

${ a }$ is the first term and

$d$ is the common difference

$\because { a }_{ t }={ a }+(t-1)d\\ { a }_{ 2 }+{ a }_{ 5 }-{ a }_{ 3 }=10,\\ \implies ({ a }+d)+({ a }+4d)-({ a }+2d)=10\\ \implies { a }+3d=10\quad ------(i)\\a_2+a_9=17\\ \implies { a }+d+{ a }+8d=17\\ \implies 2{ a }+9d=17\quad-----(ii)\\ 2\times (i)-(ii)\\ \implies -3d=3\\ \implies d=-1$

Putting value in

$(ii)$

${ a }-3=10\\ \implies { a }=13$

Answer,

${ a }=13$ &

$d=-1$

Find the common difference of the A.P.: $0,\cfrac { 1 }{ 4 } ,\cfrac { 1 }{ 2 } ,\cfrac { 3 }{ 4 } ,...$

Given A.P is,

$0,\frac{1}{4},\frac{1}{2},\frac{3}{4}…$

$\Rightarrow$ first term of this A.P is

$a_{1}=0$

$\Rightarrow$ second term of this A.P is

$a_{2}=\cfrac{1}{4}$

$\Rightarrow$ third term of this A.P is

$a_{3}=\cfrac{1}{2}$

$\Rightarrow$ fourth term of this A.P is

$a_{4}=\cfrac{3}{4}$

common difference of an A.P is given by

$d=a_{n+1}-a_{n}$

putting

$n=1$ in above equation

$d=a_{2}-a_{1}=\dfrac{1}{4}-0=\dfrac{1}{4}$

lly, if

$n=2$

then

$d=a_{3}-a_{2}=\dfrac{1}{2}-\dfrac{1}{4}=\dfrac{1}{4}$

hence, common difference

$d=\dfrac{1}{4}$

Find the first term and the difference of an arithmetic progression if the sum of its first five even terms is equal to $15$ and the sum of the first three terms is equal to 3.

${\textbf{Step -1: Finding the terms required}}{\text{.}}$

${\text{Let the first term of the }}AP{\text{ be }}a,{\text{and the common difference be }}d.$

${\text{So, the terms of the }}AP{\text{ can be written as,}}$

$a,a + d,a + 2d,a + 3d,a + 4d,a + 5d,a + 6d,a + 7d,a + 8d,a + 9d,a + 10d....$

${\text{The first five even terms will be,}}a,a + 2d,a + 4d,a + 6d{\text{ and }}a + 8d.$

${\text{and the first three terms are,}}a,a + d{\text{ and }}a + 2d.$

${\textbf{Step -2: Finding the first term and the common difference}}{\text{.}}$

${\text{We are given that the sum of first five even terms is 15,so we can write}}$

$a + a + 2d + a + 4d + a + 6d + a + 8d = 15$

$5a + 20d = 15$

$a + 4d = 3...(i)$

${\text{Also, the sum of first three terms is 3 we can write}}$

$3a + 3d = 3$

$a + d = 1...(ii)$

${\text{Solving,(}}i){\text{ and }}(ii){\text{,}}$

$4d + 1 - d = 3$

$3d = 2 \Rightarrow d = \dfrac{2}{3}$

$a = \dfrac{1}{3}$

${\textbf{Thus, the first term of the AP is }}\mathbf{\dfrac{1}{3}{\text{ and the common difference is }}\dfrac{2}{3}.}$

Find the sum of the following arithmetic progressions:
$-26,-24,-22,....$ to $36$ terms.

Given A.P is

$-26,-24,-22,...…..$

number of terms of A.P is

$n=36$

first term of this A.P is

$a_{1}=-26$

second term of this A.P is

$a_{2}=-24$

common difference

$d=a_{2}-a_{1}=-24-(-26)=2$

we know that sum of n term of an A.P is given by

$S_{n}=\frac{n}{2}\bigg[2a +(n-1)d)\bigg]$

$\implies S_{36}=\frac{36}{2}\bigg[2\times -26 +(36-1)\times 2)\bigg]$

$\implies S_{36}=18\bigg[-52 +35\times 2)\bigg]$

$\implies S_{36}=18\bigg[-52 +70)\bigg]$

$\implies S_{36}=18\bigg[18\bigg]$

$\implies S_{36}=324$

hence the sum of

$36$ terms of given A.P is

$324$

Find the sum of first $22$ terms of an A.P in which $d=22$ and ${a}_{22}=149$ .

Given,

$22$ nd term of A.P

$a_{22}=149$

common difference

$d=22$

number of terms

$n=22$

we know that nth term of an A.P is given by

$a_{n}=a_{1}+(n-1)d$

hence 22nd term is given as

$a_{22}=a_{1}+(22-1)\times 22$

put

$a_{22}=149$

$\implies 149=a_{1}+21\times 22$

$\implies a_{1}+462=149$

$\implies a_{1}=149-462=-313$ first term of A.P

sum of n terms of an A.P is given by

$S_{n}=\dfrac{n}{2}(a_{1}+a_{n})$

put

$n=22; \ a_{1}=-313 \ and \ a_{22}=149$

$\implies S_{n}=\dfrac{22}{2}(-313+149)$

$\implies S_{n}=11\times -164$

$\implies S_{n}=-1804$

hence sum of first

$22$ terms of A.P is

$-1804$

The first term of an A.P is $2$ and the last term is $50$ . The sum of all these terms is $442$ . Find the common difference.

Given:

$a=2,a_n=50$

$S_n=\dfrac{n}{2}[a+a_n]=442$

$a_n=a+(n-1)d\Rightarrow 50=2+(n-1)d\Rightarrow 48=(n-1)d$ ...(1)

$442=\dfrac{n}{2}[2+50]$

$n=2\times \dfrac{442}{2+50}=17$

From (1)

$48=(n-1)d$

$48=(17-1)d$

$\therefore d=3$

Find the sum of the following arithmetic progressions:
$41,36,31,.....$ to $12$ terms.

Given A.P is

$41,36,31,...…..$

number of terms of A.P is

$n=12$

first term of this A.P is

$a_{1}=41$

second term of this A.P is

$a_{2}=36$

common difference

$d=a_{2}-a_{1}=36-41=-5$

we know that sum of n term of an A.P is given by

$S_{n}=\frac{n}{2}\bigg[2a +(n-1)d)\bigg]$

$\implies S_{12}=\dfrac{12}{2}\bigg[2\times 41 +(12-1)\times -5\bigg]$

$\implies S_{12}=6\bigg[82 +(11)\times -5)\bigg]$

$\implies S_{12}=6\bigg[82-55\bigg]$

$\implies S_{12}=6\bigg[27\bigg]$

$\implies S_{12}=162$

hence the sum of 12 terms of given A.P is

$162.$

If the sum of a certain number of terms starting from first term of an A.P is $25,22,19,.....$ is $116$ . Find the last term.

Given A.P is

$25,22,19,...…..$

sum of

$n$ terms of A.P is

$S_{n}=116$

first term of this A.P is

$a_{1}=25$

second term of this A.P is

$a_{2}=22$

common difference

$d=a_{2}-a_{1}=22-25=-3$

we know that sum of n term of an A.P is given by

$S_{n}=\dfrac{n}{2}\bigg[2a +(n-1)d)\bigg]$

$\implies S_{n}=\dfrac{n}{2}\bigg[2\times 25 +(n-1)\times -3)\bigg]$

$\implies S_{n}=\dfrac{n}{2}\bigg[50 -3n+3)\bigg]$ .

$\implies S_{n}=\dfrac{n}{2}\bigg[53-3n\bigg]$

put value of

$S_{n}=116$ in above equation

$\implies 116=\frac{n}{2}\bigg[53-3n\bigg]$

$\implies \bigg[53n-3n^{2}\bigg]=232$

$3n^{2}-53n+232=0$

by solving the above quadratic equation we get

$n=\bigg(53\pm \sqrt{(-53)^{2}-4\times 3 \times 232}\bigg)/6$

$n=(53\pm5)/6$

$n=\dfrac{58}{6}=9.6666$ which is not possible since n must be an integer.

$n=\dfrac{48}{6}=8$

hence the sum of 8 term of this A.P is 116.

we know that sum of n term is also given by

$S_{n}=\dfrac{n}{2}(a+l)$ where l is the last term of A.P

put value of

$S_{n}=116;a=25;n=8$ we get

$116=\dfrac{8}{2}(25+l)$

$25+l=29$

$\implies l=29-25=4$

hence last term of A.P is

$4$

Find the sum of the following arithmetic progressions:
$50,46,42,.....$ to $10$ terms

Given A.P is

$50,46,42,...…..$

number of terms of A.P is

$n=10$

first term of this A.P is

$a_{1}=50$

second term of this A.P is

$a_{2}=46$

common difference

$d=a_{2}-a_{1}=46-50=-4$

we know that sum of n term of an A.P is given by

$S_{n}=\frac{n}{2}\bigg[2a +(n-1)d)\bigg]$

$\implies S_{10}=\frac{10}{2}\bigg[2\times 50 +(10-1)\times -4\bigg]$

$\implies S_{10}=5\bigg[100 +(9)\times -4)\bigg]$

$\implies S_{10}=5\bigg[100-36\bigg]$

$\implies S_{10}=5\bigg[64\bigg]$

$\implies S_{10}=320$

hence the sum of

$10$ terms of given A.P is

$320$

Find the sum to $n$ terms of the A.P $5,2,-1,-4,-7,.....$

Given A.P is

$5,2,-1,-4,-7,...…..$

number of terms of A.P is

$n$

first term of this A.P is

$a_{1}=5$

second term of this A.P is

$a_{2}=2$

common difference

$d=a_{2}-a_{1}=2-5=-3$

we know that sum of n term of an A.P is given by

$S_{n}=\dfrac{n}{2}\bigg[2a +(n-1)d)\bigg]$

$\implies S_{n}=\dfrac{n}{2}\bigg[2\times 5 +(n-1)\times -3)\bigg]$

$\implies S_{n}=\dfrac{n}{2}\bigg[10 -3n+3)\bigg]$

hence the sum of n terms of given A.P is .

$\implies S_{n}=\dfrac{n}{2}\bigg[13-3n\bigg]$

How many terms of the A.P $63,60,57,....$ must be taken so that their sum is $693$ ?

Given A.P is

$63,60,57,...…..$

sum of n terms of A.P is

$S_{n}=693$

first term of this A.P is

$a_{1}=63$

second term of this A.P is

$a_{2}=60$

common difference

$d=a_{2}-a_{1}=60-63=-3$

we know that sum of n term of an A.P is given by

$S_{n}=\dfrac{n}{2}\bigg[2a +(n-1)d)\bigg]$

$\implies S_{n}=\dfrac{n}{2}\bigg[2\times 63 +(n-1)\times -3)\bigg]$

$\implies S_{n}=\dfrac{n}{2}\bigg[126 -3n+3)\bigg]$ .

$\implies S_{n}=\dfrac{n}{2}\bigg[129-3n\bigg]$

put value of

$S_{n}=693$ in above equation

$\implies 693=\dfrac{n}{2}\bigg[129-3n\bigg]$

$\implies \bigg[129n-3n^{2}\bigg]=1386$

$3n^{2}-129n+1386=0$

by solving the above quadratic equation we get

$n=\bigg(129\pm \sqrt{(-129)^{2}-4\times 3 \times 1386}\bigg)/6$

$n=(129\pm3)/6$

for minus sign

$n=\dfrac{126}{6}=21$

$n=\dfrac{132}{6}=22$

hence the sum of

$21$ or

$22$ term of this A.P is

$693$ .

the sum is equal for

$21$ and

$22$ term because

$22$ th term of this A.P is

$0$

since addition of zero does not change the sum

Find the sum of the arithmetic progressions: $3, \dfrac{9}{2}, 16, \dfrac{15}{2},......$ to $25$ terms

Given A.P is

$3,\dfrac{9}{2},16,\dfrac{15}{2}..…..$

number of terms of A.P is

$n=25$

first term of this A.P is

$a_{1}=3$

second term of this A.P is

$a_{2}=\dfrac{9}{2}$

common difference

$d=a_{2}-a_{1}=\dfrac{9}{2}-3=\frac{3}{2}$

we know that sum of n term of an A.P is given by

$S_{n}=\dfrac{n}{2}\bigg[2a +(n-1)d)\bigg]$

$\implies S_{25}=\dfrac{25}{2}\bigg[2\times 3 +(25-1)\times \dfrac{3}{2}\bigg]$

$\implies S_{25}=12.5\bigg[6 +(24)\times \dfrac{3}{2}\bigg]$

$\implies S_{25}=12.5\bigg[6+36\bigg]$

$\implies S_{25}=12.5\bigg[42\bigg]$

$\implies S_{25}=525$

hence the sum of

$25$ terms of given A.P is

$525$

Find the sum of the following arithmetic progressions:
$1,3,5,7,....$ to $12$ terms

Given A.P is

$1,3,5,7,...…..$

Number of terms of A.P is

$n=12$

First term of this A.P is

$a_{1}=1$

Second term of this A.P is

$a_{2}=3$

Common difference

$d=a_{2}-a_{1}=3-1=2$

We know that sum of

$n$ term of an A.P is given by:

$S_{n}=\dfrac{n}{2}\bigg[2a +(n-1)d)\bigg]$

$S_{12}=\dfrac{12}{2}\bigg[2\times 1 +(12-1)\times 2)\bigg]$

$S_{12}=6[2+22]$

$S_{12}=144$

Hence, the sum of given A.P is

$144$ .

Find the sum of all integers between $84$ and $719$ , which are multiples of $5$ .

All integers between

$84$ and

$719$ , which are multiple of

$5$ are

$85,90,95,......715$

which forms an A.P

first term of this A.P is

$a_{1}=85$

second term of this A.P is

$a_{2}=90$

last term of this A.P is

$a_{n}=715$

common difference

$d=a_{2}-a_{1}$

$\implies d=90-85=5$ .

$n$ th term of this A.P is given by

$a_{n}=a_{1}+(n-1)d$

put

$a_{n}=715;a_{1}=85 \ and \ d=5$ in above equation we get,

$\implies 715=85+(n-1)5$

$\implies 5n-5+85=715$

$\implies 5n=715-80=635$

$n=\dfrac{635}{5}=127$ number of terms in this A.P

now, sum of these n=127 terms is given by

$S_{n}=\dfrac{n}{2}(a_{1}+a_{n})$

put values of

$n=127 ; a_{1}=85; a_{n}=715$ we get

$S_{127}=\dfrac{127}{2}(85+715)$

$\implies S_{127}=\dfrac{127}{2}\times 800$

$\implies S_{127}=127\times 400$

$\implies S_{127}=50800$

hence the sum of all integers between

$84$ and

$719$ which are multiple of

$5$ , is

$S_{127}=50800$

Show that the sum of all odd integers between $1$ and $1000$ which are divisible by $3$ is $83667$ .

lAll odd numbers between

$1$ and

$1000$ which are divisible by

$3$ , are

$3,9,15,......999$

which forms an A.P

first term of this A.P is

$a_{1}=3$

second term of this A.P is

$a_{2}=9$

last term of this A.P is

$a_{n}=999$

common difference

$d=a_{2}-a_{1}$

$\implies d=9-3=6$ .

nth term of this A.P is given by

$a_{n}=a_{1}+(n-1)d$

put

$a_{n}=999;a_{1}=3 \ and \ d=6$ in above equation we get,

$\implies 999=3+(n-1)6$

$\implies 6n-6+3=999$

$\implies 6n=999+3=1002$

$n=\dfrac{1002}{6}=167$ number of terms in this A.P

now, sum of these n=167 terms is given by

$S_{n}=\frac{n}{2}(a_{1}+a_{n})$

put values of

$n=167; a_{1}=3; a_{n}=999$ we get

$S_{167}=\dfrac{167}{2}(3+999)$

$\implies S_{167}=\dfrac{167}{2}\times 1002$

$\implies S_{167}=167\times 501$

$\implies S_{167}=83667$

hence the sum of all odd numbers between 1 and 1000 which are divisible by

$3$ , is

$S_{167}=83667$

Find the sum of all integers between $50$ and $500$ , which are divisible by $7$ .

All integers between 50 and 500, which are divisible by 7 are

$56,63,70,...…,497$

which forms an A.P

first term of this A.P is

$a_{1}=56$

second term of this A.P is

$a_{2}=63$

last term of this A.P is

$a_{n}=497$

common difference

$d=a_{2}-a_{1}$

$\implies d=63-56=7$ .

nth term of this A.P is given by

$a_{n}=a_{1}+(n-1)d$

put

$a_{n}=497;a_{1}=56 \ and \ d=7$ in above equation we get,

$\implies 497=56+(n-1)7$

$\implies 7n-7+56=497$

$\implies 7n=497-49=448$

$n=\dfrac{448}{7}=64$ number of terms in this A.P

now, sum of these

$n=64$ terms is given by

$S_{n}=\dfrac{n}{2}(a_{1}+a_{n})$

put values of

$n=64 ; a_{1}=56; a_{n}=497$ we get

$S_{64}=\dfrac{64}{2}(56+497)$

$\implies S_{64}=\dfrac{64}{2}\times 553$

$\implies S_{64}=32\times 553$

$\implies S_{64}=17696$

hence the sum of all integers between

$50$ and

$500$ which are divisible by

$7$ , is

$S_{64}=17696$

Find the sum of all odd numbers between $100$ and $200$

All odd numbers between $100$ and $200$ are

$101,103,105,......199$

which forms an $A.P$

first term of this A.P is $a_{1}=101$

second term of this A.P is $a_{2}=103$

last term of this A.P is $a_{n}=199$

common difference

$d=a_{2}-a_{1}$

$\implies d=103-101=2$ .

$n^{th}$ term of this $A.P$ is given by

$a_{n}=a_{1}+(n-1)d$

put $a_{n}=199;a_{1}=101$ and $d=2$ in above equation we get,

$\implies 199=101+(n-1)2$

$\implies 2n-2+101=199$

$\implies 2n=199-99=100$

$n=\dfrac{100}{2}=50$ number of terms in this A.P

now, sum of these n=50 terms is given by

$S_{n}=\dfrac{n}{2}(a_{1}+a_{n})$

put values of $n=50 ; a_{1}=101; a_{n}=199$ we get

$S_{50}=\dfrac{50}{2}(101+199)$

$\implies S_{50}=\dfrac{50}{2}\times 300$

$\implies S_{50}=25\times 300$

$\implies S_{50}=7500$

hence the sum of all odd numbers between 100 and 200, is $S_{50}=7500$

Find the sum of all natural numbers between $1$ and $100$ , which are divisible by $3$ .

$\textbf{Step 1: Find number of terms using nth term formula}$

$\text{All natural numbers between 1 and 100, which are divisible by 3 are }$

$\text{3,6,9,......99 which forms an A.P}$

$\text{first term of this A.P is }$

$a_{1} = 3$

$\quad \text{......eqn(1)}$

$\text{second term of this A.P is }$

$a_{2} = 6$

$\text{last term of this A.P is }$

$a_{n} = 99$

$\text{common difference = d = }$

$a_{2}-a_{1}$

$\Rightarrow d = 6-3 = 3$

$\quad \quad \quad \quad \quad \quad \quad \text{......eqn(2)}$

$\text{We know that, nth term of an A.P is given by }$

$a_{n}=a_{1}+(n-1)d$

$\text{put}$

$a_{n}=99;a_{1}=3$

$\text{and }$

$d=3$

$\text{ in above equation we get,}$

$\Rightarrow 99 = 3+(n-1)3$

$\Rightarrow 3n-3+3 = 99$

$\Rightarrow 3n= 99$

$\Rightarrow n = \dfrac{99}{3}$

$\Rightarrow n = 33$

$\quad \text{......eqn(3)}$

$\textbf{Step 2: Substitute n value in Sum of n terms in A.P. formula}$

$\text{We know that Sum of n terms is given by}$

$S_{n}=\dfrac{n}{2}(a_{1}+a_{n})$

$\Rightarrow S_{33}=\dfrac{33}{2}(3+99)$

$\quad \textbf{[From eqn(1), (2) and (3)]}$

$\Rightarrow S_{33}=\dfrac{33}{2}\times 102$

$\Rightarrow S_{33}=33\times 51$

$\Rightarrow S_{33}=1683$

$\textbf{Hence, the sum of all natural numbers between $$1$$ and $$100$$, which are divisible by 3 is $\boldsymbol {S_{22}}$=1683}$

Identify if a given sequence of numbers is an arithmetic progression or not.
a) $8,17,26,35,...$
b) $-4,-9,-16,-25,..$

(a)

$8,17,26,35$

We can see that

$17-8=26-17=35-26=9=d$

$\therefore$ it is an

$AP$

(b)

$-4,-9,-16,-25$

We can see

$-9+4\neq-16+9\neq-25+16\neq d$

$\therefore$ We can see that there is no common difference between the sequence

$\therefore$ it is not an

$AP$ .

Find the sum of the first $15$ terms of the following sequences having $n$ th term as
${ b }_{ n }=5+2n$

Formula,

$S_n=\dfrac{n}{2}(a+l)$

Given,

$a_n=5+2n$

$a_1=5+2(1)=7$

$l=a_{15}=5+2(15)=35$

$S_{15}=\dfrac{15}{2}(7+35)$

$\therefore S_{15}=315$

Which of the following sequences forms an A.P.
i) 0, 2, 0, 2,..............
ii) 11, 22, 33, 44,.................

$i)$

$0,2,0,2,\dots\dots$

Since, the common difference between the numbers is not constant, so it is not an

$A.P.$

$ii)$

$a=11,\\d=11.$

Since, the common difference between the numbers is constant

Hence, given sequence is an

$A.P.$

If sum of first 6 terms of an AP is 36 and that of the first 16 terms is 256, then find the sum of first 10 terms.

We have the sum of first

$n$ terms of an AP,

$S_n=\dfrac{n}{2}[2a+(n-1)d]$

Given,

$36=\dfrac{6}{2}[2a+(6-1)d]$

$12=2a+5d$ ---------(1)

$256=\dfrac{16}{2}[2a+(16-1)d]$

$32=2a+15d$ ---------(2)

Subtracting, (1) from (2)

$32-12=2a+15d-(2a+5d)$

$20=10d \ \implies d=2$

Substituting for

$d$ in (1),

$12=2a+5(2)=2(a+5)$

$6=a+5 \ \implies a=1$

$\therefore$ The sum of first

$10$ terms of an AP,

$S_{10}=\dfrac{10}{2}[2(1)+(10-1)2]$

$S_{10}=5[2+18]$

$S_{10}=100$

This is the sum of the first

$10$ terms

Write down the common difference and the first term for the following arithmetic progressions.
a) $7,13,19,25,...$
b) $-12,-4,4,12,...$

(a)

$7,13,19,25...$

$a=7->$ first term

$d=13-7=19-13=6->$ common difference

(b)

$-12,-4,4,12.....$

$a=-12,->$ first term

$d=-12-(-4)=4-(-4)=8->$ common difference

Find the sum of first 25 terms of an AP whose nth term is 1 - 4n.

Given,

$n^{th}$ term

$T_n=1-4n$

put,

$n=1$ ,

$T_1=a=1-4(1)=-3$

put,

$n=2$ ,

$T_2=1-4(2)=-7$

Common difference,

$d=T_2-T_1=-7-(-3)=-4$

So, we have

$a=-3 , \ d=-4,\ n=25$ , to find the sum.

Sum,

$S_n= \dfrac{n}{2}(2a+(n-1)d)$

$S_{25}= \dfrac{25}{2}(2(-3)+(25-1)(-4))$

$S_{25}= \dfrac{25}{2}(-112)=25\times(-51)$

$S_{25}=-1275$

This is the sum.

Find the minimum number of terms of the AP 64, 60, 56,... so that their sum is 540.

We can see that

$d=60-64=-4\\a=64$

We know that ,

Sum of first terms,

$S_n=\dfrac{n}{2}(2a+(n-1)d)\\ \Rightarrow 540=\dfrac{n}{2}(2\times64+(n-1)\times(-4))$

$\Rightarrow 540=64n-2n^2+2n$

$\Rightarrow n^2-33n+270=0$

$\Rightarrow n^2-15n-18n+270=0$

$\Rightarrow n(n-15)-18(n-15)=0$

$\Rightarrow (n-15)(n-18)=0$

$\Rightarrow n=15,18$

Since we need a minimum number of terms therefore

$n=15$

The sum of three numbers in A.P. is $21$ and the sum of their squares is $197$ . Find the middle number.

Solution:-

Let the terms are

$a-d, a, a+d$

The sum of three numbers in A.P. is 21

$\therefore \; sum = \left( a-d \right) + a + \left( a+d \right) = 3a = 21$

$\Rightarrow \; a = 7$

Second condition:-

The sum of their squares is 197.

$\therefore \; {\left( a + d \right)}^{2} + {a}^{2} + {\left( a - d \right)}^{2} = 197$

${a}^{2} + {d}^{2} - 2ad + {a}^{2} + {a}^{2} + {d}^{2} + 2ad = 197$

$\Rightarrow \; 3{a}^{2} + 2{d}^{2} = 197$

$3 \times {7}^{2} + 2{d}^{2} = 197$

$\Rightarrow \; 147 + 2{d}^{2} = 197$

$\Rightarrow \; 2{d}^{2} = 18$

$d = 3$

so the series is-

$a - d = 7 - 3 = 4$

$a = 7$

$a + d = 7 + 3 = 10$

Hence the series is

$4, 7, 10$ and the middle no. is

$7$ .

Is the following sequence an $AP$ ? If true, find the common difference $d$ and write three more terms.
$-1.2, -3.2, -5.2, -7.2...$

$-1.2,\,-3.2,\,-5.2,\,-7.2$

$\Rightarrow$ Difference between second and first term

$=-3.2-(-1.2)=-3.2+1.2=-2$

$\Rightarrow$ Difference between third and second term

$=-5.2-(-3.2)=-5.2+3.2=-2$

$\Rightarrow$ Difference between fourth and third term

$=-7.2-(-5.2)=-7.2+5.2=-2$

$\Rightarrow$ Since, difference is same, it is an

$A.P$

$\Rightarrow$ Common difference

$=d=-2$

$\Rightarrow$ We have to find next three terms. We are given

$4$ terms.

$\Rightarrow$ We have to find

$5^{th},\,6^{th}$ and

$7^{th}$ terms.

$\Rightarrow$

$5^{th}$ term

$=4^{th}\,term+d=-72+(-2)=-9.2$

$\Rightarrow$

$6^{th}$ term

$=5^{th}\,term+d=-9.2+(-2)=-11.2$

$\Rightarrow$

$7^{th}$ term

$=6^{th}\,term+d=-11.2+(-2)=-13.2$

Hence

$5^{th},\,6^{th}$ and

$7^{th}$ terms are

$-9.2,\,-11.2,\,-13.2$

Find the common difference of AP whose $n^{th}$ term is $6n + 2$ .

Let the first term of the AP be

$a$ and common difference be

$d.$

${ n }^{ th }term=6n+2\\\Rightarrow a+(n-1)d=6n+2\\ \Rightarrow (a-d)+nd=2+6n\\ \Rightarrow a-d=2,d=6\\\Rightarrow a=8$

Hence, the common difference is equal to

$6.$

Find the sum to $n$ terms of the series:
$1\times 2\times 3+2\times 3\times 4+3\times 4\times 5+.....$

$\displaystyle{S=1\times 2\times 3+2\times 3\times 4+3\times 4\times 5.......n(n+1)(n+2)\\ S=\sum _{ r=1 }^{ r=n }{ r(r+1) } (r+1)\\ S=\sum _{ r= }^{ n }{ { r }^{ 3 }+ } { r }^{ 2 }+r\\ S=\sum _{ r= }^{ n }{ { r }^{ 3 } } +\sum _{ r= }^{ n }{ { r }^{ 2 } } +\sum _{ r= }^{ n }{ r } \\ S={ \left( \frac { n(n+1) }{ 2 } \right) }^{ 2 }+\frac { n(n+1)(2n+1) }{ 6 } +\frac { n(n+1) }{ 2 } \\ S=\frac { { n }^{ 4 }+{ n }^{ 2 }+2{ n }^{ 3 } }{ 4 } \frac { 2{ n }^{ 3 }+3{ n }^{ 2 }+n }{ 6 } +\frac { { n }^{ 2 }+n }{ 2 } \\ S=\frac { { 3(n }^{ 4 }+{ n }^{ 2 }+2{ n }^{ 3 })+2(2{ n }^{ 3 }+3{ n }^{ 2 }+n)+6({ n }^{ 2 }+n) }{ 12 } \\ S=\frac { 3{ n }^{ 4 }+10{ n }^{ 3 }+14{ n }^{ 2 }+8n }{ 12 } }$

Check whether the following numbers are in A.P or not.
$2, 4, 8, 16 ,\dots$

Given Series,

$2,4,8,16...$

The numbers are said to be in AP if the difference between any two consecutive terms is constant.

Here,

$4-2=2$

$8-4=4$

$16-8=8$

Hence, this is not in AP as the common difference is not constant.

In an A.P. sum of first $n$ terms is given by $4n^2+3n$ . Then find the third term.

Given in an A.P. sum of first

$n$ terms is given by

$4n^2+3n$ .

We know the third term

$=$ the sum of first three terms

$-$ the sum of first two terms. and it is

$=4.3^2+3.3-(4.2^2+3.2)=4(9-4)+3=23$ .

If $a=8$ , $t_n=62$ , $S_n=20$ , find $n$ .

$T_n=a+(n-1)d$

$62=8+(n-1)d$

$54=(n-1)d$ ...(1)

$S_n=\dfrac{n}{2}[2a+(n-1)d]$

$20=\dfrac{n}{2}[2(8)+(n-1)d]$

$40=n[16+(n-1)d]$

From (1)

$40=n[16+54]$

$40=n(70)$

$\therefore n=\dfrac{4}{7}$

On $1^{st}$ Jan $2016$ , Sanika decides to save $Rs.\ 10$ , $Rs.\ 11$ on second day, $Rs.\ 12$ on third day. If she decides to save like this, then on $31^{st}$ Dec $2016$ what would be her total saving?

The money saved at first day is ${\rm{Rs}}\;10$ , at second day ${\rm{Rs}}\;11$ , at third day ${\rm{Rs}}\;12$ and so on.

Since the year 2016 is a leap year, therefore the total number of days in a leap year is 366.

Thus, the money saved by her will form an A.P.,

$10 + 11 + 12 + \cdots \left( {{\rm{upto}}\;{\rm{31st}}\;{\rm{dec}}} \right)$

Here,

$a = 10$ , $d = 1$ and $n = 366$

So, the sum of the above A.P. is,

${S_n} = \dfrac{n}{2}\left[ {2a + \left( {n - 1} \right)d} \right]$

$= \dfrac{{366}}{2}\left[ {2\left( {10} \right) + \left( {366 - 1} \right)1} \right]$

$= 70455$

Therefore, the total saving made by her is $70455.$

Find the common difference $d$ and write three more terms of an $AP$ :
$2,\dfrac {5}{2},3, \dfrac {7}{2}$

$2,\,\dfrac{5}{2},\,3,\,\dfrac{7}{2},\,.....$

$\Rightarrow$ Difference between second and first term

$=\dfrac{5} {2}-2=\dfrac{5-4}{2}=\dfrac{1}{2}$

$\Rightarrow$ Difference between third and second term

$=3-\dfrac{5}{2}=\dfrac{6-5}{2}=\dfrac{1}{2}$

$\Rightarrow$ Difference between fourth and third term

$=\dfrac{7}{2}-3=\dfrac{7-6}{2}=\dfrac{1}{2}$

Since difference is same, it is an

$AP$

$\Rightarrow$ Common difference

$=d=\dfrac{1}{2}$

$\Rightarrow$ Now, we have to find next three terms. So, we have to find

$5^{th},\,6^{th}$ and

$7^{th}$ terms.

$\Rightarrow$

$5^{th}$ term

$=4^{th}$ term +

$d=\dfrac{7}{2}+\dfrac{1}{2}=\dfrac{8}{2}=4$

$\Rightarrow$

$6^{th}$ term

$=5^{th}$ term +

$d=4+\dfrac{1}{2}=\dfrac{8+1}{2}=\dfrac{9}{2}$

$\Rightarrow$

$7^{th}$ term

$=6^{th}$ term +

$d=\dfrac{9}{2}+\dfrac{1}{2}=\dfrac{10}{2}=5$

Hence,

$5^{th},\,6^{th},$ and

$7^{th}$ terms are

$4,\,\dfrac{9}{2},\,5$

Is the following sequence an $AP$ ? If true, find the common difference $d$ and write three more terms.
$-10, -6, -2, 2,$

$-10,\,-6,\,-2,\,2$

$\Rightarrow$ Difference between second and first term

$=-6-(-10)=-6+10=4$

$\Rightarrow$ Difference between third and second term

$=-2-(-6)=-2+6=4$

$\Rightarrow$ Difference between fourth and third term

$=2-(-2)=2+2=4$

$\Rightarrow$ Since, difference is same, it is an

$A.P$

$\Rightarrow$ Common difference

$=d=4$

$\Rightarrow$ We have to find next three terms. We are given

$4$ terms.

$\Rightarrow$ We have to find

$5^{th},\,6^{th}$ and

$7^{th}$ terms.

$\Rightarrow$

$5^{th}$ term

$=4^{th}\,term+d=2+4=6$

$\Rightarrow$

$6^{th}$ term

$=5^{th}\,term+d=6+4=10$

$\Rightarrow$

$7^{th}$ term

$=6^{th}\,term+d=10+4=14$

Hence

$5^{th},\,6^{th}$ and

$7^{th}$ terms are

$6,\,10\,14$

The ${30^{th}}$ term of the $A.P \ series : 10,7,4....$ is $-b$ ,
what is the value of $b?$

Consider the given A.P. series

$10, 7, 4........$

$a=10$

$d=7-10=-3$

$n=30$

Find ${{a}_{30}}$

We know that, ${{a}_{n}}=a+\left( n-1 \right)d$

${{a}_{30}}=10+\left( 30-1 \right)\times \left( -3 \right)$

${{a}_{30}}=10-87$

${{a}_{30}}=-77$

Comparing $-b=-77 \Rightarrow b=77$

Hence, this is the answer.

Check if given series is $AP$ or not? If it is an $AP$ , find the common difference $d$ and write three more terms.
$3, 3+\sqrt {2}, 3+2\sqrt {2}, 3+3\sqrt {2},.$

$3,\,3\sqrt{2},\,3+2\sqrt{2},\,3+3\sqrt{2}$

$\Rightarrow$ Difference between second and first term

$=3+\sqrt{2}-3=\sqrt{2}$

$\Rightarrow$ Difference between third and second term

$=(3+2\sqrt{2})-(3+\sqrt{2})$

$=3+2\sqrt{2}-3-\sqrt{2}$

$=\sqrt{2}$

$\Rightarrow$ Difference between fourth and third term

$=(3+3\sqrt{2})-(3+2\sqrt{2})$

$=3+3\sqrt{2}-3-2\sqrt{2}$

$=\sqrt{2}$

$\Rightarrow$ Since, difference is same, it is an

$A.P$

$\Rightarrow$ Common difference

$=d=\sqrt{2}$

$\Rightarrow$ We have to find next three terms. We are given

$4$ terms.

$\Rightarrow$ We have to find

$5^{th},\,6^{th}$ and

$7^{th}$ terms.

$\Rightarrow$

$5^{th}$ term

$=4^{th}\,term+d=3+3\sqrt{2}+\sqrt{2}=3+4\sqrt{2}$

$\Rightarrow$

$6^{th}$ term

$=5^{th}\,term+d=3+4\sqrt{2}+\sqrt{2}=3+5\sqrt{2}$

$\Rightarrow$

$7^{th}$ term

$=6^{th}\,term+d=3+5\sqrt{2}+\sqrt{2}=3+6\sqrt{2}$

Hence

$5^{th},\,6^{th}$ and

$7^{th}$ terms are

$3+4\sqrt{2},\,3+5\sqrt{2},\,3+6\sqrt{2}$

In an $A.P$ $17^{th}$ term is $7$ more then is $10^{th}$ term. Find the common difference ?

Given,

$T_{17}=7+T_{10}$

$T_n=a+(n-1)d$

$a+16d=7+a+9d$

$16d-9d=7$

$7d=7$

$\therefore d=1$

common difference is equal to 1

How many terms of the series $-9, -6, -3, ...$ must be taken that the sum may be $66$ ?

$S_n=\dfrac{n}{2}\left [ 2a+(n-1)d \right ]$

$66=\dfrac{n}{2}\left [ 2(-9)+(n-1)3 \right ]$

$132=n (3n-21)$

$3n^2-21n-132=0$

$n^2-7n-44=0$

$(n-11)(n+4)=0$

$n=11,-4$

$\therefore n=11$ terms of series must be taken

If the following sequence is an AP, then find the common difference.
$2,4,6,8$

$\begin{array}{l} 2,4,6,8...... \\ a=2 \\ d={ t_{ 2 } }-{ t_{ 1 } } \\ =4-2 \\ =2 \\ { d_{ 2 } }={ t_{ 3 } }-{ t_{ 2 } } \\ =6-4 \\ =2 \\ { d_{ 3 } }=8-6 \\ =2 \\ \therefore 2,4,6,8......is\, \, an\, \, A.P\, \, with\, \, common\, \, difference\left( d \right) =2 \end{array}$

Is the following sequence an $AP$ ? If true, find the common difference $d$ and write three more terms.
$0.2, 0.22, 0.222, .0.2222,..$

$0.2,\,0.22,\,0.222,\,0.2222$

$\Rightarrow$ Difference between second and first term

$=0.22-0.2=0.02$

$\Rightarrow$ Difference between third and second term

$=0.222-0.22=0.002$

$\Rightarrow$ Since, difference is not same, it is not an

$A.P$

If the sum of the first $14$ terms of an AP is $1050$ and its first term is $10$ , find the $20^{th}$ term.

$S_{14} = 1050$

$a = 10$

$S_{n} = \dfrac{n}{2}[2a+(n-1)d]$

$1050 = \dfrac{14}{2}[2 \times 10 + (14-1)d]$

$\dfrac{1050}{7} = [20+14d-d]$

$150 -20 = 13d$

$130 = 13d$

$d = 10$

The

$20^{th}$ term is

$a_{20} = a+(n-1)d$

$= 10+(20-1)10$

$\Rightarrow 10+190$

$a_{20} \Rightarrow 200$

Is the following sequence an $AP$ ? If true, find the common difference $d$ and write three more terms.
$0, -4, -8, -12,$

$0,\,-4,\,-8,\,-12$

$\Rightarrow$ Difference between second and first term

$=-4-0=-4$

$\Rightarrow$ Difference between third and second term

$=-8-(-4)=-8+4=-4$

$\Rightarrow$ Difference between fourth and third term

$=-12-(-8)=-12+8=-4$

$\Rightarrow$ Since, difference is same, it is an

$A.P$

$\Rightarrow$ Common difference

$=d=-4$

$\Rightarrow$ We have to find next three terms. We are given

$4$ terms.

$\Rightarrow$ We have to find

$5^{th},\,6^{th}$ and

$7^{th}$ terms.

$\Rightarrow$

$5^{th}$ term

$=4^{th}\,term+d=-12+(-4)=-16$

$\Rightarrow$

$6^{th}$ term

$=5^{th}\,term+d=-16+(-4)=-20$

$\Rightarrow$

$7^{th}$ term

$=6^{th}\,term+d=-20+(-4)=-24$

Hence

$5^{th},\,6^{th}$ and

$7^{th}$ terms are

$-16,\,-20,\,-24$

How many terms of the A.P -6, $- \frac{{11}}{2}, - 5$ .......are needed to give the sum -25?

Given,

$a=-6$

$d=-\dfrac{11}{2}-(-6)=\dfrac{1}{2}$

Formula,

$S_n=\dfrac{n}{2}[2a+(n-1)d]$

$-25=\dfrac{n}{2}\left [ 2(-6)+(n-1)\dfrac{1}{2} \right ]$

$-50=n\left [ \dfrac{-24+n-1}{2} \right ]$

$n^2-25n+100=0$

$(n-20)(n-5)=0$

$\therefore n=5,20$

Therefore the number of terms required is

$5$ or

$20$

Find the sum of all odd numbers of four digits which are divisible by $9$ .

The four-digit odd numbers that are divisible by

$9$ are

$1017,1035,..9999$

The sequence forms an

$AP$ with

$a=1017,d=18$

$L$ is the last term of the series.

$L=a+(n-1)d$

$9999=1017+(n-1)18$

$n=500$

Sum

$S_{n}=\dfrac{n}{2}\left [ 2a+(n-1)d \right ]$

$S_{500}=\dfrac{500}{2}(1017+9999)=2754000$

For a given A.P, $T_7 = 12$ and $T_{12} = 72 ,$ then $d=$ _______

We know that the formula for

$n^{th}$ term of an A.P is :

$T_n=a+(n-1) d$

$T_7=12$

$a+(7-1)d=12$

$a+6d=12$ ……..

$(1)$

$T_{12}=72$

$a(12-1)d=72$

$a+11d=72$ ……….

$(2)$

Subtracting

$(1)$ from

$(2)$ , we get

$5d=60$

$\Rightarrow d=12$

Is the following sequence an A.P. ? If yes, then find the common difference.
$2, 4, 6, 8, ...$

Given that

$2, 4, 6, 8,...…$ is AP

Here

$a_1$ = 2

$a_2 = 4$

Common difference

$d = a_2 - a_1$

$=4-2$

$=2$

$\therefore$ The given sequence is in AP and common difference is

$2$ .

Find the common difference of an $A.P.$ whose $n^{th}$ term is $3n+7$ .

$T_n=3n+7$

$T_1=3\times 1+7=10$

$T_2=3\times 2+7=13$

$d=T_2-T_1$

$d=13-10$

$d=3$

common difference

$=3$

$2,\dfrac {5}{2},3\dfrac {7}{2},....$

$2, \dfrac{5}{2}, 3\dfrac{7}{2}$

$\Rightarrow 2, \dfrac{5}{2}, \dfrac{13}{2}$

$a_2-a_1=\dfrac{5}{2}-2=\dfrac{1}{2}$

$a_3-a_2=\dfrac{13}{2}-\dfrac{5}{2}=\dfrac{7}{2}$

$a_2-a_1\neq a_3-a_2$

This is not

$AP$ .

Find the common difference of the A.P. $y-7, y-2, y+3$ , _________.

$\left( { y-7 } \right) ,\left( { y-2 } \right) ,\left( { y+3 } \right) \, \, are\, \, in\, \, A.P \\ Then,\, \, common\, \, difference=\left( { y-2 } \right) -\left( { y-7 } \right) \\ Therefore\, \, common\, \, difference=y-2-y+7=5\, \, \, \, Ans.$

Find the sum of first $18$ terms of the A.P. $\dfrac{1}{3}, \dfrac{4}{3}, \dfrac{7}{3}, \dfrac{10}{3},...$

$A.P:\frac{1}{3},\frac{4}{3},\frac{7}{3},\frac{10}{3},.....$

$a=\dfrac{1}{3}$ ,

$d=\dfrac{4}{3}-\dfrac{1}{3}$

$=\dfrac{3}{3}$

$=1,n=18$

$S_{n}$ =

$\frac{n}{2}(2a+(n-1)d)$

$\Rightarrow S_{18}=\frac{18}{2}\left ( 2(\frac{1}{3})+(18-1)1 \right )$

$S_{18}$ =

$9\left ( \frac{2}{3}+17 \right )$

$S_{18}$ = 9

$\left ( \frac{2+51}{3} \right )$

$S_{18}$ =3

$\times$ 53

$S_{18}$ =159

Find the sum of the following A.P
$2,7,12,.....$ to $10$ terms

$2,7,12,--------10,$ terms

$\therefore a= 2, d = 5, n = 10$

$S_n = \dfrac{n}{2}[2a+(n-1)d]$

$S_{10}=\dfrac{10}{2}\left ( 2(2)+(10-1)5 \right )$

$=5(4+9\times 5)$

$=5(4+45)$

$=5\times 49$

$=245$

$200$ logs are in the stacked given manner. $20$ logs in the bottom row, $19$ in the next row, $18$ in the row next to it and so on. In how many rows are the $200$ logs place and how many logs are in the top row?

From the given question, we have an AP as given below:

$20, 19, 18, 17, ........$

$\therefore a= 20, d = -1, n = ?$

Also

$S_n = 200$

$200=\dfrac {n}{2}(2a+(n-1)d)$

$200=\dfrac {n}{2}(2(20)+(n-1)(-1))$

$400=n(40+1-n)$

$400=n(41-n)$

$400=41n-n^2$

$n^2-41n+400=0$

$n^2-25n-16n+400=0$

$n(n-25)-16(0-25)=0$

$n=16$ or

$n=25$

When

$n= 16$

$a_n =a+15d$

$=20-15$

$=5$

When

$n=25$

$a_n=a+25d$

$=20-25$

$=-5$

Son

$n = 25$ is not possible.

$\therefore \$ there are

$5$ logs in ten rows.

Find the first term and common difference of the given AP $\displaystyle \frac { 3 } { 2 } , \frac { 1 } { 2 } , - \frac { 1 } { 2 } , - \frac { 3 } { 2 } , \dots$

First term

$a_1=\dfrac{3}{2}$

Common difference

$d=a_2-a_1=\dfrac{1}{2}-\dfrac{3}{2}=-1$

The sum of a series of terms in A.P. isIf the first term is 2 and the last term is 14, find the common difference.

Let the number of terms in the series be

$n$

Given that the sum of the series of terms in A.P. is

$S_n=128$

Given that the first term is

$a=2$

and last term is

$a_n=14$

We know that the sum of the terms in A.P. is given by

$S_n=\dfrac n2(a+a_n)$

$\implies 128=\dfrac n2(2+14)$

$\implies \dfrac n2(16)=128$

$\implies n=16$

We know that

$a_n=a+(n-1)d$

$\implies 14=2+(16-1)d$

$\implies 15d=12$

$\implies d=\dfrac{12}{15}=\dfrac 45$

Therefore, the common difference is

$\dfrac 45$ .

If in an A.P., ${T}_{7}=18,{T}_{18}=7$ ,then find ${T}_{101}$

$T_{7}=18=a+(7-1)d$

$a+6d=18$ _______

$(1)$

$T_{18}=7=a+(18-1)d$

$a+17d=7$ _______

$(2)$

$(1)-(2)$

$a+6d-a-17d=18-7$

$-11d=11$

$d=-1$

$a-6=18\Rightarrow a=24$

$T_{101}=a+100d$

$=24-100$

$=-76$

Find the sum of all $2$ -digit odd positive numbers.

$11,13,15,-------99$

$\therefore a= 11, d = 2, a_n = 99$

$\therefore$

$99=11+(n+1)2$

$88=2(n-1)$

$44+1=n$

$n=45$

$S_n=\dfrac{n}{2}(a+l)=\dfrac{45}{2}(11+99)$

$=\dfrac{45}{2}\times 110$

$=45\times 55$

$=2475$

How many terms of the A.P: $24,21,18,....$ must be taken so that their sum is $78$ ?

$\Rightarrow S_{n}=\dfrac{n}{2}\left [ 2a+(n-1)d \right ]$

$\Rightarrow$

$78=\dfrac{n}{2}(2a+(n-1)d)$

$\Rightarrow$

$78=\dfrac{n}{2}\left ( 2(24)+(n+1)(-3) \right )$

$\Rightarrow$

$156=n(48-3n+3)$

$\Rightarrow$

$156=n(51-3n)$

$\Rightarrow$

$156=51n-3n^{2}$

$\Rightarrow$

$3n^{2}-51n+156=0$

$\Rightarrow$

$3n^{2}-12n-39n+156=0$

$\Rightarrow$

$3n(n-4)-3q(n-4)=0$

$\Rightarrow$

$n = 4$ or

$n =\dfrac{39}{3}=13$

Find the value of $k$ for which $k, 2k-1$ and $2k+1$ are in $A.P$ .

Given,

$k, 2k-1$ and

$2k+1$ are in A.P.

$\Rightarrow 2k-1-k=2k+1-2k+1$

$k-1=2$

$\therefore k=3$

Hence, this is the answer.

Find the common difference and $99th$ term of the arithmetic progression :
$7\dfrac { 3 }{ 4 } ,9\dfrac { 1 }{ 2 } ,11\dfrac { 1 }{ 4 } ,\dots \dots \dots \dots \dots \dots$ .

$7\dfrac { 3 }{ 4 } ,9\dfrac { 1 }{ 2 } ,11\dfrac { 1 }{ 4 } ,\dots \dots \dots \dots \dots \dots$ .Given,A.P

i.e., $31/4, 19/2, 45/4,$ …….

So,

$a = 31/4$

Common difference, $d = 19/2 – 31/4 = (38 – 31)/ 4 = 7/4$

Then the general term of the A.P

$t_n = a + (n – 1)d$

$t_n = 31/4 + (n – 1)(7/4) = 31/4 + 7n/4 – 7/4 = 7n/4 + 31/4 – 7/4 = 7n/4 + (31 – 7)/4 = 7n/4 + (24)/4$

$t_n = 7n/4 + 6$

Hence, the $99th$ term is $7(99)/4 + 6 = 693/4 + 6 = 717/4$

Find the sum of
$3+8+13+18+....+n$ terms

$3+8+13+18+.....$ (n terms)

The given expression is an A.P.

first term

$=a=3$

common difference

$=d=5$

Sum of n terms

$=S_n=\dfrac{n}{2}[2a+(n-1)d]$

$=\dfrac{n}{2}[2(3)+(n-1)5]$

$=\dfrac{n}{2}[6+5n-5]$

$=\dfrac{n}{2}[5n+1]$

$=\dfrac{5n^2}{2}+\dfrac{n}{2}$ .

1209104_1237431_ans_3a09c016f479473a88de9f8aecf045c2.jpg

Find the sum of all odd integers between $2$ and $100$ divisible by $3$ .

$\textbf{Step-1: Find }$ $\mathbf{n^{th}}$ $\textbf{term}$

${\text{The series forms an AP as there is a common difference between each term}}$

${\text{with first term = 3 and common difference = 6}}$

${\text{As we can see the last term is 99, then the value of the nth term is 99 }}$

${\text{So, }}{a_n} = 99$

${\textbf{Step -2: Through }}{a_n}{\textbf{ find the number of terms by putting all the values}}$

${a_n} = 99$

$\Rightarrow a + (n - 1)d = 99$

$\Rightarrow 3 + (n - 1)6 = 99$

$\Rightarrow 6(n - 1) = 96$

$\Rightarrow n - 1 = 16$

$\Rightarrow n = 17$

${\textbf{Step -3: Sum of all the numbers in the series is given by the formula}}$

${S_n} = \dfrac{n}{2}(a + 1)$

${S_{17}} = \dfrac{{17}}{2}(3 + 99) = 867$

${\textbf{Hence, The required sum is 867}}$

Find the sum of the following AP $1,3,5,7.............199$

AP is

$1,3,5,7.... 199$

$a=1, d=2$ and last term

$l=199$

$t_n=a+(n-1)d\\ \Rightarrow 199=1+(n-1)\times2\\ \Rightarrow 2n=200\\n=100\\ \therefore sum=\cfrac{n}{2}[a+l]=\cfrac{100}{2}[1+199]\\ =\cfrac{100}{2}\times200=10000$

Find the value of K so that $(K+2), (4K - 6)$ and $(3K - 6)$ are three continuous terms of AP.

Given

$(K+2), (4K - 6)$ and

$(3K - 6)$ are three continuous terms of AP

As the difference between any two consecutive terms of A.P is constant.

$\Rightarrow (4k-6)-(k+2)=(3k-6)-(4k-6)$

$\Rightarrow 3k-8=-k$

$\Rightarrow 4k=8$

$\Rightarrow k=2$ .

The first term of an $A.P.$ is $5$ , the common difference is $3$ and the last term is $80$ , find the number of terms.

$\textbf{Step -1: Find the number of terms in the given A.P.}$

$\text{Let there be }n\text{ terms in the A.P.}$

$\text{So, the given last term will be the nth term of the A.P., i.e. }T_n =80$

$\text{Formula for the nth term is,}$

${T_n=a+(n-1)d}$

${\text{where }a=\text{First term and }d=\text{Common difference of the A.P.}}$

$\text{Here, it is given }a=5\text{ and }d=3$

$\text{Putting all the values in the above formula, we get}$

$\Rightarrow 80=5+(n-1)3$

$\Rightarrow 3(n-1)=75$

$\Rightarrow 3n-3=75$

$\Rightarrow 3n=78$

$\Rightarrow n=26$

$\textbf{Hence, the number of terms in the given A.P. is }\mathbf{26}.$

Determine value of $k$ so that $3k-2$ , $4k-6$ and $k+2$ are three consecutive terms of an $AP.$

Given,

$(3k-2), (4k-6)$ and

$(k+2)$ are in

$A.P$

So,

$2(4k-6)=3k-2+k+2$

$8k-12=4k$

$4k=12$

$k=3$

Hence, this is the answer.

Find the sum of the series: $31, 32, ...., 50$

Given sequence is

$31, 32, ...., 50$

It is an AP with first term

$a= 31$

and, common difference

$d=32-31= 1$

Let, the number of terms be

$n$

We know that the

$n^{th}$ term,

$a_{n}$

$=a+(n-1)d$

$\Rightarrow 50=31+(n-1)\times1$

$\Rightarrow 50-31=n-1$

$\Rightarrow 50-31+1=n$

$\Rightarrow n=20$

Therefore, the sum of terms,

$S_{n}=\dfrac{n}{2}[2a+(n-1) d]$

$\Rightarrow S_{n}= \dfrac{20}{2}[2 \times 31+(20-1) \times 1]$

$=10[62+19]$

$=810$

Hence, sum of given sequence is

$810$ .

If the 12th term of an AP is -13 and the sum of first four terms is 24, what is the sum of the first 10 terms?

2040851_1361475_ans_141595260976412da4a2a33b6bdec8e1.jpg

Find the sum of $90$ terms of A.P $4,\,8,\,12,...$

$a=4,\,\,d=8-4=4$

${S}_{n}=\dfrac{n}{2}\left[2a+\left(n-1\right)d\right]$

${S}_{n}=\dfrac{90}{2}\left[2\times 4+\left(90-1\right)\times 4\right]$

$=45\left[4+89\times 2\right]$

$=45\left[2\left(2+89\right)\right]$

$=90\times 91=8190$

Determine the AP whose $3^{rd}$ term is $5$ and the $7th$ term is $9$ .

$\textbf{Step 1: Form equations applying the formula for general term of an AP.}$

$\text{Let the first term = a}$

$\text{and the common difference = d}$

$\text{It is given that, third term is 5.}$

$\therefore a+2d=5 ......(1)$

$\text{And the seventh term is 9.}$

$\therefore a+6d=9......(2)$

$\textbf{Step 2: Solve the equations.}$

$\text{Subtracting eq(1) from eq(2)}$

$\Rightarrow (a+6d)-(a+2d)=9-5$

$\Rightarrow a+6d-a-2d=4$

$\Rightarrow 4d=4$

$\Rightarrow d=1$

$\text{Putting the value of d in eq(1)}$

$\Rightarrow a+2\times 1=5$

$\Rightarrow a+2=5$

$\Rightarrow a=5-2$

$\Rightarrow a=3$

$\textbf{Hence, the required AP is 3,4,5,6,7........}$

Find the sum of three digits numbers which are divisible by $11$

The least

$3$ digit number that is divisible by

$11$ is

$a=110$

The highest

$3$ digit number that is divisible by

$11$ is

$l=990$

$d=11$

Last term is

$l=a+(n-1)d$

$990=110+(n-1)11$

$880=(n-1)11$

$n-1=\dfrac{880}{11}$

$n-1=80\Rightarrow n=81$

The Sum of the series is given as

$S_n = \dfrac{n}{2}[2a+(n-1)d]$

$S_{81} = \dfrac{81}{2}[2(110)+(81-1)11]$

$=\dfrac{81}{2}[220+880]$

$=81\times 550=44550$

Find the sum to n terms of the A.P., whose $k^{th}$ term is $5k+1$ .

$a_{k}=a+(k-1)d=5k+1$

$\Rightarrow a+kd-d=5k+1$

By compairing, d=5 & a-d=1

a=1+d

a=1+5=6

$S_{n}=\frac{n}{2}[2a+(n-1)d]$

$S_{n}=\frac{n}{2}[12+(n-1)5]$

$S_{n}=\frac{n}{2}[5n+7]$

1180278_1307256_ans_5ac80e032d294058bb80f8829ba78876.jpg

Find the common difference of the A.P. given below:
$0.6, 1.7, 2.8, 3.9,.....$

Given the A.P. is

$0.6, 1.7, 2.8, 3.9,.....$ .

We know that, the common difference

$(d)$ is the difference between any two consecutive terms of an A.P.

$\therefore \ d=1.7-0.6=1.1$

Hence, the common difference of the given A.P. is

$1.1$ .

Is $184$ a term of the sequence $3, 7, 11$ , ... ?

Here, the given sequence is

$A.P$

$a=3,d=7-3=11-7=4$

Let,

$a_{n}=184$

General term :

$a_n=a+(n-1)d$

$a+(n-1)d=184$

$3+(n-1) \times 4 =184$

$4n=185$

$n=46\dfrac{1}{4}$

Since,

$n$ is not a natural number. So,

$184$ is not a term of the given sequence.

The common difference for the sequence: $3, -1, -5, -9....$ is $-b$ , then what is the value of $b?$

Common difference

$d = a_2 - a_1$

$= -1 - 3$

$=-4$

Comparing

$-b=-4$

$\Rightarrow b=4$

Find the value of $k$ , If $x, 2x+k, 3x+5$ are consecutive terms in A.P.

$x,2x+k,3x+5$ are in A.P

$\Rightarrow 2x+k-x=3x+5-2x-k$

$\Rightarrow x+k=x+5-k$

$\Rightarrow k=5-k$

$\Rightarrow 2k=5$

$\therefore k=\dfrac{5}{2}$

For what value of $k$ will $k+9,2k-1$ and $2k+7$ are the consecutive terms of an A.P?

Let

$k+9=a$

$2k-1=b$

$2k+7=c$

To be in AP,

$a+c=2b$

$k+9+2k+7=2(2k-1)$

$\Rightarrow$

$3k+16=4k-2$

$\Rightarrow$

$3k-4k=-2-16$

$\Rightarrow$

$-k=-18$

$\therefore k=18$

For

$k=18$ , the terms

$k+9,2k-1,2k+7$ are in A.P

Find the common difference of an AP in which ${ a }_{ 18 }-{ a }_{ 14 }=32$

1975257_1499322_ans_d4334e4db0e940cb8939ad192438285e.jpg

State with reason, whether the sequence $12,14,16,18,22,24,2,28,32,34,36,38,$ is an $\text{A.P.}$ or not.

The given sequences are not in A.P

Because

Here

$a=12$

$d=14-12=2$

$d=16-14=2 ; d=18-16=2$

$d=18-22=4$

The common difference in the sequence is not constant for each term.

sometimes it is

$2$ or

$4.$

Is the given sequence 0.2, 0.22, 0.222, 0.2222.... an A.P.?

Given sequence is

$0.2,\ 0.22,\ 0.222,\ 0.2222,\ .......$

We know that, for a sequence to be an

$A.P.$ , the difference between any consecutive terms must be equal.

Here,

$0.22 - 0.2 = 0.02$

$0.222 - 0.22 = 0.002$

$0.2222 - 0.222 = 0.0002$

Since the difference between two consecutive terms is not equal, the given sequence is not an

$A.P.$

The first and the last term of an arithmetic progression are $5$ and $45$ respectively. If the sum of all its terms is $400$ , find its common difference.

1870617_1544265_ans_ea6f9c020a8e420b882b456a9c683976.jpg

The $9$ th term of an AP is $-32$ and the sum of its $11$ th and $13$ th terms is $-94$ . Find the common difference of the AP.

Let

$a$ be the first term and

$d$ be the common difference of an AP.

nth term

$=a_n=a+(n-1)d$

Given:

$9$ th term of an AP is

$-32$ and the sum of its

$11$ th and

$13$ th terms is

$-94$

Now,

$a_9=a+8d=-32$ .......

$(1)$

$a_{11}=a+10d$

$a_{13}=a+12d$

Sum of

$11$ th and

$13$ th terms:

$a_{11}+a_{13}=a+10d+a+12d$

$-94=2a+22d$

$a+11d=-47$ .........

$(2)$

Subtracting

$(1)$ from

$(2)$ , we have

$3d=-47+32=-15$

$d=-5$

Common difference is

$-5$ .

Find the sum of all odd integers from $1$ to $201$ .

$n^{th}$ term of AP is given by,

$T_{n}= a+(n-1)d$

$a =$ First term

$d =$ Common difference

$n =$ number of terms

Sum formula

$S_{n}=\dfrac{n}{2}\left [ 2a+(n-1)d \right ]$

Required sum

$=1+3+5+7+.....+201$

$a=1, d=2$

$T_n=201$

$1+(n-1)\times 2=201$

$\Rightarrow n=101$

$\therefore S_n=\dfrac{101}{2}\times (2+200)$

$=(101\times 101)$

$=10201$ .

Find $10$ th term of the A.P. $1, 4, 7, 10,...$ .

We know

$n^{th}$ term of an

$AP$ with first term

$'a'$ common difference

$'d'$

$a_{n}=a+(n-1)d$

In given

$AP: 1, 4, 7$

$a=1, d=3$

$10^{th}$ term

$=a+9d$

$=1+27$

$=28$

Write the common difference of an A.P. the sum of whose first $n$ terms is $\dfrac{P}{2}n^2+Qn$ .

We know that,

$S_n = \dfrac{n}{2} [2a + (n - 1)d ]$

$....(i)$

Let us rewrite the given expression in the above form,

$S_n=\dfrac{P}{2} n^2+Qn$

$=\dfrac{n}{2}(2Q+Pn)$

$=\dfrac{n}{2}(2Q+P(n-1)+P)$

$=\dfrac{n}{2}\left[2\left(Q+\dfrac{P}{2}\right)+P(n-1)\right]$

$....(ii)$

Comparing

$(i)$ and

$(ii)$ we get,

$a=Q+\dfrac{P}{2}$

$d=P$

Hence, common difference,

$d=P.$

The sum of first $7$ terms of an AP is $10$ and that of next $7$ terms is $17$ . Find the AP.

Sum formula for AP

$S_{n}=\dfrac{n}{2}\left [ 2a+(n-1)d \right ]$

$a =$ First term

$d =$ Common difference

$n =$ number of terms

$S_7=10$ and

$S_{14}=(17+10)=27$

$\therefore \dfrac{7}{2}\times [2a+6d]=10$

$\Rightarrow 7a+21d=10$ ........(i)

and

$\dfrac{14}{2}\times [2a+13d]=27$

$\Rightarrow 14a+91d=27$ .......(ii)

Solving (i) and (ii) for

$a$ and

$d.$

we get,

$a=1,d=\dfrac 1 7$

so required series is

$1+1\dfrac{1}{7}+1\dfrac{2}{7}+1\dfrac{3}{7}+....$ .

Write the sum of first n even natural numbers.

We know, Sum formula

$S_{n}=\dfrac{n}{2}\left [ a+l \right ]$

$a =$ First term

$n =$ number of terms

$a_n = n^{th}$ term

$l=$ last term

Given sum

$=2+4+6+8+....+2n$

$=\dfrac{n}{2}(2+2n)=n(n+1)$ .

The $7$ th term of an AP is $-4$ and its $13$ th term is $-16$ . Find the AP.

Let us say

$a$ be the first term and

$d$ be the common difference of an AP.

$a_n=a+(n-1)d$

$a_7=a+(7-1)d$

$=a+6d=-4$ ...........

$(1)$

And

$a_{13}=a+12d=-16$ ........

$(2)$

Subtracting equation

$(1)$ from

$(2)$ , we get

$6d=-16-(-4)=-12$

From

$(1)$ ,

$a+6d=-4$

$a+(-12)=-4$

$a=-4+12=8$

$a=8, d=-2$

AP will be

$8, 6, 4, 2, 0,...$ .

The $4$ th term of an AP is $11$ . The sum of the $5$ th and $7$ th terms of this AP is $34$ . Find its common difference.

Let

$a$ be the first term and

$d$ be the common difference of an AP.

$a_n=a+(n-1)d$

$a_4=a+(4-1)d=a+3d$

$a+3d=11$ .......

$(1)$

Now,

$a_5=a+4d$ and

$a_7=a+6d$

Now,

$a_5+a_7=a+4d+a+6d=2a+10d$

$2a+10d=34$

$a+5d=17$ ........

$(2)$

Subtracting

$(1)$ from

$(2)$ , we get

$2d=17-11=6$

$d=3$

The common difference

$=3$ .

How many terms of the AP $21, 18, 15,....$ must be added to get the sum $0$ ?

AP is

$21, 18, 15,...$

$a=21$ ,

$d=18-21=-3$

Sum of terms

$=S_n=0$

$\dfrac{n}{2}[2a+(n-1)d]=0$

$\dfrac{n}{2}[2(21)+(n-1)d]=0$

$\dfrac{n}{2}[45-3n]=0$

$[45-3n]=0$

$n=15$ (number of terms)

Thus,

$15$ terms of the given AP sums to zero.

If the sum of n terms of an A.P. is $nP+\dfrac{1}{2}n(n-1)Q$ , where P and Q are constants, find the common difference.

We have,

$S_n=nP+\dfrac{1}{2}n(n-1)Q\Rightarrow S_{n-1}=(n-1)P+\dfrac{1}{2}(n-1)(n-2)Q$

Let

$a_n$ be the

$n^{th}$ term. Then,

$a_n=S_n-S_{n-1}$

$\Rightarrow a_n=\left\{nP+\dfrac{1}{2}n(n-1)Q\right\}-\left\{(n-1)P+\dfrac{1}{2}(n-1)(n-2Q\right\}$

$\Rightarrow a_n=P+\dfrac{1}{2}(n-1)\{n-(n-2)\}Q$

$\Rightarrow a_n=P+(n-1)Q$

$\Rightarrow a_{n-1}=P+(n-2)Q$

Let d be the common difference. Then,

$d=a_n-a_{n-1}=\{P+(n-1)Q\}-\{P+(n-2)Q\}=Q$ .

Which of the following lists of numbers form an A.P.? If they form an A.P., find the common difference $d$ :
(iii) $2,4,8,16, \dots$

(i)

$4,10,16,22, \dots$

From the question, it is given that,

First term,

$a=4$

$\begin{aligned}\text { then, difference } d &=10-4=6 \\& 16-10=6 \\& 22-16=6\end{aligned}\\$

Therefore, common difference,

$d=6$

Hence, the numbers form A.P.

(ii)

$-2,2,-2,2, \dots$

From the question, it is given that,

First term,

$a=-2$

then, difference

$d=-2-2=-4$

$\begin{array}{l}-2-2=-4 \\2-(-2)=2+2=4\end{array}\\$

Therefore, common difference

$d$ is not the same in the given numbers.

Hence, the numbers do not form A.P.

(iii)

$2,4,8,16, \dots$

From the question, it is given that,

First term,

$a=2$

then, difference

$d=4-2=2$

$\begin{array}{l}8-4=4 \\16-8=8\end{array}\\$

Therefore, common difference

$d$ is not the same in the given numbers.

Hence, the numbers do not form A.P.

In an AP, it is given that $S_5+S_7=167$ and $S_{10}=235$ , then find the AP, where $S_n$ denotes the sum of its first $n$ terms.

Let

$a$ be the first term and

$d$ be the common difference of the AP.

$S_5=\dfrac{n}{2}[2a+(n-1)d]$

$=\dfrac{5}{2}[2a+(5-1)d]\\$

$=\dfrac{5}{2}[2a+4d]$

Similarly,

$S_7=\dfrac{7}{2}[2a+6d]$

and

$S_{10}=\dfrac{10}{2}[2a+9d]=5(2a+9d)$

Now,

$\dfrac{5}{2}(2a+4d)+\dfrac{7}{2}(2a+6d)=167$

$5a+10d+7a+21d=167$

$12+31d=167$ .........(i)

and

$5(2a+9d)=235$

$2a+9d=47$ .......(ii)

Multiply (i) by (i) and (ii) by

$6$ ,

$12a+31d=167$

$12a+54d=282$

- - -

_________________

$-23d=-115\Rightarrow d=\dfrac{-115}{-23}=5$

From (i),

$12a+31\times 5=167$

$12a+155=16\Rightarrow 12a=167-155$

$12a=12\Rightarrow a=\dfrac{12}{12}=1$

Which implies:

$a=1$ and

$d=5$

Therefore, the AP is

$1, 6, 11, 16,....$ .

In an AP, the first term is $22$ , $n$ th term is $-11$ and sum of first $n$ terms is $66$ . Find $n$ and hence find the common difference.

Let

$n$ be the total number of terms and

$d$ be the common difference.

Given:

First term

$=a=22$

$n^{th}$ term or last term

$l=-11$

Sum of all terms

$=S_n=66$

$S_n=\dfrac{n}{2}[a+l]$

$66=\dfrac{n}{2}[22+(-11)]$

$n=12$

There are

$12$ terms in the AP.

Since nth term is

$-11$ , so

$a_n=a+(n-1)d$

$-11=22+(12-1)d$

$d=-3$

Therefore, the Common difference is

$-3$ and the number of terms is

$12$ .

The first and the last terms of an AP are $5$ and $45$ respectively. If the sum of all its terms is $400$ , find the common difference and the number of terms.

Let

$n$ be the total number of terms and

$d$ be the common difference.

Given:

First term

$=a=5$

Last term

$=l=45$

Sum of all terms

$=S_n=400$

$S_n=n/2[a+l]$

$400=n/2[5+45]$

$n/2=400/50$

$n=16$

There are

$16$ terms in the AP.

Therefore,

$45$ is the

$16$ th term of the AP.

$45=a+(16-1)d$

$45=5+15d$

$40=15d$

$15d=40$

$d=8/3$

Common difference

$=d=8/3$

Common difference is

$8/3$ and the number of terms are

$16$ .

Find the sum of first n even natural numbers.

First n even natural numbers:

$2, 4, 6, 8, 10, ......, n$

Here,

$a=2, d=4-2=2$

Sum

$=S_n=\dfrac{n}{2}[2a+(n-1)d]$

$=S_n=\dfrac{n}{2}[2(2)+(n-1)2]$

$=n(n+1)$ .

Find the sum of all odd numbers between $0$ and $50$ .

Odd numbers between

$0$ and

$50$ are

$1, 3, 5, 7, 9, ...., 49$

Here,

$a=1, d=3-1=2, l=49$ .

We have

$l= a+(n-1)d$

$49=1+(n-1)\times 2$

$49-1=2(n-1)\Rightarrow 2(n-1)=48$

$n-1=\dfrac{48}{2}=24$

$n=24+1=25$

Sum of odd numbers:

$S_n=\dfrac{n}{2}[a+l]$

$=\dfrac{25}{2}(1+49)$

$=\dfrac{25}{2}(50)$

$=625$ .

In an AP, the first term is $-4$ , the last term is $29$ and the sum of all its terms is $150$ . Find its common difference.

Let

$d$ be the common difference.

Given:

First term

$=a=-4$

Last term

$=l=29$

Sum of all the terms

$=S_n=150$

$S_n=n/2[a+l]$

$150=n/2[-4+29]$

$n=12$

There are

$12$ terms in total.

Therefore,

$29$ is the

$12$ th term of the AP.

Now,

$29=-4+(12-1)d$

$29=-4+11d$

$d=3$

The common difference is

$3$ .

What is the common difference of an AP in which $a_{27}-a_7=84?$

Given:

$a_{27}-a_{7}=84$

We know, nth term of a A.P.

$=a_n=a+(n-1)d$

$[a+26d]-[a+6d]=84$

$20d=84$

$d=4.2$ .

Find an AP whose $4$ th term is $9$ and the sum of its $6$ th and $13$ th terms is $40$ .

Let

$a$ be the first term and

$d$ be the common difference.

Given:

$4$ th term

$=a_4=9$

Sum of

$6$ th and

$13$ th terms

$=a_6+a_{13}=40$

Now,

$a_4=a+(4−1)d$

$9=a+3d$

$a=9−3d$ ....... (1)

And

$a_6+a_{13}=40$

$a+5d+a+12d=40$

$2a+17d=40$

$2(9−3d)+17d=40$ (using (1))

$d=2$

From (1)

$:a=9−6=3$

Required AP

$=3,5,7,9,....$

For the following A.P.s, write the first term 'a' and the common difference 'd':
(i) $3,1,-1,-3, \dots$
(ii) $1 / 3,5 / 3,9 / 3,13 / 3, \dots$
(iii) $-3.2,-3,-2.8,-2.6, \dots .$

(i)

$3,1,-1,-3, \dots$

From the question,

The first term

$a=3$

Then, difference

$d=1-3=-2$

$\begin{array}{l}-1-1=-2 \\-3-(-1)=-3+1=-2\end{array}\\$

Therefore, common difference

$d=-2$

(ii)

$1 / 3,5 / 3,9 / 3,13 / 3, \dots$

From the question,

The first term

$a=1 / 3$

Then, difference

$d=5 / 3-1 / 3=(5-1) / 3=4 / 3$

$\begin{array}{l}9 / 3-5 / 3=(9-5) / 3=4 / 3 \\13 / 3-9 / 3=(13-9) / 3=4 / 3\end{array}\\$

Therefore, common difference

$d=4 / 3$

(iii)

$-3.2,-3,-2.8,-2.6, \dots .$

From the question, The first term

$a=-3.2$

Then, difference

$d=-3-(-3.2)=-3+3.2=0.2$

$\begin{array}{l}-2.8-(-3)=-2.8+3=0.2 \\-2.6-(-2.8)=-2.6+2.8=0.2\end{array}$

Therefore, common difference

$d=0.2$

(i) How many terms of the A.P. 25, 22, 19, … are needed to give the sum 116? Also, find the last term.
(ii) How many terms of the A.P. 24, 21, 18, … must be taken so that the sum is 78? Explain the double answer.

$(i)$
From the question it is given that,
First term

$a=25$
Common difference

$d=22-25=-3$
Sum

$=116$

We know that, the sum of first

$n$ terms of an A.P. is

$S_{n}=\dfrac n 2(2 a+(n-1) d)$

$116=\dfrac n 2(2 a+(n-1) d)$

By cross multiplication, we get:

$232=n((2 \times 25)+(n-1)(-3))$

$\Rightarrow 232=n(50-3 n+3)$

$\Rightarrow 232=n(53-3 n)$

$\Rightarrow 232=53 n-3 n^{2}$

$\Rightarrow 3 n^{2}-53 n+232=0$

$\Rightarrow 3 n^{2}-24 n-29 n+232=0$

$\Rightarrow 3 n(n-8)-29(n-8)=0$

$\Rightarrow (n-8)(3 n-29)=0$

$n-8=0$

$n=8$
or

$3 n-29=0$

$3n=29$

$n=\dfrac{29 }{ 3}$

$n$ cannot be a fraction.

$\mathrm{So}, \mathrm{n}=8$

$\begin{aligned}\text { Then, } a_n &=a+(n-1) d \\&a_8 =25+(8-1)(-3) \\&=25+7(-3) \\&=25-21 \\&=4\end{aligned}\\$

Hence,

$8$ terms are required to give the sum

$116$ and the last term is

$4$ .

$(ii)$
From the question, it is given that,
First-term

$a = 24$
Common difference

$d = 21 – 24 = - 3$
Sum

$= 78$

We know that, the sum of first

$n$ terms of an A.P. is

$S_{n}=\dfrac n 2(2 a+(n-1) d)$

Hence,

$78=\dfrac n 2(2 a+(n-1) d)$
By cross multiplication,

$\begin{array}{l}156=n((2 \times 24)+(n-1)(-3)) \\156=n(48-3 n+3) \\156=n(51-3 n) \\156=51 n-3 n^{2} \\3 n^{2}-51 n+156=0 \\3 n^{2}-12 n-39 n+156=0 \\3 n(n-4)-39(n-4)=0\end{array}\\$

$(n-4)(3 n-39)=0$
If

$n-4=0$

$n=4$
or

$3 n-39=0$

$\begin{array}{l}3 n=39 \\n=\dfrac{39} {3} \\n=13\end{array}\\$
Now we have to consider both values

$So, n=4$

$\begin{aligned}\text {Then, } a_n =a+(n-1) d \\a_4 =24+(4-1)(-3) \\=24+3(-3) \\=24-9 \\=15 \\n=13 \\\text { Then, } a_n =a+(n-1) d \\a_{13} =24+(13-1)(-3) \\=24+12(-3) \\=24-36 \\=-12 \\\text { So, }(12+9+6+3+0+(-3)+(-6)+(-9)+(-12)) =0\end{aligned}\\$
Hence, the sum of

$5^{\text {th }}$ term to

$13^{\text {th }}$ term is

$0$ .

Determine the A.P. whose fifth term is 19 and the difference of the eighth term from the thirteenth term is 20.

From the question it is given that,

$\begin{array}{l}T_{5}=19 \\T_{8}-T_{13}=20\end{array}\\$

We know that,

$T_{n}=a+(n-1) d$

$\mathrm{So}, \mathrm{T}_{5}=\mathrm{a}+4 \mathrm{d}=19 \quad \ldots[ \text { equation (i)} ]\\$

$T_{13}-T_{8}=(a+12 d)-(a+7 d) \quad \ldots[\text { equation (ii) }]\\$

$\begin{array}{l}20=a+12 d-a-7 d \\20=5 d \\d=20 / 5 \\d=4\end{array}\\$

Now, substitute value of d in equation (i) we get,

Then,

$T_{5}=a+4 d$

$\begin{array}{l}19=a+4(4) \\a=19-16 \\a=3\end{array}\\$

Therefore, A.P. is

$3+4=7,7+4=11,11+4=15$

Hence, the A.P. is

$3,7,11,15, \ldots$

In an A.P., the sum of the first 10 terms is 150, and the sum of the next 10 terms is 550. Find the A.P.

From the question it is given that,

The sum of the first 10 terms

$=-150$

The sum of the next 10 terms

$=-550$

A.P

$=?$

We know that,

$S_{n}=(n / 2)[2 a+(n-1) d]$

$\begin{array}{l}S_{10}=(n / 2)[2 a+(10-1) d] \\-150=(10 / 2)[2 a+9 d] \\-150=5[2 a+9 d] \\-150=10 a+45 d\end{array}\\$

Then,

$S_{20}=S_{10}+S_{10}$

$\begin{array}{l}\begin{aligned}=&-150-550 \\=&-700\end{aligned} \\\begin{array}{l}S_{20}=(20 / 2)[2 a+19 d] \\-700=10(2 a+19 d) \\-700=20 a+190 d\end{array}\end{array}\\$

Now, multiplying equation(i) by 2 we get,

$20 a+90 d=-300\\$

Subtract equation (iii) from equation (ii),

$(20 a+190 d)-(20 a+90 d)=-700-(-300)\\$

$\begin{array}{l}20 a+190 d-20 a-90 d=-700+300 \\100 d=-400 \\d=-400 / 100\end{array}$

$d = -4$

Substitute the value of d in equation (i) we get,

$\begin{array}{l}10 a+45(-4)=-150 \\10 a-180=-150 \\10 a=-150+180 \\10 a=30 \\a=30 / 10 \\a=3 \\a_{2}=3+(-4)=3-4=-1 \\a_{3}=-1+(-4)=-1-4=-5 \\a_{3}=-5+(-4)=-5-4=-9\end{array}$

Therefore, A.P. is 3, -1, -5, -9, …

(i) The first term of an A.P. is 5, the last term is 45 and the sum isFind the number of terms and the common difference.
(ii) The sum of the first 15 terms of an A.P. is 750 and its first term isFind its 20th term.

(i) The first term of an A.P. is 5, the last term is 45 and the sum is 400.

From the question, it is given that,

First term

$a=5$

Last term

$=45$

Then, sum

$=400$ We know that,

last term =

$a+(n-1) d$

$\begin{array}{l}\qquad \begin{aligned}45=5+(n-1) d \\(n-1) d=45-5 \\(n-1) d=40\end{aligned} \\\begin{array}{l}\text { So, } S_{n}=(n / 2)(2 a+(n-1) d) \\400=(n / 2)((2 \times 5)+40) \\800=n(10+40) \\800=50 n \\n=800 / 50 \\n=16\end{array}\end{array}\\$

(ii) The sum of the first 15 terms of an A.P. is 750 and its first term is 15.

From the question, it is given that,

First-term a = 15

Therefore, sum of first n terms of an A.P. is given by,

$\begin{array}{l}S_{n}=(n / 2)(2 a+(n-1) d) \\S_{15}=(15 / 2)(2 a+(15-1) d) \\750=(15 / 2)(2 a+14 d) \\(750 \times 2) / 15=2 a+14 d \\100=2 a+14 d\end{array}\\$

Dividing both the side by 2 we get

$50=a+7 d\\$

Now, substitute the value a,

$\begin{array}{l}50=15+7 d \\7 d=50-15 \\7 d=35 \\d=35 / 7 \\d=5 \\\begin{aligned}\text { So, } 20^{\text {th }} \text { term } a_{20} &=a+19 d \\&=15+19(5) \\&=15+95 \\&=110\end{aligned}\end{array}\\$

If the $8^{\text {th }}$ term of an A.P. is 31 and the $15^{\text {th }}$ term is 16 more than its $11^{\text {th }}$ term, then find the A.P.

From the question, it is given that,

$a_{8}=31\\$

$a_{15}=$ the

$15^{\text {th }}$ term is 16 more than its

$11^{\text {th }}$ term

$=a_{11}+16$

we know that,

$a_{n}=a+(n-1) d$

$\mathrm{So}, \mathrm{a}_{8}=\mathrm{a}+7 \mathrm{d}=31 \quad \ldots[ \text { equation (i) ] }\\$

$\begin{array}{l}a_{15}=a+14 d=a+10 d+16 \\14 d-10 d=16 \\4 d=16 \\d=16 / 4 \\d=4\end{array}\\$

Now substitute the value of

$\mathrm{d}$ in equation (i) we get,

$\begin{array}{l}a+(7 \times 4)=31 \\a+28=31 \\a=31-28 \\a=3 \\\text { So }, 3+4=7,7+4=11,11+4=15\end{array}\\$

Therefore, A.P. is

$3, 7, 11, 15, ...$

Determine the A.P. whose third term is 16 and the $7^{\text {th }}$ term exceeds the $5^{\text {th }}$ term by 12

${\textbf{Step -1: Establishing Relation between first term of A.P and Common difference}}.$

${\text{Suppose x is the first term}}.$

${\text{d is the common difference}}.$

${\text{so, given }}{{\text{3}}^{{\text{rd}}}}{\text{ term is 16 and}}$

${{\text{7}}^{{\text{th}}}}{\text{ term}} = {{\text{5}}^{{\text{th}}}}{\text{ term + 12}}.$

${\text{So we can say,}}$

${{\text{3}}^{{\text{rd}}}}{\text{ term}} = {{\text{a}}_3} = 16.$

$\Rightarrow {\text{a}} + (3 - 1) = 16.$

$\Rightarrow {\text{a}} + 2{\text{d}} = 16{\text{ - - - - - - - - (i)}}.$

${{\text{a}}_7} = {{\text{a}}_5} + 12.$

$\Rightarrow {\text{a}} + (7 - 1){\text{d}} = {\text{a}} + (5 - 1){\text{d}} + 12.$

$\Rightarrow {\text{a}} + 6{\text{d}} = {\text{a}} + 4{\text{d}} + 12{\text{ - - - - - - - - - (ii)}}.$

${\textbf{Step -2: Solving equations to calculate a and d}}.$

$\left( {{\text{ii}}} \right) \Rightarrow {\text{a}} + 6{\text{d}} - {\text{a}} - 4{\text{d}} = 12.$

$\Rightarrow 2{\text{d}} = 12.$

$\Rightarrow {\text{d}} = \dfrac{{12}}{2} = 6.$

${\text{Putting d}} = 6{\text{ in }}\left( {\text{i}} \right) \Rightarrow {\text{a}} + 2.{\text{d}} = 16.$

$\Rightarrow {\text{a}} = 16 - 12.$

$= 4.$

${\text{So the AP will be a}} + {\text{d , a}} + {\text{2d }}...........$

${\text{AP will be 4, 4 + 6, 4 + 2.6}}{\text{}}...............$

$= 4,10,16,22,............$

${\textbf{Hence, the AP will be 4,10,16,22 }}{\text{.....}}$

(i) If the common difference of an A.P. is -3 and the $18^{\text {th }}$ term is $-5,$ then find its first term.
(ii) If the first term of an A.P. is -18 and its 10 th term is zero, then find its common difference.

(i) If the common difference of an A.P. is -3 and the

$18^{\text {th }}$ term is

$-5,$ then find its first term.

From the question it is given that,

The

$18^{\text {th }}$ term

$=-5$

Then, common difference

$d=-3$

$\begin{aligned}T_{n}=& a+(n-1) d \\So, & T_{18}=a+(18-1) d \\&-5=a+(18-1)(-3) \\&-5=a+(17)(-3) \\&-5=a-51 \\& a=51-5 \\& a=46\end{aligned}\\$

Therefore, first term

$a=46$

(ii) If the first term of an A.P. is -18 and its 10 th term is zero, then find its common difference.

From the question, it is given that,

The

$10^{\text {th }}$ term

$=0$

Then, first term

$a=-18$

$T_{n}=a+(n-1) d\\$

So,

$\begin{array}{l}T_{10}=a+(10-1) d \\0=-18+(10-1) d \\0=-18+9 d \\9 d=18\end{array}$

$\begin{array}{l}d=18 / 9 \\d=2\end{array}\\$

Therefore, common difference

$d=2$

The first and the last terms of an A.P. are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?

From the question it is give that,

First term

$a=17$

Last term

$= 350$

Common difference

$d=9$

We know that,

$T_{n}=a+(n-1) d$

$\begin{array}{l}350=17+(n-1) \times 9 \\350-17=9 n-9 \\333+9=9 n \\342=9 n \\n=342 / 9\end{array}\\$

$n = 38$

$\begin{aligned}S_{n} &=(n / 2)(2 a+(n-1) d) \\&S_{38}=(38 / 2)((2 \times 17)+(38-1) d) \\&=19(34+(37 \times 9)) \\&=19(34+333) \\&=19 \times 367 \\&=6973\end{aligned}$

The $19^{\text {th }}$ term of an A.P. is equal to three times its $6^{\text {th }}$ term. If its $9^{\text {th }}$ term is $19,$ find the A.P.

From the question it is given that,

$a_{19}=19^{\text {th }}$ term of an A.P. is equal to three times its

$6^{\text {th }}$ term

$=3 a_{6}$

$a_{9}=19$

As we know,

$a_{n}=a+(n-1) d$

$a_{9}=a+8 d=19\\$

Then,

$a_{19}=3(a+5 d)$

$\begin{array}{l}a+18 d=3 a+15 d \\3 a-a=18 d-15 d \\2 a=3 d\end{array}\\$

$a=(3 / 2) d\\$

Now substitute the value of a in equation (i) we get,

$\begin{array}{l}(3 / 2) d+8 d=19 \\(3 d+16 d) / 2=19 \\(19 / 2) d=19 \\d=(19 \times 2) / 19 \\d=2\end{array}\\$

To find out the value of a substitute the value of

$d$ in equation (i)

$\begin{array}{l}a+8 d=19 \\a+(8 \times 2)=19 \\a+16=19 \\a=19-16 \\a=3\end{array}\\$

Therefore, A.P. is

$3,5,7,9, \dots$

Find the sum of the two middlemost terms of the following AP:
$-4 / 3,-1,-2 / 3, \dots, 4 \dfrac{1}{3}\\$

From the question,

$\text { Last term }\left(n^{\text {th }}\right)=4 \dfrac{1}{3}=\dfrac{13} { 3}$

First term

$a=-\dfrac{4} {3}$

Then, difference

$d=-1-(-\dfrac{4 }{ 3})=-1+\dfrac{4} {3}=\dfrac{-3+4 }{3}=\dfrac{1} { 3}$

Therefore, common difference

$d=\dfrac{1} {3}$

We know that,

$T_{n}=a+(n-1) d$

$\dfrac{13}{ 3}=-\dfrac{4}{ 3}+(n-1)(\dfrac{1}{ 3})$

$\dfrac{13} {3}+\dfrac{4} { 3}=\dfrac{1} { 3} n-\dfrac{1} { 3}$

$\dfrac{13}{ 3}+\dfrac{4}{ 3}+\dfrac{1}{ 3}=\dfrac{1} { 3} n$

$\dfrac{13+4+1} {3}=\dfrac{1} { 3} n$

$\dfrac{18}{ 3}=\dfrac{1}{ 3} n$

$6=\dfrac{1}{ 3} n$

$n=6 \times 3 =18$

So, middle term is

$\dfrac{18} {2}$ and

$\dfrac{18} {2}+1=9^{\text {th }}$ and

$10^{\text {th }}$ term

$\begin{aligned}\text { Then }, a_{9}+a_{10} &=a+8 d+a+9 d \\&=2 a+17 d\end{aligned}\\$

Now substitute the value of

$'a'$ and

$'d'$ .

$=2(-\dfrac{4} { 3})+17(\dfrac{1}{ 3})$

$=-\dfrac{8}{ 3}+\dfrac{17}{ 3}$

$=\dfrac{-8+17}{ 3}$

$=\dfrac{9} {3}=3$

Therefore, the sum of the two middlemost terms of the

$A.P\ is\ 3.$

If the $8th$ term of an AP is $31$ and the $15th$ term is $16$ more than the $11th$ term, find the AP.

Let

$a$ be the first term and

$d$ be the common difference of the AP.

Genereal term of an

$A.P. \Rightarrow a_n=a+(n-1)d$

We have,

$a_{8} = 31$ and

$a_{15} = 16 + a_{11}$

$\implies a+7d=31$ and

$a+ 14d =16 +a + 10d$

$\implies a+ 7d =31$ and

$4d = 16$

$\implies a+7d=31$ and

$d=4 \implies a+7\times 4=31$

$\implies a+ 28=31 \implies a=3$

Hence, the AP is

$a$ ,

$a+d$ ,

$a+2d$ ,

$a+ 3d$ ...

i.e.,

$3$ ,

$7$ ,

$11$ ,

$15$ ,

$19$ , ...

Which of the following form of an A.P.? Justify your answer.
0, 2, 0, 2, ....

Hint:- In an A.P. common difference between each consecutive terms will always be equal.

Given:-

Sequence:-

$0, 2, 0, 2, ....$

Here,

Second term

$-$ first term

$=2-0=2$

Third term

$-$ second term

$=0-2=-2$

Fourth term

$-$ third term

$=2-0=2$

Since, all of the differences are not equal to each other

Hence, the given sequence doesn't form an A.P.

The sum of first $n$ natural numbers is given by
$\cfrac { 1 }{ 2 } {n}^{2}+\cfrac { 1 }{ 2 } n$ . Find
The sum of natural numbers from $11$ to $30$

Given that sum of first

$n$ natural numbers

$=\cfrac { 1 }{ 2 } {n}^{2}+\cfrac { 1 }{ 2 } n$
The sum of natural numbers from

$11$ to

$30$

$=$ Sum of first

$30$ natural numbers

$-$ sum of first

$10$ natural numbers.

$=[\cfrac { 1 }{ 2 } \times {(30)}^{2}+\cfrac { 1 }{ 2 } \times 30]-[\cfrac { 1 }{ 2 } \times {(10)}^{2}_\cfrac { 1 }{ 2 } \times 10]$

$=\cfrac{900}{2}+\cfrac{30}{2}-\cfrac{100}{2}-\cfrac{10}{2}=410$

Which of the following form of an A.P.? Justify your answer.
$2, 2^2, 2^3, 2^4, .....$

Hint:- In an A.P. common difference between each consecutive terms will always be equal.

Given:-

Sequence:-

$2, 2^2, 2^3, 2^4, .....$

Here,

Second term

$-$ first term

$=2^2-2=4-2=2$

Third term

$-$ second term

$=2^3-2^2=8-4=4$
Fourth term

$-$ third term

$=2^4-2^3=16-8=8$

Since, all of the differences are not equal to each other

Hence, the above sequence doesn't form an A.P.

The taxi fare after each km, when the fare is Rs.15 for the first km and Rs 8 for each additional km, dies not form an A.P., as the total fare (in Rs) after each km is 15, 8, 8, 8,.... Is the statement true $\because$ Give reasons.

Hint:- Forming an A.P. sequence and analyzing that the common difference between each consecutive terms of an A.P. will always be same.

Given:-

Fare for first km

$=$ first term

$=a_1=a=15$
fare for each additional km

$=8$

Step 1: Finding the general fare sequence formed for each km

First km fare

$=15$

Second km fare

$=15+ 8 \times ( 1)=23$ .......

$1$ due to additional

$1$ km travelled aside from the first km

Third km fare

$=15 + 8\times (2)=31$ .......

$2$ due to additional

$2$ km travelled aside from the first km

Fourth km fare

$=15 + 8\times (3)=39$ .......

$3$ due to additional

$3$ km travelled aside from the first km

So, the sequence becomes

$15,23,31,39.....$

Step 2 : Contradicting the fare statement given in question
As per question the total fare (in rs) after each km is

$15, 8, 8, 8,....$
However, we can see the fare sequence is coming out to be

$15,23,31,39.....$

So, the sequence given in question is wrong.

Step 3: Finding the common difference from the obtained sequence

$15,23,31,39.....$

Second term

$-$ first term

$=a_2-a_1=23-15=8$
Third term

$-$ second term

$=a_3-a_2=31-23=8$
Fourth term

$-$ third term

$=a_4-a_3=39-31=8$

As we can see that the common difference between each consecutive terms are equal, so, the fare sequence forms an A.P.

Final step: As the common difference of the fare sequence

$15,23,31,39.....$ between each consecutive terms are equal, so, the fare sequence forms an A.P.

In which of the following situations do the list of numbers involved form an A.P.?
Give reasons for your answers.
The fee charged from a student every month by a school for the whole session, when the monthly fee is Rs. 400.

The fee charged from a student every month by a school is Rs. 400. So, the fee charged from a student the whole session is 400, 400, 400, 400,.... As

$d_1=d_2=d_3=d_{12}=0$ so, the series of numbers is an A.P.

Which of the following form of an A.P.? Justify your answer.
$\dfrac{1}{2}, \dfrac{1}{3}, \dfrac{1}{4}, ....$

Hint:- In an A.P. common difference between each consecutive terms will always be equal.

Given:-

Sequence:-

$\dfrac 12, \dfrac{1}{3}, \dfrac{1}{4}, .....$

Here,

Second term

$-$ first term

$=\dfrac 13-\dfrac 12=\dfrac {-1}{6}$

Third term

$-$ second term

$=\dfrac 14-\dfrac 13=\dfrac {-1}{12}$

Since, both of the differences are not equal to each other

Hence, the above sequence doesn't form an A.P.

Which of the following form of an A.P.? Justify your answer.
11, 22, 33, ....

Hint:- In an A.P. common difference between each consecutive terms will always be equal.

Given:-

Sequence:-

$11,22,33 .....$

Here,

Second term

$-$ first term

$=22-11=11$

Third term

$-$ second term

$=33-22=11$

Since, both of the differences equal to each other

Hence, the above sequence forms an A.P.

For the A.P. $-3, -7, -11, ....$ , can we find directly $a_{30}-a_{20}$ without actually finding $a_{30}$ and $a_{20}$ ? Give reasons for your answer.

Hint:- Use the general term formul for

$n^{th}$ term of an AP,

$a_n = a + (n-1)d$ and relations between them.

Given:-

$\text {a=first term,} \ (Let)$
$a_n$ $\text {=nth term}, (Let)$
$\text {d=common difference between all the terms} \ (Let)$

Sequence : $−3,−7,−11,.....$

Step 1: Finding the common difference from the given terms

$d=-7-(-3)=4=-11-(-7)$

$\therefore d=-4$

Step 2: Replacing the value of $30$ for $n$ in the general term to get $a_{30}$

$a_{30} = a + (30 - 1)d = a + (30 - 1)d = a + 29d$

Step 3: Replacing the value of $20$ for $n$ in the general term to get $a_{20}$

$a_{20} = a + (20 - 1)d = a + 19d$

Step 4: Finding the difference between $a_{30} - a_{20}$

$a_{30} - a_{20} = (a + 29d) - (a+19d) = 10d=10 \times (-4)=-40$

Final Step: Hence,

$a_{30} - a_{20} = - 40$ . So, we can directly find them as first term completely gets cancelled during subtraction operation between the two terms.

Which of the following form of an A.P.? Justify your answer.
$\sqrt{3}, \sqrt{12}, \sqrt{27}, \sqrt{48},....$

Hint:- In an A.P. common difference between each consecutive terms will always be equal.

Given:-

Sequence:-

$\sqrt {3}, \sqrt {12}, \sqrt {27}, \sqrt {48}, .....$

Here,

Second term

$-$ first term

$=\sqrt {12}-\sqrt 3=2\sqrt 3-\sqrt 3=\sqrt 3$

Third term

$-$ second term

$=\sqrt {27}-\sqrt {12}=3\sqrt 3-2\sqrt 3=\sqrt 3$

Fourth term

$-$ third term

$=\sqrt {48}-\sqrt {27}=4\sqrt 3-3\sqrt 3=\sqrt 3$

Since, all of the differences are equal to each other

Hence, the above sequence forms an A.P.

Which of the following form of an A.P.? Justify your answer.
1, 1, 2, 2, 3, 3,....

Hint:- In an A.P. common difference between each consecutive terms will always be equal.

Given:-
Sequence:-

$1, 1, 2, 2, 3, 3,....$

Here,
Second term

$-$ first term

$=1-1=0$
Third term

$-$ second term

$=2-1=1$
Fourth term

$-$ third term

$=2-2=0$
Fifth term

$-$ fourth term

$=3-2=1$
Sixth term

$-$ fifth term

$=3-3=0$

Since, all of the differences are not equal to each other
Hence, the above sequence doesn't form an A.P.

Is 0 a term of the A.P. 31, 28, 25, .... $\because$ Justify your answer.

Hint:- The general term of A.P.

$\{a_n=a+(n-1)d\}$ with its terms will be used for the problem.

Given:-
First term

$=a_1=a=31$

$n= \text {sequence no. of the term}$

$d=\text {common difference between consecutive terms}$
Sequence

$: 31,28,25,....$

Step 1: Finding the common difference 'd' from the terms

$a_2-a_1=a_3-a_2$

$\Rightarrow 28-31=25-28=-3$

Step 2: Using the general term formula to get the value of 'n' by replacing ' $a_n=0$ ' in the formula

$a_n=a+(n-1)d$

$\Rightarrow 0=31+(n-1) (-3)$

$\Rightarrow 0=31-3n+3$

$\Rightarrow 3n=34$

$\Rightarrow n=\dfrac {34}3$

As, n does not have an integer value, So 0 can't be a term in the above sequence.

Final step: So, 0 can't be term in the sequence as it's term number is not an integral value.

Determine the A.P. whose 5th term is 19 and the difference of the $8^{th}$ term from the $13^{th}$ term is 20.

Main concept used:

(i)

$a_n = a + (n - 1)d$ (ii) Solution of linear eqn.

Given:

$a_5 = 19, a_13 - a_8 = 20$

Let us consider an A.P. whose 1st term and common difference are a and d respectively.

$a_5 = 19$ [Given]

$\Rightarrow \ \ a + (5 -1)d = 19$

$\Rightarrow \ \ a + 4d = 19$ ...(i)

Also,

$a_{13} - a_9 = 20$ [Given]

$\Rightarrow \ \ a + (13 - 1)d - [a + (8 - 1)d] = 20$

$\Rightarrow \ \ a + 12d - [a + 7d] = 20$

$\Rightarrow \ \ a + 12d - a - 7d = 20$

$\Rightarrow \ \ 5d = 20$

$\Rightarrow \ \ d = \frac{20}{5}$

$\Rightarrow \ \ d = 4$

Now,

$a + 4d = 19$ [From (i)]

$\Rightarrow \ \ a + 4 \times 4 = 19$

$\Rightarrow \ \ a = 19 - 16 = 3$

A.P. is given by

$a, a + d, a + 2d, a + 3d, ....$

Hence, the correct required A.P. is

$3, 7, 11, 15, ....$

Find a, b and c such that the following numbers are in A.P. : a, 7, b, 23, c.

We have

$d_1 = a_2 - a_1 = 7 - a$

$d_2 = a_3 - a_2 = b - 7$

$d_3 = a_4 - a_3 = 23 - b$

$d_4 = a_5 - a_4 = c - 23$

As list of numbers is in A.P.,

$d_1 = d_2 = d_3 = d_4$

Now.

$d_2 = d_3$

$\Rightarrow \ \ b - 7 = 23 - b$

$b + b = 30$

$\Rightarrow \ \ 2b = 30$

$\Rightarrow \ \ b - 15$

Now,

$d_2 = d_1$

$\Rightarrow \ \ b - 7 = 7 - a$

$\Rightarrow \ \ 15 - 7 = 7 - a$

$\Rightarrow \ \ 8 = 7 - a$

$a = 7 - 8 = -1$

Now,

$d_4 = d_2$

$\Rightarrow \ \ c - 23 = b - 7$

$\Rightarrow \ \ c = 23 + 15 - 7 = 38 - 7$

$\Rightarrow \ \ c = 31$

Hence,

$a = -1, b = 15$ and

$c = 31$ .

In which of the following situations do the list of numbers involved form an A.P.?
Give reasons for your answers.
The fee charged every month by a school from classes I to XII, when the monthly fee for class I is Rs. 250, and it increases by Rs 50 for the next higher class.

Fee for Ist class = Rs 250
Fee for IInd class = Rs (250+50)= Rs. 300
Fee for IIIrd class = Rs (300+50)= Rs. 350
Fee for IV class = Rs (350+50)= Rs. 400

$\therefore 250, 300, 350, 400,...$ is a series consisting of 12 terms.
So,

$d_1 = 350-250 = Rs. 50, d_2 = 350-300 = Rs 50, d_3 = 400-350=Rs 50$

$\because d_1=d_2=d_3=50$
So, the list of numbers 250, 300, 350, 400, .... is in A.P.

The sum of the 5th and the 7th terms of an A.P. is 52, and the 10th term isFind the A.P.

Consider an A.P. whose first term and common difference are a and d respectively.

According to the question,

$a_5 + a_7 = 52$

$\Rightarrow a + (5-1) d + a + (7-1) d = 52 \ \ \ [\because a_n = a + (n-1) d]$

$\Rightarrow 2a + 4d + 6d = 52$

$\Rightarrow a + 5d = 26$ ....(i)

Also,

$a_{10} = 46$ [Given]

$\Rightarrow a + (10-1) d = 46$

$\Rightarrow a + 9d = 46$ ....(ii)

Subtract (ii) from (i)

$-4d = -20$

$\Rightarrow d = 5$

Now, a + 5d = 26 [From (i)]

$\Rightarrow a = 1$

A.P. is given by a, a+ d , a + 2d, ....

Hence, the required A.P. is given by 1, 6,11, 16, ...

Write the first three terms of the A.P.s when a and d are as given below:
$a = \sqrt{2}, d = \frac{1}{\sqrt{2}}$

Here,

$a = \sqrt{2}, d = \dfrac{1}{\sqrt{2}}$

We know that

$a_n = a + (n - 1)d$

$\Rightarrow \ \ a_n = \sqrt{2} + (n - 1) \dfrac{1}{\sqrt2} = \sqrt2 + \dfrac{n}{\sqrt2} - \dfrac{1}{\sqrt2} = \sqrt2 - \dfrac{1}{\sqrt2} + \dfrac{n}{\sqrt2}$

$\Rightarrow \ \ a_n = \dfrac{2 - 1 + n}{\sqrt2}$

$\Rightarrow \ \ a_n = \dfrac{1 + n}{\sqrt2}$

$\therefore \ \ a_1 = \dfrac{1 + 1}{\sqrt2} = \dfrac{2}{\sqrt2} = \dfrac{2}{\sqrt2} \times \dfrac{\sqrt2}{\sqrt2} = \dfrac{2\sqrt2}{2} = \sqrt2$ ,

$a_2 = \dfrac{1 + 2}{\sqrt2} = \dfrac{3}{\sqrt2} = \dfrac{3}{\sqrt2} \times \dfrac{\sqrt2}{\sqrt2} = \dfrac{3\sqrt2}{2}$

and

$a_3 = \dfrac{1 + 3}{\sqrt2} = \dfrac{4}{\sqrt2} = \dfrac{4}{\sqrt2} \times \dfrac{\sqrt2}{\sqrt2} = \dfrac{4\sqrt2}{2} = 2\sqrt2$

Hence, the first three terms are

$\sqrt2, \dfrac{3\sqrt2}{2}$ and

$2\sqrt2$ .

The 26th, 11th and the last term of an A.P. are 0, 3 and $-\frac{1}{5}$ respectively. Find the common difference and the number of terms.

Consider an A.P. whose first term, common difference and last term are a, d and an respectively.

Given:

$a_{26} = 0, a_{11} = 3$ and

$a_n = -\frac{1}{5}$

$a_{26} = 0$ [Given]

$\Rightarrow \ \ a + (26 - 1)d = 0$

$\Rightarrow \ \ a + 25d = 0$ ...(i)

$a_{11} = 3$ [Given]

$\Rightarrow \ \ a + (11 - 1)d = 3$

$a + 10d = 3$ ...(ii)

$a_n = -\frac{1}{5}$

$\Rightarrow \ \ a + (n - 1)d = -\frac{1}{5}$ ...(iii)

On subtracting eqn (ii) from eqn (i) we get

$15d = -3$

$\Rightarrow d = -\frac{3}{15} = -\frac{1}{5}$

From (ii),

$a + 10 d = 3$

$\Rightarrow a + 10 (-\frac{1}{5}) = 3$

$a = 5$

$\therefore$ From (iii),

$a + (n-1) d = -\frac{1}{5}$

$\Rightarrow 5 + (n-1)(-\frac{1}{5}) = -\frac{1}{5}$

Multiplying both sides by 5, we get

$\Rightarrow 25 - (n-1) = -1$

$n-1 = 26$

$n = 27$

Hence, the common difference and number of terms in the A.P. are

$-\frac{1}{5}$ and

$27$ respectively.

Write the first three terms of the A.P.s when a and d are as given below:
$a = \frac{1}{2}, d = \frac{-1}{6}$

Here

$a = \dfrac{1}{2}, d = \dfrac{-1}{6}$

We know that

$a_n = a + (n-1) d$

$\Rightarrow a_n = \dfrac{1}{2} + (n-1) \Big( \dfrac{-1}{6} \Big)\\$

$\Rightarrow a_n = \dfrac{1}{2} - \dfrac{n}{6} + \dfrac{1}{6} = \dfrac{1}{2} + \dfrac{1}{6}-\dfrac{n}{6} = \dfrac{3 + 1 - n}{6}\\$

$\Rightarrow a_n = \dfrac{4-n}{6}$

$\therefore a_1 = \dfrac{4-1}{6} = \dfrac{1}{2}, a_2 = \dfrac{4-2}{6} = \dfrac{1}{3}, a_3 = \dfrac{4-3}{6} = \dfrac{1}{6}$

Hence, the required first three terms are

$\dfrac{1}{2}, \dfrac{1}{3}$ and

$\dfrac{1}{6}$ .

Write the first three terms of the A.P.s when a and d are as given below:
$a = -5, d = -3$

Here,

$a= -5, d = -3$

We know that

$a_n = a + (n - 1)d$

$\Rightarrow \ \ a_n = -5 + (n - 1)(-3) = -5 -3n + 3 = -2 - 3n$

$\Rightarrow \ \ a_n = -(2 + 3n)$

$\therefore \ \ a_1 = -[2 + 3(1)] = -[2 + 3] = -5$

$a_2 =-[2 + 3 \times 2] = -[2 + 6] = -8$

$a_3 = -[2 + 3 \times 3] = -[2+9] = -11$

Hence, the first three terms are -5, -8 and -11.

In which of the following situations do the list of numbers involved form an A.P.?
Give reasons for your answers.
The amount of money in the account of Varun at the end of every year when Rs 1000 is deposited at simple interest of $10\%$ per annum.

$SI =\dfrac{PRT}{100}=\dfrac{1000 \times 10 \times 1}{100} = Rs 100$
So, Rs 100 is credited at the end of each year in the account of Varun.
Money in the beginning of 1st year (deposited) = Rs 1000
Money at the end of 1st year when interest credited = 1000 + 100 = Rs 1100
Money at the end of 2nd year = 1100 + 100 = Rs 1200
Money at the end of 3rd year = 1200 + 100 = Rs 1300
Money at the end 4th year = 1300 + 100 = Rs 1400
Amount of money at the end of each year starting initially from 1st year is given by 1000, 1100, 1200, 1300, 1400 ...

$\therefore d_1=d_2=d_3=d_4=100$
So, the list of numbers is an A.P.

The first term of an $A.P.$ is $-5$ and last term is $45$ . If the sum of the terms of the $A.P.$ is $120$ , then find the number of terms and the common difference.

Let us consider an

$A.P.$ whose first term and common difference are

$a$ and

$d$ respectively.

Here,

$a = -5, a_n = 45, S_n = 120$
Now,

$S_n = \dfrac{n}{2} [2a + (n-1) d ] = \dfrac{n}{2}[a + a + (n-1) d]$

$\Rightarrow S_n = \dfrac{n}{2} [a + a_n ] \quad\quad[a_n = last \ term]$

$\Rightarrow 120 = \dfrac{n}{2}[-5+45]$

$\Rightarrow 120 = \dfrac{n}{2} \times 40$

$\Rightarrow n = \dfrac{120 \times 2}{40} = 6$

$\Rightarrow n = 6$

Hence, the number of terms

$= 6$

Now,

$a_n = a + (n-1)d$

$\Rightarrow 45= -5 + (6-1) d$

$\Rightarrow 45 + 5 = 5d$

$\Rightarrow 5d= 50$

$\Rightarrow d = 10$
Hence, the number of terms and the common difference of the

$A.P.$ are

$6$ and

$10$ respectively.

If $S_n$ denotes the sum of first n terms of an A.P., prove that $S_{12} = 3(S_8 - S_4)$ .

Consider an A.P. whose first term and common difference are 'a' and 'd' respectively.

$S_n = \frac{n}{2}[2a + (n-1) d ]$

$\Rightarrow S_{12} =\frac{12}{2} [2a + (12 -1 ) d]$

$\Rightarrow S_{12} = 6 [2a + 11d]$ ...(i)
And

$S_8 = \frac{8}{2} [2a + (8-1) d]$

$\Rightarrow S_8 = 4 [2a + 7d]$ ....(ii)
And

$S_4 = \frac{4}{2} [2a + (4-1)d ]$

$\Rightarrow S_4 = 2[2a + 3d]$ .....(iii)
Now,

$3(S_8 - S_4) = 3 [4(2a + 7d) - 2 (2a + 3d)]$ [Using eqns (ii) and (iii)]
= 3 [ 4a + 22d]

$= 3 \times 2 [ 2a + 11 d]$

$= 6[2a + 11d] = S_{12}$ [Using eqns (i)]

$\therefore RHS = LHS$
Hence, proved.

Yasmeen saves Rs.32 during the first month, Rs.36 in the second month and Rs.40 in $3^{rd}$ month. if she continues to save in this manner, in how many months will she save Rs.2000 ?

During I month, savings of Yasmeen = Rs 32
During II month, savings of Yasmeen = Rs 36
During III month, savings of Yasmeen = Rs 40
During IV month, savings of Yasmeen =Rs 44
Total savings = Rs. 2000

$\therefore 32 + 36 + 40 + 44 + ... =2000$
Also, a = 32, d = 36 - 32 = 4
Now,

$S_n = 2000$

$\Rightarrow \dfrac{n}{2} [2a + (n-1) d] = 2000$

$\Rightarrow n [2(32)+(n-1)4] = 2000 \times 2$

$\Rightarrow n [ 64 + 4n -4 ] = 4000$

$\Rightarrow 4n [n + 15] = 4000$

$\Rightarrow n^2 + 15 n -1000 = 0$

$\Rightarrow n^2 + 40 n - 25 n -1000 = 0$

$\Rightarrow n ( n + 40) -25 (n + 40) = 0$

$\Rightarrow (n + 40 ) (n - 25) = 0$

$\Rightarrow n = -40 \ or \ n = 25$
Since n can not be negative.

$\therefore$ rejecting n = -40, we have n = 25.
Hence, in 25 months she shaves Rs, 2000.

Split 207 into three parts such that these are in A.P. and the product of the two smaller parts is 4623.

Main concept used: If the sum of three consecutive terms of an AP is given so term: be considered as (a - d), a, (a + 1).
Consider an A.P. whose three consecutive terms are (a - d), a, (a + d).
According to the question.
(a - d) + a + (a + d) = 207

$\Rightarrow 3a = 207$

$\Rightarrow a = 69$
Also, (a-d) (a) = 4623

$\Rightarrow (69 - d) 69 = 4623$

$69 - d = 67$

$d = 2$
So, A.P. = (a-d), a, (a + d)

$= (69-2), 69, (69 + 2)$

$= 67, 69, 71$
Hence, 207 can be divided into 67, 69, 71 which form three terms of an A.P.

Find the sum of the two middle most terms of an A.P. $\dfrac{-4}{3}, -1, \dfrac{-2}{3}, ..., 4\dfrac{1}{3}$ .

Main concept used (i) Finding the numbers of terms, i.e., n (ii) median of n

Given A.P. is

$\dfrac{-4}{3}, -1, \dfrac{-2}{3}, ..., \dfrac{13}{3}$ .

Here,

$a = \dfrac{-4}{3}, d = \dfrac{-1}{1} - (\dfrac{-4}{3}) = \dfrac{-1}{1} + \dfrac{4}{3}$

$\Rightarrow d = \dfrac{1}{3}$

And,

$a_n = \dfrac{13}{3}$

$\Rightarrow a + (n-1) d = \dfrac{13}{3}$

$\Rightarrow \dfrac{-4}{3}+ (n-1) (\dfrac{1}{3}) = \dfrac{13}{3}$

$\Rightarrow n -1 = 13 + 4$

$\Rightarrow n = 18$

So, the middle most terms in 18 terms =

$(\dfrac{18}{2} ) th$ and

$(\dfrac{18}{2} ) th + 1$

= 9th and 10 th terms are middle most

So, the required sum =

$a_9 + a_{10}$

$= a + (9-1) d + a + (10-1) d$

$= 2a + 8d + 9d = 2a + 17d = 2(\dfrac{-4}{3}) + 17 (\dfrac{1}{3}) = \dfrac{-8+17}{3} = 3$

Hence, the sum of two middle most terms, i.e.,

$a_9 + a_{10} = 3$

How many numbers lie between 10 and 300, which when divided by 4 leave a reminder 3?

Main concept used: Find the least and the largest required number between 10 and 300 and make an A.P.
The least number between 10 and 300 which leaves remainder 3 after dividing by 4 is 11. The largest number between 10 and 300 which leaves remainder 3 on dividing by 4 is 296 + 3 = 299.
So, 1st term or number = 11, llnd term or number = 15
IlIrd term or number = 19, last term or number = 299

$\therefore$ A.P. becomes 11, 15, 19 , .... , 299
Here,

$a_n = 299, a = 11 , d = 15-11 = 4, n= ?$
Now, a + (n - 1) d = 299

$\Rightarrow 11 + (n-1) 4 = 299$

$\Rightarrow n-1 = 72$

$\Rightarrow n = 73$
Hence, the required numbers between 10 and 300, which when divided by 4 leave a remainder 3 are 73.

Kanika was given her pocket money on Jan.She puts Rs.1 on day 1, Rs. 2 on day 2, Rs.3 on clay 3, and continued doing so till the end of the month, from this money into her piggy bank. She also spent Rs.204 of her pocket money, and found that at the end of the month she still had Rs.100 with her. flow much was her pocket money for the month?

Let the pocket money of Kanika for the month be 2 x.
Out of x, the money which she deposited in piggy bank and spent = Rs 204
Money put in piggy bank from Jan. 1 to Jan. 31 = 1 + 2 + 3 + 4 + ... + 31
So, a = 1, d = 1. n = 31
Now,

$S_{31} = \dfrac{31}{2} [2(1) + (31-1)(1)]$

$= \dfrac{31}{2} [2 + 30]$

$\Rightarrow S_{31} = \dfrac{31 \times 32}{2} = 31 \times 16 \Rightarrow S_{31} = 496$

$\therefore$ Money deposited in piggy bank = Rs 496
Money spent = Rs 204
Money which she still have = Rs 100

$\therefore x - 496 - 204 = 100$

$\Rightarrow x = 100 + 496 + 204= 800$
Hence, her monthly pocket money is Rs. 800.

Find whether 55 is a term of the A.P. : 7, 10, 13, .... or not. If yes, find which term it is.

Main concept used: 55 will be nth term of the given A.P. if value of n is a natural number.
Here, a = 7, d= 10 - 7 = 3
Let 55 be the nth term of the given A.P.

$\therefore a_n = 55$ [Assumed]

$\Rightarrow 7 + (n-1) 3= 55$ [Rs.

$a_n = a + (n-1) d$ ]

$(n-1) 3 = 55-7$

$\Rightarrow (n-1) =\frac{48}{3}$

$\Rightarrow (n-1) = 16$

$\Rightarrow n = 17$ , which is a natural number.
Hence, 55 is the 17th term of the given A.P.

How many terms of the A.P.: -15, -13, -11, ...., are needed to make the sum -55?

Given A.P. is

$-15, -13, -11, ....$

$\therefore S_n = -55, a = -15, n = ?$

$d = -13 - (-15) = -13 + 15 = 2$

$d = 2$
But

$S_n$

$= -55$

$\Rightarrow \frac{n}{2}[2a + (n-1)d] = -55$

$\Rightarrow n [2(-15) + (n-1) 2] = -55 \times 2$

$\Rightarrow n [-30 + 2n -2 ] + 110 = 0$

$\Rightarrow -30 n + 2n^2 -2 n + 110 0$

$\Rightarrow n^2 - 16 n + 55 = 0$

$\Rightarrow n^2 - 11n -5n + 55 = 0$

$\Rightarrow n(n-11) -5 (n-11) = 0$

$\Rightarrow (n-11)(n-5) = 0$

$\Rightarrow n = 11 \ or \ n = 5$
So,

$5$ or

$11$ terms of A.P. are needed to make the sum

$-55$

In an A.P., if $S_n = n(4n + 1)$ then find the A.P.

Main concept used :

$a_1 = S_1 , a_2 = S_2 - S_1, a_3 = S_3 - S_2$

$S_n = n (4n +1) = 4n^2 + n$ [Given]

$a_n = S_n - S_{n-1}$

$\Rightarrow a_n = [4n^2 + n] -[4(n-1)^2 + (n-1)]$

$\Rightarrow 4n^2 + n = [4(n^2 + 1 - 2n ) + n-1]$

$\Rightarrow 4n^2 + n - 4n^2 + 7n - 3$

$\Rightarrow a_n = 8n - 3$

$\therefore a_1 = 8(1) -3 = 8-3 = 5$

$a_2= 8(2) - 3 = 13$

$a_3 = 8(3) -3 = 21$

$a_4 = 8(4) - 3 = 29$
Hence the required A.P. is 5, 13, 21, 29,...

For the following sequence, write the first term and common difference if it is an AP:
$6,3,0,-3,$ $...$

In general, for an AP

$a_1,a_2,....,a_n$ , we have

$d = a_{k + 1} - a_k$

where

$a_{k + 1}$ and

$a_k$ are the

$(k + 1)^{th}$ and

$k^{th}$ terms respectively

For the sequence of numbers:

$6,3,0,-3,...$

$a_2 - a_1 = 3 - 6 = -3$

$a_3 - a_2 = 0 - 3 = -3$

$a_4 - a_3 = -3 - 0 = -3$

Here, the difference of any two consecutive terms in each case is

$-3$ .

So,the given sequence is an

$AP$ whose first term is

$6,$ and the common difference is

$-3$ .

Jaspal Singh repays his total loan of Rs.118000 by paying every month starting with the first installment of Rs.If he increases the installment by Rs.100 every month, what amount will be paid by him in the $30^{th}$ installment? What amount of loan does he still have to pay after the $30^{th}$ installment?

Monthly installment paid by Jaspal Singh are 1000, 1100, 1200.... 30 terms

$\therefore$ a = 1000, d =100,

$a_n = ?$ , n - 30 ]

$\Rightarrow a_n = a + (n -1)d = 1000 + (30 - 1) 100$
= 100[10 + 29]= 3900
So, the amount paid by him in 30th instalment = Rs. 3900.
Total amount of all 30 instalments paid = 1000 + 1100 + 1200 + .....+ 3900
Here, a= 1000, d= 100, n = 30

$\therefore S_n = \dfrac{n}{2}[2a+(n-1)d]$

$\Rightarrow S_{30} = \dfrac{30}{2} [ 2 \times 1000 + (30-1) 100]$

$= 15 [2000 + 2900]$

$\Rightarrow S_{30} = 15 \times 4900 = Rs 73500$
So. the loan amount left after 30th instalment = Rs 118000 - Rs 73500 =Rs 44500
Hence, he still has to pay Rs 44500 after 30th instalment.

$-1.2,-3.2,-5.2,-7.2,...$

We have,

$a_2 - a_1 = -3.2 - (-1.2) = -3.2 + 1.2 = -2.0$

$a_3 - a_2 = -5.2 - (-3.2) = -5.2 + 3.2 = -2.0$

$a_4 - a_3 = -7.2 - (-5.2) = -7.2 + 5.2 = -2.0$

i.e.

$a_{k + 1} - a_k$ is the same every time

So, the given list of numbers forms an AP with the common

difference

$d = -2$

Now, we have to find the next three terms.

We have

$a_1 = -1.2 ,a_2 = -3.2,a_3 = -5.2$ and

$a_4 = -7.2$

Now,we will find

$a_5,a_6$ and

$a_7$

So,

$a_5 = -7.2 + (-2) = -7.2 - 2.0 = -9.2$

$a_6 = -9.2 + (-2) = -9.2 - 2.0 = -11.2$

and

$a_7 = -11.2 + (-2) = -11.2 - 2.0 = -13.2$

Hence,the next three terms are

$-9.2,-11.2$ and

$-13.2$

For the following sequence, write the first term and common difference if it is an AP:
$147,148,149,150,$ $...$

In general,for an AP

$a_1,a_2,....,a_n,$ we have

$d = a_{k + 1} - a_k$

where

$a_{k + 1}$ and

$a_k$ are the

$(k + 1)^{th}$ and

$k_{th}$ terms respectively.

For the list of numbers:

$147,148,149,150,...$

$a_2 - a_1 = 148 - 147 = 1$

$a_3 - a_2 = 149 - 148 = 1$

$a_4 - a_3 = 150 - 149 = 1$

Here,the difference of any two consecutive terms in each case is

$1.$

So,the given list is an AP whose first term

$a$ is

$147,$ and common difference

$d$ is

$1.$

Check whether the following list of numbers form A.P. or not. If they form an A.P., find the common difference $d$ :
$-2,2,-2,2,-2,...$

We have,

$a_2 - a_1 = 2 - (-2) = 2 + 2 = 4$

$a_3 - a_2 = -2 - 2 = -4$

$a_4 - a_3 =2 - (-2) = 2 + 2 = 4$

i.e.

$a_{k + 1} - a_k$ is not same every time.

So,the given list of numbers do not forms an AP.

Check whether the following list of numbers form an A.P. or not. If they form an A.P., find the common difference $d$ and also write its next three terms.
$a,2a,3a,4a,...$

We have,

$a_2 - a_1 = 2a - a = a$

$a_3 - a_2 = 3a - 2a = a$

$a_4 - a_3 = 4a - 3a = a$

i.e.

$a_{k + 1} - a_k$ is the same every time

So,the given list of numbers forms an AP with the common

difference

$d = a$

Now,we have to find the next three terms.

We have

$a_1 = a ,a_2 = 2a,a_3 = 3a$ and

$a_4 = 4a$

Now,we will find

$a_5,a_6$ and

$a_7$

So,

$a_5 = 4a + a =5a$

$a_6 = 5a + a = 6a$

and

$a_7 = 6a + a = 7a$

Hence,the next three terms are

$5a,6a$ and

$7a$

$4,10,16,22,...$

We have,

$a_2 - a_1 = 10 - 4 = 6$

$a_3 - a_2 = 16 - 10 = 6$

$a_4 - a_3 = 22 - 16 = 6$

i.e.

$a_{k + 1} - a_k$ is the same every time

So,the given list of numbers forms an AP with the common

difference

$d = 6$

For the following sequence, write the first term and common difference if it is an AP:
$-3.1,-3.0,-2.9,-2.8,$ $...$

In general,for an AP

$a_1,a_2,....,a_n,$ we have

$d = a_{k + 1} - a_k$

where

$a_{k + 1}$ and

$a_k$ are the

$(k + 1)^{th}$ and

$k_{th}$ terms respectively

For the list of numbers:

$-3.1,-3.0,-2.9,-2.8,...$

$a_2 - a_1 = -3.0 - (-3.1) = -3.0 + 3.1 = 0.1$

$a_3 - a_2 = -2.9 - (-3.0) = -2.9 +3.0 = 0.1$

$a_4 - a_3 = -2.8 - (-2.9) = -2.8 + 2.9 = 0.1$

Here,the difference of any two consecutive terms in each case is

$0.1$

So,the given list is an AP whose first term

$a$ is

$-3.1,$ and common difference

$d$ is

$0.1$

The students of a school decided to beautify the school on the Annual Day by fixing colourful flags on the straight passage of the school. They have 27 flags to be fixed at intervals of every 2 m. The flags are stored at the position of the middle most flag. Ruchi was given the responsibility of placing the flags.
Ruchi kept her hooks where the flags were stored. She could carry only one flag at a time. How much distance did she cover in completing this job and returning back to collect her books ? What is the maximum distance she travelled carrying a flag ?

27 flags are to be fixed at intervals of 2 m.
Position of the middle must flag =

$\dfrac{27+1}{2}$ th flag =

$\dfrac{28}{2}$ th flag = 14th flag
This means that 13 flags are to be fixed before the middlemost 14th flag and 13 flags are to be fixed after the 14th flag.
Distance between flags = 2m
Distance covered in placing the first flag = 2 + 2 = 4 m
Distance covered to place the 2nd flag = 4 + 4 = 8 m
Distance covered to place the 3rd flag = 6 + 6 = 12 m
So, the total distance covered to place 13 flags on either side is given by

$S_{13} = 4 + 8 + 12 + ... 13$ terms
Here, a =4, d = 4 , n= 13

$\therefore S_n = \dfrac{n}{2}[2a + (n-1)d]$

$\Rightarrow S_{13} = \dfrac{13}{2}[2(4) + (13-1)(4)]$

$= \dfrac{13}{2}[8+48] = \dfrac{13}{2}\times 56 = 13 \times 28$

$\Rightarrow S_{13} = 364$
Distance covered by Ruchi for other side 13 flags = 364 m
Hence, the total distance to place 27 flag and pick up her books =

$364 \times 2 = 728 m$
Maximum distance which she travelled carrying a flag = Distance covered in fixing 1st or 27th flag =

$(13 \times 2) m = 26 m$ .

The sum of the first five terms of an A.P. and the sum of the first seven terms of the same A.P. isIf the sum of the first ten terms of this A.P. is 235, find the sum of its first twenty terms.

${\textbf{Step -1:Convert the given data into mathematical equation.}}$

${\text{We have given sum of first five terms of an A}}{\text{.P}}{\text{. and sum of first 7 terms of a same A}}{\text{.P}}{\text{. is 167}}{\text{.}}$

$\Rightarrow {S_5} + {S_7} = 167 \ldots \left( 1 \right)$

${\text{Let a and d be the first term and common difference of an A}}{\text{.P}}{\text{.}}$

${\text{So, equation }}\left( 1 \right)$ ${\text{can be written as:}}$

$\Rightarrow\dfrac{5}{2}\left[ {2a + \left( {5 - 1} \right)d} \right] + \dfrac{7}{2}\left[ {2a + \left( {7 - 1} \right)d} \right] = 167$ $\mathbf{\left[\because {{S_n} = {\dfrac{n}{2}\left[ {2a + \left( {n - 1} \right)d} \right]}} \right]}$

$\Rightarrow 5\left[ {2a + 4d} \right] + 7\left[ {2a + 6d} \right] = 167 \times 2$

$\Rightarrow 10a + 20d + 14a + 42d = 334$

$\Rightarrow 24a + 62d = 334$

$\Rightarrow 12a + 31d = 167 \ldots \left( 2 \right)$

${\text{Also, it is given that, sum of first 10 terms of the same A}}{\text{.P}}{\text{. is 235}}{\text{.}}$

$\Rightarrow {S_{10}} = 235$

$\Rightarrow \dfrac{{10}}{2}\left[ {2a + \left( {10 - 1} \right)d} \right] = 235$ $\mathbf{\left[\because {{S_n} = {\dfrac{n}{2}\left[ {2a + \left( {n - 1} \right)d} \right]}} \right]}$

$\Rightarrow 5\left[ {2a + 9d} \right] = 235$

$\Rightarrow 2a + 9d = 47 \ldots \left( 3 \right)$

${\textbf{Step -2:Solve the obtained equations }}\left(\mathbf 2 \right)\& \left(\mathbf 4 \right)$

${\text{Multiply equation}}\left( 3 \right){\text{by }}6{\text{ and subtract it from equation }}\left( 2 \right)$

$\Rightarrow 12a + 31d - 6\left( {2a + 9d} \right) = 167 - 6\left( {47} \right)$

$\Rightarrow 12a + 31d - 12a - 54d = 167 - 282$

$\Rightarrow 31d - 54d = 167 - 282$

$\Rightarrow - 23d = - 115$

$\Rightarrow d = 5$

${\text{Substitute the value of }}d{\text{ in equation }}\left( 3 \right){\text{ we get}}$

$\Rightarrow 2a + 9\left( 5 \right) = 47$

$\Rightarrow 2a + 45 = 47$

$\Rightarrow 2a = 47 - 45$

$\Rightarrow 2a = 2$

$\Rightarrow a = 1$

${\textbf{Step 3:Using the known values of }}\mathbf a{\textbf{ and }}\mathbf d{\textbf{ to find the sum of first }}\mathbf {20}{\textbf{ numbers in A.P.}}$

$\Rightarrow {S_{20}} = \dfrac{{20}}{2}\left[ {2 \times 1 + \left( {20 - 1} \right)5} \right]$ $\mathbf{\left[\because {{S_n} = {\dfrac{n}{2}\left[ {2a + \left( {n - 1} \right)d} \right]}} \right]}$

$\Rightarrow {S_{20}} = 10\left[ {2 + \left( {19} \right)5} \right]$

$\Rightarrow {S_{20}} = 10\left[ {97} \right]$

$\Rightarrow {S_{20}} = 970$

${\textbf{Hence, the sum of first twenty numbers of the A.P. is 970.}}$

If the number of terms of an A.P. is $2n +3,$ then find the ratio of the sum of odd terms to the sum of even terms.

Given: Total number of terms

$= 2n + 3$

Let the first term

$= a$

and the common difference

$= d$

Then,

$a_k = a + (k - 1)d ....(i)$

Let

$S_1$ and

$S_2$ denote the sum of all odd terms and the sum of

all even terms respectively.

$2n+3$ terms number of odd terms and even terms are

$n+2$ and

$n+1$ respectively.

Then,

$S_1 = a_1 + a_3 + a_5 ...+ a_{2n + 3}$

$= \dfrac{n + 2}{2} \{a_1 +a_{2n +3} \}$

$= \dfrac{n + 2}{2} \{a + a +(2n + 3 - 1)d \}$

[using

$(i)$ ]

$= \dfrac{n + 2}{2} \{2a + 2nd + 2d \}$

$= (n + 2) (a + nd + d) ...(ii)$

And,

$S_2 =a_2 + a_4 + a_6 +... + a_{2n + 2}$

$= \dfrac{n + 1}{2} \{a_2 + a_{2n + 2}\}$

$= \dfrac{n + 1}{2} [(a + d) + \{a + (2n + 2 - 1)d]$

[using

$(i)$ ]

$= \dfrac{n + 1}{2} \{2a + 2nd + 2d\}$

$= (n + 1)(a + nd + d) ...(iii)$

$\therefore \dfrac{S_1}{S_2} = \dfrac{(n + 2)(a + nd+d)}{(n+1)(a + nd+d)} \\= \dfrac{n + 2}{n + 1}$

If the sum of $n$ terms of an A.P. is $3n^2 + 5n$ and its $m^{th}$ term
is $164,$ find the value of $m.$

$S_n = 3n^2 + 5n$

Taking

$n = 1,$ we get

$S_1 = 3(1)^2 + 5(1)$

$\Rightarrow S_1 = 3 + 5$

$\Rightarrow S_1 = 8$

$\Rightarrow a_1 = 8$

Taking

$n = 2,$ we get

$S_2 = 3(2)^2 + 5(2)$

$\Rightarrow S_2 = 12 + 10$

$\Rightarrow S_2 = 22$

$\therefore a_2 = S_2 - S_1 = 22 - 8 = 14$

Taking

$n = 3,$ we get

$S_3 = 3(3)^2 + 5(3)$

$\Rightarrow S_3 = 27 + 15$

$\Rightarrow S_3 = 42$

$\therefore a_3 = S_3 - S_2 = 42 - 22 = 20$

So,

$a = 8,$

$d = a_2 - a_1 = 14 - 8 = 6$

Now, we have to find the value of

$m$

$a_n = a + (n - 1)d$

$\Rightarrow a_m = 8 + (m - 1)6$

$\Rightarrow a_m = 8 + 6m - 6$

$\Rightarrow 164 = 2 + 6m$

$\Rightarrow 162 = 6m$

$\Rightarrow m = 27$

Find the number of terms of the A.P.
$41, 38, 35, ..., 8?$

Here,

$a = 41, d = 38 - 41 = -3$ and

$a_n = 8$

Where

$a_n = a + (n - 1)d$

$\Rightarrow 8 = 41 + (n -1)(-3)$

$\Rightarrow 8 = 41 - 3n + 3$

$\Rightarrow 8 = 44 - 3n$

$\Rightarrow 8 - 44 = -3n$

$\Rightarrow -36 = -3n$

$\Rightarrow n = \dfrac{-36}{-3} = 12$

Hence, the number of the terms in the given AP is

$12$

Find the number of terms of the A.P.
$7, 11, 15, ..., 139?$

Here,

$a = 7, d = 11 - 7 = 4$ and

$a_n = 139$

Where

$a_n = a + (n - 1)d$

$\Rightarrow 139 = 7 + (n -1)(4)$

$\Rightarrow 139 = 7 + 4n - 4$

$\Rightarrow 139 = 3 + 4n$

$\Rightarrow 139 - 3 = 4n$

$\Rightarrow 136 = 4n$

$\Rightarrow n = \dfrac{136}{4} = 34$

Hence, the number of the terms in the given AP is

$34$

Check whether $1^2,2^2,3^2,4^2,....$ is an AP or not.

We have,

$a_2 - a_1 = 2^2 - (1)^2 = 4 - 1 = 3$

$a_3 - a_2 = 3^2 - (2)^2 = 9 - 4 = 5$

$a_4 - a_3 = 4^2 - (3)^2 = 16 - 9 = 7$

i.e.

$a_{k + 1} - a_k$ is not same every time.

So,the given list of numbers do not forms an AP.

Which term of the A.P. $4, 9, 14, ...\ \ is\ 89?$ Also, find its sum.

Let

$a_n = 89$

$= 4, 9, 14, ...89$

Here First term

$, a = 4$

Common difference

$, d = 14 - 9 = 5$

$nth$ term of an AP is

$a_n = 89$

We know that,

$a_n = a + (n - 1)d$

$\Rightarrow 89 = 4 + (n - 1)5$

$\Rightarrow 89 - 4 =(n - 1)5$

$\Rightarrow 85 = (n - 1)5$

$\Rightarrow 17 = n - 1$

$\Rightarrow 17+1 = n$

$\Rightarrow 18 = n$

So,

$89$ is the

$18^{th}$ term of the given AP

Now, we find the sum of

$4 + 9 + 14 + ...+ 89$

We know that,

$S_n = \dfrac{n}{2}[2a + (n - 1)d]$

$\Rightarrow S_{18} = \dfrac{18}{2}[2 \times 4 + (18 - 1)5]$

$\Rightarrow S_{18} = 9[8 +17 \times 5]$

$\Rightarrow S_{18} = 9[8 + 85]$

$\Rightarrow S_{18} = 9 \times 93$

$\Rightarrow S_{18} = 837$

Hence, the sum of the given AP is

$837.$

How many terms of the A.P. $-6, -\dfrac{11}{2}, -5 ...$ are needed to get the sum $-25?$

A.P

$= -6, -\dfrac{11}{2}, -5 ...$

Here,

$a =-6,$

$d = -\dfrac{11}{2} - -(6) = \dfrac{-11 + 12 }{2} = \dfrac{1}{2}$

and

$S_n = -25$

We know that,

$S_n = \dfrac{n}{2}[2a + (n - 1)d]$

$\Rightarrow -25 = \dfrac{n}{2}[2 \times (-6) + (n - 1)\left(\dfrac{1}{2}\right)]$

$\Rightarrow -25 = \dfrac{n}{2}\left[\dfrac{-24 + n - 1}{2}\right]$

$\Rightarrow -25 = \dfrac{n}{4}[-25 + n]$

$\Rightarrow -100 = n[-25 + n]$

$\Rightarrow n^2 - 25n + 100 = 0$

$\Rightarrow n^2 -20n -5n + 100 = 0$

$\Rightarrow n(n - 20) - 5(n - 20) = 0$

$\Rightarrow n - 5 = 0$ or

$n =20$

$\Rightarrow n = 5$ or

$n = 20$

So,

$n = 5$ or

$20$

If the sum of first $m$ terms of an A.P. is the same as the sum of its first $n$ terms, show that the sum of its first $(m + n)$ terms is zero

Let the first term be

$a$ and common difference of the given

AP is

$d.$

Given:

$S_m = S_n$

$\Rightarrow \dfrac{m}{2}[2a + (m - 1)d] = \dfrac{n}{2} [2a +(n - 1)d]$

$\Rightarrow 2am + md(m - 1) = 2an + nd(n - 1)$

$\Rightarrow 2am - 2an + m^{2}d - md -n^{2}d + nd = 0$

$\Rightarrow 2a (m - n) + d[(m^2 - n^2) - (m - n)] = 0$

$\Rightarrow 2a (m - n) + d[(m - n)(m + n) - (m - n)] = 0$

$\Rightarrow (m - n) [2a + \{(m +n) - 1\}d] = 0$

$\Rightarrow 2a + (m + n - 1)d = 0 \ [\because m - n \ne 0] ...(i)$

Now,

$S_{m + n} = \dfrac{m + n}{2} [2a + {(m + n) - 1}d] = 0$

$\Rightarrow S_{m + n} = \dfrac{m + n}{2} \times 0$ [using

$(i)$ ]

$\Rightarrow S_{m + n} = 0$

Hence proved

How many terms of the A.P. $3, 5, 7,9, ...$ must be added to
get the sum $120?$

$AP = 3,5,7,9,...$

Here,

$a = 3, d = 5 - 3 = 2$ and

$S_n = 120$

We know that,

$S_n = \dfrac{n}{2}[2a + (n - 1)d]$

$\Rightarrow 120 = \dfrac{n}{2}[2 \times 3 + (n - 1)(2)]$

$\Rightarrow 120 = \dfrac{n}{2}[6 + 2n - 2]$

$\Rightarrow 120 = \dfrac{n}{2}[4 + 2n]$

$\Rightarrow 120 = n[2 + n]$

$\Rightarrow n^2 + 2n - 120 = 0$

$\Rightarrow n^2 + 12n - 10n - 120 = 0$

$\Rightarrow n(n + 12) - 10(n + 12) = 0$

$\Rightarrow(n - 10)(n + 12) = 0$

$\Rightarrow n - 10 = 0$ or

$n + 12 = 0$

$\Rightarrow n = 10$ or

$n = -12$

But number of terms can't be negative.So,

$n = 10$

Hence,for

$n = 10$ the sum is

$120$ for the given AP.

Find the number of terms of the A.P.
$6, 10, 14, 18, ..., 174?$

Here,

$a = 6, d = 10 - 6 = 4$ and

$a_n = 174$

Where

$a_n = a + (n - 1)d$

$\Rightarrow 174 = 6 + (n -1)(4)$

$\Rightarrow 174 = 6 + 4n - 4$

$\Rightarrow 174 = 2 + 4n$

$\Rightarrow 174 - 2 = 4n$

$\Rightarrow 172 = 4n$

$\Rightarrow n = \dfrac{172}{4} = 43$

Hence, the number of the terms in the given AP is

$43$

$15, 12, 9, 6, ….$

$15, 12, 9, 6$ , ….

Finding the difference between the terms,

$d_1 = 12 – 15 = -3$

$d_2 = 9 – 12 = -3$

$d_3 = 6 – 9 = -3$

As $d_1 = d_2 = d_3$ , the given sequence is in arithmetic progression.

$-10, -6, -2, 2...$

$a_1=10,a_2=-6,a_3=2,a_4=2$

$a_2-a_1=-6-(-10)=4$

$a_3-a_4=-2-(-6)=4$

$a_4-a_3=-6-(-10)=4$

$\therefore a_{k+1}-a_k$ is same everytime

$\therefore$ The given list of numbers form an AP with commom difference,

$d=4$

$\therefore$ The next three terms are

$2+4=6$

$6+4=10$

$10+4=14$

$\therefore$ The terms are

$-10,-6,-2,2,6,10,14,....$

$0.6, 1.7, 2.8, 3.9....$

$a_1=0.6,a_2=1.7$

$d=a_2-a_1=1.7-0.6=1.1$

$\therefore$ The first term,

$a_1=0.6$
The common difference,

$d=1.1$

For the following AP, write the first term and the common difference:
$3,1, -1, -3...$

$\sqrt{2},\sqrt{8},\sqrt{18},\sqrt{32},.....$

$\sqrt{2}, 2\sqrt{2}, 3\sqrt{2}, 4\sqrt{2},5\sqrt{2},6\sqrt{2},7\sqrt{2},.....$ ;

$\sqrt{2},\sqrt{8},\sqrt{18},\sqrt{32},.....$

$\Rightarrow \sqrt{2},2\sqrt{2},3\sqrt{2},4\sqrt{2},.....$

$a_1=\sqrt{2},a_2=2\sqrt{2},a_3=3\sqrt{2},a_4=4\sqrt{2}$

$a_2-a_1=2\sqrt{2}-\sqrt{2}=\sqrt{2}$

$a_3-a_2=3\sqrt{2}-2\sqrt{2}=\sqrt{2}$

$a_4-a_3=4\sqrt{2}-3\sqrt{2}=\sqrt{2}$

$\therefore a_{k+1}-a_k$ is same everytime

$\therefore$ The given list of numbers form an AP with commom difference,

$d=a$

$\therefore$ The next three terms are

$a_5 =4\sqrt{2}+\sqrt{2}=5\sqrt{2}$

$a_6=5\sqrt{2}+\sqrt{2}=6\sqrt{2}$

$a_7 = 6\sqrt{2}+\sqrt{2} =7\sqrt{2}$

Find the common difference of the following AP:
$-10, -6, -2, 2,...$

The given sequence is an A.P.

$\therefore$ Common difference

$=$ second term

$-$ first term

$=(-6)-(-10)$

$=4$

Check whether the following sequence is an A.P. or not. If it is an A.P., find the common difference.
$2,\dfrac{5}{2},3,\dfrac{7}{2},...$

The given sequence is,

$2,\dfrac{5}{2},3,\dfrac{7}{2},...$

$d_1=\dfrac{5}{2}-2=\dfrac{1}{2}$

$d_2=3-\dfrac{5}{2}=\dfrac{1}{2}$

$d_3=\dfrac{7}{2}-3=\dfrac{1}{2}$

Now,

$d_1= d_2 = d_3$

So, the given sequence is an A.P.

The common difference of the given A.P. is

$\dfrac{1}{2}$ .

$\sqrt{3},\sqrt{6},\sqrt{9},\sqrt{12},.....$

AP;

$\sqrt{3},\sqrt{6},\sqrt{9},\sqrt{12},.....$

$a_1=\sqrt{3},a_2=\sqrt{6},a_3=\sqrt{9},a_4=\sqrt{12}$

$a_2-a_1=\sqrt{6}-\sqrt{3}$

$a_3-a_2=\sqrt{9}-\sqrt{6}=3-\sqrt{6}$

$a_4-a_3=\sqrt{12}-\sqrt{9}=2\sqrt{3}-\sqrt{3}$

$a_2-a_1 \neq a_3-a_2 \neq a_4-a_3$

$\therefore a_{k+1}-a_k$ is not same everytime

$\therefore$ The given list of numbers does not form an AP.

$\dfrac{1}{3},\dfrac{5}{3},\dfrac{9}{3},\dfrac{13}{3},....$

$a_1=\dfrac{1}{3},a_2=\dfrac{5}{3}$

$d=a_2-a_1=\dfrac{5}{3}-\dfrac{1}{3}=\dfrac{5-1}{3}=\dfrac{4}{3}$

$\therefore$ The first term,

$a_1=\dfrac{1}{3}$

The common difference,

$d=\dfrac{4}{3}$

Check whether the following sequence is an arithmetic progression or not:
$1/2, 1/3, 1/4, 1/5, ….$

$1/2, 1/3, 1/4, 1/5, ….$

Finding the difference between the terms,

$d_1 = 1/3 – 1/2 = -1/6$

$d_2 = 1/4 – 1/3 = -1/12$

$d_3 = 1/5 – 1/4 = -1/20$

As $d1 \neq d2 \neq d3$ , the given sequence is not in arithmetic progression.

Find the first term and common difference for the A.P.
$127,135,143,151,..$

First term

$=127$

Common difference

$=$ second term

$-$ first term

$=135-127$

$=8$

Find the common difference of the following AP:
$0,-4,-8,-12,..$

The given sequence is an A.P.

$\therefore$ Common difference

$=$ second term

$-$ first term

$=(-4)-(-0)$

$=-4$

Find the common difference of the following AP:
$-\dfrac{1}{5},-\dfrac{1}{5},-\dfrac{1}{5},...$

The given sequence is an A.P.

$\therefore$ Common difference

$=$ second term

$-$ first term

$=\left(-\dfrac{1}{5}\right) - \left(-\dfrac{1}{5}\right)$

$=0$

Check whether the following sequence is $A.P?$ If it is an A.P., then find the common difference.
$127,132,137,....$

The given sequence is an A.P., as common difference is same.

Common difference

$=$ second term

$-$ first term

$=(132)-(127)$

$=5$

Find the first term and common difference for the A.P.
$0.6,0.9,1.2,1.5,...$

Given first term

$=0.6$ , second term

$=0.9$

Common difference

$=$ second term

$-$ first term

$=0.9-0.6$

$=0.3$

Find the first term and common difference for the $A.P$ .
$5,1,-3,-7,...$

First term

$=5$

Common difference

$=$ second term

$-$ first term

$=1-5$

$=-4$

Write the correct number in the given boxes on the basis of the following A.P.
$70, 60, 50, 40, ...$
Here $t_{1}=\square, t_{2}=\square, t_{3}=\square ,....$
$\therefore a=\square, d=\square$

Given AP is

$70, 60, 50, 40, ...$

Here

$t_{1}=\boxed{70}, t_{2}=\boxed{60}, t_{3}=\boxed{50} ,....$

$a$ is nothing but the first term of an A.P.

Common difference is the difference between two consecutive terms.

$d=60-70$

$\Rightarrow x=-10$

$\therefore a=\boxed{70}, d=\boxed{-10}$

Find the first term and common difference for the A.P.
$\dfrac{1}{4}, \dfrac{3}{4},\dfrac{5}{4},\dfrac{7}{4},...$

First term

$=\dfrac{1}{4}$

Common difference

$=$ second term

$-$ first term

$=\dfrac{3}{4}-\dfrac{1}{4}\\$

$=\dfrac{1}{2}$

Write the correct number in the given boxes on the basis of the $A.P:$ $-3, -8, -13, -18, ....$

Here $t_{3}=\square, t_{2}=\square, t_{4}=\square, t_{1}=\square,$ $t_{2}-t_{1}=\square, t_{3}-t_{2}=\square$

$\therefore a=\square, d=\square$

Given AP is

$-3, -8, -13, -18,...$

Here

$a=\boxed{-3};$

$d=\boxed{-5}$

Therefore

$t_{3}=\boxed{13},\$

$t_{2}=\boxed{-8},\$

$t_{4}=\boxed{-18},\$

$t_{1}=\boxed{-3}$

$t_{2}-t_{1}=-8-(-3)=\boxed{-5},$

$t_{3}-t_{2}=-13-(-8)=\boxed{-5}$

If the sum of $n$ term of an A.P is $3n^{2} + 5n$ and its $m^{th}$ term is 164 , find the value of m

$Given$ :

$3n^{2} + 5n$ ..............(1)

$and\space$

$m^{th} term = 164$

$\Rightarrow 164 = a + (m - 1) d ......... (2)$

$Substitute\space n = 1\space , 2\space in\space ( 1)we\space get\space$

$S_{1} = 3 (1)^{2} + 5 (1) = 3 + 5 = 8$
and

$S_{2} = 3 (2)^{2} + 5 (2) = 12 + 10 = 22$

$We\space know\space that\space$

$S_{1}$

$= \space first\space term\space = a\space and$

$S_{2} =$

$Sum\space of\space two\space terms\space$ .

$\therefore S_{1} = 8 = a \space and\space a + (a + d) = 22$

$\Rightarrow d = 6$

$Substituting\space the\space value\space of\space a,\space d\space in\space (2) \space , we\space get\space$

$164 = 8 +(m -1)(6)$

$\implies 164=8 + 6m - 6 = 2 + 6m$

$\Rightarrow 162 = 6m \Rightarrow m = \dfrac{162}{6} = 27$

How many terms of A.P , $- 6 , \frac{-11}{2} , -5$ .......... are needed to give the sum - 25 ?

$Given$

$a_{1} = - 6 , d = -\dfrac{11}{2} - (-6) = \dfrac{1}{2}$

$and$

$S_{n} = - 25$

$We\space have$

$S_{n} = \dfrac{n}{2} \left [ 2a + (n - 1) d \right ]$

$\Rightarrow - 25 = \dfrac{n}{2}\left [ 2 (-6)+ (n - 1)\left ( \dfrac{1}{2} \right ) \right ]$

$-25\times 4=n(-24+n-1)$

$n^2-25n+100=0$

$(n-5)(n-20)=0$

$n=5, \space n=20$

Check whether the following sequence is an AP or not. If it is an AP, find the common difference 'd' and write three more terms.

$2, \dfrac{5}{2}, 3, \dfrac{7}{2},......$

$2, \dfrac{5}{2}, 3, \dfrac{7}{2},.....$

$d = a_{2} - a_{1} = \dfrac{5}{2} - \dfrac{2}{1} = \dfrac{5 - 4}{2} = \dfrac{1}{2}$

$d = a_{3} - a_{2} = \dfrac{3}{1} - \dfrac{5}{2} = \dfrac{6 - 5}{2} = \dfrac{1}{2}$

Here 'd' is constant.

$\therefore$ the given list numbers form an AP.

Next three terms are:

$4, \dfrac{9}{2}, 5$

For the following APs, write the first term and the common difference :
$3, 1, -1, -3,......$

$3, 1, -1, -3$

First term,

$a = 3,$

Common difference,

$d = a_{2} - a_{1} = 1 - 3$

$d = -2.$

Define arithmetic progression .

Let

$a_{1} ,a_{2},a_{3}$ be a sequence if

$a_{2} - a_{1} = a_{3} - a_{2} = a_{4} - a_{3}........$ i . e , the difference between any two consecutive terms is always same constant , then the sequence is called an arithmetic progression . (AP). The constant difference

$a_{2} - or a_{3} - a_{2}$ etc is called common difference and it is denoted by 'd' .

For the following APs, the common difference is ____.
$\dfrac{1}{2}, \dfrac{1}{2}, \dfrac{1}{2}, \dfrac{1}{2},.....$

$\dfrac{1}{2}, \dfrac{1}{2}, \dfrac{1}{2}, \dfrac{1}{2},.....$

First term,

$a = \dfrac{1}{2}$

Common difference,

$d = a_{2} - a_{1}$

$= \dfrac{1}{2} - \dfrac{1}{2}$

$d = 0$

Find the common difference 'd' of the following AP:
$-1.2, -3.2, -5.2, -7.2$

$-1.2, -3.2, -5.2, -7.2$

$d = a_{2} - a_{1} = -3.2 - (-1.2) = -3.2 + 1.2$

$d = -2$

$d = a_{3} - a_{2} = -5.2 - (-3.2) = -5.2 + 3.2$

$d = -2$

Here d is constant.

$\therefore$ This is an Arithmetic Progression.

Check whether the following sequence of an AP or not:
$1^{1}, 5^{2}, 7^{2}, 73,....$

$1^{1}, 5^{2}, 7^{2}, 73,....$

$1, 25, 49, 73,......$

$a_{1}, a_{2} = 25, a_{3} = 49, a_{4} = 73$

$d = a_{2} - a_{1} = 25 - 1$

$d = 24$

$d = a_{3} - a_{2} = 49 - 25$

$d = 24$

$d = a_{4} - a_{3} = 73 - 49$

$d = 24$

Here 'd' is constant.

$\therefore$ Given set of numbers form an A.P.

$2, 4, 8, 16,.....$

$2, 4, 8, 16.......$

$d = a_{2} - a_{1} = 4 - 2 = 2$

$d = a_{2} - a_{1} = 8 - 4 = 4$

Here 'd' is not constant.

$\therefore$ the given list of numbers does not form an AP.

Let the sum of $n, 2n, 3n$ terms of an A.P. be $S_{1} , S_{2}$ and $S_{3}$ respectively, show that $S_{3} = 3 (S_{2} - S_{2})$

Let 'a' be the first term of d be the common difference of A.P

$\therefore S_{1} = \dfrac{n}{2} \left [ 2a + (n - 1) d \right ]$

$S_{2} = \dfrac{2n}{2} \left [ 2a + ( 2n - 1)d \right ]$

$S_{3} = \dfrac{3n}{2} \left [ 2a + ( 3n - 1) d \right ]$

$(2) - (1) \Rightarrow S_{2} - S_{1}$

$= \dfrac{2n}{2} \left [ 2a + (2n - 1)d \right ] - \dfrac{n}{2} \left [ 2a + (n- 1)d \right ]$

$= \dfrac{n}{2} \left [ 2a + ( 2n - 1)d \right ] - \dfrac{n}{2}\left [ 2a +(n - 1) d \right ]$

$= \dfrac{n}{2} \left [ 2a + 3nd - d \right ]$

In an AP: given $a_{3} = 15, S_{10} = 125,$ find 'd' and $a_{10}$ .

$a_{3} = a + 2d = 15$

$\therefore a = 15 - 2d$

$S_{n} = \dfrac{n}{2} [2a + (n - 1)d]$

$S_{10} = \dfrac{10}{2} [2 (15 - 2d) + (10 - 1)d] = 125$

$= 5[30 - 4d + 9d] = 125$

$= 5[30 + 5d] = 125$

$150 + 25d = 125$

$25d = 125 - 150$

$25d = -25$

$d = \dfrac{-25}{25}$

$\therefore d = -1.$

Substituting the value of 'd'

$a = 15 - 2d$

$= 15 - 2(-1)$

$= 15 + 2$

$\therefore a = 17.$

$\therefore a_{10} = a + 9d$

$= 17 + 9(-1)$

$=17 - 9$

$\therefore a_{10} = 8$

In an AP:
given $a = 2, d = 8, S_{n} = 90,$ find 'n' and $a_{11}.$

$S_{n} = \dfrac{n}{2} [2a + (n - 1)d]$

$= \dfrac{n}{2} [2 \times 2 + (n - 1)8] = 90$

$\dfrac{n}{2} [4 + 8n - 8] = 90$

$n (8n - 4) = 90 \times 2$

$8n^{2} - 4n = 180$

$2n^{2} - n - 45 = 0$

$2n^{2} - 10n + 9n - 45 = 0$

$2n(n - 5) + 9(n - 5) = 0$

$(n - 5)(2n + 9) = 0$

$n - 5 = 0$ then

$n = 5$

$\therefore a_{n} = a + (n - 1)d$

$a_{5} = 2 + (5 - 1)8$

$= 2 + 4 \times 8$

$= 2 + 32$

$\therefore a_{5} = 34$

In an AP, given $a_{12} = 37, \ d = 3,$ find 'a' and $S_{12}.$

$a + (n - 1)d = a_{n}$

$a + (12 - 1)3 = 37$

$a + 11 \times 3 = 37$

$a + 33 = 37$

$\therefore a = 37 - 33$

$\therefore a = 4$

$S_{n} = \dfrac{n}{2} [a + a_{n}]$

$S_{12} = \dfrac{12}{2} [4 + 37]$

$= 6[4 + 37]$

$\therefore S_{2} = 246$

In an AP:
given $a_{n} = 4, d = 2, S_{n} = -14.$ Find 'n' and a.

$a_{n} = a + (n - 1)d = 4$

$a + (n - 1)2 = 4$

$a + 2n - 2 = 4$

$a + 2n = 4 + 2$

$a = 2n = 6$ ............(i)

$S_{n} = \dfrac{n}{2} [a + a_{n}] = 210$

$\dfrac{n}{2} [-2n + 6 + 4] = -14$

$\dfrac{n}{2} [-2n + 10] = -14$

$-2n^2 + 10n = -28$

$-2n^2 + 10n + 28 = 0$

$2n^2 - 10n - 28 = 0 - 14$

$2n^2 - 5n - 14 = 0$

$n^2 - 7n + 2n - 14 = 0$

$n(n - 7) + 2(n - 7) = 0$

$(n - 7)(n + 2) = 0$

$n - 7 = 0$ then

$n = 7$

$a = -2n + 6$

$= -2 \times 7 + 6$

$- 14 + 6$

$\therefore a = -8$

$\therefore n = 7, a = -8.$

In an AP:
given $a_n = 28, S_9 = 144$ and there are total $9$ terms. Find 'a'.

$S_{n} = \dfrac{n}{2} [a + a_{n}]$

$S_{9} = \dfrac{9}{2} [ a + 28] = 144$

$\dfrac{9}{2} [a + 28] = 144$

$a + 28 = 144 \times \dfrac{2}{9}$

$a + 28 = 32$

$a = 32 - 28$

$\therefore a = 4.$

Find the number of terms in the following AP:
$7, 13, 19, .........201$

$7, 13, 19,............, 201$

$a = 3, d = 13 - 7 = 6, a_{n} = 201, n = ?$

$a_{n} = a + (n - 1) d$

$3 + (n - 1) 6 = 201$

$3 + 6n - 6 = 201$

$6n - 3 = 201$

$6n = 204$

$n = \dfrac{204}{6}$

$\therefore n = 34$

In an AP:
given $a = 3, n = 8, S = 192,$ find 'd'.

$S_{n} = \dfrac{n}{2}[2a + (n - 1)d]$

$S_{8} = \dfrac{8}{2} [2 \times 3 + (8 - 1)d] = 192$

$\dfrac{8}{2} [6 + 7 \times d] = 192$

$4(6 + 7d) = 192$

$6 + 7d = 48$

$7d = 48 - 6$

$7d = 42$

$d = \dfrac{42}{7}$

$\therefore d = 6$

In an AP, given $d = 5, S_{9} = 72,$ find 'a' and $a_{9}.$

$S_{n} = \dfrac{n}{2} [2a + (n - 1)d]$

$S_{9} = \dfrac{9}{2} [2 \times a + (9 - 1)5] = 72$

$\dfrac{9}{2} [2a + 8 \times 5] = 72$

$\dfrac{9}{2}[2a + 40] = 72$

$2a + 40 = 72 \times \dfrac{2}{9}$

$2a + 40 = 16$

$2a = 16 - 40$

$2a = -24$

$a = \dfrac{-24}{2}$

$\therefore a = -12$

$a_{9} = a + (n - 1)d$

$= -12 + (9 - 1)(5)$

$= -12 + 8 \times 5$

$= -12 + 40$

$\therefore a_{9} = 28$

In an AP:
given $a = 8, a_{n} =S_{n} = 210,$ find 'n' and 'd'.

$S_{n} = \dfrac{n}{2} [a + a_{n}] = 210$

$\dfrac{n}{2}[8 + 62] = 210$

$\dfrac{n}{2} \times 70 = 21$

$n = 210 \times \dfrac{2}{70}$

$\therefore n = 6$

$a_{n} = 62$

$a_{6} = a + 5d = 62$

$8 + 5d = 62$

$5d = 62 - 8$

$5d = 54$

$d = \dfrac{54}{5}$

The third term of an A.P is $8$ and the ninth term of the A.P exceeds three times the third term by $2$ find the sum of its first $19$ terms.

We know that for an AP, nth term,

$a_n = a+(n-1)d$ , where

$a$ &

$d$ are the first term and common difference of an AP.

Since,

$a_{3} = 8$ (given)

$\therefore a + 2d = 8$ ........(i)

$a_{9} = 3(a_3) + 2$ (given)

$a + 8d = 3(8) + 2$ [by eqn (i)]

$a + 8d = 26$

$a + 2d + 6d = 26$

$8 + 6d = 26(a + 2d = 28)$

$6d = 26 - 8$

$6d = 18$

$d = \dfrac{18}{6}$

$d = 3$

Put

$d = 3$ in eqn (i)

$a + 2(3) = 8$

$a + 6 = 8$

$a = 8 - 6$

$a = 2$

$n = 19$

$S_{n} = \dfrac{n}{2} \left (2a + (n - 1)d \right )$

$S_{19} = \dfrac{19}{2} (2 \times 2 + (19 - 1)3)$

$= \dfrac{19}{2} (4 + (18)3) = \dfrac{19}{2} (4 + 54)$

$= \dfrac{19}{2} (58) = 19 \times 29$

$S_{19} = 551$

Find the number of terms in the following A.P.:
$100, 96, 92,.........,12$

$100, 96, 92, ..........., 12$

$a = 100 , d = a_{2} - a_{1}, d = 96 - 100 = -4$

$a_{n} = 12 \,\&\, n = ?$

$a_{n} = a + (n - 1)d$

$12 = 100 + (n - 1)d$

$12 - 100 = (n - 1) \times -4$

$-88 = (n - 1) \times -4$

$\dfrac{-88}{-4} = n - 1$

$n - 1 = 22$

$n = 22 + 1$

$n = 23$

If sum of $n$ terms of A.P. $1,6,11,...$ is $148$ , then find number of terms and last term.

We have

$S_n=\dfrac{n}{2}[2a+(n-1)d]$

$148=\dfrac{n}{2}[2+(n-1)5]$

$⇒296=n[5n−3]$

$⇒5n^2-3n-296=0$

$5n^2 −40n+37n−296=0$

$⇒5n(n−8)−37(n−8)=0$

$⇒(5n−37)(n−8)=0$

$∴n=8$

$no.\ of\ terms =8$

$l=a+(n−1)d$

$⇒l=1+(8−1)5$

$⇒l=1+35$

$∴l=36$

the last term is

$36$

Sum of $n$ terms of any A.P. is $n^2 + 2n$ . Find the first term and common difference.

The formula for sum of

$n$ terms of an

$A.P.$ is given by,

$S_n=\dfrac{n}{2}[2a+(n-1)d]\dots (1)$

$S_n=n^2+2n \dots (2)$

Comparing equation

$(1)$ &

$(2)$ , we get

$\dfrac{n}{2}[2a+(n-1)d]=n^2+2n$

$2an+n^2d-nd=2n^2+4n$

$(2a-d)n+n^2d=4n+2n^2$

On comparing coefficients of

$n^2$ in the above equation:

$d=2$

On comparing coefficients of

$n$ in equation

$(3)$ , we have:

$2a−d=4$

$2a=4+d$

$2a=4+2$

$2a=6$

$a=3$

Therefore, the first term,

$a=3$ and the common difference,

$d=2$ .

In an AP whose first term is $2,$ the sum of first five terms is one fourth the sum of the next five terms show that $T_{20} = -112$

$a = 2, S_{5} = \dfrac{1}{4}[S_{10} - S_{5}], T_{20} = -112$

$S_{n} = \dfrac{n}{2} [2a + (n - 1)d]$

$S_{5} = \dfrac{5}{2} [2(2) + (5 - 1)d]$

$S_{5} = \dfrac{5}{2} [4 + 4d]$

$S_{5} = 10 + 10d$ .....(i)

$S_{10} = \dfrac{10}{2} [2(2) + (10 - 1)d]$

$S_{10} = 5[4 + 9d]$

$S_{10} = 20 + 45d$ .......(ii)

$S_{5} = \dfrac{1}{4} [S_{10} - S_{5}]$

$10 + 10d = \dfrac{1}{4} [20 + 45d - 10 - 10d]$

[from (i) & (ii)]

$40 + 40d = [10 + 35d]$

$40d - 35d = 10 - 40$

$5d = -30$

$d = \dfrac{-30}{5} = -6$

$\boxed{d = -6}$

$T_{20} = a + 19d$

$= 2 + 19(-6)$

$= 2 - 114$

$T_{20} = -112$

In an arithmetic progression the sum of first $10$ terms is $175$ and the sum of the next $10$ terms is $475$ find the arithmetic progression.

$S_{10} = 175, S_{11 \,to \,20} = 475$

$S_{20} = S_{1 \,to \,10} + S_{11 \,to \,20}$

$S_{20} = 175 + 475$

$\boxed{S_{20} = 650}$
We know that,

$S_{n} = \dfrac{n}{2} [2a + (n - 1)d]$
If

$n = 10$

$S_{10} = \dfrac{10}{2} [2a + (10 - 1)d]$

$175 = 5 [2a + 9d]$

$2a + 9d = 35$ ...........(i)
If

$n = 20$

$S_{20} = \dfrac{20}{2} [2a + (20 - 1)d]$

$650 = 10 [2a + 19d]$

$2a + 19d = 65$ .......(ii)
from eqn. (i) & (ii), we get

$2a + 9d = 35$

$2a + 19d = 65$

$(-) \,(-) \,(-)$

$..........$

$0 - 10d = -30$

$\boxed{\therefore d = 3}$
from eqn. (i)

$2a + 9d = 35$

$2a = 35 - 9(3)$

$= > \boxed{2a = 8} \,\,\boxed{a = 4}$
General form of A.P is

$a, a + d, a + 2d, a + 3d.....$

$4, 4 + 3, 4 + 2(3), 4 + 3(3)......$

$4, 7, 10, 13.....$ are in A.P.

From the following sequence which are in A.P?
(i) 2, 6, 11, 17,...
(ii) 1, 1.4, 1.8, 2.2,...
(iii) -7, -5, -3, -1,...
(iv) 1, 8, 27, 64,...

Given sequence will be in A.P. Only if common difference of two consecutive terms is same.

S.N	Given sequence	Difference between first and second term	Differences between second and third term	The given sequence are in A.P. or not
(i)	2, 6, 11, 17,...	6 - 2 = 4	11 - 6 = 5	No
(ii)	1, 1.4, 1.8, 2.2,...	1.4 - 1 = 0.4	1.8 - 1.4 = 0.4	Yes
(iii)	-7, -5, -3, -1,...	(-5) - (-7) = -5 + 7 = + 2	(-3) - (-5) = - 3 + 5 = +2	Yes
(iv)	1, 8, 27, 64,...	8 - 1 = 7	27 - 8 = 19	No

Find the common difference of an AP in which $a_{18} - a_{14} = 32$

By the general term of an A.P.

we know that. when

$a=first \ term$

$n=number \ of \ terms \ in \ the \ A.P.$

$d=common \ difference$

general term

$=a+(n-1)d$

$a_{18} - a_{14} = 32$

$(a + 17d) - (a + 13d) = 32$

$a + 17d - a - 13d = 32$

$4d = 32$

$d = \dfrac{32}{4}$

$d = 8$

Check whether the following sequence is an AP or not. If it is an AP, then find its common difference and write few next terms.
$2, \dfrac{5}{2}, 3, \dfrac{7}{2}...$

Given series

$2, \dfrac{5}{2}, 3, \dfrac{7}{2}...$

Here

$a-1=2, a_2=\dfrac{5}{2}, a_3=3, a_4=\dfrac{7}{2}$

Difference between two consecutive terms

$(d)$ :

$d=a_2-a_1 =\dfrac{5}{2}-2=\dfrac{5-4}{2}=\dfrac{1}{2}$

$d=a_3-a_2=3-\dfrac{5}{2}=\dfrac{6-5}{2}=\dfrac{1}{2}$

$a_4-a_3=\dfrac{7}{3}-3=\dfrac{7-6}{2}=\dfrac{1}{2}$

$\therefore$ Difference between two consecutive is same,

$d=\dfrac{1}{2}$

$\therefore$ Given series is A.P

Next four terms are

$a_5=\dfrac{7}{2}+ \dfrac{1}{2}=\dfrac{8}{2}=4$

$a_6=4+\dfrac{1}{2}=\dfrac{8+1}{2}=\dfrac{9}{2}$

$a_7=\dfrac{9}{2}+\dfrac{1}{2}=\dfrac{10}{2}=5$

$a_8=5+\dfrac{1}{2}=\dfrac{11}{2}$

Hence

$d=\dfrac{1}{2}$ and next four terms of series are

$4,\dfrac{9}{2},5$ and

$\dfrac{11}{2}$

Find the first term and common difference for the following A.P
$-7,-9,-11,-13$

Given A.P is

$-7,-9,-11,-13$
First term

$(a_1)=-7$
Common difference

$(d)=a_2-a_1$

$=-9-(-7)=-2$
Thus,

$a_1=-7$ and

$d=-2$

Find the first term and common difference for the following A.P
$3,2,-7,-12,...$

Given A.P is

$3,-2,-7,-12,...$
First term

$(a_1)=3$
Common difference

$(d)=a_2-a_1$

$=-2-3$

$=-5$
Thus,

$a_1=3$ and

$d=-5$

Find the first term and common difference for the following A.P
$6,9,12,15,..$

Given A.P is

$6,9,12,15,..$
First term

$(a_1)=6$
Common difference

$(d)=a_2-a_1$

$=9-6=3$
Thus,

$a_1=6$ and

$d=3$

$\dfrac{-1}{2},\dfrac{-1}{2},\dfrac{-1}{2},\dfrac{-1}{2},....$

Given series

$\dfrac{-1}{2},\dfrac{-1}{2},\dfrac{-1}{2},\dfrac{-1}{2},....$
Here

$a_1=\dfrac{-1}{2}, a_2=\dfrac{-1}{2}, a_3=\dfrac{-1}{2}, a_4=\dfrac{-1}{2}$
Difference between two consecutive terms

$(d)$ :

$d=a_2-a_1 =\dfrac{-1}{2} - \left(\dfrac{-1}{2} \right)=\dfrac{-1}{2}+\dfrac{1}{2}=0$

$=a_3-a_2=-\dfrac{1}{2}- \left(-\dfrac{1}{2}\right)=-\dfrac{1}{2}+\dfrac{1}{2}=0$

$a_4-a_3=-\dfrac{1}{2}- \left(-\dfrac{1}{2}\right)=-\dfrac{1}{2}+\dfrac{1}{2}=0$

$\therefore$ Difference between two consecutive is same,

$d=0$

$\therefore$ Given series is A.P
Next four terms are

$Fifth \ term a_5=a_4+d$

$=-\dfrac{1}{2}+0=\dfrac{1}{-2}$

$a_6-a_5+d$

$=-\dfrac{1}{2}+0=\dfrac{1}{-2}$

$a_7=a_6+d$

$=-\dfrac{1}{2}+0=\dfrac{1}{-2}$

$a_8=a_7+d$
Hence common difference

$d=0$ and next four terms are

$\dfrac{-1}{2},\dfrac{-1}{2},\dfrac{-1}{2}$ and

$\dfrac{-1}{2}$

Third term of an $A.P.$ Is $16$ and $7^{th}$ term is $12$ more than $5^{th}$ term, then find $AP$ .

Let first term of

$A.P.$ is

$a$ and common difference is

$d$ and we know that nth term,

$a_n = a+(n-1)d$
Given

$a_{3}=16$

$a+(3-1)d=16$

$\Rightarrow a+2d=16 ...(i)$
According to question,

$a_{7}=12-a_{5}$

$\Rightarrow a_{7}-a_{5}=12$

$[a+(7-1)d]-[a+(5-1)d]=12$

$\Rightarrow a_{7}+6d-a-4d=12$

$\Rightarrow a+6d-a-4d=12$

$\Rightarrow 2d=12$

$d=\dfrac{12}{2}=6$
Substituting value of

$d$ in equation

$(i)$

$a+2(6)=16$

$\therefore a=16-12=4$

$AP. a, a+d, a+2d ,...$

$=4,4+6,4+2\times 6,....$

$=4,10,16,....$
Hence, required

$A.P.$ is

$4,10,16,22,...$

Find the first term and common difference for the following A.P
$3,1,-1,-3,..$

Given A.P is

$3,1,-1,-3,..$
First term

$(a_1)=3$
Common difference

$(d)=a_2-a_1$

$=1-3=-2$
Thus,

$a_1=3$ and

$d=-2$

Find the first term and common difference for the following A.P
$\dfrac{3}{2},\dfrac{1}{2},\dfrac{-1}{2},\dfrac{-3}{2},...$

Given A.P is

$\dfrac{3}{2},\dfrac{1}{2},\dfrac{-1}{2},\dfrac{-3}{2},...$
First term

$(a_1)=\dfrac{3}{2}$
Common difference

$(d)=a_2-a_1$

$=\dfrac{1}{2}-\dfrac{3}{2}$

$=\dfrac{1-3}{2}=\dfrac{-2}{2}$

$=-1$
Thus,

$a_1=$ and

$d=-1$

Find the first term and common difference for the following A.P
$-1,\dfrac{1}{4},\dfrac{3}{2},..$

Given A.P is

$-1,\dfrac{1}{4},\dfrac{3}{2},..$
First term

$(a_1)=-1$
Common difference

$(d)=a_2-a_1$

$=\dfrac{1}{4}-(-1)$

$=\dfrac{1}{4}+1$

$=\dfrac{1+4}{4}=\dfrac{5}{4}$
Thus,

$a_1=-1$ and

$d=\dfrac{5}{4}$

Find the first term and common difference for the following A.P
$1,-2,-5,-8...$

Given

$A.P$ is

$1,-2,-5,-8...$
First term

$(a_1)=1$
Common difference

$(d)=a_2-a_1$

$=-2-(1)$

$=-3$
Thus,

$a_1=1$ and

$d=-3$

Find the sum of first $51$ terms of $AP$ in which $II^{nd}$ and $III^{rd}$ term are $14$ and $18$ respectively.

Second term of A.P

$a_2=14$
and third term

$a_3=18$

$\therefore$ common difference

$d=a_3-a_2$

$=18-14=4$
Again,

$\because II^{nd}$ term

$=14$

$\therefore a+d=14$

$\Rightarrow a+4=14$

$\Rightarrow a=14-4$

$\Rightarrow a=10$

$\because a=10,d=4$
Then, sum of

$n$ terms

$S_n=\dfrac{n}{2}[2a+(n-1)d]$

$\therefore S_{51}=\dfrac{51}{2}[2\times 10+(51-1)4]$

$=\dfrac{51}{2}[20+50\times 4]$

$=\dfrac{51}{2}[20+200]$

$=\dfrac{51}{2}\times 220=51\times 110=5610$
Hence, sum of

$5$ terms of given A.P

$=5610$

$a,2a,3a,4a$

Given series

$a,2a,3a,4a$
Here

$a_1=a, a_2=a_2, a_3=a_3, a_4=4a$
Difference between two consecutive terms

$(d)$ :

$=a_2-a_1 =2a-a=a$

$=a_3-a_2=3a-2a=a$

$=a_4-a_3=4a-3a=a$

$\therefore$ Difference is the same
Common difference

$d=a$ and given series is an A.P.
Then

$5^{th}$ term

$a_5=a_4+d$

$=4a+a=5a$

$6^{th}$ term

$a_6=a_5+d$

$=5a+a=6a$

$7^{th}$ term

$a_7=a_6+d$

$=6a+a=7a$

$8^{th}$ term

$a_8=a_7+d$

$=7a+a=8a$
Hence, common difference

$d=a$ and next four terms of series are

$5a,6a,7a$ and

$8a$

Find the number of terms
How many terms of the $A.P,:63,60,57,....$ must be taken to give a sum of $693$ ?

Give.

$A.P,:63,60,57,....$
First term

$(a)=63$
Common difference

$(d)=60-63=-3$
Let number of terms be

$n$

$S_n=693$
We know that

$S_n=\dfrac{n}{2}[2a+(n-1)d]$

$\Rightarrow 693=\dfrac{n}{2}[2\times 63+(n-1)(-3)]$

$\Rightarrow 693=\dfrac{n}{2}[126-3n+3]$

$\Rightarrow 1386=n(129-3n)$

$\Rightarrow 1386=129n-3n^2$

$\Rightarrow 3n^2-129n+1386=0$

$\Rightarrow n^2-43n+462=0$

$\Rightarrow n^2-21n-22n+462=0$

$\Rightarrow n(n-21)-229n-21)=0$

$\Rightarrow (n-21)(n-22)=0$

$\Rightarrow n-21=0$ or

$n-22=0$

$n=21$ or

$n=22$
By taking

$21$ or

$22$ terms of given A.P. we will get sum

$693$ .

Check whether the following sequence is an A.P. or not:
$a,a^2,a^3,a^4,...$

Given series

$a,a^2,a^3,a^4,...$
Here

$a_1=a, a_2=a^2, a_3=a^3, a_4=a^4$
Difference between two consecutive terms

$(d)$ :

$=a_2-a_1 =a^2-a=a(a-1)$

$=a_3-a_2=a^3-a^2=a^2(a-1)$

$\therefore$ Difference is not same
i.e

$a_2-a_1 \ne a_3 -a_2$
Hence, given series is not A.P

$3,3+\sqrt 2, 3+2 \sqrt 2, +3+ 3\sqrt 2,...$

Given series

$3,3+\sqrt 2, +3+2 \sqrt 2, +3+3 \sqrt 2,...$

Here

$a_1=3, a_2=3+\sqrt 2, a_3=3+\sqrt 2, a_4=+3\sqrt 2$

Difference between two consecutive terms

$(d)$ :

$=a_2-a_1 =(3+\sqrt 2)-3=\sqrt 2$

$=a_3-a_2=(3+2\sqrt 2)-(3+\sqrt 2)=\sqrt 2$

$=a_4-a_3=(3+2\sqrt 2)-(3+\sqrt 2)=\sqrt 2$

$\therefore$ Difference is the same

Common difference

$d=\sqrt 2$ and given series is an A.P.

Then

$5^{th}$ term

$a_5=a_4+d$

$=3+3\sqrt 2+\sqrt 2$

$3+\sqrt 2(3+1)=3+4\sqrt 2$

$6^{th}$ term

$a_6=a_5+d$

$=3+4\sqrt 2+\sqrt 2$

$3+\sqrt 2(4+1)=3+5\sqrt 2$

$7^{th}$ term

$a_7=a_6+d$

$=3+5\sqrt 2+\sqrt 2$

$3+\sqrt 2(5+1)=3+6\sqrt 2$

$8^{th}$ term

$a_8=a_7+d$

$=3+6\sqrt 2+\sqrt 2$

$=3+\sqrt 2(6+1)=3+7\sqrt 2$

Hence, common difference

$d=\sqrt 2$ and next four terms of series are

$3+4\sqrt 2,3+5\sqrt 2,3+6\sqrt 2$ and

$3+7\sqrt 2$

The first and last term of an $A.P$ are $17$ and $350$ respectively. If common difference is $9$ then find number of terms in $AP$ . and their sum.

Given:
First term

$(a)=17$
Last term

$(l)=a_n=350$
and common difference

$(d)=9$

$\because a_n=350$

$a+(n-1)d=350$

$\Rightarrow 17+(n-1)9=350$

$\Rightarrow 9(n-1)=350-17=333$

$\Rightarrow n-1=\dfrac{333}{9}=37$

$\therefore n=38$
Now,

$S_n$ =

$\dfrac{n}{2}(a+1)$

$=\dfrac{38}{2}(17+350)$

$=19\times 367=6973$

Hence,

$n = 38$ & sum of term

$S_n = 6973$

The first term of $A.P$ is $8,n^{th}$ terms is $33$ and sum of first $n$ terms is $123$ , then find $n$ and common difference $d$ .

First term

$(a)=8$

$n^{th}$ term

$(a_n)=33$
sum of

$n$ terms

$(S_n)=123$

$\because n^{th}$ term

$a_n=a+(n-1)d$

$\Rightarrow 33=8+(n-1)d$

$\Rightarrow (n-1)d=33-8$

$\Rightarrow (n-1)d=25$ ...........(i)
Now, sum of

$n$ terms

$S_n=\dfrac{n}{2}[2a+(n-1)d]$

$\Rightarrow 123=\dfrac{n}{2}[2\times 8+25]$ [from equation (i)]

$\Rightarrow 123=\dfrac{n}{2}(16+25)$

$\Rightarrow 123 =\dfrac{n}{2}\times 41$

$\Rightarrow n=\dfrac{123\times 2}{41}$

$\Rightarrow n=6$
Put the value of

$n$ in equation (i)

$\Rightarrow (6-1)d=25$

$\Rightarrow 5d=25$

$\Rightarrow d=5$
Thus,

$n=6$ and

$d=5$

Check whether the following sequence is an A.P. or not:
$\sqrt 3,\sqrt 6,\sqrt 9,\sqrt {12},...$

Given series

$\sqrt 3,\sqrt 6,\sqrt 9,\sqrt {12},...$
Here

$a_1=\sqrt 3, a_2=\sqrt 6, a_3=\sqrt 9, a_4=\sqrt {12}$
Difference between two consecutive terms

$(d)$ :

$=a_2-a_1 =\sqrt 6-\sqrt 3=\sqrt 3(\sqrt 2-1)=0.717$

$=a_3-a_2=\sqrt 9-\sqrt 6=\sqrt 3(\sqrt 3-\sqrt 2)=0.530$

$\therefore$ Difference is not same
i.e

$a_2-a_1 \ne a_3 -a_2$
Hence, given series is not A.P

In an Arithmetic Progression (AP) the fourth and sixth terms are $8$ and $14$ respectively. Find the first term.

Given, In an Arithmetic Progression (AP) the fourth and sixth terms are

$8$ and

$14$ respectively.

We know for AP

$n^{th}$ term is given by,

$a_{n}= a+(n-1)d$

where,

$a =$ First term

$d =$ Common difference

$n =$ number of terms

$a_n = n^{th}$ term

Here,

$a_4=8\Rightarrow a+3d=8$ ........(i)

$a_6=14\Rightarrow a+5d=14$ ........(ii)

Subtracting (i) and (ii), we have

$2d=6\Rightarrow d=3$

From (i), we have

$a+3(3)=8\Rightarrow a=8-9=-1$

Hence, first term=

$-1$

Find the $16^{th}$ term of the A.P. $7,11,15,19...$ Find the sum of the first $6$ terms.

2159367_1984617_ans_4b7a2e3a8fd44187aa91aac69bba7ea9.jpg

The difference between $a_{30}$ and $a_{20}$ for the AP $-3, -7, -11$ is $'d'$ , then $\dfrac{|d|}{10}$ equals

We know that the

$n$ th term of A.P is

$a_n=a+(n-1)d$ where

$a$ is the first term,

$n$ is the number of terms and

$d$ is the common difference.

In the given A.P, the first term is

$a=-3$ and the common difference is:

$d=a_2-a_1=-7-(-3)=-7+3=-4$

Now, we find

$a_{20}$ and

$a_{30}$ as follows:

$a_{ 20 }=-3+(20-1)(-4)=-3+(19\times -4)=-3-76=-79$

$a_{ 30 }=-3+(30-1)(-4)=-3+(29\times -4)=-3-116=-119$

Subtract

$a_{20}$ from

$a_{30}$ as shown below:

$a_{ 30 }-a_{ 20 }=-119-(-79)=-40$

So, the difference between

$a_{20}$ and

$a_{30}$ is

$-40$ .

$\therefore$

$\dfrac{|d|}{10}$ =

$4$ .

If a, b, c are the ${ p }^{ th },{ q }^{ th }$ and ${ r }^{ th }$ terms of an AP, then prove that $a(q-r)+b(r-p)+c(p-q)=0$

1896587_1442000_ans_b2b6402068414a209e2b036707981034.jpg

A meeting hall has $20$ seats in the first row, $24$ seats in the second row, $28$ seats in the third row, and so on and has in all $30$ rows. How many seats are there in the meeting hall?

First row

$=20$ , second row

$=24$ , third row

$=28$

So, the A.P is

$20, 24, 28,\dots$

$a=20$

$d=24-20=4$

$n=30$

By using the formula of the sum of the first

$n$ terms of an A.P,

$\begin{aligned}{}{S_n} &= \frac{n}{2}[2a + (n - 1)d]\\{S_{30}} &= \frac{{30}}{2}[2 \cdot 20 + (30 - 1)4]\\ &= 15[40 + 29 \cdot 4] \\&= 15[156]\\ &= 2340\end{aligned}$

So, total seats in the theater are equal to

$2340$ .

Sonal and Amole made a sequence of tile designs from square white tiles surrounding one square purple tile. The purple tiles come in many sizes. Three of the designs are shown below.
Draw a graph using the first five pairs of numbers in your table.

From the given diagrams, we can conclude that the given data forms Arithmetic Progression series. The graph is plotted as above.

When side of purple tile is

$1$ , number of white tiles on border is

$8$

When side of purple tile is

$2$ , number of white tiles on border is

$12$

When side of purple tile is

$3$ , number of white tiles on border is

$16$

Thus, using formula of AP to find further values of number of white tiles on border.

${ a }_{ n }={ a }_{ 1 }+\left( n-1 \right) d$

1) When

$n=4$ ,

${ a }_{ 3 }=8+\left( 4-1 \right) \times 4$

$\therefore { a }_{ 3 }=8+12=20$

2) When

$n=5$ ,

${ a }_{ 4 }=8+\left( 5-1 \right) \times 4$

$\therefore { a }_{ 4 }=8+16=24$

If $d$ be the common difference of an A.P. and $S_n$ be the sum of its $n$ terms, then prove that $d = S_n - 2S_{n -1} + S_{n - 2}$

Given:

$S_n$ be the sum of

$n$ terms and

$d$ be the common difference.

then

$S_n = \dfrac{n}{2} [2a + (n - 1)d]$

To Prove

$d = S_n - 2S_{n -1} + S_{n - 2}$

Taking

$RHS$

$\Rightarrow S_n - 2S_{n -1} + S_{n - 2}$

$= \dfrac{n}{2} [2a + (n - 1)d] - 2 \times \dfrac{n - 1}{2}[2a + (n - 1 -1)d]$

$+ \dfrac{n - 2}{2}[2a + (n - 2 -1)d]$

$= \dfrac{n}{2} [2a + (n - 1)d] - [\dfrac{2(n -1)}{2} [2a + (n - 2)d]] + \dfrac{n - 2}{2}[2a + (n - 3)d]$

$= \dfrac{2an + n(n - 1)d - 4a(n - 1) - 2(n - 1)(n - 2)d + 2a (n - 2) + (n - 2)(n - 3)d}{2}$

$= \dfrac{1}{2}[2an + n^{2}d - nd - 4an + 4a - 2n^{2}d + 4nd + 2nd - 4d + 2an - 4a + n^{2}d$

$-3nd - 2nd + 6d]$

$= \dfrac{1}{2} [2d]$

$= d$

$= LHS$

Hence Proved

Arithmetic Progressions - Class 10 Maths - Extra Questions

Find the 20th20^{th} term of the AP whose 7th7^{th} term is 24 less than the 11th11^{th} term, first term being 12.

Is 0 a term of the AP: 31, 28, 25, ...? If true then enter 11 and if false then enter 00

Find the eighteenth term of the A.P. 1,7,13,19,..........1, 7, 13, 19, ..........

Find the sum of all three digit natural numbers which are divisible by 7.7.

Find the common difference the following A.P1,4,7,10,13,16,..1, 4, 7, 10, 13, 16,..

The difference between any two consecutive interior angles of a polygon is \displaystyle {5} ^ {o}\displaystyle {5} ^ {o} . If the smallest angle is \displaystyle {120} ^ {o}\displaystyle {120} ^ {o}, find the number of the sides of the polygon.

A man starts repaying a loan as first installment of Rs. 100100. If he increases the installment by Rs 55 every month. what amount he will pay in the 30^{th}30^{th} installment?

Find the sum of the first 4040 positive integers divisible by 66

The 17^{th}17^{th} term of an APAP exceeds its 10^{th}10^{th} term by 77. Find the common difference.

Obtain the sum of the first 5656 terms of an A.P whose 18^{th}18^{th} and 39^{th}39^{th} terms are 5252 and 148148 respectively.

Find the eleventh term of the A.P.7,13,19,25,........7,13,19,25,........

Check whether the following sequence is an A.P. or not.1,3,6,10,....1,3,6,10,....

Check whether the following sequence is an A.P. or not?1, 4, 7, 10, ...1, 4, 7, 10, ...

Check whether 13, 19, 25, 31, ............ form an A.P.

The 11^{th}11^{th} term and the 21^{st}21^{st} term of an A.P. are 1616 and 2929 respectively, then find the first term and common difference.

Find the ninth term of the A.P.: 3, 7, 11, 153, 7, 11, 15...... .

Find the term t_{15}t_{15} of an A.P.:4, 9, 14, .....4, 9, 14, .....

For the given A.P. 5, 10, 15, 20 ____Find the common difference (d).

Check whether the following sequence is an A.P. or not:2, 6, 10, 14, .....2, 6, 10, 14, .....

Write any two arithmetic progressions with common difference 55.

Write any two arithmetic progressions with common difference 33.

Write any two arithmetic progressions with common difference 22.

Find the term t_{13}t_{13} of an A.P.4, 9, 14, ....4, 9, 14, ....

There is an auditorium with 3535 rows of seats. There are 2020 seats in the first row, 2222 seats in the second row, 2424 seats in the third row and so on. Find the number of seats in the twenty-third row.

For an A.P., t_{3} = 8t_{3} = 8 and t_{4} = 12t_{4} = 12. Find the common difference dd.

For the given A. P. 10, 15, 20, 25,10, 15, 20, 25,......., find the common difference 'dd'.

In a given A.P. a=8,{T}_{n}=33,{S}_{n}=123a=8,{T}_{n}=33,{S}_{n}=123. Find dd and nn.

Check whether the following sequence is an AP or not:3m - 1, 3m - 3, 3m - 5, ....3m - 1, 3m - 3, 3m - 5, ....

If t_{n} = 3n + 5t_{n} = 3n + 5, then find A.P.

Find the first term and common difference of the following APsv(i) 5, 2, -1, -4, ....5, 2, -1, -4, ....(ii) \dfrac {1}{2}, \dfrac {5}{6}, \dfrac {7}{6}, \dfrac {3}{6}, ...., \dfrac {17}{6}\dfrac {1}{2}, \dfrac {5}{6}, \dfrac {7}{6}, \dfrac {3}{6}, ...., \dfrac {17}{6}

Write the common difference of the A.P. 7, 5, 3, 1, -1, -3, .........

Write any two arithmetic progressions with common difference 44.

In an A.P. the first term is 22, the last term is 2929, and the sum is 155155, then find the common difference.

Find the common difference of an AP: { 1 }^{ 2 },{ 5 }^{ 2 },{ 7 }^{ 2 },73,....{ 1 }^{ 2 },{ 5 }^{ 2 },{ 7 }^{ 2 },73,....

For the following arithmetic progressions write the first term aa and the common difference dd:0.3,0.55,0.80,1.05,....0.3,0.55,0.80,1.05,....

For the following arithmetic progressions write the first term aa and the common difference dd:\cfrac { 1 }{ 5 } ,\cfrac { 3 }{ 5 } ,\cfrac { 5 }{ 5 } ,\cfrac { 7 }{ 5 } ,.....\cfrac { 1 }{ 5 } ,\cfrac { 3 }{ 5 } ,\cfrac { 5 }{ 5 } ,\cfrac { 7 }{ 5 } ,.....

Find the common difference of the A.P.: 1.,2.0,2.2,2.4,.....1.,2.0,2.2,2.4,.....

Find the common difference of am AP: -225,-425,-625,-825,.....-225,-425,-625,-825,.....

Find the common difference of the A.P. and write the next two terms: 75,67,59,51,.....75,67,59,51,.....

For the following arithmetic progressions write the first term aa and the common difference: -5,-1,3,7,....-5,-1,3,7,....

For the following arithmetic progressions write the first term aa and the common difference dd:-1.1,-3.1,-5.1,-7.1,.....-1.1,-3.1,-5.1,-7.1,.....

Find the common difference of the A.P.: 119,136,153,170,.....119,136,153,170,.....

The nnth term of an A.P is 6n+26n+2. Find the common difference.

The first and the last terms of an A.P are 77 and 4949 respectively. If the sum of all its terms is 420420, find its common difference.

Find the common difference and write the next three terms of the A.P. 3, -2, -7, -12,....3, -2, -7, -12,....

Find the value of xx for which \left( {5x + 2} \right),\left( {4x - 1} \right)\;and\;(x + 2)\left( {5x + 2} \right),\left( {4x - 1} \right)\;and\;(x + 2) are in A.P

State whether the given list of numbers is an arithmetic progression or not. a) 13,20,27,34,... a) 13,20,27,34,... b) 6,16,26,35,... b) 6,16,26,35,...

Find the value of kk , for which 2k + 7 , 6k - 22k + 7 , 6k - 2 and 8k + 48k + 4 are 33 consecutive terms of an AP.

Find the sum of the following APAP.-37,-33,-29,.....,-37,-33,-29,....., to 1212 terms

If in an AP, the sum of first 10 terms is -150 and the sum of its next 10 terms is -550. Find the AP.

For the A.P. -1.1,\ -3.1,\ -5.1,\ -7.1,......-1.1,\ -3.1,\ -5.1,\ -7.1,...... write the first term and the common difference.

In an A.P., if t_7=13t_7=13 and {S_{14}} = 203{S_{14}} = 203, find S_8S_8.

Write the expression for the common difference of anA.PA.P whose first term is aa and nthnth term is bb.

If a=2a=2 and d=4d=4 , then S_{20} =S_{20} = _______.

If sum of first pp terms of an AP is equal to the sum of first qq terms, then find the sum of the first (p+q)(p+q) terms.

Find the common difference dd and write three more terms if the following sequence is an AP:2, 4, 8, 16,.2, 4, 8, 16,.

In an arithmetic progression of which aa is the first term. If the sum of the first ten terms is zero and the sum of next ten terms is -200-200 then find the value of aa.

The {25^{th}}{25^{th}} term of APAP - 5,\dfrac{{ - 5}}{2},0,\dfrac{5}{2}............ \ \ - 5,\dfrac{{ - 5}}{2},0,\dfrac{5}{2}............ \ \ is -b-b, then what is the value of b?b?

Show that sequence of following n^{th}n^{th} terms ,are not in A.P.\dfrac{n}{n+1}\dfrac{n}{n+1}

Find the sum of n terms of the series (a^2+b)+({ a }^{ 2 }+2b)+({ a }^{ 2 }+3b)+....(a^2+b)+({ a }^{ 2 }+2b)+({ a }^{ 2 }+3b)+....

The first term and the last term of an A.P are 1717 and 350350 respectively. If the common difference is 99. How many terms are there and what is their sum.

Find the common difference in the following pattern:(a) 4,7,10,13(b) 5,9,13,17,21,25

Find the 20th term of the progression.-12,-5,2,9,16,23,30,....-12,-5,2,9,16,23,30,....

Find the common difference of the following A.P.:i) 3,1,-1,-3,......3,1,-1,-3,......ii) -5,-1,3,7,.....-5,-1,3,7,.....

The ratio of the sums of m and n terms of an A.P. is { m }^{ 2 }:{ n }^{ 2 }{ m }^{ 2 }:{ n }^{ 2 }. Show that the ratio of { m }^{ th }{ m }^{ th } and { n }^{ th }{ n }^{ th } term is (2m - 1) : (2n - 1).

Check whether the following sequence is an AP or not:-1.2,-3.2,-5.2,-7.2-1.2,-3.2,-5.2,-7.2...

Is the given Progression arithmetic progression?2, 6, 7, 10, 12, 15,.........2, 6, 7, 10, 12, 15,.........

Is the given progression arithmetic progression?-1, -3, -5, -7,.........-1, -3, -5, -7,.........

What is the common difference of an A.P. in which a_{24}-a_{17}=-28a_{24}-a_{17}=-28?

Is the given Progression arithmetic progression?Why2, 3, 5, 7, 8, 10, 15,.........2, 3, 5, 7, 8, 10, 15,.........

Is the given sequence 2,4,8,162,4,8,16 form an A.P. If it forms an AP, find the common difference dd

Find the common difference of the following AP:3.3 + \sqrt { 2, } 3+2\sqrt { 2 } ,3+3\sqrt { 2 } 3.3 + \sqrt { 2, } 3+2\sqrt { 2 } ,3+3\sqrt { 2 }

Find the first term aa and the common difference dd of A.P. : -5, -1, 3, 7, .....-5, -1, 3, 7, .....

Which term of the sequence 72, 70, 68, 6672, 70, 68, 66, ... is 40 40 ?

Is the sequence \sqrt{3},\sqrt{6},\sqrt{9},\sqrt{12},......\sqrt{3},\sqrt{6},\sqrt{9},\sqrt{12},...... from an Arithmetic Progression?Give reason.

Check whether the following sequence is an AP or not:1,3,9,27,....1,3,9,27,....

Is the given sequence an AP? If it forms an AP, find the common difference dd and write the next three terms.0,-4, -8 ,-120,-4, -8 ,-12....

For the following A.P's write the first term and common difference:\dfrac{3}{2},\dfrac{1}{2},-\dfrac{1}{2},-\dfrac{3}{2},......\dfrac{3}{2},\dfrac{1}{2},-\dfrac{1}{2},-\dfrac{3}{2},......

Is the given sequence 3,3+\sqrt { 2 } ,3+2\sqrt { 2 } ,3+3\sqrt { 2 }3,3+\sqrt { 2 } ,3+2\sqrt { 2 } ,3+3\sqrt { 2 } form an APs? If it forms an AP, find the common difference dd and write the next three terms.

Find the $20^{th}$ term of the AP whose $7^{th}$ term is 24 less than the $11^{th}$ term, first term being 12.

Is 0 a term of the AP: 31, 28, 25, ...?
If true then enter $1$ and if false then enter $0$

Find the eighteenth term of the A.P. $1, 7, 13, 19, ..........$

Find the sum of all three digit natural numbers which are divisible by $7.$

Find the common difference the following A.P
$1, 4, 7, 10, 13, 16,..$

The difference between any two consecutive interior angles of a polygon is $\displaystyle {5} ^ {o}$ . If the smallest angle is $\displaystyle {120} ^ {o}$ , find the number of the sides of the polygon.

A man starts repaying a loan as first installment of Rs. $100$ . If he increases the installment by Rs $5$ every month. what amount he will pay in the $30^{th}$ installment?

Find the sum of the first $40$ positive integers divisible by $6$

The $17^{th}$ term of an $AP$ exceeds its $10^{th}$ term by $7$ . Find the common difference.

Obtain the sum of the first $56$ terms of an A.P whose $18^{th}$ and $39^{th}$ terms are $52$ and $148$ respectively.

Find the eleventh term of the A.P.
$7,13,19,25,........$

Check whether the following sequence is an A.P. or not.
$1,3,6,10,....$

Check whether the following sequence is an A.P. or not?
$1, 4, 7, 10, ...$

The $11^{th}$ term and the $21^{st}$ term of an A.P. are $16$ and $29$ respectively, then find the first term and common difference.

Find the ninth term of the A.P.: $3, 7, 11, 15$ ...... .

Find the term $t_{15}$ of an A.P.:
$4, 9, 14, .....$

For the given A.P. 5, 10, 15, 20 ____
Find the common difference (d).

Check whether the following sequence is an A.P. or not:
$2, 6, 10, 14, .....$

Write any two arithmetic progressions with common difference $5$ .

Write any two arithmetic progressions with common difference $3$ .

Write any two arithmetic progressions with common difference $2$ .

Find the term $t_{13}$ of an A.P.
$4, 9, 14, ....$

There is an auditorium with $35$ rows of seats. There are $20$ seats in the first row, $22$ seats in the second row, $24$ seats in the third row and so on. Find the number of seats in the twenty-third row.

For an A.P., $t_{3} = 8$ and $t_{4} = 12$ . Find the common difference $d$ .

For the given A. P. $10, 15, 20, 25,$ ......., find the common difference ' $d$ '.

In a given A.P. $a=8,{T}_{n}=33,{S}_{n}=123$ . Find $d$ and $n$ .

Check whether the following sequence is an AP or not:
$3m - 1, 3m - 3, 3m - 5, ....$

If $t_{n} = 3n + 5$ , then find A.P.

Find the first term and common difference of the following APsv
(i) $5, 2, -1, -4, ....$
(ii) $\dfrac {1}{2}, \dfrac {5}{6}, \dfrac {7}{6}, \dfrac {3}{6}, ...., \dfrac {17}{6}$

Write any two arithmetic progressions with common difference $4$ .

In an A.P. the first term is $2$ , the last term is $29$ , and the sum is $155$ , then find the common difference.

Find the common difference of an AP: ${ 1 }^{ 2 },{ 5 }^{ 2 },{ 7 }^{ 2 },73,....$

For the following arithmetic progressions write the first term $a$ and the common difference $d$ :
$0.3,0.55,0.80,1.05,....$

For the following arithmetic progressions write the first term $a$ and the common difference $d$ :
$\cfrac { 1 }{ 5 } ,\cfrac { 3 }{ 5 } ,\cfrac { 5 }{ 5 } ,\cfrac { 7 }{ 5 } ,.....$

Find the common difference of the A.P.: $1.,2.0,2.2,2.4,.....$

Find the common difference of am AP: $-225,-425,-625,-825,.....$

Find the common difference of the A.P. and write the next two terms: $75,67,59,51,.....$

For the following arithmetic progressions write the first term $a$ and the common difference: $-5,-1,3,7,....$

For the following arithmetic progressions write the first term $a$ and the common difference $d$ :
$-1.1,-3.1,-5.1,-7.1,.....$

Find the common difference of the A.P.: $119,136,153,170,.....$

The $n$ th term of an A.P is $6n+2$ . Find the common difference.

The first and the last terms of an A.P are $7$ and $49$ respectively. If the sum of all its terms is $420$ , find its common difference.

Find the common difference and write the next three terms of the A.P. $3, -2, -7, -12,....$

Find the value of $x$ for which $\left( {5x + 2} \right),\left( {4x - 1} \right)\;and\;(x + 2)$ are in A.P

State whether the given list of numbers is an arithmetic progression or not.
$a) 13,20,27,34,...$
$b) 6,16,26,35,...$

Find the value of $k$ , for which $2k + 7 , 6k - 2$ and $8k + 4$ are $3$ consecutive terms of an AP.

Find the sum of the following $AP$ .
$-37,-33,-29,.....,$ to $12$ terms

For the A.P. $-1.1,\ -3.1,\ -5.1,\ -7.1,......$ write the first term and the common difference.

In an A.P., if $t_7=13$ and ${S_{14}} = 203$ , find $S_8$ .

Write the expression for the common difference of an $A.P$ whose first term is $a$ and $nth$ term is $b$ .

If $a=2$ and $d=4$ , then $S_{20} =$ _______.

If sum of first $p$ terms of an AP is equal to the sum of first $q$ terms, then find the sum of the first $(p+q)$ terms.

Find the common difference $d$ and write three more terms if the following sequence is an AP:
$2, 4, 8, 16,.$

In an arithmetic progression of which $a$ is the first term. If the sum of the first ten terms is zero and the sum of next ten terms is $-200$ then find the value of $a$ .

The ${25^{th}}$ term of $AP$ $- 5,\dfrac{{ - 5}}{2},0,\dfrac{5}{2}............ \ \$ is $-b$ ,
then what is the value of $b?$

Show that sequence of following $n^{th}$ terms ,are not in A.P.
$\dfrac{n}{n+1}$

Find the sum of n terms of the series $(a^2+b)+({ a }^{ 2 }+2b)+({ a }^{ 2 }+3b)+....$

The first term and the last term of an A.P are $17$ and $350$ respectively. If the common difference is $9$ . How many terms are there and what is their sum.

Find the common difference in the following pattern:
(a) 4,7,10,13
(b) 5,9,13,17,21,25

Find the 20th term of the progression.
$-12,-5,2,9,16,23,30,....$

Find the common difference of the following A.P.:
i) $3,1,-1,-3,......$
ii) $-5,-1,3,7,.....$

The ratio of the sums of m and n terms of an A.P. is ${ m }^{ 2 }:{ n }^{ 2 }$ . Show that the ratio of ${ m }^{ th }$ and ${ n }^{ th }$ term is (2m - 1) : (2n - 1).

Check whether the following sequence is an AP or not:
$-1.2,-3.2,-5.2,-7.2$ ...

Is the given Progression arithmetic progression?
$2, 6, 7, 10, 12, 15,.........$

Is the given progression arithmetic progression?
$-1, -3, -5, -7,.........$

What is the common difference of an A.P. in which $a_{24}-a_{17}=-28$ ?

$2, 3, 5, 7, 8, 10, 15,.........$

Is the given sequence an A.P. If it forms an AP, find the common difference $d$

Find the common difference of the following AP:
$3.3 + \sqrt { 2, } 3+2\sqrt { 2 } ,3+3\sqrt { 2 }$

Find the first term $a$ and the common difference $d$ of A.P. : $-5, -1, 3, 7, .....$

Which term of the sequence $72, 70, 68, 66$ , ... is $40$ ?

Is the sequence $\sqrt{3},\sqrt{6},\sqrt{9},\sqrt{12},......$ from an Arithmetic Progression?Give reason.

Check whether the following sequence is an AP or not:
$1,3,9,27,....$

Is the given sequence an AP? If it forms an AP, find the common difference $d$ and write the next three terms.
$0,-4, -8 ,-12$ ....

For the following A.P's write the first term and common difference: $\dfrac{3}{2},\dfrac{1}{2},-\dfrac{1}{2},-\dfrac{3}{2},......$

Is the given sequence form an APs? If it forms an AP, find the common difference $d$ and write the next three terms.

Check whether the following the sequence is an AP or not:
$-10, -6, -2, 2$ ....

How many terms of the A.P. $-6, - \frac{11}{2}, -5, .....$ are needed to give the sum $-25$ ??

$0.2,0.22,0.222...$

$5, 9, 12, 18, ….$