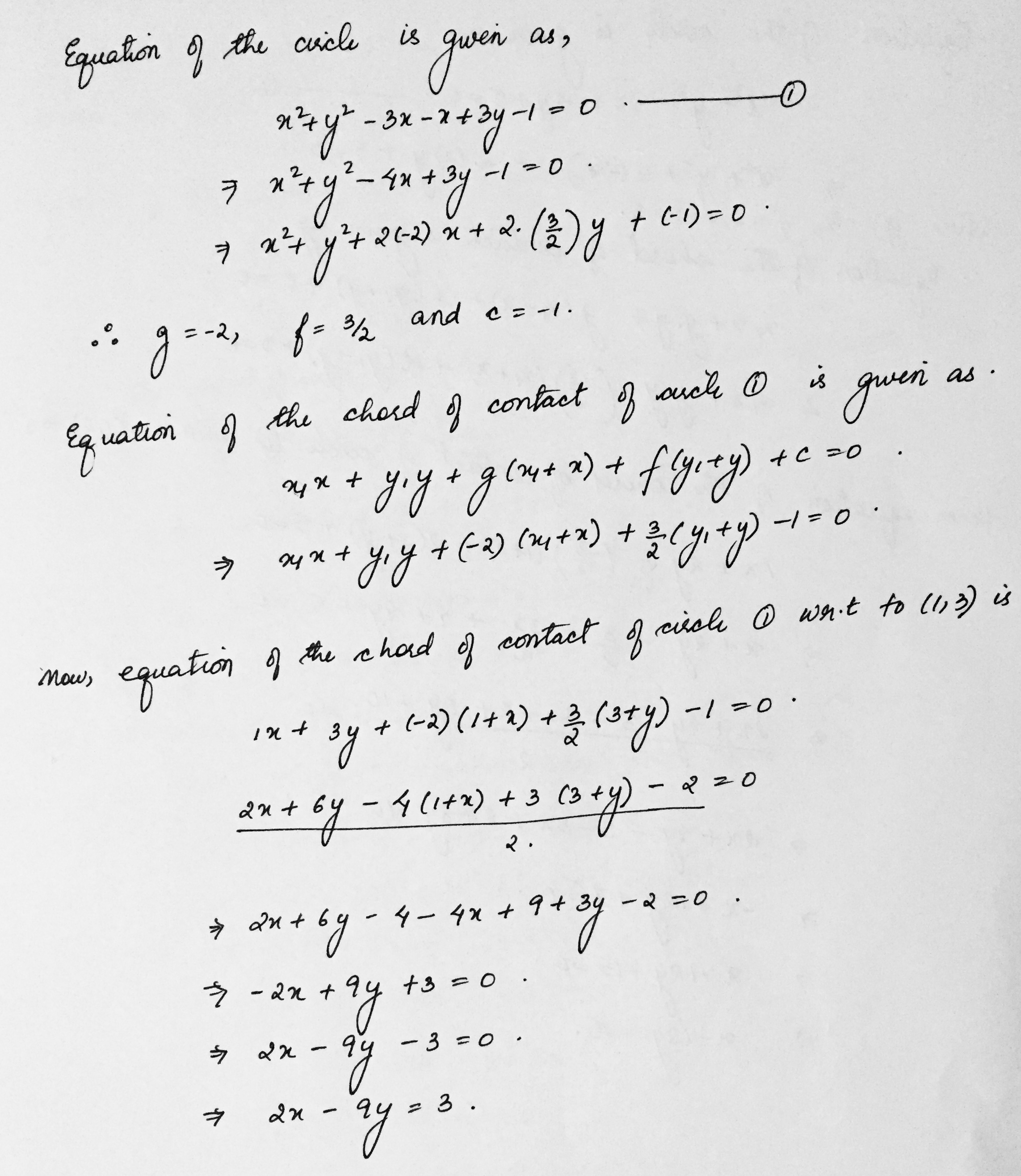Circles - Class 10 Maths - Extra Questions

Draw two tangents from a point $$5$$ cm away from the centre of a circle of radius $$3$$ cm.

Given, a circle of radius $$3$$ cm whose Centre is $$O$$ and a point P $$,  5$$ cm away from its centre.

STEPS OF CONSTRUCTION: 

$$1.$$Draw circle with $$O$$ as centre and radius $$= 3 cm.$$ Take a point $$P$$ such  that $$OP= 5 cm.$$
$$2. $$Draw the bisector of $$OP$$ which intersect $$OP$$ at $$M.$$
$$3. $$Taking $$M$$ as centre and $$MO$$ as radius, draw a dotted circle. Let this circle cuts the given circle $$A$$ and $$B.$$
$$4.$$Join $$PA$$ & $$PB$$.
$$5. $$Thus , $$PA$$ & $$PB$$ are the required tangents. By measurement using scale $$PA= PB = 4 cm.$$

1316380_1068946_ans_8b7409dc3d2e4a1383c37f9350ce6d1b.png


Maximum number of tangents that can be drawn from an external point to a circle is ______ .

The tangent of a circle is a special case of the secant when the two end points of the corresponding chord coincide.
From an external point $$P$$, only two tangents ($$PA$$ and $$PB$$) can be drawn. 
Also, both the drawn tangents are equal in length.

Hence, maximum $$2$$ tangents can be drawn from an external point to a circle.

639114_611098_ans.png


How many tangents can be drawn on the circle of radius $$5\ \text{cm}$$ from a point lying outside the circle at distance $$9\ \text{cm}$$ from the center.

Number of tangents that can be drawn to a circle from a point lying outside the circle is two.
Since, distance between the center and the point ($$9\ \text{cm}$$) is greater than the radius ($$5\ \text{cm}$$), the point lies outside the circle. Hence, two tangents can be drawn on the circle. 

629522_603952_ans_6119ae7f64ae4b9ba26d32d0da26c143.png


i) A circle can have ___ parallel tangents.
ii) The point common to the tangent and the circle is called _____.

i) A circle can have two parallel tangents.
ii) The point common to the tangent and the circle is called the point of contact.


What is the locus of the centre of a wheel of a bicycle going straight along a level road.

The locus of the centre of a wheel, which is going straight along a level road will be a straight line parallel to the road at a distance equal to the radius of the wheel.
1796986_1832813_ans_c626dd938aa74db7b3ade64d590f75d1.png


Find the equation of the tangent to the circle $$\displaystyle x^{2}+y^{2}-30x+6y+109=0$$ at (4, -1)

Equation of tangent is 
$$\displaystyle 4x+(-y)-30\left ( \frac{x+4}{2} \right )+6\left ( \frac{y+(-1)}{2} \right )+109=0$$
or      $$ 4x - y - 15x - 60 + 37 - 3 + 109 = 0 or -11x + 2y + 46 = 0$$
or     $$11x - 2y - 46 = 0$$
Hence the required equation of the tangent is $$11x - 2y - 46 = 0$$ 


The number of tangents that can be drawn to a circle at a given point on it is

Consider given the two dice,

If the point is on the circle then number of tangent $$= 1$$

If the point is outside the circle then number of tangent$$=2$$

If the point is in the circle then number of tangent $$=$$ none

 

Hence, this is the answer.



From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the perimeter of the triangle PCD in cm.

From the graph, we find some conclusion-

$$PA=PB=10$$cm

$$CE=CA$$

$$DE=DB$$

Perimeter of $$\Delta PCD$$ is,

$$=PC+PD+CD$$

$$\Rightarrow PC+PD+CE+ED$$

$$\Rightarrow PC+PD+CA+DB$$

$$\Rightarrow (PC+CA)(PD+DB)$$

$$\Rightarrow PA+PB$$

$$\Rightarrow 10+10$$

$$\Rightarrow 20$$ cm.

1458599_427348_ans_7797fef64bd241dcb1f1f40ac46b37a1.png


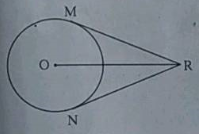
In the ddjoining figure $$O$$ is the centre of the circle. Forom point $$R\ seg\ RM$$  and $$seg\ RN$$ are tengent segment touching the circle at $$M$$ and $$N$$. If $$(OR)=10\ cm$$ and radius of the circle $$=5\ cm$$, then
What is the measure os $$\angle MRN$$?
1377688_8b78c8444d434feb8e61babd539a1bf1.png

We have $$OM=5$$cm ad $$OR=10$$cm
In rightangled $$\triangle{OMR},$$
$${OR}^{2}={OM}^{2}+{MR}^{2}$$
$$\Rightarrow MR=\sqrt{{OR}^{2}-{OM}^{2}}=\sqrt{{10}^{2}-{5}^{2}}=\sqrt{100-25}=\sqrt{75}=5\sqrt{3}$$cm
Tangent segments drawn from an external point to a circle are congruent.
$$\therefore MR=NR=5\sqrt{3}$$cm
In right angled $$\triangle{OMR}$$
$$\tan{\angle{MRO}}=\dfrac{OM}{MR}$$
$$=\dfrac{5}{5\sqrt{3}}=\dfrac{1}{\sqrt{3}}$$
$$\Rightarrow \tan{\angle{MRO}}=\tan{{30}^{\circ}}$$
Thus, the measure of $$\angle{MRO}$$ is $${30}^{\circ}$$
In right angled $$\triangle{ONR}$$
$$\tan{\angle{NRO}}=\dfrac{ON}{NR}$$
$$=\dfrac{5}{5\sqrt{3}}=\dfrac{1}{\sqrt{3}}$$
$$\Rightarrow \tan{\angle{NRO}}=\tan{{30}^{\circ}}$$
Thus, the measure of $$\angle{NRO}$$ is $${30}^{\circ}$$
$$\therefore \angle{MRN}=\angle{MRO}+\angle{NRO}={30}^{\circ}+{30}^{\circ}={60}^{\circ}$$
Thus, the measure of $$\angle{MRN}$$ is $${60}^{\circ}$$


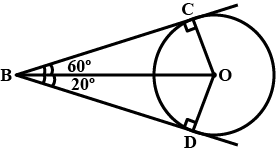
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that $$\angle DBC = {120^0}$$ prove that BC+BD=BO, i.e, BO=2BC.

Sol. Given : A circle with centre O.

Tangents BC and BD are drawn from an external point B such that $$\angle DBC = 120^{\circ}$$

To prove : $$BC + BD = BO, $$ i.e., $$BO = 2BC$$

Construction : join $$OB, OC $$ and $$OD$$.

Proof : In $$\Delta OBC$$ and $$\Delta OBD$$, we have

$$OB = OB$$ [common]

$$OC = OD$$ [Raddi of same circle]

$$BC = BD$$ [Tangents from an external point are equal in length ] __(i)

$$\therefore \Delta OBC \cong \Delta OBD$$ [By SSS criterion of congruence]

$$\Rightarrow \angle OBC = \angle OBD (CPCT)$$

$$\therefore \angle OBC = \dfrac{1}{2} \angle DBC = \dfrac{1}{2} \times 120^{\circ} $$ [ $$\because \angle CBD = 120^{\circ}$$ given]

$$\Rightarrow \angle OBC = 60^{\circ}$$

OC and BC are radius and tangent respectively at contact point C.

So, $$\angle OCB = 90^{\circ}$$

Now, in right angle $$\Delta OBC = 60^{\circ}$$

$$\therefore cos 60^{\circ} = \dfrac{BC}{BO}$$

$$\Rightarrow \dfrac{1}{2} = \dfrac{BC}{BO}$$

$$\Rightarrow OB = 2 BC$$

Hence, proved (ii) part,

$$\Rightarrow OB = BC + BC$$

$$\Rightarrow OB = BC + BD $$ [$$\because BC =BD$$ from (i)]

Hence, proved.

1791821_1458800_ans_255966551fee44788fd0f37fae1b9ede.png


Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60 .

$${\textbf{Step  - 1: Finding various angles}}{\text{.}}$$

                  $${\text{As we have to make to angle between the tangents equal to 60}}^\circ $$

                  $${\text{and the tangents subtend an angle of 90}}^\circ {\text{ at its point of contact}}{\text{.}}$$

                  $${\text{We can write, that the sum of all the angles of a quadrilateral is equal to 360}}^\circ {\text{,}}$$

                  $${\text{So for the quadrilateral we have the three angles equal to 60}}^\circ ,90^\circ ,{\text{and 90}}^\circ $$

                  $${\text{Therefore,the angle subtended by the pair of tangents at the centre will be }}$$

                  $$360^\circ  - 90^\circ  - 90^\circ  - 60^\circ  = 120^\circ $$

$${\textbf{Step  - 2: Drawing the figure}}{\text{.}}$$

                 

$${\textbf{Hence, the pair of the tangents can be drawn as above}}{\text{.}}$$



Two tangents PA and PB are drawn to a circle with centre O, such that $$\angle APB=120^\circ$$ Prove that $$OP=AP+BP=2AP$$

Given: O is the centre of the circle. PA and PB are tangents drawn to a circle and ∠APB = 120°.

To prove: OP = 2AP

Proof:

In ΔOAP and ΔOBP,

OP = OP    (Common)

∠OAP = ∠OBP  (90°) (Radius is perpendicular to the tangent at the point of contact)
OA = OB  (Radius of the circle)

∴ ΔOAP is congruent to ΔOBP (RHS criterion)

∠OPA = ∠OPB = 120°/2 = 60° (CPCT)
In ΔOAP,
cos∠OPA = cos 60° = AP/OP
Therefore, 1/2 =AP/OP
Thus, OP = 2AP

Hence, proved.



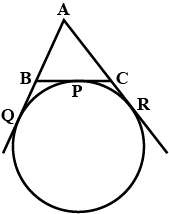
A circle touches the side $$BC$$ of $$\triangle\ ABC$$ at $$P$$ and touches $$AB$$ and $$AC$$ produced at $$Q$$ and $$R$$ respectively. Prove that $$AQ=\dfrac{1}{2}$$ (perimeter of $$\triangle\ ABC$$).
1330880_d5a7a5fea66244749fa9986eafb0fdf8.png

Given:A circle touching the side $$BC$$ of $$\triangle{ABC}$$ at $$P$$ and $$AB$$,$$AC$$ produced at $$Q$$ and $$R$$ respectively.

Proof: Lengths of tangents drawn from an external point to a circle are equal.

$$\Rightarrow AQ = AR, BQ = BP, CP = CR$$.

Perimeter of $$\triangle{ABC}=AB + BC + CA$$

$$= AB +\left(BP + PC\right)+\left(AR – CR\right)$$

$$=\left(AB + BQ\right)+\left(PC\right)+\left(AQ – PC\right)$$ since $$\left[AQ = AR, BQ = BP, CP = CR\right]$$

$$= AQ + AQ$$

$$= 2AQ$$

$$\Rightarrow AQ =\dfrac{1}{2}$$(Perimeter of $$\triangle{ABC}$$)

$$\therefore AQ$$ is the half of the perimeter of $$\triangle{ABC}$$


Write the name of the common point of the tangent to a circle and the circle.

The common point of the tangent to a circle and the circle is called the point of contact.


Which term will you use for a line that intersects a circle at two distinct points?

The term used for a line that intersects a circle at two distinct points is secant. When a line touches a circle at only one point it is known as tangent.


How many tangents can a circle have?

$${\textbf{Step1: Find the number of tangents to the circle from the given points. }}$$

              $${\text{ Circle is the locus of the points equidistant from given points, which is the center of the circle }}$$

               $${\text{and tangent is the line that intersects a circle at one point only.}}$$

              $${\text{ As circle has infinite points so there will be infinite tangents can be drawn on these points}}$$ 

              $${\text{ which touches at only one point.}}$$

$${\textbf{Therefore, a circle can have an infinite number of tangents .}}$$        


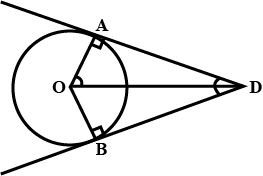
$$DA$$ and $$DB$$ are the triangle drwan from  D, to the  circle with centre $$O$$, at A and B respectively $$\angle ADO = 35^\circ$$ find $$\angle AOB$$
1529218_b96a331b4e414c2abc36bec25b786b3e.png

We are given,
Circle of centre $$O$$ is having radius $$OA$$ and $$OB$$ (r)
Now, In $$\Delta OAD$$ & $$\Delta OBD$$ is equal as two sides are equal and one angle is equal  $$(OA = OB = r)$$ and $$OD$$ also 
$$m\angle OAD = m \angle OBD = 90^o$$
Now, given that $$m\angle OBD = 90^o$$
Now, given that $$m \angle ADO = 35^o$$
then $$m\angle AOD = ?$$
$$\Delta AOD, m \angle AOD + m \angle ADO + m \angle OAD = 180^o$$
$$m\angle AOD = 180 - m \angle OAD - m \angle ADO$$
$$m \angle AOD = 180 - 90 - 35 = 55^o$$ 
So, $$m\angle AOB = m \angle AOD + m \angle DOB$$
                        $$= 55^o + 55^o$$
$$m \angle AOB = 110^o$$

1493219_1529218_ans_eb99b5c0f81b4e1fa8d5799c21dbd6a0.png


Pair of tangents are drawn from point (1,3) to circle  $${ x }^{ 2 }+{ y }^{ 2 }-3x-x+3y-1=0$$ Find  line joining their point of contact  

Equation of the circle is given as,
$$x^2+y^2-3x-x+3y-1=0$$ ……………..$$(1)$$
$$\Rightarrow x^2+y^2-4x+3y-1=0$$
$$\Rightarrow x^2+y^2+2(-2)x+2.\left(\dfrac{3}{2}\right)y+(-1)=0$$
$$\therefore g=-2$$, $$f=\dfrac{3}{2}$$ and $$c=-1$$
Equation of the chord of contact of circle $$(1)$$ is given as
$$x_1x+y_1y+g(x_1+x)+f(y_1+y)+c=0$$
$$\Rightarrow x_1x+y_1y+(-2)(x_1+x)+\dfrac{3}{2}(y_1+y)-1=0$$
Now, equation of the chord of contact of circle $$(1)$$ wrt to $$(1, 3)$$
$$1x+3y+(-2)(1+x)+\dfrac{3}{2}(3+y)-1=0$$
$$2x+6y-4(1+x)+3(3+y)-2=0$$
__________________________________
                       $$2$$
$$\Rightarrow 2x+6y-4-4x+9+3y-2=0$$
$$\Rightarrow -2x+9y+3=0$$
$$\Rightarrow 2x-9y-3=0$$
$$\Rightarrow 2x-9y=3$$.

1215675_1300969_ans_2cb011034e1b48248997ae8fa3fcdb78.JPG


How many tangents can be drawn at a point on a circle ?

Only one tangent can be drawn from a point on the circle
Every other line intersect the circle at two points which won't be a tangent
1795328_1815673_ans_c6f48f0fac564444a03d703a9f5a5211.png


Draw two concentric circles of radii $$3 \,cm$$ and $$5 \,cm.$$ Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.

Steps of construction:
(i) Draw two concentric circles $$C_1, C_2$$ of radii $$3 \,cm$$ and $$5 \,cm$$ respectively taking 'O' as centre.
(ii) Draw perpendicular bisector AB of OT. T is any point on $$C_2.$$
(iii) Draw circle $$C_3$$ taking radius $$TM = OM$$ and $$M$$ as centre.
(iv) Circle $$C_3$$ intersect the circle $$C_1$$ at P and Q. Join TP and TQ. These are the required tangents. $$TP = TQ = 4.1 \,cm$$ by measuring.

Mathematically length of tangent: Join OP. OP and TP are radius and tangent respectively at contact point P. So, $$\angle TPO = 90^\circ.$$
By Pythagoras theorem in $$\Delta TPO,$$
$$PT^2 = OT^2 - OP^2 = 5^2 - 3^2 = 25 - 9 = 16$$
$$\Rightarrow PT = 4 \,cm$$
Difference in measurement and by mathematical calculation 
$$PT = 4.1 \,cm - 4 \,cm = 0.1 \,cm.$$


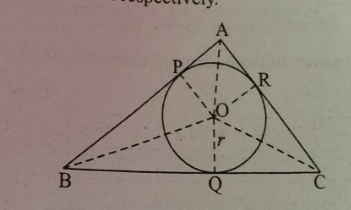
In figure, the sides  AB,  BC and CA of triangle ABC touch a circle with centre 0 and radius r at P.  Q and R respectively.
Prove That : 
(i)  AB+CQ=AC+BQ
(ii) Area $$(\Delta ABQ=\frac{1}{2}$$  (Perimeter of $$(\Delta ABC)\times r$$
1582989_f356141fb3934fac95e824989ca3a885.PNG


2173000_1582989_ans_71369e9dcad64cb3a2802c108f504b34.jpeg


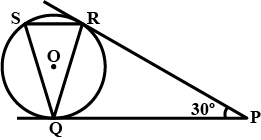
In the given figure,  tangents $$PQ$$ and $$PR$$ are drawn from an external point p to a circle with center $$O$$, such that $$\angle RPQ=30^{\circ}$$. A chord $$RS$$ is drawn parallel to the tangent $$PQ$$. Find $$\angle RQS.$$

971375_aedcb8095ea042c3aa9aa52a4d73744e.png


1570510_971375_ans_99a8ec3d198147ca917a817416ee48b4.jpg


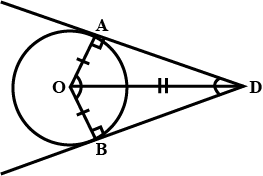
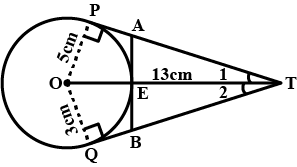
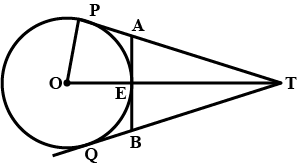
In the given figure, O is the centre of a circle of radius 5 cm, T is a point such that OT= 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.
1516190_e68a3f38695e43fb8eaa2f4e91b7ee9a.png

$$OP = OQ = 5 cm$$

$$OT = 13 cm$$

$$OP$$ and $$PT$$ are radius and tangent respectively at contact point P.

$$\therefore \angle OPT = 90^{\circ}$$

So, by pythagoras theorem, in right angled $$\Delta OPT$$,

$$PT^2 = OT^2 - OP^2 = 13^2 - 5^2 = 169 - 25 = 144$$

$$\Rightarrow PT = 12 cm$$

$$AP$$ and $$AE$$ are two tangents from an external point A to a circle.

$$\therefore AP = AE$$

$$AEB$$ is tangent and $$OE$$ is radius at contact point E.

So, $$AB \bot OT$$ ___(i)

So, by Pythagoras theorem, in right angled. $$\Delta AET$$.

$$AE^2 = AT^2 - ET^2$$

$$\Rightarrow AE^2 = (PT - PA)^2 - [TO - OE]^2$$

$$=(12 - AE)^2 - (13 - 5)^2$$

$$\Rightarrow AE^2 = (12)^2 + (AE)^2 - 2 (12) (AE) - (8)^2$$

$$\Rightarrow AE^2 - AE^2 + 24 AE = 144 - 64$$

$$\Rightarrow 24 AE = 80$$

$$\Rightarrow AE = \dfrac{80}{24} cm$$

$$\Rightarrow AE = \dfrac{10}{3} cm$$

REF. IMAGE

In $$\Delta TPO $$ and $$\Delta TQO$$,

$$OT = OT$$ [common]

$$PT = QT$$ [Tangents from T]

$$OP = OQ$$ [Radii of same circle]

$$\therefore \Delta TPO \cong \Delta TQO$$ [By SSS criterion of congruence]

$$\Rightarrow \angle 1 = \angle 2 $$ ___(ii) [CPCT]

In $$\Delta ETA $$ and $$\Delta ETB$$,

$$ET = ET$$ [Common]

$$\angle TEA = \angle TEB  = 90^{\circ}$$ [From (i)]

$$\angle 1 = \angle 2$$ [CPCT] [From (ii)]

$$\therefore \Delta ETA \cong \Delta ETB$$ [By ASA criterion of congruence]

$$\Rightarrow AE = BE$$ [CPCT]

$$\Rightarrow AB = 2 AE = 2 \times \dfrac{10}{3}$$

$$\Rightarrow AB = \dfrac{20}{3} cm$$

Hence, the required length is $$\dfrac{20}{3} cm$$.

1804487_1516190_ans_a7fea1e0002d4770b10122e7a1979cb7.png


Class 10 Maths Extra Questions