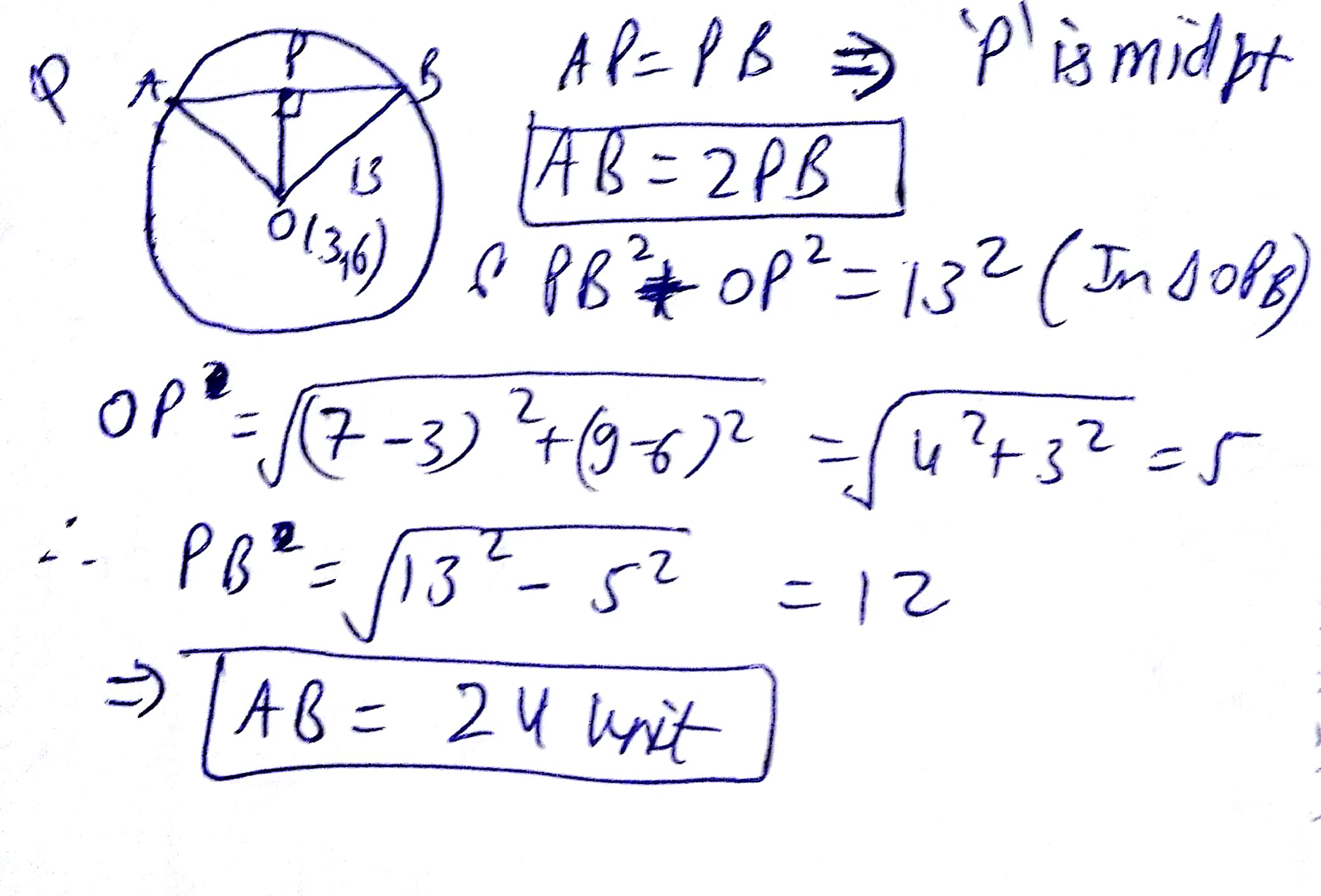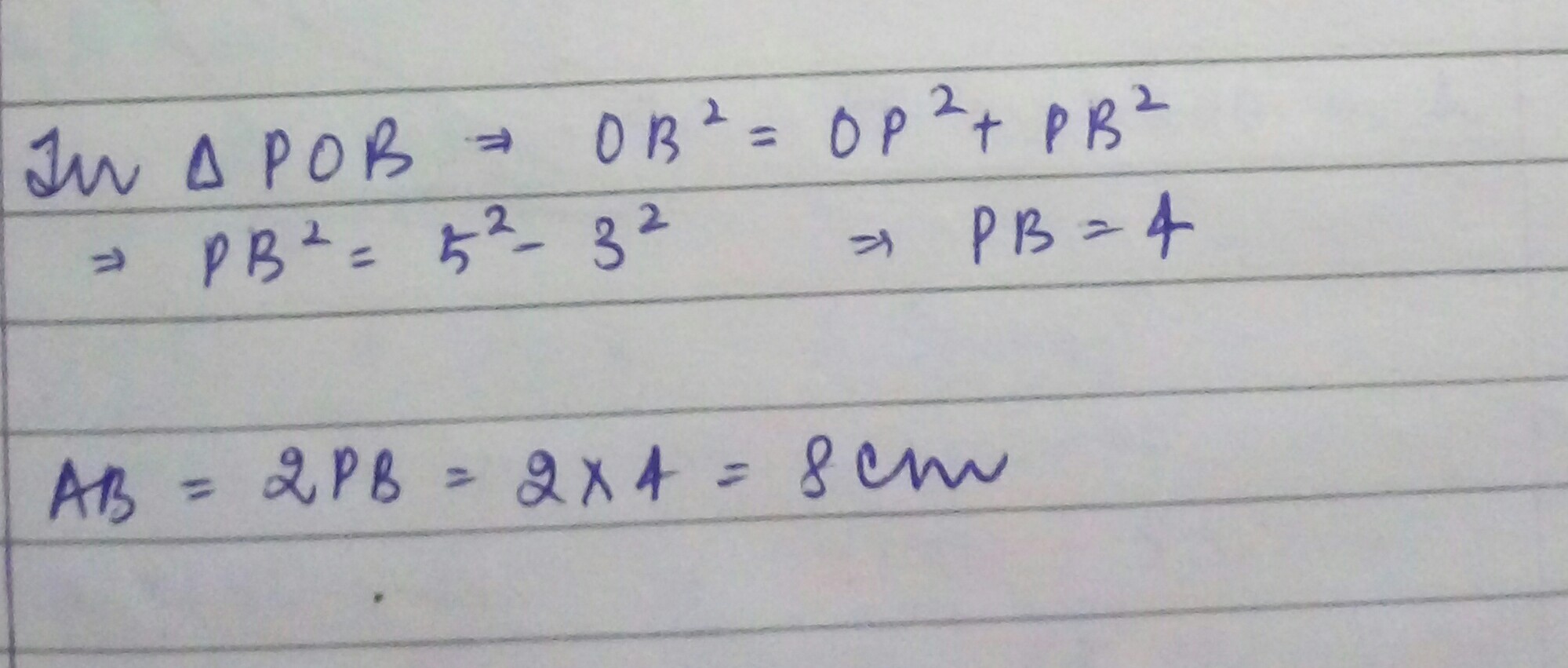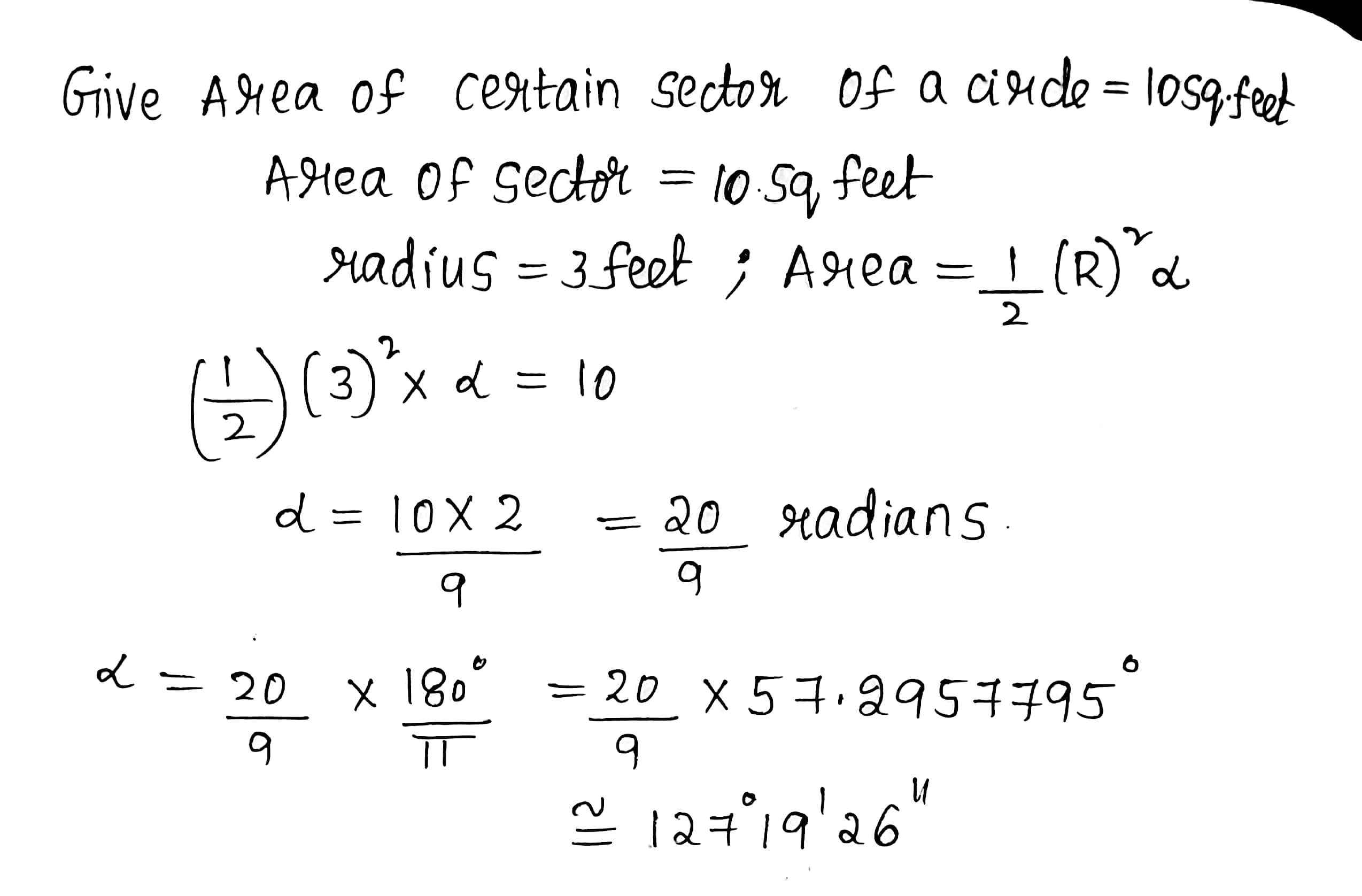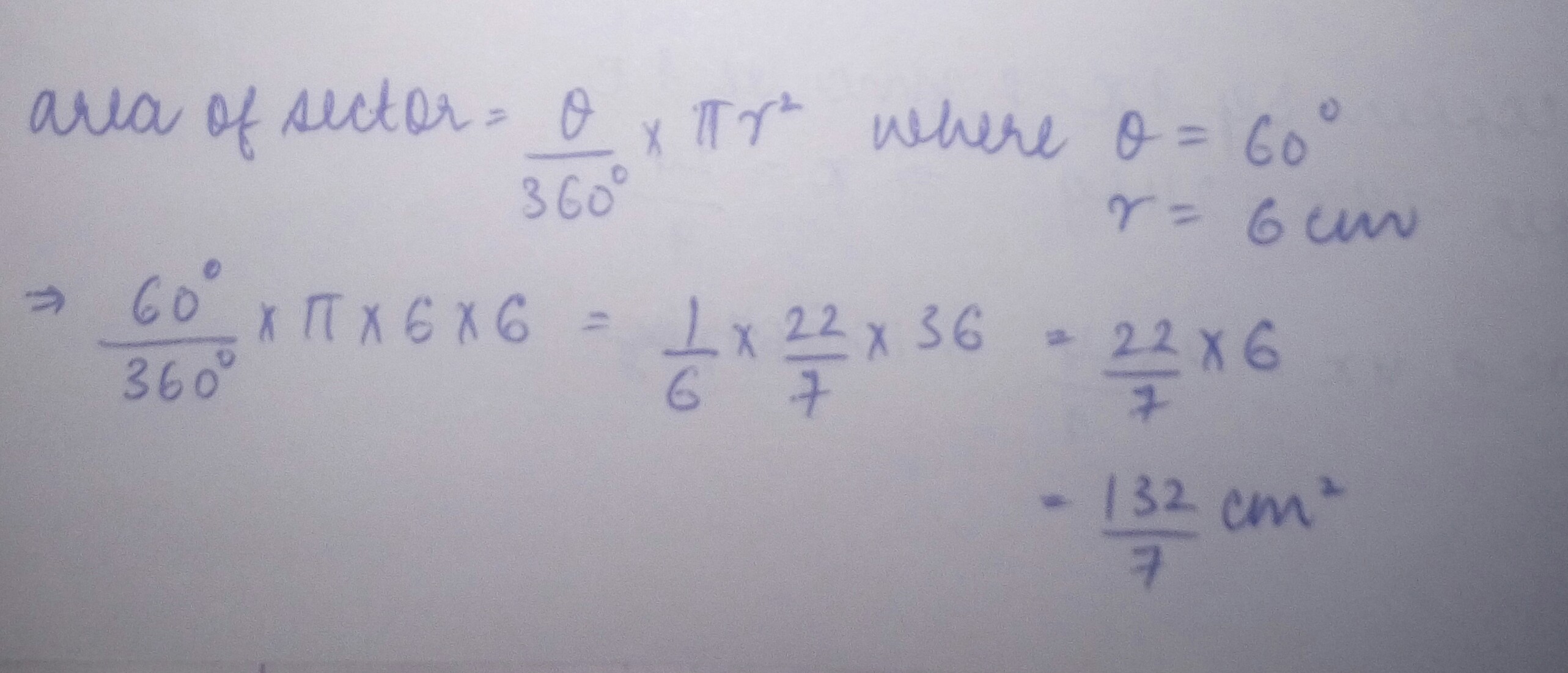Circles - Class 9 Maths - Extra Questions
If an arc of a circle subtends an angle of $${60}^{o}$$ at the centre and if the area of minor sector is $$231{cm}^{2}$$, then find the radius of the circle.
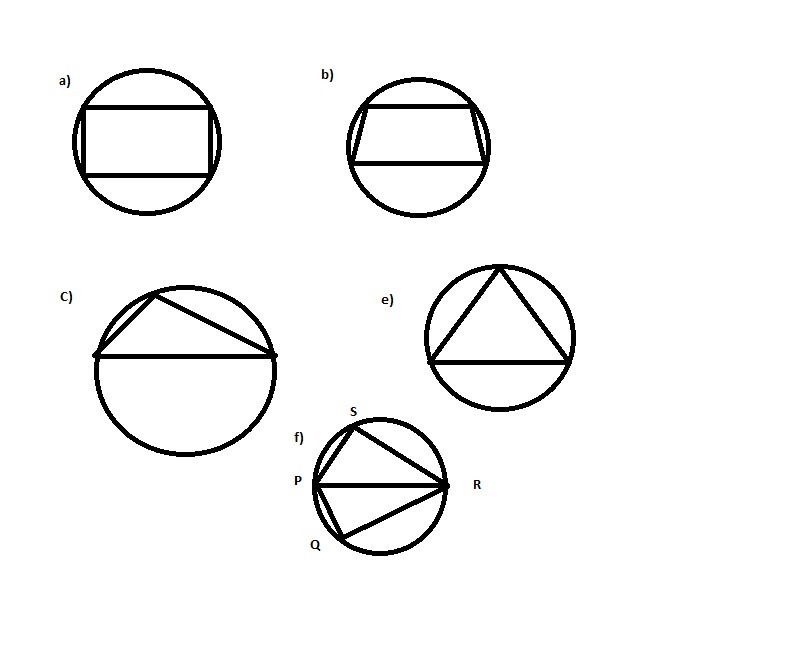
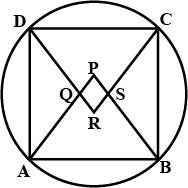
For each of the following, draw a circle and inscribe the figure given. If a polygon of the given type can't be inscribed, write not possible.
(a) Rectangle
(b) Trapezium
(c) Obtuse triangle
(d) Non-rectangular parallelogram
(e) Acute isosceles triangle
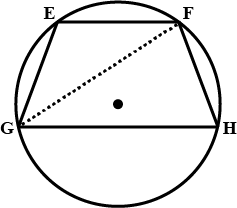
(f) A quadrilateral PQRS with $${PR}$$ as diameter.
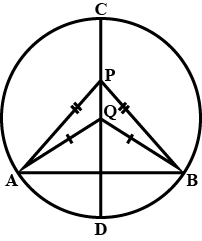
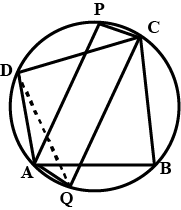
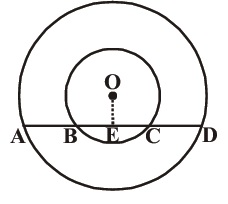
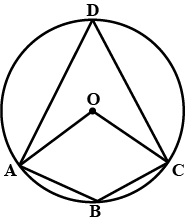
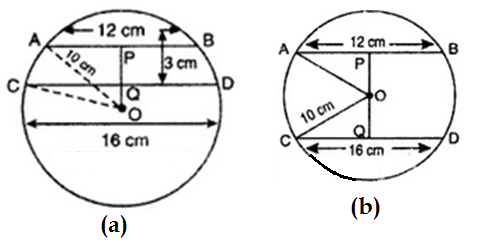
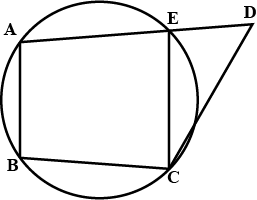
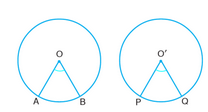
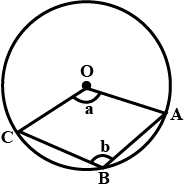
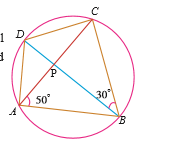
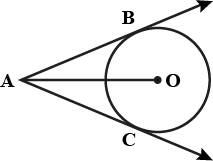
Why the given circles are equal?
If a quadrilateral is cyclic, then sum of each pair of opposite angles is $$180^o$$.
The minute hand of a watch is $$1.5\ cm$$ long. How far does it move in $$40$$ minutes? (use $$\pi =\dfrac{22}{7}$$)
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
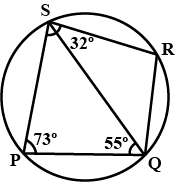
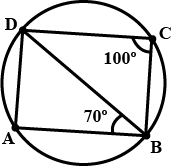
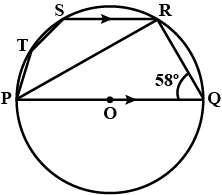
PQRS is a cyclic quadrilateral. Given $$\angle$$QPS $$=73^o$$, $$\angle$$PQS$$=55^o$$ and $$\angle$$PSR$$=82^o$$, calculate $$\angle$$QRS.
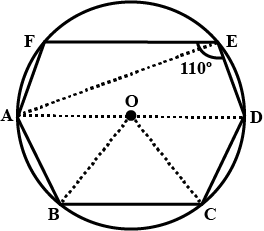
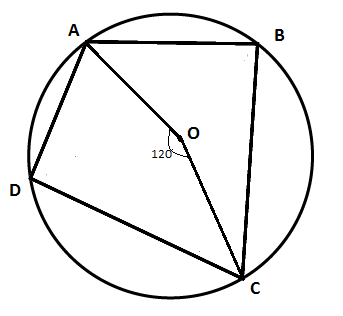
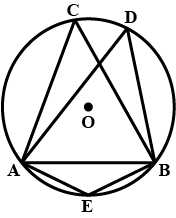
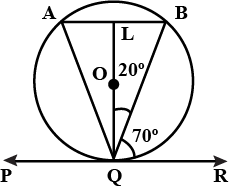
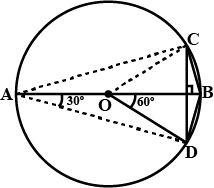
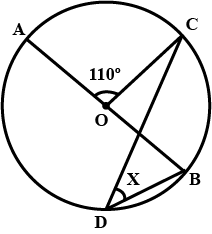
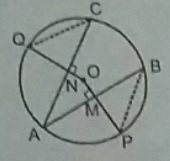
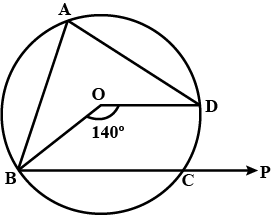
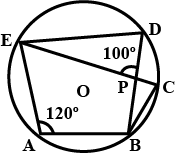
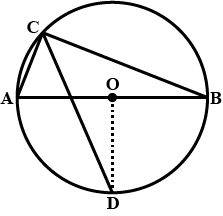
In the figure, given alongside, $$AOB$$ is a diameter of the circle and $$\angle{AOC}={110}^{o}$$. Find $$\angle{BDC}$$.
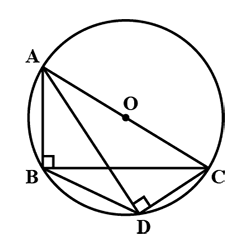
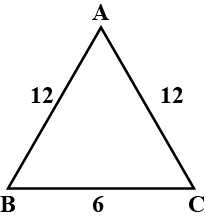
The radius of the circle passing through the vertices of the triangle $$ABC$$, is
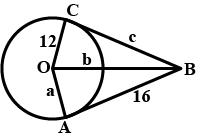
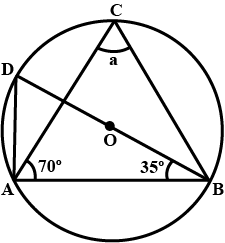
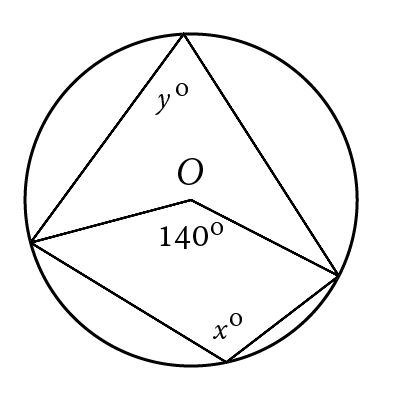
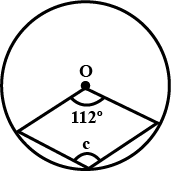
Find a, b, c in the given figure.
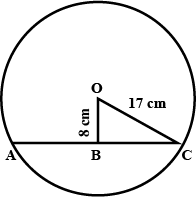
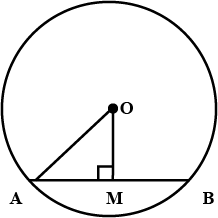
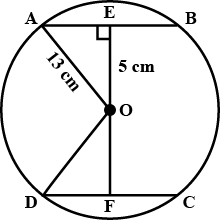
The radius of a circle is $$17.0$$ cm and the length of perpendicular drawn from its centre to a chord is $$8.0$$ cm. Calculate the length of the chord.
In a circle of radius $$21$$ cm, an arc subtends an angle of $$60^o$$ at the center, then find the length of the arc.
A chord of length 6 cm is drawn in a circle of radius 5 cm. Calculate its distance from the centre of the circle.
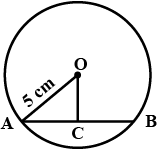
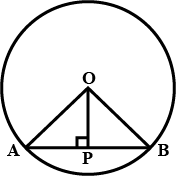
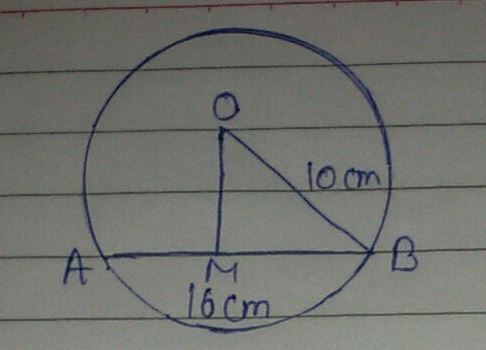
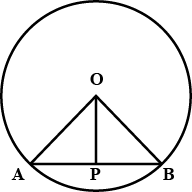
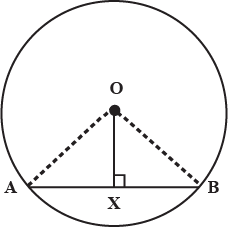
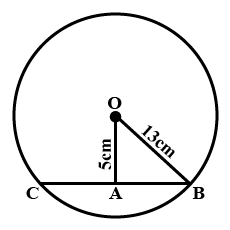
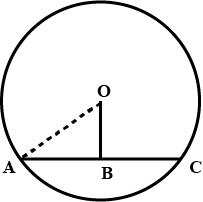
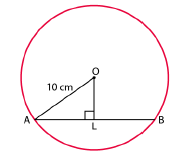
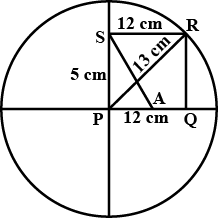
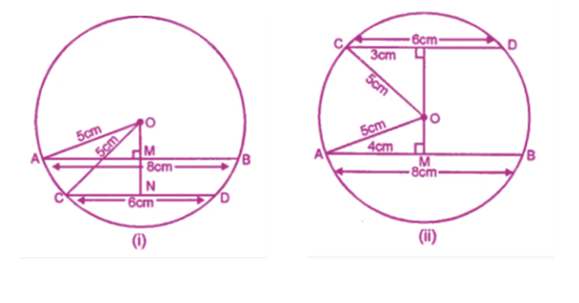
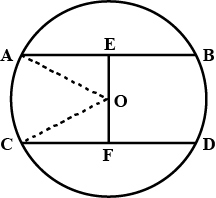
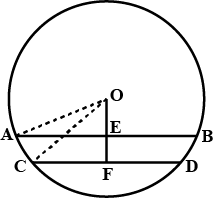
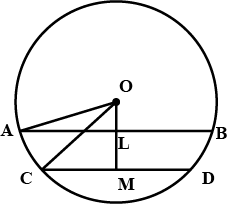
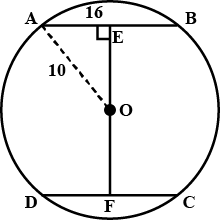
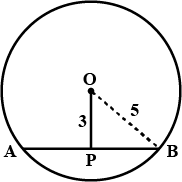
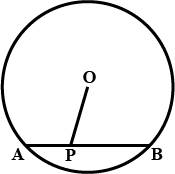
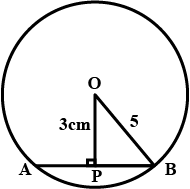
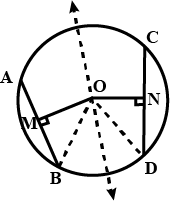
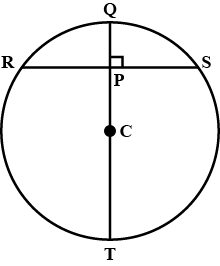
In the given figure, $$O$$ is the centre of the circle $$OB=5\ \text{cm}$$. Distance from $$O$$ to chord $$AB$$ is $$ 3\ \text{cm}$$. Find the length of $$AB$$.
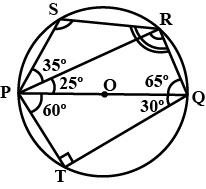
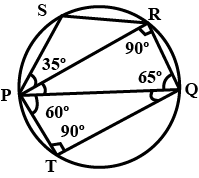
If $$\angle{PQR}={65}^{o},\angle{QPT}={60}^{o},\angle {SPR}={35}^{o}$$, find the value of:
(i) $$\angle {QPR}$$ (ii) $$\angle {PRS}$$ (iii) $$\angle {PSR}$$ (iv) $$\angle {PQT}$$.
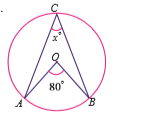
In the given fig. AOB is a diameter of the circle with centre with centre o and $$\angle AOC = 100^o $$, find $$\angle BOC$$.
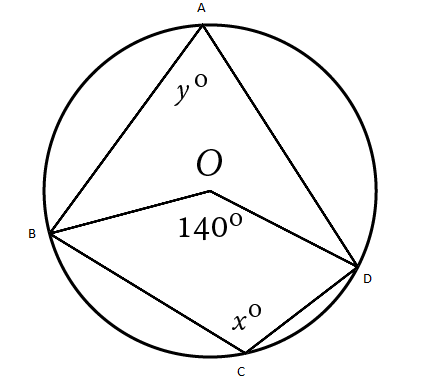
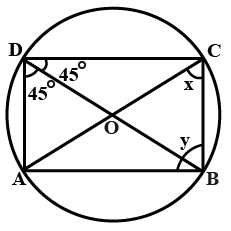
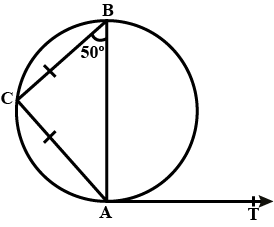
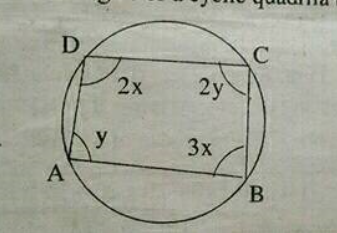
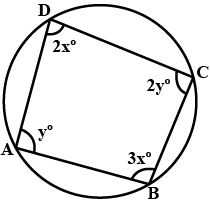
In the given figure, $$ABCD$$ is a cyclic quadrilateral. Find $$x$$ and $$y$$.

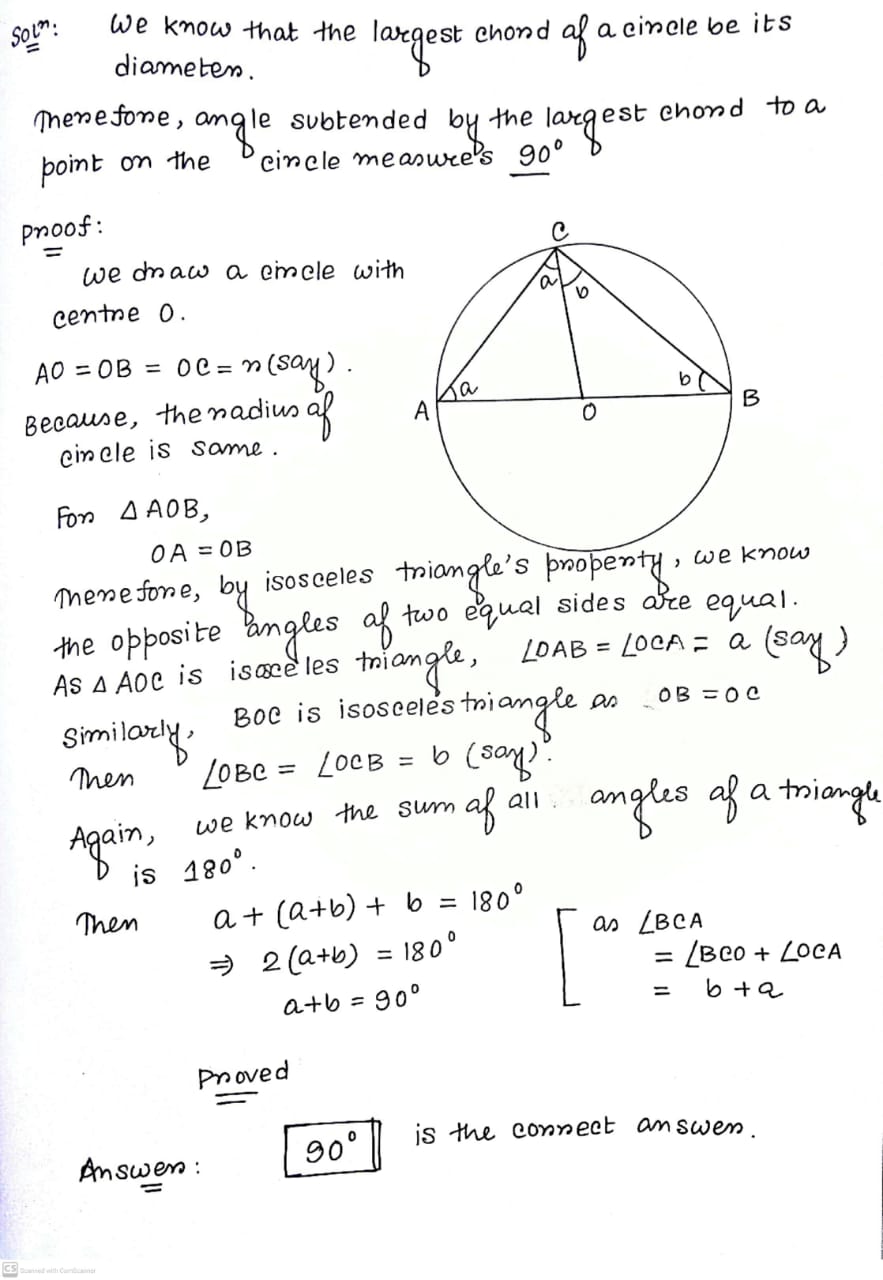
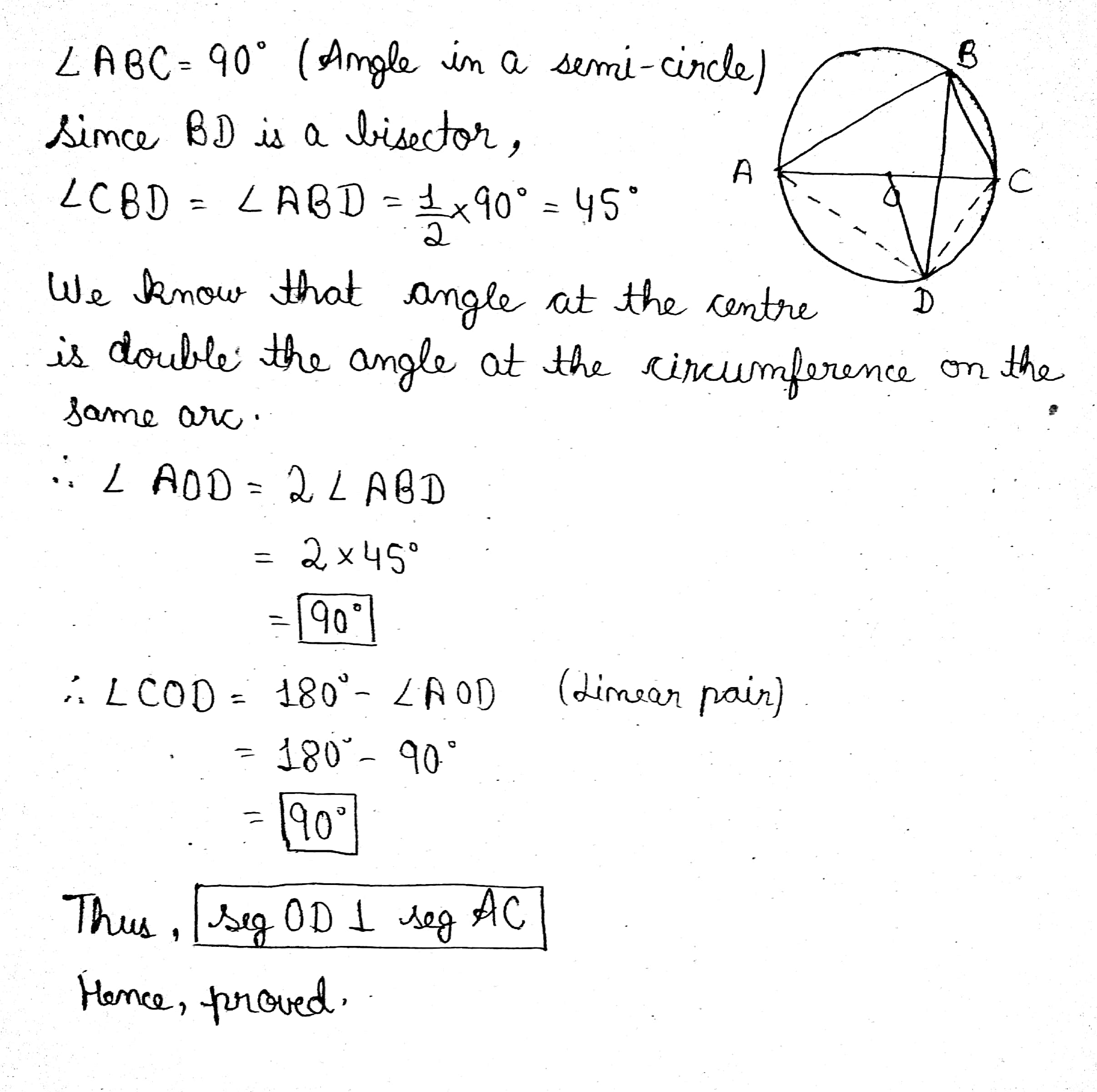
Prove that the angle subtend in a semi circle is always $$90^{o}$$
Radius of circle is $$10\ cm$$. There are two chords of length $$16\ cm$$ each. What will be the distance of these chords form the centre of the circle?
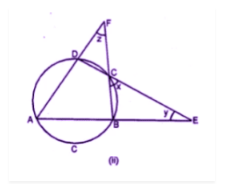
In figure $$\angle ADE$$ and $$\angle ABC$$ differ by $$15^{\circ }$$, Find $$\angle CAE$$
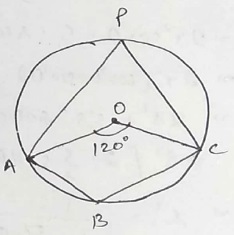
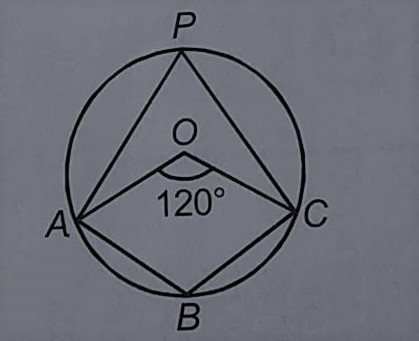
In the given figure, if $$m \angle A O C = 120 ^ { \circ }$$,then the measure of $$\angle A B C$$ is
Radius of a circle is 34 cm and the distance of the chord from the center is 30 cm, find the length of the chord.
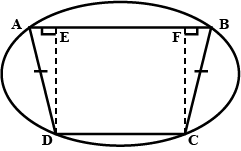
In the given figure, $$AB=AC$$. Prove that $$DECB$$ is an isosceles trapezium.
What is the distance of the chord of length $$16\ cm$$ from the centre of circle, if its radius is $$10\ cm$$?
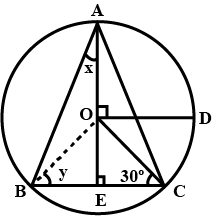
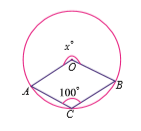
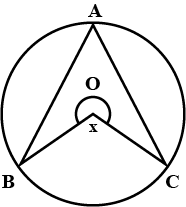
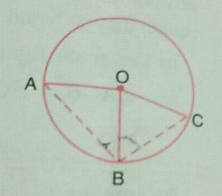
$$O$$ is the centre of the circle. $$\angle{A}={50}^{o}$$, find $$x$$
Prove by vector method that the angle in a semcircle is right amgle.
The length of a chord of a circle of $$16.8$$ cm, radius is $$9.1$$ cm. Find its distance from the centre.
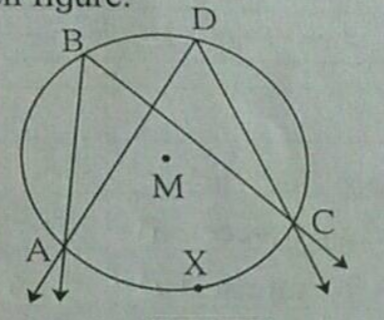
Complete the proof of the theorem 'Angles in the same arc are congruent' with the help of given figure.
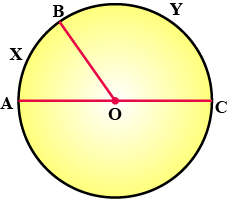
Arc intercepted by $$\angle A B C =$$
Arc intercepted by $$\angle A D C =$$
$$=\dfrac { 1 }{ 2 } m({ arc }AXC)......(I)$$
$$=\dfrac { 1 }{ 2 } m({ arc }AXC)......(II)$$
From $$(I)$$ and $$(II)$$
$$\therefore \angle A B C \cong \angle A D C$$
The length of chord of radius $$25cm$$ and Distance at $$7cm$$ is
A circle with centre 'O' has a radius $$\sqrt { 2 } $$ cm, it is divided into two segments by a chord AB of length 2 cm. Prove that the angle subtended by the chord at a point 'P' in the major segment is $${ 45 }^{ 0 }$$.
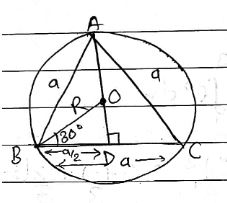
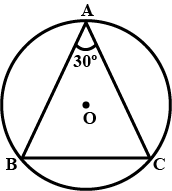
In the given figure, ABC is a triangle , in which $$\angle BAC$$ = 30 . Show that the length of BC is equal to the radius of the circumcircle of ABC , whose centre is O .
Show that the angle in a semi circle in a right angle
Find the length of chord of circle with radius $$5cm$$ and distance from center $$2cm$$
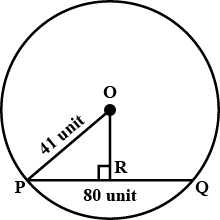
Radius of a circle with centre $$O$$ is $$41$$ units. Length of a chord $$P$$ is $$80$$ units, find the distance of the chord from the centre of the circle.
Two concentric circles are of radii $$8cm$$ and $$5cm$$.Find the length of the chords of the larger circle which touches the smaller circle.
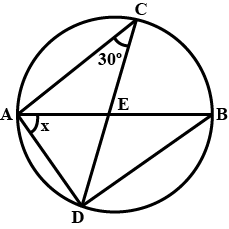
Calculate: $$\angle ABC$$
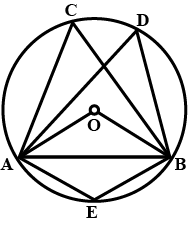
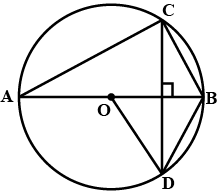
In the figure given below, O is the centre of the circle and triangle ABC is equilateral. Find $$\angle AEB$$
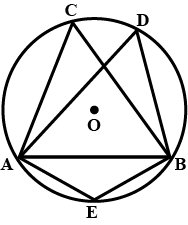
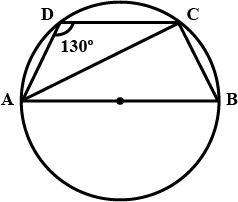
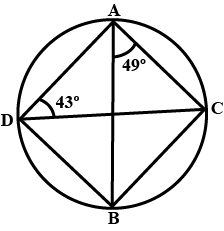
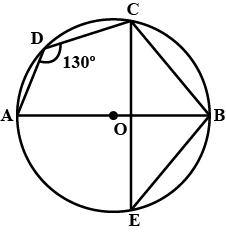
$$ABCD$$ is a cyclic quadrilateral in a circle with centre $$O$$. If $$\angle ADC = 130^{\circ}$$, find $$\angle BAC$$.
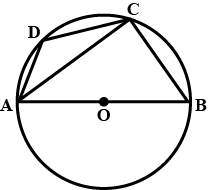
Calculate: $$\angle ACB$$
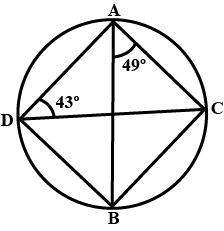
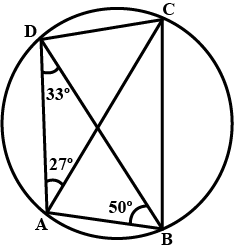
In $$ABCD$$ is a cyclic quadrilateral in which $$\angle DAC = 27^{\circ}, \angle DBA = 50^{\circ} and \angle ADB = 33^{\circ}$$. Calculate $$\angle CAB$$
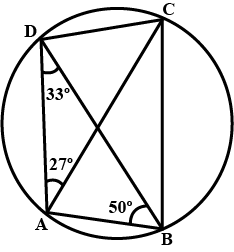
What is the locus of a points inside a circle and equidistant from two fixed points on the circumference of the circle.
In $$ABCD$$ is a cyclic quadrilateral in which $$\angle DAC = 27^{\circ}, \angle DBA = 50^{\circ} and \angle ADB = 33^{\circ}$$. Calculate $$\angle DBC$$
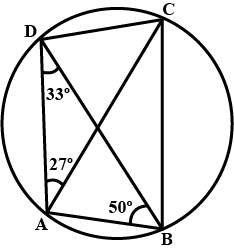
Calculate: $$\angle CDB$$
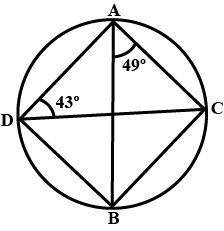
Solve the following question:
$$\Box ABCD$$ is cyclic . If $$\angle B = 110^{\circ}$$, then find measure of $$\angle D$$.
Value of $$\pi$$ is ____ approximately.
$$ABCD$$ is a cyclic quadrilateral in which $$AB$$ and $$DC$$ on being
produced, meet at $$P$$ such that $$PA = PD$$. Prove that $$AD$$ is
parallel to $$BC$$.
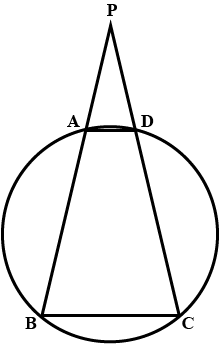
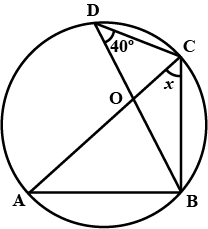
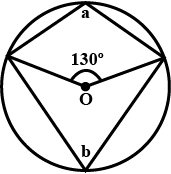
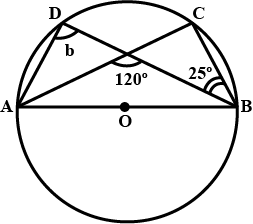
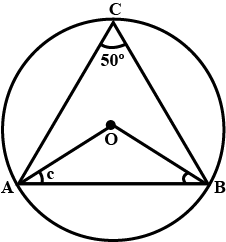
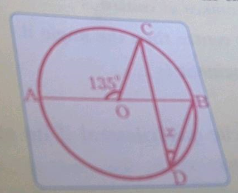
The figure given below, shows a circle with centre $$O$$. Given: $$\angle AOC = a$$ and $$\angle ABC = b$$. Find the relationship between $$a$$ and $$b$$
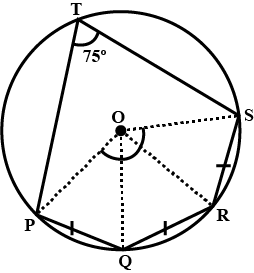
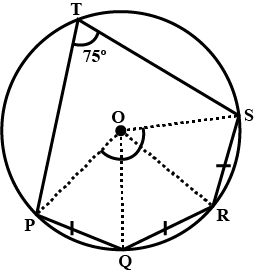
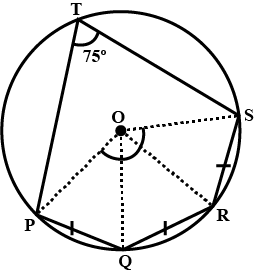
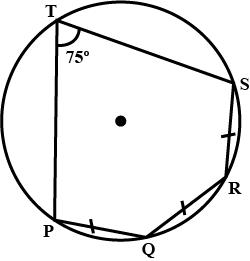
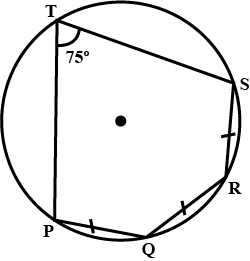
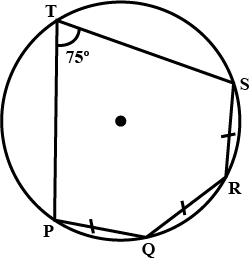
The given figure show a circle with centre $$O$$. Also, $$PQ = QR = RS$$ and $$\angle PTS = 75^{\circ}$$. Calculate $$\angle POS$$
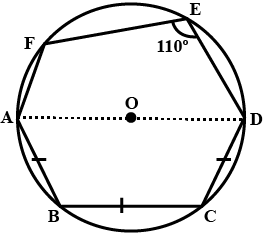
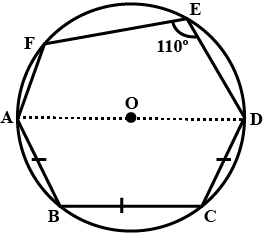
In the following figure, $$AD$$ is the diameter of the circle with centre $$O$$. Chords $$AB$$, $$BC$$ and $$CD$$ are equal. If $$\angle DEF = 110^{\circ}$$, calculate $$\angle FAB$$
The given figure show a circle with centre $$O$$. Also, $$PQ = QR = RS$$ and $$\angle PTS = 75^{\circ}$$. Calculate $$\angle PQR$$
In the following figure, $$AD$$ is the diameter of the circle with centre $$O$$. Chords $$AB$$, $$BC$$ and $$CD$$ are equal. If $$\angle DEF = 110^{\circ}$$, calculate $$\angle AFE$$
In the figure given alongside, $$AB || CD$$ and $$O$$ is the center of the circle. If $$\angle ADC = 25^{\circ}$$; find the $$\angle AEB$$. Give reasons in support of your answer.

In the following figure, $$O$$ is the centre of the circle. Find the values of $$a$$ and $$b$$.
The given figure show a circle with centre $$O$$. Also, $$PQ = QR = RS$$ and $$\angle PTS = 75^{\circ}$$. Calculate $$\angle QOR$$
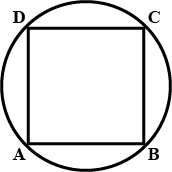
Prove that the rhombus, inscribed in a circle, is a square.
In the given circle with diameter $$AB$$, find the value of $$x$$.
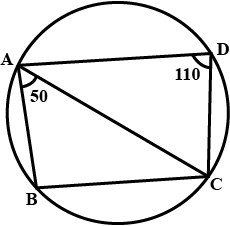
In the figure, given below, find $$\angle ADC$$. Show steps of your working.

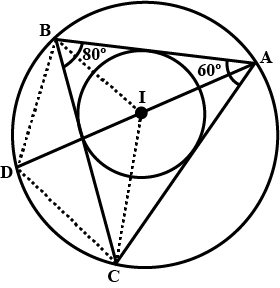
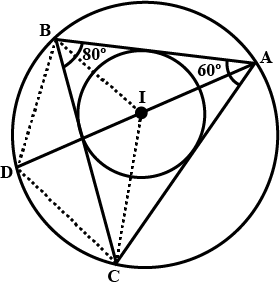
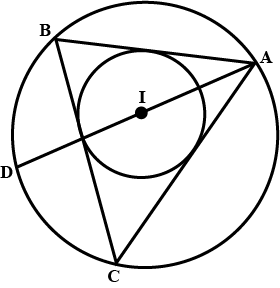
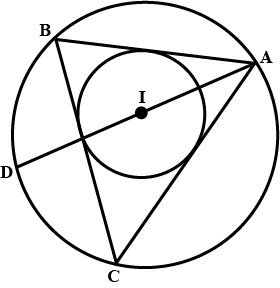
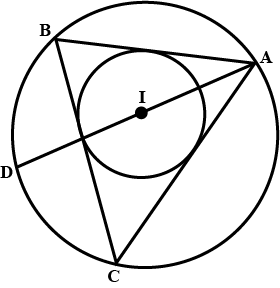
If $$I$$ is the incentre of triangle $$ABC$$ and $$AI$$ when produced meets the circumcircle of triangle $$ABC$$ in point $$D$$. If $$\angle BAC = 66^{\circ}$$ and $$\angle ABC = 80^{\circ}$$. Calculate $$\angle DBC$$
In the given figure, $$AB = AD = DC = PB$$ and $$\angle DBC = x^{\circ}$$. Determine, in terms of $$x$$:
(i) $$\angle ABD$$, (ii) $$\angle APB$$.
Hence or otherwise, prove that $$AP$$ is parallel to $$DB$$.
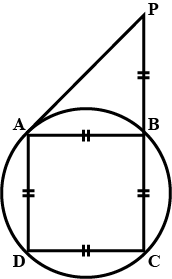
In the given figure, $$AB$$ is the diameter of the circle with centre $$O$$. If $$\angle ADC = 32^{\circ}$$, find $$\angle BOC$$.
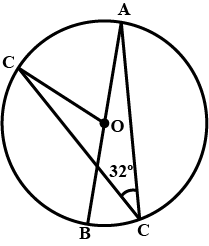
In the figure, given below, find $$\angle BCD$$. Show steps of your working.

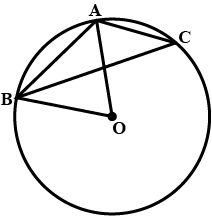
In the given figure, $$AB$$ is a side of a regular six-sided polygon and $$AC$$ is a side of a regular eight-sided polygon inscribed in the circle with centre $$O$$. calculate the sizes of $$\angle ACB$$
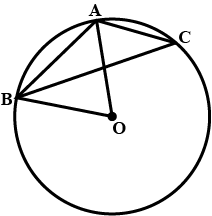
In the given figure, $$AB$$ is a side of a regular six-sided polygon and $$AC$$ is a side of a regular eight-sided polygon inscribed in the circle with centre $$O$$. calculate the sizes of $$\angle AOB$$
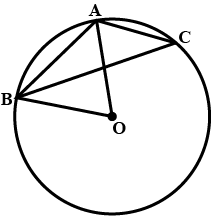
If $$I$$ is the incentre of triangle $$ABC$$ and $$AI$$ when produced meets the circumcircle of triangle $$ABC$$ in point $$D$$. If $$\angle BAC = 66^{\circ}$$ and $$\angle ABC = 80^{\circ}$$. Calculate $$\angle IBC$$
In the given figure, $$AB$$ is a side of a regular six-sided polygon and $$AC$$ is a side of a regular eight-sided polygon inscribed in the circle with centre $$O$$. calculate the sizes of $$\angle ABC$$
In the figure, given below, find $$\angle ABC$$. Show steps of your working.

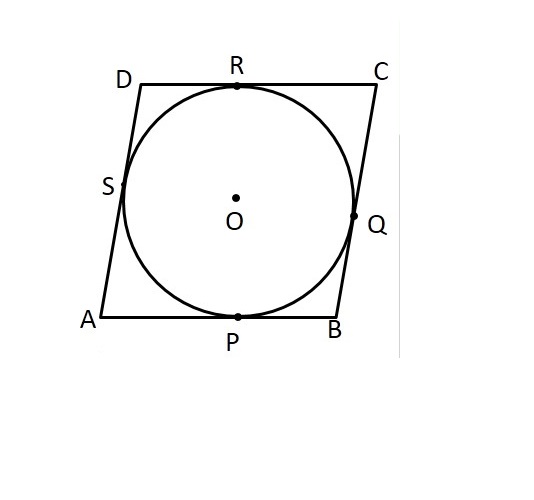
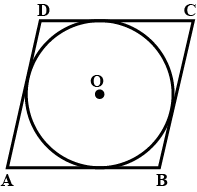
If the sides of a parallelogram touch a circle , prove that the parallelogram is rhombus
In the following figure, $$O$$ is the center of the circle. Find the values of $$b$$
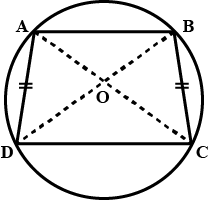
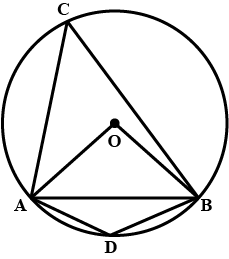
OABC is a rhombus whose three vertices A, B and C lie on a circle with center O.
If the are of the rhombus is $$32 \sqrt{3} cm^{2}$$, find the radius of the circle.
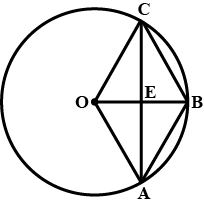
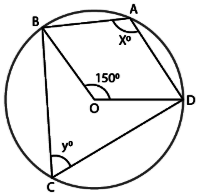
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If $$\angle DCQ = 40^{\circ}$$ and $$\angle ABD = 60^{\circ}$$, find
$$\angle DBC$$
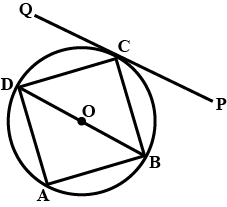
In the following figure, $$O$$ is the center of the circle. Find the values of $$d$$
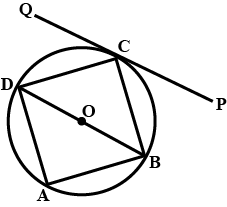
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If $$\angle DCQ = 40^{\circ}$$ and $$\angle ABD = 60^{\circ}$$, find
$$\angle BCP$$
In the following figure, $$O$$ is the center of the circle. Find the values of $$a$$
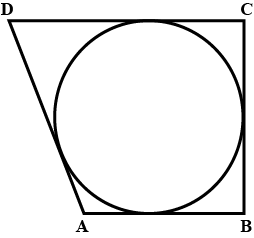
If the side of quadrilateral ABCD touch a circle, prove that AB + CD = BC + AD
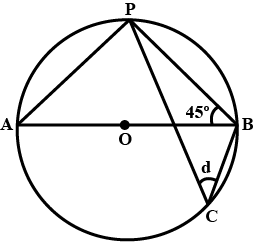
In the following figure, $$O$$ is the center of the circle. Find the values of $$c$$
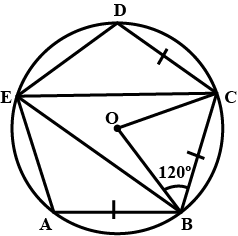
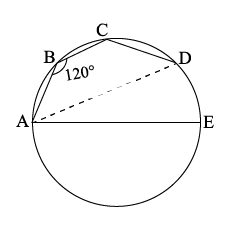
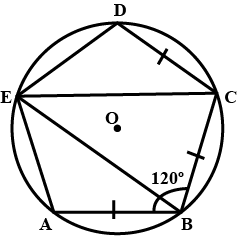
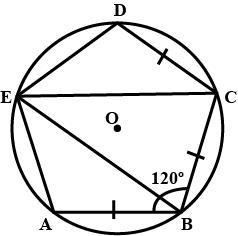
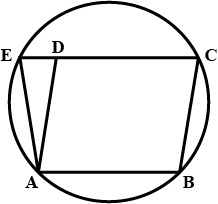
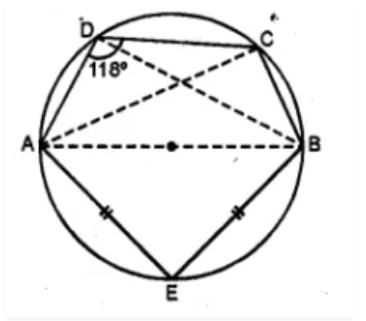
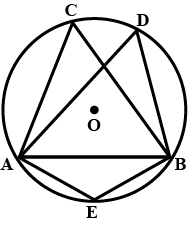
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle $$ABC = 120^{\circ}$$
Calculate :
$$\angle BED$$
The following figure shows a circle with center O .
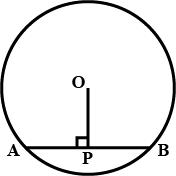
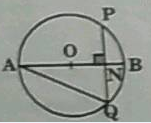
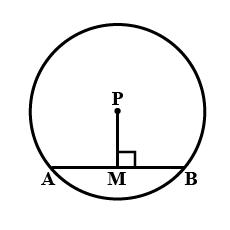
If OP is perpendicular to AB , prove that AP = BP
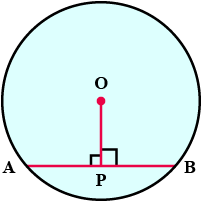
Prove that , if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
ABCDE is a cyclic pentagon with centre of its circumcircle at point O such that AB = BC = CD and angle $$ABC = 120^{\circ}$$
Calculate :
$$\angle BEC$$
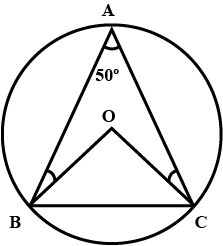
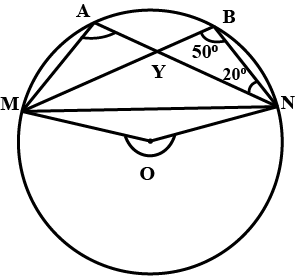
O is the center of the circle. If $$ \displaystyle \angle BAC=50^{\circ}$$, find $$\angle OBC $$
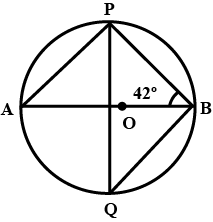
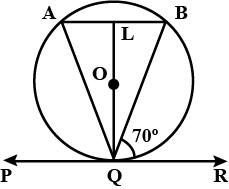
In the given figure, calculate the measure of $$ \displaystyle \angle PQB $$.
If $$ABCD$$ is a cyclic quadrilateral such that $$\displaystyle \angle A=90^{\circ},\,\angle B=70^{\circ}$$ and $$\angle C=90^{\circ}$$, then $$\angle D$$ in degrees is:
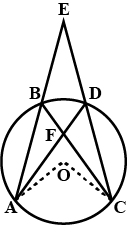
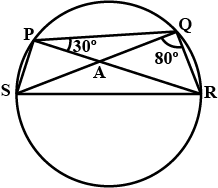
If A, B, C, D are four points such that $$\displaystyle \angle BAC=30^{\circ}\,and\,\angle BDC=60^{\circ}$$ thenprove that D is the centre of the circle through A, B and C
D is the centre of the circle through A, B and C
$$AB$$ and $$AC$$ are two equal chords of a circle. Prove that the bisector of the $$\angle BAC$$ passes through the centre of the circle.
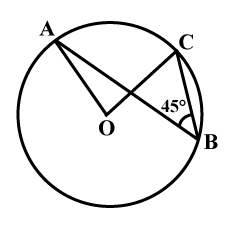
In given figure, $$\displaystyle \angle ABC=45^{\circ},$$ find $$\angle AOC$$.
The radius of a circle is $$12$$ cm. If a chord of length $$12$$ cm is drawn then find the area of the smaller segment.
If $$AB = 8$$ cm, $$BC = 6$$ cm and $$\angle ABC = 90^o$$ , then the radius of the circle passing through the points $$A, B$$ and $$C$$ is :
A chord of a circle is equal to its radius Find the angles subtended by this chord at a point in major segment
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle circumscribing it at the points P and Q prove that PQ is a diameter of the circle
In given figure, $$\displaystyle \angle ACB=40^{\circ}.$$ Find $$\displaystyle \angle AOB.$$
If a pair of opposite sides of a cyclic quadrilateral are equal prove that its diagonals are also equal
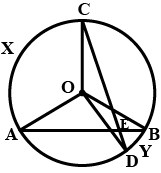
In Fig. 10.19 AB and CD are two chords of a circle intersecting each other at point E Prove that $$\displaystyle \angle AEC=\frac{1}{2}$$(Angle subtended by arc CXA at centre + angle subtended by arc DYB at the centre)
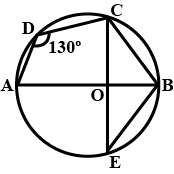
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and $$\displaystyle \angle ADC=130^{\circ}$$ Find $$\displaystyle \angle ABC $$ (in degrees)
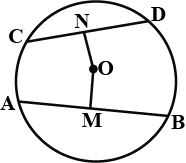
If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
In the given figure,$$\displaystyle \angle ADC=130^{\circ}$$ and chord $$BC$$ = chord $$BE$$. Find $$\displaystyle \angle CBE$$ (in degrees)
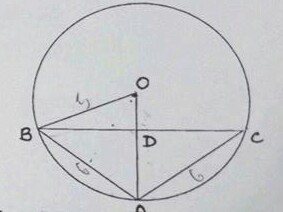
In the given figure, O is the center of the circle BD = OD and $$\displaystyle CD\perp AB$$. Find $$\displaystyle \angle CAB$$ (in degrees)
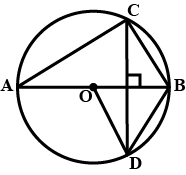
$$ABCD$$ is a cyclic quadrilateral and $$O$$ is the centre of the circle through $$A, B, C$$ and $$D$$. If $$\angle AOC = 120^o$$, find $$\angle ADC$$.
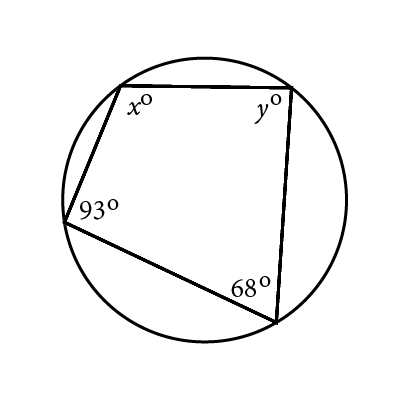
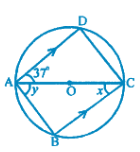
Find the value of $$y$$.
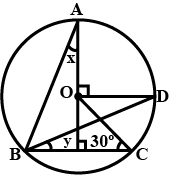
In given figure, O is the centre of the circle $$\displaystyle \angle BCO=30^{\circ}$$ Find x and y
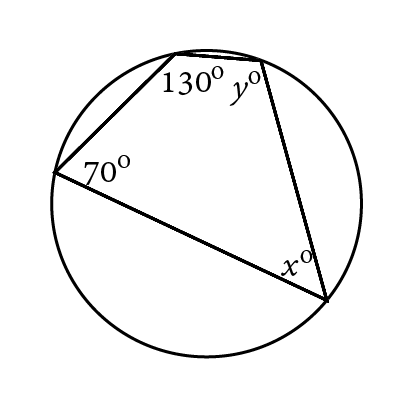
Find the value of $$x$$.
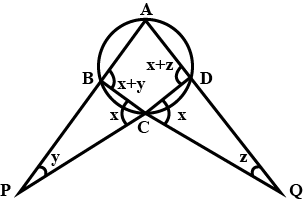
A chord $$PQ$$ of a circle is parallel to the tangent drawn at a point $$R$$ of the circle. Prove that $$R$$ bisects the arc $$PRQ.$$
If a line intersects two concentric circles with centre $$A$$ in points $$P, Q, R$$ and $$S$$ respectively, then prove that $$PQ = RS$$.
Find the value of $$x$$ in the given figure in degrees.
Suppose you are given a circle. Give a construction to find its centre.
Two chords, PQ and PR of a circle are equal. Prove that the bisector of $$\angle RPQ$$ passes through the centre of the circle.
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
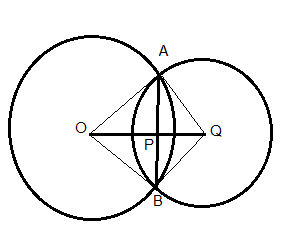
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
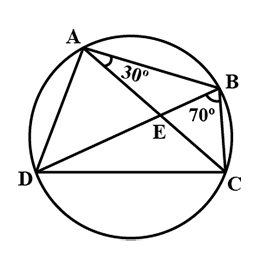
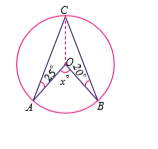
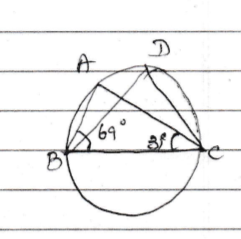
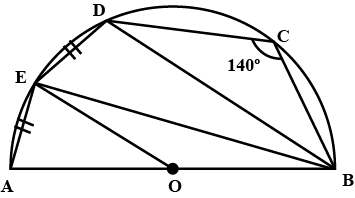
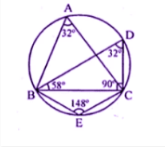
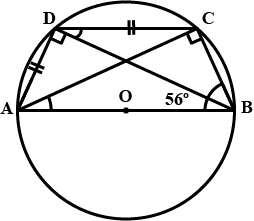
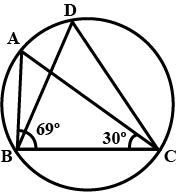
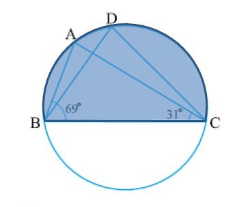
In the figure, $$\angle{ABC}={69}^{o}, \angle{ACB}={31}^{o}$$, find $$\angle{BDC}$$.
$$ABC$$ and $$ADC$$ are two right triangles with common hypotenuse $$AC$$. Prove that $$\angle{CAD}=\angle{CBD}$$.
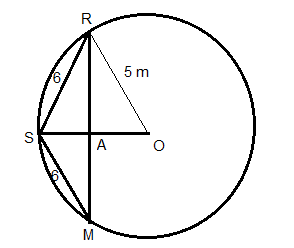
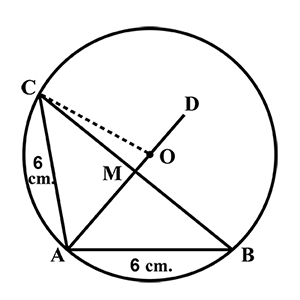
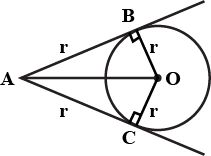
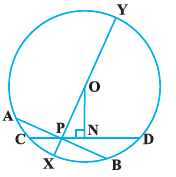
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius $$5\ m$$ drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is $$6\ m$$ each, what is the distance between Reshma and Mandip?
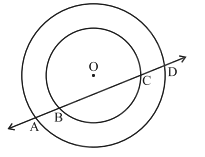
If a line intersects two concentric circles (circles with the same centre) with centre $$O$$ at $$A,B,C$$ and $$D$$, prove that $$AB=CD$$ (see figure)
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
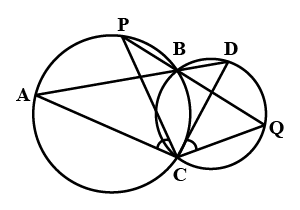
Two circles intersect at two points $$B$$ and $$C$$. Through $$B$$, two line segments $$ABD$$ and $$PBQ$$ are drawn to intersect the circles at $$A, D$$ and $$P, Q$$ respectively (see figure). Prove that $$\angle{ACP}=\angle{QCD}$$.
$$ABCD$$ is a cyclic quadrilateral whose diagonals intersect at a point $$E$$. If $$\Delta {DBC}={70}^{o}$$, $$\Delta {BAC}$$ is $${30}^{o}$$, find $$\angle\ {BCD}$$. Further if $$AB=BC$$, find $$\angle\ {ECD}$$.
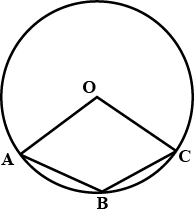
In the figure $$A,B$$ and $$C$$ are three points on a circle with centre $$O$$ such that $$\angle {BOC}={30}^{o}$$ and $$\angle {AOB}={60}^{o}$$. If $$D$$ is a point on the circle other than the arc $$ABC$$, find $$\angle {ADC}$$.

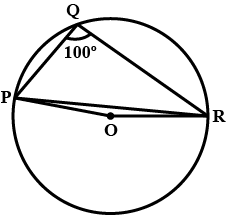
In the figure, $$\angle {PQR}={100}^{o}$$, where $$P, Q$$ and $$R$$ are points on a circle with centre $$O$$. Find $$\angle{OPR}$$.
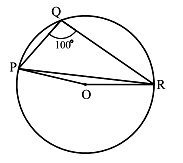
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
$$ABCD$$ is a parallelogram. The circle through $$A, B$$ and $$C$$ intersect $$CD$$ (produced if necessary) at $$E$$. Prove that $$AE=AD$$.
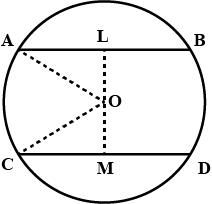
The lengths of two parallel chords of a circle are $$6$$ cm and $$8$$ cm. If the smaller chord is at distance $$4$$ cm from the centre, what is the distance of the other chord from the centre?
Prove that a cyclic parallelogram is a rectangle.

Bisectors of angles $$A, B$$ and $$C$$ of a triangle $$ABC$$ intersect its circumcircle at $$D, E$$ and $$F$$ respectively. Prove that the angles of the triangles $$DEF$$ are $${90}^{o}-\dfrac{1}{2}A$$, $${90}^{o}-\dfrac{1}{2}B$$ and $${90}^{o}-\dfrac{1}{2}C$$.
Two chords $$AB$$ and $$CD$$ of lengths $$5\ cm$$ and $$11\ cm$$ respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between $$AB$$ and $$CD$$ is $$6\ cm$$, find the radius of the circle.
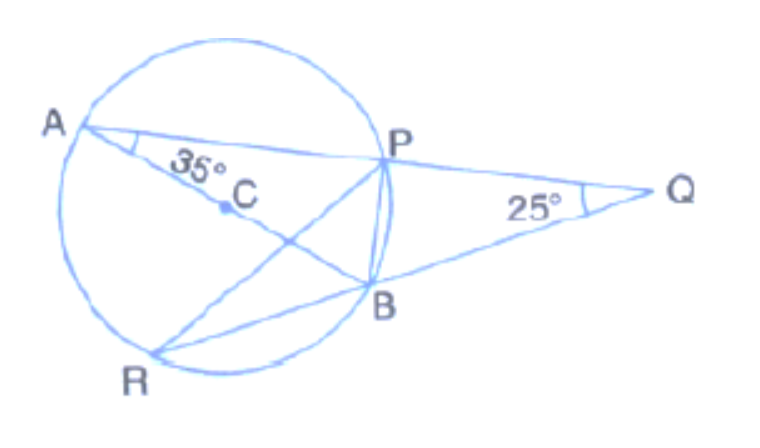
Let the vertex of an angle $$ABC$$ be located outside a circle and let the sides of the angle intersect equal chords $$AD$$ and $$CE$$ with the circle. Prove that $$\angle{ABC}$$ is equal to half the difference of the angles subtended by the chords $$AC$$ and $$DE$$ at the centre.
In any triangle $$ABC$$, if the angle bisector of $$\angle{A}$$ and perpendicular bisector of $$BC$$ intersect, prove that they intersect on the circumcircle of the triangle $$ABC$$.
The centre of a circle of radius 13 units is the point (3, 6). P(7, 9) is a point inside the circle. APB is a chord of the circle such that AP = PB. Calculate the length of AB.
In a circle whose radius is $$8$$cm, a chord is drawn at a point $$3$$ cm. from the centre of the circle. The chord is divided into two segments by a point on it. If one segment of the chord is $$9$$ cm, What is the length of the other segment?
In the figure, 'O' is the centre of the circle and OM, On are the perpendiculars from the centre to the chords PQ and RS. If OM = ON and PQ = 6 cm. Find RS.
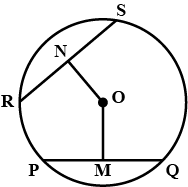
In the figure, $$\angle DBC = 58^{\circ}. BD$$ is a diameter of the circle. Calculate $$\angle BEC$$ (in degrees).
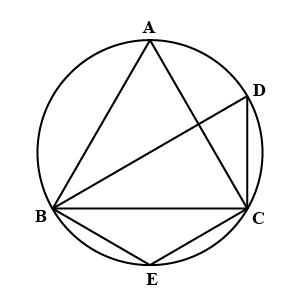
Find the values of $$x$$ and $$y$$ in the figure given above.
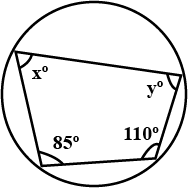
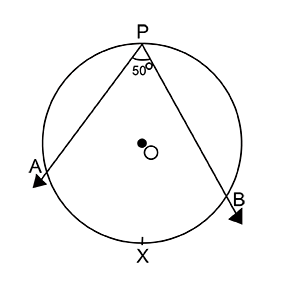
In the given figure, if $$\angle APB={ 50 }^{ o }$$, find the $$m(arcAXB)$$.
As shown in the figure below, two concentric circles are given and line $$PQ$$ is the tangent at point $$R$$. Prove that $$R$$ is the mid point of seg $$PQ$$.

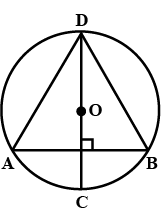
In the adjacent figure, AB is a chord of circle with centre O. CD is the diameter perpendicular to AB. Show that AD = BD.
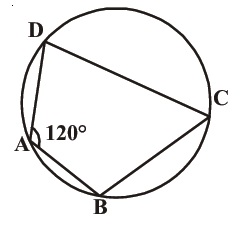
In the figure, $$\angle A= 120^o$$ then find $$\angle C$$?
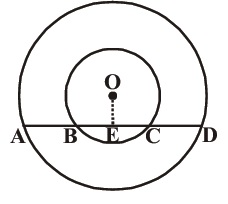
In the given above figure, there are two concentric circles with centre 'O'. Chord AD of the bigger circle intersects the smaller circle at B and C. Show that AB = CD.
In the figure given below $$\square ABCD$$ is a cyclic quadrilateral. Chord $$AB \cong $$ chord $$BC$$, chord $$AD \cong $$ chord $$CD$$. If $$\angle ADC = 3x^o$$ and $$\angle ABC = 2x^o$$, then find the measure of $$\angle B$$ and $$\angle D$$.
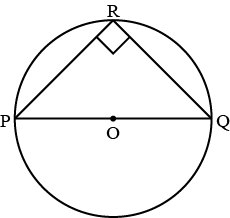
Let $$O$$ be the centre of a circle, with $$PQ$$ as a diameter, then prove that $$\angle PRQ = 90^o$$ (OR) Prove that angle subtended by semi-circle is $$90^o$$.
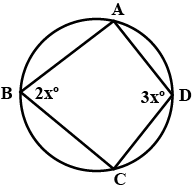
What is the value of $$x$$ from the given figure?
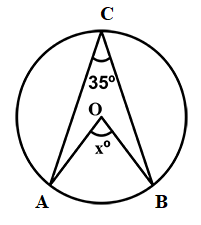
Find the value of x in the following figure.
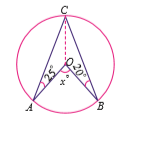
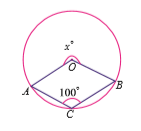
Find the value of x in the following figure.
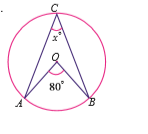
Find the value of x in the following figure.
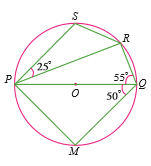
In the figure at left, PQ is a diameter of a circle with centre O. If $$\angle PQR = 55^o, \angle SPR = 25^o$$ and $$\angle PQM = 50^o$$.
Find (i) $$\angle QPR$$,
(ii)$$\angle QPM$$ and
(iii) $$\angle PRS$$.
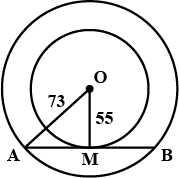
Two concentric circles having radii $$73$$ and $$55$$ are given. The chord of circle having a greater radius touches the smaller circle. Find the length of this chord.
In the Fig. O is the centre of a circle and $$\angle ADC = 120^o$$. Find the value of x.
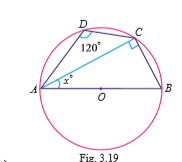
In the figure at right, ABCD is a cyclic quadrilateral whose diagonals intersect at P such that $$\angle DBC = 30^o $$ and $$\angle BAC = 50^o$$.
Find (i) $$\angle BCD$$ (ii) $$\angle CAD$$
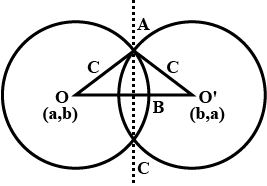
Prove that the length of the common chord of the two circles whose equations are $$(x - a)^{2} + (y - b)^{2} = c^{2}$$ and $$(x - b)^{2} + (y - a)^{2} = c^{2}$$ is $$\sqrt {4c^{2} - 2(a - b)^{2}}$$.
Hence find the condition that the two circles may touch.
In circle of radius $$5cm, AB$$ and $$AC$$ are the two chords such that $$AB=AC=6cm$$. Find the length of chord $$BC$$.
Find the length of the chord joining the points in which the straight line $$\dfrac {x}{a} + \dfrac {y}{b} = 1$$ meets the circle $$x^{2} + y^{2} = r^{2}$$.
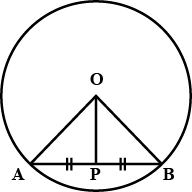
The perpendicular from the centre of a circle to a chord bisects the chord.
In the figure, radius of the circle with centre at $$O$$ is $$6$$ centimetres. And $$PA=4cm,PB=5cm$$. Find the length of $$OP$$.
In the figure, C is the centre of the circle and $$\angle ABD = 30^o$$
a) What is the measure of $$\angle ACD$$?
b) If $$\angle ABD = \angle CAB$$ and $$AB = 6 cm$$, find the radius of the circle.

Prove that perpendicular drawn from the centre of circle to the chord will bisect it.
Prove that the line of centres of two intersecting circles bisects their common chord.
$$\overline{AB}$$ and $$\overline{CD}$$ are chords of a circle with radius r. AB=2 CD and the perpendicular distance of $$\overline{CD}$$ from the centre is twice perpendicular distance of $$\overline{CD}$$ from the centre is twice perpendicular distance of $$\overline{AB}$$ from the centre. Prove that $$r=\dfrac{\sqrt{5}}{2}CD$$.
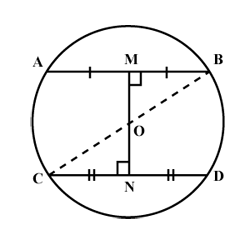
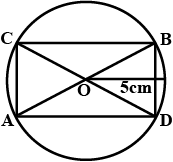
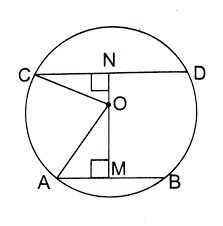
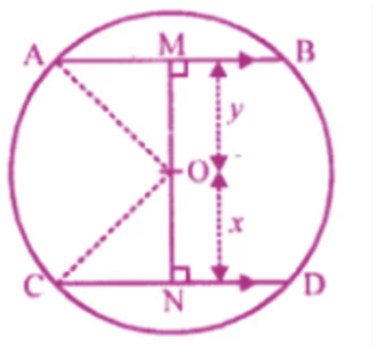
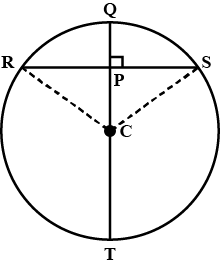
In the given figure, $$O$$ is the centre of the circle. $$AB$$ and $$CD$$ are two chords of the circle. $$OM$$ is perpendicular to $$AB$$ and $$ON$$ is perpendicular to $$CD$$. $$AB = 24\ cm, OM = 5\ cm, ON = 12\ cm$$. Find the:
(i) radius of the circle.
(ii) length of chord $$CD$$.
In figure, shown a sector OAP of a circle with centre O, containing $$\angle\theta, $$ AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is $$r\left[\tan\theta+\sec\theta+ \dfrac{\pi\theta}{180^0}-1\right].$$

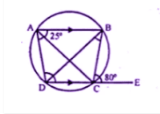
$$PQRS$$ is a cyclic quadrilateral. Given $$\angle$$QPS $$=73^\circ$$, $$\angle PQS =55^\circ$$ and $$\angle PSR =82^\circ$$, calculate $$\angle RQS.$$
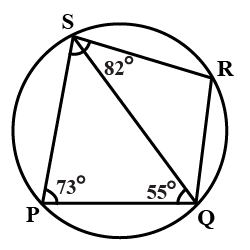
In the given figure, $$O$$ is the centre of a circle. If $$AB$$ and $$AC$$ are chords of the circle such that $$AB = AC$$ and $$OP\perp AB, OQ \perp AC$$, prove that $$PB = QC$$.
Find the length of an arc of the circle which subtends an angle of $$117^\circ$$ at the radius of the circle is $$40$$ cm.
Prove the following
Angle in a semi circle is a right angle.
An equilateral triangle is inscribed in a circle of radius $$6$$ cm. Find its side.
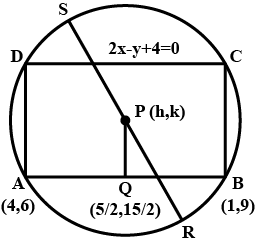
If $$2x \, - \, y \, + \, 4 \, = \, 0$$ is a diameter of a circle which circumscribes a rectangle ABCD. If the co-ordinates of $$A,B$$ are $$(4,6)$$ and $$(1,9)$$ , find the area of ABCD , and show that it is a square.
A square is inscribed in the circle $$x^2 \, + \, y^2 \, - \, 10x \, - \, 6y \, + \, 30 \,= \, 0$$ One side of the square is parallel to $$y \, = \, x \, + \, 3$$ Then determine the co-ordinates of its vertices.
A circle circumscribed a square of side $$a$$ centimeter. Find the area of the circle.
Find the equations of circles which passes through the vertices of the triangle formed by the line
x + y + 1 = 0 , 3x +y - 5 = 0 and 2x + y - 5 = 0 z
If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, then the four points lie on the same circle (i.e. they are concyclic).
The angle subtended on a semicircle is a right angle.
If an isoceles triangle $$ABC$$ in which $$AB=AC=6\ cm$$ is inscribed in a circle of radius $$9\ cm$$, find the area of triangle.
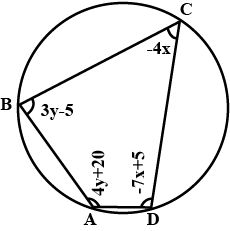
If $$A B C D$$ is a cyclic quadrilateral and $$ \angle A =
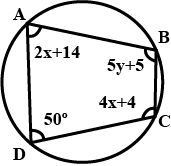
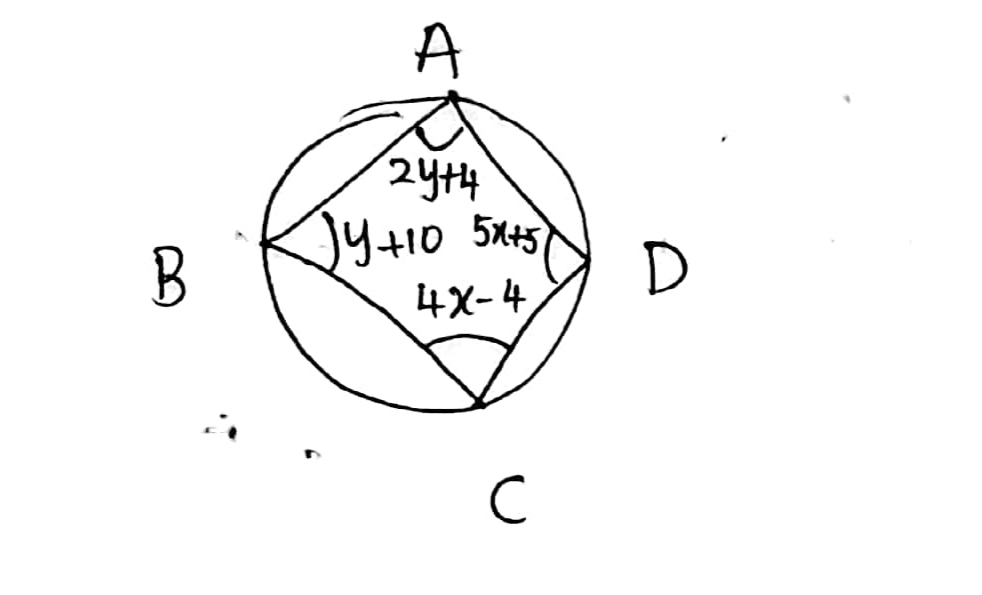
4y +20^o; \angle B = 3y -5^o; \angle C =-4x, \angle D = -7x+5^o$$, then find the value of $$x$$ and $$y$$.
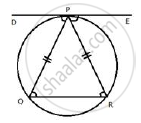
In fig $$3.38$$ $$\triangle QRS$$ is an equilateral triangle. Prove that,
A. $$\text{arc}\ RS\cong \text{arc}\ QS\cong \text{arc}\ QR$$B. $$m(\text{arc}\ QRS)={240}^{\circ}$$.
In two concentric circle, prove that all chords of the outer circle which touch the inner are of equal length.
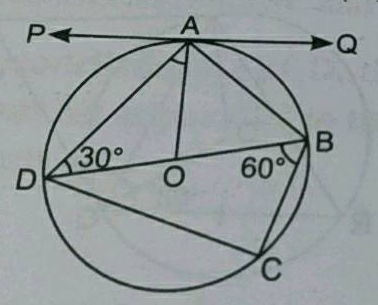
In the given figure, $$PQ$$ is a tangent to a circle at $$A, DB$$ is the diameter and $$O$$ is the centre of the circle. If $$\angle ADB = 30^o \,\, and \,\, \angle CBD = 60^o$$, calculate:
i) $$\angle QAB$$
ii) $$\angle PAD$$
iii) $$\angle CDB$$
In the given figure, if $$AB=AC,$$ prove that $$BE=EC.$$
OR
$$ABC$$ is an isosceles triangle in which $$AB=AC,$$ circumscribed about a circle, as shown in the given Figure. Prove that the base is bisected by the point of contact.
AB, CD are the chords of a circle with center O.
The chords interected E. AE=4cm, DE=3cm, EC=8cm and EB=x cm, find x, OE and the area of the circle.
Show that all the chords of the curve $$ { 3x }^{ 2 }-{ y }^{ 2 }-2x+4y=0$$ which subtend a right angle at the origin ?
Find the length of the chord $$x-y-3=0$$ of the circle $$x^{2}+y^{2}-x+3y-22=0$$
Find $$x$$:
$$AB$$ and $$CD$$ are two equal chords of a circle with centre $$O$$ which intersect each other at right angle at point $$P$$. If $$OM \bot AB$$ and $$ON \bot CD$$ ; show that $$OMPN$$ is a square
Find the coordinates of the points where the circle $$x^2+y^2+4x-4y-5=0$$ intersects the x-axis.
The line joining the mid-points of two chords of a circle passes through its centre. Prove that the chords are parallel.
In the following figure, the line ABCD is perpendicular to PQ ; where P and Q are the centres of the circles. Show that:
i) AB = CD
ii) AC = BD
Find the coordinates of the points where the circle $$x^2+y^2+4x-4y-5=0$$ intersects the y-axis.
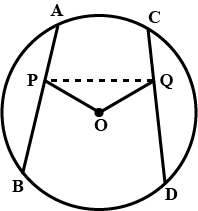
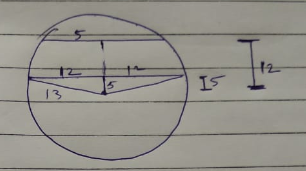
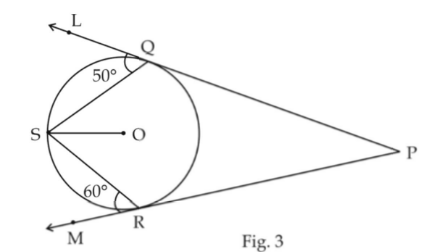
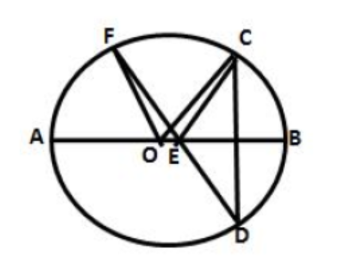
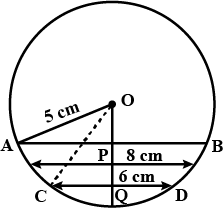
In the diagram, $$O$$ is the centre of the circle. Given that $$OQ=5\ cm \ and \ AN=8\ cm$$, find the length of $$PQ$$.
In the given figure, the lengths of arcs $$AB\ and\ BC$$ are in the ratio $$3:\ 2$$.
If $$\angle\ AOB=96^{o}$$, find
$$\angle\ BOC$$
$$\angle\ ABC$$
Calculate the length of a chord which is at a distance of $$12\ \text{cm}$$ from the center of a circle of radius $$13\ \text{cm}$$
Quadrilateral $$ MRPN$$ is cyclic. If $$\angle {R}={(5x-13)}^{o},\angle N={(4x+4)}^{o}$$, find measures of $$\angle {R}$$ and $$\angle {N}$$.
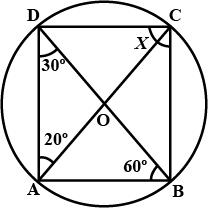
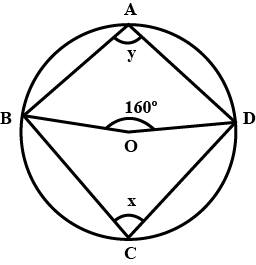
$$O$$ in the centre & $$\angle BOD=160^{o}$$ find the value of $$x$$ and $$y$$.
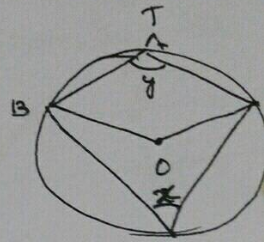
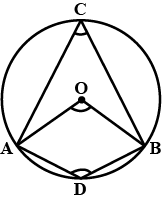
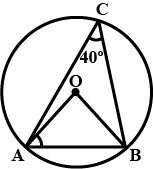
$$O$$ is the centre of the circle. $$\angle AOB = 60^\circ$$. Then,
$$\angle ACB =$$ ______
$$\angle ADB =$$ ______
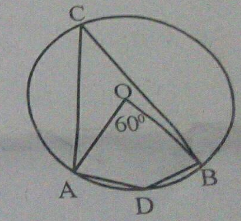
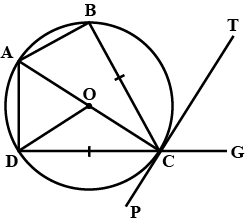
In the given figure, $$AT$$ is a tangent. $$AC=BC$$ and $$\angle {ABC}={50}^{o}$$. Find the $$\angle {BAT}$$.
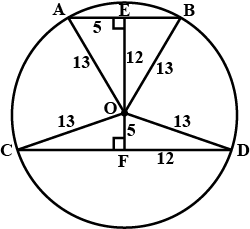
In the figure, $$O$$ is the centre of the circle with radius $$13cm$$. $$OP\bot AB$$, $$OQ\bot CD$$, $$AB\parallel CD$$
$$AB=24cm$$ and $$CD=20cm$$. Determine $$PQ$$.

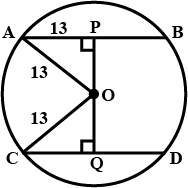
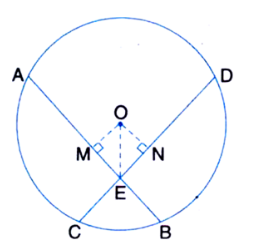
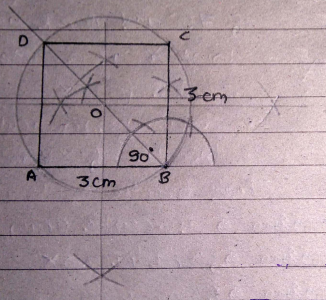
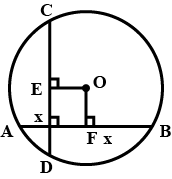
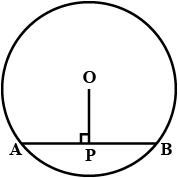
In the figure O is the centre of the circle OB$$=$$5 cm , Distance from O to cord AB is 3 cm. Find the length of AB.
Find the values of $$x$$ and $$y$$ in figure.
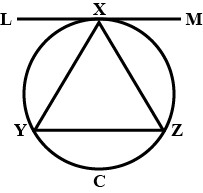
In figure, $$KXM$$ is a tangent to the circumcircle $$C$$ of $$\triangle {XYZ}$$ such that $$LM\parallel YZ$$. Show that $$XY=XZ$$
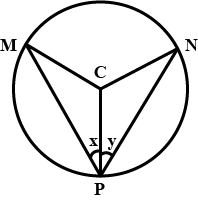
In figure (not to scale), the points M, R, N, S, Q are concyclic. Find $$\angle PQR+\angle OPR+\angle NMS+\angle OSN$$, if 'O' is centre of circle.

In the figure (not to scale), the points M, R, N, S, Q are concylic.
Find $$\angle PQR+\angle OPR+\angle NMS+\angle OSN$$, if 'O' is centre of circle.

In the following figure, $$O$$ is centre of the circle and $$\Delta ABC$$ is equilateral.
Find :
(i) $$\angle ADB$$
(ii) $$\angle AEB$$
Tangent at $$P$$ to the circumcircle of triangle $$PQR$$ is drawn. If this tangent is parallel to side $$QR$$ show that $$\triangle{PQR}$$ is an isosceles triangle.
$$O$$ is the centre of the circle, Find $$\angle{CBD}$$
in the given figure, AB and CD are two equal chords of a circle, with the center O.
IF P is the mid-point of chord AB .Q is the mid- point of chord CD and $$\angle POQ = {150^ \circ },\,find\,the\,\angle APQ.$$
Prove that angle in a segment greater than a semi-circle is less than a right angle
Two parallel chords in a circle are $$10\ cm$$ and $$24\ cm$$ long. If the radius of the circle is $$13\ cm$$, find the distance between the chords if thay lie on the opposite sides of the center
Rehman is making a wheel using spokes. He wants to fix equal spokes in such a way that the angles between any pair of consecutive spokes are equal. Help him by completing the following table
Calculate the angle between a pair of consecutive spokes on a wheel with 15 spokes.

In the figure, $$ABCD$$ is a cyclic quadrilateral with $$BC=CD$$. $$TC$$ is tangent to the circle at point $$C$$ and $$DC$$ is produced to point $$G$$. If $$\angle {BCG}={108}^{o}$$ and $$O$$ is the centre of the circle, find:
(i) $$\angle BCT$$
(ii)$$\angle DOC$$
(i) $$\angle BCT$$
(ii)$$\angle DOC$$
Two parallel chords in a circle are $$10\ cm$$ and $$ 24\ cm$$ long. If the radius of the circle is $$13\ cm\ $$, find the distance between the chords if they lie on the same side of the centre.
Two arcs of the same length subtend angles of $$60^{o}$$ and $$75^{o}$$ at the centres of the circles. What is the ratio of radii of two circles?
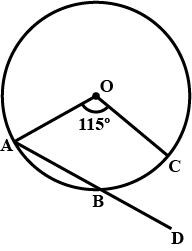
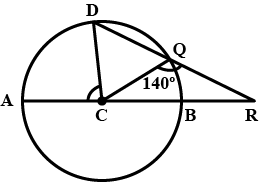
In the figure $$A B$$ is the diameter and $$C$$ is the centre of the circle.Also $$C Q = Q R$$ and $$\angle C Q R = 140 ^ { \circ } .$$ Find $$\angle D C A$$ .
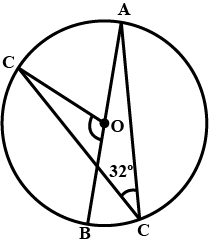
In the given figure $$\angle{ABC}={69}^{\circ}$$, $$\angle{ACB}={31}^{\circ}$$.Find $$\angle{BDC}$$
Seg $$PM$$ and Seg $$PN$$ are congruent chords of a circle with centre $$C$$. Show that the ray $$PC$$ is the bisector of $$\angle NPM$$
IN the given figure,if PQR is a tangent to the circle at q. whose centre is O and AB is a chord parallel to pr such that $$\angle BQR =70^o$$, then find $$\angle AQB$$
O is the centre of a circle in which AB and AC are congruent chords. Radius OP is perpendicular to chord AB and radius OQ is perpendicular to chord AC. If $$\angle PBA={ 30 }^{ \circ }$$, show that PB is parallel to QC.
$$ABCD$$ is such a quadrilateral that $$A$$ is the centre of the circle passing through $$B, C$$ and $$D$$. Prove that
$$\angle CBD+\angle CDB=\dfrac{1}{2}\angle BAD$$
In figure, line $$PR$$ touches the circle at point $$Q$$. Answer the following with the help of the figure:
What is the sum of $$\angle TAQ$$ and $$\angle TSQ$$?
Find the length of a chord which is at a distance of $$5\ cm$$ from the centre of a circle of radius $$13\ cm$$.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
From the figure, find all the four angles of the cyclic quadrilateral.
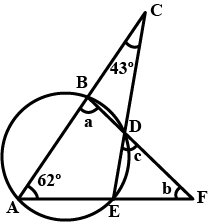
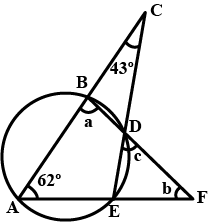
In the given figure if $$\angle ACE = 43^\circ $$ and $$\angle CAF = 62^\circ $$, find the value of $$a,\,b$$ and $$c$$.
Find the area of the quadrant of a circle whose circumference is $$44\ cm$$.
In fig.$$3$$, $$\mathrm { PQ }$$ and $$\mathrm { PR }$$ are tangents to the circle with centre $$\mathrm { O }$$ and $$\mathrm { S }$$ is a point on the circle such that $$\angle S Q L = 50 ^ { \circ }$$ and $$\angle S R M = 60 ^ { \circ } .$$ Find $$\angle Q S R .$$
Find the equations of the circles passing through two points on y-axis at distances 3 from the origin and having radius 5.
A circular park of radius $$20\ m$$ is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone his hands to talk each other. Find the length of the string of each phone.
Find the sum of the angles in the four segments exterior to a cyclic quadrilateral.
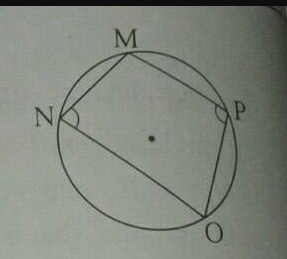
In the given figure, $$ MNOP $$ is a cyclic quadrilateral.
If $$ \angle P=4x+12 $$ and $$ \angle N=3x+28 $$, then find the value of $$x$$ and also the measures of $$ \angle P$$ and $$\angle N $$.
Prove that, the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
In the figure, $$O$$ is the center of the circle, $$AB$$ and $$AC$$ are tangents. Radius of the circle is $$r$$ and $$l(AB)=r$$, Prove that $$ ABOC$$ is a square.
Find the value of $$x+y$$
In a cyclic quadrilateral ABCD, if $$\angle A - \angle C = {60^ \circ }$$, prove that the smaller of two is $${60^ \circ }$$.
In the figure $$O$$ is the centre of the circle $$OB=5cm$$. Distance from $$O$$ to Chord $$AB$$ is $$3cm$$. Find the length of $$AB$$.
If $$O$$ is the centre of the circle, find the value of $$x$$ in the following figure.
$$A,B,C,D,E$$ in that order are points on a circle such that $$AE$$ is a diameter. Find $$\angle CDE$$ if $$\angle ABC=120^{o}$$
Angle subtended by the largest chord to a point on the circle measures
Prove that the angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle .
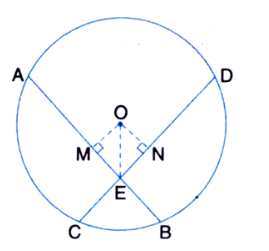
Prove that Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).
In the given figure,
point $$O$$ is the centre of the circle
show that $$\angle AOC = \angle AFC + \angle AEC$$
The radius of a circle with centre O is $$7 \text{ cm}$$ . Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major segments.
In the adjoining figure, AB and AC are two equal chords of a circle of radius 5 cm . If AB = AC = 6 cm , find the length of chord BC
Draw a circle and any two of its diameters.If you join the ends of these diameters, what is the figure obtained?
P is the centre of the circle and its radius is 10 cm. Distance of a chord AB from the centre is 6 cm. Find the length of chord AB,
If two equal chords of a circle intersect each other, then prove that the segments of one chord are equal to corresponding segment of the other chord.
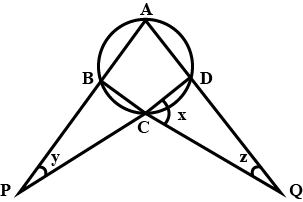
A pair of opposite sides of a cyclic quadrilateral are equal. Prove that its diagonal are also equal.
The line drawn from center of circle to bisect a chord is perpendicular to the chord. Is this true? If true enter 1 else 0.
Calculate the angles $$x,y$$ and $$ z$$ if: $$\dfrac {x}{3}=\dfrac {y}{4}=\dfrac {z}{5}$$
In a circle with radius $$13$$ cm, two equal chords are at a distance of $$5$$ cm from the centre. Find the length of the chords.
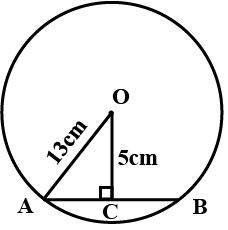
From the given figure, find $$\angle ADB$$ .
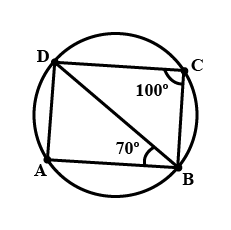
The radius of the circle is $$10\text{ cm}$$ and the length of one of its chords is $$12\text{ cm}$$, then the distance of the chord from the center is
In the figure, $$ABCD$$ is a cyclic quadrilateral.. If $$\angle BCD = 100^o$$ and $$\angle ABD = 70^o$$, find $$\angle ADB$$.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of quadrilateral, prove that it is a rectangle.
$$C$$ is the centre of the circle whose radius is $$10$$ cm. Find the distance of the chord from the centre, if the length of the chord is $$12$$ cm.
$$\angle PQR=100^ \circ$$, where $$P,Q$$ and $$R$$ are points on a circle with centre $$O$$. Find $$\angle OPR$$
ABCD is a parallelogram. The circle through A, B and C intersects CD (produce if necessary) at E. Prove that AE=AD.
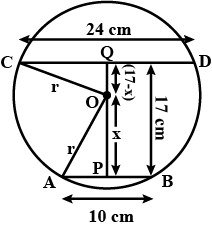
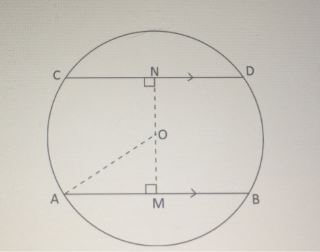
In the given diagram 'O' is the centre of the circle and AB is parallel to CD. AB=24 cm and distance between the chords AB and CD is 17 cm. If the radius of the circle is 13 cm, find the length of the chord CD.
In a circle of radius $$21cm$$ , an arc subtends an angle of $$60^o$$ at the centre.Find
(i) The length of the arc
(ii) Area of sector.
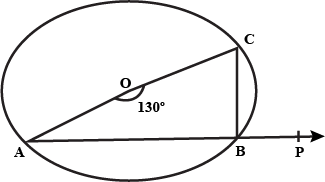
In given fig. O is centre of the circle if $$\angle AOC={ 130 }^{ o }$$ then find $$\angle ABC$$.
In the given figure, ABCD is a cyclic quadrilateral, AE is drawnn parallel to CD and BA is produced. If $$\angle ABC = 92^\circ$$ and $$\angle FAE = 20^\circ$$, then $$\angle BCD$$ is equal to

If the figure, O is the centre of the circle If $$\angle ACB={ 30 }^{ \circ },find\angle OAB.$$

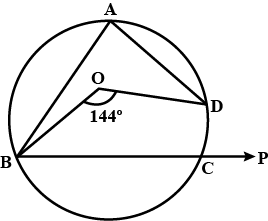
In the given figure, $$O$$ is the centre, the cirlcle. The angle subended by the are $$BCD$$ at the centre is $$144^o$$, $$BC$$ is produced to $$P$$. Determine $$\angle BAD$$ and $$\angle DCP$$
In a circle of radius 21 cm, an arc students an angle of $${ 60 }^{ \circ }$$ at the centre. Find :
Area of sector formed by the arc.
Fill in the blanks:
An arc is a ______ when its ends are the ends of a diameter.
Find the length of a chord which is at a distance of $$4\ cm$$ from the centre of the circle of radius $$6\ cm$$.
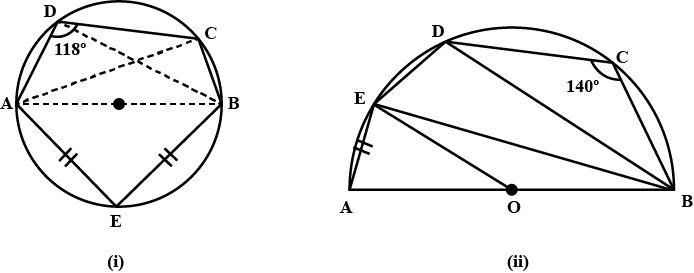
In the figure (ii) given below, AB is the diameter of the semicircle ABCDE with center O. If AE=ED and $$\angle BCD=140^{\circ}$$, find $$\angle AED$$ and $$\angle EBD$$. Also prove that OE is parallel to BD.
Fill in the blanks:
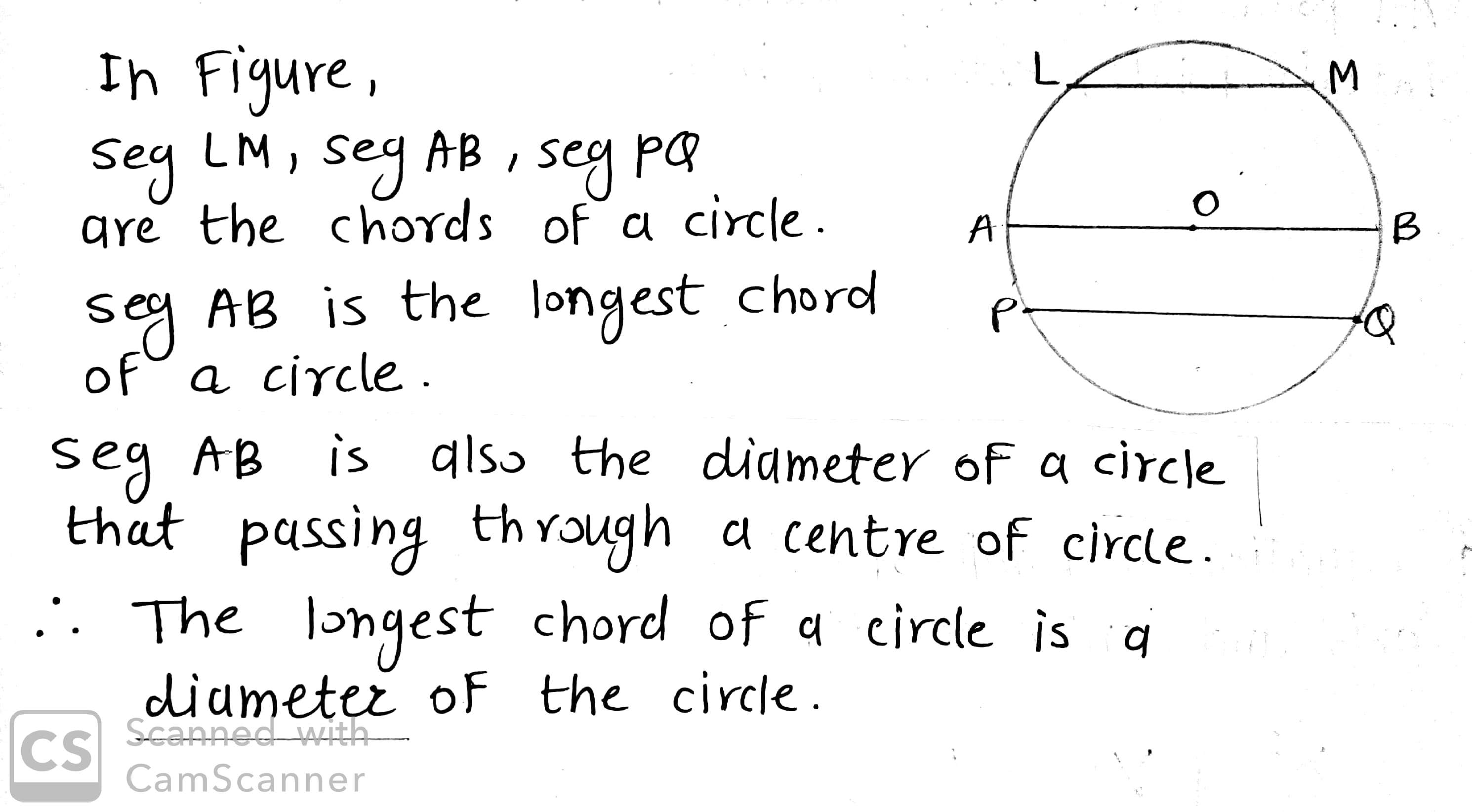
The longest chord of a circle is a _____ of the circle.
If diagonals of a cyclic quadrilateral are diameter of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
In figure, $$\angle$$PQR$$=100^o$$, where P, Q and R are points on a circle with centre O. Find $$\angle$$OPR.
In the figure '$$O$$' is the centre of the circle and $$A, B, C, D, E$$ are the points on it $$\angle EAB = 120^o, \angle EPD = 100^o$$. Write the measures of $$\angle EDB, \angle ECB$$ and $$\angle DBC$$.
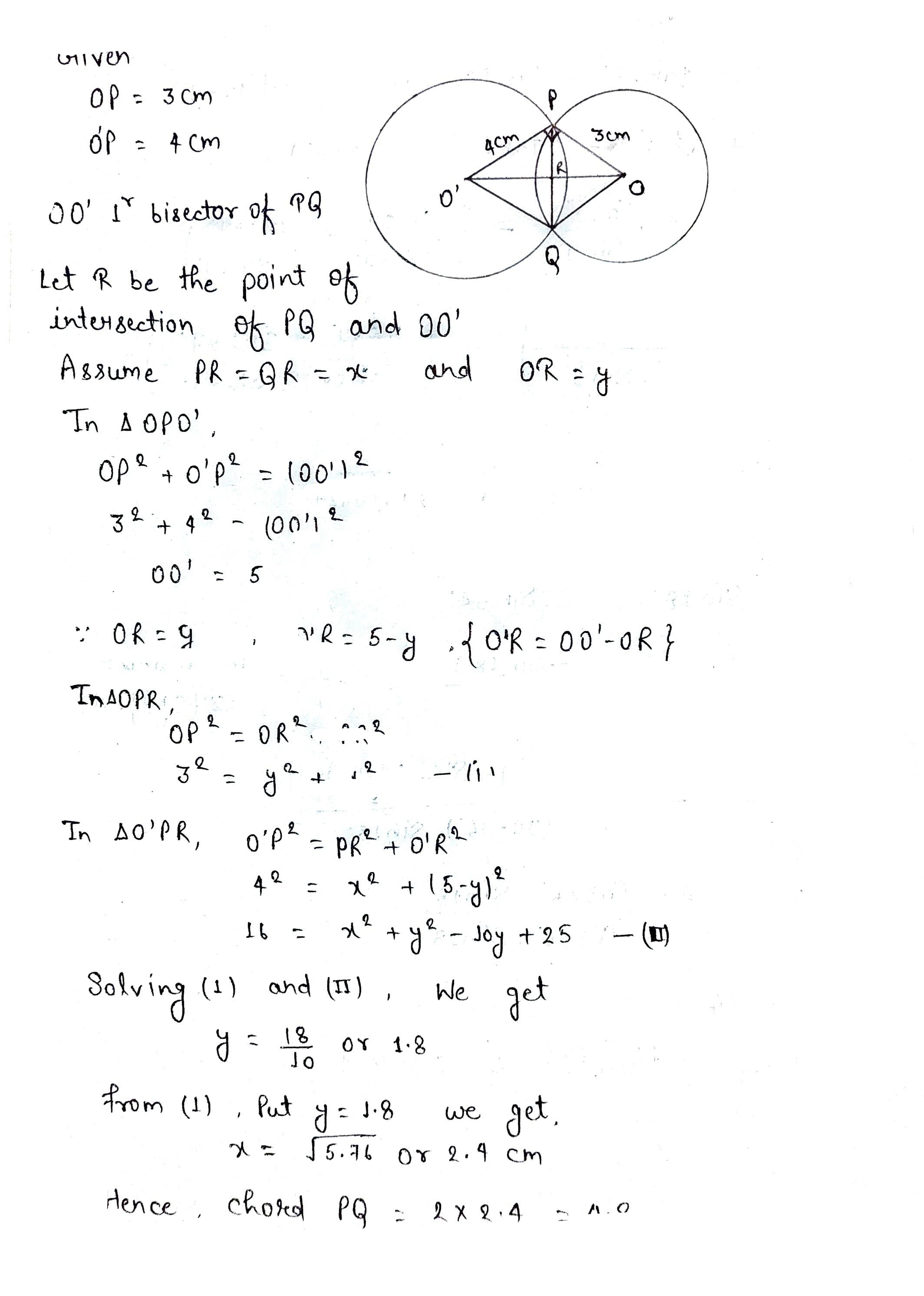
Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. find the length of the common chord PQ.
$$\angle ACB=?$$
If the length of a chord of a circle is equal to its radius, then find the angle subtended by it at the minor arc of the circle.
Prove that a diameter of a circle which bisect a chord of the circle also bisect the angle subtended by the chord at the centre of the circle.
A chord of length $$16\ cm$$ is drawn in a circle of radius $$10\ cm$$. Find the distance of the chord from the centre of the circle.
A chord of length $$30\ cm$$ is drawn at a distance of $$8\ cm$$ from the centre of a circle. Find out the radius of the circle.
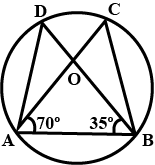
In Fig., $$O$$ is the centre of the circle. If $$\angle BOD=160^{o}$$, find the values of $$x$$ and $$y$$.
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
If the arcs of the same length in two circles subtend angles $${75}^{o}$$ and $${120}^{o}$$ at the centre, find the ratio of their radii.
Fill in the blanks:
Every point on a circle is __________ from its centre.
Find the length of a chord which is at a distance of $$3\ cm$$ from the centre of a circle of radius $$5\ cm$$
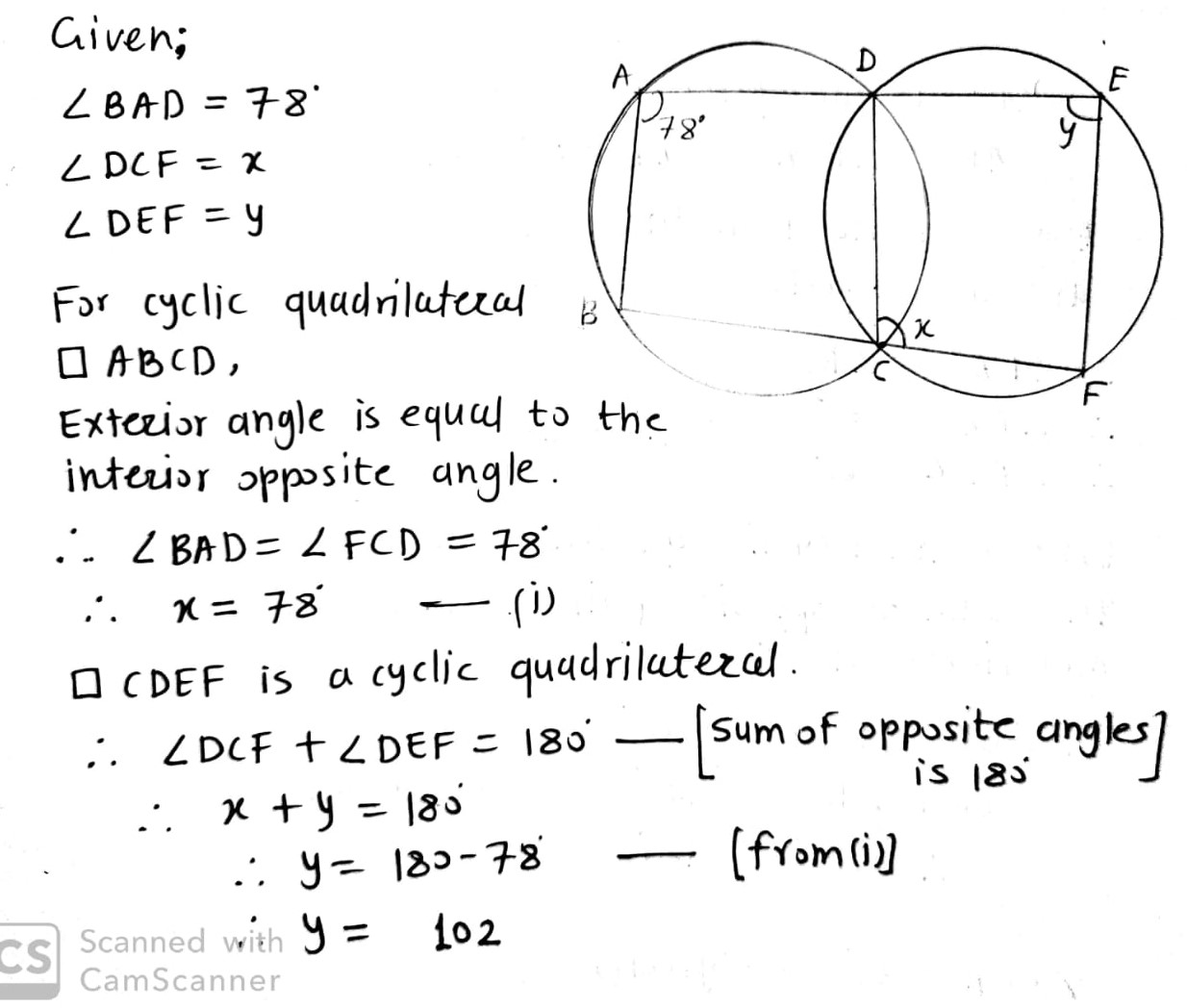
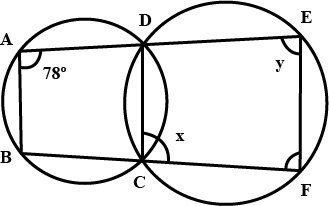
In Fig., $$\angle BAD=78^{o}, \angle DCF=x^{o}$$ and $$\angle DEF=y^{o}$$. Find the values of $$x$$ and $$y$$
In the given figure, $$BD=DC$$ and $$\angle CBD=30^o$$, find $$\angle BAC$$.
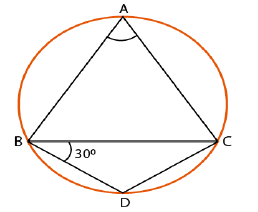
In the given figure, $$ABCD$$ is a cyclic quadrilateral whose diagonal intersect at $$P$$ such that $$\angle DBC=60^o$$ and $$\angle BAC =40^o$$. Find $$\angle BCD$$.

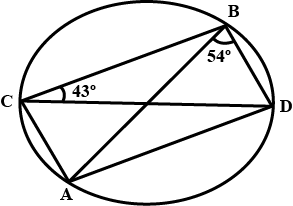
In the given figure, $$\angle ABD =54^o$$ and $$\angle BCD=43^o$$, calculate
$$\angle BDA$$
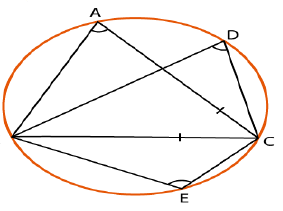
In the given figure, $$\triangle ABC$$ is equilateral. Find $$\angle BEC$$
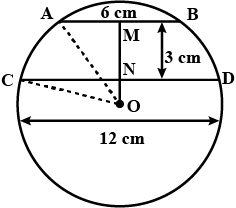
In a circle of radius $$5\ cm, AB$$ and $$CD$$ are two parallel chords of lengths $$8\ cm$$ and $$6\ cm$$ respectively.
Calculate the distance between the chords if they are on the same side of the centre
In the adjoining figure, $$ABCD$$ is a cyclic quadrilateral in which $$\angle BCD=100^o$$ and $$\angle ABD=50^o$$. Find $$\angle ADB$$.
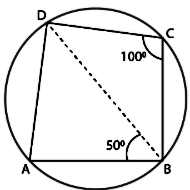
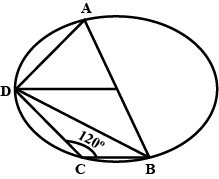
In the given figure, $$O$$ is the center of the circle and is $$ABC$$ subtends an angle $$130^o$$ at the center. If $$AB$$ extended to $$P$$, find $$\angle PBC$$.
Prove that two different circles cannot intersect each other at more than two points.
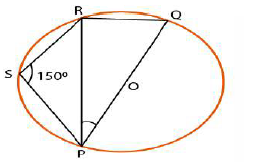
In the figure, $$POQ$$ is a diameter abd $$OQRS$$ is a cyclic quadrilateral. If $$\angle PSR=150^o$$, find $$\angle RPQ$$.
In a circle of radius $$5\ cm, AB$$ and $$CD$$ are two parallel chords of lengths $$8\ cm$$ and $$6\ cm$$ respectively.
Calculate the distance between the chords if they are on opposite sides of the centre.
In a cyclic quadrilateral $$ABCD$$, if $$(\angle B -\angle D)=60^o$$, show that the smaller of the two is $$60^o$$.
Two parallel chords of a circle, which are on the same side of the centre, subtend angles of $$72^o$$ and $$144^o$$ respectively at the centre. Prove that the perpendicular distance between the chords is half the radius of the circle.
In the given figure, $$AB$$ is a diameter of a circle with centre $$O$$ and $$DO || CB$$. If $$\angle BCD =120^{\circ}$$, calculate $$\angle BAD$$. Also, show that $$\triangle AOD$$ is an equilateral triangle.
If $$O$$ is the center of the circle, find the value of x in each of the following figures (using the given information):
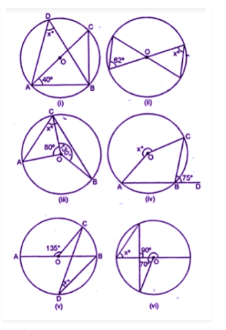
(a) In the figure (i) given below, calculate the values of $$x$$ and $$y$$.
(b) In the figure (ii) given below, $$O$$ is the centre of the circle. Calculate the values of $$x$$ and $$y$$.
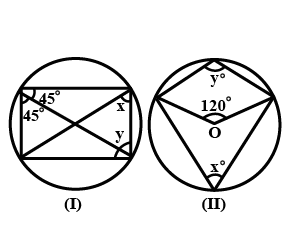
The area of a certain sector of a circle is $$10$$ square feet; if the radius of the circle be $$3$$ feet , find the angle of the sector. [Assume that $$\pi = 3.14159....,\dfrac{1}{\pi}=.31831$$ and $$\log \pi =.49715$$]
In the given figure, $$O$$ is the centre of circle and $$\angle DAB =50^o$$. Calculate the values of $$x$$ and $$y$$.
In the given figure, $$O$$ is the centre of circle. If $$\angle AOD=140^o$$ and $$\angle CAB=50^o$$, calculate
$$\angle EDB$$
In the given figure, $$ABCD$$ is a quadrilateral in which $$AD=BC$$ and $$\angle ADC =\angle BCD$$. Show that the points $$A, B, C, D$$ lie on a circle.
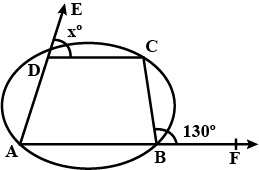
In the given figure, sides $$AB$$ of cyclic quadrilateral $$ABCD$$ are produced to $$E$$ and $$F$$ respectively. If $$\angle CBF=130^o$$ and $$\angle CDE=x^o$$, find the value of $$x$$.
In the given figure, $$AB$$ is parallel to $$DC, ∠BCE = 80^o$$ and $$∠BAC = 25^o$$. Find:
$$(i) ∠CAD \quad(ii) ∠CBD \quad(iii) ∠ADC$$
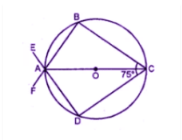
In the given figure, $$AB$$ is a diameter of the circle whose centre is $$O$$. Given that $$\angle ECD=\angle EDC= 32^{\circ }$$. Calculate
(i) $$\angle CEF$$
(ii) $$\angle COF$$
In the given figure, $$AB$$ is a diameter of the circle $$APBR$$. $$APQ$$ and $$RBQ$$ are straight lines, $$\angle A=35^{\circ }$$ and $$\angle Q=25^{\circ }$$. Find (i)$$\angle PRB\quad$$ (ii) $$\angle PRR\quad$$ (iii)$$\angle BPR$$
If $$O$$ is the centre of the circle, find the value of $$x$$.
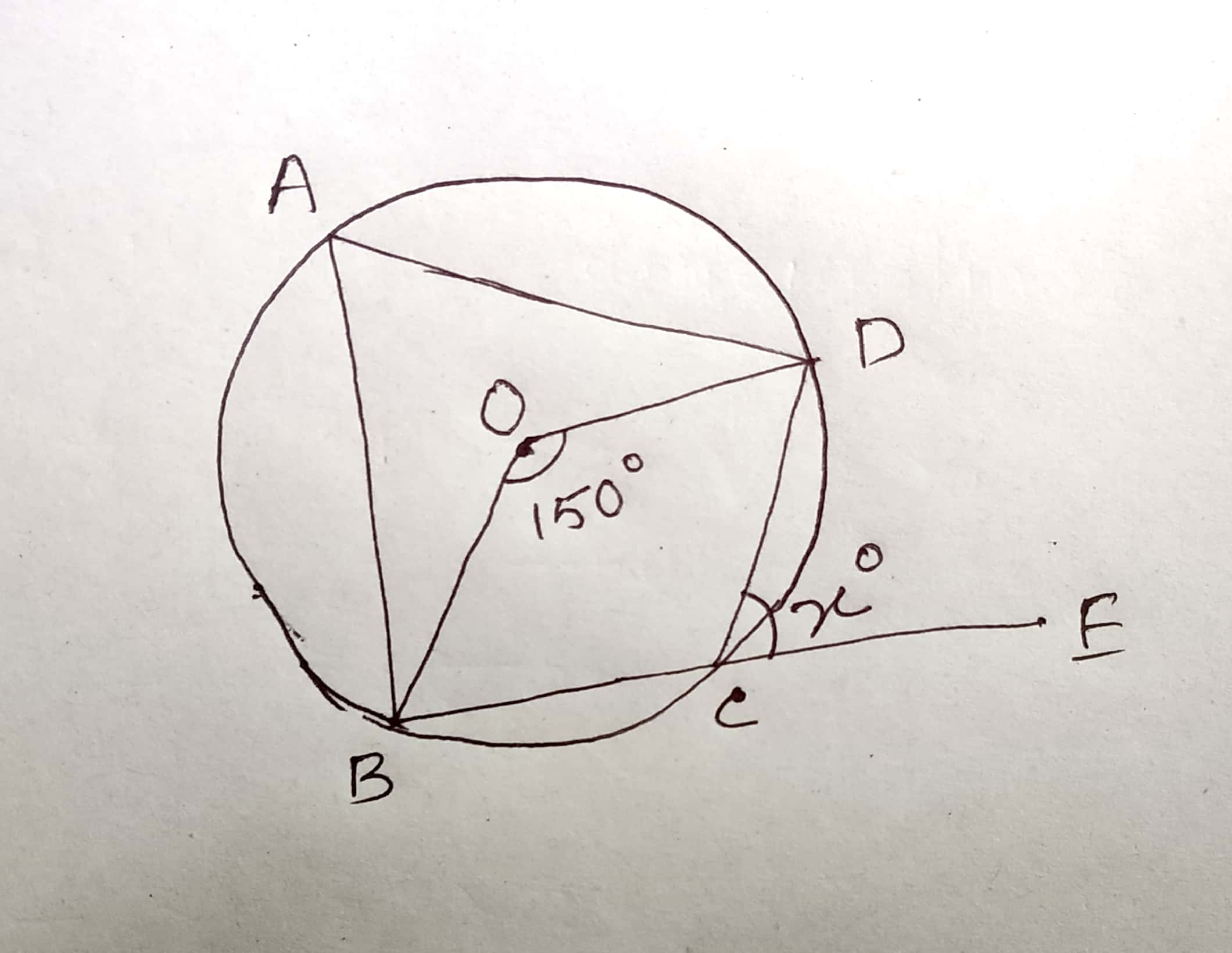
In the figure given, $$M, A, B, N$$ are points on a circle having centre $$O$$. $$AN$$ and $$MB$$ cut at $$Y$$. If $$\angle NYB = 50^{\circ }$$ and $$\angle YNB = 20^{\circ }$$, find $$\angle MAN$$ and the reflex angle $$MON$$.
In the figure (i) given below, AC is a diameter of the given circle and $$\angle BCD= 75^{\circ }$$ Calculate the size of
(i)$$\angle ABC$$
(ii)$$\angle EAF$$
In the figure given below, $$ABCD$$ is a cyclic quadrilateral. If $$∠ADC = 80^o$$ and $$∠ACD = 52^o$$, find the value of $$∠ABC $$.
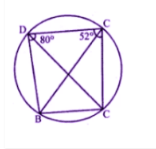
(a) In the figure (i) given below, $$ABCD$$ is a parallelogram. A circle passes through A and D and cuts AB at $$E$$ and DC at $$F$$. Given that $$BEF = 80$$, find $$ABC$$.
(b) In the figure (ii) given below, ABCD is a cyclic trapezium in which AD is parallel to BC and $$B = 70$$, find:
$$(i)BAD (ii) DBCD.$$
In the figure given, $$O$$ is the center of the circle. $$∠AOE =150^o$$ , $$ ∠DAO = 51^o$$. Calculate the values of $$∠BEC$$ and $$∠EBC$$.
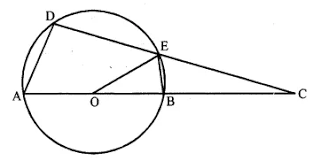
In the figure, (i) given below, if $$∠DBC = 58°$$ and BD is a diameter of the circle, calculate:
$$(i) ∠BDC \qquad(ii) ∠BEC \qquad (iii) ∠BAC$$
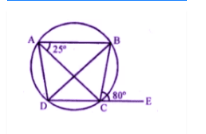
In Figure, the quadrilateral $$ ABCD $$ circumscribes a circle with centre $$ O.$$ If $$ \angle AOB =115^o $$, then find $$ \angle COD $$
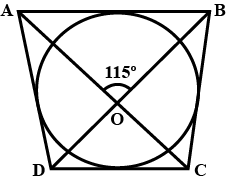
In the figure given below, $$PQ$$ is a diameter. Chord $$SR$$ is parallel to $$PQ$$. Given $$∠PQR = 58°$$, calculate $$(i) ∠RPQ\qquad (ii) ∠STP$$
What is the angle subtended at the centre of a circle of radius $$10\ cm$$ by an arc of length $$5\pi \ cm$$?
The largest square that can be drawn in a circle has a side whose length is 0.707 times the diameter of the circle. By this rule, find the length of the side of such a square when the diameter of the circle is(a) 14.35 cm (b) 8.63 cm
In the given figure, sides $$AB$$ and $$DC$$ of a cyclic quadrilateral $$ABCD$$ are produced to meet at $$E$$, the sides $$AD$$ and $$BC$$ are produced to meet at $$F$$. If $$x : y : z = 3 : 4 : 5,$$ find the values of $$x, y$$ and $$z$$.
(a) In the figure (i) given below, triangle $$ABC$$ is equilateral. Find $$∠BDC$$ and $$∠BEC$$. (b) In the figure (ii) given below, AB is a diameter of a circle with center $$O$$. OD is perpendicular to AB and $$C$$ is a point on the arc DB. Find $$∠BAD$$ and $$∠ACD$$
In the figure given, $$AB$$ is a diameter of the circle. If $$AE = BE$$ and $$∠ADC = 118^o$$, find $$(i) ∠BDC \qquad (ii) ∠CAE$$
In the figure given, $$O$$ is the center of the circle. If $$∠BAD = 30°$$, find the values of $$p, q$$ and $$r$$.
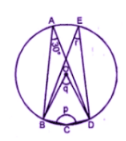
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
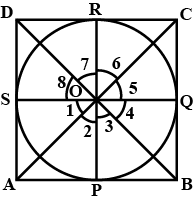
In the figure, O is the centre of the circle. Find the size of each lettered angle:
PQRS is a rectangle inscribed in a quadrant of a circle of radius $$13\,cm.$$ A is any point on PQ. If $$PS = 5 \,cm,$$ then ar(PAS)$$ = 30 \,cm^2.$$Write True or False and justify your answer:
The angles of cyclic quadrilateral $$ABCD $$ are $$ \angle A -= ( 6x + 10)^0 , \angle B =( 5x)^0 , \angle c = (x +y )^0 , \angle D = ( 3y - 10)^0 $$ find the $$ X $$ and $$ Y $$ and hence the values of four angles.
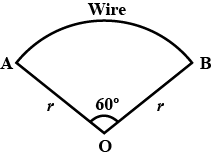
A piece of wire $$20 \,cm$$ long is bent into the form of an arc of a circle substending an angle of $$60^\circ$$ at its centre. Find the radius of the circle.
$$AB$$ and $$CD$$ are two parallel chords of a circle of lengths $$10\ cm$$ and $$4\ cm$$ respectively. If the chords lie on the same side of the centre and the distance between them is $$3\ cm$$, find the diameter of the circle.
In a circle of radius 5 cm, AB and CD are two parallel chords of length 8 cm and 6 cm respectively. Calculate the distance between the chords if they are on :
(i) the same side of the centre.
(ii) the opposite sides of the centre.
In the figure, O is the centre of the circle. Find the size of each lettered angle:
If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides , prove that the quadrilateral so formed is cyclic .
In Figure, $$AOB$$ is a diameter of the circle, $$C , D$$ and $$E$$ are any three points on the semi-circle . Find the value of $$ \angle ACD +\angle BED$$.
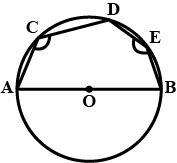
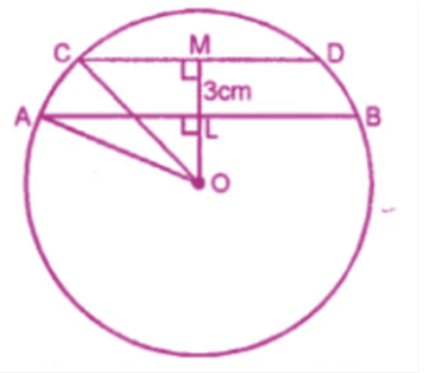
In the adjoining figure, AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
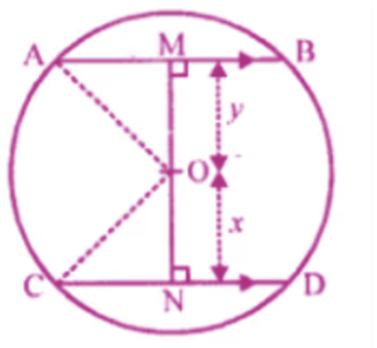
In $$ABCD$$ is a cyclic quadrilateral in which $$\angle DAC = 27^{\circ}, \angle DBA = 50^{\circ} and \angle ADB = 33^{\circ}$$. Calculate $$\angle DCB$$
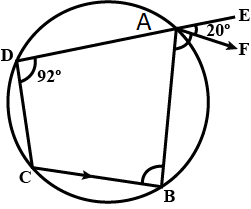
In the given figure, $$ABCD$$ is a cyclic quadrilateral. $$AF$$ is drawn parallel to $$CB$$ and $$DA$$ is produced to point $$E$$. If $$\angle ADC = 92^{\circ}$$, $$\angle FAE = 20^{\circ}$$; determine $$\angle BCD$$.
In each of the following figure, $$O$$ is the centre of the circle. Find the value of $$c$$.
If arcs APB and CQD of a circle are congruent, then find the ratio of AB : CD
If $$I$$ is the incentre of triangle $$ABC$$ and $$AI$$ when produced meets the circumcircle of triangle $$ABC$$ in point $$D$$. If $$\angle BAC = 66^{\circ}$$ and $$\angle ABC = 80^{\circ}$$. Calculate $$\angle BIC$$
Prove that, in a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal.
If all sides of a parallelogram touch a circle , then that parallelogram is .....
In the figure given below, O is the centre of the circle and triangle ABC is equilateral. Find $$\angle ADB$$
ABCD is a cyclic quadrilateral in which BC parallel to AD angle $$ADC = 110^{\circ}$$ and angle $$BAC = 50^{\circ}$$. Find angle DCA
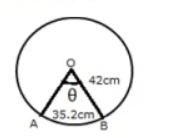
An acr of a circle of radius $$ 42 cm $$ has a length $$ 35.2 cm. $$ Find the angle subtended by the arc at the centre of the circle.
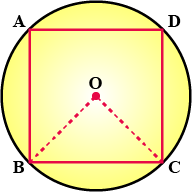
In the given figure, a square is inscribed in a circle with centre $$O$$.
Find:
$$\angle BOD$$
Is $$BD$$ a diameter of the circle?
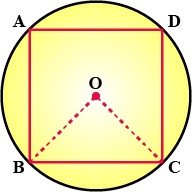
In the given figure, a square is inscribed in a circle with centre $$O$$.
Find:
$$\angle COD$$
Is $$BD$$ a diameter of the circle?
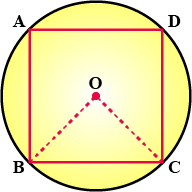
In the given figure, a square is inscribed in a circle with centre $$O$$.
Find:
$$\angle OCB$$
Is $$BD$$ a diameter of the circle?
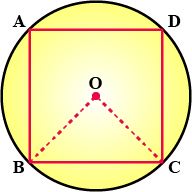
In the given figure, a square is inscribed in a circle with centre $$O$$.
Find:
$$\angle BOC$$
Is $$BD$$ a diameter of the circle?
In the given figure, ABCD is a cyclic quadrilateral, PQ is tangent to the circle at point C and BD is its diameter. If $$\angle DCQ = 40^{\circ}$$ and $$\angle ABD = 60^{\circ}$$, find $$\angle ADB$$
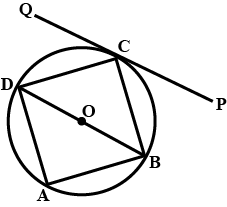
In cyclic quadrilateral $$ABCD,$$ $$\angle A = 3 \angle C$$ and $$\angle D = 5 \angle B.$$ Find the measure of each angle of the quadrilateral.
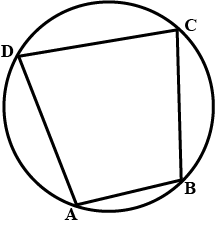
In a circle of radius $$17\ cm$$, two parallel chords of length $$30\ cm$$ and $$16\ cm$$ are drawn. Find the distance between the chords, if both chords are :
On the opposite sides of the centre,
In a circle of radius $$17\ \text{cm}$$, two parallel chords of length $$30\ \text{cm}$$ and $$16\ \text{cm}$$ are drawn. Find the distance between the chords, if both chords are on the same sides of the centre.
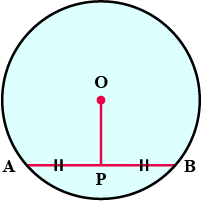
The given figure shows a circle with center $$O$$ . $$P$$ is mid - point of chord $$AB$$ .
Show that $$OP$$ is perpendicular to $$AB$$
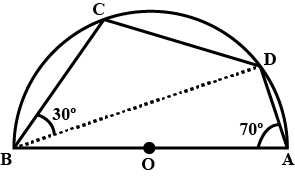
In the given figure, C and D are points on the semi - circle described on AB as diameter. Given angle $$BAD = 70^{\circ}$$, and angle $$DBC = 30^{\circ}$$, calculate angle BDC.
In a circle of radius $$10\ cm, AB$$ and $$CD$$ are two parallel chords of lengths $$16\ cm$$ and $$12\ cm$$ respectively. Calculate the distance between the chords, if they are on:
The same side of the centre.
The radius of a circle is $$13\ cm$$ and the length of one its chords is $$24\ cm$$. Find the distance of the chord from the centres.
Prove that any three points on a circle cannot be collinear.
In the given figure, $$AOC$$ is the diameter of the circle, with centre $$O$$. If arc $$AXB$$ is half of arc $$BYC$$, find $$\angle BOC$$.
In the given figure, line $$PR$$ touches the circle at point $$Q$$. Answer the following questions with the help of the figure.
(1) What is the sum of $$\angle TAQ$$ and $$\angle TSQ$$?
(2) Find the angles which are congruent to $$\angle AQP$$.
(3) Which angles are congruent to $$\angle QTS$$?
(4) $$\angle TAS = 65^{o}$$, find the measure of $$\angle TQS$$ and arc $$TS$$.
(5) If $$\angle AQP = 42^{o}$$ and $$\angle SQR = 58^{o}$$ find measure of $$\angle ATS$$.

In the given figure, chord $$EF ||$$ chord $$GH$$. Prove that, chord $$EG$$ chord $$FH$$. Fill in the blanks and write the proof.
In the given figure, $$\Box PQRS$$ is cyclic. side $$PQ \cong$$ side $$RQ$$. $$\angle PSR = 110^{o}$$, Find-
(1) measure of $$\angle PQR$$
(2) $$m(arc\, PQR)$$
(3)$$ m(arc\, QR) $$
(4) measure of $$\angle PRQ $$
In the given figure, seg $$AB$$ is a diameter of a circle with centre $$O$$. The bisector of $$\angle ACB$$ intersects the circle at point $$D$$. Prove that, seg $$AD \cong$$ seg $$BD$$. Complete the following proof by filling in the blanks.
In a circle of radius $$10\ cm, AB$$ and $$CD$$ are two parallel chords of lengths $$16\ cm$$ and $$12\ cm$$ respectively. Calculate the distance between the chords, if they are on:
The opposite sides of the centre.
In the given figure , C is the centre seg $$ OT $$ is a diameter $$CT = 13 , CP = 5 ,$$ find the length of chord RS
Prove that the parallelogram circumscribing a circle is a rhombus .
In a circle with radius $$13 cm$$, two equal chords are at a distance of $$5 cm$$ from the centre. Find the length of the chords.
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angle at the center of the circle.
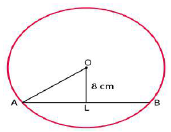
Radius of a circle with centre $$O$$ is $$41$$ units. Length of a chord $$PQ $$ is $$80$$ units, find the distance of the chord from the centre of the circle.
Find the radius of the circle in which a central angle of $$60^{o}$$ intercepts an arc of length
$$37.4\ cm \left(Use\ \pi=\dfrac{22}{7}\right)$$
A quadrilateral $$ABCD$$ is draw to circumscribe a circle (see the fig . given below ) . Prove that $$AB + CD = AD + BC $$
In the given figure , $$P$$ is the centre of the circle. Chord $$AB$$ and chord $$CD$$ intersect on the diameter at the point $$E$$ If $$\angle AEP \cong \angle DEP $$ then prove that $$ AB = CD$$
The radius of the circle is $$10\; cm$$. There are two chords of length $$16\; cm$$ each. What will be the distance of these chords from the center of the circle?
A circle of radius $$6cm$$ is inscribed in a square as shown in the given figure Find the shaded region.

ABCD is a cyclic quadrilateral . Find the angles of the cyclic quadrilateral
If $$AB = 6 cm$$, $$CD = 12 cm$$ are two chords of a circle and are parallel and lie at same side of center of circle of distance between $$AB$$ and $$CD$$ is $$3 cm$$, then find radius of circle.
Find the area of a square inscribed in a circle of radius $$a$$
Prove that the circle drawn with any side of a rhombus as diameter., passes through the point of intersection of its diagonals.
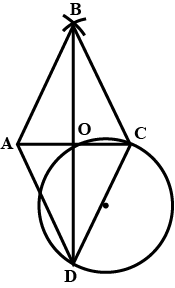
$$AC$$ and $$BD$$ are chords of a circle which bisect each other. Prove that
$$ABCD$$ is a rectangle.
The lengths of two parallel chords of a circle are $$6cm$$ and $$8cm$$. If the smaller chord is at distance $$4cm$$, from the center, what is the distance of the other chord from the center?

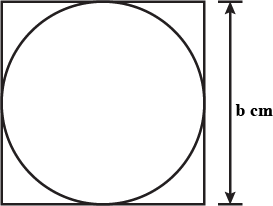
Find The area of the circle inscribed in a square of side $$b\ cm$$
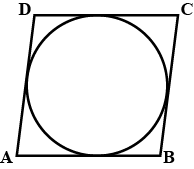
It $$AB = 10 cm, CD = 24 cm$$ are two chords of a circle. $$AB || CD$$ and distance between $$AB$$ and $$CD$$ is $$17 cm$$. Find the radius of circle.
In the figure, $$\angle ADC = 130^{0}$$ and chord $$BC =$$ chord $$BE$$, Find $$\angle CBE$$.
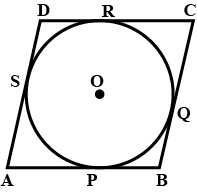
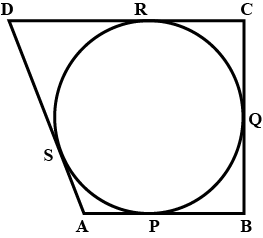
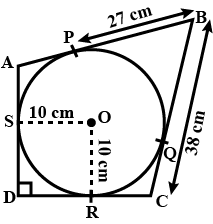
In the figure, a circle touches all the four sides of a quadrilateral $$ABCD$$. If $$AB = 8 cm BC = 6$$ cm and $$AD = 5$$ cm, then find $$CD$$.
In the given figure, a circle with center O, is Inscribed in quadrilateral $$ABCD$$ such that it touches the sides $$AB, BC, CD$$ and $$AD$$ at point $$P, Q, R$$ and $$S$$ respectively. If radius of circle is $$10$$ cm, BC = 38$$ cm, PB = 27$$ cm and $$AD \perp CD$$, then find the length of $$CD$$. [CBSE 2013]
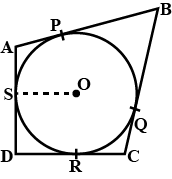
In following figure from exterior point $$'P'$$ two tangent line $$PA$$ and $$PB$$ touches the circle at $$A$$ and $$B$$, then prove that $$PAOB$$ is a cyclic quadrilateral where $$O$$ is the (RBSE Solutions. com) center of circle.
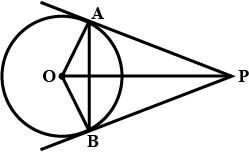
A circle with center $$'O'$$ touches all the four sides of a quadrilateral $$ABCD$$ internally in such a way that $$AB$$ is divided in the ration 3 : 1 and $$ AB = 8$$ cm, then find the radius of circle if $$OA = 10$$ m.
In a circle of radius $$10 cm$$, length of two parallel chords are $$12 cm$$ and $$16 cm$$ respectively. Find the distance between $$AB$$ and $$CD$$ of chords are (a) same side of center (b) on opposite sides of center.
A circle touches all the sides of a quadrilateral. Prove that the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.
Figure, in a cyclic quadrilateral $$ABCD$$ diagonal $$AC$$ bisects the angle $$C$$. Then prove that
diagonal $$BD$$ is
parallel to tangent $$PQ$$ of a circle which passes through the points $$A$$.
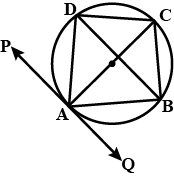
If the vertices of a quadrilateral $$ABCD$$ lie on circle and $$AB = CD$$, then prove that $$AC = BD$$.
An angle of a cyclic quadrilateral is given find its opposite angle.
$$70^{0}$$
If in cyclic quadrilateral $$ABCD, AD || BC$$, then Prove that $$\angle A = \angle D$$.
An angle of a cyclic quadrilateral is given find its opposite angle.
$$112\frac{1}{2}^{0}$$
An angle of a cyclic quadrilateral is given find its opposite angle.
$$135^{0}$$
In figure, $$AOB$$ is diameter of circle and $$C,D$$ and $$E$$ are any three points on semicircle, find $$\angle ACD + \angle BED$$
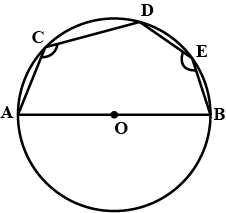
An angle of a cyclic quadrilateral is given find its opposite angle.
$$\frac{3}{5}$$ right angle.
Find opposite angle of cyclic quadrilateral if one angle is $$\frac{2}{7}$$ of other.
Find opposite angle of cyclic quadrilateral if one angle is $$\frac{11}{4}$$ of other.
An angle of a cyclic quadrilateral is given find its opposite angle.
$$165^{0}$$
In figure, find all the four angles of cyclic.
Prove that angle bisectors of cyclic quadrilaterals formed a cyclic quadrilateral.
If $$P, Q,$$ and $$R$$ arc mid points of sides $$BC, CA$$ and $$AB$$ of a triangle $$ABC$$, respectively and $$AD \perp BC$$, then Prove that $$P, Q, R, D$$ are cyclic.
$$ABCD$$ is a parallelogram. A circles passes through $$A$$ and $$B$$ and cuts $$AD$$ at $$P$$ and $$BC$$ at $$Q$$. Prove that $$P, Q, C$$ and $$D$$ arc cyclic.
If in a cyclic quadrilateral $$ABCD$$, opposite angle bisectors intersects at points $$P$$ and $$Q$$ of circumcircle of this quadrilateral, then Prove that $$PQ$$ is diameter of the circle.
In figure, $$O$$ is center of circle, $$BD = OD$$ and $$CD \perp AB$$, then find $$\angle CAB$$
$$ABCD$$ is a cyclic quadrilateral produced $$AB$$ and $$DC$$ meet at $$E$$. Prove that $$\Delta EBC$$ and $$\Delta EDA$$ arc similar.
Two circles of radius $$5 cm$$ and $$4 cm$$ cut each other at $$A$$ and $$B$$. If common chord $$AB=6 cm$$, then find distance between their centers.
Two diameters of a circle intersect at $$90^{0}$$, prove that by joining their internal points, quadrilateral so formed will be a square.
Prove that If one pair of opposite angles of a quadrilateral is supplementary, then quadrilateral is cyclic.
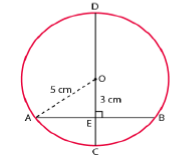
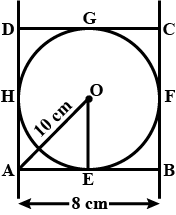
In fig. $$AN = 8 cm$$ and $$CD = 6 cm$$ are two parallel chords of a circle with center $$O$$, find the distance between these chords
In figure, $$PARS$$ is cyclic quadrilateral whose diagonal intersect at $$A$$ if $$\angle SQR = 80^{0}$$ and $$\angle QPR = 30^{0}$$, then find $$\angle SRQ$$.
Write the formula to find the area of the cyclic quadrilateral.
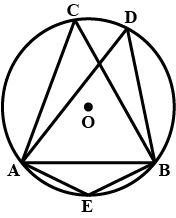
In the given figure, $$ABCDE$$ is a pentagon inscribed in a circle such that $$AC$$ is a diameter and side $$BC||AE$$. If $$\angle BAC = 50^0$$, find giving reasons $$\angle ACB$$.
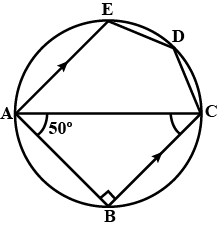
Find $$x$$, for the following diagram:
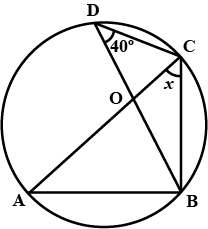
Find $$x$$, for the following diagram:
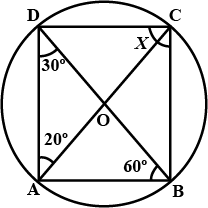
If the internal opposite angle is $$51^0$$, then find the external angle of a cyclic quadrilateral.
Suppose two chords of a circle are equidistant from the centre of the circle. Prove that the chords have equal length.
Prove that the bisectors of the four interior angles of a quadrilateral form a cyclic quadrilateral.
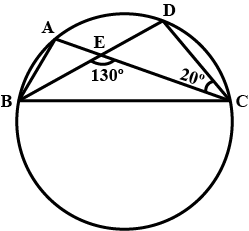
In the figure, $$A, B, C$$ and $$D$$ are four points on a circle. $$AC$$ and $$BD$$ intersect at a point $$E$$, such that $$\angle{BEC}={130}^{o}$$ and $$\angle{ECD}={20}^{o}$$. Find $$\angle{BAC}$$.
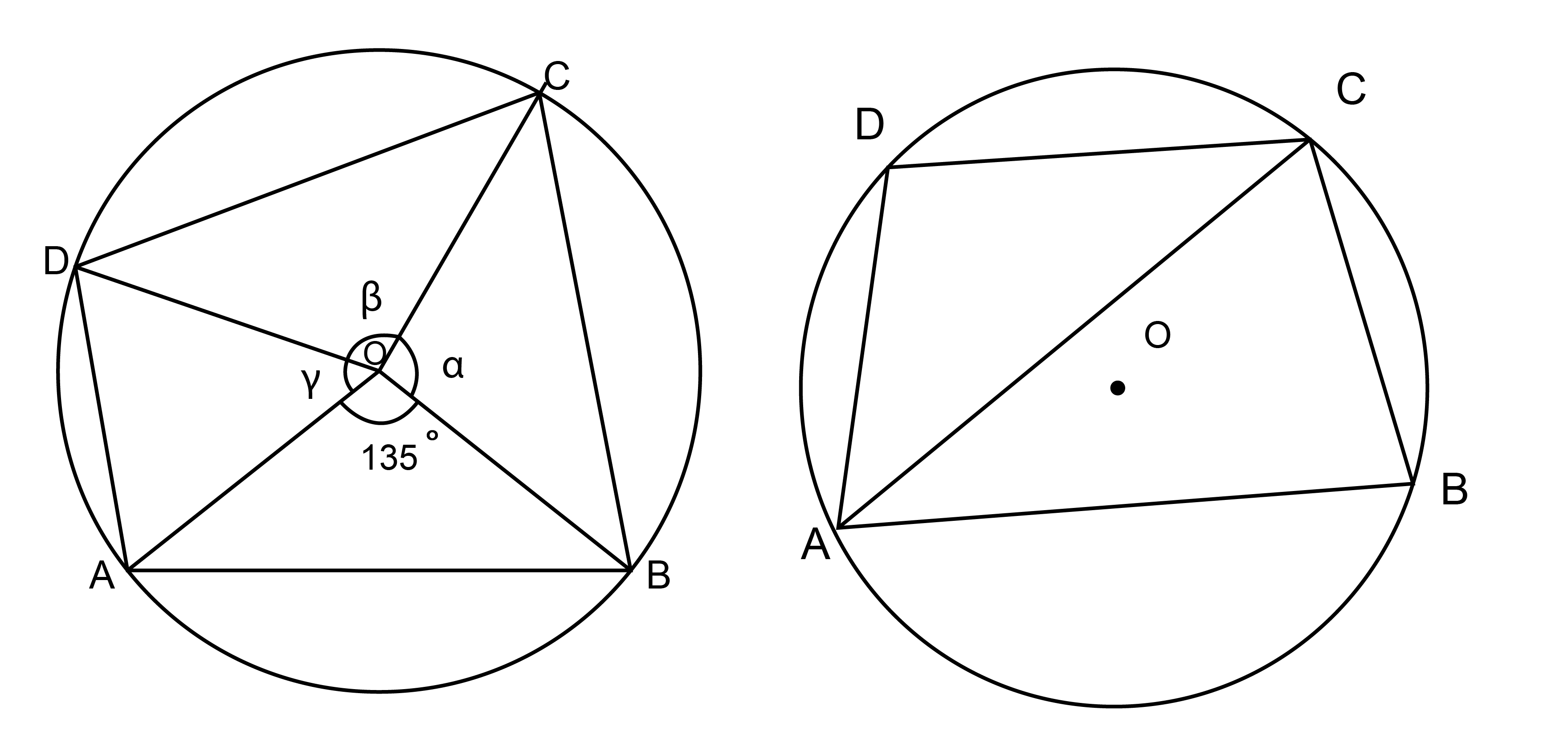
Let $$ABCD$$ be a quadrilateral inscribed in a circle. Suppose $$AB=\sqrt{2+\sqrt{2}}$$ and $$AB$$ subtends $$135^{\circ}$$ at the centre of the circle. Find the maximum possible area of $$ABCD$$.
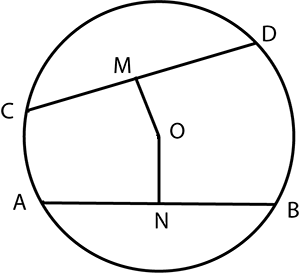
Prove that out of all the chords which passing through any point circle, that chord will be smallest which is perpendicular on diameter which passes through that point.
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
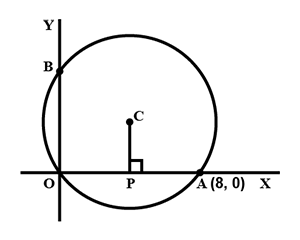
In the figure the radius of the circle centred at C isThe circle passes through the point A(8, 0). If PC is perpendicular to x axis, find the coordinates of the points P, B and C.
In the figure given, $$O$$ is the centre of the circle. $$AB$$ and $$CD$$ are two chords of the circle. $$OM$$ is perpendicular to $$CD$$ and $$ON$$ is perpendicular to $$AB$$. $$AB = 24\ cm, ON = 5\ cm, OM = 12\ cm$$. Find the length of chord $$CD$$
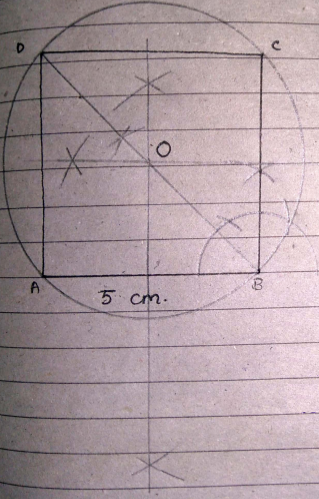
Construct a square of side length $$5$$cm and inscribe it in a circle.
Construct a square inscribed in a circle of radius $$3$$ cm.
Suppose $$AB = BC$$, $$\angle ABC = 68^o$$ , $$DA$$ and $$DB$$ are the tangents to the circle with centre O, for the trianlge $$ABC$$
Calculate the measure of $$\angle ACB$$
Prove that the quadrilateral $$ABCD$$ shown in the figure is a cycle quadrilateral.
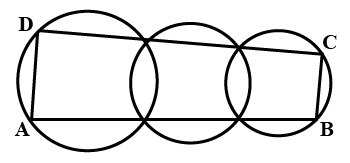
In figure, AB and CD diameters of the circle. Also AC = 4 cm and $$m \angle DPB = 45^o$$.
(a) Find $$m\angle DQB$$.
(b) Find the radius of the circle.

Prove that opposite sides of a quadrilateral circmscribing a circle subtend supplementary angles at the centre of the circle.
Prove that the line joining the mid-points of two parallel chords of a circle passes through the centre.
Find the area of a sector of a circle with radius $$6$$cm if angle of the sector is $$60^o$$.
In the given figure , O is the center of the circle. If $$\angle AOB = {140^o}$$ and $$\angle OAC = {50^o}$$; find :
$$(i) \angle ACB,$$
$$(ii) \angle OBC,$$
$$(iii) \angle OAB,$$
$$(iv) \angle CBA.$$
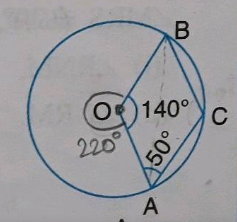
In the circle, $$AB$$ is a diameter, chords $$AD=DC$$ and $$\angle ABC=56^{o}$$. Find $$\angle CBD$$ and $$\angle DAB$$
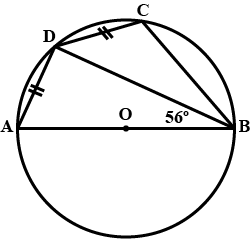
In the figure, seg AC is a diameter of the circle with centre O.Bisector of $$ \angle ABC $$ intersects the circle at D.
Prove that,$$ seg OD \bot seg AC $$
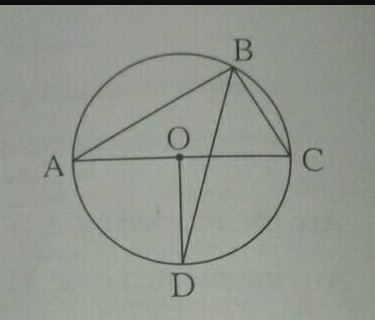
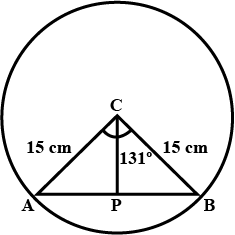
The radius of a circle is given as 15 cm and chord AB subtends an angle of $$131^\circ $$ at the centre C of the circle.Using trigonometry ,calculate :
(i) the length of AB ;
(ii) the distance of AB from the centre C
In cyclic quadrilateral $$ ABCD$$, if $$\angle A: \angle C=5: 4$$, find $$\angle A$$.
Prove that the equation of the circle circumscribing the triangle formed by the sides whose equations are 2x + y - 3 = 0 , 3x - y - 7 = 0 and x - 2y + 1 = 0 is $$x^2 \, + \, y^2 - $$ 5x - y + 4 = 0
In the given figure $$AB$$ is the diameter where $$AP=12$$ cm $$PB=16$$cm taking the value of $$\pi=3$$ find the perimeter of the shaded region
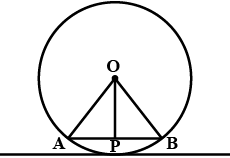
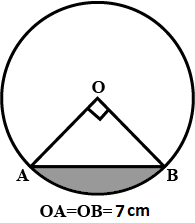
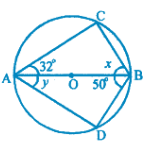
Radius of a circle with center $$O$$ is $$5\ cm$$ . Distance of a chord $$AB$$ from the center is $$3\ cm$$. Find the length of $$AB$$ .
Two parallel chords of lengths $$30\ cm$$ and $$16\ cm$$ are drawn on the opposite sides of the centre of a circle of radius $$17\ cm$$. Find the distance between the chords.
Draw a circle with centre C and radius 3.4 cm. Draw any chord $$\overline{AB}.$$ Construct the perpendicular bisector of $$\overline{AB}$$ and examine if it passes through C.
If the quadrilateral can be the inscribed in a circle , prove that the angle between its diagonals is $$ \sin ^{-1}[2\sqrt{(s-a)(s-b)(s-c)(s-d)}\div (ac +bd)]$$.
If the same quadrilateral can also be circumscribed about a circle, prove that this angle is then.
$$\cos^{-1}\dfrac{ac-bd}{ac+bd}$$.
$$A, B, C$$ and $$D$$ lie on the circle, centre $$O.BD$$ is a diameter and PAT is the tangent at $$A$$. Angle $$ABD = 58^{\circ}$$ and angle $$CDB = 34^{\circ}$$.
Find (a) angle $$ACD$$, (b) angle $$ADB$$ (c) angle $$DAT$$
If a square in inscribed in a circle, find the ratio of the areas of the circle and the square.
In a circle of radius 5 inches, the area of a certain segment is 25 square inches. Find graphically the angle that is subtended at the centre by the area of the segment.
Class 9 Maths Extra Questions
- Areas Of Parallelograms And Triangles Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Heron'S Formula Extra Questions
- Introduction To Euclid'S Geometry Extra Questions
- Linear Equations In Two Variable Extra Questions
- Lines And Angles Extra Questions
- Number Systems Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadrilaterals Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions