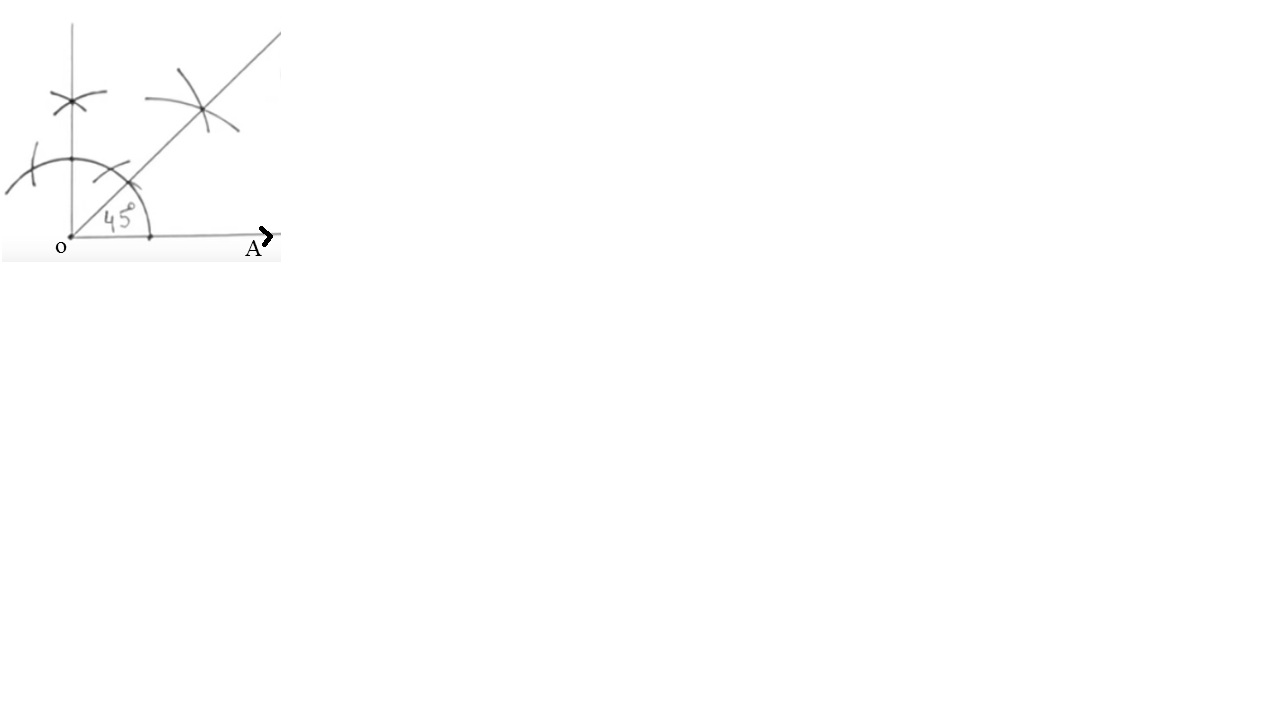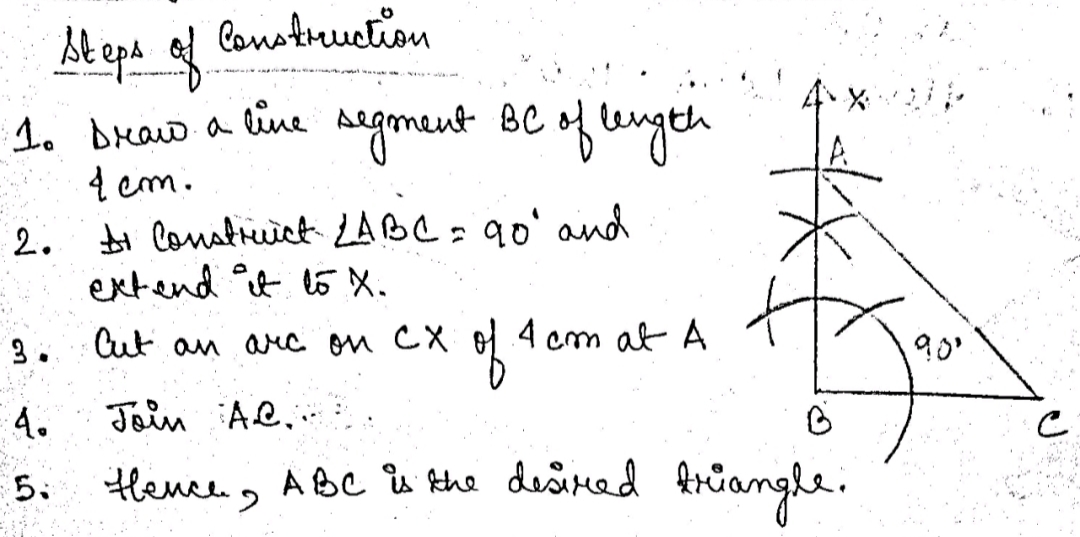Constructions - Class 9 Maths - Extra Questions
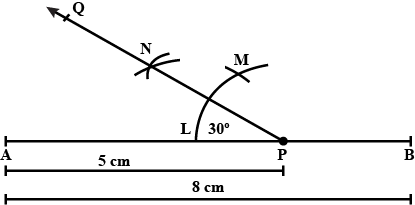
Construct a scalene triangle $$ABC,$$ given base $$AB=3\ cm,$$ base angle $$=90^o$$ and sum of the lengths $$BC+AC=9\ cm$$.
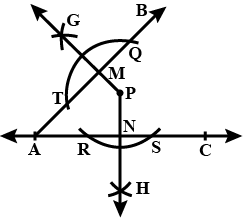
Draw $$\angle ABC$$ of measure $$110^{\circ}$$ and bisect it.
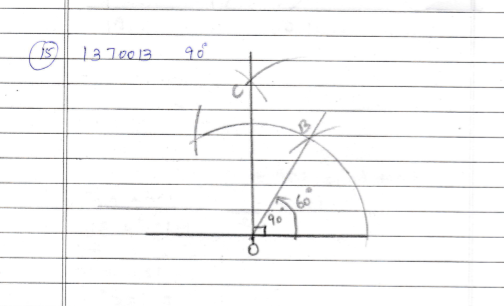
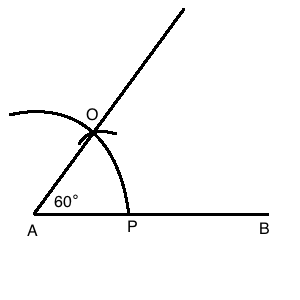
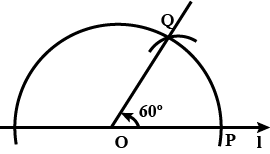
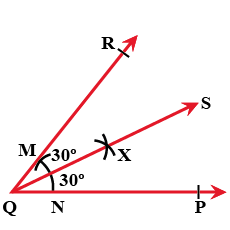
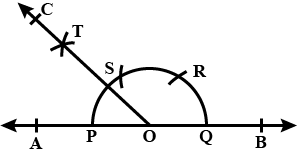
Construct a bisector of an angle of $$60^o$$.
Draw $$\angle ABC$$ of measure $$115^{\circ}$$ and bisect it.
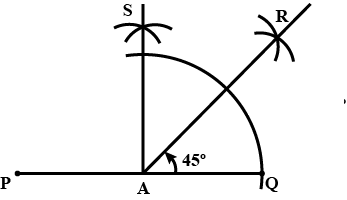
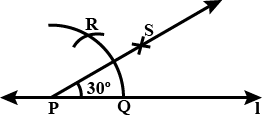
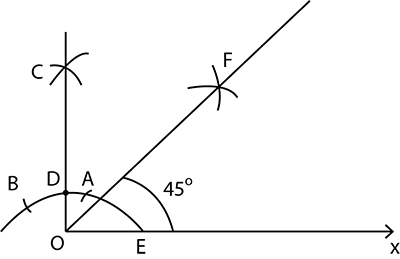
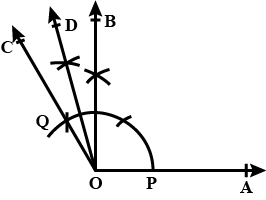
Construct an angle of $$45^o$$ using compass.
Draw the following angles using ruler and compasses. Also label them.
$$45^{o}$$
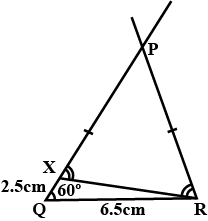
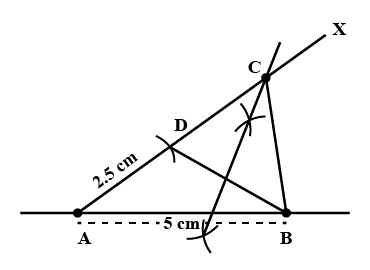
Construct $$\Delta PQR$$, such that $$QR = 6.5cm$$, $$\angle PQR = {60^0}$$ and $$PQ - PR = 2.5cm$$.
The construction of $$\Delta P Q R$$ given that $$Q R = 5.2 \mathrm\ { cm }$$ angle $$Q= 50^{\circ}$$. Is it possible when the difference of $$PQ$$ and $$PR$$ is $$3.5\ cm$$? justify.
Draw the following angles using ruler and compasses. Also label them.
$$90^{o}$$
How many of the given letters have perpendicular lines?
MATHS
Draw an angle of measure $$45^{o}$$ and bisect it.
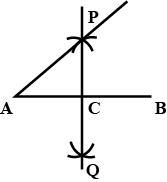
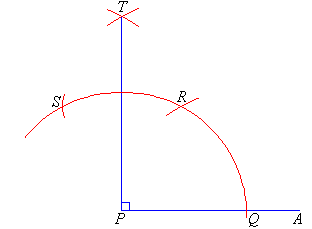
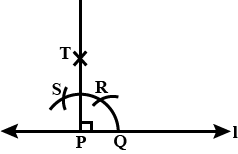
Draw a right angle.
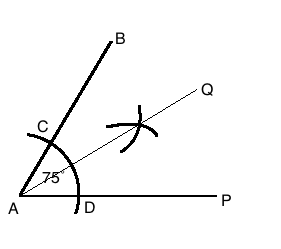
Draw $$\angle POQ$$ of measure $$75^{o}$$ and find its line of symmetry.
Draw the following angles using ruler and compasses. Also label them.
$$30^{\circ}$$
Draw a line segment $$XY=7 cm$$ and draw $$\angle AXY={ 90 }^{ \circ }$$
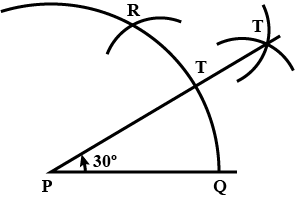
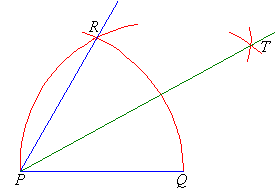
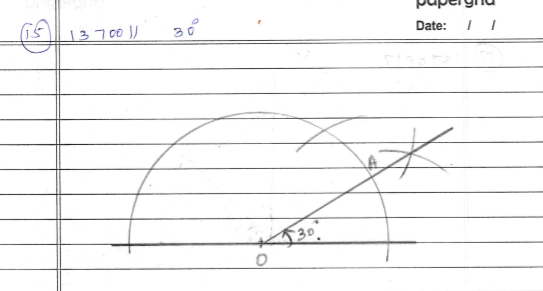
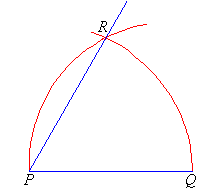
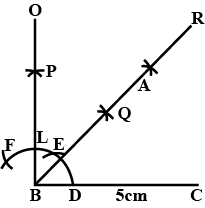
Construct the angle of $$30^{o}$$ using a ruler and compass.
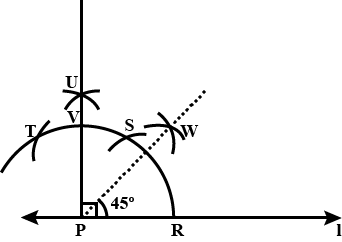
Construct an angle of the measure $$45^{\circ}$$ with ruler and compasses.
Construct with ruler and compasses, angle of the following measure:
$$30^{o}$$
Construct angles of following measures using ruler and compasses.
$$90^{o}$$
What is an angle bisector ?
Construct with ruler and compasses, angle of the following measure:
$$90^{o}$$
Construct angles of following measures using ruler and compasses.
$$60^{o}$$
Construct a bisector of an angle.
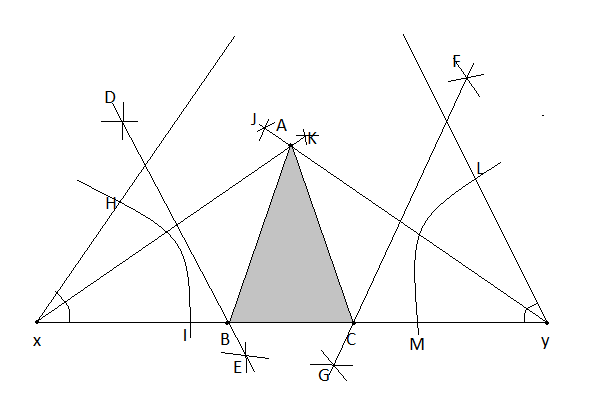
Construct a triangle ABC whose perimeter 12 cm and who base angles are $${ 50 }^{ \circ }$$ and $${ 80 }^{ \circ }$$.
Construct with ruler and compasses, angle of following measures.
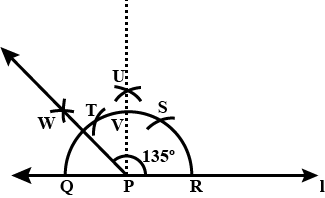
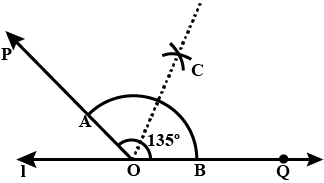
$$135^o$$.
Construct an angle of $$45^\circ$$ at the initial point of a given ray OA, using a ruler and compasses.
Construct with ruler and compasses, angle of following measures.
$$60^o$$.
Construct with ruler and compasses, angle of following measures.
$$90^o$$.
Draw an angle of measure $$135^o$$ and bisect it.
Construct with ruler and compasses, angle of following measures.
$$30^o$$.
Construct with ruler and compasses, angle of following measures.
$$120^o$$.
Draw a right angle and construct its bisector.
Construct with ruler and compasses, angle of following measures.
$$45^o$$.
Draw an angle of $$ 45 ^ { \circ } , $$ using a pair of compasses.
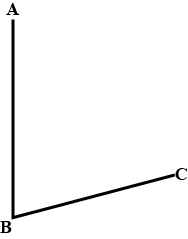
In this question, use a straight edge and compasses only and show all your construction arcs. Construct the bisector of angle ABC.
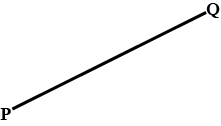
In this question, use a straight edge and compasses only and show all your construction arcs. Construct the perpendicular bisector of PQ.
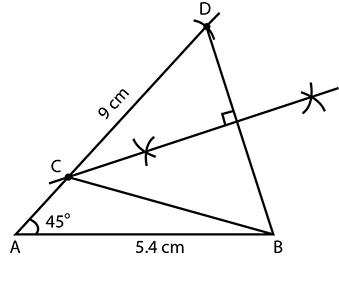
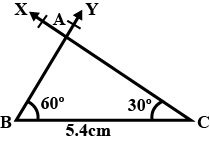
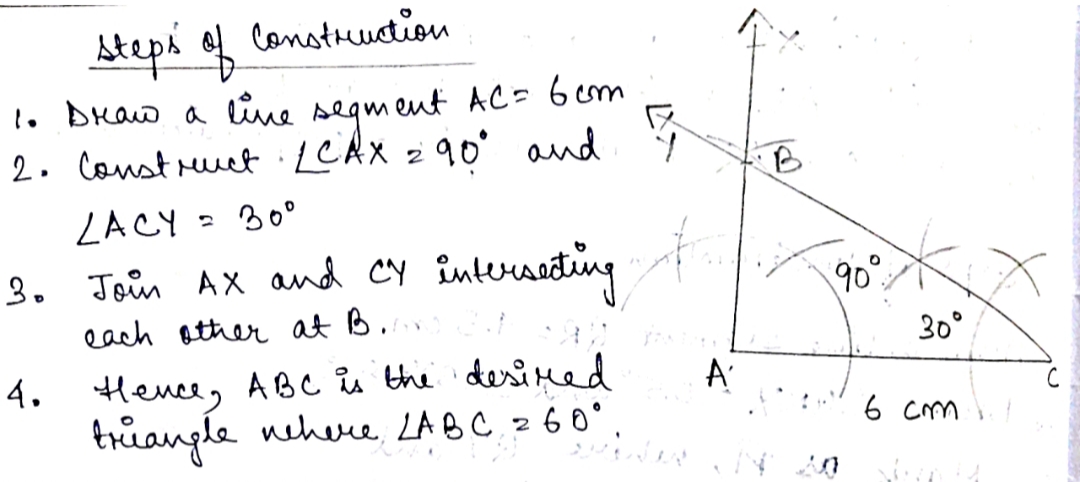
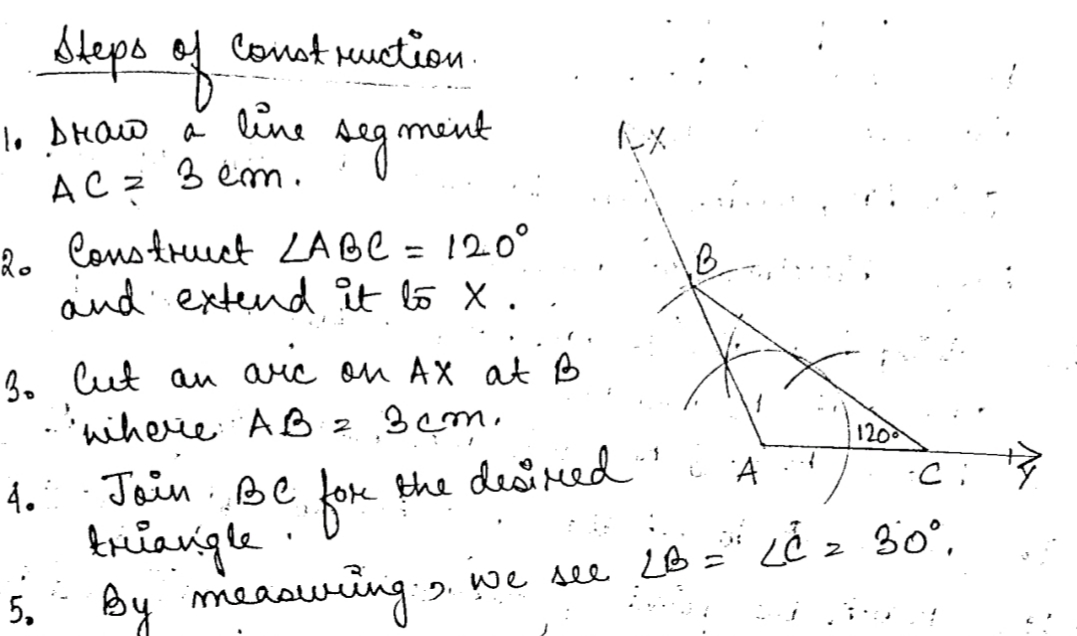
Construct a $$\triangle ABC$$ in which: $$AB= 5.4\ cm$$, $$\angle CAB= 45^{0}$$ and $$AC\, +\, BC= 9\ cm$$.Then the length of $$AC$$ (in $$cm.$$) is:
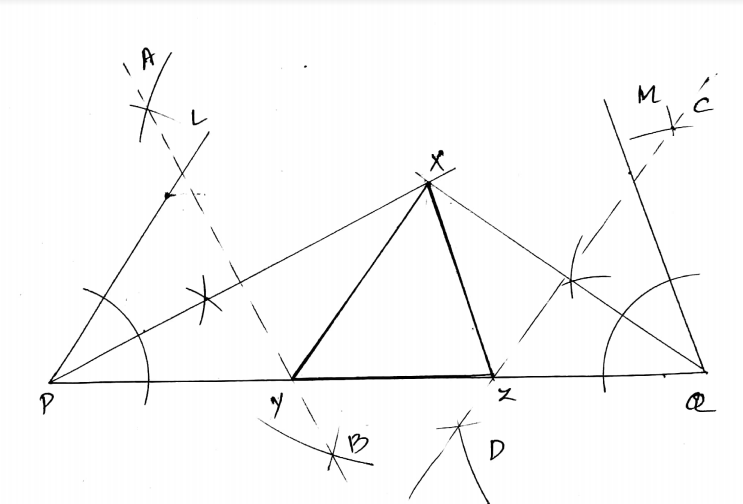
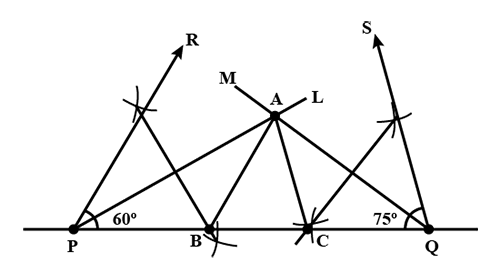
Construct a triangle $$PQR$$ in which $$\angle Q = 60^o$$ and $$\angle R = 45^o$$ and $$PQ + QR + PR = 11\ cm$$.
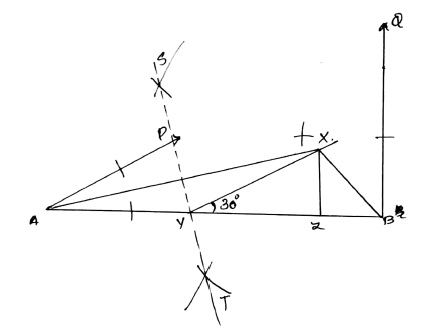
Construct a $$\triangle ABC$$ in which $$AC= 5\ cm$$, and $$\angle BAC= 60^{\circ}$$ and $$AB\, -\, BC= 1.2\ cm$$.
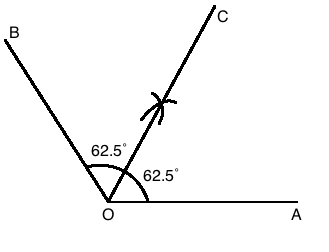
Construct the bisector of an angle $$75^o$$.
Construct an angle of $$60^o$$ using compass.
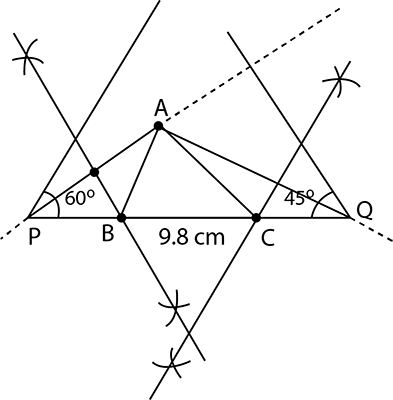
Construct a triangle whose perimeter is $$9.8\ cm$$ and the base angles are $$45^\circ$$ and $$60^\circ$$.
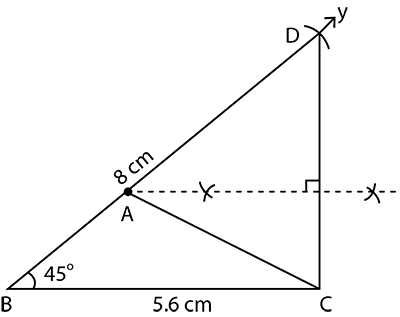
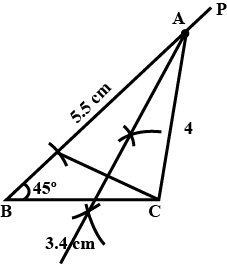
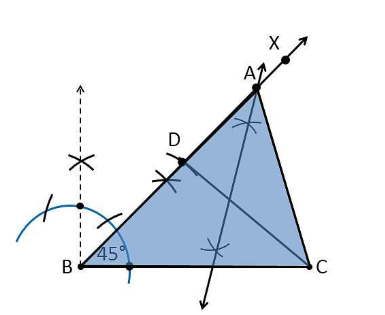
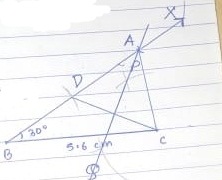
Construct a triangle ABC in which $$ \displaystyle BC=5.6 $$ $$cm$$, $$ \displaystyle \angle B=45^{\circ} $$ and $$ \displaystyle AB+AC=8\ cm $$.
Construct a $$\triangle$$ $$PQR$$, such that $$\angle$$ Q=$$70^o$$, $$\angle R=70^o$$ and $$PQ+QR+RP$$ $$=10$$ cm.
Construct a triangle ABC in which $$BC = 6\ cm, \angle A = \displaystyle 45^{\circ}$$ and median $$AD = 5\ cm$$.
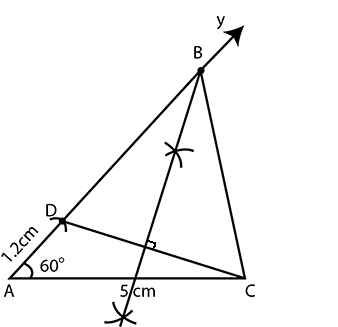
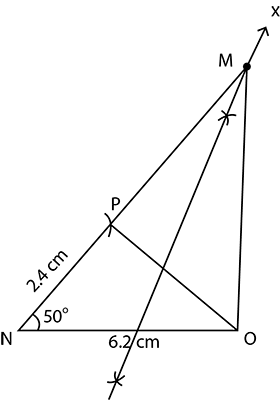
Construct $$\triangle MNO$$ such that $$NO = 6.2\ cm$$, $$\angle N = 50^\circ$$ and $$MO - MN = 2.4\ cm.$$
Perimeter of $$\triangle ABC$$ is 14cm, AB=4.5 cm and $$\angle A = 80^o$$. Construct $$\triangle ABC$$.
Construct an angle of $$30^o$$ using compass.
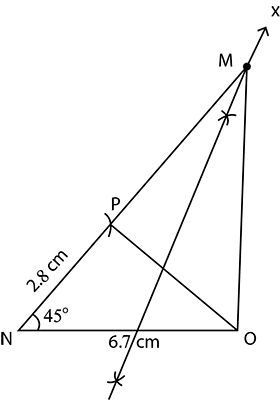
Construct $$\triangle MNO$$ where base $$NO = 6.7\ cm$$, $$\angle MNO = 45^\circ$$ and $$MO-MN = 2.8\ cm.$$
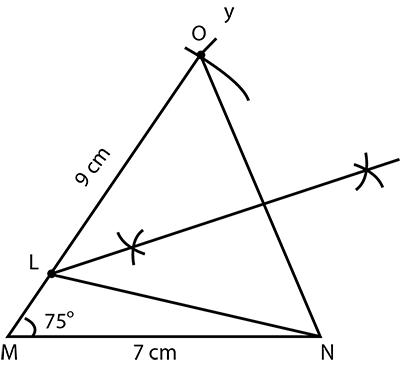
Construct $$\triangle LMN$$ in which base $$MN= 7\ cm$$, $$\angle LMN=75^\circ$$ and $$LM+LN = 9\ cm.$$
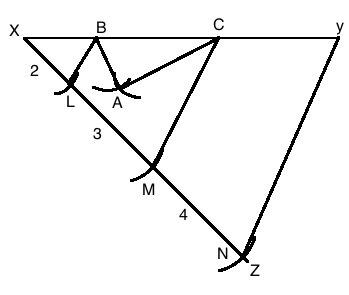
Construct a triangle $$XYZ$$ in which $$\angle {Y}={30}^{o}$$, $$\angle {Z}={90}^{o}$$ and $$XY+ZX+YZ=11cm$$.
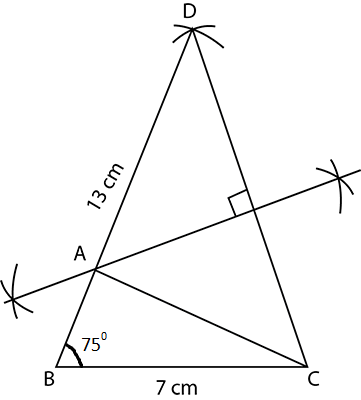
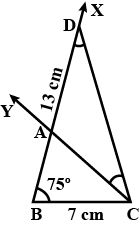
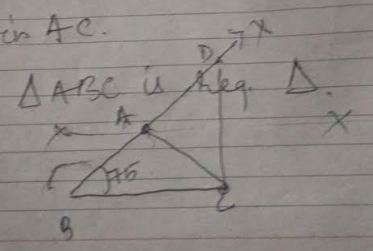
Construct a triangle $$ABC$$ in which $$BC=7cm$$, $$\angle {B}={75}^{o}$$ and $$AB+AD=13\ cm$$.
Construct $$\triangle PQR$$ such that perimeter of $$\triangle PQR$$ is $$16\ cm$$ and $$\angle Q=90^\circ$$ and $$QR = 5\ cm.$$
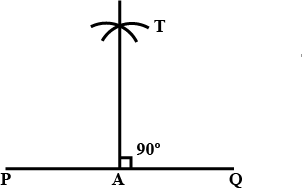
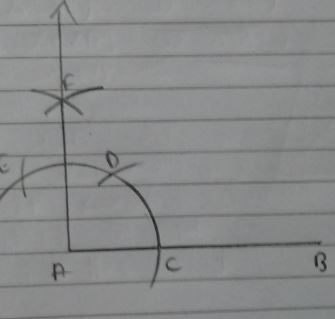
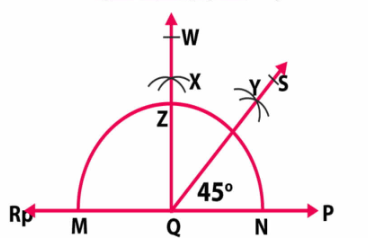
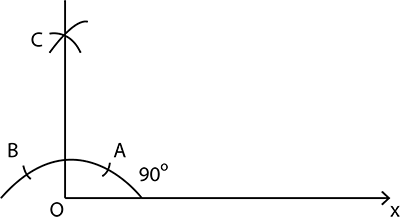
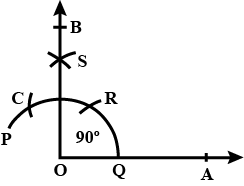
Construct an angle of $${90}^{\circ}$$ at the initial point of a given ray and justify the construction.
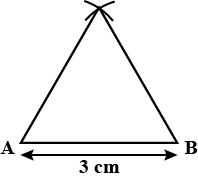
Construct an equilateral triangle, given its side $$=3 cm$$ and justify the construction.
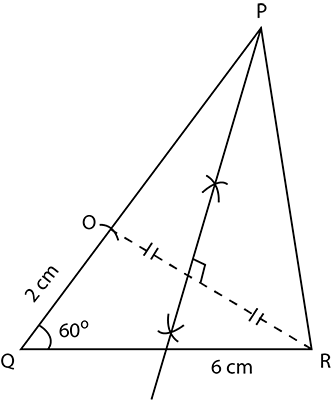
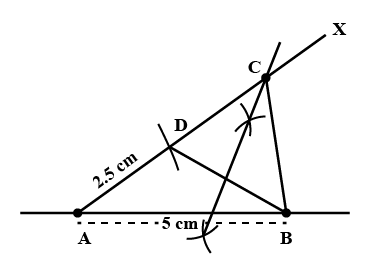
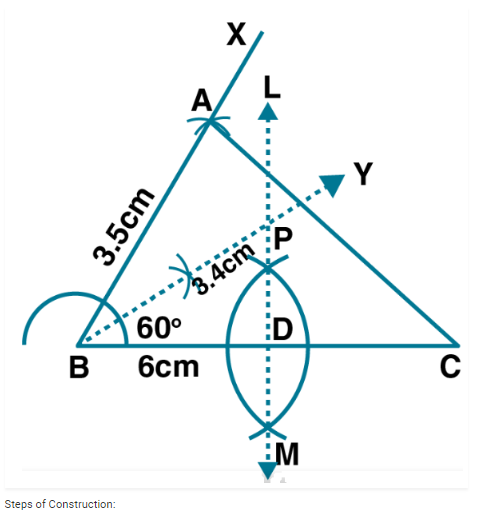
Construct a triangle $$PQR$$ in which $$QR=6cm$$, $$\angle {Q}={60}^{o}$$ and $$PQ-PO=2cm$$.
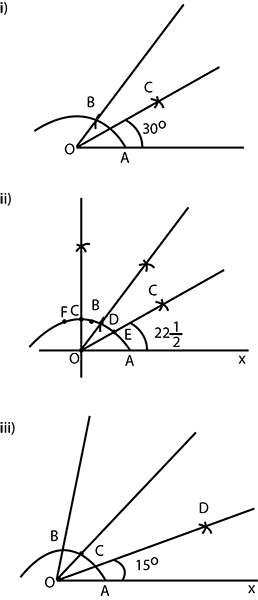
Construct the angles of the following measurements:
$$(i) {30}^{\circ}$$
$$(ii) {22\cfrac{1}{2}}^{\circ}$$
$$(iii) {15}^{\circ}$$
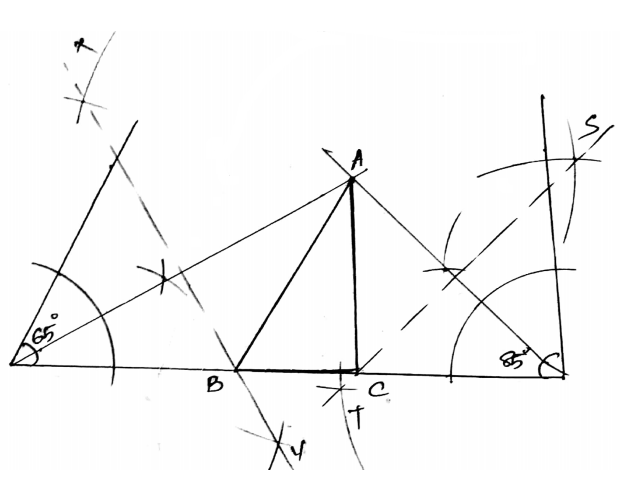
Construct a triangle $$ABC$$ whose perimeter $$12 cm$$ and whose base angles are $$65^{\circ}$$ and $$85^{\circ}$$
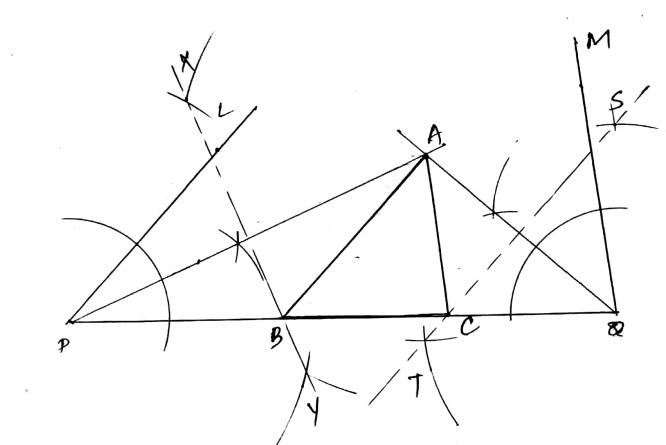
Construct a triangle $$ABC$$ whose perimeter $$12 cm$$ and whose base angles are $$50^{\circ}$$ and $$80^{\circ}$$
Construct triangle $$ABC$$ in which $$BC = 3.4 cm, AB - AC = 1.5 cm$$ and $$\angle B = 45^{\circ}$$
Construct a triangle $$ABC$$, whose perimeter is $$12 cm$$ and whose sides are in the ratio $$3 : 4 : 5$$
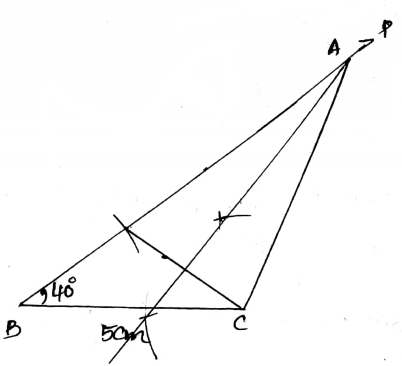
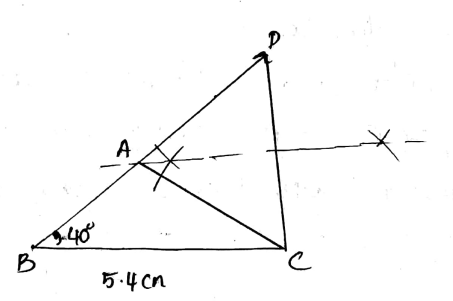
Construct triangle $$ABC$$ in which $$BC = 5 cm, AB - AC = 2.8 cm$$ and $$\angle B = 40^{\circ}$$
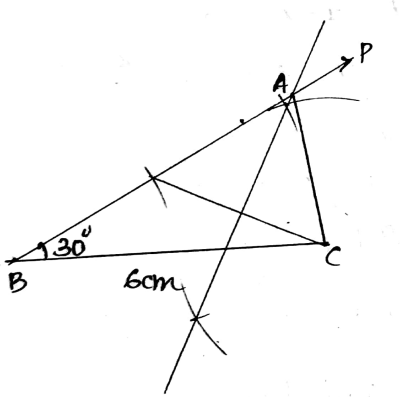
Construct triangle $$ABC$$ in which $$BC = 6 cm, AB - AC = 3.1 cm$$ and $$\angle B = 30^{\circ}$$
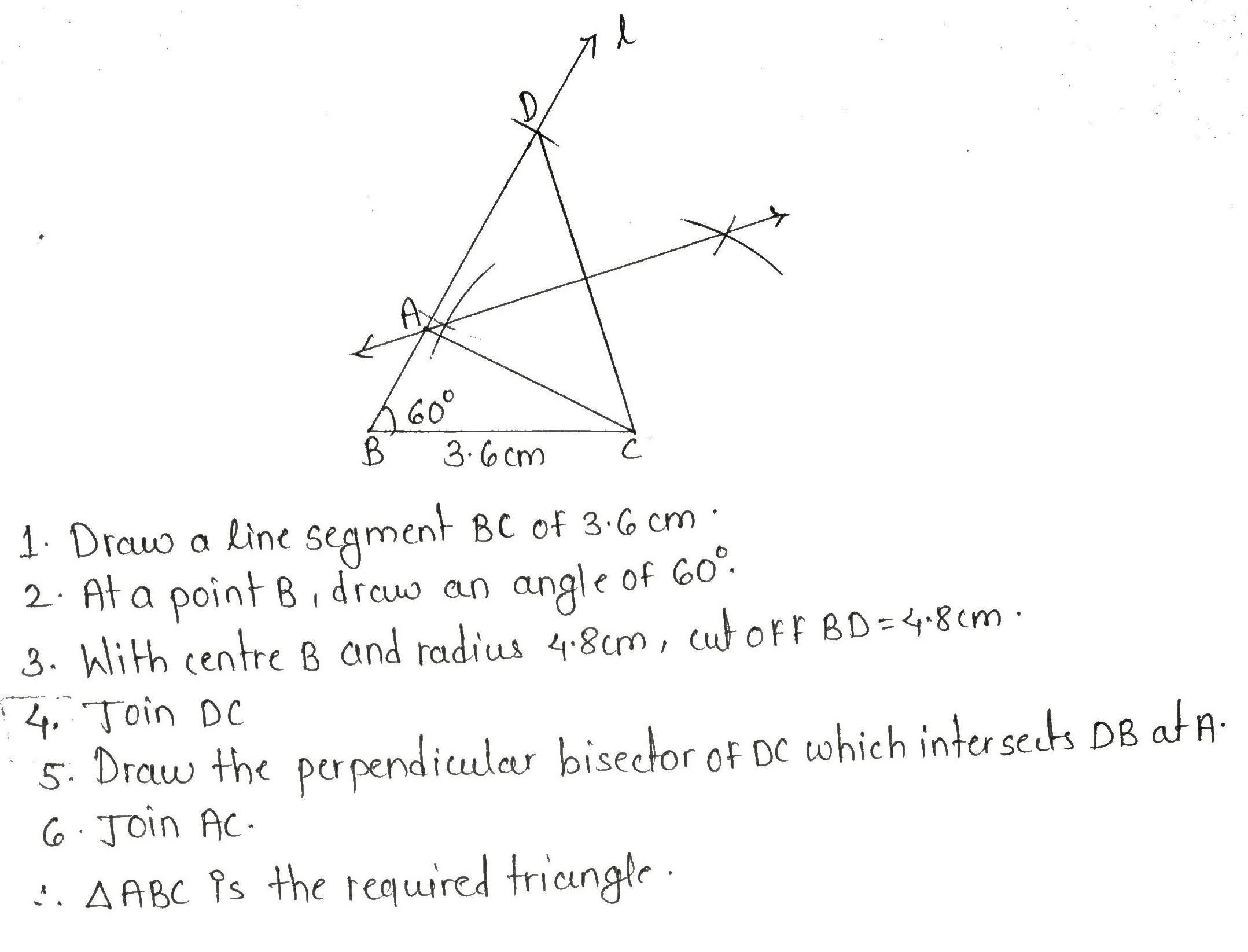
Construct a triangle $$ABC$$ in which $$BC = 3.6 cm, AB + AC = 4.8 cm$$ and $$\angle B = 60^{\circ}$$
Construct a triangle $$ABC$$ in which $$AB=5.6 cm, BC = 5.4 cm$$ and $$\angle B = 40^{\circ}$$
Construct a triangle $$ABC$$, whose perimeter is $$12 cm$$ and whose sides are in the ratio $$2 : 3 : 4$$.
Construct a triangle $$XYZ$$ whose perimeter $$15\ cm$$ and whose base angles are $$60^{\circ}$$ and $$70^{\circ}$$
Draw $$\angle ABC$$ of measure $$120^{\circ}$$ and bisect it.
Construct a triangle $$ABC$$ in which $$AB = 5.8\ cm, BC + CA = 8.4\ cm$$ and $$\angle B = 60^{\circ}$$
Using a ruler and compass only.
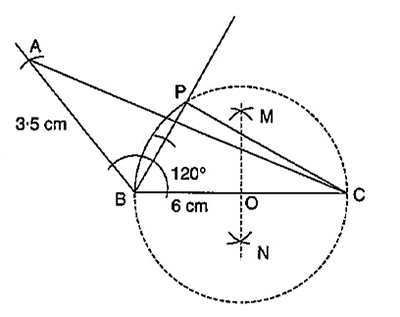
(i) Construct a $$\triangle ABC$$ with the following data.
$$AB=3.5\ cm, BC=6\ cm$$ and $$\angle ABC=120^\circ$$
(ii) In the same diagram, draw a circle with $$BC$$ as diameter. Find a point $$P$$ on the circumference of the circle which is equidistant from $$AB$$ and $$BC$$.
(iii) Measure $$\angle BCP$$.
Construct a triangle $$ABC$$ in which base $$AB = 5 cm, \angle A = 30^{\circ}$$ and $$AC - BC = 2.5 cm$$
Construct a triangle $$ABC$$ whose perimeter is $$12.5 cm$$ and whose base angles are $$60^{\circ}$$ and $$75^{\circ}$$
Construct an angle of $${45}^{o}$$ and bisect it.
Draw $$\angle$$ ABC of measure $$125^o$$ and bisect it.
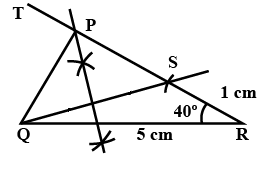
Construct a triangle $$PQR$$ in which $$QR=5\ cm,\angle R=40^{o}$$ and $$PR-PQ=1\ cm$$.
Construct a triangle $$ABC$$ in which $$BC=7cm,\angle{B}={75}^{o}$$ and $$AB+AC=13cm$$
Construct an angle of $${90}^{o}$$ at the initial point of a given ray and justify the construction.
If the measure of an angle is equal to $${225}^{\circ}$$, then find the fraction of one complete turn?
Construct $$\triangle ABC$$ in which $$BC=6.3\ cm$$ $$\angle B=75^{o}$$ and $$AB+AC=9\ cm$$.
Construct $$\triangle XYZ$$ in which $$\angle Y=30^{o}, \angle Z=60^{o}$$ and $$XY+YZ+ZX=10\ cm$$.
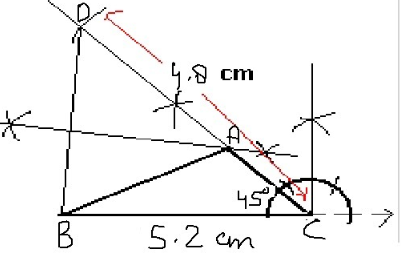
Write the steps to construct $$\triangle ABC$$, in which $$BC=5.2\ cm$$, $$\angle ACB={45}^{\circ}$$ and perimeter of $$\triangle ABC$$ is $$10\ cm$$.
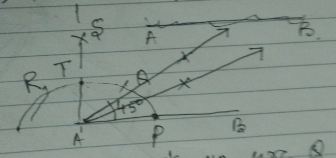
Construct an angle of $${45}^{o}$$ at the initial point of a given ray and justify the construction.
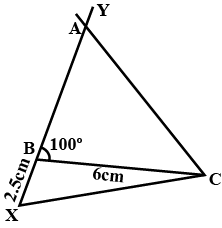
Construct $$\Delta ABC$$, such that $$BC = 6cm$$,$$\angle ABC = {100^0}$$ and $$AC - AB = 2.5cm$$.
Construct an angle of $$45^{\circ}$$ at the initial point of a given point of a given ray and justify the construction.
Construct an angle of $$90^{o}$$ at the point of a given ray and justify the construction.
Draw the following angles using ruler and compasses. Also label them.
$$60^{o}$$
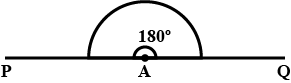
Draw the following angles using ruler and compasses. Also label them.
$$180^{o}$$
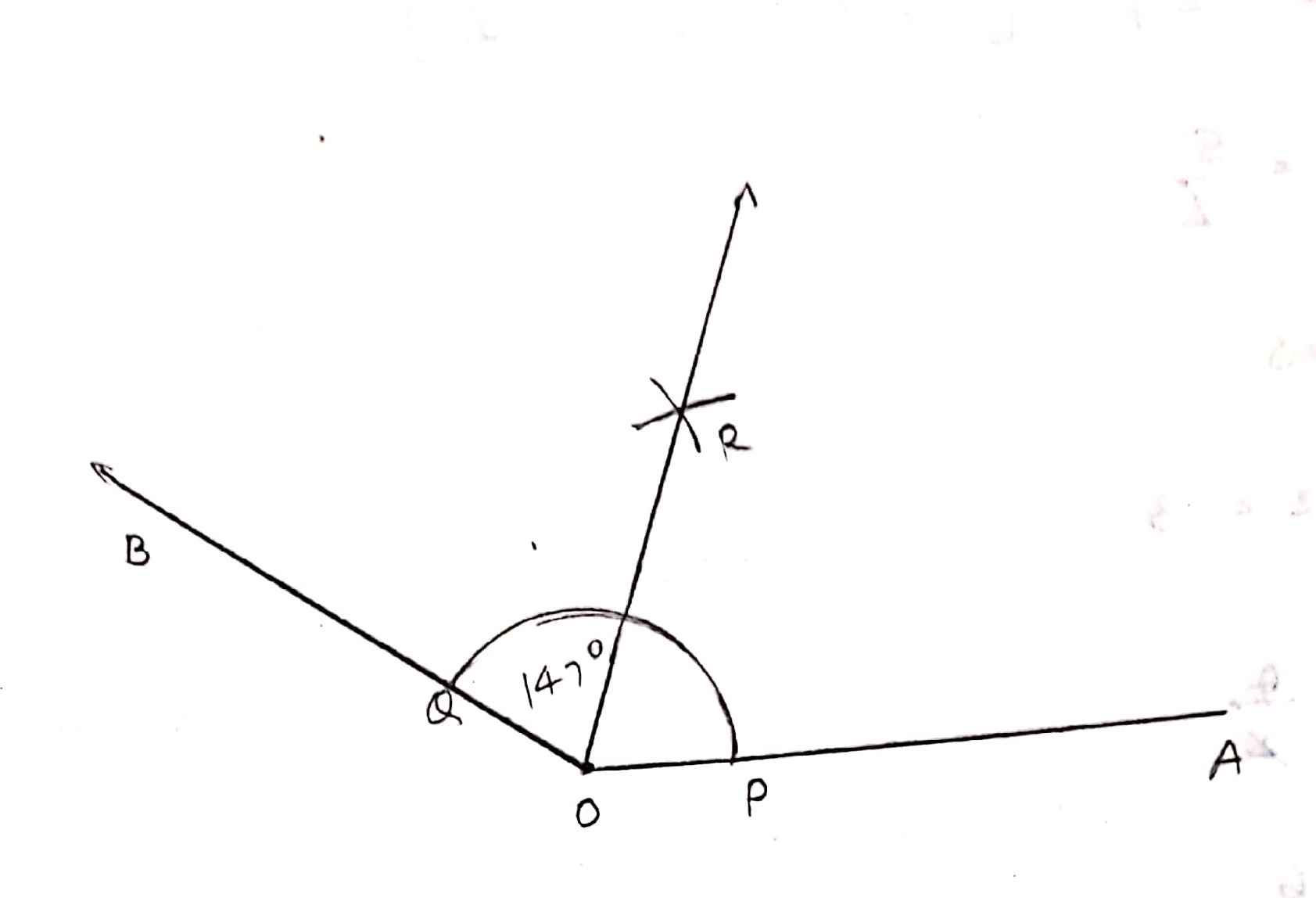
Draw an angle of measure $${147^ \circ }$$ and construct its bisector.
Draw an angle of measure $${147}^{\circ}$$ and construct its bisector
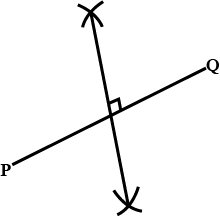
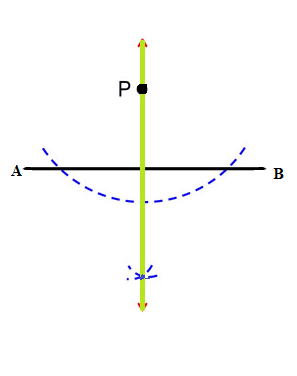
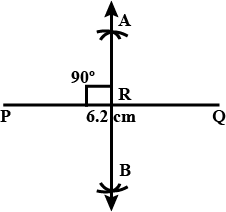
Draw a line segment $$PQ=6.2\ cm$$. Draw the perpendicular bisector of $$PQ$$.
Construct a triangle $$ABC$$ in which $$BC=8$$cm,$$\angle{B}={45}^{\circ}$$ and $$AB-AC=3.5$$cm
Construct a $$\triangle ABC$$ in which $$BC=5.6\ cm, \angle B=30^{o}$$ and the difference between the other sides is $$3\ cm$$.
Construct triangle $$ABC$$ having given $$BC=7\ cm,\ AB-AC=1\ cm$$ and $$\angle\ ABC=45^{o}$$.
Construct a perpendicular line from point $$p$$ to any line $$AB$$.
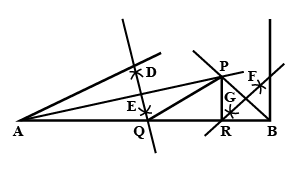
Use ruler and compasses only for this question.
Construct a $$\triangle ABC,\,AB=3.5cm,\,BC=6cm,\,\&\,\angle ABC=60^\circ$$
Mark the point P which is equidistant from $$AB$$, $$BC$$ and also equidistant from $$B$$ and $$C$$.
Construct a triangle ABC in which $$BC=8cm,\angle B={ 45 }^{ \circ }andAB-AC=3.5cm.$$
Draw an angle of $$60^\circ,$$ using a pair of compasses. Bisect it to make an angle of $$30^\circ.$$
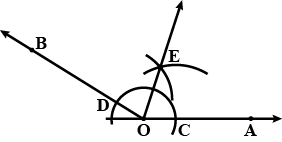
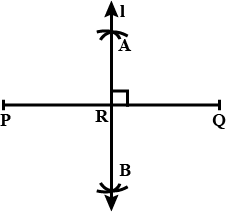
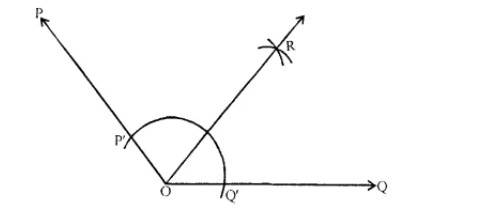
Draw any angle with vertex $$O$$. Take a point $$A$$ on one of its arms and $$B$$ on another such that $$OA=OB$$. Draw the perpendicular bisectors of $$\overline{OA}$$ and $$\overline{OB}$$. Let them meet at $$P$$. Is $$PA=PB$$?
Without using set-squares or protractor construct:
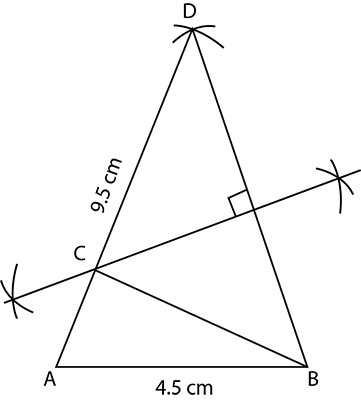
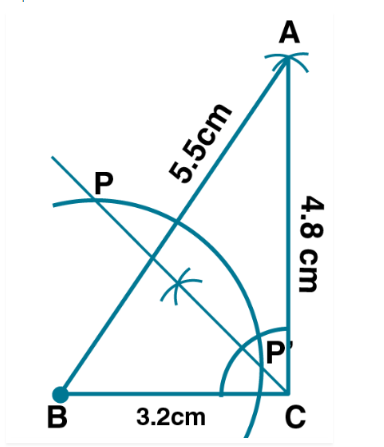
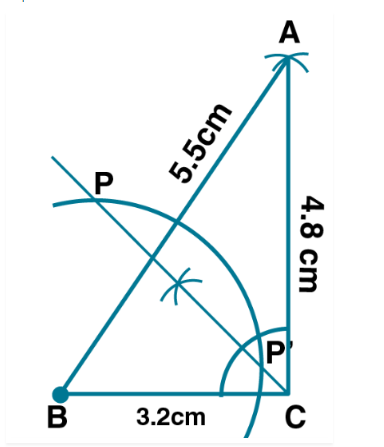
Triangle $$ABC$$, in which $$AB = 5.5$$ cm, $$BC = 3.2$$ cm and $$CA = 4.8$$ cm.
Draw the locus of a point which moves so that it is equidistant from the sides $$BC$$ and $$CA.$$
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If L is the mid-point of BC, prove that $$LM=LN$$.
Construct a $$\Delta ABC$$ in which BC=5 cm, $$\angle B=45$$ and AB-AC=2.8cm
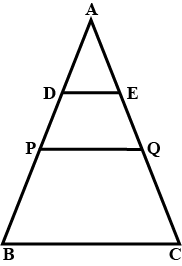
$$ABC$$ is a triangle. $$D$$ is a point on $$AB$$ such that $$AD=\dfrac{1}{4}AB$$ and $$E$$ is a point on $$AC$$ such that $$AE=\dfrac{1}{4}AC$$. Prove that $$DE=\dfrac{1}{4}BC$$.
Draw a right triangle having hypotenuse of length $$5.4$$cm, and one of the acute angles of measure $$30^o$$.
Draw an angle of measure $$127^{\circ}$$ and construct its bisector.
Without using set-squares or protractor construct:
construct a $$\triangle ABC,\,AB=5.5cm,\,BC=3.2cm,\,\&\,AC=4.8cm$$
Find the locus which is equidistant from sides $$BC\,\&\,AC$$ and also at a distance of $$2.5cm$$ from $$B$$
Mark the point of intersection of the loci with the letter $$P$$ and measure $$PC$$.
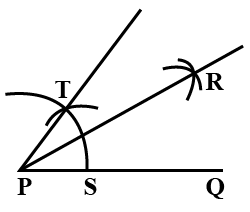
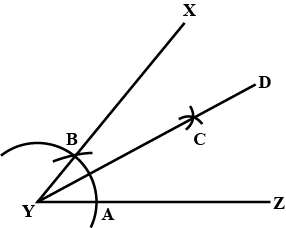
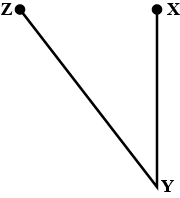
Bisect the $$ \angle XYZ $$ and write the steps of construction as well.
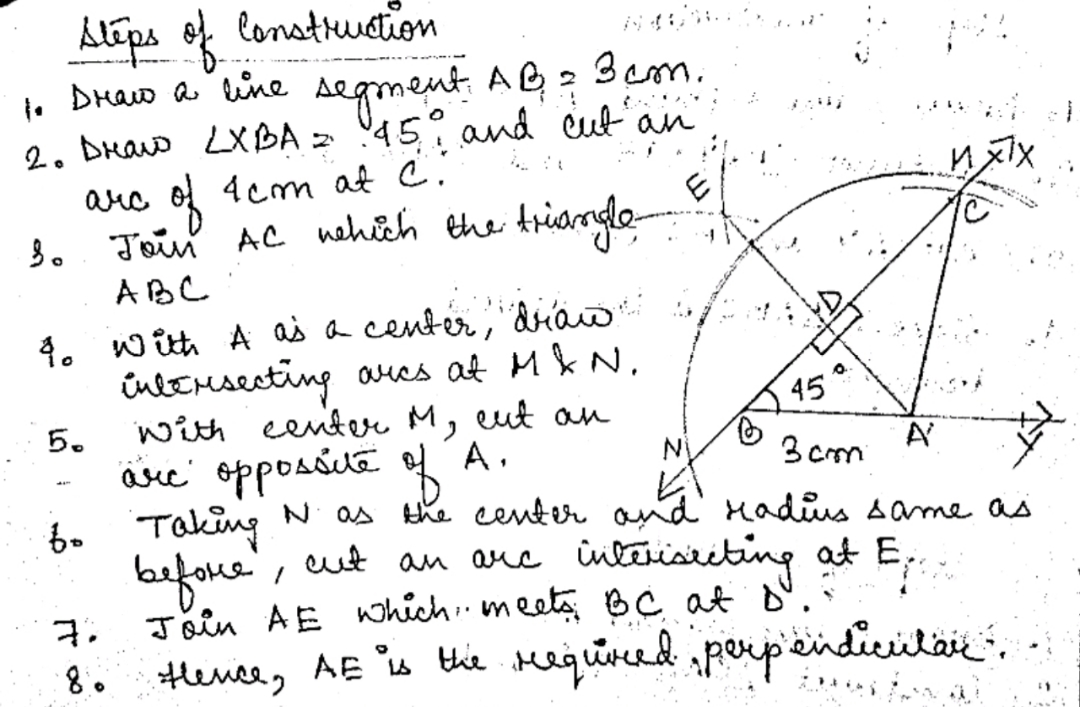
Draw a line segment $$ AB=8\ cm. $$ Mark a point $$ P $$ in $$ AB $$ so that $$ AP =5\ cm . $$ At $$ P $$, construct $$\angle APQ=30^\circ.$$
Construct angle $$ABC=45^o$$ in which $$BC=5cm$$ and $$AB=4.6cm$$.
Construct an angle of $${45}^{\circ}$$ from a horizontal line and justify the construction.
Using a protractor, draw $$ \angle BAC $$ of measure $$ 45^{\circ}$$. Take a point P in the interior of $$ \angle BAC.$$ From P draw line segments PM and PN such that $$ PM \perp AB$$ and $$ PN \perp AC$$, Measure $$ \angle MPN.$$
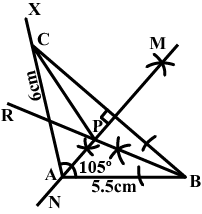
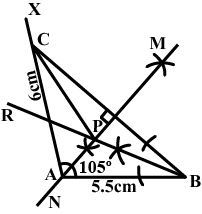
Construct a triangle $$ABC$$ with $$AB=5.5\ cm,AC=6\ cm$$ and $$\angle BAX=105^{o}$$
Hence :
Construct the locus of point equidistant from $$B$$ and $$C$$.
In triangle $$ABC$$; angle $$A=90^{o}$$, side $$AB=x\ cm,\ AC=(x+5)\ cm$$ and area $$=150\ cm^{2}$$. Find the sides of the triangle.
Construct a triangle $$ABC$$ with $$AB=5.5\ cm,AC=6\ cm$$ and $$\angle BAX=105^{o}$$
Hence :
Construct the locus of points equidistant from $$BA$$ and $$BC$$ .
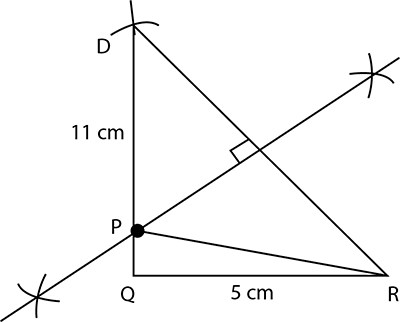
Construct a $$ \triangle A B C $$ in which B C = 3.6 cm, A B = 5 cm and A C = 5.4 cm. Draw the perpendicular bisector of the side B C.
Construct a triangle XYZ in which $$\angle Y$$ = $${30}^0$$ , $$\angle Z$$ = $${90}^0$$ and XY + YZ + ZX = 11 cm .
Draw a triangle ABC in which BC$$=4$$cm, AB$$=3$$cm and $$\angle B=45^o$$. Also, draw a perpendicular from A on BC.
Construct $$\Delta$$ABC in which AB$$=6.4$$cm, $$\angle A=45^o$$ and $$\angle B=60^o$$.
Construct the following angles with the help of ruler and compasses only:$$150^{\circ}$$
Construct the following angles with the help of ruler and compasses only:$$105^{\circ}$$
Draw $$\Delta$$ABC in which AC$$=6$$cm, $$\angle A=90^o$$ and $$\angle B=60^o$$.
Draw $$\Delta$$ABC in which $$\angle C=90^o$$ and $$AC=BC=4$$cm.
Using ruler and compasses only, draw a right angle.
Draw $$\Delta$$PQR in which $$\angle Q=80^o$$, $$\angle R=55^o$$ and $$QR=4.5$$cm. Draw the perpendicular bisector of side QR.
Draw $$\Delta$$ABC in which $$\angle A=120^o$$, AC$$=$$AB$$=3$$cm. Measure $$\angle B$$ and $$\angle C$$.
Class 9 Maths Extra Questions
- Areas Of Parallelograms And Triangles Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Heron'S Formula Extra Questions
- Introduction To Euclid'S Geometry Extra Questions
- Linear Equations In Two Variable Extra Questions
- Lines And Angles Extra Questions
- Number Systems Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadrilaterals Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions