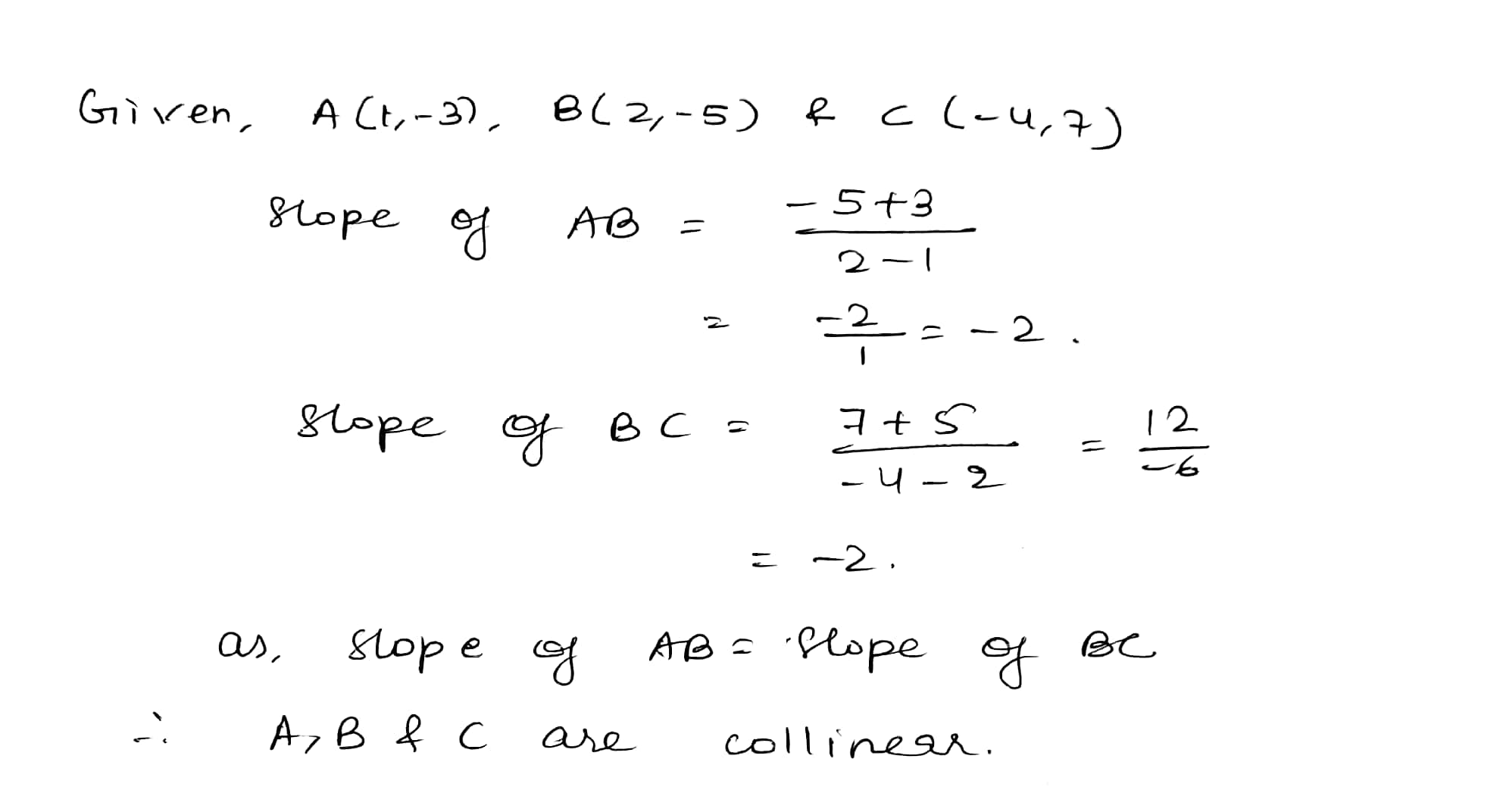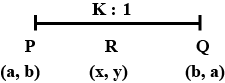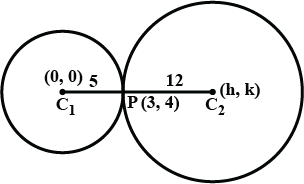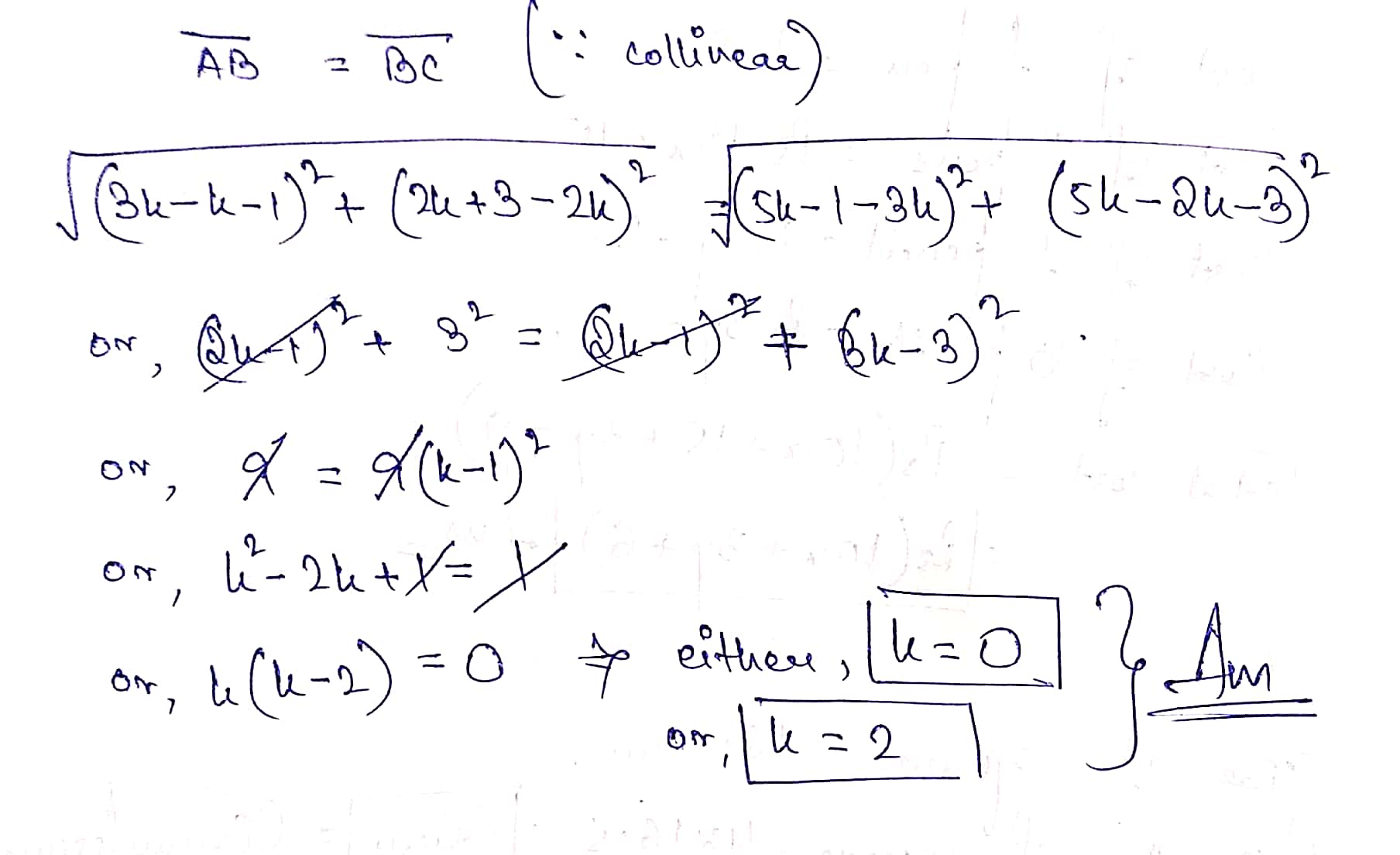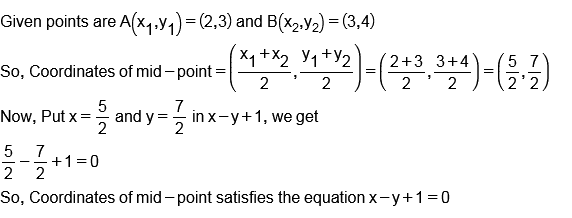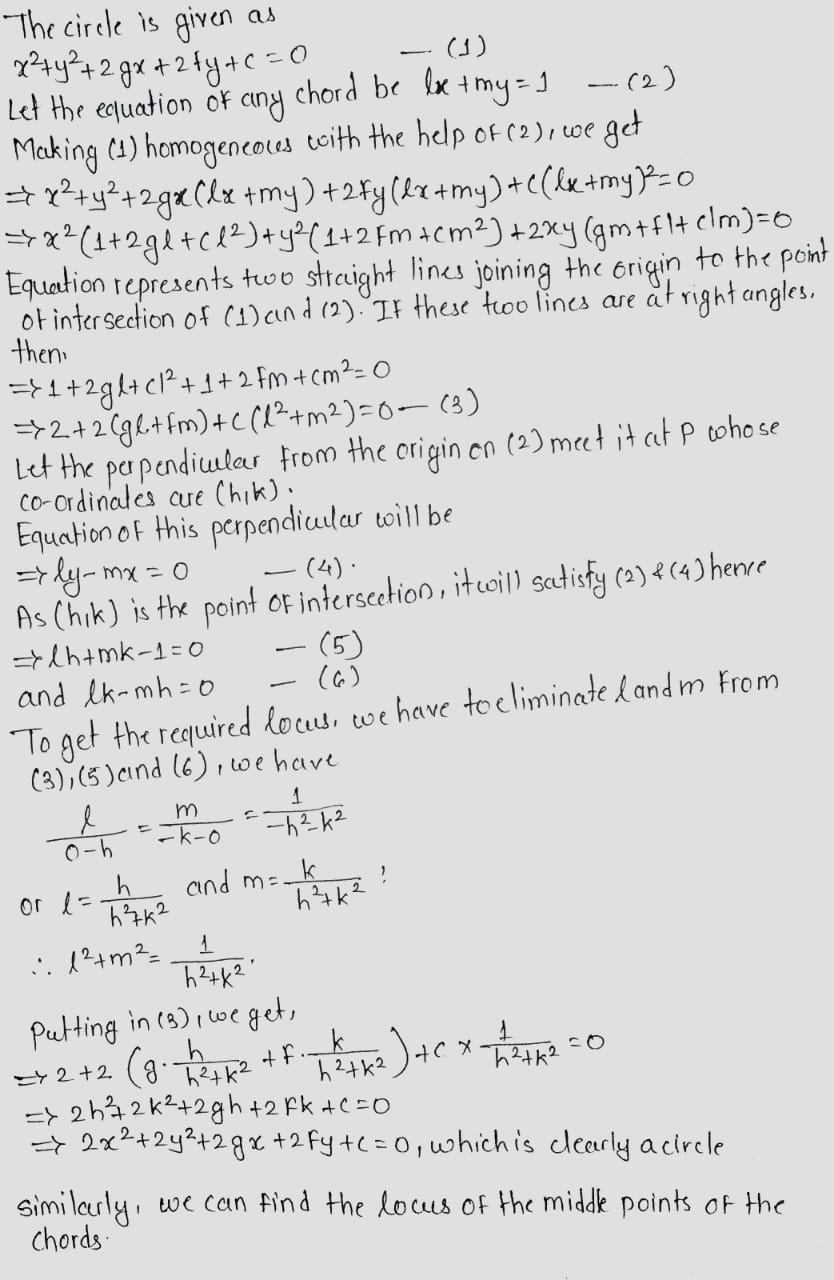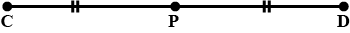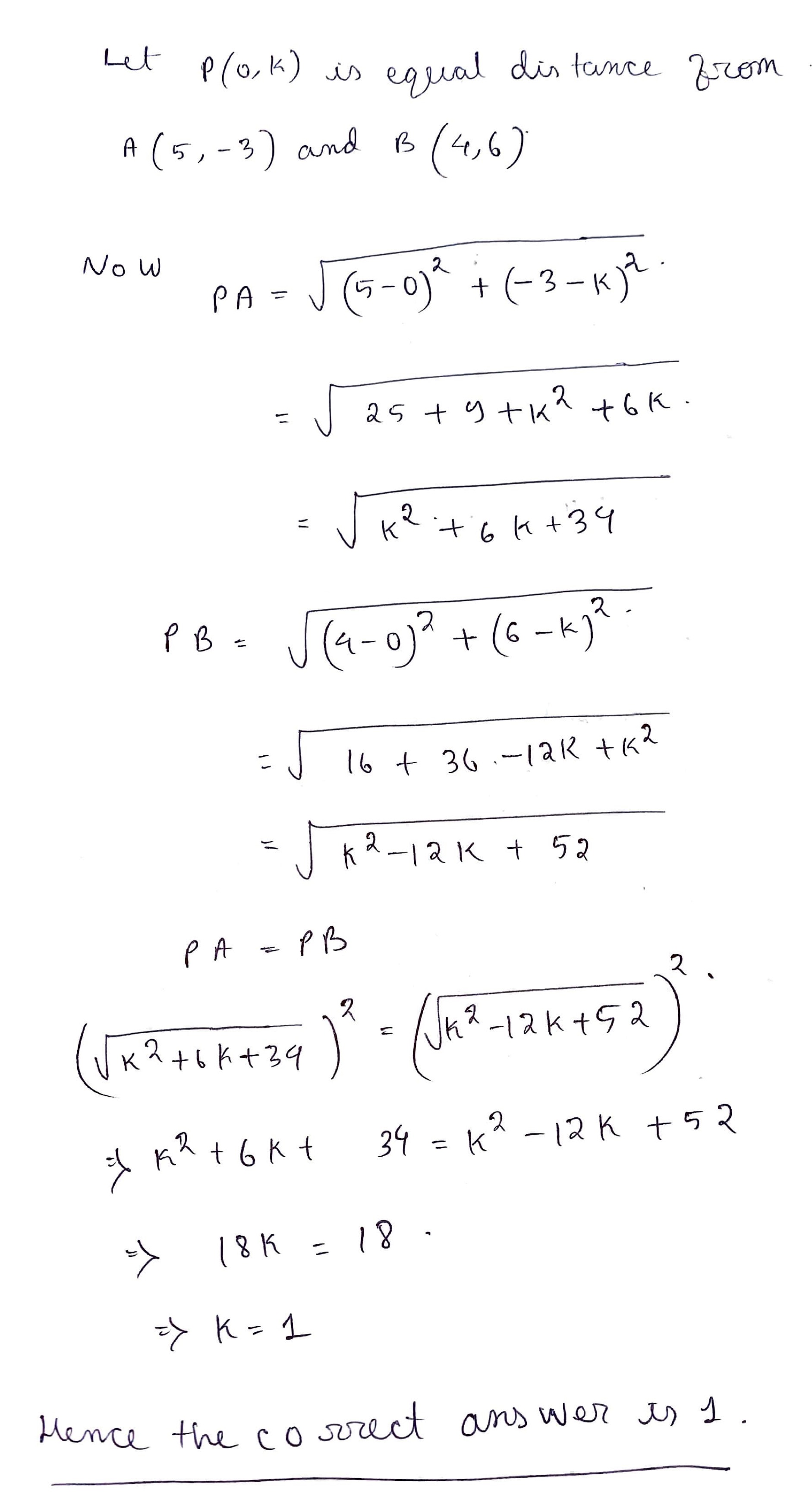Coordinate Geometry - Class 10 Maths - Extra Questions
If the points(-3, 6), (-9, a) and (0, 15) are colliner then find a
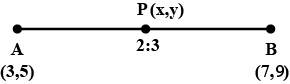
Find the coordinates of the point which divides the line segment joining the points $$(5,-2)$$ and $$(9,6)$$ in the ratio $$3:1$$.
Find the midpoint of the segment connecting the points (a,b) and (3a, c)
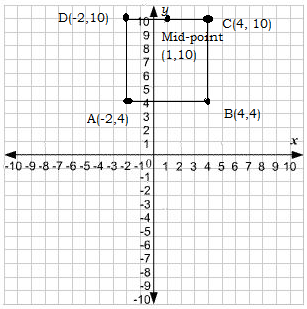
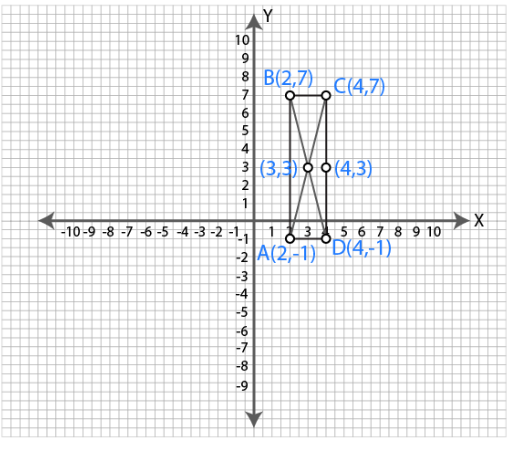
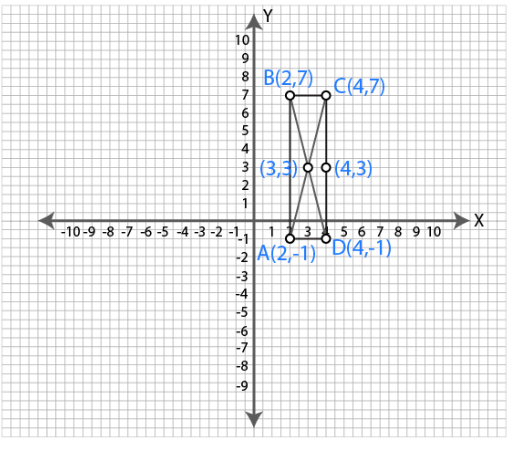
Find the coordinates of the mid-point of the line segment joining the points $$(2, 3)$$ and $$(4, 7)$$.
Find the distance between the points $$(3,0)$$ and $$(0,4)$$ without using the distance formula.
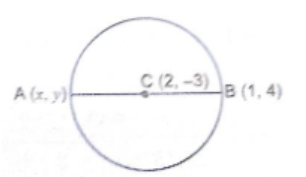
Find the co-ordinates of a point $$A$$, where $$AB$$ is the diameter of a circle, whose centre is $$(2, - 3)$$ and $$B$$ is $$(1, 4)$$.
Find the midpoint of the line segment joining the points $$(3,0)$$ and $$(-1,4)$$.
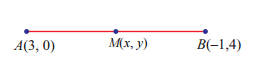
Prove that the coordinates, x and y, of the middle point of the line joining the point (2,3) to the point (3, 4) satisfy the equation
$$x-y + 1=0$$.
Find the coordinates of the point which divides the line joining the points $$\left(1, 3\right)$$ and $$\left(2, 7\right)$$ in the ratio $$3 : 4$$.
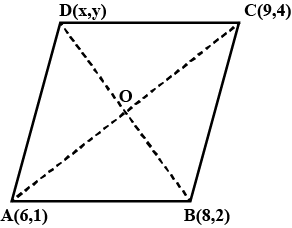
If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, find the value of p.
Find the co ordinates of the midpoint line joining of $$A\left(3,2\right)$$ and $$B\left(5,4\right)$$.
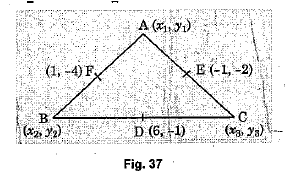
Find the sum of 'x' co-ordinates of the vertices of a triangle if the mid-points of its sides be the points $$(6, -1), (-1,-2)and(1,-4)$$
$$\dfrac{x_2 \, + \, x_3}{2} \, = \, 6,\dfrac{y_2 \, + \, y_3}{2} \, = \, -1.$$
$$\therefore \, x_2 \, + \, x_3 \, = \, 12, \, x_3 \, + \, x_1 \, = \, -2, \, x_1 \, + \, x_2 \, = \, 2.$$
$$\therefore \, 2(x_1 \, + \, x_2 \, + \, x_3) \, = \, 12.$$
or $$x_1 \, + \, x_2 \, + \, x_3 \, = \, 6$$
$$\therefore \, x_2 \, + \, x_3 \, = \, 12, \, x_3 \, + \, x_1 \, = \, -2, \, x_1 \, + \, x_2 \, = \, 2.$$
$$\therefore \, 2(x_1 \, + \, x_2 \, + \, x_3) \, = \, 12.$$
or $$x_1 \, + \, x_2 \, + \, x_3 \, = \, 6$$
Find the co-ordinates of the mid-point of the line joining the points $$(2, 3)$$ and $$(4, 7)$$.
Find the coordinates of the point which divides the line segment joining the points(6,3) and (-4,5) in the ratio 3:2 internally.
Find the coordinates of the point which divides internally the join of the points
a) $$(8,9)$$ and $$(-7,4)$$ in the ratio $$2:3$$
b) $$(1,-2)$$ and $$(4,7)$$ in the ratio $$1:2$$.
If $$(a, b)$$ is the mid-point of the line segment joining the points $$A (10, -6), B (k, 4)$$ and $$a - 2b = 18$$, find the value of $$k$$ and the distance AB.
If the points $$A(-2, -1), B(1, 0), C(a, 3)$$ and $$D(1, b)$$ form a parallelogram $$ABCD$$, find the value of $$a$$ and $$b$$.
Given $$A\left( {4, - 3} \right)$$, $$B\left( {8,5} \right)$$. Find the coordinates of the point that divides segment $$\text AB$$ in two equal parts.
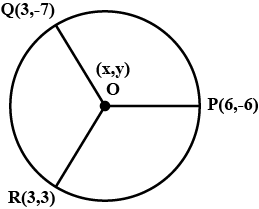
A(2,3,7), B (-1,3,2) and C (p,5,r) are vertices of a triangle. If the median through A is equally inclined to the co-ordinate axes then find the co-ordinates of the midpoint of BC in terms of p and r.
Find the mid point of line joining $$(2,3)$$ and $$(-6,5)$$.
Find the value of $$a$$, for which point $$P( a , 2 )$$ is the midpoint of the lines segment joining the points $$Q ( - 5,4 )$$ and $$R ( - 1,0 )$$ .
Find the other point if the origin is mid point of them and one vertex is $$(4,3)$$
Find the co-ordinates of points which divides the line segment joining the points $$(-2,5)$$ and $$(6,8)$$ in the ratio $$3:2$$ internally.
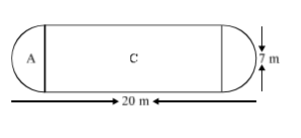
The shape of a garden is rectangular in the middle and semicircular at the ends.Find the axes of the garden?
$$A$$ and $$B$$ are the points $$(2,0)$$ and $$(0,2)$$ respectively. Find the coordinates of point $$P$$ if it is the mid point.
Find the ratio in which the point $$P$$ whose abscissa is $$3$$ divides the line joining $$A(6,5)$$ and $$B(-1,4)$$ and hence find the coordinates of $$P$$.
Find the ratio in which the line joining A(6,5) & B(4, -3) is divided by the y =2, Also find the coordinate of the point of divisions.
Find the mid-points of the line segment joining the points.$$\left( {a,b} \right)$$ and $$\left( {a + 2b,2a - b} \right)$$
The mid point of $$(2,3)$$ and $$(3,4)$$ is
Find the area of the triangle whose vertices are (3,8),(-4,2) and (5,-1). If the area is $$\left ( \dfrac a2 \right )$$ sq. units, then what will be the value of $$a$$?
If A and B are $$(-2, -2)$$ and $$(2, -4)$$, respectively, find the coordinates of P such that $$AP = \dfrac{3}{7} AB$$ and P lies on the line segment AB.
If the midpoints of the line segment joining the points $$P ( 6 , b - 2 )$$ and $$( -2 , 4)$$ is $$( 2 , - 3 ) ,$$ find the value of $$b .$$
$$P(6,b-2), Q=(-2,4)$$
midpoint of PQ is $$(2,-3)$$
$$x=2$$ $$y=-3$$
$$y=\frac{y_{1}+y_{2}}{2}$$, Acording to midpoint formula
$$-3=\frac{b-2+4}{2}$$
$$-6=b+2$$
$$\therefore b=-8$$
Find the mid point of $$(9,0)$$ and $$(5,4)$$
Solve the following :
Find the co-ordinates of midpoint of the segment joining the points $$(22, 20) $$ and $$(0,16)$$.
If the area of the triangle with vertices at the points: $$(2,7),(1,1) \ and \ (10,8)$$is $$\left (\dfrac {b}{2}\right )$$ sq. uts.Then what is the value of b?
If the points $$A(a, -11), B(5, b), C(2, 15)$$ and $$D(1, 1)$$ and the vertices of a parallelogram $$ABCD$$, find the values of $$a$$ and $$b$$.
Draw a quadrilateral in the Cartesian plane, whose vertices are (-4, 5), (0, 7), (5, -5) and (-4, -2). Also, find its area
Let ABCD be the quadrilateral with vertices are (-4, 5), (0, 7), (5, -5) and (-4, -2).
Then, by plotting A, B, C and D on the Cartesian plane and joining AB, BC, CD and DA the given quadrilateral can be drawn as
To find the area of quadrilateral ABCD, we draw one diagonal, say AC.
Accordingly, area (ABCD) = area ($$\triangle$$ ABC) + area ($$\triangle$$ ACD)
We know that the area of a triangle whose vertices are $$\left ( x_1, y_1 \right ), \left ( x_2, y_2 \right )$$ and $$\left ( x_3, y_3 \right )$$ is
$$\dfrac{1} {2} \left | x_1\left (y_2 - y_1 \right ) + x_2 \left (y_3 - y_1 \right ) + x_3 \left (y_1 - y_2 \right )\right |$$
Therefore, area of $$\triangle ABC$$
$$= \dfrac{1} {2} \left | -4\left (7 + 5 \right ) + 0 \left (-5 - 5 \right ) + 5 \left (5 - 7 \right ) unit^{2}\right |$$
$$= \dfrac{1} {2} \left | -4\left (12 \right ) + 5 \left (-2 \right ) \right | unit^{2}$$
$$= \dfrac{1} {2} \left | -48 -10\right | unit^{2}$$
$$= \dfrac{1} {2} \left | -58\right | unit^{2}$$
$$= \frac{1} {2} 58\ unit^{2}$$
$$ = 29\ unit^{2}$$
Area of $$\triangle ACD$$
$$= \dfrac{1} {2} \left | -4\left (7 + 5 \right ) + 0 \left (-5 - 5 \right ) + 5 \left (5 - 7 \right ) unit^{2}\right |$$
$$= \dfrac{1} {2} \left | -4\left (-5 + 2 \right ) + 5 \left (-2 - 5\right ) + (-4) \left (5 - 5\right )\right | unit^{2}$$
$$= \dfrac{1} {2} \left | -4\left (-3 \right ) + 5 \left (-7 \right ) + (-4) \left (10\right )\right | unit^{2}$$
$$= \dfrac{1} {2} \left | 12 - 35 - 40\right | unit^{2}$$
$$= \dfrac{1} {2} \left | -63\right | unit^{2}$$
$$= \dfrac{63} {2} unit^{2}$$
Thus, area (ABCD) = $$\left (29 + \dfrac{63} {2} \right )\ unit^{2} = \dfrac{58 + 63} {2}\ unit^{2} = \dfrac{121} {2}\ unit^{2}$$
Then, by plotting A, B, C and D on the Cartesian plane and joining AB, BC, CD and DA the given quadrilateral can be drawn as
To find the area of quadrilateral ABCD, we draw one diagonal, say AC.
Accordingly, area (ABCD) = area ($$\triangle$$ ABC) + area ($$\triangle$$ ACD)
We know that the area of a triangle whose vertices are $$\left ( x_1, y_1 \right ), \left ( x_2, y_2 \right )$$ and $$\left ( x_3, y_3 \right )$$ is
$$\dfrac{1} {2} \left | x_1\left (y_2 - y_1 \right ) + x_2 \left (y_3 - y_1 \right ) + x_3 \left (y_1 - y_2 \right )\right |$$
Therefore, area of $$\triangle ABC$$
$$= \dfrac{1} {2} \left | -4\left (7 + 5 \right ) + 0 \left (-5 - 5 \right ) + 5 \left (5 - 7 \right ) unit^{2}\right |$$
$$= \dfrac{1} {2} \left | -4\left (12 \right ) + 5 \left (-2 \right ) \right | unit^{2}$$
$$= \dfrac{1} {2} \left | -48 -10\right | unit^{2}$$
$$= \dfrac{1} {2} \left | -58\right | unit^{2}$$
$$= \frac{1} {2} 58\ unit^{2}$$
$$ = 29\ unit^{2}$$
Area of $$\triangle ACD$$
$$= \dfrac{1} {2} \left | -4\left (7 + 5 \right ) + 0 \left (-5 - 5 \right ) + 5 \left (5 - 7 \right ) unit^{2}\right |$$
$$= \dfrac{1} {2} \left | -4\left (-5 + 2 \right ) + 5 \left (-2 - 5\right ) + (-4) \left (5 - 5\right )\right | unit^{2}$$
$$= \dfrac{1} {2} \left | -4\left (-3 \right ) + 5 \left (-7 \right ) + (-4) \left (10\right )\right | unit^{2}$$
$$= \dfrac{1} {2} \left | 12 - 35 - 40\right | unit^{2}$$
$$= \dfrac{1} {2} \left | -63\right | unit^{2}$$
$$= \dfrac{63} {2} unit^{2}$$
Thus, area (ABCD) = $$\left (29 + \dfrac{63} {2} \right )\ unit^{2} = \dfrac{58 + 63} {2}\ unit^{2} = \dfrac{121} {2}\ unit^{2}$$
What point on the x-axis is equidistant from the points $$(7,6)$$ and $$(-3,4)$$?
Determine whether the point is collinear.
$$L(-2,3),M(1,-3),N(5,4)$$
Given $$M$$ is the mid-point of $$AB$$ , find the co-ordinates of :
$$B$$ ; if $$ A = (3 , -1) $$ and $$ M = (-1 , 3) $$.
Find a point on the y-axis which is equidistant from the points $$(5,2)$$ and $$(-4,3)$$
Verify whether the following points are collinear or not:
$$A (1, -3), B (2, -5), C (-4, 7)$$
The line segment joining the points $$A (3, 2)$$ and $$B (5,1)$$ is divided at the point P in the ratio $$1:2$$ and it lies on the line $$3x -18y + k = 0.$$ Find the value of $$k$$.
Column II gives the coordinates of the point P that divides the line segment joining the points given in column I, match them correctly
The co-ordinates of the midpoint P of segment AB with A $$\equiv$$ (3.5, 9.5), B $$\equiv$$ $$(-1.5, 0.5)$$ is $$(1,a)$$, then the value of a is _____
$$A (-3, 2)$$ and B (5, 4) are the end points of a line segment, find the sum of coordinates of the mid points of the line segment.
A line is such that its segment between the axes is bisected at the point $$(23, 27),$$ the product of the intercepts made by the line on the coordinate axes is
Also, find the value of $$m$$ if, coordinates of the point of intersection of the diagonals of the square $$ABCD$$ is $$(1,m)$$
Plot the points, $$A, C$$ and $$D$$. Join them using straight lines to complete the square.
Hence, B $$=(4,4)$$.
Draw the diagonals $$AC$$ and $$BD$$.
Since the diagonals of a square bisect each other, the co-ordinates of the point of intersection of the diagonals of the square $$ABCD$$ is given as
Draw the diagonals $$AC$$ and $$BD$$.
Since the diagonals of a square bisect each other, the co-ordinates of the point of intersection of the diagonals of the square $$ABCD$$ is given as
$$(x,y)=\left(\dfrac{-2+4}{2},\dfrac{4+10}{2}\right)$$
$$\implies (x,y)=(1,7)$$
$$\therefore$$ the value of $$m$$ is $$7$$.
The co-ordinates of the mid-point of CD is $$(1,m)$$.
Value of $$m$$ is
Plot the points, A, C and D. Join them using straight lines to complete the square. Hence B $$=(4,4)$$.
Mid point of CD $$=(1,10)$$
Mid point of CD $$=(1,10)$$
Find the abscissa of the point which divides the line segment joining the points $$(6, 3)$$ and $$(-4, 5)$$ in the ratio $$3 : 2$$ internally.
The area of a triangle is $$5$$. Two of its vertices are $$(2, 1)$$ and $$(3, -2)$$. The third vertex lies on $$y = x + 3$$. Find the third vertex.
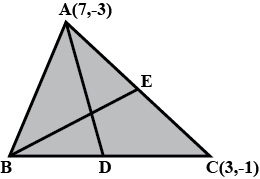
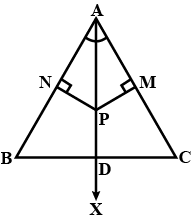
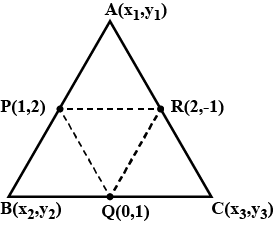
In the adjoining figure, $$D,\,E,\,F$$ are the midpoints of the sides $$BC,\,CA\;and\;AB$$ of $$\Delta ABC$$. If $$BE\;and\;DF$$ intersect at $$X$$ while $$CF\;and\;DE$$ intersect at $$Y$$, prove that $$XY=\displaystyle\frac{1}{4}BC$$.
Find the midpoint of the segment connecting the points $$(6,4)$$ and $$(3,-4)$$.
1111
The base of an equilateral triangle with side $$2a$$ lies along the $$y$$-axis such that the mid-point of the base is at the origin. Find vertices of the triangle.
Let $$ABC$$ be the given equilateral triangle with side $$2a $$
$$\displaystyle \Rightarrow AB=BC=CA=2a$$
Since base, $$BC$$ lies on the $$y$$-axis with mid-point at origin $$O$$.
So, the coordinates of point $$B$$ are $$(0,a)$$ and the coordinates of $$C$$ are $$(0,-a)$$
We know that the line joining a vertex of an equilateral triangle with the mid-point of its opposite side is perpendicular.
Hence, vertex $$A$$ lies on $$x$$-axis.
On applying Pythagoras theorem $$\triangle ABC$$, we get
$$\displaystyle \Rightarrow (2a)^{2}= x^{2}+a^{2} $$
$$\displaystyle \Rightarrow 4a^{2}-a^{2}=x^{2}$$
$$\displaystyle \Rightarrow x^{2}= 3a^{2}$$
$$\displaystyle \Rightarrow x = \pm \sqrt{3a}$$
$$\displaystyle \therefore $$ coordinates of point $$A$$ are $$\displaystyle (\pm \sqrt{3a},0) $$ or $$\displaystyle ( -\sqrt{3a},0) $$
Thus, the vertices of the given equilateral triangle are $$(0,a)(0,-a)$$ and $$\displaystyle ( \sqrt{3a},0) $$ or $$(0,a)(0,-a)$$ and $$\displaystyle ( -\sqrt{3a},0) $$
$$\displaystyle \Rightarrow AB=BC=CA=2a$$
Since base, $$BC$$ lies on the $$y$$-axis with mid-point at origin $$O$$.
$$\displaystyle \Rightarrow OB=OC=a$$
So, the coordinates of point $$B$$ are $$(0,a)$$ and the coordinates of $$C$$ are $$(0,-a)$$
We know that the line joining a vertex of an equilateral triangle with the mid-point of its opposite side is perpendicular.
Hence, vertex $$A$$ lies on $$x$$-axis.
So, let the coordinates of point $$A$$ be $$(x,0)$$
On applying Pythagoras theorem $$\triangle ABC$$, we get
$$\displaystyle (AC)^{2}= (OA)^{2}+(OC)^{2} $$
$$\displaystyle \Rightarrow (2a)^{2}= x^{2}+a^{2} $$
$$\displaystyle \Rightarrow 4a^{2}-a^{2}=x^{2}$$
$$\displaystyle \Rightarrow x^{2}= 3a^{2}$$
$$\displaystyle \Rightarrow x = \pm \sqrt{3a}$$
$$\displaystyle \therefore $$ coordinates of point $$A$$ are $$\displaystyle (\pm \sqrt{3a},0) $$ or $$\displaystyle ( -\sqrt{3a},0) $$
Thus, the vertices of the given equilateral triangle are $$(0,a)(0,-a)$$ and $$\displaystyle ( \sqrt{3a},0) $$ or $$(0,a)(0,-a)$$ and $$\displaystyle ( -\sqrt{3a},0) $$
The two opposite vertices of a square are $$(-1, 2)$$ and $$(3, 2)$$. Find the coordinates of the other two vertices.
Let $$ABCD$$ is a square where two opposite vertices are $$A(-1,2) and C(3,2)$$.
Let B$$(x,y)$$ and D$$(x_1.y_1)$$ ids the other two vertices.
In Square $$ABCD$$
$$AB=BC=CD=DA$$
Hence $$AB=BC$$
$$\Rightarrow \sqrt{(x+1)^2+(y-2)^2}=\sqrt{(3-x)^2+(2-y)^2}$$ [by distance formula]
Squaring both sides
$$\Rightarrow (x+1)^2+(y-2)^2=(3-x)^2+(2-y)^2$$
$$\Rightarrow x^2+2x+1+y^2+4-4y=9+x^2-6x+4+y^2-4y$$
$$\Rightarrow 2x+5=13-6x$$
$$\Rightarrow 2x+6x=13-5$$
$$\Rightarrow 8x=8$$
$$\Rightarrow x=1$$
In $$\triangle ABC ,\angle B=90^{\circ}$$ [all angles of square are $$90^{\circ}$$]
Then according to the Pythagorean theorem
$$AB^2+BC^2=AC^2$$
As $$AB=BC$$
$$\therefore 2AB^2=AC^2$$
$$\Rightarrow 2\left(\sqrt{x+1)^2+(y-2)^2} \right)^2=\left(\sqrt{(3-(-1))^2+(2-2)^2}\right)^2$$
$$\Rightarrow 2((x+1)^2+(y-2)^2)=(3+1)^2+(2-2)^2$$
$$\Rightarrow 2(x^2+2x+1+y^2+4-4y)=(4)^2$$
Put the value of $$x=1$$
$$\Rightarrow 2(1^1+2\times 1+1+y^2+4-4y)=16$$
$$\Rightarrow 2(y^2-4y+8)=16$$
$$\Rightarrow 2y^2-8y+16=16$$
$$\Rightarrow 2y^2-8y=0$$
$$\Rightarrow 2y(y-4)=0$$
$$\Rightarrow (y-4)=0$$
Hence $$y=0$$ or $$4$$.
As diagonals of a square are equal in length and bisect each other at $$90^{\circ}$$
Let $$P$$ is the midpoint of $$AC$$
$$\therefore \, $$CO-ordinates of $$P=\left(\dfrac{3-1}{2},\dfrac{2+2}{2}\right)=(1,2)$$
P is also the midpoint of $$BD$$
then co-ordinates of mid-point of $$BD$$=co-ordinates of $$P$$
$$\Rightarrow (x_1,y_1)=1,2$$
$$\therefore x_1=1,y_1=2$$
Then other two vertices of square $$ABCD$$ are $$(1,0)$$ or $$(1, 4)$$ and $$(1,2)$$.
Prove that the diagonals of a rectangle ABCD, with vertices A$$(2, -1)$$, B$$(5, -1)$$, C $$(5, 6)$$ and D $$(2, 6)$$, are equal and bisect each other.
$$\Delta ADC$$ and $$\Delta BDC$$ are right angled triangle with AD and BC are hypotenuse.
$$AC^2=AB^2+DC^2$$
$$AC^2=(5-2)^2+(6+1)^2=9 + 48 = 58$$ sq.unit
$$BD^2 = DC^2+CB^2$$
$$BD^2 = (5-2)^2+(-1-6)^2=9+49=58$$ sq.unit
Hence, both the diagonals are equal in length.
In $$\Delta ABO$$ and $$\Delta CDO$$
Since, $$\angle OAB = \angle OCD$$, $$\angle OBA = \angle ODC$$ (Both are alternate interior angles of parallel lines)
and $$AB = CD$$
Therefore $$\Delta ABO \cong \Delta CDO$$
$$\Rightarrow AO = CO$$ and $$BO = DO$$
Therefore, Both diaginals bisects each other.
Find the ratio in which the line segment joining the points $$A(3,- 3)$$ and $$B(- 2, 7)$$ is divided by the x-axis. Also find the coordinates of the point of division.
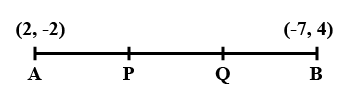
Let P and Q be the points of trisection of the line segment joining the points A$$(2, -2)$$ and B$$(-7, 4)$$ such that P is nearer to A. Find the coordinates of P and Q.
Since $$P$$ and $$Q$$ be the points of trisection of the line segment joining the points A$$(2, -2)$$ and B$$(-7, 4)$$ such that $$P$$ is nearer to $$A$$.
Therefore, $$P$$ divides line segment in the ratio $$1:2$$ and $$Q$$ divides in $$ 2:1$$ as shown in the figure.
Using section formula,
Coordinates of $$P$$ = $$\left[\dfrac{mx_2+nx_1}{m+n}, \dfrac{my_2+ny_1}{m+n}\right]$$
= $$\left[\dfrac{1(-7)+2(2)}{1+2},
\dfrac{1(4)+2(-2)}{1+2}\right]$$
= $$\left[\dfrac{-3}{3},
\dfrac{0}{3}\right]$$
= $$\left[-1, 0\right]$$
Coordinates of Q =$$\left[\dfrac{2(-7)+1(2)}{2+1}, \dfrac{2(4)-1(-2)}{2+1}\right]$$
= $$\left[\dfrac{-12}{3}, \dfrac{6}{3}\right]$$
= $$\left[-4, 2\right]$$
Find the ratio in which the $$y-$$axis divides the line segment joining the points $$(-4, -6)$$ and $$(10, 12)$$. Also, find the coordinates of the point of division.
If the coordinates of points $$A$$ and $$B$$ are $$(-2, -2)$$ and $$(2, -4)$$ respectively, find the coordinates of $$P$$ such that $$AP = \dfrac{3}{7} AB$$, where $$P$$ lies on the line segment $$AB$$.
The coordinates of the midpoint of the line segment joining the points $$\left( 2a+2,3 \right) $$ and $$\left( 4,2b+1 \right) $$ are $$\left( 2a,2b \right) $$. Find the values of $$a$$ and $$b$$.
Prove that the points $$(-7, -3), (5, 10), (15, 8)$$ and $$(3, -5)$$ taken in order are the vertices of a parallelogram.
If $$M (4, 5)$$ is the mid-point of the line segment $$AB$$ and co-ordinates of $$A$$ are $$(3, 4)$$, then find the co-ordinates of point $$B$$.
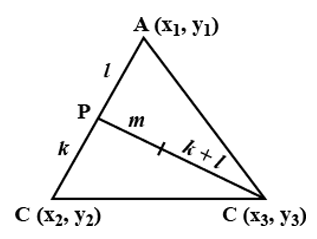
The coordinates of the vertices of a triangle are $$\left({x}_{1}, {y}_{1}\right)$$, $$\left({x}_{2}, {y}_{2}\right)$$ and $$\left({x}_{3}, {y}_{3}\right)$$. The line joining the first two is divided in the ratio $$l : k$$, and the line joining this point of division to the opposite angular point is then divided in the ratio $$m : k+l$$. Find the coordinates of the latter point of section.
Using the section formula, if a point $$(x,y)$$ divides the line joining the points $$({ x }_{ 1 },{ y }_{ 1 })$$ and $$({ x }_{ 2 },{ y }_{ 2 })$$ in the ratio $$ m:n $$, then
$$(x,y) = \left( \dfrac { m{ x }_{ 2 } + n{ x }_{ 1 } }{ m + n },\dfrac { m{ y }_{ 2 } + n{ y }_{ 1 } }{ m + n } \right) $$
Then the coordinates of the point $$P$$ that divides $$AB$$ in $$l:k$$ will be
$$\left( \dfrac { l{ x }_{ 2 }+k{ x }_{ 1 } }{ l+k } ,\dfrac { l{ y }_{ 2 }+k{ y }_{ 1 } }{ l+k } \right) $$
The coordinates of point which divides $$PC$$ in $$m:k+l$$ will be
$$\left\{ \dfrac { m{ x }_{ 3 }+(k+l)\dfrac { l{ x }_{ 2 }+k{ x }_{ 1 } }{ (l+k) } }{ m+k+l } ,\dfrac { m{ y }_{ 3 }+(k+l)\dfrac { l{ y }_{ 2 }+k{ y }_{ 1 } }{ (l+k) } }{ m+k+l } \right\} \\ \Rightarrow \left( \dfrac { k{ x }_{ 1 }+l{ x }_{ 2 }+m{ x }_{ 3 } }{ m+k+l } ,\dfrac { k{ y }_{ 1 }+l{ y }_{ 2 }+m{ y }_{ 3 } }{ m+k+l } \right) $$
A line intersects the y-axis and x-axis at points P and Q respectively. If (2, -5) is the mid point of PQ, then find the coordinates of P and Q.
A, B, C, D... are n points in a plane whose coordinates are $$(x_1, y_1), (x_2, y_2), (x_3, y_3), ...... AB$$ is bisected in the point $$G_1; G_2C$$ is divided at $$G_3$$ in the ratio $$1:2; G_3D$$ is divided at $$G_4$$ in the ratio $$1:3; G_4E$$ at $$G_5$$ in the ratio 1 : 4, and so on until all the points are exhausted. Show that the coordinates of the final point so obtained are
$$\dfrac{x_1+x_2+x_3+.....+x_n}{n}$$ and $$\dfrac{y_1+y_2+y_3+...+y_n}{n}$$
[This point is called the Centre of Mean Position of the n given points.]
From points on the circle $${ x }^{ 2 }+{ y }^{ 2 }=a^{ 2 }$$, tangents are drawn to the hyperbola $${ x }^{ 2 }-{ y }^{ 2 }=a^{ 2 }$$. Prove that the locus of the mid-points of the chord of the contact is the curve $${ \left( { x }^{ 2 }-{ y }^{ 2 } \right) }^{ 2 }=a^{ 2 }\left( { x }^{ 2 }+{ y }^{ 2 } \right) $$
If $$A$$ and $$B$$ are two points having coordinates $$(-2,-2)$$ and $$(2,-4)$$ respectively, find the coordinates of $$P$$ such that $$AP=\cfrac{3}{7}AB$$.
$$A(4,2),B(6,5)$$ and $$C(1,4)$$ are the vertices of $$\triangle {ABC}$$.
(i) The median from $$A$$ meets $$BC$$ at $$D$$. Find the coordinates of the point $$D$$.
(ii) Find the coordinates of point $$P$$ on $$AD$$ such that $$AP:PD=2:1$$
If the coordinates of the mid-points of the sides of a triangle are $$(1,1), (2,-3)$$ and $$(3,4)$$, find its vertices.
If the coordinates of the mid-points of the sides of a triangle be $$(3,-2),(-3,1)$$ and $$(4,-3)$$, then find the coordinates of its vertices.
We have mid point formula,
Point $$P(X,Y)=\left(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)$$
$$\Rightarrow$$ $$\dfrac{x+a}{2}=3\Rightarrow x+a=6$$
$$\Rightarrow$$ $$\dfrac{y+b}{2}=-2\Rightarrow y+b=-4$$
$$\Rightarrow$$ $$\dfrac{a+p}{2}=-3\Rightarrow a+p=-6$$
$$\Rightarrow$$ $$\dfrac{b+q}{2}=1\Rightarrow b+q=2$$
$$\Rightarrow$$ $$\dfrac{x+p}{2}=4\Rightarrow x+p=8$$
$$\Rightarrow$$ $$\dfrac{y+q}{2}=-3\Rightarrow y+q=-6$$
Consider, $$x+a=6$$ and $$a+p=-6$$
$$\Rightarrow$$$$x-6-p=6$$
$$\Rightarrow$$$$x-p=12,x+p=8$$
On solving;
$$\Rightarrow p=8-10=-2$$
$$\therefore 2x=20$$ $$\Rightarrow x=10$$
$$\therefore$$ $$a=-10+6= -4$$
Now,
$$y+q= -6$$
$$\Rightarrow -b-4+q= -6$$
$$\Rightarrow -b+q= -6+4$$
$$\Rightarrow$$ $$q-b= -2$$ $$\Rightarrow b-q=2 $$ and also $$b+q =2$$
on solving;
$$2b = 4$$
$$\Rightarrow b= 2$$
$$\therefore y= -4-2= -6$$
$$y+q=-6$$
$$\Rightarrow q=-6+6=0$$
$$\therefore$$ Coordinate of vertices of $$\bigtriangleup$$ABC are
$$A(10,-6), B(-4,2), C(-2,0)$$
Find the distance of the point (1, 2) from the midpoint of the line segment joining the points (6, 8) and (2, 4).
If $$A$$ and $$B$$ are $$(1,4)$$ and $$(5,2)$$ respectively, find the coordinates of $$P$$ when $$\dfrac{AP}{BP}= \dfrac{3}{4}$$.
If 3 $$\cos$$ $$\theta$$ = 1, find the value of $$\dfrac{6 \sin^2 \theta \, + \, \tan^2 \theta}{4 \cos \theta}$$
Show that the mid-point of the line segment joining the points $$(5,7)$$ and $$(3,9)$$ is also the mid-point of the line segment joining the points $$(8,6)$$ and $$(0,10)$$.
If $$R(x,y)$$ is a point on the line segment joining the points $$P(a,b)$$ and $$Q(b,a)$$, then prove that $$x+y=a+b$$
Given that, $$R(x,y)$$ divides $$PQ$$ in the ratio $$k:1$$
Then we have,
$$R(X,Y)=\left(\dfrac{kx_1+x_2}{k+1}, \dfrac{ky_1+y_2}{k+1}\right)$$
Here, $$x_1=a,y_1=b, \ x_2=b,y_2=a$$
Then $$ P( {x,y} ) = \left( {\dfrac{{bk + a}}{{k + 1}},\dfrac{{ak + b}}{{k + 1}}} \right)$$
$$ \Rightarrow x = \dfrac{{bk + a}}{{k + 1}}{\text{ }}$$ and $${\text{y = }}\left( {\dfrac{{ak + b}}{{k + 1}}} \right)$$
$$ \Rightarrow kx + x = bk + a{\text{ }}$$ and $${\text{yk + y = ak + b}}$$
$$ \Rightarrow k\left( {x - b} \right) = a - x{\text{ }}$$ $$ \Rightarrow {\text{k}}\left( {y - a} \right) = b - y$$
$$ \Rightarrow k = \dfrac{{a - x}}{{x - b}}{\text{ }}$$ ---(i) $$ \Rightarrow {\text{k = }}\left( {\dfrac{{b - y}}{{y - a}}} \right)$$ ---(ii)
from (i) and (ii)
$$\dfrac{{a - x}}{{x - b}} = \dfrac{{b - y}}{{y - a}}$$
$$ \Rightarrow ay - {a^2} - xy + ax = bx - {b^2} + by - xy$$
$$ \Rightarrow \left( {a - b} \right)y + \left( {a - b} \right)x - \left( {{a^2} - {b^2}} \right) = 0$$
$$ \Rightarrow \left( {a - b} \right)[y + x - \left( {a + b} \right)] = 0$$
$$ \Rightarrow x + y - \left( {a + b} \right) = 0$$
$$ \Rightarrow x + y = a + b$$
Hence proved
Determine the equation of the right bisector of the line joining the points $$A(-1,2)$$ & $$B(-3,4)$$
The sides of a triangle $$ABC$$ are as under $$: AB : 2x+3y=29$$ and $$AC : x+2y=16$$. If the mid-point of $$BC$$ is $$(5,6)$$ then find the equation of $$BC$$.
The line $$BC$$ is $$(y-6)=m(x-5)$$$$\dfrac { x-5 }{ \cos { \theta } } =\dfrac { y-6 }{ \sin { \theta } } =\overset { { r }_{ , } }{ C } \overset { { \quad \quad -r } }{ \quad B } \quad$$
$$\therefore\quad C\left( r\cos { \theta } +5,r\sin { \theta } +6 \right)$$ lies on $$AC$$
$$B\left( -r\cos { \theta } +5,-r\sin { \theta } +6 \right)$$ lies on $$AB$$
$$\therefore\quad r\left( \cos { \theta } +2\sin { \theta } \right) =-1$$
and $$ r\left( 2\cos { \theta } +3\sin { \theta } \right) =-1$$
Dividing, we get
$$\cos { \theta } +2\sin { \theta } =2\cos { \theta } +3\sin { \theta }$$
$$\therefore\quad \tan { \theta } =-1$$ and hence the line $$BC$$ is $$x+y=11$$
Find the co - ordinates of the circles $$ x^2 \, + \, y^2 \, - \, 4x \, - \, 2y \, = \, 4$$ and $$ x^2 \, + \, y^2 \, - \, 12x \, - \, 8y \, = \, 12$$ touch each other. Also find equations of common tangents touching the circles in distinct points.
From given equation, we get
$$C_1(2
\, , \, 1) \, , \, r_1 \, = \, 3 \, , \,C_2(6 \, , \, 4) \, , \, r \, =
\, 8 \, , \, C_1C_2 \, = \, 5 \, = \, r_2 \, - \, r_1$$
Hence the circles touch internally. The common tangent being
$$S_1\, - \, S_2 $$ = 0 or 4x + 3y + 4 =0.
and common normal $$C_1 \, C_2$$ is 3x - 4y - 2 = 0
Solving these, the point of contact is $$\left (-\dfrac{2}{5} \, , \, -\dfrac{4}{5} \right )$$
The point
of contact can also be found by ratio formula. Since the circle
touch internally there will be no direct common tangents.
Find the length of the medians of a $$\triangle $$ ABC whose vertices are A(7, -3), B(5, 3) and C(3, -1).
If $$A$$ and $$B$$ are $$(-2, -2)$$ and $$(2, -4)$$, respectively, find the coordination of $$P$$ such that $$AP = \dfrac{3}{7}AB$$ and $$P$$ lies on the line segment $$AB$$.
Let $$\left( {x,y} \right)$$ be the coordinates of P.
As, $${\rm{AP}} = \dfrac{3}{7}{\rm{AB}}$$, then,
$${\rm{AP}} = \dfrac{3}{7}\left( {{\rm{AP}} + {\rm{PB}}} \right)$$
$$7{\rm{AP}} = 3{\rm{AP}} + 3{\rm{PB}}$$
$${\rm{4AP}} = {\rm{3PB}}$$
$$\dfrac{{{\rm{AP}}}}{{{\rm{PB}}}} = \dfrac{3}{4}$$
So, the point P divides the line segment in the ratio $$3:4$$.
By section formula,
$$x = \dfrac{{{m_1}{x_2} + {m_2}{x_1}}}{{{m_1} + {m_2}}},y = \dfrac{{{m_1}{y_2} + {m_2}{y_1}}}{{{m_1} + {m_2}}}$$
$$x = \dfrac{{3\left( 2 \right) + 4\left( { - 2} \right)}}{{3 + 4}},y = \dfrac{{3\left( { - 4} \right) + 4\left( { - 2} \right)}}{{3 + 4}}$$
$$x = \dfrac{{ - 2}}{7},y = \dfrac{{ - 20}}{7}$$
So, the coordinates of P are $$\left( { - \dfrac{2}{7}, - \dfrac{{20}}{7}} \right)$$.
Find the co-ordinate of the midpoint of the line segment joining points $$(4, 7)$$ and $$(2, -3)$$.
Show that $$A(6,4),B(5,-2)$$ and $$C(7,-2)$$ are the vertices of an isosceles triangle. Also, find the length of the median through $$A$$.
Find the point on the x-axis which is equidistant from (5,7) & (2 ,4).
Find the image of the point (3,8) with respect to the line $$x+3y=7$$ assuming the line to be a plane mirror.
Let $$Q(h,k)$$ be the image of point $$P(3,8)$$ in the line $$x+3y=7$$.
Since line $$AB$$ is a mirror,
1) Point $$P$$ and $$Q$$ are at equal distance from line $$AB$$, i.e., $$PR = QR$$, i.e., $$R$$ is the mid-point of $$PQ.$$
2) Image is formed perpendicular to mirror i.e., line PQ is perpendicular to line AB.
Since R is the midpoint of PQ.
Mid point of $$PQ$$ joining $$(3,8)$$ and $$(h,k)$$ is $$\left (\dfrac{h+3}{2},\dfrac{k+8}{2}\right )$$
Coordinate of point R = $$\left (\dfrac{h+3}{2},\dfrac{k+8}{2}\right )$$
Since point R lies on the line AB.
Therefore,
$$\left (\dfrac{3+h}{2}\right )+3\left (\dfrac{8+k}{2}\right )=7$$
$$h+3k=-13$$ ....(1)
Also, $$PQ$$ is perpendicular to $$AB.$$
Therefore,
Slope of $$PQ$$ $$\times$$ Slope of $$AB = -1$$
Since, slope of $$AB =$$ $$-\dfrac{1}{3}$$
Therefore, slope of $$PQ =$$ $$3$$
Now, PQ is line joining $$P(3,8)$$ and $$Q(h,k).$$
Slope of PQ = $$3=\dfrac{k-8}{h-3}$$
$$3h-k=1$$ ........(2)
Solving equation 1 and 2, we get,
$$h=-1$$ and $$k=-4$$
Hence, image is $$Q(-1,-4)$$.
If $$A(3,y)$$ is equidistant from points $$P(8,-3)$$ and $$Q(7,6)$$, find the vaue of $$y$$ and find the distance $$AQ$$
given that $$A(5,4),B(-3,-2)$$ and $$C(1,-8)$$ are the vertices of a $$\triangle ABC$$
Find: (i) the slope of median $$AD$$
(ii) the slope of altitude $$BM$$.
The point which divides the line joining the points $$(1, 3)$$ and $$(2, 7)$$ in the ratio $$3:4$$ is
Let P be the required point.
Using the section formula, if a point $$(x,y)$$ divides the line joining the points $$({ x }_{ 1 },{ y }_{ 1 })$$ and $$({ x }_{ 2 },{ y }_{ 2 })$$ in the ratio $$ m:n $$, then
$$(x,y) = \left( \dfrac { m{ x }_{ 2 } + n{ x }_{ 1 } }{ m + n },\dfrac { m{ y }_{ 2 } + n{ y }_{ 1 } }{ m + n } \right) $$
Since, $$m:n=3:4$$
Therefore, we have
$$P=\dfrac {6+4}{3+4}, \dfrac {21+12}{3+4}$$
$$P=\dfrac {10}{7}, \dfrac {33}{7}$$
Find the coordinates of the point which divides the line joining the points $$(4, -3)$$ and $$(8, 5)$$ in the ratio $$3:1$$ internally.
We are given,
$$ (x_{1}, y_{1}) = (4, -3)$$ & $$1(x_{2}, y_{2}) = (8,5)$$
Let (x,y)coordinates which divides the line joining the point $$(x_{1},y_{1})$$
and $$ (x_{2}, y_{2})$$ in ratio $$m:n = 3:1 $$ internally.
So,$$ (x,y) = \left ( \dfrac{mx_{2}+nx_{1}}{m+n},\dfrac{my_{2}+ny_{1}}{m+n} \right )$$
$$ = \left ( \dfrac{3(8)+1(4)}{3+1}, \dfrac{3(5)+1(-3)}{3+1} \right )$$
$$ = \left ( \dfrac{28}{4},\dfrac{12}{4} \right )$$
$$ (x,y) = (7,3)$$
The coordinates of the midpoint of the sides of a $$\triangle ABC$$ are $$D(2,1),\ E(5,3),\ F(3,7)$$. Find the length and equation of its sides.
If $$Q$$ is mid-point of line segment $$AB$$ and $$P$$ is mid-point of $$QB$$, then show that $$PB=\dfrac14AB$$
$$(-2.4),(4.8),(10.7)$$ and $$(11.-5)$$ are the vertices of a quadrilateral. Show that the quadrilateral obtained on joining the mid-points of its sides, is a parallelogram.
$${\textbf{Step -1: Find the slopes of a parallel sides}}{\textbf{.}}$$
$${\text{Let }}EFGH{\text{ be the mid points of the quadrilateral }}ABCD.$$
$${\text{Coordinate of the mid - point formula are found using the formula }}\left( {\dfrac{{{x_2} - {x_1}}}{2},\dfrac{{{y_2} - {y_1}}}{2}} \right).$$
$${\text{Slope of }}FG = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$$
$$ = \dfrac{{\dfrac{{15}}{2} - 6}}{{7 - 1}}$$
$$ = \dfrac{3}{{2\left( 6 \right)}}$$
$$ = \dfrac{1}{4}$$
$${\text{Slope of }}EH = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$$
$$ = \dfrac{{1 + \dfrac{1}{2}}}{{\dfrac{{21}}{2} - \dfrac{9}{2}}}$$
$$ = \dfrac{3}{{\left( {\dfrac{{12}}{2}} \right)}}$$
$$ = \dfrac{1}{4}$$
$$\therefore FG\parallel EH{\text{ }}\left[ {\because {\text{ slopes are equal}}} \right]$$
$${\textbf{Step -2: Now, find out the slopes for the other pair of parallel sides}}{\textbf{.}}$$
$${\text{Slope of }}EF = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$$
$$ = \dfrac{{6 + \dfrac{1}{2}}}{{1 - \dfrac{9}{2}}}$$
$$ = \dfrac{{13}}{2} \times - \dfrac{2}{7}$$
$$ = - \dfrac{{13}}{7}$$
$${\text{Slope of }}FG = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$$
$$ = \dfrac{{\dfrac{{15}}{2} - 1}}{{7 - \dfrac{{21}}{2}}}$$
$$ = \dfrac{{13}}{2} \times - \dfrac{2}{7}$$
$$ = - \dfrac{{13}}{7}$$
$$\therefore EP\parallel GH{\text{ }}\left[ {\because {\text{ slopes are equal}}} \right]$$
$${\textbf{Hence, the slope of opposite sides slope are equal, i}}{\textbf{.e}}{\textbf{. }}\mathbf{\therefore EFGH}{\textbf{ is a parallelogram}}{\textbf{.}}$$
Find the area of triangle formed by joining the mid point sides of the $$\bigtriangleup ABC$$ whose vertices are A (0,-1) B (2,1) C(0,3) Find the ratio of this area to the area of $$\bigtriangleup ABC$$.
If the mid-point of the line joining $$(3,4)$$ and $$(k,7)$$ is $$(x,y)$$ and $$2x+2y+1=0$$, find the value of $$k$$.
Since $$(x,y)$$ is the mid-point,
By midpoint formula,
$$x=\dfrac{3+k}{2}$$
$$y=\dfrac{4+7}{2}=\dfrac{11}{2}$$
Again,
the above coordinates should satisfy this line, $$2x+2y+1=0$$
So, $$2\times\dfrac{3+k}{2}+2\times\dfrac{11}{2}+1=0$$
$$3+k+11+1=0$$
$$3+k+12=0$$
$$k+15=0$$
$$k=-15$$
The coordinates of $$A$$ and $$B$$ are $$(-3,\alpha)$$ and $$(1,\alpha+4)$$ and the mid point of $$\overline {AB}$$ is $$P(-1,1)$$. Find the value of $$\alpha$$
Find the ratio in which $$(-8,3)$$ divides the join of points $$(2,-2)$$and$$(-4,1).$$
Point $$B$$ on line segment joining the points $$A(1,2)$$ and $$B(3,-2)$$ divides $$AB$$ in the ratio $$1:1$$. Then the coordinates of $$D$$ are __________
If $$C$$ is a point lying on the line segment $$AB$$ joining $$A(1, 1)$$ and $$B(2, - 3)$$ such that $$3AC = CB$$, then find the coordinates of $$C$$.
The coordinates of the mid-point of the line joining the points $$(3p, 4)$$ and $$(-2, 2q)$$ are $$(5, p)$$. Find the values of $$p$$ and $$q$$.
The mid-points of the sides $$BC, CA$$ and $$AB$$ of $$\triangle ABC$$ are $$D(2, 1), E(-1, -3)$$ and $$P(4, 0)$$ respectively. Find the co-ordinates of $$A, B$$ and $$C$$.
The line joining the points $$A(-3,-10)$$ and $$B(-2,6)$$ is divided by the point $$P$$ such that $$\dfrac {PB}{AB}=\dfrac {1}{5}$$, find the co-ordinate of $$P$$.
Find the coordinates of the points which divides initially the join of the points.
$$(a)\,(8,9)$$ and $$(-7,4)$$ in the ratio $$2:3;$$
$$(b)\,(1,-2)$$ and $$(4,7)$$ in the ratio $$1:2$$
Find the point on the x-axis which is a equidistant from $$ (5 ,4)$$ and $$(-2, 3)$$.
If a vertex of a triangle is $$A\left(1,1\right)$$ and the midpoints of two sides through $$A$$ are $$\left(-1,2\right)$$ and $$\left(3,2\right)$$, then find its centroid.
If the midpoint of the line segment joining the points p(b,-2) and Q(-2,4)is (2,3). Find the value of b
If the midpoints of sides of a triangle are $$(3,4),(4,6)$$ and $$(5,7)$$, find the vertices of the triangle.
Let the vertices of triangle be $$\left( { { x_{ 1 } }, { y_{ 1 } } } \right) ,\, \left( { { x_{ 2 } }, { y_{ 2 } } } \right)$$ and $$\left( { { x_{ 3 } },{ y_{ 3 } } } \right)$$.
By using the given information in the question,
$$\dfrac { { { x_{ 1 } }+{ x_{ 2 } } } }{ 2 } =3 \\ \Rightarrow { x_{ 1 } }+{ x_{ 2 } }=6\quad\quad\quad \dots(1)$$
Similarly,
$${ x_{ 2 } }+{ x_{ 3 } }=8\quad\quad\quad\dots(2) \\ { x_{ 3 } }+{ x_{ 1 } }=10\quad\quad\quad \dots(3)$$
By using equation $$(1),$$
$${ x_{ 2 } }=6-{ x_{ 1 } }$$
Substitute the above value of $$x_2$$ in equation $$(2)$$
$$6-{ x_{ 1 } }+{ x_{ 3 } }=8 \\ \Rightarrow { x_{ 3 } }-{ x_{ 1 } }=2\quad\quad\quad \dots(4)$$
Add equations $$(4)$$ and $$(3)$$,
$$2{ x_{ 3 } }=12\, \\ \therefore { x_{ 3 } }=6$$
And,
$${ x_{ 1 } }=4 \left( { \text{from}\;\; 4 } \right) \\ { x_{ 2 } }=6-{ x_{ 1 } }$$
$$=6-4$$
$$=2 $$
By using the same method value of $$y_1=5,y_2=3$$ and $$y_3=9$$ are calculated.
Vertices of triangle are $$(4,5),(2,3),(6,9).$$
Three vertices of a parallelogram $$ABCD$$ taken in order are $$A(3, 6), B(5, 10)$$ and $$C(3, 2)$$
the coordinate of the fourth vertex $$D$$.
Determine whether the points $$\mathrm { L } ( 2,5 ) , \mathrm { M } ( 3,3 ) ,$$$$N ( 5,1 )$$ are collinear.
One end of the diameter of a circle is $$(6,9)$$ and the centre is $$(0,0)$$. Find the co-ordinate of the other end of the diameter.
Find the co-ordinates of the point which divides the line segment joining points $$(1, -3)$$ and $$(-3, 9)$$ in the ratio $$1:3$$ internally.
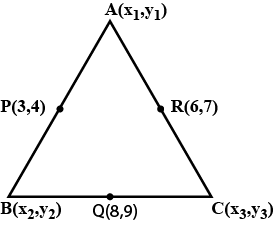
In the figure $$\triangle ABC, D, E, F$$ are the midpoint of sides $$BC, CA$$ and $$AB$$ respectively. Show that
$$BDEF$$ is parallelogram
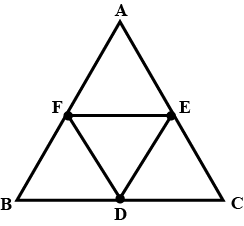
The midpoints of the sides $$BC, CA$$ and $$AB$$ of a $$\triangle ABC$$ are $$D(3, 4), E(8, 9)$$ and $$F(6, 7)$$ respectively. Find the coordinates of the vertices of the triangle.
The base of an equilateral triangle with side $$2a$$ lies along the $$y$$ -axis such that the mid-point of the base is at the origin. Find vertices of the triangle.
Let $$ABC$$ be the given equilateral triangle with side $$2a$$.
Accordingly, $$AB= BC = CA = 2a$$
Assume that base $$BC$$ lies along the y-axis such that the mid-point of $$BC$$ is at the origin.
i.e., $$BO = OC = a$$, where O is the origin.
Now, it is clear that the coordinates of point $$C$$ are $$(0, a)$$, while the coordinates of point B are $$(0, -a)$$.
It is known that the line joining a vertex of an equilateral triangle with the mid-point of its opposite side is perpendicular.
Hence, vertex A lies on the y-axis.
REF.IMAGE
On applying pythagoras theorem to $$\Delta AOC$$, we obtain
$$(AC)^2 = (OA)^2 + (OC)^2$$
$$\Rightarrow (2a)^2 = (OA)^2 + a^2$$
$$\Rightarrow 4a^2 - a^2 = (OA)^2$$
$$\Rightarrow (OA)^2 = 3a^2$$
$$\Rightarrow OA = \sqrt{3} a$$
$$\therefore$$ Coordinates of point $$A = (\pm \sqrt{3}a, 0)$$
Thus, the vertices of the given equilateral are $$(O, a), (0, -a)$$ and $$(\sqrt{3}a, 0)$$ or $$(0, a), (0, -a)$$ and $$(-\sqrt{3}a , 0)$$
Show that $$\left(3,2\right),\left(2,-3\right),\left(0,0\right)$$ are the vertices of a right angled triangle using distance formula.
Find the midpoint of the line segment joining $$\left(1,2\right)$$ and $$\left(3,4\right)$$
If the three vertices of a parallelogram are $$\left(3,1\right),\left(2,4\right)$$ and $$\left(3,5\right)$$, find the fourth vertex.
In what ratio is the line segment joining the points $$\left(-4,2,5\right)$$ and $$\left(1,-7,6\right)$$ is divided by the $$XZ$$ plane ?Also, find the co-ordinates of the point of division.
In a $$\triangle{ABC},\,c{\cos}^{2}{\dfrac{A}{2}}+a{\cos}^{2}{\dfrac{C}{2}}=\dfrac{3b}{2},\,$$ then show that $$a,b,c$$ are in A.P
Find the centre of circle passing through $$A\left(0,1\right),B\left(2,3\right),C\left(-2,5\right)$$ is
If the mid-point of the line segments joining the points $$(6,a-2)$$ and $$(-2,4)$$ is $$(2,-4)$$, then find the value of $$a$$
If $$PQ=6$$cm is a straight line and a perpendicular bisector is drawn to the line $$PQ$$ and $$A$$ is the midpoint of $$PQ$$ and if $$PA=3$$cm, then find $$AQ$$
The centroid of a triangle $$ABC$$ is at the point $$\left(1,2,1\right)$$.If the coordinates of $$A$$ and $$B$$ are $$\left(2,-4,6\right)$$ and $$\left(-1,6,-5\right)$$ respectively.Find the coordinates of the point $$C$$
The point $$P$$ has a co-ordinate $$(2, -5)$$ and Mid point of $$PQ$$ is $$(4,3)$$
Write down the co-ordinates of $$Q$$
Find the value of $$p$$ if the point $$A(2,2)$$ is mid point of $$(3,p)$$ and $$(p,3)$$
If the midpoint of the line joining the points P(6, b-2) and Q(-2,4) is (2,-3), find the value of 'b'.
If the points $$A(k+1, 2k)$$, $$B(3k, 2k+3)$$ and $$C(5k-1, 5k)$$ are collinear, then find the value of k.
If point (-4,6) divides the line seqment AB with A (-6,10) & B (r,s) in the ratio 2 : 1, then find $$r$$ and $$s$$.
If the distance of $$P(x, y)$$ from $$A(5, 1)$$ and $$B(-1, 5)$$ are equal then pove that $$3x=2y$$.
If the point $$A(x, 2)$$ is equidistant from the points $$B(8, -2)$$ and $$C(2, -2)$$, find the value of x. Also, find the length of AB.
If the points $$A(4, 3)$$ and $$B(x, 5)$$ lie on a circle with the centre $$O(2, 3)$$, find the value of x.
Find the point on the y-axis which is equidistant from the points $$A(6, 5)$$ and $$B(-4, 3)$$.
Find the point on the x-axis which is equidistant from the points $$(2, -5)$$ and $$(-2, 9)$$.
If $$P(x, y)$$ is a point equidistant from the points $$A(6, -1)$$ and $$B(2, 3)$$, show that $$x-y=3$$.
If the points $$P(x, y)$$ is equidistant from the points $$A(5, 1)$$ and $$B(-1, 5)$$, prove that $$3x=2y$$.
Using the distance formula, show that the given points are collinear.
$$(-1, -1), (2, 3)$$ and $$(8, 11)$$.
If the point $$A(0, 2)$$ is equidistant from the points $$B(3, p)$$ and $$C(p, 5)$$, find the value of p. Also, find the length of AB.
Find the coordinates of the point which divides the join of $$A(-1, 7)$$ and $$B(4, -3)$$ in the ratio $$2:3$$.
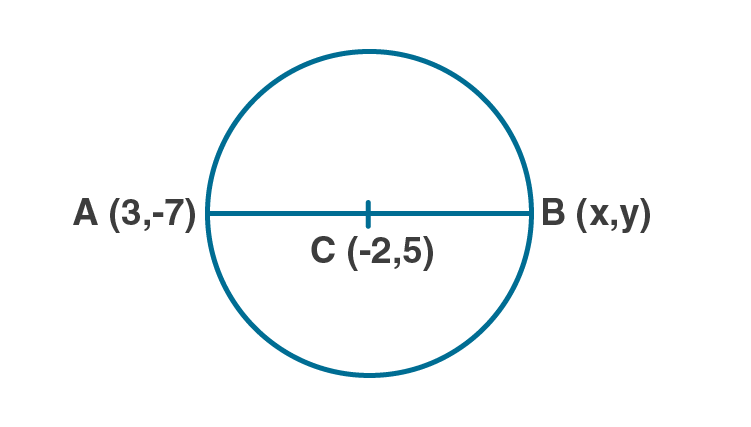
The line segment joining $$A(-2, 9)$$ and $$B(6, 3)$$ is a diameter of a circle with centre C. Find the coordinates of C.
The midpoint of the line segment joining $$A(2a, 4)$$ and $$B(-2, 3b)$$ is $$C(1, 2a+1)$$. Find the values of a and b.
Using the distance formula, show that the given points are collinear.
$$(-2, 5), (0, 1)$$ and $$(2, -3)$$.
Find the coordinated of the midpoint of the line segemnt joining $$A(3, 0)$$ and $$B(-5, 4)$$.
Find the coordinates of the midpoint of the line segment joining $$P(-11, -8)$$ and $$Q(8, -2)$$.
Point A lies on the line segment PQ joining $$P(6, -6)$$ and $$Q(-4, -1)$$ in such a way that $$PA/PQ=2/5$$. If the point A also lies on the line $$3x+k(y+1)=0$$, find the value of k.
Find the coordinates of the point which divides the join of $$A(-5, 11)$$ and $$B(4, -7)$$ in the ratio $$7:2$$.
If $$(2, p)$$ is the midpoint of the line segment joining the points $$A(6, -5)$$ and $$B(-2, 11)$$, find the value of p.
Find the coordinates of a point A, where AB is a diameter of a circle with centre $$C(2, -3)$$ and the other end of teh diameter is $$B(1, 4)$$.
For what value of y are points $$P(1, 4), Q(3, y)$$ and $$R(-3, 16)$$ are collinear?
For what values of k are the points $$A(8, 1), B(3 -2k)$$ and $$C(k, -5)$$ collinear.
For what value of x are the points $$A(-3, 12)$$, $$B(7, 6)$$ and $$C(x, 9)$$ collinear?
Points $$A(-1, y)$$ and $$B(5, 7)$$ lie on a circle with centre $$O(2, -3y)$$. Find the values of y.
Find a relation between x and y, if the points $$A(2, 1), B(x, y)$$ and $$C(7, 5)$$ are collinear.
If $$a\neq b\neq c$$, prove that $$(a, a^2), (b, b^2), (0, 0)$$ will not be collinear.
Find the value of y for which the points $$A(-3, 9), B(2, y)$$ and $$C(4, -5)$$ are collinear.
Prove that the points $$A(a, 0), B(0, b)$$ and $$C(1, 1)$$ are collinear, if $$\dfrac1a+\dfrac1b=1$$.
If the points $$P(-3, 9), Q(a, b)$$ and $$R(4, -5)$$ are collinear and $$a+b=1$$, find the values of a and b.
If the point $$P(k-1, 2)$$ is equidistant from the points $$A(3, k)$$ and $$B(k, 5)$$, find the values of k.
If the points $$C(k, 4)$$ divides the join of $$A(2, 6)$$ and $$B(5, 1)$$ in the ratio $$2:3$$, then find the value of k.
If $$P(x, y)$$ is equidistant from the points $$A(7, 1)$$ and $$B(3, 5)$$, find the relation between $$x$$ and $$y.$$
Find the lengths of the medians AD and BE of $$\Delta ABC$$ whose vertices are $$A(7, -3), B(5, 3)$$ and $$C(3, -1)$$.
Vertices of $$\Delta ABC$$ are $$A(7, -3), B(5, 3)$$ and $$C(3, -1)$$
From figure: BE and AD are the medians of triangle.
Find Coordinates of E and D:
Coordinates of E$$=\left(\dfrac{3+7}{2}, \dfrac{-1-3}{2}\right)$$
$$=(5, -2)$$
Coordinates of $$D=\left(\dfrac{3+5}{2}, \dfrac{-1+3}{2}\right)$$
$$=(4, 1)$$
Find AD and BE using distance formula:
$$AD=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
$$=\sqrt{(7-4)^2+(3+1)^2}$$
$$=\sqrt{3^2+4^2}$$
$$=\sqrt{9+16}$$
$$=\sqrt{25}$$
$$=5$$ units.
and $$BE=\sqrt{(5-5)^2+(3+2)^2}=\sqrt{0^2+5^2}$$
$$=\sqrt{25}=5$$ units
Therefore, $$BE=5$$ units and $$AD=5$$ units.(both are equal)
If the points $$A(4, 3)$$ and $$B(x, 5)$$ lie on the circle with centre $$O(2, 3)$$, find the value of x.
Three vertices of a rectangle $$\displaystyle ABCD$$ are $$\displaystyle A (3, 1), B (-3, -1)$$ and $$\displaystyle C (-3, 3)$$. Plot these points on the graph paper and find the coordinates of the fourth vertex $$\displaystyle D$$. Also, find the area of the rectangle $$\displaystyle ABCD$$.
From the graph,
The coordinates of point $$\displaystyle D$$ are $$\displaystyle (3, 3)$$.
Area of rectangle $$\displaystyle ABCD = l \times b =AB \times BC$$
On further calculation we get
Area of rectangle $$\displaystyle ABCD = 6 \times 2$$
Area of rectangle $$\displaystyle ABCD = 12 $$ sq. units
Prove that the diagonals of a rectangle ABCD with vertices $$A(2, -1), B(5, -1), C(5, 6)$$ and $$D(2, 6)$$ are equal and bisect each other.
Vertices of a rectangle ABCD are $$A(2, -1), B(5, -1), C(5, 6)$$ and $$D(2, 6)$$
To prove: Diagonals of the rectangle are equal and bisect each other.
Diagonal AC
$$=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
$$=\sqrt{(5-2)^2+(6+1)^2}$$
$$=\sqrt{9+49}$$
$$=\sqrt{58}$$
Diagonal BD
$$\sqrt{(5-2)^2+(-1-6)^2}$$
$$=\sqrt{3^2+(-7)^2}$$
$$=\sqrt{58}$$
AC and BD are equal in length. Thus, Diagonals are equal.
Now,
Consider that O is the midpoint of AC then its cooridnate are
Midpoint formula:
$$(x, y)=\left(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)$$
$$=((2+5)/2, (-1+6)/2)$$
$$=(7/2, 5/2)$$
If point O divides AC in the ratio $$m:n$$, then
$$\dfrac{7}{2}=\dfrac{mx_2+nx_1}{m+n}=\dfrac{m\times 2+n\times 5}{m+n}$$
$$=\dfrac{2m+5n}{m+n}$$
$$7m+7n=4m+10n$$
$$7m-4m=10n-7n$$
$$\Rightarrow 3m=3n$$
$$m=n$$
Which shows, O is the midpoint of diagonals.
Find the point on x-axis which is equidistant from points $$A(-1, 0)$$ and $$B(5, 0)$$.
If the points $$A(2, 3), B(4, k)$$ and $$C(6, -3)$$ are collinear, find the value of k.
Prove that the coordinates, $$x$$ and $$y$$, of the middle point of the line joining the point $$(2, 3)$$ to the point $$(3, 4)$$ satisfy the equation $$x - y + 1 = 0.$$
Find the areas of the quadrilaterals the coordinate of whose angular points, taken in order, are
$$(1 , 1) , (3 , 4) , (5 , -2) ,$$ and $$(4 , -7).$$
Find the areas of the quadrilaterals the coordinate of whose angular points, taken in order, are
$$(-1 , 6) , (-3 , -9) , (5 , -8) ,$$ and $$(3 , 9).$$
Find the locus of the foot of the perpendicular let fall from the origin upon any chord of the circle $$x^{2} + y^{2} + 2gx + 2fy + c = 0$$ which subtends a right angle at the origin.
Find also the locus of the middle points of these chords.
If the points $$A(1,2), B(0,0)$$ and $$C(a, b)$$ are collinear, then what is the relation between $$a$$ and $$b?$$
Write the coordinates of a point on $$x-$$ axis which is equidistant from the points $$(-3,4)$$ and $$(2,5)$$,
If $$(1,2),(4, y),(x, 6)$$ and (3,5) are the vertices of a parallelogram taken in order, find $$x$$ and $$y$$
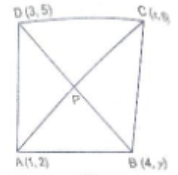
If $$Q(0,1)$$ is equidistant from $$P(5,-3)$$ and $$R(x, 6),$$ find the value of $$x$$. Also, find the distances $$QR$$ and $$PR$$.
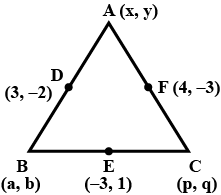
The base $${BC}$$ of an equilateral triangle $${ABC}$$ lies on $${y}$$ -axis. The coordinates of point $${C}$$ are $$(0,-3)$$. The origin is the mid-point of the base. Find the coordinates of the points $$A$$ and $$B$$. Also, find the coordinates of another point $$D$$ such that $$BACD$$ is a rhombus.
Since,
$$O$$ is the mid-point of the base $$BC$$.
$$\therefore $$ Coordinates of point $$B$$ are $$(0,3)$$
So, $${BC}=6\text { units }$$
Let the coordinates of point $$A$$ be $$(x, 0)$$
Using distance formula,
$$AB=\sqrt{(0-x)^{2}+(3-0)^{2}}=\sqrt{x^{2}+9} $$
$$BC=\sqrt{(0-0)^{2}+(-3-3)^{2}}=\sqrt{36}$$
Also, $$A B=B C \quad[\therefore \Delta{ABC}$$ is an equilateral triangle $$]$$
$$\Rightarrow \sqrt{x^{2}+9}=\sqrt{36} $$
$$\Rightarrow x^{2}+9=36$$
$$\Rightarrow x^{2}=27$$
$$\Rightarrow x=-3 \sqrt{3} \text { or } x=3 \sqrt{3} $$
$$\Rightarrow x=\mp 3 \sqrt{3}$$
$$\therefore$$ Coordinates of point $$A=(3 \sqrt{3}, 0)$$
And, Coordinates of point $$D=(-3 \sqrt{3}, 0)$$
Find the coordinates of a points $$A,$$ where $$A B$$ is the diameter of a circle whose centre is $$(2,-3)$$ and $$B$$ is $$(1,4)$$.
If the points $$A(-2,1), B(a, b)$$ and $$C(4,-1)$$ are collinear and $$a-b=1,$$ find the value of $$a$$ and $$b$$.
Find the coordinates of the point which divides the line segment joining $$(-1,7)$$ and $$(4,-3)$$ in the ratio $$2: 3$$.
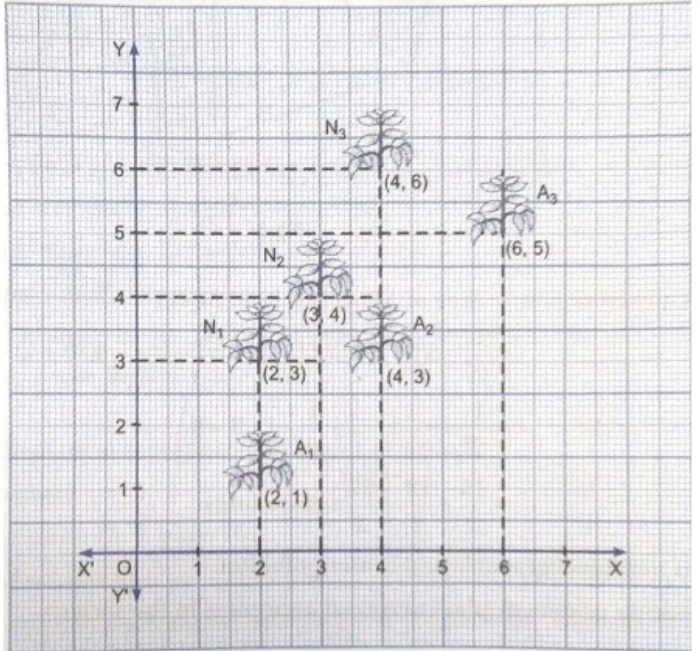
Aadya and Nitya planted some trees in a square garden as shown in the Figure, both arguing that they have planted them in a straight line. Find out who is correct? Justify your decision. (N stands for Nitya and A for Aadya)
If $$A$$ and $$B$$ are $$(-2,-2)$$ and $$(2,-4),$$ respectively, find the coordinates of $$P$$ such that $$A P=\dfrac{3}{7} A B$$ and $$P$$ lies on the line segment $$A B$$.
Find the point on the $$x-$$ axis which is equidistant from $$(2,-5)$$ and $$(-2,9)$$
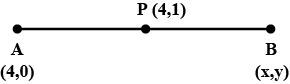
The point $$P(4,1)$$ divides the line segment joining the points $$A(2,2)$$ and $$B$$ in the ratio of $$3:5$$. Find the point $$B$$.
The mid-point of the line segment joining the points $$(3m,6)$$ and $$(-4,3n)$$ is $$(1,2m-1)$$. Find the values of $$m$$ and $$n$$.
$$AB$$ is a diameter of a circle with centre $$C(2,5)$$. If point $$A$$ is $$(3,7)$$. Find:
(i) the length of radius $$AC$$.
(ii) the coordinates of $$B$$.
(i) Length of radius $$AC = d(A,C)$$
Co-ordinates of $$A = (3,-7)$$
Co-ordinates of $$C = (-2,5)$$
Here $$x_{1} = 3, y_{1} = -7, x_{2} = -2, y_{2} = 5$$
By distance formula, $$d(A,C) = \sqrt{[(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}]}$$
= $$\sqrt{[(-2-3)^{2}+(5-(-7))^{2}]}$$
= $$\sqrt{[(-5)^{2}+(12)^{2}]}$$
= $$\sqrt{[25+144]}$$
= $$\sqrt{169}$$
= $$13$$
Hence the radius is $$13$$ units.
(ii) Given $$AB$$ is the diameter and $$C$$ is the centre of the circle.
$$\therefore$$ By midpoint formula, $$-2 = (x+3)/2$$
$$\Rightarrow -4 = x+3$$
$$\Rightarrow x = -4-3 = -7$$
$$\therefore$$ By midpoint formula, $$5 = (-7+y)/2$$
$$\Rightarrow 10 = -7+y$$
$$\Rightarrow y = 10+7 = 17$$
Hence the co-ordinates of $$B$$ are $$(-7,17)$$.
The co-ordinates of two points $$A$$ and $$B$$ are $$(3,3)$$ and $$(12,7)$$ respectively. $$P$$ is a point on the line segment $$AB$$ such that $$AP : PB = 2 : 3$$. Find the co-ordinates of $$P$$.
The point $$P$$ divides the line segment joining the points $$A(– 2,1)$$ and $$B(1,4)$$ in the ratio of $$2 : 1$$. Calculate the co-ordinates of the point $$P$$.
Find the co-ordinates of the mid-point of the line segments joining the following pairs of points:
$$(a + 3, 5b),(2a 1, 3b + 4)$$.
Find the co-ordinates of the mid-point of the line segments joining the following pair of points:
$$(2, 3)$$, $$( 6,7)$$.
Find the co-ordinates of the mid-point of the line segments joining the following pairs of points:
$$(5,11),(4,3)$$.
The coordinates of the midpoint of the line segment $$PQ$$ are $$(1,–2)$$. The coordinates of $$P$$ are $$(–3,2)$$. Find the coordinates of $$Q$$.
The line segment joining $$A(3,1)$$ and $$B(5,4)$$ is a diameter of a circle whose center is $$C$$. find the co-ordinates of the point $$C$$.
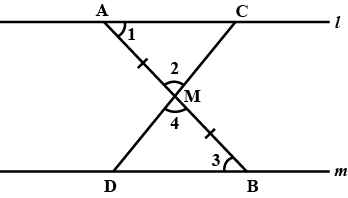
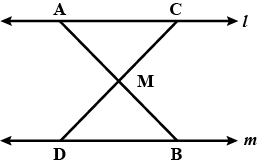
In the above figure, $$l \parallel m$$ and $$M$$ is the mid-point of a line segment $$AB$$. Show that $$M$$ is also the mid-point of any line segment $$CD$$, having its end points on $$l$$ and $$m$$, respectively.
In $$\triangle \ AMC$$ and $$\triangle \ BMD$$, we have
$$\angle 1= \angle 3$$ [Alt. $$\angle s$$ because $$ l \parallel m$$]
$$\angle 2 = \angle 4$$ [Vert. opp. $$\angle s$$]
$$AM=BM$$ [Given]
$$\therefore$$ $$\triangle \ AMC \cong \triangle \ BMD$$ [By ASS congruence rule]
$$\therefore $$ $$ CM=DM $$ [CPCT]
Hence, $$M$$ is also the mid-point of $$CD$$.
$$\angle 1= \angle 3$$ [Alt. $$\angle s$$ because $$ l \parallel m$$]
$$\angle 2 = \angle 4$$ [Vert. opp. $$\angle s$$]
$$AM=BM$$ [Given]
$$\therefore$$ $$\triangle \ AMC \cong \triangle \ BMD$$ [By ASS congruence rule]
$$\therefore $$ $$ CM=DM $$ [CPCT]
Hence, $$M$$ is also the mid-point of $$CD$$.
Find a point which is equidistant from the points $$ A(-5 , 4) $$ and $$ B(-1 , 6) $$. How many such points are there ?
If the point $$A(2 , -4) $$ is equidistant from $$ P(3 , 8) $$ and $$Q(-10 , y) $$ then find the value of $$y$$. Also find distance PQ.
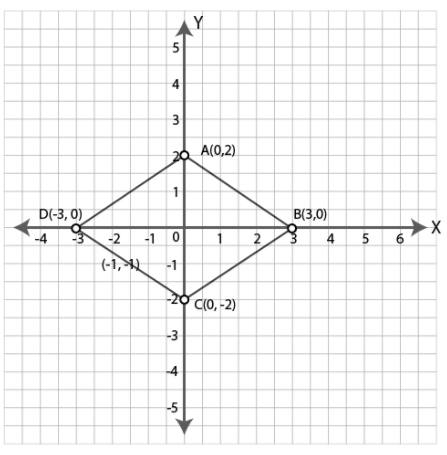
Plot the points $$(0,2), (3,0), (0, -2)$$ and $$(-3,0)$$ on a graph paper. Join these points (in order). Name the figure so obtained and find the area of the figure obtained.
Given points are $$(0,2), (3,0), (0,-2)$$ and $$(-3,0).$$
The points are plotted in the graph below.
The quadrilateral obtained is a rhombus.
$$BD$$ and $$AC$$ are the diagonals of the rhombus.
Area of a rhombus $$= 1/2 ×d_1×d_2$$
Where $$d_1$$ and $$d_2$$ are the length of diagonals.
$$AC = 4$$ units [from graph]
$$BD = 6$$ units [from graph]
Area of rhombus $$ABCD = 1/2 ×BD×AC$$
$$= 1/2 ×6×4$$
$$= 12 sq. units.$$
Hence the area is $$12 sq. units.$$
The points are plotted in the graph below.
The quadrilateral obtained is a rhombus.
$$BD$$ and $$AC$$ are the diagonals of the rhombus.
Area of a rhombus $$= 1/2 ×d_1×d_2$$
Where $$d_1$$ and $$d_2$$ are the length of diagonals.
$$AC = 4$$ units [from graph]
$$BD = 6$$ units [from graph]
Area of rhombus $$ABCD = 1/2 ×BD×AC$$
$$= 1/2 ×6×4$$
$$= 12 sq. units.$$
Hence the area is $$12 sq. units.$$
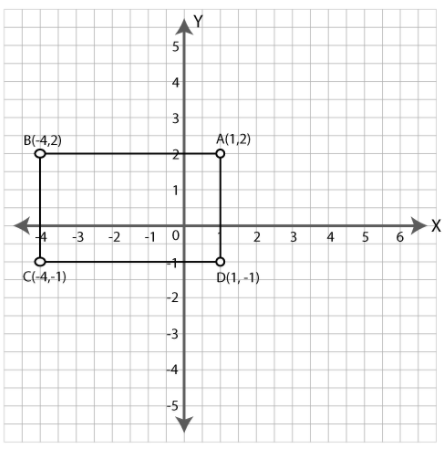
Plot the points $$A (1,2), B (-4,2), C (-4, -1)$$ and $$D (1, -1).$$ What kind of quadrilateral is $$ABCD$$ ? Also find the area of the quadrilateral $$ABCD.$$
Given points are $$A (1,2), B (-4,2), C (-4, -1)$$ and $$D (1, -1).$$
The points are plotted in the graph below.
$$ABCD$$ is a rectangle.
Area of rectangle $$ABCD =$$ length ×breadth
$$= AB×AD$$
$$= (1-(-4))×(2-(-1))$$
$$= 5×3$$
$$= 15 sq. units.$$
The points are plotted in the graph below.
$$ABCD$$ is a rectangle.
Area of rectangle $$ABCD =$$ length ×breadth
$$= AB×AD$$
$$= (1-(-4))×(2-(-1))$$
$$= 5×3$$
$$= 15 sq. units.$$
If $$Q(0, 1)$$ is equidistant from $$P (5, -3)$$ and $$R (x, 6)$$ find the values of $$x$$.
The $$x-coordinate$$ of a point $$P$$ is twice its y-coordinate. If $$P$$ is equidistant from the points $$Q (2, -5)$$ and $$U (-3, 6)$$, then find the coordinates of $$P.$$
Write the co-ordinates of the vertices of a rectangle which is $$6$$ units long and $$4$$ units wide if the rectangle is in the first quadrant, its longer side lies on the $$x-axis$$ and one vertex is at the origin.
The rectangle which is $$6$$ units long and $$4$$ units wide is shown in the graph.
Rectangle is in the first quadrant.
Longer side lies on $$x -axis$$ and one vertex is at origin.
Coordinates of the rectangle are $$A(0,0), B(6,0), C(6,4)$$ and $$D(0,4).$$
Rectangle is in the first quadrant.
Longer side lies on $$x -axis$$ and one vertex is at origin.
Coordinates of the rectangle are $$A(0,0), B(6,0), C(6,4)$$ and $$D(0,4).$$
Find the co-ordinates of point which divides the line segment joining the points $$ A (4,-3) $$ and $$ B(8,5) $$ in the ratio 3: 1 internally.
Find the coordinates of the point $$ R $$ on the line segment joining the points $$ P(-1 , 3) $$ and $$ Q(2 , 5) $$ such that $$ PR = \dfrac{3}{5} PQ $$.
$$ PR = \dfrac{3}{5} PQ $$
$$ \Rightarrow \, \dfrac{5}{3} = \dfrac{PQ}{PR} $$
$$ \Rightarrow \, \dfrac{5}{3} = \dfrac{PR + RQ}{PR} $$
$$ \Rightarrow \, \dfrac{3}{5} = \dfrac{PR}{PR} + \dfrac{RQ}{PR} $$
$$ \Rightarrow \, \dfrac{QR}{PR} = \dfrac{5}{3} - 1 = \dfrac{5 - 3}{3} $$
$$ \Rightarrow \, \dfrac{QR}{PR} = \dfrac{2}{3} $$
or $$ \dfrac{PR}{QR} = \dfrac{3}{2} $$ or $$ PR : QR = 3 : 2 $$
$$ \therefore \, m_1 = 3 $$ and $$ m_2 = 2 $$
Now , the coordinates of point $$ R $$ are given by
$$ x = \dfrac{m_1 (x_2) + m_2(x_1)}{m_1 + m_2} $$ and $$ y = \dfrac{m_1(y_2) + m_2(y_1)}{m_1 + m_2} $$
$$ \Rightarrow \, x = \dfrac{3(2) + 2(-1)}{3 + 2} = \dfrac{6 - 2}{5} $$
$$ \Rightarrow \,y = \dfrac{3(5) + 2(3)}{3 + 2} = \dfrac{15 + 6}{5} $$
$$ \Rightarrow \, x = \dfrac{4}{5} $$
$$ \Rightarrow \, y = \dfrac{21}{5} $$
Hence , the required coordinates of $$ R $$ are $$ \left ( \dfrac{4}{5} , \dfrac{21}{5} \right ) $$
If $$P (2, -1), Q (3, 4), R (-2, 3)$$ and $$S (-3, -2)$$ be four points in a plane, show that $$PQRS$$ is a rhombus but not a square. Find the area of the rhombus.
Show that the points $$(0, 1), (- 2, 3), (6, 7)$$ and $$(8, 3)$$, taken in order, are the vertices of a rectangle.
Also find its area.
Examine whether the points $$(1, -1), (-5, 7)$$ and $$(2, 6)$$ are equidistant from the point $$(-2, 3)$$ ?
Find the point on y-axis which is equidistant from point $$(-5, -2)$$ and $$(3, 2)$$.
1. Three vertices of a rectangle are $$A (2, -1), B (2, 7)$$ and $$C(4, 7)$$. Plot these points on a graph and hence use it to find the co-ordinates of the fourth vertex $$D$$
Also find the co-ordinates of
(i) the mid-point of $$BC$$
What is the area of the rectangle?
Given three vertices of a rectangle are $$A (2, -1), B (2, 7) and C(4, 7).$$
These points are marked on the graph shown below.
Join the points to form rectangle $$ABCD.$$
Also join the diagonals $$AC$$ and $$BD$$
The coordinates of fourth vertex $$D$$ is $$(4,-1)$$
(i) The midpoint of $$BC$$ is $$(3,7).$$
Area of rectangle $$=AB\times BC$$
$$=8\times 2$$
$$16sq.units$$
These points are marked on the graph shown below.
Join the points to form rectangle $$ABCD.$$
Also join the diagonals $$AC$$ and $$BD$$
The coordinates of fourth vertex $$D$$ is $$(4,-1)$$
(i) The midpoint of $$BC$$ is $$(3,7).$$
Area of rectangle $$=AB\times BC$$
$$=8\times 2$$
$$16sq.units$$
Find the point on x-axis which is equidistant from the following pair of points:
$$(3, 2)$$ and $$(-5, -2)$$
Find the point on x-axis which is equidistant from the following pair of points:
$$(2, -5)$$ and $$(-2, 9)$$
1. Three vertices of a rectangle are $$A (2, -1), B (2, 7)$$ and $$C(4, 7)$$. Plot these points on a graph and hence use it to find the co-ordinates of the fourth vertex $$D$$
Also find the co-ordinates of
(iii) the point of intersection of the diagonals.
What is the area of the rectangle?
Given three vertices of a rectangle are $$A (2, -1), B (2, 7) and C(4, 7).$$
These points are marked on the graph shown below.
Join the points to form rectangle $$ABCD.$$
Also join the diagonals $$AC$$ and $$BD$$
The coordinates of fourth vertex $$D$$ is $$(4,-1)$$
(iii)The point of intersection of diagonals is $$(3,3).$$
Area of the rectangle $$ABCD = AB×BC$$
$$= 8×2$$
$$= 16 sq.$$ units.
These points are marked on the graph shown below.
Join the points to form rectangle $$ABCD.$$
Also join the diagonals $$AC$$ and $$BD$$
The coordinates of fourth vertex $$D$$ is $$(4,-1)$$
(iii)The point of intersection of diagonals is $$(3,3).$$
Area of the rectangle $$ABCD = AB×BC$$
$$= 8×2$$
$$= 16 sq.$$ units.
2. Three vertices of a parallelogram are $$A (3, 5), B (3, -1)$$ and $$C (-1, -3)$$. Plot these points on a graph paper and hence use it to find the coordinates of the fourth vertex $$D$$. Also find the coordinates of the mid-point of the side $$CD$$. What is the area of the parallelogram?
Given $$A (3, 5), B (3, -1)$$ and $$C (-1, -3)$$ are the three vertices of a parallelogram.
These points are marked on the graph shown below.
Join the points to form parallelogram $$ABCD.$$
The coordinates of fourth vertex $$D$$ is $$(-1,3).$$
The coordinates of midpoint of $$CD$$ is $$(-1,0)$$.
Area of parallelogram $$ABCD =$$ Base ×height
$$= AB×EF$$
$$= 6×4$$
$$= 24 sq.$$ units.
Hence the area of the parallelogram is $$24 sq.$$ units.
These points are marked on the graph shown below.
Join the points to form parallelogram $$ABCD.$$
The coordinates of fourth vertex $$D$$ is $$(-1,3).$$
The coordinates of midpoint of $$CD$$ is $$(-1,0)$$.
Area of parallelogram $$ABCD =$$ Base ×height
$$= AB×EF$$
$$= 6×4$$
$$= 24 sq.$$ units.
Hence the area of the parallelogram is $$24 sq.$$ units.
If the point $$(x, y)$$ on the tangent is equidistant from the points $$(2, 3)$$ and $$(6, -1),$$ find the relation between x and y.
If $$A(4, -8), B(3, 6)$$ and $$C(5, -4)$$ are the vertices of a $$\Delta ABC, D$$ is the mid-point of BC and P is a point on AD joined such that $$\dfrac{AP}{PD} = 2,$$ find the coordinates of P.
Find the centre of a circle passing through the points $$(6, -6), (3, -7)$$ and $$(3, 3).$$
If the point $$(x, y)$$ be equidistant from the points $$(a + b, b - a)$$ and $$(a - b, a + b),$$ prove that $$\dfrac{a - b}{a + b} = \dfrac{x - y}{x + y}$$
Find the coordinates of the point which divides the join of $$(-1, 7)$$ and $$(4, -3)$$ internally in the ratio $$2 : 3.$$
If p divides the join of $$A(-2, -2)$$ and $$B(2, -4)$$ such that $$\dfrac{AP}{AB} = \dfrac{3}{7},$$ find the coordinates of P.
The coordinates of the middle points of the sides of a triangle are $$(1, 1), (2, 3)$$ and $$(4, 1),$$ find the coordinates of its vertices.
If the points $$(10, 5), (8, 4)$$ and $$(6, 6)$$ are the mid-points of the sides of a triangle, find its vertices.
Find the coordinates of a point A, where AB is the diameter of a circle whose center is $$(2, -3)$$, and B is $$(1, 4)$$
A quadrilateral has the vertices at the point $$(-4, 2), (2, 6), (8, 5)$$ and $$(9, -7).$$ Show that the mid-point of the sides of this quadrilateral are the vertices of a parallelogram.
One end of a diameter of a circle is at $$(2, 3)$$ and the center is $$(-2, 5),$$ find the coordinates of the other end of the diameter.
Find the area of the quadrilateral whose vertices are
Given $$(0, 0), (6, 0), (4, 3)$$ and $$(0, 3)$$
Find the area of the quadrilateral whose vertices are
Given $$(1, 0), (5, 3), (2, 7)$$ and $$(-2, 4)$$
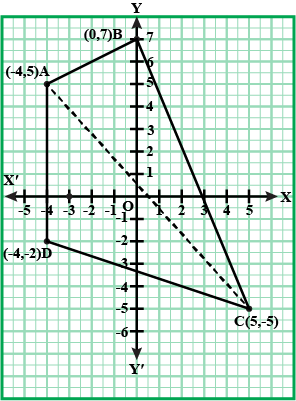
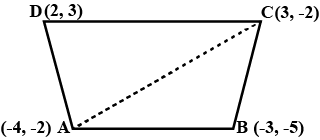
Find the area of the quadrilateral whose vertices are $$(-4, 5), (0, 7), (5, -5)$$ and $$(-4, -2)$$.
Given:-
$$\;(-4, 5), (0, 7), (5, -5)$$ and $$(-4, 2)$$ are the vertices of quadrilateral.
To Find:-
Find the area of the quadrilateral.
Let us Assume,
$$A(x_1, y_1) = (-4, 5)$$
$$B(x_2, y_2) = (0, 7)$$
$$C(x_3, y_3) = (5, -5)$$
$$D(x_4, y_4) = (4, -2)$$
Let us join $$AC$$ to form two triangles $$\triangle ABC$$ and $$\triangle ACD$$.
$$\text{Area of triangle}= \dfrac{1}{2} \left [ x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right ]$$
Then, area of the triangle $$ABC$$,
$$ar(\triangle ABC) = \dfrac{1}{2} | -4 (7 + 5) + 0(-5 - 5) + 5(5 - 7) |$$
$$= \dfrac{1}{2} [-48 + 0 - 10]$$
$$= \dfrac{1}{2} [-58]$$
$$= \dfrac{58}{2}\text{ sq. units}$$ [Negative sign will be ignored as area cannot be negative]
Area of the triangle $$ACD$$,
$$ar(\triangle ACD)= \dfrac{1}{2} [ -4 (-5 + 2) + 5(-2 - 5) -4(5 + 5)]$$
$$= \dfrac{1}{2} [ -4(-3) + 5(-7) - 4(10)]$$
$$= \dfrac{1}{2} [ 12 - 35 - 40 ]$$
$$= \dfrac{1}{2} [ -63]$$ [Negative sign will be ignored as area cannot be negative]
$$= \dfrac{63}{2}\text{ sq. units}$$
$$ar(ABCD) \;= ar(ABC)+ ar(ACD)$$
$$= \dfrac{58}{2} + \dfrac{63}{2} $$
Hence, area of quadrilateral $$ABCD$$ is equal to $$\dfrac{121}{2}\text{ sq. units}.$$
Find the area of the quadrilateral whose vertices are
$$(1, 1), (7, -3), (12, 2)$$ and $$(7, 21)$$
Find the area of the quadrilateral whose vertices are
Given $$(-5, 7), (-4, -5), (-1, -6)$$ and $$(4, 5)$$
The line joining the points $$ A (-3 , -10) $$ and $$ B(-2 , 6) $$ is divided by the point P such that $$ \dfrac{PB}{AB} = \dfrac{1}{5} $$ . Find the co-ordinates of $$P$$.
Find the mid-point of the line segment joining the points :
$$ (-6 , 7) $$ and $$ (3 , 5)$$
Points A and B have co-ordinates $$(3, 5)$$ and $$(x, y)$$ respectively. The mid-point of AB is $$(2, 3)$$. Find the values of $$x$$ and $$y$$.
If the area of the quadrilateral whose angular points taken in order are $$(1, 2), (-5, 6), (7, -4)$$ and $$(h, -2)$$ be zero, show that $$h = 3.$$
Calculate the co-ordinates of the point P which divides the line segment joining the points $$ A(-4 , 6) $$ and $$ B(3 , -5) $$ is the ratio $$ 3 : 2 $$.
P is a point on the line joining $$ A (4 , 3) $$ and $$ B ( -2 , 6) $$ such that $$ 5AP = 2BP $$. Find the co-ordinates of $$P$$.
Calculate the co-ordinates of the point P which divides the line segment joining thr points $$ A(1 , 3) $$ and $$ B(5 , 9) $$ is the ratio $$ 1 : 2 $$.
Find the mid-point of the line segment joining the points :
$$ (5 , -3) $$ and $$ (-1 , 7) $$
Find the coordinates of midpoint of the segment joining the points (22, 20) and (0, 16).
Determine whether the point is collinear.
$$A(1,-3),B(2,-5),C(-4,7)$$
Determine whether the point is collinear.
P(−2,3),Q(1,2),R(4,1)
Determine whether the point is collinear.
$$R(0, 3), D(2, 1), S(3, -1) $$
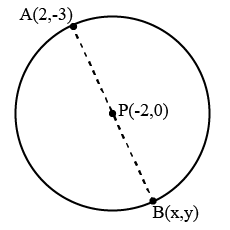
Point P is the centre of the circle and AB is a diameter . Find the coordinates of point B if coordinates of point A and P are (2,-3) and (-2, 0) respectively.
Centre $$= P(-2, 0)$$
Diameter has $$A(2, -3)$$ on one end and $$B(x, y)$$ on the other.
The centre point $$P$$ divides $$AB$$ in two equal parts.
So, using the midpoint formula,
$$-2=\dfrac{2+x}{2}$$
$$\Rightarrow -4=2+x$$
$$\Rightarrow x=-6$$
And also,
$$0=\dfrac{-3+y}{2}$$
$$\Rightarrow 0=-3+y$$
$$\Rightarrow y=3$$
$$(x,y)=(-6,3)$$
Find the co-ordinate of point $$A $$ which divides segment $$PQ$$ in the ratio $$a : b,$$ where $$P(2, 6), Q(-4, 1), a : b = 1 : 2 $$.
Find the point on the X-axis which is equidistant from A(-3, 4) and B(1, -4).
Determine whether the following point is collinear. A(-1, -1), B(0, 1), C(1, 3)
Point P is the midpoint of seg CD. If $$CP = 2.5$$, find $$l(CD)$$.
We have $$l(CP) = 2.5.$$
Since, P is the midpoint of seg CD, then
∴ $$l(CD) = 2 \times l(CP) = 2 \times 2.5 = 5$$
So, the length of CD is $$5$$.
Determine whether the given point is collinear.
$$P(1,2),Q\left(2,\dfrac{8}{5}\right),R\left(3,\dfrac{6}{5}\right)$$
Determine whether the following point is collinear. $$A(-4,4),K(-2,\dfrac{5}{2}),N(4,-2)$$
Determine whether the following point is collinear. P(2,-5),Q(1,-3),R(-2,3)
Find the coordinates of the midpoint of the line segment joining $$P(0,6)$$ and $$Q(12,20). $$
Determine whether the given point is collinear.
$$L(1,2),M(5,3), N(8,6)$$
Determine whether the following point is collinear. R(1,-4),S(-2,2),T(-3,4)
Find the value of x for which the points ( x , -1 ) , (2,1) and (4,5) are collinear
If A and B are $$(-2 , -2)$$ and $$(2 , -4)$$ respectively, find the coordinates of P such that $$AP = \dfrac{3}{7}$$ AB and P lies on the line segment AB.
In each of the following find the value of 'k', for which the points are collinear.
$$(8, 1) , (k , -4) , (2 , 5)$$
Find a relation between 'x' and 'y' such that the point (x , y) is equidistant from the point $$(3 , 6)$$ and $$(-3 , 4)$$.
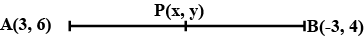
Find the coordinates of the point which divides the join of $$(-1 , 7)$$ and $$(4 , -3)$$ in the ratio $$ 2 : 3$$.
If $$Q(0 , 1)$$ is equidistant from $$P(5 , -3)$$ and $$R(x , 6)$$ , find the value of $$x$$. Also find the distances QR and PR.
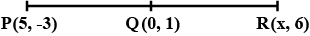
Find the point on the x-axis which is equidistant from $$(2 , -5) $$ and $$(-2 , 9)$$.
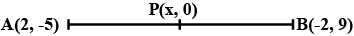
In each of the following find the value of 'k', for which the points are collinear.
$$(7 , -2) , (5, 1) , (3 , k) $$
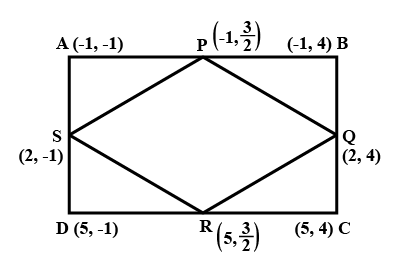
ABCD is a rectangle formed by the points $$A(-1 , -1) , B(-1 , 4) , C(5 , 4) $$ and $$D(5 , -1) $$. P , Q , R and S are the mid points of AB , BC , CD and DA respectively. Is the quadrilateral PQRS a square ? a rectangle ? or a rhombus ? Justify your answer.
Given :
$$A \rightarrow (-1 , 1) , B \rightarrow (-1 , 4) , C \rightarrow (5 , 4) $$ & $$ D \rightarrow (5 , -1)$$ Co-ordinates of midpoint $$ = \left ( \dfrac{x_{1} + x_{2}}{2} , \dfrac{y_{1} + y_{2}}{2} \right ) $$
Co-ordinates of P are
$$ = \left (\dfrac{-1 - 1}{2} , \dfrac{-1 + 4}{2} \right ) = \left ( -1 , \dfrac{3}{2} \right ) $$
Co-ordinates of Q
$$ = \left ( \dfrac{-1 + 5}{2} , \dfrac{4 + 4}{2} \right ) = (2 , 4 ) $$
Co-ordinates of R
$$ = \left ( \dfrac{5 + 5}{2} , \dfrac{-1 + 4}{2} \right ) = \left ( 5 , \dfrac{3}{2} \right ) $$
Co-ordinates of S
$$ = \left (\dfrac{-1 + 5}{2} , \dfrac{-1 - 1}{2} \right ) = (2 , -1) $$
Distance formula
$$ = \sqrt{(x_{2} - x_{1})^{2} + (y_2 - y_1)^{2}} $$
$$PQ = \sqrt{(2 + 1)^{2} + \left (4 - \dfrac{3}{2} \right )^2} = \sqrt{9 + \dfrac{25}{4}} $$
$$ = \sqrt{\dfrac{36 + 25}{4}} = \dfrac{\sqrt{61}}{2} $$
$$QR = \sqrt{(5 - 2)^{2} + \left ( \dfrac{3}{2} - 4 \right )^{2}} = \sqrt{(3)^{2} + \left (\dfrac{3 - 8}{2} \right )^{2}} $$
$$ = \sqrt{9 + \dfrac{25}{4}} = \sqrt{\dfrac{36 + 25}{4}} = \dfrac{\sqrt{61}}{2} $$
$$RS = \sqrt{(2 - 5)^{2} + \left ( -1 - \dfrac{3}{2} \right )^{2}} = \sqrt{9 + \dfrac{25}{4}} $$
$$ = \sqrt{\dfrac{36 + 25}{4}} = \sqrt{\dfrac{61}{4}} = \dfrac{\sqrt{61}}{2} $$
$$SP = \sqrt{(2 + 1)^{2} + \left (-1 - \dfrac{3}{2} \right )^{2}} = \sqrt{\dfrac{9}{1} + \dfrac{25}{4}} $$
$$ = \sqrt{\dfrac{36 + 25}{4}} = \sqrt{\dfrac{61}{4}} = \dfrac{\sqrt{61}}{2} $$
$$ \therefore \, PQ = QR = RS = SP $$
$$ \therefore PQRS $$ is either square (or) Rhombus
Diagonal $$PR$$
$$ PR = \sqrt{(5 + 1)^{2} + \left ( \dfrac{3}{2} - \dfrac{3}{2} \right )^{2}} = \sqrt{(6)^2} = 6 $$
and Diagonal $$QS$$
$$ = \sqrt{(2 - 2)^2 + (4 + 1)^2} = \sqrt{(5)^2} = 5 $$
$$PR \neq QS $$
$$ \therefore $$ Diagonal are not equal
Therefore , $$PQRS $$ is a rhombus
$$A \rightarrow (-1 , 1) , B \rightarrow (-1 , 4) , C \rightarrow (5 , 4) $$ & $$ D \rightarrow (5 , -1)$$ Co-ordinates of midpoint $$ = \left ( \dfrac{x_{1} + x_{2}}{2} , \dfrac{y_{1} + y_{2}}{2} \right ) $$
Co-ordinates of P are
$$ = \left (\dfrac{-1 - 1}{2} , \dfrac{-1 + 4}{2} \right ) = \left ( -1 , \dfrac{3}{2} \right ) $$
Co-ordinates of Q
$$ = \left ( \dfrac{-1 + 5}{2} , \dfrac{4 + 4}{2} \right ) = (2 , 4 ) $$
Co-ordinates of R
$$ = \left ( \dfrac{5 + 5}{2} , \dfrac{-1 + 4}{2} \right ) = \left ( 5 , \dfrac{3}{2} \right ) $$
Co-ordinates of S
$$ = \left (\dfrac{-1 + 5}{2} , \dfrac{-1 - 1}{2} \right ) = (2 , -1) $$
Distance formula
$$ = \sqrt{(x_{2} - x_{1})^{2} + (y_2 - y_1)^{2}} $$
$$PQ = \sqrt{(2 + 1)^{2} + \left (4 - \dfrac{3}{2} \right )^2} = \sqrt{9 + \dfrac{25}{4}} $$
$$ = \sqrt{\dfrac{36 + 25}{4}} = \dfrac{\sqrt{61}}{2} $$
$$QR = \sqrt{(5 - 2)^{2} + \left ( \dfrac{3}{2} - 4 \right )^{2}} = \sqrt{(3)^{2} + \left (\dfrac{3 - 8}{2} \right )^{2}} $$
$$ = \sqrt{9 + \dfrac{25}{4}} = \sqrt{\dfrac{36 + 25}{4}} = \dfrac{\sqrt{61}}{2} $$
$$RS = \sqrt{(2 - 5)^{2} + \left ( -1 - \dfrac{3}{2} \right )^{2}} = \sqrt{9 + \dfrac{25}{4}} $$
$$ = \sqrt{\dfrac{36 + 25}{4}} = \sqrt{\dfrac{61}{4}} = \dfrac{\sqrt{61}}{2} $$
$$SP = \sqrt{(2 + 1)^{2} + \left (-1 - \dfrac{3}{2} \right )^{2}} = \sqrt{\dfrac{9}{1} + \dfrac{25}{4}} $$
$$ = \sqrt{\dfrac{36 + 25}{4}} = \sqrt{\dfrac{61}{4}} = \dfrac{\sqrt{61}}{2} $$
$$ \therefore \, PQ = QR = RS = SP $$
$$ \therefore PQRS $$ is either square (or) Rhombus
Diagonal $$PR$$
$$ PR = \sqrt{(5 + 1)^{2} + \left ( \dfrac{3}{2} - \dfrac{3}{2} \right )^{2}} = \sqrt{(6)^2} = 6 $$
and Diagonal $$QS$$
$$ = \sqrt{(2 - 2)^2 + (4 + 1)^2} = \sqrt{(5)^2} = 5 $$
$$PR \neq QS $$
$$ \therefore $$ Diagonal are not equal
Therefore , $$PQRS $$ is a rhombus
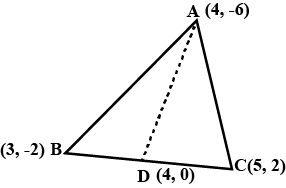
You have studied Class IX, (Chapter 9 , Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify this result for $$ \Delta ABC$$ whose vertices are $$A(4 , -6) , B(3 , -2) $$ and $$C((5 , 2)$$.
Find the centre of a circle passing through the points $$(6 , -6) , (3 , -7)$$ and $$(3 , 3)$$.
Let $$A \rightarrow (6 , -6) , B \rightarrow (3 , -7) $$ and $$C \rightarrow (3 , 3) $$
$$IA = IB = IC $$ [Radii of circle]
$$ \sqrt{(x - 6)^{2} + (y + 6)^{2}} = \sqrt{(x - 3)^{2} + (y + 7)^{2}} $$ $$ = \sqrt{(x - 3)^{2} + (y - 3)^{2}} $$
Squaring
$$(x - 6)^{2} + (y + 6)^{2} = (x - 3)^{2} + (y + 7)^{2} $$
$$x^{2} - 12x + 36 + y^{2} + 12y + 36 $$ $$ = x^{2} - 6x + 9 + y^{2} + 14y + 49 $$
$$x^{2} - x^{2} + y^{2} - y^{2} - 12x + 6x + 12y - 14y + 72 - 58 = 0 $$
$$-6x - 2y = -14 $$
$$IA = IB = IC $$ [Radii of circle]
$$ \sqrt{(x - 6)^{2} + (y + 6)^{2}} = \sqrt{(x - 3)^{2} + (y + 7)^{2}} $$ $$ = \sqrt{(x - 3)^{2} + (y - 3)^{2}} $$
Squaring
$$(x - 6)^{2} + (y + 6)^{2} = (x - 3)^{2} + (y + 7)^{2} $$
$$x^{2} - 12x + 36 + y^{2} + 12y + 36 $$ $$ = x^{2} - 6x + 9 + y^{2} + 14y + 49 $$
$$x^{2} - x^{2} + y^{2} - y^{2} - 12x + 6x + 12y - 14y + 72 - 58 = 0 $$
$$-6x - 2y = -14 $$
divide by $$-2$$
$$3x + y = 7 \rightarrow (1) $$
$$(x - 3)^{2} + (y + 7)^{2} = (x - 3)^{2} + (y - 3)^{2} $$
$$y^{2} + 49 + 14y = y^{2} + 9 - 6y $$
$$ y^{2} - y^{2} + 14y + 6y = 9 - 49 $$
$$20 y = -40$$
$$y = -2 $$
Putting $$y = -2 $$ in eqn (1) $$3x + y = 7 $$
$$3x - 2 = 7 $$
$$3x = 7 + 2 $$
$$3x = 9 $$
$$x = \dfrac{9}{3} = 3 $$
$$ x = 3 $$
Thus $$ I(x , y) \rightarrow (3 , -2) $$
Hence, the center of a circle is $$(3 , -2) $$
$$3x + y = 7 \rightarrow (1) $$
$$(x - 3)^{2} + (y + 7)^{2} = (x - 3)^{2} + (y - 3)^{2} $$
$$y^{2} + 49 + 14y = y^{2} + 9 - 6y $$
$$ y^{2} - y^{2} + 14y + 6y = 9 - 49 $$
$$20 y = -40$$
$$y = -2 $$
Putting $$y = -2 $$ in eqn (1) $$3x + y = 7 $$
$$3x - 2 = 7 $$
$$3x = 7 + 2 $$
$$3x = 9 $$
$$x = \dfrac{9}{3} = 3 $$
$$ x = 3 $$
Thus $$ I(x , y) \rightarrow (3 , -2) $$
Hence, the center of a circle is $$(3 , -2) $$
Find the area of the quadrilateral whose vertices , taken in order are $$(-4 , -2) , (-3 , -5) , (3, -2) $$ and $$(2 , 3) $$
Write the coordinates of intersection points of $$x=\pm 4$$ and $$y \pm 3$$ and find the area of rectangle so formed .
Given,$$x=\pm 4$$
and $$y=\pm 3$$
Equation of line $$AB$$ is $$y=+3$$
Equation of line $$AD$$ is $$y=+4$$
Then coordinates of point $$A$$ of intersection of lines $$AB$$ and $$AD=(4,3)$$
For the coordinates of point $$B$$
Equation of line $$AB \Rightarrow =+3$$
Equation of line $$BC \Rightarrow =-4$$
Coordinates of point $$B$$ of their intersection $$=(-4,3)$$
For the coordinates of point $$C$$,
Equation of line $$BC \Rightarrow x=-4$$
Equation of line $$CD \Rightarrow y=-3$$
Coordinates of point $$C$$ of their intersection $$=(-4,-3)$$
For the coordinates of point $$D$$, equation of line $$CD \Rightarrow y=-3$$
Equation of line $$AD \Rightarrow x=+4$$
Coordinates of point $$C$$ of their intersection $$=(4,-3)$$
Thus coordinates of point $$B,C$$ and $$D$$ are respectively
$$(4,3),(-4,3),(-4,-3)$$ and $$(4,-3)$$
Then,
length of $$AB=\sqrt{(-4-4)^2+(3-3)^2}$$
$$=\sqrt{(-8)^2+0^2}=8$$
and length of $$BC=\sqrt{(-4+4)^2+(-3-3)^2}$$
$$=\sqrt{(0)^2+(-6)^2}=8$$
$$=6$$
Thus area of rectangle $$ABCD$$
$$=length \times breadth$$
$$=8 \times 6$$
$$=48\ sq. units$$
and $$y=\pm 3$$
Equation of line $$AB$$ is $$y=+3$$
Equation of line $$AD$$ is $$y=+4$$
Then coordinates of point $$A$$ of intersection of lines $$AB$$ and $$AD=(4,3)$$
For the coordinates of point $$B$$
Equation of line $$AB \Rightarrow =+3$$
Equation of line $$BC \Rightarrow =-4$$
Coordinates of point $$B$$ of their intersection $$=(-4,3)$$
For the coordinates of point $$C$$,
Equation of line $$BC \Rightarrow x=-4$$
Equation of line $$CD \Rightarrow y=-3$$
Coordinates of point $$C$$ of their intersection $$=(-4,-3)$$
For the coordinates of point $$D$$, equation of line $$CD \Rightarrow y=-3$$
Equation of line $$AD \Rightarrow x=+4$$
Coordinates of point $$C$$ of their intersection $$=(4,-3)$$
Thus coordinates of point $$B,C$$ and $$D$$ are respectively
$$(4,3),(-4,3),(-4,-3)$$ and $$(4,-3)$$
Then,
length of $$AB=\sqrt{(-4-4)^2+(3-3)^2}$$
$$=\sqrt{(-8)^2+0^2}=8$$
and length of $$BC=\sqrt{(-4+4)^2+(-3-3)^2}$$
$$=\sqrt{(0)^2+(-6)^2}=8$$
$$=6$$
Thus area of rectangle $$ABCD$$
$$=length \times breadth$$
$$=8 \times 6$$
$$=48\ sq. units$$
Prove that $$(x_1,y_1)$$ will be coordinates of mid point of section cut by line.
$$\dfrac{x}{2x_1}+\dfrac{y}{2y_1}=1$$
Let straight line cuts $$x$$ and $$y$$ axis of point $$B$$ and $$A$$ coordinates of points $$A$$ and $$B$$ are $$(0,2y_1)$$
and $$(2x_1,0)$$ then their mid point bill be $$\left(\dfrac{0+2x_1}{2},\dfrac{0+2y_1}{2}\right)$$ or $$(x_1,y_1)$$.
and $$(2x_1,0)$$ then their mid point bill be $$\left(\dfrac{0+2x_1}{2},\dfrac{0+2y_1}{2}\right)$$ or $$(x_1,y_1)$$.
If points (3,K) and (K,5) are equidistant from point (0,2), then find the value of K.
Prove that the points (1,1), (-2,7) and (3,-3) are collinear.
Find the length of that part of line $$x \sin a+y \cos a= \sin 2 \alpha$$ which cuts axis at mid point. Also, find the coordinate of mid point of this part.
$$x \sin a+y \cos a= \sin 2 \alpha$$
$$\Rightarrow x \sin a+y \cos a= 2\sin \alpha \cos \alpha$$
$$\Rightarrow \dfrac{x \sin \alpha}{2 \sin \alpha \cos \alpha}+\dfrac{x \cos \alpha}{2 \sin \alpha \cos \alpha}=1$$
$$\Rightarrow \dfrac{x}{2 \cos \alpha}+\dfrac{y}{2 \sin \alpha}=1$$
Thus intercept of $$x-$$axis $$=2$$ $$\cos \alpha$$ and intercept at $$y-axis=2 \sin \alpha$$ coordinated of point $$A$$ and $$B$$ are $$(2 \cos \alpha, 0)$$ and $$(0,2 \sin \alpha)$$
$$\therefore AB=\sqrt{(0-2 \cos \alpha)^2+(2 \sin \alpha-0)^2}$$
$$=\sqrt{4\cos^2 \alpha+4\sin^2 \alpha}$$
$$=\sqrt{4(\cos^2 \alpha+\sin^2 \alpha)}$$ $$(\because cos^2 \alpha+\sin^2 \alpha=1)$$
$$=\sqrt 4=2$$
and coordinates of mid point of $$AB$$ are
$$= \left( \dfrac{2 \cos \alpha +0}{2}, \dfrac{0+2 \sin \alpha}{2}\right)$$ or $$(\cos \alpha, \sin \alpha)$$
Thus, length of middle part cut of axis by given line is $$2$$ unit and coordinates of mid point are $$(\cos \alpha, sin \alpha)$$
$$\Rightarrow x \sin a+y \cos a= 2\sin \alpha \cos \alpha$$
$$\Rightarrow \dfrac{x \sin \alpha}{2 \sin \alpha \cos \alpha}+\dfrac{x \cos \alpha}{2 \sin \alpha \cos \alpha}=1$$
$$\Rightarrow \dfrac{x}{2 \cos \alpha}+\dfrac{y}{2 \sin \alpha}=1$$
Thus intercept of $$x-$$axis $$=2$$ $$\cos \alpha$$ and intercept at $$y-axis=2 \sin \alpha$$ coordinated of point $$A$$ and $$B$$ are $$(2 \cos \alpha, 0)$$ and $$(0,2 \sin \alpha)$$
$$\therefore AB=\sqrt{(0-2 \cos \alpha)^2+(2 \sin \alpha-0)^2}$$
$$=\sqrt{4\cos^2 \alpha+4\sin^2 \alpha}$$
$$=\sqrt{4(\cos^2 \alpha+\sin^2 \alpha)}$$ $$(\because cos^2 \alpha+\sin^2 \alpha=1)$$
$$=\sqrt 4=2$$
and coordinates of mid point of $$AB$$ are
$$= \left( \dfrac{2 \cos \alpha +0}{2}, \dfrac{0+2 \sin \alpha}{2}\right)$$ or $$(\cos \alpha, \sin \alpha)$$
Thus, length of middle part cut of axis by given line is $$2$$ unit and coordinates of mid point are $$(\cos \alpha, sin \alpha)$$
Prove that the points (1,-2),(3,9),(1,2) and (-1,0) are the vertices of a square.
Let, A(1,-2), B(3,9), C(1,2) and D(-1,0) are the vertices of a square
Now,
$$AB=\sqrt {(1-3)^2+(-2-0)^2}$$
$$=\sqrt {(-2)^2+(-2)^2}$$
$$=\sqrt {4+4} = \sqrt {8}$$
$$BC=\sqrt{(1-3)^2+(2-0)^2}$$
$$=\sqrt{(-2)^2+2^2}$$
$$=\sqrt {4+4}= \sqrt {8}$$
$$CD=\sqrt{(-1-1)^2+(0-2)^2}$$
$$=\sqrt {(-2)^2+(-2)^2}$$
$$=\sqrt {4+4} = \sqrt {8}$$
$$DA=\sqrt{(1+1)^2+(-2-0)^2}$$
$$=\sqrt {4+4} = \sqrt {8}$$
Again diagonal,
$$AC =\sqrt {(1-1)^2+(2+2)^2}$$
$$=\sqrt {0+4^2} = \sqrt{16} = 4$$
$$BD=\sqrt{(-1-3)^2+(0-0)^2}$$
$$=\sqrt {0+4^2} = \sqrt{16} = 4$$
$$\therefore AB=BC=CD=DA = \sqrt{8}$$ and diagonal AC = diagonal BD.
Hence ABCD is a square and given points are vertices of a square.
Hence,
Now,
$$AB=\sqrt {(1-3)^2+(-2-0)^2}$$
$$=\sqrt {(-2)^2+(-2)^2}$$
$$=\sqrt {4+4} = \sqrt {8}$$
$$BC=\sqrt{(1-3)^2+(2-0)^2}$$
$$=\sqrt{(-2)^2+2^2}$$
$$=\sqrt {4+4}= \sqrt {8}$$
$$CD=\sqrt{(-1-1)^2+(0-2)^2}$$
$$=\sqrt {(-2)^2+(-2)^2}$$
$$=\sqrt {4+4} = \sqrt {8}$$
$$DA=\sqrt{(1+1)^2+(-2-0)^2}$$
$$=\sqrt {4+4} = \sqrt {8}$$
Again diagonal,
$$AC =\sqrt {(1-1)^2+(2+2)^2}$$
$$=\sqrt {0+4^2} = \sqrt{16} = 4$$
$$BD=\sqrt{(-1-3)^2+(0-0)^2}$$
$$=\sqrt {0+4^2} = \sqrt{16} = 4$$
$$\therefore AB=BC=CD=DA = \sqrt{8}$$ and diagonal AC = diagonal BD.
Hence ABCD is a square and given points are vertices of a square.
Hence,
Find that the points on the X axis, which is equidistant from points (-2,-5) and (2,-3).
If points $$(2,-3), (\lambda, -2)$$ and $$(0,5)$$ are collinear, then find $$\lambda$$
Find that the points on the Y axis, which is equidistant from points (-5,-2) and (3,2).
Find the mid point of joining the points (22,20) and (0,16).
Find the coordinate points of which divides the line segment joining the point (3,5) and (7,9) in the ratio 2:3 internally.
$$x_1=3\,,\,y_1=5\,,\,m_1=2$$
$$x_2=7\,,\,y_2=9\,,\,m_2=3$$
Let point P(x,y) divides the line segment joining the points $$A(3,5)$$ and $$B(7,9)$$ in the ratio $$2:3$$ internally.By the formula of internal division.
$$x=\dfrac{m_1x_2+m_2x_1}{m_1+m_2}$$
$$=\dfrac{(2)(7)+(3)(3)}{2+3}$$
$$=\dfrac{14+9}{5} = \dfrac {23}{5} = 4\dfrac{3}{5}$$
and
$$y=\dfrac{m_1y_2+m_2y_1}{m_1+m_2}$$
$$=\dfrac{(2)(9)+(3)(5)}{2+3}$$
$$=\dfrac{18+15}{5} = \dfrac{33}{5}=6\dfrac{3}{5}$$
Hence, the co-ordinates of P is $$(4\dfrac{3}{5},6\dfrac{3}{5})$$
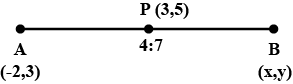
If the point $$ P(3,5)$$ divides the line segment which joins $$ A(-2,3) $$ and $$B (x,y)$$ in the ratio $$ 4:7 $$ internally, then find the co-ordinates of $$B.$$
By section formula, we know $$(x,y)=\bigg(\dfrac{mx_2+nx_1}{m+n},$$ $$\dfrac{my_2+ny_1}{m+n}\bigg)$$
Equating the coordinates of point $$P$$
$$\Rightarrow 3=\dfrac{(4)(x)+(7)(-2)}{4+7}$$
$$\Rightarrow 3=\dfrac{4x-14}{11}$$
$$\Rightarrow 4x-14=33$$
$$\Rightarrow 4x=33+14$$
$$\Rightarrow x=\dfrac{47}{4}$$
And
$$\Rightarrow 5=\dfrac{(4)(y)+(7)(3)}{4+7}$$
$$\Rightarrow 5=\dfrac{(4)(y)+(7)(3)}{4+7}$$
$$\Rightarrow 5=\dfrac{4y+21}{11}$$
$$\Rightarrow 4y = 55-21$$
$$\Rightarrow y=\dfrac{34}{4} = \dfrac{17}{2}$$
Hence the co-ordinates of point $$B=\left (\dfrac{47}{4},\dfrac{17}{2}\right )$$
Hence the co-ordinates of point $$B=\left (\dfrac{47}{4},\dfrac{17}{2}\right )$$
How we will find the point in side BC of $$\Delta ABC$$ which is equidistant from sides AB and AC?
In $$\Delta ABC$$, draw AX, bisector of $$\angle A$$ which cuts BC at D.
Take any point P on AX. Draw $$\perp$$ PN and PM from P to AB and P to AC respectively.
PN $$\perp$$ AB and PM $$\perp$$ AC
From $$\Delta APN$$ and $$\Delta APM$$
$$\angle PNA = \angle PMA = 90^o$$ (By construction)
$$\angle PAN = \angle PAM$$ (AX is bisector of $$\angle A$$)
AP = AP (Common)
by A.A.S. rule
$$\Delta APN \cong \Delta APM$$
$$\Rightarrow$$ PN = PM (By CPCT)
Thus P is equidistant from AB and AC.
$$\therefore$$ Any point on AX will be equidistant from AB and AC.
Therefore point D on line BC, will be equidistant from AB and AC.
Take any point P on AX. Draw $$\perp$$ PN and PM from P to AB and P to AC respectively.
PN $$\perp$$ AB and PM $$\perp$$ AC
From $$\Delta APN$$ and $$\Delta APM$$
$$\angle PNA = \angle PMA = 90^o$$ (By construction)
$$\angle PAN = \angle PAM$$ (AX is bisector of $$\angle A$$)
AP = AP (Common)
by A.A.S. rule
$$\Delta APN \cong \Delta APM$$
$$\Rightarrow$$ PN = PM (By CPCT)
Thus P is equidistant from AB and AC.
$$\therefore$$ Any point on AX will be equidistant from AB and AC.
Therefore point D on line BC, will be equidistant from AB and AC.
Prove that the midpoint of a line segment which joins the points (5,7) and (3,9) is the same as the mid point of the line segment which joins the points (8,6) and (3,10).
Prove that, the points (1,5),(2,3), and (-2,-11) are not collinear.
Find the midpoint of the line segment joining the point (-3,4) and point (7,5).
Find the type of quadrilateral, If its vertices are (1,4),(-5,4),(-5,-3) and (1,-3)
Let the vertices of quadrilateral are $$ \mathrm{A}(1,4), \mathrm{B}(-5,4) \mathrm{C}(-5,-3) $$ and $$ \mathrm{D}(1,-3) $$ respectively.
Then Hence, $$ A B=C D $$, and $$ B C $$ = DA and Diagonal BD = Diagonal AC
$$ \begin{aligned} A B &=\sqrt{(-5-1)^{2}+(4-4)^{2}} \\ &=\sqrt{(-6)^{2}+(0)^{2}} \\ &=\sqrt{36}=6 \\ B C &=\sqrt{(-5+5)^{2}+(-3-4)^{2}} \\ &=\sqrt{0+(-7)^{2}}=\sqrt{49}=7 \\ C D &=\sqrt{[1-(-5)]^{2}+[(-3)+(-3)]^{2}} \\ &=\sqrt{(1+5)^{2}+(-3+3)^{2}} \\ &=\sqrt{(6)^{2}} \\ &=6 \\ D A &=\sqrt{(1-1)^{2}+(4+3)^{2}} \\ &=\sqrt{0+(7)^{2}} \\ &=\sqrt{49}=7 \end{aligned} $$
$$ \begin{aligned} \text { Diagonal } \mathrm{BD} &=\sqrt{(1+5)^{2}+(-3-4)^{2}} \\ &=\sqrt{36+49} \\ &=\sqrt{85} \end{aligned} $$
$$\begin{array}{l}\begin{aligned}\text { Diagonal } A C &=\sqrt{(-5-1)^{2}+(-3-4)^{2}} \\&=\sqrt{(-6)^{2}+(-7)^{2}} \\&=\sqrt{36+49} \\&=\sqrt{85}\end{aligned}\end{array}$$
Hence, these points are the vertices of rectangle.
Then Hence, $$ A B=C D $$, and $$ B C $$ = DA and Diagonal BD = Diagonal AC
$$ \begin{aligned} A B &=\sqrt{(-5-1)^{2}+(4-4)^{2}} \\ &=\sqrt{(-6)^{2}+(0)^{2}} \\ &=\sqrt{36}=6 \\ B C &=\sqrt{(-5+5)^{2}+(-3-4)^{2}} \\ &=\sqrt{0+(-7)^{2}}=\sqrt{49}=7 \\ C D &=\sqrt{[1-(-5)]^{2}+[(-3)+(-3)]^{2}} \\ &=\sqrt{(1+5)^{2}+(-3+3)^{2}} \\ &=\sqrt{(6)^{2}} \\ &=6 \\ D A &=\sqrt{(1-1)^{2}+(4+3)^{2}} \\ &=\sqrt{0+(7)^{2}} \\ &=\sqrt{49}=7 \end{aligned} $$
$$ \begin{aligned} \text { Diagonal } \mathrm{BD} &=\sqrt{(1+5)^{2}+(-3-4)^{2}} \\ &=\sqrt{36+49} \\ &=\sqrt{85} \end{aligned} $$
$$\begin{array}{l}\begin{aligned}\text { Diagonal } A C &=\sqrt{(-5-1)^{2}+(-3-4)^{2}} \\&=\sqrt{(-6)^{2}+(-7)^{2}} \\&=\sqrt{36+49} \\&=\sqrt{85}\end{aligned}\end{array}$$
Hence, these points are the vertices of rectangle.
If in any plane there are four points $$ \mathrm{P}(2,-1), \mathrm{Q}(3,4), \mathrm{R}(-2,3) $$ and $$ \mathrm{S}(-3,-2), $$ then provethat PQRS is not a square but a rhombus.
Let four points $$ \mathrm{P}(2,-1), \mathrm{Q}(3,4), \mathrm{R}(-2,3) $$ and $$ \mathrm{S}(-3,-2) $$ are in a plane.
$$ \begin{aligned} \mathrm{PQ} &=\sqrt{(3-2)^{2}+(4-(-1))^{2}} \\ &=\sqrt{(1)^{2}+(4+1)^{2}} \\ &=\sqrt{25+1}=\sqrt{26} \\ \mathrm{QR} &=\sqrt{(-2-3)^{2}+(3-4)^{2}} \\ &=\sqrt{(-5)^{2}+(-1)^{2}} \\ &=\sqrt{25+1}=\sqrt{26} \\ \mathrm{RS} &=\sqrt{(-3-(-2))^{2}+(-2-3)^{2}} \\ &=\sqrt{(-3+2)^{2}+(-5)^{2}} \\ &=\sqrt{1+25}=\sqrt{26} \\ \mathrm{SP} &=\sqrt{(2-(-3))^{2}+(-1-(-2))^{2}} \\ &=\sqrt{(2+3)^{2}+(-1+2)^{2}} \\ &=\sqrt{(5)^{2}+(1)^{2}} \\ &=\sqrt{25+1}=\sqrt{26} \end{aligned} $$
$$ \begin{array}{l}\begin{aligned} \text { Diagonal } \mathrm{PR} &=\sqrt{(2-(-2))^{2}+(-1-3)^{2}} \\ &=\sqrt{(2+2)^{2}+(-4)^{2}} \\ &=\sqrt{16+16} \\ &=\sqrt{32} \\ &=4 \sqrt{2} \\ \text { Diogonal } \mathrm{SQ} &=\sqrt{(-3-3)^{2}+(-2-4)^{2}} \\ &=\sqrt{(-6)^{2}+(-6)^{2}} \\ &=\sqrt{36+36} \\ &=\sqrt{72} \\ &=6 \sqrt{2} \end{aligned} \\ \because P Q=\mathrm{QR}=\mathrm{RS}= S P=\sqrt{26}\end{array} $$
And diagonal PR $$ \neq $$ diagonal SQ
since diagonals are also equal in a square but here diagonals are not equal. Hence PQRS is not square but a rhombus.
$$ \begin{aligned} \mathrm{PQ} &=\sqrt{(3-2)^{2}+(4-(-1))^{2}} \\ &=\sqrt{(1)^{2}+(4+1)^{2}} \\ &=\sqrt{25+1}=\sqrt{26} \\ \mathrm{QR} &=\sqrt{(-2-3)^{2}+(3-4)^{2}} \\ &=\sqrt{(-5)^{2}+(-1)^{2}} \\ &=\sqrt{25+1}=\sqrt{26} \\ \mathrm{RS} &=\sqrt{(-3-(-2))^{2}+(-2-3)^{2}} \\ &=\sqrt{(-3+2)^{2}+(-5)^{2}} \\ &=\sqrt{1+25}=\sqrt{26} \\ \mathrm{SP} &=\sqrt{(2-(-3))^{2}+(-1-(-2))^{2}} \\ &=\sqrt{(2+3)^{2}+(-1+2)^{2}} \\ &=\sqrt{(5)^{2}+(1)^{2}} \\ &=\sqrt{25+1}=\sqrt{26} \end{aligned} $$
$$ \begin{array}{l}\begin{aligned} \text { Diagonal } \mathrm{PR} &=\sqrt{(2-(-2))^{2}+(-1-3)^{2}} \\ &=\sqrt{(2+2)^{2}+(-4)^{2}} \\ &=\sqrt{16+16} \\ &=\sqrt{32} \\ &=4 \sqrt{2} \\ \text { Diogonal } \mathrm{SQ} &=\sqrt{(-3-3)^{2}+(-2-4)^{2}} \\ &=\sqrt{(-6)^{2}+(-6)^{2}} \\ &=\sqrt{36+36} \\ &=\sqrt{72} \\ &=6 \sqrt{2} \end{aligned} \\ \because P Q=\mathrm{QR}=\mathrm{RS}= S P=\sqrt{26}\end{array} $$
And diagonal PR $$ \neq $$ diagonal SQ
since diagonals are also equal in a square but here diagonals are not equal. Hence PQRS is not square but a rhombus.
If co-ordinate of one end and the midpoint of a line segment are (4,0) and (4,1) respectively, then find the co-ordinate of other ends of the line segment.
Let co-ordinate of side A is (4,0) and co-ordinate of side $$ B $$ is $$ (x, y) $$ of line segment $$ A B . $$ The co-ordinate ofmid point P is (4,1)
By mid point formula
$$x=\dfrac{x_{1}+x_{2}}{2}$$
$$\begin{aligned}4 &=\dfrac{4+x}{2} \\\Rightarrow \quad 4+x &=8 \\x &=8-4=4 \\\text { and } \quad y &=\dfrac{y_{1}+y_{2}}{2}\end{aligned}$$
$$\begin{aligned}1 &=\dfrac{0+y}{2} \\\Rightarrow \quad y &=2\end{aligned}$$
Hence, co-ordinate of point $$ B $$ is (4,2)
By mid point formula
$$x=\dfrac{x_{1}+x_{2}}{2}$$
$$\begin{aligned}4 &=\dfrac{4+x}{2} \\\Rightarrow \quad 4+x &=8 \\x &=8-4=4 \\\text { and } \quad y &=\dfrac{y_{1}+y_{2}}{2}\end{aligned}$$
$$\begin{aligned}1 &=\dfrac{0+y}{2} \\\Rightarrow \quad y &=2\end{aligned}$$
Hence, co-ordinate of point $$ B $$ is (4,2)
If mid points of sides of a triangle is (1,2),(0,-1) and (2,-1) , then find its vertices.
Let $$ P(1,2), Q(0,-1) $$ and $$ R(2,-1) $$ are mid point of sides of given triangle and coordinate of vertices of triangleare $$ \mathrm{A}\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right), \mathrm{B}\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right) $$ and $$ \mathrm{C}\left(\mathrm{x}_{3}, \mathrm{y}_{3}\right) $$ respectively.
since, co-ordinate of mid point $$ P $$ is (1,2) of $$ A\left(x_{1}, y_{1}\right) $$ and $$ B\left(x_{2}, y_{2}\right) $$ then $$ 1=\dfrac{x_{1}+x_{2}}{2} $$ and $$ 2=\dfrac{y_{1}+y_{2}}{2} $$
$$ \Rightarrow x_{1}+x_{2}=2 \ldots$$(i)
and $$ y_{1}+y_{2}=4 \ldots $$ (ii)
since $$ \mathrm{Q}(0,-1) $$ is the midpoint of $$ \mathrm{B}\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right) $$ and $$ \mathrm{C}\left(\mathrm{x}_{3}, \mathrm{y}_{3}\right) $$
$$ \mathrm{So}^{\dfrac{x_{2}+x_{3}}{2}}=0, \dfrac{y_{2}+y_{3}}{2}=-1 $$
$$ \Rightarrow x_{2}+x_{3}=0 \ldots $$ (iii)
and $$ y_{2}+y_{3}=-2 \ldots$$(iv)
since $$ \mathrm{R}(2,-1) $$ is the mid point of $$ \mathrm{A}\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right) $$ and $$ \mathrm{C}\left(\mathrm{x}_{3}, \mathrm{y}_{3}\right) $$
So $$ \dfrac{x_{1}+x_{3}}{2}=2, \dfrac{y_{1}+y_{3}}{2}=-1 $$
$$ \Rightarrow x_{1}+x_{3}=4 \ldots(v) $$
and $$ y_{1}+y_{3}=-2 \ldots$$(vi)
adding equation (i), (iii) and (v) $$ 2 x_{1}+2 x_{2}+2 x_{3}=6 $$
$$ =x_{1}+x_{2}+x_{3}=3 \ldots $$ (vii)
Adding equation (ii), (iv) and (vi) $$ 2 y_{1}+2 y_{2}+2 y_{3}=0 $$
$$ y_{1}+y_{2}+y_{3}=0 \ldots$$(viii)
Put the value of equation (i) in equation (vii)
$$ x_{1}+x_{2}+x_{3}=3 $$
$$ 2+x_{3}=3 $$
$$ x_{3}=3-2=1 $$
Put the value of equation (ii) in equation (viii)
$$ y_{1}+y_{2}+y_{3}=0 $$
$$ 4+y_{3}=0 $$
$$ y_{3}=-4 $$
Hence, co-ordinate of point $$ C\left(x_{3}, y_{3}\right)=(1,-4) $$
Subtract equation (iii) from equation (vii)
$$\begin{array}{lllllll}x_1 &+&x_2&+&x_3&=&3 \\&&x_2&+&x_3&=&0 \\&-&&-&&&- \\\hline x_1&&&&&=&3\end{array}$$
Subtract eq (iv) from eq (viii)
$$\begin{array}{lllllll}y_1 &+&y_2&+&y_3&=&0 \\&&y_2&+&y_3&=&-2 \\&-&&-&&&+ \\\hline \hline y_1&&&&&=&2\end{array}$$
Hence, co-ordinate of point $$ A\left(x_{1}, y_{1}\right)=(3,2) $$
Again subtract equation ( $$ \mathrm{v} $$ ) from equation (vii)
$$\begin{array}{llllllll}&x_1 &+&x_2&+&x_3&=&3 \\&&&x_2&+&x_3&=&4 \\-&&-&&-&&&- \\\hline &&&x_2&&&=&-1\end{array}$$
Subtract equation (vi) from equation (viii)
$$\begin{array}{lllllll}y_1 &+&y_2&+&y_3&=&0 \\y_1&&&+&y_3&=&-2 \\&-&&-&&&+ \\\hline \hline &&y_2&&&=&2\end{array}$$
Hence, co-ordinate (-1,2)
Hence, the vertices of triangle are $$(1,-4),(3,2)$$ and $$(-1,2)$$ Respectively.
since, co-ordinate of mid point $$ P $$ is (1,2) of $$ A\left(x_{1}, y_{1}\right) $$ and $$ B\left(x_{2}, y_{2}\right) $$ then $$ 1=\dfrac{x_{1}+x_{2}}{2} $$ and $$ 2=\dfrac{y_{1}+y_{2}}{2} $$
$$ \Rightarrow x_{1}+x_{2}=2 \ldots$$(i)
and $$ y_{1}+y_{2}=4 \ldots $$ (ii)
since $$ \mathrm{Q}(0,-1) $$ is the midpoint of $$ \mathrm{B}\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right) $$ and $$ \mathrm{C}\left(\mathrm{x}_{3}, \mathrm{y}_{3}\right) $$
$$ \mathrm{So}^{\dfrac{x_{2}+x_{3}}{2}}=0, \dfrac{y_{2}+y_{3}}{2}=-1 $$
$$ \Rightarrow x_{2}+x_{3}=0 \ldots $$ (iii)
and $$ y_{2}+y_{3}=-2 \ldots$$(iv)
since $$ \mathrm{R}(2,-1) $$ is the mid point of $$ \mathrm{A}\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right) $$ and $$ \mathrm{C}\left(\mathrm{x}_{3}, \mathrm{y}_{3}\right) $$
So $$ \dfrac{x_{1}+x_{3}}{2}=2, \dfrac{y_{1}+y_{3}}{2}=-1 $$
$$ \Rightarrow x_{1}+x_{3}=4 \ldots(v) $$
and $$ y_{1}+y_{3}=-2 \ldots$$(vi)
adding equation (i), (iii) and (v) $$ 2 x_{1}+2 x_{2}+2 x_{3}=6 $$
$$ =x_{1}+x_{2}+x_{3}=3 \ldots $$ (vii)
Adding equation (ii), (iv) and (vi) $$ 2 y_{1}+2 y_{2}+2 y_{3}=0 $$
$$ y_{1}+y_{2}+y_{3}=0 \ldots$$(viii)
Put the value of equation (i) in equation (vii)
$$ x_{1}+x_{2}+x_{3}=3 $$
$$ 2+x_{3}=3 $$
$$ x_{3}=3-2=1 $$
Put the value of equation (ii) in equation (viii)
$$ y_{1}+y_{2}+y_{3}=0 $$
$$ 4+y_{3}=0 $$
$$ y_{3}=-4 $$
Hence, co-ordinate of point $$ C\left(x_{3}, y_{3}\right)=(1,-4) $$
Subtract equation (iii) from equation (vii)
$$\begin{array}{lllllll}x_1 &+&x_2&+&x_3&=&3 \\&&x_2&+&x_3&=&0 \\&-&&-&&&- \\\hline x_1&&&&&=&3\end{array}$$
Subtract eq (iv) from eq (viii)
$$\begin{array}{lllllll}y_1 &+&y_2&+&y_3&=&0 \\&&y_2&+&y_3&=&-2 \\&-&&-&&&+ \\\hline \hline y_1&&&&&=&2\end{array}$$
Hence, co-ordinate of point $$ A\left(x_{1}, y_{1}\right)=(3,2) $$
Again subtract equation ( $$ \mathrm{v} $$ ) from equation (vii)
$$\begin{array}{llllllll}&x_1 &+&x_2&+&x_3&=&3 \\&&&x_2&+&x_3&=&4 \\-&&-&&-&&&- \\\hline &&&x_2&&&=&-1\end{array}$$
Subtract equation (vi) from equation (viii)
$$\begin{array}{lllllll}y_1 &+&y_2&+&y_3&=&0 \\y_1&&&+&y_3&=&-2 \\&-&&-&&&+ \\\hline \hline &&y_2&&&=&2\end{array}$$
Hence, co-ordinate (-1,2)
Hence, the vertices of triangle are $$(1,-4),(3,2)$$ and $$(-1,2)$$ Respectively.
$$ \mathrm{A}(4,2), \mathrm{B}(6,5) $$ and $$ \mathrm{C}(1,4) $$ are the vertices of triangle $$ \mathrm{ABC}, \mathrm{AD} $$ is a median through point A meet BC at point D, find the co-ordinate of D.
Find the value of $$ x $$ which is equidistant from the points $$ A(6,5) $$ and $$ B(-4,5) $$.
Find the point on $$ \mathrm{x} $$ -axis which is equidistant from (-2,5) and (2,-3)
If point $$ \mathrm{P}(2,4) $$ is equidistant from the points $$ \mathrm{A}(5, \mathrm{K}) $$ and $$ \mathrm{B}(\mathrm{K}, 7) $$, then find the value of K.
If the points $$ \mathrm{A}(6,1), \mathrm{B}(8,2), \mathrm{C}(9,4) $$ and $$ \mathrm{D}(\mathrm{x}, \mathrm{y}) $$ are vertices of parallelogram respectively, then find the point $$ D(x, y) $$.
Let point $$ \mathrm{A}(6,1), \mathrm{B}(8,2), \mathrm{C}(9,4) $$ and $$ \mathrm{D}(\mathrm{x}, \mathrm{y}) $$ are the vertices of parallelogram.
$$ \therefore $$ Diagonals of a parallelogram bisects each other.
So,
$$ = $$ co-ordinate of mid point diagonal AC $$ \Rightarrow\left(\dfrac{6+9}{2}, \dfrac{1+4}{2}\right)=\left(\dfrac{8+x}{2}, \dfrac{2+y}{2}\right) $$
$$ \Rightarrow \quad\left(\dfrac{15}{2}, \dfrac{5}{2}\right)=\left(\dfrac{8+x}{2}, \dfrac{2+y}{2}\right) $$
comparing $$ \dfrac{8+x}{2}=\dfrac{15}{2} $$ and $$ \dfrac{2+y}{2}=\dfrac{5}{2} $$
$$ \Rightarrow 8+x=15 $$ and $$ 2+y=5 $$
$$ \Rightarrow x=15-8 $$ and $$ y=5-2 $$
$$ \Rightarrow x=7 $$ and $$ y=3 $$
Hence, co-ordinate of point $$D(7, 3)$$
$$ \therefore $$ Diagonals of a parallelogram bisects each other.
So,
$$ = $$ co-ordinate of mid point diagonal AC $$ \Rightarrow\left(\dfrac{6+9}{2}, \dfrac{1+4}{2}\right)=\left(\dfrac{8+x}{2}, \dfrac{2+y}{2}\right) $$
$$ \Rightarrow \quad\left(\dfrac{15}{2}, \dfrac{5}{2}\right)=\left(\dfrac{8+x}{2}, \dfrac{2+y}{2}\right) $$
comparing $$ \dfrac{8+x}{2}=\dfrac{15}{2} $$ and $$ \dfrac{2+y}{2}=\dfrac{5}{2} $$
$$ \Rightarrow 8+x=15 $$ and $$ 2+y=5 $$
$$ \Rightarrow x=15-8 $$ and $$ y=5-2 $$
$$ \Rightarrow x=7 $$ and $$ y=3 $$
Hence, co-ordinate of point $$D(7, 3)$$
Find the co-ordinate of point P on the line segment joining the points $$ A(-2,-2) $$ and $$B(2,-4)$$ such that $$ \mathrm{AP}=\dfrac{3}{7} \mathrm{AB} $$ and point $$ \mathrm{P} $$ lies on line segment $$ \mathrm{AB} $$.
Using the section formula, if a point $$(x,y)$$ divides the line joining the points $$({ x }_{ 1 },{ y }_{ 1 })$$ and $$({ x }_{ 2 },{ y }_{ 2 })$$ in the ratio $$ m:n $$, then
$$(x,y) = \left( \dfrac { m{ x }_{ 2 } + n{ x }_{ 1 } }{ m + n },\dfrac { m{ y }_{ 2 } + n{ y }_{ 1 } }{ m + n } \right) $$
Given $$ A P=\dfrac{3}{7} A B \ldots$$(i)
But $$ P B=A B-A P $$
$$ =A B-\dfrac{3}{7} A B $$
$$ =\dfrac{7 A B-3 A B}{7} $$
$$ \mathrm{PB}=\dfrac{4}{7} \mathrm{AB} \ldots$$(ii)
From equation (i) and (ii),
$$ \mathrm{AP}: \mathrm{PB}=\dfrac{3}{7} \mathrm{AB}: \dfrac{4}{7} \mathrm{AB} $$
$$ A P: P B=3: 4 $$
$$ \therefore $$ Hence point $$ P $$ divides point $$ A $$ and $$ B $$ in the ratio 3: 4 respectively.
$$ \therefore $$ Hence coordinates of point $$ P $$ are
$$\begin{array}{c}x=\dfrac{3 \times 2+4 \times(-2)}{3+4} \\=\dfrac{6-8}{7}=\dfrac{-2}{7}\end{array}$$
and $$ y=\dfrac{3 \times(-4)+4 \times(-2)}{3+4} $$
$$=\dfrac{-12-8}{7}=\dfrac{-20}{7}$$
Hence coordinate of point $$ P=\left(\dfrac{-2}{7}, \dfrac{-20}{7}\right) $$
$$ A P: P B=3: 4 $$
$$ \therefore $$ Hence point $$ P $$ divides point $$ A $$ and $$ B $$ in the ratio 3: 4 respectively.
$$ \therefore $$ Hence coordinates of point $$ P $$ are
$$\begin{array}{c}x=\dfrac{3 \times 2+4 \times(-2)}{3+4} \\=\dfrac{6-8}{7}=\dfrac{-2}{7}\end{array}$$
and $$ y=\dfrac{3 \times(-4)+4 \times(-2)}{3+4} $$
$$=\dfrac{-12-8}{7}=\dfrac{-20}{7}$$
Hence coordinate of point $$ P=\left(\dfrac{-2}{7}, \dfrac{-20}{7}\right) $$
If the co-ordinates of the midpoints of the sides of the triangle are (3,4),(8,9), and $$ (6, 7)$$ respectively. Find the co-ordinate of vertices of the triangle. (NCERT Exemplar Problem)
Let mid points of sides of triangle are $$ P(3,4), Q(8,9) $$ and $$ R(6,7) $$ respectively.
Let $$ A\left(x_{1}, y_{1}\right) B\left(x_{2}, y_{2}\right) $$ and $$ C\left(x_{3}, y_{3}\right) $$ be the vertices of the triangle ABC.
since $$ P(3,4) $$ is the mid point of $$ A\left(x_{1}, y_{1}\right) $$ and $$ B\left(x_{2}, y_{2}\right) $$
$$ 3=\dfrac{x_{1}+x_{2}}{2} $$ and $$ 4=\dfrac{y_{1}+y_{2}}{2} $$
$$ x_{1}+x_{2}=6 $$ and $$ y_{1}+y_{2}=8 \ldots$$(i)
since $$ Q(8,9) $$ is the mid point of $$ B\left(x_{2}, y_{2}\right) $$ and $$ C\left(x_{3}, y_{3}\right) $$
So $$ 8=\dfrac{x_{2}+x_{3}}{2} $$ and $$ 9=\dfrac{y_{2}+y_{3}}{2} $$
$$ x_{2}+x_{3}=16 ; y_{2}+y_{3}=18 \ldots . .( $$ ii $$ ) $$
since $$ \mathrm{R}(6,7) $$ is the mid point of $$ \mathrm{A}\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right) $$ and $$ \mathrm{C}\left(\mathrm{x}_{3}, \mathrm{y}_{3}\right) . $$
So $$ 6=\dfrac{x_{1}+x_{3}}{2} $$ and $$ 7=\dfrac{y_{1}+y_{3}}{2} $$
$$ \Rightarrow x_{1}+x_{3}=12 $$ and $$ y_{1}+y_{3}=14 \ldots$$(iii)
Adding equation (i), (ii) and (iii) $$ 2 x_{1}+2 x_{2}+2 x_{3}=34 $$
and $$ 2 y_{1}+2 y_{2}+2 y_{3}=40 $$
$$ \Rightarrow x_{1}+x_{2}+x_{3}=17 \ldots$$(iv)
and $$ y_{1}+y_{2}+y_{3}=20 $$
Subtract equation (i) from equation (iv).
$$ x_{1}+x_{2}+x_{3}-x_{1}-x_{2}=17-6 $$
and $$ y_{1}+y_{2}+y_{3}-y_{1}-y_{2}=20-8 $$
$$ \Rightarrow \mathrm{x}_{3}=11 $$ and $$ \mathrm{y}_{3}=12 $$
subtract equation (ii) from equation (iv)
$$ x_{1}+x_{2}+x_{3}-x_{2}-x_{3}=17-6 $$
and $$ y_{1}+y_{2}+y_{3}-y_{2}-y_{3}=20-8 $$
$$ \Rightarrow x_{1}=1 $$ and $$ y_{1}=2 $$
subtract equation (iii) from equation (iv)
$$ x_{1}+x_{2}+x_{3}-x_{1}-x_{3}=17-12 $$
and $$ y_{1}+y_{2}+y_{3}-y_{1}-y_{3}=20-14 $$
$$ \Rightarrow x_{2}=5 $$ and $$ y_{2}=6 $$
Hence, the co-ordinate of vertices of triangle $$ \mathrm{A}(1,2) \mathrm{B}(5,6) $$ and $$ \mathrm{C}(11,12) $$
Let $$ A\left(x_{1}, y_{1}\right) B\left(x_{2}, y_{2}\right) $$ and $$ C\left(x_{3}, y_{3}\right) $$ be the vertices of the triangle ABC.
since $$ P(3,4) $$ is the mid point of $$ A\left(x_{1}, y_{1}\right) $$ and $$ B\left(x_{2}, y_{2}\right) $$
$$ 3=\dfrac{x_{1}+x_{2}}{2} $$ and $$ 4=\dfrac{y_{1}+y_{2}}{2} $$
$$ x_{1}+x_{2}=6 $$ and $$ y_{1}+y_{2}=8 \ldots$$(i)
since $$ Q(8,9) $$ is the mid point of $$ B\left(x_{2}, y_{2}\right) $$ and $$ C\left(x_{3}, y_{3}\right) $$
So $$ 8=\dfrac{x_{2}+x_{3}}{2} $$ and $$ 9=\dfrac{y_{2}+y_{3}}{2} $$
$$ x_{2}+x_{3}=16 ; y_{2}+y_{3}=18 \ldots . .( $$ ii $$ ) $$
since $$ \mathrm{R}(6,7) $$ is the mid point of $$ \mathrm{A}\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right) $$ and $$ \mathrm{C}\left(\mathrm{x}_{3}, \mathrm{y}_{3}\right) . $$
So $$ 6=\dfrac{x_{1}+x_{3}}{2} $$ and $$ 7=\dfrac{y_{1}+y_{3}}{2} $$
$$ \Rightarrow x_{1}+x_{3}=12 $$ and $$ y_{1}+y_{3}=14 \ldots$$(iii)
Adding equation (i), (ii) and (iii) $$ 2 x_{1}+2 x_{2}+2 x_{3}=34 $$
and $$ 2 y_{1}+2 y_{2}+2 y_{3}=40 $$
$$ \Rightarrow x_{1}+x_{2}+x_{3}=17 \ldots$$(iv)
and $$ y_{1}+y_{2}+y_{3}=20 $$
Subtract equation (i) from equation (iv).
$$ x_{1}+x_{2}+x_{3}-x_{1}-x_{2}=17-6 $$
and $$ y_{1}+y_{2}+y_{3}-y_{1}-y_{2}=20-8 $$
$$ \Rightarrow \mathrm{x}_{3}=11 $$ and $$ \mathrm{y}_{3}=12 $$
subtract equation (ii) from equation (iv)
$$ x_{1}+x_{2}+x_{3}-x_{2}-x_{3}=17-6 $$
and $$ y_{1}+y_{2}+y_{3}-y_{2}-y_{3}=20-8 $$
$$ \Rightarrow x_{1}=1 $$ and $$ y_{1}=2 $$
subtract equation (iii) from equation (iv)
$$ x_{1}+x_{2}+x_{3}-x_{1}-x_{3}=17-12 $$
and $$ y_{1}+y_{2}+y_{3}-y_{1}-y_{3}=20-14 $$
$$ \Rightarrow x_{2}=5 $$ and $$ y_{2}=6 $$
Hence, the co-ordinate of vertices of triangle $$ \mathrm{A}(1,2) \mathrm{B}(5,6) $$ and $$ \mathrm{C}(11,12) $$
If $$ \mathrm{M}(4,5) $$ is a mid point of line segment $$ \mathrm{AB} $$ and co-ordinate of $$ \mathrm{A} $$ is (3,4) , then find theco-ordinate of point B.
Prove that points 4(1,1) $$ \mathrm{B}(-2,7) $$ and $$ \mathrm{C}(3,-3) $$ are collinear
Find the center of a circle passing through the points (6,-6),(3,-7) and (3,3) (NCERT)
Let $$ O(x, y) $$ is a center of circle.
The circle of center 0 is passes through the points $$ P(6,-6), Q(3,-7) $$ and $$ R(3,3) $$ respectively.
$$\because$$ since radius of circle is same
$$ \therefore \mathrm{OP}=\mathrm{OQ}=\mathrm{OR} $$
or $$ \mathrm{OP}^{2}=\mathrm{OQ}^{2}=\mathrm{OR}^{2} $$
Now $$ \mathrm{OP}^{2}=\mathrm{OQ}^{2} $$
$$ \Rightarrow(x-6)^{2}+(y+6)^{2}=(x-3)^{2}+(y+7)^{2} $$
$$ \Rightarrow x^{2}-12 x+36+y^{2}+12 y+36=x^{2}-6 x+9+y^{2}+14 y+49 $$
$$ \Rightarrow-12 x+6 x+12 y-14 y+72-58=0 $$
$$ \Rightarrow-6 x-2 y+14=0 $$
$$ \Rightarrow 3 x+y-7=0 \ldots$$(i)
Now $$ \mathrm{OQ}^{2}=\mathrm{OR}^{2} $$
$$ \Rightarrow(x-3)^{2}+(y+7)^{2}=(x-3)^{2}+(y-3)^{2} $$
$$ \Rightarrow(y+7)^{2}=(y-3)^{2} $$
$$ \Rightarrow y^{2}+49+14 y=y^{2}+9-6 y $$
$$ \Rightarrow 20 y=-40 $$
$$ \Rightarrow y=\dfrac{-40}{20}=-2 $$
Put the value of y in equation (i)
$$ 3 x-2-7=0 $$
$$ \Rightarrow 3 x-9=0 $$
$$ \Rightarrow 3 x=9 $$
$$ \Rightarrow x=\dfrac{9}{3}=3 $$
Hence, required center is $$(3,-2)$$ .
The circle of center 0 is passes through the points $$ P(6,-6), Q(3,-7) $$ and $$ R(3,3) $$ respectively.
$$\because$$ since radius of circle is same
$$ \therefore \mathrm{OP}=\mathrm{OQ}=\mathrm{OR} $$
or $$ \mathrm{OP}^{2}=\mathrm{OQ}^{2}=\mathrm{OR}^{2} $$
Now $$ \mathrm{OP}^{2}=\mathrm{OQ}^{2} $$
$$ \Rightarrow(x-6)^{2}+(y+6)^{2}=(x-3)^{2}+(y+7)^{2} $$
$$ \Rightarrow x^{2}-12 x+36+y^{2}+12 y+36=x^{2}-6 x+9+y^{2}+14 y+49 $$
$$ \Rightarrow-12 x+6 x+12 y-14 y+72-58=0 $$
$$ \Rightarrow-6 x-2 y+14=0 $$
$$ \Rightarrow 3 x+y-7=0 \ldots$$(i)
Now $$ \mathrm{OQ}^{2}=\mathrm{OR}^{2} $$
$$ \Rightarrow(x-3)^{2}+(y+7)^{2}=(x-3)^{2}+(y-3)^{2} $$
$$ \Rightarrow(y+7)^{2}=(y-3)^{2} $$
$$ \Rightarrow y^{2}+49+14 y=y^{2}+9-6 y $$
$$ \Rightarrow 20 y=-40 $$
$$ \Rightarrow y=\dfrac{-40}{20}=-2 $$
Put the value of y in equation (i)
$$ 3 x-2-7=0 $$
$$ \Rightarrow 3 x-9=0 $$
$$ \Rightarrow 3 x=9 $$
$$ \Rightarrow x=\dfrac{9}{3}=3 $$
Hence, required center is $$(3,-2)$$ .
$$A(a+1, a-1)$$, $$B(a^{2}+1, a^{2}-1)$$ and $$C(a^{3}+1, a^{3}-1)$$ are given points. $$D(11, 9)$$ is the mid point of $$AB$$ and $$E(41, 39)$$ is the mid point of $$BC$$. If $$F$$ is the mid point of $$AC,$$ then $$\dfrac{(BF)^{2}}{81}$$ is equal to
Without using distance formula, show that point $$(-2, -1), (4, 0), (3, 3)$$ and $$(-3, 2)$$ are the vertices of a parallelogram.
If $$M$$ is the mid-point of $$AB$$, find the co-ordinates of:
a) $$A$$ if the coordinates of $$M$$ and $$B$$ are $$M(2,8)$$ and $$B(-4,19)$$ and
b) $$B$$ if the coordinates of $$A$$ and $$M$$ are $$A(-1,2)$$, $$M(-2,4)$$.
If $$( 10,5 ), ( 8,4 )$$ and $$( 6,6 )$$ be the mid-points of the sides of a triangle, find the coordinates of the vertices.
Let's say $$D,\ E$$ and $$F$$ are the midpoints of $$AB,\ BC$$ and $$AC$$ and coordinate of vertices $$A,B,C$$ be $$(x,y),\ (a,b)$$ and $$(p,q)$$ respectively.
For points $$(x_1,y_1)$$ and $$(x_2,y_2)$$ we define the midpoint as,
Point $$P(X,Y)=\left(\dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2}\right)$$
For mid point $$D$$ of $$AB,$$
$$\dfrac{x+a}{2}=10$$
$$\Rightarrow x+a=20$$
$$\dfrac{y+b}{2}=5$$
$$\Rightarrow y+b=10$$
For midpoint $$D$$ of $$BC,$$
$$\dfrac{a+p}{2}=6$$
$$\Rightarrow a+p=12$$
$$\dfrac{b+q}{2}=6$$
$$\Rightarrow b+q=12$$
For midpoint $$F$$ of $$AC,$$
$$\dfrac{x+p}{2}=8$$
$$\Rightarrow x+p=16$$
$$\dfrac{y+q}{2}=4$$
$$\Rightarrow y+q=8$$
Consider, $$x+a=20$$ and $$a+p=12$$
$$x+12-p=20$$
$$\Rightarrow x-p=8$$
Now, we have,
$$x-p=8,x+p=16$$
On solving;
$$x=12$$ and $$p=4$$
Now, we have $$x=12$$ and $$x+a=20$$. So,
$$12+a=20$$
$$\Rightarrow a=8$$
Consider, $$y+q=8$$ and $$q+b=12$$
$$y+12-b=8$$
$$\Rightarrow y-b=-4$$
Now, we have,
$$y-b=-4,y+b=10$$
On solving;
$$y=3$$ and $$b=7$$
Now, we have $$y=3$$ and $$y+q=8$$. So,
$$3+q=8$$
$$\Rightarrow q=5$$
Hence, the coordinates of the vertices will be $$A(12,3),\ B(8,7),\ C(4,5).$$
Find k if (0, k) is equidistant from (5, -3) and (4, 6)
Three consecutive vertices of a parallelogram ABCD are A$$\left(3,-1,2\right)$$, B$$\left(1,2,-4\right)$$ and C$$\left(-1,1,2\right)$$. Find the coordinates of the fourth vertex D.
Three consecutive vertices of a parallelogram $$ABCD$$ are $$A\left(-2,3,5\right),\,B\left(-3,2,1\right)$$ and $$C\left(3,5,1\right)$$.Find the fourth vertex $$D$$
Three consecutive vertices of a parallelogram $$ABCD$$ are $$A\left(5,2\right),\,B\left(3,5\right)$$ and $$C\left(2,3\right)$$.Find the fourth vertex $$D$$
Show that the perpendicular from the origin upon the straight line joining the points
$$(a \ cos \ \alpha, a \ sin \ \alpha)$$ and $$(a \ cos \ \beta, a \ sin \ \beta)$$
bisects the distance between them.
The mid-points of the sides of a triangle are $$(3, 4), (4, 6)$$ and $$(5, 7).$$ Find the coordinates of the vertices of the triangle.
Find a point on the x-axis , which is equidistant from the point $$ ( 7 ,6) $$ and $$(3,4)$$
A point $$P(2,-1)$$ is equidistant from the points $$(a,7)$$ and $$(-3,a)$$. Find $$a$$.
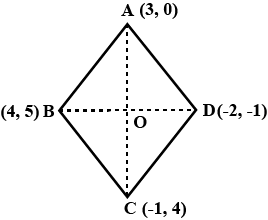
Find the area of a rhombus if its vertices are $$(3 , 0) , (4 , 5) , (-1 , 4) $$ and $$(-2 , -1) $$ taken in order.[Hint: Area of a rhombus $$ = \dfrac{1}{2} $$ (product of its diagonals)
Class 10 Maths Extra Questions
- Areas Related To Cricles Extra Questions
- Arithmetic Progressions Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Introduction To Trigonometry Extra Questions
- Pair Of Linear Equations In Two Variables Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadratic Equations Extra Questions
- Real Numbers Extra Questions
- Some Applications Of Trigonometry Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions