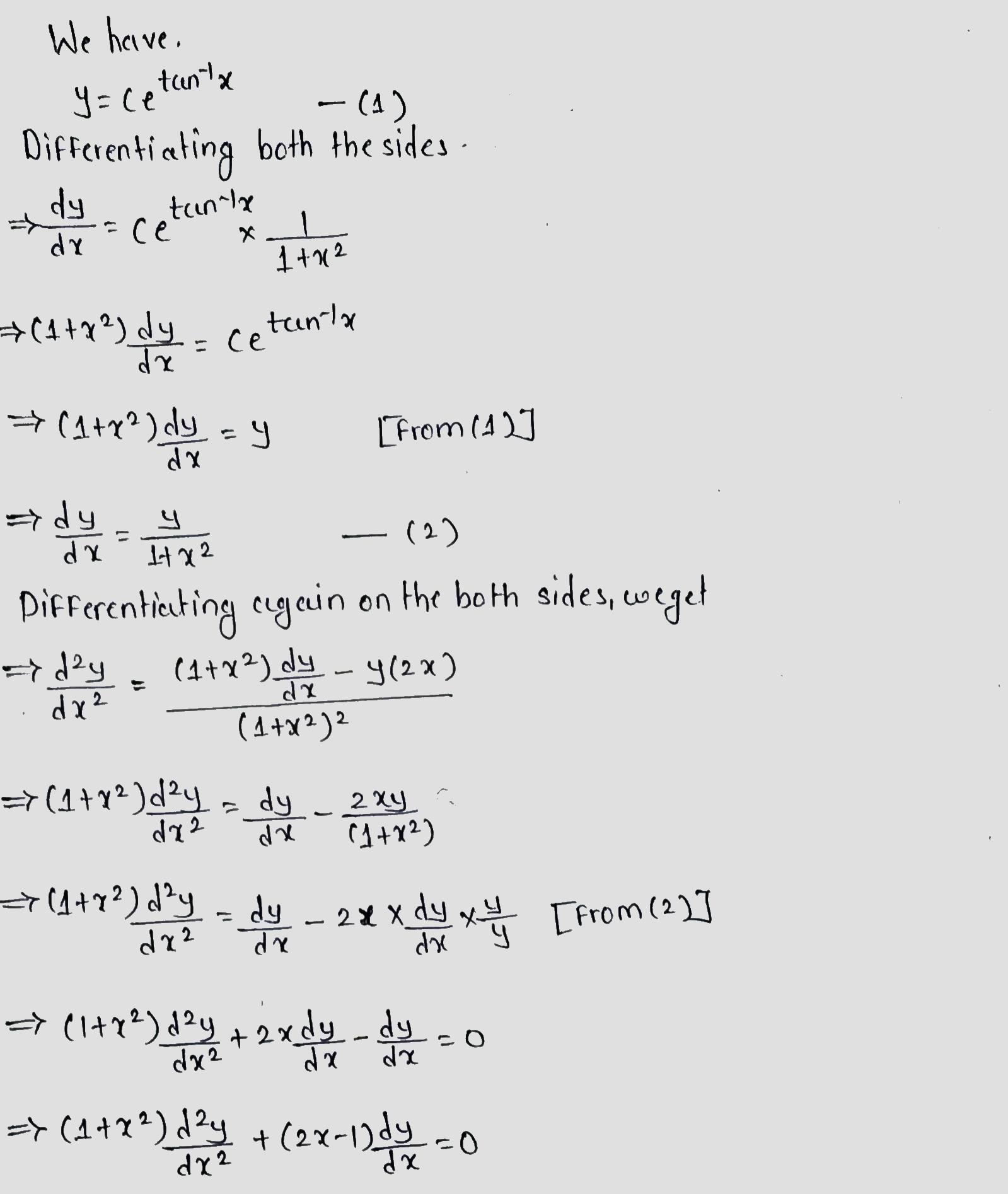Differential Equations - Class 12 Engineering Maths - Extra Questions
Find the order and degree of the differential equations.
a) $$y ^ { \prime \prime } + 3 y ^ { \prime ^ { 2 } } + y ^ { 3 } = 0$$
b) $$\left( \dfrac { d y } { d x } \right) ^ { 2 } + \dfrac { 1 } { d y d x } = 2$$
c) $$\dfrac { d ^ { 2 } y } { d x ^ { 2 } } + 4 y = 0$$
$$\cos \left( \frac { d y } { d x } \right) = a ( a \in \mathbf { R } ) ; y = 1$$ when $$x = 0$$.Find $$y$$?
Show that $$y=cx+\dfrac{a}{c}$$ is a solution of the differential equation $$y=x\dfrac{dy}{dx}+\dfrac{a}{\dfrac{dy}{dx}}$$.
Write the integrating factor of the differential equation:
$$\cos x\dfrac{dy}{dx}+y=\sin x; 0\le x <\dfrac{\pi}{2}$$.
Find the integrating factor of $$\cfrac { dy }{ dx } +\cfrac { y }{ x } ={ x }^{ 2 }$$.
Find the differential coefficient of $$\tan ^{ -1 }{ x } $$ w.r to $$x$$.
Consider the following equation, $$\dfrac {dy}{dx} + P(x)y = Q(x)$$
(i) If two particular solutions of given equation $$u(x)$$ and $$v(x)$$ are known, find the general solution of the same equation in terms of $$u(x)$$ and $$v(x)$$.
(ii) If $$\alpha$$ and $$\beta$$ are constants such that the linear combinations $$\alpha \cdot u(x) + \beta \cdot v(x)$$ is a solution of the given equation, find the relation between $$\alpha$$ and $$\beta$$.
(iii) If $$w(x)$$ is the third particular solution different from $$u(x)$$ and $$v(x)$$ then find the ratio $$\dfrac {v(x) - u(x)}{w(x) - u(x)}$$.
Find the general solution of the differential equation:
$$xdy-ydx=\sqrt { { x }^{ 2 }+{ y }^{ 2 } } dx$$
Verify that $$y=4sin 3x$$ is the solution of the differential equation $$\frac{{{d^2}y}}{{d{x^2}}} + 9y = 0$$.
Find order and degree of the following differential equations .
(i) $$\dfrac{dy}{dx} + y = \dfrac{1}{\dfrac{dy}{dx}}$$
(ii)$$_e\left[\dfrac{dy}{dx}-\dfrac{d^3y}{dx^3}\right] = ln \left[\dfrac{d^5y}{dx^5}+ 1\right]$$
(iii)$$\left[(\dfrac{dy}{dx})^{1/3} + y \right]^2 = \dfrac{d^2y}{dx^2}$$
Find the particular solution of the difference equation
$$(1-y^{2})(1+\log x)dx+2xydy=0$$
given that $$y=0$$ when $$x=1$$
Solve: $$\cos^2x\dfrac{dy}{dx}+y=\tan x$$.
Find the order of the differential equation obtained by eliminating the arbitrary constants $$b$$ and $$c$$ from $$xy=ce^{x}+be^{-x}+x^{2}$$.
Solve: $$\dfrac{dy}{dx}=cos(x+y)+sin(x+y)$$
If $$y=(cos^{-1}x)^2$$, prove that $$(1-x^2)\dfrac{d^2y}{dx^2}-x\dfrac{dy}{dx}-2=0$$. Hence find $$y_2$$ when $$x=0$$.
If $${ x }^{ y }={ e }^{ x-y }$$, show that $$\dfrac { dy }{ dx } =\dfrac{y\log{x}}{x\left(\log{x}+1\right)}$$
Write the order of the differential equation $$1+\left(\dfrac{dy}{dx}\right)^2=7\left(\dfrac{d^2y}{dx^2}\right)^3$$.
Show that $$xy=ae^x+be^{-x}+x^2$$ is a solution of the differential equation $$x\dfrac{d^2y}{dx^2}+2\dfrac{dy}{dx}-xy+x^2-2=0$$.
Verify that $$y = A\cos 2x - B\sin 2x$$ is the general solution of the differential equation $$\dfrac {d^{2}y}{dx^{2}} + 4y = 0$$.
Verify that $$y = ce^{\tan^{-1}x}$$ is a solution of the differential equation $$(1 + x^{2}) \dfrac {d^{2}y}{dx^{2}} + (2x - 1) \dfrac {dy}{dx} = 0$$.
The number of arbitrary constants in the general solution of a differential equation of order three is ______ .
Solve the following differential equation:
$$x^{2} \dfrac {dy}{dx} = y^{2} + 2xy$$
Given that : $$y = 1$$, when $$x = 1$$.
Find the particular solution of the differential equation $$\dfrac{dy}{dx} = \dfrac{x(2logx + 1)}{sin y + y cos y}$$ given that $$y = \dfrac{\pi}{2}$$ where x = 1.
Class 12 Engineering Maths Extra Questions
- Continuity And Differentiability Extra Questions
- Determinants Extra Questions
- Differential Equations Extra Questions
- Integrals Extra Questions
- Inverse Trigonometric Functions Extra Questions
- Relations And Functions Extra Questions
- Three Dimensional Geometry Extra Questions
- Vector Algebra Extra Questions