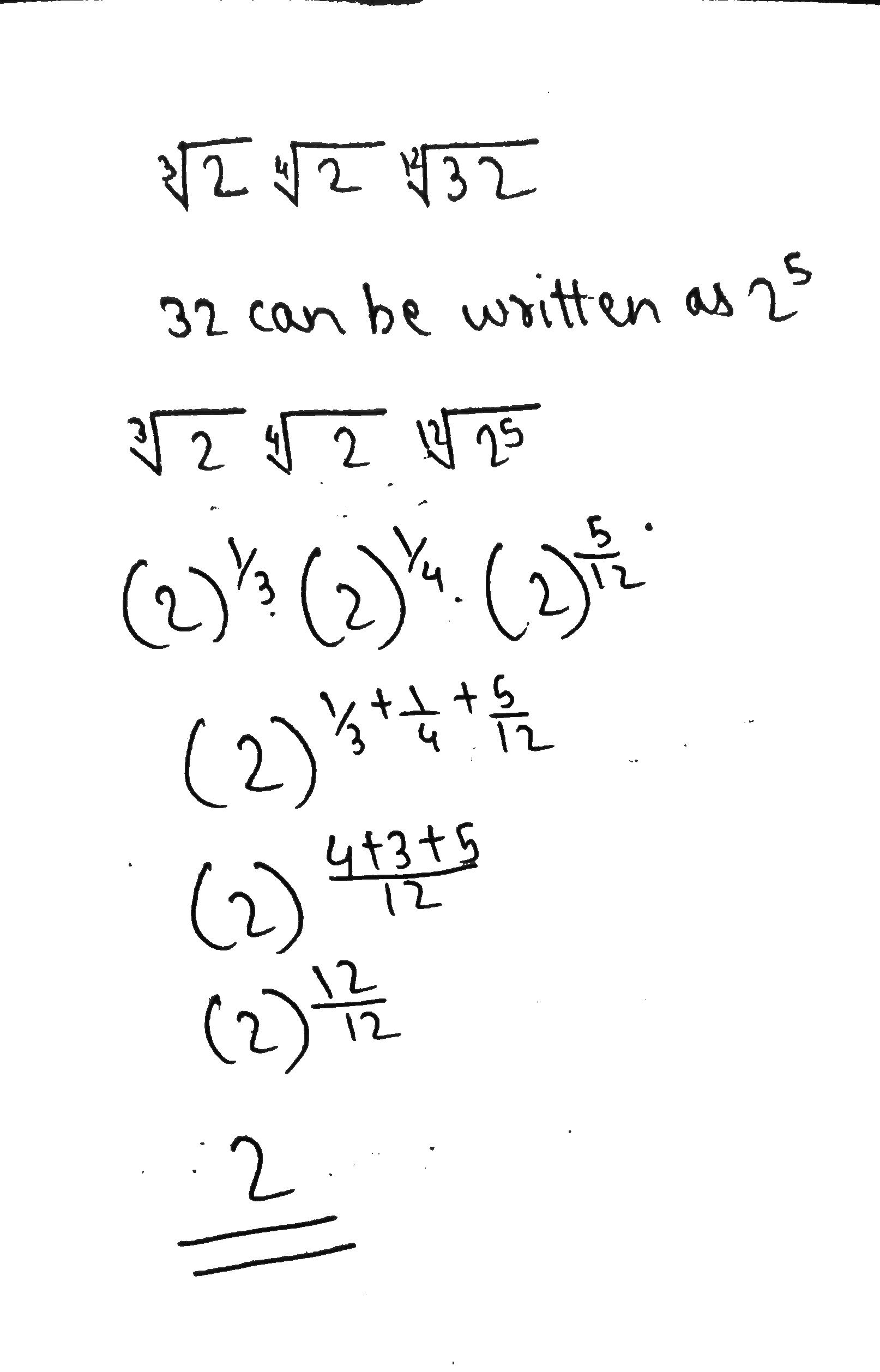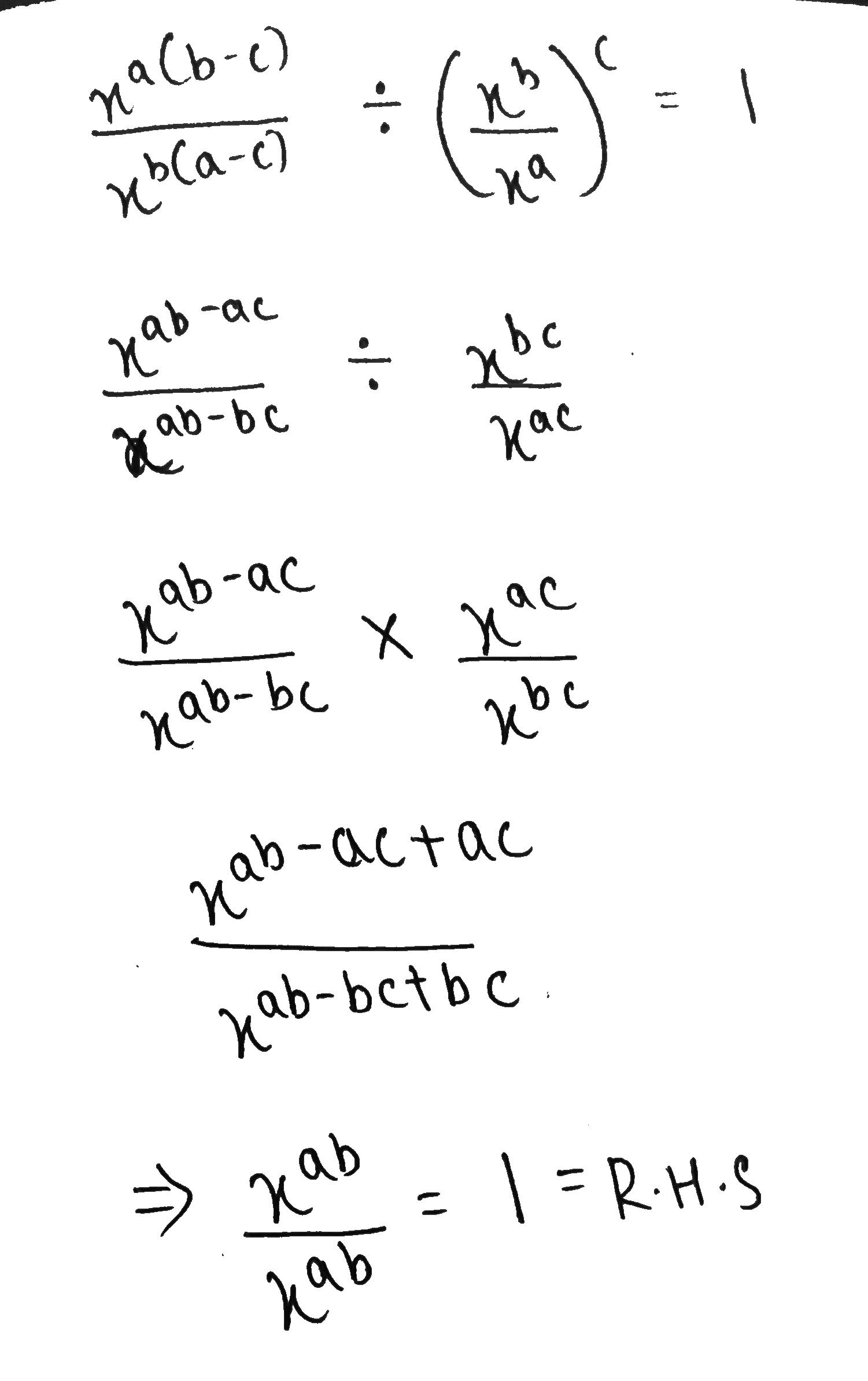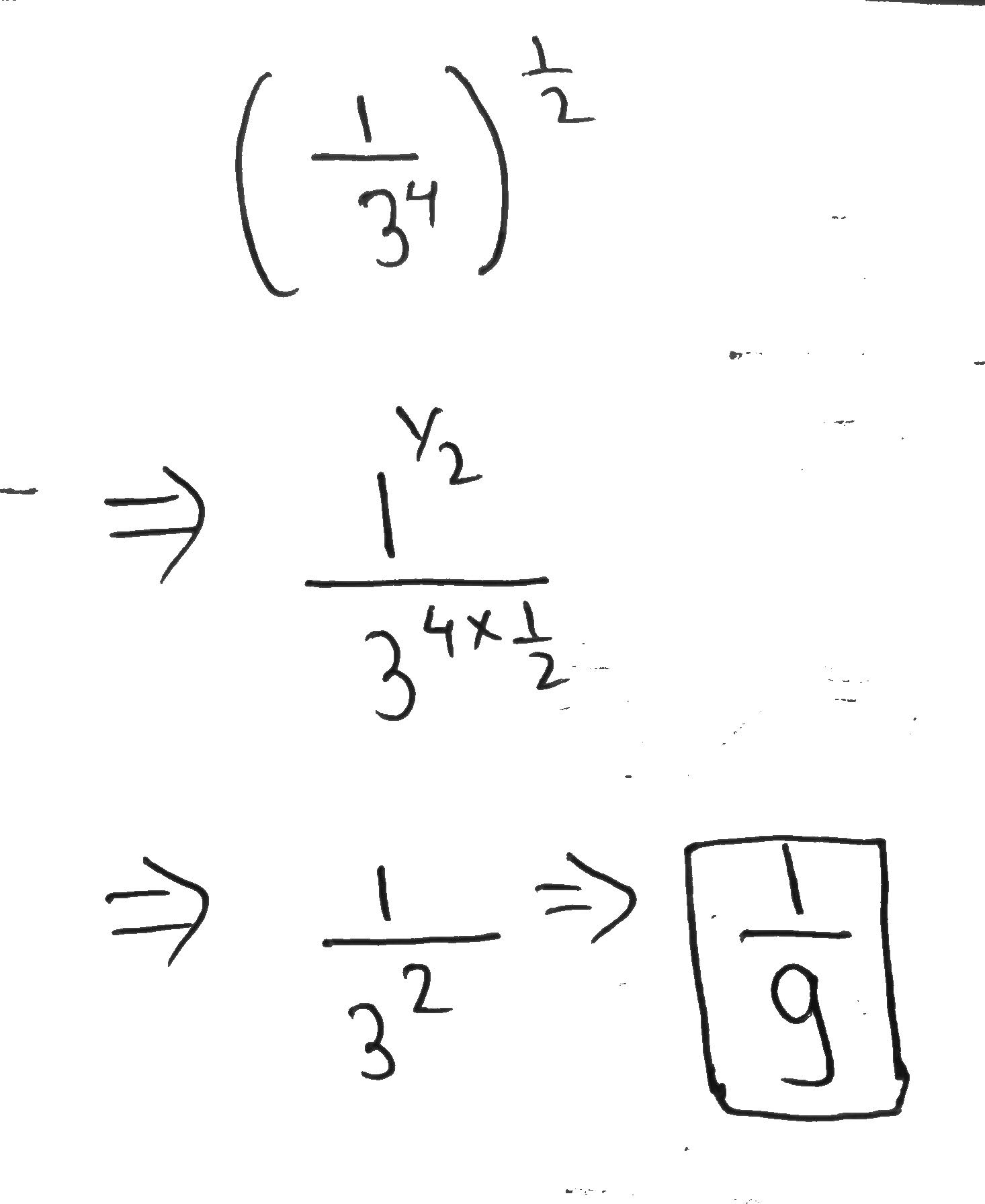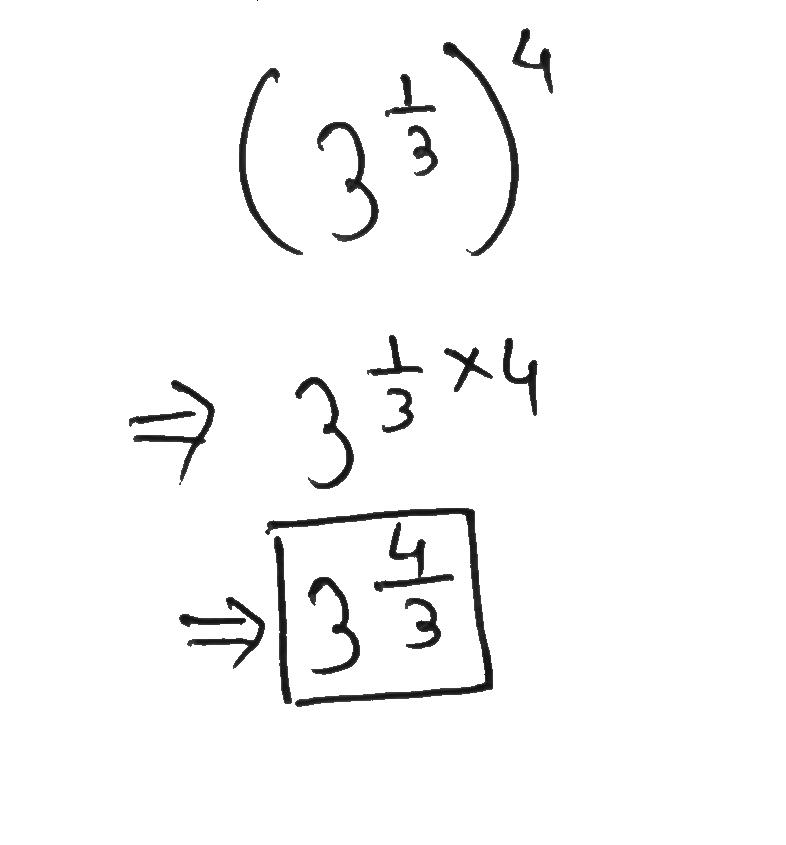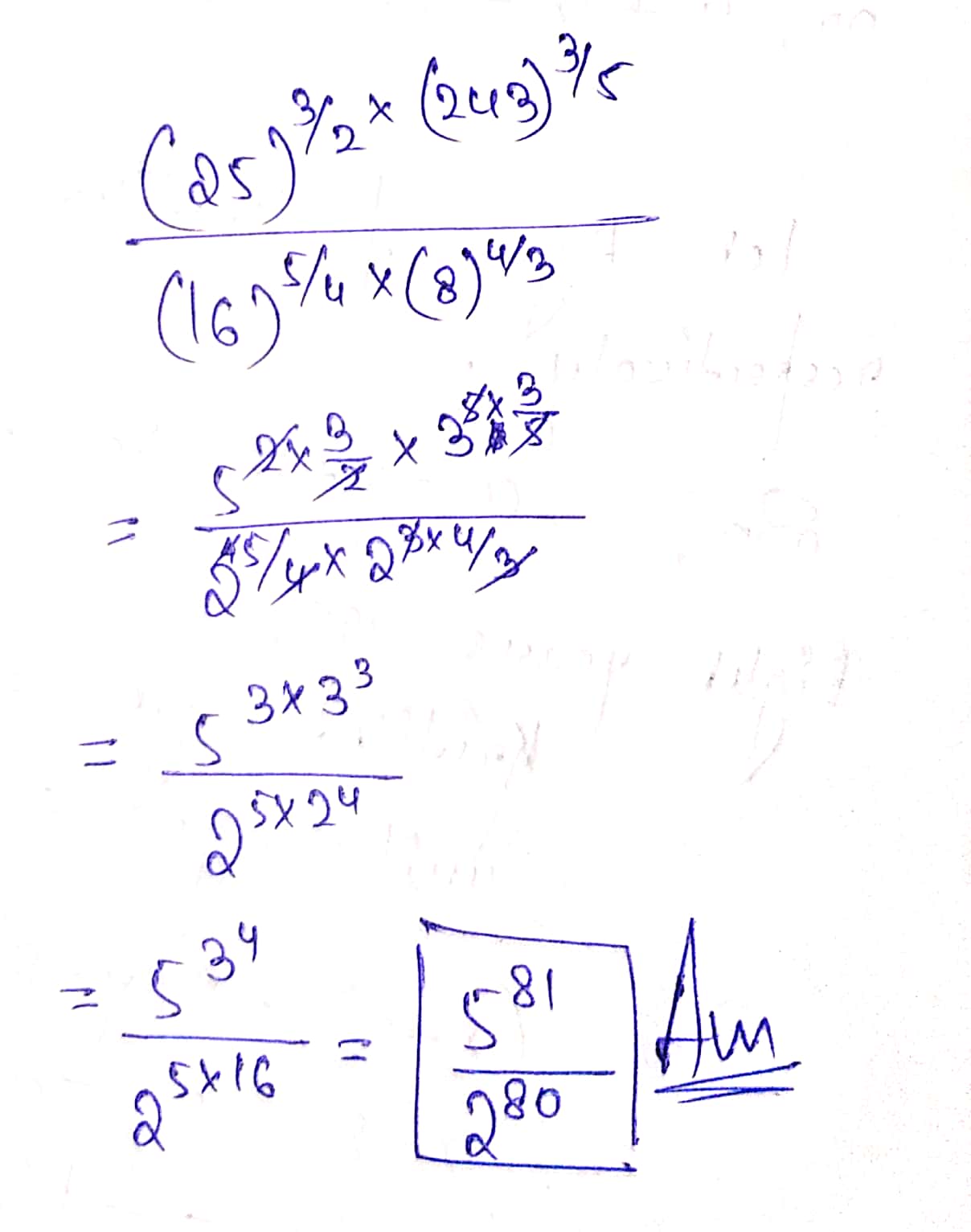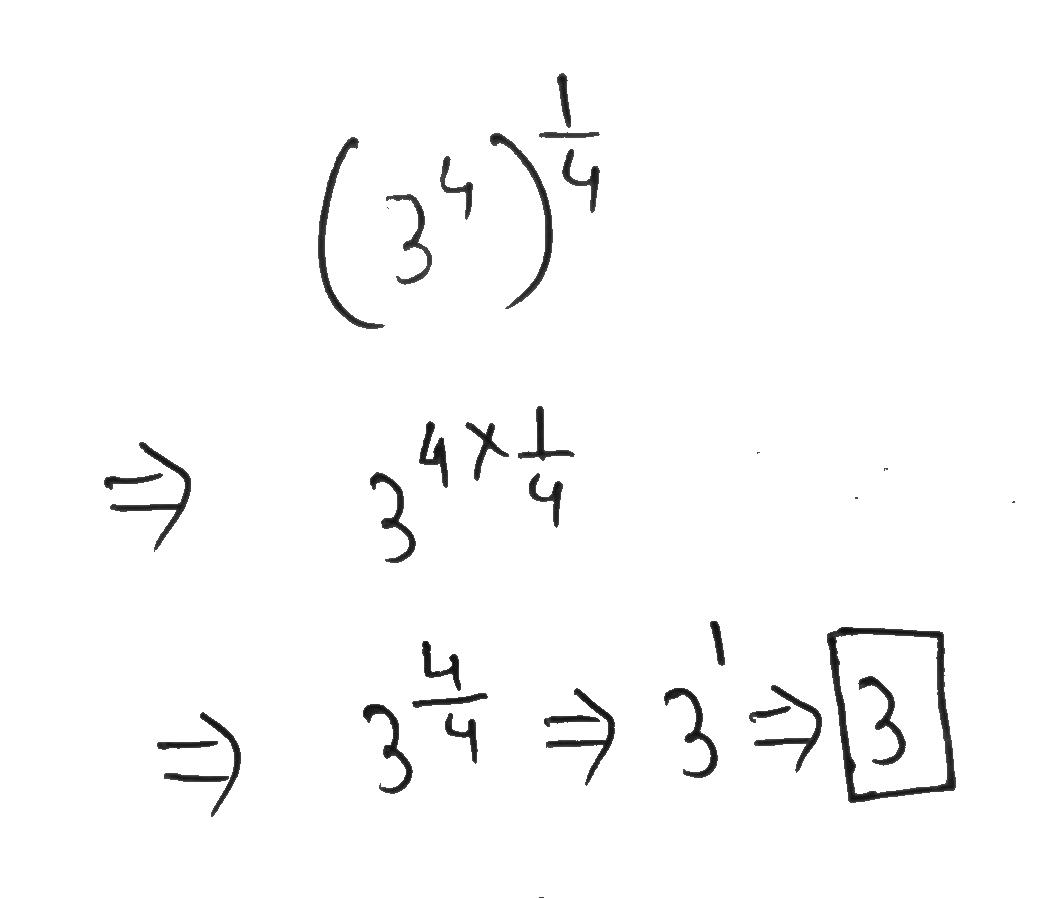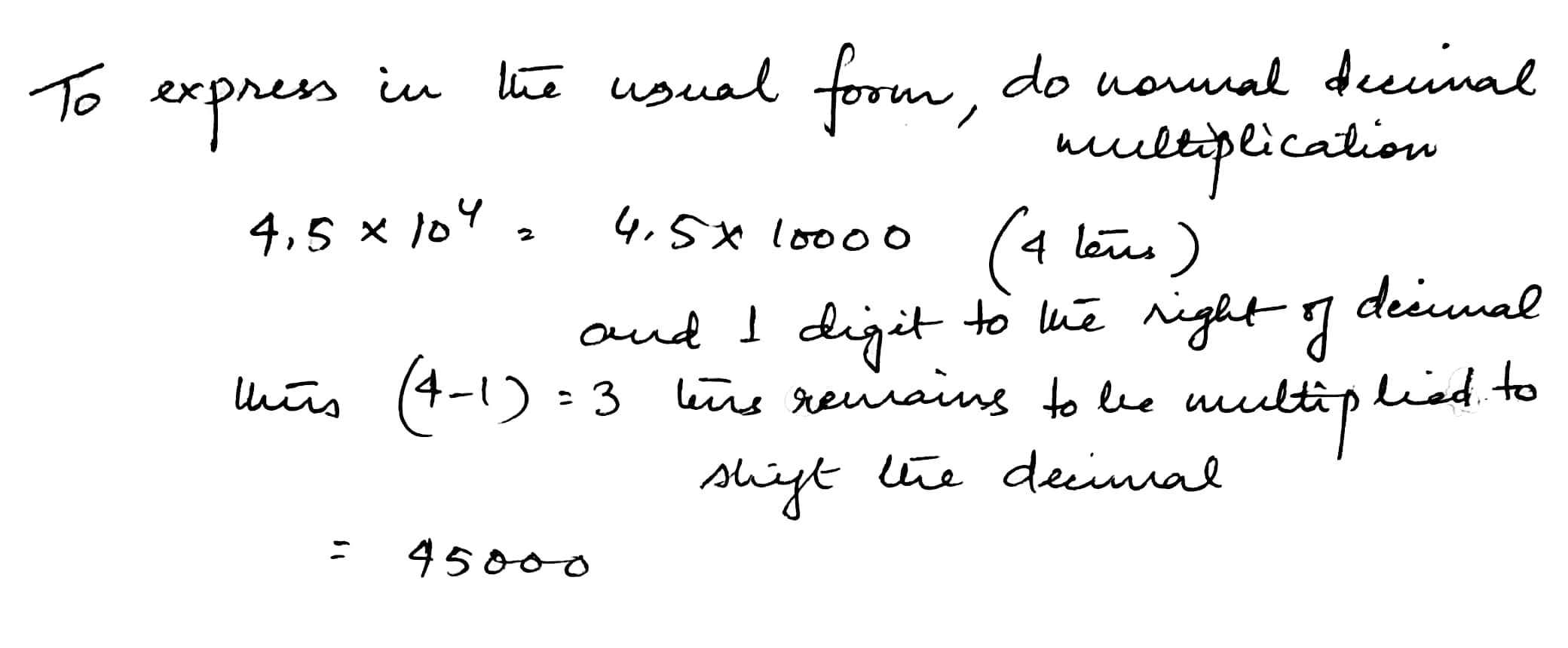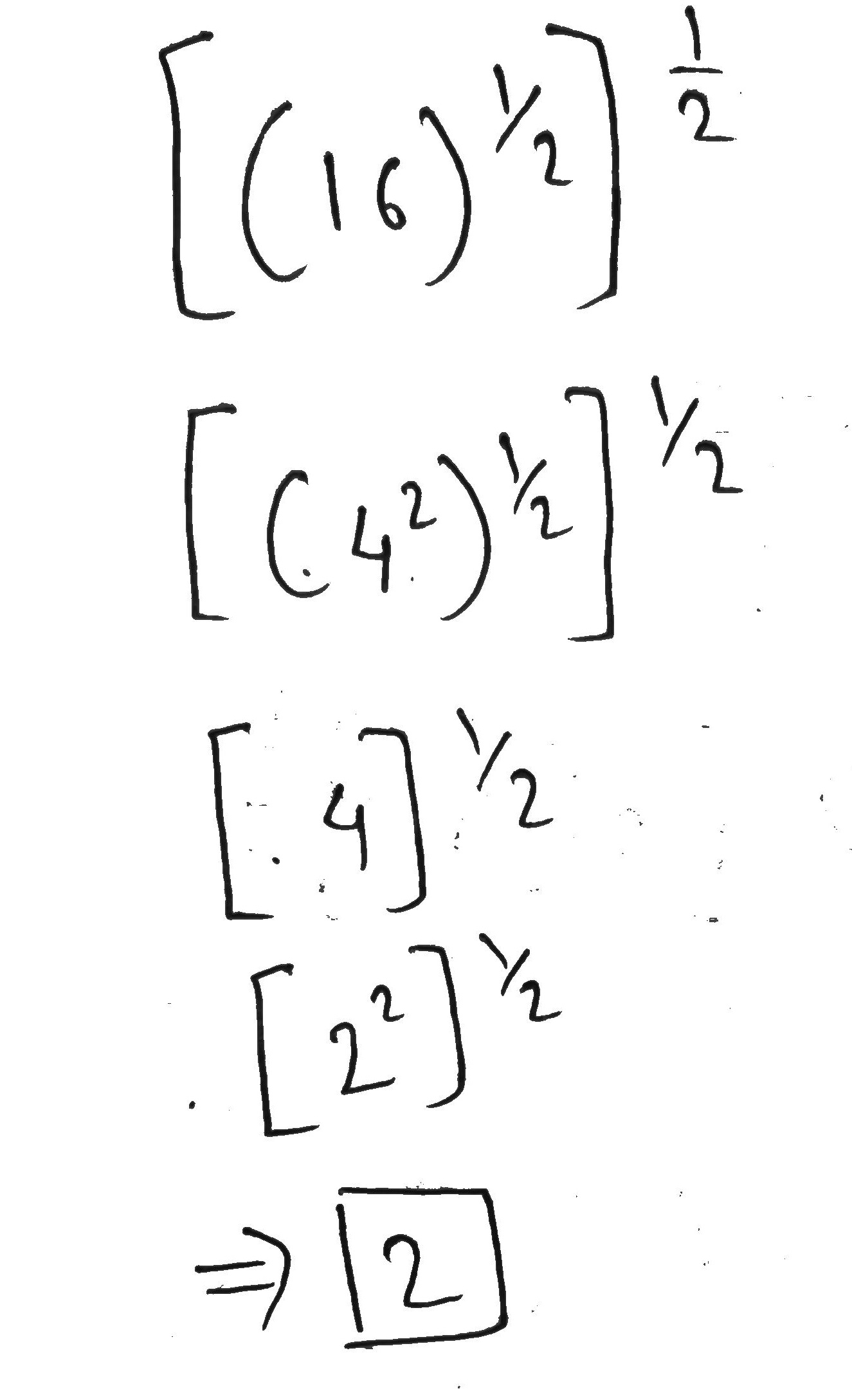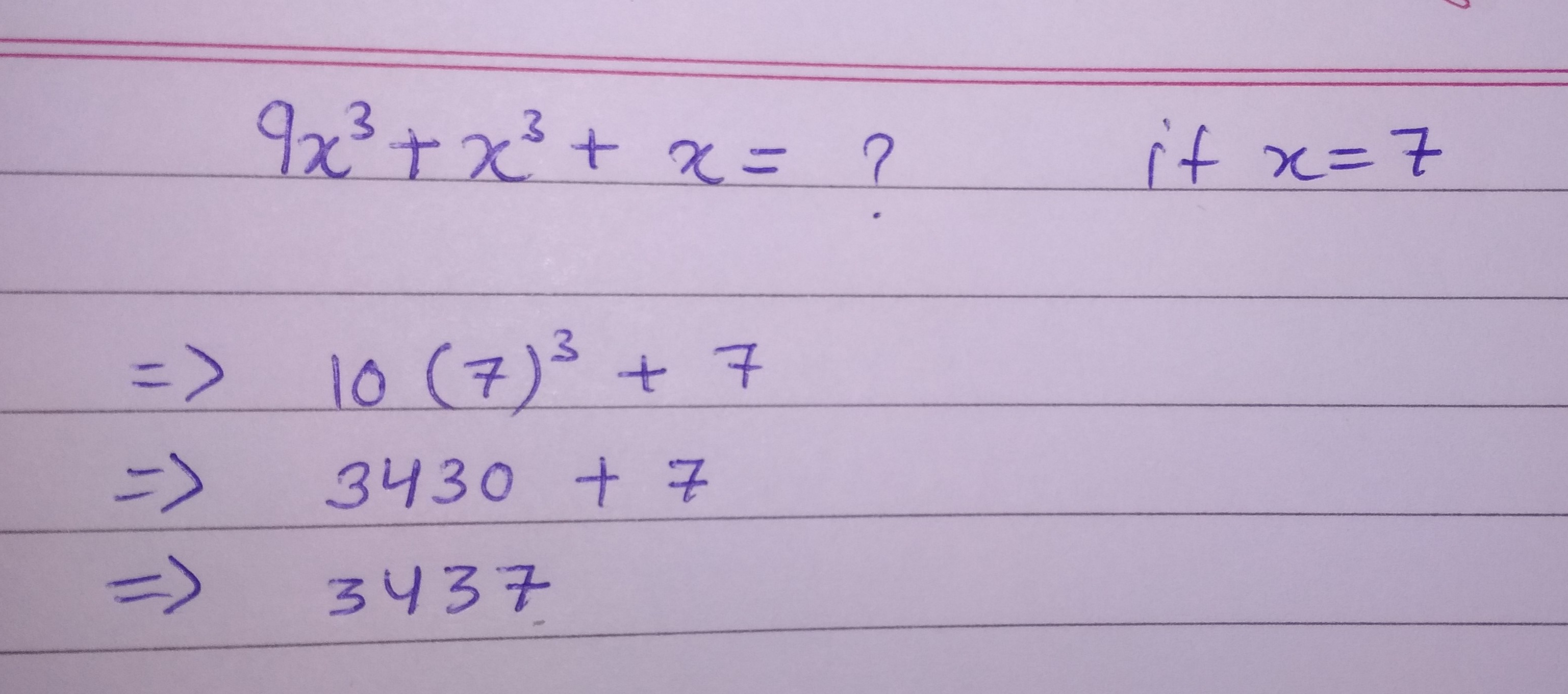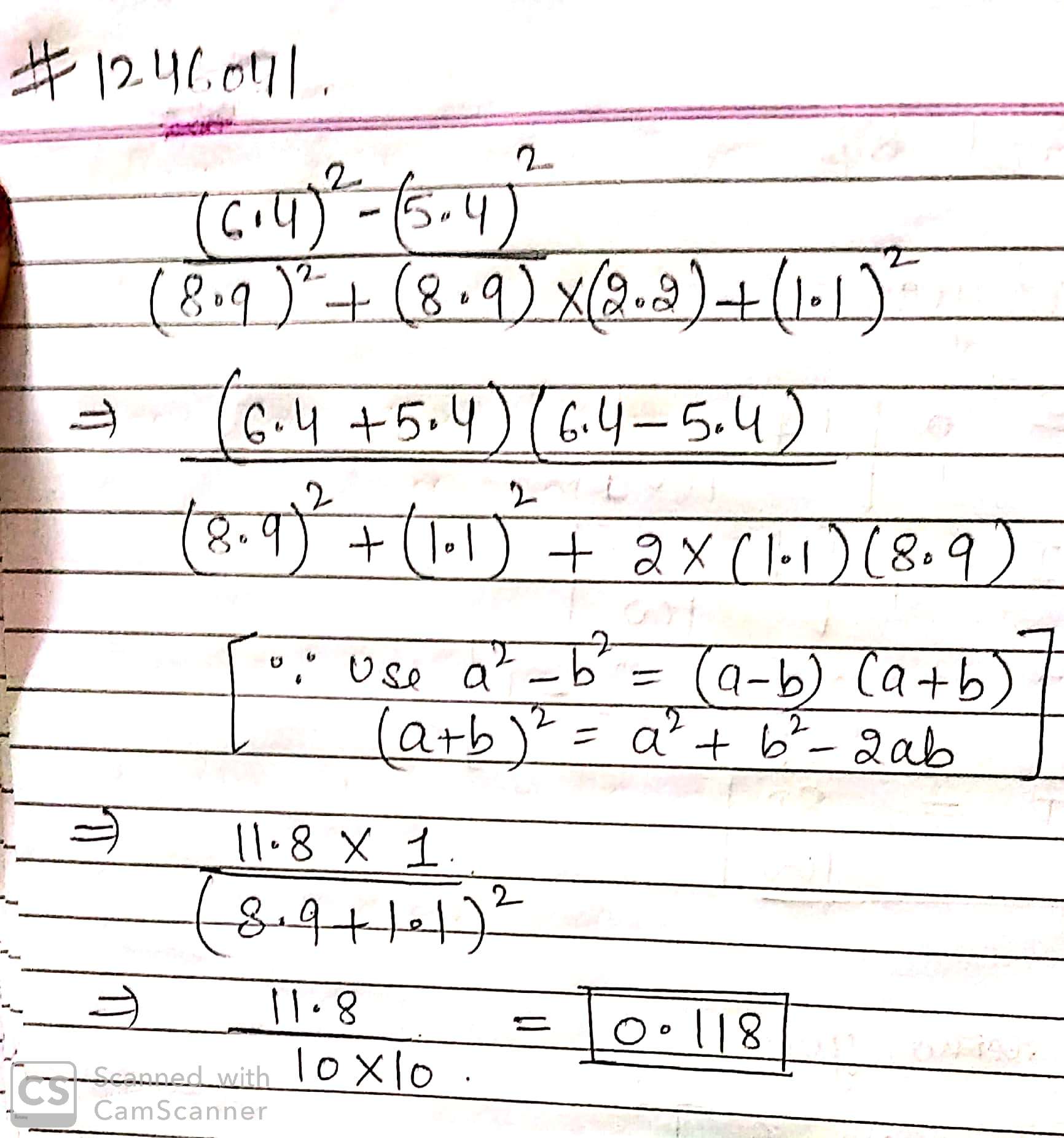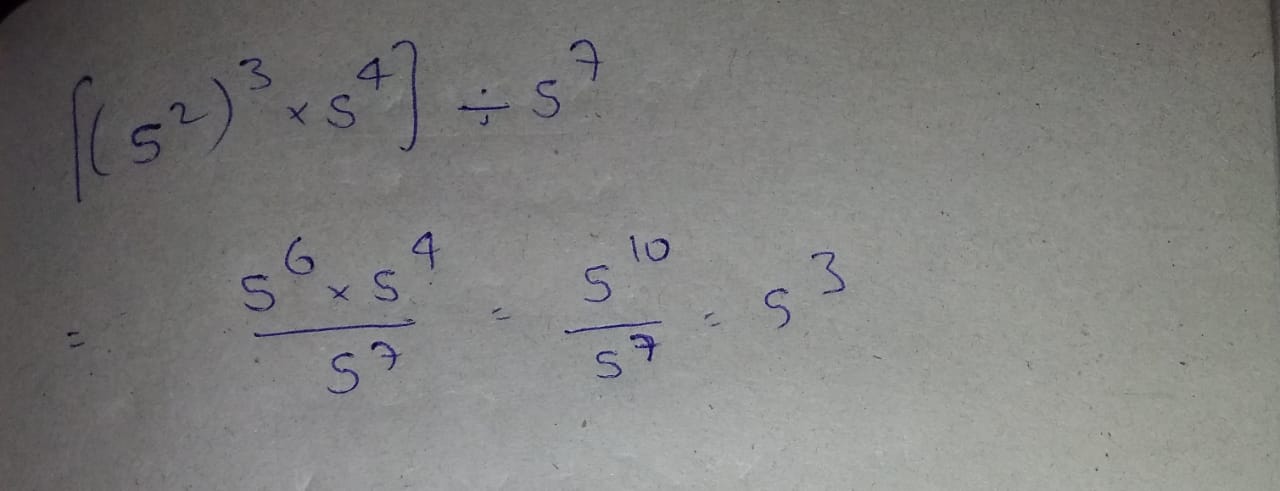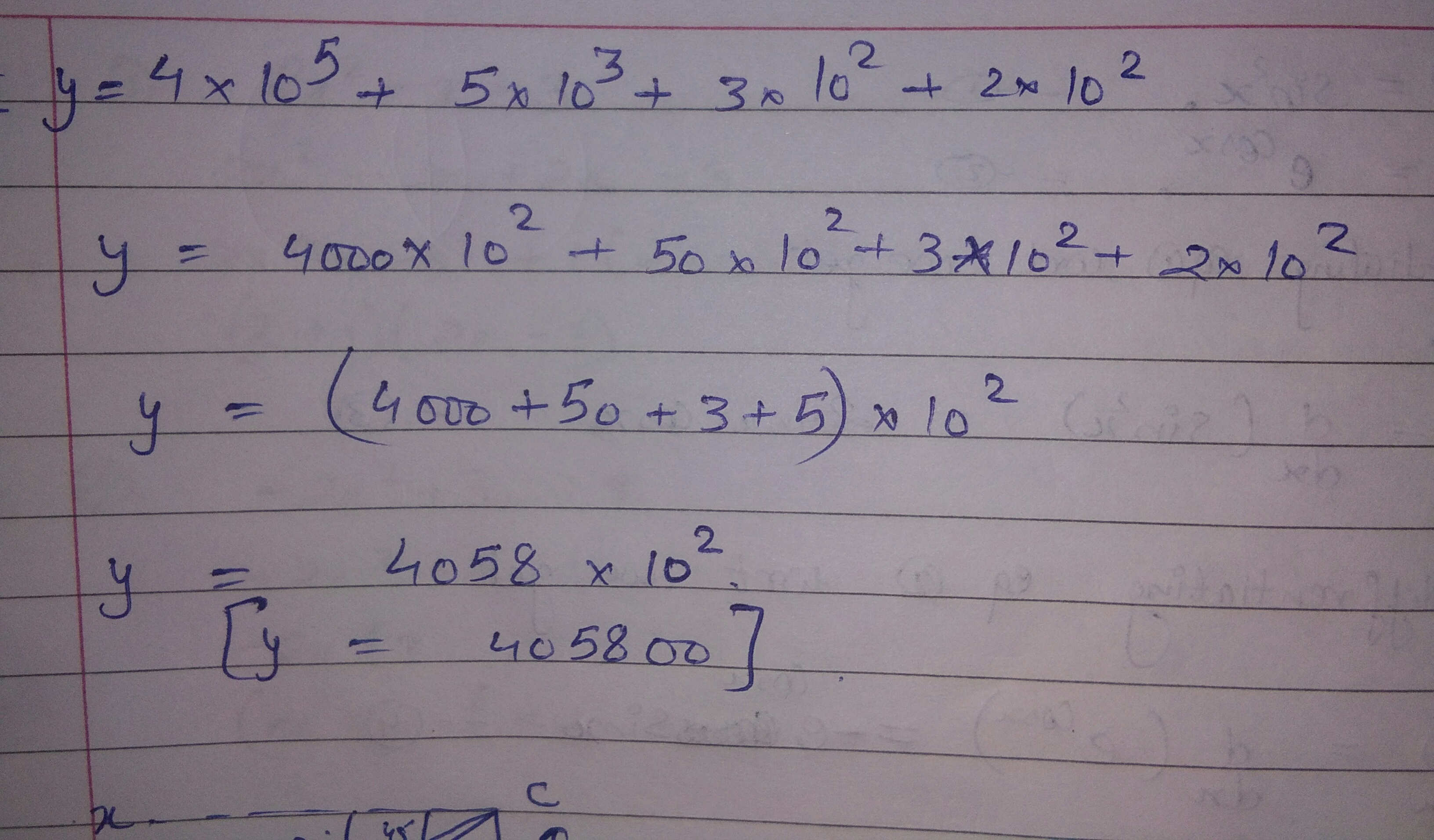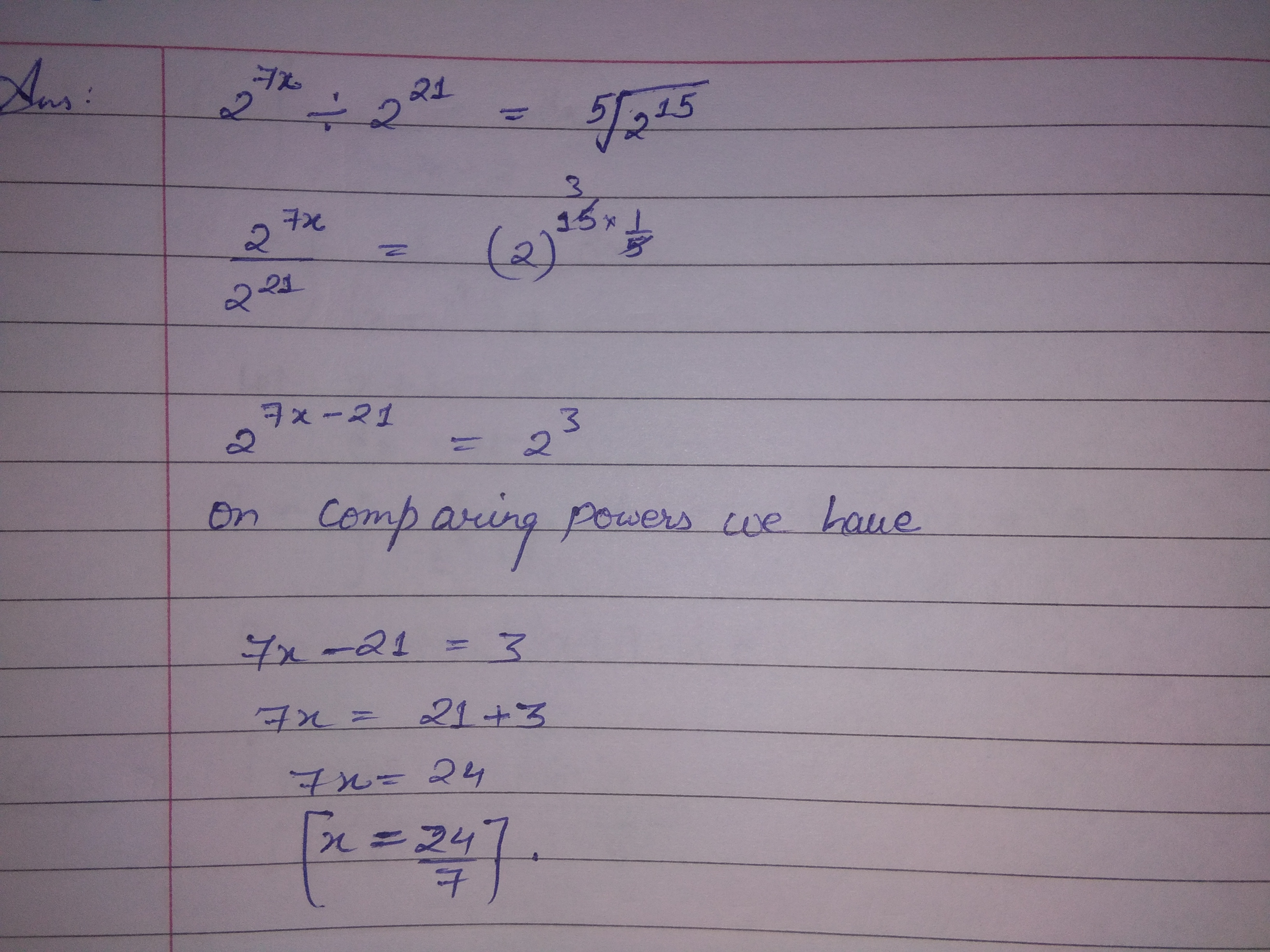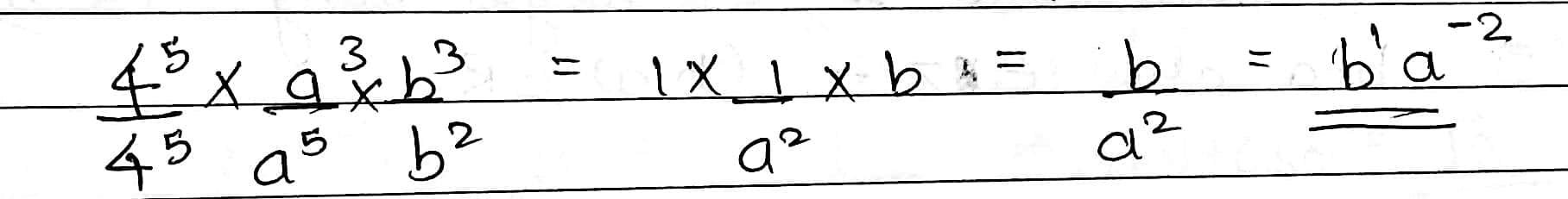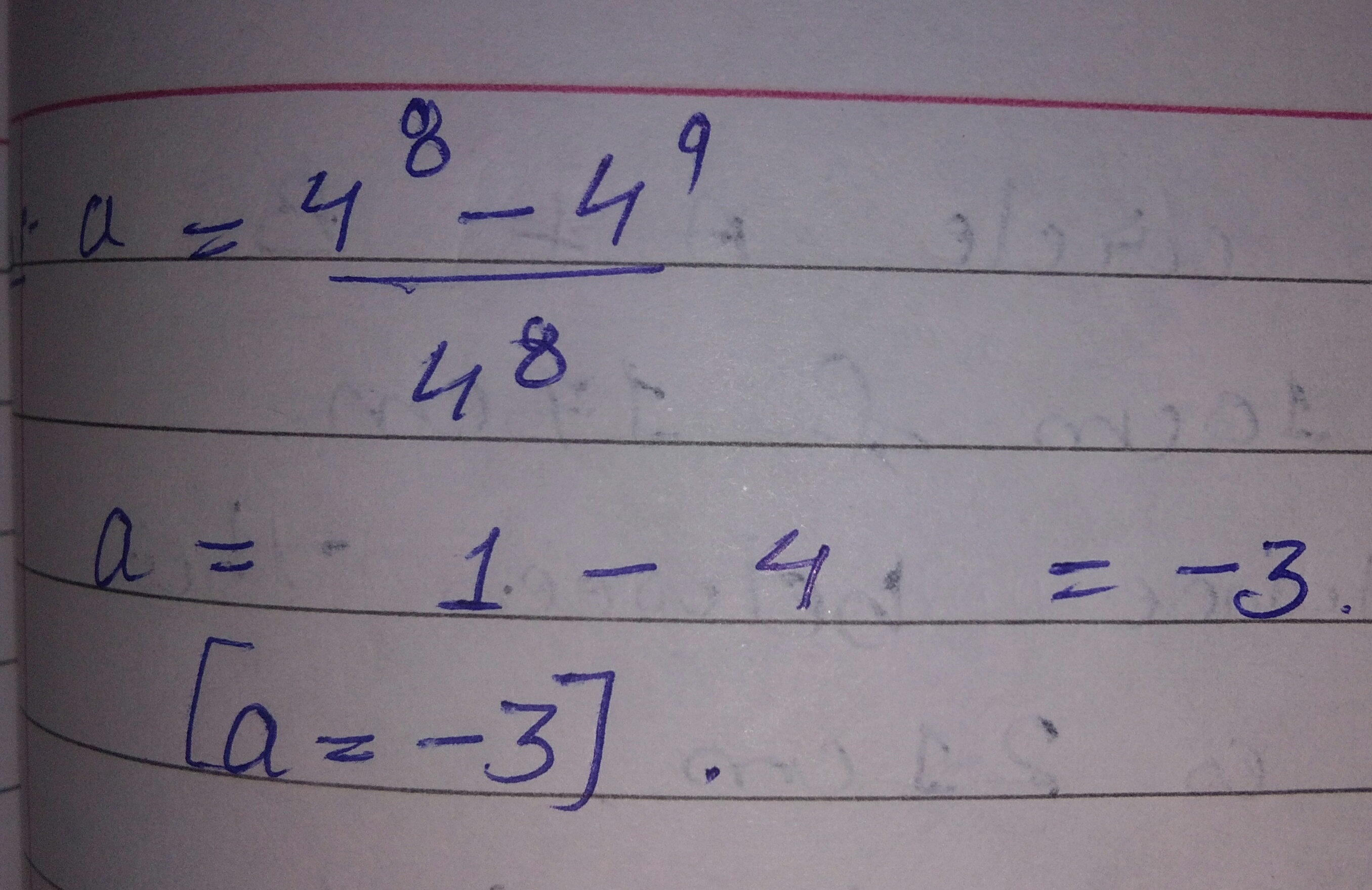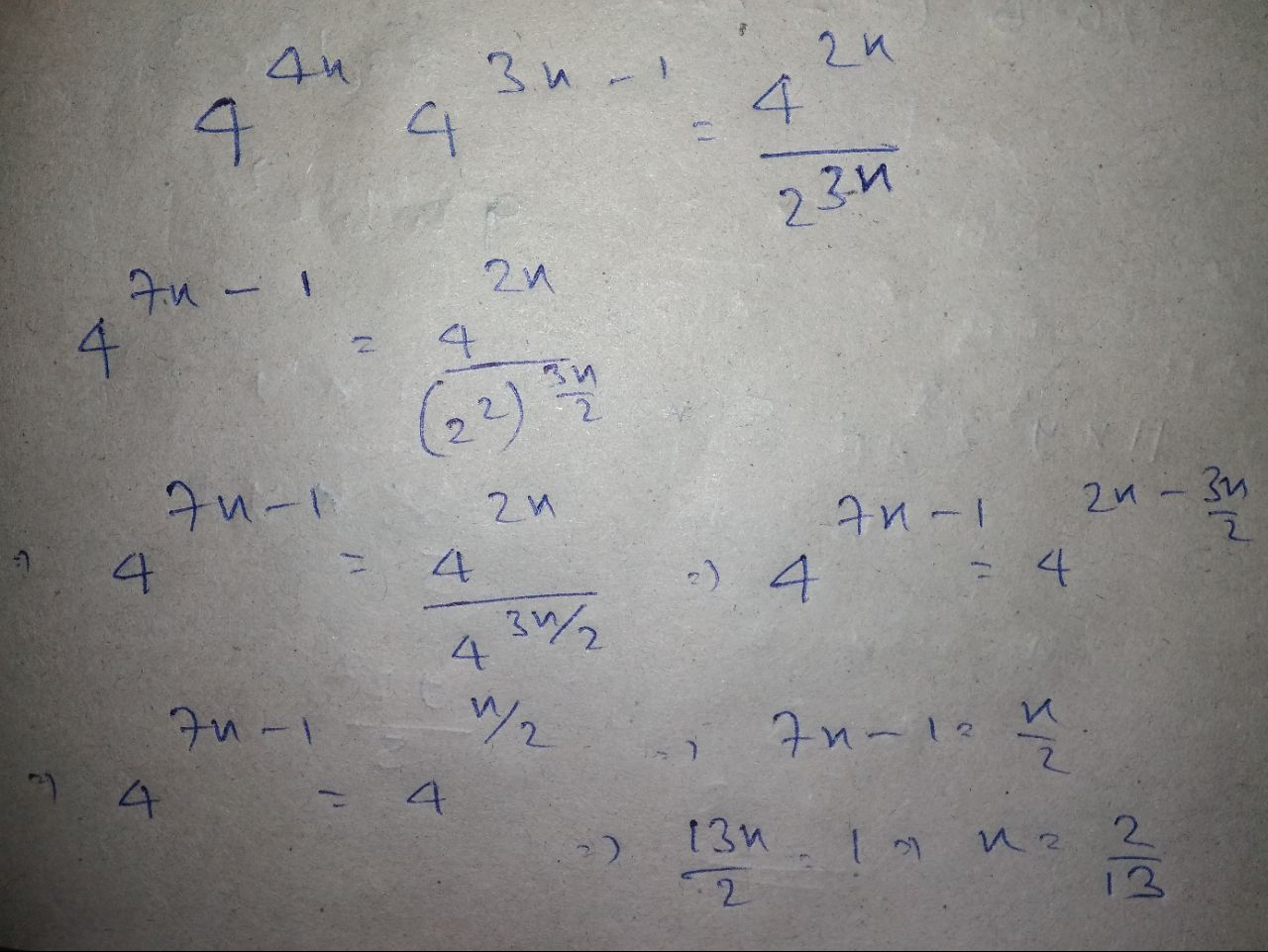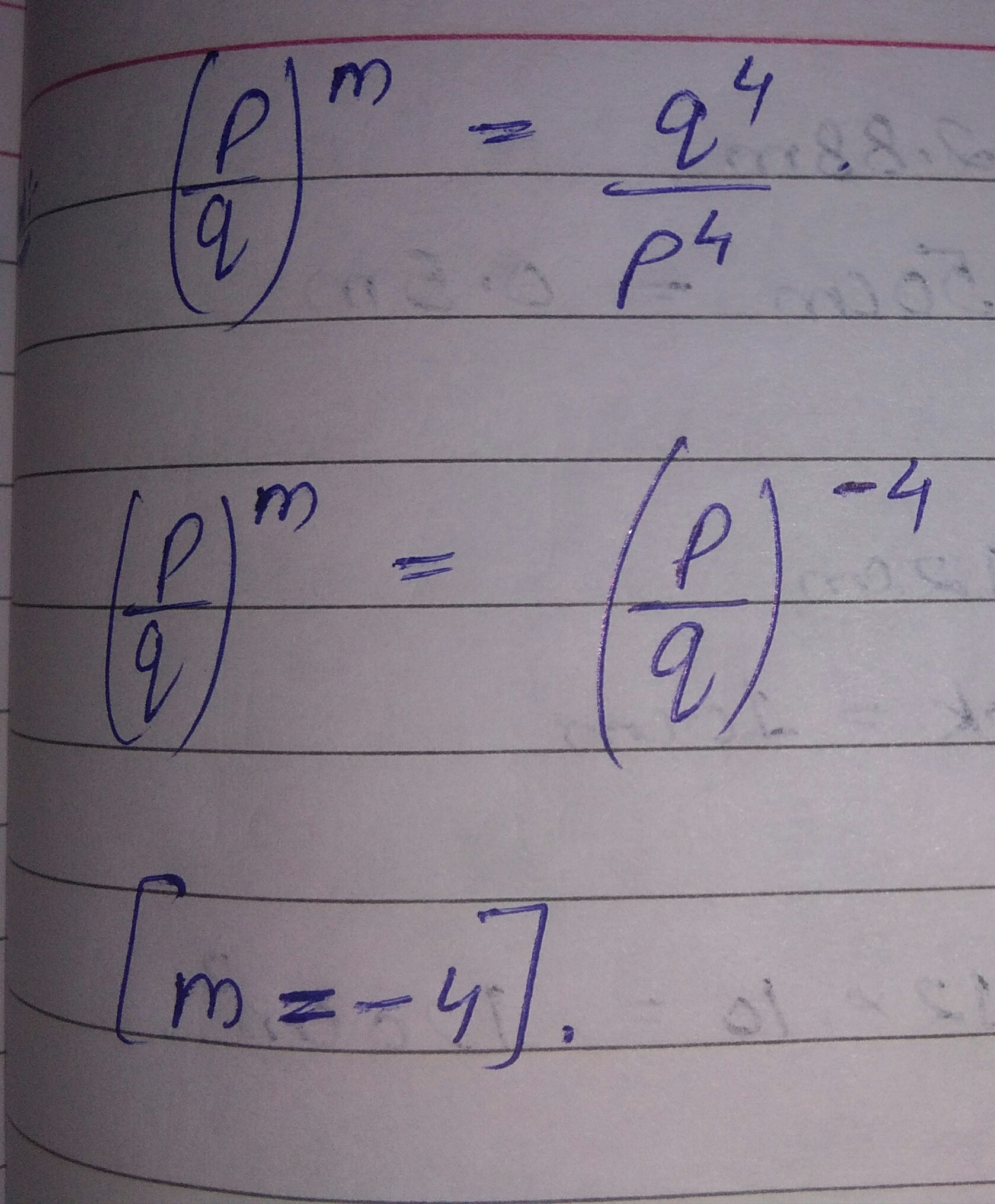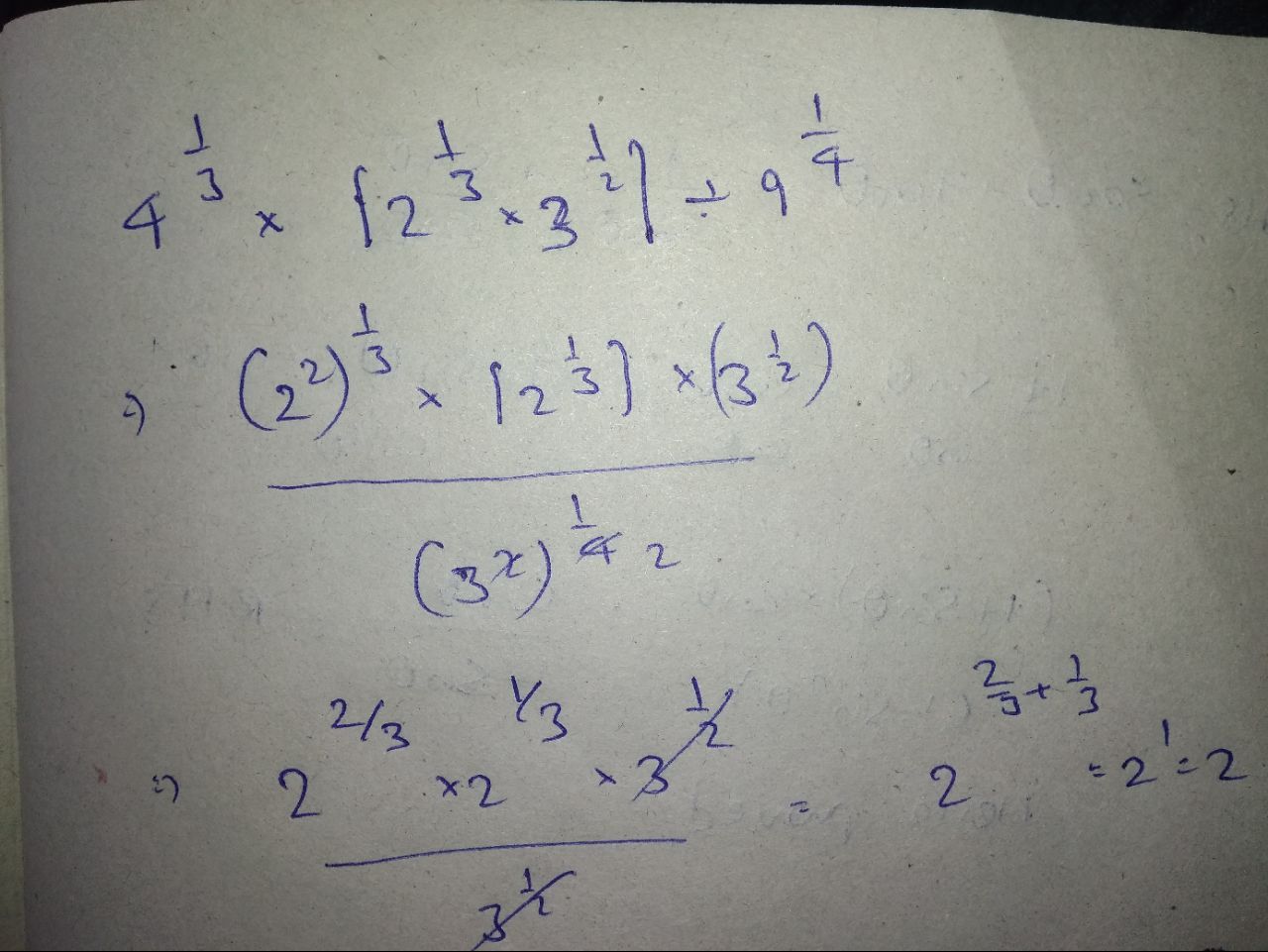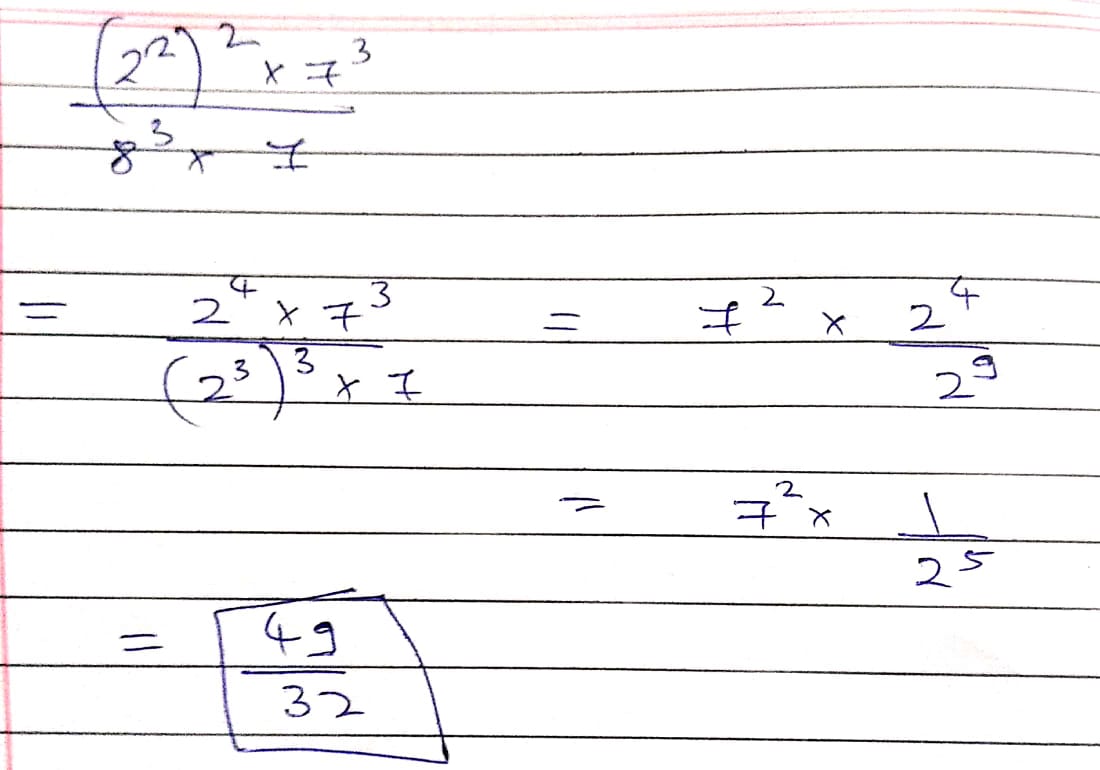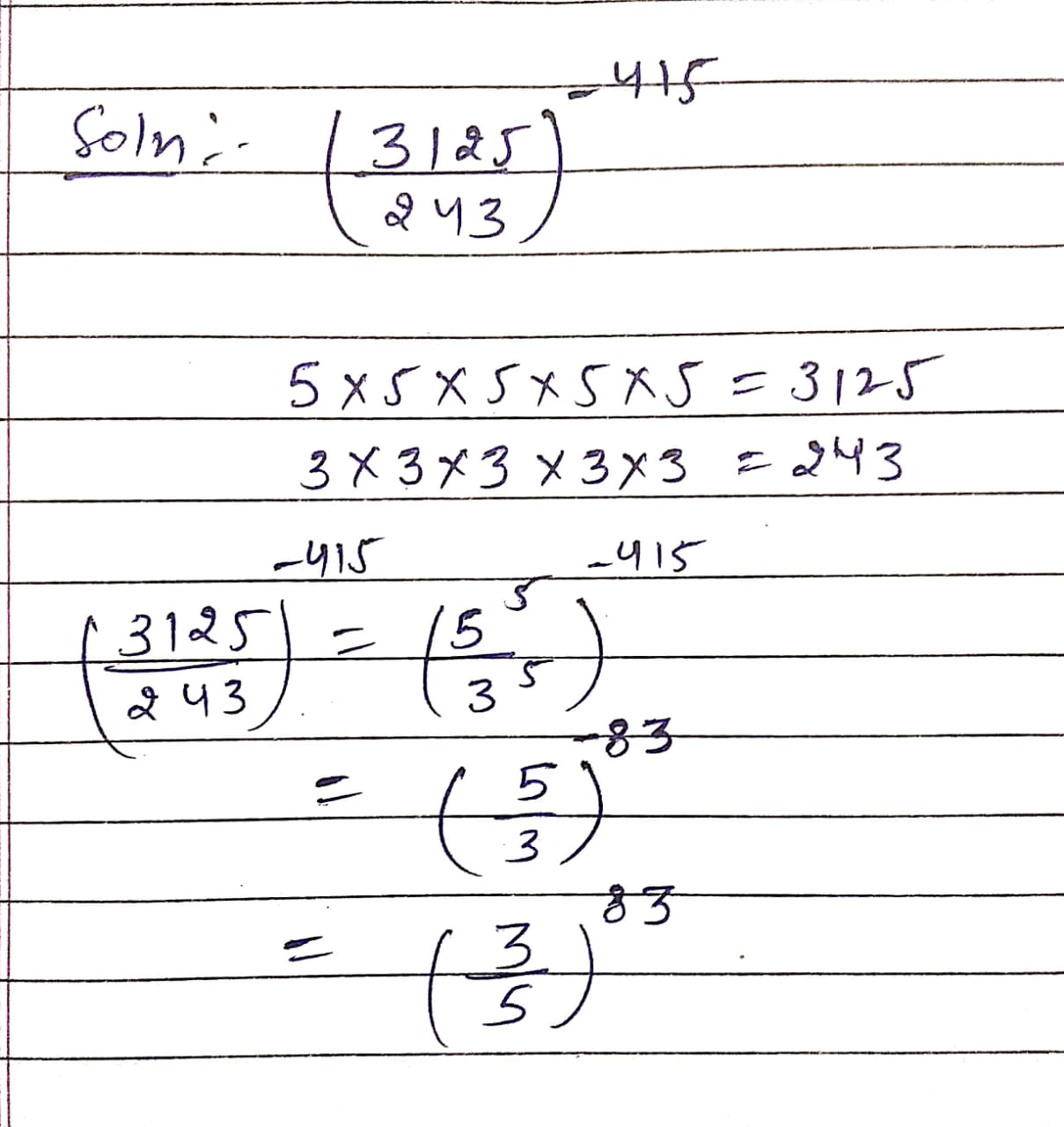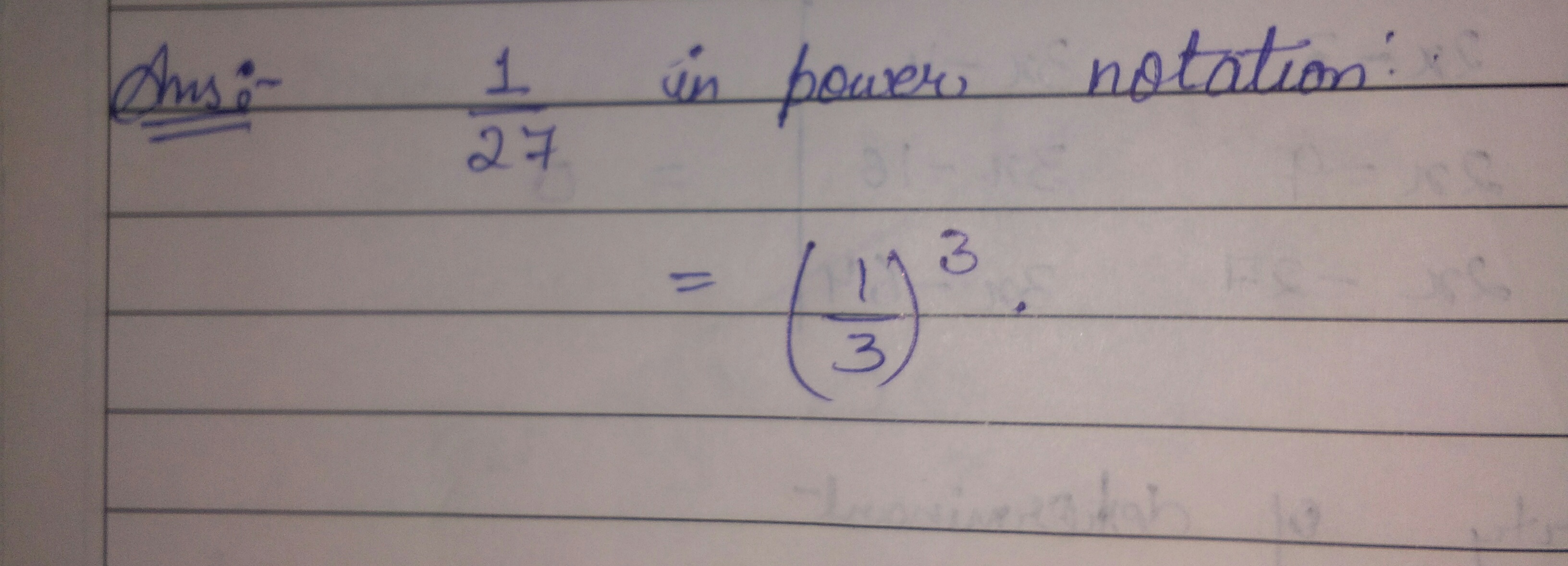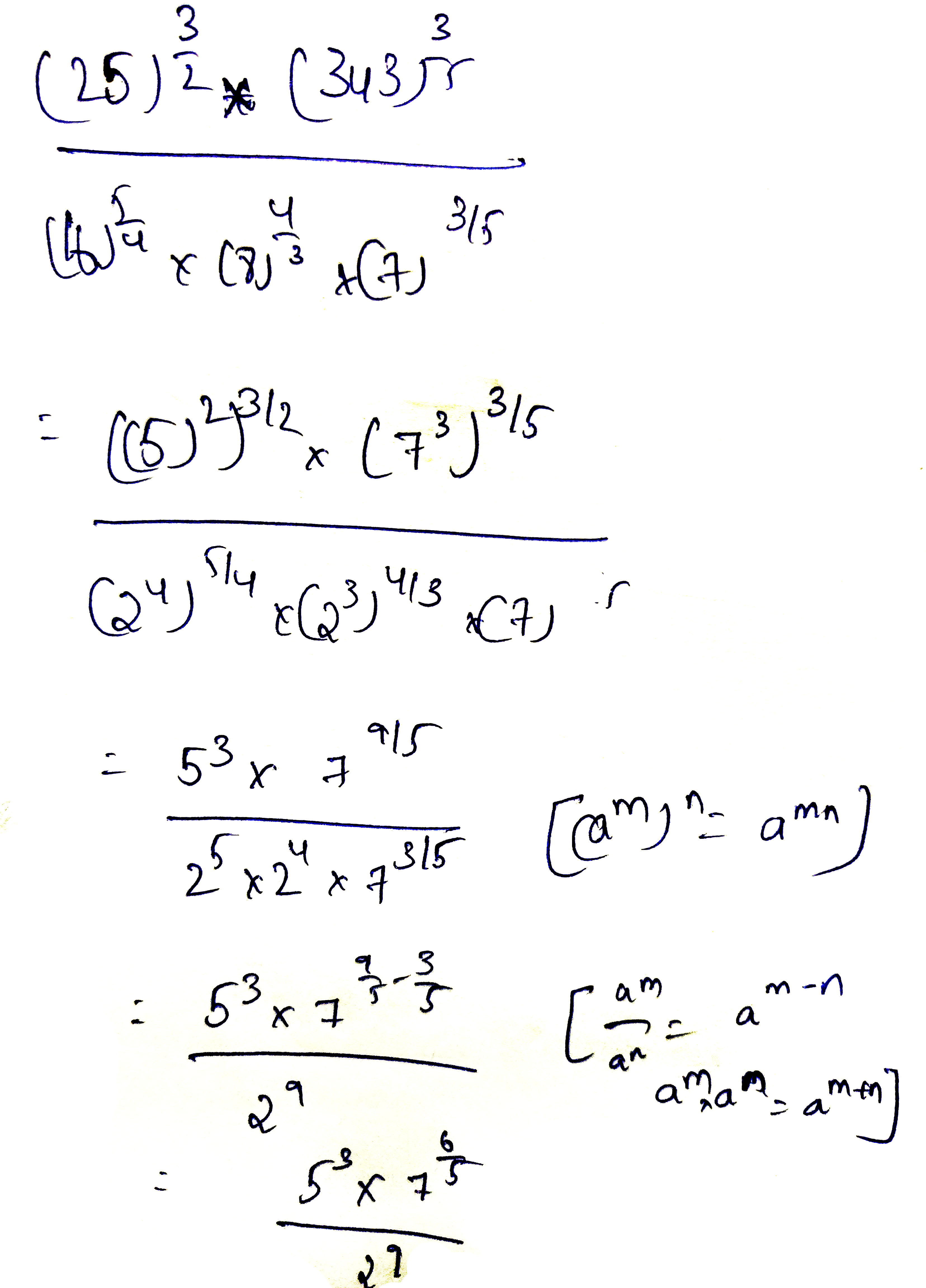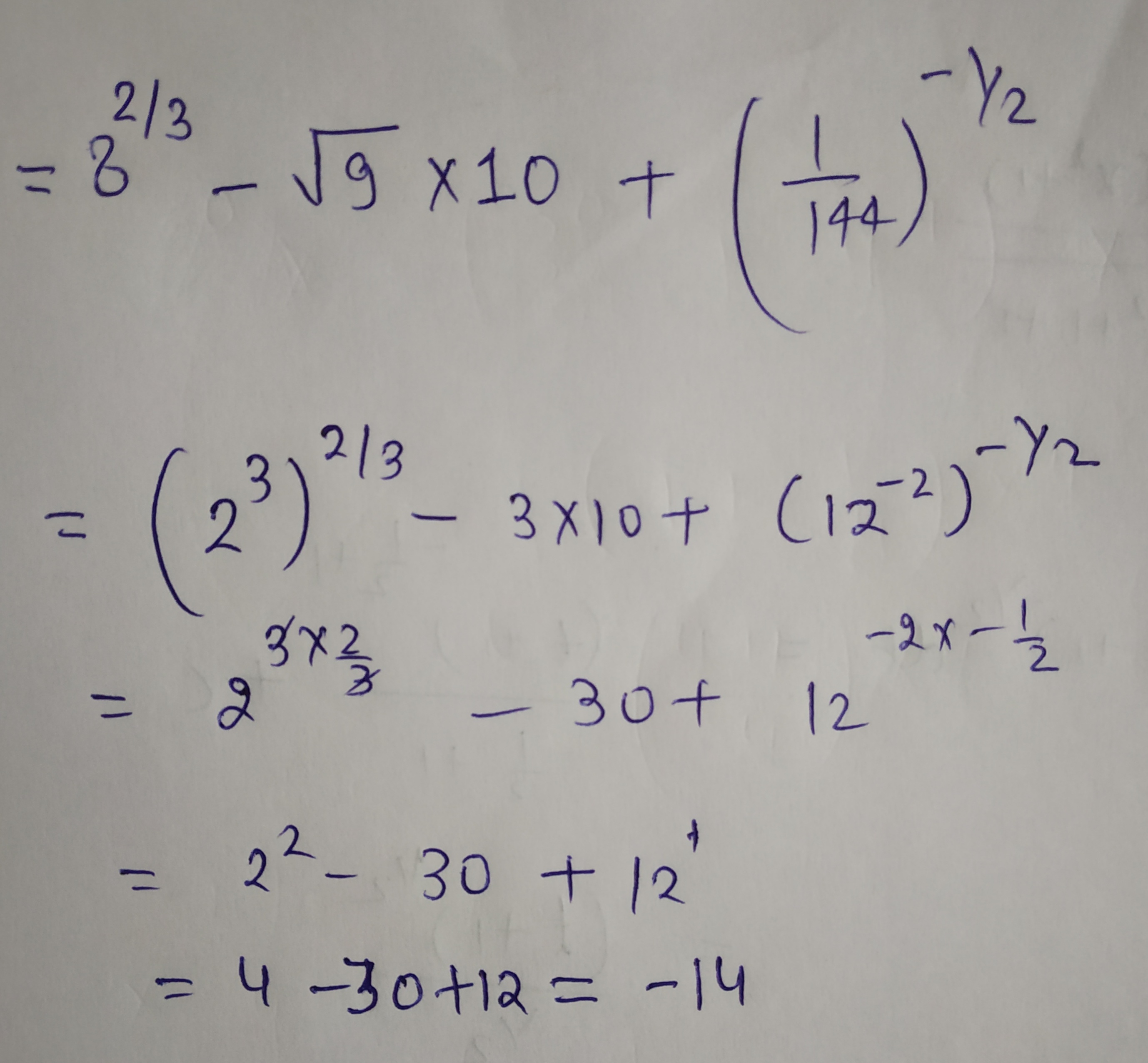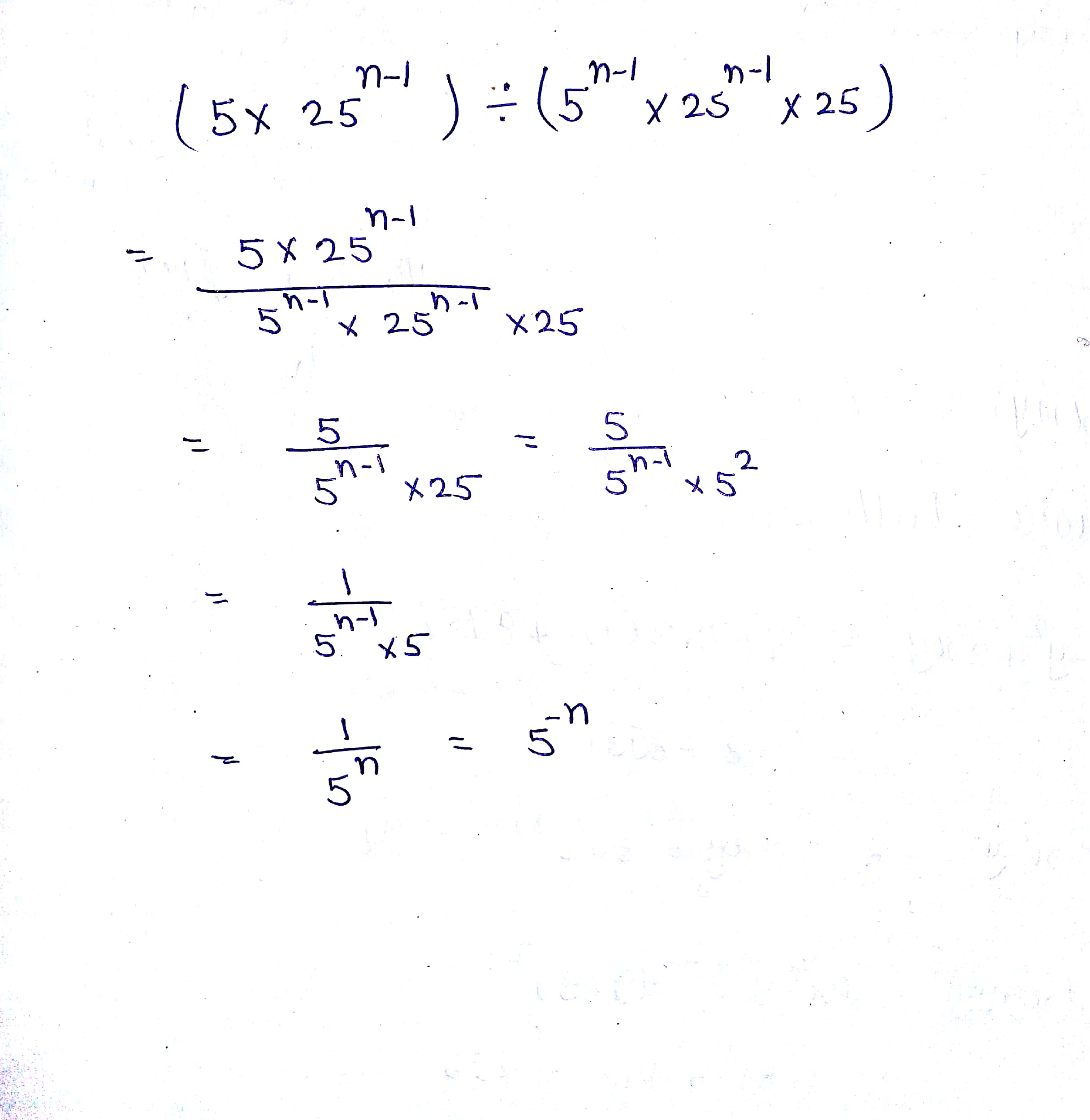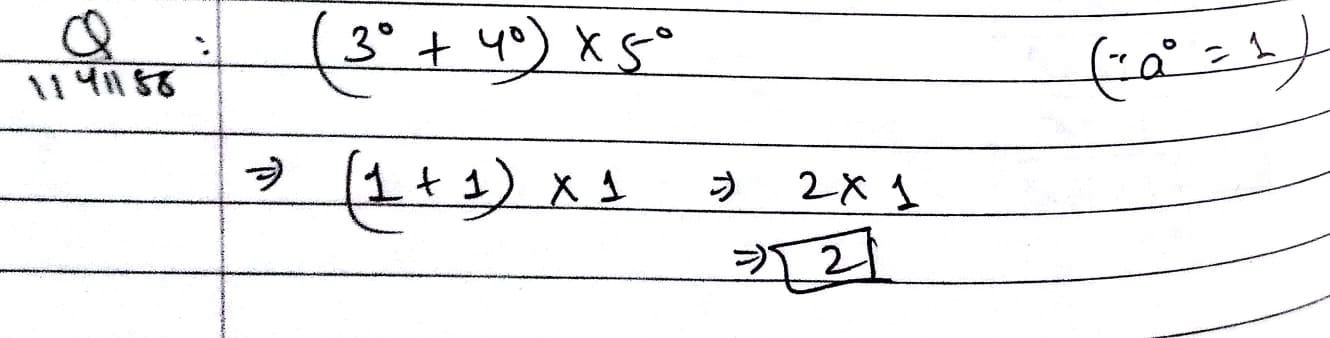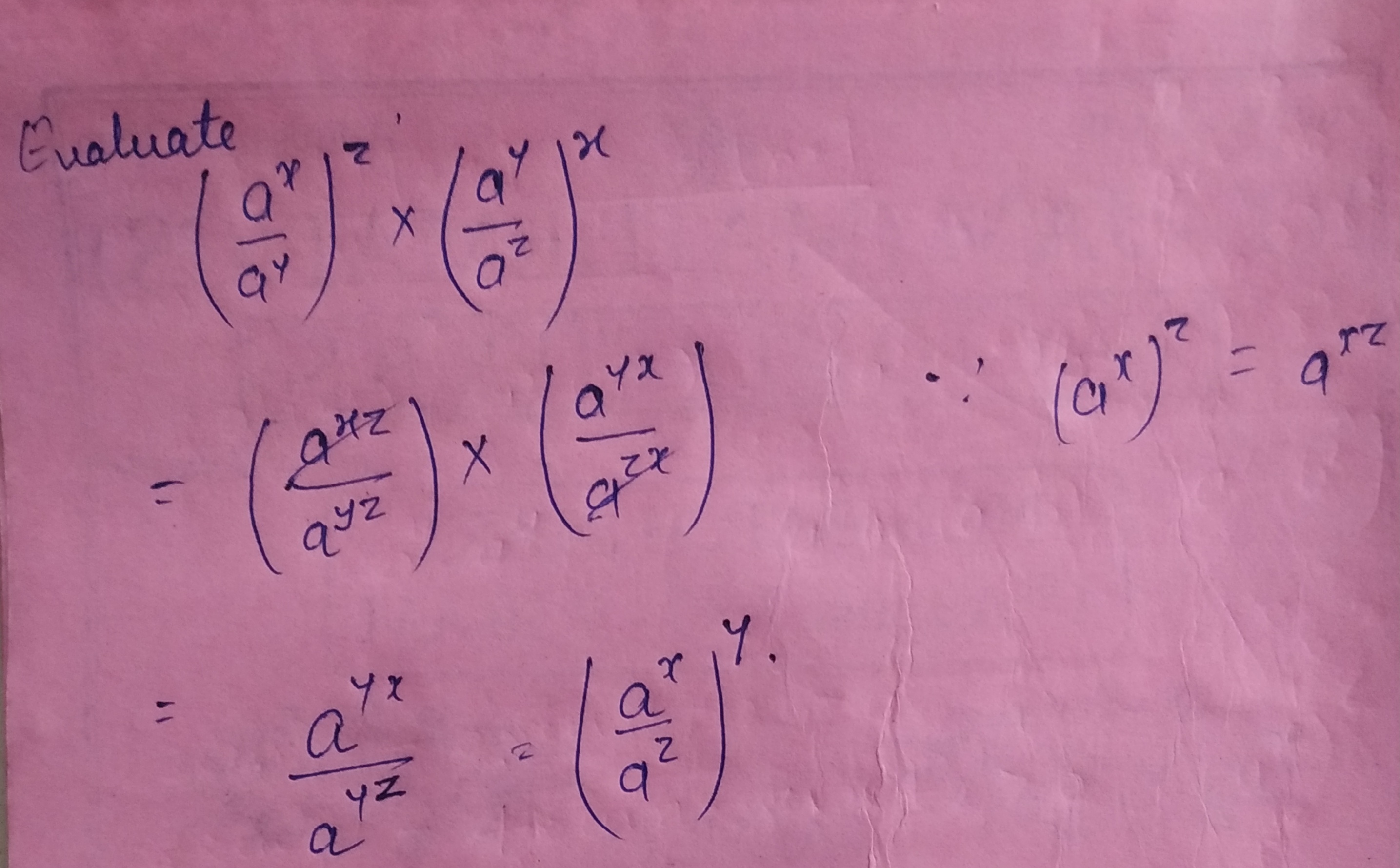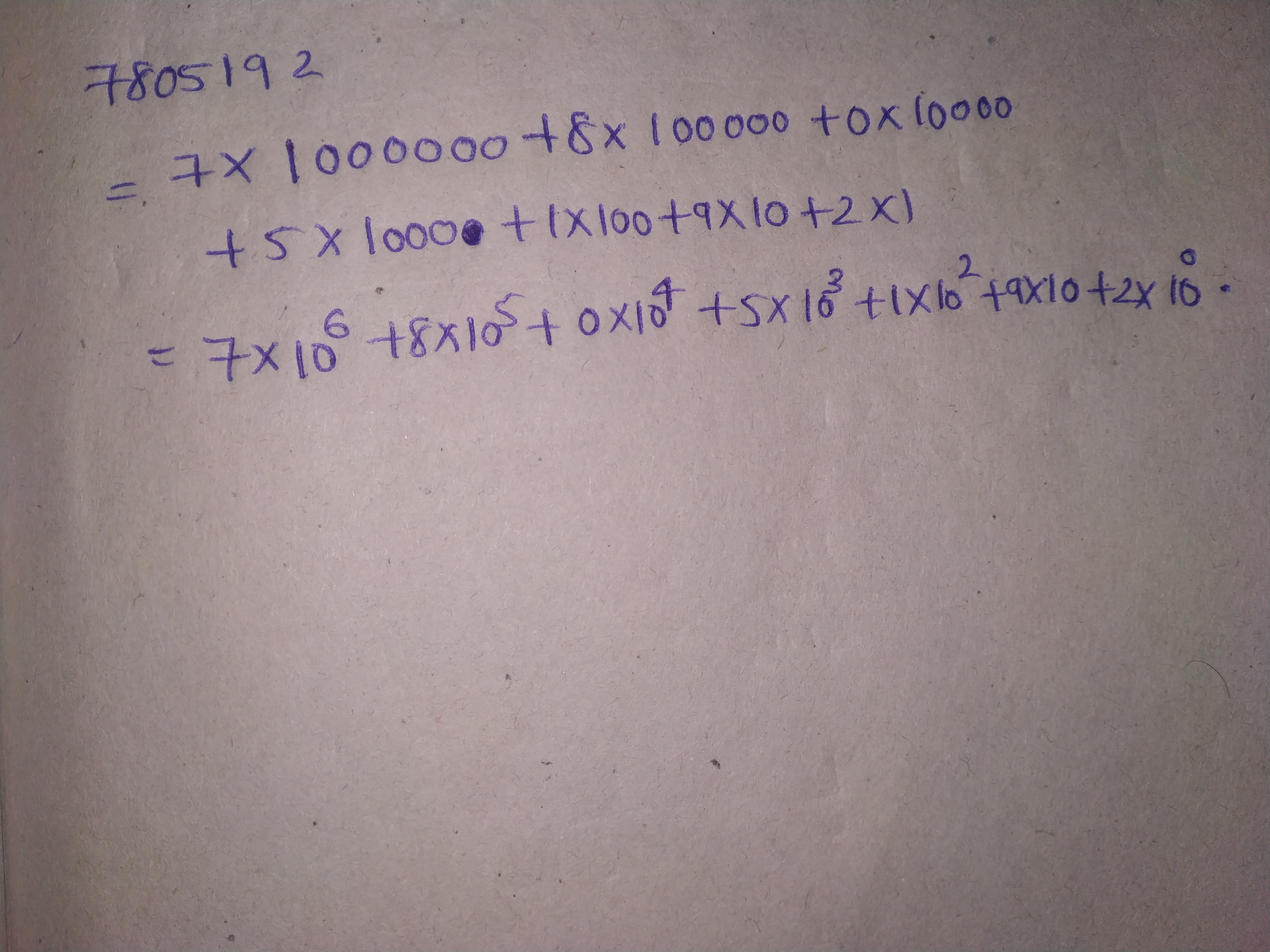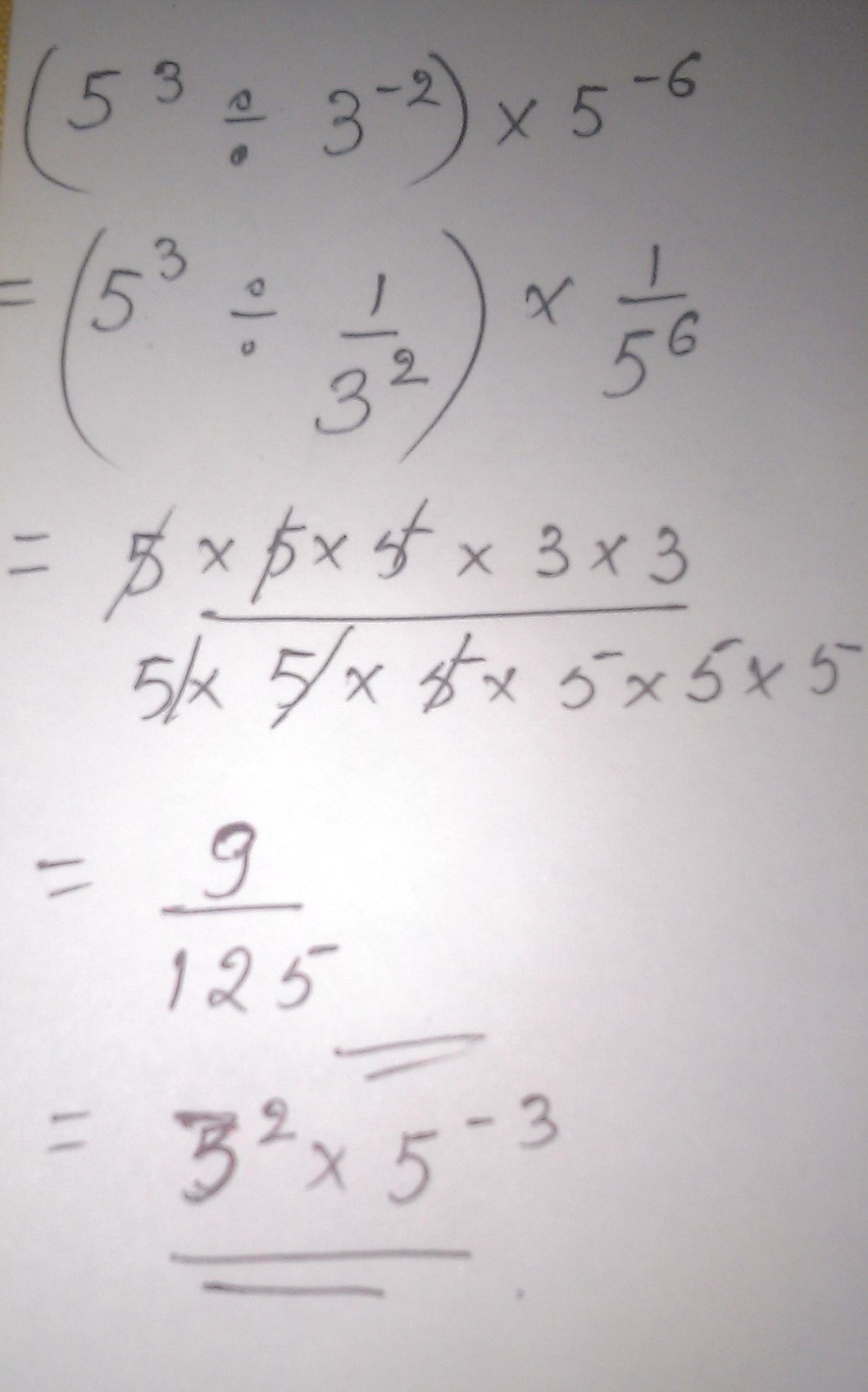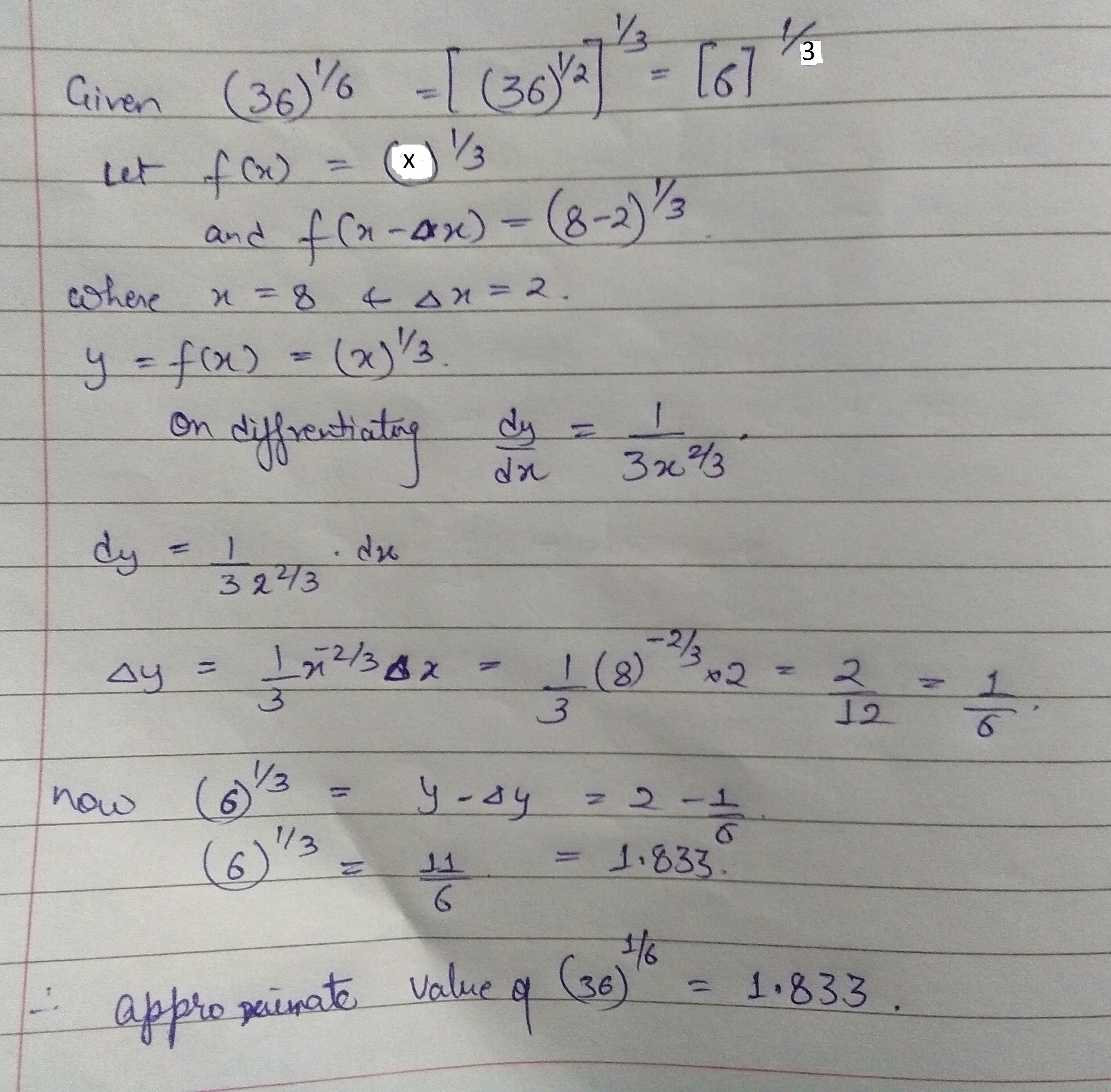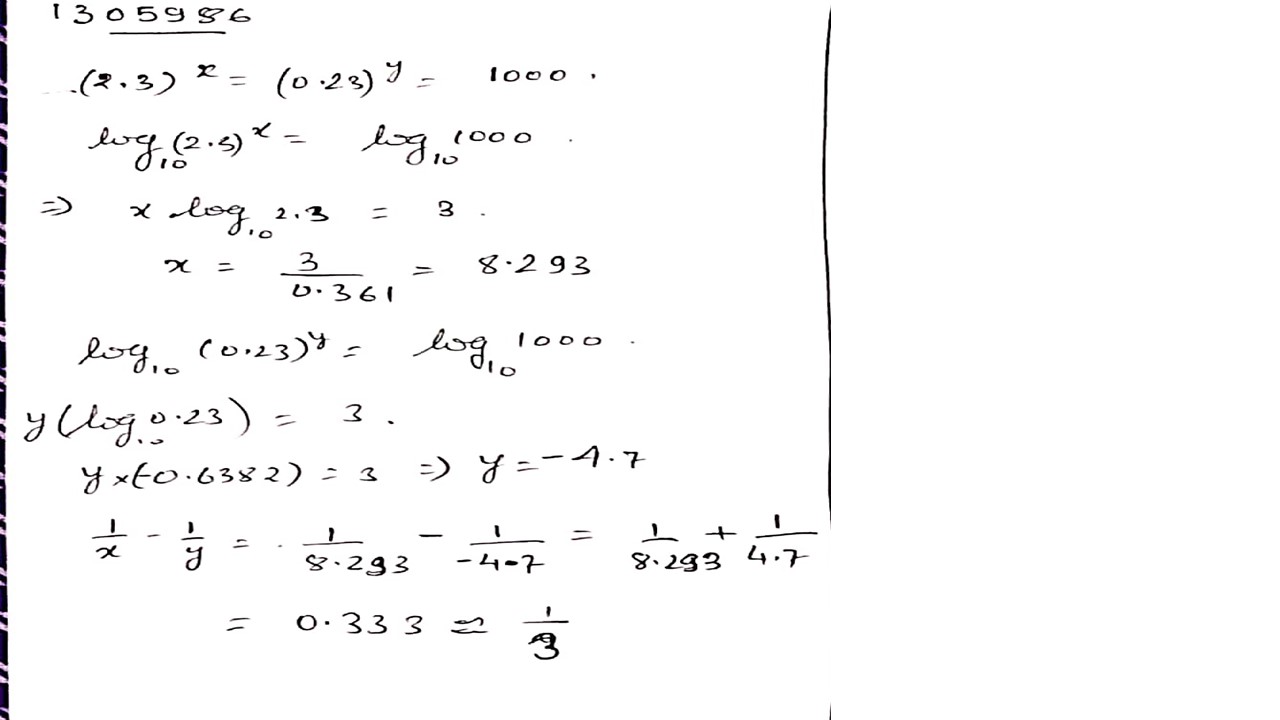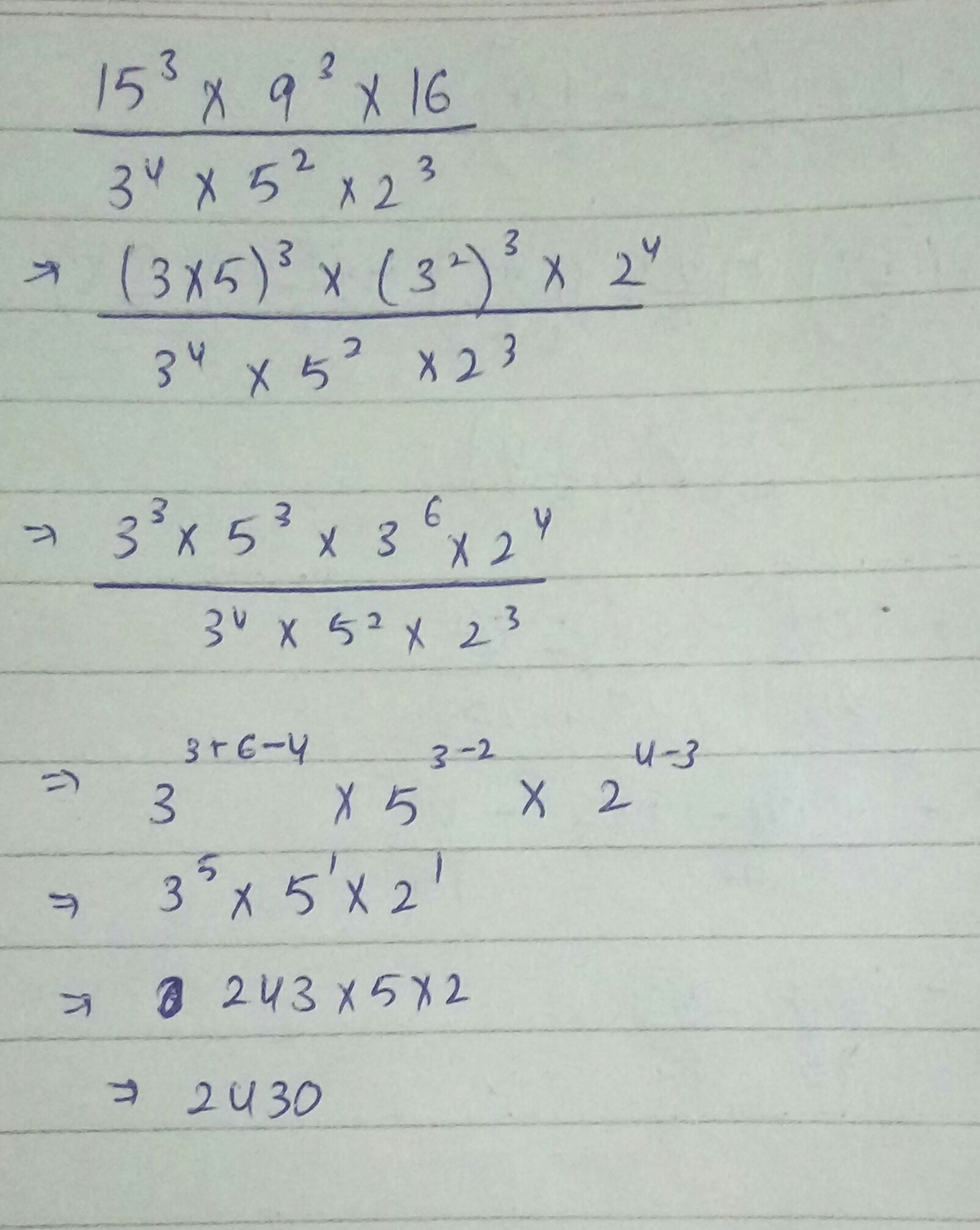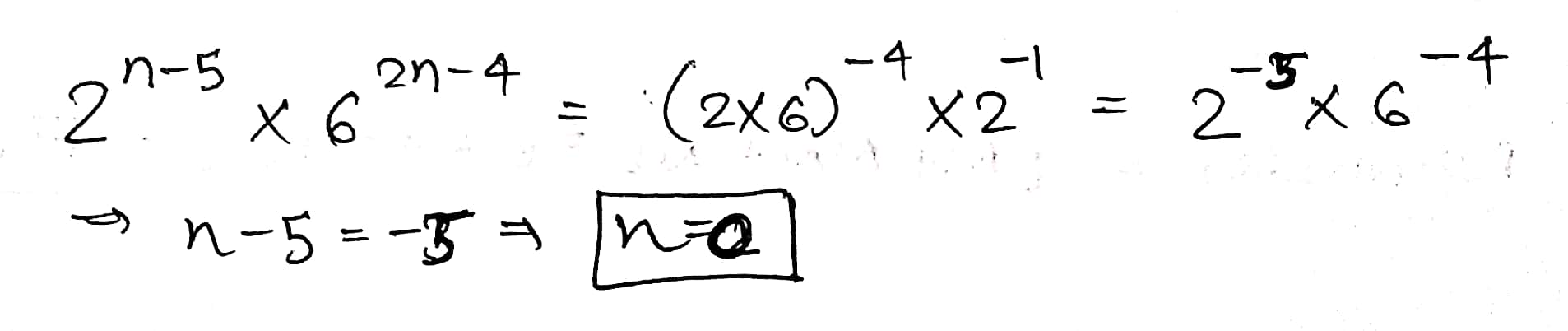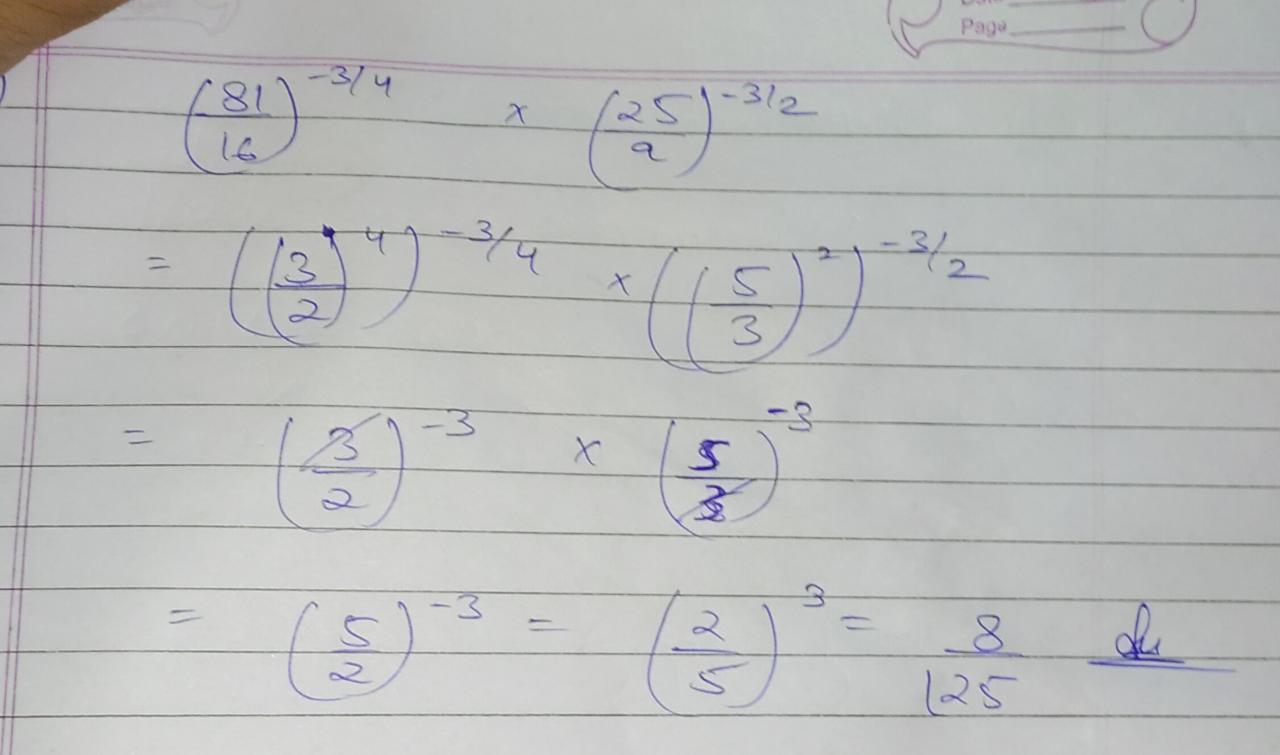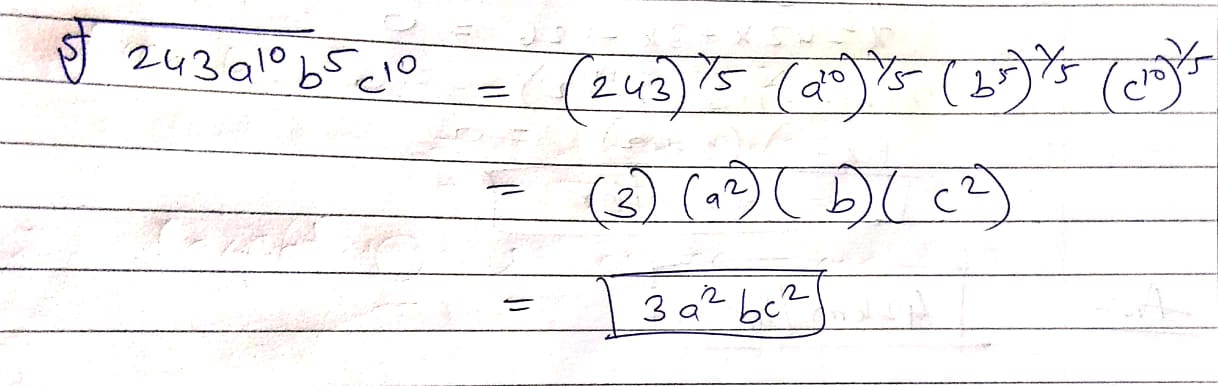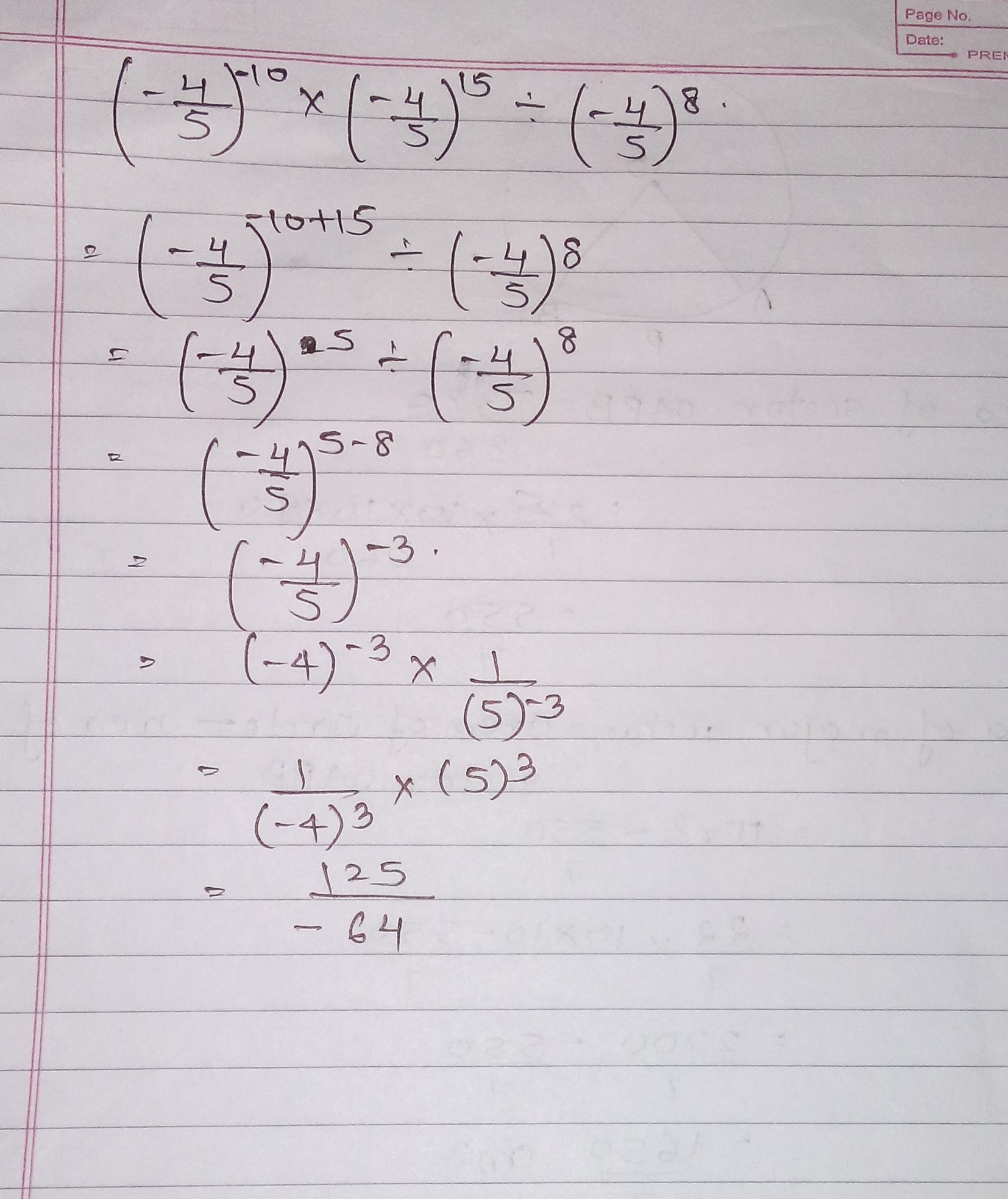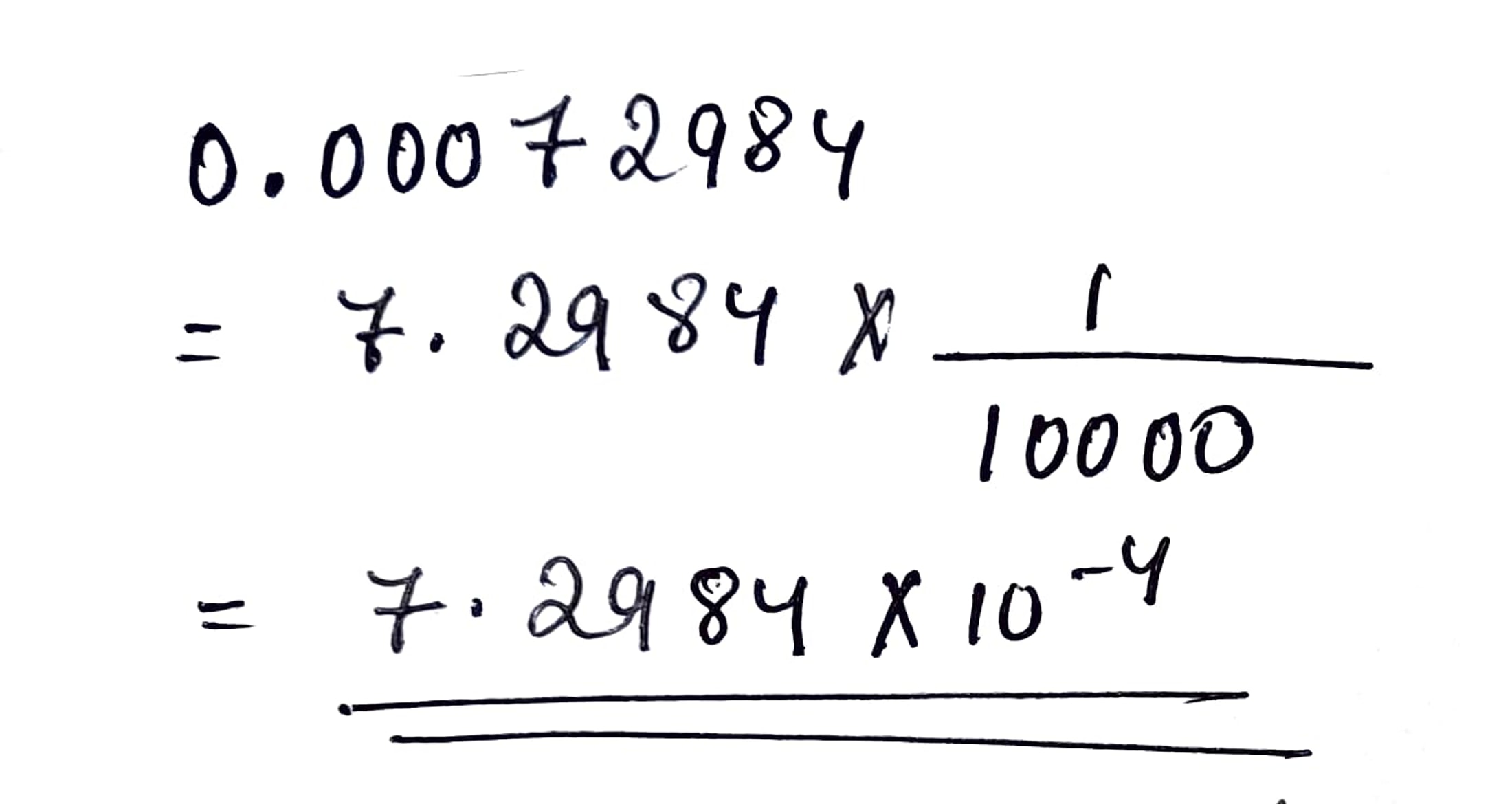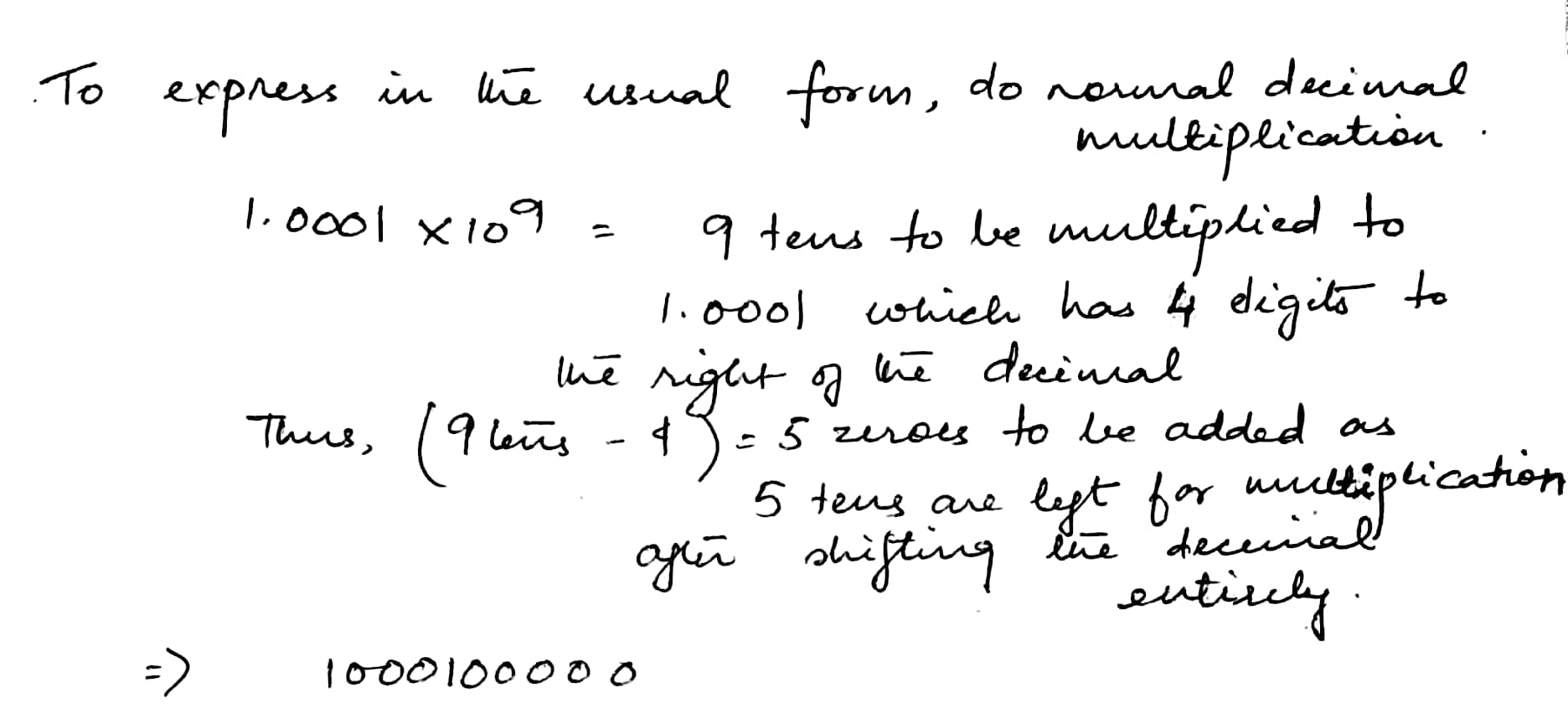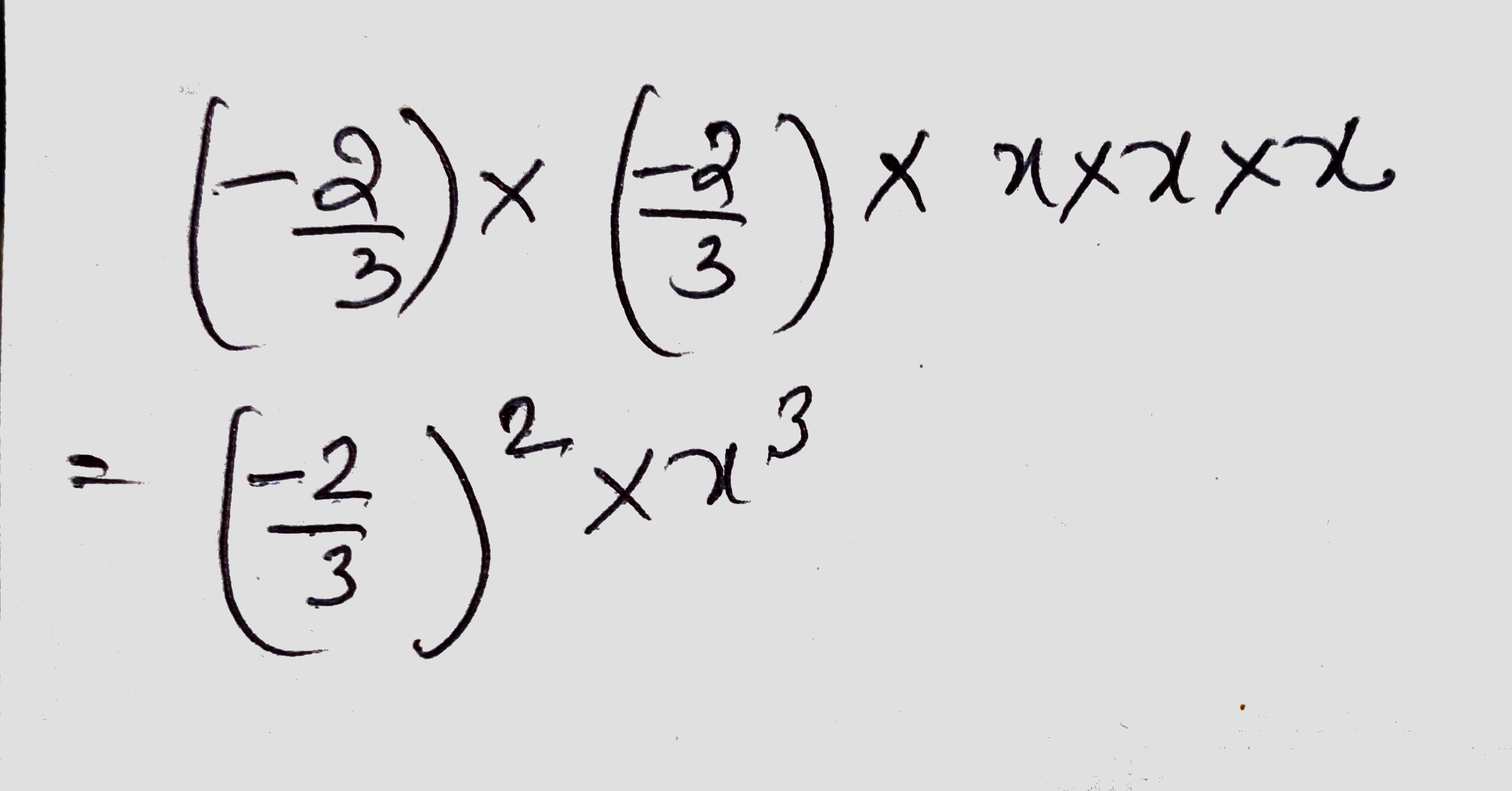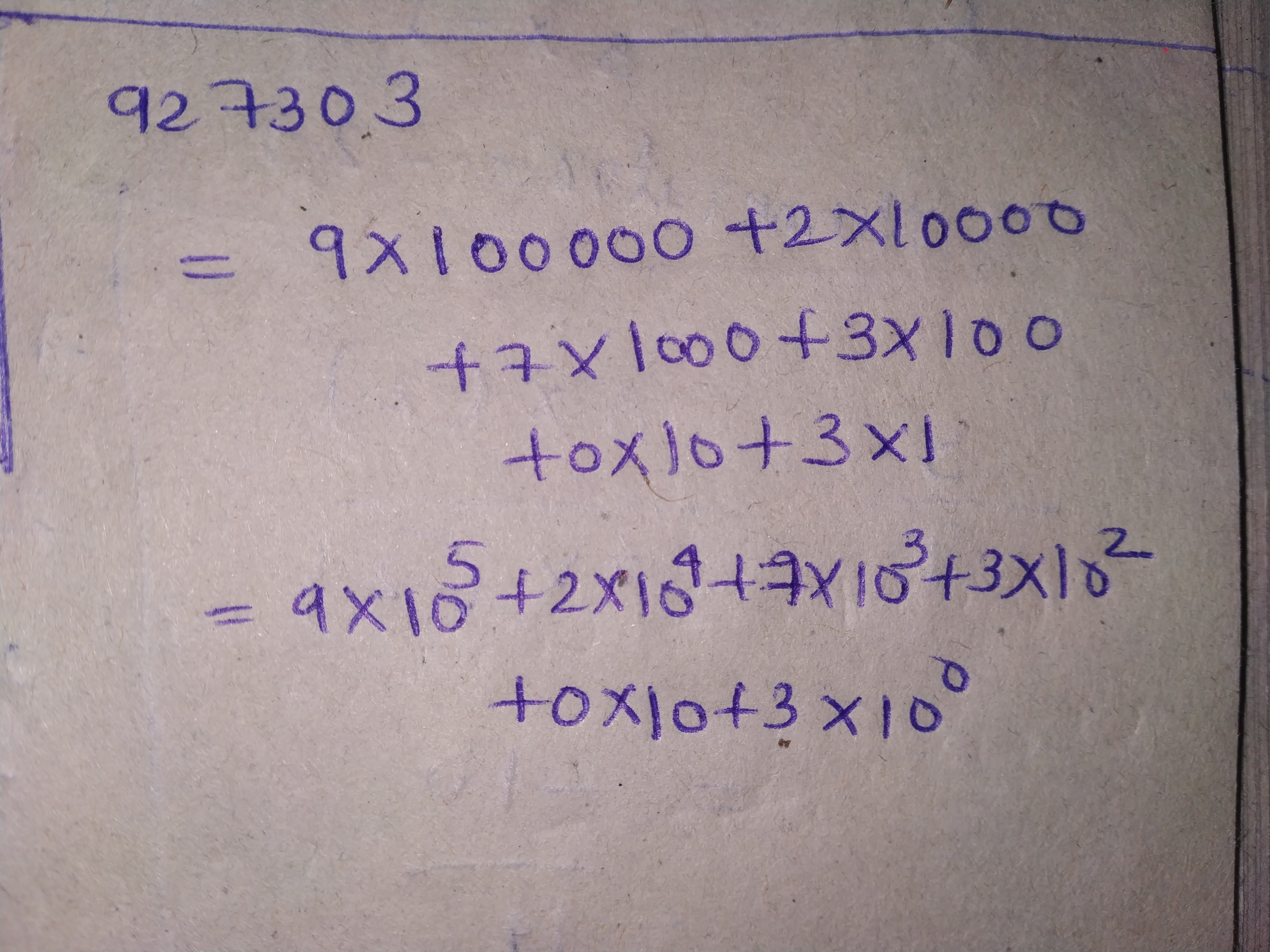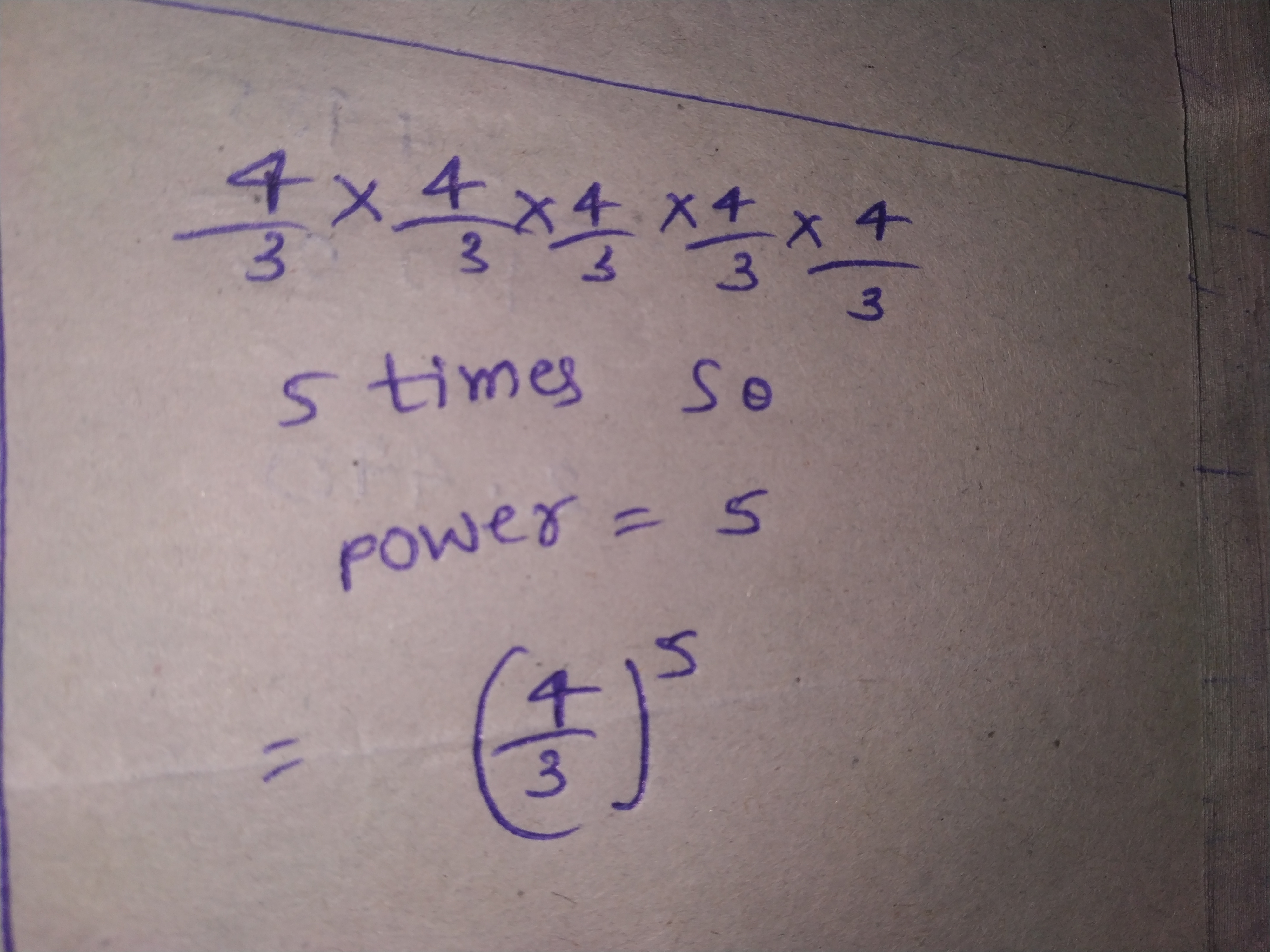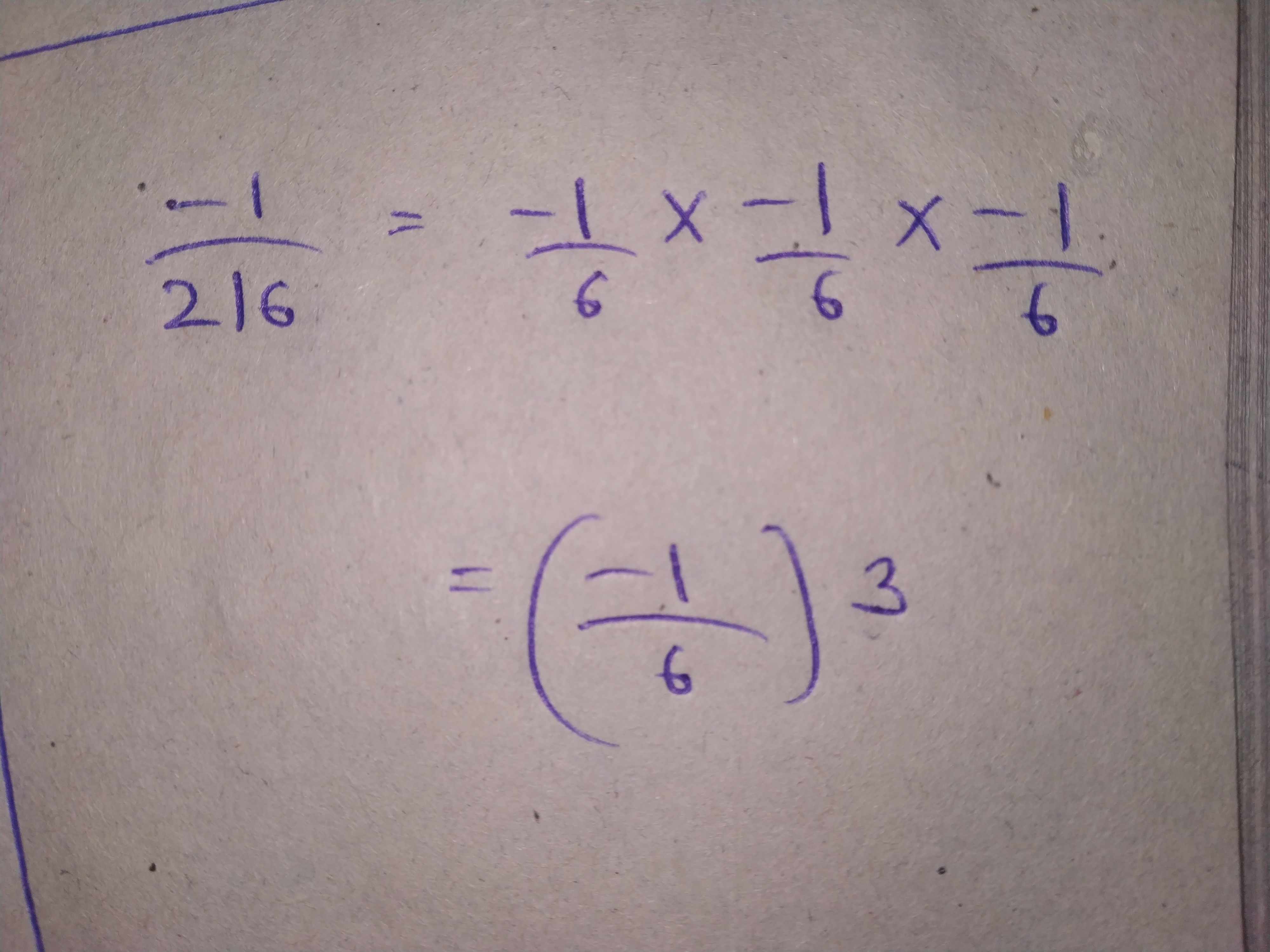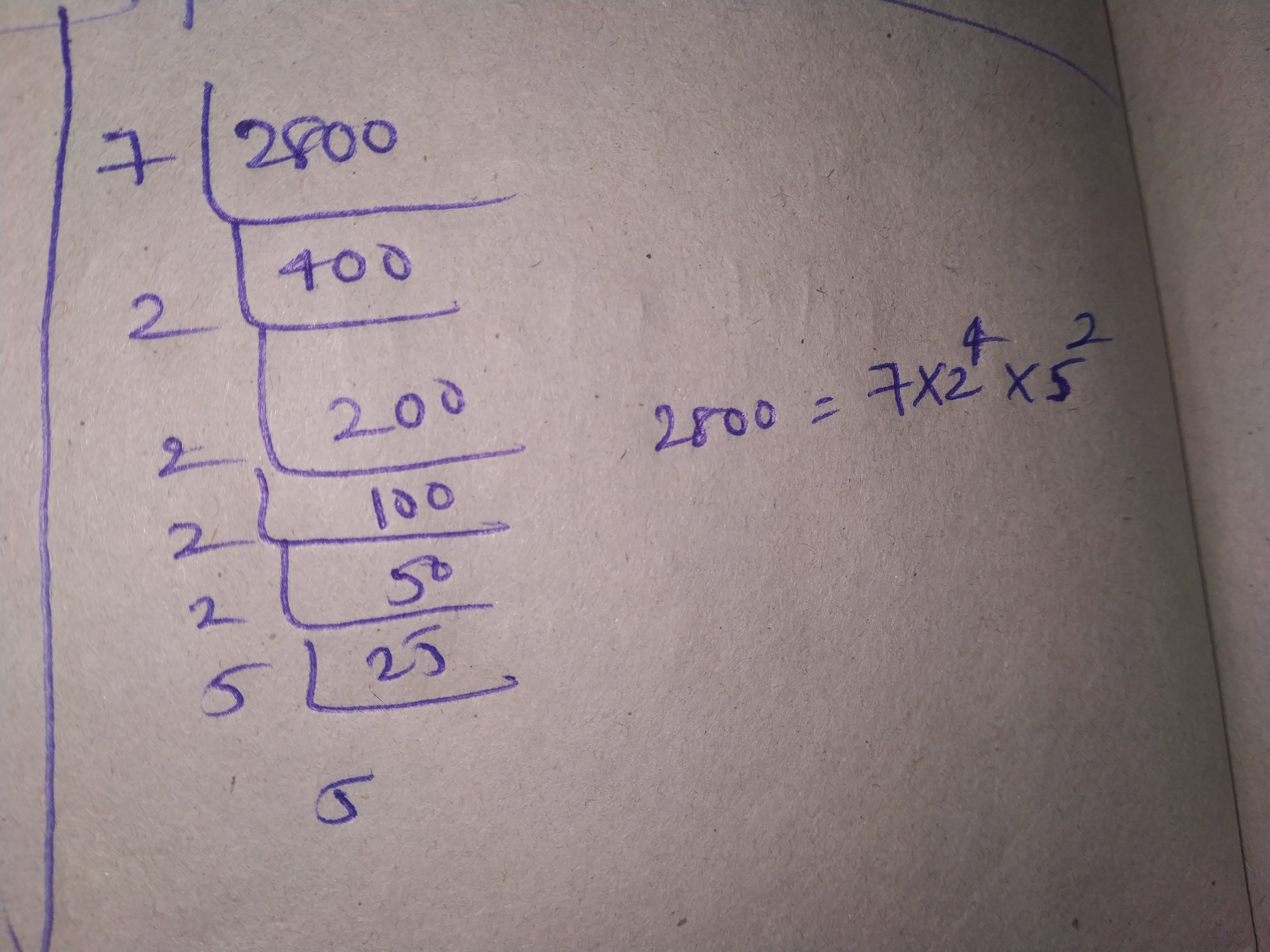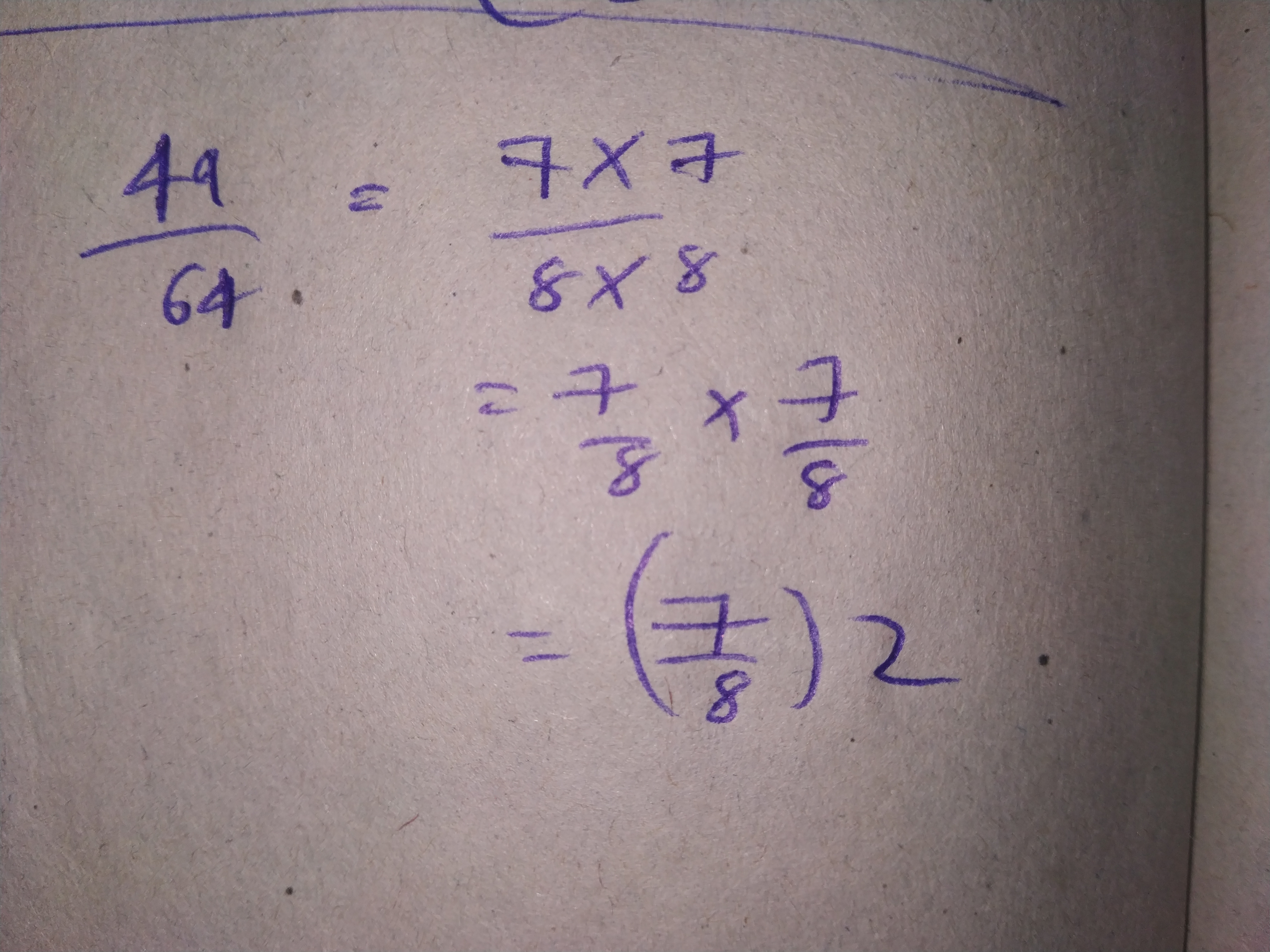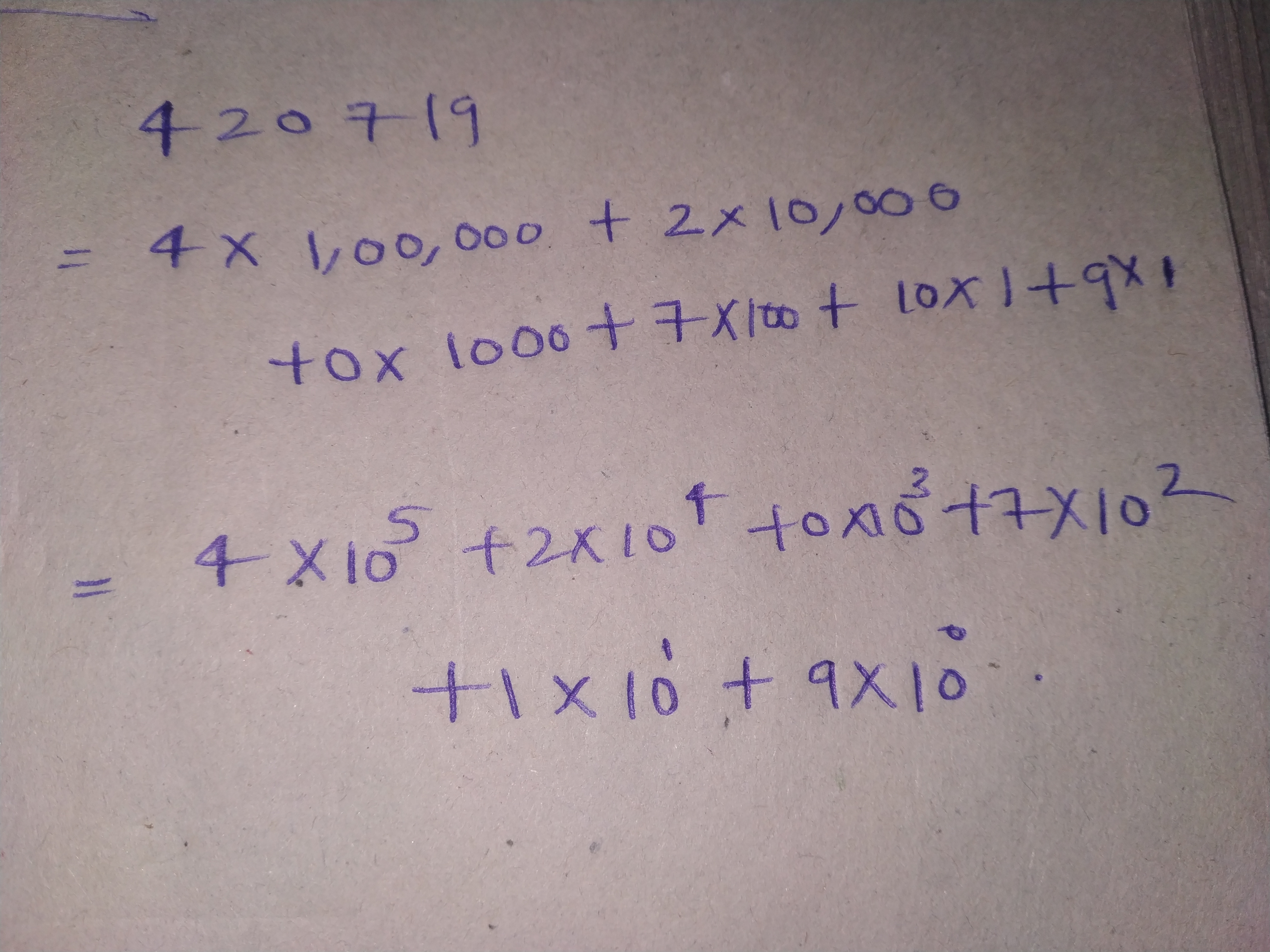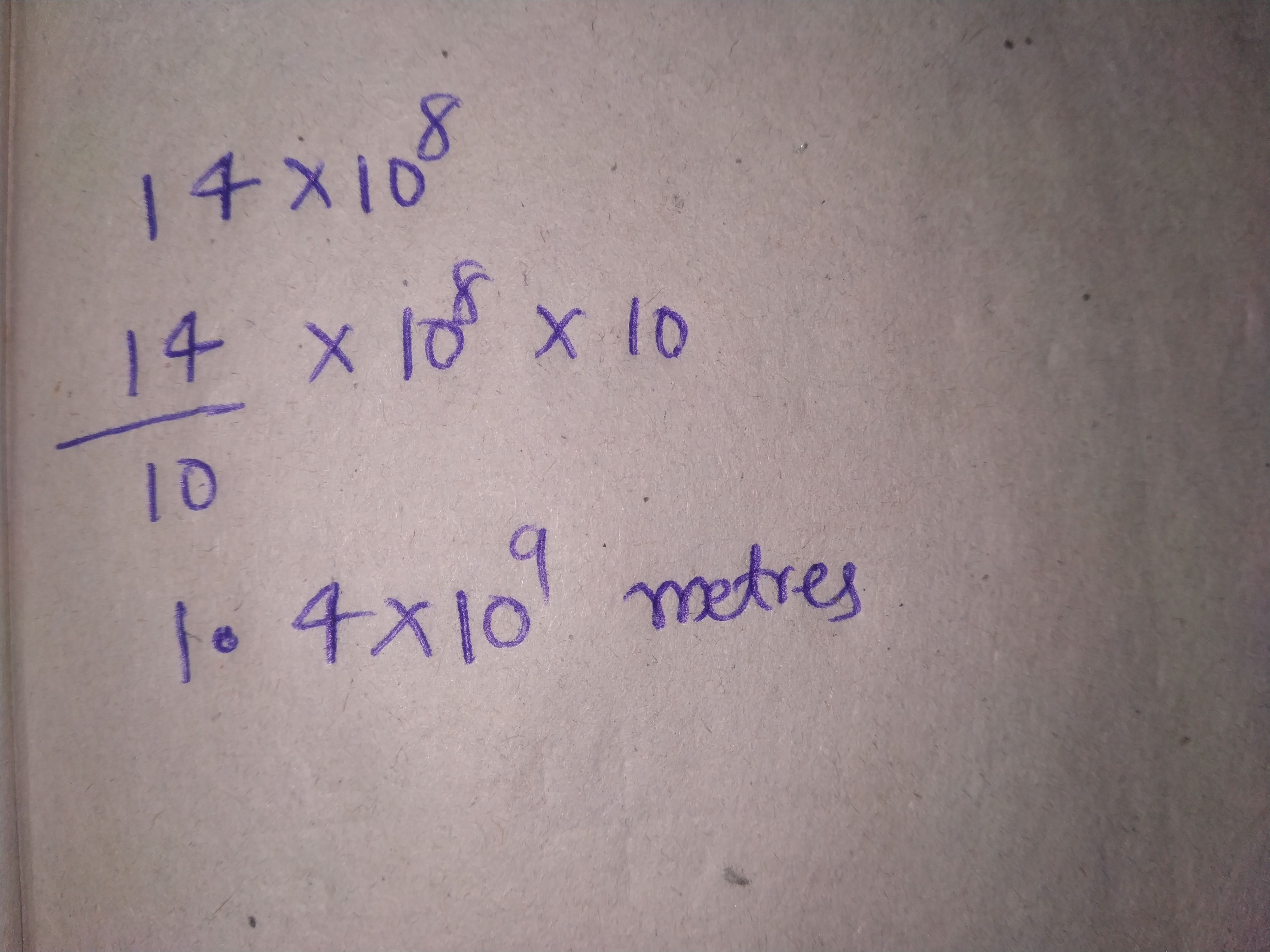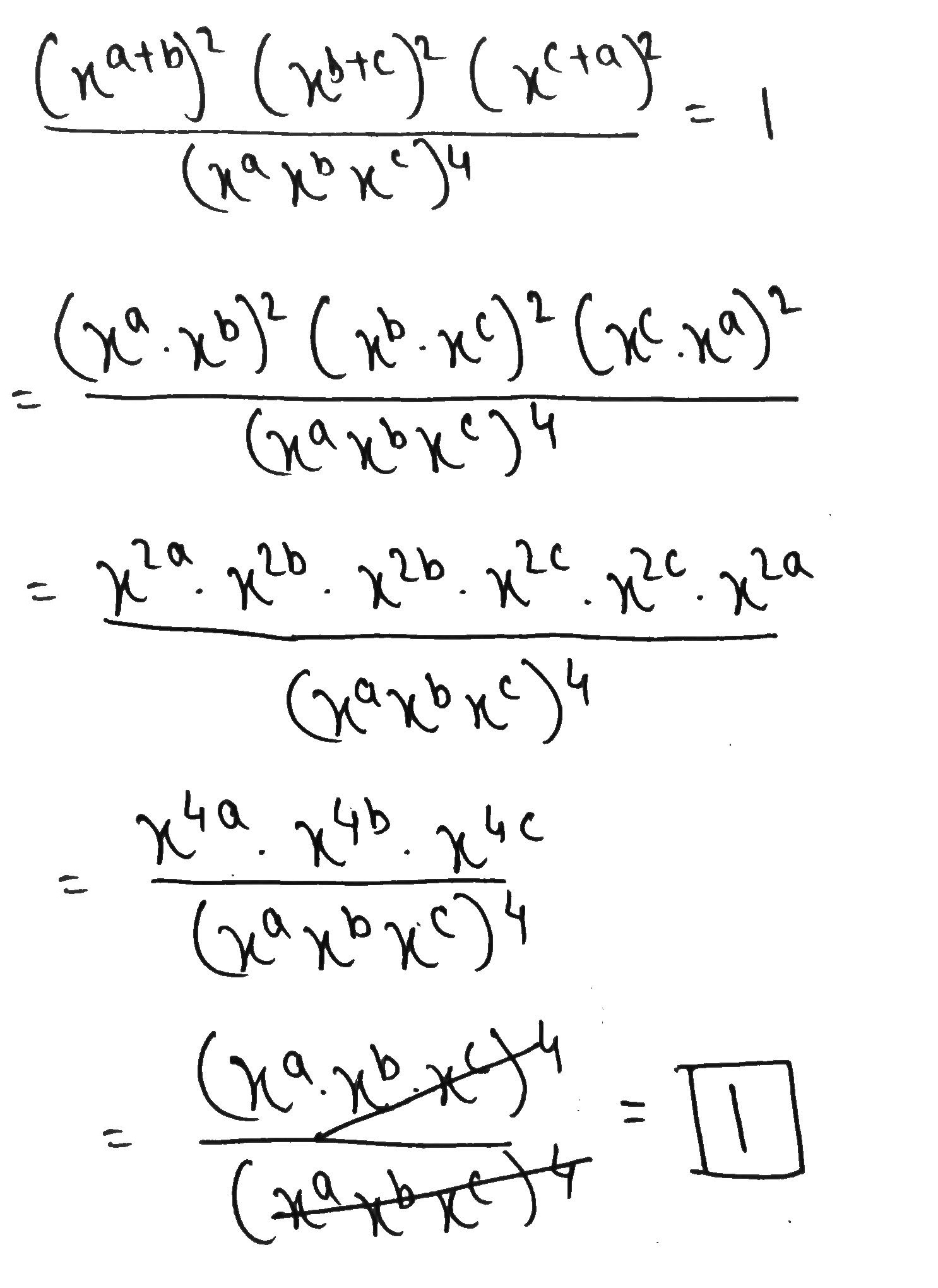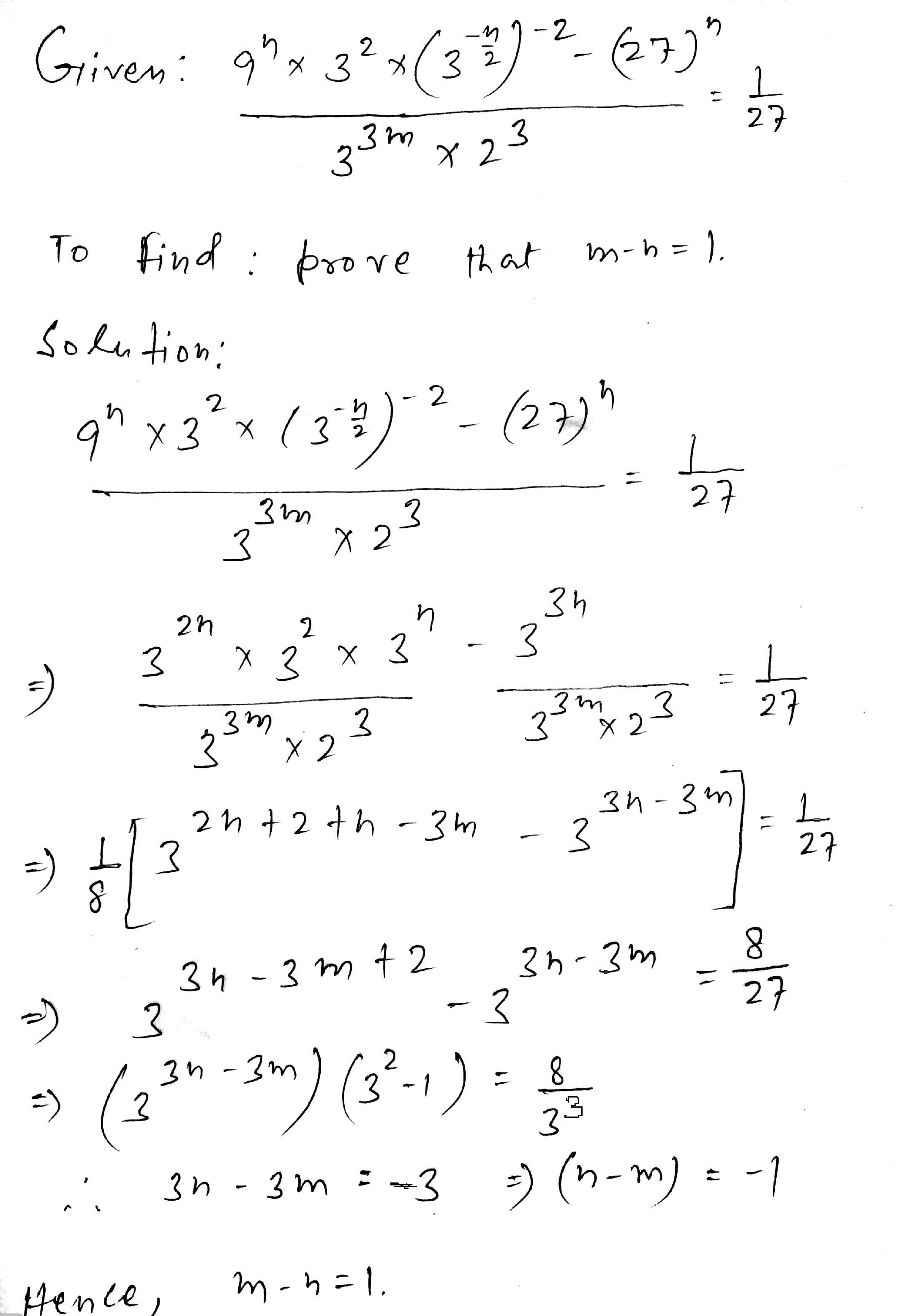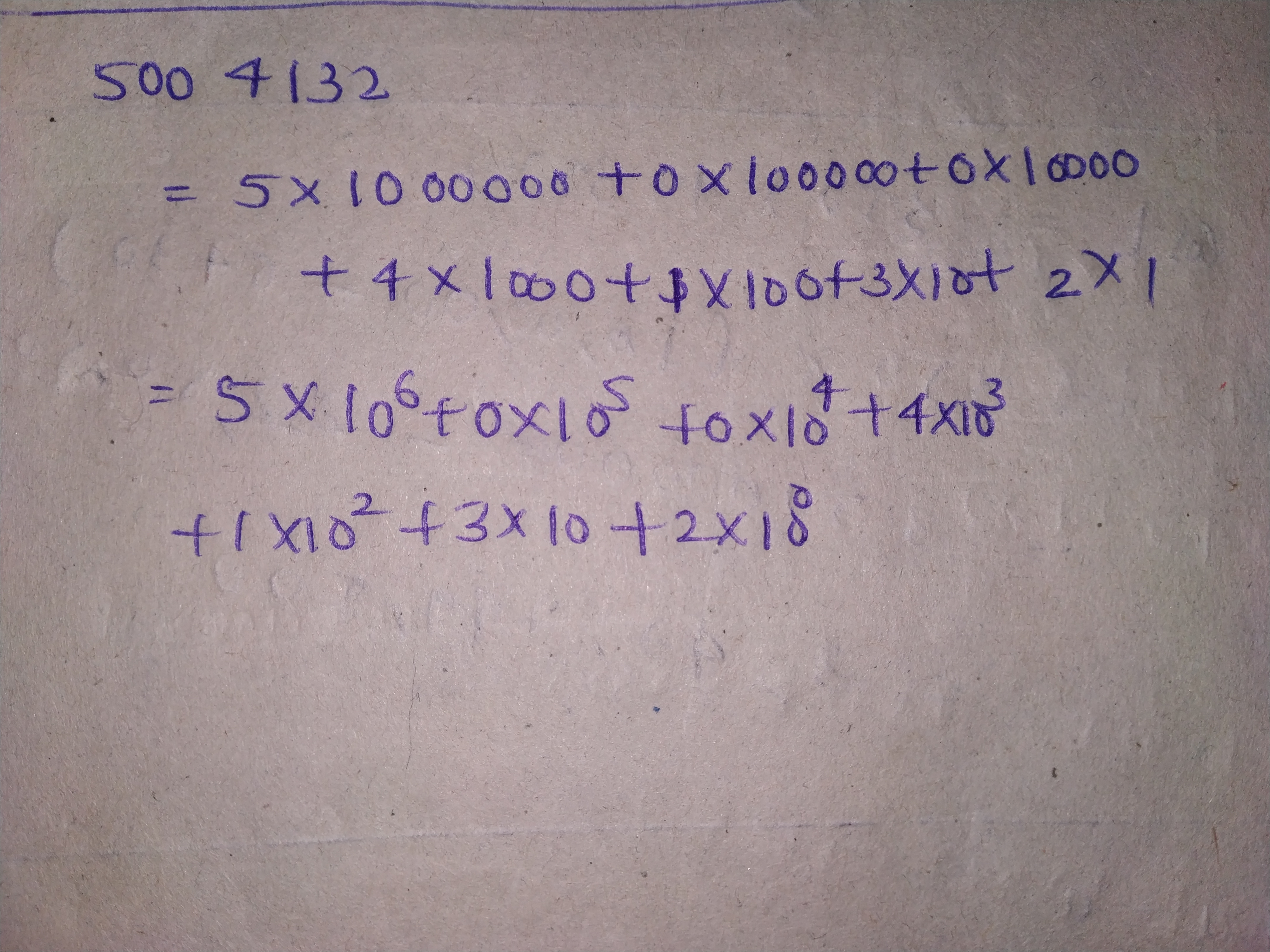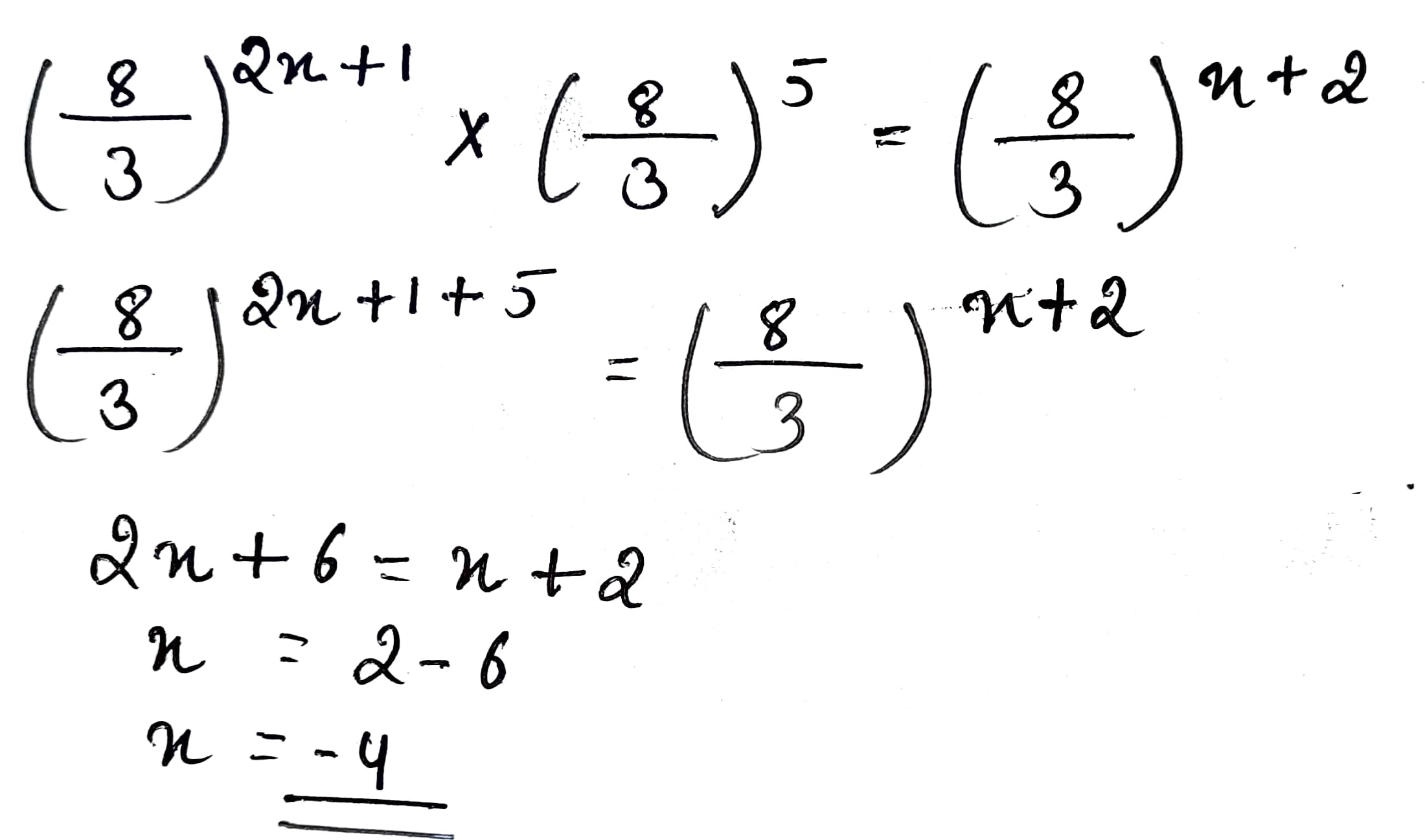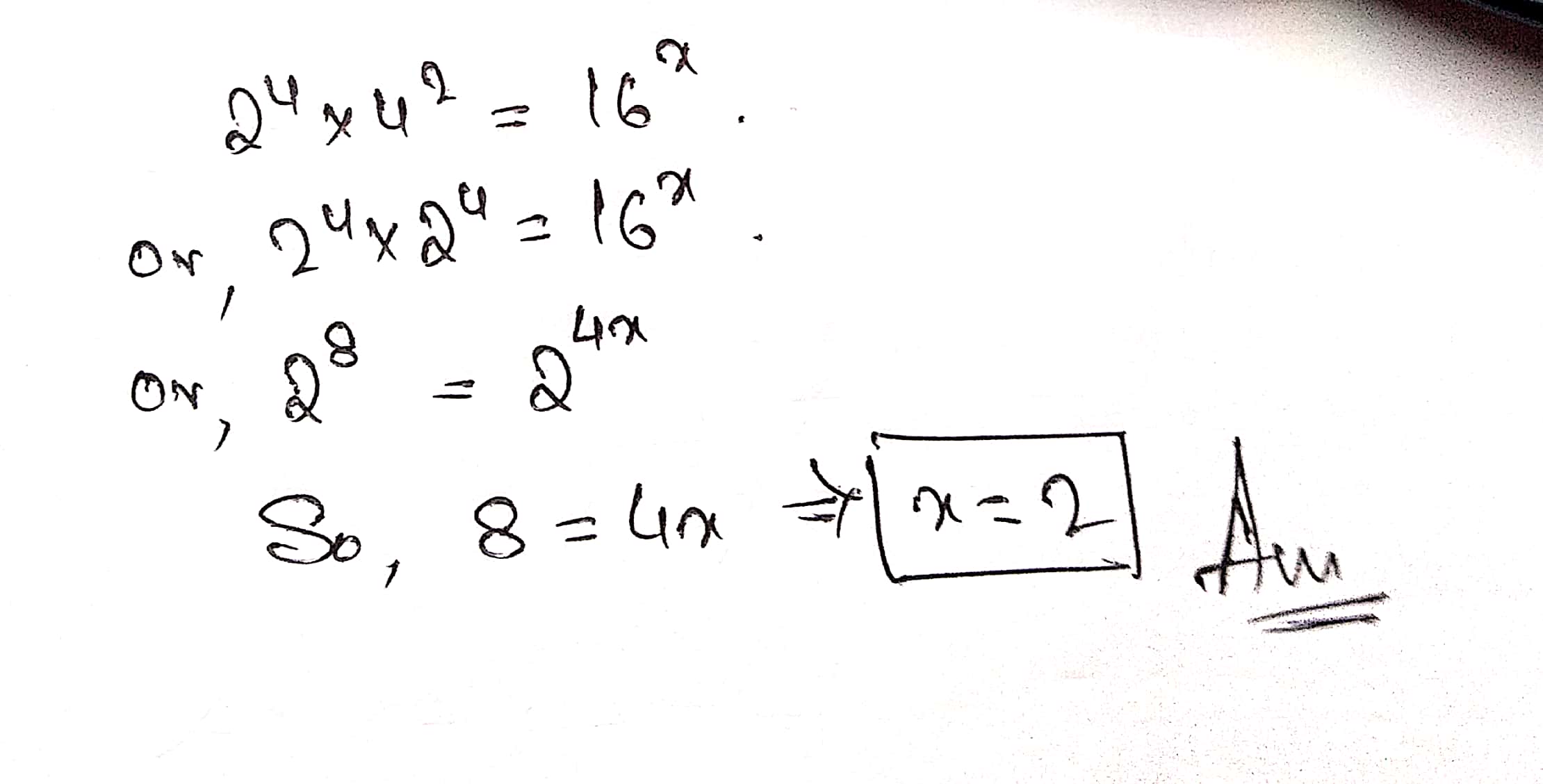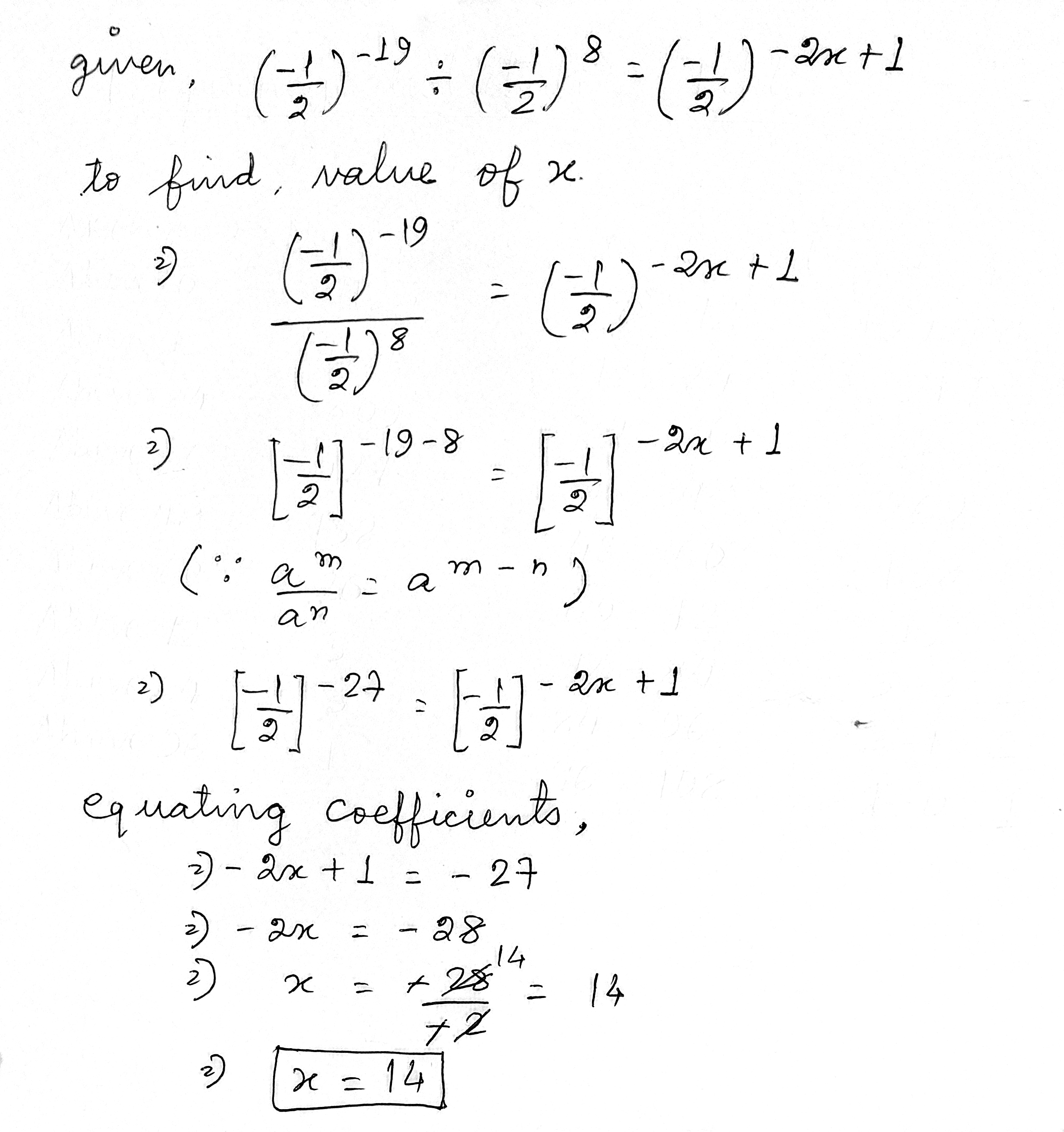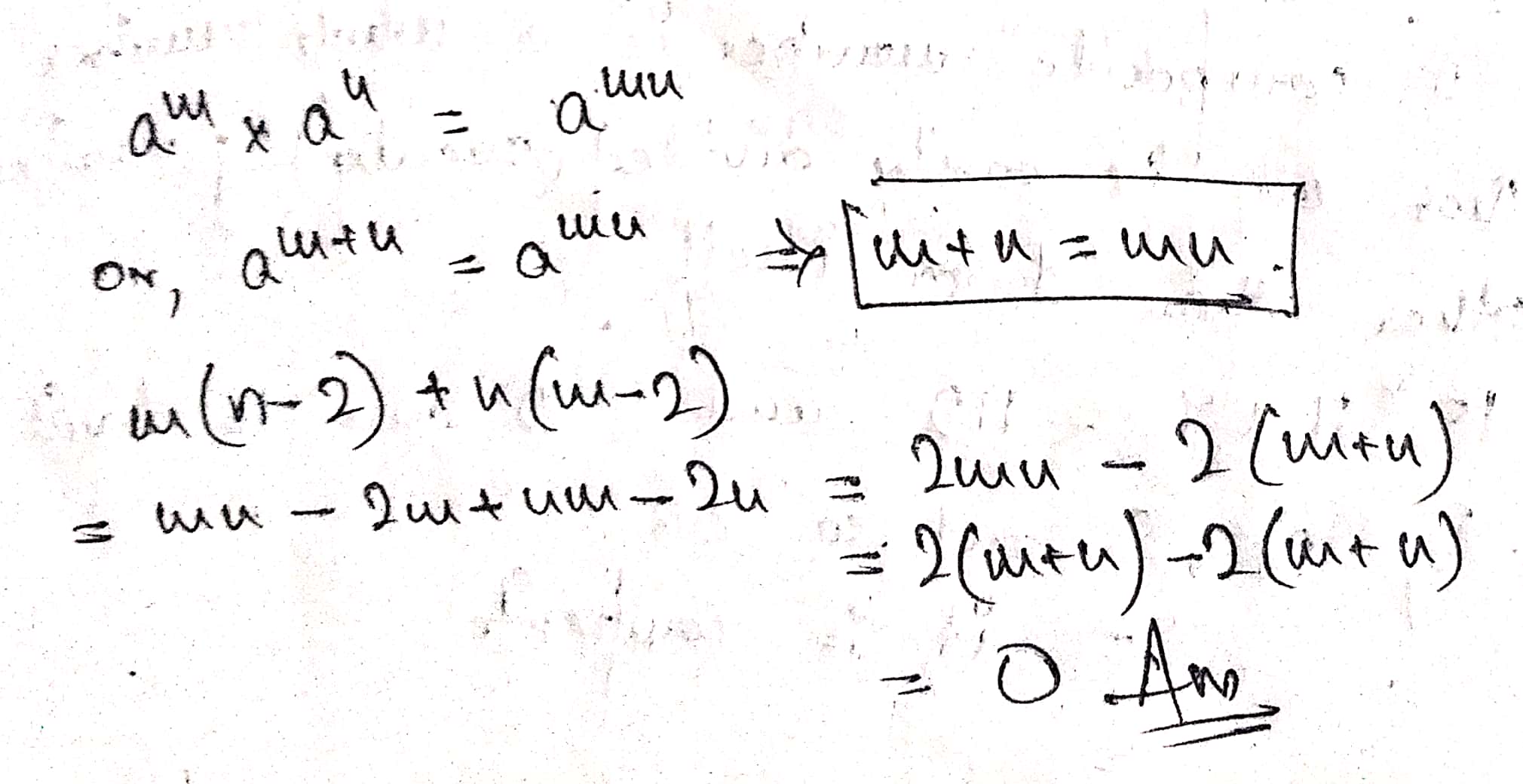Class 7 Maths - Exponents And Powers

Solve: $$\dfrac{\left(\dfrac{7}{12}\right)^8}{\left(\dfrac{14}{6}\right)^8}$$.

Now,

$$\dfrac{\left(\dfrac{7}{12}\right)^8}{\left(\dfrac{14}{6}\right)^8}$$

$$=\dfrac{\left(\dfrac{7}{12}\right)^8}{\left(\dfrac{7}{3}\right)^8}$$

$$=\left(\dfrac{3}{12}\right)^8$$

$$=\left(\dfrac{1}{4}\right)^8$$

Solve: $$0.00000000 657 \times 10^{15}$$

Now,

$$0.00000000657 \times 10^{15}$$

$$=657\times 10^{-11} \times 10^{15}$$

$$=657\times 10^{4}$$

$$=657,0000$$

Solve: $$\left(\dfrac {5^{-4}}{5^{-6}}\right)\times5^{3}$$

$$\left(\dfrac{5^{- 4}}{5^{- 6}}\right) \times {5^3}$$

$$ = \left( {{5^{ - 4 + 6}}} \right) \times {5^3}$$

$$ = {5^2} \times {5^3}$$

$$ = {5^5}$$

$$ = 3125$$

Evaluate using product rule properties: $$27 \times 3$$=

$$27\times3 =(30-3)\times3$$

$$=30\times3 - 3\times3$$

$$=90-9=81$$

Express the following as a rational number:
$$(5/7)^{-1}\times (7/4)^{-1}$$

We know that,
$$=(5/7)^{-1}=(7/5)^1$$ $$...[\because (a/b)^{-n}=(b/a)^n]$$
$$=(7/4)^{-1}=(4/7)^1$$ $$...[\because (a/b)^{-n}=(b/a)^n]$$
$$=(7/5)\times (4/ 7)$$
$$=(7\times 4)/(5\times 7)$$
On simplifying,
$$=(1\times 4)/(5\times 1)$$
$$=4/5$$

Express the following as a rational number:
$$(1/4)^{-4}$$

We know that,

$$=(1/4)^{-4}=(4/1)^4$$ $$...[\because (a/b)^{-n}=(b/a)^n]$$

$$=(4^4 /1^4)$$

$$=(256/1)$$

$$=256$$

Express the following as a rational number:
$$(-3)^{-1}\times (1/3)^{-1}$$

We know that,
$$=(-3)^{-1}=(-1/3)^1$$ $$...[\because (a/b)^{-n}=(b/a)^n]$$
$$=(1/3)^{-1}=(3/1)^1$$ $$...[\because (a/b)^{-n}=(b/a)^n]$$
$$=(-1/3)\times (3\times 1)$$
$$=(-3/3)$$
$$=-1$$

Find the value of the following:
$$ \left( \dfrac{2}{3} \right)^4$$

$$ \left( \dfrac{2}{3} \right)^4 = \dfrac{2}{3} \times \dfrac{2}{3} \times \dfrac{2}{3} \times\dfrac{2}{3} =\dfrac{2 \times 2 \times 2 \times 2 }{3 \times 3 \times 3 \times 3 } = \dfrac{16}{81}$$

Fill in the blanks to make the statements true.
The square of 500 will have ______ zeroes.

The square of 500 will have $$\underline{4}$$ zeroes.
beacause $$500^2=250000$$

Simplify:
$$\bigg(\dfrac{3}{2}\bigg)^{-1} \div \bigg(\dfrac{-2}{5}\bigg)^{-1}$$

$$\bigg(\dfrac{3}{2}\bigg)^{-1} \div \bigg(\dfrac{-2}{5}\bigg)^{-1}$$

$$=\bigg(\dfrac{2}{3}\bigg)^{1} \div \bigg(\dfrac{5}{-2}\bigg)^{1}$$

$$=\dfrac{2}{3} \times \dfrac{-2}{5}$$

$$=\dfrac{-4}{15}$$

Simplify:
$$\bigg(-\dfrac{3}{5}\bigg)^{-3}$$

$$\bigg(-\dfrac{3}{5}\bigg)^{-3}$$

$$=\bigg(-\dfrac{-5}{3}\bigg)^{3}$$ $$\bigg[\because \bigg(\dfrac{1}{a}\bigg)^{-1} =a^1\bigg]$$

$$=\dfrac{(-5) \times (-5)\times (-5)}{3 \times 3 \times 3}$$

$$=\dfrac{-125}{27}$$

Fill in the blanks:
$$\bigg(\dfrac{5}{13}\bigg)^{{10}} \div\bigg[\bigg(\dfrac{5}{13}\bigg)^3\bigg]^2 = \bigg(\dfrac{5}{13}\bigg)^{......}$$

$$\bigg(\dfrac{5}{13}\bigg)^{{10}} \div\bigg[\bigg(\dfrac{5}{13}\bigg)^3\bigg]^2 = \bigg(\dfrac{5}{13}\bigg)^{{10}} \div\bigg(\dfrac{5}{13}\bigg)^6$$

$$= \bigg(\dfrac{5}{13}\bigg)^{10-6}$$

$$= \bigg(\dfrac{5}{13}\bigg)^4$$

Fill in the blanks:
In the expression $$(-5)^{9}$$, exponent = ........ and base = ........

In the expression $$(-5)^{9}$$, exponent =$$9$$ and base = $$(-5)$$

Simplify and write the exponential form with negative exponent:
$$(-7)^3 \times (1/-7)^{-9}\div (-7)^{10}$$

$$(-7)^3 \times (1/-7)^{-9}\div (-7)^{10}$$

Let us simplify

$$(-7)^3 \times (1/-7)^{-9}\div (-7)^{10}\\=(-7)^3 \times (-7)^9 \div (-7)^{10}$$

$$=(-7)^{3+9-10}$$

$$=(-7)^2$$

$$=(1/-7)^{-2}$$

The exponential form is $$(1/-7)^{-2}$$

Express the number appearing in the following statement in standard form:
The diameter of a wire on a computer chip is $$0.000003$$ m.

The diameter of a wire on a computer chip is $$0.000003$$ m.
It is expressed in standard form as $$3.0\times10^{-6}$$ m. In standard form, the number should be of the form $$a\times 10^k$$ where $$1\leq a< 10$$ .

Express the number appearing in the following statement in standard form:
The thickness of a piece of paper is $$0.0016$$ cm.

The thickness of a piece of paper is $$0.0016$$ cm;

It can be expressed in standard form as $$1.6\times10^{-3}\ cm$$

Express the number appearing in the following statement in standard form:
Mass of molecule of hydrogen gas is about $$0.00000000000000000000334$$ tons.

Mass of molecule of hydrogen gas is about $$0.00000000000000000000334$$ tons; it is expressed in standard form as $$=3.34\times10^{-21}$$ tons

Express the number appearing in the following statement in standard form:
The distance form the Earth of the Sun is $$149,600,000,000\ m$$.

The distance form the Earth of the Sun is expressed in standard form as $$149,600,000,000\ m=1.496\times 10^{11}$$

Express the number appearing in the following statement in standard form:
The human body has $$1$$ trillion cells which vary in shapes and size.

Human body has $$1$$ trillion cells which vary in shapes and sizes; it is expressed in standard form as $$1,000,000,000,000=10^{12}$$

Express $$1024$$ as a power of $$2$$.

The given number is $$1024$$

Using prime factorisation, it can be written as,
$$1024 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^{10}$$

1739986_1826175_ans_23b4823861534b8c95b820394c419311.png

Express
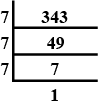
343 as a power of 7.

1343 as a power of 7.
It can be written as above
So we get
$$343 = 7 \times 7 \times 7= 7^3$$
1739992_1826176_ans_6654b07303cd45008b495c9331815718.png

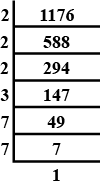
Express each of the following in exponential form:
1176

It can be written as above
so we get
$$1176 = 2 \times 2 \times 2 \times 3 \times 7 \times 7 = 2^3 \times 3 \times 7^2 $$
1739962_1826011_ans_250aee193fdb4a0f98049ff606984388.png

1739962_1826011_ans_250aee193fdb4a0f98049ff606984388.png

Express each of the following in exponential form:
1250

It can be written as above
so we get
$$1250 = 2 \times 5 \times 5 \times 5 \times 5 = 2 \times 5^4$$
1739943_1826004_ans_36548dc007694a5a9d0fd9267cc193b4.png

Which is greater:
$$5^4$$ or $$4^3$$

$$5^4$$ or $$4^5$$
It can be written as
$$5^4 = 5 \times 5 \times 5 \times 5 = 625$$
$$4^5 = 4 \times 4 \times 4 \times 4 \times 4 = 1024$$
Hence, 1024 is greater than 625 i.e $$4^5 >5^4 $$

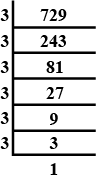
Express
729 as a power of 3

729 as a power of 3.
It can be written as above
So we get
729 = 3 \times 3 \times 3 \times 3 \times 3 \times 3 = 3^6$$
1739997_1826177_ans_d3c171d3d0d74249bbfcc17e9c7645d0.png

1739997_1826177_ans_d3c171d3d0d74249bbfcc17e9c7645d0.png

Evaluate
$$2^3 \div 2^8$$

$$2^3 \div 2^8$$
It can be written as
$$= 2^3/2^8$$
On further calculations
$$2^{3 - 8}$$
So we get
$$=2^{-5}$$
$$=\dfrac{1}{2^5}$$

Fill in the blanks
If index $$= 3x$$ and base $$= 2y, $$the number = ………

In the number $$a^b$$ , $$a$$ is base and $$b$$ is index.

If index $$= 3x$$ and base $$= 2y$$, the number $$= 2y^{3x}$$

Evaluate
$$(2^6)^0$$

$$(2^6)^0$$
It can be written as
$$2^{6\times 0}$$
On further calculations
$$=2^0$$
So we get
$$=1$$

Evaluate
$$(3^5 \times 4^7 \times 5^8)^0$$

$$(3^5 \times 4^7 \times 5^8)^0$$

It can be written as

$$=3^{5 \times 0} \times 4^{7\times 0} \times 5^{8 \times 0}$$

On further calculations

$$=3^{0}\times 4^0 \times 5^0$$

so we get

$$=1 \times 1 \times 1$$

$$=1$$

Evaluate
$$2^8 \div 2^3$$

$$2^8 \div 2^3$$
It can be written as
$$= 2^8/2^3$$
On further calculations
$$2^{8 - 3}$$
$$2^5$$

Fill in the blanks
If index = 3x and base = 2y, the number =

If index = 3x and base = 2y, the number = $$2y^{3x}$$

Evaluate
$$(3^0)^6$$

$$(3^0)^6$$
It can be written as
$$=3^0 \times 6$$
On further calculations
$$=3^0$$
so we get
$$=1$$

Simplify, giving answers with positive index:
$$(a^{10})^{10} (1 ^6)^{10}$$

$$(a^{10})^{10} (1 ^6)^{10}$$

It can be written as

$$=a^{10 \times 10}.1^{60}$$

On further calculation

$$=a^{100} . a^{60}$$

So we get

$$=a^{100}$$

Evaluate:
$$\left ( \frac{5}{4} \right )^{2}$$

$$\big(\frac54\big)^2=\dfrac{5^2}{4^2}=\dfrac{25}{16}=1\dfrac9{16}$$

Express $$10,100,1000,10000,100000$$ is exponential form.

Evaluate:
$$\left ( 1\frac{1}{4} \right )^{2}$$

$$(1\frac14)^2=\big(\frac54\big)^2=\dfrac{5^2}{4^2}=\dfrac{25}{16}=1\dfrac9{16}$$

Express each of the following as a product of prime factors only in exponential form:
$$729\times 64$$

$$729\times 64={3}^{6}\times {2}^{6}$$

Express the following as a rational number:
$$(1/3)^{-1}$$

We have:

$$(1/3)^{-1}=(-6/1)^{-1}$$

$$=(3/1)^1$$ $$....[\because (a/b)^{-n}=(b/a)^n]$$
$$=3$$

Simplify the product $$\sqrt[3]{2}\times \sqrt[4]{2}\times \sqrt[12]{32}$$.

1683045_1715615_ans_6d3f5418a1c5435a8f603f1c5f025167.jpg

Prove that $$\dfrac{x^{a(b-c)}}{x^{b(a-c)}}\div \left(\dfrac{x^b}{x^a}\right)^c=1$$.

1674390_1715626_ans_3d1e6c3f2bc247cb845554dbf0fbcacc.jpg

Simplify $$\left(\dfrac{1}{3^4}\right)^{\tfrac{1}{2}}$$.

1680364_1715578_ans_7e5d0b3485f14217a1383371e5c91ea3.jpg

Simplify $$\left(3^{\tfrac{1}{3}}\right)^4$$.

1680362_1715577_ans_b7459c97a7c0406d9c7c056b4818dc34.jpg

Simplify $$\dfrac{(25)^{\dfrac{3}{2}\times (243)^{\dfrac{3}{5}}}}{(16)^{\frac{5}{4}\times (8)^{\dfrac{4}{3}}}}$$

1318501_1586758_ans_2cbf66cecaa446fcb5ddaa1b5b292da3.jpg

Simplify and express the following as a rational number:
$$(-7/8)^{-3} \times (-7/8)^{2}$$

We have,
$$=(-7/8)^{(-3+2)}$$ $$...[ \left\{ (a/b)^m \times (a/b)^n\right\} =(a/b)^{m-n}$$
$$=(-7/8)^{(-1)}$$

$$=(-8/7)^1$$

$$=(-8/7)$$

Express the following as a rational number:
$$(-2)^{-3}$$

We know that,

$$=(-2)^{-3}=(-1/2)^3$$ $$...[\because (a/b)^{-n}=(b/a)^n]$$

$$=(-1^3 /2^3)$$

$$=(-1/8)$$

Express the following as a rational number:
$$5^{-3}$$

We know that,
$$=(5)^{-3}=(1/5)^3$$ $$...[\because (a/b)^{-n}=(b/a)^n]$$
$$=(1^3 /5^3)$$
$$=(1/125)$$

Simplify and express the following as a rational number:
$$(4/9)^6 \times (4/9)^{-4}$$

We have,
$$=(4/9)^{(6+(-4))}$$ $$...[ \left\{ (a/b)^m \times (a/b)^n\right\} =(a/b)^{m-n}$$
$$=(4/9)^{(6-4)}$$
$$=(4/9)^2$$
$$=(4^2 /9^2)$$
$$=(16/81)$$

Express the following as a rational number:
$$(4)^{-1}$$

We have:

$$(4^{-1}=(4/1)^{-1}$$

$$=(1/4)^1$$ $$....[\because (a/b)^{-n}=(b/a)^n]$$
$$=(1/4)$$

Express the following as a rational number:
$$(-3/4)^{-3}$$

We know that,
$$=(-3/4)^{-3}=(-4/3)^3$$ $$...[\because (a/b)^{-n}=(b/a)^n]$$
$$=(-4^3 /3^3)$$
$$=(-64/27)$$

Solve for $$x$$ when $$2^{2x+1}+2^9=2^{10}$$

Given,

$$2^{2x+1}+2^9=2^{10}$$

or, $$2^{2x+1}=2^{10}-2^{10}$$

or, $$2^{2x+1}=2^9$$

or, $$2x+1=9$$

or, $$2x=8$$

or, $$x=4$$.

If $$27^{x}=\dfrac{9}{3^{x}}$$, find x.

We have, $$27^{x}=\dfrac{9}{3^{x}}$$

$$\Rightarrow (3^{3})^{x}=\dfrac{3^{2}}{3^{x}}$$

$$\Rightarrow 3^{3x}=3^{2-x}$$

$$\Rightarrow 3x=2-x$$

$$\Rightarrow 4x=2$$

$$\Rightarrow x=\dfrac{1}{2}$$

Express each of the following as a product of prime factors only in exponential form:
$$270$$

$$270=2\times {3}^{5}\times 5$$

Express the following numbers in standard from:
$$846\times 10^7$$

1514834_1671221_ans_ce90fe8494f94ce3b0bbb67874098462.jpg

Express the following as a rational number:
$$(-8/5)^3$$

We have,

$$(-8/5)^3=(-8^3/5^3)$$

$$= (-8\times -8\times -8)/(5\times 5\times 5)$$
$$=(-512/125)$$

Simplify $$(3^4)^{\tfrac{1}{4}}$$.

1680358_1715575_ans_d5cd91d56efb40718cadbdb82fb889ca.jpg

Express the following as a rational number:
$$(1/6)^3$$

We have,

$$(1/6)^3=(1^3/6^3)$$

$$=(1\times 1\times 1)/(6\times 6\times 6)$$
$$=(1/216)$$

Express the following as a rational number:
$$(-13/11)^2$$

We have,

$$(-13/11)^2=(-13^2/11^2)$$

$$=(-13\times -13)/(11\times 11)$$
$$=(169/121)$$

Write the following numbers in the usual form:
$$4.5\times 10^4$$

1520638_1671234_ans_34e74d11f2da44ada2b49cb7fa8c9fdd.jpg

Express the following in a rational number:
$$(-1/2)^5$$

We have,

$$(-1/2)^5=(-1^5/2^5)$$

$$=(-1\times -1\times -1\times -1\times -1)/(2\times 2\times 2\times 2\times 2)$$
$$=(-1/32)$$

Evaluate $$\left[(16)^{\dfrac{1}{2}}\right]^{\dfrac{1}{2}}$$.

1680984_1715610_ans_35cc1774b3fd4602a75aa502f9a66c1c.jpg

Finf the value of $$m$$: $$\displaystyle \left ( \frac{-2}{3} \right )^4 \times \left ( \frac{-2}{3} \right )^3 \times \left ( \frac{-2}{3} \right )= \left(\dfrac{-2}{3}\right)^m$$

$$\displaystyle \left ( \frac{-2}{3} \right )^4 \times \left ( \frac{-2}{3} \right )^3 \times \left ( \frac{-2}{3} \right )$$
$$=\left(\dfrac{-2}{3}\right)^{4+3+1}$$
$$=\left(\dfrac{-2}{3}\right)^{8}$$

Simplify the following using law of exponents.
$$[(\dfrac{-5}{6})^2]^5$$

$$(\dfrac{-5}{6})^{10}=\dfrac{(-5)^{10}}{6^{10}}=\dfrac{5^{10}}{6^{10}}$$

Express the following as a rational number:
$$(2/3)^5$$

We have,

$$(2/3)^5=(2^5/3^5)$$

$$=(2\times 2\times 2\times 2\times 2)/(3\times 3\times 3\times 3\times 3)$$
$$=(32/243)$$

Simplify the following using law of exponents.
$$(10^2)^3$$

we know,

$$(a^{m})^{n}=a^{mn}$$

so,

$$(10^{2})^{3}$$

$$=10^{6}$$

$$=1000000$$

Simplify
$${11^{{2 \over 3}}} \times {11^{{1 \over 3}}}$$

$$11^{\frac{2}{3}}\times 11^{\frac{1}{3}}=11^{\frac{2}{3}+\frac{1}{3}}=11^{1}=11$$

Simplify
$${13^{{1 \over 5}}} \times {17^{{1 \over 5}}}$$

$$13^{1/5}\times 17^{1/5}=(13\times 17)^{1/5}=\sqrt[5]{221}$$

Prove that $$\dfrac{x^{a(b-c)}}{x^{b(a-c)}}\div \left(\dfrac{x^{bc}}{x^{ac}}\right)=1$$

$$\displaystyle{\frac { { x }^{ a(b-c) } }{ { x }^{ b(a-c) } } \div \frac { { x }^{ bc } }{ { x }^{ ac } } \\ ={ x }^{ a(b-c)-b(a-c) }\div { x }^{ bc-ac }\\ ={ x }^{ ab-ac-ba+bc }\div { x }^{ bc-ac }\\ ={ x }^{ bc-ac }\div { x }^{ bc-ac }\\ =1}$$

If $$(-4)^8 \div (-4)^4$$ is $${(-4)^{m}}$$, then find the value of $$m$$.

$$(-4)^8 \div (-4)^4$$$$=\dfrac { { -4 }^{ 8 } }{ { -4 }^{ 4 } } $$
$$= { -4 }^({ 8-4 })$$

$$ ={-4}^{4}$$

Therefore $$4$$ = $$m$$

Express the number $$4.5 \times 10^3$$ in usual form:

$$4.5\times{ 10 }^{ 3 } = 4.5\times1000 \\\ \ \ \ \ \ \ \ \ \ \ \ \ \ = 4500$$

Evaluate : $$\displaystyle \left[ \left( \frac{-4}{3} \right)^2 \right]^3$$

$$\displaystyle \left( \frac{-4}{3} \right)^6$$
= $$\displaystyle \frac{-4}{3} \times \frac{-4}{3} \times \frac{-4}{3} \times \frac{-4}{3} \times \frac{-4}{3} \times \frac{-4}{3}$$
= $$\displaystyle \frac{4096}{729}$$
$$\therefore \displaystyle \left[ \left( \frac{-4}{3} \right)^2 \right]^3 = \frac{4096}{729}$$

Which is larger $${ \left( 2.5 \right) }^{ 6 }$$ or $${ \left( 1.25 \right) }^{ 12 }$$?

We write $$\quad { \left( 2.5 \right) }^{ 6 }={ \left( \cfrac { 5 }{ 2 } \right) }^{ 6 }=\cfrac { { 5 }^{ 6 } }{ { 2 }^{ 6 } } $$. Similarly, you may obtain
$${ \left( 1.25 \right) }^{ 12 }=\quad { \left( \cfrac { 5 }{ 4 } \right) }^{ 12 }=\cfrac { { 5 }^{ 12 } }{ { 4 }^{ 12 } } =\cfrac { { 5 }^{ 12 } }{ { 2 }^{ 24 } } $$
Thus you have to check which of the numbers $$\cfrac { { 5 }^{ 6 } }{ { 2 }^{ 6 } } $$, $$\cfrac { { 5 }^{ 12 } }{ { 2 }^{ 24 } } $$ is larger. Equivalently, you must determine the larger number between $${5}^{6}$$ and $${2}^{18}$$ (why?).
However, $${5}^{2}=25< 32={2}^{5}$$. Hence
$${ 5 }^{ 6 }={ \left( { 5 }^{ 2 } \right) }^{ 3 }<{ \left( { 2 }^{ 5 } \right) }^{ 3 }={ 2 }^{ 15 }<{ 2 }^{ 18 }$$
Thus
$$\cfrac { { 5 }^{ 12 } }{ { 2 }^{ 24 } } =\cfrac { { 5 }^{ 6 } }{ { 2 }^{ 18 } } \times \cfrac { { 5 }^{ 6 } }{ { 2 }^{ 6 } } <\cfrac { { 5 }^{ 6 } }{ { 2 }^{ 6 } } $$
Hence $${ \left( 1.25 \right) }^{ 12 }<{ \left( 2.5 \right) }^{ 6 }$$

Write the following numbers without scientific notation:
(A) $$1.234\times { 10 }^{ 5 }$$
(B) $$5.45\times { 10 }^{ -3 }$$

$$1.234 \times {10}^{5} = 123,400$$
$$5.45 \times {10}^{-3} = 0.00545$$

Simplify $$\cfrac { { \left( 1024 \right) }^{ 3 }\times { \left( 81 \right) }^{ 4 } }{ { \left( 243 \right) }^{ 2 }\times { \left( 128 \right) }^{ 4 } } $$

Observe $$1024={2}^{10}$$, $$81={3}^{4}$$, $$243={3}^{5}$$, and $$128={2}^{7}$$. Hence the expression is
$$\cfrac { { \left( { 2 }^{ 10 } \right) }^{ 3 }\times { \left( { 3 }^{ 4 } \right) }^{ 4 } }{ { \left( { 3 }^{ 5 } \right) }^{ 2 }\times { \left( { 2 }^{ 7 } \right) }^{ 4 } } =\cfrac { { \left( 2 \right) }^{ 30 }\times { \left( 3 \right) }^{ 16 } }{ { \left( 3 \right) }^{ 10 }\times { \left( 2 \right) }^{ 28 } } $$
$$={ 2 }^{ 30-28 }\times { 3 }^{ 16-10 }={ 2 }^{ 2 }\times { 3 }^{ 6 }=2916$$

Suppose $$b$$ is a positive integer such that $$\cfrac { { 2 }^{ 4 } }{ { b }^{ 2 } } $$ is also an integer. What are the possible values of $$b$$?

Given b will be a positive integer

$$\dfrac { { 2 }^{ 4 } }{ { b }^{ 2 } } $$ will be integer so the possible values of b will be

when b=1

$$\dfrac { { 2 }^{ 4 } }{ { 1 }^{ 2 } } =\dfrac { 16 }{ 1 } =16$$

when b=2

$$\dfrac { { 2 }^{ 4 } }{ { 2 }^{ 2 } } =\dfrac { 16 }{ 4 } =4$$

when b=3

$$\dfrac { { 2 }^{ 4 } }{ { 3 }^{ 2 } } =\dfrac { 16 }{ 9 } =1.77$$

when b=4

$$\dfrac { { 2 }^{ 4 } }{ { 4 }^{ 2 } } =\dfrac { 16 }{ 16 } =1$$

possible values of b will be 1,2,4

as when b is 3 $$\dfrac { { 2 }^{ 4 } }{ { b }^{ 2 } } $$ is not an integer and when b exceeds 4 again it will not be an integer.

Express the number $$1728$$ in the exponential form:

The factors of 1728 are $$ {2}\times{2}\times{2}\times{2}\times{2}\times{2}\times{3}\times{3}\times{3}$$

1728 can be expressed in exponential form as

$${ 2 }^{ 6 }\times { 3 }^{ 3 }=1728$$

Simplify: $$\cfrac { { 2 }^{ 3 }\times { 3 }^{ 2 }\times { 5 }^{ 4 } }{ { 3 }^{ 3 }\times { 5 }^{ 2 }\times { 2 }^{ 4 } } $$

Given that: $$\dfrac { { 2 }^{ 3 }\times { 3 }^{ 2 }\times { 5 }^{ 4 } }{ { 3 }^{ 3 }\times { 5 }^{ 2 }\times { 2 }^{ 4 } } $$

$$=\dfrac { { 5 }^{ 4 }\times { 5 }^{ -2 } }{ { 2 }^{ 4 }\times { 2 }^{ -3 }\times { 3 }^{ 3 }\times { 3 }^{ -2 } } $$ .........Using [$$a^{m_1}\times...\times a^{m_n} =a^{m_1+.......m_n}$$ and $$ a^{-m} = \dfrac{1}{a^m}$$ ]

$$=\dfrac { { 5 }^{ 2 } }{ { 2 }^{ 1 }\times { 3 }^{ 1 } } =\dfrac { 25 }{ 6 } $$

Simplify:
$$\cfrac { { \left( 15 \right) }^{ -3 }\times { \left( -12 \right) }^{ 4 } }{ { 5 }^{ -6 }\times { 36 }^{ 2 } } $$

$$\cfrac { { \left( 15 \right) }^{ -3 }\times { \left( -12 \right) }^{ 4 } }{ { 5 }^{ -6 }\times { 36 }^{ 2 } } $$

$$=\cfrac { { \left( 5\times 3 \right) }^{ -3 }\times { \left( -12 \right) }^{ 4 } }{ { 5 }^{ -6 }\times { \left( 12\times 3 \right) }^{ 2 } } $$

$$=\cfrac { { 5 }^{ -3 }\times { 3 }^{ -3 }\times { \left( -12 \right) }^{ 4 } }{ { 5 }^{ -6 }\times { 12 }^{ 2 }\times { 3 }^{ 2 } } $$ (using$${ (xy)}^{n}={x}^{n}.{y}^{n}$$

$$={ 5 }^{ \left( -3+6 \right) }\times { 3 }^{ \left( -3-2 \right) }\times { \left( -12 \right) }^{ \left( 4-2 \right) }$$

$$=\cfrac { { 5 }^{ 3 }\times { \left( -12 \right) }^{ 2 } }{ { 3 }^{ 5 } } $$

$$=\cfrac { 125\times 144 }{ 243 } $$

$$=\cfrac { 2000 }{ 27 } $$

Simplify:
$$\cfrac { { 6 }^{ 8 }\times { 5 }^{ 3 } }{ { 10 }^{ 3 }\times { 3 }^{ 4 } } $$

$$\dfrac { { 6 }^{ 8 }\times { 5 }^{ 3 } }{ { 10 }^{ 3 }\times { 3 }^{ 4 } } $$

$$=\dfrac { { \left( 3\times 2 \right) }^{ 8 }\times { 5 }^{ 3 } }{ { \left( 2\times 5 \right) }^{ 3 }\times { 3 }^{ 4 } } $$

$$=\dfrac { { 3 }^{ 8 }\times { 2 }^{ 8 }\times { 5 }^{ 3 } }{ { 2 }^{ 3 }\times { 5 }^{ 3 }\times { 3 }^{ 4 } } $$ ......(using$${ (xy)}^{n}={x}^{n}.{y}^{n}$$)

$$={ 3 }^{ \left( 8-4 \right) }\times { 2 }^{ \left( 8-3 \right) }\times { 5 }^{ \left( 3-3 \right) }$$ ......(using $$\cfrac{{x}^{n}}{{x}^{m}}={x}^{n-m}$$)

$$={ 3 }^{ 4 }\times { 2 }^{ \left( 5 \right) }\times { 5 }^{ 0 }$$

$$=81\times 32\times 1$$

$$=2592$$

simplify in exponent form:
$$36{a^4}{b^6}{c^3}\root 6 \of {108} $$

$$36a^{4}b^{6}c^{3}\sqrt[6]{108}=2^{2}\times 3^{2}\times (2^{2}\times 3^{3})^{1/6}a^{4}b^{6}c^{3}=2^{2+\dfrac{1}{3}}\times 3^{2+\dfrac{1}{2}}\times a^{4}b^{6}c^{3}=2^{7/3}\cdot 3^{5/2}\cdot a^{4}b^{6}c^{3}$$

Express the following as a rational number:
$$(-2/3)^{-1}$$

We have:

$$(-2/3)^{-1}=(-2/3)^{-1}$$

$$=(3/-2)^1$$ $$....[\because (a/b)^{-n}=(b/a)^n]$$
$$=(-3/2)$$

Which is larger: $$({3}^{4}\times {2}^{3})$$ or $$({2}^{5}\times {3}^{2})$$?

Given that: $$\left( { 3 }^{ 4 }\times { 2 }^{ 3 } \right) =\left( 81\times 8 \right) =648$$ .........Using [$$a^{m_1}\times...\times a^{m_n} =a^{m_1+.......m_n}$$ ]

And $$\left( { 2 }^{ 5 }\times { 3 }^{ 2 } \right) =\left( 32\times 6 \right) =192$$ .........Using [$$a^{m_1}\times...\times a^{m_n} =a^{m_1+.......m_n}$$

$$\therefore $$ $$648>192$$

Hence $$\left( { 3 }^{ 4 }\times { 2 }^{ 3 } \right) >\left( { 2 }^{ 5 }\times { 3 }^{ 2 } \right) $$

Simplify:
$$\cfrac { { \left( { 2 }^{ 5 } \right) }^{ 6 }\times { \left( { 3 }^{ 3 } \right) }^{ 2 } }{ { \left( { 2 }^{ 6 } \right) }^{ 5 }\times { \left( { 3 }^{ 2 } \right) }^{ 3 } } $$

$$\dfrac {({2}^{5})^{6}\times {({3}^{3})}^{2}}{({2}^{6})^{5}\times {({3}^{2})}^{3}}$$

$$=\dfrac{(2^6)^{5}\times (3^2)^{3}}{(2^6)^{5}\times (3^2)^{3}}$$

$$=\dfrac{(2^6)^{5}\times (3^2)^{3}\times (3^2)^{-3}\times (2^6)^{-5}}{1}$$

$$=(2^6)^{5-5}\times (3^2)^{3-3}$$

$$=(2^6)^0\times (3^2)^0=1$$

Hence, $$\dfrac {({2}^{5})^{6}\times {({3}^{3})}^{2}}{({2}^{6})^{5}\times {({3}^{2})}^{3}}=1$$

What is the least positive integer $$n$$ such that $$\cfrac { { \left( 30 \right) }^{ 3 } }{ { \left( 35 \right) }^{ 2 } } n$$ is also integer?

$$\dfrac{(30)^3}{(35)^2}n$$

$$=\dfrac{(2\times 3\times 5)^3}{(7 \times 5)^2}n$$

$$=\dfrac{2^3\times 3^3\times 5^3}{7^2 \times 5^2}n$$

$$=\dfrac{2^3\times 3^3\times 5^{3-2}}{7^2}n$$

$$=\dfrac{2^3\times 3^3\times 5}{7^2}n$$

To get the result as integer, the denominator should be reduced to $$1$$ and that is possible only when we have $$7^2$$ in the numerator.

Since, $$n$$ is not given we can take it $$7^2$$ to get the final result as integer.

$$\dfrac{2^3\times 3^3\times 5\times 7^{2}}{7^2}=2^3\times 3^3\times 5$$ is an integer.

Thus, the value of $$n=7^2=49$$.

Simplify: $$\dfrac {2^{1/2}}{4^{1/6}}$$

Observe
$$4^{1/6} = (2^{2})^{1/6} = 2^{2\times (1/6)} = 2^{1/3}$$
Hence
$$\dfrac {2^{1/2}}{4^{1/6}} = \dfrac {2^{1/2}}{2^{1/3}} = 2^{(1/2) - (1/3)} = 2^{1/6}$$.

Find the value of $$(81^{1/2}\times 8^{2/3}\times 32^{2/5})^{1/2}$$

Observe $$81 = 3^{4}$$. Hence
$$81^{1/2} = (3^{4})^{1/2} = 3^{4\times (1/2)} = 3^{2} = 9$$.
Similarly,
$$8^{2/3} = (2^{3})^{2/3} = 2^{3\times (2/3)} = 2^{2} = 4$$,
$$32^{2/5} = (2^{5})^{2/5} = 2^{5\times (2/5)} = 2^{2} = 4$$.
Thus we get
$$(81^{1/2} \times 8^{2/3}\times 32^{2/5})^{1/2} = (9\times 4\times 4)^{1/2} = (144)^{1/2} = \sqrt {144} = 12$$.

Rakesh solved some problems of exponents in the following way. Do you agree with the solutions? If not why? Justify your argument.
$$\cfrac { { x }^{ 3 } }{ { x }^{ 2 } } ={ x }^{ 4 }$$

No, I do not agree with the solution provided by Rakesh

By theory of exponent we know that

$$\dfrac{x^{a}}{x^{b}}=x^{a-b}$$

$$\therefore \dfrac{x^{3}}{x^{2}}=x^{3-2}=x^{1} =x\neq x^{4}$$

The correct answer is $$x$$, which is justified above.

Rakesh solved some problems of exponents in the following way. Do you agree with the solutions? If not why? Justify your argument.
$$3{ x }^{ -1 }=\cfrac { 1 }{ 3x } $$

No, I do not agree with the Rakesh

By Theory of equations,3We know that :

$$3x-1=\frac{3}{x}=LHS$$ ____ (1)

$$RHS=3x$$ ______ (2)

Hence clearly $$LHS\neq RHS$$

Hence proved

Find the value of $$(1000\pi)^{2/3}\times (512\pi)^{4/3}$$

Observe $$1000 = 2^{3}\times 5^{3}$$ and $$512 = 2^{9}$$. Hence
$$(1000\pi)^{2/3} \times (512\pi)^{4/3} = (2^{3}5^{3} \pi)^{2/3} \times (2^{9}\pi)^{4/3}$$
$$= (2^{3})^{2/3} \times (5^{3})^{2/3} \times (\pi)^{2/3} \times (2^{9})^{4/3} \times (\pi)^{4/3}$$
$$= 2^{2} \times 5^{2} \times 2^{12} \times (\pi)^{2/3} \times (\pi)^{4/3}$$
$$= 2^{14}5^{2} (\pi)^{(2/3) + (4/3)} = 409600\pi^{2}$$.

Simplify and obtain a numerical value $${ (32) }^{ -\tfrac45 }$$.

Given: $$E = 32^{-\tfrac45}$$

The expression becomes

$$E = {(2^5)}^ \tfrac{-4}{5}$$

$$= {2}^ {5 \times \tfrac{-4}{5}}$$

$$= {(2)}^{-4}$$$$= \dfrac{1}{16}$$

Prove that :
(i) $$\dfrac {3^{x + 1}}{3^{x(x + 1)}}\times \left (\dfrac {3^{x}}{3}\right )^{x + 1} = 1$$
(ii) $$\left (\dfrac {x^{m}}{x^{m}}\right )^{m + n} \cdot \left (\dfrac {x^{n}}{x^{l}}\right )^{n + l}\cdot \left (\dfrac {x^{l}}{x^{m}}\right )^{l + m} = 1$$

(i)$$\dfrac{3^{x+1}}{3^{x(x+1)}}\times \left ( \dfrac{3^{x}}{3} \right )^{x+1}$$

$$=\dfrac{3^{x+1}}{3^{x(x+1)}}\times \dfrac{3^{x(x+1)}}{3^{x+1}}$$ ..... [Using power rule of exponents]

$$=1$$

So LHS=RHS

(ii)$$\left ( \dfrac{x^{m}}{x^{n}} \right )^{m+n}.\left ( \dfrac{x^{n}}{x^{l}} \right )^{n+l}.\left ( \dfrac{x^{l}}{x^{m}} \right )^{l+m}$$

=$$\left ( x^{m-n} \right )^{m+n}\times \left ( x^{n-l} \right )^{n+l}\times \left ( x^{l-m} \right )^{l+m}$$ ...... [Using quotient rule of exponents]

=$$(x^{m^{2}-n^{2}})\times (x)^{n^{2}-l^{2}}\times (x)^{l^{2}-m^{2}}$$ ...... [Using power rule of exponents]

=$$x^{m^{2}-n^{2}+n^{2}-l^{2}+l^{2}-m^{2}}=x^{0}=1$$

So LHS=RHS

The value of $${ \left( 0.001 \right) }^{ \tfrac13 }$$ is

$${(0.001)}^\tfrac { 1 }{ 3 } =({ { (0.1) }^{ 3 } })^{ \tfrac { 1 }{ 3 } }={ (0.1) }^{ 3\times\tfrac { 1 }{ 3 } }=0.1$$

Find the value of $$(-10{m}^{2}{n}^{2})\times(-20\ m{n}^{15})$$ for $$m=1.2$$ and $$n=-1$$.

$$\left( { - 10{m^2}{n^2}} \right) \times \left( { - 20m{n^{15}}} \right)$$

$$ = 200{m^3}{n^{17}}$$

$$ = 200{\left( {1.2} \right)^3}{\left( { - 1} \right)^{17}}$$

$$ = \cfrac{{ - 200 \times 12 \times 12 \times 12}}{{10 \times 10 \times 10}}$$

$$ = - \cfrac{{3456}}{{10}}$$

$$ = - 345.6$$

If $$10^{2x}=25$$ then find $$10^{-x}$$.

Given,

$$10^{2x}=25$$

or, $$(10^x)^2=25$$

or, $$10^x=\sqrt{25}$$

or, $$10^x=5$$

or, $$10^{-x}=5^{-1}$$

or, $$10^{-x}=\dfrac{1}{5}$$

If $$a^{x-1} = bc, b^{y-1} = ac, c^{z-1} = ab$$, then find the value of $$xy + yz + zx - xyz$$.

We have,

$$ {{a}^{x-1}}=bc $$

$$ \dfrac{{a}^{x}}{a}=abc $$

$$ {{a}^{x}}=abc $$

$$ a={{\left( abc \right)}^{1/x}} $$ $$\dots(1)$$

Similarly,

$$ b={{\left( abc \right)}^{1/y}} $$ $$\dots(2)$$

$$ c={{\left( abc \right)}^{1/z}} $$ $$\dots(3)$$

Multiply $$(1),(2),(3)$$

$$ abc={{\left( abc \right)}^{1/x}}.{{\left( abc \right)}^{1/y}}.{{\left( abc \right)}^{1/z}} $$

$$ abc={{\left( abc \right)}^{1/x+1/y+1/z}} $$

$$ \therefore\ \cfrac{1}{x}+\cfrac{1}{y}+\cfrac{1}{z}=1 $$

$$ \dfrac{xy+yz+zx}{xyz}=1 $$

$$ xy+yz+zx=xyz $$

$$ xy+yz+zx-xyz=0 $$

Hence, this is the answer.

Write each of the following in scientific notation:
(i) $$92.43$$
(ii) $$0.9243$$
(iii) $$9243$$
(iv) $$924300$$
(v) $$0.009243$$
(vi) $$0.09243$$

(i)

92.43 == 9.243 × 10¹
(ii)

0.9243= 9.243 × 10^-1
(iii)

9243= 9.243 × 10³
(iv)

924300 = 9.243 × 10⁵
(v)

0.009243= 9.243 × 10^-3
(vi)

0.09243
= 9.243 × 10^-2

Find the value of the following:
$$\left [\left (\dfrac {2}{3}\right )^{2} \right ]^{2}$$

$$\left [\left (\dfrac {2}{3}\right )^{2}\right ]^{2} = \left (\dfrac {2}{3}\right )^{2\times 2} = \left (\dfrac {2}{3}\right )^{4} = \dfrac {2^{4}}{3^{4}} = \dfrac {16}{81}$$

Write the value of $$0.2642E05+0.3781E05$$.

The given format of number is known as E-Notation.

$$0.2642E05=0.2642\times { 10 }^{ 5 }=26420$$

$$0.3781E05=0.3781\times { 10 }^{ 5 }=37810$$

Hence, $$0.2642E05+0.3781E05=26420+37810=64230$$

$$64230=0.6423\times { 10 }^{ 5 }$$

$$0.6423\times { 10 }^{ 5 }=0.6423E05$$

Thus, the sum is $$0.6423E05$$

Simplify :

$$\dfrac{{{8^{3a}} \times {2^5} \times {2^{2a}}}}{{4 \times {2^{11a}} \times {2^{ - 2a}}}}$$

We have,

$$\dfrac{{{8^{3a}} \times {2^5} \times {2^{2a}}}}{{4 \times {2^{11a}} \times {2^{ - 2a}}}}$$

$$\Rightarrow \dfrac{{{(2^3)^{3a}} \times {2^5} \times {2^{2a}}}}{{2^2 \times {2^{11a-2a}} }}$$

$$\Rightarrow \dfrac{{{2^{9a}} \times {2^{5+2a}}}}{{2^2 \times {2^{9a}} }}$$

$$\Rightarrow \dfrac{{ {2^{5+2a+9a}}}}{{ {2^{9a+2}} }}$$

$$\Rightarrow \dfrac{{ {2^{5+11a}}}}{{ {2^{9a+2}} }}$$

$$\Rightarrow 2^{5+11a-9a-2}$$

$$\Rightarrow 2^{2a+3}$$

$$\Rightarrow 2^{2a}\times 2^3$$

$$\Rightarrow 8\times 2^{2a}$$

Hence, this is the answer.

Simplify:
$$(c^{-2})^{2/3} \times c^{3/2} \div c^{-3}$$ is equal to $$c^{\frac {p}{q}}$$ . If p snd q are co prime fiind the value of $$p+q$$.

We have,

$$ {{\left( {{c}^{-2}} \right)}^{2/3}}\times {{c}^{3/2}}\div {{c}^{-3}}={{c}^{\frac{p}{q}}} $$

$$ {{c}^{-4/3}}\times {{c}^{3/2}}\times {{c}^{3}}={{c}^{\frac{p}{q}}} $$

$$ {{c}^{-4/3}}\times {{c}^{9/2}}={{c}^{\frac{p}{q}}} $$

$$ {{c}^{\left( 27-8 \right)/6}}={{c}^{\cfrac{p}{q}}} $$

$$ {{c}^{\frac{19}{6}}}={{c}^{\frac{p}{q}}} $$

$$ \therefore p=19,q=6 $$

So, $$p+q=19+6=25$$

Hence, this is the answer.

Find the radix of the scale in which the numbers denoted by $$479,698,907$$ are in arithmetical progression.

For $$(479)_b, (698)_b,(907)_b$$ to be in Arithmetic Progression

$$\Rightarrow(479)_b+(907)_b=2(678)_b$$

$$\Rightarrow (9+7b+4b^2)+(7+9b^2)=2(8+9b+6b^2)$$

$$\Rightarrow b^2-11b=0$$

$$\Rightarrow b=11$$

Simplify:
$$(3r^2)\times (9r^2)^{3/2} \div (27r^{-3})^{1/3}$$ and find the power of $$r$$

We have,
$$(3r^2)\times (9r^2)^{3/2}\div(27r^{-3})^{1/3}$$

$$\Rightarrow (3r^2)\times ((3r)^2)^{3/2}\div(3^3r^{-3})^{1/3}$$

$$\Rightarrow (3r^2)\times (3r)^{3}\div(3r^{-1})$$

$$\Rightarrow \dfrac {(3r^2)\times (3r)^{3}}{(3r^{-1})}$$

$$\Rightarrow (3r^2)\times (3^3r^3)\times(3^{-1}r)$$

$$\Rightarrow 27r^6$$

So, the power of $$r$$ is $$6$$.

Hence, this is the answer.

Express the following in exponential form
(i) $$\log_{2} 128 = 7$$
(ii) $$\log_{10} 0.0001 = -4$$
(iii) $$\log_{8} 16 = \dfrac{4}{3}$$

$$1)\log _{2}128=7\implies 2^{7}=128$$

$$2)\log _{10}0.0001=-4\implies 10^{-4}=0.0001$$

$$3)\log _{8}16=\dfrac{4}{3}\implies 8^{4/3}=16$$

$$[(-3)^2]^5$$ = ..............

$${\textbf{Step -1: Solve using exponents}}{\textbf{.}}$$

$${\left[ {{{\left( { - 3} \right)}^2}} \right]^5}$$

$$ = {\left[ { - 3 \times - 3} \right]^5}$$

$$ = {\left( 9 \right)^5}$$

$$ = 9\times 9\times 9\times 9\times 9$$

$$ = 59,049$$

$${\textbf{Hence, the value of }}{\mathbf{{\left[ {{{\left( { - 3} \right)}^2}} \right]^5}}}{\textbf{ is }}{\mathbf{59,049.}}$$

Solve for $$x$$:
$$3^{\large{\frac{x}{5}}}+3^{\large{\frac{x-10}{10}}}=84$$.

Now,

$$3^{\large{\frac{x}{5}}}+3^{\large{\frac{x-10}{10}}}=84$$

or, $$\left(3^{\large{\frac{x}{10}}}\right)^2+\dfrac{3^{\large{\frac{x}{10}}}}{3}=84$$

or, $$3.\left(3^{\large{\frac{x}{10}}}\right)^2+3^{\large{\frac{x}{10}}}-3.84=0$$

or, $$3.\left(3^{\large{\frac{x}{10}}}\right)^2+28.3^{\large{\frac{x}{10}}}-27.3^{\large{\frac{x}{10}}}-3.84=0$$

or, $$\left(3.3^{\large{\frac{x}{10}}}+28\right)\left(3^{\large{\frac{x}{10}}}-9\right)=0$$

We have, $$\left(3.3^{\large{\frac{x}{10}}}\right)\ne -28$$ so $$\left(3^{\large{\frac{x}{10}}}-9\right)=0$$ or, $$\dfrac{x}{10}=2$$ or, $$x=20$$.

Solve: $$4^x-9.2^x+2^3=0$$.

Now,

$$4^x-9.2^x+2^3=0$$

or, $$4^x-9.2^x+8=0$$

or, $$4^x-8.2^x-2^x+8=0$$

or, $$2^x(2^x-8)-1(2^x-8)=0$$

or, $$(2^x-1)(2^x-8)=0$$

or, $$2^x=1$$ or ,$$2^x=8$$

or, $$x=0$$ or, $$x=3$$.

Express in exponential notation:
A) $${ \left( -\dfrac { 7 }{ 2 } \right) }^{ 11 }\times { \left( -\dfrac { 7 }{ 2 } \right) }^{ 5 }$$

B) $${ \left( \dfrac { 13 }{ 17 } \right) }^{ 4 }\div { \left( \dfrac { 13 }{ 17 } \right) }^{ 7 }$$

$$\displaystyle{{ \left( -\frac { 7 }{ 2 } \right) }^{ 11 }\times { \left( -\frac { 7 }{ 2 } \right) }^{ 5 }\\ ={ \left( -\frac { 7 }{ 2 } \right) }^{ 11+5 }\\ ={ \left( -\frac { 7 }{ 2 } \right) }^{ 16 }\\ { \left( \frac { 13 }{ 17 } \right) }^{ 4 }\div { \left( \frac { 13 }{ 17 } \right) }^{ 7 }\\ ={ \left( \frac { 13 }{ 17 } \right) }^{ 4-7 }\\ ={ \left( \frac { 13 }{ 17 } \right) }^{ -3 }\\ ={ \left( \frac { 17 }{ 13 } \right) }^{ 3 }}$$

If $$a^x=b,b^y=c,c^z=a$$ then show that $$xyz=1$$.

$$a^x=b$$......(1), $$b^y=c$$......(2), $$c^z=a$$......(3).

Now putting the value of $$c$$ from (2) in (3) we get,

$$b^{yz}=a$$

Now using the value of $$b$$ from (1) in the above equation we get,

$$a^{xyz}=a$$

or, $$xyz=1$$.

Simply with the help of exponential notation :
(i) $${({2^2} \times {3^3})^2}$$
(ii) $${\left( {{{15} \over {16}}} \right)^3} \div {\left( {{9 \over 8}} \right)^2}$$

(i)$$\implies (2^2)^2\times (3^3)^2$$ $$\because(a^m)^n=a^{mn}$$

$$=2^4\times3^6 = 11664$$

(ii)$$\implies \dfrac{5^3\times3^3}{(2^4)^3}\times\dfrac{(2^3)^2}{(3^2)^2}$$

$$=\dfrac{5^3}{3\times2^6} = 0.6510$$

Find the value of $$\sqrt[5]{32^4}$$.

Now,

$$\sqrt[5]{32^4}$$

$$=\sqrt[5]{(2^5)^4}$$

$$=\sqrt[5]{2^{20}}$$

$$=2^{\large{\frac{20}{5}}}$$

$$=2^4=16$$

Prove that: $$\dfrac{\left(\dfrac{a}{b}\right)^m}{\left(\dfrac{a}{b}\right)^n} = \left(\dfrac{a}{b}\right)^{m-n}$$

We have,

$$\dfrac{\left(\dfrac{a}{b}\right)^m}{\left(\dfrac{a}{b}\right)^n} $$

$$=\dfrac{a^m.b^n}{a^nb^m}$$

$$=\dfrac{a^{m-n}}{b^{m-n}}$$

$$=\left(\dfrac{a}{b}\right)^{m-n}$$

Simplify:
$$\left[ { 4 }^{ 0 }+{ 4 }^{ 2 }-{ 2 }^{ 5 } \right] \times { 3 }^{ -2 }$$

$$=\left[ {{4^0} + {4^2} - {2^5}} \right] \times {3^{ - 2}}$$

$$=\left[ {1 + 16 - 32} \right] \times \dfrac{1}{9}$$

$$ = \left( {17 - 32} \right) \times \dfrac{1}{9}$$

$$ = - 15 \times \dfrac{1}{9}$$

$$ = - \dfrac{5}{3}$$

Simplify:
$$\left[ \left( 2 \right) ^{ -1 }+\left( 4 \right) ^{ -1 }+\left( 3 \right) ^{ -1 } \right] ^{ -1 }$$

$${\left[ {{{\left( 2 \right)}^{ - 1}} + {{\left( 4 \right)}^{ - 1}} + {{\left( 3 \right)}^{ - 1}}} \right]^{ - 1}}$$

$$={\left( {\cfrac{1}{2} + \cfrac{1}{4} + \cfrac{1}{3}} \right)^{ - 1}}$$

$$ = {\left( {\cfrac{{6 + 3 + 4}}{{12}}} \right)^{ - 1}}$$

$$ = {\left( {\cfrac{{13}}{{12}}} \right)^{ - 1}}$$

$$ = \cfrac{{12}}{{13}}$$

Find the value of $${4^{ - 3}}$$ in fractional form:

$$4^{-3}=\dfrac {1}{4^{3}}=\dfrac {1}{64}$$

Simplify:
$$\left[ \left( 4 \right) ^{ -1 }-\left( 5 \right) ^{ -1 } \right] ^{ 2 }\times \left( \dfrac { 5 }{ 8 } \right) ^{ -1 }$$

$${\left[ {{{\left( 4 \right)}^{ - 1}} - {{\left( 5 \right)}^{ - 1}}} \right]^2} \times {\left( {\cfrac{5}{8}} \right)^{ - 1}}$$

$$ = {\left( {\cfrac{1}{4} - \cfrac{1}{5}} \right)^2} \times {\left( {\cfrac{5}{8}} \right)^{ - 1}}$$

$$ = \left( {\cfrac{{5 - 4}}{{20}}} \right) \times \cfrac{8}{5}$$

$$ = \cfrac{1}{{20}} \times \cfrac{8}{5}$$

$$ = \cfrac{2}{{25}}$$

Find $$n$$
$$\left( \dfrac { 2 }{ 3 } \right) ^{ 3 }\times \left( \dfrac { 2 }{ 3 } \right) ^{ 5 }=\left( \dfrac { 2 }{ 3 } \right) ^{ n-2 }$$

$${\left( {\dfrac{2}{3}} \right)^3} \times {\left( {\dfrac{2}{3}} \right)^5} = {\left( {\dfrac{2}{3}} \right)^{n - 2}}$$

$$ \Rightarrow {\left( {\dfrac{2}{3}} \right)^8} = {\left( {\dfrac{2}{3}} \right)^{n - 2}}$$

$$ \Rightarrow n - 2 = 8$$

$$ \Rightarrow n = 10$$

Evaluate :$$\sqrt {\dfrac{1}{4}} + {\left( {0.01} \right)^{ - \dfrac{1}{2}}} - {\left( {27} \right)^{^{\dfrac{2}{3}}}}$$

Given equation is,

$$\sqrt{ \dfrac{1}{4}}+( 0.01)^{-\cfrac{1}{2}}-\left ( 27 \right )^\cfrac{2}{3}$$

$$=\dfrac{1}{2}+\left ( \dfrac{1}{0.01} \right )^\cfrac{1}{2}-\left ( (3 )^3 \right )^\cfrac{2}{3}$$

$$=\dfrac{1}{2}+\sqrt{\dfrac{100}{1}}-\left ( (3 )^3 \right )^\cfrac{2}{3}$$

$$=\dfrac{1}{2}+10-\left ( 3 \right )^2$$

$$=\dfrac{1}{2}+10-9$$

$$=\dfrac{3}{2}$$

Hence, the value is $$\dfrac{3}{2}$$.

Simplify:
$$\left[ \left( 5 \right) ^{ 2 }-\left( \dfrac { 1 }{ 4 } \right) ^{ -2 } \right] \times \left( \dfrac { 3 }{ 4 } \right) ^{ -2 }$$

$$\left[ {{{\left( 5 \right)}^2} - {{\left( {\cfrac{1}{4}} \right)}^{ - 2}}} \right] \times {\left( {\cfrac{3}{4}} \right)^{ - 2}}$$

$$ = \left[ {25 - {{\left( 4 \right)}^2}} \right] \times {\left( {\cfrac{4}{3}} \right)^2}$$

$$ = \left( {25 - 16} \right) \times \cfrac{{16}}{9}$$

$$ = 9 \times \cfrac{{16}}{9}=16$$

If $$x=(100)^{a}, y=(10000)^{b}$$ and $$z=(10)^{c}$$, express $$\log \dfrac {10\sqrt {y}}{x^{2}z^{3}}$$ in terms of $$a,b,c$$

$$x=(100)^{a}$$

Take log both sides,

$$\log x=\log 100^{a}$$

$$\log x=a\log 100$$

$$\log x=a\log 10^{2}$$

$$\log x=2a$$ .................. (1)

$$y=(10000)^{b}$$

$$\log y=\log 10000^{b}$$

$$\log y=b\log 10000$$

$$\log y=b\log 10^{4}$$

$$\log y=4b$$ ................ (2)

$$z=(10)^{c}$$

$$\log z=\log 10^{c}$$

$$\log z=c\log 10$$

$$\log z=c$$ .................... (3)

$$\displaystyle \log \frac{10\sqrt{y}}{x^{2}z^{3}}$$$$=\log 10\sqrt{y}-\log x^{2}z^{3}$$

$$=\log 10+\log \sqrt{y}-\log x^{2}-\log z^{3}$$

$$=1+\dfrac{1}{2}\log y-2\log x-3\log z$$

$$\displaystyle \log \frac{10\sqrt{y}}{x^{2}z^{3}}$$$$=1+2b-4a-3c$$

Find the value of $${\left( {6561} \right)^{0.25}}$$

$${\left( {6561} \right)^{0.25}}$$

$${\left( {{9^4}} \right)^{0.25}}$$

$${9^{4 \times {{24} \over {100}}}}$$

$${9^{4 \times {1 \over 4}}}$$

$${9^1}$$

$$9$$

$${ \left( { 2 }^{ 3 } \right) }^{ 4 }={ \left( { 2 }^{ 2 } \right) }^{ x }$$, find $$x$$.

$$\begin{array}{l} { \left( { { 2^{ 3 } } } \right) ^{ 4 } }={ \left( { { 2^{ 2 } } } \right) ^{ x } } \\ \Rightarrow { 2^{ 12 } }={ 2^{ 2x } } \\ \Rightarrow 2x=12 \\ \Rightarrow x=6 \end{array}$$

Express each of the following numbers using expotential notation:
i) $$512$$
ii) $$343$$
iii) $$729$$
iv) $$3125$$

We have,

i) $$512=2^8$$

ii) $$343=7^3$$

iii) $$729=9^3$$

iv) $$3125=25^2\times 5=5^5$$

Find the highest power of $$p$$ when $$81p^4 -1$$ is divided by $$3p-1$$.

We have

$$81p^4-1=(3p)^4-1^4=(3p-1)(3p+1)\{(3p)^2+1\}$$.

Now, $$\dfrac{(81p^4)-1}{3p-1}=(3p+1)\{(3p)^2+1\}=(3p)^3+(3p)^2+(3p)+1$$.

So the highest power of $$p$$ in the quotient is $$3$$.

Simplify: $$\dfrac{8^5}{8^3}$$

Now,

$$\dfrac{8^5}{8^3}$$

$$=8^{5-3}$$

$$=8^2$$

$$=64$$.

Solve: $${\left( {25} \right)^2}$$

625

Express the following in exponential form
(i)$$-1331$$

(ii)$$\dfrac{-64}{125}$$

(iii)$$\dfrac{-345}{1024}$$

(i) $$-1331=-11\times -11\times -11 ={\left(-11\right)}^{3}$$

(ii)$$\dfrac{-64}{125} = \dfrac{2\times 2\times 2\times 2\times 2\times 2}{-5\times -5\times -5}$$

$$\Rightarrow \dfrac{-64}{125} =\dfrac{{2}^{6}} {{\left(-5\right)}^{3}}$$

(iii)$$ \dfrac{-345}{1024} = \dfrac{-5\times 69}{2\times 512} =\dfrac{-5\times 3\times 23}{{2}^{2}\times 256}$$

$$\Rightarrow \dfrac{-345}{1024}=\dfrac{-5\times 3\times 23}{{2}^{10}}$$

Calculate:
$$\dfrac{{{4^3} \times {6^6} \times {2^5}}}{{{2^3} \times {4^2} \times {3^2}}}$$

$$\dfrac{{{4^3} \times {6^6} \times {2^5}}}{{{2^3} \times {4^2} \times {3^2}}}$$

$$=\dfrac{{{4^3} \times {(3 \times 2)^6} \times {2^5}}}{{{2^3} \times {4^2} \times {3^2}}}$$

$$=\dfrac{{{4^3} \times {3^6} \times {2^{11}}}}{{{2^3} \times {4^2} \times {3^2}}}$$

$$= (4)\times(3^4)\times(2^8)$$

$$=82944$$

Simplify $$\sqrt[4]{(81)^{-2}}$$.

$$\sqrt[4]{(81)^{-2}}\\=81^{(\frac{-2}{4})}\\=81^{(\frac{-1}{2})}\\=(3^4)^{(\frac{-1}{2})}\\=3^{-2}\\=(\frac{1}{9})$$

Simplify:
$${2^{\cfrac{2}{3}}}{.2^{\cfrac{1}{5}}}$$

$$2^{\cfrac{2}{3}}. 2^{\cfrac{1}{5}}$$

Sine we know that

$$x^{n}.x^{m}=x^{(m+n)}$$

$$2^{\cfrac{2}{3}}. 2^{\cfrac{1}{5}}= 2^{\cfrac{2}{3}+\cfrac{1}{5}}$$

Let's Solve the power as we have addition of unlike frcations

$$\dfrac{2}{3}+\dfrac{1}{5}$$

So, first find the lcm of 3 and 5, which would be 15

$$=\dfrac{2\times 5+1\times 3}{15}$$

$$=\dfrac{10+3}{15}$$

$$=\dfrac{13}{15}$$

Therefore, $$2^{\cfrac{2}{3}+\cfrac{1}{5}}=2^{\cfrac{13}{15}}$$

or we can say

$$2^{\cfrac{2}{3}}. 2^{\cfrac{1}{5}}=2^{\cfrac{13}{15}}$$

Find the value of $$x$$ for the given equation $${\left( {\dfrac{3}{4}} \right)^3}{\left( {\dfrac{4}{3}} \right)^{ - 7}} = \left( {\dfrac{3}{4}} \right)2x$$

We have,

$${{\left( \dfrac{3}{4} \right)}^{3}}\times {{\left( \dfrac{4}{3} \right)}^{-7}}=\left( \dfrac{3}{4} \right)\times 2x$$

$$ {{\left( \dfrac{3}{4} \right)}^{3}}\times {{\left( \dfrac{3}{4} \right)}^{7}}=\left( \dfrac{3}{4} \right)\times 2x $$

$$ {{\left( \dfrac{3}{4} \right)}^{3}}\times {{\left( \dfrac{3}{4} \right)}^{6}}=2x $$

$$ {{\left( \dfrac{3}{4} \right)}^{9}}=2x $$

$$ x=\dfrac{1}{2}{{\left( \dfrac{3}{4} \right)}^{9}} $$

Hence, the value of $$x$$ is $$\dfrac{1}{2}{{\left( \dfrac{3}{4} \right)}^{9}}$$.

If $$a=2,$$ $$b=3$$ find the value of $$(ab)^a$$.

Given ,

$$a=2$$ and $$b=3$$

$$=$$ $${ (ab) }^{ a }$$

$$=$$ $${ ((2)(3)) }^{ 2 }$$

$$=$$ $${ (6) }^{ 2 }$$

$$=$$ $$36$$

$$81$$ in exponential form as
a) base $$9$$
b) base $$3$$

$$81\Rightarrow 9 \times 9 \Rightarrow 3\times 3\times 3\times 3$$

$$(i) \ 81=9\times 9=9^2$$

$$(ii)\ 81=3\times 3\times 3\times 3=3^4$$

Find the value of n when :
i) $$5^{2n} \times 5^3 = 5^9$$
ii) $$8 \times 2^{n + 2} = 32$$

(1)

$$5^{2n}\times 5^{3}=5^{9}$$

Apply law of exponents $$x^{a}\times x^{b}=x^{a+b}$$

$$5^{2n+3}=5^{9}$$

$$\Rightarrow 2n+3=9$$

$$2n=9-3$$

$$2n=6$$

$$n=3$$

(2)

$$8\times 2^{n+2}=32$$

$$2^{3}\times 2^{n+2}=2^{5}$$

Apply law of exponents $$x^{a}\times x^{b}=x^{a+b}$$

$$2^{3+n+2}=2^{5}$$

$$2^{n+5}=2^{5}$$

$$\Rightarrow n+5=5$$

$$n=5-5$$

$$n=0$$

Solve
$$\dfrac{4^5 a^8b^3}{ 4^5 a^5b^2}$$

$$\dfrac{4^{5}a^{8}b^{3}}{4^{5}a^{5}b^{2}}=4^{5-5}a^{8-5}b^{3-2}$$

$$=4^{0}a^{3}b^{1}$$

$$=a^{3}b$$

Simplify:
$${\left( { - 3} \right)^4} \times {\left( {\dfrac{5}{3}} \right)^4} $$

Consider the given expression,

$$ \Rightarrow {{\left( -3 \right)}^{4}}\times {{\left( \dfrac{5}{3} \right)}^{4}} $$

$$ \because \,-x=-1\times x $$

$$ \Rightarrow {{\left( -3 \right)}^{4}}\times {{\left( \dfrac{5}{3} \right)}^{4}}={{\left( -1\times 3 \right)}^{4}}\times {{3}^{4}}\times \dfrac{{{5}^{4}}}{{{3}^{4}}}={{\left( -1 \right)}^{4}}\dfrac{{{5}^{4}}}{1} $$

$$ \because \,{{\left( -1 \right)}^{4}}=1 $$

$$ \Rightarrow {{\left( -1 \right)}^{4}}\dfrac{{{5}^{4}}}{1}=\dfrac{{{5}^{4}}}{1}={{5}^{4}} $$

Hence, this is the answer .

Find the value of $$4^3$$

$$\textbf{Step-1:}$$ $$\textbf{Finding}$$ $${4^3}$$

$$\textbf{Step-2:}$$ $${4^3 = }$$ $${4} \times {4} \times {4 = 64}$$

$$\textbf{Hence, }$$ $${4^3 = 64}$$

Solve:$$\dfrac{{{3^0} \times {5^2}}}{{{3^4} \times {5^3} \times {2^4}}}$$

We have,

$$=\dfrac{{{3}^{0}}\times {{5}^{2}}}{{{3}^{4}}\times {{5}^{3}}\times {{2}^{4}}}$$

$$ =\dfrac{1}{{{3}^{4}}\times 5\times {{2}^{4}}} $$

$$ =\dfrac{1}{81\times 5\times 16} $$

$$ =\dfrac{1}{81\times 80} $$

$$ =\dfrac{1}{6480} $$

Hence, the value is $$\dfrac{1}{6480}$$.

Find the value of : $${\left( { - \dfrac{1}{{27}}} \right)^{ - \dfrac{2}{3}}}$$

We have,

$${{\left( -\dfrac{1}{27} \right)}^{-\frac{2}{3}}}$$

$$ ={{\left( -\dfrac{1}{{{\left( 3 \right)}^{3}}} \right)}^{-\frac{2}{3}}} $$

$$ ={{\left( -{{\left( 3 \right)}^{-3}} \right)}^{-\frac{2}{3}}} $$

$$ ={{\left( -\left( 3 \right) \right)}^{2}} $$

$$ =9 $$

Hence, the value is $$9$$.

Find the value of $$\left(\frac{9}{8}\right)^{-3}\times \left(\frac{8}{9}\right)^{-2}$$

$$(\frac{9}{8})^{-3}\times(\frac{8}{9})^{-2}\\=(\frac{8}{9})^3\times(\frac{9}{8})^2\\=(\frac{8}{9})\times(\frac{8}{9})\times(\frac{8}{9})\times(\frac{9}{8})\times(\frac{9}{8})\\=(\frac{8}{9})$$

$$a = \dfrac{{{2^{x - 1}}}}{{{2^{-x - 2}}}}$$ and $$b = \dfrac{{{2^{ - x}}}}{{{2^{x + 1}}}}$$, find the value of $$x$$.

We have,

$$ a=\dfrac{{{2}^{x-1}}}{{{2}^{-x-2}}} $$

$$ a={{2}^{x-1}}\times {{2}^{-\left( -x-2 \right)}} $$

$$ a={{2}^{x-1+x+2}} $$

$$ a={{2}^{2x+1}} $$

$$ 2x+1={{\log }_{2}}a $$

$$ 2x={{\log }_{2}}a-1 $$

$$ x=\dfrac{1}{2}\left( {{\log }_{2}}a-1 \right) $$

Since,

$$b=\dfrac{{{2}^{-x}}}{{{2}^{x+1}}}$$

$$ b={{2}^{-x}}\times {{2}^{-\left( x+1 \right)}} $$

$$ b={{2}^{-x-x-1}} $$

$$ b={{2}^{-2x-1}} $$

$$ -2x-1={{\log }_{2}}b $$

$$ -2x=1+{{\log }_{2}}b $$

$$ x=-\dfrac{1}{2}\left( 1+{{\log }_{2}}b \right) $$

Hence, the values of x are $$\dfrac{1}{2}\left( {{\log }_{2}}a-1 \right)$$ and $$-\dfrac{1}{2}\left( 1+{{\log }_{2}}b \right)$$.

Find the value of x , if
$${(\dfrac{5}{7})^6}{(\dfrac{7}{5})^{ - 9}} = {(\dfrac{5}{7})^{3x}}$$

Given

$${ \left( \dfrac { 5 }{ 7 } \right) }^{ 6 }.{ \left( \dfrac { 7 }{ 5 } \right) }^{ -9 }={ \left( \dfrac { 5 }{ 7 } \right) }^{ 3x }$$

$${ \Rightarrow \left( \dfrac { 5 }{ 7 } \right) }^{ 6 }\times { \left( \dfrac { 5 }{ 7 } \right) }^{ 9 }={ \left( \dfrac { 5 }{ 7 } \right) }^{ 3x }$$

$${ \Rightarrow \left( \dfrac { 5 }{ 7 } \right) }^{ 6+9 }={ \left( \dfrac { 5 }{ 7 } \right) }^{ 3x }$$ ---since base is same, powers add up

$${ \Rightarrow \left( \dfrac { 5 }{ 7 } \right) }^{ 15 }={ \left( \dfrac { 5 }{ 7 } \right) }^{ 3x }$$

$$\Rightarrow 15=3x$$ ---since base is same, we can compare powers

$$\therefore x=5$$

Simplify :
$$(-5)^4 + (2)^3$$

$$(-5)^{4}+(2)^{3}$$

$$=(-5)(-5)(-5)(-5)+(2)(2)(2)$$

$$=625+8$$

$$=633$$

Show that
$$\dfrac{{{{\left( {{3^a}} \right)}^2} \times {{\left( {{2^{a - 2}}} \right)}^2}}}{{{9^{a - 1}} \times {4^{a + 2}}}} = \dfrac{9}{{256}}$$

$$\dfrac{(3^a)^2\times(2^{a-2})^2}{9^{a-1}\times4^{a+2}}$$

$$=\dfrac{9^a\times4^{a-2}}{9^{a-1}\times4^{a+2}}$$

$$=9^{a-(a-1)}4^{(a-2)-(a+2)}$$

$$=9^14^{-4}=\dfrac{9}{256}$$

Solve $$84{ a }^{ 2 }{ b }^{ 5 }\div 12{ a }^{ 2 }{ b }^{ 2 }$$

$$\cfrac { 84{ a }^{ 2 }{ b }^{ 5 } }{ 12{ a }^{ 2 }{ b }^{ 2 } }$$

$$ =7{ b }^{ 3 }$$

What is $${10^{ - 10}}$$ equals to

$$ \because a^{-b} = \dfrac{1}{a^{-b}}$$

$$\therefore 10^{-10} = \dfrac{1}{10^{10}}$$

Find Y-
$$27^y = \dfrac{9}{{{3^y}}}$$.

We have,

$${{27}^{y}}=\dfrac{9}{{{3}^{y}}}$$

$$ {{\left( {{3}^{3}} \right)}^{y}}=\dfrac{9}{{{3}^{y}}} $$

$$ {{3}^{3y}}\times {{3}^{y}}=9 $$

$$ {{3}^{4y}}={{3}^{2}} $$

$$ 4y=2 $$

$$ 2y=1 $$

$$ y=\dfrac{1}{2} $$

Hence, the value of $$y$$ is $$\dfrac{1}{2}$$.

Express in the form of $$a^{m}b^{m}c^{m}$$ as appropriate: $$343\times 216$$

$$216=6^3=2^3\times 3^3$$

$$343=7^3$$

$$343\times 216=7^3\times 2^3\times 3^3$$

$$a^mb^mc^m=7^3\times 2^3\times 3^3.$$

$$a=a,b=2,c=3,m=3.$$

Simplify $$11^{8} \div 11^{2}$$

We have,

$$ \Rightarrow {{11}^{8}}\div {{11}^{2}} $$

$$ \Rightarrow \dfrac{{{11}^{8}}}{{{11}^{2}}} $$

$$ \Rightarrow {{11}^{6}} $$

Hence, this is the answer.

If $${\left( {\frac{5}{9}} \right)^{ - 4}} \times {\left( {\frac{7}{5}} \right)^{ - 4}} = \left( {\frac{p}{q}} \right)$$, find $${\left( {\frac{p}{q}} \right)^{ - 2}}$$

Given,

$$(\dfrac{5}{9})^-4\times(\dfrac{7}{5})^-4=(\dfrac{p}{q})$$

$$=>(\dfrac{7}{9})^-4=(\dfrac{p}{q})$$

$$=>\dfrac{p}{q}=(\dfrac{9}{5})^4$$

Now,

$$(\dfrac{p}{q})^-2=((\dfrac{9}{7})^4)^-2$$

$$=>(\dfrac{9}{7})^2$$

$$=>\dfrac{81}{49}$$

Find value of $$12x^{3}+x^{2}+x$$ if $$x=7$$

Given: $$12x^3+x^2+x$$

At $$x=7$$,

$$=12(7)^3+(7)^2+7$$

$$=12 \times 343+49+7$$

$$=4116+49+7=4172$$

If $$a= b^{2x}, b= c^{2y} $$ & $$c= a^{2z} $$, prove that xyz= $$\frac{1}{8}$$

$$a=b^{2x}\\a=(c^{2y})^{2x}\\or\>a=c^{4xy}\\or\>a=(a^{2z})^{4xy}\\or\>a=a^{8xyz}\\\therefore 8xyz=1\\\therefore xyz=(\frac{1}{8})$$

Find $$x$$, if $${\left( {{3^6}} \right)^4} = {3^{12x}}$$

$${ { (3 }^{ 6 }) }^{ 4 }$$ $$={ 3 }^{ 12x }$$

$${ 3 }^{ (6)(4) }$$$$={ 3 }^{ 12x }$$

$${ 3 }^{ 24 }$$$$={ 3 }^{ 12x }$$

By comparing ,

$$24=12x$$

$$x=2$$

Write the base and exponent of the following :
$$ \left( \dfrac {-4}{7} \right)^6 $$

Base = $$ \dfrac {-4}{7} $$
Exponent = $$6$$

Write the base and exponent of the following :
$$ \dfrac{-2}{3} $$

Base = $$ \dfrac{-2}{3} $$
Exponent = $$1$$

Express the following in exponential form :
$$ \left( \dfrac {9}{2} \right)^4 $$

$$\left(\dfrac{9}{2}\right)^{4}= \left(\dfrac{8+1}{2}\right)^{4}\Rightarrow \left(4+\dfrac{1}{2}\right)^{4}= \left(4+\dfrac{1}{2}\right)^{2} \left(4+\dfrac{1}{2}\right)^2$$

$$=((2^{2})^{2}+2\times 2^{2}\times \dfrac{1}{2}+ \left(\dfrac{1}{2}\right)^{2})^{2}$$

$$=(2^{4}+2^{2}+2^{-2})^{2}$$

$$\left(\dfrac{9}{2}\right)^{4}=2^{8}+2^{4}+2^{-4}+2.2^{4}.2^{2}+2.2^{2}2^{-2}+2.2^{4}.2^{-2}$$

$$=2^{8}+2^{4}+2^{-4}+2^{7}+2+2^{3}$$

$$\left(\dfrac{9}{2}\right)^{4}=2^{8}+2^{7}+2^{4}+2^{3}+2+2^{-4}$$

Express the following in exponential form :
$$ \left( \dfrac {-7}{8} \right)^3 $$

$$(\dfrac{-7}{8})^{3}\Rightarrow (\dfrac{-7-1+1}{8})^{3}\Rightarrow (\dfrac{-8+1}{8})^{3}\Rightarrow (-1+\dfrac{1}{8})^{3}$$

$$\Rightarrow (-1)^{3}+(\dfrac{1}{8})^{3}+3(-1)(\dfrac{1}{8})(-1+\dfrac{1}{8})$$

$$\Rightarrow -1+\dfrac{1}{8^{3}}+\dfrac{3}{8}[\dfrac{7}{8}]$$

$$\Rightarrow -1+8^{-3}+3^{1}\times 7^{1}\times 8^{-2}$$

$$(\dfrac{-7}{8})^{3}=-1+2^{-3\times 3}+3^{1}\times 7^{1}\times 2^{-2\times 3}$$

$$(\dfrac{-7}{8})^{3}=-1+2^{-9}+3\times 7\times 2^{-6}$$

Write the base and exponent of the following :
$$ \left( \dfrac {2}{9} \right)^5 $$

Base = $$ \dfrac {2}{9} $$
Exponent = $$5$$

Write the base and exponent of the following :
$$ \left( \dfrac {15}{19} \right)^3 $$

Base = $$ \dfrac {15}{19} $$
Exponent = $$3$$

Express the following in exponential form.
$$\dfrac{9}{2}\times \dfrac{9}{2}\times \dfrac{9}{2}\times \dfrac{9}{2}\rightarrow\left(\dfrac{9}{2}\right)^4$$.

$$\Bigg( \cfrac{9}{2} \Bigg)^4 = \cfrac{3^8}{2^4}$$

if $$4^x - 4^{x-1} = 24 $$ then find the value of $$(2x)^x . $$

$$4^{x}-4^{x-1}=24$$

$$\Rightarrow 4^{x}-\dfrac{4^{x}}{4}=24$$

$$\dfrac{3}{4}(4^{x})=24$$

$$\Rightarrow (2^{2x})=32$$

$$\Rightarrow 2^{2x}=2^{5}$$

$$2x=5$$

$$\Rightarrow x=\dfrac{5}{2}$$

$$(2x)^{x}=(5)^{\frac{5}{2}}\Rightarrow (\sqrt{5})^{5}\Rightarrow 5.5\times \sqrt{5}\Rightarrow 25\sqrt{5}$$

$$\therefore (2x)^{x}=25\sqrt{5}$$

Express the following in exponential form :
$$ \left( \dfrac {5}{6} \right)^2 $$

$$ \left ( \dfrac{5}{6} \right )^{2} =\left ( \dfrac{6-1}{6} \right )^{2}=\left ( 1-\dfrac{1}{6} \right )^{2}$$

=$$1+\left ( \dfrac{1}{6} \right )^{2} - \dfrac{2}{6}$$

$$=1+\dfrac{1}{6^{2}} - \dfrac{1}{3}$$

$$\left ( \dfrac{5}{6} \right )^{2} = $$$$1+6^{-2}-3^{-1}$$

Solve : $$\dfrac{7525}{5^2} + 3125 \, \times \, 5^{-4} - 105 \, \times \, 2 = ?$$

$$\cfrac{7525}{5^{2}}+3125\times 5^{-4}-105\times 2$$

$$=\cfrac{7525}{5^{2}}+\cfrac{3125}{5^{4}}-210$$

$$=\cfrac{7525}{25}+\cfrac{3125}{625}-210$$

$$=301+5-210$$

$$=306-210$$

$$=96$$

Simplify:
$$16^{\frac{3}{2}}$$

$$ { 16^{ \frac { 3 }{ 2 } } } \\ ={ \left( { { 4^{ 2 } } } \right) ^{ \frac { 3 }{ 2 } } } \\ =4^{ 3 } \\ =64 $$

Simplify:
$$32^{\frac{1}{5}}$$

$$ { 32^{ \frac { 1 }{ 5 } } } \\ ={ \left( { { 2^{ 5 } } } \right) ^{ \frac { 1 }{ 5 } } } \\ =2 $$

Express the following in exponential form :
$$ \left( \dfrac {11}{12} \right)^6 $$

$$\left (\dfrac{11}{12}\right)^6$$

$$\Rightarrow \left (1-\dfrac{1}{2}\right)^6$$

$$\Rightarrow \left [1+ ^6C_1\left (\dfrac{-1}{12}\right)+ ^6C_2\left (\dfrac{-1}{12}\right)^2+ ^6C_3\left (\dfrac{-1}{12}\right)^3+ ^6C_4\left (\dfrac{-1}{12}\right)^4+ ^6C_5\left (\dfrac{-1}{12}\right)^5+ ^6C_6\left (\dfrac{-1}{12}\right)^6\right]$$

$$\Rightarrow \left[ 1+6\left( \dfrac { -1 }{ 12 } \right) +15{ \left( \dfrac { -1 }{ 12 } \right) }^{ 2 }+20{ \left( \dfrac { -1 }{ 12 } \right) }^{ 3 }+15{ \left( \dfrac { -1 }{ 12 } \right) }^{ 4 }+6{ \left( \dfrac { -1 }{ 12 } \right) }^{ 5 }+{ \left( \dfrac { -1 }{ 12 } \right) }^{ 6 } \right] $$

$$\Rightarrow \left [1-\dfrac{1}{2}+15\left [\dfrac{1}{12^2}+\dfrac{1}{12^4}\right]\dfrac{1}{12^6}-\dfrac{6}{12^5}-\dfrac{20}{12^3}\right]$$

$$\boxed{\left (\dfrac{11}{12}\right)^6\Rightarrow \left [\dfrac{1}{2}+\dfrac{15}{12^2}+\dfrac{15}{12^4}+\dfrac{1}{12^6}-\dfrac{6}{12^5}-\dfrac{20}{12^3}\right]}$$

Express the following in exponential form :
$$ \left( 1.8 \right)^7 $$

$$(1.8)^7$$

$$\Rightarrow \ (1+(0.8)^7$$

$$\Rightarrow \ [1+ ^7C_1(0.8)+ ^7C_2(0.8)^2+ ^7C_3(0.8)^3+ ^7C_4(0.8)^4+^7C_5(0.8)^5+ ^7C_6(0.8)^6+ ^7C_7(0.8)^7]$$

$$\Rightarrow [1+7(0.8)+21(0.8)^2+35(0.8)^3+35(0.8)^4+21(0.8)^5+7(0.8)^6+(0.8)]$$

$$\boxed{(0.8)^7=(1+(0.8)^7+21((0.8)^2+(0.8)^6)+7((0.8)+(0.8)^6)+35((0.8)^4+(0.8)^5))}$$

Find the value of $${ \left[ { \left( 16 \right) }^{ \frac { 1 }{ 2 } } \right] }^{ \frac { 1 }{ 2 } }$$

$${ \left[ { \left( 16 \right) }^{ \frac { 1 }{ 2 } } \right] }^{ \frac { 1 }{ 2 } }$$

Now,

$${ \left[ { \left( 16 \right) }^{ \frac { 1 }{ 2 } } \right] }^{ \frac { 1 }{ 2 } }$$

$$={ { \left( 16 \right) }^{ \frac { 1 }{ 2 }\times{ \frac { 1 }{ 2 } } } }$$

$$={ { \left( 16 \right) }^{ \frac { 1 }{ 4 } } }$$

$$={ { \left( 2 \right) }^{4\times \frac { 1 }{ 4 } } }$$

$$=2^1$$

$$=2$$

Hence, the required value is $$1$$ .

Prove that : $$\left(\dfrac{2^a}{2^b} \right)^{(a +b)} . \left(\dfrac{2^b}{2^c} \right)^{(b + c)} . \left(\dfrac{2^c}{2^d} \right)^{(c + d)}.\left(\dfrac {2^d}{2^a}\right)^{(d+a)} = 1$$

$$\left ( \dfrac{2^a}{2^b} \right )^{(a+b)}\cdot\left ( \dfrac{2^b}{2^c} \right )^{(b+c)}\cdot\left ( \dfrac{2^c}{2^d} \right )^{(c+d)}\cdot\left ( \dfrac{2^d}{2^a} \right )^{(d+a)}$$

$$=\left ( 2^{(a-b)} \right )^{(a+b)}\cdot\left ( 2^{(b-c)} \right )^{(b+c)}\cdot\left ( 2^{(c-d)} \right )^{(c+d)}\cdot\left ( 2^{(d-a)} \right )^{(d+a)}$$

$$=2^{(a^2-b^2)}\cdot2^{(b^2-c^2)}\cdot2^{(c^2-d^2)}\cdot2^{(d^2-a^2)} $$

$$=2^{(a^2-b^2+b^2-c^2+c^2-d^2+d^2-a^2)}$$

$$=2^0$$

$$=1$$

Simplify:
$$625^{\frac{1}{4}}$$

$${ 625^{ \frac { 1 }{ 4 } } } \\ ={ \left( { { 5^{ 4 } } } \right) ^{ \frac { 1 }{ 4 } } } \\ =5 $$

Simplify:
$$243^{\frac{2}{5}}$$

$$ { 243^{ \frac { 2 }{ 5 } } } \\ ={ \left( { { 3^{ 5 } } } \right) ^{ \frac { 2 }{ 5 } } } \\ ={ 3^{ 2 } } \\ =9 $$

Find the value of K if $${5^6}\times{5^k} = {\left( 5 \right)^{3k}}$$

$$5^6\times5^k =5^{6+k}$$

Now, $$5^{6+k}=5^{3k}\Rightarrow 6+k=3k\Rightarrow k=3$$

Evaluate $$8^{9}\div8^{3}$$

$$8^{9}\div 8^{3}$$

$$=\dfrac{8^{9}}{8^{3}}\rightarrow $$ Law of Exponents $$\left(\dfrac{a^{m}}{a^{n}}=a^{m-n}\right)$$

$$=8^{9-3}$$

$$=8^{6}$$

$$=(512) \times (512)$$

$$=262144$$

Is $${\left( {{a^m}} \right)^n} = {\left( {{a^n}} \right)^m}$$ Explain.

Show that $$(a^{m})^{n}=(a^{n})^{m}$$

Taking LHS.

$$=(a^{m})^{n}$$

$$=a^{mn}$$ (According to properties of exponets)

Taking $$RHS$$.

$$=(a^{n})^{m}$$

$$=a^{nm}$$ (According to properties of exponents)

$$=a^{mn}$$

$$=LHS$$

$$LHS=RHS$$

$$\dfrac{\left ( -3^{2} \right )\times \left ( -6^{2} \right )\times 7^{2}}{\left ( 12 \right )^{1}\times \left ( 14 \right )^{2}}$$

$$\dfrac{{\left( -3 \right)}^{2} \times {\left( -6 \right)}^{2} \times {\left( 7 \right)}^{2}}{{\left( 12 \right)}^{1} \times {\left( 14 \right)}^{2}}$$

$$= \dfrac{\left( -3 \times -3 \right) \times \left( -6 \times -6 \right) \times \left( 7 \times 7 \right)}{\left( 12 \right) \times \left( 14 \times 14 \right)}$$

$$= \dfrac{9 \times 6}{2 \times 2 \times 2}$$

$$= \dfrac{9 \times 3}{2 \times 2}$$

$$= \dfrac{27}{4}$$

Hence the correct answer is $$\dfrac{27}{4}$$.

Express $$\dfrac{1.5 \times 10^6}{2.5 \times 10^{-4}}$$ in the standard form.

$$\frac {1.5\times 10^6}{2.5 \times 10^{-4}}$$

$$=\frac {15\times 10^6}{25\times 10^{-4}}$$

$$=\frac {3}{5}\times 10^{6+4}$$

$$=\frac {3}{5}\times 10^{10}$$

$$ = 0.6 \times 10^{10}$$

$$\therefore \frac {1.5\times 10^6}{2.5\times10^{-4}}= 0.6 \times 10^{10}$$

Simplify: $$125^{\frac{2}{3}}$$.

$$(125)^{\dfrac{2}{3}}$$

$$=(5^3)^{\dfrac{2}{3}}$$

$$=(5)^{3\times \dfrac{2}{3}}$$

$$=5^2$$

$$=25$$

$$\therefore (125)^{\dfrac{2}{3}}=25$$.

Find the value of $$\sqrt{\left(81\right)^{-2}}$$.

$$\begin{aligned}{}\sqrt {{{\left( {81} \right)}^{ - 2}}} &= {\left[ {{{\left( {81} \right)}^{ - 2}}} \right]^{\frac{1}{2}}}\\ &= {\left( {81} \right)^{ - 2 \times \frac{1}{2}}}\\& = {\left( {81} \right)^{ - 1}}\\ &= \frac{1}{{81}}\end{aligned}$$

Find $$9x^3 + x^3 + x =$$? if $$x = 7$$.

Very easy , just simplification
1111520_1205642_ans_6e48b9a62f144c1d8a157e0857783c55.jpg

Write the following numbers in the usual form:
$$4.83\times 10^7$$

To express the give number in the usual form, we need to perform multiplication as follows:

$$4.83\times 10^7=4.83\times 10000000$$

$$=48300000$$

Express each of the following numbers using exponential notations:

$$512$$
$$343$$
$$729$$
$$3125$$

$$(i)\ 512=(256\times 2)=(16)^2\times 2$$

$$\therefore \ 512=2^9$$

$$(ii)\ 343=7(49)=7(7)^2=7^3$$

$$\therefore \ 343=7^3$$

$$(iii)\ 729=9(81)=9(9)^2=9^3=(3^2)^3=3^6$$

$$\therefore \ 729=9^3=3^6$$

$$(iv)\ 3125=5(625)=5(25)^2=5(5^2)^2=5\times 5^9=5^5$$

$$\therefore \ 3125=5^5$$

If $$2^{n}=1024$$, then $$n=?$$

$${ 2 }^{ n }=1024={ 2 }^{ 10 }\\ \Rightarrow n=10$$

Solve:
$$\dfrac{{2}^{8}\times {a}^{6}}{{4}^{3}\times {a}^{3}}$$

$$\cfrac { { 2 }^{ 8 }\times { a }^{ 6 } }{ { 4 }^{ 3 }\times { a }^{ 3 } } \\ =\cfrac { { 2 }^{ 8 }\times { a }^{ 6 } }{ { ({ 2 }^{ 2 }) }^{ 3 }\times { a }^{ 3 } } \\ =\cfrac { { 2 }^{ 8 }\times { a }^{ 6 } }{ { 2 }^{ 6 }\times { a }^{ 3 } } \\ ={ 2 }^{ 8-6 }.{ a }^{ 6-3 }\\ ={ 2 }^{ 2 }.{ a }^{ 3 }$$

If $$\frac{(2^{-a})^{-2}8^{a}+32^{a}}{2^{3b}4}=2^{-4}$$, then 3b - 5 a =

$$\dfrac{(2^{-a})^{-2}\cdot (2^3)^a+(2^5)^a}{2^{3b}\cdot (2^2)}=2^{-4}$$

$$\dfrac{2^{2a}\cdot 2^{3a}+2^{5a}}{2^{3b}\cdot 2^2}=2^{-4}$$

$$\dfrac{2^{5a}+2^{5a}}{2^{2+3b}}$$

$$=\dfrac{2.2^{5a}}{2^{2+3b}}$$

$$=\dfrac{2^{5a+1}}{2^{2+3b}}$$

$$=2^{-4}$$

$$\Rightarrow 2^{(5a+1)-(2+3b)}=2^{-4}$$

$$\Rightarrow 5a-1-3b=-4$$

$$\Rightarrow 5a-3b=-3$$

$$\Rightarrow 3b-5a=3$$.

1192195_1195861_ans_3665bf9ef5e8496fbbd9a7e80388afca.jpg

If $$27^{n}=81$$, find $$\dfrac {27}{4}\times n\dfrac {3n}{4}$$

$$27^n=81\Longrightarrow 3^{3n}=3^{4}\Longrightarrow 3n=4\Longrightarrow n=\cfrac{4}{3}$$

$$\cfrac{27}{4}\times n\times \cfrac{3n}{4}=\cfrac{27}{4}\times \cfrac{4}{3}\times \cfrac{3}{4}\times \cfrac{4}{3}=9$$

Simplify :- 62.5×(10)−122.5×(10)8

$$\dfrac{62.5\times{10}^{-12}}{2.5\times {10}^{8}}$$

$$=\dfrac{62.5\times 10\times{10}^{-12}}{10\times2.5\times {10}^{8}}$$ (Multiplying and Dividing by $$10$$ )

$$=\dfrac{6.25\times {10}^{1-12}}{2.5\times{10}^{8}}$$ using $${a}^{m}\times{a}^{n}={a}^{m+n}$$

$$=\dfrac{{\left(2.5\right)}^{2}\times{10}^{-11}}{2.5\times {10}^{8}}$$ using $$\dfrac{{a}^{m}}{{a}^{n}}={a}^{m-n}$$

$$=2.5\times{10}^{-11-8}$$

$$=2.5\times {10}^{-19}$$

Solve:
$$3a^2 \times 8a^4$$

$$3a^2\times 8a^4$$

$$ 24a^{ 2+4 } \quad \dots (a^{ m }\times a^{ n } =a^{ m+n })$$

$$ 24a^{ 6 } $$

Simplify $$\dfrac{7^{-5}\times 10^{-5}\times 75}{5^{-7}\times (14)^{-5}}$$

$$\dfrac{7^{-5} \times 10^{-5} \times 75}{5^{-7} \times 14^{-5}} = \dfrac{5^7 \times 14^{5} \times 75}{7^5 \times 10^5}$$

$$= \dfrac{5^7 \times 2^5 \times 7^5 \times 5^2 \times 3}{7^5 \times 2^5 \times 5^5}$$

$$= \dfrac{5^4 \times 3}{1}$$

$$ = 1875$$

Solve : $$[1-\left\{1-(1-n)^{-1}\right\}]^{-1}$$

A] $$ [1-\left \{ 1-(1-n)^{-1} \right \}]^{-1}$$

$$ = [1-\left \{1- (\frac{1}{1-n} )\right \}]^{-1}$$

$$ = [1-\left \{ \frac{1-n-1}{1-n} \right \}]^{-1}$$

$$ = [1-\left \{ \frac{-n}{1-n} \right \}]^{-1}$$

$$ = \left \{ \frac{1-n+n}{1-n} \right \}^{-1} = [\frac{1}{1-n}]^{-1} = 1 - n$$

1191443_1292281_ans_2a52e2622a2645fe9245c3ea6a900d0f.jpg

Solve
$$\dfrac{6^{7}}{2^{3}\times 3^{7}}$$

$$\dfrac{6^{7}}{2^{3}\times 3^{7}}\Rightarrow \dfrac{(2\times 3)^{7}}{2^{3}\times 3^{7}}\Rightarrow \dfrac{2^{7}\times 3^{7}}{2^{3}\times 3^{7}}$$

$$\Rightarrow 2^{7-3}\Rightarrow 2^{4}$$

$$\Rightarrow 16$$

If $$ b = \sqrt [ n ] { a ^ { m } }$$, then will $$a = \sqrt [ m ] { b ^ { n } }$$.

$$b=\sqrt[n] {a^m}=a^{m/n}\implies a=b^{n/m}=\sqrt[m]{b^ n}$$

How to calculate the value of $$10^{2}$$?

$$\begin{array}{l} { 10^{ 2 } } \\ =10\times 10 \\ =100 \end{array}$$

Hence, this is the answer.

$$a^ {x}=b^ {y}=c^ {x}$$ and $$b^ {2}=ac$$ prove that $$y=\dfrac {2xz}{x+z}$$

Given,

$$a^x=b^y=c^z$$

$$\rightarrow a^x=b^y=c^z=k$$

$$a=k^{\frac{1}{x}}$$

$$b=k^{\frac{1}{y}}$$

$$c=k^{\frac{1}{z}}$$

$$b^2=ac$$

$$\Rightarrow (k^{\frac{1}{y}})^2=k^{\frac{1}{x}}\times k^{\frac{1}{z}}$$

$$k^{\frac{2}{y}}=k^{\frac{1}{x}+\frac{1}{z}}$$

$$k^{\frac{2}{y}}=k^{\frac{x+z}{xz}}$$

$$\dfrac{2}{y}=\dfrac{x+z}{xz}$$

$$\Rightarrow y=\dfrac{2xz}{x+z}$$

Hence Proved.

Write the base and exponent of
$$(2xy)^{3}$$

$${\left( {2xy} \right)^3} \Rightarrow base = 2xy$$

exponent$$=3.$$

Find the value of :-
$$\cfrac{{{{\left( {6.4} \right)}^2} - {{\left( {5.4} \right)}^2}}}{{{{\left( {8.9} \right)}^2} + \left( {8.9} \right) \times \left( {2.2} \right) + {{\left( {1.1} \right)}^2}}}$$

1324258_1246041_ans_f13b7fa31d584703b7389faa9d87849c.jpg

Write the base and exponent of
$$(7y)^{2}$$

$${\left( {7y} \right)^2} \Rightarrow base = 7y$$

exponent $$=2.$$

Simplify and express the result in power notation with a positive exponent.
$$\left( \dfrac { 1 } { 2 ^ { 3 } } \right) ^ { 2 }$$

Let $$a= \left(\dfrac{1}{2^3}\right)^{2} = \dfrac{1}{2^{3\times2}}$$

$$ = \dfrac{1}{2^{6}}$$

$$a =\left (\dfrac{1}{2}\right)^{6} $$

$$\therefore \left(\dfrac{1}{2^3}\right)^{2} =\left (\dfrac{1}{2}\right)^{6} $$

Express in exponential form:$$0.000169$$

$$0.000169=\dfrac{169}{1000000}$$

$$=\dfrac{169}{{10}^{6}}$$

$$=169\times{10}^{-6}$$

$$=1.69\times{10}^{2}\times{10}^{-6}$$

$$=1.69\times{10}^{-4}$$

Find the value of $$3 ^ { 2 } \times 3 ^ { 4 } \times 3 ^ { 3 } = ? $$

$$\begin{array}{l} { 3^{ 2 } }\times { 3^{ 4 } }\times { 3^{ 3 } } \\ =9\times 81\times 27 \\ =19683 \end{array}$$

Evaluate
$$(-6)^8 \div (-6)^2$$

Now,

$$(-6)^8 \div (-6)^2$$

$$=(-6)^{8-2}$$

$$=(-6)^6$$.

Find the value of $$x,$$ if $$(5)^{x-3} \times (3)^{2x-8}=225$$

Given equation can be rewritten as,

$$5^{x-3}\times 3^{2x-8}=225$$

$$5^{x-3}\times 3^{2x-8}=25\times 9$$

$$5^{x-3}\times 3^{2x-8}=5^{2}\times 3^{2}$$

Now, on comparing LHS and RHS of the above equation we get,

$$x-3=2$$ and $$2x-8=2$$

Both equations results $$x=5.$$

solve $$[(5^2)^3 \times 5^4] \div 5^7$$

$$[(5^{2})^{3}\times 5^{4}]\div 5^{7}$$

$$=\frac{5^{6}\times 5^{4}}{5^{7}}=\frac{5^{10}}{5^{7}}=5^{3}$$

1190619_1325187_ans_51af797fbe6e432e848d9a39e771f25a.jpeg

The exponential form of $$\dfrac{-64}{125}$$ is

$$\dfrac{-64}{125}$$

$$=\dfrac{(-4)\times(-4)\times(-4)}{(5)\times(5)\times(5)}$$

$$=\left \{ \dfrac{-4}{5} \right \}^3$$

Solve the following equation for x :
$$4^{2x}=\dfrac{1}{32}$$

$$\textbf{Simplify the equation to have same bases on both sides}$$

$$(2^2)^{2x} = \cfrac{1}{2^5}$$

$$2^{4x} = 2^{-5}$$

$$\text{As bases are same, the powers can be equated,hence}$$

$$4x=-5$$

$$x=\cfrac{-5}{4}$$

$$\textbf{Hence the value of}\ \mathbf x\ \textbf{is found to be}\ \mathbf{\cfrac{-5}{4}}$$

Solve
$${ \left( \dfrac { 5 }{ 3 } \right) }^{ -4 }\times { \left( \dfrac { 5 }{ 3 } \right) }^{ -5 }$$

$${\left(\dfrac{5}{3}\right)}^{-4}\times{\left(\dfrac{5}{3}\right)}^{-5}$$

$$={\left(\dfrac{5}{3}\right)}^{-4-5}$$ since $${a}^{m}\times {a}^{n}={a}^{m+n}$$

$$={\left(\dfrac{5}{3}\right)}^{-9}$$

$$={\left(\dfrac{3}{5}\right)}^{9}$$ since $$\dfrac{1}{{a}^{m}}={a}^{-m}$$

$$=\dfrac{{3}^{9}}{{5}^{9}}$$ since $${\left(\dfrac{a}{b}\right)}^{m}=\dfrac{{a}^{m}}{{b}^{m}}$$

$$=\dfrac{19683‬}{1953125‬}$$

Using laws of exponents, simplify and write the answer in exponential form :
$$\dfrac {{ 6 }^{ 15 }} {{ 6 }^{ 10 }}$$

Given $$\dfrac {{ 6 }^{ 15 }} {{ 6 }^{ 10 }}$$

Let $$a=\dfrac{{6}^{15}}{{6}^{10}}$$

As we know that, $$\dfrac{{a}^{m}}{{a}^{n}}={a}^{m-n}$$

$$a={6}^{15-10}$$

$$a={6}^{5}=7776$$

$$\therefore \dfrac {{ 6 }^{ 15 }} {{ 6 }^{ 10 }}=7776$$

Express $$27^{-2}$$ as a power with base $$3$$.

$${27}^{-2}$$ $$={\left(3\times 3\times 3\right)}^{-2}$$

$$={\left({3}^{3}\right)}^{-2}$$

$$={3}^{-6}$$

Using laws of exponents, simplify and write the answer in exponential form: $$a^{ 4 }\times b^{ 4 }$$

Given $${a}^{4}\times{b}^{4}$$

We know that, $${a}^{m}\times{b}^{m}={\left(ab\right)}^{m}$$

$${a}^{4}\times{b}^{4}={\left(ab\right)}^{4}$$

$$4\times 10^{5}+5\times 10^{3}+3\times 10^{2}+2\times 10^{2}=$$

$$y=4\times 10^5+5\times 10^3+3\times 10^2+2\times 10^2$$

$$y=4000\times 10^2+50\times 10^2+3\times 10^2+2\times 10^2$$

$$y=(4000+50+3+5)\times 10^2$$

$$y=4058\times 10^2$$

$$[y=405800]$$.

1204177_1393969_ans_f4dcdab39cca4da2b8fc75f169360747.JPG

Solve:
$$2^{7x}\div 2^{21}=\sqrt[5]{2^{15}}$$

$$2^{72} \div 2^{21} = \sqrt[5]{2^{15}}$$

$$\dfrac{2^{7x}}{2^{21}} = (2)^{15\times \frac{1}{15}}$$

$$2^{7x-21} = 2^3$$

On comparing power we have

$$7x-21 = 3$$

$$7x = 21+3$$

$$7x=24$$

$$\left[x = \dfrac{24}{7}\right]$$

1204160_1398292_ans_a7102d75bfea440d834a03031cb86c17.jpg

Simplify and express following in exponential form :
$$\dfrac{4^{5}\times a^{3}b^{3}}{4^{5}\times a^{5}b^{2}}$$

$$\dfrac{4^5}{4^5}\times \dfrac{a^3}{a^5}\times \dfrac{b^3}{b^2}=1\times \dfrac{1}{a^2}\times b=\dfrac{b}{a^2}=b^1a^{-2}$$.
1207978_1392482_ans_ea7343def4a145e1b59783d1237de2f6.jpg

1207978_1392482_ans_ea7343def4a145e1b59783d1237de2f6.jpg

What is the value of $$\dfrac{4^{8}-4^{9}}{4^{8}}$$?

$$a = \dfrac{4^8 - 4^9}{4^8}$$

$$a = 1 - 4$$

$$a=-3$$

1204152_1398772_ans_68058a1480d946228988595befb94d11.JPG

Write the following in standard form $$0.00000564$$.

Standard form is given as, $$N\times 10^n$$ where, $$1\leq N<10$$

To convert the given number into the standard form, move decimal point $$6$$ places to the right.

$$0.00000564 =5.64 \times 10^{-6}$$

Solve $${ (-2) }^{ x }=-128$$.

$$(-2)^x=-128$$
$$(-2)^x=(-2)^7$$
By comparing the power on both sides, we get
$$x=7$$

Let us solve :
$$4^{4x}.4^{3x-1}=\dfrac{4^{2x}}{2^{3x}}$$

$$4^{4x}4^{3x-1}=\dfrac{4^{2x}}{2^{3x}}$$

$$4^{7x-1}=\dfrac{4^{2x}}{(2^2)^{\dfrac{3x}{2}}}$$

$$4^{7x-1}=\dfrac{4^{2x}}{4^{3x/2}}$$

$$\Rightarrow 4^{7x-1}=4^{2x-\dfrac{3x}{2}}$$

$$\Rightarrow 4^{7x-1}=4^{x/2}$$

$$=7x-1=\dfrac{x}{2}$$

$$=\dfrac{13x}{2}=1$$

$$x=\dfrac{2}{13}$$.

1215857_1400537_ans_1c08de42043943ba872a9aa974c92c66.jpg

Find the value of x for which $$7^{10}\times$$ $$7^8$$ = $$\left ( \dfrac{1}{7} \right )^x$$

$$7^{10}\times $$ $$7^8$$ = $$\left ( \dfrac{1}{7} \right )^x$$

$$\implies 7^{10+8}=(7^{-1})^ x$$

$$\implies 7^{18}=7^{-x}$$

$$\implies x=-18$$

Find the product of $$3 ^ { 1 / 2 }$$ and $$\sqrt { 3 }$$.

To find the product of $$3^{\frac{ 1 }{ 2} }$$ and $$\sqrt { 3 }$$

Now,

product $$=(3)^{\frac{1}{2}}\times \sqrt{3}$$

$$=(3)^{\frac{1}{2}}\times(3)^{\frac{1}{2}}$$

$$=(3)^{\frac{1}{2}+\frac{1}{2}}$$

$$=3^1$$

$$=3$$

Hence, the product is $$3$$.

Find the value of m if $$\left ( \dfrac{p}{q} \right )^{m}=\dfrac{q^{4}}{p^{4}}$$

$$\left(\dfrac{p}{q}\right)^m=\dfrac{q^4}{p^4}$$

$$\left(\dfrac{p}{q}\right)^m=\left(\dfrac{p}{q}\right)^{-4}$$

$$[m=-4]$$.

1204148_1399182_ans_7b242060f53742c09843ee2cc89fbc34.JPG

Write exponential form for $$ 8 \times 8 \times 8 \times 8 $$ taking base as 2

$$\textbf{Step-1: Apply laws of indices.}$$

$$\text{Given expression can be written as}$$

$$8\times 8\times 8\times 8=2^{3}\times 2^3\times 2^3\times 2^3=2^{3+3+3+3}=2^{12}$$ $$ [ \textbf{If}$$$$\boldsymbol{ \ a^m \times \ b^n}$$ $$\textbf{then}$$ $$\ \boldsymbol{ a^{m+n}}]$$

$$\textbf{Hence, answer is}$$ $$\ \boldsymbol{2^{12}}$$

Let us solve :
$$49^{x}=7^{3}$$

$$49^x=7^3$$

$$\Rightarrow (7^2)^x=7^3$$

$$\Rightarrow 7^{2x}=7^3$$

$$\Rightarrow 2x=3$$ $$[\because a^m=a^n \implies m=n]$$

$$x=\dfrac{3}{2}$$.

Write the base and the exponential :
$$3^{4}$$

The given number is $$3^4$$.

Then base is $$3$$ and exponential is $$4$$

Prove that:
$$4^{\dfrac {1}{3}}\times [2^{\dfrac {1}{3}}\times 3^{\dfrac {1}{2}}]\div 9^{\dfrac {1}{4}}$$.

$$4^{\dfrac{1}{3}}\times \left[2^{\dfrac{1}{3}}\times 3^{\dfrac{1}{2}}\right]\div 9^{\dfrac{1}{4}}$$

$$\Rightarrow \dfrac{(2^2)^{\dfrac{1}{3}}\times\left[2^{\dfrac{1}{3}}\right]\times (3^{\dfrac{1}{2}})}{(3^2)^{\dfrac{1}{4}}}$$

$$\Rightarrow \dfrac{2^{\dfrac{2}{3}}\times 2^{\dfrac{1}{3}}\times 3^{\dfrac{1}{2}}}{3^{\dfrac{1}{2}}}=2^{\dfrac{2}{3}+\dfrac{1}{3}}=2^1=2$$.

1210943_1399264_ans_c57365c978c545d2be344e725a6e8aaf.jpg

Divide
$$8\sqrt { 15 } $$ by $$2\sqrt { 3 } $$.

$$8\sqrt{15}\div 2\sqrt{3}$$

$$=\dfrac{8\times \sqrt{5\times 3}}{2\sqrt{3}}$$

$$=\dfrac{8\times\sqrt{3}\times\sqrt{5}}{2\sqrt{3}}$$

$$=4\sqrt{5}$$

Express each of the following as product of powers of their prime factors:
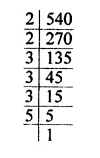
$$540$$

$$540={2}^{2}\times{3}^{3}\times 5$$

Write the value of $$(\frac{x^{a}}{x^{b}})^{a+b}\times (\frac{x^{b}}{x^{c}})^{b+c}\times (\frac{x^{c}}{x^{a}})^{c+a}$$

As we know that

$$\dfrac{a^m}{a^n}=a^{m-n}$$ and also $$(a+b)(a-b)=a^2-b^2$$

$$\bigg(\dfrac{x^a}{x^b}\bigg)^{a+b}\times \bigg(\dfrac{x^b}{x^c}\bigg)^{b+c}\times \bigg(\dfrac{x^c}{x^a}\bigg)^{c+a}=(x^{a-b})^{a+b}\times (x^{b-c})^{b+c}\times (x^{c-a})^{c+a}=x^{a^2-b^2}\times x^{b^2-c^2}\times x^{c^2-a^2}=x^{a^2-b^2+b^2-c^2+c^2-a^2}=x^{0}=1$$

Simplify
$$\dfrac { (2^{ 2 })^{ 2 }\times 7^{ 3 } }{ { 8 }^{ 3 }\times 7 } $$

1320781_1505041_ans_f43496a53d5542938ae2c699ad42f900.jpeg

Compare the following numbers:
$$4\times{10}^{14};3\times{10}^{17}$$

$$4\times{10}^{14};3\times{10}^{17}$$
On comparing the exponents of base $$10$$
$$4\times{10}^{14}< 3\times{10}^{17}$$

Find value of $${ \left( -\dfrac { 1 }{ 27 } \right) }^{ -\tfrac { 2 }{ 3 } }$$.

Solution:- given

$$ = \left ( \dfrac{-1}{27} \right )^{\tfrac{-2}{3}}$$

$$ = \left [ \left ( \dfrac{-1}{27} \right )^2 \right ]^{\tfrac{-1}{3}} = \left ( \dfrac{1}{27^{2}} \right )^{\tfrac{-1}{3}}=\dfrac{ 1}{\left ( \dfrac{1}{27^{2}} \right )^{\tfrac{1}{3}}}$$

$$=(27^{2})^{\frac{1}{3}}$$

$$= (3)^{2} = 9 (Ans)$$

Simplify and express the following in exponential form:
$${2}^{0}\times{3}^{0}\times{4}^{0}$$

$${2}^{0}\times{3}^{0}\times{4}^{0}=1\times 1\times 1=1$$
$$[\because {a}^{0}=1]$$

Express each of the following as product of powers of their prime factors:
$$3,600$$

$$3,600={2}^{4}\times{3}^{2}\times{5}^{2}$$

Solve $$\frac { 6 ^ { 4 } \times 36 \times 216 } { 6 ^ { 7 } }$$

$$\dfrac{6^4\times 36\times 216}{6^7}=\dfrac{6^4\times 6^2\times 6^3}{6^7}=\dfrac{6^{4+2+3}}{6^7}=\dfrac{6^9}{6^7}=6^{9-7}=6^2=36$$

Simplify:$${8}^{\tfrac{2}{3}}$$

$${8}^{\tfrac{2}{3}}$$

$$={\left({2}^{3}\right)}^{\tfrac{2}{3}}$$

$$={2}^{3\times\tfrac{2}{3}}$$.............. since $${\left({a}^{m}\right)}^{n}={a}^{mn}$$

$$={2}^{2}=4$$

Write $$2016$$ in standard form.

The standard form is $$2.016\times{10}^{3}$$

Write the following numbers in the usual form:
$$302\times 10^{6}$$

$$302\times 10^{6}$$ = $$3.02 × 100 × 10^6 = 3.02 × 10^8$$

Express the following as a rational number:
$$\left(\dfrac{-4}{7}\right)^3$$

The given number can be expressed as a rational number as follows;

$$\left(\dfrac{-4}{7}\right)^3$$$$=\left(\dfrac{-4^3}{7^3}\right)$$

$$=\left(\dfrac{(-4)\times (-4)\times (-4)}{7\times 7\times 7}\right)$$

$$=\left(\dfrac{-64}{343}\right)$$

Express the following as a rational number:
$$(-6)^{-1}$$

We have:

$$(-6)^{-1}=(-6)^{-1}$$

$$=(1/-6)^1$$ $$....[\because (a/b)^{-n}=(b/a)^n]$$
$$=(-1/6)$$

Simplify the following and express as a rational number:
$$(3/2)^4\times (1/5)^2$$

We have,
$$(3^4 /2^4)=(3\times 3\times 3\times 3)/(2\times 2\times 2\times 2)=(81/16)$$
$$(1^2/5^2)=(1\times 1)/(5\times 5)=(1/25)$$
Then,
$$=(81/16)\times (1/25)$$
$$=(81\times 1)/(16/25)$$
$$=(81/400)$$

Express the following as a rational number:
$$(-1)^9$$

We have,
$$(-1)^9=(-1^9)$$
$$=(-1\times -1\times -1\times -1\times -1\times -1 \times -1\times -1\times -1)$$

$$=(-1)$$

Which can also be written as

$$=(-1)/1$$

Simplify the following and express as a rational number:
$$(2/3)^2\times (-3/5)^3\times (7/2)^2$$

We have,
$$(2^2 /3^2)=(2\times 2)/(3\times 3)=(4/9)$$
also $$(-3/5)^3=(-3\times -3\times -3)/(5\times 5\times 5)=(-27/125)$$
and $$(7^2 /2^2)=(7\times 7)/(2\times 2)=(49/4)$$
Then,
$$=(4/9)\times (-27/125)\times (49/4)$$
$$=(4\times 27\times 49)/(9\times 125\times 4)$$
By simplifying
$$=(1\times -3\times 49)/(1\times 125\times 1)$$
$$=(-147/125)$$

Simplify the following and express as a rational number:
$$\left\{ (-3/4)^3- (-5/2)^3\right\} \times 4^2$$

We have,
$$=\left\{ -3^3/4^3 )-(5^3 /2^3)\right\} \times 16$$

$$=\left\{ (-27/64)-(-125/8)\right\} \times 16$$

First we find the difference of $$\left\{ (-27/64)-(125/8)\right\}$$

LCM of $$64$$ and $$8$$ is $$64$$

$$\Rightarrow (-27\times 1)/(64\times 1)=(-27/64)$$

and $$\Rightarrow (125\times 8)/(8\times 8)=(1000 /64)$$

Now,

$$=(1000-(-27))/64$$
$$=(1000+27)/64$$

$$=(973/64)$$

So,

$$=(973/64)\times 16$$
$$=(973/4)$$

Simplify the following and express as a rational number:
$$(-1/2)^5\times 2^3 \times (3/4)^2$$

We have,
$$(-1^5 /2^5)=(-1\times -1\times -1\times -1\times -1)/(2\times 2\times 2\times 2\times 2)=(-1/32)$$
$$(2)^3=(2\times 2\times 2)=8$$
$$(3^2 /4^2)=(3\times 3)/(4\times 4)=(9/16)$$
Then,
$$=(-1/32)\times 8\times (9/16)$$
$$=(-1\times 8\times 9)/(32\times 1\times 16)$$
By simplifying
$$=(-1\times 1\times 9)/(32\times 1\times 2)$$
$$=(-9/64)$$

Simplify the following and express as a rational number:
$$(-2/3)^5\times (-3/7)^3$$

We have,
$$(-2^5 /3^5)=(-2\times -2\times -2\times -2\times -2)/(3\times 3\times 3\times 3\times 3)=(-32/243)$$
$$(-3^3/7^3)=(-3\times -3\times -3)/(7\times 7\times 7)=(-27/343)$$
Then,
$$=(-32/243)\times (-27/343)$$
$$=(-32\times -27)/(243/343)$$
$$=(32/3087)$$

Fill in the blanks to make the statement true:
$$(213 \times 657)^{-1} = 213^{-1} \times ...............$$

$$(213 \times 657)^{-1} = 213^{-1} \times 657^{-1}$$

Simplify and express the following as a rational number:
$$(\dfrac{4}{3})^{-3} \times (\dfrac{4}{3})^{-2}$$

We have,
$$=(\dfrac{4}{3})^{(-3+(-2))}$$ $$...[ \left\{ (\dfrac{a}{b})^m \times (\dfrac{a}{b})^n\right\} =(\dfrac{a}{b})^{m-n}$$

$$=(\dfrac{4}{3})^{(-3-2)}$$

$$=(\dfrac{4}{3})^{-5}$$

$$=(\dfrac{3}{4})^5$$

$$=(\dfrac{3^5}{4^5})$$

$$=\dfrac{1024}{243}$$

$$=\dfrac{243}{1024}$$

Write the prime factorization of the following number in exponential form:
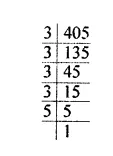
$$405$$

$$405 = 3\times 3\times 3\times 3 \times 5 = 3^4 \times 5^1$$

1771801_1801088_ans_df1275a7279a4a028569fbc100cb9b4c.PNG

Write the prime factorization of the following number in exponential form:
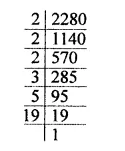
$$2280$$

$$2280 = 2 \times 2 \times 2 \times 3 \times 5 \times 19 = 2^{3} \times 3^1 \times 5^1 \times 19^1$$

1771810_1801094_ans_b0c82fdf50da4bdab3ddb377c6af819a.PNG

Write the prime factorization of the following number in exponential form:
$$540$$

$$540 = 2\times 2 \times 3\times 3\times 3 \times 5 = 2^2 \times 3^3 \times 5^1$$

1771805_1801091_ans_b5b1bc2d371e4ba4bada66eac94e403b.PNG

Write the prime factorization of the following number in exponential form:
$$360$$

$$360 = 2\times 2 \times 2 \times 3\times 3 \times 5= 2^3 \times 3^2 \times 5$$

1771798_1801083_ans_eb25225aebb1460a988c211df701dc4f.PNG

Write the prime factorization of the following number in exponential form:
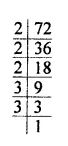
$$72$$

$$72 = 2\times 2 \times 2 \times 3\times 3 = 2^3 \times 3^2$$

1771794_1801080_ans_8606d63a1e154cb386c3f9dc37fc6d14.PNG

Simplify : $$(256)^{-\left (4^{-\frac {3}{2}}\right )}$$

$$(256)^{-\left (4^{-\frac {3}{2}}\right )} $$

We know that $$ a^{m^{n}}=a^{mn}$$

So,

$$\Rightarrow (2^{8})^{\left(-4\right)\times \left(-\frac{3}{2}\right)} $$

$$\Rightarrow 2^{8\times 4 \times \frac{3}{2}}=2^{8\times2\times 3}=2^{48}$$

Write the prime factorization of the following number in exponential form:
$$3600$$

$$3600 =2\times 2\times 2\times 2 \times 3 \times 3 \times 5 \times 5 = 2^4 \times 3^2 \times 5^2$$

1771813_1801098_ans_7139e24084c9487a868462454293fcb0.PNG

Fill in the blanks:
$$(-3)^8 \div (-3)^5 = (-3)^{.....}$$

$$(-3)^8 \div (-3)^5 = (-3)^{8-5} = (-3)^3$$

Express the number appearing in the following statement in scientific notation (or standard form):

In a galaxy there are $$100000000000$$ stars on an average.

$$\textbf{Step 1: Given}$$

A number $$100000000000$$

$$\textbf{Step 2: Required to find}$$

To express $$100000000000$$ in its standard form

$$\textbf{Step 3: Any number that we can write as a decimal number, between 1.0 and 10.0, multiplied by a power of 10, is said to be in standard form. }$$

$$100000000000$$ can be written as $$1\times 100000000000$$

And $$100000000000$$ has $$11$$ zeroes

$$\therefore 100000000000 = 10^{11}$$

$$\Rightarrow 1 \times 100000000000 = 1 \times 10^{11}$$

$$\textbf{Step 4: Conclusion}$$

$$100000000000$$ in its standard form is $$1 \times 10^{11}$$

In a galaxy, there are on an average $$ 1.0 \times 10^{11}$$ stars.

Write the prime factorization of the following number in exponential form:
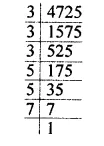
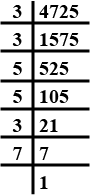
$$4725$$

$$4725 = 3\times 3\times 3\times 5 \times 5 \times 7 =3^3 \times 5^2 \times 7^1$$
1771815_1801099_ans_4047912710c04293974a36c9761d1605.PNG

Write $$1.205 \times 10^5$$ in the usual decimal notation.

$$1.205 \times 10^5 = 120500$$

Write the prime factorization of the following number in exponential form:
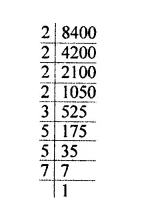
$$8400$$

$$8400 = 2\times 2\times 2\times 2 \times 3 \times 5 \times 5 \times 7 = 2^4 \times 3^1 \times 5^2 \times 7^1$$

1771817_1801100_ans_a7fd352bc81f4066aea45ad881d23e5c.PNG

1771817_1801100_ans_a7fd352bc81f4066aea45ad881d23e5c.PNG

Fill in the blanks:
In $$5^2 = 25,$$ base = .......... and index = ...........

In $$5^2 = 25,$$ base = $$5$$. and index = $$2$$

Evaluate:
$$(-1)^{4}$$

Evaluate:
$$2^{1}$$

$$2^1=2$$ (By laws of exponent)

Evaluate:
$$0^{3}$$.

$$0^3=0$$

Find the sum of $$8 \times {10}^{13}$$ and $$12.3 \times {10}^{12}$$ and express the answer in scientific notation.

Given numbers are $$8 \times {10}^{13}$$ and $$12.3 \times {10}^{12}$$
$$= 8 \times {10}^{13}+ 12.3 \times {10}^{12}$$
$$= 8 \times {10}^{13}+ 1.23 \times 10 \times {10}^{12}$$
$$= 8 \times {10}^{13} + 1.23 \times {10}^{12+1}$$
$$= 8 \times {10}^{13} + 1.23 \times {10}^{13}$$
$$= (8+1.23) \times {10}^{13} $$
$$= 9.23 \times {10}^{13}$$

Fill in the blank with "equal to " or "greater than" or "less than"
$$39 \times {10}^4 $$ is _______ $$3.9 \times {10}^5$$

Since, we have
$$39 \times {10}^4 $$ and $$3.9 \times {10}^5$$
$$\Rightarrow 39 \times 10000 $$ and $$3.9 \times 100000$$
$$\Rightarrow 390000 $$ and $$390000$$
Hence both are equal.

Which of the following numbers is least?
$$3.47 \times {10}^4 $$, $$34.7 \times {10}^4$$ and $$347 \times {10}^4$$

Given numbers are $$3.47 \times {10}^4 $$, $$34.7 \times {10}^4$$ and $$347 \times {10}^4$$
$$3.47 \times {10}^4 = 3.47 \times 10000 = 34700$$
$$34.7 \times {10}^4 = 34.7 \times 10000 = 347000$$
And
$$347 \times {10}^4 = 347 \times 10000 = 3470000$$
Clearly, $$3400$$ is least number.

Choose the correct answers for number in exponential form $$9^8$$

In $$9^8$$, $$9$$ is the base and $$8 $$ is the exponent.

Fill in the blank:
The value of exponential $$5^4$$ is _____.

$$5^4 = 5 \times 5 \times 5 \times 5 = 625$$

Write the exponential form when base is $$11$$ and exponent is $$7$$.

The exponential form when base is $$11$$ and exponent is $$7$$, is given by $$11^7$$.

Fill in the blank:
The base in the exponential $$6^2 $$ is ____.

In $$6^2 $$, $$6$$ is the base.

Exponent of $$a^{5}\, \times\, a^0\, \times\, a^5$$ is equal to

We have $$a^{5}\times a^{0} \times a^{5}$$
By using law $$a^{m} \times a^{n}= a^{m+n}$$, we get
$$=a^{5+0+5}$$
$$=a^{10}$$
$$=10$$

Simplify
$$\cfrac { { 15 }^{ 4 }\times { 14 }^{ 2 } }{ { 21 }^{ 3 }\times { 10 }^{ 3 } } $$

The numerator is
$${ 15 }^{ 4 }\times { 14 }^{ 2 }={ \left( 3\times 5 \right) }^{ 4 }\times { \left( 2\times 7 \right) }^{ 2 }={ 3 }^{ 4 }\times { 5 }^{ 4 }\times { 2 }^{ 2 }\times { 7 }^{ 2 }\quad $$
Similarly the denominator is
$${ 21 }^{ 3 }\times { 10 }^{ 3 }={ \left( 7\times 3 \right) }^{ 3 }\times { \left( 2\times 5 \right) }^{ 3 }={ 7 }^{ 3 }\times { 3 }^{ 3 }\times { 2 }^{ 3 }\times { 5 }^{ 3 }$$
The given expression is therefore
$$\cfrac { { 3 }^{ 4 }\times { 5 }^{ 4 }\times { 2 }^{ 2 }\times { 7 }^{ 2 } }{ { 7 }^{ 3 }\times { 3 }^{ 3 }\times { 2 }^{ 3 }\times { 5 }^{ 3 } } ={ 3 }^{ 4-3 }\times { 5 }^{ 4-3 }\times { 2 }^{ 2-3 }\times { 7 }^{ 2-3 }=\cfrac { 3\times 5 }{ 2\times 7 } =\cfrac { 15 }{ 14 } $$

Express the following numbers using scientific notation:
(A) $$1,234.56$$
(B) $$0.0876$$

$$1,234.56 = 1.23456 \times {10}^{3}$$
$$0.0876 = 8.76 \times {10}^{-2}$$

Simplify: $${ \left( \cfrac { 2 }{ 5 } \right) }^{ -3 }\times { \left( \cfrac { 25 }{ 4 } \right) }^{ -2 }$$

$$\cfrac{25}{4}=\cfrac{5\times 5}{2\times 2}=\cfrac{{5}^{2}}{{2}^{2}}$$
$${ \left( \cfrac { 2 }{ 5 } \right) }^{ -3 }\times { \left( \cfrac { 25 }{ 4 } \right) }^{ -2 }={ \left( \cfrac { 2 }{ 5 } \right) }^{ -3 }\times { \left( \cfrac{{5}^{2}}{{2}^{2}} \right) }^{ -2 }$$
$$\left( \because { \left( { a }^{ m } \right) }^{ n }={ a }^{ mn } \right) $$
$$\cfrac{{5}^{3}}{{2}^{3}}\times \cfrac{{2}^{4}}{{5}^{4}}={5}^{3-4}\times {2}^{4-3}$$
As $$\left( \because { a }^{ -m }=\cfrac { 1 }{ { a }^{ m } } \right) $$
$$={5}^{-1}\times {2}^{1}=\cfrac{2}{5}$$

Simplify: $$\cfrac { { \left( { 5 }^{ -3 } \right) }^{ 2 }\times { \left( { 3 }^{ 4 } \right) }^{ } }{ { \left( { 3 }^{ -2 } \right) }^{ -3 }\times { \left( { 5 }^{ 3 } \right) }^{ -2 } } $$

The given expression $$\dfrac { (5^{ -3 })^{ 2 }\times 3^{ 4 } }{ (3^{ -2 })^{ -3 }\times (5^{ 3 })^{ -2 } }$$ can be simplified as follows:

$$\dfrac { (5^{ -3 })^{ 2 }\times 3^{ 4 } }{ (3^{ -2 })^{ -3 }\times (5^{ 3 })^{ -2 } } \quad \quad \quad \\ =\dfrac { 5^{ -6 }\times 3^{ 4 } }{ 3^{ 6 }\times 5^{ -6 } } \quad \quad \quad \quad \left( \because \quad \left( x^{ m } \right) ^{ n }=x^{ m\times n } \right) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ =\dfrac { 5^{ -6 } }{ 5^{ -6 } } \times \dfrac { 3^{ 4 } }{ 3^{ 6 } } \\ =5^{ -6-(-6) }\times 3^{ 4-6 }\quad \quad \quad \quad \quad \quad \left( \because \quad \dfrac { x^{ m } }{ x^{ n } } =x^{ m-n } \right)$$

$$=5^{ -6+6 }\times 3^{ -2 }\\ =5^{ 0 }\times \dfrac { 1 }{ 3^{ 2 } } \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left( \because \quad \dfrac { 1 }{ x } =x^{ -1 } \right) \\ =1\times \dfrac { 1 }{ 3^{ 2 } } \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \left( \because \quad x^{ 0 }=1 \right) \\ =\dfrac { 1 }{ 9 }$$

Hence $$\dfrac { (5^{ -3 })^{ 2 }\times 3^{ 4 } }{ (3^{ -2 })^{ -3 }\times (5^{ 3 })^{ -2 } }=\dfrac {1}{9}$$.

Simplify:
$$\cfrac { { \left( 0.22 \right) }^{ 4 }\times { \left( 0.222 \right) }^{ 3 } }{ { \left( 0.2 \right) }^{ 5 }\times { \left( 0.2222 \right) }^{ 2 } } $$

$$\dfrac { { \left( 0.22 \right) }^{ 4 }\times { \left( 0.222 \right) }^{ 3 } }{ { \left( 0.2 \right) }^{ 5 }\times { \left( 0.2222 \right) }^{ 2 } } $$

$$=\dfrac { { \left( 1.1\times 0.2 \right) }^{ 4 }\times { \left( 1.11\times 0.2 \right) }^{ 3 } }{ { \left( 0.2 \right) }^{ 5 }\times { \left( 1.111\times 0.2 \right) }^{ 2 } } $$

$$=\dfrac { { \left( 1.1 \right) }^{ 4 }\times { \left(0.2 \right) }^{ 4 }\times { \left( 1.11 \right) }^{ 3 }\times { \left( 0.2 \right) }^{ 3 } }{ { \left( 0.2 \right) }^{ 5 }\times { \left( 1.111 \right) }^{ 2 }\times { \left( 0.2 \right) }^{ 2 } } $$

$$=\dfrac { { \left( 0.2 \right) }^{ 7 }\times { \left( 1.11 \right) }^{ 3 }\times { \left( 1.1 \right) }^{ 4 } }{ { \left( 0.2 \right) }^{ 7 }\times { \left( 1.111 \right) }^{ 2 }} $$

$$=\dfrac { { \left( 0.2 \right) }^{ 7 }\times { \left( 1.11 \right) }^{ 3 }\times { \left( 1.1 \right) }^{ 4 } }{ { \left( 0.2 \right) }^{ 7 }\times { \left( 1.01 \times 1.1\right) }^{ 2 } } $$

$$=\dfrac { { \left( 0.2 \right) }^{ 7 }\times { \left( 1.11 \right) }^{ 3 }\times { \left( 1.1 \right) }^{ 4 } }{ { \left( 0.2 \right) }^{ 7 }\times { \left( 1.01 \right) }^{ 2 }\times { \left( 1.1 \right) }^{ 2 } } $$

$$=\dfrac { { \left( 0.2 \right) }^{ 7-7 }\times { \left( 1.11 \right) }^{ 3 }\times { \left( 1.1 \right) }^{ 4-2 } }{ { \left( 1.01 \right) }^{ 2 } } $$

$$=\dfrac { { \left( 0.2 \right) }^{ 0 }\times { \left( 1.11 \right) }^{ 3 }\times { \left( 1.1 \right) }^{ 2 } }{ { \left( 1.01 \right) }^{ 2 } } $$

$$=\dfrac { { \left( 1.11 \right) }^{ 3 }\times { \left( 1.1 \right) }^{ 2 } }{ { \left( 1.01 \right) }^{ 2 } } $$

Find all positive integers $$m,n$$ such that $${ \left( { 3 }^{ m } \right) }^{ n }={ 3 }^{ m }\times { 3 }^{ n }\quad $$

Suppose, $$(3^m)^{n}=3^{m}\times 3^{n}$$

$$\implies (3)^{mn}=(3)^{m+n}$$

$$\implies mn=m+n$$

$$\implies mn-m-n=0$$

$$\implies mn-m-n+1-1=0$$

$$\implies m(n-1)-(n-1)=1$$

$$\implies (m-1)(n-1)=1$$

$$\implies m-1=1$$ and $$n-1=1$$

$$\implies m=2$$ and $$n=2$$

Can it happen that for some integer $$m\ne 0$$, $${ { \left( \cfrac { 4 }{ 25 } \right) }^{ m } }={ \left( \cfrac { 2 }{ 5 } \right) }^{ { m }^{ 2 } }\quad $$?

We need to find $$m\neq 0$$ so that $${ { \left( \cfrac { 4 }{ 25 } \right) }^{ m } }={ \left( \cfrac { 2 }{ 5 } \right) }^{ { m }^{ 2 } }\quad $$

Suppose, $${ { \left( \cfrac { 4 }{ 25 } \right) }^{ m } }={ \left( \cfrac { 2 }{ 5 } \right) }^{ { m }^{ 2 } }\quad $$

$$\implies \left(\dfrac{2^{2}}{5^{2}}\right)^{m}=\left(\dfrac{2}{5}\right)^{m^2}$$

$$\implies \dfrac{(2^{2})^{m}}{(5^{2})^{m}}=\dfrac{(2)^{m^2}}{(5)^{m^2}}$$

$$\implies \dfrac{(2)^{2m}}{(5)^{2m}}=\dfrac{(2)^{m^2}}{(5)^{m^2}}$$

$$\implies \left(\dfrac{2}{5}\right)^{2m}=\left(\dfrac{2}{5}\right)^{m^2}$$

$$\implies 2m=m^2$$

$$\implies m^2 - 2m=0$$

$$\implies m=0,2$$

$$\implies m=2$$ ........ $$\because m\neq 0$$

Hence, $$\left(\dfrac{4}{25}\right)^{m}=\left(\dfrac{2}{5}\right)^{m^2}$$ for $$m=2$$

Simplify:
$$\cfrac { { \left( 0.0006 \right) }^{ 9 } }{ { \left( 0.015 \right) }^{ -4 } } $$

$$\dfrac { { \left( 0.0006 \right) }^{ 9 } }{ { \left( 0.015 \right) }^{ -4 } } $$

$${ =\left( 0.0006 \right) }^{ 9 }\times { \left( 0.015 \right) }^{ 4 }$$

$${ =\left( 6\times 10^{-4} \right) }^{ 9 }\times { \left( 15\times 10^{-3} \right) }^{ 4 }$$

$$=(6)^{9}\times (10)^{-36}\times (15)^{4}\times (10^{-12} )$$

$$=\dfrac { { 6 }^{ 9 }\times { 15 }^{ 4 } }{ { 10 }^{ 36 }\times { 10 }^{ 12 } } $$

$$=\dfrac { (2\times 3)^{9}\times (5\times 3)^{4}}{(5\times 2)^{36}\times (5\times 2)^{ 12 } } $$

$$=\dfrac { { 2 }^{ 9 }\times { 3 }^{ 9 }\times { 5 }^{ 4 }\times { 3 }^{ 4 } }{ { 5 }^{ 36 }\times { 2 }^{ 36 }\times { 5 }^{ 12 }\times { 2 }^{ 12 } } $$

$$=\dfrac { { 3 }^{ \left( 9+4 \right) } }{ { 2 }^{ \left( 36+12-9 \right) }\times { 5 }^{ \left( 36+12-4 \right) } } $$

$$=\dfrac { { 3 }^{ 13 } }{ { 2 }^{ 39 }\times { 5 }^{ 44 } } $$

If $${ \left( { 2 }^{ m } \right) }^{ 4 }={ 4 }^{ 6 }$$, find the value of $$m$$.

$${ \left( { 2 }^{ m } \right) }^{ 4 }={ 4 }^{ 6 }$$

$${ 2 }^{ m4 }={ \left( { 2 }^{ 2 } \right) }^{ 6 }$$

$${ 2 }^{ m4 }={ 2 }^{ 12 }$$

$$4m=12$$

$$m=\dfrac { 12 }{ 4 } =3$$

Simplify:
$${ \left( 1.8 \right) }^{ 6 }\times { \left( 4.2 \right) }^{ -3 }$$

$${ \left( 1.8 \right) }^{ 6 }\times { \left( 4.2 \right) }^{ -3 }$$

$$=\dfrac { { \left( 1.8 \right) }^{ 6 } }{ { \left( 4.2 \right) }^{ 3 } } $$

$$=\dfrac { { \left( 1.8 \right) }^{ 6 }\times (10)^{6} \times { \left( 10 \right) }^{ 3 } }{ { (4.2)}^{3}\times (10)^{6}\times (10)^{3}}$$

$$=\dfrac { { \left( 1.8 \times 10\right) }^{ 6 }\times { \left( 10 \right) }^{ 3 } }{ { \left( 4.2\times 10 \right) }^{ 3 }\times { \left( 10 \right) }^{ 6 } } $$

$$=\dfrac { { \left( 18 \right) }^{ 6 }\times { \left( 10 \right) }^{ 3 } }{ { \left( 42 \right) }^{ 3 }\times { \left( 10 \right) }^{ 6 } } $$

$$=\dfrac { { \left( 6\times 3 \right) }^{ 6 }\times { \left( 10 \right) }^{ 3 } }{ { \left( 7\times 6 \right) }^{ 3 }\times { \left( 10 \right) }^{ 6 } } $$

$$=\dfrac { { 6 }^{ 6 }\times { 3 }^{ 6 }\times { 10 }^{ 3 } }{ { 7 }^{ 3 }\times { 6 }^{ 3 }\times { 10 }^{ 6 } } $$

$$=\dfrac { { 6 }^{ \left( 6-3 \right) }\times { 3 }^{ 6 } }{ { 7 }^{ 3 }\times { 10 }^{ \left( 6-3 \right) } } $$

$$=\dfrac { { 6 }^{ 3 }\times { 3 }^{ 6 } }{ { 7 }^{ 3 }\times { 10 }^{ 3 } } $$

$$=\dfrac {(2\times 3)^{ 3 }\times { 3 }^{ 6 } }{ { 7 }^{ 3 }\times (2\times 5)^{ 3 } } $$

$$=\dfrac { { 2 }^{ 3 }\times { 3 }^{ 3 }\times { 3 }^{ 6 } }{ { 7 }^{ 3 }\times { 2 }^{ 3 }\times { 5 }^{ 3 } } $$

$$=\dfrac { { 2 }^{ 3-3 }\times { 3 }^{ 3+6 } }{ { 7 }^{ 3 }\times { 5 }^{ 3 } } $$

$$=\dfrac { { 3 }^{ 9 } }{ { 7 }^{ 3 }\times { 5 }^{ 3 } } $$

$$=\dfrac { 19683 }{ 42875 } $$

Which is larger: $$0.25^4$$ or $$0.35^3$$

We use the simple observation: If $$a$$ and $$b$$ are non zero numbers then $$a< b$$ its equivalent to $$\cfrac{a}{b}< 1$$.
Write $$0.25=\cfrac { 1 }{ 4 } $$ and $$0.35=\cfrac { 35 }{ 100 } =\cfrac { 7 }{ 20 } $$. We have to compare $$\cfrac { 1 }{ { 4 }^{ 4 } } $$ and $$\cfrac { { 7 }^{ 3 } }{ { 20 }^{ 3 } } $$. But $${ 20 }^{ 3 }={ \left( 4\times 5 \right) }^{ 3 }={ 4 }^{ 3 }\times { 5 }^{ 3 }$$. Thus we see that
$$\cfrac { { \left( 0.25 \right) }^{ 4 } }{ { \left( 0.35 \right) }^{ 3 } } =\cfrac { { 4 }^{ 3 }\times { 5 }^{ 3 } }{ { 4 }^{ 4 }\times { 7 }^{ 3 } } =\cfrac { { 5 }^{ 3 } }{ 4\times { 7 }^{ 3 } } <1$$
since $$5< 7$$. Thus $${ \left( 0.25 \right) }^{ 4 }<{ \left( 0.35 \right) }^{ 3 }$$

Find the value of the following:
$$\left (\dfrac {-1}{2}\right )^{5}$$

$$\left (\dfrac {-1}{2}\right )^{5} = \dfrac {-1}{32}$$

Simplify: $$10^{9} \div 10^{6}$$

$$10^{9}\div 10^{6} = 10^{9 - 6} = 10^{3}$$

Simplify: $$(2^{5})^{2}$$

$$(2^{5})^{2} = 2^{5\times 2} = 2^{10} = 1024$$

Is $$\cfrac { { \left( { 10 }^{ 4 } \right) }^{ 3 } }{ { 5 }^{ 13 } } $$ an integer? Justify your answer.

Consider, $$\dfrac { { \left( { 10 }^{ 4 } \right) }^{ 3 } }{ { 5 }^{ 13 } } $$

$$=\dfrac { { 10 }^{12} }{ { 5 }^{(12+1)} } $$

$$=\dfrac { { \left( 5\times 2 \right) }^{ 12 } }{ { 5 }^{ 12 }\times 5^{1} } $$

$$=\dfrac { { 5 }^{ 12 }\times { 2 }^{ 12 } }{ { 5 }^{ 12 }\times 5^{1}} $$

$$=\dfrac { { 2 }^{ 12 } }{ 5 } $$

$$=\dfrac { 4096 }{ 5 } $$

$$=819.2$$

Hence, it is not an integer as it contains decimal.

Simplify:
$$\left [\left \{(3^{5/2} \times 5^{3/4})\div 2^{-5/4}\right \} \div \left \{16\div (5^{2}\times 2^{1/4} \times 3^{1/2})\right \}\right ]^{1/5}$$

$$[\{(3^{5/2} \times 5^{3/4} ) \div 2^{-5/4} \} \div \{16 \div (5^2 \times 2^{1/4} \times 3^{1/2})\}]^{1/5}$$

$$\Rightarrow \left[\left\{\dfrac{3^{3/5} \times 5^{3/4}}{2^{-5/4}}\right\} \div \left\{ \dfrac{16}{5^2\times 2^{1/4} \times 3^{1/2}}\right\}\right]^{1/5}$$

$$ \Rightarrow \left [ \left \{ 3^{5/2}\times5^{3/4}\times2^{5/4} \right \}\div \dfrac{16}{5^{2}\times 2^{1/4}\times 3^{1/2}} \right ]^{1/5} $$

$$\Rightarrow \left[\dfrac{3^{5/2} \times 5^{3/4} \times 2^{5/4} \times 5^2 \times 2^{1/2} \times 3^{1/2}}{16}\right]^{1/5}$$

$$\Rightarrow \left[\dfrac{3^3 \times 5^{3/4+2} \times 2^{5/4+1/4} }{2^4}\right]^{1/5}$$

$$\Rightarrow \left[\dfrac{3^3 \times 5^{11/4} \times 2^{3/2}}{2^4}\right]^{1/5}$$

$$\Rightarrow \left[\dfrac{3^3 \times 5^{11/4}}{2^{(4-3/2)}}\right]^{1/5}$$ $$\Rightarrow \left[\dfrac{3^3\times 5^{11/4}}{2^{5/2}}\right]^{1/5}$$

$$\Rightarrow \dfrac{(3^3 \times 5^{11/4})^{1/5}}{\sqrt{2}}$$ $$\Rightarrow \dfrac{3^{3/5} \times 5^{11/20}}{\sqrt{2}}$$

Simplify the following using laws of indices:
$$(6.25)^{0.5}\times 10^{2}\times (100)^{-1/2}$$

Given, $$ (6.25)^{0.5} \times 10^2 \times (100)^{- 1/2}$$

$$=$$ $$ (6.25)^{0.5} \times 10^2 \times (10^2)^{- 1/2}$$

$$=$$ $$ (6.25)^{0.5} \times 10^2 \times (10)^{- 1}$$ Using $$[(A^m)^n = A^{mn}]$$

$$=$$ $$ (6.25)^{0.5} \times 10^1 $$ Using $$[A^m \times A^n = A^{m+n}]$$

$$=$$ $$ ((2.5)^2)^{0.5} \times 10^1 $$

$$=$$ $$ (2.5)^1 \times 10^1 $$ Using $$[(A^m)^n = A^{mn}]$$

$$=$$ $$2.5 \times 10$$

$$=$$ $$25$$

Find the value of the expression
$$\left [3^{1/3}\left \{5^{-1/2} \times 3^{-1/3} \times (225^{2})^{1/3} \right \}^{-1/2}\right ]^{6}$$

Solution:

$$\left[3^{1/3}\{5^{-1/2}\times3^{-1/3}\times(225^2)^{1/3}\}^{-1/2}\right]^6$$

$$=\left[3^{1/3}\{5^{-1/2}\times3^{-1/3}\times(15)^{4/3}\}^{-1/2}\right]^6$$

$$=\left[3^{1/3}\{5^{-1/2}\times3^{-1/3}\times5^{4/3}\times3^{4/3}\}^{-1/2}\right]^6$$

$$=\left[3^{1/3}\{5^{5/6}\times3\}^{-1/2}\right]^6$$

$$=\left[3^{1/3}\times5^{-5/12}\times3^{-1/2}\right]^6$$

$$=\left[3^{-1/6}\times5^{-5/12}\right]^6$$

$$=3^{-1}\times5^{-5/2}$$

Write the given $$\sqrt [3]{108}$$ in its simplest form

We can write $$\sqrt[3]{108} $$ as

$$\sqrt[3]{108} =\sqrt[3]{ 2^2 \times 3^3}$$

$$\therefore \sqrt[3]{108}=3 \sqrt[3]{4} $$ [After simplification]

Write the given surd $$\sqrt [4]{5000}$$ in its simplest form

To simplify $$\sqrt[4]{500}$$ we may proceed as follows by splitting the number into its prime factors.

$$\sqrt[4]{500}$$ $$=$$ $$\sqrt[4]{2 \times 2 \times 2 \times 5 \times 5 \times 5 \times 5}$$

$$\space$$ $$ \space$$ $$\space$$ $$ = $$ $$\sqrt[4]{5 \times 5 \times 5 \times 5} $$ $$ \times$$$$\sqrt[4]{2 \times 2 \times 2 }$$

$$\space$$ $$ \space$$ $$\space$$ $$ = $$ $$ 5$$$$\sqrt[4]{2 \times 2 \times 2 }$$

$$\space$$ $$ \space$$ $$\space$$ $$ = $$ $$ 5$$$$\sqrt[4]{8}$$

Write the given surd $$\sqrt {76}$$ in its simplest form

We can write $$\sqrt{76}$$ as

$$\sqrt{76} =\sqrt {2 \times 2 \times 19}$$

$$\therefore \sqrt{ 76}=2 \sqrt{19}$$ [Taking $$2$$ outside from the square root]

Express the following information in the standard form:
Size of the bacteria is $$0.0000004$$ m

Size of the bacteria is $$0.0000004$$ m

In standard form,

Size of the bacteria is $$4\times{10}^{-7}$$ m

Simplify $$\left(\frac{3125}{243}\right) ^{-415}$$

1310719_1032763_ans_1e0207387ae9403e966f77fbcf3fad7c.jpeg

Simplify: $$\root 4 \of {\root 3 \of {{2^2}} } $$

$$\sqrt[4]{\sqrt[3]{2^{2}}}=(2^{2})^{\dfrac{1}{4}\times \dfrac{1}{3}}=2^{1/6}$$

Simplify the following expression.

$$(8p^{-3})^{2/3} \times (4p^2)^{3/2} \div p^{-3}$$ and find the power of $$p$$

We have,

$$(8p^{-3})^{2/3}\times (4p^2)^{3/2}\div p^{-3}$$

$$\dfrac {(8p^{-3})^{2/3}\times (4p^2)^{3/2}} {p^{-3}}$$

$$\Rightarrow (2^3\times p^{-3})^{2/3}\times ((2p)^2)^{3/2}\times p^{3}$$

$$\Rightarrow (2\times p^{-1})^{2}\times (2p)^{3}\times p^{3}$$

$$\Rightarrow (4\times p^{-2})\times 8p^3\times p^{3}$$

$$\Rightarrow (32\times p^{-2})\times p^6$$

$$\Rightarrow (32\times p^{-2+6})$$

$$\Rightarrow 32\times p^{4}$$

So, the power of $$p$$ is $$4$$.

Hence, this is the answer.

Simplify: $$(x^{0})^{4}$$

$$(x^{0})^{4} = (1)^{4} = 1 [\because a^{0} = 1]$$

Simplify: $$(2\times 3)^{4}$$

$$(2\times 3)^{4} = 6^{4} = 1296$$
(or) $$(2\times 3)^{4} = 2^{4}\times 3^{4} = 16\times 81 = 1296$$

Simplify: $$\left (\dfrac {3}{2}\right )^{5}$$

$$\left (\dfrac {3}{2}\right )^{5} = \dfrac {3^{5}}{2^{5}} = \dfrac {243}{32}$$

Simplify the following using law of exponents.
$$\dfrac{(-6)^9}{(-6)^5}$$

we know,

$$\dfrac{a^{m}}{a^{n}}=a^{m-n}$$

so,

$$\dfrac{(-6)^{9}}{(-6)^{5}}=(-6)^{9-5}$$

$$=(-6)^4$$

$$=(6)^4$$

$$=1296$$

Simplify the following using law of exponents.
$$(3^2)^2$$

we know,

$$(a^{m})^{n}=a^{mn}$$

So,

$$(3^{2})^{2}=3^{2*2}$$

$$=3^{4}$$

$$=81$$

Solve the following equation:
$$\displaystyle\, \left ( \dfrac{5}{3} \right )^{x + 1}\cdot \left ( \dfrac{9}{25} \right )^{x^2 + 2x - 11} = \left ( \dfrac{5}{3} \right )^9$$

$$\bigg(\dfrac{5}{3}\bigg)^{x+1}\cdot\bigg(\dfrac{9}{25}\bigg)^{x^{2}+2{x}-11}=\bigg(\dfrac{5}{3}\bigg)^{9}$$

$$\bigg(\dfrac{5}{3}\bigg)^{x+1-2{x^{2}}-4{x}+22}=\bigg(\dfrac{5}{3}\bigg)^{9}$$

$$-2{x^{2}}-3{x}+23=9$$

$$2{x^{2}}+3{x}-14=0$$

$$2{x^{2}}+4{x}-7{x}-14=0\implies x=-2,\dfrac{7}{2}$$

Represent the following mixed infinite decimal periodic fractions as common fractions $$(1 4)$$
$$\displaystyle\frac{\sqrt[3]{a^5 b^{1/2}}\sqrt[4]{a^{-1}}}{(a^2 \sqrt[5]{ab^3})^2}$$

The given equation is

$$\dfrac { \sqrt [ 3 ]{ { a }^{ 5 }{ b }^{ 1/2 } } \sqrt [ 4 ]{ { a }^{ -1 } } }{ { ({ a }^{ 2 }\sqrt [ 5 ]{ a{ b }^{ 3 } } ) }^{ 2 } } $$

$$\Rightarrow =\dfrac { { a }^{ 5/3 }{ b }^{ 1/6 }{ a }^{ -1/4 } }{ { (a }^{ 2 }{ a }^{ 1/5 }{ b }^{ 3/5 } } $$[since $${ ({ a }^{ m }) }^{ n }={ a }^{ mn }$$]

$$\Rightarrow \dfrac { { a }^{ 5/3 }{ b }^{ 1/6 }{ a }^{ -1/4 } }{ { (a }^{ 2 }{ a }^{ 1/5 }{ b }^{ 3/5 } } ={ a }^{ 5/3-2-1/5-1/4 }{ b }^{ 1/6-3/5 }={ a }^{ -47/60 }{ b }^{ -13/30 }$$

Represent the following mixed infinite decimal periodic fractions as common fractions:
Simplify the following expressions.
$$\displaystyle\frac{(\sqrt[5]{a^{4/3}})^{3/2}}{(\sqrt[5]{a^4})^3} \cdot \frac{(\sqrt{a \sqrt[3]{a^2b}})^4}{(\sqrt[3]{a\sqrt{b}})^4}$$

The given equation is

$$\dfrac { { (\sqrt [ 5 ]{ { a }^{ 4/3 } } ) }^{ 3/2 } }{ { (\sqrt [ 5 ]{ { a }^{ 4 } } ) }^{ 3 } } \dfrac { { (\sqrt { { a }^{ 3 }\sqrt { { a }^{ 2 }b } } ) }^{ 4 } }{ { (\sqrt [ 3 ]{ a\sqrt { b } } ) }^{ 4 } } $$

$$\dfrac { { (\sqrt [ 5 ]{ { a }^{ 4/3 } } ) }^{ 3/2 } }{ { (\sqrt [ 5 ]{ { a }^{ 4 } } ) }^{ 3 } } \dfrac { { (\sqrt { { a }^{ 3 }\sqrt { { a }^{ 2 }b } } ) }^{ 4 } }{ { (\sqrt [ 3 ]{ a\sqrt { b } } ) }^{ 4 } } \Rightarrow =\dfrac { { a }^{ (\dfrac { 4 }{ 3\times 5 } \times \dfrac { 3 }{ 2 } ) } }{ { a }^{ (\dfrac { 4\times 3 }{ 5 } ) } } \dfrac { { a }^{ (\dfrac { 3\times 4 }{ 2 } +\dfrac { 2\times 4 }{ 2\times 2 } ) }{ b }^{ \dfrac { 4 }{ 2\times 2 } } }{ { a }^{ 4/3 }{ b }^{ \dfrac { 4 }{ 2\times 2 } } } $$

Now add all the powers of a and b we get

$$\Rightarrow \dfrac { { a }^{ (\dfrac { 4 }{ 3\times 5 } \times \dfrac { 3 }{ 2 } ) } }{ { a }^{ (\dfrac { 4\times 3 }{ 5 } ) } } \dfrac { { a }^{ (\dfrac { 3\times 4 }{ 2 } +\dfrac { 2\times 4 }{ 2\times 2 } ) }{ b }^{ \dfrac { 4 }{ 2\times 2 } } }{ { a }^{ 4/3 }{ b }^{ \dfrac { 4 }{ 2\times 2 } } } =\dfrac { { a }^{ 2/5 } }{ { a }^{ 12/5 } } \dfrac { { a }^{ 8 }b }{ { a }^{ 4/3 }b } ={ a }^{ (\dfrac { 2 }{ 5 } + 8-\dfrac { 12 }{ 5 } -\dfrac { 4 }{ 3 } ) }{ b }^{ 0 }$$

$$={ a }^{ 14/3 }$$

If $$ (7+4 \sqrt3)^n = p + \beta , $$ where $$n$$ and $$p$$ are positive integers, and $$ \beta$$ a proper fraction, show that $$ ( 1 - \beta ) ( p + \beta ) = 1 $$

given that

$$(7+4\sqrt{3})^{n}=p+\beta$$ ...........................(1)

where $$\beta$$ is a proper fraction $$0<\beta<1$$

$$(7-4\sqrt{3})^{n}=\beta'$$

where $$\beta$$ is a proper fraction

$$0<\beta' <1$$

sum of $$\beta$$ & $$\beta '$$ must be 1.

$$\beta+\beta '=1$$

$$(7-4\sqrt{3})^{n}=\beta'=1-\beta$$ . .................(2)

multiplying eqn (1) & (2)

$$(7+4\sqrt{3})^{n}\times[(7-4\sqrt{3})^{n}]=(p+\beta).(1-\beta)$$

$$[(49-48)^{n}]=(p+\beta).(1-\beta)$$

$$1=(p+\beta).(1-\beta)$$ n is positive integer

Hence proved

Simplify the following using law of exponents.
$$\dfrac{(4)^6}{(4)^3}$$

we know,

$$\dfrac{a^{m}}{a^{n}}=a^{m-n}$$

so,

$$\dfrac{4^{6}}{4^{3}}=4^{6-3}$$$$=4^{3}$$$$=64$$

Solve the following equation:
$$\displaystyle\, 9^{|3x - 1|} = 3^{8x - 2}$$

$$9^{\mid 3{x}-1\mid}=3^{8{x}-2}$$

$$3^{2\mid 3{x}-1\mid}=3^{8{x}-2}$$

$$\mid 3{x}-1\mid=4{x}-1$$

$$3{x}-1=\pm (4{x}-1)$$

$$\implies x=0,\dfrac{2}{7}$$

Solve the following equations.
$$\displaystyle\, 3.4^x + \frac{1}{3} \cdot 9^{x + 2} = 6.4^{x + 1} - \frac{1}{2} \cdot 9^{x + 1}$$

$$3.4^{ x }+\cfrac { 1 }{ 3 } \cdot 9^{ x+2 }=6.4^{ x+1 }-\cfrac { 1 }{ 2 } \cdot 9^{ x+1 }$$

$$\Rightarrow { 3.4 }^{ x }+\cfrac { 1 }{ 3 } \cdot { 9 }^{ x }\cdot { 9 }^{ 2 }={ 6.4 }^{ x }\cdot 4-\cfrac { 1 }{ 2 } { 9 }^{ x }\cdot 9$$

$$\Rightarrow { 3.4 }^{ x }-{ 24.4 }^{ x }=\cfrac { -81 }{ 3 } \cdot { 9 }^{ x }-\cfrac { 9 }{ 2 } \cdot { 9 }^{ x }$$

$$\Rightarrow { 4 }^{ x }\left( 3-24 \right) =-{ 9 }^{ x }\left( 27+\cfrac { 9 }{ 2 } \right) $$

$$\Rightarrow { 4 }^{ x }\left( -21 \right) =-{ 9 }^{ x }\cdot \cfrac { 63 }{ 2 } $$

$$\Rightarrow \cfrac { { 4 }^{ x } }{ { 9 }^{ x } } =\cfrac { 63 }{ 2 } \times \cfrac { 1 }{ 21 } $$

$$\Rightarrow \cfrac { { 2 }^{ 2x } }{ { 3 }^{ 2x } } =\cfrac { 3 }{ 2 } $$

$$\Rightarrow { \left( \cfrac { 2 }{ 3 } \right) }^{ 2x }={ \left( \cfrac { 2 }{ 3 } \right) }^{ -1 }$$

$$\Rightarrow 2x=7$$

$$x=-\cfrac { 1 }{ 2 } $$ Solved

$$4^x \, - \, 3^{x \, - \, \dfrac{1}{2}} \, = \, 3^{x \, + \, \dfrac{1}{2}} \, - \, 2^{2x \, - \, 1}$$ find the value of x

The given equation can be re-written as
$$2^{2x} \, + \, 2^{2x \, - \, 1} \, = \, 3^{x - 1/2} \, + \, 3^{x + 1/2}$$
$$2^{2x}\left(1 \, + \, \dfrac{1}{2}\right) \, = \, 3^x \left(\dfrac{1}{\sqrt{(3)}} \, + \, \sqrt{3}\right)$$
or $$3.2^{2x - 1} \, = \, 4. 3^{x \, - \, 1/2}$$
or $$2^{2x - 3} \, = \, 3^{x -3/2}$$
Now by trial, $$x \, = \, \dfrac{3}{2}$$ is one solution
Now taking logarithm to the base 10, we get
$$(2x - 3) \, log_{10}2 \, = \, \left(x \, - \, \dfrac{3}{2}\right)log_{10}3$$
or $$(2 log 2 - log 3)x = $$\dfrac{3}{2}(2log 2 \, - \, log 3)$$
This also gives $$x \, = \, \dfrac{3}{2}$$
Hence $$x \, = \, \dfrac{3}{2}$$is the only solution

Multiply -
$$\sqrt {27{a^3}{b^2}{c^4}} \times \root 3 \of {128{a^7}{b^9}{c^2}} \times \root 6 \of {729a{b^{12}}{c^2}} $$

$$\sqrt{27a^3b^2c^4}\sqrt[3]{128a^7b^9c^2}\sqrt[6]{729ab^{12}c^2}$$

-------------------------------------------------

$$\sqrt{27a^3b^2c^4}=3\sqrt{3}bc^2a^{\frac{3}{2}}$$

-----------------------------------------------------

$$\sqrt[3]{128a^7b^9c^2}=4\sqrt[3]{2}b^3\sqrt[3]{a^7c^2}$$

-----------------------------------------------------

$$\sqrt[6]{729ab^{12}c^2}=3b^2\sqrt[6]{ac^2}$$

---------------------------------------------------

$$=3\sqrt{3}bc^2a^{\frac{3}{2}}\cdot \:4\sqrt[3]{2}b^3a^{\frac{7}{3}}c^{\frac{2}{3}}\cdot \:3b^2\sqrt[6]{a}\sqrt[3]{c}$$

$$=4\sqrt[3]{2}\cdot \:3^{\frac{5}{2}}b^3b^2bc^2a^{\frac{3}{2}}a^{\frac{7}{3}}\sqrt[6]{a}c^{\frac{2}{3}}\sqrt[3]{c}$$

$$=4\sqrt[3]{2}\cdot \:3^{\frac{5}{2}}a^4b^3b^2bc^2c^{\frac{2}{3}}\sqrt[3]{c}$$

$$=4\sqrt[3]{2}\cdot \:3^{\frac{5}{2}}a^4b^6c^2c^{\frac{2}{3}}\sqrt[3]{c}$$

$$=4\sqrt[3]{2}\cdot \:3^{\frac{5}{2}}a^4b^6c^3$$

$$=3^2\cdot \:4\sqrt[3]{2}\sqrt{3}a^4b^6c^3$$

$$=36\sqrt[3]{2}\sqrt{3}(a^4b^6c^3)$$

Solve the following equation:
$$\displaystyle 81^{\sin^2 \, x} \, + \, 81^{\cos^2 \, x} \, = \, 30 $$

$$81^{\sin^{2}x}+81^{\cos^{2}x}=30\implies 81^{\sin^{2}x}+81^{1-\sin^{2}x}=30$$

$$(81^{\sin^{2}x})^{2}-30(81^{\sin^{2}x})+81=0\implies 81^{\sin^{2}x}=3,27\implies 3^{4\sin^{2}x}=3,3^{3}$$

$$\sin^{2}x=\dfrac{1}{4},\dfrac{3}{4}\implies x=n\pi+(-1)^{n}\dfrac{\pi}{6},m\pi+(-1)^{m}\dfrac{\pi}{3},$$

Evaluate $$\dfrac{{{{(36)}^{\dfrac{{ - 7}}{2}}} - {{(36)}^{\dfrac{{ - 9}}{2}}}}}{{{{\left( {36} \right)}^{\dfrac{{ - 5}}{2}}}}}.$$

$$ \Rightarrow \,\,\dfrac{{{{36}^{\dfrac{{ - 7}}{2}}} - {{36}^{\dfrac{{ - 9}}{2}}}}}{{{{\left( {36} \right)}^{\dfrac{{ - 5}}{2}}}}}$$
$$ \Rightarrow \,\,\dfrac{{{{\left( 6 \right)}^{2 \times \dfrac{{ - 7}}{2}}} - {{\left( 6 \right)}^{2 \times \dfrac{{ - 9}}{2}}}}}{{{{\left( 6 \right)}^{2 \times \dfrac{{ - 5}}{2}}}}}$$
$$ \Rightarrow \,\,\dfrac{{{6^{ - 7}} - {6^{ - 9}}}}{{{6^{ - 5}}}}$$
$$ \Rightarrow \,\,\dfrac{{{6^{ - 7}}}}{{{6^{ - 5}}}} - \dfrac{{{6^{ - 9}}}}{{{6^{ - 5}}}}$$
$$ = {6^{ - 7 + 5}} - {6^{ - 9 + 5}}$$
$$ = {6^{ - 2}} - {6^{ - 4}}$$
$$ = \dfrac{1}{{{6^2}}} - \dfrac{1}{{{6^4}}}$$
$$ = \dfrac{{{6^2} - 1}}{{{6^4}}}$$

$${27^x} = {\dfrac{9} {{3^x}}}$$ find $$x$$

$${ 27 }^{ x }=\cfrac { 9 }{ { 3 }^{ x } } \\ { 3 }^{ 3x }\times{ 3 }^{ x }=9\\ { 3 }^{ 4x }={ 3 }^{ 2 }\\ 4x=2\\ x=\cfrac { 1 }{ 2 } $$

Solve the following equations. $$\left (\displaystyle\, 7.3^{x + 1} - 5^{x + 2} \right ) = \left (3^ {x + 4} - 5 ^{x + 3} \right )$$

$$7.{ 3 }^{ x+1 }-{ 5 }^{ x+2 }={ 3 }^{ x+4 }-{ 5 }^{ x+3 }$$

$$\Rightarrow 7\cdot { 3 }^{ x }\cdot 3-{ 5 }^{ x }\cdot { 5 }^{ 2 }={ 3 }^{ x }\cdot { 3 }^{ 4 }-{ 5 }^{ x }\cdot { 5 }^{ 3 }$$

$$\Rightarrow 21\cdot { 3 }^{ x }-{ 5 }^{ x }\cdot 25={ 3 }^{ x }\cdot 81-{ 5 }^{ x }\cdot 125$$

$$21\cdot { 3 }^{ x }-{ 3 }^{ x }\cdot 81={ 5 }^{ x }\cdot 25-{ 5 }^{ x }\cdot 125$$

$$\Rightarrow { 3 }^{ x }\left( 21-18 \right) ={ 5 }^{ x }\left( 25-125 \right) $$

$$\Rightarrow \cfrac { { 3 }^{ x } }{ { 5 }^{ x } } =\cfrac { 100 }{ 60 } $$

$$\Rightarrow { \left( \cfrac { 3 }{ 5 } \right) }^{ x }=\cfrac { 5 }{ 3 } $$

$$\Rightarrow { \left( \cfrac { 3 }{ 5 } \right) }^{ x }={ \left( \cfrac { 3 }{ 5 } \right) }^{ -1 }$$

$$\therefore x=-1$$

Simplify: $$2\root 5 \of {\root 4 \of {{{({2^3})}^4}} } $$

$$2\sqrt[5]{\sqrt[4]{(2^{3})^{4}}}$$

$$=2\sqrt[5]{2^{3}}$$

$$=2.2^{\dfrac{3}{5}}$$

$$=2^{\dfrac{8}{5}}$$

Prove that
$${\dfrac{a + b + c}{{a^{ - 1}}{b^{ - 1}} + {b^{ - 1}}{c^{ - 1}} + {c^{ - 1}}{a^{ - 1}}}} = abc$$

Consider,

$$\dfrac{a + b + c}{{a^{ - 1}}{b^{ - 1}} + {b^{ - 1}}{c^{ - 1}} + {c^{ - 1}}{a^{ - 1}}}$$

$$=\dfrac{a + b + c}{{\dfrac{1}{ab}} + {\dfrac{1}{bc}} + {\dfrac{1}{ca}}}$$-----since $$x^{-1}=\dfrac{1}{x}$$

$$=\dfrac{a + b + c}{{\dfrac{c}{abc}} + {\dfrac{a}{abc}} + {\dfrac{b}{cab}}}$$ -----Multiply and divide each terms in the denominator by the missing terms. i.e., $$c,a,b$$ respectively

$$=\dfrac{a + b + c}{\dfrac{c+a+b}{abc}}$$

$$=\dfrac{1}{\dfrac{1}{abc}}$$

$$=abc$$

Hence proved.

Solve: $$\left( \cfrac{125}{343} \right)^{1/3}$$

$$\left( \cfrac{125}{343} \right)^{1/3} \\ =\left( \cfrac{5^3}{7^3} \right)^{1/3} \\ =\left( \cfrac{5}{7} \right)^{3 \times \cfrac{1}{3}} \\ =\cfrac{5}{7}$$

Simplify:
$$\left(\dfrac{x^b}{x^c}\right)^a$$$$\times\left(\dfrac{x^c}{x^a}\right)^b$$$$\times\left(\dfrac{x^a}{x^b}\right)^c$$

Now,

$$\left(\dfrac{x^b}{x^c}\right)^a$$$$\times\left(\dfrac{x^c}{x^a}\right)^b$$$$\times\left(\dfrac{x^a}{x^b}\right)^c$$

$$=(x^{b-c})^a\times(x^{c-a})^b\times(x^{a-b})^c$$

$$=x^{(ab-ac+bc-ab+ac-bc)}$$

$$=x^0$$

$$=1$$.

Simplify : $$2^{\frac{1}{4}} . 4^{\frac{1}{8}} . 8^{\frac{1}{16}} . 16^{\frac{1}{32}} ......$$

$$2^\dfrac14 \times 2^\dfrac28 \times 2^\dfrac 3{16}\times 2^\dfrac4{32}\times 2^\dfrac5{64}......$$

$$P=(2)^{\left(\dfrac14+\dfrac28+\dfrac3{16}+\dfrac4{32}+\dfrac5{64}+....\right)}$$

$$P=(2)^S$$ ……………… $$(1)$$

Where $$S=\dfrac14+\dfrac28+\dfrac3{16}+\dfrac4{32}+\dfrac5{64}+....\infty$$ ..... $$(2)$$

$$S \times \left(\dfrac12 \right) = \dfrac 18+\dfrac 2{16}+\dfrac 3{32}+\dfrac 4{64}+....+\infty$$ ……. $$(3)$$

On subtracting equation $$(3)$$ from $$(2)$$, we get

$$\dfrac S2=\dfrac 14+\dfrac18+\dfrac 1{16}+\dfrac1{32}+\dfrac {1}{64}+.....\infty$$.

$$\dfrac S2=\dfrac a{1-r} = \dfrac {\dfrac 14}{1–\dfrac 12}$$.

$$\dfrac S2 =\dfrac 14×\dfrac 21.$$

$$\dfrac S2 = \dfrac 12$$

$$S = 1$$

Put $$S=1$$ in eq.$$(1)$$.

$$P =(2)^S.$$

$$P =(2)^1$$

$$P = 2$$

Convert into power notation
$$\dfrac { 1 }{1000 }$$

1302493_1040695_ans_f5646624d549460a853a0616d93739c1.JPG

Find m.
$$\dfrac { { \left( 3 \right) }^{ 2m+1 } }{ 27 } ({ 9 }^{ 2 })={ \left( \left( { -3 }^{ 8 } \right) { 3 }^{ 4 } \right) }^{ 5 }$$ ?

$$(\frac{(3)^{2m+1})}{27})\times9^2=((-3)^8 3^4)^5\\(\frac{3^{2m+1}}{3^3})\times3^4=(3^{12})^5\\3^{2m+1+4-3}=3^{60}\\2m+2=60\\\therefore m = 29$$

Convert into power notation
$$\dfrac {-1 }{32 }$$

$$\dfrac{-1}{32}=\dfrac{-1^5}{2^5}=\left[\dfrac{-1}{2}\right]^5$$

Convert into power notation
$$\dfrac {-1 }{343 }$$

$$\dfrac{-1}{343}=\dfrac{-1^3}{7^3}=\left[\dfrac{-1}{7}\right]^3$$

Convert in to power notation
$$\dfrac{1}{27}$$

1302492_1040685_ans_5a787a742c5e4baea67b5a26bf22c6ee.JPG

Convert into power notation
$$\dfrac { -27 }{125 }$$

Given number is $$\dfrac{-27}{125}$$

We can write $$-27$$ as $$(-3)\times (-3)\times (-3)$$ which is $$(-3)^3$$.

Similarly, we can write $$125$$ as $$(5)\times (5)\times (5)$$ which is $$(5)^3$$.

$$\therefore \ \dfrac{-27}{125}=\left[\dfrac{-3}{5}\right]^3$$

If $$\dfrac{9^n \times 3^2 \times 3^n - (27)^n}{3^{3m} \times 2^3} = 3^{-3}$$, prove that $$(m - n) = 1$$.

Consider given the equation,

$$ \dfrac{{{9}^{n}}\times {{3}^{2}}\times {{3}^{n}}-{{(27)}^{n}}}{{{3}^{3m}}\times {{2}^{3}}}={{3}^{-3}} $$

$$ \dfrac{{{9.3}^{2\times }}^{n}{{.3}^{n}}-{{({{3}^{3}})}^{n}}}{{{3}^{3m}}\times {{2}^{3}}}={{3}^{-3}} $$

$$ \dfrac{{{9.3}^{3n}}-{{3}^{3n}}}{{{3}^{3m}}\times {{2}^{3}}}={{3}^{-3}} $$

$$ \dfrac{{{8.3}^{3n}}}{{{3}^{3m}}\times {{2}^{3}}}={{3}^{-3}} $$

$$ \dfrac{{{3}^{3n}}}{{{3}^{3m}}}={{3}^{-3}} $$

$${{3}^{3n-3m}}={{3}^{-3}}$$

By comparing of power both sides,

$$ 3n-3m=-3 $$

$$ n-m=-1 $$

$$ m-n=1 $$

Hence,proved

Convert into power notation
$$\dfrac { -1 }{64 }$$

$$\dfrac{-1}{64}=\dfrac{-1^3}{8^3}=\left[\dfrac{-1}{8}\right]^3$$

Convert into power notation
$$\dfrac {49 }{81}$$

$$\dfrac{49}{81}=\dfrac{7^2}{9^2}=\left[\dfrac{7}{9}\right]^2$$

Convert into power notation
$$156$$

Given number is $$156$$

$$156=2\times2\times3\times13$$

$$156=2^2\times3\times13$$

Convert into power notation
$$343$$

1302494_1040697_ans_0bb1242795d84f518e9be47585a34d5d.JPG

If $$x=y^{2}$$, $$y=z^{2}$$, $$z=p^{2}$$ where $$p =2^{36} \times 9^{48}$$, then $$\sqrt{x}$$ is_____

$$p=2^{36} \times (3^2)^{48}=2^{36} \times (3)^{96}$$

As $$z=p^2\Rightarrow z=(2^{36})^2 \times (3^{96})^2=2^{72} \times 3^{192}$$

similarly, $$y=z^2=2^{72} \times 3^{192}=2^{144} \times 3^{384}$$

and $$x=y^2\Rightarrow \sqrt x=y=2^{144} \times 3^{384}$$

Let $$a+b+c=0$$, then find the value of $$\sqrt[bc]{\dfrac{x^{a^2}}{x^{bc}}}$$$$\times\sqrt[ca]{\dfrac{x^{b^2}}{x^{ca}}}$$$$\times\sqrt[ab]{\dfrac{x^{c^2}}{x^{ab}}}$$.

Given,

$$a+b+c=0$$

or, $$a+b=-c$$.....(1).

Cubing both sides we get,

$$a+b)^3=-c^3$$

or, $$a^3+b^3+3ab(a+b)=-c^3$$

or, $$a^3+b^3+c^3=3abc$$.......(2) [ Using (1)].

Now,

$$\sqrt[bc]{\dfrac{x^{a^2}}{x^{bc}}}$$$$\times\sqrt[ca]{\dfrac{x^{b^2}}{x^{ca}}}$$$$\times\sqrt[ab]{\dfrac{x^{c^2}}{x^{ab}}}$$

$$=\sqrt[bc]{{x^{a^2-bc}}}$$$$\times\sqrt[ca]{{x^{b^2-ac}}}$$$$\times\sqrt[ab]{{x^{c^2-ab}}}$$

$$=x^{\left(\dfrac{a^2}{bc}+\dfrac{b^2}{ca}+\dfrac{c^2}{ab}-3\right)}$$

$$=x^{\dfrac{a^3+b^3+c^3-3abc}{abc}}$$

$$x^{3abc-3abc}$$

$$=x^0$$ [ Using (2)]

$$=1$$.

Simplify:
$$\dfrac{m^{2} -n^{2}}{(m + n)^{2}} \times \dfrac{m^{2} +mn + n^{2}}{m^{3} - n^{3}}$$

$$\dfrac{m^2 - n^2}{(m+n)^2}\times\dfrac{m^2 + mn +n^2}{m^3 - n^3}$$

$$=\dfrac{(m+n)(m-n)}{(m+n)^2}\times\dfrac{m^2 + mn +n^2}{(m-n)(m^2 +mn+ n^2)}$$

$$=\dfrac{m - n}{m+n}\times\dfrac{1}{m - n}$$

$$=\dfrac{1}{m+n}.$$

Formule:

$$a^2 - b^2 = (a + b)(a - b)$$

$$a^3 - b^3 = (a - b)(a^2 + ab + b^2)$$

Convert into power notation
$$169$$

$$169=13\times 13=13^2$$

Evaluate $$\dfrac { \left( { 3 }^{ -2 } \right) ^{ 2 }\times \left( { 5 }^{ 2 } \right) ^{ -3 }\times \left( { t }^{ -3 } \right) ^{ 1 } }{ \left( { 3 }^{ -2 } \right) ^{ 5 }\times \left( { 5 }^{ 3 } \right) ^{ -2 }\times \left( { t }^{ -4 } \right) ^{ 3 } } $$

$$\cfrac{{{{\left( {{3^{ - 2}}} \right)}^2} \times {{\left( {{5^2}} \right)}^{ - 3}} \times {{\left( {{t^{ - 3}}} \right)}^1}}}{{{{\left( {{3^{ - 2}}} \right)}^5} \times {{\left( {{5^3}} \right)}^{ - 2}} \times {{\left( {{t^{ - 4}}} \right)}^3}}}$$

$$ = \cfrac{{{3^{ - 4}} \times {5^{ - 6}} \times {t^{ - 3}}}}{{{3^{ - 10}} \times {5^{ - 6}} \times {t^{ - 12}}}}$$

$$ = {3^6} \times {t^9}$$

$$ = 729{t^9}$$

Simplify:
$$\left(\dfrac{5^{-1} \times 7^2}{5^2 \times 7^{-4}}\right)^{7/2} \times \left(\dfrac{5^2 \times 7^3}{5^3 \times 7^{-5}}\right)^{-5/2}$$.

$$\textbf{Apply the properties of the exponent and power}$$

We have, $${\left( {\frac{{{5^{ - 1}} \times {7^2}}}{{{5^2} \times {7^{ - 4}}}}} \right)^{\frac{7}{2}}} \times {\left( {\frac{{{5^2} \times {7^3}}}{{{5^3} \times {7^{ - 5}}}}} \right)^{ - \frac{5}{2}}}$$

$$ = {\left( {{5^{ - 1 - 2}} \times {7^{2 + 4}}} \right)^{\frac{7}{2}}} \times {\left( {{5^{2 - 3}} \times {7^{3 + 5}}} \right)^{ - \frac{5}{2}}}$$ $$\boldsymbol{[\because {\left( {{a^m}} \right)^n} = {a^{mn}}]}$$

$$ = {\left( {{5^{ - 3}}} \right)^{\frac{7}{2}}} \times {\left( {{7^6}} \right)^{\frac{7}{2}}} \times {\left( {{5^{ - 1}}} \right)^{\frac{{ - 5}}{2}}} \times {\left( {{7^8}} \right)^{\frac{{ - 5}}{2}}}$$

$$ = {5^{\frac{{ - 21}}{2}}} \times {7^{21}} \times {5^{\frac{5}{2}}} \times {7^{ - 20}}$$ $$\boldsymbol { { [\because \left( {{a^m}} \right)^n} = {a^{mn}]}}$$

$$ = {5^{ - 8}} \times 7$$

$$ = \frac{7}{{{5^8}}}$$

$$\textbf{Hence, the answer is}$$ $$\boldsymbol{\frac{7}{{{5^8}}}.}$$

Write in exponential form: $${2}^{3}+{2}^{5}+{2}^{6}-{2}^{2}$$

$$2^3+2^5+2^6-2^2$$

Take $$2^2$$ common

$$\Rightarrow 2^2(2^1+2^3+2^4-2^0)$$

$$\Rightarrow 2^2(2+8+16-1)$$

$$\Rightarrow 2^2(25)$$

$$\Rightarrow 2^2\times 5^2$$

Therefore, $$\Rightarrow 2^3+2^5+2^6-2^2=2^2\times 5^2$$

Solve:

$$\sqrt {{2^{x + 3}}} = 16$$

$$\sqrt {2^{x+3}}=16$$

$$2^{x+3}=(2^4)^2$$

$$\Rightarrow \ 2^{x+3}=2^8$$

when bases are equal power and also equal

$$\Rightarrow x+3=8$$

$$\therefore {x=5}$$

Value of $$\dfrac{(81)^{3\times6}\times (9)^{2\times 7}}{(81)^{4\times 2}\times (3)}$$ is?

$$\cfrac{(81)^{3.6}\times (9)^{2.7}}{(81)^{4.2}\times(3)}$$

$$\cfrac{((3)^4)^{3.6}\times((3)^2)^{2.7}}{((3)^4)^{4.2}\times (3)}$$

$$\cfrac{(3)^{4\times3\times6} \times(3)^{2\times2\times7}}{(3)^{4\times4\times2}\times(3)}$$

$$\cfrac{(3)^{72} \times(3)^{28}}{(3)^{32}\times(3)}$$

$$\cfrac{(3)^{72+28}}{(3)^{32+1}}$$

$$(3)^{100-33}=(3)^{67}$$ Ans.

Simplify:- $$\left[\dfrac {(-3)^{2}}{2}\right]^{3}$$

$${\left[ {\dfrac{{{{\left( { - 3} \right)}^2}}}{2}} \right]^3} = {\left( {\dfrac{9}{2}} \right)^3}$$

$$ = \dfrac{{729}}{8}$$

Solve $$\frac{8^{x} + 27^{x}}{12^{x} +18^{x}} =\frac{7}{6}$$

$$\dfrac{8^{x} + 27^{x}}{12^{x} +18^{x}} =\dfrac{7}{6}$$

By hit and Trial Method

Put $$x=1$$

$$\dfrac{8 + 27}{12 +18} =\dfrac{35}{30}=\dfrac76$$

$${ \left( 64 \right) }^{ 2/3 }+\sqrt [ 3 ]{ 125 } +{3}^{o}+\dfrac { 1 }{ { 2 }^{ -5 } } +{ \left( 27 \right) }^{ -2/3 }\times { \left( \dfrac { 25 }{ 9 } \right) }^{ -12 }$$

Let the problem $${\left( {{\rm{64}}} \right)^{{\rm{2}}/{\rm{3}}}} + \sqrt[3]{{{\rm{125}}}} + {{\rm{3}}^{\rm{o}}} + \frac{{\rm{1}}}{{{{\rm{2}}^{ - {\rm{5}}}}}} + {\left( {{\rm{27}}} \right)^{ - {\rm{2}}/{\rm{3}}}} \times {\left( {\frac{{{\rm{25}}}}{{\rm{9}}}} \right)^{ - {\rm{1/2}}}}$$

$$={\left( {4 \times 4 \times 4} \right)^{\frac{2}{3}}} + \sqrt[3]{{{{\rm{5}}^3}}} + {\rm{1}} + {2^5} + \left( {\frac{1}{{{{\left( {{\rm{3}} \times {\rm{3}} \times {\rm{3}}} \right)}^{\frac{2}{3}}}}}} \right) \times {\left( {\frac{{\rm{9}}}{{{\rm{25}}}}} \right)^{\frac{1}{2}}}$$

$$={\left( 4 \right)^2} + 5 + {\rm{1}} + 32 + \left( {\frac{1}{{{{\left( {\rm{3}} \right)}^2}}}} \right) \times \left( {\frac{{\rm{3}}}{{\rm{5}}}} \right)$$

$$=16+5+1+32+\frac{1}{15}$$

$$=54+\frac{1}{15}$$

$$=\frac{811}{15}$$

Exponential
$${(34)}^{3}$$

The given term can be written as $${\left( {34} \right)^3} = {\left( {2 \times 17} \right)^3}$$

$$ = {2^3} \times {17^3}$$

$$ = 8 \times 4913$$

$$ = 39304$$

If the radian measures of two angles of a triangle are as given below . find the radian measure and the degree measure of the third angle then.
$$\dfrac{3\pi}{5},\dfrac{4\pi}{15}$$

We have two angles of the triangle

$$\dfrac{3\pi}{5},\dfrac{4\pi}{15}$$

Let the third angle be $$x$$

So, $$\dfrac{3\pi}{5}+\dfrac{4\pi}{15}+x=\pi\Rightarrow \pi-\dfrac{13\pi}{15}=\dfrac{2\pi}{15}rad$$

In Angle $$x=\dfrac{2\times180}{15}=24^\circ$$

If
$${ 2 }^{ 3 }\frac{2}{3}^x=8\frac { 8 }{ 27 }$$
Find the value of $$x$$?

$$2^{3}\left(\dfrac{2}{3}\right)^{2}=8\dfrac{8}{27}$$

$$\therefore 8\left(\dfrac{2}{3}\right)^{x}=8\dfrac{8}{27}$$

$$\therefore \left(\dfrac{2}{3}\right)^{x}=\dfrac{8}{27}$$ ....... $$(1)$$

Now $$\dfrac{8}{27}=\left(\dfrac{2}{3}\right)^{3}$$

$$\therefore$$ from $$(1)$$ & $$(2)$$

$$x=3$$

Given $$4725={ 3 }^{ a }{ 5 }^{ b }{ 7 }^{ c }$$, find
i) the integral values of a,b and c.
ii) the value of $${ 2 }^{ -a }{ 3 }^{ b }{ 7 }^{ c }$$

From division alorithm it is evident that,

$$4725=3\times 3\times 3\times 5\times 5\times 7$$

$$\Rightarrow 4725={ 3 }^{ 3 }\times { 5 }^{ 2 }\times { 7 }^{ 1 }$$

$$\Rightarrow a=3,b=2,c=1$$

ii) $${ 2 }^{ -a }{ 3 }^{ b }{ 7 }^{ c }={ 2 }^{ -3 }\times { 3 }^{ 2 }\times { 7 }^{ 1 }$$

$$=\cfrac { 9\times 7 }{ 8 } \\=\cfrac { 63 }{ 8 } $$

1034100_1078801_ans_59f0cb958d03400a8186915881a1433d.png

Express positive exponents$${(\dfrac {5}{7})}^{-3}$$ and $${2}^{-5}$$

The positive exponent is obtained by reversing the given term which makes the power positive.

Therefore, the positive exponent of $${\left( {\cfrac{5}{7}} \right)^{ - 3}}$$ is,

$${\left( {\cfrac{7}{5}} \right)^3} = \cfrac{{{7^3}}}{{{5^3}}}$$

The positive exponent of $${\left( 2 \right)^{ - 5}}$$ is,

$${\left( {\cfrac{1}{2}} \right)^5} = \cfrac{1}{{{2^5}}}$$

Simplify:
$$\dfrac{{{{3}^{30}} + {3^{29}} + {3^{25}}}}{{{3^{31}} + {{3}^{30}} - {3^{29}}}} + \dfrac{{{2^{30}} + {2^{29}} + {2^{25}}}}{{{2^{31}} + {2^{30}} - {2^{29}}}}$$

We have,

$$=\dfrac{{{3}^{30}}+{{3}^{29}}+{{3}^{25}}}{{{3}^{31}}+{{3}^{30}}-{{3}^{29}}}+\dfrac{{{2}^{30}}+{{2}^{29}}+{{2}^{25}}}{{{2}^{31}}+{{2}^{30}}-{{2}^{29}}}$$

$$ =\dfrac{{{3}^{25}}\left( {{3}^{5}}+{{3}^{4}}+1 \right)}{{{3}^{29}}\left( {{3}^{2}}+3-1 \right)}+\dfrac{{{2}^{25}}\left( {{2}^{5}}+{{2}^{4}}+1 \right)}{{{2}^{29}}\left( {{2}^{2}}+2-1 \right)} $$

$$ =\dfrac{\left( 243+81+1 \right)}{{{3}^{4}}\left( 9+3-1 \right)}+\dfrac{\left( 32+16+1 \right)}{{{2}^{4}}\left( 4+2-1 \right)} $$

$$ =\dfrac{325}{{{3}^{4}}\times 11}+\dfrac{49}{{{2}^{4}}\times 5} $$

$$ =\dfrac{325}{81\times 11}+\dfrac{49}{16\times 5} $$

$$ =\dfrac{325}{891}+\dfrac{49}{80} $$

$$ =\dfrac{325\times 80+49\times 891}{891\times 80} $$

$$ =\dfrac{26000+43659}{71280} $$

$$ =\dfrac{69659}{71280} $$

Hence, the value is $$\dfrac{69659}{71280}$$.

Simplify and find the value of x:-
$${e^{x + 2\log x}}$$

Let $$a=e^{x+2\log x}$$ $$\Rightarrow$$ Here $$\log x=\log_{e^{x}}$$

$$=e^{x}, e^{2\log x}$$ $$-[e^{a+b}=e^{a}\times e^{b}]$$

$$=e^{x}\times e^{\log x^{2}}$$ $$-[e^{\log b}=b^{\log e}]$$

$$=e^{x}\times (x^{2})^{\log e}$$ $$-[\log e=1]$$

$$a=x^{2}e^{x}$$

$$e^{x+2\log x}=x^{2}e^{x}$$

Solve : $$\dfrac{25^{\frac{3}{2}} \times 343^{\frac{3}{5}}}{16^{\frac{5}{4}} \times 8^{\frac{4}{3}} \times 7^{\frac{3}{5}}}$$

1053856_1084841_ans_1eb07ad07a414d6c89195210412a917c.png

$$\left(\dfrac{5}{7}\right)^3\times \left(\dfrac{21}{25}\right)^2$$.

$$=\left(\dfrac{5}{7}\right)^{3}\times \left(\dfrac{21}{25}\right)^{3}$$

$$=\dfrac{5^{3}}{7^{3}}\times \dfrac{7^{3}\times 3^{3}}{5^{6}}\Rightarrow \left(\dfrac{3}{5}\right)^{3}$$

The number of zeroes at the end of the sum $${101^{11}} - 1$$

$$101\times 101=10201$$

$$(101)^{2}=1030301$$

$$(101)^{4}=104060401$$

there is one pattern that in all the powers of $$101$$ last three digits

$$M01$$ where $$M$$ is a non zero digit.

So at the end of $$(101)^{n}-1$$

last three digits are $$M00$$

then there are $$2$$ zeroes at the end.

Express the following in exponential form:
(i) $$6 \times 6 \times 6 \times 6$$ (ii) $$t \times t$$ (iii) $$b \times b \times b \times b$$
(iv) $$5 \times 5 \times 7 \times 7 \times 7$$ (v) $$2 \times 2 \times a \times a$$ (vi) $$a \times a \times a \times c \times c \times c \times c \times d$$

Now,

(i) $$6 \times 6 \times 6 \times 6=6^4$$.

(ii) $$t \times t=t^2$$.

(iii) $$b \times b \times b \times b=b^4$$

(iv) $$5 \times 5 \times 7 \times 7 \times 7=5^2\times7^3$$

(v) $$2 \times 2 \times a \times a=2^2\times a^2$$

(vi) $$a \times a \times a \times c \times c \times c \times c \times d=a^3\times c^4\times d$$

If $$a=2-\sqrt{5}/2+\sqrt{5}$$ and $$b=2+\sqrt{5}/2-\sqrt{5}$$ find $$(a+b)^3$$.

given $$a=2- \dfrac{\sqrt{5}}{2} +\sqrt{5}$$ and

$$ b=2+ \dfrac{\sqrt{5}}{2} -\sqrt{5}$$

so, $$a+b = 2- \dfrac{\sqrt{5}}{2} + \sqrt{5}+2+ \dfrac{\sqrt{5}}{2} -\sqrt{5}$$

$$=4$$

$$\therefore (a+b)^{3}=4^{3}=64$$

Simplify
$${8^{\frac{2}{3}}} - \sqrt 9 \times 10 + {\left( {\frac{1}{{144}}} \right)^{ - \frac{1}{2}}}$$

1315436_1062892_ans_392a3eb906a0417595a8bf83f5cc3553.jpg

Write the base and exponent of the following :
$$ \left( \dfrac {-1}{3} \right)^3 $$

Base = $$ \dfrac {-1}{3}$$
Exponent = $$3$$

Express the following in exponential from: $$ \dfrac{4}{3}\times \dfrac{4}{3}\times \dfrac{4}{3}\times \dfrac{4}{3}\times \dfrac{4}{3}$$

We have $$\dfrac{4}{3}\times \dfrac{4}{3}\times \dfrac{4}{3}\times \dfrac{4}{3}\times \dfrac{4}{3}$$

$$i.e\ \dfrac{4}{3}$$ multiplied $$5$$ times

So,

The power is to be raised to $$5$$

$$\Rightarrow \left(\dfrac{4}{3}\right)^5$$

What we should multiply with $$ \dfrac {\sqrt{x^3} \sqrt[3]{x^5}}{\sqrt[5]{x^3}} . \sqrt[30]{x^{77}}$$ to get $$1$$

$$\dfrac{\sqrt{x^3}.\sqrt[3]{x^{5}}}{\sqrt[5]{x^{3}}}.\sqrt[30]{x^{77}}\times (K)=1$$

we have to find K.

$$\Rightarrow \dfrac{x^{\dfrac{3}{2}}.x^{\dfrac{5}{3}}}{x^{\dfrac{3}{5}}}.x^{\dfrac{77}{30}}.K=1$$

$$\Rightarrow x^{\left[\dfrac{3}{2}+\dfrac{5}{3}+\dfrac{77}{30}-\dfrac{3}{5}\right]}\times K=1$$

$$\Rightarrow x^{\left[\dfrac{45+50+77-18}{30}\right]}\times K=1$$

$$\Rightarrow x^{\left[\dfrac{172-18}{30}\right]}\times K=1$$

$$\Rightarrow x^{\left(\dfrac{154}{30}\right)}\times K=1$$

$$\Rightarrow K=x^{\dfrac{-154}{30}}$$

$$\Rightarrow K=x^{\dfrac{-77}{15}}$$

$$\Rightarrow K=(\sqrt[15]{x^{-77}})$$

Evaluate; $$\dfrac {^{3}\sqrt {-125 \times 343}}{^{3}\sqrt {(-27)}\times (-64)}$$

$$\dfrac { \sqrt [ 3 ]{ -125\times 343 } }{ \sqrt [ 3 ]{ -27}\left( -64 \right) } =\dfrac { 7\times \left( -5 \right) }{ -3\times -64 } =\dfrac { -35 }{ 192 } $$

Simplify and express of the following in exponential form.
$$25^4\div 5^3$$.

$$\begin{matrix} { 25^{ 4 } }\div { 5^{ 3 } } \\ \Rightarrow { \left( { { 5^{ 2 } } } \right) ^{ 4 } }\div { 5^{ 3 } }\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \left[ { \because { a^{ x } }\div { a^{ y } }={ a^{ x-y } } } \right] \\ \Rightarrow { 5^{ 8 } }\div { 5^{ 3 } } \\ \Rightarrow { 5^{ 8-3 } }={ 5^{ 5 } } \\ \end{matrix}$$

Simplify and express the following in the positive exponent form.
$$\left( 5{ \times 25 }^{ n-1 } \right) \div \left( { 5 }^{ n-1 }{ \times 25 }^{ n-1 }\times 25 \right)$$

1136204_1113424_ans_9810a2d849284f3fb7ecb64fc0ad93d0.jpg

Solve for $$x$$:
$$2^{2x+1}+2^9=2^{10}$$.

Now,

$$2^{2x+1}+2^9=2^{10}$$

or, $$2^{2x+1}=2^{10}-2^9$$

or, $$2^{2x+1}=2^9$$

or, $$2x+1=9$$

or, $$2x=8$$

or, $$x=4$$.

Write the base and exponent of the following :
$$ (-15)^4$$

Given number $$(-15)^4$$

Base $$= -15 $$
Exponent $$=4$$

If $$(a^m)^m=a^m$$, then m =

$$(a^m)^m=a^{m^2}$$

and $$a^{m^2}=a^m\Rightarrow m^2=m\Rightarrow m=0,1$$

Find the value of :
$$(3^{0}+4^{0})\times 5^{0}$$

1142077_1141158_ans_5b1ab657a6124f458e0ae137b875553e.jpg

Simplify :
$$128^{\dfrac{-2}{7}}-(625^{-3})^{\dfrac{-1}{4}}+ {14(2401)^{\dfrac{-1}{4}}}$$

$$ 128^{\frac {-2}{7}} - { 625^{-3}} ^{\times{\frac {-1}{4}}} + 14(2401)^\frac{-1}{4}$$

$$\implies {2^7 }^{\times{\frac {-2}{7}}} - { {5^{4\times}}^{-3}} ^{\times{\frac {-1}{4}}} + 14({7^4})^\frac{-1}{4}$$

$$ \implies \dfrac{1}{4} +125+ \dfrac {14}{7}$$

$$\implies \dfrac {509}{4}$$

Express the following numbers in the exponential form:

(i) $$1728$$

(ii) $$\dfrac{1}{512}$$

(iii) $$0.000169$$

(i) $$1728 =12\times 12 \times 12$$

$$ = 12^3$$

(ii) $$\dfrac{1}{512} = \dfrac{1}{2\times 2 \times 2 \times 2 \times 2\times 2\times 2\times 2\times 2}$$

$$ = 2^{-9}$$

(iii) $$0.000169 = 0.013 \times 0.013$$

$$=(0.013)^2$$

Solve the following equation and find the value of $$m$$ in $$3^{m}=\left[\dfrac{1}{9}\right]$$.

$${3}^{m}=\cfrac{1}{9}$$

$${3}^{m}={3}^{-2}$$ ($$\cfrac{1}{9}=\cfrac{1}{{3}^{2}}$$)

$$m=-2$$

Write the following numbers using base $$10$$ and exponents:
(i) $$12345$$
(ii) $$1010.0101$$
(iii) $$0.1020304$$

(i) $$12345_{(10)}$$

$$= 1\times 10^4 + 2\times 10^3 + 3\times 10^2 + 4\times 10^1 + 5\times 10^0$$

$$= 10^4 + 2\times 10^3 + 3\times 10^2 + 4\times 10^1 + 5$$

(ii) $$1010.0101_{(10)} = 1\times 10^3+0\times 10^2+1\times 10^1+0\times 10^0+0\times \dfrac{1}{10}+1\times \dfrac{1}{10^2} + 0 \times \dfrac{1}{10^3} + 1 \times \dfrac{1}{10^4}$$

$$=10^3 + 10^1 + \dfrac{1}{10^2} + \dfrac{1}{10^4}$$

(iii) $$0.102030^4_{(10)} = 1\times \dfrac{1}{10} + 0 \times \dfrac{1}{10^2} + 2 \times \dfrac{1}{10^3} + 0 \times \dfrac{1}{10^4} + 3 \times \dfrac{1}{10^5}+0\times \dfrac{1}{10^6} + 4 \times \dfrac{1}{10^7}$$

$$=\dfrac{1}{10} +2\times \dfrac{1}{10^3} + 3 \times \dfrac{1}{10^5} + 4\times \dfrac{1}{10^7}$$

Value of $$x$$, satisfying $${(\sqrt{3}+1)}^{2x}+{(\sqrt{3}-1)}^{2x}={2}^{3x}$$, is equal to

Given,

$$(\sqrt{3}+1)^{2x}+(\sqrt{3}-1)^{2x}=2^{3x}$$

$$\Rightarrow \left\{(\sqrt{3}+1)^{2}\right\}^{x}+\left\{(\sqrt{3}-1)^{2}\right\}^{x}=2^{3x}$$

$$\Rightarrow (4+2\sqrt{3})^{x}+(4-2\sqrt{3})^{x}=2^{3x}$$

$$\Rightarrow 2^{x}(2+\sqrt{3})^{x}+2^{x}(2-\sqrt{3})^{x}=2^{3x}$$

$$\Rightarrow (2+\sqrt{3})^{x}+(2-\sqrt{3})^{x}=2^{2x}$$

Clearly given equation satisfied only for $$x=1$$

$$\therefore$$ Number of value of $$x$$ is $$1$$

Solve the following equation and find the value of m in $$7^{m}=343$$

$${7}^{m}=343.....(1)$$

Now $$343-7\times 7\times 7={7}^{3}....(2)$$

from (1) and (2)

$$m=3$$

Evaluate $$\left( \frac { a ^ { x } } { a ^ { y } } \right) ^ { z } \times \left( \frac { a ^ { y } } { a ^ { z } } \right) ^ { x }$$

Evaluate

$$(\frac{a^{x}}{a^{y}})\times (\frac{a^{y}}{a^{z}})^{x}$$

$$=(\frac{a^{xz}}{a^{yz}})\times (\frac{a^{yx}}{a^{zx}})$$ $$\because (a^{x})^{z}=a^{xz}$$

$$=\frac{a^{yz}}{a^{yz}}=(\frac{a^{x}}{a^{z}})^{y}$$

1110174_1181411_ans_1fa3c50395f845dca7fc6e9d9d61b885.jpg

Prove $$\left(\dfrac{2^a}{2^b} \right)^{a + b} \times \left(\dfrac{2^b}{2^c} \right)^{b + c} \times \left(\dfrac{2^c}{2^a} \right)^{c + a} = 1$$

$$\Big (\dfrac{2^a}{2^b}\Big )^{a+b}\times \Big (\dfrac{2^b}{2^c}\Big )^{b+c}\times \Big (\dfrac{2^c}{2^a}\Big )^{c+a}=(2^{a-b})^{a+b}+(2^{b-c})^{b+c}+(2^{c-a})^{c+a}$$ (since, $$\dfrac{a^m}{a^n}=a^{m-n}$$)

$$=2^{(a-b)(a+b)}\times 2^{(b-c)(b+c)}\times 2^{(c-a)(c+a)}$$ (since, $$(a^m)n=a^{mn}$$)

$$=2^{(a^2-b^2)}\times 2^{(b^2-c^2)}\times 2^{(c^2-a^2)}$$

$$=2^{a^2-b^2+b^2-c^2+c^2-a^2}$$ (since, $${a^m}\times {a^n}=a^{m+n}$$)

$$=2^0=1$$

Find $${\left( {\dfrac{{16}}{{100}}} \right)^{ - 1/2}}$$

$${\left(\dfrac{16}{100}\right)}^{-\frac{1}{2}}$$

$$={\left(\dfrac{100}{16}\right)}^{\frac{1}{2}}$$

$$={\left({\left(\dfrac{10}{4}\right)}^{2}\right)}^{\frac{1}{2}}$$

$$=\dfrac{10}{4}=\dfrac{5}{2}$$

Express the following in exponential form:
$$b\times b\times b\times b$$

$$\begin{array}{l} b\times b\times b\times b \\ = { b^{ 1+1+1+1 } } \\ = { b^{ 4 } } \end{array}$$

What number should $${(-3)}^{7}$$ be divided by so that the quotient may be equal to $${(-3)}^{4}$$?

Let the number be $$x$$ by which $$(-3)^7$$ is divided

$$\Rightarrow \dfrac{(-3)^7}{x}=(-3)^4$$

$$\Rightarrow \dfrac{(-3)^7}{(-3)^4}=x$$

$$\Rightarrow x=(-3)^{7-4}$$

$$\Rightarrow x=(-3)^{3}=-27$$

Therefore the number is -27

Solve
$$3.2\times { 10 }^{ 6 }\times 4.1\times { 10 }^{ -1 }$$

$$3.2\times 10^6\times 4.1\times 10^{-1}$$

$$\dfrac{32}{10}\times 10^6\times \dfrac{41}{10}\times \dfrac{1}{10}$$

$$32\times 41\times 10^6\times 10^{-3}$$

$$32\times 41\times 10^{6-3}$$

$$1312\times 10^3$$

$$=1312000$$.

Find the value of $$x$$ so that-
$${3}^{2}\times{(-4)}^{2}={(-12)}^{2x}$$

$$3^2\times (-4)^2=(-12)^{2x}$$

$$9\times 16=(-12)^{2x}$$

$$144=(-12)^{2x}$$

As $$12^2=144$$

So $$(-12)^2=144$$

So $$x=1$$.

Simplify:
$${ \left[ { \left( \dfrac { 2 }{ 3 } \right) }^{ 2 } \right] }^{ 3 }\times { \left( \dfrac { 2 }{ 3 } \right) }^{ -4 }\times { 3 }^{ -1 }\times \dfrac { 1 }{ 6 } $$

$$\left[ \left( \dfrac{2}{3}\right)^2\right]^3 \times \left( \dfrac{2}{3}\right)^{-4}\times \left( \dfrac{1}{3}\right)\times \dfrac{1}{6}=\dfrac{2^6\times 2^{-4}\times 1}{3^6\times 36{-4}\times 3\times 2\times 3}$$

$$=\dfrac{2}{3^4}$$

$$=\dfrac{2}{81}$$

Hence, the answer is $$\dfrac{2}{81}.$$

Prove that $$\left( \frac { 1 } { x ^ { a - b } } \right) ^ { \frac { 1 } { a - c } } \left( x ^ { \frac { 1 } { b - c } } \right) ^ { \frac { 1 } { b - a } } \left( x ^ { \frac { 1 } { c - a } } \right) ^ { \frac { 1 } { c - b } } = 1$$

$$\\Let\>LHS=y\\then\>y=(\frac{1}{x^{(a-b)(a-c)}})(\frac{1}{x^{(b-c)(b-a)}})(\frac{1}{x^{(c-a)(c-b)}})\\then\\y^{(a-b)(b-c)(c-a)}=x^{-(b-c)}x^{-(c-a)}x^{-(a-b)}\\=x^{-b+c-c+a-a+b}\\=x^0=1\\\therefore\>y=1=RHS(proved)$$

$${a}^{\cfrac{4}{3}}\div {a}^{-\cfrac{2}{3}}=$$

Given

$$a^{\dfrac{4}{3}}\div a^{-\dfrac{2}{3}}=\dfrac{a^{\dfrac{4}{3}}}{a^{-\dfrac{2}{3}}}$$

$$=a^{\dfrac{4}{3}-\left(-\dfrac{2}{3}\right)}$$

$$=a^{\dfrac{4}{3}+\dfrac{2}{3}}$$

$$=a^{\dfrac{4+2}{3}}$$

$$=a^{\dfrac{6}{3}}$$

$$=a^2$$

If $$\left(x^{n^2}\right)^n=\left(x^{2^n}\right)^2$$ then prove that $$\sqrt[n+1]{n^3}=2$$.

Given,

$$\left(x^{n^2}\right)^n=\left(x^{2^n}\right)^2$$

$$\left(x^{n^2\times n}\right)=\left(x^{2^n\times 2}\right)$$

$$\left(x^{n^3}\right)=\left(x^{2^{n+1}}\right)$$

As the bases are same, equating the powers

$$n^3=2^{n+1}$$

Taking $$(n+1)^{th}$$ root on both sides

$$\sqrt[n+1]{n^3}=2$$

Hence, proved

Find the greatest:
$$2^{300},3^{200}$$.

We have,

$$2^{300}$$

$$=(2^3)^{100}$$

$$=8^{100}$$.

And

$$3^{200}$$

$$=(3^2)^{100}$$

$$=9^{100}$$.

So it is clear that $$3^{200}>2^{300}$$.

$$(9^{\dfrac43}\div 27^{\dfrac23})\times 3^{\dfrac32}$$

$$\left[ { { 9 }^{ \dfrac { 4 }{ 2 } } }\div { 27 }^{ { 2 }_{ 3 } } \right] \times { 3 }^{ \dfrac { 3 }{ 2 } }=\left[ { 3 }^{ { 2\times 4 }_{ 2 } }\div { 3 }^{ 3\times \dfrac { 2 }{ 3 } } \right] \times { \left( \sqrt { 3 } \right) }^{ 2\times \dfrac { 3 }{ 2 } }$$

$$=\left[ { 3 }^{ 4 }\div { 3 }^{ 2 } \right] \times \left( { \sqrt { 3 } }^{ 3 } \right) $$

$$=\left( 81\div 9 \right) \times 3\sqrt { 3 } =9\times 3\sqrt { 3 } $$

$$=27\sqrt { 3 } $$

Solve: $${\left( {81} \right)^{ - 1/4}} \times \sqrt[4]{{81}}$$

$${ (81) }^{ \cfrac { -1 }{ 4 } }\times \sqrt { 81 } \\ ={ (3) }^{ 4\times \cfrac { -1 }{ 4 } }\times 9\\ ={ (3) }^{ -1 }\times 3\\ =\cfrac { 1 }{ 3 } \times 3\\ =1$$

Solve
$$\dfrac { 1.5\times { 10 }^{ 6 } }{ 2.5\times { 10 }^{ -4 } }$$

$$\dfrac{1.5\times 10^6}{2.5\times 10^{-4}}$$

$$\Rightarrow \dfrac{1.5}{2.5}\times 10^{6+4}$$

$$\dfrac{1.5}{2.5}\times 10^{10}$$

$$\dfrac{15}{10}\times \dfrac{10}{25}\times 10^{10}$$

$$\dfrac{3}{5}\times 10^{10}$$

$$=6000000000$$.

Write the following numbers in the expanded exponential forms: 7805192

1518065_1676715_ans_af14237b45a54bc18f33c152f0821dba.jpg

Evaluate :
$$\dfrac{3^{4}\times 12^{3}\times 36}{2^{5}\times 6^{3}}$$

$$\begin{array}{l}\dfrac{{{3^4} \times {{12}^3} \times 36}}{{{2^5} \times {6^3}}} = \dfrac{{{3^4} \times {{\left( {{2^2} \times 3} \right)}^3} \times \left( {{2^2} \times {3^2}} \right)}}{{{2^5} \times {{\left( {2 \times 3} \right)}^3}}}\\ = \dfrac{{{3^4} \times {2^6} \times {3^9} \times {2^2} \times {3^2}}}{{{2^5} \times {2^3} \times {3^3}}}\\ = {3^{4 + 9 - 2 - 3}} \times {2^{6 + 2 - 5 - 3}}\\ = {3^8} \times {2^0}\\ = {3^8}\\ = 6561\end{array}$$

Write the following in the form of $$4 ^ { n } :$$
$$(i) 16$$ $$(ii) 8$$

$$i). 16=4^2$$

$$ii). 8=4^{3/2}$$ on solving $$ \left( 4^3\right)^{1/2}=64^{1/2}=8$$

Hence, solved.

Solve the equation $$9^{x+2}-6\times3^{x+1}+1=0$$

$$9^{x+2}-6\times 3^{x+1}+1=0$$

$$9^2\times 9^x-6\times 3^1\times 3^x+1=0$$

$$81\times (3\times 3)^x-6\times 3\times 3^x+1$$

$$81\times 3^x\times 3^x-18\times 3^x+1=0$$

Put $$3^x=k$$

$$81\times k\times k-18\times k+1=0$$

$$81k^2-18k+1=0$$

$$81k^2-(9\times 9)k+1=0$$

$$81k^2-9k-9k+1=0$$

$$9k(9k-1)-1(9k-1)=0$$

$$(9k-1)(9k-1)=0$$

$$k=1/9$$

$$3^x=1/9=(3^2)^{-1}=3^{-2}$$

$$\therefore x=-2$$.

$$(5^{3}\div 3^{-2})\times 5^{-6}$$

$$(5^3\div 3^{-2})\times 5^{-6}$$

$$=\left(5^3\div \dfrac{1}{3^2}\right)\times \dfrac{1}{5^6}$$

$$=\dfrac{5\times 5\times 5\times 3\times 3}{5\times 5\times 5\times 5\times 5\times 5}$$

$$=\dfrac{9}{125}$$

$$=3^2\times 5^{-3}$$.

1155511_1282193_ans_058f3d836b0542e48a9fc7f2c4e63015.jpg

Simplify and express in exponential form: $$\left[ \left( \dfrac { - 3 } { - 5 } \right) ^ { 4 } \right] ^ { 3 }$$

Let $$a= \left [ \left ( \dfrac{-3}{-5} \right )^{4} \right ]^{3}$$

$$ = \left [ \left ( \dfrac{3}{5} \right )^{4} \right ]^{3}$$

$$a = \left ( \dfrac{3}{5} \right )^{12}$$

$$ \left [ \left ( \dfrac{-3}{-5} \right )^{4} \right ]^{3}= \left ( \dfrac{3}{5} \right )^{12}$$

Find the approximant value of $$(36)^{\dfrac{1}{6}}$$.

Given $$(36)^{\frac{1}{6}}=[(36)^{\frac{1}{2}}]^{\frac{1}{3}}=[6]^{\frac{1}{3}}$$

Let $$f(x)=(x)^{\frac{1}{3}}$$

and $$f(x-\Delta x)=(8-2)^{\frac{1}{3}}$$

where x=8 & $$\Delta x=2$$

$$y=f(x)=(x)^{\frac{1}{3}}$$

on differentiating $$\frac{d}{dx}=\frac{1}{3x^{\frac{2}{3}}}$$

$$dy=\frac{1}{3x^{\frac{2}{3}}}dx$$

$$\Delta y=\frac{1}{3}x^{\frac{-2}{3}}\Delta x=\frac{1}{3}(8)^{\frac{-2}{3}}\times 2=\frac{2}{12}=\frac{1}{6}$$

now $$(6)^{\frac{1}{3}}=y-\Delta y=2-\frac{1}{6}$$

$$(6)^{\frac{1}{3}}=\frac{11}{6}= 1.833$$

$$\therefore $$ appropriate value of $$(36)^{\frac{1}{6}}=1.833$$

1206611_1366058_ans_e4c58669f1ea45be83c60f1baaced884.JPG

Simplify:
$$\left(\dfrac{625}{256}\right)^{-\dfrac{3}{4}}$$.

Now,

Let $$a=\left(\dfrac{625}{256}\right)^{-\dfrac{3}{4}}$$

$$=\left(\dfrac{5^4}{4^4}\right)^{-\dfrac{3}{4}}$$

$$=\left(\dfrac{5}{4}\right)^{-3}$$

$$=\left(\dfrac{4}{5}\right)^{3}$$

$$a=\dfrac{64}{125}$$.

$$\therefore \left(\dfrac{625}{256}\right)^{-\dfrac{3}{4}}=\dfrac{64}{125}$$

If $${5}^{a}={25}^{5}$$ then $$a$$ is equal to

Given : $${5}^{a}={25}^{5}$$

$$\Rightarrow {5}^{a}={\left({5}^{2}\right)}^{5}$$

$$\Rightarrow {5}^{a}={5}^{10}$$

Equating the powers with the same base, we get

$$\therefore \,a=10$$

Solve:$${5}^{3x+1}={25}^{x+2}$$

Given : $${5}^{3x+1}={25}^{x+2}$$

$$\Rightarrow {5}^{3x+1}={\left({5}^{2}\right)}^{x+2}$$

$$\Rightarrow {5}^{3x+1}={5}^{2x+4}$$

Equating the powers with the same base, we get

$$\Rightarrow \,3x+1=2x+4$$

$$\Rightarrow 3x-2x=4-1=3$$

$$\therefore x=3$$

The population of India is $$125,00000000$$. Write in exponential form.

$$125,00000000=125\times 100000000$$

$$=125\times {10}^{8}$$

$$=1.25\times 100\times {10}^{8}$$

$$=1.25\times {10}^{2+8}$$

$$=1.25\times {10}^{10}$$

If $${\left( {2.3} \right)^x} = {\left( {0.23} \right)^y} = 1000$$ then find the value of $$\frac{1}{x} - \frac{1}{y}.$$

$$(2.3)^{x}=(0.23)^{y}= 1000$$

$$log_{10}(2.5)^{x}=log_{10}1000$$

$$\Rightarrow x-log_{10}2.3 =3$$

$$x=\frac{3}{0.361}= 8.293$$

$$log_{10}(0.23)^{y}=log_{10}1000$$

$$y(log_{10}0.23)=3$$

$$y\times (-0.6382)=3\Rightarrow y=-4.7$$

$$\frac{1}{x}-\frac{1}{y}=\frac{1}{8.293}-\frac{1}{-4.7}=\frac{1}{8.293}+\frac{1}{4.7}$$

$$= 0.333 \approx \frac{1}{3}$$

1213374_1305986_ans_f210696908fe4372be883586b3c6775e.JPG

Solve:$${2}^{{x}^{2}}:{2}^{2x}=8:1$$

$${2}^{{x}^{2}}:{2}^{2x}=8:1$$

$$\dfrac{{2}^{{x}^{2}}}{{2}^{2x}}=\dfrac{8}{1}$$

We know that, $$\dfrac{{a}^{m}}{{a}^{n}}={a}^{m-n}$$

$$\Rightarrow {2}^{{x}^{2}-2x}={2}^{3}$$

Since bases are same we can equate the powers.

$$\Rightarrow {x}^{2}-2x=3$$

$$\Rightarrow {x}^{2}-2x-3=0$$

$$\Rightarrow {x}^{2}-3x+x-3=0$$

$$\Rightarrow x\left(x-3\right)+\left(x-3\right)=0$$

$$\Rightarrow \left(x-3\right)\left(x+1\right)=0$$

$$\Rightarrow x=3,\,-1$$

Using laws of exponents, simplify and write the answer in exponential form: $${ \left( { 3 }^{ 4 } \right) }^{ 3 }$$

Given $${\left({3}^{4}\right)}^{3}$$

using $${\left({a}^{m}\right)}^{n}={a}^{mn}$$

$${\left({3}^{4}\right)}^{3}$$$$={3}^{12}$$

$${ e }^{ \left( 1+{ sin }^{ 2 }x+{ sin }^{ 4 }x+....\infty \right) log2 }=16$$ then

We have,

$$ {{e}^{\left( 1+{{\sin }^{2}}x+{{\sin }^{4}}x+......\infty \right)\log 2}}=16 $$

$$ \Rightarrow \left( 1+{{\sin }^{2}}x+{{\sin }^{4}}x+.....\infty \right)\log 2=\log 16 $$

Now,

$$\left( 1+{{\sin }^{2}}x+{{\sin }^{4}}x+.....\infty \right)$$ series is G.P.

So, First term

$$ a=1 $$

$$ r\left( \text{Common}\,\text{ratio} \right)=\dfrac{{{\sin }^{2}}x}{1} $$

$$ r={{\sin }^{2}}x $$

The sum of this series is

$$ {{S}_{\infty }}=\dfrac{a}{1-r} $$

$$ =\dfrac{1}{1-{{\sin }^{2}}x} $$

$$ =\dfrac{1}{{{\cos }^{2}}x} $$

$$ ={{\sec }^{2}}x $$

So,

$$ {{\sec }^{2}}x\log 2=\log 16 $$

$$ \Rightarrow {{\sec }^{2}}x\log 2=\log {{2}^{4}} $$

$$ \Rightarrow {{\sec }^{2}}x\log 2=4\log 2 $$

Now comparing and we get,

$$ {{\sec }^{2}}x=4 $$

$$ {{\sec }^{2}}x={{2}^{2}} $$

$$ \sec x=2 $$

$$ \operatorname{secx}=sec\dfrac{\pi }{6} $$

$$ x=\dfrac{\pi }{6} $$

Hence, this is the answer.

Simplify: $$\dfrac{15^{3}\times 9^{3}\times 16}{3^{4}\times 5^{2}\times 2^{3}}$$

$$ \frac{15^{3}\times 9^{3}\times 16}{3^{4}\times 5^{2}\times 2^{3}}$$

$$ \Rightarrow \frac{(3\times 5)^{3}\times (3^{2})^{3}\times 2^{4}}{3^{4}\times 5^{2}\times 2^{3}}$$

$$ \Rightarrow \frac{3^{3}\times 5^{3}\times 3^{6}\times 2^{2}}{3^{4}\times 5^{2}\times 2^{3}}$$

$$ \Rightarrow 3^{3+6-4}\times 5^{3-2}\times 2^{4-3}$$

$$ \Rightarrow 3^{5}\times 5^{1}\times 2^{1}$$

$$\Rightarrow 243\times 5\times 2$$

$$\Rightarrow 2430$$

1215209_1354286_ans_c243a9033b4646f89c0e8e4fb4ce2ca0.jpg

Which is greatest $${2}^{12}$$ or $${3}^{8}$$

We have the inequality,$${a}^{m}>{b}^{n}$$ if $$a>b,\,\,m<n$$

We have $$3>2,\,\,8<12$$

Hence $${3}^{8}>{2}^{12}$$

$$\therefore\,\,{3}^{8}$$ is the greatest.

Find the value of $$x$$ if $${0.6}^{x}{\left(\dfrac{25}{9}\right)}^{{x}^{2}-12}={\left(\dfrac{27}{125}\right)}^{3}$$

$$\Rightarrow {\left(\dfrac{6}{10}\right)}^{x}{\left(\dfrac{25}{9}\right)}^{{x}^{2}-12}={\left(\dfrac{27}{125}\right)}^{3}$$

$$\Rightarrow {\left(\dfrac{3}{5}\right)}^{x}{\left(\dfrac{{5}^{2}}{{3}^{2}}\right)}^{{x}^{2}-12}={\left(\dfrac{{3}^{3}}{{5}^{3}}\right)}^{3}$$

$$\Rightarrow {\left(\dfrac{3}{5}\right)}^{x}{\left(\dfrac{5}{3}\right)}^{2{x}^{2}-24}={\left(\dfrac{3}{5}\right)}^{9}$$

$$\Rightarrow\dfrac{{3}^{x}}{{5}^{x}}\times\dfrac{{5}^{2{x}^{2}-24}}{{3}^{2{x}^{2}-24}}=\dfrac{{3}^{9}}{{5}^{9}}$$

$$\Rightarrow \dfrac{{3}^{x-2{x}^{2}+24}}{{5}^{x-2{x}^{2}+24}}=\dfrac{{3}^{9}}{{5}^{9}}$$

Equating the powers with the same base, we get

$${3}^{x-2{x}^{2}+24}={3}^{9}$$ and $${5}^{x-2{x}^{2}+24}={5}^{9}$$

$$\Rightarrow x-2{x}^{2}+24=9$$ and $$x-2{x}^{2}+24=9$$

$$\Rightarrow -2{x}^{2}+x+24-9=0$$ and $$-2{x}^{2}+x+24-9=0$$

$$\Rightarrow -2{x}^{2}+x+15=0$$ and $$-2{x}^{2}+x+15=0$$

$$\Rightarrow 2{x}^{2}-x-15=0$$

$$\Rightarrow 2{x}^{2}-6x+5x-15=0$$

$$\Rightarrow 2x\left(x-3\right)+5\left(x-3\right)=0$$

$$\Rightarrow \left(x-3\right)\left(2x+5\right)=0$$

$$\Rightarrow x=3,\,\dfrac{-5}{2}$$

Find the value of $$x$$
$${ \left( \dfrac { 5 }{ 3 } \right) }^{ -4 }\times { \left( \dfrac { 5 }{ 3 } \right) }^{ -5 }={ \left( \dfrac { 5 }{ 3 } \right) }^{ 3x }$$

$${\left(\dfrac{5}{3}\right)}^{-4}\times{\left(\dfrac{5}{3}\right)}^{-5}={\left(\dfrac{5}{3}\right)}^{3x}$$

$$\Rightarrow {\left(\dfrac{5}{3}\right)}^{-4-5}={\left(\dfrac{5}{3}\right)}^{-4}$$ using $${a}^{m}\times {a}^{n}={a}^{m+n}$$

Since bases are same, we can equate the powers

$$\Rightarrow -3x=-9$$

$$\Rightarrow x=\dfrac{-9}{-3}=3$$

$$\therefore x=3$$

Find the unit's place in the expansion $${2}^{2007}$$

The unit's place digit of $${2}^{2007}$$

$$\Rightarrow2^1=2$$; $$2^2=4$$ ; $$2^3=8$$ ; $$2^4=16$$

And thus the cycle of the unit's place is repeated after every $$4^{th}$$ power of $$2$$

$$=$$The unit's place digit of $${2}^{4\left(501\right)+3}$$

$$=$$The unit's place digit of $${2}^{3}$$

$$=8$$

If $${3}^{x+y}=81$$ and $${81}^{x-y}=3$$, then find the values of $$x$$ and $$y$$

$${3}^{x+y}=81$$ and $${81}^{x-y}=3$$

$$\Rightarrow \,{3}^{x+y}={3}^{4}$$ and $${3}^{4x-4y}={3}^{1}$$

Equating the terms withthe same bases,

$$x+y=4$$ ......$$(1)$$

$$4x-4y=1$$ ......$$(2)$$

$$(2)+4\times(1)$$ we get

$$\Rightarrow 4x-4y+4x+4y=4-4$$

$$\Rightarrow 8x=0$$

$$\therefore x=0$$

Put $$x=0$$ in $$(1)$$ we get

$$x+y=4$$

$$\Rightarrow y=4$$

$$\therefore \,x=0,\,y=4$$

Find the unit's place in the expansion $${7}^{131}$$

The unit's place digit of $${7}^{131}$$

$$\Rightarrow7^1=7$$; $$7^2=49$$ ; $$7^3=343$$ ; $$7^4=2401$$

And thus the cycle of the unit's place is repeated after every $$4^{th}$$ power of $$7$$

$$\therefore$$ The unit's place digit of $${7}^{4\left(32\right)+3}$$

$$=$$The unit's place digit of $${7}^{3}$$

$$=3$$

Using laws of exponents, simplify and write the answer in exponential form: $$\dfrac{{\left({5}^{2}\right)}^{3}}{{5}^{3}}$$

$$\dfrac{{\left({5}^{2}\right)}^{3}}{{5}^{3}}$$

Let $$a=\dfrac{{\left({5}^{2}\right)}^{3}}{{5}^{3}}$$

using $${\left({a}^{m}\right)}^{n}={a}^{mn}$$

$$a=\dfrac{{5}^{6}}{{5}^{3}}$$

using $$\dfrac{{a}^{m}}{{a}^{n}}={a}^{m-n}$$

$$a={5}^{6-3}$$

$$a={5}^{3}=125$$

Find the unit's place in the expansion $${3}^{2006}$$

The unit's place digit of $${3}^{2006}$$

$$\Rightarrow3^1=3$$; $$3^2=9$$ ; $$3^3=27$$ ; $$3^4=81$$

And thus the cycle of the unit's place is repeated after every $$4^{th}$$ power of $$3$$

$$=$$The unit's place digit of $${3}^{4\left(501\right)+2}$$

$$=$$The unit's place digit of $${3}^{2}$$

$$=9$$

Solve :
$$[{(2^{-1})^{-1}}^{-1}]^{-1}$$

$$[{(2^{-1})^{-1}}^{-1}]^{-1}$$

$$={(2^{-1})^{-1}}^{-1} $$

$$=(2^{-1})^{-1}$$

$$=2^{1}=2$$

$$9x+5={ e }^{ 10b }$$
$$9x+5=2.688\times { 10 }^{ 43 }$$

2048920_1398190_ans_5fd11a5b9b9b4d38b6c2f92e016cbd44.jpg

Find the value of $$n$$, where $$n$$ is an integer and $$2^{n-5}\times 6^{2n-4}=\dfrac{1}{12^{4}\times 2}$$

$$2^{n-5}\times 6^{2n-4}=(2\times 6)^{-4}\times 2^{-1}=2^{-5}\times 6^{-4}$$

$$\Rightarrow n-5=-5\Rightarrow n=0$$.

1214810_1396418_ans_77df5c049f78489d98dd72e7f29849e9.jpg

Evaluate:
$$\dfrac {3\times 27^{n+1}+9\times 3^{n-1}}{8\times 3^{3n}-5\times 27^{n}}$$

$$\dfrac {3\times 27^{n+1}+9\times 3^{n-1}}{8\times 3^{3n}-5\times 27^{n}}=\dfrac{3\times 27^{n}\times 27+9\times 3^{n-1}}{8\times 3^{3 n}-5\times 3^{3 n}}=\dfrac{3^{3 n+4}+3^{n+1} }{3^{3 n+1}}=3^3+3^{-2 n}=27+\dfrac{1}{9^n}$$

Using laws of exponents, simplify and write the answer in exponential form: $$\dfrac{{8}^{t}}{{8}^{2}}$$

Given $$\dfrac{{8}^{t}}{{8}^{2}}$$

Let $$a=\dfrac{{8}^{t}}{{8}^{2}}$$

using $$\dfrac{{a}^{m}}{{a}^{n}}={a}^{m-n}$$

$$={8}^{t-2}$$

$$={\left({2}^{3}\right)}^{t-2}$$

using $${\left({a}^{m}\right)}{n}={a}^{mn}$$

$$a={2}^{3t-6}$$

$$\dfrac{{8}^{t}}{{8}^{2}}={2}^{3t-6}$$

If $$a=3,\,b=7,$$ then find the value of $${a}^{b}-{b}^{a}$$

Given that, $$a=3,\,b=7,$$

To find : $${a}^{b}-{b}^{a}$$

$${a}^{b}-{b}^{a}={3}^{7}-{7}^{3}$$ (where $$a=3,\,b=7$$)

$$=3\times 3\times 3-7\times 7\times 7$$

$$=9\times 3-49\times 7$$

$$=27-343=-316$$

$$\therefore {a}^{b}-{b}^{a}=-316$$

Find the value of $$m-n$$ such that $$a^m=a^n$$.

Given,

$$a^m=a^n$$

$$\dfrac{a^m}{a^n}=1$$

We know that, $$\dfrac{{a}^{m}}{{a}^{n}}={a}^{m-n}$$

$$a^{m-n}=1$$

$$a^{m-n}=a^0$$

As the bases are same, equating the powers

$$m-n=0$$.

Evaluate $$\sqrt [ 4 ]{ \cfrac { 256 }{ 625 } } -\sqrt { \cfrac { 9 }{ 25 } } $$

$$\sqrt[4]{\dfrac{256}{625}}-\sqrt{\dfrac{9}{25}}\\\sqrt [4]{\dfrac{4^4}{5^4}}-\sqrt{\dfrac{3^2}{5^2}}\\\dfrac 45-\dfrac 35=\dfrac 15$$

Change $$8.3705\times 10^{6}$$ in usual form.

The usual form of the number $$8.3705\times 10^{6}$$ is $$\dfrac{83705}{10000}\times 10^6=8370500$$.

Find the value of $$n$$ :
$$\left(\dfrac{3}{2}\right)^{6}\times\left(\dfrac{3}{2}\right)^{2n+1}\times \left(\dfrac{3}{2}\right)^{-3}=1$$

Now,

$$\left(\dfrac{3}{2}\right)^{6}\times\left(\dfrac{3}{2}\right)^{2n+1}\times \left(\dfrac{3}{2}\right)^{-3}=1$$

or, $$\left(\dfrac{3}{2}\right)^{2n+1+6-3}=\left(\dfrac{3}{2}\right)^0$$

or, $$2n+4=0$$

or, $$n=-2$$.

$$\dfrac { (2{ p }^{ 2 }{ q }^{ 9 })^{ 2 }(4pq)^{ 3 } }{ (4{ p }^{ 6 }{ q }^{ 10 })^{ 2 } } $$

$$\dfrac{{\left(2{p}^{2}{q}^{9}\right)}^{2}{\left(4pq\right)}^{3}}{{\left(4{p}^{6}{q}^{10}\right)}^{2}}$$

$$=\dfrac{{2}^{2}\times{p}^{4}\times{q}^{18}\times {\left({2}^{2}\right)}^{2}\times{p}^{3}\times{q}^{3}}{{\left({2}^{2}\right)}^{2}\times{p}^{12}\times {q}^{20}}$$

$$=\dfrac{{2}^{2}\times{p}^{4}\times{q}^{18}\times {2}^{4}\times{p}^{3}\times{q}^{3}}{{2}^{4}\times{p}^{12}\times {q}^{20}}$$

$$={2}^{2+4-4}\times{p}^{4+3-12}\times{q}^{18+3-20}$$

$$={2}^{2}\times{p}^{-5}\times{q}^{1}$$

$$=\dfrac{4q}{{p}^{5}}$$

Express $$512$$ in exponential form

We can express $$512$$ as

$$512=2\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times 2$$

$$512={2}^{9}$$

Express in exponential form:
$$\sqrt [ 3 ]{ { xy }^{ 2 } } \div { x }^{ 2 }y\\ $$

$$={\left(x{y}^{2}\right)}^{\frac{1}{3}}\div{x}^{2}y$$

$$=\dfrac{{x}^{\frac{1}{3}}{y}^{\frac{2}{3}}}{{x}^{2}y}$$

$$={x}^{\frac{1}{3}-2}{y}^{\frac{2}{3}-1}$$

$$={x}^{\frac{1-6}{3}}{y}^{\frac{2-3}{3}}$$

$$={x}^{\frac{-5}{3}}{y}^{\frac{-1}{3}}$$

Find the values:
$$2^{3+\log_{2}3}$$

$$2^{3+\log_2 3}=2^3\times 2^{\log_2 3}=8\times 3^{\log _2 2}=8\times 3=24$$

$${\left( {{{81} \over {16}}} \right)^{{{ - 3} \over 4}}} \times {\left( {{{25} \over 9}} \right)^{{{ - 3} \over 2}}}$$

1305781_1418728_ans_de65da5c551e464eb21b4398170aa2b1.jpeg

Express the following numbers in standard from:
$$3759\times 10^{4}$$

$$3759\times 10^{4}$$ = $$3.759 × 1000 × 10^4 $$ = $$3.759 × 10^7$$

Simplify: $$ (81 / 16)^{-3 / 4} \times\left[(25 / 9)^{-3 / 2} \div(5 / 2)^{-3}\right] $$

$$(81/16)^{-3/4}\times [(25/9)^{-3/2}\div (5/2)^{-3}]=\bigg(\dfrac{3^4}{2^4}\bigg)^{-3/4}\times \bigg[\bigg(\dfrac{5^2}{3^2}\bigg)^{-3/2}\div \bigg(\dfrac{5}{2}\bigg)^{-3}\bigg]=\bigg(\dfrac{3}{2}\bigg)^{-3}\times \bigg[\bigg(\dfrac{5}{3}\bigg)^{-3}\div \bigg(\dfrac{5}{2}\bigg)^{-3}\bigg]$$

$$=\bigg(\dfrac{2}{3}\bigg)^3\times \bigg[\bigg(\dfrac{3}{5}\bigg)^3\div \bigg(\dfrac{2}{5}\bigg)^3\bigg]=\bigg(\dfrac{2^3}{3^3}\bigg)\times \bigg(\dfrac{3^3}{5^3}\bigg)\times \bigg(\dfrac{5^3}{2^3}\bigg)=1$$

Solve : $${ 3 }^{ 5}\times { 3 }^{ -6 }$$

$${3}^{5}\times{3}^{-6}$$

$$={3}^{5-6}$$ using $${a}^{m}\times {a}^{n}={a}^{m+n}$$

$$={3}^{-1}$$

$$=\dfrac{1}{3}$$ using $${a}^{-m}=\dfrac{1}{{a}^{m}}$$

Simplify $$\sqrt [4]{81}-8\sqrt [3]{216}+15\sqrt [3]{8}+\sqrt {225}$$

$$\sqrt [4]{81}-8\sqrt [3]{216}+15\sqrt [3]{8}+\sqrt {225}=\sqrt[4]{3^4}-8\sqrt[3]{6^3}+15\sqrt[3]{2^3}+\sqrt{15^2}=3-8\times 6+15\times 2+15=3-48+30+15=0$$

Solve for $$x$$.
$$5^{x+1}$$ + $$5^{1-x}$$ = 26

$$\textbf{Hint: Assume}$$ $$\boldsymbol{{5^x} = y}$$ $$\textbf{and solve}$$

$$\textbf{Solve the quadratic in variable}$$ $$\boldsymbol{y}$$

Given, $${5^{x + 1}} + {5^{1 - x}} = 26$$

Let $${5^x} = y$$

$$ \Rightarrow 5y + \frac{5}{y} = 26$$

$$ \Rightarrow 5{y^2} + 5 = 26y$$

$$ \Rightarrow 5{y^2} - 26y + 5 = 0$$

$$ \Rightarrow 5{y^2} - 25y - y + 5 = 0$$ [Split the middle term for factorisation]

$$ \Rightarrow 5y\left( {y - 5} \right) - \left( {y - 5} \right) = 0$$

$$ \Rightarrow y = \frac{1}{5},5$$

$$ \Rightarrow x = - 1,1$$

$$\textbf{Hence, the value of}$$ $$\boldsymbol{x}$$ $$\textbf{is -1 and 1.}$$

Solve : $$\dfrac { { 3 }^{ -5 }\times{ 10 }^{ -5 }\times {125} }{ { 5 }^{ -7 }\times { 6 }^{ -5 } } $$

$$\dfrac { { 3 }^{ -5 }\times{ 10 }^{ -5 }\times {125} }{ { 5 }^{ -7 }\times { 6 }^{ -5 } } $$

$$=\dfrac{{3}^{-5}\times{\left(2\times 5\right)}^{-5}\times{5}^{3}}{{5}^{-7}\times{\left(2\times 3\right)}^{-5}}$$

$$=\dfrac{{3}^{-5}\times{2}^{-5}\times{5}^{-5}\times{5}^{3}}{{5}^{-7}\times{2}^{-5}\times{3}^{-5}}$$

$$={3}^{-5+5}\times{2}^{-5+5}\times{5}^{-5+3+7}$$

$$={3}^{0}\times{2}^{0}\times{5}^{5}$$

$$={5}^{5}=3125$$

Prove that : $$\frac{2^{30}+2^{29}+2^{28}}{2^{31}+2^{30}-2^{29}}=\frac{7}{10}$$

$${\textbf{Hint: Use the formula}} $$ $$\mathbf{\dfrac{{{a^m}}}{{{a^n}}} = {a^{m - n}}}$$

$$\textbf{Step - 1: Take common the least power of 2 in both the numerator and the denominator of L.H.S.}$$

$$\text{L.H.S.}$$

$$= \dfrac{{{2^{30}} + {2^{29}} + {2^{28}}}}{{{2^{31}} + {2^{30}} - {2^{29}}}} $$

$$=\dfrac{{{2^{28}}({2^2} + 2 + 1)}}{{{2^{29}}({2^2} + 2 - 1)}}$$

$$\textbf{Step - 2: Use Laws of Exponents.}$$

$$\dfrac{{{2^{28}}({2^2} + 2 + 1)}}{{{2^{29}}({2^2} + 2 - 1)}} = \dfrac{{{2^{28}}(4 + 2 + 1)}}{{{2^{29}}(4 + 2 - 1)}} $$

$$ = \dfrac{{{2^{28}}(7)}}{{{2^{29}}(5)}} $$

$$ = \dfrac{7}{{{2^{29 - 28}}(5)}} $$ $$\mathbf{[\because \dfrac{{{a^m}}}{{{a^n}}}}$$ $$\mathbf{= {a^{m - n}}]} $$

$$= \dfrac{7}{{2\times5}} $$

$$ = \dfrac{7}{{10}} $$

$$\text{= R.H.S.}$$

$$\textbf{Hence Proved.}$$

Simplify $$\sqrt [ 5 ]{ 243{ a }^{ 10 }{ b }^{ 5 }{ c }^{ 10 } } $$

1311614_1438871_ans_930c0149c3274153b542b2e5e2acf3b9.jpeg

Express in exponential form: $$\dfrac { 81 }{ 625 } $$

Given

$$\dfrac{81}{625}$$

$$=\dfrac{9^{2}}{25^{2}}$$

$$=\dfrac{{(3^{2})^2}}{(5^{2})^{2}}$$

$$=\dfrac{3^{4}}{5^{4}}$$

$$={\left(\dfrac{3}{5}\right)}^4$$

Evaluate : $$\left (\dfrac{-4}{5}\right)^{-10} \times \left (\dfrac{-4}{5}\right)^{15} \div \left (\dfrac{-4}{5}\right)^{8}$$

$$ (\frac{-4}{5})^{-10} \times (\frac{-4}{5})^{15} \div (\frac{-4}{5})^{8}$$

$$ = (\frac{-4}{5})^{-10+15} \div (\frac{-4}{5})^{8}$$

$$ = (\frac{-4}{5})^{5} \div (\frac{-4}{5})^{8}$$

$$ = ( \frac{-4}{5})^{5-8}$$

$$ = ( \frac{-4}{5})^{-3}$$

$$ (-4)^{-3} \times \frac{1}{(5)^{3}}$$

$$ \frac{1}{(-4)^{3}} \times (5)^{3}$$

$$ = \frac{125}{64}$$

1227053_1503818_ans_176f13884a914adea954819689510d63.jpg

Evaluate using law of exponents: $$25^{4}\div 5^{3}$$

As we know that

$$(a^m)^n=a^{m\times n},\dfrac{a^m}{a^n}=a^{m-n}$$

$$25^4\div 5^3=\dfrac{25^{4}}{5^3}=\dfrac{(5^2)^4}{5^3}=\dfrac{5^{2\times 4}}{5^3}=\dfrac{5^8}{5^3}=5^{8-3}=5^5=3125$$

By what number should $${ 3 }^{ -4 }$$ be multiplied so that the products is $$729$$

Let the number be $$a$$

$$3^{-4}\times a=729$$

$$3^{-4}\times a=(27)^{2}$$

$$3^{-4}\times a=3^6$$

$$a=\dfrac{3^6}{3^{-4}}$$

$$a=3^{10}$$

The numbers is $$3^{10} = 59049$$

Given $$ 4725 = 3^{a}5^{b}7^{c}, $$ find the value of $$ 2^{a}3^{b}7^{c} $$

Given,

$$4725$$

$$=3\times 3\times 3\times 5\times 5\times 7$$

$$=3^3\times 5^2\times 7$$

$$\therefore 4725=3^3\times 5^2\times 7$$

Given, $$4725=3^a\times 5^b\times 7^c$$

comparing both, we get,

$$a=3,b=2,c=1$$

Given,

$$2^{a}3^b7^c$$

$$=2^{3}3^27^1$$

$$=8\times9\times7$$

$$=504$$

If $$ 5^{3x} = 125$$ and $$10^{y} = 0.001$$ then find x + y.

Given,

$$5^{3x}=125$$

$$5^3=5^{3x}=125$$

By comparing powers

$$\Rightarrow 3=3x$$

$$\therefore x=1$$

Now $$10^y=0.001$$

$$10^{-3}=10^y=0.001$$

By comparing powers

$$\therefore y=-3$$

$$\therefore x+y=1-3=-2$$

Express each of the following as a product of prime factors only in exponential form:
$$768$$

The given number is $$7688$$.

The number can be represented as a product of its prime factors as:

$$768=2\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times 3$$

We can add the powers of the same factor to represent the product in exponential form.

$$\therefore \ 768={2}^{8}\times 3$$

Prove that :
$$ \left ( \dfrac{x^{a}}{x^{b}} \right )^{a^{2}+ab+b^{2}}\times \left ( \dfrac{x^{b}}{x^{c}} \right )^{b^{2}+bc+c^{2}}\times \left ( \dfrac{x^{c}}{x^{a}} \right )^{c^{2}+ca+a^{2}} = 1 $$

Given,

$$\left (\dfrac{x^a}{x^b} \right )^{a^2+ab+b^2}\times \left (\dfrac{x^b}{x^c} \right )^{b^2+bc+c^2}\times \left (\dfrac{x^c}{x^a} \right )^{c^2+ca+a^2}$$

$$=\left (x^{a-b} \right )^{a^2+ab+b^2}\times \left ( x^{b-c} \right )^{b^2+bc+c^2}\times \left ( x^{c-a} \right )^{c^2+ca+a^2}$$

$$=x^{a^3+a^2b+ab^2-a^2b-ab^2-b^3}\times x^{b^3+b^2c+bc^2-cb^2-bc^2-c^3}\times x^{c^3+c^2a+ca^2-c^2a-ca^2-a^3}$$

$$=x^{a^3-b^3}\times x^{b^3-c^3}\times x^{c^3-a^3}$$

$$=x^{a^3-b^3+b^3-c^3+c^3-a^3}$$

$$=x^0$$

$$=1$$ $$[hence \, proved]$$

Express the following numbers in standard from:
$$0.00072984$$

2039761_1671226_ans_5e337806ecaa443c94e4ffe48004a2ee.jpg

Write the given expression in the product form.
$$9xy^2z^2$$

We know that,

$$b^{n}$$ = $$b\times b\times b\times\dots\times b$$ upto $$n$$ terms.

So, given expression can be written as,

$$9xy^{2}z^{2} = 9 \times x\times y\times y \times z\times z $$

$$3.25\times 10^{2}$$ in the usual form is $$325$$

Enter 1 if it is True or 0 if it is False

$$3.25\times 10^{2}$$ = $$3.25 × 100 = 325 $$

$$3\times 10^{8}$$ in the usual form is $$300000000$$
Enter 1 if it is True or 0 if it is False.

$$3\times 10^{8}$$ = $$ 3 × 100000000= 300000000$$

Write the given expression in the product form.
$$6x^7y$$.

We know that,

$$b^{3}$$ = $$b\times b\times b$$.

So,

$$6x^{7}y = 6\times x\times x\times x\times x\times x \times x\times x\times y$$.

Write the following numbers in the usual form:
$$5.8\times 10^2$$

$$5.8 \times {10}^2 = 5.8 \times 100 $$

$$= 580$$

Write the following numbers in the usual form:
$$3.61492\times 10^6$$

1520706_1671241_ans_d0ae9a7c1ab84136b14bf7499dadf5ae.jpg

Write the given product in exponential form.
$$5\times a\times a\times a \times b\times b\times c\times c\times c$$.

We know that if a number say $$b$$ is multiplied two times, that is, $$b\times b$$ can be written as $$b^2$$.

Similarly,

$$5\times a\times a\times a = 5^{1} \times a^{3}$$.

Thus,

$$5\times a\times a\times a\times b\times b\times c\times c \times c =$$ $$ 5^1\times a^ 3 \times b^2 \times c ^ 3 $$.

$$=5a^{3}b^{2}c^{3}$$

Write the given expression in the product form.
$$7a^3b^4$$.

We know that if a number say $$b$$ is multiplied three times.

Hence, $$b\times b\times b$$ can be written as $$b^3$$.

$$b^3$$ = $$b\times b\times b$$

So,

$$ a^{3} = a \times a \times a$$

$$ b^{4} = b \times b \times b \times b $$

Thus,

$$7a^{3}b^{4} = 7 \times a \times a\times a \times b\times b\times b\times b$$.

Write the following numbers in the usual form:
$$1.0001\times 10^9$$

1520639_1671238_ans_0bc900910c644c70b6c890d9b793e42c.jpg

Express each of the following in exponential from:$$ (-2)\times (-2)\times(-2)\times (-2) \times a \times a \times a $$

1515099_1676090_ans_c564fcd36cc84cc0a76aab25ad629b03.jpg

Express the following in exponential form: $$ \dfrac{-5}{7}\times \dfrac{-5}{7}\times \dfrac{-5}{7}\times \dfrac{-5}{7}$$

We have $$\dfrac{-5}{7}\times \dfrac{-5}{7}\times \dfrac{-5}{7}\times \dfrac{-5}{7}$$

$$i.e\ \dfrac{-5}{7}$$ multiplied $$4$$ times

So,

The power is to be raised to $$4$$

$$\Rightarrow \left(\dfrac{-5}{7}\right)^4$$

$$\Rightarrow \left(\dfrac{-1\times5}{7}\right)^4$$

$$\Rightarrow (-1)^4\left(\dfrac{5}{7}\right)^4$$

$$\Rightarrow \left(\dfrac{5}{7}\right)^4$$

Express each of the following in exponential from: $$ \left ( \dfrac{-2}{3} \right )\times \left ( \dfrac{-2}{3} \right )\times x \times x \times x $$

1539642_1676092_ans_0b2b55add513413781d48a4bfc39af76.jpeg

Write the following numbers in the expanded exponential forms: 927303

1518363_1676722_ans_5417b472456c487ebf0ab9965054c94c.jpg

In a large hall there are $$4x^2$$ rows of benches. If each row has $$5x^2y^3$$ benches and each bench can accommodate $$xy^2$$ persons, determine the total number of persons if its is full up to its capacity.

Given,

Number of rows in the hall $$= 4x^{2}$$.

Number of benches in each row $$= 5x^{2}y^{3}$$.

Number of people in each bench $$= xy^{2}$$.

Total number of persons $$=$$ number of rows in the hall $$\times$$ number of benches in each row $$\times$$ number of people in each bench.

$$ = 4x^{2} \times 5x^{2}y^{3} \times xy^{2}$$

$$ = 20x^{5}y^{5}$$.

Simplify: $$ \left ( \dfrac{-2}{3} \right )^{4}$$

Now,

$$\left(\dfrac{-2}{3}\right)^4$$

$$=\dfrac{2^4}{3^4}=\dfrac {2\times 2\times 2\times 2}{3\times 3\times 3\times 3}$$

$$=\dfrac{16}{81}$$.

Express each of the following in exponential from: $$ \dfrac{4}{3}\times \dfrac{4}{3}\times \dfrac{4}{3}\times \dfrac{4}{3}\times \dfrac{4}{3}$$

1516017_1676061_ans_211eba02b67248718c145cf895b4351c.jpg

Express the following in exponential form: $$ x\times x \times x\times x \times a \times a \times b \times b \times b$$

We have,

$$= x\times x \times x\times x \times a \times a \times b \times b \times b$$

$$x\times x \times x\times x\Rightarrow x$$ is multiplied $$4$$ times

So, $$x\times x \times x\times x\Rightarrow x^4$$

$$a \times a \times\Rightarrow a$$ is multiplied $$2$$ times

So, $$a \times a \times\Rightarrow a^2$$

$$ b \times b \times b\Rightarrow b$$ is multiplied $$3$$ times

So, $$ b \times b \times b\Rightarrow b^3$$

Hence, $$x\times x \times x\times x \times a \times a \times b \times b \times b=x^4a^2b^3$$

Write down the given expression in the product form.
$$10a^3b^3c^3$$.

We know that if a number say $$b$$ is multiplied three times. That is, $$b\times b\times b$$ can be written as $$b^3$$.

=> $$b^{3}$$ = $$b\times b\times b$$.

Thus,

$$10 a^{3}b^{3}c^{2} = 10 \times a \times a \times a \times b \times b\times b\times c \times c \times c $$.

Express each of the following rational numbers in power notation:
$$ -\dfrac{1}{216}$$

1516288_1676226_ans_7fc51dcf3cfb490a88cfd46bcba390ba.jpg

Write $$ 9 \times 9 \times 9 \times 9\times 9 $$ in exponential form with base 3.

Given $$ 9 \times 9 \times 9 \times 9 \times 9 $$

$$ = (9)^{5} $$
$$ = (3^2)^{5} $$
$$ = 3^{10} $$

Write the following number in the expanded exponential forms: 20068

We have

$$20068=2\times 10000+0\times1000+0\times100+6\times10+8\times1\\=2\times10^4+0\times10^3+0\times10^2+6\times10^1+8\times10^0$$

Express each of the following numbers as a product of powers of their prime factors: 2800

1516257_1676188_ans_a7a4355c6f034d32b866f0a38a9a17d4.jpg

Express each of the following rational numbers in power notation:
$$ \dfrac{49}{64} $$

1516282_1676220_ans_6599d9fbd4b8403182597f65524c4e1d.jpg

Write the following numbers in the expanded exponential forms: 420719

1518047_1676712_ans_5ef9746fccb24cc48c4e101f8d2bc30f.jpg

Express the following number as a product of powers of their prime factors: 2800

We are given the number $$2800$$

Prime factorization of $$2800 = 2 \times 2 \times 2 \times 2 \times 5 \times 5 \times 7$$

$$=2^4\times5^2\times7$$

Express the following number as a product of powers of their prime factors: 450

Prime factorization of $$450$$

$$450 = 2 \times 225$$

$$450 = 2 \times 3\times 75$$

$$450 = 2 \times 3 \times 3 \times 25$$

$$450 = 2\times 3 \times 3 \times 5 \times 5$$

Therefore $$ 450=2\times 3^2\times 5^2$$

Express the number appearing in the standard form:

Diameter of the Sun is $$1,400,000,000$$ metres.

1518043_1676685_ans_b381d71a40364ec081242317ecf4d8ae.jpg

If x is a positive real number and exponents are rational numbers, simplify $$\left(\dfrac{x^b}{x^c}\right)^{b+c-a}\times \left(\dfrac{x^c}{x^a}\right)^{c+a-b}\times \left(\dfrac{x^a}{x^b}\right)^{a+b-c}$$.

1683048_1715628_ans_c02c153da0ba4b5c98c1a3ef58175ef0.jpg

Prove that $$\dfrac{(x^{a+b})^2(x^{b+c})^2(x^{c+a})^2}{(x^ax^bx^c)^4}=1$$.

1674393_1715627_ans_b99d713e1c224ff08106765ad2c00911.jpg

If $$\dfrac{9^n\times 3^2\times (3^{-\tfrac{n}{2}})^{-2}-(27)^n}{3^{3m}\times 2^3}=\dfrac{1}{27}$$, prove that $$m-n=1$$.

1886463_1715629_ans_2358126b939d4a0080eaec9a6bc38635.jpg

Write the following numbers in the expanded exponential forms: 5004132

1518296_1676718_ans_c2ff44ad5bb949f58438843b8219ba88.jpg

What number must be subtracted from
$$1,02,59756$$ to get $$77,63,835$$ ?

First number $$= 1,02,59,756$$

Second number $$=x$$

Resultant number $$= 77,63,835$$

From the question,
$$1,02,59,756-x=77,63,835$$

$$x=1,02,59,756-77,63,835$$

$$x=24,95,921$$

$$10259756$$
$$- 7763835$$
$$----$$
$$2495921$$
$$---$$
The number to be subtracted from first number to obtain the resultant number

The sale receipt of a company during a year was $$Rs.30587850.$$ Next year it increased by $$Rs.6375490.$$ What was the total sale receipt of the company during these two years ?

Sale in the first year $$= Rs.30587850$$
Sale increased in the next year by $$= Rs.6375490$$
$$\therefore$$ Sale in the second year
$$= Rs.30587850 + Rs.6375490$$
$$= Rs.36963340$$
Total sale for the two years $$=Rs.30587850+Rs.36963340= Rs.67551190$$

Express the following as a rational number:
$$((5)^{-1}-(7)^{-1})^{-1}$$

We know that,
$$=(5)^{-1}=(1/5)^1$$ $$...[\because (a/b)^{-n}=(b/a)^n]$$
$$=(7)^{-1}=(1/7)^1$$ $$...[\because (a/b)^{-n}=(b/a)^n]$$
Now subtract,
$$=\left\{ (1/5)-(1/7)\right\}^{-1}$$
$$=\left\{ (7-5)/35\right\}^{-1}$$ $$...[LCM$$ of $$5$$ and $$7$$ is $$35]$$
$$=\left\{ 2/35\right\}^{-1}$$
$$=\left\{ 35/2\right\}$$

Express $$16/81$$ and $$-16/81$$ as powers of a rational number.

As $$16=4\times 4$$
And $$81=9\times 9$$
Now use, $$\left( \dfrac ab\right)^m =\dfrac{a^m}{b^m}$$
$$\therefore \dfrac{16}{81}=\dfrac{4^2}{9^2}=\left( \dfrac 49\right)^2$$
$$\therefore \dfrac{-16}{81}=\dfrac{-(4^2)}{9^2}=-\left( \dfrac 49 \right)^2$$

Solve the following:
$$\left( \dfrac 12 \right)^{-2}\div \left( \dfrac 12\right)^{-3}$$

Use $$a^m \div a^n =(a)^{m-n}$$
$$\left( \dfrac{1}{2}\right)^{-2}\div \left( \dfrac{1}{2}\right)^{-3}=\left( \dfrac{1}{2}\right)^{-2-(-3)}=\left( \dfrac{1}{2}\right)^{-2+3}=\left( \dfrac{1}{2}\right)^{1}= \dfrac{1}{2}$$
$$\left( \dfrac{1}{2}\right)^{-2}\div \left( \dfrac{1}{2}\right)^{-3}=\dfrac 12$$

Express $$27/64$$ and $$-27/64$$ as powers of a rational number.

$$\because 27=3\times 3\times 3=3^3$$
$$\Rightarrow -27=-3\times -3\times -3=(-3)^3$$
$$\Rightarrow 64=4\times 4\times 4=4^3$$
Now use, $$\left( \dfrac{a}{b}\right)^m=\dfrac{a^m}{b^m}$$
$$\therefore \dfrac{27}{64}=\dfrac{3^3}{4^3}=\left( \dfrac 34\right)^3$$
$$\therefore \dfrac{-27}{64}=\dfrac{(-3)^3}{4^3}=\left( \dfrac{-3}{4}\right)^3$$

Simplify :
$$(2^5 \div 2^8) \times 2^{-7}$$

Use $$a^m \div a^n =(a)^{m-n}$$ and $$a^m \times a^n =a^{m+n}$$ and $$a^{-m}=\dfrac{1}{a^m}$$
$$\therefore (2^5+2^8)\times (2)^{-7}=(2)^{5-8}\times (2)^{-7}$$
$$=(2)^{-3}\times (2)^{-7}$$
$$=(2)^{-3-7}=(2)^{-10}=\dfrac{1}{2^{10}}=\dfrac{1}{1024}$$

Express as a power of a rational number with negative exponent.
$$(2^5 \div 2^8)\times 2^{-7}$$

Use $$a^m \div a^n =(a)^{m-n}$$ and $$a^m \times a^n =a^{m+n}$$
$$(2^5\div2^8)\times 2^{-7}=(2^{5-8})\times 2^{-7}=2^{-3}\times 2^{-7}=2^{-3-7}=2^{-10}$$

The usual form of $$2.39461 \times 10^6$$ is _______.

Usual for of the given number will be,

$$2.39461 \times 10^6 = 2.39461 \times 10 \times 10 \times 10 \times 10 \times 10 \times 10$$

$$ =23,94,610$$

Simplify :
$$(2^{-1}+4^{-1}+6^{-1}+8^{-1})^x=1$$

Given, $$(2^{-1}+4^{-1}+6^{-1}+8^{-1})^x=1$$
Use, $$a^{-m}=\dfrac{1}{a^m}$$
$$\Rightarrow \left( \dfrac 12 +\dfrac 14 +\dfrac 16+\dfrac 18 \right)^x=1$$
$$\Rightarrow \left( \dfrac{12+6+4+3}{24}\right)^x=1$$
$$\Rightarrow \left( \dfrac{25}{24}\right)^x=1$$
This can be possible only if $$x=0$$ because $$a^0=1$$.

Find the value of $$x^{-3}$$ if $$x=(100)^{1-4}\div (100)^0$$.

Given, $$x=(100)^{1-4}\div (100)^0$$

Use $$a^m \div a^n =(a)^{m-n}$$

$$\Rightarrow x=(100)^{-3}\div (100)^0$$

$$\Rightarrow x=(100)^{-3-0}$$

$$\Rightarrow x=(100)^{-3}$$

Now use, $$(a^m)^n=(a)^{mn}$$

$$x^{-3}=[(100)^{-3}]^{-3}\\\ \ \ \ \ =(100)^9$$

The usual form of $$3.41 \times 10^6$$ is _______.

$$3410000$$

$$\Rightarrow 3.41 \times 10^6 =3.14 \times 10 \times 10 \times 10 \times 10 \times 10 \times 10$$

$$\Rightarrow 3.41 \times 10^6 =3410000$$

$$3^5 \div 3^{-6}$$ can be simplified as ________ .

Using $$a^m \div a^n=a^{m-n}$$

$$3^5 \div 3^{-6}=3^{5-(-6)}=3^{5+6}=3^{11}$$

To add the numbers given in the standard form, we first convert them into numbers with _____ exponents.

Equal

To add the numbers given in the standard form, we first convert them into numbers with "equal" exponents.

The usual form for $$2.3 \times 10^{-10}$$ is _____.

$$ \dfrac{2.3}{10^{10}} =\dfrac{2.3}{10000000000}= 0.00000000023$$

The value of $$3 \times 10^{-7}$$ is equal to _______.

$$0.0000003$$
$$\dfrac{3}{10^7}=\dfrac{3}{10000000}=0.0000003$$

On dividing $$8^5$$ by ________ we get $$8$$

Using $$a^m \div a^n=a^{m-n}$$

$$8^5\div 8=8^5\div 8^1=8^{5-1}=8^4$$

Mass of Mars is $$6.42\times 10^{29}\ kg$$ and mass of the Sun is $$1.99\times 10^{30}\ kg$$. What is the total mass?

The mass of Mars $$=6.42\times 10^{29}\ kg$$

The mass of the Sun $$=1.99\times 10^{30}\ kg$$

Total mass of Mars and the Sun combined

$$=6.42\times 10^{29}+1.99\times 10^{30}$$

$$=6.42\times 10^{29}+19.9\times 10^{-1}\times10^{30}$$

$$=6.42\times 10^{29}+19.9\times 10^{29}\cdots\cdots[\because a^m\times a^n=a^{m+n}]$$

$$=(6.42+19.9)\times 10^{29}\ kg$$

$$=26.32\times 10^{29}\ kg$$

By what number should $$\left( \dfrac{-3}{2}\right)^{-3}$$ be divided so that the quotient may be $$\left( \dfrac{4}{27}\right)^{-2}$$?

Let $$\left( \dfrac{-3}{2}\right)^{-3}$$ is divided by $$x$$ to get quotient $$\left( \dfrac {4}{27}\right)^{-2}$$
Then,
$$\left( \dfrac{-3}{2}\right)^{-3}\div x=\left( \dfrac{4}{27}\right)^{-2}$$

$$x=\left( \dfrac{-3}{2}\right)^{-3}\div\left( \dfrac{2^2}{3^3}\right)^{-2}=\left( \dfrac{-3}{2}\right)^{-3}\div \dfrac{(2)^{-4}}{(3)^{-6}}$$

$$=\left( \dfrac{-3}{2}\right)^{-3}\times \dfrac{(3)^{-6}}{(2)^{-4}}$$

[ Use $$a^m \times a^n =a^{m+n}$$]

$$=\dfrac{(-3)^{-3}\times (3)^{-6}}{2^{-3}\times 2^{-4}}=\dfrac{-3^{-9}}{2^{-7}}$$

Now use, $$a^{-m}=\dfrac{1}{a^m}$$ and $$(a^m)^n=(a)^{mn}$$
Therefore ,
$$\dfrac{-3^{-9}}{2^{-7}}=-\dfrac{2^7}{3^9}$$

A new born bear weights $$4\ kg$$. How many kilograms might a five year old bear weight if its weight increases by the power of $$2$$ in $$5$$ years?

Weight of new born year $$=4\ kg$$

Its weight increases by the power of $$2$$ in $$5$$ years

So, Weight of bear in $$5$$ yr$$=\text{weight of bear at present}^2=(4)^2=16\ kg$$.

This table shows the mass of one atom for five chemical elements. Use it to answer the question given.
Element Mass of atom $$(kg)$$
Titanium $$7.95\times 10^{-26}$$
Lead $$3.44\times 10^{-25}$$
Silver $$1.79\times 10^{-25}$$
Lithium $$1.15\times 10^{-26}$$
Hydrogen $$1.674\times 10^{-27}$$
Which element is lighter, Silver or Titanium?

Arrangement of masses of atoms in the same power of $$10$$ is given by-

Element Mass of atom $$(kg)$$

Titanium $$7.95\times 10^{-26}$$

Lead $$3.44\times 10^{-25}=34.4\times 10^{-26}$$

Silver $$1.79\times 10^{-25}=17.9\times10^{-26}$$

Lithium $$1.15\times 10^{-26}$$

Hydrogen $$1.674\times 10^{-27}=0.1674\times10^{-26}$$

So, comparing in this form, we get

$$\text{Silver}=17.9\times 10^{-26}>\text{ Titanium }=7.95\times 10^{-26}$$

therefore, titanium is lighter.

Planet $$A$$ is at a distance of $$9.35\times 10^6\ km$$ from Earth and planet $$B$$ is $$6.27\times 10^7\ km$$ from Earth. Which planet is nearer to Earth?

Distance between planet $$A$$ and Earth $$=9.35\times 10^6\ km$$. Distance between planet $$B$$ and Earth $$=6.27\times 10^7\ km$$

For finding difference between above two distances, we have to change both in same exponent of $$10$$, i.e.,

$$9.35\times 10^6=9.35\times10^6\times \cfrac{10}{10}=0.935\times 10^7\ km$$

As $$6.27\times 10^7\ km$$ is greater than $$0.935\times10^7\ km$$, means Planet $$B$$ is farther than planet $$A$$.

So, planet $$A$$ is nearer to Earth.

By what number should $$(-15)^{-1}$$ be divided so that quotient may be equal to $$(-15)^{-1}$$?

Let $$(-15)^{-1}$$ be divided by $$x$$ to get quotient $$(-15)^{-1}$$
So, $$\dfrac{(-15)^{-1}}{x}=(-15)^{-1}$$
$$\Rightarrow \dfrac{(-15)^{-1}}{(-15)^{-1}}=x$$
$$\Rightarrow x=(-15)^{-1+1}[ \because a^m \div a^n =(a)^{m-n}]$$
$$\Rightarrow x=(-15)^0=1\ [ \because a^0 =1]$$

$$\Big\{\Big[6^2 +(8^2)^{\frac{1}{2}}\Big]\Big\}^3$$

As per question,
$$\Big\{\Big[6^2 +(8^2)^{\frac{1}{2}}\Big]\Big\}^3 = \{36 + 8\}^3 = (44)^3 = 85184$$

This table shows the mass of one atom for five chemical elements. Use it to answer the question given.
Element Mass of atom $$(kg)$$
Titanium $$7.95\times 10^{-26}$$
Lead $$3.44\times 10^{-25}$$
Silver $$1.79\times 10^{-25}$$
Lithium $$1.15\times 10^{-26}$$
Hydrogen $$1.674\times 10^{-27}$$
Which is the heaviest element?

Arrangement of masses of atoms in the same power of $$10$$ is given by-

Element Mass of atom $$(kg)$$

Titanium $$7.95\times 10^{-26}$$

Lead $$3.44\times 10^{-25}=34.4\times 10^{-26}$$

Silver $$1.79\times 10^{-25}=17.9\times10^{-26}$$

Lithium $$1.15\times 10^{-26}$$

Hydrogen $$1.674\times 10^{-27}=0.1674\times10^{-26}$$

So, comparing in this form, we get

The heaviest element is Lead $$=34.4\times 10^{-26}$$kg

Use the properties of exponents to varify that the statement is true.
$$25(5^{n-2})=5^n$$

$$\mathrm{LHS}$$ $$=25(5^{n-2})=5^2 \left(\cfrac{5^n}{5^2}\right)\cdots\cdots\{\because a^{m-n}=\cfrac{a^m}{a^n}\}$$

$$=5^2 \times 5^n \times \dfrac{1}{5^2}=5^n =\mathrm{RHS}$$

Hence,

$$25(5^{n-2})=5^n$$ proved.

Find a single repeater machine that will do the same work as the hook -up.

A machine $$(\times x^y)$$ with input $$a$$ will give an output $$ax^y$$

When, multiple such machines are hooked up their stretching powers are multiplied.

Machine $$1$$ is $$(\times 7^{10})$$

Machine $$2$$ is $$(\times 7^{50})$$

Machine $$3$$ is $$(\times 7^1)$$

As per the law of exponent- $$a^m \times a^n =a^{m+n}$$

So,

The work that can be performed by the given repeater machine is equal to $$7^{10}\times 7^{50} \times 7^1 =7^{10+50+1}=7^{61}$$.

Hence, $$(\times 7^{61})$$ is the single machine that can perform the same amount of work as given hooked up machines

Find the value of:
$$(-3\dfrac{1}{2})^{3}$$

$$(-3\dfrac{1}{2})^{3}=(\dfrac{-7}{2})^{3}$$

$$=\dfrac{-7}{2}\times \dfrac{-7}{2}\times \dfrac{-7}{2}$$

$$=\dfrac{-343}{8}$$

$$=-42\dfrac{7}{8}$$

This table shows the mass of one atom for five chemical elements. Use it to answer the question given.
Element Mass of atom $$(kg)$$
Titanium $$7.95\times 10^{-26}$$
Lead $$3.44\times 10^{-25}$$
Silver $$1.79\times 10^{-25}$$
Lithium $$1.15\times 10^{-26}$$
Hydrogen $$1.674\times 10^{-27}$$
List all five elements in order from lightest to heaviest.

Arrangement of masses of atoms in the same power of $$10$$ is given by-

Element Mass of atom $$(kg)$$

Titanium $$7.95\times 10^{-26}$$

Lead $$3.44\times 10^{-25}=34.4\times 10^{-26}$$

Silver $$1.79\times 10^{-25}=17.9\times10^{-26}$$

Lithium $$1.15\times 10^{-26}$$

Hydrogen $$1.674\times 10^{-27}=0.1674\times10^{-26}$$

So, comparing in this form, we get

Arrangement of elements from lightest to heaviest-

$$\text{Hydrogen < Lithium < Titanium < Silver < Lead}$$

The given table shows the crop production of a state in the year $$2008$$ and $$2009$$. Observe the table table given below and answer the given questions.
Crop $$2008$$ Harvest
( Hectare) Increase/ decrease
( Hectare ) in $$2009$$
Bajra $$1.4\times 10^3$$ $$-100$$
Jowar $$1.7\times 10^6$$ $$-440,000$$
Rice $$3.7\times 10^3$$ $$-100$$
Wheat $$5.1\times 10^5$$ $$+190,000$$
For which crop(s) did the production decrease?

Negative in increase / decrease column means decrease in crop production.

So, from the given table we can figure out that $$\text{bajra, jowar and rice}$$ crop's production is negative that is decreased.

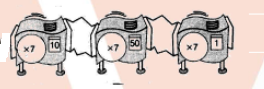
Find three repeater machines that will do the same work as $$a(\times 64)$$ machine. Draw them, or describe those using exponents.

Repeater Machine is a hypothetical machine which automatically enlarges items several times.

As $$2, 4$$, and $$8$$ are the possible factor of $$64$$.

So, $$2^6=64, 4^3=64$$ and $$8^2 =64$$

So the repeater machines that will do same work as $$( \times 64)$$ will be $$( \times 2^6), ( \times 4^3)$$ and $$( \times 8^2)$$

All three are shown in diagram with base written as $$(\times a)$$ and multiplicity at side of base.

Example, for $$(\times2^6)$$, $$2$$ is base and $$6$$ is its multiplicity.

1678482_1793334_ans_00f1ca3219a54a698fc758c820af83e7.png

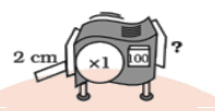
What will the following machine do to a $$2\ cm$$ long piece of chalk?

Repeater Machine is a hypothetical machine which automatically enlarges items several times.

In given machine $$(\times1)$$ gives us base $$1$$ and $$100$$ is its multiplicity.

So, it will stretch the object by $$(\times1^{100})=\times1$$

That is object will remain as it is.

So, if we insert $$2\ cm$$ long piece of chalk in that machine, the piece of chalk remains the same.

At the end of the $$20th$$ century, the world population was approximately $$6.1\times 10^9$$ people. Express this population in usual form. How would you say this number in words?

In standard form of a number we put decimal after first digit and remaining power is written as power of $$10$$

Given at the end of the $$20^{th}$$ century, the world population was approx $$6.1\times 10^9$$, which is standard form

So,

Population of people in usual form $$=6.1\times 10^{9}=6100,000,000$$.

Thus, the population of the people is six thousand one hundred million.

The volume of the Earth is approximately $$7.67\times 10^{-7}$$ times the volume of the Sun. Express this figure in usual form.

In standard form of a number we put decimal after first digit and remaining power is written as power of $$10$$

Given, volume of the Earth $$=7.67\times 10^{-7}$$ times the volume of the Sun, is in the standard form.

In usual form we have to add $$7$$ more decimals because of $$10^{-7}$$

So,

Usual form of $$7.67\times 10^{-7}=0.000000767$$

We have placed decimal $$7$$ places towards the left of original position.

Sanchay put a $$1\ cm$$ stick of gum through $$a(1\times 3^{-2})$$ machine. How long was the stick when it came out ?

If input to $$a$$ is given to $$\times x^y$$ machine then output is $$ax^y$$

Length of the stick of gum that Sanchay put through the

$$( \times 3^{-2})$$ machine $$=1\ cm$$

Negative (-) sign is power states that the given machine is a shrinking machine.

Hence, Output= $$1\times \dfrac {1}{3^2}=1\times \dfrac 19=\dfrac 19\ cm$$

Therefore, the length of the stick when it came out is $$\dfrac 19\ cm$$

What happens when $$1\ cm$$ worms are sent through these hook-ups?

If $$a$$ is input to $$\times x^y$$ machine then output will be $$a\times x^y$$

When two such machines are hooked up, output of one is input to other.

So, for overall output their stretching power multiplies.

So,

If we send $$1\ cm$$ worms through hooked machines $$( \times 2^{-1})$$ and $$( \times 2^{-2})$$, result will be -

$$1\times \dfrac 12 \times \dfrac {1}{2\times 2}=\dfrac{1}{2\times 4}=\dfrac 18\ cm=0.125\ cm$$

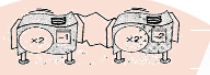
Find a single machine that will do the same job as the given hook-up.
$$A(\times 2^4)$$ machine followed by $$\left[ \times \left( \dfrac{1}{2}\right)^2\right]$$ machine.

A machine $$(\times x^y)$$ with input $$a$$ will give an output $$ax^y$$

When, two such machines are hooked up their stretching powers are multiplied.

$$(\times 2^4)$$ machine is followed by a $$\left[ \times\left( \dfrac{1}{2}\right)^2\right]$$ machine.

Therefore, the result will be - $$\times2^4\times \left(\cfrac12\right)^2=2\times 2\times 2\times 2\times \dfrac 12 \times \dfrac 12=4=2^2$$

So, a single machine $$(\times2^2)$$ or machine $$(\times 4^1)$$ will do same job as that of given hooked up machines

For the hook-up, Find the output for $$3\ unit$$ input work
Is other single repeater machine possible which can produce same amount of work.

A machine $$(\times x^y)$$ with input $$a$$ will give an output $$ax^y$$

When, multiple such machines are hooked up their stretching powers are multiplied.

Machine $$1$$ is $$(\times 2^3)$$

Machine $$2$$ is $$(\times 3^2)$$

As per the law of exponent- $$a^m \times a^n =a^{m+n}\ \&\ \cfrac{a^m}{a^n}=a^{m-n}$$

So,

The work that can be performed by the given repeater machine for $$3\ unit$$ input is equal to $$3\times2^3 \times 3^2=3\times8\times 9=3\times72=216\ unit$$

The work that can be performed by the given repeater machine is equal to $$2^3 \times 3^2=8\times 9=72$$

So, $$(\times72^1)$$ repeater machine is possible which can produce work equal to given hooked up machines.

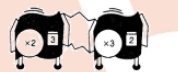
If possible, find a hook-up of prime base number machine that will do the same work as the given stretching machine. Do not use $$(\times 1)$$ machines.

Total work of the single machine $$=\times99$$

We have to find a hook-up of prime base number machine that will do the same work as the given stretching machine.

So, let's find prime factors of $$99$$

$$\Rightarrow 99=11\times9=11\times3^2$$

Where, $$11$$ and $$3$$ are prime factors and they are also not equal to $$1$$

So, machines with base $$11$$, power $$1$$ and base $$2$$, power $$2$$ can be used to hook up to produce same work as that of machine $$(\times 99)$$

Hence, prime base machines hooked up are $$(\times 11^1)$$ and $$(\times 3^2)$$

If possible, find a hook-up of prime base number machine that will do the same work as the given stretching machine. Do not use $$(\times 1)$$ machines.

Total work of the single machine $$=\times1111$$

We have to find a hook-up of prime base number machine that will do the same work as the given stretching machine.

So, let's find prime factors of $$1111$$

$$\Rightarrow 1111=11\times101$$

Where, $$11$$ and $$101$$ are prime factors and they are also not equal to $$1$$

So, machines with base $$11$$, power $$1$$ and base $$101$$, power $$1$$ can be used to hook up to produce same work as that of machine $$(\times 1111)$$

Hence, prime base machines hooked up are $$(\times 11^1)$$ and $$(\times 101^1)$$

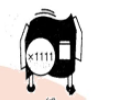
Find a repeater machine that will do the same work as a $$\left( \times \dfrac{1}{8}\right)$$ machine.

Total work of the single machine $$=\times\dfrac 18$$

We have to find a machine that will do the same work as the given stretching machine.

So, let's find prime factors of $$\dfrac 18$$

$$\Rightarrow \dfrac {1}{8}=\dfrac {1}{2}\times \dfrac {1}{2}\times \dfrac {1}{2}=\left( \dfrac 12 \right)^3$$

So, machine with base $$\dfrac {1}{2}$$, power $$3$$ and can be used produce same work as that of machine $$(\times \cfrac18)$$

Hence, required machines is $$\left(\times\left(\cfrac12\right)^3\right)$$

Find the two repeater machines that will do the same work as $$(\times 81)$$ machine.

Total work of the single machine $$=\times81$$

We have to find two machines that will do the same work as the given stretching machine.

So, let's find prime factors of $$81$$

$$\Rightarrow 81=9^2=3^{2\times2}=3^4$$

So, machines with base $$9$$, power $$2$$ and base $$3$$, power $$4$$ can be used produce same work as that of machine $$(\times 81)$$

Hence, two required machines are $$(\times 9^2)$$ and $$(\times3^4)$$

If possible, find a hook-up of prime base number machine that will do the same work as the given stretching machine. Do not use $$(\times 1)$$ machines.

Total work of the single machine $$=100$$

We have to find a hook-up of prime base number machine that will do the same work as the given stretching machine.

So, let's find prime factors of $$100$$

$$\Rightarrow 100=25\times4=5^2\times2^2$$

Where, $$5$$ and $$2$$ are prime factors and their power is also not equal to $$1$$

So, machines with base $$5$$ and $$2$$ and power of both $$2$$ can be used to hook up to produce same work as that of machine $$(\times 100)$$

Hence, prime base machines hooked up are $$(\times 5^2)$$ and $$(\times 2^2)$$

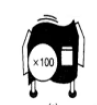
Neha needs to stretch some sticks to $$25^2$$ times their original lengths, but her $$(\times 25)$$ machine is broken. Find a hook-up of two repeater machines that will do the same work as $$(\times 25^2)$$ machine. To get started, think about the hook-up you could use to replace the $$(\times 25)$$ machine.

A machine $$(\times x^y)$$ with input $$a$$ will give an output $$ax^y$$

When, multiple such machines are hooked up their stretching powers are multiplied.

Here,

The single machine $$( \times 25^2)$$ will do the work $$=25 \times 25=625=5\times 5\times 5\times 5=5^2\times 5^2$$

So, we can use two same hooked up machines $$(\times5^2)$$ to produce same work because $$5^2\times 5^2=25^2$$

Therefore, the hooked up machine $$( \times 5^2)$$ and $$( \times 5^2)$$ can be replaced by $$(\times 25)$$ machine.

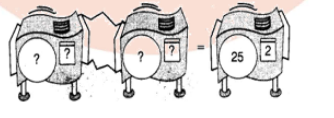
Express the following in exponential form:
$$\dfrac{-125}{343}$$

For making exponential form we need factors of both numearator and denominator with same power

Given, $$\dfrac{-125}{343}$$

Since, $$-125=(-5)^3$$ and $$343=(7)^3$$

So, Exponential form of $$\dfrac{-125}{343}=\dfrac{(-5)^3}{(7)^3}=\left( \dfrac{-5}{7}\right)^3$$

Express the following in exponential form:
$$\dfrac{400}{3969}$$

For making exponential form we need factors of both numearator and denominator with same power

Given, $$\cfrac{400}{3969}$$

$$400=(20)^2$$

$$3969=9\times441=9\times21\times21=9\times3\times7\times3\times7=(63)^2$$

So, Exponential form of $$\dfrac{400}{3969}=\dfrac{(20)^2}{(63)^2}=\left( \dfrac{20}{63}\right)^2$$

Compare the following numbers:
$$3.7662 \times 10^{17}$$, $$3.7671 \times 10^{17}$$

Here $$10^{17}$$ is multiplied in both and $$7671 $$ > $$7662$$

$$3.7671 \times 10^{17}$$ > $$3.7662 \times 10^{17}$$

Find $$x$$.
$$\left( -\dfrac 17\right)^{-5}\div \left( -\dfrac 17\right)^{-7}=(-7)^x$$

$$\left( -\dfrac 17\right)^{-5}\div \left( -\dfrac 17\right)^{-7}=(-7)^x$$

As per the law of exponents: $$a^m \div a^n =(a)^{m-n}$$

Therefore, $$\left( -\dfrac {1}{7}\right)^{-5-(-7)}=(-7)^x$$

$$\Rightarrow\left( -\dfrac {1}{7}\right)^{-5+7}=(-7)^x$$

$$\left(-\dfrac{1}{7}\right)^{2}=(-7)^x$$

$$(-7)^{-2}=(-7)^x\cdots\cdots\left(\because a^{-m}=\cfrac1{a^m}\right)$$

When we compare the powers of $$(-7)$$, we get $$x=-2$$

The distance between the Sun and the Earth is $$1.496\times 10^8\ km$$ and distance between the Earth and the Moon is $$3.84\times 10^8\ m$$. During solar eclipse the Moon comes in between the Earth and the Sun. What is the distance between the Moon and the Sun at that particular time?

The distance between the sun and the earth is $$1496\times 10^8\ m$$

As $$1\ km=1000\ m$$

$$\Rightarrow1.496\times 10^8\ km=1.496\times 10^8\times 10^3\ m=1496\times 10^8\ m$$

And $$3.84\times 10^8\ m$$ is the distance between the earth and the moon.

During solar eclipse the Moon comes in between the Earth and the Sun.

So,

$$\text{Distance between moon and the sun = distance of earth from sun - distance of earth from the moon}$$

$$=(1496\times 10^8-3.84\times 10^8)\ m$$

$$=(1496-3.84)\times10^8$$

$$=1492.16\times 10^8\ m$$.

Express the following in exponential form:
$$\dfrac{-1296}{14641}$$

For making exponential form we need factors of both numearator and denominator with same power

On making the factors of $$1296$$, we get,

$$1296=12\times108=12\times12\times9=2^4\times 3^4=6^4$$

Similarly, we make factors of $$14641$$, we get,

$$\Rightarrow 14641=11\times1331=11\times11\times121=11^4$$,

Exponential form of $$\dfrac{-1296}{14641}=-\dfrac{(6)^4}{(11)^4}=-\left( \dfrac{6}{11}\right)^4$$

By what number should $$(-15)^{-1}$$ be divided so that the quotient may be equal to $$(-5)^{-1}$$?

$${\textbf{Step - 1 : Assume the number and form equation as per given condition}}{\text{.}}$$

$${\text{Suppose the number is }x,\text{ such that }}{\left( { - 15} \right)^{ - 1}} \div {x = \;}{\left( { - 5} \right)^{ - 1}}$$

$$ \Rightarrow - \dfrac{1}{{15}} \div {x = } - \dfrac{1}{5}.$$

$${\textbf{Step - 2 : Solve and calculate the number}}{\text{.}}$$

$$ \Rightarrow \dfrac{{ - \dfrac{1}{{15}}}}{{x}} = - \dfrac{1}{5}$$

$$ \Rightarrow \dfrac{1}{{15}} = \dfrac{{x}}{5}$$

$$ \Rightarrow {x = }\dfrac{5}{{15}}$$

$$ \Rightarrow {x = } \dfrac{1}{3}.$$

$${\textbf{Hence, the required number is }}\dfrac{\mathbf{1}}{\mathbf{3}}.$$

Express the following in exponential form:
$$\dfrac{-625}{10000}$$

For making exponential form we need factors of both numearator and denominator with same power

Given, $$\cfrac{-625}{10000}$$

$$625=25\times25=(5)^4$$

and $$10000=(10)^4$$

So, Exponential form of $$\cfrac{-625}{10000}=-\cfrac{(5)^4}{(10)^4}=-\left( \dfrac{1}{2}\right)^4$$

Find the value of $$(-6)^{4}$$

$$(-6)^4 = (-6) \times (-6) \times (-6) \times (-6) = 1296$$

Find the value of $$(\frac{-2}{3})^{5}$$

$$\displaystyle (\frac{-2}{3})^{5} = \dfrac{-2}{3} \times \dfrac{-2}{3} \times \dfrac{-2}{3} \times \dfrac{-2}{3} \times \dfrac{-2}{3}$$

$$=\dfrac{(-2) \times (-2) \times (-2) \times (-2) \times (-2)}{3 \times 3 \times 3\times 3 \times 3}$$

$$=\dfrac{-32}{243}$$

In the expression $$3^7$$, base = ........ and exponent = ........

In the expression $$3^7$$, base = $$3$$ and exponent = $$7$$.

Find the value of $$(-2)^{9}$$

$$(-2)^{9} = (-2) \times (-2) \times (-2) \times (-2) \times (-2) \times (-2) \times (-2) \times (-2) \times (-2) \times =-512 $$

Find the value of $$5^{5}$$

$$5^5 = 5 \times 5 \times 5 \times 5 \times 5 =3125$$

Find the number from the expanded form:
$$8 \times 10^7 + 3 \times 10^4 + 7 \times 10^3+ 5 \times 10^2+8 \times 10^1$$

$$8 \times 10^7 + 3 \times 10^4 + 7 \times 10^3+ 5 \times 10^2+8 \times 10^1$$

$$=80000000+30000+7000+500+80$$

$$=80037580$$

Find the number from the expanded form:
$$4 \times 10^5 + 5 \times 10^3 + 3 \times 10^2 + 2 \times 10^0$$

$$4 \times 10^5 + 5 \times 10^3 + 3 \times 10^2 + 2 \times 10^0$$

$$=400000+5000+300+2\times 1$$

$$=405302$$

Identify the greater number in $$4^5$$ or $$5^4$$

$$4^5 = 4\times 4\times 4\times 4\times 4 = 1024$$

$$5^4 = 5\times 5\times 5\times 5 =625$$

$$4^5$$ is greater

Fill in the blanks:
In the expression ($$\frac{2}{5})^{11}$$, base = ...... and exponent = .......

Fill in the blanks:
In the expression $$(\frac{2}{5})^{11}$$, base =$$\big(\dfrac{2}{5}\big)$$ and exponent = $$11$$

Compare the following numbers:
$$1.439 \times 10^{12}$$, $$1.4335 \times 10^{12}$$

$$1.439 >1.4335$$

$$\implies$$ $$1.439 \times 10^{12} > 1.4335 \times 10^{12}$$

Compare the following numbers:
$$5.976 \times 10^{24}$$, $$8.689 \times 10^{23}$$

Here in $$5.976 \times 10^{24}$$, $$10^{24}$$ is greater then $$10^{23}$$ in $$8.689 \times 10^{23}$$

$$5.976 \times 10^{24}$$ > $$8.689 \times 10^{23}$$

Simplify:
$$\bigg(\dfrac{-1}{2}\bigg)^{5} \times 2^6 \times \bigg(\dfrac{3}{4}\bigg)^{3}$$

$$\bigg(\dfrac{-1}{2}\bigg)^{5} \times 2^6 \times \bigg(\dfrac{3}{4}\bigg)^{3}$$

$$=\dfrac{(-1)^5}{2^5} \times 2^6 \times \dfrac{3^3}{4^3}$$

$$=\dfrac{(-1)^5}{2^5} \times 2^6 \times \dfrac{3^3}{(2^2)^3}$$

$$ = \dfrac{(-1)^5 }{2^5} \times 2^6 \times \dfrac{3^3}{2^6}$$

$$=\dfrac{-1 \times 3}{2^5}$$

$$=\dfrac{-1 \times 27}{32}$$

$$=\dfrac{-27}{32}$$

Simplify and write the exponential form with negative exponent:
$$5^{3}\times (4/5)^3$$

Let us simplify

$$5^{3}\times (4/5)^3=5^{3}\times (4^3 /5^3)$$

$$=5^{3-3}\times 4^3$$

$$=5^0 \times 4^3$$

$$=1\times 4^3$$

$$=(1/4)^{-3}$$

The exponential form is $$(1/4)^{-3}$$

Write the following numbers in expanded from using exponents:
$$2789.453$$

Given number is $$2789.453$$

The expanded from of

$$2789.453=2\times 10^3 +7\times 10^2 +8\times 10^1 +9\times 10^0 +4\times 10^{-1} +5\times 10^{-2} +3\times 10^{-3}$$

Simplify and write the following exponential form:
$$3^{-5}\times 3^2\div 3^{-6}+(2^2 \times 3)^2 +\left(\dfrac{2}{3}\right)^{-1}+2^{-1} +\left(\dfrac{1}{19}\right)^{-1}$$

Let us simplify,

$$3^{-5}\times 3^2\div 3^{-6}+(2^2 \times 3)^2 +\left(\dfrac{2}{3}\right)^{-1}+2^{-1} +\left(\dfrac{1}{19}\right)^{-1}$$

$$=3^{-5}\times 3^2\times 3^{6}+(2^2 \times 3)^2 +\left(\dfrac{2} {3}\right)^{-1}+2^{-1} +\left(\dfrac{1}{19}\right)^{-1}$$ $$[\because a \div b= a \times b^{-1} ]$$

$$=3^{-5+2+6}+(2^4 \times 3^2)+\dfrac{3}{2}+\dfrac{1}{2}+19^1$$ $$[\because a^m \times a^n=a^{m+n}$$ and $$ \left(\dfrac{a}{b}\right)^{-1}=\dfrac{b}{a}]$$

$$=3^3 +(16\times 9)+\dfrac{4}{2}+19$$

$$=27+144+2+19$$

$$=192$$

The exponential form is $$192$$.

Simplify and write in exponential form with positive exponent:
$$\dfrac{[8^{-1}\times 5^3]}{2^{-4}}$$

Let us simplify

$$\dfrac{[8^{-1}\times 5^3]}{2^{-4}}=\dfrac{[(2^3)^{-1}\times 5^3]}{2^{-4}}$$

$$=\dfrac{[2^{-3}\times 5^3]}{2^{-4}}$$

$$=2^{-3+4}\times 5^3$$

$$=2^1\times 5^3$$

$$=2\times 5\times 5\times 5$$

$$=2\times5^3$$

The exponential form is $$2\times5^3$$

Simplify and write in exponential form with positive exponent:
$$(2/7)^2\times (7/2)^{-3}\div \left\{(7/5)^{-2}\right\}^{-4}$$

$$(2/7)^2\times (7/2)^{-3}\div \left\{(7/5)^{-2}\right\}^{-4}$$

Let us simplify

$$(2/7)^2\times (7/2)^{-3}\div \left\{(7/5)^{-2}\right\}^{-4}= (2/7)^2\times (7/2)^{3}\div (7/5)^{8}$$

$$(2/7)^2 \times (2/7)^3 \times (5/7)^8$$

$$=(2^2/7^2)\times (2^3 /7^3)\times (5^8 /7^8)$$

$$=(2^{2+3}/7^{2+3})\times (5^8/7^8)$$

$$=(2^5 /7^5)\times (5^8 /7^8)$$

$$=\dfrac{(2^5 \times 5^8)}{ 7^{5+8}}$$

$$=\dfrac{(2^5 \times 5^8)}{7^{13}}$$

The exponential form is $$\dfrac{(2^5 \times 5^8)}{7^{13}}$$

Simplify and write the exponential form with negative exponent:
$$[(3/7)^{-2}]^{-3}$$

Let us simplify

$$[(3/7)^{-2}]^{-3}=(3/7)^{-2\times -3}$$

$$=(3/7)^6$$

$$=(7/3)^{-6}$$

The exponential form is $$(7/3)^{-6}$$

Simplify and write in exponential form with positive exponent:
$$(4/5)^2 \times 5^4\times (2/5)^{-2}\div (5/2)^{-3}$$

$$(4/5)^2 \times 5^4\times (2/5)^{-2}\div (5/2)^{-3}\\=((2^2)^2 /5^2) \times 5^4 \times (2^{-2}/5^{-2})\times (2^{-3}/5^{-3})$$

$$=\dfrac{(2^4 \times 5^4 \times 2^{-2} \times 2^{-3}) }{ (5^2 \times 5^{-2}\times 5^{-3})}$$

$$=2^{4-2-3}\times 5^7$$

$$=\dfrac{5^7 }{2^1}$$

The exponential form is $$\dfrac{5^7} 2$$

Write the following number in expanded from using exponents:
$$3007.805$$

Given number is $$3007.805$$

The expanded from of

$$3007.805=2\times 10^3 +7\times 10^0 +8\times 10^{-01} +5\times 10^{-3}$$

Simplify and write the following exponential form:
$$((-2)^3)^2 +5^{-3}\div 5^{-5}-(-1/2)^0$$

$$((-2)^3)^2 +5^{-3}\div 5^{-5}-(-1/2)^0$$

Let us simplify,

$$((-2)^3)^2 +5^{-3}\div 5^{-5}-(-1/2)^0 = (-2)^6 +1/5^3 \div 1/5^5 -1$$

$$=64+1/5^3 \times 5^5 -1$$

$$=64+5^{5-3}-1$$

$$=64+5^2 -1$$

$$=64+25-1$$

$$=88$$

The exponential form is $$88$$.

Simplify and write the exponential form with negative exponent:
$$(5/9)^{-2}\times (5/3)^2\div (1/5)^{-2}$$

Let us simplify

$$(5/9)^{-2}\times (5/3)^2\div (1/5)^{-2}$$

$$=(5^{-2}/9^{-2})\times (5^2 /3^2)\div (1/5^{-2})$$

$$=\dfrac{(5^{-2}\times 5^2 \times 5^{-2})}{ (3^2)^{-2}\times 3^2 1}$$

$$=\dfrac{(5^{-2\times 2-2})} {(3^2)^{-2}\times (3^{-4+2})}$$

$$=\dfrac{5^{-1}}{3^{-2}}$$

$$=(5/3)^{-2}$$

The exponential form is $$(5/3)^{-2}$$

Simplify and write the exponential form with negative exponent:
$$2^{-1}\bigg [\bigg( \dfrac 53\bigg)^4 +\bigg( \dfrac 35\bigg) ^{-2}\bigg ]\div \dfrac {17}{9}$$

$$2^{-1}\bigg[\bigg(\dfrac 53\bigg)^4 +\bigg(\dfrac 35\bigg)^{-2}\bigg]\div \dfrac {17}{9}$$

$$= 2^{-1} \bigg[\bigg(\dfrac{5^{4}}{3^{4}}\bigg)+\bigg(\dfrac{3^{-2}}{5^{-2}}\bigg)\bigg] \div \dfrac{17}{9}$$

$$=2^{-1} \bigg[\bigg(\dfrac{5^{4}}{3^{4}}\bigg)+\bigg(\dfrac{5^{2}}{3^{2}}\bigg)\bigg] \div \dfrac{17}{9}$$

$$=\dfrac{1}{2} \bigg[\bigg(\dfrac{625}{81}\bigg)+\bigg(\dfrac{25}{91}\bigg)\bigg]\times \dfrac{9}{17}$$

$$=\dfrac12 \times \dfrac{850}{81}\times \dfrac{9}{17}$$

$$=\dfrac{25}{9}$$

$$=\bigg(\dfrac{5}{3}\bigg)^{2}$$

$$=\bigg(\dfrac{3}{5}\bigg)^{-2}$$

The exponential form is $$\bigg(\dfrac 35\bigg)^{-2}$$

Express the number appearing in the following statement in standard form:
A helium atom has a diameter of $$22/100000000000$$ m.

A helium atom has a diameter of $$22/100000000000$$ m;

it is expressed in standard form as $$22\times10^{-12}=2.2\times10^{-10}$$

Express the number appearing in the following statement in standard form:
The mass of a proton is $$0.000000000000000000000001673$$ gram.

The mass of a proton is $$0.000000000000000000000001673$$ gram, it is expressed in standard form as $$1.673\times10^{-24}$$ gram.

The number of red blood cells per cubic millimeter of blood is approximately $$5.5$$ million. If the average body contains $$5$$ liters of blood, what is the total number of red cell in the body? $$\left(1\ liter=1,00,000\ mm^{3}\right)$$

Given:

Red blood per cubic millimeter $$=5.5$$ million $$=5.5\times 10^{6}$$

Red blood in $$5$$ litres of blood $$=5.5\times 10^{6}\times 5\times 10^{5}(1\ litre=10^{5}\ mm)$$

$$=27.5\times 10^{6+5}$$

$$=27.5\times 10^{11}$$

$$=27.5\times 10\times 10^{11}$$

$$=27.5\times 10^{12}$$

$$\therefore$$ Total number of red blood cells in the body is $$2.75\times 10^{12}$$.

Express the number appearing in the following statement in standard form:
Express $$7$$ hectares in $$cm^{2}$$.

Express $$7$$ hectares in $$cm^{2}$$. it is expressed in standard form as

$$7$$ hectares$$=7\times 10000\ m^{2}$$

$$=7\times 10000\times 100\times 100\ cm^{2}$$

$$=700000000\ cm^{2}$$

$$=7.0\times 10^{8}\ cm^{2}$$

Compare the following:
Size of a plant cell to the diameter of a wire on a computer chip.
Given size of plant cell $$=0.00001275\ m=1.275\times 10^{-5}\ m$$
Diameter of a wire on a computer chip $$=0.000003\ m=3.0\times 10^{-6}\ m$$

Given

size of plant cell $$=0.00001275\ m=1.275\times 10^{-5}\ m$$

Diameter of a wire on a computer chip $$=0.000003\ m=3.0\times 10^{-6}\ m$$

Size of a plant cell: diameter of a wire on a computer chip

$$1.275\times 10^{-5}: 3.0\times 10^{-6}$$

$$12.75: 3.00$$

Size of plant cell is $$4$$ times of diameter of wire.

Compare the following:
The thickness of a piece of paper to the diameter of wire on a computer chip.
Given Thickness of a piece of paper $$=0.0016\ cm$$
Diameter of a wire on a computer chip $$=0.000003\ m$$

Given

size of plant cell $$=0.00001275\ m=1.275\times 10^{-5}\ m$$

Thickness of a piece of paper $$=0.0016\ cm=1.6\times 10^{-3}cm$$

Diameter of a wire on a computer chip $$=0.000003\ m=3.0\times 10^{-6}\ m$$

Thickness of a piece of paper: diameter of wire on a computer chip

$$1.6\times 10^{-3}:3.0\times 10^{-6}\times 100\ cm$$

$$1.6\times 1000: 300$$

$$16:3$$

Approximately $$5$$ times is the thickness of paper to diameter of wire.

Express the number appearing in the following statement in standard form:
The speed of light is $$300,000,000\ m/sec$$.

The speed of light is $$300,000,000\ m/sec$$: it expressed in standard form as $$3.0\times10^{8}m/sec$$

Express the number appearing in the following statement in standard form:
A sugar factory has annual sales of $$3$$ billion $$720$$ million kilograms of sugar.

A sugar factory has annual sales of $$3$$ billion $$720$$ million kilograms of sugar, it is expressed in standard form as

Annual sale of a sugar factory $$=3$$ billion

$$720$$ million kilograms sugar $$=3,720,000,000 kg=3.72\times 10^{9}\ kg$$

Express the number appearing in the following statement in standard form:
Express $$3$$ years in seconds.

To express $$3$$ years in seconds,

It is expressed in standard form as

$$3$$ years$$= 3\times 365\ days$$

$$=3\times 365\times 24\ hours$$

$$=3\times 365\times 24\times 60\ minutes$$

$$=3\times 365\times 24\times 60\times 60\ seconds$$

$$=94608000\ seconds$$

$$=9.4608\times 10^{7}\ seconds$$

Compare the following:
Size of a plant cell to the thickness of a piece of paper.
Given size of plant cell $$=0.00001275\ m=1.275\times 10^{-5}\ m$$
Thickness of a piece of paper $$=0.0016\ cm=1.6\times 10^{-3}cm$$

Given

size of plant cell $$=0.00001275\ m=1.275\times 10^{-5}\ m$$

Thickness of a piece of paper $$=0.0016\ cm=1.6\times 10^{-3}cm=1.6\times 10^{-5}m$$

Size of a plant cell to the thickness of a piece of paper

$$1.275\times 10^{-5}: 1.6\times 10^{-5}$$

Size of plant cell $$=1.2/1.6=3/4$$ times of thickness of paper.

Which is greater:
$$2^3$$ or $$3^2$$

$$2^3$$ or $$3^2$$
It can be written as
$$2^3 = 2 \times 2 \times 2 = 8$$
$$3^2 = 3 \times 3$$
Hence, 9 is greater than 8 i.e $$3^2 > 2^3$$

Express each of the following in exponential form:
$$1350$$

Factorize the given number

$$1350=2\times 675$$

$$1350=2\times 3\times 225$$

$$1350=2\times 3\times 3\times 75$$

$$1350=2\times 3\times 3\times 5\times 15$$

$$1350=2\times 3\times 3\times 5\times 5\times 3$$

Thus,

$$1350=2\times 3^3\times 5^2$$

Express each of the following in exponential form:
3600

It can be written as above
so we get
$$3600 = 2 \times 2 \times 2 \times 2 \times 3 \times 3 \times 5 \times 5 = 2^4 \times 3^2 \times 5^2$$
1739949_1826009_ans_a96d8d538d754da3b2f9f354c7c266cb.png

1739949_1826009_ans_a96d8d538d754da3b2f9f354c7c266cb.png

Express each of the following in exponential form:
512

It can be written as above
so we get
$$512 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^9$$
1739938_1825993_ans_7f33a5aaf32b4ff69388f9d438f1b7cd.png

1739938_1825993_ans_7f33a5aaf32b4ff69388f9d438f1b7cd.png

Which is greater:
$$4^3$$ or $$3^4$$

$$4^3$$ or $$3^4$$
It can be written as
$$4^3 = 4 \times 4 \times 4 = 64$$
$$3^4 = 3 \times 3 \times 3 \times 3 = 81$$
Hence, 81 is greater than 64 i.e $$3^4 >4^3 $$

Which is greater:
$$2^5$$ or $$5^2$$

$$2^5$$ or $$5^2$$
It can be written as
$$2^5 = 2 \times 2 \times 2 \times 2\times 2 = 32$$
$$5^2 = 5 \times 5 = 25$$
Hence, 32 is greater than 25 i.e $$2^5 >5^2 $$

Simplify, giving answers with positive index:
$$(2a^3)^4 (4a^2)^2$$

$$(2a^3)^4 (4a^2)^2$$

It can be written as

$$=(2a^3)^4(4a^2)^2$$

On further calculation

$$= 2^4 a^3 \times 4. 2^{2 \times 2}. a^{2 \times 2}$$

So we get

$$= 2^4 a^{12}. 2^4 a^4$$

Here

$$= 2^{4 + 4}. a^{12} + 4$$

$$= 2^8 a^{16}$$

We get

$$= 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times a^{16}$$

$$= 256 a^{16}$$

Simplify, giving answers with positive index:
$$(10^2)^3 (x ^8)^{12}$$

$$(10^2)^3 (x ^8)^{12}$$

It can be written as

$$=10^{2 \times 3}. x^{8 \times 12}$$

On further calculation

$$=10^6x^{96}$$

Express in simplest exponential form:
$$25*125$$.

$$25*125$$
$$5^{2}*5^{3}=5^{2+3}=5^{5}$$
$$\therefore$$ Exponential form of $$25*125$$ is $$5^{5}$$.

Express in simplest exponential form:
$$16*64$$

$$16*64$$
$$=2^{4}*2^{6}=2^{4+6}=2^{10}$$.
$$\therefore$$ Exponential form of $$16*64$$ is $$2^{10}$$.

$$9^{0}\times 4^{-1}\div 2^{-4}$$

$$(\dfrac{2}{3})^{-4}\times (\dfrac{27}{8})^{-2}$$ $$ =(\dfrac{2}{3})^{-4}\times \left ( \dfrac{3^{3}}{2^{8}} \right )^{-2}$$ $$\dfrac{2^{-4}}{3^{-4}} \times \dfrac{3^{-6}}{2^{-6}}=\dfrac{2^{-4}}{2^{-6}}\times \dfrac{3^{-6}}{3^{-4}}$$ $$=2^{-4+6}\times \dfrac{1}{3^{-4}+6}=\dfrac{2^{2}}{3^{2}}=\dfrac{4}{9}$$

Express in simplest exponential form:
$$128\div 32$$

$$128\div 32$$
$$=2^{7}\div 2^{5}=\dfrac{2^{7}}{2^{5}}=2^{7-5}=2^{2}$$
$$\therefore$$ Exponential form of $$128\div 32$$ is $$2^{2}$$.

Can you find two integers $$m,n$$ such that $${ 2 }^{ m+n }={ 2 }^{ mn }$$?

Equating the powers of $$2^{ m+n }=2^{ mn }$$ that is $$m+n=mn$$.

Now we have to find such integers so that the sum of the integers is equal to their product and those integers are $$0$$ and $$2$$:

Let us first take $$m=2$$ and $$n=2$$, we get

$$2+2=2\times 2$$

$$\Rightarrow4=4$$

which is true

Now take $$m=0$$ and $$n=0$$, we get

$$0+0=0\times 0$$

$$\Rightarrow0=0$$

which is true

Hence the integers are $$m=0,2$$ and $$n=0,2$$.

Simplify the following using laws of indices:
$$(3^{-\tfrac 12} \times 2^{-\tfrac 13}) \div (3^{-\tfrac 34} \times 2^{-\tfrac 56})$$

The given expression $$\left( 3^{ -\tfrac { 1 }{ 2 } }\times 2^{ -\tfrac { 1 }{ 3 } } \right) \div \left( 3^{ -\tfrac { 3 }{ 4 } }\times 2^{ -\tfrac { 5 }{ 6 } } \right)$$ can be simplified as follows:

$$\left( 3^{ -\tfrac { 1 }{ 2 } }\times 2^{ -\tfrac { 1 }{ 3 } } \right) \div \left( 3^{ -\tfrac { 3 }{ 4 } }\times 2^{ -\tfrac { 5 }{ 6 } } \right) \\ =\left( 3^{ -\tfrac { 1 }{ 2 } }\div 3^{ -\tfrac { 3 }{ 4 } } \right) \times \left( 2^{ -\tfrac { 1 }{ 3 } }\div 2^{ -\tfrac { 5 }{ 6 } } \right) \\ =3^{ -\tfrac { 1 }{ 2 } -\left( -\tfrac { 3 }{ 4 } \right) }\times 2^{ -\tfrac { 1 }{ 3 } -\left( -\tfrac { 5 }{ 6 } \right) }\quad \quad \quad \quad \quad \quad \quad \quad \left( \because \quad x^{ m }\div x^{ n }=x^{ m-n } \right)$$

$$=3^{ -\tfrac { 1 }{ 2 } +\tfrac { 3 }{ 4 } }\times 2^{ -\tfrac { 1 }{ 3 } +\tfrac { 5 }{ 6 } }\quad \\ =3^{ \tfrac { -2+3 }{ 4 } }\times 2^{ \tfrac { -2+5 }{ 6 } }\quad \quad \quad \quad \quad \quad \\ =3^{ \tfrac { 1 }{ 4 } }\times 2^{ \tfrac { 3 }{ 6 } }\\ =3^{ \tfrac { 1 }{ 4 } }\times 2^{ \tfrac { 1 }{ 2 } }$$

$$=3^{ \tfrac { 1 }{ 4 } }\times 2^{ \tfrac { 2 }{ 4 } }\\ =(3\times 2^{ 2 })^{ \tfrac { 1 }{ 4 } }\\ =(3\times 4)^{ \tfrac { 1 }{ 4 } }\\ =12^{ \tfrac { 1 }{ 4 } }$$

Hence $$\left( 3^{ -\tfrac { 1 }{ 2 } }\times 2^{ -\tfrac { 1 }{ 3 } } \right) \div \left( 3^{ -\tfrac { 3 }{ 4 } }\times 2^{ -\tfrac { 5 }{ 6 } } \right)=12^{\tfrac {1}{4}}$$

Express the following in exponential form:
$$t\times t$$

$$\begin{matrix} t\times t={ t^{ 2 } } \\ It\, \, is\, \, { ex }ponential\, \, form \\ \end{matrix}$$

In a particular year, a company manufactured 8570435 bicycles and next year it
manufactured 8756430 bicycles. In which year more bicycles were manufacture and by how many?

1975313_1336673_ans_e389f614836f437bae93e3bab4ac4631.jpg

Find $$x$$, if
$$\left (\dfrac {8}{3}\right)^{2x+1} \times \left (\dfrac {8}{3}\right)^{5} = \left (\dfrac {8}{3}\right)^{x+2}$$

2039758_1671188_ans_79e291200db647a5a98b3284753e18a6.jpg

If $$2^4\times 4^2=16^x$$, then find the value of x.

1311451_1586257_ans_3265b8ecf48244b89b8c54b2778a0256.jpg

Find $$x$$, if
$$\left (\dfrac {-1}{2}\right)^{-19} \div \left (\dfrac {-1}{2}\right)^{8} = \left (\dfrac {-1}{2}\right)^{-2x+1}$$

2039752_1671164_ans_2f1efae9c95a4f77bc1ad473e4402c45.jpg

Find $$x$$, if
$$\left (\dfrac {3}{2}\right)^{-3} \times \left (\dfrac {3}{2}\right)^{5} = \left (\dfrac {3}{2}\right)^{-2x+1}$$

2039753_1671167_ans_4c7bce49a9164525bc8142e88d835672.jpg

Find $$x$$, if
$$\left (\dfrac {5}{4}\right)^{-x} \div \left (\dfrac {5}{4}\right)^{-4} = \left (\dfrac {5}{4}\right)^{5}$$

2039756_1671183_ans_aa189552a0c14797bbb9c15c0a4c9a03.png

If $$\displaystyle a^m\cdot a^n=a^{mn}$$, then $$m(n-2)+n(m-2)$$ is?

1298387_1579091_ans_606ca23a95964cefb0e6482a6487e17b.jpg

Element	Mass of atom $$(kg)$$
Titanium	$$7.95\times 10^{-26}$$
Lead	$$3.44\times 10^{-25}$$
Silver	$$1.79\times 10^{-25}$$
Lithium	$$1.15\times 10^{-26}$$
Hydrogen	$$1.674\times 10^{-27}$$

Crop	$$2008$$ Harvest ( Hectare)	Increase/ decrease ( Hectare ) in $$2009$$
Bajra	$$1.4\times 10^3$$	$$-100$$
Jowar	$$1.7\times 10^6$$	$$-440,000$$
Rice	$$3.7\times 10^3$$	$$-100$$
Wheat	$$5.1\times 10^5$$	$$+190,000$$

Exponents And Powers - Class 7 Maths - Extra Questions

Solve: $$\dfrac{\left(\dfrac{7}{12}\right)^8}{\left(\dfrac{14}{6}\right)^8}$$.

Solve: $$0.00000000 657 \times 10^{15}$$

Solve: $$\left(\dfrac {5^{-4}}{5^{-6}}\right)\times5^{3}$$

Evaluate using product rule properties: $$27 \times 3$$=

Express the following as a rational number:$$(5/7)^{-1}\times (7/4)^{-1}$$

Express the following as a rational number:$$(1/4)^{-4}$$

Express the following as a rational number:$$(-3)^{-1}\times (1/3)^{-1}$$

Find the value of the following:$$ \left( \dfrac{2}{3} \right)^4$$

Fill in the blanks to make the statements true.The square of 500 will have ______ zeroes.

Simplify:$$\bigg(\dfrac{3}{2}\bigg)^{-1} \div \bigg(\dfrac{-2}{5}\bigg)^{-1}$$

Simplify:$$\bigg(-\dfrac{3}{5}\bigg)^{-3}$$

Fill in the blanks:$$\bigg(\dfrac{5}{13}\bigg)^{{10}} \div\bigg[\bigg(\dfrac{5}{13}\bigg)^3\bigg]^2 = \bigg(\dfrac{5}{13}\bigg)^{......}$$

Fill in the blanks:In the expression $$(-5)^{9}$$, exponent = ........ and base = ........

Simplify and write the exponential form with negative exponent:$$(-7)^3 \times (1/-7)^{-9}\div (-7)^{10}$$

Express the number appearing in the following statement in standard form:The diameter of a wire on a computer chip is $$0.000003$$ m.

Express the number appearing in the following statement in standard form:The thickness of a piece of paper is $$0.0016$$ cm.

Express the number appearing in the following statement in standard form:Mass of molecule of hydrogen gas is about $$0.00000000000000000000334$$ tons.

Express the number appearing in the following statement in standard form:The distance form the Earth of the Sun is $$149,600,000,000\ m$$.

Express the number appearing in the following statement in standard form:The human body has $$1$$ trillion cells which vary in shapes and size.

Express $$1024$$ as a power of $$2$$.

Express343 as a power of 7.

Express each of the following in exponential form:1176

Express each of the following in exponential form:1250

Which is greater:$$5^4$$ or $$4^3$$

Express729 as a power of 3

Evaluate$$2^3 \div 2^8$$

Fill in the blanks If index $$= 3x$$ and base $$= 2y, $$the number = ………

Evaluate$$(2^6)^0$$

Evaluate$$(3^5 \times 4^7 \times 5^8)^0$$

Evaluate$$2^8 \div 2^3$$

Fill in the blanks If index = 3x and base = 2y, the number =

Evaluate$$(3^0)^6$$

Simplify, giving answers with positive index:$$(a^{10})^{10} (1 ^6)^{10}$$

Evaluate: $$\left ( \frac{5}{4} \right )^{2}$$

Express $$10,100,1000,10000,100000$$ is exponential form.

Evaluate: $$\left ( 1\frac{1}{4} \right )^{2}$$

Express each of the following as a product of prime factors only in exponential form:$$729\times 64$$

Express the following as a rational number:$$(1/3)^{-1}$$

Simplify the product $$\sqrt[3]{2}\times \sqrt[4]{2}\times \sqrt[12]{32}$$.

Prove that $$\dfrac{x^{a(b-c)}}{x^{b(a-c)}}\div \left(\dfrac{x^b}{x^a}\right)^c=1$$.

Simplify $$\left(\dfrac{1}{3^4}\right)^{\tfrac{1}{2}}$$.

Simplify $$\left(3^{\tfrac{1}{3}}\right)^4$$.

Simplify $$\dfrac{(25)^{\dfrac{3}{2}\times (243)^{\dfrac{3}{5}}}}{(16)^{\frac{5}{4}\times (8)^{\dfrac{4}{3}}}}$$

Simplify and express the following as a rational number:$$(-7/8)^{-3} \times (-7/8)^{2}$$

Express the following as a rational number:$$(-2)^{-3}$$

Express the following as a rational number:$$5^{-3}$$

Simplify and express the following as a rational number:$$(4/9)^6 \times (4/9)^{-4}$$

Express the following as a rational number:$$(4)^{-1}$$

Express the following as a rational number:$$(-3/4)^{-3}$$

Solve for $$x$$ when $$2^{2x+1}+2^9=2^{10}$$

If $$27^{x}=\dfrac{9}{3^{x}}$$, find x.

Express each of the following as a product of prime factors only in exponential form:$$270$$

Express the following numbers in standard from:$$846\times 10^7$$

Express the following as a rational number:$$(-8/5)^3$$

Simplify $$(3^4)^{\tfrac{1}{4}}$$.

Express the following as a rational number:$$(1/6)^3$$

Express the following as a rational number:$$(-13/11)^2$$

Write the following numbers in the usual form:$$4.5\times 10^4$$

Express the following in a rational number:$$(-1/2)^5$$

Evaluate $$\left[(16)^{\dfrac{1}{2}}\right]^{\dfrac{1}{2}}$$.

Finf the value of $$m$$: $$\displaystyle \left ( \frac{-2}{3} \right )^4 \times \left ( \frac{-2}{3} \right )^3 \times \left ( \frac{-2}{3} \right )= \left(\dfrac{-2}{3}\right)^m$$

Simplify the following using law of exponents.$$[(\dfrac{-5}{6})^2]^5$$

Express the following as a rational number:$$(2/3)^5$$

Simplify the following using law of exponents.$$(10^2)^3$$

Simplify $${11^{{2 \over 3}}} \times {11^{{1 \over 3}}}$$

Simplify$${13^{{1 \over 5}}} \times {17^{{1 \over 5}}}$$

Prove that $$\dfrac{x^{a(b-c)}}{x^{b(a-c)}}\div \left(\dfrac{x^{bc}}{x^{ac}}\right)=1$$

If $$(-4)^8 \div (-4)^4$$ is $${(-4)^{m}}$$, then find the value of $$m$$.

Express the number $$4.5 \times 10^3$$ in usual form:

Evaluate : $$\displaystyle \left[ \left( \frac{-4}{3} \right)^2 \right]^3$$

Which is larger $${ \left( 2.5 \right) }^{ 6 }$$ or $${ \left( 1.25 \right) }^{ 12 }$$?

Write the following numbers without scientific notation:(A) $$1.234\times { 10 }^{ 5 }$$(B) $$5.45\times { 10 }^{ -3 }$$

Simplify $$\cfrac { { \left( 1024 \right) }^{ 3 }\times { \left( 81 \right) }^{ 4 } }{ { \left( 243 \right) }^{ 2 }\times { \left( 128 \right) }^{ 4 } } $$

Suppose $$b$$ is a positive integer such that $$\cfrac { { 2 }^{ 4 } }{ { b }^{ 2 } } $$ is also an integer. What are the possible values of $$b$$?

Express the number $$1728$$ in the exponential form:

Simplify: $$\cfrac { { 2 }^{ 3 }\times { 3 }^{ 2 }\times { 5 }^{ 4 } }{ { 3 }^{ 3 }\times { 5 }^{ 2 }\times { 2 }^{ 4 } } $$

Simplify:$$\cfrac { { \left( 15 \right) }^{ -3 }\times { \left( -12 \right) }^{ 4 } }{ { 5 }^{ -6 }\times { 36 }^{ 2 } } $$

Simplify:$$\cfrac { { 6 }^{ 8 }\times { 5 }^{ 3 } }{ { 10 }^{ 3 }\times { 3 }^{ 4 } } $$

simplify in exponent form:$$36{a^4}{b^6}{c^3}\root 6 \of {108} $$

Express the following as a rational number:
$$(5/7)^{-1}\times (7/4)^{-1}$$

Express the following as a rational number:
$$(1/4)^{-4}$$

Express the following as a rational number:
$$(-3)^{-1}\times (1/3)^{-1}$$

Find the value of the following:
$$ \left( \dfrac{2}{3} \right)^4$$

Fill in the blanks to make the statements true.
The square of 500 will have ______ zeroes.

Simplify:
$$\bigg(\dfrac{3}{2}\bigg)^{-1} \div \bigg(\dfrac{-2}{5}\bigg)^{-1}$$

Simplify:
$$\bigg(-\dfrac{3}{5}\bigg)^{-3}$$

Fill in the blanks:
$$\bigg(\dfrac{5}{13}\bigg)^{{10}} \div\bigg[\bigg(\dfrac{5}{13}\bigg)^3\bigg]^2 = \bigg(\dfrac{5}{13}\bigg)^{......}$$

Fill in the blanks:
In the expression $$(-5)^{9}$$, exponent = ........ and base = ........

Simplify and write the exponential form with negative exponent:
$$(-7)^3 \times (1/-7)^{-9}\div (-7)^{10}$$

Express the number appearing in the following statement in standard form:
The diameter of a wire on a computer chip is $$0.000003$$ m.

Express the number appearing in the following statement in standard form:
The thickness of a piece of paper is $$0.0016$$ cm.

Express the number appearing in the following statement in standard form:
Mass of molecule of hydrogen gas is about $$0.00000000000000000000334$$ tons.

Express the number appearing in the following statement in standard form:
The distance form the Earth of the Sun is $$149,600,000,000\ m$$.

Express the number appearing in the following statement in standard form:
The human body has $$1$$ trillion cells which vary in shapes and size.

Express
343 as a power of 7.

Express each of the following in exponential form:
1176

Express each of the following in exponential form:
1250

Which is greater:
$$5^4$$ or $$4^3$$

Express
729 as a power of 3

Evaluate
$$2^3 \div 2^8$$

Fill in the blanks
If index $$= 3x$$ and base $$= 2y, $$the number = ………

Evaluate
$$(2^6)^0$$

Evaluate
$$(3^5 \times 4^7 \times 5^8)^0$$

Evaluate
$$2^8 \div 2^3$$

Fill in the blanks
If index = 3x and base = 2y, the number =

Evaluate
$$(3^0)^6$$

Simplify, giving answers with positive index:
$$(a^{10})^{10} (1 ^6)^{10}$$

Evaluate:
$$\left ( \frac{5}{4} \right )^{2}$$

Evaluate:
$$\left ( 1\frac{1}{4} \right )^{2}$$

Express each of the following as a product of prime factors only in exponential form:
$$729\times 64$$

Express the following as a rational number:
$$(1/3)^{-1}$$

Simplify and express the following as a rational number:
$$(-7/8)^{-3} \times (-7/8)^{2}$$

Express the following as a rational number:
$$(-2)^{-3}$$

Express the following as a rational number:
$$5^{-3}$$

Simplify and express the following as a rational number:
$$(4/9)^6 \times (4/9)^{-4}$$

Express the following as a rational number:
$$(4)^{-1}$$

Express the following as a rational number:
$$(-3/4)^{-3}$$

Express each of the following as a product of prime factors only in exponential form:
$$270$$

Express the following numbers in standard from:
$$846\times 10^7$$

Express the following as a rational number:
$$(-8/5)^3$$

Express the following as a rational number:
$$(1/6)^3$$

Express the following as a rational number:
$$(-13/11)^2$$

Write the following numbers in the usual form:
$$4.5\times 10^4$$

Express the following in a rational number:
$$(-1/2)^5$$

Simplify the following using law of exponents.
$$[(\dfrac{-5}{6})^2]^5$$

Express the following as a rational number:
$$(2/3)^5$$

Simplify the following using law of exponents.
$$(10^2)^3$$

Simplify
$${11^{{2 \over 3}}} \times {11^{{1 \over 3}}}$$

Simplify
$${13^{{1 \over 5}}} \times {17^{{1 \over 5}}}$$

Write the following numbers without scientific notation:
(A) $$1.234\times { 10 }^{ 5 }$$
(B) $$5.45\times { 10 }^{ -3 }$$

Simplify:
$$\cfrac { { \left( 15 \right) }^{ -3 }\times { \left( -12 \right) }^{ 4 } }{ { 5 }^{ -6 }\times { 36 }^{ 2 } } $$

Simplify:
$$\cfrac { { 6 }^{ 8 }\times { 5 }^{ 3 } }{ { 10 }^{ 3 }\times { 3 }^{ 4 } } $$

simplify in exponent form:
$$36{a^4}{b^6}{c^3}\root 6 \of {108} $$

Express the following as a rational number:
$$(-2/3)^{-1}$$

Simplify:
$$\cfrac { { \left( { 2 }^{ 5 } \right) }^{ 6 }\times { \left( { 3 }^{ 3 } \right) }^{ 2 } }{ { \left( { 2 }^{ 6 } \right) }^{ 5 }\times { \left( { 3 }^{ 2 } \right) }^{ 3 } } $$

Rakesh solved some problems of exponents in the following way. Do you agree with the solutions? If not why? Justify your argument.
$$\cfrac { { x }^{ 3 } }{ { x }^{ 2 } } ={ x }^{ 4 }$$

Rakesh solved some problems of exponents in the following way. Do you agree with the solutions? If not why? Justify your argument.
$$3{ x }^{ -1 }=\cfrac { 1 }{ 3x } $$

Prove that :
(i) $$\dfrac {3^{x + 1}}{3^{x(x + 1)}}\times \left (\dfrac {3^{x}}{3}\right )^{x + 1} = 1$$
(ii) $$\left (\dfrac {x^{m}}{x^{m}}\right )^{m + n} \cdot \left (\dfrac {x^{n}}{x^{l}}\right )^{n + l}\cdot \left (\dfrac {x^{l}}{x^{m}}\right )^{l + m} = 1$$

Write each of the following in scientific notation:
(i) $$92.43$$
(ii) $$0.9243$$
(iii) $$9243$$
(iv) $$924300$$
(v) $$0.009243$$
(vi) $$0.09243$$

Find the value of the following:
$$\left [\left (\dfrac {2}{3}\right )^{2} \right ]^{2}$$

Simplify :

$$\dfrac{{{8^{3a}} \times {2^5} \times {2^{2a}}}}{{4 \times {2^{11a}} \times {2^{ - 2a}}}}$$

Simplify:
$$(c^{-2})^{2/3} \times c^{3/2} \div c^{-3}$$ is equal to $$c^{\frac {p}{q}}$$ . If p snd q are co prime fiind the value of $$p+q$$.

Simplify:
$$(3r^2)\times (9r^2)^{3/2} \div (27r^{-3})^{1/3}$$ and find the power of $$r$$

Express the following in exponential form
(i) $$\log_{2} 128 = 7$$
(ii) $$\log_{10} 0.0001 = -4$$
(iii) $$\log_{8} 16 = \dfrac{4}{3}$$

Solve for $$x$$:
$$3^{\large{\frac{x}{5}}}+3^{\large{\frac{x-10}{10}}}=84$$.

Express in exponential notation:
A) $${ \left( -\dfrac { 7 }{ 2 } \right) }^{ 11 }\times { \left( -\dfrac { 7 }{ 2 } \right) }^{ 5 }$$

B) $${ \left( \dfrac { 13 }{ 17 } \right) }^{ 4 }\div { \left( \dfrac { 13 }{ 17 } \right) }^{ 7 }$$

Simply with the help of exponential notation :
(i) $${({2^2} \times {3^3})^2}$$
(ii) $${\left( {{{15} \over {16}}} \right)^3} \div {\left( {{9 \over 8}} \right)^2}$$

Simplify:
$$\left[ { 4 }^{ 0 }+{ 4 }^{ 2 }-{ 2 }^{ 5 } \right] \times { 3 }^{ -2 }$$

Simplify:
$$\left[ \left( 2 \right) ^{ -1 }+\left( 4 \right) ^{ -1 }+\left( 3 \right) ^{ -1 } \right] ^{ -1 }$$

Simplify:
$$\left[ \left( 4 \right) ^{ -1 }-\left( 5 \right) ^{ -1 } \right] ^{ 2 }\times \left( \dfrac { 5 }{ 8 } \right) ^{ -1 }$$

Find $$n$$
$$\left( \dfrac { 2 }{ 3 } \right) ^{ 3 }\times \left( \dfrac { 2 }{ 3 } \right) ^{ 5 }=\left( \dfrac { 2 }{ 3 } \right) ^{ n-2 }$$

Simplify:
$$\left[ \left( 5 \right) ^{ 2 }-\left( \dfrac { 1 }{ 4 } \right) ^{ -2 } \right] \times \left( \dfrac { 3 }{ 4 } \right) ^{ -2 }$$

Express each of the following numbers using expotential notation:
i) $$512$$
ii) $$343$$
iii) $$729$$
iv) $$3125$$

Express the following in exponential form
(i)$$-1331$$

(ii)$$\dfrac{-64}{125}$$

(iii)$$\dfrac{-345}{1024}$$

Calculate:
$$\dfrac{{{4^3} \times {6^6} \times {2^5}}}{{{2^3} \times {4^2} \times {3^2}}}$$

Simplify:
$${2^{\cfrac{2}{3}}}{.2^{\cfrac{1}{5}}}$$

$$81$$ in exponential form as
a) base $$9$$
b) base $$3$$

Find the value of n when :
i) $$5^{2n} \times 5^3 = 5^9$$
ii) $$8 \times 2^{n + 2} = 32$$

Solve
$$\dfrac{4^5 a^8b^3}{ 4^5 a^5b^2}$$