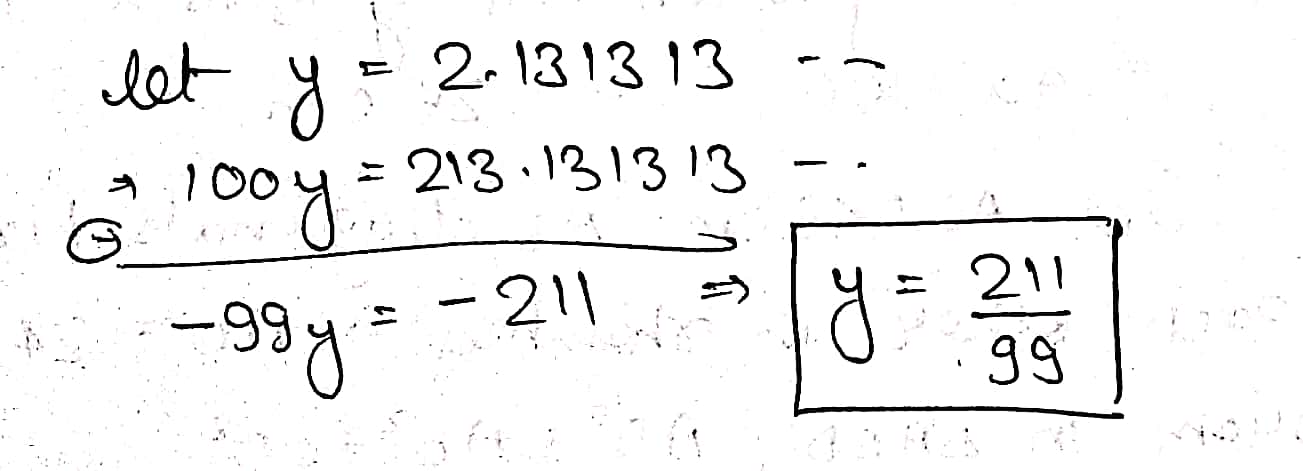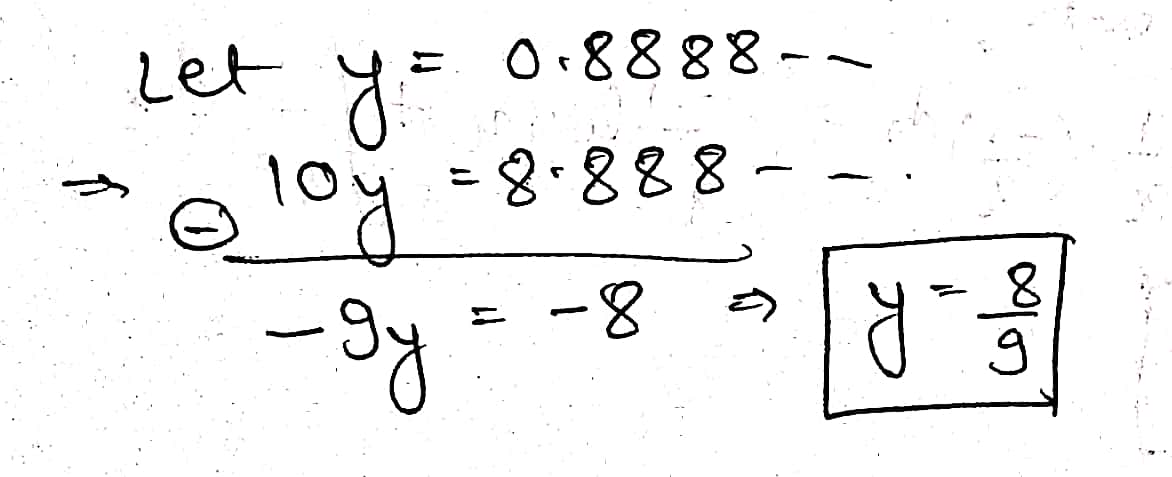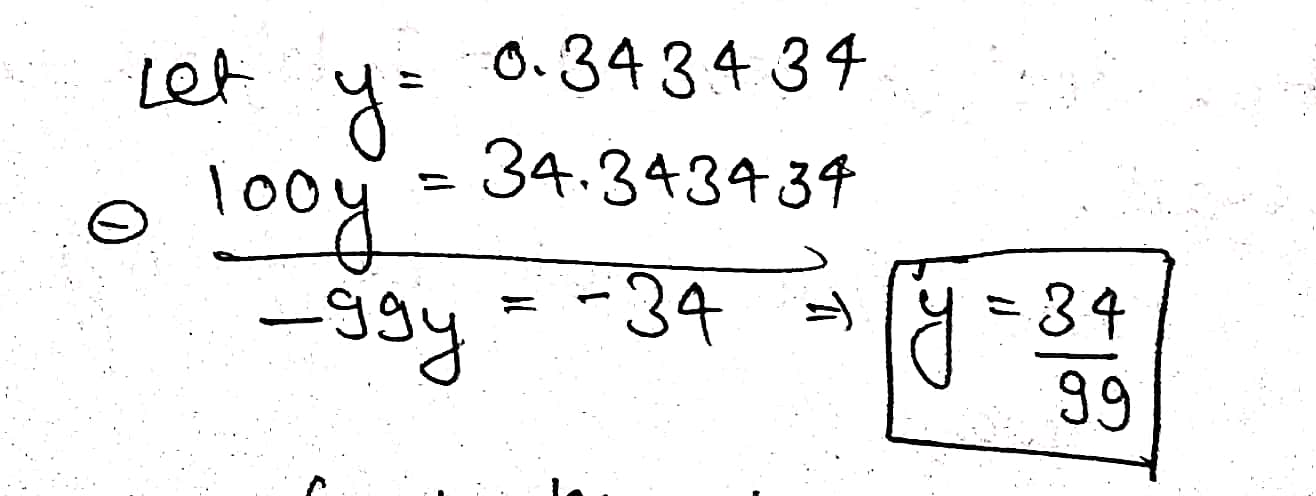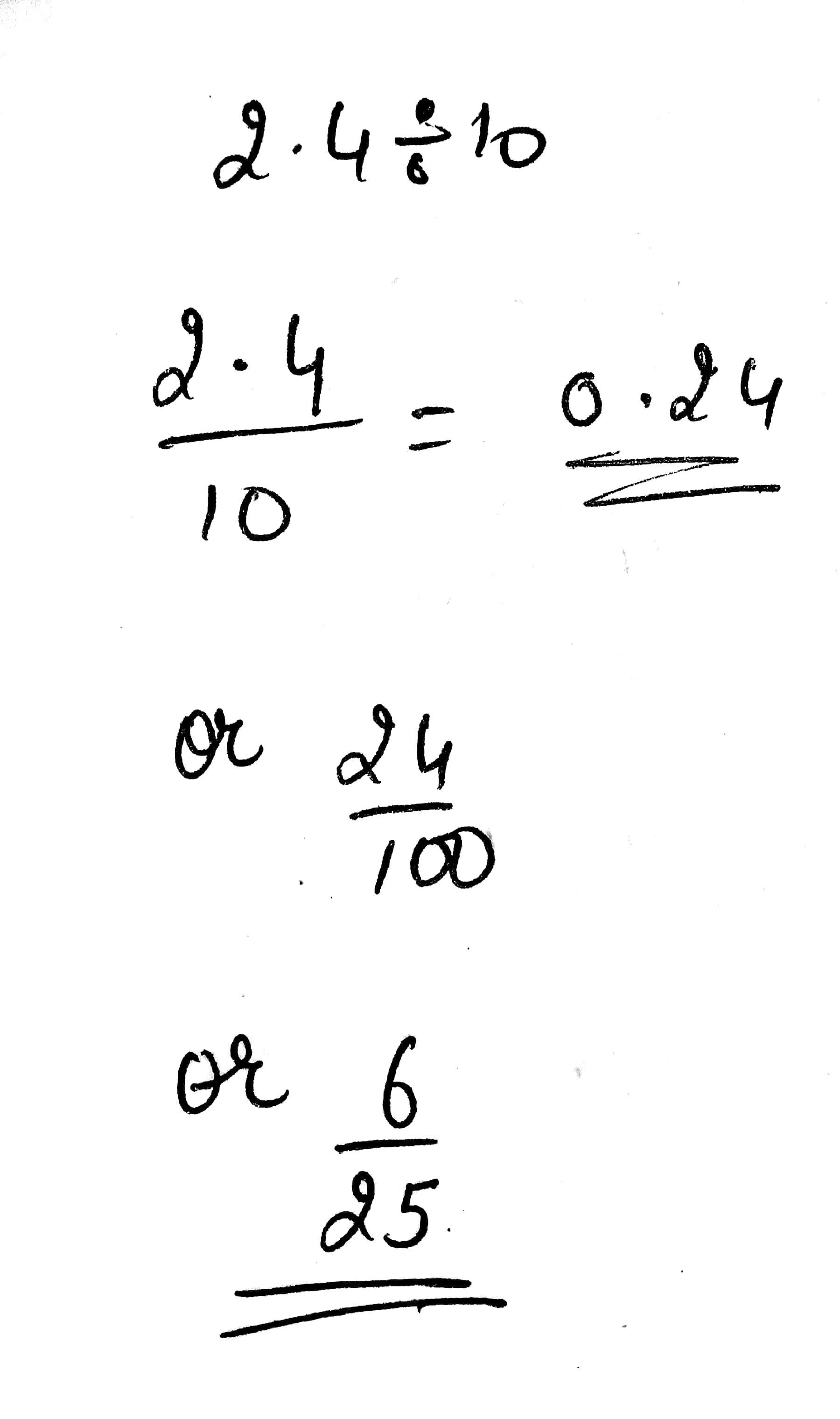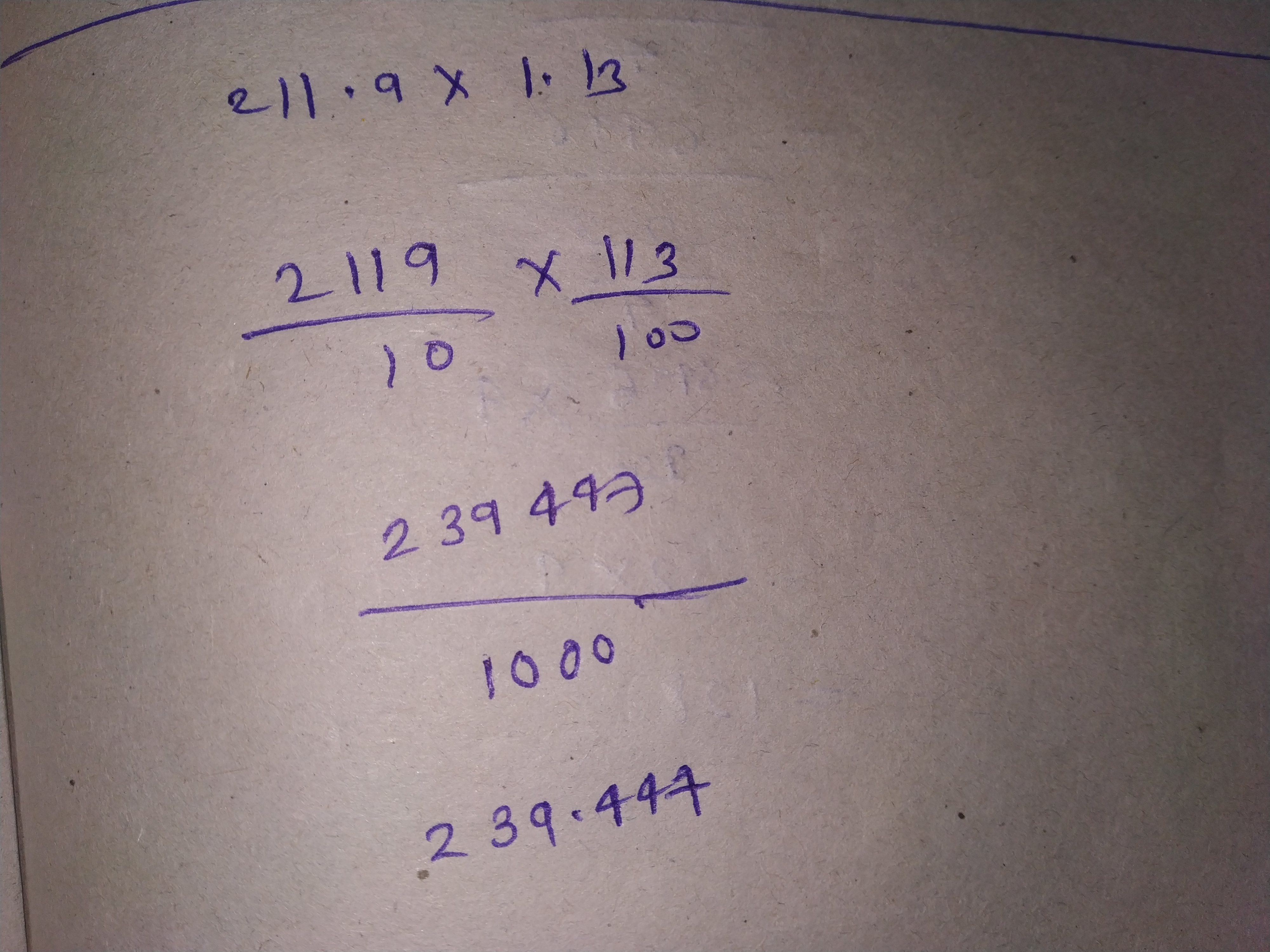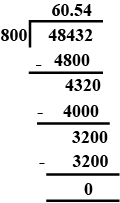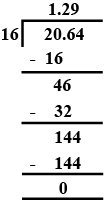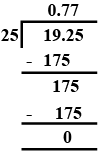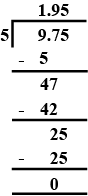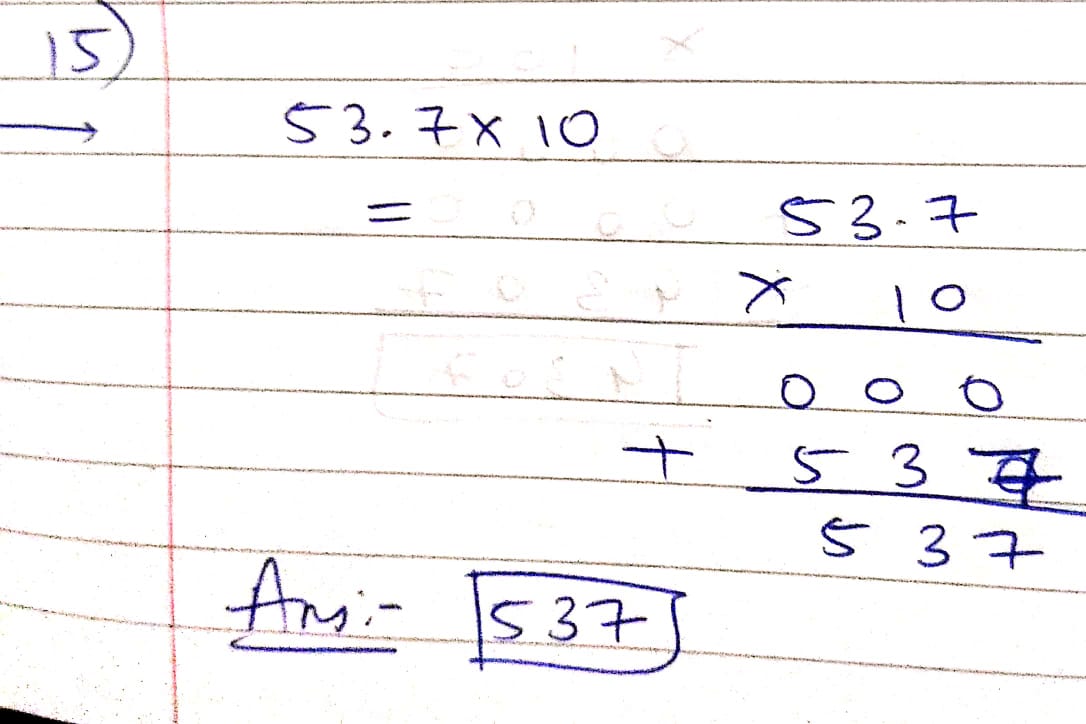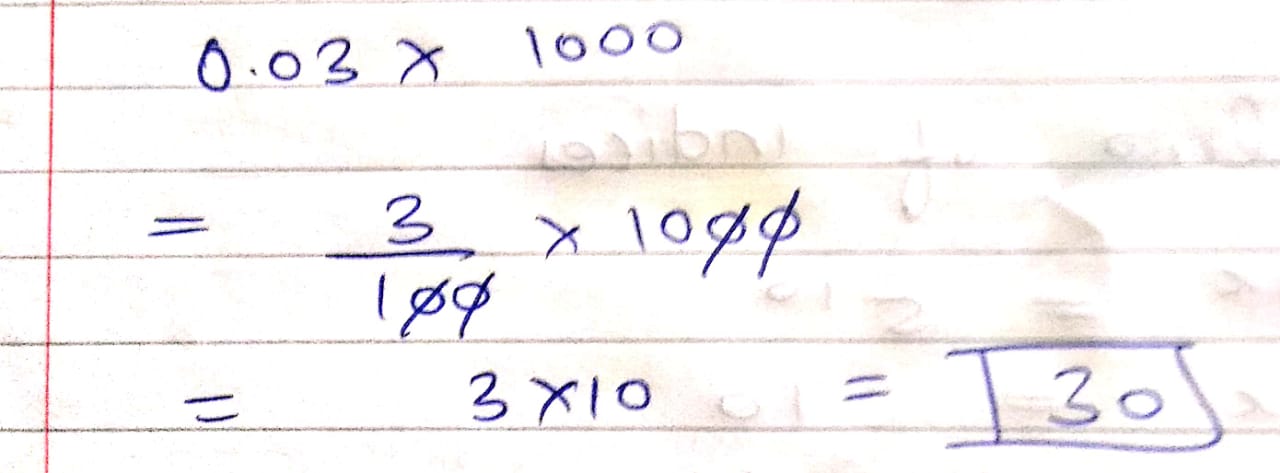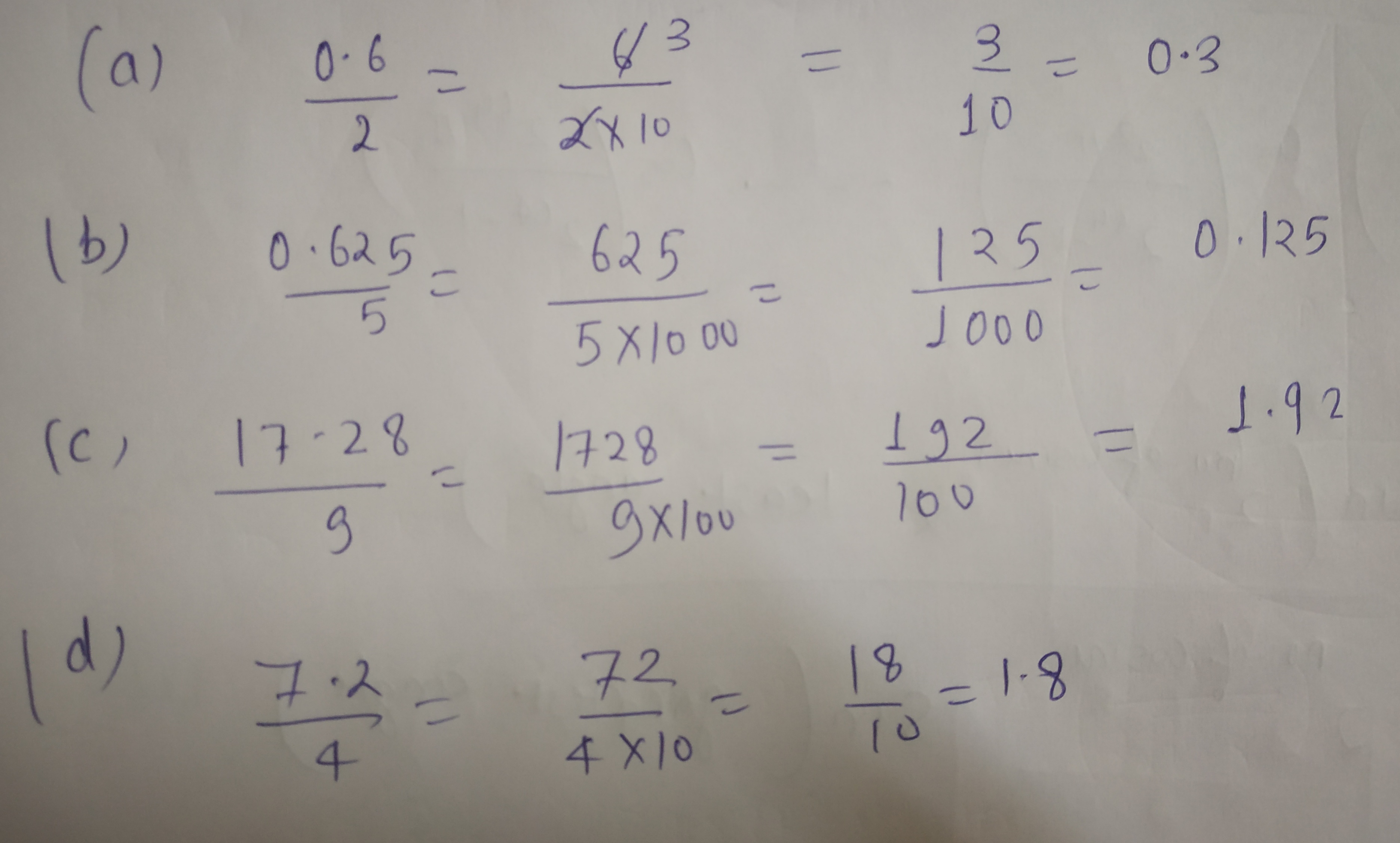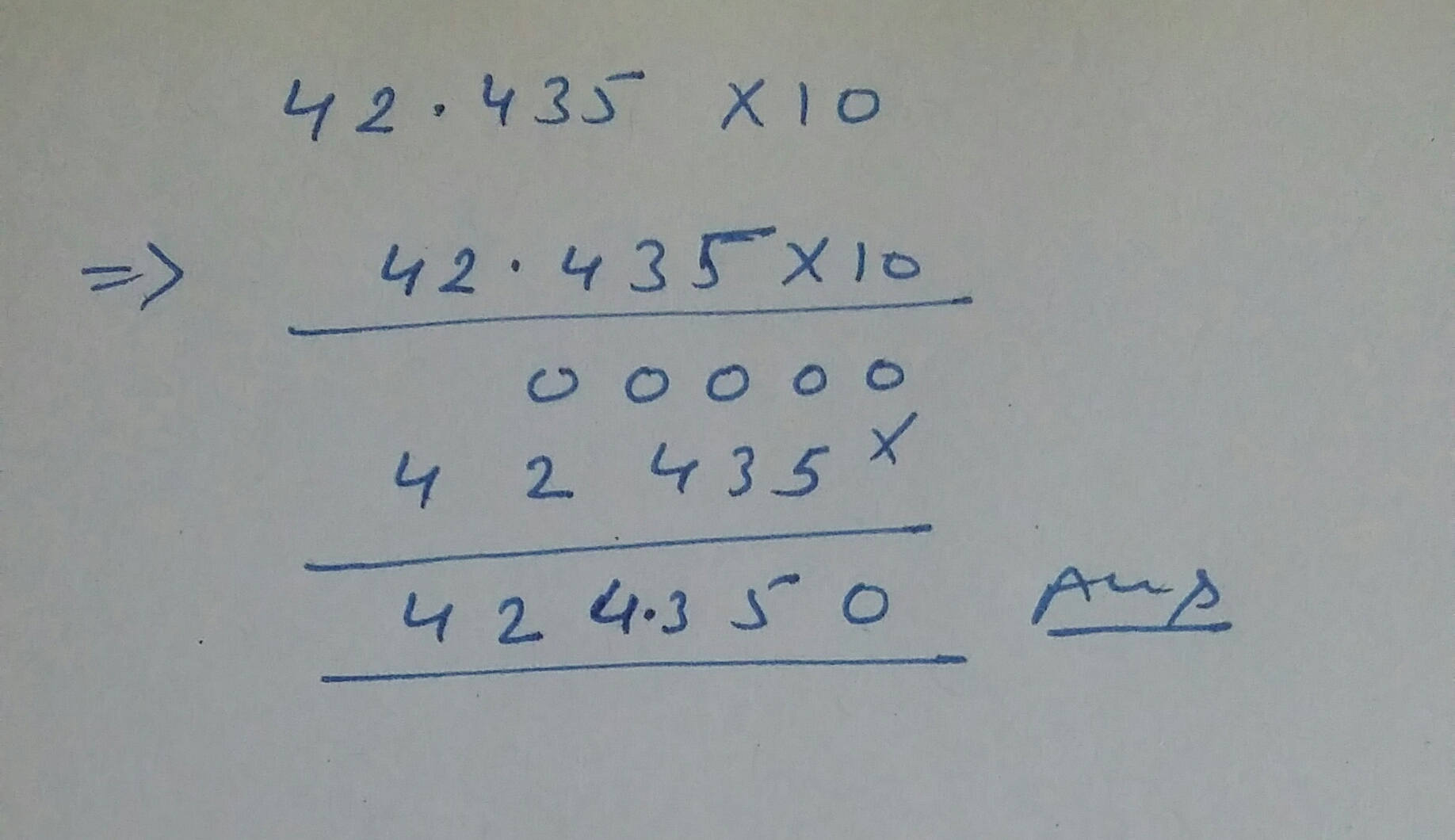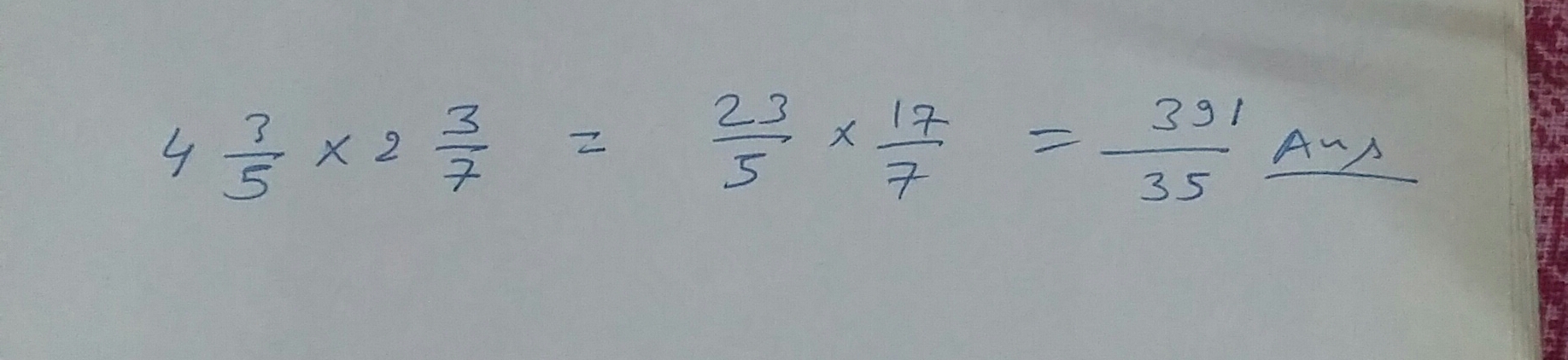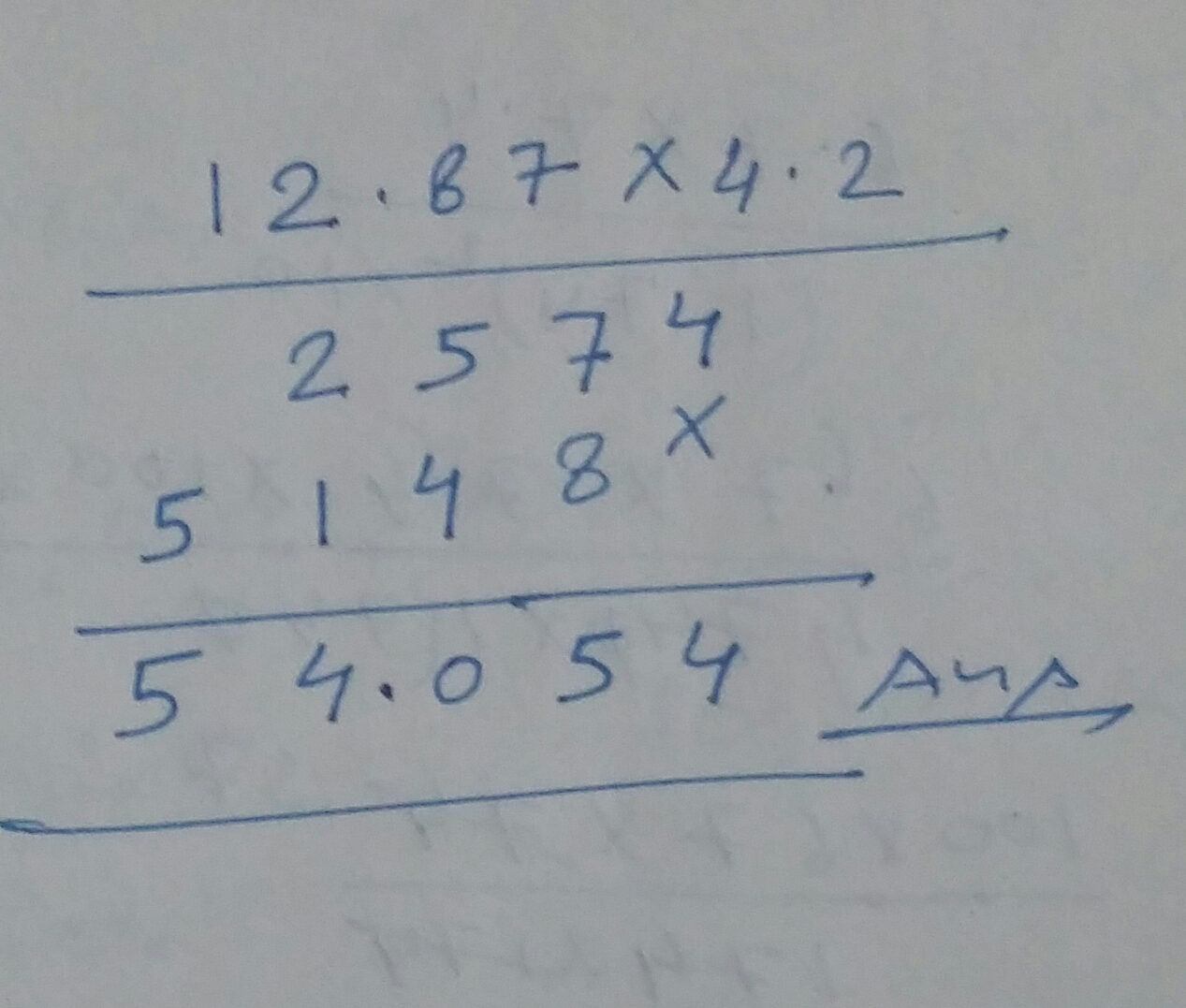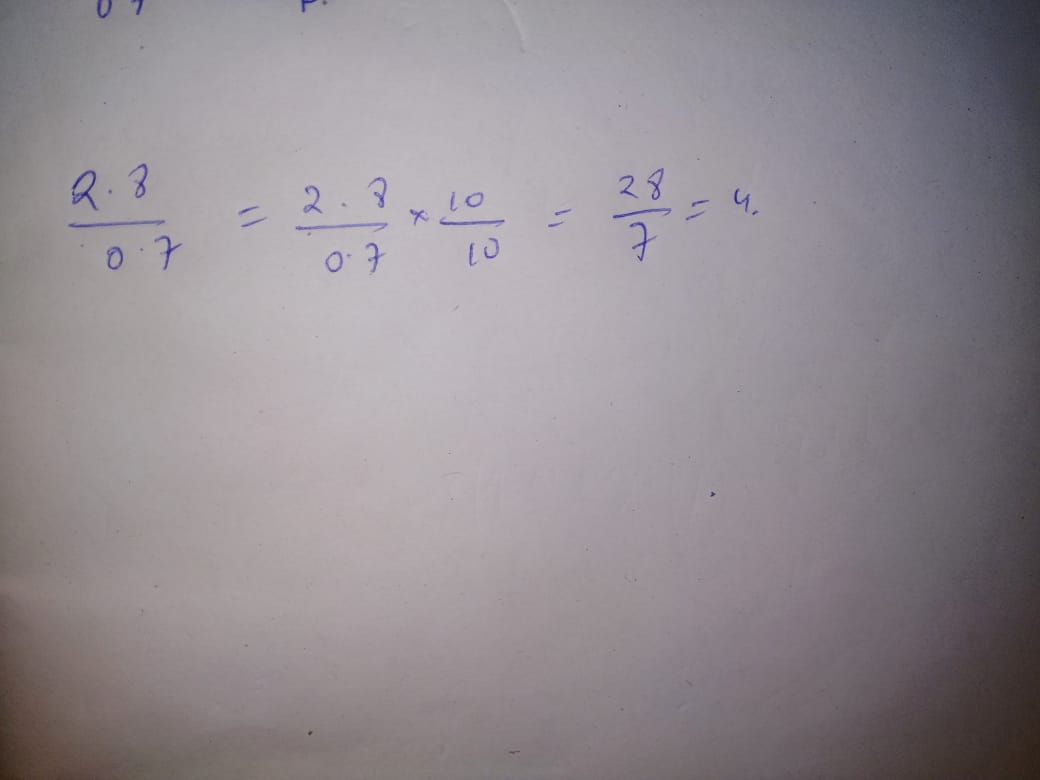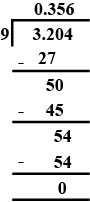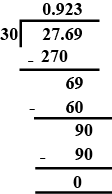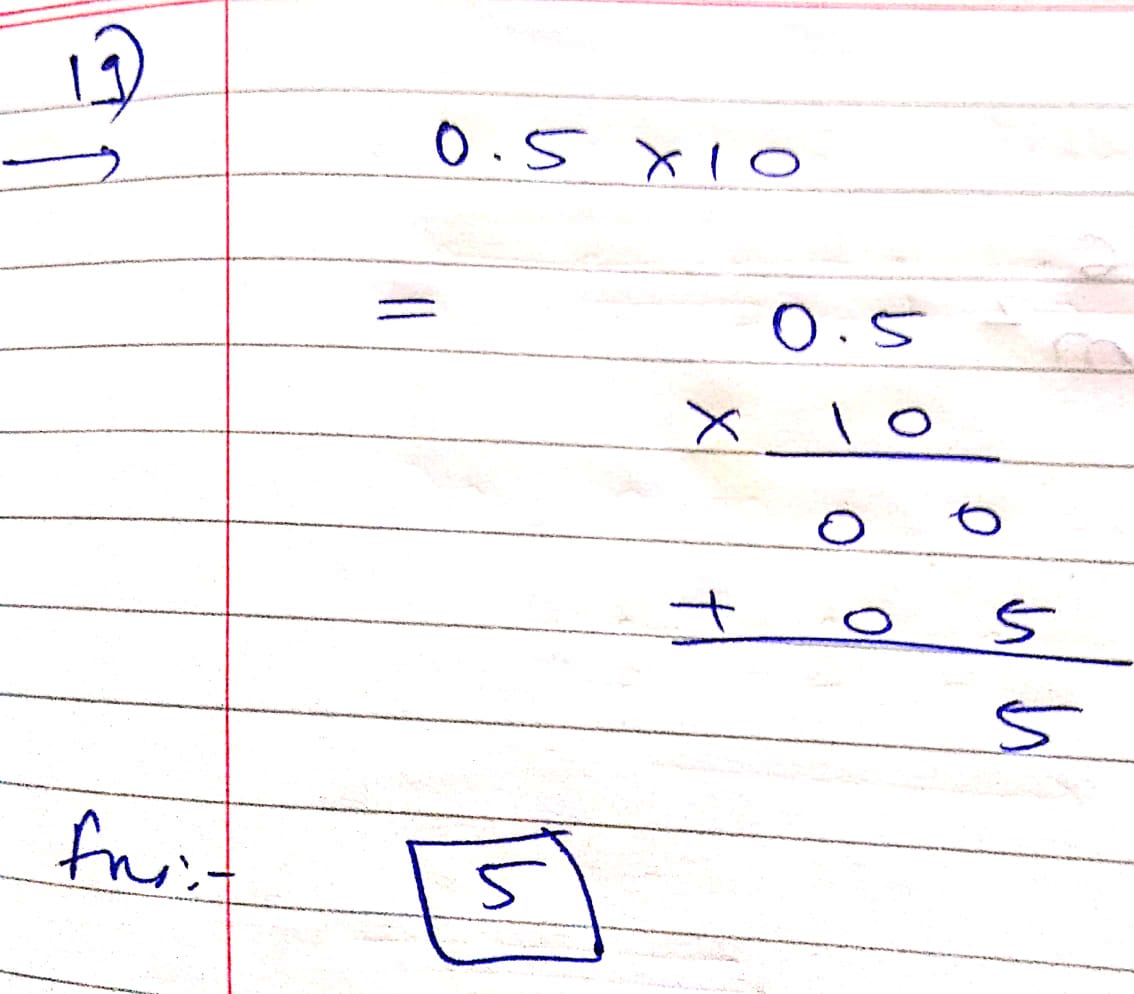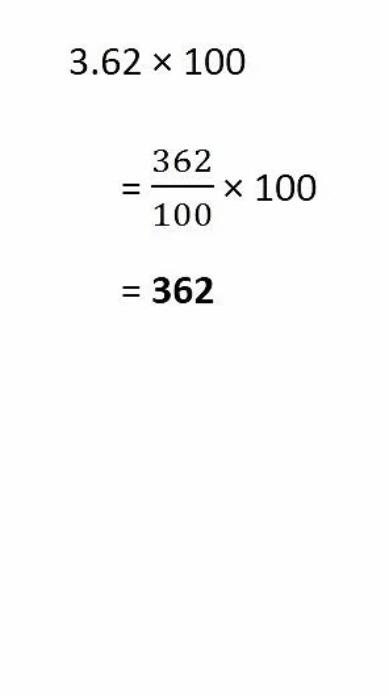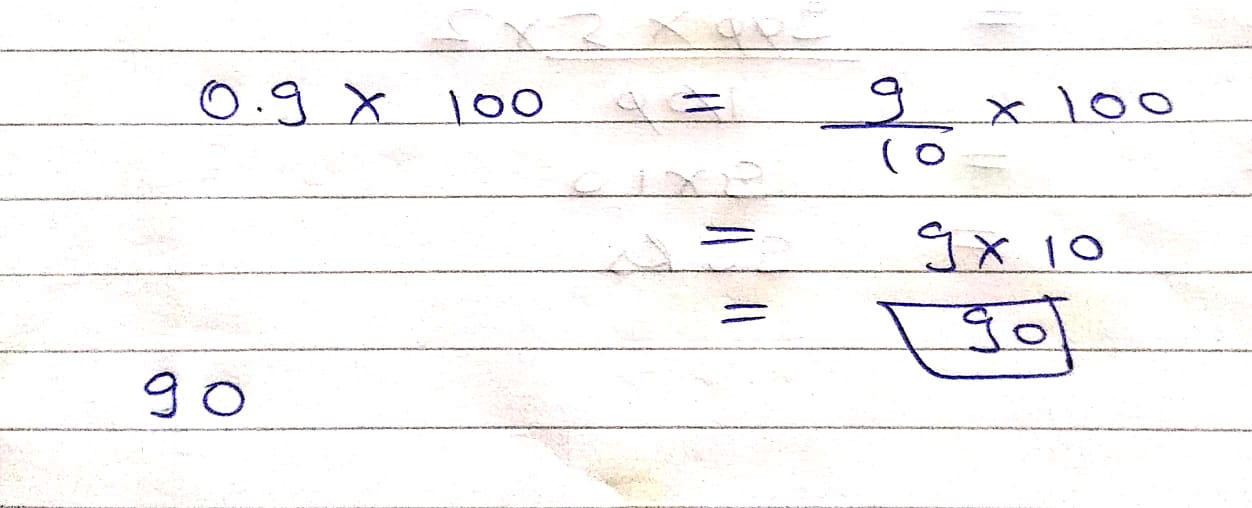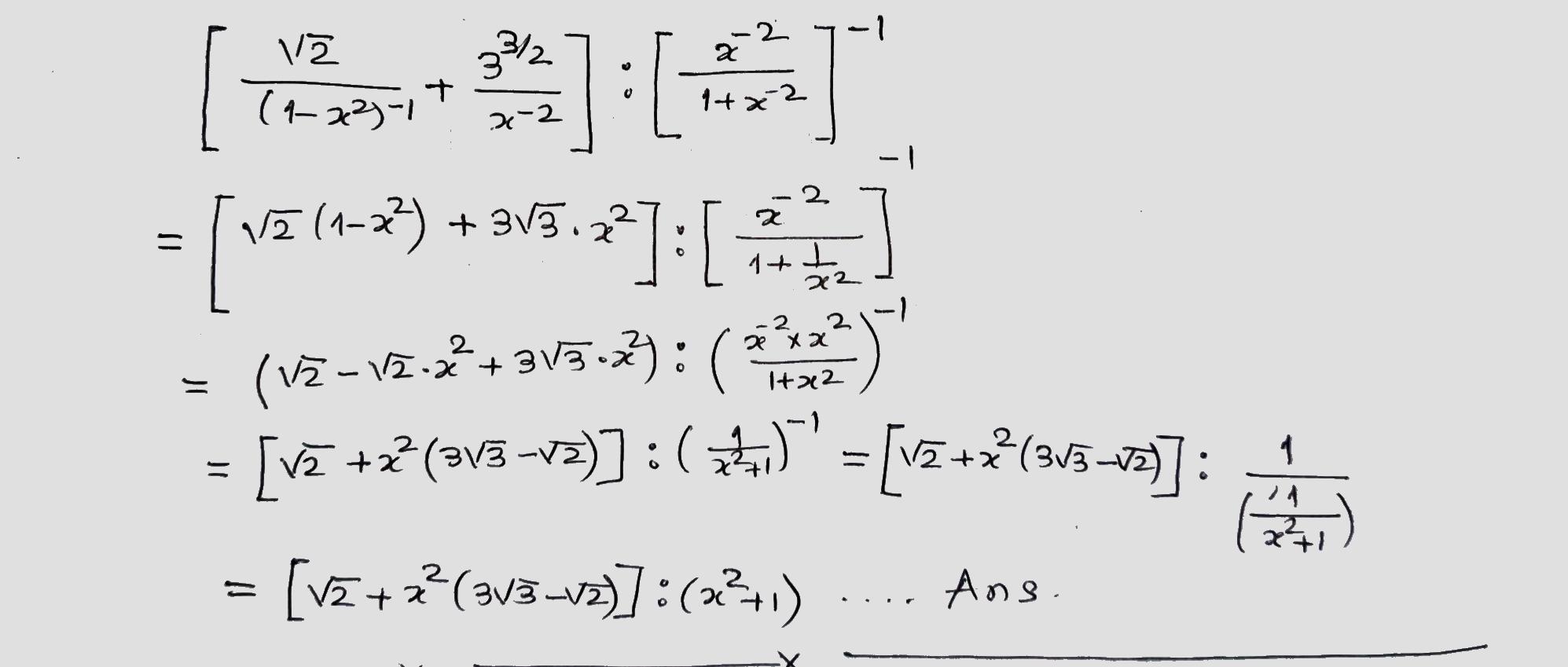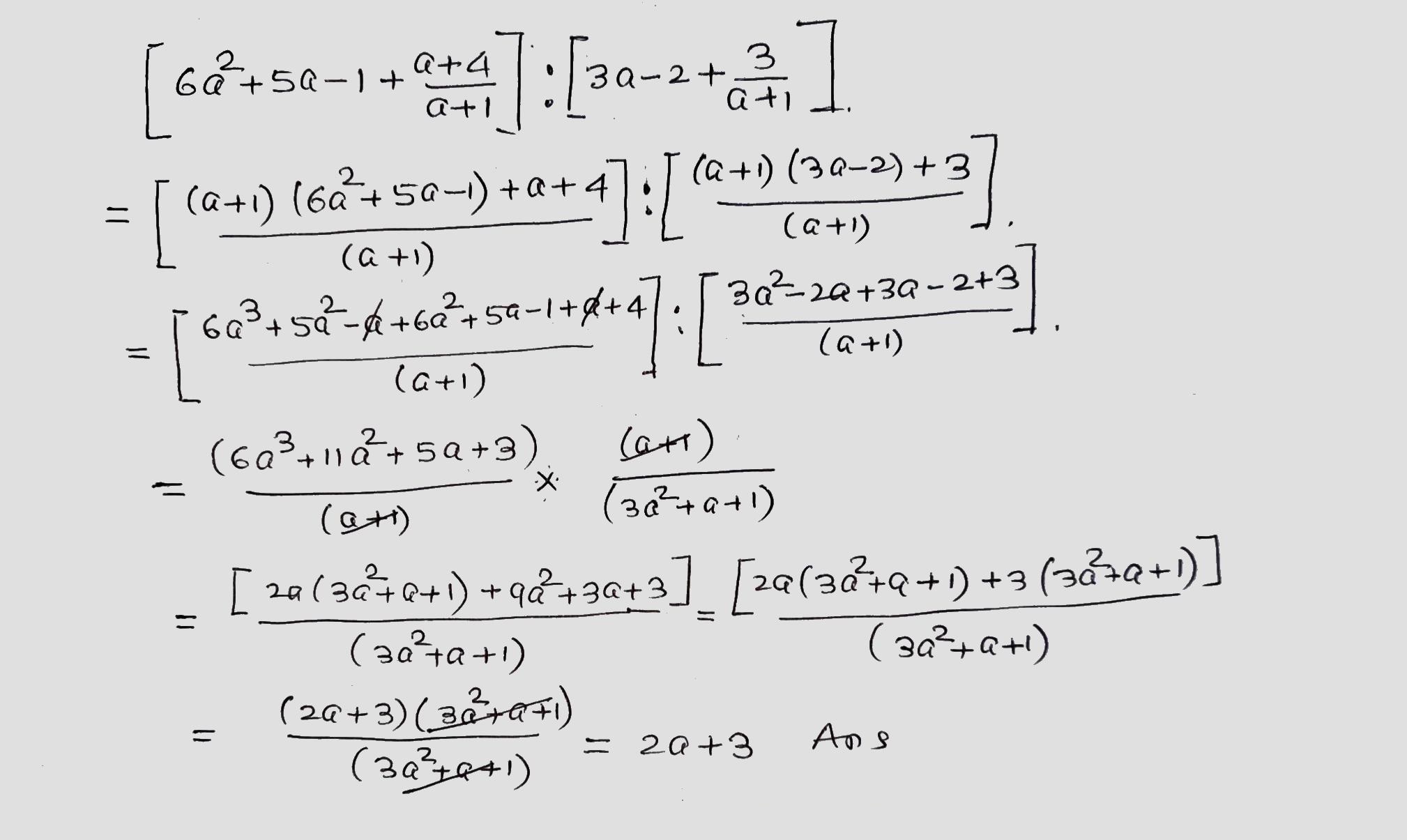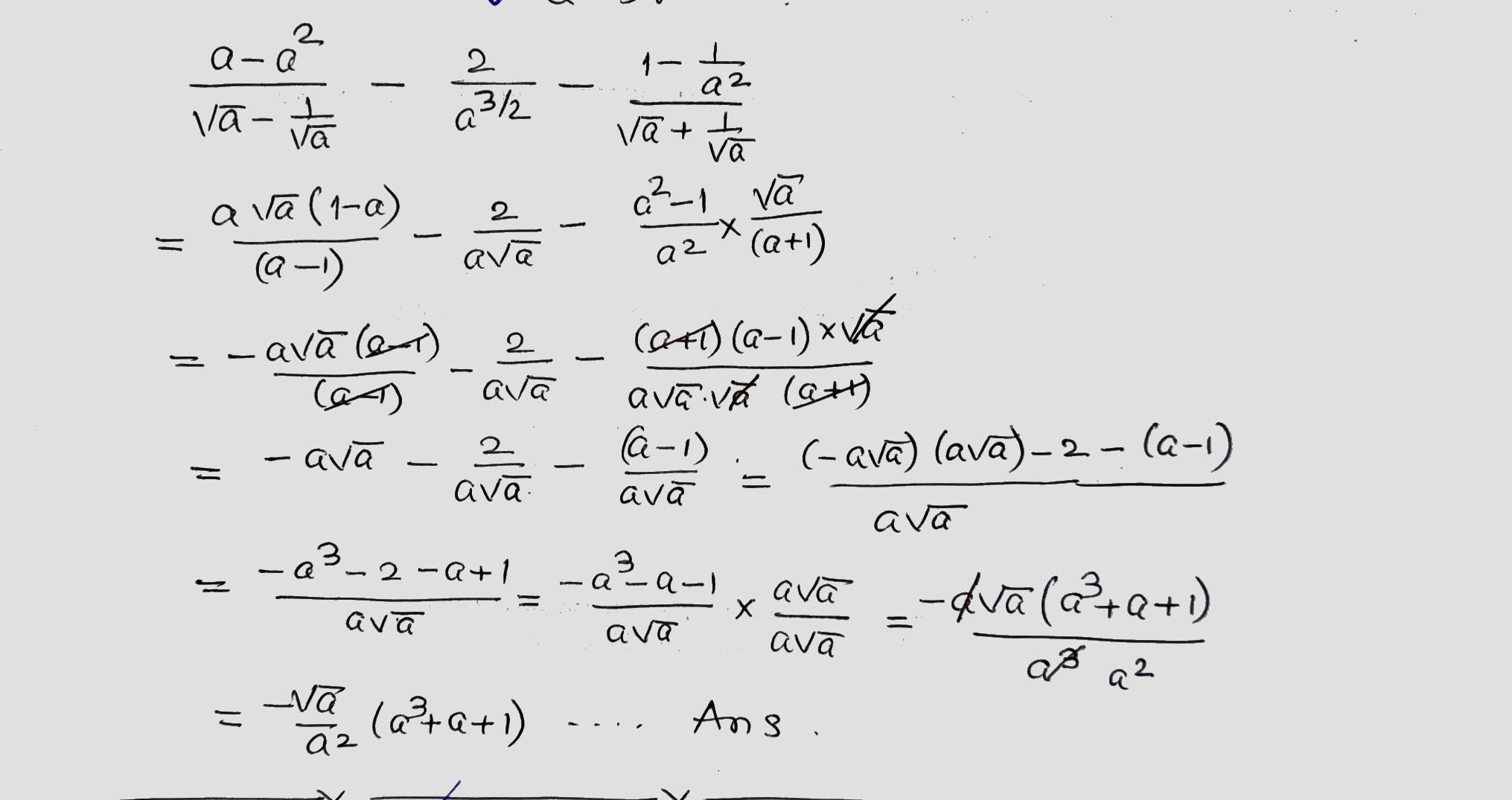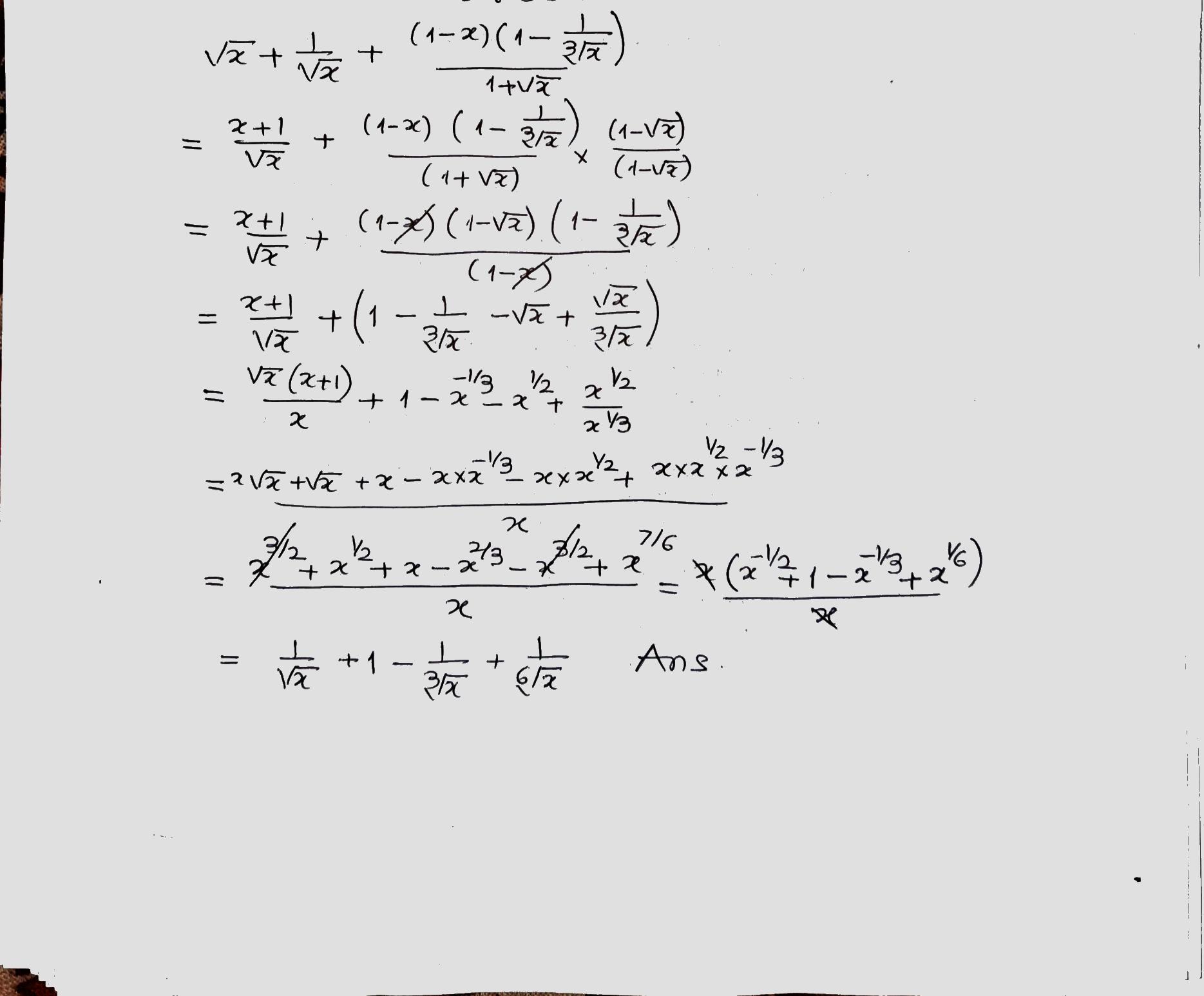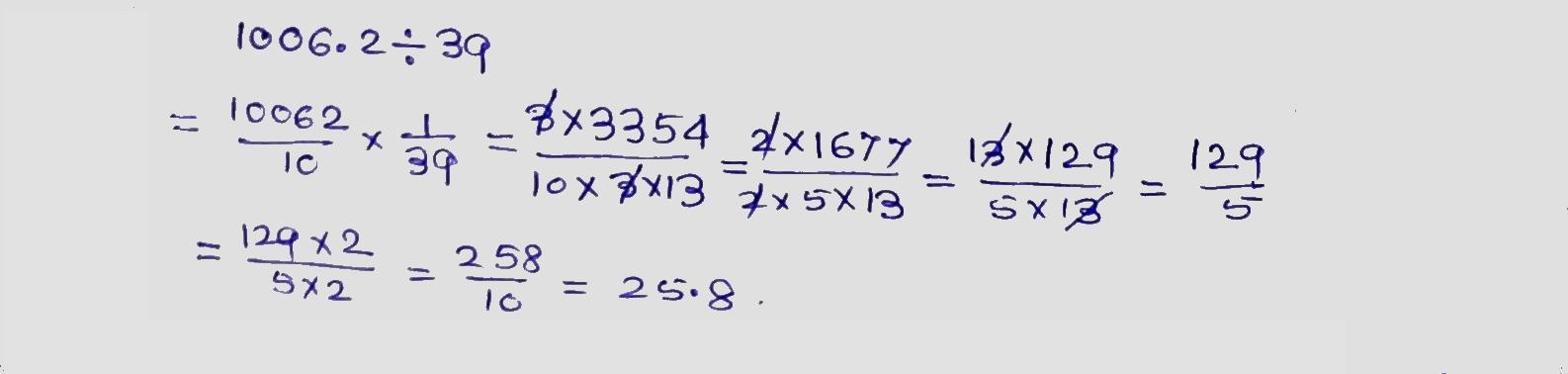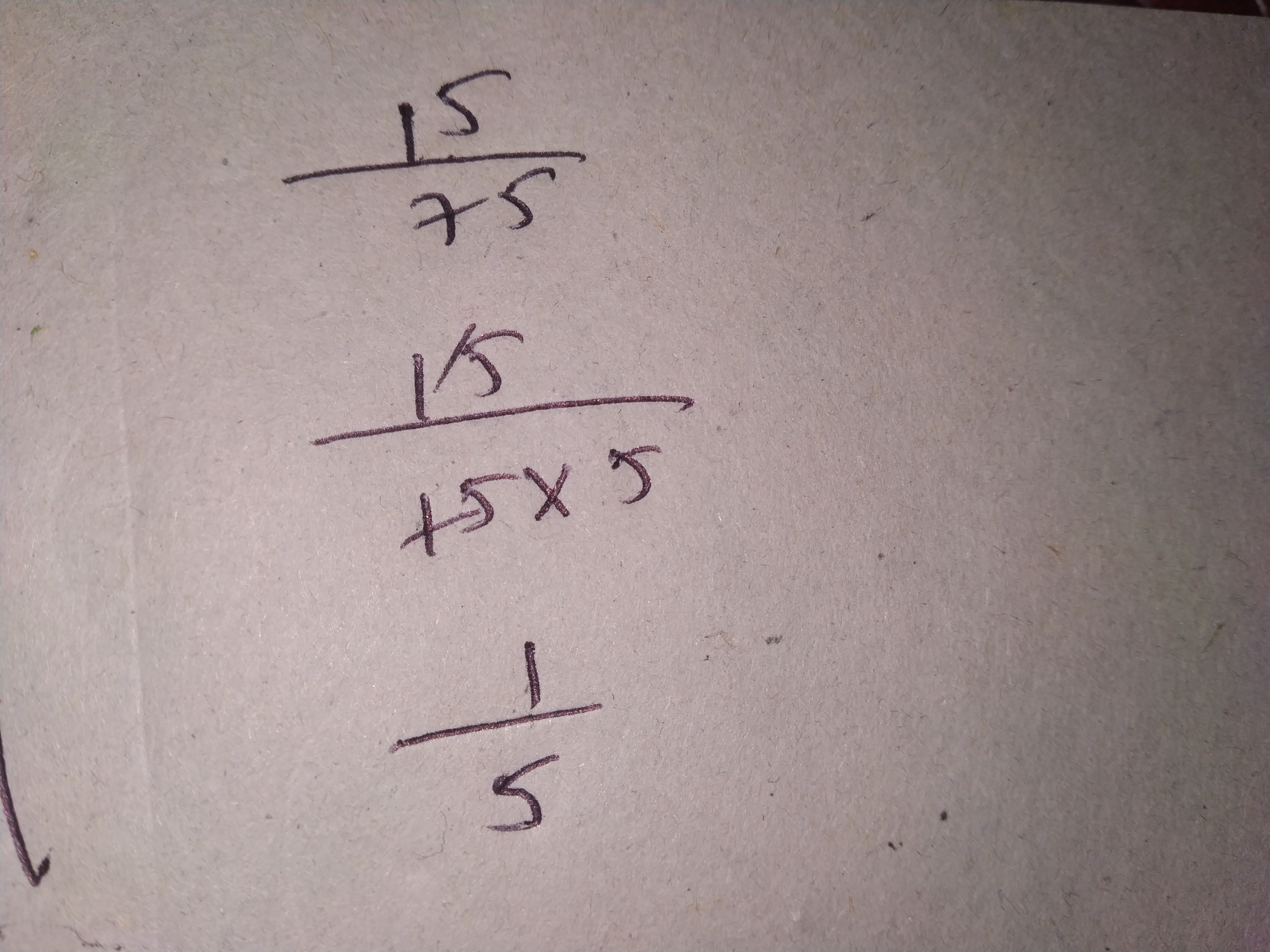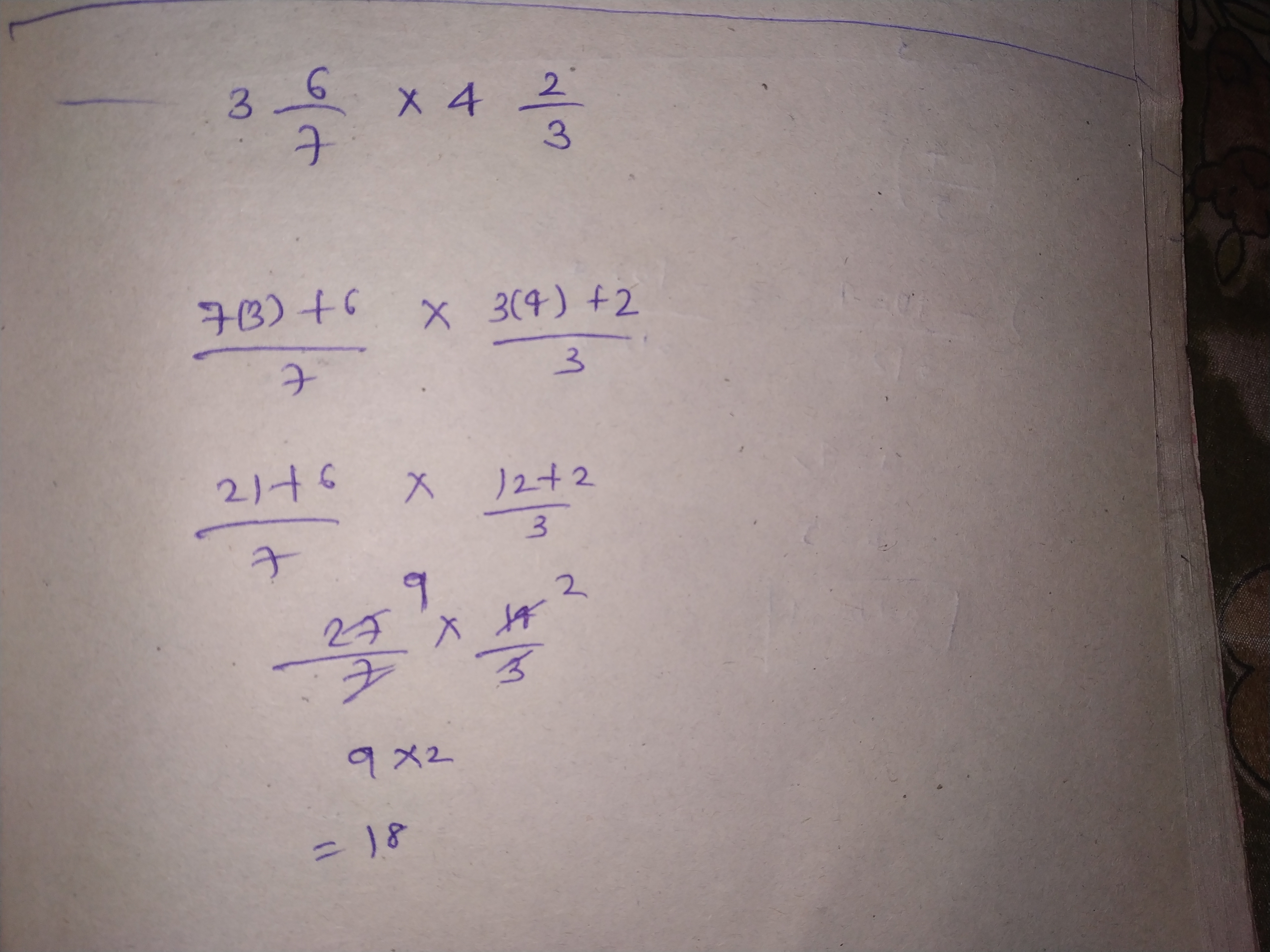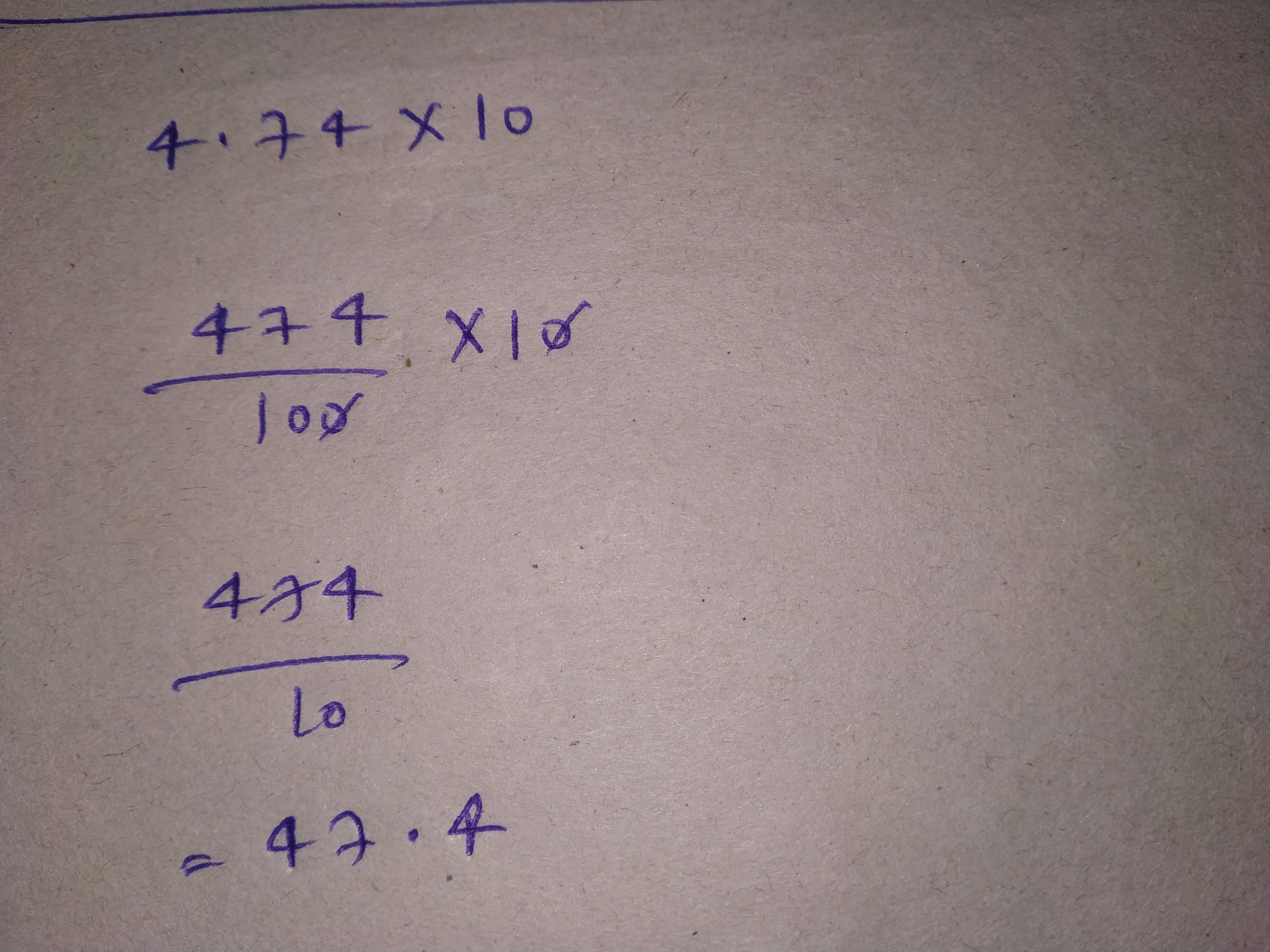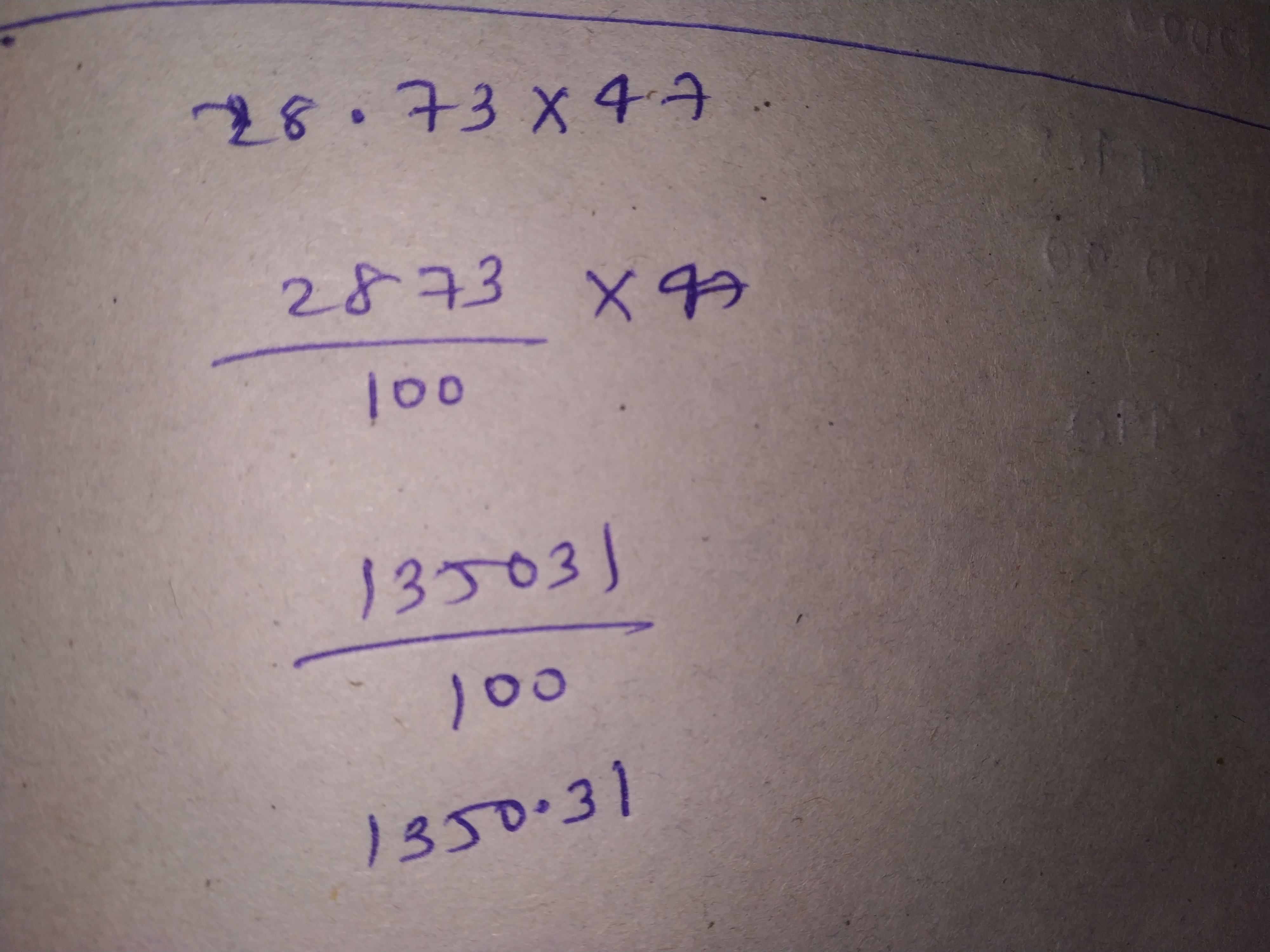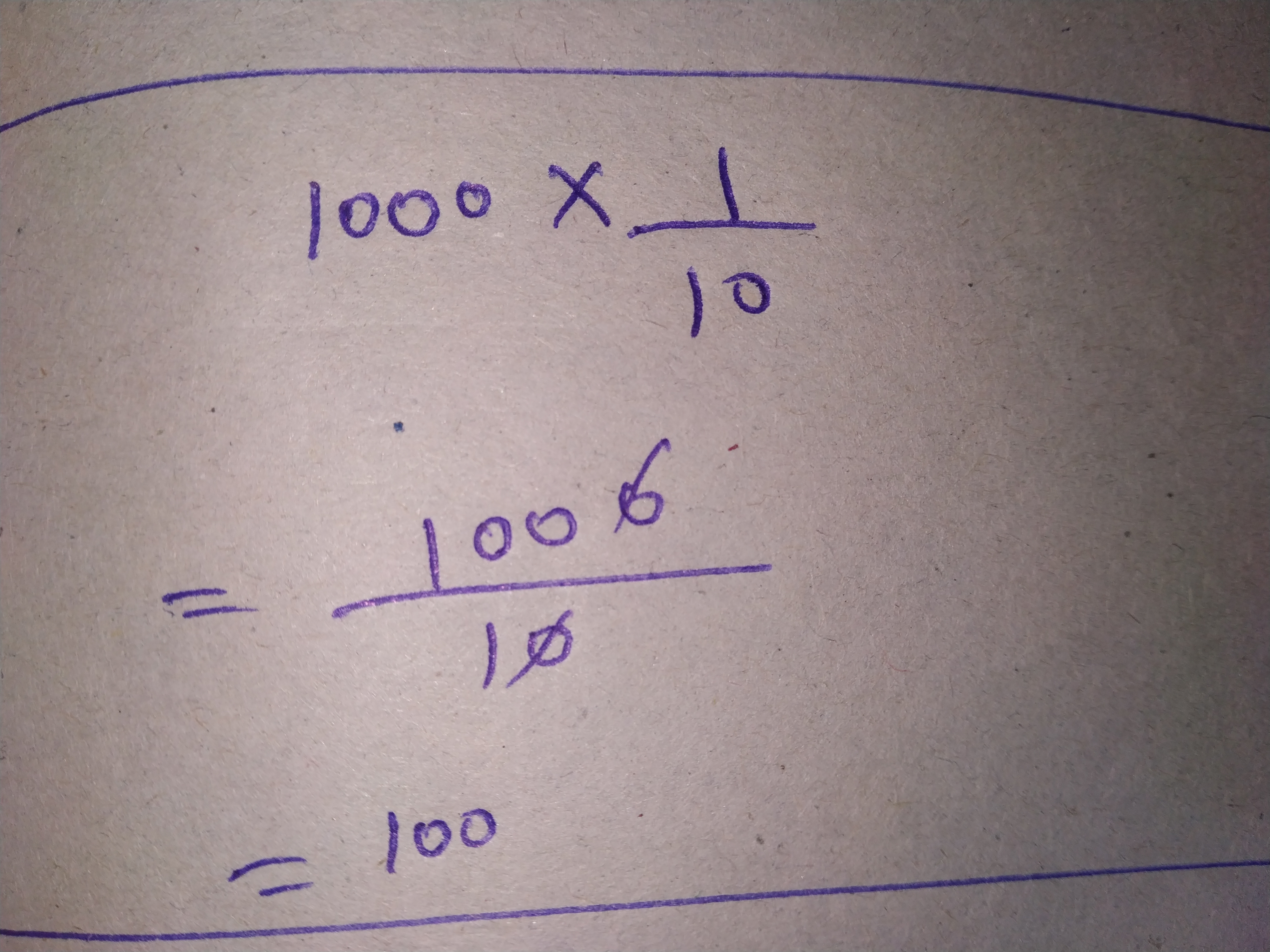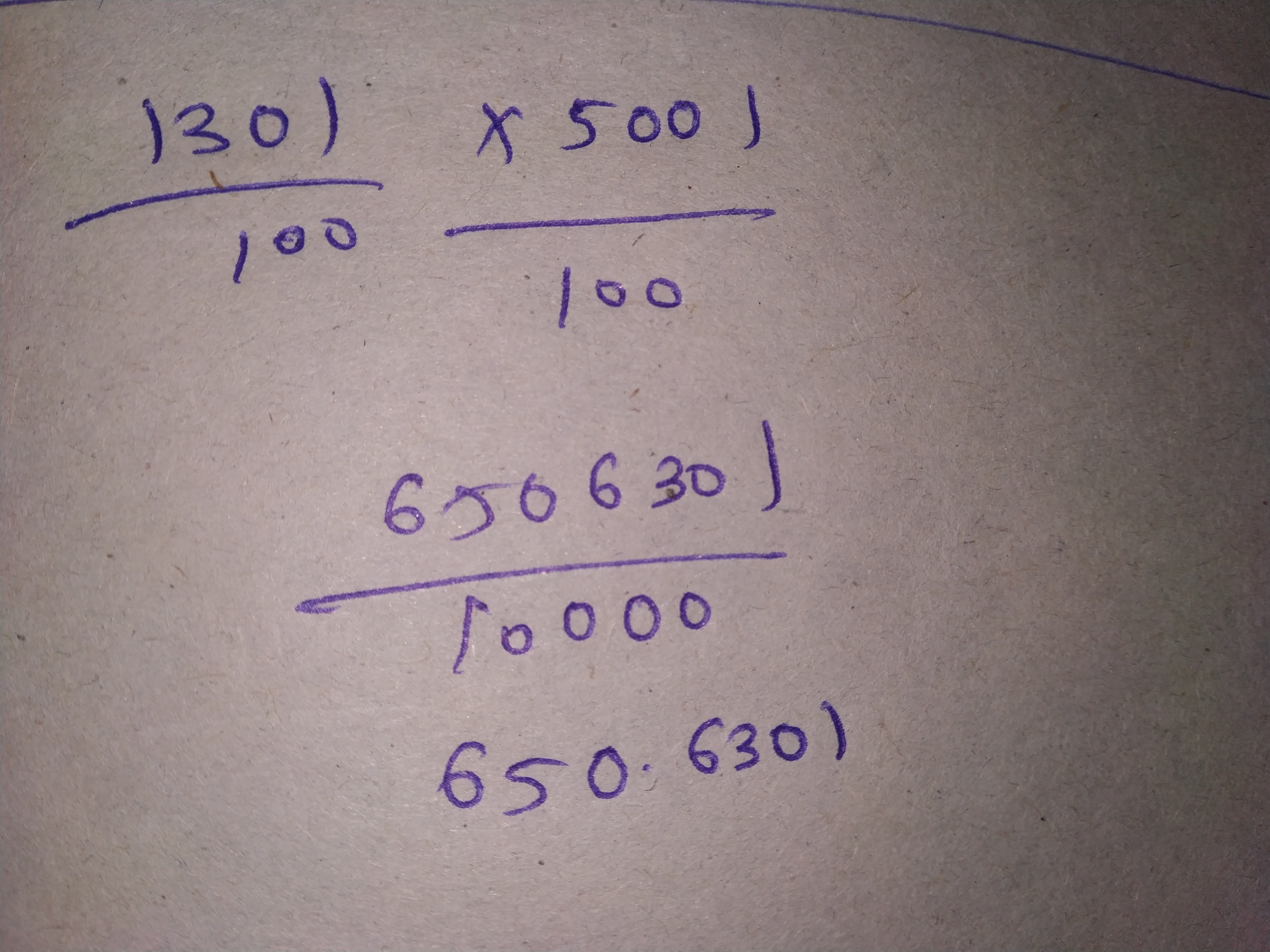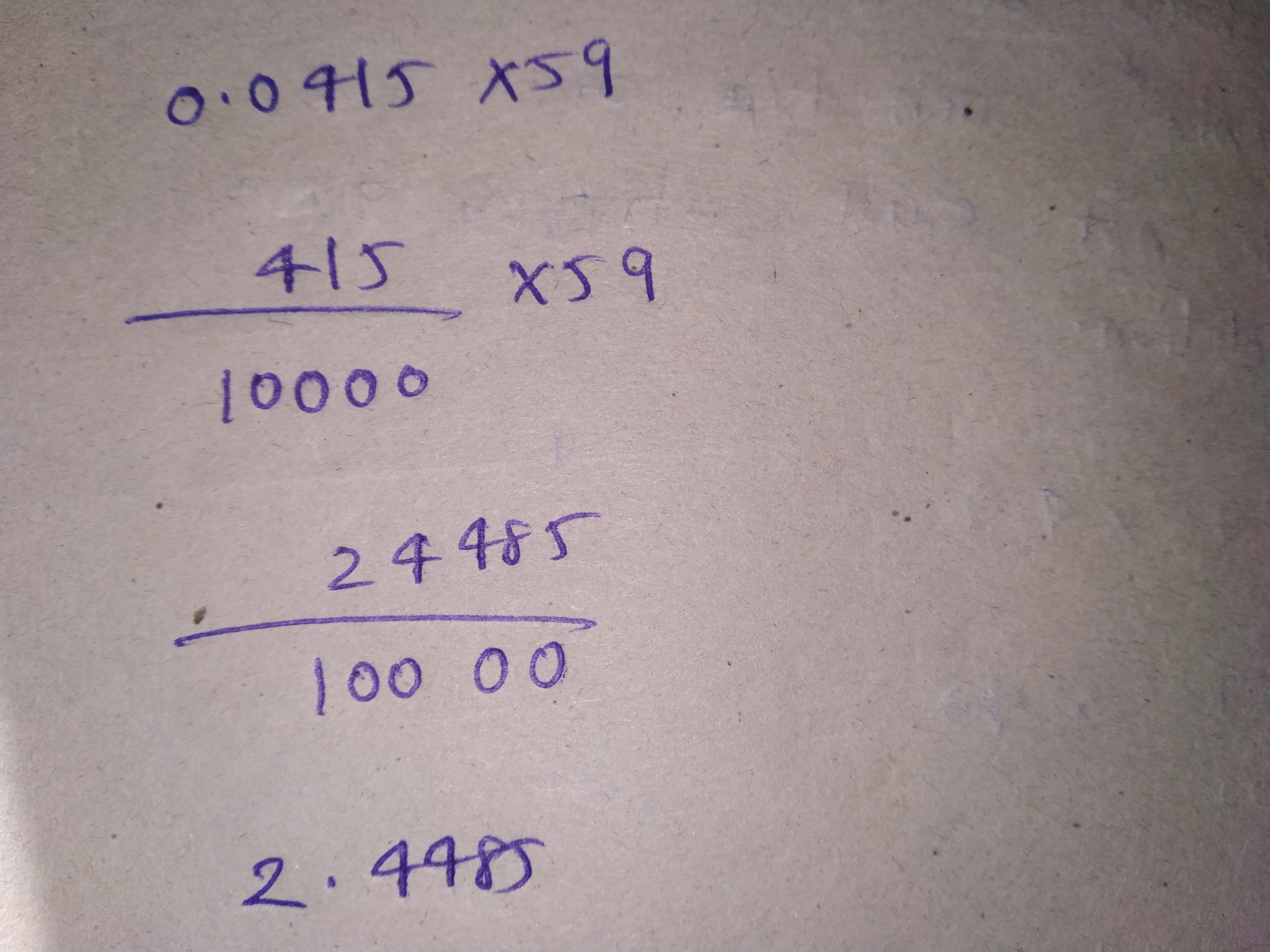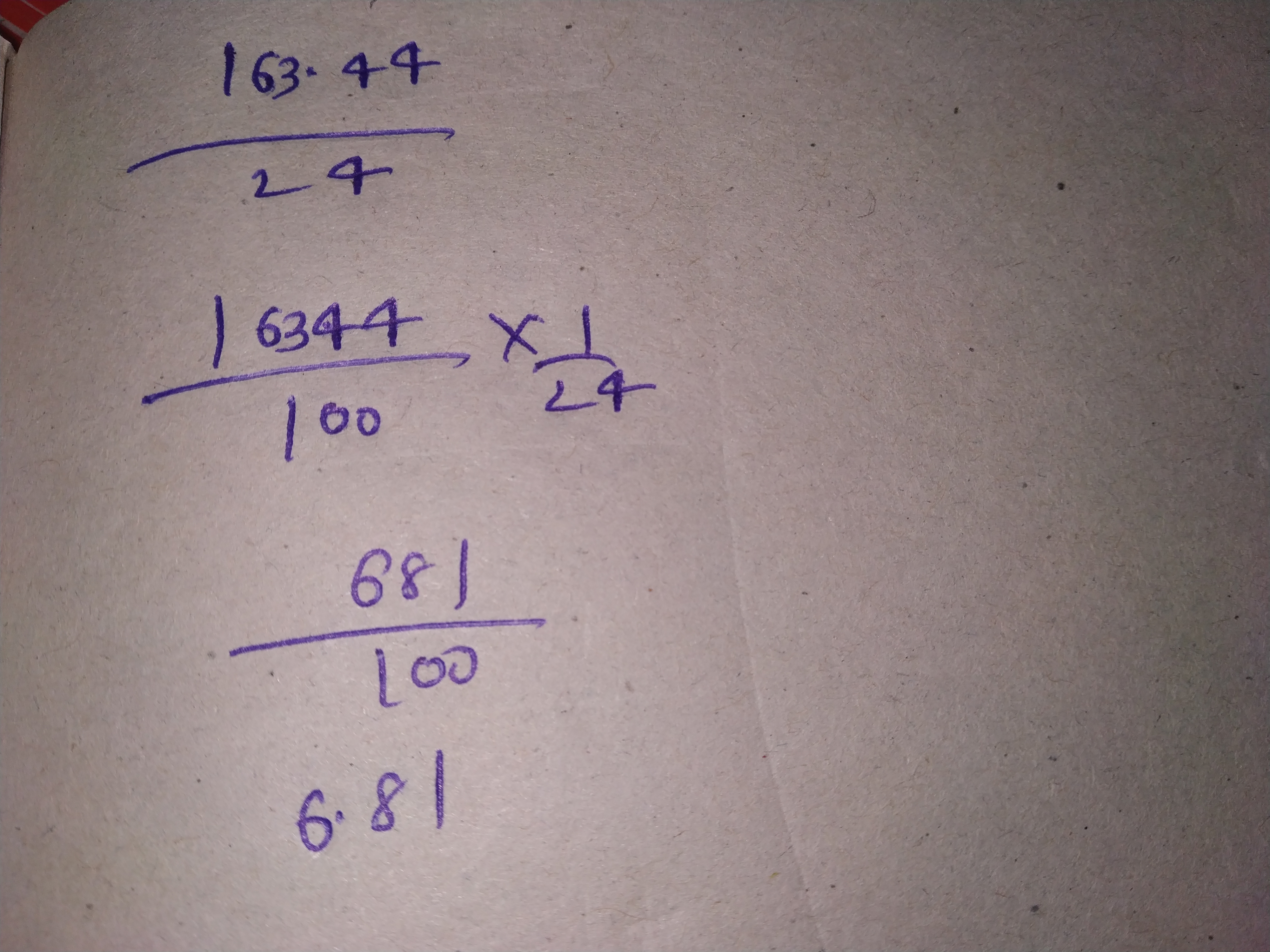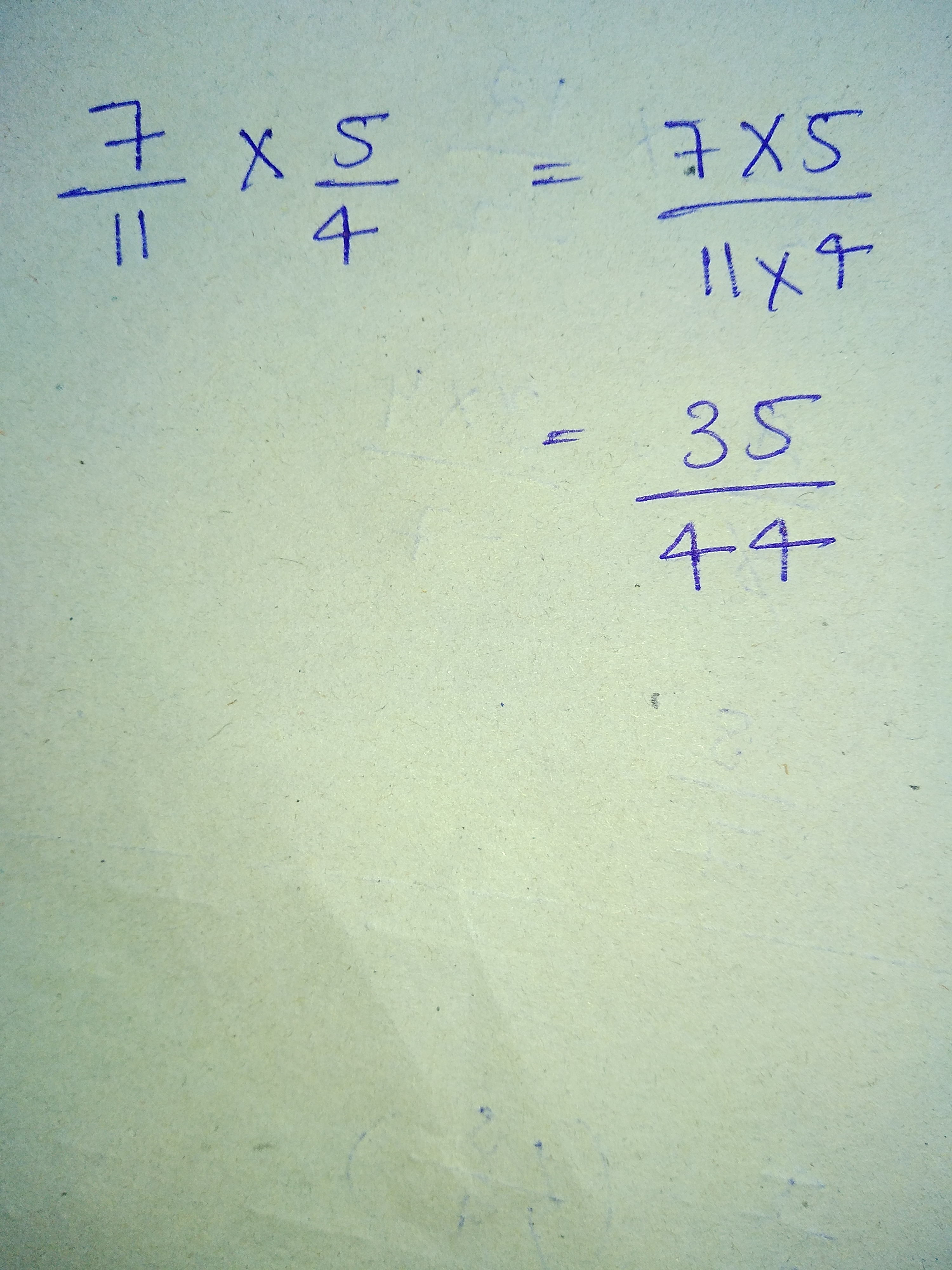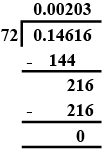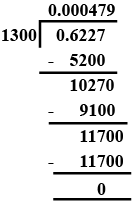Fractions And Decimals - Class 7 Maths - Extra Questions
$$23.2\div 100 =x$$. Find $$1000x$$
Convert the given mixed fractions into improper
$$2\dfrac {1}{5}$$
Convert the given mixed fractions into improper
$$2\dfrac {1}{2}$$
Convert the given mixed fractions into improper
$$3\dfrac {1}{6}$$
Convert the given mixed fractions into improper
$$7\dfrac {2}{9}$$
Convert the given mixed fractions into improper
$$6\dfrac {1}{10}$$
Convert the given mixed fractions into improper
$$4\dfrac {2}{3}$$
Find $$2\dfrac{1}{2}%$$ of $$320$$ people.
find : $$2.5 \times 0.3$$
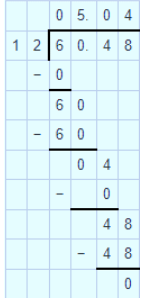
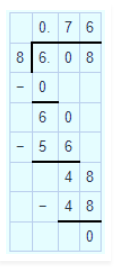
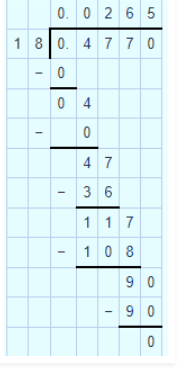
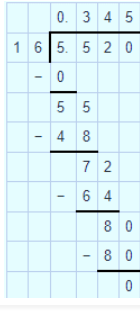
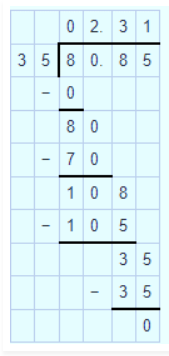
$$18.368\div 14$$.
Divide each of the given numbers by $$10,100,1000$$ and 10000$$:$$$$2.1$$$$8.64$$$$5.01$$$$0.0906$$$$0.125$$$$111.11$$
$$8.64$$
$$5.01$$
$$0.0906$$
$$0.125$$
$$111.11$$
Solve : $$0.5\times 0.05$$
Solve
(i) $$1.5\times 0.3$$
Solve: $$1.07\times 0.02$$
Solve: $$4.3\times 3.4$$
Solve: $$0.1\times 47.5$$
Solve:$$10.05\times 1.05$$
Solve : $$70.01\times 1.1$$
Find:
$$0.2\times 6$$
Find
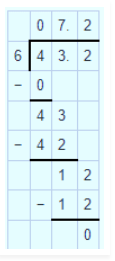
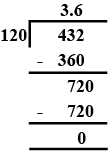
$$651.2 \div 4$$
Convert the following into a vulgar fraction:
$$2.\overline { 13 } $$
Let $$y=2.131313$$
$$\Rightarrow 100y=213.131313$$
$$-99y=-211$$
$$\Rightarrow y=\dfrac{211}{99}$$.
Fill in the blank.
$$1.1 \times 100=$$______
Convert the following into a vulgar fraction:
$$0.\bar { 8 } $$
Let $$y=0.8888$$
$$\Rightarrow 10y=8.888$$
$$-9y=-8$$
$$\Rightarrow y=\dfrac{8}{9}$$.
Multiply : $$0.1\times 51.7$$
Simplify:$$9\displaystyle \dfrac{5}{10} $$
Convert the following into a vulgar fraction:
$$0.\overline { 34 } $$
Let $$y=0.343434$$
$$100y=34.343434$$
$$-99y=-34$$
$$\Rightarrow y=\dfrac{34}{99}$$.
Fill in the blank.
$$0.345 \times 1000=$$______
Fill in the blank.
$$5.9 \times 1000=$$_____
Fill in the blank.
$$10.056 \times 100=$$______
Fill in the blank.
$$5.76 \times 10=$$________
What is the value when $$442.36\ km$$ is divided by $$2$$.
What is $$10$$ times of $$50.30 $$kg.
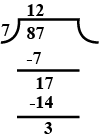
Convert $$ \dfrac{87}{7} $$ into mixed fraction.
$$ \therefore \dfrac {87}{7}$$ in mixed fraction $$= 12 \dfrac {3}{7} $$
To multiply a decimal number by 1000, we move
the decimal point in the number to the right by three places.
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, (a + a^{1/2} b^{1/2})(a + b)^{-1}(\sqrt{a}(\sqrt{a} -\sqrt{b})^{-1} - (\frac{\sqrt{a} + \sqrt{b}}{\sqrt{b}})^{-1})$$
Convert the following into a vulgar fraction:
$$0.\bar { 6 } $$
$$2.4\div 10=$$
Simplify:
$$3.24\div 0.0016$$
Divide $$0.57$$ by $$10$$.
Find:
$$211.9 \times 1.13$$
Divide $$54.25$$ by $$10$$.
Divide $$0.004$$ by $$10$$.
Divide:
$$0.45$$ by $$9$$
Divide $$0.48$$ by $$100$$.
Divide:
$$40.32$$ by $$9.6$$
Divide $$0.71$$ by $$1000$$.
Divide $$3.8$$ by $$1000$$.
Divide $$74.3$$ by $$100$$.
Divide $$0.7$$ by $$100$$.
Divide:
$$217.44$$ by $$9$$
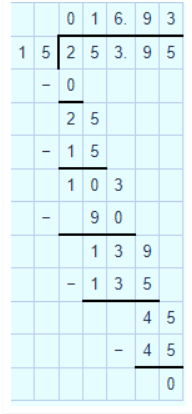
Divide: $$319.2$$ by $$2.28$$
Divide $$29.5$$ by $$1000$$.
Divide:
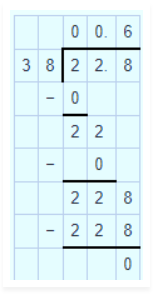
$$31.92$$ by $$228$$
Divide:
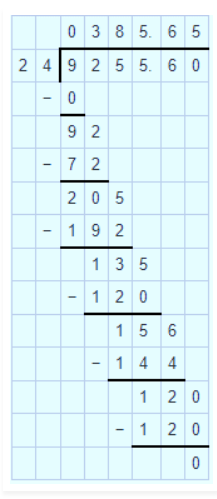
$$403.2$$ by $$96$$
Divide:
$$0.765$$ by $$0.9$$
Divide:
$$15.68$$ by $$20$$
Divide:
$$ 0.08 \quad by \quad 10 $$
Divide:
$$ 23.4 \quad by \quad 100 $$
Divide:
$$ 137.2 \quad by \quad 100 $$
Divide:
$$ 32.56 \quad by \quad 10 $$
Divide:
$$ 0.062 \quad by \quad 10 $$
Express the following improper fractions as mixed fractions:
$$25/6$$
Express the following improper fractions as mixed fractions:
18/5
Express the following mixed fractions as improper fractions:
$$3 \dfrac{1}{4}$$
Express the following improper fractions as mixed fractions:
$$22/5$$
Express the following improper fractions as mixed fractions:
$$38/5$$
Multiply each number by $$(i)10, (ii)100, (iii)1000 :$$
$$0.112$$
Multiply each number by $$10,100,1000 :$$
$$0.5$$
Multiply:
$$0.568$$ by $$6.4 $$
Express the following mixed fractions as improper fractions:
$$12\dfrac{ 7}{11}$$
Multiply each number by $$(i)10, (ii)100, (iii)1000 :$$
$$4.8$$
Multiply:
16.32 by 28
Divide:
$$324.76$$ by $$1000$$
Divide:
4.8432 by 0.08
$$4.8432$$ by $$0.08 $$
It can be written as
$$ 4.8432 \div 0.08 $$
Multiplied by $$10000$$
So we get
$$ 48432 \div 800=60.54$$
It can be written as
$$ 4.8432 \div 0.08 $$
Multiplied by $$10000$$
So we get
$$ 48432 \div 800=60.54$$
Evaluate :
$$ 0.125 \div 25 $$
$$ 0.125 \div 25 $$
We get
$$ 0.125 \div 25=0.005 $$
We get
$$ 0.125 \div 25=0.005 $$
Multiply each number by $$(i)10, (ii)100, (iii)1000 :$$
$$16.27$$
Evaluate:
$$ 5.897 \times 2.3 $$
Multiply each number by $$(i)10, (ii)100, (iii)1000 :$$
$$234.8 $$
Evaluate :
$$ 20.64 \div 16 $$
$$ 20.64 \div 16 $$
We get
$$20.64 \div 16=1.29$$
We get
$$20.64 \div 16=1.29$$
Divide:
$$27.918$$ by $$9$$
Multiply each number by $$(i)10, (ii)100, (iii)1000 :$$
$$0.0359$$
Evaluate :
$$ 19.25 \div 25 $$
$$ 19.25 \div 25 $$
We get
$$19.25 \div 25=0.77$$
We get
$$19.25 \div 25=0.77$$
Evaluate :
$$ 257.894 \div 0.169 $$
$$ 257.894 \div 0.169 $$
Multiplying by 1000
$$ 257894 \div 169=1526 $$
Multiplying by 1000
$$ 257894 \div 169=1526 $$
Solve : $$ 13 \dfrac{5}{6} \times 1\dfrac{5}{26}$$
Divide the following numbers by $$10, 100$$ and $$1000$$ ( orally):
$$3.45$$
Evaluate :
$$ 9.75 \div 5 $$
$$ 9.75 \div 5 $$
We get
$$ 9.75 \div 5 =1.95 $$
We get
$$ 9.75 \div 5 =1.95 $$
For the celebration class $$VII$$ bought sweets for $$Rs.740.25$$ and cold drink for $$Rs.70$$. If $$35$$ students contributed equally what amount was contributed by each student.
Fill in the blank.
$$32.4 \times 10=$$______
Fill in the blank.
$$0.369 \times 10=$$________
Fill in the blank.
$$2.35 \times 1000=$$____
Fill in the blank.
$$0.25 \times 100=$$_____
Divide $$0.043$$ by $$10$$.
$$8.892\div 19=x$$. Find $$1000x$$
$$324.4\div 100 =x$$. Find $$1000x$$
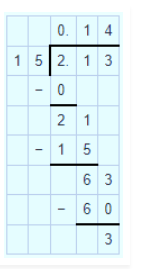
$$35.7\div 10 =x$$. Find $$100x$$
If $$0.24\div 0.6=x$$. Find $$10x$$
Find $$1.5\div 0.05=$$
If cost of a pen is $$Rs. 6.25$$ then the cost of $$14$$ such pens is
Find $$3.6\div 0.6$$.
$$0.2\div 10 =x$$. Find $$100x$$
Solve $$6.69\div 3=x$$. Find $$100x$$
Solve : $$\dfrac{9}{46} \times 7\dfrac{2}{3}$$
$$2.214 \div 18=x$$. Find $$1000x$$
Express the septenary fraction $$\cfrac{1552}{2626} $$ as a denary vulgar fraction in its lowest terms.
Solve the following:
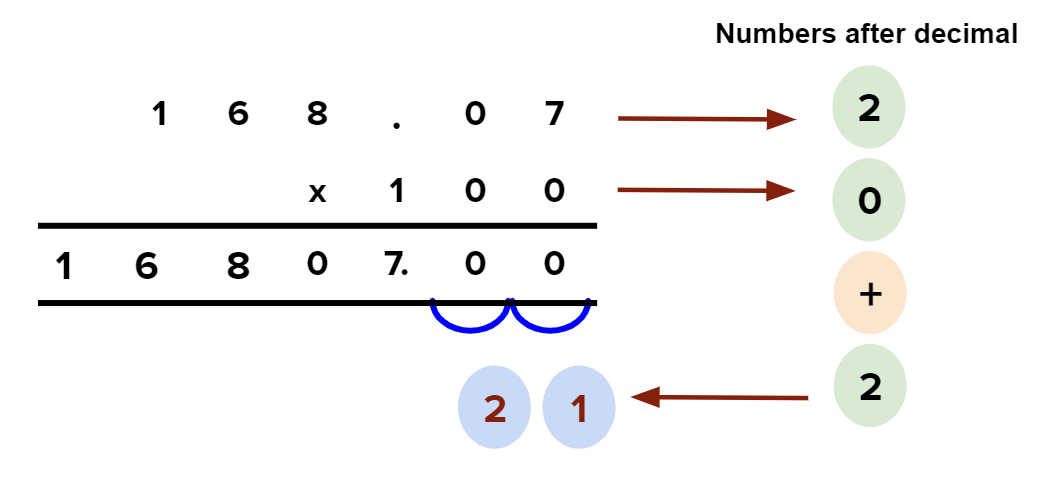
$$168.07\times 100$$
Solve the following:
$$131.1\times 100$$
Solve the following:
$$53.7\times 10$$
Solve the following:
$$36.8\times 10$$
Solve the following:
$$21.3\times 10$$
Solve the following:
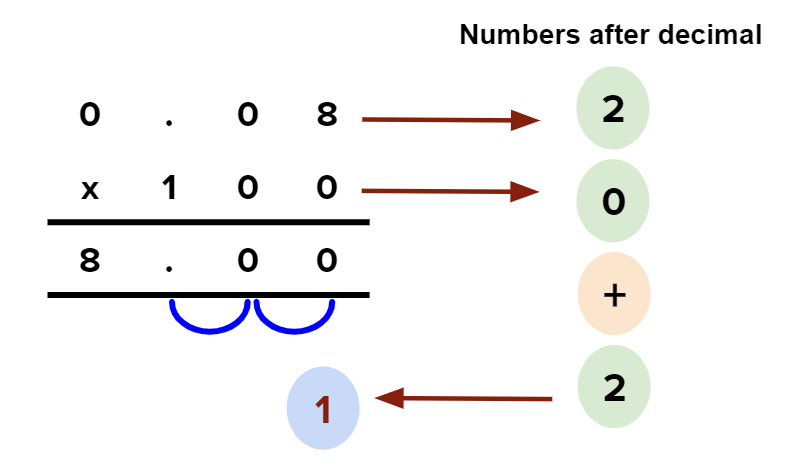
$$0.08\times 100$$
Solve the following:
$$0.03\times 1000$$
Solve the following:
$$88.5\div 0.15$$
$$\dfrac {6}{15}\times \dfrac {5}{18}=$$ $$\dfrac {x}{9}$$. Find x.
Solve $$50\dfrac{1}{2}\times 49\dfrac{1}{2}$$.
$$\dfrac {9}{10}\times \dfrac {5}{9}\times \dfrac {15}{25}=$$ $$\dfrac {x}{10}$$. Find x.
Calculate $$4.203\times 15000$$.
Calculate $$0.035\times 1200$$.
Evaluate $$2.25\times 4$$.
$$3.4\times 10 =$$ ________.
$$2.97\times 100 =$$ _______.
$$3.4\times 1000 =$$ _______.
Calculate $$3.5\times 24$$.
$$0.46\times 100 =$$ _________.
$$0.5\times 10 =$$ ____________.
Calculate $$6.54\times 50$$.
$$0.25\times 1000 =$$ __________.
Solve $$2.1\times 100 =$$ ______.
Calculate $$7.604\times 0$$.
$$14.63\div 11=x$$. Find $$100x$$
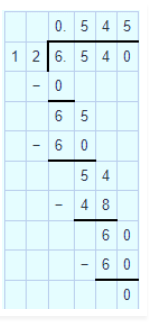
$$13.92\div 12=x$$. Find $$100x$$
$$48.3\div 14=x$$. Find $$100x$$
$$45.645 \div 15=x$$. Find $$1000x$$
$$39.39\div 13=x$$. Find $$100x$$
Solve $$2.24\times 100 =$$ ______.
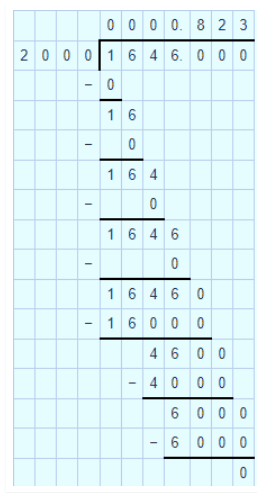
$$24.6\div 100 =x$$. Find $$1000x$$
Hitesh and Hiral goes to market to buy some items for their home. Rate of items are in kg. Answer the following question on its base. How much is the price of $$4\ kg$$ Rice in rupees?
$$620.5 \div 10 =x$$. Find $$100x$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \frac{x^{1/2} + 1}{x + x^{1/2} + 1} : \frac{1}{x^{1/2} - 1}$$
Divide $$3.96$$ by $$4$$
Convert each of the following into mixed fraction :
$$(1)\dfrac{17}{5}$$ $$(2)\dfrac{62}{7}$$ $$(3)\dfrac{101}{8}$$
$$(4)\dfrac{95}{13}$$ $$(5)\dfrac{81}{11}$$ $$(6)\dfrac{87}{16}$$
$$(7)\dfrac{113}{12}$$ $$(8)\dfrac{117}{20}$$
Simplify $$7\dfrac {1}{2} \times 3\dfrac {1}{3}$$
Evaluate $$9\dfrac {1}{11}\times 10\dfrac {1}{12}$$
Find the value of :
(i) $${(82)^2} - {(18)^2}$$
(ii) $$\,\,{(128)^2} - {(72)^2}$$
(iii) $$\,197 \times 203\,\,$$
(iv) $$\dfrac{{198 \times 198 - 102 \times 102}}{{96}}$$
(v) $$(14.5 \times 15.3)\,$$
(vi) $$\,\,\,\,\,{(8.63)^2} - {(1.37)^2}$$
Solve $$45.30 \div 15$$
Multiply: $$\dfrac { 4 }{ 5 } \times 6\dfrac { 1 }{ 4 } $$
Find
(i) $$0.4\, \div \,\,2$$
(ii) $$0.35\, \div \,\,5$$
(iii) $$2.48\, \div \,\,4$$
(iv) $$65.4\, \div \,\,6$$
(v) $$651.2\, \div \,\,4$$
(vi) $$14.49\, \div \,\,7$$
(vii) $$3.96\, \div \,\,4$$
(viii) $$0.80\, \div \,\,5$$
Find
(i) $$7.9\, \div \,1000$$
(ii) $$128.9\, \div \,10$$
Work out the following division.
a. $$0.6\div2$$
b. $$0.625 \div 5$$
c. $$17.28 \div 9$$
d. $$7.2 \div 4$$
Rishi bought six school bags for Rs. $$712.02$$. What is the cost of each bag?
solve:
(i)$$6\frac{1}{4}\div 1\frac{1}{3}$$
(ii) $$12\div 1\frac{3}{4}$$
(iii)$$\frac{1}{3}\times 2\frac{1}{3}$$
Multiply:
$$2.57$$ by $$1.8$$
Find the product of $$\dfrac {12}{15} $$ & $$\dfrac {14 }{ 10}$$
$$\cfrac{0.036}{4}$$
Find the value of
$$3.852\div 1.8$$
Multiply:
$$1.5$$ by $$0.9$$
$$4\frac { 1 }{ 2 } \quad :\quad 1\frac { 1 }{ 8 } $$
Solve: $$42.435 \times 10=?$$
$$ 42.435\times 10 $$
$$ \Rightarrow 42.435\times 10 $$
______________
$$ 00000 $$
$$ 42435\times $$
______________
$$ 424.350 $$ Ans
Convert $$4\dfrac{11}{7}$$ into improper fraction:
Solve:$$4\dfrac{3}{5}\times 2\dfrac{3}{7}=\dfrac{23}{5}\times \dfrac{17}{7}= ?$$
$$\displaystyle 4\frac{3}{5}\times 2\frac{3}{7} = \frac{23}{5}\times \frac{17}{7} = \frac{391}{35} $$ Ans
Find the product :
$$3.762\times 10$$
$$6.4 \div 0.4$$
Simplify: $$5 \dfrac { 1 } { 6 } - 3 \dfrac { 1 } { 4 } + 3 \dfrac { 1 } { 3 } + 4$$
Solve:$$12.87 \times 4.2$$
$$ 12.87\times 4.2$$
__________
$$2574$$
$$5148 \times $$
__________
$$ 54.054$$ Ans
A student in a school pays $$3\frac { 1 }{ 5 } $$ as a fund. If the amount collected is $$406\frac { 2 }{ 5 } $$, find the number of students in the school.
Divide : $$3\dfrac{1}{2}\div \dfrac{3}{14}$$
$$ 3\frac{1}{2}\div \frac{3}{14} $$
$$ \Rightarrow \frac{7}{2}\times \frac{14}{3} = \frac{49}{3} $$
Simplify
$$2\dfrac {2}{7} \div 1\dfrac {4}{11} \times 2\dfrac {4}{9}$$
If in mixed fraction form $$\dfrac {19}{6}$$ is equal to $$3\dfrac {x}{6}$$, then what is the value of $$x$$ ?
Find the product :
$$19.638\times 10$$
Divide the following
$$2.8 \div 0.7$$
Solve $$\dfrac { 7 }{ 8 } +\dfrac { 5 }{ 12 } \times \dfrac { 9 }{ 10 } -\dfrac { 1 }{ 4 } $$.
Write these numbers in order, starting with the smallest.
$$0.55$$ $$\dfrac{6}{11}$$ $$54\dfrac{1}{2}\%$$
_______ $$<$$ _______ $$<$$ _______
Find :
$$211.02 \times 4$$
Find:
$$20.1\times 4$$
Find :
$$1.3\times 10$$
Find :
$$0.05\times 5$$
Find:
$$153.7\times 10$$
Find :
$$2.71\times 5$$
Find :
$$2\times 0.86$$
Find :
$$11.2\times 0.15$$.
Find :
$$1.3\times 3.1$$.
Find :
$$168.07\times 10$$.
Find :
$$0.2\times 316.8$$.
Find :
$$0.5\times 10$$.
Find :
$$156.1\times 100$$.
Find :
$$31.3\times 100$$.
Find :
$$0.08\times 10$$
Divide:
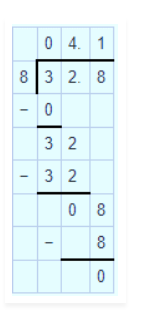
$$ 43.2 \quad by \quad 6 $$
Perform the division by considering the dividend a whole number.
When the division of the whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$43.2 \div 6$$
$$43.2 \div 6=7.2$$
When the division of the whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$43.2 \div 6$$
$$43.2 \div 6=7.2$$
Divide:
$$ 60.48 \quad by \quad 12 $$
Perform the division by considering the dividend a whole number.
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 60.48 \div 12 $$
$$ \therefore 60.48 \div 12 = 5.04 $$
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 60.48 \div 12 $$
$$ \therefore 60.48 \div 12 = 5.04 $$
Divide:
$$ 117.6 \quad by \quad 21 $$
Perform the division by considering the dividend a whole number.
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 117.6 \div 21 $$
$$ \therefore 117.6 \div 21 = 5.6 $$
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 117.6 \div 21 $$
$$ \therefore 117.6 \div 21 = 5.6 $$
Divide:
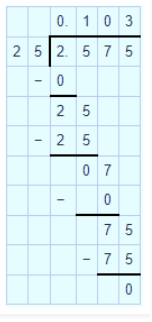
$$ 2.575 \quad by \quad 25 $$
Perform the division by considering the dividend a whole number.
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 2.575 \div 25 $$
$$ \therefore 2.575 \div 25 = 0.103 $$
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 2.575 \div 25 $$
$$ \therefore 2.575 \div 25 = 0.103 $$
Divide:
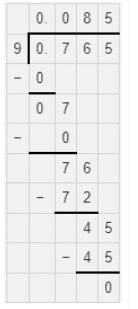
$$ 0.765 \quad by \quad 9 $$
Perform the division by considering the dividend a whole number.
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 0.765 \div 9 $$
$$ \therefore 0.765 \div 9 = 0.085 $$
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 0.765 \div 9 $$
$$ \therefore 0.765 \div 9 = 0.085 $$
Find the product: $$\dfrac{5}{8}$$ $$\times$$ $$\dfrac{4}{7}$$
Divide:
$$ 6.08 \quad by \quad 8 $$
Perform the division by considering the dividend a whole number.
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 6.08 \div 6 $$
$$ \therefore 6.08 \div 6 = 0.76 $$
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 6.08 \div 6 $$
$$ \therefore 6.08 \div 6 = 0.76 $$
Divide:
$$ 217.44 \quad by \quad 18 $$
Perform the division by considering the dividend a whole number.
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 217.44 \div 18 $$
$$ \therefore 217.44 \div 18 = 12.08 $$
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 217.44 \div 18 $$
$$ \therefore 217.44 \div 18 = 12.08 $$
Evaluate the following:
$$12.08\times 9.3$$
Evaluate the following:
$$238.06\times 7.5$$
Evaluate the following:
$$3.7\times 4.5$$
Work out the following:
$$72.8\div 0.04$$
Work out the following:
$$8.64\div 3.6$$
Multiply the following number by $$10, 100$$ and $$1000$$ orally:
$$.234$$
Work out the following:
$$0.144\div 0.02$$
Multiply the following number by $$10, 100$$ and $$1000$$ orally:
$$3.45$$
Work out the following:
$$70.756\div 4$$
Work out the following:
$$2.46\div 6$$
Evaluate the following:
$$0.79\times 32.4$$
Work out the following:
$$3.016\div 8$$
Convert the following mixed number into improper fractions :
$$(i) 7\dfrac{2}{11}$$
$$(ii) 3\dfrac{5}{48}$$
$$(iii)13\dfrac{7}{64}$$
$$(iv) 7\dfrac{2}{3}$$
Divide the following numbers by $$10, 100$$ and $$1000$$ ( orally):
$$23.01$$
Evaluate the following :
$$(i) \dfrac{2}{5} \times \dfrac{3}{7}$$
$$(ii) \dfrac{3}{5} \times \dfrac{8}{9}$$
$$(iii) 7 \times 1\dfrac{2}{3}$$
Divide the following numbers by $$10, 100$$ and $$1000$$ ( orally):
$$4.7$$
Multiply:
$$0.943$$ and $$62$$
If length of one bed-cover is $$2.1 m,$$ find the total length of $$17$$ bed-covers.
Multiply:
$$5.6$$ and $$8$$
Multiply:
$$38.46$$ and $$9$$
Multiply:
$$0.0453$$ and $$35$$
Multiply:
$$7.5$$ and $$2.5$$
Multiply:
$$0.87$$ by $$10$$
Multiply:
$$6.4$$ by $$1000$$
Multiply:
$$2.948$$ by $$100$$
Multiply:
$$5.8$$ by $$4$$
Divide:
$$12.8$$ by $$4$$
Divide:
$$7.8$$ by $$100$$
Evaluate:
$$ 0.01 \times 0.001 $$
Divide:
4.32 by 1.2
$$4.32$$ by $$1.2$$
It can be written as
$$ 4.32 \div 1.2$$
Multiplying by 100
$$432 \div 120=3.6$$
It can be written as
$$ 4.32 \div 1.2$$
Multiplying by 100
$$432 \div 120=3.6$$
Divide:
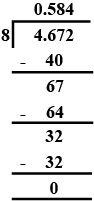
4.672 by 8
$$4.672$$ by $$8 $$
It can be written as
$$4.672\div8=0.584$$
It can be written as
$$4.672\div8=0.584$$
Divide:
$$54.9$$ by $$10$$
Multiply:
5.037 by 8
Multiply:
$$4.6$$ by $$2.1 $$
Evaluate:
$$ 0.894 \times 87 $$
Evaluate :
$$ 3.204 \div 9 $$
$$ 3.204 \div 9 $$
We get
$$3.204 \div 9=0.356$$
We get
$$3.204 \div 9=0.356$$
Evaluate :
$$ 27.69 \div 30 $$
$$ 27.69 \div 30 $$
We get
$$27.69 \div 30=0.923$$
We get
$$27.69 \div 30=0.923$$
Evaluate :
$$ 4.4064 \div 4 $$
Divide:
$$7.644$$ by $$1.4$$
$$7.644$$ by $$1.4$$
It can be written as
$$ 7.644 \div 1.4 $$
Multiplying by $$1000$$
$$ 7644 \div 1400=5.46$$
It can be written as
$$ 7.644 \div 1.4 $$
Multiplying by $$1000$$
$$ 7644 \div 1400=5.46$$
If we multiply the fractions $$\displaystyle\frac{1}{2}$$ and $$\displaystyle\frac{1}{3}$$ we will get $$\displaystyle\frac{1}{6}$$ .If true enter 1 else 0.
Solve the following:
$$0.5\times 10$$
Solve the following:
$$3.62\times 100$$
A motor bike covers a distance of $$62.5km$$ consuming one litre of petrol. How much distance does it cover for $$10$$ litres of petrol? (In km)
Solve the following:
$$0.9\times 100$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\left ( \frac{\sqrt{2}}{(1 - x^2)^{-1}} + \frac{3^{3/2}}{x^{-2}} \right ) : \left ( \frac{x^{-2}}{1 + x^{-2}} \right )^{-1}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\frac{0.23 (7) + \frac{43}{450}}{0.5 (61) - \frac{113}{495}}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\left ( \frac{1}{a} + \frac{1}{b} - \frac{2c}{ab} \right )(a + b + 2c): \left ( \frac{1}{a^2} + \frac{1}{b^2} + \frac{2}{ab} - \frac{4c^2}{a^2 b^2} \right )$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\left ( 6a^2 + 5a - 1 + \frac{a + 4}{a + 1} \right ) : \left ( 3a - 2 + \frac{3}{a + 1} \right )$$
Remove the irrationality in the denominator.
$$\displaystyle\frac{1}{1 + \sqrt{2} + \sqrt{3}}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle( \sqrt{\sqrt{3} + \sqrt{2}} - (\sqrt{3} - \sqrt{2})^{1/2}) ((\sqrt{3} + \sqrt{2})^{1/2} + \sqrt{\sqrt{3} - \sqrt{2}})^{-1} - \cos \frac{5\pi }{4}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\frac{x^{1/2} + x^{-1/2}}{1 - x} + \frac{1 - x^{-1/2}}{1 + \sqrt{x}}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \frac{2 \sqrt{b}}{\sqrt{a} + \sqrt{b}} + \left ( \frac{a^{3/2} + b^{3/2}}{\sqrt{a} + \sqrt{b}} - \frac{1}{(ab)^{-1/2}} \right )(a - b)^{-1}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \frac{a - a^2}{a^{1/2} - a^{-1/2}} - \frac{2}{a^{3/2}} - \frac{1 - a^{-2}}{a^{1/2} + a^{-1/2}}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\frac{a \sqrt{a} + b \sqrt{b}}{(\sqrt{a} + \sqrt{b})(a - b)} + \frac{2\sqrt{b}}{\sqrt{a} + \sqrt{b}} - \frac{\sqrt{ab}}{a -b}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, x^{1/2} + x^{-1/2} + \frac{(1 - x)(1 - x^{-1/3})}{1 + \sqrt{x}}$$
$$1006.2 \div 39$$
Express $$32.12\bar{35}$$ in the form of $$\dfrac{p}{q}$$ where $$p$$ and $$q$$ are integers.
Convert each of the following into mixed fraction :
$$(1)\frac{17}{5}$$ $$(2)\frac{62}{7}$$ $$(3)\frac{101}{8}$$ $$(4)\frac{95}{13}$$
$$(5)\frac{81}{11}$$ $$(6)\frac{87}{16}$$ $$(7)\frac{113}{12}$$ $$(8)\frac{117}{20}$$
Find $$0.1\times 71.3$$
In order to make a shirt $$2\,m\,\,\,25\,cm$$ cloth is needed. What length of cloth is required to make $$18$$ such shirt ?
Find: $$100.01\times 0.01$$
Find $$101.01 \times 0.01$$
Find $$0.2\times 312.4$$
$$5.04 \div 0.8=?$$
Find $$3.3\times 0.3$$
In mixed fraction form $$\dfrac {35}{9}$$ is equal to $$3\dfrac {y}{9}$$.
What is the value of $$y$$ ?
Solve:
$$84.9 \div 30$$
$$14.9\div 0.64$$.
Find :
1) $$\dfrac{2}{5} \times \dfrac{1}{8}$$
ii) $$\dfrac{1}{5} \times \dfrac{3}{4}$$
iii) $$\dfrac{5}{8} \times \dfrac{8}{15}$$
$$2\dfrac {1}{2}:3\dfrac {1}{3} > 3.5:4.5$$
State true or false.
Draw representations to multiply :
(a) $$3$$ and $$2.6$$
(b) $$4$$ and $$1.3$$
Multiply of the following numbers by $$10,\ 100$$ and $$1000$$ :
(i) $$3.9$$
(ii) $$2.89$$
(iii) $$0.0829$$
(iv) $$40.3$$
(v) $$0.3725$$
Express the following as improper fractions:
$$10\dfrac {3}{5}$$
The following fractions represent just three different numbers. Separate them in to three groups of equal fractions by changing each one to its simplest form:
$$\dfrac {15}{75}$$
Change the following fraction into its simplest form:
$$\dfrac {4}{25}$$
Multiply :
$$3\dfrac{1}{8}$$ $$\times 4\dfrac{10}{11}$$
Find the product:
$$3\dfrac{6}{7}\times 4\dfrac{2}{3}$$
Find the product:
$$7\dfrac{1}{2}\times 2\dfrac{4}{15}$$
Find the product:
$$4.74\times 10$$
Find the product:
$$42.5 \times 100$$
Find the product:
$$0.0054 \times 10$$
Find the product:
$$0.45 \times 10$$
Find the product:
$$35.853 \times 100$$
Find the product:
$$12.075 \times 100$$
Find the product:
$$0.0529 \times 1000$$
Find the product:
$$28.73 \times 47$$
Find the product:
$$20.708 \times 1000$$
Find the product:
$$100 \times 0.005$$
Find the product:
$$1000 \times 0.1$$
Find:
$$13.01 \times 50.01$$
Divide $$142.45$$ by $$10$$.
Find the product:
$$0.0415 \times 59$$
Divide $$3.45$$ by $$10$$.
Find the area of a square plot of land whose each side measures $$8\dfrac {1}{2}$$ meters.
Divide:
$$16.64$$ by $$20$$
Divide:
$$164.6$$ by $$200$$
Divide:
$$403.80$$ by $$30$$
Divide:
$$163.44$$ by $$24$$
Multiply:$$\dfrac{7}{11}$$ by $$\dfrac{5}{4}$$
Find the product :
$$ 7.54 \times 10 $$
Find the product :
$$ 2.397 \times 100 $$
Find the product :
$$ 0.08 \times 100 $$
Find the product :
$$ 6.83 \times 100 $$
Find the product :
$$ 0.7 \times 10 $$
Find the product :
$$ 0.83 \times 10 $$
Find the product :
$$ 73.92 \times 10 $$
Find the product :
$$ 84.003 \times 10 $$
Find the product :
$$ 0.032 \times 10 $$
Find the product :
$$ 0.076 \times 1000 $$
Find the product :
$$ 6.25 \times 1000 $$
Find the product :
$$ 0.03 \times 100 $$
Find the product:
$$ 4.8 \times 1000 $$
Find the product :
$$ 5.4 \times 1.6 $$
Find the product :
$$ 0.182 \times 1000 $$
Find the product :
$$ 0.06 \times 1000 $$
Find the product :
$$ 0.6 \times 100 $$
Find the product :
$$ 6.7314 \times 1000 $$
Find the product :
$$ 3.65 \times 19 $$
Find the product :
$$ 7.6 \times 2.4 $$
Find the product :
$$ 0.54 \times 0.27 $$
Multiply the two decimal without the decimal point just like whole numbers.
$$ \therefore 54 \times 27 = 1458 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ =4 $$
$$ \therefore 0.54 \times 0.27 = 0.1458 $$
$$ \therefore 54 \times 27 = 1458 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ =4 $$
$$ \therefore 0.54 \times 0.27 = 0.1458 $$
Find the product :
$$ 6.032 \times 124 $$
Find the product :
$$ 0.0146 \times 69 $$
Find the product :
$$ 3.45 \times 6.3 $$
Multiply the two decimal without the decimal point just like whole numbers.
$$ \therefore 345 \times 63 = 21735 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ =3 $$
$$ \therefore 3.45 \times 6.3 = 21.735 $$
$$ \therefore 345 \times 63 = 21735 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ =3 $$
$$ \therefore 3.45 \times 6.3 = 21.735 $$
Find the product :
$$ 0.854 \times 12 $$
Find the product :
$$ 0.00125 \times 327 $$
Find the product :
$$ 4.125 \times 86 $$
Find the product :
$$ 36.73 \times 48 $$
Find the product :
$$ 104.06 \times 75 $$
Find the product :
$$ 0.623 \times 0.75 $$
Multiply the two decimal without the decimal point just like whole numbers.
$$ \therefore 623 \times 75 = 46725 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ = 5 $$
$$ \therefore 0.623 \times 0.75 = 0.46725 $$
$$ \therefore 623 \times 75 = 46725 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ = 5 $$
$$ \therefore 0.623 \times 0.75 = 0.46725 $$
Find the product :
$$ 0.06 \times 0.38 $$
Multiply the two decimal without the decimal point just like whole numbers.
$$ \therefore 6 \times 38 = 228 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ =4 $$
$$ \therefore 0.06 \times 0.38 = 0.0228 $$
$$ \therefore 6 \times 38 = 228 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ =4 $$
$$ \therefore 0.06 \times 0.38 = 0.0228 $$
Divide:
$$ 4.7 \quad by \quad 100 $$
Find the product :
$$ 54.5 \times 1.76 $$
Multiply the two decimal without the decimal point just like whole numbers.
$$ \therefore 547 \times 176 = 95920 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ = 3 $$
$$ \therefore 54.5 \times 1.76 = 95.92 $$
$$ \therefore 547 \times 176 = 95920 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ = 3 $$
$$ \therefore 54.5 \times 1.76 = 95.92 $$
Find the product :
$$ 1.245 \times 6.4 $$
Multiply the two decimal without the decimal point just like whole numbers.
$$ \therefore 1245 \times 64 = 79680 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ = 4 $$
$$ \therefore 1.245 \times 6.4 = 7.9680 $$
$$ \therefore 1245 \times 64 = 79680 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ = 4 $$
$$ \therefore 1.245 \times 6.4 = 7.9680 $$
Find the product :
$$ 0.014 \times 0.46 $$
Multiply the two decimal without the decimal point just like whole numbers.
$$ \therefore 14 \times 46 = 644 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ = 5 $$
$$ \therefore 0.014 \times 0.46 = 0.00644 $$
$$ \therefore 14 \times 46 = 644 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ = 5 $$
$$ \therefore 0.014 \times 0.46 = 0.00644 $$
Find the product :
$$ 0.568 \times 4.9 $$
Multiply the two decimal without the decimal point just like whole numbers.
$$ \therefore 568 \times 49 = 27832 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ =4 $$
$$ \therefore 0.568 \times 4.9 = 2.7832 $$
$$ \therefore 568 \times 49 = 27832 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ =4 $$
$$ \therefore 0.568 \times 4.9 = 2.7832 $$
Find the product :
$$ 6.54 \times 0.09 $$
Multiply the two decimal without the decimal point just like whole numbers.
$$ \therefore 654 \times 9 = 5886 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ =4 $$
$$ \therefore 6.54 \times 0.09 = 0.5886 $$
$$ \therefore 654 \times 9 = 5886 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ =4 $$
$$ \therefore 6.54 \times 0.09 = 0.5886 $$
Find the product :
$$ 3.87 \times 1.25 $$
Multiply the two decimal without the decimal point just like whole numbers.
$$ \therefore 387 \times 125 = 48375 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ =4 $$
$$ \therefore 3.87 \times 1.25 = 4.8375 $$
$$ \therefore 387 \times 125 = 48375 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ =4 $$
$$ \therefore 3.87 \times 1.25 = 4.8375 $$
Find the product :
$$ 0.045 \times 2.4 $$
Multiply the two decimal without the decimal point just like whole numbers.
$$ \therefore 45 \times 24 = 1080 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ = 4 $$
$$ \therefore 0.045 \times 2.4 = 0.108 $$
$$ \therefore 45 \times 24 = 1080 $$
Mark the decimal point in the product in such a way that the number of decimal places in the product is equal to the sum of the decimal place in the given decimals.
Sum of decimal places in the given decimals $$ = 4 $$
$$ \therefore 0.045 \times 2.4 = 0.108 $$
Divide:
$$ 131.6 \quad by \quad 10 $$
Divide:
$$ 0.3 \quad by \quad 100 $$
Divide:
$$ 0.34 \quad by \quad 10 $$
Divide:
$$ 4.38 \quad by \quad 10 $$
Divide:
$$ 0.58 \quad by \quad 100 $$
Multiply:
$$\cfrac98$$ by $$\cfrac{32}3$$
Multiply:
$$\cfrac34$$ by $$\cfrac57$$
Divide:
$$ 4.6 \quad by \quad 1000 $$
Divide:
$$ 354.16 \quad by \quad 1000 $$
Divide:
$$ 38.9 \quad by \quad 1000 $$
Divide:
$$ 1286.5 \quad by \quad 1000 $$
Simplify: $$=\dfrac{3}{20}\times $$ $$\dfrac{4}{5}$$
Divide:
$$ 0.8 \quad by \quad 1000 $$
Divide:
$$ 0.02 \quad by \quad 100 $$
Divide:
$$ 0.768 \quad by \quad 16 $$
We perform the division by considering the dividend and divisor a whole number.
When the division in this form is complete.
we, subtract number of decimal points in dividend from number of decimal point in divisor. and that many decimal points we put in quotient of division.
So, we have,
$$ 0.768 \div 16 $$
Now, we will do division $$768\div 16$$
$$768\div16=\cfrac{768}{16}=48$$
Decimal points in dividend=$$3$$
Decimal points in divisor=$$0$$
subtraction=$$3-0=3$$
So, we will put $$3$$ decimal points in our answer $$48$$
$$\therefore 0.768 \quad by \quad 16 =0.048$$
Divide:
$$ 0.477 \quad by \quad 18 $$
Perform the division by considering the dividend a whole number.
When the division of thr whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
Proceeding as above, We get
$$ 0.477 \div 18 = 0.0265 $$
When the division of thr whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
Proceeding as above, We get
$$ 0.477 \div 18 = 0.0265 $$
Divide:
$$ 0.3322 \quad by \quad 11 $$
Perform the division by considering the dividend a whole number.
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 0.3322 \div 11 $$
$$ \therefore 0.3322 \div 11 = 0.0302 $$
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 0.3322 \div 11 $$
$$ \therefore 0.3322 \div 11 = 0.0302 $$
Divide:
$$ 403.8 \div 30 $$
The above question can be written as,
$$ 403.8 \div 30 =\dfrac{403.8}{30} $$
Multiplying both numerator and denominator by 10, we get,
$$ = \dfrac{403.8 \times 10}{30 \times 10}=\dfrac{4038}{300}$$
By long division (as shown in image), We get
$$ 403.8\div30=\dfrac{4038 }{300} = 13.46 $$
$$ 403.8 \div 30 =\dfrac{403.8}{30} $$
Multiplying both numerator and denominator by 10, we get,
$$ = \dfrac{403.8 \times 10}{30 \times 10}=\dfrac{4038}{300}$$
By long division (as shown in image), We get
$$ 403.8\div30=\dfrac{4038 }{300} = 13.46 $$
Divide:
$$ 6.54 \hspace{2mm} by \hspace{2mm}12$$
Perform the division by considering the dividend a whole number.
When the division of the whole part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
When the division of the whole part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
Proceeding as above, We get
$$ 6.54 \div 12 = 0.545 $$
Divide:
$$ 1.001 \quad by \quad 14 $$
Perform the division by considering the dividend a whole number.
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
Proceeding as above, We get
$$ 1.001 \div 14 = 0.0715 $$
Divide:
$$ 16.46 \div 20 $$
The above question can be written as,
$$ 16.46\div20=\dfrac{16.46 }{ 20 } $$
Multipling both numerator and denominator by 100 we get,
$$ = \dfrac{ 16.46 \times 100}{ 20 \times 100} $$
$$ = \dfrac{1646 }{ 2000 } $$
$$ 16.46\div20=\dfrac{16.46 }{ 20 } $$
Multipling both numerator and denominator by 100 we get,
$$ = \dfrac{ 16.46 \times 100}{ 20 \times 100} $$
$$ = \dfrac{1646 }{ 2000 } $$
By long division (as shown in image), we get
$$ 16.46\div20=\dfrac{ 1646 }{ 2000 } = 0.823 $$
$$ 16.46\div20=\dfrac{ 1646 }{ 2000 } = 0.823 $$
Divide:
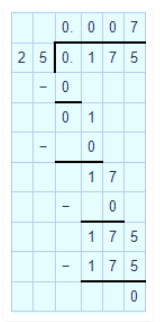
$$ 0.175 \quad by \quad 25 $$
Perform the division by considering the dividend a whole number.
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 0.175 \div 25 $$
$$ \therefore 0.175 \div 25 = 0.007 $$
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
we have,
$$ 0.175 \div 25 $$
$$ \therefore 0.175 \div 25 = 0.007 $$
Divide:
$$ 5.52 \quad by \quad 16 $$
Perform the division by considering the dividend a whole number.
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
Proceeding as above, We get
$$ 5.52 \div 16 = 0.345 $$
When the division of whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
Proceeding as above, We get
$$ 5.52 \div 16 = 0.345 $$
Divide:
$$ 2.13 $$ by $$ 15 $$
Perform the division by considering the dividend a whole number.
When the division of the whole-part of the dividend is complete, put the decimal point in the quotient and proceed with the division as in case of whole numbers.
$$ \therefore 2.13 \div 15 = 0.14 $$
$$ \therefore 2.13 \div 15 = 0.14 $$
Find the product:
$$\left(3\cfrac{6}{7}\right) \times\left(4\cfrac{2}{3}\right)$$
Divide:
$$ 18.08 \div 400 $$
$$\dfrac{18.08}{400} = 0.0452 $$
Find the product:
$$\left(4\cfrac{1}{8} \right)\times\left(2\cfrac{10}{11}\right)$$
Divide:
$$ 3.28 \div 0.8 $$
Find the product:
$$\left(9\cfrac{1}{2}\right) \times\left(1\cfrac{9}{19}\right)$$
Find the product:
$$\left(5\cfrac{5}{6}\right)\times\left(1\cfrac{5}{7}\right)$$
Divide:
$$ 156.8 \div 200 $$
The above question can be written as,
$$ \Rightarrow ( \dfrac{156.8} {200} ) $$
Multiply by 10 for both numerator and denominator, then we get,
$$ = \dfrac{ ( 156.8 \times 10)} { ( 200 \times 10) }$$
$$=\dfrac{1568}{2000}$$
$$ =0.784 $$
Divide:
$$ 12.8 \div 500 $$
$$12.8\div 500= 0.0256 $$
Divide:
$$ 19.2 \div 80 $$
The above question can be written as,
$$ 19.2 \div 80 =\dfrac{19.2}{80} $$
Multiplying both numerator and denominatorby 10, we get,
$$ = \dfrac{19.2 \times 10}{ 80 \times 10} $$
$$ = \dfrac{192 }{800} $$
$$ 19.2 \div 80 =\dfrac{19.2}{80} $$
Multiplying both numerator and denominatorby 10, we get,
$$ = \dfrac{19.2 \times 10}{ 80 \times 10} $$
$$ = \dfrac{192 }{800} $$
By long division (as shown in image), We get
$$ 19.2 \div80 =\dfrac{192}{800}= 0.24 $$
$$ 19.2 \div80 =\dfrac{192}{800}= 0.24 $$
Divide:
$$ 0.8085 \quad by \quad 0.35 $$
Divide:
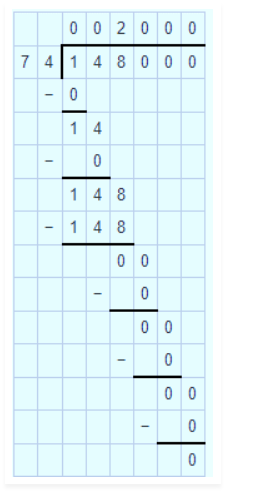
$$ 148 \quad by \quad 0.074 $$
$$\dfrac{148}{0.074}=2000$$
Divide:
$$ 6.612 \quad by \quad 11.6 $$
Divide:
$$ 21.976 \quad by \quad 1.64 $$
Divide:
$$ 0.288\ by\ 0.9 $$
Divide:
$$ 11.04 \quad by \quad 1.6 $$
Divide:
$$ 0.076 \quad by \quad 0.19 $$
Divide:
$$ 16.578 \quad by \quad 5.4 $$
Divide:
$$ 25.395 by 1.5 $$
Divide:
$$ 0.228$$ by $$0.38 $$
The total cost of $$ 24 $$ chairs is $$ 9255.60.$$ Find the cost of each chair.
The number of chairs $$ = 24 $$
The cost of $$ 24 $$ chairs is = ₹$$ 9255.60$$
Then the cost of each chair = $$\dfrac{9255.60}{24}$$
$$ \therefore $$ the cost of each chair is ₹$$ 385.65 $$
The cost of $$ 24 $$ chairs is = ₹$$ 9255.60$$
Then the cost of each chair = $$\dfrac{9255.60}{24}$$
$$ \therefore $$ the cost of each chair is ₹$$ 385.65 $$
$$ 8 \frac{2}{7} $$ Is equal to the improper fraction_____.
Write $$ \dfrac{129}{8} $$ as a mixed fraction.
We have
$$ \dfrac {192}{8} = 16 \dfrac {1}{8} $$
Grip size of a tennis racquet is $$ 11 \dfrac{9}{80} cm $$. Express the size as an improper fraction.
Convert the following fractions into mixed fractions:
(i) $$\dfrac{73}{8}$$
(ii) $$\dfrac{94}{13}$$
When 0.004 is divided by 0.02964, what will be the quotient?
Convert the following fractions into improper fractions :
(i) $$2 \dfrac{7}{9}$$
(ii) $$5 \dfrac{4}{11}$$
Find the following:
(i) $$10.8 \div 4$$
(ii) $$126.35 \div 7$$
(iii) $$22.5 \div 1.5$$
(iv) $$4.28 \div 0.02$$
(v) $$3.645 \div 1.35$$
(vi) $$0.728 \div 0.04$$
(vii) $$13.06 \div 0.08$$
(viii) $$58.635 \div 4.5$$
Multiply each of the following numbers by $$10, 100$$ and $$1000$$ (orally):
(i) $$5.9$$
(ii) $$3.76$$
(iii) $$0.549$$
Find the following:
(i) $$2.7 \times 4$$
(ii) $$2.71 \times 5$$
(iii) $$2.5 \times 0.3$$
(iv) $$2.3 \times 4.35$$
(v) $$238.06 \times 7.5$$
(vi) $$0.79 \times 32.4$$
(vii) $$1.07 \times 0.02$$
(viii) $$10.05 \times 1.05$$
What is the cost of 27.5 m of cloth at 53.50 per metre?
What will be the total length of cloth required to make $$5$$ shirts, if $$2.15 m$$ of cloth is needed for each shirt?
The cost of a fountain pen is $$Rs 13.25$$. Find the cost of $$8$$ such pens.
Find the area of a rectangle whose length is $$5.7 \ cm$$ and breadth is $$3.5 \ cm$$.
If $$Rs. 242.46$$ are to be distributed among $$6$$ children equally, find the share of each.
$$83$$ note-books are sold at $$Rs 15.25$$ each. Find the total money (in rupees) obtained by selling these note-books.
The cost of one metre cloth is $$Rs. 38.50$$. Find the cost of $$3.6$$ m cloth.
The length of an iron rod is $$10.32 m$$. The rod is divided into $$4$$ pieces of equal lengths. Find the length of each piece.
The cost of $$25$$ identical articles is $$Rs 218.25.$$ Find the cost of one article
If the product of two decimal numbers is $$38.745$$ and one of the numbers is $$2.7$$, find the other.
Change the following mixed fractions to improper fractions:
(i) $$2\frac { 1 }{ 5 } $$
(ii) $$3\frac { 1 }{ 4 } $$
(iii) $$7\frac { 1 }{ 8 } $$
(iv) $$2\frac { 1 }{ 11 } $$
Express the following improper fractions as mixed fractions:
$$7/4$$
Express the following mixed fractions as improper fractions:
$$2 \dfrac{5}{48}$$
Express the following mixed fractions as improper fractions:
$$2 \dfrac{4}{9}$$
Express the following mixed fractions as improper fractions:
$$7 \dfrac{5}{13}$$
Express the following as improper fractions:
a) $$7\dfrac{3}{4}$$ b) $$5\dfrac{6}{7}$$ c) $$2\dfrac{5}{6}$$ d) $$10\dfrac{5}{3}$$ e) $$9\dfrac{3}{7}$$ f)$$8\dfrac{4}{9}$$
Evaluate :
$$ 0.14616 \div 72 $$
$$ 0.14616 \div 72 $$
We get
$$0.14616 \div 72=0.00203 $$
We get
$$0.14616 \div 72=0.00203 $$
Evaluate :
$$ 0.6227 \div 1300 $$
$$ 0.6227 \div 1300 $$
We get
$$0.6227 \div 1300=0.000479$$
We get
$$0.6227 \div 1300=0.000479$$
Express the following as mixed fraction:
a) $$\displaystyle \frac{20}{3}$$ b) $$\displaystyle \frac{11}{5}$$ c) $$\displaystyle \frac{17}{7}$$ d) $$\displaystyle \frac{28}{5}$$ e) $$\displaystyle \frac{19}{6}$$ f) $$\displaystyle \frac{35}{9}$$
a) $$\displaystyle \frac{20}{3}$$ b) $$\displaystyle \frac{11}{5}$$ c) $$\displaystyle \frac{17}{7}$$ d) $$\displaystyle \frac{28}{5}$$ e) $$\displaystyle \frac{19}{6}$$ f) $$\displaystyle \frac{35}{9}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\frac{2b + a - \frac{4a^2 - b^2}{a}}{b^3 + 2ab^2 - 3a^2b} \cdot \frac{a^3b - 2a^2b^2 + ab^3}{a^2 - b^2}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\left ( \frac{1}{a - \sqrt{2}} - \frac{a^2 + 4}{a^3 - \sqrt{8}} \right ) : \left ( \frac{a}{\sqrt{2}} + 1 + \frac{\sqrt{2}}{a} \right )^{-1}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\frac{(5 \sqrt{3} + \sqrt{50})\, (5 - \sqrt{24})}{\sqrt{75} - 5 \sqrt{2}}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\left ( \frac{1}{3} \right )^{-10}\, \cdot 27^{-3} + 0.2^{-4} \cdot 25^{-2} + (64^{-1/9})^{-3}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \frac{\sqrt{x} + 1}{1 + \sqrt{x} + x} : \frac{1}{x^2 - \sqrt{x}}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \left ( \frac{1}{m - \sqrt{mn}} + \frac{1}{m + \sqrt{mn}} \right )\cdot \frac{m^3 - n^3}{m^2 + mn + n^2}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \left ( \frac{a^{1/2} + 2}{a + 2a^{1/2} + 1 } - \frac{a^{1/2} - 2}{a - 1} \right ) \cdot \frac{a^{1/2} + 1}{a^{1/2}}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \frac{a -b}{a + b + 2\sqrt{ab}} : \frac{a^{-1/2} - b^{-1/2}}{a^{-1/2} + b^{-1/2}}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \frac{b -x}{\sqrt{b} - \sqrt{x}} - \frac{b^{3/2} - x^{3/2}}{b - x}$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\,(x + \sqrt{x^2 - 1})^2 + (x + \sqrt{x^2 - 1})^{-2} + 2 (1 -2x^2)$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\,\left ( \frac{x^{1/2} + y^{1/2}}{x^{1/2} - y^{1/2}} - \frac{x^{1/2} - y^{1/2}}{x^{1/2} + y^{1/2}} \right ) (y^{-1/2} - x^{-1/2})$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \left ( \frac{3}{\sqrt{1 + a}} + \sqrt{1 -a} \right ) : \left ( \frac{3}{\sqrt{1 - a^2}} + 1 \right )$$
A flower garden is 22.50 m long. Sheela wants to make a border along one side using bricks that are 0.25 m long. How many bricks will be needed?
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \left ( \frac{\sqrt{a}}{2} - \frac{1}{2 \sqrt{a}} \right )^2 \left ( \frac{\sqrt{a} - 1}{\sqrt{a} + 1} - \frac{\sqrt{a} + 1}{\sqrt{a} - 1} \right )$$
Represent the following mixed infinite decimal periodic fractions as common fractions:
$$\displaystyle\, \left ( \frac{P^{3/2} + q^{3/2}}{p - q} - \frac{p - q}{P^{1/2} + q^{1/2}} \right )\left ( \sqrt{pq} \frac{\sqrt{p} + \sqrt{q}}{p - q} \right )^{-1}$$
Class 7 Maths Extra Questions
- Algebraic Expressions Extra Questions
- Comparing Quantities Extra Questions
- Data Handling Extra Questions
- Exponents And Powers Extra Questions
- Fractions And Decimals Extra Questions
- Integers Extra Questions
- Lines And Angles Extra Questions
- Perimeter And Area Extra Questions
- Practical Geometry Extra Questions
- Rational Numbers Extra Questions
- Simple Equations Extra Questions
- Symmetry Extra Questions
- The Triangle And Its Properties Extra Questions
- Visualising Solid Shapes Extra Questions