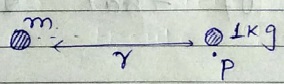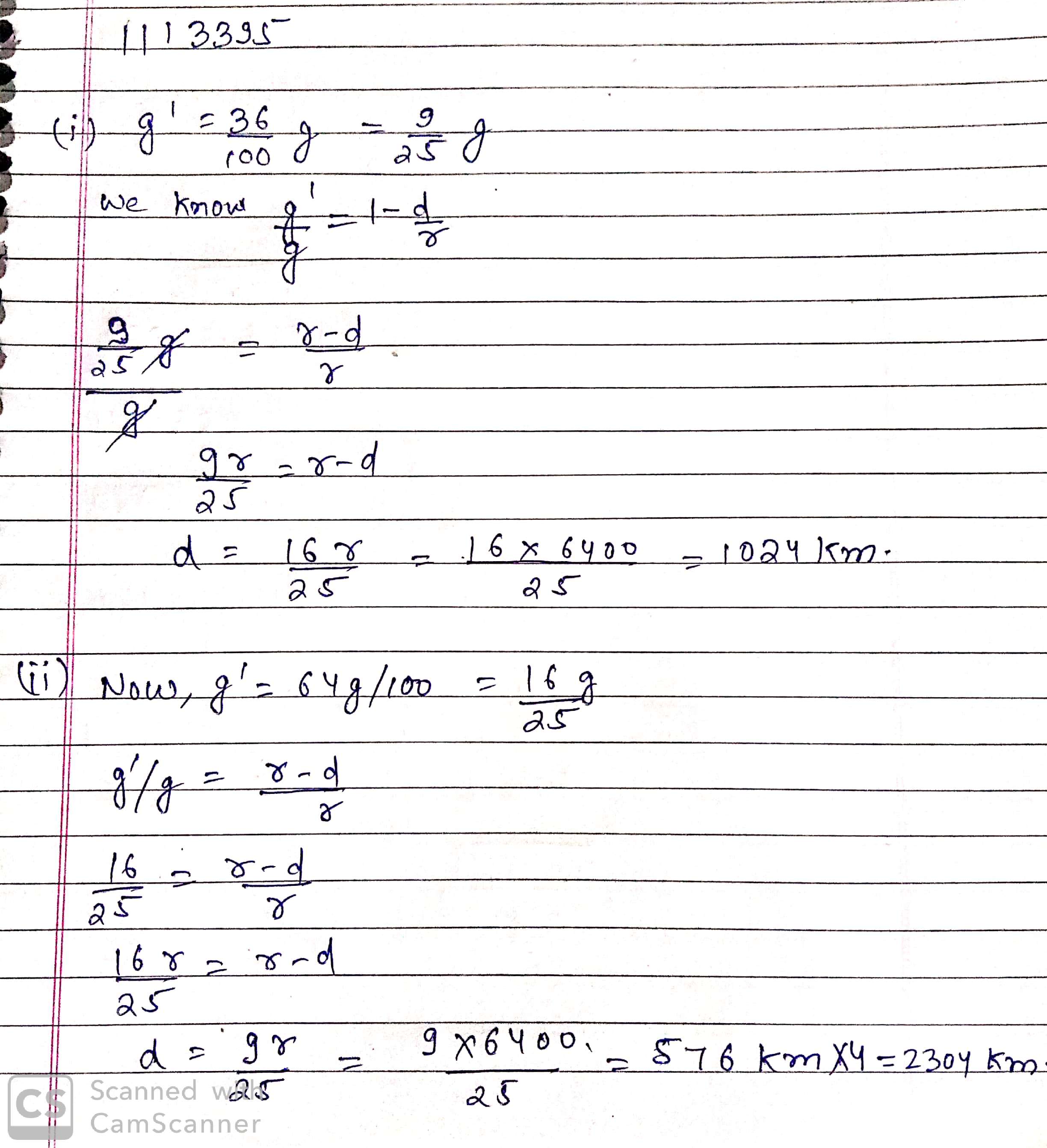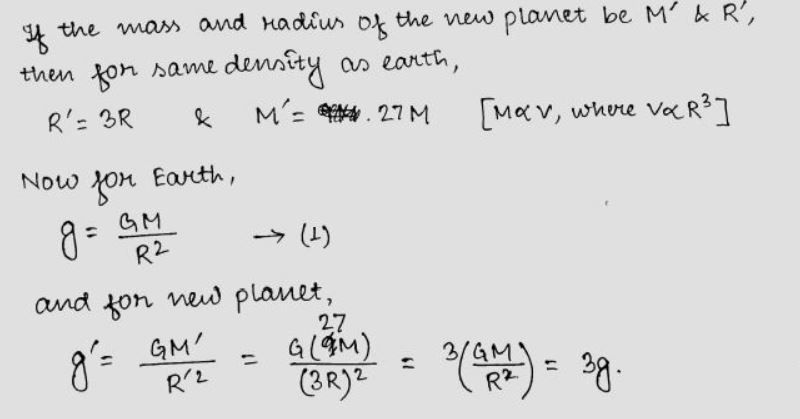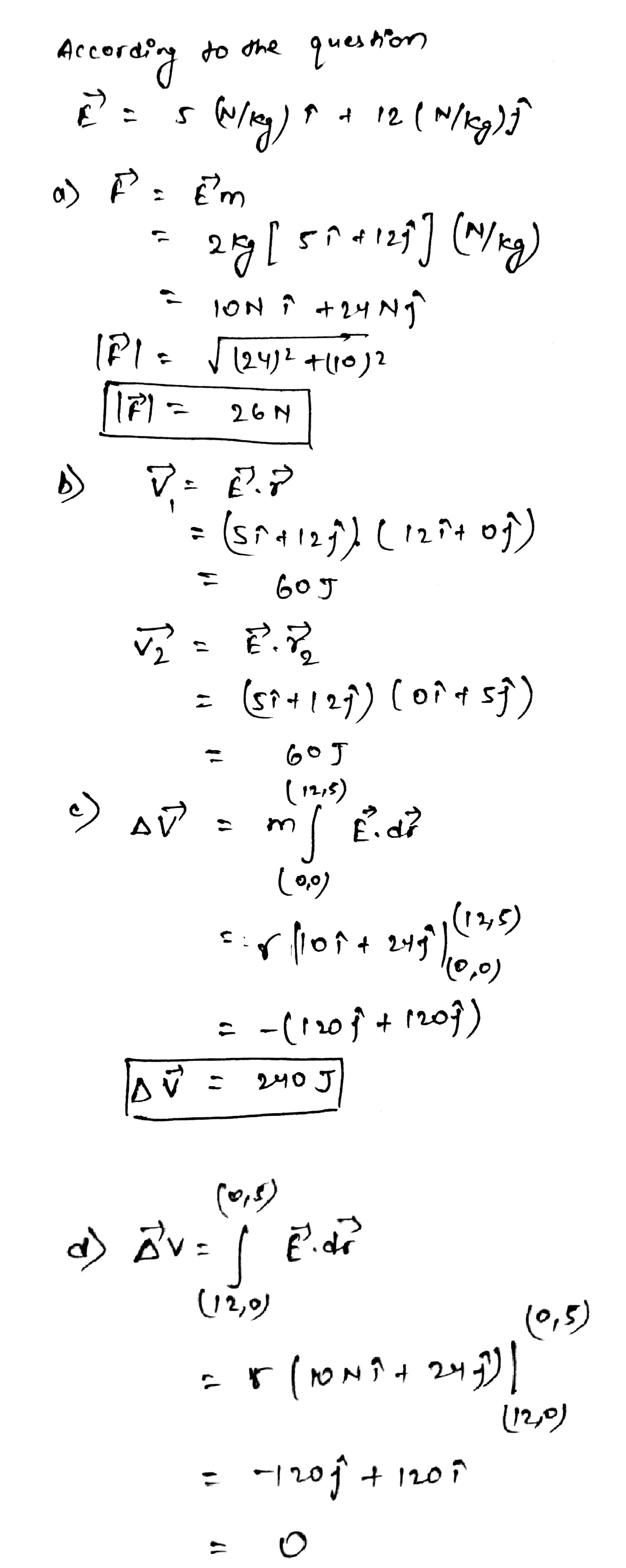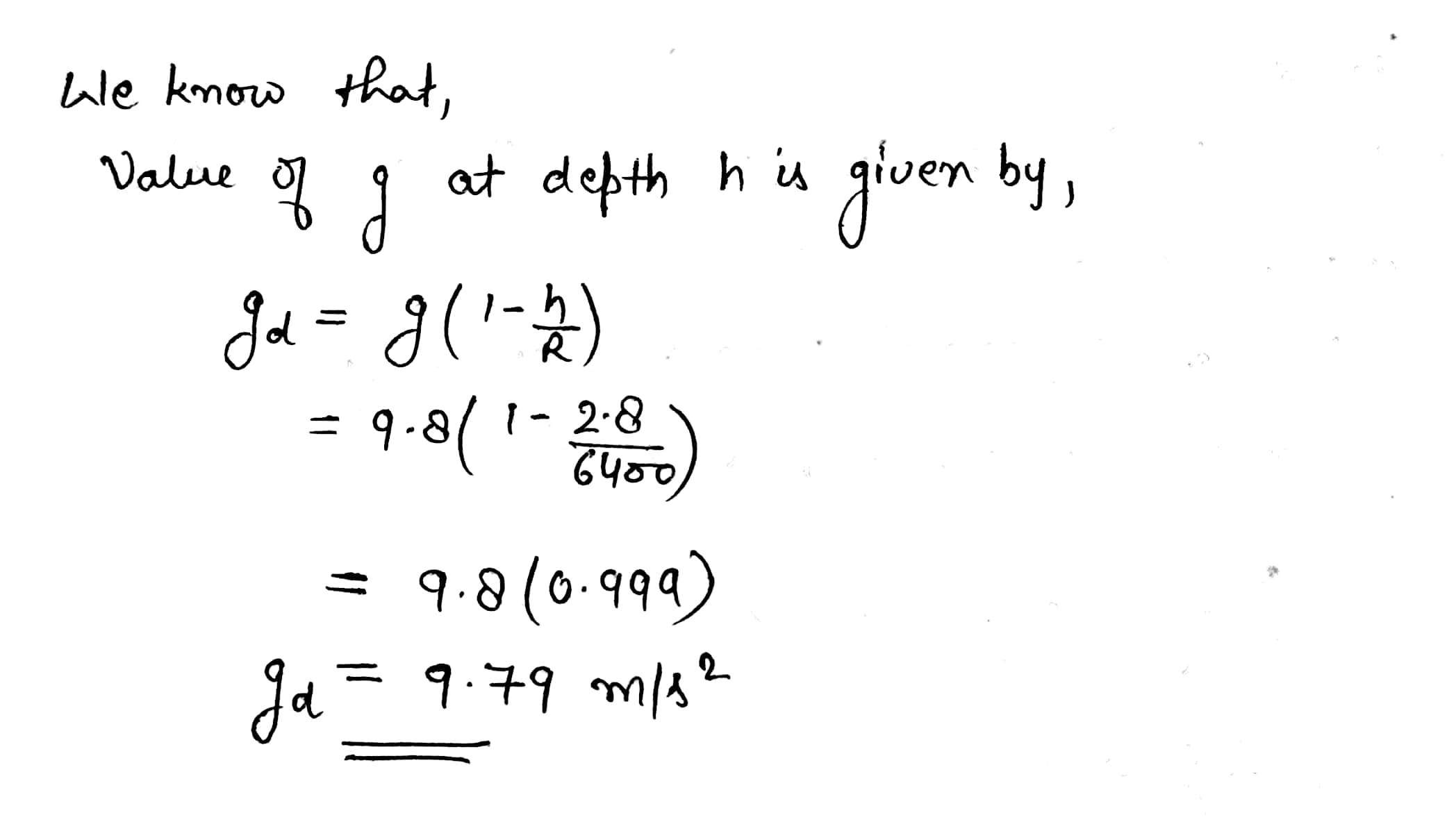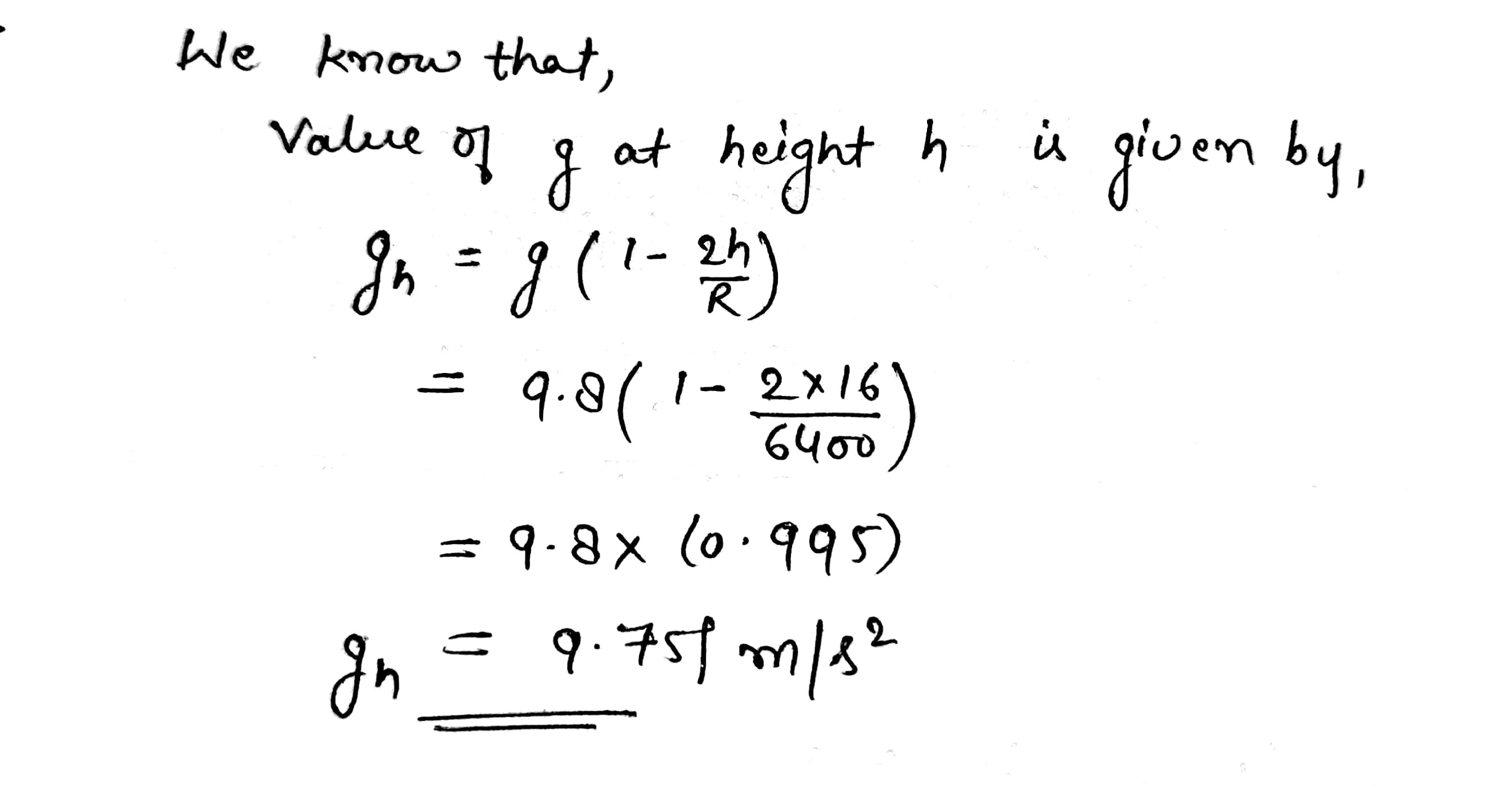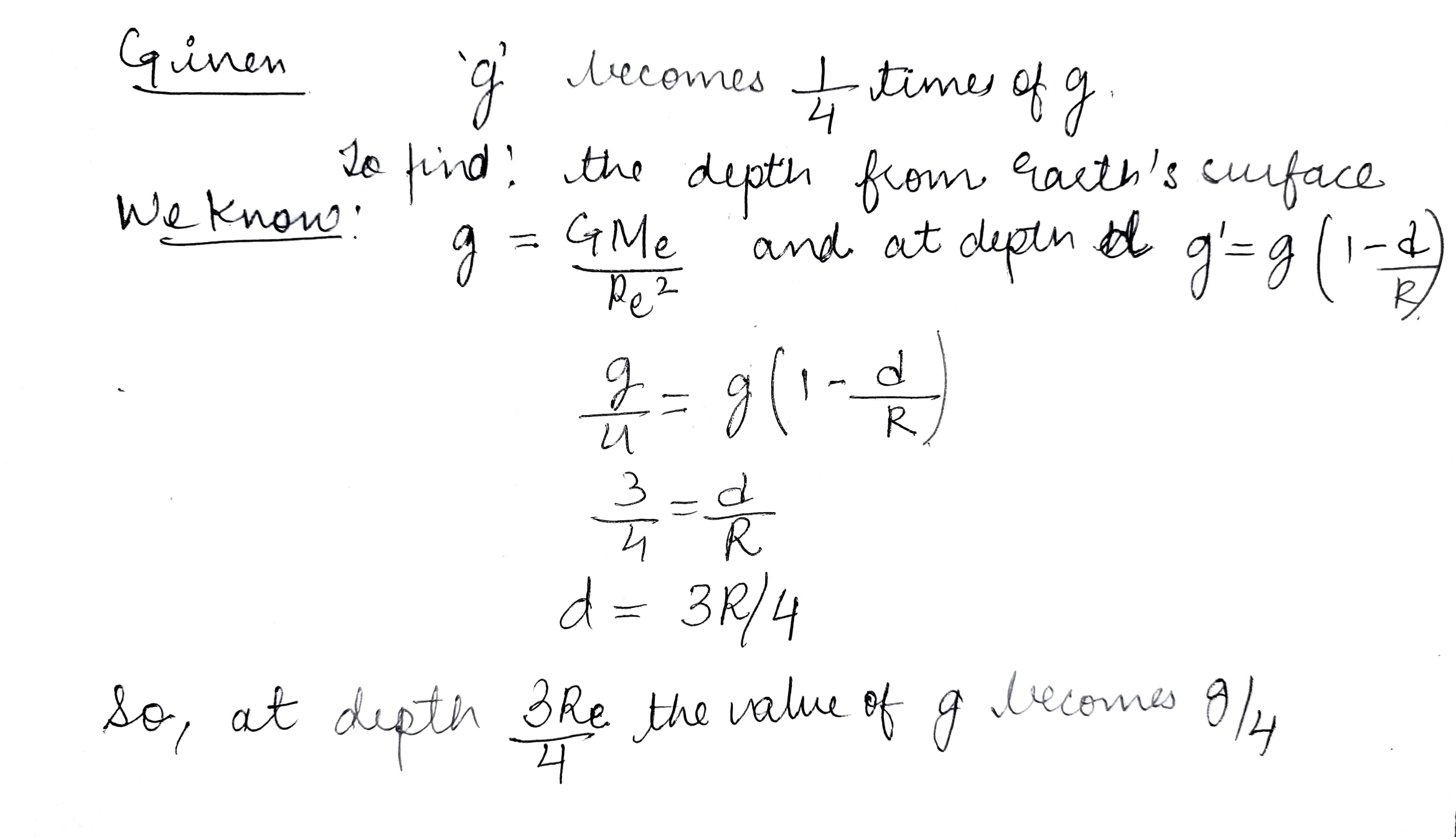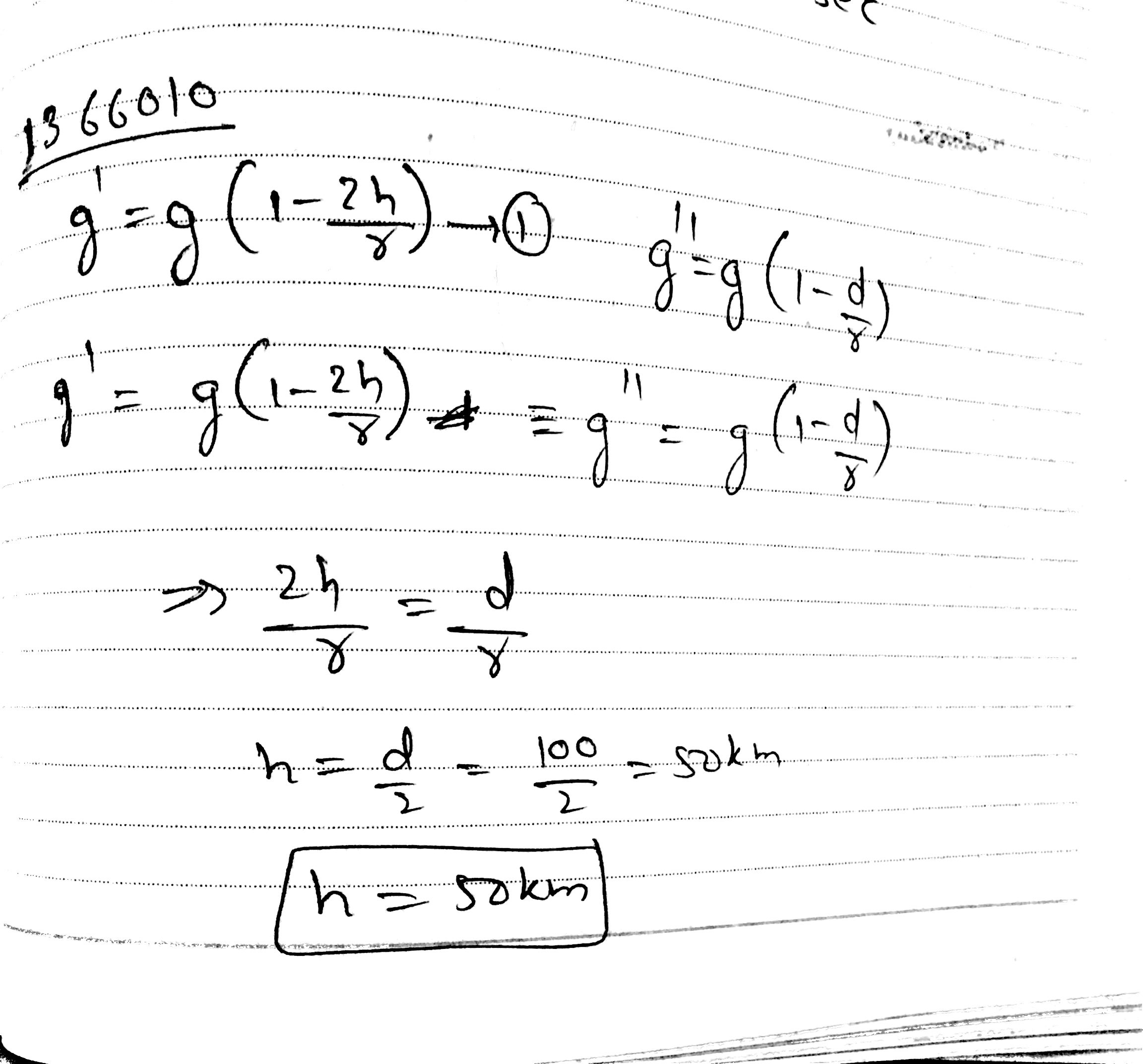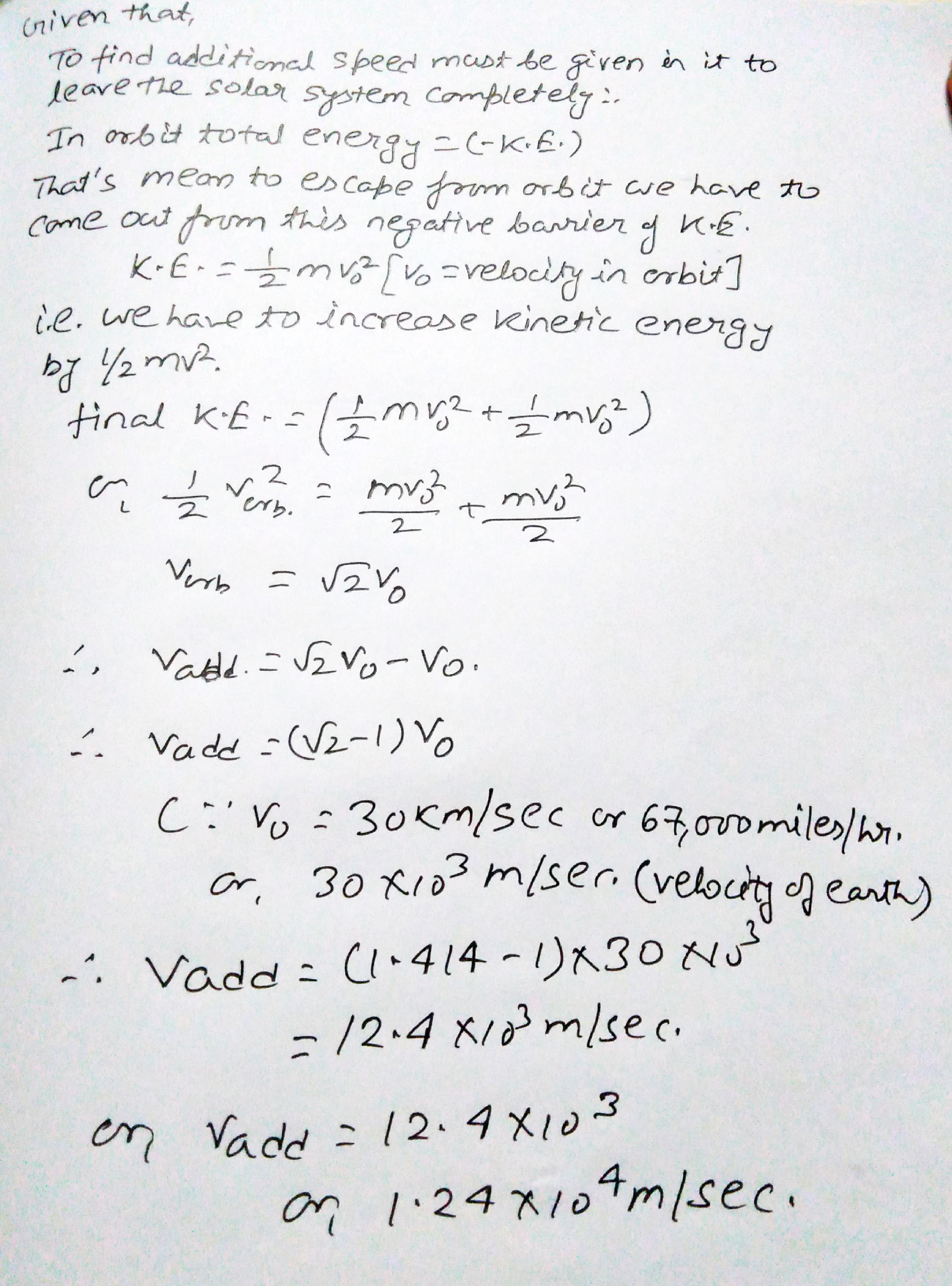Gravitation - Class 11 Engineering Physics - Extra Questions
A body weighs 100 N at a distance $$\dfrac {R}{4}$$ from the center of the earth. Find its weight at height of $$ 9 R$$ from the surface of the earth ($$R$$=Radius of earth and answer in SI unit )?
At what depth (in terms of the radius of earth) the acceleration due to gravity will be$$\dfrac {2g}{5}$$?
Fill up the blank with suitable words.
Value of universal gravitational constant G = _______________.
What is the weight of a body placed at the centre of the earth?
Potential due to a point mass $$m$$ at a distance $$r$$ is $$V = -\dfrac {GM}{r}$$.
Find the acceleration due to gravity of the moon at a point $$1000\,km$$ above the moon's surface. The mass of the moon is $$7.4\times 10^{22}\,kg$$ and its radius is $$1740\,km$$.
The acceleration due to gravity _______ with an increase in height and depth.
What is the geometrical interpretation of infinity for gravitational field and gravitational potential?
The acceleration due to gravity on the surface of the earth will be maximum at ________ and minimum at _________
Find what will be the change in the value of $$g$$ while going $$h$$ height over the earth's surface where $$h$$ is in the order of $$Re$$.
Find the acceleration due to gravity on a point which is above half the radius of earth, from surface?[take g = $$10 m/s^{2}$$on earth's]
At noon, the sun and the earth pull the objects on the earth's surface in opposite directions. At midnight, the gm and the earth pull these objects in the same direction. Is the weight of an object, as measured by a string balance on the earth's surface, more at midnight as compared to its weight at noon?
Derive the effect of gravity due to depth.
Name the scientist who gave the three laws of planetary motion.
Where is acceleration due to gravity on earth minimum ?
Where is the acceleration due to gravity on earth maximum ?
At what height above the earth's surface, the value of $$g$$ is same as that at a depth of $$100km$$?
Hint: Take $$g_{h}=g_{d}$$.
What will be the velocity of the stone on reaching the ground? (Take g = $$10 m / s^{2}$$)
At what height (in terms of radius of earth) the acceleration due to gravity will be:
(a) $$\dfrac {g}{2}$$ (b) $$\dfrac {4g}{9}$$ (c) $$\dfrac {g}{100}$$
Are the equations of motion applicable to bodies projected vertically up with any velocity, say $$8\ km\ s^{-1}$$, for determining the maximum height? And why?
Match column I with column II.
A spaceship is launched into a circular orbit close to the Earth's surface. The additional velocity has to be imparted to the spaceship to overcome the gravitational pull?
Match the following :
Considering the earth to be a homogeneous sphere but keeping in mind its spin, Match the following :
Calculate the distance from the surface of the earth at which the acceleration due to gravity is the same below and above the surface of the earth.
Value of $$g$$ on the surface of earth is $$9.8 m/s^{2}$$. Value of $$g$$ on the surface of earth is $$9.8 m/s^{2}$$. At height $$h = R$$ from the surface the value of $$g$$ is $$\dfrac{g}{x}$$. Find $$x$$.
If a body be projected vertically upward from the surface of the earth so as to reach a height $$nR$$ above the surface; the increase in its potential energy is $$\left (\displaystyle\frac{n}{n+a} \right )mgR$$ ,where $$a = $$ ?
The velocity with which it must be projected is $$\sqrt{\displaystyle\frac{2ngR}{n+1}}$$ ,where $$R$$ is the radius of the earth and $$m$$ the mass of body.
What is the kinetic energy needed to project a body of mass $$m$$ from the surface of the earth to infinity. Radius of earth is $$R$$ and acceleration due to gravity on earth's surface is $$g$$.
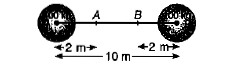
In the figure masses $$400 kg$$ and $$100 kg$$ are fixed. How much work must be done to move a $$1 kg$$ mass from point $$A$$ to point $$B$$?
Value of $$g$$ on the surface of earth is $$9.8 m/s^{2}$$. Find acceleration due to gravity at depth $$h =\displaystyle\frac{R}{2}$$ from the surface ($$R =$$ radius of earth).
Does the escape speed of a body from the earth depend on (a) The mass of the body, (b) The location from where it is projected, (c) The direction of projection, (d) The height of the location from where the body is launched?
Assuming the earth to be a sphere of uniform mass density, how much would a body weigh (in N) half way down to the center of the earth if it weighed 250 N on the surface ?
Choose the correct alternative :
(a) Acceleration due to gravity increases/decreases with increasing altitude.
(b) Acceleration due to gravity increases/decreases with increasing depth (assume the earth to be a sphere of uniform density).
(c) Acceleration due to gravity is independent of mass of the earth/mass of the body.
(d) The formula $$-G\,Mm(1/r_2-1/r_1)$$ is more/less accurate than the formula $$mg(r_2-r_1)$$ for the difference of potential energy between two points $$r_2$$ and $$r_1$$ distance away from the center of the earth.
As you have learnt in the text, a geostationary satellite orbits the earth at a height of nearly 36,000 km from the surface of the earth. What is the potential due to earth's gravity at the site of this satellite ? (Take the potential energy at infinity to be zero). Mass of the earth = $$6.0 \times 10^{24}\ kg$$, radius = 6400 km.
A body weighs $$63 $$N on the surface of the earth. What is the gravitational force (in N) on it due to the earth at a height equal to half the radius of the earth ?
Calculate the distance below and above the surface of the earth, at which the value of acceleration due to gravity becomes $${ 1 }/{ 4 }$$th that at earth's surface?
Match the following
Match the following :
Mention the effect of altitude and depth on the value of acceleration due to gravity. Give the corresponding mathematical relation.
A planet is moving around the Sun in a circular orbit of circumference $$C$$. The work done on the planet by the gravitational force $$F$$ of the Sun is $$kFC$$, then the value of $$k$$ is
If the Earth were made of wood, the mass of wooden earth is $$10$$% as much as it is now without the change in its diameter.
Calculate the escape velocity of space shot from the surface of wooden earth.
Radius of earth: $$R = 6400\ km$$
Mass of earth: $$M = 6\times 10^{24}kg$$
Constant of gravitation: $$G = 6.67\times 10^{-11}Nm^{2}/kg^{2}$$
What the decrease in weight ofa body of mass 600 kg when it is taken in a mine of depth 5000 m ? [Radius of earth a 6400 km, g = 9.8 $$m/s^2$$]
Why does the value of 'g' decrease as we go deep inside a mine (or the Earth)?
Derive an expression for acceleration due to gravity at depth '$$h$$' below earth's surface.
The escape velocity of a body from the surface of the earth is $$11.2km/s$$. If a satellite were to orbit close to the surface, what would be its critical velocity?
If the density of the earth is doubled to that of its original value, the radius remaining the same, what will be the change in acceleration due to gravity?
A rocket starts vertically upward with speed $$v_0$$. Show that its speed $$v $$ at height $$h$$ is given by $$v_0^2-v^2=\dfrac{2gh}{1+\dfrac{h}{R}}$$, hence $$R$$ is the radius of the Earth.
A pendulum clock is accurate at a place where $$g = 9.8\ m/s^{2}$$. Find the value of $$g$$ at another place where clock becomes slow by $$24$$ seconds in a day $$(24\ hrs)$$.
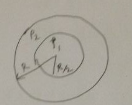
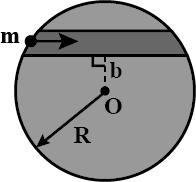
A straight tunnel is dug into the earth as shown in figure at a distance $$b$$ from its center. A ball of mass $$m$$ is dropped from one of its ends. Find the time it takes to reach the other end is approximately.
It has been considered that during the formation of earth,$$H_2$$ gas was available on our planet.Due to excessively high temperature during the formation of earth, $$H_2$$ gas escaped out of the planet.If average escaping velocity of $$H_2$$ is $$1.1 \times 10^6 cm/sec$$, what was the temperature at the time of earth formation.
What is the decrease in weight of a body of mass $$500\ Kg$$ when it is taken into a mine of depth $$1000\ Km$$?
(Radius of earth $$\text{R= 6400 km, g = 9.8 m/s}^2$$)
(a) Find the height from the earth's surface where $$g$$ will be $$25\%$$ of its value on the surface of earth. ($$R=6400\ Km$$).
(b) Find the percentage decrease in the value of $$g$$ at a depth $$h$$ from the surface of earth.
(b) Find the percentage decrease in the value of $$g$$ at a depth $$h$$ from the surface of earth.
The value of acceleration due to gravity is $$980 cm s^{-2}$$. What will be its value if the unit of length is kilometer and that of time is minute?
Two particles of masses $$m$$ and $$M$$ are initially at rest at an infinite distance apart. They move towards each other and gain speeds due to gravitational attraction. Find their speeds when the separation between the masses becomes equal to $$d$$.
Find the height from the earth's surface where g will be $$25\%$$ of its value on the surface of earth (R$$=6400$$km). (b) Find the percentage increase in the value of g at a depth h from the surface of earth.
How much the surface of earth does the acceleration due to gravity reduce by $$36\%$$ of its value on the surface of earth? Radius of earth $$=6400$$km.
The distance of planet Jupiter from the Sun is $$5.2$$ times that of the earth. Find the period of revolution of Jupiter around the Sun.
Gravitational potential energy of interaction of a system of two particles of masses $$m_{1}$$ and $$m_{2}$$ separated by a distance $$r$$
$$U = -\dfrac {Gm_{1}m_{2}}{r}$$.
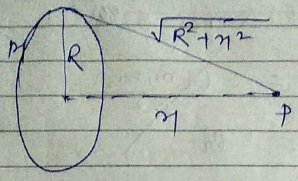
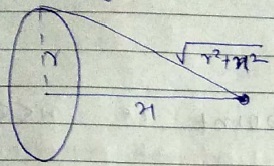
Potential due to a thin ring at a distance $$x$$.
$$V = -\dfrac {GM}{\sqrt {R^{2} + x^{2}}}$$
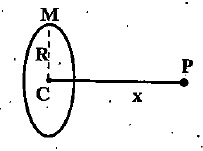
Field at a distance $$x$$ due to a circular ring, $$E_{G} = \dfrac {-GM}{\sqrt {(R^{2} + x^{2})^{3}}}$$.
The masses and the radii of the earth and the moon are $$M_{1}, R_{1}$$ and $$M_{2}, R_{2}$$ respectively. Their centres are at a distance $$d$$ apart. Find the minimum speed with which a particle of mass $$m$$ should be projected from a point midway between the two centres so as to escape it to infinity.
Discuss the variation of acceleration due to gravity with depth. What happens to $$g$$ at the centre of the earth?
Give the dimensional formula for Gravitational constant $$G$$.
At what height above the earth's surface the value of $$g$$ is same as that at a depth of $$100km$$? (Take $${g}_{h}={g}_{d}$$)
At a certain height above the earth surface the gravitational acceleration is 4% of its value at the surface of the earth find the height above the earth surface:
What is the gravitational potential energy?
Find the percentage decrease in the acceleration due to gravity when a body is taken from the surface of earth to a height of $$64\ km$$ from its surface. [Take $$R_{e} = 6.4\times 10^{6}m]$$.
As the altitude, increases how do the weight and mass of the body vary?
A planet has twice the mass of earth and of identical size. What will be the height above the surface of the planet where its acceleration due to gravity reduces by $$36%$$ of its value on its surface?
The question is "A man of mass $$55 kg $$climbs upstairs to reach the springboard which is 6m above the surface of a swimming pool. He jumps up into the air, $$3 m$$ above the springboard, before falling into the pool. If the force exerted by water on the man is $$1500 N$$, the maximum depth of the man in water will be"
The acceleration due to gravity at a place is $$0.2 m/s^ 2.$$ Find its height above the earth's surface.
How far away from the centre of the earth does the acceleration due to gravity will be reduced by $$1$$% of its value at the earth's surface?
Radius of earth $$R = 6400 km$$.
Derive an expression for acceleration due to gravity at a place below the surface of earth
At what depth below the surface does the acceleration due to gravity becomes $$70\%$$ of its value on the surface of earth?
How much below the surface of the earth does the acceleration due to gravity. (i) Reduces to $$36$$% (ii) Reduce by $$36$$% of its value on the surface of earth? (Take $${R}_{e}=6400km$$)
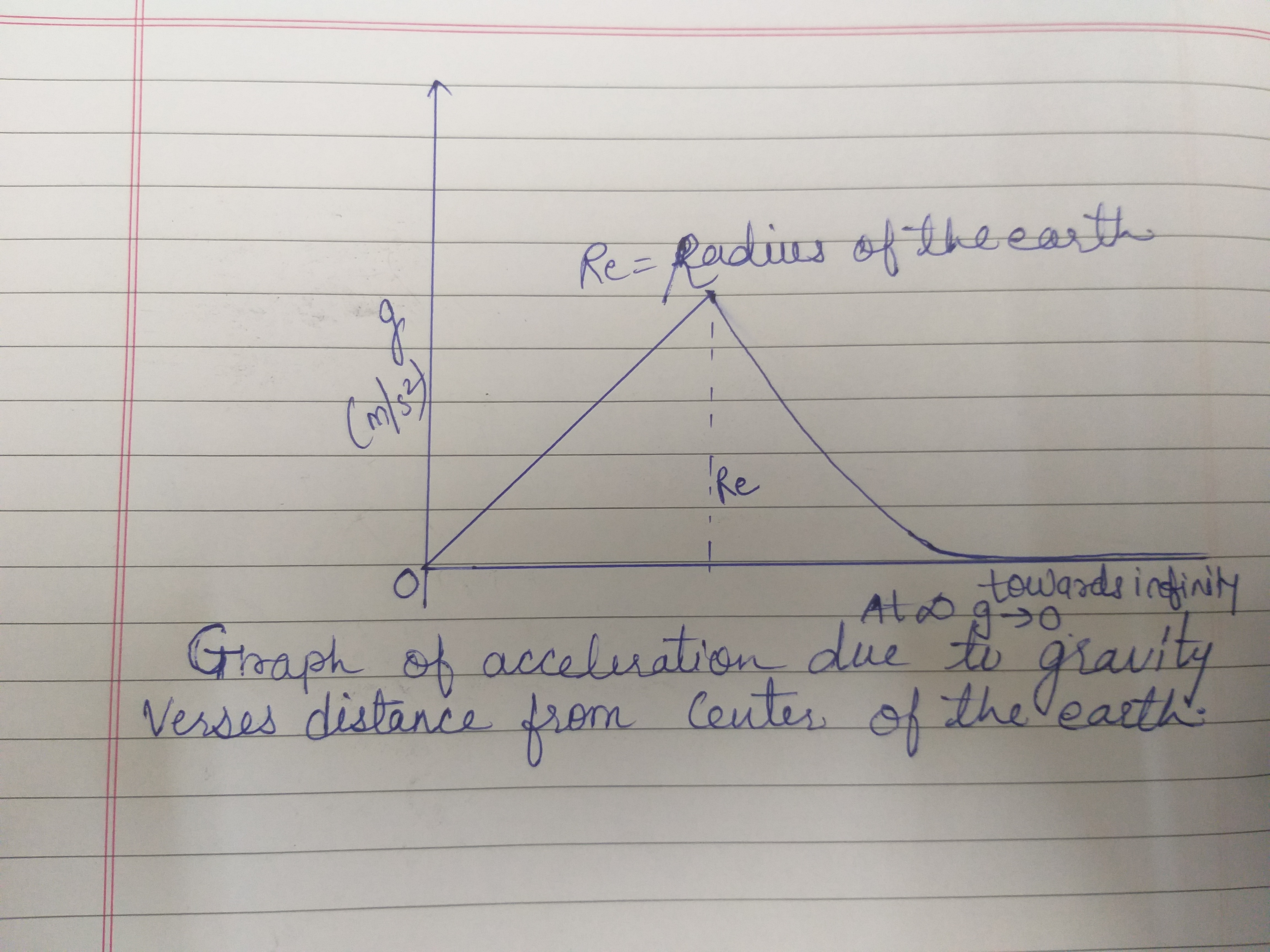
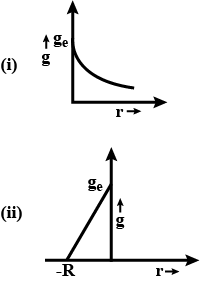
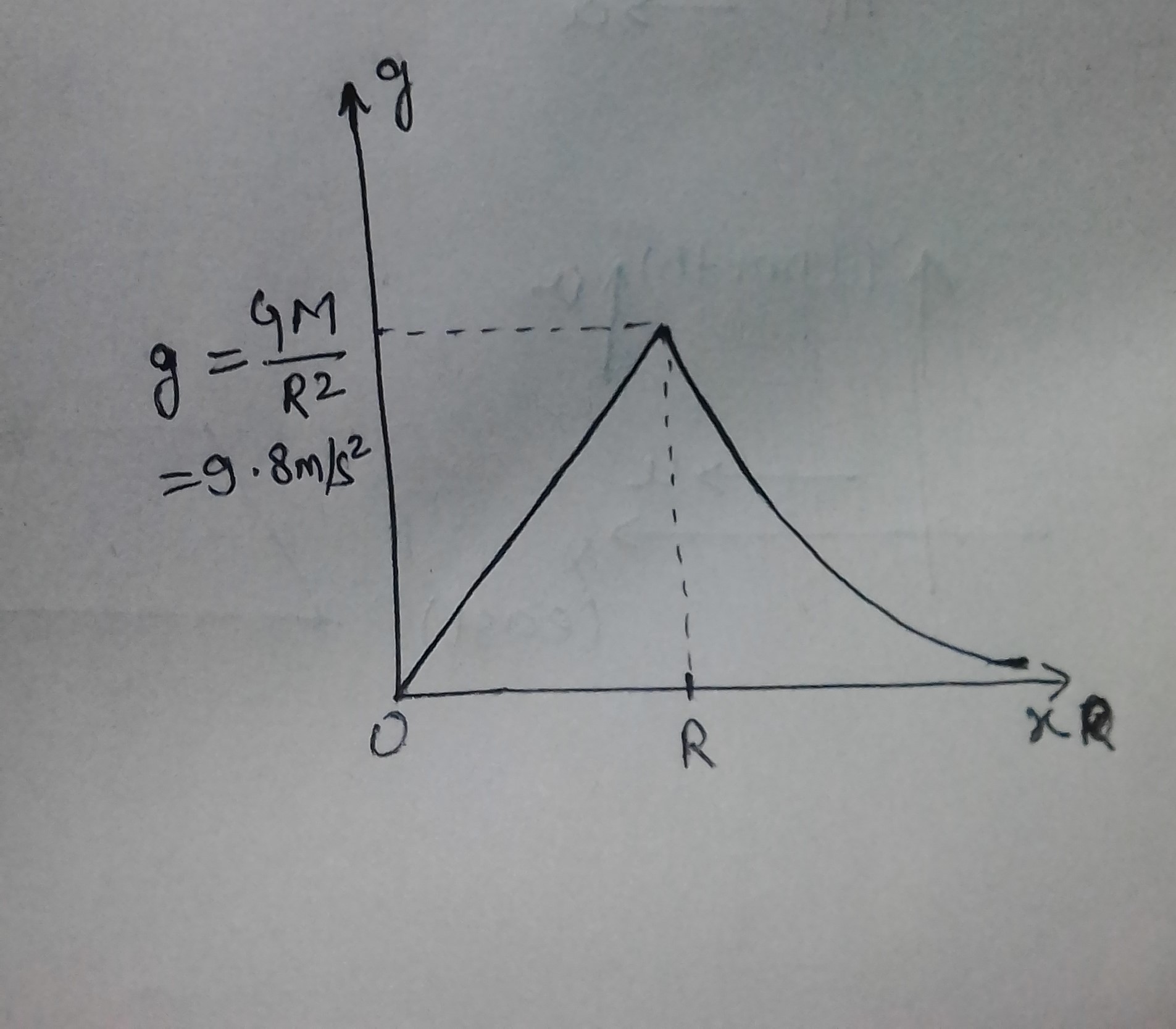
Plot a graph showing the variation of acceleration due to gravity with the distance from the centre of the earth.
The Earth may be regarded as a spherically shaped uniform core of density $$\rho_1$$ and radius $$\dfrac{R}{2}$$ surrounded by a uniform shell of thickness $$\dfrac{R}{2}$$ and density $$\rho_2$$. Find the ratio of $$\dfrac{\rho_1}{\rho_2}$$ if the acceleration due to gravity is the same at surface as at depth $$\dfrac{R}{2}$$ from the surface.
Compare the weight of a body when it is
(i) 200km above the surface of the Earth and (ii) 200km below the surface of the earth.A radius of the Earth is $$6400$$km
The gravitational potential energy of a body at a distance r from the center of the earth is U. The gravitational force at that point is?
Imagine a new planet having the same density as that of earth but it is 3
times bigger than the earth in size. If the acceleration due to
gravity on the surface of earth is g and that on the surface of the new
planet is g' then that would be the relation between them ?
Assuming the earth to be a sphere of uniform density, how much could a body weigh at a height equal to radius of earth when it weighs 250 N on the surface of the earth.
At what height the acceleration due to gravity will be reduced by 36 % its value o the surface of the earth?
A space ship is launched into a circular orbit close to the Earth's surface. What additional velocity has now to be imparted to the space ship in the orbit to overcome the gravitational pull ?
(Radius of Earth = 6400 km:g= 9.8 $$ms^{-2}$$
The height above the earth's surface does the acceleration due to gravity fall to $$1\%$$ of its value at the earth's surface is KR. Then the value of K is_____(K is an integer)
Calculate the distance from the surface of the earth at which above and below the surface acceleration due to gravity is the same.
If the radius of the earth shrinks by $$2.0 \%$$, mass remaining constant, then how would the value of acceleration due to gravity change. ?
What will be the weight of a $$120$$kg body if it is taken to $$2000$$km above earth surface?
What is escape velocity? Obtain an expression for it.
Suppose the gravitational potential due to a small system is $$k /r^ 2$$ at a distance r from it. What will be the gravitational field ? Can you think of any such system? What happens if there were negative masses?
A person is painting his house walls. He stands on a ladder with a bucket containing paint in one hand and a brush in other. Suddenly the bucket slips from his hand and falls down on the floor. If the bucket with the paint had a mass of $$0.6\ kg$$ and was at a height of $$2.0\ m$$ at the time it slipped, how much gravitational potential energy is lost together with the paint?
Explain why the value of $$g$$ is zero at the center of the earth.
A sky lab of mass 200 kg has to be lifted from one circular orbit of radius 2R to another circular orbit of radius 3R. Calculate the minimum energy required if $$R_E=6.37 \times 10^6 m$$ and acceleration due to gravity on earth's surface$$=9.8 ms^{-2}$$
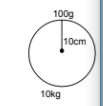
A particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
A satellite orbiting certain planet has apogee $$R_1$$ and perigee equal to $$R_2$$, then find the minimum kinetic energy that should be given to the satellite to the satellite to enable it to escape the planet.

Find the height over the earth's surface at which the weight of a body becomes half of its value at the surface.
Find the acceleration due to gravity in a mine of depth 640 m if value at the surface is $$ 9.800 m/s^2 $$.The radius of the earth is 6400 km.
What is the acceleration due to gravity on the top of Mount Everest? Mount Everest is the highest mountain peak of the world at the height of 8848 m. The value at sea level is $$ 9.80 m/s^2 $$
The gravitational field in a region is given by $$\vec { E } =\left( 5N/kg \right) \vec { i } +\left( 12N/Kg \right) \vec { j } $$
(a) Find the magnitude of gravitational force acting on a particle of mass 2 kg placed at the origin.(b) Find the potential at the points (12 m,0) and (0,5) if the change in gravitational potential energy if the potential at the origin is taken to be zero. (c) Find the change in gravitational potential energy if a particle of mass 2kg is taken from the origin to the point $$(12m,5m)$$ (d) Find the change in potential energy if the particle is taken from $$(12m.0)$$ to $$(0,5m)$$
Mile-high building. In 1956, Frank Lloyd Wright proposed the construction of a mile-high building in Chicago. Suppose the building had been constructed . Ignoring Earth's rotation, find the change in your weight if you were to ride an elevator from the street level, where you weigh 600 N, to the top of the building.
A body has a weight of 10 kg on the surface of earth. What will be its weight when taken to the centre of the earth?
Derive an expression for the work required to move an earth satellite of mass m from a circular orbit of radius $$2R_E$$ to one of radius $$3R_E.$$
At what altitude above Earth's surface would the gravitational acceleration be $$4.9 m/s^{2}$$?
Match the Column
As the altitude of a body increases, do the weight and mass both vary?
What is the value of gravitation constant G (i) on the earth, and (ii) on the moon?
Two homogeneous spheres, $$S_1$$ and $$S_2$$ , have equal masses but different radii, $$R_1$$ and $$R_2.$$ If the acceleration of gravity on the surface of sphere S is $$g_1$$ , what is the acceleration of gravity on the surface of sphere $$S_2$$ ?
(a)What is the the value of $$g_h$$ , acceleration due to gravity at height $$h$$, from earth surface, How can we approximate it for small values of $$h$$.
Derive an expression for the acceleration due to gravity on the surface of the earth. State factors on which g depends . How does it vary with depth ? Where is it maximum on the surface of the earth ?
If we go deeper inside the earth , what will change : weight or mass or both , and why ?
Out of aphelion and perihelion , where is the speed of the earth more and why ?
State the value of universal gravitational constant. What was its value back In 1947?
What is the direction of areal velocity of the earth around the sun ?
In Fig, the scale on which the 60 kg pysicist stands reads 220 N. How long will the cantaloupe take to reach the floor if the physicist drops it (from rest relative to himself ) at a height of 2.1 m above the floor
Draw aerial velocity versus time graph for mars.
A ball is thrown vertically upwards. It returns 6s later. Calculate
the initial velocity of the ball. (Take g = $$9.8 m / s^{2}$$)
A ball is thrown vertically upwards. It does to a height 20m and then returns to the ground. Taking acceleration due to gravity g to be $$10 m / s^{2}$$, find:
The initial velocity of the ball
Define escape velocity with respect to earth. What do $$R$$ and $$g$$ indicates in the mathematical formula of escape velocity?
Write the numerical value of gravitational constant G with its S.I unit.
Define gravitational constant G.
How long will a stone take a fall to the ground from the top a building 80m high
A body is dropped from the top of a tower. It acquires a velocity $$20$$m/s on reaching the ground. Calculate the height of the tower. (Take g = $$9.8 m / s^{2}$$)
A ball is thrown vertically upwards. It returns 6s later. Calculate:
the greatest height reached by the ball,
A ball is thrown vertically upwards. It does to a height 20m and then returns to the ground. Taking acceleration due to gravity g to be $$10 m / s^{2}$$, find:
The total time of journey of the ball.
Answer the following question
What is escape velocity ?
A pebble is dropped freely in a well from its top. It takes the $$20s$$ fro the pebble to reach the water surface in the well. Taking $$g=10m/s^2$$ and speed of sound $$= 330m/s.$$ find the depth of water surface,
A stone is dropped freely from the top of a tower and it reaches the ground is 4s. Taking g = $$10 m / s^{2}$$, calculate the height of the tower.
A ball is thrown vertically upwards from the top of a tower with an initial velocity of 19.6 m/s. the ball reaches the ground after 5s. Calculate:
the height of the tower,
Define gravitational potential and give its unit in S.I.
How much would be the increase in the potential energy if a body of mass $$m$$ is taken to a height $$R$$ equal to the radius of the Earth ?
If Earth is a hollow sphere ; then what would be the mass of an object at a depth $$10\,km$$ below the Earth's surface ?
Calculate the escape velocity on the Moon. Given Earth's radius is $$4$$ times the radius of Moon and mass of Earth is $$80$$ times of the Moon.
At how much above the Earth's surface , the value of gravitational acceleration would be $$10$$ % less than that on the surface ?
What will be the weight of the book whose mass is $$500$$ gm, placed at c height equal to the radius of the earth?
Assuming the earth to be a sphere of uniform mass density , how much would a body weigh halfway down to the centre of the earth if it weighed 250 N on the surface ?
Acceleration due to gravity increases / decreases with increasing altitude .
Acceleration due to gravity increasing / decreasing with the increasing depth (assume the earth to be a sphere of uniform density ).
Derive an expression for gravitational potential energy.
A body weight 63 N on the surface of the earth . What is the gravitational force on it due to the earth at a height equal to half the radius of the earth ?
Calculate the acceleration due to gravity
At a depth 2.8 km below surface of the earth. (Radius of the earth is 6400 km and acceleration due to gravity on the surface of the earth $$g = 9.8 m/s^{2}$$).
Does the escape speed of a body from the earth depend on ?
the location from where it is projected ,
Find the height at which the acceleration due to gravity is 1% less than its value on the surface of the earth. Radius of the earth $$6400 km$$.
Calculate the acceleration due to gravity
At a height 16 km above Earth's surface.
An astronaut inside a small space ship orbiting the earth cannot detect gravity . If the space station orbiting around the earth has a large size , can be hop to detect gravity ?
What is the difference between gravitational potential energy and gravitation potential ? Derive an expression for gravitational potential energy.
How does g vary with height above the surface of earth?
Give the expression for the escape velocity .
Explain the variation of 'g' with
height.
What is the escape velocity of a body ?
Write the expression for acceleration due to gravity at a height (altitude ) 'h'
Define Universal gravitational constant G. What is the dimensional formula G?
Mention the relation between escape velocity and Orbiting velocity
Define gravitational potential and field intensity. Give their units . Also, write relation between them.
Write the expression for acceleration due gravity at a depth h below Earth's surface
Where does a body experience maximum weight on the earth? What is the reason?
While Jumping on a cement floor, we weigh less than what weighs on cement floor. Why?
A planet's radius is reduced by 5%, with its mass unchanged . What is the percentage change in 'g'?
Find the expression for the weight of the body at centre of Earth.
Suppose if the body is moved from the surface of the earth to the centre. What happens?
Where on the earth does a body experience minimum weight? What is the reason?
Find the height at which g is the same as that at depth R/2
Is the potential energy of an object on the surface of Earth zero?
What will be the value of $$g$$ at the centre of the earth?
Is it possible for the weight of a body to be zero?
During the rotation of a giant wheel, a person experiences loss of weight on the descent. Explain why.
What will be the weight of a body at the center of earth.
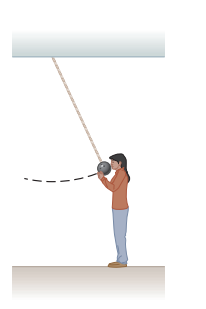
A bowling ball is suspended from the ceiling of a lecture hall by a strong cord. The ball drawn away from its equilibrium position and released from rest at the tip of the demonstrator's nose as show n Figure The demonstrator remains stationary Would this demonstrator be safe if the ball were given a push from its starting position at her nose?
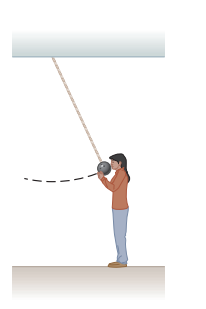
One person drops a ball from the top of a building while another person at the bottom observes its motion. Will these two people agree o(a) n the value of the gravitational potential energy of the ball Earth system (b) On the change in potential energy? (C)On the kinetic energy of the ball at some point inits motion?
What is the weight of the body when it is at the center of the earth? Give reasons.
A bowling ball is suspended from the ceiling of a lecture hall by a strong cord. The ball drawn away from its equilibrium position and released from rest at the tip of the denominator's nose as show n Figure The demonstrator remains stationary Explain why the ball does not strike her on its return swing.
Newton’s law of universal gravitation is represented by
$$F=\frac{GMm}{r^{2}}$$
where $$F$$ is the magnitude of the gravitational force exerted by one object on another, $$M$$ and $$m$$ are the masses of the objects, and $$r$$ is a distance. Force has the SI units $$kg.m/s^{2}$$. What is the SI unit of the proportionality constant $$G$$?
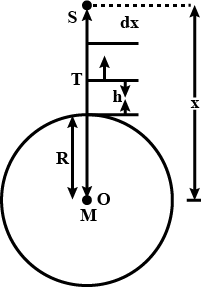
lmagine a vertical mine shaft of depth x metres located near the equator (of earth). A plumb line is hanging in the shaft and a stone is dropped from rest next to it. The stone will not fall parallel to the plumb line, but will deviate in easterly direction by an amount of y metres.
Given $$\omega $$ is angular speed of earth and $$g$$ is acceleration due to gravity)
If y$$=\dfrac{\omega g}{n}\left ( \dfrac{2x}{g} \right )^{\dfrac{3}{2}} $$ find n.
At what height (in km) over the Earth's pole the free-fall acceleration decreases by one percent?
A particle of mass $$m$$ was transferred from the centre of the base of a uniform hemisphere of mass $$M$$ and radius $$R$$ into infinity. What work was performed in the process by the gravitational force exerted on the particle by the hemisphere?
Assuming earth to be spherical, at what approximate height (in km) above the north pole, value of $$g$$ is same as that on the earth's surface at equator?
A rocket is fired 'vertically' from the surface of mars with a speed of $$2\ kms^{-1}$$. If 20% of its initial energy is lost due to martian atmospheric resistance, how far (in km) will the rocket go from the surface of mars before returning to it ? Mass of mars = $$6.4 \times 10^{23}\ kg$$; radius of mars = 3395 km; $$G = 6.67 \times 10^{-11}\ Nm^2kg^{-2}$$.
A planet has a core and on outer shell of radii $$R$$ and $$2R$$ respectively. The density of the core is $$x$$ and that of outer shell is $$y$$. The acceleration due to gravity at the surface of planet is same as that at depth $$R$$. The ratio of $$x$$ and $$y$$ is $$\dfrac{n}{3}$$. Find $$n$$.
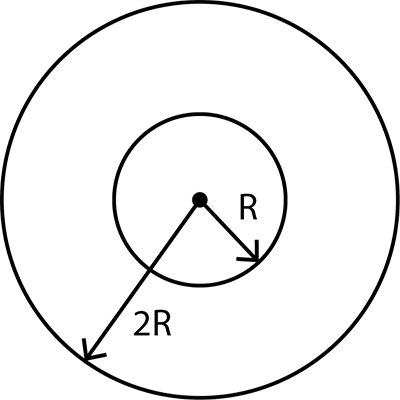
Earth radius is $$R$$ and spin angular velocity of Earth is $$\omega$$. At what height above the North pole the acceleration due to gravity will be same as that at the equation? ($$g$$ is acceleration due to gravity at North pole).
Draw graphs showing the variation of acceleration due to gravity with (a) height above the earth's surface, (b) depth below the earth's surface.
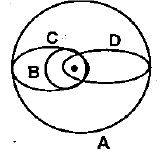
The given figure shows several possible elliptical orbits of a satellite. Then match the following
A small body starts falling onto the Sun from a distance equal to the radius of the Earth. The initial velocity of the body is equal to zero in the heliocentric reference frame. If the time taken by the body to fall into the sun is $$6.45 \times 10^{k}$$. Then $$k$$ is
A small body of super dense material, whose mass is half of the earth (but whose size is very small compared to the size of the earth), starts from rest at a height $$H$$ above the earths surface, and reaches the earths surface in time $$t$$. Calculate time $$t$$ assuming that $$H$$ is very small compared to the radius of the earth. Acceleration due to gravity near the surface of the earth is $$g$$.
At what height the acceleration due to gravity will be reduced to $$36\%$$ of its value on the surface of the earth?
At which height above earth's surface value of $$'g'$$ is same as in a mine $$100 km $$ deep.
If the distance of Earth from the Sun were half the present value, how many days will make one year?
Plot a graph showing the variation of acceleration due to gravity with the center of the earth.
The weight of a body on the surface of earth is $$250\ N$$. Calculate its weight at distance equal to half of the radius of earth below the surface of earth. (Radius of earth $$= 6400\ km$$).
What is gravitational potential energy? Explain with the help of an example.
Calculate the value of the acceleration due to gravity at a place $$3,200 km$$ above the surface of the earth.
The moon is observed from two diametrically opposite points A and B on earth. The angle subtended at the moon by two directions of observation is $${1^ \circ }54'$$. The diameter of the earth is $$1.276 \times {10^7}m$$ . Calculate the distance of moon from earth.
At which height from the surface of the Earth, The acceleration due to gravity is the same as at a depth 160 km below the surface of Earth. Radius of Earth is 6400 km
At what depth from earth's surface does the acceleration due to gravity becomes $$\dfrac{1}{4}$$ times that of its value at surface?
Discuss the variation of g with
(a) altitude (b) depth
At which height above earth surface is the value of 'g' same as in a 100 km deep mine?
On a planet whose size is the same and mass 4 times as that of the earth, find the energy needed to lift a 2 kg mass vertically upwards through 2 m distance in joule. The value of g on the surface of earth is 10 $${ ms }^{ -2 }$$ ?
How the value of g varies with height.
The gravitational field in a region is given by $$ E = (2 \hat{i} + 3\hat{j}) $$N/kg. Show that no work is done by the gravitational field when a particle is moved on the line 3 y + 2 x = 5
What is the unit of G ?
A star like the sun has several bodies moving around it at different distances. consider that all of them are moving in circular orbits. Let $$ r $$ be the distance of the body from the center of the star and let its linear velocity be $$ v$$ angular velocity $$ \omega $$ kinetic energy $$ K$$ . gravitational potential energy $$ U $$, total energy $$ E $$ and angular momentum $$ l $$. as the radius $$ r $$ of the orbit increases, determine which of the above quantities increase and which ones decrease.
Calculate the height at which the acceleration due to gravity becomes $$\left ( \dfrac{1}{16} \right )^{th}$$ of its value on the surface. (radius of the earth 6400 km).
Show the velocity of body released from a height r from centre of Earth (r > R) is $$R [2g \left ( \dfrac{1}{R} - \dfrac{1}{r} \right )]^{1/2}$$ when it reaches the Earth's surface is, where R is radius of Earth.
A spacecraft is in an orbit around the sun that coincides with the orbit of the earth. What additional speed must be given it if it is leave the solar system completely ?
At what height over the Earth's pole the free-fall acceleration decreases by one per cent; by half?
Define gravitational potential energy. Calculate the change in the potential energy in sending a particle to height $$h$$ from the Earth's surface . When $$ h << R $$ discuss about the changes in potential energy.
Two bodies of masses $$ M_1 $$ and $$ M_2$$ are kept at a distance $$d$$ from each other. Prove that the point at which the intensity of the gravitational field is zero, the gravitational potential will be :
$$ V = \dfrac{-G}{d} [M_1 + M_2 + 2\sqrt{M_1 M_2}] $$
Jonathan is riding a bicycle and encounters a hill of height $$h$$. At the base of the hill, he is travelling at a speed $$\nu_i$$. When he reaches the top of the hill, he is travelling at a speed $$\nu_f$$. Jonathan and his bicycle together have a mass $$m$$ Ignore friction in the bicycle mechanism and between the bicycle tries and the road What is the change in potential energy stored in Jonathan's body during this process?
What is the minimum speed, relative to the Sun, necessary for a spacecraft to escape the solar system if it starts at the Earth's orbit?
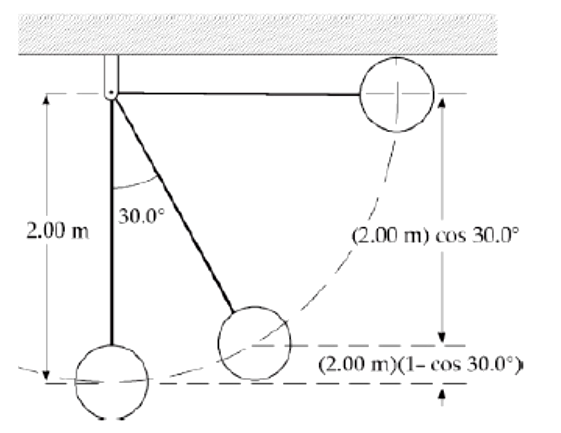
A $$400N$$ child is in a swing that is attached to a pair of ropes $$2.00 m$$ long. Find the gravitational potential energy of the childEarth system relative to the childs lowest position when (a) the ropes are horizontal, (b) the ropes make a $$30.0^{0}$$ angle with the vertical, and (c) the child is at the bottom of the circular arc.
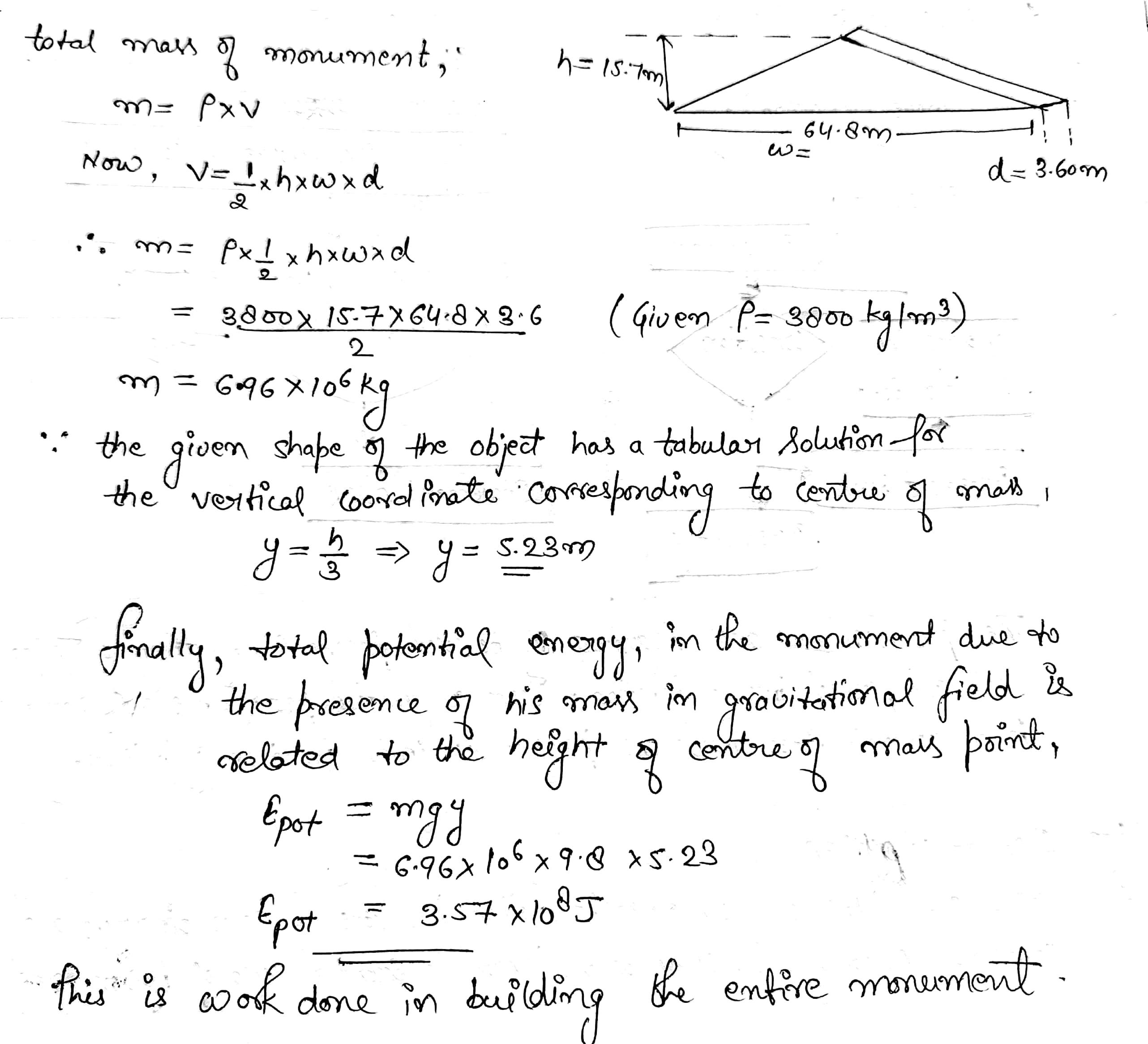
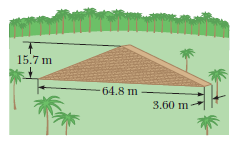
Explorers in the jungle find an ancient monument in the shape of a large isosceles triangle as shown in Figure $$P9.47$$. The monument is made from tens of thousands of small stone blocks of density $$3\ 800 kg/m^3$$. The monument is $$15.7\ m$$ high and $$64.8\ m$$ wide at its base and is everywhere $$3.60\ m$$ thick from front to back.Before the monument was built many years ago, all the stone blocks lay on the ground. How much work did laborers do on the blocks to put them in position while building the entire monument? Note: The gravitational potential energy of an objectEarth system is given by $$Ug = Mgy_{CM}$$, where M is the total mass of the object and $$y_{CM}$$ is the elevation of its center of mass above the chosen reference level.
Evaluate this difference for $$h=6.00\ m$$, a typical height for a two-story building.
A small block of mass $$m=200\ g$$ is released from rest at point $$A$$ along the horizontal diameter on the inside of a frictionless, hemispherical bowl of radius $$R=30.0\ cm$$ Fig. calculate the gravitational potential energy of the block-Earth system when the block is at point $$A$$ relative to point
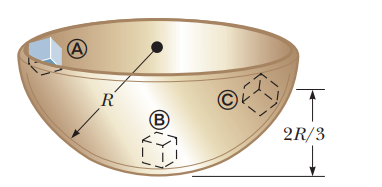
(i) Rank the gravitational accelerations you would measure for the following falling objects: (a) a $$2kg$$ object $$5 cm$$ above the floor, (b) a $$2kg$$ object $$120 cm$$ above the floor, (c) a $$3kg$$ object $$120 cm$$ above the floor, and (d) a $$3kg$$ object $$80 cm$$ above the floor. List the one with the largest magnitude of acceleration first. If any are equal, show their equality in your list. (ii) Rank the gravitational forces on the same four objects, listing the one with the largest magnitude first. (iii) Rank the gravitational potential energies (of the objectEarth system) for the same four objects, largest first, taking $$y = 0$$ at the floor.
Class 11 Engineering Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Physical World Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work,Energy And Power Extra Questions