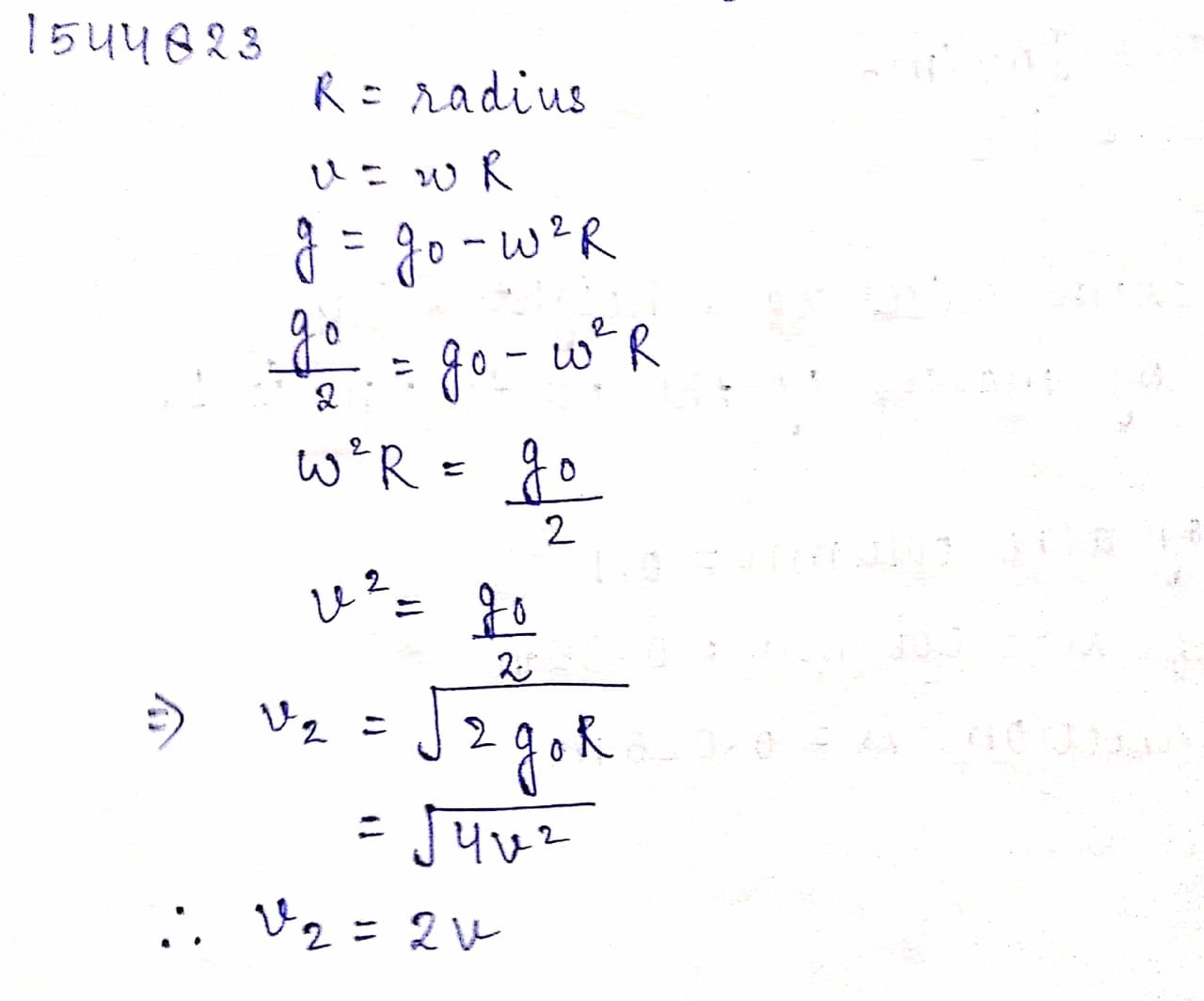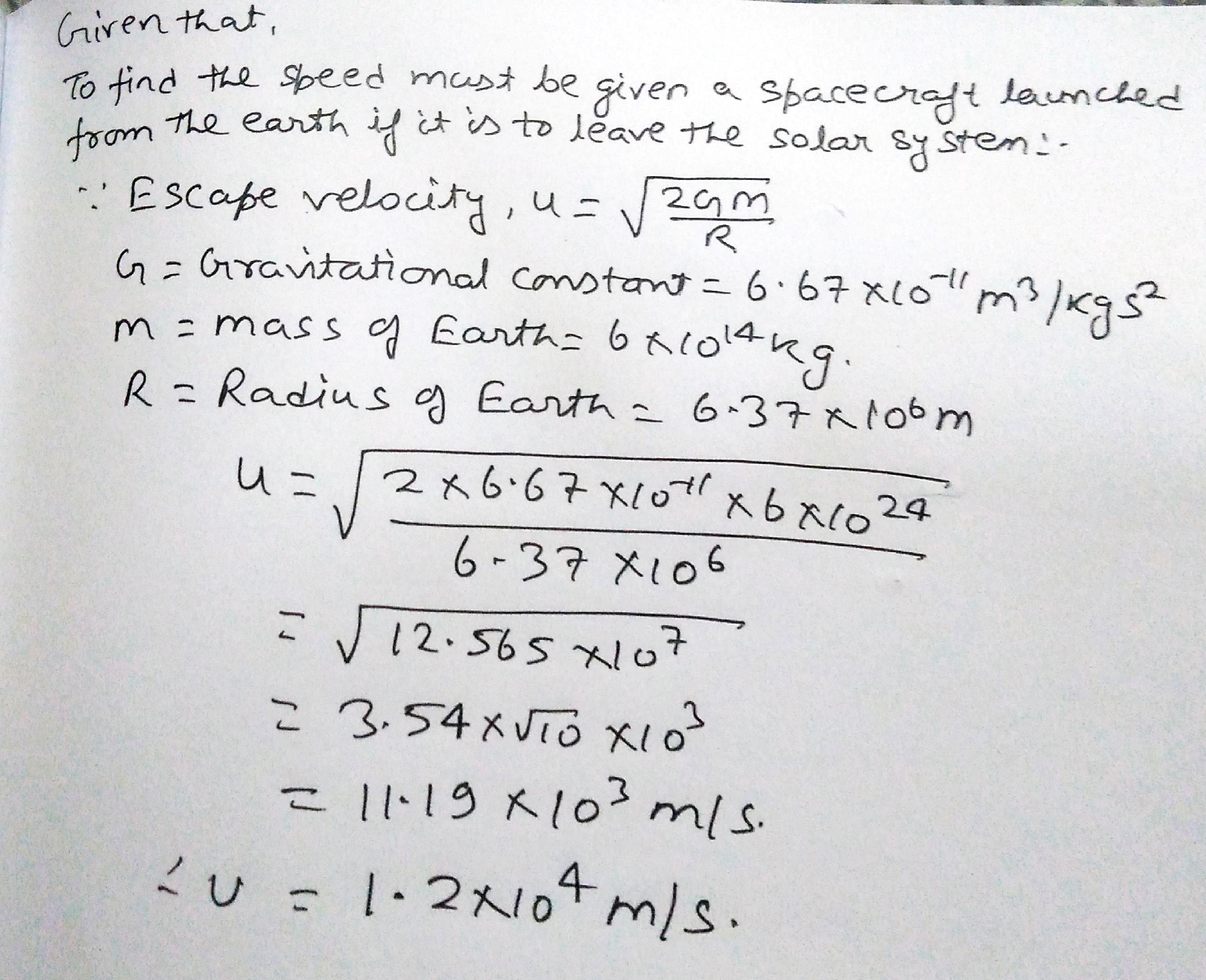Gravitation - Class 11 Medical Physics - Extra Questions

Review. At what temperature would the average speed of helium atoms equal (a) the escape speed from the Earth, $$1.12 \times 10^4 m/s$$, and (b) the escape speed from the Moon, $$2.37 \times 10^3 m/s?$$ Note: The mass of a helium atom is $$6.64 \times 10^{-27} kg$$.


1892496_1859898_ans_8da932937dd64ceca7f18cbc6865de8b.jpeg


What are the factors that decide the value of escape velocity?

The factors that decide the value of escape velocity are:
1) The escape velocity depends on the mass of the planet or moon that a spacecraft is blasting off the earth.
2) Apart from these the escape velocity also depends on the value of gravitational pull.


What is meant by escape velocity? Write the relation between escape velocity and orbital velocity.

Escape velocity is the lowest velocity which a body must have in order to escape the gravitational attraction of a particular planet or other object.
The relation between escape velocity and orbital velocity is given by V$$_{e}$$ = $$\sqrt{2}$$V$${o}$$ where V$$_{e}$$ is the escape velocity and V$$_{o}$$ is the orbital velocity. Thus the escape velocity is root-two times the orbital velocity.



What is escape velocity? Obtain an expression for it

Escape velocity is defined as the minimum initial velocity that will take a body away above the surface of a planet when it is projected vertically upwards.
Therefore the body must have total energy as zero at his velocity so that it can reach the gravity free region of the planet with exactly zero kinetic energy.
Hence $$\dfrac{1}{2}mv_{e}^2-\dfrac{GMm}{R}=0$$ 
$$\implies v_e=\sqrt{\dfrac{2GM}{R}}$$


Define escape velocity. Mentions its expression.

Escape velocity at any planet is defined as the minimum velocity of a body required to go out of the gravitational field of that planet.
for a planet having mass M and radius R is given as $$ \sqrt[2]{2GM/R}$$ 




The escape velocity of a projectile on the earth's surface is $$11.2km{s}^{-1}$$. A body is projected out with thrice this speed. What will be the speed of the body far away from the earth, that is, at infinity? Ignore the presence of sun and other planets

Escape velocity from Earth is $${v_{esc}} = 11.2km{s^{ - 1}}$$
Projection Velocity = $${v_p} = 3{v_{esc}}$$
Mass of projectile m, is projected with velocity $${v_f}$$
Total energy of projectile on Earth = $$\frac { 1 }{ 2 } m{ v_{ p } }^{ 2 }-\frac { 1 }{ 2 } m{ v_{ esc } }^{ 2 }$$
Gravitational potential energy far away from Earth is zero, so the total energy of projectile far away from the Earth will be = $$\dfrac { 1 }{ 2 } { v_{ f } }^{ 2 }$$
From the law of conservation of energy,
$$\begin{array}{l} \dfrac { 1 }{ 2 } m{ v_{ p } }^{ 2 }-\dfrac { 1 }{ 2 } m{ v_{ esc } }^{ 2 }=\dfrac { 1 }{ 2 } m{ v_{ f } }^{ 2 } \\ { v_{ f } }=\sqrt { { v_{ p } }^{ 2 }-{ v_{ esc } }^{ 2 } } =\sqrt { 3{ v_{ esc } }^{ 2 }-{ v_{ esc } }^{ 2 } } =\sqrt { 8 } { v_{ esc } } \\ { v_{ f } }=\sqrt { 8 } \times 11.2=31.68km{ s^{ -1 } } \end{array}$$


A spherical uniform planet is rotating about its axis. The velocity of a point on its equator is V. Due to the rotation of planet about its axis the acceleration due to gravity g at equator is 1/2 of g at poles. The escape velocity of a particle on the pole of planet in terms of V.


1359662_1544823_ans_c2207196989645c285e7672808ae8972.jpg


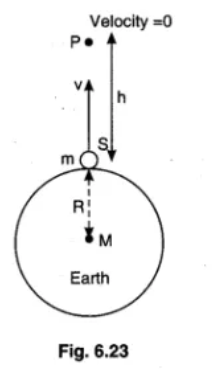
Small, glassy button like objects called tektites are found strewn over areas in various locations over the earth. One view of the origin of tektites is that they were ejected from the moon by the impact of meteorites on the lunar surface. At what minimum speed must a body be ejected from the lunar surface if it is to reach the earth ?

Hint : A minimum speed tektite must have negligible speed when it passes through a certain point on its moon-earth trajectory.

Here we have to evaluate the escape velocity of a particle from moon
Now $$v_e = \sqrt{\dfrac{2GM_m}{R}}$$
Now, Mass of moon  $$M_m = 7.3 \times 10^{22} \ kg$$
Radius of moon $$R= 1737 km = 1737 \times 10^3\ m$$
$$G = 6.67 \times 10^{-11} \ Nm^2kg^{-2}$$
Putting all these we get $$v_e \approx 2330 \ m/s$$
So, $$v_{min} \approx 2330 \ m/s$$


Derive formula for velocity of projection.

Projection Velocity 
The minimum velocity to throw an object vertically upwards to a definite height is called the projection velocity."

Suppose , if an object having mass (m) is projected with v velocity to a height (h) from the Earth's surface , when the body is thrown upwards then body's kinetic energy is changed into its gravitational potential energy. Hence, from the law of conservation of energy.

Total energy of the body at the surface of the Earth (S) = Total energy of body at point P at height h 

or    $$ K_S + U_S = K_P + U_P $$ 

$$ \dfrac{1}{2} mv^2 + U_S = 0 + U_P $$ 

$$ \therefore $$     $$ \dfrac{1}{2} mv^2 = U_P - U_S = \Delta U $$ 

$$ \dfrac{1}{2} mv^2 = \dfrac{mgh}{\left  [ 1 + \dfrac{h}{R}  \right  ]} $$ 

or       $$ v^2 = \dfrac{2gh}{\left  [1 + \dfrac{h}{R}  \right  ]} $$      .........(1) 

or       $$ v = \sqrt{\dfrac{2gh}{\left  [ 1 + \dfrac{h}{R}  \right  ]}} $$   ...........(2) 

This is the formula for the projection velocity of a body going to a height h from the surface of the Earth.
The maximum height (h) gained by the object from equation (1) is ;
    $$ 2gh = v^2 \left  [ 1 + \dfrac{h}{R}  \right  ] = \dfrac{v^2 (R + h)}{R} $$ 

or       $$ 2ghR = v^2R + v^2h $$ 

or     $$ 2ghR - v^2h = v^2R $$ 

or      $$ h (2gR - v^2) = v^2R $$ 

     $$ h = \dfrac{v^2R}{(2gR - v^2)} $$                 ...............(3) 

This is the maximum height 

If $$ 2gR >> v^2 $$  then $$ h = \dfrac{v^2R}{2gR} $$ 

 $$ \therefore $$            $$ h = \dfrac{v^2}{2g} $$             .............(4) 
1753569_1832982_ans_29a73e669ebb4117a270f9a543077338.png


If an object has just enough energy to escape from the earth, it will not escape from the solar system because of the attraction of the sun. Use equation for escape velocity $$\upsilon_e = \sqrt {2GM_E / R_E}$$ with $$M_S$$ replacing $$M_E$$ and the distance to the sun $$r_S$$ replacing $$R_E$$ to calculate the speed $$\upsilon_{eS}$$ needed to escape from the sun's gravitational field for an object at the surface of the earth. Neglect the attraction of the earth. Show that if $$\upsilon_e$$ is the speed needed to escape from the earth, neglecting the sun, then the speed of an object at the earth's surface needed to escape from the solar system is given by $$\upsilon_{e, solar}^2 = \upsilon_e^2 + \upsilon_{eS}^2 ,$$ and calculate $$\upsilon _{e,solar}.$$

The energy required to escape from earth is $$E_1 = \dfrac{1}{2}mv_e^2$$
The energy required to escape from sun's gravitational field at the surface of earth is $$E_2 = \dfrac{1}{2}mv_{eS}^2$$
So, the energy required to escape from solar system $$E = E_1 + E_2$$
Also, $$E = \dfrac{1}{2}mv_{e,solar}^2$$
So, $$\dfrac{1}{2}mv_{e,solar}^2 = \dfrac{1}{2}mv_e^2 + \dfrac{1}{2}mv_{eS}^2$$
$$or, v_{e,solar}^2 = v_e ^2 + v_{eS}^2$$ (proved)

Now, $$v_e = 11.2 \ km/s$$
Now, $$v_{eS} = \sqrt{\dfrac{2GM_s}{r_s}}$$
$$M_s = 2 \times 10^{30} \ kg, r_s = 15 \times 10^{10} \ m$$(roughly the distance of an object on the surface of earth to the sun) that gives $$v_{eS} = 42.2 \ km/s$$
And from the above relation we get $$v_{e,solar} = 43.7 \ km/s$$


At what altitude above Earth's surface would the gravitational acceleration be  $$ 4.9 m/s^{2} $$

Acceleration due to gravity at height h is given by 

$$g_h=\dfrac{GM}{(R+h)^2}$$

we know $$g=GM/R^2=9.8\,m/s^2$$

so $$GM/2R^2=4.9\,m/s^2$$
putting in $$g_h=\dfrac{GM}{(R+h)^2}$$

$$\dfrac{GM}{2R^2}=\dfrac{GM}{(R+h)^2}$$

$$\implies R+h=\sqrt 2 R$$

$$h=0.414 R$$, where $$R$$ is the radius of earth.



The values of g at six distances A, B, C, D, E and F from the surface of the earth are found to be $$3.08 m/s^2, 9.2.3 m/s^2, 0.57 m/s^2, 7.34 m/s^2, 0.30 m/s^2$$ and $$1.49 m/s^2$$, respectively.
(a) n Arrange these values of g according to the increasing distances from the surface of the earth (keeping the value of g nearest to the surface of the earth first)
(b) If the value of distance F be 10000 km from the surface of the earth, state whether this distance is deep. inside the earth or high up in the sky. Give reason for your answer.

(a) 9.23 $$m/s^2$$, 7.34  $$m/s^2$$, 3.08  $$m/s^2$$, 1.49  $$m/s^2$$, 0.57  $$m/s^2$$, 0.30  $$m/s^2$$
(b) This distance F of 10000 km is high up in the sky. The distance of 10000 km cannot be deep inside the earth because the radius of earth is only about 6400km and the value of g at the centre of earth becomes zero.


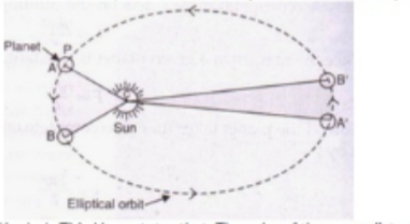
State and explain Kepler's laws of planetary motion. Draw diagrams to illustrate these laws.

Kepler's first law: The planets move in elliptical orbits around the sun, with the sun at one of the two foci of the elliptical orbit. This law means that the orbit of a planet around the sun is an ellipse and not an exact circle. An elliptical path has two foci, and the sun is at one of the two foci of the elliptical path.
Kepler's Second law states that: Each planet revolves around the sun in such a way that the line joining the planet to the sun sweeps over equal areas in equal intervals of time. This means that a planet does not move with constant speed around the sun. The speed is greater when the planet is nearer the sun, and less when the planet is farther away from the sun.
Kepler's Third Law states that: The cube of the mean distance of a planet from the sun is directly proportional to the square of time it takes to move around the sun.
$$r^3 \propto T^2$$
1611297_1763580_ans_8d9b0e79e3744ca7889c6949be3d89eb.jpg


A ball is thrown vertically upwards with an initial velocity of 49 m/s. Calculate:
the maximum height attained,(Take g = $$9.8 m / s^{2}$$)

Given: $$initial\, velocity\, u=49m/s$$
Assume $$‘h’$$ to be the height, velocity $$= 0m/s$$ at the greatest height
We know from the equation of motion,
$$v^2-u^2=2gh$$
$$\Rightarrow 0-(49)^2 = 2(-9.8)(h)$$
$$\Rightarrow h=\dfrac{(49)^2 }{19.6}$$
$$\Rightarrow h=122.5m$$


A body falls from the top of a building and reaches the ground 2.5s later. How high is the building? (Take g = $$9.8 m / s^{2}$$)

Given: $$g=9.8m/s^2, t=2.5s$$
Assume $$‘h’$$ to be the height of the building
We know from the equation of motion,
$$H=ut + \dfrac{1}{2} gt^2$$
$$H= \dfrac{1}{2} gt^2$$
$$H=\dfrac{1}{2} (9.8)(2.5)^2$$
$$=30.6m$$



The potential energy of $$3\,kg$$ body is $$ -54\,J$$. Calculate its escape velocity.

Given 
potential energy on the Earth's surface $$ U_i = -54 J $$ 
mass of the body $$ m = 3 \,kg $$ 
If the body escapes , then its potential energy at infinity $$ U_f = 0 $$ 
Escape energy $$ = U_f - U_i = 0 - (-54) = 54 J $$ 
or $$ \dfrac{1}{2} mv_{e}^{2} = 54 $$
or $$ v_e = \sqrt{\dfrac{2 \times 54}{m}} = \sqrt{\dfrac{2 \times 54}{3}} = \sqrt{36} $$ 
or $$ v_e = 6\,ms^{-1} $$ 


Does the escape speed of a body from the earth depend on ?
The height of the locations from where the body is lunched 

Escape velocity of a  body from earth is given by v =$$\sqrt{2gR}$$ 
g = Acceleration due to  Gravity 
R = Radius of earth 
No, it depends on the gravitational potential energy which depends on the height. Since g changes with height.  The escape velocity also depends on height 


The change in the value of  'g' at a height 'h' and depth 'd' is same . Assuming h and d are both very small compared to radius of Earth . Find  ratio of h with respect to d.

Comparing (1) and (2) we can write 
$$2h =d $$$$\Rightarrow \dfrac{h}{d}=\dfrac{1}{2}$$
If the change in the value of g at height h above earth surface is the same as that at depth x i.e.
$$g- g_h  = g - g_x$$ 
$$\dfrac{2gh}{R} = \dfrac{gx}{R}$$ 
 $$∴x=2h$$


What speed must be given a spacecraft launched from the earth if it is to leave the solar system ?
Hint : The spacecraft is launched from a moving platform.


1874716_1746660_ans_d3c0a4a4144b4813ab2ebd41aaff796d.jpg


Class 11 Medical Physics Extra Questions