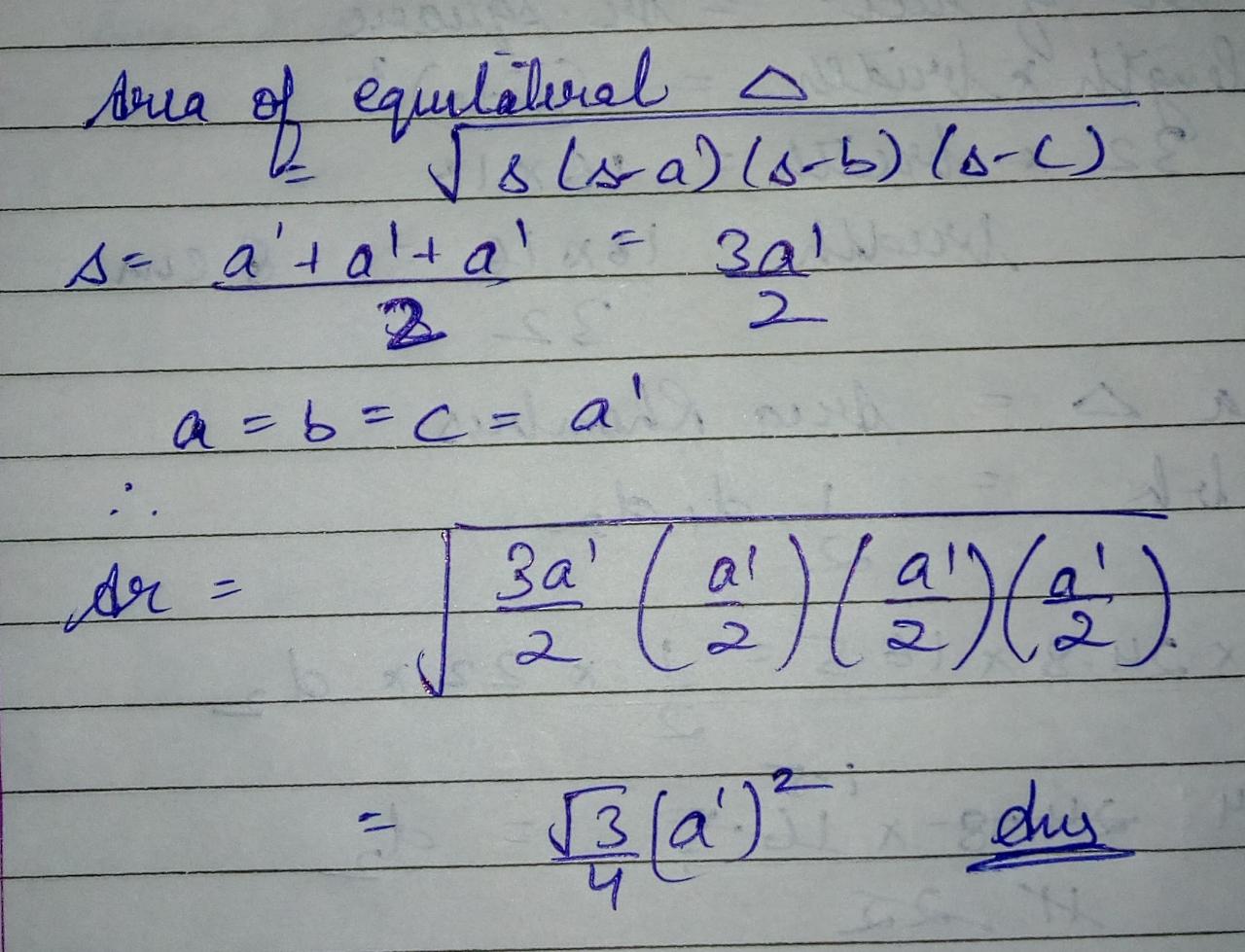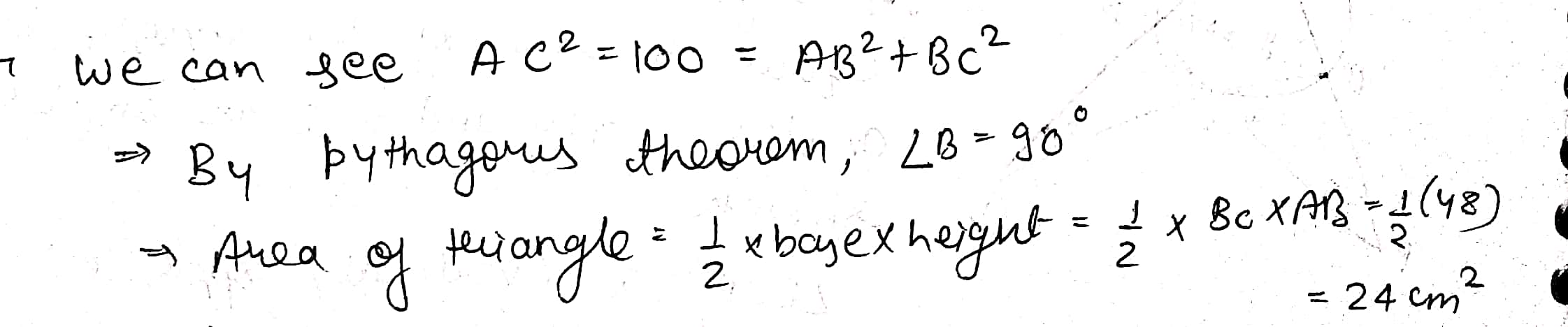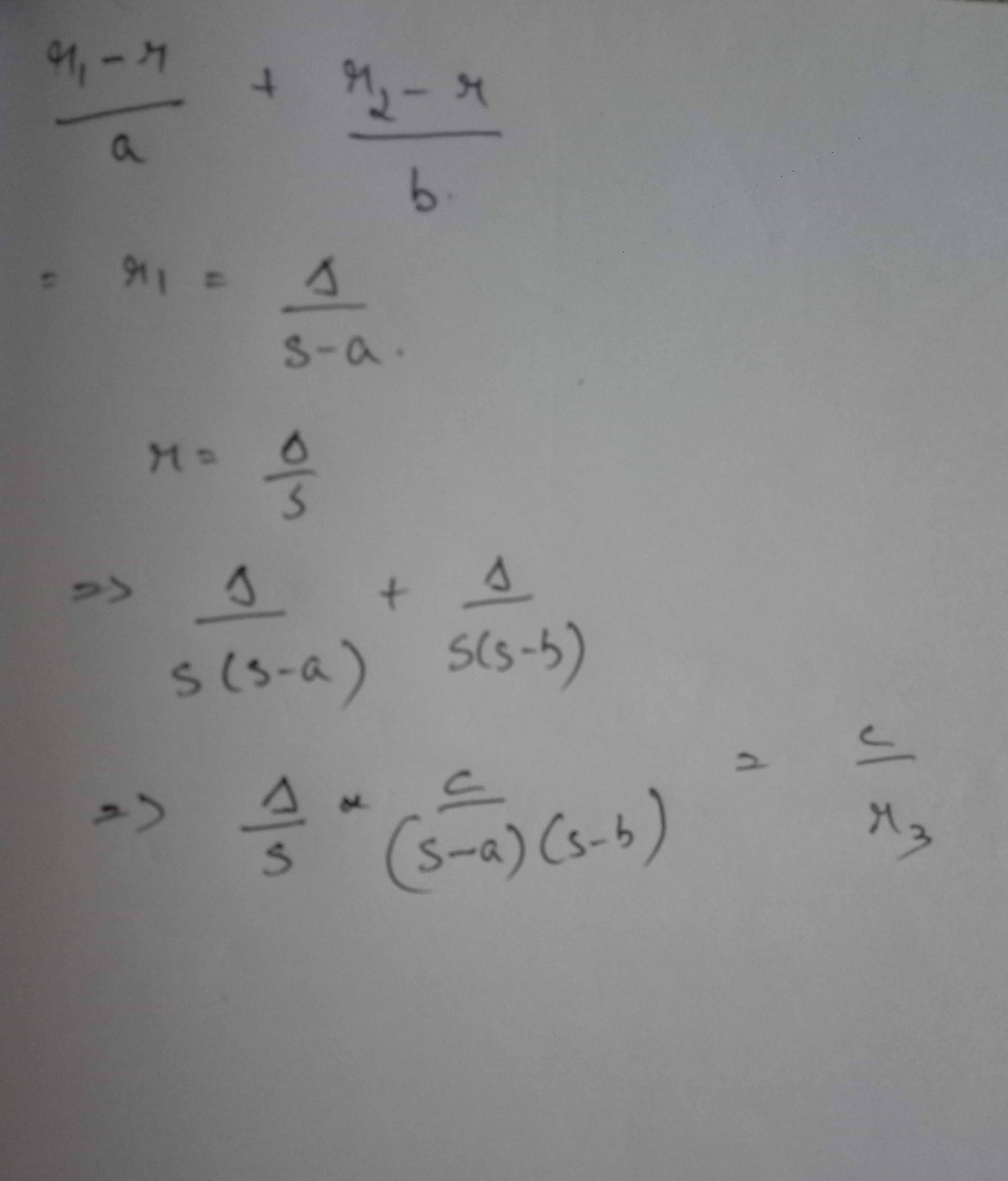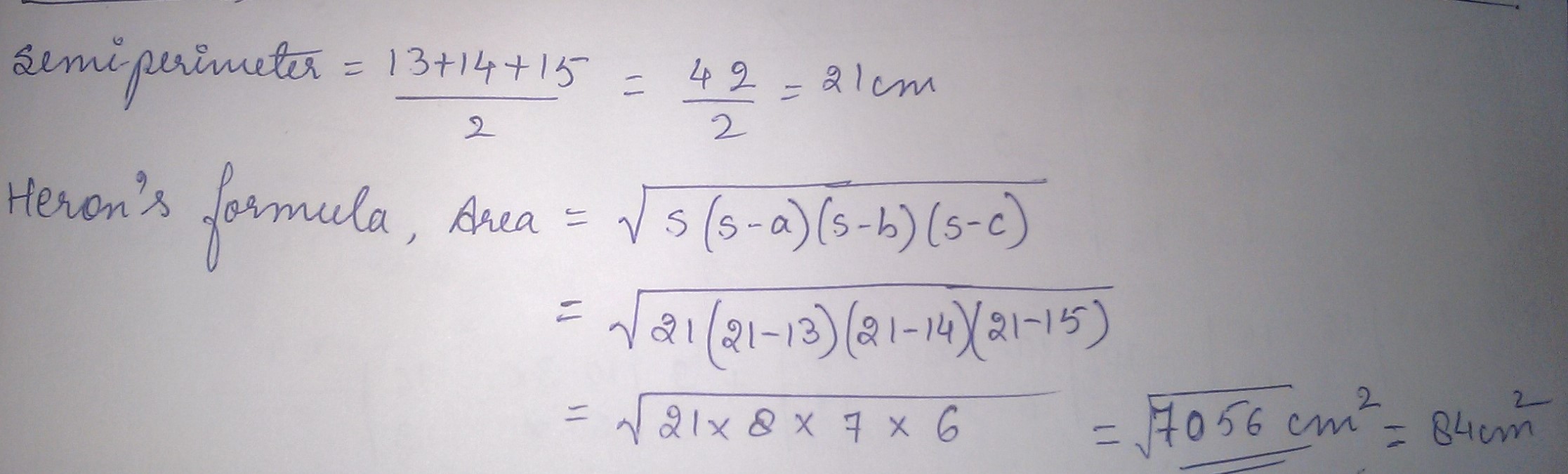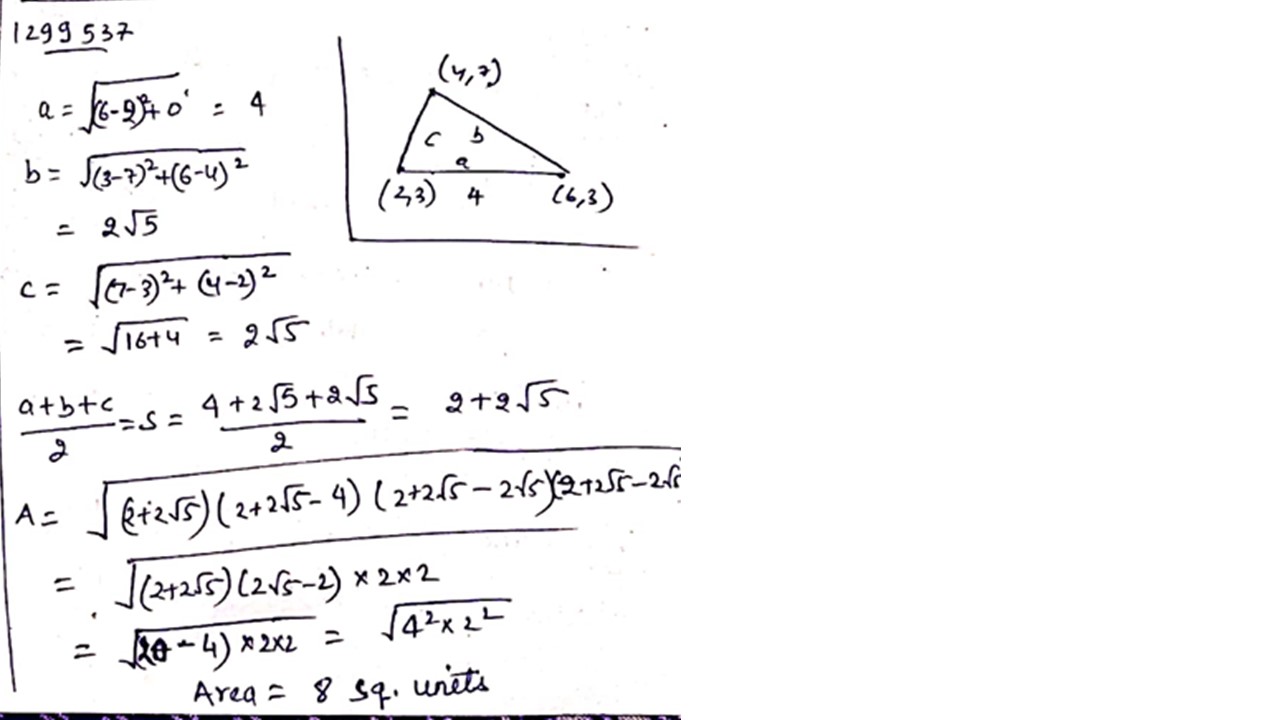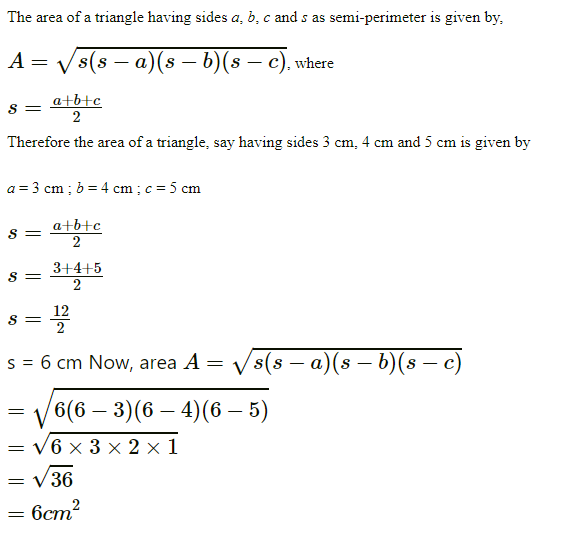Heron'S Formula - Class 9 Maths - Extra Questions
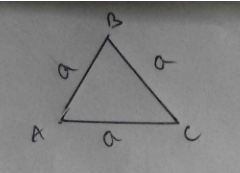
Find area of an equilateral triangle whose each side is $$ a^{\prime} $$.
The area of an equilateral triangle is $$( 16 \times \sqrt { 3 } ) \mathrm { cm } ^ { 2 }$$.Find the length of each side of triangle.
Sides of a triangle are $$70$$ cm, $$80$$ cm and $$90$$ cm. Find its area.
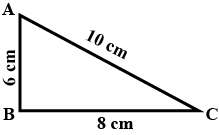
The area of the triangle whose sides are $$6,8,10$$ is ..........
The longest side of a right angled triangle is 125 m and one of the remaining two sides is 100 m. Find its area using Heron's formula.
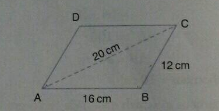
In a parallelogram $$ABCD,\ AB=16\ cm, BC=12\ cm$$ and diagonal $$AC=20\ cm$$. Find the area of the parallelogram.
The sides of a triangle are $$12$$cm,$$16$$cm and $$20$$cm. Find its area.
Find the perimeter of triangle with sides :
$$6 cm, 7cm, 3cm$$
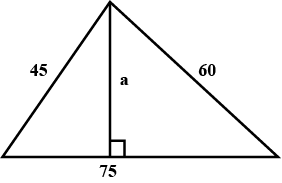
Find the area of the triangle whose sides are 42 cm, 34 cm and 20 cm in length. Find the height corresponding to the longest side.
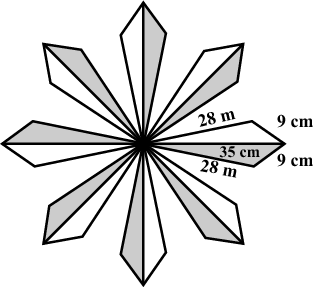
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9cm, 28cm and 35cm. Find the cost of polishing the tiles at the rate of 50p per $$c{m^2}$$.
Find the area of the triangle whose sides are 50 m, 78 m and 112 m and also find the length of the perpendicular from the opposite vertex to the side of length 112 m.
Write the Heron's formula used to calculate the area of a triangle whose side are $$a, b$$ and $$c$$.
Side of a triangle in the ratio $$7:12:8$$ and its perimeter is $$270$$ cm, find its area.
Find the cost of laying grass in a triangular field of sides $$50 m, 65 m$$ and $$65 m$$ at the rate of $$Rs 7$$ per $$m^2$$.
Find the area of a triangle two sides of which are $$18$$ cm and $$10$$ cm and the perimeter is $$42$$ cm.
From a point in the interior of an equilateral triangle, perpendiculars are drawn on the three sides. The lengths of the perpendiculars are $$14 cm$$, $$10 cm$$ and $$6 cm$$. Find the area of the triangle.
Find the area of triangle whose sides are $$4 \ cm,6 \ cm,8 \ cm$$
Find the area of the following triangle.
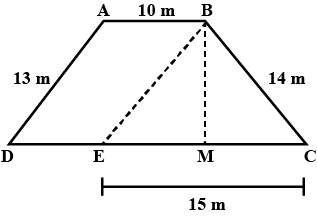
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are $$13 m$$, $$14 m$$ and $$15 m$$. The advertisements yield an earning of $$Rs.\ 2000$$ per $$m^2$$ a year. A company hired one of its walls for $$6$$ months. How much rent did it pay?
The sides of a triangle are $$119,111$$ and $$92$$ yards; prove that its area is $$10$$ sq. yards less than an acre.
Find the area of the isosceles triangle whose
i) each of the equal sides is 8 cm and the base is 9 cm;
Write Heron's formula.
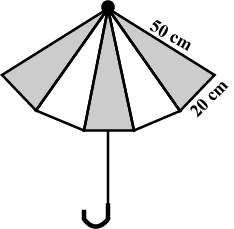
An umbrella is made by stitching $$10$$ triangular pieces of cloth of $$5$$ different colour each piece measuring $$20$$cm, $$50$$cm and $$50$$cm. How much cloth of each colour is required for one umbrella?
The sides of the triangle are $$78m$$, $$112m$$ and $$50m$$ respectively. What is the area of the triangle?
Find the area of a $$\Delta $$ whose sides are $$8\ m$$, $$17\ m$$ and $$15\ m.$$
Prove: In $$\Delta ABC$$ $$\dfrac{{{r_1} - r}}{a} + \dfrac{{{r_2} - r}}{b} = \dfrac{c}{{{r_3}}}$$
Find the area of the triangle with sides $$35 cm, 54 cm$$ and $$61 cm$$.
The base of an isosceles triangle is $$10$$ cm and one of its equal sides is $$13$$ cm. Find its area using Heron's Formula.
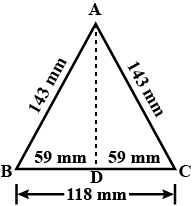
An isosceles triangle has a base $$118 mm$$ long and two equal sides are each $$143 mm$$ long. calculate the are of the triangle.
Give an triangle with an area of $$3.94$$ sq.units a perimeter of $$16$$ units and sides $$a=3$$ units, $$b=7$$ units. Find $$c$$ in units.
The semi- perimeter of a triangle is $$96 cm$$ and its sides are in the ratio $$3:4:5.$$ Find the area of the triangle.
The sides of $$\Delta $$ are $$6 cm$$ ,$$8cm$$,$$10cm$$ find its area using heron's formulas
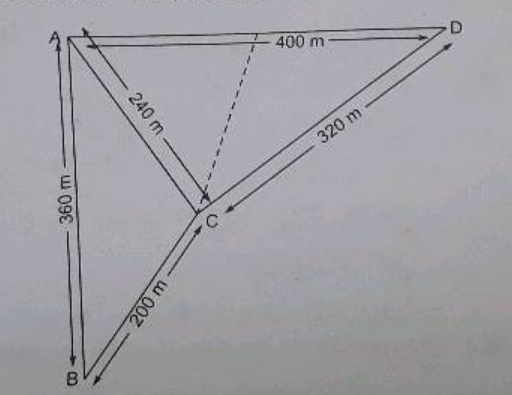
A farmer has a triangular field with sides 240 m and 360 m, where he grew wheat. In another triangular field with sides 240 m, 320 m and 400 m adjacent to the previous field, he wanted to grow potatoes and onions. He divided the field into two parts by joining the mid point of the longest side to the opposite vertex and grew potatoes in one part and onions in the other part. How much area (in hectares) has been used for wheat, potatoes and onions ?
The perimeter of an isosceles triangle is equal to $$\text{14 cm}$$, the ratio of the lateral side to the base is $$5:4$$, then the area of the triangle is:
Find area of the triangle with sides 5 cm, 12 cm, 13 cm.
The sides of a triangular field are in the ratio $$5:3:4$$ and its perimeter is $$180m$$. Find:
(i) its area
(ii) altitude of the triangle corresponding to its largest side
(iii) the cost of levelling the field at the rate of Rs. $$10$$ per square metre
An umbrella is made by stitching $$6$$ triangular pieces of cloth of red and black colours each measuring $$20$$cm, $$50$$cm, and $$50$$cm. How much cloth of each colour is required for umbrella?
Find the area of an isosceles triangle each of whose equal sides measures $$13\ cm$$ and whose base measures $$20\ cm$$.
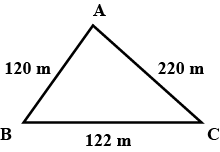
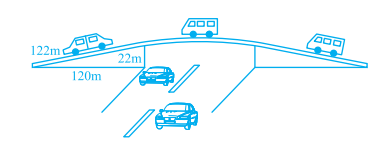
The triangular side walls of a flyover have been used for advertisements.The sides of the walls are $$122m, 22m, 120m$$. The advertisements yield an earning of RS. $$5000$$ per $${m}^{2}$$. A company hired one of its walls for $$3$$ months. How much rent did it pay?
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 13 m, 14 m and 15 m. The advertisements yield an earning of Rs 2000 per $$m^2$$ a year. A company hired one of its walls for 6 months. How much rent did it pay?
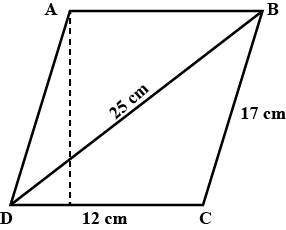
Find the area of a parallelogram given in Fig. 12.Also find the length of the altitude from vertex A on the side DC.(in $$cm^2$$)
The perimeter of a triangle is 50 cm. One side of a triangle is 4 cm longer than the smaller side and the third side is 6 cm less than twice the smaller side, then the area of the triangle is $$20 \sqrt{30} cm^2$$
If true then enter $$1$$ and if false then enter $$0$$
Find the area of a triangle in $${mm}^2$$, whose sides are: $$18\>mm, 24\> mm$$ and $$30\> mm$$.
Find the area of a triangle in $${cm}^2$$, whose sides are: $$10\>cm, 24\>cm$$ and $$26\>cm$$
The sides of a triangle are 16 cm, 12 cm and 20 cm. Find area of the triangle
The lengths of the sides of a triangle are in the ratio $$4 : 5 : 3$$ and its perimeter is $$96$$ cm. Find its area (in sq. cm).
If a triangle with sides (in units) of measure $$a, b$$ and $$c$$ has an area of $$'A'\ sq\ units$$ and a triangle with sides measuring $$a+b, b+c, c+a$$ has an area of $$'1'\ sq\ units$$, then prove that $$T\ge 4A$$.
The sides of a triangular field are in the ratio $$ 5 : 3 : 4 $$ and its perimeter is $$180$$ m, then find the altitude of the triangle corresponding to its largest side (in $$m.$$)
The sides of a triangular field are in the ratio $$ 5 : 3 : 4 $$ and its perimeter is $$180$$ m, then find the cost of levelling the field at the rate of Rs. $$10$$ per square meter.
Find the area of a triangle in cm$$^2$$; whose sides are: $$21\>cm, 28\> cm$$ and $$35\> cm$$.
The lengths of the sides of a triangle are in the ratio $$ 3 : 4 : 5 $$. Find the area of the triangle if its perimeter is $$144\ cm$$ .
The area of a triangle is $$57\ sq.\ cm$$. If the two sides are $$8\ cm$$ and $$19\ cm$$ respectively, then what is the third side approximately?
Find the length of the perpendicular from the vertex opposite to the side $$72$$ m of the triangular field, whose other two sides are $$30$$ m and $$78$$ m.
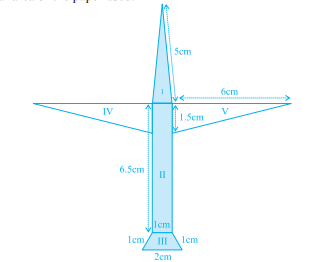
Radha made a picture of an aeroplane with coloured paper as shown in Fig $$12.15$$. Find the total area of the paper used.
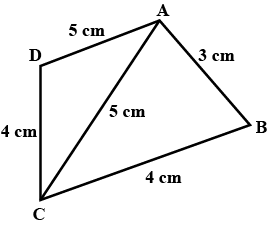
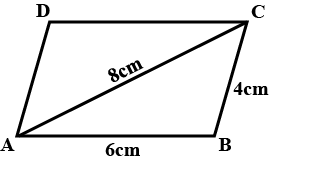
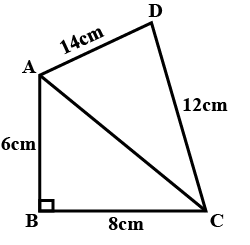
Find the area of a quadrilateral $$ABCD$$ in which $$AB=3\ cm$$, $$BC=4\ cm$$, $$CD=4\ cm$$, $$DA=5\ cm$$ and $$AC=5\ cm$$
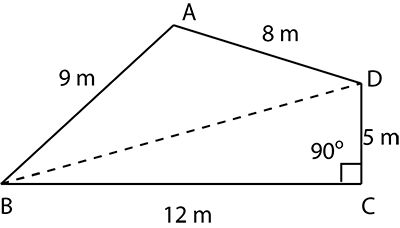
A park, in the shape of a quadrilateral $$ABCD$$, has $$\angle{C}={90}^{o}$$, $$AB=9\ m$$, $$BC=12\ m$$, $$CD=5\ m$$ and $$AD=8\ m$$. How much area does it occupy?
An isosceles triangle has perimeter $$30cm$$ and each of the equal sides is $$12cm$$. Find the area of the triangle.
Find the area of a triangle two sides of which are $$18\ cm$$ and $$10\ cm$$ and the perimeter is $$42\ cm$$.
Find the area of a triangle whose sides are $$16$$ cm, $$19$$ cm, and $$21$$ cm in length.
In an isosceles triangle , length of the congruent sides is 13 cm and its base is 10 cm . Find the distance between the vertex opposite the base and the centroid
A traffic signal board, indicating $$'SCHOOL\ AHEAD'$$, is an equivalent triangle with side '$$a$$'. Find the area of the signal board, using Heron's formula. If its perimeter is $$180\ cm$$, what will be the area of the signal board?
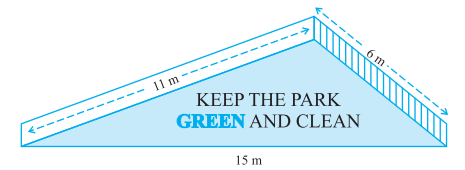
There is a slide on a park. One of its side walls has been painted in some colour with a message "KEEP THE PARK GREEN AND CLEAN" (see figure). If the sides of the wall are $$15\ m, 11\ m$$ and $$6\ m$$, find the area painted in colour.
Sides of a triangle are in the ratio of $$12:17:25$$ and its perimeter is $$540\ cm$$. Find its area.
The triangular side walls of a flyover have been used for advertisements. The sides of the walls are $$122 \ m, 22 \ m$$ and $$120 \ m$$ (see figure). The advertisements yield an earning of $$Rs.5000 \ per \ {m}^{2}$$ per year. A company hired one of its walls for $$3$$ months. How much rent did it pay?
An umbrella is made by stitching $$10$$ triangular pieces of cloth of two different colours (see figure), each piece measuring $$20\ cm,\ 50\ cm$$ and $$50\ cm$$. How much cloth of each colour is required for the umbrella?
A kite in the shape of square with a diagonal $$32cm$$ and an isosceles triangle of base $$8cm$$ and sides $$6cm$$ each is to be made of three different shades as shown in figure. How much paper if each shade has been used in it?
A floral design on a floor is made up of $$16$$ tiles which are triangular, the sides of the triangle being $$9\ cm$$, $$28\ cm$$ and $$35\ cm$$ (see figure). Find the cost of polishing the tiles at the rate of $$50\ p$$ per $${cm}^{2}$$.
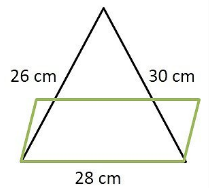
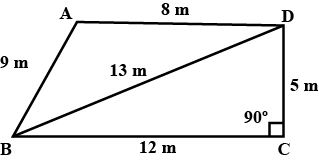
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are $$26cm, 28cm$$ and $$30cm$$ and the parallelogram stands on the base $$28cm$$, find the height of the paraollelogram.
In $$\Delta ABC$$, BC=11 cm, CA=13 cm and the median to side AB is 10 cm. The area of the $$\Delta^{le}$$ is:
Find area of a triangle whose sides measures 13 cm,14cm,15cm.
Find the area of a triangle if its sides are $$9 cm , 12cm\ and\ 15cm $$
$$\dfrac{r_1}{(s \, - \, b) \, (s \, - \, c)} \, + \, \dfrac{r_2}{(s \, - \, c) \, (s \, - \, a)} \, + \, \dfrac{r_3}{(s \, - \, a) \, (s \, - \, b)} \, = \, \dfrac{3}{r}$$
Find the area of $$\triangle$$ two sides are $$18\ cm$$, $$10\ cm$$ if perimeter is $$42\ cm$$
The sides of a triangle are $$x, x + 1, 2x - 1$$ and its area is $$x\sqrt{10}$$. What is the value of $$x$$?
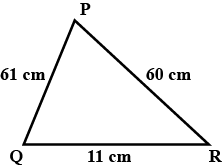
A triangle has sides of $$35\ cm, 54\ cm$$ and $$61\ cm$$ long. Find its area and its smallest altitude.
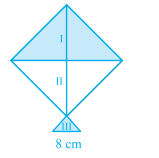
A kite in the shape of a square with a diagonal $$40\ \text{cm}$$ and an isosceles triangle of base $$10\ \text{cm}$$ and equal sides $$13\ \text{cm}$$ each, is to be made up of three different shades as shown in the figure. How much paper of each shade has been used to make the kite?
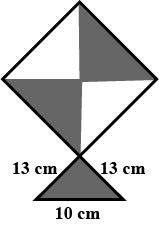
The perimeter of right angled triangle is $$12$$ cm and its hypotenuse is of length $$5$$ cm. Find the other two sides and calculate its area. Verify the result using heron' formula.
Each of equal sides of an isosceles triangle is 4 cm greater than its height. If the base of the triangle is 24 cm, calculate the perimeter and the area of the triangle.
The length of the sides of a triangle are in the ratio $$3:4:5$$ and its perimeter is $$144$$ cm. Find the area of the triangle and the height corresponding to the longest side
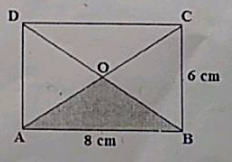
In the given figure, $$ABCD$$ is a rectangle, where $$AB = 8$$ cm, $$BC = 6$$ cm and the diagonals bisect each other at $$O$$. Find the area of the shaded region by Heron's formula.
A school started a campaign against the habit of taking junk food. Ten students were asked to prepare banners in a triangular shape. The sides of the banner are $$112, 78$$ AND $$50\ cm$$. if cost of banners is $$Rs 3$$ per $$100\ cm2$$, find the total cost of banners. What valye is being promoted in this question?
find the area of the triangle whose are (-5,-1) (3,-5) (5,2).
Find the area of triangle between the co-ordinate axis of line $$3x-4y-12=0$$
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are $$26cm, 28cm$$ and $$30cm$$ and the parallelogram stands on the base $$28cm$$, find the height of the parallelogram.
Find the area of triangle with sides 3 cm, 7 cm and 8 cm.
Find the area of this $$\triangle$$ by hero's formula.
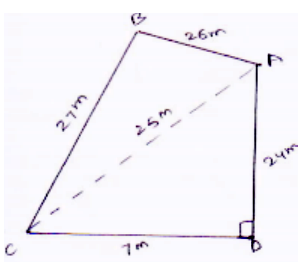
The sides of quadrangular field taken in order are $$26,27,7,24m$$ respectively. The angle contained by the last $$2$$ sides is a right angle. Find its area.
Find the area of a triangle with sides $$a=3cm, b=2cm, c=4cm$$.
If base of an isosceles triangle is $$12\ cm$$ and its perimeter is $$35\ cm$$, find the area of the triangle.
Derive a formula for area of equilateral triangle in terms of its side using Heron's formula.
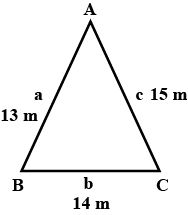
Find the area of triangle whose sides are $$13$$ cm, $$14$$ cm and $$15$$ cm.
The area of a parallelogram with a base $$24 \text{ cm}$$ is equal to the area of a triangle of sides $$10 \text{ cm},\ 24 \text{ cm}$$ and $$26 \text{ cm}$$. Find the altitude of the parallelogram.
Get the formula $$\triangle =\sqrt {s(s-a)(s-b)(s-c)}$$ for the area of a triangle by use of vectors.
Using Heron's formula, find the area of a triangle whose sides are $$5\ cm, 12\ cm$$ and $$13\ cm$$.
Find the area of the triangle whose vertices are $$(1, 2), (3, 7)$$ and $$(5, 3)$$,
Find the altitude of the triangle if its area is $$25\ acres$$ and base is $$20\ m$$.
A parallelogram has sides $$6\ cm$$ and $$4\ cm$$ and one of its diagonals is $$8\ cm$$ then its area is:-
Find the area of the triangle in which $$a=91\ m,\ b=98\ m,\ c=105\ m$$, where $$a,b,c$$ are sides of triangle.
Find the area of the triangle in which $$a=52\ cm,\ b=56\ cm,\ c=60\ cm$$, where $$a,b,c$$ are sides of triangle.
Find the area of a triangle plot whole side are $$61$$ cm, $$60$$ cm, $$11$$ cm
Find the area of a triangle whose sides are 13 cm, 14 cm and 15 cm.
A park is in the shape of quadrilateral $$ABCD$$ as shown. Given that angle $$C=90^{o}$$ Also, $$AB=9\ m,\ BC=12\ m,\ CD=5\ m$$ and $$AD=8\ m$$. Using Pythagoras Theorem find the length of diagonal $$BD$$. Also, find the total area of the given quadrilateral by using Heron's Formula.
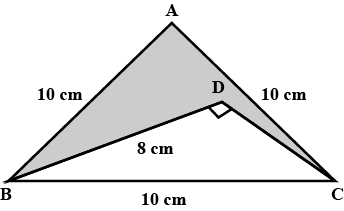
An isosceles triangle has perimeter $$30\ cm$$ and each of the equal side is $$12\ cm$$. Find the area of the triangle.
Find the area of a triangle whose sides re in the ratio $$5:12:13$$ and its perimeter is $$60\ cm$$.
What is Heron's formula?
Plot the points $$(2,3)(6,3)and(4,7)$$ in a graphsheet.join them to make it a triangle find the area of the triangle
The sides of a triangle-shaped sheet are $$5\ cm$$, $$12\ cm$$ and $$13\ cm$$. Find the cost of painting on the sheet at the rate of $$Rs.\ 30\ per\ cm^ {2}$$.
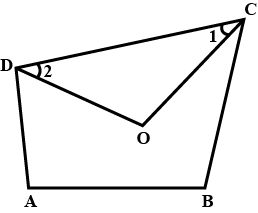
In a quadrilateral ABCD, CO and DO are the bisectors of $$\angle C$$ and $$\angle D$$ respectively. Prove that $$\angle COD=\dfrac{1}{2}(\angle A+\angle B)$$.
Calculated the area of the triangle whose are 18 cm, 24 cm and 30 cm in length. also find the length of the altitude corresponding is the smallest side.
Find the area of the triangle whose side are 42 cm, 34 cm and 20 cm in length. hence find the height corresponding to the longest side.
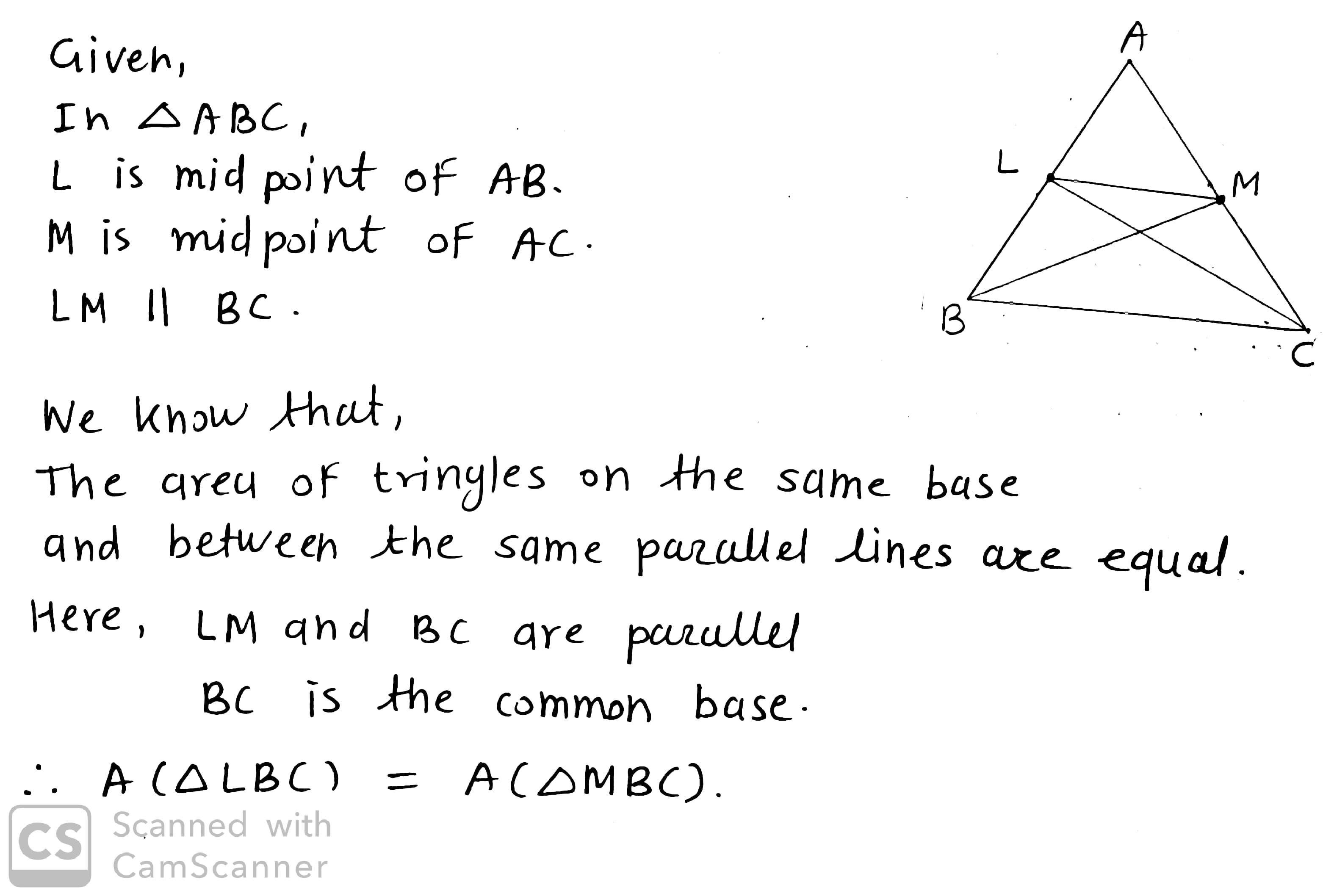
In a $$\triangle ABC$$, if $$L$$ and $$M$$ are points on $$AB$$ and $$AC$$ respectively such that $$LM||BC$$.Prove that:
$$ar(\triangle LBC)=ar (\triangle MBC)$$
Find the area and perimeter of an isosceles right triangle, each of whose equal sides measures 10 cm. [Given: $$\sqrt{2} = 1 .41$$]
Find the area of the triangle whose sides are 18 cm, 24 cm and 30 cm. Also, find the height corresponding to the smallest side.
Each of the equal sides of an isosceles triangle measures 2 cm more than its height, and the base of the triangle measures 12 cm. Find the area of the triangle.
The height of an equilateral triangle is 6 cm. Find its area. [Take $$\sqrt{3} = 1 .73$$]
If the area of an equilateral triangle is $$ 81\sqrt{3}cm^{2}$$, find its height.
The base of a right-angled triangle measures 48 cm and its hypotenuse measures 50 cm. Find the area of the triangle.
In the given figure, $$\Delta ABC$$ is an equilateral triangle the length of whose side is equal to 10 cm, and $$\Delta DBC$$ is right-angled at D and $$BD = 8\,cm.$$ Find the area of the shaded region. [Take $$\sqrt{3} = 1.732.$$]
Each side of an equilateral triangle is 10 cm. Find (i) the area of the triangle and (ii) the height of the triangle.
The sides of a triangle are in the ratio $$5: 12 : 13,$$ and its perimeter is 150 m. Find the area of the triangle.
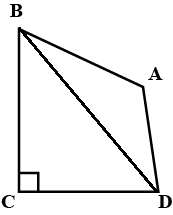
In Fig., area of triangle PQR is $$20\, cm^2$$ and area of triangle PQS is $$44\, cm^2$$. Find the length RS. if PQ is perpendicular to QS and QR is $$5\,cm$$.

The sides of a quadrilateral $$ABCD$$ taken in order are $$6\ cm,\ 8\ cm,\ 12\ cm$$, and $$14\ cm$$ respectively and the angle between the first two sides is a right angle. Find its area. (Use $$\sqrt{6}=2.45$$)
Using Herons formula, find the area of an equilateral triangle the length of whose one side is x.
Find the area of a triangle whose sides are
29 cm, 20 cm , and 21 cm
Find the area of a triangle whose sides are
3 cm,4 cm, and 5 cm
The perimeter of a triangular field is $$540\text{ m}$$ and its sides are in the ratio of $$25: 17: 12$$. Find the area of the field. Also, find the cost of plowing the field at $$\text{Rs. } 5 \text{ per m}^2$$.
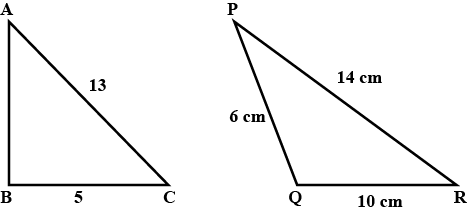
In the given triangles of Fig, perimeter of triangle ABC $$=$$ perimeter of triangle PQR. Find the area of triangle ABC.
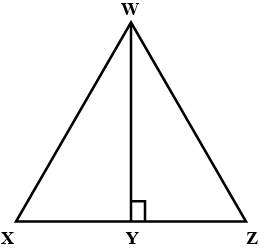
The ratio of the area of triangle WXY to the area of triangle WZY is 3:4 (Fig). If the area of triangle WXZ is 56 $$cm^2$$ end WY $$=8\, cm$$, find the lengths of XY and YZ.
The perimeter of an isosceles triangle is 32cm. The ratio of the equal side to its base is 3:Find the area of the triangle.
An umbrella is made by stitching $$12$$ triangular pieces of cloth, each measuring $$(50\ cm\times 20\ cm \times 50\ cm)$$. Find the area of the cloth used in it.

If the perimeter of an equilateral triangle is 36 cm,calculate its area
Find the area of a triangle whose sides are $$12$$ cm, $$9.6$$ cm, and $$7.2$$ cm
Find the area of an equilateral triangle whose side is 8 cm. Give your answer correct to two decimal places.
How much paper of yellow shade is needed in $$cm^2$$ to make a kite given in Fig, in which ABCD is a square with diagonal 44 cm.

The legs of a right triangle are 12 cm and 5 cm long. Find the distance between the centres of the inscribed and the circumscribed circle.
Find to the three places of decimals the radius of the circle whose area is the sum of the areas of two triangles whose sides are $$35, 53, 66$$ and $$33, 56, 65$$ measured in centimetres. (Use $$\pi$$ = 22/7).
A triangular park in a city has dimensions $$30m\times 26m\times 28m$$. A gardener has to plant grass inside the park at $$Rs.150\quad per\quad { m }^{ 2 }$$. Find the amount to be paid to the gardener.
In the given figure, ABC is a right angle triangle right-angled at A. Find the area of shaded region, if AB = $$6$$m, BC = $$10$$m and O is the centre of the incircle of triangle ABC (Use $$\pi = 3.14$$)
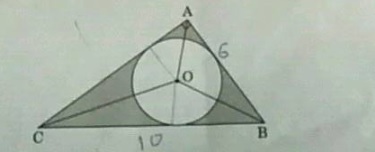
Find the area of a triangle whose sides are $$8$$ cm, $$15$$ and $$17$$ cm.
A field is in the shape of a trapezium whose parallel sides are $$25\ m$$ and $$10\ m$$. The non-parallel sides are $$14\ m$$ and $$13\ m$$. Find the area of the field.
Find the area of a triangle field of sides $$18$$, $$24$$m and $$30$$m. Also find the altitude corresponding to the shortest side.
If each sides of a triangle is double, then find the ratio of area of the new triangle thus formed and the given triangle.
A park, in the shape of a quadrilateral $$ABCD$$, has $$\angle{C}={90}^{o}, AB=9\ m, BC=12\ m, CD=5\ m$$ and $$AD=8\ m$$. How much area does it occupy?
Find the area of a triangle whose sides. are $$18$$ $$cm$$ , $$10$$ $$cm $$ and $$14$$ $$cm$$.
$$\triangle ABC \sim \triangle PQR,M$$ is mid point of $$BC$$ and $$N$$ is mid point of $$QR$$. If the area of $$\triangle AC=100\ cm^{2}$$, the area of $$\triangle PQR=144\ cm^{2}$$ and $$AM=4\ cm$$, then find the length of $$PN$$
Find the area of the triangle in which
a = 13 m, b = 14 m and c = 15 m
In the triangle $$ABC$$ with vertices $$A(2,\ 3),\ B(4,\ -1)$$ and $$C(1,\ 2)$$. find the equation and the length of the altitude from the vertex $$A$$.
Find the area of a triangle whose sides are 34 cm, 20 cm and 42 cm . hence the length of the altitude corresponding to the shortest side.
In figure $$ABCD$$ is a $$||^{gm}$$. $$O$$ is any point on $$AC$$. $$PQ||AB$$ and $$LM||AD$$. Prove that $$ar(||^{gm} DLOP)=ar (||^{gm} BMOQ)$$.
Class 9 Maths Extra Questions
- Areas Of Parallelograms And Triangles Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Heron'S Formula Extra Questions
- Introduction To Euclid'S Geometry Extra Questions
- Linear Equations In Two Variable Extra Questions
- Lines And Angles Extra Questions
- Number Systems Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadrilaterals Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions