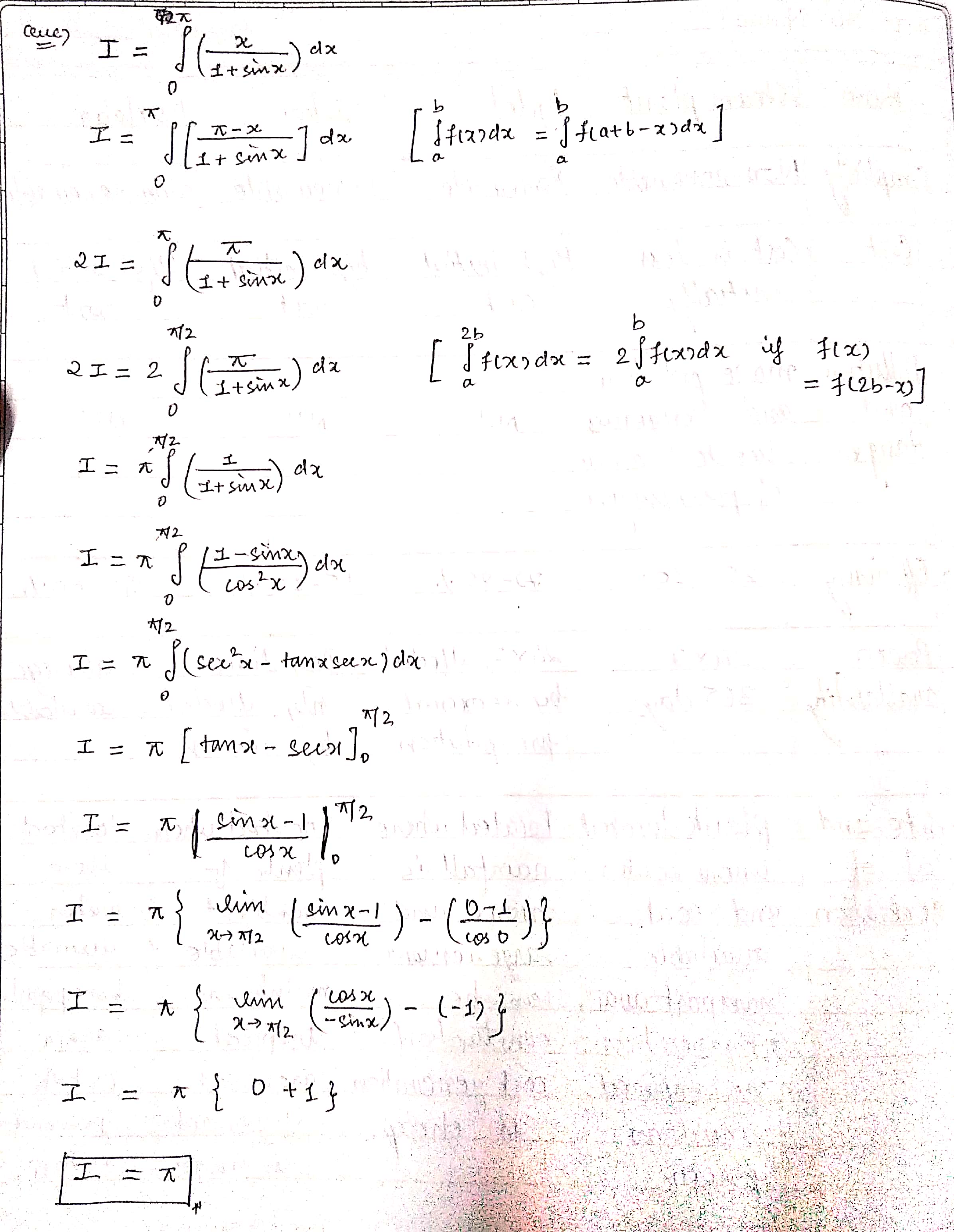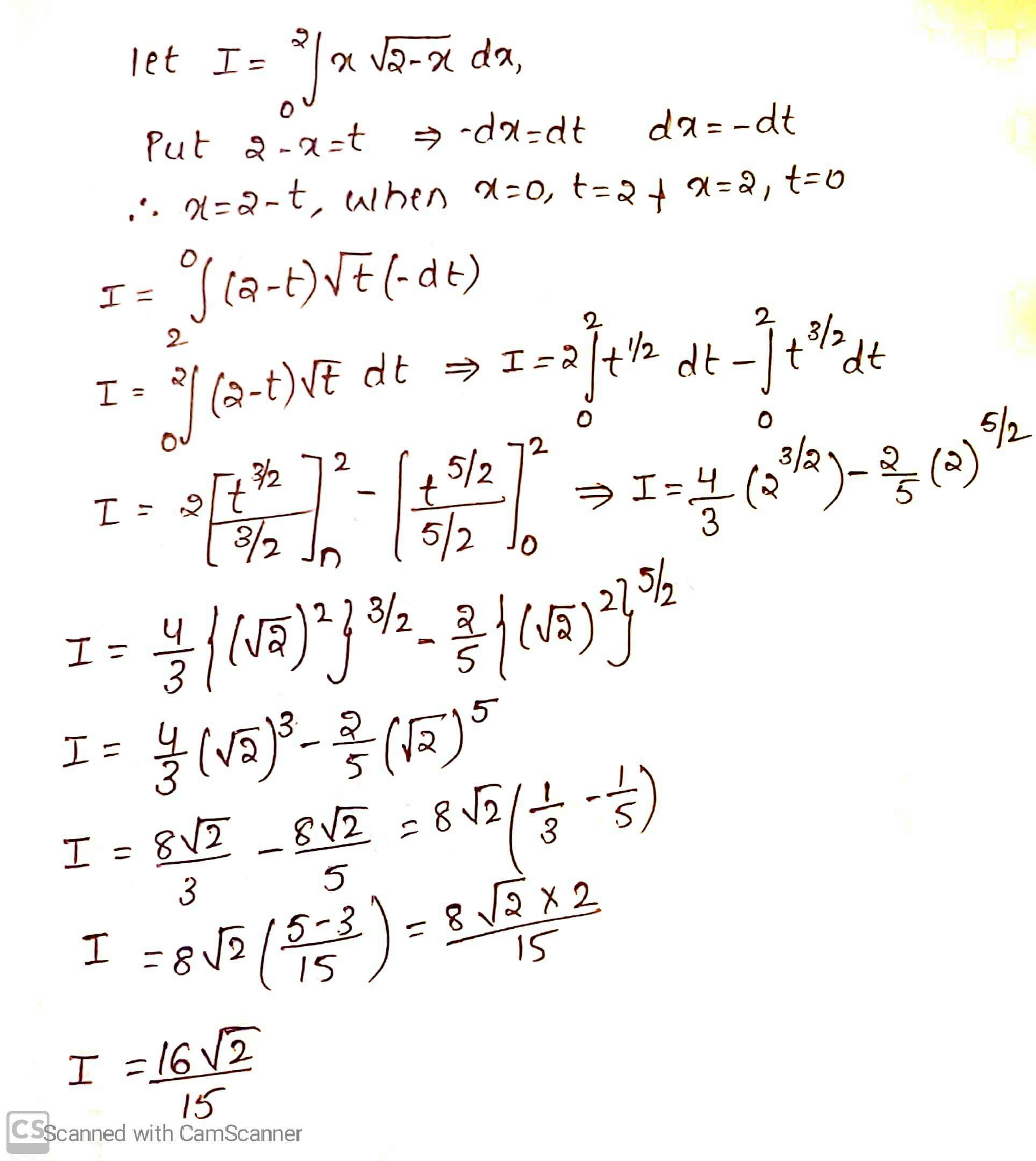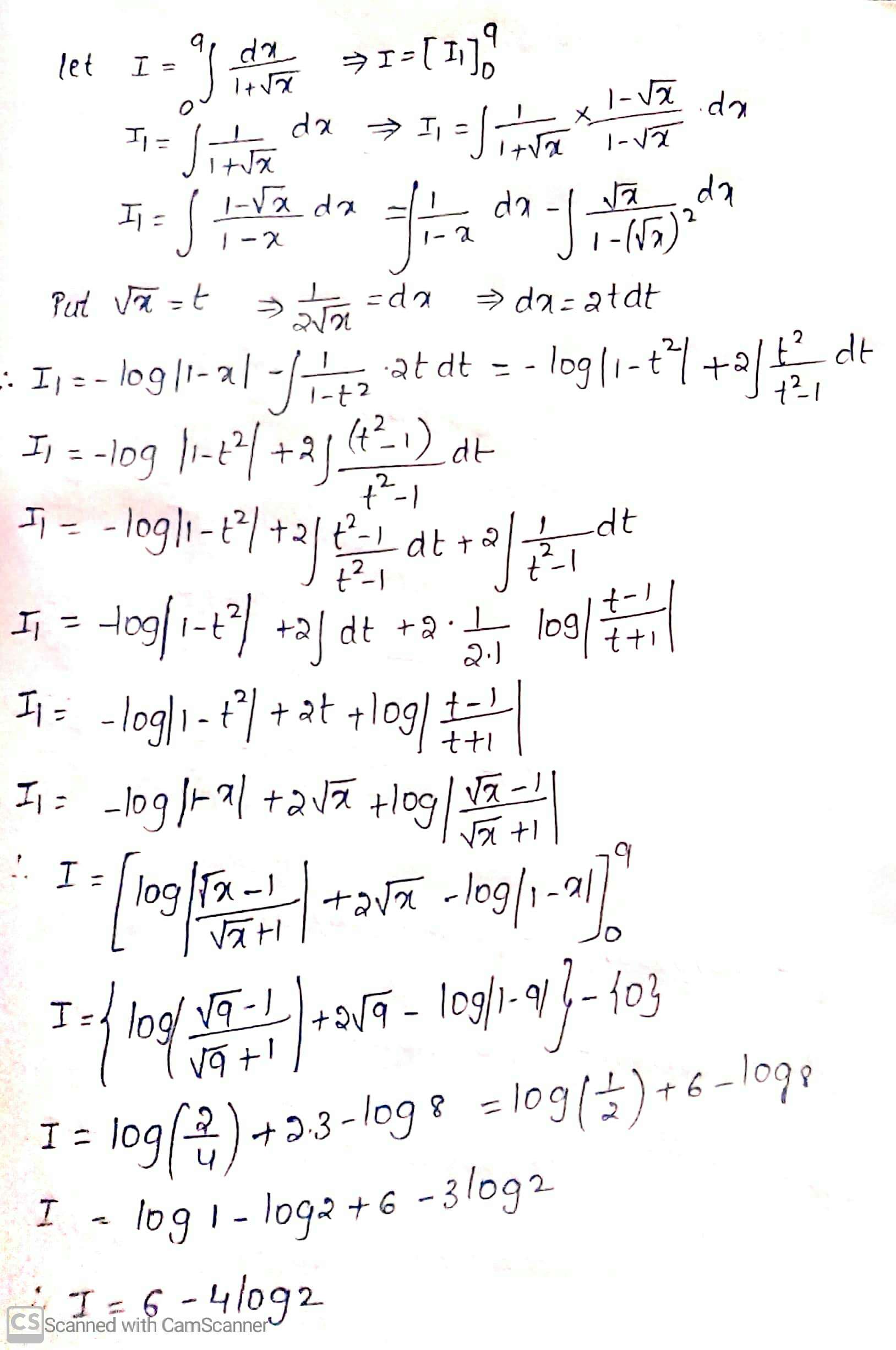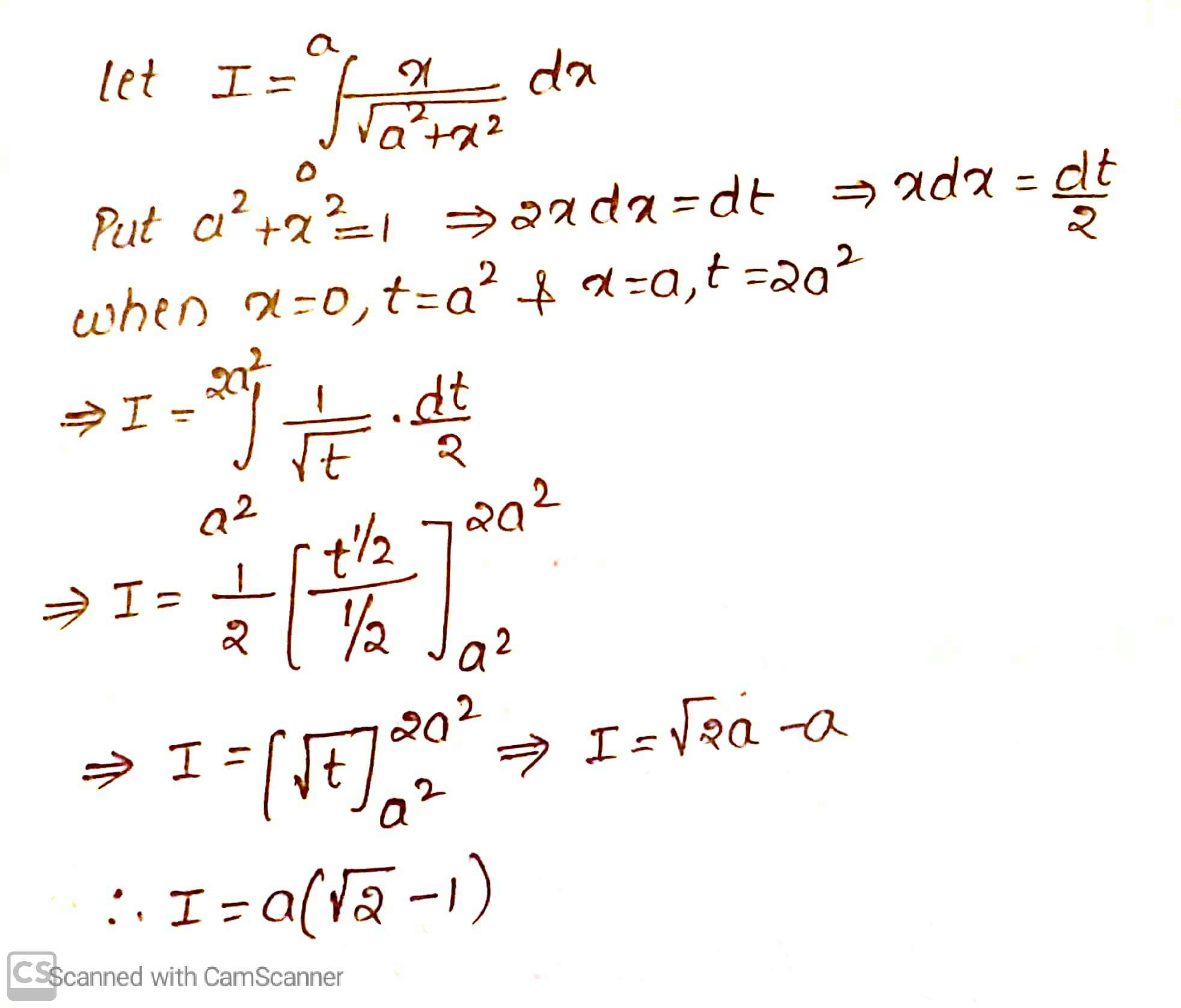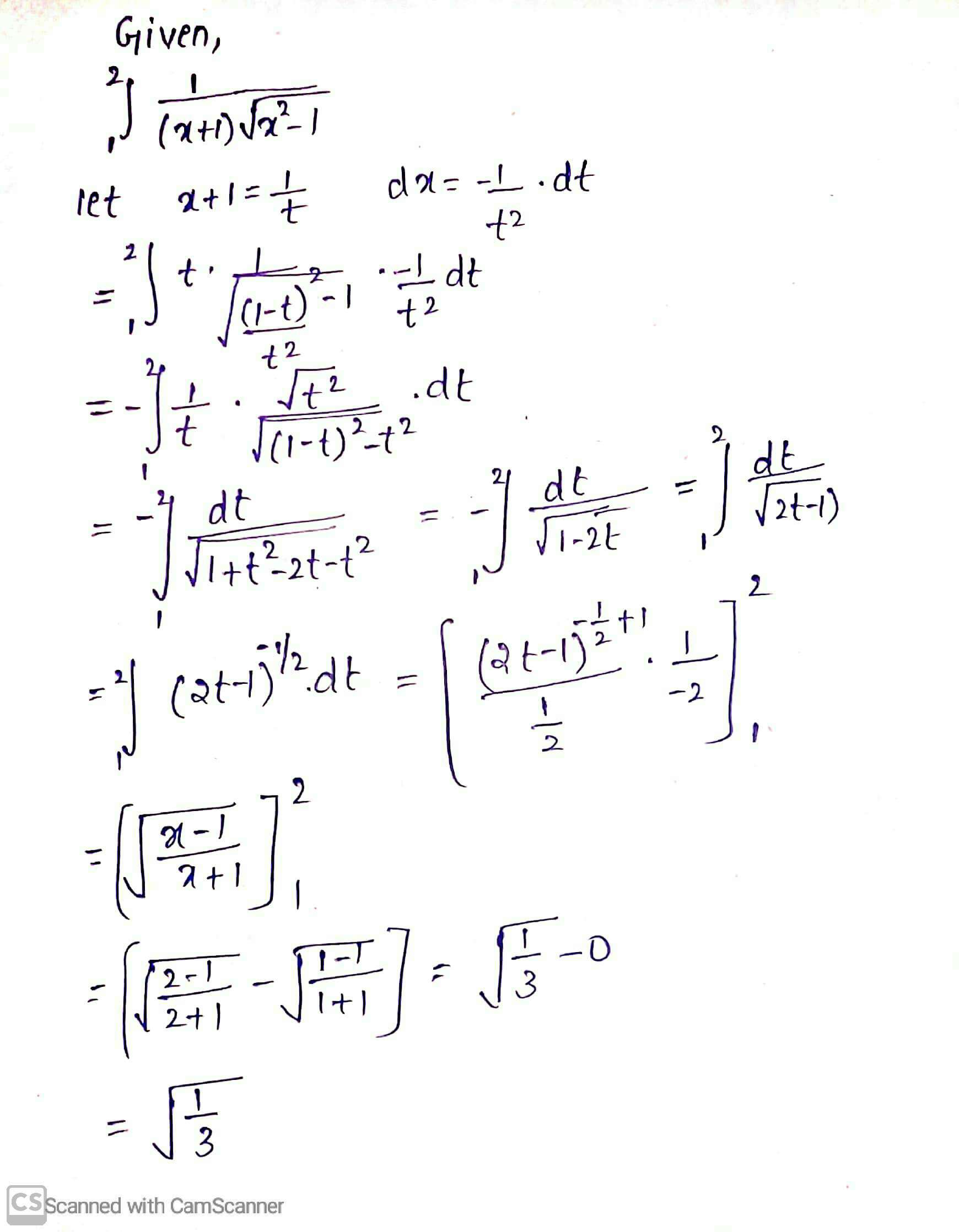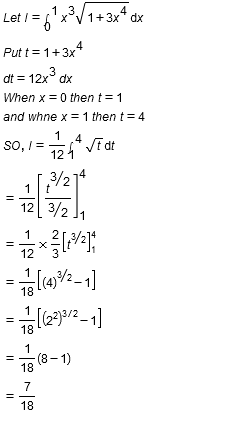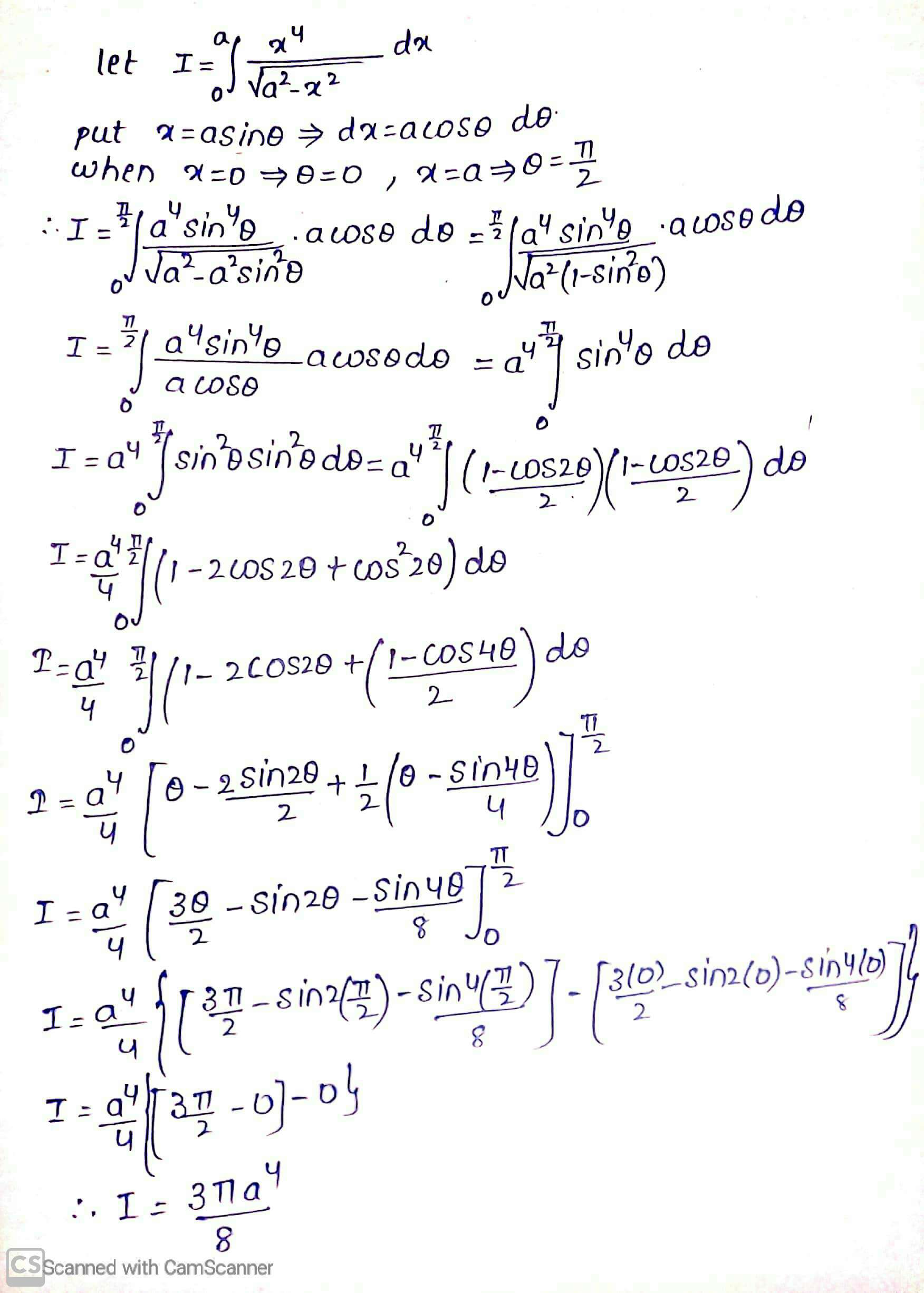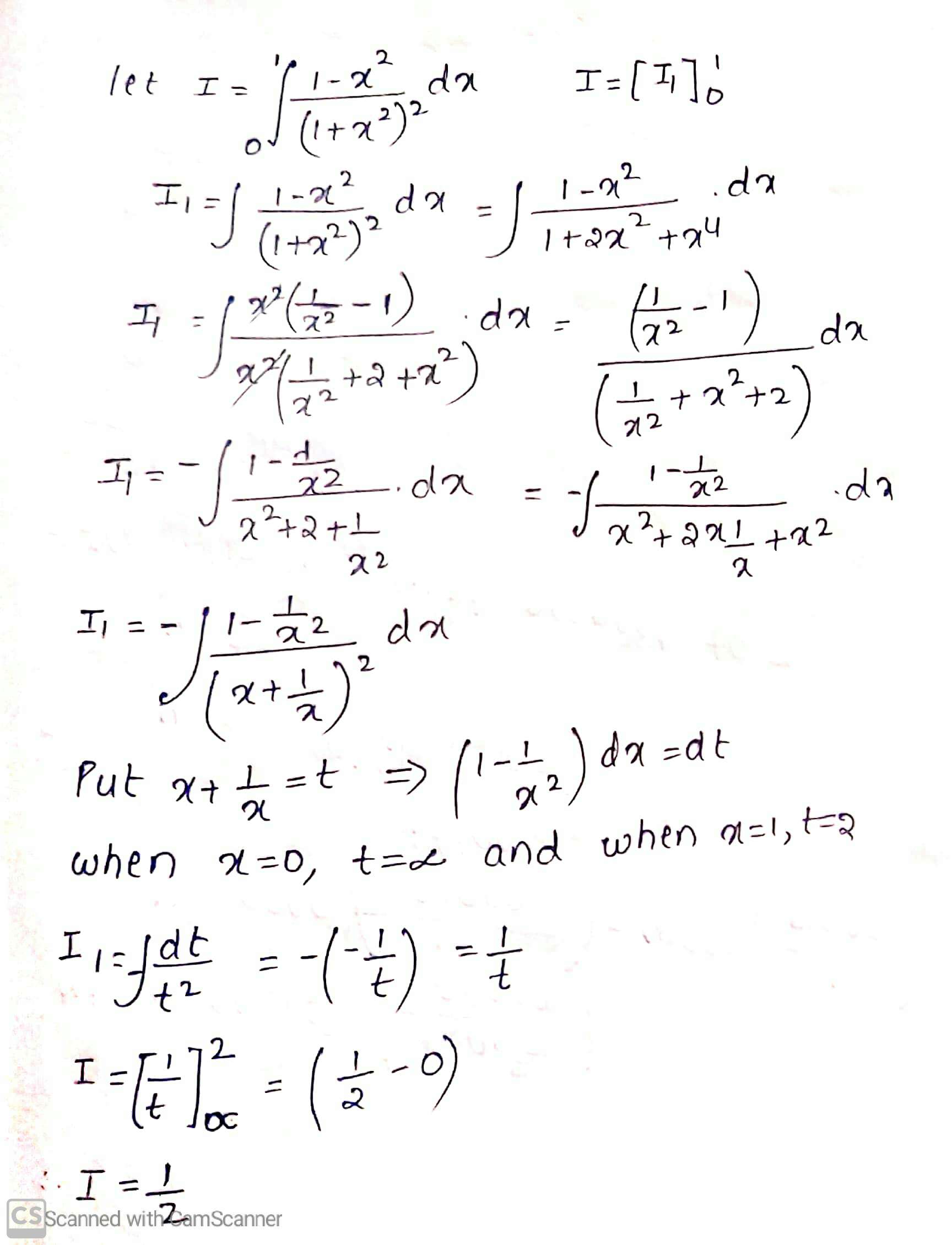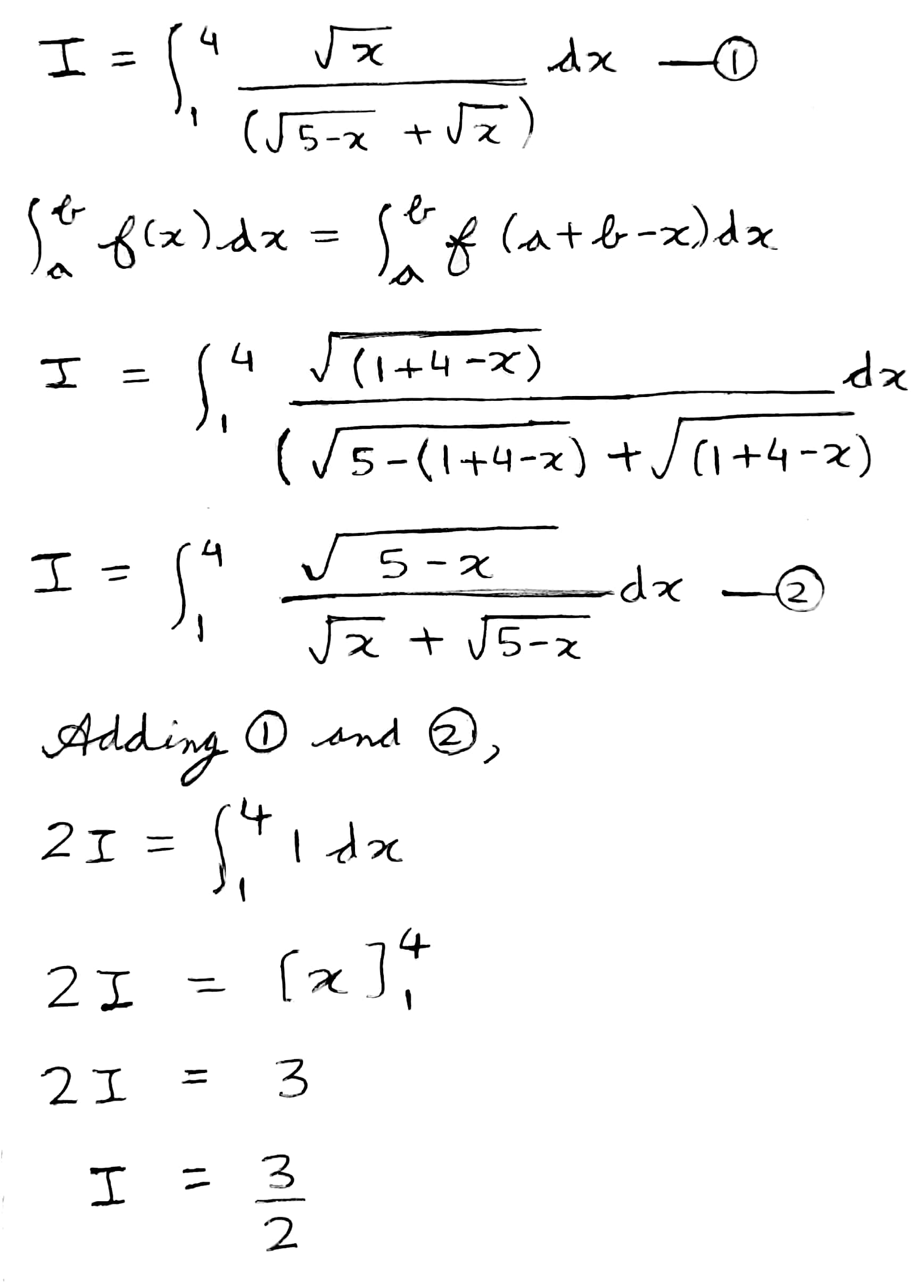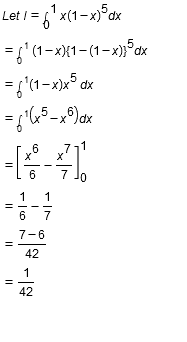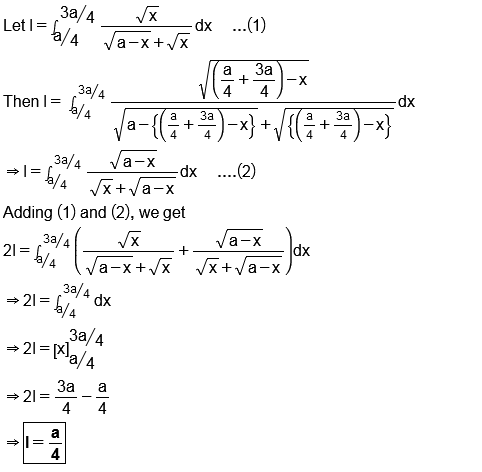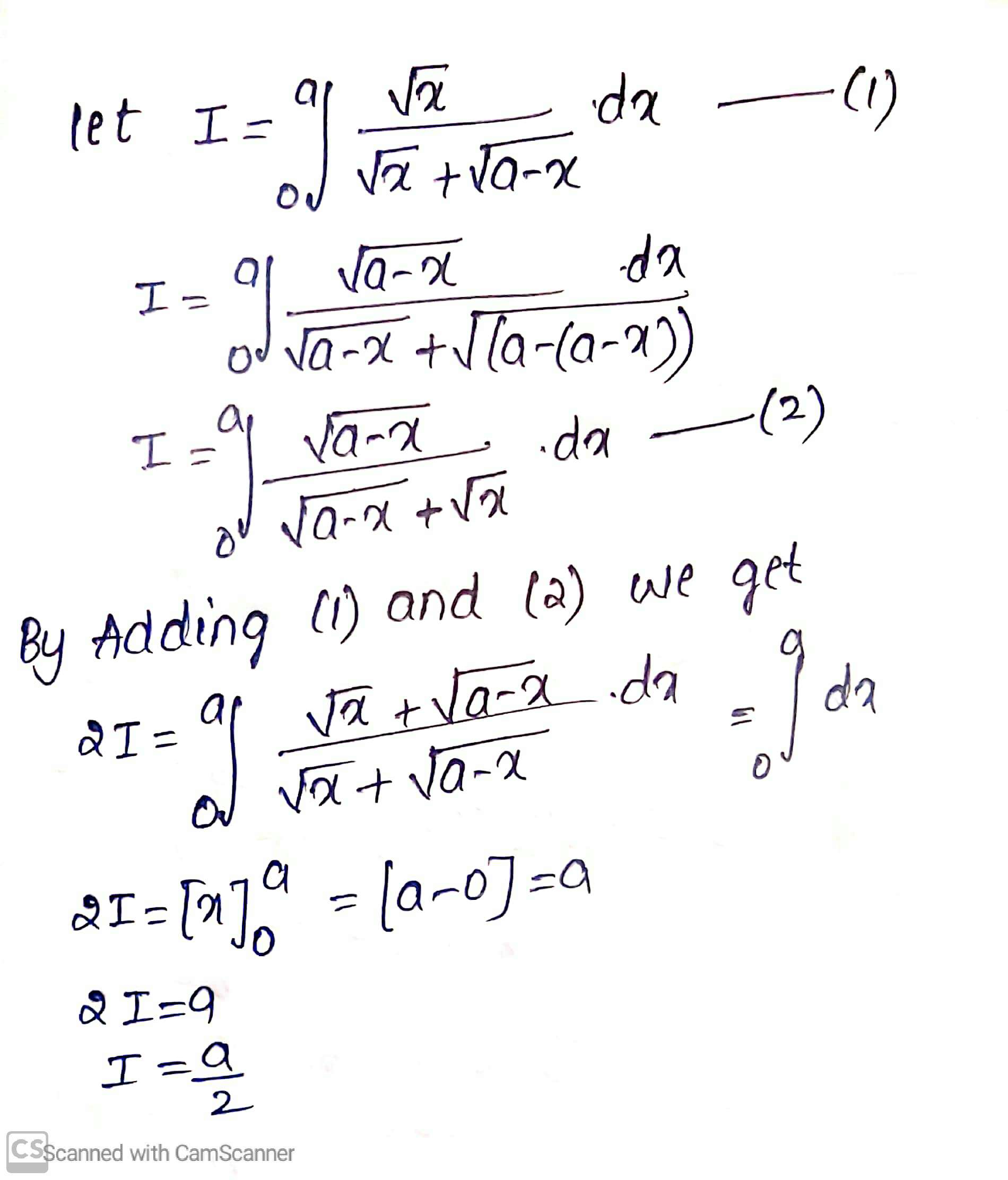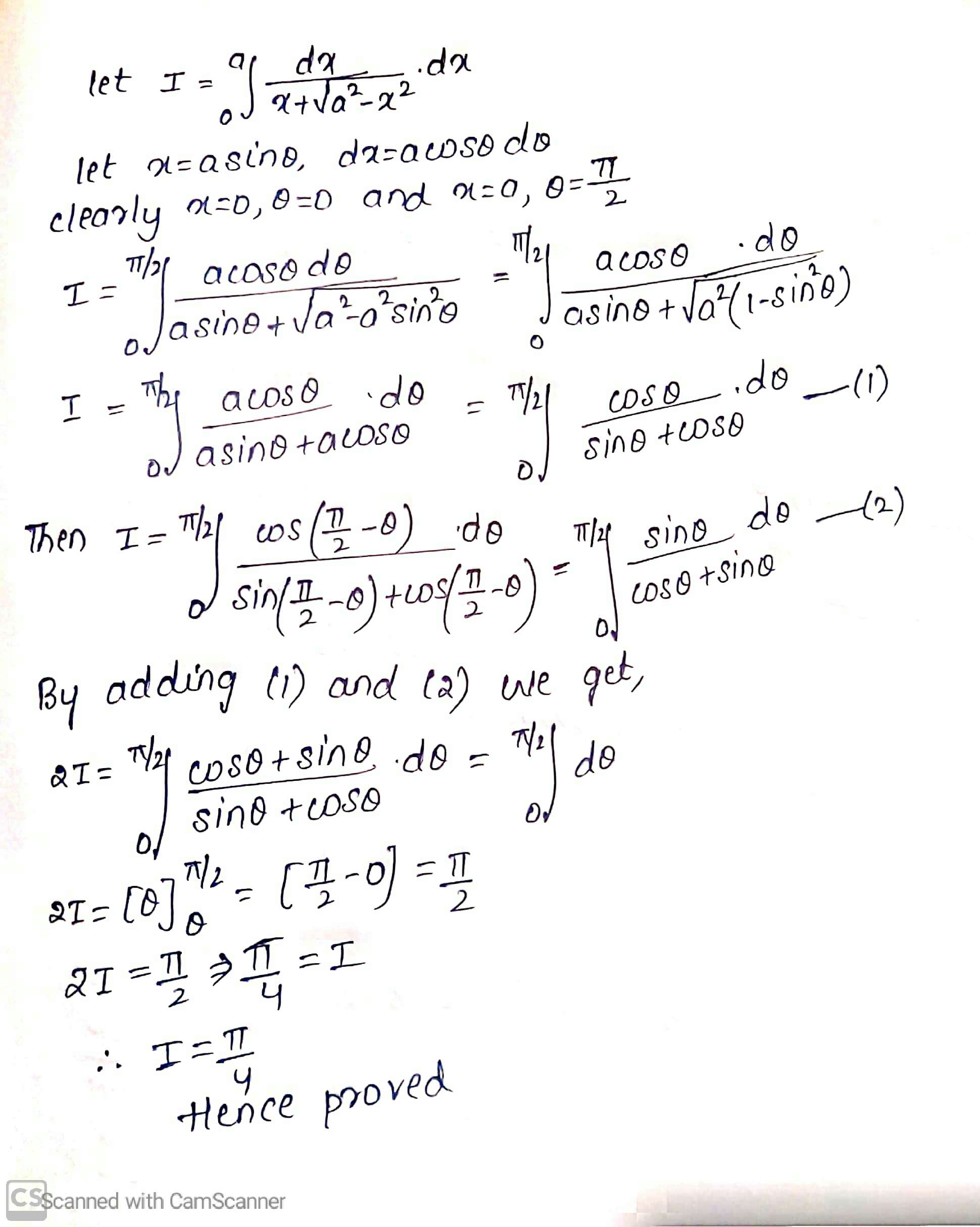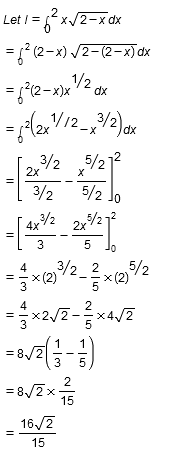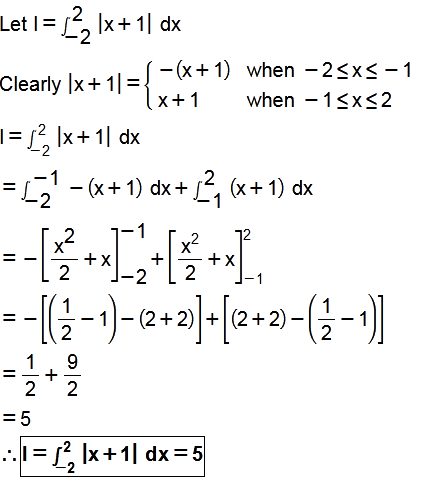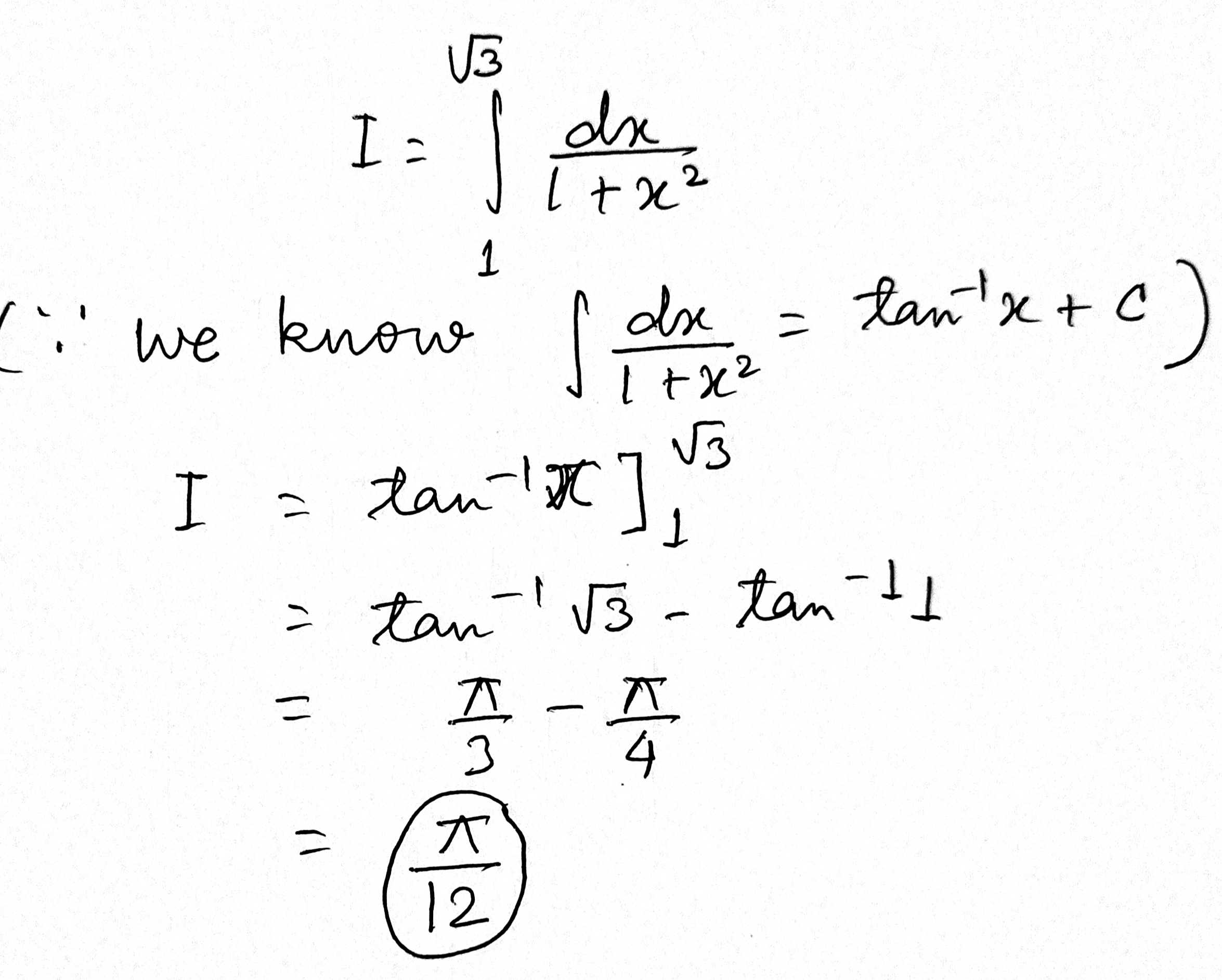Integrals - Class 12 Engineering Maths - Extra Questions

The value  of the definite integral, $$I = \int _{ 0 }^{ \sqrt { 10 }  }{ \dfrac { x }{ { e }^{ { x }^{ 2 } } }  } dx$$ is equal to 

$$I = \displaystyle \int_0^{\sqrt{10}} \frac{x}{e^{x^2}}dx \quad x^2 = t $$

$$  \displaystyle \Rightarrow 2x . dx = dt \Rightarrow x \, dx = \frac{dt}{2} $$ 

$$ I = \displaystyle \int_0^{\sqrt{10}} \frac{dt}{2\times e^t} =\frac{1}{2}\int_0^{\sqrt{10}} e^{-t} \, dt $$

$$ I \displaystyle =\frac{-1}{2}[e^{-t}]_0^{\sqrt{10}} = \frac{-1}{2}[e^{-x^2}]_0^{\sqrt{10}} $$

$$I \displaystyle =\frac{-1}{2} \left[e^{-10}- e^0\right] = \frac{-1}{2}\left[[\frac{1}{e^2}]^5 - 1\right] $$

$$ \displaystyle = 0.499 $$





$$\displaystyle \int_0^{2\pi}\cos^5x\,\,dx$$

$$I=\int _{ 0 }^{ 2\pi  }{ \cos ^{ 5 }{ x }  } dx.......(i)\\ I=\int _{ 0 }^{ 2\pi  }{ \cos ^{ 5 }{ (2\pi -x) }  } dx\\ I=-\int _{ 0 }^{ 2\pi  }{ \cos ^{ 5 }{ x }  } dx.....(ii)$$
Adding$$(i)$$ and $$(ii)$$
$$\Rightarrow 2I=0\\ \Rightarrow I=0$$


Write the value of $$\displaystyle\int \dfrac{1-\sin x}{\cos^2x}dx$$

$$I=\int \dfrac{1-\sin x}{\cos^2x} dx$$

$$I=\int (\dfrac{1}{\cos^2x}-\dfrac{\sin x}{\cos^2x})dx$$

$$=\int \sec^2x dx-\int \sec x \tan x \ dx$$
$$=\tan x -\sec x +C$$


$$\sqrt{2}\displaystyle \int _{ 0 }^{ 2\pi  }{ \sqrt { 1-\sin { x }  } dx } =$$

$$\sqrt 2 \int_0^{2\pi } {\sqrt {1 - \sin x} } dx$$
$$ = \mathop \smallint \nolimits^ \sqrt 2 \sin \left( {\frac{{2x - \pi }}{4}} \right){\mkern 1mu} {\rm{d}}x$$

$$ =  - {2^{\frac{3}{2}}}\cos \left( u \right)$$

$$ =  - {2^{\frac{3}{2}}}\cos \left( {\frac{{2x - \pi }}{4}} \right)$$

$$ = \sqrt 2 \mathop \smallint \nolimits^ \sqrt {1 - \sin \left( x \right)} {\mkern 1mu} {\rm{d}}x$$

$$ = \sqrt 2 \mathop \smallint \nolimits^ \sqrt {1 - \sin \left( x \right)} {\mkern 1mu} {\rm{d}}x$$

$$ =  - 4\cos \left( {\frac{{2x - \pi }}{4}} \right) + C$$

$$\sqrt 2 \int_0^{2\pi } {\sqrt {1 - \sin x} dx}  = 8$$




Prove that:
$$\displaystyle \int_{0}^{\pi}\dfrac {xdx}{1+\sin x} = \pi$$

$$I=\displaystyle\int_0^{\pi}\left(\dfrac{x}{1+\sin x}\right)dx$$
$$I=\displaystyle\int_0^{\pi}\left[\dfrac{x}{1+\sin x}\right]dx$$                              $$\left[\displaystyle\int_a^b f(x)dx=\displaystyle\int_a^b  f(a+b-x)dx\right]$$
$$2I=\displaystyle\int_0^{\pi}\left(\dfrac{x}{1+\sin x}\right)dx$$
$$2I=\displaystyle\int_0^{\pi}\left[\dfrac{x}{1+\sin x}\right]dx$$  $$\left[\displaystyle\int_a^{2b}f(x)dx=2\int_a^bf(x)dx if f(x )=7(2b-x) \right]$$
$$I=\displaystyle\int_0^{\pi/2}\left(\dfrac{1}{1+\sin x}\right)dx$$
$$I=\displaystyle\int_0^{\pi/2}\left(\dfrac{1-\sin x}{\cos^2x}\right)dx$$
$$I=\displaystyle\int_0^{\pi/2}(\sec^2x-\tan x\sec x)dx$$
$$I=\pi [\tan x- \sec x]^{\pi/2}_0$$
$$I=\pi\left|\dfrac{\sin x-1}{\cos x}\right|^{\pi/2}_0$$
$$I=\pi\left\{\displaystyle\lim_{x\rightarrow \pi/2}\left(\dfrac{\sin x-1}{\cos x}\right)\left(\dfrac{0-1}{\cos 0}\right)\right\}$$
$$I=\pi\left\{\displaystyle\lim_{x\rightarrow \pi/2}\left(\dfrac{\cos x}{-\sin x}\right)-(-1)\right\}$$
$$I=\pi\left\{0+1\right\}$$
$$I=\pi$$.

1173018_1346787_ans_16ec191de5294914a2a5e91f4a67b447.jpg


Evaluate the following definite integral:

$$\displaystyle\int_{4}^{12}x\ dx$$

$$\displaystyle\int_{4}^{12}x\ dx$$

$$\implies\left.\dfrac {x^2}2\right|_4^{12} $$

$$\implies\dfrac {12^2}2 -\dfrac {4^2}2$$

$$\implies\dfrac {144}2-\dfrac {16}2$$

$$\implies72-8=64$$ 



Evaluate the following definite integral:
$$\displaystyle\int_{0}^{\pi/2} \sin x \cos x\ dx$$ 

consider, $$I=\displaystyle\int_{0}^{\pi/2} \sin x \cos x\ dx$$ 

Let $$t=\sin x \implies dt=\cos x dx $$

$$x \to 0 \to \pi/2$$ 

$$t \to 0 \to 1$$ 

$$\Rightarrow I= \displaystyle \int _0^1 t \ dt $$ 

$$\Rightarrow$$ $$ \left [\dfrac {t^2}2 \right] _0^1 =\dfrac 12$$



Evaluate the following definate integral:
$$\displaystyle\int_{0}^{2} 3x+2\ dx$$

consider, $$I=\displaystyle\int_{0}^{2} 3x+2\ dx$$

$$I=\left[ 3\dfrac{x^2}2+2x \right]_0^2$$ 

$$I=6+4-0-0=10$$



$$\displaystyle \int_{0}^{1}\frac{dx}{(1+x)\sqrt{(2+x-x^{2})}}=\frac{1}{k}\sqrt{2}$$. Find the value of $$k$$.

Let $$\displaystyle I=\int { \dfrac { 1 }{ \left( 1+x \right) \sqrt { 2+x-{ x }^{ 2 } }  }  } =\int { \dfrac { 1 }{ \sqrt { \dfrac { 9 }{ 4 } -{ \left( x-\dfrac { 1 }{ 2 }  \right)  }^{ 2 } } \left( x+1 \right)  } dx } $$

Substitute $$\displaystyle x-\dfrac { 1 }{ 2 } =t\Rightarrow dx=dt$$

$$\displaystyle I=\int { \dfrac { 1 }{ \left( t+\dfrac { 3 }{ 2 }  \right) \sqrt { \dfrac { 9 }{ 4 } -{ t }^{ 2 } }  }  } dt$$

Substitute $$\displaystyle t=\dfrac { 3 }{ 2 } \sin { u } \Rightarrow dt=\dfrac { 3\cos { u }  }{ 2 } dx$$

$$\displaystyle \therefore I=\int { \dfrac { 1 }{ \dfrac { 3\sin { u }  }{ 2 } +\dfrac { 3 }{ 2 }  }  } dt$$

Substitute $$\displaystyle p=\tan { \dfrac { u }{ 2 }  } \Rightarrow dp=\dfrac { 1 }{ 2 } \sec ^{ 2 }{ \dfrac { u }{ 2 } du } $$

$$\displaystyle \therefore I=\int { \dfrac { 4 }{ 3{ p }^{ 2 }+6p+3 } dp } =4\int { \dfrac { 1 }{ { \left( \sqrt { 3 } p+\sqrt { 3 }  \right)  }^{ 2 } } dp } $$

$$\displaystyle =-\dfrac { 4 }{ 3p+3 } =\dfrac { 2\left( x-2 \right)  }{ 3\sqrt { -{ x }^{ 2 }+x+2 }  } $$

$$\displaystyle \therefore \int _{ 0 }^{ 1 }{ \dfrac { 1 }{ \left( 1+x \right) \sqrt { 2+x-{ x }^{ 2 } }  } dx } =\dfrac { \sqrt { 2 }  }{ 3 } $$


Integrate $$\displaystyle\int _{ 0 }^{ 1 }{ \sin ^{ -1 }{ \left( \dfrac { 2x }{ 1+{ x }^{ 2 } }  \right) dx }  }$$

Let,
$$I = \int_0^1 {si{n^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right)dx} $$
Let $$x=tan{\theta}$$
$$dx=sec^2{\theta}d{\theta}$$
When,  $$x=0, {\theta}=0$$ & $$x=1, {\theta}=\frac{\pi}{4}$$
Now,
$$I = \int_0^{\frac{\pi }{4}} {2\theta .{{\sec }^2}\theta .d\theta } $$
Integrating by parts , Taking $$sec^2{\theta}$$ as a first function.
$$=\dfrac{\pi}{2}-\log 2$$


Evaluate: $$\displaystyle \int _{ 0 }^{ 1 }{ \frac { { x }^{ 4 }{ \left( 1-x \right)  }^{ 4 } }{ 1+{ x }^{ 2 } }  } dx$$

Consider the given integral.

$$I=\int_{0}^{1}{\dfrac{{{x}^{4}}{{\left( 1-x \right)}^{4}}}{1+{{x}^{2}}}}dx$$

$$ I=\int_{0}^{1}{\dfrac{{{x}^{4}}{{\left( 1-x \right)}^{2}}{{\left( 1-x \right)}^{2}}}{1+{{x}^{2}}}}dx $$

$$ I=\int_{0}^{1}{\dfrac{{{x}^{4}}\left( 1+{{x}^{2}}-2x \right)\left( 1+{{x}^{2}}-2x \right)}{1+{{x}^{2}}}}dx $$

$$ I=\int_{0}^{1}{\dfrac{{{x}^{4}}\left( 1+{{x}^{2}}-2x+{{x}^{2}}+{{x}^{4}}-2{{x}^{3}}-2x-2{{x}^{3}}+4{{x}^{2}} \right)}{1+{{x}^{2}}}}dx $$

$$ I=\int_{0}^{1}{\dfrac{{{x}^{4}}\left( 1+6{{x}^{2}}+{{x}^{4}}-4{{x}^{3}}-4x \right)}{1+{{x}^{2}}}}dx $$

$$ I=\int_{0}^{1}{\dfrac{\left( {{x}^{4}}+6{{x}^{6}}+{{x}^{8}}-4{{x}^{7}}-4{{x}^{5}} \right)}{1+{{x}^{2}}}}dx $$

$$ I=\int_{0}^{1}{\dfrac{\left( {{x}^{8}}-4{{x}^{7}}+6{{x}^{6}}-4{{x}^{5}}+{{x}^{4}} \right)}{{{x}^{2}}+1}}dx $$

$$ I=\int_{0}^{1}{\left( {{x}^{6}}-4{{x}^{5}}+5{{x}^{4}}-4{{x}^{2}}+4-\dfrac{4}{1+{{x}^{2}}} \right)}dx $$

$$ I=\left[ \dfrac{{{x}^{7}}}{7}-\dfrac{4{{x}^{6}}}{6}+\dfrac{5{{x}^{5}}}{5}-\dfrac{4{{x}^{3}}}{3}+4x-4{{\tan }^{-1}}x \right]_{0}^{1} $$

$$ I=\left[ \dfrac{1}{7}-\dfrac{4}{6}+\dfrac{5}{5}-\dfrac{4}{3}+4-4{{\tan }^{-1}}\left( 1 \right)-\left[ 0 \right] \right] $$

$$ I=\left[ \dfrac{1}{7}-\dfrac{2}{3}+1-\dfrac{4}{3}+4-4{{\tan }^{-1}}\left( \tan \dfrac{\pi }{4} \right) \right] $$

$$ I=\left[ \dfrac{1}{7}-\dfrac{2}{3}-\dfrac{4}{3}+5-\dfrac{4\pi }{4} \right] $$

$$ I=\left[ \dfrac{1}{7}-2+5-\pi  \right] $$

$$ I=\left[ \dfrac{1}{7}-3-\pi  \right] $$

$$ I=-\left( \dfrac{20}{7}+\pi  \right) $$

 

Hence, this is the answer.


$$\displaystyle\int^1_0\cot^{-1}(1+x^2-x)dx$$.

\begin{array}{l} \int  _{ 0 }^{ 1 }{ { { \tan   }^{ -1 } } }(\frac { { x+\left( { 1-x } \right)  } }{ { 1+{ x^{ 2 } }-x } } )dx \\ \int  _{ 0 }^{ 1 }{ { { \tan   }^{ -1 } } }(\frac { { x-\left( { -1+x } \right)  } }{ { 1+x\left( { x+1 } \right)  } } )dx \\ \int  _{ 0 }^{ 1 }{ \left[ { { { \tan   }^{ -1 } }x-{ { \tan   }^{ -1 } }\left( { x-1 } \right)  } \right]  }dx \\ \int  _{ 0 }^{ 1 }{ { { \tan   }^{ -1 } }xdx }-\int  _{ 0 }^{ 1 }{ { { \tan   }^{ -1 } } }\left( { x-1 } \right) dx \\ \left[ { \frac { 1 }{ { 1+{ x^{ 2 } } } }  } \right] _{ 0 }^{ 1 }+\left[ { \frac { 1 }{ { \left[ { 1+\left( { x-1 } \right)  } \right]  } }  } \right] _{ 0 }^{ 1 } \\ \left( { \frac { 1 }{ 2 } -1 } \right) -\left( { 1-\frac { 1 }{ 2 }  } \right)  \\ -\frac { 1 }{ 2 } -\frac { 1 }{ 2 } =-1 \end{array}


Prove that $$\displaystyle\int^{\tan x}_{1/e}\dfrac{t}{1+t^2}dt+\displaystyle\int^{\cot x}_{1/e}\dfrac{1}{t(1+t^2)}dt=1$$.

To prove $$\int _{ \cfrac { 1 }{ e }  }^{ \tan { x }  }{ \cfrac { t }{ 1+{ t }^{ 2 } } dt } +\int _{ \cfrac { 1 }{ e }  }^{ \cot { x }  }{ \cfrac { 1 }{ t(1+{ t }^{ 2 }) } dt } $$
Let $${ I }_{ 1 }=\int _{ \cfrac { 1 }{ e }  }^{ \tan { x }  }{ \cfrac { t }{ 1+{ t }^{ 2 } } dt } \\ { I }_{ 2 }=\int _{ \cfrac { 1 }{ e }  }^{ \cot { x }  }{ \cfrac { 1 }{ t(1+{ t }^{ 2 }) } dt } $$
and $$I={ I }_{ 1 }+{ I }_{ 2 }$$
also, $$\int _{ \cfrac { 1 }{ e }  }^{ \cot { x }  }{ \cfrac { 1 }{ t(1+{ t }^{ 2 }) } dt } $$
Let $$t=\cfrac { 1 }{ z } $$
$$dt=\cfrac { -1 }{ { z }^{ 2 } } dz$$
So, $${ I }_{ 1 }=\int _{ e }^{ \tan { x }  }{ \cfrac { -zdz }{ { z }^{ 2 }(1+\cfrac { 1 }{ { z }^{ 2 } } ) }  } =\int _{ \tan { x }  }^{ e }{ \cfrac { zdz }{ 1+{ z }^{ 2 } }  } $$
So, $${ I }_{ 2 }=\int _{ \tan { x }  }^{ e }{ \cfrac { tdt }{ 1+{ t }^{ 2 } }  } $$
So, $$I={ I }_{ 1 }+{ I }_{ 2 }$$
$$I=\int _{ \cfrac { 1 }{ e }  }^{ e }{ \cfrac { tdt }{ 1+{ t }^{ 2 } }  } \\ =\cfrac { 1 }{ 2 } \int _{ \cfrac { 1 }{ e }  }^{ e }{ \cfrac { 2t }{ 1+{ t }^{ 2 } } dt } \\ I=\cfrac { 1 }{ 2 } { \log { (1+{ t }^{ 2 }) }  }_{ \cfrac { 1 }{ e }  }^{ e }\\ I=\cfrac { 1 }{ 2 } \log { (1+{ e }^{ 2 }) } -\cfrac { 1 }{ 2 } \log { (1+\cfrac { 1 }{ { e }^{ 2 } } ) } \\ I=\cfrac { 1 }{ 2 } [\log { (\cfrac { 1+{ e }^{ 2 } }{ 1+\cfrac { 1 }{ { e }^{ 2 } }  } ) } ]\\ I=\cfrac { 1 }{ 2 } \log { { e }^{ 2 } } \\ I=\cfrac { 1 }{ 2 } \times 2\\ I=1$$


Evaluate:
$$\int _ { 0 } ^ { \pi / 4 } \dfrac { \sin x + \cos x } { 9 + 16 \sin 2 x } d x$$

$$ \displaystyle \int_{0}^{\pi/4} \dfrac{sinx+cosx}{9+16sin2x}dx $$
express deno. in terms of sinx-cosx.

$$ sin 2x = 1-(sinx-cosx)^{2}$$
$$ \displaystyle \Rightarrow \int_{0}^{\pi/4} \dfrac{sinx+cosx}{9+16(1-(sinx-cosx)^{2})}dx$$

$$ \displaystyle \Rightarrow \int_{0}^{\pi/4} \dfrac{sinx+cosx}{25-16(sinx-cosx^{2})}dx$$

Put $$sinx - cosx = t $$

$$ \displaystyle I = \int_{-1}^{0}\dfrac{dt}{25-16t^{2}}$$
$$ \displaystyle = \frac{1}{16} \times \dfrac{1}{2.\dfrac{5}{4}}[log\dfrac{5/4+t}{5/4-t}]_{-1}^{0}$$

$$ = \dfrac{1}{40}log 9.$$


Evaluate:
$$\displaystyle \int\limits_2^0 {\dfrac{1}{{\sqrt {4 - x^2} }}} dx$$


1353297_1270642_ans_b8aa8492c8844000812c3ac00ff12a7b.PNG


EVALUATE 
$$ \int_{2}^{3} \frac{1}{x+5} d x $$

$$\displaystyle\int ^{3}_{2}\dfrac{1}{x+5}d x=[\ln |x+5|]^3_2=\ln |3+5|-\ln |2+5|=\ln 8-\ln 7=\ln \dfrac{8}{7}$$


Evaluate the definite integral:
$$\displaystyle\int_{0}^{1}\dfrac{1-x^{2}}{(1+x^{2})^{2}}dx$$

$$I=\displaystyle\int_{0}^{1}\dfrac{1-x^{2}}{(1+x^{2})^{2}}dx$$

Dividing by $$x^2$$ in both numerator and denominator 

$$I=\displaystyle\int_{0}^{1}\dfrac{\dfrac{1} {x^{2}}-1}{\left(x+\dfrac{1}{x}\right)^{2}}\ dx$$

 Let $$x+\dfrac{1}{x}=t$$.

 Then, $$d\left(x+\dfrac{1}{x}\right)=dt\Rightarrow \left(1-\dfrac{1}{x^{2}}\right)dx=dt$$

Clearly, 

$$x=0\Rightarrow t=\infty$$

$$x=1\Rightarrow t=2$$

$$\therefore \displaystyle\int_{\infty}^{2}-\dfrac{1}{t^{2}}dt=\left[\dfrac{1}{t}\right]_{\infty}^{2}=\dfrac{1}{2}$$


Evaluate: $$\displaystyle\int \dfrac {1}{2x+3}dx$$


Let $$t=2x+3 \implies dt=2 dx$$

$$\Rightarrow \displaystyle \int \dfrac 1{2t }dt $$

$$\Rightarrow \dfrac12 \log t$$ 

$$\Rightarrow \dfrac12[\log 2x+3]$$ 


Evaluate the following integrals:
$$\int { \sqrt { 2{ x }^{ 2 }+3x+4 }  } dx$$

Let $$I=\displaystyle\int \sqrt{2 x^2+3 x+4} d x$$

        $$=\displaystyle\int \sqrt{2\left(x^2+2(x)\bigg(\dfrac{3}{4}\bigg)+2\right)}$$

        $$=\sqrt{2}\displaystyle\int \sqrt{x^2+2(x)\bigg(\dfrac{3}{4}\bigg)+\bigg(\dfrac{3}{4}\bigg)^2-\bigg(\dfrac{3}{4}\bigg)^2+2}\ d x$$

       $$=\sqrt{2}\displaystyle\int \sqrt{\bigg(x+\dfrac{3}{4}\bigg)^2+\dfrac{23}{16}}\ d x$$                                                        $$(\because (a+b)^2=a^2+2 a b+b^2)$$

Put $$t=x+\dfrac{3}{4}\implies d t=d x$$

$$I=\sqrt{2}\displaystyle\int \sqrt{t^2+\bigg(\dfrac{\sqrt{23}}{4}\bigg)^2}\ d t$$

As we know that

$$\displaystyle\int \sqrt{a^2+x^2} d x=\dfrac{x}{2}\sqrt{x^2+a^2}+\dfrac{a^2}{2}\ln |x+\sqrt{x^2+a^2}|+C$$

Here $$a=\dfrac{\sqrt{23}}{4}$$

$$\implies I=\sqrt{2}\left(\dfrac{t}{2}\sqrt{t^2+\dfrac{23}{16}}+\dfrac{23/16}{2}\ln \left|t+\sqrt{t^2+\dfrac{23}{16}}\right|+C\right)$$

$$\implies I=\dfrac{1}{2}\bigg(x+\dfrac{3}{4}\bigg)\sqrt{2\bigg(x+\dfrac{3}{4}\bigg)^2+\dfrac{23}{16}}+\dfrac{23\sqrt{2}}{32}\ln \left|x+\dfrac{3}{4}+\sqrt{\bigg(x+\dfrac{3}{4}\bigg)^2+\dfrac{23}{16}}\ \right|+C$$

$$\implies I=\dfrac{1}{8}(4  x+3)\sqrt{2 x^2+3 x+4}+\dfrac{23\sqrt{2}}{32}\ln \left|x+\dfrac{3}{4}+\sqrt{x^2+\dfrac{3}{2} x+2}\ \right|+C$$


Evaluate the following integral:
$$\int { \left( x+1 \right)  } \sqrt { 2{ x }^{ 2 }+3 } dx$$

Let $$I=\displaystyle\int (x+1)\sqrt{2 x^2+3}\ d x$$

$$\implies I=\displaystyle\int (x+1)\sqrt{2\bigg(x^2+\dfrac{3}{2}\bigg)}\ d x$$

$$\implies I=\sqrt{2}\displaystyle\int (x+1)\sqrt{x^2+\dfrac{3}{2}}\ d x$$

$$\implies I=\sqrt{2}\displaystyle\int x\sqrt{x^2+\dfrac{3}{2}}\ d x+\sqrt{2}\displaystyle\int \sqrt{x^2+\bigg(\sqrt{\dfrac{3}{2}}\bigg)^2}\ d x$$

As we know that

$$\displaystyle\int \sqrt{a^2+x^2} d x=\dfrac{x}{2}\sqrt{x^2+a^2}+\dfrac{a^2}{2}\ln |x+\sqrt{x^2+a^2}|+C$$

$$\implies I=\sqrt{2}\displaystyle\int x\sqrt{x^2+\dfrac{3}{2}}\ d x+\sqrt{2}\left(\dfrac{x}{2}\sqrt{x^2+\dfrac{3}{2}}+\dfrac{3/2}{2}\ln \bigg| x+\sqrt{x^2+\dfrac{3}{2}}\ \bigg|\right)+C$$

Put $$x^2+\dfrac{3}{2}=y\implies 2 x d x=d y\implies x d x=\dfrac{dy}{2}$$

$$\implies I=\sqrt{2}\displaystyle\int \sqrt{y}\times \dfrac{d y}{2}+\dfrac{x}{\sqrt{2}}\sqrt{x^2+\dfrac{3}{2}}+\dfrac{3}{2\sqrt{2}}\ln \bigg| x+\sqrt{x^2+\dfrac{3}{2}}\ \bigg|+C$$

$$\implies I=\dfrac{1}{\sqrt{2}}\displaystyle\int \sqrt{y}\ d y+\dfrac{x}{\sqrt{2}}\sqrt{x^2+\dfrac{3}{2}}+\dfrac{3}{2\sqrt{2}}\ln \bigg| x+\sqrt{x^2+\dfrac{3}{2}}\ \bigg|+C$$  

$$\implies I=\dfrac{1}{\sqrt{2}}\times \dfrac{y^{3/2}}{3/2}+\dfrac{x}{\sqrt{2}}\sqrt{x^2+\dfrac{3}{2}}+\dfrac{3}{2\sqrt{2}}\ln \bigg| x+\sqrt{x^2+\dfrac{3}{2}}\ \bigg|+C$$                    $$\left(\because \displaystyle\int x^n\ d x=\dfrac{x^{n+1}}{n+1}+c\right)$$


$$\implies I=\dfrac{\sqrt{2}}{3}\ y^{3/2}+\dfrac{\sqrt{2}x}{2}\sqrt{x^2+\dfrac{3}{2}}+\dfrac{3}{2\sqrt{2}}\ln \bigg| x+\sqrt{x^2+\dfrac{3}{2}}\ \bigg|+C$$   

$$\implies I=\dfrac{\sqrt{2}}{3}\ \left(x^2+\dfrac{3}{2}\right)^{3/2}+\dfrac{\sqrt{2}x}{2}\sqrt{x^2+\dfrac{3}{2}}+\dfrac{3}{2\sqrt{2}}\ln \bigg| x+\sqrt{x^2+\dfrac{3}{2}}\ \bigg|+C$$             $$\left(\because y=x^2+\dfrac{3}{2}\right)$$

$$\implies I=\dfrac{\sqrt{2}}{3}\ \left(\dfrac{2 x^2+3}{2}\right)^{3/2}+\dfrac{x}{2}\sqrt{2 x^2+3}+\dfrac{3}{2\sqrt{2}}\ln \bigg| x+\sqrt{x^2+\dfrac{3}{2}}\ \bigg|+C$$      

$$\implies I=\dfrac{1}{6}\ \left(2 x^2+3\right)^{3/2}+\dfrac{x}{2}\sqrt{2 x^2+3}+\dfrac{3}{2\sqrt{2}}\ln \bigg| x+\sqrt{x^2+\dfrac{3}{2}}\ \bigg|+C$$      


Evaluate the following integrals:
$$\int { \sqrt { 2ax-{ x }^{ 2 } }  } dx\quad $$

Let $$I=\displaystyle\int \sqrt{2 a x-x^2}\ d x$$

$$\implies I=\displaystyle\int \sqrt{-(-2(a)(x)+x^2)}\ d x$$

$$\implies I=\displaystyle\int \sqrt{a^2-(a^2-2(a)(x)+x^2}\ d x$$

$$\implies I=\displaystyle\int \sqrt{a^2-(a-x)^2}\ d x$$

Put $$t=a-x\implies d t=-d x$$

$$\implies I=-\displaystyle\int \sqrt{a^2-t^2}\ d t$$

As we know that

$$\displaystyle\int \sqrt{a^2-x^2}\ d x=\dfrac{x}{2}\sqrt{a^2-x^2}+\dfrac{a^2}{2}\text{sin}^{-1} \left(\dfrac{x}{a}\right)+C$$

$$I=-\dfrac{t}{2}\sqrt{a^2-t^2}-\dfrac{a^2}{2}\text{sin}^{-1} \left(\dfrac{t}{a}\right)+C$$

$$I=-\dfrac{a-x}{2}\sqrt{a^2-(a-x)^2}-\dfrac{a^2}{2}\text{sin}^{-1} \left(\dfrac{a-x}{a}\right)+C$$

$$I=\dfrac{1}{2}(x-a)\sqrt{2 a x-x^2}-\dfrac{a^2}{2}\text{sin}^{-1} \left(\dfrac{a-x}{a}\right)+C$$


Evaluate the following definite integral:

$$\displaystyle\int_{0}^{\pi/4}\sin^{3}2t\cos 2t\ dt$$.


Consider, $$I=\displaystyle\int_{0}^{\pi/4}\sin^{3}2t\cos 2t\ dt$$

Let $$\sin 2t=u$$. 

Then, 

$$d(\sin 2t)=du$$ 

$$\Rightarrow 2\cos 2t\ dt=du$$ 

$$\Rightarrow \cos 2t dt=\dfrac{1}{2}du$$

Also, 

$$t=0\Rightarrow u=\sin 0=0$$ 

$$t=\dfrac{\pi}{4}$$ 

$$\Rightarrow u=\sin\dfrac{\pi}{2}=1$$

$$\therefore I=\dfrac{1}{2}\displaystyle\int_{0}^{1}u^{3}du$$ 

$$I=\dfrac{1}{8}\left[u^{4}\right]_{0}^{1}=\dfrac{1}{8}$$



Evaluate the following integral:
$$\displaystyle\int^2_0x\sqrt{2-x}dx$$.


1548009_1706409_ans_ee11ccf7842548df99ee6e8d91cd53db.jpg


Evaluate the following integral:
$$\displaystyle\int^9_0\dfrac{dx}{(1+\sqrt{x})}$$.


1548623_1706440_ans_1a2af81ff3da463dbbb5ee56f765851e.jpg


Evaluate the following integral:
$$\displaystyle\int^3_2\dfrac{(2-x)}{\sqrt{5x-6-x^2}}dx$$.


1548628_1706450_ans_0b7eb7ecd8ef425e87a283aafc1259e6.jpg


Evaluate the following integral:
$$\displaystyle\int^a_0\dfrac{x}{\sqrt{a^2+x^2}}dx$$.


1548008_1706408_ans_668d63b38a7d4e62abcbbf5702c12e88.jpg


Evaluate the following integral:
$$\displaystyle\int^2_1\dfrac{dx}{(x+1)\sqrt{x^2-1}}$$.


1548626_1706445_ans_0c04428214c7465c87342ae3e304f78c.jpg


Evaluate the following integral:
$$\displaystyle\int^1_0x^3\sqrt{1+3x^4}dx$$.


1546857_1706441_ans_9ec97e3304b94dee9076cf63d5a4d806.jpg


Evaluate the following integral:
$$\displaystyle\int^a_0\dfrac{x^4}{\sqrt{a^2-x^2}}dx$$.


1548006_1706407_ans_7cbfdb6903e4402b97fee10092688f13.jpg


Evaluate the following integral:
$$\displaystyle\int^1_0\dfrac{(1-x^2)}{(1+x^2)^2}dx$$.

$$\therefore I=\dfrac12$$
1548625_1706444_ans_06e905af0bb24e839eef368784f9fd8c.jpg


Prove that $$\displaystyle\int^4_1\dfrac{\sqrt{x}}{(\sqrt{5-x}+\sqrt{x})}dx=\dfrac{3}{2}$$.


1548747_1706591_ans_71e83b25ba9846c59774ec55dabf0ac6.jpg


Prove that $$\displaystyle\int^1_0x(1-x)^5dx=\dfrac{1}{42}$$.


1546876_1706527_ans_aa38366ff8964ef68f0fe50d5e81be85.jpg


Prove that $$\displaystyle\int^{\infty}_0\dfrac{x}{(1+x)(1+x^2)}dx=\dfrac{\pi}{4}$$.


1548816_1706554_ans_734f2bd1b54341b3a87ef641bc38ad8e.jpg


Prove that $$\displaystyle\int^{3a/4}_{a/4}\dfrac{\sqrt{x}}{(\sqrt{a-x}+\sqrt{x})}dx=\dfrac{a}{4}$$.


1564749_1706587_ans_91f130031cab4805b774f5c9c8b59594.png


Prove that $$\displaystyle\int^8_0|x-5|dx=17$$.


1549298_1706610_ans_caa28685b8d149898fac0e2943a8bcf9.jpg


Prove that $$\displaystyle\int^a_0\dfrac{\sqrt{x}}{(\sqrt{x}+\sqrt{a-x})}dx=\dfrac{a}{2}$$.


1548822_1706558_ans_32e7ce247af74b30a5cdbd11bd2809b4.jpg


Prove that $$\displaystyle\int^a_0\dfrac{dx}{x+\sqrt{a^2-x^2}}=\dfrac{\pi}{4}$$.


1548819_1706556_ans_a30516ff255e428f9d08334b579dbde7.jpg


Prove that $$\displaystyle\int^2_0x\sqrt{2-x}dx=\dfrac{16\sqrt{2}}{15}$$.


1546883_1706530_ans_302bf98eef7c433791acdd4115f33839.jpg


Prove that $$\displaystyle\int^2_{-2}|x+1|dx=5$$.


1564788_1706608_ans_42d8688e808d46ada7da35b4838f5622.png


The value of the integral $$  9999\displaystyle \int_{0}^{\infty }\displaystyle \frac{dx}{\left ( x+\sqrt{1+x^{2}} \right )^{100}} $$ is

Let $$\displaystyle I=9999\int _{ 0 }^{ \infty  } \frac { dx }{ \left( x+\sqrt { 1+x^{ 2 } }  \right) ^{ 100 } } $$

Put $$\log { \left( x+\sqrt { 1+x^{ 2 } }  \right)  } =t$$
$$\Rightarrow \left( x+\sqrt { 1+x^{ 2 } }  \right) ={ e }^ t$$
$$\Rightarrow \ { { x }^{ 2 }+1 } ={ e }^{ 2t }-2x{ e }^{ t }+{ x }^{ 2 }$$
$$\displaystyle \therefore x=\frac { { e }^{ 2t }-1 }{ 2{ e }^{ t } } =\frac { { e }^{ t }+{ e }^{ -t } }{ 2 } $$
$$\Rightarrow dx=\dfrac { { e }^{ t }-{ e }^{ -t } }{ 2 } dt$$

when $$x\rightarrow 0,t\rightarrow 0$$ and $$x\rightarrow \infty ,t\rightarrow \infty $$

$$\displaystyle \therefore I=9999\int _{ 0 }^{ \infty  }{ \left( \frac { { e }^{ t }+{ e }^{ -t } }{ 2{ e }^{ 100t } }  \right) dt } =\frac { 9999 }{ 2 } \int _{ 0 }^{ \infty  }{ \left( { e }^{ -99t }+{ e }^{ -101t } \right) dt } $$

$$\displaystyle =\frac { 9999 }{ 2 } \lim _{ a\rightarrow \infty  }{ { \left( \frac { { e }^{ -99t } }{ -99 } -\frac { { e }^{ -101t } }{ 101 }  \right)  }_{ 0 }^{ a } } $$

$$\displaystyle =\frac { 9999 }{ 2 } \lim _{ a\rightarrow \infty  }{ \left( \frac { 1 }{ -99{ e }^{ 99a } } -\frac { 1 }{ 101{ e }^{ 101a } } -\frac { 1 }{ -99 } +\frac { 1 }{ 101 }  \right)  } $$

$$\displaystyle =\frac { 9999 }{ 2 } \left( \frac { 1 }{ 99 } +\frac { 1 }{ 101 }  \right) =100$$


Let $$\displaystyle I=\int_{0}^{1}\frac{dx}{\sqrt{4-x^{2}-x^{3}}}$$ and $$\displaystyle I_{1}=\int_{0}^{1/2}\frac{dx}{\sqrt{1-x^{4}}}$$

As $$0\leq x\leq 1\Rightarrow 4-x^{ 2 }\geq 4-x^{ 2 }-x^{ 3 }\geq 4-2x^{ 2 }\Rightarrow \int _{ 0 }^{ 1 } \frac { dx }{ \sqrt { 4-x^{ 2 } }  } \leq I\leq \int _{ 0 }^{ 1 } \frac { dx }{ \sqrt { 4-2x^{ 2 } }  } $$
$$\int _{ 0 }^{ 1 } \frac { dx }{ \sqrt { 4-x^{ 2 } }  } =\left. \sin ^{ -1 } \frac { x }{ 2 }  \right| _{ 0 }^{ 1 }=\frac { \pi  }{ 6 } \\ \int _{ 0 }^{ 1 } \frac { dx }{ \sqrt { 4-2x^{ 2 } }  } =\frac { 1 }{ \sqrt { 2 }  } \int _{ 0 }^{ 1 } \frac { dx }{ \sqrt { 2-x^{ 2 } }  } =\left. \frac { 1 }{ \sqrt { 2 }  } \sin ^{ -1 } \frac { x }{ \sqrt { 2 }  }  \right| _{ 0 }^{ 1 }=\frac { \pi  }{ 4\sqrt { 2 }  } $$
And as $$0\leq x\leq 1/2\Rightarrow \sqrt { 1-x^{ 2 } } \leq \sqrt { 1-x^{ 4 } } \leq 1$$
$$\Rightarrow \frac { 1 }{ 2 } =\int _{ 0 }^{ 1/2 } 1dx\leq I_{ 1 }\leq \int _{ 0 }^{ 1/2 } \frac { dx }{ \sqrt { 1-x^{ 2 } }  } =\frac { \pi  }{ 6 } $$
A) $$I<\frac { \pi  }{ 4\sqrt { 2 }  } <\frac { \pi  }{ 4 } <1$$
B) $$I>\frac { \pi  }{ 6 } >\frac { 1 }{ 2 } >\frac { 1 }{ 4 } $$
C) $${ I }_{ 1 }<\frac { \pi  }{ 6 } <\frac { \pi  }{ 4 } <1$$
D) $${ I }_{ 1 }>\frac { 1 }{ 2 } >\frac { 1 }{ 4 } $$


Find : $$\displaystyle \int_{0}^{\tfrac {\pi}{2}} \dfrac {dx}{4 + 5\cos x} dx$$

Let $$I = \displaystyle \int _0^{\tfrac{\pi}{2}} \cfrac{dx}{4 + 5\cos x}$$
Substituting $$\cos x = \cfrac{1 - \tan^2{\dfrac{x}{2}}}{1 + \tan^2{\dfrac{x}{2}}}$$, we have
$$I = \displaystyle \int _0^{\tfrac{\pi}{2}} \cfrac{\left(1 + \tan^2{\cfrac{x}{2}}\right)dx}{9 - \tan^2{\cfrac{x}{2}}}$$
Let $$t = \tan{\cfrac{x}{2}}$$
$$\Rightarrow 2dt = \left(1 + \tan^2{\cfrac{x}{2}}\right) dx$$
$$\therefore I = \displaystyle \int _0^{1} \cfrac{2dt}{9 - t^2}$$
$$\therefore I = \displaystyle \int _{0}^{1} \cfrac{(3 + t + 3 - t)}{3(3 + t)(3 - t)}$$
$$= \displaystyle \int _0^{1} \cfrac{dt}{3(3 - t)} + \displaystyle \int _0^{1} \cfrac{dt}{3(3 + t)}$$
$$= [\ln(3 - t)]_0^{1} \times \cfrac{-1}{3} + [\ln(3 + t)]_0^{1} \times \cfrac{1}{3}$$
$$= (\ln 3 - \ln 2 + \ln 4 - \ln 3) \times \cfrac{1}{3}$$
$$= \cfrac{1}{3} \times \ln 2$$


$$\int _{ 0 }^{ \pi /4 }{ \frac { (sinx+cosx) }{ 9+16sin2x }  } dx$$

$$I=\displaystyle\int_{0}^{\frac{\pi}{4}}{\dfrac{\sin{x}+\cos{x}}{9+16\sin{2x}}dx}$$
Let $$\sin{x}-\cos{x}=t$$
$$\left(\cos{x}+\sin{x}\right)dx=dt$$
Again $${\left(\sin{x}-\cos{x}\right)}^{2}={t}^{2}$$
$$\Rightarrow {\sin}^{2}{x}+{\cos}^{2}{x}-2\sin{x}\cos{x}={t}^{2}$$
$$\Rightarrow 1-\sin{2x}={t}^{2}$$
$$\Rightarrow \sin{2x}=1-{t}^{2}$$
When $$x=0\Rightarrow t=\sin{0}-\cos{0}=-1$$
When $$x=\dfrac{\pi}{4}\Rightarrow t=\sin{\dfrac{\pi}{4}}-\cos{\dfrac{\pi}{4}}=\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{2}}=0$$
$$\therefore  I=\displaystyle\int_{-1}^{0}{\dfrac{dt}{9+16\left(1-{t}^{2}\right)}}$$
$$=\displaystyle\int_{-1}^{0}{\dfrac{dt}{9+16-16{t}^{2}}}$$
$$=\displaystyle\int_{-1}^{0}{\dfrac{dt}{25-16{t}^{2}}}$$
$$=\dfrac{1}{16}\displaystyle\int_{-1}^{0}{\dfrac{dt}{\dfrac{25}{16}-{t}^{2}}}$$
$$=\dfrac{1}{16}\left[\dfrac{1}{2\times\dfrac{5}{4}}\log{\left|\dfrac{\dfrac{5}{4}+t}{\dfrac{5}{4}-t}\right|}\right]_{-1}^{0}$$
$$=\dfrac{1}{4}\left[\dfrac{1}{10}\log{\left|\dfrac{5+4t}{5-4t}\right|}\right]_{-1}^{0}$$
$$=\dfrac{1}{40}\left[\log{\left|\dfrac{5+0}{5-0}\right|}-\log{\left|\dfrac{5-4}{5+4}\right|}\right]$$
$$=\dfrac{1}{40}\left[\log{1}-\log{\left(\dfrac{1}{9}\right)}\right]$$
$$=\dfrac{1}{40}\left[0+\log{9}\right]$$
$$=\dfrac{\log{9}}{40}$$


$$\int^2_1 \dfrac{x}{\sqrt{2x^2+1}} dx$$

$$\displaystyle\int_{1}^{2}{\dfrac{xdx}{\sqrt{2{x}^{2}+1}}}$$
$$=\dfrac{1}{4}\displaystyle\int_{1}^{2}{\dfrac{4xdx}{\sqrt{2{x}^{2}+1}}}$$
Let $$t=2{x}^{2}+1\Rightarrow dt=4xdx$$
$$=\dfrac{1}{4}\displaystyle\int_{1}^{2}{\dfrac{dt}{\sqrt{t}}}$$
$$=\dfrac{1}{4}\displaystyle\int_{1}^{2}{{t}^{\frac{-1}{2}}dt}$$
$$=\dfrac{1}{4}\left[\dfrac{{t}^{\frac{-1}{2}+1}}{\dfrac{-1}{2}+1}\right]_{1}^{2}$$
$$=\dfrac{2}{4}\left[\sqrt{t}\right]_{1}^{2}$$
$$=\dfrac{1}{2}\left(\sqrt{2}-1\right)$$


Evaluate: $$ \int_{1}^{\sqrt{3}} \frac{d x}{1+x^{2}} $$


2040901_1453406_ans_4c8ff73261304a4d89d036f06b10a3b3.jpg


Evaluate: $$\displaystyle \int_{0}^{\frac{\pi}{2}} \dfrac{\sin x \cdot \cos x}{1+\sin^4 x}\cdot dx$$.

$$\displaystyle \overset{\pi/2}{\underset{0}{\int}} \frac{\sin x \cdot \cos x}{1 + \sin^4 x} \cdot dx$$.
Let $$\sin^2 n = t$$
$$2 \sin x \,\cos x \,dx = dt$$
When $$x = 0, t = 0$$

           $$x = \dfrac{\pi}{2}, t = 1$$

$$= \dfrac{1}{2} \displaystyle \overset{dt/2}{\underset{1 + t^2}{\int}} \frac{dt}{1 + t^2}$$

$$= \dfrac{1}{2} \displaystyle \overset{1}{\underset{0}{\int}} \frac{dt}{1 + t^2}$$

$$= \dfrac{1}{2} [\tan^{-1} - \tan^{-1} 0]$$

$$= \dfrac{1}{2} \left[\dfrac{\pi}{4} - 0 \right]$$

$$= \dfrac{\pi}{8}$$


If the value of the definite integral$$\int_{0}^{207} C_{7} x^{200} \cdot(1-x)^{7} d x$$ is equal to $$\dfrac{1}{k}$$ where $$k \in N\\$$, thenthe value of $$k / 26$$ is

(8) Let $$I=\int_{0}^{1} 207 C_{7} \cdot \underbrace{x^{200}}_{I I} \cdot \underbrace{(1-x)^{7}}_{I} d x\\$$
$$\begin{aligned}I=^{207} C_{7}[\left.\underbrace{(1-x)^{7} \cdot \dfrac{x^{201}}{201}}\right|_{0} ^{1}&\left.+\dfrac{7}{201} \int_{0}^{1}(1-x)^{6} \cdot x^{201} d x\right] \\&=^{207} C_{7}: \dfrac{7}{201} \int_{0}^{1}(1-x)^{6} \cdot x^{201} d x\end{aligned}\\$$
Integrating by parts again 6 more times
$$\begin{array}{l}=^{207} \mathrm{C}_{7} \cdot \dfrac{7 !}{201.202 .203 .204 .205 .206 .207} \int_{0}^{1} x^{207} d x \\=\dfrac{(207) !}{7 !(200) !} \cdot \dfrac{7 !}{201.202 \cdots 207} \cdot \dfrac{1}{208} \\=\dfrac{(207) !}{(207) ! 7 !} \cdot \dfrac{7 !}{208}=\dfrac{1}{208}=\dfrac{1}{k} \Rightarrow k=208\end{array}\\$$


Class 12 Engineering Maths Extra Questions