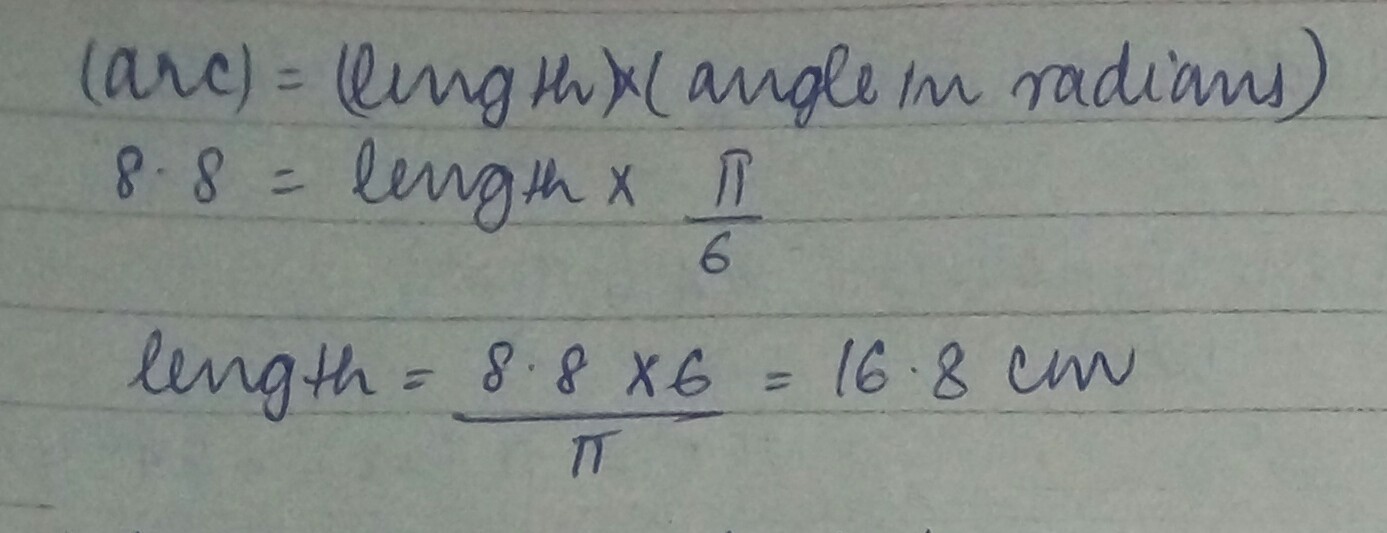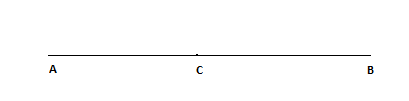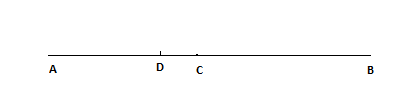Introduction To Euclid'S Geometry - Class 9 Maths - Extra Questions

What is the different between n theorem and an axiom ?

A statement where proof is required is called theorem whereas a basic fact where proof is not required is called an axiom
example :
Theorem - Pythagoras theorem
Axiom - A line can be drawn through two points


In  triangle ABC , $$A(0,8)\ B(2,4)\ C=(6,8)$$. Find equation of altitudes.


1110740_1172510_ans_035b29cd7afa48088b327dbdfb1fa855.jpeg


What is need for introducing axioms?

The Greek mathematicians faced a great difficulty while developing geometry as pure deductive science. They has to depend on certain primitive notions like points, line, planes and space. But this was not enough to deduce every thing. They had to set up certain statements whose validity was accepted unquestionably. Thus there was a need of introducing axioms. 


How would you rewrite Euclid's fifth postulate so that it would be easier to understand ? 

$${\textbf{Step - 1: Easier way}}$$
                $${\text{For every line L and for every point P not lying on L there exist a unique line m passing}}$$
                $${\text{through P and parallel to l}}$$
                $${\text{In an easier way we can say that there exists a line which passes through point P and that is}}$$
                $${\text{parallel to line L}}$$
                $${\text{Or, two straight lines intersect each other if a straight line passing through them has}}$$
                $${\text{interior angles less than right angles}}$$

2182503_1868806_ans_77472264eccb45b1858fdcb340a4984d.png


Does Euclid's fifth postulate imply the existence of parallel lines ? Explain.
1868809_9466817dd9f24f1f8d9b1f2a41e78630.PNG

$$'n'$$ is a straight line which intersects $$I$$ and $$m$$ straight lines. 
$$\angle 1 + \angle 4 < 180^0$$ and $$\angle 2 + \angle 3 > 180^0$$. 
If $$I$$ and $$m$$, produced by the side of $$\angle 1$$ and $$\angle 4$$ they meet at $$p$$. 
If $$\angle 1 + \angle 4 < 180^0$$ and $$\angle 2 + \angle 3 > 180^0$$, 
then $$I$$ and $$m$$ straight lines do not meet even produced, means they are parallel lines. 
1957543_1868809_ans_36cfd0cdc7f9463c96de520c827e582c.PNG


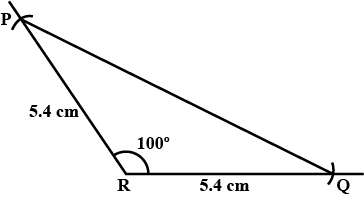
Construct  $$\Delta  PQR $$ such that  $$\angle R=100^o, QR = RP = 5.4 \,cm$$.


Draw a line, from one end, make angle $$100^o$$ by the protector and mark it as $$\angle R$$. From $$R$$ mark point at $$5.4$$cm on both lines and join the points mark them as $$P$$ and $$Q.$$


1142285_705207_ans_067bac166ff94aa4b811563481a001a4.png


What is the need of introducing axioms?

Earlier Greek Mathematician has to depends on some factors like point, straight lines, plane etc. But this was not enough to prove everything. They had to assembled certain statement whose validity was absolute, Thus there was a need of introducing axioms.


In figure given, if AC$$=$$BD, show that AB$$=$$CD. State the Euclid's postulate/axiom used for the same.
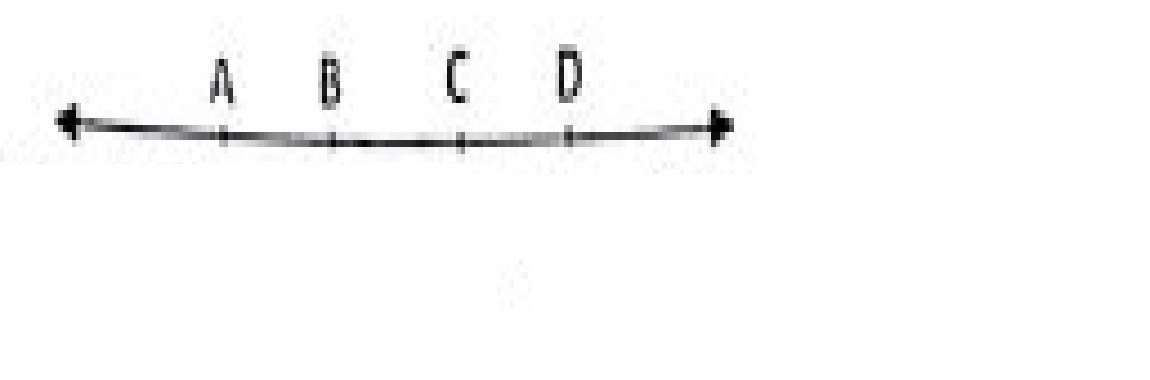
1126197_416a9fe2316842f18669910757f6bd2f.jpg

$$AC = BD$$
If two lines are collinear then  they are equal.(By euclid axiom)
$$AB + BC = BC + CD$$
$$AB = CD$$



Why is Axiom 5, in the list of Euclid's axioms, considered a 'universal truth' ? (Note that the question is not about the fifth postulate). 


2175001_1868801_ans_1e7a9f18ef7d4b9fb314740e60bb3729.jpg


Why is axiom 5, in the list of Euclid's axions; considered as a 'universal truth'? (Note that the question is not about the fifth postulate.)

Euclid's Axiom 5 states that. "The whole is greater than the part."
Since this is true for anything in any part of the world. So, this is a universal truth.


What are undefined objects in Euclids geometry?

Euclids Geometry has three undefined objects called point, line and plane.
Hence, point, line and plane are undefined objects.


Write three un-defined terms of geometry

 We have three undefined terms: point, line and plane. From these three undefined terms, all other terms in Geometry can be defined. 
In Geometry, we define a point as a location and no size. 
A line is defined as something that extends infinitely in either direction but has no width and is one dimensional while a plane extends infinitely in two dimensions.


How many books are there in Euclid's Elements?

There are $$13$$ books in Euclid's Elements.


In the adjoining figure, if $$\angle COA - \angle BOC = 50^o$$, find these angles.
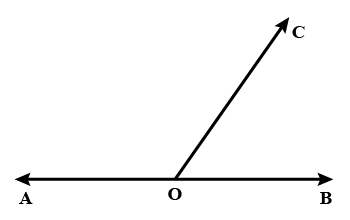
558829_6613538766584cc3a2884d657537e01e.png

In the figure,
$$\angle COA - \angle BOC=50^{o}$$ ....... $$(i)$$ [Given]
We know that, $$\angle BOC+\angle COA=180^{o}$$
$$\implies \angle BOC+50^{o}+\angle COA=180^{o}$$
$$\implies 2\angle BOC=180^{o}-50^{o}=130^{o}$$
$$\implies \angle BOC=65^{o}$$
From $$(i)$$,
$$\angle COA -65^{o}=50^{o}$$
$$\implies \angle COA=115^{o}$$
Hence, $$\angle BOC=65^{o}$$ and $$ \angle COA=115^{o}$$


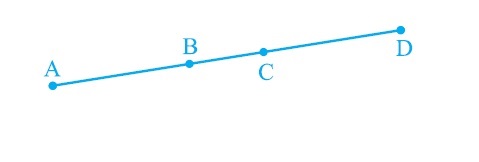
If $$A, B, C$$ are three points on a line and $$B$$ lies between $$A$$ and $$C$$, then prove that $$AC - AB = BC$$
569717_295298e573b74224a719616ddd7bfc58.png

Given $$B$$ is a point which lies on the line $$AC$$
$$\therefore$$ From Euclid's postulate,
$$AB+BC=AC$$
$$\Rightarrow{AC-AB=BC}$$
Hence, proved.


In the figure given below, show that length $$AH > AB + BC + CD$$
569704_783d0fd762754befa43fe6b6046215e1.png

$$AH=AB+BC+CD+DE+EF+FG+GH$$
$$\Rightarrow AB+BC+CD$$ is a part of $$AH$$
According to Euclid's fifth axiom the whole thing is greater then a part
$$\therefore AH>AB+BC+CD$$


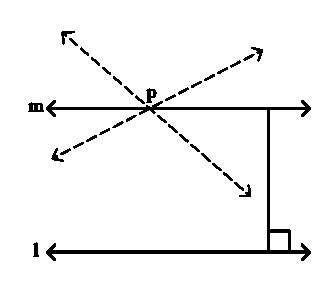
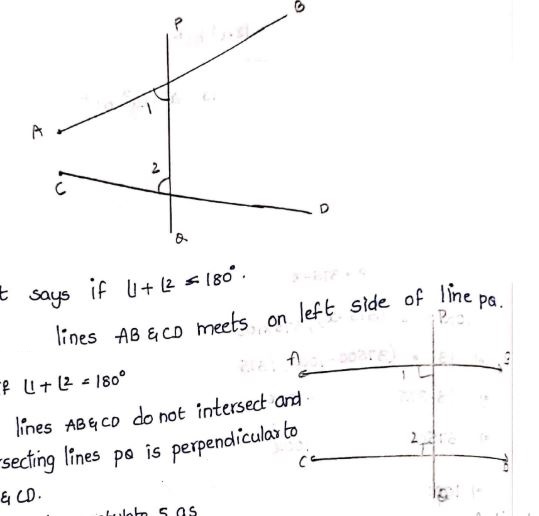
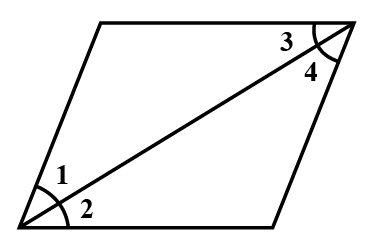
In the adjacent figure, if $$\angle 1 = \angle 3, \angle 2 = \angle 4$$ and $$\angle 3 = \angle 4$$, write the relation between $$\angle 1$$ and $$\angle 2$$ using an Euclid's postulate
569713_e67272d418c24d4ebf1d459c47bb603e.png

Given,
      $$\angle{1}=\angle{3}$$
      $$\angle{2}=\angle{4}$$
$$_____________$$
$$\angle{1}+\angle{2}=\angle{3}+\angle{4}$$
From $$1st$$ postulate of Euclid,
      The things which are equal to equal this are equal to one another.
$$\Rightarrow\angle{1}=\angle{2}$$
$$\Rightarrow\angle{1}=\angle{2}=\angle{3}=\angle{4}$$

881691_569713_ans_c72848b76434471385c056631a2a261d.png


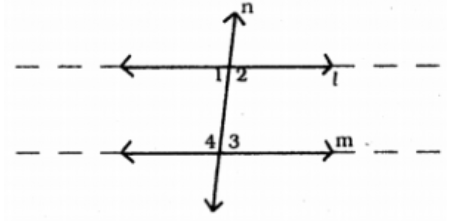
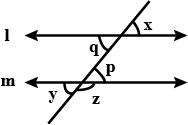
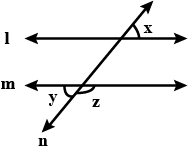
Line $$ l ||$$ Line $$m$$ , Line $$n$$ is the transversal. If $$ \angle x = 45^o , $$ find $$ \angle y $$ and $$ \angle z . $$
1109874_e665a4d612464944be65ff2fa6a528be.png

$$\angle x=\angle p$$ (corresponding angle)
$$\angle p=\angle y$$ (verticlly opposite angle)
$$\boxed{\angle y = \angle x = 45^o}$$
$$\angle y=\angle z=180^0$$ (supplementary angle)
$$\boxed{\angle z=180-45=135^0}$$

1048666_1109874_ans_1feb0f26cc014af9bf8f4230839f3823.png


Define Euclid's fifth Axiom.

  1. If a straight line crossing two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if extended indefinitely, meet on that side on which are the angles less than the two right angles.

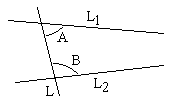
1325916_1064973_ans_a7d177f248a440dbac0ad10963262727.png


State Euclid's fifth postulate. Using the same write the pairs of angles, having the Sum less than $$180^{o}$$. (from the figure given)
1040060_37a9402e5d3b4de9ae7afa2bafc98f16.PNG

If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles I.e, $$180^{\circ}$$ , then the two straight lines, if produced indefinitely meet on that side on which sum of angles is less than two right angles.

Here, $$\angle3 + \angle6 < 180^{\circ}$$


Solve each of the following question using appropriate Euclid' s axiom: 
look at the figure, and show that 
Length AH > sum of lengths of $$AB + BC + CD$$. 
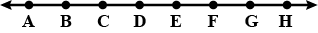
1794375_79921524bbed4bc880405928b93d0936.png

We see the AB, BC and CD are parts of line.
Now, AB + BC + CD = AD ....(1)
& AD is the part of line AH
By Euclid's axiom 5, the whole is greater than the part, 
so, AH > AD
i.e. Length AH > sum of length of AB + BC + CD [Using (1)]


Where will the hand of a clock stop if it 
a)Starts at $$12$$ and makes $$\frac{1}{2}$$ of a revolution, clockwise?
b)Starts at $$2$$ and makes $$\frac{1}{2}$$ of a revolution, clockwise?
c)Starts at $$5$$ and makes $$\frac{1}{4}$$ of a revolution, clockwise?
d)Starts at $$5$$ and makes $$\frac{3}{4}$$ of a revolution, clockwise?

$$\dfrac 12 $$ revolution clockwise exceeds the time by $$6$$ hrs so $$12$$ becomes $$6$$

$$\dfrac 12 $$ revolution clockwise exceeds the time by $$6$$ hrs so $$2$$ becomes $$8$$

$$\dfrac 14 $$ revolution clockwise exceeds the time by $$3$$ hrs so $$5$$ becomes $$8$$

$$\dfrac 34 $$ revolution clockwise exceeds the time by $$9$$ hrs so $$5$$ becomes $$2$$



In the figure, if AC$$=$$BD, use an Euclid's Axiom to show that AB$$=$$CD. 
1064980_cb5630fd2f004df0b3c7329bbe2e8696.png


1325999_1064980_ans_9ef11940a4424944bce6bd42403ade0b.jpg


Solve the equation $$a - 15 = 25$$ and state the axiom used.

Axiom : If equals are added to the equals, the wholes are equal.
That is, if $$a=b$$ and $$c=d$$, then $$a+c=b+d$$

In the given equation,

$$a-15=25$$

Add $$15$$ both sides,

$$a-15+15=25+15$$

$$a=40$$


Name three undefined terms of geometry.

$$Point, Line\ and\ Plane$$


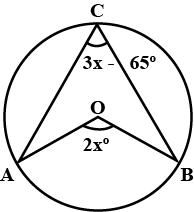
In the given figure $$A,B,C$$ are three points on the circle, $$O$$ is its centre. If $$\angle AOB=2x^{\circ}$$ and $$\angle ACB=3x-65^{\circ}$$, find the value of $$x$$. 
1133145_02e8965eb5ef4fc6b6f22abe2bc614e1.png

According to the problem,

$$\frac {1}{2} \angle AOB = \angle ACB$$

we know, 
[SINCE THE ANGLE SUBTENDED BY AN ARC AT THE CENTRE IS DOUBLE THE ANGLE SUBTENDED BY IT AT ANY POINT ON THE REMAINING PART OF THE CIRCLE]

hence, 

$$3x - 65 = \dfrac {1}{2} \times 2x$$

$$2x = 65$$

$$x = {{32.5}^\circ}$$


Give two equivalent versions of Euclid's fifth postulate.

The two equivalent versions of Euclid's fifth postulate are,

1. For every line $$l$$ and for every point $$p$$ not lying on $$l$$, there exists a unique line $$m$$ passing through $$p$$ and parallel to $$l$$.

2. Two distinct intersecting lines cannot be parallel to the same line.


If $$A$$ pendulum swings through an angle of $$30^{o}$$ and describes an are of $$8.8\ cm$$ in length. Find the length of pendulum.

(arc)=(length) $$\times$$ (angle in radians)
8. 8 = length$$\times \frac{\pi }{6}$$
length = $$\frac{8.8\times 6}{\pi }=16.8 cm$$

1195889_1344054_ans_5e6918f1320d4e828ab9ed460f63384d.jpg


In the given figure, AD=CDAD=CD.
1133630_9f0a3035cebb48c38bf5b8275efaefe6.png

In $$\triangle{ABD} \; \& \; \triangle{CBD}$$, all the three parts stated below are equal.
$$AD = CD \; \left( \text{Given} \right)$$
$$AB = CB \; \left( \text{Given} \right)$$
$$BD = BD \; \left( \text{Common side} \right)$$


In a conversation, Anand said his savings of the month is same as that of Raju, Pankaj replied he also saves as much his monthly savings of Anand and Pankaj ? Write the Euclid's axiom for this situation. 

Let the savings of Anand of a month be $$x$$.
Since Raju's savings is same as Anand's saving.
Then, Raju's savings $$= x$$
Anand's savings = Raju's savings........$$\left(i\right)$$
Pankaj's savings$$=$$ Raju's savings.........$$\left(ii\right)$$
From eq$$\left(i\right)$$ and $$\left(ii\right)$$
Anand's savings$$=$$ Pankaj's savings.This is the relation between them.
Since, things which are equal to the same thing are equal to one another. This is the euclid axiom which has been used.


Solve each of the following question using appropriate Euclid' s axiom: 
It is known that $$x + y = 10$$ and that $$x= z$$. Show that $$z + y = 10$$? 

It is known that $$x + y = 10$$ and that $$x = z$$.
$$\therefore \ \  x + y = z + y$$ [$$\therefore$$ By Euclid's axiom 2, if equals are added to equals, the wholes are equal] 
$$\Rightarrow 10= y + z$$ [Using (1), $$x + y = 10$$) 
Hence. $$z + y = 10$$.


Study the following statement: 
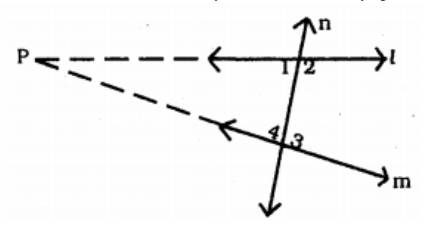
"Two intersecting lines cannot be perpendicular to the same line". Check whether it is an equivalent version to the Euclid's fifth postulate. [Hint: Identify the two intersecting lines 1 and m and the line n in the above statement.] 

Two intersecting lines cannot be both perpendicular to the same line because if two lines l and m are perpendicular to the same line n. then 1 and m must be parallel. 
The given statement is not an equivalent version of Euclid's fifth postulate. 


Solve each of the following question using appropriate Euclid' s axiom: 
Two salesmen make equal sales during the month of August. In September, each salesman doubles his sale of the month of August. Compare their sales in September. 

Let the sales of two salesmen in the month of August be x and y. As, they make equal sale during the month of August, x = y. In September, each salesman double his sale of the month of August, So 2x = 2y. 
Now, by Euclid's axiom, thing which are double of the same things are equal to one another. 
Hence, we can say that in the month of September also, two salesmen make equal sales.


Read the following axioms:
(i) Things which are equal to the same thing are equal to one another.
(ii) If equals are added to equals, the wholes are equal.
(iii) Things which are double of the same thing are equal to one another.
Check whether the given system of axioms Is consistent or inconsistent.  

The given system of axioms is consistent because (i), (ii) and (iii) are Euclid's axiom.


Read the following statement: 
An equilateral triangle is a polygon made up of three line segments out of which two line segments are equal to the third one and all its angles are $$60^0$$ each. 
Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all sides and all angles are equal in a equilateral triangle? 

The term need to be defined are: 
Polygon: A simple closed figure made up of three or more line segments. 
Line segment: Part of a line with two end points. 
Line: Undefined term. 
Point: Undefined term. 
Angle: A figure formed by two rays with a common initial point. 
Acute angle: Angle whose measure is between $$0^0$$ and $$90^0$$. 
Undefined terms used are: Line, Point Justification: 
Two line segments are equal to third line segment 
Therefore, all three sides of an equilateral triangle are equal All its angle are $$60^0$$ each. Therefore, all angles are equal (by Euclid's first axiom, things which are equal to same things are equal to one another.) 
Hence, we can say that all sides and all angles are equal in an equilateral triangle. 


How would you rewrite Euclid's fifth postulate so that it would be easier to understand?

$$\textbf{Step -1: Defining }$$
                $${\text{For every line L and for every point P not lying on L there exist a unique }}$$ 
                $${\text{line m passing through P and}}$$
                $${\text{parallel to l}}$$
$${\textbf{Step -2: Easier way}}$$
                $${\text{In an easier way we can say that there exists a line which passes through point P and that is}}$$
                $${\text{parallel to line L}}$$
                $${\text{Or, two straight lines intersect each other if a straight line passing through them has}}$$
                $${\text{interior angles less than right angles}}$$
$$\textbf{Hence , this is required answer .}$$


In the figure, if $$AC=BD$$, then prove that $$AB=CD$$.
463630.jpg

Given, 
$$AC = BD$$    ... (i)
$$AC = AB + BC$$    ……(ii) (Point $$B$$ lies between $$A$$ and $$C$$)
$$ BD = BC + CD$$    … (iii)   (Point $$C$$ lies between $$B$$ and $$D$$)
Now, 
substituting (ii) and (iii) in (i), we get
$$\Rightarrow AB + BC = BC + CD$$
$$\Rightarrow AB + BC – BC = CD$$
$$\Rightarrow AB = CD$$

Hence, $$AB = CD$$.


If a point $$C$$ lies between two points $$A$$ and $$B$$ such that $$AC=BC$$, then prove that $$AC=\dfrac{1}{2}AB$$. Explain by drawing the figure.

As given $$AC=BC$$......eq $$(1)$$

From equation $$(1)$$

$$AC=BC$$

Adding $$AC$$ on both sides,

$$AC+AC=BC+AC$$

$$2AC=AB$$  $$(\because BC+AC=AB)$$

$$\therefore AC=\dfrac{1}{2}AB$$

490210_463628_ans.png


Point $$C$$ is the mid-point of line segment $$AB$$, prove that every line segment has one and only one mid-point.

$$AC = BC$$     ... $$(i)$$

If possible, let $$D$$ be another mid-point of $$AB$$.

$$AD = DB$$    ... $$(ii)$$

Subtracting $$(ii)$$ from $$(i)$$

$$AC –AD = BC – DB$$

$$ DC = -DC$$    $$(\because AC-AD = DC and CB-DB = -DC)$$

$$ DC + DC = 0$$

$$ 2DC = 0$$

$$DC = 0$$

So, $$C$$ and $$D$$ coincide.

Thus, every line segment has one and only one mid-point.

490212_463629_ans.png


Consider two 'postulates' given below:
(i) Given any two distinct points $$A$$ and $$B$$, there exists a third point $$C$$ which is in between $$A$$ and $$B$$.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are there postulates consistent? Do they follow from Euclid's postulates? Explain.

There are several undefined terms which we should keep in mind. They are consistent, because they deal with two different situations:

(i) says that the given two points $$A$$ and $$B$$, there is a point C lying on the line in between them;

(ii) says that given $$A$$ and $$B$$, we ca take $$C$$ not lying on the line through $$A$$ and $$B$$.

These ‘postulates’ do not follow from Euclid’s postulates. However, they follow from axiom stated as given two distinct points; there is a unique line that passes through them.



How would you rewrite Euclid's fifth postulate so that it would be easier to understand?

$$\textbf{Step 1 : Defining}$$
                 $$\text{Euclid's fifth postulate: Given a line L and a point P not on the line , exactly one line can be drawn }$$ 
                 $$\text{through P which is parallel to L.}$$
                 
$$\textbf{Step 2: Re-writing}$$
                $$\text{For every line 'L' and for every point 'P' not lying on 'L' . there exist a unique line 'm' passing through }$$
                $$\text{'P' and parallel to 'l'. This is called 'Playfairs Axiom'} $$
                $$\text{1. 'L' is a ln=ine and 'P' is a point not lying on 'L'}$$
                $$\text{2. We can draw infinite lines through 'P' but there is only one line unique which is parallel to 'L' and }$$ 
                     $$\text{passes through 'P'}$$
                $$\text{3. Take any point on 'L' and draw a line to 'm'. Measure the distances.}$$
                $$\text{4. We know that it is the same everywhere, so these lines 'L' and 'm' do not meet anywhere.}$$
                $$\text{5. Hence, two lines 'L' and 'm' are parallel}$$
$$\textbf{Hence , Euclid's 5th postulate can be re-written as above }$$


Does Euclid's fifth postulate imply the existence of parallel lines? Explain.

The sum of the interior angles will be equal to sum of the two right angles then two lines will not meet each other on either sides and therefore they will be parallel to each other.


Why is Axiom $$5$$, in the list of Euclid's axioms, considered as a 'universal truth'? (Note that the question is not about the fifth postulate.)

Axiom $$5$$ states that the whole is greater than the part. 
This axiom is known as a universal truth because it holds true in any field, and not just in the field of mathematics. 
Let us take two cases: one in the field of mathematics and one other than that.
Case I
Let t represent a whole quantity and only $$a, b, c$$ are parts of it.
$$t = a + b + c$$
Clearly, $$t$$ will be greater than all of its parts $$a, b$$ and $$c$$.
Therefore, it is rightly said that the whole is greater than the part.

Case II
Let us consider continent Asia. Then, let us consider a country India which belongs to Asia. India is a part of Asia and it can also be observed that Asia is greater than India. That is why we can say that the whole is greater than the part. This is true for anything in any part of the world and is thus a universal truth.


Using Euclid's division algorithm, find whether the pair of numbers $$231,396$$ are coprime or not.

$$\Rightarrow 396 = 1 × 231 + 165$$


$$\Rightarrow 231 = 1 × 165 + 66$$


 $$\Rightarrow 165 = 2 × 66 + 33$$


 $$\Rightarrow 66 = 2 × 33 + 0$$


 ∴ The $$HCF$$ of $$231, 396$$ is $$33$$ not $$1$$, so they are not co-prime.



List five Euclid's postulates.

Axiom $$1:$$ Given two distinct points, there is a unique line that passes through them. 
Axiom $$2 :$$ A terminated line can be produced indefinitely.
Axiom $$3:$$ A circle can be drawn with any center and any radius. 
Axiom $$4:$$ All right angles are equal to one another. 
Axiom $$5:$$ If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.


State Euclid division Lemma.

$$\textbf{Step -1: Stating Euclid's Division Lemma}.$$

                 $$\text{According to Euclid’s Division Lemma if we have two positive integers a and b,}$$ 

                 $$\text{then there exist unique integers q and r which satisfies the condition a = bq + r, where 0 ≤ r < b.}$$

                 $$\text{Mathematically, we can express this as }$$

                 $$\text{Dividend}=(\text{Divisor}\times\text{Quotient})+\text{Remainder}$$

$$\textbf{Hence, Euclid's division lemma is stated.}$$


Give an example for the following axiom from your experience:
  •  When equals are added to equals then the resultant are equal

It is logically true, as addition of equals will become equals. 
For example: $$2+3=4+1$$ and $$1+5=4+2$$
The addition of these two equalities will give
$$2+3+1+5=4+1+4+2\Rightarrow 11=11$$



What is the difference between an axiom and a postulate?

Axioms are generally true for any field in science, while a postulate can be specific on a particular field.
It is impossible to prove from other axioms, while postulates are provable to axioms. 


Formulate the Euclid's $${5^{th}}$$ postulate in a simpler manner.

Postulate 5 : If a straight line falling on two straight lines makes that interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.

Here two right angles means $$180^{\circ}$$.

Ref. image I

It says if $$\angle 1 +\angle 2 = 180^{\circ}$$.

There lines AB & CD meets on left side of line PQ. 

If $$ \angle 1 +\angle 2 = 180^{\circ}$$

Then lines AB & CD do not intersect and intersecting lines PQ is perpendicular to AB & CD.          Ref. image II

We rewrite postulate 5 as

"straight lines intersecting

(i) There is a line through P which is parallel to (i) and (ii) there is only on such line.

(ii) Two distinct intersecting lines cannot be parallel to the same line.

1463365_1455948_ans_ae6badce674a4096950d6c222c9b993a.jpg


Euclid's division lemma states that for two positive integers a and b, there exists unique integers q and rr such that $$a=bq+r$$, where r must satisfy $$0\le r\le b$$ is this statement true?

required conditions
$$0\le r<b$$
$$a$$ is the quotient, $$b$$ is the divisor $$a$$ is divided and $$r$$ is remainder 
Remainder cannot be more than divisor


Write any two axioms given by Euclid.

First Axiom: Things which are equal to the same thing are also equal to one another.

Second Axiom: If equals are added to equals, the whole is equal.


Consider two 'postulates' given below :
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid's postulates? Explian. 

There are many undefined terms for students. They are consistent, because they deal with two different situations. 
(i) When two points A and B ar given, C is in between two. 
(ii) When two points A and B are given take point C which passes through A and B. 
These postulates do not follow from Euclid's postulates. But they follow Axiom 2.1 


Fill in the blanks with similar/not similar :
Reduced and Enlarged photographs of an object are ...............................

Reduced and Enlarged photographs of an object are similar.


Solve the Equation $$U-5=15$$ and state the axiom that you use here.

u - 5 = 15

=> u = 15 + 5

=> u = 20

The Axiom used above is Transposition according to which when a number is shifted to the other side sign changes.


Answer the following :
1) how many dimensions does a solid have ?
2)how many books are there in euclid's elements?
3)write the number of faces of a cube and a cuboid?
4) what is the sum of the interior angles of a triangle ?
5)write three undefined terms of geometry .

1)A solid shape have three dimensions namely length, breadth and height.
2)13 books
3)There are 6 faces in cube and cuboid
4)Sum of interior  angle of triangle is 180 degree
5)These words are point, line and plane, and are referred to as the "three undefined terms of geometry".


Class 9 Maths Extra Questions