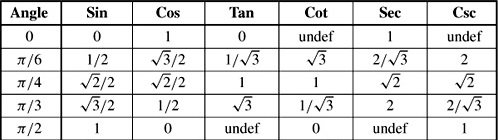
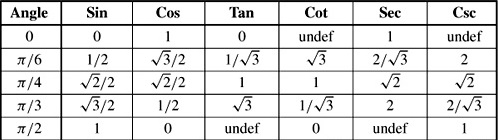
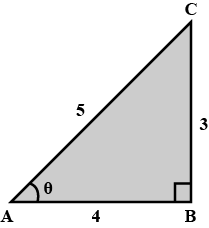
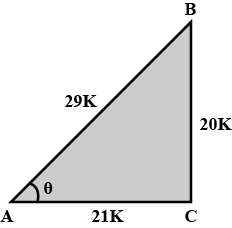
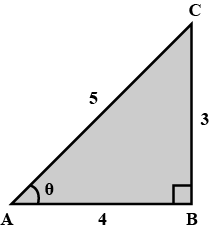
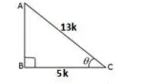
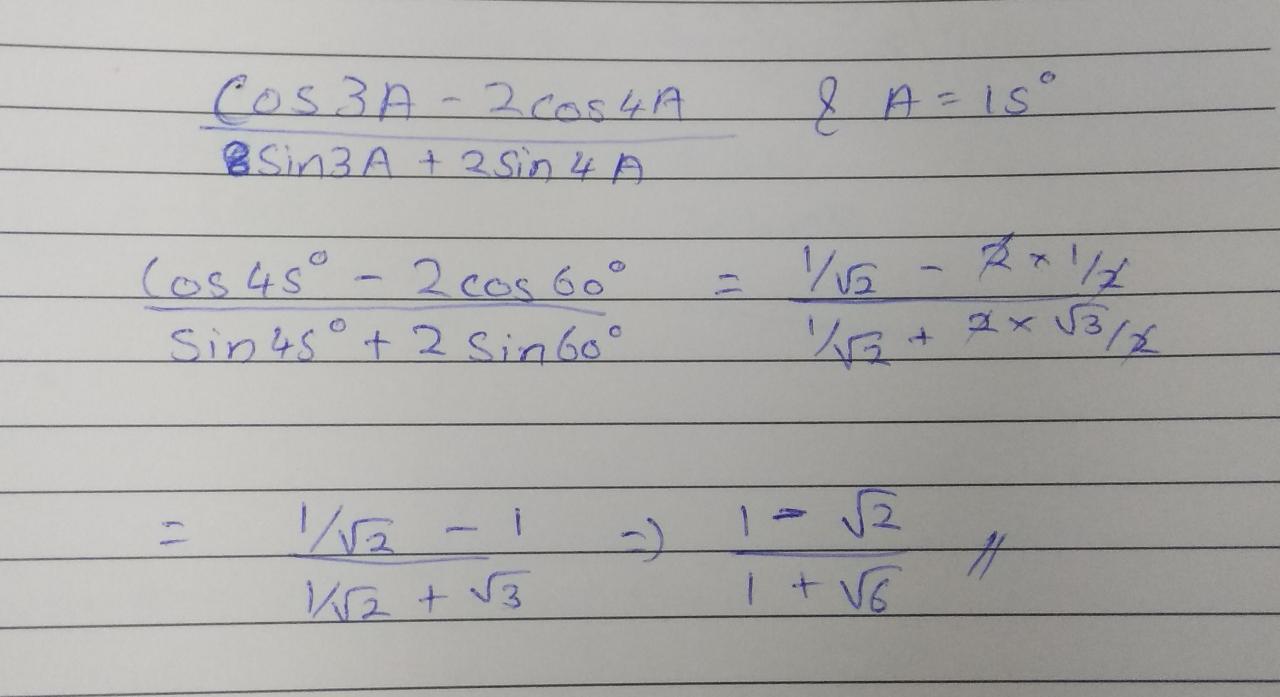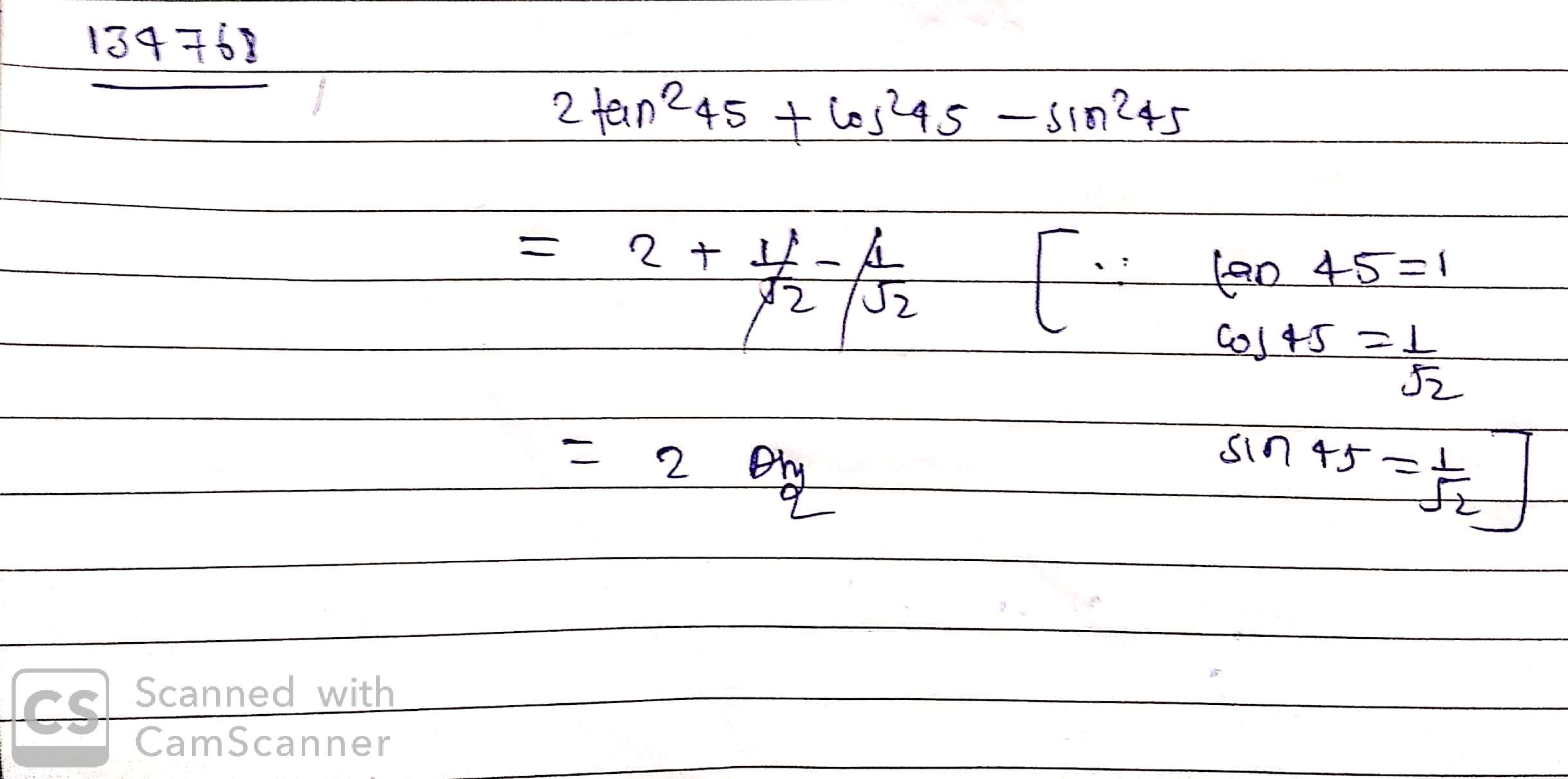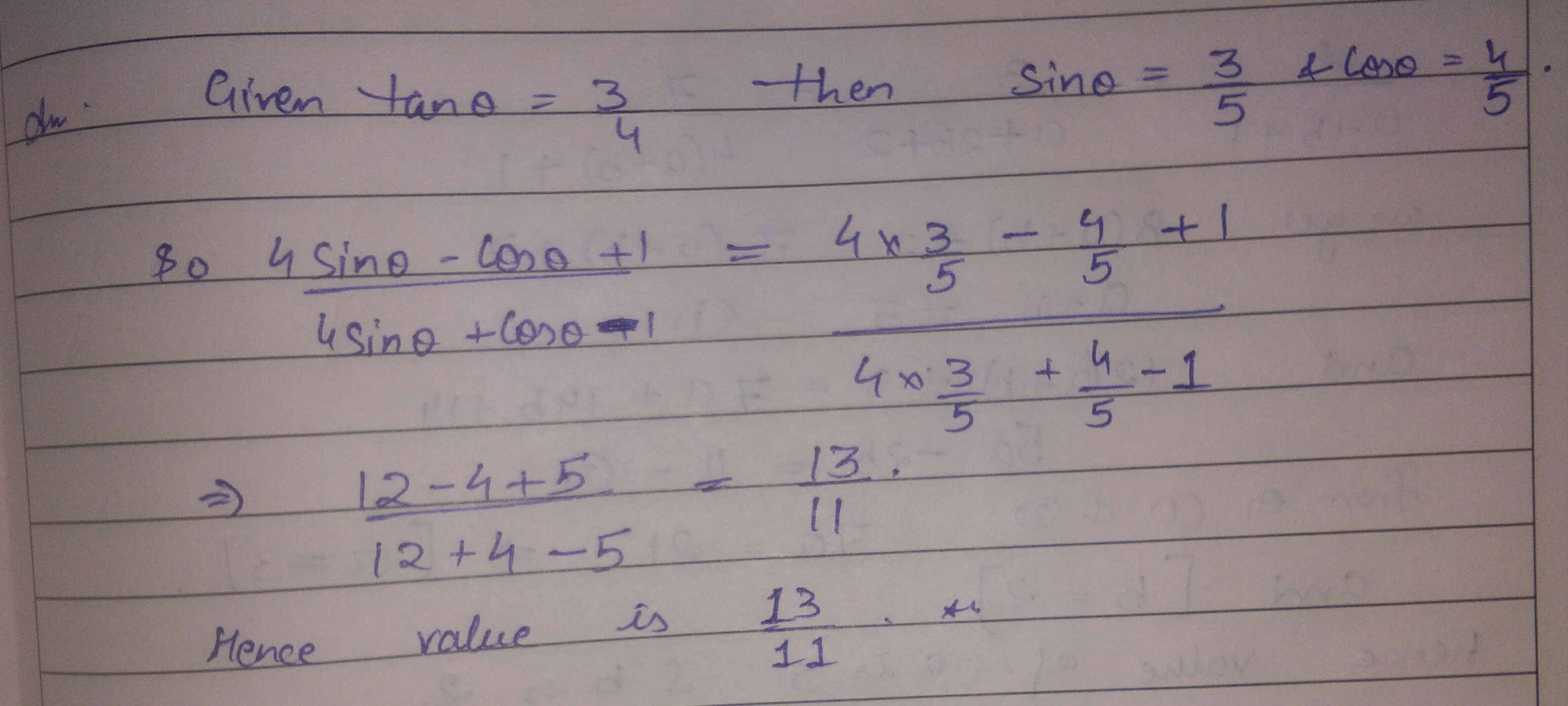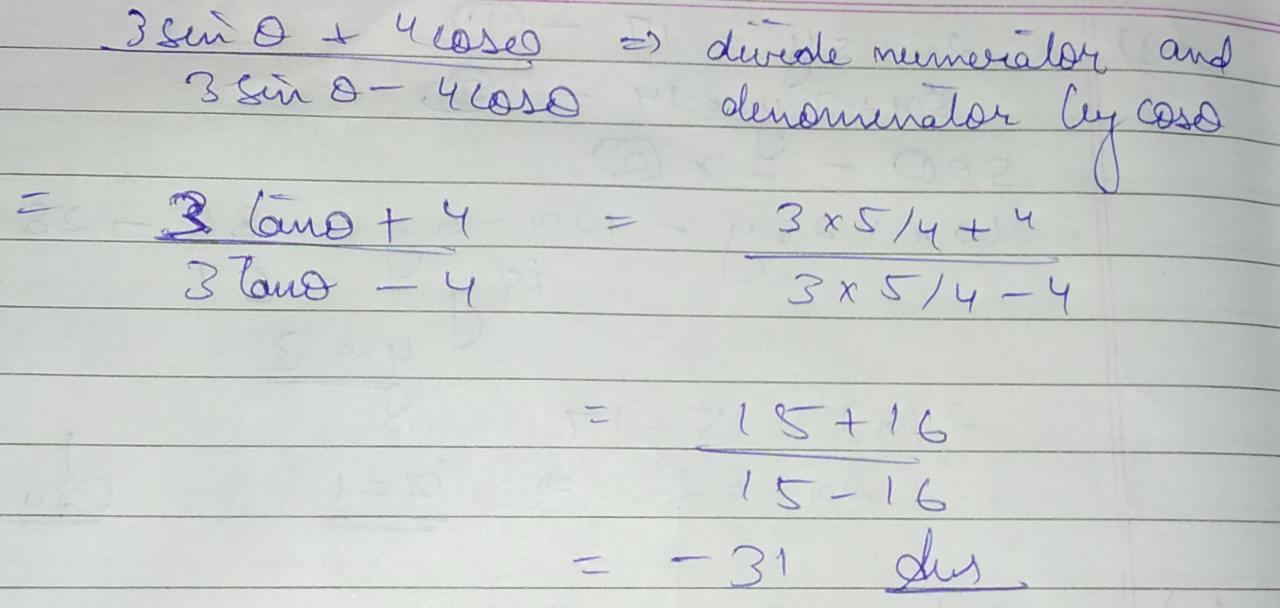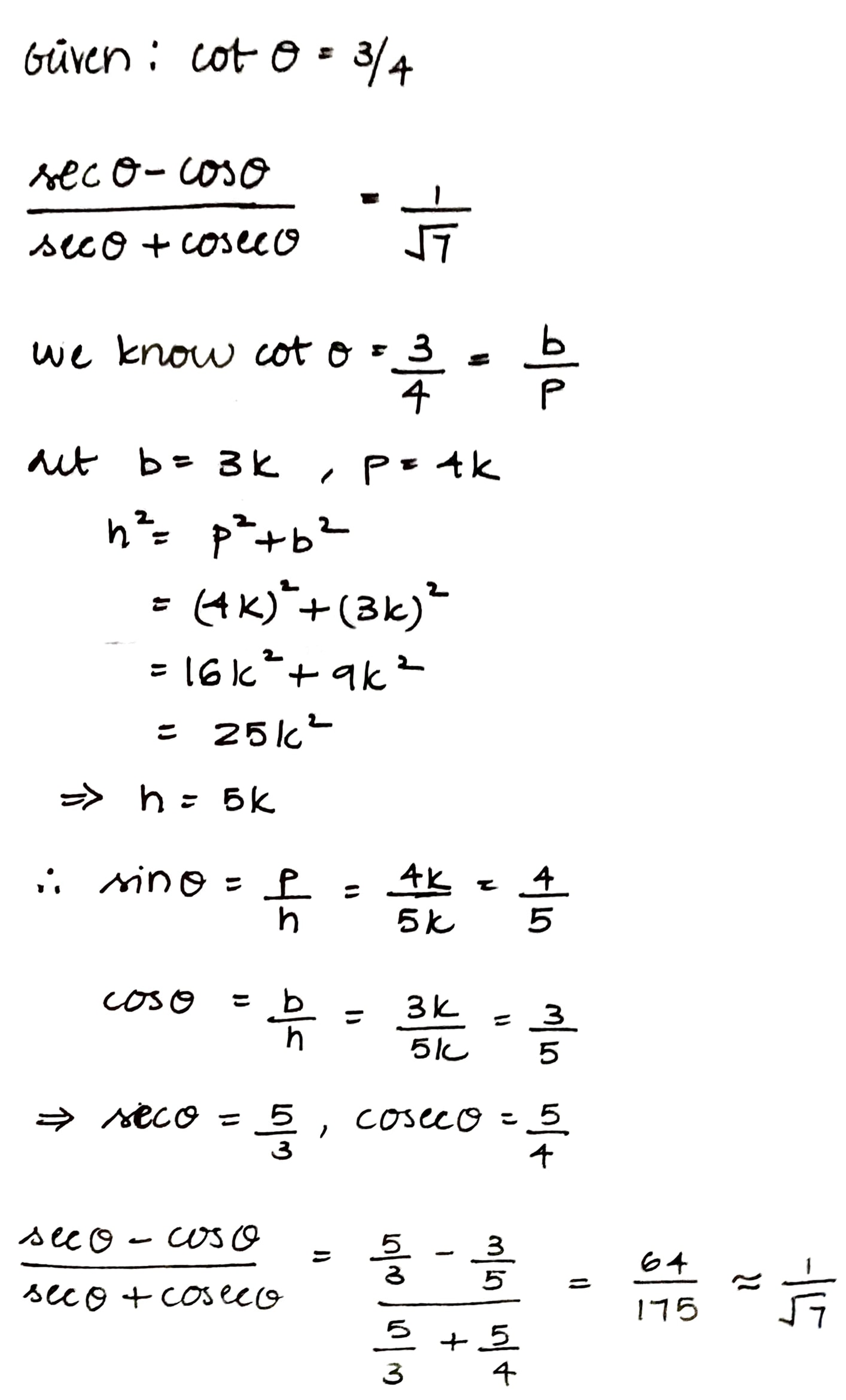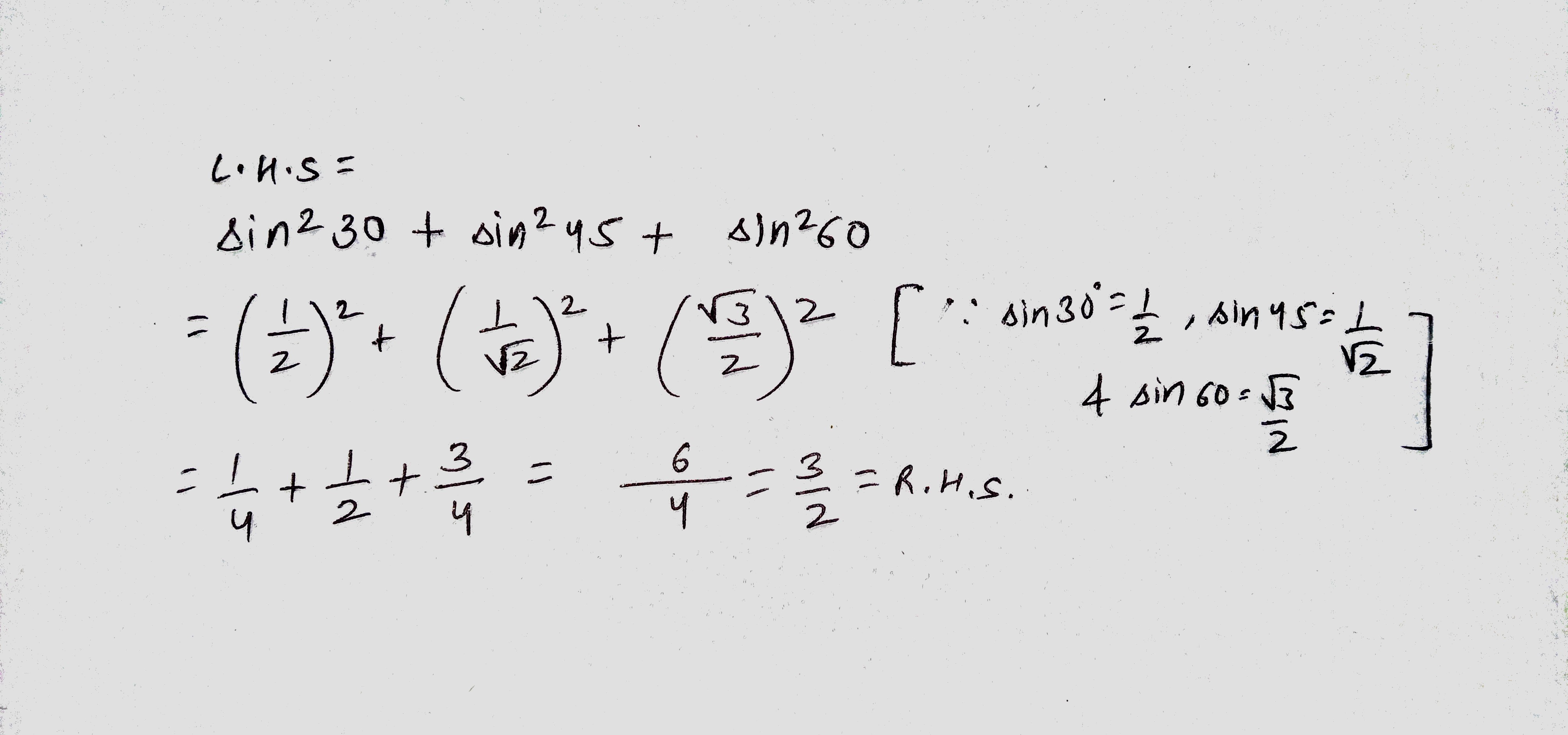Introduction To Trigonometry - Class 10 Maths - Extra Questions
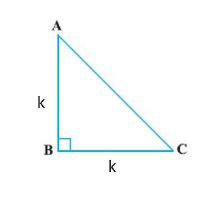
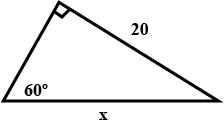
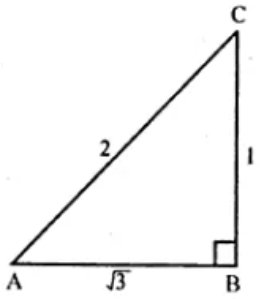
Find value of 10x
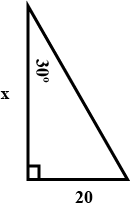
Value of 100x is 3464,
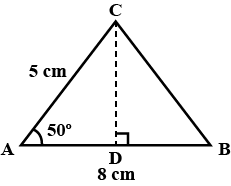
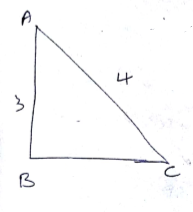
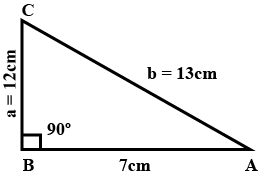
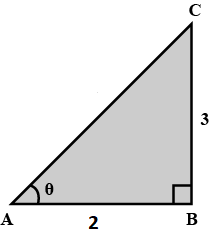
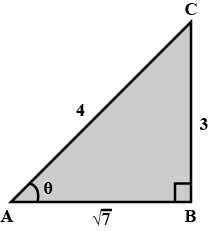
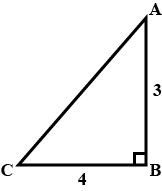
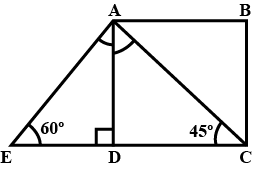
From the given figure, find the value of m if, tan C is $$\displaystyle \frac{m}{4}$$.
$$\displaystyle\,\frac{1\,-\,cos\,2\,A}{sin\,2\,A}\,=\,tan\,2A$$
If above statement is true then mention answer as 1, else mention 0 if false
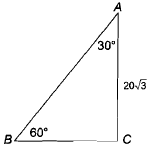
Find side $$c$$ of the triangle $$ABC$$, given that $$\displaystyle A=30^{0},B=60^{0}$$ and $$\displaystyle b=20\sqrt{3}$$
If $$2\cos { \theta } =1$$ and $$\theta$$ is acute angle, then what is $$ \theta $$ equal to?
Find the value of the following:
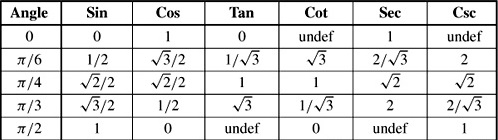
$$\tan ^{ 2 }{ { 60 }^{ o } } +2\tan ^{ 2 }{ { 45 }^{ o } } $$
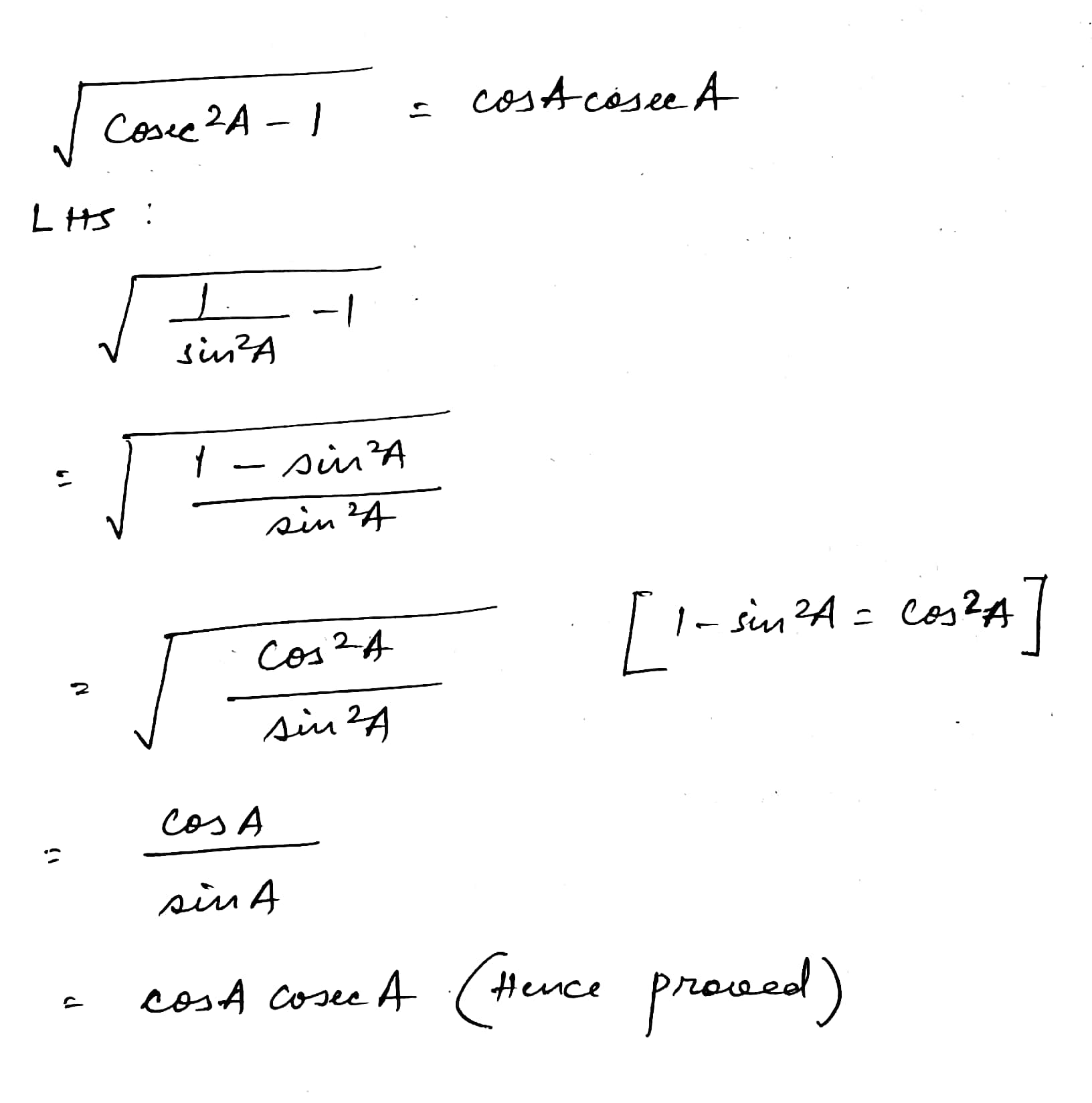
Prove that $$\cos { \theta } \cdot cosec \ { \theta } =\cot { \theta } $$
Find the value of $$\sin ^{ 2 }{ { 45 }^{ o } } +\cos ^{ 2 }{ { 45 }^{ o } } $$.
Find the value of $${ \left( \sin { \theta } +\cos { \theta } \right) }^{ 2 }+{ \left( \sin { \theta } -\cos { \theta } \right) }^{ 2 }$$
If $$\cos{\theta}=1$$, then find the value of acute angle $$\theta$$.
$$\sin{\left({60}^{\circ}+{30}^{\circ}\right)}=$$ _______.
$$(1 + \tan A \cdot \tan B)^{2} + (\tan A - \tan B)^{2} = \sec^{2}A \cdot \sec^{2}B$$.
Find the value of $$\sin^{2}30^{\circ} + \cos^{2} 60^{\circ}$$
Prove that $$\sin^2A + \dfrac{1}{1 + \tan^2A} = 1$$.
Prove that $$(1 + \cot^2A) \sin^2A = 1$$.
Prove the following :
(iv) $$\dfrac{\cos(90^{\circ} \, - \, A) \sin (90^{\circ} \, - \, A)}{\tan(90^{\circ} \, - \, A)} = \, \sin^2 \, A$$
Prove that $$cosec \theta \sqrt{1 - \cos^2 \theta} = 1$$.
Evaluate the following :
$$\dfrac{cos 37^{\circ}}{sin 53^{\circ}}$$
Evaluate the following :
$$\dfrac{\tan 10}{\cot 80}$$
Evaluate the following :
$$\dfrac{\sec 11}{\text{cosec} 79}$$
$$\dfrac{\sec 11}{\text{cosec} 79}$$
Prove that $$(\sec \theta + \cos \theta) (\sec \theta - \cos \theta) = \tan^2 \theta + \sin^2\theta$$.
Prove that $$(\sec^2\theta - 1) (co\sec^2\theta - 1) = 1$$
Evaluate the following :
$$\dfrac{tan 54^{\circ}}{cot 36^{\circ}}$$
Evaluate the following:
$$\dfrac{2 \tan 53^{\circ}}{\cot 37^{\circ}} \, - \, \dfrac{\cot 80^{\circ}}{\tan 10^{\circ}}$$
$$\dfrac{2 \tan 53^{\circ}}{\cot 37^{\circ}} \, - \, \dfrac{\cot 80^{\circ}}{\tan 10^{\circ}}$$
Verify that $$\cot ^{ 2 }{ {60}^{o} } +\sin ^{ 2 }{ {45}^{o} } +\sin ^{ 2 }{ {30}^{o} } +\cos ^{ 2 }{ {90}^{o} } =\dfrac { 13 }{ 12 }$$
If $$\tan { \theta } =\dfrac { 20 }{ 21 }$$, then prove that $$\dfrac { 1-\sin { \theta } +\cos { \theta } }{ 1+\sin { \theta } +\cos { \theta } } =\dfrac { 3 }{ 7 }$$
Express each of the following in trigonometric ratios of angles between $$0^{\circ} \, and \, 45^{\circ}$$ :
$$sin 85^{\circ} \, + \, cosec 85^{\circ}$$
$${ \left( \tan { x } +\cot { x } \right) }^{ 2 }=\sec ^{ 2 }{ x+\csc ^{ 2 }{ x } }$$
Prove that:$$\dfrac{1+\sec A}{\sec A}=\dfrac{\sin^2 A}{1-\cos\,A}$$
Calculate : $${ \left( \cos { 40 } \right) }^{ 2 }+{ \left( \sin { 40 } \right) }^{ 2 }$$
Prove that $$\dfrac{{\cot A - \cos A}}{{\cot A + \cos A}} = \dfrac{{\cos ecA - 1}}{{\cos ecA + 1}}$$
Prove that: $$\dfrac{1}{\sec A-1}+\dfrac{1}{\sec A+1}=2 \csc A \cot A$$
Prove that $$\dfrac {1+\cos \theta}{\sin^{2}\theta}=\dfrac {1}{1-\cos \theta}$$
Evaluate
$$\dfrac{tan 45^o}{cosec 30^o} + \dfrac{sec 60^o}{cot 45^o} - \dfrac{5 sin 90^o}{2 cos 0^o}$$
Evaluate : $$\sin^{2}90.\cos^{2} 45+4 \tan^{2}30+\dfrac {1}{2}\sin^{2}a-2 \cos^{2}90+\dfrac {1}{24}$$
Simplify:
$$\dfrac {\sin \theta.\csc (90-\theta).\tan \theta}{\csc (90-\theta).\cos \theta.\cot (90-\theta)}$$
For any angle of measure $$\theta$$ prove that $$1+\tan^2\theta =\sec^2\theta$$.
Find the value of $$\dfrac{\cos 30^o \tan 60^o + \sin 60^o \cos 60^o}{cosec \,30^o \sec 60^o - cosec \,60^o \cot 30^o}$$
Prove that: $$\sqrt {\sec^{2}A+\csc^{2}A}=\tan A+\cot A$$
If $$A = 15^o$$, verify that $$4 \sin 2 A . \cos 4 A . \sin 6 A = 1$$
Evaluate
$$\sin^{2}\theta(\tan^{2}\theta+1)=\sec^{2}\theta-1$$
Evaluate
$$\tan\theta.\sin\theta+\cos\theta=\sec\theta$$
Simplify: $$\dfrac{{{\text{sec}}{{\text { x}}^{\text{}}}{\text{ + tan}}{{\text{ x}}^{\text{}}}}}{{{\text{sec}}{{\text{ x}}^{\text{}}}{\text{ - tan}}{{\text { x}}^{\text{}}}}}$$
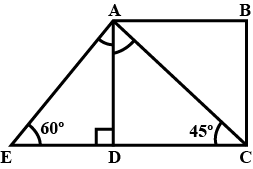
In the figure, find the value of $$BC$$
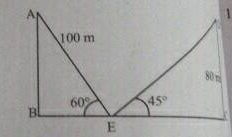
Solve $$\dfrac{{\cos {{45}^ \circ }}}{{\sec {{30}^ \circ } + {\mathop{\rm cosec}\nolimits} {{30}^ \circ }}}$$
Find value of:
$$3\cos ^{ 2 }{ { 30 }^{ o } } +\sec ^{ 2 }{ { 30 }^{ o } } +2\cos ^{ 2 }{ { 0 }^{ o } } +3\sin ^{ 2 }{ { 90 }^{ o } } -\tan ^{ 2 }{ { 60 }^{ o } } $$
Evaluate: $$\dfrac{\cos\ 3A-2\cos(4A)}{\sin\ 3A+2\sin(4A)}$$; when $$A=15^{o}$$
Solve:-
$$\dfrac{{2\tan {{45}^ \circ }}}{{1 + {{\tan }^2}{{45}^ \circ }}}$$
Prove that $$\cos \theta \sin(90^o-\theta)+\sin \theta \cos(90^o-\theta)=1$$
Without using trigonometric tables, evaluate the following: $$\left ( \sin 35^{0}\cos 55^{0}+\cos 35^{0}\sin 55^{0} \right )/\left ( cosec^{2}10^{0}-\tan ^{2}80^{0} \right )$$.
Prove that following identities, where the angles involved are acute angles for which the trigonometric ratios as defined: $$\left ( 1+\tan ^{2}A \right )\left ( 1-\sin A \right )\left ( 1+\sin A \right )=1$$.
Verify that
$$\tan^{2} 30^{\circ} + \tan^{2} 45^{\circ} + \tan^{2} 60^{\circ} = 4\dfrac {1}{3}$$.
A $$15 m$$ long ladder touches the top of vertical wall. If this ladder makes an angle of $$60^{0}$$ with the wall, then height of the wall is :
REF.Image
$$sin60^{\circ}=\frac{AB}{AC}=\frac{AB}{15}$$
$$AB=15 sin 60^{\circ}=\frac{15\sqrt{3}}{2}m$$
Prove that following identities, where the angles involved are acute angles for which the trigonometric ratios as defined: $$1/\left ( 1+\cos A \right )+1/\left ( 1-\cos A \right )=2cosec^{2}A$$.
Verify that
$$\cos 45^{\circ} \cos 60^{\circ} - \sin 45^{\circ} \sin 60^{\circ} = -\dfrac {\sqrt {3} - 1}{2\sqrt {2}}$$.
Verify that
$$cosec^{2} 45^{\circ} \cdot \sec^{2} 30^{\circ} \cdot \sin^{3} 90^{\circ} \cdot \cos 60^{\circ} = 1\dfrac {1}{3}$$.
Find the value of $$\cfrac{\tan 47^{0}}{\cot 43^{0}}$$
Simplify: $$(1 + \tan^{2} \theta) (1 - \sin \theta) (1 + \sin \theta)$$.
State true or false:$$\sin^2A+ \cos^2A= 1$$
If $$\sin A, \cos A$$ and $$\tan A$$ are in geometric progression, then $$\cot^6A-\cot^2A=........$$
$$\tan 30^{\circ} \: \cot 30^{\circ}=$$
$$\text{cosec}\, ^{2} 60^{0}-\tan ^{2} 30^{0}=$$
If the angle $$\theta = 60^{\circ}$$ and $$\displaystyle cos \theta = \frac{1}{2}$$, find the value of sec $$\theta$$.
Find the value of : $$\displaystyle \dfrac{2 \tan 53^o}{\cot 37^o} - \dfrac{\cot 80^o}{\tan 10^o}$$
If $$\displaystyle \sin \theta = \cfrac{\sqrt{2}}{3}, \cos \theta = \cfrac{1}{3}$$, then $$\displaystyle \tan \theta = \sqrt{m}.$$ The value of $$m$$ is
If $$\displaystyle tan \theta = \frac{2}{5}$$, then $$\displaystyle cot \theta = \frac{p}{2}$$, $$p$$ is
If $$\tan 2A = \cot (A - 18^o)$$ then find the value of A where (2A) and $$(A - 18^o)$$ are acute angles
The value of $$\displaystyle \left ( \dfrac{\tan 60^{0}+1}{\tan 60^{0}-1} \right )^{2}= \dfrac{1+\cos 30^{0}}{1-\cos 30^{0}}$$
if true then enter $$1$$ and if false then write $$0$$
if true then enter $$1$$ and if false then write $$0$$
The value of $$\displaystyle \tan \left ( 2 \times 30^{0}\right )= \frac{2 \tan 30^{0}}{1-\tan ^{2} 30^{0}}$$
if true then enter $$1$$ and if false then write $$0$$
if true then enter $$1$$ and if false then write $$0$$
The value of $$\cos ^{2} 30^{0}-\sin ^{2} 30^{0}= \cos 60^o$$
If above statement is true then enter $$1$$ and if false then write $$0$$.
$$\sin ^{2} 30^{0}+\cos ^{2} 30^{0}$$
The value of $$\cos 30^{\circ} \cos 60^{\circ}-\sin 30^{\circ} \sin 60^{\circ} $$ is equal to
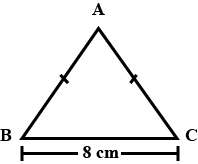
$$ABC$$ is an isosceles right-angled triangle. Assuming $$AB= BC= x$$, find the value of each of the following trigonometric ratios:$$\sin 45^{0}$$ is $$\displaystyle \frac{1}{\sqrt{2}}$$
If true then enter $$1$$ and if false then enter $$0$$
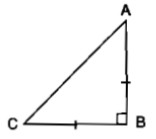
If true then enter $$1$$ and if false then enter $$0$$
Find the value of $$\text{cosec}^{2} 45^{o}-\cot^{2} 45^{o}$$.
The value of $$\displaystyle \cos \left ( 2 \times 30^{0}\right )= \frac{1-\tan ^{2} 30^{0}}{1+\tan ^{2} 30^{0}}$$
If true then enter $$1$$ and if false then write $$0$$
If true then enter $$1$$ and if false then write $$0$$
The value of $$\displaystyle \sin \left ( 2 \times 30^{0}\right )= \frac{2\tan 30^{0}}{1+\tan ^{2} 30^{0}}$$
if true then enter $$1$$ and if false then write $$0$$
if true then enter $$1$$ and if false then write $$0$$
If $$A= 30^{0}$$, then the value of$$\sin \left ( 60^{0}+A \right )-\sin \left ( 60^{0}-A \right )= \sin A$$If true then enter $$1$$ and if false then write $$0$$
If $$\tan \theta= \cot \theta $$ and $$0^{0}\leq \theta \leq 90^{0}$$, state the value of $$\theta$$ in degrees
The value of $$\sin 60^{0}=2 \sin 30^{0} \cos 30^{0}$$
if true then enter $$1$$ and if false then write $$0$$
if true then enter $$1$$ and if false then write $$0$$
If $$\sqrt{3}= 1.732$$, (correct to two decimal places) the value of $$\sin 60^{0}$$ is $$0.87.$$If true then enter $$1$$ and if false then enter $$0$$.
If $$\sqrt{3}= 1.732$$, (correct to two decimal places) the value of $$\sin 60^{0}$$ is $$0.87.$$
If true then enter $$1$$ and if false then enter $$0$$.
If $$x= 15^{0}$$, evaluate:
$$\displaystyle 12 \sin 3x \cos 3x+5 \tan ( 2x+ 15^{0})-3 \cot ^{2}3x$$
If $$\sin x= \cos x$$ and $$x$$ is acute, state the value of $$x$$ in degrees.
If $$A= 60^{0}$$ and $$B= 30^{0}$$, find the value of $$\left ( \sin A \cos B+ \cos A\sin B \right )^{2}+\left ( \cos A \cos B-\sin A \sin B \right )^{2}$$
If $$x= 15^{0}$$, evaluate:
$$4 \cos 2x \sin 4x\tan 3x-1$$
If $$\sqrt{3}= 1.732$$, find (correct to two decimal places) the value of the following:
$$\displaystyle \dfrac{2}{\tan 30^{0}}$$ is $$3.46$$
If true then enter $$1$$ and if false then enter $$0$$
$$\displaystyle \dfrac{2}{\tan 30^{0}}$$ is $$3.46$$
If true then enter $$1$$ and if false then enter $$0$$
If $$A= 30^{0}$$, then$$\displaystyle \cos 2A= \cos ^{2} A-\sin ^{2} A= \dfrac{1-\tan ^{2}A}{1+\tan ^{2}A}$$If true enter 1 else 0
Given $$A= 60^{0}$$ and $$B= 30^{0}$$, then
$$\displaystyle \tan \left ( A-B \right )= \dfrac{\tan A-\tan B}{1+\tan A \tan B}$$If true enter 1 else 0
If $$A= 30^{0}$$, then $$2\cos ^{2} A-1= 1-2\sin ^{2}A$$If true enter 1 else 0
If $$A=B= 45^{0}$$, then $$\sin \left ( A-B \right )=\sin A \cos B-\cos A \sin B$$If true enter 1 else 0
Solve: $$\sec 4A$$ $$= \csc (A-20^{\circ}$$)
$$\displaystyle \cos ^2\ 10^{\circ}-\sin^2 80+\tan ^2 45^{\circ}$$
State true or false
Given $$A= 60^{0}$$ and $$B= 30^{0}$$, then$$\sin \left ( A+B \right )= \sin A\cos B+\cos A\sin B$$
If true enter 1 else 0
Given $$A= 60^{0}$$ and $$B= 30^{0}$$, then
$$\sin \left ( A+B \right )= \sin A\cos B+\cos A\sin B$$
Find the value of: $$\displaystyle \sqrt{\frac{1-\sin ^{2}60^{0}}{1-\cos ^{2}60^{0}}}$$ is $$\displaystyle \frac{1}{\sqrt{m}}$$, m is
Given $$A= 60^{0}$$ and $$B= 30^{0}$$, then
$$\cos \left ( A-B \right )= \cos A\cos B+\sin A\sin B$$If true or false:
If $$A= 60^{0}$$ and $$B= 30^{0}$$; $$\displaystyle \frac{\sin \left ( A-B \right )}{\sin A \sin B}= \cot B-\cot A$$
If true enter 1 else 0
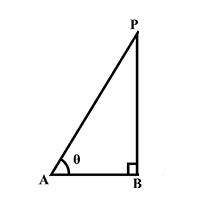
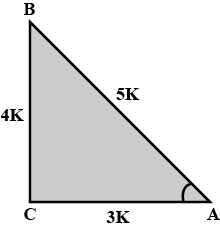
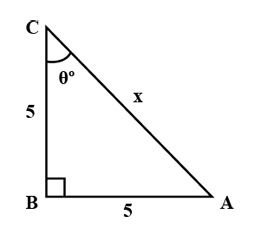
Refer to the triangle given in figure.$$\sec C$$ is $$\displaystyle \frac{3\sqrt{2}}{m}$$, m is
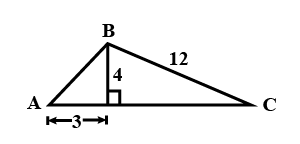
Consider the following figure:
$$\sin B$$ is $$\displaystyle \frac{12}{m}$$, m is
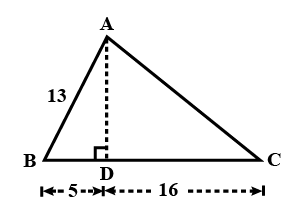
$$\displaystyle 3-\sin ^2 48^{\circ}+\cos ^2 42^{\circ}$$
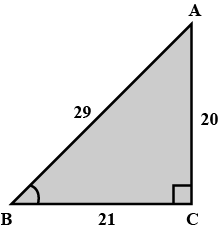
Consider the following figure:
$$\tan C$$ is $$\displaystyle \frac{m}{4}$$, m is
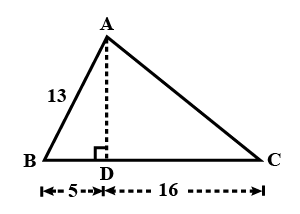
Refer to the triangle given in the figure.
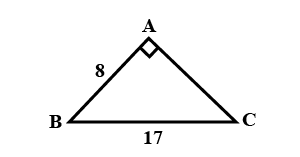
If $$\cos A$$ is equal to $$\displaystyle \frac{m}{5}$$, find $$m$$.
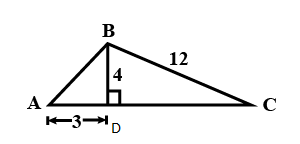
If $$\cos A$$ is equal to $$\displaystyle \frac{m}{5}$$, find $$m$$.
If $$\cos A$$ is $$\displaystyle \frac{3}{m}$$, then m is
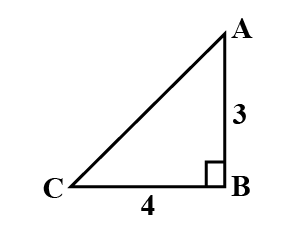
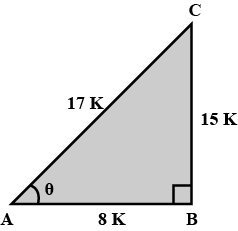
From the following figure, find the values of:
$$\sec ^{2}B\, -\, \tan ^{2}B$$
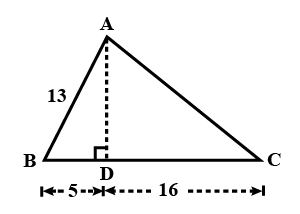
If $$\sin C$$ is $$\displaystyle \frac{1}{m}$$, then $$m$$ is:
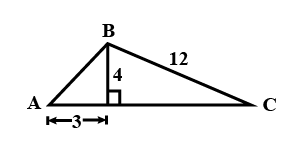
Refer to the triangle given in figure.
If $$cosec\: A$$ is $$\displaystyle \cfrac{5}{m}$$, then $$m$$ is:
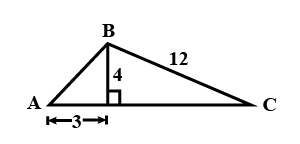
Also find the value of : $$\sin B\cdot \cos C\, +\, \cos B\cdot \sin C$$.
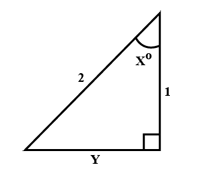
From the figure, $$\sin x^{0}$$ is $$\displaystyle \frac{\sqrt{m}}{2}$$. The value of $$m$$ is:
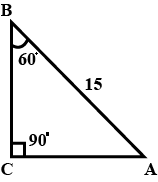
In triangle $$ABC$$, $$AD$$ is perpendicular to $$BC$$. $$\sin B= 0.8$$, $$BD = 9$$ cm and $$\tan C= 1$$. Find the length of $$AB$$
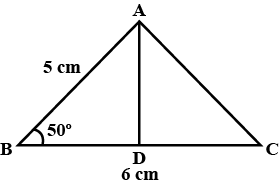
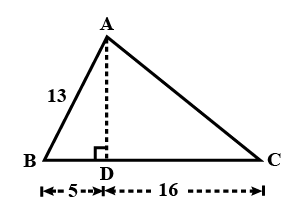
In triangle $$ABC$$, $$AB= AC= 15$$ cm and $$BC= 18$$ cm. Find :
m if $$\sin C$$ is $$\displaystyle \dfrac{4}{m}$$,
m if $$\sin C$$ is $$\displaystyle \dfrac{4}{m}$$,
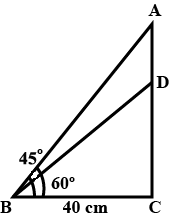
Find the length of $$AD$$. If $$\angle ABC = 60^{\circ},\ \angle DBC = 45^{\circ}$$ and $$BC = 40\ cm.$$
From the following figure, find the value of:
$$\sin ^{2}C\, +\, \cos ^{2}C$$
From the following figure, find the value of:
$$\cos ^{2}A\, +\, \sin ^{2}A$$
Find $$AB$$, if:
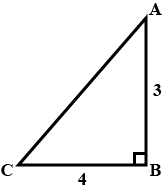
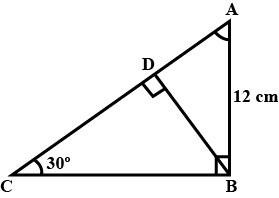
Find $$AC$$
Find $$AB$$
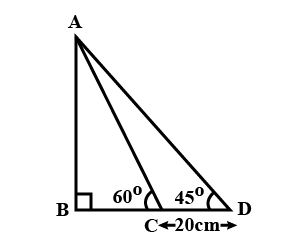
The value of $$BC$$ in the closest integer (in cm.) is:
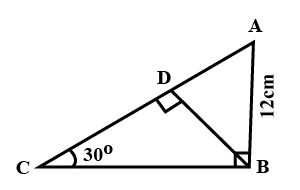
$$Find \space BC \space and \space AB$$
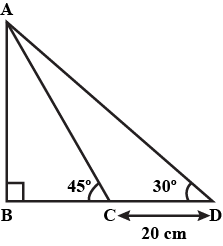
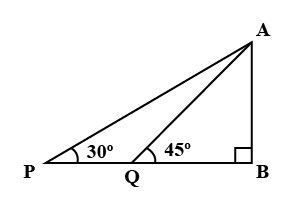
Find $$PQ$$, if $$\displaystyle AB = 150\ m, \angle P = 30^{\circ}$$ and $$\displaystyle \angle Q = 45^{\circ}$$
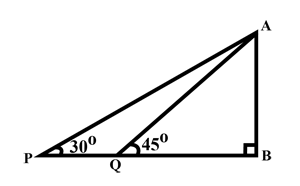
From the given figure, find the value of $$m$$, if cos A $$=\displaystyle \dfrac{3}{m}$$,
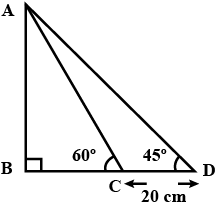
If $$\tan x^{\circ} = \dfrac {5}{12}, \tan y^{\circ} = \dfrac {3}{4}$$ and $$AB = 48\ m$$; find the length of $$CD$$.
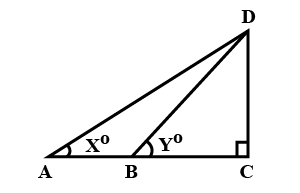
From the given figure, find the value of $$\sin^{2}B\, +\, \cos^{2}B$$
In the following figure; angle $$\displaystyle B=90^{\circ},\angle ADB=30^{\circ}$$ and $$\displaystyle \angle ACB=60^{\circ}$$.
If $$\displaystyle CD = 40\ m$$, then $$AB$$ is 34.64 m
If true then enter $$1$$ and if false then enter $$0$$
cos A is $$\displaystyle \frac{12}{m}$$, m is
sin A is $$\displaystyle \frac{m}{13}$$, m is
From the given figure, find the value of sin B.cos C + cos B.sin C
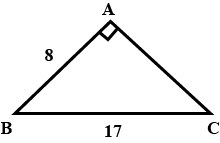
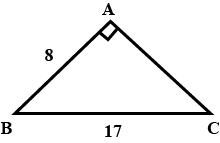
sin B is $$\displaystyle \frac{m}{5}$$, m is
In triangle $$ABC$$, $$AD$$ is perpendicular to $$BC$$.If $$\sin B = 0.8, BD = 9 cm$$ and $$\tan C = 1$$. Find the length of $$AB$$
Given :
In $$\triangle ABC$$, $$AD \perp BC$$,
$$\sin B = 0.8$$,
$$\tan C = 1$$,
$$BD = 9$$
In $$\triangle ABD$$,
$$\sin B = 0.8$$
$$\cos^2 B = 1 - \sin^2 B = 1 - (0.8)^2$$
$$\cos B = (0.6)^2$$
$$\cos B = 0.6$$
$$\cos B = \dfrac{BD}{AB}$$
$$AB = \dfrac{BD}{0.6}$$
$$AB = \dfrac{9}{0.6} = 15$$
Also, using Pythagoras theorem,
$$AB^2 = AD^2 + BD^2$$
$$15^2 = 9^2 + AD^2$$
$$AD = 144$$
$$AD = 12$$ cm
Now, In $$\triangle ACD$$
$$\tan C = 1 = \dfrac{P}{B} = \dfrac{AD}{CD}$$
$$AD = CD = 12$$ cm
Using Pythagoras theorem,
$$AD^2 + CD^2 = AC^2$$
$$12^2 + 12^2 = AC^2$$
$$AC = 12\sqrt{2}$$ cm
In $$\triangle ABD$$,
$$\sin B = 0.8$$
$$\cos^2 B = 1 - \sin^2 B = 1 - (0.8)^2$$
$$\cos B = (0.6)^2$$
$$\cos B = 0.6$$
$$\cos B = \dfrac{BD}{AB}$$
$$AB = \dfrac{BD}{0.6}$$
$$AB = \dfrac{9}{0.6} = 15$$
Also, using Pythagoras theorem,
$$AB^2 = AD^2 + BD^2$$
$$15^2 = 9^2 + AD^2$$
$$AD = 144$$
$$AD = 12$$ cm
Now, In $$\triangle ACD$$
$$\tan C = 1 = \dfrac{P}{B} = \dfrac{AD}{CD}$$
$$AD = CD = 12$$ cm
Using Pythagoras theorem,
$$AD^2 + CD^2 = AC^2$$
$$12^2 + 12^2 = AC^2$$
$$AC = 12\sqrt{2}$$ cm
If $$\sin\, 30^{\circ}\, \cos\, 30^{\circ}$$ is $$\displaystyle \dfrac{\sqrt{3}}{m}$$, then $$m$$ is:
If $$3 \tan A - 5 \cos B =$$ $$\sqrt{3}$$ and $$B =$$ $$90^{\circ}$$, find the value of $$A$$ in degrees.
AB is 17.32 cm
If true then enter $$1$$ and if false then enter $$0$$
Find PQ, if AB = 150 m, $$\angle P\, =\, 30^{\circ}\, and\, \angle Q\, =\, 45^{\circ}$$
Ab is 47.32 cm
If true then enter $$1$$ and if false then enter $$0$$
$$\cos^{2}\, 10^{\circ}\, -\, \sin^{2}\, 80^{\circ}\, +\, \tan^{2}\, 45^{\circ}$$
AB is 27.32 cm
If true then enter $$1$$ and if false then enter $$0$$
$$sin\,x^{\circ}$$ is $$\displaystyle\,\frac{\sqrt{3}}{m}$$
value of m is
The value of $$x$$ is $$m\sqrt{2}$$, so $$m$$ is equal to:
Use $$cos\,x^{\circ}$$ to find the value of y.
If $$\sec A \tan B+\tan A \sec B=91$$, then the value of $$(\sec A \sec B+\tan A \tan B)^2$$ is equal to
If $$\displaystyle \cos \theta =\frac{3}{4}$$ then the value of $$\displaystyle \sqrt{\frac{\sec \theta -cosec \theta }{\sec \theta +cosec \theta }}$$ is ____
Find the value of $$\displaystyle \frac{2\sin 68^{\circ}}{\cos 22^{\circ}}-\frac{2\cot 15^{\circ}}{5\tan 75^{\circ}}-\frac{3\tan 45^{\circ}\tan 20^{\circ}\tan 40^{\circ}\tan 50^{\circ}\tan 70^{\circ}}{5}$$.
Find the value of $$\displaystyle \frac{\cot 54^{\circ}}{\tan 36^{\circ}}+\frac{\tan 20^{\circ}}{\cot 70^{\circ}}-2$$.
The value of $$\displaystyle \cos ^{2}5^{0}+\cos ^{2}10^{0}+\cos ^{2}15^{0}+\cos ^{2}20^{0}+\cos ^{2}70^{0}+\cos ^{2}75^{0}+\cos ^{2}80^{0}+\cos ^{2}85^{0}$$ is equal to
Eliminate $$\theta$$, $$\displaystyle x=a\cos ^{3}\theta\ y=b\sin ^{3}\theta $$
Find the relation obtained by eliminating $$\displaystyle \theta $$ from the equations $$x = r$$ $$\displaystyle \cos \theta +s\sin \theta $$ and $$y=r$$$$\displaystyle \sin \theta -s\cos \theta $$
Show that : (i) $$\tan 48^{\circ} \tan 23^{\circ} \tan 42^{\circ} \tan 67^{\circ} = 1$$ (ii) $$\cos 38^{\circ} \cos 52^{\circ} - \sin 38^{\circ} \sin 52^{\circ} = 0$$.
Evaluate:
(i) $$\displaystyle \frac { \sin { { 1 }8^{ \circ } } }{ \cos { { 72 }^{ \circ } } } $$
(ii) $$\displaystyle \frac { \tan { { 26 }^{ \circ } } }{ \cot { { 64 }^{ \circ } } } $$
(iii) $$\displaystyle \cos { { 48 }^{ \circ } } -\sin { 42^{ \circ } } $$
(iv) $$\displaystyle \csc \ { 31 }^{ \circ }-\sec { { 59 }^{ \circ } } $$
If $$\cos{x} = \dfrac{24}{25}$$, then $$\sec{x} = $$
If $$\sin { \theta } =\cfrac { 1 }{ 2 } $$ and $$\cos { \theta } =-\cfrac { \sqrt { 3 } }{ 2 } $$, find the values of the other 4 trignometric functions.
If $$cosec\ {x} = \dfrac{25}{15}$$, $$\sin{x} =$$
If $$\tan{x} = \dfrac{7}{24}$$, $$\cot{x} = $$
If $$\cot{A} = \dfrac{8}{15}$$ and $$\sin{A} = \dfrac{15}{17}$$ then, $$\cos{A} =$$
If $$\sin{x} = \dfrac{3}{5}$$, then $$\text{ cosec} \ x = ?$$
What trigonometric ratios of angles from $${0}^{o}$$ to $${90}^{o}$$ are not defined?
The trigonometric table of all the functions with all values are shown in the above table:
Hence, from the above table we observe that between $$0^o$$ to $$90^o$$, the below trigonometric functions are equal to not defined.
$$\tan { \dfrac { \pi }{ 2 } } =\csc { { 0 }^{ o } } =\cot { { 0 }^{o } } =\sec { \dfrac { \pi }{ 2 } }=$$ Not defined
Find the value of '$$x$$'
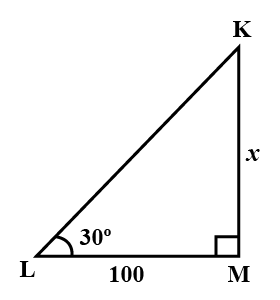
Find the value of '$$x$$'
If $$A={ 60 }^{ o },B={ 30 }^{ o }$$ then prove that $$\cos { \left( A+B \right) } =\cos { A } \cos { B } -\sin { A } \sin { B } $$
What trigonometric ratios of angles from $${0}^{o}$$ to $${90}^{o}$$ are equal?
The trigonometric table of all the functions with all values are shown in the above table:
Hence, from the above table we observe that between $$0^o$$ to $$90^o$$, the below trigonometric functions are equal.
$$\sin { \dfrac { \pi }{ 2 } } =\csc { \dfrac { \pi }{ 2 } } =1$$
$$\cos { { 0 }^{ o } } =\sec { { 0 }^{ o } } =1$$
$$\sin { \dfrac { \pi }{ 4 } } =\cos { \dfrac { \pi }{ 4 } } =\dfrac { \sqrt { 2 } }{ 2 }$$
$$\sec { \dfrac { \pi }{ 4 } } =\csc { \dfrac { \pi }{ 4 } } =\sqrt { 2 }$$
$$\tan { \dfrac { \pi }{ 4 } } =\cot { \dfrac { \pi }{ 4 } } =1$$
What trigonometric ratios of angles from $${0}^{\circ}$$ to $${90}^{\circ}$$ are equal to $$0$$?
Hence, from the given table we observe that between $$0^o$$ to $$90^o$$, the below trigonometric functions are equal to $$0$$.
$$\sin { { 0 }^{ o } } =\tan { { 0 }^{ o} } =\cos { \cfrac { \pi }{ 2 } } =\cot { \cfrac { \pi }{ 2 } } =0$$
If $$A={ 60 }^{ o }$$ and $$B={ 30 }^{ o }$$, then prove that $$\tan { \left( A-B \right) } =\dfrac { \tan { A } -\tan { B } }{ 1+\tan { A } \tan { B } } $$
What trigonometric ratios of angles from $${0}^{o}$$ to $${90}^{o}$$ are equal to $$1$$?
The trignometric table of all the functions with all values are shown in the above table:
Hence, from the above table we observe that between $$0^o$$ to $$90^o$$, the below trignometric functions are equal to $$1$$.
$$\sin { \dfrac { \pi }{ 2 } } =\cos { { 0 }^{ o } } =\csc { \dfrac { \pi }{ 2 } } =\sec { { 0 }^{ o } } =\tan { \dfrac { \pi }{ 4 } } =\cot { \dfrac { \pi }{ 4 } } =1$$
Prove that $$\cos { \theta } \cdot \text{cosec} { \theta } =\cot { \theta } $$
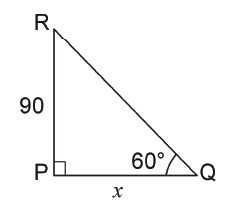
Find the value of '$$x$$'
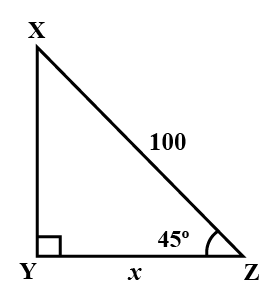
Prove that $$\dfrac { \sin { \theta } }{ 1-\cot { \theta } } +\dfrac { \cos { \theta } }{ 1-\tan { \theta } } =\cos { \theta } +\sin { \theta } $$.
Evaluate without using trigonometric tables
$$\cos^226^\circ+\cos\,64^\circ \sin\,26^\circ+\dfrac{\tan\,36^\circ}{\cot\,54^\circ}$$
Without using tables evaluate $$3\cos 80^o.\text{cosec}\, 10^o+2\sin 59^o.\sec 31^o$$.
If $$\cos { 7A } =\sin { \left( A-{ 6 }^{ o } \right) } $$, where $$7A$$ is an acute angle. Find the value of $$A$$.
Without using trigonometric tables evaluate :$$\dfrac { \sin { { 63 }^\circ } }{ \cos { { 27 }^\circ } } +\dfrac { \cos { { 39 }^\circ } }{ \sin { { 51 }^\circ } } -\sin { { 23 }^\circ } \cdot \sec { { 67 }^\circ } +\csc ^{ 2 }{ { 30 }^\circ } $$
If $$\cos{\theta}=\dfrac{1}{2}$$, then find the value of acute angle $$\theta$$.
Prove that: $$\dfrac {\cos A}{1 + \sin A} + \tan A = \sec A$$
If $$\theta = 60^{\circ}$$, find the value of $$\cos \theta$$
Prove that $$\displaystyle \frac{\tan^2\theta}{(\sec\,\theta-1)^2}=\frac{1+\cos\,\theta}{1-\cos\,\theta}$$
Without using trigonometric tables, evaluate $$\sin^{2} 34^{\circ} + \sin^{2} 56^{\circ} + 2\tan 18^{\circ} \tan 72^{\circ} - \cot^{2} 30^{\circ}$$
Verify the following equalities.
$$\cos 60^{\circ} = 1 - 2\sin^{2} 30^{\circ} = 2\cos^{2} 30^{\circ} - 1$$
Verify the following equalities.
$$\sin^{2}30^{\circ} + \cos^{2} 30^{\circ} = 1$$
Verify the following equalities.
$$\cos 90^{\circ} = 1 - 2\sin^{2} 45^{\circ} = 2\cos^{2} 45^{\circ} - 1$$
Prove that $$\sqrt {\dfrac {1 + \cos \theta}{1 - \cos \theta}} = cosec \theta + \cot \theta$$
Prove that
$$\dfrac {\sin (90^{\circ} - \theta)}{1 + \sin \theta} + \dfrac {\cos \theta}{1 - \cos (90^{\circ} - \theta)} = 2\sec \theta$$
Verify the following equalities.
$$1 + \tan^{2} 45^{\circ} = \sec^{2} 45^{\circ}$$
Verify the following equalities.
$$\tan^{2} 60^{\circ} - 2\tan^{2} 45^{\circ} - \cot^{2} 30^{\circ} + 2\sin^{2} 30^{\circ} + \dfrac {3}{4} cosec^{2} 45^{\circ} = 0$$
Verify the given equalities.
$$\sin 30^{\circ} \cos 60^{\circ} + \cos 30^{\circ} \sin 60^{\circ} = \sin 90^{\circ}$$
Verify the following equalities.
$$\dfrac {1 - \tan^{2} 60^{\circ}}{1 + \tan^{2} 60^{\circ}} = 2\cos^{2} 60^{\circ} - 1$$
Verify the following equalities.
$$4\cot^{2} 45^{\circ} - \sec^{2} 60^{\circ} + \sin^{2} 60^{\circ} + \cos^{2} 60^{\circ} = 1$$
Simplify $$\dfrac {\cos 80^{\circ}}{\sin 10^{\circ}} + \cos 59^{\circ} cosec 31^{\circ}$$
Verify the following equalities.
$$\dfrac {\sec 30^{\circ} + \tan 30^{\circ}}{\sec 30^{\circ} - \tan 30^{\circ}} = \dfrac {1 + \sin 30^{\circ}}{1 - \sin 30^{\circ}}$$
Verify the following equalities.
$$\dfrac {\cos 60^{\circ}}{1 + \sin 60^{\circ}} = \dfrac {1}{\sec 60^{\circ} + \tan 60^{\circ}}$$
Show that: $$\tan 35^{\circ} \tan 60^{\circ} \tan 55^{\circ} \tan 30^{\circ} = 1$$
Prove that: $$\sec^2\theta =1+\tan^2\theta$$.
Let $$\Delta ABP$$ is a right angle triangle, where $$\angle B=90^o$$.
By applying Pythagoras theorem, in $$\Delta ABP$$,
$$PA^2=PB^2+AB^2$$
Dividing both sides by $$AB^2$$
$$\Rightarrow \displaystyle\frac{PA^2}{AB^2}=\frac{PB^2}{AB^2}+\frac{AB^2}{AB^2}$$
Let $$\angle PAB=\theta$$.
so, $$\tan\theta=\dfrac{PB}{AB}.....(1)$$
and, $$\sec\theta=\dfrac{PA}{AB}......(2)$$
By applying Pythagoras theorem, in $$\Delta ABP$$,
$$PA^2=PB^2+AB^2$$
Dividing both sides by $$AB^2$$
$$\Rightarrow \displaystyle\frac{PA^2}{AB^2}=\frac{PB^2}{AB^2}+\frac{AB^2}{AB^2}$$
$$\Rightarrow \left(\displaystyle\frac{PA}{AB}\right)^2=\left(\displaystyle\frac{PB}{AB}\right)^2+\left(\displaystyle\frac{AB}{AB}\right)^2$$ [from $$(1)$$ and $$(2)$$]
$$\Rightarrow (\sec\theta)^2=(\tan\theta)^2+1$$
$$\Rightarrow \sec^2\theta =\tan^2\theta +1$$.
$$\Rightarrow \sec^2\theta =\tan^2\theta +1$$.
$$Hence, proved$$.
Length of two sides of a triangle are $$6$$ centimetres and $$5$$ centimetres. If their included angle is $${50}^{o}$$. What is the area of the triangle?
Also find the length of its third side.
$$\left( \sin { { 50 }^{ o } } =0.77,\cos { { 50 }^{ o } } =0.64,\tan { { 50 }^{ o } } =1.19 \right) $$
Consider the following figure of triangle:
Area of triangle $$=\cfrac { 1 }{ 2 } \times BC\times AD=\cfrac { 1 }{ 2 } \times 6\times AD=3\times AD$$
From right-angled $$\triangle{ABD}$$,
$$\sin { { 50 }^{ o } } =\cfrac { AD }{ AB } $$
$$AD=AB\times \sin { { 50 }^{ o } } =5\times 0.77=3.85cm$$
Thus, area of triangle $$3\times 3.85=11.55{cm}^{2}$$
Now, $$\cos { { 50 }^{ o } } =\cfrac { BD }{ AB } \quad $$
$$\Rightarrow BD=AB\times \cos { { 50 }^{ o } } =5\times 0.64=3.2cm$$
Thus, $$DC=6-3.2=2.8cm$$
$$\Rightarrow AC=\sqrt { { (2.8) }^{ 2 }+{ (3.85) }^{ 2 } } =\sqrt { 7.84+14.82 } =\sqrt { 22.66 } cm\quad \quad $$
Area of triangle $$=\cfrac { 1 }{ 2 } \times BC\times AD=\cfrac { 1 }{ 2 } \times 6\times AD=3\times AD$$
From right-angled $$\triangle{ABD}$$,
$$\sin { { 50 }^{ o } } =\cfrac { AD }{ AB } $$
$$AD=AB\times \sin { { 50 }^{ o } } =5\times 0.77=3.85cm$$
Thus, area of triangle $$3\times 3.85=11.55{cm}^{2}$$
Now, $$\cos { { 50 }^{ o } } =\cfrac { BD }{ AB } \quad $$
$$\Rightarrow BD=AB\times \cos { { 50 }^{ o } } =5\times 0.64=3.2cm$$
Thus, $$DC=6-3.2=2.8cm$$
$$\Rightarrow AC=\sqrt { { (2.8) }^{ 2 }+{ (3.85) }^{ 2 } } =\sqrt { 7.84+14.82 } =\sqrt { 22.66 } cm\quad \quad $$
In $$\Delta ABC, $$ AB = 8 cm, AC = 5 cm and $$m \angle A = 50^o$$. Then
(a) What is the length of the perpendicular from C to AB?
(b) Find the length of BC.
$$[sin 50^o = 0.7660, cos 50^o = 0.6428, tan 50^o = 1.1918]$$
Let CD be perpendicular from C to AB.
(a) In $$\Delta ACD$$,
$$sin 50^o = \dfrac{CD}{AC} \Rightarrow 0.7660 = \dfrac{CD}{5}$$
$$\Rightarrow CD = 0.7660 \times 5 = 3.83 cm$$
(b) $$cos 50^o = \dfrac{AD}{AC} \Rightarrow 0.6428 = \dfrac{AD}{5}$$
$$\Rightarrow AD = 0.6428 \times 5 = 3.214$$
DB = AB - AD = (8 - 3.214) cm = 4.786 cm
In right triangle CDB,
$$BC^2 = CD^2 + DB^2$$
$$= (3.83)^2 + (4.786)^2$$
$$= 14.67 + 22.91$$
$$= 37.58$$
$$\Rightarrow BC = \sqrt{37.58} cm$$
(a) In $$\Delta ACD$$,
$$sin 50^o = \dfrac{CD}{AC} \Rightarrow 0.7660 = \dfrac{CD}{5}$$
$$\Rightarrow CD = 0.7660 \times 5 = 3.83 cm$$
(b) $$cos 50^o = \dfrac{AD}{AC} \Rightarrow 0.6428 = \dfrac{AD}{5}$$
$$\Rightarrow AD = 0.6428 \times 5 = 3.214$$
DB = AB - AD = (8 - 3.214) cm = 4.786 cm
In right triangle CDB,
$$BC^2 = CD^2 + DB^2$$
$$= (3.83)^2 + (4.786)^2$$
$$= 14.67 + 22.91$$
$$= 37.58$$
$$\Rightarrow BC = \sqrt{37.58} cm$$
Without using trigonometric tables, evaluate the following:
$$2\left (\dfrac {\cos 58^{\circ}}{\sin 32^{\circ}}\right ) - \sqrt {3}\left (\dfrac {\cos 38^{\circ} \text{cosec }52^{\circ}}{\tan 15^{\circ} \tan 60^{\circ} \tan 75^{\circ}}\right )$$.
Evaluate : $$\displaystyle \, \frac{cosec 13^{\circ}}{\sec 77^{\circ}} \, - \, \frac{\cot 20^{\circ}}{\tan 70^{\circ}}$$
Calculate
$$\displaystyle\, \frac{\sin \, \alpha}{\sin^3 \, \alpha \, + \, \cos^3 \, \alpha}$$ if $$\tan$$ $$\alpha$$ =2.
If $$\cos\theta +\sin\theta =\sqrt{2}\cos\theta$$, show that $$\cos\theta -\sin\theta=\sqrt{2}\sin\theta$$
Show that:$$\left( 1+\cot { A } +\tan { A } \right) \left( \sin { A } -\cos { A } \right) =\cfrac { \sec { A } }{\text{cosec} ^{ 2 }{ A } } -\cfrac {\text{cosec }{ A } }{ \sec ^{ 2 }{ A } } =\sin { A } \tan { A } -\cot { A } \cos { A } $$
Prove that $$\dfrac{\tan^2A}{1 + \tan^2A} + \dfrac{\cot^2A}{1 +\cot^2A} = 1$$
Prove that $$\dfrac{\tan A \, + \, \tan B}{\cot A \, + \, \cot B} \, = \, \tan A \, \tan B$$
Prove the following statements.
$$\dfrac {\cot A + \tan B}{\cot B + \tan A} = \cot A \tan B$$.
Evaluate the following : sin $$45^{\circ}$$ sin $$30^{\circ}$$ + cos $$45^{\circ}$$ cos $$30^{\circ}$$
Prove that $$\tan^2A + \cot^2A = \sec^2A.cosec^2A \, - \, 2$$
Prove that $$\dfrac{\cos^2 \theta}{\sin \theta} - cosec \theta + \sin \theta = 0$$.
Evaluate $$\sin 60^{\circ} \cos 30^{\circ} + \cos 60^{\circ} \sin 30^{\circ}$$.
Evaluate the following :
cos $$60^{\circ}$$ cos $$45^{\circ}$$ - sin $$60^{\circ}$$ sin $$45^{\circ}$$
Prove that $$\dfrac{(1 + \tan^2\theta) \cot \theta}{co\sec^2 \theta} = \tan \theta$$
Prove that $$\dfrac{\sin 70^{\circ}}{\cos 20^{\circ}} + \dfrac{\text{cosec} 20^{\circ}}{\sec 70^{\circ}} - 2 \cos 70^{\circ} \text{cosec} 20^{\circ} = 0$$
Express the following in terms of trigonometric ratios of angles lying between $$0^\circ$$ and $$45^\circ$$:
$$\cot 85^\circ + \cos 75^\circ$$
If $$A = 30^{\circ}$$ and $$B = 60^{\circ}$$, verify that
(i) $$\sin(A + B) = \sin A \cos B + \cos A \sin B$$
(ii) $$\cos(A + B) = \cos A \cos B - \sin A \sin B$$
Express the following in terms of trigonometric ratios of angles lying between 0 and 45:
$$\text{cosec} 54^0 + \sin 72^0$$
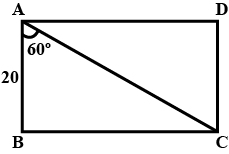
In a rectangle ABCD, $$AB = 20$$ cm, $$\angle$$BAC = $$60^{\circ}$$, calculate side $$BC$$ and diagonals $$AC, BD$$.
In $$\triangle ABC$$, from the above figure
$$\tan60^\circ=\dfrac{BC}{AB}=\sqrt3$$
$$\sqrt3=\dfrac{BC}{20}$$
$$\therefore \ BC=20\sqrt3 \ cm$$
$$\cos60^\circ=\dfrac{AB}{AC}=\dfrac{1}{2}$$
$$\dfrac{1}{2}=\dfrac{20}{AC}$$
$$\therefore \ AC=40 \ cm$$
In a rectangle, the two diagonals are equal.
$$\therefore \ AC=BD=40 \ cm$$
In a right $$\triangle \text{ABC}$$, right angled at $$\text{C}$$, if $$\angle \text{B} = 60^{\circ}$$ and $$\text{AB} = 15$$ units. Find the remaining angles and sides.
Given:
$$\triangle ABC$$ is right angled at $$C, \ \angle{B}=60^\circ$$
$$\angle{C}=90^\circ$$
We know that,
In triangle $$ABC$$, $$\angle{A}+\angle{B}+\angle{C}=180^\circ$$
$$60^\circ+\angle{A}+90^\circ=180^\circ$$
$$\angle{A}=30^\circ$$
We have,
$$\sin{A}=\dfrac{CB}{AB}$$
$$\sin30^\circ=\dfrac{CB}{15}$$
$$\dfrac{1}{2}\times 15 = CB$$
$$CB=7.5 \text{ units}$$
From Pythagoras theorem,
$$AB^2=AC^2+BC^2$$
$$15^2=AC^2+\left(\dfrac{15}{2}\right)^2$$
$$AC^2=225-\left(\dfrac{225}{4}\right)$$
$$AC^2=225\left(\dfrac{3}{4}\right)$$
$$AC=\dfrac{15\sqrt{3}}{2}\text{ units}$$
Prove the following :$$\dfrac{\cos(90^{\circ} \, - \, \theta) \, \sec \, (90^{\circ} \, - \, \theta) \, \tan \, \theta}{\text{cosec}(90^{\circ} \, - \, \theta) \, \sin(90^{\circ} \, - \, \theta) \, \cot(90^{\circ} \, - \, \theta)} \, + \ \dfrac{\tan(90^{\circ} \, - \, \theta)}{\cot \, \theta} \, = \, 2$$
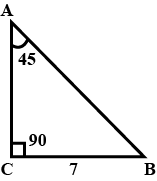
If $$\Delta ABC$$ is a right triangle such that $$\angle C = 90^{\circ}, \, \angle A = 45^{\circ}$$ and $$BC = 7$$ units. Find $$\angle B, AB$$ and $$AC$$.
$$\triangle ABC$$ is $$right \, angled$$ at $$C$$
$$\angle{C}=90^\circ, \angle{A}=45^\circ$$
We know that,
In triangle $$ABC$$, $$\angle{A}+\angle{B}+\angle{C}=180^\circ$$
$$45^\circ+\angle{B}+90^\circ=180^\circ$$
$$\angle{B}=45^\circ$$
It's a scalene triangle.
$$\therefore BC=AC=7 units$$
From Pythagoras theorem,
$$AB^2=AC^2+BC^2$$
$$AB^2=7^2+7^2=98$$
$$AB=7\sqrt2$$
Prove that $$\sin 48^{\circ} \sec 42^{\circ} + \cos 48^{\circ} \text{cosec} 42^{\circ} = 2$$
Prove that: $$\tan 20^{\circ} \tan 35^{\circ} \tan 45^{\circ} \tan 55^{\circ} \tan 70^{\circ} = 1$$
Prove that: $$\dfrac{{\tan \theta }}{{1 - \cot \theta }} + \dfrac{{\cot \theta }}{{1 - \tan \theta }} = 1 + \sec \theta\ {cosec}\ \theta $$
If $$3x\sin 60^o.\cos^2 30^o=\dfrac{\tan^2 45^o.\sec 60^o}{cosec 60^o.\sin 45^o}$$, then find the value of $$x$$.
If $$a \cos \theta - b \sin \theta = x$$ and $$a \sin \theta + b \cos \theta = y$$ then find $$\dfrac{a^{2} + b^{2}}{x^{2} + y^{2}}$$.
Express each of the following in trigonometric ratios of angles between $$0^{\circ} \, and \, 45^{\circ}$$ :
$$sin 72^{\circ} \, + \, cot 72^{\circ}$$
Prove that :
$$sin 35^{\circ} \, sin 55^{\circ} \, - \, cos 35^{\circ} \, cos 55^{\circ} \, = \, 0$$
The value of $$\left( 1+\cos { \dfrac { \pi }{ 8 } } \right) \left( 1+\cos { \dfrac { 3\pi }{ 8 } } \right) \left( 1+\cos { \dfrac { 5\pi }{ 8 } } \right) \left( 1+\cos { \dfrac { 7\pi }{ 8 } } \right) =\dfrac { a }{ 256 } $$. Find a.
Find the value of:
$$\dfrac{1 + \cos A -\sin A}{1 + \cos A +\sin A} -\sec A + \tan A$$
Prove that $$\dfrac{1+2\cos^2\,A}{1+3\cot^2\,A}=\sin^2\,A$$
Find the value of $$(\sin \theta + \sec \theta)^{2} + (\cos \theta + \text{cosec} \theta)^{2} - (1 + \sec \theta \text{cosec} \theta)^{2}$$
If $$cosec^{6} \theta -cot^{6} = a cot^{4}\theta + b cot^{2}\theta + c$$ then a + b + c =
If $$\dfrac{\tan^3\alpha}{1+\tan^2\alpha}= \sec\alpha \sin\alpha- a \sin\alpha \cos\alpha$$. Find $$a$$
If $$x= r \cos\theta. \sin\phi, y= \sin\theta . \sin\phi, z= r \cos\phi$$ Prove that $$x^2+y^2+z^2=r^2$$
Prove that $$\sqrt { \dfrac { \sin { A } +1 }{ 1-\sin { A } } } +\sqrt { \dfrac { 1-\sin { A } }{ \sin { A } +1 } } =2\sec { A }$$
Solve: $$\cos^{2}\theta +\cos^{2}\theta \cot^{2}\theta-\cot^{2}\theta$$
$$ \dfrac { \cos { x } }{ { \left( \cos { x } +\sin { x } \right) }^{ 2 } }$$
If $$(\sec A+ \tan A -1)(\sec A-\tan A+1)= a\tan A$$.Find $$a$$
If $$\dfrac{\tan\theta}{(1+\tan^2\theta)^2}+ \dfrac{\cot\theta}{(1+ \cot^2\theta)^2}= m\sin \theta \cos\theta$$. Find $$m$$
If $$\sin\theta =\dfrac{3}{4} $$, show that $$\sqrt{\dfrac{\text{cosec}^2\theta - \cot^2\theta}{\sec^2\theta-1}}=\dfrac{\sqrt m}{3}.$$.Find $$m$$
If $$\sin \theta=\cfrac {3}{4}$$
$$\sqrt {\cfrac {\csc^2\theta-\cot^2\theta}{\sec^2\theta-1}}=\cfrac {\sqrt{m}}{3}$$ Find m.
$$AC^2=AB^2+BC^2$$
$$16=9+BC^2$$
$$\Rightarrow BC=\sqrt {7}$$
(Refer to Image)
$$\sin\theta=\cfrac {3}{4}=\cfrac {AB}{AC}$$
$$\csc\theta=\cfrac {AC}{AB}=\cfrac {4}{3}$$
$$\cot\theta=\cfrac {\sqrt 7}{3}=\cfrac {BC}{AB}$$
$$\sec\theta=\cfrac {AC}{BC}=\cfrac {4}{\sqrt7}$$
$$\Rightarrow\sqrt{\cfrac {\csc^2\theta-\cot^2\theta}{\sec^2\theta-1}}=$$$$\sqrt {\cfrac {\left(\cfrac {4}{3}\right)^2-\left(\cfrac {\sqrt {7}}{3}\right)^2}{\left(\cfrac {4}{\sqrt {7}}\right)^2-1}}$$
$$=\sqrt {\cfrac {\cfrac {16}{9}-\cfrac {7}{9}}{\cfrac {16}{7}-1}}$$
$$=\sqrt {\cfrac {\cfrac{9}{9}}{\cfrac {9}{7}}}$$
$$=\sqrt {\cfrac {7}{9}}$$
$$=\cfrac{\sqrt{7}}{3}$$
$$\therefore m=7$$
$$si{n^2}{30^ \circ } + co{s^2}60 + {\tan ^2}{45^ \circ } + se{c^2}{60^ \circ } - co{\sec ^2}{30^ \circ } = \frac{3}{2}$$
If $$\dfrac{\sin\theta - \cos\theta +1}{\sin\theta + \cos\theta -1}= \dfrac{m}{\sec\theta - \tan\theta},$$ Find $$m$$
If $$x= \text{cosec}A + \cos A $$ and $$y= \text{cosec}A- \cos A$$ then prove that $$\left(\dfrac{2}{x+y}\right) ^2+ \left(\dfrac{x-y}{2}\right)^2-1=0$$.
If $${\cos}^{4}{\theta}+{\cos}^{2}{\theta}=1$$ then show that
i) $${\sec}^{4}{\theta}-{\sec}^{2}{\theta}=1$$
ii) $${\cot}^{4}{\theta}-{\cot}^{2}{\theta}=1$$
If $$A+ B =90^{\circ}$$ then prove $$\displaystyle \sqrt{\frac{ \tan A\tan B + \tan A\cot B}{\sin A \sec B} -\frac{\sin^{2}B}{\cos^{2}A}} = \tan A$$
Solve $$7cos^{2}\theta + 3 sin^{2}\theta =4$$.
Evaluate
$$\dfrac{{\sin {{90}^ \circ }}}{{\cos {{45}^ \circ }}} + \dfrac{1}{{\cos ec{{30}^ \circ }}}$$
Prove $$\dfrac{1+\cos{A}+\sin{A}}{1+\cos{A}-\sin{A}}=\dfrac{1+\sin{A}}{\cos{A}}$$
If $$\tan\theta =\dfrac{1}{\sqrt{7}}$$, show that $$\dfrac{cosec^2\theta -\sec^2\theta}{cosec^2\theta +\sec^2\theta}=\dfrac{3}{4}$$.
$$2x\tan ^{ 2 }{ { 60 }^{ o }+3x\sin ^{ 2 }{ { 30 }^{ o } } } =\dfrac { 27\cos ^{ 2 }{ { 45 }^{ o } } }{ 4\sin ^{ 2 }{ { 60 }^{ o } } } $$
Prove: $$1- \dfrac{cos^2A}{1+SinA}= SinA.$$
Prove:$$\cfrac{{\cot \theta - \cos \theta }}{{\cot \theta + \cos \theta }} = \cfrac{{{\mathop{\rm cosec}\nolimits} \theta - 1}}{{{\mathop{\rm cosec}\nolimits} \theta + 1}}$$
If $$\cot x =2$$, find the value of $$\dfrac{(2+2\sin x)(1-\sin x)}{(1+\cos x)(2-2\cos x)}$$
$$\dfrac{2}{3}\text{cosec}^258^0 -\dfrac{2}{3}\cot 58^0 \tan32^0-\dfrac{5}{3}\tan 13^0\tan37^0\tan45^0\tan53^0\tan 77^0=-m$$.Find $$m$$
$${\sec ^4}x - {\sec ^2}x = {\tan ^4}x + {\tan ^2}x$$
Prove:$$\left( {1 + \,{{\tan }^2}\,\theta } \right)\,{\sin ^2}\,\theta \, = \,{\tan ^2}\,\theta $$
Prove: $$\sec ^{ 4 }{ \theta } -\tan ^{ 4 }{ \theta } =2\sec ^{ 2 }{ \theta } -1$$
Prove that $$\dfrac{\sin \theta-\cos \theta+1}{\sin \theta+ \cos \theta-1}=\dfrac{1}{\sec \theta- \tan \theta }$$ [use the identity $$\sec^{2} \theta=1+\tan^{2} \theta$$.]
Prove that $$\dfrac{2}{1-\sin A}\times \dfrac{1}{1+\sin A}=2\sec^2 A$$
Evaluate $$\dfrac {2\cos^{2}90^{o}+4\cos^{2}45^{o}+\tan^{2}60^{o}+3csc^{2}60^{o}+1}{3csc 60^{o}-\dfrac {7}{2}\sec^{2}45^{o}+2\csc 30^{o}-1}$$
If $$\sec{\theta}=x+\cfrac{1}{4x}$$ then prove $$\sec{\theta}+\tan{\theta}=2x$$
Evaluate:
$${ \sin }^{ 2 }{ 5 }^{ o }+{ \sin }^{ 2 }{ 10 }^{ o }+..........{ \sin }^{ 2 }{ 85 }^{ o }$$ ?
Prove: $${ \left( \tan { \theta } +\sec { \theta } \right) }^{ 2 }+{ \left( \tan { \theta } -\sec { \theta } \right) }^{ 2 }=\cfrac { 2\left( 1+\sin ^{ 2 }{ \theta } \right) }{ \cos ^{ 2 }{ \theta } } $$
$$\tan^{2}{\phi}-\sin^{2}{\phi}=\tan^{2}{\phi}.\sin^{2}{\phi}$$
Solve :
$$2\tan^{2}{45^{0}}+\cos^{2}{45^{0}}-\sin^{2}{45^{0}}$$
Solve $${\sec ^6}x - {\tan ^6}x - 3{\sec ^2}x.{\tan ^2} $$
To prove that
$$\left(\dfrac {1}{\sec^{2}x-\cos^{2}x}+\dfrac {1}{\csc^{2}x-\sin^{2}x}\right)\sin^{2}x.\cos^{2}x$$
$$=\dfrac {1-\sin^{2}x \cos^{2}x}{2+\sin x\cos^{2}x}$$
Find the values of the trigonometric ratio
$$\tan \theta=11$$
Show that $$(\text{cosec}{\theta}-\cot{\theta})^{2}=\dfrac{1-\cos{\theta}}{1+\cos{\theta}}$$
$$\dfrac{\cos{A}-1}{2-\sec^{2}{A}}=\dfrac{\cot{A}}{1+\tan{A}}$$Find A.
If $$x=a\sin\theta$$ and $$y=b\tan\theta$$, then prove that $$\dfrac{a^{2}}{x^{2}}-\dfrac{b^{2}}{y^{2}}=1$$.
Express $$\sec{\theta}$$ in terms of $$\cot{\theta}$$
If $$x=r\sin A\cos C, y=r\sin A\sin C$$ and $$z=r\cos A$$, prove that $$r^{2}=x^{2}+y^{2}+z^{2}$$.
If $$\dfrac{\cos{A}}{\cos{B}}=m$$ and $$\dfrac{\cos{A}}{\sin{B}}=n.$$Prove:- $$\left(m^{2}+n^{2}\right)\cos^{2}B=n$$
Show that $$\dfrac{{\tan A}}{{1 - \cot A}} + \dfrac{{\cot A}}{{1 - \tan A}} = 1 + \sec A cosecA$$
Prove that $$\dfrac { 1 + \cos A } { \sin A } + \dfrac { \sin A } { 1 + \cos A } = 2 \csc A$$
LHS = $$ \frac{1+cosA}{sinA}+\frac{sinA}{1+cosA}$$
$$ = \frac{(1+cosA)^{2}+sin^{2}A}{sinA(1+cosA)}$$
$$ = \frac{1+2cosA+cos^{2}A+sin^{2}A}{sinA(1+cosA)}$$
$$ = \frac{1+2cosA+1}{sinA(1+cosA)}[sin^{2}A+cos^{2}A = 1 ]$$
$$ = \frac{2+2cosA}{sinA(1+cosA)}$$
$$ = \frac{2[1+cosA]}{sinA(1+cosA)}$$
$$ = \frac{2}{sinA}$$
$$ = 2 cosec A = RHS $$
LHS = RHS
Hence proved.
Evaluate:
$$\tan ^{ 2 }{ { 30 }^{ o } } \sin { { 30 }^{ o } } +\cos { { 60 }^{ o } } \sin ^{ 2 }{ { 90 }^{ o } } \tan ^{ 2 }{ { 60 }^{ o } } -2\tan { { 45 }^{ o } } \cos ^{ 2 }{ { 0 }^{ o } } \sin { { 90 }^{ o } } $$
Given $$sec\: \theta = \dfrac {13}{12}$$, calculate all other trigonometric ratios
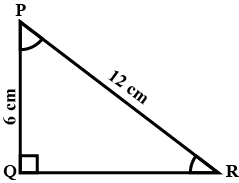
In fig. $$ \triangle PQR$$ right angled at $$Q,PQ=6cm$$ and $$PR=12cm$$. Determine $$\angle QPR$$ and $$\angle PRQ$$.
Given $$PQ=6\ cm$$
$$PR=12\ cm$$
$$\sin R=\dfrac{PQ}{PR}$$
$$=\dfrac{6}{12}=\dfrac{1}{2}$$
$$\sin R=\sin 30^o$$
$$R=30^o$$
$$\angle PRQ=30^o$$
As $$\angle P+\angle Q+\angle R=180^o$$
$$\angle P+90^o+30^o=180^o$$
$$\angle P=180^o-120^o$$
$$\angle P=60^o$$
$$\angle QPR=60^o$$ & $$\angle PRQ=30^o$$
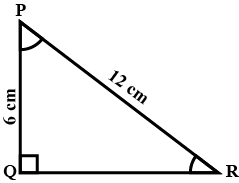
If $$\tan \theta + \sec \theta =1.5$$, find $$\sin \theta$$.
Evaluate $$\dfrac { \sin 18 ^ { \circ } } { \cos 72 ^ { \circ } }$$.
Prove that: $$\cfrac { \sin { \theta } }{ \left( 1-\cot { \theta } \right) } +\cfrac { \cos { \theta } }{ \left( 1-\tan { \theta } \right) } =\cos { \theta } +\sin { \theta } $$
Evaluate : $$\dfrac{ cos 22^0}{sin 68^0}$$
If $$4tan\theta =3$$, evaluate $$\left( \dfrac { 4sin\theta -cos\theta +1 }{ 4sin\theta +cos\theta -1 } \right) $$
If $$\cot\theta=3x-\dfrac{1}{12x}$$ then show that $$\csc\theta+\cot\theta=6x$$ or $$-\dfrac{1}{6x}$$.
Evaluate : $$\dfrac { 4 }{ { cot }^{ 2 }{ 30 }^{ 0 } } +\dfrac { 1 }{ { sin }^{ 2 }{ 30 }^{} } -2{ cos }^{ 2 }{ 45 }^{ 0 }-{ sin }^{ 2 }{ 0 }^{ 0 }$$
If $$\cot \theta=\dfrac {15}{8}$$, find $$\cos \theta$$ and $$\csc \theta$$.
Find the value of $$6\tan^{ 2 }\theta -6\sec^{ 2 }\theta $$.
Evaluate :
$$\left( 3-\cot{ 30 }^{ \circ } \right) -{ \tan }^{ 3 }{ 60 }^{ \circ }+2\tan{ 60 }^{ \circ }$$
Prove that :
$$(\sin\theta+\cos\theta)(\tan\theta+\cot\theta)=\sec\theta+\csc\theta$$.
The value of $$tan^2 60^{0}$$ is ?
Evaluate:
$$\sin {25^0}\cos {65^0} + \cos {25^0}\;\sin {65^0}$$
If $$A$$ and $$B$$ are acute angles such that $$\tan A = \dfrac {1}{3}$$, $$\tan B = \dfrac{1}{2}$$ and $$\tan(A + B) = \dfrac {\tan A + \tan B}{1 - \tan A \tan B}$$, show that $$A + B = 45^{\circ}$$.
If in $$\Delta A B C , \angle B = 90 ^ { \circ } , a = 12 \mathrm { cm } , b = 13 \mathrm { cm } ,$$ then write all the trigonometric ratios for $$\angle A$$ and $$\angle C$$
Given that $$ \angle B = 90^{\circ} , AC = 13\ cm , BC = 12\ cm $$
$$ \because $$ $$AB^{2} + BC^{2} = AC^{2} $$
$$ \Rightarrow $$ $$AB = \sqrt{AC^{2} - BC^{2}} $$
$$ = \sqrt{(13)^{2} - (12)^{2}} $$
$$ = \sqrt{169 - 144} = \sqrt{25} $$
$$ = 5\ cm $$
For acute angle $$A$$ , the value of trigonometric ratios are
$$ \sin A = \dfrac{BC}{AC} = \dfrac{12}{13} , \cos A = \dfrac{AB}{AC} = \dfrac{5}{13} $$,
$$\tan A = \dfrac{BC}{AB} = \dfrac{12}{5} $$
$$ cosec A = \dfrac{AC}{BC} = \dfrac{13}{12} , \sec A = \dfrac{AC}{AB} = \dfrac{13}{5} $$
$$ \cot A = \dfrac{AB}{BC} = \dfrac{5}{12} $$
$$ \because $$ $$AB^{2} + BC^{2} = AC^{2} $$
$$ \Rightarrow $$ $$AB = \sqrt{AC^{2} - BC^{2}} $$
$$ = \sqrt{(13)^{2} - (12)^{2}} $$
$$ = \sqrt{169 - 144} = \sqrt{25} $$
$$ = 5\ cm $$
For acute angle $$A$$ , the value of trigonometric ratios are
$$ \sin A = \dfrac{BC}{AC} = \dfrac{12}{13} , \cos A = \dfrac{AB}{AC} = \dfrac{5}{13} $$,
$$\tan A = \dfrac{BC}{AB} = \dfrac{12}{5} $$
$$ cosec A = \dfrac{AC}{BC} = \dfrac{13}{12} , \sec A = \dfrac{AC}{AB} = \dfrac{13}{5} $$
$$ \cot A = \dfrac{AB}{BC} = \dfrac{5}{12} $$
Without using tables, evaluate:
$$ 4 \tan 60 ^ { \circ } \sec 30 ^ { \circ } + \dfrac { \sin 31 ^ { \circ } \sec 59 ^ { \circ } + \cot 59 ^ { \circ } \cot 31 ^ { \circ } } { 8 \sin ^ { 2 } 30 ^ { \circ } - \tan ^ { 2 } 45 ^ { \circ } } $$
In $$\Delta { ABC } ,$$ if $$\dfrac { \cos { A } } { a } = \dfrac { \cos { B } } { b },$$ then show that it is an isosceles triangle.
If the angles $$(2x-10)^{\circ}$$ and $$(x-5)^{\circ}$$ are complementary angles, find $$x (in \, degrees).$$
If $$\tan \theta = \dfrac { 5 } { 4 },$$ then find the value of $$\dfrac { 3 \sin \theta + 4 \cos \theta } { 3 \sin \theta - 4 \cos \theta }.$$
If sec $$ \theta = 5/4 $$, show that $$ \left( \dfrac { sin\theta -2cos\theta }{ tan\theta -cos\theta } \right) = \dfrac{12}{7} $$
$$sec \theta = \dfrac{5k }{ (4k)} = \dfrac{5}{4}$$ and $$cos \theta = \dfrac{4}{5}$$
Where k is any positive.
By pythagoras theorem:
$$AC^2 = AB^2 + BC^2$$
$$BC^2 = AC^2 - AB^2$$
$$= 25k^2 + 16k^2$$
$$ BC = 3k$$
Find $$ sin \theta,tan \theta$$ and $$cot \theta $$ using their definitions:
$$ sin \theta = \dfrac{ perpendicular}{hypotenuse }= \dfrac{3}{5}$$
$$ tan \theta = \dfrac{perpendicular}{base} = \dfrac{3}{4} $$
$$ cot \theta =\dfrac{ 1 }{tan \theta} = \dfrac{4}{3} $$
Now,
LHS $$= \left( \dfrac { sin\theta -2cos\theta }{ tan\theta -cot\theta } \right) $$
$$= \dfrac { \frac { 3 }{ 5 } -2\times \frac { 4 }{ 5 } }{ \frac { 3 }{ 4 } -\frac { 4 }{ 3 } } $$
$$LHS= \dfrac { \frac { 3-8 }{ 5 } }{ \frac { 9-16 }{ 12 } } $$
$$ LHS= \dfrac{12}{7}$$
$$LHS= RHS$$
If tan $$ \theta = \dfrac{20}{21} $$ ,show that $$ \left( \dfrac { 1-sin\theta +cos\theta }{ 1+sin\theta +cos\theta } \right) = \dfrac{3}{7} $$
$$ tan \theta = \dfrac{20 k}{21k} $$
Where k is any positive.
By pythagoras theorem.
$$AC^2 = AB^2 + BC^2 $$
$$ 441k^2 + 400 k^2$$
$$ AC = 29 k$$
Find $$sin \theta$$ and $$cos \theta $$ using their definitions.
$$ sin \theta = \dfrac{perpendicular }{ hypotenuse} = \dfrac{20}{29 }$$
$$ cos \theta = \dfrac{ base}{hypotenuse} = \dfrac{21}{29}$$
Now,
LHS $$ =\left( \dfrac { 1-sin\theta +cos\theta }{ 1+sin\theta +cos\theta } \right) $$
LHS $$ =\left( \dfrac { 1-sin\theta +cos\theta }{ 1+sin\theta +cos\theta } \right) $$
$$= \dfrac { 1-\frac { 20 }{ 20 } +\frac { 21 }{ 20 } }{ 1+\frac { 20 }{ 20 } +\frac { 21 }{ 20 } } $$
$$LHS= \dfrac{30}{70}$$
$$LHS=\dfrac{ 3}{7}$$
$$LHS=RHS$$
Hence proved
If tan $$ \theta = \dfrac{1}{ \sqrt 7}$$ show that $$ \dfrac{(cosec^2\theta - sec^2 \theta)}{cosec^2 \theta + sec^2 \theta)} = \dfrac{3}{4} $$
In a right $$ \triangle ABC $$, right-angled at $$B$$, if $$\tan A = 1,$$ then verify that, $$2 sin A. cos A = 1$$
Consider $$ \triangle ABC $$ to be right angled triangle at $$B.$$
angle $$C = 90$$ degree
Again, $$tan A =\dfrac {\sin A}{\cos A}$$
$$ sin A = cos A$$ .... using (1)
By Pythagoras theorem:
$$ AC^2 = BC^2 + AB^2 $$
$$AC^2 = 2BC^2$$
$$\left(\dfrac{AC}{BC}\right)^2 = 2\\$$
angle $$C = 90$$ degree
Given : $$tan A = 1$$ ...(1)
$$tan A = 1 = \dfrac{BC}{AB}$$
$$AB = BC$$
$$tan A = 1 = \dfrac{BC}{AB}$$
$$AB = BC$$
Again, $$tan A =\dfrac {\sin A}{\cos A}$$
$$ sin A = cos A$$ .... using (1)
By Pythagoras theorem:
$$ AC^2 = BC^2 + AB^2 $$
$$AC^2 = 2BC^2$$
$$\left(\dfrac{AC}{BC}\right)^2 = 2\\$$
or $$\dfrac{AC}{BC} = $$ $$ \sqrt 2 $$
$$ cosec\ A$$ $$ = \sqrt 2 $$
or $$\sin A = \dfrac 1{\sqrt2} $$
$$\cos A = \dfrac 1{\sqrt2} $$Now,
$$ 2 \sin A \cos A $$
$$ 2 \sin A \cos A $$
$$=2 \times \dfrac 1{\sqrt2} \times \dfrac 1 { \sqrt2 } $$
$$ = 2\times \dfrac 12 $$
$$= 1$$
= RHS
$$ = 2\times \dfrac 12 $$
$$= 1$$
= RHS
In a $$ \triangle ABC $$ angle B = 90 degree, AB = 12 cm and BC = 5 cm
Find (i) cos A (ii) cosec A (iii) cos C (iv) cosec C
From figure: $$ \triangle ABC is $$ a right angled triangle
$$AC^2 = BC^2 + AB^2$$
$$AC^2 = (5)^2 + (12)^2$$
$$AC^2 = 25 + 144$$
$$ AC^2 = 169 = (13)^2 $$
or $$AC = 13 $$
Now from figure,
$$i. \cos A = \dfrac{AB}{AC} =\dfrac{ 12}{13}$$
$$ii. \csc A = \dfrac{AC}{BC} = \dfrac{13}{5}$$
$$iii. \cos C = \dfrac{BC}{AC} = \dfrac{5}{13}$$
$$iv. \csc C = \dfrac{AC}{AB} = \dfrac{13}{12}$$
Hence, proved.
If 3 cot $$ \theta = 2 $$ ,show that $$ \left( \dfrac { 4sin\theta -3cos\theta }{ 2sin\theta +6cos\theta } \right) = \dfrac{1}{3} $$
Given : $$ 3 \cot \theta = 2 $$
or $$\cot \theta = \dfrac 23 $$
Where $$k$$ is any positive.
By Pythagoras theorem:
$$AC^2 = AB^2 + BC^2$$
Find $$\sin \theta$$ and $$\cos \theta $$ using their definitions:
$$ \cos \theta = \dfrac{perpendicular }{hypotenuse} = \dfrac 3 { \sqrt {13}} $$
Now,
LHS
$$= \left( \dfrac { 4sin\theta -cos\theta }{ 2sin\theta +6cos\theta } \right) =
\dfrac { 4\times \dfrac { 3 }{ \sqrt { 13 } } -3\times \dfrac { 2 }{ \sqrt { 13 } } }{ 2\times \dfrac { 3 }{ \sqrt { 13 } } +6\times \dfrac { 2 }{ \sqrt { 13 } } } $$
$$ = \dfrac { \dfrac { 12-6 }{ \sqrt { 13 } } }{ \dfrac { 6+12 }{ \sqrt { 13 } } } $$
$$ = \dfrac 13$$
= RHS
or $$\cot \theta = \dfrac 23 $$
Where $$k$$ is any positive.
By Pythagoras theorem:
$$AC^2 = AB^2 + BC^2$$
$$AC^2 = 2^2 + 3^2$$
$$AC =$$ $$ \sqrt {13} $$Find $$\sin \theta$$ and $$\cos \theta $$ using their definitions:
$$ \cos \theta = \dfrac{perpendicular }{hypotenuse} = \dfrac 3 { \sqrt {13}} $$
$$ \sin \theta = \dfrac{base }{hypotenuse} = \dfrac 2 { \sqrt {13}} $$
LHS
$$= \left( \dfrac { 4sin\theta -cos\theta }{ 2sin\theta +6cos\theta } \right) =
\dfrac { 4\times \dfrac { 3 }{ \sqrt { 13 } } -3\times \dfrac { 2 }{ \sqrt { 13 } } }{ 2\times \dfrac { 3 }{ \sqrt { 13 } } +6\times \dfrac { 2 }{ \sqrt { 13 } } } $$
$$ = \dfrac { \dfrac { 12-6 }{ \sqrt { 13 } } }{ \dfrac { 6+12 }{ \sqrt { 13 } } } $$
$$ = \dfrac 13$$
= RHS
If cot $$ \theta = 3/4,$$ show that
$$ \left( \frac { sec\theta -cos\theta }{ sec\theta +cosec\theta } \right) = \frac{1}{\sqrt{7}} $$
If sin $$ \theta = \dfrac34, $$ show that $$ \sqrt { \dfrac { cosec^ 2\theta -cot^ 2\theta }{ sec^ 2\theta -1 } } = \dfrac{\sqrt{7}}{3} $$.
Given: sin $$ \theta = \dfrac34 $$
or $$ sin \theta = \dfrac{3k}{4k} $$
Where $$k$$ is any positive.
By pythagoras theorem.
$$AC^2 = AB^2 + BC^2 $$
$$ 16k^2 = AB^2 + 9k^2$$
$$ AB = \sqrt 7 $$
Find $$ sec \theta$$ and $$cot \theta $$ using their definitions:
$$ sec \theta = \dfrac{hypotenuse}{base} = \dfrac4{\sqrt 7} $$
$$ cot \theta = \dfrac{base}{perpendicular} = \dfrac{\sqrt7} 3$$
$$ = \sqrt { \dfrac { \left( \dfrac { 4 }{ 3 } \right) ^ 2-\left( \dfrac { \sqrt { 7 } }{ 3 } \right) ^ 2 }{ \left( \dfrac { 4 }{ \sqrt { 7 } } \right) ^ 2-1 } } $$
or $$ sin \theta = \dfrac{3k}{4k} $$
Where $$k$$ is any positive.
By pythagoras theorem.
$$AC^2 = AB^2 + BC^2 $$
$$ 16k^2 = AB^2 + 9k^2$$
$$ AB = \sqrt 7 $$
Find $$ sec \theta$$ and $$cot \theta $$ using their definitions:
$$ sec \theta = \dfrac{hypotenuse}{base} = \dfrac4{\sqrt 7} $$
$$ cot \theta = \dfrac{base}{perpendicular} = \dfrac{\sqrt7} 3$$
Now,
LHS =
$$ \sqrt { \dfrac { cosec^ 2\theta -cot^ 2\theta }{ sec^ 2\theta -1 } } $$
LHS =
$$ \sqrt { \dfrac { cosec^ 2\theta -cot^ 2\theta }{ sec^ 2\theta -1 } } $$
$$ = \sqrt { \dfrac { \left( \dfrac { 4 }{ 3 } \right) ^ 2-\left( \dfrac { \sqrt { 7 } }{ 3 } \right) ^ 2 }{ \left( \dfrac { 4 }{ \sqrt { 7 } } \right) ^ 2-1 } } $$
$$ = \sqrt { \dfrac { \dfrac{16}9-\dfrac79 }{ { \dfrac{16}7-1 } } } $$
$$= \dfrac { \sqrt { 7 } }{ 3 } $$
= RHS
= RHS
If $$ cos \theta = \dfrac{3}{5} $$, show that $$ \dfrac { \left( sin\theta -cot\theta \right) }{ 2tan\theta } = \dfrac{3}{160} $$
Given : $$ \cos \theta = \dfrac{3}{5} $$
$$ \cos \theta = \dfrac{(3k)}{(5k)} = \dfrac{AC}{AB} $$
Where k is any positivity
By Pythagoras theorem:
$$AB^2 = BC^2 + AC^2 $$
$$BC = 4k$$
$$BC = 4k$$
Find $$ sin \theta \ \ tan \theta \ \ and \ \ cot \theta $$ using their definitions:
$$ sin \theta = \dfrac{perpendicular}{hypotenuse }= \dfrac{4}{5} $$
$$tan \theta = \dfrac{perpendicular}{base} = \dfrac{4}{3} $$
$$cot \theta = \dfrac{ 1}{tan \theta }= \dfrac{3}{4} $$
$$cot \theta = \dfrac{1}{tan \theta} = \dfrac{3}{4} $$
Now
LHS= $$ \dfrac { \left( sin\theta -cot\theta \right) }{ 2tan\theta } $$
= $$ \dfrac{4/5-3/4}{2(4/3)} $$
$$= \dfrac{3}{160}$$
$$LHS=RHS $$
If $$ tan \theta = 4/3 $$, show that $$(sin \theta + cos \theta) = 7/5 $$
In a $$ \triangle ABC $$, in which $$ \angle = 90^o , \angle ABC = \theta^o, BC = 21 $$ units, $$AB = 29$$ units, show that $$ (cos^2 \theta - sin^2 \theta ) = \dfrac{41}{841} $$
Draw a triangle using given instructions:
From figure : $$ \triangle ABC$$ is a right angled triangle
$$AB^2 = AC^2 + BC^2$$
$$(29)^2 = AC^2 + (21)^2$$
$$841 = AC^2 + 441$$
$$ AC^2 = 400$$
or $$AC = 20$$
Find $$\sin \theta$$ and $$\cos \theta $$
$$ sin \theta = \dfrac{AC}{AB} = \dfrac{20}{29}\\$$
$$ cos \theta = \dfrac{BC}{ AB} = \dfrac{21}{29} $$
Now :
LHS = $$ cos^2\theta - sin^2 \theta $$
$$= {\left(\dfrac{21}{29}\right)}^2 - {\left(\dfrac{20}{29}\right)}^2\\$$
$$ = \dfrac{41}{841}$$
= RHS
Hence proved.
From figure : $$ \triangle ABC$$ is a right angled triangle
$$AB^2 = AC^2 + BC^2$$
$$(29)^2 = AC^2 + (21)^2$$
$$841 = AC^2 + 441$$
$$ AC^2 = 400$$
or $$AC = 20$$
Find $$\sin \theta$$ and $$\cos \theta $$
$$ sin \theta = \dfrac{AC}{AB} = \dfrac{20}{29}\\$$
$$ cos \theta = \dfrac{BC}{ AB} = \dfrac{21}{29} $$
Now :
LHS = $$ cos^2\theta - sin^2 \theta $$
$$= {\left(\dfrac{21}{29}\right)}^2 - {\left(\dfrac{20}{29}\right)}^2\\$$
$$ = \dfrac{41}{841}$$
= RHS
Hence proved.
If sec $$ \theta = \dfrac{17}{8}, $$ verify that $$ \dfrac{3-4 sin^2 \theta}{4 cos^2 \theta - 3} = \dfrac{3- tan^2 \theta}{1 - 3tan^2 \theta} $$
Given : $$ sec \theta = 17/8 $$
or $$sec \theta = 17 k/8 k $$
Where k is any positive.
By pythagoras theorem:
$$AC^2= AB^2 + BC^2$$
$$BC^2= AC^2 - AB^2$$
$$BC^2= 289k^2 - 64k^2$$
or $$sec \theta = 17 k/8 k $$
Where k is any positive.
By pythagoras theorem:
$$AC^2= AB^2 + BC^2$$
$$BC^2= AC^2 - AB^2$$
$$BC^2= 289k^2 - 64k^2$$
$$BC^2=225 k^2$$
$$BC = 15 k$$
Find sin $$ \theta$$ and $$cos \theta $$using their definition:
$$ sin \theta = $$ $$\dfrac{perpendicular}{hypotenuse} = \dfrac{15}7$$
$$ cos \theta $$ $$= \dfrac{base }{hypotenuse} =\dfrac{ 15}8 $$
Now,
LHS
$$ \dfrac{ 3-4 sin^ 2 \theta }{ 4cos^ 2\theta -3 } $$
$$ \dfrac { 3-4\times \left( \dfrac { 15 }{ 17 } \right) ^ 2 }{ 4\times \left( \dfrac { 8 }{ 17 } \right) ^ 2-3 } =\dfrac { 3-\dfrac { 4\times 225 }{ 289 } }{ 4\times \dfrac { 64 }{ 289 } -3 } $$
$$= \dfrac{(867-900)}{(256-867)}$$
$$= \dfrac{33}{611}$$
RHS:
$$ \dfrac{3-tan^2\theta}{1-3tan^2\theta} $$
$$ \dfrac { 3-\dfrac { 225 }{ 64 } }{ 1-3\times \dfrac { 225 }{ 64 } } =\dfrac { \dfrac { 3\times 64-225 }{ 64 } }{ \dfrac { 64-3\times 225 }{ 64 } } $$
$$= \dfrac{(19-225)}{(64-675)}$$
$$=\dfrac{33}{611}$$
LHS = RHS
Verified.
$$BC = 15 k$$
Find sin $$ \theta$$ and $$cos \theta $$using their definition:
$$ sin \theta = $$ $$\dfrac{perpendicular}{hypotenuse} = \dfrac{15}7$$
$$ cos \theta $$ $$= \dfrac{base }{hypotenuse} =\dfrac{ 15}8 $$
Now,
LHS
$$ \dfrac{ 3-4 sin^ 2 \theta }{ 4cos^ 2\theta -3 } $$
$$ \dfrac { 3-4\times \left( \dfrac { 15 }{ 17 } \right) ^ 2 }{ 4\times \left( \dfrac { 8 }{ 17 } \right) ^ 2-3 } =\dfrac { 3-\dfrac { 4\times 225 }{ 289 } }{ 4\times \dfrac { 64 }{ 289 } -3 } $$
$$= \dfrac{(867-900)}{(256-867)}$$
$$= \dfrac{33}{611}$$
RHS:
$$ \dfrac{3-tan^2\theta}{1-3tan^2\theta} $$
$$ \dfrac { 3-\dfrac { 225 }{ 64 } }{ 1-3\times \dfrac { 225 }{ 64 } } =\dfrac { \dfrac { 3\times 64-225 }{ 64 } }{ \dfrac { 64-3\times 225 }{ 64 } } $$
$$= \dfrac{(19-225)}{(64-675)}$$
$$=\dfrac{33}{611}$$
LHS = RHS
Verified.
If $$3 \cot \theta = 4 $$, show that $$\dfrac{(1-\tan^2 \theta)}{(1+\tan^2 \theta)}=(\cos^2 \theta - \sin^2 \theta) $$.
Given: $$3 \cot \theta = 4 $$
or $$\cot \theta = \dfrac {4k} {3k} $$
Where $$k$$ is any positive.
By pythagoras theorem ;
$$AC^2 = AB^2 + BC^2 $$
$$= 16k^2 + 9k^2$$
$$AC = 5 k$$
Find $$\sin \theta$$ and $$\cos \theta $$ using their definition
Now,
LHS = $$ \dfrac{(1-tan^2 \theta )}{(1+tan^2 \theta )} \\$$
$$= \dfrac { 1-\left( \dfrac 34 \right) ^ 2 }{ 1+\left( \dfrac 3 4 \right) ^ 2 } \\$$
$$= \dfrac { 1-\dfrac 9{16} }{ 1+\dfrac 9{16} } =\dfrac { 7 }{ 16 } \times \dfrac { 16 }{ 25 } $$
$$= \dfrac{7}{25}$$
Again,
RHS = $$ (cos^2 \theta -sin^2 \theta ) $$
$$ = \left( \dfrac { 4 }{ 5 } \right) ^ 2-\left( \dfrac { 3 }{ 5 } \right) ^ 2 $$
$$= \dfrac{16}{25} - \dfrac9{25}\\$$
$$= \dfrac 7{25}$$
Therefore, RHS = LHS
Hence proved.
or $$\cot \theta = \dfrac {4k} {3k} $$
Where $$k$$ is any positive.
By pythagoras theorem ;
$$AC^2 = AB^2 + BC^2 $$
$$= 16k^2 + 9k^2$$
$$AC = 5 k$$
Find $$\sin \theta$$ and $$\cos \theta $$ using their definition
$$ \cos \theta = \dfrac{perpendicular }{hypotenuse} = \dfrac 4 5 $$
$$ \sin \theta = \dfrac{base }{hypotenuse} = \dfrac 35 $$
Now,
LHS = $$ \dfrac{(1-tan^2 \theta )}{(1+tan^2 \theta )} \\$$
$$= \dfrac { 1-\left( \dfrac 34 \right) ^ 2 }{ 1+\left( \dfrac 3 4 \right) ^ 2 } \\$$
$$= \dfrac { 1-\dfrac 9{16} }{ 1+\dfrac 9{16} } =\dfrac { 7 }{ 16 } \times \dfrac { 16 }{ 25 } $$
$$= \dfrac{7}{25}$$
Again,
RHS = $$ (cos^2 \theta -sin^2 \theta ) $$
$$ = \left( \dfrac { 4 }{ 5 } \right) ^ 2-\left( \dfrac { 3 }{ 5 } \right) ^ 2 $$
$$= \dfrac{16}{25} - \dfrac9{25}\\$$
$$= \dfrac 7{25}$$
Therefore, RHS = LHS
Hence proved.
Without using trigonometric tables, prove that:
$$\tan ^{ 2 }{ { 66 }^{ o } } -\cot ^{ 2 }{ { 24 }^{ o } } =0$$
Without using trigonometric tables, prove that:
$$\left( \sin { { 65 }^{ o } } +\cos { { 25 }^{ o } } \right) \left( \sin { { 65 }^{ o } } -\cos { { 25 }^{ o } } \right) =0$$
Without trigonometric tables, prove that:
$$\cos { { 54 }^{ o } } \cos { { 36 }^{ o } } -\sin { { 54 }^{ o } } \sin { { 36 }^{ o } } =0\quad $$
Without using trigonometric tables, prove that:
$$\sin ^{ o }{ { 48 }^{ o } } +\sin ^{ o }{ { 42 }^{ o } } =1$$
Without using trigonometric tables, prove that:
$$co\sec ^{ 2 }{ { 72 }^{ o } } -\tan ^{ 2 }{ { 18 }^{ o } } =1$$
Without using trigonometric tables, prove that:
$$\cos ^{ 2 }{ { 57 }^{ o } } -\sin ^{ 2 }{ { 33 }^{ o } } =0$$
Without trigonometric tables, prove that:
$$\sin { { 53 }^{ o } } \cos { { 37 }^{ o } } +\cos { { 53 }^{ o } } \sin { { 37 }^{ o } } =1$$
Without trigonometric tables, prove that:
$$\sec { { 70 }^{ o } } \sin { { 20 }^{ o } } +\cos { { 20 }^{ o } } co\sec { { 70 }^{ o } } =2$$
Without using trigonometric tables, prove that:
$$\cos ^{ 2 }{ { 75 }^{ o } } +\cos ^{ 2 }{ { 15 }^{ o } }=1 $$
Without trigonometric tables, prove that:
$$\sin { { 35 }^{ o } } \sin { { 55 }^{ o } } -\cos { { 35 }^{ o } } \cos { { 55 }^{ o } } =0$$
Without trigonometric tables, prove that:
$$\left( \sin { { 72 }^{ o } } +\cos { { 18 }^{ o } } \right) \left( \sin { { 72 }^{ o } } -\cos { { 18 }^{ o } } \right) =0$$
Prove that:$$\sec^{2}\theta \textrm{cosec}^{2}\theta = \tan^{2}\theta + \cot^{2}\theta + 2$$
Prove the following statement:
$$(\sec A + \cos A) (\sec A - \cos A) = \tan^{2}A + \sin^{2}A$$.
Prove that
$$\cfrac { \cos { { 80 }^{ o } } }{ \sin { { 10 }^{ o } } } +\cos { { 59 }^{ o } } co\sec { { 31 }^{ o } } =2$$
Prove the following statements.
$$\dfrac {1 + \tan^{2}A}{1 + \cot^{2}A} = \dfrac {\sin^{2}A}{\cos^{2}A}$$.
Prove that,
$$\dfrac {\sec A - \tan A}{\sec A + \tan A} = 1 - 2\sec A \tan A + 2\tan^{2}A$$.
Without trigonometric tables, prove that:
$$\tan { { 48 }^{ o } } \tan { { 23 }^{ o } } \tan { { 42 }^{ o } } \tan { { 67 }^{ o } } =1$$
Prove that
$$\cfrac { \sin { { 70 }^{ o } } }{ \cos { { 20 }^{ o } } } +\cfrac { co\sec { { 20 }^{ o } } }{ \sec { { 70 }^{ o } } } -2\cos { { 70 }^{ o } } co\sec { { 20 }^{ o } } =0$$
Prove that
$$\cfrac { 2\sin { { 68 }^{ o } } }{ \cos { { 22 }^{ o } } } -\cfrac { 2\cot { { 15 }^{ o } } }{ 5\tan { { 75 }^{ o } } } -\cfrac { 3\tan { { 45 }^{ o } } \tan { { 20 }^{ o } } \tan { { 40 }^{ o } } \tan { { 50 }^{ o } } \tan { { 70 }^{ o } } }{ 5 } =1\quad $$
Prove the following statements.
$$\sqrt {co\sec^{2}A - 1} = \cos A\cdot \csc A$$.
Prove the following statements.
$$\tan^{2}A - \sin^{2}A = \sin^{4} A \sec^{2}A$$.
Prove that following identities, where the angles involved are acute angles for which the trigonometric ratios as defined: $$\left ( 1-\tan ^{2}A \right )/\left ( \cot ^{2}A-1 \right )=\tan ^{2}A$$.
If $$\tan A=1/\sqrt{3}$$, find all other trigonometric ratios of angle $$A$$.
Prove that following identities, where the angles involved are acute angles for which the trigonometric ratios as defined: $$\cos \theta /\left ( 1-\tan \theta \right )-\sin ^{2}\theta /\left ( \cos \theta -\sin \theta \right )=\cos \theta +\sin \theta $$.
Prove that:
$$\left (\dfrac {1}{\sec^{2}\alpha - \cos^{2}\alpha} + \dfrac {1}{\text{cosec}^{2}\alpha - \sin^{2}\alpha}\right ) \cos^{2} \alpha \sin^{2}\alpha = \dfrac {1 - \cos^{2} \alpha \sin^{2} \alpha}{2 + \cos^{2} \alpha \sin^{2} \alpha}$$.
Without using trigonometric tables, evaluate the following: $$\left ( \sin 29^{0}/cosec61^{0} \right )+2\cot 8^{0}\cot 17^{0}\cot 45^{0}\cot 73^{0}\cot 82^{0}-3\left ( \sin ^{2}38^{0}+\sin ^{2}52^{2} \right )$$.
Without using trigonometric tables, evaluate the following: $$\frac{cosec^{2}\left ( 90-\theta \right )-\tan ^{2}\theta }{2\left ( \cos ^{2}48^{0}+\cos ^{2}42^{0} \right )}-\frac{2\tan ^{2}30^{0}\sec ^{2}52^{0}\sin ^{2}38^{0}}{cosec^{2}70^{0}-\tan ^{2}20^{0}}$$.
Show that $$\dfrac {4}{3} \cot^{2} 30^{\circ} + 3\sin^{2} 60^{\circ} - 2cosec^{2} 60^{\circ} - \dfrac {3}{4} \tan^{2} 30^{\circ} = 3\dfrac {1}{3}$$.
Verify that
$$\sin^{2} 30^{\circ} + \sin^{2} 45^{\circ} + \sin^{2} 60^{\circ} = \dfrac {3}{2}$$.
Prove the following statement.
$$\dfrac {\cos A cosec A - \sin A \sec A}{\cos A + \sin A} = cosec A - \sec A$$.
Show that
$$ \tan 48^{\circ} \tan 16^{\circ} \tan 42^{\circ} \tan 74^{\circ} = 1 $$
Prove the following identities:
$$\dfrac{sec A -1}{secA +1} = \dfrac{1-cosA}{1+ cosA}$$
Show that
$$ \cos 36^{\circ} \cos 54^{\circ} - \sin 36^{\circ} \sin 54^{\circ} = 0 $$
Prove the following identities:
$$\dfrac{1+sinA}{1-sinA}= \dfrac{cosec A + 1}{cosec A -1}$$
Evaluate:
$$3 \dfrac{sin 72^\circ}{cos 18^\circ}- \dfrac{sec 32^\circ}{cosec58^\circ}$$
Evaluate
$$ \sin 15^{\circ} \sec 75^{\circ} $$
Evaluate
$$ \tan 26^{\circ} \tan 64^{\circ} $$
If $$\sec \theta =\cfrac{13}{5}$$, show that $$\cfrac { 2\sin { \theta } -3\cos { \theta } }{ 4\sin { \theta } -9\cos { \theta } } =3$$
we know that
$$\sec { \theta } =\cfrac { hypotenuse }{ base } $$
$$\sec { \theta } =\cfrac { 13 }{ 5 } \Rightarrow \cfrac { H }{ B } =\cfrac { 13 }{ 5 } \Rightarrow \cfrac { AC }{ BC } =\cfrac { 13 }{ 5 } \quad \quad $$
Let $$ BC=5k$$ and $$AC=13k$$
where $$k$$ is any positive integer
In right angled $$\triangle ABC$$ we have
$$\Rightarrow { \left( AB \right) }^{ 2 }+{ \left( BC \right) }^{ 2 }={ \left( AC \right) }^{ 2 }\Rightarrow { \left( AB \right) }^{ 2 }+{ \left( 5k \right) }^{ 2 }={ \left( 13k \right) }^{ 2 }\Rightarrow { \left( AB \right) }^{ 2 }={ 169k }^{ 2 }+{ 25k }^{ 2 }\quad \quad $$ (Pythagoras theorem)
$${ \left( AB \right) }^{ 2 }={ 144k }^{ 2 }\Rightarrow AB=\pm 12k$$
(taking positive sqaureroot as side cannot be negative)
Now we have to find the other trigonometric ratios
$$\sin { \theta } =\cfrac { Perpendicular }{ hypotenuse } =\cfrac { AB }{ AC } =\cfrac { 12k }{ 13k } =\cfrac { 12 }{ 13 } ;\cos { \theta } =\cfrac { base }{ hypotenuse } =\cfrac { BC }{ AC } =\cfrac { 5k }{ 13k } =\cfrac { 5 }{ 13 } \quad $$
$$LHS=\cfrac { 2\sin { \theta } -3\cos { \theta } }{ 4\sin { \theta } -9\cos { \theta } } =\cfrac { 2\left( \cfrac { 12 }{ 13 } \right) -3\left( \cfrac { 5 }{ 13 } \right) }{ 4\left( \cfrac { 12 }{ 13 } \right) -9\left( \cfrac { 5 }{ 13 } \right) } =\cfrac { 9 }{ 3 } =3=RHS$$
$$\sec { \theta } =\cfrac { hypotenuse }{ base } $$
$$\sec { \theta } =\cfrac { 13 }{ 5 } \Rightarrow \cfrac { H }{ B } =\cfrac { 13 }{ 5 } \Rightarrow \cfrac { AC }{ BC } =\cfrac { 13 }{ 5 } \quad \quad $$
Let $$ BC=5k$$ and $$AC=13k$$
where $$k$$ is any positive integer
In right angled $$\triangle ABC$$ we have
$$\Rightarrow { \left( AB \right) }^{ 2 }+{ \left( BC \right) }^{ 2 }={ \left( AC \right) }^{ 2 }\Rightarrow { \left( AB \right) }^{ 2 }+{ \left( 5k \right) }^{ 2 }={ \left( 13k \right) }^{ 2 }\Rightarrow { \left( AB \right) }^{ 2 }={ 169k }^{ 2 }+{ 25k }^{ 2 }\quad \quad $$ (Pythagoras theorem)
$${ \left( AB \right) }^{ 2 }={ 144k }^{ 2 }\Rightarrow AB=\pm 12k$$
(taking positive sqaureroot as side cannot be negative)
Now we have to find the other trigonometric ratios
$$\sin { \theta } =\cfrac { Perpendicular }{ hypotenuse } =\cfrac { AB }{ AC } =\cfrac { 12k }{ 13k } =\cfrac { 12 }{ 13 } ;\cos { \theta } =\cfrac { base }{ hypotenuse } =\cfrac { BC }{ AC } =\cfrac { 5k }{ 13k } =\cfrac { 5 }{ 13 } \quad $$
$$LHS=\cfrac { 2\sin { \theta } -3\cos { \theta } }{ 4\sin { \theta } -9\cos { \theta } } =\cfrac { 2\left( \cfrac { 12 }{ 13 } \right) -3\left( \cfrac { 5 }{ 13 } \right) }{ 4\left( \cfrac { 12 }{ 13 } \right) -9\left( \cfrac { 5 }{ 13 } \right) } =\cfrac { 9 }{ 3 } =3=RHS$$
Evaluate
$$ \dfrac{\tan 36^{\circ}}{\cot 54^{\circ}} $$
$$2 \dfrac{tan57^\circ}{cot 33^\circ} - \dfrac{cot 70^\circ}{tan20^\circ} - \sqrt{2} cos 45^\circ$$
$$\dfrac{cot^2 41^\circ}{tan^2 49^\circ} - 2 \dfrac{sin^2 75^\circ}{cos^2 15^\circ} $$
Find the value of:
$$\dfrac{3 sin 72^\circ}{ cos 18^\circ} - \dfrac{sec 32^\circ}{cosec 58^\circ}$$
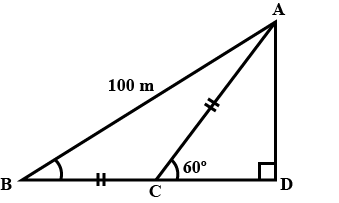
Find $$AD$$(Refer figure)
$$\dfrac{5 \ sin 66^\circ}{cos 24^\circ}- \dfrac{2 \ cot 85^\circ}{tan 5^\circ}$$
$$sin 27^\circ \ sin 63^\circ- cos 63^\circ \ cos 27^\circ$$
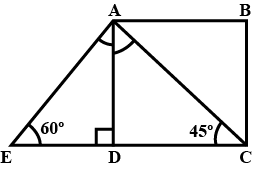
In the given figure, $$AB$$ and $$EC$$ are parallel to each other. Sides $$AD$$ and $$BC$$ are $$2\ cm$$ each and are perpendicular to $$AB$$.
Given that $$\angle AED = 60^{\circ}$$ and $$\angle ACD = 45^{\circ}$$. Calculate $$AB$$.
Find the length of $$AB$$.
Evaluate:
$$sec 26^\circ \ sin 64^\circ + \dfrac{cosec 33^\circ}{sec 57^\circ}$$
Evaluate:
$$2 \left( \dfrac{tan 35^\circ}{cot 55^\circ} \right)^2+ \left(\dfrac{cot 55^\circ}{tan 35^\circ} \right)^2 - 3 \left( \dfrac{sec 40^\circ}{cosec 50^\circ} \right)$$
Find $$AD$$.(Refer figure)
Evaluate: $$\dfrac{\cos 22^{0}}{\sin68^{0}}$$
Find $$AD$$.(Refer figure)
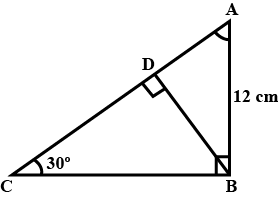
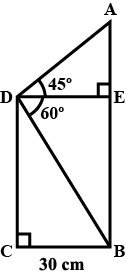
Find $$BC$$.(Refer figure)
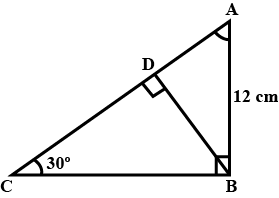
Refer given figure, Find $$AB$$ and $$BC$$
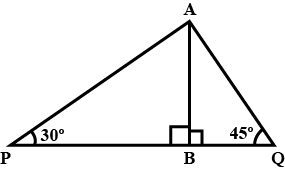
Find $$PQ$$, if $$AB = 150\ m, \angle P = 30^{\circ}$$ and $$\angle Q = 45^{\circ}$$.
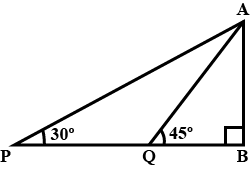
Refer given figure, Find $$AB$$ and $$BC$$.
Find $$PQ$$, if $$AB = 150\ m, \angle P = 30^{\circ}$$ and $$\angle Q = 45^{\circ}$$.
In the given figure, $$AB$$ and $$EC$$ are parallel to each other. Sides $$AD$$ and $$BC$$ are $$2\ cm$$ each and are perpendicular to $$AB$$.
Given that $$\angle AED = 60^{\circ}$$ and $$\angle ACD = 45^{\circ}$$. Calculate: $$AE$$.
In the given figure, $$AB$$ and $$EC$$ are parallel to each other. Sides $$AD$$ and $$BC$$ are $$2\ cm$$ each and are perpendicular to $$AB$$.
Given that $$\angle AED = 60^{\circ}$$ and $$\angle ACD = 45^{\circ}$$. Calculate $$AC$$.
Find $$AC$$.(Refer figure)
Evaluate:
$$\dfrac{\cos55^{0}}{\sin35^{0}}+\dfrac{\cot35^{0}}{\tan55^{0}}$$
Evaluate:
$$\dfrac{\cot54^{0}}{\tan36^{0}}+\dfrac{\tan20^{0}}{\cot70^{0}}-2$$
Evaluate:
$$\sin42^{0}\sin48^{0}-\cos42^{0}\cos48^{0}$$
Show that:
$$\sin42^{0}\sec48^{0}+\cos42^{0}cosec48^{0}=2$$
Evaluate:
$$\dfrac{2\tan53^{0}}{\cot37^{0}}-\dfrac{\cot80^{0}}{\tan10^{0}}$$
Evaluate: $$\dfrac{\sec75^{0}}{cosec15^{0}}$$
Evaluate:
$$3\dfrac{\sin72^{0}}{\cos18^{0}}-\dfrac{\sec32^{0}}{cosec58^{0}}$$
Show that:
$$\tan10^{0}\tan15^{0}\tan75^{0}\tan80^{0}=1$$
Evaluate:
$$\dfrac{\sin80^{0}}{\cos10^{0}}+\sin59^{0}\sec31^{0}$$
Evaluate: $$\dfrac{\tan47^{0}}{\cot43^{0}}$$
What is the meaning of trigonometry?
Evaluate:
$$2\dfrac{\tan57^{0}}{\cot33^{0}}-\dfrac{\cot70^{0}}{\tan20^{0}}-\sqrt{2}\cos45^{0}$$
Find the value of the following :
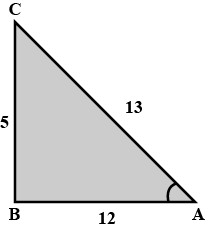
$$\dfrac{\cos 37^o}{\sin 53^o}$$
Evaluate :
$$ cos 48^0 - sin 42^0 $$
Find the value of the following :
$$\dfrac{\cos 19^o}{\sin 71^o}$$
Find the value of the following :
$$\cot 34^o- \tan 56^o$$
Evaluate:
$$\dfrac{\cos70^{0}}{\sin20^{0}}+\dfrac{\cos59^{0}}{\sin31^{0}}-8\sin^{2}30^{0}$$
Find the value of the following :
$$\dfrac{\tan 10^o}{\cot 80^o}$$
Evaluate:
$$\left( \dfrac{\sin 27^o}{\cos 63^o} \right)^2 + \left( \dfrac{\cos 63^o}{\sin 27^o}\right)^2$$
Prove that
$$ \sin \theta \, cosec \theta + \cos \theta \sec \theta = 2 $$.
Solve:
$$\sqrt {\dfrac {\sec \theta +1}{\sec \theta -1}}=\cot \theta +\csc \theta $$
Find the value of the following :
$$ \dfrac{\sin 36^o}{\cos 54^o} - \dfrac{\sin 54^o}{\cos 36^o}$$
Evaluate:
$$\sin 70^o \sin 20^o - \cos 20^o \cos 70^o$$
Evaluate:
$$\dfrac{2 \cos 67^o}{\sin 23^o}- \dfrac{\tan 40^o}{\cot 50^o}- \cos 60^o$$
Evaluate:
$$\left( \dfrac{\sin 35^o}{\cos 55^o} \right)^2 + \left( \dfrac{\cos 55^o}{\sin 35^o}\right)^2 -2 \cos 60^o$$
Prove :
$$\tan \theta + \tan \left( {{{90}^ \circ } - \theta } \right) = \sec \theta \sec \left( {{{90}^ \circ } - \theta } \right)$$
If $$\displaystyle \frac {9x}{\cos\theta}+\frac {5y}{\sin\theta}=56$$ and $$\displaystyle \frac {9x \sin\theta}{\cos^2\theta}-\cfrac {5y \cos\theta}{\sin^2\theta}=0$$, then the value of $$[(9x)^{2/3}+(5y)^{2/3}]^3$$ is
Express the trigonometric ratios $$\sin A, \sec A$$ and $$\tan A$$ in terms of $$\cot A$$.
If $$\text{cosec} \theta -\sin \theta =m$$ and $$\sec \theta - \cos \theta =n$$, then find the value of $$(m^{2}n)^{2/3} + (mn^{2})^{2/3}. $$
Class 10 Maths Extra Questions
- Areas Related To Cricles Extra Questions
- Arithmetic Progressions Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Introduction To Trigonometry Extra Questions
- Pair Of Linear Equations In Two Variables Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadratic Equations Extra Questions
- Real Numbers Extra Questions
- Some Applications Of Trigonometry Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions