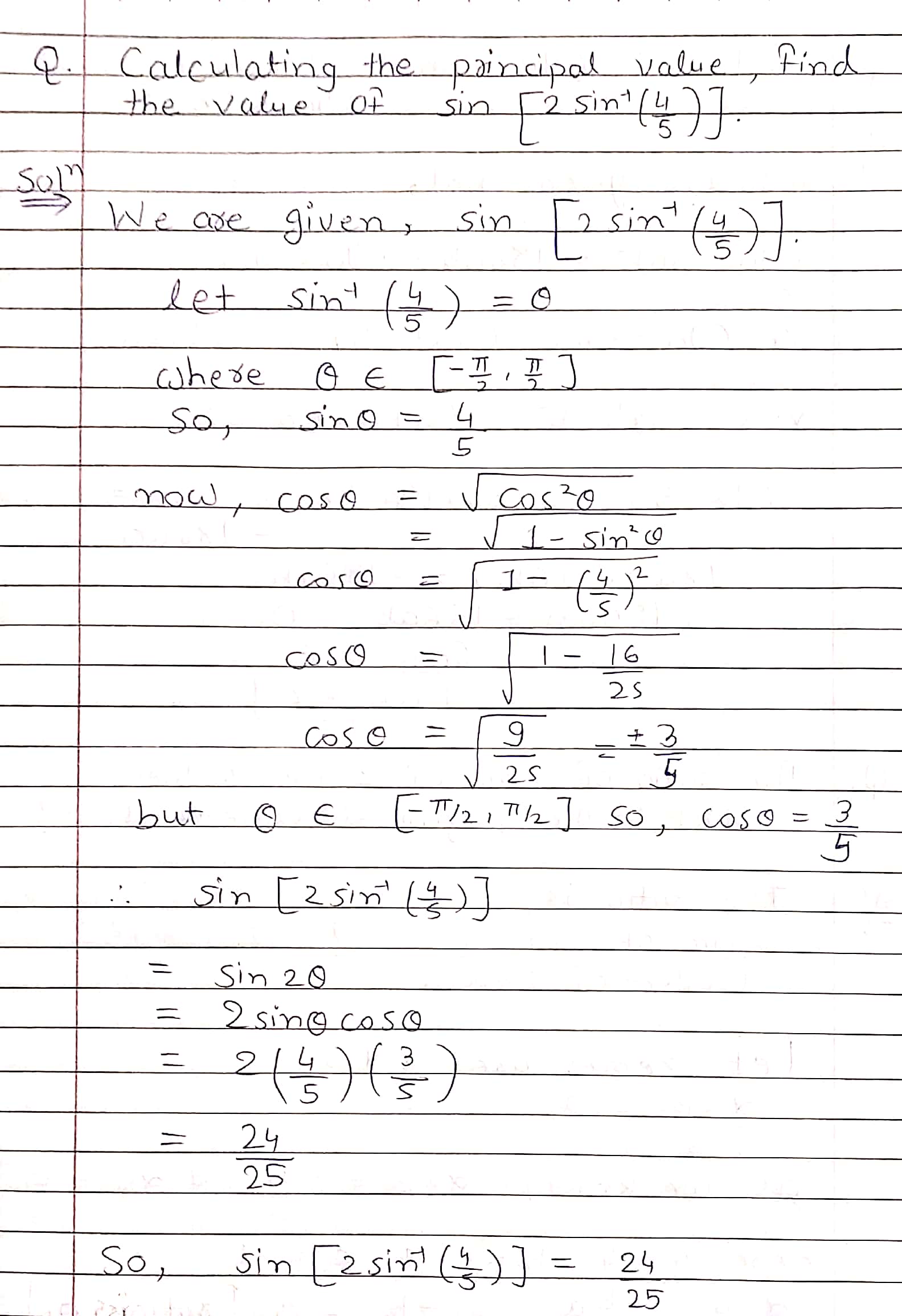Inverse Trigonometric Functions - Class 12 Engineering Maths - Extra Questions

$$\sin^{-1} x + \cos^{-1} x =$$ ________

$$\sin^{-1} x + \cos^{-1} x = \cfrac{\pi}{2}$$ when $$x \in [-1,1]$$


If $$xy < 1$$, $$\tan ^{ -1 }{ x } +\tan ^{ -1 }{ y } =$$ _______.

Let $$\theta = \tan^{-1}x + \tan^{-1}y$$
Taking $$\tan$$ on both sides,
$$\tan \theta$$ $$=\tan(\tan^{-1}x+\tan^{-1}y)\\=\cfrac{\tan(\tan^{-1}x)+\tan(\tan^{-1}y)}{1-\tan(\tan^{-1}x)\tan(\tan^{-1}y)}\\=\cfrac{x+y}{1-xy}$$
Therefore, $$\theta = \tan^{-1}\left(\dfrac{x+y}{1-xy}\right)$$


Prove that $$\tan ^{ -1 }{ (1) } +\tan ^{ -1 }{ (2) } +\tan ^{ -1 }{ (3) } =\pi $$

Let  $$\tan^{-1}(1)=x$$
$$\Rightarrow 1=\tan x$$

Let  $$\tan^{-1}(2)=y$$
$$\Rightarrow 2=\tan y$$

Let  $$\tan^{-1}(3)=z$$
$$\Rightarrow 3=\tan z$$

$$\tan \left ( x+y+z \right )=\cfrac{\tan x+\tan y+\tan z-\tan x.\tan y.\tan z}{1-\tan x.\tan y-\tan x.\tan z-\tan y.\tan z}$$

$$=\cfrac{1+2+3-1\times 2\times 3}{1-1\times 2-1\times 3-2\times 3}$$

$$=0$$

$$\Rightarrow x+y+z=\pi $$

 $$\tan^{-1}(1)+\tan^{-1}(2)+\tan^{-1}(3)=\pi $$

(  $$x+y+z$$  cannot be equal to zero, because
 $$\tan^{-1}(1)+\tan^{-1}(2)+\tan^{-1}(3)$$ will have some value greater than zero )


If $$f : \left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right) \rightarrow (-\infty, \infty)$$ is defined by $$f(x) = \tan x$$, then $$f^{-1}( \sqrt{3}) =$$

Given, $$f : \left(-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right) \rightarrow (-\infty, \infty)$$ is defined by $$f(x)=\tan x$$.
This function $$f(x)$$ is one-one and onto in the given domain and range.
So it is invertible and and the inverse is defined by $$f^{-1}(y)=\tan^{-1}y$$ for $$y\in (-\infty,\infty)$$.
So $$f^{-1}(\sqrt{3})=\tan^{-1}(\sqrt{3})=\dfrac{\pi}{3}$$. [ Since $$\tan 60^o=\sqrt{3}$$].


If $${\sin ^{ - 1}}\sqrt {1 + x + {x^2}}  + {\tan ^{ - 1}}\sqrt {x + {x^2}}  = \dfrac{\pi }{2}$$
$$then\,x = $$

$${\tan ^{ - 1}}\sqrt {{x^2} + x}  + {\sin ^{ - 1}}\sqrt {{x^2} + x + 1}  = \pi /2 \to (i)$$
$${\tan ^{ - 1}}\sqrt {{x^2} + x}  = \theta $$
$$\sqrt {{x^2} + x}  = \tan \theta $$
$$\sec \theta  = \sqrt {1 + {{\tan }^2}\theta } $$
$$ = \sqrt {1 + {x^2} + x} $$
$$\cos \theta  = \dfrac{1}{{\sqrt {1 + {x^2} + x} }}$$
$${\cos ^{-1}}\left( {\dfrac{1}{{\sqrt {1 + {x^2} + x} }}} \right) + {\sin ^{ - 1}}\left( {\sqrt {{x^2} + x + 1} } \right) = \pi /2$$
$${\cos ^{ - 1}}\alpha  + {\sin ^{ - 1}}\alpha  = \dfrac{\pi}{2}$$ is possible when,
$$\dfrac{1}{{\sqrt {1 + {x^2} + x} }} = \sqrt {{x^2} + x + 1} $$
$${x^2} + x + 1 = 1$$
$${x^2} + x = 0$$
$$x(x + 1) = 0$$
$$x = 0$$, $$x = 1$$


Simplify  $$\sin (\sin^{-1}(\dfrac {1}{5})+\cos^{-1}(x))=1$$

$$\begin{array}{l} \sin  \left( { { { \sin   }^{ -1 } }\dfrac { 1 }{ 5 }  } \right) +{ \cos ^{ -1 }  }x=1 \\ \Rightarrow \dfrac { 1 }{ 5 } +{ \cos ^{ -1 }  }x=1 \\ \Rightarrow { \cos ^{ -1 }  }x=1-\dfrac { 1 }{ 5 }  \\ \Rightarrow { \cos ^{ -1 }  }x=\dfrac { 4 }{ 5 }  \\ x=\cos  \dfrac { 4 }{ 5 }  \end{array}$$


Solve $$\sin^{-1}\sqrt {x}$$

$$\int {{{\sin }^{ - 1}}\sqrt x } $$
putting $$x=t^2$$
$$dx=2tdt$$
$$ =2 \int {{{\sin }^{ - 1}}t \times tdt} $$
Integrating by parts taking $$\sin ^{-1}t$$ as first function.
$$ = 2\left[ {{{\sin }^{ - 1}}t \times \dfrac{{{t^2}}}{2} - \int {\dfrac{1}{{\sqrt {1 - {t^2}} }} \times \dfrac{{{t^2}}}{2}dt} } \right]$$
$$= {t^2}{\sin ^{ - 1}}t + \int {\frac{{1 - {t^2} + 1}}{{\sqrt {1 - {t^2}} }}dt}  = {t^2}{\sin ^{ - 1}}t + \int {\sqrt {1 - {t^2}} dt}  - \int {\dfrac{{dt}}{{\sqrt {1 - {t^2}} }}} $$
$$= {t^2}{\sin ^{ - 1}}t + \dfrac{t}{2}\sqrt {1 - {t^2}}  + \dfrac{1}{2}{\sin ^{ - 1}}t - {\sin ^{ - 1}}t + C$$
$$ = {t^2}{\sin ^{ - 1}}t + \dfrac{t}{2}\sqrt {1 - {t^2}}  - \dfrac{1}{2}{\sin ^{ - 1}}t + C$$
$$ = x{\sin ^{ - 1}}\sqrt x  + \dfrac{{\sqrt x }}{2}\sqrt {1 - x}  - \dfrac{1}{2}{\sin ^{ - 1}}\sqrt x  + C$$



If $$ \tan^{-1} \left (\dfrac{1}{2i^2}\right) = t $$, then $$\tan t$$ equals 

$$\sum_{i=1}^{\infty }\tan^{-1}\left ( \dfrac{1}{2i^2} \right )=t$$

$$\tan^{-1}\left ( \dfrac{1}{2i^2} \right )=t$$

$$\Rightarrow \tan t=\left ( \dfrac{1}{2i^2} \right )=\dfrac{-1}{2}$$



Prove $$\tan^{-1} \dfrac{3}{4} + \tan^{-1} \dfrac{3}{5} - \tan^{-1} \dfrac{8}{19} = \dfrac{\pi}{4}$$.

Formula to be used:
$$\tan^{-1}a+\tan^{-1}b+\tan^{-1}c=\tan^{-1}\left [ \dfrac {a+b+c-abc}{1-ab-bc-ca} \right ]$$

$$\tan^{-1}\dfrac{3}{4}+\tan^{-1}\dfrac{3}{5}+\tan^{-1}\dfrac{8}{19}=\tan^{-1}\left [ \dfrac {\dfrac{3}{4}+\dfrac{3}{5}+\dfrac{8}{19}-\dfrac{3}{4}\dfrac{3}{5}\dfrac{8}{19}}{1-\dfrac{3}{4}\dfrac{3}{5}-\dfrac{3}{5}\dfrac{8}{19}-\dfrac{8}{19}\dfrac{3}{4}} \right ]$$

$$\tan^{-1}\dfrac{3}{4}+\tan^{-1}\dfrac{3}{5}+\tan^{-1}\dfrac{8}{19}=\tan^{-1}\left [ \dfrac {\dfrac{425}{380}} {\dfrac{425}{380}}  \right ]$$

$$\tan^{-1}\dfrac{3}{4}+\tan^{-1}\dfrac{3}{5}+\tan^{-1}\dfrac{8}{19}=\tan^{-1}1$$

$$\tan^{-1}\dfrac{3}{4}+\tan^{-1}\dfrac{3}{5}+\tan^{-1}\dfrac{8}{19}=\dfrac{\pi}{4}$$



Evaluate : $$\cos \left[ {{\cos }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)+\dfrac{\pi
}{6} \right] $$

Consider the given expression.

$$ \Rightarrow \cos \left[ {{\cos }^{-1}}\left( -\dfrac{\sqrt{3}}{2} \right)+\dfrac{\pi }{6} \right] $$

$$ \Rightarrow \cos \left[ {{\cos }^{-1}}\left( \cos \dfrac{5\pi }{6} \right)+\dfrac{\pi }{6} \right] $$

$$ \Rightarrow \cos \left[ \dfrac{5\pi }{6}+\dfrac{\pi }{6} \right] $$

$$ \Rightarrow \cos \left( \pi  \right) $$

$$ \Rightarrow -1 $$

 

Hence, this is the required result.


If $${\sin ^{ - 1}}x = \dfrac{\pi }{5}$$, for some $$x \in \left( { - 1,1} \right)$$, then find the value of $${\cos ^{ - 1}}x$$.

We have,

$${{\sin }^{-1}}x=\dfrac{\pi }{5}$$    …….. (1)

 

We know that

$${{\sin }^{-1}}x+{{\cos }^{-1}}x=\dfrac{\pi }{2}$$

 

From equation (1), we get

$$ \dfrac{\pi }{5}+{{\cos }^{-1}}x=\dfrac{\pi }{2} $$

$$ {{\cos }^{-1}}x=\dfrac{\pi }{2}-\dfrac{\pi }{5} $$

$$ {{\cos }^{-1}}x=\dfrac{5\pi -2\pi }{10} $$

$$ {{\cos }^{-1}}x=\dfrac{3\pi }{10} $$

 

Hence, this is the answer.



Solve $${\sin ^{ - 1}}\left( {\cos x} \right)$$

Let,

  $$ y={{\sin }^{-1}}\left( \cos x \right) $$

 $$ \Rightarrow y={{\sin }^{-1}}\sin \left( \dfrac{\pi }{2}-x \right) $$

 $$ \Rightarrow y=\dfrac{\pi }{2}-x $$

Hence, this is the answer.


Evaluate: $$\tan^{-1}\sqrt{3}-\sec^{-1}(-2)+cosec^{-1}\dfrac{2}{\sqrt{3}}$$.

$$\tan^{-1} \sqrt{3} - \sec^{-1} (-2) + cosec^{-1} \cfrac{2}{\sqrt3}$$
$$\cfrac{\pi}{3} -\cfrac{2\pi}{3}+\cfrac{\pi}{3}$$
$$\implies 0$$


Prove that $$\displaystyle \sin \cot^{-1} \tan \cos^{-1} x = \sin cosec^{-1} \cot \tan^{-1} x = x$$ where $$\displaystyle x \: \epsilon \: \left ( 0, \: 1 \right ]$$

Let $$x=cos\theta$$. where $$cos\theta\epsilon(0,1]$$
Hence $$\theta\epsilon [0,\dfrac{\pi}{2})\cup(\dfrac{3\pi}{2},2\pi]$$.
Then
$$sin(cot^{-1}(tan(cos^{-1}(x))))$$
$$=sin(cot^{-1}(tan(cos^{-1}(cos\theta))))$$
$$=sin(cot^{-1}(tan\theta))$$
$$=sin(\dfrac{\pi}{2}-tan^{-1}(tan\theta))$$

$$=sin(\dfrac{\pi}{2}-\theta)$$

$$=cos\theta=x$$ ...(i)
Similarly 
$$sin(cosec^{-1}(cot(tan^{-1}x)))$$
Let $$x=tan\theta$$. where $$tan\theta\epsilon (0,1]$$
Hence $$\theta\epsilon (0,\dfrac{\pi}{4}]\cup(\pi,\dfrac{5\pi}{4}]$$
Then
$$sin(cosec^{-1}(cot(tan^{-1}x)))$$
$$=sin(cosec^{-1}(cot(tan^{-1}tan\theta)))$$
$$=sin(cosec^{-1}(cot\theta))$$
$$=\dfrac{1}{cosec(cosec^{-1}(cot\theta))}$$

$$=\dfrac{1}{cot\theta}$$

$$=tan\theta$$
$$=x$$.


Write the function in the simplest form:
$$\displaystyle { \tan }^{ -1 }\frac { 1 }{ \sqrt { { x }^{ 2 }-1 }  } ,\left| x \right| >1$$

$$\displaystyle { \tan }^{ -1 }\frac { 1 }{ \sqrt { { x }^{ 2 }-1 }  } ,\left| x \right| >1$$

Put $$\displaystyle x=cosec\theta \Rightarrow \theta ={ cosec }^{ -1 }x$$

$$\displaystyle \therefore \quad { \tan }^{ -1 }\frac { 1 }{ \sqrt { { x }^{ 2 }-1 }  } ={ \tan }^{ -1 }\frac { 1 }{ \sqrt { { cosec }^{ 2 }\theta -1 }  } $$

$$\displaystyle ={ \tan }^{ -1 }\left( \frac { 1 }{ \cot { \theta  }  }  \right) ={\tan }^{ -1 }\left( \tan { \theta  }  \right) $$

$$\displaystyle =\theta ={ cosec }^{ -1 }x$$

$$=\dfrac { \pi  }{ 2 } -{ \sec }^{ -1 }x$$     ...$$\left[\because { cosec }^{ -1 }x+{ \sec }^{ -1 }x=\dfrac { \pi  }{ 2 }  \right] $$


Prove: $$\displaystyle 2{ \tan }^{ -1 }\frac { 1 }{ 2 } +{ \tan }^{ -1 }\frac { 1 }{ 7 } ={ \tan }^{ -1 }\frac { 31 }{ 17 } $$

$$\text{L.H.S.}\displaystyle =2{ \tan }^{ -1 }\frac { 1 }{ 2 } +{ \tan }^{ -1 }\frac { 1 }{ 7 } $$

$$\displaystyle={ \tan }^{ -1 }\left(\frac { 2.\frac { 1 }{ 2 }  }{ 1-{ \left( \frac { 1 }{ 2}  \right)  }^{ 2 } } \right)+{ \tan }^{ -1 }\frac { 1 }{ 7 }$$

$$= \tan ^{ -1 } \left(\dfrac { 1 }{ \frac 34} \right)  + \tan ^{ -1 } \dfrac { 1 }{ 7 } $$

$$\displaystyle ={ \tan }^{ -1 }\frac { 4 }{ 3 } +{ \tan }^{ -1 }\frac { 1 }{ 7 } $$

$$\displaystyle={ \tan }^{ -1 } \left(\dfrac { \dfrac { 4 }{ 3 } +\dfrac { 1 }{ 7 }  }{ 1-\dfrac {4 }{ 3 } .\dfrac { 1 }{ 7 }  } \right)$$

$$\displaystyle ={ \tan }^{ -1 }\dfrac { \left( \dfrac { 28+3 }{ 21 }  \right)  }{ \left( \dfrac { 21-4 }{ 21 }  \right)  } $$

$$\displaystyle ={ \tan }^{ -1 }\frac { 31 }{ 17 } =\text{R.H.S.}$$


Prove: $$\displaystyle { \tan }^{ -1 }\frac { 2 }{ 11 } +{ \tan }^{ -1 }\frac { 7 }{ 24 } ={ \tan }^{ -1 }\frac { 1 }{ 2 } $$

$$\text{L.H.S.}\displaystyle ={ \tan }^{ -1 }\frac { 2 }{ 11 } +{ \tan }^{ -1 }\frac { 7 }{ 24 } $$ 

$$\displaystyle ={ \tan }^{ -1 }\dfrac { \dfrac { 2 }{ 11 } +\dfrac { 7 }{ 24 }  }{ 1-\dfrac
{ 2 }{ 11 } .\dfrac { 7 }{ 24 }  }$$,        .....$$\left[\because { \tan }^{ -1 }x+{ \tan }^{ -1 }y={ \tan }^{ -1 }\dfrac { x+y }{ 1-xy }  \right] $$

$$\displaystyle ={ \tan }^{ -1 }\dfrac { \dfrac { 48+77 }{ 11\times 24 }  }{ \dfrac { 11\times 24-14 }{ 11\times 24 }  } $$

$$\displaystyle ={ \tan }^{ -1 }\frac { 48+77 }{ 264-14 } ={ \tan }^{ -1 }\frac { 125 }{
250 } ={ \tan }^{ -1 }\frac { 1 }{ 2 } $$

$$=\text{R.H.S.}$$


If $$\displaystyle { \tan }^{ -1 }\frac { x-1 }{ x-2 } +{ \tan }^{ -1 }\frac { x+1 }{ x+2 } =\frac {\pi  }{ 4 } $$, then find the value of $$x$$.

$$\displaystyle { \tan }^{ -1 }\frac { x-1 }{ x-2 } +{ \tan }^{ -1 }\frac { x+1  }{ x+2 } =\frac { \pi  }{ 4 }  $$          ...Given

$$\displaystyle \Rightarrow { \tan }^{ -1 }\left[ \dfrac { \dfrac { x-1 }{ x-2 } +\dfrac {x+1 }{ x+2 }  }{ 1-\left( \dfrac { x-1 }{ x-2 }  \right) \left( \dfrac { x+1 }{ x+2 }  \right)  }  \right] =\dfrac { \pi  }{ 4 } $$

$$\displaystyle \Rightarrow { \tan }^{ -1 }\left[ \dfrac { \left( x-1 \right) \left( x+2 \right) +\left( x+1 \right) \left( x-2 \right)  }{ \left( x+2 \right) \left( x-2 \right) -\left( x-1 \right) \left( x+1 \right)  }  \right] =\frac { \pi  }{ 4 } $$

$$\displaystyle \Rightarrow { \tan }^{ -1 }\left[ \frac { { x }^{ 2 }+x-2+{ x }^{ 2}-x-2 }{ { x }^{ 2 }-4-{ x }^{ 2 }+1 }  \right] =\frac { \pi  }{ 4 } $$

$$\displaystyle \Rightarrow { \tan }^{ -1 }\left[ \frac { 2{ x }^{ 2 }-4 }{ -3 }  \right] =\frac { \pi  }{ 4 } $$

$$\displaystyle \Rightarrow \tan { \left[ { \tan }^{ -1 }\frac { 4-{ 2x }^{ 2 } }{ 3 } \right]  } =\tan { \frac { \pi  }{ 4 }  } $$

$$\displaystyle \Rightarrow \frac { 4-{ 2x }^{ 2 } }{ 3 } =1$$

$$\displaystyle \Rightarrow 4-2{ x }^{ 2 }=3$$

$$\displaystyle \Rightarrow 2{ x }^{ 2 }=4-3=1$$

$$\displaystyle \Rightarrow x=\pm \frac { 1 }{ \sqrt { 2 }  } $$


If $$\displaystyle \sin { \left( { \sin }^{ -1 }\frac { 1 }{ 5 } +{ \cos }^{ -1 }x \right)  } =1$$, then find the value of $$x$$.

$$\displaystyle \sin { \left( { \sin }^{ -1 }\frac { 1 }{ 5 } +{ \cos }^{ -1 }x \right)  } =1$$

$$\Rightarrow \displaystyle  { \left( { \sin }^{ -1 }\frac { 1 }{ 5 } +{ \cos }^{ -1 }x \right)  } =\sin^{-1}(1)=\frac{\pi}{2}$$

$$\Rightarrow \displaystyle \sin^{ -1 }\frac { 1 }{ 5 }=\frac{\pi}{2}-\cos^{-1}x=\sin^{-1}x$$

$$\displaystyle \therefore x=\frac{1}{5}$$


Find the value of $$\displaystyle \tan { \frac { 1 }{ 2 }  } \left[ { \sin }^{ -1 }\frac { 2x }{ 1+{ x }^{ 2 } } +{ \cos }^{ -1 }\frac { 1-{ y }^{ 2 } }{ 1+{ y }^{ 2 } }  \right] ,\left| x \right| <1,y>0$$ and $$xy<1$$

Let $$\displaystyle x=\tan { \theta  } \Rightarrow \theta ={ \tan }^{ -1 }x$$

$$\displaystyle\therefore { \sin }^{ -1 }\frac { 2x }{ 1+{ x }^{ 2 } } ={ \sin }^{-1 }\left( \frac { 2\tan { \theta  }  }{ 1+{ \tan }^{ 2 }\theta  }  \right) ={ \sin }^{ -1 }\left( \sin2\theta  \right) =2\theta =2{ \tan }^{ -1 }x$$

Let $$\displaystyle y=\tan { \phi  } \Rightarrow \phi ={ \tan }^{ -1 }y$$

$$\displaystyle\therefore { \cos }^{ -1 }\frac { 1-{ y }^{ 2 } }{ 1+{ y }^{ 2 } }={ \cos }^{ -1 }\left( \frac { 1-{ \tan }^{ 2 }\phi  }{ 1{ +\tan }^{ 2 }\phi  }  \right) ={ \cos }^{ -1 }\left( \cos { 2\phi  }  \right) =2\phi =2{ \tan }^{ -1 }y$$

$$\displaystyle \therefore \tan { \frac { 1}{ 2 }  } \left[ { \sin }^{ -1 }\frac { 2x }{ 1+{ x }^{ 2 } } +{ \cos }^{-1 }\frac { 1-{ y }^{ 2 } }{ 1+{ y }^{ 2 } }  \right] $$

$$\displaystyle = \tan { \frac { 1 }{ 2 }  } \left[ 2{ \tan }^{ -1 }x+2{ \tan }^{ -1 }y \right] $$

$$\displaystyle =\tan { \left[ { \tan }^{ -1 }x+{ \tan }^{ -1 }y \right]  } $$

$$\displaystyle =\tan { \left[ { \tan }^{ -1 }\left( \frac { x+y }{ 1-xy }  \right)  \right]  } =\frac { x+y }{ 1-xy } $$


Prove: $$\displaystyle \frac { 9\pi  }{ 8 } -\frac { 9 }{ 4 } { \sin }^{ -1 }\frac { 1 }{ 3 }=\frac { 9 }{ 4 } { \sin }^{ -1 }\frac { 2\sqrt { 2 }  }{ 3 } $$

$$\displaystyle L.H.S.=\frac { 9\pi  }{ 8 } -\frac { 9 }{ 4 } { \sin }^{ -1 }\frac { 1 }{ 3 } $$

$$\displaystyle =\frac { 9 }{ 4 } \left( \frac { \pi  }{ 2 } -{ \sin }^{ -1 }\frac { 1 }{ 3 }  \right) $$

$$\displaystyle=\frac { 9 }{ 4 } \left( { \cos }^{ -1 }\frac { 1 }{ 3 }  \right) .....(1)$$ 

Now, let $$\displaystyle { \cos }^{ -1 }\frac{ 1 }{ 3 }=x $$. 

Then, $$\displaystyle \cos { x } =\frac { 1 }{ 3 } \Rightarrow \sin { x } =\sqrt { 1-{ \left( \frac { 1 }{ 3 }  \right)  }^{ 2 } } =\frac { 2\sqrt { 2 }  }{ 3 } $$

$$\displaystyle \therefore x={ \sin }^{ -1 }\frac { 2\sqrt { 2 }  }{ 3 } \Rightarrow {
\cos }^{ -1 }\frac { 1 }{ 3 } ={ \sin }^{ -1 }\frac { 2\sqrt { 2 }  }{ 3 } $$

$$\displaystyle \therefore \text{L.H.S.}=\frac { 9 }{ 4 } { \sin }^{ -1 }\frac { 2\sqrt { 2 }  }{ 3 } =\text{R.H.S.}$$


If $$A=\dfrac{1}{1}\cot^{-1}\left(\dfrac{1}{1}\right)+\dfrac{1}{2}\cot^{-1}\left(\dfrac{1}{2}\right)+\dfrac{1}{3}\cot^{-1}\left(\dfrac{1}{3}\right)$$ and $$B=1\cot^{-1}1+2\cot^{-1}2+3\cot^{-1}3$$ then $$|B-A|$$ is equal to $$\dfrac{a\pi}{b}+\dfrac{c}{d}\cot^{-1}3$$ where $$a, b, c, d \in N$$ and are in their lowest form then $$a + b + c+d$$ equal to 

Given, $$A=\dfrac{1}{1}\cot^{-1}\left(\dfrac{1}{1}\right)+\dfrac{1}{2}\cot^{-1}\left(\dfrac{1}{2}\right)+\dfrac{1}{3}\cot^{-1}\left(\dfrac{1}{3}\right)$$ and $$B=1\cot^{-1}1+2\cot^{-1}2+3\cot^{-1}3$$

We know that $$\cot^{-1}\dfrac{1}{x}=\tan^{-1}x\ \forall\ x>0$$

$$\Rightarrow  A = \tan^{-1}1 + \dfrac{1}{2}\tan^{-1}2 + \dfrac{1}{3}\tan^{-1}3$$

Also, $$\tan^{-1}1=\cot^{-1}1=\dfrac{\pi}{4}$$

$$\therefore |B-A| = |\cot^{-1}1 + 2\cot^{-1}2 + 3\cot^{-1}3 -(\tan^{-1}1 + \dfrac{1}{2}\tan^{-1}2 + \dfrac{1}{3}\tan^{-1}3)|$$

$$\therefore |B-A| = |2\cot^{-1}2 + 3\cot^{-1}3 -\dfrac{1}{2}\tan^{-1}2 - \dfrac{1}{3}\tan^{-1}3|$$

Consider $$\tan^{-1}2=x$$

$$\therefore \tan x=2$$

$$\therefore \sin x = 2\sqrt{1-\sin ^2x}$$

$$\therefore 5\sin ^2x=4$$

$$\therefore \sin x=\dfrac{2}{\sqrt{5}}\implies x=\dfrac{7\pi}{20}$$

Also, $$\tan^{-1}x+\cot^{-1}x=\dfrac{\pi}{2}$$

$$\therefore |B-A| = |2(\dfrac{\pi}{2}-\dfrac{7\pi}{20}) + 3\cot^{-1}3 -\dfrac{7\pi}{40} - \dfrac{1}{3}(\dfrac{\pi}{2}-\cot^{-1}3)|$$

$$\therefore |B-A| = |\dfrac{3\pi}{10} -\dfrac{7\pi}{40} - \dfrac{\pi}{6}+ 3\cot^{-1}3 +\dfrac{1}{3}\cot^{-1}3|$$

$$\therefore |B-A| = |-\dfrac{\pi}{24}+ \dfrac{10}{3}\cot^{-1}3|$$

$$\therefore |B-A| = -\dfrac{\pi}{24}+ \dfrac{10}{3}\cot^{-1}3$$                            $$\left(\because \cot^{-1}3>\dfrac{\pi}{24}\right)$$

$$\therefore a+b+c+d=-1+24+10+3=36$$



Solve the equation: $$\tan^{-1}x+2\cot^{-1}x=\displaystyle\frac{2\pi}{3}$$.

$$\tan ^{-1}x+2\cot ^{-1}x=\displaystyle\frac{2\pi}{3}$$
$$\tan ^{-1}x+\cot ^{-1}+\cot ^{-1}x=\displaystyle\frac{2\pi}{3}$$
$$\displaystyle\frac{\pi}{2}+\cot ^{-1}x=\displaystyle\frac{2\pi}{3}$$
$$\cot ^{-1}x=\displaystyle\frac{2\pi}{3}-\frac{\pi}{2}$$
$$\cot ^{-1}x=\displaystyle\frac{\pi}{6}$$
$$x=\cot \displaystyle\frac{\pi}{6}$$
$$x=\sqrt{3}$$.


Write the simplest form of $$\tan^{-1}\left (\dfrac {\cos x - \sin x}{\cos x + \sin x}\right ), 0 < x < \dfrac {\pi}{2}$$.

Given:
$$\tan^{-1} \left (\dfrac {\cos x - \sin x}{\cos x + \sin x}\right ) = \tan^{-1}\left (\dfrac {1 - \dfrac {\sin x}{\cos x}}{1 + \dfrac {\sin x}{\cos x}}\right )$$
$$= \tan^{-1} \left (\dfrac {1 - \tan x}{1 + \tan x}\right )$$
$$= \tan^{-1} \left (\dfrac {\tan \dfrac {\pi}{4} - \tan x}{1 + \tan \dfrac {\pi}{4} \cdot \tan x}\right )$$
$$= \tan^{-1} \left (\tan \left (\dfrac {\pi}{4} - x\right )\right )$$
$$\therefore \tan^{-1} \left (\dfrac {\cos x - \sin x}{\cos x + \sin x}\right ) = \dfrac {\pi}{4} - x$$.


Write $$\tan ^{ -1 }{ \left[ \cfrac { \sqrt { 1+{ x }^{ 2 } } -1 }{ x }  \right]  } ,x\neq 0$$ in the simplest form.

Let $$x=\tan { \theta  } $$
$$\tan ^{ -1 }{ \left[ \cfrac { \sqrt { 1+{ x }^{ 2 } } -1 }{ x }  \right]  } =\tan ^{ -1 }{ \left[ \cfrac { \sec { \theta  } -1 }{ \cfrac { \sin { \theta  }  }{ \cos { \theta  }  }  }  \right]  } $$
                                           $$=\tan ^{ -1 }{ \left( \cfrac { 1-\cos { \theta  }  }{ \sin { \theta  }  }  \right)  } $$
                                           $$=\tan ^{ -1 }{ \left( \cfrac { 2\sin ^{ 2 }{ \theta /2 }  }{ 2\sin { \theta /2 } \cos { \theta /2 }  }  \right)  }$$
                                           $$ =\tan ^{ -1 }{ \left( \tan { \theta /2 }  \right)  } $$
                                           $$=\theta /2=\cfrac { 1 }{ 2 } \tan ^{ -1 }{ x } $$


If $$\sin \left (\sin^{-1} \dfrac {1}{5} + \cos^{-1} x\right ) = 1$$ then find the value of $$x$$.

Given $$\sin \left (\sin^{-1} \left (\dfrac {1}{5}\right ) + \cos^{-1}x\right ) = 1$$
$$\Rightarrow \sin^{-1} \left (\dfrac {1}{5}\right ) + \cos^{-1} x = \sin^{-1}(1)$$
$$\sin^{-1}\left (\dfrac {1}{5}\right ) + \cos^{-1}x = \dfrac {\pi}{2}$$
$$\therefore \cos^{-1} x = \dfrac {\pi}{2} - \sin^{-1} \left (\dfrac {1}{5}\right )$$
$$x = \cos \left (\dfrac {\pi}{2} - \sin^{-1} \left (\dfrac {1}{5}\right )\right )$$
$$x = \sin \left (\sin^{-1} \left (\dfrac {1}{5}\right )\right )$$
or $$x = \dfrac {1}{5}$$.


Inverse circular functions,Principal values of $${ sin }^{ -1 }x,{ cos }^{ -1 }x,{ tan }^{ -1 }x$$.
$${ tan }^{ -1 }x+{ tan }^{ -1 }y={ tan }^{ -1 }\frac { x+y }{ 1-xy } $$,      $$xy<1$$
       $$\pi +{ tan }^{ -1 }\frac { x+y }{ 1-xy } $$,         $$xy>1$$.
(a) $${ cos }^{ -1 }\left( cos\frac { 7\pi  }{ 6 }  \right) $$
(b) $${ cos }^{ -1 }\left( cos\frac { 4\pi  }{ 3 }  \right) $$

(a) $${ cos }^{ -1 }cos\left( \dfrac { 7\pi  }{ 6 }  \right) =\dfrac { 7\pi  }{ 6 } $$ is wrong, as $$7\pi /6$$ is greater than $$\pi $$.
Here $$\dfrac { 7\pi  }{ 6 } =2\pi -\dfrac { 5\pi  }{ 6 } $$ so that $$\dfrac { 5\pi  }{ 6 } $$ lies between $$0$$ and $$\pi $$
$$\therefore $$  $${ cos }^{ -1 }cos\left( \dfrac { 7\pi  }{ 6 }  \right) ={ cos }^{ -1 }cos\left( 2\pi -\dfrac { 5\pi  }{ 6 }  \right) $$
      $$={ cos }^{ -1 }cos\left( \dfrac { 5\pi  }{ 6 }  \right) =\dfrac { 5\pi  }{ 6 } $$.
(b) $${ cos }^{ -1 }cos\dfrac { 4\pi  }{ 3 } ={ cos }^{ -1 }cos\left( 2\pi -\dfrac { 2\pi  }{ 3 }  \right) $$
        $$={ cos }^{ -1 }cos\dfrac { 2\pi  }{ 3 } =\dfrac { 2\pi  }{ 3 } $$.


Inverse circular functions,Principal values of $${ sin }^{ -1 }x,{ cos }^{ -1 }x,{ tan }^{ -1 }x$$.
$${ tan }^{ -1 }x+{ tan }^{ -1 }y={ tan }^{ -1 }\frac { x+y }{ 1-xy } $$,      $$xy<1$$
       $$\pi +{ tan }^{ -1 }\frac { x+y }{ 1-xy } $$,         $$xy>1$$.
(a) $${ tan }^{ -1 }\frac { 2mn }{ { m }^{ 2 }-{ n }^{ 2 } } +{ tan }^{ -1 }\frac { 2pq }{ { p }^{ 2 }-{ q }^{ 2 } } ={ tan }^{ -1 }\frac { 2MN }{ { M }^{ 2 }-{ N }^{ 2 } } $$
where $$M=mp-nq,N=np+mq$$
(b) $$\frac { 2 }{ 3 } { tan }^{ -1 }\frac { 3m{ n }^{ 2 }-{ m }^{ 3 } }{ { n }^{ 3 }-3{ m }^{ 2 }n } +\frac { 2 }{ 3 } { tan }^{ -1 }\frac { 3p{ q }^{ 2 }-{ p }^{ 3 } }{ { q }^{ 3 }-3{ p }^{ 2 }q } ={ tan }^{ -1 }\frac { 2MN }{ { M }^{ 2 }-{ N }^{ 2 } } $$
Where $$M=-mp+nq,N=np+mq$$ and all the letters are $$+ive$$ quantities.

(a) Dividing $${ T }_{ 1 },{ T }_{ 2 }$$ and $${T}_{3}$$ by $${m}^{2},{p}^{2}$$ and $${M}^{2} $$respectively, $$2{ tan }^{ -1 }x={ tan }^{ -1 }\dfrac { 2x }{ 1-{ x }^{ 2 } } $$
L.H.S.$$=2{ tan }^{ -1 }\dfrac { n }{ m } +2{ tan }^{ -1 }\dfrac { q }{ p } $$
          $$=2{ tan }^{ -1 }\dfrac { pn+mq }{ pm-nq } =2{ tan }^{ -1 }\dfrac { N }{ M } =$$R.H.S.
(b) Dividing above and below by $${n}^{3}$$ in $${T}_{1}$$ and $${q}_{3}$$ in $${T}_{2}$$ and $${M}^{2}$$ in $${T}_{3}$$, we get
$$\dfrac { 2 }{ 3 } ,3{ tan }^{ -1 }\dfrac { m }{ n } +\dfrac { 2 }{ 3 } ,3{ tan }^{ -1 }\dfrac { p }{ q } =2{ tan }^{ -1 }\dfrac { N }{ M } $$
L.H.S.$$=2\left[ { tan }^{ -1 }\dfrac { (m/n)+(p/q) }{ 1-(m/n)(p/q) }  \right] $$
         $$=2{ tan }^{ -1 }\dfrac { np+mq }{ nq-mp } =2{ tan }^{ -1 }\dfrac { N }{ M } =$$R.H.S.


Solve the equation $$ \tan^{-1} \sqrt{x^2+x}+\sin^{-1} \sqrt{x^2+x+1}=\dfrac{\pi}{2}$$

$$\tan^{-1}\sqrt{x^{2}+x}+\sin^{-1}\sqrt{x^{2}+x+1}=\dfrac{\pi }{2}$$

$$\tan^{-1}\sqrt{x^{2}+x}=\dfrac{\pi }{2}-\sin^{-1}\sqrt{x^{2}+x+1}$$

$$\tan^{-1}\sqrt{x^{2}+x}=\cos^{-1}\sqrt{x^{2}+x+1}$$


Apply  $$\tan^{-1}y=\cos^{-1}\dfrac{1}{\sqrt{1+y^{2}}}$$  on R.H.S.

$$\cos^{-1}\dfrac{1}{\sqrt{1+(\sqrt{x^{2}+x})^{2}}}=\cos^{-1}\sqrt{x^{2}+x+1}$$

$$\cos^{-1}\dfrac{1}{\sqrt{x^{2}+x+1}}=\cos^{-1}\sqrt{x^{2}+x+1}$$

$$\Rightarrow \dfrac{1}{\sqrt{x^{2}+x+1}}=\sqrt{x^{2}+x+1}$$

$$x^{2}+x+1=1$$

$$x^{2}+x=0$$

$$x(x+1)=0$$

$$x=0,-1$$


If $$ \cot^{-1} \left( \frac{\sqrt{1+ \sin x}+ \sqrt{ 1- \sin x}}{\sqrt{1+\sin x}-\sqrt{1- \sin x}}\right) =\dfrac{x}{m}, x \in \left(0, \frac{\pi}{4}\right)$$.Find $$m$$

$$\\0<x<(\frac{\pi}{4})\\hence\>0<(\frac{x}{2})<(\frac{\pi}{8})\\\>and\>so\>sin\>(\frac{x}{2})<cos(\frac{x}{2})\>\\\therefore\>\sqrt{1+sinx}=\sqrt{sin^2(\frac{x}{2})+cos^2(\frac{x}{2})+2sin(\frac{x}{2})cos(\frac{x}{2})}\\=sin(\frac{x}{2})+cos(\frac{x}{2})\\and\>\sqrt\>{1-sinx}=cos(\frac{x}{2})-sin(\frac{x}{2})\\\>hence\>given\>expression\>in\>question\>\\\>=cot^-1[(\frac{\sqrt{sin(\frac{x}{2})+cos(\frac{x}{2})+cos(\frac{x}{2})-sin(\frac{x}{2})}}{\sqrt{sin(\frac{x}{2})+cos(\frac{x}{2})-cos(\frac{x}{2})+sin(\frac{x}{2})}})]\\=cot^{-1}(cot(\frac{x}{2}))\\=(\frac{x}{2})\>hence\>m\>=2$$



If $$(Tan^{-1}x)^2+(Cot^{-1}x)^2=\dfrac{5\pi^2}{8},then$$ x=

$$(\tan^{-1}x)^2+(\dfrac{\pi}{2}-\tan^{-1}x)^2=\dfrac{5\pi^2}{8}$$
Put $$\tan^{-1}x=c$$
$$\therefore 2c^2+\dfrac{\pi^2}{4}-\pi c-\dfrac{5\pi^2}{8}=0$$
$$\therefore 16c^2-8\pi c-3\pi^2=0$$
$$\therefore 16c^2-12\pi c+4\pi c-3\pi^2=0$$
$$(4c-3\pi)(4c+\pi)=0$$
$$c=\dfrac{3\pi}{4},\dfrac{-\pi}{4}$$
$$\tan^{-1}x=\dfrac{3\pi}{4},\dfrac{-\pi}{4}$$
$$x=\tan\dfrac{3\pi}{4},\tan\dfrac{-\pi}{4}$$
$$x=-1,1$$


find the value of the following: 
$$(i) \ \sin^{-1}(\frac{-1}{2})$$
$$(ii) \ \cos^{-1}(\frac{\sqrt{3}}{2})$$
$$(iii) \ \text{cosec}^{-1}(2)$$
$$(iv)  \ \tan^{-1} ({-\sqrt{3}})$$
$$(v) \ \cos^{-1}(\frac{-1}{2})$$
$$(vi)  \tan^{-1} (-1)$$

i) $$\sin^{-1}(\cfrac{-1}{2})$$
$$=-\sin^{-1}(\cfrac{1}{2})$$
$$=\cfrac{-\pi}{6}$$

ii) $$\cos^{-1}(\cfrac{\sqrt 3}{2})$$=$$\cfrac{\pi}{6}$$

iii) $$\csc^{-1}(2)=\sin^{-1}(\cfrac{1}{2})=\cfrac{\pi}{6}$$

iv) $$\tan^{-1}(-\sqrt 3)=-\tan^{-1}(\sqrt 3)=-\cfrac{\pi}{3}$$

v) $$\cos^{-1}(\cfrac{-1}{2})=\cfrac{2\pi}{3}$$
 vi) $$\tan^{-1}=\cfrac{-\pi}{4}$$


Differentiate  $$\cos^{-1}(4x^{2} -3x); x \epsilon (\frac{1}{2}, 1)$$ 

$$\dfrac{d}{dx}\cos^{-1}(4x^{2} -3x)\\=\dfrac{-1}{\sqrt{1-(4x^{2} -3x)^2}}.\dfrac{d}{dx}(4x^2-3x)=\dfrac{-1}{\sqrt{1-(4x^{2} -3x)^2}}.(8x-3)$$


Solve the following for $$x:\tan^{-1}\left(\dfrac{x-2}{x-3}\right)+\tan^{-1}\left(\dfrac{x+2}{x+3}\right)=\dfrac{\pi}{4},|x|<1$$


1314728_1035338_ans_57b3307b9bf14728a4941aae91b57bce.jpeg


Simplify : $$\cot^{-1} [\sqrt{1 + x^2} - x]$$

$$\cot ^{-1}\left [ \sqrt{1+x^{2}} -x\right ]$$

Let  $$x=\cot\theta $$

$$\cot ^{-1}\left [ \sqrt{1+\cot^{2}\theta } -\cot\theta \right ]$$

$$=\cot ^{-1}\left [ \text{cosec} \theta  -\cot\theta \right ]$$

$$=\cot ^{-1}\left [ \dfrac{1}{\sin \theta }  -\dfrac{\cos \theta }{\sin \theta } \right ]$$

$$=\cot ^{-1}\left ( \dfrac{1-\cos \theta }{\sin \theta } \right )$$

$$=\cot ^{-1}\left ( \dfrac{2\sin ^{2}\dfrac{\theta }{2} }{2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2} } \right )$$

$$=\cot ^{-1}\left ( \tan\dfrac{\theta }{2} \right )$$

$$=\cot ^{-1}\left ( \cot\left ( \dfrac{\pi }{2}-\dfrac{\theta }{2} \right ) \right )$$

$$=\dfrac{\pi }{2}-\dfrac{\theta }{2}$$

$$=\dfrac{\pi }{2}-\dfrac{\cot^{-1}x }{2}$$


Does $$\sin^{-1} \left(\dfrac{2}{\sqrt{5}} \right) = \tan^{-1} (2)$$ & please give value.

$$\sin^{-1}\left ( \dfrac{2}{\sqrt{5}} \right )= x$$
$$\sin x=\dfrac{2}{\sqrt{5}}$$
$$\cos x=\dfrac{\sqrt{5-2^{2}}}{\sqrt{5}}$$ =$$ \dfrac{1}{\sqrt{5}}$$
$$\cos x=\dfrac{1}{\sqrt{5}}$$
$$\tan x=\dfrac{\dfrac{2}{\sqrt{5}}}{\dfrac{1}{\sqrt{5}}}$$
$$\tan x=2$$
$$\tan^{-1}z=x$$
$$\therefore \sin\left ( \dfrac{2}{\sqrt{5}} \right )=\tan^{-1}(2)$$


Find the domain and range of the real function $$\cfrac { x+2 }{ { x }^{ 2 }-8x-4 } $$

Let $$f\left( x \right) =\cfrac { x+2 }{ { x }^{ 2 }-8x-4 } =y\rightarrow 1$$
If $${ x }^{ 2 }-8x-4=0$$
$$x=\cfrac { 8\pm \sqrt { 64+16 }  }{ 2 } =\cfrac { 8\pm 4\sqrt { 5 }  }{ 2 } $$
$$=4\pm 2\sqrt { 5 } $$
At $$x=4\pm 2\sqrt { 5 } ,{ x }^{ 2 }-8x-4=0\quad \therefore f\left( x \right) $$ is not defined
Domain of $$f(x)$$ is $$R-\left\{ 4-2\sqrt { 5 } ,4+2\sqrt { 5 }  \right\} $$
$$1\Rightarrow y\left( { x }^{ 2 }-8x-4 \right) =x+2$$
$$y{ x }^{ 2 }-(1+8y)x-\left( 4y+2 \right) =0$$
As x is always real, Discriminant of above equation must be $$\ge 0$$
$${ (1+8y) }^{ 2 }+4y(4y+2)\ge 0$$
$$64{ y }^{ 2 }+16y+1+16{ y }^{ 2 }+8y\ge 0$$
$$80{ y }^{ 2 }+24y+1\ge 0$$
Factorize above equation,
$$y=\cfrac { -24\pm \sqrt { 526-320 }  }{ 160 } $$
$$=\cfrac { -1 }{ 4 } $$ or $$\cfrac { -1 }{ 20 } $$
$$\therefore \left( 4y+1 \right) \left( 20y+1 \right) \ge 0$$
$$\therefore y\le \cfrac { -1 }{ 20 } $$ or $$y\ge \cfrac { -1 }{ 4 } $$
$$\therefore $$ Range of $$f\left( x \right) =\left( -\infty ,\cfrac { -1 }{ 20 }  \right] \bigcup { \left[ \cfrac { -1 }{ 4 } ,\infty  \right)  } $$


Solve  $$y=\tan ^{ -1 }{ \cfrac { 5ax }{ a^{ 2 }-6{ x }^{ 2 } }  } $$, find $$\cfrac { dy }{ dx } $$

$$y=\tan ^{ -1 }{ \left( \cfrac { 5ax }{ { a }^{ 2 }-6{ x }^{ 2 } }  \right)  } $$
$$\tan { y } =\cfrac { 5ax }{ { a }^{ 2 }-6{ x }^{ 2 } } \quad \ast \sec ^{ 2 }{ y } -\tan ^{ 2 }{ y } =1$$
$$\left( \sec ^{ 2 }{ y }  \right) \cfrac { dy }{ dx } =\cfrac { 5a\left( { a }^{ 2 }-6{ x }^{ 2 } \right) -\left( -12x \right) \left( 5ax \right)  }{ { \left( { a }^{ 2 }-6{ x }^{ 2 } \right)  }^{ 2 } } $$
$$\left[ 1+{ \left( \cfrac { 5ax }{ { a }^{ 2 }-6{ x }^{ 2 } }  \right)  }^{ 2 } \right] \cfrac { dy }{ dx } =\cfrac { 5{ a }^{ 3 }-30a{ x }^{ 2 }+60a{ x }^{ 2 } }{ { \left( { a }^{ 2 }-6{ x }^{ 2 } \right)  }^{ 2 } } $$
$$\left[ \cfrac { { a }^{ 4 }+36{ x }^{ 4 }+13{ a }^{ 2 }{ x }^{ 2 } }{ { \left( { a }^{ 2 }-6{ x }^{ 2 } \right)  }^{ 2 } }  \right] \cfrac { dy }{ dx } =\cfrac { 5{ a }^{ 3 }+30a{ x }^{ 2 } }{ { \left( { a }^{ 2 }-6{ x }^{ 2 } \right)  }^{ 2 } } $$
$$\left[ \left( { a }^{ 4 } \right) +36{ x }^{ 4 }+13{ a }^{ 2 }{ x }^{ 2 } \right] \cfrac { dy }{ dx } =5a\left( { a }^{ 2 }+6{ x }^{ 2 } \right) $$
$$\left( { a }^{ 2 }+9{ x }^{ 2 } \right) \left( { a }^{ 2 }+4{ x }^{ 2 } \right) \cfrac { dy }{ dx } =5a\left( { a }^{ 2 }+6{ x }^{ 2 } \right) $$
$$\therefore \cfrac { dy }{ dx } =\cfrac { 5a\left( { a }^{ 2 }+6{ x }^{ 2 } \right)  }{ \left( { a }^{ 2 }+9{ x }^{ 2 } \right) \left( { a }^{ 2 }+4{ x }^{ 2 } \right)  } $$
$$\cfrac { dy }{ dx } =\cfrac { 3a\left( { a }^{ 2 }+4{ x }^{ 2 } \right) +2a\left( { a }^{ 2 }+9{ x }^{ 2 } \right)  }{ \left( { a }^{ 2 }+9{ x }^{ 2 } \right) \left( { a }^{ 2 }+4{ x }^{ 2 } \right)  } $$
$$\therefore \cfrac { dy }{ dx } =\cfrac { 3a }{ { a }^{ 2 }+9{ x }^{ 2 } } +\cfrac { 2a }{ { a }^{ 2 }+4{ x }^{ 2 } } $$


Calculating the principal value, find the value of $$\sin\left[2\sin^{-1}\left(\dfrac{4}{5}\right)\right]$$.

We are given, $$ sin \left [ 2xin^{-1}\left ( \dfrac{4}{5} \right ) \right ]$$
Let $$ sin^{-1}\left ( \dfrac{4}{5} \right ) = \theta $$
where $$ \theta \epsilon  \left [ -\dfrac{\pi }{2}, \dfrac{\pi}{2} \right ]$$
So, $$ sin \theta = \dfrac{4}{5}$$
now, $$ cos\theta  = \sqrt{cos^{2}\theta}$$
$$ = \sqrt{1-sin^{2}\theta}$$
$$ cos \theta = \sqrt{1-\left ( \dfrac{4}{5} \right )^2}$$
$$ cos \theta = \sqrt{1-\dfrac{16}{25}}$$
$$ cos \theta = \sqrt{\dfrac{9}{25}} = \pm \dfrac{3}{5}$$
but $$ \theta \epsilon  \left [ -\pi/2, \pi/2 \right ] $$ so, $$ cos \theta = \dfrac{3}{5}$$
$$ \therefore sin \left [ 2sin^{-1}\left ( \dfrac{4}{5} \right ) \right ]$$
$$ = sin 2\theta $$
$$  = 2sin \theta \,cos \theta $$
$$ = 2\left ( \dfrac{4}{5} \right )\left ( \dfrac{3}{5} \right )$$
$$ = \dfrac{24}{25}$$
So, $$ sin \left [ 2 sin^{-1} \dfrac{4}{5} \right ] = \dfrac{24}{25}$$

1180647_1069989_ans_edd5770c9aba4fd0a8398412b9837e0b.jpg


Find  $$\sin ^{ -1 }{ \left( \cfrac { \sqrt { 3 } +1 }{ 2\sqrt { 2 }  }  \right)  } $$=

We know that $$\sin 75^0=\dfrac{\sqrt 3 +1}{2\sqrt 2}$$

$$\Rightarrow  75^0=\sin ^{-1}(\dfrac{\sqrt 3 +1}{2\sqrt 2})$$


Therefore, $$\Rightarrow  \sin ^{-1}(\dfrac{\sqrt 3 +1}{2\sqrt 2})=75^0$$


Prove that $${\sin ^{ - 1}}\dfrac{3}{5} - {\sin ^{ - 1}}\dfrac{8}{{17}} = {\cos ^{ - 1}}\left( {\dfrac{{84}}{{85}}} \right)$$ 

L.H.S

$${{\sin }^{-1}}\dfrac{3}{5}-{{\sin }^{-1}}\dfrac{8}{12}$$

 

We know that

$${{\sin }^{-1}}x-{{\sin }^{-1}}y={{\sin }^{-1}}\left\{ x\sqrt{1-{{y}^{2}}}-y\sqrt{1-{{x}^{2}}} \right\}$$

 

Therefore,

$$ ={{\sin }^{-1}}\left\{ \dfrac{3}{5}\sqrt{1-{{\left( \dfrac{8}{17} \right)}^{2}}}-\dfrac{8}{17}\sqrt{1-{{\left( \dfrac{3}{5} \right)}^{2}}} \right\} $$

$$ ={{\sin }^{-1}}\left\{ \dfrac{3}{5}\sqrt{1-\dfrac{64}{289}}-\dfrac{8}{17}\sqrt{1-\dfrac{9}{25}} \right\} $$

$$ ={{\sin }^{-1}}\left\{ \dfrac{3}{5}\sqrt{\dfrac{225}{289}}-\dfrac{8}{17}\sqrt{\dfrac{16}{25}} \right\} $$

$$ ={{\sin }^{-1}}\left\{ \dfrac{3}{5}\times \dfrac{15}{17}-\dfrac{8}{17}\times \dfrac{4}{5} \right\} $$

$$ ={{\sin }^{-1}}\left\{ \dfrac{45}{85}-\dfrac{32}{85} \right\} $$

$$ ={{\sin }^{-1}}\left\{ \dfrac{13}{85} \right\} $$

$$ ={{\cos }^{-1}}\left( \dfrac{84}{85} \right) $$

 

Hence, proved.



$$2{\tan ^{ - 1}}\left( {\frac{{1 + x}}{{1 - x}}} \right) + {\sin ^{ - 1}}\left( {\frac{{1 - {x^2}}}{{1 + {x^2}}}} \right) = $$

$$2\tan ^{ -1 }{ \left( \dfrac { 1+x }{ 1-x }  \right)  } +\sin ^{ -1 }{ \left( \dfrac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } }  \right)  } $$

$$\tan ^{ -1 }{ \left( \dfrac { 1+x }{ 1-x }  \right)  } +\tan ^{ -1 }{ \left( \dfrac { 1+x }{ 1-x }  \right)  } +\sin ^{ -1 }{ \left( \dfrac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } }  \right)  } $$

$$\tan ^{ -1 }{ \left( \dfrac { \dfrac { 2+2x }{ 1-x }  }{ 1-{ \left( \dfrac { 1+x }{ 1-x }  \right)  }^{ 2 } }  \right)  } +\sin ^{ -1 }{ \left( \dfrac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } }  \right)  } $$

$$\tan ^{ -1 }{ \left( \dfrac { 2+2x\left( 1-x \right)  }{ -4x }  \right)  } +\sin ^{ -1 }{ \left( \dfrac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } }  \right)  } $$

$$-\tan ^{ -1 }{ \left( \dfrac { 1+{ x }^{ 2 } }{ 2x }  \right)  } +\sin ^{ -1 }{ \left( \dfrac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } }  \right)  } $$

We know that, 
$$\tan ^{ -1 }{ \left( \dfrac { 1-{ x }^{ 2 } }{ 2x }  \right)  } $$ $$=\sin ^{ -1 }{ \left( \dfrac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } }  \right)  } $$

$$\Rightarrow -\sin ^{ -1 }{ \left( \dfrac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } }  \right)  } +\sin ^{ -1 }{ \left( \dfrac { 1-{ x }^{ 2 } }{ 1+{ x }^{ 2 } }  \right)  } =0$$


Prove
$$4\tan^{-1}\left(\dfrac{1}{5}\right)-\tan^{-1}\left(\dfrac{1}{70}\right)+\tan^{-1}\left(\dfrac{1}{99}\right)=\dfrac{\pi}{4}$$.

To be proved : $$4 \tan^{-1}\dfrac{1}{5}-\tan^{-1}\left(\dfrac{1}{70}\right)+ \tan^{-1}\left(\dfrac{1}{99}\right)=\dfrac{\pi }{4}$$
We know that $$2\tan^{-1}x= \tan^{-1}\left(\dfrac{2x}{1-x^{2}}\right)$$
So, $$2 \tan^{-1}\dfrac{1}{5}=\tan^{-1}\left(\dfrac{2\times \dfrac{1}{5}}{1-\left(\dfrac{1}{5}\right)^{2}}\right)= \tan^{-1}\left(\dfrac{5}{12}\right)$$
$$LHS : 4 \tan^{-1}\dfrac{1}{5}+ \tan^{-1}\dfrac{1}{99}-\tan^{-1}\dfrac{1}{70}$$
$$\displaystyle =\left(2 \tan^{-1}\frac{1}{5}-\tan^{-1}\frac{1}{70}\right)+\left(2 \tan^{-1}\frac{1}{5}-\tan^{-1}\frac{1}{70}\right)+\left(2\tan^{-1}\frac{1}{5}+\tan^{-1}\frac{1}{99}\right)$$
$$\displaystyle =\left(\tan^{-1}\frac{5}{12}-\tan^{-1}\frac{1}{70}\right)+\left(\tan^{-1}\frac{5}{12}+\tan^{-1}\frac{1}{99}\right)$$
$$\displaystyle= \tan^{-1}\left(\dfrac{\dfrac{5}{12}-\dfrac{1}{70}}{1+\left(\dfrac{5}{12}\right)\left(\dfrac{1}{70}\right)}\right)+\tan^{-1}\left(\dfrac{\dfrac{5}{12}+\dfrac{1}{99}}{1-\left(\dfrac{5}{12}\right)\left(\dfrac{1}{99}\right)}\right)$$
$$\left(\because \tan^{-1}x+\tan^{-1}y= \tan^{-1}\left(\dfrac{x+y}{1-xy}\right)\right)$$
$$= \tan^{-1}\left(\dfrac{2}{5}\right)+\tan^{-1}\left(\dfrac{3}{7}\right)$$
$$=\tan^{-1}\left(\dfrac{\dfrac{2}{5}+\frac{3}{7}}{1-\dfrac{6}{35}}\right)= \tan^{-1}(1)$$
$$=\dfrac{\pi }{4}$$


Find the value of $$\sin\left(\dfrac{1}{2}\cot^{-1}\left(-\dfrac{3}{4}\right)\right)$$.

$$\begin{matrix} \sin  \left( { \frac { 1 }{ 2 } { { \cot   }^{ -1 } }\left( { \frac { { -3 } }{ 4 }  } \right)  } \right)  \\ let\, \, \, \frac { 1 }{ 2 } { \cot ^{ -1 }  }\left( { \frac { { -3 } }{ 4 }  } \right) =\theta  \\ { \cot ^{ -1 }  }\left( { \frac { { -3 } }{ 4 }  } \right) =2\theta  \\ \cot  2\theta =\frac { { -3 } }{ 4 }  \\ \therefore \tan  2\theta =\frac { { -4 } }{ 3 }  \\ Then\, \, \,   \sin  \left( \theta  \right)=\dfrac{-2}{\sqrt13}   \end{matrix}$$


if$$\int \sin^{-1}\left ( \dfrac{2x+2}{\sqrt{4x^2+8x+13}} \right )dx$$$$=(x + 1)tan^{-1}\left ( \dfrac{2x+2}{3}\right )$$+$$\lambda$$$$ln(4x^2+8x+13)$$+$$C$$
then find the value of - 4$$\lambda$$

77292

Given 

$$\sin ^ {-1} \left( \dfrac {2x+2}{\sqrt{4x^2+8x+13}}\right)$$

$$\sin ^ {-1} \left( \dfrac {2x+2}{\sqrt{(2x+2)^2+(3)^2}}\right)$$

$$\tan ^ {-1} \left( \dfrac {2x+2}{3}\right)$$

$$ \displaystyle \int \tan ^ {-1} \left( \dfrac{2(x+1)}3\right) dx$$

Put $$ t=1+x \implies dt=dx$$ 

$$ \displaystyle \int  \tan ^ {-1} \left( \dfrac {2t}3\right)$$

Integrating by parts

$$ \implies \displaystyle \tan ^ {-1} \dfrac {2t}3 \int dt-\int\left( \dfrac d{dt}\tan ^ {-1}\dfrac {2t}3 \times \int dt\right)$$

$$ \implies \displaystyle t\tan ^ {-1} \dfrac {2t}3 -\int\left( \dfrac 1{1+\dfrac{4t^2}9} \times \dfrac 23 t \right) dt$$

$$ \implies \displaystyle t\tan ^ {-1} \dfrac {2t}3 - \dfrac 68\int\left( \dfrac {8tdt}{9+{4t^2}} \right) dt$$

$$ \implies \displaystyle t\tan ^ {-1} \dfrac {2t}3 - \dfrac 34 \ln (9+4t^2)+c $$

$$ \implies \displaystyle (1+x)\tan ^ {-1} \dfrac {2x+2}3 - \dfrac 34 \ln (4x^2+4x+13)+c $$

$$ \implies \lambda= \dfrac{-3}4 $$

$$ \implies -4\lambda =3 $$

 





If $$0< \cos^{-1} x< 1$$ and $$1+\sin (\cos^{-1}x)+\sin^{2}(\cos^{-1}x)+\sin^{3} (\cos^{-1}x)+.........\infty =2,$$ then find $$2\sqrt{3}x.$$

We have $$1+sin (cos^{-1}x)+sin^{2}(cos^{-1}x)+.........\infty =2$$

This is an infinite $$GP$$

$$\Rightarrow \dfrac{1}{1-sin\left ( cos^{-1}x \right )}=2\Rightarrow \dfrac{1}{2}=1-sin \left ( cos^{-1}x \right )$$

$$\Rightarrow sin (cos^{-1}x)=\dfrac{1}{2}$$

$$\Rightarrow cos^{-1}x=\dfrac{\pi }{6}       \therefore x=\dfrac{\sqrt{3}}{2} Ans.$$

$$\Rightarrow 2\sqrt{3}x=2\sqrt{3}\times\dfrac{\sqrt{3}}{2}=3$$


Find the number of values of $$x$$ of the form $$6n$$, where $$n$$ is an integer , in the domain of the function  $$f(x)=x\ln|x-1|+\displaystyle \frac{\sqrt{64-x^{2}}}{\sin x}$$

Considering the domain, we get
$$|x-1|>0$$
$$\Rightarrow x \neq 1$$
And
$$64-x^{2}\geq0$$
$$x^{2}\leq64$$
$$x\leq|8|$$
$$-8\leq x\leq 8$$
Hence
domain is
$$x\epsilon [-8,1)\cup(1,8]$$
Also, 
$$sin x \neq 0$$
Hence, $$x \neq k\pi$$
Hence the number of the form $$6n$$ are
$$-6,6$$
Hence there will be two numbers of the form 6n.
Hence answer is 2.


If $$ \displaystyle 0< \cos ^{-1}x< 1 $$ and  $$ \displaystyle 1+\sin(\cos^{-1}x)+\sin^{2}(\cos^{-1}x)+\sin^{3}(\cos^{-1}x)+...infinity= 2$$ then the value of  $$ \displaystyle 12 x^{2}$$ is

The above equation is an infinite G.P
Hence sum of the G.P will be 
$$S$$ $$=\dfrac{a}{1-r}$$
$$=\dfrac{1}{1-\sin(\cos^{-1}(x))}$$ ...(i)
Let $$\cos^{-1}(x)=y$$
$$\therefore \cos y=x$$
$$\sin y=\pm\sqrt{1-x^{2}}$$
$$y=\sin^{-1}(\pm\sqrt{1-x^{2}})$$
$$=\pm \sin^{-1}(\sqrt{1-x^{2}})$$
Substituting in the equation, gives us 
$$=\dfrac{1}{1\pm\sqrt{1-x^{2}}}$$
$$=2$$
$$2\pm2 \sqrt{1-x^{2}}=1$$
$$2-1=\pm2 \sqrt{1-x^{2}}$$

$$\dfrac{1}{2}=\pm\sqrt{1-x^{2}}$$
Squaring both sides, we get 

$$\dfrac{1}{4}=1-x^{2}$$

$$x^{2}=\dfrac{3}{4}$$
Hence, $$12x^{2}$$ $$=12\times\dfrac{3}{4}$$ $$=9$$.


If the domain of the function $$\displaystyle f(x)= \sqrt{3\cos^{-1}(4x)-\pi} $$ is [a,b] then the value of $$ \displaystyle (4a+64b)$$ is

$$3cos^{-1}(4x)-\pi$$
Now the domain of $$cos^{-1}(x)=[-1,1]$$
Similarly
$$\Rightarrow$$
$$cos^{-1}(4x)\rightarrow[0,\pi]$$
$$x\rightarrow [\dfrac{-1}{4},\dfrac{-1}{4}]$$
Now
$$\sqrt{3cos^{-1}(4x)-\pi}\geq0$$

$$\Rightarrow 3cos^{-1}(4x)\geq\pi$$

$$\Rightarrow cos^{-1}(4x)\geq\dfrac{\pi}{3}$$

$$\Rightarrow 4x\leq\dfrac{1}{2}$$
$$x\leq\dfrac{1}{8}$$
Hence domain is
$$x\epsilon[\dfrac{-1}{4},\dfrac{1}{8}]$$
Thus,
$$4a+64b$$
$$=-1+8$$
$$=7$$


If $$\displaystyle x= \sin^{-1}(a^{6}+1)\cos^{-1}(a^{4}+1)-\tan^{-1}(a^{2}+1),a\epsilon R$$ , then the value of $$\displaystyle \sec^{2}x$$ is


Let $$a=0$$
We get
$$x=sin^{-1}(1)cos^{-1}(1)-tan^{-1}(1)$$

$$=\dfrac{\pi}{2}.0-\dfrac{\pi}{4}$$

$$=\dfrac{-\pi}{4}$$
Hence 
$$sec(x)=\sqrt{2}$$
$$\Rightarrow sec^{2}(x)=2$$


If range of the function $$ \displaystyle f(x)= \sin^{-1}x+2\tan^{-1}x+x^{2}+4x+1$$ is $$[p,q]$$, then the value of $$(p+q)$$ is

Now the domain of $$sin^{-1}(x)$$ is $$[-1,1]$$
Hence the domain of the above function is $$[-1,1]$$ since the domain of $$tan(x)$$ is $$(-\infty,\infty)$$ and the rest is a linear function.
Hence
Domain is $$[-1,1]$$
Now
$$f(1)=\dfrac{\pi}{2}+2\dfrac{\pi}{4}+1+4+1$$
$$=\pi+6$$.
$$f(-1)=\dfrac{-\pi}{2}-2\dfrac{\pi}{4}+1-4+1$$
$$=-\pi-2$$
Hence
$$p+q$$
$$=\pi+6+(-\pi-2)$$
$$=6-2$$
$$=4$$


Prove that   

$$2\tan^{-1} \dfrac {1}{2} + \tan^{-1}\dfrac {1}{7} = \tan^{-1} \dfrac {31}{17}$$

Consider  L.H.S$$=2{\tan}^{-1}{\left(\dfrac{1}{2}\right)}+{\tan}^{-1}{\left(\dfrac{1}{7}\right)}$$

We know that,
 $$2{\tan}^{-1}{A}={\tan}^{-1}{\left(\dfrac{2A}{1-{A}^{2}}\right)}$$

$$={\tan}^{-1}{\left(\dfrac{2\times \dfrac{1}{2}}{1-{\left(\dfrac{1}{2}\right))}^{2}}\right)}+{\tan}^{-1}{\left(\dfrac{1}{7}\right)}$$

$$={\tan}^{-1}{\left(\dfrac{1}{1-\dfrac{1}{4}}\right)}+{\tan}^{-1}{\left(\dfrac{1}{7}\right)}$$

$$={\tan}^{-1}{\left(\dfrac{1}{\dfrac{4-1}{4}}\right)}+{\tan}^{-1}{\left(\dfrac{1}{7}\right)}$$

$$={\tan}^{-1}{\left(\dfrac{1}{\dfrac{3}{4}}\right)}+{\tan}^{-1}{\left(\dfrac{1}{7}\right)}$$

$$={\tan}^{-1}{\left(\dfrac{4}{3}\right)}+{\tan}^{-1}{\left(\dfrac{1}{7}\right)}$$

We know that 
$${\tan}^{-1}{A}+{\tan}^{-1}{B}={\tan}^{-1}{\left(\dfrac{A+B}{1-AB}\right)}$$

$$={\tan}^{-1}{\left(\dfrac{\dfrac{4}{3}+\dfrac{1}{7}}{1-\dfrac{4}{3}\times\dfrac{1}{7}}\right)}$$

$$={\tan}^{-1}{\left(\dfrac{\dfrac{28+3}{21}}{1-\dfrac{4}{21}}\right)}$$

$$={\tan}^{-1}{\left(\dfrac{\dfrac{31}{21}}{\dfrac{21-4}{21}}\right)}$$

$$={\tan}^{-1}{\left(\dfrac{31}{17}\right)}=$$R.H.S

Hence proved.


Prove that $$\tan^{-1} \left [\dfrac {\sqrt {1 + x} + \sqrt {1 - x}}{\sqrt {1 + x} - \sqrt {1 - x}}\right ] = \dfrac {\pi}{4} + \dfrac {1}{2} \cos^{-1} x, 0 < x < 1$$

For this we have to put $$x= \cos 2\theta$$

From LHS we get,

$$\tan^{-1}\left (\dfrac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}  \right )$$

Put $$x=\cos 2\theta$$

$$\tan^{-1}(\dfrac{\sqrt{1+\cos2 \theta}-\sqrt{1-\cos2 \theta}}{\sqrt{1+\cos2 \theta}+\sqrt{1-\cos2 \theta}})  .......1$$ 

Since we know that 

$$\cos2 \theta= 2\cos^2 \theta-1$$ or $$1-2\sin^2 \theta$$

Put this value in equation 1 then we get

$$=\tan^{-1}(\dfrac{\sqrt{ 2\cos^2 \theta}-\sqrt{2\sin^2 \theta}}{{ \sqrt{2\cos^2 \theta}}-\sqrt{2\sin^2 \theta}})$$

$$\tan^{-1}(\dfrac{{\sqrt{2}\cos \theta-\sqrt2\sin \theta}}{{\sqrt{2}\cos \theta+\sqrt2\sin \theta}})$$

$$\tan^{-1}(\dfrac{\sqrt{2}}{\sqrt{2}})(\dfrac{{\cos \theta-\sin \theta}}{{\cos \theta+\sin \theta}})$$

$$=(\dfrac{\cos \theta-\sin \theta}{\cos \theta+\sin \theta})$$

dividing by $$\cos \theta$$

$$\tan{-1}(\dfrac{\dfrac{\cos \theta}{\cos \theta}-\dfrac{\sin \theta}{\cos \theta}}{\dfrac{\cos \theta}{\cos \theta}-\dfrac{\sin \theta}{\cos \theta}})$$

$$\tan^{-1}(\dfrac{1- \tan \theta}{1+\tan \theta})$$

$$\tan^{-1}(\dfrac{1- \tan \theta}{1+1.\tan \theta})$$

$$\tan^{-1}(\dfrac{1- \tan \theta}{1+\tan\dfrac{\pi}{4}\tan \theta})$$     [since  $$\tan\dfrac{\pi}{4}=1$$]

By using $$\tan(x+y)= \dfrac{\tan x-\tan y}{1+\tan x.\tan y}$$
Thus, Put this value

 $$x=\dfrac{\pi}{4} $$ and $$y= \theta$$

$$\tan^{-1}\tan(\dfrac{\pi}{4}- \theta)$$

$$=\dfrac{\pi}{4}- \theta ......2$$
\since we know that

$$x=\cos2 \theta$$

$$\cos^{-1}=2 \theta$$

$$\dfrac{1}{2}\cos^{-1}x= \theta$$

Put this value in equation $$2$$ then we get

$$=\dfrac{\pi}{4}-\dfrac{1}{2}\cos^{-1}x$$

Hence RHS proved.


The number of real solutions of the equation
$$\sin^{-1}\left(\displaystyle\sum^{\infty}_{i=1}x^{i+1}-x\displaystyle\sum^{\infty}_{i=1}\left(\displaystyle\dfrac{x}{2}\right)^i\right)=\dfrac{\pi}{2}-\cos^{-1}\left(\displaystyle\sum^{\infty}_{i=1}\left(-\displaystyle\frac{x}{2}\right)^i-\displaystyle\sum^{\infty}_{i=1}(-x)^i\right)$$ lying in the interval  $$\left(-\displaystyle\frac{1}{2}, \frac{1}{2}\right)$$ is

$$\displaystyle\sum^{\infty}_{i=1}x^{i+1}=\frac{x^2}{1-x}$$
$$\displaystyle\sum^{\infty}_{i=1}\left(\displaystyle\frac{x}{2}\right)^i=\frac{x}{2-x}$$
$$\displaystyle\sum^{\infty}_{i=1}\left(-\displaystyle\frac{x}{2}\right)^i=\frac{-x}{2+x}$$
$$\displaystyle\sum^{\infty}_{i=1}(-x)^{i}=\frac{-x}{1+x}$$
To have real solutions
$$\displaystyle\sum^{\infty}_{i=1}x^{i+1}-x\displaystyle\sum^{\infty}_{i=1}\left(\displaystyle\frac{x}{2}\right)^i=\displaystyle\sum^{\infty}_{i=1}\left(\displaystyle\frac{-x}{2}\right)^i-\displaystyle\sum^{\infty}_{i=1}(-x)^i$$
$$\displaystyle\frac{x^2}{1-x}-\frac{x^2}{2-x}=\frac{-x}{2+x}+\frac{x}{1+x}$$
$$x(x^3+2x^2+5x-2)=0$$
$$\therefore x=0$$ and let $$f(x)=x^3+2x^2+5x-2$$
$$f\left(\displaystyle\frac{1}{2}\right)\cdot f\left(\displaystyle -\frac{1}{2}\right) < 0$$
Hence two solutions exist.


Using principal values, evaluate the following
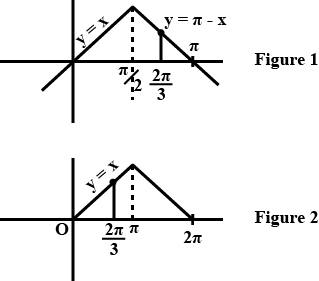
$$\cos^{-1}(\cos\dfrac{2\pi}{3})$$+ $$\sin^{-1}(\sin\dfrac{2\pi}{3})$$

$$\cos^{-1}(\cos \cfrac{2\pi}{3})+\sin^{-1}(\sin \cfrac{2\pi}{3})$$
Figure 1 represents graph of $$\sin^{-1}\sin x$$
Figure 2 represents graph of $$\cos^{-1}\cos x$$
Hence, $$\cos^{-1}\cos\cfrac{2\pi}{3}+\sin^{-1}\sin\cfrac{2\pi}{3}$$
$$=\cfrac{2\pi}{3}+\pi-\cfrac{2\pi}{3}$$
$$=\cfrac{2\pi}{3}+\cfrac{\pi}{3}=\pi$$



1016966_1018950_ans_b4224ab6349a4a838d35e961b9ee45b5.png


$$\dfrac{d}{dx}\sin ^{-1}\left(2x\sqrt{1-x^2}\right)=.......|x|>\dfrac{1}{\sqrt{2}}$$

Let $$y= \sin^{-1}(2x\sqrt {1-x^2}) \quad |x|>\dfrac{1}{\sqrt 2}$$
Let $$x=\sin \theta $$
$$\Rightarrow 1-x^2 = 1-\sin^\theta = \cos^2 \theta $$
$$\Rightarrow y = \sin^{-1}(2\sin \theta \sqrt {\cos^2 \theta })$$
$$= \sin^{-1} (2 \sin \theta |\cos \theta |)$$
$$=\sin^{-1}(\sin 2\theta)$$

Now $$|x|> \dfrac{1}{\sqrt 2}$$ 
$$\Rightarrow \theta \in \left[\dfrac{-\pi}{2}, \dfrac{-\pi}{4}\right)\cup \left(\dfrac{\pi}{4},\pi/2\right]$$
$$\Rightarrow 2\theta \in \left[-\pi, -\dfrac{\pi}{2}\right) \cup \left( \pi/2, \pi \right]$$
$$\Rightarrow y  = \sin^{-1}(\sin 2 \theta ) = \begin{cases} -\pi -2\theta \quad \quad \quad \quad \quad 2\theta \in [-\pi ,\dfrac { -\pi  }{ 2 } ) \\ +\pi -2\theta \quad \quad \quad \quad \quad 2\theta \in (\pi/2 ,\pi ] \end{cases}$$

$$\Rightarrow y= \begin{cases} -\pi -2\sin^{-1}x \quad \quad \quad \quad \quad x \in [-1 ,-\dfrac { 1  }{ \sqrt {2} } ) \\ \pi -2\sin^{-1}x \quad \quad \quad \quad \quad \quad x \in ( \dfrac{1}{\sqrt 2} ,1 ] \end{cases}$$

$$\Rightarrow \dfrac{dy}{dx} = -2\ \dfrac{1}{\sqrt {1-x^2}}$$
$$\Rightarrow \dfrac{dy}{dx} = \dfrac{-2}{\sqrt {1-x^2}}$$






















Find the value of $$\sin (\cfrac{1}{4}\sin^{-1}\cfrac{\sqrt 63}{8})$$

$$\sin (\cfrac{1}{4}\sin^{-1}\cfrac{\sqrt 63}{8})$$
Let $$\cfrac{1}{4} \sin^{-1}\cfrac{\sqrt 63}{8}=\theta$$
$$\Rightarrow \sin 4\theta=\cfrac{\sqrt 63}{8}=2\sin 2\theta$$


Prove that $$\tan^{-1}\dfrac{1}{7}+\tan^{-1}\dfrac{1}{13}-\tan^{-1}\dfrac{2}{9}=0$$

Simplifying the LHS of $${\tan ^{ - 1}}\frac{1}{7} + {\tan ^{ - 1}}\frac{1}{{13}} - {\tan ^{ - 1}}\frac{2}{9} = 0$$

$${\tan ^{ - 1}}\frac{1}{7} + {\tan ^{ - 1}}\frac{1}{{13}} - {\tan ^{ - 1}}\frac{2}{9} = {\tan ^{ - 1}}\left( {\frac{{\frac{1}{7} + \frac{1}{{13}}}}{{1 - \frac{1}{7} \times \frac{1}{{13}}}}} \right) - {\tan ^{ - 1}}\frac{2}{9}$$

$$ = {\tan ^{ - 1}}\left( {\frac{{20}}{{90}}} \right) - {\tan ^{ - 1}}\left( {\frac{2}{9}} \right)$$

$$ = {\tan ^{ - 1}}\left( {\frac{2}{9}} \right) - {\tan ^{ - 1}}\left( {\frac{2}{9}} \right)$$

$$ = 0$$

$$ = {\rm{RHS}}$$

Hence proved.



$${\sin ^{ - 1}}\sqrt {1 + x + {x^2}}  + {\tan ^{ - 1}}\sqrt {x + {x^2}}  = \frac{\pi }{2}$$
$$then\,x = $$


2041482_1048663_ans_1badae781dc648fbae1c72961dcad22d.jpg


$$\tan^{-1}\left(\dfrac{5-x}{6x^2-5x-3}\right)$$.

$$\begin{matrix} { \tan ^{ -1 }  }\left( { \dfrac { { 3-x } }{ { 6{ x^{ 2 } }-5x-3 } }  } \right)  \\ compare\, \, it\, \, with\, , \, { \tan ^{ -1 }  }\left( { \dfrac { { a-b } }{ { 1+ab } }  } \right)  \\ \Rightarrow 1+ab=6{ x^{ 2 } }-5x-3 \\ \Rightarrow 6{ x^{ 2 } }-5x-3=1+ab\, \, \, \Rightarrow 6{ x^{ 2 } }-5x-4=ab \\ \Rightarrow \left( { 3x-4 } \right) \left( { 2x+1 } \right) =ab \\ Also\, \, 5-x=2x+1-\left( { 3x-4 } \right)  \\ i.e,\, \, \, a=2x+1\, \, \, \, \, \, \, \, \, \, b=3x-4 \\ { \tan ^{ -1 }  }\left( { \dfrac { { a-b } }{ { 1+ab } }  } \right) \, \, \, =\, \, { \tan ^{ -1 }  }a+{ \tan ^{ -1 }  }b \\ \Rightarrow \boxed { { { \tan   }^{ -1 } }\left( { 2x+1 } \right) +{ { \tan   }^{ -1 } }\left( { 3x-4 } \right)  }  \\  \end{matrix}$$


$$\cot^{-1} \dfrac {1 - x}{1 + x}$$.

Let $$x = \tan \theta ,\,\theta  = {\tan ^{ - 1}}x$$

$$\begin{array}{l} ={ \cot ^{ - }  }\left[ { \dfrac { { 1-\tan  \theta  } }{ { 1+\tan  \theta  } }  } \right]  \\ ={ \cot ^{ - }  }\left[ { \tan  \left( { \dfrac { \pi  }{ 4 } -\theta  } \right)  } \right]  \\ ={ \cot ^{ - }  }\left[ { \cot  \left( { \dfrac { \pi  }{ 2 } -\dfrac { \pi  }{ 4 } +\theta  } \right)  } \right]  \\ ={ \cot ^{ - }  }\cdot \cot  \left[ { \dfrac { \pi  }{ 4 } +\theta  } \right]  \\ =\dfrac { \pi  }{ 4 } +\theta  \\ =\dfrac { \pi  }{ 4 } ={ \tan ^{ - }  }x \end{array}$$


$$\tan^{-1}\left(\dfrac{4x}{1+5x^2}\right)+\tan^{-1}\left(\dfrac{2+3x}{3-2x}\right)$$.

$$\begin{matrix} { \tan ^{ -1 }  }\left( { \frac { { 4x } }{ { 1+5{ x^{ 2 } } } }  } \right) +{ \tan ^{ -1 }  }\left( { \frac { { 2+3x } }{ { 3-2x } }  } \right)  \\ \Rightarrow { \tan ^{ -1 }  }\left( { \frac { { 5xd-x } }{ { 1+5x\cdot x } }  } \right) +\, { \tan ^{ -1 }  }\left( { \frac { { \frac { 2 }{ 3 } +x } }{ { 1-\frac { 2 }{ 3 } \cdot x } }  } \right)  \\ \Rightarrow { \tan ^{ -1 }  }5x-{ \tan ^{ -1 }  }x+{ \tan ^{ -1 }  }\frac { 2 }{ 3 } +{ \tan ^{ -1 }  }x \\ \Rightarrow { \tan ^{ -1 }  }\left( { \frac { { 5x+\frac { 2 }{ 3 }  } }{ { 1-\frac { { 10x } }{ 3 }  } }  } \right)  \\ \Rightarrow { \tan ^{ -1\,  }  }\left( { \frac { { 15x+2 } }{ { 3-10x } }  } \right)  \\  \\  \\  \end{matrix}$$


Find the value of $$\sin{\left[\dfrac{1}{2}\cot^{-1}{\left(\dfrac{-3}{4}\right)}\right]}$$.

$$\sin \left[ \dfrac{1}{2}\cot ^{-1}\left( -\dfrac{3}{4}\right)\right]$$
Let $$\theta=\cot^{-1}\left( -\dfrac{3}{4}\right)$$
$$\Rightarrow \cot \theta =\dfrac{-3}{4}$$
so, $$\cos \theta =\dfrac{-3}{5}$$
$$\Rightarrow \theta =\cos^{-1}\left( \dfrac{-3}{5}\right)$$
$$\therefore \sin \left[ \dfrac{1}{2}\cot^{-1}\left( -\dfrac{3}{4}\right)\right]=\sin\left[ \cos^{-1}\left( -\dfrac{3}{5}\right)\right].....\left(1\right)$$
we know that :
$$\Rightarrow \cos \theta =1-2\sin^2\left( \dfrac{\theta}{2}\right)$$
$$\Rightarrow \sin \dfrac{\theta}{2}=\sqrt{\dfrac{1-\cos\theta}{2}}$$
using this we can simplify $$\left( 1\right)$$ as 
$$\Rightarrow \sin \left[ \dfrac{\cos^{-1}\left(\dfrac{-3}{5}\right)}{2}\right]=\sqrt{\dfrac{1-\cos\left( \cos^{-1}\left(\dfrac{-3}{5}\right)\right)}{2}}$$
                                           $$=\sqrt{\dfrac{1-\left(\dfrac{-3}{5}\right)}{2}}$$

                                           $$=\sqrt{\dfrac{1+\dfrac{3}{5}}{2}}$$

                                           $$=\sqrt{\dfrac{8}{10}}$$

                                           $$=\sqrt{\dfrac{4}{5}}$$

$$\therefore \sin\left[ \dfrac{1}{2}\cot^{-1}\left(\dfrac{-3}{4}\right)\right] =\sqrt{\dfrac{4}{5}}$$
Hence, the answer is $$\sqrt{\dfrac{4}{5}}.$$


Class 12 Engineering Maths Extra Questions