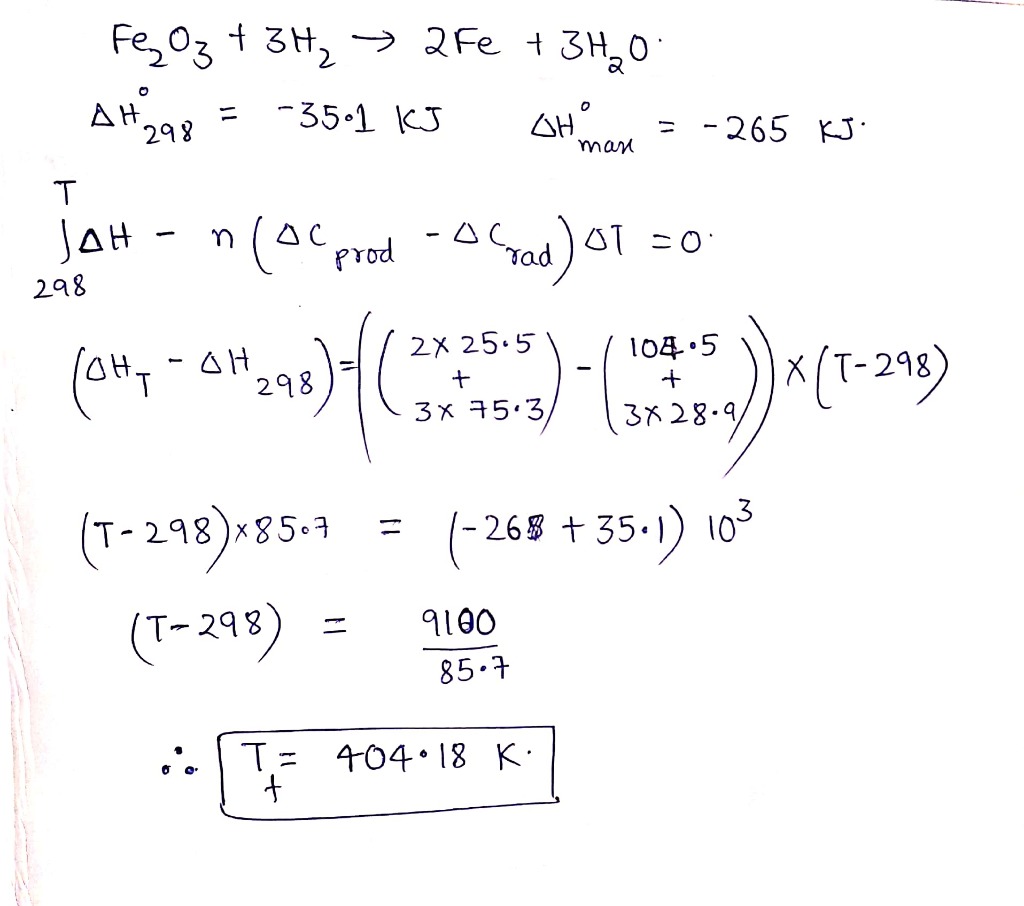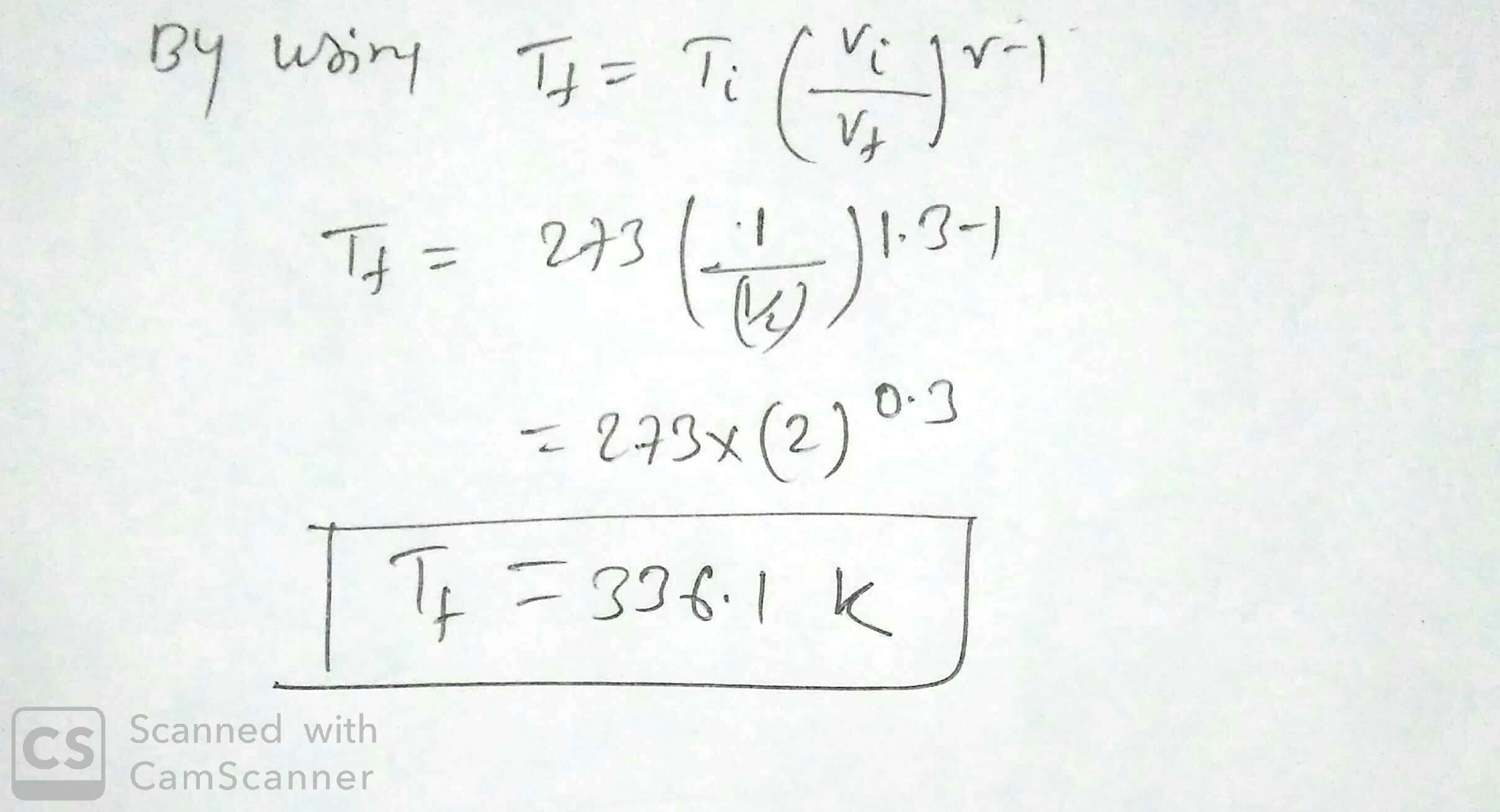Kinetic Theory - Class 11 Engineering Physics - Extra Questions

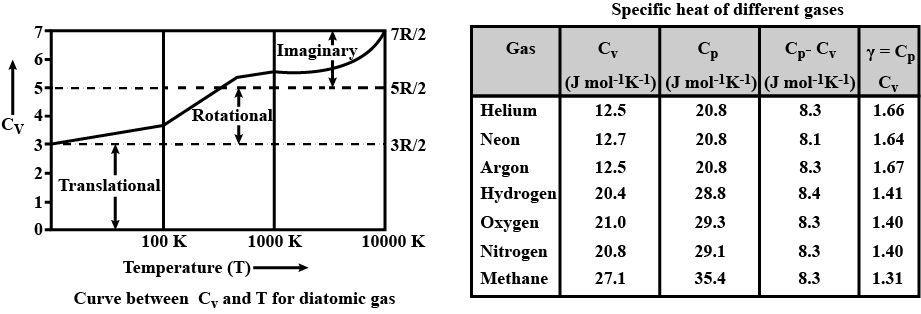
The heat capacity of a diatomic gas is higher than that of a mono-atomic gas.If true enter 1 else 0

The heat capacity of a diatomic gas is higher than that of a mono-atomic gas.
For ideal mono atomic gas $$C_p   = \frac {5}{2} R $$, $$C_v=\frac {3}{2}R $$
For ideal di atomic gas $$C_p = \frac {7}{2} R $$, $$C_v =\frac {5}{2}R $$


Molecules of a gas has -------------- intermolecular spaces.    (maximum / minimum)  

Maximum
Molecules of a gas has maximum intermolecular spaces.
Due to this the molecules are free to move any where within the confined region.
Therefore they take the shape of the container in which they are kept, and also their volume changes.
Therefore, Gases have no definite volume and size.



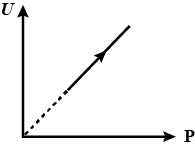
In the graph shown, U is the internal energy of gas and $$\rho$$ the density. Corresponding to given graph match the following two columns
216767_741fd2f94de54e68b03d5d2abc9e6644.png

Since, Internal energy is increasing therefore, temperature is increasing.
density is increasing therefore, volume is decreasing.
Now V decreasing , T increasing
from ideal gas equation PV=nRT
P is increasing
since P is increasing ratio T/V is increasing 
therefore,
A-2,B->3,C->2,D->2


State the law of equipartition of energy.

Law of equipartition of energy states that for a dynamical system in thermal equilibrium the total energy of the system is shared equally by all the degrees of freedom. The energy associated with each degree of freedom per molecule is $$\dfrac{1}{2}kT$$, where $$k$$ is the Boltzmann’s constant.

For example, for a monoatomic molecule each molecule has 3 degrees of freedom.  According to kinetic theory of gases, the mean kinetic energy of a molecule is $$\dfrac{3}{2}kT$$.



When the hydrogen atom in going from $$n=5$$ to $$n=1$$ state, its recoil speed is nearly

When the hydrogen atom is going from $$n=5$$ to $$n=1$$ state its recoil speed is nearly
Solution
We know that, momentum is given by equation
$$P=\cfrac{h}{\lambda}\\ \Rightarrow m\times V=\cfrac{h}{\lambda}\\V=\cfrac{h}{\lambda\times m}\rightarrow(1)$$
For hydrogen atom emits photon during transition from $$n=5$$ to $$n=1$$
$$\cfrac{1}{\lambda}=R(\cfrac{1}{n^2_1}-\cfrac{1}{n_2^2})$$
$$R=$$ Rydberg's constant $$=1.097\times10^7m^{-1}$$
$$\Rightarrow\cfrac{1}{\lambda}=R(\cfrac{1}{1^2}-\cfrac{1}{5^2})\\ \lambda=\cfrac{25}{24\times1.097\times10^{7}}=948\times10^{-8}m$$
Substituiting in equation $$(1)$$ we get,
mass of proton$$=1.6\times10^{-27}kg$$
$$\Rightarrow v=\cfrac{6.62\times10^{-34}m^2Kg/s}{1.\times10^{-27}\times9.48\times10^{-8}}\\ \quad=4.36m/s$$




$$C_p - C_v$$ for an ideal gas is ______.

For an ideal gas,
$$\triangle H=Q_P=nC_P\triangle T$$               $$\triangle U=Q_V=nC_V\triangle T$$
$$\triangle H= \triangle U+R\triangle T$$
$$nC_p\triangle T=nC_V\triangle T+R\triangle T$$
$$n\triangle T(C_P-C_V)=R\triangle T\longrightarrow C_P-C_V=R$$


What is the name of h & what is the value?

We know that,

$$h$$= plank constant

And value of plank constant is

$$h=6.67\times {{10}^{31}}$$

Hence, this is the required solution 



The value of rotational K.E. at temperature T of one gram molecules of a diatomic gas will be-

According to law of equipartition of energy, a molecule can have$$\frac { 1 }{ 2 } KT$$ energy per degree of freedom.

A diatomic molecule has two rotational degrees of freedom. Hence the total rotational kinetic energy is $$KT$$.



Calculate the average molecular kinetic energy:
Per kilogram, of oxygen at $$27^{o}C$$
($$R=8320J/ Kmol K$$, Avogadro's number $$=6.03\times 10^{26}m$$ molecules /$$K mole$$)

$$E=PV=nRT$$
    $$=1\times 8320\times 6.03\times { 10 }^{ 26 }\times 300$$
    $$=1.505\times { 10 }^{ 33 }J.$$


What is the kinetic energy of an object?

Kinetic energy (KE) of an object is the energy possess by the object because of its motion.

$$KE=\dfrac{1}{2}mv^2$$

where,
$$m=$$ mass of the object.
$$v=$$ velocity of the object.


What is the average translational kinetic energy of a molecule of an ideal gas at temperature of $$27^{\circ}C$$

Translational kinetic energy is given by the formula

$${ E }_{ T }=\dfrac { 3 }{ 2 } kT$$

$${ E }_{ T }=\dfrac { 3 }{ 2 } (1.38X{ 10 }^{ -23 })(300)=6.21X{ 10 }^{ -21 }J$$

Answer is $$6.21X{ 10 }^{ -21 }J$$


The average speed of all the molecules in a gas at a given instant is zero, whereas the average velocity of all the molecules is zero. Explain why?

Molecules of a gas  move randomly, hence average velocity is zero since velocity is a vector quantity.

There is a speed distribution  for the molecules, average speed will be non zero.


What is the average kinetic energy per atom of each gas ?

Since both Helium and Neon are monoatomic gases, degree of freedom for each gas is f=3. From ideal gas theory, average kinetic energy is equal to the thermal energy. Hence

$$KE=\dfrac { f }{ 2 } kT=\dfrac { 3 }{ 2 } (1.38X{ 10 }^{ -23 })(300)=6.21X{ 10 }^{ -21 }J/atom$$

Answer is $$6.21X{ 10 }^{ -21 }J$$


If $$x\, \times\, 10^{-2}\,$$ moles of helium at temperature 300 K and 1.00 atm pressure are needed to make the internal energy of the gas 100 J. Find $$x$$ (Round off to the nearest integer)

The internal energy of a monoatomic gas (He) is:
$$IE = \dfrac{3}{2}nRT$$
$$100 = \dfrac{3}{2}n(8.314)(300)$$
$$n = 2.67 \times 10^{-2}$$
2.67 gets rounded out to 3


A sample of helium gas is at a temperature of 300 K and a pressure of 0.5 atm. What is the average kinetic energy of a molecule of a gas?

Average kinetic energy of an ideal gas is equal to its thermal energy. Since, for helium, degrees of freedom is 3 as there is only translational motion possible in three directions. Hence,

$$KE=U=\dfrac { f }{ 2 } kT=\dfrac { 3 }{ 2 } (1.3807X{ 10 }^{ -23 })(300)=6.21X{ 10 }^{ -21 }J$$

Answer is $$6.21X{ 10 }^{ -21 }J$$


For any distribution of speeds $$V_{rms}\, \geq\, V_{av}$$. Is this statement true or false?

As per Maxwell's speed distribution, various speeds are given by,

$${ v }_{ rms }=\sqrt { \dfrac { 3RT }{ M }  } $$

$${ v }_{ av }=\sqrt { \dfrac { 8RT }{ \pi M }  } $$

Now, since $$3\pi >8$$. Hence $$3>\dfrac { 8 }{ \pi  } $$.

This implies that $${ v }_{ rms }\ge { v }_{ av }$$ where equality holds at 0K.

Thus the given statement is true.


A $$2.00\ mL$$ volume container contains $$50\ mg$$ of gas at a pressure of $$100\ kPa$$. The mass of each gas particle is $$8.0\, \times\, 10^{-26}\  kg$$. Find the average translational kinetic energy of each particle.

Mass of one mole of gas will be

$$M=(8X{ 10 }^{ -23 })(6.022X{ 10 }^{ 23 })g=48.18g$$

Thus number of moles will be

$$n=\dfrac { m }{ M } =\dfrac { 0.05 }{ 48.18 } =1.04X{ 10 }^{ -3 }$$

Thus temperature is $$T=\dfrac { PV }{ nR } =\dfrac { { 10 }^{ 5 }(2X{ 10 }^{ -6 }) }{ (1.04X{ 10 }^{ -3 })(8.314) } =23.13K$$

Translational energy per particle is

$$e=\dfrac { 3 }{ 2 } kT=\dfrac { 3 }{ 2 } (1.38X{ 10 }^{ -23 })(23.13)=4.88X{ 10 }^{ -22 }J$$

Answer is $$4.88X{ 10 }^{ -22 }J$$


Match the followung two columns for 2 moles of an ideal diatomic gas at room temperature T.

For a diatomic molecule, there are three degrees of freedom for translation.
Thus translational kinetic energy=$$n\dfrac{f}{2}RT$$
$$=2\times\dfrac{3}{2}RT=3RT$$
For a diatomic molecule, there are 2 degress of freedom for rotation.
Thus rotational kinetic energy=$$n\dfrac{f}{2}RT$$
$$=2\times \dfrac{2}{2}RT=2RT$$
Total degrees of freedom of a diatomic molecule=$$6$$
Thus total internal energy of the molecule=$$n\dfrac{f}{2}RT$$
$$=2\times \dfrac{6}{2}RT=6RT$$


Match following

(A) For $$O_2$$ (a diatomic gas)$$\Upsilon = 1.4$$ and $$C_P = \frac { 7 }{ 2 }R$$.
(B) For $$N_2$$ (a diatomic gas) $$C_P = \frac { 7 }{ 2 }R$$
(C) For $$CO_2$$ $$C_V = \frac { 9 }{ 2 }R$$
(D) For the mixture $$1  mol O_2 + 2  mol  O_3$$ $$C_V = \frac { 17 }{ 6 }R$$
Here: $$C_P$$ = heat  capacity  at constant pressure 
$$C_V$$ = heat  capacity  at constant volume
$$\Upsilon = C_P/C_V$$


Match following

(A) For $$O_2$$ (a diatomic gas),  $$\Upsilon = 1.4$$ and $$C_P =\displaystyle  \frac { 7 }{ 2 }R$$.
(B) For $$N_2$$ (a diatomic gas), $$\Upsilon = 1.4$$ and $$C_P =\displaystyle  \frac { 7 }{ 2 }R$$
(C) For $$CO_2,CH_4$$ $$\Upsilon = 1.33$$
(D) For the mixture $$1  mol O_2 + 2  mol  O_3$$ $$\Upsilon = 1.33$$
Here: $$C_P$$ = heat  capacity  at constant pressure 
$$C_V$$ = heat  capacity  at constant volume
$$\Upsilon = C_P/C_V$$


Heat capacity of a diatomic gas is higher than that of monoatomic gas.
If true enter 1, else enter 0.

True.

Let us give the same amount of energy to the mono- and di-atomic gases. 

The mono-atomic gas will spend all energy on translation and result in temperature rise. 

The di-atomic gas will spend that energy on translational as well as rotational motion. This way, the translational component gets lesser fraction of the same energy, causing lower temperature rise compared to the mono-atomic gas. 

So, to have same temperature rise, we need to give the di-atomic gas more energy. In other words, it has more specific heat.


The ratio of average translational kinetic energy to rotational kinetic energy of a diatomic molecule at temperature T is x/y.
then value of x+y is...........

For a diatomic molecule, the three translation direction contribute 1/2 kT per molecule, and for each molecule there are also two axes of rotation, contributing rotational kinetic energy in the amount of 1/2 kT each.
So total translational kinetic energy $$=(3/2)kT$$ & total rotational kinetic energy $$=(2/2)kT$$.
So, the ratio of average translational kinetic energy to rotational kinetic energy of a diatomic molecule at temperature T is (3/2).
So sum of ratio is 3+2 = 5


The ratio of a specific heats of a gas is 9/7, then the number of degrees of freedom of the gas molecules for translation motion is:

The ratio of a specific heats of a gas is 9/7, then the number of degrees of freedom of the gas molecules for translation motion is 3.We will use the standard formula $$\dfrac{(f+2)}{f} = \gamma$$.On cross multi plication and solving we get $$f=7$$,but total translational will be 3 only.


Calculate the kinetic energy of $$10$$ gram of Argon molecules at $$127^\circ C$$.
[Universal gas constant $$R=8320{ J }/{ }\ mol\ K$$. Atomic weight of Argon $$=40kg/ mol$$]

Given : $$m=10g=10\times { 10 }^{ -3 }kg$$

           $$T=273+127=400K$$
            $$R=8320{ J }/{  }mol.K$$
            $$M=40{ kg }/{ }mol$$
Kinetic energy per unit mass $$=\dfrac { 3 }{ 2 } \dfrac { RT }{ M }$$

                                              $$ =\dfrac { 3\times 8320\times 400 }{ 2\times 40 }$$
                                               $$ =15\times 8320$$

                                               $$=1.248\times { 10 }^{ 5 }{ J }/{ kg }$$

The kinetic energy of $$10\times { 10 }^{ -3 }kg$$ of Argon at $$127^\circ C$$
                                           $$=1.248\times { 10 }^{ 5 }\times 10\times { 10 }^{ -3 }$$
                                           $$=1248J$$


Calculate the average molecular kinetic energy :
(a) per kilomole,             (b) per kilogram, of oxygen at $$27^\circ C$$.
($$R=8320{ J }/{ K }moleK$$, Avogadro's number $$=6.03\times { 10 }^{ 26 }{ molecules }/{ K }mole$$)

(a) $$KE=\dfrac { 3RT }{ 2N }$$, where $$ R=8320{ J }/{ K }mole$$, $$T=27+273=300K$$ and $$N=$$ Avogadro number $$=6.03\times { 10 }^{ 26 }{ molecules }/{ K }mole$$

or, $$KE=\dfrac { 3\left( 8320 \right) 300 }{ 2\left( 6.03\times { 10 }^{ 26 } \right)  } $$

        $$=\dfrac { { \left( 4160 \right)  }^{ } }{ \left( 0.67\times { 10 }^{ 24 } \right)  } $$

        $$=62\times { 10 }^{ -22 }{ J }/{ molecule }$$
(b) $$K.E.=\left( \dfrac { 3 }{ 2 }  \right) kT$$

or, $$K.E.=\left( \dfrac { 3 }{ 2 }  \right) \left( 1.38\times { 10 }^{ -23 }{ J }/{ K } \right) \left( 27+273 \right) K=6.21\times { 10 }^{ -21 }{ J }/{ molecule }$$.


The specific heat at constant volume for a gas is $$0.075\ cal/g$$ and at constant pressure it is $$0.125\ cal/g$$. Calculate:
(i) the molecular weight of gas,
(ii) atomicity of gas 

(i) $${C}_{P}-{C}_{V}=\cfrac{R}{M}$$ where $$M=$$ molecular weight of gas
$$0.125-0.075=\cfrac{1.987}{M}$$
$$M=39.74=40$$
(ii) $$\cfrac{{C}_{P}}{{C}_{V}}=\gamma$$
$$\gamma=\cfrac{0.125}{0.075}=1.66$$


Specific heat of a monoatomic gas at constant volume is $$315\ J\ kg^{-1} K^{-1}$$ and at a constant pressure is $$525\ J\ kg^{-1} K^{-1}$$. Calculate the molar mass of the gas.

$$C_{P} = M\times 525$$ and $$C_{V} = M\times 315$$
where, $$M$$ is the molecular mass.
$$C _{P} - C_{V} = R(R = 8.314\ K\ K^{-1} mol^{-1})$$
$$M\times 525 - M \times 315 = 8.314$$
$$M (525 - 315) = 8.314$$
$$M = \dfrac {8.314}{210} = 0.0396\ kg\ mol^{-1} = 39.6\ g\ mol^{-1}$$


If the average distance between collisions of nitrogen molecules at $$NTP$$ is $$9.44 \times {10}^{-6}\ cm$$, what is the time between collisions?
Given $$R=8.31 \times {10}^{3}\ J/k\ mol\ K$$

Given mean free path $$\lambda =9.44\times { 10 }^{ -6 }cm$$
$$\Rightarrow$$ Time between collision $$=\dfrac { \lambda  }{ { V }_{ rms } } $$
$$\Rightarrow$$ Where, $${ V }_{ rms }=\sqrt { \dfrac { 3RT }{ M }  } =\sqrt { \dfrac { 3\times 8.31\times { 10 }^{ 3 }\times 293 }{ 28 }  } $$
                                                $$=510.7m/s$$
$$\Rightarrow$$ Time between collision $$=\dfrac { 9.44\times { 10 }^{ -8 }m }{ 510.7 } =1.8\times { 10 }^{ -10 }s.$$
Hence, solve.


Explain the inter-conversion of the three states of matter in terms of force attraction and K.E of the molecules.

The inter-conversion of states of matter:
In terms of forces of attraction:
The forces of attraction decrease as the solid changes to liquid then the gases.
$$Solid \to Liquid \to Gases$$
$$ \to $$
Forces of attraction decreased.

In terms of kinetic energy:
Kinetic energy will increases when solid changes to liquids than to gaseous state, because of particles will absorb energy and K.E. increases.
$$Solid \to Liquid \to Gases$$
$$ \to $$
kinetic energy increases.


State the applications of compressibility of gases in our day-today life.

Application of compressibility of gases in our day to day life:

1) Gaseous form of CNG and LPG gas can be stored in a cylinder by compression.

2) $$C{O_2}$$ [Carbon dioxide] gas is compressed and dissolved in cold drinks.



Find the average kinetic energy per molecule at temperature $$T$$ for an equimolar mixture of two ideal gases $$A$$ and $$B$$ where $$A$$ is monoatomic and $$B$$ is diatomic.

No. of degrees of freedom per molecule for $$A = 3$$
No. of degrees of freedom per molecule for $$B = 5$$
Since, the mixture is equimolar, the average kinetic energy per molecule will be the simple average of the two values i.e. $$\left (\dfrac {3 + 5}{2}\right )kT = 4kT$$, where $$k$$ is Boltzmann's constant.


The average translational kinetic energy of air molecules is $$0.040eV$$ ($$1eV=1.6\times {10}^{-19}J$$). Calculate the temperature of the air. Boltzman's constant $$k=1.38\times {10}^{-23}J{K}^{-1}$$

Given 
the average translational $$KE=0.040eV$$
                                           $$ =  6.4 \times {10^{ - 21}}J$$
$$\begin{array}{l} k=1.38\times { 10^{ -23 } }J{ k^{ -1 } } \\ T=? \end{array}$$

the average translational kinetic energy
$$\begin{array}{l} KE=\dfrac { 3 }{ 2 } \times K\times T \\ 6.4\times { 10^{ -21 } }=\dfrac { 3 }{ 2 } \times 1.38\times { 10^{ -23 } }\times T \\ T={ 309.1^{ \circ  } }C \end{array}$$


Find the number of degrees of freedom of molecules in a gas if its heat capacities are $$ C_v = 650 \ J Kg^{-1} K^{-1} $$ and $$C_p = 910 \ J Kg^{-1} K^{-1}$$.

The relation between $$\gamma $$(ratio of specific heats) and degree of freedom $$f$$ is

$$ \gamma =1+\dfrac{2}{f}..........(1) $$

$$ \gamma =\dfrac{{{c}_{p}}}{{{c}_{v}}} $$

$$ \gamma =1.4 $$

Put this in equation (1)

$$ 1.4-1=\dfrac{2}{f} $$

$$ 0.4=\dfrac{2}{f} $$

$$ f=5 $$

So the degree of freedom of the gas is 5. Hence, the gas is diatomic.



$$0.040$$ $$g$$ of He is kept in a closed container initially at $$100.0C$$. The container is now heated. Neglecting the expansion of the container, calculate the temperature at which the internal energy is increased by $$12$$ $$J$$. [ R = $$\dfrac {25}{3}$$ j - $$moi^{-1}$$ - $$k^{-1}$$]

The mass of the Helium $$m = 0.040 g$$
The initial temperature of the container is $$ T = 100^{\circ} C$$
The molecular mass of the helium is $$ M_{He} = 4g$$

The internal energy of the gas molecules:
$$U = \dfrac{3}{2} nRt $$

$$= \dfrac{3}{2} \times \dfrac{m}{M} \times RT $$ 

According to the question
$$\dfrac{3}{2} \times \dfrac{m}{M} \times RT + 12 = \dfrac{3}{2} \times \dfrac{m}{M} \times RT'$$

$$\Rightarrow 1.5 \times 0.01 \times 8.3 \times 373 = 12 = 1.5 \times 0.01 \times 8.3 \times T'$$

$$\Rightarrow T' = \dfrac{58.4385}{0.1245} $$

$$= 469.3855 K = 196.3^{\circ} C \approx 196^{\circ} C$$


Calculate the max. work done by system in an irreversible (single step) adiabatic expression of 1 mole of a polyatomic gas from 300K pressure 10 atm to 1 atm.($$\gamma$$ = 1.33)

According to the problem:
Let us consider the work done for adiabatic irreversible expansion
$$w = n{C_v}\left( {{T_2} - {T_1}} \right)$$
for $${T_2}$$
$$\left( {\frac{{{T_2}}}{{{T_1}}}} \right) = {\left( {\frac{{{P_2}}}{{{P_1}}}} \right)^{\left[ {1 - \frac{1}{\gamma }} \right]}}$$
implies that
$${T_2} = T \times {\left( {\frac{1}{{10}}} \right)^{\left[ {1 - \frac{1}{{1.33}}} \right]}}$$
$$ = 300 \times 1.175$$
$$ = 525K$$
To find cv:
$$\gamma  - 1 = \frac{R}{{CV}}$$
or
$$Cv = \frac{{8.314}}{{1.33 - 1}}$$
$$ = 25.19$$
substitute in equation,
$$w = 5.5KJmo{l^{ - 1}}$$


For a gas, $$\gamma=9/7$$. What is the number of degrees of freedom of the molecules of the gas?

Given,
$$\gamma  = \frac{9}{7}$$
Now,
$$\begin{array}{l} \gamma =\frac { 9 }{ 7 }  \\ \Rightarrow \gamma =\frac { { f+2 } }{ f }  \\ \Rightarrow \frac { { f+2 } }{ f } =\frac { 9 }{ 7 }  \\ \Rightarrow f=7 \end{array}$$
$$\therefore$$ Degree of freedom is $$7$$.


The kinetic energy of $$1\ kg$$ of oxygen at $$300\ K$$ is $$1.356 \times 10^{6}\ J$$. Find the kinetic energy of $$4\ kg$$ of oxygen at $$400\ K$$.

Given:Let $${m}_{1}$$ be the mass of oxygen$$=1$$kg
and $${T}_{1}$$ be the kinetic energy$$=300$$K
K.E is $${E}_{1}=1.356\times{10}^{6}$$J
Let $${m}_{2}$$ be the mass of oxygen$$=4$$kg
and $${T}_{2}$$ be the kinetic energy$$=400$$K
To find:K.E is $${E}_{2}$$
K.E$$E=\dfrac{3m}{2M}RT$$
$${E}_{1}=\dfrac{3{m}_{1}}{2M}R{T}_{1}$$     ......$$(1)$$
$${E}_{2}=\dfrac{3{m}_{2}}{2M}R{T}_{2}$$     ......$$(2)$$
$$\dfrac{{E}_{2}}{{E}_{1}}=\dfrac{{m}_{2}}{{m}_{1}}.\dfrac{{T}_{2}}{{T}_{1}}$$
$$=\dfrac{4\times 400}{1\times 300}=\dfrac{16}{3}$$
$${E}_{2}={E}_{1}\times\dfrac{16}{3}$$
$$=1.356\times{10}^{6}\times\dfrac{16}{3}=7.232\times{10}^{6}$$J



Volume of vessel A is twice the volume of vessel B. Both are filled with the same gas. If the gas in A is at twice the temperature and twice the pressure to the gas in B, what is the ratio of gas molecules in A and B?


1357276_1586906_ans_057ef4dd1c6a4f20aa9d4fc4c4b12ad0.jpg


State law of equipartition of energy. Use this law of equipqrtition to calculate specific heats of monoatomic , diatomic and triatomic gases.


1357337_1586903_ans_bce634f68b9940769dd9e1924996c32e.jpg


A gas of molecular weight $$40$$ has a specific heat $$0.075\ cal/g/deg$$ at a constant volume. What is the $$C_v$$ value for it and what is the atomicity of the gas?

Sp. heat at constant volume $$=0.075\ cal/g-degree$$

$$C_v=0.075\ cal/ g^oc \times 40\ g/mole =3cal/ mol^oc$$

$$\dfrac{R}{\gamma -1}=3$$

$$\dfrac{R}{\gamma-1}=3\Rightarrow \gamma -1=\dfrac{2}{3}\Rightarrow \gamma=\dfrac{2}{3}+1=5/3=1.67\Rightarrow monoatomic\ gas$$.



The molar heat capacities of water , $$ H_{2 (g)} $$ and $$ O_{2(g)} $$ are $$ 18 , 6.76 $$ and $$ 6.62 \,cal $$ respectively . the heat of formation of water at $$ 25^{\circ} \,C $$ is $$ -68.4\,kcal $$ . Calculate its heat of fomation at $$ 90^{\circ} \,C $$ .


1986404_1744659_ans_457a7793b5e64b5f84b372daca1fab2c.jpg


An ideal gas undergoes isothermal compression from an initial volume of $$4.00\ m^3$$ to a final volume of $$3.00\ m^3$$. There is $$3.50$$ mol of the gas, and its temperature is $$10.0^oC$$.
How much energy is transferred as heat between the gas and its environment?

The internal energy change $$\Delta E_{int}$$ vanishes when $$\Delta T=0$$ so that the First Law of Thermodynamic leads to $$Q=W=-2.37\ kJ$$. The negative value implies that the heat transfer is from the sample to its environment.


One way to keep the contents of a garage from becoming too cold on a night when a severe subfreezing temperature is forecast is to put a tub of water in the garage. If the mass of the water is $$125\ kg$$ and its initial temperature is $$20^oC$$,
how much energy must the water transfer to its surroundings in order to freeze completely.

The water ( of mass $$m$$ ) releases energy in two steps, first by its temperature from $$20^oC$$ to $$0^oC$$, and then by freezing into ice. Thus the total energy transferred from the water to the surroundings is
$$Q=C_Wm\Delta T+L_pm=(4190\ J/kg. K)(125\ kg)(20^oC)+(333\ kJ/kg)(125\ kg)=5.2\times 10^7\ J$$.


Specific heat of $$Li(s), \ Na(s), \ K(s), \ Rb(s)$$ and $$Cs(s)$$ at $$398\ K$$ are $$3.57,\ 1.23,\ 0.756, \ 0.363$$ and $$0.243\ Jg^{-1}K^{-1}$$ respectively. Compute the molar heat capacity of these elements and identify any periodic trend. If there is trend, use it to predict the molar heat capacity of $$Fr$$.

Molar heat capacity $$= $$ At. wt. $$\times$$ specific heat.

Molar heat capacity (in $$J \ mol^{-1}KT^{-1}$$)of:
$$Li(s) = 3.57 \times 6.94 = 24.78$$
$$Na(s) = 1.23 \times 22.99 = 28.28$$
$$K(s) = 0.756 \times 39.10 = 29.56$$
$$Rb(s) = 0.363 \times 85.47 = 31.03$$
$$Cs(s) = 0.242 \times 132.91 = 32.16$$

There is a trend plotting these values with atomic number, the extrapolation of graph gives the value of $$Fr(s) = 33.5\ J \ mol^{-1}K^{-1}$$


For the reduction of ferric oxide by hydrogen,
$$Fe_{2}O_{3(s)} + 3H_{2(g)} \rightarrow 2Fe_{(s)} + 3H_{2}O_{(l)}$$; $$\Delta H^o_{298}= -35.1\ kJ$$.
The reaction was found to be too exothermic to be convenient. It is desirable that $$\Delta H^o$$ should be at most $$-26\ kJ$$. At what temperature it is possible.
$$C_{P\ Fe_{2} O_{3}}=104.5$$, $$C_{p\ Fe(s)} = 25.5$$, $$C_{p\ H_{2}O_{(|)}} = 75.3$$,
$$C_{p \ H_{2(g)}} =28.9$$ (All in $$J/mol^{-1}$$ )


1759679_1746814_ans_5b964d6b91bf4a3da0b5cd161f2c6197.jpg


1 g of arsenic dissolved in 86 g of benzene brings down the freezing point to $$ 5.31 ^0C $$ from $$ 5.50 ^0 C $$. If $$ K_f $$ of benzene is $$ 4.9 \frac { ^0C}{m} $$, the atomicity of the molecule is :  ( Atomic mass of  As = 75 ) 

$$ \Delta T_f = K_f m $$

$$ 0.19 = 4.9 \times \dfrac { \dfrac {1}{M} }{ \dfrac {86}{1000} } \Rightarrow  0.19 = 4.9 \times  \dfrac {1000}{ M \times 86} \Rightarrow M = \dfrac { 4.9 \times 1000}{ 86 \times 0.19 } = 300. $$

$$Atomicity  = \dfrac {300}{75} = 4 $$ 


The heat of reaction for, $$C_{10}H_{8(s)} + 12O_{2(g)} \rightarrow 10CO_{2(g)} + 4H_{2}O_{(1)} $$ at constant volume is $$- 1228.2\ kcal$$ at $$25^oC$$. Calculate the heat of reaction at constant pressure at $$25^oC.$$

Heat of reaction at constant pressure is represented by $$\Delta H$$

Heat of reaction at constant volume is represented by $$\Delta U$$

Given​: $$\Delta U = -1228.2$$ kcal

Since $$\Delta H = \Delta U + \Delta nRT$$

In the given reaction $$\Delta n = 10-12 = -2$$
$$R = 2$$ cal/mol K

$$\Delta H = -1228.2 +(-2/1000)(2\times 298) = -1229.4$$ kcal


Suppose $$12.0\ g$$ of oxygen $$(O_2)$$ gas is heated at constant atmospheric pressure from $$25.0^o$$ to $$125^oC$$.
How much energy is transferred to the oxygen as heat? (The molecules rotate but do not oscillate).

This is a constant pressure with a diatomic gas, so we used. We note a charge of Kelvin temperature is numerically the same as a change of Celsius degrees.
$$Q=nC_P \Delta T=\left(\dfrac 72 R \right)\Delta T=(0.375\ mol)\left(\dfrac 72 \right)(8.3.1\ J/mol.K)(100\ K)=1.09\times 10^3 J$$.


Under constant pressure, temperature of $$2.00\ mol$$ of an ideal monatomic gas is raised $$15.0\ K$$. What are
the change $$\Delta E_{int}$$ in the internal energy of the gas.

Since the process is a constant pressure expansion,
$$W=p\Delta V=nR \Delta T=(2.02\ mol)(8.31\ J/mol.K)(15\ K)=249\ J$$
Now $$C_{p}=\dfrac{5}{2}R$$ in this case, so $$Q=nC_{p}\Delta T=+623\ J$$ 
The change in the internal energy is $$\Delta E_{int}=Q-W=+374\ J$$.


Calculate the number of degrees of freedom of molecules of hydrogen in $$1cc$$ of hydrogen gas at NTP.

hydrogen molecule is diatomic so it has $$3$$ translational degree of freedom and $$2$$ rotational.
So degree of freedom in $${H}_{2}$$ molecule $$=3+2=5$$
for number of molecule in $$1cc$$
$$22.4lit=22400cc$$ $${H}_{2}$$ gas at STP has $$=6.023\times {10}^{23}$$ molecule
$$1cc$$ $${H}_{2}$$ gas at STP has $$=\cfrac{6.023}{22400}\times {10}^{23}$$ molecule $$=2.688\times {10}^{19}$$
so total degree of freedom $$=5\times 2.688\times {10}^{19}$$
$$=13.440\times {10}^{19}=1.344\times {10}^{20}$$


We give $$70\ J$$ as heat to a diatomic gas, which then expands at constant pressure. he gas molecules rotate but do not oscillate. By how much does the internal energy of the gas increase?

Referring to equation , we have
$$\Delta E_{int}=nC_V \Delta T=\dfrac 52 nR\Delta T$$
$$Q=nC_P \Delta T=\dfrac 72 nR\Delta T$$
Dividing the equations, we obtain
$$\dfrac {\Delta E_{int}}{Q}=\dfrac 57$$
Thus, the given value $$Q=70\ J$$ leads to $$\Delta E_{int}=50\ J$$ 


The difference between $$C_{p}$$
and $$C_{v}$$ can be derived using the empirical relation $$H=U +\mathbf{p}
\mathbf{V}$$. Calculate the difference between $$\mathbf{C}_{\mathbf{p}}$$ and $$\mathbf{C}_{\mathbf{v}}$$
for 10 moles of an ideal gas.

We can write
equation for heat, $$q$$ at constant volume as $$q_{r}=\Delta U=C_{1} \Delta T$$
at constant pressure as $$q_{p}=\Delta H=C_{p} \Delta T$$



$$C_{p}-C_{v}=R$$
for 1 mole of a gas



For $$n$$
mole of a gas



$$C_{p}-C_{v}-n
R-10 \times 4.184 J=41.84 J$$



Suppose $$4.00$$ mol of an ideal diamotic gas, with molecular reaction rotation but not oscillation experienced a temperature increase of $$60.0\ K$$ under constant-pressure conditions. What are the change $$\Delta E_{int}$$ in internal energy of the gas?

The change in the internal energy is given by $$\Delta E_{int}=nC_V \Delta T$$, where $$C_V$$ is the specific heat at constant volume. For a diatomic ideal gas $$C_V =\dfrac 52 R$$, so
$$\Delta E_{int}=\dfrac 52 n R\Delta T=\dfrac 52 (4.00\ mol)(8.31\ J/mol.K)(60.0\ K)=4.99\times 10^3 J$$.


When $$20.9\ J$$ was added as heat to a particular ideal gas, the volume of the gas changed from $$50.0\ cm^{3}$$ to $$100\ cm^{3}$$ while the pressure remained at $$1.00\ atm$$
By how much did the internal energy of the gas change ? If the quantity of gas present was $$2.00\times 10^{-3}\ mol$$.

According to the first law of thermodynamics $$Q=\Delta E_{int}+W$$. When the pressure a constant $$W=p\Delta V$$. So
$$\Delta E_{int}=Q-p\Delta V=20.9\ J-(1.01\times 10^{5}Pa)(100\ cm^{3}-50\ cm^{2})\left(\dfrac{1\times 10^{-6}m^{3}}{1\ cm^{3}}\right)=15.9\ J$$


Suppose $$1.00\ L$$ of a gas with $$\gamma =1.30$$, initially at $$273\ K$$ and $$1.00\ atm$$, is suddenly compressed adiabatically to half its volume. Find its final temperature.


1697698_1770441_ans_06853a914bbe47b09cb6372c7fa7fd92.jpg


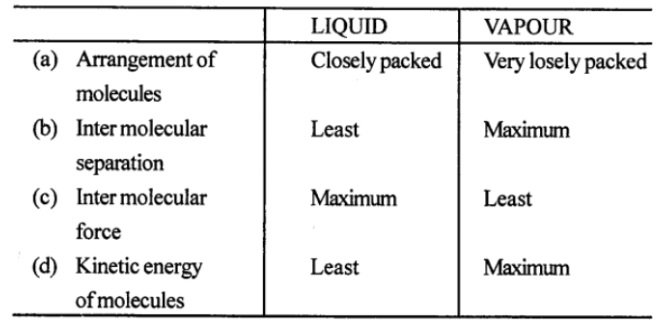
Distinguish between liquid and vapour (or gas) states of matter on the basis of following factors
(a) Arrangement of molecules
(b) Inter-molecular separation
(c) Inter-molecular force, and 
(d) Kinetic energy of molecules

DISTINCTION BETWEEN LIQUID AND VAPOUR ON THE BASES OF:
1692481_1802318_ans_389693a51a054dd6995ccf263ca7be19.jpg


What is boiling ? Explain it on the basis of molecular motion ?

BOILING : "The change of liquid to vapours on heating at a constant temperature is called BOILING".
$$KE = \dfrac{1}{2} MV^2.$$ more the speed of molecules more is the kinetic energy. Heating of the liquid increases the average K.E. of liquid molecules and molecules acquire sufficient K.E. needed to overcome the force of attraction of other molecules. These molecules start leaving the liquid not only at the surface but also near the walls of the containing vessel and bubbles are seen on the walls of vessel. This causes the agitation in the whole of the liquid and this is called boiling.


What is the degree of freedom for an airplane flying in the sky ?

An airplane can have independent velocities in three directions (X, Y, Z). Hence, the degree of freedom is $$3.$$


Why does bubbles appear when a liquid is heated ?

When a liquid is heated formation of vapours takes place which appear in the form of bubbles.



Give the relation between degree of freedom (f) and $$\gamma.$$

$$\gamma = \left ( 1 + \dfrac{2}{f} \right )$$ where f = degree of freedom


State the main postulates of kinetic theory of matter. 

According to this theory, any substance whether solid, liquid or gas is made up of tiny particles called atoms, molecules or ions which are in constant motion is called kinetic theory of matter. The main postulates of kinetic theory of matter are:
            1. Matter is composed of very small particles called atoms or molecules.
            2. The constituent particles of a kind of matter are identical in all respects.
            3. These particles have spaces between them which is known as interparticular or intermolecular space.
            4. There exists a force of attraction between the particles of matter which holds them together. This force of attraction is known as interparticular or intermolecular force of attraction.
            5. Particles of matter are always in a state of random motion and possess kinetic energy, which increases with an increase in temperature and vice-versa.


Give the value of Cp for a diatomic gas.

For a diatomic gas,
$$C_{p} = \dfrac{7}{2}R,$$ where R = Universal gas constant.


Which energy gained due to the moment of molecule? Potential energy / Kinetic, energy.

Kinetic energy  gained due to the moment of molecule


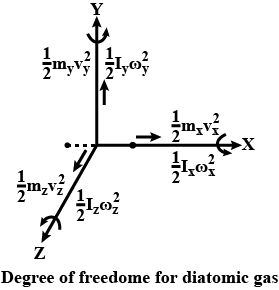
What do you understand by degree of freedom ?

A degree of freedom is an independent physical parameter in the formal description of the state of a physical system.
 In three-dimensional space, three degrees of freedom are associated with the movement of a particle.
 A diatomic gas molecule thus has six degrees of freedom. This set may be split in terms of translations, rotations, and vibrations of the molecule. The centre of mass motion of the whole molecule accounts for three (3) degrees of freedom. Also, the molecule has two rotational degrees of motion and one vibrational degree of freedom.
1756444_1833939_ans_6d5f02f610c64cc3a42cf45bf714ff03.png


A gas contained in a cylinder surrounded by a thick layer of insulating material is quickly compressed has there been a transfer of heat ?

No. There's no any transfer of heat energy, as the cylindrical vessel is surrounded by an insulating material, which doesn't allow heat transfer.


On what factors do the degrees of freedom depend?

The degrees of freedom depends upon
(i) the number of atoms forming a molecule
(ii) the structure of the molecule
(iii) the temperature of the gas.


Find the kinetic energy of $$5$$ liters of a gas at STP, given the standard pressure, is $$1.013 \times 10^5\, N/m^2$$.

$$P=1.013 \times 10^5\, N/m^2,\,V=5\,litres=5 \times 10^{-3}\,m^3$$

$$E=\dfrac{3}{2}PV$$

$$=\dfrac{3}{2}(1.013 \times 10^5\, N/m^2)(5 \times 10^{-3}\,m^3)$$

$$=7.5 \times 1.013 \times 10^2\,J$$

$$=7.597 \times 10^2\,J$$

This is the required energy.


Mention the conditions under which a real gas obeys the ideal gas equation.

A real gas obeys ideal gas equation when the temperature is very high and pressure is very low. [Note: Under these conditions, the density of a gas is very low. Hence, the molecules, on average, are far away from each other. The intermolecular forces are then not of much consequence.]


A gas contained in a cylinder surrounded by a thick layer of insulating material is quickly compressed has work been done ?

Yes. Work is always done when a gas is compressed by any external agent, no matter what type of system is there.


How many degrees of freedom have the gas molecules, if under standard conditions the gas density is $$\rho= 1.3 \ mg/cm^3$$ and the velocity of sound propagation in it is $$v = 330 \ m/s$$.

From the formula 
$$v = \sqrt{\frac{\gamma p}{\rho}}, \ \gamma  = \frac{pV^2}{p}$$
If i = number of degrees of freedom of the gas then 
$$C_p = C_V +RT $$ and $$C_V = \frac{i}{2} RT$$
$$\gamma =  \frac{C_p}{C_V} = 1 + \frac{2}{i}$$ or $$i = \frac{2}{\gamma -1} = \frac{2}{\frac{\rho v^2}{p}-1}$$


Find the mass and the number of degrees of freedom of molecules of freedom of molecules in a gas if its heat capacities are known: $$c_v =  0.65 \ J/(g.K)$$ and $$c_p = 0.91 \ J/(g.K)$$.

Given specific heats $$C_p, C_v$$ (per unit mass)
$$M(C_p - C_V) = R$$ or, $$M = \frac{R}{C_p - C_V}$$
Also $$\gamma  = \frac{C_p}{C_V} = \frac{2}{i} +1  $$, or, $$i = \frac{2}{\frac{C_p}{C_V} 1} = \frac{2C_V}{C_p - C_V}$$


A solar cooker and a pressure cooker both are used to cook food. Treating them as thermodynamic systems, discuss the similarities and differences between them.

Solar cooker:
$$\cdot$$ Solar cooker was invented by Horace Benedict de saussure in $$1767.$$
$$\cdot$$ Solar cooker is a device used to cook food by using no fuel, instead of sunlight.
$$\cdot$$ Solar cookers use a parabolic reflector to collect the rays of the sun and focus them at the cooker to heat it and cook the food in the cooker.
$$\cdot$$ Today the solar cookers are a little bit expensive than pressure cookers.
$$\cdot$$ Big solar cookers can be used to make food for people on a larger scale.
Pressure Cooker-
$$\cdot$$ Pressure cooker was invented by Denis papin.
$$\cdot$$ Pressure cookers are the most common cookers used in our houses and can be found in every house.
$$\cdot$$ Pressure cookers require water to convert it into steam for raising the internal temperature and pressure that permits quick cooking.
$$\cdot$$ Pressure cooker are cheaper than solar cookers.
$$\cdot$$ Pressure cookers requires a fuel for heating the liquid inside them


When a gas is heated, its temperature increases. Explain this phenomenon on the basis of the kinetic theory of gases.

Molecules of a gas are in a state of continuous random motion. They possess kinetic energy. When a gas is heated, there is an increase in the average kinetic energy per molecule of the gas. Hence, its temperature increases (the average kinetic energy per molecule being proportional to the absolute temperature of the gas).


Using the Maxwell distribution function, calculate the mean velocity projection ($$v_x$$) and the mean value of the modulus of this projection ($$| v_x |$$) if the mass of each molecule is equal to $$m$$ and the gas temperature is $$T$$.

$$<v_x> = 0$$ by symmetry 
$$<|v_x|> = \displaystyle \int\limits_{-\infty}^{\infty} |v_x| e^{-\frac{mv_x^2}{2kT}} \Big/ \int\limits_o^{\infty} \frac{-mv_x^2}{e \ 2kT} dv_x = \int\limits_o^{\infty} v_x \frac{-mv_x^2}{e \ 2kT} \Big/ \int\limits_o^{\infty} \frac{-mv^2}{e \ 2kT} dv_x$$
$$  = \displaystyle \sqrt{\frac{2kT}{m}} \int\limits_o^{\infty}  ue^{-u^2} du \Big/ \int\limits_o^{\infty}e^{-u^2} du$$
$$  = \displaystyle \sqrt{\frac{2kT}{m}} \int\limits_o^{\infty}  \frac{1}{2} e^{-x} dx \Big/ \int\limits_o^{\infty}e^{-x} \frac{dx}{2\sqrt{x}}$$
$$= \displaystyle \sqrt{\frac{2kT}{m}} \Gamma (1) \Big/ \Gamma \Big( \frac{1}{2}\Big) = \sqrt{\frac{2kT}{m\pi}}$$


How long will a $$2\ kW$$ heater take to boil $$2\ L$$ of water taken at $$25^oC$$? Given that the average specific heat of water in the range $$25^o C-100^oC$$ is $$4.184\ JK^{-1}g^{-1}$$.

$$2\ L$$ of water $$=2000\ cm^3=2000\ g(d_{H_2O}=1\ g\ cm^{-3})$$
$$\therefore$$ Heat required by $$2\ L$$ of water to raise its temperature from $$25^oC$$ to $$100^oC$$
$$=m \times C \times \Delta T$$
$$=(2000\ g)\times (4.184\ JK^{-1}g^{-1})\times (100-25)\ K$$
$$=627600\ J$$

Heat supplied by $$2\ kW$$ heater $$=2000\ Js^{-1}$$
$$( \because 1\ W=1\ Js^{-1})$$

$$\therefore$$ Time required to supply the required heat
$$=\dfrac {627600\ J}{2000\ Js^{-1}}\simeq 314\ s$$
$$=5\ min\ 14\ s$$.


Find the statistical weight of the most probable distribution of $$N = 10$$ identical molecules over two halves of the cylinder's volume. Find also the probability of such a distribution.

The statistical weight is 
$$N_{C_{N/2}} = \frac{N!}{N/2! \dfrac{N}{2}!}  = \dfrac{10 \times 9 \times 8 \times 7 \times  6}{8 \times  4 \times 3 \times 2} = 252$$

The probability distribution is
$$N_{C_{N/2}} 2^{-N}= 252 \times 2^{-10} = 24.6 \%$$


Using the Maxwell distribution function, determine the pressure exerted by gas on a wall, if the gas temperature is $$T$$ and the concentration of molecules is $$n$$. 

Let, $$dn(v_x) = n \Big( \frac{m}{2\pi kT}\Big)^{1/2} e^{-mv_x^2/2kT} dv_x$$
be the number of molecules per unit volume with x component of velocity in the range $$v_x$$ to $$v_x+ dv_x$$
Then
$$\displaystyle p= \int\limits_0^{\infty} 2v_x. v_x dn(v_x)$$
$$\displaystyle p= \int\limits_0^{\infty} 2v_x^2 n \Big( \frac{m}{2\pi kT}\Big)^{1/2} e^{-mv_x^2/2kT} dv_x$$
$$ = 2mn \frac{1}{\sqrt{\pi}}\frac{2kT}{m} \displaystyle \int\limits_0^{\infty} u^2 e^{-u^2} du$$
$$\frac{4}{\sqrt{\pi}} nkT . \displaystyle \int\limits_0^{\infty} xe^{-x}\frac{dx}{2\sqrt{x}} = nkT$$


Making use of the Maxwell distribution function, calculate the number $$v$$ of gas molecules reaching a unit area of a wall per unit time, if the concentration of molecules is equal to $$n$$, the temperature to $$T$$, and the mass of each molecule is $$m$$. 

Here $$vdA$$ = No. of molecules hitting an area $$dA$$ of the wall per second.
$$\displaystyle = \int\limits_{0}^{\infty} dN (v_x) v_x dA$$
or, $$\displaystyle v = \int\limits_{0}^{\infty}  n \Big( \frac{m}{2\pi K T} \Big)^{1/2} \ e^{-\frac{mv^2_x}{2kTv_x} } dv_x$$
$$\displaystyle  = \int\limits_{0}^{\infty} \frac{n}{\sqrt{\pi}} \Big( \frac{2kT}{m}\Big)^{1/2} e^{-u^2} udu$$
$$ = \
frac{1}{2}n \sqrt{\frac{2kT}{m\pi}} = n \sqrt{\frac{kT}{2 m \pi}} = \frac{1}{4} n <v>$$,
(where $$<V> = \sqrt{\frac{8kT}{m\pi}}$$


From the Maxwell distribution function find ($$v_x^2$$), the mean value of the squared $$v_x$$ projection of the molecular velocity in a gas at a temperature $$T$$. The mass of each molecule is equal to $$m$$.

$$<v_x^2> = \displaystyle \int\limits_{0}^{\infty} v_x^2 e^{-\frac{mv_x^2}{2kT}} dv_x \Big/ \int\limits_0^{\infty} \frac{-mv_x^2}{e \ 2kT} dv_x$$
$$= \frac{2kT}{m} \displaystyle \int\limits_{0}^{\infty} xe^{-x} \frac{dx}{2\sqrt{x}}  \ \Big/  \int\limits_{0}^{\infty} e^{-x} \frac{dx}{2\sqrt{x}}$$
$$= \frac{2kL}{m} \Gamma \Big(\frac{3}{2} \Big) \ \Big/  \Gamma \Big( \frac{1}{2} \Big) = \frac{kT}{m}$$


Why does a diatomic gas have a greater energy content per mole than a monatomic gas at the same temperature?


1883744_1859597_ans_f381df98e97d4a0aaa84ce0320bb7ace.jpeg


Making the use of the Maxwell distribution function, find $$(1/v)$$, the mean value of a reciprocal of the velocity of molecules in an ideal gas at temperature T, if the mass of each molecule is equal to $$m$$. Compare  the value obtained with the reciprocal of the mean velocity. 

$$\Big< \frac{1}{v} \Big>  = \displaystyle \int\limits_0^{\infty}\Big( \frac{m}{2\pi kT} \Big)^{3/2} e^{-\frac{mv^2}{2kT}} 4\pi v^2 dv \frac{1}{v}$$
$$ = \Big( \frac{m}{2\pi kT}\Big)^{3/2} 4\pi \frac{1}{2} \frac{2kT}{m}\displaystyle \int\limits_0^{\infty} e^{-x} dx$$
$$ = 2\Big(\frac{m}{2\pi kT}\Big)^{1/2} = \Big( \frac{2m}{\pi kT}\Big)^{1/2}=  \Big( \frac{16}{\pi^2} \frac{m\pi}{8kT}\Big)^{1/2} = \frac{4}{\pi <v>}$$


A light container having a diatomic gas enclosed with in is moving with velocity $$v$$. Mass of the gas is $$M$$ and number of moles is $$n$$.
  1. What is the kinetic energy of gas with respect to centre of mass of the system?
  2. What is the kinetic energy of gas with respect to ground?

1. respect to center of mass of the system, that is, frame of the container, kinetic energy will be equal to the thermal energy of the gas.

Since the gas is diatomic, there will be three translational degrees of freedom and two rotational degrees of freedom, hence,

$${ K }_{ C }=n\dfrac { f }{ 2 } RT=\dfrac { 5 }{ 2 } nRT$$

2. With respect to the ground, kinetic energy is given by the formula,

$$K={ K }_{ C }+\dfrac { 1 }{ 2 } M{ v }_{ c }^{ 2 }=\dfrac { 5 }{ 2 } nRT+\dfrac { 1 }{ 2 } M{ v }^{ 2 }$$


A diatomic is expanded according to $${ PV }^{ 3  }= $$ constant under very high temperature (Assume vibration mode active). Calculate the molar heat capacity of gas (in cal/mol K) in this process:

Molar heat capacity ($$C_p$$) is the amount of heat required to change the temperature of 1 mol of the substance by unit degree.
$${ C }_{ p }=\dfrac { dH }{ dT }$$

and $$dH=q=dU-w$$

Also, $$ \Rightarrow \dfrac { dH }{ dT } =\dfrac { dU }{ dT } -\dfrac { w }{ dT }$$

or, $${ C }_{ P }={ C }_{ V } -\dfrac { w }{ dT }$$

For 1 mole of diatomic gas at high temperature

$$\\ { C }_{ V }=\dfrac { dU }{ dT } =\dfrac { 7 }{ 2 } R$$

and $$dw=-PdV$$

Given, $$P{ V }^{ 3 }=k$$

$$\therefore dw=-k.{ V }^{ -3 }dV$$ 

$$w=-k\int _{ { V }_{ 1 } }^{ { V }_{ 2 } }{ { V }^{ -3 } } dV=\dfrac { 1 }{ 2 } k({ V }_{ 2 }^{ -2 }-{ V }_{ 1 }^{ -2 })$$ 

$$w=\dfrac { 1 }{ 2 } \left( P{ V }_{ 2 }-P{ V }_{ 1 } \right) =\dfrac { 1 }{ 2 } RdT$$

On substitution, $${ C }_{ P }={ C }_{ V }-\dfrac { 1 }{ 2 } R=\dfrac { 7 }{ 2 } R-\dfrac { 1 }{ 2 } R=3R$$

Answer is: $${ C }_{ P }=5.96\  cal\  mo{ l }^{ -1 }K$$


Calculate 
  1. the average kinetic energy of translation of an oxygen molecule at $$27^\circ C$$,
  2. the total kinetic energy of an oxygen molecule at $$27^\circ C$$,
  3. the total kinetic energy in joule of one mole of oxygen at $$27^\circ C$$.
Given Avogadro's number$$=6.02\times 10^{23}$$ and Boltzmann's constant$$=1.38\times 10^{-23}\:J/(mol-K)$$.

1. An oxygen molecule has three translational degrees of freedom, thus the average translational kinetic energy of an oxygen molecule at $$27^\circ C$$ is given as

$$\displaystyle E_T=\frac{3}{2}kT=\frac{3}{2}\times 1.38\times 10^{-23}\times 300$$

$$=6.21\times 10^{-21}\:J/mol$$

2.  An oxygen molecule has total five degrees of freedom, hence its total kinetic energy is given as

$$\displaystyle E_T=\frac{5}{2}kT=\frac{5}{2}\times 1.38\times 10^{-23}\times 300$$

$$=10.35\times 10^{-21}\:J/mol$$

3. Total kinetic energy of one mole of oxygen is its internal energy, which can be given as

$$\displaystyle U=\frac{f}{2}\mu RT=\frac{5}{2}\times 1\times 8.314\times 300=6235.5\:J/mol$$


The pressure of a gas in a 100 mL container is 200 kPa and the average translation kinetic energy of each gas particle is $$6\, \times\, 10^{-21}$$. Find the number of gas particles in the container. How many moles are there in the container ?

The total translational kinetic energy is given by

$$E=\dfrac { 3 }{ 2 } nRT=\dfrac { 3 }{ 2 } PV$$

Also, since energy of one particle is $$e$$, let the total number of particles be N. Then

$$E=Ne$$

Hence, 

$$Ne=\dfrac { 3 }{ 2 } PV$$

$$N=\dfrac { 3 }{ 2e } PV$$

$$N=\dfrac { 3(2X{ 10 }^{ 5 })(0.1X{ 10 }^{ -3 }) }{ 2(6X{ 10 }^{ -21 }) } =5X{ 10 }^{ 21 }$$ particles.

Also, number of moles will be

$$n=\dfrac { N }{ { N }_{ A } } =\dfrac { 5X{ 10 }^{ 21 } }{ 6.023X{ 10 }^{ 23 } } =8.3X{ 10 }^{ -3 }$$ mol.


One mole of a non-linear triatomic gas is heated in a closed rigid container from $$500^{\circ}C$$ to $$1500^{\circ}C$$. The amount of energy required is $$500xR$$ if the vibrational degree of freedom become effective only above $$1000^{\circ}C$$. Find the value of $$x$$.

$$\displaystyle Q=C_{V_{1}}(1000-500)+C_{V_{2}}(1500-1000)$$

$$Q=\displaystyle (\frac{3R}{2}+\frac{3R}{2})\times500+(\frac{3R}{2}+\frac{3R}{2}+3R)(500)$$

$$Q=\displaystyle 1500\:R+3000\:R=4500\:R$$

Therefore, value of $$x= 9$$.


What is the total random translational energy of the molecules in one mole of this gas ?

Translational energy of one molecule is given by

$${ E }_{ T }=\dfrac { 3 }{ 2 } kT$$

Thus, for one mole,

$${ E }_{ T }=\dfrac { 3 }{ 2 } { N }_{ A }kT=\dfrac { 3 }{ 2 } RT$$

Thus, $${ E }_{ T }=\dfrac { 3 }{ 2 } (8.314)(300)=3740J$$

Answer is $$3740J$$


If K is the average kinetic energy per atom, find $$x$$, such that $$x=K\times{10}^{23}$$

Average kinetic energy per atom be e.

Hence, $$e=\dfrac { 3 }{ 2 } kT$$

$$e=\dfrac { 3 }{ 2 } (1.38X{ 10 }^{ -23 })(160)=3.31X{ 10 }^{ -21 }J$$

Answer is $$3.31X{ 10 }^{ -21 }J$$


An ideal gas occupies $$2$$ $$cubic meters$$ at a pressure of $$2$$ $$atm$$. Taking $$1$$ atm. $$= 10^5$$ $$Pa$$, find the energy density of the gas.

Ideal gas volume$$=2cc$$
Pressure $$2atm\\=2\times10^5Ps\\=2\times10^5 N/m^2$$
Energy density$$=\rho=\cfrac{P}{V}\\ \quad=\cfrac{2\times10^5m/s}{2\times(10^{-2})^3}\\ \quad=10^{11}Kg/m^3$$



A sheet of $$15.0  g$$ of gold at $$25.0C$$ is placed on a $$30.0  g$$ sheet of copper at $$45.0C$$. What is the final temperature of the two metals assuming that no heat is lost to the surroundings. The specific heats of gold and copper are $$0.129  { J }/{ gC }$$ and $$0.385  { J }/{ gC }$$ respectively.

Heat lost copper = heat gain by gold
$$30\times 0.385\left( 318-T \right) =15\times 0.129\left( T-298 \right) $$
final temperature $$T = 315.1 K$$
                            $$T = 42.1C$$


Nitrogen gas is filled in an insulated container. If $$\alpha$$ fraction of moles dissociates without exchange of any energy, then the fractional change in its temperature is

A formula of internal energy at temperature T and no of a mole of gas n is  $$n{ C }_{ v }T$$ .
where Cv is molar heat capacity at constant volume.
N₂ is diatomic molecule so, $$Cv = 5R/2 $$
Let initial temperature is T₁ and number of mole of N₂ is n 
Then, internal energy $${ E } = n × 5R/2 × T₁$$
$$⇒T₁ = 2E/5nR -------(1)$$
after dissociation of N₂ gas ; 
$$N₂ ----------> 2N $$
at t = 0
number of mole of $$N₂ = n $$
number of moles of $$N = 0 $$
After dissociation by α fractional , 
number of moles of $$N₂ gas = n(1 - α) $$
number of moles of $$N = 2nα $$
Now, Let temperature be T₂ after dissociation ,
Then, internal energy $${ E } = energy of \ N₂ + energy of \ N $$
$$E = n(1 - α) × 5R/2 × T₂ + 2nα × 3R/2 × T₂ [ N is \ monoatomic \ so, Cv = 3R/2]$$
$$E = T₂nR/2[ 5(1 - α) + 6α ] = nRT₂[5 + α]/2 $$
$$T₂ = 2E/nR[5 + α] ------(2)$$
Now, fractional change in temperature is $$\dfrac { { T }_{ 2 }-{ T }_{ 1 } }{ { T }_{ 1 } } $$
Fraction change $$=\cfrac{2E}{nR}{5 + α} -\dfrac{ 2E}{5nR }$$
$$= {1/(5+α) - 1/5}/{1/5}$$
$$= -α/(5 + α) $$
Hence, fractional change in temperature is $$-α/(5 + α)$$


Oxygen is filled in a closed metal jar of volume $$1.0\times 10^{-3}\ m^{3}$$ at a pressure of $$1.5\times 10^{5}$$ Pa and temperature $$400\ K$$. The jar has a small leak in it. The atmospheric pressure is $$1.0\times 10^{5}$$ Pa and the atmospheric temperature is $$300\ K$$. Find the mass of the gas that leaks out by the time the pressure and the temperature inside the jar equalize with the surrounding.

The volume of the metal jar is $$V_1 = 1 \times 10^{-3}  m^3$$
The pressure of the gas is $$P_1 = 1.5 \times 10^5 Pa$$
The temperature of the gas in container is $$T_1 = 400 k$$

Using the ideal gas equation:
$$P_1V_1 = n_1R_1T_1$$

$$n_1 = \dfrac{P_1 V_1}{R_1 T_1} = \dfrac{1.5 \times 10^5 \times 10^{-3}}{8.3 \times 400}$$

$$n_1 = \dfrac{1.5}{8.3 \times 4}$$
The mass of the gas present in container is:
$$m_1 = \dfrac{1.5}{8.3 \times 4} \times m $$

$$= \dfrac{1.5}{8.3 \times 4} \times 32 = 1.4457 \cong 1.446$$

After the gas is leaked, 
$$P_2 = 1 \times 10^5 Pa \,\,\, , V_2 = 1 \times 10^{-3} m^3 \,\,\, ,T_2 = 300 k$$

Again using the ideal gas equation:
$$P_2V_2 = n_2R_2T_2$$

$$n_2 = \dfrac{P_2V_2}{R_2 T_2} $$

$$= \dfrac{10^5 \times 10^{-3}}{5.3 \times 300} = \dfrac{1}{3 \times 8.3} = 0.040$$
The mass present in after after leakage is:
$$\therefore m_2 = 0.04 \times 32 = 1.285$$

The mass of the gas leaked from container is:
$$\Delta m = m_1 - m_2 = 1.441 - 1.285  = 0.160$$

$$ \delta \cong 0.16 g$$


Two moles of an ideal monoatomic gas at $$27^{o}$$C occupies a volume of $$V$$. If the gas is expanded adiabatically to the volume $$2\ V$$, then the work?

$$w=−P({ V }_{ 2 }–{ V }_{ 1 })$$
 $$PV=nRT$$
 $$P=\frac { nRT }{ V } $$
 $$W=-\left( \frac { nRT }{ V }  \right) (2V-V)$$
 $$W=-nRT$$
 $$n=2$$
 $$T=273+27=300$$


Hydrogen gas is contained in a closed vessel at 1 atm (100 kPa) and 300 K. (a) Calculate the mean speed of the molecules (b) Suppose the molecules strike the wall with this speed making an average angle of $$45^{\circ}$$ with it. How many molecules strikes each square meter of the wall per second?

$$P = 1 atm = 10^5 $$ pascal     $$T = 300 k $$    $$M = 2g = 2 \times 10^{-3} kg$$

(a) 
The average velocity of the gas molecules is:
$$V_{avg} = \sqrt{\dfrac{8 RT}{\pi M}} $$

$$= \sqrt{\dfrac{8 \times 8.3 \times 300}{3.14 \times 2 \times 10^{-3}}} = 1781.004 \Rightarrow 1780 m/s$$

(b) 
When molecule strike at angle $$45^{\circ}$$
No of molecules striking per unit area
$$= \dfrac{force}{\sqrt{2} mv \times Area} = \dfrac{Pressure}{\sqrt{2} m v}$$

$$= \dfrac{\dfrac{10^5}{\sqrt{2} \times 2 \times 10^{-3} \times 1780}}{6 \times 10^{23}} = \dfrac{3}{\sqrt{2} \times 1780} \times 10^{31}$$

$$= 1.19 \times 10^{-3} \times 10^{31} = 1.19 \times 10^{28}  \cong 1.2 \times 10^{28}$$


Consider a classroom that is roughly $$8.21m\times 10m\times 3m$$. Initially $$T=290K$$ and $$P=1$$ atm. There are $$50$$ people in the class, each losing energy to the room at the average rate of $$166W$$. Assume that the walls, ceiling, floor, and furniture are perfectly insulated and do not absorb any heat. Also assume that all the doors and windows are tightly closed to prevent any exchange of air from the surrounding. How long (in sec) will the physical chemistry examination last if the professor (Mr. Neeraj Kumar) has foolishly agreed to dismiss the class when the air temperature in the room reaches body temperature, $$310K$$?
For air, $${ C }_{ P,m }=7R/2, \left[ R=0.0821L-atm/K-mol=8.3J/K-mol \right] $$


1958982_1679483_ans_37841d1d10574b0886391e3f8022b8df.jpg


A molecule of a gas, filled in a discharge tube, gets ionized when an electron is detached from it. An electric field of $$5.0 kV m^{-1}$$ exists in the vicinity of the event. (a) Find the distance travelled by the free electron in $$1 \mu s$$ assuming no collision. (b) If the mean free path of the electron is $$1.0 mm$$, estimate. the time of transit of the free electron between successive collisions. 

$$E = 5\, kV/m = 5\times 10^3 \, V/m$$
$$t=1 \, \mu s = 1 \times 10^{-6} s$$ 

$$F= qE = 1.6 \times 10^{-9} \times 5 \times 10^{3}$$

$$a =\dfrac {qE}{m}=\dfrac {1.6 \times 5 \times 10^{-16}}{9.1 \times 10^{-31}}$$

a) S = distance travelled
$$ = \frac {1}{2} at^2 = 439.56 \, m = 440 \, m$$

b) $$d= 1\, mm = 1 \times 10^{-3}\, m$$
$$ 1 \times 10^{-3}=\dfrac {1}{2}\times \dfrac {1.6 \times 5 }{9.1} 10^5 \times t^2$$

$$\Rightarrow t^2 =\dfrac {9.1}{0.8\times 5}\times 10^{-18}\Rightarrow t = 1.508 \times 10^{-9}\, sec \Rightarrow 1.5 \, ns$$


When $$229 \,J$$ of energy is supplied as heat at constant pressure to $$3.0$$ mole of argon gas, the temperature of the sample increases by $$2.55 \,K$$. Calculate the molar heat capacities at constant volume and constant pressure of the gas.

undefined
1986423_1746359_ans_0e6a61997ef1410c94d25f3b959f2556.jpg


The specific heat at constant volume for a gas $$0.075\ cal/g$$ and at constant pressure is $$0.125\ cal/g$$. Calculate:
(i) The molecular weight of gas,
(ii) Atomicity of gas,
(iii) No. of atoms of gas in its $$1$$ mole.


1759689_1746826_ans_ee732f3b17dd4925bbecb0d8fa982f98.jpg


 (a) For two particles with speeds $$ v_{1} $$ and $$ v_{2} $$ , show that $$ v_{rms} \geq v_{av.} $$ , regardless of the numerical values of $$ v_{1} $$ and $$ v_{2} $$ . then show that $$ v_{rms} > v_{av.} $$ if $$ v_{1} \neq v_{2} . $$ (b) Suppose that for a collection of $$ N $$ particles you know . Another particle , with speed $$ u $$ , is added to the collection of particles . If the new rms and average speeds are denoted a $$ {v}'_{rms}$$ and $$ {v}'_{av.} $$ , show that                                
                               $$\displaystyle {v}'\,_{rms} = \sqrt{\dfrac{Nv^{2}_{rms} + u^{2}}{N + 1}} $$ 
   
and                        $$ {v}'_{rms} = \dfrac{Nv_{av.} + u}{N + 1} $$ 
(c) Use the expressions in part (b) to show that $$ {v}'_{rms} > {v}'_{av.} $$ , regardless of the numerical value of $$ u $$. (d) Explain why your results for (a) and (c) together show that $$ v_{rms} > v_{av.}$$ for any collection of particles if the particles do not all have the same speed .


1638873_1739162_ans_c8cd1161f34b42a09ee433d9d77458d7.jpg


The volume of an ideal gas is adiabatically reduced from $$200\ L$$ to $$74.3\ L$$. The initial pressure and temperature are $$1.00\ atm$$ and $$300\ K$$. The final pressure is $$4.00\ atm$$. Is the gas monotonic, diatomic, or polyatomic?

Adiabatic Equation , $$p_i V_i^{\gamma}=p_fV_f^{\gamma}$$, leads to 
$$p_f =p_i \left( \dfrac{v_i}{V_f}\right)^{\gamma}\Rightarrow 4.00\ atm=(1.00\ atm)\left( \dfrac{200\ L}{74.3\ L}\right)^{\gamma}$$
which can be solved to yield
$$\gamma =\dfrac{\ln (p_f/p_t)}{\ln (V_i/V_f)}=\dfrac{\ln (1.00 \ atm)}{\ln (200\ L/74.3\ L)}=1.4=\dfrac{7}{5}$$.
This implies that the gas is diatomic.


An adiabatic vessel contains $$ n_{1}=3 $$ mole of diatomic gas. Moment of inertia of each molecule is $$ I=2.76 \times 10^{-46} \mathrm{kg} $$ $$ \mathrm{m}^{2} $$ and root-mean-square angular velocity is $$ \omega_{0}=5 \times $$ $$ 10^{12} \mathrm{rad} / \mathrm{s} . $$ Another adiabatic vessel contains $$ n_{2}=5 \mathrm{mole} $$ of a monatomic gas at a temperature $$ 470 \mathrm{K} $$. Assume gases to be ideal, calculate root-mean-square angular velocity of diatomic molecules when the two vessels are connected by a thin tube of negligible volume. Boltzmann constant $$ k=1.38 \times 10^{-23} \mathrm{J} / $$ molecule.

We know according to the law of equipartition of energy, each gas molecule has $$ 1 / 2 kT $$ energy associated with each of its degrees of freedom. As a diatomic gas molecule has two rotational degrees of freedom, the final temperature of the system is

$$T_{f}=\dfrac{f_{1} n_{1} T_{1}+f_{2} n_{2} T_{2}}{f_{1} n_{1}+f_{2} n_{2}}.....(i)$$
Here for diatomic gas,

$$f_{1}=5, \quad n=3 \quad \text { and } \quad T_{1}=250 \mathrm{K}$$
For monatomic gas

$$f_{2}=3, \quad n_{2}=5 \quad \text { and } \quad T_{2}=470 \mathrm{K}$$Thus from Eq. (i),

$$T_{f}=\dfrac{5 \times 3 \times 250+3 \times 5 \times 470}{5 \times 3+3 \times 5}=360 \mathrm{K}$$

Thus a final mixture of the two gases is at temperature $$ 360 \mathrm{K}. $$ If final RMS angular velocity of diatomic gas molecules is 

$$ \omega_{\mathrm{rms }f}, $$ according to law of equipartition of energy, we have $$\dfrac{1}{2} I \omega_{\operatorname{rms} f}^{2} =k T$$

or

$$\omega_{\operatorname{rms} f} =\sqrt{\dfrac{2 k T}{I}}$$

$$=\sqrt{\dfrac{2 \times 1.38 \times 10^{-23} \times 360}{2.76 \times 10^{-46}}}$$

$$\omega_{\mathrm{rms}f} =6 \times 10^{12} \mathrm{rad} / \mathrm{s}$$


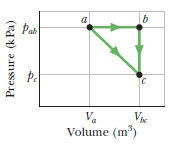
One mole of an ideal diatomic gas goes from $$a$$ to $$c$$ along the diagonal path in Fig . The scale of the vertical axis is set by $$p_{ab}=5.0\ kPa$$ and $$p_{c}=2.0\ kPa$$, and the scale of the horizontal axis is set by $$V_{bc}=4.0\ m^{3}$$ and $$V_{a}=2.0\ m^{3}$$. During the transition,
What is the change in internal energy of the gas.
1770449_6905798f1389453a9464888702d07c95.png

Two formulas (other than the first law of thermodynamics) will be of use to us. It is straightforward to show that for any process that is deplcted as a straight line on the $$pV$$ diagram, the worl is
$$W_{straight}=\left(\dfrac{p_{i}+p_{f}}{2}\right)\Delta V$$
which includes as special cases, $$W=p\Delta V$$ for constant pressure processes and $$W=0$$ for constant volume process. 
$$E_{int}=n\left(\dfrac{f}{2}\right)RT=\left(\dfrac{f}{2}\right)pV$$
where we have used the ideal gas law in the last step. We emphasize that in order to obtain work and energy in joules, pressure should be in pascals $$(N/m^{2})$$ and volume should be in cubic meters. The degrees of freedom for a diatomic gas is $$f=5$$
The internal energy change is 
$$E_{int\ c}=E_{int\ a}=\dfrac{5}{2}(p_{c}V_{c}-p_{a}V_{a})=\dfrac{5}{2}((2.0\times 10^{3}Pa)(4.0\ m^{3})-(5.0\times 10^{3}Pa)(2.0\ m^{3}))=-5.0\times 10^{3}\ J$$


Show that the number of collisions a molecule makes per second , called the collision frequency , $$ f $$ , is given by $$ f = \bar{v}/l_{m} $$ , and thus $$ f = 4\sqrt{2} \pi r^{2} \bar{v} N / V $$                   


1662935_1739169_ans_17234db832a44757a099c8982ef64c7f.jpg


Calculate the average molecular kinetic energy (i) per kmol (ii) per kg (iii) per molecule of oxygen at $$127^\circ C$$, given that the molecular weight of oxygen is $$32$$, R is $$8.31 J\,mol^{-1}K^{-1}$$ and Avogadros number $$N_A$$ is $$6.02 \times 10^{23}$$ molecules $$mol^{-1}$$.

$$T = 273 + 127 = 400\,K$$

molecular weight $$= 32$$

 ∴ molar mass $$=\,32 kg/kmol$$, 

$$R = 8.31\,Jmol^{-1}K^{-1}$$, 

$$N_A = 6.02 \times 10^{23}$$ molecules $$mol^{-1}$$

i) The average molecular kinetic energy per kmol of oxygen = the average kinetic energy per mol of oxygen $$\times 1000$$

$$=\dfrac{3}{2}RT \times 1000 =\dfrac{3}{2}(8.31)(400)(10^3)\dfrac{J}{kmol}$$

$$=(600)(8.31)(10^3)=4.986 \times 10^6\,J/kmol$$

(ii) The average molecular kinetic energy per kg of oxygen

$$=\dfrac{3}{2}\,\dfrac{RT}{M_0}=\dfrac{4.986 \times 10^6\,J/kmol}{32kg/kmol}$$

$$=1.558 \times 10^5\,J/kg$$

(iii) The average molecular kinetic energy per molecule of oxygen

$$=\dfrac{3}{2}\,\dfrac{RT}{N_A}=\dfrac{4.986 \times 10^6\,J/kmol}{6.022 \times 10^{23}molecule/mole}$$

$$=8.282 \times 10^{-21}\,J/molecule$$



What is meant by degree of freedom. Explain the specific heats for monoatomic, diatomic and polyatomic gases.

A degree of freedom is an independent physical parameter in the formal description of the state of a physical system. 
In three-dimensional space, three degrees of freedom are associated with the movement of a particle. 
A diatomic gas molecule thus has six degrees of freedom. This set may be split in terms of translations, rotations, and vibrations of the molecule. The centre of mass motion of the whole molecule accounts for three (3) degrees of freedom. Also, the molecule has two rotational degrees of motion and one vibrational degree of freedom. Since in a monoatomic gas, each molecule of the gas have only translatory motion and hence its degree of freedom is $$3$$, i. e., $$f = 3$$, Then from equations (14.78), (14.79) and (14.81)
$$C_v = \dfrac{f}{2}R = \dfrac{5}{2}R$$
$$C_p = \left ( \dfrac{fr}{2} + 1 \right ) R = \left ( \dfrac{5}{2} + 1 \right ) R = \dfrac{7}{2}R$$
and $$\gamma = \left ( 1 + \dfrac{2}{f} \right ) = \left ( 1 + \dfrac{2}{5} \right ) = \dfrac{7}{5} = 1.4$$
We know that each molecule of a diatomic gas is made up of two molecules, in which degree of freedom of each molecule is is $$5$$, i.e., $$f = 5$$
From equations (14.78), (14.79) and (14.81),
$$C_v = \dfrac{f}{2}R = \dfrac{5}{2}R$$
$$C_p = \left ( \dfrac{fr}{2} + 1 \right ) R = \left ( \dfrac{5}{2} + 1 \right ) R = \dfrac{7}{2}R$$
and $$\gamma = \left ( 1 + \dfrac{2}{f} \right ) = \left ( 1 + \dfrac{2}{5} \right ) = \dfrac{7}{5} = 1.4$$
Since a polyatomic has three degrees of freedom each of translation and rotation. Also, there is some definite number of vibrational degrees of freedom (fv). Then, total degree of freedom per molecule (f),
$$f = 3 + 3 + fv = 6 + fv$$
From equations (14.78), (14.79) and (14.81),
$$C_v = \dfrac{f}{2}R = \dfrac{(6 + fv)}{2}R = \left ( 3 + \dfrac{fv}{2} \right )R$$
$$C_p = \left ( \dfrac{f}{2} + 1 \right )R = \left ( \dfrac{6 + fv}{2} + 1 \right )R = \left (4 + \dfrac{fv}{2} \right )R$$
and $$\gamma = \left (1 + \dfrac{2}{5} \right ) = \left (1 + \dfrac{2}{6 + frv} \right ) = \dfrac{8 + fv}{6 + fv}$$
If $$fv = 0,$$ then $$C_{v} = 3\,R; C_p = 4\,R$$ and $$\gamma = 1.33$$
The graph plotted between Cv and T for diatomic gases, is shown in Fig. 14.7. We see that the temperature increases, the gas absorbs heat through the translational, rotational and vibrational ways.
1756538_1833962_ans_4761eb93c7024814805f518de10e0a4c.png


A gas is to be expanded from initial state $$i$$ to final state $$f$$ along either path $$1$$ or path $$2$$ on a $$P-V$$ diagram. Path $$1$$ consists of three steps: an isothermal expansion ( work is $$40\ J$$ in magnitude),  an adiabatic expansion ( work is $$20\ J$$ in magnitude), and another isothermal expansion ( work is $$30\  J$$ in magnitude ). Path $$2$$ consists of two steps: a pressure reduction at constant volume and an expansion at constant pressure. What is the change in the internal energy of the gas along the path $$2$$?

The aim of this problem is to emphasize what it meant for the internal energy to be a state function. Since path 1 and path 2 start and stop at the same places, then the internal energy change along path 1 is equal to that along path 2. Now, during isothermal processes ( involving an ideal gas ) the internal energy change is zero, so the only step in path 1 that we need to examine is step 2. From the equation of the internal energy it immediately yields $$-20\ J$$ as the answer for the internal energy change.


State the law of equipartition of energy and hence calculate the molar specific heat of mono- and diatomic gases at constant volume and constant pressure.

The Law of equipartition of energy states that for a dynamical system in thermal equilibrium the total energy of the system is shared equally by all the degrees of freedom. The energy associated with each degree of freedom per molecule is $$\dfrac{1}{2}kT$$, where k is the Boltzmann’s constant.

For example, for a monoatomic molecule, each molecule has $$3$$ degrees of freedom. According to the kinetic theory of gases, the mean kinetic energy of a molecule is $$\dfrac{3}{2}kT$$.

Specific heat capacity of Monatomic gas:

The molecules of a monatomic gas have $$3$$ degrees of freedom.

The average energy of a molecule at temperature T is $$\dfrac{3KBT}{2}$$

The total internal energy of a mole is: $$\dfrac{3KBT}{2} \times N_A$$

The molar specific heat at constant volume $$C_v$$ is

For an ideal gas,

$$C_v$$ (monatomic gas) $$=\dfrac{dU}{dT}=\dfrac{3RT}{2}$$

For an ideal gas, $$C_p - C_v = R$$

where $$C_p$$ is molar specific heat at constant pressure.

Thus, $$C_p = \dfrac{5R}{2}$$

Specific heat capacity of Diatomic gas:

The molecules of a monatomic gas have $$5$$ degrees of freedom, $$3$$ translational, and $$2$$ rotational.

The average energy of a molecule at temperature T is $$\dfrac{5K_BT}{2}$$

The total internal energy of a mole is: $$\dfrac{5K_BT}{2} \times N_A$$

The molar specific heat at constant volume $$C_v$$ is

For an ideal gas,

Cv (monatomic gas) $$= \dfrac{dU}{dT}=\dfrac{5RT}{2}$$

For an ideal gas, $$C_p - C_v = R$$

where $$C_p$$ is molar specific heat at constant pressure. 

Thus, $$C_p =\dfrac{7R}{2}$$



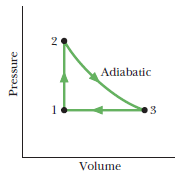
Figure shows a cycle undergone by $$1.00\ mol$$ of an ideal monatomic gas. The temperatures are $$T_1=300\ K, T_2=600\ K$$, and $$T_3=445\ K$$. For $$3\to 1$$, what is $$\Delta E_{int}$$?
1770484_1222bd8f21d84a3a9864cc6616de6f6f.png

In the following, $$C=\dfrac{3}{2}R$$ is the molar specific heat at constant volume, $$C_p=\dfrac{5}{2}R$$ is the molar specific heat at constant pressure, $$\Delta T$$ is the temperature change, and $$n$$ is the number of moles.
The process $$1\to 2$$ takes place at constant volume.
The change in the internal energy is 
The change in the internal energy is 
$$\Delta E_{int}=nC_v\Delta T=\dfrac{3}{2}nR\Delta T=\dfrac{3}{2}(1.00\ mol)(8.31\ J/ mol.K)(300\ K-455\ K)=-1.93\times 10^3\ J$$.


A vessel contains $$N$$ molecules of an ideal gas. Dividing mentally the vessel into two halves $$A$$ and $$B$$, find the probability that the half $$A$$ contains $$n$$ molecules. Consider the cases when $$N = 5$$ and $$n = 0, 1, 2, 3, 4, 5$$. 


1897878_1852376_ans_a3b9c732ca8d4fba990af17c98b77a2c.jpg


Show that the average value of $$c^3$$ of a Maxwellian gas is $$4\pi^{-1/2}(2kT/m)^{3/2}$$.

By definition, the average value of $$c^3$$ is:

$$\displaystyle c^3=\dfrac{1}{n}\int^{\infty}_{\rho}c^3dn=\int^{\infty}_0 4\pi a^3 e^{-bc}c^5dc$$

$$\displaystyle =\dfrac{4\pi a^3}{b^3}\,\left[Since\,\int^{\infty}_0 e^{-bc^2}c^5dc=\dfrac{1}{b^3}\right]$$

$$=\dfrac{4\pi}{b^3}(\dfrac{b}{\pi})^{3/2}[Since\,\,,a\sqrt{\dfrac{b}{n}}]$$

$$=\dfrac{4}{\sqrt{\pi}b^{3/2}}=\dfrac{4}{\sqrt{\pi}}(\dfrac{2kT}{m})^{3/2}$$  [Since, $$b=m/2kT$$]


In 1801, Humphry Davy rubbed together pieces of ice inside an ice house. He made sure that nothing in the environment was at a higher temperature than the rubbed pieces. He observed the production of drops of liquid water. Make a table listing this and other experiments or processes to illustrate each of the following situations. (a) A system can absorb energy by heat, increase in internal energy, and increase in temperature. (b) A system can absorb energy by heat and increase in internal energy without an increase in temperature. (c) A system can absorb energy by heat without increasing in temperature or in internal energy. (d) A system can increase in internal
energy and in temperature without absorbing energy by heat. (e) A system can increase in internal energy without absorbing energy by heat or increasing in temperature.

(a) Warm a pot of coffee on a hot stove. 
(b) Place an ice cube at $$0^0C$$ in warm water the ice wiII absorb energy while melting, but not increase in temperature. 
(c) Let a high-pressure gas at room temperature slowly expand by pushing on a piston. Energy comes out of the gas by work in a  constant-temperature expansion as the same quantity of energy flows by heat in from the surroundings. 
(d) Warm your hands by rubbing them together. H eat your tepid coffee in a microwave oven. Energy input by work, by electromagnetic radiation, or by other means, can all alike produce a temperature increase. 
(e) Davy's experiment is an example of this process. 


A spherical rubber balloon inflated with air is held stationary, with its opening, on the west side, pinched shut. (a) Describe the forces exerted by the air inside and outside the balloon on sections of the rubber. (b) After the balloon is released, it takes off toward the east, gaining speed rapidly. Explain this motion in terms of the forces now acting on the rubber.  (c) Account for the motion of a skyrocket taking off from its launch pad.

(a) The air inside pushes outward on each patch of rubber, exerting a force perpendicular to that section of area. The air outside pushes perpendicularly inward, but not quite so strongly. 

(b) As the balloon takes off, all of the sections of rubber feel essentially the same outward forces as before, but the now-open hole at the opening on the west side feels no force – except for a small amount of drag to the west from the escaping air. The vector sum of the forces on the rubber is to the east.
The small-mass balloon moves east with a large acceleration.

 (c) Hot combustion products in the combustion chamber push outward on all the walls of the chamber, but there is nothing for them to push on at the open rocket nozzle. The net force exerted by the gases on the chamber is up if the nozzle is pointing down. This force is larger than the gravitational force on the rocket body, and makes it accelerate upward.


Class 11 Engineering Physics Extra Questions