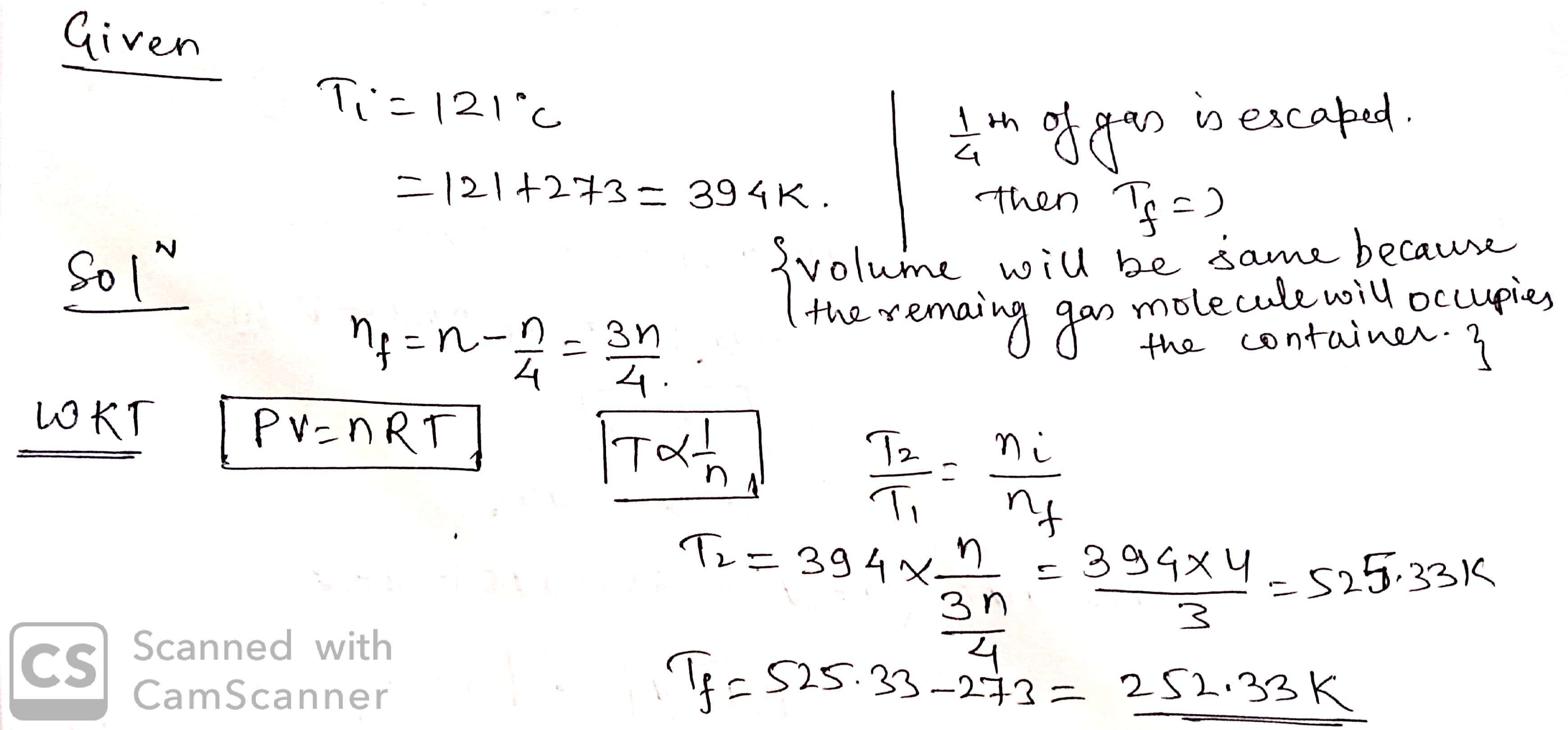Kinetic Theory - Class 11 Medical Physics - Extra Questions
Gas A four times denser than gas B. Find the ratio between their rates of diffusion.
State Charles law at constant pressure and constant volume
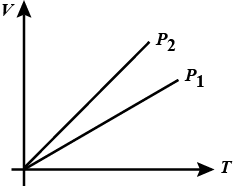
State whether $$P_1\, >\, P_2$$ or $$P_2\, >\, P_1$$ for given mass of a gas ?
An ideal gas is taken through a complete cycle in three steps: adiabatic expansion with work equal to $$125\ J$$, isothermal contraction at $$325\ K$$ and increase in pressure at constant volume.
Is it transferred to or from the gas?
The temperature of $$3.00$$ mol of a gas with $$C_v=6.00$$ cal/mol $$K$$ is to be raised $$50.0\ K$$. If the process is at constant volume, If the process is at constant pressure, what are $$\Delta K$$?
An ideal gas initially at $$300\ K$$ is compressed at a constant pressure of $$25\ N/m^2$$ from a volume of $$3.0\ m^3$$ to a volume of $$1.8\ m^3$$. In the process $$75\ J$$ is lost by the gas as heat. What are the change in internal energy of the gas?
Two ideal gas thermometers A and B use oxygen and hydrogen respectively. The following observations are made
| Temperature | Pressure thermometer A | Pressure thermometer B |
| Triple-point of water | $$1.250\times 10^5 Pa$$ | $$0.200\times 10^5Pa$$ |
| Normal melting point of sulphur | $$1.797\times 10^5Pa$$ | $$0.287\times 10^5 Pa$$ |
(b) What do you think is the reason behind the slight difference in answers of thermometers A and B ? (The thermometers are not faulty) What further procedure is needed in the experiment to reduce the discrepancy between the two readings ?
Describe an experiment to verify the Boyles law.
How will you show that air supports burning?
Fill in the empty values of the cells in the table:
| $$V_1$$ | $$T_1$$ | $$V_2$$ | $$T_2$$ | |
| A | 840 K | 1070 ml | 147 K | |
| B | 3250 ml | $$475^0$$ | $$50^0$$ | |
| C | 10 Litre | 15 Litre | $$50^0$$ |
The volume of an air bubble becomes three times as it rises from the bottom of a lake to its surface. Assuming atmospheric pressure to be 75 cm of Hg and the density of water to be 1/10 of the density of mercury, the depth of the lake.
The temperature of $$3.00$$ mol of a gas with $$C_v=6.00$$ cal/mol $$K$$ is to be raised $$50.0\ K$$. If the process is at constant volume, If the process is at constant pressure, what are $$W$$?
The temperature of $$3.00$$ mol of a gas with $$C_v=6.00$$ cal/mol $$K$$ is to be raised $$50.0\ K$$. If the process is at constant volume, If the process is at constant pressure, what are $$Q$$.
During a compression at a constant pressure of $$250\ Pa$$, the volume of an ideal gas decreases from $$0.80\ m^3$$ to $$0.20\ m^3$$. The initial temperature is $$360\ K$$, and the gas loses $$210\ J$$ as heat. What are the final temperature of the gas?
An ideal gas initially at $$300\ K$$ is compressed at a constant pressure of $$25\ N/m^2$$ from a volume of $$3.0\ m^3$$ to a volume of $$1.8\ m^3$$. In the process $$75\ J$$ is lost by the gas as heat. What are the final temperature of the gas?
When air is pumped into a cycle tyre the volume and pressure of the air in the tyre both are increased. What about Boyle's law in this case?
We have $$0.5g$$ of hydrogen gas in a cubic chamber of size $$3cm$$ kept at NTP. The gas in the chamber is compressed keeping the temperature constant till a final pressure of $$100atm$$. Is one justified in assuming the ideal gas law, in the final state? (Hydrogen molecules can be consider as sphere of radius $$1\mathring {A}$$)
An ideal gas under goes adiabatic expansion to twice original volume. If the gas was initially at $$40^\circ C,$$ calculate its temperature after the process.
$$[Take \,1 = \dfrac{5}{3}]$$
A gas is found to obey $$PV^{2} = Constant.$$ The initial volume and temperature of the gas are $$V_{i}$$ and $$T_{i}$$ respectively. If the final volume of the gas is $$V_{f},$$ find its final temperature $$(T_{f}).$$
State and explain Charles law.
Review. At 25.0 m below the surface of the sea, where the temperature is $$5.00^0C$$, a diver exhales an air bubble having a volume of $$1.00 CM^3$$. If the surface temperature of the sea is $$20.0^0C$$, what is the volume of the bubble just before it breaks the surface?
One mole of an ideal gas goes through a process in which the entropy of the gas changes with temperature $$T$$ as $$S = aT + + C_v$$, In $$T$$, where $$a$$ is a positive constant. $$C_v$$, is the molar heat capacity of this gas at constant volume. Find the volume dependence of the gas temperature in this process if $$T = T_0$$ at $$V = V_0$$.
A room of volume V contains air having equivalent molar mass M (in g/mol). If the temperature of the room is raised from $$T_1$$ to $$T_2$$, what mass of air will leave the room? Assume that the air pressure in the room is maintained at $$ P_0$$.
Air in a thundercloud expands as it rises. If its initial temperature is 300 K and no energy is lost by thermal conduction on expansion, what is its temperature when the initial volume has doubled?
We have two vessels of equal volume, one filled with hydrogen and the other with an equal mass of Helium. The common temperature is $$27^{\circ}C$$.
If the temperature of Helium is kept at $$27^{\circ}C$$ and that of hydrogen is changed, at what temperature will its pressure become equal to that of helium? The molecular weights of hydrogen and helium are $$2$$ and $$4$$ respectively.
A gas is filled in a container of volume V at 121C. To what temperature should it be heated in order that $$\frac {1 }{4 }$$th of the gas may escape out of the vessel?
An air bubble of volume $$20\ cm^3$$ is at the bottom of a lake $$40\ m$$ deep, where the temperature is $$4.0^oC$$. The bubble rises to the surface, which is at a temperature of $$20^oC$$. Take the temperature of the bubble's air to be the same as that of the surrounding water. Just as the bubble reaches the surface, what is its volume?
In the temperature range $$310\ K$$ to $$330\ K$$, the pressure $$p$$ of a certain nonideal gas is related to volume $$V$$ and temperature $$T$$ by
$$p=(24.9\ J/K)\dfrac{T}{V}-(0.00662\ J/K^2)\dfrac{T^2}{V}$$.
How much work is done by the gas if its temperature is raised from $$315\ K$$ to $$325\ K$$ while the pressure is held constant?
Give the laws of Boyle, Charles, Gay-Lussac and Dalton by writing the postulates of kinetic theory of gases.
Class 11 Medical Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work, Energy And Power Extra Questions