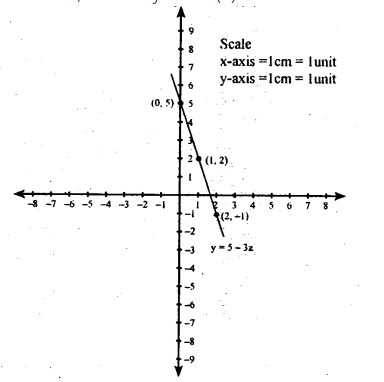
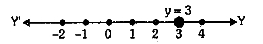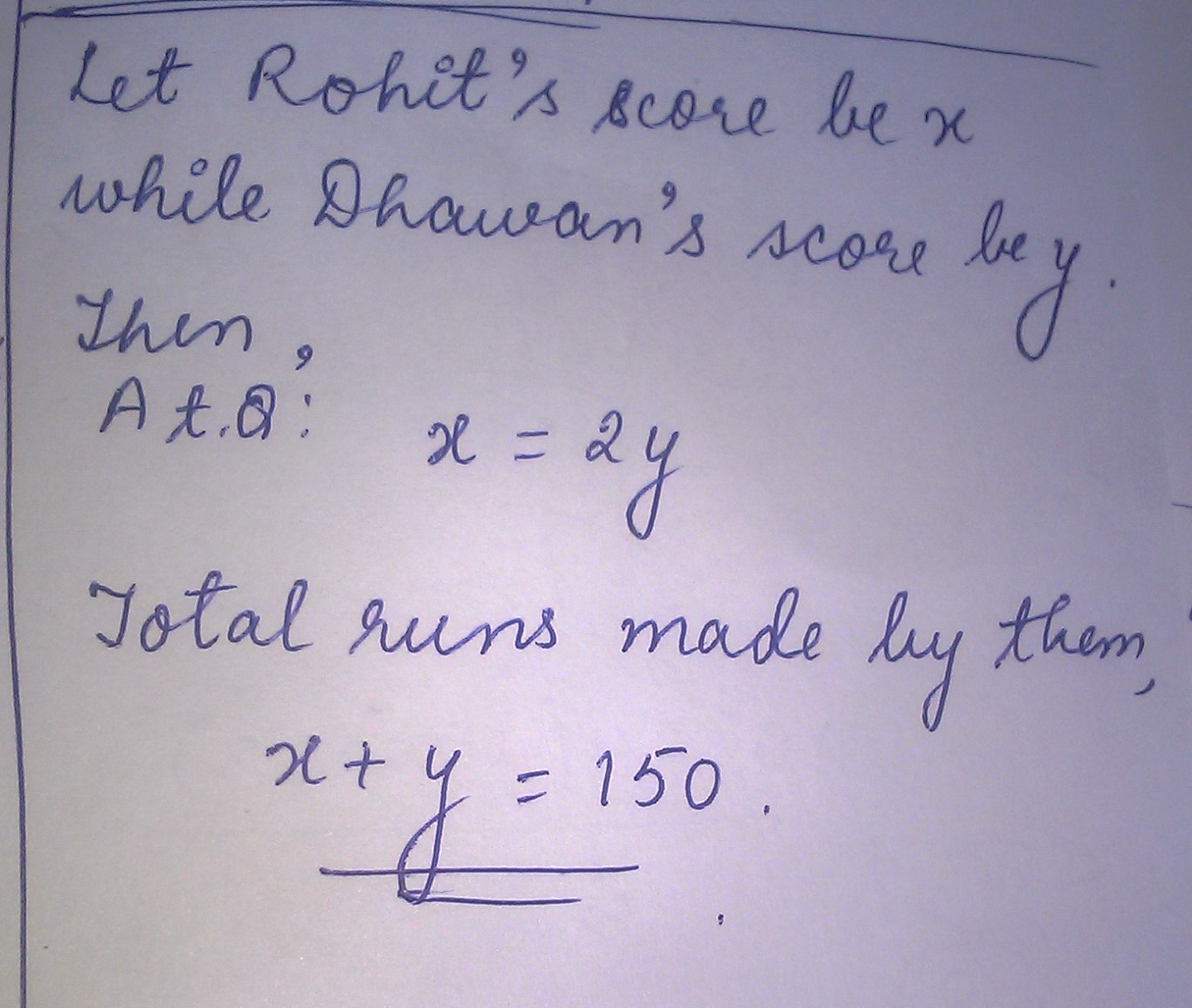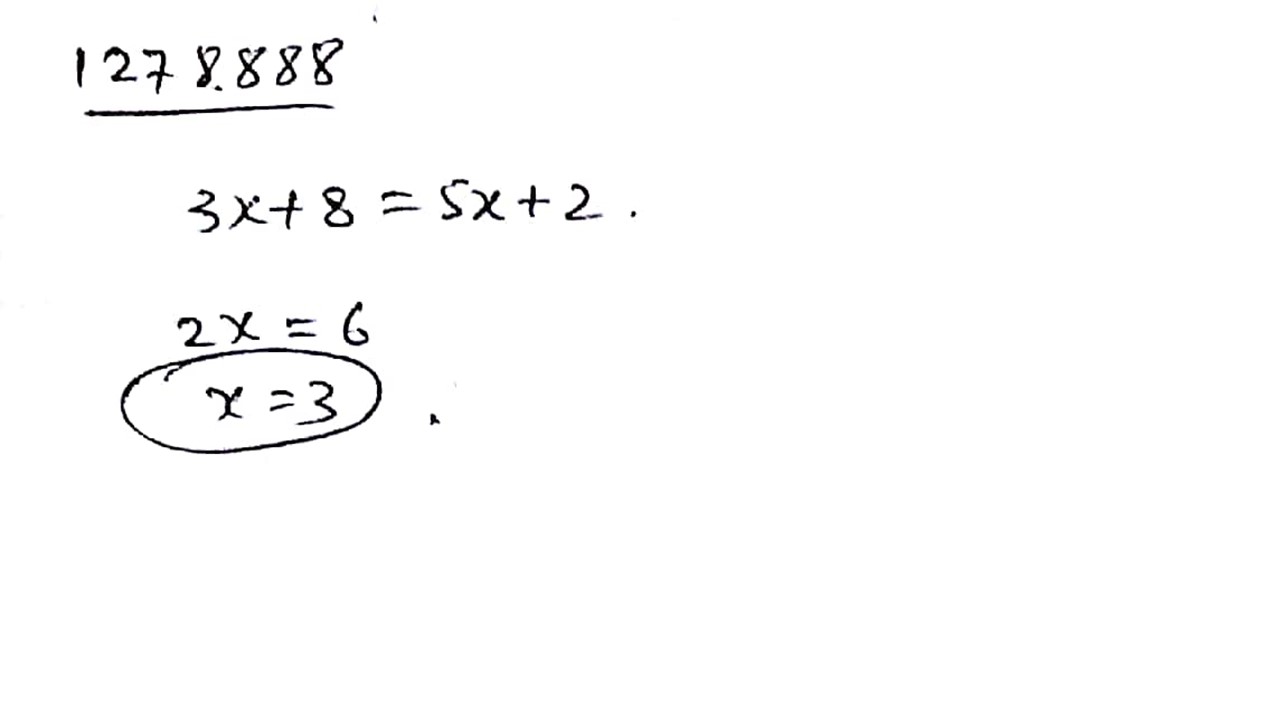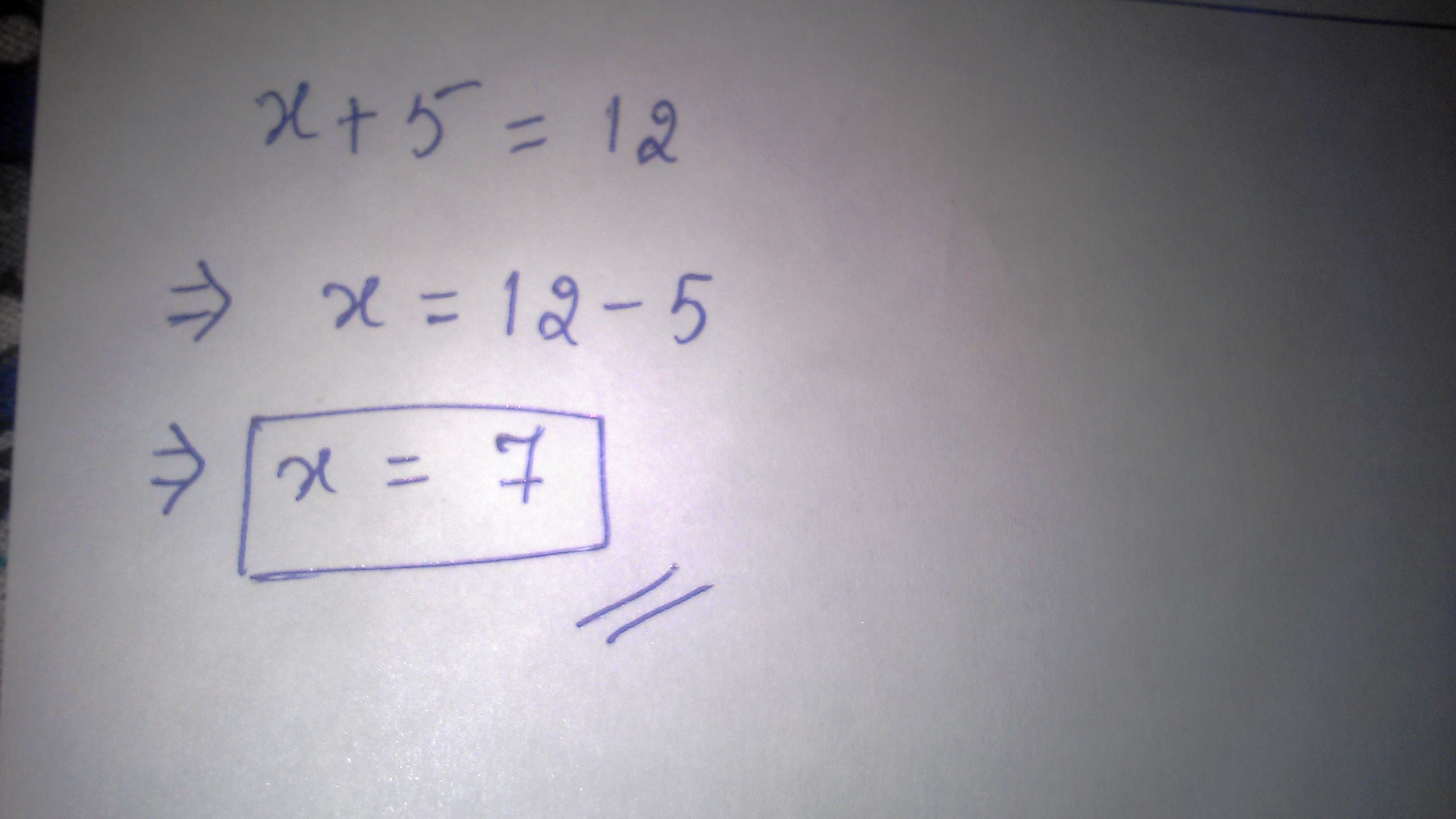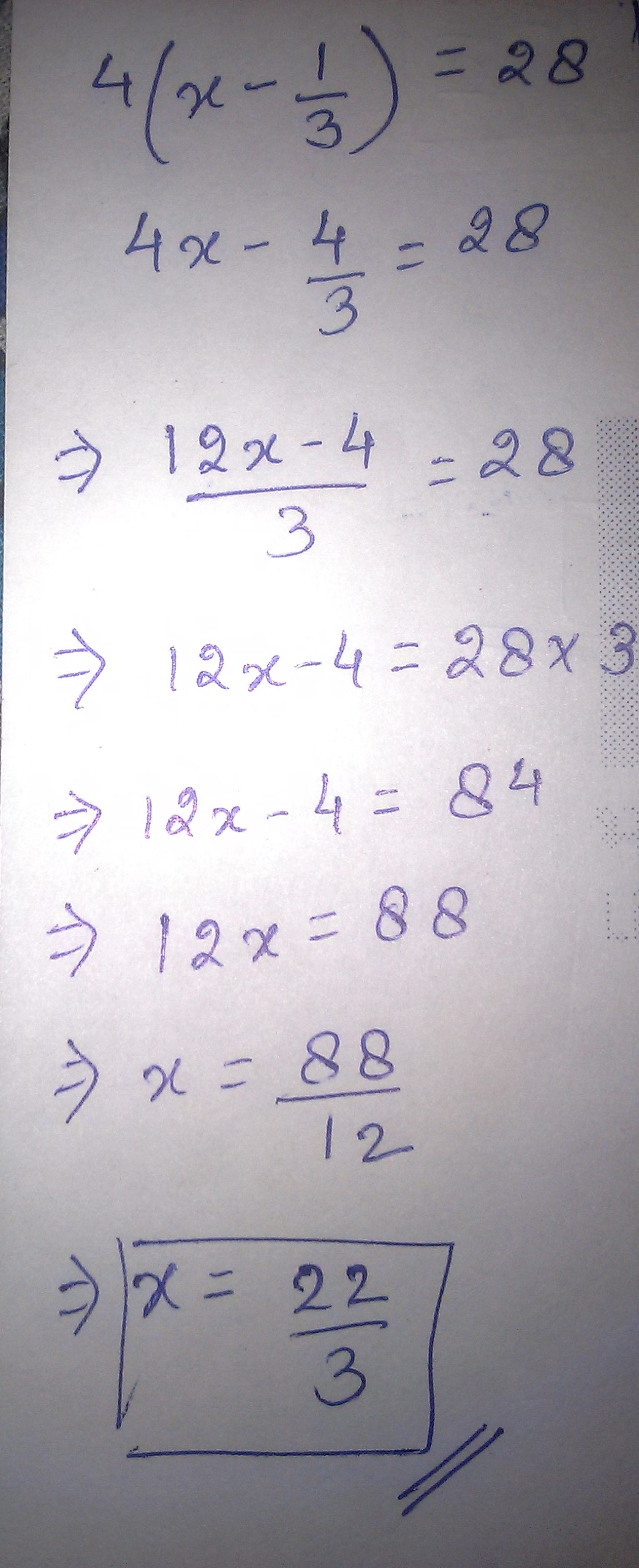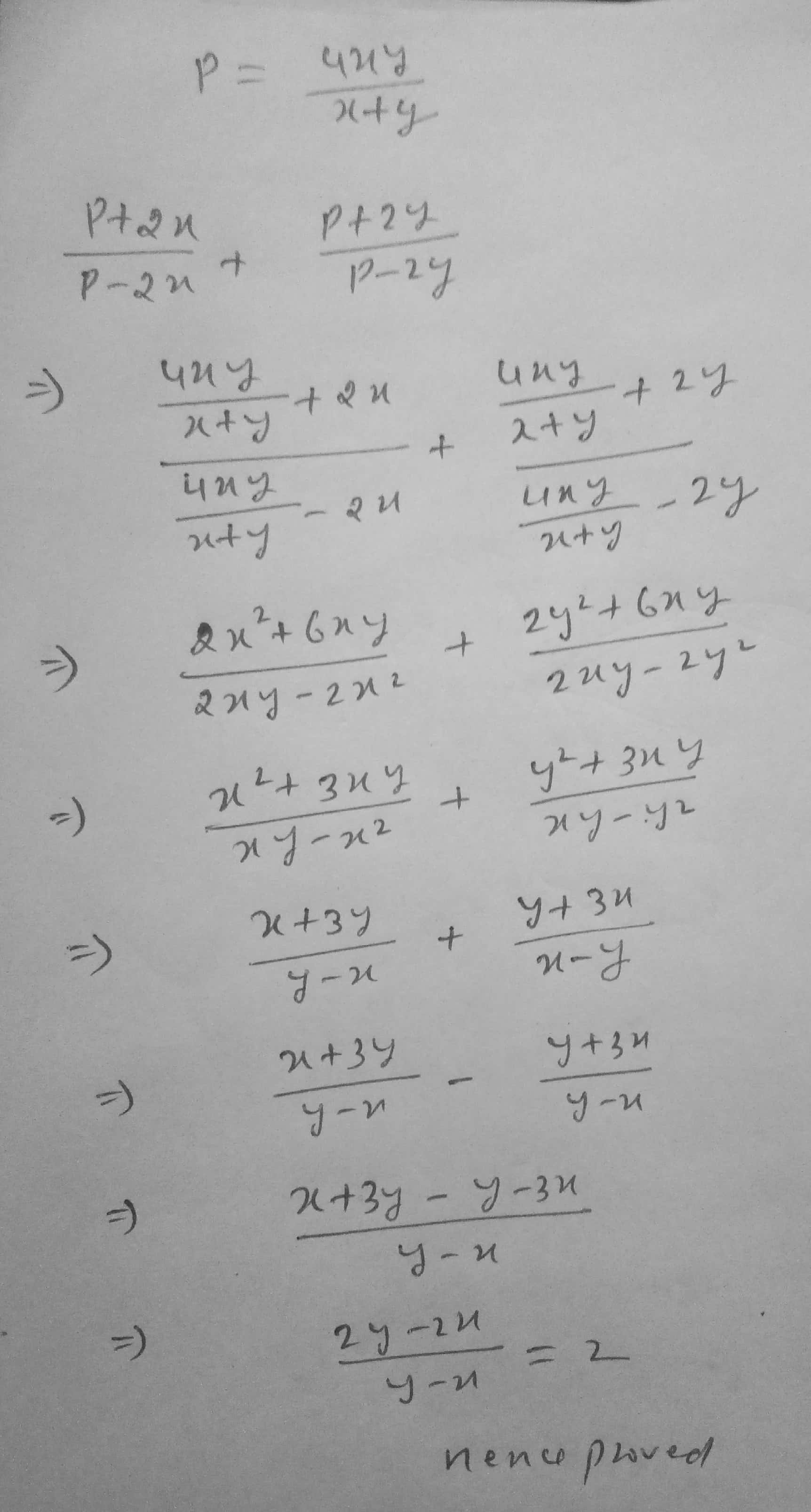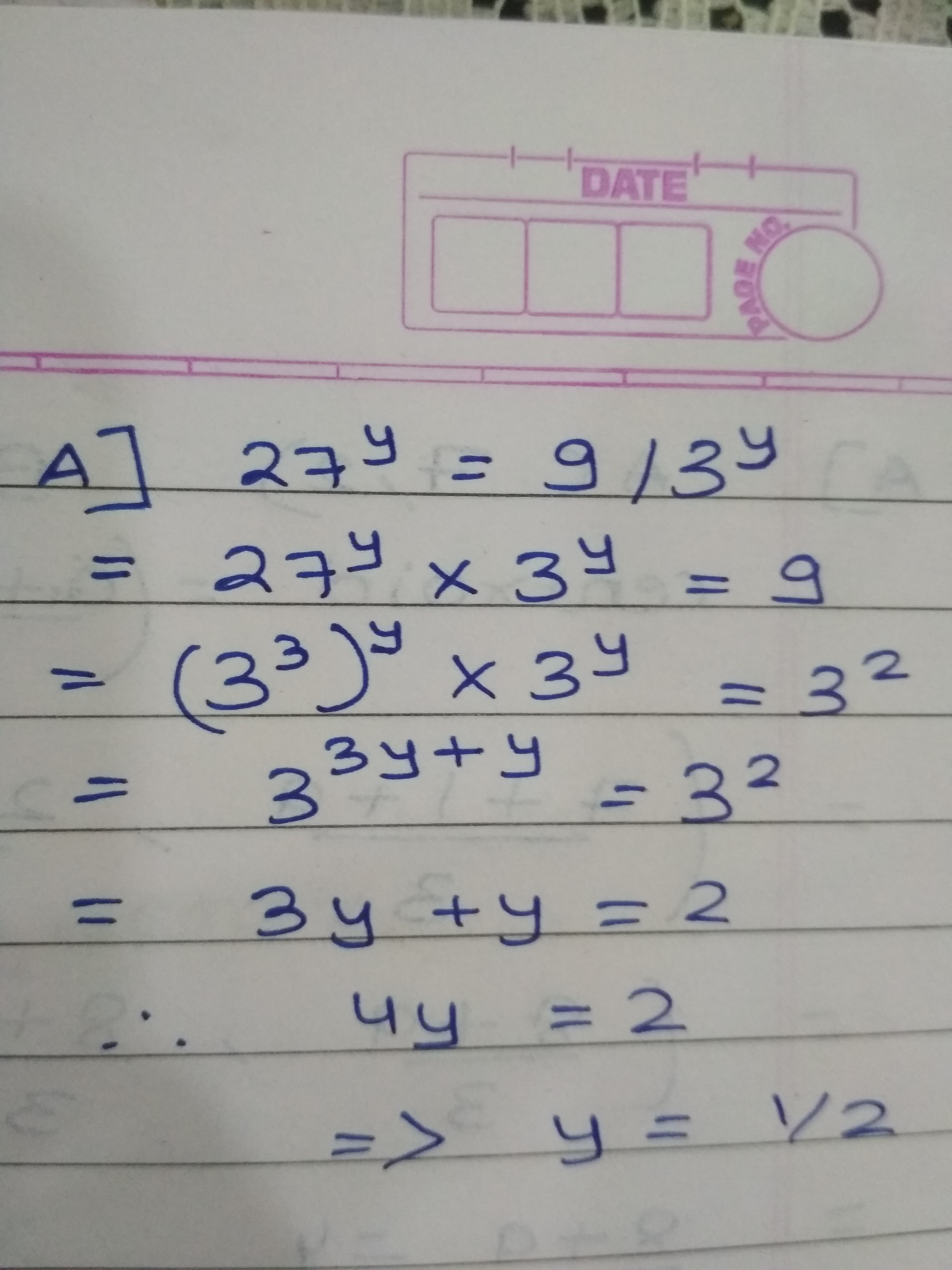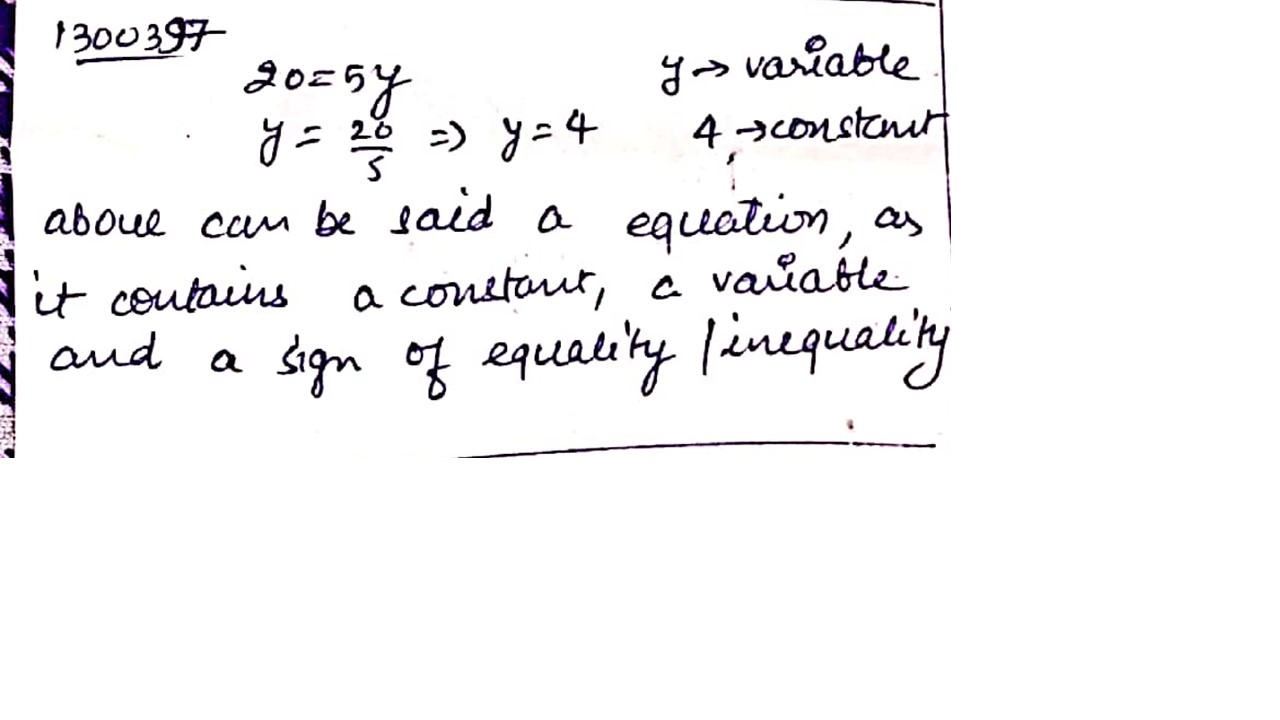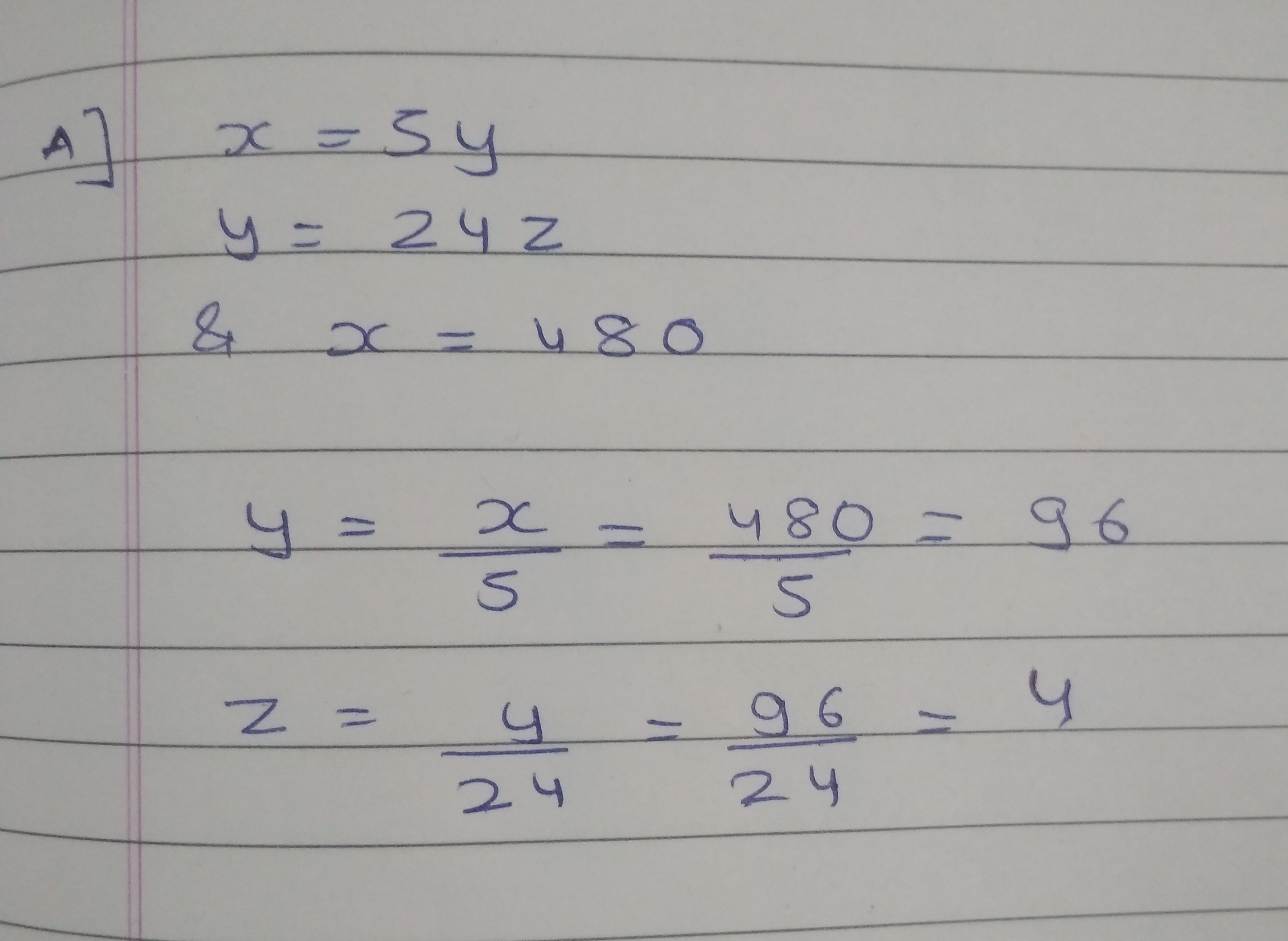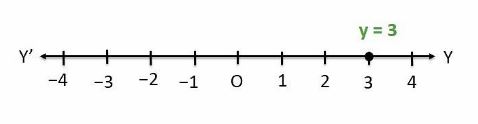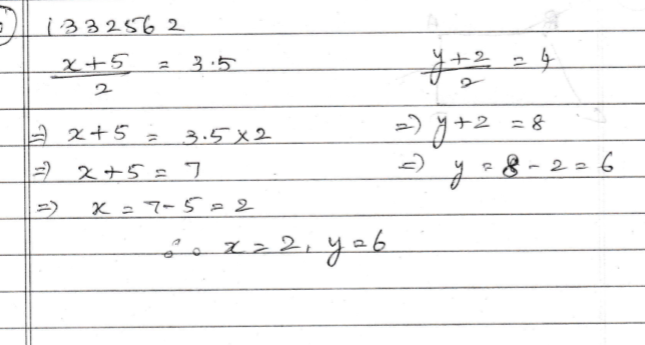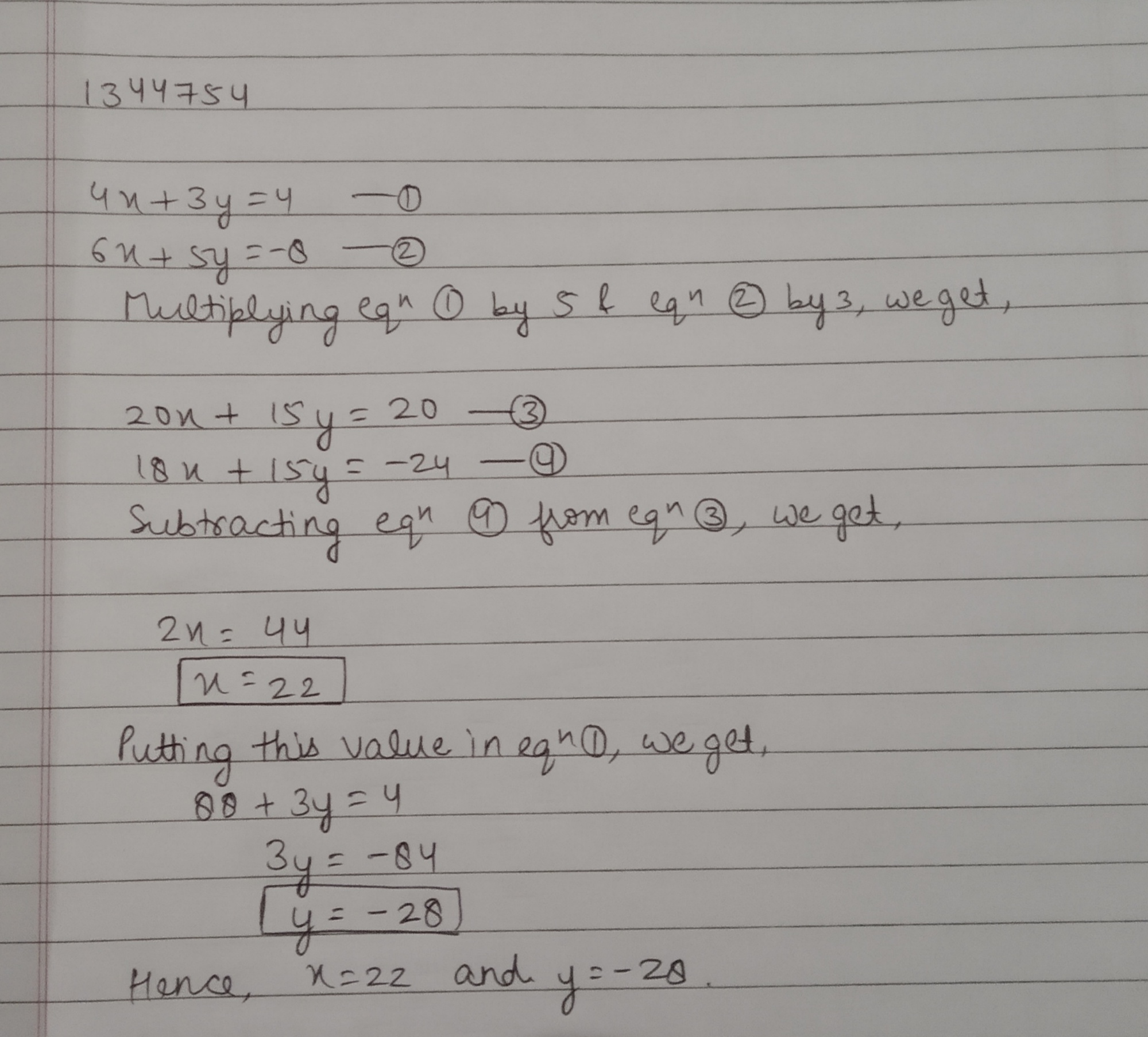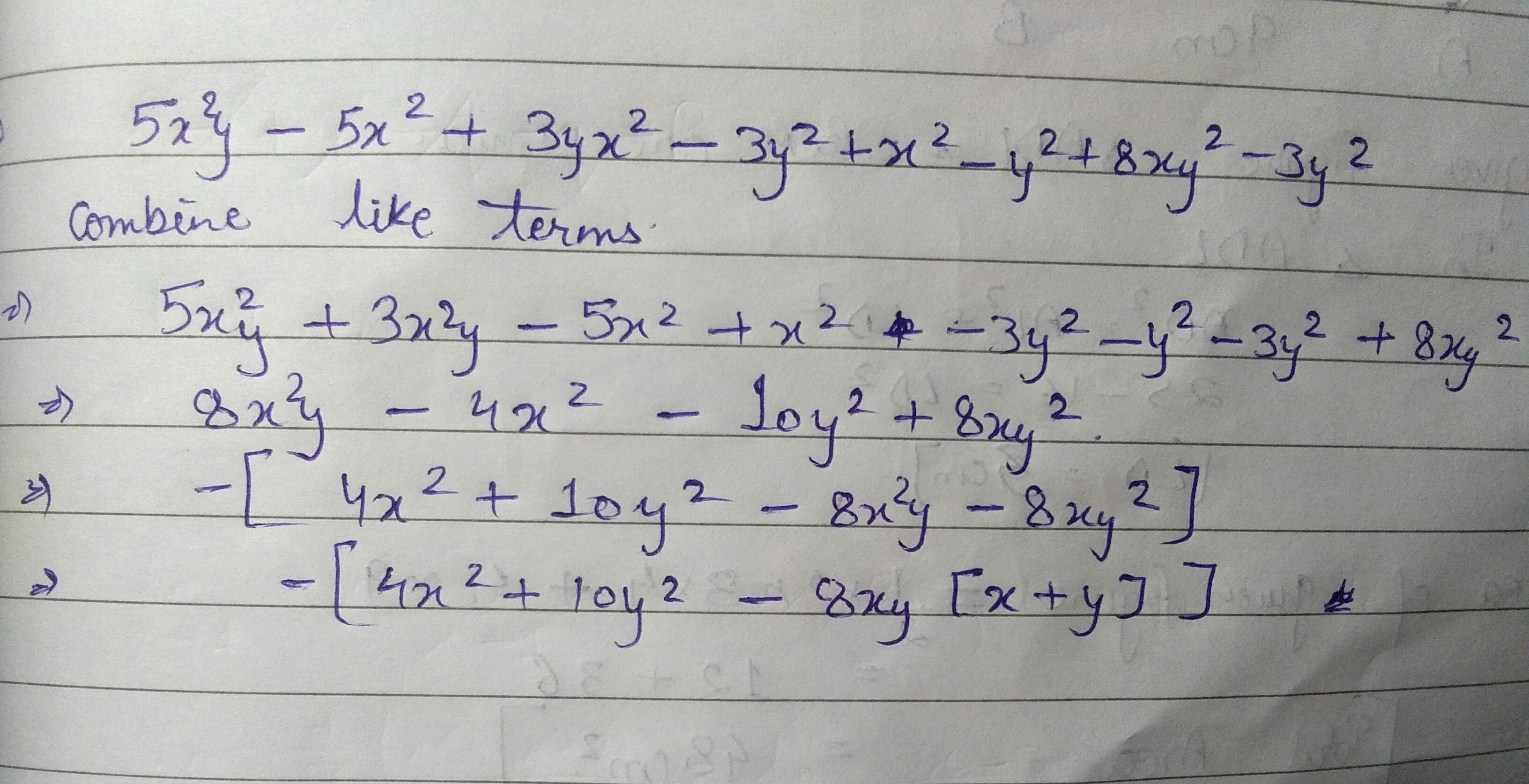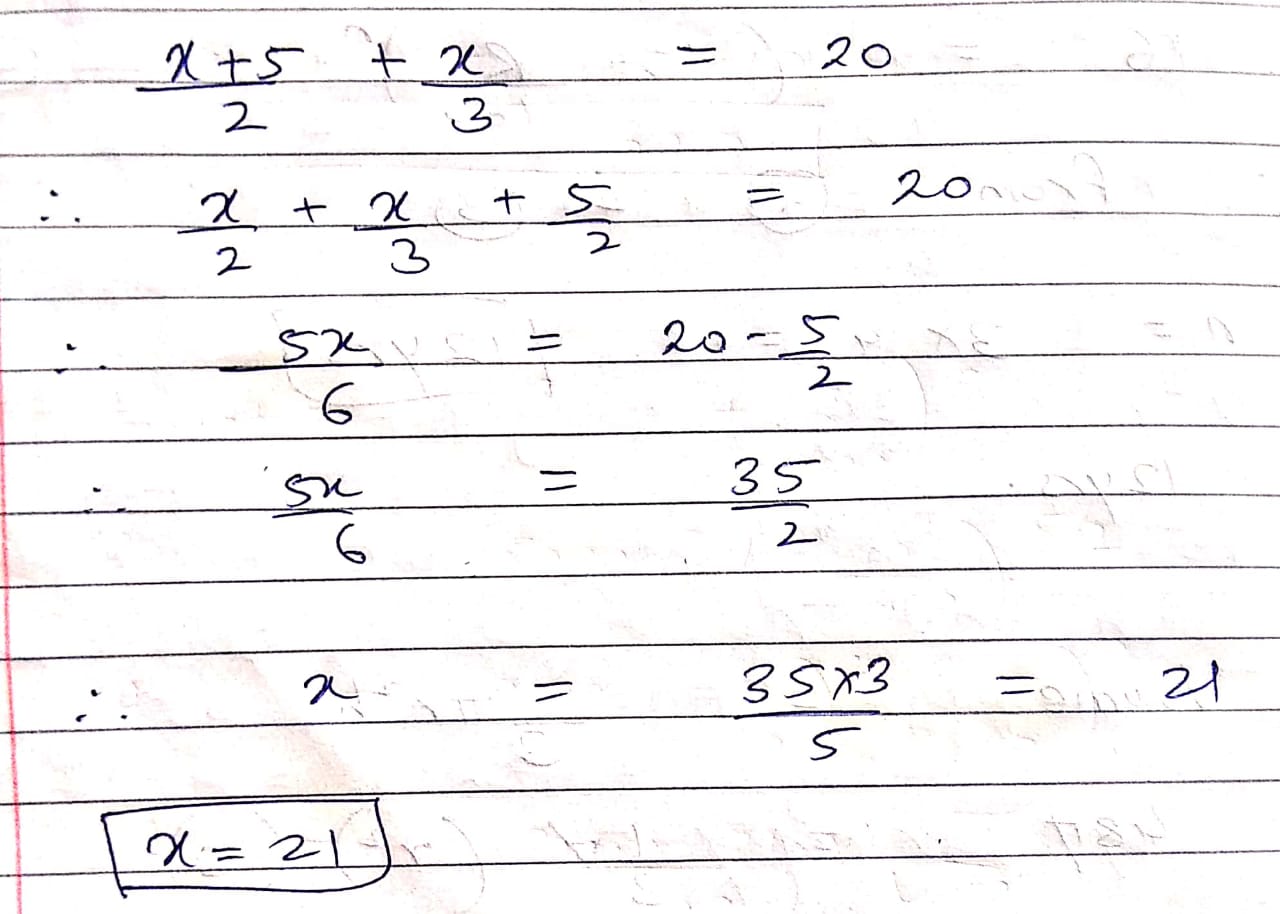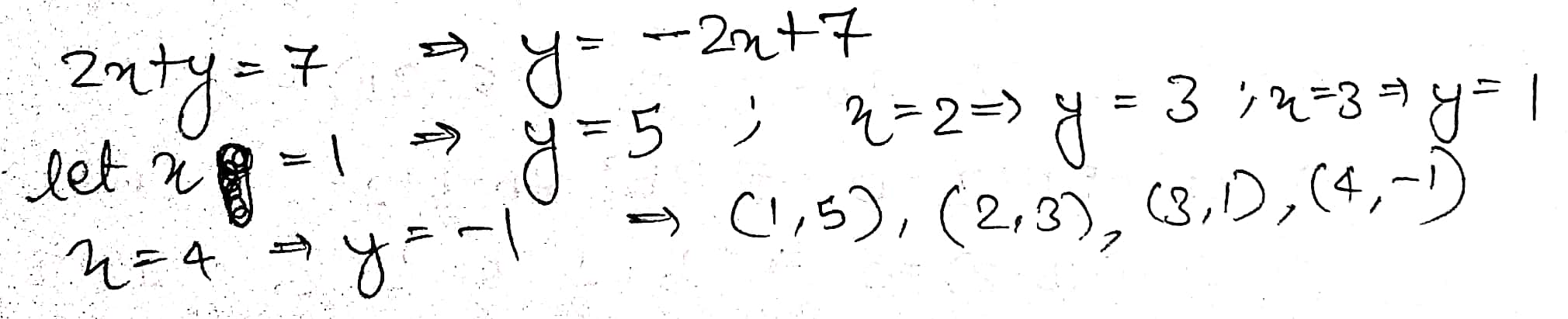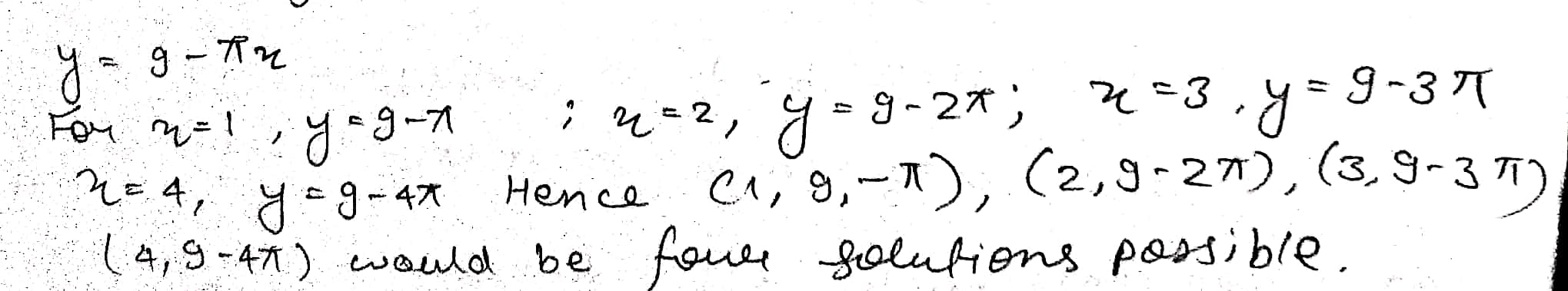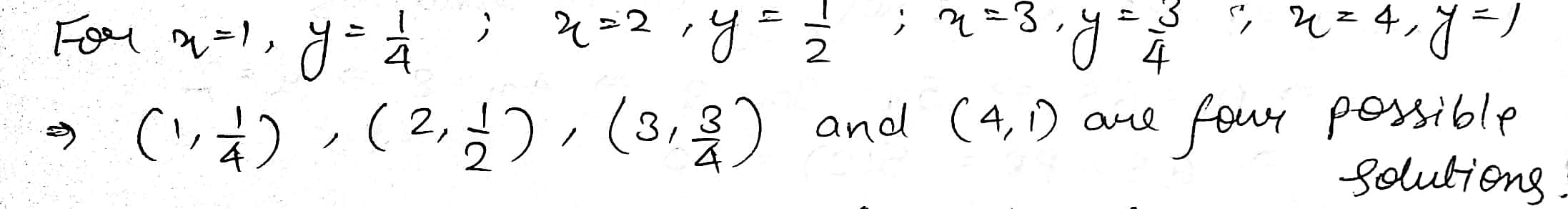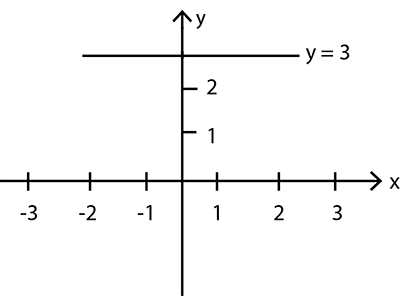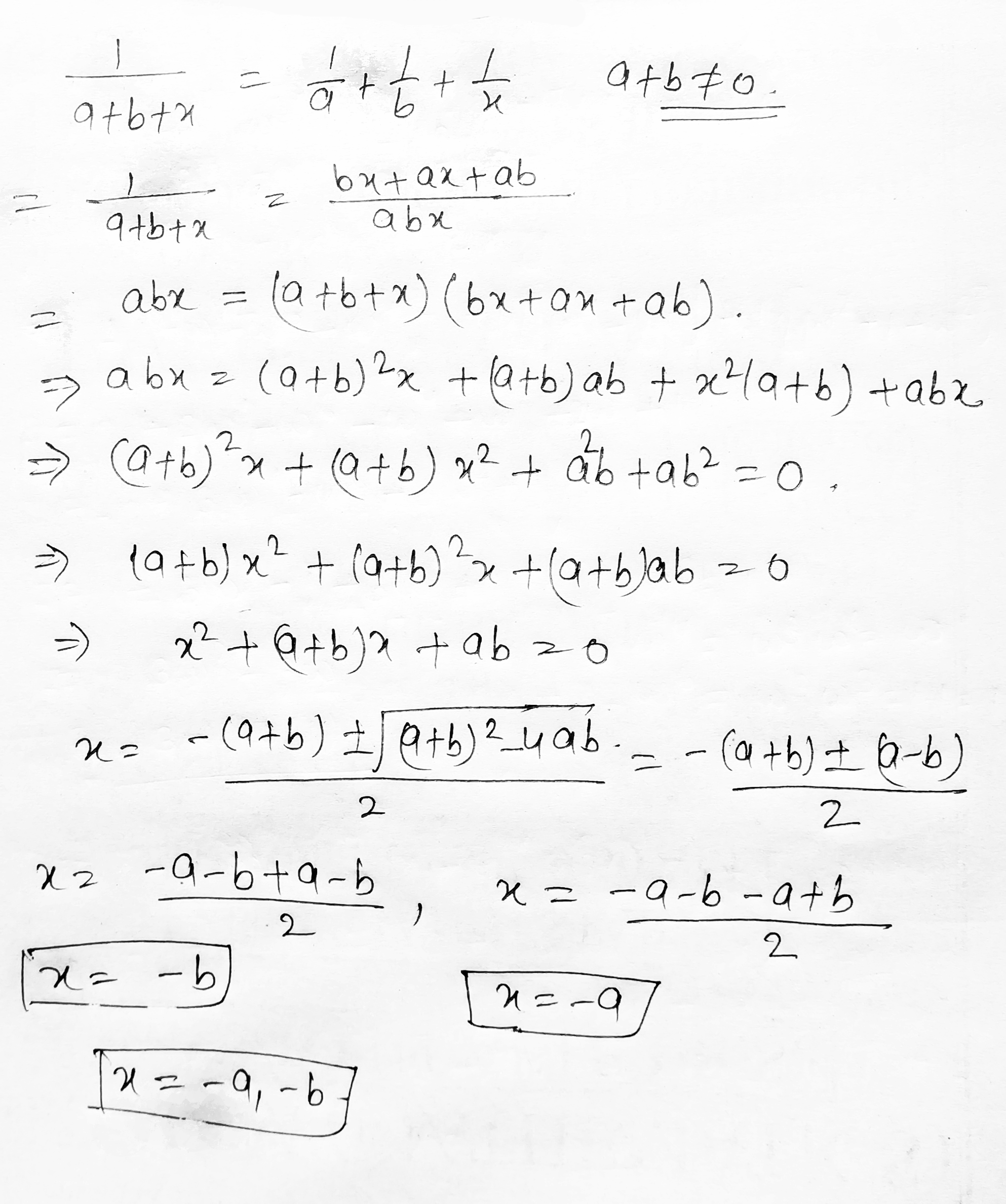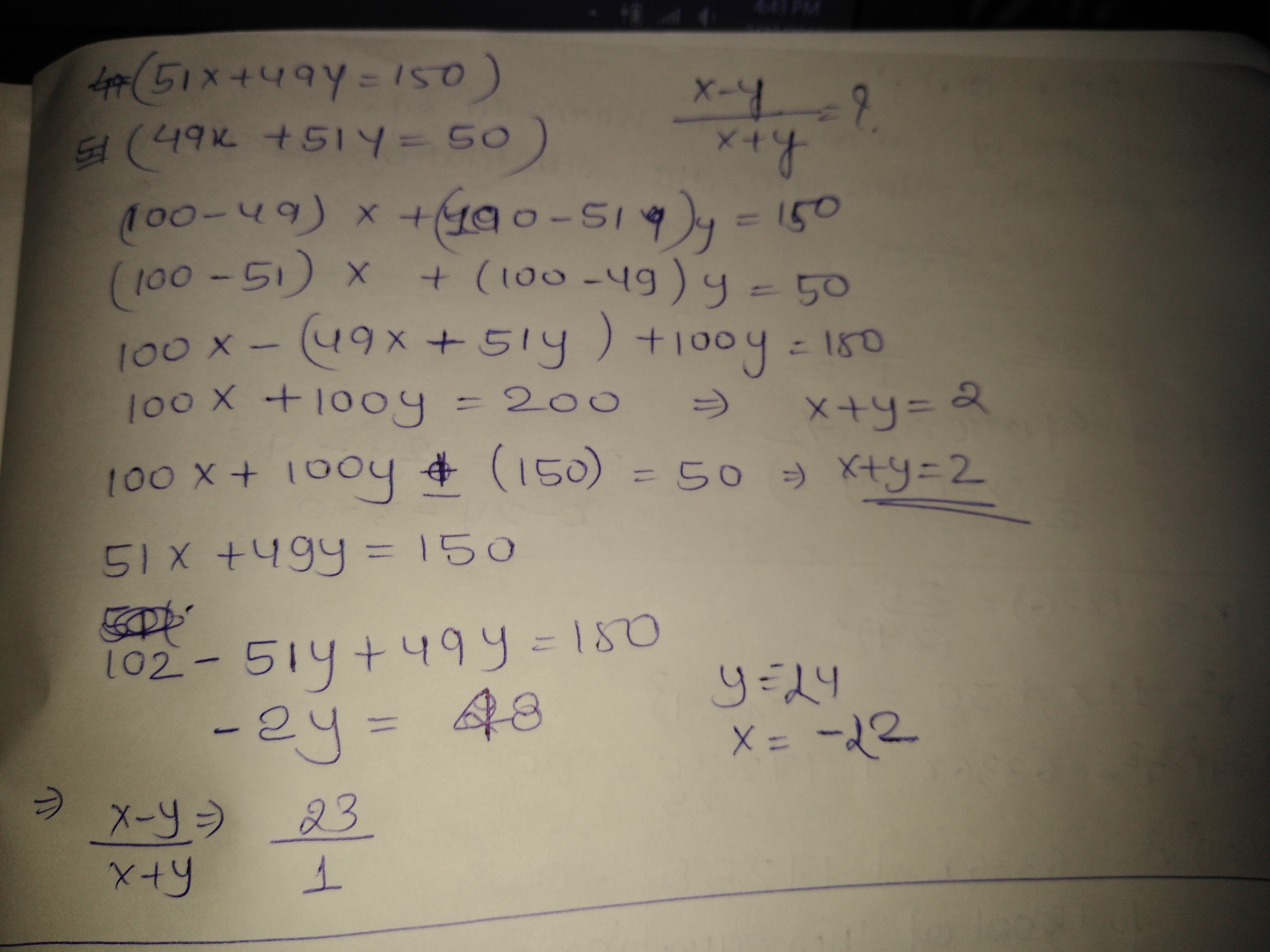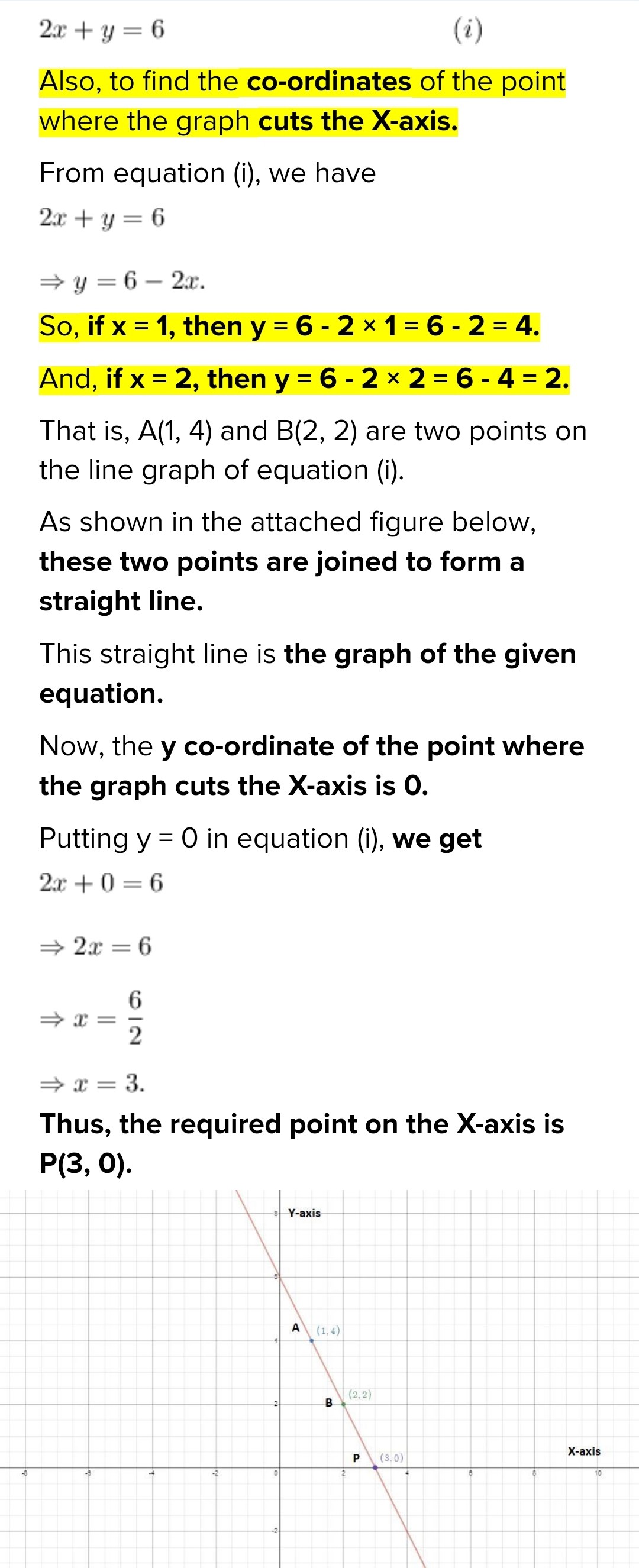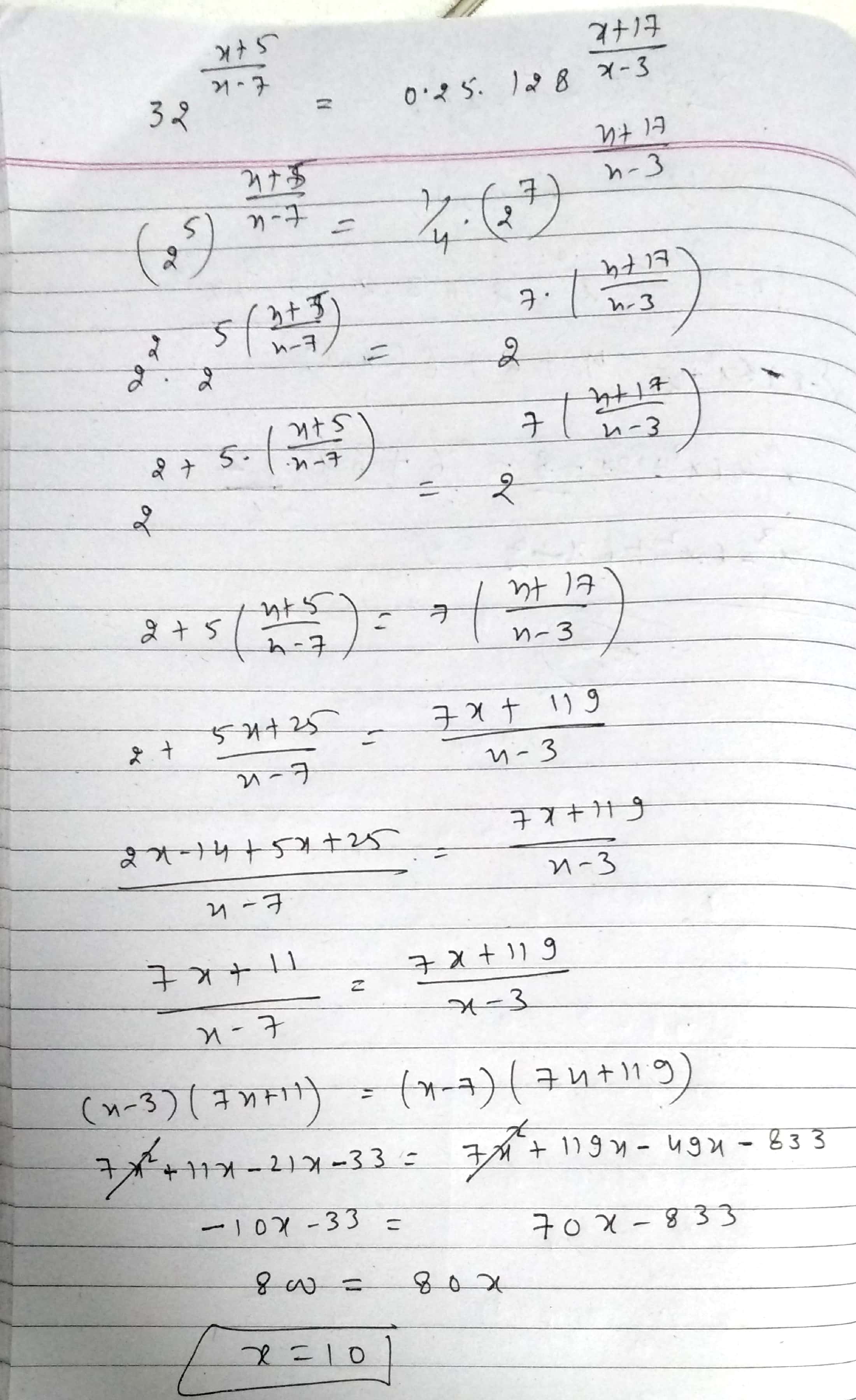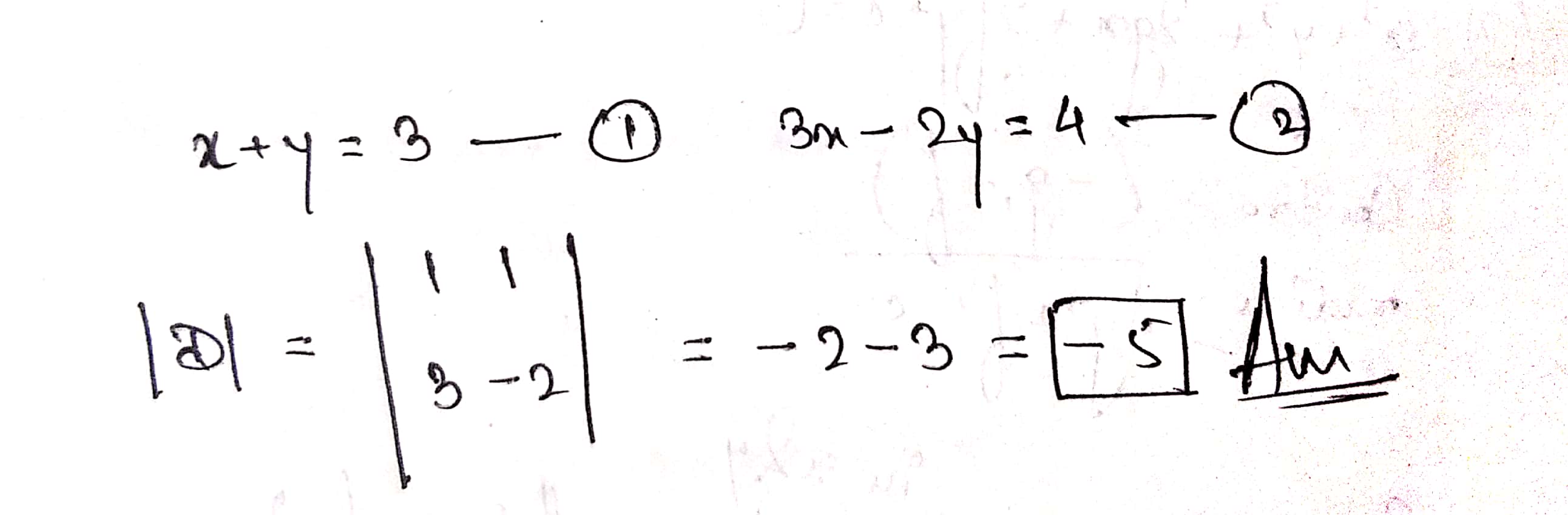Linear Equations In Two Variable - Class 9 Maths - Extra Questions
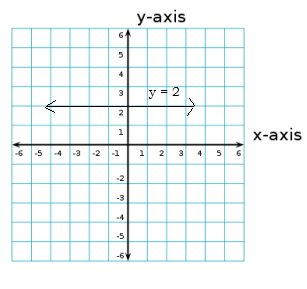
$$y - 2 = 0$$ is parallel to $$x$$-axis.If true enter 1 else 0.
The graph for the linear equation $$2y - 5 = 0 $$ is parallel to $$x$$-axis.If true enter 1 else 0.
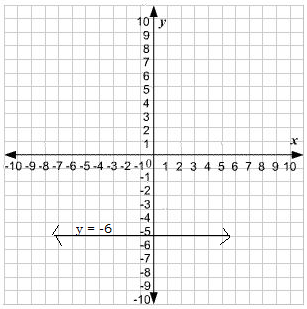
$$y + 6 = 0$$ is parallel to $$x$$-axis.If true enter 1 else 0.
The cost of notebook is twice the cost of a pen. Write a linear equation in two variable to represent this statement.
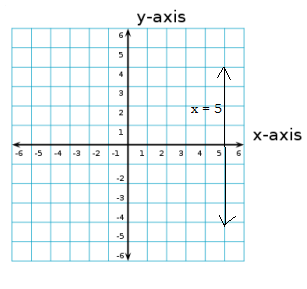
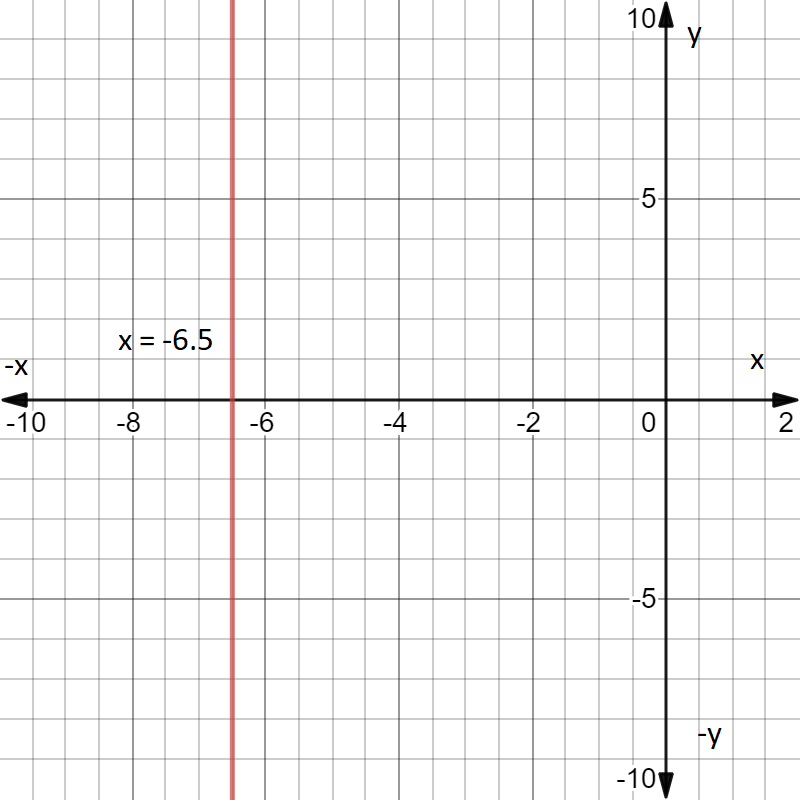
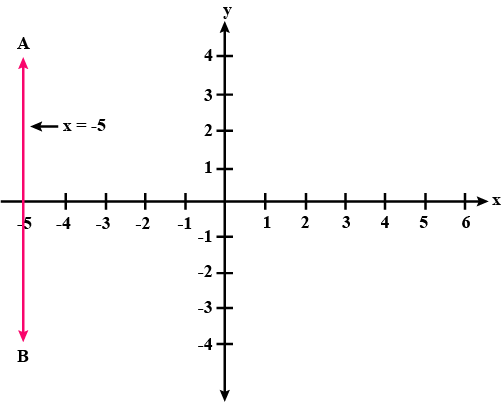
$$x - 5 = 0$$ is parallel to $$y-$$axis. Find the value of $$x$$ co-ordinate where it crosses $$x-axis$$.
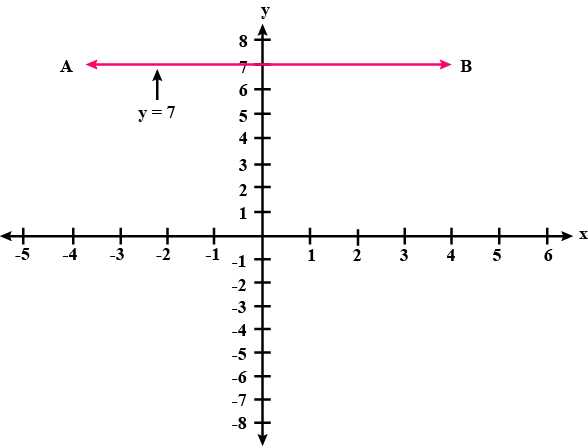
Give the geometric representation of $$y = 3$$ as an equation in one variable.
Give the geometric representation of $$x = -\dfrac{9}{2}$$ in one variable.
A greeting card costs Rs.$$3$$ and a ream of photocopy paper costs Rs.$$8$$. Amir paid Rs.$$32$$ for $$x$$ cards and $$y$$ reams of paper. Write a linear equation based on the information above.
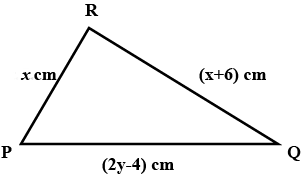
The perimeter of $$\triangle PQR$$ is $$30 cm$$.
Write a linear equation in two variables based on the information given above.
The length and width of a rectangle is $$4x cm$$ and $$y cm$$ respectively. If its length is $$3 cm$$ longer than its width, write an equation involving $$x$$ and $$y$$.
Express the following linear equation in the form of ax + by + c = 0 and indicate the value of a, b and c.
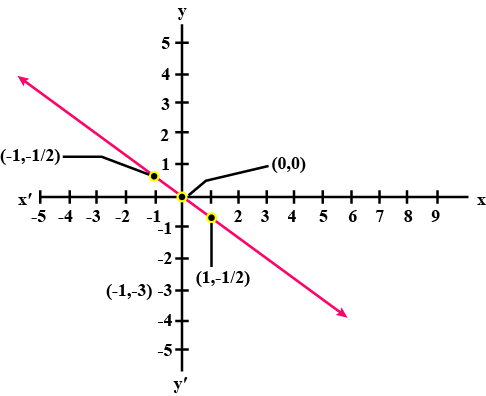
$$y = \dfrac{-3}{2} x$$
Given the function $$h$$ such that $$h(x)=x^2+kx+5$$ and $$h(3)=2$$. Find the value of $$k$$.
Write each of the following in the form of ax + by + c = 0 and find the value of a, b and c
(i) x = - 5
(ii) y = 2
(iii) 2x = 3
(iv) 5y = -3
Express the following linear equation in the form of ax + by + c = 0 and indicate the value of a, b and c.
$$2x = - 5y$$
Express each of the following equations in the form of $$ax + by + c= 0$$ and write the values of a, b and c.
$$\dfrac{x}{2} + \dfrac{y}{2} = \dfrac{1}{6}$$
Hema's age is 4 times the age of Mary. Write a linear equation in two variables to represent this information.
Express each of the following equations in the form of $$ax + by + c= 0$$ and write the values of a, b and c.
$$3x = y$$
Express the following linear equation in the form of ax + by + c = 0 and indicate the value of a, b and c.
$$\dfrac{x}{3} + \dfrac{y}{4} = 7$$
Express the following linear equation in the form of ax + by + c = 0 and indicate the value of a, b and c.
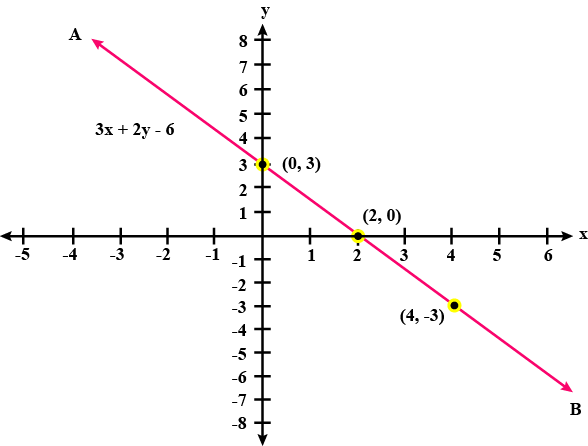
$$8x + 5y - 3 = 0$$
Sachin and Sehwag scored $$137$$ runs together. Express the information in the form of an equation.
Express the following linear equation in the form of ax + by + c = 0 and indicate the value of a, b and c.
$$\dfrac{y}{7} = 3$$
Express the following statements as a linear equation in two variable.
The cost of a pencil is Rs. 2 and one ball point pen costs Rs.Sheela pays Rs. 100 for the pencils and pens she purchased.
Express the following statements as a linear equation in two variable.
The cost of a ball pen is Rs. 5 less than half the cost of a fountain pen.
Express the following statements as a linear equation in two variable
The sum of two numbers is 34.
Express the following linear equation in the form of $$ax + by + c = 0$$ and indicate the values of $$a, b$$ and $$c$$ .
$$y - 2 = 0$$
Express the following statements as a linear equation in two variable.
Bhargavi got 10 more marks than double of the marks of Sindhu.
Express the following statements as a linear equation in two variable.
Yamini and Fatima of class IX together contributed Rs. 200/- towards the Prime Minister's Relief Fund.
Express the following linear equation in the form of ax + by + c = 0 and indicate the value of a, b and c.
2x = 5
Express the following linear equation in the form of ax + by + c = 0 and indicate the value of a, b and c.
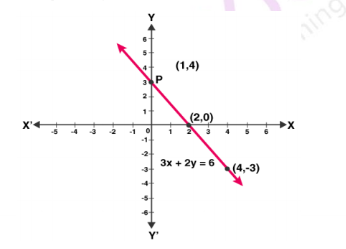
$$3x + 5y = 12$$
Write the linear equations in two variables using '$$x$$' and '$$y$$' to represent the following information :
"The sum of the two numbers is $$30$$."
Determine whether $$(4, 6)$$ is the solution of linear equation $$x + y = 10$$.
By using two variables, write the following statement in mathematical form:
"The cost of two tables and five chairs is Rs. $$2,200.$$"
The sum of two numbers is $$28$$. Write this information in linear equation of two variable. (Use variable $$x$$ and $$y$$)
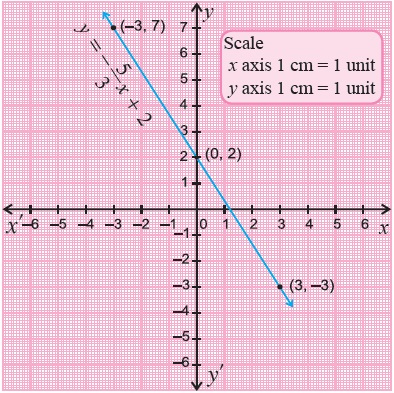
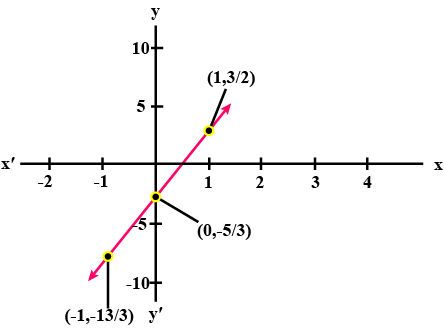
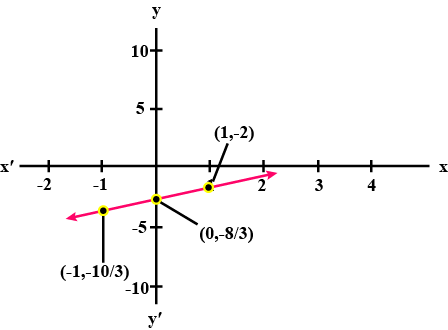
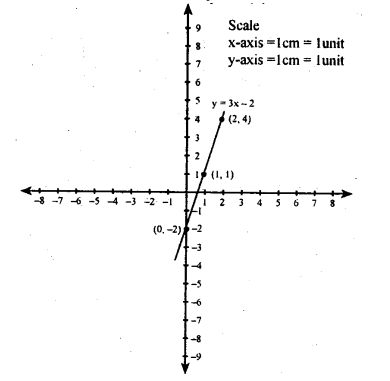
Draw the graph of the line $$y=-\dfrac{5}{3}x+2$$.
Write any one linear equation using the variables '$$x$$' and '$$y$$'.
Write any one linear equation using the variables $$x$$ and $$y$$.
In linear equation x + y = 5, if x = 3, then find the value of y.
Write the following equation in the general form of a linear equation in two variables:
$$7x = 3y + 23$$
Write L.H.S and R.H.S of the following simple equations:
$$4z+1=8$$
Find the limits within which $$c$$ must lie in order that the equation $$19x+14y=c$$ may have six solutions, zero solutions being excluded.
Prove that the coefficient of $$ x^r $$ in the expansion of $$ (1-4x)^{- \frac{1}{2} } $$ in $$ \dfrac {|\underline{2r}|}{(|\underline{r}|)^2} $$
Write L.H.S and R.H.S of the following simple equations:
$$7m=14$$
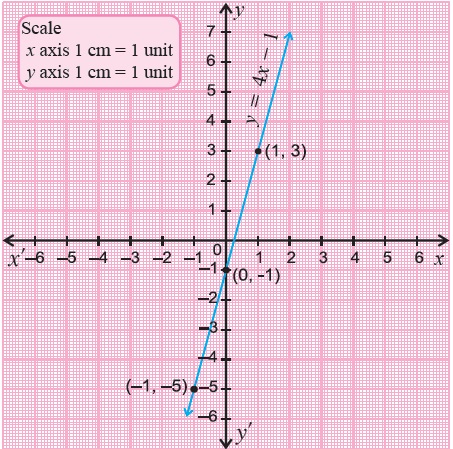
Draw the graph of $$y=4x-1$$.
Solve the following equation without transposing:
$$x+5=9$$
Write L.H.S and R.H.S of the following simple equations:
$$5p+3=2p+9$$
Write L.H.S and R.H.S of the following simple equations:
$$8=q+5$$
Write L.H.S and R.H.S of the following simple equations:
$$2x=10$$
Write L.H.S and R.H.S of the following simple equations:
$$2x-3=9$$
Solve the following equation.
$$\sqrt[4]{1+5x}+\sqrt[4]{5-y}=3, 5x-y=11$$.
Romila went to a stationary stall and purchased $$2$$ pencils and $$3$$ erasers for Rs. $$9$$. Her friend Sonali saw the new variety of pencils and erasers with Romila, and she also bought $$4$$ pencils and $$6$$ erasers of the same kind for Rs. $$18$$. Represent this situation algebraically.
The diameter of front and rear wheels of a tractor are $$80cm$$ and $$2m$$ respectively. Find the number of revolutions that rear wheel will make in covering distance in which the front wheel makes $$1400$$ revolutions.
Solve the following linear equations for $$x$$ and $$y$$$$3x+2y=5$$
$$2x-3y=7$$
$$2x-3y=7$$
The temperature of certain place fell by $$2^0$$C ( a charge of -$$2^0$$C ) each day for a week. What is the change of temperature over the whole week?
Solve the following equations :
$$\cfrac{x-ab}{a+b} + \cfrac{x-ac}{a+c} + \cfrac{x-bc}{b+c}$$ = a+ b + c
There are 'a' trees in the village Lat. If the number of trees increases every year by 'b', then how many trees will there be after 'x' years?
After $$12$$ years, Kanwar shall be $$3$$ times as old as I was $$4$$ years ago. Find my present age.
A man is twice as old as his son. Twelve years ago, the man was thrice as old as his son. Find their present ages.
Given $$A= 2(a
+b)h $$ find $$a$$ if $$A=144, b=1, h=12$$
Find the value of $$k$$ for which the system of equations $$kx+y=2, x+ky=1$$ is undefined.
State which of the following are equation (with variable). Given reasons for your an mention which variable is used from the equation with a variable.
$$9x+6=12$$
Express the given statements in the form of linear equations in two variables.
$$1$$ is added to the numerator and $$4$$ is subtracted from the denominator, the fraction becomes 1.
State which of the following are equation (with variable). Given reasons for your an mention which variable is used from the equation with a variable.
$$5x=0$$
A train $$100
m$$ long is moving with a velocity of $$60 km /hr$$. Find the time it takes to
cross the bridge one km long
Verify $$a-(-b)=a+b$$ for the following value of $$a$$ and $$b$$.(i). $$a=28,b=1$$(ii). $$a=118,b=125$$(iii). $$a=75,b=84$$(iv). $$a=28,b=1$$
The sum of the two digits of a $$2-$$digit number is $$9$$. When the digits are reversed, the number deceases by $$9$$. Find the original number.
What will be the ratio of the ages after 5 years?
Rina lost her weights inn the ratio 5:Her original wights was 80 kg. What is her new weight.
A works twice as fast as B. They work together and complete a job in 8 days. How long would A take to complete the job?
State which of the following are equation (with variable). Given reasons for your an mention which variable is used from the equation with a variable.
$$17q+3=54$$
Find the values of $$x$$ and $$y$$ if:
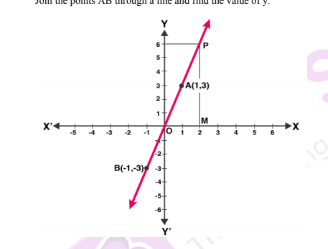
$$(x - 1, y + 3) = (4, 4)$$.
Solve $$\dfrac{{2x - 3}}{5} + \dfrac{{x + 3}}{4} = \dfrac{{4x + 1}}{7}$$
Solve $$10p\, - \,\left( {3p - 4} \right)\, = \,4\left( {p + 1} \right)\, + \,9$$
Solve:$$8x+4=3(3c-1)+7$$
Solve $$\dfrac{p}{4} + \dfrac{p}{3} = 55 - \dfrac{{p + 40}}{{50}}$$
Express the following statement as a linear equation in two variables.
"Seetha got $$8$$ mark more than double of the marks of Ramya"
In the given expression $$-2y+3x=14$$, express $$y$$ is terms of $$x$$.
If four is subtracted from $$3$$ times the square of a number to get $$6$$. Write this in the form of a linear equation.
Solve for $$x$$ and $$y$$:
$$\dfrac{6}{x -1} - \dfrac{3}{y - 2} = 1$$
$$\dfrac{5}{x-1} + \dfrac{1}{y-2} =2$$, where $$x \neq 1, y \neq 2$$.
Solve the equation $$\dfrac {x}{3}+2=2x-3y$$
Factorize the following using appropriate identities:
(i)$$9x^2+6xy+y^2$$
(ii)$$4y^2-4y+1$$
(iii)$$x^2-\dfrac{y^2}{100}$$
Solve $$2x+3=5x+6$$ & represent it as
i) One variableii) Two variable
The marks of Urmila of $$4$$ subjects are $$52,70,66,60$$ respectively. If the total average marks is equal to $$60$$. How many marks should urmila obtain in fifth subject.
Find $$k$$, if $$kx+3y=5$$ passes through $$(1,5)$$.
Solve: $$\dfrac{2x}{7} + \dfrac{x - 1}{5} = \dfrac{x}{3} + \dfrac{x}{7}$$.
Solve following equation:
$$x^2 + \dfrac{x}{\sqrt{2}} + 1 = 0$$
Find the value of $$x$$ in terms of $$y$$ $$4x-4y-20=0$$
Give two equations passing through $$(3,10)$$
Write two different linear equation in two variables.
Solve $$ \frac{1}{2}\,(0)\,+100=x$$
Which of the following is not a linear equation in one variable ? why?
$$2x-1=\dfrac{3}{2}$$
$$x+3y=5$$
$$a=0$$
Solve the following question using a systematic method
1) 7x=28
2) 2x+7=13
3) -y+36=32
4) 2y-6=8
Father is thrice as old as his son. The sum of their ages is $$88$$ years. Find their ages.
Write a linear equation in two variables x and y such that at $$x=4, y=4$$.
The cost of $$2kg$$ of apples and $$3kg$$ of grapes is Rs. $$190$$. Represent this information as linear equation in two variables.
Simplify:
$${\left( {2x + y} \right)^3} + {\left( {2x - y} \right)^3}.$$
The present age of $$A$$ and $$B$$ are in the ratio $$4:5$$. Ten years ago their ages were in the ratio $$3:4$$. What are their present ages?
Write the standard or general form of linear equation with two variables.
Find the value of $$20 + {\left( {27} \right)^{\frac{{ - 1}}{3}}}$$
If $$x:y=1:7$$ and $$y:z=4:5$$, find
$$x:z$$
Given Munnus's age to be $$x$$ years, ca you guess what $$(x-2)$$ may show .can you guess what $$(x+4)$$ may show? what $$(3x+7)$$ may show?
Solve $$\dfrac{{5x}}{3} + \dfrac{2}{5} = 1$$
Meera's mother, in four times as old as Meera. After $$5$$ years, her mother will be three times as old as she will be then. What are their present ages.
The points $$A(a,b)$$ and $$B(b,0)$$ lie on the line $$y=8x+3$$ then(i)Find the value if $$a\ and\ b$$
(ii)Determine if $$(2,0)$$ is a solution of $$y=8x+3$$.
(ii)Determine if $$(2,0)$$ is a solution of $$y=8x+3$$.
simplify
$$3x + \dfrac{1}{2} = \dfrac{3}{8} + \dfrac{x}{8}$$
(i) $$3(Y+3)+4=28$$. Find Y.
If $$2x+8=-2$$, find the value of $$4x+5$$.
Solve: $$4(2 - x) = 8$$
x-5=6
$$\frac{1}{10}-\frac{7}{x}=35$$
Identify like terms in the following:
$$10pq,7p,8q,-{ p }^{ 2 }{ q }^{ 2 },-7qp,100q,-23,12{ p }^{ 2 }{ q }^{ 2 },-5{ p }^{ 2 },41,2405p,78qp,13{ p }^{ 2 }{ q }^{ 2 },{ q }{ p }^{ 2 },701{ p }^{ 2 }$$
$$......$$ contains only one variable with highest power $$1$$.A) Simple equation
B) linear equation
C) Linear polynomial
D) multi equation
Identify like terms in the following:
$$-{ xy }^{ 2 },-4{ yx }^{ 2 },-{ 8x }^{ 2 },2{ xy }^{ 2 },{ 7y,-{ 11x }^{ 2 },11yx,-{ 20x }^{ 2 }y,-6{ x }^{ 2 },{ y,-{ 2xy,3x } } }$$
Find the value of y in terms of x:
$$2x+3y+5=0$$
Find $$x$$:
$$\dfrac { 5 - x } { 5 + x } = \dfrac { 2 } { 5 }$$
Solve
$$5x = 7x - \frac{{10}}{7}$$
Obtain pair of linear equations in two variables: In a cricket match, rohit makes his score twice Dhawan's scored. Both of them together make a total score 150 runs.
The cost of a toy elephant is the same as cost of $$3$$ balls. Express the statement as a linear equation in two variables.
Find the value of the unknown variable in the following equation.
$$\dfrac{-7p+13}{6}=2p-1$$
Solve the following equation without transporting $$3x + 8 = 5x + 2$$.
Write constant term
$$2x^2-x$$
If $$3x-2y=24$$ and $$2x-3y=18$$ then find $$x+y$$ and $$x-y$$
Solve $$3(y+8)=10(y-4)+8$$.
Find x:x+5=12
Write constant term
$$x^2y+xy^2+5xy-4$$
$$4(x-\frac{1}{3})=28$$
State which of the following are equation (with a variable) given reason and tell your answer. identify the variable from the equation with a variable.
$$\dfrac{4}{2} = 2$$
State which of the following are equation (with a variable) given reason and tell your answer. identify the variable from the equation with a variable.
$$5\times 4-8=2x$$
State which of the following are equation (with a variable) given reason and tell your answer. Identify the variable from the equation with a variable.
$$2n+1=11$$
Write one solution of the equation $$2x+y=10$$.
State which of the following are equation (with a variable) given reason and tell your answer. identify the variable from the equation with a variable.
$$2m<30$$
State which of the following are equation (with a variable) given reason and tell your answer. identify the variable from the equation with a variable.
$$x-2=0$$
If $$p = \frac{{4xy}}{{x + y}}$$
Prove that :
$$\frac{{p + 2x}}{{p - 2x}} + \frac{{p + 2y}}{{p - 2y}} = 2$$
Simplify $$27^{y}=9/3^{y}$$, find $$y$$.
State which of the following are equation (with a variable) given reason and tell your answer. identify the variable from the equation with a variable.
$$(7*3)-19=8$$
State which of the following are equation (with a variable) given reason and tell your answer. identify the variable from the equation with a variable.
$$20=5y$$
Verify that $$x = 2 , y = - 1 ,$$ is a solution of the linear equation $$7 x + 3 y = 11$$
$$X$$ is $$5\ $$ of $$y$$, $$y$$ is $$24%$$ of $$z$$. If $$x=480$$, find the values of $$y$$ and $$x$$
The cost of $$2$$ pencils is same as the cost of $$5$$ erasers. Express the statement as a linear equation in two variables.
Find the values of $$x$$ in the following diagram.
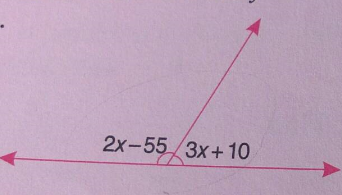
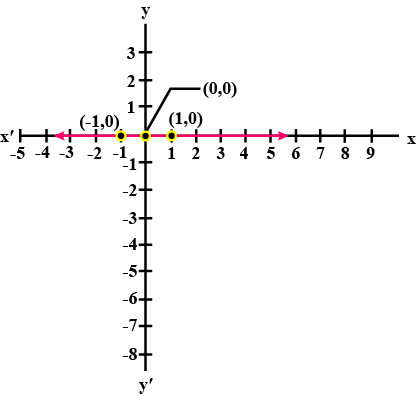
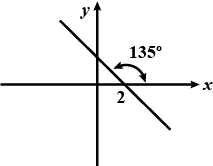
Give the geometrical representation of the equation $$y = 3$$ as an equation.
(i) In one variable
Find the solution of the equation $$\cfrac{{p - 3}}{{1.5p + 9}} = \cfrac{{ - 7}}{5}$$.
Solve the following linear equation :
$$\dfrac{2(x+1)}{3}=\dfrac{3(x-2)}{5}$$
Solve for $$x$$ and $$y$$$$\dfrac { x + 5 } { 2 } = 3.5$$ and $$ \dfrac { y + 2 } { 2 } = 4$$
Find the product
(ii) $$\left( 2x-3y \right) \left( 2x+3y \right) \left( { 4x }^{ 2 }+{ 9y }^{ 2 } \right) $$
Solve:
$$4p - 3 = 13\left( {p - 4} \right)$$
Solve the following
$$3x+y=-2$$ & $$x+y=2$$
Convert $$x+6y=6$$ in the form of $$y=mx+c$$
Find x, y in:
$$4x+3y-4=0$$
$$6x+5y+8=0$$
If x = 4, find the value of 5x.
$$2+\sqrt { x } =9$$ the value of x ?
By using variables $$x$$ and $$y$$ form any two linear equation in two variable.
Simplify combining like terms:
$$5x^{2}y-5x^{2}+3yx^{2}-3y^{2}+x^{2}-y^{2}+8xy^{2}-3y^{2}$$
Solve :$${ (0.7p-0.6q) }^{ 2 }$$
Solve $$\dfrac { x+5 }{ 2 } +\dfrac { x }{ 3 } =20$$
Solve:
$$\dfrac{5}{x}+\dfrac{1}{x}=2$$
Find p if $$\dfrac23p=\dfrac32$$
Express 15 = 2x in the form of ax + by + c = 0 and find the values of a , b, c.
Solve the following equation for x :$$\sqrt{(\dfrac{3}{5})^{1-2x}}=4\dfrac{17}{27}$$
Solve:$$ x+7=10$$
Write four solution for each of the following equation:
$$2x+y=7$$
Write four solution for each of the following equation:
$$\pi x+y=9$$
Write four solutions for each of the following equations:
$$x=4y$$
If $$\left( {x + \dfrac{1}{x}} \right):\left( {x - \dfrac{1}{x}} \right) = 5:4\ $$ then the value of $$x$$ is
if $$\dfrac{4}{a}+\dfrac23=\dfrac{22}{15} $$ find $$a$$
Find x if $$\dfrac 1x+\dfrac 3x=1$$
solve $$ 4x=28$$
Ram covered a distance of 200km in 10 hrs . The first part of his journey is covered by auto ,then he hired a car .The speed of the auto and car is 15 km/hr and 30 km /hr resp. Find the ratio of distance covered by auto and car
Rs. 69 were divided among 115 students so that each girl gets 50 paise less than a boy. Thus each boy received twice the paise as each girl received. The number of girls in the class is:
Check whether the following is solution of the equation $$x-2y=4$$ or not
$$\left(2, 0\right)$$
Find b
$$\dfrac { 2b }{ 3 } -5=3$$
Solve $$\dfrac { { x }^{ 2 }-(x+1)(x+2) }{ 5x+1 } =6$$
Rearrange the formula to make $$w$$ the subject
$$5w-3y+7=0$$
Check whether the following is solution of the equation $$x-2y=4$$ or not:
$$\left(\sqrt{2}, 4\sqrt{2}\right)$$
Solve :- $$\dfrac {y-4} {3} + 3y = 4$$
Solve : $$\dfrac { 2 x - 1 } { 3 } - \dfrac { x + 2 } { 2 }=0$$
Check whether the following equation is with a variable or not. In case of an equation with a variable, identity the variable.
$$17+x=5$$
State which of the following are equations with a variable. In case of an equation with a variable, identity the variable.
$$2b-3=7$$
Show that the points $$A (1,2), B (-1,-16)$$ and $$C (0, -7)$$ lies on the graph of the linear equation $$y= 9x - 7.$$
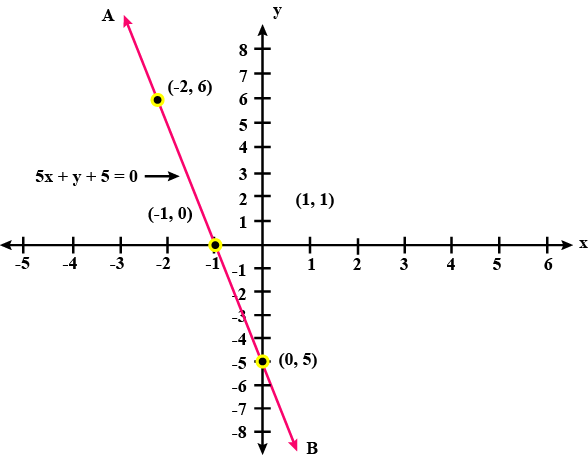
Draw the graph for each equation, given below: $$5x + y + 5 = 0$$.
State which of the following are equations with a variable. In case of an equation with a variable, identity the variable.
$$\dfrac 93 =3$$
Write any three linear equations in two variables using the variables $$x$$ and $$y?$$
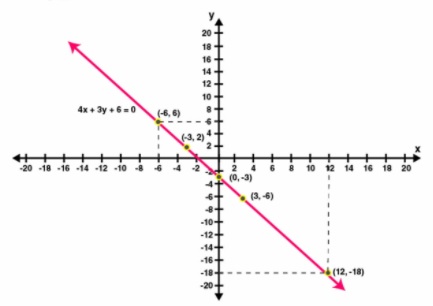
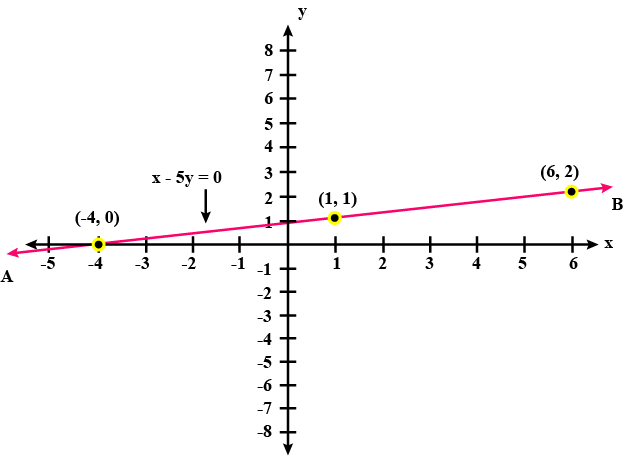
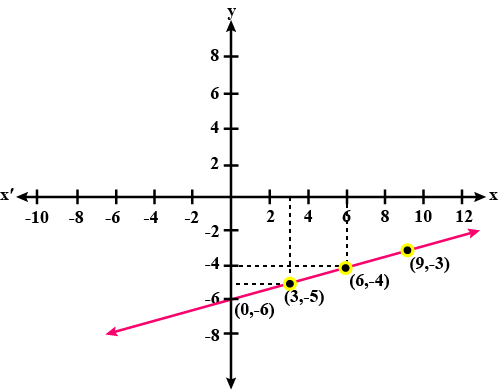
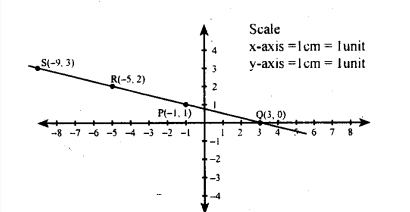
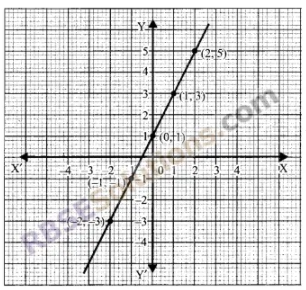
For the graph given below, write down their x-y equation
The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.
If the point $$\left(3, 4\right)$$ lies on the graph of the equation $$3y=ax+7$$, find the value of $$a$$.
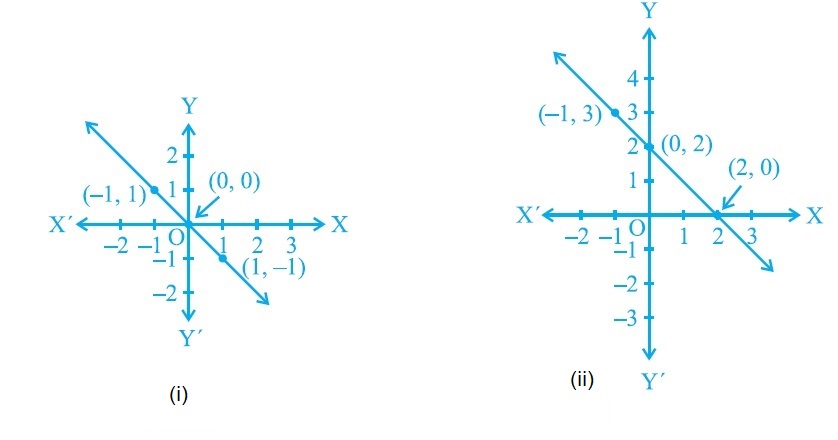
From the choices given below, choose the equation whose graphs are given in Fig. (i) and Fig. (ii).
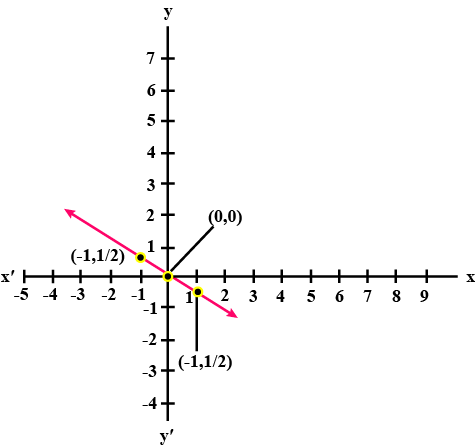
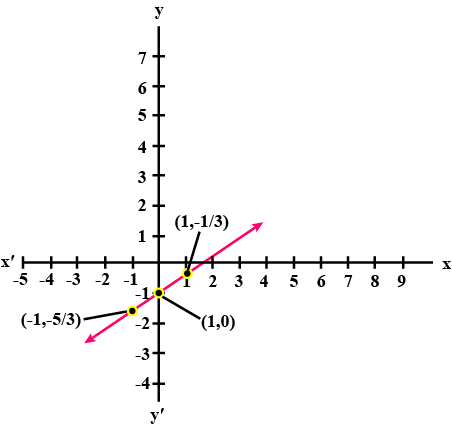
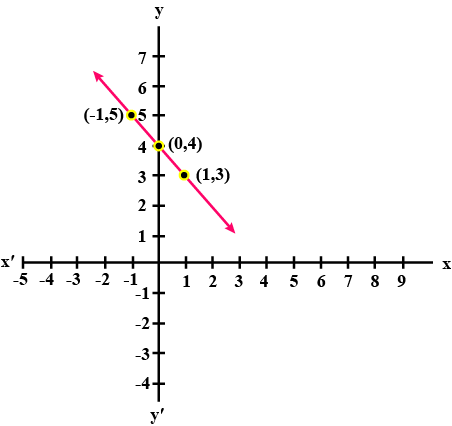
For fig. (i) For fig. (ii) (i) $$y=x$$ (i) $$y=x+2$$ (ii) $$x+y=0$$ (ii) $$y=x-2$$ (iii) $$y=2x$$ (iii) $$y=-x+2$$ (iv) $$2+3y=7x$$ (iv) $$x+2y=6$$
| For fig. (i) | For fig. (ii) |
| (i) $$y=x$$ | (i) $$y=x+2$$ |
| (ii) $$x+y=0$$ | (ii) $$y=x-2$$ |
| (iii) $$y=2x$$ | (iii) $$y=-x+2$$ |
| (iv) $$2+3y=7x$$ | (iv) $$x+2y=6$$ |
The taxi fare in a city is as follows: For the first kilometre, the fare is $$8$$ and for the subsequent distance it is $$5$$ per km. Taking the distance covered as $$x$$ km and total fare as Rs.$$y$$, write a linear equation for this information and draw its graph.
Express the following linear equations in the form $$ax+by+c=0$$ and indicate the values of $$a, b$$ and $$c$$ in each case:
(i) $$2x+3y=9.3\overline { 5 } $$
(ii) $$x-\dfrac{y}{5}-10=0$$
(iii) $$-2x+3y=6$$
(iv) $$x=3y$$
(v) $$2x=-5y$$
(vi) $$3x+2=0$$
(vii) $$y-2=0$$
(viii) $$5=2x$$
(ii) $$x-\dfrac{y}{5}-10=0$$
(iii) $$-2x+3y=6$$
(iv) $$x=3y$$
(v) $$2x=-5y$$
(vi) $$3x+2=0$$
(vii) $$y-2=0$$
(viii) $$5=2x$$
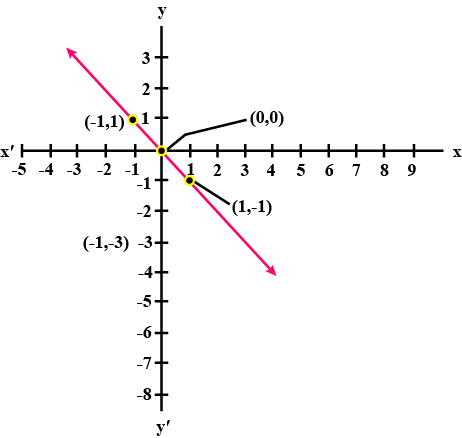
Give the geometric representations of $$y=3$$ as an equation
(i) in one variable
(ii) in two variable
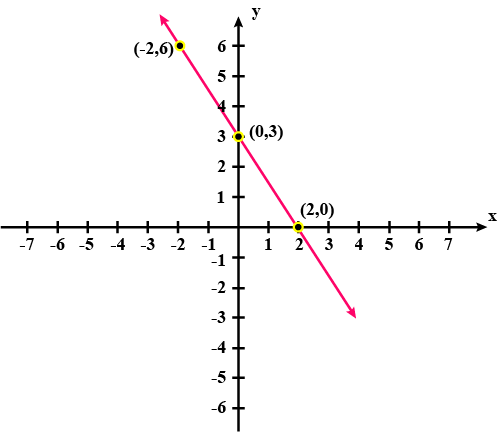
Yamini and Fatima, two students of Class $$IX$$ of a school, together contributed $$Rs.100$$ towards the Prime Minister's Relief Fund to help the earthquake victims. Write a linear equation which satisfies this data. (You many take their contributions as $$Rs.x$$ and $$Rs.y$$.) Draw the graph of the same.
Express each of the following equations in the form of $$ax + by + c= 0$$ and write the values of a, b and c.
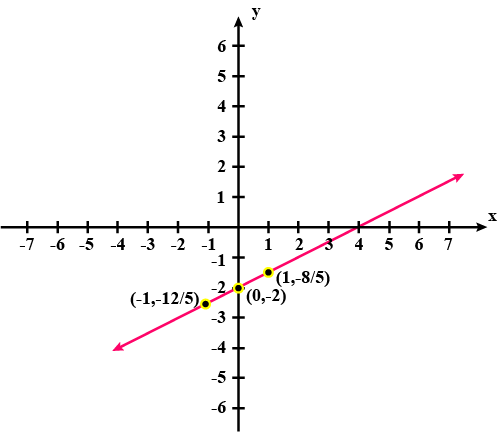
$$x - 5 = \sqrt 3 y$$
A number is 27 more than the number obtained by reversing its digits. If its unit's and ten's digits are x and y respectively, write the linear equation representing the above statement.
$$A, B$$ and $$C$$ lie on a line, as shown. The length of $$\overline{AB}$$ is $$(x-4)$$ and the length of $$\overline{AC}$$ is $$(x+6)$$. What is the length of $$\overline{BC}$$?
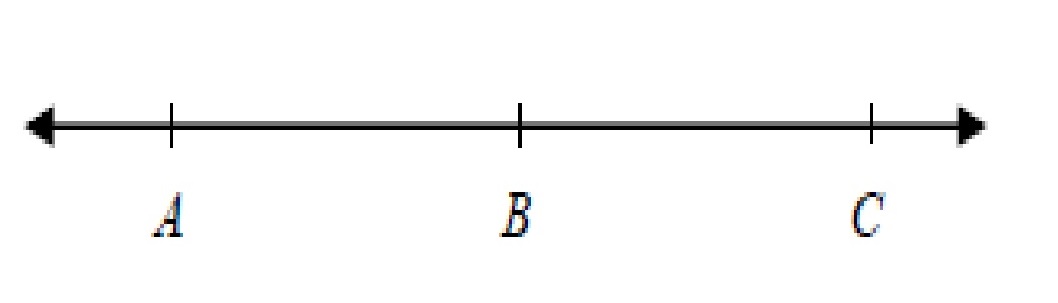
Prove that $$ (1+x)^n = 2^n \left\{ 1-n \dfrac{1-x}{1+x} +\dfrac{n(n+1)}{1 \cdot 2 } \left( \dfrac {1-x}{1+x} \right)^2 \cdot \cdot \cdot \right\} $$
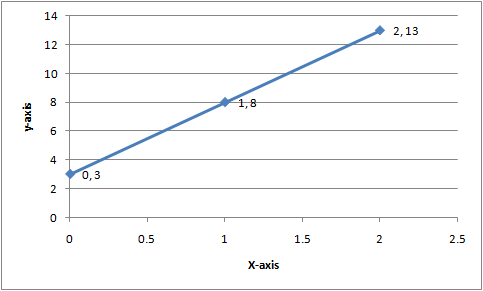
Draw the graph of y = 7x.
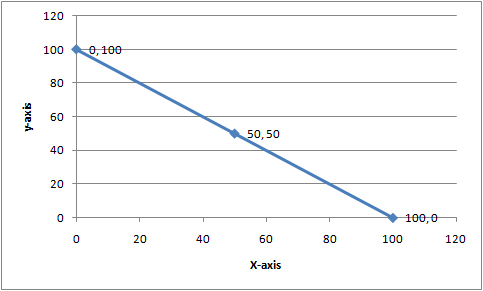
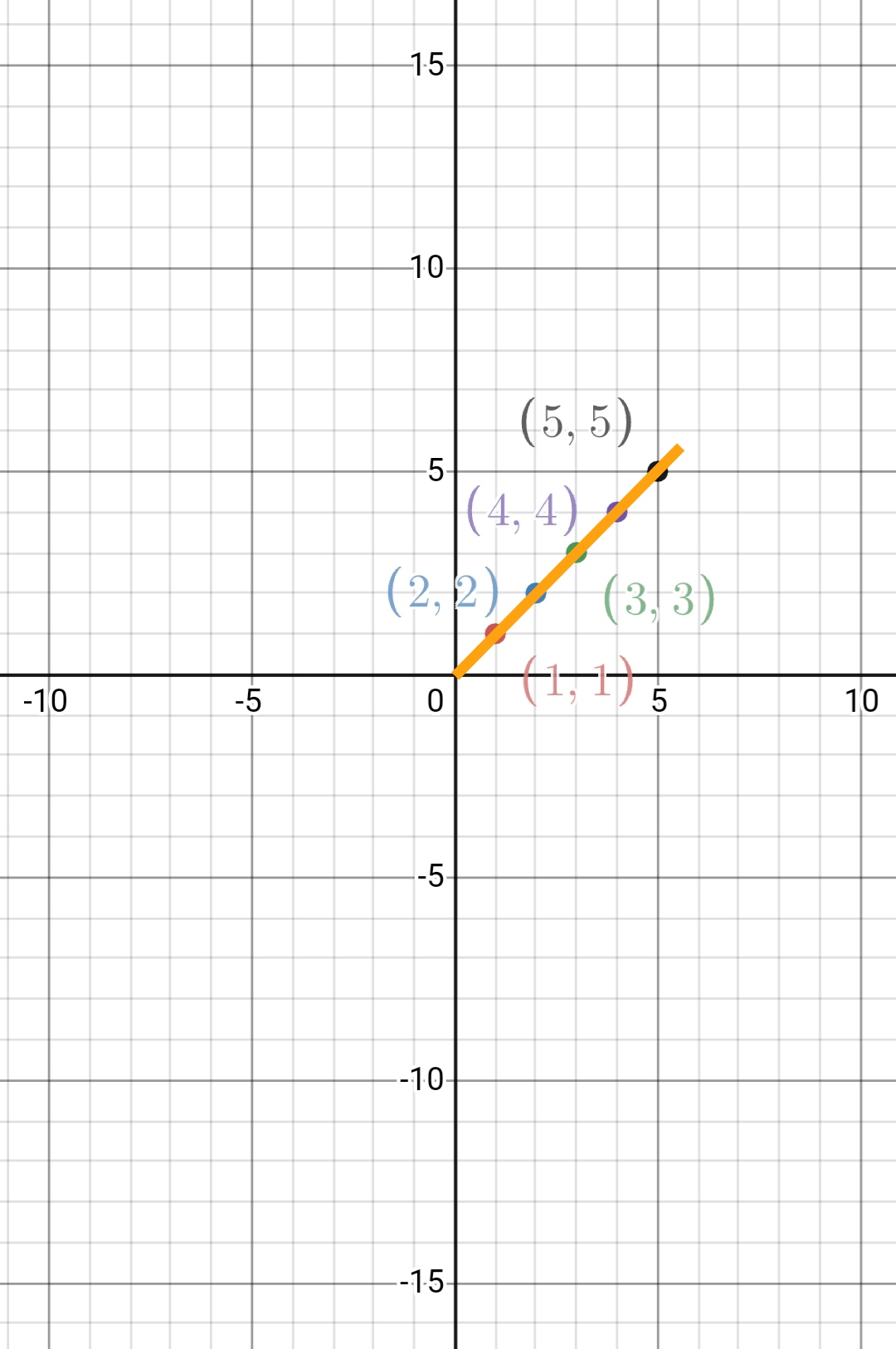
Draw a linear graph for the following data.
| x | 1 | 2 | 3 | 4 | 5 |
| y | 1 | 2 | 3 | 4 | 5 |
Express the following linear equation in the form of ax + by + c = 0 and indicate the value of a, b, c.
$$28 x - 35 y = -7$$
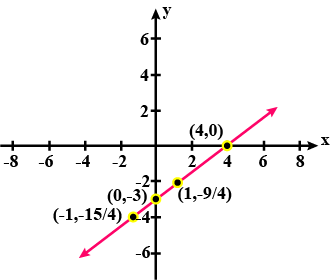
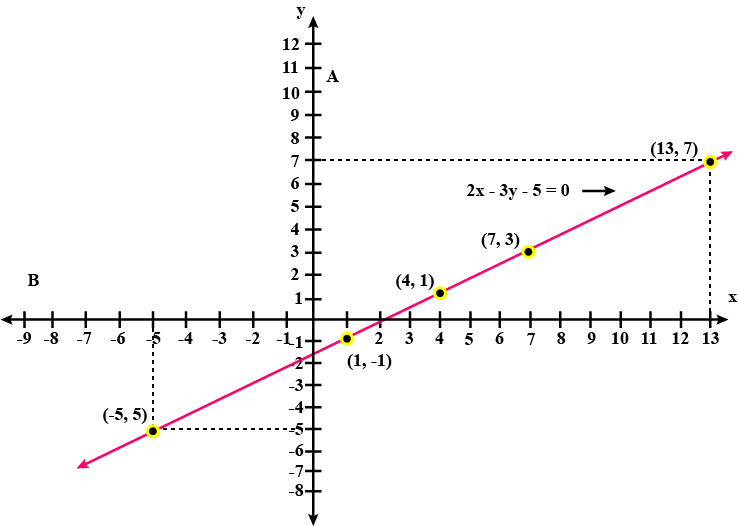
Represent $$3x - 7 = 0$$ in the form of $$ax+by+c=0$$ and find the values of $$a$$,$$b$$ and $$c$$
If x be so small that its square and higher powers may be neglected, find the value of :
$$ \dfrac { \left( 1 + \dfrac{2}{3} x \right)^{-5} \times (4+3x)^{ \frac{1}{2} } } { (4+x)^{\frac{3}{2} } } $$
The sum of a two digit number and the number obtained by reversing the order of its digits isIf the digits in unit's and ten's place are 'x' and 'y' respectively.
If $$x$$ be so small that its square and higher powers may be neglected, find the value of :
$$ \sqrt{4-x} \cdot \left( 3 - \dfrac {x}{2} \right)^{-1} $$
If $$x$$ be so small that its square and higher powers may be neglected, find the value of :
$$ (1-7x)^{\frac{1}{3}} (1+2x)^{-\frac{3}{4}} $$
In a class test $$(+3)$$ marks are given for every correct answer and $$(-2)$$ marks are given for every incorrect answer and no marks for not attempting any question. (i) Radhika scored $$20$$ marks. If she has got $$12$$ correct answers, how many questions has she attempted incorrectly? (ii) Mohini scores $$(-5)$$ marks in this test, though she has got $$7$$ correct answers How many questions has she attempted incorrectly.
How many two- digits positive integers N have the property that the sum of N and the number obtained by reversing the order of the digits of is a perfect square
Form a pair of linear equations in two variables for the following information.
"There are some $$50$$ paisa and $$25$$ paisa coins in a bag. The total number of coins are $$140$$ and the value of all coins is $$Rs. 50$$."
Ten students of class X took part in Mathematics quiz. If the number of girls is $$4$$ more than the number of boys. Represent this situation algebraically.
Find all numbers x such that
$$\left | x \, + \, 1 \right | \, - \,|x|\, + \, 3|x \, - \, 1||x \, - \, 2| \, = \, x \, + \, 2$$
solve: $$
\dfrac{{5x + 4}}
{4} - \dfrac{{3x - 2}}
{2} = 5
$$
Solve the following linear equation :
$$\dfrac{x}{2} + 7x - 6 = 7x + {1 \over 4}$$
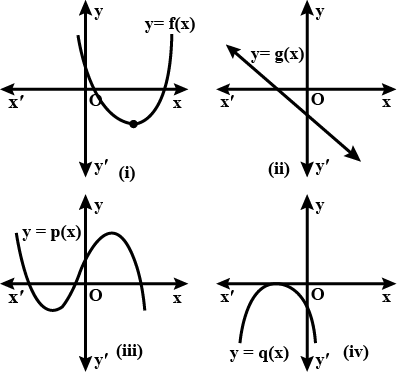
If each one of the following graphs are the graph of a polynomial, then identify which one corresponds to a linear polynomial and which one corresponds to a quadratic polynomial?
A bag contains $$25$$ paise and $$50$$ paise coins whose total value is $$Rs.\ 30$$. If the number of $$25\ paise$$ coins is four times that of $$50\ paise$$ coins, find the number of each type of coins.
Solve the following linear equation :
$$2x - \dfrac{1 }{3} = \dfrac{1 }{5} - x$$
Solve for x: $$\cfrac{p+q-x}{r} +\cfrac{q+r-x}{p} + \cfrac{r+p-x}{q} +\cfrac{4x}{p+q+r}$$ =1
Aftab tells his daughter, "Seven years ago, I was seven times as old as you were then. Also, Three years from now, I shall be there times as old as you will be." Represent this situation algebraically.
The cost of a notebook is twice the cost of a pen. Write a linear equation in two variable to represent this statement.
( Take the cost of a notebook to be $$Rs.x$$ and that of a pen to be $$Rs. y$$ ).
The sum of a two digit number and the number obtained by reversing the digits is $$66$$. If the digit of the number differ by $$2$$, find the number. How many such numbers are there?
Solve $$\dfrac{{x - b - c}}{a} + \dfrac{{x - c - a}}{b} + \dfrac{{x - a - b}}{c} = 3$$
$${\dfrac{3t - 2} 4} - {\dfrac{2t + 3} 3} = {\dfrac2 3} - t$$
Reducing equation to simple from :-$$\dfrac{6x+1}{3}=\dfrac{x-3}{6}$$
Find the value of $$y$$:
$$15(y-4) - 2(y-9) + 5(y+6)=0$$
Represent the solution of each of the following inequalities on the real number line:
$$4x - 1 > x + 11$$
If $$\dfrac{1}{5} - x = -\dfrac{4}{5}$$, then $$x$$ is ...............
A ball falls from a height of 100 mts. on a floor. If in each rebound, it describe (4/5)th height of the previous falling height, then the total distance travelled by the ball before it come to rest is
At a certain time in a deer park, the number of heads and the number of legs of deers and human visitors were counted and it was found there were $$39$$ heads & $$132$$ legs. If the number of deers and human visitors in the park are $$'d'$$ and $$ 'h'$$ respectively, Then find $$\left|\dfrac{d-h}{3}\right|$$.
Solve following equation:
$$x^2 - x + 2 = 0$$
Raju's salary was first increased by $$10$$%, then decreased by $$20$$%. If the latest salary is Rs.$$17600$$, then find his original salary.
what is linear equation?with example.
Solve the equation:
$$\dfrac{{\sqrt {4x + 1} + \sqrt {x + 3} }}{{\sqrt {4x + 1} - \sqrt {x + 3} }} = \dfrac{4}{1}$$
If $$4a - 3 = 13,$$ then find the value of $$10{a^2} - 5a + 6.$$
Solve the given equation $$\dfrac{9x+7}{2}-\left(x-\dfrac{x-2}{7}\right)=36$$
if $$p(x)=2x+3$$, then find $$P(1),P(3),P(-3)$$ and $$P(-1)$$
$$\dfrac{8x-3}{3x}=2$$.
The sum of the ages of Anup and his father isWhen he will be as old as his father now, he will be five times as old as his son Anuj is now. Also, Anuj will be eight years older than Anup is now at that time. What are their ages right now?
If $$\dfrac{\sqrt{11}-\sqrt{7}}{\sqrt{11}+\sqrt{7}}=x-y\sqrt{77}$$, find the values of $$x$$ and $$y$$ ?
Solve $$x+\dfrac{x}{2}+\dfrac{x}{3} <11$$
Simplify $$3x(4x-5)+3$$ and find its value for $$x=3$$.
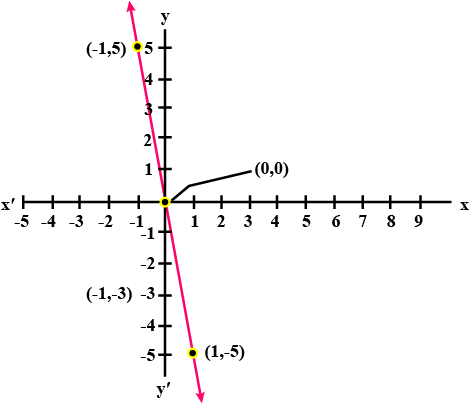
Give the geometrical representation of $$2x+5=0$$ as an equation in two variables.
Find the coefficient of the term independent of x in $$\left(x-\dfrac{1}{x^2}\right)^{3n}$$.
$$x = \dfrac{a^n - a^{-n}}{a^n + a^{-n}}$$ then n =
Pooja and Ritu can do a piece of work in $$17\cfrac { 1 }{ 7 } $$ days. If one day work of Pooja be three fourth of one day work of Ritu; find in how many days each will do the work alone.
People of sundargram planted tree in the village garden. Some of the trees were fruit trees. The number of non-fruit trees were two more than three times the number of fruits trees. What was the number of fruit trees planted if the number of non-fruit trees planted was $$77$$ ?
Twice of the numerator of a fraction is $$1$$ more than the denominator. If $$5$$ is added to both numerator and denominator, the fraction is $$\dfrac{7}{60}$$ more than the original one. Find the original fraction.
Give the geometrical representation of $$2x+5=0$$ as an equation in one variable.
Give the equations of two lines passing through $$(2, 14)$$. How many more such lines are there, and why?
A lending library has a fixed per day charge for the first three days and an additional charge for each day thereafter. Arushi paid Rs. 27 for a book kept for seven days. The fixed charges are Rs. x per day and additional charges are Rs. y per day. Write the linear equation representing the above information.
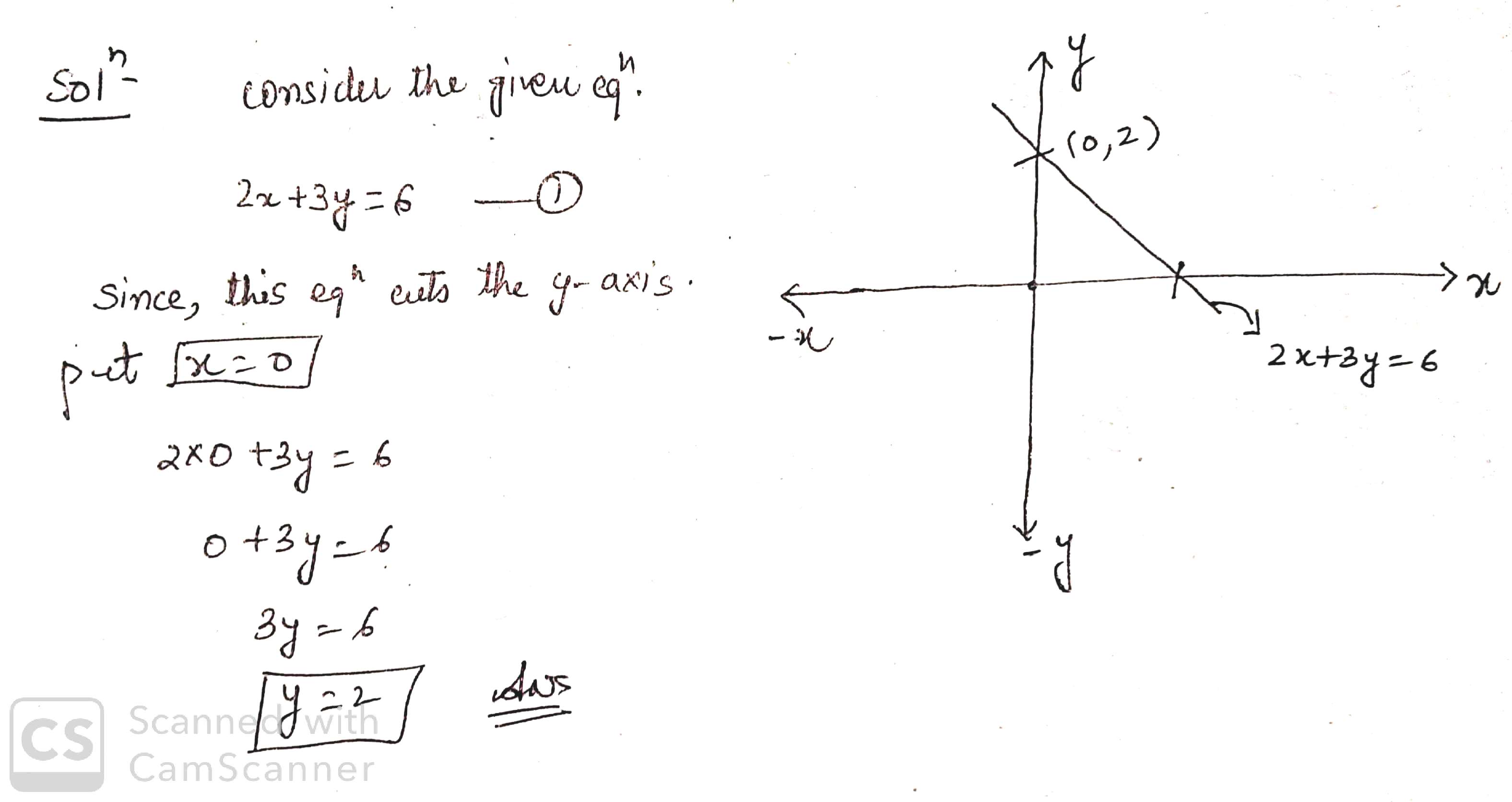
Find the point where the graph of the linear equation $$2x + 3y = 6$$ cuts the y-axis.
Find $$x$$
$$2x+3 = 3x+5$$
Add: $$3mn, - 5mn,8mn, - 4mn$$
$$\dfrac{1}{2} $$ of a boat is under water. When $$\dfrac{1}{5}$$ of it is pulled out, 2 ft is still under water. What is the height of the boat?
Simplify the equation: $$\dfrac { 1 } { a + b + x } = \dfrac { 1 } { a } + \dfrac { 1 } { b } + \dfrac { 1 } { x } ; a + b \neq 0$$
Solve for $$x$$ and $$y.$$
$$\begin{array}{l}\dfrac{x}{b} + \dfrac{y}{a} = 2 , \, ax - by = {a^2} - {b^2}\end{array}$$
$$\begin{array}{l}\dfrac{x}{b} + \dfrac{y}{a} = 2 , \, ax - by = {a^2} - {b^2}\end{array}$$
Find the equations of the two lines through the origin which
intersect the line $$\dfrac{{x - 3}}{2} = \dfrac{{y - 3}}{1} = \dfrac{z}{1}$$at angle of $$\dfrac{\pi }{3}$$each.
If $$51x+49y=150$$ and $$49x+51y=50$$ then obtain the value of $$x-y:x+y$$
Solve to find $$x$$:
$$\displaystyle {{3x} \over 5} - 4 = 8$$
'When $$5$$ is subtracted from the length and breadth of the rectangle, the perimeter becomes $$26$$.' What is the mathematical form of the statement
Solve for x: $$x-12=9$$
Solve the equation $$2x + 6 < 12$$
Solve:$$5 = 6 + 11x$$
Simplify$$\dfrac { 25 }{ 4 } { x }^{ 2 }-\dfrac { { y }^{ 2 } }{ 9 } $$
The ratio of girls and boys are in a class is $$1:3$$.Set up an equation between the students of class and boys .
Solve it :-
$$\frac{7}{{x - 5}} = \frac{5}{{x - 7}}$$
Solve:$$0.16\left( {5x - 2} \right) = 0.4x + 7$$
Solve the following simultaneously equation using elimination method
$$4m+6n=54; 3m+2n=28$$
A number consist of two digits, the difference of whose digits is $$5$$. If $$8$$ times the number is equal to $$3$$ times the number obtained by reversing the digits, Find the number.
Solve
$$5x-4y=12,for(y)$$
Find values of a,b and c:$$a-b+2c=0$$
$$a+2b-c=0$$
Solve for $$\displaystyle x , 2 \left( \frac { 2 x + 3 } { x - 3 } \right) - 25 \left( \frac { x - 3 } { 2 x + 3 } \right) = 5$$
What must be subtracted from $$\frac{{ - 2}}{3}{x^2} + \frac{3}{2}xy + 2{y^2}$$ to get $$3{x^2} - 2xy - \frac{7}{2}{y^2}$$
If $${ x }^{ 2 }-ax+b=0$$ and $${ x }^{ 2 }-bx+a=0$$, then find $$a+b$$.
If $$12x+13y=29$$ and $$13x+12y=21$$ find $$x+y$$
The sum of two numbers is $$4000$$. If $$15\%$$ of one is equal to $$25\%$$ of the other, find the numbers.
The linear equations that converts Fahenheit $$(^{o}F)$$ to Celsius $$(^{o}C)$$ is given by the relation:
$$^{o}C=\dfrac {5^{o}F-160}{9}$$
What is the numerical value of the temperature is same in both the scale?
Solve $$\cfrac { 1 }{ x } -\cfrac { 4 }{ y } =2,\cfrac { 1 }{ x } -\cfrac { 3 }{ y } =9$$ by reducing it into the pair of linear equations
Draw the graph of the equation $$y=3x$$
If the number obtained by interchanging the digits of a two digit number is 18 more than the original number and the sum of the digits is 8 then what is the original number?
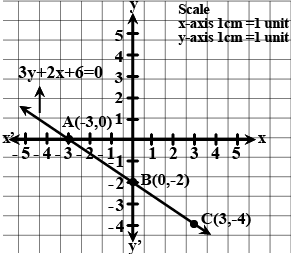
Draw the graph of the equation $$2x+3y+6=0$$
Solve and verify the result :
$$3x-5=13$$
Give the geometric representation of $$y=3$$ as an equation in two variables.
The sum of the digits of a two digit number is $$13$$. The number obtained by interchanging the digits of the given number exceeds the number by $$27$$. Find the number.
For what value of $$y,10 y=50$$ satisfy the equation.
State which of the following are equations (with a variable). Give reasons for your answer. Identify the variable from the equations with a variable.
$$17=x+7$$
Construct a word problem on simultaneous linear equation in two variables so that the value of one of the variables will be $$10$$ ( person, rupees, metres, years etc) and solve it.
Find the product:$$\left(2x-\dfrac{3}{y}\right)\left(2x+\dfrac{3}{y}\right)$$
Solve $$\cfrac { 4m+2 }{ 6m+10 } =\cfrac { 1 }{ 2 } $$.
Solve:$$2y+9\ge 4$$
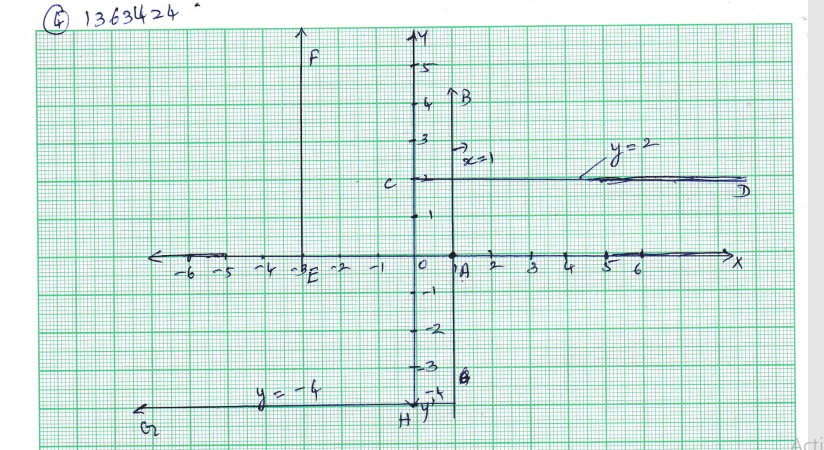
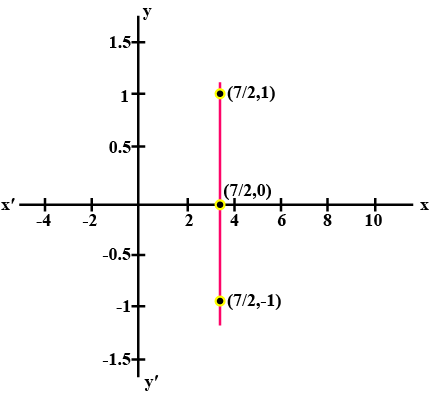
Draw the graph of the equation $$x=1,\,y=2,\,x+3=0,\,y+4=0$$$$x=1$$ is the line $$AB$$ parallel to $$y-$$axis at a distance of $$1$$ units to the right of the origin $$O$$
Find the equation of the straight line which is parallel to $$2x-9y=11$$ and makes $$x-$$intercept $$4$$ units.
Solve: $$15(y-4) -2(y-9)+5(y+6)=0$$
$$2$$ tables and $$3$$ chairs cost Rs.$$2000$$.Where as $$3$$ tables and $$2$$ chairs cost Rs.$$2500$$.Find the total cost of $$1$$ table and $$5$$ chairs.
Solve:
$$\dfrac{6}{x}-\dfrac{3}{x}=1; x\neq 0$$
Solve:$$-3\le\,4-\dfrac{7x}{2}\le\,2$$
Find the equation of the straight line which is parallel to $$x-5y=9$$ and makes $$x-$$intercept $$4$$ units.
Let $$x+y=5$$ and $$x-y=3$$ then find the value of $$\dfrac{x}{2}.\dfrac{y}{2}$$
$$x+y=17\\2x-y=-2$$
Draw the graph of each of the following linear equations in two variables:
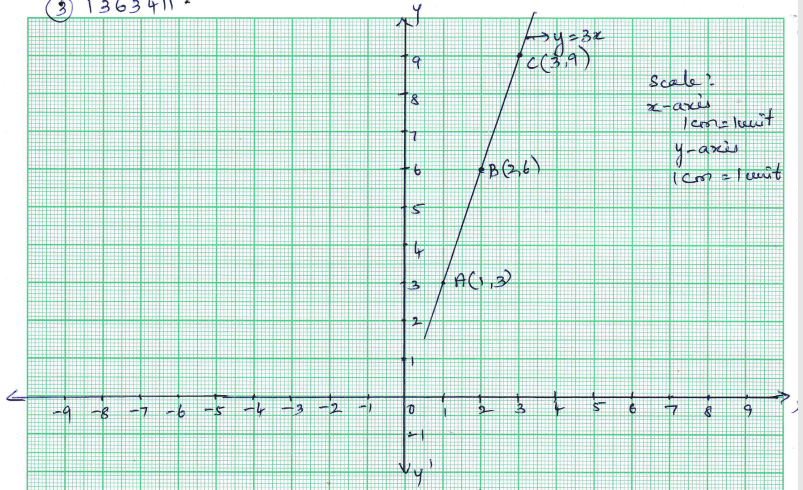
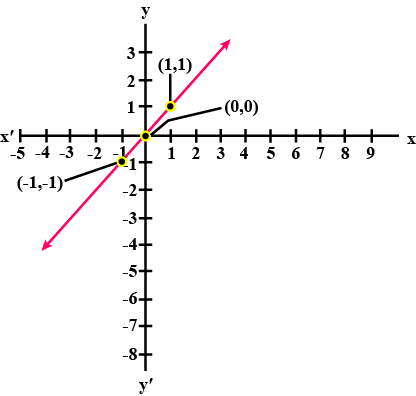
$$y=3x$$
Find the value of $$\dfrac{a-2}{3}+\dfrac{a-1}{2}+\dfrac{a+5}{6}=1$$
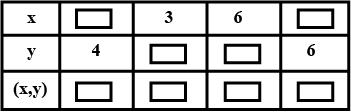
Points are to be recognised on X-Y plane to draw graph of equation $$2x + 3y = 12$$. So fill the boxes given below and identify points.
Draw the graph of each of the following linear equations in two variables:
$$x-y=2$$
Solve:$$8x+5>12$$
Sudhir's present age is $$5$$ more than three times of age of Viru. Amit's age is half the age of Sudhir. If the ratio o the sum of Sudhir's and Viru's age to three times Amit's age is $$5:6$$, then find Viru's age.
The sum of a two consecutive numbers isthen find the numbers
What must be added to $$2x-4x+9$$ to get $$5x-13$$
If there are 50 Mangoes in a box, how will you write the total number of mangoes in terms of the number of boxes? ( Use b for the number of boxes).
Find the equation of the perpendicular bisector of the line joining $$\left(-5,-6\right)$$ and $$\left(2,-2\right)$$
Prove $$4$$ is the root of $$2x-3-5=0$$.
Check whether the following is solution of the equation $$x-2y=4$$ or not: $$\left(1, 1\right)$$
Check whether the point $$\left(4, 0\right)$$ satisfies the equation $$x-2y=4$$ or not.
One third of a number added to itself gives $$8$$. Find the number.
Solve for X :
$$\dfrac 1{2x+5}=\dfrac 43$$
The value of $$x$$ if $$\dfrac 12x+\dfrac 14x=\dfrac 16$$
$$\dfrac{2}{3}rd$$ of a number is $$20$$ less than original number. Find the original number.
One pen costs $$Rs\ 15$$ and one pencil costs $$Rs\ 3$$. What is the total cost of $$x$$ pens and $$y$$ pencils
A rabbit covers a distance of $$10$$ metres, in which it covers $$y$$ metres distance by walking in slow motion and the remaining by $$x$$ jumps, each jump contains $$2$$ metres. Express this information in linear equation.
Solve:$$3x - 2 = 19$$
Find $$x$$: $$\dfrac { 7x+ 5 }{ 5 } =7x$$
Solve:$$3t + 25.8 = -4.2$$
Find $$m$$ in $$\dfrac{{5m}}{2} - 4=0.$$
Verify by substitution that the root of $$3x - 5 = 7 $$ is $$x = 4 $$.
Show that $$3$$ is the root of $$2(x+4)=14$$.
$$\text{Solve : }$$$$5 y = 15$$
If the point $$(2, -2)$$ lies on the graph of the linear equation $$5x + ky = 4$$, find the value of $$k$$.
Natasha thinks of number and subtracts $$\dfrac{2}{3}$$ from it and multiplies the result by $$9$$. The product now obtained is $$7$$ times the numbers she thought of. What is the number?
Draw the graph of each of equations given below. Also, find the coordinates of the points where the graph cuts the coordinate axes:
$$6x - 3y = 12$$.
Draw the graph of each of the following linear equations in two variables:
$$2y = -x + 1$$.
Solve for $$x$$: $$7x-3=0$$
Classify the following polynomials as polynomials in one-variable, two variables etc.:
$$x^{2} - 2tx + 7t^{2} - x + t$$.
Verify by substitution that the root of $$3 + 2x = 9$$ is $$x = 3$$.
Draw the graph of each of the following linear equations in two variables:
$$y = 2x$$.
Verity by substitution that the root of $$8 - 7y = 1$$ is $$y = 1$$.
Draw the graph of each of equations given below. Also, find the coordinates of the points where the graph cuts the coordinate axes:
$$3x + 2y + 6 = 0$$.
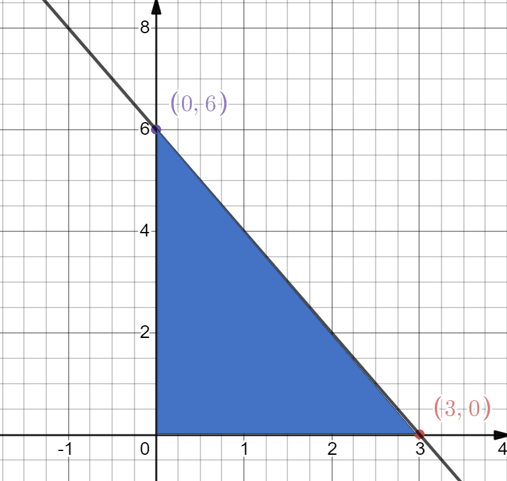
Draw the graph of the equation $$2x + y = 6$$. Shade the region bounded by the graph and the coordinate axes. Also, find the area of the shaded region.
Draw the graph of each of equations given below. Also, find the coordinates of the points where the graph cuts the coordinate axes:
$$-x + 4y = 8$$.
Solve the equation $$2y - 1 = y + 1$$ and represent it graphically on the coordinate plane.
Draw the graph of $$y = |x| + 2$$.
If the point $$(a, 2)$$ lies on the graph of the linear equation $$2x - 3y + 8 = 0$$, find the value of $$a$$.
Find the value of $$k$$ for which the point $$(1, -2)$$ lies on the graph of the linear equation $$x - 2y + k = 0$$.
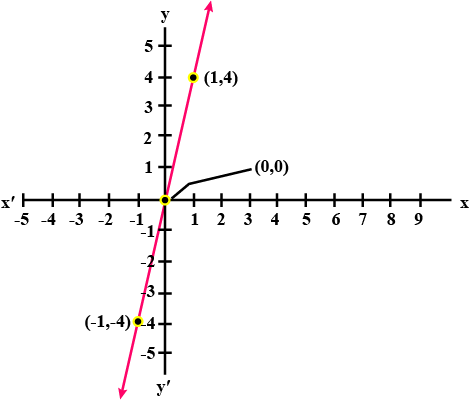
Give the geometrical representation of $$2x + 13 = 0$$ as an equation in two variables.
Solve the equation $$3x - 2 = 2x + 3$$ and represent the solution on the number line.
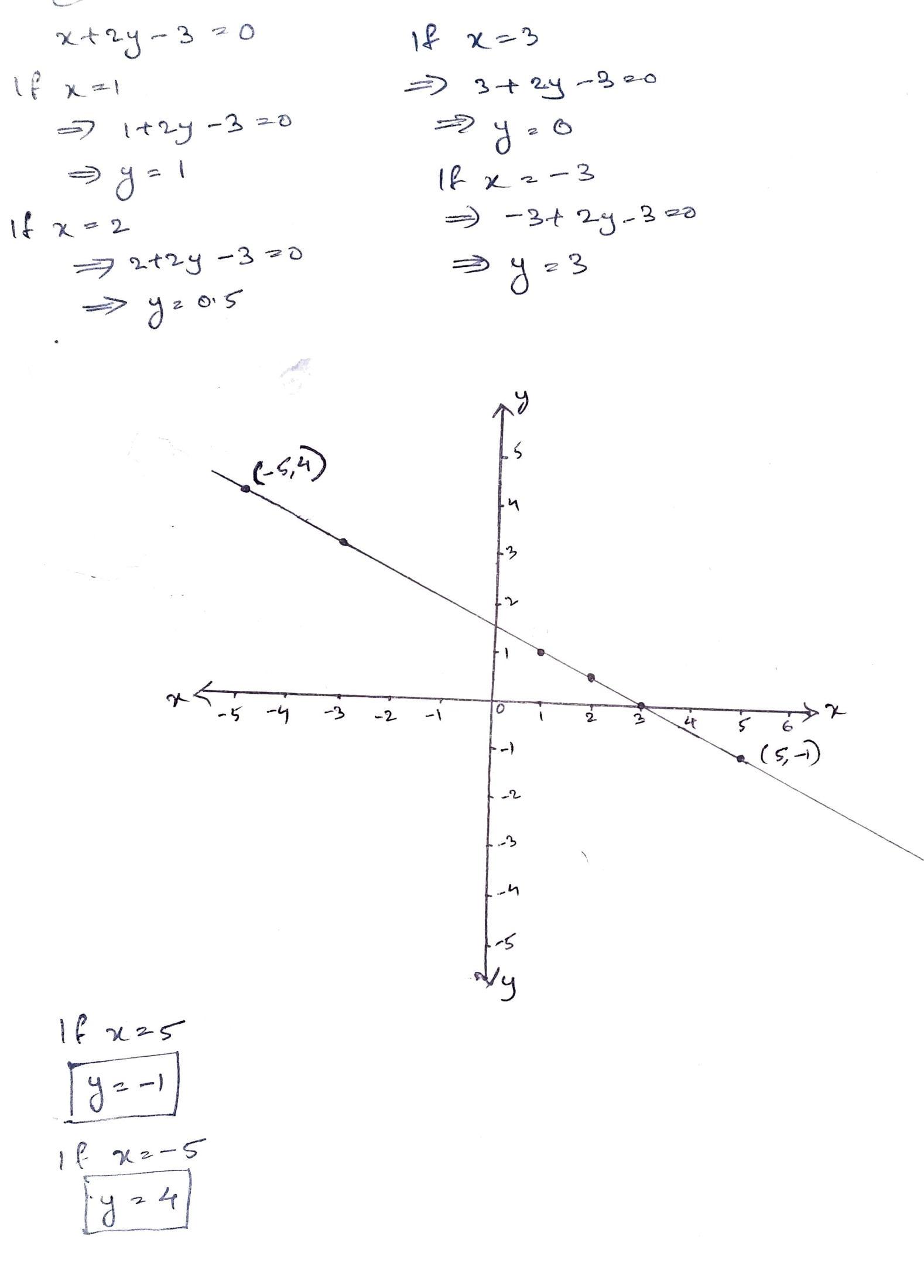
Draw the graph of the equation $$x+2y-3=0$$
From your graph,find the value of $$y$$ when
(i) $$x = 5$$
(ii) $$x = -5$$
State which of the following are equations with a variable. In case of an equation with a variable, identity the variable.
$$5\times 4-8=31$$
Draw the graph of the equation, $$2x + y = 6$$
Find the coordinates of the graph cut the x-axis.
State which of the following are equations with a variable. In case of an equation with a variable, identity the variable.
$$(y-7)> 5$$
State which of the following are equations with a variable. In case of an equation with a variable, identity the variable.
$$7\times 3x-19=2$$
Draw the graph of the equation $$y = 3x$$
From your graph, find the value of y when
$$(i)x=2$$
$$ (ii) x =-2$$
Draw the graph of the equation, $$3x+2y = 6$$
Find the coordinates of the point where the graph cuts the y-axis
Draw the graph of the equation, $$2x - 3y = 5$$
From your graph find
(i) The value of y when $$x = 4$$
(ii) The value of x when $$y = 3$$
State which of the following are equations with a variable. In case of an equation with a variable, identity the variable.
$$7=11\times 5-12\times 4$$
Draw the graphs of linear equations $$y = x$$ and $$y = -x$$ on the same Cartesian plane. What do you observe?
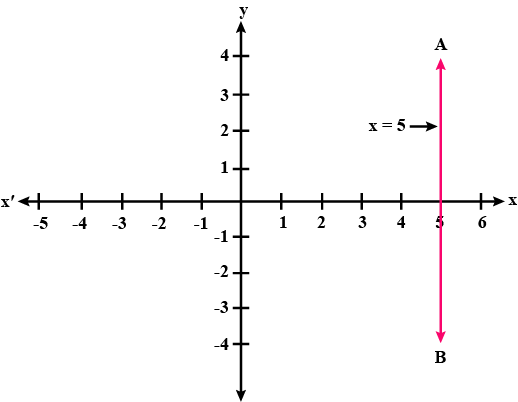
The line represented by $$ x= 7 $$ parallel to $$ x-axis $$ . justify whether the statement is true or not.
Find the solution of the linear equation $$x+2y =8$$ which represents a point on
(i) x-axis (ii) y-axis
If the point (3,4) lies on the graph of $$3y = ax + 7,$$ then find the value of a.
There are Some students in two examination halls $$ A $$ and $$ B $$ . To make the number of students equal in each hall $$ 10$$ students are sent from $$ A$$ to $$ B $$. But if $$ 20 $$ students are sent from $$ B $$ to $$ A$$ , the number of students in $$ A $$ becomes double the number of students in $$ B $$ find the numbers of students in the two halls.
Draw the graph of the linear equation whose solutions are represented by the points having the sum of coordinates as $$10$$ units.
Draw the graph for the linear equation given below: $$y = -2x$$.
Draw the graph for the linear equation given below: $$y = -x$$.
Draw the graph for the linear equation given below: $$5x + y = 0$$.
Draw the graph for each linear equation given below: $$4x - y = 0$$.
Draw the graph for each linear equation given below:
$$2x - 7 = 0$$.
Draw the graph for each linear equation given below: $$y = 0$$.
Draw the graph for the linear equation given below: $$x + 2y = 0$$.
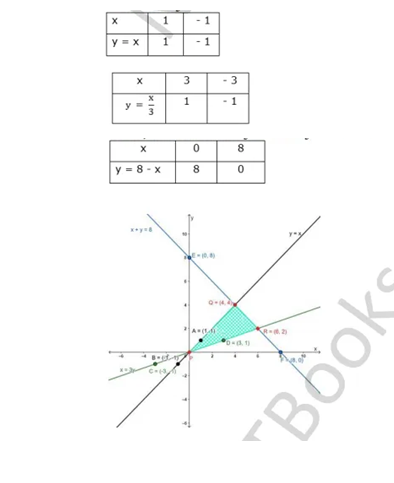
Use a single graph paper and draw the graph of the following equations. Obtain the vertices of the triangle so formed: $$y = x; 3y = x$$ and $$x + y = 8$$
Draw the graph for each linear equation given below: $$y = 3x$$.
Draw the graph for the linear equation given below: $$y = x$$.
Draw the graph for the linear equation given below: $$x = -2y$$.
Draw the graph for the each linear equation given below: $$y = \dfrac {2x}{3} - 1$$.
Draw the graph for the each linear equation given below: $$y = -x + 4$$.
Draw the graph for the linear equation given below: $$y = 4x - \dfrac {5}{2}$$.
Draw the graph for the linear equation given below: $$3x + 2y = 0$$.
Draw the graph for the linear equation given below: $$2x - 3y = 4$$.
Draw the graph for the each linear equation given below: $$y = 2x + 3$$.
Draw the graph for the each linear equation given below: $$y = \dfrac {3x}{2} + \dfrac {2}{3}$$.
Draw the graph for the linear equation given below: $$\dfrac {x - 1}{3} - \dfrac {y + 2}{2} = 0$$.
Draw the graph for the linear equation given below: $$x - 3 = \dfrac {2}{5} (y + 1)$$.
Draw the graph of equation $$x + 2y - 3 = 0$$. From the graph, find:
(i) $$x_{1}$$, the value of $$x$$, when $$y = 3$$
(ii) $$x_{2}$$, the value of $$x$$, when $$y = -2$$.
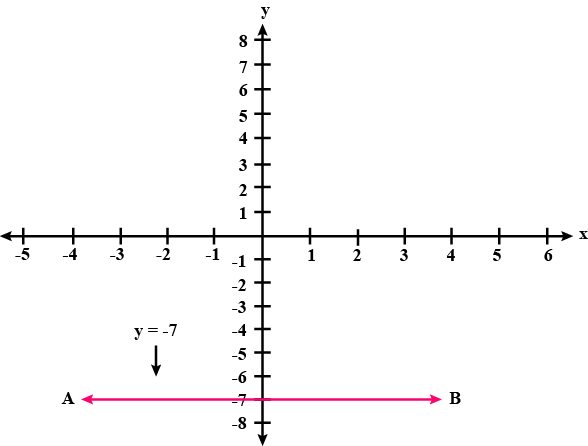
Draw the graph for each equation, given below: $$y + 7 = 0$$.
Draw the graph for each equation, given below: $$x + 5 = 0$$.
Draw the graph for each equation, given below: $$y = 7$$.
Draw the graph for the equation given below:
$$2x - 5y = 10$$
Also, find the co-ordinates of the points where the graph (line) drawn meets the co-ordinates axes.
Draw the graph of the equation $$3x - 4y = 12$$.
Use the graph drawn to find:
(i) $$y_{1}$$, the value of $$y$$, when $$x = 4$$.
(ii) $$y_{2}$$, the value of $$y$$, when $$x = 0$$.
Draw the graph for the equation given below:
$$3x + 2y = 6$$
Also, find the co-ordinates of the points where the graph (line) drawn meets the co-ordinates axes.
Draw the graph for the linear equation given below: $$x + 5y + 2 = 0$$.
Draw the graph for each equation, given below: $$3x + 2y = 6$$.
Draw the graph for each equation, given below: $$x = 5$$.
Draw the graph of the equation $$2x - 3y - 5 = 0$$
(i) $$x_{1}$$, the value of $$x$$, when $$y = 7$$
(ii) $$x_{2}$$, the value of $$x$$, when $$y = -5$$.
Draw the graph of the equation $$4x + 3y + 6 = 0$$
From the graph, find:
(i) $$y_{1}$$, the value of $$y$$, when $$x = 12$$
(ii) $$y_{2}$$, the value of $$y$$, when $$x = -6$$.
Draw the graph for each equation, given below: $$x - 5y + 4 = 0$$.
Draw the graph of the equation given below
$$ x + y = 2 $$
Draw the graph of the equation given below
$$ 2x + y = 1 $$
Complete the following table to draw the graph of $$2x - 6y = 3$$
| $$\textbf{x} $$ | -5 | x |
| $$\textbf{y}$$ | x | 0 |
| $$\textbf{(x,y)}$$ | (-5,x) | (x,0) |
Draw the graph (straight line) given by equation $$x - 3y = 18$$. If the straight line drawn passes through the points $$(m, -5)$$ and $$(6, n)$$; find the values of $$m$$ and $$n$$.
Draw the graph of the equation given below
$$ 3x - y = 0 $$
Draw the graphs of the following straight lines.
$$4y=-x+3$$
Draw the graphs of the following straight lines.
$$3y=1$$
Draw the graphs of the following straight lines.
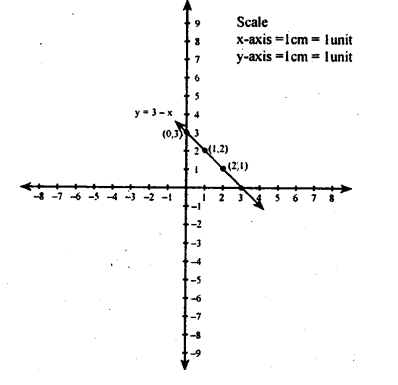
$$y=3-x$$
Draw the graphs of the following straight lines.
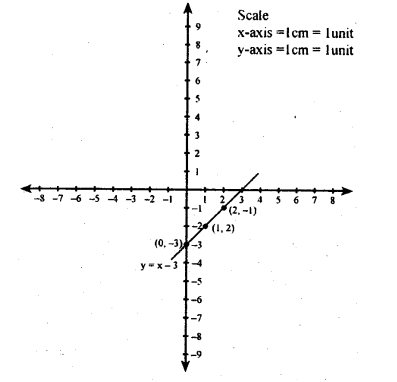
$$y=x-3$$
Draw the graphs of the following straight lines.
$$3y=4x+1$$
Draw the graphs of the following straight lines.
$$y=3x-2$$
Give the geometric representations of $$2x + 9 = 0$$ as an equation.
(ii) in two variable
Draw the graph of each of the following linear equations in two variables:
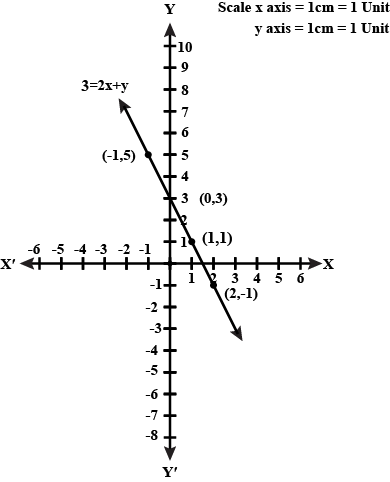
$$ 3 = 2x + y$$
Draw the graphs of the following straight lines.
$$y=5-3x$$
Draw the graphs of the following straight lines.
$$x=4$$
By taking the values of $$x = -2$$ to $$x = 2$$ and also included value of x for the equation $$y = 2x + 1.$$ Form the and draw the graph of the equation.
Construct $$3$$ equations starting with $$x=-2$$.
Two candidates A and B contest an election. A gets 46% of the valid votes and is defeated by 1600 votes. Find the total number of valid votes cast in the election ?
Express the following linear equations in the form ax + by + c = 0 and indicate the value of a, b and c in each case :
i) $$2x + 3y = 9.3 \bar{5}$$
ii) $$x - \dfrac{y}{5} - 10 = 0$$
iii) -2x + 3y = 6
What is the sum of $$2x-y$$ and $$3y -2x$$ ?
Express the following linear equation in the form $$ax+by+c=0$$ and indicate the values of $$a,b$$ and $$c$$ in each case :
$$2x+3y=9.35$$
Find the solution of given problem $$\dfrac{3}{4}(7x-1)-\left(2x-\dfrac{1-x}{2}\right)=x+\dfrac{3}{2}$$.
Solve the following equations.
$$\displaystyle\, 32^{\frac{x + 5}{x - 7}} = 0.25 \cdot 128^{\frac{x + 17}{x - 3}}$$
Express the following linear equation in the form $$ax+by+c=0$$ and indicate the values of $$a,b$$ and $$c$$ in each case :
$$5=2x$$
$$A$$ and $$B$$ can dig a trench in $$20$$ days. If $$B$$ is twice as good as $$A$$ in his work, in how many days can A alone complete the work?
If $$x + y = 3,\,\,\,3x - 2y - 4 = 0$$, then find coefficient determinant(D).
Solve:$$\dfrac{3}{x+y}+\dfrac{2}{x-y}=2$$; $$\dfrac{9}{x+y}-\dfrac{4}{x-y}=1$$
Solve : $$3 x = 27$$
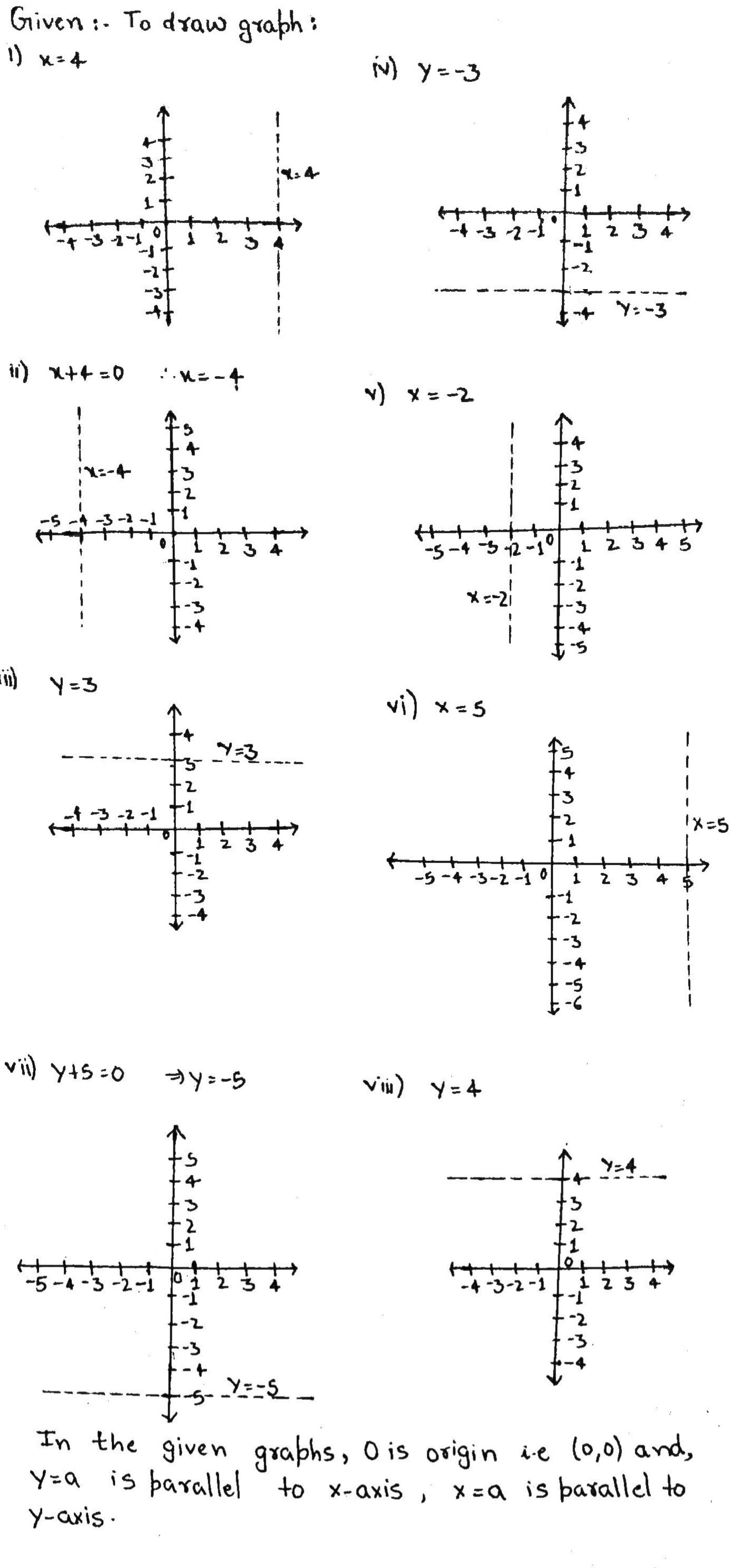
Draw the graph of each of the following equations.
(i) x = 4
(ii) x+4 = 0
(ii) y = 3
(iv) y = -3
(v) x =-2
(vi) x=5
(vii) y+5 = 0
(viii) y = 4
Solve : $$4 x - 30 = 0$$
Class 9 Maths Extra Questions
- Areas Of Parallelograms And Triangles Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Heron'S Formula Extra Questions
- Introduction To Euclid'S Geometry Extra Questions
- Linear Equations In Two Variable Extra Questions
- Lines And Angles Extra Questions
- Number Systems Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadrilaterals Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions