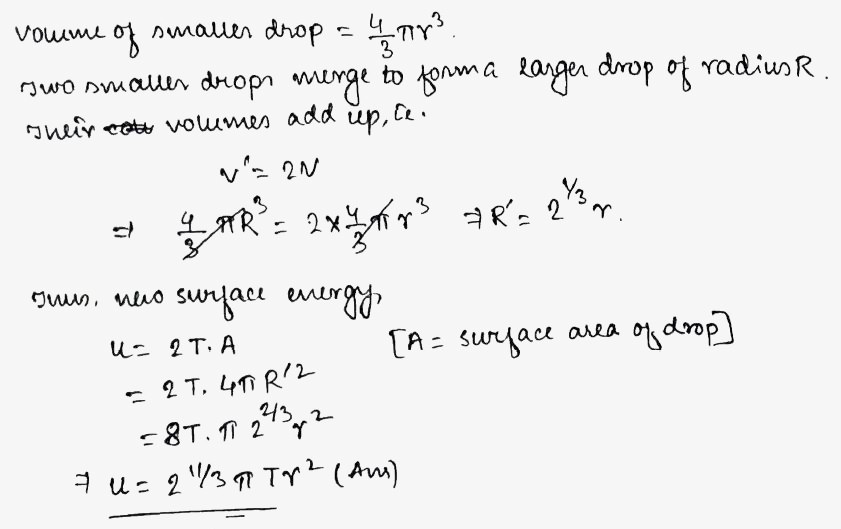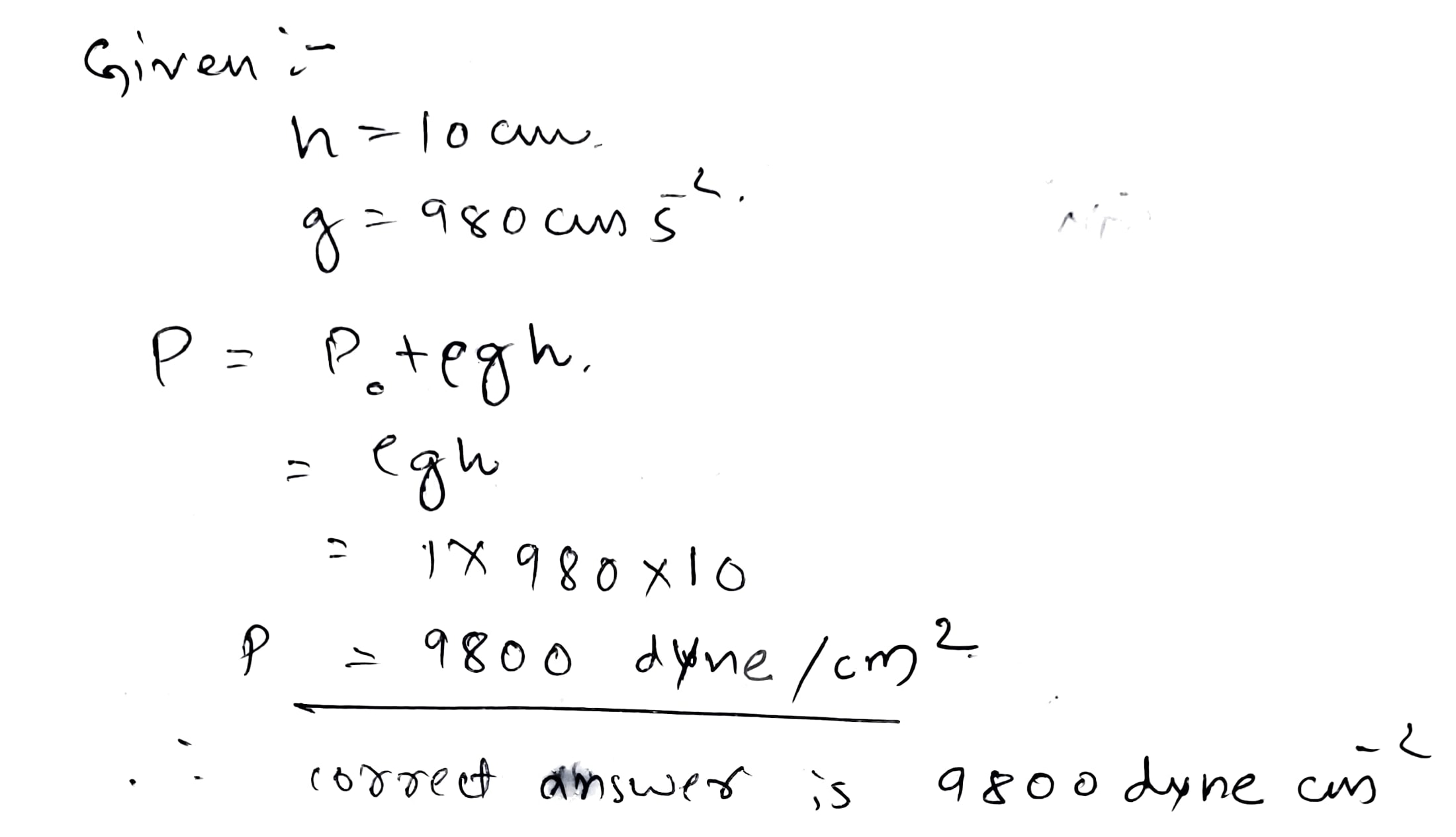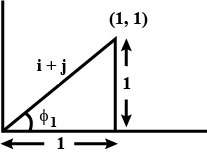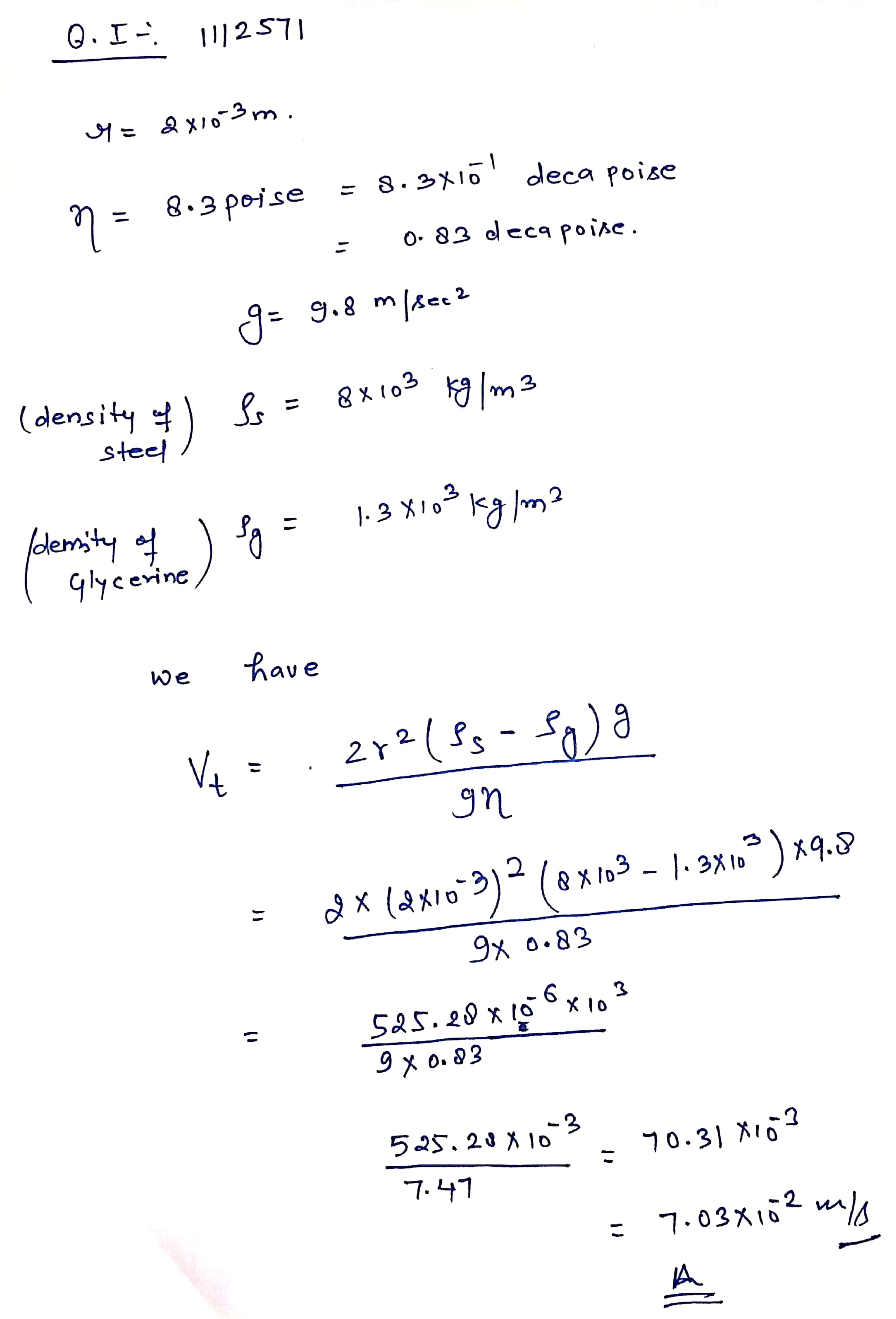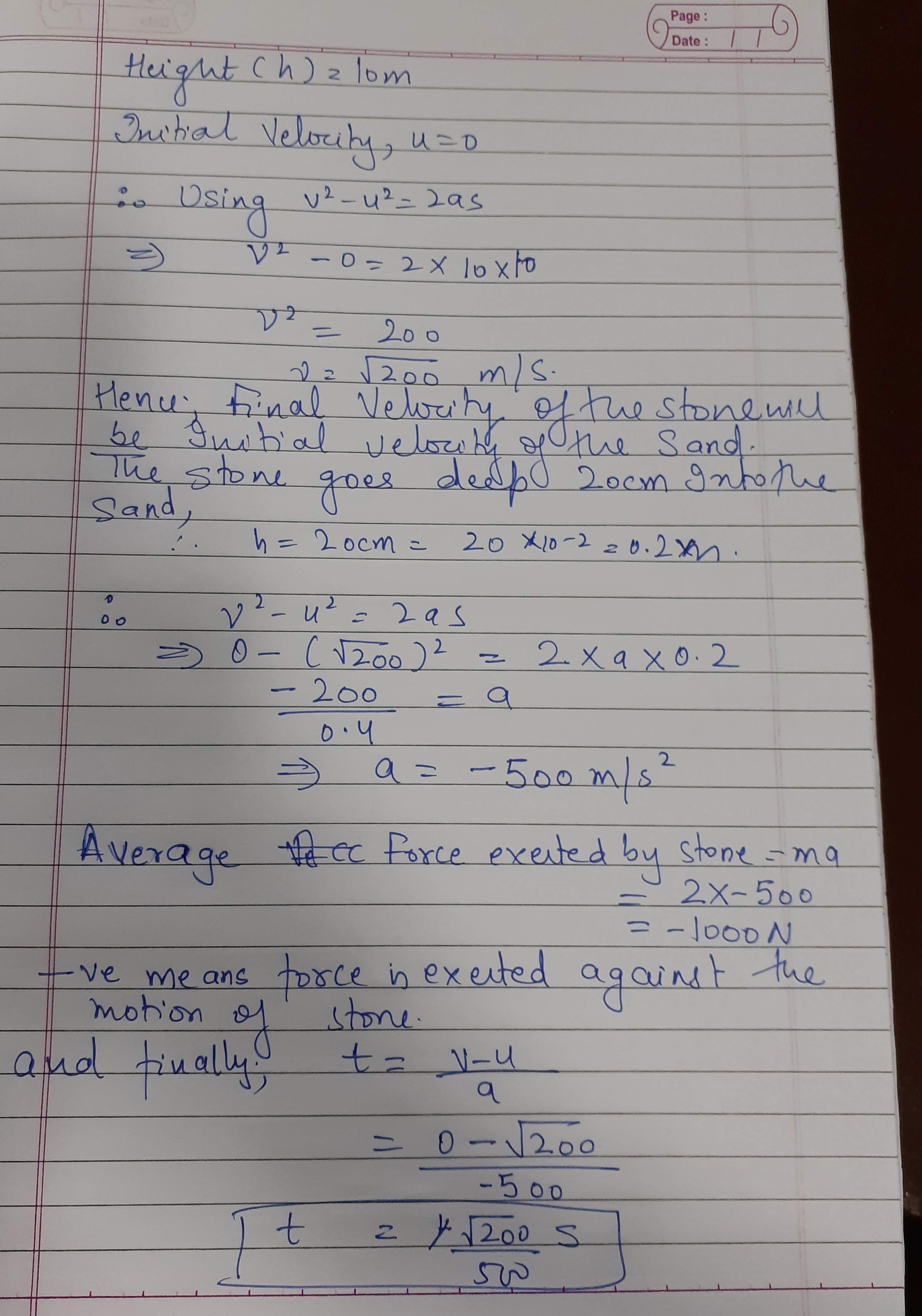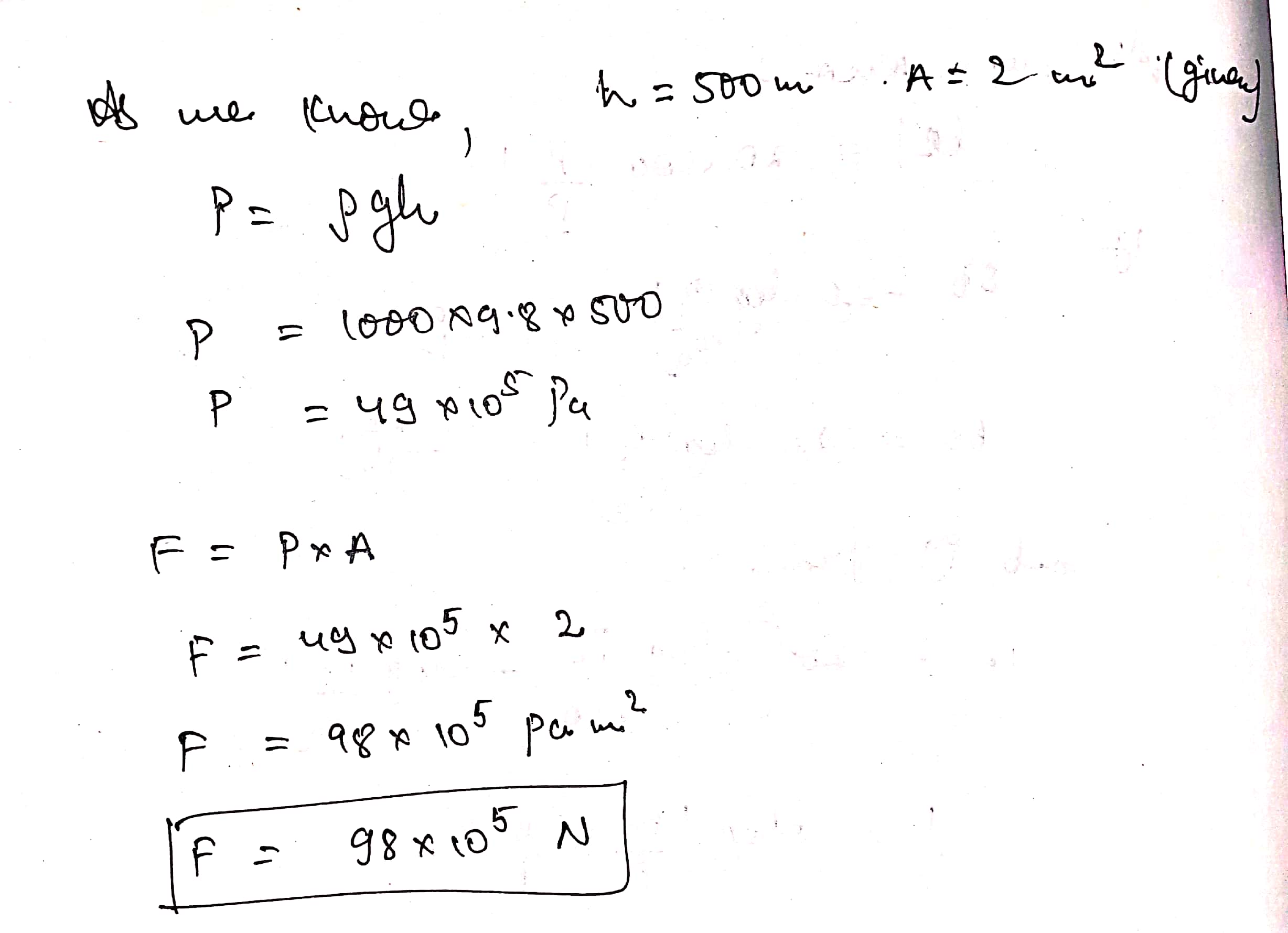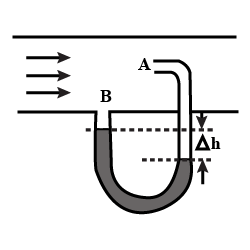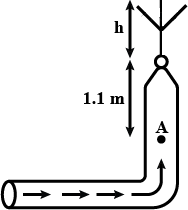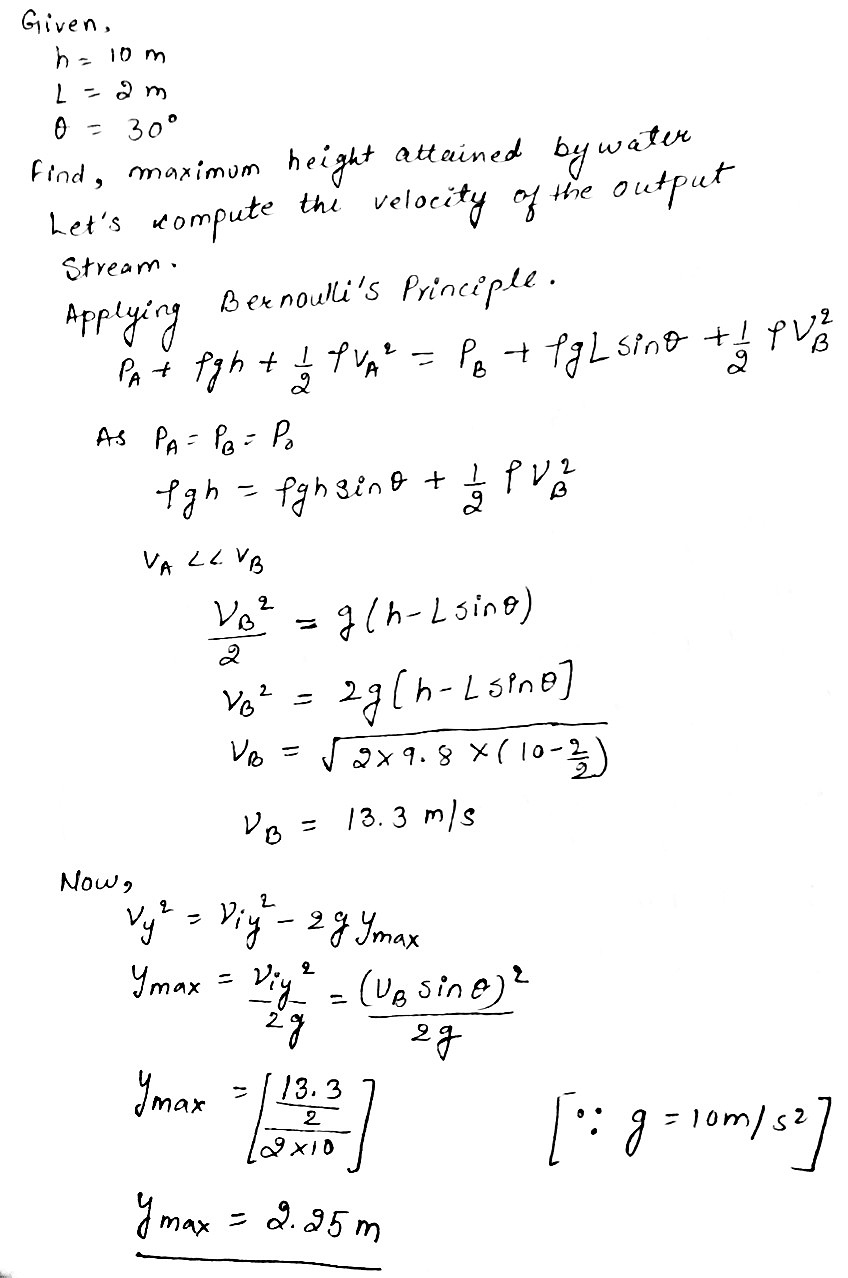Class 11 Engineering Physics - Mechanical Properties Of Fluids

List 2 shows five systems in which two objects are labelled as X and Y. Also in each case a point P is shown. List 1 gives some statements about X and/or Y. Match these statements to the appropriate system(s) from List 2.

1. constant velocity, thus net force=0,

${ F }_{ X }=Mg$

Since X is fixed, PE does not change.

Since Y loses PE (KE constant), ME reduces

Since weight does not pass through P,

$\tau\neq 0$ .

2.Force on Y by

$Z=mg$ downwards. Thus,

${ F }_{ X }=Mg$

Since going up,

${ PE }_{ X }$ increases, ME increases

Since weight through center,

$\tau = 0$

${ F }_{ X }=$ resultant of tensions (mg each) and

$mg\neq Mg$ . Going down, PE decreases, ME decreases.

Weight does not pass through P,

$\tau \neq 0$

4.a decreases, thus

${ F }_{ x }<Mg$

As Y decreases, X increases, so PE increases. Isolated system, thus ME=constant and

$\tau \neq 0$ .

5. a=0, thus

${ F }_{ x }=Mg$ .

As Y decreases, X increases, so PE increases. Due to viscous force, ME decreases,

$\tau \neq 0$

Answer is A

$\rightarrow$ (1,5) B

$\rightarrow$ (2,4,5) C

$\rightarrow$ (1,3,5) D

$\rightarrow$ (2).

The type of flow in which there is a regular gradient of velocity in going from one layer to the next is called laminar flow.
If true enter 1, for false enter 0.

Due to No-slip condition, velocity across the section is not uniform. Velocity gradient and hence, the shear stress gradient is established at right angles to the direction of flow.

ans : 1

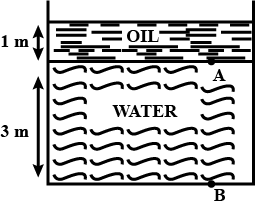
What force does water exert on the base of a house tank of base area $1.5 m^2$ when it is filled with water up to a height of 1 m?
[Density of water is $10^3 kg m^{-3}$ and $g=10 m s^{-2}]$

Given, base area of tank (A)

$=1.5 m^2$
Height of the tank

$=1m$
Density of water (D)

$=10^3 k gm^{-3}$
Force executed by water

$=pressure\times area$

$=h d g \times A$

$=1\times 10^3\times 10\times 1.5$

$=1.5\times 10^4N$

The press plungers of a Bramah (hydraulic) press is $40cm^2$ in cross-section and is used to lift a load of mass $800 kg$ . What minimum force is required to be applied to the pump plunger if its cross-sectional area is $0.02 m^2$ ?

According to pascal's law, pressure acting on press plunger

$=$ pressure acting on pump plunger.

$=\dfrac {800\times g}{40\times 10^{-4}m^2}$

$\Rightarrow \therefore F=\dfrac {800\times 9.8\times 0.02}{40\times 10^{-4}}$

$=39200 N$

At what depth below the surface of water total pressure would be equal to $1.5$ atmosphere?
$1\;atmosphere=10^5\;Nm^{-2}$ .

Total pressure at depth

$h$ below the water surface

$=atmospheric\;pressure+water\;pressure$ .
Let atmospheric pressure be

$P$ . Then, total pressure

$=1.5\;P$

$\therefore\;1.5\;P=P+hdg\Rightarrow hdg=0.5\;P$

$\Rightarrow h=\displaystyle\frac{0.5\,P}{dg}=\displaystyle\frac{0.5\times10^5\;Nm^{-2}}{(10^3\,kgm^{-2})\times9.8\;ms^{-2}}$

$=\displaystyle\frac{5\times10^5}{10^3\times98}m=\displaystyle\frac{500}{98}m=5.1\;m$

Why does a soft convertible top on a car bulges when the car travels at high speeds.

The air moving over the top causes an area of low pressure, and the higher pressure inside the car pushes the soft top up.

Sometimes you see a fountain of water rucshing out of the leaking joints (or holes) in the pipes of main water supply line in the city. Why does it happen?

It is due to the high pressure exerted by water on the sides (or walls) of the pipes.

Why do the tyres of a bicycle feel hard when air is filled in the tubes inside them.

When air is pumped into a bicycle tube, the tube gets inflated due to the air pressure exerted by the collisions of gas molecules in air with the inner walls of the rubber tube. This air pressure makes the tyres feel hard.

What makes a balloon get inflated when air is filled in it?

When air is filled in a balloon then the number of the molecules of air inside the balloon increases. As a result more collisions of molecules take place with the walls. This gives rise to high air pressure on the walls which causes the balloon to expand and get inflated.

What is the height of mercury which exerts the same pressure as $20\;cm$ of water column? Take density of mercury as $13.6\;g/cc$ .

Pressure exerted by mercury column

$(P_m)=h_1d_1g(say)$
Pressure exerted by water column

$(P_w)=h_2d_2g(say)$
Given,

$P_m=P_w\Rightarrow h_1d_1g=h_2d_2g\Rightarrow h_1=\displaystyle\frac{h_2d_2}{d_1}$

$\Rightarrow h_1=\displaystyle\frac{(20\times10^{-2})m\times10^3\;kg\,m^{-3}}{(13.6\times10^3)kg\,m^{-3}}$

$=1.48\times10^{-2}\,m=1.48\;cm$ .

The areas of the pistons in a hydraulic machine are $5{cm}^{2}$ and $625{cm}^{2}$ . What force on the smaller piston will support a load of $1250N$ on the larger piston?

${ F }_{ 1 }=1250N\quad \quad \quad \quad { A }_{ 1 }=625{ cm }^{ 2 }$

${ F }_{ 2 }=xn\quad \quad \quad \quad \quad { A }_{ 2 }=5{ cm }^{ 2 }$

Since pressure is constant.

$\dfrac { { F }_{ 1 } }{ { A }_{ 1 } } =\dfrac { { F }_{ 2 } }{ { A }_{ 2 } } \Rightarrow \dfrac { 1250 }{ 625 } =\dfrac { x }{ 5 } \Rightarrow \boxed { x=10N }$

In hydraulic machine, the two pistons are of area of cross section in the ratio $1:10$ . What force is needed on the narrow piston to overcome a force of $100N$ on the wider piston?

${ F }_{ 1 }=100N\quad \quad \quad { A }_{ 1 }=10{ m }^{ 2 }$

${ F }_{ 2 }=xN\quad \quad \quad { A }_{ 2 }=1{ m }^{ 2 }$

Since pressure = constant

hence,

$\dfrac { { F }_{ 1 } }{ { A }_{ 1 } } =\dfrac { { F }_{ 2 } }{ { A }_{ 2 } } \Rightarrow \dfrac { 100 }{ 10 } =\dfrac { x }{ 1 }$

$\boxed { x=10N }$

If mercury height in a glass tube is $50cm$ , find the pressure.

If mercury height in a glass tube is 50cm then it won't effect the atmospheric pressure & hence pressure will be 1 atm.

A hydraulic machine exerts a force of $900N$ on a piston of diameter $1.80cm$ . The output force is exerted on a piston of diameter $36cm$ . What will be the output force?

${ F }_{ 1 }=900N\quad \quad \quad \quad { F }_{ 2 }=xN$

${ r }_{ 1 }=0.9cm\quad \quad \quad \quad { r }_{ 2 }=18cm$

from Pascals law

${ P }_{ 1 }={ P }_{ 2 }$

$\dfrac { { F }_{ 1 } }{ { A }_{ 1 } } =\dfrac { { F }_{ 2 } }{ { A }_{ 2 } } \Rightarrow { F }_{ 2 }={ F }_{ 1 }\times \dfrac { { r }_{ 2 }^{ 2 } }{ { r }_{ 1 }^{ 2 } } =\dfrac { 90000\times 18\times 18 }{ 0.9\times 0.9 }$

$\boxed { { F }_{ 2 }=36\times { 10 }^{ 4 }N }$

The radii of the press plunger and the pump plunger are in the ratio $30:4$ . If an effort of $32kgf$ acts on the pump plunger. Find the maximum effort the press plunger can overcome. ( in kgf)

$\dfrac { { r }_{ 1 } }{ { r }_{ 2 } } =\dfrac { 30 }{ 4 } \quad \quad \quad \quad \& \quad { F }_{ 2 }=32kgf$

to find

${ F }_{ 1 }$

Since from pascals law

${ P }_{ 1 }={ P }_{ 2 }\Rightarrow \dfrac { { F }_{ 1 } }{ { A }_{ 1 } } =\dfrac { { F }_{ 2 } }{ { A }_{ 2 } } \Rightarrow { F }_{ 1 }={ F }_{ 2 }\times \dfrac { { A }_{ 1 } }{ { A }_{ 2 } } ={ F }_{ 2 }\times { \left( \dfrac { { r }_{ 1 } }{ { r }_{ 2 } } \right) }^{ 2 }$

${ F }_{ 1 }=32\times \dfrac { { 15 }^{ 2 } }{ 4 } =1800kgf$

The space above the mercury column in a barometer contains_____ (mercury, water) vapour.

The space above mercury collumn in a barometer is filled with mercury vapour & it compresses based on pressure at other end.

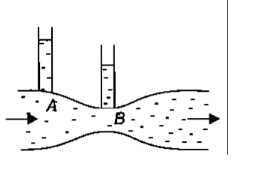
What is a Venturimeter? On what principle does the Venturimeter work?

Ventutimeter

$-$ device used to measure flow rate of a fluid through a pipe.

It is used on application of Bernoullis principle (equation).

Why do snow shoes stop you from sinking it into snow ?

1310668_1138740_ans_47e1857b4f784556a0fcaf6d386543a7.jpg

Two small drops each of radius r coalesce to form a larger drop. Find energy of the new drop. (surface tension is T)

Volume of smaller drop

$= \dfrac{4}{3}\pi r^{3}$

two smaller drops merge to forms larger drop of radius R.

their volumes add up, i.e.

${V}' = 2V$

$\Rightarrow \dfrac{4}{3}\pi R^{3} = 2 \times \dfrac{4}{3 }\pi r^{3} \Rightarrow {R}' = 2^{1/3}r.$

thus, new surface energy,

$u = 2T.A$ [A = Surface area of drop]

$= 2T.4\pi {R}'2$

$= 8T. \pi 2^{2/3}r^{2}$

$\Rightarrow u = 2^{11/3}\pi Tr^{2}$ (Ans)

1069070_1166560_ans_fae9b5936dc145f3bd4534178032eecb.png

The average mass that must be lifted by a hydraulic press is 80 kg. If the radius of the larger piston is five times that of the smaller piston, what is the minimum force that must be applied?

According to the question,

The mass to be lifted is

$80\,kg$

Since, the force needed to lift iit up is

$=80 \times 9.8$

$=784\,N$

Let the radius of the larger position is

$= {R_1}$

the radius of the smaller piston is

$= {R_2}$

We given that,

${R_1} = 5{R_2}$

The area of the larger piston is

$= {A_1} = \pi {R_1}^2$

The area of the smaller piston is

$= {A_2} = \pi {R_2}^2$

${A_1} = 25{A_2}$

Let the pressure

$= \frac{F}{A}$

According to the Pascal's Law,

The pressure will be applied the same

${P_1} = {P_2}$

$\frac{{{F_1}}}{{{A_1}}} = \frac{{{F_2}}}{{{A_2}}}$

$\frac{{{F_1}}}{{25{A_2}}} = \frac{{{F_2}}}{{{A_2}}}$

$\frac{{{F_1}}}{{25}} = {F_2}$

The area of the larger piston is larger therefore water will exert more force on the larger piston.

Since the area of the larger piston is

$25$ times larger, therefore minimum force we need to apply on the smaller piston is

$\frac{1}{{25}}$ times the force required,

the minimum force is required is

$= \frac{1}{{25}} \times 784$

$= 31.36\,N$

Hence, the minimum force that must be applied is

$31.36\,N$

Answer the following question in brief.
A plastic cube is released in water. Will it sink of come to the surface of water ?

The plastic cube is going to float on the surface of water as its density is less than that of water.

Answer the following question in brief.
Why do the load carrying heavy vehicles have large number of wheels?

We know,

$Pressure = \dfrac{Force}{Area}$
So, greater the area of contact between two surfaces, lesser will be the pressure. So, the load carrying heavy vehicles have large number of wheels so that the pressure on the road is reduced due to larger contact area. Also, using large number of wheels ensures that the force due to the load is shared among the tyres and no single tyre is under stress.

In the arrangement shown, a car of certain mass 'm' is in equilibrium by applying a force of 25 N. If the density of liquid taken is $0.9 cm^{-3}$ , then find the mass of the car.

Let m be the mass of the car

$\dfrac {m}{400\times 10^{-4}}=\dfrac {25}{5\times 10^{-4}}+8\times 0.9\times 10^3\times 9.8$

$\dfrac {m}{400\times 10^{-4}}=\dfrac {25\times 10^{-1}}{5\times 10^{-4}}$

$M=492 kg$

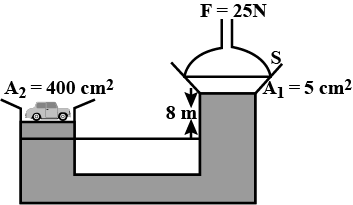
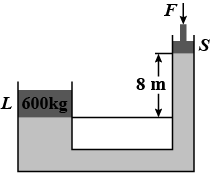
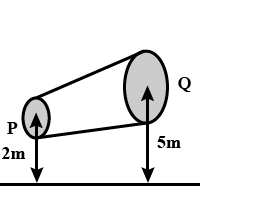
For the system shown in the figure, the cylinder on the left at $L$ has a mass of $600 kg$ and a cross sectional area of $800 \ { cm }^{ 2 }$ . The piston on the right, at $S$ , has a cross sectional area $25 { cm }^{ 2 }$ and negligible weight. If the apparatus is filled with oil. ( $\rho= 75 gm/{ cm }^{ 3 }$ ) Find the force $F$ required to hold the system in equilibrium.

Now pressure at

$8 m$ level will be same at both the end

$\dfrac{F}{a_1}+\rho gh=\dfrac{600\times g}{a_2}$

$a_1=25\times 10^{-4} \ m^2$ ,

$a_2=800\times 10^{-4} \ m^2$

$\dfrac{F}{a_1}+750\times g\times 8=\dfrac{600\times g}{a_2}$

we get

$F=37.5 N$

$x=75$

A spherical ball of density $\rho$ and radius $0.003 m$ is dropped into a tube containing a viscous fluid filled up to the $0 cm$ mark as shown in the figure. Viscosity of the fluid $=1.2160 { N.m }^{ -2 }$ and its density ${ \rho }_{ L }={ \rho }/2=1260 kg.{ m }^{ -3 }$ . Assume the ball reaches a terminal speed by the $10 cm$ mark. Find the time taken (in sec) by the ball to traverse the distance between the $10 cm$ and $20 cm$ mark. (g=acceleration due to gravity $= 10 m{ s }^{ -2 }$

We know that terminal velocity

$v=\dfrac{2(\rho_{metal}-\rho_{fluid})gR^2}{9\mu}$

Here, R=

$3\times 10^{-3} m$

Putting the value we get ,

$\rho_{metal}-\rho_{fluid}=\rho_{metal}/2$

We know that terminal velocity

$v=\dfrac{21260\times g\times 9\times 10^{-6}}{18\times 1.2160}$

$v=2\times 10^{-2} m/s$

Distance traveled =10 cm =0.1m

$t=\dfrac{0.1}{v}=5\ sec$

A cylindrical vessel open at the top is $20 cm$ high and $10 cm$ in diameter. A circular hole whose cross-sectional area $1{ cm }^{ 2 }$ is cut at the centre of the bottom of the vessel. Water flows from a tube above it into the vessel at the rate $100{ cm }^{ 3 }{ s }^{ -1 }$ . The height of water in the vessel under steady state (in cm) is

When the steady state is reached, rate of outflow of water will be equal to inflow of water.

$\Rightarrow$ Rate of outflow = 100 cm

$^3$

$\because$ Rate of inflow = 100 cm

$^3$

$\Rightarrow av=100$ cm

$^3$ , where

$a$ is the cross-section area of circular

hole and

$v$ is the velocity of water coming out of the hole.

$\Rightarrow a \sqrt{2gh} =100$ cm

$^3 \because v=\sqrt{2gh}$ using Torricelli's theorem.

$\Rightarrow 1 \times \sqrt{2gh} =100$ cm

$^3$

$\Rightarrow \sqrt{2gh} =100$ cm

$^3$

$2gh=10000 \\\Rightarrow 2 \times 1000 \times h =10000 \\\Rightarrow h=5 cm$

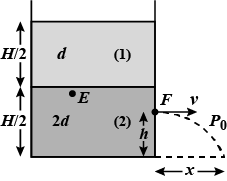
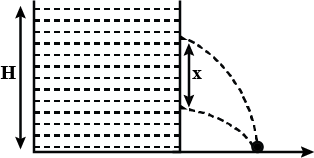
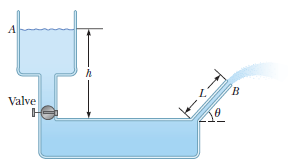
The height $h$ at which the hole should be punched so that the liquid travels the maximum distance $x_m$ initially is given as $\frac {x}{4}H$ . Find $x$ .

Using Bernoulli's equation,

$\dfrac{dgH}{2} + 2dg(\dfrac{H}{2}-h) + P_o = P_o + \dfrac{\rho v^2}{2}$

$v = \sqrt{\dfrac{3gH-4gh}{4}}$

Now, using kinematics,

Time to reach ground $t=\sqrt{2h/g}$

$x = vt = \sqrt{\dfrac{3Hh-4h^2}{2}}$

For the maximum horizontal distance x,
$\dfrac {dx}{dh}=\Rightarrow \dfrac {d}{dh}(3Hh-4h^2)^{\dfrac {1}{2}}=0$
or $\dfrac {1}{2}(3Hh-4h^2)^{-\dfrac {1}{2}}\times (3H-8h)=0$
This gives $3H-8h=0\Rightarrow h=\dfrac {3H}{8}$
This is the length of the liquid for which the range is maximum, i.e.,
$h\rightarrow h_m=\dfrac {3H}{8}$
The maximum horizontal distance is given by
$x_m=\sqrt {(3H-4h_m)h_m}$
$=\sqrt {\left \{\left (3H-4\dfrac {3H}{8}\right )\dfrac {3H}{8}\right \}}=\dfrac {3}{4}H$

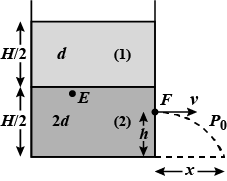
Determine the horizontal distance $x$ traveled by the liquid initially is given as $=\sqrt {(3H-xh)h}$ . Find $x$ .

Let the equivalent depth of liquid (1) of density

$d$ in terms of density

$2d$ which gives the same pressure as liquid (1) at interface, i.e.,

$\dfrac {H}{2}dg=H'(2d)g$ which gives

$H'=\dfrac {H}{4}$
Hence, depth of the liquid above opening

$($ in terms of depth of liquid of density

$2d),$

$H'+\left (\dfrac {H}{2}-h\right )=\dfrac {H}{4}+\left (\dfrac {H}{2}-h\right )$

$H_{net}=\left (\dfrac {3H-4h}{4}\right )$
And velocity of efflux is given by

$v=\sqrt {2g H_{net}}$

$v=\sqrt {\left (\dfrac {3H-4h}{2}\right )g}$
Time taken by the liquid to fall through a vertical height

$h$ is given by

$H=\dfrac {1}{2}gt^2\Rightarrow t=\sqrt {\dfrac {2h}{g}}$
Therefore, horizontal distance traversed by liquid is

$x=vt=\sqrt {\dfrac {(3H-4h)g}{2}}\times \sqrt {\dfrac {2h}{g}}$

$=\sqrt {(3H-4h)h}$

Calculate the energy spent in spraying a drop of mercury of radius $R$ into $N$ droplets all of same size. If the surface tension of mercury is $T$ .

Let the radius of the small droplets be

$r$ and

$\rho$ be the density of mercury.

Mass of the drop must be equal to the total mass of the droplets.

$\therefore$

$\rho \times \dfrac{4\pi}{3}R^3 = N \times \dfrac{4\pi}{3} r^3 \times \rho$

$\implies R^3 =N r^3$

Change in surface area

$\Delta A = N \times 4\pi r^2 -4\pi R^2 = 4\pi (N r^2 - R^2)$

$\therefore$ Energy spent

$E =T \Delta A =4\pi T (Nr^2 - R^2)$

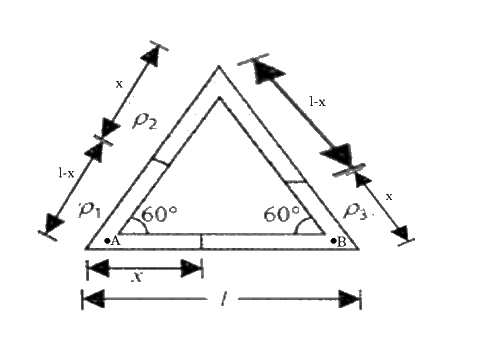
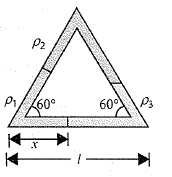
A rectangular tube of uniform cross section has three liquids of densities $\rho_1, \rho_2$ and $\rho_3$ . Each liquid column has length l equal to length of sides of the equilateral triangle. Find the length x of the liquid of density $\rho_1$ in the horizontal limb of the tube, if the triangular tube is kept in the vertical plane

Pressure at point A

$P_A = \rho_2 (x sin 60^o) g + \rho_1 (l-x) sin60^o g$

Pressure at point B

$P_B = \rho_2 (l-x ) sin 60^o g + \rho_3 (x sin60^o) g$

But

$P_A = P_B$

$\therefore$

$\rho_2 (x sin 60^o) g + \rho_1 (l-x) sin60^o g$

$= \rho_2 (l-x ) sin 60^o g + \rho_3 (x sin60^o) g$

$2\rho_2 -(\rho_1 +\rho_3) x = (\rho_2 - \rho_1)l$

$\implies$

$x = \dfrac{(\rho_2 - \rho_1)l}{2\rho_2 - (\rho_1 + \rho_3)}$

An open capillary tube contains a drop of water. When the tube is in its vertical position, the drop forms a column with a length of $2cm$ . The internal diameter of the capillary tube is $1mm$ . Determine the radii of curvature of the upper and lower meniscus in each case. Consider the wetting to be complete. Surface tension of water $=0.0075N/m$

When capillary is in vertical position, thge upper meniscus is concave and pressure due to surface tension

$P_s=\frac{2T}{R_1}$

is directed vertically upward,

$R_1$ being radius of curvature of upper

meniscus. When wetting is complete

$P_1=\frac{2T}{r}$

$r$ being radius of the capillary tube

$=\frac{D}{2}=\frac12 mm$

$R_1=r=0.5\,mm$ in each case.

We have

$P_1=\frac{2T}{r}=\frac{2\times 75\times 10^{-3}}{0.5\times 10^{-3}}=300\,N/m^2$

The hydrostatic pressure

$P_2=h\rho g$ is always directed downwards.

$h=2\,cm$

$P_2=h\rho g=2\times 10^{-2} \times 10\times 10^3=200\,N/m^2$

Clearly

$P_1>P_2$ . That is resulting pressure is directed upward. For

equilibrium, the pressure due to lower meniscus should be downward. This

makes the lower meniscus concave downwards. Then,

$P_1-P_2=\frac{2T}{R_2}$

$300-200=\frac{2\times 75 \times 10^{-3}}{R_2}$

$R_2=\frac{2\times 75\times 10^{-3}}{100}=1.50\times 10^{-3}\,m=1.50\,mm$

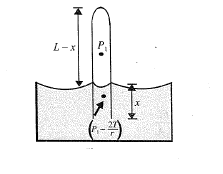
A force of $50 kgf$ is applied to the smaller piston of a hydraulic machine. Neglecting friction, The force exerted on the large piston, if the diameters of the piston are $5 cm$ and $25 cm$ respectively is $'X' \ N$ . Find $\cfrac{X}{250}$

We know that Pressure on both the Piston should be same,

$\therefore Pressure \ on \ smaller \ Piston = Pressure \ on \ larger \ Piston$

$\cfrac{Force \ on \ smaller}{Area \ of \ smaller} = \cfrac{Force \ on \ larger}{Area \ of \ larger}$

$\therefore \ Force \ on \ Larger = \cfrac{Force \ on \ smaller}{Area \ of \ smaller} \times {Area \ of \ larger}$

$\Rightarrow \cfrac{50}{2.5 \times 2.5 \times 3.14} \times 12.5 \times 12.5 \times 3.14 = 1250 kgf$

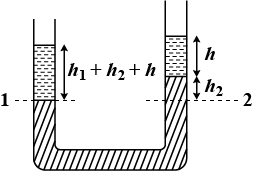
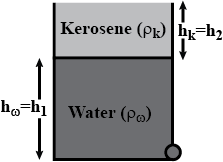
A U-tube of uniform cross-sectional area and open to the atmosphere is partially filled with mercury.Water is then poured into both arms. If the equilibrium configuration of the tube is as shown in figure with $h_{2} = 1.0 cm$ , determine the value of $h_{1}$ .

$P_{1}=P_{2}$

$\therefore$

$P_{0}+\rho _{w}g\left ( h_{1}+h_{2}+h \right )=P_{0}+\rho _{w}gh+\rho _{Hg}gh_{2}$

$\therefore$

$\displaystyle h_{1}=\frac{\left ( \rho _{Hg}-\rho _{w} \right )h_{2}}{\rho _{w}}$

$\displaystyle =\frac{\left ( 13.6-1 \right )\left ( 1.0 \right )}{1}$

$=12.6$ cm

For the system shown in figure, the cylinder on the left, at L, has a mass of 600 kg and a cross-sectional area of $800 cm^{2}$ . The piston on the right, at S, has cross-sectional area $25 cm^{2}$ and negligible weight. If the apparatus is filled with oil $(p = 0.78 g/cm^{3})$ what is the force F required to hold the system in equilibrium?

Let

$A_{1}$ =area of cross-section on LHS and

$A_{2}$ =area of cross-section on RHS
Then,

$\displaystyle \frac{F}{A_{2}}+\rho gh=\frac{Mg}{A_{1}}$

$\therefore$

$\displaystyle F=A_{2}\left [ \frac{Mg}{A_{1}}-\rho gh \right ]$

$\displaystyle =\left ( 25\times 10^{-4} \right )\left [ \frac{600\times 9.8}{800\times 10^{-4}}-780\times 9.8\times 8 \right ]$

$=31$ N

What is the time required for the same amount of water to flow out if the water level in tank is maintained always at a height of $1 m$ from orifice?

Rate of flow of water

$Q=a\sqrt{2gH}=$ constant
Total volume of water V=AH

$\therefore$ Time take to empty the tank with,constant rate

$\displaystyle t=\frac{V}{Q}=\frac{AH}{a\sqrt{2gH}}$

$\displaystyle =\frac{400\times 1}{\sqrt{2\times 9.8\times 1}}$

$=90$ s

$=1.5$ min

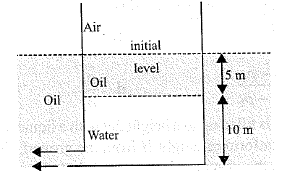
A tank having a small circular hole contains oil on top of water. It is immersed in a large tank of the same oil. Water flows through the hole. What is the velocity of this flow initially? When the flow stops, what would be the position of the oil-water interface in the tank from the bottom. The specific gravity of oil is $0.5.$

(a)

$\Delta p=h\left ( \rho _{w}-\rho _{0} \right )g=\left ( 10 \right )\left ( 1000-500 \right )9.8$

$=49000$ N/m

$^{2}$
Now,

$\displaystyle \Delta P=\frac{1}{2}\rho _{w}v_{2}$

$\therefore$

$\displaystyle v=\sqrt{\frac{2\Delta P}{\rho _{w}}}$

$\displaystyle =\sqrt{\frac{2\times 49000}{1000}}$

$=9.8$ m/s
The flow will stop when,
(b)

$\left ( 10+5 \right )\rho _{0}g=5\rho _{0}g+h\rho _{w}g$

$10\rho _{0}=h\rho _{w}$

$\therefore$

$\displaystyle h=\frac{10\times 500}{1000}$

$=5$ m
i.e., flow will stop when the water-oil interface is at a height of 5.0 m.

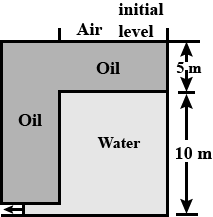
What is the time required to empty the tank through the orifice at the bottom?

Time taken to empty the tank (has been derived in theory) is

$\displaystyle t=\frac{2A}{a\sqrt{2g}}\sqrt{H}$
Given,

$\displaystyle \frac{A}{a}=400$
Substituting the values we have,

$\displaystyle t=\frac{2\times 400}{\sqrt{2\times 9.8}}\sqrt{1}$

$=180$ s

$=3$ min

A siphon tube is discharging a liquid of specific gravity $0.9$ from a reservoir as shown in the figure find the velocity of the liquid through the siphon.

Using the Bernoulli theorem,

$\displaystyle P_{A}-\frac{1}{2}\rho v^{2}+\rho gh=P_{D}$

But

$P_{A}=P_{D}=P_{0}$

$\therefore$

$\displaystyle \frac{1}{2}\rho v^{2}=\rho gh$

$\therefore$

$v=\sqrt{2gh}$

Here,

$h$ = (4+1)= 5 m

$\therefore$

$v=\sqrt{2\times 9.8\times 5}$

$=9.9$ m/s

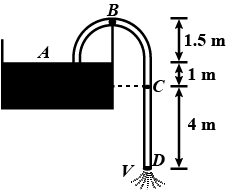
initial speed (in m/s) with which the water flows from the orifice.

Area of orifice

$A_o = 10^{-4}$

$m^2$

Area of the surface

$A = \pi r^2 = \pi \times 1^2 = 3.14$

$m^2$

$\implies A_o<< A$

Velocity of water flows

$v = \sqrt{2gh}$ for

$A_o << A$

$\implies v = \sqrt{2\times 10 \times 5} = 10$

$m/s$

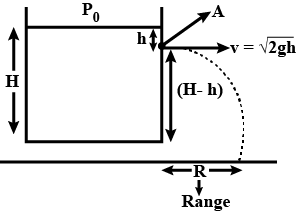
Three holes $A, B$ and $C$ are made at depths $1m, 2 m$ and $5 m$ as shown. Total height of liquid in the container is $8 m$ . Let v is the speed with which liquid comes out of the hole and $R$ the range on ground.Match the following two columns

Velocity with which liquid comes out is

$v=\sqrt{2gh_t}$ where

$h_t$ is height from the top of liquid.

Now as

$h_{tA}<h_{tB}<h_{tC}$ , so

$v_A<v_B<v_C$ So

$v$ is maximum for point

$C$ and minimum for

$A$ .

The range on ground is given as

$R=v\times\sqrt{2h_b/g}=2\sqrt{h_th_b}$ , where

$h_b$ is height from the bottom of liquid.

$h_{tA}h_{bA}<h_{tB}h_{bB}<h_{tC}h_{bC}$ , so,

$R_A<R_B<R_C$ So

$R$ is also maximum for point

$C$ and minimum for

$A$ .

Thus correct match is A-3, B-1, C-3, A-1.

A long cylindrical tank of cross-sectional area $0.5m^{2}$ is filled with water. It has a small hole at a height $50 cm$ from the bottom. A movable piston of cross-sectional area almost equal to $0.5 m^{2}$ is fitted on the top of the tank such that it can slide in the tank freely. A load of $20 kg$ is applied on the top of the water by piston, as shown in the figure. Calculate the speed of the water jet with which it hits the surface when piston is $1 m$ above the bottom. (Ignore the mass of the piston).

Given

$A=0.5\\W=20kg\\H=1m\\h=50cm$

By the Bernoulli theorem:

$\displaystyle \frac{1}{2}\rho v^{2}=\rho gh+\frac{mg}{A}$

Here,

$h=1.0-0.5=0.5$ m,

A=Area of pistone=0.5 m

$^{2}$

$\therefore$

$\displaystyle v=\sqrt{2gh+\frac{2mg}{\rho A}}$

$\displaystyle =\sqrt{2\times 9.8\times 0.5+\frac{2\times 20\times 9.8}{10^{3}\times 0.5}}$

$=3.25$ m/s

$\therefore$ Speed with which it hits the surface is

${v}'=\sqrt{v^{2}+2g{h}'}$

$=\sqrt{\left ( 3.25 \right )^{2}+\left ( 2\times 9.8\times 0.5 \right )}$

$=4.51$ m/s

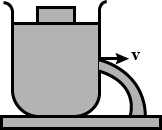
A siphon tube is discharging a liquid of specific gravity $0.9$ from a reservoir as shown in the figure find the pressure at the highest point $B$ .

Applying Bernoulli's equation at A and B,

$\displaystyle P_{A}+0+0=P_{B}+\frac{1}{2}\rho v^{2}+\rho g\left ( 1.5 \right )$
or

$\displaystyle P_{0}=P_{B}+\frac{1}{2}\rho v^{2}+1.5\rho g$

$\therefore$

$\displaystyle P_{B}=1.01\times 10^{5}-\frac{1}{2}\times 900\times \left ( 9.9 \right )^{2}-1.5\times 900\times 9.8$

$=4.36\times 10^{4}$ Pa

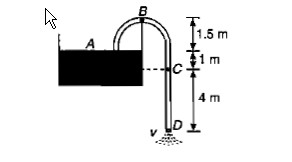
A siphon tube is discharging a liquid of specific gravity $0.9$ from a reservoir as shown in the figure. Find the pressure at point $C$ .

Applying Bernoulli's equation at A and C,

$\displaystyle P_{0}=P_{c}+\frac{1}{2}\rho v^{2}-\rho g\left ( 1.0 \right )$

$\therefore$

$\displaystyle P_{C}=P_{0}+\rho g-\frac{1}{2}\rho v^{2}$

$\displaystyle =1.01\times 10^{5}+900\times 9.8-\frac{1}{2}\times 900\times \left ( 9.9 \right )^{2}$

$=6.6\times 10^{4}$ Pa

initial speed with which water strikes the ground.

Let the discharge velocity be v

$v=\sqrt{2gh}=\sqrt{2\times 10\times 5}=10m/s$

Let say it strikes the ground with

$v_1$ velocity

$v_1^2-v^2=2gH$

$v_1^2=10^2+2\times 10\times 5$

$v_1=14.14m/s$

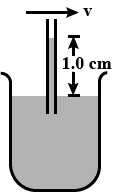
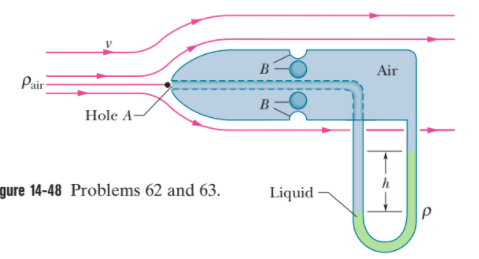
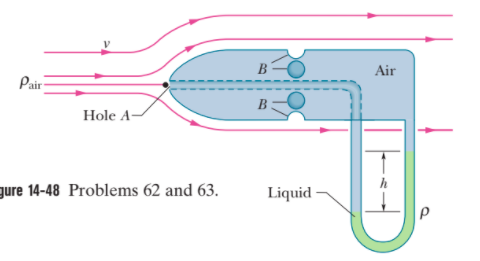
When air of density $1.3 kg/m^{3}$ flows across the top of the lobe shown in the accompanying figure, water rises in the lobe to a height of $1 .0 cm$ . What is the speed of the air?

$\displaystyle \frac{1}{2}\rho _{air}v^{2}=\rho _{w}gh_{w}$

$\displaystyle v=\sqrt{\frac{2\rho _{w}gh_{w}}{\rho _{air}}}$

$\displaystyle =\sqrt{\frac{2\times 10^{3}\times 10\times 10^{-2}}{1.3}}$

$=12.4$ m/s

Water flows through the tube as shown in figure. The areas of cross-section of the wide and the narrow portions of the tube are $5 cm^{2}$ and $2cm^{2}$ respectively. The rate of flow of water through the tube is $500cm^{3}/s$ . Find the difference of mercury levels in the U-tube.

$A_{1}v_{1}=A_{2}v_{2}=$ rate of flow of water

$5v_{1}=2v_{2}=500$ cm

$^{3}$ /s

$\therefore$

$v_{1}=100$ cm/s

$=1.0$ m/s

$v_{2}=250$ cm/s

$=2.5$ m/s

$\displaystyle \frac{1}{2}\rho _{w}\left ( v_{2}^{2}-v_{1}^{2} \right )=\rho _{Hg}gh_{Hg}$

$\therefore$

$\displaystyle h_{Hg}=\frac{\rho _{w}\left ( v_{2}^{2}-v_{1}^{2} \right )}{2\rho _{Hg}g}$

$\displaystyle =\frac{10^{3}\left ( 6.25-1 \right )}{2\times 13.6\times 10^{3}\times 9.8}$

$=0.0196$ m

$=1.96$ cm

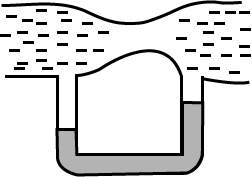
time taken to empty the tank to half its original value. $(g = 10 m/s ^{2})$

$\displaystyle t=\frac{2A}{a\sqrt{2g}}\left [ \sqrt{H}-\sqrt{\frac{H}{2}} \right ]$

$\displaystyle =\frac{2\times \pi \times \left ( 1 \right )^{2}}{10^{-4}\sqrt{2\times 10}}\left [ \sqrt{5}-\sqrt{2.5} \right ]$

$=9200$ s

What is the pressure drop (in mm Hg) in the blood as it passes through a capillary 1 mm long and $2\mu m$ in radius if the speed of the blood through the centre of the capillary is 0.66 mm/s ? (The viscosity of whole blood is $4 \times 10^{-3}$ poise).

See the expression of maximum velocity at centre of tube,

$\displaystyle v_{max}=\frac{\left ( p_{1}-p_{2} \right )R^{2}}{4\eta L}$

$\therefore$

$\displaystyle \left ( P_{1}-P_{2} \right )=\frac{4\eta Lv_{max}}{R_{4}}$

$\displaystyle =\frac{\left ( 4\times 4\times 10^{-3} \right )\left ( 10^{-3} \right )\left ( 0.66\times 10^{-3} \right )}{\left ( 2\times 10^{-6} \right )^{2}}$

$=2.64\times 10^{3}$ N/m

$^{2}$ =

$h\rho g$

$\displaystyle h=\frac{2.64\times 10^{3}}{\rho g}$

$\displaystyle =\frac{2.64\times 10^{3}}{13.6\times 10^{3}\times 9.81}$ m of Hg

$=0.0195$ m of Hg

$=19.5$ mm of Hg

The area of cross-section of a large tank is $0.5 m^{2}$ It has an opeoing near the bottom having area ofcross-section $1 cm^{2}$ , A load of 20 kg is applied on the water at the top. Find the velocity of the water coming out of the opening at the time when the height of water level is 50 cm above the bottom. (Takeg $= 10m/s^{2})$

$\displaystyle \left ( \frac{Mg}{A} \right )+\rho gh=\frac{1}{2}\rho v^{2}$

$\therefore$

$\displaystyle v=\sqrt{\frac{2Mg}{\rho A}+2gh}$

$\displaystyle =\sqrt{\frac{2\times 20\times 10}{0.5\times 10^{3}}+2\times 10\times 0.5}$

$=3.28$ m/s

Water flows through a horizontal lobe as shown in figure , If the difference of heights of water column in the vertical lobes is $2 cm$ and the areas of cross-section at A and B are $4 cm^{2}$ and $2cm^{2}$ respectively. Find the rate of flow of water across any section.

$\displaystyle \frac{1}{2}\rho v_{B}^{2}-\frac{1}{2}\rho v_{A}^{2}=\rho g\left ( h_{A}-h_{B} \right )$
or

$v_{B}^{2}-v_{A}^{2}=2g\left ( h_{A}-h_{B} \right )$

$=2\times 10\times 0.02$
or

$v_{B}^{2}-v_{A}^{2}=0.4$ m

$^{2}$ /s

$^{2}$ (i)

$v_{A}A_{A}=v_{B}A_{B}$
or

$4v_{A}=4v_{B}$

$\therefore$

$v_{B}=2v_{A}$
Solving Eqs. (i) and (ii), we get

$v_{A}=0.363$ m/s
Volume flow rate

$=v_{A}A_{A}$

$=\left ( 0.365 \right )\left ( 4\times 10^{-4} \right )$

$=1.46\times 10^{-4}$ m

$^{3}$ /s

$=146$ cm

$^{3}$ /s

A water barrel stands ona table of heighth. lf a small hole is punched in the side of the barrel at its base, it is found that the resultant stream of water strikes the ground at a horizontal distance R from the barrel.What is the depth of water in the barrel?

Let the depth of water in the barrel be

$H$ .

$\therefore$ Velocity of water coming out of the barrel

$v = \sqrt{2gH}$

Also the horizontal range where the water strikes the ground

$R =v \times \sqrt{\dfrac{2h}{g}}$

$\therefore$

$R = \sqrt{2gH} \times \sqrt{\dfrac{2h}{g}}$

$R^2 = 4hH$

$\implies$

$H =\dfrac{R^2}{4h}$

Water is flowing smoothly through a closed-pipe system. At one point the speed of the water is $3.0 m/s$ ,while at another point $1.0 m$ higher the speed is $4.0 m/s$ . If the pressure is $20kPa$ at the lower point, what is the pressure at the upper point? What would the pressure at the upper point be if the water were to stop flowing and the pressure at the lower point were $18 kPa$ ?

(i)

$\displaystyle p_{1}+\frac{1}{2}\rho v_{1}^{2}+\rho gh_{1}=p_{2}+\frac{1}{2}\rho v_{2}^{2}+\rho gh_{2}$

$\displaystyle \left ( 20\times 10^{3} \right )+\frac{1}{2}\times 10^{3}\times \left ( 3 \right )^{2}+0=p_{2}+\frac{1}{2}\times 10^{3}\times \left ( 4 \right )^{2}+10^{3}\times 10\times 1$

$\therefore$

$p_{2}=6.5\times 10^{3}$ N/m

$^{2}$ =

$6.5$ kPa
(ii) Again applying the same equation, we have:

$\left ( 18\times 10^{3} \right )+0+0=p_{2}+0+\left ( 10^{3} \right )\left ( 10 \right )\left ( 1 \right )$

$\Rightarrow$

$p_{2}=8\times 10^{3}$ N/m

$^{2}$

$=8$ kPa

A typical river-borne silt particle has a radius of $20 \mu m$ and a density of $2 \times 10^{3} kg/m^{3}$ . The viscosity of water is $1.0\ \text{milli-poise}$ . Find the terminal speed with which such a particle will settle to the bottom of a motionless volume of water.

Using

$\displaystyle V=\frac{2}{9}\frac{r^{2}\left ( \rho -\sigma \right )g}{\eta }$

$\eta =1.0$ m

$Pi=1.0\times 10^{-3}Pi$

$\displaystyle =\frac{2}{9}\frac{\left ( 20\times 10^{-6} \right )^{2}\times \left ( 2\times 10^{3}-10^{3} \right )\times 9.8}{1.0\times 10^{-3}}$

$=0.882$ mm/s

Two equal drops of water are falling through air with. steady velocity v. If the drops coalesced, what will be the new velocity ?

When the two equal drops coalesces, volume of water remains same and a bigger drop is formed. Lets say

$r$ is radius of drop before these combine and

$R$ is radius after these combine.

We have

$2 \times \dfrac{4}{3} \pi r^3 =\dfrac{4}{3} \pi R^3 \\\Rightarrow R=2^{1/3}r$

and we know that terminal velocity

$V_T \propto$ radius

$^2$ , so we have

$\dfrac{V_T'}{V_T}=\dfrac{R^2}{r^2}$

$\Rightarrow V_T' =\left (\dfrac{R}{r} \right)^2 V_T$

$= (2^{1/3})^2 v$

$=2^{2/3}v\ \text{m/s}$

Velocity of a viscous liquid in long cylinder of radius R at a distance $R_{1}$ from centre is $V_{1}$ Find the velocity of the liquid as a function of the distance r from the axis of the cylinder,

$\displaystyle v=\frac{p_{1}-p_{2}}{4\eta L}\left ( R^{2}-r^{2} \right )$ (i)

$\displaystyle v_{1}=\frac{P_{1}-P_{2}}{4\eta L}\left ( R^{2}-R_{1}^{2} \right )$ (ii)
Dividing Eq. (i) by Eq. (ii) we get

$\displaystyle v=\left ( \frac{R^{2}-r^{2}}{R^{2}-R_{1}^{2}} \right )v_{1}$

Find the pressure exerted by a man weighing $90\;kg$ on the ground.
(a) when he is standing on one of his feet having an area of $90\;cm^2$ .
(b) when he is lying flat. The area of his body in contact with the ground is $0.9\;m^2$ . Given $g=10\;ms^{-2}$ .

Force exerted by the man (thrust)

$=mg$

$=90\;kg\times10\;ms^{-2}=900\;kg\;ms^{-2}=900\;N$
(a) pressure exerted by man while standing

$=\displaystyle\frac{Force}{Area}$

$=\displaystyle\frac{900\;N}{\begin{pmatrix}\displaystyle\frac{90}{10000}\end{pmatrix}m^2}=\displaystyle\frac{900\times10000}{90}Nm^{-2}=10^5\;Nm^{-2}$
(b) Pressure exerted by man while lying

$=\displaystyle\frac{Force}{Area}=\displaystyle\frac{900\;N}{0.9\;m^2}=\displaystyle\frac{9000\;N}{9\;m^2}=1000\;Nm^{-2}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=10^3\;Nm^{-2}$

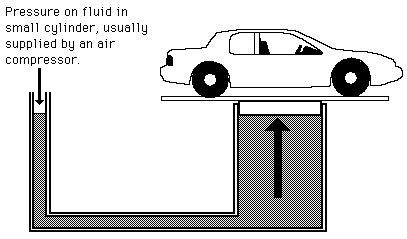
State a device that utilises 'Pascal's law' and also explain how it works.

Frequently used hydraulic lift in automobile stores and repair shops is a practical application of Pascal's law.
In its case the base of vehicle platform is one with larger area and other platform has low area so less force is applied on platform and still manages to lift heavy an automobiles.

$P=\frac { { F }_{ 1 } }{ a_{ 1 } } =\frac { { F }_{ 2 } }{ { a }_{ 2 } } \quad$

What is the pressure exerted by a woman weighing $500\;N$ standing on one heel of area of $1\;cm^2$ ?

Force exerted by the women = Her weight =

$500\;N$
Area on which force acts

$=1\;cm^2=\begin{pmatrix}\displaystyle\frac{1}{100}m\end{pmatrix}^2$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\displaystyle\frac{1}{10000}m^2$

$\therefore\;Pressure=\displaystyle\frac{Force}{Area}=\displaystyle\frac{500\;N}{\displaystyle\frac{1}{10000}m^2}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=500\times10000\;Nm^{-2}=5\times10^6\;Nm^{-2}$ .

A glass is filled with water up to its brim and a thick hand card placed on top of it. Now keeping the card tightly closed and pressed with palm, the glass full of water is inverted and placed upside down. The palm is gently removed from the card. It is observed that the piece of card dose not fall off the glass though the glass is full of water and its whole weight is exerting pressure on the card. Why does it happen?

The card does not fall because the atmospheric pressure from underneath acts upwards and is greater than the downward pressure exerted by the weight of the water.

How can a scuba diver keep from floating back to the surface of the water?

By adding weights.

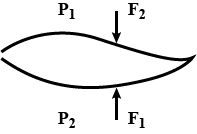
In a test experiment on a model airplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are $70\ ms^{-1}$ and $63\ ms^{-1}$ respectively. What is the lift on the wing if its area is $2.5$ m $^2$ ? Take the density of air to be $1.3\ kgm^{-3}$ .

$\textbf{Step 1: Apply Bernouli equation [Refer Fig.]}$

$P_{1} + \dfrac{1}{2} \rho v_{1}^{2} = P_{2} + \dfrac{1}{2} \rho v_{2}^{2}$

$(h_{1} = h_{2})$

$\Rightarrow$

$(P_{2} - P_{1}) = \dfrac{1}{2} \rho (v_{1}^{2} - v_{1}^{2})$

$....(1)$

$\textbf{Step 2: Force Calculation}$

$F_{1} =$ Net upward force

$= P_{2} A$

$;$

$F_{2} =$ Net downward force

$= P_{1} A$

$\Rightarrow$

$F_{\text{net}} = F_{1} - F_{2} = (P_{2} - P_{1}) A$

Using equation

$(1)$

$F = \dfrac{1}{2} \rho (v_{1}^{2} - v_{2}^{2}). A$

Putting given values

$F = \dfrac{1}{2} \times 1.3 (kg/m^3)\times ((70m/s)^2 - (63m/s)^2) \times 2.5(m^2)\$

$= 1512.87\ N$

2114374_419464_ans_c01d3f859a3c441489f30667adfe307c.png

A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm $^2$ . What maximum pressure would the smaller piston have to bear ?

Pressure on the piston

$P = \dfrac{F}{A}$

Force

$F=m\times a$

$=3000\times 9.8$

$=29400\ N$

Area of cross section

$A = 425\times 10^{-4}sq\, m$

Therefore the pressure

$P=\displaystyle \frac{3000\times 9.8}{425\times 10^{-4}}=6.92\times 10^{5}Pa$ .

What will be the pressure in $dyne$ ${cm}^{-2}$ , due to a water column of height $12.5cm$ ? ( $g=980cm$ ${s}^{-2}$ ) (density of water ${10}^{3}kg$ ${m}^{-3}$ ).

Pressure at the bottom of the water collumn is

$P=Po+\rho gh={ 10 }^{ 6 }+1\times 980\times 12.5$

$= 1012250 \ dyne \ { cm }^{ -2 }$

What is the magnitude of force required(in $Newton$ ) to produce a pressure of $37500 \ Pa$ in an area of $300 \ {cm}^{2}$ ?

Pressure

$P = 37500 \ Pa$ Area

$A= { 300cm }^{ 2 }=3\times { 10 }^{ -2 }{ m }^{ 2 }$

Since,

Pressure

$P= \dfrac { Force }{ Area } \Rightarrow Force\ F=P\times A = 37500\times 3\times { 10 }^{ -2 } \ N$

Hence, Force

$F = 1125 \ N$

A man weighing $50kgf$ is standing on a wooden plank of $1m\times 0.5m$ . The pressure exerted by it on the ground will be ___________ (in Pa)

Given,

Mass

$= 50kg$

Dimension of wooden plank=

$1\ m\times 0.5\ m$

Weight,

$F = mg$

$F= 50\times 10$

$F=500\ N$

Area

$= 1\times0.5 = 0.5{ m }^{ 2 }$ .

Pressure =

$\dfrac { Force }{ Area }$

Pressure =

$\dfrac { 500 }{ 0.5 } =1000\ Pa$

What will be the pressure in dyne ${cm}^{-2}$ , due to a water column of height $10cm$ ? [take $g=980cm/{s}^{2}$ ] (density of water $={10}^{3}kg$ ${m}^{-3}$ ).

1966104_512604_ans_ec02bf5104b34c5eb44f2211f9ef5b50.jpg

A brick with dimensions of $20cm\times 10cm\times 5cm$ has a weight $500gwt$ . Calculate the pressure exerted by brick when the pressure is greatest?

1917980_512909_ans_a434376f556e46d49bb24ec9a6522df9.jpg

The press plungers of a braman (hydraulic) press is $40\ cm^{2}$ in cross-section and is used to lift a load of mass $800\ kg$ . What minimum force will be required to be applied on the pump plunger if its cross-sectional area is $0.02\ m^{2}$ ?

Pressure at Plunger is

$P=\dfrac{weight}{area}$

$Weight=800\times 9.8=7840N$

Area

$A=40cm^2=40\times10^{-4}m^2$

$P=\dfrac{7840}{40\times10^{-4}}=196\times 10^4Nm^{-2}$

Now at pump plunger required pressure is

$P=196\times 10^{4}Nm^{-2}$

Let the force require be F.

Area,

$a=0.02m^2$

$P=\dfrac{F}{a}$

$F=p\times a=196\times 10^4\times 0.02=39200N$

Force exerted by a truck is $500000N$ and the pressure on the ground is $2500000Pa$ . Calculate the area of contact of tyres with ground?

Force =

$5\times { 10 }^{ 5 }N$ . Pressure = 2500000

${ P }_{ a }$

Since, Pressure

$=\dfrac { Force }{ Area } \Rightarrow Area=\dfrac { 5\times { 10 }^{ 5 } }{ 25\times { 10 }^{ 5 } }$

Area = 0.2

${ m }^{ 2 }$ (for all four tyres)

& for single tyre area of contact is 0.05

${ m }^{ 2 }$

A block wood is kept on table top. The mass wooden block is $5kg$ and its dimensions are $40cm\times 20cm\times 10cm$ . Find the pressure exerted by the wooden block on the table top, if it is made to lie on the table top with its sides of dimension:
(a) $20cm\times 10cm$ and
(b) $40cm\times 20cm$

pressure=force/area

(a) pressure= (5x9.8)/(0.2x0.1)=2450 pa

(b) pressure=(5x9.8)/ (0.4x0.2)=612.5 pa

A force of $50kgf$ is applied to the smaller piston of a hydraulic machine. Neglecting friction, find the force exerted on the large piston, the diameters of the piston being $5cm$ and $24cm$ respectively.

$Area1=\dfrac { \Pi { 5 }^{ 2 } }{ 4 } \quad \quad \quad \quad { F }_{ 1 }=50kgf$

$Area2=\dfrac { \Pi { 24 }^{ 2 } }{ 4 } \quad \quad \quad \quad { F }_{ 2 }=x\quad kgf.$

Since Pressure is constant.

So,

$\dfrac { { F }_{ 1 } }{ { A }_{ 1 } } =\dfrac { { F }_{ 2 } }{ { A }_{ 2 } } \Rightarrow \dfrac { x }{ \dfrac { \Pi { 24 }^{ 2 } }{ 4 } } =\dfrac { 50 }{ \dfrac { \Pi { 5 }^{ 2 } }{ 4 } }$

$x=\dfrac { { 50 }^{ 2 }\times { 24 }^{ 2 } }{ 25 } =576\times 2$

$\boxed { x=1152\quad kgf }$

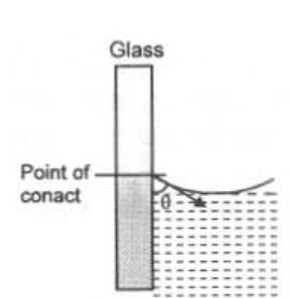
Draw a neat, labelled diagram for a liquid surface in contact with a solid, when the angle of contact is acute.

The figure represents a fluid in contact with solid glass. The liquid wets the solid and as such the angle of contact i.e. the angle between the surface of the solid and the tangent drawn to the free surface of the liquid at the point of contact , is acute.

A hydraulic lift at a service station can lift cars with a mass of $3500\ kg$ . The area of cross section of the piston carrying the load is $500\ cm^{2}$ . What pressure does the smaller piston experience? $g = 9.8 m/s^{2}.$

Pressure =

$\dfrac { Force }{ Area } =\dfrac { 3500\times 9.8 }{ 500\times { 10 }^{ -4 }N/{ m }^{ 2 } } =6.86\times { 10 }^{ 5 }N/{ m }^{ 2 }$

Two spherical soap bubbles collapses. If $V$ is the consequent change in volume of the contained air and $S$ is the change in the total surface area and $T$ is the surface tension of the soap solution, then if relation between $P_{0}, V, S$ and $T$ are $\lambda P_{0}V + 4ST = 0$ , then find $\lambda$ ? (If $P_{0}$ is atmospheric pressure): Assume temperature of the air remain same in all the bubbles.

$\left( \triangle P\right)_{soap \;bubble }=\dfrac{4T}{R}$

Let radii of two spherical bubbles be

$r_1\;\&\;r_2$ respectively.

Now, as two collapse to form a single.

then,

$\Rightarrow \left( P+\dfrac{4T}{r_1}\right)\dfrac{4}{3}\pi r_1^3+\left( P+\dfrac{4T}{r_2}\right)\left( \dfrac{4}{3}\pi r_2^3\right)=\left( P+\dfrac{4T}{R}\right) \dfrac{4}{3}\pi R^3$

$\Rightarrow PV+\dfrac{4T}{3}\left( 4\pi r_1^2+4\pi r^2_2-4\pi R^2\right)=0$

$\Rightarrow 3PV=4TS=0$

Hence, the answer is

$3PV=4TS=0.$

Two cylindrical vessels of equal cross-sectional area $A$ contain water upto heights $h_{1}$ and $h_{2}$ . The vessels are interconnected so that the levels in them become equal. Calculate the work done by the force of gravity during the process. The density of water is $\rho$ .

Since total volume remains constant, the final height of the liquid is:

$\cfrac { { h }_{ 1 }+{ h }_{ 2 } }{ 2 } =H$

Initial potential energy of container

$A{ h }_{ 1 }\rho g\times \cfrac { { h }_{ 1 } }{ 2 } +A{ h }_{ 2 }\rho g\times \cfrac { { h }_{ 2 } }{ 2 } \\ =\cfrac { A\rho g }{ 2 } \left[ { h }_{ 1 }^{ 2 }+{ h }_{ 2 }^{ 2 } \right]$

Final potential energy

$=2\times A\rho \left( \cfrac { { h }_{ 1 }+{ h }_{ 2 } }{ 2 } \right) \times \left( \cfrac { { h }_{ 1 }+{ h }_{ 2 } }{ 2 } \right) g\\ =\cfrac { A\rho g }{ 2 } { \left( { h }_{ 1 }+{ h }_{ 2 } \right) }^{ 2 }$

Work done

$={ P }_{ f }-{ P }_{ i }\\ =\cfrac { A\rho g }{ 2 } \left[ { 2h }_{ 1 }{ h }_{ 2 } \right]$

$W=A\rho g{ h }_{ 1 }{ h }_{ 2 }$

If $A$ denotes the area of free surface of a liquid and $h$ the depth of an orifice of area of cross-section $a,$ below the liquid surface, then find the velocity $v$ of flow through the orifice.

Since velocity

$=\sqrt{2gh}$

and by the equation of continuity,

${A}_{1}{v}_{1}={A}_{2}{v}_{2}$

So,

$v=\cfrac{a}{A}\sqrt{2gh}$

The diameter of a piston $P_{2}$ is $50\ cm$ and that of a piston $P_{1}$ is $10\ cm$ . What is the force exerted on $P_{2}$ when a force of $1\ N$ is applied on $P_{1}$ ?

$\dfrac { { A }_{ 1 } }{ { A }_{ 2 } } =\dfrac { { D }_{ 1 }^{ 2 } }{ { D }_{ 2 }^{ 2 } } =\dfrac { 1 }{ 25 }$

Since, Pressure = constant

${ P }_{ 1 }={ P }_{ 2 }$

$\dfrac { { F }_{ 1 } }{ { F }_{ 2 } } =\dfrac { { A }_{ 1 } }{ { A }_{ 2 } } =\dfrac { 1 }{ 25 }$

$1=\dfrac { { F }_{ 2 } }{ 25 } \Rightarrow \boxed { { F }_{ 2 }=25N }$

A container is filled with liquid upto height $H$ as shown in figure. There are $2$ holes in the container such that water coming out from them have same range. If the range of water coming out of the holes is half of maximum range, then find the distance $x$ between these holes.

Range

$=2\sqrt{(H-h)h}$

So,

${R}_{max}=H$

According to question,

$R=\cfrac{H}{2}=2\sqrt{(H-h)h}$

$\Rightarrow \cfrac{H}{4}=\sqrt{(H-h)h}$

$\Rightarrow \cfrac{H^{2}}{16}=(H-h)h$

$\Rightarrow \cfrac{H^{2}}{16}-Hh+h^{2}=0$

$\Rightarrow h=\cfrac{1\pm \sqrt{1-4\times 1\times \cfrac{1}{16}}}{2}H=\cfrac{1\pm \cfrac{\sqrt{3}}{2}}{2}H= \left(\cfrac{1}{2}-\cfrac{\sqrt{3}}{4}\right)H= 0.067H$

and

$x+2h=H$

$\Rightarrow x=H-2h=0.866H$

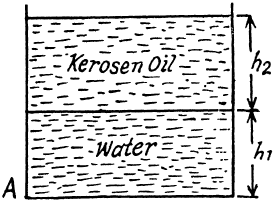
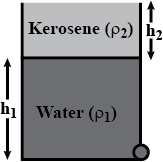
The figure shows two immiscible liquids (Kerosens and water). Kerosene has density $\rho_{2}$ and water has density $\rho_{1}$ . Find the velocity of water flow.

Applying Bernaulis theoram

${ P }_{ 0 }+{ \rho }_{ 2 }g{ h }_{ 2 }+{ \rho }_{ 1 }g{ h }_{ 1 }={ P }_{ 0 }+\cfrac { 1 }{ 2 } { \rho }_{ 1 }{ v }^{ 2 }\\ v=\sqrt { \cfrac { 2g\left( { \rho }_{ 1 }{ h }_{ 1 }+{ \rho }_{ 2 }{ h }_{ 2 } \right) }{ { \rho }_{ 1 } } } \\$

A fixed container of height $'H'$ with large cross-sectional area $'A'$ is completely filled with water. orifice of cross-sectional area $'a'$ are made, one at the bottom and the other on the vertical wall container at a distance $H/2$ from the top of the container. Find the time taken by the water level of a height of $H/2$ to get reduced to ground level .

$t=\cfrac { A }{ a } \left( \sqrt { { H }_{ 1 } } -\sqrt { { H }_{ 2 } } \right) \sqrt { \cfrac { 2 }{ g } }$

$t_{ 1 }$ -time taken to reduce water level to

$\cfrac { H }{ 2 }$ when only upper orifice is open

$t_{ 1 }=\cfrac { A }{ a } \left( \sqrt { { H } } \right) \sqrt { \cfrac { 2 }{ g } } \\ t_{ 1 }=\cfrac { A }{ a } \sqrt { \cfrac { 2H }{ g } }$

Similarly,

$t_{ 2 }=\cfrac { A }{ a } \left( \sqrt { { H } } -\sqrt { \cfrac { H }{ 2 } } \right) \sqrt { \cfrac { 2 }{ g } } \\ \quad =\cfrac { A }{ a } \left( \cfrac { \sqrt { 2 } -1 }{ \sqrt { 2 } } \right) \sqrt { \cfrac { 2H }{ g } }$

$T$ -time taken when both are open

$\cfrac { 1 }{ T } =\cfrac { 1 }{ t_{ 1 } } +\cfrac { 1 }{ t_{ 2 } } \\ T=\cfrac { \cfrac { \sqrt { 2 } -1 }{ \sqrt { 2 } } \sqrt { \cfrac { 2H }{ g } } }{ 1+\cfrac { \sqrt { 2 } -1 }{ \sqrt { 2 } } } \\ T=\cfrac { \sqrt { 2 } -1 }{ 2\sqrt { 2 } -1 } \sqrt { \cfrac { 2H }{ g } }$

A tank is filled with water up to a height $H$ . Water is let out of a hole $P$ from one of the walls, at a depth $D$ below the surface of the water. Express the range of the efflux $x$ in terms of $H$ and $D$ .

Time taken to fall the liquid

$t=\sqrt { \cfrac { 2\left( H-D \right) }{ g } } \\ v=\sqrt { 2gD } \\ x=\sqrt { 2gD } \times \sqrt { \cfrac { 2\left( H-D \right) }{ g } } \\ x=2\sqrt { D\left( H-D \right) }$

Two vertical parallel glass plates are partially submerged in water. The distance between the plates is d and the length is L. Assume that the water between the plates does not reach the upper edges of the plates and that the wetting is complete. To what height will the water rise? $(\rho =$ density of water and $\sigma =$ surface tension of water).

R.E.F image

Let F be the face carved

due to surface tension

$F = TL$

Capillary use can found out

as the rise of fluid due

to surface forces

Let h be the use from

the surface

Using newton's laws, we can found the Weight

Surface tension force = weight of fluid

$2\sigma = \rho \times (d\&h)\times g$

$h = \dfrac{2\sigma }{\rho h_{g}d}$

$h = \dfrac{2\sigma }{\rho gd}$

1145720_873823_ans_920ff597f7654fbba67b49d602ff1b86.jpg

A large cylindrical tank of cross-sectional are $1m^{2}$ is filled with water. It has a small hole at a height of $1m$ from the bottom. A movable piston of mass 5kg is fitted on top of the tank such that it can slide in the tank freely. A load of 45kg is applied on the top of water piston as shown in figure. Find the value of v when piston is 7m above the bottom( $g=10m/s^{2}$ )

Applying Bernaulis theorem on upper and lower part of the vessel

${ P }_{ 0 }+50\times 10\times 1+1000\times 10\times 7=\cfrac { 1 }{ 2 } \rho { v }^{ 2 }+{ P }_{ 0 }\\ v=\sqrt { \cfrac { \left( 500+70000 \right) 2 }{ 1000 } } \\ v=\sqrt { \cfrac { 705 }{ 5 } } \\ v=\sqrt { 352.5 } \\ v=18.8m/s$

Spherical particles of pollen are shaken up in water and allowed to settle. The depth of water is $2 \, \times \,10^{-2}$ m. What is the diameter of the largest particles remaining in suspension one hour later? Density of pollen = $1.8 \, \times \, 10^3 \, kg \, m^{-3}$ , viscosity of water = $1 \, \times \, 10^{-2}$ poise and density of water = $1 \, \times \, 10^{3} \, kg \, m^{-3}.$

Terminal velocity,

$v\, \, = \, \, \dfrac{2 \, r^2 }{9} \, \dfrac{(\rho-\sigma)g}{\eta}$

But we know V =

$v \, = \, \dfrac{s}{t}$

$\therefore \, \dfrac{s}{t} \, = \, \dfrac{2}{9} \, \dfrac{r^2(p \, - \, \sigma)}{\eta} \, \Rightarrow \, r^2 \, \dfrac{9s}{2t} \, \dfrac{\eta}{(p \, - \, \sigma)g}$

Given

$S \, = \, 2 \, \times 10 ^2 \, \,m, \, \, t =\,1 \,\,h \, = \,3600s$

$\therefore \, \eta \, =\,1\times10^{-2}posie\, = \,1 \times10^{-3} m^{-1}\, s^{}-1$

Substituting given values, we get

$r^{2} \, = \, \dfrac{9}{2} \, \times \, \dfrac{2 \, \times \, 10^{-2}}{3600} \, \times \, \dfrac{1 \, \times \, 10^{-3}}{(1.8 \, \times \, 10^{3} \, -1 \, \times \, 10^3) \, \times \, 10} \, = \, \dfrac{9}{36} \, \times \, \dfrac{1}{8} \, \times \,10^{-10}$

$\dfrac{1}{32}\times 10^{-10}$

$\therefore r = \sqrt{\dfrac{100}{30}} \times 10^{-6}m = 1.77 \times 10^{^{-6}} m$

Diameter D = 2r =

$2 \times 1.77\mu m = 3.54 \mu m$

A capillary tube is dipped in water vertically. It is long enough for the water to rise to the maximum height h in the tube. The length of portion immersed in water is l < h. The lower end of the tube is closed and then the tube is taken out and opened again. Will all the water flow out of tube? Explain.

No, the water will not flow out. When the tube is taken out, a convex meniscus is formed and force due to surface tension comes into play in the upward direction which keeps the water column remaining in the tube will be l + h

The end of a capillary tube with a radius r is immersed in water. Is mechanical energy conserved when the water rises in the tube? The tube is sufficiently long. If not, calculate the energy change.

In the equilibrium position (

$\theta \, = 0 \,$ for water and glass)

$2\pi rT = \, cos \theta \, = \pi r^{2}hpg$
or

$h= \, \frac{2 T}{\rho gr}$
Work done by surface tension =

$\left (2\pi rT \right ) \times h = \frac{4\pi T^{2}}{pg}$
The potential energy of water in the tube, U = (

$\pi r^{2}hp$ )gh/2; it is multiplied by h/2 because the centre of gravity of the water and the capillary tube is at a height h/2
U =

$\dfrac{2\pi T^{2}}{pg}$
Thus, it is seen that the mechanical energy is not conserved.
Therefore, mechanical energy loss =

$\dfrac{4\pi T^{2}}{pg}- \dfrac{2\pi T^{2}}{pg} = \dfrac{4\pi T^{2}}{pg}$
This energy is converted into heat.

If a 5 cm long capillary tube with 0.1 mm internal diameter, open at both ends, is slightly dipped in water having surface tension 75 dyne/cm, state whether:
water will overflow out of the upper end of capillary. Explain your answer.

Given the surface tension of water,

T = 75 dyne/cm

Radius r = 0.1/2 mm = 0.05 mm = 0.005 mm

$density \ \rho = 1 gm / cm^3$ , angle of contact,

$\theta = \,0^\circ$

Let h be the height to which water rise in capillary tube

Then

$h \, = \dfrac{2Tcos \theta }{rpg} \, =\,\dfrac{2 \times 75 \times cos 0^{\circ}} {0.005 \times 1 \times 981} cm \, =\,30.58 cm$

But the length of capillary tube, h = 5 cm

c. The water will not overflow out of the upper end of the capillary. It will rise only up to the upper end of the capillary

The liquid meniscus will adjust its radius of curvature R in a such a way that

$R^1h^1 \,=\,Rh \left [ hR = \dfrac{2T}{\rho g} \,= \,constant \right ]$

Where R is the radius of curvature liquid meniscus would possess if the capillary tube were of sufficient length

$R^1\, =\,\dfrac{Rh}{h} \,=\,\dfrac{rh}{h^1} \left [ R \,= \,\dfrac{r}{cos\theta} \,=\,\dfrac {r}{cos 0^{\circ}} \,= r \right ]$

$= \,\dfrac{0.005 \times 30.58}{5} \,= \,0.0306 \,cm$

Two liquid gets coming out of the small holes at $P$ and $Q$ intersect at the point $R$ . Find the position of $R$ if we maintain the liquid level constant.

${ v }_{ p }=\sqrt { 2gh }$

${ v }_{ r }=\sqrt { 2g.2h } =\sqrt { 4gh }$

${ y }_{ p }-h=\cfrac { 1 }{ 2 } g{ t }^{ 2 }\quad \quad \left[ { t }^{ 2 }=\cfrac { { x }_{ p }^{ 2 } }{ { v }_{ p }^{ 2 } } =\cfrac { { x }_{ p }^{ 2 } }{ 2gh } \right]$

${ y }_{ p }=h+\cfrac { 1 }{ 2 } g.\cfrac { { x }_{ q }^{ 2 } }{ 4gh }$

(Image 1)

Similarly,

${ y }_{ q }={ y }_{ q }={ y }_{ 0 }$ &

${ x }_{ p }={ x }_{ q }={ x }_{ 0 }$

$\Rightarrow h+\cfrac { 1 }{ 2 } g.\cfrac { { x }_{ 0 }^{ 2 } }{ 2gh } =2h+\cfrac { 1 }{ 2 } g\cfrac { { x }_{ 0 }^{ 2 } }{ 4gh }$

$h=\cfrac { 1 }{ 2 } g\cfrac { { x }_{ 0 }^{ 2 } }{ gh } \times \left( \cfrac { 1 }{ 2 } -\cfrac { 1 }{ 4 } \right)$

(Image 2)

$\Rightarrow { x }_{ 0 }^{ 2 }=8{ h }^{ 2 }$

${ x }_{ 0 }=2\sqrt { 2 } h\Rightarrow { y }_{ 0 }=h+\cfrac { 1 }{ 4h } .28{ h }^{ 2 }\Rightarrow y=3h$

1144958_985007_ans_9a42caffb36843ba8ffbb94775589489.png

The area of cross section of the wider tube shown in fig. is 900 cm $^2$ . If the body standing on the position weighs 45 kg, find the difference in the levels of water in the two tubes.

Given that,

m= 45 kg = 45000g

A = 900 cm²

Ρ = 1000 kg/m³ = 1 g/cm³

Let, the difference in the height of the water level be $h\ units$ .

Now,

According to the figure

${{P}_{a}}+h\rho g={{P}_{a}}+\dfrac{mg}{A}$

$h=\dfrac{m}{A\rho }$

Put the values of all elements

$h=\dfrac{45\times 1000}{900\times 1}$

$h=50\,cm$

Hence, the difference in the levels of water in the two tubes is $50\$ cm.

The flow rate of a water from a tap of diameter $1.25\ cm$ is $0.48\ L/min$ . If the coefficient of viscosity of water is $10^{-3}\ Pa\ s$ , what is the nature of flow of water?

Let the speed of the flow be V.

The diameter of the tap = d

= 1.25 cm

= 1.25

$\times 10^{-2}$ m

Density of water =

$\rho = 10^3 kg$

$m^{-3}$

viscosity =

$\eta = 10^{-3}$ Pa s

The volume of the water flowing out per second is

Q =

$V \times \frac{\pi d^2}{4}$

V =

$\frac{4Q}{d^2\pi}$

The Reynolds number is given by

R =

$\frac{\rho Vd}{\eta}$

$\frac{4\rho Q}{\pi d \eta}$

$\frac{4 \times 10^3 \times Q}{3.14 \times 1.25 \times 10^{-2} \times 10^{-3}}$

$1.019 \times 10^8 Q$

Hence the flow is turbulent.

Water is flowing through a horizontal tube. The pressure of the liquid in the portion where velocity is $2\ m/s$ is $2\ m$ of $Hg$ . What will be the pressure in the portion where velocity is $4\ m/s$

According to Bernoulli,s principle

$P_1 + \dfrac{1}{2}\rho v_1^2+\rho gh_1$

$=P_2+ \dfrac{1}{2}\rho v_2^2+\rho gh_2$

$\Rightarrow$

$2 mHg+ \dfrac{1}{2}\rho (2)^2$

$=P_2+ \dfrac{1}{2}\rho (4)^2$

$\Rightarrow P_2 = \dfrac{1}{2}\times 10 ^3(2^2-4^2) +2mHg$

$\Rightarrow P_2 =-6000 +2 Hg$

$\Rightarrow -\dfrac{6000}{101325}(0.76)mHg +2mHg$

$\Rightarrow P_2 = 1.955$ m of Hg

The pressure of liquid column ____________ with the depth of column.

The pressure of the liquid column will increase with the depth of the column.

Pressure in a liquid column varies as,

$P = h\rho g$

Calculate the amount of energy evolved when $8$ droplets of water of radius $0.5\ mm$ each combine into one. Surface tension of water is $72\ dyne\ c{m}^{-1}$ .

The volume surface of the droplet which spherical in shape is given as

$V = \frac{4}{3}\pi {R^3}$

The volume of the eight droplet is

$V = 8 \times \frac{4}{3}\pi {\left( {0.5} \right)^3}$

On equation the above two equation we get the radius of the combined droplet

The radius is $1\;mm$

The surface energy of the droplet will be

$\Delta E = 8 \times 4\pi {\left( {\frac{1}{2} \times \frac{1}{{1000}}} \right)^2} \times 0.072 - 4\pi {\left( {\frac{1}{{1000}}} \right)^2} \times 0.072$

The energy evolved will be ${\rm{9 \times 1}}{{\rm{0}}^{{\rm{ - 7}}}}{\rm{J}}$

Two cylindrical vessels fitted with pistons A and B of area of cross section 8 $cm^2$ and 320 $cm^2$ respectively are joined at their bottom by a tube and they are completely filled with water. When a mass of 4 kg is placed on piston A, find: (i) the pressure on piston A , (ii) the pressure on piston B, and (iii) the thrust on piston B.

Given

Force applied to the smaller piston A

$=4\ kg$

Area of cross section of piston A

$=8\ cm^2$

Area of cross section of piston B

$=320\ cm^2$

(i) Pressure acting on piston A in the downwar direction

$=\frac {Thrust }{Area}$

$=\frac{4}{8}=0.5\ kg/cm^2$

$\therefore$ Pressure acting on piston A

$=0.5\ kg/cm^2$

(ii) according to pascal's law

Pressure acting on piston A= Pressure acting on piston B

$=0.5\ kg/cm^2$

(iii) Thrust acting on piston B in the upward direction

$=Presuure\times Area\ of B$

$=4\times\frac{32}{8}=160\ kg$

$\therefore$ Thrust acting on piston B in the upward direction

$=160\ kg$

find the angle of ${\phi _1}$ .

$\tan {\phi _1} = \dfrac{1}{1}$

$\tan {\phi _1} = 1\,\,\,\,\,\,\tan {45^ \circ } = 1$

$So,\,\,\tan {45^ \circ } = 1$

$\therefore {\phi _1} = {45^ \circ }$
1157115_1058448_ans_5dffcd1110c94b388e6132c17cb3d4dd.png

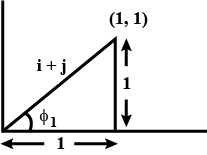
If an oil drop of density $0.95\times 10^{3}\ kg\ m^{-3}$ and radius $10^{-4}\ cm$ is falling in air whose density is $1.3\ kg\ m^{-3}$ and coefficient of viscosity is $18\times \ 10^{-6}\ kg\ m^{-1}s^{-1}$ . Calculate the terminal speed of the drop.

1380316_1113192_ans_044831d259084b64a9b12fd213ed7e07.jpg

What will be the terminal velocity of a steel ball of radius $2\ mm$ in glycerine?

1328078_1112571_ans_b30b622dc28e4580acdd299699e08268.jpg

A wind speed 40 m/s blows parallel to the roof of a house. The area of the roof is $250 m^2$ Assuming that the pressure inside the house is atmospheric pressure,the force exerted by the wind on the roof and the direction of the force will be:

Let p₁ and p₂ are pressure inside and outside the roof and v₁ and v₂ are velocities of the wind inside and outside the roof.

According to Bernoulli’s theorem

${{p}_{1}}+\dfrac{1}{2}\rho v_{1}^{2}={{p}_{2}}+\dfrac{1}{2}\rho v_{2}^{2}$

${{p}_{1}}-{{p}_{2}}=\dfrac{1}{2}\times 1.2\times ({{40}^{2}}-0)$

${{p}_{1}}-{{p}_{2}}=960\,N/{{m}^{2}}$

Force is

$F=({{p}_{1}}-{{p}_{2}})A=960\times 250$

$24\times {{10}^{4}}\,N$

Water is flowing through a horizontal tube $4\ km$ in $4\ cm$ in radius at a rate of $20\ litre\ s^{-1}$ Calculate the pressure required to maintain the flow in terms of the height of mercury column.?

1343656_1112137_ans_842bab2f4a8d4a1fb286661b7203eff9.jpg

Rain drops, each of radius r, are falling through air with steady velocity v. If eight drops coalesce to form a big drop, then the big drop so formed will fall with velocity ?

Falling with uniform speed means the drops have acheived terminal speed. Let us find the radius R of the bigger drop in terms of the radius r of the smaller drop. We use conservation of volume to arrive at the result.

$8\times \dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi R^3\Rightarrow R=2r$

Now terminal speed is directly proportional to square of radius,

$\therefore \dfrac{v}{v'}=\dfrac{r^2}{R^2}=\dfrac{r^2}{(2T)^2}$

$\Rightarrow v'=4v$

$\therefore$ Big drop will fall with velocity

$4v$ .

A horizontal pipe line carries water in a streamline flow. At a point along the tube where the cross-sectional area is $10^{-2}$ $m^2$ , the water velocity is $2$ $ms^{-1}$ and the pressure is $8000$ Pa. The pressure of water at another point where the cross-sectional area is $0.5\times 10^{-2}m^2$ is?

$P_1 - P_2 = \cfrac{1}{2}\rho (v_2^2 - v_1^2)$

$\cfrac{1}{2} \rho (v_2^2 - v_1^2)$

$\cfrac{1}{2} \rho v_1^2(\cfrac{v_2^2}{v_1^2}-1)$

$\cfrac{1}{2} \times 1000 \times (\cfrac{100}{25} -1)$

$P_2-8000 = 1500$

$P_2 = 9500$ Pa

The density of the atmosphere at sea level is $1.29kg/{m}^{3}$ and $g=9.8m/{s}^{2}$ . Assume that both do not change with altitude, how high should the atmosphere extend?

Given,

$\rho =1.29kg/m^3$

$P=1\times 10^5 Pa$ atmospheric pressure

$g=9.8m/s^2$

The pressure,

$P=\rho gh$

$h=\dfrac{P}{\rho g}=\dfrac{1\times 10^5}{1.29\times 9.8}$

$h=7.910 km$

Two identical vessels with their bases at same level each contains a liquid of density $\rho$ . The height of the liquid in one vessel in $h_1$ and that in other is $h_2$ , the area of either bases is $A$ . What is the work done by the gravity in equalizing the levels when two vessels are connected?

1336716_1122580_ans_22bcb893dcfc407a95e5a498316dc9da.jpg

Two drops of equal radii are falling through air with a terminal velocity of $5\ cm\ s^{-1}$ . If they coalesce into one drop, what will be the terminal velocity of the new drop?

Let

$x$ be the radius of each drop

The terminal velocity

$(v)=\dfrac {2}{9}.r^2 \dfrac {(\rho 5)g}{4}$

where

$5$ and

$4$ are the density and vescosity at are respectively

$\rho$ is the density of the drop

Volume at each drop

$=\dfrac {4}{3}\times r^3$

The volume of coalesed drop

$=2\times \dfrac {4}{3}\times r^2 =\dfrac {4}{3}\times \left (2^{1/3}r\right)^3$

So Radius of collapsed drop

$=(2)^{1/3}r$

$\therefore$ Now the terminal velocity at the collapsed drop

$v=4(2^{1/3}r)^2 =2^{2/3}4r^2 =2^{2/3}v$

$\therefore \$ Hence the terminal velocity of the collapsed drop is

$7.94\ cm/s$

Show that the pressure in a fluid at rest in same at all points if we ignore gravity.

Pascal's first law states pressure in a fluid is same at all points. Consider a small cube containing fluid, and forces on each face be

$F_1, F_2$ …..

Considering Equilibrium,

$\displaystyle\sum F_x=0$

$\displaystyle\sum F_y=0$

$\displaystyle\sum M=0$

$\Rightarrow \displaystyle F_1=F_2$

$\Rightarrow F_3=F_4$

$\Rightarrow F_1=F_2=F_3=F_4$

Now areas of each surface is A, so:-

$\dfrac{F_1}{A}=\dfrac{F_2}{A}=\dfrac{F_3}{A}=\dfrac{F_4}{A}$

$\Rightarrow P_1=P_2=P_3=P_4$ .

A body of mass $2 kg$ is let fall from top of a $10 m$ tall building. It lands on a sandy patch of ground and burries itself $20 cm$ deep in the sand. Find the average resistance offered to it by the sand. Also find the approximate time of penetration.

1310568_1139062_ans_bd863e08659f41cab5579759a1262cae.jpg

In a venturimeter, the diameter of the pipe is $4\ cm$ and that of constriction is $3\ cm$ . The heights of the liquid of density $1.5\ gm/cc$ in the pressure tube is $20\ cm$ at the pipe and $5\ cm$ at the constrictions. What is the discharge rate of water flowing inside the pipe?

1310740_1138599_ans_2eff1e09b36e4bc3af5972273d0f5847.jpg

Derive expression for terminal velocity when a ball of radius r is dropped thrugh a liquid of viscousity $\eta$ and density $\rho$ .

1059097_1162318_ans_e5ebe04b7d1e4b4e8c535031317cd486.png

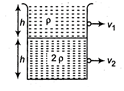
Equal volumes of two immiscible liquids of densities p and 2p are filled in a vessel as shown in the figure. Two small holes are punched at depth $\dfrac{h}{2}$ and $\dfrac{3h}{2}$ from the surface of lighter liquid. If ${{v}_{1}}$ and ${{v}_{2}}$ are the velocities of efflux at these holes, then $\dfrac{{{v}_{1}}}{{{v}_{2}}}$ will be:

We have,

${{v}_{1}}=\sqrt{2g\times \left( \dfrac{h}{2} \right)}$

${{v}_{1}}=\sqrt{gh}$

Now, by using Bernoulli’s theorem

$\rho gh+2\rho g\left( \dfrac{h}{2} \right)=\dfrac{1}{2}\left( 2\rho \right)v_{2}^{2}$

${{v}_{2}}=\sqrt{2gh}$

Now, the value of $\dfrac{{{v}_{1}}}{{{v}_{2}}}$

$\dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{\sqrt{gh}}{\sqrt{2gh}}$

$\dfrac{{{v}_{1}}}{{{v}_{2}}}=\dfrac{1}{\sqrt{2}}$

Hence, this is the required solution

Water rises to a height of 10 cm in a capillary tube and mercury falls to a depth of the same capillary tube. If the density of water is 1 gm/c.c and its angle of contact is $0^{\circ}$ , then the ratio of such of two liquids is ( cos $135^{\circ}$ =0.7)

Let a liquid of density ρ rise a height h in a capillary of raduis r, then we can write

hrρg = 2Tcosθ

where T is surface tension of that liquid and θ is angle of contact.

Let Tm and Tw be the surface tension of water and mercury.

Tm/Tw = [(3.112 * 13.6)/(10 * 1)] * [cos0 / cos(135)]

θw is the angle of contact of water 0 degrees

= 5.98

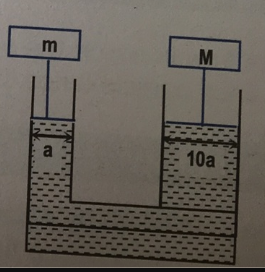
When the system shown in the adjoining fig. is in equilibrium and the areas of cross sec. of the small and big piston are $'a'$ and $'10a'$ , then what is the value of $m/M$ ?

The pressure at the smaller and larger pistons is equal.

So,

$P_1 =P_2$

$\dfrac{F_1}{A_1} = \dfrac{F_2}{A_2}$

$\dfrac{mg}{a} = \dfrac{Mg}{10a}$

$\implies \ \dfrac{m}{M} = \dfrac{1}{10}$

What is the effect of temperature on angle of contact?

It means

$,$ if the temperature increases

$,$ angle of contact decreases due to decrease cohesive force and if the temperature decreases

$,$ angle of contact increases due to increase cohesive force

$.$

Calculate the work done in blowing a soap bubble from a radius of $2\ cm$ to $3\ cm$ . The surface tension of the soap solution is $30\ dyne\ cm^{-1}$ .

Water is flowing through a pipe of non unifrom cross section. at the point when the velocity of flow is 35 cm/s, the pressure is 1 cm of mercury. What is the pressure at the point where the velocity of flow is 65 cm/s?(0.887 cm of mercury)

According to Bernoulli's eqn.

$P + pgh + \dfrac{1}{2}pv^2 = constant$

$1g+0.5p35^2=1gh+0.565^2$

$gh=1\times 10\times 1+0.5\times 1\times 35^2-0.5\times 1\times 65^2$

$gh=1490cm$

$h=\dfrac{1490}{10}=149cm$

The flow rate of water from a tap of diameter $1.25$ cm is $0.48$ $L/min$ . the coefficient of viscosity of water is ${ 10 }^{ -3 }$ $Pa-s$ . After sometime, the flow rate is increased to $3$ $L/min$ . Characterize the flow for both the flow rates.

Let the speed of the flow be v and the area of tap be

$d = 1.2$ cm. The volume of the water flowing out per second is

$Q = v \times \pi d^2 /4$

$v = 4Q/d^2$
Reynold’s number is

$R_e = 4P^22 / \pi d\eta$

$= 4 \times 10^3kg/m^3\times Q/(3.14 \times 1.2 \times 10^{-2}m \times 10^{-1}Pa\,s)$

$= 1.061 \times 10^8 m^{-3}s$

$Q = 1.061 \times 10^8Q$
Initially,

$Q = 0.48\,L/min = 8.0\,cm^3/s$

$= 8.00 \times 10^{-6}m^3/s$
we obtain

$R =484.8$
Since this is below 1000, the flow is steady.
After sometime when

$Q = 4L/min$ ,

$= 66.67\,cm^3/s$

$= 6.67 \times 10^{-5}\,m^3s^{-1}$
we obtain

$R = 1.061 \times 10^8 \times 6.67 \times 10^{-5}$

$= 7076.9$
The flow now is turbulent.

The area of a man's foot is $80\ \mathrm { cm } ^ { 2 }$ . How much pressure will the man exert on the ground, while standing, if the weight is $800\ N$ ?

Area of foot

$A=80\ cm^2$

$\Rightarrow A=\dfrac{80}{10000}m^2$

Weight

$F = 800\ N$

$\text{Pressure}=\dfrac{weight}{Area}$

$\Rightarrow P=\dfrac{800}{80/10000}$

$\Rightarrow P=98000$ Pascals.

What is the pressure on a swimmer 10 m below the surface of a lake?

Let atmospheric pressure

$=P_o=1.05\times 10^5$ Pa

Pressure

$10$ m below surface of lake,

$P=P_o+\displaystyle\rho gh$

$=1.05\times 10^5+1000\times 9.8\times 10$

$-1.99\times 10^5Pa$

$=2$ atm (

$\rho\rightarrow$ Density of water

$=1000$ kg

$/m^3$ ,

$g=9.8m/s^2$

$h\rightarrow$ Depth

$=10$ m).

1167841_1330204_ans_16aa1d57d3554380a80c0bb107022ad4.jpg

Write any two practical applications of stoke's law.

Applications of Stoke's law are as follows:
Rain drop do not acquire alarmingly high velocity during their free fall. If this does not happen a person moving in rain would get hurt.
While jumping from an airplane, parachute helps us to land safely on the earth.
It is used to determine the value of charge on an electron. (Millikan’s oil drop method)

If pressure at half depth of a lake is equal to $2/3$ pressure at the bottom of the lake that what is the depth of the lake

According to the question,

pressure at half depth of lake

$=\dfrac{2}{3}$ (Pressure at bottom of lake)

$P_0+\rho g\dfrac{h}{2}=\dfrac{2}{3}(\rho gh+P_0)$

$(P_0+\rho g\dfrac{h}{2})3=2(\rho gh+P_0)$

$[P_0=10^5Pa, \rho =10^3kg/m^3]$

$3P_0+\dfrac{3}{2}\rho gh=2\rho gh+2P_0$

$P_0=\left(2-\dfrac{3}{2}\right)\rho gh$

$P_0=\dfrac{\rho gh}{2}$

$h=\dfrac{2P_0}{\rho g}=\dfrac{2\times 10^{5}Pa}{10^3kg/m^3\times 10m/s^2}=20m$ .

1197322_1399915_ans_5a04dc1e03c441e983f753b7644caa1f.jpg

The height of mercury in a barometer is 760 mm, then the atmospheric pressure is $\left[ g=9.8m/{ s }^{ 2 } \right]$

2050733_1399954_ans_b1f6faafd3534162958ce661cad3497b.jpg

Find the force exerted by the water on a $2\ m^{2}$ plane surface of a large stone placed at the bottom of a sea $500\ m$ deep. Does the force depend on the orientation of the surface?

1669718_1712435_ans_4ec7ad1368414562bf46ae2d86d82644.jpeg

A beaker of liquid accelerates from rest, on a horizontal surface, with acceleration $a$ to the right.
How does the pressure vary with depth below the surface?

$P = P_0 + \rho gh$

where

$h$ is the depth

Hovering over the pit of hell, the devil observed that as a student falls past ( with terminal velocity ), the frequency of the scream decreases from $842$ to $820\ Hz$ .
Find the speed of descent of the student.

When the student is coming towards the devil:

$f'=f(\dfrac{v}{v-v_s})=842$

When the student has gone past the devil:

$f''=f(\dfrac{v}{v+v_s})=820$

Dividing both the equations we get,

$\dfrac{v+v_s}{v-v_s}=\dfrac{842}{820}$

n calculation we get,

$v_s=\dfrac{11\times v}{831}=\dfrac{11\times 340}{831}=4.5\,m/s$

A rocket ejects the fuel (hot gases) of density $\rho$ from the chamber which is maintained at a pressure ${P}_{1}$ , say. The atmospheric pressure is ${P}_{0}$ . If the base area of the cylindrical chamber is ${A}_{1}$ and the area of the hole through which hot gases escape from the rocket is ${A}_{2}$ , find $(a)$ velocity of efflux of the fuel, $(b)$ thrust exerted on the rocket given by the escaping fuel.

$a.$ Let us consider two points

$1$ and

$2$ . Applying Bernoulli's equation, we have

${P}_{1}+\dfrac{1}{2}{\rho}{v}_{1}^{2}+{\rho}{gh}_{1}={P}_{2}+\dfrac{1}{2}{\rho}{v}_{2}^{2}+{\rho}{gh}_{2}$

Since

${\rho}{g}\left({h}_{1}-{h}_{2}\right)={\rho}{gh}$ is negligible compared to

${P}_{1}={P}$ (Pressure inside the chamber) and

${P}_{2}={P}$ (atmospheric pressure),

we have

${P}+\dfrac{1}{2}\rho{v}_{1}^{2}={P}_{0}+\dfrac{1}{2}{\rho}{v}_{2}^{2}$

$(i)$

Equation of continuity gives

${A}_{1}{v}_{1}={A}_{2}{v}_{2}$

$(ii)$

Since

${v}_{1}=\left({A}_{2}/{A}_{1}\right){v}_{2}$ and

${A}_{2}\||{A}_{1}$ , we can ignore

${v}_{1}$ when compared to

$v$
Then Eq.

$(i)$ gives

${v}_{2}=\sqrt{\frac{2\left(P-P_{0}\right)}{\rho}}$

$b.$ The impact force of the ejected gas is given as

${F}={\rho}{A}_{2}{v}_{2}^{2}$
where

${v}_{rel}={v}_{2}=\sqrt{\frac{2\left(P-P_{0}\right)}{\rho}}$

Then, we have

$F=2A_{2}\left(P-P_{0}\right)$ .

1555569_1735920_ans_ec066f05a94b4404952c9bb152e03ee8.JPG

Bernoulli's equation can be written in the following different forms (Column I). Column II lists certain units each of which pertains to one of the possible forms of the equation. Match the unit associated with each of the equation.

Kinetic energy is

$1/2 \,mv^2$ . Hence,

$\dfrac{v^2}{2g} = \dfrac{\left(\dfrac{1}{2} mv^2\right)}{mg}$

is energy per unit weight.

$\dfrac{\rho v^2}{2} = \dfrac{\left(\dfrac{1}{2}\right)}{m\rho}$

is energy per unit volume and

$\dfrac{v^2}{2} = \dfrac{\dfrac{1}{2} mv^2}{m}$
is energy per unit mass.

A pressure of 10 Pa acts on an area of $3.0 m^2$ . What is the force acting on the area? What force will be exerted by the application of same pressure if the area is made one-third?

$Pressure = \frac{Force}{Area}$

$Force = Area \times pressure$

$= 3 \times 10$

$= 30 N$
If the area is made one-third i.e.

$1m^2$ , then the force would be

$Pressure = \frac{Force}{Area}$

$Force = Area \times pressure$

$= 1 \times 10$

$= 10 N$

A partially evacuated airtight container has a tight-fitting lid of surface area $77\hspace{0.05cm}m^2$ and negligible mass. If the force required to remove the lid is $480\hspace{0.05cm}N$ and the atmospheric pressure is $1.0 \times 10^5\hspace{0.05cm}Pa$ , what is the internal air pressure?

The magnitude

$F$ of the force required to pull the lid off is

$F=(p_{\circ}-p_{i})A$ , where

$p_{\circ}$ is the pressure outside the box,

$p_{i}$ is the pressure inside, and

$A$ is the area of the lid. Recalling that

$1\hspace{0.05cm}N/m^2=1\hspace{0.05cm}Pa$ , we obtain

$p_{i}=p_{\circ}-\dfrac{F}{A}=1.0\times10^5\hspace{0.05cm}pa-\dfrac{480\hspace{0.05cm}N}{77\times10^{-4}\hspace{0.05cm}m_{2}}=3.8\times10^4\hspace{0.05cm}Pa$ .

Water flows through a fire hose of diameter $6.35\ cm$ at a rate of $0.0120\ m^{3}/s$ .
The fire hose ends in a nozzle with an inner diameter of $2.20\ cm$ . What is the speed at which the water exists the nozzle?

As we know,

$v=\dfrac{Q}{A}=\dfrac{flow \ rate}{area}$

$v=\dfrac{0.120}{\pi (1.1)^2\times10^{-4}}=31.6\ m/s$

The plastic tube in Figure has across-sectional area of $5.00\hspace{0.05cm}cm^2$ .The tube is filled with water until the short arm (of length $d= 0.800\hspace{0.05cm}m$ ) is full. Then the short arm is sealed and more water is gradually poured into the long arm. If the seal will pop off when the force on it exceeds $9.80\hspace{0.05cm}N$ , what total height of water in the long arm will put the seal on the verge of popping?

1750523_1770687_ans_facab5449ca64f868847366d05ac00d3.jpg

Why would an aircraft be unable to fly on the moon?

An aircraft needs air because air moving under the wings of aircraft is strong enough to hold it up and air is also required to burn the fuel in aircraft engines.Since there is no air on moon,an aircraft cannot fly on moon.

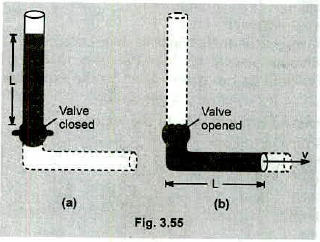
An incompressible, nonviscous fluid initially rests in the vertical portion of the pupe shown in Fig $3.55$ (a) where $L=2.00\ m$ . When the valve is opened, the fluid flows into the horizontal section of the pipe. What is the speed of the fluid when all of its is in the horizontal section as in Fig $3.55$ (b)? Assume that the cross-sectional area of the entire pipe is constant.

1668438_1746039_ans_586f4eff41fc4d72aee32a39798bc633.jpeg

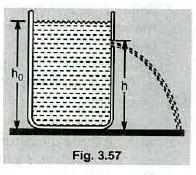
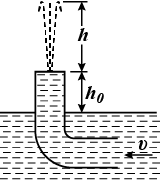
A large storage tank is filled to a height $h_{0}$ . The tank is punctured at a height $h$ above the bottom of the tank (Fig $3.57$ ). Find an expression for how far from the tank the exiting stream lands.

1668447_1746042_ans_6c1e9c074f2248a2bbcffaa49af5c4e4.jpeg

An office window has dimensions $3.4\hspace{0.05cm}m$ by $2.1\hspace{0.05cm}m$ . As a result of the passage of a storm, the outside air pressure drops to $0.96\hspace{0.05cm}atm$ , but inside the pressure is held at $1.0\hspace{0.05cm}atm$ . What net force pushes out on the window?

The pressure difference between two sides of the window results in a net force acting on the window.
The air inside pushes outward with a force given by

$p_{i}A$ , where

$p_{i}$ is the pressure inside the room and

$A$ is the area of the window. Similarly, the air on the outside pushes inward with a force given by

$p_{\circ}A$ , where

$p_{\circ}$ is the pressure outside. The magnitude of the net force is

$F=(p_{i}-p_{\circ})A$ . With

$1\hspace{0.05cm}atm=1.013\times10^5\hspace{0.05cm}Pa$ , the net force is

$F=(p_{i}-p_{\circ})A=(1.0\hspace{0.05cm}atm-0.96\hspace{0.05cm}atm)(1.013\times10^5\hspace{0.05cm}Pa/atm)(3.4\hspace{0.05cm}m)(2.1\hspace{0.05cm}m)=2.9\times10^4\hspace{0.05cm}N$ .

What should be the ratio of area of cross section of the master cylinder and wheel cylinder of a hydraulic brake so that a force of 15N can be obtained at each of its brake show by exerting a force of 0.5N on the pedal ?

Consider thew ratio of cross-section of the master cylinder and wheel cylinder be

$X_{1} :X_{2}$
Let the force applied on pedal be

$F^{1}=0.5N$
And the force applied on brake shoe
We know from the hydraulic machine,
Pressure on narrow piston = pressure on broader piston

$\dfrac{f_{1}}{x_{1}} = \dfrac{f_{2}}{x_{2}}$

$\Rightarrow \dfrac{f_{1}}{f_{2}} = \dfrac{x_{1}}{x_{2}}$

$\Rightarrow \dfrac{X_{1}}{X_{2}} = \dfrac{0.5}{15}$

$\Rightarrow \dfrac{X_{1}}{X_{2}} = 1/30$

$\Rightarrow$ Hence, the ratio is 1:30

A vessel contain water up to a height of 1.5m.Taking the density of water $10^{3}kg m^{-3}$ acceleration due to gravity $9.8ms^{-2} and area of base vessel$ 100^{2}, calculate ;
the pressure and

To calculate pressure:
Given: h = 1.5m, p = 1000, g = 9.8m/

$s ^{2}$
P = h p g
=

$1.5\times 1000\times 9.8$
= 14700Pa

A normal force of $200 N$ acts on an area of $0.02 m^2$ Find the pressure in pascal.

Pressure =

$\dfrac {Force}{Area}$

$= \dfrac { 200N}{0.02 m^2}$

$= \dfrac { 200 \times 100}{2} = 10,000 N/m^2$ or

$10,000$ Pascal

A man first swims in sea water and then in river water. Where does he find it easier to swim and why?

The man will find it easier to swim to swim in sea water as the density of sea water is more than that of the river water. Therefore, his weight is balanced in sea water with lesser part of his immersed inside it.

A block of iron of mass 7.5 kg and of dimension $12cm\times8cm\times 10cm$ is kept on a table top on its base of side $12cm \times8cm$ . Calculate :
pressure exerted on the table top. Take 1kg = 10N

To calculate pressure exerted
Pressure = thrust/area
=75/0.0096
=7182.5Pa

A pitot tube on a high-altitude aircraft measures a differential pressure of 180 Pa. What is the aircrafts airspeed if the density of the air is $$0.031\hspace{0.05cm} kg/m^3?

We use the formula

$v=\sqrt{\dfrac{2\vartriangle p}{\rho_{air}}}$
$$v=\sqrt{\dfrac{2(180\hspace{0.05cm}Pa)}{0.031\hspace{0.05cm}kg/m^3}}
=1.1\times 10^2\hspace{0.05cm}m/s$$

Water is moving with a speed of $5.0\hspace{0.05cm}m/s$ through a pipe with a cross-sectional area of $4.0\hspace{0.05cm}cm^2$ . The water gradually descends 10 m as the pipe cross-sectional area increased to $8.0\hspace{0.05cm}cm^2$ . (a)What is the speed at the lower level?
(b)If the pressure at the upper level is $1.5\times 10^5 \hspace{0.05cm}Pa$ , what is the pressure at the lower level?

(a) We use the equation of continuity:

$A_{1}v_{1}=A_{2}v_{2}$ . Here

$A_{1}$ is the area of the pipe at the top and

$v_{1}$ is the speed of the water there;

$A_{2}$ is the area of the pipe at the bottom and

$v_{2}$ is the speed of the water there. Thus

$v_{2}=(A_{1}/A_{2})v_{1}=[(4.0\hspace{0.05cm}cm^2)/(8.0\hspace{0.05cm}cm^2)]()=2.5\hspace{0.05cm}m/s$
(b) We use the Bernoulli equation:

$p_{1}+\dfrac{1}{2}\rho v_{1}^2+\rho gh_{1}=p_{2}+\dfrac{1}{2}\rho v_{2}^2+\rho gh_{2},$
where

$\rho$ is the density of water,

$h_{1}$ is its initial altitude, and

$h_{2}$ is its final altitude. Thus,

$p_{2}=p_{1}+\dfrac{1}{2}\rho (v_{1}^2-v_{2}^2)+\rho g(h_{1}-h_{2}) =1.5\times 10^5\hspace{0.05cm}Pa +\dfrac{1}{2}(1000\hspace{0.05cm}kg/m^3)\bigg[ (5.0\hspace{0.05cm}m/s^2)^2-(2.5\hspace{0.05cm}m/s)^2\bigg] +(1000\hspace{0.05cm}kg/m^3)(9.8\hspace{0.05cm}m/s^2)(10\hspace{0.05cm}m)=2.6\times 10^5\hspace{0.05cm}Pa$

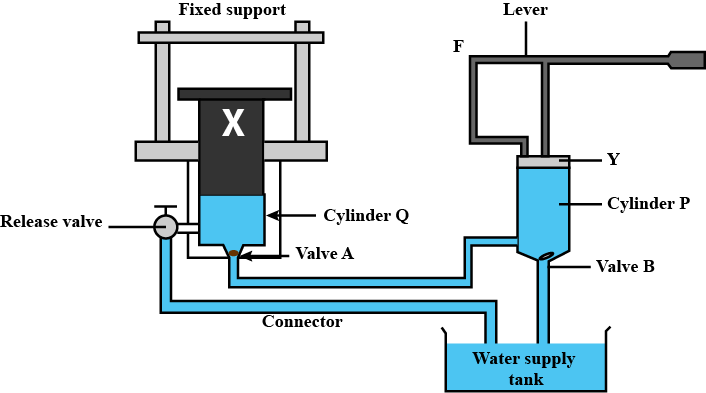
The diagram in figure shows a device which makes use of the principal of transmission of pressure.
Name the parts labelled by the letters X and Y.

X - press plunger
Y - Pump plunger

Two cylindrical vessels fitted with pistons A and B of area section $8cm^{2}$ and $320cm^{2}$ respectively are joined at their bottom by a tube and they are completely filled with water. When a mass of $4kg$ is placed on piston A, find the pressure on piston A,

$\text{Given that the force applied to the smaller piston A is 4 kg}$

$\text{Area of cross section of piston A=8cm}^{2}$

$\text{Area of cross section of piston B=320cm}^2$

$\text{Pressure acting on piston A in the downward direction =}\dfrac{\text{Thrust}}{\text{Area}}$

$=\dfrac{4kg}{8cm^2}$

$\therefore \text{Pressure A=0.5kg cm}^{-2}$

A hammer exerts a force of 1.5 N on each of the two nails A and B. The area of cross section of to of nail A is $2mm^{2}$ while that of nail B is $6mm^{2}$ . Calculate pressure on each nail in pascal.

1887433_1810526_ans_7f8c4a6bf7f34b319f0c3a458e8ccb45.jpg

What force is applied on a piston of area of cross section $2cm^{2}$ to obtain a force $150N$ on the piston of area of cross section $12cm^{2}$ in a hydraulic machine?

1962719_1810570_ans_4af2c2d6d4464e4ea2b27378723f6b82.jpg

Write the numerical value of the atmospheric pressure on the surface of the earth in pascal.

$1.013 \times 10 Pa.$

Why is the meant by the statement 'the atmospheric pressure at a place is $76$ cm of Hg ? State its value in Pa.

1887449_1810417_ans_87a80a90a7374e8daa1c6107049772cf.jpg

The areas of pistons in a hydraulic machine are $5 cm^{2} and 625 cm^{2}$ What force on the smaller piston will support a load of 1250N on the larger piston? State any assumption which you make in your calculation.
Assumption:There is no friction and no leakage of liquid.

Given:
Area of narrow piston =

$5 cm^{2} = A_{1}$ , Let force applied be

$F_{1}$ ,
Area of wider piston =

$625 cm^{2} = A_{2}$ , let force applied be

$F_{2}$ =1250N
We know from the hydraulic machine,

$\dfrac{F_{1}}{A_{1}}=\dfrac{F_{2}}{A_{2}}$

$\Rightarrow \dfrac{F_{1}}{5} = \dfrac{1250}{625}$

$\Rightarrow F_{1} = 10N$

Explain shape of meniscus for different liquids in capillary.

We know that, the height rises in the capillary tube,

$h = \frac{2T \cos \theta} {r \space p \space g}$

For pure water, the value of angle of

$\theta$ is very small.

$\therefore \cos \theta \approx 1$

$\Rightarrow h = \frac{2T} {r \space p \space g}$

where r is the radius of the capillary tube.

A clean capillary tube of uniform bore is fixed vertically with its lower end dipping into water taken in a beaker. A needle N is also fixed with the capillary tube as shown in the figure. The tube is raised or lowered until the tip of the needle just touches the water surface.

A travelling microscope M is focused on the meniscus of the water in the capillary tube. The reading

$R_1$ corresponding to the lower meniscus is noted. The microscope is lowered and focused on the tip of the needle and the corresponding reading is taken as

$R_2$ . The difference between

$R_1$ and

$R_2$ gives the capillary rise h.

The radius of the capillary tube is determined using the travelling microscope. If p is the density of water then the surface tension of water is given by

$T = \frac{rhpg} {2}$

where g is the acceleration due to gravity.

When a liquid rises in a capillary tube, the weight of the liquid column of density p inside the tube is supported by the surface tension (upward) acting around the circumference of the points of contact.

$T = \frac{r \left(h + \frac{r} {3} \right)} {2 \cos \theta}$

where

$h \rightarrow$ height of the liquid column above the liquid meniscus

$p \rightarrow$ density of the liquid

$r \rightarrow$ inner radius of the capillary tube

1754875_1833449_ans_fc63ddcc1ca34437b4fd6caaa52d7df6.png

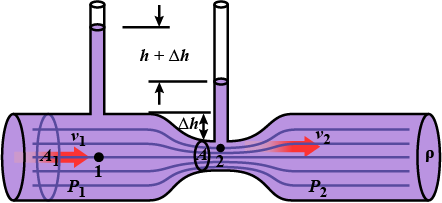
Derive a formula to measure the rate of flow of a liquid through venturi meter.

Venturi meter :

This device is used to measure velocities and mass rate of flow of liquid at the different cross-sections of a pipe. It consists of a constriction inserted in a pipe line and have tapers at the inlet and outlet, so that turbulence is avoided. See fig. 11.21.

Let at the cross-sectional areas

$A_1$ and

$A_2$ , the velocities are

$v_1$ and

$v_2$ respectively.

From the equation of continuity,

$A_1 v_1 - = A_2 v_2$

From Bernoulli's theorem,

$P_1 + \frac{1} {2} v^{2}_1 = P_2 + \frac{1} {2} v^{2}_2$

or,

$P_1 - P_2 = \frac{1} {2} \left(v^{2}_2 - v^{2}_1 \right)$

$\Rightarrow \left(P_1 - P_2 \right) = \frac{1} {2} \left(\frac{A^{2}_1 v^{2}_1} {A^{2}_2} - v^{2}_1 \right)$

$\Rightarrow \left(P_1 - P_2 \right) = \frac{1} {2} v^{2}_1\left(\frac{A^{2}_1 - A^{2}_2} {A^{2}_2} \right)$

$v_1 = A_2 \left[\frac{2\left(P_1 - P_2 \right)} {\left(A^{2}_1 - A^{2}_2 \right)} \right]^{1/2}$ ...........(11.17)

But,

$A_1v_1 = \Delta V$

where

$\Delta V \rightarrow$ Volume that flows through a cross-section per second.

$\therefore \Delta V = A_2 A_1 \left[\frac{2 \left(P_1 - P_2 \right)} {\left(A^{2}_1 - A^{2}_2 \right)} \right]^{1/2}$ ..........(11.18)

$\Delta V = A_1 A_2 \left[\frac{2gh} {A^{2}_1 - A^{2}_2 } \right]^{1/2}$ ..........(11.19)

1754799_1833420_ans_bc65784902dd4309909196637dd3f3e9.png

What is the effect on angle of contact on mixing soap solution in water?

The angle of contact decreases.

Water is flowing through a non-uniform cross-sectional area pipe. In pipe where the velocity of water is 0.4 m/s, pressure 0.1 m of mercury. A another place, where velocity of water is 0.5 m/s, calculate the value of pressure.

Given,

$v_1 = 0.4 \space ms^{-1}, v_2 = 0.5 \space ms^{-1}$

$P_1 = 0.1 \space m$ of mercury

$= 0.1 \times 13.6 \times 10^{3} \times 9.8 \space Nm^{-2}$

$P_2 = ?, p= 10^{3} \space k gm^{-3}$

From Bernoulli's theorem

$P_2 + \dfrac{1} {2} pv^{2}_2 = P_1 + \dfrac{1} {2} pv^{2}_1$

$P_2 = P_1 + \dfrac{1} {2} pv^{2}_1 - \dfrac{1} {2} pv^{2}_2$

$= P_1 + \dfrac{1} {2} p \left( v^{2}_1 v^{2}_2 \right)$

$= 0.1 \times 13.6 \times 10^{3} \times 9.8 + \dfrac{1} {2} \times 10^{3} \left[\left( 0.4\right)^{2} - \left( 0.5\right)^{2}\right]$

$= 13.328 \times 10^{3} + \dfrac{1} {2} \times 10^{3} \left[ 0.16 - 0.25\right]$

$= 10^{3} \left[ 13.328 - 0.045\right]$

$= 13.283 \times 10^{3} \space Nm^{-2}$

$= 0.0996 \space m$ of mercury

$= 9.96 \space cm$ of mercury.

Name the forces which are responsible for shape of liquid surface in a capillary tube.

The adhesive force and cohesive force are responsible for shape of liquid surface in a capillary tube.

When the adhesive force > the cohesive force, the shape of the liquid surface is concave.

If the adhesive force < the cohesive force, the shape of the liquid surface is convex.

If the adhesive force - the cohesive force, the shape of the liquid surface is flat.

Why does the speed of a liquid increase and its pressure decrease when a liquid passes through a constriction in a horizontal pipe?

Consider a horizontal constricted tube.
Let

$A_1$ and

$A_2$ be the cross-sectional areas at points 1 and 2, respectively. Let

$v_1$ and

$v_2$ be the corresponding flow speeds. p is the density of the fluid in the pipeline. By the equation of continuity,

$v_1A_1 = v_2A_2$ ....(1)

$\therefore \ \ \frac{v_2}{v_1} = \frac{A_1}{A_2} > 1$

$(\because \ \ A_1 > A_2)$
Therefore, the speed of the liquid increases as it passes through the constriction. Since the meter is assumed to be horizontal, from Bernoulli's equation we get,

$P_1 = \frac{1}{2} \rho v^2_1 = P_2 + \frac{1}{2} \rho^2_2$

$\therefore \ \ P_1 + \frac{1}{2} \rho v ^2_1 = P_2 + \frac{1}{2} \rho v^2_1 \bigg(\frac{A_1}{A_2}\Bigg)^2$ .....[from eq.(1)]

$\therefore \ \ p_1 - p_2 = \frac{1}{2} pv^2_1 \bigg[\bigg(\frac{A_1}{A_2}\bigg)^2 - 1\bigg]$ ...(2)
Again, since

$A_1 > A_2$ , the bracketed term is positive so that

$p_1 > p_2$ . Thus, as the fluid passes through the constriction or throat, the higher speed results in lower pressure at the throat.
1765027_1841633_ans_575724d8145c4c668b445c124d57d1d5.png

1765027_1841633_ans_575724d8145c4c668b445c124d57d1d5.png

A force of 1 kN is applied on a road surface by the tyre of a car. If the contact area of the tyre is $10\,cm^2$ , find the pressure on the contact area.

Given:

Force applied is

$1\ kN=1000\ N$

Contact area is

$10\ cm^2=10\times 10^{-4}\ m^2$

We know that,

$Pressure=\dfrac{Force}{Area}$

$\therefore Pressure=\dfrac{1000\ N}{10 \times 10^{-4}\,m^2}=10^6\,Pa$

The pressure of water inside a closed pipe is $3 \times 10^5 \ N/m^2$ . This pressure reduces to $2 \times 10^5 \ N/m^2$ on opening the valve of the pipe. Calculate the speed of water flowing through the pipe..[Density of water $1000 kg/m^0$ ].

$p_1 = 3 \times 10^5 Pa, v_1 = 0, p_2 = 2 \times 10^5 Pa,\ \rho =10^3 kg/m^3$

Assuming the potential head to be zero, i.e., the pipe to be horizontal, the Bernoulli equation is

$p_1 + \dfrac{1}{2}\rho v_1^2 = p_2 + \dfrac{1}{2}\rho v_2^2$

$v_2^2 = \dfrac{2(p_1 - p_2)}{\rho}$ .....[

$\because v_1=0$ ]

$= \dfrac{2(3-2)\times 10^5}{10^3} = 200$

$\therefore v_2 = 10\sqrt{2} = 14.14$

Explain why:
Water with detergent dissolved in it should have small angles of contact.

The cloth has narrow spaces in the form of capillaries. The rise of liquid in a capillary tube is directly proportional to cos θ. If θ is small cos θ will be large. Hence capillary rise will be more so that the detergent will penetrate more in cloth and hence gets dissolved.

Fill in the blanks using the word(s) from the list appended with each statement:
For the model of a plane in a wind tunnel, turbulence occurs at a .. speed for turbulence for an actual plane (greater / smaller).

1881381_1844556_ans_febac450ca674283a3775c8e21039d17.jpg

With what velocity does water flow out of an orifice in a tank with gauge pressure $4 \times 10^5 \ N/m^2$ before the flow starts? Density of water = $1000 \ kg/m^3$ .

$\rho - \rho_0 = 4 \times 10^5 Pa, \rho = 10^3$
If the orifice is at a depth h from the water surface in a tank, the gauge pressure there is

$\rho - \rho_0 = h\rho g$ ....(1)
By Toricelli's law of efflux, the velocity of efflux,

$v = \sqrt{2gh}$ ...(2)
Substituting for h from Eq.(1),

$v = \sqrt{2g \dfrac{rho - \rho_0}{\rho g}} = \sqrt{2\dfrac{\rho - \rho_0}{\rho}} = \sqrt{\dfrac{2(4 \times 10^5)}{10^3}}= 20\sqrt{2} = 28.28 m/s$ .

An air bubble of radius $0.2 \ mm$ is situated just below the water surface. Calculate the gauge pressure. Surface tension of water = $7.2 \times 10^{-2} \ N/m$

Given: Radius of bubble =

$0.2 mm \ or \ 0.2 \times (10)^{-3}$ m
Surface tension of water =

$7.2 \times (10)^{-2}$ N/m
We know that, excess pressure inside a air bubble in a liquid is given by
Where,
t = surface tension of liquid
r = radius of bubble
Thus,
Excess pressure =

$\frac{2\times 7.2 \times (10)^{-2}}{0.2 \times (10)^{-3}} = \frac{2 \times 72}{2 \times (10)^{-1}} = 72 \times (10)^1 = 720 n/m$

Explain why
The angle of contact of mercury with glass Is obtuse, while that of water with glass is acute.

When a small quantity of liquid is poured on solid, three interfaces, namely liquid – air, solid – air, and solid-liquid are formed. The surface tension corresponding to theses three layers is $S_{LA}$ , $S_{SA}$ , and $S_{SL}$ respectively. Let $\theta$ be the angle of contact between the liquid and solid.

The molecules in the region, where the three interfaces meet are in equilibrium. It means that net force acting on them is zero. For the molecule at K to be in equilibrium, we have
$S_{SL} + S_{LA} cos \theta = S_{SA}$ or $cos \theta =\dfrac{S_{SA}−S_{SL}}{S_{LA}}$ In case of mercury-glass, $S_{SA} < S_{SL}$ , therefore cos θ is negative or $\theta > 90^\circ$ i.e. (obtuse). In case of water-glass $S_{SA} > S_{SL}$ , therefore $cos\,\theta$ is positive or $\theta < 90^\circ$ (acute).

1773579_1844543_ans_e9769a99851f454f804689a3230fe123.png

Find the pressure $200 \ m$ below the surface of the ocean if pressure on the free surface of liquid is one atmosphere. (Density of sea water = $1060 \ kg/m^3$ )

$h - 200m$

$p - 1060kg/m^3$

$g - 9.8m/s^2$

$Patm:- 1.013 \times 10 \ N/m2$
FORMULA:

$P = P_0 + hpg$
=

$1.013 \times 10 + 200 \times 1060 \times 9.8$
=

$21.789 \times 10^5 N/m^2$

The speed of water is $2 \ m/s$ through a pipe of internal diameter $10 \ cm$ . What should be the internal diameter of the nozzle of the pipe if the speed of the water at nozzle is $4 \ m/s$ ?

Data:

$d_1 = 10 cm = 0.1 m, v_1 = 2m/s, v_2 = 4 m/s$
By the equation of continuity, the ratio of the speed is

$\frac{v_1}{v_2} = \frac{A_2}{A_1} = \Big( \frac{d_2}{d_1} \Big)^2$

$\therefore \ \frac{d_2}{d_1} = \sqrt{\frac{v_1}{v_2}} = \sqrt{\frac{2}{4}} = \frac{1}{\sqrt{2}} = 0.707$

$\therefore d_2 = 0.707d_1 = 0.707(0.1m) = 0.0707m$

Explain why water with detergent dissolved in it should have small angles of contact.

Cloth has narrow spaces inform of capillaries. The rise of liquid in a capillary tube is directly proportional to cos e.

$\theta \propto \dfrac{1}{cos \theta}$ . Hence e should be less in order that detergent penetrates more in clothes.

Derive an expression for the velocity of the fluid at a wide neck in a venturi meter.

Speed of fluid flowing through tube at broad neck

$= V_1$
Speed of fluid flowing through tube at narrow neck

$= V_2$
By equation of continuity,

$A_1V_1 = A_2V_2$

$V_2 =\dfrac{A_1V_1}{A_2}=\dfrac{AV_1}{a}$
From Bernoulli’s equation,

$P_1+\dfrac{1}{2}\rho {V_1}^2=P_2+\dfrac{1}{2}\rho {V_2}^2$
From Bernoulli’s equation,

$P_1-P_2=+\dfrac{1}{2}\rho {V_1}^2\Bigg(\dfrac{A_2}{a_2}-1\Bigg)$

$P_1-P_2=\rho_m gh=+\dfrac{1}{2}\rho {V_1}^2\Bigg(\dfrac{A_2}{a_2}-1\Bigg)$

$\therefore V_1=\sqrt{\dfrac{2\rho_m gh}{\rho}}\Bigg(\dfrac{A_2}{a_2}-1\Bigg)^{-1/2}$

What is a venturi meter? Name two applications.

Venturi meter is a device to measure the flow speed of the incompressible fluid. The principle is used in filter pumps, Bunsen burner, atomizer.

State Stokes law? What are the factors on which viscous drag depends?

Stoke’s law states the backward dragging force (F) acting on a small spherical body of radius r, moving through a medium having a coefficient of viscosity η and velocity v is given by
$F = 6\pi \eta rv$
viscous drag (F) depends on

coefficient of viscosity of the medium η
the velocity of the body (v)
the radius of the spherical body (r)

What is terminal velocity? What are the factors on which terminal velocity depends?

The terminal velocity of an object is the maximum constant velocity acquired by the object while falling freely in a viscous medium.
Terminal velocity (v) of an object of radius (r) density moving through a viscous medius of viscosity $\eta$ and density $\rho_0$ is given by
$v=\dfrac { 2 }{ 9 } \dfrac {r^2}{ \eta } \left( \rho -\rho_0 \right)g$
Hence, terminal velocity depends on

radius of the object
coefficient of viscosity of the medium
density of the object.
density of the medium

An open tank contains water up to a depth of $3m$ and above it an oil of sp.gr $0.9$ for a depth of $1m$ . Find pressure intensity
at the interface of two liquids
at the bottom of the tank.

Height of water, $z_1 = 3\,m$
Height of oil, $z_2 = 1\,m$
Density of oil
= Sp.gr of oil $\times$ Density of water
$= 0.9 \times 1000\,kg/m^3 = 9000\,kg/m^3$
$=\rho_2$
Density of water $= \rho_1 =1000\,kg/m^3$

1. At the interface, i.e., at A,
$P=\rho_2 g \times z_2 = 900 \times 9.81 \times 1$

$= 8829\,N/m^2$

2. At the bottom i.e., at B,
$p =\rho_2gz_2 + \rho_1gz_1$
$= 900 \times 9.81 \times 1 + 1000 \times 9.81 \times 3$

$= 8829 + 29430 = 38259\,N/m$

1776649_1845093_ans_d241c56b77f342b8851b68120bbbeaab.png

A hole of area $2$ mm opens near the bottom of a large water storage tank and a stream of water shoots from it. If the top of the water in the tank is to be kept $30$ m above leaking point, how much water in liters Is should be added to the reservoir tank to keep this level? Take $g = 10\,m/s^2$

Velocity of the outflowing water

$v =\sqrt{2gh}=\sqrt{2 \times 10 \times 30}= 24.49\,m/s$
Quantity of water flowing out per sec.

$= av = 10^{-5} \times 4 \times 24.49$

$= 97.96 \times 10^{-6}$

$= 9.796 \times 10^{-}5 \times 10^3\,litres/s$

$= 97.96\,ml/s$ .

Diameter of a ball A is thrice that of B. What will be the ratio of their terminal velocities in the water?

Terminal velocity × (rad. of ball)2 Required ratio is

$\dfrac{3^2}{1} = 9$

Define terminal velocity. Give reasons why a sphere attains this velocity. Derive a relation for the terminal velocity.

The constant velocity with which a body drops down after initial acceleration in a dense liquid or fluid is called terminal velocity. This is attained when the apparent weight is compensated by the viscous force. It is given by
$v = \dfrac{2}{9}\dfrac{r^2g}{\eta}(\rho−\sigma)$ , where $\sigma$ and $\rho$ are densities of the body and liquid respectively, $\eta$ is the coefficient of viscosity of liquid and r is the radius of the spherical body.
The net force on the sphere becomes zero as the viscous force equals the apparent weight.
Consider a long column of dense liquid-like glycerine. As the ball is dropped in it, the forces experienced are;

weight $= mg =\dfrac{4}{3}\pi r^3 \rho g$ , where ρ is the density of the ball.
upthrust $= U =\dfrac{4}{3}\pi r^3 \rho g$ , where $\rho_1$ is the density of the liquid.
viscous force $F_v = 6 \pi \eta \rho v$

What do you mean by the angle of contact of a liquid with a solid surface? What are the factors that affect it?

The angle made by the tangent drawn to the meniscus from the point of contact with the walls of the container measured from within the liquid is called the angle of contact. It depends on the atmospheric pressure, adhesive and cohesive forces of the liquid in the tube.

Why is there a continuous flow of water the valve is opened?

Here, it is due to the working of the pump, which is an external source of power, that the potential difference was maintained and the flow of water was made possible continuously.

Calculate the total energy possessed by one kg of water at a point where pressure is $30\,gm\,wt/sq.mm$ . The velocity of $0.1\, ms^{-1}$ and height is $60$ cm above the ground.

Given,

$P = 30\,g\,wt/sq.mm$

$=\dfrac{30}{1000} \times 9.8 \times 10^6N/m^2$

$v = 0.1ms^{-1}\,h = 0.6\,m$
Total energy per unit mass

$\dfrac{P}{\rho} + gh + 1/2 v^2$

$=\dfrac{30\times9.8\times 10^3}{103} + 9.8 \times 0.6 + 1/2 \times (0.1^)2$

$= 294 + 5.88 + 0.005$

$= 299.885\,J.$

On which law, hydraulic break works? Name other three devices that works on the basis of this law. State the law.

Hydraulic break works on the basis of Pascal's law. Other devices are hydraulic jack, hydraulic press and excavator.

Pascal law: The pressure applied at any point of a liquid at rest in a closed system, will be experienced equally at all parts of the liquid.

In the bottom of a vessel with mercury there is a round hole of diameter $d = 70 \mu m$ . At what maximum thickness of the mercury layer will the liquid still not flow out through this hole?

The pressure just inside the hole will be less than the outside pressure by

$4\alpha /d$ . This can support a height h of Hg where

$\rho g h = \frac{4\alpha}{d}$ or

$h = \frac{4\alpha}{\rho g d}$

$= \frac{4 \times 490 \times 10^{-3}}{3.6 \times 10^3 \times 9.8 \times 70 \times 10^{-6}} = \frac{200}{13.6 \times 70} = 21 m \ of \ Hg$

When a drop of mercury of radius R is split into n similar drops, What is the change in surface energy? Assume as the surface tension of the mercury.

Volume of initial mercury drop

$= \dfrac{4}{3} \pi R^3$
r = radius of smaller drops,
volume conservation

$\Rightarrow \dfrac{4}{3} \pi R^3 =n\dfrac{4}{3} \pi r^3$

$r = Rn^{-1/3}$
Initial Surface Energy

$= \sigma \times$ surface area

$= \sigma \times 4\pi R^2$
Final Surface Energy

$= n \times \sigma \times 4πr^2$

$= n\sigma 4\pi[Rn^{-1/3}]^2$

$= n\sigma 4\pi R^2n^{-2/3}$

$= n^{1/3}4\sigma \pi R^2$
Change in surface energy

$= 4\sigma \pi R^2[1 – n^{1/3}]$

Are you able to balance with 1N at Y?

Now increase the weight at Y and find out the weight required to bring both the ends to the same level.

Water flows through a horizontal pipe of varying cross-section. If the pressure is $1$ cm of mercury when the velocity is $0.35$ m/s. Find the pressure at a point where velocity is $0.65$ m/s.

$1^{st}$ point,

$P_1 = 1$ cm of mercury

$= 0.01m$ of Hg.

$= 0.01 \times (13.6 \times 10^3) \times 9.8\,P a$ ;

$v_1 = 0.35$ m/s
At the second nd point,

$p_2 = ?$

$v_2 = 0.65$ m/s and

$\rho = 10^3\,hg/m^3$ .
According to Bernoulli’s theorem,

$p_1 + 1/2 (\rho \mathrm{V}_{1}^{2}) = p_2 + 1/2 (\rho \mathrm{V}_{2}^{2})$
or

$P_2 = P_1 + 1/2 (\rho\left(v_{2}^{2}-v_{1}^{2}\right))$

$= 0.01 \times 13.6 \times 103 \times 9.8 – 1/2 \times 10^3 \times [(0.65)^2 – (0.35)^2]$

$= 1182.8\, Pa \Rightarrow (\frac{1182.8}{9.8\left(13.6 \times 10^{3}\right)})$

$= 0.00887\,m$ of Hg.

Press slightly on the end X. What do you observe.

When we press slightly on the end X, Y rises up.

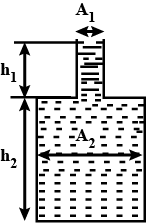
The container shown in the figure below is filled with a liquid of density $\rho$ . Note that the container has height $h_1$ and area of cross-section $A_1$ for the upper half height $h_2$ and area of cross-section $A_2$ for the lower half. Find:
The pressure at the base of the container.
Force exerted by the liquid on the base of the container.

1. The pressure at the base of the container is due to the liquids both at the upper and lower half.
∴ $P_{Total} = P_1 + P_2$
$P_{Total} = ρgh_1 + ρgh_2$
$P_{Total} = \rho g(h_1 + h_2)$

2. Force exerted on the bottom of the container,
$P = P_{Total} \times A_2$
$F = \rho g(h_1 + h_2) \times A_2$ .

The area of one end of a U-tube is $0.01 \,m^2$ and that of the other end the force $1 \,m^2$ , When a force was applied on the liquid at the first end?

As we know that pressure head remains constant at a particular horizontal level

$A_1=0.01 \,m^2$

$A_2=1 \,m^2$

$F_1=?$

$P_1 = P_2$

$F2=20000 \,N$

$\dfrac{F_1}{F_2}=\dfrac{A_1}{A_2}$

$F_1=F_2\times \dfrac{A_1}{A_2}=20000\times \dfrac{0.01}{1}=200 \,N$

Find the pressure in an air bubble of diameter $d = 4.0 \mu m$ , located in water at a depth $h = 5.0 m$ . The atmospheric pressure has tho standard value $P_0$ .

The pressure has terms due to hydrostatic pressure and capillarity and they add

$p = p_0 + \rho g h + \dfrac{4\alpha}{d}$

$p = \Big( 1 + \dfrac{5 \times 9.8 \times 10^3}{10^5} + \dfrac{4 \times .73 \times 10^{3}}{4 \times 10^{-6}} \times 10^{-5}\Big) atoms = 2.22 \ atom.$

You are a passenger on a spacecraft. For your survival and comfort, the interior contains air just like that at the surface of the Earth. The craft is coasting through a very empty region of space. That is, nearly perfect vacuum exists just outside the wall. Suddenly, a meteoroid pokes a hole, about the size of a large coin, right through the wall next to your seat. (a) What happens?
(b) Is there anything you can or should do about it?

1981269_1866197_ans_1961bf57037c42e49f84aa27d41a131f.png

Let us suppose that a planet of mass M and radius r is surrounded by an atmosphere of constant density, consisting of a gas of molar mass R.Determine the temperature T of the atmosphere on the surface of the planet if the height of the atmosphere is $h\,(h << r)$ .

Pressure of atmosphere varies as,

$P={ P }_{ o }{ e }^{ -\dfrac { mgz }{ kT } }$ .

Scale height of the atmosphere is defined as height at which pressure falls to

$\dfrac { 1 }{ e }$ of its value at sea level.

Hence,

$h=\dfrac { kT }{ mg }$

$T=\dfrac { mgh }{ kT }$

Since,

$g=\dfrac { GM }{ { r }^{ 2 } }$

$T=\dfrac { mGMh }{ k{ r }^{ 2 } }$

Since,

$k=\dfrac { R }{ { N }_{ A } }$

T

$=\dfrac { \mu GMh }{ R{ r }^{ 2 } }$

Find the increment of the free energy of the surface layer when two identical mercury droplets, each of diameter $d = 1.5 \ mm$ , merge isothermally.

When two mercury drops each of diameter d merge, the resulting drop has diameter

$d_1$

where

$\dfrac{\pi }{6} d_1^3 = \dfrac{\pi}{6} d^3 \times 2$

or,

$d_1 = 2^{1/3} d$

The increase in free energy is

$\Delta F = \pi 2^{2/3} d^2 \alpha - 2\pi d^2 \alpha = 2\pi d^2 \alpha (2^{-1/3} - 1) = -1.43 \mu J$

Answer the question:
The diagram shows a simple mercury barometer, used to measure atmospheric pressure.
Atmospheric pressure decreases.
Which row states what happens to the pressure at point P and what happens to the level L ?
Pressure at P level L
A decreases falls
B decreases rises
C stays the same falls
D stays the same rises

There is no mercury at point P

If atmospheric pressure decreases, pressure at point P also decreases

Pressure at L =

$p_o$ same as atmospheric pressure.

To balance that decreased pressure, Level L falls.

Hence option A is correct.

Review. Inside the wall of a house, an L-shaped section of hot-water pipe consists of three parts: a straight, horizontal piece h = 28.0 cm long; an elbow; and a straight, vertical piece = 134 cm long. A stud and a second story floorboard hold the ends of this section of copper pipe stationary. Find the magnitude and direction of the displacement of the pipe elbow when the water flow is turned on, raising the temperature of the pipe from $18.0^0C$ to $46.5^0C$ .

The horizontal section expands according to

$\Delta L =\alpha L_i\Delta T$ .

$\Delta x =[17 \times 10^{-6} (^0C)^{-1}](28.0 cm)( 46.5^0C - 18.0^0C)$

$=1.36 \times 10^{-2} cm$
The vertical section expands similarly by

$\Delta y =[17 \times 10^{-6}(^0C)^{-1}](134 cm)(28.5^0C) =6.49 \times 10^{-2} cm$
The vector displacement of the pipe elbow has magnitude

$\Delta r=\sqrt{\Delta x^2 +\Delta y^2}=\sqrt{(0.136 mm)^2 +(0.649 mm)^2} =0.663 mm$
and is directed to the right below the horizontal at angle

$\theta =tan^{-1} (\dfrac{\Delta y}{\Delta x}) =tan^{-1}( \dfrac{0.649 mm}{0.136 mm}) =78.2^0$

$\Delta r =0.663 mm$ to the right at

$78.2^0$ below the horizontal

A backyard swimming pool with a circular base of diameter $6.00\ m$ is filled to depth $1.50\ m$ .
Find the absolute pressure at the bottom of the pool.

1979746_1866968_ans_727f7b9346304cdfab1fa792e56eb3d8.jpeg

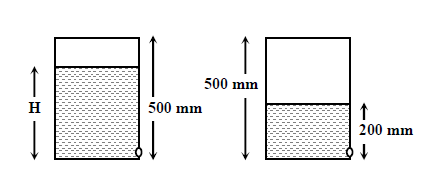
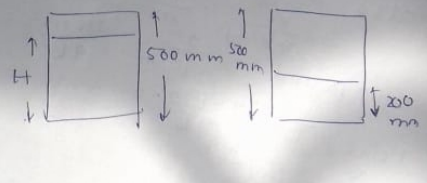
A cylindrical vessel of height $500 \ mm$ has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it upto height $H$ . Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with the height of water column being $200 \ mm$ . Find the fall in height (in mm) of water level due to the opening of the orifice.
[Take atmospheric pressure $=1.0\times 10^{5}\mathrm{N}/\mathrm{m}^{2}$ , density of water $=1000\mathrm{k}\mathrm{g}/\mathrm{m}^{3}$ and $\mathrm{g}=10\mathrm{m}/\mathrm{s}^{2}$ Neglect any effect of surface tension.]

Pressure due to falling water level at

$200 mm$ is

$P+\rho gh= P_0$

$P=10^5-(1000)(10)(0.2)=98\times 10^3 N/m^2$

now,

$P_0V_0=PV$

$10^5[A(0.5-H)]=98\times 10^3[A(0.5-0.2)]$

where

$A=$ cross-sectional area of a vessel.

$0.5-H=0.294$

$\Rightarrow H=0.206 m= 206 mm$

The fall in height (in mm) of water level

$=206-200=6$

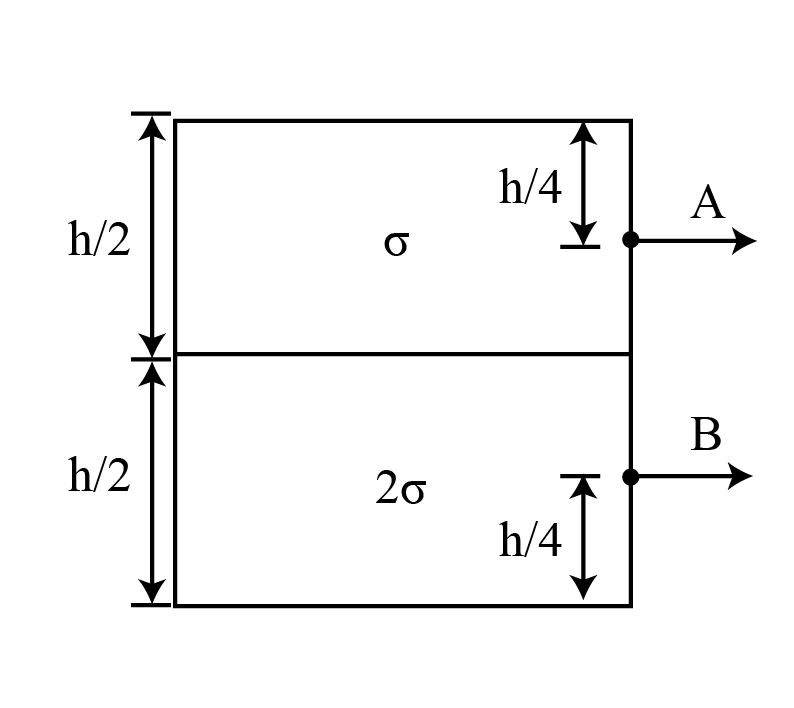
A large tank is filled with two liquids of specific gravities $2\sigma$ and $\sigma$ . Two holes are made on the wall of the tank as shown. Find the ratio of the distances from $O$ of the points on the ground where the jets from holes $A$ & $B$ strike.

Since there is no acceleration in horizontal direction, we have
$\text{S(distance travelled)} \propto \text{vt (velocity of efflux} \times \text{time taken by the jet to reach the bottom)}\\\Rightarrow \dfrac { { S }_{ 1 } }{ { S }_{ 2 } } =\dfrac { { v }_{ 1 }{ t }_{ 1 } }{ v_{ 2 }{ t }_{ 2 } } \quad \quad \quad \quad .......(I)$
For the top hole $v_1 =\sqrt {2g \left(\dfrac{h}{4}\right)} = \sqrt{\dfrac{gh}{2}}\quad \quad \quad \quad .......(II)$
Time taken by the jet reach the bottom from the first hole ${ t }_{ 1 }=\sqrt { \dfrac { 2\left( h-\dfrac { h }{ 4 } \right) }{ g } } =\sqrt { \dfrac { 3h }{ 2g } } \quad \quad \quad .......(III)$
Applying Bernoulli's theorem for the bottom hole, we have
$\sigma g\left( \dfrac { h }{ 2 } \right) +2\sigma g\left( \dfrac { h }{ 4 } \right) =\dfrac { 1 }{ 2 } (2\sigma )v_{ 2 }^{ 2 }\\ \Rightarrow v_{ 2 }=\sqrt { gh } \quad \quad \quad .......(IV)$
Time taken by the jet reach the bottom from the second hole ${ t }_{ 2 }=\sqrt { \dfrac { 2\left( \dfrac { h }{ 4 } \right) }{ g } } =\sqrt { \dfrac { h }{ 2g } } \quad \quad \quad .......(V)$
From $(I)$ , $(II)$ , $(III)$ , $(IV)$ and $(V)$ , we have
$\dfrac { { S }_{ 1 } }{ { S }_{ 2 } } =\dfrac { { v }_{ 1 }{ t }_{ 1 } }{ v_{ 2 }{ t }_{ 2 } } =\dfrac { \left( \sqrt { \dfrac { gh }{ 2 } } \right) \times \left( \sqrt { \dfrac { 3h }{ 2g } } \right) }{ \left( \sqrt { gh } \right) \times \left( \sqrt { \dfrac { h }{ 2g } } \right) } =\dfrac { \sqrt { 3 } }{ \sqrt { 2 } } \\\Rightarrow \boxed{x=3}$

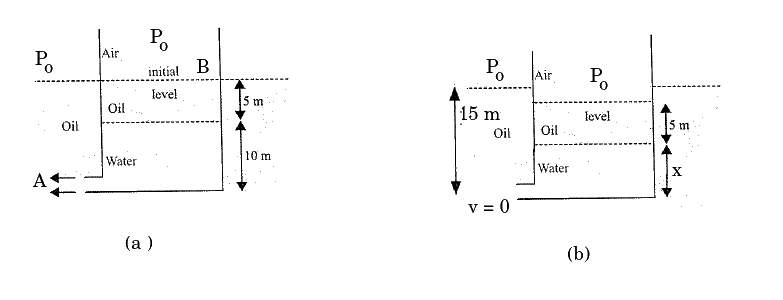
A tank with a small orifice contains oil on top of water. It is immersed in a large tank of the same oil. Water flows through the hole. Assuming the level of oil outside the tank above orifice does not change. a. What is the velocity of this flow initially? b. When the flow stops, what would be the position of the oil-water interface in the tank? c. Determine the time at which the flow stops. Density of oil $=800 kg/m^3$ .

Given :

$\rho_o = 800 kg/m^3$

$\rho_w = 1000 kg/m^3$

Consider figure (a) :

Let the velocity of the flow of water at A be

$v$ .

Pressure at A

$P_A = P_o + \rho_o g (15)$

Assuming the velocity of top oil surface inside the tank is zero.

Applying Bernoulli's theorem at A and B :

$P_A + \dfrac{1}{2}\rho_w v^2 = P_B + [\rho_o g (5) + \rho_w g (10)]$

$\therefore$

$(P_o + 800 g (15)) + \dfrac{1}{2}\times 1000 v^2 = P_o + [800 g (5) + 1000 g (10)]$

$\therefore$

$v^2 = 40$

$\implies v = 6.3 m/s$

(b) Consider figure (b):

Let the water-oil interface be at a height

$x$ from the bottom of tank when the velocity of flow is zero i.e v =0.

Applying Bernoulli's theorem at A and B :

$P_A = P_B + [\rho_o g (5) + \rho_w g (x)]$ (v = 0)

$\therefore$

$P_o + 800 g (15) = P_o + [800 g (5) + 1000 g (x)]$

$\implies x =8$ m

$t$ i.e

$S = 2$ m

Using

$S = ut + \dfrac{1}{2}gt^2$ where

$u = 0$

$\therefore$

$2 = \dfrac{1}{2} \times 10 t^2$

$\implies t = \sqrt{\dfrac{2}{5}}$ s

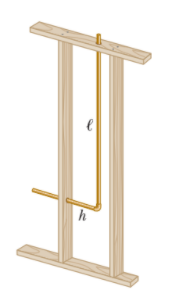
A bent tube is lowered into a water stream as shown in figure above. The velocity of the stream relative to the tube is equal to $v=2.5\:m/s$ . The closed upper end of the tube located at the height $h_0=12\:cm$ has a small orifice. The height $h$ the water jet spurt?

Let the velocity of the water jet, near the orifice be

$v^\prime$ , then applying Bernoulli's theorem,

$\displaystyle\dfrac{1}{2}\rho v^2=h_0\rho g+\dfrac{1}{2}\rho v^2$

or,

$v^\prime=\sqrt{v^2-2gh_0}$ (1)

Here the pressure term on both sides is the same and equal to atmospheric pressure.

Now, if it rises upto a height

$h$ , then at this height, whole of its kinetic energy will be converted into potential energy. So,

$\displaystyle\dfrac{1}{2}\rho{v^\prime}^2=\rho gh$ or

$\displaystyle h=\dfrac{{v^\prime}^2}{2g}$

$\displaystyle=\dfrac{v^2}{2g}-h_0=20\:cm$ , [using equation (1)]

$n$ drops of water, each of radius $2\ mm$ , fall through air at a terminal velocity of $8\ cm/s$ . If they coalesce to form a single drop, then the terminal velocity of the combined drop is $32\ cm/s$ . The value of $n$ is

$\dfrac {4}{3} \pi R^{3} = n\times \dfrac {4}{3} \pi r^{3}$
or

$R^{3} = nr^{3}$ or

$R = n^{1/3} r$
or

$R = 2\pi^{1/3} mm$

$v_{0}\propto r^{2}, v_{0}' \propto R^{2}$
Now,

$\dfrac {v'_{0}}{v_{0}} = \dfrac {R^{2}}{r^{2}} = \dfrac {4n^{2/3}}{4} f$
or

$\dfrac {32}{8} = n^{2/3}$ or

$n^{2/3} = 4$
or

$n = 4^{3/2} = \sqrt {64}$
or

$n = 8$ .

A wide vessel with a small hole in the bottom is filled with water and kerosene. Neglecting the viscosity, find the velocity of the water flow, if the thickness of the water layer is equal to $h_1=30\:cm$ and that of the kerosene layer to $h_2=20\:cm$ .

Since, the density of water is greater than that of kerosene oil, it will collect at the bottom. Now, pressure due to water level equals

$h_1\rho_1g$ and pressure due to kerosene oil level equals

$h_2\rho_2g$ . So, net pressure becomes

$h_1\rho_1g+h_2\rho_2g$ .

From Bernoulli's theorem, this pressure energy will be converted into kinetic energy while flowing through the whole

$A$ .
i.e.

$\displaystyle h_1\rho_1g+h_2\rho_2g=\dfrac{1}{2}\rho_1v^2$
Hence

$\displaystyle v=\sqrt{2\left(h_1+h_2\dfrac{\rho_2}{\rho_1}\right)g}=3\:m/s$

A Pitot tube (Shown in figure above) is mounted along the axis of a gas pipeline whose cross-sectional area is equal to $S$ . Assuming the viscosity to be negligible, the volume of gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to $\Delta h$ , and the densities of the liquid and the gas are $\rho_0$ and $\rho$ respectively.

Applying Bernoulli's theorem for the point

$A$ and

$B$ ,

$\displaystyle P_A=P_B+\frac{1}{2}\rho v^2$ as,

$v_A=0$

or,

$\displaystyle\frac{1}{2}\rho v^2=P_A-P_B=\Delta h\rho_0g$

So,

$\displaystyle v=\sqrt{\frac{2\Delta h\rho_0g}{\rho}}$

Thus, rate of flow of gas,

$\displaystyle Q=Sv=S\sqrt{\frac{2\Delta h\rho_0g}{\rho}}$

The gas flows over the tube past it at

$B$ . But at

$A$ the gas becomes stationary as the gas will move into the tube which already contains gas.
In applying Bernoulli's theorem we should remember that:

$\displaystyle\frac{p}{\rho}+\frac{1}{2}v^2+gz$ is constant along a streamline.

In the present case, we are really applying Bernoulli's theorem somewhat indirectly. The streamline at

$A$ is not the streamline at

$B$ . Nevertheless the result is correct. To be convinced of this, we need only apply Bernoulli's theorem to the streamline that goes through

$A$ by comparing the situation at

$A$ with that above

$B$ on the same level. In steady conditions, this agrees with the result derived because there cannot be a transverse pressure differential.

A side wall of a wide open tank is provided with a narrowing tube (figure shown above) through which water flows out. The cross-sectional area of the tube decreases from $S=3.0\:cm^2$ to $s=1.0\:cm^2$ . The water level in the tank is $h=4.6\:m$ higher than that in the tube. Neglecting the viscosity of the water, find the horizontal component of the force tending to pull the tube out of the tank (in $N$ ). Round off to the closest integer.

Consider narrowing tube made off rings arranged across it's length.

where

$p_p$ is the pressure at

$P$ and

$p_0$ is the atmospheric pressure which is the pressure just outside of

$B$ . The force on the nozzle tending to pull it out from diagram is

$dF=P \times dA sin\theta; \;P=p_p-p_O; dA=2\pi y ds$

$F=\int{(p_p-p_O)\sin{\theta}2\pi yds}$

where

$y$ is the radius at the point

$P$ distant

$x$ from the vertex

$O$ .We have subtracted

$p_0$ which is the force due to atmospheric pressure the factor

$\sin{\theta}$ gives horizontal component of the force and

$ds$ is the length of the element of nozzle surface,

$ds=dx\sec{\theta}$

Suppose the radius at

$A$ is

$R$ and it decreases uniformly to

$r$ at

$B$ where

$S=\pi R^2$ and

$s=\pi r^2$ . Assume also that the semi vertical angle at 0 is

$\theta$ . Then

$\displaystyle\dfrac{R}{L_2}=\dfrac{r}{L_1}=\dfrac{y}{x}$

$\displaystyle y=r+\dfrac{R-r}{L_2-L_1}(x-L_1)$

Suppose the velocity with which the liquid flows out is

$V$ at

$A$ , at

$B$ and

$u$ at

$P$ . Then by the equation of continuity

$\pi R^2V=\pi r^2v=\pi y^2u$

The velocity

$v$ of efflux is given by

$v=\sqrt{2gh}$

and Bernoulli's theorem gives

$\displaystyle p_p+\dfrac{1}{2}\rho u^2=p_0+\dfrac{1}{2}\rho v^2$

$\displaystyle\tan{\theta}=\dfrac{R-r}{L_2-L_1}$

Thus

$\displaystyle F=\int_{L_1}^{L_2}{\dfrac{1}{2}(v^2-u^2)\rho 2\pi y\dfrac{R-r}{L_2-L_1}dx}$

$\displaystyle=\pi\rho\int_r^R{v^2\left(1-\dfrac{r^4}{y^4}\right)ydy}$

$\displaystyle=\pi\rho v^2\dfrac{1}{2}\left(R^2-r^2+\dfrac{r^4}{R^2}-r^2\right)=\rho gh\left(\dfrac{\pi{(R^2-r^2)}^2}{R^2}\right)$

$\displaystyle=\rho gh\dfrac{{(S-s)}^2}{S}=6.02\:N$ on putting the values.

Note: If we try to calculate

$F$ from the momentum change of the liquid flowing out will be wrong even as regards the sign of the force.

There is of course the effect of pressure at

$S$ and

$s$ but quantitative derivation of

$F$ from Newton's law is difficult.

When a sphere of radius $r_1=1.2\ \text{mm}$ moves in glycerin, the laminar flow is observed if the velocity of the sphere does not exceed $v_1=23\ \text{cm/s}.$ At what minimum velocity $v_2\ ($ in $\mu\ \text{m/s}\ )$ of a sphere of radius $r_2=5.5\ \text{cm}$ will the flow in water become turbulent? The viscosities of glycerin and water are equal to $\eta_1=13.9\:P$ and $\eta_2=0.011\:P$ respectively.

We know that Reynold's number for turbulent flow is greater than that on laminar flow.

Now,

$\displaystyle (R_e)_l=\dfrac{\rho vd}{\eta}=\dfrac{2\rho_1v_1r_1}{\eta_1}$ and

$\displaystyle (R_e)_t=\dfrac{2\rho_2v_2r_2}{\eta_2}$

But,

$(R_e)_t\ge(R_e)_l$

$\displaystyle {v_2}_{min}=\dfrac{\rho_1v_1r_1\eta_1}{\rho_2r_2\eta_2}=5\:\mu m/s$ on putting the values.

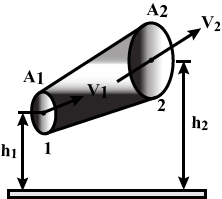
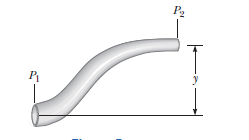
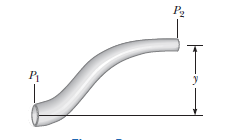
A non-viscous liquid of constant density $1000 kg/m^{3}$ flows in a streamline motion along a tube of variable cross section, The tube is kept inclined in the vertical plane as shown in the figure, The area of cross-section of the tube at two points P and Q at heights of $2 m$ and $5 m$ are respectively $4 \times 10^{-3} m^{2}$ and $8 \times 10^{-3}m^{2}$ . The velocity of the liquid at point $P$ is $1 m/s.$ Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q, Take $g = 9.8 m/s^{"2}$

Given:

$A_{1}=4\times 10^{-3}$ m

$^{2}$ ,

$A_{2}=8\times 10^{-3}$ m

$^{2}$

$h_{1}=2$ m,

$h_{2}=5$ m

$v_{1}=1$ m/s
and

$\rho =10^{3}$ kg/m

$^{3}$
From continuity equation, we have

$A_{1}v_{1}=A_{2}v_{2}$
or

$\displaystyle v_{2}=\left ( \frac{A_{1}}{A_{2}} \right )v_{1}$

$\displaystyle v_{2}=\left ( \frac{4\times 10^{-3}}{8\times 10^{-3}} \right )$ (m/s)

$\displaystyle v_{2}=\frac{1}{2}$ m/s

Applying Bernoulli's equation at sections 1 and 2

$\displaystyle p_{1}+\frac{1}{2}\rho v_{1}^{2}+\rho gh_{1}=p_{2}+\frac{1}{2}\rho v_{2}^{2}+\rho gh_{2}$
or

$\displaystyle P_{1}-P_{2}=\rho g\left ( h_{2}-h_{1} \right )+\frac{1}{2}\rho \left ( v_{2}^{2}-v_{1}^{2} \right )$ (i)

(i) Work done per unit volume by the pressure as the fluid flows from P to Q.

$W_{1}=p_{1}-p_{2}$

$=\rho g\left ( h_{2}-h_{1} \right )+\frac{1}{2}\rho \left ( v_{2}^{2}-v_{1}^{2} \right )$ [From Eq. (i)]

$\displaystyle =\left \{ \left ( 10^{3} \right )\left ( 9.8 \right )\left ( 5-2 \right )+\frac{1}{2}\left ( 10 \right )^{3}\left ( \frac{1}{4}-1 \right ) \right \}$ J/m

$^{3}$

$=\left [ 29400-375 \right ]$ J/m

$^{3}$ =

$29025$ J/m

$^{3}$

(ii) Work done per unit volume by the gravity as the fluid flows from P to Q.

$W_{2}=\rho g\left ( h_{2}-h_{1} \right )=\left \{ \left ( 10^{3} \right )\left ( 9.8 \right )\left ( 5-2 \right ) \right \}$ J/m

$^{3}$

$W_{2}=29400$ J/m

$^{3}$

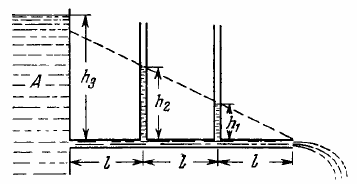
In the arrangement shown in figure above viscous liquid whose density is $\rho=1.0\:g/cm^3$ flows along a tube out of a wide tank $A$ . Find the velocity (in m/s) of the liquid flow, if $h_1=10\:cm$ , $h_2=20\:cm$ , and $h_3=35\:cm$ . All the distances $l$ are equal.

The loss of pressure head in travelling a distance

$l$ is seen from

the middle section to be

$h_2-h_1=10\:cm$ . Since

$h_2-h_1=h_1$ in

our problem and

$h_3-h_2=15\:cm=5+h_2-h_1$ , we see that a pressure

head of

$5\:cm$ remains incompensated and must be converted into

kinetic energy, the liquid flow out. Thus

$\displaystyle\frac{\rho v^2}{2}=\rho g\Delta h$ where

$\Delta h=h_3-h_2$

Thus

$v=\sqrt{2g\Delta h}=1\:m/s$

On the opposite sides of a wide vertical vessel filled with water two identical holes are opened, each having the cross-sectional area $S=0.50\:cm^2$ . The height difference between them is equal to $\Delta h=51\:cm$ . If the resultant force of reaction of the water flowing out of the vessel.

Let the velocity of water, flowing through

$A$ be

$v_A$ and that through

$B$ be

$v_B$ , then discharging rate through

$A=Q_A=Sv_A$ and similarly through

$B=Sv_B$ .
Now, force of reaction at

$A$ ,

$F_A=\rho Q_Av_A=\rho Sv_B^2$

Hence, the net force,

$F=\rho S(v_A^2-v_B^2)$ as

$\vec{F_A}\uparrow\downarrow\vec{F_B}$ (1)
Applying Bernoulli's theorem to the liquid flowing out of

$A$ we get

$\displaystyle P_0+\rho gh=P_0+\dfrac{1}{2}\rho v_A^2$

and similarly at

$B$

$\displaystyle P_0+\rho g(h+\Delta h)= P_0+\dfrac{1}{2}\rho v_B^2$

Hence

$\displaystyle(v_B^2-v_A^2)\dfrac{\rho}{2}=\Delta h\rho g$

Thus

$\displaystyle F=2\rho gS\Delta h=0.50\:N$

A rectangular tank of height $6 m$ filled with water is placed near the bottom of an incline of angle $\displaystyle 30^{\circ}$ . At height $x$ from bottom a small hole is made (as shown in figure ) such that stream coming out from hole strikes the inclined plane normally. Find $x$ in meter .

The velocity of stream when it gets out of the hole is

$V_o = \sqrt {2g(6-x)}$

Now lets say that the stream strikes the inclined plane after t seconds,

the horizontal component of the velocity will still be,

$V_x = V_0$

Now, the angle of incline is

$30^o$ , so the stream will be forming an angle of

$90-30 = 60^o$ on striking the inclined plane.

Now,

$V_y/V_x = \tan 60^o = \sqrt 3$

Therefore,

$V_y = \sqrt 3 V_x = \sqrt 3 V_0$

Since, the initial velocity in the vertical direction is

$0$ ,

$V_y = 0 + gt$

$gt = \sqrt 3 V_0$

Therefore, t =

$\sqrt 3 V_0 /g$

Now, the distance travelled in the vertical direction will be,

$x - 0.5 gt^2$

Or, distance =

$x - 0.5 g \times 3 V_0^2 / g^2$

Distance travelled in the horizontal direction =

$V_0 t$

The two distances are related as,

$y/x = \tan 30^o$

$x - 0.5 gt^2 = \sqrt {1/3} V_0 t$

Solving, this,

$x = 5h/6 = 5 m$

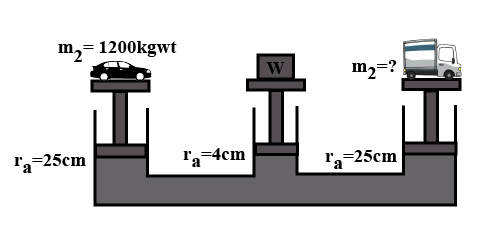
In the figure shown, cylinder 'A' has pump piston, whereas B and C cylinders have lift pistons. If the maximum weight that can be placed on the pump piston is $50\ kgwt$ what is the maximum weight that can be lifted by the piston in the cylinder 'B'. Find the total mechanical advantage. (Take $g = 10\ m\ s^{-2})$

Using pascal law , Pressure at piston A= pressure at piston B

$\dfrac{F_A}{\pi r_a^2} = \dfrac{F_B}{\pi r_b^2}$

$\dfrac{50g}{\pi 4^2}=\dfrac{mg}{\pi (25)^2}$

$m=1953.12kg$

Mechanical advantage

$\dfrac{total\,weight}{total \,effort}=\dfrac{1200+1953.12}{50}=63.06$

A cylindrical vessel of height $500$ mm has an orifice(small hole at its bottom). The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being $200$ mm. Find the fall in height (in mm) of water level due to opening of the office. [Take atmospheric pressure $=1.0\times 10^5N/m^2$ , density of water $=1000$ kg $/m^3$ and $g=10m/s^2$ . Neglect any effect of surface tension].

A cylinder vessel of high

$h=500mm$

$P=P_0-\rho gh\\ \quad=98\times10^3 N/m^2\\P_0V_0=PV$

(according to Charles and Boyle's law)

$10^5{A(500-H)}=98\times10^3{A(500-200)}\\500A\times 10^5-AH\times 10^5=9.8\times10^3A\times 500-98\times 10^3\times A\times 200\\500A\times10^5+98\times10^3A\times200=98\times 10^3A\times500+AH\times 10^5\\A(500\times10^5+98\times200\times10^3)=A(98\times10^3\times500+H\times10^5)\\H=206mm\\Level \quad fall=206-200mm\\ \quad\quad=6mm$

1218712_769485_ans_98358b96f7004ecd86a597dfe5a5c9b4.png

The figure shows two immiscible liquids(Kerosene and water). Kerosene has density $\rho_2$ and water has density $\rho_1$ . Find the velocity of water flow.

Density of Kerosene

$=\rho_2$ water density

$=\rho_1$

Let, the height water

$=h_1$

and the height of Kerosene

$=h_2$ respectively

The velocity of water flow through hole in the bottom is given by

$v=\sqrt{2g[h_1+h_2(\rho_2\rho_1)]}$

Water shoots out a pipe and nozzle as shown in the figure. The cross-sectional area for the tube at point $A$ is four times that of the nozzle. The pressure of water at point $A$ is $41\times 10^{3}Nm^{-2}$ (guage). If the height $'h'$ above the nozzle to which water jet will shoot is $x/10$ meter than $x$ is. (Neglect all the losses occurred in the above process) $[g= 10m/s^{2}]$ .

Cross sectional area at point

$4A(tube)$

Cross sectional area at point

$=A(nozle)$

The pressure at a point A is

$=41\times10^3N/m^2$

The height above the nozzle

$=x+\cfrac{x}{10}\\=\cfrac{11x}{10}\\g=10m/s^2\\P=h\rho g\\41\times10^3=\cfrac{11x}{10}\times10\times\cfrac{m}{1.1}\\x=\cfrac{41\times10^3}{10}\\x=41\times10^2m$

1217616_766402_ans_7ab7cb3d46504e2080afd699c7aa0b25.png

Water stands at a height H in a tall cylinder (see figure). Two holes A and B are made on the sides of the cylinder. If hole A is at a height $h$ above the ground, what is the height of hole B above the ground so that the two streams of water emerging from holes A and B strikes the ground at the same point?

Given,

Water stands at a height

$=H$

Solution

ranges are same then two holes

$(1)\quad h$ above

Let, t is time taken by the jet to travel the vertical height

$H$ from bottom of the cylinder and

$v$ is the velocity steam of steam of water.

$H=\cfrac{1}{2}gt^2\rightarrow(1)\\t=\sqrt{\cfrac{2H}{g}}\rightarrow(2)\\v=\sqrt{2gh}\rightarrow(3)$

The horizontal distance R travelled by stream

$V_t=\cfrac{(2gh)^{1/2}}{(2gH)^{1/2}}\rightarrow(4)$

Solving equation

$(4)$ we get

$h$ (depth of water in the cylinder)

$=\cfrac{R^2}{4H}$

R be the radius of the hole of B.

If n identical water droplets falling under gravity with terminal velocity v coalesce to form a single drop which has the terminal velocity $4$ v, find the number n.

No of identical water dropletts falling falling under gravity

$=n$

Thermal velocity

$=V$

And then coalesce to form a single drop

The thermal velocity

$==4V$

Find n

The terminal velocity of an object is directly proportional to the square of the radius of the drop. The volume of the small drop is

$\cfrac{4}{3}\pi r^3$ . The volume of the bigger drop formed by collection of

$N$ drops is

$N\cfrac{4}{3}\pi R^3$

(R be the radius of the bigger droplet and r be the radius of the smaller droplet)

Thus the radius of the bigger drop is

$R=N^{1/3}\times r(\cfrac{V_2}{V_1})\\ \quad=(\cfrac{R}{r})^2)(\cfrac{V_2}{V_1})\\ \quad=(\cfrac{r-N^{1/3}}{r})^2\times\cfrac{V_2}{V_1}\\=N^{2/3}4V\\=N^{2/3}V\\N=8$

Find the pressure in the circular water pipe shown in the figure .

$P_0$ = atmospheric pressure

Taking

$2$ reference since

$x$ and

$y$ .

For

$X$

$P_{left}=P_A-(0.8\times g\times 5)-(1.59\times g\times 7)$

$P_{right}=P_b-(0.8\times g\times 15)$

$P_{left}=P_{right}$

$\Rightarrow P_A-P_B=g(0.8\times 5+1.59\times 7-0.8\times 15)$ ......(1)

For

$y$ and

$z$

$P_{left}=P_c-(0.8\times 5\times g)$

$P_{right}=P_0-(1.51\times 5\times g)$

$P_{left}=P_{right}$

$\Rightarrow P_c-P_0=(0.8\times 5\times g)-(1.59\times 5\times g)$ .......(2)

Solving (1) and (2) (

$P_c=P_B$ because on the same reference line)

$P_A-P_B=g(4+11.13-12)$

$P_e-P_0=g(4-7.95)$

$\overline{\quad P_A=P_0-g(0.82)}$

$\Rightarrow \boxed{P_A=(P_0-8.2)}$

1115965_806162_ans_59e98bcaca2640ea9d09157a294354a9.png

Water is filled to a height of $2.5\ m$ in a container lying at rest on a horizontal surface as shown in the figure. The bottom of the container is square shaped of side $\sqrt { 3 }\ m$ and its top is open. There is a very small hole in the vertical wall of the container near the bottom. A small cap closes the hole. The hole gets opened when pressure near the bottom becomes more than $4\times { 10 }^{ 4 }$ pascal.
(a) What minimum acceleration can be given to the container in the positive $x-$ direction so that the cap will came out of the hole? Assume water dose not spill out of container when the container accelerates.
(b) Find the velocity of efflux as soon as the container starts moving with the acceleration calculate in part (a) of the question.

(Image )

${ P }_{ 0 }=\left( l+h \right) \rho g$

$\tan { \theta } =\cfrac { l }{ \sqrt { 3 } }$

$l=\sqrt { 3 } \tan { \theta }$

$l=\sqrt { 3 } .\cfrac { a }{ g }$

${ P }_{ 0 }=\sqrt { 3 } \cfrac { a }{ g } .\rho g+h\rho g$

${ P }_{ 0 }=\sqrt { 3 } a\rho +h\rho g\quad \quad \left[ { \rho }_{ water }=1000{ ㎏ }/{ ㎥ } \right]$

$4\times { 10 }^{ 4 }=\sqrt { 3 } a\rho +h\rho g$

Comparing water volume:

$\sqrt { 3 } \times 2.5=\sqrt { 3 } h+\cfrac { 1 }{ 2 } \sqrt { 3 } .l$

$\cfrac { 25 }{ 10 } =h+\cfrac { \sqrt { 3 } a }{ 2g } \Rightarrow h=2.5-\cfrac { \sqrt { 3 } }{ 2 } \cfrac { a }{ g }$

$4\times { 10 }^{ 4 }=\sqrt { 3 } a\times { 10 }^{ 3 }+\left( 2.5-\cfrac { \sqrt { 3 } a }{ 2g } \right) { 10 }^{ 3 }\times g$

$40=\sqrt { 3 } a+2.5g-\cfrac { \sqrt { 3 } }{ 2 } a\Rightarrow 40=2.5g+\cfrac { \sqrt { 3 } }{ 2 } a$

$a=\cfrac { 30 }{ \sqrt { 3 } } \Rightarrow a=10\sqrt { 3 } m/s^2$

Velocity of efflux

According to Bernouli's principle,

${ P }_{ 0 }+\cfrac { 1 }{ 2 } \rho { v }_{ 2 }^{ 2 }={ P }_{ 0 }+0+\cfrac { 1 }{ 2 } \rho { v }_{ 1 }^{ 2 }$

$4\times { 10 }^{ 4 }=\cfrac { 1 }{ 2 } \rho \left( { v }_{ 1 }^{ 2 }-{ v }_{ 2 }^{ 2 } \right)$

By equation of continuity,

${ A }_{ 1 }{ v }_{ 1 }={ A }_{ 2 }{ v }_{ 2 }$

$4\times { 10 }^{ 4 }=\cfrac { 1 }{ 2 } \times 1000\left( { v }_{ 1 }^{ 2 }-\cfrac { { A }_{ 1 }^{ 2 }{ v }_{ 1 }^{ 2 } }{ { A }_{ 2 }^{ 2 } } \right) \Rightarrow 80={ v }_{ 1 }^{ 2 }\left( \cfrac { { A }_{ 1 }^{ 2 } }{ { A }_{ 2 }^{ 2 } } \right)$

$80={ v }_{ 1 }^{ 2 }\quad \quad \left[ \cfrac { { A }_{ 1 } }{ { A }_{ 2 } } \approx 0 \right] \quad \left[ \because \left( { A }_{ 1 }<<{ A }_{ 2 } \right) \right]$

${ v }_{ 1 }=\sqrt { 80 } =4\sqrt { 5 } m/s$

1094868_984958_ans_8772922e6ca14e76ab6625d443228375.png

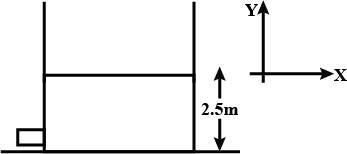
Two tubes of length ${ l }_{ 1 }$ , ${ l }_{ 2 }$ and radius ${ r }_{ 1 }$ , ${ r }_{ 2 }$ are connected in series, and allowed to carry a liquid $\eta$ through it. If ${ p }_{ 1 }$ and ${ p }_{ 2 }$ are the pressure at the two extreme ends, calculate the pressure at the junction.

$\cfrac { dv }{ dt } =\cfrac { \pi { r }^{ 4 }\left( \Delta P \right) }{ 8\eta l }$

$\eta$ - coeffiecient of viscosity

Let the pressure of the junction is

$P$

Since the pipe is connected to each other then rate of flow must be same.

${ \left( \cfrac { dv }{ dt } \right) }_{ 1 }={ \left( \cfrac { dv }{ dt } \right) }_{ 2 }\\ \Rightarrow \cfrac { \pi { r }_{ 1 }^{ 4 }\left( { P }_{ 1 }-P \right) }{ 8\eta { l }_{ 1 } } -\cfrac { \pi { r }_{ 2 }^{ 4 }\left( { P-P }_{ 2 } \right) }{ 8\eta { l }_{ 2 } } \\ \Rightarrow { l }_{ 1 }{ r }_{ 1 }^{ 4 }\left( { P }_{ 1 }-P \right) ={ l }_{ 2 }{ r }_{ 2 }^{ 4 }\left( { P-P }_{ 2 } \right) \\ \Rightarrow { l }_{ 2 }{ { r }_{ 1 }^{ 4 }P }_{ 1 }-{ l }_{ 2 }{ { r }_{ 1 }^{ 4 }P }={ l }_{ 1 }{ { r }_{ 2 }^{ 4 }P }-{ l }_{ 2 }{ { r }_{ 2 }^{ 4 }P }\\ \Rightarrow \left( { r }_{ 1 }^{ 4 }{ l }_{ 2 }+{ r }_{ 2 }^{ 4 }{ l }_{ 1 } \right) P={ r }_{ 1 }^{ 4 }{ l }_{ 2 }{ P }_{ 1 }+{ r }_{ 2 }^{ 4 }{ l }_{ 1 }{ P }_{ 2 }\\ \Rightarrow P=\dfrac { { r }_{ 1 }^{ 4 }{ l }_{ 2 }{ P }_{ 1 }+{ r }_{ 2 }^{ 4 }{ l }_{ 1 }{ P }_{ 2 } }{ { r }_{ 1 }^{ 4 }{ l }_{ 2 }+{ r }_{ 2 }^{ 4 }{ l }_{ 1 } }$

Find the area of a body which experiences a pressure of $50,000\ Pa$ by a thrust of $100\ N$ .

Pressure on the body =

$50,000 pa$

Force or thrust =

$100 N$

To find,

Area of the body =?

We know that,

Pressure =

$\dfrac{Force }{Area}$

By substituting the values we get,

$a = \dfrac{100 }{50,000 }$

$a = 0.002 m^2$

How much force should be applied on an area of $10^{-4} m^2$ to get a pressure of $15 Pa$ ?

The applied force is given as,

$F = PA$

$F = 15 \times {10^{ - 4}}$

$F = 0.0015\;{\rm{N}}$

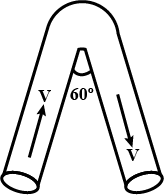
There is a uniform tube of cross-section area . A Liquid of density $\rho$ is flowing in the tube flowing with uniform speed $v$ . Wat will be the force applied by liquid at the bend ? $\theta=^{o}$

toward x-dircetion, Angle bisect into half, as show in fgure

Inlet velocity ${{V}_{i}}$ = outlet velocity ${{V}_{o}}$ = $V$

Change in velocity in y-direction, $\Delta {{V}_{y}}={{V}_{o}}\sin {{30}^{o}}-{{V}_{i}}\sin {{30}^{o}}=0$

Change in velocity in x-direction, $\Delta {{V}_{x}}={{V}_{o}}\cos {{30}^{o}}-\left( -{{V}_{o}}\cos {{30}^{o}} \right)=2{{V}_{o}}\dfrac{\sqrt{3}}{2}=\sqrt{3}{{V}_{o}}$

Rate of fluid flow, $\overset{\bullet }{\mathop{m}}\,=\rho AV$

$Force=rate\,of\,change\,of\,momentum=\overset{\bullet }{\mathop{m}}\,\Delta V$

$Force=\,\rho AV.\,\sqrt{3}\,V=\sqrt{3}\,\rho A{{V}^{2}}$

Hence, force on tube is $\sqrt{3}\,\rho A{{V}^{2}}$

1024014_1082561_ans_d3a35fabe85d46c68cbf0f0d592a2a86.png

Explain the relation between the area of contact and pressure exerted on a body.

The pressure is force exerted by a body per unit area.

$P = \dfrac{F}{A}$

From the above equation we can see that the force is inversely proportional to that of the area. We can see by physical example how the pressure exerted by the body depends on the area.

When we walk in high heels the area of the contact of the heels with the surface is very small and hence the pressure exerted will be very high so is the pressure exerted on the body.

The doctor prescripts to a patient an infusion of $30 mg/h$ . You gave a bag of $200 mg$ in $50 ml$ . At what rate $(ml/min)$ do you set the pump?

Rate of infusion $= 30\;{\rm{mg/h}}$

We have a bag of $200\;{\rm{mg}}$ in $50\;{\rm{ml}}$ .

Rate of pump setting $= 30 \times \dfrac{{50}}{{200}} = 7.5\;{\rm{ml/h}}$

Do liquids exert pressure on the sides of the container they are kept in? Justify.

The liquid is less dense s compared to the solid. They have less tensile strength in them and hence they can’t keep themselves in shape as solid do. Liquid tend to flow from higher level to lower level to the gravity.

If the liquid is stored in the cylinder it requires an external force.

Also the molecules of the liquid keep on vibrating and thus exert pressure on the wall of the container.According to the Newton’s law every action has equal and opposite reaction.

An aeronautical engineer observed that on the upper and lower surfaces of the wings of an aeroplane, the speed of the air are $90m/s$ & $72 m/s$ respectively. What is the left on the wing if its area is $3.2 m^2$ density of air is $0.29 kg/m^3$

The pressure difference is given as,

$\Delta P = \frac{1}{2}\rho \left( {{V_2}^2 - {V_1}^2} \right)$

$\Delta P = \frac{1}{2} \times 0.29\left( {{{\left( {90} \right)}^2} - {{\left( {72} \right)}^2}} \right)$

$\Delta P = 422.82\;{\rm{N/}}{{\rm{m}}^2}$

The lift on the wing is given as,

$F = \Delta P \times A$

$F = 422.82 \times 3.2$

$F = 1353.024\;{\rm{N}}$

A small hole is made at the bottom of a symmetrical jar, as shown in figure. A liquid is filled into the jar up to a certain height. The rate of fall of liquid is independent of the level of liquid in the jar. The surface of jar is a surface of revolution of the curve $y=kx^{n}$ . The value of $n$ is ?

1310810_1138534_ans_7dc32d309cc9402a9a96481b3be59ec0.jpg

A solid cube of dimensions $50\ cm \times 50\ cm$ and weighing $25\ N$ placed on a table. Calculate the pressure exerted on the table.

The magnitude of the pressure

$(P)$ exerted by an object on a given surface is equal to its weight

$(F)$ acting in the direction perpendicular to that surface divided by the total surface area of contact

$(A)$ between the object and the surface.

$P=\dfrac{F}{A}=\dfrac{F}{a^2}$

where

$a$ is the dimension of the cube.

Given that

$a = 50\ cm= 0.5\ m , F= 25\ N$

$\implies P=\dfrac{25}{0.5\times 0.5}$

$\implies P=100\ Pa$

Air stream horizontally across an aeroplane wing of area 3m $^{2}$ weighing 250 kg. The air speed is 60 m/s and 45 m/s over respectively. What is the lift on the wing ? (Density of air 1.293 g/1)

$\Delta P=\dfrac{1}{2}\rho(v_2^2-v_1^2)$

Lift

$=L=\Delta P A=\dfrac{1}{2}\rho(v_2^2-v_1^2)A$

$\implies L=\dfrac{1}{2}\times 1.293\times (60^2-45^2)\times 3$

$\implies L=3054.7N$

A water hose 2 cm in diameter is used to fill a 20 litre bucket. If it takes 1 minute to fill the bucket, then the speed v at which the water the water leaves the hose is,

$\textbf{Hint:}$ Use the volumetric flow rate equation.

$\textbf{Explanation:}$ Volumetric flow rate

$V=Avt=area\times velocity\times time$

$v=\dfrac{V}{At}$

$v=\dfrac{20\times 10^{-3}}{\pi \dfrac{(0.02)^2}{4}\times 60}$

$v=1.06m/s$

Find the terminal velocity of a steel ball of diameter $0.2 cm$ when it falls through a tube filled with glycerin. $(g=9.8m/s^2$ ,density of steel $=8000 kg/m63$ ,density of glycerin $=1.33 g/cm^3, \eta =8.33$ poise $=0.833 Ns/m^2$ )

Given :

$\sigma = 8000 \ kg/m^3$

$\rho = 1330 \ kg/m^3$

Radius of ball

$r = \dfrac{d}{2} = \dfrac{0.2 \ cm}{2} = 0.1 \ cm = 10^{-3} \ m$

Terminal velocity

$v = \dfrac{2gr^2 (\sigma - \rho)}{9\eta}$

$v = \dfrac{2\times 9.8\times (10^{-3})^2 (8000-1330 )}{9\times 0.833} = 1.74\times 10^{-2} \ m/s = 1.74 \ cm/s$

Water follows through a tube shown in the figure. The areas of cross-section at $A$ and $B$ are $1\ cm^{2}$ and $0.5\ cm^{2}$ respectively. The height difference between $A$ and $B$ is $5\ cm$ . If the speed of water at $A$ s $10\ cm/s$ . find (a) the speed at $B$ and (b) the difference in pressure at $A$ and $B$ .

1669684_1353974_ans_752a373e60104ff6ae48cecb07f45f4a.jpeg

The area of cross section of the wider tube shown in Fig. is $900 cm^{2}$ . If the body standing on the position weighs $45 kg$ , find the difference in the levels of water in the two tubes.

1669688_1376237_ans_ea111402d8724d418ce1f3a00b869646.jpeg

Velocity of flow of water in a horizontal pipe is $10.0\ m\ s^ {-1}$ . Find the velocity-head of water. $(g=10.00\ ms^ {-2})$

Given that,

velocity of flow of water $v{\rm{ }} = {\rm{ }}10.0{\rm{ }}m/s$

From Bernoulli's equation, Velocity head of water is given by:

${V_h} = \dfrac{{{v^2}}}{{2g}}$

Here, g = acceleration due to gravity = $9.8m/{s^2}$

Put the value into the formula

${V_h} = \dfrac{{{{(10m/s)}^2}}}{{2 \times 9.8m/s^2}}$

${V_h} = 5.10m$

Hence, Velocity head of water ${V_h} = 5.10m$

Water is flowing through a cylinderical pipe of cross-sectional area 0.09 $\quad \pi \quad m^{ 2 }$ at a speed of 1.0 m $s^{ -1 }$ . If the diameter of the pipe is halved , then find the speed of the flow of water through it .

2047312_1393686_ans_ee4d9ad215aa4919b475ee33e88f3f60.jpg

The thrust due to atmospheric pressure on us is around 15 tonne. How we withstand such a thrust?

2048977_1398039_ans_9fd3ae57458847cd9c5db2e4c0ae9e15.jpeg

8 Rain Drops of radius 1 mm each falling down of Terminal velocity 5 m/s Combine to from a bigger drop. find the Terminal velocity of bigger drop .

2047328_1393837_ans_70b997c6fa8045379cf420acc244f73c.jpeg

A cemented wall of thickness one metre can withstand a side pressure of ${ 10 }^{ 5 }{ Nm }^{ -2 }$ . What should be the thickness of the side wall at the bottom of a water dam of depth 100 m.take density of water = ${ 10 }^{ 3 }{ kg\quad m }^{ -3 }$ and g= $9.8{ ms }^{ -2 }$

2048965_1397945_ans_7da92998eadb49bc888f4a4c8737fad0.jpg

Calculate total energy per unit mass possessed by water at a point where the pressure is $0.1 \times 10^5 \ N/m^2$ , velocity 0.02 m/s and height of water level from the ground is 10 cm. (Density of water = $1000 \ kg/m^3 , \ g= 9.8 \ m/s^2$ ).

1876646_1527939_ans_e41b99949c6f40a5942e010960a8b0f9.jpg

The contact angle between water and glass is $0^o$ . When water is poured in a glass to the maximum of its capacity, the water surface is convex upward. The angle of contact in such a situation is more than $90^o$ . Explain.

Due to the surface tension, the surface of the liquid acts as a stretched membrane. So even if some more water than the rim level of the glass is poured into it, the stretched water surface which holds the glass rim due to adhesion becomes convex upward and the contact angle between the water and the glass becomes more than 90° in this situation.

The zero degrees angle of contact for water and the glass is for the situation when the water level is below the rim level of the glass. In some special situations, the angle of contact may change.

In a vessel is a liquid, density of which increases with depth $y$ from its surface according to the law $\rho ={ \rho }_{ 0 }+ky$ , where ${ \rho }_{ 0 } = 1.0 g/cm^3$ and $k = 0.01 g/cm^4$ . Two balls connected with an inextensible thread of length $15 cm$ are dropped in the liquid. Volume of each ball is $1.0 cm^3$ and their masses are $1.2 g$ and $1.4 g$ . At what depth will these balls settle in equilibrium?

1643162_1731068_ans_05e9c469a3c242229e429852cb2f6f0e.jpg

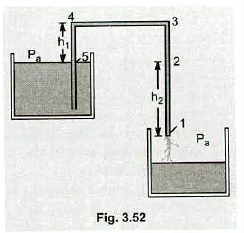
A pipe of uniform cross-section is used to siphon an ideal fluid of density $\rho$ from one tank to another, as shown below. The lower end of the pipe is above the liquid level in the receiving tank. If the atmospheric pressure is $P_{a}$ , find (a) the speed of the fluid as it passes through the pipe; (b) the pressure of the fluid at points $1,2,3,4$ and $5$ . (The value of $P_{a}$ is essentially the same at the both ends of the pipe).

(a)Taking the level of water in the upper container as the reference level.

Applying Bernoulli's equation at both the ends of the pipe:

$P_a+\dfrac{1}{2}\rho v_1^2+\rho g (0)=P_a+\dfrac{1}{2}\rho v^2+\rho g(-h_2)$

If we consider the container area is big enough such that

$v_1=0$

We get,

$\dfrac{1}{2}\rho v^2=\rho gh_2\Rightarrow v=\sqrt{2gh_2}$

(b)

$P_1=atmospheric\, pressure=P_a$

$P_2=P_a-\rho g h_2$

$P_3=P_a+\rho g (h_1-h_2)$

$P_4=P_3$ because they are at the same level

$P_5=P_a$

A cylindrical bucket of liquid (density $\rho$ ) is rotated about its symmetry axis, which is vertical. If the angular velocity is $\omega$ , show that the pressure at a distance $r$ from the rotation axis is
$P = P_0 +\dfrac {1}{2} \rho \omega^2 r^2$ ,
where $P_0$ is the pressure at $r=0$ ,

1651118_1745824_ans_e1a1f2efce3845b4934d88f851ab8062.jpg

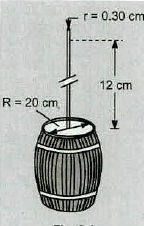
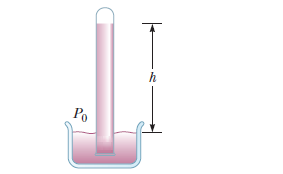
In working out his principle, Pascal showed dramatically how force can be multiplied with fluid pressure. He placed a long thin tube of $0.30\ cm$ radius vertically into a $20\ cm$ radius wine barrel. He found that when the barrel was filled with water and the tube filled to a height of $12\ cm$ , the barrel burst. Calculate
The mass of fluid in the tube.

we know

$V=Ah$

where

$A$ is the cross section Area and h is the height .

here

$h=12\,m=1200\,cm$

and

$A=\pi r^2$

$A=3.14\times(0.30)^2 \,cm^2=0.385\,cm^2$

Therefore,

$V=461.8 \,cm^3 = 0.4618 \,L$

also

$m=\rho V$

water density is

$\rho =1 kg/L$

$m=0.4618\,kg$

at the bottom of the tube:

$F=mg=9.8\times0.4618=4.53\,N$

which acts on area

$A=0.385 cm^2$

but the barrel lid has area

$B=\pi R^2=3.14\times 20^2$

$B=2642.08 cm^2$

so force on entire lid is

$F=4.53\times 2642.08/0.385$

$F=31087.3\,N$

which is equivalent to weight of mass

$M=F/g=3169\,kg$

so mass of the fluid is

$3169\,kg$

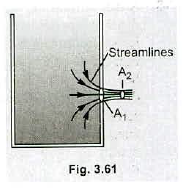
Sketch in Fig $3.61$ is a thin walled tank having a small circular hole of area $A_{1}$ in its side. As you can see from the sketch, the cross-sectional area of the water jet emerging from the hole does not have constant area $A_{1}$ because this would require the streamlines to have sharp kinks in them where they pass through the hole. Instead the cross-sectional area of the jet diminishes for some distance after the jet leaves the hole. The area attains a minimum value $A_{2}$ where the streamlines are essentially parallel to one another. The location is called the vena contracta (Latin for narrow conduit). A detailed analysis is very difficult, even for the simplest case of circular hole in a thin plate. But, for this case, the result is $A_{2}=\pi/(2+\pi)=0.611\ A_{1}$ . If the hole is circular with radius $1.20\ cm$ and the depth of the hole below the water surface is $2.5\ m$ , what is the volume flux $dV/dt$ through the hole?

1694332_1746052_ans_8a7b1c071a8b481781691f7c0aabf7ee.jpg

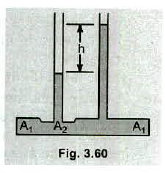
The device shown in Fig $3.60$ can be used as flowmeter. The horizontal man pipe has a cross-sectional area $A_{1}$ except at the constriction where the area is $A_{2}$ . When an ideal fluid flows through the main pipe, there is a difference $H$ in the fluid levels in the two small vertical standpipes (a) Show that the flow speed $v_{1}$ at any point in the main pipe except at the constriction is
$v_{1}=\dfrac{\sqrt{2gh}}{\sqrt{\dfrac{A_{1}^{2}}{A_{2}^{2}}}-1}=\dfrac{A_{2}}{\sqrt{A_{1}^{2}-A_{2}^{2}}}\sqrt{2gh}$
(b) Show that the volume flux in the main pipe is
$\dfrac{dV}{dt}=\dfrac{A_{1}A_{2}}{\sqrt{A_{1}^{2}-A_{2}^{2}}}\sqrt{2gh}$

1661364_1746050_ans_4b6f3de35e8540faa48819bfc371c4c9.jpg

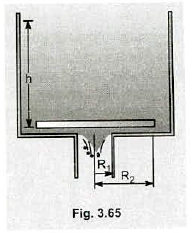
The liquid-filled tank illustrated in Fig $3.65$ has a drain of radius $R_{1}$ at the bottom. The drain is covered with a large circular plate of radius $R_{2}$ , with $R_{2}>>R_{1}$ . The space between the plate and the bottom of the tank is quite narrow, so the drain does not fill with liquid. Show that the pressure in the space between the plate and the bottom of the tank is
$P=P_{atm}+\rho gh\left(1-\dfrac{R_{1}^{2}}{r^{2}}\right)$
where $r$ is the distance from the axis of the drain $(R_{1}<r<R_{2}), h$ is the depth of the liquid in the tank, and $\rho$ the density of the liquid.

1678528_1746063_ans_6e06b907c16a49168b5c27a42b560150.jpg

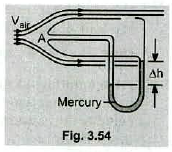
A Pitot tube can be used to determine the velocity of air flow by measuring the difference between the total pressure and the static pressure (Fig: $3.54$ ). If the fluid in the tube is mercury, whose density is $\rho_{Hg}=13600\ kg/m^{3}$ , and if $\Delta h=5.00\ cm$ , find the speed to air flow. (Assume that the air is stagnant at point $A$ , and take $\rho_{air}=1.2\ kg/m^{3}$ )

1668432_1746037_ans_1826355979bc4259b1d40e698c369b1c.jpeg

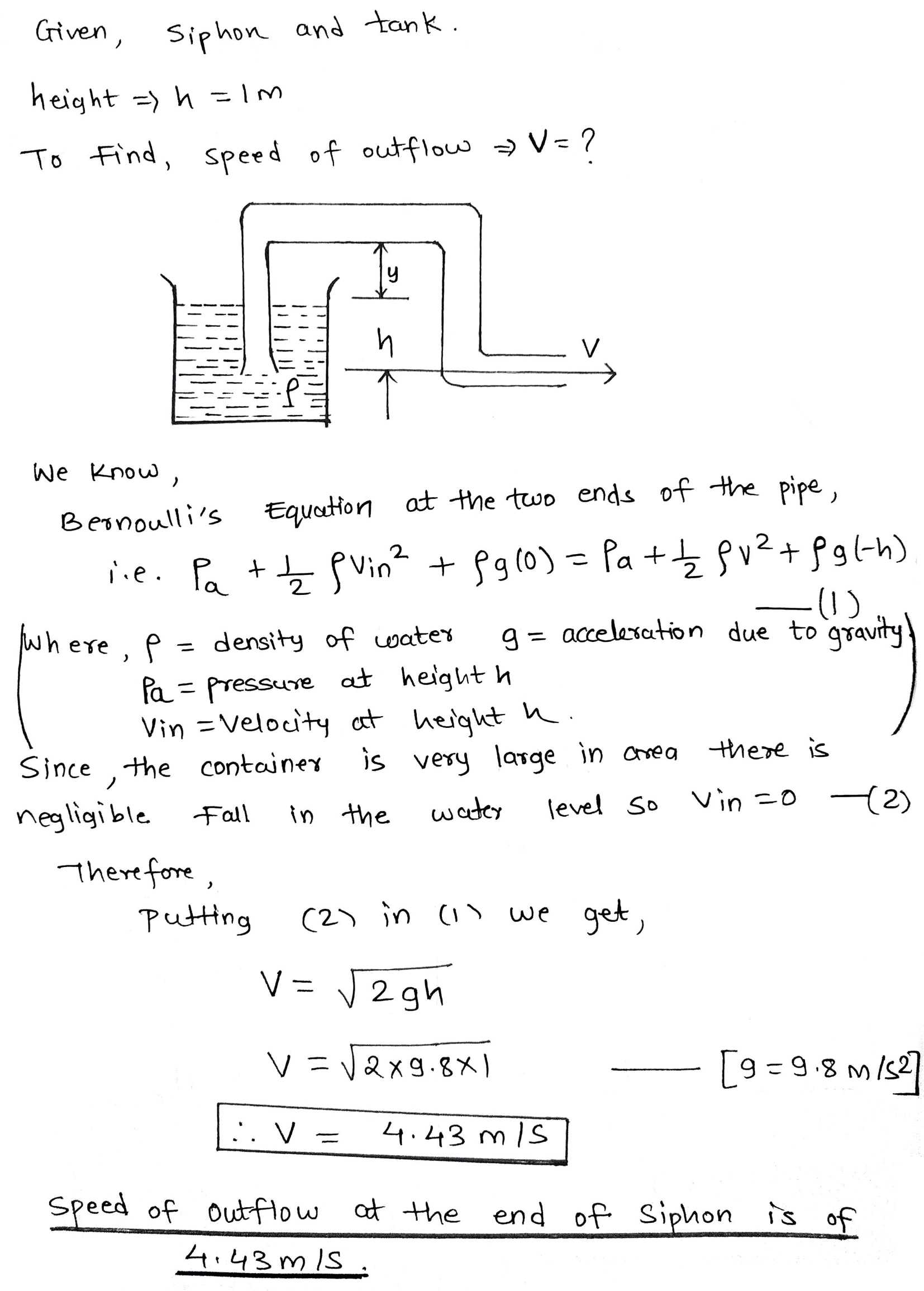
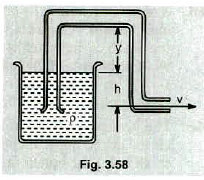
A siphon is used to drain water from a tank,as illustrated in Fig $3.58$ . The siphon has a uniform diameter. Assume steady flow without friction (a) If the distance $h=1.00\ m$ , find the speed of outflow at the end of the siphon (b) What is the limitation on the height of the top of the siphon above the water surface> (For the flow of liquid to be continuous the pressure must not drop below the vapour pressure of the liquid.)

Using Bernoulli's Equation at the two ends of the pipe we can get:

$P_a+\dfrac{1}{2}\rho v_{in}^2+\rho g(0)=P_a+\dfrac{1}{2}\rho v^2+\rho g(-h)$

Since the container is very large in area there is negligible fall in the water level so

$v_{in}=0$

From here we get ,

$v=\sqrt{2gh}=\sqrt{2\times 9.8\times 1}=4.43\,m/s$

The traditional theory for centuries was that gravity pulling the liquid down on the exit side of the siphon resulted in reduced pressure at the top of the siphon. For continuous flow, the pressure inside the pipe must not drop below the vapour pressure of the liquid.

In 1654 Otto von Guericke, inventor of the air pump, gave a
demonstration before the noble-men of the Holy Roman Empire in
which two teams of eight horses could not pull apart two evacuated brass hemispheres. (a) Assuming the hemispheres have (strong) thin walls so that R in Figure may be considered both the inside and outside radius, show that the force required to pull apart
the hemispheres has magnitude $F=\pi R^2 \vartriangle p$ , where $\vartriangle p$ is the difference between the pressures outside and inside the sphere.
(b) Taking R as 30 cm, the inside pressure as 0.10 atm, and the outside pressure as 1.00 atm, find the force magnitude the teams of
horses would have had to exert to pull apart the hemispheres. (c) Explain why one team of horses could have proved the point just as well if the hemispheres were attached to a sturdy wall.

(a) The pressure difference results in forces applied as shown in the figure. We consider a team of horses pulling to the right. To pull the sphere apart, the team must exert a force at least as great as the horizontal component of the total force determined by "summing" (actually, integrating) these force vectors.
We consider a force vector at an angle

$\theta$ . Its leftward component is

$\vartriangle\hspace{0.05cm}p\hspace{0.05cm}cos{\theta}dA$ ,where

$dA$ is the area element for where the force is applied. We make use of the symmetry of the problem and let

$dA$ be that of a ring of constant

$\theta$ on the surface. The radius of the ring is

$r=Rsin{\theta}$ , where

$R$ is the radius of the sphere. If the angular width of the ring is

$d\theta$ , in radians, then its width is

$Rd\theta$ and its area is

$dA=2\ piR^2sin{\theta} d\theta$ .Thus the net horizontal component of the force of the air is given by

$F_{h}=2 \pi R^2 \vartriangle p\textstyle \int_{0}^{\pi/2} sin{\theta}cos{\theta}d\theta= \pi R^2\vartriangle p sin^2 {\theta}\mid_{0}^{\pi/2}=\pi R^2 \vartriangle p$ .
(b) We use

$1\hspace{0.05cm}atm=1.01\times10^5\hspace{0.05cm}Pa$ to show that

$\vartriangle p =0.90\hspace{0.05cm}atm=9.09\times10^4\hspace{0.05cm}Pa$ .The sphere radius is

$R=0.30\hspace{0.05cm}m$ ,so

$F_{h}=\pi(0.30\hspace{0.05cm}m)^2(9.09\times10^4\hspace{0.05cm}Pa)=2.6\times10^4\hspace{0.05cm}N$ .
(c) One team of horses could be used if one half of the sphere is attached to a sturdy wall. The force of the wall on the sphere would balance the force of the horses.

An airplane has a mass of $1.60\times 10^{4}\ kg$ and each wing has an area of $40.0\ m^{2}$ . During level flight the pressure on the lower wing surface is $7.00\times 10^{4}\ Pa$ . Determine the pressure on the upper wing surface.

1668440_1746041_ans_0348ad0dc46141458ae28f794a16667f.jpeg

The bends during flight. Anyone who scuba dives are advised not to fly within the next $24\hspace{0.05cm} h$ because the air mixture for diving can introduce nitrogen to the bloodstream. Without allowing the nitrogen to come out of solution slowly, any sudden air-pressure reduction (such as during aeroplane ascent) can result in the nitrogen forming bubbles in the blood, creating the bends, which can be painful and even fatal. Military special operations forces are especially at risk. What is the change in pressure on such a special-op soldier who must scuba dive at a depth of $20\hspace{0.05cm} min$ seawater one day and parachute at an altitude of $7.6\hspace{0.05cm}km$ the next day? Assume that the average air density within the altitude range is $0.87\hspace{0.05cm}kg/m^3$

Using the equation

$p_{2}=p_{1}+\rho g(y_{1}-y_{2})$ , we find the gauge pressure to be

$p_{gauge}=\rho gh$ , where

$\rho$ is the density of the fluid medium, and

$h$ is the vertical distance to the point where the pressure is equal to the atmospheric pressure.
The gauge pressure at a depth of

$20\hspace{0.05cm}m$ in seawater is

$p_{1}=\rho_{sw}gd=(1024\hspace{0.05cm}kg/m^3)(9.8\hspace{0.05cm}m/s^2)(20\hspace{0.05cm}m)=2.00\times 10^5\hspace{0.05cm}Pa$ .
On the other hand, the gauge pressure at an altitude of

$7.6\hspace{0.05cm}km$ is

$p_{2}=\rho_{air}gd=(0.87\hspace{0.05cm}kg/m^3)(9.8\hspace{0.05cm}m/s^2)(7600\hspace{0.05cm}m)=6.48\times 10^4\hspace{0.05cm}Pa$ .
Therefore, the change in pressure is

$\vartriangle p=p_{1}-p_{2}=2.00\times10^5\hspace{0.05cm}Pa-6.48\times10^4\hspace{0.05cm}Pa \thickapprox 1.4\times10^5\hspace{0.05cm}Pa$ .

Two cylindrical vessels fitted with pistons A and B area of cross section $8 cm^{2}$ and $320 cm^{2}$ respectively, are joined at their bottom by a tube and they are completely filled with water. When a mass of 4 kg is placed on piston A,find
the thrust on piston B,

1962712_1810569_ans_d090001954bb4739b906c57210011dd9.jpg

Two cylindrical vessels fitted with pistons A and B area of cross section $8 cm^{2}$ and $320 cm^{2}$ respectively, are joined at their bottom by a tube and they are completely filled with water. When a mass of 4 kg is placed on piston A,find
the pressure on piston A,

1962702_1810567_ans_bb810f5b04de42cab1a65b0407e62ee6.jpg

A block of iron of mass 7.5 kg and of dimensions 12cm $12cm \times 8cm \times 10cm$ is kept on a table top on its base of side $12cm \times 8cm$ . Calculate :
pressure exerted on the table top. Take 1kgf = 10N.

1962645_1810532_ans_f10450084eb144c8879256cae99d5261.jpg

Figure shows a brick of weight $2 kgf$ and dimensions $20 cm \times 10 cm \times 5 cm$ placed in three different positions on the ground . find the pressure exerted by the brick in each case.

Case (A)
Area of base = area of top =

$L \times B$

$20 cm \times 10 cm=200 cm^2$

$P = \dfrac { Thrust }{A} = \dfrac { 2 kgf }{ 200 cm^2} = \dfrac {1}{100}= 0.01 kgf cm^{-2}$

Case (B)

Area of base = area of top

$5 cm \times 10 cm = 50 cm^2$
pressure exerted =

$P = \dfrac {F}{A} = \dfrac { 2 kgf}{ 50 cm^2} = 0.04$

$P = 0.04 kgf cm^{-2}$

Case (C)

Weight of brick

$F = 2kgf$
Area of base

$= L \times B$

$= 20 cm \times 5 cm = 100 cm^2$
Pressure exerted =

$\dfrac {F}{A} = \dfrac {2}{100} = 0.02 kgf cm^{-2}$

A pitot tube is used to determine the air-speed of an airplane. It consists of an outer tube with a number of
small holes B (four are shown) that allow air into the tube; that tube is connected to one arm of a U-tube. The other arm of the U-tube is connected to hole A at the front end of the device, which points in the direction the plane is headed. At A the air becomes
stagnant so that $v_{A}=0$ . At B, however, the speed of air presumably equals the airspeed $v$ of the plane (a) Use Bernoullis equation
to show that $v=\sqrt{\dfrac{2\rho gh}{\rho_{air}}}$ , where $\rho$ is the density of the liquid in the U-tube and $h$ is the difference in the liquid levels in that tube.
(b) Suppose that the tube contains alcohol and level difference $h$ is 26.0 cm. What is the plane's speed relative to the air? The density of the air is $1.03\hspace{0.05cm}kg/m^3$ and that of alcohol is $810\hspace{0.05cm} kg/m^3$

(a) Bernoull's equation gives

$p_{A}=p_{b}+\dfrac{1}{2}\rho_{air}v^2$ . Howeveer,

$\vartriangle=p_{A}-p_{B}=\rho gh$ in order to balance the pressure in the two arms of the U-tube. Thus

$\rho gh=\dfrac{1}{2}\rho_{air}v^2$ , or

$v=\sqrt{\dfrac{2\rho gh}{\rho_{air}}}$ .
(b) The plane's speed relative to the air is

$v=\sqrt{\dfrac{2\rho gh}{\rho_{air}}}=\sqrt{\dfrac{2(810\hspace{0.05cm}kg/m^3)(9.8\hspace{0.05cm}m/s^2)(0.260\hspace{0.05cm}m)}{1.03\hspace{0.05cm}kg/m^3}}=63.3\hspace{0.05cm}m/s$

Two cylindrical vessels fitted with pistons A and B area of cross section $8 cm^{2}$ and $320 cm^{2}$ respectively, are joined at their bottom by a tube and they are completely filled with water. When a mass of 4 kg is placed on piston A,find
the pressure on piston B,

1962693_1810568_ans_69fe1543375c4af4b248d20a52f22db4.jpg

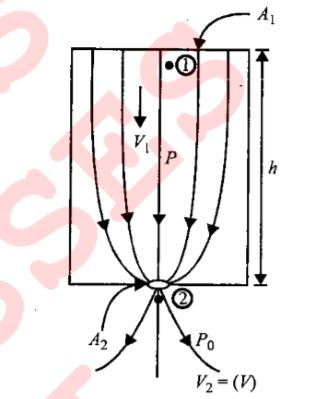
A tank is filled with water to a height H. At a depth h from the free surface, a hole is made so that the water comes out of it. What is the velocity of efflux? Also, what are the maximum range and the position of the hole for the same? Find the time taken by a water molecule to reach the ground. Determine the horizontal length covered by the molecule.

Take two points at the same height (H- h) from ground one inside and one outside the hole. Applying Bernoulli’s theorem for the points, we have

$(\frac{P_{0}+h p g}{\rho g}) + 0 + (H – h) = (H – h) + (\frac{v^{2}}{2 g}+\frac{P_{0}}{\rho g})$
On Solving, we get,

$v = (\sqrt{2 \mathrm{gh}})$
The velocity of efflux thus depends on the depth of which the hole is made from the surface of the liquid. Time taken to reach
ground

$= t = (\sqrt{\frac{2(\mathrm{H}-\mathrm{h})}{\mathrm{g}}}),$
Since

$v =(\sqrt{2 \mathrm{gh}})$ is horizontal and

$ax = 0$ ;

$R = vt = (\sqrt{2 \mathrm{gh}}) (\sqrt{\frac{2(\mathrm{H}-\mathrm{h})}{\mathrm{g}}})$

$R = (2 \sqrt{\mathrm{h}(\mathrm{H}-\mathrm{h})})$
To maximise Range,

$(\frac{\mathrm{d} \mathrm{R}}{\mathrm{dh}}) = 0$
i.e., h = H/2
Maximum Range,

$(R_{\max }=2 \sqrt{\frac{H}{2}(H-H / 2)}=H).$
1776717_1845220_ans_7b7c3842002948ccba11f8354a628474.png

What should be the ratio of area of cross section of the master cylinder and wheel cylinder of a hydraulic brake so that a force of 15N can be obtained at each of its brake show exerting a force of 0.5N on the pedal?

1962673_1810557_ans_667903771c79429bb2e8eecff437ee57.jpg

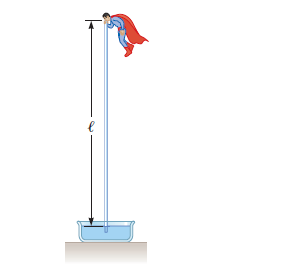
Why is the following situation impossible? Figure shows Superman attempting to drink cold water through a straw of length $\ell=12.0\ m$ . The walls of the tabular straw are very strong and do not collapse. With his great strength, he achieves maximum possible suction and enjoys drinking the cold water.

1979690_1866940_ans_3c52a260e37d4497a32098148ce9cd29.jpg

Blaise Pascal duplicated Torricelli's barometer using a red Bordeaux wine, of density $984\ kg.m^3$ , as the working liquid.
Would you expect the vacuum above the column to be as good as for mercury ?

1979741_1866963_ans_7bcb02b853a74bc1ba67cc5b5b1abea4.jpg

A jet plane having a cabin of length $l-50\ m$ flies along the horizontal with an acceleration $a=1 \ m/s^2$ The air density in the cabin is $\rho=1.2 \times 10^{-3}\ g/cm^3$
What is the difference between the atmospheric pressure and the air pressure exerted on the ears of the passengers sitting in the front, middle, and rear parts of the cabin?

The air layer of thickness

$\Delta x$ at a distance

$x$ form the front of the cabin experiences the force of pressure

$[p (x+ \Delta x) -p (x)]S,$
where

$S$ is the cross-sectional area of the cabin SInce air is at rest relative to the cabin, the equation of motion for the mass of air under consideration has the form

$\rho S \Delta xa= [p(x+ \Delta x) - p(x)]S$
Making

$\Delta x$ tend to zero, we obtain

$\dfrac{dp}{dx}= \rho a$
whence

$p(x) = p_1 + \rho ax$
Since the mean pressure in the cabin remains unchanged and equal to the atmospheric pressure

$\rho_0$ the constant

$p_1$ can be found from the condition

$p_0 = p_1 + \dfrac{\rho a l}{2}$ ,
where

$l$ is the length of the cabin. Thus in the middle and near parts of the cabin, the pressure is equal to the atmospheric pressure, while in the front and rear parts of the cabin, the pressure is lower and higher than the atmospheric pressure by

$\Delta p\ \dfrac{\rho a l}{2} \simeq 0.03 \ Pa$ respectively

Normal atmospheric pressure is $1.013 \times 10^5\ Pa$ . The approach of a storm causes the height of a mercury barometer to drop by $20.0\ mm$ from the normal height. What is the atmospheric pressure?

1979725_1866954_ans_e24f8dc2b791489cbc568e254be6c458.jpg

Find the free energy of the surface layer of
(a) a mercury droplet of diameter $d = 1 4 \ mm$ ;
(b) a soap bubble of diameter $d = 6.0 \ mm$ if the surface tension of the soap water solution is equal to $\alpha = 45 \ mN/m$ .

(a) The free energy per unit area being

$\alpha$ ,

$F = Surface\ tension \times A=\alpha\ \pi d^2 = 3 \mu J$

(b)

$F = \alpha\ 2\pi d^2$ because the soap bubble has two surfaces. Substitution gives

$F = 10 \mu J$

Calculate the absolute pressure at the bottom of a freshwater lake at a point whose depth is $27.5\ m$ . Assume the density of the water is $1.00 \times 10^3 \ kg/m^3$ and that the air above is at a pressure of $101.3\ kPa$ .

1979687_1866938_ans_ef075089243f4b70b587b6c681fe06c6.jpg

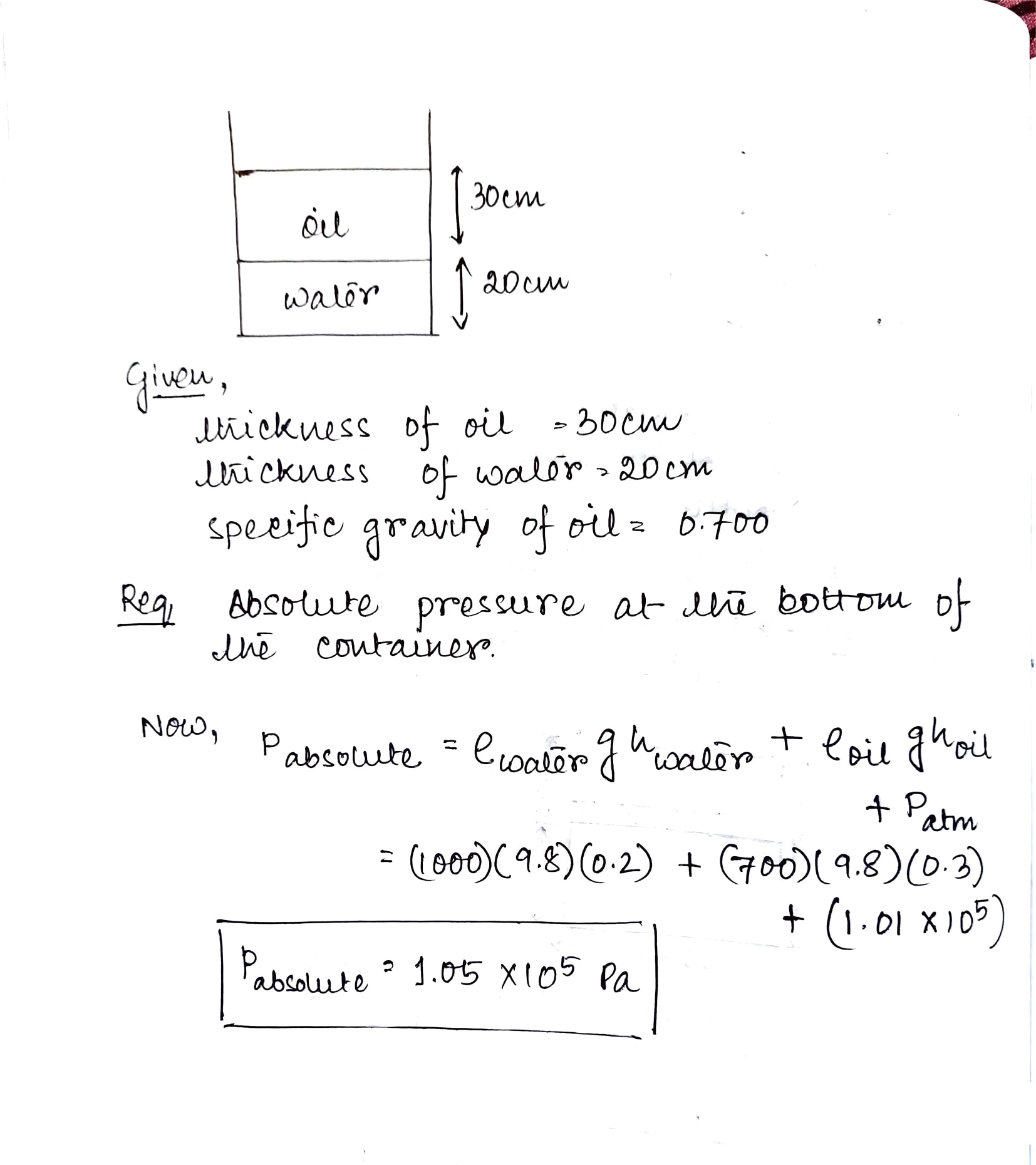
A container is filled to a depth of $20.0\ c$ with water. On top of the water floats a $30.0-cm$ -thick layer of oil with specific gravity $0.700$ . What is the absolute pressure at the bottom of the container?

1979698_1866944_ans_766d56c649bc4cb4b011ada26be41a4e.jpg

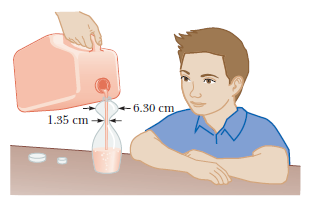
A child loves to watch as you fill a transparent plastic bottle with shampoo (Fig above). Every horizontal cross section of the bottle is circular, but the diameters of the circles have different values. You pour the brightly colored shampoo into the bottle at a constant rate of $16.5 cm^{3}/s$ . At what rate is its level in the bottle rising (a) at a point where the diameter of the bottle is $6.30 cm$ and (b) at a point where the diameter is $1.35 cm$ ?

Observe in Fig. in question that the radius of the horizontal cross section of the bottle is a relative maximum or minimum at the two radii cited in the problem; thus, we recognize that as the liquid level rises, the time rate of change of the diameter of the cross section will be zero at these positions.

The volume of a particular thin cross section of the shampoo of thickness

$h$ and area

$A$ is

$V = Ah$ , where

$A = \pi r^{2} = \pi D^{2}/4$ . Differentiate the volume with respect to time:

$\frac{dV}{dt}=A\frac{dh}{dt}+h\frac{dA}{dt}=A\frac{dh}{dt}+h\frac{d}{dt}(\pi r^{2})=A\frac{dh}{dt}+2\pi hr\frac{dr}{dt}$

Because the radii given are a maximum and a minimum value,

$dr/dt = 0$ , so

$\frac{dV}{dt}+A\frac{dh}{dt}=Av\rightarrow v=\frac{1}{A}\frac{dV}{dt}=\frac{1}{\pi D^{2}/4}\frac{dV}{dt}=\frac{4}{\pi D^{2}}+\frac{dV}{dt}$

where

$v = dh/dt$ is the speed with which the level of the fluid rises.

(a) For

$D = 6.30 cm$ ,

$v=\frac{4}{\pi (6.30cm)^{2}}(16.5cm^{3}/s)=0.529cm/s$

(d) For

$D=1.35cm$

$v=\frac{4}{\pi(1.35cm)^{2}}(16.5cm^{3}/s)=11.5cm/s$

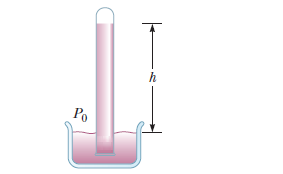
Blaise Pascal duplicated Torricelli's barometer using a red Bordeaux wine, of density $984\ kg.m^3$ , as the working liquid.
What was the height $h$ of the wine column for normal atmospheric pressure?

1979740_1866962_ans_b1fe1ba4bced49db813db272b3a8f483.jpg

Bring the ends X and to the same level. Place a slotted weight of $1N (100 gwt)$ at the end of X. What happens at the end Y?

When we place a slotted weight of

$1N$ at the end of

$X$ then the Y end rises because pressure is exerted on it.

A large storage tank, open at the top and filled with water, develops a small hole in its side at a point $16.0\ m$ below the water level. The rate of flow from the leak is found to be $2.50\times 10^{-3}\ m^3/ min$ . Determine the diameter of the hole.

1979807_1867024_ans_8ce6c3149b3142f5905e691634ae53f0.jpg

A tank with a flat bottom of area $A$ and vertical sides is filled to a depth $h$ with water. The pressure is $P_0$ at the top surface.
What is the absolute pressure at the bottom of the tank?

1979752_1866971_ans_0ca54db1192c48cb833d2314e9bbcdaf.jpeg

Figure shows a stream of water in steady flow from a kitchen faucet. At the faucet, the diameter of the stream is $0.960\ cm$ . The stream fills a $125-cm^3$ container in $16.3\ s$ . Find the diameter of the stream $13.0\ cm$ below the opening of the faucet.

1980522_1867034_ans_9610432fb7ca43a9b095c38787ebe671.jpg

Water moves through a constricted pipe in steady, ideal flow. At the lower point shown in the figure, the pressure is $P_1=1.75 \times 10^4\ Pa$ and the pipe diameter is $6.00\ cm$ . At another point $y=0.250\ m$ higher, the pressure is $P_2=1.20\times 10^4\ Pa$ and the pipe diameter is $3.00\ cm$ . Find the volume flow rate through the pipe.

1980511_1867032_ans_04e93153988840629f899a86b9668fea.jpg

A light balloon is filled with $400\ m^3$ of helium at atmospheric pressure.
At $0^oC$ , the balloon can lift a payload of what mass ?

1979768_1866981_ans_a940af5285254e4d987c7b10ed4af650.jpg

A backyard swimming pool with a circular base of diameter $6.00\ m$ is filled to depth $1.50\ m$ .
Two persons with combined mass $150\ kg$ enter the pool and float quietly there. No water overflows. Find the pressure increase at the bottom of the pool after they enter the pool and float.

1979749_1866969_ans_f6b36754a83a417998e9488ed69810f4.jpeg

Water moves through a constricted pipe in steady, ideal flow. At the lower point shown in the figure, the pressure is $P_1=1.75 \times 10^4\ Pa$ and the pipe diameter is $6.00\ cm$ . At another point $y=0.250\ m$ higher, the pressure is $P_2=1.20\times 10^4\ Pa$ and the pipe diameter is $3.00\ cm$ . Find the speed of flow in the upper section.

1980509_1867029_ans_c0ddb62ac2fb4fd48ef06d89f3326db8.jpg

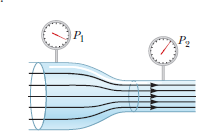
Water flowing through a garden hose of diameter $2.74\ cm$ fills a $25-L$ bucket in $1.50\ min$ .
What is the speed of the water leaving the end of the hose?

1979802_1867017_ans_3175ce3c74bb4268b411414e04788240.jpg

A tank with a flat bottom of area $A$ and vertical sides is filled to a depth $h$ with water. The pressure is $P_0$ at the top surface.
Suppose an object of mass $M$ and density less than the density of water is placed into the tank and floats. Now overflows. What is the resulting increase in pressure at the bottom of the tank?

1979754_1866972_ans_f97ca275f9344f14a0294713967856ce.jpeg

A large storage tank, open at the top and filled with water, develops a small hole in its side at a point $16.0\ m$ below the water level. The rate of flow from the leak is found to be $2.50\times 10^{-3}\ m^3/ min$ . Determine the speed at which the water leaves the hole and the diameter of the hole.

1979805_1867023_ans_45efd73885e24aa28fa26ba2a4e1b4d9.jpg

In ideal flow, a liquid of density $850\ kg/m^3$ moves from a horizontal tube of radius $1.00\ cm$ into a second horizontal tube of radius $0.500\ cm$ at the same elevation as the first tube. The pressure differs by $\Delta P$ between the liquid in one tube and the liquid in the second tube. Evaluate the volume flow rate for $\Delta P=12.0\ kPa$ .

1980565_1867068_ans_04fcb8ed7db546e991f441dab6d1e438.jpg

In ideal flow, a liquid of density $850\ kg/m^3$ moves from a horizontal tube of radius $1.00\ cm$ into a second horizontal tube of radius $0.500\ cm$ at the same elevation as the first tube. The pressure differs by $\Delta P$ between the liquid in one tube and the liquid in the second tube. Evaluate the volume flow rate for $\Delta P=6.00\ kPa$

1980561_1867066_ans_a0412825aa7142cb8799f599f2fce5b1.jpg

The Venturi tube discussed in example and shown in figure may be used as a fluid flowmeter. Suppose the device is used at a service station to measure the flow rate gasoline $( \rho =7.00 \times 10^2\ kg/m^3)$ through a hose having an outlet radius of $1.20\ cm$ . If the difference in pressure is measured to be $P_1 -P_2=1.20\ kPa$ and the radius of the inlet tube to the meter is $2.40\ cm$ , find the fluid flow rate in cubic meters per second.

1980573_1867072_ans_8a5d9877d8a84921bb69f81bb2493ddc.jpg

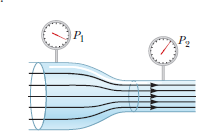
An airplane has a mass of $1.60\times 10^{4}kg$ , and each wing has an area of $40.0\ m^{2}$ . During level flightly, the pressure on the lower wing surface is $7.00\times 10^{4}Pa$
Suppose the lift on the airplane were due to a pressure difference alone. Determine the pressure on the upper wing surface.

1980585_1867100_ans_1a6aa31ef0e545508f611999bcc7700b.jpg

In ideal flow, a liquid of density $850\ kg/m^3$ moves from a horizontal tube of radius $1.00\ cm$ into a second horizontal tube of radius $0.500\ cm$ at the same elevation as the first tube. The pressure differs by $\Delta P$ between the liquid in one tube and the liquid in the second tube. Find the volume flow rate as a function of $\Delta P$ .

1980560_1867065_ans_f8a2da3fd464466b9eb29f8ddd237f6f.jpg

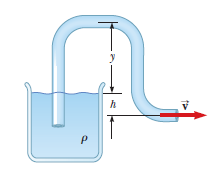
A village maintains a large tank with an open top, containing water for emergencies. The water can drain from the tank through a hose of diameter $6.60\ cm$ . The hose ends with a nozzle of diameter $2.20\ cm$ . A rubber stopper is inserted into the nozzle. The water level in the tank is kept $7.50\ m$ above the nozzle.Calculate the gauge pressure of the flowing water in the hose just behind the nozzle.

1980529_1867040_ans_7480847e28b943d78f1f59596d337223.jpg

The Venturi tube discussed in example and shown in figure may be used as a fluid flowmeter. Suppose the device is used at a service station to measure the flow rate gasoline $( \rho =7.00 \times 10^2\ kg/m^3)$ through a hose having an outlet radius of $1.20\ cm$ . If the difference in pressure is measured to be $P_1 -P_2=1.20\ kPa$ and the radius of the inlet tube to the meter is $2.40\ cm$ , find the speed of the gasoline as it leaves the hose.

1980570_1867070_ans_c97762aab4f8409f831dc6efe3f32ad8.jpg

What if? Model the rising stream as an ideal fluid in streamline flow. Use Bernoulli's equation to determine the speed of the water as it leaves ground. How does the answer from part (a) compare with the answer from part (b)?

1980580_1867079_ans_00ac97ba85014b6b961a790f7e2ba5ec.jpg

What if? Model the rising stream as an ideal fluid in streamline flow. Use Bernoulli's equation to determine the speed of the water as it leaves ground. What is the pressure ( above atmospheric ) in the heated underground chamber if its depth is $175\ m$ ? Assume the chamber is large compared with the geyser's vent.

1980581_1867082_ans_abce95b62d33426b967ff9aba070d34d.jpg

A village maintains a large tank with an open top, containing water for emergencies. The water can drain from the tank through a hose of diameter $6.60\ cm$ . The hose ends with a nozzle of diameter $2.20\ cm$ . A rubber stopper is inserted into the nozzle. The water level in the tank is kept $7.50\ m$ above the nozzle. The stopper is removed. What mass of water flows from the nozzle in $2.00\ h$ ?

1980528_1867039_ans_d5131b0734504511a7c9b46f7667b6c9.jpg

A siphon is used to drain water from a tank as illustrated in Figure $P14.53$ . Assume steady flow without friction.
What If? What is the limitation on the height of the top of the siphon above the end of the siphon?
Note: For the flow of the liquid to be continuous, its pressure must not drop below its vapor pressure. Assume the water is at $20.0^{o}C$ , at which the vapor pressure is $2.3\ k\ Pa$ .

1980590_1867105_ans_d0c9036b9beb4f488a03f7c625f5b6e8.jpg

Calculate the absolute pressure at an ocean depth of $1\ 000\ m$ . Assume the density of seawater is $1\ 030\ kg/m^3$ and the air above exerts a pressure of $101.3\ kPa$ .

1980602_1867112_ans_09148d4ff8314ea48fcbd361c4e82f91.jpg

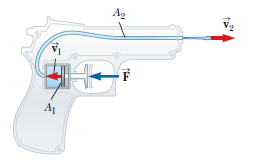
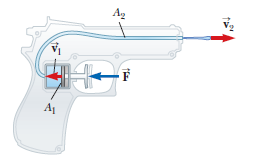
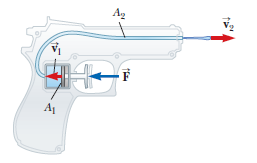
In a water pistol, a piston drives water through a large tube of area $A_1$ into a smaller tube of area $A_2$ as shown in Figure $P14.78$ . The radius of the large tube is $1.00\ cm$ and that of the small tube is $1.00\ mm$ . The smaller tube is $3.00\ cm$ above the larger tube.
What is the pressure at the nozzle?

1980663_1867179_ans_a5230736aa0340fe91257b687bc38056.JPG

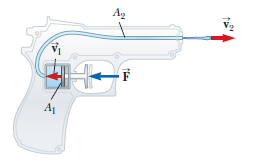
In a water pistol, a piston drives water through a large tube of area $A_1$ into a smaller tube of area $A_2$ as shown in Figure $P14.78$ . The radius of the large tube is $1.00\ cm$ and that of the small tube is $1.00\ mm$ . The smaller tube is $3.00\ cm$ above the larger tube.
If the desired range of the stream is $8.00\ m$ , with what speed $v_2$ must the stream leave the nozzle?

1980660_1867176_ans_35c00342e8f24474895ba9abf54d3276.jpg

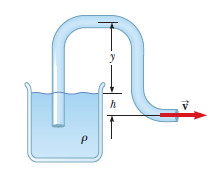
A siphon is used to drain water from a tank as illustrated in Figure $P14.53$ . Assume steady flow without friction.
If $h=1.00\ m$ , find the speed of outflow at the end of the siphon.
Note: For the flow of the liquid to be continuous, its pressure must not drop below its vapor pressure. Assume the water is at $20.0^{o}C$ , at which the vapor pressure is $2.3\ k\ Pa$ .

1980587_1867104_ans_cac3dc804d4342d9a99bd8879d034a31.jpg

Water is forced out of a fire extinguisher by air pressure as shown in Figure $P14.63$ . How much gauge air pressure in the tank is required for the water jet to have a speed of $30.0\ m/s$ when the water level is $0.500\ m$ below the nozzle?

1980625_1867131_ans_bc63a85c14d645a58081a78ac511ba77.jpg

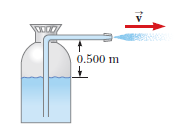
Figure $P14.61$ shows a value separating a reservoir from a water tank. If this valve is opened. what is the maximum height above point $B$ attained by the water stream coming out of the right side of the tank? Assume $h=10.0\ m, L=2.00\ m$ , and $\theta=30.0^{o}$ , and assume the cross-sectional area at $A$ is very large compared with that at $B$ .

1980621_1867128_ans_37929cc08dd34daf89d0a592041d3105.jpg

In a water pistol, a piston drives water through a large tube of area $A_1$ into a smaller tube of area $A_2$ as shown in Figure $P14.78$ . The radius of the large tube is $1.00\ cm$ and that of the small tube is $1.00\ mm$ . The smaller tube is $3.00\ cm$ above the larger tube.
If the pistol is fired horizontally at a height of $1.50\ m$ , determine the time interval required for the water to travel from the nozzle to the ground. Neglect air resistance and assume atmospheric pressure is $1.00\ atm$ .

1980655_1867172_ans_10964947214149deb705b51c8926eba3.jpg

The Bernoulli effect can have important consequences for the design of buildings. For example, wind can blow around a skyscraper at remarkably high speed, creating low pressure. The higher atmospheric pressure in the still air inside the buildings can cause windows to pop out. As originally constructed, the John Hancock Building in Boston popped windowpanes that fell many stories to the sidewalk below.
What If? If a second skyscraper is built nearby, the airspeed can be especially high where wind passes through the narrow separation between the buildings. Solve part (a) again with a wind speed of $22.4\ m/s$ , twice as high.

1980596_1867109_ans_58fd5f367c43495da95f3b1ac935384a.jpg

A helium-filled balloon (whose envelope has a mass of $m_{b}=0.250\ kg$ ) is tied to a uniform string of length $l=2.00\ m$ and mass $m=0.050.0\ kg$ . The balloon is spherical with a radius of $r=0.400\ m$ . When released in air of temperature $20^{o}C$ and density $\rho_{air}=1.20\ kg/m^{3}$ , it lifts a length $h$ of string and then remains stationary as shown in Figure $P14.60$ . We wish to find the length of string lifted by the balloon.
Find the length $h$ numerically.

1980620_1867126_ans_254e64e06eb749e38fc3a110408aab86.jpg

Show that the variation of atmospheric pressure with altitude is given by $P=P_{0}e^{-\alpha y}$ , where $\alpha=\rho_{0}g/P_{0}, P_{0}$ is atmospheric pressure at some reference level $y=0$ , and $\rho_0$ is the atmospheric density at this level. Assume the decrease in atmospheric pressure over an infinitesimal change in altitude (so that the density is approximately uniform over the infinitesimal change) can be expressed from Equation $14.4$ as $dP = -\rho g\ dy$ . Also assume the density of air is proportional to the pressure, which, as we will see in Chapter $20$ , is equivalent to assuming the temperature of the air is the same at all altitudes.

1980757_1867205_ans_31af0ab11d1247d3b9b41d088bb63b6b.jpg

In a water pistol, a piston drives water through a large tube of area $A_1$ into a smaller tube of area $A_2$ as shown in Figure $P14.78$ . The radius of the large tube is $1.00\ cm$ and that of the small tube is $1.00\ mm$ . The smaller tube is $3.00\ cm$ above the larger tube.
Find the pressure needed in the larger tube.

1980680_1867180_ans_6d33324452974ca2b19996aac9aa4e79.JPG

The water supply of a building is fed through a main pipe $6.00\ cm$ in diameter. A $2.00-cm$ diameter faucet tap, located $2.00\ m$ above the main pipe, is observed to fill a $25.0-L$ container in $30.0\ s$ .
What is the speed at which the water leaves the faucet?

1980687_1867184_ans_fbe52c6c7b094f1c91d15b678f41a7e8.jpg

	Pressure at P	level L
A	decreases	falls
B	decreases	rises
C	stays the same	falls
D	stays the same	rises

Mechanical Properties Of Fluids - Class 11 Engineering Physics - Extra Questions

List 2 shows five systems in which two objects are labelled as X and Y. Also in each case a point P is shown. List 1 gives some statements about X and/or Y. Match these statements to the appropriate system(s) from List 2.

The type of flow in which there is a regular gradient of velocity in going from one layer to the next is called laminar flow.If true enter 1, for false enter 0.

What force does water exert on the base of a house tank of base area 1.5m21.5 m^2 when it is filled with water up to a height of 1 m?[Density of water is 103kgm−310^3 kg m^{-3} and g=10ms−2]g=10 m s^{-2}]

The press plungers of a Bramah (hydraulic) press is 40cm240cm^2 in cross-section and is used to lift a load of mass 800kg800 kg. What minimum force is required to be applied to the pump plunger if its cross-sectional area is 0.02m20.02 m^2?

At what depth below the surface of water total pressure would be equal to 1.51.5 atmosphere?1\;atmosphere=10^5\;Nm^{-2}1\;atmosphere=10^5\;Nm^{-2}.

Why does a soft convertible top on a car bulges when the car travels at high speeds.

Sometimes you see a fountain of water rucshing out of the leaking joints (or holes) in the pipes of main water supply line in the city. Why does it happen?

Why do the tyres of a bicycle feel hard when air is filled in the tubes inside them.

What makes a balloon get inflated when air is filled in it?

What is the height of mercury which exerts the same pressure as 20\;cm20\;cm of water column? Take density of mercury as 13.6\;g/cc13.6\;g/cc.

The areas of the pistons in a hydraulic machine are 5{cm}^{2}5{cm}^{2} and 625{cm}^{2}625{cm}^{2}. What force on the smaller piston will support a load of 1250N1250N on the larger piston?

In hydraulic machine, the two pistons are of area of cross section in the ratio 1:101:10. What force is needed on the narrow piston to overcome a force of 100N100N on the wider piston?

If mercury height in a glass tube is 50cm50cm, find the pressure.

A hydraulic machine exerts a force of 900N900N on a piston of diameter 1.80cm1.80cm. The output force is exerted on a piston of diameter 36cm36cm. What will be the output force?

The radii of the press plunger and the pump plunger are in the ratio 30:430:4. If an effort of 32kgf32kgf acts on the pump plunger. Find the maximum effort the press plunger can overcome. ( in kgf)

The space above the mercury column in a barometer contains_____ (mercury, water) vapour.

What is a Venturimeter? On what principle does the Venturimeter work?

Why do snow shoes stop you from sinking it into snow ?

Two small drops each of radius r coalesce to form a larger drop. Find energy of the new drop. (surface tension is T)

The average mass that must be lifted by a hydraulic press is 80 kg. If the radius of the larger piston is five times that of the smaller piston, what is the minimum force that must be applied?

Answer the following question in brief.A plastic cube is released in water. Will it sink of come to the surface of water ?

Answer the following question in brief.Why do the load carrying heavy vehicles have large number of wheels?

In the arrangement shown, a car of certain mass 'm' is in equilibrium by applying a force of 25 N. If the density of liquid taken is 0.9 cm^{-3}0.9 cm^{-3}, then find the mass of the car.

The height hh at which the hole should be punched so that the liquid travels the maximum distance x_mx_m initially is given as \frac {x}{4}H\frac {x}{4}H. Find xx.

Determine the horizontal distance xx traveled by the liquid initially is given as =\sqrt {(3H-xh)h}=\sqrt {(3H-xh)h}. Find xx.

Calculate the energy spent in spraying a drop of mercury of radius RR into NN droplets all of same size. If the surface tension of mercury is TT.

A force of 50 kgf50 kgf is applied to the smaller piston of a hydraulic machine. Neglecting friction, The force exerted on the large piston, if the diameters of the piston are 5 cm5 cm and 25 cm25 cm respectively is 'X' \ N'X' \ N. Find \cfrac{X}{250}\cfrac{X}{250}

A U-tube of uniform cross-sectional area and open to the atmosphere is partially filled with mercury.Water is then poured into both arms. If the equilibrium configuration of the tube is as shown in figure with h_{2} = 1.0 cmh_{2} = 1.0 cm, determine the value of h_{1}h_{1} .

What is the time required for the same amount of water to flow out if the water level in tank is maintained always at a height of 1 m1 m from orifice?

What is the time required to empty the tank through the orifice at the bottom?

A siphon tube is discharging a liquid of specific gravity 0.9 0.9 from a reservoir as shown in the figure find the velocity of the liquid through the siphon.

initial speed (in m/s) with which the water flows from the orifice.

Three holes A, BA, B and CC are made at depths 1m, 2 m1m, 2 m and 5 m5 m as shown. Total height of liquid in the container is 8 m8 m. Let v is the speed with which liquid comes out of the hole and RR the range on ground.Match the following two columns

A siphon tube is discharging a liquid of specific gravity 0.9 0.9 from a reservoir as shown in the figure find the pressure at the highest point BB.

A siphon tube is discharging a liquid of specific gravity 0.9 0.9 from a reservoir as shown in the figure. Find the pressure at point CC.

initial speed with which water strikes the ground.

When air of density 1.3 kg/m^{3}1.3 kg/m^{3} flows across the top of the lobe shown in the accompanying figure, water rises in the lobe to a height of 1 .0 cm1 .0 cm. What is the speed of the air?

time taken to empty the tank to half its original value.(g = 10 m/s ^{2}) (g = 10 m/s ^{2})

What is the pressure drop (in mm Hg) in the blood as it passes through a capillary 1 mm long and 2\mu m2\mu m in radius if the speed of the blood through the centre of the capillary is 0.66 mm/s ? (The viscosity of whole blood is 4 \times 10^{-3}4 \times 10^{-3} poise).

Water flows through a horizontal lobe as shown in figure , If the difference of heights of water column in the vertical lobes is 2 cm2 cm and the areas of cross-section at A and B are 4 cm^{2}4 cm^{2} and 2cm^{2}2cm^{2} respectively. Find the rate of flow of water across any section.

A water barrel stands ona table of heighth. lf a small hole is punched in the side of the barrel at its base, it is found that the resultant stream of water strikes the ground at a horizontal distance R from the barrel.What is the depth of water in the barrel?

Two equal drops of water are falling through air with. steady velocity v. If the drops coalesced, what will be the new velocity ?

Velocity of a viscous liquid in long cylinder of radius R at a distance R_{1}R_{1} from centre is V_{1}V_{1} Find the velocity of the liquid as a function of the distance r from the axis of the cylinder,

Find the pressure exerted by a man weighing 90\;kg90\;kg on the ground.(a) when he is standing on one of his feet having an area of 90\;cm^290\;cm^2.(b) when he is lying flat. The area of his body in contact with the ground is 0.9\;m^20.9\;m^2. Given g=10\;ms^{-2}g=10\;ms^{-2}.

State a device that utilises 'Pascal's law' and also explain how it works.

What is the pressure exerted by a woman weighing 500\;N500\;N standing on one heel of area of 1\;cm^21\;cm^2?

How can a scuba diver keep from floating back to the surface of the water?

A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm^2^2. What maximum pressure would the smaller piston have to bear ?

What will be the pressure in dynedyne {cm}^{-2} {cm}^{-2}, due to a water column of height 12.5cm12.5cm? (g=980cmg=980cm {s}^{-2}{s}^{-2}) (density of water {10}^{3}kg{10}^{3}kg {m}^{-3}{m}^{-3}).

What is the magnitude of force required(in NewtonNewton) to produce a pressure of 37500 \ Pa37500 \ Pa in an area of 300 \ {cm}^{2}300 \ {cm}^{2}?

A man weighing 50kgf50kgf is standing on a wooden plank of 1m\times 0.5m1m\times 0.5m. The pressure exerted by it on the ground will be ___________ (in Pa)

What will be the pressure in dyne {cm}^{-2}{cm}^{-2}, due to a water column of height 10cm10cm? [take g=980cm/{s}^{2}g=980cm/{s}^{2}] (density of water={10}^{3}kg={10}^{3}kg {m}^{-3}{m}^{-3}).

A brick with dimensions of 20cm\times 10cm\times 5cm20cm\times 10cm\times 5cm has a weight 500gwt500gwt. Calculate the pressure exerted by brick when the pressure is greatest?

The press plungers of a braman (hydraulic) press is 40\ cm^{2}40\ cm^{2} in cross-section and is used to lift a load of mass 800\ kg800\ kg. What minimum force will be required to be applied on the pump plunger if its cross-sectional area is 0.02\ m^{2}0.02\ m^{2}?

Force exerted by a truck is 500000N500000N and the pressure on the ground is 2500000Pa2500000Pa. Calculate the area of contact of tyres with ground?

A force of 50kgf50kgf is applied to the smaller piston of a hydraulic machine. Neglecting friction, find the force exerted on the large piston, the diameters of the piston being 5cm5cm and 24cm24cm respectively.

Draw a neat, labelled diagram for a liquid surface in contact with a solid, when the angle of contact is acute.

A hydraulic lift at a service station can lift cars with a mass of 3500\ kg3500\ kg. The area of cross section of the piston carrying the load is 500\ cm^{2}500\ cm^{2}. What pressure does the smaller piston experience? g = 9.8 m/s^{2}.g = 9.8 m/s^{2}.

Two cylindrical vessels of equal cross-sectional area AA contain water upto heights h_{1}h_{1} and h_{2}h_{2}. The vessels are interconnected so that the levels in them become equal. Calculate the work done by the force of gravity during the process. The density of water is \rho\rho.

If AA denotes the area of free surface of a liquid and hh the depth of an orifice of area of cross-section a,a, below the liquid surface, then find the velocity vv of flow through the orifice.

The diameter of a piston P_{2}P_{2} is 50\ cm50\ cm and that of a piston P_{1}P_{1} is 10\ cm10\ cm. What is the force exerted on P_{2}P_{2} when a force of 1\ N1\ N is applied on P_{1}P_{1}?

A container is filled with liquid upto height HH as shown in figure. There are 22 holes in the container such that water coming out from them have same range. If the range of water coming out of the holes is half of maximum range, then find the distance xx between these holes.

The figure shows two immiscible liquids (Kerosens and water). Kerosene has density \rho_{2}\rho_{2} and water has density \rho_{1}\rho_{1}. Find the velocity of water flow.

A tank is filled with water up to a height HH. Water is let out of a hole PP from one of the walls, at a depth DD below the surface of the water. Express the range of the efflux xx in terms of HH and DD.

The end of a capillary tube with a radius r is immersed in water. Is mechanical energy conserved when the water rises in the tube? The tube is sufficiently long. If not, calculate the energy change.

If a 5 cm long capillary tube with 0.1 mm internal diameter, open at both ends, is slightly dipped in water having surface tension 75 dyne/cm, state whether:water will overflow out of the upper end of capillary. Explain your answer.

Two liquid gets coming out of the small holes at PP and QQ intersect at the point RR. Find the position of RR if we maintain the liquid level constant.

The area of cross section of the wider tube shown in fig. is 900 cm^2^2. If the body standing on the position weighs 45 kg, find the difference in the levels of water in the two tubes.

The flow rate of a water from a tap of diameter 1.25\ cm1.25\ cm is 0.48\ L/min0.48\ L/min. If the coefficient of viscosity of water is 10^{-3}\ Pa\ s10^{-3}\ Pa\ s, what is the nature of flow of water?

Water is flowing through a horizontal tube. The pressure of the liquid in the portion where velocity is 2\ m/s2\ m/s is 2\ m2\ m of HgHg. What will be the pressure in the portion where velocity is 4\ m/s4\ m/s

The pressure of liquid column ____________ with the depth of column.

Calculate the amount of energy evolved when 88 droplets of water of radius 0.5\ mm0.5\ mm each combine into one. Surface tension of water is 72\ dyne\ c{m}^{-1}72\ dyne\ c{m}^{-1}.

find the angle of {\phi _1}{\phi _1}.

What will be the terminal velocity of a steel ball of radius 2\ mm2\ mm in glycerine?

A wind speed 40 m/s blows parallel to the roof of a house. The area of the roof is 250 m^2 250 m^2 Assuming that the pressure inside the house is atmospheric pressure,the force exerted by the wind on the roof and the direction of the force will be:

Water is flowing through a horizontal tube 4\ km4\ km in 4\ cm4\ cm in radius at a rate of 20\ litre\ s^{-1}20\ litre\ s^{-1} Calculate the pressure required to maintain the flow in terms of the height of mercury column.?

Rain drops, each of radius r, are falling through air with steady velocity v. If eight drops coalesce to form a big drop, then the big drop so formed will fall with velocity ?

The density of the atmosphere at sea level is 1.29kg/{m}^{3}1.29kg/{m}^{3} and g=9.8m/{s}^{2}g=9.8m/{s}^{2}. Assume that both do not change with altitude, how high should the atmosphere extend?

Two drops of equal radii are falling through air with a terminal velocity of 5\ cm\ s^{-1}5\ cm\ s^{-1}. If they coalesce into one drop, what will be the terminal velocity of the new drop?

The type of flow in which there is a regular gradient of velocity in going from one layer to the next is called laminar flow.
If true enter 1, for false enter 0.

What force does water exert on the base of a house tank of base area $1.5 m^2$ when it is filled with water up to a height of 1 m?
[Density of water is $10^3 kg m^{-3}$ and $g=10 m s^{-2}]$

The press plungers of a Bramah (hydraulic) press is $40cm^2$ in cross-section and is used to lift a load of mass $800 kg$ . What minimum force is required to be applied to the pump plunger if its cross-sectional area is $0.02 m^2$ ?

At what depth below the surface of water total pressure would be equal to $1.5$ atmosphere?
$1\;atmosphere=10^5\;Nm^{-2}$ .

What is the height of mercury which exerts the same pressure as $20\;cm$ of water column? Take density of mercury as $13.6\;g/cc$ .

The areas of the pistons in a hydraulic machine are $5{cm}^{2}$ and $625{cm}^{2}$ . What force on the smaller piston will support a load of $1250N$ on the larger piston?

In hydraulic machine, the two pistons are of area of cross section in the ratio $1:10$ . What force is needed on the narrow piston to overcome a force of $100N$ on the wider piston?

If mercury height in a glass tube is $50cm$ , find the pressure.

A hydraulic machine exerts a force of $900N$ on a piston of diameter $1.80cm$ . The output force is exerted on a piston of diameter $36cm$ . What will be the output force?

The radii of the press plunger and the pump plunger are in the ratio $30:4$ . If an effort of $32kgf$ acts on the pump plunger. Find the maximum effort the press plunger can overcome. ( in kgf)

Answer the following question in brief.
A plastic cube is released in water. Will it sink of come to the surface of water ?

Answer the following question in brief.
Why do the load carrying heavy vehicles have large number of wheels?

In the arrangement shown, a car of certain mass 'm' is in equilibrium by applying a force of 25 N. If the density of liquid taken is $0.9 cm^{-3}$ , then find the mass of the car.

The height $h$ at which the hole should be punched so that the liquid travels the maximum distance $x_m$ initially is given as $\frac {x}{4}H$ . Find $x$ .

Determine the horizontal distance $x$ traveled by the liquid initially is given as $=\sqrt {(3H-xh)h}$ . Find $x$ .

Calculate the energy spent in spraying a drop of mercury of radius $R$ into $N$ droplets all of same size. If the surface tension of mercury is $T$ .

A force of $50 kgf$ is applied to the smaller piston of a hydraulic machine. Neglecting friction, The force exerted on the large piston, if the diameters of the piston are $5 cm$ and $25 cm$ respectively is $'X' \ N$ . Find $\cfrac{X}{250}$

A U-tube of uniform cross-sectional area and open to the atmosphere is partially filled with mercury.Water is then poured into both arms. If the equilibrium configuration of the tube is as shown in figure with $h_{2} = 1.0 cm$ , determine the value of $h_{1}$ .

What is the time required for the same amount of water to flow out if the water level in tank is maintained always at a height of $1 m$ from orifice?

A siphon tube is discharging a liquid of specific gravity $0.9$ from a reservoir as shown in the figure find the velocity of the liquid through the siphon.

Three holes $A, B$ and $C$ are made at depths $1m, 2 m$ and $5 m$ as shown. Total height of liquid in the container is $8 m$ . Let v is the speed with which liquid comes out of the hole and $R$ the range on ground.Match the following two columns

A siphon tube is discharging a liquid of specific gravity $0.9$ from a reservoir as shown in the figure find the pressure at the highest point $B$ .

A siphon tube is discharging a liquid of specific gravity $0.9$ from a reservoir as shown in the figure. Find the pressure at point $C$ .

When air of density $1.3 kg/m^{3}$ flows across the top of the lobe shown in the accompanying figure, water rises in the lobe to a height of $1 .0 cm$ . What is the speed of the air?

time taken to empty the tank to half its original value. $(g = 10 m/s ^{2})$

What is the pressure drop (in mm Hg) in the blood as it passes through a capillary 1 mm long and $2\mu m$ in radius if the speed of the blood through the centre of the capillary is 0.66 mm/s ? (The viscosity of whole blood is $4 \times 10^{-3}$ poise).

Water flows through a horizontal lobe as shown in figure , If the difference of heights of water column in the vertical lobes is $2 cm$ and the areas of cross-section at A and B are $4 cm^{2}$ and $2cm^{2}$ respectively. Find the rate of flow of water across any section.

Velocity of a viscous liquid in long cylinder of radius R at a distance $R_{1}$ from centre is $V_{1}$ Find the velocity of the liquid as a function of the distance r from the axis of the cylinder,

Find the pressure exerted by a man weighing $90\;kg$ on the ground.
(a) when he is standing on one of his feet having an area of $90\;cm^2$ .
(b) when he is lying flat. The area of his body in contact with the ground is $0.9\;m^2$ . Given $g=10\;ms^{-2}$ .

What is the pressure exerted by a woman weighing $500\;N$ standing on one heel of area of $1\;cm^2$ ?

A hydraulic automobile lift is designed to lift cars with a maximum mass of 3000 kg. The area of cross-section of the piston carrying the load is 425 cm $^2$ . What maximum pressure would the smaller piston have to bear ?

What will be the pressure in $dyne$ ${cm}^{-2}$ , due to a water column of height $12.5cm$ ? ( $g=980cm$ ${s}^{-2}$ ) (density of water ${10}^{3}kg$ ${m}^{-3}$ ).

What is the magnitude of force required(in $Newton$ ) to produce a pressure of $37500 \ Pa$ in an area of $300 \ {cm}^{2}$ ?

A man weighing $50kgf$ is standing on a wooden plank of $1m\times 0.5m$ . The pressure exerted by it on the ground will be ___________ (in Pa)

What will be the pressure in dyne ${cm}^{-2}$ , due to a water column of height $10cm$ ? [take $g=980cm/{s}^{2}$ ] (density of water $={10}^{3}kg$ ${m}^{-3}$ ).

A brick with dimensions of $20cm\times 10cm\times 5cm$ has a weight $500gwt$ . Calculate the pressure exerted by brick when the pressure is greatest?

The press plungers of a braman (hydraulic) press is $40\ cm^{2}$ in cross-section and is used to lift a load of mass $800\ kg$ . What minimum force will be required to be applied on the pump plunger if its cross-sectional area is $0.02\ m^{2}$ ?

Force exerted by a truck is $500000N$ and the pressure on the ground is $2500000Pa$ . Calculate the area of contact of tyres with ground?

A force of $50kgf$ is applied to the smaller piston of a hydraulic machine. Neglecting friction, find the force exerted on the large piston, the diameters of the piston being $5cm$ and $24cm$ respectively.

A hydraulic lift at a service station can lift cars with a mass of $3500\ kg$ . The area of cross section of the piston carrying the load is $500\ cm^{2}$ . What pressure does the smaller piston experience? $g = 9.8 m/s^{2}.$

Two cylindrical vessels of equal cross-sectional area $A$ contain water upto heights $h_{1}$ and $h_{2}$ . The vessels are interconnected so that the levels in them become equal. Calculate the work done by the force of gravity during the process. The density of water is $\rho$ .

If $A$ denotes the area of free surface of a liquid and $h$ the depth of an orifice of area of cross-section $a,$ below the liquid surface, then find the velocity $v$ of flow through the orifice.

The diameter of a piston $P_{2}$ is $50\ cm$ and that of a piston $P_{1}$ is $10\ cm$ . What is the force exerted on $P_{2}$ when a force of $1\ N$ is applied on $P_{1}$ ?

A container is filled with liquid upto height $H$ as shown in figure. There are $2$ holes in the container such that water coming out from them have same range. If the range of water coming out of the holes is half of maximum range, then find the distance $x$ between these holes.

The figure shows two immiscible liquids (Kerosens and water). Kerosene has density $\rho_{2}$ and water has density $\rho_{1}$ . Find the velocity of water flow.

A tank is filled with water up to a height $H$ . Water is let out of a hole $P$ from one of the walls, at a depth $D$ below the surface of the water. Express the range of the efflux $x$ in terms of $H$ and $D$ .

If a 5 cm long capillary tube with 0.1 mm internal diameter, open at both ends, is slightly dipped in water having surface tension 75 dyne/cm, state whether:
water will overflow out of the upper end of capillary. Explain your answer.

Two liquid gets coming out of the small holes at $P$ and $Q$ intersect at the point $R$ . Find the position of $R$ if we maintain the liquid level constant.

The area of cross section of the wider tube shown in fig. is 900 cm $^2$ . If the body standing on the position weighs 45 kg, find the difference in the levels of water in the two tubes.

The flow rate of a water from a tap of diameter $1.25\ cm$ is $0.48\ L/min$ . If the coefficient of viscosity of water is $10^{-3}\ Pa\ s$ , what is the nature of flow of water?

Water is flowing through a horizontal tube. The pressure of the liquid in the portion where velocity is $2\ m/s$ is $2\ m$ of $Hg$ . What will be the pressure in the portion where velocity is $4\ m/s$

Calculate the amount of energy evolved when $8$ droplets of water of radius $0.5\ mm$ each combine into one. Surface tension of water is $72\ dyne\ c{m}^{-1}$ .

find the angle of ${\phi _1}$ .

What will be the terminal velocity of a steel ball of radius $2\ mm$ in glycerine?

A wind speed 40 m/s blows parallel to the roof of a house. The area of the roof is $250 m^2$ Assuming that the pressure inside the house is atmospheric pressure,the force exerted by the wind on the roof and the direction of the force will be:

Water is flowing through a horizontal tube $4\ km$ in $4\ cm$ in radius at a rate of $20\ litre\ s^{-1}$ Calculate the pressure required to maintain the flow in terms of the height of mercury column.?

The density of the atmosphere at sea level is $1.29kg/{m}^{3}$ and $g=9.8m/{s}^{2}$ . Assume that both do not change with altitude, how high should the atmosphere extend?

Two drops of equal radii are falling through air with a terminal velocity of $5\ cm\ s^{-1}$ . If they coalesce into one drop, what will be the terminal velocity of the new drop?

A body of mass $2 kg$ is let fall from top of a $10 m$ tall building. It lands on a sandy patch of ground and burries itself $20 cm$ deep in the sand. Find the average resistance offered to it by the sand. Also find the approximate time of penetration.

Derive expression for terminal velocity when a ball of radius r is dropped thrugh a liquid of viscousity $\eta$ and density $\rho$ .

Water rises to a height of 10 cm in a capillary tube and mercury falls to a depth of the same capillary tube. If the density of water is 1 gm/c.c and its angle of contact is $0^{\circ}$ , then the ratio of such of two liquids is ( cos $135^{\circ}$ =0.7)

When the system shown in the adjoining fig. is in equilibrium and the areas of cross sec. of the small and big piston are $'a'$ and $'10a'$ , then what is the value of $m/M$ ?

Calculate the work done in blowing a soap bubble from a radius of $2\ cm$ to $3\ cm$ . The surface tension of the soap solution is $30\ dyne\ cm^{-1}$ .

The flow rate of water from a tap of diameter $1.25$ cm is $0.48$ $L/min$ . the coefficient of viscosity of water is ${ 10 }^{ -3 }$ $Pa-s$ . After sometime, the flow rate is increased to $3$ $L/min$ . Characterize the flow for both the flow rates.

The area of a man's foot is $80\ \mathrm { cm } ^ { 2 }$ . How much pressure will the man exert on the ground, while standing, if the weight is $800\ N$ ?

If pressure at half depth of a lake is equal to $2/3$ pressure at the bottom of the lake that what is the depth of the lake

The height of mercury in a barometer is 760 mm, then the atmospheric pressure is $\left[ g=9.8m/{ s }^{ 2 } \right]$

Find the force exerted by the water on a $2\ m^{2}$ plane surface of a large stone placed at the bottom of a sea $500\ m$ deep. Does the force depend on the orientation of the surface?

A beaker of liquid accelerates from rest, on a horizontal surface, with acceleration $a$ to the right.
How does the pressure vary with depth below the surface?

Hovering over the pit of hell, the devil observed that as a student falls past ( with terminal velocity ), the frequency of the scream decreases from $842$ to $820\ Hz$ .
Find the speed of descent of the student.

A pressure of 10 Pa acts on an area of $3.0 m^2$ . What is the force acting on the area? What force will be exerted by the application of same pressure if the area is made one-third?

Water flows through a fire hose of diameter $6.35\ cm$ at a rate of $0.0120\ m^{3}/s$ .
The fire hose ends in a nozzle with an inner diameter of $2.20\ cm$ . What is the speed at which the water exists the nozzle?

A large storage tank is filled to a height $h_{0}$ . The tank is punctured at a height $h$ above the bottom of the tank (Fig $3.57$ ). Find an expression for how far from the tank the exiting stream lands.

A vessel contain water up to a height of 1.5m.Taking the density of water $10^{3}kg m^{-3}$ acceleration due to gravity $9.8ms^{-2} and area of base vessel$ 100^{2}, calculate ;
the pressure and

A normal force of $200 N$ acts on an area of $0.02 m^2$ Find the pressure in pascal.

A block of iron of mass 7.5 kg and of dimension $12cm\times8cm\times 10cm$ is kept on a table top on its base of side $12cm \times8cm$ . Calculate :
pressure exerted on the table top. Take 1kg = 10N

The diagram in figure shows a device which makes use of the principal of transmission of pressure.
Name the parts labelled by the letters X and Y.

Two cylindrical vessels fitted with pistons A and B of area section $8cm^{2}$ and $320cm^{2}$ respectively are joined at their bottom by a tube and they are completely filled with water. When a mass of $4kg$ is placed on piston A, find the pressure on piston A,

A hammer exerts a force of 1.5 N on each of the two nails A and B. The area of cross section of to of nail A is $2mm^{2}$ while that of nail B is $6mm^{2}$ . Calculate pressure on each nail in pascal.

What force is applied on a piston of area of cross section $2cm^{2}$ to obtain a force $150N$ on the piston of area of cross section $12cm^{2}$ in a hydraulic machine?