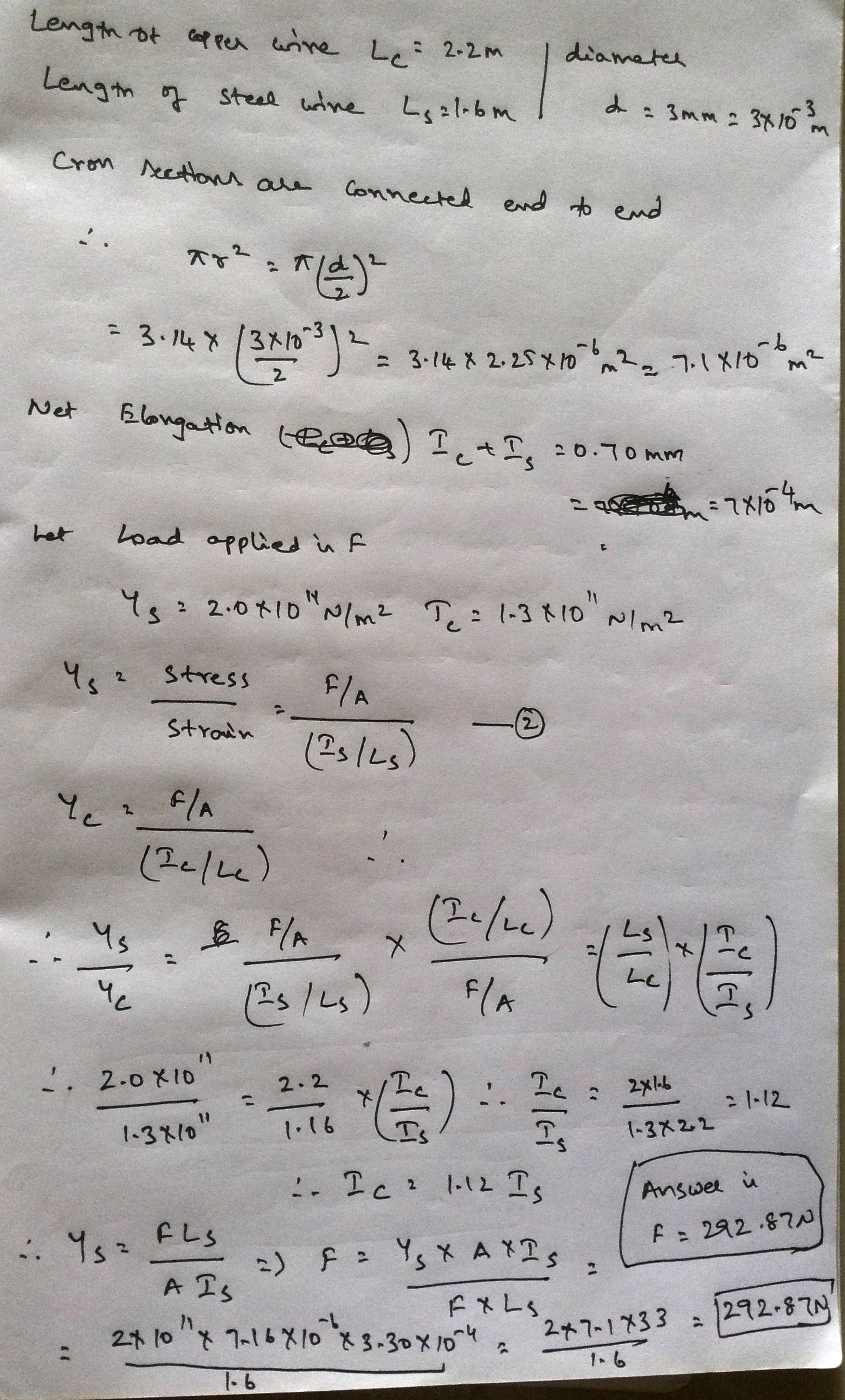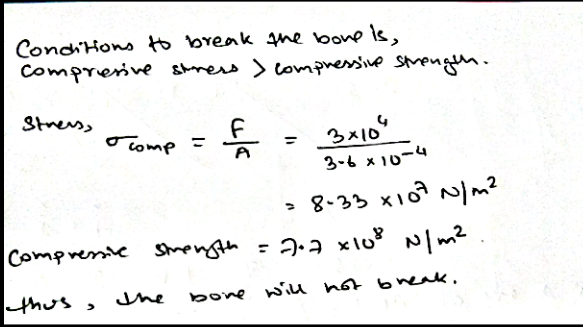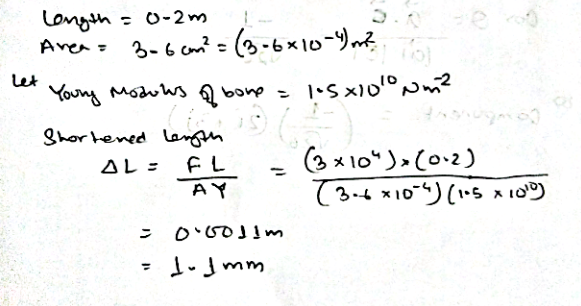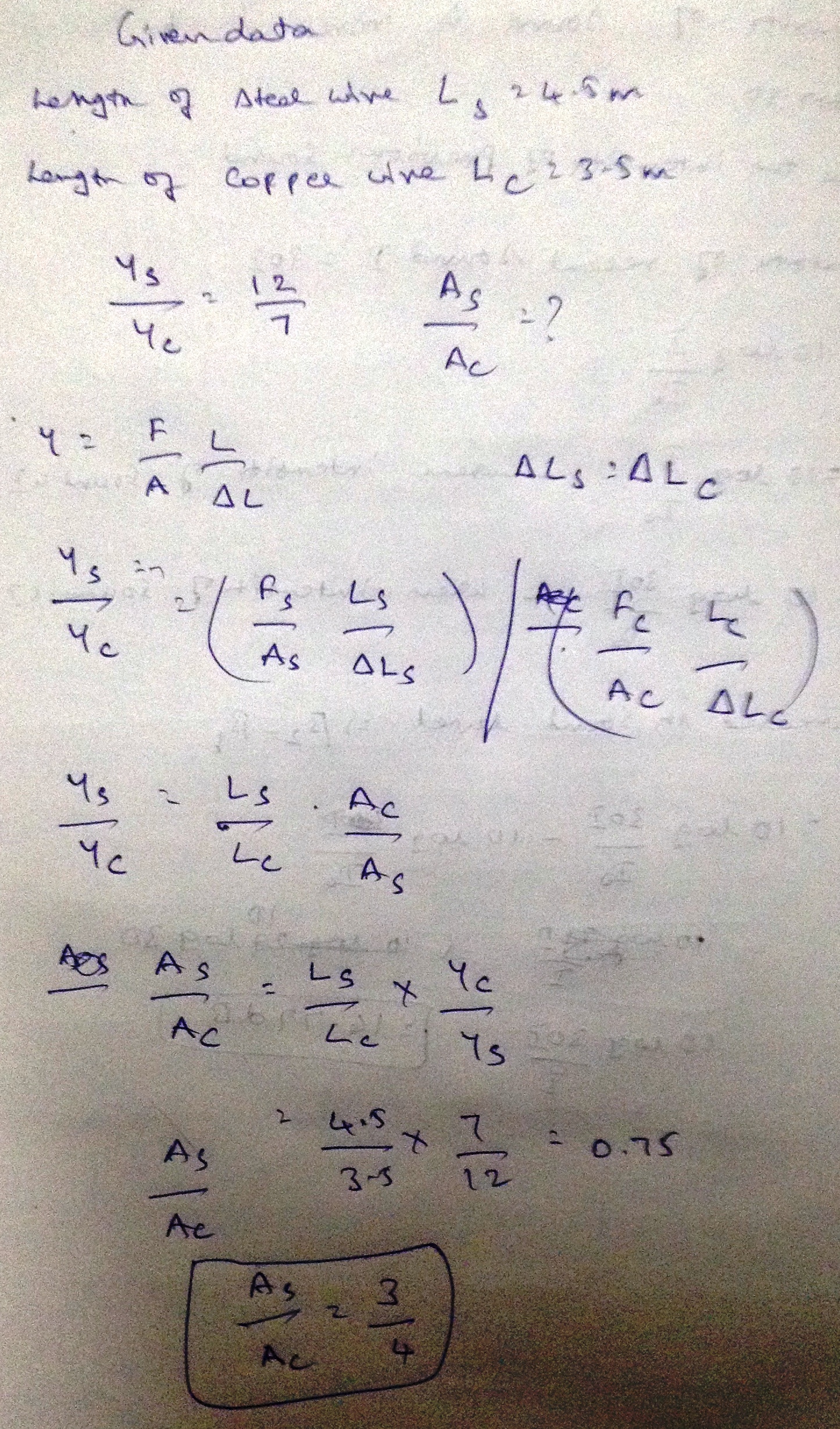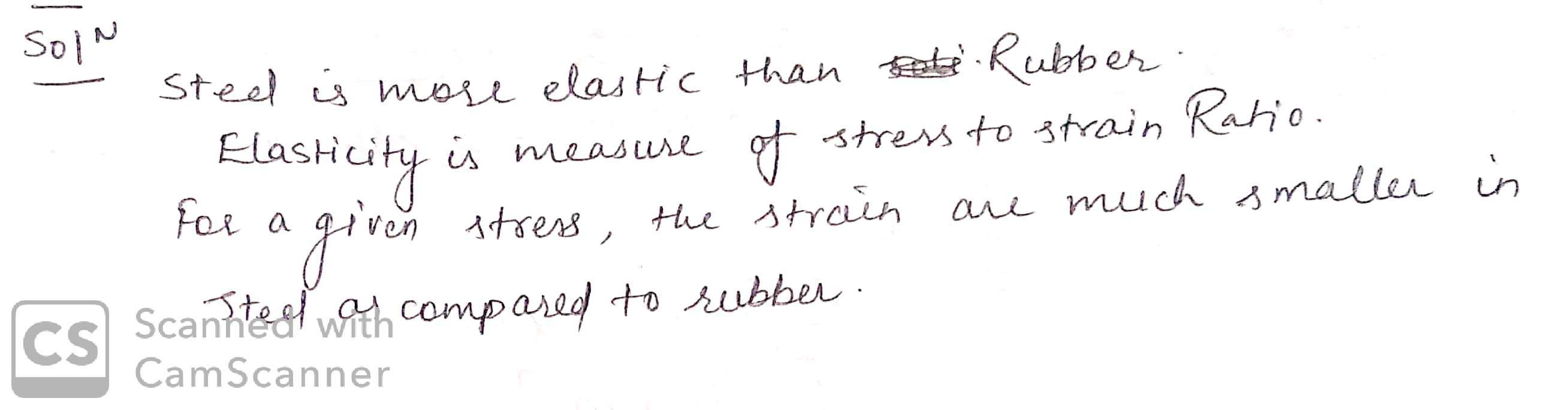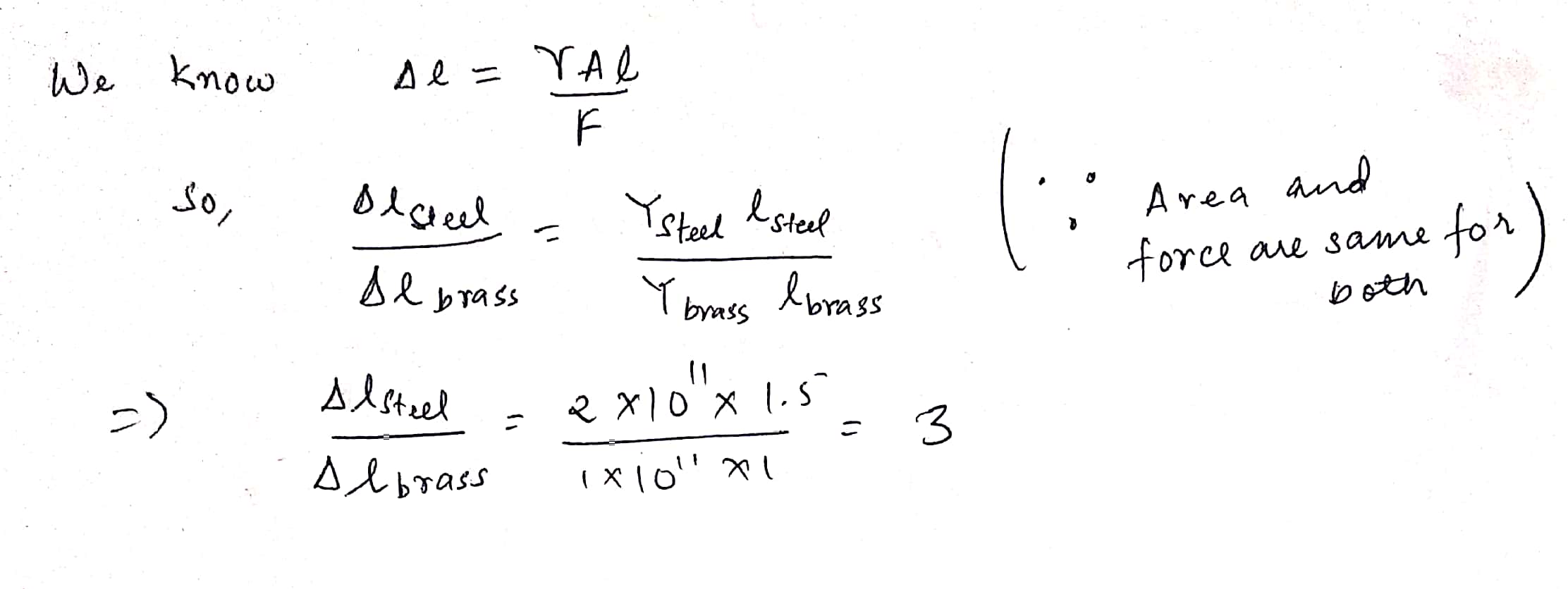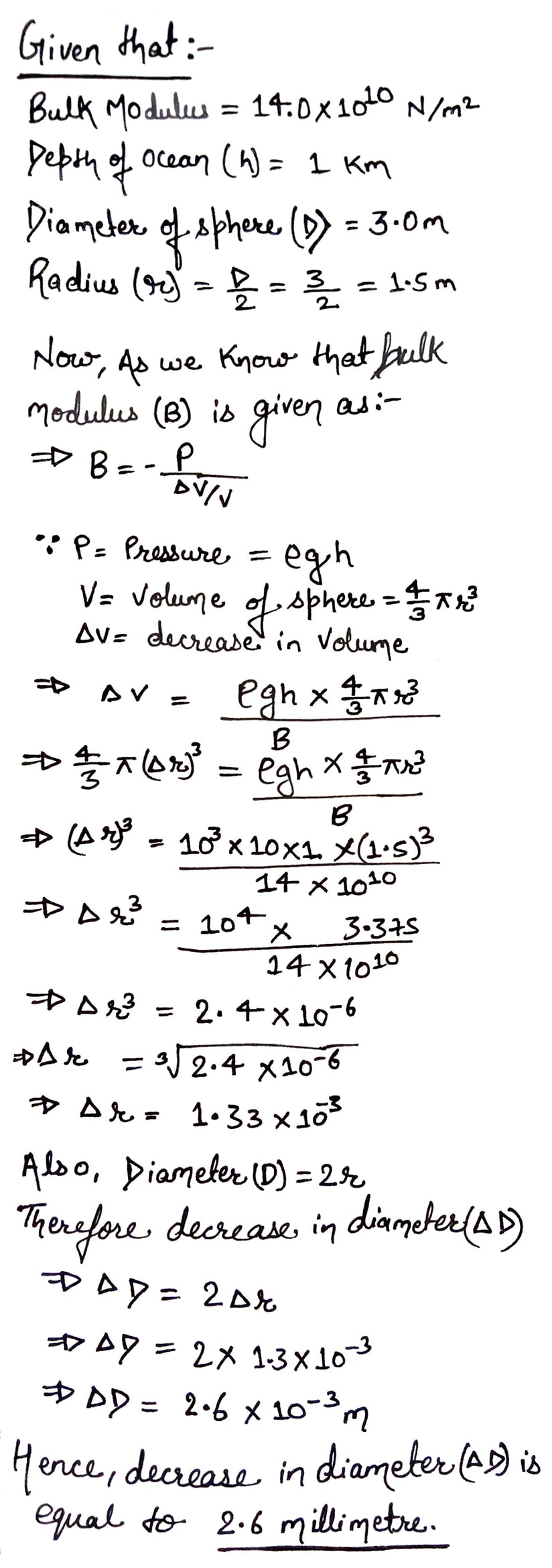Mechanical Properties Of Solids - Class 11 Engineering Physics - Extra Questions
A steel wire of diameter $$0.5$$ mm and Young modulus $$2 \times 10^{11} N m^{-2}$$ carries a load of mass M. The length of the wire with the load is $$1.0$$ m, A Vernier scale with $$10$$ divisions is attached to the end of this wire. Next to the steel wire is a reference wire to which a main scale, of least count $$1.0$$ mm is attached. The $$10$$ divisions of the Vernier scale correspond to $$9$$ divisions of the main scale. Initially, the zero of Vernier scale coincides with the zero of main scale division. If the load on the steel wire is increased by 1.2 kg, the vernier scale division which coincides with a main scale division is __________. [Take g = $$10 ms^{-2}$$ and $$\pi = 3.2$$]
Is a substance which can be compressed soft or hard?
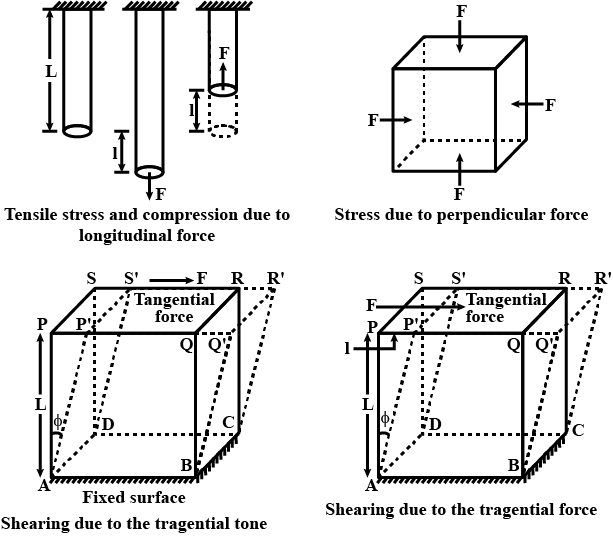
What are stress and strain?
Which is more hard, sponge or iron?
Define Young's modulus.
Stress and pressure have the same dimensions but pressure is not the same as stress. Why?
A cube is subjected to a uniform volume compression. If the side of the cube decreases by 1% the bulk stain is
Define elasticity.
Define Poisson's ratio.
Define bulk modulus of elasticity. Give its units and dimensions.
Is stress a vector quantity?
What is stress?
Is stress a vector quantity ?
What is elasticity ?
Fill in the blanks:
On pulling a string, its _______ increases.
What is strain?
What is the ratio of lateral strain to a longitudinal strain called?
Define stress .
Define strain .
Which is more elastic , rubber or iron ?
If the elastic deformation energy of a steel rod of mass $$m=3.1\:kg$$ stretched to a tensile strain $$\varepsilon=1.0\times{10}^{\displaystyle-3}$$ is $$x$$,then value of $$100x$$ is:
If the volume density of the elastic deformation energy in fresh water at the depth of $$h=1000\:m$$ is $$x\; KJ/m^3$$, find the value of $$\dfrac{x}{5}$$.(rounded off to nearest integer)
A cast iron column has an internal diameter of $$200\ mm$$. What should be the minimum external diameter (in m) so that it may carry a load of $$1.6\ millionN$$ without the stress exceeding $$90\ N/mm^{2}$$? (round off your answer to nearest integer)
$$\boxed{copper}\boxed{steel}$$A steel wire and a copper wire of equal length and equal cross-sectional area are joined end to end and the combination is subjected to a tension. If the ratio of the strains developed is $$\dfrac{x}{20}$$. Find $$x$$. (Y of steel $$ = 2 \times10^{11} N/m^{2}$$ and Y of copper = $$1.3 \times 10^{11} N/m^{2})$$
Two wires $$A$$ and $$B$$ of same dimensions are stretched by same amount of force. Young's modulus of $$A$$ is twice that of $$B$$. Which wire will get more elongation? Enter 1 for A and 2 for B.
The stress at the centre of the wire,
Let $$T$$ be the tension at the centre of the wire and $$S$$ be the cross-sectional area.
$$T = M_1 a_o$$
$$T = \rho (A \frac{L}{2}) a_o$$
$$\therefore$$ $$T/S = \rho \dfrac{L}{2}a_o$$
Stress $$T/S = \rho \dfrac{L}{2}a_o$$
A rod $$100 cm$$ long and of $$2 cm \times 2 cm$$ cross-section is subjected to a pull of $$1000 kg$$ force. Modulus of elasticity of the material is $$2.0 \times 10^{6}kg/cm^{2}$$. If the elongation of the rod is $$x$$ mm, find the value of $$40x$$.
Total elongation of the wire.
Let the tension acting on dx element of wire be $$T_x$$ and due to this the elongation in that element be $$\delta x$$
$$T_x = M_x a_o$$
$$T_x = \rho (S x)a_o$$ ...........(1)
From Hooke's law, $$Y = \dfrac{T_x dx}{S \delta x}$$ $$\implies \delta x = \dfrac{T_x dx}{SY}$$
$$\therefore$$ Total increment $$\int \delta x = \int_0^L \dfrac{T_x }{SY} dx$$
$$\therefore$$ $$\Delta L = \int_0^L \dfrac{\rho a_o}{Y} xdx $$
OR $$\Delta L = \dfrac{\rho a_o}{Y} \times \dfrac{x^2}{2}\bigg|_0^L$$ $$\implies$$ $$\Delta L = \dfrac{\rho a_o L^2}{2 Y}$$
A wire of length $$I$$, area of cross-section $$A$$ and Young's modulus of elasticity $$Y$$ is stretched by a longitudinal force $$F$$. The change in length is $$\Delta l$$. Match the following two columns.
Compute the bulk modulus of water from the following data: Initial volume = 100.0 litre, Pressure increase = 100.0 atm ($$1 atm = 1.013 \times 10^5 Pa$$), Final volume = 100.5 litre. Compare the bulk modulus of water with that of air (at constant temperature). Explain in simple terms why the ratio is so large.
A steel wire of length 4.7 m and cross-sectional area $$3.0 \times 10^{-5} m^2$$ stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of $$4.0 \times 10^{-5} m^2$$ under a given load. What is the ratio of the Youngs modulus of steel to that of copper ?
What is the density of water at a depth where pressure is 80.0 atm, given that its density at the surface is $$1.03 \times 10^3 kg m^{-3}$$ ?
A steel cable with a radius of 1.5 cm supports a chairlift at a ski area. If the maximum stress is not to exceed $$10^8 N m^{-2}$$, what is the maximum load the cable can support ?
Determine the volume contraction of a solid copper cube, $$10\ cm$$ on an edge, when subjected to a hydraulic pressure of $$7.0 \times 10^6 Pa$$. (Bulk modulus of copper, $$B=140 \times 10^{9}Pa$$)
A 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1.0 m, is whirled in a vertical circle with an angular velocity of 2 rev/s at the bottom of the circle. The cross-sectional area of the wire is 0.065 $$cm^2$$. Calculate the elongation of the wire when the mass is at the lowest point of its path.
Compute the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of $$10$$ atm.
How much should the pressure on a litre of water to be changed to compress it by 0.10% ? (Bulk modulus of water, $$B = 2.2\times 10^9Nm^{-2}$$)
Distinguish between elastic and plastic materials.
Define the terms
(a) Plastic
(b) Adhesive
A steel wire having cross-sectional area $$1.5\ mm^2$$ when stretched by a load produces a lateral strain $$1.5 \times 10^{-5}$$. Calculate the mass attached to the wire. $$(Y_{steel} = 2 \times 10^{11} N/m^2,\,\, Poisson's\,\, ratio \,\,a = 0.291, g = 9.8 m/s^2)$$
Why should you not use an elastic measuring tape to measure distances? What would be some of the problems you would face in telling someone about a distance you measured with an elastic tape?
Two bar $$A$$ and $$B$$ of circular cross section and of same volume made of the same material are subjected to tension. If the diameter of $$A$$ is half that of $$B$$ and if the force applied to both the rods is the same and it is within the elastic limit. What will be the ratio of extension of $$A$$ to that of $$B$$?
A steel wire of length $$2$$m is hanging from a rigid horizontal support. How much energy is stored in it when a load of $$5$$ kg is suspended on it? If the load is increased to $$10$$ kg then by how much the energy stored will increase? ($$Y=2\times 10^{11}N/m^2$$, area of cross-section $$=10^{-6}m^2$$).
The maximum stress that can be applied to the material of a wire employed to suspend an elevator is $$\cfrac { 3 }{ \pi } \times { 10 }^{ 8 }\ N/{ m }^{ 2 }$$. If the mass of the elevator is $$900\ kg$$ and it moves up with an acceleration of $$2.2\ m/{s}^{2}$$ then calculate the minimum radius of the wire.
When the load applied to a suspended wire is increased from 3 kg-wt to 5 kg-wt; the elongation increases from 0.6 mm to 1 mm. How much work is done during the extention of the wire.
A copper wire of length 2.2 m and a steel wire of length 1.6 m. both of diameter 3.0 mm, are connected end to end.When stretched by a load, the net elongation is found to be 0.70 mm. Obtain the load applied.
LONGITUDINAL STRAIN: When a body is subjected to an axial tensile or compressive load, there is an axial deformation in the length of the body. The ratio of axial deformation to the original length of the body is known as Longitudinal (or linear strain) OR The longitudinal strain is also defined as the deformation of the body per unit length in the direction of applied load.
STRAIN = Change in length / Original Length
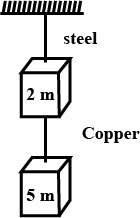
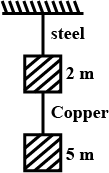
If the ratio of diameters, lengths and Young's modulus of steel and copper wires shown in the figure are p,q, and s respectively, then the corresponding ratio of increase in their lengths would be ____.
A copper wire of negligible mass, 1 m length and cross-sectional area $$l0^{-6} \, m^2$$ is kept on a smooth horizontal table with one end fixed. A ball of mass 1 kg is attached to the other end. The wire and the ball are rotating with an angular velocity of 20 rad/s. If the elongation in the wire is $$10^{-3}$$ m.
a. Find the Young's modulus of the wire (in terms of $$\times \, 10^{11} \, N/m^2)$$.
When a weight W is hung from one end of a wire of length L (other end being fixed) , the length of the wire increases byIf the same wire is passed over a pulley and two weights W each are hung at the two ends, what will be the total elongation in the wire?
A load of $$10\ kN$$ is supported from a pulley which in turn is supported by a rope of sectional area, $$1 \, \times \,10^3 \, mm^2$$ and modulus of elasticity $$10^3 \, N mm^{-2}$$, as shown in Fig. 5.Neglecting the friction at the pulley, determine the deflection of the load is $$x+0.75mm$$. Find $$x$$
A catapult consists of two parallel rubber strings, each of lengths 10 cm and cross-sectional area 10 $$mm^2.$$ When stretched by 5 cm, it can throw a stone of mass 100 gm to a vertical height of 25 m. Determine Young's modulus of elasticity of rubber.
Stress and pressure are both forces per unit area. Then in what respect does stress differ from pressure?
A rod of uniform cross-sectional area A and length L has a weight W. It is suspended vertically from a fixed support. If the material of the rod is homogeneous and its modulus of elasticity is I. then determine the total elongation produced in the rod due to its own weight.
Two vertical rods of equal lengths, one of steel and the other of copper, are suspended from the ceiling, at a distance l apart and are connected rigidly to a rigid horizontal bar at their lower ends. If $$A_S$$ and $$A_C$$ be their respective cross-sectional areas, and $$Y_S$$ and $$Y_C$$, their respective Young's moduli of elasticities, where should a vertical force F be applied to the horizontal bar in order that the bar remains horizontal?
Two rods A and B. each of equal length but different materials are suspended from a common support as shown in the figure. The roads A and B can support a maximum load of $$W_1$$ = 600 N and $$W_2$$ = 6000 N, respectively. If their cross-sectional areas are $$A_1$$ = $$10 mm^2$$ and $$A_2$$ = 1000 $$mm^2,$$ respectively, then identify the stronger material.
A steel wire of $$4.0$$m in length is stretched through $$2.0$$ mm. The cross-sectional area of the wire is $$2.0$$ $$mm^2$$. If Young's modulus of steel is $$2.0\times 10^{11} N/m^2$$ find (i) the energy density of wire (ii) the elastic potential energy stored in the wire.
A copper rod with length $$1.4$$m and area of cross-section of $$2cm^2$$ is fastened to a steel rod with length L and cross-sectional area $$1 cm^2$$. The compound rod is subjected to equal and opposite pulls of magnitude $$6.00\times 10^4$$ N at its ends.
What is the strain in each rod? $$[Y_{steel}=2\times 10^{11}Pa; Y_{CU}=1.1\times 10^{11}Pa]$$.
A steel wire of length $$7\ m$$ and cross section $$1\ {mm}^{2}$$ is hung from a rigid support with a steel weight of volume $$1000\ cc$$ hanging from the other end. Find the decreases in the length of wire, when steel weight is completely immersed in water.
$$({Y}_{steel}=2\times {10}^{11}{N/m}^{2})$$
Density of water$$=1\ g/c.c)$$
A wire stretches by a certain amount under a load. If the load & radius both are increased to $$4$$ time . Find the stress cause in the wire.
The length of a wire increases by $$1$$% on loading a $$2kg$$ weight on it. Calculate the linear strain in the wire.
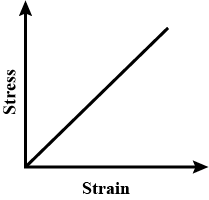
Which of the following is the graph showing stress-strain variation for elastomers?
The corect option is 1
Strees is proportional to strain,
So,the graident will be the straight line
Why is it difficult to hold a school bag having a strap made of thin and strong string?
Find the increase in pressure required to decrease volume of mercury by $$0.001\%$$. (Bulk modulus of mercury = $$2.8 \times 10^{10} \ N/m^2$$)
A solid brass sphere of volume 0.305 $$m^3$$ is dropped in ocean, where water pressure is $$2 \times 10^7 \ N/m^2$$. The bulk modulus of water is $$6.1 \times 10^{10} \ N/m^2$$. What is the change in volume of sphere?
The length of wire increases by 9 mm when weight of 2.5 kg is hung from the free end of wire. If all conditions are kept the same and the radius of wire is made thrice the original radius, find the increase in length.
A uniform steel wire of length $$3m$$ and are of cross section $$2mm^2$$ is extended through $$3mm$$ Calculate the energy stored in the wire, if the elastic limit is not exceeded
Calculate the percentage increase in length of a wire of diameter $$2\ mm$$ stretched by force of $$1\ kg$$. Youngs modulus of the material of wire $$15\times 10^{10}\ N\ m^{-1}$$.
A structural steel rod has a radius of $$10\ mm$$ and a length of $$1.0\ m$$. A $$100\ kN$$ force stretches it along its length. Calculate (a) stress, (b) elongation, and (c) strain on the rod. Young's modulus, of structural steel is $$2.0\times 10^{11}N\ m^{2}$$
Two wires $$A$$ and $$B$$ of radius $$2r$$ and $$r$$ respectively are joined and a force $$F$$ is applied at the end. The length of each wire is $$L$$. Their Youngs modulus are Y and 2Y respectively. Find the net elongation.
A metal sphere is lowered into a sea upto a depth of $$5000\ m$$. Bulk modulus of material of the sphere is $${ 10 }^{ 11 }\quad N/{ m }^{ 2 }$$. The percentage change in the diameter of the sphere is (Take density of water as$$1000\quad kg/{ m }^{ 3 }$$ and $$g=10 m/{ s }^{ 2 }$$).
A piece of copper having a rectangular cross-section of $$15.2mm\times 19.1mm$$ is pulled in tension with $$44,500N$$ force, producing only elastic deformation.Calculate the resulting strain? Shear modulus of elasticity of copper is $$42\times 10^9N/m^2$$.
What force is required to stretch a copper wire $$1\ cm^{2}$$ in cross-section to double its length? $$Y$$ for copper is $$1.26\times 10^{12}\ dyne\ cm^{-2}$$
Find stress, strain and Young modulus of elasticity in the case of a wire $$1.5\ m$$ long & $$1mm$$ in cross section, if it is increased by $$1.55\ mm$$ in length when a weight of $$10\ kg$$ is suspended from it.
Which is more elastic: water or air, why?
A copper wire is stretched by 0.5 % of its length. Calculate the energy stored per unit of its volume $$Y = 12 \times {10^{10}}N/{m^2}$$ .
A $$40kg$$ boy whose leg bones are $$4cm^2$$ in area and $$50cm$$ long falls through a height of $$50cm$$ without breaking his leg bones. If the bones can stand a stress of $$0.9 \times 10^8 N/m^2$$. Calculate Young's Modulus for the material of the bone
Two persons pull a rope towards themselves. Each person exerts a force of $$100$$N on the rope. Find the Young modulus of the material of the rope if it extends in length by $$1$$cm. (Original length of the rope $$=2$$m and the area of cross section $$=2$$ $$cm^2$$).
If a compressive force $$3.0\times 10^{4}\ N$$ is exerted on the end of $$20\ cm$$ long done of cross-sectional area $$3.6cm^{2}$$
(a) Will the bone break and Given, Compressive strength of bone$$=7.7\times 10^{8}Nm^{-2}$$ and Young's modulus of bone $$=1.5\times 10^{-2}Nm^{-2}$$?
If a compressive force $$3.0\times 10^{4}\ N$$ is exerted on the end of $$20\ cm$$ long done of cross-sectional area $$3.6cm^{2}$$
(b) if if not, how much will it shorten?
A composite wire consits of a steel wire of length $$1.5\ m$$ and a copper wire of length $$2.0\ m$$, with a uniform cross-sectional area of $$2.5\ \times 10^{-5}\ m^{2}$$. It is loaded with a mass of $$200\ kg$$. Find the extension produced. Young's modulus of copper is $$1.0\ \times 10^{11}\ N\ m^{-2}$$ and that of steel is $$2.0\ \times 10^{11}\ N\ m^{-2}$$.
Take $$g=9.8\ m\ s^{-2}$$
The tension due to the load
will oemain same in the composite
wire. So, the tensile stress in
both rods is same.
Tensile stress $$ = \dfrac{Load}{Area\,of\,section} = \dfrac{200\times 9.8}{2.5\times 10^{-5}} $$
$$ \Rightarrow $$ stress $$ = 7.84\times 10^{7}N/m^{2} $$
So, let the elongations in the
st and lee wire be $$\Delta l_{1} $$ and $$ \Delta l_{2} $$
Then,
As $$ r = \dfrac{T.stress}{strain} $$
For st wire
$$ \Rightarrow 2\times 10^{11} = \dfrac{7.84\times 10^{7}}{\dfrac{\Delta l_{1}}{1.5}} $$
$$ \Rightarrow \Delta l_{1} = 5.88\times 10^{-4}m $$
For Lr wire
$$ \Rightarrow 10^{11} = \dfrac{7.84\times 10^{7}}{\dfrac{\Delta l_{2}}{2}} $$
$$ \Rightarrow \Delta l_{2} = 1.508\times 10^{-3}m $$
So, extension in composite rod $$ = \Delta l_{1}+\Delta l_{2} $$
$$ = 2.156\,mm $$
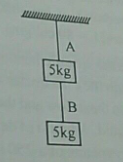
Two identical wire $$A$$ & $$B$$ of same material are loaded as shown in figure. If the elongation in wire $$B$$ is $$1.5\ mm$$, what is the elongation in $$A$$. (Mass of $$A$$ & $$B$$ can be neglect)
What is Poisson's ratio ?
A structure steel rod has a radius of $$10\ mm$$ and a length of $$1.0\ m$$. A $$100\ kN$$ force stretches it along its length. Calculate $$(a)$$ stress. $$(b)$$ elongation. and $$(c)$$ strain on the rod. Young's modulus, of stricture steel is $$2.0\ \times 10^{11}\ N\ m^{-2}$$.
A uniform cylindrical wire of length $$4m$$ and diameter $$0.6mm$$ is stretched by a certain force such that its length is increased by $$4 mm$$. If the Poisson's ratio of the material is $$0.3$$ then, calculate the change in diameter of the wire.
Find the charge in volume which $$1 m^3$$ water with undergo when taken from the surface to bottom of se $$1 Km$$ given the bulk modulus of elasticity of water is $$20,000 N/m^2$$
a steel wire of length $$4.5m$$ and a copper wire of length $$3.5m$$ are stretched same amount under a given load. if ratio of young's modulo of steel to that of coppers is $$\frac{{12}}{7}$$, then what is the ratio of cross sectional area of steel wire to copper wire ?
If a stretching force $$F1$$ is applied on a vertical metal wire then its length is $$L1$$ and if force $$F2$$ is applied on it then its length becomes $$1.2$$. The real length of wire is?
A vertical metal cylinder of radius $$2 cm$$ and length $$2 m$$ is fixed at the lower end and a load of $$100 kg$$ is put on it. Find (a) the stress (b) the strain and (c) the compression of the cylinder. Young modulus of the metal = $$2 \times 10^{11} N m^{-2}$$
Why is steel is more elastic than rubber?
If the ratio of diameters, lengths and Young's modulus of steel and copper wires shown in the figure are p, q and s respectively, then the corresponding ratio of increase in their lengths would be
A wire elengates by lmm when a weight w is hanged than it . If wire goes over a pulley and 2 weights W each are huge at two ends. What will be elongations of wire is mm?
The breaking stress of aluminium is $$7.5\times 1{ 0}^{ 7 }N{ m}^{ -2 } $$ . Find the greatest length of aluminium wire that can hang vertically without breaking . Density of aluminium is $$ 2.7\times 1{ 0}^{ 3 }{ Kgm}^{ -3 } $$.
What do you mean by elastic bodies and plastic.
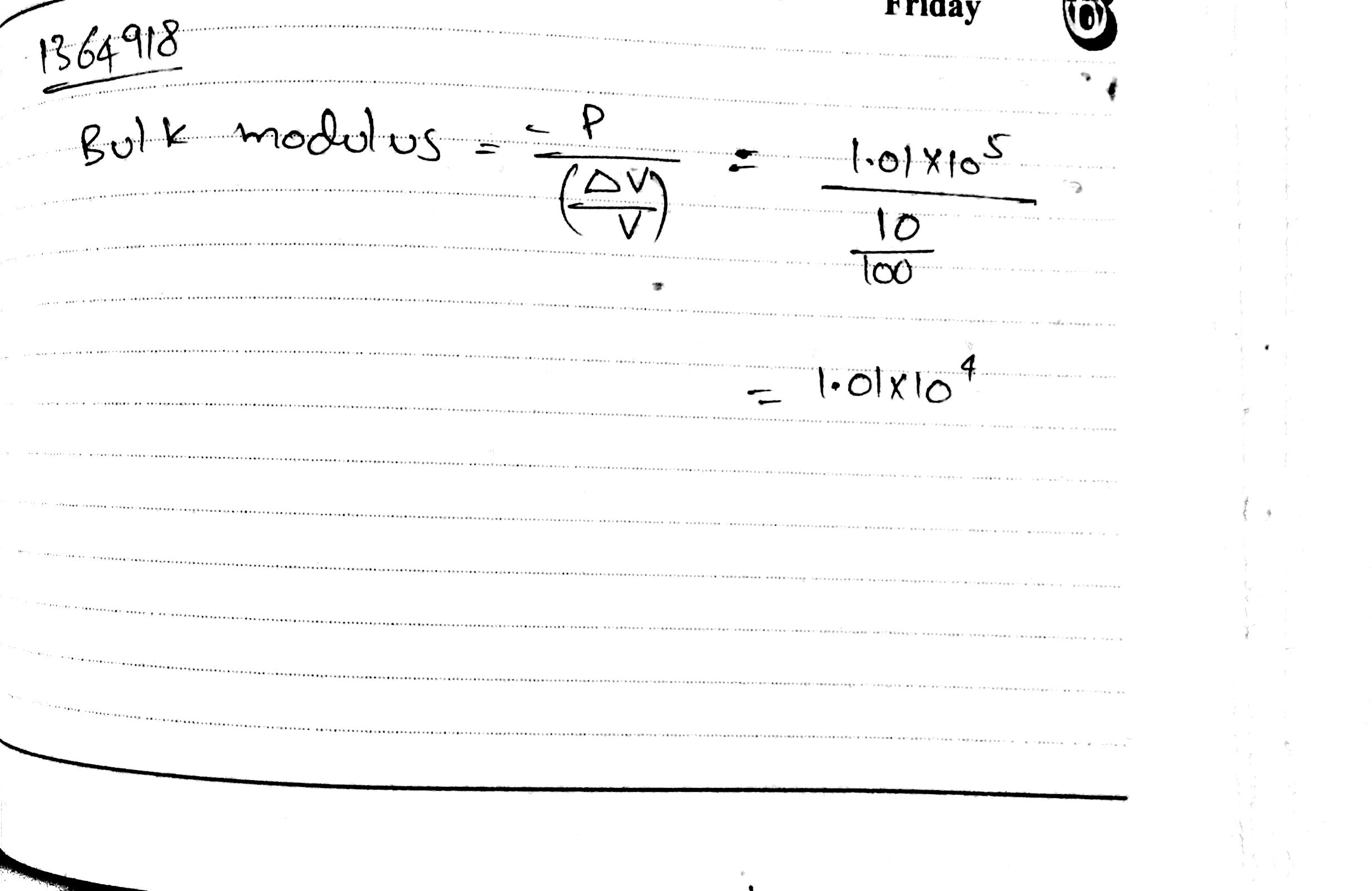
Pressure on an object increases from $$ 1.01 \times 10 ^{5} $$Pa. Its volume decreases by $$10 \text{%}$$ constant temperature. Bulk modulus of material is....
A steel ball initially at a pressure of $$1.0\times 10^{5} Pa$$ is heated from $$20^{\circ}C$$ to $$120^{\circ}C$$ keeping its volume constant. Find the pressure inside the ball. Coefficient of linear expansion of steel $$= 12\times 10^{-6}/^{\circ}C$$ and bulk modulus of steel $$= 1.6\times 10^{11} N/m^{2}$$.
Steel is more elastic as compare to rubber why?
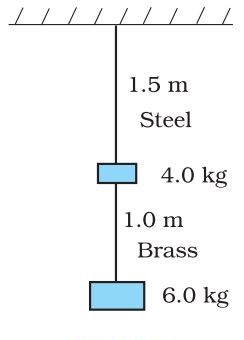
Two wires of diameter $$0.25\ cm$$, one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is $$1.5\ m$$ and that of brass of $$1.0\ m$$. Young's modulus of steel is $$2.0\times 10^{11} Pa$$ and that of brass is $$1.0\times 10^{11} Pa$$. Compute the ratio of elongations of steel and brass wires. $$\left (\dfrac {l_{steel}}{l_{brass}} = ? \right )$$.
Define Bulk modulus.
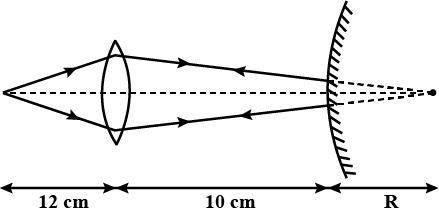
A point object is placed at a distance of $$12 cm$$ on the principal axis of a convex lens of focal length $$10 cm$$. A convex mirror is placed coaxially on the other side of the lens at a distance of $$10 cm$$. If the final image coincides with the object, sketch the ray diagram and find the focal length of the convex mirror.
We kow that
$$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$$ (len's formula)
Given that
$$f = 10cm$$ of convex lens
$$u = 20 cm$$ from lens
$$v = (10cm + R)$$ from lens
$$R = $$ Radius curvature of mirror
When a light incident on the mirror that way it will meet on the center of the mirror, then it will be retracing the path.
So, $$\dfrac{1}{v}- \dfrac{1}{u} =\dfrac{1}{f}$$
$$\dfrac{1}{10 +R}- \dfrac{1}{(-12)} = \dfrac{1}{10}$$
$$\dfrac{1}{10 + R} = \dfrac{1}{10} - \dfrac{1}{12}$$
$$\dfrac{1}{10 + R} = \dfrac{6 - 5}{60}$$
$$R = 50cm$$
Focal length of mirror os $$\left(\dfrac{R}{2} = \dfrac{50}{2} cm\right) 25cm$$
Prove that if an object under pressure is raised in temperature but not allowed to expand , the increase in pressure is $$ \Delta p = B\beta \,\Delta T , $$ where the bulk modulus $$ B $$ and the average coefficient of volume expansion $$ \beta $$ are both assumed positive and constant.
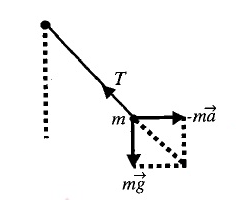
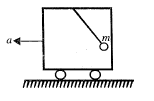
A bob of mass $$m$$ hangs from the ceiling of a smooth trolley car which is moving with a constant acceleration $$a$$. If Young's modulus, radius and length of the string are $$Y, r$$ and $$l$$, respectively, find the (a) stress in the string and (b) extension of the string when it makes a constant angle relative to vertical.
Relative to the accelerating frame (trolley car), the forces acting on the bob are as shown in the figure.
Then $$T = m\sqrt {a^{2} + g^{2}}$$
Since the string is light, same tension is felt at all points of the string.
Putting the area of cross section of the string $$A = \pi r^{2}$$ in the formula
Stress, $$\sigma = \dfrac {F'}{A}$$
where $$F' = T = m\sqrt {a^{2} + g^{2}}$$
Then $$T = m\sqrt {a^{2} + g^{2}}$$
Since the string is light, same tension is felt at all points of the string.
Putting the area of cross section of the string $$A = \pi r^{2}$$ in the formula
Stress, $$\sigma = \dfrac {F'}{A}$$
where $$F' = T = m\sqrt {a^{2} + g^{2}}$$
$$\sigma = \dfrac {m\sqrt {g^{2} + d^{2}}}{\pi r^{2}}$$
b. As $$Y = \dfrac {F/A}{\triangle l/l} = \dfrac {\sigma l}{\triangle l}$$
which gives $$\triangle l =\dfrac {\sigma l}{Y}$$
Hence, $$\triangle l = \dfrac {m|\vec {a} - \vec {g}|l}{\pi r^{2}Y} = \dfrac {m(\sqrt {g^{2} + a^{2}})l}{\pi r^{2} Y}$$.
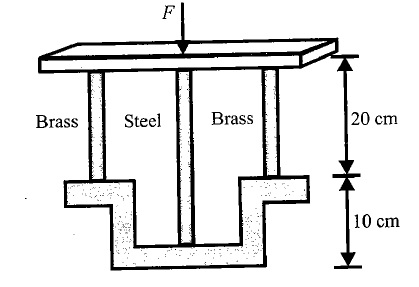
A steel rod of length $$l_{1} = 30\ cm$$ and two identical brass rod of length $$l_{2} = 20\ cm$$ each support a light horizontal platform as shown in the figure. Cross-sectional area of each of the three rods is $$A = 1\ cm^{2}$$.
A vertically downward force $$F = 5000\ N$$ is applied on the platform.
Young's modulus of elasticity for steel $$Y_{s} = 2\times 10^{11} Nm^{-2}$$ and brass $$Y_{b} = 1\times 10^{11} Nm^{-2}$$
Find stress (in $$MPa$$) developed in
(i) Steel rod (ii) Brass rod
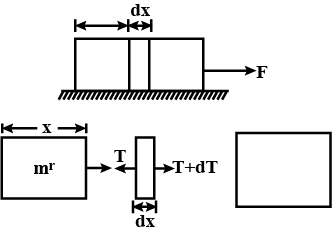
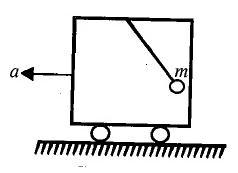
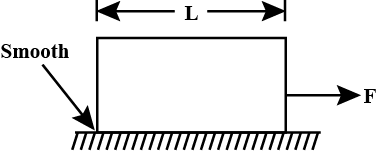
A uniform rod of length $$L$$ and density $$\rho$$ is being pulled along a smooth floor with a horizontal acceleration $$a$$ (see figure). The magnitude of the stress at the transverse cross section through the mid-point of the rod is _______.
After a fall, a $$95$$ kg rock climber finds himself dangling from the end of a rope that had been $$15$$ m long and $$9.6$$ mm in diameter but has stretched by $$2.8$$ cm. For the rope, calculate (a) the strain, (b) the stress, and (c) Young’s modulus.
a) What is the difference between gravitational potential energy and elastic potential energy ? Give one example of a body having gravitational potential energy and another having elastic potential energy.
b) If $$784\,J$$ of work was done in lifting a $$20\,kg$$ mass , calculate the height through which it was lifted.
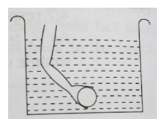
A hollow plastic ball is taken to the bottom through the water and released (see adjoining figure).
(a) What happens to the ball?
(b) Give a reason for this phenomenon.
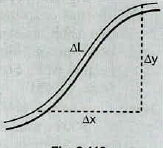
In this problem you will derive an expression for the potential energy for a segment of a string carrying a travelling wave. The potential energy of a segment equals the work done by the tension in stretching the string, which is $$\Delta U=F(\Delta l-\Delta x)$$, where $$F$$ is the tension, $$\Delta l$$ is the length of the stretched segment and $$\Delta x$$ is the original length. From the figure we see that
$$\Delta l=\sqrt{(\Delta x)^2+(\Delta y)^2}=\Delta x \left\{ 1+\left( \dfrac{\Delta y}{\Delta x}\right)^2\right\}^{1/2}$$
a) Use the binomial expansion to show that $$\Delta l-\Delta x \sim \dfrac{1}{2}\left( \dfrac{\Delta y}{\Delta x}\right)^2\Delta x$$ and therefore $$\Delta u=\dfrac{1}{2}F\left( \dfrac{\Delta y}{\Delta x}\right)^2\Delta x$$
Calculate the stress developed inside a tooth cavity filled with copper when hot tea at temperature of $$57^{\circ} \mathrm{C}$$ is drunk. You can take body (tooth) temperature to be $$37^{\circ} \mathrm{C}$$ and $$\alpha=1.7 \times 10^{-5} / \mathrm{K} .$$ Bulk modulus for copper $$=140 \times 10^{9} \mathrm{N} / \mathrm{m}^{2}$$
A steel rod of length $$2l$$, cross sectional area A and mass M is set rotating in a horizontal plane about an axis passing through the centre. If Y is the Young's moulus for steel, find the extension in the length of the rod. (Assume the rod is uniform.)
Centripetal force acting on this element,
$$dF=dm.x\omega^2$$
$$dF=\left(\dfrac{M}{2l}\right)dx.x\omega^2$$
Here, $$dF$$ is provided by tension in element $$dx$$ of the rod due to elasticity.
Let tension in the rod be $$F$$ at a distance $$x$$ from the axis of rotation.
$$F$$ is due to centripetal force acting on all the elements from $$x$$ to $$l$$, i.e
$$\displaystyle F=\dfrac{M\omega^2}{2l}\int^l_x xdx=\dfrac{M\omega^2}{4l}(l^2-x^2)$$
If $$d(r)$$ is the extension in the element of length $$dx$$ at position $$x$$, then,
$$\displaystyle d(r)=\dfrac{Fdx}{YA}\left[\because y=\dfrac{F/A}{d(r)/dx}\right]$$
Hence, extension in the half of the rod (from axis to point $$A$$) is given by
$$\displaystyle \Delta r=\int^l_0d(r)=\int^l_0\dfrac{Fdx}{YA}$$
$$=\dfrac{M\omega^2}{4YAl}\left[l^2(x)-\dfrac{x^3}{3}\right]^l_0=\dfrac{M\omega^2}{4YAl}[l^3-\dfrac{l^3}{3}]=\dfrac{M\omega^2l^2}{6YA}$$
Hence, total extension in entire rod of length $$2l$$.
$$2\Delta=\dfrac{M\omega^2l^2}{3YA}$$
$$\therefore$$ Total change in length $$=\dfrac{2}{3YA}\mu\omega^2l^2$$
First we have to consider a small element on the rod of mass dm to find tension in the rod at this element and then calculate for the whole rod.Let us consider an element of width dx at a distance x from the given axis of rotation as shown in the diagram.
A wooden block is kept on a table top. The mass of the wooden block is 5 kg and its dimensions are 40 cm x 20 cm x 10 cm. Find the pressure exerted by the wooden block on the table top if it is made to lie on the table top with its sides of dimensions (a) 20 cm x 10 cm and (b) 40 cm x 20 cm.
What is the Bulk modulus for a perfect rigid body ?
A truck is pulling a car out of a ditch by means of a steel cable that is $$9.1 m $$ long and has a radius of 5 mm. When the car just begins to move, the tension in the cable is $$800 N$$. How much has the cable stretched ? ( Young's modulus for steel us $$\times 10^{11} N.m^{-2}$$)
What is Poisson's ratio?
Explain stress, strain, the limit of elasticity, and describe various strains produced in a material.
A substance is in equilibrium position in its original form due to the effect of interatomic forces.
When an external force is applied on any substance then as a result there is a change in the shape or size or both of the substance and internal reactive force is produced in the substance.
When external forces are removed then due to internal reactive forces the substance regains its original configuration.
Internal reactive forces are also called restoring forces.
Restoring forces are equal in magnitude to the external forces but opposite in direction. In equilibrium position; the internal reactive force or the restoring force per unit cross-sectional area originated due to strain is called stress.
In the position of equilibrium the value of reactive force is equal to the external force applied on a unit area; i.e.
$$ \begin{aligned} \text { Stress } &=\dfrac{\text { Magnitude of reactive force }}{\text { Area }} \\ &=\dfrac{\text { Magnitude of external force }}{\text { Area }} \end{aligned} $$
If $$ \mathrm{A} $$ is the area of cross-section of the body and working external force is $$ \mathrm{F} $$, then
Stress $$ =\mathrm{F} / \mathrm{A} $$
The unit of stress in M.K.S. system is N.m-2 (Newton/metre $$ ^{2} $$ ) and its dimensional formula is $$ \left[\mathrm{M}^{1} \mathrm{L}^{-1} \mathrm{T}^{-2}\right] $$.
When any external force works on a solid then its dimensions can be changed in three types.
Hence, stress are of three types:
(a) Longitudinal stress
(b) Normal (volume) stress.
(c) Shearing (Tangential) stress.
(a) Longitudinal Stress: When the deforming force is applied along the length of an object such as a cylinder, then the reactive force acting on the longitudinal cross-sectional area of the object is called longitudinal stress. If the length increases in the direction of force then restoring force is called tensile stress and in case of compression it is called compressive stress. In both cases, the length of the cylinder changes.
If $$ F $$ is the force acting on the cylinder and its cross-sectional area is A then;
Longitudinal stress $$ =\dfrac{F}{A}\left[\mathrm{Nm}^{-2}\right] $$
(b) Normal (volume) Stress: When uniform force is applied in the perpendicular direction to the surfaces of an object; then there is change produced in the volume. The reactive normal force in unit area acting opposite to the change in volume is called normal stress. If the volume decreases then it is called compressive stress and if the volume increases it is called tensile stress.
Normal stress $$ =\dfrac{F}{A}\left[\mathrm{N} \cdot \mathrm{m}^{-2}\right] $$
(c) Tangential Stress or Shearing Stress: If one surface of a body is kept stable (by frictional force) and a deforming linear force $$ F $$ is applied on a surface opposite to it (as shown in diagram 10.4 ); then the perpendicular surface to the stable surface rotates by angle $$ \Phi $$ due to which there is a change in the shape of the body. Due to tangential force shearing stress is produced.
The tangential reactive force applied in unit area opposite to shearing is called tangential stress or shearing stress. This stress is produced in the body due to change or distortion. If tangential force is $$ \mathrm{F} $$ working on across sectional area A then;
When deforming force is applied an any object then there is a change in its length or volume or shape. The proportional change produced in the shape and size of an object due to the deforming force is called strain.
It is a dimensionless quantity.
According to deformation strain have a three types.
(a) Longitudinal strain
(b) Volume strain
(c) Shearing strain
(a) Longitudinal Strain: The change produced in the unit length or the proportional change produced in the length of an object due to the effect of external force is called the longitudinal strain
longitudinal strain $$ =\dfrac{\text { Change in length }}{\text { Original length }}=\dfrac{l}{L} $$
If the length of the object increases after applying external force then it is called tensile strain and if the length of the object decreases after applying external force it is called compressive strain.
(b) Volume Strain : The change produced in the unit volume of the object after applying external force is called volume strain. If $$ \Delta \mathrm{V} $$ is the change in volume of an object of volume $$ \mathrm{V} $$ then
Volume Strain $$ =\dfrac{\text { Change in volume }}{\text { Original volume }}=\dfrac{\Delta V}{V} $$
Volume strain is less in solids and liquids but is more in gases.
(c) Shearing Strain: If there is change only in the form or shape of an object by applying external tangential force and the length and volume remain unchanged then this type of strain is called shearing strain.
In the figure (10.5) surface $$ A B C D $$ is stable and force $$ F $$ is acting on surface PQRS, due to which surface
PQRS deviates by angle $$ \Phi $$ from stable surface ABCD.
Angle $$ \Phi $$ is called shearing angle and it is the measure of shearing strain.From $$ \Delta P A P^{\prime} $$
$$\tan \phi=\dfrac{P P^{\prime}}{P A}=\dfrac{l}{L}$$
If $$ \phi $$ is small then $$ \tan \phi=\phi $$
Shearing strain $$ = $$ Shearing angle $$ =\phi=\dfrac{l}{L} $$.
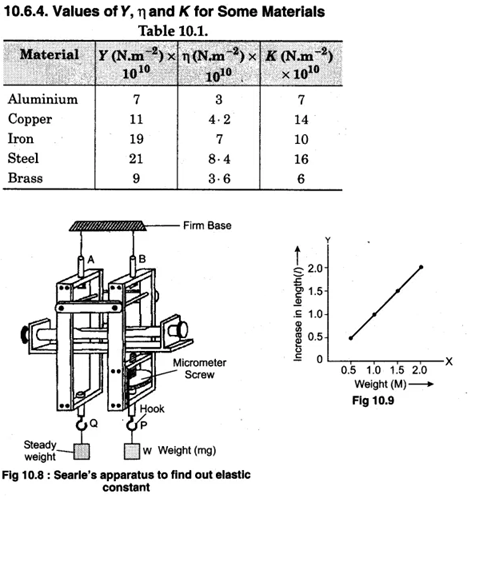
Define Young's modulus of elasticity, modulus of rigidity and Bulk modulus of elasticity. Calculate Young's; modulus of elasticity by Searle's experiment method.
The ratio of longitudinal stress to longitudinal strain is called Young's modulus of elasticity in the elasticity limit.It is represented by $$ \mathrm{Y} $$.
Young's modulus of elasticity $$ Y=\dfrac{\text { Longitudinal stress }}{\text { Longitudinal strain }} $$
If on any wire of longitudinal cross-sectional area A a tensile force $$ F $$ is applied then its initial length $$ L $$ and change in length is I, then,
Longitudinal Strain $$ =\dfrac{\text { Change in length }}{\text { Original length }}=\dfrac{l}{L} $$ and
Longitudinal stress $$ =\dfrac{\text { Deforming force }}{\text { Area of cross-section }}=\dfrac{F}{A} $$
Therefore, Young's modulus of elasticity;
$$\begin{array}{|l|}\hline Y=\dfrac{F / A}{l / L}=\dfrac{F L}{A l} \\\hline\end{array}$$
If $$l=L \text { and } A=1 \mathrm{m}^{2}$$
Then,$$Y=F$$
If $$ r $$ is the radius of the wire and the mass $$ M $$ is hanging on it then;
$$A=\pi r^{2} \quad \text { and } \quad F=M g$$
Therefore; $$Y=\dfrac{M g L}{\pi r^{2} l}$$
In MKS system the unit of $$ Y $$ is $$ \mathrm{Nm}^{-2} $$.
The value of $$ Y $$ is calculated only for solids and it is a characteristic of solids.
When on every point of the surface of any object a perpendicular and equal force i. e., pressure is applied then the volume of the object changes but nature or form does not change. This type of strain can be in all the three types of states of any material such as solid, liquid and gas. The change in the unit volume of the object is called 'volume strain' and the normal force (pressure) applied to the unit area of the object is called 'normal stress'. In the limit of elasticity, the ratio of normal stress to volume strain is called bulk modulus of elasticity. It is represented by K.
Bulk modulus of elasticity $$ K=\dfrac{\text { Normal stress }}{\text { Volume strain }} $$
If the material having surface area A; an equal normal deforming force $$ \mathrm{F} $$ is applied on all the surfaces of the material; then due to this there is no change in the shape of the material but there is AV change in the original volume $$ \mathrm{V} $$ then
$$ K=\dfrac{F / A}{-\Delta V / V}=\dfrac{-F V}{A \Delta V}=-\dfrac{P V}{\Delta V} $$
Negative sign shows that if pressure is increased then volume decreases and when pressure is decreased then volume increases i. e., the signs of $$ \mathrm{P} $$ and $$ \Delta \mathrm{V} $$ are opposite.
Inverse of bulk modulus of elasticity is called compressibility. Therefore; Compressibility $$ =\dfrac{1}{K} $$ If $$ \Delta V=V $$ and $$ A=1 \mathrm{m}^{2} $$ then $$ K=F=P $$
Hence, by quantitative form within the limit of elasticity the perpendicular and uniform applied force on any unit transverse cross-sectional area; by which the volume of the object reduces to half of its initial volume; is equal to the bulk modulus of elasticity of that material.
For solids the value of bulk modulus of elasticity is very high than liquids and for liquids the value is muchhigher than gases. In this way solids are less compressible and gases are more compressible.It is defined as the ratio of tangential stress to the shearing strain; within the elastic limit. It is represented by $$ \eta $$
Therefore, $$ \eta=\dfrac{\text { Tangential stress }}{\text { Shearing strain }} $$
Tangential stress $$ =F / A $$
Shearing strain $$ \phi=l / L $$
$$\therefore \quad \eta=\dfrac{F / A}{l / L}=\dfrac{F L}{A l} \quad \text { or } \quad \eta=\dfrac{F}{A \phi}$$
Here, $$ l $$ is not the change in length but the displacement of the layer in the direction of $$ F $$.
From table 10.1 we understand that the value of modulus of rigidity (n) is less than Young's modulus ofelasticity (Y) i.e., stretching or compressing an object (material) is more tough than deforming its shape.
For metals, Young's modulus of elasticity is more. Therefore, to generate small difference in length of thesematerials; more force is required. Steel is more elastic than copper, brass and aluminium. Due to this reasonthe machines used for heavy works and structural designs give more preference to steel.Set Before Numerical ExamplesFactors Affecting Elasticity
The elasticity of a material is affected by the following factors:
(i) Effect of annealing: Annealing means heating and then cooling gradually. The process of annealingresults into the formation of larger crystal gains. Here, the elasticity of the material decreases.
(ii) Effect of the impurities present in the material : The elasticity of the material can be increased ordecreased by adding impurities in it depending on the nature of impurities.
(iii) Effect of hammering and rolling : Hammering and rolling leads to breaks up the crystal grains into thesmaller peices. Thus the elasticity of the materials is increased.
(iv) Effect of temperature: The elasticity of the materials decrease with increase in temperature.
In Searle's experiment there is a rectangular frame of metal. As shown in figure (10.8) on a rigid base two wires A and B of same material have hook P and Q hanged. One end of the spirit level is attached to the frame P and second end is at the screw of the spherometer. The spherometer screw can be rotated up and down along a vertical pitch and along with it rotates the spirit level. The hanged weight $$ \mathrm{W} $$ from hook $$ \mathrm{P} $$ is astable weight which does produce twist in the wire. The hook from Q has a hanger.
When any weight is placed on the string (wire) A then its length increases and the independent end of spirit level moves downwards. By rotating the spherometer the spirit level is brought in the horizontal position.
By reading the initial reading and the final reading the distance travelled by the spherometer is calculated. This distance is the increased length due to weight.
For different weights, by experiment, the increase in length is calculated. A graph is drawn by taking weight (M) on $$ \mathrm{X} $$ -axis and increase (I) on $$ \mathrm{Y} $$ -axis.
Suppose, the initial length of the wire A is L and applied mass is $$ \mathrm{M}, \mathrm{r} $$ is the radius of the wire and increase in length is I then;
$$\begin{array}{l}\therefore \quad \text { Stress }=\dfrac{F}{a}=\dfrac{M g}{\pi r^{2}} \\\text { Strain }=\dfrac{l}{L} \\\therefore \quad Y=\dfrac{\text { Stress }}{\text { Strain }}=\dfrac{M g L}{\pi r^{2} l}\end{array}$$
The value of $$ \dfrac{M}{l} $$ is calculated from graph. From graph the value of $$ \left(\dfrac{M}{l}\right) ; $$ value of $$ r $$ is from screw gauge and value of L from metre scale can be calculated and kept in the formula and the value of Young's modulus of elasticity is calculated.
The weight applied should not be more than the limit of elasticity. The limit of elasticity is dependent on the material and its radius.
What do you understand by elasticity?
Tn a wire by producing $$ 4 \times 10^{-4} $$ linear strain a $$ 4.8 \times 10^{7} \mathrm{Nm}^{-2} $$ stress is produced. Calculate Young's modulus of elasticity of the material.
What do you understand by the perfectly elastic, plastic, and rigid bodies? Discuss their limits.
What is the property called by which the body regains its original shape and size after the removal of deforming force?
What is Poisson's ratio? Define its limits.
Explain stress, strain, and modulus of elasticity and define Young's modulus of elasticity.
The ratio of radius of two wires of same material is 2: 1 If they are stretched by applying similar force then what would be the ratio of the stress generated?
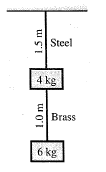
From any rigid base a steel wire of length $$ 2 \mathrm{m} $$ and weight $$ 3 \mathrm{g} $$ a weight of $$ 2.5 \mathrm{kg} $$ is hanged. The increase in length of the steel wire is $$ 2.5 \mathrm{mm} $$. If the density of the steel wire is $$ 7.8 \times 103 \mathrm{kg} / \mathrm{m}^{3} $$ then calculate theYoung's modulus of elasticity.
A copper wire of transverse cross section of $$ 0.8 \mathrm{cm}^{2} $$ is tied at both the ends rigidly. If the temperature of thewire is reduced by $$ 20^{\circ} \mathrm{C} $$ then calculate the tension in the wire. Young's modulus of elasticity of copper is 11 $$ \times 10^{10} \mathrm{Nm}^{-2} $$ and coefficient of expansion is $$ 17 \times 10^{-6} /{ }^{\circ} \mathrm{C} $$
A 5 m long steel rod is tied between two rigid bases. Steel's linear modulus of elasticity $$ =12 \times 10^{-6} /^{\circ} \mathrm{C} $$ and $$ \mathrm{Y} $$$$ =2 \times 10^{11} \mathrm{Nm}^{-2} $$. Calculate the stress produced in the rod if the temperature is increased by $$ 40^{\circ} \mathrm{C} $$.[Hint : Increase in length $$ \mid=\alpha \mathrm{L} \text { t }] $$
A material breaks by the stress of $$ 10^{9} \mathrm{N} . \mathrm{m}^{-2} $$; if the density of the material is $$ 3 \times 10^{3} \mathrm{kg} \mathrm{m}^{-3} $$ then calculate that length of the wire; which on hanging by its own weight breaks.
For a steel wire of $$ 4.7 \mathrm{m} $$ length and transverse cross section of $$ 3.0 \times 10^{-5} \mathrm{m}^{2} $$ and a copper wire of length $$ 3.5 \mathrm{m} $$ and $$ 4.0 \times 10^{-5} \mathrm{m}^{2} $$, the increase in length of both is same when same value of weights are hangedfrom the wires. What is the ratio of steel and copper's Young's modulus of elasticity?
A wire of length $$ 0-5 \mathrm{m} $$ and diameter $$ 2 \mathrm{mm} $$ is tied at one end and is twisted at the other end by $$ 0.8 \mathrm{rad} $$ Calculate the shearing strain on the surface of the wire. [Hint: Shearing strain $$ \left.\phi=\dfrac{r}{l} \otimes\right] $$
Given, $$ L=0.5 \mathrm{m} $$
$$ r=\dfrac{D}{2}=\dfrac{2 \mathrm{mm}}{2}=1 \mathrm{mm}=1 \times 10^{-3} \mathrm{m} $$
$$\theta=0.8 \mathrm{rad}$$
From the figure
$$ \begin{aligned} & \phi=\dfrac{\Delta r}{L} \text { and } \theta=\dfrac{\Delta r}{r} \\ \therefore \quad \dfrac{\phi}{\theta} &=\dfrac{\Delta r / L}{\Delta r / r}=\dfrac{r}{L} \\ \therefore \quad & \phi=\dfrac{r}{L} \theta \end{aligned} $$
Hence shearing strain,
$$\begin{aligned}\phi &=\dfrac{1 \times 10^{-3}}{0.5} \times 0.8=\dfrac{8}{5} \times 10^{-3} \\&=1.6 \times 10^{-3} \mathrm{rad} \\or \quad \phi &=1.6 \times 10^{-3}\left(\dfrac{180}{\pi}\right)^{0}\end{aligned}$$
$$\begin{array}{l}=\dfrac{1.6 \times 10^{-3} \times 180}{3.14} \\=9.17 \times 10^{-2}=0.0917=\mathbf{0} \mathbf{0 9 2}^{\circ}\end{array}$$
Two wires are made up of the same material (metal). Length of the first wire is half the length of the second wire, and its diameter is double the diameter of the second wire. If the same weights are hanged from the wires then what would be the ratio of increase in the length of the wires?
A solid rubber ball when taken from the surface to the bottom of a 200 m deep lake the volume of the ball reduces by $$ 0.1 \% $$. Density of water of the lake $$ =1.0 \times 10^{3} \mathrm{kg} / \mathrm{m}^{3} $$. Calculate the Bulk modulus of elasticity of rubber, $$ \left(\mathrm{g}=10 \mathrm{m} / \mathrm{s}^{2}\right) $$
Two wires of a diameter 0.25 cm . one made of steel and other made of brass are loaded as shown in fig 9.13 , The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m
Computer the elongations of steel and the brass wires.
If a wire is replaced by another similar wire but of half the diameter . What is the effect on
Max load it can sustain .
If a wire is replaced by another similar wire but of half the diameter . What is the effect on
Increase in the length for a given load,
What is the Bulk modulus of an incompressible object ?
If the length of the wire is made 2 times , what is the effect on the increase in length under same load ?
Define Modulus of elasticity .
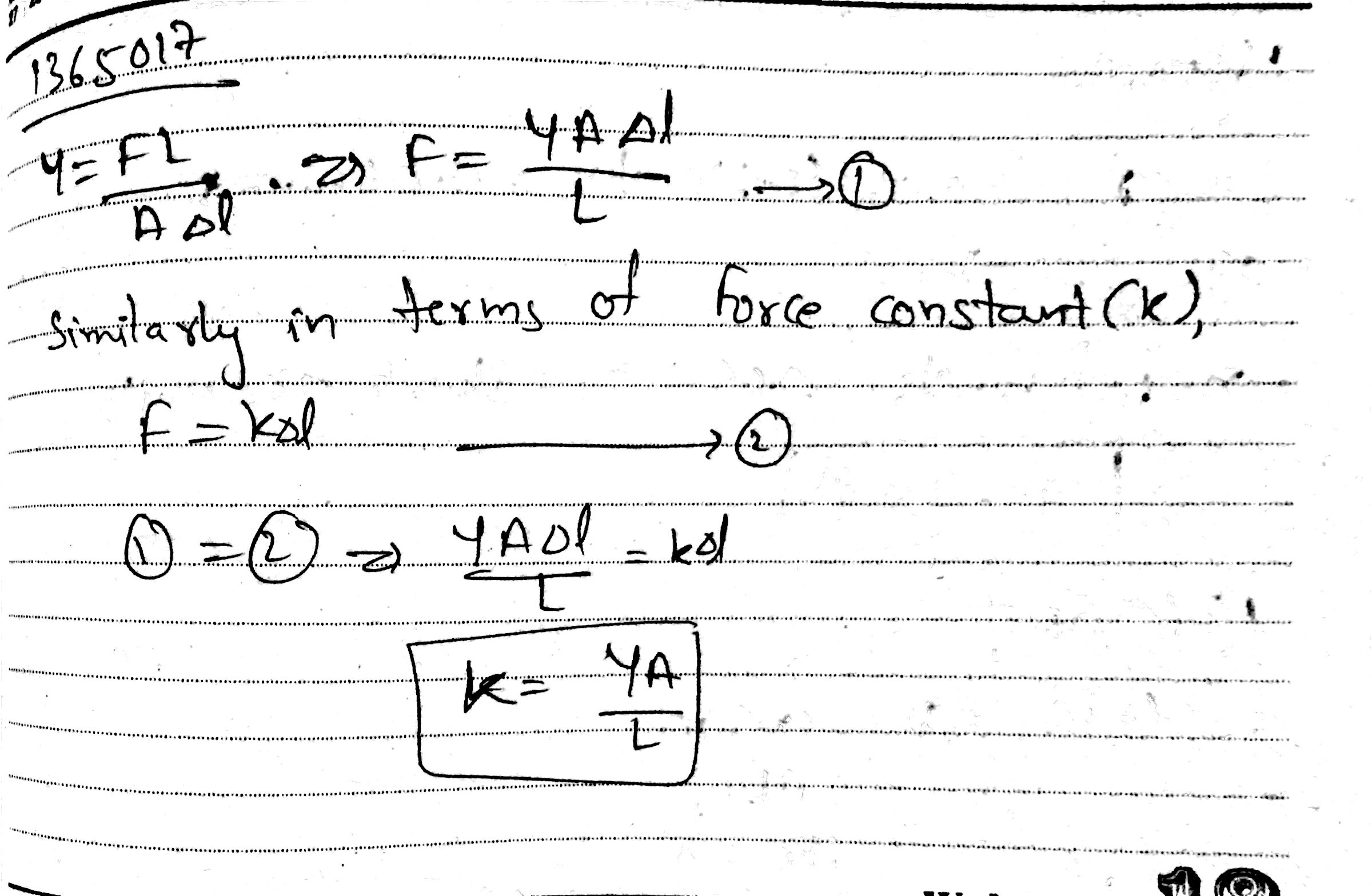
Mention the expression for Young's modulus in the case of a stretched string .
What is a perfectly elastic and inelastic body ?
How much should the pressure on a liter of water be changed to compress it by 0.10%.
Four indentical hollow cylindrical columns of mild steel support a big structure of mass 50,000 kg . The inner and outer of each column are 30 and 60 cm respectively . Assuming the load distributing to be uniform , calculate the compressional strain of each
When the pressure on a sphere increases by 50 atm than its volume decreases by 0.02% .Find Bulk modulus.
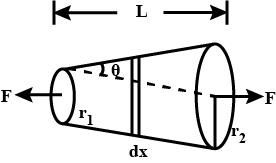
Consider a tapered wire as shown .Find the extension if Y is its Young's modulus
A cube of side 3 cm Is subjected to shearing force .The toop of cube is sheared through 0.012 cm with respect to bottom face . If cube is made of a material of shear modulus $$ 2.1 \times 10^{10} Nm^{-2}$$ then find:
Shearing stress
The Young's modulus of a wire of length L and radius 'r' is Y . If length is reduced to L /3 and Radius r /4 .What will be its ratio of extension ?
The Young's modulus of a materials is Y .It has an area A and length 'L' .Now if a is made $$ \dfrac{A}{16}$$ and length L/What is the new Young's modulus ?
Define stress and strain and derive their units .Write one limitation of Hooke's Law.
What is the percentage increase in length of a wire of dimeter 12.5 mm stretched by a weight of $$1000 kg\omega t $$ ? $$\left [ Given Y = 12.5 \times 10^{11}dyne/sq .cm \right ]$$
A cube of side 3 cm Is subjected to shearing force .The toop of cube is sheared through 0.012 cm with respect to bottom face . If cube is made of a material of shear modulus $$ 2.1 \times 10^{10} Nm^{-2}$$ then find :
Shearing strain
When a wire is stretched by a certain force its elongation is 'a' .If the the second wire having daouble - radius and 4 -times length .Find its elongation .
The length of a metal is $$ L_{1} $$ when a force is $$ F_{1} $$ is applied on it and its length is $$ L_{2} $$ when applied force is $$ F_{2} $$ . Find the original length of wire .
A metal rod is tied vertically . If the breaking stress is $$ 5.4 \times 10^{9} Nm^{-2}$$ and density $$ 5.4 \times 10^{3} kg /m^{3}$$ .Find the maximum length of rod that can be held without breaking .
The relationship between the impressibility $$\beta $$ and the elastic constants $$E$$ and $$\mu$$.
Show that Poisson's ratio $$\mu$$ cannot exceed $$1/2$$.
A glider of mass $$m$$ is free to slide along a horizontal air track. It is pushed against a launcher at one end of the track. Model the launcher as a light spring of force constant $$k$$ compressed by a distance $$x$$. The glider us released from rest.
Show that the glider attains a speed of $$v=x(k/m)^{1/2}$$.
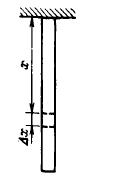
The elongation $$\Delta l$$ of the rod due to its own weight.
If the extension of the string when it makes a constant angle relative to vertical is $$\cfrac { 2m\sqrt { { g }^{ 2 }+{ a }^{ 2 } } }{ x\pi { r }^{ 2 }Y } l$$. Find $$x$$.
Here the net force on the bob is $$\displaystyle F=\sqrt{(ma)^2+(mg)^2}=m\sqrt{a^2+g^2}$$
Stress in the string is $$\displaystyle S=\frac{F}{A}=\frac{m\sqrt{a^2+g^2}}{\pi r^2}$$
If $$\Delta l$$ be the extension of string , Young modulus $$\displaystyle Y=\frac{F/A}{\Delta l/l}=\frac{Fl}{A\Delta l}$$
$$\displaystyle \therefore \Delta l=\frac{Fl}{AY}= \frac{m\sqrt{a^2+g^2} l}{\pi r^2 Y}$$ thus, $$x=2$$
Stress in the string is $$\displaystyle S=\frac{F}{A}=\frac{m\sqrt{a^2+g^2}}{\pi r^2}$$
If $$\Delta l$$ be the extension of string , Young modulus $$\displaystyle Y=\frac{F/A}{\Delta l/l}=\frac{Fl}{A\Delta l}$$
$$\displaystyle \therefore \Delta l=\frac{Fl}{AY}= \frac{m\sqrt{a^2+g^2} l}{\pi r^2 Y}$$ thus, $$x=2$$
Two wires of diameter $$0.25\ cm$$, one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is $$1.5\ m$$ and that of brass is $$1.0\ m$$. Young's modulus of steel is $$2.0\times {10}^{11}Pa$$ and that of brass is $$1.0\times {10}^{11}Pa$$. If the ratio of elongations of steel and brass wires $$\dfrac {{\Delta l }_{ steel } }{ { \Delta l }_{ brass } } = \dfrac{x}{4} $$, find $$x$$.
When operating, the ride has a maximum angular speed of $$\dfrac{\sqrt { 19 }}{5}rad/s$$. How much is the rod stretched (in $$\mu m$$) then?
A copper wire of negligible mass, $$1m$$ length and cross-sectional area $$ { 10 }^{ -6 }{ m }^{ 2 }$$ is kept on a smooth horizontal table with one end fixed. A ball of mass $$1kg$$ is attached to the other end. The wire and the ball are rotating with an angular velocity of $$20 \ rad/s$$. If the elongation in the wire is $${10}^{-3}m$$. Find the Young's modulus of the wire (in terms of $$10^{11}N/m^2$$)
A sphere of radius $$10\ cm$$ and mass $$25\ kg$$ is attached to the lower end of a steel wire of length $$5 \ m$$ and diameter $$4\ mm$$ which is suspended from the ceiling of a room. The point of support is $$521\ cm$$ above the floor. When the sphere is set swinging as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position in $$m/s$$. $$(Y_{steel}=2\times10^{11}\ N/m^{2})$$
A steel bolt is inserted into a copper tube as shown in figure. Find the forces induced in the bolt and in the tube when the nut is turned through one revolution. Assume that the length of the tube is $$l$$, the pitch of the bolt thread is $$h$$ and the cross-sectional areas of the steel bolt and the copper tube are $${A}_{s}$$ and $${A}_{c}$$, respectively
A cylindrical steel wire of 3 m length is to stretch no more than 0.2 cm when a tensile force of 400 N is applied to each end of the wire. What minimum diameter is required for the wire?
$$Y_{steel} =2.1\times 10^{11} N/m^{2}$$
Find the increment in the length of a steel wire of length $$5\ m$$ and radius $$6\ mm$$ under its own weight.Density of steel $$=8000kg/m^{3}$$ and Young's modulus of steel $$=2 \times10^{11}\ N/m^{2}$$. What is the energy stored in the wire? $$(Take\ g = 9.8m/s^{2}).$$
Find out the elongation in the block shown if mass, area of cross-section and young modulus of the block are m, A and Y respectively
Acceleration $$\displaystyle a=\frac{F}{m}$$ then T = m'a where $$\displaystyle \Rightarrow m'=\frac{m}{\ l }x$$
T $$\displaystyle T=\frac{m}{\ l }\times \frac{F}{m}=\frac{Fx}{\ l }$$
Elongation in element 'dx' = $$\displaystyle \frac{Tdx}{AY}$$
Total elongation $$\displaystyle \delta =\int_{0}^{l}\frac{Tdx}{AY}d=\int_{0}^{l}\frac{Fxdx}{A\ l Y}=\frac{F\ l }{2AY}$$
Note : Try this problem if friction is given between block and surface ($$\displaystyle \mu $$ = friction coefficient) and Case I F < $$\displaystyle \mu $$mg II F > $$\displaystyle \mu $$mg
Ans In both cases answer will be $$\displaystyle =\frac{F\ l }{2AY}$$
T $$\displaystyle T=\frac{m}{\ l }\times \frac{F}{m}=\frac{Fx}{\ l }$$
Elongation in element 'dx' = $$\displaystyle \frac{Tdx}{AY}$$
Total elongation $$\displaystyle \delta =\int_{0}^{l}\frac{Tdx}{AY}d=\int_{0}^{l}\frac{Fxdx}{A\ l Y}=\frac{F\ l }{2AY}$$
Note : Try this problem if friction is given between block and surface ($$\displaystyle \mu $$ = friction coefficient) and Case I F < $$\displaystyle \mu $$mg II F > $$\displaystyle \mu $$mg
Ans In both cases answer will be $$\displaystyle =\frac{F\ l }{2AY}$$
A $$5 m$$ long cylindrical steel wire with radius $$2 \times 10^{-3}$$ m is suspended vertically from a rigid support and carrics a bob of mass 100 kg at the other end. If the bob gets snapped, calculate the change in temperature of the wire ignoring radiation losses. $$(Take\ g= 10m/s^{2})$$(For the steel wire: Young's $$modulus = 2.1 \times 10^{11} N/m^{2}$$; Density $$= 7860kg/m^{3}$$ Specific heat= $$420J/kg^{}C)$$
A 6 kg weight is fastened to the end of a steel wire of unstretched length 60 cm. It is whirled in a vertical~~ circle and has an angular velocity of 2 rev/s at the bottom of the circle. The area of cross-section of the. i wire is $$0.05 cm^{2}$$. Calculate the elongation of the wire when the weight is at the lowest point of the path . Young's modulus of steel $$= 2\times 10^{11}$$ N/m^{2} .
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in Fig. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires. Given youngs modulus of steel = $$ 2 \times {10}^{-11} Pa $$ and that of brass is $$ 0.9 \times {10}^{-11} Pa$$
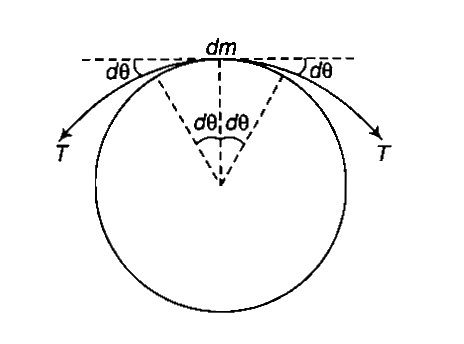
A uniform ring of radius R and made up of a wire ofcross-sectional radius r is rotated about its axis witha frcquency f If density of the wire is p and Young's modulus is Y. Find the fractional change in radiusof the ring .
Let $$T$$ be the tension in the ring.
From figure, net radial component of the tension $$T' = 2T sin(d\theta)$$
As $$d\theta$$ is very small, thus $$sin (d\theta) \approx d\theta$$
$$\implies$$ $$T' = 2T d\theta$$
Mass of the ring $$m = \rho \times (\pi r^2) (2\pi R)$$
Mass of the small element of the ring $$dm = \dfrac{m}{2\pi} (2d\theta) = \dfrac{m d\theta}{\pi}$$
$$\therefore$$ $$dm = \dfrac{2\pi^2 r^2 R\rho d\theta }{\pi} = 2\pi r^2 R \rho d\theta$$
Also $$T' = (dm) R w^2$$ where $$w =2\pi f$$
$$\therefore$$ $$2T (d\theta) = 2\pi r^2 R \rho (d\theta) \times R(2\pi f)^2$$ $$\implies T = 4\pi^3 R^2 r^2 \rho f^2$$
Elongation in the length of the ring $$\delta = 2\pi (R + \Delta R) - 2\pi R =2\pi \Delta R$$
$$\therefore$$ Strain in the ring $$\epsilon =\dfrac{\delta}{2\pi R} = \dfrac{\Delta R}{R}$$
From Hooke's law $$Y = \dfrac{T}{A \epsilon}$$ where $$A =\pi r^2$$
$$\therefore$$ $$Y =\dfrac{4\pi^3 R^2 r^2 f^2 \rho}{\pi r^2 \times \Delta R/R}$$ $$\implies \Delta R =\dfrac{4\pi^2 R^3 f^2 \rho}{Y}$$
A wire of density '$$\rho$$' and Youngs modulus '$$Y$$' is stretched between two rigid supports separated by a distance '$$L$$' under tension '$$T$$'. Derive an expression for its frequency in fundamental mode. Hence show that $$\eta=\cfrac { 1 }{ 2L } \sqrt { \cfrac { Yl }{ \rho L } } $$, where symbol have their usual meanings.
When the length of a simple pendulum is decreased by $$20cm$$, the period changes by $$10$$%. Find the original length of the pendulum.
A 30.0 kg hammer, moving with speed speed 20.0 $$ms^{-1}$$, strikes a steel Spike 2.30 cm in diameter. The hammer rebounds with speed 10.0 $$ms^{-1}$$ after 0.110 s .What is the average Strain in the Spike during the impact?
Calculate the work done in stretching steel wire of length 2m and of cross sectional area 0.0225 $$mm^2$$, when a load of 100 N is applied slowly to its free end. (Young's modulus of steel = 20 x $$10^{10}N/m^2$$)
A bar is subjected to axial forces as shown. If E is the modulus of elastically of the bar and A is its cross-section area. Its elongation will be.
One end of a wire $$2\ m$$ long and $$0.2\ {cm}^{2}$$ in cross-section is fixed to a ceiling and a load of $$4.8\ kg$$ is attached to the free end. Find the extension of the wire. Young's modulus of steel $$=2.0 \times {10}^{11}\ N/{m}^{2}$$. Take $$g=10\ m/{s}^{2}$$.
A copper wire $$4\ m$$ long has diameter of $$1\ mm$$, if a load of $$10\ kg$$ wt is attached at other end. What extension is produced, if Poisson's ratio is $$0.26$$? How much lateral compression is produced in it? $$(Y_{cu} = 12.5 \times \ 10^{10}N/m^2)$$.
Poisson`s ratio of a material is $$0.5$$ applied to wire of this material, these in the cross-section area increase in the length is.
Estimate the change in the density of water in ocean at a depth of $$400$$ m below the surface. The density of water at the surface $$=1030$$ kg $$m^{-3}$$ and the bulk modulus of water $$=2\times 10^9$$N $$m^{-2}$$.
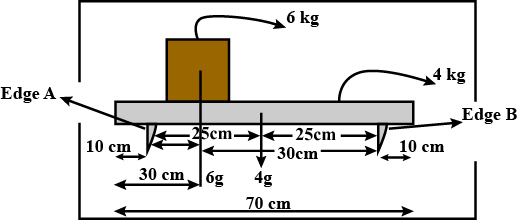
A metal bar 70 cm long and 4.00 kg in mass supported on two knife--edges placed 10 cm from each end. A 6.00 kg load is suspended at 30 cm from one end. Find the reactions at the knife-edges. (Assume the bar to be of uniform cross section and homogeneous.)
To find the normal reaction due to edges we will use the concept of moment of force about a point.
Since system is in equilibrium i.e. rod is balanced about edges, therefore we have
Applying equilibrium condition of moment about the point A (edge A)
Moment of normal reaction of edge B about A= Moment of rod about A$$\times$$ Moment of 6 kg mass about A
$$N_B\times50=4g\times25+6g\times20$$
here $$N_B$$ is a normal reaction due to edge B in upward direction
$$4g$$ is weight of the rod in downward direction
$$6g$$ is weight of the mass in downward direction
therefore,
$$N_B=\dfrac{(100+120)g}{50}=\dfrac{220}{50}g=\dfrac{22}{5}g=4.4g$$
Similarly, applying equilibrium condition of moment about the point B (edge B)
We get
$$N_A\times50=4g\times25+6g\times30$$
$$N_A=\dfrac{(100+180)g}{50}=\dfrac{280}{50}g=\dfrac{28}{5}g=5.6g$$
Therefore, normal reaction on the edges is 4.4g and 5.6g, where g is acceleration due to gravity.
A wire of lenth L suppleid heat to raise its temperature by T.if y is the coefficient of volume expansion of the wire and Young`s modulus of the wire then the energy density stored in the wire is.
A copper wire of length $$2.2m$$ and a steel wire of length $$1.6m$$, both of diameter $$3.0mm$$, are connected end to end. When stretched by a load, the net elongation is found to be $$0.70mm$$. Obtain the load applied.
$$\sigma _{cu}=\sigma_{st}\quad r=\dfrac {3}{2}=1.5\ mm$$
$$\left [\gamma_{cy}\times \dfrac {\Delta l}{l}\right]_{cu} =\left [\gamma_{st}.\dfrac {\Delta l}{l}\right]_{st}$$
$$11\times 10^{11}\times \dfrac {\Delta l_{cu}}{2.2}=2\times 10^{11} \times \dfrac {\Delta l_{st}}{1.6}$$
$$\dfrac {\Delta l_{cu}}{\Delta l_{st}}=\dfrac {40}{16}=2.5......(1)$$
$$\Delta l_{cu}+ \Delta l_{st}=0.7\times 10^{-3}m$$,
from equation $$(1)$$ & $$(2)$$
$$2.5 (\Delta l)_{st} + (\Delta l)_s =0.7\times 10^{-3}m$$
$$(\Delta l)_{st} =2\times 10^{-4}m$$
$$(\Delta l)_{cu}=5\times 10^{-4}m$$
we know that
$$\gamma =\dfrac {stress}{strain}=\dfrac {F\times l}{A\times \Delta l}\Rightarrow F=\dfrac {\gamma A\Delta l}{l}$$
$$F=\dfrac {1.1\times 10^{11}\times \pi \times (1.5\times 10^{-3})^2 \times 5\times 10^{-4}}{2.2}$$
$$=\dfrac {1.1\times 51\times (1.5)^2 \times 10^{11}\times 10^{-6}\times 10^{-4\times 5}}{2.2}$$
$$=176.78\ N$$
A steel wire of length 4m and diameters 5mm is stretched by 5kg weight find the change in it's diameter if $$y = 0.4 \times 10^{12}dyne/cm^2$$ and $$\sigma = 0.3$$
What mass must be suspended from a steel wire $$2m$$ long and $$1\ mm$$ in diameter to stretch it by $$1\ mm$$ Given Youngs modulus of steel $$2\times{10}^{12}$$ $$dyne/{ cm }^{ 2 },\ g=981\ cm/{ s }^{ 2 }$$.
A sphere of mass 20kg is suspended by a metal wire of unstretched length 4 m and diameter 1mm.When is equilibrium, there is a clear gap of 2mm between the so that the wire makes an angle $$\theta $$ with the vetical and is released.find the maximum value of $$\theta $$ so that the sphere does not rub the floor.young modulus of the metal of the wire is $$2.0 \times {10^{11}}N{m^{ - 2}}$$.make appropriate approximations.
In determination of young modulus of elasticity of wire, a force is applied and extension is recorded. Initial length of wire is $$1 \mathrm { m } $$ . The curve between extension and stress is depicted then young modulus of wire will be:
Two wires are made of the same material and have the same volume . However wire 1 has cross section area A and wire 2 has cross-section area 3A . If the length of wire 1 increases by$$\bigtriangleup x$$ on applying force F, how much force is needed to stretch wire 2 by the same amount ?
A material has normal density $$\rho$$ and bulk modulus K. Find the increase in the density of the material when subjected to an external pressure P from all sides.
A uniform wire of length $$1\ m$$ and radius $$0.028\ cm$$ is employed to raise a stone of density $$2500\ kg/{m}^{3}$$ immersed in water. Find the change in elongation of wire when the stone is raised out of water. $$\left [mass of stone =5\ kg,\ Y of material of wire = 2\times {10}^{11}\ N/{m}^{2}\right]$$
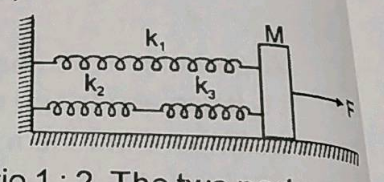
The springs shown in the figure are all unstretched in the begining when a man starts pulling the block. The man exerts a constant force F on the block. Find the amplitude and the frequency of the motion of the block.
Two light wires made up of the same material (Young Modulus, Y) have length $$L$$ each and radii $$R$$ and $$2R$$ respectively, They are joined together and suspended from a rigid support. Now a weight $$W$$ attached to the free end of the joint wire as shown in the figure. Find the elastic potential energy stored in the system due to the extension of the wire.
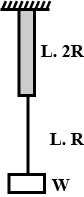
A steel wire of radius 0.4 x$$
10^{-3}
$$ m and length 1 m is tightly clamped between points A and B which are separated by 1 m and in the same horizontal plane. A mass is hung from the middle point of the wire such that the middle point sags by 2 cm from the original position. Compute the mass of body. $$
\left(Y_{\text { steel }}=20 \times 10^{10} \mathrm{N} / \mathrm{m}\right)
$$ (Ans. : M = 0.6566 kg.)
Cross-sectional area of a wire of length L is A. Young's modulus of a material is Y. If the wire acts as a spring what is the value of force constant?
The elastic limit of steel is $$8 \times 10^8 Nm^{-2}$$ and its Young modulus $$2 \times 10^{11}Nm^{-2}$$. Find the maximum elongation of a half-metre steel wire that can be given without exceeding the elastic limit.
A steel wire of diameter 0.4 mm is heated upto $$25{ 0 }^{ o }C$$ and then rigidity clamped at its ends when hot. Calculate the pull exerted on the clamps when it cools to $${ 50 }^{ o }C$$.
[Coefficient of linear expansion of steel is $$2\times { 10 }^{ -5 }/^{ o }C$$, $$Y = 22\times { 10 }^{ 11 }N/{ m }^{ 2 }]$$
Mention the expression for young's modulus in terms of radius
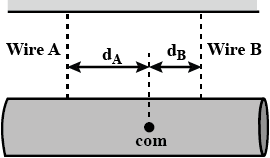
In fig. 12-13 a 103 kg uniform log hangs by two steel wires. A and B, both of radius 1.20 mm. Initially wire A was 2.50 m long and 2.00 mm shortest then wire B. The log is now horizontal. what are the magnitude of the forces on it from
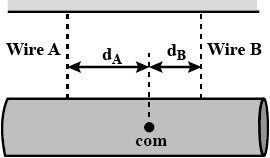
What is the ratio $${ d }_{ A }/{ d }_{ s }$$?
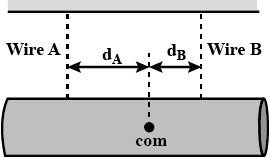
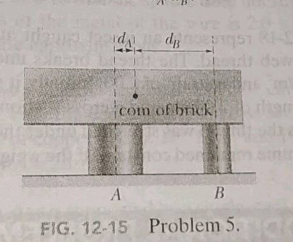
In fig 12-15 a lead brick rests horizontally on cylinders A and B. The areas of the top faces of the cylinders are related by $${ A }_{ A }={ 2A }_{ B }$$; the Young's moduli of the cylinders are related by $${ E }_{ A }={ 2E }_{ B }$$ The cylinders had identical lengths before the brick was placed on them. What fraction of the brick's mass is supported
By cylinder B? The horizontal distances between the center of mass of the brick and the centerlines of the cylinders are $${ d }_{ A }$$ for cylinder A and $${ d }_{ B }$$ for cylinder B. What is the ratio $${{d}_{A}}/{{d}_{B}}$$ ?
In fig. 12-13 a 103 kg uniform log hangs by two steel wires. A and B, both of radius 1.20 mm. Initially wire A was 2.50 m long and 2.00 mm shortest then wire B. The log is now horizontal. what are the magnitude of the forces on it from Wire B?
In Fig. 12-13, a 103 kg uniform log hangs by two steel wires. A and B, both of radius 1.20 mm. Initially, wire A was 2.50 m long and 2.00 mm shorter than wire B. The log is now horizontal. What are the magnitudes of the forces on it from
Wire B ?
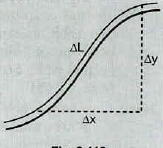
In this problem you will derive an expression for the potential energy for a segment of a string carrying a travelling wave. The potential energy of a segment equals the work done by the tension in stretching the string, which is $$\Delta U=F(\Delta l-\Delta x)$$, where $$F$$ is the tension, $$\Delta l$$ is the length of the stretched segment and $$\Delta x$$ is the original length. From the figure we see that
$$\Delta l=\sqrt{(\Delta x)^2+(\Delta y)^2}=\Delta x \left\{ 1+\left( \dfrac{\Delta y}{\Delta x}\right)^2\right\}^{1/2}$$
b) Show that $$\Delta U\sim \dfrac{1}{2}FK^2A^2 \cos^2( kx-\omega t)\Delta x$$.
A copper wire of negligible mass, $$1\ m$$ length and cross sectional area $$10^{-6} m^{2}$$ is kept on a smooth horizontal table with one end fixed. A ball of mass $$1\ kg$$ is attached to the other end. The wire and the ball are rotating with an angular velocity of $$20\ rad/s$$. If the elongation in the wire is $$10^{-3} m$$.
(i) Find the Young's modulus of the wire (in terms of $$\times 10^{11} N/m^{2})$$.
(ii) If for the same wire as stated above, the angular velocity is increased to $$100\ rad/s$$ and the wire breaks down, find the breaking stress (in terms of $$\times 10^{10} N/m^{2})$$.
An amusement park ride consists of airplane shaped cars attached to steel rods. Each rod has a length of $$20.0\ m$$ and a cross-sectional area of $$8.00\ cm^{2}$$. Young's modulus for steel is $$2\times 10^{11} N/m^{2}$$.
(a) How much is the rod stretched (in mm) when the ride is at rest? (Assume that each car plus two people seated in it has a total weight of $$2000\ N$$).
(b) When operating, the ride has a maximum angular speed of $$\sqrt {19}/5 rad/s$$. How much is the rod stretched (in mm) then?
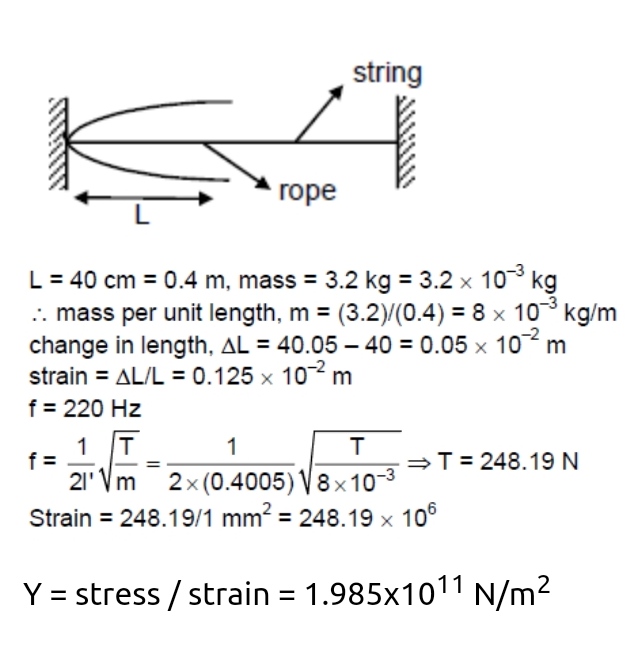
Ab $$40 cm$$ wire having a mass of $$3.2 g$$ is stretched between two fixed supports $$40.05 cm$$ apart. In its fundamental mode, the wire vibrates at $$220 Hz$$. If the area of cross section of the wire is $$1.0 mm^2$$, find its Young modulus.
A 14 . 5 kg mass , fastened to the end of a steel wire of understand length 1.0 m , is whirled in a vertical circle with an angular velocity of 2 rev/s at the bottom of the circle . The cross - sectional area of the wire is $$ 0.065 cm^{2} $$ . Calculate the elongation of the wire when the mass is the lowest point of its path .
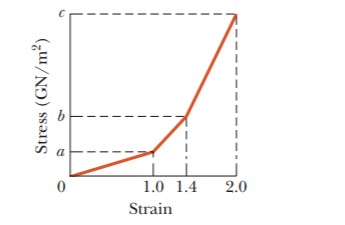
The figure shows an approximate plot of stress versus strain for a spider-web thread, out to the point of breaking at a strain of $$2.00$$. The vertical axis scale is set by values $$a = 0.12 GN/m^2$$, $$b = 0.30 GN/m^2$$ , and $$c = 0.80 GN/m^2$$ . Assume that the thread has an initial length of 0.80 cm, an initial cross-sectional area of $$8.0\times10^{12} m^2$$, and (during stretching) a constant volume. The strain on the thread is the ratio of the change in the thread’s length to that initial length, and the stress on the thread is the ratio of the collision force to that initial cross-sectional area. Assume that the work done on the thread by the collision force is given by the area under the curve on the graph. Assume also that when the single thread snares a flying insect, the insect’s kinetic energy is transferred to the stretching of the thread. (a) How much kinetic energy would put the thread on the verge of breaking? What is the kinetic energy of (b) a fruit fly of mass $$6.00$$ mg and speed $$1.70$$ m/s and (c) a bumblebee of mass $$0.388$$ g and speed $$0.420$$ m/s? Would (d) the fruit fly and (e) the bumble bee break the thread?
A steel wire of length 4.7 m cross - section $$3.0 \times 10^{-5}m^{2}$$ stretches by the same amount as a copper wire of length 3.5 m and cross - sectional area of $$4.0 \times 10^{-5}m^{2} $$ under a given load . What is the ratio of the Young's modulus of steel of that of copper ?
A stone of mass m is tied to an elastic string of negligible mass and string constant k. The unstretched of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point P. Initially, the stone is at the same level as the point P. The stone is dropped vertically from point Q
(a) Find the distance y from the top when the mass comes to rest for an instant, for the first time.
(b) What is the maximum velocity attained by the stone in this drop?
(c) What shall be the nature of the motion after the stone has reached its lowest point?
(a) A steel wire of mass $$\mu$$ per unit length with a circular cross section has a radius of $$0.1 cm$$. The wire is of length $$10 m$$ when measured lying horizontal, and hangs from a hook on the wall. A mass of $$25 kg $$ is hung from the free end of the wire. Assuming the wire to be uniform and lateral strains << longitudinal strains, find the extension in the length of the wire. The density of steel is $$7860 kg m^{-3}$$ ( Young's modules $$Y = 2 \times 10^{11} N.m^{-2}$$)
(b) If the yield strength of steel is $$2.5 \times 10^8 N.m^{-2}$$, what is the maximum weight that can be hung at the lower end of the wire ?
A horizontal aluminum rod $$4.8$$ cm in diameter projects $$5.3$$ cm from a wall. A $$1200 $$kg object is suspended from the end of the rod. The shear modulus of aluminum is $$3.0 1010 \,N/m^2$$. Neglecting the rod’s mass, find (a) the shear stress on the rod and (b) the vertical deflection of the end of the rod.
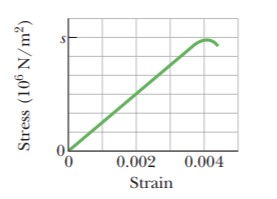
Figure shows the stress-strain curve for a material. The scale of the stress axis is set by $$s = 300$$, in units of $$10^6 N/m^2$$. What are (a) Young’s modulus and (b) the approximate yield strength for this material?
Anvils made of single crystals of diamond , with the shape as shown in fig . are used to investigate behaviour of materials under very high pressures . Flat faces at the narrow end of the anvil have diameter of 0.50 mm , and the wide ends are subjected to a compressional force of 50,000 N . What is the pressure at the tip of the anvil ?
A wire of length L and radius r is clamped rigidly at one end . When the other end of the wire is pulled by a force f, its length increase by l . Another wire of the same material of length $$2L$$ and radius $$2r$$, is pulled by a force $$2f$$. Find the increase in length of this wire.
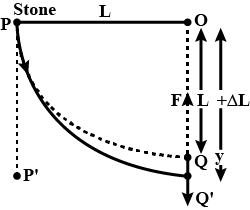
A person hoists one of the two loads of equal mass at constant velocity $$v$$. At the moment when the two loads are at the same height $$h$$, the upper pulley is released ( is able to rotate without friction like the tower pulley ).
Indicate the load which touches the floor first after a certain time $$t$$, assuming that the person continues to slack the rope at the same constant velocity $$v$$. The masses of the pulleys and the ropes and the elongation of the ropes should be neglected.
A solid sphere of brass ( bulk modulus of $$14.0\times 10^{10}\ N/m^2 $$) with a diameter of $$3.00\ m$$ is thrown into the ocean. By how much does the diameter of the sphere decrease as it sinks to a depth of $$1.00\ km$$?
A rubber string of mass $$m$$ and rigidity $$k$$ is suspended at one end.
Determine the elongation $$\Delta l$$ of the string.
We write the equilibrium condition for a small segment of the string which had the length $$\Delta x$$ before suspension and was at a distance $$x$$ from the point of suspension :
$$\dfrac mL \Delta xg +T ( x+\Delta x) T(x)$$.
where $$L$$ is the length of the rubber string in the unstretched state. Thus, it is clear that after the suspension the tension will uniformly decrease along the string from $$mg$$ to zero.
Therefore, the elongations per units length for small equal segments of the string in the unstressed state after the suspension will also linearly decrease from the maximum value to zero. For this reason, the half-sum of the elongations of two segments of the string symmetric of the central segment which experiences the tension $$mg/2$$. Consequently, the elongation $$\Delta l$$ of the string will be such as if it were acted upon by the force $$mg/2$$ at the point of suspension and at the lower end, and the string were weightless; hence
$$\Delta l=\dfrac {mg}{2k}$$.
$$\dfrac mL \Delta xg +T ( x+\Delta x) T(x)$$.
where $$L$$ is the length of the rubber string in the unstretched state. Thus, it is clear that after the suspension the tension will uniformly decrease along the string from $$mg$$ to zero.
Therefore, the elongations per units length for small equal segments of the string in the unstressed state after the suspension will also linearly decrease from the maximum value to zero. For this reason, the half-sum of the elongations of two segments of the string symmetric of the central segment which experiences the tension $$mg/2$$. Consequently, the elongation $$\Delta l$$ of the string will be such as if it were acted upon by the force $$mg/2$$ at the point of suspension and at the lower end, and the string were weightless; hence
$$\Delta l=\dfrac {mg}{2k}$$.
Staring from rest, a $$64.0-kg$$ person bungee jumps from a tethered hot air balloon $$65.0 m$$ above the ground. The bungee cord has negligible mass and unstretched length $$25.8 m$$ One end is tied to the basket of the balloon and the other end to a harness around the person's body. The cord is modeled as a spring that obeys Hooke's law with a spring constant of $$N/m$$ and the person's body is modeled as a particle. the hot-air balloon does not move. Plot a graph of the gravitational elastic and total potential energies as functions of $$y$$
A light spring has unstressed length $$15.5 cm$$. It is described by Hookes law with spring constant $$4.30 N/m$$. One end of the horizontal spring is held on a fixed vertical axle, and the other end is attached to a puck of mass m that can move without friction over a horizontal surface. The puck is set into motion in a circle with a period of $$1.30 s$$. (a) Find the extension of the spring $$x$$ as it depends on $$m$$. Evaluate $$x$$ for (b) $$m = 0.070 0 kg$$, (c) $$m = 0.140 kg$$, (d) $$m = 0.180 kg$$, and (e) $$m = 0.190 kg$$. (f) Describe the pattern of variation of $$x$$ as it depends on $$m$$.
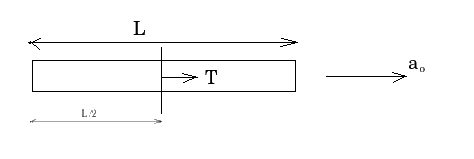
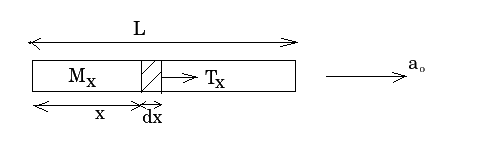
A uniform elastic plank moves over a smooth horizontal plane due to a constant force $$F_o$$ distributed uniformly over the end face. The surface of the end face is equal to $$S$$, and Young's modulus of the material to $$E$$. Find the compressive strain of the plank in the direction of the acting force.
A rubber string 10 m long is suspended from a rigid support at one end.Calculate extension of the string due to its own weight .The density of rubber is $$ 1.5 \times 10^{3} kg / m^{3} $$and $$ Y_{rubber} = 5 \times 10^{6}Nm^{-2}$$
Class 11 Engineering Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Physical World Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work,Energy And Power Extra Questions