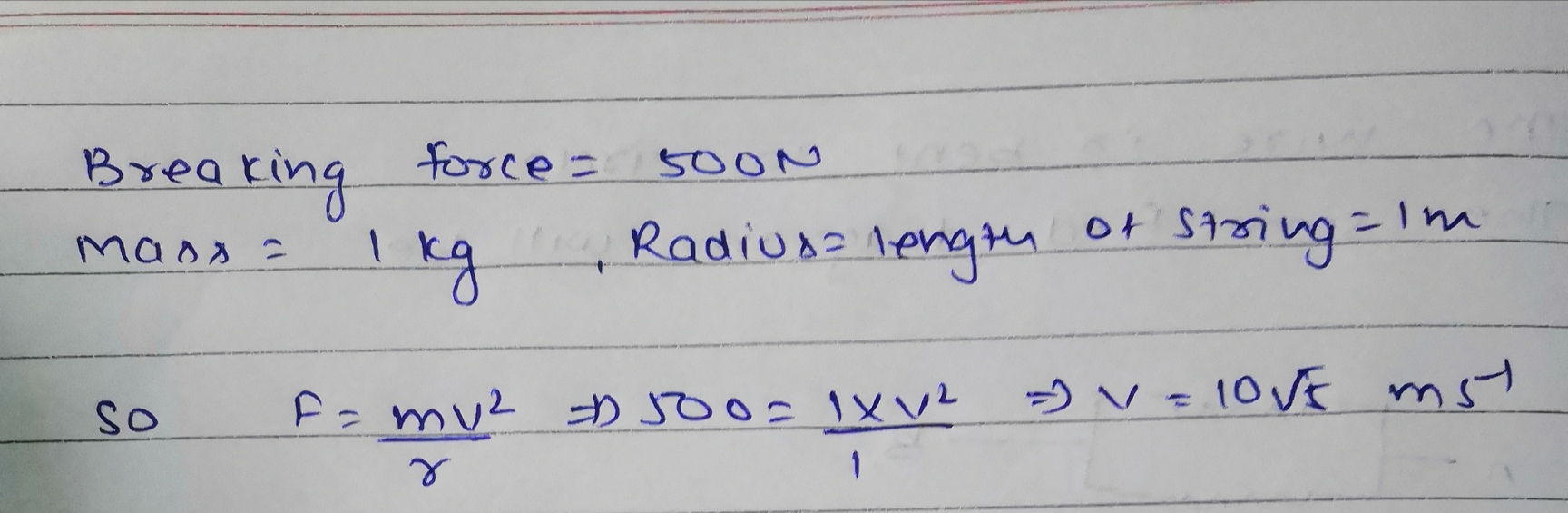Mechanical Properties Of Solids - Class 11 Medical Physics - Extra Questions
A rubber tube is longer when suspended vertically than when placed horizontally on a table. Explain?
Four identical hollow cylindrical columns of mild steel support a big structure of mass 50,000 kg. The inner and outer radii of each column are 30 and 60 cm respectively. Assuming the load distribution to be uniform, calculate the compressional strain of each column.
A uniform steel rod of $$5{ mm }^{ 2 }$$ cross section is heated from $$0^\circ C$$ to $$25^\circ C$$. Calculate the force which must be exerted to prevent it from expanding. Also calculate strain.
($$\alpha$$ for steel $$ =12\times { { 10 }^{ -6 } }/{^\circ C }$$ and $$\gamma$$ for steel $$ =20\times { 10 }^{ 10 }{ N }/{ { m }^{ 2 } }$$)
A steel wire of diameter $$1\times { 10 }^{ -3 }m$$ is stretched by a force of $$20N$$. Calculate the strain energy per unit volume. ($$Y$$ steel $$=2\times { 10 }^{ 11 }{ N }/{ { m }^{ 2 } }$$)
Find the increase in pressure required to decrease the volume of a water sample by $$0.01\%$$. Bulk modulus of water $$=2.1\times 10^9N m^{-2}$$.
A stone of mass $$1\ Kg$$ is attached to one end of a string of length $$1\ m$$ and breaking strength $$500\N$$, and is whirled in a horizontal circle on a frictionless table top. The other end of the string is kept fixed. Find the maximum speed the stone can attain, without breaking the string.
What is Plasticity?
The pressure at a point varies from $$99980\ Pa$$ to $$100020\ Pa$$, due to a simple harmonic sound wave. The amplitude and wavelength of the wave are $$5\times{10}^{-6 }m$$ and $$40\ cm$$, respectively. Find the bulk modulus of air.
A solid copper cube has an edge length of $$85.5$$ cm. How much stress must be applied to the cube to reduce the edge length to $$85.0$$ cm? The bulk modulus of copper is $$1.4 \times 10^{11} N/m^2$$
Compute the fractional change in volume of a glass slab , when subjected to hydraulic pressure of 10 atm .
A steel cable with a radius of 1.5 cm support a chair lift at a ski area . If the maximum stress is not exceed $$ 10 ^{8}N m^{2} $$ , What is the maximum load the cable can support ?
Compute the bulk modulus of water from the following data : Intial Volume = 100 . 0 liter .Pressure increase = 100.0 atm $$ \left ( 1 atm = 1.013 \times 10^{5} Pa \right ),$$ Final Volume = 1000.5 litre .Compare the bulk modulus of water with that of air (at constant temperature ) . Explain in simple terms why the ratio is so large .
A cube of side 3 cm Is subjected to shearing force .The toop of cube is sheared through 0.012 cm with respect to bottom face . If cube is made of a material of shear modulus $$ 2.1 \times 10^{10} Nm^{-2}$$ then find
Force applied .
A cube of 5 cm has its upper face displaced by 0.2 by a force of 8 N .Find Shear Modulus , Stress and Strain .
Column I
(order of magnitude in Pa)
A smooth uniform string of natural length $$l$$,cross-sectional area $$A$$ and Young's modulus $$Y$$ is pulled aling its length by a force $$F$$ on a horizontal surface. If the elastic potential energy stored in the string is $$U=\cfrac { { F }^{ 2 }l }{ xAY } $$. Find $$x$$.
A ball of mass 'm' drops from a height 'h' which sticks to mass-less hanger after striking. Neglect overturning, find out the maximum extension in the rod. Assuming rod is massless.

Find the depth of a lake at which density of water is 1% greater than at the surface. Given compressibility K = 50 x $$\displaystyle 10^{-6}$$ /atm
A load $$1$$ kg produces a certain extension in the wire of length $$3$$ m and radius $$5 \times 10^{-4}$$ m. How much will be the lateral strain produced in the wire? $$\left( { Y } = 7.48 \times 10 ^ { 10 } { N } / { m } ^ { 2 } \text { and } \sigma = 0.291 \right)$$
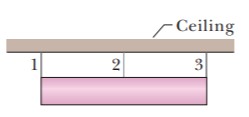
The figure shows a $$300$$ kg cylinder that is horizontal. Three steel wires support the cylinder from a ceiling. Wires 1 and 3 are attached at the ends of the cylinder, and wire 2 is attached at the center. The wires each have a cross-sectional area of $$2.00 \times 10^6 m^2$$. Initially (before the cylinder was put in place) wires 1 and 3 were $$2.0000$$ m long and wire 2 was $$6.00$$ mm longer than that. Now (with the cylinder in place) all three wires have been stretched. What are the tension in (a) wire 1 and (b) wire 2?
A rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) Of equal lengths as shown in Fig. The cross - sectional areas of wires A ad B are $$ 1.0 mm ^{2} $$ and $$2.0 mm^2$$ respectively . At what point along the rod should a mass m be suspended in order to produce. (a) equal stresses and (b) equal strain in both steel and aluminium wires.$$\gamma_{steel}=2×10^{11} Nm^{-2}$$ and $$\gamma_{aluminium}=7×10^{10}Nm^{-2}$$

Class 11 Medical Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work, Energy And Power Extra Questions