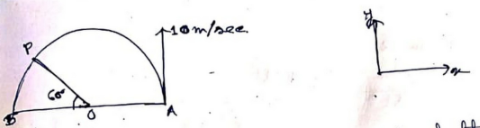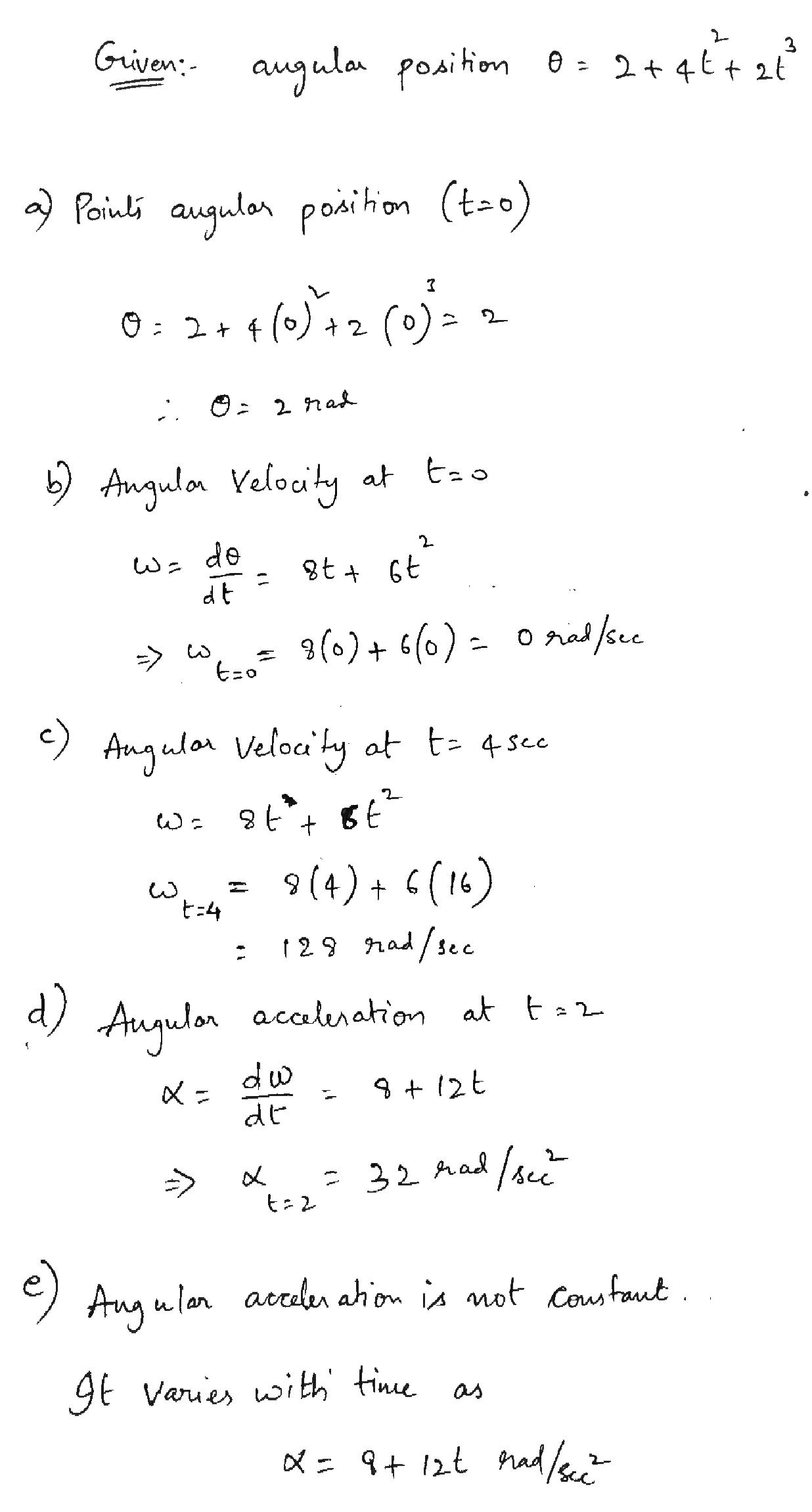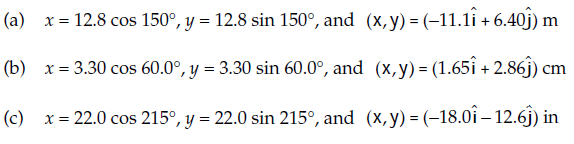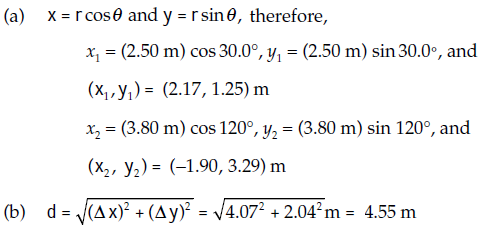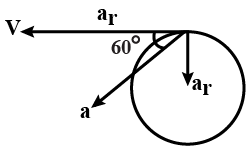Motion In A Plane - Class 11 Engineering Physics - Extra Questions
State whether 'speed' is a scalar or vector?
State whether 'Force' is a scalar or vector?
State whether 'Pressure' is a scalar or vector?
Define curvilinear motion.
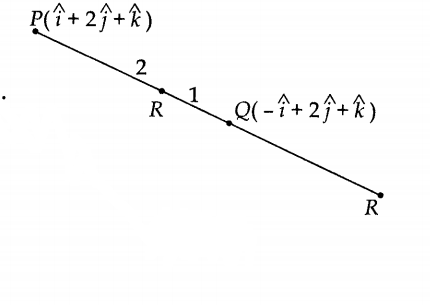
If $$\overline {p} = \hat {i} - 2\hat {j} + \hat {k}$$ and $$\overline {q} = \hat {i} + 4\hat {j} - 2\hat {k}$$ are position vectors of points $$P$$ and $$Q$$, find the position vector of the point $$R$$ which divides segment $$PQ$$ internally in the ratio $$2 : 1$$
Fill in the blanks.
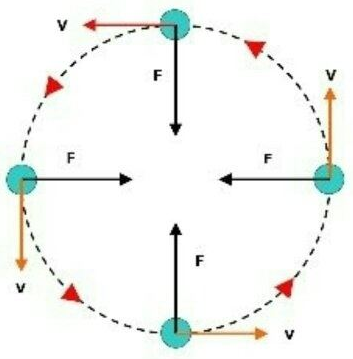
At any point in a circular motion the direction of linear velocity of the particle is _______.
At any point in a circular motion, the direction of the linear velocity of the particle is tangential to the circular path.
Find the magnitude of the vector which starts at the point $$2\hat { i } +\hat { j } -3\hat { k } $$ and ends at $$4\hat { i } -\hat { j } -\hat { k } $$.
What is a unit vector?
$$\textbf{Explanation:}$$
$$\bullet$$A vector is type of quantity that has both magnitude and direction.
$$\bullet$$Unit vector has word unit in it which means that its magnitude is 1. Because it has direction, it is also known as direction vector. Unit vectors are generally represented by symbol cap ‘^’.
What is the value of linear velocity. If $$\overrightarrow \omega= 3 \hat i + 4 \hat j + \hat k$$ and $$\overrightarrow r = 5 \hat i - 6 \hat j + 6 \hat k$$
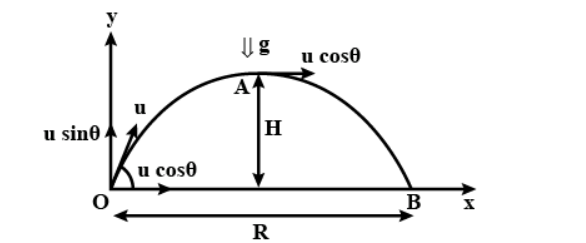
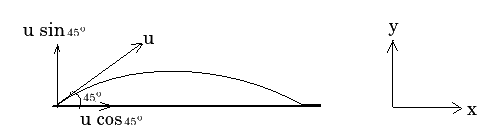
What is a projectile? Give example.
Find a unit vector in direction of $$\overset{\rightarrow}{A}=5\hat{i}+\hat{j}-2k$$
$$\hat{i}$$ and $$\hat{j}$$ are unit vectors along x- and y-axis respectively.
(a) What is the magnitude and direction of the vectors $$(\hat{i} + \hat{j})$$ and $$(\hat{i} - \hat{j})$$?
(b) What are the componets of a vector $$\overrightarrow{B} = 2\hat{i} + 3\hat{j}$$ along the direction of $$(\hat{i} + \hat{j}$$ and $$(\hat{i} - \hat{j})$$?
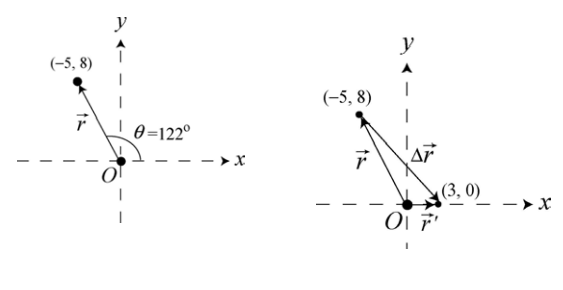
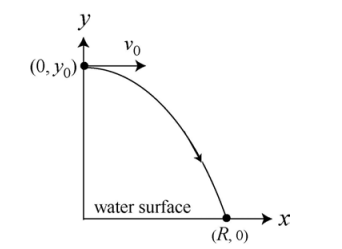
Locating position vector of a point object
Define scalar quantity.
If the position vector $$\overrightarrow a$$ of a point (12,n) is such that $$|\overrightarrow a |=13$$, find the value of n.
Which of the following is a scalar quantity?Mass, velocity, force, acceleration
Find the vector joining the points $$P(2,3,0)$$ and $$Q(-1,-2,-4)$$ directed from $$P$$ to $$Q$$.
A metal cylinder is melted and whole mass is cast in the shape of a cube. What happens to the density? Give reasons.
If the position vector of a point $$(-4, -3)$$ be $$ \vec{a}$$ , find $$\left | \vec{a} \right |.$$
If the position vector $$\overrightarrow a$$ of a point $$(12,n)$$ is such that $$|\overrightarrow a|=13$$, find the value of $$n$$.
Complete the following sentences and explain them .
When an object is in uniform circular motion , its ......changes at every point .
If the position vector of a point $$R$$ which divides the line segment joining points $$ P(\hat{i}+2\hat{j}+\hat{k}) $$ and $$ Q (-\hat{i}+\hat{j}+\hat{k}) $$ in the ratio $$2:1$$ internally is $$ -\dfrac{1}{3}\hat{i}+\dfrac{a}{3}\hat{j}+\hat{k} $$.
What is the value of $$a$$?
Angular momentum is
State whether speed is a scalar or a vector quantity. Give reason for your choice.
Classify the following quantities into Scalar and Vector quantities.
Distance, Displacement, Time, Speed, Velocity, Acceleration.
What is a projectile? Give an example.
Can the magnitude of a vector have a negative value? Explain
An object is suspended from the ceiling of a lift by means of a string. When the lift starts moving in the upward direction the string breaks and the object falls int the lift. Explain giving reasons.
Two solid bodies rotate about stationary mutually perpendicular intersecting axes with constant angular velocities $$\omega_1=3\:rad/s$$ and $$\omega_2=4\:rad/s$$. Find the angular velocity and angular acceleration of one body relative to the other.
Prove that the distance s metres, which a body falling from rest covers in time t seconds is 4.9 times the square of the time t.
A wheel rotating with uniform angular acceleration covers $$50$$ rev in the first five seconds after the start. If the angular acceleration at the end of five seconds is $$x\pi rad/s^2$$, find the value of $$x$$.
A wheel starting from rest is uniformly accelerated at $$ 4 rad/s^{2}$$ for $$10 s$$. It is allowed to rotate uniformly for the next $$10 s $$ and is finally brought to rest in the next $$10 s.$$ The total angle rotated by the wheel is $$\theta$$ (in rad). Find the value of $$\dfrac{\theta}{100}$$.
$$\omega = \alpha \times t = 4 \times 10 = 40 rad$$
$$ \theta =$$ Area under $$ \omega-t $$ graph ....(1)$$\displaystyle =\frac{1}{2} (10 \times40)+ (10 \times 40) + \dfrac{1}{2}(10 \times40)$$
$$=800 rad$$
$$=800 rad$$
A body rotates about a fixed axis with an angular acceleration $$1 rad/s^{2}$$. The angle (in radians), it rotates during the time in which its angular velocity increases from $$ 5 rad/s $$ to $$15 rad/s$$ is given by $$10^x$$. Then $$x$$ is :
A solid body rotates about a stationary axis according to the law $$\theta= 6t - 2t^{3}$$. Here $$\theta$$ is in radian
and $$t$$ in seconds.
Hint: If $$Y= y(t)$$, then mean/average value of $$y$$ between $$t_{1}$$, and $$t_{2}$$ is $$\displaystyle < Y > \frac{\int_{t_{1}}^{t_{2}}Y(t)dt}{t_{2}-t_{1}}$$. The angular acceleration at the moment when the body stops is $$-x \sqrt{3}$$. Find $$x$$.
Is it necessary to express all angles in radian only while using the equation $$\displaystyle \omega =\omega _{0}+\alpha t?$$Write '1' for YES and '2' for NO.
A wheel starting from rest is uniformly accelerated with $$\alpha = 2 rad/s ^{2}$$ for $$5 s.$$ It is then allowed to rotate uniformly for the next two seconds and is finally brought to rest in the next $$5 s.$$ Find the total angle rotated by the wheel in radians.
$$ \theta= $$ Area under $$ \omega t $$ graph
$$\displaystyle =\frac{1}{2} (12+2) (10) =70 rad$$
$$\displaystyle =\frac{1}{2} (12+2) (10) =70 rad$$
If the magnitude of its angular speed at $$t = 3.0s$$ is $$x rad/s$$, find $$2x$$.
A body rotating at $$20\ rad/s$$ is acted upon by a constant torque providing it a deceleration of $$2\ rad/s^{2}$$. At what time will the body have kinetic energy same as the initial value if the torque continues to act?
The angle rotated by the disc before stopping.
If it turns an angle of $$y\ rad$$ in these $$3 s$$, then $$2y$$ is equal to $$250 + x$$. Find $$x$$.
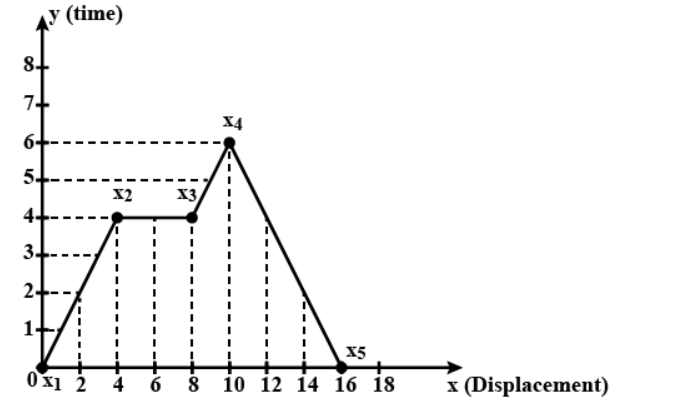
Using following data, draw time-displacement graph for a moving object.
| Time (s) | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| Displacement (m) | 0 | 2 | 4 | 4 | 4 | 6 | 4 | 2 | 0 |
$$\textbf{Step 1: Displacement Vs time graph [Refer Fig.]} $$
$$\textbf{Step 2: Average Velocity Calculation } $$
We know that the slope of the displacement time graph gives us the velocity.
For first four seconds
$$< V_1> = \dfrac{x_2-x_1}{t_2-t_1} = \dfrac{4-0}{4-0}\ m/s $$
$$< V_1>=1\,m/s$$
For next $$4$$ seconds
$$< V_2> = \dfrac{x_3-x_2}{t_3-t_2} = \dfrac{4-4}{8-4}\ m/s $$
$$< V_2>=0\,m/s$$
For last $$6$$ seconds
$$< V_3> = \dfrac{x_5-x_4}{t_5-t_4} = \dfrac{0-6}{16-10}\ m/s $$
$$< V_3>=-1\,m/s$$
Position vector (with respect to centre), velocity vector and acceleration vector of a particle in circular motion are $$\displaystyle \vec{r}= \left ( 3\hat{i}-4\hat{j} \right )m, \vec{v}= \left ( 4\hat{i}-a\hat{j} \right )ms^{-1}\:and\:\vec{a}= \left ( -6\hat{i}+b\hat{j} \right )ms^{-2}$$ respectively. Speed of particle is constant. Match the following two columns.
The velocity-time graph of a particle moving along X-axis is shown in figure. Match the entries of Column I with entries of Column II.
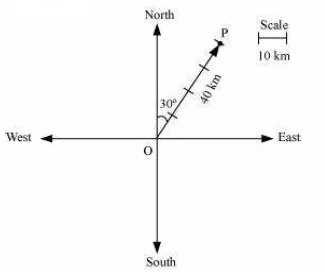
Represent graphically a displacement of $$40\ km$$, $$30^o$$ east of north.
Here, vector $$\vec {OP}$$ represents the displacement of $$40$$ km,$$ 30^o$$ East of North.
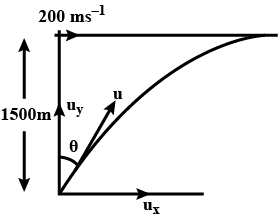
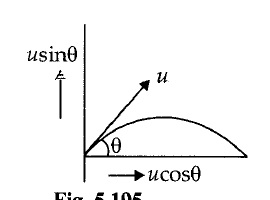
A fighter plane flying horizontally at an altitude of $$1.5\ km$$ with speed $$720\ km/h$$ passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed $$600\ ms^{-1}$$ to hit the plane ? At what minimum altitude should the pilot fly the plane to avoid being hit ? ($$Take\ g = 10\ ms^{-2}$$)
Height of the fighter plane $$= 1.5 km = 1500$$ m
Speed of the fighter plane, $$v = 720 km/h = 200$$ m/s
Let be the angle with the vertical so that the shell hits the plane. The situation is shown in the given figure.
Muzzle velocity of the gun, $$u = 600$$ m/s
Time taken by the shell to hit the plane $$= t$$
Horizontal distance travelled by the shell $$= u_xt$$
Distance travelled by the plane $$= vt$$
The shell hits the plane. Hence, these two distances must be equal.
$$u_xt = vt$$
$$u \ Sin\ \theta = v$$
$$Sin \ \theta = v / u$$
$$= 200 / 600 = 1/3 = 0.33$$
$$\theta= Sin^{-1}(0.33) = 19.50$$
In order to avoid being hit by the shell, the pilot must fly the plane at an altitude (H) higher than the maximum height achieved by the shell for any angle of launch.
$$H_{max} = u^2 sin^2 (90 - \theta)/2g = 600^2/(2 \times 10) = 16 km$$
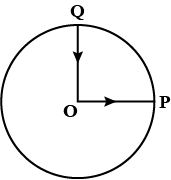
A cyclist starts from the center O of a circular park of radius 1 km, reaches the edge P of the park, then cycles along the circumference, and returns to the center along QO as shown in Fig. If the round trip takes 10 min, what is the
(a) Net displacement,(b) Average velocity, and
(c) The average speed of the cyclist?
Read each statement below carefully and state, with reasons and examples, if it is true or false :
A scalar quantity is one that ;
(a) is conserved in a process.(b) can never take
negative values
(c) must be dimensionless.
(d) does not vary from
one point to another in space.
(e) has the same value for observers with different orientations of axes.
A scalar quantity is one that ;
(b) can never take negative values
(c) must be dimensionless.
(d) does not vary from one point to another in space.
(e) has the same value for observers with different orientations of axes.Obtain equation of angular velocity as a function of time for rotating bodies with constant angular acceleration from the first principles.
The angular speed of a motor wheel is increased from $$1200\ rpm$$ to $$3120\ rpm$$ in $$16$$ seconds. $$(i)$$ What is its angular acceleration to be uniform? $$(ii)$$ How many revolutions does the engine make during this time?
Show that the area of the triangle contained between the vectors $$\textbf a$$ and $$\textbf b$$ is one half of the magnitude of $$\textbf{a} \times \textbf{b}$$.
Consider two vectors OK = vector $$|a| $$and OM = vector$$ |b|$$, inclined at an angle $$\theta$$ as shown in the following figure.
In $$\triangle OMN,$$ we can write the relation:
$$sin\theta=\dfrac{MN}{OM}=\dfrac{MN}{\left|\vec{b}\right|}$$
$$\implies MN=\left|\vec{b}\right| sin\theta$$
$$\left|\vec{a}\times \vec{b}\right|=\left|\vec{a}\right| \left| \vec{b}\right| sin\theta$$
$$=OK\times MN\\ =2\times \dfrac{1}{2}\times OK\times MN$$
$$=2\times $$ Area of $$\triangle OMK$$
$$\implies $$ Area of $$\triangle$$ $$OMK=\dfrac{1}{2}\times \left| \vec{a}\times \vec{b}\right|$$
Consider the diagram of the trajectory of a thrown tomato. At what point is the potential energy greatest?
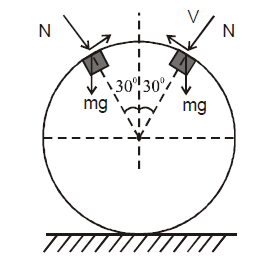
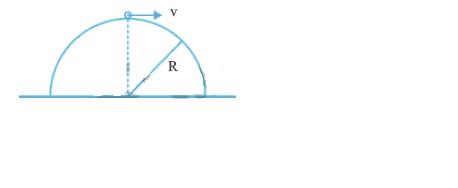
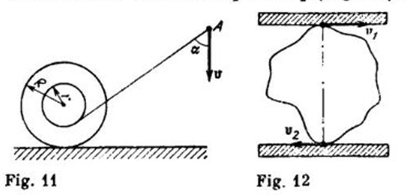
A small metal washer is placed on the top of a hemisphere of radius R. What minimum horizontal velocity should be imparted to the washer to detach it from the hemisphere at the initial point of motion?
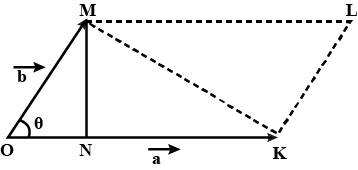
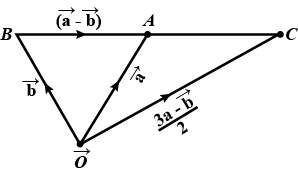
Show that the position vector of the point $$P$$, which divides the line joining the points $$A$$ and $$B$$ having position vector $$\overrightarrow{a}$$ and $$\overrightarrow{b}$$ internally in the ratio $$m : n$$ is $$\dfrac{m\overrightarrow{b}+n\overrightarrow{a}}{m+n}$$.
$$\vec { r } $$ divides $$\vec { a } ,\vec { b } $$ in ratio $$\lambda :1$$
$$\vec { PB } $$ is parallel to $$\vec { AP } $$
$$\vec { AP } =\lambda \vec { PB }
$$\vec { OP } -\vec { OA } =\lambda (\vec { OB } -\vec { OP } )$$
$$\vec { r } -\vec { a } =\lambda (\vec { b } -\vec { r } )$$
$$\vec { r } (\lambda +1)=\lambda \vec { b } +\vec { a } $$
$$\vec { r } =\dfrac { m\vec { b } +n\vec { a } }{ m+n } $$
What will be the $$\theta _{max}$$ for which the distance of particle from thrower always increases upto the end of path again at ground?
Two particles start moving from the same position on a circle of radius 20 cm with speed $$40\pi$$m/s and $$36\pi$$m/s respectively in the same direction. Find the time after which the particles will meet again.
The two graphs of a given projectile show that variation of vertical velocity component with time and with horizontal displacement. What is the x-compound of velocity in m/s?
Why is the motion of a body moving with a constant speed around a circular path said to be accelerated?
A particle starts at $$A$$ with initial speed $${v_0} = 10m/sec$$. It moves along a circular path under the action of a variable force which is always directed towards $$B.$$ $$A$$ and $$B$$ are end of a diameter. Find its speed (in m/sec) when it reaches $$P.$$
The potentila moves along a circular path
Therefore at any time $$t$$, the position coordinates of the potential may be expressed
as
$$\left. \begin{matrix} x=r\cos { wt } \\ y=r\sin { wt } \end{matrix} \right\} .....\left( 1 \right) $$
where $$(x,y)$$ is the coordinate of the potential with respect to enter at the origin to is the angular velocity
Now if the mass of the potential is $$m$$, the equation of motion is
$$m\dfrac {d^2x}{dx^2}=-F(t)....(2)$$
$$-F(t)$$ is the variable force directed towards $$B$$
and $$m\dfrac {d^2y}{dt^2}=0$$
mass no force is playing along $$y$$ direction Now From $$(1)$$
$$\left. \begin{matrix} \dfrac { dx }{ dt } =-wr\sin { wt } \\ \dfrac { { d }^{ 2 }x }{ { dt }^{ 2 } } =-{ w }^{ 2 }r\cos { wt } \end{matrix} \right\} .....\left( 4 \right) $$
$$\left. \begin{matrix} \dfrac { dy }{ dt } =-wr\cos { wt } \\ \dfrac { { d }^{ 2 }y }{ { dt }^{ 2 } } =-{ w }^{ 2 }r\sin { wt } \end{matrix} \right\} .....\left( 5 \right) $$
From $$(2)$$
$$\dfrac {d^2x}{st^2}=-\dfrac {F(t)}{m}$$
Comparing, $$(2)$$ and $$(4)$$, the simplest option is
$$\dfrac {F(t)}{m}=w^2 r\cos wt$$
$$\Rightarrow \ F(t)=mw^2 r \cos wt$$
Putting this from of $$F(t)$$
$$\dfrac {d^2r}{dt^2}=-w^2 r \cos wt$$
Velting
$$\dfrac {dr}{dt}=\displaystyle \int_0^t (d^2r/ dt^2)dt$$
$$=\displaystyle \int_0^t\dfrac {d}{dt} \left (\dfrac {dx}{dt}\right)dt$$
$$=\left [\dfrac {dx}{dt}\right]_0^t$$
$$-[wr\sin wt]_0^t$$
$$=-wr \sin \dfrac {2\pi}{3}.....(6)$$
$$\dfrac {dy}{dt}=[wr\cos wt]_0^t$$
$$=wr \cos \dfrac {2\pi}{3}-10....(7)$$
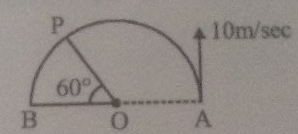
A ball is projected from the origin. The $$x$$ and $$y-$$ coordinates of its displacement are given by $$x=3t$$ and $$y=4t-{ 5t }^{ 2 }$$. Find the velocity of projection (in $${ m/s }$$)
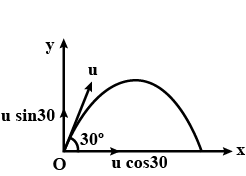
A body is projected with a velocity of 60 $${ ms }^{ -1 }$$ at 30$$^{o}$$ to horizontal.
| Column I | Column II | ||
| i. | Initial velocity vector | a. | $$60 \sqrt{3} \hat{i} + 40 \hat{j}$$ |
| ii. | Velocity after 3 s | b. | $$30 \sqrt{3}\hat{i} + 10 \hat{j}$$ |
| iii. | Displacement after 2 s | c. | $$30 \sqrt{3} \hat{i} + 30 \hat{j}$$ |
| iv. | Velocity after 2 s | d. | $$30 \sqrt{3} \hat{i}$$ |
$$\textbf{Step 1: Initial velocity vector[Refer Fig.]}$$
$$\vec {u} = u_{x}\hat {i} + u_{y} \hat {j}$$
$$= (u\cos 30^o)\hat {i} + (u \sin 30^o)\hat {j}$$
$$= (60 \cos 30^o) \hat {i} + (60 \sin 30^o)\hat {j}$$
$$\boxed{\vec {u} = (30\sqrt {3})\hat {i} + (30)\hat {j} \ m/s}\rightarrow $$Option (c)
$$\textbf{Step 2: Velocity after t= 3 s}$$
In $$x$$ direction $$u_{x} = 30\sqrt {3} m/s$$
Velocity in x-direction will not change as there is no acceleration in $$x$$ direction, therefore $$v_x=u_{x}$$
In $$y$$ direction $$a_{y} = -10\ m/s^{2}\ ; t = 3s$$; $$u_{y} = 30\ m/s$$
Since acceleration is constant, therefore applying equation of motion
$$v_{y} = u_{y} + at$$
$$\Rightarrow$$ $$v_{y} = 30 - 10\times 3\ m/s = 0\ m/s$$
$$\boxed{V = 30\sqrt {3} \hat {i} \ m/s}\rightarrow $$Option (d)
$$\textbf{Step 3: Displacement after t= 2 s}$$
In x direction: $$a_x=0$$
$$s_{x} = u_{x}t+ \dfrac{1}{2}a_xt^2 = 30\sqrt {3} \times 2\hat {i}+0$$ $$ = 60\sqrt {3} \hat {i} \ m$$
In $$y$$ direction applying equation of motion
$$s_{y} = u_{y}t + \dfrac {1}{2}a_{y} t^{2}$$ $$= 30\times 2 - \dfrac {1}{2} (10) (2)^{2}$$
$$s_{y} = 40 \hat {j} \ m$$
$$\therefore$$ $$\boxed{s = (60\sqrt {3} \hat {i} + 40\hat {j})m}\rightarrow$$Option (a)
$$\textbf{Step 4: Velocity after 2s }$$
In $$y$$ direction applying equation of motion as the acceleration is constant.
$$v_{y} = u_{y} + a_{y}t$$ $$= 30 - 10\times 2\ m/s$$
$$= 10\ m/s$$
$$\therefore$$ $$\boxed{v = (30\sqrt {3} \hat {i} + 10\hat {j}) m/s}\rightarrow$$Option (b)
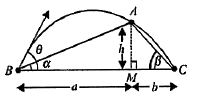
A particle is projected over a triangle from one extremity of its horizontal base. Grazing over the vertex, it falls on the other extremity of the base. If $$a$$ and $$b$$ are the base angles of the triangle and $$\theta$$ the angle of projection, prove that $$tan\,\theta = tan\,\alpha+\tan\,\beta$$
Let $$ABC$$ be the triangle with base $$BC$$. Let $$h$$ be the height of the vertex $$A$$ above $$BC$$. If $$AM$$ is the perpendicular drawn on base $$BC$$ from vertex $$A$$, then $$tan \,\alpha = h/a$$ and $$tan\, \beta = h/b$$, where $$BM =a$$ and $$CM = b$$.
Since $$A (a, h)$$ lies on the trajectory of the projectile,
$$\displaystyle y = x\,tan \theta \left ( 1- \frac{x}{R} \right )$$ ..(i)
Therefore, it should satisfy (i) i.e.,
$$\displaystyle h =a\,tan \theta \left ( 1- \frac{a}{a+b}\right )$$
[$$\therefore$$ Range, $$R = a + b$$]
$$\displaystyle \frac{h}{a} =tan \theta \left [ \frac{b}{a+b} \right ]$$
$$\displaystyle \Rightarrow tan \theta = \frac{h}{a} + \frac {h}{b} \,\,\,\,\, = tan \alpha + tan \beta$$
Hence, proved.
Since $$A (a, h)$$ lies on the trajectory of the projectile,
$$\displaystyle y = x\,tan \theta \left ( 1- \frac{x}{R} \right )$$ ..(i)
Therefore, it should satisfy (i) i.e.,
$$\displaystyle h =a\,tan \theta \left ( 1- \frac{a}{a+b}\right )$$
[$$\therefore$$ Range, $$R = a + b$$]
$$\displaystyle \frac{h}{a} =tan \theta \left [ \frac{b}{a+b} \right ]$$
$$\displaystyle \Rightarrow tan \theta = \frac{h}{a} + \frac {h}{b} \,\,\,\,\, = tan \alpha + tan \beta$$
Hence, proved.
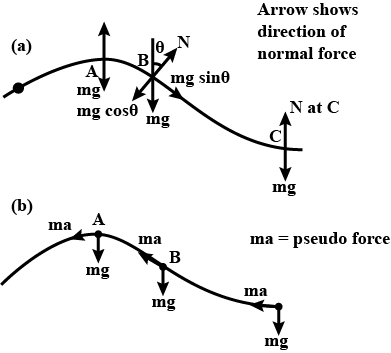
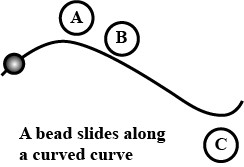
A bead slide freely along a curve wire lying on a horizontal surface at constant speed as shown in Fig.
a. Draw the vectors representing the force exerted by the wire on the bead at points A, B and C.
b. Suppose the bead in fig. speeds up with constant tangential acceleration as it moves towards the right. Draw the vectors representing the force on the bead at point A, B, and C.
a. R.E.F image
Arrow shown direction of Normal force
b. R.E.F image
ma = parallels force
A particle is projected train a point on the level ground and its height is $$h$$ when at horizontal distances $$a$$ and $$2a$$ from its point of projection. Find the velocity of projection.
A body is projected from the bottom of a smooth inclined plane with a velocity of 20 $$ms^{-1}$$. If it is just sufficient to carry it to the top in 4 s, find the inclination and height of the plane.
Time taken to reach top$$=4sec$$
Let inclination of plane $$\theta$$ and length $$h$$ We know $$v=u+at$$
Final velocity, $$v=0,t=4sec,a=-mg\sin\theta\\mg\sin\theta=\cfrac{2}{4}\Rightarrow mg\sin\theta=5...(i)$$
Also, $$s=ut+\cfrac{1}{2}at^2\\h=20\times4-\cfrac{1}{2}mg\sin\theta(4)^2\\h=80-8\sin\theta mg\\mg\sin\theta=5[using equation(i)]\\h=80-8\times5\\h=40m$$
By conservation of energy,
Gain in potential energy$$=loss in K.E\\mgh_1=\cfrac{1}{2}mv^2\\h_1=h\sin\theta\\m\times10\times40\sin\theta=\cfrac{1}{2}m(20)^2\\ \sin\theta=\cfrac{400}{2\times40\times10}\\ \sin\theta=\cfrac{1}{2}\\ \theta=30$$
A small sphere of mass $$m = 1 kg$$ is moving with a velocity $$(4\hat{i} - \hat{j})m/s$$. It hits fixed smooth wall and rebounds with velocity $$(\hat{i} + 3\hat{j})m/s$$. The coefficient of restitution between the sphere and the wall is $$n/16$$. Find the value of $$n$$.
A particle moves in a semicircular path of radius R from O to A as shown in the Fig. Then it moves parallel to z-axis covering a distance R upto B. Finally it moves along BC parallel to y-axis through a distance 2R. Find the ratio of D/s.
The distance D, that is the length of the actual path covered by the particle(0A'ABC) as shown in Fig.
D = length of the semicircle OA'A + length AB + length BC. This gives D = $$\pi$$R + R +
2R = ($$\pi$$ + 3)R.
Since OA = 2R,AB = R, and BC = 2R, the coordinates of C can be given as C = (2R, R,2R). Then the position of C is expressed as:
$$\vec{r}_c$$ = 2R$$\hat{i}$$ + R$$\hat{j}$$ + 2R$$\hat{k}$$
As $$\vec{s}$$(=$$\vec{OC}$$) = $$\vec{r}_c$$ - $$\vec{r}_0$$, substituting $$\vec{r}_c$$ and $$\vec{r}_0$$ = 0$$\hat{i}$$ +0$$\hat{j}$$ +0$$\hat{k}$$,
we obtain $$\vec{s}$$ = (2$$\hat{i}$$ + $$\hat{j}$$ + 2$$\hat{k}$$)R.
Its magnitude |$$\vec{s}$$| = ($$\sqrt{2^1 + 1^2 + 2^2}$$R = 3R
Hence, $$\dfrac{D}{s}$$ = $$\dfrac{(\pi + 3)R}{3R}$$ = $$\dfrac{\pi + 3}{3}$$
D = length of the semicircle OA'A + length AB + length BC. This gives D = $$\pi$$R + R +
2R = ($$\pi$$ + 3)R.
Since OA = 2R,AB = R, and BC = 2R, the coordinates of C can be given as C = (2R, R,2R). Then the position of C is expressed as:
$$\vec{r}_c$$ = 2R$$\hat{i}$$ + R$$\hat{j}$$ + 2R$$\hat{k}$$
As $$\vec{s}$$(=$$\vec{OC}$$) = $$\vec{r}_c$$ - $$\vec{r}_0$$, substituting $$\vec{r}_c$$ and $$\vec{r}_0$$ = 0$$\hat{i}$$ +0$$\hat{j}$$ +0$$\hat{k}$$,
we obtain $$\vec{s}$$ = (2$$\hat{i}$$ + $$\hat{j}$$ + 2$$\hat{k}$$)R.
Its magnitude |$$\vec{s}$$| = ($$\sqrt{2^1 + 1^2 + 2^2}$$R = 3R
Hence, $$\dfrac{D}{s}$$ = $$\dfrac{(\pi + 3)R}{3R}$$ = $$\dfrac{\pi + 3}{3}$$
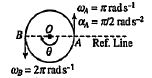
Two particles $$A$$ and $$B$$ move on a circle. Initially particles $$A$$ and $$B$$ are diagonally opposite to each other. Particle $$A$$ moves with angular velocity $$\pi\,rad\,s^{-1}$$ and angular acceleration $$\pi /2\,rad\,s^{-2}$$ and particle B move with constant angular velocity $$2 \pi\,rad\,s^{-2}$$. Find the time after which both the particles $$A$$ and $$B$$ will collide.
Suppose the angle between $$OA$$ and $$OB$$ = $$\theta$$. Then the rate of change of $$\theta$$,
$$\theta =\omega_B - \omega_A = 2\pi - \pi =\pi\,rad\,s^{-2}$$
$$\theta =\omega_B - \omega_A = 2\pi - \pi =\pi\,rad\,s^{-2}$$
$$\theta =\alpha_B-\alpha_A=-\dfrac{\pi}{2}rad\,s^{-2}$$
If the angular displacement is $$\Delta \theta$$, then
$$\displaystyle \Delta \theta = \dot { \theta} t+\dfrac{1}{2} \ddot { \theta} t^2$$
For $$A$$ and $$B$$ to collide angular displacement, $$\Delta \theta = \pi$$.
$$\displaystyle \Rightarrow \,\,\,\pi = \pi t +\dfrac{1}{2} \left ( \dfrac{-\pi}{2} \right ) t^2 \,\,\Rightarrow\,t^2 -4t + 4 = 0\,\Rightarrow\,t=2\,s$$
$$\displaystyle \Delta \theta = \dot { \theta} t+\dfrac{1}{2} \ddot { \theta} t^2$$
For $$A$$ and $$B$$ to collide angular displacement, $$\Delta \theta = \pi$$.
$$\displaystyle \Rightarrow \,\,\,\pi = \pi t +\dfrac{1}{2} \left ( \dfrac{-\pi}{2} \right ) t^2 \,\,\Rightarrow\,t^2 -4t + 4 = 0\,\Rightarrow\,t=2\,s$$
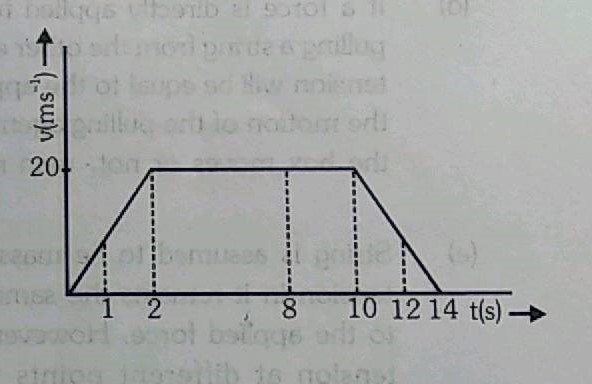
A person of mass M kg is standing on a lift. If the lift moves vertically upwards according to given v-t graph then find out the weight of the man at the following instants :(g=10m/$$s^2$$)
(i) t = 1 second
(ii) t= 8 seconds
(iii) t= 12 seconds
An object of mass 2 kg attached to a wire of length 5 m is revolved in a horizontal circle. If it makes 60 r.p.m. final its
(a) Angular speed
(b) Linear speed
(c) Centripetal acceleration
(d) Centripetal force.
What is a projectile? Derive an equation of the path of a projectile
The angular displacement of an object having uniform circular motion is $$\frac { \pi }{ 4 } $$ rad in every 3 s.Find the frequency of revolution.
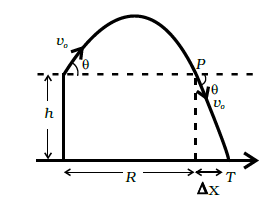
A stone is thrown from a bridge at an angle of $${30}^{o}$$ down with the horizontal with a velocity of $$25\ m/s$$. If the stone strikes the water after $$2.5$$ seconds, then calculate the height of the bridge from the water surface. $$(g=9.8\ {m/s}^{2})$$
A particle of mass $$5g$$ is moving in a circle of radius $$0.5m$$ with an angular velocity of $$6rad/s$$. Find (i) the change in linear momentum in half a revolution (ii) the magnitude of the acceleration of the particle.
A rod rotating with uniform angular $$\omega=3.5\ rad/s$$ is found at angular positive: $$\theta=-6.4\ rad$$ when $$t=3$$ seconds. With is its angular when $$t=12$$ seconds?
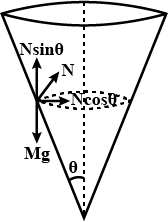
A particle describe a horizontal circle on the smooth inner surface of a conical funnel. The height of the circle above the vertex is $$9.8$$cm. Find the speed of the particle (Take $$g=9.8ms^2$$)
Since mg is in the downward direction so the gravitational force and $$nsin \theta$$ is the balance that force
$$Nsin \theta=mg........1$$
$$Ncos \theta=\dfrac{mv^2}{R}...................2$$ R is the radius of the circle.
Dividing equation 1 and 2 then we get,
$$\dfrac{Nsin \theta}{N cos \theta}=tan \theta=\dfrac{gE}{v^2}$$
$$tan \theta=\dfrac{R}{h}=\dfrac{gR}{v^2}$$ Where h is the height of the plane from the vertex,
$$v^2=gh\Rightarrow v=\sqrt{gh}=\sqrt{0.098\times9.8}=0.98m/s$$
Derive the equation of time taken by a ball, when it is thrown at a angle $$\Theta$$ with the horizontal.
Time of flight:
The time taken in whole projectile motion is known as time of flight.
Let Time of flight= T
applying $$\frac{{{v_t} - {v_i}}}{t} = a$$ in vertical direction
= $$\frac{{v\sin \theta - \left( { - v\sin \theta } \right)}}{t} = g$$ ( taken downward +ve)
$$\therefore T = \frac{{2v\sin \theta }}{g}$$
The time taken in whole projectile motion is known as time of flight.
Let Time of flight= T
applying $$\frac{{{v_t} - {v_i}}}{t} = a$$ in vertical direction
= $$\frac{{v\sin \theta - \left( { - v\sin \theta } \right)}}{t} = g$$ ( taken downward +ve)
$$\therefore T = \frac{{2v\sin \theta }}{g}$$
A bicycle wheel starts at rest and has a constant angular acceleration $$\alpha$$.At time $$t$$ ,it has roated through an angle $$\theta $$ and has an angular velocity $$\omega$$.What are $$\omega$$ and $$\alpha$$ in term of $$\theta $$ and $$t$$
What is a projectile? Derive an equation of the path of a projectile.
$$x = x\cos \,\theta t$$
$$t = \frac{x}{{x\cos \theta }}\, \cdots \left( i \right)$$
or, $$y = x\sin \theta t - \frac{1}{2}g{t^2}$$
or, $$y = x\sin \theta \frac{x}{{\cos \theta }} - \frac{1}{2}g{\left( {\frac{x}{{x\cos \theta }}} \right)^2}$$
or, $$y = x\tan \theta - \frac{1}{2}g\frac{{{x^2}}}{{{x^2}{{\cos }^2}\theta }}$$
or, $$y = x\tan \theta - \frac{g}{{2{x^2}{{\cos }^2}\theta }}.{x^2}$$
Equation of projectile.
$$t = \frac{x}{{x\cos \theta }}\, \cdots \left( i \right)$$
or, $$y = x\sin \theta t - \frac{1}{2}g{t^2}$$
or, $$y = x\sin \theta \frac{x}{{\cos \theta }} - \frac{1}{2}g{\left( {\frac{x}{{x\cos \theta }}} \right)^2}$$
or, $$y = x\tan \theta - \frac{1}{2}g\frac{{{x^2}}}{{{x^2}{{\cos }^2}\theta }}$$
or, $$y = x\tan \theta - \frac{g}{{2{x^2}{{\cos }^2}\theta }}.{x^2}$$
Equation of projectile.
Which force is required to maintain a body in uniform circular motion?
Can a vector have zero component along a line and still have nonzero magnitude?
Express the magnitude of $$\vec{a} \times \vec{b}$$ in terms of scalar products.
A particle is travelling in a circular path of radius $$4\ m$$. At certain instant the particle is moving at $$20\ m/s$$ and its acceleration is at an angle of $${37}^{o}$$ from the direction to the centre of the circle as seen from the particle.
(i) At what rate is the speed of the particle increasing?
(ii) What is the magnitude of the acceleration?
Find vector of magnitude $$9$$ equality inclined to the coordinate axes ?
To how much angel does the earth revolve around sun in 2 days?
A man projects a coin upwards from the gate of a uniform moving train. The path of coin for the man will be
Prove that the vectors $$2\hat{i} - 3\hat{j} - \hat{k}$$ and $$-6\hat{i} + 9\hat{j} + 3\hat{k}$$ are parallel.
Define following :
Position vector
The position of an object moving along x-axis is given by x = $$a + bt^2$$ where a = 8.5 m, b = 2.5 $$ms^{-2}$$ and t is measured in seconds. What is its velocity at t = 0 s and t = 2.0 s.?
The position vectors of the points $$A, B, C$$ and $$D$$ are $$3\hat {i} - 2\hat {j} - \hat {k}, 2\hat {i} + 3\hat {j} - 4\hat {k}, -\hat {i} + \hat {j} + 2\hat {k}$$ and $$4\hat {i} + 5\hat {j} + \lambda \hat {k}$$ respectively. If the points $$A, B, C$$ and $$D$$ lie on a plane, find the value of $$\lambda$$.
Give example where (a) the velocity of a particle is zero but its acceleration is not zero, (b) the velocity is opposite in direction to the acceleration, (c) the velocity is perpendicular to the acceleration.
Show that the path of a projectile is a parabola
Let a body is projected with speed $$u m/s$$ inclined $$\theta $$ with horizontal line$$.$$
Then$$,$$ vertical component of $$u,$$ $${u_y} = u\cos \theta $$
Horizontal component of $${u_x} = u\sin \theta $$
acceleration on horizontal$$,$$ $$ax=0$$
acceleration on vertical$$,$$ $$ay=-g$$
Now$$,$$ use formula
$$X = {u_x}t$$
$$X = u\cos \theta .t$$
$$t = X/u\cos \theta $$--------------------------$$(1)$$
Again$$,$$ $$y = {u_y}t + 1/2{a_y}{t^2}$$
$$y = u\sin \theta t - 1/2g{t^2}$$
put equation $$(1)$$ here$$,$$
$$y = u\sin \theta \times x/u\cos \theta - 1/2g{t^2} \times {x^2}/{u^2}{\cos ^2}\theta $$
$$ = \tan \theta x - 1/2g{x^2}/{u^2}{\cos ^2}$$
$$y = \tan \theta .x - 1/2g{x^2}/{u^2}{\cos ^2}\theta $$
this equation is similar to standard equation of parabola $$y = a{x^2} + bx + c$$ her$$,$$ $$a,b$$and $$c$$ are constant
So$$,$$ A projectile motion is parabolic motion$$.$$
A particle rotates along a circle of radius $$ R = \sqrt { 2 } $$ m with an angular acceleration $$ \alpha=\dfrac { \pi }{ 4 } rad/s^2 $$ starting from rest. Calculate the magnitude of average velocity of the particle over the time it rotates a quarter circle.
$$\textbf{Step 1: Time required to cover quarter circle (t)}$$ $$\textbf{[Refer Fig.]}$$
Suppose the particle goes from A to B as shown in the figure.
Angular displacement, $$\theta=\dfrac{\pi}{2}$$
Initial angular speed, $$\omega_o=0$$
Since Angular acceleration $$(\alpha)$$ is constant
$$\therefore$$ Applying equation of motion in rotation
$$\theta=\omega_o t+\dfrac{1}{2}\propto t^2$$
$$\Rightarrow\ \ \dfrac{\pi}{2}=0+\dfrac{1}{2}\,\dfrac{\pi}{4}t^2$$
$$\Rightarrow\ \ t=2s$$
$$\textbf{Step 2: Average velocity calculation }$$
$$|\vec{V_{avg}}|=\dfrac{\text{Displacement}}{\text{time}}$$
From figure, Displacement(shortest distance between A and B) $$=\sqrt{R^2+R^2}$$ $$=\sqrt{2}R$$
$$\Rightarrow\ \ |\vec{V_{avg}}|=\dfrac{\sqrt{2}R}{2\ s}=\dfrac{\sqrt{2}\sqrt{2}}{2}\,m/s$$$$=1\,m/s$$
Hence the magnitude of average velocity of the particle over the time it rotates a quarter circle is $$1\,m/s$$.
A particle thrown vertically up from the ground,returns to the ground level. show the nature of its position- time and velocity-time graphs.
When a body is thrown vertically upward, after some time the
particle reaches a maximum point and then begins to fall. Then from the above
figure, x is the displacement of particle. AB shows the displacement as the
body goes up and BC shows the variation when the body comes down after reaching
a maximum value. Figure (1)
Let v-t graph shows the variation of velocity with time. Figure (2)
A body is projected horizontally from the top of a cliff with a velocity of $$10m/s$$. What time elapses before the horizontal and vertical velocities become equal? $$g = 10m/{s^2}.\left( {1s} \right)$$
A rotating wheel has a speed of $$1200$$ rpm and the it is made to slow down at a constant rate at $$2rad/s^2$$.The number of revolution it makes before coming to rest will be:
Find a unit vector perpendicular to the vectors $$\vec{A}=4\hat{i}-\hat{j}+3\hat{k}$$ and $$\vec{B}=-2\hat{i}+\hat{j}-2\hat{k}$$.
A wheel starting from rest is uniformly accelerated at $$ 4\ rad/s^2 $$ for 10 seconds. It is allowed to rotate uniformly for the next 10 seconds and is finally brought to rest in the next 10 seconds. Find the total angle rotated by the wheel.
Initial angular velocity, $${{\omega }_{o}}=0$$
Displacement in first 10 sec
$${{\theta }_{1}}={{\omega }_{0}}{{t}_{1}}+\dfrac{1}{2}{{\alpha }_{1}}t_{1}^{2}=0+\dfrac{1}{2}\times 4\times {{10}^{2}}=200\,rad$$
Angular velocity after 10 sec
$$ {{\omega }_{1}}={{\omega }_{o}}+{{\alpha }_{1}}{{t}_{2}} $$
$$ {{\omega }_{1}}=0+4\times 10=40\,rad{{s}^{-1}} $$
Displacement in next 10 sec
$${{\theta }_{2}}={{\omega }_{1}}t=40\times 10=400\,rad$$
Deceleration in later 10 sec
$$ {{\omega }_{2}}={{\omega }_{1}}+{{\alpha }_{2}}{{t}_{3}} $$
$$ {{\alpha }_{2}}=\dfrac{{{\omega }_{2}}-{{\omega }_{1}}}{{{t}_{3}}}=\dfrac{0-40}{10}=-4\,rad{{s}^{-1}} $$
Displacement in later 10 sec
$$ {{\theta }_{2}}={{\omega }_{1}}{{t}_{3}}+\dfrac{1}{2}{{\alpha }_{2}}{{t}_{3}} $$
$$ {{\theta }_{2}}=40\times 10+\dfrac{1}{2}\times \left( -4 \right)\times 10 $$
$$ {{\theta }_{3}}=200\,rad $$
Total angular displacement, $${{\theta }_{total}}={{\theta }_{1}}+{{\theta }_{2}}+{{\theta }_{3}}=200+400+200=800\,rad$$
Hence, total angular displacement is $$800\,rad$$
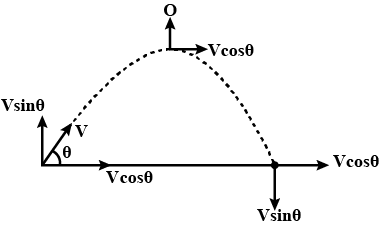
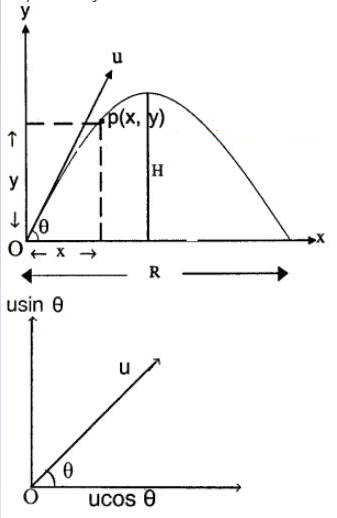
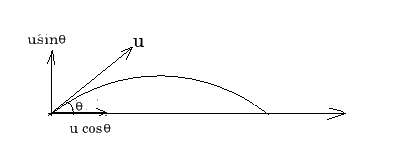
A projectile is thrown at an angle $$ \theta $$ from the horizontal with velocity 'u' under the gravitation field of the earth. Derive expressions for its:a)Time of its flightb)Heightc)Horizontal Range
$$\textbf{Step 1: Time of flight calculation [Refer Fig.]}$$
For calculation of time of flight, we always apply equations of motion in vertical direction.
Since vertical acceleration $$g$$ is constant, therefore applying equation of motion in $$y$$ direction
Motion from O to B:
$$S_{y} =$$ Total displacement in $$y = 0$$; $$u_{y} = u\sin \theta; \ a_{y} = -g$$
$$S_{y} = u_{y}t + \dfrac {1}{2} a_{y} t^{2}$$
$$\Rightarrow$$ $$0 = u\sin \theta \ t - \dfrac {1}{2} gt^{2}$$
$$\Rightarrow$$ $$t = \dfrac {2u\sin \theta}{g}$$
$$\textbf{Step 2: Horizontal range in x direction}$$
$$u_{x} = u\cos \theta; a_{x} = 0; s_{x} = R$$
Since acceleration is zero in $$x$$ direction
So, $$S_{x} = u_{x}t $$
$$\Rightarrow$$ $$R = u\cos \theta\times \dfrac {2u\sin \theta}{g}$$
$$\Rightarrow$$ $$R = \dfrac {u^{2} \sin 2\theta}{g}$$
$$\textbf{Step 3: Maximum height}$$
From Figure, at maximum height only horizontal component of velocity is present, vertical component becomes zero,
So, Applying $$eq^{n}$$ of motion in $$y$$ direction between $$OA$$
$$u_{y} = u\sin \theta; v_{y} = 0, a_{y} = -g$$, $$s_{y} = H$$
$$v_{y}^{2} - u_{y}^{2} = 2a_{y} s_{y}$$
$$\Rightarrow$$ $$0^{2} - (u\sin \theta)^{2} = -2gH$$
$$\Rightarrow$$ $$H = \dfrac {u^{2}\sin^{2}\theta}{2g}$$
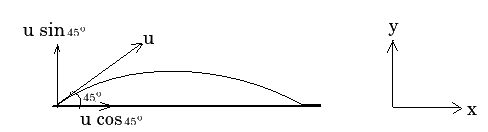
Find the velocity of a projectile at the highest point, if it is projected with a speed $$15$$ m $$s^{-1}$$, in the direction $$45^o$$ above horizontal. [take $$g=10 m s^{-2}$$]
The speed of a motor increases from $$600 \,rpm$$ to $$1200 \,rpm$$ in $$20 \,sec$$. What is its angular acceleration and how many evolution does it make during this time.
If the image formed by a lens for all positions of an object placed in front it is always erect and diminished What is the nature of this lens? Draw a ray diagram to justify your answer. If the numerical value of the power of this lens of 10 D, What is its focal length in the Cartesian system ?
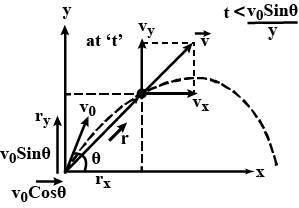
A small particle of mass $$m$$ is projected at an angle $$\theta $$ with the $$x-axis$$ with an initial velocity $${v_0}$$ in the $$x-y$$ plane shown in the figure . At a time $$t < \frac{{{v_0}\sin \theta }}{g},$$ the angular momentum of the particle is
at time $$t=\dfrac {v_0 sin \theta }{g}$$
$$v_y= v_0 sin \theta -g\left ( \dfrac {v_0 sin \theta }{g} \right )$$
$$\Rightarrow v_y=0$$
So,
at $$t= \dfrac {v_0 sin \theta }{g}$$, the particle will be at maximum height
So,
for time $$t < \dfrac {v_0 sin \theta }{g}$$
$$v_y = v_0 sin \theta -gt$$
$$v_x = v_0 cos \theta $$
$$\Rightarrow \vec{v}=v_x \hat{i}+ v_y\hat{j}$$
$$ \vec{v} =v_o cos \theta \hat{i} + (v_0 sin \theta - gt)\hat{j} $$
And,
$$ r_x = v cos \theta t$$
and $$r_y = v sin \theta -\dfrac {1}{2}gt^2$$
$$\Rightarrow \vec{r}= r_x \hat{i}+r_y\hat{j}$$
$$\vec{r}= v cos t \hat{i}+(v sin \theta -\dfrac {1}{2} gt^2)\hat{k}$$
Now, we know that angular momentm $$(\vec{L})$$
$$\vec{L} = \vec{P} \times \vec{r}$$
$$ \vec{L} =m \vec{v}\times \vec{r}$$
$$ = m (v_x \hat{i}+v_y\hat{j})\times (v_x\hat{i}\times r_y\hat{j})$$
$$= m [v_xr_y\hat{k}-v_yr_x\hat{k}]$$
$$\Rightarrow \vec{L}= m (v_x\times r_y-v_y r_x)\hat{k}$$
$$= m [v_0 cos \theta (v sin \theta -\dfrac {1}{2}gt^2)-(v_0 sin \theta -gt)v_0 cos \theta t]\hat{k}$$
$$= m [ v_0^2 cos \theta -\dfrac {v_0 cos \theta gt^2}{2}-v^2 sin \theta cos \theta + v_0 cos \theta gt^2]\hat{k}$$
$$\Rightarrow \vec{L}= m [v_0 cos \theta gt^2 -\frac {1}{2}v_0 cos \theta gt^2]\hat{k}$$
$$\Rightarrow \vec{L} =\dfrac {1}{2}m v_0 cos \theta gt^2 \hat{k}$$
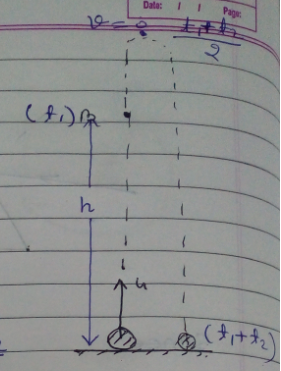
A particle is projected vertically upwards from a point A on the ground$$.$$ it makes time $${t_1}$$ to reach a point B$$,$$ but it still continues to move up $$.$$ If it takes further time $${t_2}$$ to reach the ground from point B$$.$$ Then height of point B from the ground is$$:$$
Hint:- Use equation of motion to calculate required height.
Step 1: Note the given values.
Let the height of point B be 'h' and initial velocity of particle be 'u'.
Total time of light $$=t_1+t_2$$
So, time to reach at maximum height $$=\dfrac{t_1+t_2}{2}$$
Step 2: Applying I equation of motion
$$v=u+at$$
$$0=u+(-g)\left[\dfrac{t_1+t_2}{2}\right]$$
$$\Rightarrow u=\dfrac{g(t_1+t_2)}{2}$$
Step 3: Applying II equation of motion
$$s=ut+\dfrac{1}{2}at^2$$
$$h=ut_1-\dfrac{1}{2}gt^2_1$$
$$=\dfrac{g(t_1+t_2)t_1}{2}-\dfrac{gt^2_1}{2}$$
$$\Rightarrow h=\dfrac{gt_1t_2}{2}$$.
Express the magnitude of $$\overrightarrow { a } \times \overrightarrow { b }$$ in terma of scalar products
A boy can throw a stone up to maximum height of $$10$$cm. The maximum horizontal distance that the boy can throw the same stone up to will be?
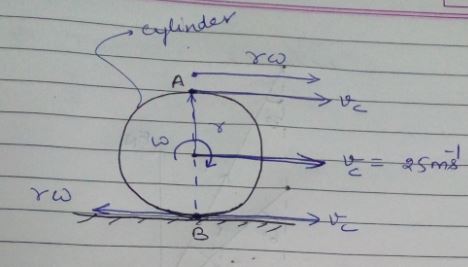
A cylinder rolls without slipping on a horizontal plane surface. If the speed of the centre is $$25\ m/s$$, what is the speed of the highest point?
Since, the cylinder is rolling without slipping
so, velocity of point $$B = 0$$
(no relative motion between cylinder and surface at point of contact B.)
$$ \Rightarrow r\omega = \vartheta _{c}$$ __ (i)
so, velocity of highest point $$ (\vartheta _{A})$$
$$ \vartheta _{A} = r \omega + \vartheta _{c}$$
from (i)
$$ \vartheta _{A} = \vartheta_{c}+\vartheta_{2}$$
$$ \vartheta_{A} = 2\vartheta_{c}$$
$$ \Rightarrow \vartheta_{A} = 2\times 25$$
$$ \Rightarrow \vartheta^{A} = 50 \,ms^{-1}$$
If $$ \overrightarrow { A } ,\overrightarrow { B } ,\overrightarrow { C } $$are they vectors, show that $$\overrightarrow { A } \times(\overrightarrow { B }+\overrightarrow { C }) = \overrightarrow { A } \times \overrightarrow { B }+\overrightarrow { A } \times\overrightarrow { C }$$
If $$\vec{a}$$ and $$\vec{b}$$ are the position vectors of A and B, respectively, find the position vector of a point C in BA produced such that BC = 1.5 BA.
Since $$\overline {OA}=\overline a$$ and $$\overline {OB}= \overline b$$
$$\therefore \overline{BA}=\overline{OA}-\overline{OB}=\overline a- \overline b$$
And $$1.5\ \overline {BA}=1.5 (\overline a- \overline b)$$
$$\therefore \overline{BA}=\overline{OA}-\overline{OB}=\overline a- \overline b$$
And $$1.5\ \overline {BA}=1.5 (\overline a- \overline b)$$
Since, $$\overline {BC}=1.5 \overline {BA}=1.5 (\overline a- \overline b)$$
$$\overline {OC} - \overline {OB}=1.5 \overline a-1.5 \overline b$$
$$\overline {OC} =1.5 \overline a-1.5 \overline b+b [\because \overline {OB} =\overline b]$$
$$=1.5 \overline a-0.5 \overline b$$
$$=\dfrac{3 \overline a- \overline b}{2}$$
Graphically, explanation of the above solution is given above
$$\overline {OC} - \overline {OB}=1.5 \overline a-1.5 \overline b$$
$$\overline {OC} =1.5 \overline a-1.5 \overline b+b [\because \overline {OB} =\overline b]$$
$$=1.5 \overline a-0.5 \overline b$$
$$=\dfrac{3 \overline a- \overline b}{2}$$
Graphically, explanation of the above solution is given above
Write vector relation between angular velocity $$(\overset{\rightarrow}{\omega})$$, tangential velocity $$(\overset{\rightarrow}{V})$$ and position vector $$(\overset{\rightarrow}{r})$$.
A juggler throws balls into air. He throws one whenever the previous one is at its highest point. How high do the balls rise if the throws $$n$$ balls each second.
Find the equation of the line parallel to $$2\bar {i}-\bar {j}+2\bar {k}$$ and which passes through point $$'A'(3\bar {i}+\bar {j}-\bar {k})$$. if P is a point on the line such that $$AP=15$$. Find the position vectors of $$P$$.
What is the angle between velocity and acceleration at the highest point of projectile motion?
Which physical quantities remain constant in U.C.M?
Find $$\overrightarrow {AB} $$, if $$A(4,3,4)$$ and $$B(2,5,0)$$.
A boy is cycling such that the wheels of the cycle are making $$140$$ revolutions per minute. If the diameter of the wheel is $$60\ cm$$, then find the speed per hour with which the boy is cycling.
Find the point of intersection of the three planes $$r \cdot a = 1, r \cdot b = 1, r \cdot c = 1$$, where a, b, c are three non coplanar vector.
Enter $$1$$ if true else $$0$$.The position vectors of points A, B and C are $$\lambda \hat{i}+3\hat{j},\, 12\hat{i}+\mu \hat{j}$$ and $$ 11\hat{i}-3\hat{j}$$ respectively. If C divides the line segment joining A and B in the ratio $$3:1,$$ then $$ \lambda =8, \mu = -5 $$.
In a Circus, a motor-cyclist having mass of $$50 kg$$ moves in a spherical cage of radius $$3 m$$. Calculate the least velocity with which he must pass the highest point without losing contact. Also calculate his angular speed at the highest point.
Given, the mass of motorcyclist $$=50 Kg$$
The radius of spherical cage $$=3m$$
for minimum velocity of $$N=0$$
$$\Rightarrow v=\sqrt{rg}=\sqrt{3\times 10}$$ (taking $$g=10m/s$$)
$$=\sqrt{30}$$
$$=5.48m/s$$
$$\therefore V_{min}=5.48m/s$$
$$=1.83rad/s$$
The radius of spherical cage $$=3m$$
Refer image.1
At highest point $$A$$
FBD of motorcyclist
Refer image. 2
At highest point $$A$$
FBD of motorcyclist
Refer image. 2
$$N+mg=\dfrac{mv^2}{r}$$
Here, $$r$$ is radius of circle, $$N$$ is Normal reacting by surface of sphere.
Here, $$r$$ is radius of circle, $$N$$ is Normal reacting by surface of sphere.
for minimum velocity of $$N=0$$
$$mg=\dfrac{mv^2}{r}\Rightarrow v^2=rg$$
$$\Rightarrow v=\sqrt{rg}=\sqrt{3\times 10}$$ (taking $$g=10m/s$$)
$$=\sqrt{30}$$
$$=5.48m/s$$
$$\therefore V_{min}=5.48m/s$$
Also $$v=rw$$.
So angular speed $$\Rightarrow w=\dfrac{v}{r}$$
$$=\dfrac{5.48}{3}$$
$$=\dfrac{5.48}{3}$$
$$=1.83rad/s$$
If the vertices A,B,C of a triangle ABC are the points with position vectors
$$ a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k},b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k},c_{1}\hat{i}+c_{2}\hat{j}+c_{3}\hat{k} $$ respectively, what are the vectors determined
by its sides? Find the length of these vectors.
If $$( -a\hat{i}+b\hat{k}) $$ is the position vector of a point $$R$$ which divides the line segment joining points $$ P(\hat{i}+2\hat{j}+\hat{k}) $$ and $$ Q (-\hat{i}+\hat{j}+\hat{k}) $$ in the ratio $$2:1$$ externally, then $$a+b$$ is equal to ___.
If $$R$$ divides $$PQ$$ externally in the ratio $$2:1$$ i.e.
$$PR:RQ = 2:1,$$ then its position vector is
$$ \dfrac{2(-\hat{i}+\hat{j}+\hat{k})-(\hat{i}+2\hat{j}+\hat{k})}{2-1} = -3\hat{i}+\hat{k} $$
Comparing with $$( -a\hat{i}+b\hat{k}) $$
we get $$a=3$$ and $$b=1$$
$$a+b= 3+1=4$$
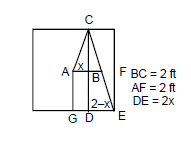
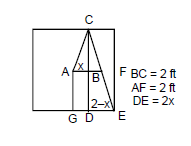
A carrom board ($$4$$ ft $$\times 4$$ ft square) has the queen at the centre. The queen, hit by the striker moves to the front edge, rebounds and goes in the hole behind the striking line. Find the magnitude of displacement of the queen from the centre to the front edge.
In $$\Delta$$ABC, $$\tan\theta =x/2$$ and $$\Delta$$DCE, $$\tan\theta =(2-x)/4\tan\theta =(x/2)=(2-x)/4=4x$$
$$\Rightarrow 4-2x=4x$$
$$\Rightarrow 6x=4\Rightarrow x=2/3$$ft
In $$\Delta$$ABC, AC$$=\sqrt{AB^2+BC^2}=\dfrac{2}{3}\sqrt{10}$$ft.
$$\Rightarrow 4-2x=4x$$
$$\Rightarrow 6x=4\Rightarrow x=2/3$$ft
In $$\Delta$$ABC, AC$$=\sqrt{AB^2+BC^2}=\dfrac{2}{3}\sqrt{10}$$ft.
A swimmer wishes to cross a 500 m wide river flowing at 5 km/h. His speed with respect to water is 3 km/h. He reaches the other shore in shortest time. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point. Find the minimum distance that he has to walk.
A carrom board ($$4$$ ft $$\times 4$$ ft square) has the queen at the centre. The queen, hit by the striker moves to the front edge, rebounds and goes in the hole behind the striking line. Find the magnitude of displacement of the queen from the front edge to the hole.
In $$\Delta$$ABC, $$\tan\theta =x/2$$ and $$\Delta$$DCE, $$\tan\theta =(2-x)/4\tan\theta =(x/2)=(2-x)/4=4x$$
$$\Rightarrow 4-2x=4x$$
$$\Rightarrow 6x=4\Rightarrow x=2/3$$ ft
In $$\Delta$$CDE, DE$$=1-(2/3)=4/3$$ft
$$CD=4$$ft. So, $$CE=\sqrt{CD^2+DE^2}=\dfrac{4}{3}\sqrt{10}$$ft.
$$\Rightarrow 4-2x=4x$$
$$\Rightarrow 6x=4\Rightarrow x=2/3$$ ft
In $$\Delta$$CDE, DE$$=1-(2/3)=4/3$$ft
$$CD=4$$ft. So, $$CE=\sqrt{CD^2+DE^2}=\dfrac{4}{3}\sqrt{10}$$ft.
A particle is projected from the ground at an angle $$30^{\circ}$$ with the horizontal with an initial speed $$20\ ms^{-1}$$. At what time after which velocity vector of projectile is perpendicular to the initial velocity? [in second]
Initial velocity $$u = u\cos \theta \hat {i} + u\sin \theta \hat {j}$$
Velocity after time $$t$$ is
$$v = u\cos \theta \hat {i} + (u\sin \theta - gt)\hat {j}$$
Since $$u$$ and $$v$$ are perpendicular to each other,
$$\vec {u}\cdot \vec {v} = 0$$
$$(u\cos \theta \hat {i} + u\sin \theta \hat {j})\times [u\cos \theta \hat {i} + (u\sin \theta - gt)\hat {j} ] = 0$$
$$u^{2}\cos^{2} \theta + u^{2}\sin^{2} \theta - u\sin \theta gt = 0$$
$$t = \dfrac {u}{g\sin \theta} = \dfrac {20}{10\times \dfrac {1}{2}} = 4s$$.
Velocity after time $$t$$ is
$$v = u\cos \theta \hat {i} + (u\sin \theta - gt)\hat {j}$$
Since $$u$$ and $$v$$ are perpendicular to each other,
$$\vec {u}\cdot \vec {v} = 0$$
$$(u\cos \theta \hat {i} + u\sin \theta \hat {j})\times [u\cos \theta \hat {i} + (u\sin \theta - gt)\hat {j} ] = 0$$
$$u^{2}\cos^{2} \theta + u^{2}\sin^{2} \theta - u\sin \theta gt = 0$$
$$t = \dfrac {u}{g\sin \theta} = \dfrac {20}{10\times \dfrac {1}{2}} = 4s$$.
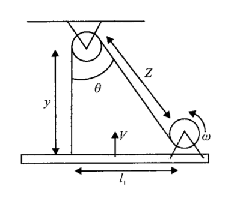
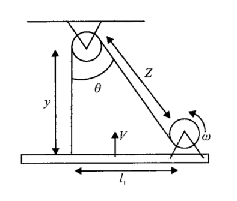
In the instant shown in diagram the board is moving up ( vertically) with velocity v. the drum radius is R and the board always remains horizontal, find the value of velocity v in terms of R $$ \theta , \omega $$
I = y+z ( total length at any time t) is given as:
$$l= y + \sqrt { y^2 +l^2} $$
$$ \dfrac {dl}{dt} = \dfrac {dy}{dt} + \dfrac {y}{ \sqrt { y^2 +l^2 } } \dfrac {dy}{dt} $$
Now, we know that for the shown case:
$$ \omega R = v( 1 + cos \theta)$$
$$v = \dfrac { \omega R}{ 1 +cos \theta} $$
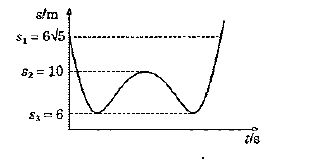
A ball is thrown vertically upwards. Its distance $$s$$ from a fixed point varies with time $$t$$ according to the following graph. Calculate velocity of projection of the ball.
A carrom board ($$4$$ft $$\times 4$$ ft square) has the queen at the centre. The queen, hit by the stricker moves to the front edge, rebounds and goes in the hole behind the striking line. Find the magnitude of displacement of the queen from the centre to the hole.
In $$\Delta$$ABC, $$\tan\theta =x/2$$ and $$\Delta$$DCE, $$\tan\theta =(2-x)/4\tan\theta =(x/2)=(2-x)/4=4x$$
$$\Rightarrow 4-2x=4x$$
$$\Rightarrow 6x=4\Rightarrow x=2/3$$ ft
In $$\Delta$$AGE, $$AE=\sqrt{AG^2+GE^2}=2\sqrt{2}$$ ft.
$$\Rightarrow 4-2x=4x$$
$$\Rightarrow 6x=4\Rightarrow x=2/3$$ ft
In $$\Delta$$AGE, $$AE=\sqrt{AG^2+GE^2}=2\sqrt{2}$$ ft.
A ball is projected from the ground with velocity $$v$$ such that its range is maximum.
| Column I | Column II |
| i. Velocity at half of the maximum height | a. $$\dfrac {\sqrt {3}v}{2}$$ |
| ii. Velocity at the maximum height | b. $$\dfrac {v}{\sqrt {2}}$$ |
| iii. Change in its velocity when it returns to the ground | c. $$v\sqrt {2}$$ |
| iv. Average velocity when it reaches the maximum height | d. $$\dfrac {v}{2}\sqrt {\dfrac {5}{2}}$$ |
$$i.\rightarrow a.; ii. \rightarrow b.; iii. \rightarrow c.; iv. \rightarrow d$$.
$$i. \rightarrow a$$. Range is maximum, when the angle of projection is $$45^{\circ}$$.
$$H = \dfrac {v^{2}}{2g}\sin^{2} 45 = \dfrac {v^{2}}{4g} .... (i)$$
Velocity, at half of the maximum height is $$v$$.
$$v'^{2} = v^{2} \sin^{2} 45 - 2g \dfrac {H}{2} = \dfrac {v^{2}}{2} - \dfrac {v^{2}}{4} \Rightarrow v' = \dfrac {\sqrt {3}v}{2}$$
$$H = \dfrac {v^{2}}{2g}\sin^{2} 45 = \dfrac {v^{2}}{4g} .... (i)$$
Velocity, at half of the maximum height is $$v$$.
$$v'^{2} = v^{2} \sin^{2} 45 - 2g \dfrac {H}{2} = \dfrac {v^{2}}{2} - \dfrac {v^{2}}{4} \Rightarrow v' = \dfrac {\sqrt {3}v}{2}$$
$$ii. \rightarrow b$$. Velocity at the maximum height
$$v' = v\cos 45\Rightarrow v' = \dfrac {v}{\sqrt {3}}$$
[Because vertical component of velocity is zero at the highest point]
$$v' = v\cos 45\Rightarrow v' = \dfrac {v}{\sqrt {3}}$$
[Because vertical component of velocity is zero at the highest point]
$$iii. \rightarrow c$$. Projection velocity
At projection point, $$v_{i} = v\cos 45\hat {i} + v\sin 45\hat {j}$$
At the point, when the body strikes the ground
$$\vec {v}_{f} = v\cos 45\hat {i} - v\sin 45\hat {j}$$
$$\triangle v = \vec {v}_{f} + (-\vec {v}_{i}) = 2 v\sin 45 (-j)$$
$$|\triangle \vec {v}| = 2v\sin 45 = v\sqrt {2}$$
At projection point, $$v_{i} = v\cos 45\hat {i} + v\sin 45\hat {j}$$
At the point, when the body strikes the ground
$$\vec {v}_{f} = v\cos 45\hat {i} - v\sin 45\hat {j}$$
$$\triangle v = \vec {v}_{f} + (-\vec {v}_{i}) = 2 v\sin 45 (-j)$$
$$|\triangle \vec {v}| = 2v\sin 45 = v\sqrt {2}$$
$$iv. \rightarrow d$$. Average velocity $$= \dfrac {Total\ displacement}{Total\ time}$$
$$Displacement = \sqrt {\left (\dfrac {R}{2}\right )^{2} + H^{2}}$$
$$\vec {v}_{av} = \dfrac {\sqrt {\dfrac {R^{2}}{4} + H^{2}}}{\dfrac {v\sin \theta}{g}} = \dfrac {\sqrt {R^{2} + 4H^{2}}}{\dfrac {2v\sin \theta}{g}}$$
$$v_{av} = \dfrac {\sqrt{ \left (\dfrac {v^{2}}{g}\right )^{2} + 4 \left (\dfrac {v^{2}}{4g}\right )^{2}}}{\dfrac {\sqrt {2}v}{g}}$$
$$v_{ag}= \dfrac {\dfrac {v^{2}}{g} \sqrt {1 + \dfrac {1}{4}}}{\dfrac {v\sqrt {2}}{g}} = \dfrac {v^{2}\sqrt {5}}{2v\sqrt {2}} = \dfrac {v}{2} \sqrt {\dfrac {5}{2}}$$.
A golfer standing on level ground hits a ball with a velocity of $$52\ ms^{-1}$$ at an angle $$\theta$$ above the horizontal. If $$\tan \theta = \dfrac {5}{12}$$, then find the time for which the ball is atleast $$15\ m$$ above the ground (take $$g = 10\ ms^{-2})$$.
Match the entries of Column I with that of Column II.
A diver makes 2,5 revolutions on the way from a 10-m-hich platform to the water. Assuming zero intial vertical velocity, find the average angular velocity during the dive.
An astronaut is tested in a centrifuge with radius 10 m and rotating according to $$0 = 0.30t^{2}$$. At t = 50 s, what are the magnitudes of the (a) angular velocity, (b) linear velocity, (c) tangential acceleration, and (d) radial acceleration?
For sport, a 12 kg armadillo runs onto a large pond of level, frictionless ice.The armadillos initial velocity is 5.0 m/s along the positive direction of an x axis.Take its initial position on the ice as being the origin.It slips over the ice while being pushed by a wind with a force of 17N in the positive direction of the y axis. In unitvector notation, what are the animals (a) velocity and (b) position vector when it has slid for 3.0s?
A positron undergoes a displacement $$\Delta \vec { r } =2.0\hat { i } -3.0\hat { j } +6.0\hat { k } $$, ending with the position vector $$\vec { r } =3.0\hat { j } -4.0\hat { k } $$, in meters. What was the positrons initial position vector?
The angular position of a point on a roatating wheel is given by $$ \theta =2.0+4.0t^{2}+2.0t^{3} $$ , where $$ \theta $$ is in radians and t is in seconds. At t=0, 'what are (a) the point's angulatr position and (b) its angular velocity (c) What is its angular velocity at t=4.0 s (d) Calculate its angular acceleration at t=2.0 s. (e) Is its angular acceleration constant
If the position of a particle is given by $$x$$ = $$ 20t - 5t^{3}$$, where $$x$$
is in meters and $$t$$ is in seconds, For what time range (positive or negative) is $$a$$ negative?
In an arcade video game, a spot is programmed to move across the screen according to $$x = 9.00t - 0.750t^{3}$$, where $$x$$ is distance in centimeters measured from the left edge of the screen and $$t$$ is time in seconds. When the spot reaches a screen edge, at either $$x$$ = 0 or $$x$$ = 15.0 cm, $$t$$ is reset to 0 and the spot starts moving again according to $$x(t)$$. At what time after starting is the spot instantaneously at rest?
A circular track has a circumference of $$3140 \,m$$ with AB as one of its diameter. A scooterist moves from A to B along the circular path with a uniform speed of $$10 \,m/s.$$ Find
(a) distance covered by the scooterist,
(b) displacement of the scooterist, and
(c) time taken by the scooterist in reaching from A to B
$$\textbf{Part (a)}$$
$$\textbf{Step 1: Distance Calculation}$$
The distance covered is the actual path length between point A and B.
Distance covered, $$D=$$ Half of the circumference $$= \dfrac{3140}{2}$$$${ = 1570m}$$
$$\textbf{Part (b)}$$
$$\textbf{Step 2: Displacement Calculation}$$
Displacement is the shortest distance between the initial and final points. Here, the shortest distance between A and B is the diameter AB.
$$d = AB$$
Circumference $$= 3140$$$$=2\pi R$$
$$\Rightarrow$$ $$R = 500m$$
$$\therefore AB = 2R$$$$=1000m$$
Displacement, $${d = 1000m}$$
$$\textbf{Part(c)}$$
$$\textbf{Step 3: Time Calculation}$$
Time taken by the scootrist in reaching from A to B:
$$t = \dfrac{Distance}{Speed}$$ $$=\dfrac{1570(m)}{10m/s}$$
$$\Rightarrow t = 157s$$
The position vector for a proton is initially $$\vec { r } =5.0\hat { i } -6.0\hat { j } +2.0\hat { k } $$ and then later is $$\vec { r } =-2.0\hat { i } +6.0\hat { j } +2.0\hat { k } $$ , all in meters. (a) What is the protons displacement vector, and (b) to what plane is that vector parallel?
The position function $$X$$ $$(t)$$ of a particle moving along an $$X$$ axis is $$X$$
= 4.0 - 6.0$$_{t}$$ $$^{2}$$, with $$X$$ in meters and $$t$$ in seconds. At what negative time and positive time does the particle pass through the origin?
A ball rolls horizontally off the top of a stairway with a speed of $$1.52 m/s$$. The steps are $$20.3 cm$$ high and $$20.3 cm$$ wide. Which step does the ball hit first?
We denote $$h$$ as the height of a step and w as the width. To hit step n, the ball must fall a distance $$nh$$ and travel horizontally a distance between $$(n – 1)w and nw$$. We take the origin of a coordinate system to be at the point where the ball leaves the top of the
stairway, and we choose the $$y$$ axis to be positive in the upward direction, as shown in the figure.
The coordinates of the ball at time $$t$$ are given by $$x={ v }_{ 0x }t$$ and $$y=-\frac { 1 }{ 2 } g{ t }^{ 2 }$$ ($${ v }_{ 0y }=0)$$.
We equate y to –nh and solve for the time to reach the level of step n:
$$t=\sqrt { \frac { 2nh }{ g } } $$
The x coordinate then is
$$x={ v }_{ 0x }\sqrt { \frac { 2nh }{ g } } =(1.52m/s)\sqrt { \frac { 2n(0.203m) }{ { 9.8m/s }^{ 2 } } } =(0.309m)\sqrt { n }. $$
The method is to try values of $$n$$ until we find one for which x/w is less than $$n$$ but greater
than $$n – 1$$. For $$n = 1, x = 0.309 m$$ and $$x/w = 1.52$$, which is greater than $$n$$. For $$n = 2, x =
0.437 m$$ and $$x/w = 2.15$$, which is also greater than $$n$$. For $$n = 3, x = 0.535 m$$ and $$x/w =
2.64$$. Now, this is less than n and greater than $$n – 1$$, so the ball hits the third step.
Note: To check the consistency of our calculation, we can substitute $$n = 3$$ into the above equations. The results are $$t = 0.353 s, y = 0.609 m$$, and $$x = 0.535 m$$. This indeed corresponds to the third step.
stairway, and we choose the $$y$$ axis to be positive in the upward direction, as shown in the figure.
The coordinates of the ball at time $$t$$ are given by $$x={ v }_{ 0x }t$$ and $$y=-\frac { 1 }{ 2 } g{ t }^{ 2 }$$ ($${ v }_{ 0y }=0)$$.
We equate y to –nh and solve for the time to reach the level of step n:
$$t=\sqrt { \frac { 2nh }{ g } } $$
The x coordinate then is
$$x={ v }_{ 0x }\sqrt { \frac { 2nh }{ g } } =(1.52m/s)\sqrt { \frac { 2n(0.203m) }{ { 9.8m/s }^{ 2 } } } =(0.309m)\sqrt { n }. $$
The method is to try values of $$n$$ until we find one for which x/w is less than $$n$$ but greater
than $$n – 1$$. For $$n = 1, x = 0.309 m$$ and $$x/w = 1.52$$, which is greater than $$n$$. For $$n = 2, x =
0.437 m$$ and $$x/w = 2.15$$, which is also greater than $$n$$. For $$n = 3, x = 0.535 m$$ and $$x/w =
2.64$$. Now, this is less than n and greater than $$n – 1$$, so the ball hits the third step.
Note: To check the consistency of our calculation, we can substitute $$n = 3$$ into the above equations. The results are $$t = 0.353 s, y = 0.609 m$$, and $$x = 0.535 m$$. This indeed corresponds to the third step.
The position of a particle moving along an $$x$$ axis is given by $$x$$ =
$$12_ {t}^ {2}$$ - $$12_{t}^{3}$$,where $$x$$ is in meters and $$t$$ is in seconds. Determine at what time is reached its maximum value?
A particle moves along a circular path over a horizontal xy coordinate system, at constant speed.At time $${ t }_{ 1 }= 4.00 s$$, it is at point ($$5.00 m, 6.00 m$$) with velocity $$(3.00 m/s)\hat { j } $$ and acceleration in the positive $$x$$ direction. At time $${ t }_{ 2}=10.0 s$$, it has velocity $$( 3.00 m/s)\hat { i } $$ and acceleration in the positive y direction. What are the (a) x and (b) y coordinates of the center of the circular path if $${ t }_{ 2 }-{ t }_{ 1 }$$ is less than one period?
If the position of a particle is given by X = 20t - 5t^{3}, where Xis in meters and t is in seconds, For what time range is a Positive?
is in meters and t is in seconds, For what time range is a Positive?
A carnival merry-go-round rotates about a vertical axis at a constant rate. A man standing on the edge has a constant speed of $$3.66 m/s$$ and a centripetal acceleration $$\vec { a } $$ of magnitude $$1.83{ m/s }^{ 2 }$$ . Position vector $$\vec { r } $$ locates him relative to the rotation axis. (a) What is the magnitude of $$\vec { r } $$? What is the direction of $$\vec { r } $$ when $$\vec { a }$$ is directed (b) due east and (c) due south?
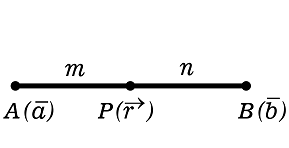
Find the position vector of a point $$R$$ which divides the line joining the two points $$P$$ and $$Q$$ with position vectors $$\bar{OP}=2\bar{a}+\bar{b}$$ and $$\bar{OQ}=\bar{a}-2\bar{b}$$, respectively, in the ratio $$1:2$$ internally
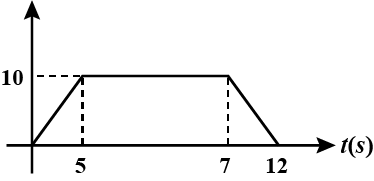
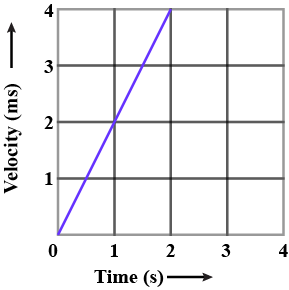
Figure shows the displacement-time graph for the motion of a body. USe it to calculate the velocity of body at $$t=1s,\ 2s$$ and $$3s$$, then the velocity-time graph for it in figure $$(b)$$.
From the graph given, the velocity can be observed,
At time,
$$t=1s,$$ velocity is $$2ms^{-1}$$
$$t=2s,$$ velocity is $$4ms^{-1}$$
$$t=3s,$$ velocity is $$6ms^{-1}$$
At time,
$$t=1s,$$ velocity is $$2ms^{-1}$$
$$t=2s,$$ velocity is $$4ms^{-1}$$
$$t=3s,$$ velocity is $$6ms^{-1}$$
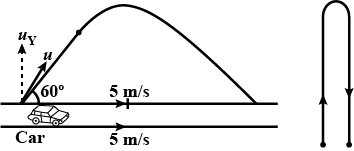
A boy throws a ball in the air at $$60^o$$ to the horizontal along a road with a speed of $$10 \,m/s$$. Another boy sitting in a passing by car observes the ball. Sketch the motion of the ball as observed by the boy in the car. If the car has a speed of $$(18kmh^{-1})$$. Give an explanation to support your diagram.
$$u = 36 \,km/h = 36 \times \dfrac{5}{15} = 10 \,m/s$$
$$u_x = u \cos 60^o = 10 \times \dfrac{1}{2} = 5 \,m/s$$
The speed of car in the direction of motion of ball $$= 18 \times \dfrac{5}{15} = 5 \,m/s.$$
If the ball is thrown by a boy when the car just passes him, then the ball and car (boy) travel (covers) equal horizontal distances as their horizontal speeds are same. But due to vertical component.
Of velocity, $$u_y = u \cos 30^o = \dfrac{10 \sqrt{3}}{2} \,m/s = 5 \sqrt{3} \,m/s$$ ball rises up and then come back. The motion of ball by the boy sitting in the car will be simple vertically up-down motion.
$$u_x = u \cos 60^o = 10 \times \dfrac{1}{2} = 5 \,m/s$$
The speed of car in the direction of motion of ball $$= 18 \times \dfrac{5}{15} = 5 \,m/s.$$
If the ball is thrown by a boy when the car just passes him, then the ball and car (boy) travel (covers) equal horizontal distances as their horizontal speeds are same. But due to vertical component.
Of velocity, $$u_y = u \cos 30^o = \dfrac{10 \sqrt{3}}{2} \,m/s = 5 \sqrt{3} \,m/s$$ ball rises up and then come back. The motion of ball by the boy sitting in the car will be simple vertically up-down motion.
Write detailed answer?
Why is the work done on object moving with uniform circular motion zero?
Which force acts on a uniform circular motion?
How does a vehicle obtain a centripetal force on a leveled circular path?
A body moves in a circle of radius 2R. What is the distance covered and displacement of the body after 2 complete rounds ?
An athlete runs along a circular track of radius 2R. What is his displacement after covering half a round ?
How much should be the angle of a projection so that the body covers the maximum distance ?
Explain uniform circular motion.
Somehow, an ant is stuck to the rim of a bicycle wheel of a diameter $$1\,m$$. While the bicycle is on a central stand, the wheel is set into rotation and it attains the frequency of $$2\,rev/s$$ in $$10$$ seconds , with uniform angular acceleration. Calculate :
(i) The number of revolutions completed by the ant in these $$10$$ seconds.
(ii) Time taken by it for first complete revolution and the last complete revolution.
What is the direction of motion (or velocity) of a body in uniform circular motion?
State, for each of the following physical quantities, if it is a scalar or a vector: volume, mass, speed, acceleration, density, number of moles, velocity, angular frequency, displacement, angular velocity.
A car which is at rest is accelerated with an acceleration of $$40 \,rad /s^2.$$ In how much time will it get the angular velocity of $$800$$ cycles / minute ?
What is projectile motion?
How do you determine the instantaneous velocity of a particle from the position-time graph?
State with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
adding any two scalars,
adding a scalar to a vector of the same dimensions,
multiplying any vector by any scalar,
multiplying any two scalars,
adding any two vectors,
adding a component of a vector to the same vector.
Pick cut the two scalar quantities in the following list: force, angular momentum, work, current, linear momentum, electric field, average velocity, magnetic moment, relative velocity.
Pick out the only vector quantity in the following list: Temperature, pressure, impulse, time, power, total, path length, energy, gravitational potential, coefficient of friction, charge.
A vector has both magnitude and direction. Does it mean that anything that has magnitude and direction is necessarily a vector? The rotation of a body can be specified by the direction of the axis of rotation, and the angle of rotation about the axis. Does that make any rotation a vector?
Which of the following is a scalar quantity? Force, momentum & Inertia.
the time dependence of the angle $$\alpha$$ between the vectors $$w$$ and $$v$$;
Read each statement below carefully and state, with reasons and examples, if it is true or false: A scalar quantity is one that
is conserved in a process
can never take negative values
must be dimensionless
does not vary from one point to another in space
has the same value for observers with different orientations of axes.
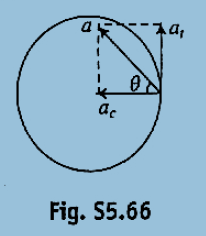
Using the condition of the foregoing problem, draw the approximate time dependence of moduli of the normal $$\omega_n$$ and tangent $$\omega_{\tau}$$, acceleration vector, as well as of the projection of the total acceleration vector $$\omega_{\nu}$$ on the velocity vector direction.
Read each statement below carefully false :
The magnitude of a vector is always a scalar,
each component of a vector is always a scalar,
the total path length is always equal to the magnitude of the displacement vector of a particle,
the average speed of a particle (defined as total path length divided by the time taken to cover the path) is either greater or equal to the magnitude of average velocity of the particle over the same Interval of time,
Three vectors not lying In a plane can never add up to give a null vector.
the equation of the point's trajectory $$y(x);$$ plot this function;
As $$\vec r=a t \vec i-b t^2 \vec j$$
So, $$x=a t, y=-b t^2$$
and therefore $$y=\dfrac{-b x^2}{a^2}$$
which is Eq. of a parabola, whose graph is shown in the Fig.
Show that the trajectory of a projectile is a parabola.
Consider a particle thrown up at an angle $$q$$ to the horizontal with a velocity $$u$$. The velocity of projection can be resolved into who component $$u \cos \theta$$ and $$u \sin \theta$$ along $$OX$$ and $$OY$$ respectively.
(Refer image)
The horizontal component remains constant while the vertical component is affected by gravity.
Let $$P(x, y)$$ be the position of the projectile after $$'t'$$ seconds.
Then distance travelled $$x'$$ along OX is given by,
$$x = \text{horizontal component of the velocity} \times \text{time}$$
$$x = u \cos 0 \times t ........(1)$$
The distance travelled along the vertical direction in same time $$'t'$$ is,
$$y = (u \sin \theta) t - 1 /2 gt^2..............(2)$$
$$Substituting, t=\dfrac{x}{u \cos \theta} from (1) in (2)$$,
$$y= u \sin \theta\dfrac{x}{u \cos \theta}-\dfrac{1}{2}g\left(\dfrac{x^2}{u^2 \cos^2 \theta}\right)$$
$$y=(\tan \theta)x-\left(\dfrac{g}{2u^2 \cos^2 \theta}\right)x^2$$
$$y=ax-bx^2...........(3) where$$
$$a=\tan \theta,b=\dfrac{g}{2u^2 \cos^2 \theta},$$ are constants
for given values of $$\theta$$, u and g.
Equation (3) represents a parabola. Therefore trajectory of a projectile is parabola.
(Refer image)
The horizontal component remains constant while the vertical component is affected by gravity.
Let $$P(x, y)$$ be the position of the projectile after $$'t'$$ seconds.
Then distance travelled $$x'$$ along OX is given by,
$$x = \text{horizontal component of the velocity} \times \text{time}$$
$$x = u \cos 0 \times t ........(1)$$
The distance travelled along the vertical direction in same time $$'t'$$ is,
$$y = (u \sin \theta) t - 1 /2 gt^2..............(2)$$
$$Substituting, t=\dfrac{x}{u \cos \theta} from (1) in (2)$$,
$$y= u \sin \theta\dfrac{x}{u \cos \theta}-\dfrac{1}{2}g\left(\dfrac{x^2}{u^2 \cos^2 \theta}\right)$$
$$y=(\tan \theta)x-\left(\dfrac{g}{2u^2 \cos^2 \theta}\right)x^2$$
$$y=ax-bx^2...........(3) where$$
$$a=\tan \theta,b=\dfrac{g}{2u^2 \cos^2 \theta},$$ are constants
for given values of $$\theta$$, u and g.
Equation (3) represents a parabola. Therefore trajectory of a projectile is parabola.
Are mass and weight are vector or scalar quantities? Why?
Does the velocity of a particle moving with a uniform speed along a circular path change?
The polar coordinates of a certain point are $$(r = 4.30 cm, \theta = 214^{0})$$. (a) Find its Cartesian coordinates $$x$$ and $$y$$. Find the polar coordinates of the points with Cartesian coordinates (b) $$(-x, y)$$, (c) $$(-2x, -2y)$$, and (d) $$(3x, -3y)$$.
For polar coordinates $$(r, θ)$$, the Cartesian coordinates are $$(x = r \cos θ , y = r \sin θ)$$, if the angle is measured relative to the $$+x$$ axis.
The instantaneous position of an object is specified by its position vector leading from a fixed origin to the location of the object, modeled as a particle. Suppose for a certain object the position vector is a function of time given by $$\vec{r} = 4\hat{i} + 3\hat{j} - 2t\hat{k}$$, where $$\vec{r}$$ is in meters and $$t$$ is in seconds. (a) Evaluate $$d\vec{r}/dt$$. (b) What physical quantity does $$d\vec{r}/dt$$ represent about the object?
Let the polar coordinates of the point $$(x, y)$$ be $$(r, \theta)$$. Determine the polar coordinates for the points (a) $$(-x, y)$$, (b) $$(-2x, -2y)$$, and (c) $$(3x, -3y)$$.
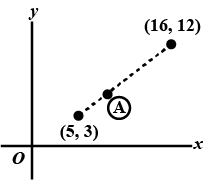
In above figure, the line segment represents a path from the point with position vector $$(5\hat{i}+ 3\hat{j})m$$ to the point with location $$(16\hat{i}+12\hat{j})m$$. Point $$A$$ is along this path, a fraction $$f$$ of the way to the destination. (a) Find the position vector of point $$A$$ in terms of $$f$$. (b) Evaluate the expression from part.(a) for $$f=0$$. (c) Explain whether the result in part (b) is reasonable. (d) Evaluate the expression for $$f = 1$$. (e) Explain whether the result in part (d) is reasonable.
The polar coordinates of a point are $$r = 5.50 m$$ and $$\theta = 240^{0}$$. What are the Cartesian coordinates of this point?
Figure below helps to visualize the $$x$$ and $$y$$ coordinates, and trigonometric functions will tell us the coordinates directly. When the polar coordinates ($$r, \theta$$) of a point $$P$$ are known, the Cartesian coordinates are found as
$$x = r \cosθ$$ and $$y = r \sinθ$$
Then,
$$x = r \cosθ = (5.50m)\cos240^{0}$$
$$= (5.50m)(−0.5) = −2.75m$$
$$y = r \sinθ = (5.50m)\sin240^{0}$$
$$= (5.50m)(−0.866) = −4.76m$$
A fly lands on one wall of a room. The lower left corner of the wall is selected as the origin of a two-dimensional Cartesian coordinate system. If the fly is located at the point having coordinates $$(2.00, 1.00)$$ m, (a) how far is it from the origin? (b) What is its location in polar coordinates?
Obtain expressions in component form for the position vectors having the polar coordinates (a) $$12.8 m, 150^{0}$$; (b) $$3.30 cm, 60.0^{0}$$; and (c) $$22.0 in., 215^{0}$$
Do not think of $$\sin θ$$ = opposite/hypotenuse, but jump right to $$y =R \sin θ$$. The angle does not need to fit inside a triangle. We find the $$x$$ and $$y$$ components of each vector using $$x = r \cos θ$$ and $$y = r \sin θ$$. In unit vector notation, $$\vec{R}=R_{x}\hat{i}+R_{y}\hat{j}$$
Two points in a plane have polar coordinates $$(2.50 m, 30.0^{0})$$ and $$(3.80 m, 120.0^{0})$$. Determine (a) the Cartesian coordinates of these points and (b) the distance between them.
Yes or no: Is each of the following quantities a vector?
(a) force,
(b) temperature,
(c) the volume of water in a can,
(d) the ratings of a TV show,
(e) the height of a building,
(f) the velocity of a sports car,
(g) the age of the Universe.
Find the scalar product of the vectors in above figure.
We must first find the angle between the two vectors. It is
$$θ = (360^{0} – 132^{0}) – (118^{0} + 90.0^{0})$$
$$= 20.0^{0}$$
Then
$$\vec{F}\cdot\vec{r} = Fr \cosθ$$
$$= (32.8 N)(0.173 m)\cos 20.0^{0}$$
or
$$\vec{F}\cdot\vec{r} = 5.33 N\cdot m = 5.33 J$$
$$θ = (360^{0} – 132^{0}) – (118^{0} + 90.0^{0})$$
$$= 20.0^{0}$$
Then
$$\vec{F}\cdot\vec{r} = Fr \cosθ$$
$$= (32.8 N)(0.173 m)\cos 20.0^{0}$$
or
$$\vec{F}\cdot\vec{r} = 5.33 N\cdot m = 5.33 J$$
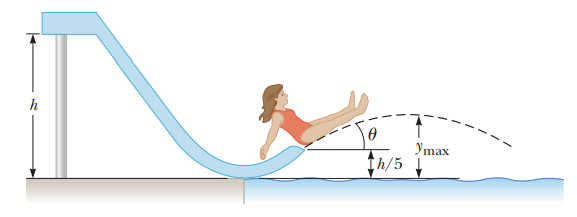
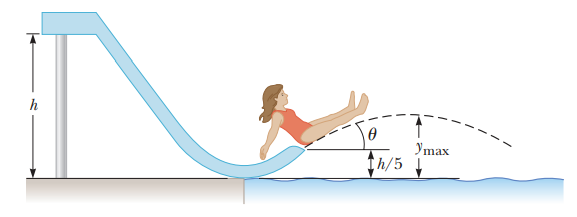
A child of mass $$m$$ starts from rest and slides without friction from a height $$h$$ along a slide next to a pool Fig. She is launched from a height $$h/5$$ into the air over the pool. We wish to find the maximum height she reaches above the water in her projectile motion Would your answers be the same if the waterslide were not frictionless? Explain
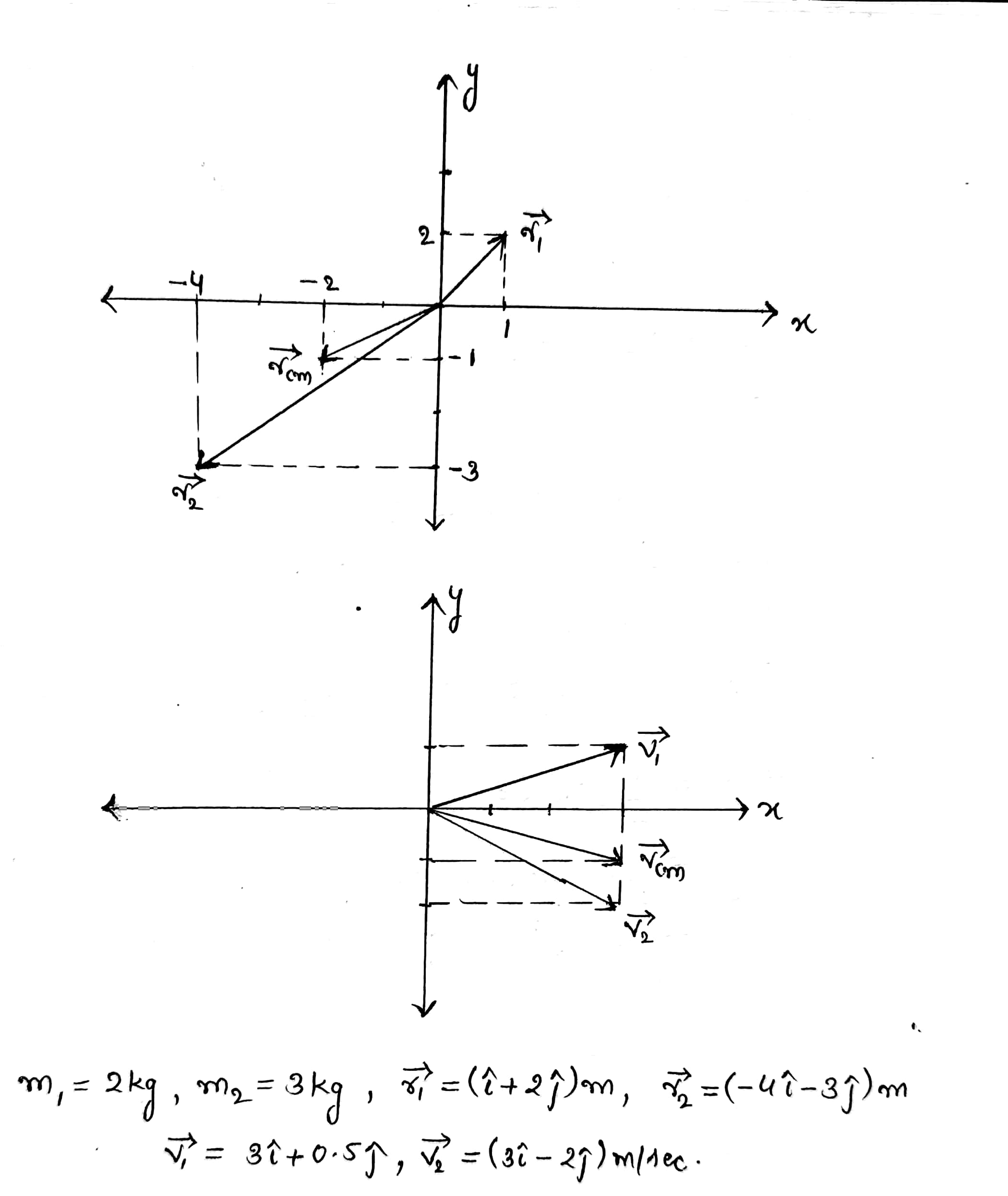
Consider a system of two particles in the $$xy$$ plane: $$m_{1}=2.00\ kg$$ is at the location $$\vec{r}_{1}=(1.00\hat{i}+2.00\hat{j})m$$ and has a velocity of $$(3.00\hat{i}+0.500\hat{j})\ m/s; m_{2}=3.00\ kg$$ is at $$\vec{r}_{2}=(-4.00\hat{i}-3.00\hat{j})\ m$$ and has velocity $$(3.00\hat{i}-2.00\hat{j})\ m/s$$.
Plot these particles on a grid or graph paper. Draw their position vectors and show their velocities.
A particle is located at the vector position $$\vec r =(4.00\hat i+6.00\hat j)m$$, and a force exerted on it is given by $$\vec F=(3.00\hat i+2.00\hat j)N$$.
Determine the position vector of one such point.
A small object with mass $$4.00\ kg$$ counterclockwise with constant angular speed $$1.50\ rad/s$$ in a circle of radius $$3.00\ m$$ centered at the origin. It starts at the point with position vector $$3.00\ \hat i\ m$$. It then undergoes an angular displacement of $$9.00\ rad$$.
In what direction is it moving?
A particle is located at the vector position $$\vec r =(4.00\hat i+6.00\hat j)m$$, and a force exerted on it is given by $$\vec F=(3.00\hat i+2.00\hat j)N$$.
Can there be another point about which the torque caused by this force on this particle will be in the opposite direction and half as large in magnitude?
A particle is located at the vector position $$\vec r =(4.00\hat i+6.00\hat j)m$$, and a force exerted on it is given by $$\vec F=(3.00\hat i+2.00\hat j)N$$.
Can such a point lie on the $$y$$ axis?
A particle is located at the vector position $$\vec r =(4.00\hat i+6.00\hat j)m$$, and a force exerted on it is given by $$\vec F=(3.00\hat i+2.00\hat j)N$$.
Can more than one such point lie on the $$y$$ axis?
A hollow cylinder of mass m= 1kg and radius $$R = \sqrt{3}m $$ is placed on a smooth horizontal surface. Two small blocks of equal mass m = 1kg are sliding on the inner surface of the cylinder without friction. At the initial moment both the blocks are moving in the vertically upward direction with speed $$u =\sqrt{56}m/ s$$ . A vertical force F is applied on the cylinder to keep it in contact with ground.What should be the minimum value of F (in newton) at the instant when $$\theta =60^o$$
$$\dfrac{mV^2}{R}=\dfrac{\sqrt{3}}{2}mg+ N$$
$$\dfrac{1}{2}mV^2=\dfrac{1}{2}mu^2=-\dfrac{\sqrt{3}}{2}mgR$$
$$\Rightarrow \dfrac{mV^2}{R}=\dfrac{mu^2}{R}-\sqrt{3}mg$$
$$\dfrac{mu^2}{R}-\sqrt{3}mg=\dfrac{\sqrt{3}}{2}mg+N$$
$$\Rightarrow N=\dfrac{mu^2}{R}-\dfrac{3\sqrt{3}}{2}mg$$
$$F_{Min}=2N\, cos\, 30^o-mg$$
$$=\dfrac{\sqrt{3}mu^2}{R}-\dfrac{9}{2}mg-mg \Rightarrow $$
$$F_{Min}=1 newton$$
In a two dimensional motion of a body prove that tangential acceleration is nothing but component of acceleration along velocity.
A particle moves in the plane xy with constant acceleration a directed along the negative y-axis. The equation of motion of the particle has the form $$\displaystyle y= px-qx^{2}$$ where p and q are positive constants. Find the velocity of the particle at the origin of co-ordinates.
A solid body starts rotating about a stationary axis with an angular acceleration $$\alpha =(2.0 \times 10^{-2}) t\: rad/s^{2}$$ , where $$t$$ is in seconds. How soon(in seconds) after the beginning of rotation will the total acceleration vector of an arbitrary point of the body form an angle $$\theta= 60^{\circ}$$ with its velocity vector?
$$\displaystyle tan 60^{\circ}=\frac{a_{r}}{a_{t}}=\frac{r \omega ^{2}}{r \alpha }$$
$$\displaystyle = \frac{ \left[ \int _{0}^{t} \alpha dt \right]^{2}}{\alpha}$$
$$\displaystyle =\frac{(0.01 t^{2})^{2}}{0.02 t}$$
Solving we get,
$$ t^{3} =346$$
$$\therefore t=7 s$$
$$\displaystyle = \frac{ \left[ \int _{0}^{t} \alpha dt \right]^{2}}{\alpha}$$
$$\displaystyle =\frac{(0.01 t^{2})^{2}}{0.02 t}$$
Solving we get,
$$ t^{3} =346$$
$$\therefore t=7 s$$
A solid body rotates about a stationary axis according to the law $$\theta= 6t - 2t^{3}$$. Here $$\theta$$ is in radian
and $$t$$ in seconds.
Hint: If $$Y= y(t)$$, then mean/average value of $$y$$ between $$t_{1}$$, and $$t_{2}$$ is $$\displaystyle < Y > \frac{\int_{t_{1}}^{t_{2}}Y(t)dt}{t_{2}-t_{1}}$$. The mean values of angular acceleration averaged over the time interval between $$t= 0 $$ and the complete stop is $$-x$$. Find $$x$$.
A particle is projected from ground with velocity $$\displaystyle 20\sqrt{2}m/s\:at\:45^{\circ}.$$ At what time particle is at height $$15\ m$$ from ground? $$\displaystyle \left ( g= 10m/s^{2} \right )$$
Given : $$u = 20\sqrt{2} m/s$$ $$a_y =-g = -10 m/s^2$$
$$\therefore$$ $$u_x = u cos45^o = 20 m/s$$ and $$u_y =u sin45^o = 20 m/s$$
y direction : $$S_y = u_yt + \dfrac{1}{2}a_yt^2$$ where $$S_y = 15$$ m
$$\therefore$$ $$15 =20 t - \dfrac{10 \times t^2}{2} $$
OR $$t^2 - 4t + 3 = 0$$
$$\implies$$ $$t = 1s $$ and $$3 s$$
Hence the particle is at height 15 m from ground after $$1$$ s and $$3$$ s
Show that there are two values of time for which a projectile is at the same height. Also show mathematically that the sum of these two times is equal to the time of flight.
From figure, $$u_y = u$$ $$sin\theta$$ $$a_y = -g$$
y-direction : $$S_y = u_y t +\dfrac{1}{2}a_y t^2$$
$$\therefore$$ $$h = (usin\theta)t - \dfrac{gt^2}{2}$$
$$\implies$$ $$t^2 -\bigg(\dfrac{2u}{g} sin\theta \bigg) t+ \dfrac{2h}{g} =0$$ ...............(1)
Equation (1) has two roots $$t_1$$ and $$t_2$$, thus there are two values of time for which a projectile is at the same height.
Sum of roots of (1) $$t_1 + t_2 = \dfrac{-b}{a} = \dfrac{2u sin\theta}{g} = T$$ (Time of flight)
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If $$\displaystyle \alpha \:and\:\beta $$ be the base angles and $$\displaystyle \theta $$ the angle of projection, prove that $$\displaystyle \tan \theta = \tan \alpha +\tan \beta .$$
$$\displaystyle \tan \alpha +\tan \beta = \frac{y}{x}+\frac{y}{R-x}$$
$$\displaystyle \tan \alpha +\tan \beta =\frac{yR}{x\left ( R-x \right )}$$ ...(i)
Equation of trajectory is
$$\displaystyle y= x\tan \theta \left [ 1-\frac{x}{R} \right ]$$
or, $$\displaystyle \tan \theta = \frac{yR}{x\left ( R-x \right )}$$ ...(ii)
From Eqs. (i) and (ii), we have
$$\displaystyle \tan \theta = \tan \alpha +\tan \beta $$
A particle is projected from ground with velocity $$\displaystyle 40\sqrt{2}\ m/s\:at\:45^{\circ}.$$ Find the displacement of the particle after 2 s. $$\displaystyle \left ( g= 10m/s^{2} \right )$$
Given : $$u = 40\sqrt{2} m/s$$ $$t =2$$ s $$a_y =-g = -10 m/s^2$$
$$\therefore$$ $$u_x = u cos45^o = 40 m/s$$ and $$u_y =u sin45^o = 40 m/s$$
x direction : $$S_x = u_xt + \dfrac{1}{2}a_x t^2$$ where $$t =2$$ s and $$a_x = 0$$
$$\therefore$$ $$S_x = 40 \times 2 + 0 = 80 $$ m
y direction : $$S_y = u_yt + \dfrac{1}{2}a_yt^2$$ where $$t =2$$ s
$$\therefore$$ $$S_y =40 \times 2 - \dfrac{10 \times 2^2}{2} = 60$$ m
$$\implies$$ Displacement of the particle $$S = \sqrt{S_x^2 + S_y^2} = \sqrt{80^2 + 60^2} = 100$$ m
A body is projected up such that its position vector with time as $$\displaystyle \vec{r}= \left \{ 3t\hat{i}+\left ( 4t-5t^{2} \right )\hat{j} \right \}m.$$ Here, t is in seconds.
Find the time and $$x-$$coordinate of particle when its $$y-$$coordinate is zero.
A ring rotates about z axis as shown in figure. The plane of rotation is xy. At a certain instant the acceleration of a particle P(shown in figure) on the ring is $$(6\hat{i}-8\hat{j})m/s^2$$. Find the angular acceleration of the ring & the angular velocity at that instant. Radius of the ring is $$2m$$.
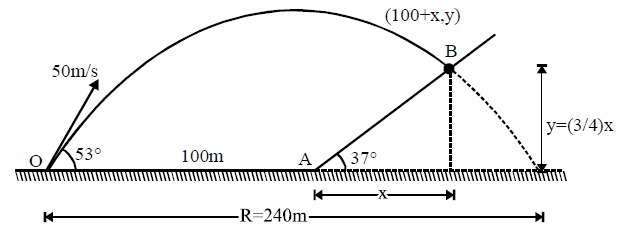
A shell is fired from point O on the level ground with velocity $$50 m/s$$ at angle $$ 53^{\circ} $$ . A hill of uniform slope $$ 37^{\circ} $$ starts from point A that is $$100 m$$ away from the point O as shown in the figure. Calculate the time of flight (in seconds).
By using $$\displaystyle y = x\,tan\,\theta = \left( 1 - \frac {x} {R} \right) $$ where $$\displaystyle R = \frac {2u^2\,sin\,\theta\,cos\,\theta} {g} $$ = 240m
$$\displaystyle \frac {3} {4} x = (100 + x)\,tan\,53^{\circ} \left[ 1 - \frac {x + 100} {240} \right] \Rightarrow x^2 + 95x - 14000 = 0 \Rightarrow x = \frac {-95 \pm \sqrt {(95)^2 + 4(14000)}} {2} $$ = 80
Required distance AB = $$\displaystyle \frac {x} {cos\,37^{\circ}} = \frac {80} {4/5} $$ = 100m
Time of fight = $$\displaystyle \frac {100 + x} {50\,cos\,53^{\circ}} = \frac {100 + 80} {50 (3/5)} $$ = 6s
A small sphere of radius $$R$$ is held against the inner surface of a larger sphere of radius $$6R$$. The masses of large and small spheres are $$4M$$ and $$M$$ respectively. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small spheres is now released. Find the co-ordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
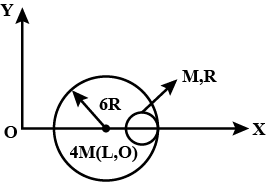
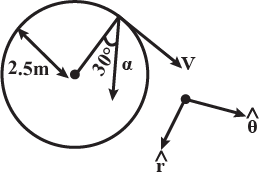
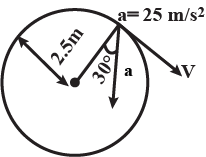
Figure shows the total acceleration and velocity of a particle moving clockwise in a circle of radius $$2.5\ m$$ at a given instant of time. At this instant, find:
(a) the radial acceleration,
(b) the speed of the particle and
(c) its tangential acceleration.
$$a=25$$ $${m/s^2}$$
General form of velocity:
$$\overrightarrow V=\dot r \hat r+r\dot \theta\hat \theta$$
where, a dot above denotes time derivative
General form of acceleration:
$$\overrightarrow a=(\ddot r-r\dot \theta^2)\hat r+(r\ddot\theta+2\dot r\dot \theta)\hat \theta$$
Since, the particle is moving in a circle,
$$\dot r=\ddot r=0$$
Now, $$(a)$$ radial acceleration:
$$a_r=a\cos\theta$$
$$\implies a_r=25\times \cos 30^o$$
$$\implies a_r=25\times \cfrac{\sqrt{3}}{2}$$
$$\implies a_r=21.650$$
Also, $$a_r=r\dot \theta^2=21.650$$
Using magnitude:
$$\dot \theta^2=\cfrac{21.650}{r}$$
$$\implies \dot\theta^2=\cfrac{21.650}{2.5}$$
$$\implies \dot\theta^2=8.66$$
$$\implies \dot\theta=2.94$$ $${rad/s}$$
$$(b)$$ Speed of the particle:
$$V=r\dot\theta$$
$$\implies V=2.5\times 2.94$$
$$\implies V=7.35$$ $${m/s}$$
$$(c)$$ Tangential acceleration:
$$a_{\theta}=a\sin 30^o$$
$$\implies a_{\theta}=25\times \cfrac{1}{2}$$
$$\implies a_{\theta}=12.5$$ $${m/s^2}$$
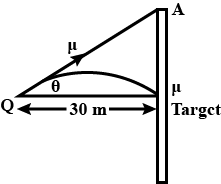
A bullet with muzzle velocity 100 m s $$^{-1}$$ is to be shot at a target 30 m away in the same horizontal line. How high above the target must the rifle be aimed so that the bullet will hit the target?
A particle starts from rest and moves in a circular motion with constant angular acceleration of $$2\ rad/s^{2}$$. Find
a. Angular velocity
b. Angular displacement of the particle after $$4\ s$$
c. The number of revolutions completed by the particle during these $$4\ s$$.
d. If the radius of the circle is $$10\ cm$$, find the magnitude and direction of net acceleration of the particle at the end of $$4\ s$$.
$$\alpha=2\,rads^{-2},\omega_1=0,t=4s$$
a.)$$\omega=\omega_1+\alpha t \Rightarrow \omega_2=0+2\times4=8rads^{-1}$$
b.)$$\theta =\omega_1t+\dfrac{1}{2}\alpha t^2 \Rightarrow \theta=0\times 4+\dfrac{1}{2}\times2\times4^2=16 rad$$
c.) $$1$$ revolution $$=2\pi \,rad \Rightarrow 1rad=\dfrac{1}{2}rev \Rightarrow 16 rad=\dfrac{16}{2\pi}rev=\dfrac{8}{\pi}rev=\dfrac{8\times7}{22}=\dfrac{28}{11}rev$$
d.) After $$4s:v=\omega_2r=8\times 10/100=0.8ms^{-1}$$
$$a_c=\dfrac{v^2}{r}=\dfrac{(0.8)^2}{10/100}=6.4ms^-2$$
Now magnitude of net acceleration,
$$a=\sqrt{a_c^2+a_t^2}=\sqrt{6.4^2+0.2^2}=\sqrt{41}ms^{-2}$$
Direstion on acceleration
$$\tan \theta=\dfrac{a_t}{a_c}=\dfrac{0.2}{6.4}=\dfrac{1}{32}\Rightarrow\theta=\tan^{-1}\left(\dfrac{1}{32}\right)$$
The circular disc rotates about its centre O on the direction shown. At a certain instant point P on the rim has an acceleration $$\vec{a}=-3\hat{i}-4\hat{j}m/s^2$$. For this instant its angular velocity is?
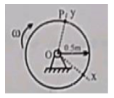
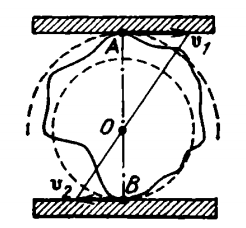
A rigid ingot is pressed between two parallel guides moving in horizontal directions at opposite velocities $${V_1}$$ and $${V_2}$$ . At a certain instant of time, the points of contact between the ingot and the guides lie on the straight line perpendicular to the direction of velocities $${V_1}$$ and $${V_2}$$ . (fig.12).
What point of the ingot have velocities equal in magnitude to $${V_1}$$ and $${V_2}$$ . at this instant?
The velocities of the points of the ingot lying on a segment $$AB$$ at a given instant uniformly vary from $$\nu_1$$ at point $$A$$ to $$\nu_2$$ at point $$B$$. Consequently, the velocity of point $$O$$ Fig. at a given instant is zaro. Hence point $$O$$ is an instantaneous centre of rotation. (Sinc the ingot is three dimensional, point $$O$$ lies on the instantaneous rotational axis which perpendicular to the plane of the figure) Clearly, at a given instant, the velocity $$\nu_1$$ corresponding to the point of the ingot lying on the circle of radius $$OA$$, while the velocity $$\nu_2$$ to points lying on the circle of radius $$OB$$. (In a three dimensional ingot, the points having such velocities lie on cylindrical surface with radii $$OA$$ and $$OB$$ respectively)
The rotating rod starts from rest and acquires a rotational speed $$\omega =600$$ rev/min in $$2$$ seconds with constant angular acceleration. The magnitude of acceleration for time t is?
The velocity vector of a particle moving in the xy plane is given by $$\vec{v}=t\hat{i}+x\hat{j}$$. If initially, the particle was at origin then the equation of trajectory of the projectile is?
The rotating rod starts from rest and acquires a rotational speed $$\omega =600$$ rev/min in $$2$$ seconds with constant angular acceleration. The time t after starting before the acceleration vector of end P makes an angle $$45^o$$ with the rod is?
Prove that there is only one and one way in which a given vector can be resolved in given directions
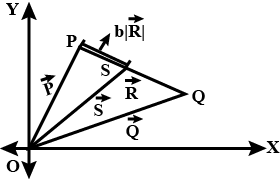
Three vectors $$\vec { P } ,\vec { Q }$$ & $$\vec { R }$$ are shown in figure let $$S$$ be any point on the vector $$\vec {R}$$, the dirt. Between $$P$$ & $$S$$ is if $$\left| \vec { R } \right|$$ find the general equation between $$P,Q$$ & $$S$$.
A ball is thrown horizontally from a point $$100\ m$$ above the ground with a speed of $$200\ m/s$$. Find (a) the time it takes to reach the ground, (b) the horizontal distance it travels before reaching the ground, (c) the velocity (direction and magnitude) with which it strikes the ground.
A projectile is launched at t=$$0$$, with velocity u at an angle with the horizontal
A ball is dropped from the roof of a tower of height h. The total distance covered by it in the last second of its motion is equal to the distance covered by it in first three seconds. What is the value of h? $$\left( {g = 10\,m/{s^2}} \right)$$
A particle is moving in a circle of radius R in such a way that at any instant the normal and tangential components of its acceleration are equal. If its speed at t = 0 is $$v_0$$, the time taken to complete the first revolution is
A man is sitting on the shore of a river. He is in the line of a $$1.0\ m$$ long boat and is $$5.5\ m$$ away from the centre of the boat. He wishes to throw an apple into the boat. If he can throw the apple only with a speed of $$10\ m/s$$, find the minimum and maximum angles of a projection for successful shot. Assume that the point of projection and the adge of the boat are in the same horizontal level.
If vectors A B and C have magnitude $$8$$,$$15$$, and $$17$$ units and A and B =C
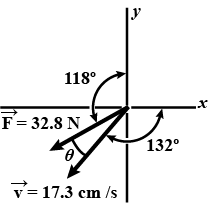
Assume $$\hat{e}_1$$ is as unit vector along the direction at $$30^oN$$ of $$E$$ and $$\hat{e}_2$$ is the unit vector along the direction at an angle $$60^oN$$ of $$W$$. $$A \ 10N$$ force acting towards south. Write down force in vector form.
A particle is moving along a circle of radius $$20/\pi$$ with constant tangential acceleration. The velocity of the particle is 80m/s at the end of 2nd revolution after motion has began. Then the tangential acceleration is
Water stands at a depth $$H$$ in a tank whose side wails are vertical. A hole is made on one of the walls at a depth $$h$$ below the water surface. Find at what distance from the foot of the wall does the emerging stream of water strike the floor?
Let $$\alpha ,\beta ,\gamma ,$$ be distinct real numbers. The points with position vectors $$\alpha \hat{i}+\beta \hat{j}+\gamma \hat{k}+,\beta \hat{i}+\gamma \hat{j}+\alpha \hat{k},\gamma \hat{i}+\alpha \hat{j}+\beta \hat{k}$$
A cannon ball is imparted an initial velocity of 30$${ ms }^{ -1 }$$ at an angle of $${ 53 }^{ o }$$ to the horizontal. Aafter some time the ball is seen to travel at an angle of $${ 37 }^{ o }$$ below horizontal.Compute the time consumed (in second) till then, upto nearest integer.
A particle moves along a circular path over a horizontal xy coordinate system, at constant speed. At time $${t_1} = 4.00$$ s, it is at point $$(5.00\,\,m,\,\,6.00\ m),$$ with velocity $$3\pi$$ $$\hat{j}$$ m/s and acceleration in the positive x direction. At time $${t_2} = 10.0\,\,s,$$ it has velocity $$-3\pi$$ $$\hat{i}$$ m/s and acceleration in the positive y direction. What are the (a) x and (b) y coordinates of the center of the circular path if $${t_2} - {t_1}$$ is less than one period?
A body is projected with a speed u m/s at an angle $$\beta $$ with the horizontal the kinetic energy at the highest point is 3/4 of the initial kinetic energy. the value of $$\beta $$ is
A projetile is projected with a speed u making an angle $$2\theta $$ with the horizontal. what is the speed when its direction of motion an angle $$\theta $$ with the horizontal
A particle is projected at $${ 60 }^{ \circ }$$ to the horizontal with a kinetic energy K The kinetic energy at the highest point is
If $$\vec{a}, \vec{b}, \vec{c}$$ are the position vectors of points A, B, C respectively. Prove that $${(\vec{b}\times\vec{c}+\vec{c}\times\vec{a}+\vec{a}\times\vec{b})}$$ is perpendicular to the plane ABC.
A watermelon seed has the following coordinates: $$x = -5.0 m$$, $$ y = 8.0 m$$ $$and$$ $$z = 0 m $$. Find its position vector (a) in unit-vector notation and as (b) a magnitude and (c) an angle relative to the positive direction of the $$x$$ axis. (d) Sketch the vector on a right-handed coordinate system. If the seed is moved to the $$xyz$$ coordinates $$(3.00 m, 0 m, 0 m)$$, what is its displacement (e) in unit-vector notation and as (f) a magnitude and (g) an angle relative to the positive $$x$$ direction?
(a) The position vector, according to Eq. 4-1, is $$r$$ $$=$$ $$(-5.0 m)\hat { i } + (8.0 m)\hat { j }$$
(b) The magnitude is $$\left| r \right|$$ $$=$$ $$\sqrt {{ x }^{2} +{ y }^{ 2 } +{z}^{ 2 }}$$ $$=$$ $$\sqrt {{(-5.0 m)}^{2} +{(8.0 m)}^{ 2 } +{(0 m)}^{ 2 }}$$ $$=$$ 9.4 m.
(c) Many calculators have polar $$↔$$ rectangular conversion capabilities that make this computation more efficient than what is shown below. Noting that the vector lies in the $$xy$$ plane and using Eq. 3-6, we obtain:
$$\theta ={ tan }^{ -1 }\left( \frac { 8.0m }{ -5.0m } \right) =-{ 58 }^{ o }\quad or\quad { 122 }^{ o }$$
where the latter possibility ($$122°$$ measured counterclockwise from the +$$x$$ direction) is chosen since the signs of the components imply the vector is in the second quadrant.
(d) The sketch is shown to the right. The vector is $$122°$$ counterclockwise from the $$+x$$ direction.
(e) The displacement is $$\Delta \vec { r } =\vec { r } -\vec { r } $$ where $$\vec { r } $$ is given in part (a) and $$\vec { r } =(3.0m)\hat { i } $$. Therefore, $$\Delta \vec { r } =(8.0m)\hat { i } -(8.0m)\hat { j } $$.
(f) The magnitude of the displacement is $$\left| \Delta \vec { r } \right| =\sqrt { { (8.0m) }^{ 2 }+{ (-8.0m) }^{ 2 } } =11m.$$
(g) The angle for the displacement, using Eq. 3.6, is $${ tan }^{ -1 }\left( \frac { 8.0m }{ -8.0m } \right) ={ -45 }^{ o }or{ 135 }^{ o }$$ where we choose the former possibility $$(−45°, or 45°$$ measured clockwise from $$+x$$) since the signs of the components imply the vector is in the fourth quadrant. A sketch of $$\Delta \vec { r } $$ is shown on the right.
(b) The magnitude is $$\left| r \right|$$ $$=$$ $$\sqrt {{ x }^{2} +{ y }^{ 2 } +{z}^{ 2 }}$$ $$=$$ $$\sqrt {{(-5.0 m)}^{2} +{(8.0 m)}^{ 2 } +{(0 m)}^{ 2 }}$$ $$=$$ 9.4 m.
(c) Many calculators have polar $$↔$$ rectangular conversion capabilities that make this computation more efficient than what is shown below. Noting that the vector lies in the $$xy$$ plane and using Eq. 3-6, we obtain:
$$\theta ={ tan }^{ -1 }\left( \frac { 8.0m }{ -5.0m } \right) =-{ 58 }^{ o }\quad or\quad { 122 }^{ o }$$
where the latter possibility ($$122°$$ measured counterclockwise from the +$$x$$ direction) is chosen since the signs of the components imply the vector is in the second quadrant.
(d) The sketch is shown to the right. The vector is $$122°$$ counterclockwise from the $$+x$$ direction.
(e) The displacement is $$\Delta \vec { r } =\vec { r } -\vec { r } $$ where $$\vec { r } $$ is given in part (a) and $$\vec { r } =(3.0m)\hat { i } $$. Therefore, $$\Delta \vec { r } =(8.0m)\hat { i } -(8.0m)\hat { j } $$.
(f) The magnitude of the displacement is $$\left| \Delta \vec { r } \right| =\sqrt { { (8.0m) }^{ 2 }+{ (-8.0m) }^{ 2 } } =11m.$$
(g) The angle for the displacement, using Eq. 3.6, is $${ tan }^{ -1 }\left( \frac { 8.0m }{ -8.0m } \right) ={ -45 }^{ o }or{ 135 }^{ o }$$ where we choose the former possibility $$(−45°, or 45°$$ measured clockwise from $$+x$$) since the signs of the components imply the vector is in the fourth quadrant. A sketch of $$\Delta \vec { r } $$ is shown on the right.
Starting from rest, a wheel has constant $$ \alpha $$ = 3.0 rad/$$ s^{2} $$ During a certain 4.0 s interval, it turns through 120 rad. How much time did it take to reach that 4.0 s interval
A disk rotated about its central axis starting from rest and accelerates with constant angular acceleration. At one time it is rotating at 10 rev/s; 60 revolutions later, its angular speed is 15 rev/s.Calculate (a) the angular acceleration, (b) the time required to complete the 60 revolutions, (c) the time required to reach the 10 rev/s angular speed, and (d) the number of revolutions from rest until the time the disk reaches the 10 rev/s angular speed.
At t=0, a flywheel has an angular velocity of 4.7 rad/s, a constant angular acceleration of 0.25 rad/$$ s^{2} $$, and a reference line at $$ \theta _{0}=0 $$. (a) Through what maximum angle $$ \theta _{max} $$ will the reference line turn in the positive direction What are the (b) first and (c) second times the reference line will be at $$ \theta =\dfrac{1}{2}\theta _{max} $$ At what b(d) negative time and (e) positive time will the reference line be at $$ \theta =10.5 rad (f) Graph $$ \theta $$ versus t, and indicate your answers.
A flywheel turns through 40 rev as it slow from an angular speed of 1.5 rad/s to a stop. (a) Assuming a constant angular acceleration , find the time for it to come to rest. (b) What is its angular acceleration (c) How much time is required for it complete the first 20 of the 40 revolutions
A vinyl record on a turntable rotates at $$ 33\dfrac{1}{3} $$ rev/min. (a) What is its angular speed in radians per second What is the linear speed of a point on the record (b) 15 cm and (c) 7.4 cm from the turntable axis
Between 1911 and 1990, the top of the leaning bell tower at Pisa, Italy, moved toward the south at an average rate of 1.2 mm/y. The tower is 55 m tall. In radians per second, what is the average angular speed of the tower's top about its base?
What are the magnitudes of (a) the angular velocity, (b) the radial acceleration, and (c) the tangential acceleration of a spaceship taking a circular turn of radius 3220 km at a speed of 29 000 km/h
Trucks can be run on energy stored in a rotating flywheel, with an electric motor getting the flywheel up to its top speed of 200 $$ \pi $$ rad/s. Suppose that one such flywheel is a solid, uniform cylinder with a mass of 500 kg and a radius of 1.0 m. (a) What is the kinetic energy of the flywheel after changing (b) If the truck uses an average power of 8,0 kW, for how many minutes can it operate between chargings
An object rotates about a fixed axis, and the angular position of a reference line on the object is given by $$0 = 0.40e^{2t}$$, where 0 is in radians and t is in seconds. Consider a point on the object that is 4.0 cm from the axis of rotation. At t = 0, what are the magnitudes of the point's (a) tangential component of acceleration and (b) radial component of acceleration?
A particle moves so that its position (in meters) as a function of time (in seconds) is $$\vec { r } =\hat { i } +4{ t }^{ 2 }\hat { j } +t\hat { k } .$$
Write expressions for (a) its velocity and (b) its acceleration as functions of time.
The acceleration of a particle moving only on a horizontal $$xy$$ plane is given by $$\vec { a } =3t\hat { i } +4t\hat { j },$$ where $$\vec { a } $$ is in meters per second squared and $$t$$ is in seconds. At $$t=0$$, the position vector $$\vec { r } =(20.0m)\hat { i } +(40.0m)\hat { j } .$$ locates the particle, which then has the velocity vector $$\vec { v } =(5.00m/s)\hat { i } +(2.00m/s)\hat { j } .$$ At $$t=4.00 s,$$ what are (a) its position vector in unit vector notation and (b) the angle between its direction of travel and the positive direction of the $$x$$ axis?
In Fig. 10-31, wheel A of radius $$r_{A} = 10$$ is coupled by belt B to wheel C of radius $$r_{C} = 25$$ cm. The angular speed of wheel A is increased from rest at a constant rate of 1.6 $$rad/s^{2}$$ . Find the time needed for wheel C to reach an angular speed of 100 rev/min, assuming the belt does not slip. (Hint : If the belt does not slip, the linear speeds at the two rims must be equal.)
The position $$\vec { r } $$ of a particle moving in an $$xy$$ plane is given by $$\vec { r } =(2.00{ t }^{ 3 }-5.00t)\hat { i } +(6.00-7.00{ t }^{ 4 })\hat { j, } $$ with $$\vec { r } $$ in meter and $$t$$ in seconds. In unit-vector notation, calculate (a) $$\vec { r } $$, (b) \vec { v }, and (c) \vec { a } for $$t=2.00s$$. (d) What is the angle between the positive direction of the $$x axis$$ and a line tangent to the particle's path at $$t = 2.00s$$
A particle leaves the origin with an initial velocity $$\vec { v } =\quad (3.00\hat { i } )m/s$$ and a constant acceleration $$\vec { a } =\quad (-1.00\hat { i } -0.500\hat { j } ){ m/s }^{ 2 }$$ . When it reaches its maximum $$x$$ coordinate, what are its (a) velocity and (b) position vector?
A lowly high diver pushes off horizontally with a speed of $$2.00 m/s$$ from the platform edge $$10.0 m$$ above the surface of the water. (a) At what horizontal distance from the edge is the diver $$0.800 s$$ after pushing off? (b) At what vertical distance above the surface of the water is the diver just then? (c) At what horizontal distance from the edge does the diver strike the water?
The initial velocity has no vertical component $$({ \theta }_{ 0 }\quad = 0 )$$ — only an x component. Eqs. (4-21) and (4-22) can be simplified to
$$x-{ x }_{ 0 }={ v }_{ 0x }t$$
$$y-{ y }_{ 0 }={ v }_{ 0y }t-\dfrac { 1 }{ 2 } g{ t }^{ 2 }=-\dfrac { 1 }{ 2 } g{ t }^{ 2 }$$
where $${ x }_{ 0 }= 0, { v }_{ 0x }={ v }_{ 0 } =+2.0m/s$$, and $${ y }_{ 0 } = +10.0 m$$ (taking the water surface to be at $$y = 0$$). The setup of the problem is shown in the figure below.
$$x-{ x }_{ 0 }={ v }_{ 0x }t$$
$$y-{ y }_{ 0 }={ v }_{ 0y }t-\dfrac { 1 }{ 2 } g{ t }^{ 2 }=-\dfrac { 1 }{ 2 } g{ t }^{ 2 }$$
where $${ x }_{ 0 }= 0, { v }_{ 0x }={ v }_{ 0 } =+2.0m/s$$, and $${ y }_{ 0 } = +10.0 m$$ (taking the water surface to be at $$y = 0$$). The setup of the problem is shown in the figure below.
(a) At $$t = 0.80s$$, the horizontal distance of the diver from the edge is
$$x={ x }_{ 0 }+{ v }_{ 0x }t=0+(2.0m/s)(0.80s)=1.60m$$
$$x={ x }_{ 0 }+{ v }_{ 0x }t=0+(2.0m/s)(0.80s)=1.60m$$
(b) Similarly, using the second equation for the vertical motion, we obtain
$$y={ y }_{ 0 }-\dfrac { 1 }{ 2 } g{ t }^{ 2 }=10.0m-\dfrac { 1 }{ 2 } (9.80m/{ s }^{ 2 })(0.80s)^{ 2 }=6.86m.$$
$$y={ y }_{ 0 }-\dfrac { 1 }{ 2 } g{ t }^{ 2 }=10.0m-\dfrac { 1 }{ 2 } (9.80m/{ s }^{ 2 })(0.80s)^{ 2 }=6.86m.$$
(c) At the instant the diver strikes the water surface, $$y = 0$$. Solving for $$t$$ using the
equation$$y={ y }_{ 0 }-\dfrac { 1 }{ 2 } g{ t }^{ 2 }$$ leads to
equation$$y={ y }_{ 0 }-\dfrac { 1 }{ 2 } g{ t }^{ 2 }$$ leads to
$$t=\sqrt { \dfrac { 2{ y }_{ 0 } }{ g } } =\sqrt { \dfrac { 2(10.0m) }{ 9.80m/{ s }^{ 2 } } } =1.43s.$$
During this time, the x-displacement of the diver is $$R = x = (2.00 m/s)(1.43 s) = 2.86 m.$$
During this time, the x-displacement of the diver is $$R = x = (2.00 m/s)(1.43 s) = 2.86 m.$$
Prove that the path of projectile motion in parabolic.
path of a projectile
let $$ OX $$ be a horizontal line on the ground and $$ OY $$ be a verticle line $$ O $$ is the origin for $$ X $$ and $$ Y $$ axis Consider that the projectile is fired with velocity u and making angle $$ \theta $$ with the horizontal form the point $$ 'O' $$ on the ground
The velocity of projection of the projectile can be resolved into the following two components
(i) $$ u_x = u co s\theta , along OX $$
(ii) $$ u_y = u sin \theta , along OY $$
As the projectile moves it covers distance along the horizontal due to the horizontal component $$u cos \theta $$ of the velocity of projection and along verticle due to the vertical component $$ u sin \theta $$ . let that any time t , the projectile reaches the point P , So that its distance along the $$ X $$ and $$ Y $$ axis are given by $$ x $$ and $$ y $$ respetively.
Motion along horizontal direction : it we neglect friction due to air, then horizontal component of the velocity i.e. $$ u cos \theta $$ will remain constant. thus
Initial velocity along the horizontal $$ u_x = u cos \theta $$
Acceleration along the horizontal $$a_x = 0 $$
The position of the projectile along X-axis at any time t is given by
$$ x = u_x t + \frac {1}{2} a_xt^2 $$
Putting $$ u_x = u cos \theta $$ and $$ a_x = 0 $$ we have
$$ x = ( u cos \theta )t + \frac {1}{2} (o)t^2 $$
or $$ x = ( u cos \theta )t $$
or $$ t = \frac {x}{u cos \theta} .......(i) $$
Motion along verticle direction:
The velocity of the projectile along the verticle goes on decreasing due to effect of gravity initial velocity along vertical $$ u_y = u sin \theta $$
Acceleration along vertical $$ a_y = - g $$
The position of the projectile along T-axis at any time t is given by
$$ y = u_yt + \frac {1}{2} a_y t^2 $$
Putting $$ u_y = u sin \theta $$ and $$ a_y = -g $$ we have
$$ y = ( u sin \theta) t + \frac {1}{2}(-g) t^2 $$
or $$ y = ( u sin \theta ) t - \frac {1}{2} gt^2 .....(2) $$
Putting the value of t from equation (1) in equation (2) we get
$$ y = ( u sin \theta ) \frac {x}{u cos \theta } - \frac {1}{2} g( \frac {x}{ u cos \theta} )^2 $$
or $$ y = x tan \theta -( \frac {g}{2u^2 cos^2 \theta })x^2 ...(3) $$
This is an equation of a parabola . hence the path of projectile projected at some angle with the horizontal direction is a parabola.
let $$ OX $$ be a horizontal line on the ground and $$ OY $$ be a verticle line $$ O $$ is the origin for $$ X $$ and $$ Y $$ axis Consider that the projectile is fired with velocity u and making angle $$ \theta $$ with the horizontal form the point $$ 'O' $$ on the ground
The velocity of projection of the projectile can be resolved into the following two components
(i) $$ u_x = u co s\theta , along OX $$
(ii) $$ u_y = u sin \theta , along OY $$
As the projectile moves it covers distance along the horizontal due to the horizontal component $$u cos \theta $$ of the velocity of projection and along verticle due to the vertical component $$ u sin \theta $$ . let that any time t , the projectile reaches the point P , So that its distance along the $$ X $$ and $$ Y $$ axis are given by $$ x $$ and $$ y $$ respetively.
Motion along horizontal direction : it we neglect friction due to air, then horizontal component of the velocity i.e. $$ u cos \theta $$ will remain constant. thus
Initial velocity along the horizontal $$ u_x = u cos \theta $$
Acceleration along the horizontal $$a_x = 0 $$
The position of the projectile along X-axis at any time t is given by
$$ x = u_x t + \frac {1}{2} a_xt^2 $$
Putting $$ u_x = u cos \theta $$ and $$ a_x = 0 $$ we have
$$ x = ( u cos \theta )t + \frac {1}{2} (o)t^2 $$
or $$ x = ( u cos \theta )t $$
or $$ t = \frac {x}{u cos \theta} .......(i) $$
Motion along verticle direction:
The velocity of the projectile along the verticle goes on decreasing due to effect of gravity initial velocity along vertical $$ u_y = u sin \theta $$
Acceleration along vertical $$ a_y = - g $$
The position of the projectile along T-axis at any time t is given by
$$ y = u_yt + \frac {1}{2} a_y t^2 $$
Putting $$ u_y = u sin \theta $$ and $$ a_y = -g $$ we have
$$ y = ( u sin \theta) t + \frac {1}{2}(-g) t^2 $$
or $$ y = ( u sin \theta ) t - \frac {1}{2} gt^2 .....(2) $$
Putting the value of t from equation (1) in equation (2) we get
$$ y = ( u sin \theta ) \frac {x}{u cos \theta } - \frac {1}{2} g( \frac {x}{ u cos \theta} )^2 $$
or $$ y = x tan \theta -( \frac {g}{2u^2 cos^2 \theta })x^2 ...(3) $$
This is an equation of a parabola . hence the path of projectile projected at some angle with the horizontal direction is a parabola.
In a jump spike, a volleyball player slams the ball from overhead and toward the opposite floor. Controlling the angle of the spike is difficult. Suppose a ball is spiked from a height of $$2.30 m$$ with an initial speed of $$20.0 m/s$$ at a downward angle of $$18.00°$$. How much farther on the opposite floor would it have landed if the downward angle were, instead, $$8.00°$$?
Two particles move along an $$x$$ axis. The position of particle 1 is given by $$x$$ = 6.00$$t^{2} + 3.00t + 2.00$$ (in meters and seconds); the acceleration of particle 2 is given by $$a = -8.00t$$ (in meters per second squared and seconds) and, at $$t = 0$$, its velocity is 20 m/s. When the
velocities of the particles match, what is their velocity?
Motion in two dimension in a plane can be studied by expression position, velocity and acceleration as vectors in Cartesian co-ordinates $$\vec { A } ={ A }_{ 2 }\hat { i } +{ A }_{ 2 }\hat { j } $$ where $$\hat { i } ,\hat { j } $$ are unit along x and y directions, respectively and $${ A }_{ 2 }$$ and $${ A }_{ 2 }$$ are corresponding components of $$\vec { A } $$ (Figure). Motion can also be studied by expressing vectors in circular polar co-ordinates $$\vec { A } ={ A }_{ 1 }\hat { r } +{ A }_{ \theta }\hat { \theta } $$
where $$\hat { r } =\frac { \vec { r } }{ \left| r \right| } =cos\theta \hat { i } +cos\theta \hat { j } $$
and $$\hat { \theta } =-sin\theta \hat { i } +cos\theta \hat { j } $$ are unit vectors along direction in which $$'r' and '\theta '.$$
(a) Express $$\hat { i } $$ and $$\hat { j } $$ in terms of $$\hat { r } and\quad \hat { \theta } $$.
(b) Show that both $$ \hat { r } and\quad \hat { \theta } $$ are unit vectors and are perpendicular to each other.
(c) Shows that $$\frac { d }{ dt } \hat { r } =\omega \hat { \theta } \quad $$ where $$\omega =\frac { d\theta }{ dt } $$ and $$\frac { d\hat { \theta } }{ dt } =-\omega \hat { r } $$
(d) For a particle moving along a spiral given by $$\vec { r } =\left| \hat { a } \right| \left| \hat { \theta } \right| \left| \hat { r } \right| $$ where $$a=1$$ (unit), find dimensions of 'a'.
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
A gun can fire shells with maximum speed $${ v }_{ 0 }$$ and the maximum horizontal range that can be achieved is $$R=\frac { { v }_{ 0 }^{ 2 } }{ g } $$.If a target farther away by distance $$\Delta x$$ (beyond R) has to be hit with the same gun as shown in the figure. Show that it could be achieved by raising the gun as shown in figure here. Shown that a it could be achieved by raising the gun to a height at least $$h=\quad \Delta x[1+\frac { \Delta x }{ R } ]$$
Hint: This problem can be approached in two different ways:
(i) Refer to the diagram : target T is at the horizont
(ii) From point P in the diagram : Projection at speed $${ v }_{ 0 }$$ at an angle $$\theta $$ below horizontal with height $$h$$ and horizontaal distance $$X=R+\Delta x$$ and below the point of projection $$y=-h$$. l range $$\Delta x.1$$
The main concept used: This problem can be solved In two different ways:
(i) The target is at horizontal distance $$(R + \Delta x)$$ and below the point of projection $$h$$ metre below i.e., $$y = -h$$.
The motion of projectile after point $$P$$ to $$T$$: projection speed is at an angle $$(-\theta)$$ i.e., $$\theta^o$$ below horizontal and vertical height covered it Is $$(-h)$$ and horizontal range $$\Delta x$$.
Solution:
$$R = \dfrac{V^2_g}{g}$$ ...(i) that it is maximum range of projectile
$$\therefore$$ The angle of projection $$\theta = 45^o$$
Let the gun is raised to a height $$h$$ from the horizontal level of target $$T$$. So that the projectile can hit the target $$T$$.
Total range of projectile must be $$= (R+ \Delta x)$$
Horizontal component of velocity at $$A = u_0 \,\cos \theta$$
The motion of the projectile from $$P$$ to $$T$$: As $$A$$ and $$P$$ are on the same level. So the magnitude of velocity will be same at $$A$$ and $$P$$.
$$\therefore$$ But the direction of velocity will be below horizontal,
so horizontal velocity at $$P = u_x \cos \theta$$
So vertical velocity at $$P = u_y = v_0 \sin \theta$$
$$h = ut + \dfrac{1}{2} at^2$$
$$h = -v_0 \sin \theta(t) + \dfrac{1}{2} gt^2$$ ...(ii)
Consider horizontal motion from $$A$$ to $$T = \text{distance} (R + \Delta x) = v_0 \cos \theta.t$$
$$t = \dfrac{R + \Delta x}{v_0 \cos \theta}$$
Substitute $$t$$ in (ii) $$h = -v_0 \sin \theta \left[\dfrac{R + \Delta x}{v_0 \cos \theta}\right] + \dfrac{1}{2} g \dfrac{(R + \Delta x)^2}{v^2_0 \cos^2 \theta}$$
$$h = -\tan \theta (R - \Delta x) + \dfrac{1}{2} \left(\dfrac{g}{v^2_0}\right) \dfrac{)R + \Delta x)^2}{1/2} \theta = 45^o$$
$$h = -(R + \Delta x) + \dfrac{1}{R} (R^2 + \Delta x^2 + 2R \Delta x) \left[\because \dfrac{g}{v^2_0} = \dfrac{1}{R}\right]$$
$$= -R - \Delta x + R + \dfrac{\Delta x^2}{R} + 2\Delta x = \Delta x + \dfrac{\Delta x^2}{R}$$
$$h = \Delta x \left[1 + \dfrac{\Delta x}{R}\right]$$ Hence proved.
(i) The target is at horizontal distance $$(R + \Delta x)$$ and below the point of projection $$h$$ metre below i.e., $$y = -h$$.
The motion of projectile after point $$P$$ to $$T$$: projection speed is at an angle $$(-\theta)$$ i.e., $$\theta^o$$ below horizontal and vertical height covered it Is $$(-h)$$ and horizontal range $$\Delta x$$.
Solution:
$$R = \dfrac{V^2_g}{g}$$ ...(i) that it is maximum range of projectile
$$\therefore$$ The angle of projection $$\theta = 45^o$$
Let the gun is raised to a height $$h$$ from the horizontal level of target $$T$$. So that the projectile can hit the target $$T$$.
Total range of projectile must be $$= (R+ \Delta x)$$
Horizontal component of velocity at $$A = u_0 \,\cos \theta$$
The motion of the projectile from $$P$$ to $$T$$: As $$A$$ and $$P$$ are on the same level. So the magnitude of velocity will be same at $$A$$ and $$P$$.
$$\therefore$$ But the direction of velocity will be below horizontal,
so horizontal velocity at $$P = u_x \cos \theta$$
So vertical velocity at $$P = u_y = v_0 \sin \theta$$
$$h = ut + \dfrac{1}{2} at^2$$
$$h = -v_0 \sin \theta(t) + \dfrac{1}{2} gt^2$$ ...(ii)
Consider horizontal motion from $$A$$ to $$T = \text{distance} (R + \Delta x) = v_0 \cos \theta.t$$
$$t = \dfrac{R + \Delta x}{v_0 \cos \theta}$$
Substitute $$t$$ in (ii) $$h = -v_0 \sin \theta \left[\dfrac{R + \Delta x}{v_0 \cos \theta}\right] + \dfrac{1}{2} g \dfrac{(R + \Delta x)^2}{v^2_0 \cos^2 \theta}$$
$$h = -\tan \theta (R - \Delta x) + \dfrac{1}{2} \left(\dfrac{g}{v^2_0}\right) \dfrac{)R + \Delta x)^2}{1/2} \theta = 45^o$$
$$h = -(R + \Delta x) + \dfrac{1}{R} (R^2 + \Delta x^2 + 2R \Delta x) \left[\because \dfrac{g}{v^2_0} = \dfrac{1}{R}\right]$$
$$= -R - \Delta x + R + \dfrac{\Delta x^2}{R} + 2\Delta x = \Delta x + \dfrac{\Delta x^2}{R}$$
$$h = \Delta x \left[1 + \dfrac{\Delta x}{R}\right]$$ Hence proved.
A graphing surprise.At time $$t = 0$$, a burrito is launched from level ground, with an initial speed of $$16.0 m/s$$ and launch angle . Imagine a position vector $$\vec { r } $$ continuously directed from the launching point to the burrito during the flight. Graph the magnitude $$r$$ of the position vector for (a) $${ \theta }_{ 0 }= 40.0$$ and (b) $${ \theta }_{ 0 }= 80.0$$. For = $${ \theta }_{ 0 }=40.0$$, (c) when does $$r$$ reach its maximum value, (d) what is that value, and how far (e) horizontally and (f) vertically is the burrito from the launch point? For $${ \theta }_{ 0 } = 80.0$$, (g) when does $$r$$ reach its maximum value, (h) what is that value, and how far (i) horizontally and (j) vertically is the burrito from the launch point?
the mean velocity vector averaged over the first $$t$$ seconds of motion, and the modulus of this vector.
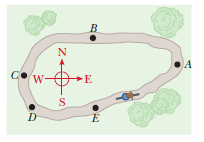
A child is practicing for a BMX race. His speed remains constant as he goes counterclockwise around a level track with two straight sections and two nearly semicircular sections as shown in the aerial view of above figure. (a) Rank the magnitudes of his acceleration at the points $$A, B, C, D$$, and $$E$$ from largest to smallest. If his acceleration is the same size at two points, display that fact in your ranking. If his acceleration is zero, display that fact. (b) What are the directions of his velocity at points $$A, B$$, and $$C$$? For each point, choose one: north, south, east, west, or nonexistent. (c) What are the directions of his acceleration at points $$A, B$$, and $$C$$?
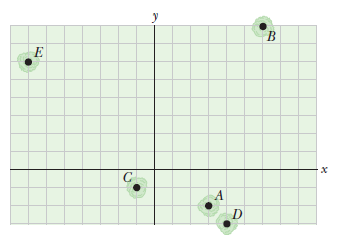
A pirate has buried his treasure on an island with five trees located at the points $$(30.0 m, 220.0 m), (60.0 m, 80.0 m), (210.0 m, 210.0 m), (40.0 m, 230.0 m)$$, and $$(270.0 m, 60.0 m)$$, all measured relative to some origin, as shown in above figure. His ships log instructs you to start at tree A and move toward tree $$B$$, but to cover only one-half the distance between $$A$$ and $$B$$. Then move toward tree $$C$$, covering one-third the distance between your current location and $$C$$. Next move toward tree $$D$$, covering one-fourth the distance between where you are and $$D$$. Finally move toward tree $$E$$, covering one-fifth the distance between you and $$E$$, stop, and dig. (a) Assume you have correctly determined the order in which the pirate labeled the trees as $$A, B, C, D$$, and $$E$$ as shown in the figure. What are the coordinates of the point where his treasure is buried? (b) What If? What if you do not really know the way the pirate labeled the trees? What would happen to the answer if you rearranged the order of the trees, for instance, to $$B (30 m, 220 m), A (60 m, 80 m), E (210 m, 210 m), C (40 m, 230 m), and D (270 m, 60 m)$$? State reasoning to show that the answer does not depend on the order in which the trees are labeled.
An ice skater is executing a figure eight, consisting of two identically shaped, tangent circular paths. Throughout the first loop she increases her speed uniformly, and during the second loop she moves at a constant speed. Draw a motion diagram showing her velocity and acceleration vectors at several points along the path of motion.
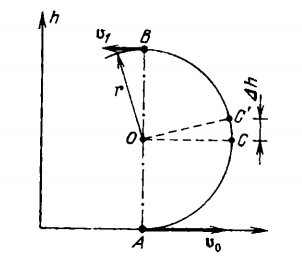
An aeroplane flying along the horizontal at a velocity $$\nu_0$$ starts too ascend describing a circle in the vertical plane. The velocity of the plane changes with height $$j$$ above the initial level of motion according to the law $$\nu_2=\nu_0^2-2a_0h$$. The velocity of the plane at the upper point of the trajectory is $$\nu_0=\nu_0/2$$
Determine the acceleration $$a$$ of the plane at the moment when its velocity is directed vertically upwards.
Let us consider the
motion of the plane starting from the moment it goes over to the circular path
Fig. By hypothesis at the upper point $$B$$ of the path, the velocity of the
plane is $$\nu_1= \nu_0/2$$, and hence the radius $$r$$ of the circle described
by the plane can be found from the relation
$$\dfrac{\nu_0^2}{4} = \nu_0^2- 2a_0.2r$$,
which is obtained from the law of motion of the
plane for $$h=2r$$. At point $$C$$ of the path where the velocity of the plane
is directed upwards, the total acceleration will be the sum of the centripetal
acceleration $$a_c= \nu_c^2 / r (\nu_c^2 = \nu_0^2 - 2a_0 r,$$ where $$\nu_C$$
is the velocity of the plane at point $$C$$) and the tangential acceleration
$$a_t$$ (this acceleration is responsible for the change in the magnitude of
the velocity).
In order to find the tangential acceleration let
us consider a small displacement of the plane from point $$C$$ to point
$$C^{'}$$ Then $$\nu_{C^{'}}^2 = \nu_0^2 -2 a_0 (r+ \Delta h)$$. Therefore,
$$\nu_{C^{'}}^2 -\nu_C^2 = -2a_0 \Delta h$$, where $$\Delta h$$ is the change
in the altitude of the plane as it goes over to point $$C^{'}$$ Let us divide
both sides of the obtained relation by the time intervals $$\Delta t$$ during
which this change takes place:
$$\dfrac{\nu^2_{C^{'}} - \nu_C^2}{ \Delta
t}=$$$$ - \dfrac{2 a_0 \Delta h}{\Delta t}.$$
Then, making point $$C^{'}$$ tend to $$C$$ and
$$\Delta t$$ to zero, we obtain
$$2a_t \nu_C =- 2 a_0 \nu_C$$
Hence $$a_t= -a_0$$. The total acceleration of
the plane at the moment when the velocity has the upward direction is then
$$a=\sqrt{ a_0^2 + \left( \dfrac{\nu_C^2}{r}
\right)^2}= \dfrac{a_0 \sqrt{109}}{3}$$
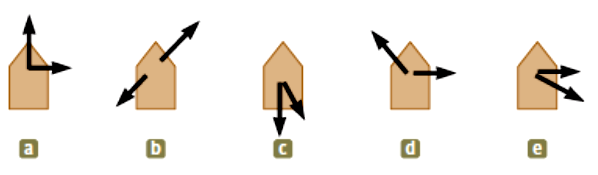
The cutting tool on a lathe is given two displacements, one of magnitude $$4 cm$$ and one of magnitude $$3 cm$$, in each one of five situations (a) through (e) diagrammed in above figure. Rank these situations according to the magnitude of the total displacement of the tool, putting the situation with the greatest resultant magnitude first. If the total displacement is the same size in two situations, give those letters equal ranks.
A radar station locates a sinking ship at range $$17.3 km$$ and bearing $$136^{0}$$ clockwise from north. From the same station, a rescue plane is at horizontal range $$19.6 km, 153^{0}$$ clockwise from north, with elevation $$2.20 km$$. (a) Write the position vector for the ship relative to the plane, letting $$\hat{i}$$ represent east, $$\hat{j}$$ north, and $$\hat{k}$$ up. (b) How far apart are the plane and ship?
A body with zero initial velocity moves down an inclined plane from a height $$h$$ and then ascends along the same plane with an initial velocity such that it stops at the same height$$h$$. In which case is the time of notion longer?
Kathy tests her new sports car by racing with Stan, an experienced racer. Both start from rest, but Kathy leaves the starting line $$1.00 s$$ after Stan does. Stan moves with a constant acceleration of $$3.50 m/s^{2}$$, while Kathy maintains an acceleration of $$4.90 m/s^{2}$$. Find (a) the time at which Kathy overtakes Stan, (b) the distance she travels before she catches him, and (c) the speeds of both cars at the instant Kathy overtakes Stan.
A small object with mass $$4.00\ kg$$ counter clockwise with constant angular speed $$1.50\ rad/s$$ in a circle of radius $$3.00\ m$$ centered at the origin. It starts at the point with position vector $$3.00\ \hat i\ m$$. It then undergoes an angular displacement of $$9.00\ rad$$. In what quadrant is the particle located, and what angle does its position vector make with the positive $$x$$ axis?
Pursued by ferocious wolves, you are in a sleight with no horses, gliding without friction across an ice-covered lake. You take an action described by the equations
$$(270\ kg)(7.50\ m/s)\hat{i}=(15.0\ kg)(-v_{1f}\hat{i})+(255\ kg)(v_{2f}\hat{i})$$
$$v_{1f}+v_{2f}=8.00\ m/s$$
Find the values of $$v_{1f}$$ and $$v_{2f}$$
A projectile is launched at some angle to the horizontal with some initial speed $$v_{i}$$, and air resistance is negligible. (a) Is the projectile a freely falling body? (b) What is its acceleration in the vertical direction? (c) What is its acceleration in the horizontal direction?
A bar on a hinge starts from rest and rotates with an angular acceleration $$\alpha=10+6t$$, where $$\alpha$$ is in $$rad/s2$$ and $$t$$ is in seconds. Determine the angle in radians through which the bar turns in the first $$4.00\ s$$.
A child of mass $$m$$ starts from rest and slides without friction from a height $$h$$ along a slide next to a pool Fig. She is launched from a height $$h/5$$ into the air over the pool. We wish to find the maximum height she reaches above the water in her projectile motion Express teh total energy of the system when the child is at the highest point in her projectile motion.
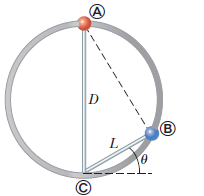
Two thin rods are fastened to the inside of a circular ring as shown in above figure. One rod of length $$D$$ is vertical, and the other of length $$L$$ makes an angle $$\theta$$ with the horizontal. The two rods and the ring lie in a vertical plane. Two small beads are free to slide without friction along the rods. (a) If the two beads are released from rest simultaneously from the positions shown, use your intuition and guess which bead reaches the bottom first. (b) Find an expression for the time interval required for the red bead to fall from point $$A$$ to point $$C$$ in terms of $$g$$ and $$D$$. (c) Find an expression for the time interval required for the blue bead to slide from point $$B$$ to point $$C$$ in terms of $$g, L$$, and $$\theta$$. (d) Show that the two time intervals found in parts (b) and (c) are equal. Hint: What is the angle between the chords of the circle $$A B$$ and $$B C$$? (e) Do these results surprise you? Was your intuitive guess in part (a) correct?
Pursued by ferocious wolves, you are in a sleight with no horses, gliding without friction across an ice-covered lake. You take an action described by the equations
$$(270\ kg)(7.50\ m/s)\hat{i}=(15.0\ kg)(-v_{1f}\hat{i})+(255\ kg)(v_{2f}\hat{i})$$
$$v_{1f}+v_{2f}=8.00\ m/s$$
Complete the statement of the problem, giving the data and identifying the unknowns.
A small object with mass $$4.00\ kg$$ counterclockwise with constant angular speed $$1.50\ rad/s$$ in a circle of radius $$3.00\ m$$ centered at the origin. It starts at the point with position vector $$3.00\ \hat i\ m$$. It then undergoes an angular displacement of $$9.00\ rad$$.
What is its new position vector? Use unit-vector notation for all vector answers.
Class 11 Engineering Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Physical World Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work,Energy And Power Extra Questions