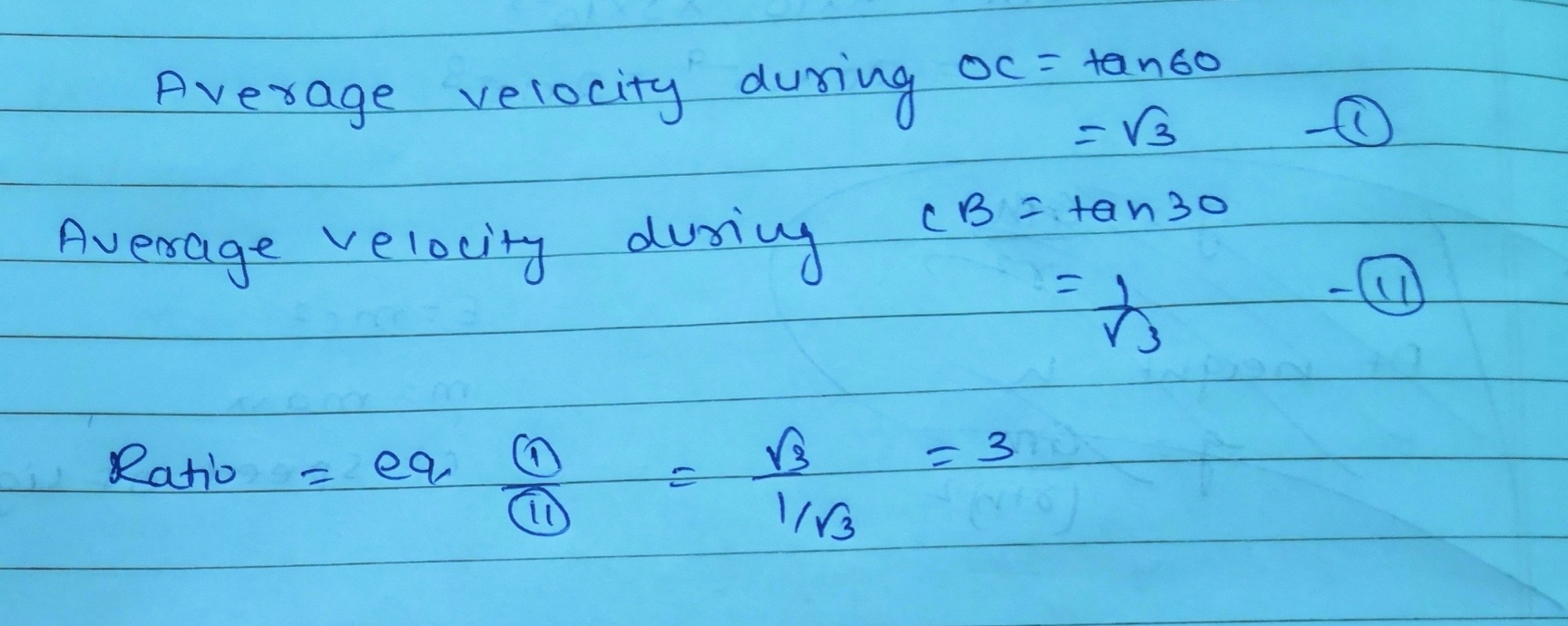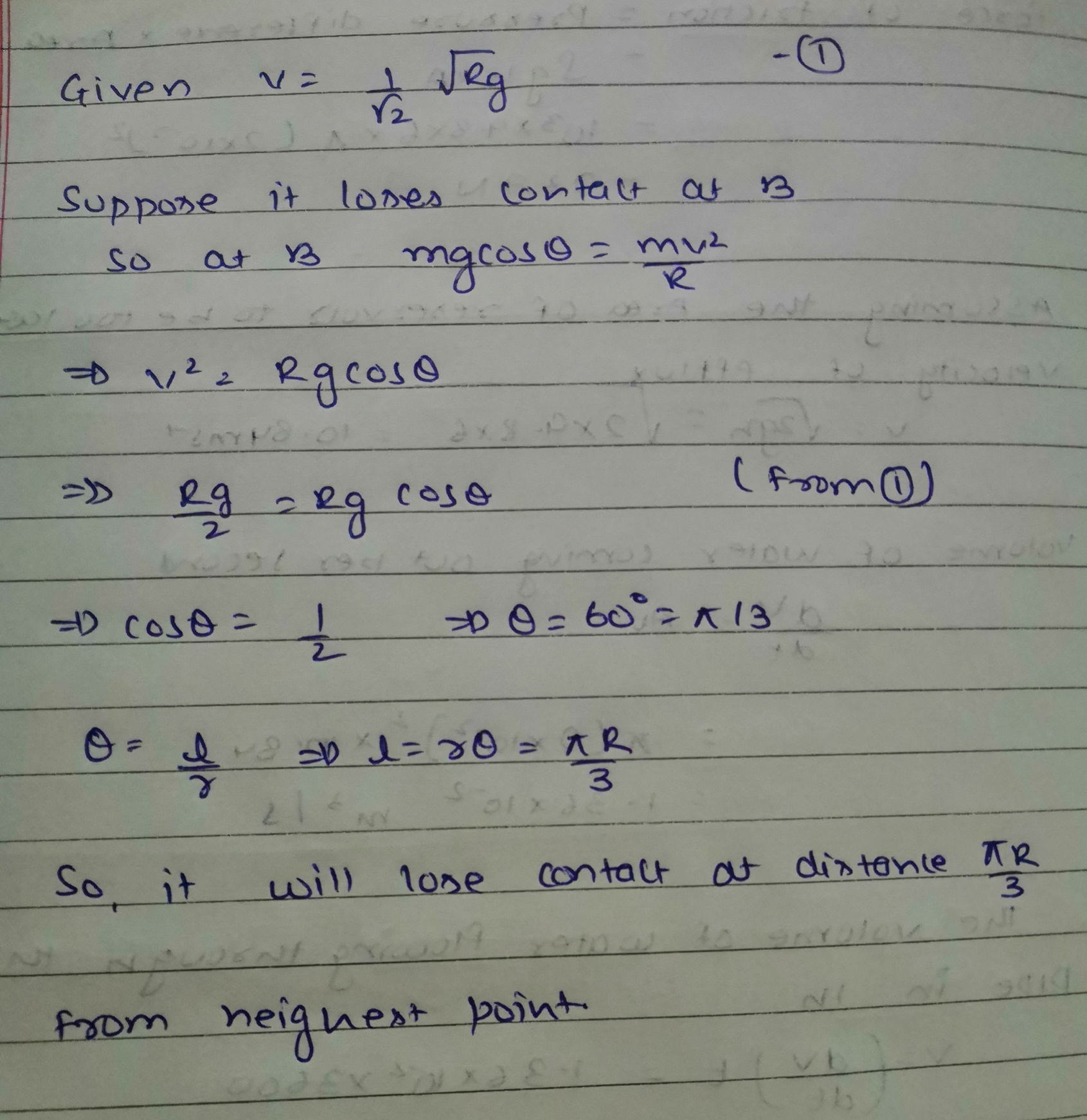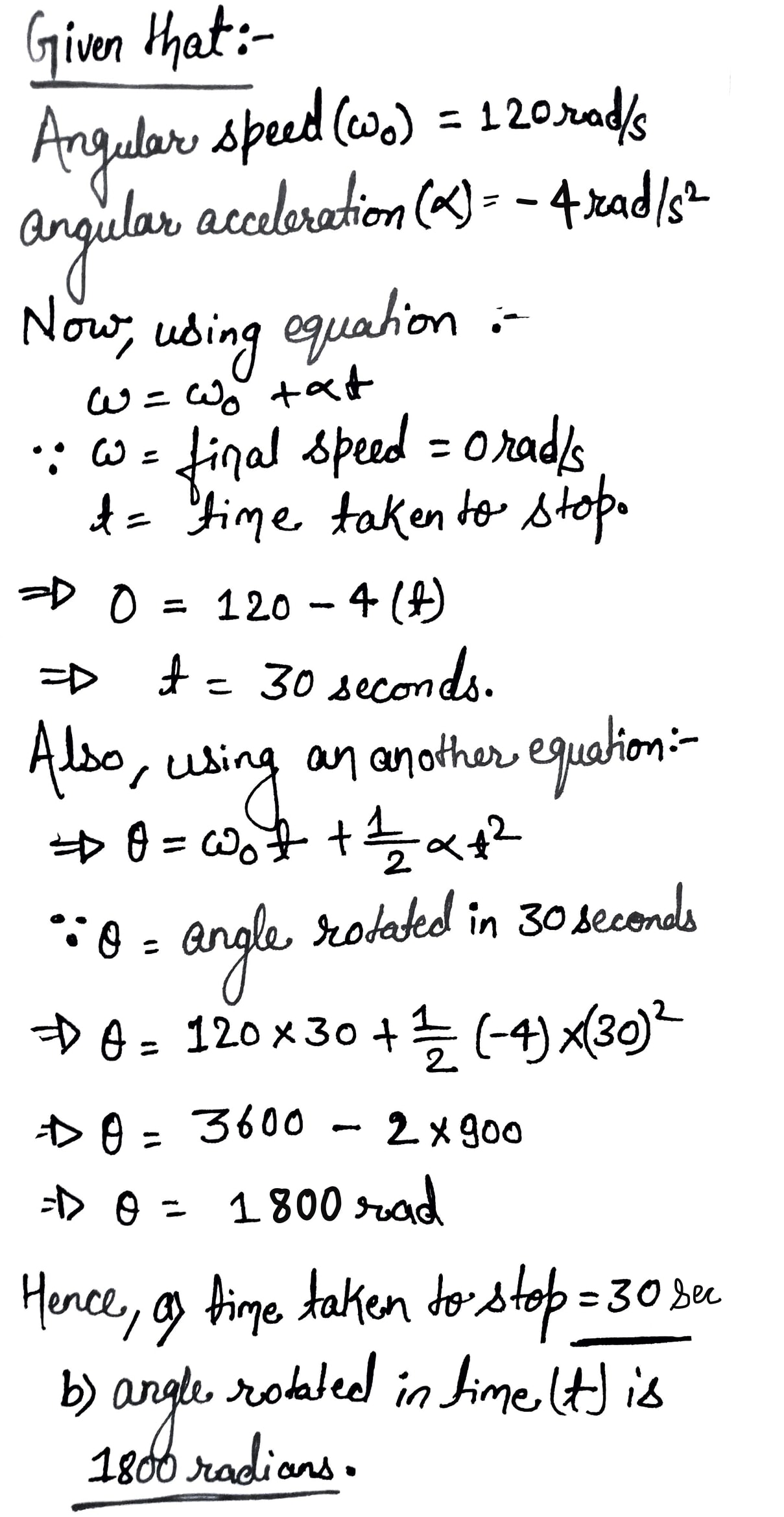Motion In A Plane - Class 11 Medical Physics - Extra Questions
A ball is thrown from the top of a tower with an initial velocity of 10 $$ms^{-1}$$ at an angle of $$30^0$$ above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. Calculate the height of the tower. (g = 10 $$ms^{-2}$$)
A ball is thrown upwards from the top of a tower 40 m high with a velocity of 10 m/s. Find the time when it strikes the ground (Take g = 10 $$m/s^{2}$$).
A particle is projected from ground at some angle to the horizontal. $$($$Assuming point of projection to be origin and the horizontal and vertical directions to be the $$x\ \&\ y$$ axis$$)$$ the particle passes through the points $$(3, 4)$$ and $$(4, 3)$$ during its motion. If the range of the particle is $$\dfrac{37}{x}\ m$$ then $$x$$ is:
The resultant of two like parallel forces 12 N and 7 N is ________.
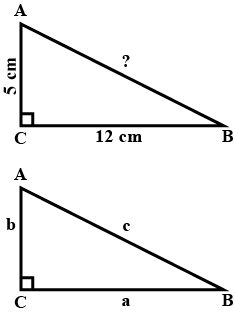
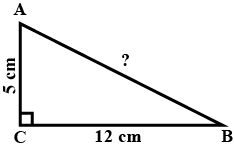
$$ \displaystyle \bigtriangleup ABC $$ is right-angled at C If AC = 5 cm and BC=12 cm find the length of AB
A car is moving with speed $$30\ m/sec$$ on a circular path of radius $$500\ m$$. Its speed is increasing at the rate of $$2\ m/sec^{2}$$. What is the net acceleration of the car at that moment (i.e the vector sum of tangential and radial acceleration)?
Two forces $$5$$kg wt and $$10$$kg wt are acting with an inclination of $$120^o$$ between them. what is the angle the resultant makes with $$10$$kg wt?
Three point charges $$+Q, + 2Q$$ and $$-3Q$$ are placed at the vertices of an equilateral triangle ABC of side L.if these charges are displaced to the mid-points $$A_1, B_1$$ and $$C_1$$ respectively find the amount of the work done in shifting the charges to the new locations.
Find a unit vector parallel to the resultant of the vectors $$\bar{A}=2\hat{i}+3\hat{J}+4\hat{k}$$ and $$\bar{B}=3\hat{i}-5\hat{J}$$.
A ball is thrown from the top of a building 45 m high with a speed 20 m s$$^{-1}$$ above the horizontal at an angle of $$30^o$$. Find
a. The time taken by the ball to reach the ground.
b. The speed of ball just before it touches the ground.
Two bullets are fired with horizontal velocities of $$50m/s$$ and $$100m/s$$ from two guns at a height of $$19.6m$$ (a) Will both the bullets strike the ground? (b) If yes, then after how much time and which bullet will strike first? (c) What would be the path of the bullets? ($$g=9.8m/{s}^{2}$$)
Two forces each of $$10\ N$$ act at an angle $${60}^{o}$$ with each other. The magnitude & direction of the resultant with respect to one of the vectors is
A projectile fired from the top of a $$40\ m$$ high cliff with an initial speed of $$50\ m/s$$ at an unknown angle. Find its speed when it hits the ground. $$(g=10\ {m/s}^{2})$$
A gun is mounted on a stationary rail road car. The mass of the car, the gun, the shells and the operator is 50m, where m is the mass of one shell. Two shells are fired one after the other along same horizontal line in same direction. If the muzzle velocity (velocity with respect to gun) of the shells is 200 m/s, then find the speed of the car after second shot.
A ball is dropped from a height, if it takes $$0.2\,s$$ to cross the last $$6\,m$$ before hitting the ground, find the height from which it is dropped. Take $$g=10\,m/s^{2}$$ (AS1)
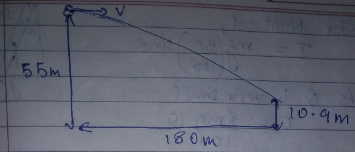
b) Two tall building face each other and are at a distance of 180 m from each other. With what velocity must a ball be thrown horizontally from a window 55 m above the ground in one building, so that it enters a window 10.9 m above the ground in the second building?
From the top of a tower $$100\ m$$ in flight ball is dropped and the same time another ball is projected vertically upward from the ground with a velocity of $$25\ m/sec$$. Find when and where the two balls will meet? $$(g=9.8\ m/sec^{2})$$
The velocity time graph of particle moving along a straight line is shown in the figure in the time interval from t=$$0$$ t=$$8$$second answer the following three questions.
A particle is projected up with an initial velocity of $$80$$ the ball will be at a height of $$96$$ from the ground after
A ball in thrown from a roof top at an angle $$45^{\circ}$$ above the horizontal. It hits the ground a few second later. At what point during its motion, does the ball have greatest acceleration?
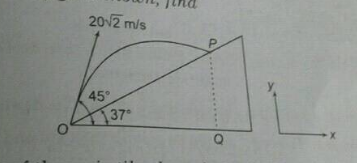
In the figure shown, find time of flight of the projectile along the inclined plane and range OP.
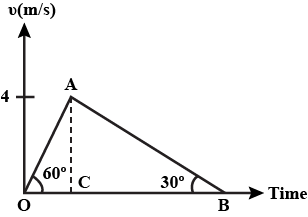
The velocity time graph of a body is shown in the Fig. The ratio of the average velocity, during the intervals OC and CB is ?
A motorcycle has to move with a constant speed on an over bridge which is in the form of a circular arc of radius $$R$$ and has a total length $$L$$. Suppose the motorcycle starts from the highest point.
(b) If the motorcycle goes at speed $$1/\sqrt{2}$$ times the maximum found in part
(a) where will it lose the contact with the road?
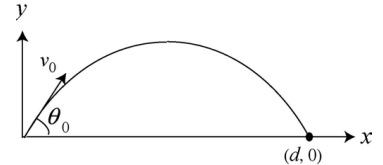
You are to launch a rocket, from just above the ground, with one of the following initial velocity vectors: (1) $$\vec { { v }_{ o } } =20\hat { i } +70\hat { j } $$ ,(2) $$\vec { { v }_{ o } } =-20\hat { i } +70\hat { j } $$, (3) $$\vec { { v }_{ o } } =20\hat { i } -70\hat { j }$$ , (4) $$\vec { { v }_{ o } } =-20\hat { i } -70\hat { j }$$ . In your coordinate system, $$x$$ runs along level ground and $$y$$ increases upward. (a) Rank the vectors according to the launch speed of the projectile, greatest first. (b) Rank the vectors according to the time of flight of the projectile, greatest first.
Shown are several curves Explain with reason, which one amongst them can be possible trajectory traced by a projectile ( neglect air friction).
A particle moves horizontally in uniform circular motion, over a horizontal $$xy$$ plane. At one instant, it moves through the point at coordinates (4.00 m, 4.00 m) with a velocity of $$5.00\hat { i } m/{ s }^{ 2 }$$ and an acceleration of $$+12.5\hat { j } m/{ s }^{ 2 }$$ . What are the (a) x and (b) y coordinates of the center of the circular path?
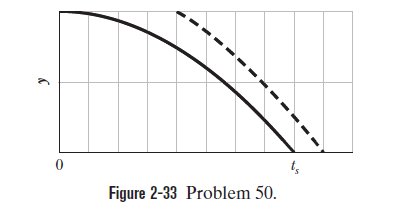
At the time $$t = 0$$, apple 1 is dropped from a bridge onto a roadway beneath the bridge; somewhat later, apple 2 is thrown down from the same height. The figure gives the vertical positions $$y$$ of the apples versus $$t$$ during the falling until both apples have hit the roadway. The scaling is set by $$t_{s} = 2.0\, s$$. With approximately what speed is apple 2 thrown down?
A car travels with speed $$30$$ km $$h^{-1}$$ for $$30$$ minute and then with speed $$40$$ km $$h^{-1}$$ for one hour. Find: The average speed of car
A point moves along an arc of a circle of radius $$R$$. Its velocity depends on the distance covered $$s$$ $$\nu=a \sqrt s$$, where $$a$$ is a constant. Find the angle $$\alpha$$ between the vector of the total acceleration and the vector of velocity as a function of $$s$$
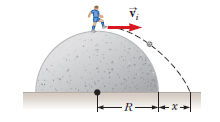
A person standing at the top of a hemispherical rock of radius $$R$$ kicks a ball (initially at rest on the top of the rock) to give it horizontal velocity $$\vec{V}_{i}$$ as shown in above figure. (a) What must be its minimum initial speed if the ball is never to hit the rock after it is kicked? (b) With this initial speed, how far from the base of the rock does the ball hit the ground?
A novice golfer on the green takes three strokes to sink the ball. The successive displacements of the ball are $$4.00 m$$ to the north, $$2.00 m$$ northeast, and $$1.00 m$$ at $$30.0^{0}$$ west of south (Fig. below). Starting at the same initial point, an expert golfer could make the hole in what single displacement?

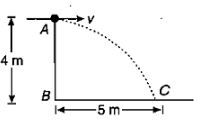
A ball rolls off the edge of a horizontal table top 4 m high. If it strikes the floor at a point 5 m horizontally away from the edge of the table, what was its speed at the instant it left the table?
The trajectories of the motion of 3 particles are shown in the figure. Match the entries of column I with the entries of column II. Neglect air resistance.
A projectile is fired horizontally with a velocity of $$98 m/s$$ from the top of a hill $$490 m$$ high. Find the horizontal range of the projectile.

A ball is thrown vertically upwards. After some time, it returns to the thrower. Draw the velocity-time graph and speed-time graph.
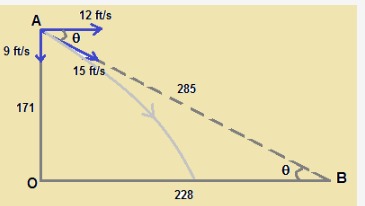
A person standing on the top of a cliff $$171\ ft$$ high has to throw a packet to his friend standing on the ground $$228\ ft$$ horizontally away. If he throws the packet directly aiming at the friend with a speed of $$15\cdot 0\ ft/s$$, how short will the packet fall?
A ball A is a projected from the ground such that its horizontal range is maximum. Another ball left it is dropped from a height equal from a height equal to the maximum range of A?
An airplane flying horizontally at a constant speed of $$350 \,km/h$$ over level ground releases a bundle of food supplies. Ignore the effect of the air on the bundle. What are the bundles initial (a) vertical and (b) horizontal components of velocity? (c) What is its horizontal component of velocity just before hitting the ground? (d) If the airplanes speed were, instead, $$450 \,km/h$$, would the time of fall be longer, shorter, or the same?
A disk, initially rotating at 120 rad/s , is slowed down with a constant angular acceleration of magnitude 4.0 rad/ $$ s^{2} $$. (a) How much time does the disk take to stop (b) Through what angle does the disk rotate during that time
A certain airplane has a speed of $$290.0 km/h$$ and is diving at an angle of $$30.0$$ below the horizontal and when the pilot releases a radar decoy (Fig. 4-33). The horizontal distance between the release point and the point where the decoy strikes the ground is $$d =700 m.$$ (a) How long is the decoy in the air? (b) How high was the release point?
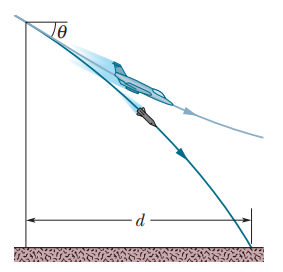
A rifle that shoots bullets at $$460 m/s$$ is to be aimed at a target $$45.7 m$$ away. If the center of the target is level with the rifle, how high above the target must the rifle barrel be pointed so that the bullet hits dead center?
A trebuchet was a hurling machine built to attack the walls of a castle under siege. A large stone could be hurled against a wall to break apart the wall. The machine was not placed near the wall because then arrows could reach it from the castle wall. Instead, it was positioned so that the stone hit the wall during the second half of its flight. Suppose a stone is launched with a speed of $${ v }_{ 0 }=28.0 m/s$$ and at an angle of $${ \theta }_{ 0 }=40.0$$. What is the speed of the stone if it hits the wall (a) just as it reaches the top of its parabolic path and (b) when it has descended to half that height? (c) As a percentage, how much faster is it moving in part (b) than in part (a)?
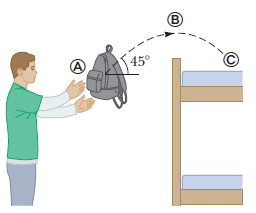
Entering his dorm room, a student tosses his book bag to the right and upward at an angle of $$45^{0}$$ with the horizontal (Fig. above). Air resistance does not affect the bag. The bag moves through point $$A$$ immediately after it leaves the students hand, through point $$B$$ at the top of its flight, and through point $$C$$ immediately before it lands on the top bunk bed.
(i) Rank the following horizontal and vertical velocity components from the largest to the smallest.
(a) $$v_{Ax}$$ (b) $$v_{Ay}$$ (c) $$v_{Bx}$$ (d) $$v_{By}$$ (e) $$v_{Cy}$$.
Note that zero is larger than a negative number. If two quantities are equal, show them as equal in your list. If any quantity is equal to zero, show that fact in your list.
(ii) Similarly, rank the following acceleration components.
(a) $$a_{Ax}$$ (b) $$a_{Ay}$$ (c) $$a_{Bx}$$ (d) $$a_{By}$$ (e) $$a_{Cy}$$.
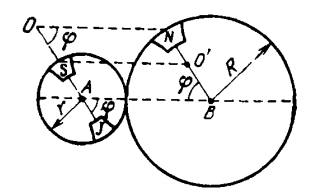
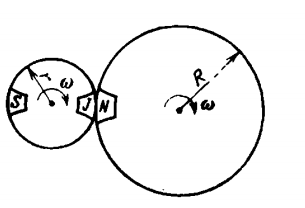
Three schoolboys, Sam, Jhon, and Nick, are on merry-go-round. Sam and John occupy diametrically opposite points on a merry-go-round of radius $$R$$. The position of the boys at the initial instant are shown in fig
Considering that the merry-go-round touch each other and rotate in the same direction at the same angular velocity $$\omega$$ determine the nature of motion of Nick from John's point of view and of Sam from Nick's point of view.
A $$1.25-kg$$ wooden block rests on a table over a large hole as in Figure $$P9.71$$. A $$5.00-g$$ bullet with an initial velocity $$v_i$$ is fired upward into the bottom of the block and remains in the block after the collision. The block and bullet rise to a maximum height of $$22.0\ cm$$.
Describe how you would find the initial velocity of the bullet using ideas you have learned in this chapter.
Class 11 Medical Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work, Energy And Power Extra Questions