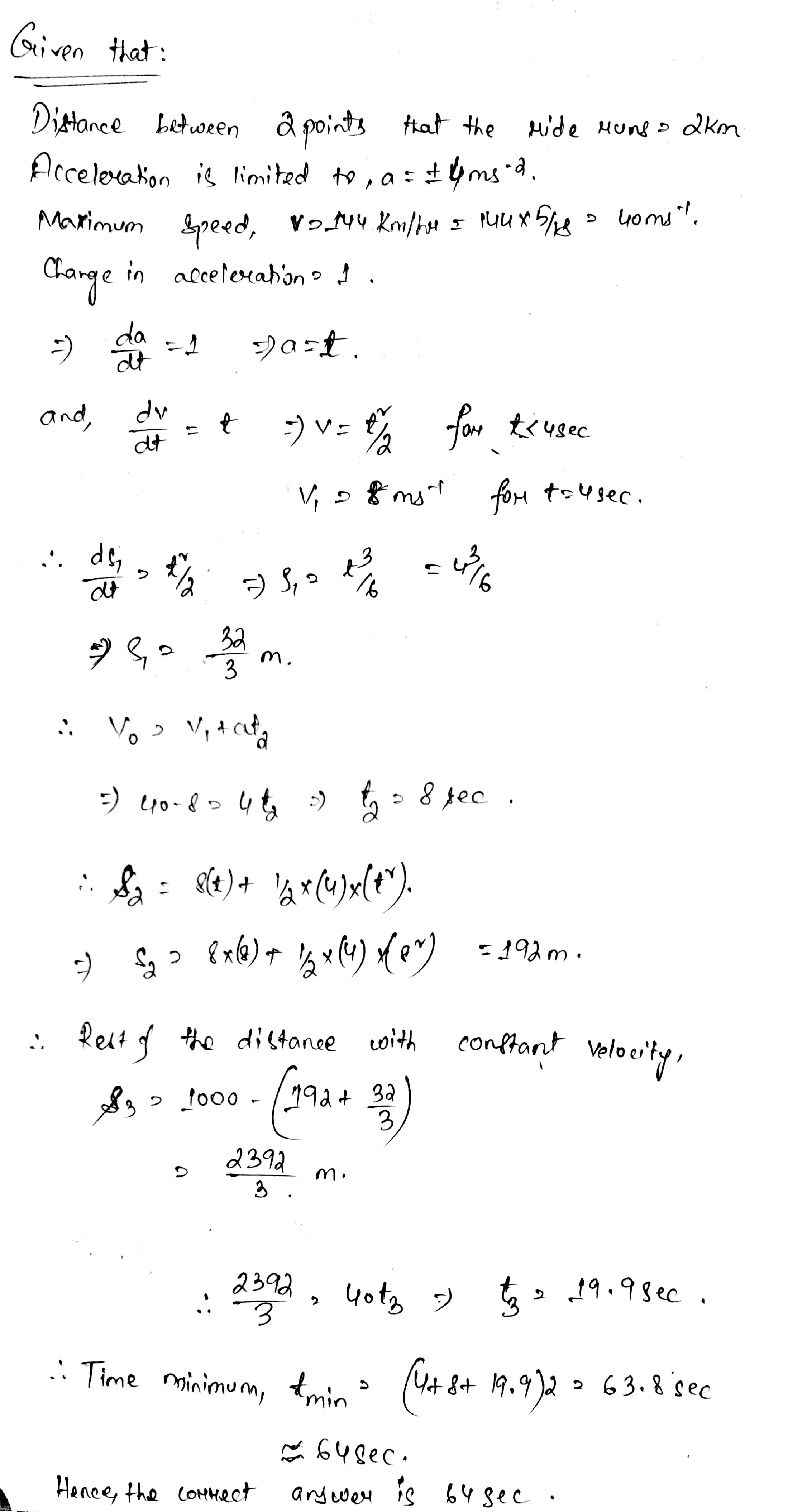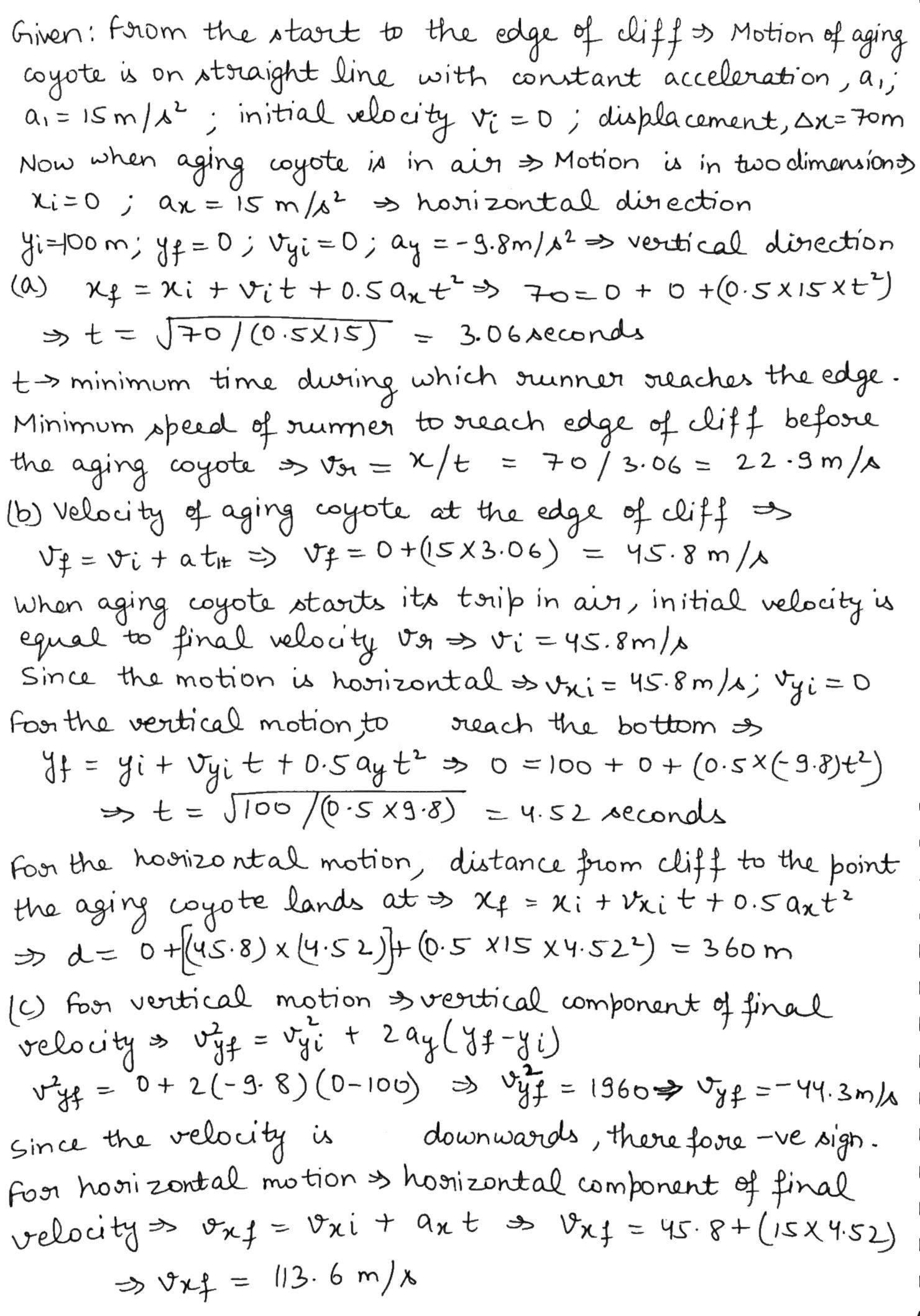Motion In A Straight Line - Class 11 Engineering Physics - Extra Questions
A car accelerates from 18 km/hr to 36 km/hr in 10 sec. Calculate its acceleration.
What do you mean by constant acceleration?
How are the states of rest and motion relative?
If $$u=6m/s$$ and $$h=1m$$. Find the final velocity($$v$$)? Take $$g=10 m/s^2$$
A motorbike initially at rest, picks up a velocity of $$72km/{h^{ - 1}}$$ over a distance of $$40m$$. Calculate (1)acceleration (2)time in which it picks up above velocity
If the velocity of a body does not change with time, its acceleration is ___.
If a vehicle is accelerated to $$5ms^{-2}$$, how much time does it take to attain a velocity of $$27ms^{-1}$$ which initially starts with $$2ms^{-1}$$?
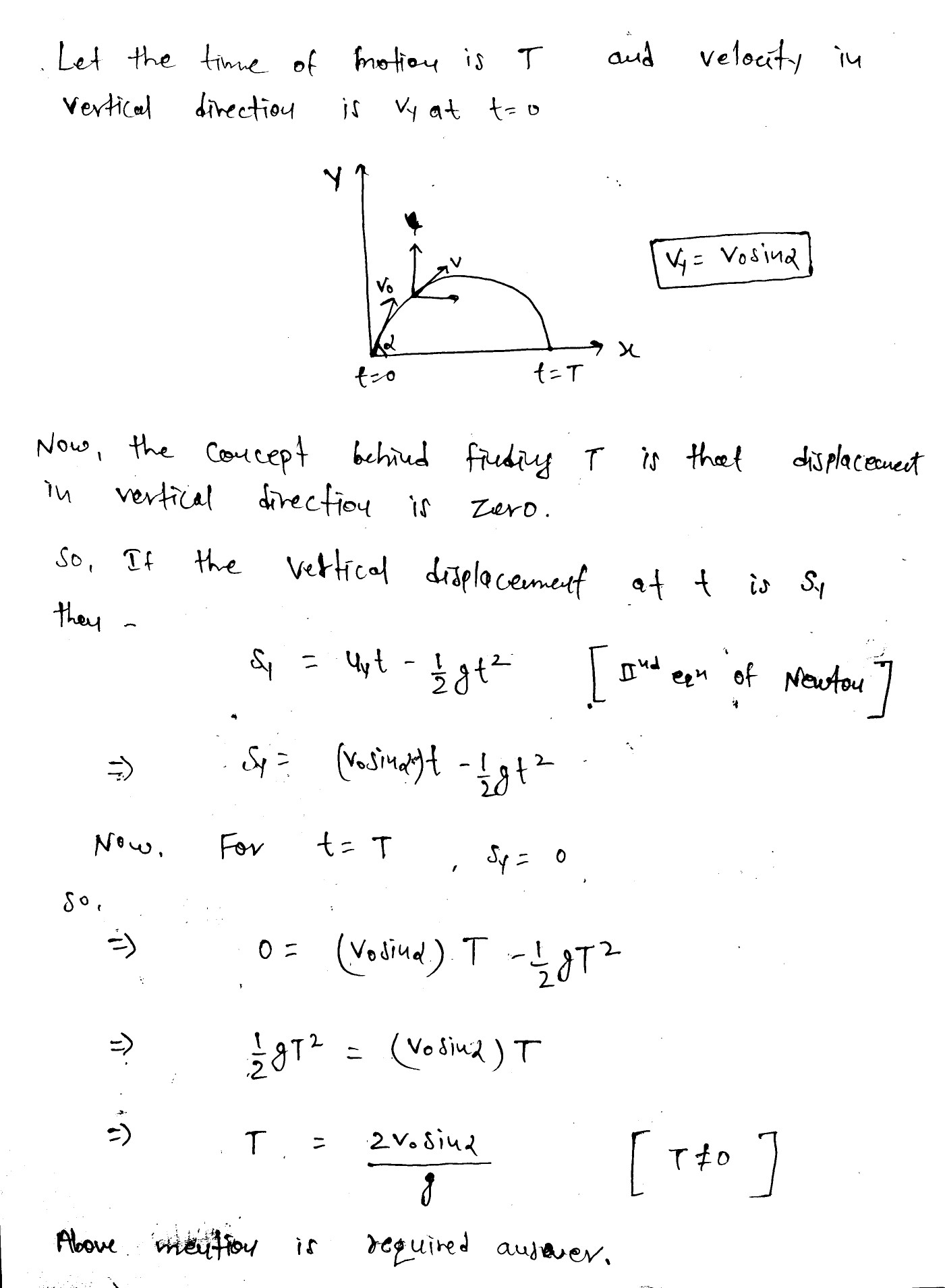
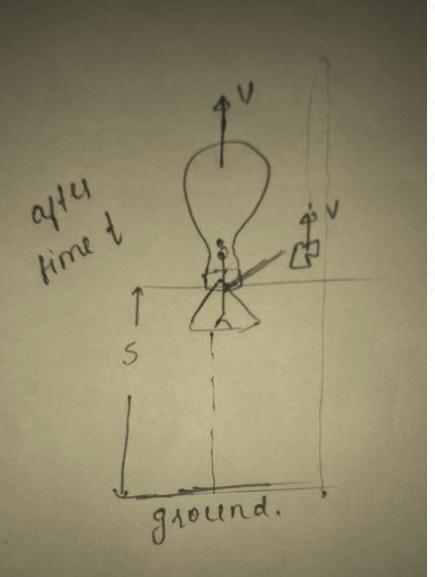
A man throws ball with the same speed vertically upwards one after the other at an interval of $$2$$ seconds. What should be the speed of the throw so that more than two balls are in the sky at any time? (Given $$g=9.8m/{s}^{2}$$)
What term is used to denote the change of velocity with time?
Given that, $$ t= 5\ s, u = 0\ m/s, s= 110\ m$$find the acceleration
Define the following:
Acceleration.
A lorry travelling with a velocity of $$30\ m/s$$ came to rest in $$5\ s$$. What is its acceleration ?
Two object $$A$$ and $$B$$ are walking with speed $$6\ km/h$$ and $$10\ km/h$$ respectively in the same direction. Find the relative displacement of $$B$$ w.r.t $$A$$ after $$4$$ hours.
A car starting from rest acquires a velocity $$180\ ms^{-1}$$ in $$0.05\ h$$. Find the acceleration.
A man on a certain planet throws up a stone of 500 gm with a velocity of 10 m/s and catches it after 8 second. What is the weight of the stone on the planet ?
Can a body exist in a state of absolute rest or of absolute motion?explain.
Define velocity and acceleration.
Ram is standing on the edge of a cliff 30 m high. He throws ball vertically up with a velocity of 10 m/s at (time) $$t = 0$$. The ball strikes the ground after the flight and does not rebound. Match the time intervals in column-I with description of motion in column-II.
Ram is standing on the edge of a cliff $$30 m$$. He throws ball vertically up with a velocity of $$10 m/s$$ at (time) $$t = 0$$. The ball strikes the ground after the flight and does not rebound. Match the time intervals in column-I with description of motion in column-II
A balloon is ascending vertically with an acceleration of $$ 0.2m/s^2 $$. Two stones are dropped from it at an interval of 2 sec. The distance (in m) between them 1.5 sec after the second stone is released is approximately 10x. The value of x is: (use $$ g=9.8 m/s^2 $$)
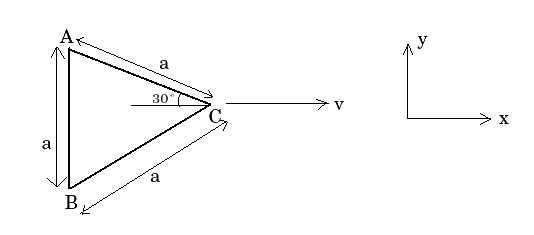
In a triangle the proper length of each side equals $$a$$. Find the perimeter of this triangle in the reference frame moving relative to it with a constant velocity $$V$$ along one of its bisectors :
Length of the rod moving parallel to the direction of velocity $$(v)$$ gets reduced by a factor of $$\sqrt{1- \beta^2}$$ of its proper length whereas the length perpendicular to the direction of velocity remains the same.
Given : $$|AB| = |AC| = |BC| = a$$ (proper length)
In the moving frame : $$A'B' = a$$
$$\vec{AC} = a cos(30) \hat{i} + a sin(30) \hat {j}$$
$$\therefore$$ $$\vec{A'C'} =[(a cos30) \sqrt{1-\beta^2} \hat{i} + a sin 30 \hat{j}] = \dfrac{ a\sqrt{3(1-\beta^2)} }{2} \hat{i} + \dfrac{a}{2} \hat{j}$$ where $$\beta =v/c$$
$$\implies$$ $$|A'C'| = \dfrac{a\sqrt{4-3\beta^2}}{2} $$
Similarly $$|B'C'| = $$ $$ \dfrac{a\sqrt{4-3\beta^2}}{2} $$
$$\therefore$$ Perimeter of the triangle $$P' = |A'B'| +|A'C'| +|B'C'| = a + $$$$ \dfrac{a\sqrt{4-3\beta^2}}{2} +$$ $$ \dfrac{a\sqrt{4-3\beta^2}}{2} $$
$$\implies$$ $$P' = a (1 + \sqrt{4-3\beta^2})$$
The velocity of a particle moving in a straight line is directly proportional to $$\dfrac{3}{4}^{th}$$ power of time elapsed. The ratio of its displacement and acceleration be $$t^{x}$$.Find $$x.$$
A particle-is projected vertically upwards with an initial velocity of 40 m/s. Find the displacement and distance covered by the particle in 6 seconds. Take g=10 m/s$$^{2}$$
The driver of a car travelling at $$52 km h^{-1}$$ applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 s. Another driver going at $$3 kmh^{-1}$$ in another car applies his brakes slowly and stops in 10 s. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied?
Hint:
Displacement of a body is given by the area under the v-t curve.
Step 1: Express the velocity of the first car in terms of time.
It is given that,
Initial Velocity of car is, $$u_1 = 52kmh^{-1} = 14.4ms^{-1}$$
Final velocity of car is, $$v_1 = 0ms^{-1}$$
Time taken by car to stop is, $$t_1 = 5s$$
Acceleration of car is goven by, $$a_1 = \dfrac{v_1 - u_1}{5}$$
$$\Rightarrow a_1 = \dfrac{0-14.4}{5} = -2.8ms^{-2}$$
Thus, By First Equation of Motion we have,
$$v_1 = u_1 + a_1t$$
$$\Rightarrow v_1 = 14.4 - 2.8t$$ ....eq.1
Step 2: Express the velocity of the second car in terms of time.
It is given that,
Initial Velocity of car is, $$u_2 = 3kmh^{-1} = 0.83ms^{-1} $$
Final velocity of car is, $$v_2 = 0ms^{-1}$$
Time taken by car to stop is, $$t_2 = 10s$$
Acceleration of car is goven by, $$a_2 = \dfrac{v_1 - u_1}{5}$$
$$\Rightarrow a_2 = \dfrac{0-0.83}{10} = -0.083ms^{-2}$$
Thus, By First Equation of Motion we have,
$$v_2 = u_2 + a_2t$$
$$\Rightarrow v_2 = 0.83 - 0.083t$$ ....eq.2
Step 3: Plotting Equations 1 and 2.
The graph for v-t for both the cars is as given:
First car - blue,
The second car - orange.
Since we know the distance traveled is the area under the speed-time curve, the area under the curve for the first car before it comes to rest is greater than the area under the curve for the second car before it comes to rest. Thus, the First car travels more distance after applying brakes.
$$\textbf{ The car moving at $$52 km/h$$ travels more distance on the application of brakes.}$$
Read each statement below carefully and state with reasons and examples, if it is true or false:
A particle in one-dimensional motion
(a) with zero speed at an instant may have non-zero acceleration at that instant.
(b) with zero speed may have non-zero velocity.
(c) with constant speed must have zero acceleration.
(d) with positive value of acceleration must be speeding up.
A particle starts from the origin at t = 0 s with a velocity of 10.0 $$\hat{j}$$ m/s and moves in the x-y plane with a constant acceleration of $$\left ( 8.0\hat{i}\,+\,2.0 \hat{j}\right )$$ m/$$s^2$$.
(a) At what time is the x- coordinate of the particle 16 m? What is the y-coordinate of the particle at that time?
(b)What is the speed of the particle at the time ?
Explain this common observation clearly : If you look out of the window of a fast moving train, the nearby trees, houses etc. seem to move rapidly in a direction opposite to the trains motion, but the distant objects (hill tops, the Moon, the stars etc.)seem to be stationary. (In fact, since you are aware that you are moving, these distant objects seem to move with you).
The position-time (x-t) graphs for two children A and B returning from their school O to their homes P and Q respectively are shown in Fig. above. Choose the correct entries in the brackets below :
(a) (A/B) lives closer to the school than (B/A)
(b) (A/B) starts from the school earlier than (B/A)
(c) (A/B) walks faster than (B/A)
(d) A and B reach home at the (same/different) time
(e) (A/B) overtakes (B/A) on the road (once/twice).
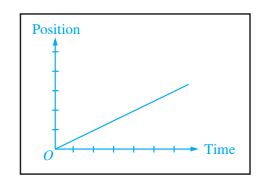
An object is moving in a straight line and its graph of position versus time is shown in above graph. Which of the following show correct relation between speed and acceleration of the object.
| SPEED | ACCELERATION | |
| (A) | Increasing | Increasing |
| (B) | Increasing | Constant but not zero |
| (C) | Constant but not zero | Increasing |
| (D) | Constant but not zero | Zero |
| (E) | Zero | Constant but not zero |
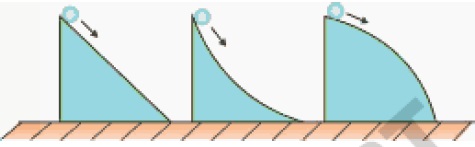
Suppose that the three ball's shown in figure start simultaneously from the tops of the hills. Which one reaches the bottom first? Explain.
1) path AFB : angles : $$tan\Theta 1=1/3,tan\Theta 1=3, sin\Theta 1=1/\sqrt{}10,sin\Theta 1=3/\sqrt{}10 $$
$$ v1 $$ at $$ F = g\,sin \Theta 1*t1,$$ v1^2$$=2gH/4 = gH/2, v1 = \sqrt{}(gH/2) $$
$$ t1 = \sqrt{}(H/2g)/(sin\Theta 1)$$ $$ t1=\sqrt{}10*sqrt(H/2g) $$
v2^2 = v1^2+2g3H/4 = 2gH sqrt(2gH) $$= sqrt(gH/2)+g\,sin\Theta 2*t2 $$
$$ t2 = (\sqrt{}10/3)\sqrt{(H/2g)} = (\sqrt{}10/3)\sqrt{(H/2g)} $$
$$ t1+t2 = 2/3*sqrt(10)*sqrt(2H/g) = 2.108*\sqrt{}(2H/g) $$
2) path ADB:
angle $$ tan\Theta = 1 \,sin\Theta = 1/\sqrt{}2 $$
$$ v2 = sqrt(2gH) = g\,sin\,\Theta *t\Rightarrow t = 1.414\sqrt{}(2H/g) $$
3) path AEB: angle: $$ tan\Theta 1=3,tan\Theta 2 = 1/3,sin\Theta 1 = 3/\sqrt{}10,tan\Theta 2=1/\sqrt{}10 $$
$$ v1 = g\,sin\Theta 1*t1=\sqrt{}(2g3H/4), t1 = \sqrt{}10*\sqrt{}(H/2g)/\sqrt{3} $$
$$ v2 = \sqrt{}(2gH) = \sqrt{}(3gH/2)+g\,sin\Theta 2*t2, t2=\sqrt{}10(H/2g)[2-\sqrt{3}] $$
$$ t1+t2 = \sqrt{}10*\sqrt{}(2H/g)(1-1/\sqrt{3}), t = 1.33\sqrt{}(2H/g) $$
4) path AOB: First vertical and then horizontal.
$$ v1=\sqrt{}(2gH), t1 = \sqrt{}(2H/g), t2= H/v1 = \sqrt{}(h/2g) $$
$$ t1+t2 = 1.5*\sqrt{}(2H/g) $$
So we can see that the ball along the path AFB takes longest time
to reach B. The ball along single straight line path, ADB takes less
time duration to reach B. For the path AEB, the time duration reduces
further to a minimum. But after a particular point, as the slope of AE
increase, the slope of EB reduces and the total time duration to
reach B increase.
An object changes its velocity from 30ms$$^{-1}$$ to 40ms$$^{-1}$$ in a time interval of 2 seconds. What is its acceleration?
Is it possible for an accelerating body to have zero velocity? Explain.
A ball is dropped from a balloon going up at a speed of $$5m/s$$. If the balloon was at a height $$60$$m at the time of dropping the ball, how long will the ball take to reach the ground?
A scooter weighing $$150$$kg together with its rider moving at $$36km/hr$$ is to take a turn of radius $$30$$m. What force on the scooter towards the center is needed to make the turn possible? Who or what provides this?
A ball is dropped from a height. If it takes $$0.200\ s$$s to cross the last $$6.00\ m$$ before hitting the ground, find the height from which it is dropped. Take $$g=10\ m/s^2$$.
The speed of a particle is constant. Will it have an acceleration? Justify with an example.
An enemy plane is at a distance of $$300$$km from a radar. In how much time the radar will be able to detect the plane? Take velocity of radio-waves as $$3\times 10^8ms^{-1}$$.
A policeman fires a bullet on a thief's car at rest. As the bullet is fired, the car starts accelerating by acceleration $$10m/{s}^{2}$$. If the speed of bullet is $$720km/h$$ and the initial distance of thief's car from policeman is $$2km$$, then after what time will the bullet hit the thief's car?
A car accelerates from $$36\ km/h$$ to $$90\ km/h$$ in $$5\ s$$ on a straight road. What was its acceleration in $$m/s^{2}$$ and how far did it travel in this time? Assume constant acceleration and direction of motion remains constant.
A shell bursts on contact with the ground and pieces from it fly in all directions with all velocities upto $$80$$ feet per second. Show that a man $$100$$ feet away is in danger for $$\dfrac {5}{\sqrt {2}}$$ second. [Use $$g = 32\ ft/ s^{2}]$$.
The speed of a car is reduced from $$90$$km/hr to $$36$$ km/hr in $$5$$ s. What is the distance travelled by car during this time interval?
At what distance from its starting point does the car overtake the truck?
In a square cut, the speed of the cricket ball changes from $$30\ { ms }^{ -1 }$$ to $$40\ { ms^{-1} }$$ during the time of its contact $$\triangle t=0.01 s$$ with the bat. If the ball is deflected by the bat through an angle of $$\theta = 90^{o}$$, find the magnitude of the average acceleration $$\left( in \times { 10 }^{ 2 }\ { ms }^{ -2 } \right)$$ of the ball during the square cut.
The acceleration of a motorcycle is given by $$a_{x}(t) = At - Br^{2}$$, where $$A = 1.50\ ms^{-2}$$ and $$B = 0.120\ ms^{-4}$$. The motorcycle is at rest at the origin at time $$t = 0$$.
Calculate the maximum velocity it attains.
Two trains P and Q are moving along parallel tracks with the same uniform speed of 20 $$ms^{-1}$$. The driver of train P decides to overtake train Q and accelerates his train by 1 $$ms^{-2}$$. After 50 s, train P crosses the engine of train Q.Find out what was the distance between the two trains initially, provided the length of each train is 400m.
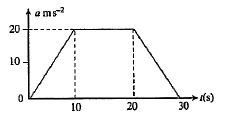
Find the average acceleration in first 20 s.
A bird flies to and fro between two cars which move with velocities $$v_{1}$$ and $$v_{2}$$. If the speed of the bird is $$v_{3}$$ and the initial distance of separation between them is d, find the total distance covered by the bird till the cars meet.
A car starts from rest and accelerates uniformly for 10 s to a velocity of 8 $$ms^{-1}$$. It then runs at a constant velocity and is finally brought to rest in 64 m with constant retardation. The total distance covered by the car is 584 m. Find the value of acceleration, retardation, and total time is taken.
(Refer to Image)
$$V= at$$
$$\Rightarrow 8= a10$$
$$\Rightarrow a= 0.8 m/s^2$$
$$V^2= U^2+2as$$
$$\Rightarrow U= 8^2+2 \times a 64$$
$$\Rightarrow a= \cfrac {-64}{2 \times 64}=-0.5 m/s^2$$
Distance travelled= Area of graph
$$\Rightarrow 584= \cfrac {1}{2} \times 10 \times 8+ 8 \times t^1+\cfrac {1}{2}\times 16\times 8$$
$$\Rightarrow 584= 40+8t^1+64$$
$$\Rightarrow 8t^1= 480$$
$$\Rightarrow t^1= 60$$
Total time= $$10+60+16= 86 s$$
A boy throws a ball with initial speed $$2\sqrt{ag}$$ at an angle $$\theta$$ to the horizontal. It strikes a smooth vertical wall and returns to his hand. Show that if the boy is standing at a distance '$$a$$' from the wall, the coefficient of restitution between the ball and the wall equals $$\dfrac{1}{( 4 sin 2\theta - 1)}$$. Also show that $$\theta$$ cannot be less than $$15^o$$.
A body moves from rest with uniform accelerations and travels 270 m in 3 sec. Find the velocity of the body 10 sec after that start.
The change in velocity of a motorbike is 54 km/hr in one minute. Calculate the acceleration in m/$${ s }^{ 2 }$$ and km/$${ hr}^{ 2 }$$
An object may appear moving to one person and at rest to another person at the same time Justify giving an example.
Is it possible that the train in which you are sitting appears to move while it is at rest?
A particle is moving along a circular path of radius $$5\ m$$ with a uniform speed $$5\ {ms}^{-1}$$. What is the magnitude of average acceleration during the interval in which particle completes half revolution?
When moving in a car the trees and buildings appear to move backwards where as the moon appears to be stationery why? does relative velocity concept fail in case of moon sun or stars.
A ball of mass $$2kg$$ is thrown vertically upwards by applying a force by hand. If the hand moves $$0.2m$$ while applying the force and the ball goes upto $$2m$$ height further, find the magnitude of the force. ($$g=10m{s}^{-1}$$)
A ball is dropped from a high rise platform at $$t=0$$ starting from rest. After 6 seconds another ball is thrown downwards from the same platform with a speed $$v$$. The two balls meet at $$t=18s$$. What is the value of $$v$$? (Take $$g=10m/{s}^{2}$$)
A car aquires a velocity of $$72\ km/h$$ in $$10\ sec$$. starting from lust. Find (a) The acceleration (b) the average velocity (c) the distance travelled in this time.
A stone of mass $$5 kg$$ falls from the top of a cliff $$50 m$$ high and buries $$1 m$$ in sand. Find the average resistance offered by the sand and the time it takes to penetrate.
The motion of a particle of mass $$m$$ is described by $$y = ut + \dfrac {1}{2} gt^2 $$ . Find the force acting on the particle.
A motor cycle moving with speed of $$5m/s$$ is subject to an acceleration of $$0.2m/{s}^{2}$$. Calculate the speed of motorcycle after 10 second, and the distance travelled in this time.
What does the path of an object look like when it is in uniform motion?
A car travels with a uniform velocity of $$25ms^{-1}$$ for $$5s$$ the brakes are then applied and the car is uniformly retarded and comes to rest in further $$10s$$ find the retardation
A body is said to be in motion if it covers equal distances in unequal intervals of time.
A car starting from rest acquires a velocity $$180ms^{-1}$$ in $$0.05h$$.Find the acceleration
A car accelerates uniformly on a straight road from rest to a speed of $$180 kmh^{-1} $$ in $$25s $$ . Find the distance covered by the car in this time-interval
A car accelerates uniformly from $$18 km \ h^{-1}$$ to $$36 km \ h^{-1}$$ in 5s.
Calculate (i) the acceleration and
(ii) the distance covered by the car at that time.
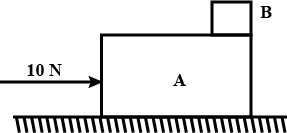
A small block B is placed on another block A of mass 5 kg and length 20 cm. Initially the block B is near the right end of block A. A constant horizontal force of 10 N is applied to the block A. All the surfaces are assumed frictionless. Find the time elapsed before the block B separates from A.
A body of mass $$0.4$$kg moving with a constant speed of $$10$$m/s to the north is subject to a constant force of $$8$$N direction toward the south for $$30s$$. Take the instant the force is applied to be $$t=0$$, the position of the body at the time to be $$x=0$$ , and predict its position at $$t=-5s,25s,100s$$.
A particle starts at the origin and move along the x axis such that its velocity $$v$$ varies with time $$t$$ as $$v=4t^3 - 2t$$, where v is in m/s and t is in second.What is the distance of the particle from the origin when its acceleration is $$46m/s^2$$?
Can a body have zero velocity and finite acceleration?
State with reasons, it is possible or impossible for an object to have :
Zero speed at an instant but non zero acceleration at the same time
A man is 9m behind the door of a train when it stands moving with acceleration $$\alpha = 2m/s^2$$ The man turns at full speed. After what time does he get into the train? What is his full speed?
A car moving at 4 kmph is to be stopped by applying brakes in the next 40 m. If the car weighs 2000 kg, what average force must be applied on it?
A train travelling at $$90km/hr$$ is brought to rest by the application of brakes in a distance of $$75m$$.find the time in which the train is brought to rest Also calculate the distance covered by the train in the first half and the second half of this time interval.
Derive an equation for the distance covered by a uniformly accelerated body in $$n^{th}$$ second of its motion. A body travels half its total path in the last second of its fall from rest. Calculate the time of its fall.
A car states from rest and acquires a velocity of $$54km/hr$$ in $$2$$ minutes. Find(i) acceleration and(ii) distance travelled by car in this time. Assume, that the motion of the car is uniform.
A car starts from rest. It moves with uniform acceleration. In $$10$$ seconds, it attains a speed of $$12\ km h^{-1}$$ a straight road. Find its acceleration.
A particle starts from the origin and moves along the $$x-$$axis such that its velocity $$v$$ varies with time $$t$$ as $$v=4t^3-2t$$, where $$v$$ is in $${m/s}$$ and $$t$$ is in $$second$$. What is the distance of the particle from the origin when its acceleration is $$46$$ $${m/s^2}$$?
A ball thrown in vertical upward direction attains maximum height of $$16m$$. At what height would its velocity be half of its initial velocity?
A particle starts from origin at$$t=0$$ when a velocity $$5.01m/s$$and moves in $$x-y$$ plane under action of a force which produces a constant acceleration of $$(3.0\hat{i}+2.0\hat{j})m/s^{2}$$
$$(a)$$ what is the $$y-$$ co-ordinate of the particle at the instant its $$x-$$ coordinate is $$84m?$$
$$(b)$$ What is the speed of the particle at this time?
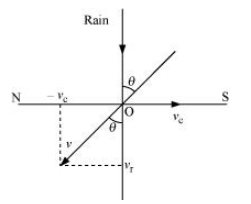
Rain is falling vertically with a speed of 30 m/s. A woman rides a bicycle with a speed of 10 m/s in the north to south direction. What is the direction in which she should hold her umbrella then?
Here,
$$v_c=$$Velocity of the cyclist
$$v_r=$$Velocity of falling rain
In order to protect herself from the rain, the women must hold her umbrella in the direction of the relative velocity (v) of the rain with respect to the women
$$v=v_r+(-v_c)$$
$$v=30+(-10)=20\ m/s$$
$$\tan\theta=\dfrac{v_c}{v_r}=\dfrac{10}{30}$$
$$\theta=\tan^{-1}\left(\dfrac{1}{3}\right)$$
$$\theta\approx 18°$$
Hence the women must hold the umbrella towards the south, at angle of nearly 18° with the vertical
What is the acceleration of a body moving with a uniform velocity?
A $$120m$$ long train is going from East to West with velocity $$10m\ s^{-1}$$ A bird, flying due East with velocity $$5m\ s^{-1}$$, crosses the train. Calculate the time taken by the bird to cross the train.
Establish the relation $$S_nth = u + \cfrac{a}{2}(2n -1)$$, where the letters have their usual meaning.
A car falls off a ledge and drops to the ground in $$ 0.5 s(g=10 ms^2) $$. calculate:
How high is the ledge from the ground?
What is its speed on striking the ground?
In a velocity-time graph the variation of velocity v versus time t gives ...........................
When does a cyclist appear to be stationary with respect to another moving cyclist?
A body covers $$100\ cm$$ in first $$2$$ seconds and $$128\ cm$$ in the next four second moving with constant acceleration. Find the velocity of the body at the end of $$8\ sec$$?
Displacement is given by $$X = 1+ 2t +3t^2$$ . Find the value of instantaneous acceleration.
Acceleration time graph of a body is shown the corresponding velocity time graph same body is
If the graph in question is divided into 3 parts then
1. For first part acceleration is positive and constant. Hence velocity during this time interval should increase. With this we can say (b) and (d) options are incorrect.
2. For second part acceleration is zero. Hence velocity should be constant. Slope in velocity time graph should be zero. This is shown by both (a) and (c)
3. For last part acceleration again is positive and constant. Hence velocity during this time interval should increase. With this we can say that (c) is correct.
On turning a corner a car driver driving at $$36\ kmh^{-1}$$, finds a child on the road $$55\ m$$ ahead. He immediately applies brakes, so as to stop within $$5\ m$$ of the child. If the retardation produced is x m$$s^{-2}$$and the time taken by the car to stop is y seconds. Find xy.
An $$NCC$$ parade is going at a uniform speed of $$6\ km/h$$ through a place under a berry tree on which a bird is sitting at a height of $$12.1\ m$$. At a particular instant the bird drops a berry. Which cadet (give the distance from the tree at the instant) will receive the berry on his uniform?
If a body is droped from a building it covers $$40$$ m in last $$2$$ sec. Find height of building$$?$$
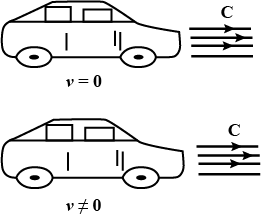
In figure , one car is at rest and velocity of light from head light is C, then velocity of light from head light for the moving car at velocity v,would be
A train starting from a railway station and moving with uniform acceleration attains a speed of $$40\ kmph$$ in $$10$$ minutes. Find its acceleration.
A car is travelling along the road at $$ 8 ms^{-1} $$. It accelerates at $$ 1 ms^{-2} $$ for a distance of 18 m. How fast is it then travelling?
A constant force of 5N is applied continuously on a body of mass 10 kg for 4 seconds. The body moves 800 cm along a straight line. What is the velocity of the body when the force was applied initially ?
Initial velocity of a car is 36 km/h. Find the final velocity of the car after 1 sec,if it goes with acceleration $$5 m/s^2$$?
The displacements is given by $$x = 2 + 4t + 5t^2$$. Find the value of instantaneous acceleration?
A ball is projected vertically up with a speed of 50 m/s. Find the maximum height, the time to reach the maximum height, and the speed at the maximum height.
$$ (g=10 m/s^2 ) $$
During the last second of its free fall, a body covers half of the total distance travelled. Calculate (i) the approximate height from which the body falls (ii) the duration of the fall.
A stone falls from a cliff and travels $$34.3 \,m$$ in the last second before it reaches the ground. Calculate the height of the cliff.
A ball thrown vertically upward returns to the thrower after 6 s. The ball is 5 m below the highest point at t = 2 s. The time at which the body will be at same position, (take g = 10$$m/s^2$$).
A bus starting from rest moves with a uniform acceleration of $$0.1 m s^2$$ for 2 minutes. find (a) the speed acquired. (b) the distance traveled.
A body starting from rest is travelling on a straight road with constant non-zero acceleration. If the speeds after covering distances $${S_1}$$ and $${S_2}$$ be $${V_1}$$ and $${V_2}$$ respectively. If $${V_2}/{V_1} = 2$$, then $${S_2}/{S_1} = N$$. Find $$N$$.
Solution
(i) While covering $$S_{1}$$ distance
$$u= 0 m/s$$ and $$V=V_{1}$$, so,
Applying third $$eq^{n}$$ of motion,
$$(V_{1})^{2}-(0)^{2}=2(S_{1})(a)$$
$$\Rightarrow (V_{1})^{2}=2S_{1}a\Rightarrow V_{1}=\sqrt{2S_{1}a}$$
(ii) While covering $$S_{2}$$ distance,
$$u=V_{1}m/s$$ and $$V=V_{2}m/s$$. so,
Applying third $$eq^{n}$$ of motion,
$$(V_{2})^{2}-(V_{1})^{2}=2(S_{2})(a)$$
$$\Rightarrow (V_{2})^{2}= 2S_{2}a+V_{1}^{2}$$
$$\Rightarrow V_{2}^{2}=2(S_{1}+S_{2})a$$
$$\Rightarrow V_{1}=\sqrt{2(S_{1}+S_{2})}a$$
As $$\dfrac{V_{2}}{V_{1}}=2$$ Let $$V_{1}=K,$$ then $$V_{2}= 2K$$
so, $$V_{1}=\sqrt{2S_{1}a}\Rightarrow S_{1}=\dfrac{V_{1}^{2}}{2a}\Rightarrow S_{1}=\dfrac{K^{2}}{2a}$$
Also, $$S_{1}+S_{2}=\dfrac{V_{2}^{2}}{2a}\Rightarrow \dfrac{K^{2}}{2a}+S_{2}=\dfrac{V_{2}^{2}}{2a}$$
$$\Rightarrow S_{2}=\dfrac{4K^{2}}{2a}-\dfrac{K^{2}}{2a}=\dfrac{3K^{2}}{2a}$$
So, $$\dfrac{S_{2}}{S_{1}}=3\Rightarrow N$$ is 3.
A ship moving with a constant acceleration of $$36km/{ h }^{ 2 }$$ in a fixed direction speeds up from $$12 km/h$$ to $$18 km/h.$$ Find the distance traversed by the ship in this period.
$$\int _ { 0 } ^ { s } d s = \int _ { 0 } ^ { t } u \cdot d t + \int _ { 0 } ^ { t } a t \cdot d t$$ Solve it
A bicycle moves with a constant velocity of $$5 km/h$$ for $$10$$ minutes and then decelerates at the rate $$1$$ $$km/{ h }^{ 2 },$$ till it stops. Find the total distance covered by the bicycle.
The acceleration due to gravity on the surface of the earthj is $$10m{s^{ - 2}}$$ . The mass of the planet Mars as compared to earth is 1/10 and radius is 1/Determine the gravitational acceleration of a body on the surface of mars.
An object experiences a constant acceleration for $$20$$s after starting from rest. If it travels a distance $$s_1$$ in the first $$10$$s and distance $$s_2$$ in the remaining $$10$$s, then the ratio of $${\dfrac{s_2}{s_1}}$$ is?
A motor boat starting from rest on a lake accelerates in a straight line at constant rate of $$3.0 \mathrm { m } / \mathrm { s } ^ { 2 }$$ for 8.0 sec. How far does the boat travel during this time
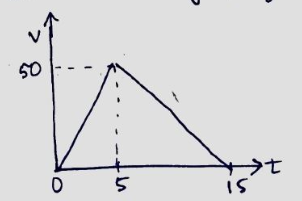
A car accelerates from rest at a constant rate 10 $$m/s^{2}$$ for some time after which it decelerates at constant rate 5 $$ m/s^{2}$$ and then comes to rest. Total time elapsed is 15 s. Calculate (1)Maximum velocity of the car (2)Average velocity of the car during deacceleration.
Suppose car acceleration for time $$t$$. So it decelerate by time $$(15-t)s.$$
Initially at rest, $$u=0$$ and come to velocity $$v$$ in time $$t!$$ use from Kinematics
for constant accim, $$(a=10m/m^2)$$
$$\Rightarrow \ v=\bot 0 t\ \rightarrow (1)$$
$$\bot$$ & $$(2)$$ gives,
$$\bot O t=5(15-t)\ \Rightarrow \ t=5\ s$$.
for constant deceleration $$(a=-5m/s)$$
$$\Rightarrow \ o=v-5(15-t)$$
$$\Rightarrow \ v=5(15-t)\ \rightarrow (2)$$
so, $$v=\bot o t=50\ m/s$$
construct $$a\ v-t$$ graph from obtained results.
From graph
$$(i)$$ max velocity $$=50\ m/s$$
$$(ii)$$ net distance travelled =area ot $$vt$$ graph
$$d=\dfrac {1}{2}\times 50 \times 15 =375\ m$$
$$\therefore $$ average velocity $$=\dfrac {d}{t}=\dfrac {375}{15}=25\ m/s$$
during deceleration distance travelled, $$d_1=\dfrac {1}{2}\times (15-5)\times 50=250m$$
$$\therefore $$ avg velocity during deceleration $$=\dfrac {d_2}{\Delta t}=\dfrac {250}{(15-5)}=25\ m/s$$
A train of length $$120\ m$$ travels at a speed of $$57\ km/h$$. In what time it will pas a man who is walking at $$3\ km/h$$ in the opposite direction?
A train starts from rest and moves with a constant acceleration of $$2.0\ m/s^{2}$$ for half a minute. the brakes are then applied and the train comes to rest in one minute. Find
the total distance moved by the train,
A distance of $$14.4$$km is covered in $$2$$ hours $$40$$minutes.FInd the speed in m/sWith this spees Sakshi goes to her school,$$240$$m away from her house and then returns back.How much time,in all, will Sakshi take?
The distance x covered by a particle in one dimensional motion varies with time t as $$x^2=at^2+2bt+c$$. If the acceleration of the particle depends on x as $$x^{-n}$$, where n is an integer, the value of n is:
The driver of a car moving at 30 $$m{ s }^{ -1 }$$ suddenly sees a truck that is moving in the same direction at 10 $$m{ s }^{ -1 }$$ and is 60 m ahead. The maximum deceleration of the car is 5 $$m{ s }^{ -2 }$$.
a. Will the collision occur if the driver's reaction time is zero? If so, when?
b. If the car driver's reaction time of 0.5 s included, what is the minimum deceleration required to avoid the collision?
A particle moves along a straight line such that its displacement S varies with time t as $$S=\alpha +\beta t+\gamma t^{ 2 }.$$
(a) What term is used to denote the change of velocity with time ?
(b) Give one word which means the same as 'moving with a negative acceleration'.
(c) The displacement of a moving object in a given interval of time is zero.
Would the distance travelled by the object also be zero ? Give reason for your answer.
(a) Write the formula for acceleration. Give the meaning of each symbol which occurs in it.
(b) A train starting from Railway Station attains a speed of $$21\, m/s$$ in one minute. Find its acceleration.
A motorcyclist starts from rest and reaches a speed of $$6\, m/s $$ after travelling with uniform acceleration for $$3\, s$$. What is his acceleration ?
A satellite goes around the earth in a circular orbit with constant speed. Is the motion uniform or accelerated?
Two diamonds begin a free fall from rest from the same height, $$1.0\
s$$ apart. How long after the first diamond begins to fall will the two
diamonds be $$10\ m$$ a part?
Define acceleration and state its SI unit. For motion along a straight line, when do we consider the acceleration to be (i) positive (ii) negative ?
Give example of a body in uniform acceleration.
Fill in the following blanks with suitable words :
It is possible for something to accelerate but not change its speed if it moves in a _______.
Where does the particle start and with what velocity?
How will the equations of motion for an object moving with a uniform velocity change?
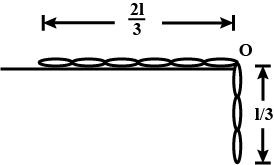
The diagram below shows the pattern of the coil on the road, dripping at a constant rate from a moving car. What information do you get from it about the motion of car?
Define acceleration. State its S.I. unit.
How does the acceleration produced by a given force depend on mass of the body? Draw a graph to show it.
If a force is applied on two bodies that have different masses, then the acceleration that is produced by them varies inversely to their individual masses.
When a graph for mass against acceleration is sketched, a hyperbola is obtained.
When a graph for mass against acceleration is sketched, a hyperbola is obtained.
A body is moving vertically upward. Its velocity changes at a constant rate from $$50\ ms^{-1}$$ to $$20\ ms^{-1}$$ in $$3\ s$$. What is the acceleration?
Two objects of masses $$m_1$$ and $$m_2$$ having the same size are dropped silmultaneously from heights $$h_1$$ and $$h_2$$ respectively. Find out the ratio of time they would take in reaching the ground. Will this ratio remain the same if (i) one of the objects is hollow and the other one is solid and (ii) both of them are hollow, size remaining the same in each case? Give reason.
Explain the meaning of the term's rest and motion.
Derive an expression for distance traveled during the nth second of motion.
OR
Derive $$s_n= u + a(n 1/2)$$
On the basis of frame of reference in how many types is the motion divided? write the names .
Define a non-inertial frame of reference.
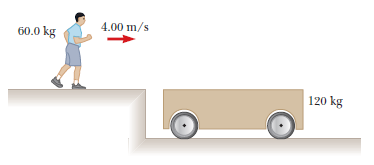
A trolley of mass $$00 kg$$ moves with a uniform speed of $$36 km$$ $$h^{-1}$$ on a frictionless track. A child of mass $$20 kg$$ runs on a trolley from one and to the other ($$10m$$ away) with a speed of $$4ms^{-1}$$ relative to the trolley in a direction opposite to the trolleys motion, and jumps out of the trolley. What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?
A uniform accelerated motion object covers $$ 65 m $$ in $$ 5th $$ second and $$ 105 m $$ in $$ 9th $$ . then how much distance will it cover in $$ 20th $$ second ? Also calculate the distance travelled in $$ 20s $$.
A particle is moving with a definite velocity then how much would be its acceleration ?
What is a velocity-time graph? What is its importance?
Derive an expression for acceleration in terms of distance travelled in two successive equal interval of time.
OR
Derive the equation $$a =\dfrac{s_2s_1}{t^2}$$
the time of motion;
If a velocity of a train which starts from rest is $$ 72 km/h (20m/s) $$ after $$ 5 $$ minutes, find out its acceleration and the distance traveled by the train in this time.
What is meant by acceleration ?
An object starting from rest travels with a uniform acceleration of $$ 5 m/s^2 $$.Calculate the velocity and distance traveled after $$ 1$$ minute?
Does a body have acceleration in the following situations? Why?
$$\bullet$$ body travelling along a straight line with uniform velocity.
$$\bullet$$ body travelling along a straight line with non-uniform velocity.
$$\bullet$$ body travelling along a circular path with uniform speed.
$$\bullet$$ body travelling along a circular path with non-uniform speed.
the time interval $$\Delta t$$ taken by the particle to return to the initial points, and the distance $$s$$ covered during that time.
If the velocity of a particle is zero, can the particles acceleration be zero? Explain
At time $$t = 0$$, a student throws a set of keys vertically upward to her sorority sister, who is in a window at distance $$h$$ above. The second student catches the keys at time $$t$$. (a) With what initial velocity were the keys thrown? (b) What was the velocity of the keys just before they were caught?
The speed of a nerve impulse in the human body is about $$100 m/s$$. If you accidentally stub your toe in the dark, estimate the time it takes the nerve impulse to travel to your brain.
If the velocity of a particle is nonzero, can the particles acceleration be zero? Explain.
The froghopper Philaenus spumarius is supposedly the best jumper in the animal kingdom. To start a jump, this insect can accelerate at $$4.00 km/s^{2}$$ over a distance of $$2.00 mm$$ as it straightens its specially adapted jumping legs. Assume the acceleration is constant. (a) Find the upward velocity with which the insect takes off. (b) In what time interval does it reach this velocity? (c) How high would the insect jump if air resistance were negligible? The actual height it reaches is about $$70 cm$$, so air resistance must be a noticeable force on the leaping froghopper.
A tennis ball of mass $$57.0\ g$$ is held just above a basketball of mass $$590\ g$$. With their centers vertically aligned, both balls are released from rest at the same time, to fall through a distance of $$1.20\ m$$, as shown in Figure.
Find the magnitude of the downward velocity with which the basketball reaches the ground.
Why is the following situation impossible? Starting from rest, a charging rhinoceros moves $$50.0 m$$ in a straight line in $$10.0 s$$. Her acceleration is constant during the entire motion, and her final speed is $$8.00 m/s$$.
A daring ranch hand sitting on a tree limb wishes to drop vertically onto a horse galloping under the tree. The constant speed of the horse is $$10.0 m/s$$, and the distance from the limb to the level of the saddle is $$3.00 m$$. (a) What must be the horizontal distance between the saddle and limb when the ranch hand makes his move? (b) For what time interval is he in the air?
You throw a ball vertically upward so that it leaves the ground with velocity $$+5.00 m/s$$. (a) What is its velocity when it reaches its maximum altitude? (b) What is its acceleration at this point? (c) What is the velocity with which it returns to ground level? (d) What is its acceleration at this point?
Describe the path of a moving body in the event that:(a) its acceleration is constant in magnitude at all times and perpendicular to the velocity.(b) its acceleration is constant in magnitude at all times and parallel to the velocity.
A particle moving in a straight line is acted upon by a force which works at a constant rate and changes its velocity from u and v over a distance x. Prove that the time taken in it is $$\displaystyle \frac{3}{2}\frac{\left ( u+v \right )x}{u^{2}+v^{2}+uv}$$
A particle moves in a straight line with constant acceleration a. The displacements of particle from origin in times $$\displaystyle t_{1}, t_{2}$$ and $$\displaystyle t_{3}$$ are $$\displaystyle s_{1}, s_{2}$$ and $$\displaystyle s_{3}$$ respectively. If time are in AP with common difference d and displacements are in GP, then prove that $$\displaystyle a=\frac{\left ( \sqrt{s_{1}-\sqrt{s_{3}}} \right )^{2}}{d^{2}}$$
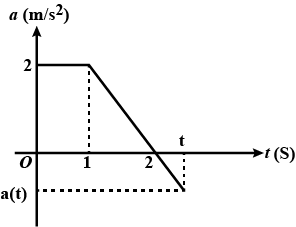
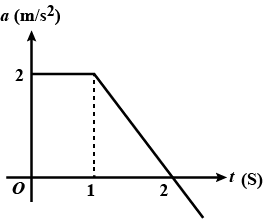
Figure shows the acceleration-time graph of a particle moving along a straight line. After what time the particle acquires its initial velocity?
From the graph, slope of oblique line $$ = \dfrac{2-0}{1-2} =-2$$ for $$t > 1$$
$$\therefore$$ from similar triangles properties between upper and lower triangle $$\frac{a}{t-2} = \frac{2} {2-1}$$ $$\implies$$ Magnitude of acceleration $$|a(t)| = 2t - 4$$ for $$t >2$$ s
Magnitude of acceleration $$|a(t)| = 2t - 4$$ for $$t>2$$ s
Area under the a-t graph gives the change in velocity of the particle during that period.
$$\therefore$$ $$\Delta V = area$$ $$of$$ $$rectangular$$ $$portion$$+ $$area$$ $$of$$ $$upper$$ $$trianle$$-$$area$$ $$of$$ $$lower$$ $$triangle$$
$$\therefore$$ $$\Delta V = 2 \times 1 + \dfrac{1}{2} \times 1 \times 2 - \dfrac{1}{2} \times (a(t)) \times (t-2)$$
$$\therefore$$ $$\Delta V = 2 \times 1 + \dfrac{1}{2} \times 1 \times 2 - \dfrac{1}{2} \times (2t-4) \times (t-2)$$
$$\implies$$ $$\Delta V = 3 - (t-2)^2$$
Let the particle acquires its initial velocity again after time $$t_1$$ i.e
change in velocity=$$0$$
$$\Delta V = 0$$ at $$t = t_1$$
$$\therefore$$ $$0 = 3 - (t_1-2)^2$$ $$\implies t_1 =2 + \sqrt{3}$$ s and $$t_1 =2- \sqrt{3}$$ s (Not possible)(Because for $$t_1 =2- \sqrt{3}$$ s Acceleration is always positive so change in velocity can not be zero)
Thus the particle acquires its initial velocity again at $$t = 2+\sqrt{3}$$ s
A car moving with constant acceleration covered the distance between two points 60.0 m apart in 6.00 s. Its speed as it passes the second point was 15.0 m/s.What was the speed at the first point?
A particle moves along the x-direction with constant acceleration. The displacement, measured form a convenient position, is 2 m at time t = 0 and is zero when t = 10 s. If the velocity of the particle is momentary zero when t = 6s, determine the acceleration a the velocity v when t = 10s.
What is the maximum height reached?
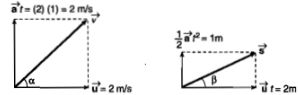
velocity and acceleration of a particle at time t=0 are $$\displaystyle \vec{u}= \left ( 2\hat{i}+3\hat{j} \right )$$ m/s and $$\displaystyle \vec{a}= \left ( 4\hat{i}+2\hat{j} \right )m/s^{2}$$ respectively. Find the velocity and displacement of particle at t=2 s.
A particle of mass 1 kg has a velocity of 2 m/s. A constant force of 2 N acts on the particle for 1 s in a direction perpendicular to its initial velocity. Find the velocity and displacement of the particle at the end of 1 second.
Let the initial speed of the particle be in x direction.
$$\therefore$$ $$u_x =2\hat{i}$$ $$ m/s$$
Given : $$M = 1 kg$$ $$t =1 $$ s $$F_y = 2 \hat{j} $$ N
x direction : $$a_x = 0$$ $$\implies$$ $$V_x =u_x = 2\hat{i}$$ $$m/s$$
Also $$S_x = u_x t = 2 \times 1 = 2 \hat{i}$$ m
y direction : $$a_y = \dfrac{F_y}{M} = 2\hat{j}$$ $$m/s^2$$
$$\therefore$$ $$V_y =u_y + a_y t = 0 + 2 \times 1 = 2\hat{j}$$ $$m/s$$
Also $$S_y = u_y t+ \dfrac{1}{2}a_yt^2 = 0 + \dfrac{1}{2} \times 2 \times 1^2 = 1 \hat{i}$$ m
Total displacement of the particle $$S = 2\hat{i} + 1 \hat{j} $$ m
$$\implies $$ $$|S| = \sqrt{2^2 + 1^2} = \sqrt{5}$$ m
Velocity of the particle $$V = 2\hat{i } + 2\hat{j}$$
$$\implies$$ $$|V| = \sqrt{2^2 + 2^2} = 2\sqrt{2}$$ $$m/s$$
What does $$\displaystyle \left | \frac{d\vec{v}}{dt} \right |\:and\:\frac{d\left | \vec{v} \right |}{dt}$$ represent?
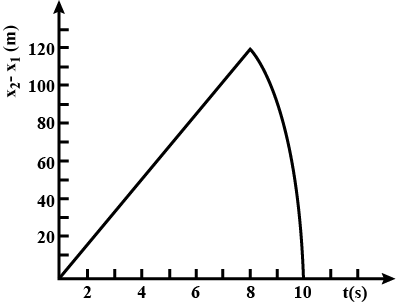
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of $$15 ms^{-1}$$ and $$30 ms^{-1}$$. Verify that the graph shown in Fig. correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take $$g = 10 m s^{-2}$$. Give the equations for the linear and curved parts of the plot.
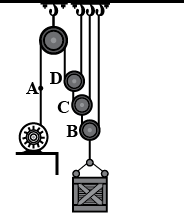
Starting from rest, the cable can be wound onto the drum of the motor at a rate of $${v}_{A}=(3{t}^{2}) \ m/s$$, where $$t$$ is seconds. Determine the time needed to lift the load $$7$$ $$m$$.
One day you, together with your class, went on a picnic. During return journey from the picnic spot to your school, your bus was traveling at scheduled average speed $$v_0$$ = 70 $$kmh^{-1}$$; suddenly, it began to rain so the driver reduced the speed and drove the bus at average speed $$v_1$$ = 60 $$kmh^{-1}$$. After the rain stopped, the driver drove the bus at average speed $$v_2$$ = 75 $$kmh^{-1}$$ to cover remaining s = 40 km and reached exactly at the scheduled time. How long did it rain?
A fun drive in an amusement park runs between two spots that are 2.0 km apart. For safety reasons, the acceleration of the drive is limited to $$\pm$$4.0 $$ms^{-2}$$, and the jerk, or the rate of change of acceleration, is limited to $$\pm$$1.0 $$ms^{-2}$$. The drive has a maximum speed of 144 $$kmh^{-1}$$. Find the shortest time taken by the drive to travel between the spots.
How many coaches are on the train than?
The exit of a school is through a corridor of width b = 3.5 m. After the school, on an average, N = 42 students pass through the corridor in 1 min and population density within the length of the corridor occupied becomes n = 0.4 students per square meter. Find the average speed of the students within the corridor.
A traffic officer receives complaints on often traffic jams at the traffic signal on the main street of a busy market. He studied the traffic pattern and to simplify calculations made reasonable assumptions that all the vehicles are identical in size and move with identical speed. He also notices that when a signal turns green, all the vehicles do not begin to move at the same time; but vehicles standing adjacent to traffic signal begin to move first after a small time delay, then next after the same time delay, and so on. At present, durations of red and the green signals are equal an average speed of traffic advancement is $$v_1$$ = 1.5 $$ms^{-1}$$. If he orders to make $$\eta$$ = 2 times the duration of green signal and leaves the duration of the red signal unchanged, what would be the average speed $$v_2$$ of the traffic advancement?
When a ball is thrown up, it reaches a maximum height $$h$$ travelling $$5$$ m in the last second. Find the velocity with which the ball should be thrown up.
A small object of mass $$0.5\ kg$$ is attached to an end of a mass less $$2\ m$$ long rope. It is rotated under gravity in a vertical circle with the other end of the rope being at the centre of the circle. The motion is started from the lowest point. Match column $$I$$ and $$II$$.
A railway track runs parallel to a road until a turn brings the road to the railway crossing. A cyclist rides along the road everyday at a constant speed 20 $$kmh^{-1}$$. He normally meets a train that travels in the same direction at the crossing. One day he was late by 25 min and met the train 10 km before the railway crossing. Find the speed of the train.
On a large slippery ground, a boy left his dog sitting and walks away with constant velocity $$v_b$$=2.0 $$ms^{-1}$$. When he reaches $$x_0$$= 199 m away from the dog, the dog decides to catch him and meet at the same speed as that of the boy. Because the ground is slippery, the dog cannot develop acceleration more than a = 2.0 $$ms^{-2}$$ in any direction. In what minimum time will the dog meet the boy?
A particle moving with uniform acceleration along a straight line ABC crosses point A at t=0 with a velocity 12 m/s, B is 40 m away from A and Cis 64 m away from A. The particle passes B at t = 4 s.
a.After what time will the particle be at C?
b.What is its velocity at C?
c.When does the particle reach A again?
d.Locate the point where the particle reverses its direction of motion.
e.Find the distance covered by the particle in the first 15 s.
Let the acceleration of the particle be a.
For motion between A and B
u= 12 m/s, s = 40 m, t = 4 s
s = ut + (1/2)a$$t^2$$
$$\Rightarrow$$ 40 = 12 x 4 + (1/2) x a x $$(4)^2$$
a = -1 $$ms^{-2}$$
For motion between A and C
64= 12t + (1/2)(-l)$$t^2$$
=> $$r^2$$ - 24t +128 = 0
=>(t- 8) (t- 16) = 0
=> t = 8 s, 16 s
A.The particle will be at C twice, at t = 8 s and t = 16 s.
B.Velocity of the particle at C
At t = 8 s. velocity of the particle v = 12 + (-1) x 8
= 4 m/s.
As the acceleration of the particle is negative, it will retard as it moves along ABC. At a point beyond C (i.e., at D), the particle will come to rest momentarily, and then it will move backwards with increasing speed. Throughout the motion, the particle decelerates, its velocity decreases continuously, velocity varies as 12,
11,10,..., 2,1,0,-1,-2-10, -11, -12, etc. Only from A to D the motion is retarded, during which speed varies as 12,11,10,..., 2,1,0. Subsequently, the particle speeds up, speed changing as 1, 2, 3,..., etc. Notice the difference between deceleration and retardation.
When the particle reaches A again, its displacement = 0
$$\therefore$$ 0= 12 $$\times$$ t + (1/2)(-1)$$t^2$$
=> t = 0, 24 s
At t = 0, velocity at A = 12 m/s,
At t = 24 s, velocity at A is 12 + (-1) x 24 = -12 m/s.
D.The particle reverses the direction of motion at D. For the motion between A and D
u = 12 m/s, v = 0, a = -1 m$$s^{-2}$$. If AD = s, from the equation $$v^2 = u^2 + 2as$$
$$(0)^2 = (12)^2$$ + 2 x (-1) x s
s = 72 m
E. After 12 s the particle comes to rest momentarily at D after covering a distance of 72 m.
Distance in subsequent 3 s
= 0 x 3 + (1/2) x (-1) x $$(3)^2$$ = 4.5 m
$$\therefore$$ d = 72 m + 4.5 m = 76.5 m
For motion between A and B
u= 12 m/s, s = 40 m, t = 4 s
s = ut + (1/2)a$$t^2$$
$$\Rightarrow$$ 40 = 12 x 4 + (1/2) x a x $$(4)^2$$
a = -1 $$ms^{-2}$$
For motion between A and C
64= 12t + (1/2)(-l)$$t^2$$
=> $$r^2$$ - 24t +128 = 0
=>(t- 8) (t- 16) = 0
=> t = 8 s, 16 s
A.The particle will be at C twice, at t = 8 s and t = 16 s.
B.Velocity of the particle at C
At t = 8 s. velocity of the particle v = 12 + (-1) x 8
= 4 m/s.
As the acceleration of the particle is negative, it will retard as it moves along ABC. At a point beyond C (i.e., at D), the particle will come to rest momentarily, and then it will move backwards with increasing speed. Throughout the motion, the particle decelerates, its velocity decreases continuously, velocity varies as 12,
11,10,..., 2,1,0,-1,-2-10, -11, -12, etc. Only from A to D the motion is retarded, during which speed varies as 12,11,10,..., 2,1,0. Subsequently, the particle speeds up, speed changing as 1, 2, 3,..., etc. Notice the difference between deceleration and retardation.
When the particle reaches A again, its displacement = 0
$$\therefore$$ 0= 12 $$\times$$ t + (1/2)(-1)$$t^2$$
=> t = 0, 24 s
At t = 0, velocity at A = 12 m/s,
At t = 24 s, velocity at A is 12 + (-1) x 24 = -12 m/s.
D.The particle reverses the direction of motion at D. For the motion between A and D
u = 12 m/s, v = 0, a = -1 m$$s^{-2}$$. If AD = s, from the equation $$v^2 = u^2 + 2as$$
$$(0)^2 = (12)^2$$ + 2 x (-1) x s
s = 72 m
E. After 12 s the particle comes to rest momentarily at D after covering a distance of 72 m.
Distance in subsequent 3 s
= 0 x 3 + (1/2) x (-1) x $$(3)^2$$ = 4.5 m
$$\therefore$$ d = 72 m + 4.5 m = 76.5 m
A thief on a bike moving with uniform velocity passes a stationary policeman who is hiding behind a bill board with a motorcycle. After a 2.0 sec. delay (reaction time) the policeman accelerates to his maximum speed of 150 km/hr in 12sec. The policeman moves with uniform speed of 150 km/hr from this instant onwards and catches up with the thief 1.5 km beyond the billboard. Find the speed of the thief in km/hr.
A balloon starts rising upwards with constant acceleration "a" and after time to second, a packet is dropped from it which reaches ground after t seconds of dropping. Determine value of t.
Velocity of packet when dropped will be same as velocity of balloon ,but as its acceleration becomes g downward,
velocity of balloon after time t will be
$$v=u+a\times 2$$
since u=0
$$v=a\times 2$$
and distance travelled by balloon will be
$$s=u\times t + \dfrac{1}{2}\times a\times t^{2}$$
$$s=0+\dfrac{1}{2}\times a\times 4$$
$$s=2a$$
so velocity of packet will also be same
for packet
$$u_{initial}=2a$$ $$ a=-g$$ . $$time=t$$ and $$s=-2a$$
$$s=u\times t + \dfrac{1}{2}\times a\times t^{2}$$
$$-2a=2a\times t +\dfrac{1}{2}\times -g\times t^{2}$$
solving above quadratic equation
$$t = \dfrac{a+\sqrt{a^2 + 8ag}}{2g}$$
this is the time required for the packet to reach ground.
A diwali rocket moves vertically up with a constant acceleration $$a_1$$ = 20/3 $$ms^{-2}$$. After sometimes, its fuel gets exhausted and then it falls freely with an acceleration $$a_2 = 10 ms^{-2}$$. If the maximum height attained by the diwali rocket is h, using graphical method, find its speed when the fuel is just exhausted. Assume h = 50 m.
Let the rocket acquire a speed v at the time when all its fuel gets exhausted. Referring to the v-t graph in Fig., the slope of OP gives the acceleration $$a_1$$.
The slope of OP gives the acceleration
$$a_1 = tan \Theta_1 = \dfrac{v}{t_1}$$ ...(i)
The slope of PQ gives the acceleration
$$-(a_2) = tan \Theta_2 = \dfrac{-v}{t_2}$$ ...(ii)
From (i) and (ii), we have
$$v = a_1t_2 = a_2 t_2$$. ...(iii)
The area under v - t graph = Area of $$\Delta$$OPQ = (1/2) OQ.PM = s
Substituting OQ = $$t_1 + t_2$$ and PM = v,
The total displacement s =(v/2)$$(t_1 + t_2$$ ...(iv)
Substituting $$t_1 = \dfrac{v}{a_1}$$ and $$t_2 = \dfrac{v}{a_2}$$ from(iii) in (iv), we have
$$s = \dfrac{v}{2}\left ( \dfrac{v}{a_1} + \dfrac{v}{a_2} \right ) $$
Finally substituting s = +h (as the area is positive), $$a_1 = \dfrac{20}{3} ms^{-2}$$ and $$a_2 = 10 ms^{-2}$$, we have
$$\displaystyle v = \sqrt{\dfrac{2a_1 a_2h}{a_1 + a_2}} = \sqrt{\dfrac{2\times (20/3) \times 10 \times 50}{\dfrac{20}{3} + 10}}$$
This yields v = 20 m/s.
The slope of OP gives the acceleration
$$a_1 = tan \Theta_1 = \dfrac{v}{t_1}$$ ...(i)
The slope of PQ gives the acceleration
$$-(a_2) = tan \Theta_2 = \dfrac{-v}{t_2}$$ ...(ii)
From (i) and (ii), we have
$$v = a_1t_2 = a_2 t_2$$. ...(iii)
The area under v - t graph = Area of $$\Delta$$OPQ = (1/2) OQ.PM = s
Substituting OQ = $$t_1 + t_2$$ and PM = v,
The total displacement s =(v/2)$$(t_1 + t_2$$ ...(iv)
Substituting $$t_1 = \dfrac{v}{a_1}$$ and $$t_2 = \dfrac{v}{a_2}$$ from(iii) in (iv), we have
$$s = \dfrac{v}{2}\left ( \dfrac{v}{a_1} + \dfrac{v}{a_2} \right ) $$
Finally substituting s = +h (as the area is positive), $$a_1 = \dfrac{20}{3} ms^{-2}$$ and $$a_2 = 10 ms^{-2}$$, we have
$$\displaystyle v = \sqrt{\dfrac{2a_1 a_2h}{a_1 + a_2}} = \sqrt{\dfrac{2\times (20/3) \times 10 \times 50}{\dfrac{20}{3} + 10}}$$
This yields v = 20 m/s.
A ball is thrown with a velocity of $$20\ m/sec$$ from top of a multistory building the height of point from were the ball is thrown in $$25\ m$$ from the ground. (i) How height is the ball rise (ii) How long will it take before hitting the ground? Take $$g=10\ m/s$$
A fighter jet plane is flying at a height of $$500\ m$$ with a velocity $$450\ h^{-1}$$. It releases a bomb when $$500\ m$$ away from the enemy post. Will the bomb hit the post ? Take $$g=10\ ms^{-2}$$.
A police inspector in a jeep is chasing a pickpocket on a straight road. The jeep is going at its maximum speed v (assumed uniform). The pickpocket rides on the motorcycle of a waiting friend when the jeep is at a distance d away, and the motorcycle starts with a constant acceleration a . Show that the pickpocket will be caught if $$v \leq \sqrt{2ad}$$
A truck moving with constant acceleration covers the distance between two points $$180\ m$$ apart in $$6\ seconds$$. Its speed as it passes the second points $$45\ m/s$$. Find
(a) its acceleration, and
(b) its speed when it was at the first point.
Let the initial speed is $$v_0$$
A to B
$$u_i = v_0 $$, $$ v = 45$$
$$t = 6$$ , $$s = 180 m$$
$$v = u + at$$
$$45 = v_0 + 6a$$ ............( 1 )
$$s = ut$$ + $$\dfrac{1}{2} at^2$$
$$180 = v_0 \times 6 + \dfrac{1}{2} \times a \times 36$$
$$30 = v_0 + 3a$$ .................( 2 )
from ( 1 ) & ( 2 ) equation
$$a = 5 m/s^2$$
$$v_0 = 15 m / s $$
so
( i ) its acceleration = $$5m/s^2$$
( ii ) its initial speed = $$15 m / s $$
A balloon is ascending at the rate of $$14\ m/s$$ at a height of $$98\ m$$ above the ground a packet is dropped from the balloon. After how much time and with velocity does it reach the ground?
An object thrown vertically upwards reaches a height of $$500\ m$$. What was its initial velocity? How long will the object take to come back to the earth? Assume $$g=10\ m/s^{2}$$
A car travels with a velocity $$10\ { ms }^{ -1 }$$ and accelerates at $$5\ { ms }^{ -2 }$$. Calculate the final velocity when it has travelled $$30\ m$$.
A parachutist bails out from an aeroplane and after drooping through a distance of $$40\ m$$, he opens the parachute and decelerates at $$2\ {m/s}^{2}$$. If he reaches the ground with a speed of $$2\ m/s$$ (i) how long he is in air. (ii) at what height did he bail out from the plane?
A person of mass $$50 kg $$ is standing in lift. What weight will he experience if the lift is moving upwards with acceleration $$ 2 m/s^2 $$
A particle starts from origin at t = 0 with velocity of 15$$\hat{i}$$ and moves in x-y plane under the action of force which produce a constant acceleration of $$15\hat{i} + 20 \hat{j}$$. Find y-coordinate of particle when x-coordinate is 180 m.
A train $$200 m $$ long crosses a bridge $$300 m $$ long. It enters the bridge with a speed of $$3 ms^{-1} $$ and leaves it with a speed of $$ 5 ms^{-1} $$. What is the time taken to cross the bridge?
Two masses $$A$$ and $$B$$ are moving in the same straight line, A moves with a uniform velocity of $$11m/sec$$, $$B$$ starts from rest at the instant when it is $$52.5$$ metres ahead of $$A$$, and moves with a uniform acceleration $$1m/{sec}^{2}$$. When will $$A$$ catch $$B$$? Explain the reason for two answers?
A person sitting in the compartment of a train moving with uniform speed throws a ball in the upward direction. What path of the ball will appear to him? What to a person standing outside the train?
A $$2kg$$ block sliding on horizontal surface with a speed of $$5 m/s$$ comes to rest after covering distance of $$5m$$ . Assuming that the retardation is uniform find $$\mu_2 $$
An object starts moving with a velocity $$6 m/s$$ and acceleration $$105 m/s^2 $$ after. What time will it acquire the velocity $$15 m/s $$ ? Find the distance traveled by the object in this time.
A Bullet is fired from a rifle with a velocity $$750 m/s$$. If length of rifle barrel is a $$60cm$$ ,calculate average velocity of the bullet ,while being accelerate in barrel. Find the time taken by the bullet to travel.
A uniform chain of mass $$m$$ and length $$l$$ is placed on a smooth table so that one-third length hangs freely as shown in the figure. Now the chain is released, with what velocity chain slips off the table?
An elevator has a mass of 4000 kg. When the tension in the supporting cable is 48000 N, What is the acceleration? Starting from rest, how far does it move in 3 s? $$(g = 10 m/s^2)$$
A body moving along the ground with a velocity of $$14 m/s $$ comes to rest due to friction after travelling a distance of $$50 cm $$ Determine the coefficient of friction between the body and the ground $$ g = 9.8 m/s^2 $$
A can travelling at a speed of 20m/sec to due north along the highway make it turns on to a side word that has due east. If takes 50 sec for the ear to comp lite the 50 sec for the end of 50 sec the ear has a speed of 15m/sec along the side road. Determine the magnitude of an acceleration over the 50 sec internal.
Initial velocity $$\vec{u}=20j$$
Final velcoity $$\vec{v}=15i$$
time $$t=50s$$
Hence acceleration is $$\vec{a}=\dfrac{\vec{v}-\vec{u}}{t}$$
$$\implies \vec{a}=\dfrac{15i-20j}{50}$$
$$\implies a=\dfrac{\sqrt{15^2+20^2}}{50}=\dfrac{25}{50}$$
$$\implies a =0.5m/s^2$$
A body starting from rest slides down a rough inclined plane of length one metre is $$2s$$ . Find $$\mu $$ if the angle of inclination of the plane to the horizontal is $$30^o (0.518) $$
A particle having initial velocity u moves with a constant acceleration a for a time $$t.$$ Find the displacement of the particle in the last $$1$$ second.
If a particle moves towards east with a velocity Q $$5ms^{-1}.$$ In 10 seconds. The velocity changes to $$5ms{-1}$$ north. Find avg. acceleration Q particle.
A particle having initial velocity u moves with a constant acceleration a for a time $$t.$$ Evaluate it for $$u= 5 m/s, a = 2 m/s $$ and $$ t =10 s. $$
The displacement s of an object is given as a function of time t
$$s = 5t^2 + 9t$$
Calculate the instantaneous velocity of object at t = 0.
A monkey is ascending a branch with constant acceleration. If the breaking strength is $$160 \% $$ of the monkey's weight, what is the maximum acceleration permitted for the monkey?
The engine of a train passes an electric pole with a velocity $$'u'$$ and the last compartment of the train crosses the same pole with a velocity $$v$$. Then find the velocity with which the mid-point of the train passes the pole. Assume acceleration to be uniform.
A police jeep on a petrol duty on national highway was moving with a speed of 54Km/hr The same direction. If finds a thief rushing up in a car at a rate of 126 Km/hr in the same direction. Police sub-inspector fired at the car of the thief with his servise revoluter with a muzzel speed of 100 m/s. with what speed will the bullet hit car of thief?
Establish the relation $$ s_nth = u\frac { a }{ 2 } \left( 2n-1 \right) $$where the letters have their usual meanings.
The power of engine of a car of mass 1200 kg is 25 kW.The minimum time required to reach a velocity of 90 Km/h by the car after starting from rest is
A ball starts required form ground with zero imitial velocity and $$ 2 m/sec^{2}$$ acceleration at$$ t =0 $$At $$t = 5s$$ a stone is dropped from ball Find time taken by stone to reach ground.
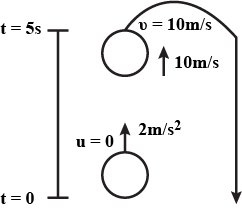
A stone is thrown vertically upward with a speed of 28 m/s.
a) Find the maximum height reached by the stone.
b) Find its velocity one second before it reaches the maximum height.
c) Does the answer of part
d) change if the initial speed is more than 28 m/s such as 40 m/s or 80 m/s?
On a two-lane road, car A is travelling with a speed of 36 km $${ h }^{ -1 }$$. Two cars B and C approach car A in opposite directions with a speed of 54 km $${ h }^{ -1 }$$ each. At a certain instant, when the distance AB is equal to AC, both being 1 km. B decides to overtake A before C does. What minimum acceleration of car B is required to avoid an accident ?
A car falls off a ledge and drops to the ground in 0.5 seconds.
Let $$g = 10 ms^{-2}$$, then
(a) What is its speed on striking the ground?
(b) What is its average speed during 0.5 second?
(c) How high is the ledge from the ground?
A body is starting from rest and is subjected to a uniform acceleration of $$10ms^{-2}$$. Determine.
- Velocity of the body at the end of $$5s$$
- Displacement of the body In the first $$3s$$
- the velocity of the body after a displacement of $$20m$$.
- Displacement of the body In the $$4^{th}$$ second of its motion (Tumkur $$05$$)
A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give an explanation to support your diagram.
v= vertical velocity of the ball given by the boy
u= velocity of the car which is equal to the horizontal velocity of the ball.
As the ball has both vertical and horizontal components of velocities it's path will be parabolic as observed by a person standing on the footpath.
Path of the ball as seen by the boy sitting in the same car will be only vertical up-down under gravity and will catch up by the boy if car is moving with constant velocity
u= velocity of the car which is equal to the horizontal velocity of the ball.
As the ball has both vertical and horizontal components of velocities it's path will be parabolic as observed by a person standing on the footpath.
Path of the ball as seen by the boy sitting in the same car will be only vertical up-down under gravity and will catch up by the boy if car is moving with constant velocity
Derive the equations of motion with the help of the graphical method.
Graphical method : Consider an object moving along a straight line with uniform acceleration a let u be the initial velocity of the object at time $$ t = 0 $$ and v be the final velocity of the object at time t . let s be the distance travelled by the object in time t.
velocity -time graph of this motion is a straight line $$ PQ $$ as shown in the figure
where $$ OP = u = RS $$
$$ OW = SQ = v $$ and
$$ OS =PR =t $$
(I) for the first equation of motion : we know that the slope of velocity -time graph of uniformly accelerated motion represents the acceleration of the object
i.e. acceleration = slope of the velocity -time graph $$ PQ $$
or $$ a = \frac {QR}{PR} = \frac { QR}{OS} $$
$$ a = \frac {SQ-SR}{OS} = \frac {v -u }{t} $$
or $$ v-u = at $$
or $$ v = u + at $$ .....(i)
This is the first equation of uniform acceterated motion.
(ii) Second equation of motion ; We know that the area under the velocity-time graph for a given time interval represents the distance covered by the uniformly accelerated object in that interval of time.
$$ \therefore $$ Distance (displacement) travelled by the object in time t is :
S = area of trapezium $$ OSQP $$
= area of rectangle $$ OSRP $$ + Area of triangle $$ PRQ $$
or $$ S = OS \times OP + \frac {1}{2} \times PR \times PQ $$
(area of rectangle = length $$ \times $$ breadth)
( Area of triangle $$ = \frac {1}{2} \times $$ Base $$ \times $$ Height )
$$ = t \times u + \frac {1}{2} \times t \times ( v- u) $$
(from the first equation of motion $$ v- u =at) $$
$$ = ut + \frac {1}{2} \times t \times at $$
Thus $$ S = ut + \frac {1}{2} at^2 ......(ii) $$
This is the second equation of uniform accelerated motion.
(iii) Third equation of motion : Distance travelled by the object in time interval t is s = area of trapezium $$OSQP $$
$$ = \frac {1}{2} ( OP + SQ) \times OS $$
$$ \because OP =SR $$
$$ = \frac {1}{2} ( SR +SQ) \times OS ........(iii) $$
Acceleration , a = slope of the velocity -time graph $$ PQ $$
or $$ a = \frac {RQ}{PR} = \frac {SQ-SR}{OS} $$
or $$ OS = \frac {SQ-SR}{a} ...........(iv) $$
Putting this value in equation (iii) we get
$$ s = \frac {1}{2} (SR + SQ) ( \frac { SQ-SR}{a} ) $$
or $$ s = \frac {1}{2a}(AQ^2 -SR^2) $$
or $$ s = \frac {1}{2a} (v^2 - u^2) $$
or $$ v^2 -u^2 = 2as $$
or $$ v^2 = u^2 +2as $$.............(v)
This the third equation of uniform accelerated motion.
velocity -time graph of this motion is a straight line $$ PQ $$ as shown in the figure
where $$ OP = u = RS $$
$$ OW = SQ = v $$ and
$$ OS =PR =t $$
(I) for the first equation of motion : we know that the slope of velocity -time graph of uniformly accelerated motion represents the acceleration of the object
i.e. acceleration = slope of the velocity -time graph $$ PQ $$
or $$ a = \frac {QR}{PR} = \frac { QR}{OS} $$
$$ a = \frac {SQ-SR}{OS} = \frac {v -u }{t} $$
or $$ v-u = at $$
or $$ v = u + at $$ .....(i)
This is the first equation of uniform acceterated motion.
(ii) Second equation of motion ; We know that the area under the velocity-time graph for a given time interval represents the distance covered by the uniformly accelerated object in that interval of time.
$$ \therefore $$ Distance (displacement) travelled by the object in time t is :
S = area of trapezium $$ OSQP $$
= area of rectangle $$ OSRP $$ + Area of triangle $$ PRQ $$
or $$ S = OS \times OP + \frac {1}{2} \times PR \times PQ $$
(area of rectangle = length $$ \times $$ breadth)
( Area of triangle $$ = \frac {1}{2} \times $$ Base $$ \times $$ Height )
$$ = t \times u + \frac {1}{2} \times t \times ( v- u) $$
(from the first equation of motion $$ v- u =at) $$
$$ = ut + \frac {1}{2} \times t \times at $$
Thus $$ S = ut + \frac {1}{2} at^2 ......(ii) $$
This is the second equation of uniform accelerated motion.
(iii) Third equation of motion : Distance travelled by the object in time interval t is s = area of trapezium $$OSQP $$
$$ = \frac {1}{2} ( OP + SQ) \times OS $$
$$ \because OP =SR $$
$$ = \frac {1}{2} ( SR +SQ) \times OS ........(iii) $$
Acceleration , a = slope of the velocity -time graph $$ PQ $$
or $$ a = \frac {RQ}{PR} = \frac {SQ-SR}{OS} $$
or $$ OS = \frac {SQ-SR}{a} ...........(iv) $$
Putting this value in equation (iii) we get
$$ s = \frac {1}{2} (SR + SQ) ( \frac { SQ-SR}{a} ) $$
or $$ s = \frac {1}{2a}(AQ^2 -SR^2) $$
or $$ s = \frac {1}{2a} (v^2 - u^2) $$
or $$ v^2 -u^2 = 2as $$
or $$ v^2 = u^2 +2as $$.............(v)
This the third equation of uniform accelerated motion.
At the instant the traffic light turns green, an automobile starts with a constant acceleration $$a$$ of $$5 \ m/s^{2}$$. At the same instant a truck, traveling with a constant speed of $$10 \ m/s$$, overtakes and passes the automobile. How fast will the automobile be traveling at that instant?
A man is standing on the top of building 100 m high. He throws two balls vertically, One at $$ t=0 $$ and other after a time interval (less than 2 seconds). The later ball is thrown at a velocity of half the first. The vertical gap between first and second ball is $$ +15 \mathrm{m} $$ at $$ \mathbf{t}=2 \mathbf{s} . $$ The gap is found to remain constant. Calculate the velocity with which balls were thrown and the exact time interval between their thrown.
Comment on the statement 'rest and motion are relative terms' . Give an example.
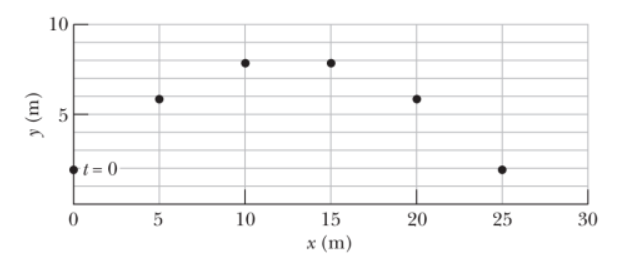
A track meet is held on a planet in a distant solar system. A shot-putter releases a shot at a point $$2.0 m$$ above ground level. A stroboscopic plot of the position of the shot is shown in Fig. 4-61,where the readings are $$0.50 s$$ apart and the shot is released at time $$t = 0$$. (a) What is the initial velocity of the shot in unit vector notation? (b) What is the magnitude of the free-fall acceleration on the planet? (c) How long after it is released does the shot reach the ground? (d) If an identical throw of the shot is made on the surface of Earth, how long after it is released does it reach the ground?
A hare and a tortoise compete in a race over a straight course $$1.00$$ km long. The tortoise crawls at a speed of $$0.200$$ m/s toward the finish line. The hare runs at a speed of $$8.00$$ m/s toward the finish line for $$0.800$$ km and then stops to tease the slow-moving tortoise as the tortoise eventually passes by. The hare waits for a while after the tortoise passes and then runs toward the finish line again at $$8.00$$ m/s. Both the hare and the tortoise cross the finish line at the exact same instant. Assume both animals, when moving, move steadily at their respective speeds. (a) How far is the tortoise from the finish line when the hare resumes the race? (b) For how long in time was the hare stationary?
A hockey player is standing on his skates on a frozen pond when an opposing player, moving with a uniform speed of $$12.0 m/s$$, skates by with the puck. After $$3.00 s$$, the first player makes up his mind to chase his opponent. If he accelerates uniformly at $$4.00 m/s^{2}$$, (a) how long does it take him to catch his opponent and (b) how far has he traveled in that time? (Assume the player with the puck remains in motion at constant speed.)
A person takes a trip, driving with a constant speed of $$89.5$$ km/h, except for a $$22.0$$ min rest stop. If the persons average speed is $$77.8$$ km/h, (a) how much time is spent on the trip and (b) how far does the person travel.
A speedboat moving at $$30.0 m/s$$ approaches a no-wake buoy marker $$100 m$$ ahead. The pilot slows the boat with a constant acceleration of $$-3.50 m/s^{2}$$ by reducing the throttle. (a) How long does it take the boat to reach the buoy? (b) What is the velocity of the boat when it reaches the buoy.
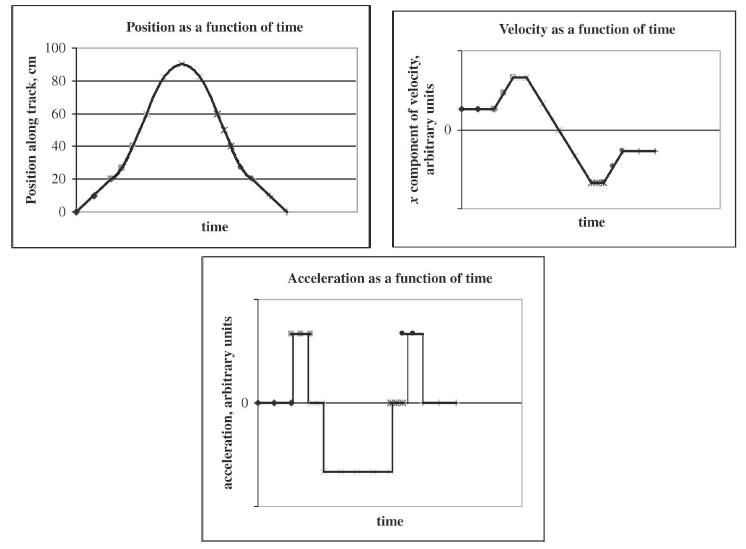
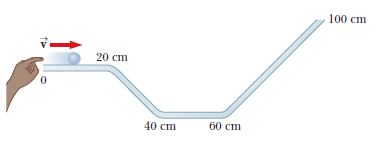
A child rolls a marble on a bent track that is $$100$$ cm long as shown in above figure. We use $$x$$ to represent the position of the marble along the track. On the horizontal sections from $$x = 0$$ to $$x = 20 cm$$ and from $$x = 40 cm$$ to $$x = 60 cm$$, the marble rolls with constant speed. On the sloping sections, the marbles speed changes steadily. At the places where the slope changes, the marble stays on the track and does not undergo any sudden changes in speed. The child gives the marble some initial speed at $$x = 0$$ and $$t = 0$$ and then watches it roll to $$x = 90 cm$$, where it turns around, eventually returning to $$x = 0$$ with the same speed with which the child released it. Prepare graphs of $$x$$ versus $$t$$, $$v_{x}$$ versus $$t$$, and $$a_{x}$$ versus $$t$$, vertically aligned with their time axes identical, to show the motion of the marble. You will not be able to place numbers other than zero on the horizontal axis or on the velocity or acceleration axes, but show the correct graph shapes.
The acceleration is zero whenever the marble is on a horizontal section. The acceleration has a constant positive value when the marble is rolling on the 20-to-40-cm section and has a constant negative value when it is rolling on the second sloping section. The position graph is a straight sloping line whenever the speed is constant and a section of a parabola when the speed changes.
A car travels along a straight line at a constant speed of $$60.0 mi/h$$ for a distance d and then another distance $$d$$ in the same direction at another constant speed. The average velocity for the entire trip is $$30.0 mi/h$$. (a) What is the constant speed with which the car moved during the second distance $$d$$ ? (b) What If? Suppose the second distance $$d$$ were traveled in the opposite direction; you forgot something and had to return home at the same constant speed as found in part (a). What is the average velocity for this trip? (c) What is the average speed for this new trip?
A speedboat travels in a straight line and increases in speed uniformly from $$v_{i} = 20.0 m/s$$ to $$v_{f} = 30.0 m/s$$ in a displacement $$x$$ of $$200 m$$. We wish to find the time interval required for the boat to move through this displacement. (a) Draw a coordinate system for this situation. (b) What analysis model is most appropriate for describing this situation? (c) From the analysis model, what equation is most appropriate for finding the acceleration of the speedboat? (d) Solve the equation selected in part (c) symbolically for the boats acceleration in terms of $$v_{i}, v_{f}$$, and $$x$$. (e) Substitute numerical values to obtain the acceleration numerically. (f) Find the time interval mentioned above.
(a) We choose a coordinate system with the $$x$$ axis positive to the right, in the direction of motion of the speedboat, as shown on the right.
(b) Since the speedboat is increasing its speed, the particle under constant acceleration model should be used here.
(c) Since the initial and final velocities are given along with the displacement of the speedboat, we use
$$v_{xf}^{2}=v_{xi}^{2}+2a\Delta x$$
(d) Solving for the acceleration of the speedboat gives
$$a=\frac{v_{xf}^{2}-v_{xi}^{2}}{2\Delta x}$$
(e) We have $$v_{i} = 20.0 m/s, v_{f} = 30.0 m/s$$, and $$x_{f} – x_{i} = Δx = 200 m$$:
$$a=\frac{v_{xf}^{2}-v_{xi}^{2}}{2\Delta x}=\frac{(30.0m/s)^{2}-(20.0m/s)^{2}}{2(200m)}=1.25m/s^{2}$$
(f) To find the time interval, we use $$v_{f} = v_{i} + at$$, which gives
$$t=\frac{v_{f}-v_{i}}{a}=\frac{30.0m/s-20.0m/s}{1.25m/s^{2}}=8.00s$$
(b) Since the speedboat is increasing its speed, the particle under constant acceleration model should be used here.
(c) Since the initial and final velocities are given along with the displacement of the speedboat, we use
$$v_{xf}^{2}=v_{xi}^{2}+2a\Delta x$$
(d) Solving for the acceleration of the speedboat gives
$$a=\frac{v_{xf}^{2}-v_{xi}^{2}}{2\Delta x}$$
(e) We have $$v_{i} = 20.0 m/s, v_{f} = 30.0 m/s$$, and $$x_{f} – x_{i} = Δx = 200 m$$:
$$a=\frac{v_{xf}^{2}-v_{xi}^{2}}{2\Delta x}=\frac{(30.0m/s)^{2}-(20.0m/s)^{2}}{2(200m)}=1.25m/s^{2}$$
(f) To find the time interval, we use $$v_{f} = v_{i} + at$$, which gives
$$t=\frac{v_{f}-v_{i}}{a}=\frac{30.0m/s-20.0m/s}{1.25m/s^{2}}=8.00s$$
A glider of length $$12.4 cm$$ moves on an air track with constant acceleration (Fig above). A time interval of $$0.628 s$$ elapses between the moment when its front end passes a fixed point $$A$$ along the track and the moment when its back end passes this point. Next, a time interval of $$1.39 s$$ elapses between the moment when the back end of the glider passes the point $$A$$ and the moment when the front end of the glider passes a second point $$B$$ farther down the track. After that, an additional $$0.431 s$$ elapses until the back end of the glider passes point $$B$$. (a) Find the average speed of the glider as it passes point $$A$$. (b) Find the acceleration of the glider. (c) Explain how you can compute the acceleration without knowing the distance between points $$A$$ and $$B$$.
An object moves with constant acceleration $$4.00 m/s^{2}$$ and over a time interval reaches a final velocity of $$12.0 m/s$$. (a) If its initial velocity is $$6.00 m/s$$, what is its displacement during the time interval? (b) What is the distance it travels during this interval? (c) If its initial velocity is $$26.00 m/s$$, what is its displacement during the time interval? (d) What is the total distance it travels during the interval in part (c)?
A body moving along a straight line with uniform acceleration covers $$23m$$ and $$35m$$ respectively In the $$5^{th}$$ and $$8^{th}$$ second of its motion calculate the distance traveled by the body in
- The $$10^{th}$$ second
- Complete $$10$$ second and what is its velocity at the end of $$6$$ seconds.
An attacker at the base of a castle wall $$3.65 m$$ high throws a rock straight up with speed $$7.40 m/s$$ from a height of $$1.55 m$$ above the ground. (a) Will the rock reach the top of the wall? (b) If so, what is its speed at the top? If not, what initial speed must it have to reach the top? (c) Find the change in speed of a rock thrown straight down from the top of the wall at an initial speed of $$7.40 m/s$$ and moving between the same two points. (d) Does the change in speed of the downward moving rock agree with the magnitude of the speed change of the rock moving upward between the same elevations? (e) Explain physically why it does or does not agree.
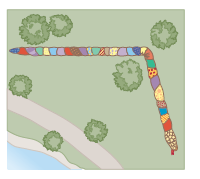
The biggest stuffed animal in the world is a snake $$420 m$$ long, constructed by Norwegian children. Suppose the snake is laid out in a park as shown in above figure, forming two straight sides of a $$105^{0}$$ angle, with one side $$240 m$$ long. Olaf and Inge run a race they invent. Inge runs directly from the tail of the snake to its head, and Olaf starts from the same place at the same moment but runs along the snake. (a) If both children run steadily at $$12.0 km/h$$, Inge reaches the head of the snake how much earlier than Olaf? (b) If Inge runs the race again at a constant speed of $$12.0 km/h$$, at what constant speed must Olaf run to reach the end of the snake at the same time as Inge?
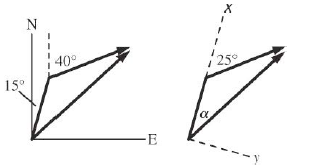
An airplane maintains a speed of $$630 km/h$$ relative to the air it is flying through as it makes a trip to a city $$750 km$$ away to the north. (a) What time interval is required for the trip if the plane flies through a headwind blowing at $$35.0 km/h$$ toward the south? (b) What time interval is required if there is a tailwind with the same speed? (c) What time interval is required if there is a crosswind blowing at $$35.0 km/h$$ to the east relative to the ground?
Consider a tall building located on Earths equator. As the earth rotates, a person on the top floor of the building moves faster than someone of the ground with respect to an inertial reference frame because the person on the ground is closer to the Earths axis. Consequently, if an object is dropped from the top floor to the ground a distance $$h$$ below, it lands east of the point vertically below where it was dropped.
How far to the east will the object land? Express your answer in terms of $$h, g$$ and the angular speed $$\omega$$ of the Earth. Ignore air resistance and assume the free-fall acceleration is constant over this range of heights.
A frictionless plane is $$10.0 m$$ long and inclined at $$35.0^{0}$$. A sled starts at the bottom with an initial speed of $$5.00 m/s$$ up the incline. When the sled reaches the point at which it momentarily stops, a second sled is released from the top of the incline with an initial speed $$v_{i}$$. Both sleds reach the bottom of the incline at the same moment. (a) Determine the distance that the first sled traveled up the incline. (b) Determine the initial speed of the second sled.
A Coast Guard cutter detects an unidentified ship at a distance of $$20.0 km$$ in the direction $$15.0^{0}$$ east of north. The ship is traveling at $$26.0 km/h$$ on a course at $$40.0^{0}$$ east of north. The Coast Guard wishes to send a speedboat to intercept and investigate the vessel. If the speedboat travels at $$50.0 km/h$$, in what direction should it head? Express the direction as a compass bearing with respect to due north.
Choose the $$x$$ axis along the $$20km$$ distance. The $$y$$ components of the displacements of the ship and the speedboat must agree:
$$(26 km/h)t \sin(40.0^{0} − 15.0^{0}) = (50 km/h)t \sin\alpha$$
$$\alpha=\sin^{-1}\left ( \frac{11.0km/h}{50km/h} \right )=12.7^{0}$$
The speedboat should head,
$$15.0^{0}+12.7^{0}=27.7^{0}$$ E of N.
$$(26 km/h)t \sin(40.0^{0} − 15.0^{0}) = (50 km/h)t \sin\alpha$$
$$\alpha=\sin^{-1}\left ( \frac{11.0km/h}{50km/h} \right )=12.7^{0}$$
The speedboat should head,
$$15.0^{0}+12.7^{0}=27.7^{0}$$ E of N.
A student throws a set of keys vertically upward to her sorority sister, who is in a window $$4.00 m$$ above. The second student catches the keys $$1.50 s$$ later. (a) With what initial velocity were the keys thrown? (b) What was the velocity of the keys just before they were caught?
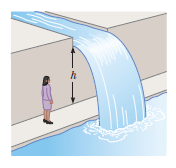
A landscape architect is planning an artificial waterfall in a city park. Water flowing at $$1.70 m/s$$ will leave the end of a horizontal channel at the top of a vertical wall $$h = 2.35 m$$ high, and from there it will fall into a pool (Fig. above). (a) Will the space behind the waterfall be wide enough for a pedestrian walkway? (b) To sell her plan to the city council, the architect wants to build a model to standard scale, which is one-twelfth actual size. How fast should the water flow in the channel in the model.
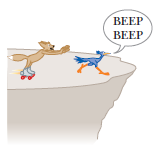
An aging coyote cannot run fast enough to catch a roadrunner. He purchases on eBay a set of jet-powered roller skates, which provide a constant horizontal acceleration of $$15.0 m/s^{2}$$ (Fig. above). The coyote starts at rest $$70.0 m$$ from the edge of a cliff at the instant the roadrunner zips past in the direction of the cliff. (a) Determine the minimum constant speed the roadrunner must have to reach the cliff before the coyote. At the edge of the cliff, the roadrunner escapes by making a sudden turn, while the coyote continues straight ahead. The coyotes skates remain horizontal and continue to operate while he is in flight, so his acceleration while in the air is $$(15.0\hat{i}- 9.80\hat{j}) m/s^{2}$$. (b) The cliff is $$100 m$$ above the flat floor of the desert. Determine how far from the base of the vertical cliff the coyote lands. (c) Determine the components of the coyotes impact velocity.
In a womens $$100m$$ race, accelerating uniformly, Laura takes $$2.00 s$$ and Healan $$3.00 s$$ to attain their maximum speeds, which they each maintain for the rest of the race. They cross the finish line simultaneously, both setting a world record of $$10.4 s$$. (a) What is the acceleration of each sprinter? (b) What are their respective maximum speeds? (c) Which sprinter is ahead at the $$6.00s$$ mark, and by how much? (d) What is the maximum distance by which Healan is behind Laura, and at what time does that occur?
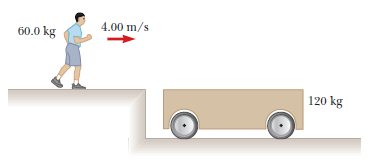
A $$60.0-kg$$ person running at an initial speed of $$4.00\ m/s$$ jumps onto a $$120-kg$$ cart initially at rest (Fig. $$P9.69$$). The person slides on the carts top surface and finally comes to rest relative to the cart. The coefficient of kinetic friction between the person and the cart is $$0.400$$. Friction between the cart and ground can be ignored.
Determine the displacement of the cart relative to the ground while the person is sliding.
Consider a tall building located on Earths equator. As the earth rotates, a person on the top floor of the building moves faster than someone of the ground with respect to an inertial reference frame because the person on the ground is closer to the Earths axis. Consequently, if an object is dropped from the top floor to the ground a distance $$h$$ below, it lands east of the point vertically below where it was dropped. Evaluate the eastward displacement for $$h=50.0\ m$$
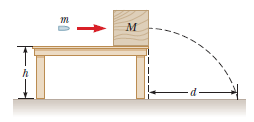
A bullet of mass m is fired into a block of mass $$M$$ initially at rest at the edge of a frictionless table of height h (Fig. $$P9.81$$). The bullet remains in the block, and after impact the block lands a distance d from the bottom of the table. Determine the initial speed of the bullet.
A $$60.0-kg$$ person running at an initial speed of $$4.00\ m/s$$ jumps onto a $$120-kg$$ cart initially at rest (Fig. $$P9.69$$). The person slides on the carts top surface and finally comes to rest relative to the cart. The coefficient of kinetic friction between the person and the cart is $$0.400$$. Friction between the cart and ground can be ignored.
Determine the displacement of the person relative to the ground while he is sliding on the cart.
A commuter train travels between two downtown stations. Because the stations are only $$1.00 km$$ apart, the train never reaches its maximum possible cruising speed. During rush hour the engineer minimizes the time interval $$\Delta t$$ between two stations by accelerating at a rate $$a_{1} = 0.100 m/s^{2}$$ for a time interval $$\Delta t_{1}$$ and then immediately braking with acceleration $$a_{2} = -0.500 m/s^{2}$$ for a time interval $$\Delta t_{2}$$. Find the minimum time interval of travel $$\Delta t$$ and the time interval $$\Delta t_{1}$$.
As soon as a traffic light turns green, a car speeds up from rest to $$50.0 mi/h$$ with constant acceleration $$9.00 mi/h/s$$. In the adjoining bicycle lane, a cyclist speeds up from rest to $$20.0 mi/h$$ with constant acceleration $$13.0 mi/h/s$$. Each vehicle maintains constant velocity after reaching its cruising speed. (a) For what time interval is the bicycle ahead of the car? (b) By what maximum distance does the bicycle lead the car?
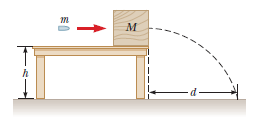
A bullet of mass $$m = 8.00\ g$$ is fired into a block of mass $$M = 250\ g$$ that is initially at rest at the edge of a table of height $$h = 1.00\ m$$ (Fig. $$P9.81$$). The bullet remains in the block, and after the impact the block lands $$d = 2.00\ m$$ from the bottom of the table. Determine the initial speed of the bullet.
The front $$1.20\ m$$ of a $$1400-kg$$ car is designed as acrumple zone that collapses to absorb the shock of a collision. If a car traveling $$25.0\ m/s$$ stops uniformly in $$1.20\ m$$,
what as a multiple of the acceleration of the car? Express the acceleration as a multiple of the acceleration due to gravity.
Class 11 Engineering Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Physical World Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work,Energy And Power Extra Questions