Motion In A Straight Line - Class 11 Medical Physics - Extra Questions
If the relation between acceleration and time for an object is given by $$a = 2t + 4t^2$$.
Calculate the position of object from the origin at $$t = 4 s$$ (At $$t = 0, v = 0, x = 0$$)
Consider a particle initially moving with a velocity of $$5 ms^{-1}$$ starts decelerating at a constant rate of $$2ms^{-2}$$. Determine the time at which the particle becomes stationary.
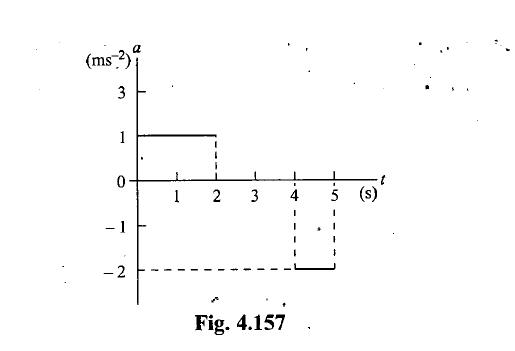
Starting at $$x=0$$, a particle moves according to the graph of $$v$$ vs $$t$$ shown in Fig. 4.Sketch a graph of the instantaneous acceleration $$a$$ vs $$t$$, indicating numerical values at significant points of the graph.
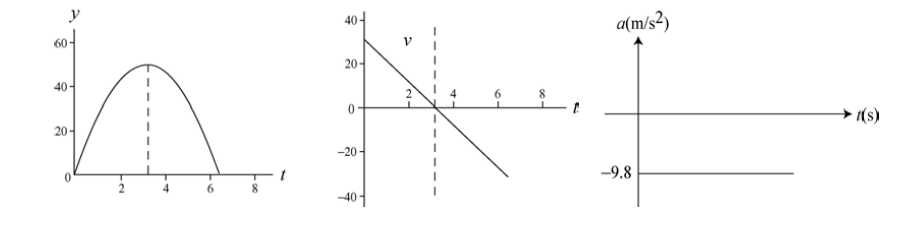
A ball is thrown vertically from ground level to rise to a maximum height of $$50\, m$$. Sketch graphs of $$y, v$$ and $$a$$ versus $$t$$ for the ball. On the first two graphs, indicate the time at which $$50\,m$$ is reached.
A vehicle is accelerating on a straight road. Its velocity at any instant is $$30\ km/h$$, after $$2s$$, it is $$33.6\ km/h$$ and after further $$2s$$, it is $$37.2\ km/h$$. Find the acceleration of vehicle in $$m/s^{2}$$. Is the acceleration uniform?
What is the acceleration time graph?
A train of length $$l=350\:m$$ starts moving rectilinearly with constant acceleration $$\omega=3.0\cdot10^{-2}\:m/s^2$$; $$t=30\:s$$ after the start the locomotive headlight is switched on (event 1), and $$\tau=60\:s$$ after that event the tail signal light is switched on (event 2) . At what constant velocity $$V$$ (in m/s) relative to the Earth must a certain reference frame $$K$$ move for the two events to occur in it at the same point? (round off your answer to the nearest integer)
A car is to be hoisted by elevator to the fourth floor of a parking garage, which is $$14$$ $$m$$ above the ground. If the elevator can have maximum acceleration of $$0.2$$ $$\displaystyle m/s^{2}$$ and maximum deceleration of $$0.1$$ $$\displaystyle m/s^{2}$$ and can reach a maximum speed of $$2.5$$ $$m/s$$, the shortest time to make the lift, starting form rest and ending at rest is $$K$$. The value of $$2K$$ will be
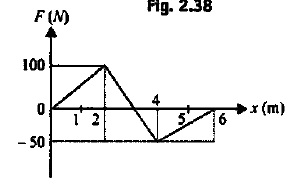
A stationary particle of mass $$m = 1.5\ kg$$ is acted upon by a variable force. The variation of force with respect to displacement is plotted in fig.
Calculate the velocity acquired by the particle after getting displaced through $$6\ m$$.
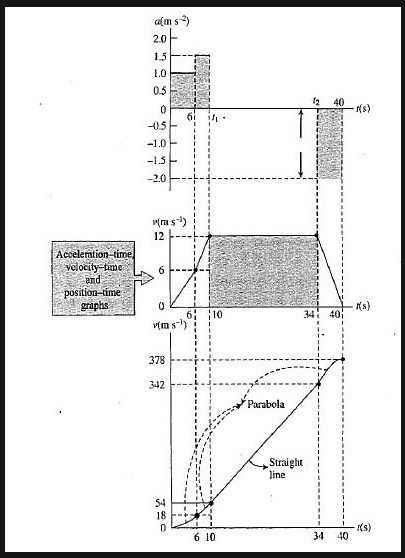
A local train leaves station A; it gains speed at the rate of 1 $$ms^{-2}$$ for first 6 s and then at the rate of 1.5 $$ms^{-2}$$ until it has reached the speed of 12 m/s. The train maintains the same speed until it approaches station B; brakes are then applied, giving the train a constant deceleration and bringing it to a stop in 6 s. If the total running time of the train is 40 s. Find (a) the distance between stations A and B. (b) Draw acceleration-time, velocity-time, and the position-time relation of motion.
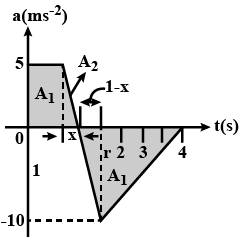
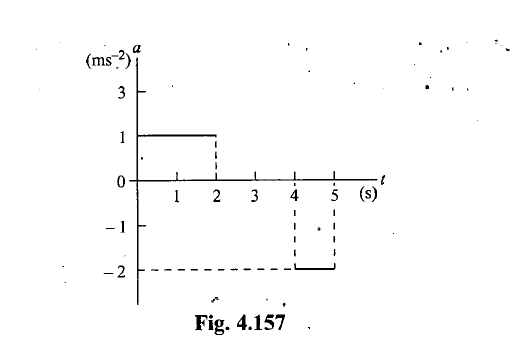
A particle moves along x-axis with an initial speed $$v_{0}$$ = $$5 ms ^{-1}$$. If its acceleration varies with time as shown in a-t graph in the figure.
a. Find the velocity of the particle at t = 4s.
b. Find the time when the particle starts moving along -x direction.

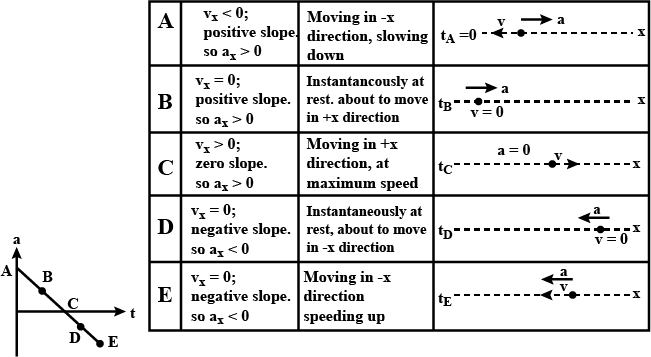
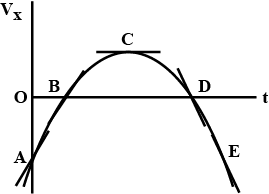
Consider the following $$v_x = t$$ graph to be parabolic. Plot the acceleration-time graph and analyze the motion of the particle from A to E.
A car starting from rest on a straight road first acceleration with $$6$$ m/s then suddenly decelerates with $$3 m/s$$ till it stops if total time of journey is $$10$$ seconds, Then the maximum speed and distance acquired by the car is:
A golf ball is hit off a tee at the edge of a cliff. Its $$x$$ and $$y$$ coordinates as functions of time are given by $$x = 18.0t$$ and $$y = 4.00t- 4.90t^{2}$$, where $$x$$ and $$y$$ are in meters and $$t$$ is in seconds. (a) Write a vector expression for the balls position as a function of time, using the unit vectors $$\hat{i}$$ and $$\hat{j}$$. By taking derivatives, obtain expressions for (b) the velocity vector $$\vec{v}$$ as a function of time and (c) the acceleration vector $$\vec{a}$$ as a function of time. (d) Next use unit-vector notation to write expressions for the position, the velocity, and the acceleration of the golf ball at $$t = 3.00 s$$.
The coordinates of an object moving in the $$xy$$ plane vary with time according to the equations $$x = 25.00 \sin \omega t$$ and $$y = 4.00 - 5.00 \cos\omega t$$, where $$v$$ is a constant, $$x$$ and $$y$$ are in meters, and $$t$$ is in seconds. (a) Determine the components of velocity of the object at $$t = 0$$. (b) Determine the components of acceleration of the object at $$t = 0$$. (c) Write expressions for the position vector, the velocity vector, and the acceleration vector of the object at any time $$t > 0$$. (d) Describe the path of the object in an $$xy$$ plot.
A rocket has total mass $$M_{i}=360\ kg$$, including $$M_{f}=330\ kg$$ of fuel and oxidizer, In interstellar space, it starts from rest at the position $$x=0$$, turns on its engine at time $$t=0$$, and puts out exhaust with relative speed $$v_{e}=1\ 500\ m/s$$ at the constant rate $$k=2.50\ kg/s$$. The fuel will last for a burn time of $$T_{b}=M_{f}/k=330\ kg/(2.5\ kg/s)=132\ s$$.
Graph the acceleration as a function of time.
Class 11 Medical Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work, Energy And Power Extra Questions