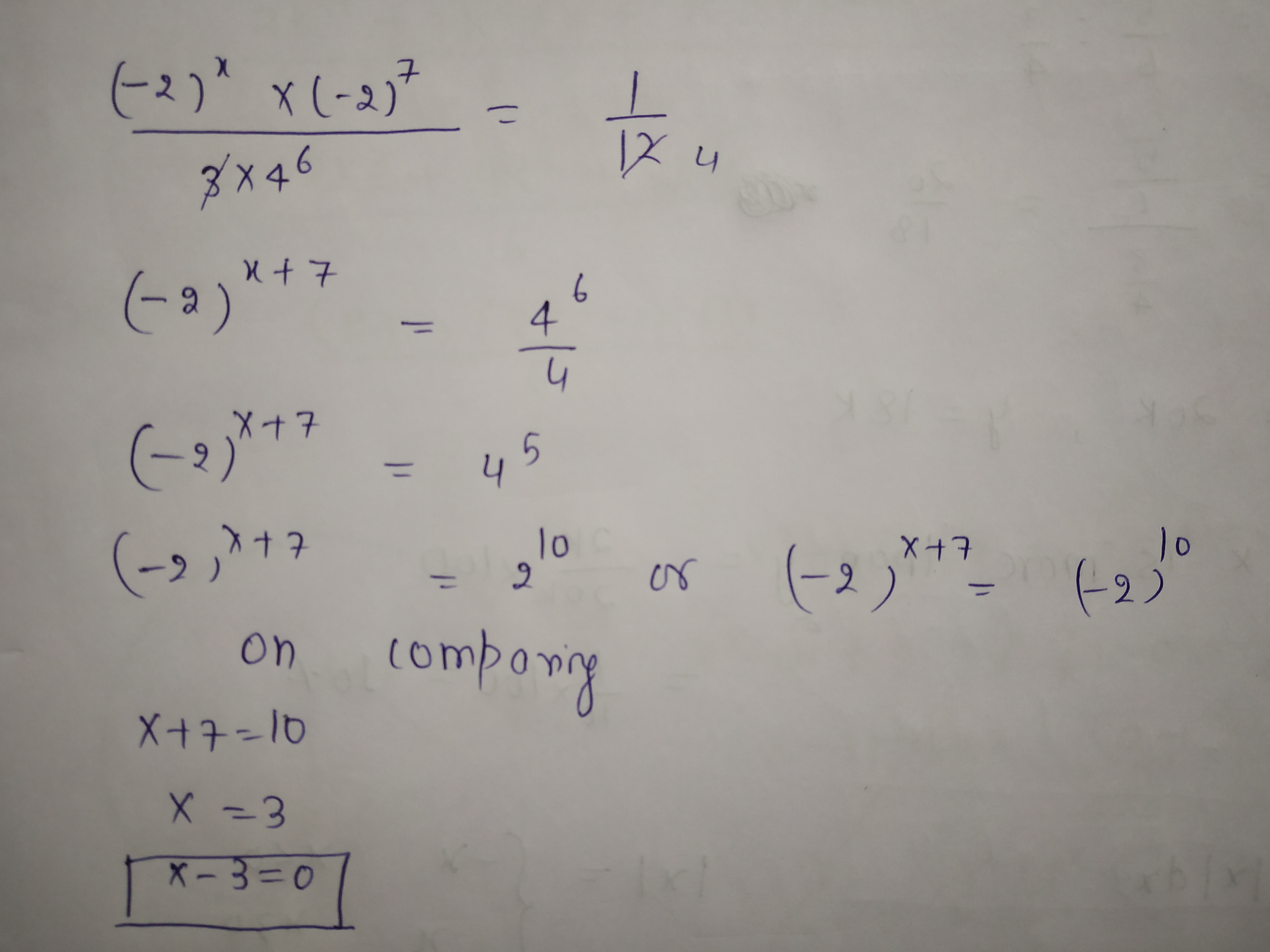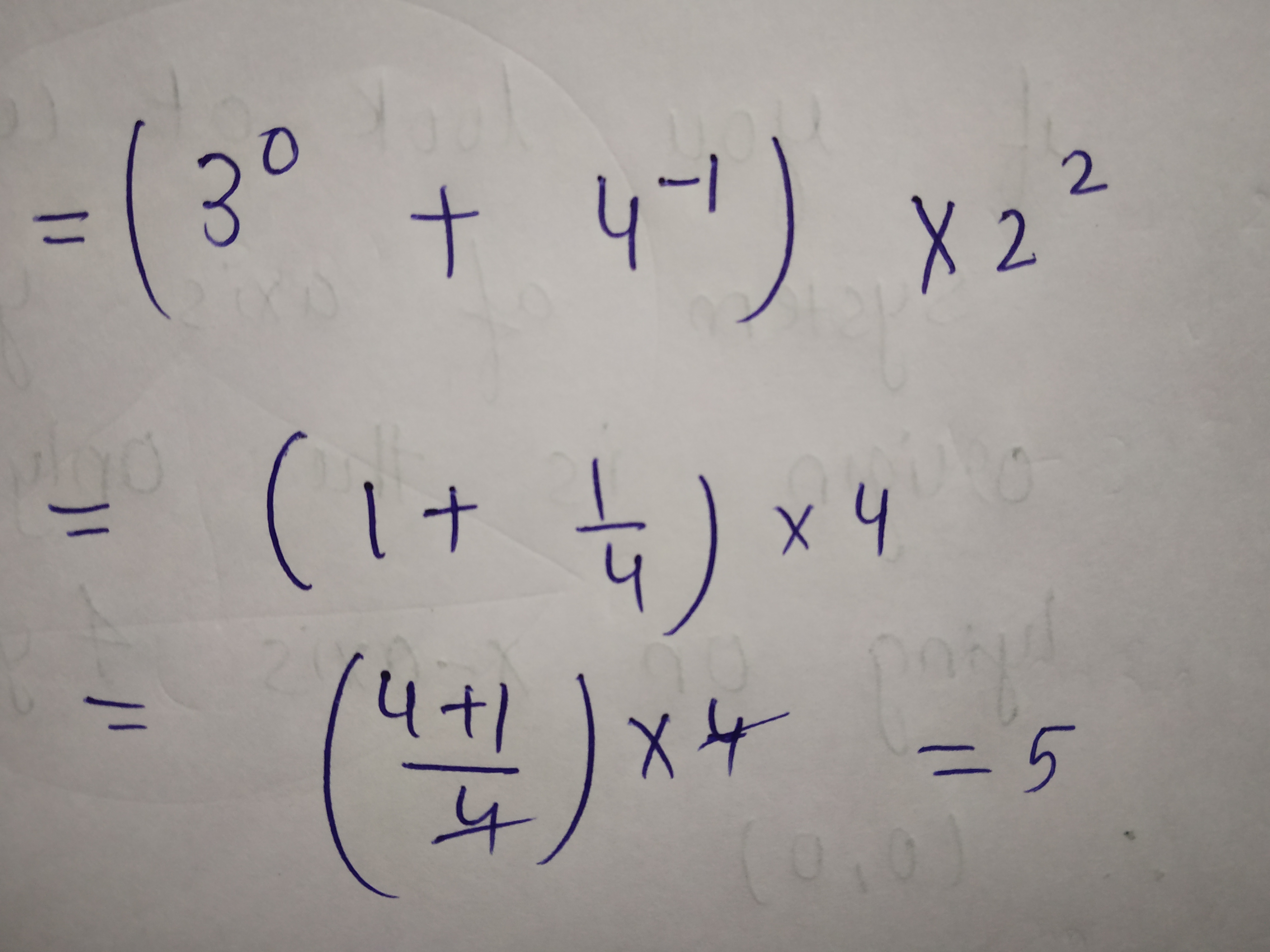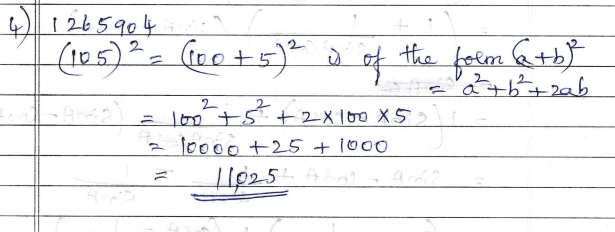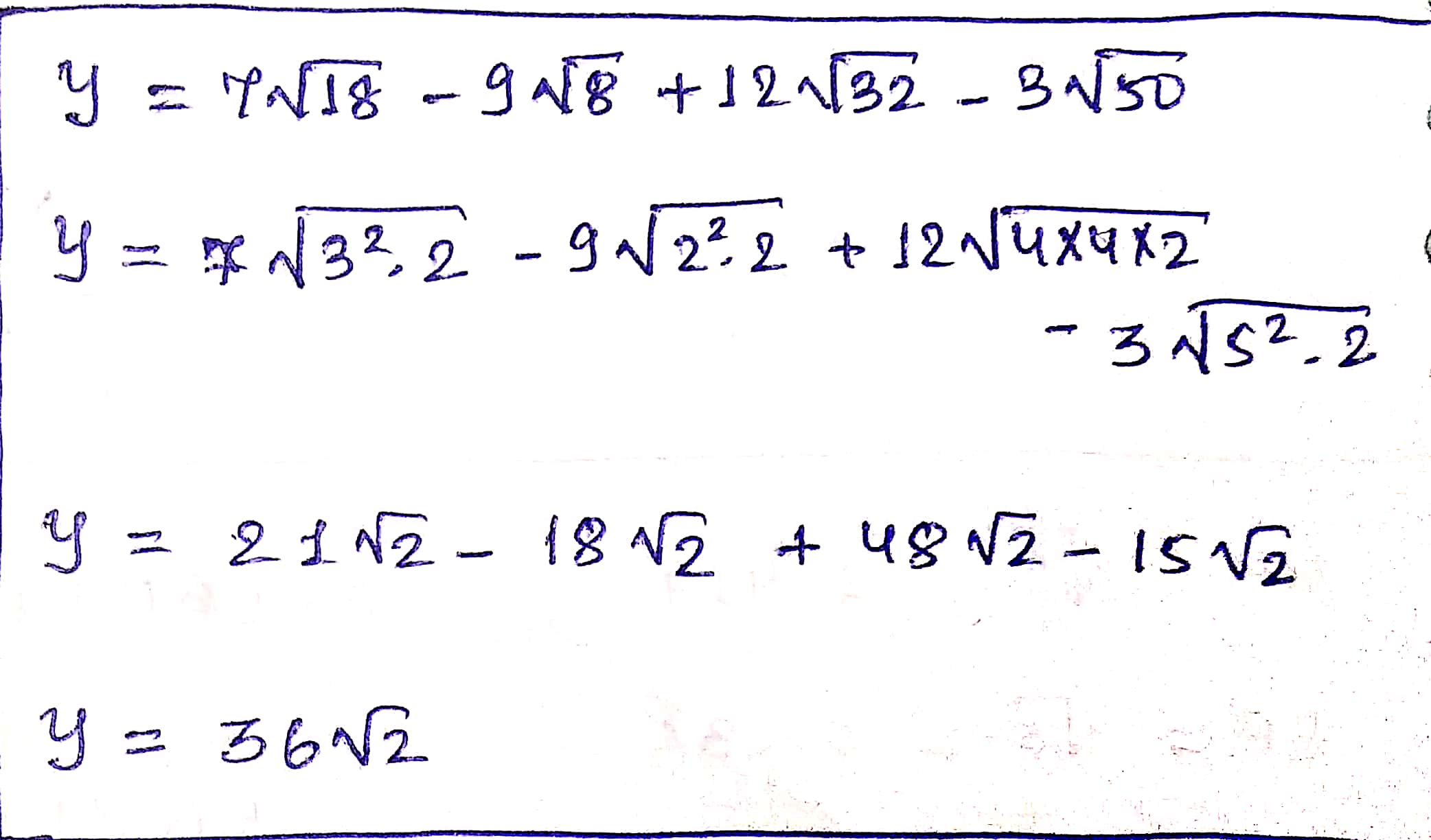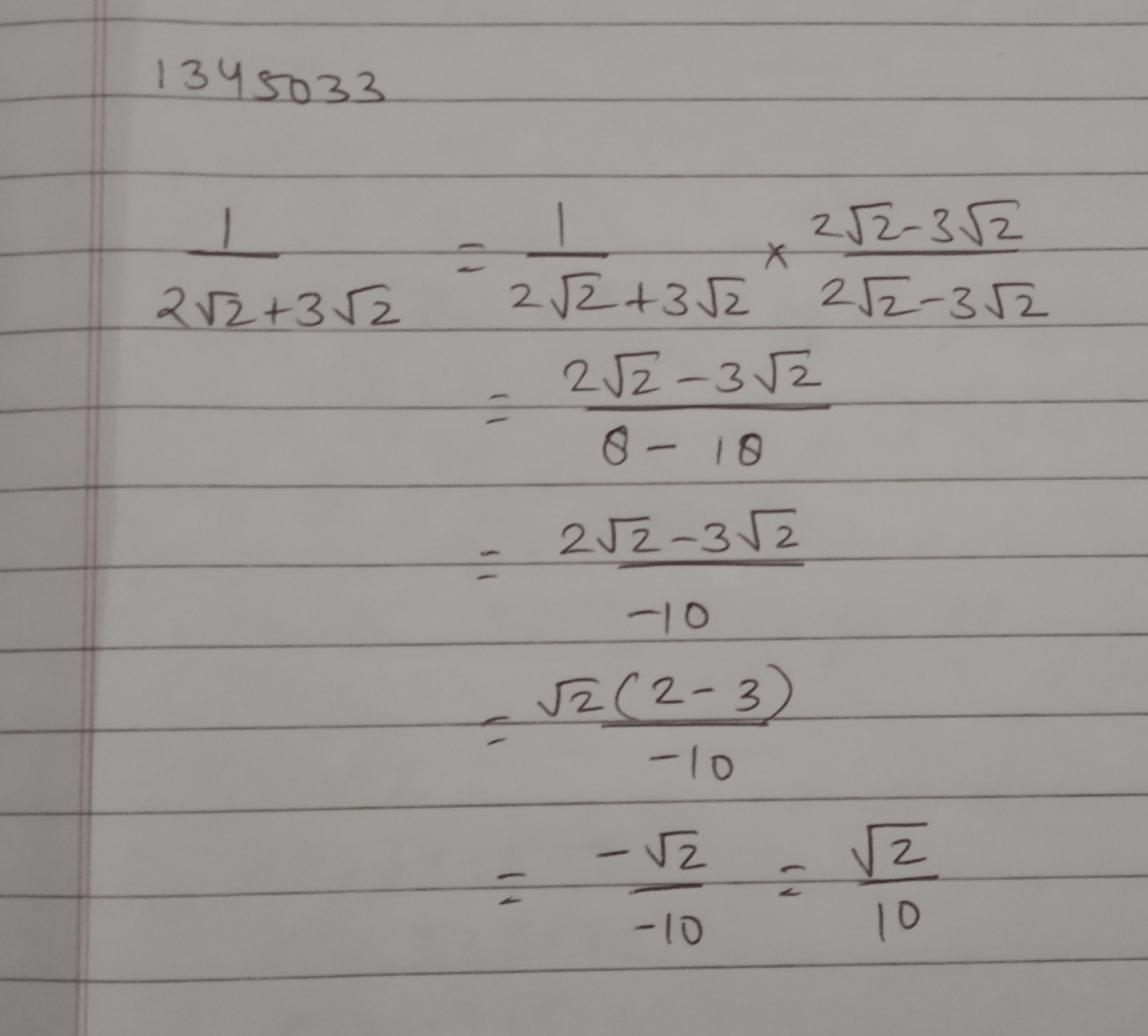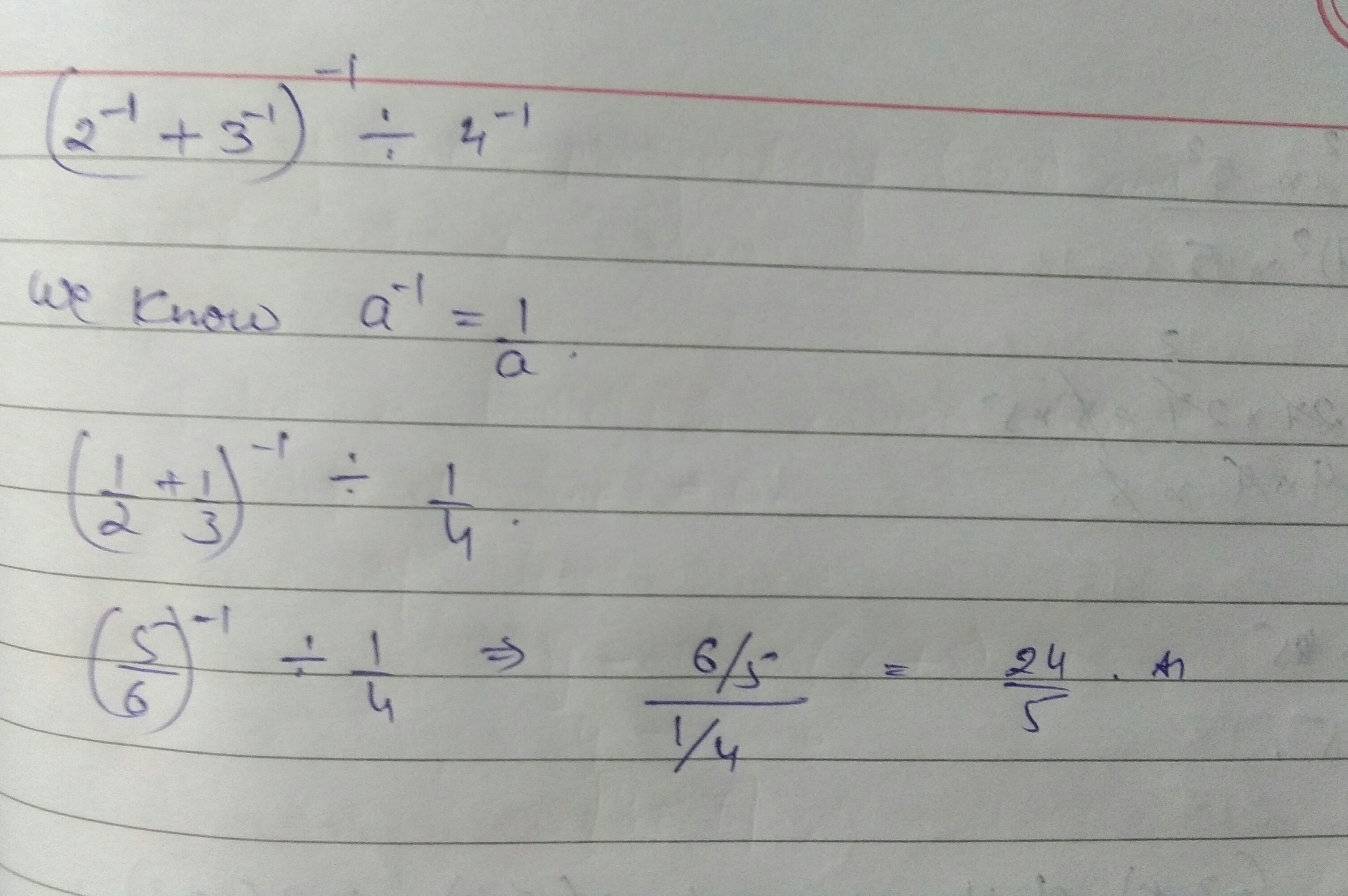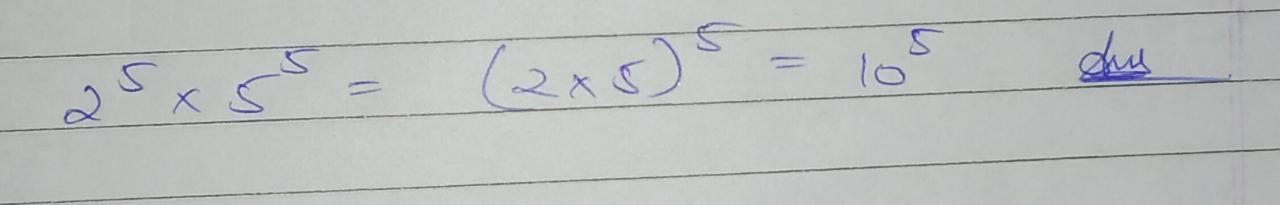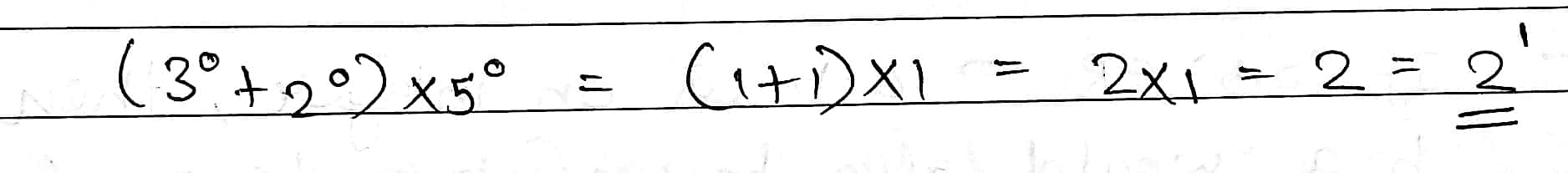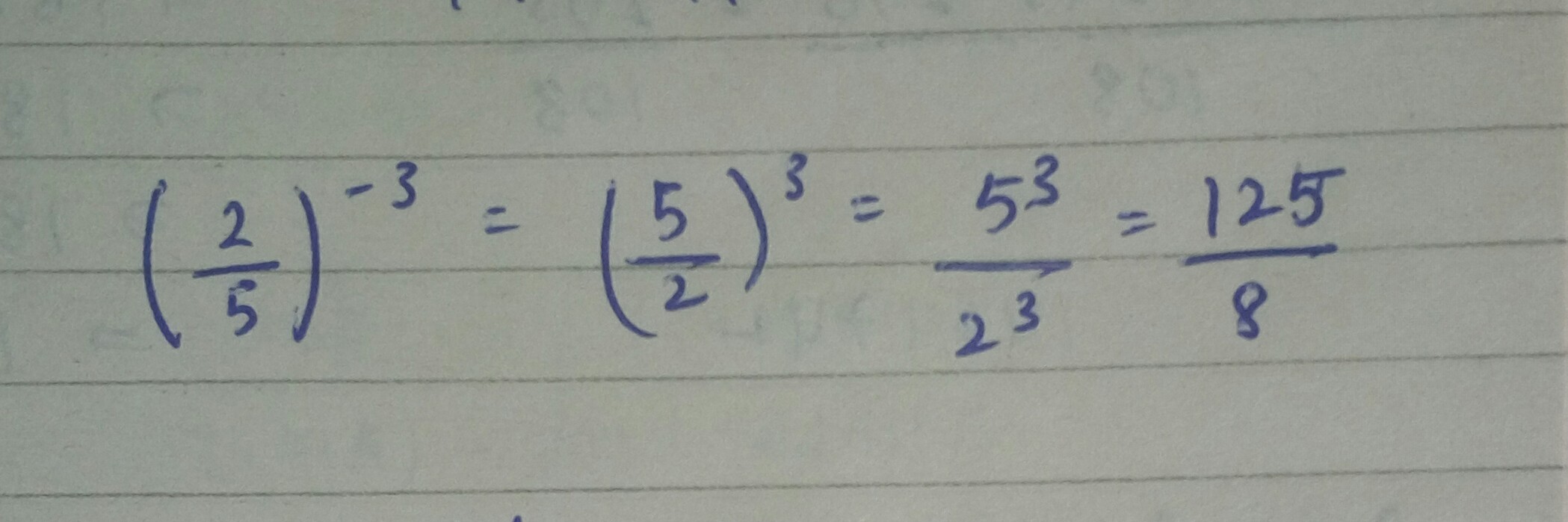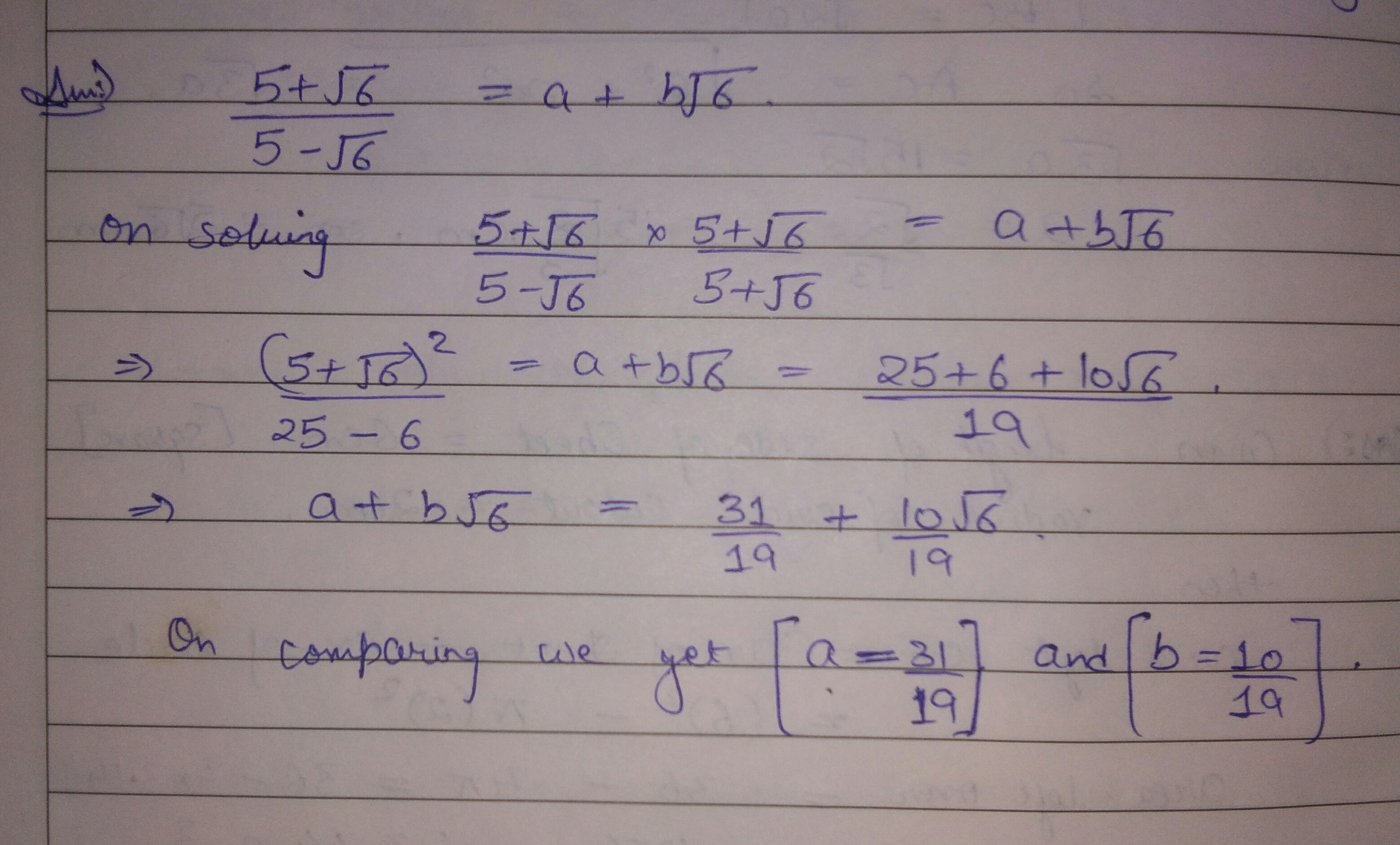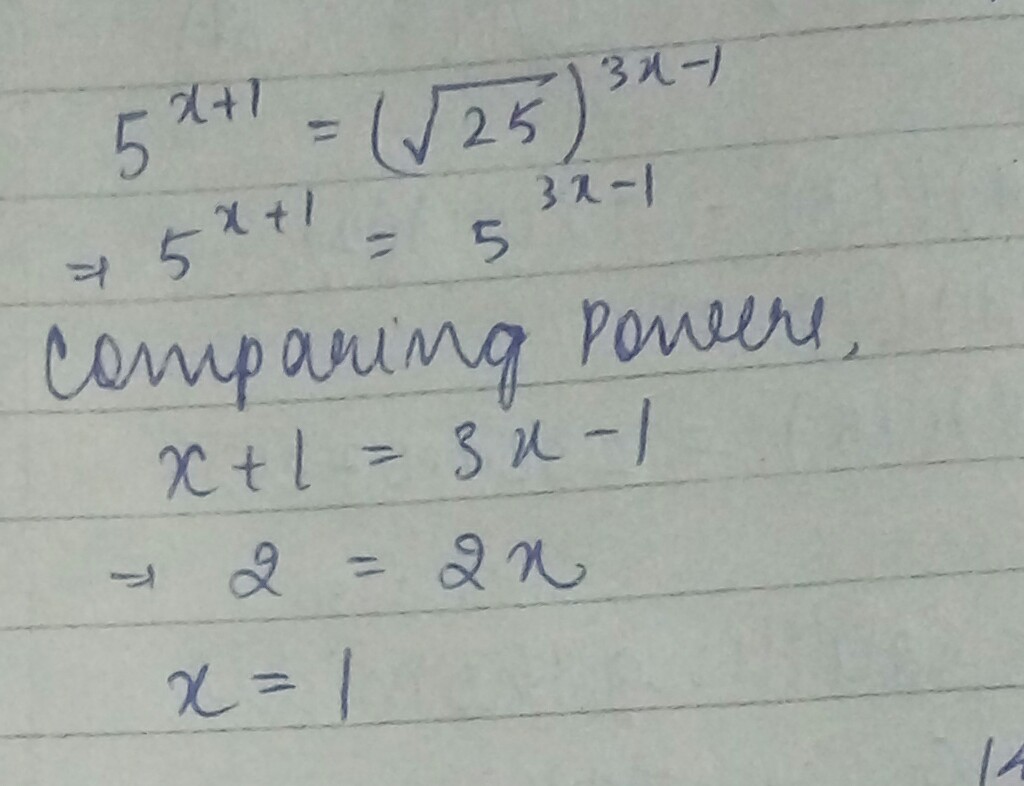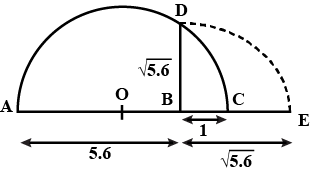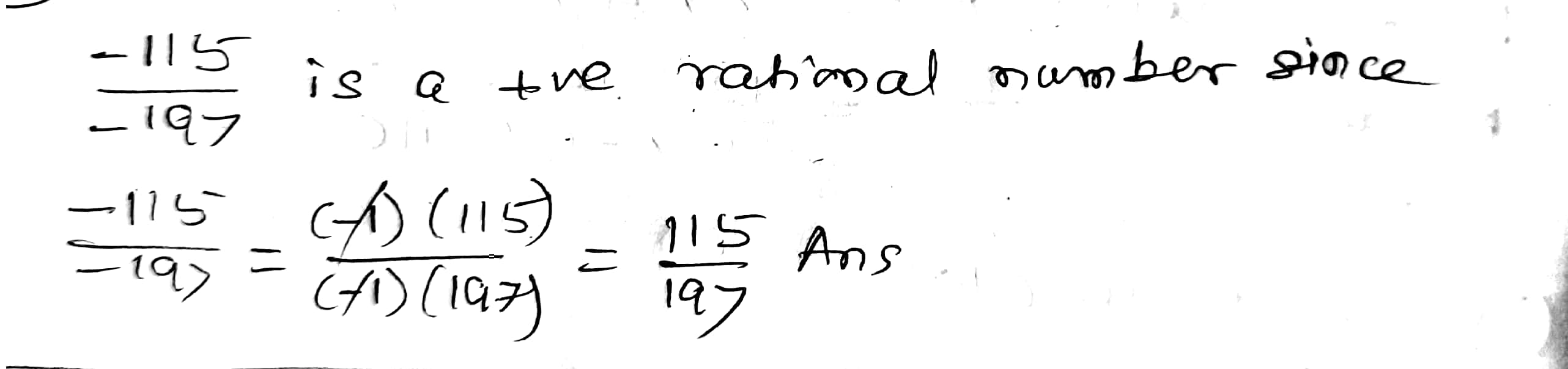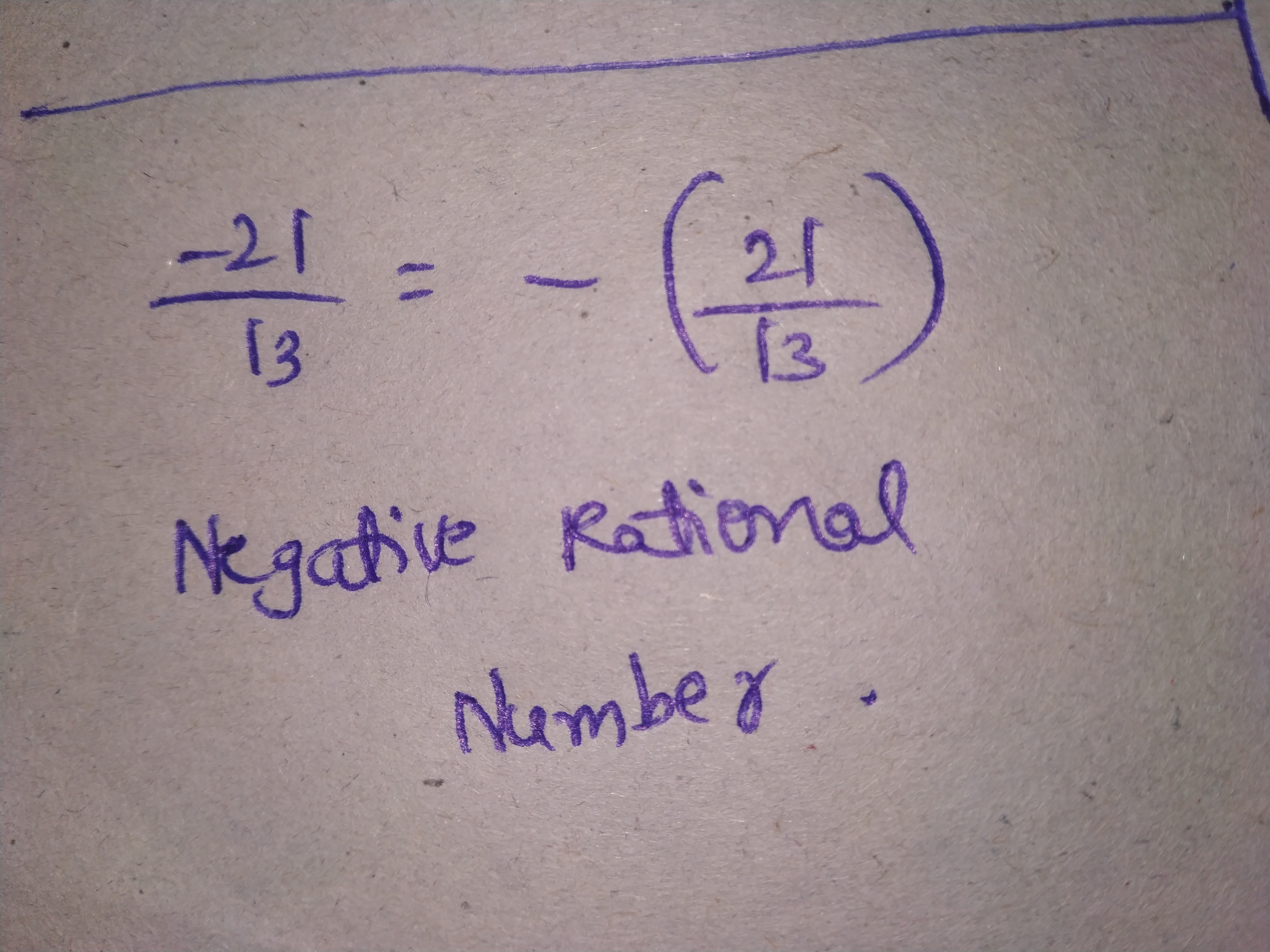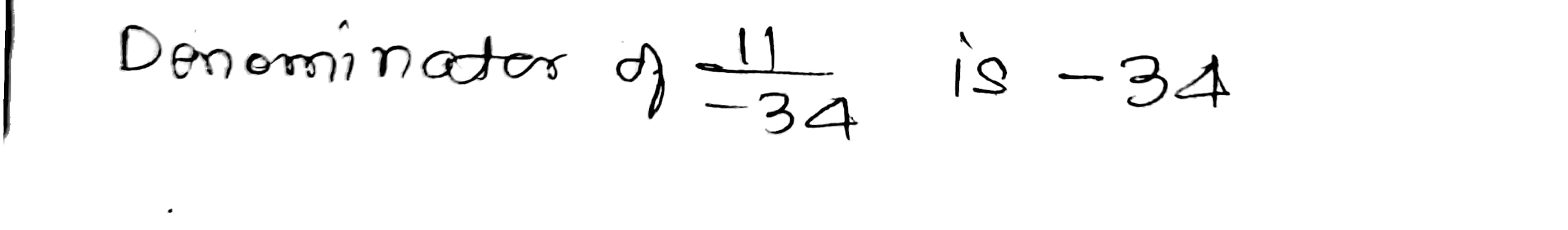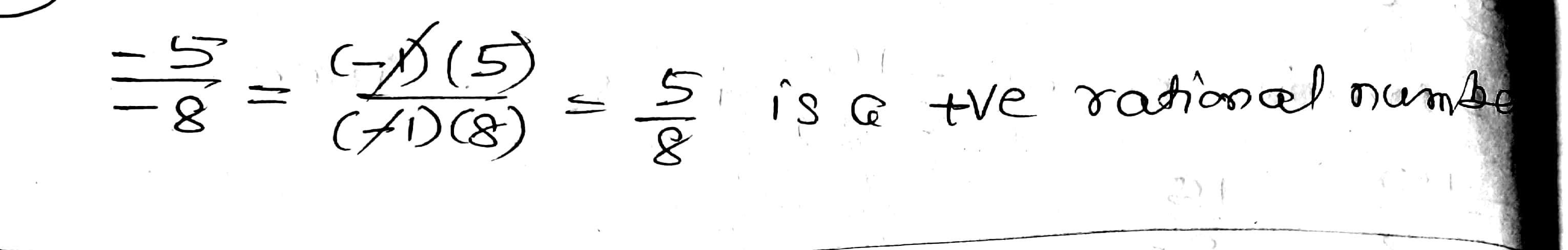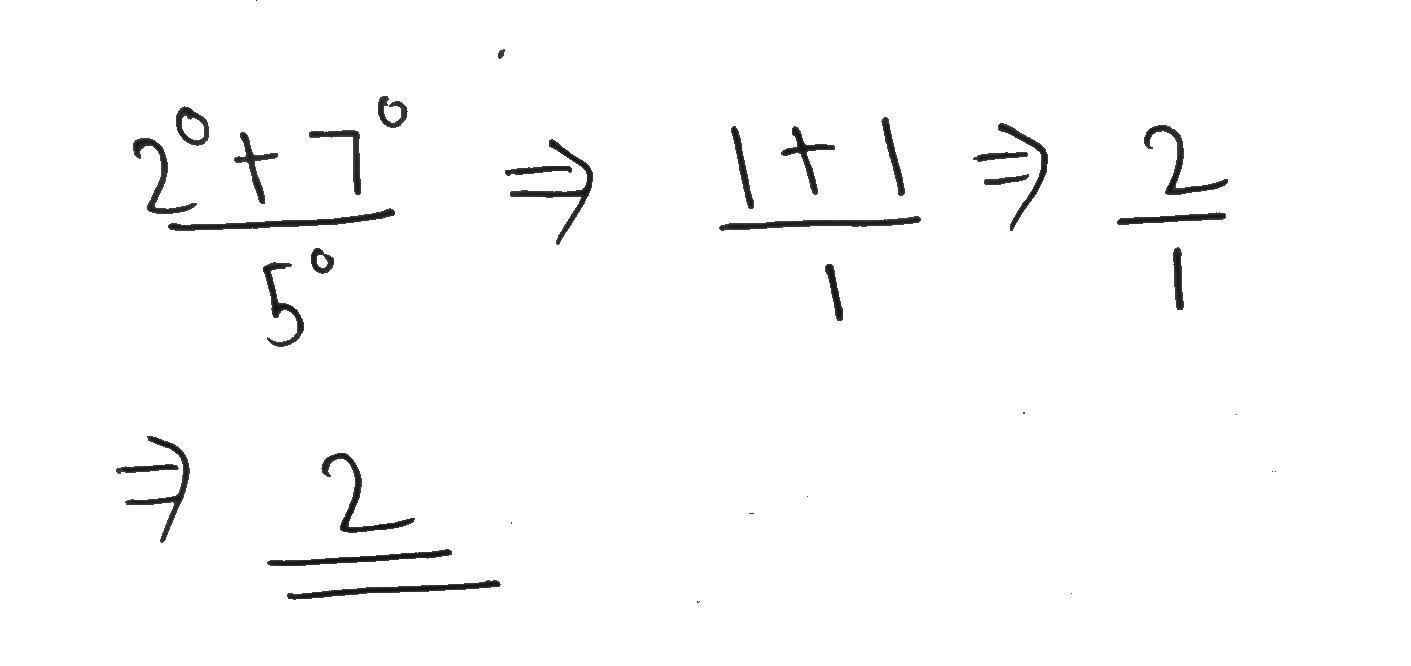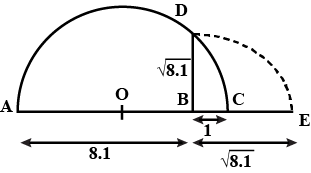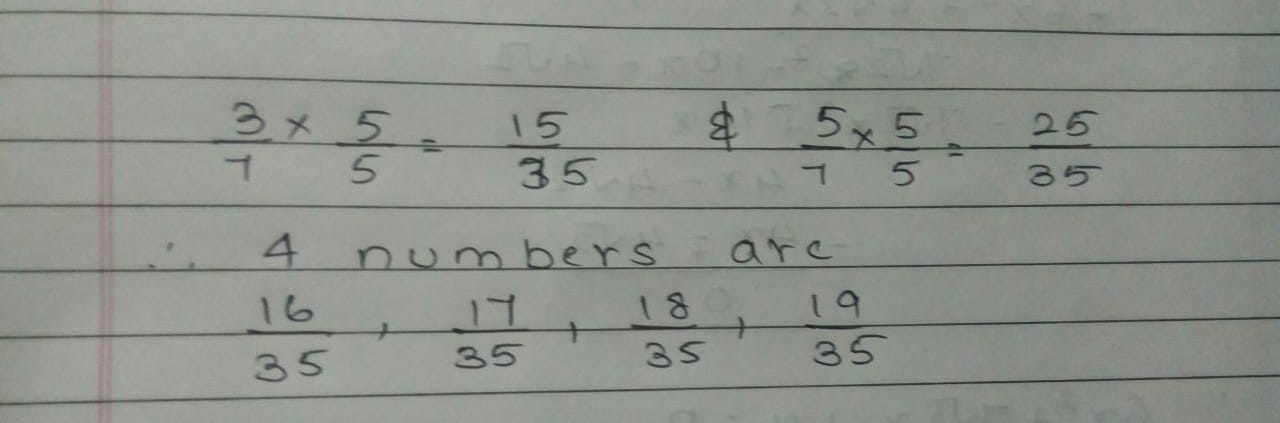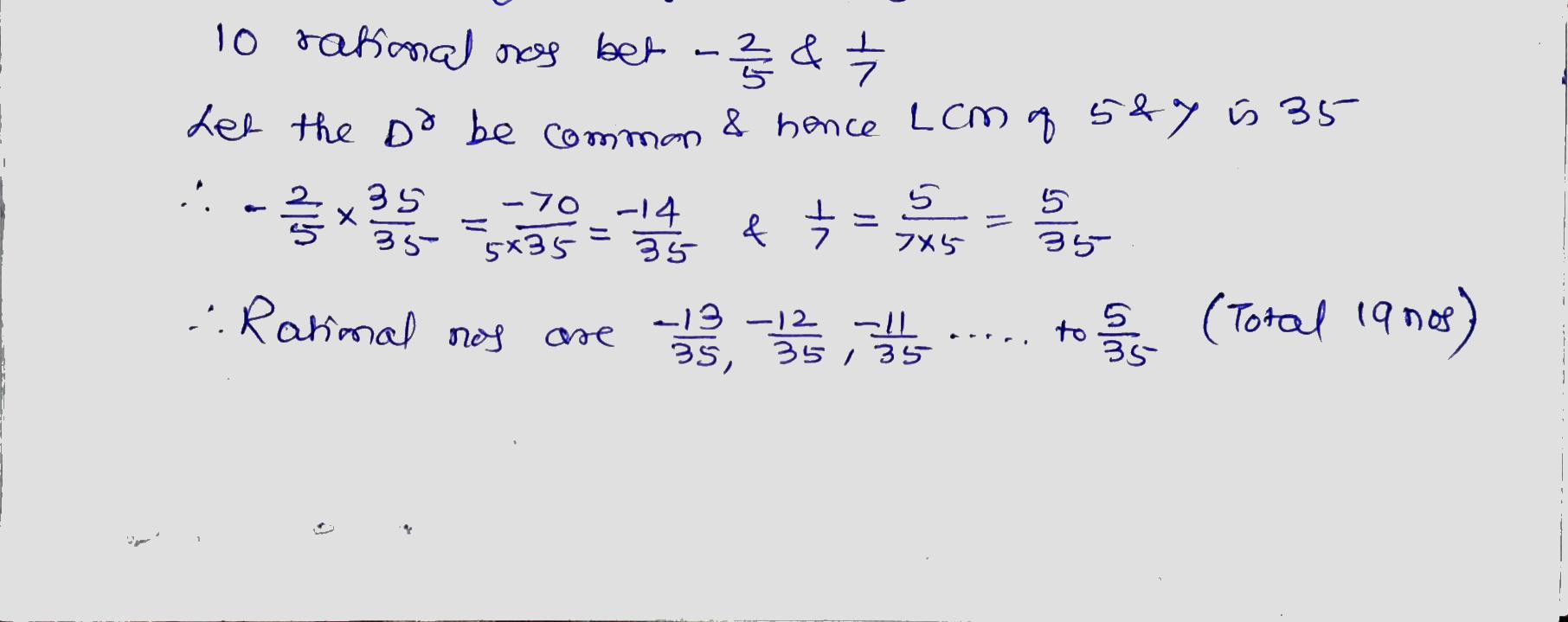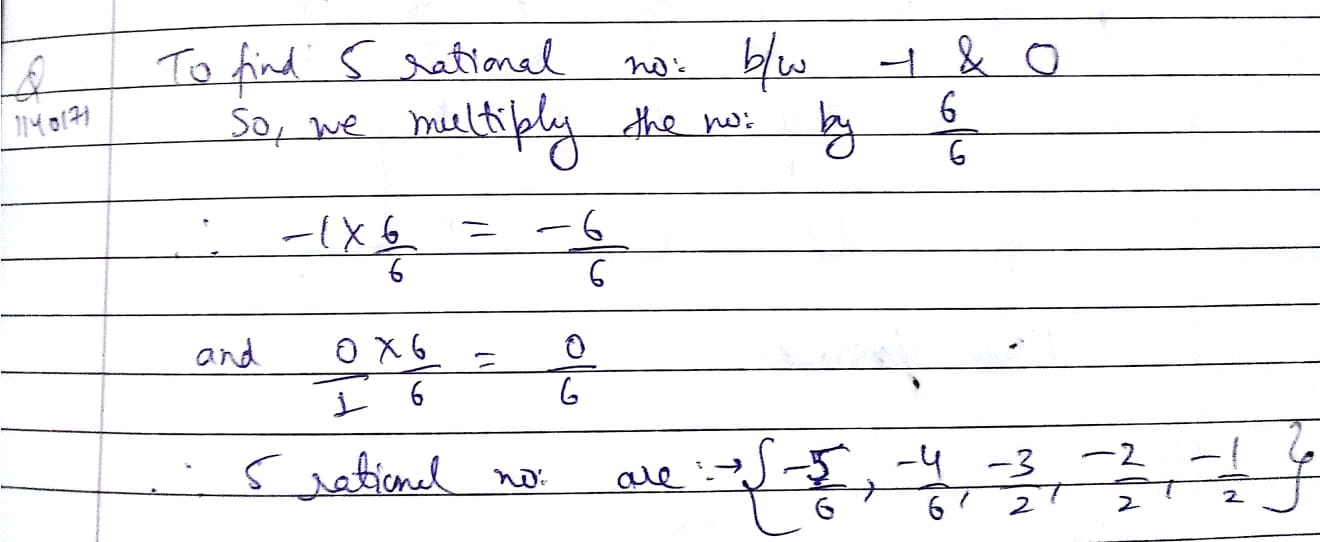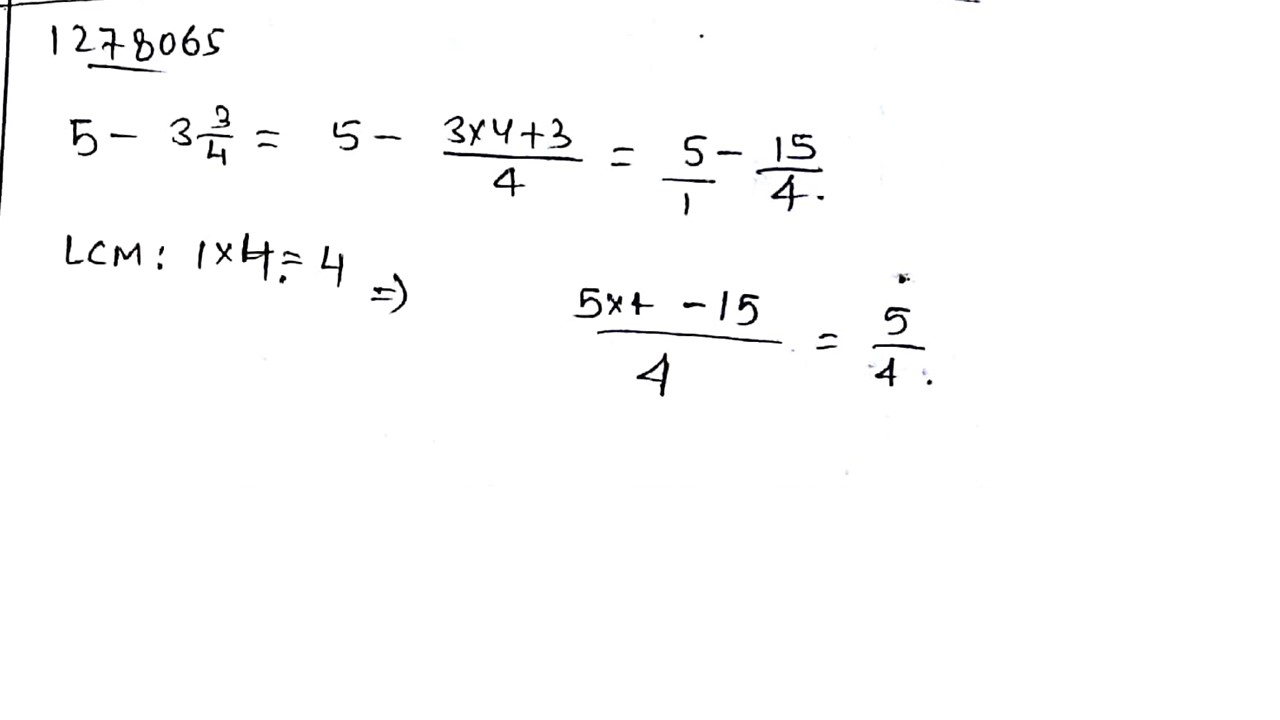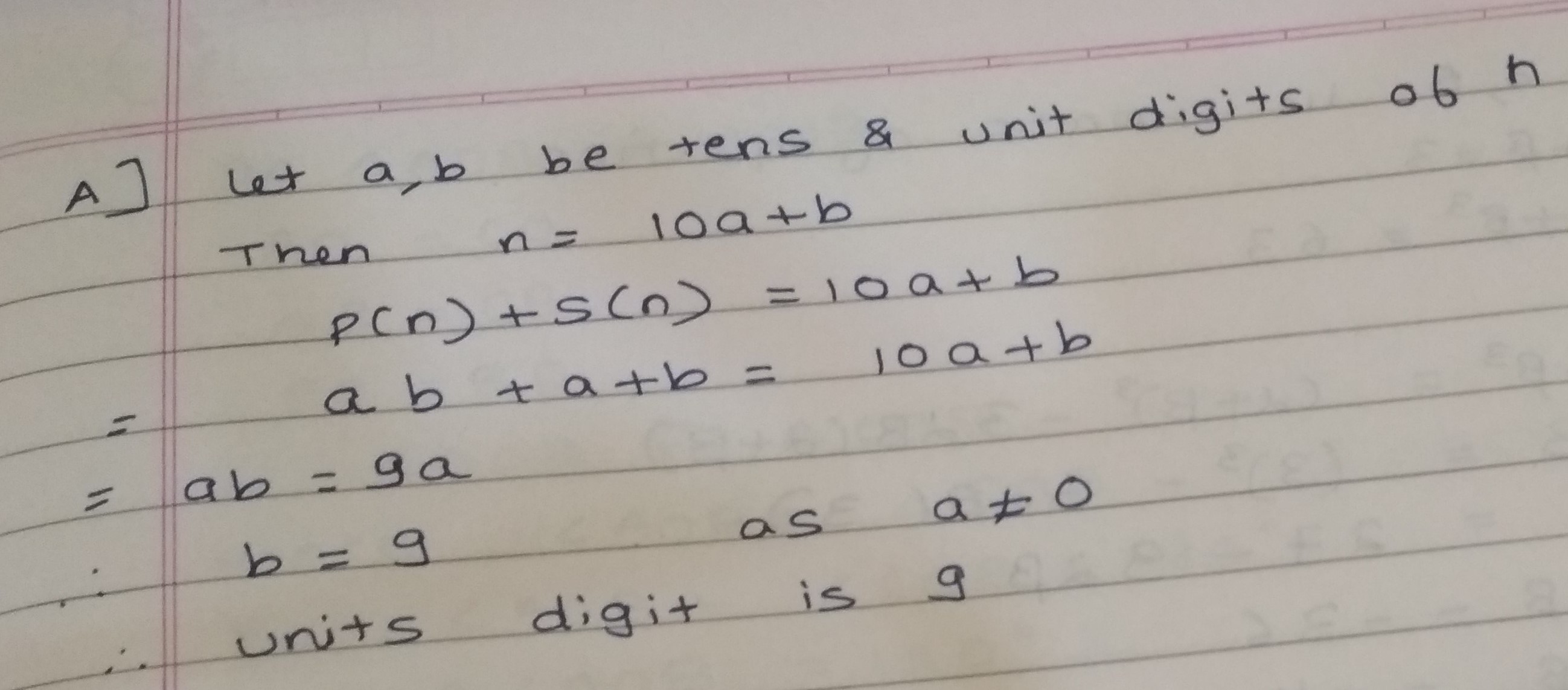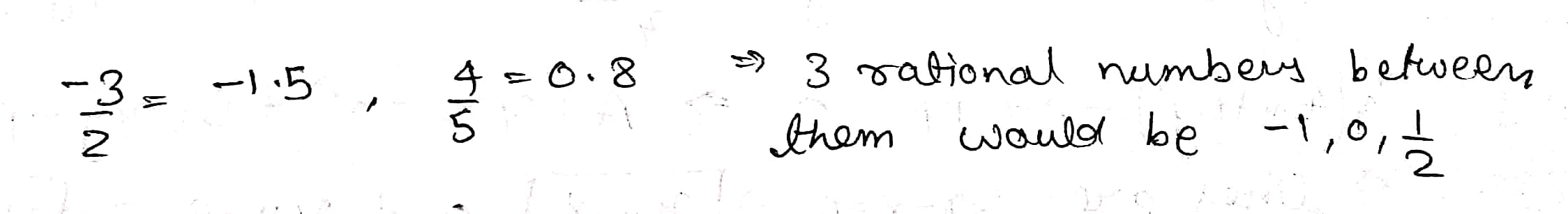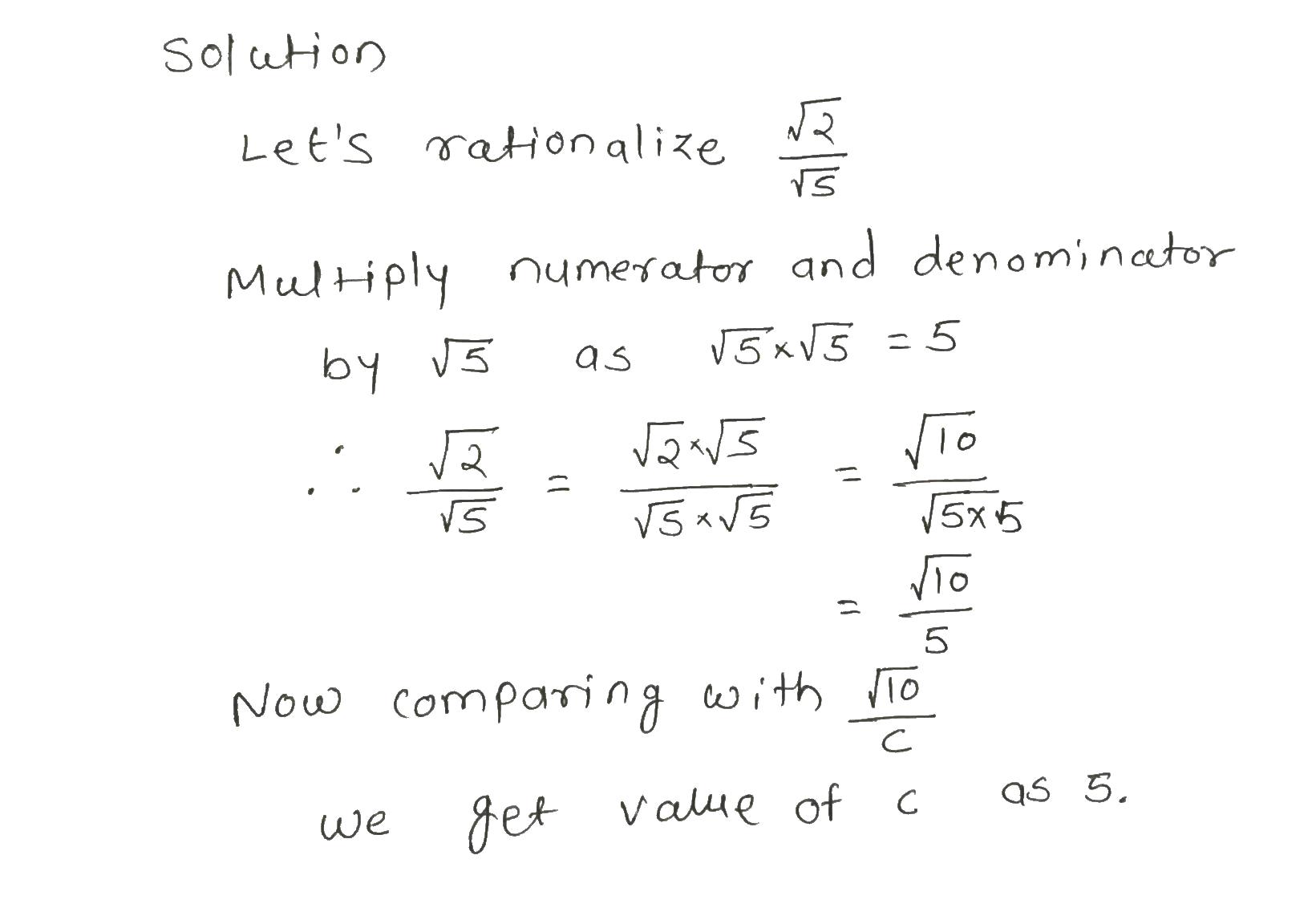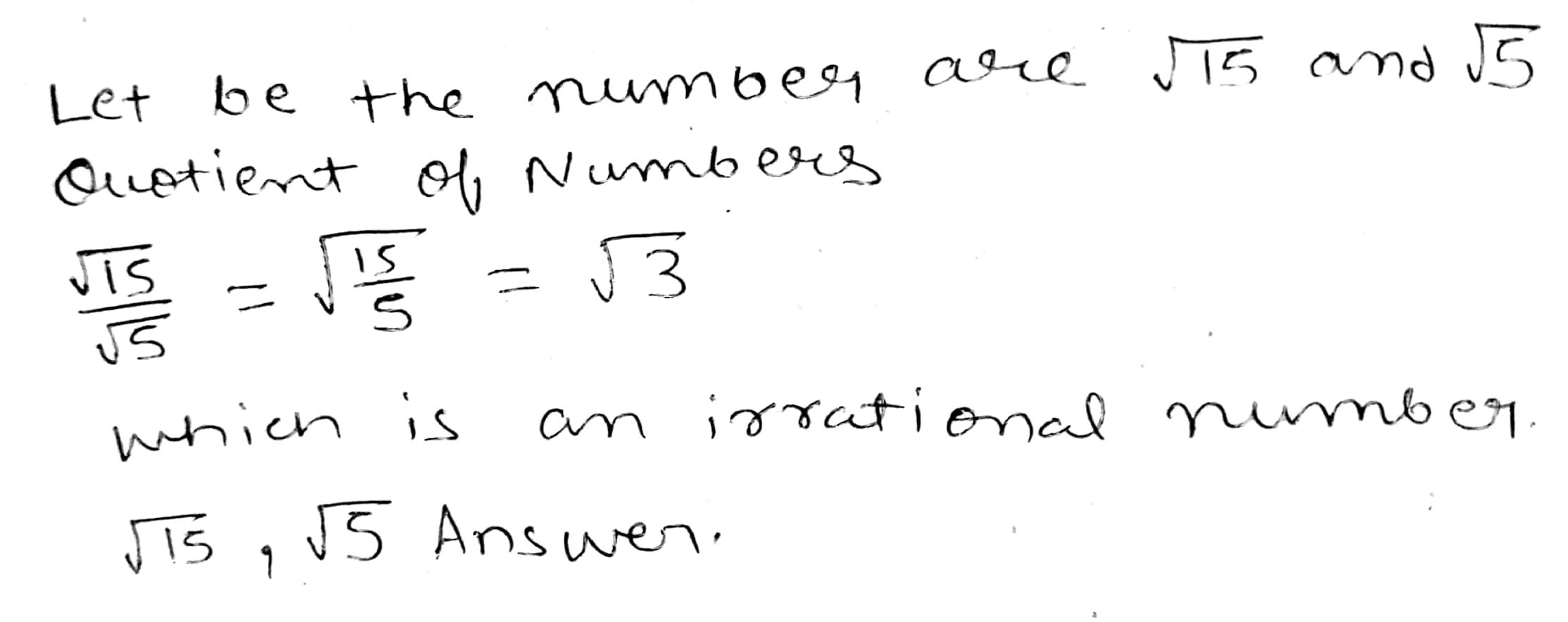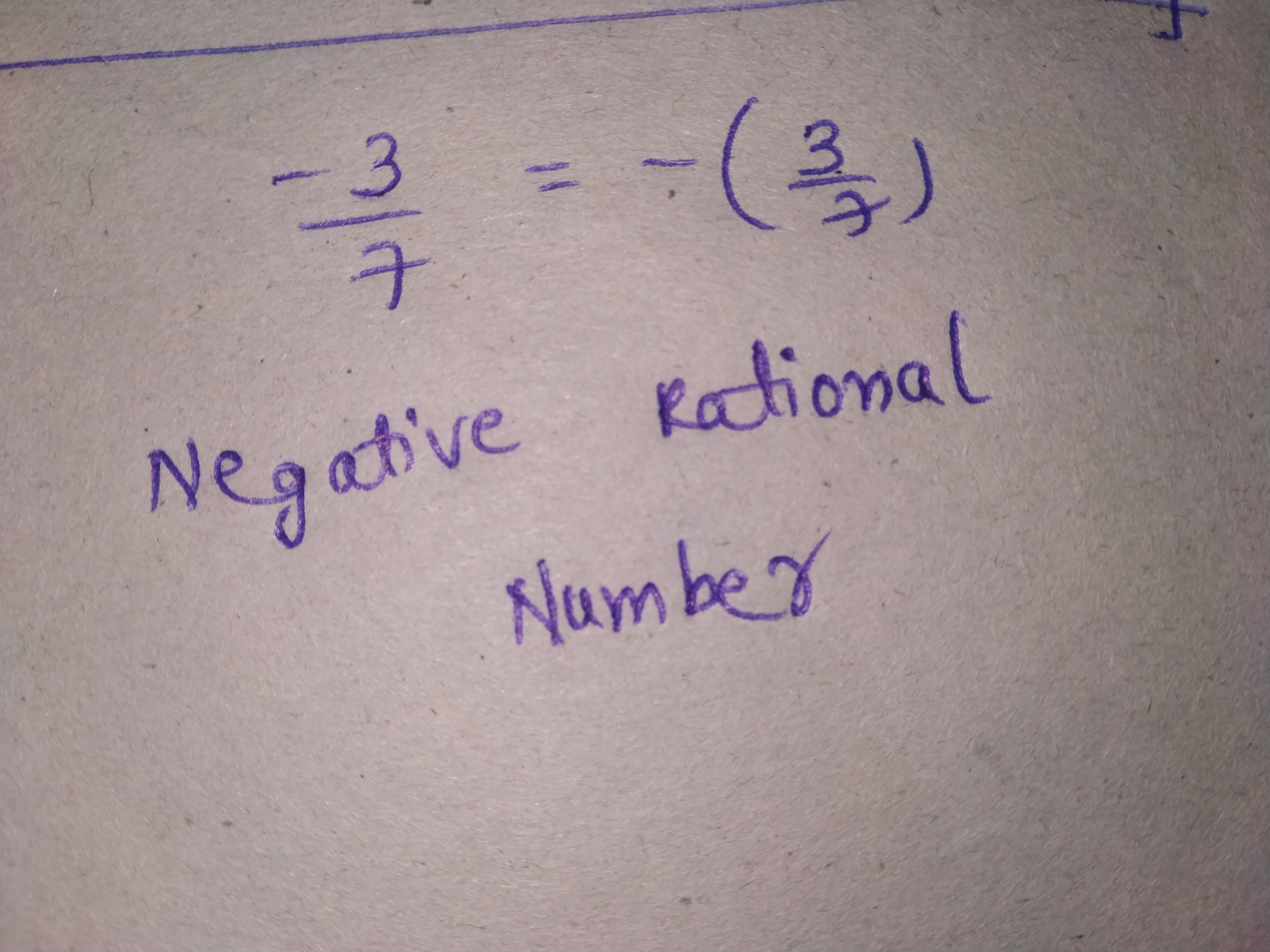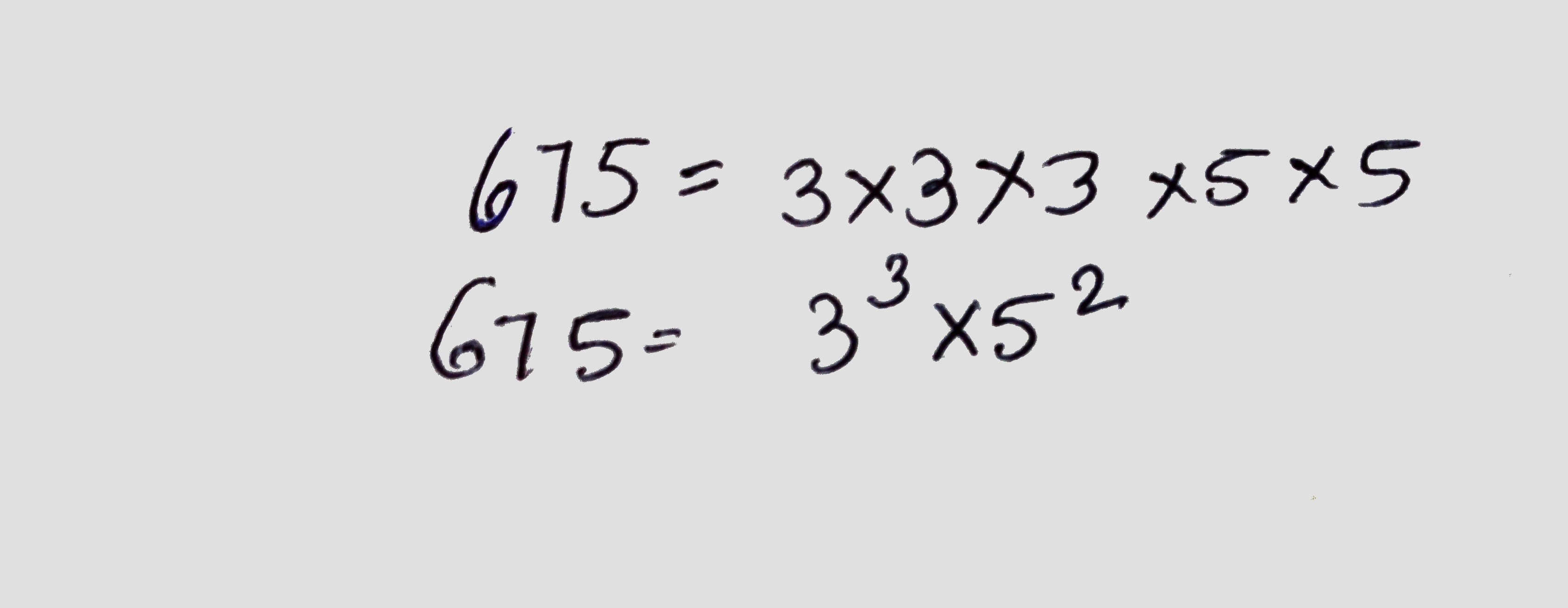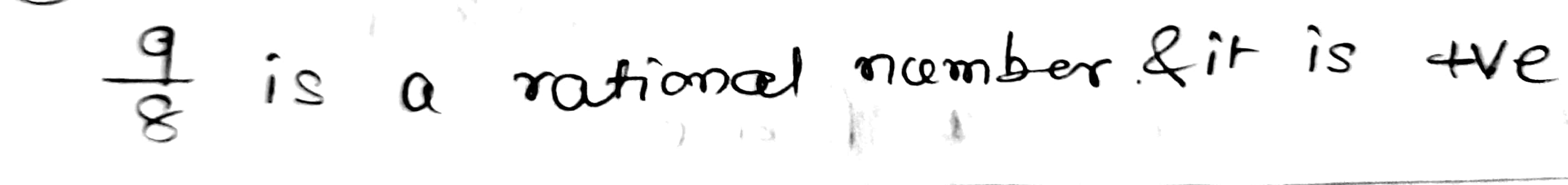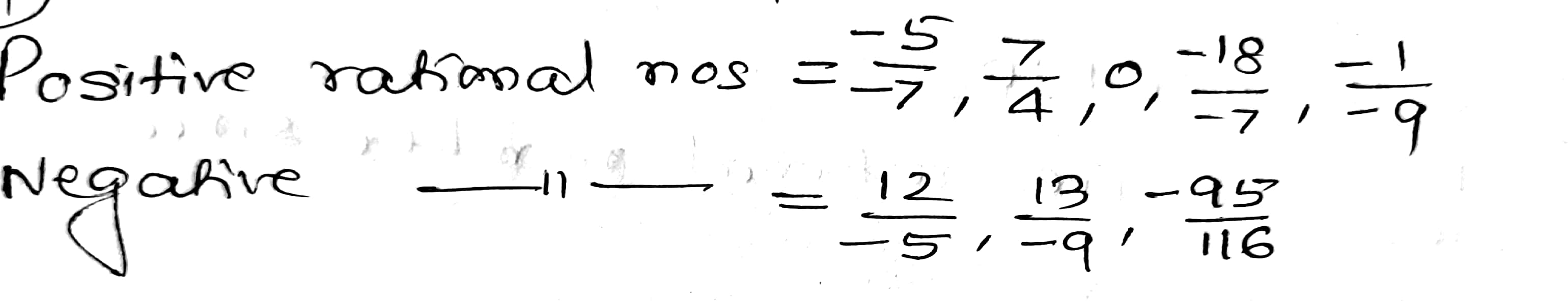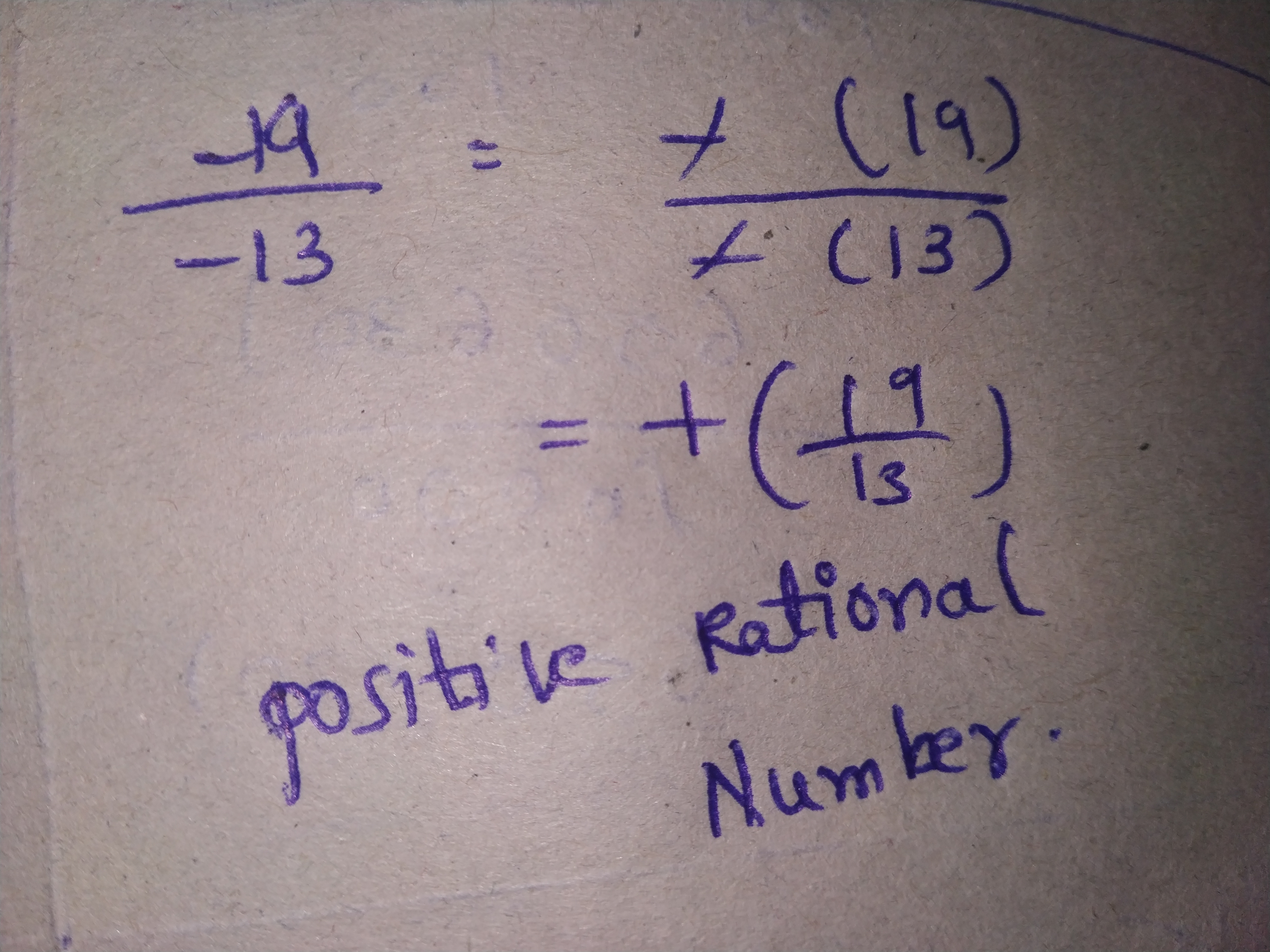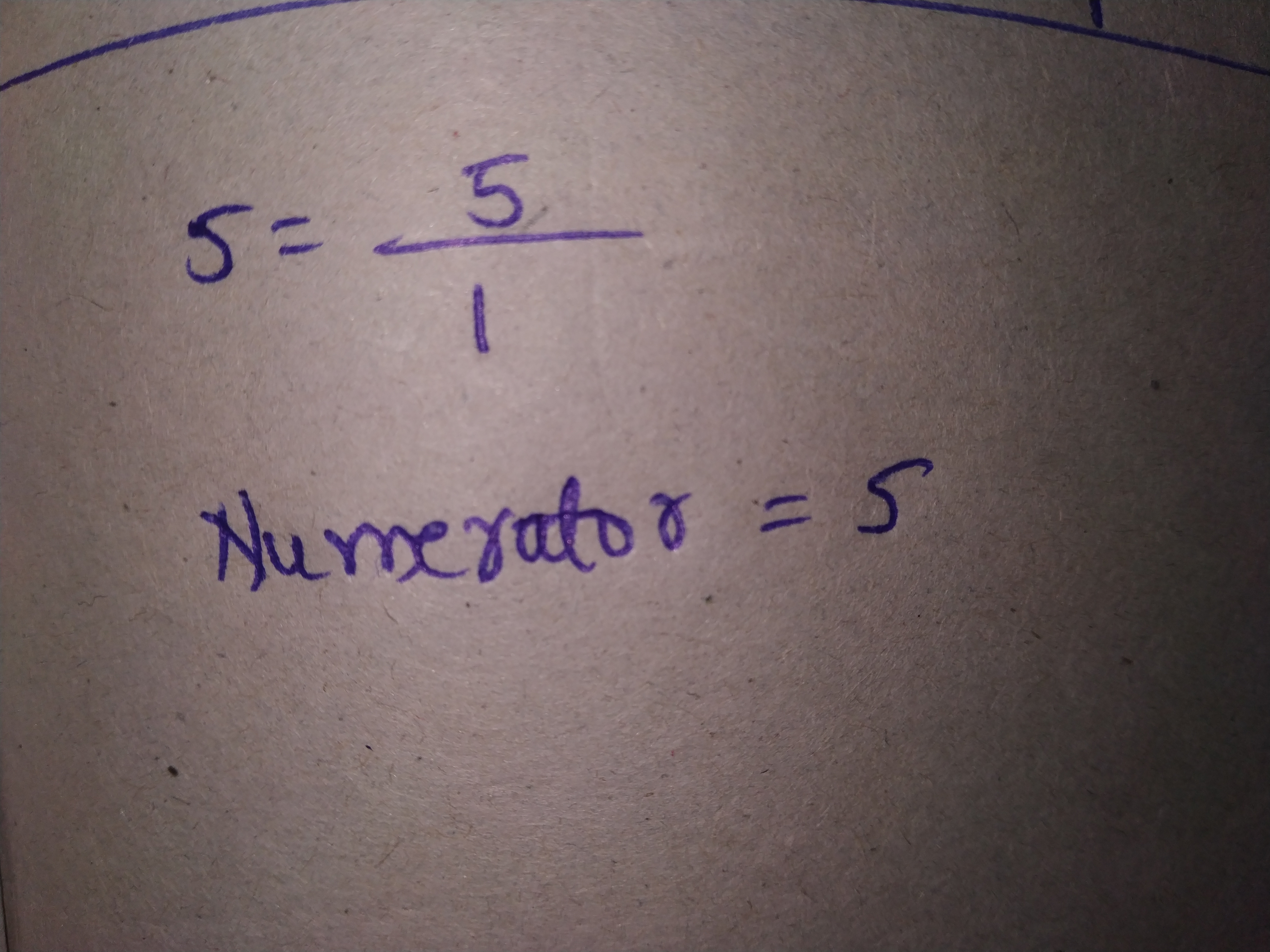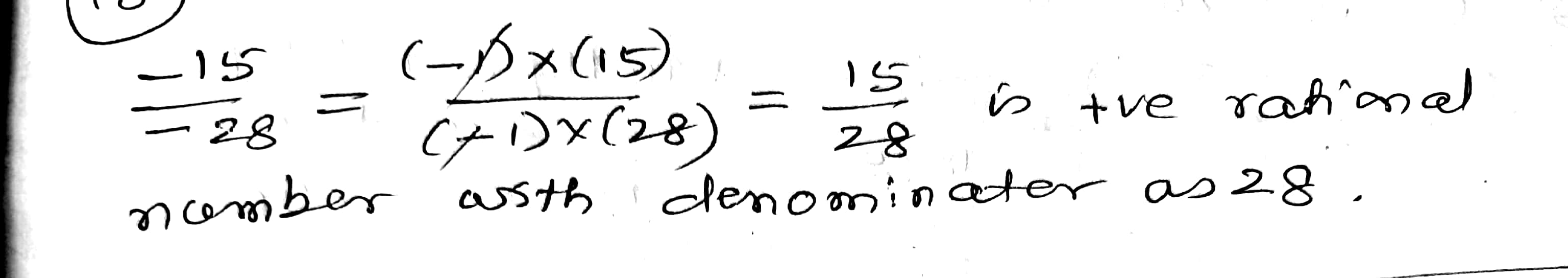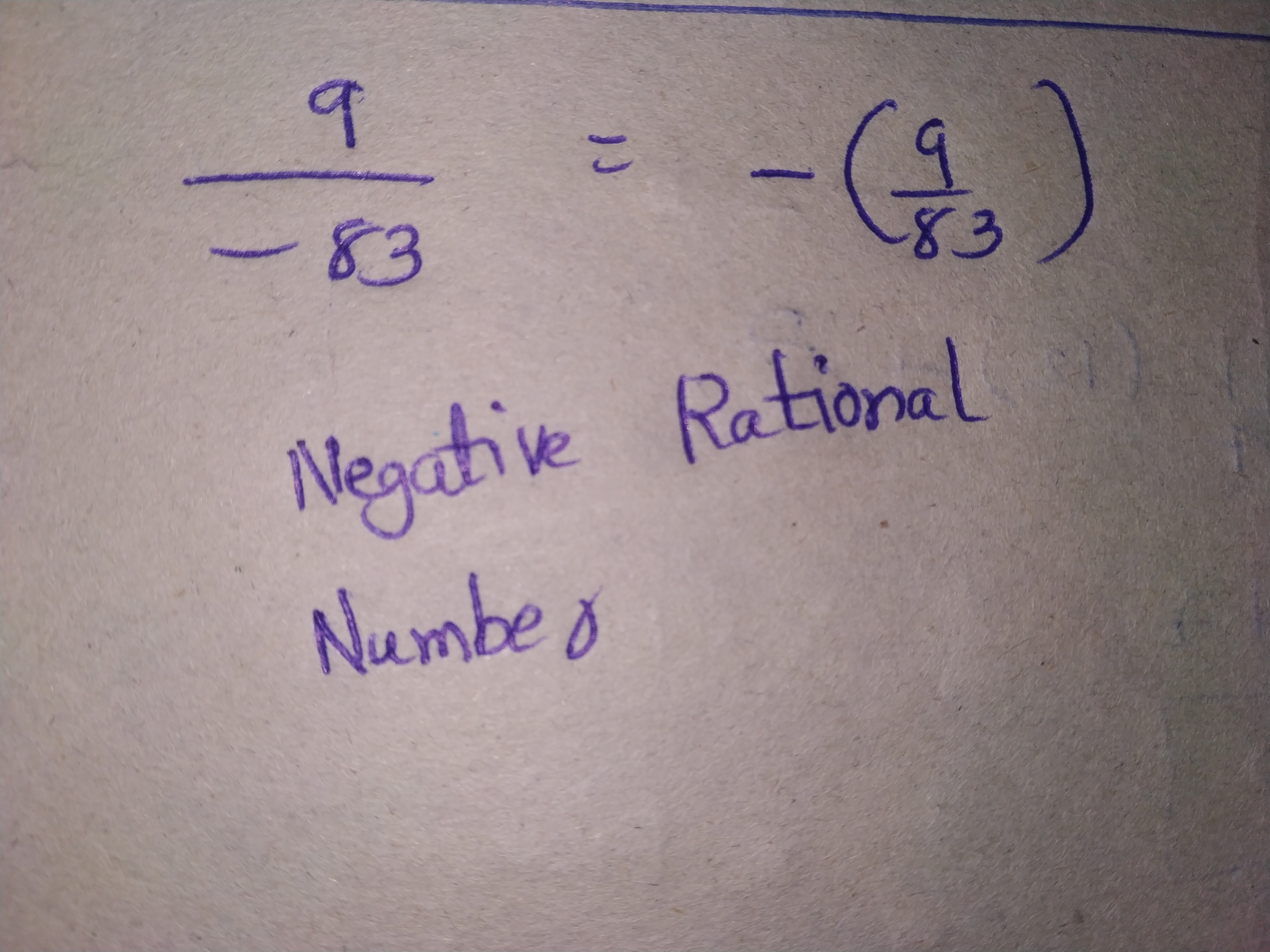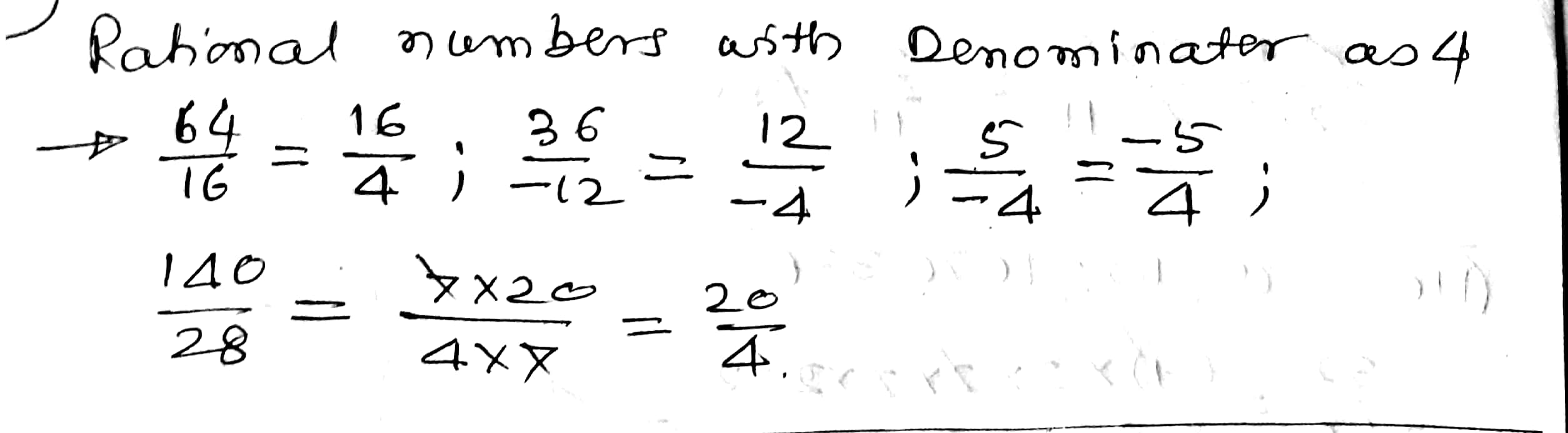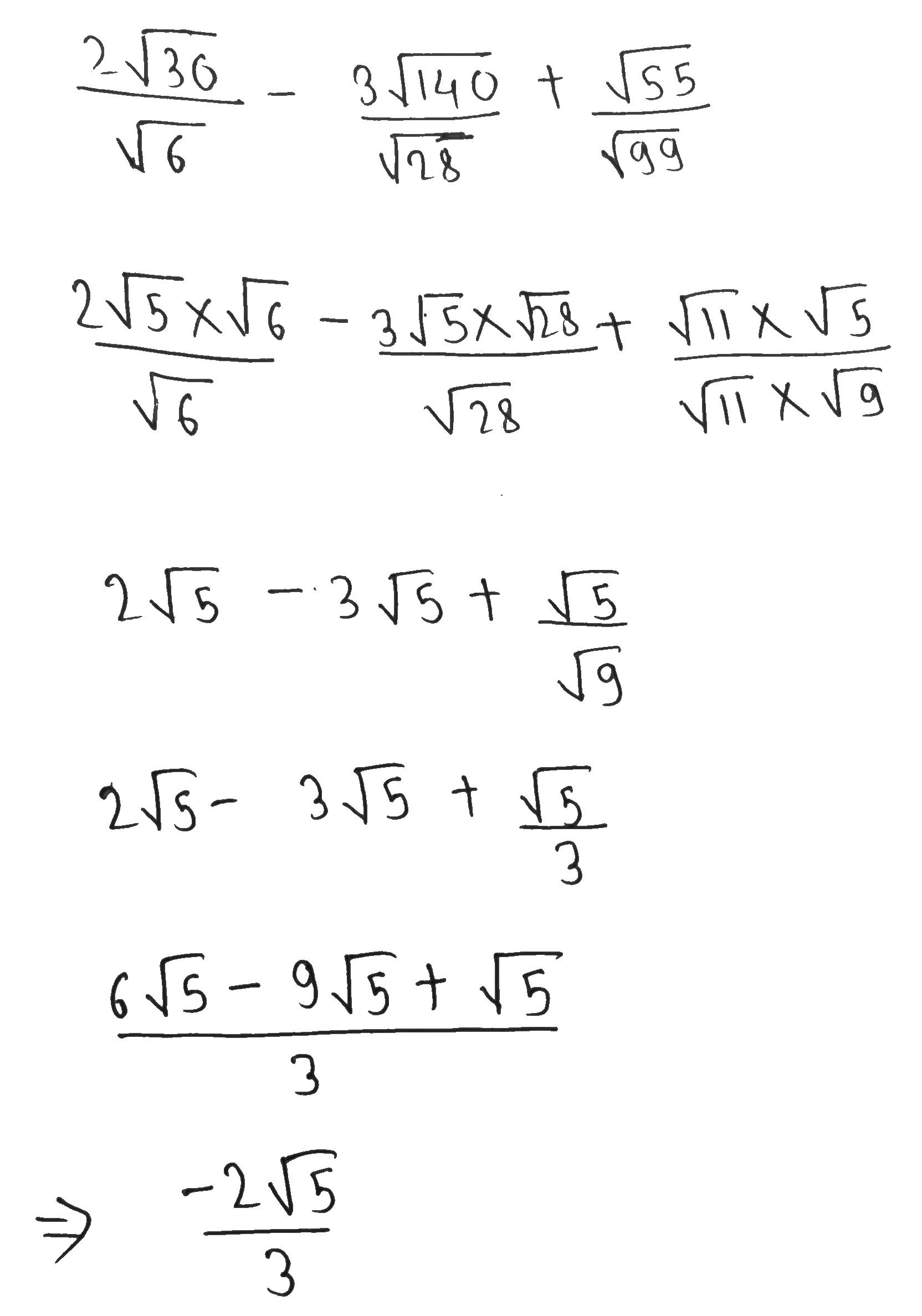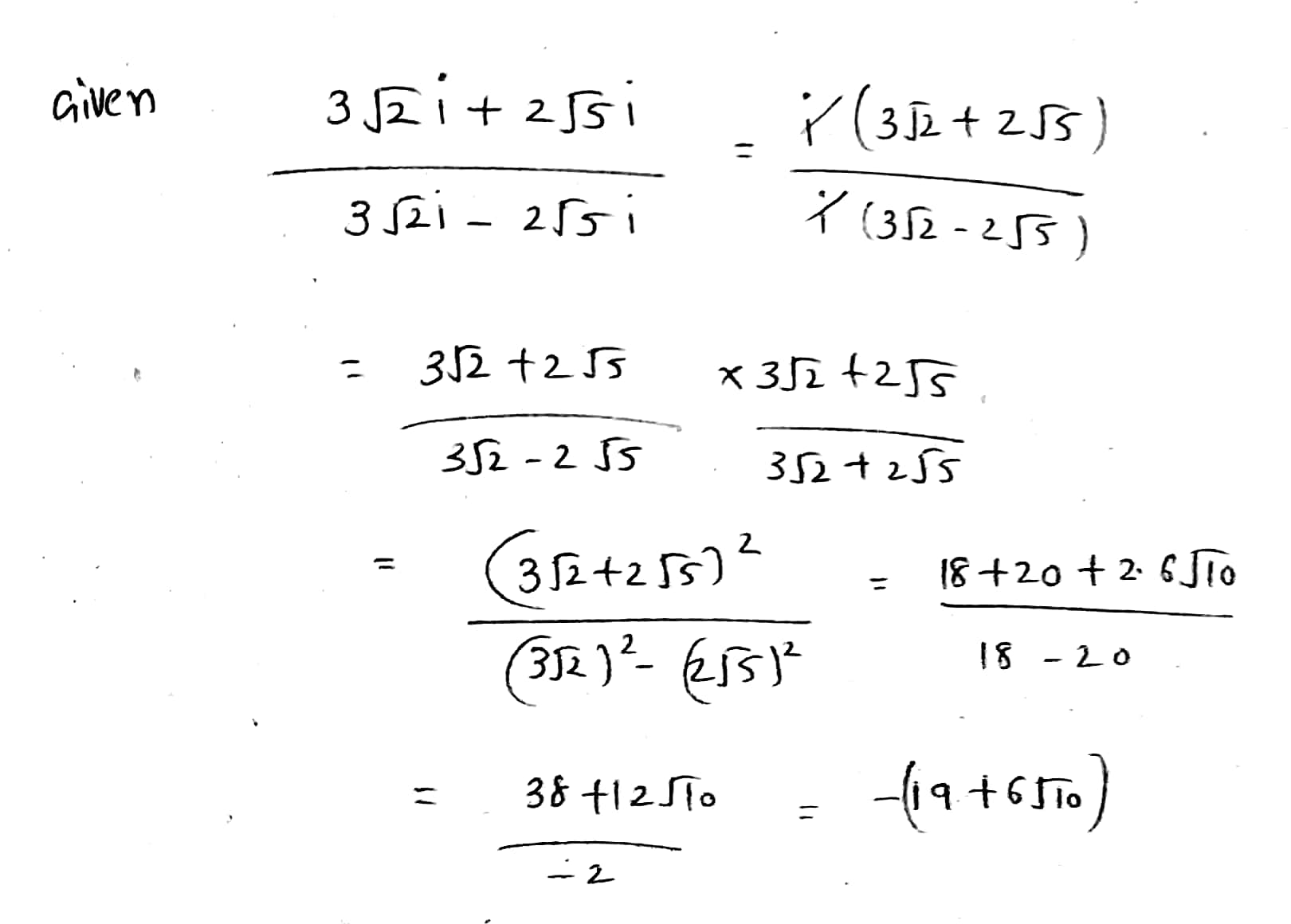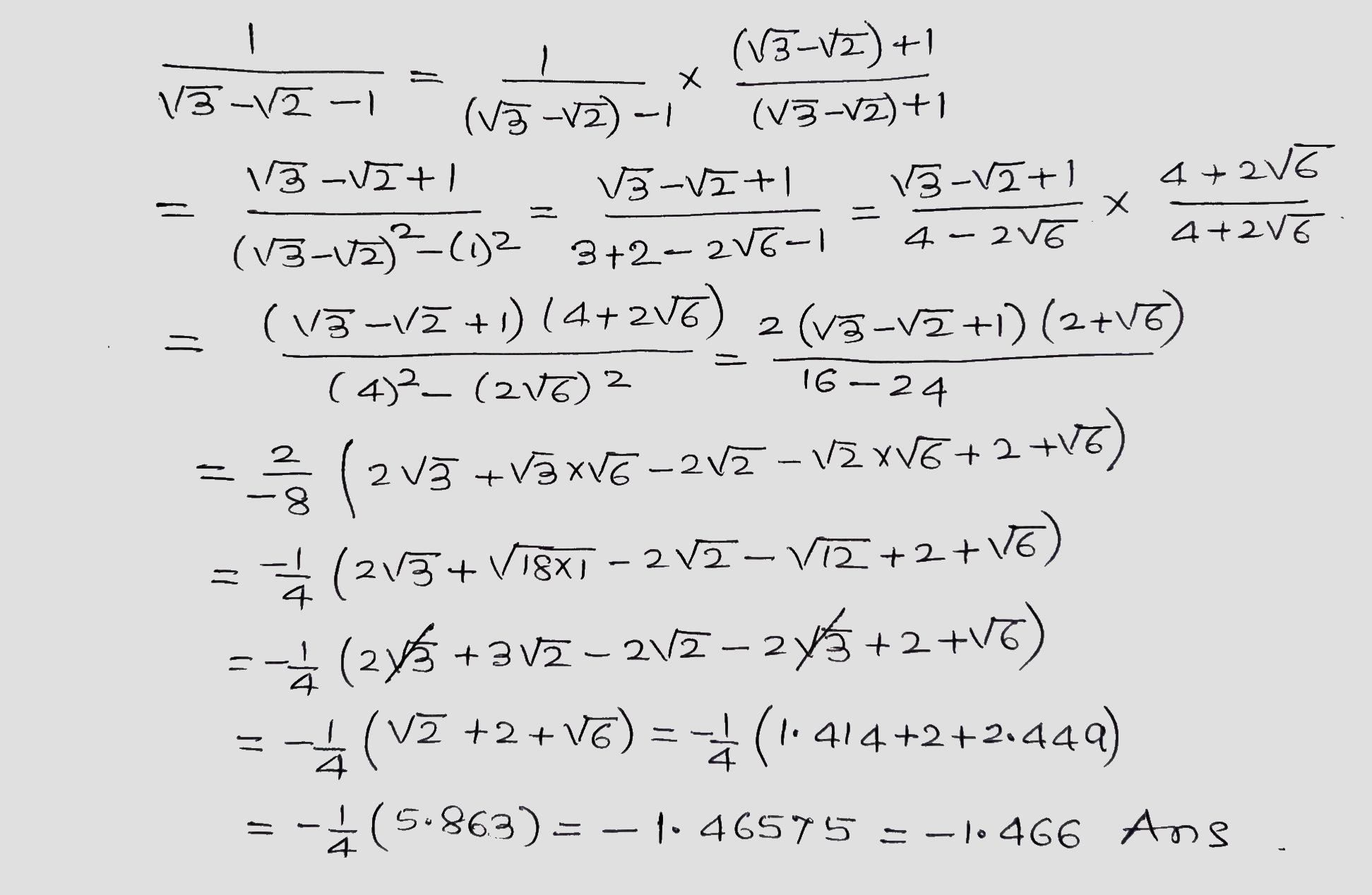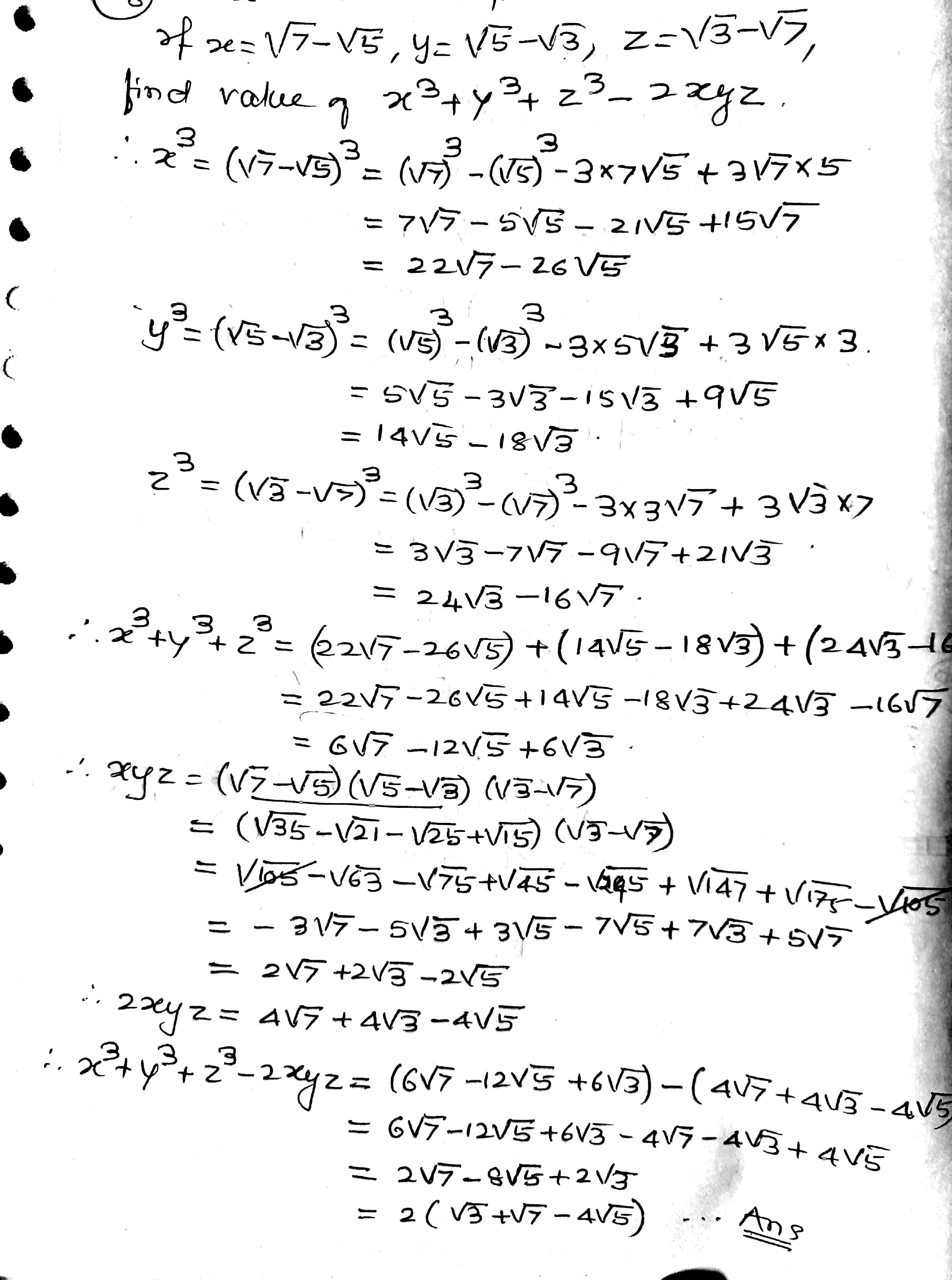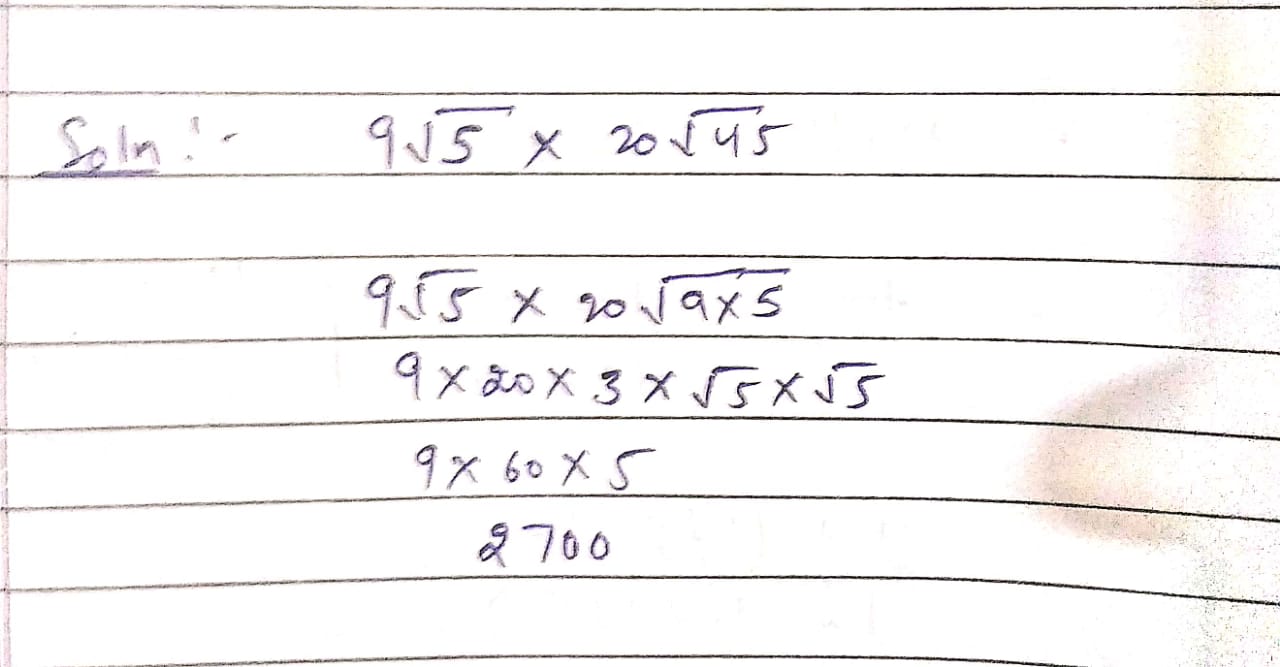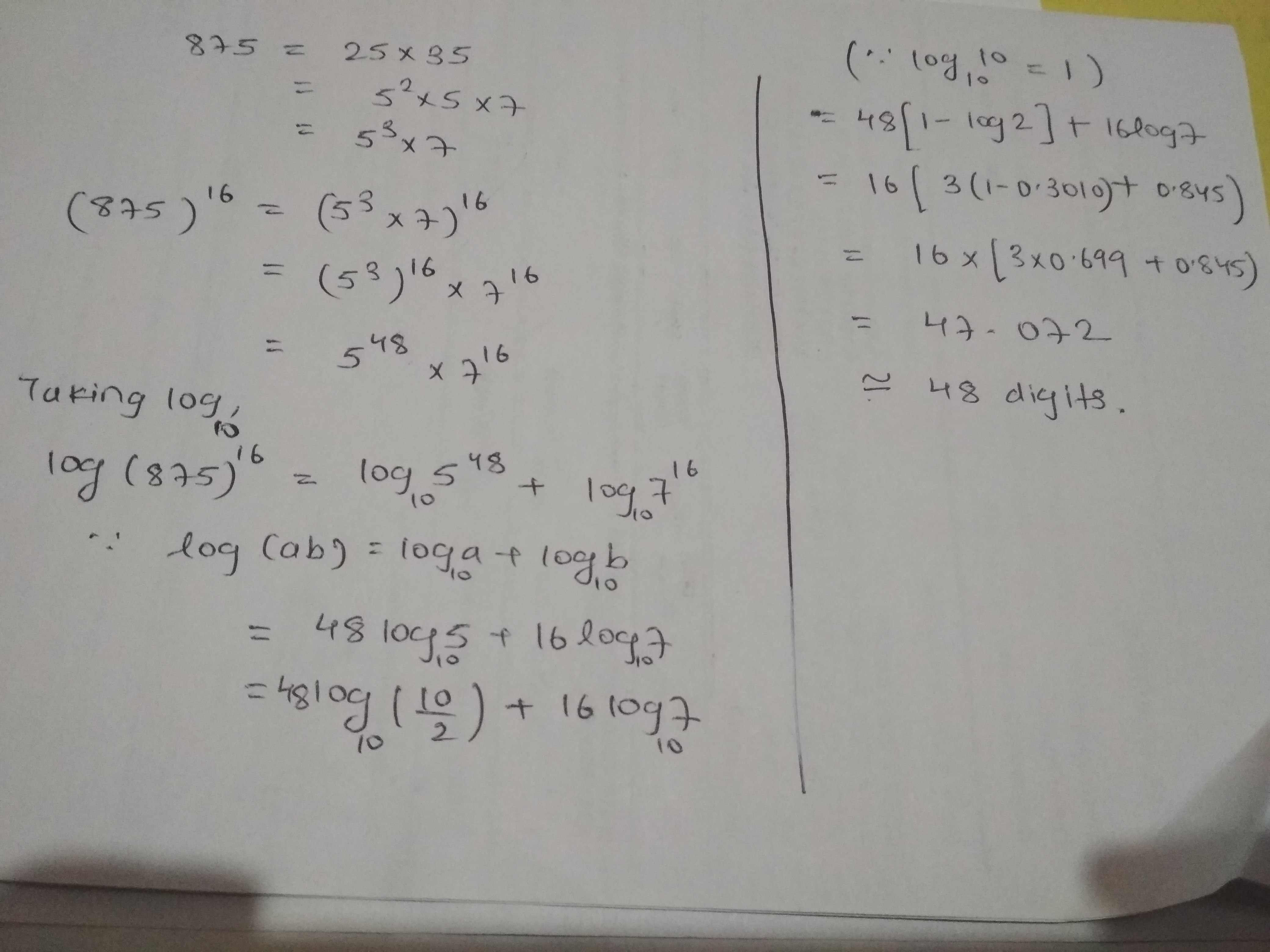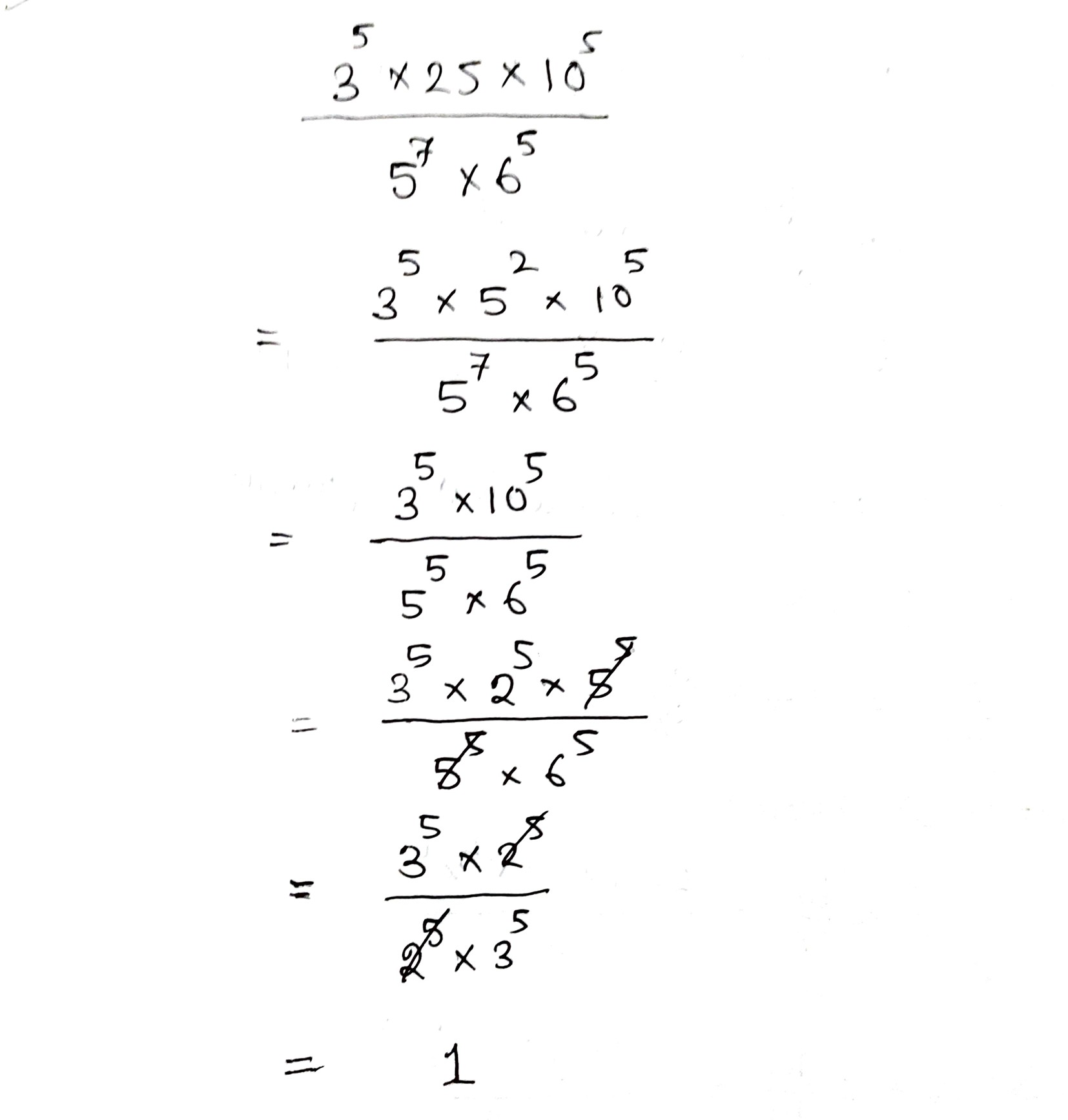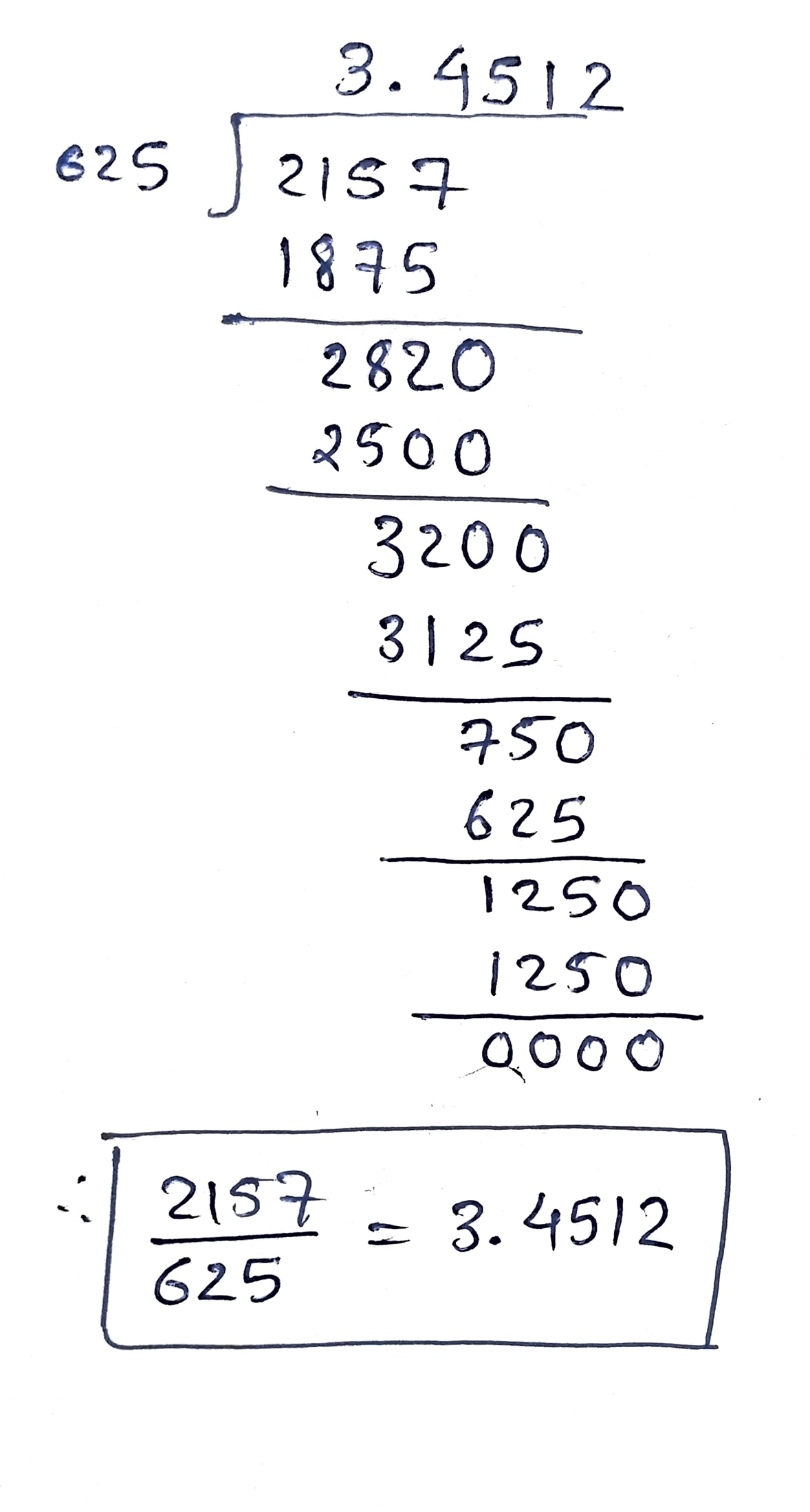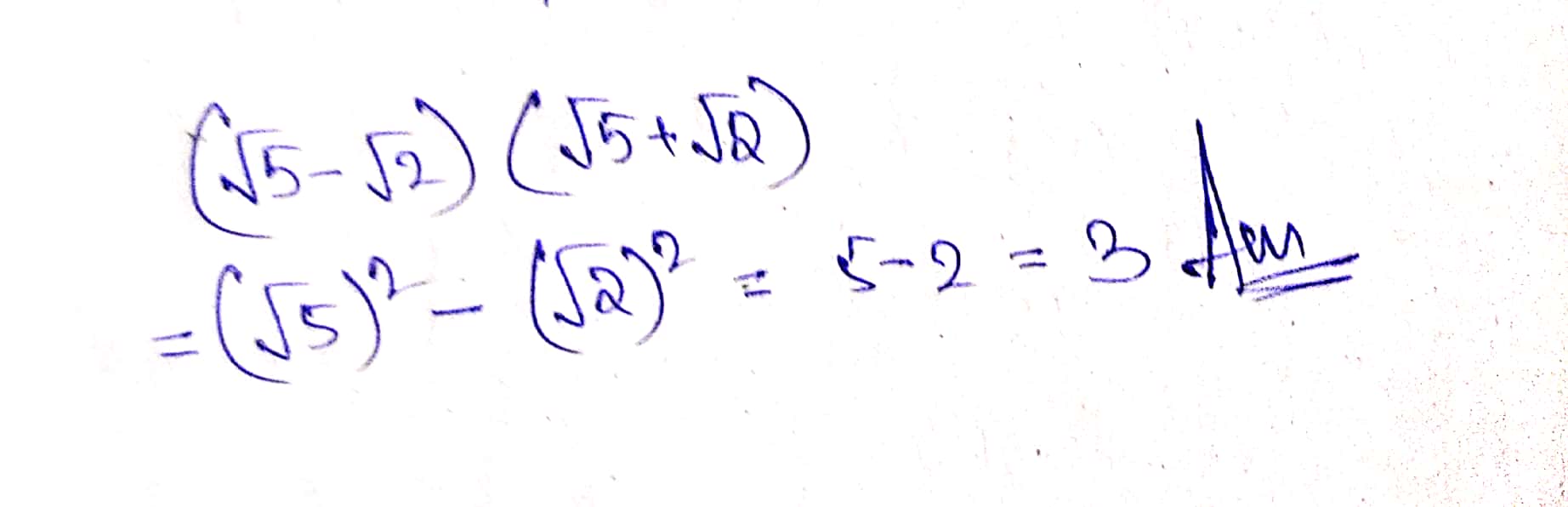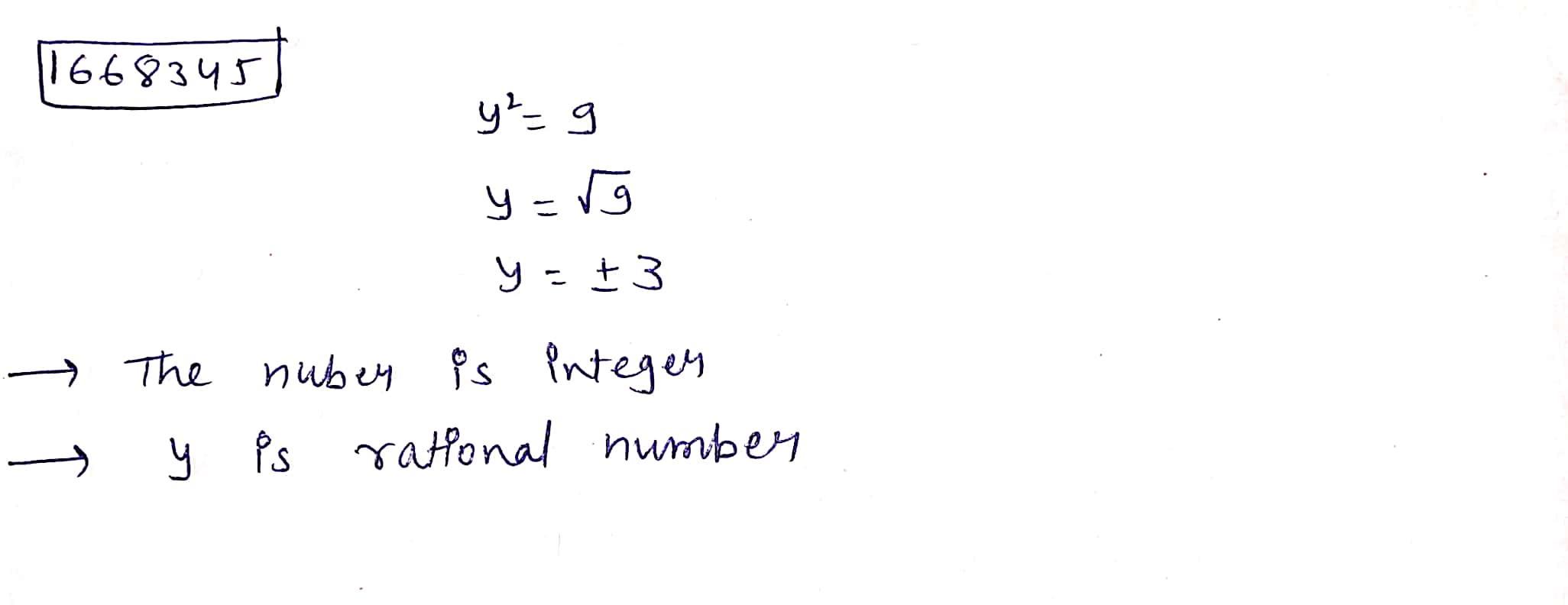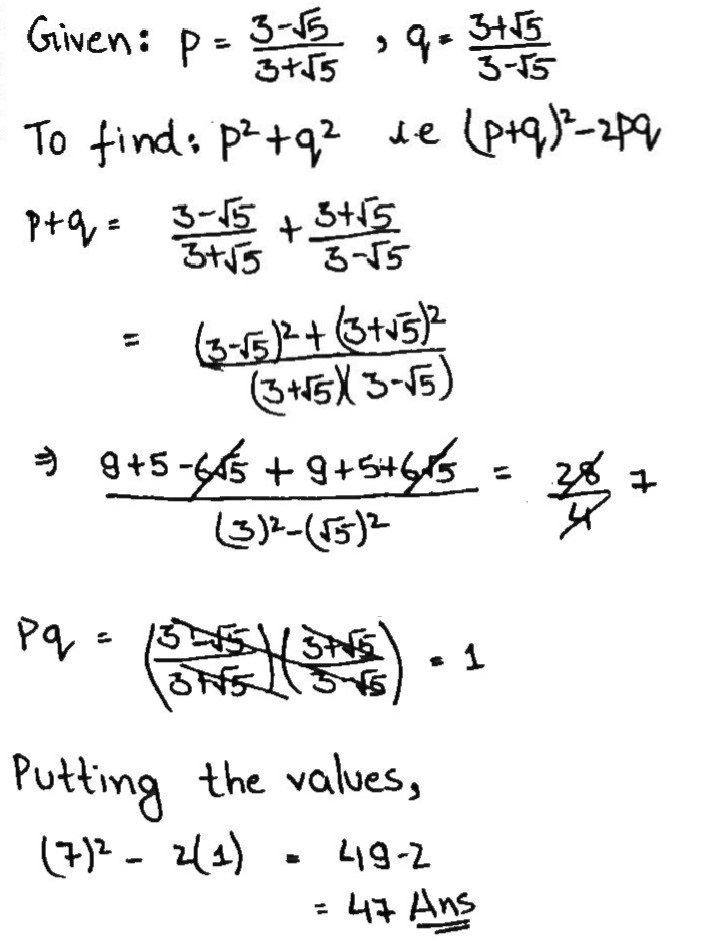Number Systems - Class 9 Maths - Extra Questions
Following are the five rational numbers which are smaller than $$2$$ $$\Rightarrow$$ $$1,\dfrac{1}{2},0,-1,\dfrac{-1}{2}$$.
If true then enter $$1$$ and if false then enter $$0$$.
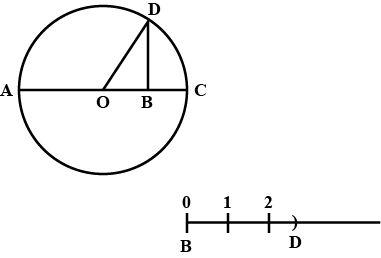
$$y^{2}=9$$
Simplify and express the result in power notation with positive exponent.
$$(-3)^4 \times \left ( \dfrac{5}{3} \right )^4$$ is $$(m)^4$$
$$m$$ is
$$m$$ is
Find the value of $$(3^{1}+4^{1}+5^{1})^{0}$$.
Find the value of.
$$(3^0+4^{-1}) \times 2^2$$
Some rational numbers are integers, if true then enter $$1$$ and if false then enter $$0$$
5$$\sqrt{3}+2\sqrt{3}$$ = 7$$\sqrt{6}$$
enter $$1$$ for true and $$0$$ for false
Is zero a rational number?
Zero can be written in the form of $$\displaystyle\ \frac{p}{q}$$, where p and q are integers and q$$\neq$$ 0?
If above statement is true then enter $$1$$ and if false then enter $$0.$$
5$$\sqrt{3} -2\sqrt{3}$$ = 3$$\sqrt{3}$$
enter $$1$$ for true and $$0$$ for false
Rationalise the denominator and simplify:If $$\displaystyle \frac{2}{\sqrt{5}+\sqrt{3}}$$ is $$\displaystyle \sqrt{m}-\sqrt{3}$$, then $$m$$ is ?
Rationalise the denominator and simplify:If $$\displaystyle \frac{3}{4-\sqrt{3}}$$ is $$\displaystyle \frac{3}{13}(4+\sqrt{m})$$, then $$m$$ is ?
Rationalise the denominator and simplify:If $$\displaystyle \frac{1}{2+\sqrt{3}}$$ is $$\displaystyle 2-\sqrt{m}$$, then $$m$$ is ?
Find the product of $$3-\sqrt{7}$$ and its conjugate.
Find the value-of $$(3^0 - 4^0)\times5^2$$:
Express as rational number $$\displaystyle \left ( \frac{-5}{7} \right )^{-3}$$ is $$\dfrac{-m}{125}$$
Value of $$m$$ is
Simplify: $$\displaystyle \left (\frac{1}{2} \right )^{-2} + \left (\frac{1}{3} \right )^{-2}+ \left (\frac{1}{4} \right )^{-2}$$
Express as a power of a rational number with positive exponent $$\displaystyle \left [ \left ( \frac{4}{5} \right )^{-2} \right ]^4$$
Answer is $$(\dfrac{5}{4})^m$$
Value of $$m$$ is
Express as rational number $$\displaystyle \left ( \frac{-5}{7} \right )^{-1}$$ is $$=\displaystyle \frac{-m}{5} $$
Value of $$m$$ is
Evaluate $$\displaystyle \left ( \frac{1}{2} \right )^{-5}$$
If $$\displaystyle \left \{ \left (\frac{3}{4} \right )^{-1} - \left (\frac{1}{4} \right )^{-1} \right \}=$$ $$- \dfrac{3}{m}$$, the the value of $$m$$ is
If $$4^{-3}$$ is $$\dfrac{1}{m}$$, then the value of $$m$$ is:
Express with positive index $$\displaystyle x^{ \frac{-1}{2}}$$
Simplify $$ \displaystyle \left ( - \frac{2}{5} \right )^{-3} \times \left ( - \frac{2}{5} \right )^{4}$$
Find the value of $$(3^0 + 4^{-1}) \times 2^2$$
Find the value of $$\displaystyle \left ( \left ( \frac{4}{7} \right )^{8} \right )^0$$.
Find the value of $$m$$:$$(2^{-1} \times 4^{-1}) + 2^{-2}=\dfrac{3}{m}$$
Simplify $$\displaystyle \left ( \frac{-3}{4} \right )^{-5} + \left ( \frac{-3}{4} \right )^{-3}$$
Find the value of $$m$$: $$\displaystyle \left ( \frac{5}{2} \right )^3 \times \left ( \frac{5}{2} \right )^7 =\left( \dfrac { 5 }{ 2 } \right) ^{ m}$$
Find $$(0.04)^{-1.5} = ?$$
The conjugate of $$3 - \sqrt {5 + x}$$ is $$3 + \sqrt {5 + x}$$. Verify
Verify that the conjugate of $$\sqrt {3} + \sqrt {2}$$ is $$\sqrt {3} - \sqrt {2}$$
Write five rational numbers which are smaller than $$2$$.
Write five rational numbers which are smaller than $$\dfrac{5}{6}$$.
Write.
(i) The rational number that does not have a reciprocal.
(ii) The rational numbers that are equal to their reciprocals.
(iii) The rational number that is equal to its negative.
Express the following with positive exponents:
$${4}^{-7}$$
Find the value of '$$x$$' such that
$${(-2)}^{x+1}\times {(-2)}^{7}={(-2)}^{12}$$
Write $$0, 7, 10, -4$$ in $$\dfrac{p}{q}$$ form
Can you guess the value of '$$x$$' when $${2}^{x}=1$$
Express the following with positive exponents:
$${ \left( \cfrac { 4 }{ 7 } \right) }^{ -3 }$$
Express the following with positive exponents:
$$\dfrac{1}{{(5)}^{-4}}$$
Give one example for the following statement:
A number which is rational but not an integer.
Classify the following number as rational or irrational.
$$5 - \sqrt {3}$$
Give one example each to the following statements.
A number which is natural number, whole number, integer and rational number
Give one example each to the following statements.
An integer which is not a whole number
Give one example each to the following statements.
A whole number which is not a natural number
Rationalise the denominator and simplify:
$$\dfrac {\sqrt {3} + \sqrt {2}}{\sqrt {3} - \sqrt {2}}$$
Number $$\dfrac {3}{625}$$ is a terminating decimal or a non-terminating repeating decimal? Write it in decimal form.
Rationalise the denominator and simplify:
$$\cfrac { \sqrt { 6 } +\sqrt { 3 } }{ \sqrt { 6 } -\sqrt { 3 } } $$
Is zero a rational number? Give reasons for your answer.
Rationalising factor of $$\left( \sqrt { x+y } \right) $$ is ____
Find the value of the following:
$$\left (\dfrac {7}{4}\right )^{0}\times 3$$
Find x$$2^{2x \, + \, 2} \, - \, 6^x \, - \, 2 \times 3 ^{2x \, + \, 2} \, = \, 0 $$
Solve the following equation:
$$\displaystyle\, \frac{0.2^{x + 0.5}}{\sqrt{5}} = \frac{(0.04)^x}{25}$$
Solve the following equations.
$$\displaystyle\, \left ( \frac{5}{12} \right )^x \cdot\left ( \frac{6}{5} \right )^{x -1} = (0.3)^{-1}$$
Is $$0.9$$ a rational number?
Solve $$17^2 \cdot 17^{-5}$$
Solve:
$$\dfrac {\sqrt{24}}{8}+\dfrac {\sqrt{54}}{9}$$.
Simplify: $$\dfrac { 25 }{ \sqrt { 5 } }$$
Find a rational number between $$\dfrac{2}{3}$$ and $$\dfrac{3}{4}$$.
Find four rational numbers between $$\dfrac{2}{3}$$ and $$\dfrac{3}{5}$$.
Write five rational numbers which are greater than $$\dfrac{-3}{2}$$.
Prove that $$\dfrac{{{{({a^{p + q}})}^2}{{({a^{q + r}})}^2}{{({a^{r + p}})}^2}}}{{{{({a^p}.{a^q}.{a^r})}^4}}} = 1$$
Find the value of $$x$$ for which$${ \left( \dfrac { 4 }{ 9 } \right) }^{ 4 }\times { \left( \dfrac { 4 }{ 9 } \right) }^{ -7 }={ \left( \dfrac { 4 }{ 9 } \right) }^{ 2x-1 }$$
How many of the following numbers are rational numbers?
(i) $$\dfrac{5}{-8}$$ (ii) $$\dfrac{-6}{11}$$ (iii) $$\dfrac{7}{15}$$ (iv) $$-3$$ (v) $$0$$ (vi) $$\dfrac{1}{0}$$
If $$\frac{{{{\left( { - 2} \right)}^x} \times {{\left( { - 2} \right)}^7}}}{{3 \times {4^6}}} = \frac{1}{{12}}$$, then the value of x-3 is
Simplify
$$(16)^{\dfrac {-1}{4}}x {^{4}\sqrt {16}}$$
Evaluate:-
$${3^3} \times \left( {243} \right)\,{\,^{ - \cfrac{2}{3}}}\,\, \times {9^{\,\, - \cfrac{1}{3}}}$$
Add $$7\sqrt 2 + 5\sqrt 3 $$ and $$\sqrt 2 - 7\sqrt 3 $$
Use the laws of exponents and simplify $${3}^{-7}+{3}^{-4}$$
Solve $${2^0} + {1^0} - {4^0} - {7^0}$$
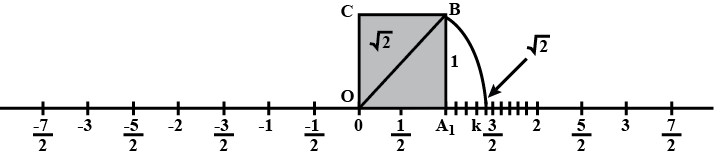
Represent $$\sqrt {4.5}$$ on the number line.
$$AB =4.5\ units\ ,\ BC=1\ unit\ ,\ OC=OD=\displaystyle \frac{5.5}{2}=2.75units$$
$$OD^{2}=OB^{2}+BD^{2}$$
$$\displaystyle (\frac{4.5+1}{2})^{2}=(\frac{4.5+1}{2}-1)^{2}+(BD)^{2}$$
$$BD^{2}=(\frac{4.5+1}{2})^{2}-(\frac{4.5-1}{2})^{2}$$
$$BD^{2}=4.5$$
$$BD=\sqrt{4.5}units$$
so the length of BD will be the required one so mark an arc of length BD on number line it will result I the required length.
Simplify $$\dfrac {(6.7\times 10^{-11})(6 \times 10^{24})(7.4 \times 10^{22})}{(3.84 \times 10^{8})^{2}}$$
Find the value of $${\left( \cfrac{6}{5} \right)}^{\dfrac{1}{2}}$$
Simplify: $$\cfrac { { 3 }^{ 5 }\times { 10 }^{ 5 }\times 2^5 }{ { 5 }^{ 7 }\times { 6 }^{ 5 } } $$
Find the co-efficient of $$a^0$$ in the expression $$a^2+3a+2$$.
Find the value to three places of decimals of each of the following. It is given that $$\sqrt {2}=1.414, \sqrt {3}=1.732, \sqrt {5}=2.236$$ and $$\sqrt {10}=3.162$$
$$\dfrac {3}{\sqrt {10}}$$
Simplify:$$2+\dfrac{\sqrt{3}}{3}$$
Find the value to three places of decimals of each of the following. It is given that $$\sqrt {2}=1.414, \sqrt {3}=1.732, \sqrt {5}=2.236$$ and $$\sqrt {10}=3.162$$
$$\dfrac {\sqrt {10}+\sqrt {15}}{\sqrt {2}}$$
Find the value to three places of decimals of each of the following. It is given that $$\sqrt {2}=1.414, \sqrt {3}=1.732, \sqrt {5}=2.236$$ and $$\sqrt {10}=3.162$$$$\dfrac{2+\sqrt {3}}{3}$$
Find the value to three places of decimals of each of the following. It is given that $$\sqrt {2}=1.414, \sqrt {3}=1.732, \sqrt {5}=2.236$$ and $$\sqrt {10}=3.162$$
$$\dfrac {\sqrt {2}-1}{\sqrt {5}}$$
$$\left( {{3^ \circ } + {4^{ - 1}}} \right) \times {2^2}$$
$${\left( {\frac{1}{2}} \right)^{ - 2}}\, + \,{\left( {\frac{1}{3}} \right)^{ - 2}}\, + \,{\left( {\frac{1}{4}} \right)^{ - 2}}$$
Write any two irrational numbers between $$0.23$$ and $$0.3$$.
Solve: $$32^{1/5}$$.
Multiply$$\sqrt 3 (\sqrt 7 - \sqrt 3 )$$
Convert into form of power. $$3 \times 3 \times 5 \times 3 \times 3 \times 5$$
Rationalise:$$\dfrac{6}{{9\sqrt 3 }}$$.
$$Write\quad 5\quad rational\quad numbers\quad smaller\quad than\quad \cfrac { 5 }{ 6 } $$
Find the five rational numbers between $$\frac{1}{6}$$ and $$\frac{1}{3}$$
Show that $$\dfrac{1}{{\left( {3 - \sqrt 8 } \right)}} - \dfrac{1}{{\left( {\sqrt 8 - \sqrt 7 } \right)}} + \dfrac{1}{{\left( {\sqrt 7 - \sqrt 6 } \right)}} - \dfrac{1}{{\left( {\sqrt 6 - \sqrt 5 } \right)}} + \dfrac{1}{{\left( {\sqrt 5 - 2} \right)}} = 5$$
Find the value of $$(-i)^{100} $$
Find $${ 1 }^{ 0 }\times { 2 }^{ 0 }+{ 3 }^{ 0 }\times { 4 }^{ 0 }+{ 5 }^{ 0 }\times { 6 }^{ 0 }$$
The value of $${(64)^{1/3}}$$
Which are two rational number between $$\dfrac{6}{5}$$ and $$\dfrac{7}{5}$$.
$$\frac{1}{{\sqrt 9 - \sqrt 8 }}$$ is equal to :
Simplify and write in exponential form
$$P^{3}\times P^{-10}$$
Simplify:$${\left( { - 4} \right)^5}{\left( { - 4} \right)^6}$$
Solve: $${{\left( \dfrac{7}{4\sqrt{3}+1}+\dfrac{7}{4\sqrt{3}-1} \right)}^{2}}$$
If $$a={x}^{m+n}.{y}^{l};b={x}^{n+l}.{y}^{m}$$ and $$c={x}^{l+m}.{y}^{n}$$ prove that : $${a}^{m-n}.{b}^{n-l}.{c}^{l-m}=1$$
Simplify $$\dfrac{13}{4}+\sqrt{3}$$
Evaluate $${2}^{3}\times {(9)}^{0}\times {3}^{3}$$
Classify the following number as rational or irrational :
$$\left( 3+\sqrt { 23 } \right) -\sqrt { 23 } $$
Is zero a rational number ? Justify
Evaluate the following expression $${\left( {\dfrac{{625}}{{81}}} \right)^{ - 1/4}}$$
Write any three rational numbers between the two numbers given below.
$$0.3$$ and $$-0.5$$
Write three rational numbers that lie between the two given numbers.
$$\dfrac{-3}{4}, \dfrac{+5}{4}$$
Write three rational numbers that lie between the two given numbers.
$$0, \dfrac{-3}{4}$$
Evaluate
$${\left( {{{17}^2} - {8^2}} \right)^{1/2}}$$
Write three rational numbers that lie between the two given numbers.
$$\dfrac{7}{9}, -\dfrac{5}{9}$$
Solve : $$4 + 4 \sqrt{3}$$
List five rational numbers between:
$$-2$$ and $$-1$$
Solve the following equation and find the value of $$m$$ in $$2^{m-3}=1$$
Insert three rational number between $$-\dfrac{1}{3}$$ and $$-\dfrac{2}{3}$$.
Find the rational number between $$\dfrac {2}{7}$$ and $$\dfrac {3}{4}$$
Write any three rational numbers between the two numbers given below.
$$-4.5$$ and $$-4.6$$
Find the value of $$({3^0} + {4^{ - 1}}) \times {2^2}$$
$$x = {\left( {\dfrac{5}{7}} \right)^{ - 5}} \times {\left( {\dfrac{7}{5}} \right)^{ - 7}}$$ then find the value of 2x + 1
Simplify:
$${2}^{3/2}$$ to $$2\sqrt{2}$$
Write any three rational numbers between the two numbers given below.
$$-2.3$$ and $$-2.33$$
Write any three rational numbers between the two numbers given below.
$$5.2$$ and $$5.3$$
Define an irrational number.
The decimal representation of $$\cfrac{6}{1250}$$ will terminate after how many places of decimal?
If $$\dfrac{p}{q}=\left(\dfrac{3}{2}\right)^{-2}\div \left(\dfrac{6}{7}\right)^{0}$$, find the value of $$\left(\dfrac{p}{q}\right)^{-3}$$
Evaluate : $$(-4)^{5}\div (4)^{8}$$
Write the rational numbers which are smaller than $$2$$.
Solve :
$$(14x^{3} \times 2x^{4} \times 8x^{8}) \div 7x^{3}.$$
Simplify the following using laws of exponents.
$${\left( {\dfrac{3}{5}} \right)^4} \times {\left( {\dfrac{3}{5}} \right)^3} \times {\left( {\dfrac{3}{5}} \right)^8}$$
Solve:
$$\left( {{2^3} \times {2^5}} \right) \div {2^8}$$
List five rational numbers between $$\dfrac{1}{2}$$ and $$\dfrac{2}{3}$$.
Insert five rational numbers between $$\dfrac { 3 }{ 5 }$$ and $$ \dfrac { 2 }{ 3 } $$
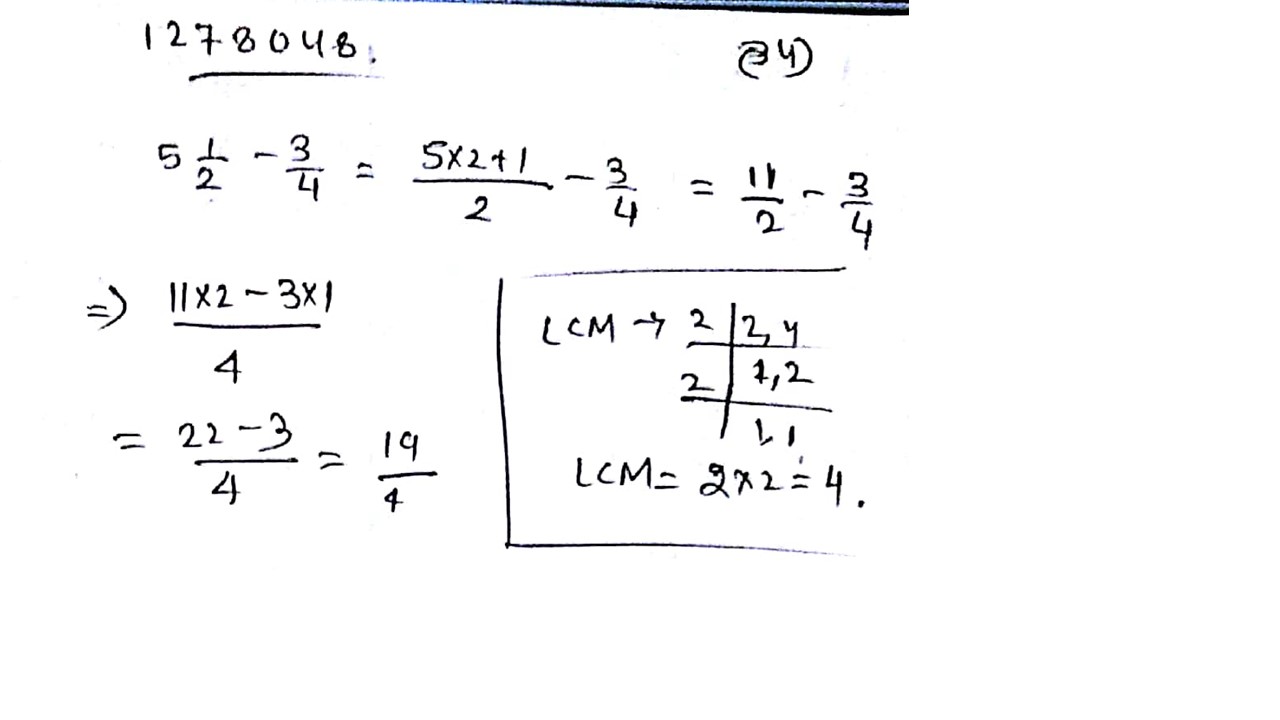
Solve: $$5\dfrac{1}{2} - \dfrac{3}{4}$$
Find the value of $${(105)^2}$$
Fill in the blanks: $$\dfrac a 8$$, so that it lies between $$\frac{3}{4}$$ and $$\frac{1}{2}$$?
Classify the following numbers as rational or irrational:
$$\dfrac{2\sqrt{7}}{7\sqrt{7}}$$
Simplify the following using laws of expressions
$$(2^{3})^{2}\times 2^{8}$$
Simplify $$(a^{3} \times a^{-2} \times a^{4})^{-2}$$
Prove that the sum of two irrational numbers given by $$3 + \sqrt { 2 }\ \& \ 3 - \sqrt { 2 }$$ is a rational number
Insert three rational numbers between $$\dfrac {1}{4}$$ and $$\dfrac {7}{8}$$.
Evaluate:
$${ \left\{ { \left( { 3 }^{ 2 }+{ 4 }^{ 2 } \right) }^{ \frac { 1 }{ 2 } } \right\} }^{ 3 }$$
Simplify the following
$$7 \sqrt{18}-9 \sqrt{8}+12\sqrt{32}-3\sqrt{50}$$
$$ y =7\sqrt{18}-9\sqrt{8}+12\sqrt{32}-3\sqrt{50}$$
$$ y =7\sqrt{3^{2},2}-9\sqrt{2^{2},2}+12\sqrt{4\times 4\times 2}-3\sqrt{5^{2}2}$$
$$ y= 21\sqrt{2}-18\sqrt{2}+48\sqrt{2}-15\sqrt{2}$$
$$ y=36\sqrt{2}$$
Rationalise it
$$\left[1-\dfrac{1}{a}\right]^3$$
solve:
$${ ({ 3 }^{ -1 } }+{ 4 }^{ -1 }+{ 5 }^{ -1 })^{ 0 }$$
Which is the rational number that is equal to its negative?
What are terminating decimals ?
Solve :
$$(4 - p)^3$$
Simplify:
$$(2^{-1}+3^{-1})^{-1}\div 4^{-1}$$
$$(2^{-1}+3^{-1})^{-1}\div 4^{-1}$$
we know $$ a^{-1}=$$ $$\frac{1}{a}.$$
$$(\frac{1}{2}+\frac{1}{3})^{-1}\div \frac{1}{4}$$
$$(\frac{5}{6})^{-1}\div \frac{1}{4}$$ $$\Rightarrow \frac{6/5}{1/4}$$ = $$ \frac{24}{5}$$
Insert a rational and an irrational number between $$2$$ and $$3$$.
Using laws of exponents, simplify and write the answer in exponential form: $${ 7 }^{ x }\times { 7 }^{ 2 }$$
Insert a rational number between $$-\dfrac { 2 }{ 5 } and+\dfrac { 1 }{ 2 } $$
Using laws of exponents, simplify and write the answer in exponential form $${ 2 }^{ 5 }\times { 5 }^{ 5 }$$
Insert a rational number between $$\dfrac {3}{4}$$ and $$1$$ without using $$\dfrac {a+b}{2}$$ formula.
Rationalise: $$5+\sqrt{3}$$
Solve
$$3 ^ { 4 } \times 2 ^ { 4 }$$
Using laws of exponents, simplify and write the answer in exponential form :
$${ 3 }^{ 2 }\times { 3 }^{ 4 }\times { 3 }^{ 8 }$$
Express the following numbers in usual form.
$$3\times {10}^{-8}$$
Rationalise:$$4+\sqrt{5}$$
Using laws of exponents, simplify and write the answer in exponential form: $${ a }^{ 3 }\times { a }^{ 2 }$$
Fill in the blanks :
If the integer $$p$$ and $$q$$ have no common divisor other than $$1$$ and $$q$$ is positive, then the rational number $$\dfrac{p}{q}$$ is said to be in........... .
Simplify and express following in exponential form :
$$({3^{0}+ 2^{0})\times 5^{0}}$$
$$(3^o+2^o)\times 5^o=(1+1)\times 1=2\times 1=2=2^1$$.
Express each of the following exponential expressions as a rational number. $${ (\dfrac { 2 }{ 5 } ) }^{ (-3) }$$
$$\left(\dfrac{2}{5}\right)^{-3}=\left(\dfrac{5}{2}\right)^3=\dfrac{5^3}{2^3}=\dfrac{125}{8}$$.
Give examples of irrational numbers between $$11$$ and $$16$$.
Simplify $$3\sqrt { 2 } +\sqrt { 8 } -\sqrt { 5 } $$.
If $$\dfrac { 5+\sqrt { 6 } }{ 5-\sqrt { 6 } } =a+b\sqrt { 6 } ,$$ then find the value of 'a' and 'b'.
Solve:
$${5^{x + 1}} = {\left( {\sqrt {25} } \right)^{3x - 1}}$$
$$5^{x+1}=(\sqrt{25})^{3x-1}$$
$$\Rightarrow 5^{x+1}=5^{3x-1}$$
comparing powers,
$$x+1=3x=1$$
$$\Rightarrow 2=2x$$
$$x=1$$
Solve:$$\dfrac{4+\sqrt3}{4-\sqrt3}+\dfrac{4-\sqrt3}{4+\sqrt3}$$
Express the following in exponential form:
$$6\times 6\times 6\times 6$$
Find the value of:
$${2}^{6}$$
Find the value of :
$${11}^{2}$$
Express $$1.27$$ in the form of $$\dfrac p q$$.
Find the value of $${5}^{4}$$
Write any four rational numbers larger than $$0$$ and smaller than $$\dfrac { 5 }{ 6 } .$$
Simplify:
$$2\times{10}^{3}$$
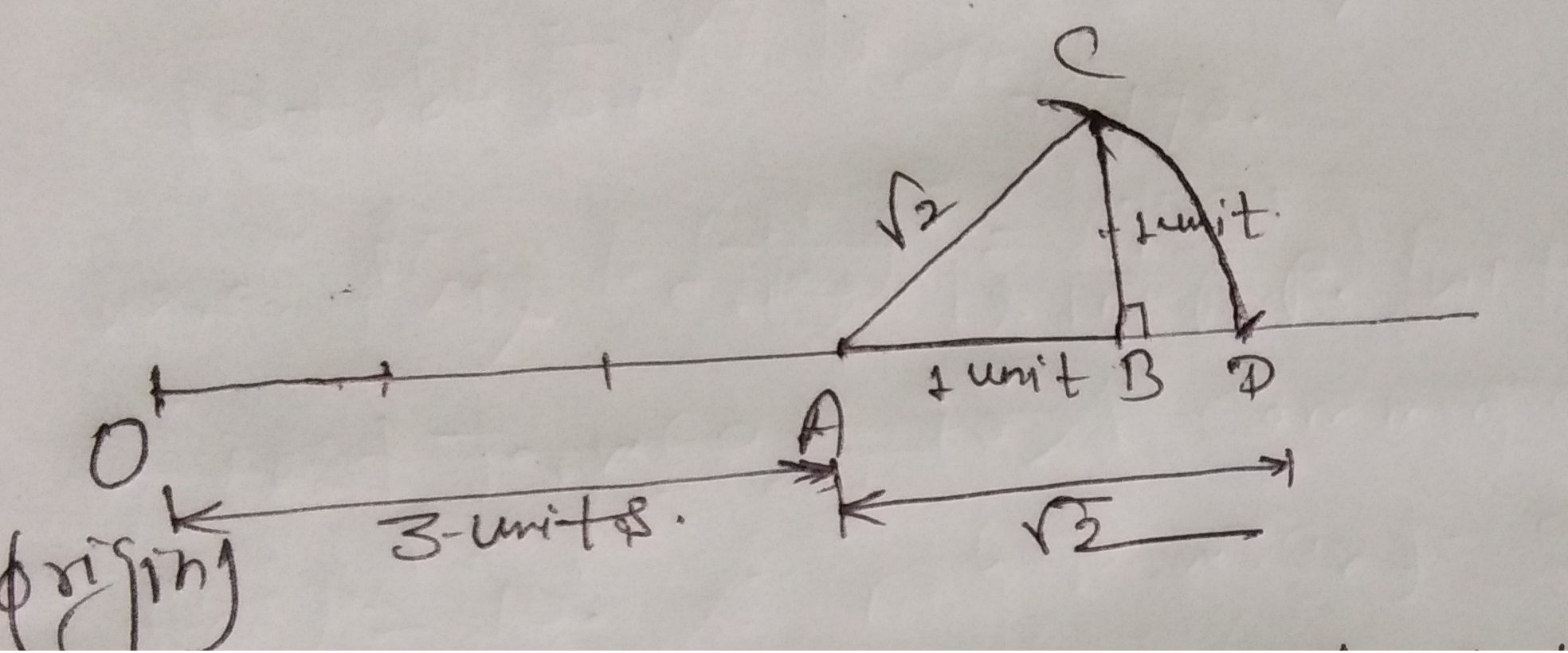
Represent geometrically $$\sqrt {5.6}$$ on the number line.
Presentation of $$\sqrt {5.6}$$ on number line:
Mark the distance $$5.6\ units$$ from a fixed points $$A$$ on a given line to obtain a point $$B$$ such that $$AB = 5.6\ units$$. From $$B$$, mark a distance of $$1\ unit$$ and mark the new points as $$C$$. Find the mid-point of $$AC$$ and mark the points as $$O$$. Draw a semicircle with centre $$O$$ and radius $$OC$$. Draw a line perpendicular to $$AC$$ passing through $$B$$ and intersecting the semicircle at $$D$$. Then $$BD = \sqrt {5.6}$$.
Now, draw an arc with centre $$B$$ and radius $$BD$$, which intersects the number line in $$E$$.
Thus, $$E$$ represent $$\sqrt {5.6}$$.
Find the value:
$${9}^{3}$$
Find five rational numbers between $$ \dfrac{-3}{5} $$ and $$ \dfrac{-1}{2} $$.
Simplify the following :
$$\dfrac{(a^{3n-9})^{6}}{a^{2n-4}} $$
Write down the value of $${17}^{0}$$
Which of the following rational numbers are negative?
$$\dfrac{-115}{-197}$$
Which of the following rational numbers are positive:
$$\dfrac{-21}{13}$$
Simplify
$$x^{0}$$
Simplify:
$${5}^{2}\times{3}^{3}$$
Simplify:
$${x}^{3}{y}^{4}\times{x}^{5}{y}^{3}$$
Write down the denominator of each of the following rational numbers:
$$\dfrac{11}{-34}$$
Which of the following rational numbers are negative?
$$\dfrac{-5}{-8}$$
Given below is a rational number or not?
$$\cfrac{5}{-8}$$
Given below is a rational number or not?
$$\cfrac7{15}$$
Express the rational number with positive denominator:
$$\dfrac{19}{-7}$$
Fill in the blanks so as to make the statement true:
If $$\dfrac{p}{q}$$ is a rational number, then $$q$$ cannot be _____
Given below is a rational number or not?
$$-3$$
Given below is a rational number or not?
$$6$$
Given below is a rational number or not?
$$\cfrac{-8}{-12}$$
Given below is a rational number or not?
$$\cfrac{-6}{11}$$
Evaluate $$\dfrac{2^0+7^0}{5^0}$$.
Write down the numerator and the denominator of the following rational number:
$$9$$
Given below is a rational number or not?
$$\cfrac10$$
Given below is a rational number or not?
$$\cfrac00$$
Write the following integer as a rational number. Write the numerator and the denominator in the following case.
$$1$$
Write down the numerator and the denominator of the following rational number:
$$\cfrac8{19}$$
Write the following integer as a rational number. Write the numerator and the denominator in the following case.
$$-3$$
Write down the numerator and the denominator of the following rational number:
$$\cfrac{-13}{15}$$
Write down the numerator and the denominator of the following rational number:
$$\cfrac{-8}{-11}$$
Write the following integer as a rational number. Write the numerator and the denominator in the following case.
$$5$$
Given below is a rational number or not?
$$0$$
Given below is a negative rational number or not?
$$\cfrac{-5}7$$
Given below is a positive rational number or not?
$$8$$
Given below is a positive rational number or not?
$$\dfrac{0}{3}$$
Given below is a negative rational number or not?
$$\cfrac4{-9}$$
Given below is a positive rational number or not?
$$\cfrac{-5}{-8}$$
Given below is a negative rational number or not?
$$ \cfrac{-15}4$$
Given below is a positive rational number or not?
$$\cfrac{37}{53}$$
Given below is a negative rational number or not?
$$\cfrac1{-2}$$
Given below is a positive rational number or not?
$$\cfrac3{-5}$$
Given below is a positive rational number or not?
$$\cfrac{-11}{15}$$
Find the value of the following:
$$6^0\times 7^0$$
Find the value of the following:
$$4^0+5^0$$
Find the value of the following:
$$8^0$$
Write the following as a rational number with positive denominator.
$$\cfrac{-8}{-19}$$
Find the value of the following:
$$(-3)^0$$
Write the following as a rational number with positive denominator.
$$\cfrac{12}{-17}$$
Write the following as a rational number with positive denominator.
$$\cfrac{1}{-2}$$
Fill in the blanks to make the statements true.
$$\dfrac{-3}{8}$$ is a ________ rational number
Write the following as a rational number with positive denominator.
$$\cfrac{11}{-6}$$
Write the following number in the form $$\dfrac{p}{q}$$, where p and q are integers.
six-eighths
Select the rational numbers from the list which are also the integers.
$$\dfrac{9}{4}, \dfrac{8}{4}, \dfrac{7}{6}, \dfrac{6}{4}, \dfrac{9}{3}, \dfrac{8}{3}, \dfrac{7}{3}, \dfrac{6}{3}, \dfrac{5}{2}, \dfrac{4}{2}, \dfrac{3}{2}, \dfrac{1}{1}, \dfrac{0}{1}, \dfrac{-1}{1}, \dfrac{-2}{1}, \dfrac{-3}{2}, \dfrac{-4}{2}, \dfrac{-5}{2}, \dfrac{-6}{2}$$
Write the following number in the form $$\dfrac{p}{q}$$, where p and q are integers.
three and half
Write the following number in the form $$\dfrac{p}{q}$$, where p and q are integers.
one-fourth
Fill in the blanks to make the statements true.
$$\dfrac{-16}{24}$$ and $$\dfrac{20}{-16}$$ represent ________ rational numbers.
Fill in the blanks to make the statements true.
$$1$$ is a ________ rational number.
$$5^0=$$.
Insert a rational number and an irrational number between the following:
$$0$$ and $$0.1$$.
Put the $$(\checkmark),$$ wherever applicable
Number | Natural Number | Whole Number | Integer | Fraction | Rational Number |
$$\dfrac{73}{71}$$ |
Put the $$(\checkmark),$$ wherever applicable
Number | Natural Number | Whole Number | Integer | Fraction | Rational Number |
$$\dfrac{19}{27}$$ |
Insert a rational number and an irrational number between the following:
$$0.15$$ and $$0.16$$.
Rationalize the denominator of the following:
$$\dfrac {\sqrt {40}}{\sqrt {3}}$$.
Rationalize the denominator of the following:
$$\dfrac {2 + \sqrt {3}}{2 - \sqrt {3}}$$.
Represent geometrically the following number on the number line:
$$\sqrt {8.1}$$.
Presentation of $$\sqrt {8.1}$$ on number line:
Mark the distance $$8.1$$ units from a fixed point $$A$$ on a given line to obtain a point $$B$$ such that $$AB = 8.1\ units$$. From $$B$$, mark a distance of $$1$$ unit and mark the new points as $$C$$. Find the mid-point of $$AC$$ and mark that point as $$O$$. Draw a semicircle with a centre $$O$$ and radius $$OC$$. Draw a line perpendicular to $$AC$$ passing through $$B$$ and intersecting the semicircle at $$D$$. Then, $$BD = \sqrt {8.1}$$.
Now, draw an arc with centre $$B$$ and radius $$BD$$, which intersects the number line in $$E$$. Thus, $$E$$ represents $$\sqrt {8.1}$$.
Mark the distance $$8.1$$ units from a fixed point $$A$$ on a given line to obtain a point $$B$$ such that $$AB = 8.1\ units$$. From $$B$$, mark a distance of $$1$$ unit and mark the new points as $$C$$. Find the mid-point of $$AC$$ and mark that point as $$O$$. Draw a semicircle with a centre $$O$$ and radius $$OC$$. Draw a line perpendicular to $$AC$$ passing through $$B$$ and intersecting the semicircle at $$D$$. Then, $$BD = \sqrt {8.1}$$.
Now, draw an arc with centre $$B$$ and radius $$BD$$, which intersects the number line in $$E$$. Thus, $$E$$ represents $$\sqrt {8.1}$$.
Rationalize the denominator of the following:
$$\dfrac {3 + \sqrt {2}}{4\sqrt {2}}$$.
Rationalize the denominator of the following:
$$\dfrac {\sqrt {3} + \sqrt {2}}{\sqrt {3} - \sqrt {2}}$$.
Rationalize the denominator of the following:
$$\dfrac {\sqrt {6}}{\sqrt {2} + \sqrt {3}}$$.
Rationalize the denominator of the following:
$$\dfrac {2}{3\sqrt {3}}$$.
Rationalize the denominator of the following:
$$\dfrac {3\sqrt {5} + \sqrt {3}}{\sqrt {5} - \sqrt {3}}$$.
Insert a rational number and an irrational number between the following:
$$2.357$$ and $$3.121$$.
Insert a rational number and an irrational number between the following:
$$0.484848$$ and $$3.623623$$.
If $$a = 2 + \sqrt {3}$$, then find the value of $$a - \dfrac {1}{a}$$.
Which of the
following are negative rational numbers?
$$\dfrac{-5}{7},
\dfrac{4}{-3}, \dfrac{-3}{-11},-6,9,0, \dfrac{-28}{5}, \dfrac{31}{7}$$
Rationalize the denominator of the following and hence evaluate by taking $$\sqrt {2} = 1.414$$ and $$\sqrt {5} = 2.236$$, upto three places of decimal.
$$\dfrac {10 - \sqrt {5}}{2}$$.
Find the values of $$a$$ in the following:
$$\dfrac {5 + 2\sqrt {3}}{7 + 4\sqrt {3}} = a - 6\sqrt {3}$$.
Rationalize the denominator of the following and hence evaluate by taking $$\sqrt {2} = 1.414, \sqrt {3} = 1.732$$ upto three places of decimal.
$$\dfrac {1}{\sqrt {3} + \sqrt {2}}$$.
Simplify and write in exponential form:
$$(2^0+3^0)4^0$$
Which of the following are positive rational numbers?
$$\dfrac{5}{8},
\dfrac{-3}{11}, \dfrac{0}{5}, 7,-4, \dfrac{-3}{-13}, \dfrac{-17}{-6}, \dfrac{9}{-20}$$
Rationalize the denominator of the following and hence evaluate by taking $$\sqrt {2} = 1.414, \sqrt {3} = 1.732$$ upto three places of decimal.
$$\dfrac {6}{\sqrt {6}}$$.
Rationalize the denominator of the following and hence evaluate by taking $$ \sqrt {3} = 1.732$$ upto three places of decimal.
$$\dfrac {4}{\sqrt {3}}$$.
Write the denominator of each of the following rational numbers :
$$ \dfrac{7}{-15} $$
Write the numerator of each of the following rational numbers :
$$ \dfrac{-85}{93} $$
Write the numerator of each of the following rational numbers :
$$0$$
Write the denominator of each of the following rational numbers :
$$ \dfrac{-18}{29} $$
Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion: $$\dfrac{1258}{625}$$.
Given, $$\dfrac{1258}{625}$$.
The denominaor, $$625 = 5 \times 5 \times 5 \times 5=5^4=2^0\times5^4$$, i.e. in the form of $$2^n\times 5^m$$
Therefore, it has a terminating decimal.
Simplify and write in exponential form:
$$3^0 \times 4^0 \times 5^0$$
Write the numerator of each of the following rational numbers :
$$ \dfrac{-125}{127} $$
Write the numerator of each of the following rational numbers :
$$ \dfrac{37}{-137} $$
Write the numerator of each of the following rational numbers :
$$2$$
Separate positive and negative rational numbers from the following :
$$ \dfrac{-3}{5} , \dfrac{3}{-5} , \dfrac{-3}{-5} , \dfrac{3}{5} , 0 , \dfrac{-13}{-3} , \dfrac{15}{-8} , \dfrac{-15}{8} $$
Express each of the following rational numbers in the standard form.
$$ \dfrac{5}{-12} $$
State true or false :
$$ \dfrac{-5}{-12} $$ is a negative rational number
False.
Express each of the following rational numbers in the standard form.
$$ \dfrac{-7}{-8} $$
$$(-5)^{0}$$
$$(4x)^{0}=?$$
Express the following rational number in the standard form.
$$ \dfrac{14}{-49}$$
Evaluate
$$(8+4+2)^{0}$$
Evaluate:
$$(4.73)^{0}$$
Write the denominator of each of the following rational numbers :
$$ \dfrac{-3}{4} $$
Is $$\frac { 3 }{ -2 } $$ a rational number? If so, how do you write it in the form conforming to the definition of a rational number ( that is, the denominator as positive integer)?
Identify whether the given number is a rational or irrational number:$$\displaystyle \frac{\sqrt{12}}{\sqrt{75}}$$
Type $$1$$ if the given number is rational,else type $$0$$1.010010001...
Type $$1$$ if the given number is a rational number ,else type $$0$$10.124124....
When denominator is rationalised, then the number $$\displaystyle \frac{5+2\sqrt{3}}{7+4\sqrt{3}}$$ becomes $$a-6\sqrt{3}$$. Find the value of $$a$$.
Ten rational numbers between $$\dfrac{-2}{5} \ and\ \dfrac{1}{2}$$ are $$\dfrac{-7}{20},\dfrac{-6}{20},\dfrac{-5}{20},\dfrac{-4}{20},\dfrac{-3}{20},\dfrac{-2}{20},\dfrac{-1}{20},0$$.....,$$\dfrac{1}{20},\dfrac{2}{20}$$
If true then enter $$1$$ and if false then enter $$0$$
Divide the following.
(i) $$6\sqrt[3]{25}$$ by $$2\sqrt{5}$$ (ii) $$25\sqrt[4]{33}$$ by $$5\sqrt[4]{11}$$ (iii) $$5\sqrt[3]{4}$$ by $$3\sqrt{2}$$
Given that $$\sqrt{3}=1.7321$$, find the correct value to 3 places of decimal of the following.$$\sqrt{192}-\dfrac{1}{2}\sqrt{48}-\sqrt{75}$$
Simplify the following.$$3\sqrt{2}+\sqrt[4]{64}+\sqrt[4]{500}+\sqrt[6]{8}$$
State wheather true or false
3$$\sqrt{9} + 3$$ = 9, enter $$1$$ for true and $$0$$ for false
Find difference between $$\displaystyle 7+5\sqrt{2}$$ and $$\displaystyle -3+5\sqrt{2}$$
If the following statement is True, enter 1 else enter 0.The difference between these two irrational numbers, $$7\, +\, 5\, \sqrt2$$ and $$-3\, +\, 5\, \sqrt2$$ is rational.
Prove that the following are irrationals:
(i) $$\frac {1}{\sqrt 2}$$
(ii) $$7\sqrt 5$$
(iii) $$6+\sqrt 2$$
Match the column
Prove that $$\frac {1}{\sqrt 3}$$ is irrational
Find the value of 'a' in the following equation:$$\displaystyle \frac{2\, +\, \sqrt3}{2\, -\, \sqrt3}\, =\, a\, +\, b\, \sqrt3$$
Solve $$\displaystyle \left[ \left( \frac{-2}{3} \right)^4 \times \left( \frac{-2}{3} \right)^2 \div \left( \frac{4}{9} \right)^3 \right]$$
What can be the maximum number of digits in the repeating block of digits in the decimal expansion of $$\displaystyle\dfrac{1}{17}$$? Perform the division to check your answer.
You know that $$\displaystyle\frac{1}{7}=0.\overline{142857}$$. Can you predict what the decimal expansions of $$\displaystyle\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}$$ are, without actually doing the long division? If so, how? (Hint: Study the remainders while finding the value of $$\frac{1}{7}$$ carefully.).
Find five rational numbers between:
(i) $$\dfrac{2}{3}\;$$ and $$\;\dfrac{4}{5}$$
(ii) $$\dfrac{-3}{2}\;$$ and $$\;\dfrac{5}{3}$$
(iii) $$\dfrac{1}{4}\;$$ and $$\;\dfrac{1}{2}$$
(ii) $$\dfrac{-3}{2}\;$$ and $$\;\dfrac{5}{3}$$
(iii) $$\dfrac{1}{4}\;$$ and $$\;\dfrac{1}{2}$$
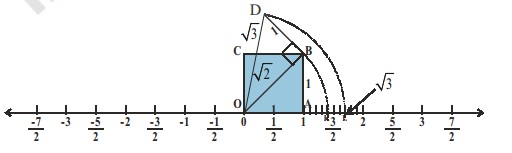
Show how $$\sqrt 5$$ can be represented on the number line.
$$\sqrt{5}=\sqrt{4+1}$$
Here $$4$$ and $$1$$ both are perfect square.
Number as $$\sqrt{4}=2$$ and $$\sqrt{1}=1$$
So draw a right angle triangle with side $$2$$ and $$1$$.
And according to Pythagoras theorem will be $$2^2+1^2=5$$
Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
State whether the following statements are true or false. Give reasons for your answers.
(i) Every natural number is a whole number.
(ii) Every integer is a whole number.
(iii) Every rational number is a whole number.
Find ten rational numbers between $$\dfrac{-2}{5}$$ and $$\dfrac{1}{2}$$.
Write five rational numbers greater than $$-2$$.
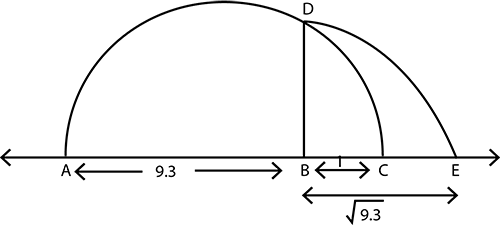
Represent $$\sqrt{9.3}$$ on the number line.
Steps:
1) Draw a line segment AB of length $$9.3$$ units.
2) Extend the line by 1 unit more such that $$BC =1$$ unit .
3) Find the midpoint of $$AC$$.
4) Draw a line BD perpendicular to AB and let it intersect the semicircle at point D.
5) Draw an arc $$DE$$ such that $$BE=BD$$.
Therefore, BE=$$\sqrt{9.3}$$ units
Simplify each of the following expressions:
(i) $$(3+\sqrt 3)(2+\sqrt 2)$$
(ii) $$(3+\sqrt 3)(3-\sqrt 3)$$
(iii) $$(\sqrt 5+\sqrt{2})^2$$
(iv) $$(\sqrt 5-\sqrt 2)(\sqrt 5+\sqrt 2)$$
Find three different irrational numbers between the rational numbers $$\displaystyle\dfrac{5}{7}$$ and $$\displaystyle\dfrac{9}{11}$$.
Write down the decimal expansions of the rational numbers which have terminating decimal expansions.
(i) $$\dfrac{13}{3125}$$ (ii) $$\dfrac{17}{8}$$ (iii) $$\dfrac{15}{1600}$$ (iv) $$\dfrac{23}{2^{3}5^{2}}$$ (v) $$\dfrac {6}{15}$$ (vi) $$\dfrac{35}{50}$$
The division of all the numbers is shown in figure.
ii) $$\dfrac{17}{8} = 2.125$$
iii) $$\dfrac{15}{1600} = 0.009375$$
iv) $$\dfrac{23}{2^{3}5^{2}} =\dfrac{23}{200}= 0.115$$
v) $$\dfrac{6}{15} = 0.4$$
vi) $$\dfrac{35}{50} = 0.70$$
Here, all the decimal expansions are terminating.
Find ten rational numbers between $$\dfrac 35$$ and $$\dfrac 34$$.
Classify the following numbers as rational or irrational:
(i) $$ \ \ 2-\sqrt 5$$ (ii) $$(3+\sqrt{23})-\sqrt {23}$$ (iii) $$\ \displaystyle\frac{2\sqrt 7}{7\sqrt {7}}$$ (iv) $$ \displaystyle\frac{1}{\sqrt 2}$$ (v) $$2\pi$$.
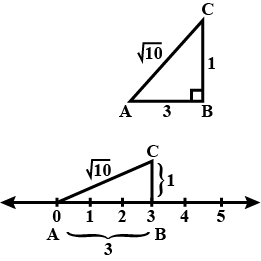
Represent $$\sqrt{8}, \sqrt{10}$$ and $$\sqrt{13}$$ on the number line
If $$x=\displaystyle\frac{\sqrt{2a+3b}+\sqrt{2a-3b}}{\sqrt{2a+3b}-\sqrt{2a-3b}}$$, the prove that $$3bx^2-4ax+3b=0$$.
Write $$5$$ rational number between $$\dfrac {2}{5}$$ and $$\dfrac {3}{5}$$, having the same denominators
Give an example of an irrational number such that its $$8^{th}$$ power is a rational number.
Find a rule to decide whether a given rational number has terminating or non-terminating decimal expansion by looking at its denominator.
Find $$5$$ irrational numbers between $$4$$ and $$5$$.
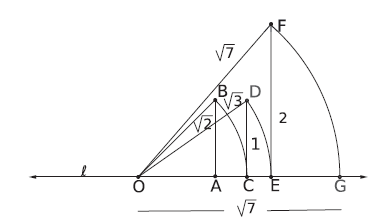
Represent $$\sqrt{7}$$ on the number line.
Let O be the origin on the line $$l$$.
Let A be on the line such that $$OA =1$$.
Draw AB perpendicular to OA at A such that $$AB = 1$$. Then
$$OB^2=OA^2+AB^2=1^2+1^2=2$$ Thus $$OB=\sqrt{2}$$.
With O as centre and OB as radius draw an arc cutting the line at C.
Then $$OC = OB = \sqrt{2}$$
Again draw CD prependicular to $$l$$ such that $$CD=1$$. Then
$$OD^2=OC^2+CD^2=2+1=3$$. Thus $$OD=\sqrt{3}$$.
Draw an arc with O as centre and OD as radius to cut $$l$$ in E. Then $$OE = OD = \sqrt{3}$$.
Draw EF prependicular to $$l$$ at E such that EF = 2 and join OF. Now
$$OF^2=OE^2+EF^2=3+4=7$$.
Hence $$OF=\sqrt{7}$$. With O as centre and OF as radius, cut $$l$$ at G.
Then $$OG=OF=\sqrt{7}$$.
Thus G represents $$\sqrt{7}$$ on the line $$l$$.
Write any three rational numbers.
Explain rational number in your own words
Write the conjugate of the binomial surd $$5 + \sqrt {3}$$.
Find five rational numbers between $$2$$ and $$3$$
Find $$10$$ rational numbers between $$-\dfrac {3}{11}$$ and $$\dfrac {8}{11}$$
Find the value of $${(-5)}^{2}$$
Find an irrational number between $$\dfrac {5}{7}$$ and $$\dfrac {7}{9}$$. How many more there may be?
Which of the following fractions have terminating decimal expansion?
$$\displaystyle \frac{1}{16}, \frac{4}{25}, \frac{22}{625}, \frac{1}{1080}$$.
Find $$12$$ rational number between $$-1$$ and $$2$$.
Find five rational numbers between $$\dfrac {2}{3}$$ and $$\dfrac {3}{5}$$
Simplify the following expressions:
$$(\sqrt {5} + \sqrt {2})^{2}$$
Locate $$\sqrt {2}$$ on number line.
By Pythagoras theorem $$OB = \sqrt {1^{2} + 1^{2}} = \sqrt {2}$$
We have seen that $$OB = \sqrt {2}$$. Using a compass with centre $$O$$ and radius $$OB$$, draw an arc on the right side to $$O$$ intersecting the
number line at the point $$K$$. Now $$K$$ corresponds to $$\sqrt {2}$$ on the number line.
Multiply $$6\sqrt {3}$$ with $$13\sqrt {3}$$
Simplify:
(a) $$\sqrt [4]{81} - \sqrt [5]{32}$$
(b) If $$2$$ is zero of the polynomial $$P(x) = 2x^2 - 3x + 5k$$, find $$K$$?
Simplify the following expressions:
$$(3 + \sqrt {3})(2 + \sqrt {2})$$
Subtract $$5\sqrt {3} + 7\sqrt {5}$$ from $$3\sqrt {5} - 7\sqrt {3}$$
Examine, whether the following number is rational or irrational:
$$(3 + \sqrt {3}) + (3 - \sqrt {3})$$.
Locate $$\sqrt {3}$$ on number line
Construct $$BD$$ of $$1$$ unit length perpendicular to $$OB$$ as fig. Join $$OD$$
By Pythagoras theorem, $$OD = \sqrt {(\sqrt {2})^{2} + 1^{2}} = \sqrt {2 + 1} = \sqrt {3}$$
Using a compass, with centre $$O$$ and radius $$OD$$, draw an arc which
intersects the number line at the point $$L$$ right side to $$0$$. Then
$$'L'$$ corresponds to $$\sqrt {3}$$. From this we can conclude that many
points on the number line can be represented by irrational numbers also.
In the same way, we can locate $$\sqrt {n}$$ for any positive integers $$n$$, after $$\sqrt {n - 1}$$ has been located.
Simplify the following expressions:
$$(\sqrt {5} - \sqrt {2})(\sqrt {5} + \sqrt {2})$$
Simplify $$\dfrac {1}{7 + 4\sqrt {3}} + \dfrac {1}{2 + \sqrt {5}}$$
Multiply the surd $$(\sqrt 5 + \sqrt 2)$$ by _____ to get a rational number.
Simplify
$$2^{\frac {2}{3}} . 2^{\frac {1}{3}}$$
Insert $$4$$ rational numbers between $$\cfrac{3}{4}$$ and $$1$$ without using $$\left (\cfrac { a+b }{ 2 }\right ) $$ formula.
Simplify: $$(2^{3})^{0}$$
Find any two rational numbers between $$ \left (-\displaystyle\frac{5}{7} \right )$$ and $$ \left (-\displaystyle\frac{2}{7} \right )$$.
Simplify:
(i) $$(-4)^{5}\div (-4)^{8}$$
(ii) $$\left (\dfrac {1}{2^{3}}\right )^{2}$$
(iii) $$(-3)^{4} \times \left (\dfrac {5}{3}\right )^{4}$$
(iv) $$\left (\dfrac {2}{3}\right )^{5}\times \left (\dfrac {3}{4}\right )^{2}\times \left (\dfrac {1}{5}\right )^{2}$$
(v) $$(3^{-7} \div 3^{10})\times 3^{-5}$$
(vi) $$\dfrac {2^{6}\times 3^{2} \times 2^{3} \times 3^{7}}{2^{8}\times 3^{6}}$$
(vii) $$y^{a - b} \times y^{b- c}\times y^{c - a}$$
(ii) $$\left (\dfrac {1}{2^{3}}\right )^{2}$$
(iii) $$(-3)^{4} \times \left (\dfrac {5}{3}\right )^{4}$$
(iv) $$\left (\dfrac {2}{3}\right )^{5}\times \left (\dfrac {3}{4}\right )^{2}\times \left (\dfrac {1}{5}\right )^{2}$$
(v) $$(3^{-7} \div 3^{10})\times 3^{-5}$$
(vi) $$\dfrac {2^{6}\times 3^{2} \times 2^{3} \times 3^{7}}{2^{8}\times 3^{6}}$$
(vii) $$y^{a - b} \times y^{b- c}\times y^{c - a}$$
Insert any two irrational numbers between $$\dfrac{4}{7}$$ and $$\dfrac{5}{7}$$.
If $$\displaystyle\frac{\sqrt{7}-1}{\sqrt{7}+1}+\frac{\sqrt{7}+1}{\sqrt{7}-1}=a+b\sqrt{7}$$, find the values of a and b.
Find the value of:
(i) $$(3^{0} + 4^{-1})\times 2^{2}$$
(ii) $$(2^{-1}\times 4^{-1}) \div 2^{-2}$$
(iii) $$\left (\dfrac {1}{2}\right )^{-2} + \left (\dfrac {1}{3}\right )^{-2} + \left (\dfrac {1}{4}\right )^{-2}$$
(iv) $$(3^{-1} + 4^{-1} + 5^{-1})^{0}$$
(v) $$\left [\left (\dfrac {-2}{3}\right )^{-2}\right ]^{2}$$
(vi) $$7^{-20} - 7^{-21}$$
(ii) $$(2^{-1}\times 4^{-1}) \div 2^{-2}$$
(iii) $$\left (\dfrac {1}{2}\right )^{-2} + \left (\dfrac {1}{3}\right )^{-2} + \left (\dfrac {1}{4}\right )^{-2}$$
(iv) $$(3^{-1} + 4^{-1} + 5^{-1})^{0}$$
(v) $$\left [\left (\dfrac {-2}{3}\right )^{-2}\right ]^{2}$$
(vi) $$7^{-20} - 7^{-21}$$
Find any two irrational numbers between $$0.15$$ and $$0.16$$.
Find any two irrational numbers between $$3$$ and $$3.5$$.
Find two rational numbers between
(i) $$\dfrac {2}{7}$$ and $$\dfrac {3}{5}$$
(ii) $$\dfrac {6}{5}$$ and $$\dfrac {9}{11}$$
(iii) $$\dfrac {1}{3}$$ and $$\dfrac {4}{5}$$
(iv) $$\dfrac {-1}{6}$$ and $$\dfrac {1}{3}$$
Classify the following numbers as rational or irrational.
(i) $$\sqrt{11}$$
(ii) $$\sqrt{81}$$
(iii) $$0.0625$$
(iv) $$0.8\overline{3}$$
(v) $$1.505500555$$....
Simplify the following using law of exponents.
$$(-7)^7\times (-7)^8$$=$$(-7)^{m}$$ .Find m
In the following equations determine whether x, y, z represent rational or irrational numbers.
(i) $$x^3=8$$
(ii) $$x^2=82$$
(iii) $$y^2=3$$
(iv) $$z^2=0.09$$
Solve the following equations.
$$\displaystyle\, 2^x \cdot 5^{x - 1} = 0.2 \cdot 10^{2 - x}$$
Simplify the following:
a) $${\left( {{a^8} \times {a^5}} \right)^0}$$
b) $${\left( {{b^2}} \right)^4} \times {b^0}$$
c) $$ - \dfrac{{{a^{ - 3}}{b^{10}}{c^8} \times b{c^8}}}{{{{\left( {{b^{ - 10}} \times {c^6}} \right)}^4}}}$$
d) $${\left[ {\dfrac{{ - {a^{ - 5}}}}{{ - {a^{10}}{b^{ - 9}}{c^{ - 7}} \times \left( {{a^{ - 15}} \times {c^0}} \right)}}} \right]^2}$$
Find (i)six (ii)sixty (iii) six hundred rational between $$\dfrac{-5}{8}$$ and $$\dfrac{3}{8}$$.
Find four rational numbers between $$\dfrac{3}{7}$$ & $$\dfrac{5}{7}$$
If $$a = \frac{1}{{\sqrt 5 - \sqrt 3 }},\,\,b = \frac{1}{{\sqrt 7 + \sqrt 5 }}$$ and $$c = \frac{1}{{\sqrt 9 - \sqrt 7 }},$$ then $$a + b + c$$ equals
$$(\sqrt{5 \, + \, 2 \sqrt{6}}) ^x \, + \, (\sqrt{5 \, - \, 2 \sqrt{6}}) ^x \, = \, 10 $$
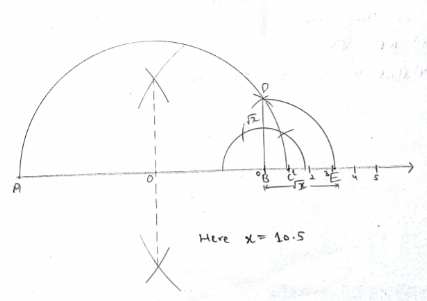
Represent $$
\sqrt {10.5}
$$ on the number line
Instructions:
1) On a straight line mark $$A$$ and $$B$$ such that $$AB=x$$.
2) Mark point $$C$$ $$1\ unit$$ away from $$B(BC=1\ unit)$$
3) Draw the $$\bot$$ bisector of $$AC$$, mark the pt of intersection as $$O$$
4) Taking $$O$$ as centre and $$OC$$ as radius draw a semicircle.
5) Draw perpendicular from $$B$$ and mark its pt of intersection with semicircle as $$D$$
6) Now $$BD=\sqrt x$$
7) Taking $$B$$ as centre and $$BD=\sqrt x$$ as radius construct an arc to make it intersect at $$E$$ on the line.
8) $$BE=\sqrt x$$
9) Start the number line from $$B$$
If $$\dfrac{\sqrt 5 + \sqrt 3 } {\sqrt 5 - \sqrt 3 } = a + b\sqrt {15} $$, find $$a$$ and $$b$$.
Five rational numbers between $$2$$ and $$1$$ are
Four rational numbers between $$\dfrac{2} {3}$$ and $$\dfrac{3} {5}$$ are
How many rational numbers are there between $$- \dfrac{3}{2}$$ and 0 with denominator as 1?
Write the multiplicative $${\left( {{{ - 7} \over {13}}} \right)^{ - 6}}$$ with a positive exponent and also with a negative exponent
Insert a rational number between $$\frac{1}{3}$$ and $$\frac{4}{5}$$ and arrange in descending order
Expand $${\left( {\sqrt 3 + \sqrt 7 } \right)^2}$$
Insert three rational number between $$4$$ and $$4.5$$.
Find the value of m and n if
$${4^{2m}} = {\left( {\root 3 \of {16} } \right)^{ - {6 \over n}}} = {\left( {\sqrt 8 } \right)^2}$$
Find the 7 rational number between -7/8 and 6/8.
Find $$3$$ rational numbers between $$\dfrac{1}{6}$$ and $$\dfrac{1}{7}$$.
$$(2\sqrt{2}+5\sqrt {3})+(\sqrt{2}-3\sqrt{3})$$
Solve$$\left( {\sqrt 8 - \sqrt 2 } \right)\left( {\sqrt 8 + \sqrt 2 } \right)$$
Insert a rational number between $$\frac{2}{9}$$ and $$\frac{3}{8}$$ and arrange in ascending order.
Let, $$f(x)=2^{nx+1}$$ then show that $$f(a).f(b).f(c)=4f(a+b+c)$$.
If $${x^2} = 5$$, then $$x$$ is a
The value of $$x$$ in
$$\left(\dfrac{1}{2}\right)^3 \times \left(\dfrac{1}{2}\right)^5 = \left(\dfrac{1}{4}\right)^x$$
Find four rational numbers between $$\dfrac{{ - 2}}{5}$$ and $$\dfrac{{ - 3}}{4}$$.
Evaluate: $$\left( \dfrac {1}{2}\times \dfrac {\sqrt {3}}{2}\right)+\left( \dfrac {1}{\sqrt {2}}\times \dfrac {1}{2}\right)$$
Find six rational number between $$\dfrac{1}{2}$$ and $$\dfrac{2}{3}$$.
Find ten rational number between $$\dfrac{-2}{5}$$ and $$\dfrac{1}{7}$$.
Simplify: $$3\sqrt [ 3 ]{ 40 } -4\sqrt [ 3 ]{ 320 } -\sqrt [ 3 ]{ 5 } $$
Solve the following :
$$\left( i \right)\,{\left( {\dfrac{{27}}{{125}}} \right)^{\dfrac{2}{3}}} \times {\left( {\dfrac{9}{{25}}} \right)^{ - \dfrac{3}{2}}}$$
$$\left( {ii} \right)\,{7^0} \times {\left( {25} \right)^{ - \dfrac{3}{2}}} - {5^{ - 3}}$$
$$\left( {iii} \right)\,{\left( {\dfrac{{16}}{{81}}} \right)^{ - \dfrac{3}{4}}} \times {\left( {\dfrac{{49}}{9}} \right)^{\dfrac{3}{2}}} \div {\left( {\dfrac{{343}}{{216}}} \right)^{\dfrac{2}{3}}}$$
Find the value of $$x$$
i) $$\left(\dfrac{4}{3} \right)^{-4} \times \left(\dfrac{4}{3} \right)^{-5} = \left(\dfrac{4}{3} \right)^{-3x}$$
ii) $$7^x \div 7^3 = 7^5$$
iii) $$4^{2x + 1} \div 16 = 64$$
Carry out the following additions of rational numbers.
$$\dfrac {5}{36}+\dfrac {6}{42}$$
Find three rational numbers between $$5$$ and $$-2$$.
Find any ten rational numbers between $$\frac{-5}{6}$$ and $$\frac{5}{8}$$.
If $$\dfrac{{{{25}^x} \times {{10}^{2x}}}}{{{4^x}}} = {5^8}$$, find $$x$$.
Solve for $$x$$ such that $$4^{2\log_2 x}=81$$.
Find an irrational number between $$0.1$$ and $$0.19$$.
Carry out the following additions of rational numbers.
$$\dfrac {11}{17}+\dfrac {13}{19}$$
Find the value to three places of decimals of each of the following. It is given that $$\sqrt {2}=1.414, \sqrt {3}=1.732, \sqrt {5}=2.236$$ and $$\sqrt {10}=3.162$$
$$\dfrac {\sqrt {5}+1}{\sqrt {2}}$$
Find $$3$$ irrational numbers between $$\dfrac {3} {8}$$ and $$\dfrac {2}{5}$$.
Simplify the expression:
$$\cfrac{{7}^{n+3}-9\times {7}^{n+1}}{31\times {7}^{n+1}-3\times {7}^{n+2}}$$
Solve :
$$\dfrac{7 + 3\sqrt{5}}{3+\sqrt{5}} - \dfrac{7 - 3\sqrt{5}}{3- \sqrt{5}} = a + \sqrt{5}b$$
If $$x = 8 + 3\sqrt 7 $$, then find the value of $${x^2} + \dfrac{1}{{{x^2}}}$$
Divide the sum of $$-\cfrac { 13 }{ 5 } $$ and $$\cfrac { 12 }{ 7 } $$ by the product of $$-\cfrac { 13 }{ 7 } $$ and $$-\cfrac { 1 }{ 2 } $$
Given $$x = 9 + 4\sqrt 5 $$ find $$\sqrt x - \dfrac{1}{{\sqrt x }} = $$?
$$\sqrt{2+\sqrt3}+\sqrt{2-\sqrt3}=?$$
simplify with steps.
Rationalise the denominators of the following:$$\dfrac{1}{{\sqrt 7 }}$$,$$\dfrac{1}{{\sqrt 7 - \sqrt 6 }}$$,$$\dfrac{1}{{\sqrt 5 + \sqrt 2 }}$$,$$\dfrac{1}{{\sqrt 7 - 2}}$$
Find 5 rational numbers between $$ - \dfrac{1}{3}$$ and $$\dfrac{1}{2}$$.
Simplify the following
$$\dfrac {\sqrt {5}-1}{\sqrt {5}+1}+\dfrac {\sqrt {5}+1}{\sqrt {5}+1}$$
Solve
$$\left( \cfrac { -5 }{ 4 } +\cfrac { 3 }{ 8 } \right) +\cfrac { -7 }{ 6 } $$
If $$\dfrac{{3 + 2\sqrt 2 }}{{3 - \sqrt 2 }} = a + b\sqrt 2 $$ , then find the values of $$a$$ and $$b$$.
If $$a = 2 + \sqrt 3 $$, then find the value of a $$a - \frac{1}{a}$$
Find $$4$$ rational numbers between $$\dfrac { 1 }{ 6 }\ and\ \dfrac { 3 }{ 8 }$$
Find five rational numbers between $$\frac{2}{5}$$ and $$\frac{3}{5}$$
List five rational numbers between: $$-1$$ and $$0$$.
After how many decimal places will the decimal expansion of the number $$\dfrac{5^3}{ 2^5^4}$$ terminate? Justify your answer without performing the actual division.
List five rational numbers between: $$-2$$ and $$-1$$.
List five rational numbers between: $$\dfrac {-4}{5}$$ and $$\dfrac {-2}{3}$$.
Represent the real numbers on the number-line
(i) $$\sqrt {10} $$
(ii) $$\sqrt {13} $$
(iii) $$\sqrt {2} $$
(iv) $$\sqrt {5} $$
(v) $$\sqrt {3} $$
Solution-
$$ \sqrt{1}<\sqrt{2}<\sqrt{4}, \sqrt{1}< \sqrt{3}<\sqrt{4}, \sqrt{4}<\sqrt{5}<\sqrt{9}, \sqrt{9}< \sqrt{10}, \sqrt{16},\sqrt{9}<\sqrt{13},\sqrt{16}.$$
Insert three rational numbers between: $$\dfrac{3}{5}$$ to $$\dfrac{7}{8}$$
List five rational numbers between :
$$\dfrac{1}{2}$$ and $$\dfrac{2}{3}$$
If $$10^{x}=64$$, what is the value of $$10^{\dfrac{x}{2}+1}$$?
Simplify
$$\sqrt {27}+\sqrt {48}-\sqrt {12}+\sqrt {75}-\sqrt {108}$$
$$\dfrac{3^{-5}\times 10^{-5}\times 125}{5^{-7}\times 6^{-5}}$$.
Simplify
$$\left[\dfrac{4}{7}\right]^{-5}\times \left[\dfrac{7}{4}\right]^{-7}$$ by giving reasons.
Solve :
$$(\sqrt{3}+\sqrt{2})^{6}-(\sqrt{3}-\sqrt{2})^{6}$$
List five rational numbers between:
$$-1$$ and $$0$$
To find 5 rational no: b/w -1 & 0
So, we multiply the no: by $$ \dfrac{6}{6} $$
$$ \therefore -1\times \dfrac{6}{6} = \dfrac{-6}{6} $$
and $$ \dfrac{0}{1}\times \dfrac{6}{6} = \dfrac{0}{6} $$
$$ \therefore $$ 5 rational no:- $$ \left \{ \dfrac{-5}{6},\dfrac{-4}{6},\dfrac{-3}{2},\dfrac{-2}{2},\dfrac{-1}{2} \right \} $$
Represent $$\sqrt{10}$$ on number line by direct method.
R.E.F image
$$ AC $$
$$ = \sqrt{10} $$
$$ = \sqrt{9+1} $$
$$ = \sqrt{3^{2}+1^{2}} $$
Write $$5$$ rational numbers between $$\dfrac{3}{5}$$ and $$\dfrac{6}{5}$$.
Simplify $$12\sqrt{18}-6\sqrt{20}-3\sqrt{50}+8\sqrt{45}$$
Find an irrational number between two numbers $$\dfrac{1}{7}$$ and $$\dfrac{2}{7}$$ and justify your answer.
Simplify:
$$\dfrac{{25 \times {t^{ - 4}}}}{{{5^{ - 2}} \times 10 \times {t^{ - 8}}}}\left( {t \ne 0} \right)$$
find the value of 'x' by using following equations $$ - \sqrt {3x} = 3 + 2$$
$$ - \sqrt {3x} = 5$$
Add $$2 + \sqrt { 3 }$$ and $$2 - \sqrt { 3 }$$
$$ 2^{5}\times2^{3} $$
Rationalise the denominator and simplify:
$$\frac{{\sqrt 3 - \sqrt 2 }}{{\sqrt 3 + \sqrt 2 }}$$
Show that $$7-\sqrt 5$$ is irrational .given that $$\sqrt 5 $$ is irrational.
What number should $${5}^{3}$$ be multiplied so that the product may be equal to $${5}^{5}$$?
Is this a negative rational number?
$$\dfrac{5}{7}$$
Write the number whose expanded form is as below:$$3 \times {10^4} + 6 \times {10^3} + 5 \times {10^2} + 8 \times {10^0}$$
$$2^{-3}\times (-7)^{-3}$$.
Simplify: $$9\sqrt {5}-3\sqrt {5}+\sqrt {125}$$
Is this a negative rational number?
$$\dfrac{6}{11}$$
Is this a negative rational number?
$$\dfrac{3}{-5}$$
Insert two rational numbers between $$\dfrac{3}{8}$$ and $$\dfrac{7}{12}$$.
Is this a negative rational number?
$$\dfrac{-2}{-9}$$
Is this a negative rational number?
$$0$$
Is this a negative rational number?
$$\dfrac{-2}{3}$$
Write whether the rational number $$\cfrac {11}{125}$$ will have a terminating decimal expansion or a non terminating repeating decimal expansion.
Insert three rational numbers between $$\dfrac {9}{11}$$ and $$\dfrac {5}{7}.$$
We are making denominator of both numbers same,so that we can easily compare both numbers.
Simplify the following using laws of exponent
$$\dfrac{(7xy\, z)^0}{[12x^2(y^8)^{-3}(z^3)^2]^{-1}}$$
Simplify the following using laws of exponent
$$-[(2)^7]^4 \div 4^4$$
Evaluate $$p^5\times p^8$$.
Solve: $$\dfrac{3}{{\sqrt 5 - \sqrt 3 }}$$
Simplify the following using laws of exponent
$$(3^2)^2 \times 3^{10}$$
Is the product of two irrational numbers always an irrational number ?
Find three rational numbers between $$4$$ and $$5$$
Solve $$\left( 2 ^ { 3 } \cdot 3 \right) \div 2 ^ { 2 } \cdot 5 ^ { 2 }$$
Classify the following number as rational or irrational :
$$(3+\sqrt{23})-\sqrt{23}$$.
$$49\times \left(-7\right)^ {m}=-343$$
Solve: $$5 - 3\dfrac{3}{4}$$
$$5-3\frac{3}{4}=5-\frac{3\times 4+3}{4}=\frac{5}{1}-\frac{15}{4}$$
$$LCM : 1\times 4=4\Rightarrow \frac{5\times 4-15}{4}=\frac{5}{4}$$
For any positive real number x, prove that there exists an irrational number y such that 0 < y < x.
Simplify the following using laws of exponents:-
$$2^{3}\times 2^{10}\times 2^{5}$$
Rationalize the denominator $$\frac{1}{{\sqrt 5 + \sqrt 6 - \sqrt {11} }}$$
Find two irrational number between $$1$$ and $$2$$.
$$n$$ is a two digit number. $$P(n)$$ is the product of the digit of $$n$$ and $$S(n)$$, is the sum of the digits of $$n$$. If $$n=P(n)+S(n)$$ then find the units digit of $$n$$.
A] Let a,b be tens & unit digits of n
Then n = 10 a + b
p(n) + s(n) = 10 a + b
= a b + a+b = 10 a +b
= a b = 9 a
$$ \therefore b = 9 $$ as $$ a \neq 0$$
$$ \therefore $$ units digit is 9
Write any two irrational number lying between $$3$$ and $$4$$.
solve : $$\left\{ \left( \dfrac { - 3 } { 2 } \right) ^ { 2 } \right\} ^ { - 3 }$$
Simplify and evaluate :
$$[2^{5}\times 2^{4}]\div 2^{3}$$
Solve:
$$\sqrt{12}+5\sqrt{4}+\sqrt{4}-\sqrt{81}$$
Find four rational Numbers between $$\dfrac{1}{2}$$ and $$\dfrac{2}{3}$$
Evaluate : $$2\sqrt[3]{4}+7\sqrt[3]{32}-\sqrt[3]{500}$$
What is the value of $$\pi$$ ?
Is $$\left(\pi-\dfrac{22}{7}\right)$$ a rational number, an irrational number or zero.
Simplify : $$\dfrac{1}{1 + \sqrt{2}}$$ + $$\dfrac{1}{\sqrt{2} + \sqrt{3}}$$ + $$\dfrac{1}{\sqrt{3} + \sqrt{5}}$$
Simplify the following :
$$2\sqrt{5}+\sqrt{125}$$
Find three rational number between $$\frac{-3}{14}$$ and $$\frac{6}{14}$$
Find three rational numbers between $$-\dfrac {3}{2}$$ and $$\dfrac {4}{5}$$.
Prove that the following are irrational.
$$\dfrac{1}{\sqrt{2}}$$
Find three rational numbers between $$\dfrac {4}{3}$$ and $$\dfrac {5}{6}$$.
Rationalise:$$5-\sqrt{3}$$
Prove that the following is irrational.
$$6+\sqrt{2}$$
Prove that the following is irrational.
$$7\sqrt{5}$$
Find a rational number between $$-\dfrac{2}{3}$$ and $$\dfrac{1}{4}$$.
$$\dfrac{1+\sqrt7}{1-\sqrt7}+\dfrac{1-\sqrt7}{1+\sqrt7}$$
Rationalise:$$4-\sqrt{5}$$
Prove that the following is irrational.
$$3+2\sqrt{5}$$
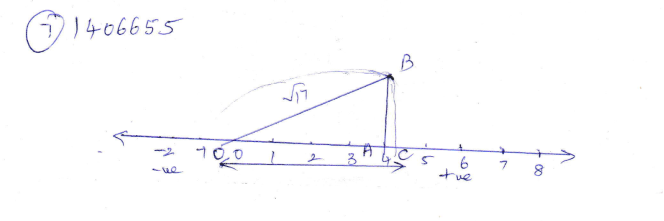
Construct $$\sqrt{17}$$ using a number line
We know that $$\sqrt{16}=4$$ and $$\sqrt{17}=\sqrt{{4}^{2}+{1}^{2}}$$
Mark point $$A$$ representing $$4$$ on number line .
Now construct $$AB$$ of unit length perpendicular to $$OA$$ .
Then taking $$O$$ as centre and $$OB$$ as radius.
Draw an arc intersecting number line at $$C$$ .
$$C$$ is represented as $$\sqrt{17}$$
Simplify:
$$\dfrac { a+\sqrt { { a }^{ 2 }-{ b }^{ 2 } } }{ a-\sqrt { { a }^{ 2 }-{ b }^{ 2 } } } + \dfrac { a-\sqrt { { a }^{ 2 }-{ b }^{ 2 } } }{ a+\sqrt { { a }^{ 2 }-{ b }^{ 2 } } }$$
Write the simplest rationalising factor of :$$\left( i \right)\sqrt {32} \;\left( {ii} \right)\sqrt {72} \;\left( {iii} \right)\root 3 \of 5 \;\left( {iv} \right)\root 5 \of 9 \left( v \right)\root 3 \of {135} $$
Rationalise:
$$\dfrac { 1 }{ x-\sqrt { x } } $$
Expand $${a^3}{b^2},{a^2}{b^3},{b^2}{a^3},{b^3}{a^2}.$$ Are they all same?
Find the value of $$a$$ and $$b$$ if $$\dfrac { \sqrt { 11 } -\sqrt { 7 } }{ \sqrt { 11 } +\sqrt { 7 } } =a-b\sqrt { 77 } $$.
Solve:
$$\dfrac { 7+3\sqrt { 5 } }{ 2+\sqrt { 5 } } -\dfrac { 7-3\sqrt { 5 } }{ 2-\sqrt { 5 } } $$
Express in exponential form:$$\dfrac { 4 }{ 5 } \times p\times p\times p\times p\times r\times r\times r\times r$$
Write two irrational numbers between '3' and '4'
List three rational numbers between $$6$$ and $$8 .$$
If rationalization of $$\dfrac{3}{2\sqrt{5}}$$ is $$\dfrac {3\sqrt{5}} {b}$$ then value of b is ___ .
Let's rationalize $$\dfrac{3}{2 \sqrt{5}}$$
Multiply numerator and denominator by $$\sqrt{5}$$ as $$\sqrt{5} \sqrt{5} = 5$$
$$\therefore \dfrac{3 \times \sqrt{5}}{2 \sqrt{5} \times \sqrt{5}} = \dfrac{3 \sqrt{5}}{2 \sqrt{25}} = \dfrac{3 \sqrt{5}}{10}$$
$$= \dfrac{3 \sqrt{5}}{10}$$
Comparing with $$\dfrac{3 \sqrt{5}}{b}$$
we get value of '$$b$$' as $$10$$
Is 5.131131113.... a rational number or irrational number?
Find three rational numbers between $$\dfrac {1}{5}$$ and $$\dfrac {1}{4}$$.
Simplify:$$a\left ( a^0 + b^0 \right )^3$$
Write down a rational number whose numerator is the largest number of two digits and denominator is the smallest number of four digits .
Simplify : $${p^{\frac{1}{2}}} \times {p^{\frac{1}{2}}}$$
Find six rational numbers between 3 and 4.
List five rational numbers between
$$\cfrac{-4}{5}$$ and $$\cfrac{-2}{3}$$
Prove that :
$$ (a^{-1}+b^{-1})^{-1} = \dfrac{ab}{a+b} $$
If rationalization of $$\dfrac{3\sqrt{2}}{\sqrt{5}}$$ is $$ \dfrac{3\sqrt{a}}{5}$$ then value of a is ___ .
If rationalization of $$\dfrac{\sqrt{2}}{\sqrt{5}}$$ is $$\dfrac {\sqrt{10}} {c}$$ then value of c is ___ .
Let's rationalize $$\dfrac{\sqrt{2}}{\sqrt{5}}$$
$$\therefore \dfrac{\sqrt{2}}{\sqrt{5}} = \dfrac{\sqrt{2} \times \sqrt{5}}{\sqrt{5} \times \sqrt{5}} = \dfrac{\sqrt{10}}{\sqrt{5 \times 5}}$$
Multiply numerator and denominator by $$\sqrt{5}$$ as $$\sqrt{5} \times \sqrt{5} = 5$$
$$\therefore \dfrac{\sqrt{2}}{\sqrt{5}} = \dfrac{\sqrt{2} \times \sqrt{5}}{\sqrt{5} \times \sqrt{5}} = \dfrac{\sqrt{10}}{\sqrt{5 \times 5}}$$
$$= \dfrac{\sqrt{10}}{5}$$
Now comparing with $$\dfrac{\sqrt{10}}{C}$$
we get value of c as $$5$$.
Define an irrational number.
Examine whether $$\sqrt{5}-2$$ is rational or irrational.
After rationalizing the denominator of $$\dfrac{1}{\sqrt{6}-\sqrt{5}}$$ and simplifying we get $$\sqrt{a}+\sqrt{5}$$ then value of $$a$$ is ___ .
The given fraction is $$\dfrac{1}{\sqrt{6} - \sqrt{5}}$$
To rationalize the denominator we can multiply both numerator and denominator by $$\sqrt{6} + \sqrt{5}$$ (the conjuate of $$\sqrt{6} - \sqrt{5}$$)
$$\therefore \dfrac{1}{\sqrt{6} - \sqrt{5}} = \dfrac{1 \times (\sqrt{6} + \sqrt{5})}{(\sqrt{6} - \sqrt{5}) (\sqrt{6} + \sqrt{5})}$$
$$= \dfrac{\sqrt{6} + \sqrt{5}}{(\sqrt{6})^2 - (\sqrt{5})^2}$$ $$.... ((a - b)(a + b) = a^2 - b^2)$$
$$= \dfrac{\sqrt{6} + \sqrt{5}}{6 - 5}$$
$$= \dfrac{\sqrt{6} + \sqrt{5}}{1} = \sqrt{6} + \sqrt{5}$$
Now, comparing $$\sqrt{6} + \sqrt{5}$$ with $$\sqrt{a} + \sqrt{5}$$,
we get the value of 'a' as $$6$$.
If rationalization of $$\dfrac{\sqrt{2}+\sqrt{5}}{\sqrt{3}}$$ is $$ \dfrac{\sqrt{a}+\sqrt{15}}{3}$$ then value of $$a$$ is ___ .
If rationalization of $$\dfrac{\sqrt{3}+1}{\sqrt{2}}$$ is $$ \dfrac{\sqrt{6}+\sqrt{a}}{2}$$ then value of a is ___ .
If rationalization of $$\dfrac{1}{\sqrt{12}}$$ is $$\dfrac {\sqrt{a}} {6}$$ then value of a is ___ .
Examine whether the following number is rational or irrational: $$0.3796$$.
Prove that :
$$ \sqrt{\dfrac{1}{4}}+(0.01)^{-1/2}-(27)^{2/3} = \dfrac{3}{2} $$
Examine, whether the following numbers are rational or irrational: $$7.478478....$$
Complete the following sentence:
Every point on the number line corresponds to a ... number which may be either ... or ...
Every point on the number line corresponds to a ... number which may be either ... or ...
Find the value of $$(3^{-1}+4^{-1}+5^{-1})^0$$
Give an example of two irrational numbers whose quotient is an irrational number.
Give an example of two irrational numbers whose quotient is a rational number.
Express each of the following as a rational number with positive denominator:
$$\dfrac{6}{-9}$$
Which of the following rational numbers are negative?
$$\dfrac{-3}{7}$$
Express each of the following numbers as a product of powers to their prime factors: 675
check the given numbers is positive or not.
$$\dfrac{9}{8}$$
Separate positive and negative rational numbers from the following rational numbers:
$$\displaystyle \frac{-5}{-7}, \frac{12}{-5}, \frac{7}{4}, \frac{13}{-9}, 0, \frac{-18}{-7}, \frac{-95}{116}, \frac{-1}{-9}$$
Which of the following rational numbers are positive:
$$\dfrac{-19}{-13}$$
Which of the following rational numbers are positive:
$$\dfrac{-8}{7}$$
Write down the numerator of each of the following rational numbers:
$$5$$
Express each of the following as a rational number with positive denominator:
$$\dfrac{-15}{-28}$$
Which of the following rational numbers are negative?
$$\dfrac{9}{-83}$$
Without actual division, show that each of the following rational number is a terminating decimal. Express in decimal form: $$ \dfrac {23}{ ( 2^3 \times 5^2)} $$.
Fill in the blanks so as to make the statement true:
If $$p$$ and $$q$$ are positive integers, then $$\dfrac{p}{q}$$ is a _____ rational number and $$\dfrac{p}{-q}$$ is a ______ rational number.
Select those rational numbers which can be written as a rational number with denominator $$4$$:
$$\displaystyle \frac{7}{8}, \frac{64}{16}, \frac{36}{-12}, \frac{-16}{17}, \frac{5}{-4}, \frac{140}{28}$$
Find $$10$$ rational numbers between $$\dfrac{7}{13}$$ and $$\dfrac{-4}{13}$$.
Find six rational numbers between $$\dfrac{-4}{8}$$ and $$\dfrac{3}{8}$$.
Express each of the following as a rational number with positive denominator:
$$\dfrac{-28}{-11}$$
Express $$392$$ as a product of its prime factors
$$392 = 2^3 \times 7^2$$
Give an example of two irrational whose sum is rational.
Without actual division, show that the following rational number has a terminating decimal form and also, express in decimal form$$\dfrac {19} { 3125}$$
Give an example of two irrationals whose product is rational.
Let $$x$$ and $$y$$ be rational and irrational numbers, respectively. Is $$x + y$$ necessarily an irrational number? Given an example in support of your answer.
Without actual division, show that the following rational number is a terminating decimal. Express in decimal form: $$\dfrac {15} {1600}$$.
Without actual division, show that each of the following rational number is a terminating decimal. Express in decimal form: $$\dfrac {17} { 320} $$.
Without actual division, show that each of the following rational number is a terminating decimal. Express in decimal form $$\dfrac {171} {800}$$.
Without actual division, show that each of the following rational number is a terminating decimal. Express in decimal form $$\dfrac {24} {125}$$.
Find four rational numbers between $$\dfrac{3}{7}$$ and $$\dfrac{5}{7}$$.
Give an example of two irrational numbers whose difference is an irrational number.
Simplify $$\dfrac{2\sqrt{30}}{\sqrt{6}}-\dfrac{3\sqrt{140}}{\sqrt{28}}+\dfrac{\sqrt{55}}{\sqrt{99}}$$.
Express with rational denominator :
$$\dfrac{3\sqrt{-2}+2\sqrt{-5}}{3\sqrt{-2}-2\sqrt{-5}}$$ .
Given, $$\sqrt{2}=1.414$$ and $$\sqrt{6}=2.449$$, find the value of $$\dfrac{1}{\sqrt{3}-\sqrt{2}-1}$$ correct to $$3$$ places of decimal.
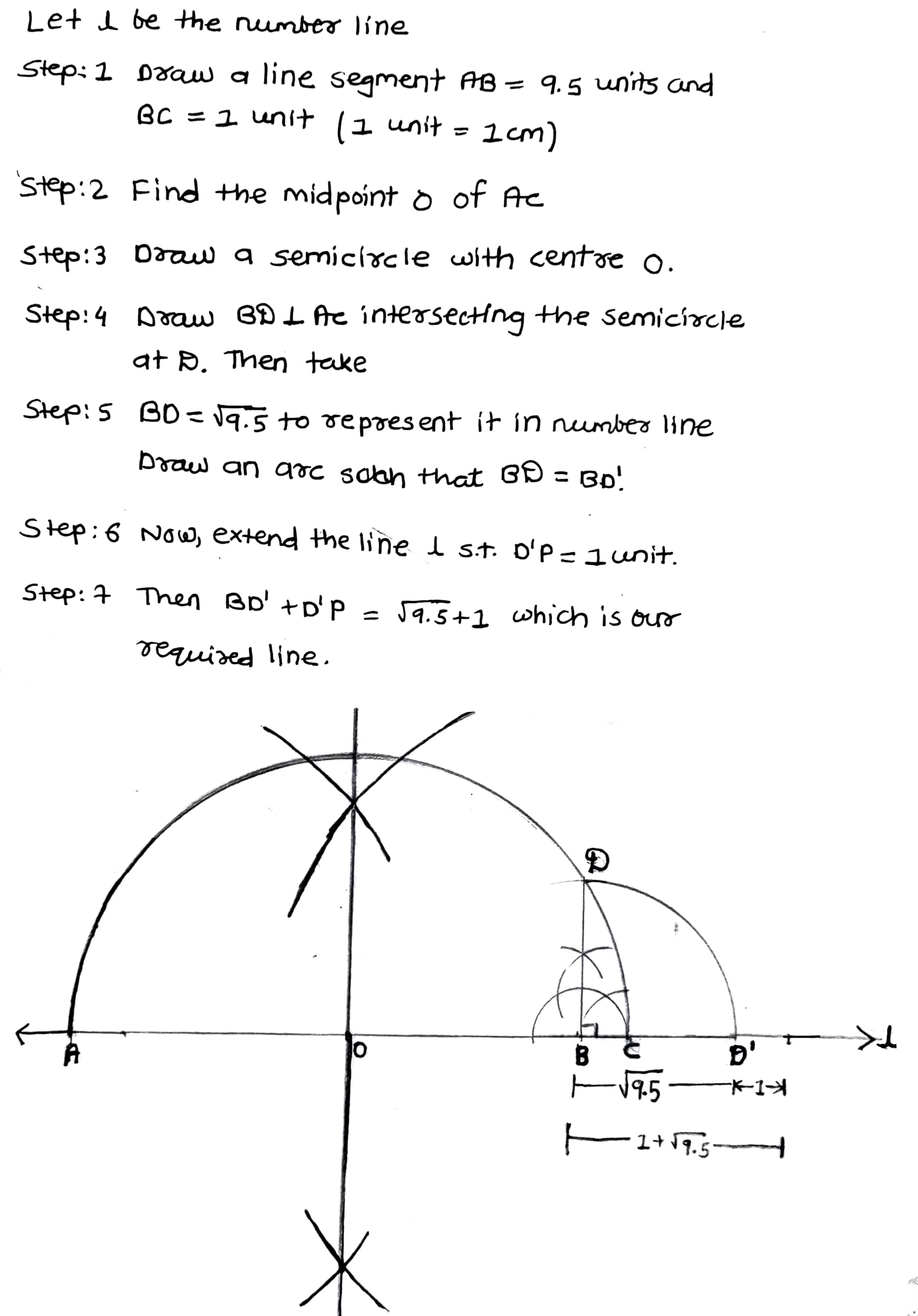
Represent $$(1+\sqrt{9.5})$$ on the number line.
Represent $$\sqrt{4.7}$$ geometrically on the number line.
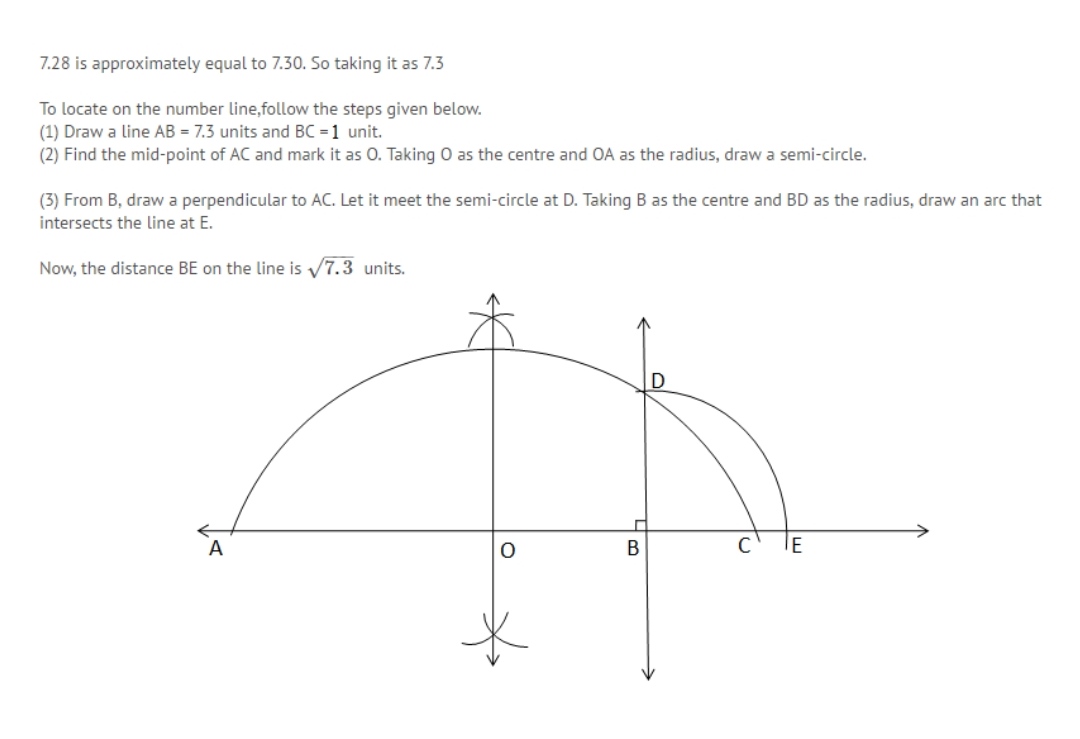
Represent $$\sqrt{7.28}$$ geometrically on the number line.
Find two irrational numbers between $$0.16$$ and $$0.17$$.
Give an example of two irrational numbers whose difference is a rational number.
Give an example of two irrational numbers, the sum of which is a rational number.
Express with rational denominator :
$$\dfrac{(a+\sqrt{-1})^{3}-(a-\sqrt{-1})^{3}}{(a+\sqrt{-1})^{2}-(a-\sqrt{-1})^{2}}$$ .
Write the following integer as a rational number. Write the numerator and the denominator in the following case.
$$-23$$
Given below is a negative rational number or not?
$$0$$
Express the following as a rational number:
$$(23/25)^0$$
Mark tick against the correct answer in each of the following:
$$(5/6)^0 =$$?
What are rational number? Give examples of five positive and negative rational numbers. Is there any rational number which is neither positive nor negative? Name it.
Given below is a negative rational number or not?
$$-6$$
Write a rational number in which the numerator is less than $$'-7\times11'$$ and the denominator is greater than $$'12+4'.$$
List four rational numbers between $$\dfrac{5}{7}$$ and $$\dfrac{7}{8}$$
In each of the following cases, write the rational number whose numerator and denominator are respectively as under:
$$5-39$$ and $$54-6$$
In each of the following cases, write the rational number whose numerator and denominator are respectively as under:
$$(-4)\times6$$ and $$8\div 2$$
In each of the following cases, write the rational number whose numerator and denominator are respectively as under:
$$35\div(-7)$$ and $$35-18$$
Solve the following:
$$2^{-2}\times 2^{-3}$$
$$a^3 \times a^{-10}$$
Find the value of $$x$$ so that
$$\left( \dfrac 53\right)^{-2}\times \left( \dfrac 53\right)^{-14}=\left( \dfrac 53\right)^{8x}$$
Simplify :
$$(-2)^3 \times (-2)^{-6}=(-2)^{2x-1}$$
By what number should we multiply $$(-29)^0$$ so that the product becomes $$(+29)^0$$.
The value of $$\left(\dfrac{1}{2^3}\right)^2$$ is equal to _______.
By multiplying $$(10)^5$$ by $$(10)^{-10}$$ we get _____.
$$5^5 \times 5^{-5}=$$______.
$$[2^{-1}+3^{-1}+4^{-1}]^0=$$ ______.
Express $$3^{-5}\times 3^{-4}$$ as a power of $$3$$ with positive exponent.
Find $$x$$ so that $$\left( \dfrac{2}{9}\right)^{3}\times \left( \dfrac{2}{9}\right)^{-6}=\left( \dfrac{2}{9}\right)^{2x-1}$$.
A half life is the amount of time that it takes for a radioactive substance to decay to one half of its original quantity.
Suppose radioactive decay causes $$300$$ grams of a substance to decrease to $$300\times 2^{-3}$$ grams after $$3$$ half-lives. Evaluate $$300\times 2^{-3}$$ to determine how many grams of the substance are left.
Explain why the expression $$300\times 2^{-n}$$ can be used to find the amount of the substance that remains after $$n$$ half-lives.
In a repeater machine with $$0$$ as an exponent, the base machine is applied $$0$$ times.
What do these machines do to a piece of chalk?
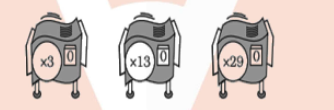
In a repeater machine with $$0$$ as an exponent, the base machine is applied $$0$$ times.
What do you think the value of $$6^o$$ is ?
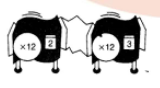
For the hook-up, determine whether there is a single repeater machine that will do the same work. If so, describe or draw it.
A machine $$(\times x^y)$$ with input $$a$$ will give an output $$ax^y$$
When, multiple such machines are hooked up their stretching powers are multiplied.
Machine $$1$$ is $$(\times 12^2)$$
Machine $$2$$ is $$(\times 12^3)$$
As per the law of exponent- $$a^m \times a^n =a^{m+n}$$
So,
The work that can be performed by the repeater machine is equal to $$12^2 \times 0.12^3=12^{5}$$.
It is described in a figure with $$12$$ as base and $$5$$ as power.
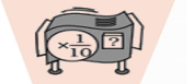
Ajay had a $$1\ cm$$ piece of gum. He put it through repeater machine given below and it came out $$\dfrac{1}{100,000}\ cm$$ long. What is the missing value?
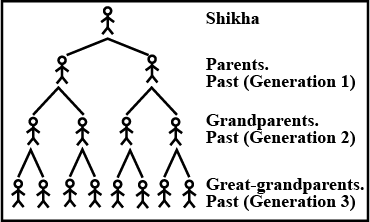
While studying her family's history. Shikha discovers records of ancestors she has had in the past $$12$$ generations. She started to make a diagram to help her figure this out. The diagram soon become very complex.
Write an equation for the number of ancestors in a given generation $$n$$.
On the basis of generations- ancestor table, the numbers of ancestors in Past generation number $$n$$ will $$2^n$$.
Insert a rational number and an irrational number between the following:
$$0.0001$$ and $$0.001$$.
Simplify :
$$4\sqrt {12}\times 7\sqrt {6}$$.
Represent geometrically the following number on the number line:
$$\sqrt {2.3}$$.
Presentation of $$\sqrt {2.3}$$ on number line:
Mark the distance $$2.3$$ units from a fixed point $$A$$ on a given line to obtain a point $$B$$ such that $$AB = 2.3$$ units. From $$B$$ mark a distance of $$1$$ unit and mark the new point as $$C$$. Find the mid-point of $$AC$$ and mark that point as $$O$$. Draw a semicircle with Centre $$O$$ and radius $$OC$$. Draw a line perpendicular to $$AC$$ passing through $$B$$ and intersecting the semicircle at $$D$$. Then, $$BD = \sqrt {2.3}$$.
Now, draw an arc with centre $$B$$ and radius $$BD$$, which intersects the number line in $$E$$. Thus, $$E$$ represents $$\sqrt {2.3}$$.
Mark the distance $$2.3$$ units from a fixed point $$A$$ on a given line to obtain a point $$B$$ such that $$AB = 2.3$$ units. From $$B$$ mark a distance of $$1$$ unit and mark the new point as $$C$$. Find the mid-point of $$AC$$ and mark that point as $$O$$. Draw a semicircle with Centre $$O$$ and radius $$OC$$. Draw a line perpendicular to $$AC$$ passing through $$B$$ and intersecting the semicircle at $$D$$. Then, $$BD = \sqrt {2.3}$$.
Now, draw an arc with centre $$B$$ and radius $$BD$$, which intersects the number line in $$E$$. Thus, $$E$$ represents $$\sqrt {2.3}$$.
If $$z^{2} = 0.04$$, find if $$z$$ is rational or irrational .
Let $$x$$ be rational and $$y$$ be irrational. Is $$xy$$ necessarily irrational? Justify your answer by an example.
Find three rational numbers between:
$$\dfrac {5}{6}$$ and $$\dfrac {6}{7}$$.
Arrange in ascending order. $$\sqrt[3]{2}, \sqrt 3, \sqrt[6] 5$$
Without actually performing the long division, state whether the following rational number have terminating or non-terminating repeating (recurring) decimal expansion: $$\frac{17}{8}$$.
Prove that $$ 3+\sqrt{5} $$ is an irrational number.
Insert five
rational numbers between:
(i) $$\dfrac{-4}{5}$$ and $$\dfrac{-2}{3}$$
(ii) $$\dfrac{-1}{2}$$ and $$\dfrac{2}{3}$$
Find ten rational numbers between $$-2/5$$ and $$1/7$$.
Fill in the blanks:
$$\bigg(-\dfrac{1}{2}\bigg)^0 + (-2)^0 =$$ ........
Rationalize the denominator of the following and hence evaluate by taking $$\sqrt {2} = 1.414$$, upto three places of decimal.
$$\dfrac {\sqrt {2}}{2 + \sqrt {2}}$$.
Find six rational numbers between $$-1/2$$ and $$5/4$$.
Simplify :
$$\dfrac {3}{\sqrt {8}} + \dfrac {1}{\sqrt {2}}$$.
Write the decimal expansion of the following number which have terminating decimal expansion:$$\dfrac{2^{2}\times7}{5^{4}}$$.
We know, $$\dfrac{2^{2}\times7}{5^{4}}=\dfrac{2^{2}\times7}{2^{0}\times5^{4}}$$
Multiplying and diving by $$2^{4}$$,
$$=\dfrac{2^{2}\times7\times2^{4}}{2^{0}\times5^{4}\times2^{4}}$$ $$=\dfrac{2^{2}\times7\times2^{4}}{1\times5^{4}\times2^{4}}$$
$$=\dfrac{7\times2^{6}}{(2\times5)^{4}}$$ $$=\dfrac{448}{(10)^{4}}$$
$$=\dfrac{448}{10000}$$ $$=0.0448$$ and it is terminating.
Write the decimal expansion of the following number which have terminating decimal expansion:$$\dfrac{27}{8}$$.
Write down a rational number with numerator $$ (-5) \times (-4) $$ and with denominator $$ (28 - 27) \times (8 - 5) $$.
Write the denominator of each of the following rational numbers :
$$ -7 $$
Write the decimal expansion of the following number which have terminating decimal expansion:$$\dfrac{6}{15}$$.
Write the decimal expansion of the following number which have terminating decimal expansion:$$\frac{64}{455}$$.
Write the decimal expansion of the following number which have terminating decimal expansion:$$\dfrac{129}{2^{2}\times5^{7}\times7^{5}}$$.
Write the decimal expansion of the following number which have terminating decimal expansion:
$$\frac{29}{243}$$.
Write the decimal expansion of the following number which have terminating decimal expansion:$$\dfrac{13}{125}$$.
Write the decimal expansion of the following number which have terminating decimal expansion:$$\dfrac{35}{50}$$.
Simplify, giving answers with positive index
$$(-3)^2(3)^3$$
Which of the following are not rational numbers :
(i) $$ -3$$
(ii) $$0$$
(iii) $$ \dfrac{0}{4} $$
(iv) $$ \dfrac{8}{0} $$
(v) $$ \dfrac{0}{0} $$
Simplify, giving answers with positive index
$$(-4x)(-5x^2)$$
$$(-6)^{0}$$
Simplify, giving answers with positive index:
$$(-2)^2 \times (0)^3 \times (3)^3$$
Evaluate
$$8^{0}+4^{0}+2^{0}$$
Evaluate
$$8^3 \times 8^{-5}\times 8^4$$
Express the following rational numbers in the standard form.
$$ \dfrac{-7}{-20} $$
$$ \dfrac{-7}{-20} $$
Simplify giving answers with positive index
$$(-a)^5 (a^2)$$
Rationalize the denominator.
$$\dfrac{2}{3\sqrt{7}}$$
Insert two irrational numbers between $$5$$ and $$6.$$
Rationalize the denominator.
$$\dfrac{1}{3\sqrt{5}+2\sqrt{2}}$$
Write a pair of irrational numbers whose difference is rational.
Rationalize the denominator.
$$\dfrac{1}{\sqrt{5}}$$
Given Universal set is
$$ \left\{-6,-5 \dfrac{3}{4},-\sqrt{4},-\dfrac{3}{5},-\dfrac{3}{8}, 0, \dfrac{4}{5}, 1,1 \dfrac{2}{3}, \sqrt{8}, 3.01, \pi, 8.47\right\} $$
From the given set, find:
Set of irrational numbers
Show that $$5+\sqrt{7}$$ is an irrational number.
Are the square roots of all positive integers irrational ? If not, give an example of the square root of a number that is a rational number.
Classify the following numbers as rational or irrational:
$$\sqrt{225}$$
Rationalize the denominator.
$$\dfrac{12}{4\sqrt{3}-\sqrt{2}}$$
Write the conjugates of the binomial surd $$3\sqrt {7} + 7\sqrt {3}$$
Write the conjugates of binomial surd given as $$\sqrt {a} + \sqrt {b}$$
Prove that $$\sqrt{2} + \sqrt{5}$$ is irrational
Find 3 irrational numbers between $$\dfrac{2}{3}$$ and $$\dfrac{3}{4}$$ using their decimal expansion.
The decimal expansions of $$\dfrac {2}{3}$$ and $$\dfrac {3}{4}$$ are as follows:
Here, the one decimal expansions are non-terminating recurring, while the other is terminating.
Hence, $$\frac {2} {3}$$ and $$\frac {3}{4}$$ are two rational numbers.
We know, between any two rational numbers, there are infinitely many irrational numbers.
An irrational number has non-terminating non-recurring decimal expansions.
Then $$3$$ different irrational number between $$\dfrac{2}{3}$$ and $$\dfrac{3}{4}$$ can be:
$$a=0.6707007000$$
$$b=0.6808008000$$
$$c=0.6909009000$$
Here we observe that $$\dfrac {2}{3}<a<b<c<\dfrac {3}{4}$$.
NOTE:
This is $$3$$ of the various possible answers. It might have different solution.
Why is 0.111222333444..., where each number appears 3 times in a row irrational?
If $$x = \sqrt {7} - \sqrt {5}, y = \sqrt {5} - \sqrt {3}, z = \sqrt {3} - \sqrt {7}$$, then find the value of $$x^{3} + y^{3} + z^{3} - 2xyz$$
Write the conjugates of the binomial surd $$10\sqrt {2} + 3\sqrt {5}$$
Write the conjugates of the binomial surds $$x + 3\sqrt {y}$$
Write the conjugates of the binomial surd $$\sqrt {8} - 5$$
Write the conjugates of the binomial surds given as $$\sqrt {x} - 2\sqrt {y}$$
Write the conjugate of the binomial surd $$x\sqrt {a} + y\sqrt {b}$$
$${\dfrac{\sqrt 3 - 1} {\sqrt 3 + 1}} = a + b\sqrt 3 $$ find $$a$$ and $$b$$
If $$x=\sqrt{2}+1$$. Find the value of $$x+\large{\frac{1}{x}}$$.
Write the conjugates of the binomial surd $$\dfrac {1}{2}x + \dfrac {1}{2}\sqrt {y}$$
Locate $$\sqrt {10}$$ on number line
We can do it by using Pythagoras Theorem.
We can write $$\sqrt { 10 }$$ as follows:
$$\sqrt { 10 } =\sqrt { 9+1 } \\ \Rightarrow \sqrt { 10 } =\sqrt { { 3 }^{ 2 }+1^2 }$$
The construction steps are as follows:
1. Take a line segment $$AO = 3$$ unit on the $$x$$-axis. (consider $$1$$ unit = $$2$$ cm)
2. Draw a perpendicular on $$O$$ and draw a line $$OC = 1$$ unit
3. Now join $$AC$$ with $$\sqrt { 10 }$$.
4. Take $$A$$ as center and $$AC$$ as radius, draw an arc which cuts the $$x$$-axis at point $$E$$.
5. The line segment $$AC$$ in the below diagram represents $$\sqrt { 10 }$$ units.
Find a point corresponding to $$3+\sqrt{2}$$ on the number line.
First plotting $$\sqrt{2}$$ on number line and then shift the origin $$3$$ units to the left will, get the point $$(3+\sqrt{2})$$ on number ilne.
Steps:-
i) Draw AB of $$1$$- unit,
ii) draw BC of length $$1$$ unit perpendicular to AB from B,
ii) take AC as radius and draw and arc which cuts horizontal line in D,
iv) thus distance AD=$$\sqrt{2}$$,
v) distance $$OD=3+\sqrt{2}$$ units.
Write the conjugate of the binomial surd $$xy\sqrt {z} + yz\sqrt {x}$$
Write the conjugates of the binomial surd $$\dfrac {1}{2} + \sqrt {2}$$
Explain with an example how irrational numbers differ from rational numbers?
Simplify
(i) $$10\sqrt{2}-2\sqrt{2}+4\sqrt{32}$$
(ii) $$\sqrt{48}-3\sqrt{72}-\sqrt{27}+5\sqrt{18}$$
(iii) $$\sqrt[3]{16}+8\sqrt[3]{54}-\sqrt[3]{128}$$.
Find $$a^{3}$$ if $${ \left( \dfrac { 2 }{ 7 } \right) }^{ a }={ \left( \dfrac { 16 }{ 21 } \right) }^{ -5 }\times { \left( \dfrac { 3 }{ 8 } \right) }^{ -5 }$$
Solve:
$$\dfrac{(-3)^{3}\times (-2)^{5}\times 7^{2}}{(-1)^{5}\times (-7)^{2}\times 2^{5}}$$
Find the value of $$8\sqrt{60}\times 5\sqrt{3}$$
Find the value of $$9\sqrt{5}\times 20\sqrt{45}$$
Solve:
$$x^{11}\div x^{15}$$
$$\cot { \left( \dfrac { 15 }{ 2 } \right) } =\sqrt { 2 } +\sqrt { 3 } +\sqrt { 4 } +\sqrt { 6 }$$
Carry out the following additions of rational numbers.
$$1\ \dfrac {2}{3}+2\ \dfrac {4}{5}$$
Find the number of digits in the numeral for $$(875)^{16}$$
$$875=25\times 35$$
$$=5^{2}\times 5\times 7$$
$$=5^{3}\times 7$$
$$(875)^{16}=(5^{3}\times 7)^{16}$$
$$=(5^{3})^{16}\times 7^{16}$$
$$=5^{48}\times 7^{16}$$
Taking $$log_{10}$$
$$log(875)^{16}=log_{10}5^{48}+log_{10}7^{16}$$
$$\therefore log (ab)= log_{10}a+log_{10}b$$
$$= 48 log_{10}5+16log_{10}7$$
$$ = 48log_{10}(\frac{10}{2})+16log_{10}7$$
$$ (\because log_{10}10=1)$$
$$=48[1-log2]+16 log 7$$
$$=16[3(1-0.3010)+0.845]$$
$$16\times [3\times 0.699+0.845]$$
$$=47.072$$
$$\simeq 48$$ digits.
Simplify and express each of the following as a rational number: $$\dfrac {3^{5}\times 25\times 10^{5}}{5^{7}\times 6^{5}}$$.
Find the smallest and greatest among $$\sqrt{7}-\sqrt{5}$$ and $$\sqrt{8}-\sqrt{6}$$
Find the Rationalising factor of $$\sqrt[3]{3}+\sqrt[3]{2}$$
Simplify:
$$2b^{6}.b^{3}.5b^{4}$$
What can you say about the product of a non-zero rational and irrational number?
Express $$\cfrac {2157}{625}$$ in decimal form and state what it is terminating or not?
$$\sqrt{6}.\sqrt{3}$$=_______
Identify the following as rational or irrational number. Give the decimal representation rational number.
$$\sqrt {\dfrac {9}{27}}$$.
The longest $$(\sqrt{5}-\sqrt{2})$$ $$(\sqrt{5}+\sqrt{2})$$
Find the value of 'a' and 'b' $$\dfrac { 7+\sqrt { 5 } }{ 7-\sqrt { 5 } } -\dfrac { 7-\sqrt { 5 } }{ 7+\sqrt { 5 } } =a+\dfrac { 7 }{ 11 } \sqrt { 5 } b$$
Find which of the variables $$x, y, z$$ and $$u$$ represent rational numbers and which irrational numbers:
$$y^{2} = 9$$.
$$y^2 = 9$$
$$y = \sqrt{9}$$
$$y = \pm 3$$
$$\rightarrow $$ The number is integer
$$\rightarrow y $$ is rational number
Rationalise the denominator of the following.
$$\dfrac{4}{2+\sqrt{3}+\sqrt{7}}$$.
Represent $$\sqrt{9.3}$$ on the number line.
It being given that $$\sqrt{2}=1.414, \sqrt{3}=1.732, \sqrt{5}=2.236$$ and $$\sqrt{10}=3.162$$, find the value to three places of decimals, of the following.
$$\dfrac{\sqrt{10}-\sqrt{5}}{\sqrt{2}}$$.
Prove that $$\sqrt{3}+\sqrt{5}$$ is an irrational number.
Find three rational number lying between $$\dfrac{3}{5}$$ and $$\dfrac{7}{8}$$. How many rational numbers can be determined between these two numbers?
There will be infinite rational numbers lying between given two rational numbers
Rationalise the denominator of the following.
$$\dfrac{3}{\sqrt{3}+\sqrt{5}-\sqrt{2}}$$.
If $$p=\dfrac{3-\sqrt{5}}{3+\sqrt{5}}$$ and $$q=\dfrac{3+\sqrt{5}}{3-\sqrt{5}}$$, find the value of $$p^2+q^2$$.
Class 9 Maths Extra Questions
- Areas Of Parallelograms And Triangles Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Heron'S Formula Extra Questions
- Introduction To Euclid'S Geometry Extra Questions
- Linear Equations In Two Variable Extra Questions
- Lines And Angles Extra Questions
- Number Systems Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadrilaterals Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions