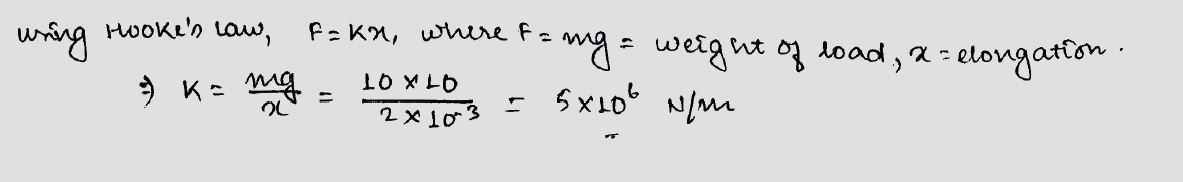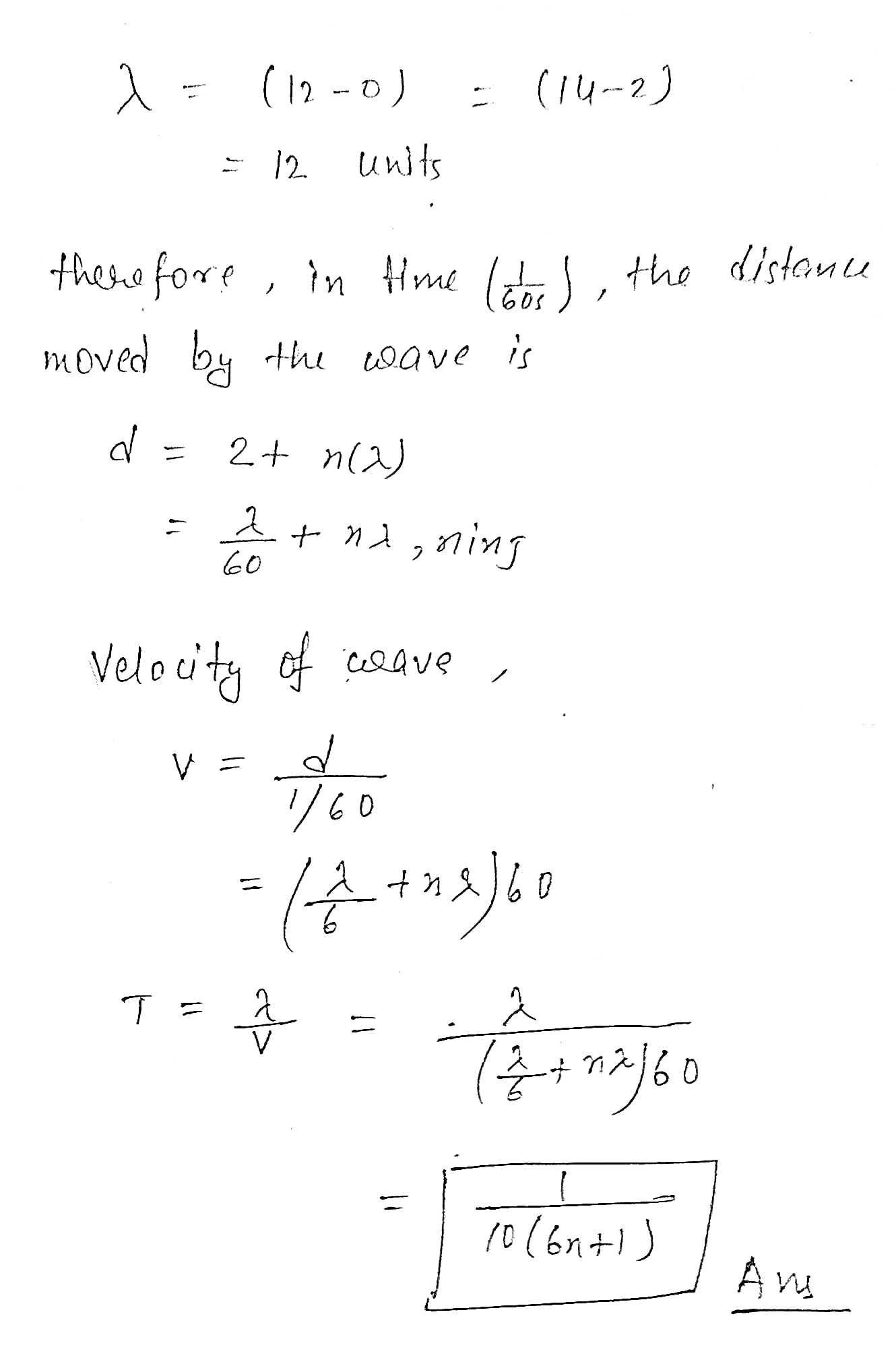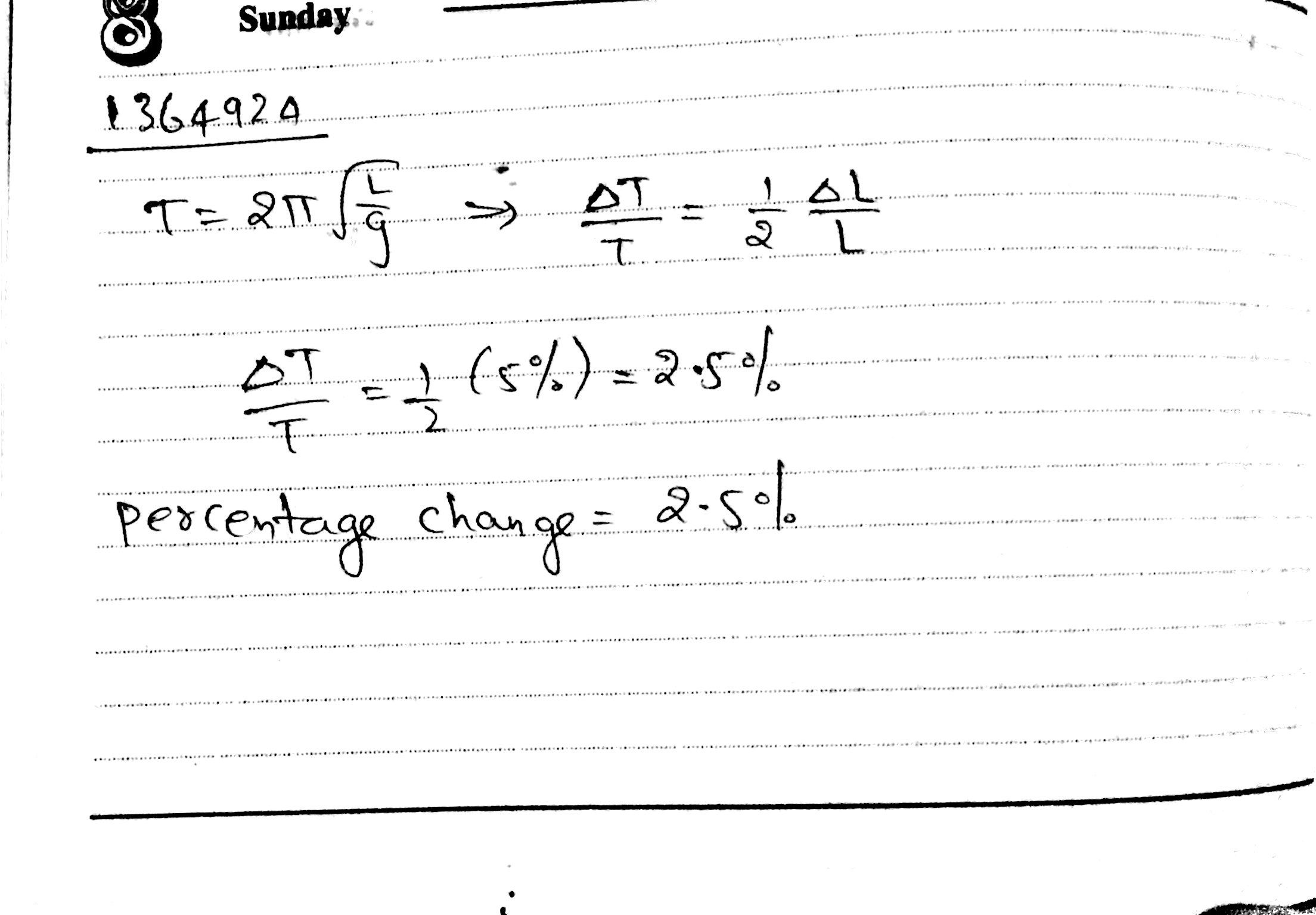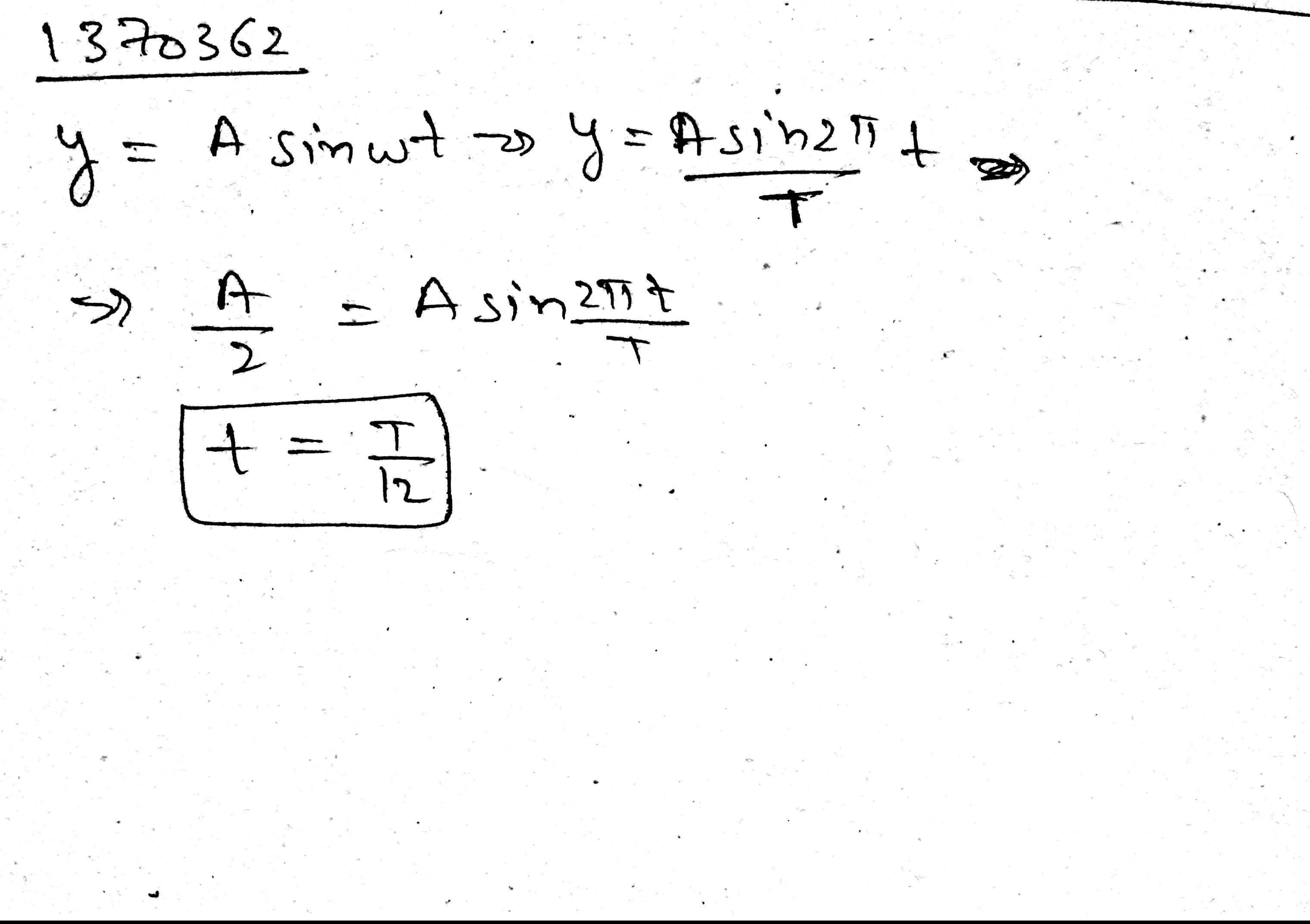Oscillations - Class 11 Engineering Physics - Extra Questions
Define Oscillatory motion.
What is a seconds' pendulum?
It takes 0.2 s for a pendulum bob to move from mean position to one end. What is the time period of pendulum?
What is centripetal force?
Write two differences between centripetal force and centrifugal force.
The velocities of a particle executing SHM are $$10\ cm/s$$ and $$8\ cm/s$$, at displacements $$4\ cm$$ and $$5\ cm$$, from mean position. Calculate the time period of the particle.
When a load of $$10\ kg$$ is suspended on a metallic wire, its length increase by $$2\ mm$$. The force constant of the wire is
using Hooke'n low, F = Kx, where F = mg weight of load,a = elongation
$$ \Rightarrow k = \dfrac{mg}{x} = \dfrac{10\times 10}{2\times 10^{3}} = 5\times 10^{6}n/m $$
The distance between two consecutive crests in a wave train produced in a string is $$5\ cm$$. If $$2$$ complete waves pass through any point per second, what is the velocity of the wave?
A particle performs a S.H.M. of amplitude 10 cm and period 12 s. What is the speed of the particle 3 s, after passing through its mean position?
A particle moves with simple harmonic motion along x-axis. At times $$t$$ and $$2t$$, its positions are given by $$x = a$$ and $$x = b$$ respectively from equilibrium position. Find the time period of oscillation.
If initially particle is at
mean position. Then,
$$x= A\, sin(\omega t)$$ is the expression
of its displacement from mean. So,
$$a= A\, sin (\omega t)$$ ____ (i)
$$b= A\, sin (2\omega t)$$ ____ (ii)
Dividing (ii) by (i), we get
$$\dfrac{sin (2 cos)}{sin (\omega t)}=\dfrac{b}{a}$$
$$\dfrac{2sin(\omega t)cos (\omega t)}{sin (\omega t)}=\dfrac{b}{a}$$
$$\Rightarrow cos(\omega t)=\dfrac{b}{2a}$$
$$\Rightarrow \omega t= cos^{-1}\left ( \dfrac{b}{2a} \right )$$
As $$\omega = 2\pi f\Rightarrow \omega =\dfrac{2\pi }{1}$$
So, $$\dfrac{2\pi t}{T}= cos^{-1}\left ( \dfrac{b}{2a} \right )$$
$$\Rightarrow T= \dfrac{2\pi t}{cos^{-1}\left ( \dfrac{b}{2a} \right )}$$
Find the mechanical energy of a blockspring system with a spring constant of $$1.3 N/cm$$ and an amplitude of $$2.4 cm$$.
What is simple pendulum?
State force law for a SHM.
When object is said to be oscillating?
What is the relation between the length of the pendulum and frequency?
If a simple pendulum oscillates $$10$$ times in $$10$$ seconds, what would be its frequency?
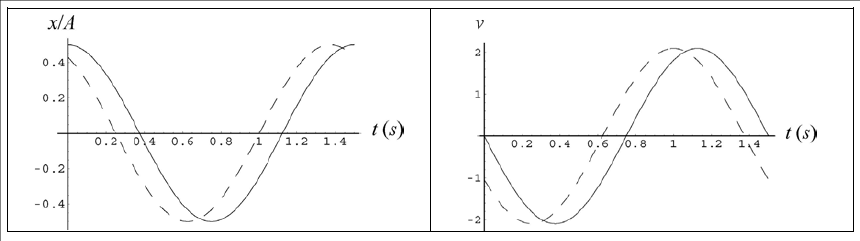
Two simple harmonic motions are denoted as $$\mathrm{S}_{1}$$ and $$\mathrm{S}_{2}$$ as below :
$$\mathrm{S}_{1}$$: $$\mathrm{x}=6\sin^2 \pi t$$
$$\mathrm{S}_{2}$$: $$\mathrm{x} (x-2)=\cos 3 \pi t$$
where $$\mathrm{x}$$ is displacement (In cm) and $$t$$ is time (In second)
For$$S_{1}:$$
$$x=6\sin^{2}\pi t$$
$$=3(1-\cos2\pi t)$$
$$\Rightarrow (x-3)=-3\cos2\pi t$$
$$\Rightarrow period=\dfrac{2\pi }{2\pi }=1second$$
Amplitude$$=3$$
Centre of oscillation is at $$x=3$$
For$$S_{2}:$$
$$x(x-2)=\cos3\pi t$$
$$\Rightarrow (x-1)^{2}=1+\cos3\pi t$$
$$=2cos^{2}\left ( \dfrac{3\pi t}{2} \right )$$
$$\Rightarrow (x-1)=\sqrt{2}\cos\dfrac{3\pi t}{2}$$
$$\Rightarrow period=\dfrac{2\pi }{\dfrac{3\pi }{2}}=\dfrac{4}{3}s$$
Amplitude$$=\sqrt{2}$$
Centre of oscillation is at $$x=1$$
$$x=6\sin^{2}\pi t$$
$$=3(1-\cos2\pi t)$$
$$\Rightarrow (x-3)=-3\cos2\pi t$$
$$\Rightarrow period=\dfrac{2\pi }{2\pi }=1second$$
Amplitude$$=3$$
Centre of oscillation is at $$x=3$$
For$$S_{2}:$$
$$x(x-2)=\cos3\pi t$$
$$\Rightarrow (x-1)^{2}=1+\cos3\pi t$$
$$=2cos^{2}\left ( \dfrac{3\pi t}{2} \right )$$
$$\Rightarrow (x-1)=\sqrt{2}\cos\dfrac{3\pi t}{2}$$
$$\Rightarrow period=\dfrac{2\pi }{\dfrac{3\pi }{2}}=\dfrac{4}{3}s$$
Amplitude$$=\sqrt{2}$$
Centre of oscillation is at $$x=1$$
What is a simple pendulum? Is the simple pendulum used in a pendulum clock? Give reason to your answer.
How do you measure the time period of a given pendulum? Why do you note the time for more than one oscillation ?
How is the time period T and frequency $$f$$ of a simple pendulum related to each other?
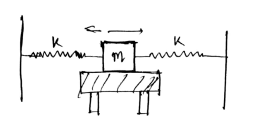
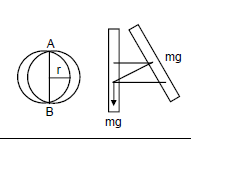
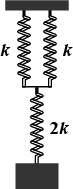
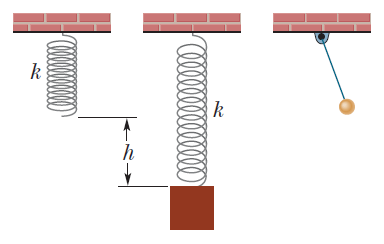
Find the period of oscillation of the system shown in Fig.
State the numerical value of the frequency of oscillation of a seconds' pendulum. Does it depend on the amplitude of oscillation?
The time period of a simple pendulum is 2 s. What is its frequency? What name is given to such a pendulum?
A body describing SHM has a maximum acceleration of $$8\pi $$ m/s$$^{2}$$ and a maximum speed of 1.6 m/s. Find the period T and the amplitude A.
A simple pendulum completes 40 oscillations in a minute. Find its frequency.
A particle moves under the force $$F\left ( x \right )=\left ( x^{2}-6x \right )N$$, where x is in meters. Show that for small displacements from the origin the force constant in the simple harmonic motion is approximately 6.
How much time does the bob of a seconds pendulum take to move from one extreme to the other extreme of its oscillation ?
If a string is wound around a pencil 50 times The total width of all the turns is 5 cm then the thickness of the string is _______ mm.
A spring balance has a scale that reads from $$0$$ to $$50 kg$$. The length of the scale is $$20 cm$$. A body suspended from this balance, when displaced and released, oscillates with period of $$0.6 s$$. What is the weight of the body ?
Obtain the differential equation of linear simple harmonic motion.
A particle having mass 10 g oscillates according to the equation $$x = (2.0\, cm) sin [(100 s^{-1}) t + \pi/6]$$. Find (a) the amplitude, the time period and the force constant (b) the position, the velocity and the acceleration at t=0.
The energy of a particle executing simple harmonic motion is given by the equation $$E=A{x}^{2}+B{v}^{2}$$ where $$x$$ is the displacement from mean position $$x=0$$ and $$v$$ is the velocity of the particle at $$x$$. Find the amplitude of $$S.H.M$$.
$$E=Ax^2+Bv^2$$
As we know that at max amplitude, V$$=0$$
$$\therefore E=Aa^2$$
Let a be amplitude
$$\therefore a^2=\dfrac{E}{A}$$
$$|a|=\sqrt{\dfrac{E}{A_1}}$$.
On the average a human heart is found to beat $$75$$ times in a minute. Calculate its beat frequency of heart and period.
A particle can move along x axis under the influence of a conservative force. The potential energy of the particle is given by $$U=5{x}^{2}-20x+2(J)$$, where $$x$$ is coordinate of the particle expressed in $$m$$. The particle is released at $$x=-3m$$. Find the maximum $$x$$ coordinate of the particle.
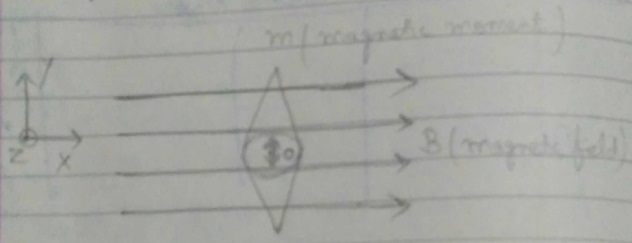
A small compass needle of magnetic moment 'm' is free to turn about an axis perpendicular to the direction of uniform magnetic field 'B'. The moment of inertia of the needle about the axis is 'I'. The needle is slightly disturbed from its stable position and then released. Prove that it executes simple harmonic motion. Hence deduce the expression for its time period.
Conditions for $$S.H.M$$ :-
$$\bullet $$ An Elastic restoring force most be there
$$\bullet $$ Acceleration $$(a)$$ of a system should be directly proportional to its displacement $$(x)$$
i.e, $$a\alpha -x$$
$$(-)$$ve sign indicate opposite to direction of motion.
External Torque on compass needle $$m\times B$$
$$M=m\theta \sin\theta $$
For $$\theta \rightarrow $$ small, $$\sin\theta \simeq \theta $$
$$\Rightarrow \boxed { T=mB\theta } \quad \longrightarrow \left( i \right) $$
Also, it rotates about centre $$O$$ due to inertia $$T=-Id\quad \longrightarrow \left( ii \right) $$ $$\left\{ d=\dfrac { { d }^{ 2 }\theta }{ { dt }^{ 2 } } =\theta \right\} $$
$$(-)$$ve indicator restoring torque.
From $$(i)$$ & $$(ii)$$
$$Il=mB\theta $$
$$\Rightarrow \boxed { l\alpha -\theta } $$ (condition of $$SHM$$)
$$\Rightarrow Il+mB\theta =0$$
Normal frequency, $$f=\dfrac { { W }_{ n } }{ 2\pi } $$
$$\boxed { { W }_{ n }=\sqrt { \dfrac { mB }{ I } } } \quad \Rightarrow \boxed { f=\dfrac { 1 }{ 2\pi } \sqrt { \dfrac { mB }{ I } } } $$
& Time period, $$\boxed { T=\dfrac { 1 }{ f } =2\pi \sqrt { \dfrac { I }{ mB } } } $$
In a sewing machine used by tailors, mention the type of motion of sewing machine parts when it runs.
a) the wheel
b) the needle
c) the cloth
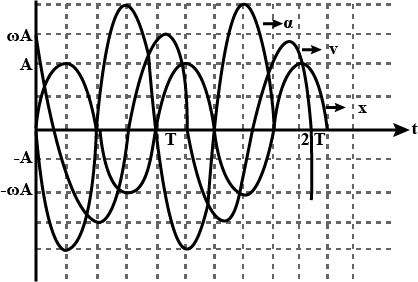
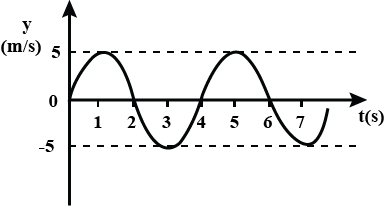
The variation of the velocity of a particle executing SHM with time is shown in the figure. Find the velocity of the particle after a phase change of $$\pi /6$$ that takes place from the instant it is at one of the extreme positions.
Fill in the blank
A point source emits sound equally in all direction in a non-absorbing medium. Two point $$P$$ and $$Q$$ are at a distance of $$9\ m$$ and $$25\ m$$ respectively from the source. The ratio of the amplitudes of the waves at $$P$$ and $$Q$$ is..
Assuming that the frequency $$\gamma$$ of a vibrating string may depend upon $$i)$$ applied force $$(F)\ ii)$$ length $$(\ell)\ iii)$$ mass per unit length $$(m)$$, prove that $$\gamma \alpha \dfrac{1}{l}\sqrt{\dfrac{F}{m}}$$ using dimensional analysis.
Determine whether or not the following quantities can be in the same direction for SHM (a) displacement and velocity (b) velocity and acceleration (c) displacement and acceleration.
A body of mass 1 gram executes a linear S.H.M. of period 1.57 s. If its maximum velocity is 0.8 m/s, then its maximum displacement from the mean position is
Calculate the velocity of the bob of a simple pendulum at its mean position if it is able to rise to a vertical height of $$10\ cm$$. Given: $$g=980\ cm{s}^{-2}$$.
The frequency $$f$$ of vibration of mass $$m$$ suspended from a spring of spring contact $$k$$ is given by $$f=c\ {m}^{x}\ {k}^{y}$$. Where $$c=$$ dimensionless constant, then find the values of $$x$$ and $$y$$.
The displacement of an object attached to a spring and executing SHM is given by $$ x= 2 \times 10^{-2} cos \pi \tau m$$. In what time the object attains maximum speed first?
A particle of mass 0.3 kg is subjected to a force $$F = - kx$$ with k = 15 N/m. What will be its initial acceleration if it is released from a point x = 20 cm?
Find time period of SHM =?
The length of scale of a spring balance which reads to $$100kg$$ is $$20cm$$.On suspending a packet from spring it oscillates with a frequency of $$5$$ oscillation second in a vertical plane. If $$g=\pi^2 m/sec^2$$. Calculate the weight of the suspended object.
$$2$$ particles are in SHM with same time period same amplitude, same mean position (parallel to each other) if maximum separation between them is $$\sqrt{3}{A}$$. Then the find phase difference between them is.
Classify the following as linear , circular, vibratory or oscillatory motion.
i) The motion of a swing.
ii) The motion of earth around the sun.
iii) The motion of a cyclist on a plain road.
iv) The motion of a falling stone
v) The motion of a plucked string of a sitar.
The bob of a simple pendulum has a mass of $$60\ g$$ and a positive charge of $$6\times 10^{-5}C$$. It makes $$30$$ oscillations is $$50\ s$$ above earth's surface. A vertical electric field pointing upward and a magnitude $$5\times 10^{4}N/C$$ is switched on. How much time will it now take to complete $$60$$ oscillations? $$(g = 10\ m/s^{2})$$.
A block of mass $$m$$ is gently attached to the spring and released at time $$t = 0$$ when the spring has its free length as shown in the figure. During subsequent motion of the block, find the variation of $$x$$ with respect to time.
$$\textbf{Hint: Block will perform Simple harmonic motion}$$
$$\textbf{Step1: Find maximum elongation in spring}$$
The spring will obviously elongate until
$$mg=kx_{max}$$
$$\Rightarrow$$$$x_{max}=\dfrac{mg}{k}$$
$$\textbf{Step2: Find variation of $$x$$ w.r.t time}$$
Thus the block execute SHM with an amplitude $$X_{max}$$
$$\Rightarrow x=x_{max}\sin(\omega t)$$
where $$\omega=\sqrt{\dfrac{k}{m}}$$
$$\Rightarrow x=\dfrac{mg}{k}.\sin \left(\sqrt{\dfrac{k}{m}}t\right)$$
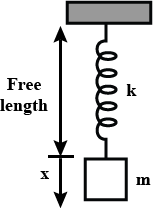
A spring having a spring constant $$1200\ Nm^{-3}$$, is mounted on a horizontal table. A mass of $$3\ kg$$ is attached to the free end of the spring. The mass is then pulled to a distance of $$2.0\ cm$$ and released. Determine maximum acceleration of mass.
A block is resting on a piston which executes simple harmonic motion with a period 2.0 s. The maximum velocity of the piston, at an amplitude just sufficient for the block to separate from the piston is
A particle is executing SHM along the x-axis given by x = A sin$$\omega t.$$ What is the mangnitude of the average acceleration of the partical between t = 0 and (T/4) s, where T is the time period of oscillation .
Two identical particles each of mass 0.5 kg are interconnected by a light spring of stiffness 100 N/m, time period of small oscillation is
A body of mass m is suspended from a spring of force constant $$K$$. Its time period is $$T$$. If an additional mass $$M$$ is attached to $$m$$, then its time period becomes $$4T$$. The value of mass $$M$$ will be
For a particle exicuiting S.H.M. equation of motion is given by $$\cfrac {d_2x}{dt^2}+4x=0$$. Calculate the time period.
Two SHM are represented by $$X_{1}a\sin (\omega t+\alpha_{1})$$ and $$X_{2}a\sin (\omega t+\alpha_{2})$$ obtain the expression for displacement and amplitude.
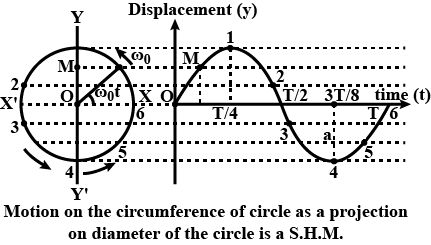
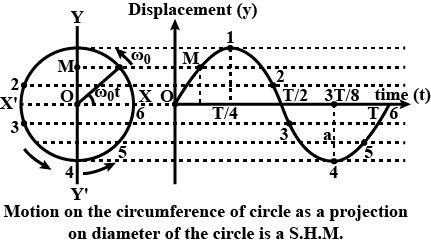
Show that linear S.H.M. is the projection of U.C.M on any diameter.
Let us consider a particle $$p$$ be in a uniform circular motion about '$$o$$' in the $$xy$$ plane
Let $$op = r$$ then $$x = r \cos \theta$$
$$y = r \sin \theta$$
here motion is uniform circular motion then $$\theta$$ increase in a constant rate $$\dfrac{\theta}{t} = \omega \Rightarrow \theta = \omega t$$
$$\therefore x = r \cos \theta \Rightarrow a r \cos \omega d$$
$$r \sin \theta \Rightarrow r \sin \omega t$$
After double integration
$$\dfrac{d^2x}{dt^2} = -\omega^2 r \cos \omega t = -\omega^2 x$$
we know
$$\dfrac{d^2 x}{dt^2} = a$$ [linear acceleration along x-axis] $$\Rightarrow a = -\omega^2 x$$
$$F = ma = -m \omega^2 x$$
$$k = m \omega^2 $$ then $$F = -kx$$
$$\therefore$$ Fore in directly proportional to the displacement, then motion in simple harmonic motion, so projection of uniform circular motion on any diameter is in linear SHM
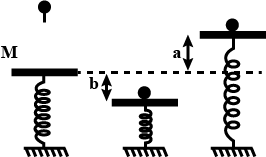
A mass M is in static equilibrium on a massless vertical spring as shown in figure A ball of mass m dropped from certain height sticks to the mass M after colliding with it. The oscillation they perform reaches to height 'a' above the original level of scales & depth 'b' below it. 1 - Find the constant of a force of the spring :2 - Find the oscillation frequency3 - What is the height above the initial level from which the mass m was dropped?
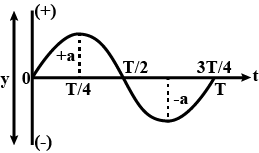
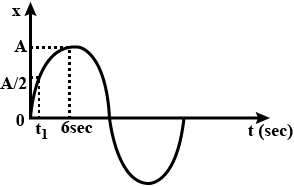
The graph below shows a particle in simple harmonic motion.From the information shown ,find the value of time $$t_1$$
Calculate the velocity of the bob of a simple pendulum at its mean position if it is able to rise to a vertically height of 10 cm. Given $$g=980cm{ s }^{ -2 }$$
It simple pendulum is mounted inside a spacecraft. What should be its time period of vibration?
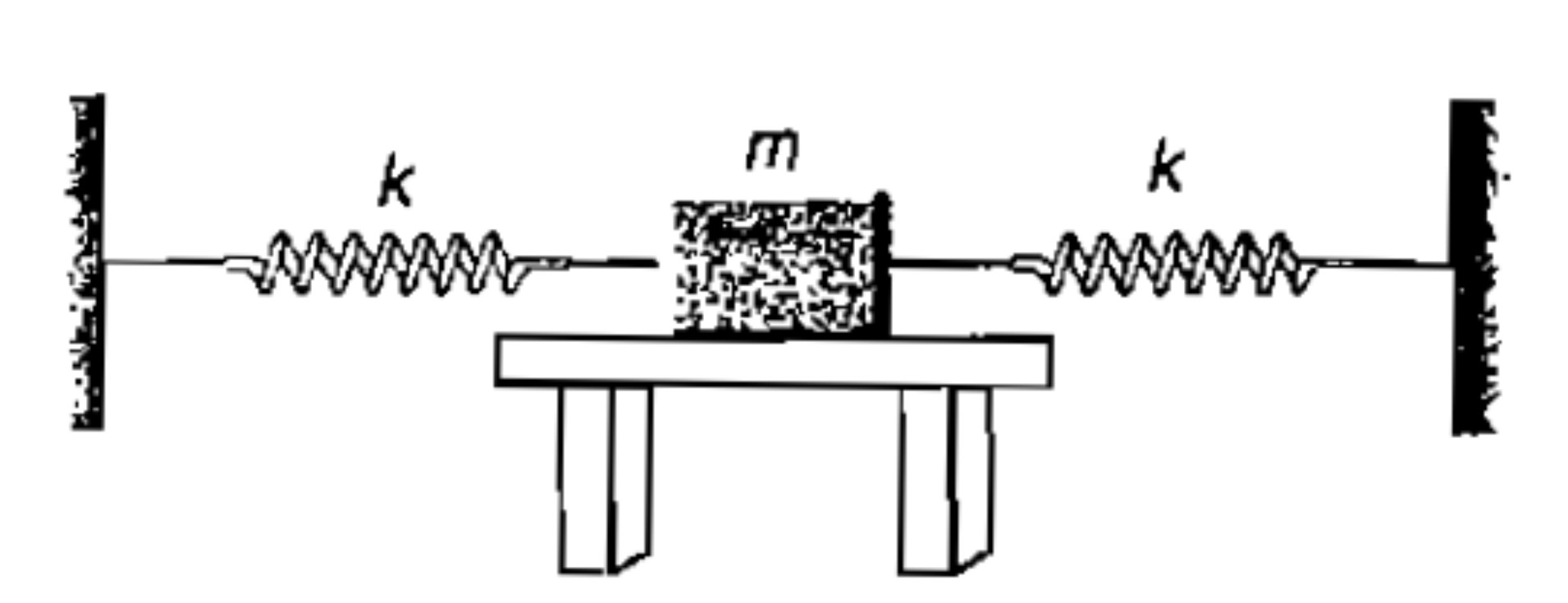
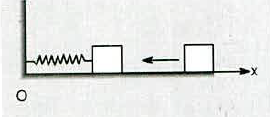
Consider the situation shown in figure. Show that if the blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. Calculate the time period.
Consider that both the blocks are displaced by x each then, by energy method
$$\dfrac{1}{2}k(2x)^2+\dfrac{1}{2}mv^2+\dfrac{1}{2}mv^2=$$ constant
$$mv^2+2kx^2=$$ constant
Taking derivative of both sides wrt t
$$m\times 2v\dfrac{dN}{dt}+2k\times 2x\dfrac{dx}{dt}=0$$
$$ma+2kx=0$$ $$\left[\dfrac{dv}{dt}=a; \dfrac{dx}{dt}=v\right]$$
$$\Rightarrow a=-\left(\dfrac{2k}{m}\right)x$$ $$[a=-\omega^2x]$$ i.e., it is SHM
$$\Rightarrow \omega =\sqrt{\dfrac{2k}{m}}$$
Thus, time period $$(T)=2\pi\sqrt{\dfrac{m}{2k}}$$
$$\left[T=\dfrac{2\pi}{\omega}\right]$$.
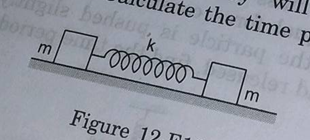
A spring store $$5J$$ of energy when stretched by $$25cm$$. It is kept vertical with the lower end fixed. A block fastened to its other end is made to undergo small oscillation. If the block makes $$5$$ oscillation each second, what is the mass of the block?
A pendulum clock giving correct time at a place where $$g= 9.8 m/s^2$$ is taken to another place where it loses $$24$$ seconds during $$24$$ hours. Find the value of g at this new place.
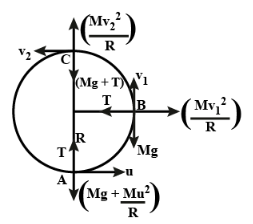
Obtain expressing of energy of a particle at different positions in the vertical circular motion.
We have to find expression of kinetic energy and potential energy at $$A,B$$ and $$C$$
At A say $$P.E=0$$
then at $$B$$ P.E = $$MgR$$
at $$C.PE=Mg(2R)$$
at $$A, K.E.=\dfrac{1}{2}Mcl^2$$
we can write
$$-MgR=\dfrac{1}{2}Mv_1^2-\dfrac{1}{2}mv^2$$
$$\Rightarrow v_1^2=u^2-2gR$$
at $$B,K.ER$$=$$ \dfrac{1}{2}mv_1^2$$
$$=\dfrac{1}{2}M(u^2-2gR)$$
$$=\dfrac{1}{2}mu^2-MgR$$
at $$C\rightarrow$$
$$K.E=\dfrac{1}{2}mv_2^2$$
we can write
$$-Mg\times 2R=\dfrac{1}{2}-Mv_2^2-\dfrac{1}{2}mu^2$$
at $$C\rightarrow K.E=\dfrac{1}{2}M(u^2-4gR)$$
$$\dfrac{1}{2}Mu^2-2MgR$$
also ,for general case $$\rightarrow$$
$$w_g$$ - was done done by gravity
$$w_g=K.E_f-K.E$$
$$\rightarrow MgR(1-\cos \theta)=\dfrac{1}{2}mv^2-\dfrac{1}{2}mv^2$$
$$\rightarrow v^2=2gR(1-\cos \theta )+u^2$$
$$K.E\,\,at\,\,\theta =\dfrac{1}{2}m\{u^2+2gR(1-\cos \theta)\}$$
$$P.E\,\,at\,\,\theta =-MgR(1-\cos\theta)$$
At A say $$P.E=0$$
then at $$B$$ P.E = $$MgR$$
at $$C.PE=Mg(2R)$$
at $$A, K.E.=\dfrac{1}{2}Mcl^2$$
we can write
$$-MgR=\dfrac{1}{2}Mv_1^2-\dfrac{1}{2}mv^2$$
$$\Rightarrow v_1^2=u^2-2gR$$
at $$B,K.ER$$=$$ \dfrac{1}{2}mv_1^2$$
$$=\dfrac{1}{2}M(u^2-2gR)$$
$$=\dfrac{1}{2}mu^2-MgR$$
at $$C\rightarrow$$
$$K.E=\dfrac{1}{2}mv_2^2$$
we can write
$$-Mg\times 2R=\dfrac{1}{2}-Mv_2^2-\dfrac{1}{2}mu^2$$
at $$C\rightarrow K.E=\dfrac{1}{2}M(u^2-4gR)$$
$$\dfrac{1}{2}Mu^2-2MgR$$
also ,for general case $$\rightarrow$$
$$w_g$$ - was done done by gravity
$$w_g=K.E_f-K.E$$
$$\rightarrow MgR(1-\cos \theta)=\dfrac{1}{2}mv^2-\dfrac{1}{2}mv^2$$
$$\rightarrow v^2=2gR(1-\cos \theta )+u^2$$
$$K.E\,\,at\,\,\theta =\dfrac{1}{2}m\{u^2+2gR(1-\cos \theta)\}$$
$$P.E\,\,at\,\,\theta =-MgR(1-\cos\theta)$$
The pendulum of a clock is replaced by a spring-mass system with the spring having spring constant $$0.1{ Nm }^{ { -1 } }.$$ What mass should be attached to the spring ?
A simple harmonic motion is represented by $$x = 10\sin (20t + 0.5)$$.
Write down its amplitude, angular frequency, frequency, time period and initial phase if displacement is measured in metres and time in second.
Define linear S.H.M. Obtain differential equation of linear S.H.M.
Linear SHM is the simplest Kind of oscillatory motion in which a body when displaced from its mean position, oscillates 'to and fro' about mean position and the restoring force (or acceleration) is always directed towards its mean position and its magnitude is directly proportional to the displacement from the mean position.
Consider particle $$P$$ moving along the circumference of a circle of radius 'a' with a uniform angular speed of $$\omega$$ in the anticlockwise direction.
Refer image .1
Particle $$P$$ along the circumference of the circle has its projection particle on diameter $$AB$$ at point $$M$$. This projection particle follows linear SHM along line $$AB$$ when particle P rotates around the circle.
Let the rotation start with initial angle $$'\alpha'$$ as shown above $$(t=0)$$
In time 't' the angle between OP and X-axis will become $$(\omega t+\alpha)$$ as shown below:
Refer image 2
Now from $$\Delta\,\,OPM=\dfrac{OM}{OP}\cos (\omega t+\alpha)$$
$$\Rightarrow \dfrac{x}{a}=\cos(\omega t+\alpha)$$
$$\Rightarrow x=a\cos (\omega t+\alpha)$$ .........(1)
Differentiating above equation with respect to time
we get velocity
$$\Rightarrow v=\dfrac{dx}{dt}=-a\omega \sin (\omega t+\alpha)$$ .........(2)
Differentiating again we get acceleration
$$\Rightarrow a=\dfrac{dv}{dt}=\dfrac{d^2x}{dt^2}-a\omega^2\cos(\omega t+\alpha)$$
$$=-a\cos(\omega t+\alpha)\omega^2$$
$$=-\omega^2x$$ ...........(3)
as $$x=a\cos (\omega t+\alpha)$$
Equation (1),(2) and (3) are differential equations for linear SHM.
A simple pendulum of length $$1 m$$ has mass $$10 g$$ and oscillates freely with amplitude of $$5 cm$$. Calculate its potential energy at extreme position.
In forced vibration $$m=10gm$$,$$f=100Hz$$ and driver force $$F=100\cos(20\pi t)$$ then what amplitude of particle.
The maximum speed and acceleration of a particle executing simple harmonic motion are $$10 cm/s$$ and $$50cm/s^2$$ Find the position(s) of the particle when the speed is $$ 8 cm/s$$.
A small block oscillates back and forth on a smooth concave surface of radius R. Find the time period of small oscillation
As this case is similar to a simple pendulum. Here normal reaction works in the place of tension. So,
$$T=2\pi \sqrt{\dfrac{R}{g}}$$
Analogus to $$T=2\pi \sqrt{\dfrac{l}{g}}$$
[simple pendulum]
A uniform rod of length l is suspended by an end and is made to undergo small oscillations. Find the length of the simple pendulum having the time period equal to that of the rod.
A pendulum suspended in a stationary lift has time period $$T_0$$.
What will be the period $$T$$ of the oscillation of the pendulum if the lift begins to lower with an acceleration equal to $$\dfrac {3}{4}g$$?
In column $$I$$ equation describing the motion of a particles are given and in column $$II$$ possible nature of the motions. Match the entries of column $$I$$ with the entries of column $$II$$.
An accurate pendulum clock is mounted on the ground floor of a high building. How much time will it lose or gain in one day if it is transferred to the top story of a building which is h = 200m higher than the ground floor? The radius of the earth is $$6.4×10^6 \ m$$
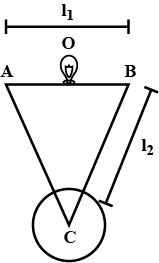
A compensated pendulum shown in fig 1.61 is in the form of an isosceles triangle of base length $$l_1$$ = 5cm and coefficient of linear expansion $$\alpha{1} = 18 \times 10^{-6}$$ and side length $$l_2$$ and coefficient of linear expansion $$\alpha{2} = 12 \times 10^{-6}$$. Find $$l_2$$ so that the distance of centra of mass of the bob from suspension centre O may remain the same at all the temperature
First, we must know what is a compensated pendulum. we've discussed that due to change in temperature the time period of a pendulum clock changes. Due to this, in pendulum clocks, to make a pendulum some specific metals are used which have a very low coefficient of expansion so that the error introduced in their time is very small. The other alternative of minimizing the error in time measurement is to use a compensated pendulum. This is a pendulum made up of two or more metals as shown in the figure.
In this case, the distance of the centre of mass from suspension point O is
$$h = \sqrt{l_2^2 - \dfrac{l_1^2}{4}}$$
When the temperature is changed by $$\triangle t$$, a new value of h will become
$$h' =\sqrt{l_2^1(1 + \alpha_2 \triangle t)^2 - \dfrac{l_1^2}{4}(1 + \alpha_1 \triangle t)^2}$$
As we require h = h', we have
$$l_2^2 - \dfrac{l_1^2}{4} = l_2^2 ( 1+ 2\alpha_2 \triangle t) - \dfrac{l_1^2}{4}(1 + 2 \alpha_1 \triangle t)$$
or $$2 \alpha_2 i_2^2 = \dfrac{l_1^2}{2}\alpha_1$$
or $$l_2 - \dfrac{l_1}{2}\sqrt {\dfrac{\alpha_1}{\alpha_2}}$$
In this case, the distance of the centre of mass from suspension point O is
$$h = \sqrt{l_2^2 - \dfrac{l_1^2}{4}}$$
When the temperature is changed by $$\triangle t$$, a new value of h will become
$$h' =\sqrt{l_2^1(1 + \alpha_2 \triangle t)^2 - \dfrac{l_1^2}{4}(1 + \alpha_1 \triangle t)^2}$$
As we require h = h', we have
$$l_2^2 - \dfrac{l_1^2}{4} = l_2^2 ( 1+ 2\alpha_2 \triangle t) - \dfrac{l_1^2}{4}(1 + 2 \alpha_1 \triangle t)$$
or $$2 \alpha_2 i_2^2 = \dfrac{l_1^2}{2}\alpha_1$$
or $$l_2 - \dfrac{l_1}{2}\sqrt {\dfrac{\alpha_1}{\alpha_2}}$$
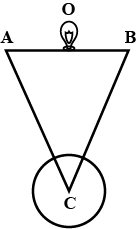
Figure 5.42 shows two snapshots of medium particles within a time interval of $$\dfrac{1}{60} \,s.$$ Find the possible time periods of the wave
An oscillating blockspring system takes $$0.75s$$ to begin repeating its motion. Find (a) the period, (b) the frequency in $$hertz$$, and (c) the angular frequency in $$radians-per-second$$.
Two particles oscillate in simple harmonic motion along a common straight-line segment of length $$A$$. Each particle has a period of $$1.5s$$, but they differ in phase by $$\pi /6rad$$. (a) How far apart are they (in terms of $$A$$ ) $$0.50s$$ after the lagging particle leaves one end of the path? (b) Are they then moving in the same direction, toward each other, or away from each other?
(a) Let, $$x_{1}=\dfrac{A}{2}\cos \left ( \dfrac{2\pi t}{T}\right)$$ be the coordinate as a function of time for particle 1 and $$x_{2}=\frac{A}{2}\cos \left ( \dfrac{2\pi t}{T}+\dfrac{\pi}{6}\right)$$
be the coordinate as a function of time for particle 2. Here $$T$$ is the period. Note that since the range of the motion is $$A$$, the amplitudes are both $$A/2$$. The arguments of the cosine functions are in radians. Particle 1 is at one end of its path $$\left (x_{1}=A/2\right)$$ when $$t = 0$$. Particle 2 is at $$A/2$$ when $$2πt/T + π/6 = 0$$ or $$t = –T/12$$. That is, particle 1 lags particle 2 by one-twelfth a period. We want the coordinates of the particles $$0.50 s$$ later; that is, at $$t = 0.50 s$$,
$$x_{1}=\dfrac{A}{2}\cos \left ( \dfrac{2\pi 0.50s}{1.5s}\right)=-0.25A$$
and, $$x_{2}=\dfrac{A}{2}\cos \left ( \dfrac{2\pi 0.50s}{1.5s}+\dfrac{\pi}{6}\right)=-0.43A$$
Their separation time at that time is $$x_{1}-x_{2}=-0.25A+0.43A=0.81A$$.
(b) The velocities of the particles are given by$$v_{1}=\dfrac{dx_{1}}{dt}=\dfrac{\pi A}{T}\sin \left ( \dfrac{2\pi t}{T} \right)$$
and, $$v_{2}=\dfrac{dx_{2}}{dt}=\frac{\pi A}{T}\sin \left ( \dfrac{2\pi t}{T}+\dfrac{\pi}{6} \right)$$.
We evaluate these expressions for $$t = 0.50 s$$ and find they are both negative-valued, indicating that the particles are moving in the same direction. The plots of $$x$$ and $$v$$ as a function of time for particle 1 (solid) and particle 2 (dashed line) are given below.
A $$1000kg$$ car carrying four $$82 kg$$ people travels over a washboard dirt road with corrugations $$4.0m$$ apart. The car bounces with maximum amplitude when its speed is $$16 km/h$$. When the car stops and the people get out, by how much does the car body rise on its suspension?
A uniform spring with $$k=8600 N/m$$ is cut into pieces $$1$$ and $$2$$ of unstretched lengths $$L_{1}=7.0cm$$ and $$L_{2}=10cm$$. What are (a) $$k_{1}$$ and (b) $$k_{2}$$? A block attached to the original spring as in above figure oscillates at $$200Hz$$. What is the oscillation frequency of the block attached to (c) piece $$1$$ and (d)piece $$2$$?
A $$0.12 kg$$ body undergoes simple harmonic motion of amplitude $$8.5 cm$$ and period $$0.20 s$$. (a) What is the magnitude of the maximum force acting on it? (b) If the oscillations are produced by a spring, what is the spring constant?
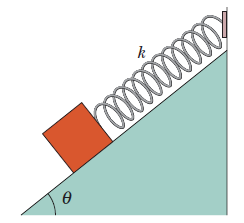
In above figure, a block weighing $$14.0 N$$, which can slide without friction on an incline at angle $$\theta =40.0^{0}$$, is connected to the top of the incline by a massless spring of unstretched length $$0.450 m$$ and spring constant $$120 N/m$$. (a) How far from the top of the incline is the blocks equilibrium point? (b) If the block is pulled slightly down the incline and released, what is the period of the resulting oscillations?
A harmonic wave is travelling in a stationary medium whose equation is given by $$y = A \,sin \,(\omega \,t - kx).$$ Find the equation of this wave w.r.t. a frame which is moving along -ve x-axis with a constant speed v w.r.t. stationary medium. Also, find speed of wave in moving frame.
A $$10g$$ particle undergoes SHM with an amplitude of $$2.0mm$$, a maximum acceleration of magnitude $$8.0*10^{3}m/s^{2}$$, and an unknown phase constant $$\phi$$. What are (a) the period of the motion, (b) the maximum speed of the particle and (c) the total mechanical energy of the oscillator? What is the magnitude of the force on the particle when the particle is at (d) its maximum displacement and (e) half its maximum displacement?
An oscillator consists of a block of mass $$0.500 kg$$ connected to a spring. When set into oscillation with amplitude $$35.0 cm$$, the oscillator repeats its motion every $$0.500 s$$. Find the (a) period, (b) frequency, (c) angular frequency, (d) spring constant, (e) maximum speed, and (f) magnitude of the maximum force on the block from the spring.
The end point of a spring oscillates with a period of $$2.0 s$$ when a block with mass $$m$$ is attached to it. When this mass is increased by $$2.0 kg$$, the period is found to be $$3.0s$$. Find $$m$$.
A spider can tell when its web has captured, say, a fly because the flys thrashing causes the web threads to oscillate. A spider can even determine the size of the fly by the frequency of the oscillations. Assume that a fly oscillates on the capture thread on which it is caught like a block on a spring. What is the ratio of oscillation frequency for a fly with mass m to a fly with mass $$2.5m$$?
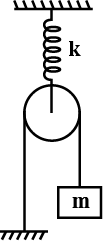
In above figure, it shows that if we hang a block on the end of a spring with spring constant $$k$$, the spring is stretched by distance $$h=2.0 cm$$. If we pull down on the block a short distance and then release it, it oscillates vertically with a certain frequency. What length must a simple pendulum have to swing with that frequency?
A $$50.0g$$ stone is attached to the bottom of a vertical spring and set vibrating. If the maximum speed of the stone is $$15.0 cm/s$$ and the period is $$0.500s$$, find the (a) spring constant of the spring, (b) amplitude of the motion and (c) frequency of oscillation.
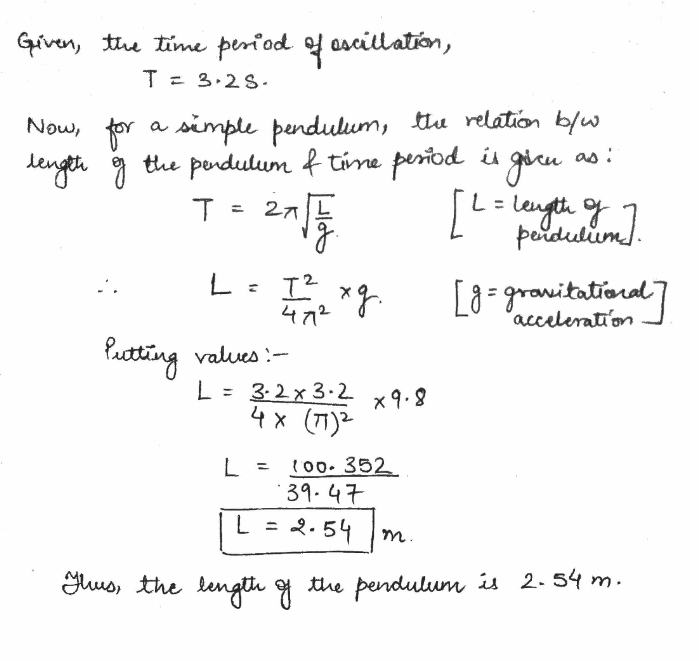
What is the length of a simple pendulum whose full swing from left to right and then back again takes $$3.2 s$$?
Two identical charged particles moving with the same speed enter a region of uniform magnetic field. If one of these enters normal to the field direction and the other enters along a direction at $$30^{o}$$ with the field, what would be the ratio of their angular frequencies.
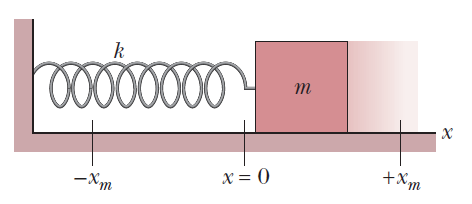
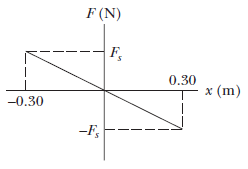
A simple harmonic oscillator consists of a $$0.50kg$$ block attached to a spring. The block slides back and forth along a straight line on a frictionless surface with equilibrium point $$x=0$$. At $$t=0$$ the block is at $$x=0$$ and moving in the positive $$x$$ direction. A graph of the magnitude of the net force $$\underset{F}{\rightarrow}$$ on the block as a function of its position is shown in above figure. The vertical scale is set by $$F_{s}=75.0N$$. What are (a) the amplitude and (b) the period of the motion, (c) the magnitude of the maximum acceleration and (d) the maximum kinetic energy?
The scale of a spring balance that reads from $$0$$ to $$15.0kg$$ is $$12.0cm$$ long. A package suspended from the balance is found to oscillate vertically with a frequency of $$2.00Hz$$. (a) What is the spring constant? (b) How much does the package weigh?
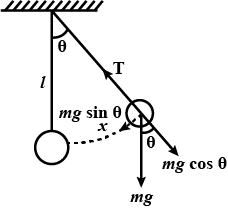
When will the motion of a simple pendulum be simple harmonic?
As consider a pendulum of length l and mass bob m is displaced by angle $$\theta$$ as shown is figure.
The restoring force $$= F = -mg \sin \theta$$
If $$\theta$$ is small then $$\sin \theta = \theta = \dfrac{arc}{radius} = \dfrac{x}{l}$$
$$\therefore F = -mg \dfrac{x}{l}$$ or $$F \alpha (-x)$$
$$(\because $$m, g, l are constants)
Hence the motion of simple pendulum will be simple harmonic for small angle $$\theta$$.
The restoring force $$= F = -mg \sin \theta$$
If $$\theta$$ is small then $$\sin \theta = \theta = \dfrac{arc}{radius} = \dfrac{x}{l}$$
$$\therefore F = -mg \dfrac{x}{l}$$ or $$F \alpha (-x)$$
$$(\because $$m, g, l are constants)
Hence the motion of simple pendulum will be simple harmonic for small angle $$\theta$$.
A tunnel is dug through the centre of the Earth. show that a body of mass 'm' when dropped from rest from one end of the tunnel will execute simple harmonic motion.
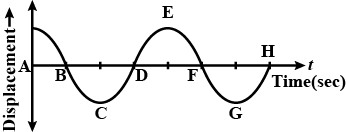
Displacement versus time curve for a particle executing S.H.M. is shown in Figure. Identify the points marked at which velocity of the oscillator is zero.
Draw a graph between displacement from mean position and time for a body executing free vibrations in vacuum.
Displacement-time graph for the free vibrations is shown above :
The pendulum shown in the figure is kept horizontal. It is released from this position. Calculate its velocity when it reaches the down most position. ($$g = 9.8 m/s^2$$)
What type of motion do the hands of a clock exhibits ?
What is the relation between oscillating frequency and total energy of a simple pendulum?
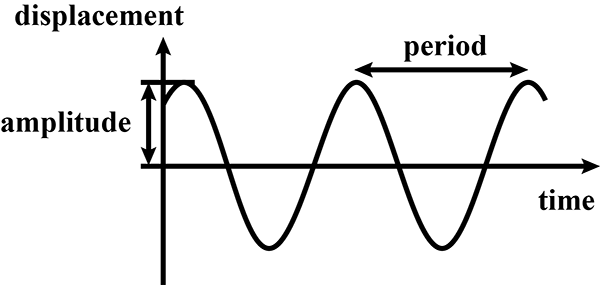
What is the maximum displacement from mean position called?
How does the spring constant varies when small and same springs are connected in: (a) series (b) parallel.
What will be the value of the time period of a simple pendulum if the amplitude is reduced to half of its original value?
What is the phase difference between the displacement and velocity in a SHM?
Explain following terms
Simple harmonic motion
Mention expression for velocity and acceleration of a particle executing SHM.
Define linear simple harmonic motion.
What is the condition for motion of a particle to be SHM?
When is the tension maximum in the string of simple pendulum?
A spring of spring constant $$k$$ is cut into two equal parts . What is the spring constant of each part?
Define simple harmonic motion (SHM). Give an example.
What is oscillation?
the moments of time at which the point reaches the extreme positions.
Explain the relation in phase between displacement, velocity, and acceleration in SHM, graphically as well as theoretically.
Let displacement X =$$A sin \omega t$$
Velocity v = $$\omega A cos \omega t$$
acceleration a = $$-\omega^2 A sin \omega T = \omega^2 A sin (\omega T + \pi)$$
Displacement and velocity have phase difference of $$\pi/2$$ radians.
v and $$\alpha$$ has $$\frac{\pi}{2}$$ radians of phase difference. $$\alpha$$ ans x has $$\pi$$ radians of phase difference.
Assume $$\omega > 1$$
Velocity v = $$\omega A cos \omega t$$
acceleration a = $$-\omega^2 A sin \omega T = \omega^2 A sin (\omega T + \pi)$$
Displacement and velocity have phase difference of $$\pi/2$$ radians.
v and $$\alpha$$ has $$\frac{\pi}{2}$$ radians of phase difference. $$\alpha$$ ans x has $$\pi$$ radians of phase difference.
Assume $$\omega > 1$$
A simple harmonic oscillator takes $$12.0 \ s$$ to undergo five complete vibrations. Find (a) the period of its motion, (b) the frequency in hertz, and (c) the angular frequency in radians per second.
If a pendulum clock keeps perfect time at the base of a mountain, will it also keep perfect time when it is moved to the top of the mountain? Explain.
The angular position of a pendulum is represented by the equation $$\theta = 0.0320 \cos \omega t$$, where u is in radians and $$\omega = 4.43 \ rad/s$$. Determine the period and length of the pendulum.
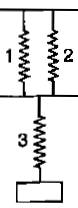
What is spring factor? Find its value in case of two springs connected in
series
parallel
Fill in the blanks:
Motion of the needle of a sewing machine is ______
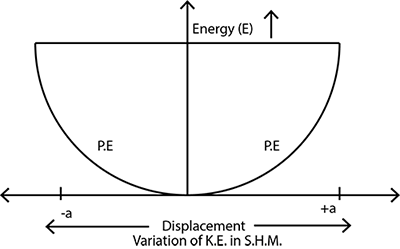
Find an expression for energy of a body vibrating in SHM.
What is SHM? Show that in SHM acceleration is directly proportional to its displacement at a give instant.
Is a bouncing ball an example of simple harmonic motion? Is the daily movement of a student from home to school and back simple harmonic motion? Why or why not?
Name the type of oscillation, D will execute.
Name the type of oscillation, C will execute.
If the length of D is made equal to C, then what difference will you notice in the oscillations of D?
A body undergoing $$SHM$$ about the origin has its equation is given by $$ x=0.2\cos 5 \pi {t}$$. Find its average speed in $$m/s$$ from $$t=0$$ to $$t=0.7\ sec$$.
Potential Energy (U) of a body of unit mass moving in a one-dimension conservative force field is given by,$${U=\left ( x^2-4x+3 \right )}$$.All units in S.I (i) Find the equilibrium position of the body.(ii) Show that oscillations of the body about this equilibrium position is simple harmonic motion & find its time period.(iii) Find the amplitude of oscillations if speed of the body at equilibrium position is $${2\sqrt{6}}$$m/s.
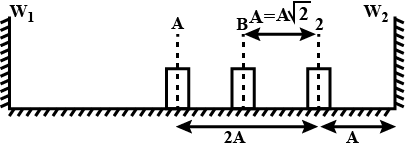
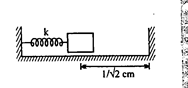
A block of mass $$0.9\ kg$$ attached to a spring of force constant $$k$$ is lying on a friction less floor.The spring is compressed by $$\sqrt{2}\ cm$$ and the block is at a distance $$\dfrac{1}{\sqrt{2}}\ cm$$ from the wall as shown in the figure. When the block is released, it makes elastic collision with the wall and its period of motion is $$0.2\ \sec$$. Find the appropriate value of $$k$$ in $$ Nm^{-1}$$
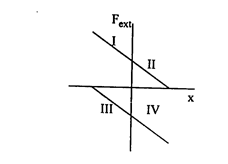
A block is executing SHM on a rough horizontal surface under the action of an external variable force.The force is plotted against the position x of the particle from the mean position
A bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.
One end of each of two identical springs, each of force-constant 0.5 N/m attached on the opposite sides of a wooden block of mass 0.01 kg. The other ends of the springs are connected to separate rigid supports such that the springs are unstretched and are collinear in a horizontal plane. To the wooden piece is fixed a pointer which touches a vertically moving plane paper. The wooden piece, kept on a smooth horizontal table is now displaced by 0.02 m along the line of springs and released. If the speed of paper is 0.1 m/s, find the equation of the path traced by the pointer on the paper and the distance two consecutive maximas on this path.
On the vertically moving paper the pointer traces out the path which gives us the equation of displacement of mass at any time $$t$$ . i.e, displacement as a function of $$t$$.
The two spring will apply some force on mass $$m$$ and it will add up. So,
$$F=-(k+k)x$$
$$\Rightarrow F=-2kx$$
$$\Rightarrow m\cfrac { { d }^{ 2 }x }{ { d }t^{ 2 } } =-2kx$$
$$\Rightarrow \cfrac { { d }^{ 2 }x }{ { d }t^{ 2 } } +(\cfrac { 2k }{ m } )x=0$$
$$\Rightarrow \cfrac { { d }^{ 2 }x }{ { d }t^{ 2 } } +\omega ^{ 2 }x=0$$
$$\cfrac { { d }^{ 2 }x }{ { d }t^{ 2 } } =$$ Acceleration of mass $$m$$.
$$\omega =\sqrt { \cfrac { 2k }{ m } } =\cfrac { 2\times 0.5 }{ 0.01 } $$
$$=\sqrt { 100 } =10rad/s$$
The general solution of this equation gives the equation of path traces out by pointer.
So,
$$x=A\quad \sin { \omega t } $$ (In general solution)
$$\Rightarrow x=0.02\sin { 10t } $$ ($$A$$= Maximum displacement from mean position $$=0.02m$$ $$2\times { 10 }^{ -2 }m$$)
Now velocity of paper is $$0.1m/s$$. And two consecutive maximum for $$x$$ occurs at time:
$${ t }_{ 1 }=\cfrac { \pi }{ 20 } sec$$ and
$${ t }_{ 2 }=\cfrac { 21\pi }{ 20 } sec$$
The time interval between two consecutive maxima:
$$\triangle t={ t }_{ 2 }-{ t }_{ 1 }=\pi sec$$
In this time paper will be moved by: $$u\triangle t=0.1\times \pi =0.1\pi m$$
in vertical direction, So it should be the distance between two consecutive maxima in the paper.
A body of mass $$200\ g$$ is in equilibrium at $$x=0$$ under the influence of a force $$F\left ( x \right )=\left ( -100x+10x^{2} \right )N$$ . If the amplitude is $$4.0\ cm,$$ by how much do we error in assuming that $$F(x)=-kx$$, at the end points of the motion.
A particle executes simple harmonic motion of period 16 s. Two seconds later after it passes through the center of oscillation its velocity is found to be 2 m/s. Find the amplitude.
An object suspended from a spring exhibits oscillations of period T. Now, the spring is cut in half and the two halves are used to support the same object, as shown in figure. Show that the new period of oscillation is T/2.
A spring is cut into three equal pieces and connected as shown in figure. By what factor will the time period of oscillation change if a block is attached before and after?
Neglecting friction, what is the amplitude of oscillations of combined body?
After collision velocity of combined blocks ($$A+C$$)
$$\displaystyle v_{0}=\frac{\left ( 3\times 0.2 \right )+\left ( 3 \right )\left ( 0.4 \right )}{3+3}=0.3 m/s$$
and velocity of block B is $$v_{2}=0.1m/s$$
The spring will compress till velocity of all the blocks become equal to the centre of mass. Applying conservation of mechanical energy,
$$\displaystyle \frac{1}{2}\left ( 3+3 \right )\left ( 0.3 \right )^{2}+\frac{1}{2}\left ( 6 \right )\left ( 0.1 \right )^{2}=\frac{1}{2}\left ( 3+3+6 \right )\left ( 0.1 \right )^{2}+\frac{1}{2}kA^{2}$$
Solving this we get, $$A=0.048 m$$
or $$A=4.8 cm$$
$$\displaystyle v_{0}=\frac{\left ( 3\times 0.2 \right )+\left ( 3 \right )\left ( 0.4 \right )}{3+3}=0.3 m/s$$
and velocity of block B is $$v_{2}=0.1m/s$$
The spring will compress till velocity of all the blocks become equal to the centre of mass. Applying conservation of mechanical energy,
$$\displaystyle \frac{1}{2}\left ( 3+3 \right )\left ( 0.3 \right )^{2}+\frac{1}{2}\left ( 6 \right )\left ( 0.1 \right )^{2}=\frac{1}{2}\left ( 3+3+6 \right )\left ( 0.1 \right )^{2}+\frac{1}{2}kA^{2}$$
Solving this we get, $$A=0.048 m$$
or $$A=4.8 cm$$
A plank with a body of mass $$m$$ placed on it starts moving straight up according to the law $$y=a\left (1 - \cos \omega t \right )$$, where $$y$$ is the displacement from the initial position, $$\omega =11$$ $$rad/s$$. What is the force that the body exerts on the plank?
A particle of mass m free to move in the x-y plane is subjected to a force whose components are $$F_{x}=-ky$$ and $$F_{y}=-ky$$, where k is a constant. The particle is released when t=0 at the point (2, 3). Prove that the subsequent motion is simple harmonic along the straight line $$2y-3x=0.$$
$$\vec{F}=-kx\hat{i}-ky\hat{j}$$
$$\vec{F}=0$$ at (0, 0)
When it is displaced to a point P whose position vector is
$$\vec{r}=x\hat{i}+y\hat{j}$$
Force on it is $$\vec{F}=-k\left ( x\hat{i}+y\hat{j} \right )=-k\vec{r}$$
Since, $$\vec{F}\propto -\vec{r}$$, motion is simple harmonic. At t=0 particle is at (2, 3)
$$\displaystyle \frac{y}{x}=\frac{3}{2}$$
or $$2y-3x=0$$
i.e., the particle will oscillate simple harmonically along this line.
$$\vec{F}=0$$ at (0, 0)
When it is displaced to a point P whose position vector is
$$\vec{r}=x\hat{i}+y\hat{j}$$
Force on it is $$\vec{F}=-k\left ( x\hat{i}+y\hat{j} \right )=-k\vec{r}$$
Since, $$\vec{F}\propto -\vec{r}$$, motion is simple harmonic. At t=0 particle is at (2, 3)
$$\displaystyle \frac{y}{x}=\frac{3}{2}$$
or $$2y-3x=0$$
i.e., the particle will oscillate simple harmonically along this line.
A particle is in linear simple harmonic motion between two points, $$A$$ and $$B, 10\ cm$$ apart. Take the direction from $$A$$ to $$B$$ as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
(a) at the end $$A$$,
(b) at the end $$B$$,
(c) at the mid point of $$AB$$ going towards $$A$$,
(d) at $$2\ cm$$ away from $$B$$ going towards $$A$$,
(e) at $$3\ cm$$ away from $$A$$ going towards $$B$$, and
(f) at $$4$$ cm away from $$B$$ going towards $$A$$.
Answer is:
a)Zero, Positive, Positive
b) Zero, Negative, Negative
c) Negative, Zero, Zero
d) Negative, Negative, Negative
e) Zero, Positive, Positive
f)Negative, Negative, Negative
Explanation:
a,b) The given situation is shown in the following figure. Points A and B are the two end points, with AB = 10 cm. O is the midpoint of the path.
A particle is in linear simple harmonic motion between the end points At the extreme point A, the particle is at rest momentarily. Hence, its velocity is zero at this point.
Its acceleration is positive as it is directed along AO. Force is also positive in this case as the particle is directed rightward.
At the extreme point B, the particle is at rest momentarily.Hence, its velocity is zero at this point.
c) The particle is executing a simple harmonic motion. O is the mean position of the particle. Its velocity at the mean position O is the maximum. The value for velocity is negative as the particle is directed leftward. The acceleration and force of a particle executing SHM is zero at the mean position.
d) The particle is moving toward point O from the end B. This direction of motion is
opposite to the conventional positive direction, which is from A and B.Hence the particle’s velocity and acceleration, and the force on it are all negative.
e) The particle is moving toward point O from the end A. This direction of motion is from A
to B, which is the conventional positive direction.Hence, the values for velocity, acceleration, and force are all positive
f)-This case is similar to the one given in (d)
A mass attached to a spring is free to oscillate, with angular velocity $$\omega$$, in a horizontal plane without friction or damping. It is pulled to a distance $$x_0$$ and pushed towards the centre with a velocity $$v_0$$ at time t =Determine the amplitude of the resulting oscillations in terms of the parameters $$\omega , x_0$$ and $$v_0$$. [Hint : Start with the equation $$x = a\displaystyle \cos \left ( \omega t+\theta \right )$$ and note that the initial velocity in negative.]
Obtain an expression for potential energy of a particle performing simple harmonic motion. Hence evaluate the potential energy (a) at mean position and (b) at extreme position. A horizontal disc is freely rotating about a transverse axis passing through its centre at the rate of $$100$$ revolutions per minute. A $$20$$ gram blob of wax falls on the disc and sticks to the disc at a distance of $$5 cm$$ from its axis. Moment of inertia of the disc about its axis passing through its centre of mass is $$2 \times {10}^{-4} kg {m}^{2}$$. Calculate the new frequency of rotation of the disc.
An oscillating particle possess both types of energies : Potential as well as kinetic. It possesses potential energy on account of its displacement from the equilibrium position.
Potential energy : Consider a particle of mass $$m$$ executing S.H.M. Let $$x$$ be its displacement from the equilibrium position at any instant $$t$$. Since in S.H.M. the force $$F$$ acting upon the particle is proportional to and opposite to the displacement $$x$$, we have
$$F=-kx$$
Where, the constant $$k$$ gives the force per unit displacement $$x$$. The force can also be express in terms of potential energy $$U$$ of the particle as :
$$F=-\dfrac { dU }{ dx }$$
Thus, $$ \dfrac { dU }{ dx } =kx$$
On integrating, we get
$$U=\dfrac { 1 }{ 2 } k{ x }^{ 2 }+C$$
Where $$C$$ is a constant. If we assume the potential energy zero in the equilibrium position, i.e.,
If $$U=0$$ at $$x=0$$, then $$C=0$$.
Therefore, $$U=\dfrac { 1 }{ 2 } k{ x }^{ 2 }$$
(P.E.) $$U=\dfrac { 1 }{ 2 } m{ \omega }^{ 2 }{ x }^{ 2 }$$
Hence from here it is clear that the potential energy of a particle doing S.H.M. is directly proportional to the square of the displacement (P.E. $$\propto { x }^{ 2 }$$).
(a) Potential energy at mean position : At mean position, velocity of a particle executing S.H.M. is maximum and displacement is minimum i.e., $$x=0$$
P.E. $$=\dfrac { 1 }{ 2 } m{ \omega }^{ 2 }{ x }^{ 2 }=0$$
(b) Potential energy at extreme position : At extreme position, velocity of a particle executing S.H.M. is minimum and displacement is maximum, i.e., $$x=\pm a$$
P.E. $$=\dfrac { 1 }{ 2 } k{ a }^{ 2 }=\dfrac { 1 }{ 2 } m{ \omega }^{ 2 }{ a }^{ 2 }$$
Given : $${ n }_{ 1 }=100r.p.m.$$
$$=\dfrac { 100 }{ 60 } =1.66r.p.s.$$
$$m=20gm=2\times { 10 }^{ -2 }kg$$
$$h=r=5cm=0.05m$$
$${ I }_{ 1 }=$$ Moment of inertia of the disclabout its axis is $$=2\times { 10 }^{ -4 }kg{ m }^{ 2 }$$
$${ I }_{ 2 }=$$ Moment of inertia of the disc about same axis with the wax.
To find : $${ n }_{ 2 }=$$ ?
From formula,
$${ I }_{ 2 }={ I }_{ 1 }+m{ r }^{ 2 }$$ [from parallel axis theorem]
$${ I }_{ 1 }{ \omega }_{ 1 }={ I }_{ 2 }{ \omega }_{ 2 }$$
$${ I }_{ 1 }\left( 2\pi { n }_{ 1 } \right) =\left( { I }_{ 1 }+m{ r }^{ 2 } \right) \left( 2\pi { n }_{ 2 } \right)$$
$$ { I }_{ 1 }{ n }_{ 1 }=\left( { I }_{ 1 }+m{ r }^{ 2 } \right) { n }_{ 2 }$$ [$$\because 2\pi$$ is cancelled out]
$$ { n }_{ 2 }=\dfrac { { I }_{ 1 }{ n }_{ 1 } }{ { I }_{ 1 }+m{ r }^{ 2 } }$$
$$ { n }_{ 2 }=\dfrac { 2\times { 10 }^{ -4 }\times 1.66 }{ 2\times { 10 }^{ -4 }+\left( 2\times { 10 }^{ -2 }\times 0.05\times 0.05 \right) } $$
$$=\dfrac { 2\times { 10 }^{ -4 }\times 1.66 }{ 2\times { 10 }^{ -4 }+0.5\times { 10 }^{ -4 } } $$
$$=\dfrac { 2\times { 10 }^{ -4 }\times 1.66 }{ 2.5\times { 10 }^{ -4 } } =1.28\cong 1r.p.s.$$
$${ n }_{ 2 }=1r.p.s.$$
In the figure shown, the spring is relaxed and mass $$m$$ is attached to the spring. The spring is compressed by $$2A$$ and released at $$t = 0$$. Mass $$m$$ collides with the wall and loses two third of its kinetic energy and returns. Starting from $$t = 0$$, find the time taken by it to come back to rest again (instant at which spring is again under maximum compression). Take $$\sqrt {\dfrac {m}{k}} = \dfrac {12}{\pi}$$.
starting point $$A$$ the time taken from $$A$$ to $$W_2(t_1)$$
$$=\dfrac{T}{4}+\dfrac{T}{12}$$
Kinetic energy before collision $$K_a=\dfrac{1}{2}k(2A)^2-\dfrac{1}{2}KA^2$$
$$=K_a=\dfrac{1}{2}K4A^2-\dfrac{1}{2}KA^2$$
$$=K_a=\dfrac{3}{2}A^2K$$
Loss two third $$K_a=\dfrac{3}{2}KA^2\times \dfrac{2}{3}$$
$$=K_a=KA^2$$
now time taken by block $$B\,w_2(f_2)=\dfrac{T}{4}+\dfrac{T}{8}$$
total time $$=t_1+t_2$$
$$=\dfrac{T}{4}+\dfrac{T}{12}+\dfrac{T}{4}+\dfrac{T}{8}$$
$$=\left(\dfrac{2}{4}+\dfrac{t}{12}+\dfrac{1}{8}\right)T$$
$$=\left(\dfrac{12+2+3}{24}\right)T=\dfrac{17}{24}T$$
$$=\dfrac{17}{24}\times 2\pi\sqrt{\dfrac{m}{k}}=\dfrac{17}{12}\pi\times \dfrac{12}{17}$$
Total time taken $$=17sec$$
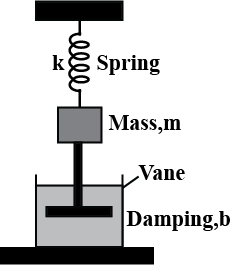
For the damped oscillator shown in Fig, the mass of the block is $$200\ g, k = 80\ N\ m^{-1}$$ and the damping constant $$b$$ is $$40\ g\ s^{-1}$$ Calculate.
(a) The period of oscillation,
(b) Time period for its amplitude of vibrations to drop to half of its initial value
(c) The time for the mechanical energy to drop to half initial value.
A particle performs $$S.H.M.$$ whose velocity is $$v_1$$ at a distance $$x_1$$ from mean position and velocity is $$v_2$$ at distance $$x_2$$ . The time period and amplitude will be.
Using the differential equation of linear S.H.M, derive an expression for the velocity of a particle performing linearly:
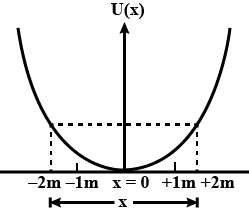
The potential energy function for a particle executing linear simple harmonic motion is given by $$U(_{x})= \frac{1}{2} \ kx^{2}$$, where $$k$$ is the force constant. For $$k= 0.5 N m^{-1}$$,the graph of $$U(x)$$ versus $$x$$ is shown in figure. Show that a particle of total energy $$1\ J$$ moving under this potential $$'turns \ back'$$ when it reaches $$x= \pm \ 2m$$.
A spring of force constant k is cut into lengths of ratio $$1:2:3$$. They are connected in series and the new force constant is k'. Then they are connected in parallel and force constant is k''. Then k':k'' is?
If the percentage increase in the length of the simple pendulum is 2% then find the percentage increase in its time period.
A simple pendulum has time period T. What will be percentage change in its time period if its amplitude is decreased by 5%:-
A particle starts its SHM. At a particular instant t=0, it is at x=$$ \frac{A}{2} $$. Find the time t taken by the particle to come back to mean position after reaching the extreme position.
In figure $$k=100 { Nm }$$, M=1kg and F=10 N. (a) Find the compression of the spring in equilibrium position. (b) A sharp blow by some external agent imparts a speed of $$2m{ s }$$ to the block towards left .Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.(c) Find the time period of the simple harmonic motion.(d) Find the amplitude.(e) Write the potential energy of the spring when the block is at the left exterme.(f) write the potential energy of the spring when the block is at the right extreme.
The answers of (b),(e)and (f) are different. Explain why this dose not violate the principle of conservation of enrgy.
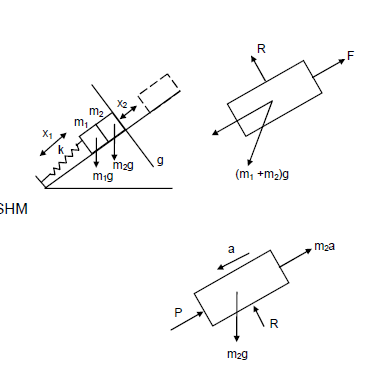
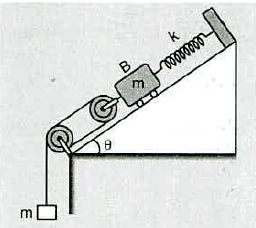
The block of mass $$m_1$$ in shown in figure is fastened to the spring and the block of mass $$m_2$$ is placed against it. (a) Find the compression of the spring in the equilibrium position. (b) The blocks are pushed a further distance $$(2/k)(m_1+m_2)g\sin\theta$$ against the spring and released. Find the position where the two blocks separate. (c) What is the common speed of blocks at the time of separation ?
(a) Due to the gravitational force on the blocks that's will equal the spring force
So,
$$kx = (m_1+m_2)g sin \theta$$
So,
$$x = \dfrac{(m_1+m_2)gsin \theta}{k}$$
Now,
(b) The blocks are further pushed $$\dfrac{2}{k}(m_1+m_2)g sin \theta$$
So, Total compression = $$\dfrac{2}{k}(m_1+m_2)g sin \theta$$
That means that The amplitude of the SHM followed will be $$\dfrac{2}{k}(m_1+m_2)g sin \theta$$
And, after the total compression in the spring will become zero that is the spring comes to it's natural length , then the blocks will leave each other's contact.
(c) By work energy theorem,
Change in Kinetic Energy = Work done by all forces,
So,
$$\dfrac{1}{2} \times (m_1+m_2) \times v^2 = \dfrac{1}{2}kx^2 - (m_1+m_2)gsin\ theta \times x$$
Therefore,
$$\dfrac{1}{2}(m_1+m_2)v^2 = \dfrac{1}{2}k{\dfrac{3}{k}(m_1+m_2)g sin \theta}^2 - (m_1+m_2)g sin \theta \times \dfrac{3}{k} (m_1+m_2) g sin \theta$$
So,
$$\Rightarrow$$ $$v = g sin \theta \sqrt{\dfrac{3(m_1+m_2)}{k}}$$
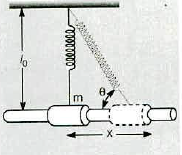
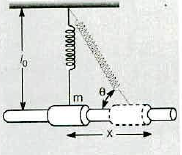
A spring with spring constant $$k$$ is attached to the mass $$m$$. i.e confined to move along a frictionless rail as shown in figure. Natural length of the spring is $$l_0$$ when mass $$m$$ is at origin of coordinate system.
Show that for small displacement $$x$$,
$$F_x =-\dfrac {k}{2l_0^2}x^3$$
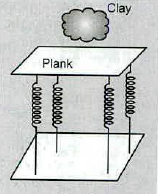
A $$1.60\ kg$$ plank is supported on four springs. A $$0.55\ kg$$ chunk of clay is held above the plank and dropped so that it hits the plank with a speed of $$1.65\ m/s$$. The clay makes an inelastic collision with the plank and the plank and clay oscillate up and down. After a long time the plank comes to rest $$6.0\ cm$$ below its original position.
What is the effective spring constant of all four spring taken together?
A hollow sphere of radius $$2 cm$$ is attached to an 18 cm long thread to make a pendulum. Find the time period of oscillation of this pendulum. How does it differ from the time period calculated using the formula for a simple pendulum ?
A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude $$2^0$$ and time period 2 s. Find (a) the radius of the circular wire, (b) the speed of the particle farthest away from the point of suspension as it goes through its mean position, (c) the acceleration of this particle as it goes through its mean position and (d) the acceleration of this particle when it' is at an extreme position. Take $$g=\pi^2\,m/s^2$$
As we know,
For a compound pendulum
a) $$T=2\pi\sqrt{\dfrac{l}{mgl}}=2\pi \sqrt{\dfrac{l}{mgr}}$$
The MI of the circular wire about the point of suspension is given by
$$\therefore I=mr^2+mr^2=2mr^2$$ is Moment of inertia about $$A$$,.
$$\therefore 2=2\pi \sqrt{\dfrac{2mr^2mgr}{}}=2\pi \sqrt{\dfrac{2r}{g}}$$
$$\Rightarrow \dfrac{2r}{g}=\dfrac{1}{\pi^2}\Rightarrow r=\dfrac{g}{2\pi^2}=0.5\pi =50cm$$.
b) $$(1/2)\omega^2-0=mgr\, \omega (1-\cos \theta)$$
$$\Rightarrow (1/2)2mr^2-\omega^2=mgr(1-\cos 2^0)$$
$$\Rightarrow \omega^2=g/r (1-\cos 2^0)$$
$$\Rightarrow \omega =0.11$$ rad/sec [putting the values of g and r]
$$\Rightarrow v=\omega \times 2r=11$$ cm/sec
c) Acceleration at the end position will be centripetal.
$$=a_n=\omega^2(2r)=(0.11)^2\times 100=1.2cm/s^2$$
The dircetion of $$a_n$$ is towards the point of suspension
d) At the extreme position the centrepetal acceleration will be zero. But the particle will still have acceleration due to the SHM.
Because, $$T=2$$ sec
Angular frequency $$\omega=\dfrac{2\pi}{T}(\pi=3.14)$$
So, angular acceleration at the extreme position,
$$\alpha=\omega^2\theta=\pi^2\times \dfrac{2\pi}{180}=\dfrac{2\pi^3}{180}[1^0=\dfrac{\pi}{180}]$$ radius
So, tangential acceleration $$=\alpha(2r)=\dfrac{2\pi^3}{180}\times 100=34cm/s^2$$
Two swings in an amusement park have length $$l_1 > l_2$$, time periods $$T_1$$ and $$T_2$$ respectively. They both are drawn a side together and released at the same instant to swing in small oscillations. After what time interval will they again be in phase with each other?
Show that if a pendulum of length $$l$$ and period $$T$$ is moved to a location where acceleration due to gravity changes by $$\Delta g$$, the change $$\Delta t$$ in the period of the pendulum is approximately.
$$\Delta T =-\dfrac {T}{2g}\Delta g$$
A physical pendulum consists of a sphere of mass $$m$$ and radius $$r$$, suspended from a string. The centre of the sphere is at a distance $$L$$ from the point of suspension. For $$r << L$$ this pendulum is treated as a simple pendulum of length $$L$$.
If $$L=1\ m$$, how large must the radius of the bob for the error to be $$1\%$$.
A spring with spring constant $$k$$ is attached to the mass $$m$$. i.e confined to move along a frictionless rail as shown in the figure. The natural length of the spring is $$l_0$$ when mass $$m$$ is at the origin of the coordinate system.
Show that the $$x-$$component of the force that the spring exerts on the mass is
$$F_x=-k[(l_0^2+x^2)^{\dfrac{1}{2}}-l_0]\ cos\theta$$
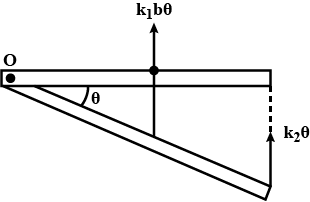
Find the angular frequency of oscillation of motion of block $$m$$ for small angular motion of rod $$BD$$. Consider the rod to be massless.
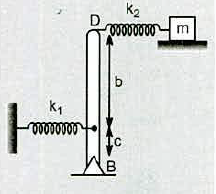
Find the natural angular frequency of the system shown in figure. Pulies are massless and friction is absent everywhere.
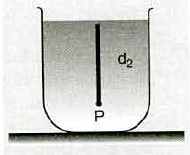
A thin rod of length $$L$$ and uniform cress-section is pivoted at its lowest point $$P$$ inside a stationary homogeneous and non viscus liquid (as shown in figure). The rod is free to rotate in a vertical plane about a horizontal axis passing through $$P$$. The density $$d_1$$ of the material of the rod is smaller than the density $$d_2$$ of the liquid. The rod is displaced by small angle $$\theta$$ from its equilibrium position and the released. Show that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters.
A pendulum clock keeps perfect time on the surface of the Earth. In which case will the error be greater. if the clock is placed at depth $$h$$ below Earth's surface or if the clock is raised to height $$h$$? Assume $$h << R_E$$.
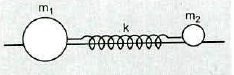
Two spheres with the masses $$m_1 $$ and $$m_2$$ can slide without friction along a thin horizontal rod as shown in the figure. The sphere are connected by a massless spring of spring constant $$k$$. The sphere are pulled in opposite directions and are then released.
A momentum of $$m_1 v_0$$ is imparted to the first sphere. What is the velocity of the centre of mass of the system? What is the energy $$E_{trans}$$, of the translation and $$E_{osc}$$ of the oscillatory motion of the system?
One end of an ideal spring is fixed to a wall at origin $$O$$ and axis of spring is parallel to $$x-$$axis. $$A$$ block of mass $$m=1\ kg$$ is attached to free end of the spring and it is performing $$SHM$$. Equation of position of the block in coordinates system shown in figure is $$x=10+3\sin (10t)$$. Here $$t$$ is in second $$x$$ in $$cm$$.
Another blocks of mass $$M=3\ kg$$. moving towards the origin with velocity $$30\ cm/sec$$ collides with the block performing $$S.H.M$$ at $$t=0$$ and gets stuck to it.
Calculate:
New equation for position of the combined body,
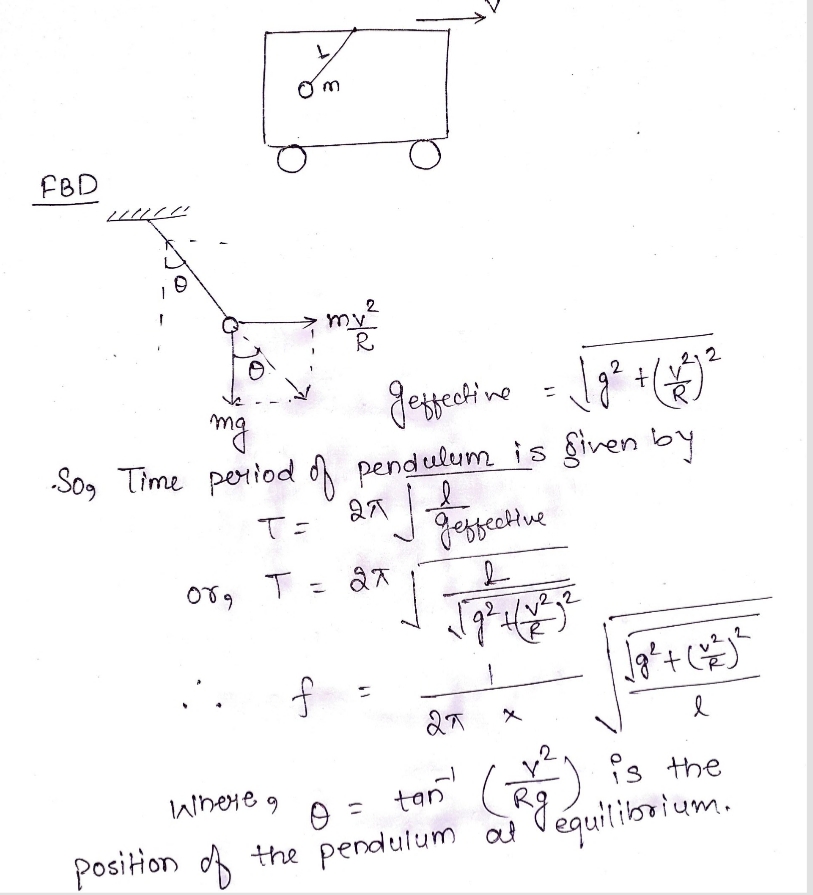
A simple pendulum of length $$L$$ and mass $$m$$ is suspended in a car that is moving with constant speed $$v$$ around a circle of radius $$R$$. What will be the frequency of oscillation and equilibrium position of the pendulum?
A rod of mass $$m$$ and length $$l$$ hinged at one end is connected by two springs contants $$k_1$$ and $$k_2$$ so that it is horizontal at equilibrium. What us the angular frequency of the system ? ( in rad/s) ( Take $$\ell=1\ m, b=1/4\ m, K_1=16\ N/m, K_2=61\ N/m)$$.
Applying torque equation about
$$\tau_{0}=t_{0}\alpha$$
$$k_{1}b\theta\times b\cos \theta+\dfrac{k_{2}l_{\theta}}{\theta}\times l\cos\theta=-\dfrac{Id^{2}\theta}{dt^{2}}$$
Here, $$I=\dfrac{ml^{2}}{3}$$, and as $$\theta$$ is small, $$\cos\theta=1$$
$$\dfrac{ml^{2}d^{2}\theta}{3dt^{2}}+(k_{1}b^{2}+k_{2}l^{2})\theta=0$$
Hence, $$\omega=\sqrt{\dfrac{3k_{1}b^{2}+k_{2}l^{2}}{ml}}$$
On substituting the value we get $$\omega=8\ rad/s$$
$$\tau_{0}=t_{0}\alpha$$
$$k_{1}b\theta\times b\cos \theta+\dfrac{k_{2}l_{\theta}}{\theta}\times l\cos\theta=-\dfrac{Id^{2}\theta}{dt^{2}}$$
Here, $$I=\dfrac{ml^{2}}{3}$$, and as $$\theta$$ is small, $$\cos\theta=1$$
$$\dfrac{ml^{2}d^{2}\theta}{3dt^{2}}+(k_{1}b^{2}+k_{2}l^{2})\theta=0$$
Hence, $$\omega=\sqrt{\dfrac{3k_{1}b^{2}+k_{2}l^{2}}{ml}}$$
On substituting the value we get $$\omega=8\ rad/s$$
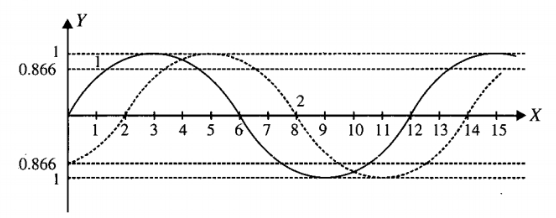
Figure 5.41 shows the position of a medium particles at $$t = 0,$$ supporting a simple harmonic wave travelling either along or opposite to the positive x-axis.
a.Write down the equation of the curve.
b. Find the angle $$'\theta '$$ made by the tangent at point P with the x-axis.
c. If the particle at P has a velocity $$v_{p} \,m/s,$$ in the negative y-direction , as shown in figure, then determine the speed and direction of the wave.
d. Find the frequency of the waves.
e. Find the displacement equation of the particle at the origin as a function of time.
f. Find the displacement equation of the wave.
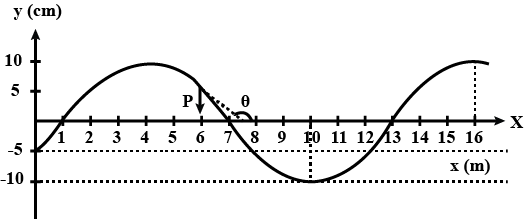
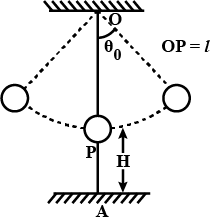
A simple pendulum of time period 1 second and length l is hung from a fixed support at O, such that the bob is at a distance H vertically above A on the ground (Figure). The amplitude is $$\theta_{o}$$. The string snaps at $$\theta = \dfrac{\theta_{o}}{2}$$. Find the time taken by the bob to bit the ground Also find distance from A where bob hits the ground. Assume $$\theta_{o}$$ to be small so that $$\sin \theta_{o} = \theta_{o}$$ and $$\cos \theta_{o} = 1$$.
The suspension system of a $$2000kg$$ automobile sags $$10 cm$$ when the chassis is placed on it. Also, the oscillation amplitude decreases by $$50$$% each cycle. Estimate the values of (a) the spring constant $$k$$ and (b) the damping constant $$b$$ for the spring and shock absorber system of one wheel, assuming each wheel supports $$500 kg$$.
Explain oscillatory motion by giving one example.
Part 1: Definition of oscillatory motion
Oscillatory motion - The to and fro motion of a body about a fixed point is called oscillatory motion.It is a type of periodic motion.
Part 2: Examples of oscillatory motion
Motion of a pendulum is the most common example of oscillatory motion.
The bob of a pendulum is always in a to and fro motion about a fixed point.
Graphically represent the displacement, velocity and acceleration for a time period of one cycle.
(i) Displacement in $$ SHM $$
The displacement of any particle at any instant in linear $$ S.H.m $$ can be represented as
$$ y=\alpha sin \omega_o t $$
Where $$ \alpha= $$ amplitude
and $$ \omega_0 $$= angular frequancy.
Therefore $$ y= \alpha sin \frac{2 \pi}{t} t $$
Putting different values of $$ t $$ in $$ Eq.(8.6), $$ we can calculate different values of $$ y $$ and get the graphical representation between time and displacement.
$$ y= \alpha sin\frac{2 \pi}{T} t $$
t 0 T/4 T/2 3T/4 T
$$ sin \frac{2\pi}{T}t $$ 0 1 0 -1 0
$$ \therefore y=a sin\frac{2 \pi}{T} t $$ 0 a 0 -a 0
The graphical representation of time and displacement from the values is shown below in Diagram $$ (8.3 ) $$.
If instantaneous displacement is
$$ y= \alpha sin (\omega_0t \pm \phi) $$
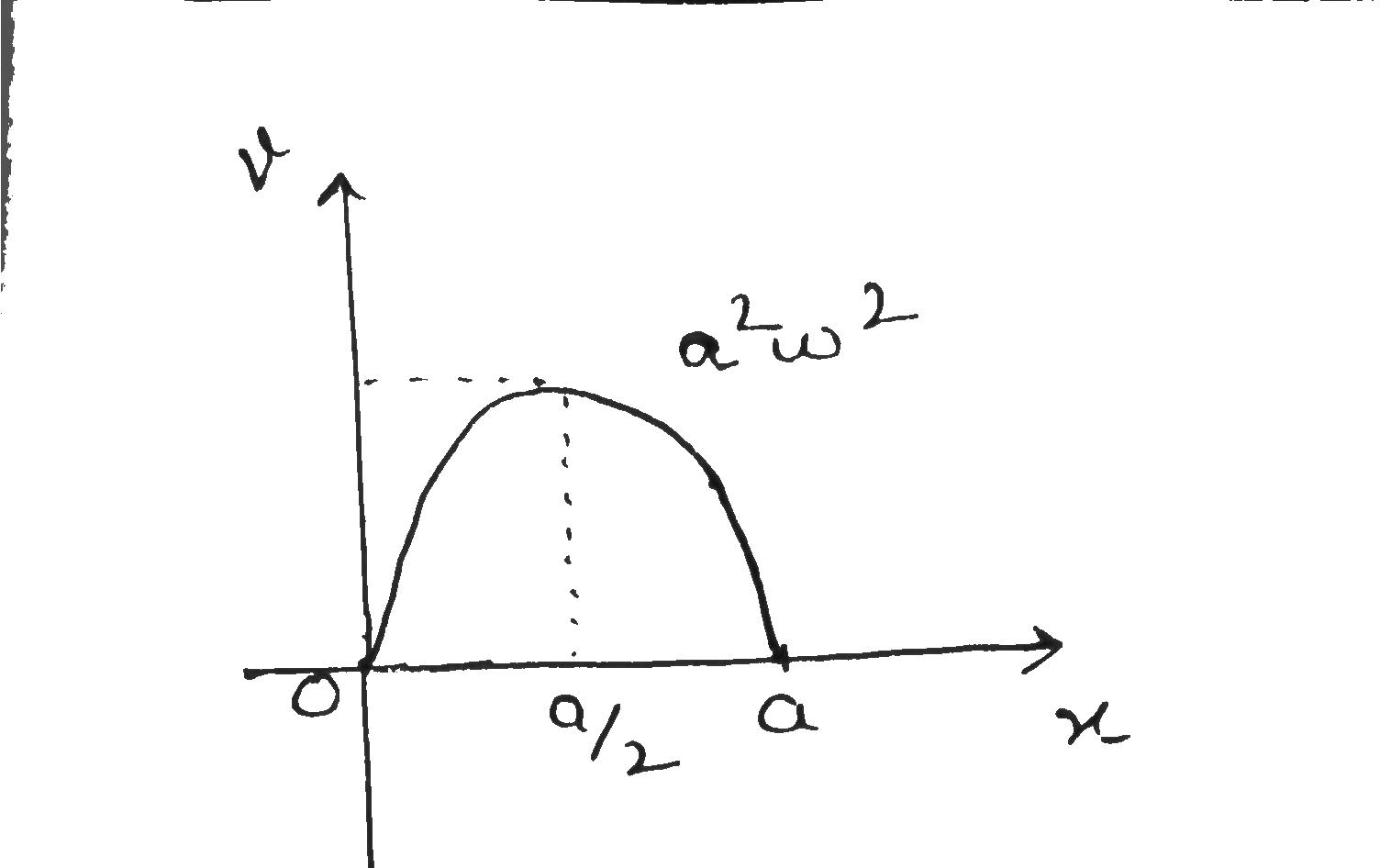
the velocity projection $$\nu_x$$ as a function of the coordinate $$x$$; draw the plot $$\nu_x\ (x)$$.
Differentiating Eqn (1) w.r.t. time
$$v_x =a\omega \cos ( 2\omega t+\pi )$$ or $$v_x^2=a^2\omega^2 \cos^2 ( 2\omega t+\pi )=a^2 \omega^2 [1-\sin^2 (2\omega t +\pi )]$$
From Eqn (1) $$\left( x-\dfrac a2 \right)^2 =\dfrac {a^2}{4}\sin^2 ( 2\omega t+\pi)$$
or, $$4\dfrac {x^2}{a^2}+1-\dfrac {4x}{a}=\sin^2 (2\omega t +\pi)$$ or $$1-\sin^2 (2\omega t+\pi )=\dfrac{4x}{a}\left( 1-\dfrac xa\right)$$
From Eqns (2) and (3), $$v_x =a^2 \omega^2 \dfrac {4x}{a}\left( 1-\dfrac xa \right)=4\omega^2 x(a-x)$$
$$v_x =a\omega \cos ( 2\omega t+\pi )$$ or $$v_x^2=a^2\omega^2 \cos^2 ( 2\omega t+\pi )=a^2 \omega^2 [1-\sin^2 (2\omega t +\pi )]$$
From Eqn (1) $$\left( x-\dfrac a2 \right)^2 =\dfrac {a^2}{4}\sin^2 ( 2\omega t+\pi)$$
or, $$4\dfrac {x^2}{a^2}+1-\dfrac {4x}{a}=\sin^2 (2\omega t +\pi)$$ or $$1-\sin^2 (2\omega t+\pi )=\dfrac{4x}{a}\left( 1-\dfrac xa\right)$$
From Eqns (2) and (3), $$v_x =a^2 \omega^2 \dfrac {4x}{a}\left( 1-\dfrac xa \right)=4\omega^2 x(a-x)$$
Calculate the percentage change in the time period of a simple pendulum in the following positions;
$$(i) $$ Increasing the length of the pendulum by $$ 5 $$ %.
$$(ii) $$ Increasing the mass of the pendulum by $$ 5 $$ %.
$$(iii) $$ Increasing the amplitude of the pendulum by $$ 5 $$ %.
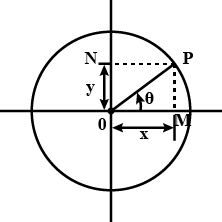
Prove that the projection of a uniform circular motion is simple harmonic motion.
The special form of simple oscillatory motion which is most simple is known as Simple Harmonic Motion. In this motion the body moves in a simple line on both the sides of its mean position. The definition of simple harmonic motion, "Simple harmonic motion is the projection on the diameter of a circle of the same motion as on the circumference of that circle."
Suppose, as shown in figure a particle of mass $$ m $$ is moving with angular speed $$ \omega_0 $$ on the circumference of a circle of radius 'a' and centre $$ O $$. At any instant, when the particle is at point $$ P, $$ then the perpendicular drwan from the position of the particle to the diameter $$ YY' $$ has its foot at point $$ M $$. When the particle doing circular motion is at point $$ X $$, then the foot point $$ M $$ of the perpendicular is moving along the diameter $$ YY'$$ abd is at point $$ O $$. When the particle is at point $$ Y $$ then the foot point $$ M $$ also reaches at $$ Y $$ point. When particle is at $$ X'$$ point then the foot point of perpendicular again comes back to $$ O $$.
The particle reaching $$ Y'$$ point the foot point of the perpendicular is also at $$ Y '$$ and after completing one cycle when the particle is at point $$ X $$ then the foot point of the perpendicular also moves from $$ Y'$$ to $$ O $$. It is clear that when any particle moving on a circular path completes one cycle then foot point $$ M $$ of the perpendicular, moves in a simple line to and fro of the centre $$ O $$ of the circle. This is the simple harmonic motion of point $$ M. $$ Therefore, projection of . the foot point of a perpendicular in uniform circular motion is simple harmonic motion.
Suppose, as shown in figure a particle of mass $$ m $$ is moving with angular speed $$ \omega_0 $$ on the circumference of a circle of radius 'a' and centre $$ O $$. At any instant, when the particle is at point $$ P, $$ then the perpendicular drwan from the position of the particle to the diameter $$ YY' $$ has its foot at point $$ M $$. When the particle doing circular motion is at point $$ X $$, then the foot point $$ M $$ of the perpendicular is moving along the diameter $$ YY'$$ abd is at point $$ O $$. When the particle is at point $$ Y $$ then the foot point $$ M $$ also reaches at $$ Y $$ point. When particle is at $$ X'$$ point then the foot point of perpendicular again comes back to $$ O $$.
The particle reaching $$ Y'$$ point the foot point of the perpendicular is also at $$ Y '$$ and after completing one cycle when the particle is at point $$ X $$ then the foot point of the perpendicular also moves from $$ Y'$$ to $$ O $$. It is clear that when any particle moving on a circular path completes one cycle then foot point $$ M $$ of the perpendicular, moves in a simple line to and fro of the centre $$ O $$ of the circle. This is the simple harmonic motion of point $$ M. $$ Therefore, projection of . the foot point of a perpendicular in uniform circular motion is simple harmonic motion.
The displacement of an oscillating particle is given by $$ x = a sin \omega t + b cos \omega t $$ where a, b and $$ \omega $$ are constants. prove that the particle performs a linear S.H.M with amplitude $$ A = \sqrt { a^2 + b^2 } $$
Question 14.
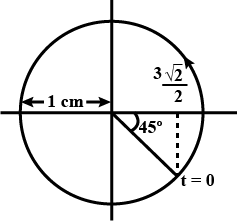
Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial $$(t = 0)$$ position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anti-clockwise in every case: (x is in cm and t is in s).
$$ x = 3 \;sin(2 \pi \;t + \pi/4)$$
$$ x = 3 \;sin(2 \pi \;t + \pi/4)$$
radius $$r = 3 cm$$
at $$t = 0, \;x = 3 \; sin \pi/4 = \dfrac{3}{2}\sqrt{2}$$
$$\omega = 2\pi \;rad/s$$
$$cos \phi _{0} = \dfrac{\dfrac{3\sqrt{2}}{2}}{3} = \dfrac{1}{\sqrt{2}}$$
$$\phi _{0} = \pm \pi/4$$
radius $$r = 3 cm$$
at $$t = 0, \;x = 3 \; sin \pi/4 = \dfrac{3}{2}\sqrt{2}$$
$$\omega = 2\pi \;rad/s$$
$$cos \phi _{0} = \dfrac{\dfrac{3\sqrt{2}}{2}}{3} = \dfrac{1}{\sqrt{2}}$$
$$\phi _{0} = \pm \pi/4$$
What is the difference between the series and parallel combination of springs? Calculate the value of effective spring constant for every combination.
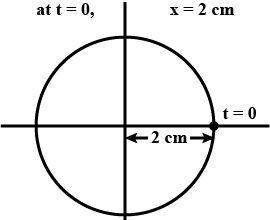
Question 15.
Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial $$(t = 0)$$ position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anti-clockwise in every case: (x is in cm and t is in s).
$$x = 2 \;cos \pi \;t$$
$$x = 2 \;cos \pi \;t$$
$$r = 2 cm$$
$$\omega = \pi \;rad/s$$
at $$t = 0, x = 2 cm$$
$$r = 2 cm$$
$$\omega = \pi \;rad/s$$
at $$t = 0, x = 2 cm$$
Prove that the foot of the perpendicular of a particle revolving with angular velocity $$ \omega 0 $$ in a circular path of radius a executes simple harmonic motion. Write the equation for this motion.
Suppose as shown in (fig) a particle of mass m is moving with angular speed $$ \omega_0 $$ on the circumference of a circle of radius 'a' and center O. At any instant, when the particle is at point P then the perpendicular drawn from the position of the particle to diameter YY' has its foot point M. When the particle doing circular motion is at point X, then the foot print M of the perpendicular is moving along the diameter YY'and is at point O. when the particle is at point T then the foot point M also reaches at Y point . when particle is at X'point then the foot print of perpendicular again comes back to O.
the particle reaching Y' point the foot point of the perpendicular is also at Y'and after completing one cycle when the particle is at point X then the foot point of the perpendicular also moves from Y' to O. it is clear that when any particle moving on a circular path completes once cycle then foot point M of the perpendicular , moves in a simple line to and fro of the center I of the circle . this is the simple harmonic motion of point M . Therefore , projection of the foot point of a perpendicular in uniform circular motion is simple harmonic motion.
Point M moving from O to T , Y to Y and Y'to O is called one complete vibration We know that in circular motion the centrifugal force on the particle ( $$ m \omega^2_0 a $$ in magnitude ) is as always towards the center of the circle . hence the force acting on the point P of the particle will be in the direction of OP .The component of force in YY' direction will be $$ ( \omega^2_0 a sin \omega_0t ) $$
From diagram $$ 8.2 sin \omega_0 t = \frac {OM}{OP} = \frac {y}{a} $$
Hence working force
$$ = [ m \omega^2_0 a ] sin \omega_0t = [ m \omega^2_0] \frac {y}{a} $$
Displacement $$ y $$ is taken positive in direction $$ OY $$ this force is in direction $$ YO $$ hence will be negative therefore
$$ F = - m \omega^2_0 y $$
$$ F = -ky .....(8.3) $$
where $$ k = m \omega^2_0 $$ is force constant .
It is clear from fig (8.3) that mass of the particle m , angular velocity $$ \omega_0 $$ are constant then as a result force is directly proportional to displacement y , and its direction its possible to displacement y . hence force $$ F $$ is called restoring force.
hence simple ha monic motion is that imaginary or oscillating motion of an object to and fro its means position in which the restoring force is
(i) Directly proportional to the displacement of the object from its mean position.
(ii) Always points ( moving) towards the mean position.
For a simple pendulum why is a spherical bob chosen.
the law of motion $$y(t),$$ where $$y$$ is the displacement of the body from the equilibrium position;
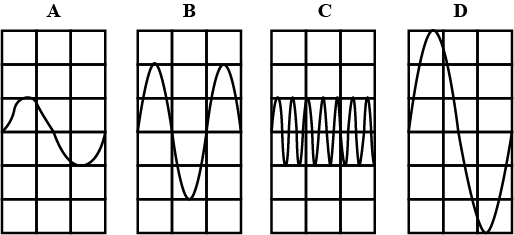
Figure shows four traces produced by an oscilloscope for different sounds. For each trace the same settings of the oscilloscope were used.
(i) In the box, write the letter A, B, C or D of the trace showing the sound with the highest pitch.
$$\square$$
(ii) Complete the statement using the letters of the traces.
the two traces that have the same amplitudes are ........... and ............
The superposition of two harmonic oscillation ofthe same direction
results in the oscillation of a point according to the law $$x=a \cos
2.1 t \cos 50.0 t$$ where $$t$$ is expressed in seconds. Find the angular frequencies of the constituent oscillation and the period with which they beat.
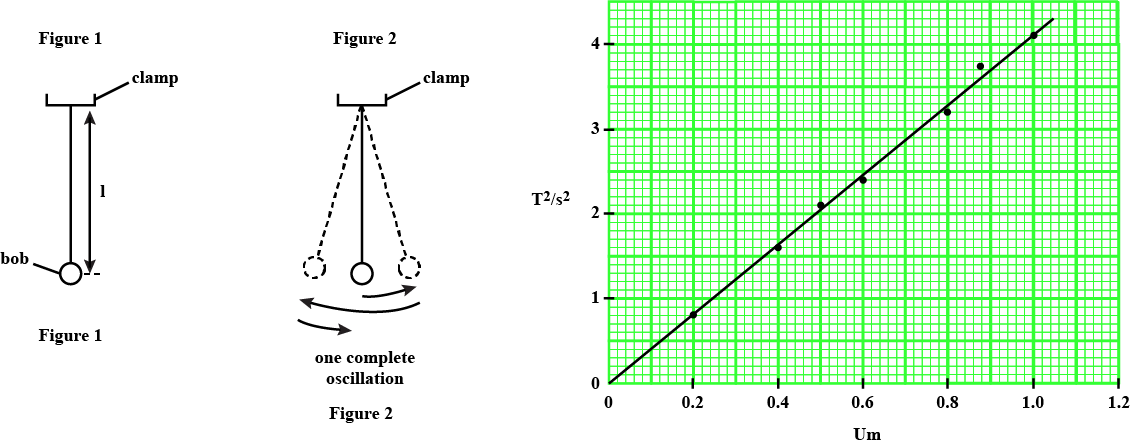
The class is investigating the oscillations of a pendulum.
Fig 5.1 and 5.2 show the apparatus.
A student measures the length l of the pendulum and takes readings of the time t for 20 complete oscillations. She calculates the period T of the pendulum. T is the time taken for one complete oscillation. She repeats the procedure for a range of lengths.
She plots a graph of $$T^2 / s^2$$ against l / m. Given figure shows the graph.
(a) Using the graph, determine the length l of a pendulum that has a period $$T = 2.0\,s.$$ Show clearly on the graph how you obtained the necessary information.
(b) Explain why measuring the time for 20 swings. rather than for 1 swing. gives a more accurate value for T.
(c) Another student investigates the effect that changing the mass m of the pendulum bob has on the period T of the pendulum.
(i) Suggest how many different masses the student should use for this laboratory experiment.
(ii) Suggest a range of suitable values for the masses.
the time dependence of the force that the body exerts on the plank if $$a=4.0\ cm;$$ plot this dependence;
potential energy $$w_{p}(x,t);$$
The velocity oscillation amplitude of particles of the medium and its ratio to the wave propagation velocity;
The initial position, velocity, and acceleration of an object moving in simple harmonic motion are $$x_i, v_i,$$ and $$a_i$$; the angular frequency of oscillation is $$\omega$$. (a) Show that the position and velocity of the object for all time can be written as
$$x(t) = x_i \cos \omega t + \left( \dfrac{v_i}{\omega} \right) \sin \omega t$$
$$v(t) = -x_i \omega \sin \omega t + v_i \cos \omega t$$
(b) Using A to represent the amplitude of the motion, show that
$$v^2 - ax= v^2_i - a_i x_i = \omega^2 A^2$$
Class 11 Engineering Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Physical World Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work,Energy And Power Extra Questions