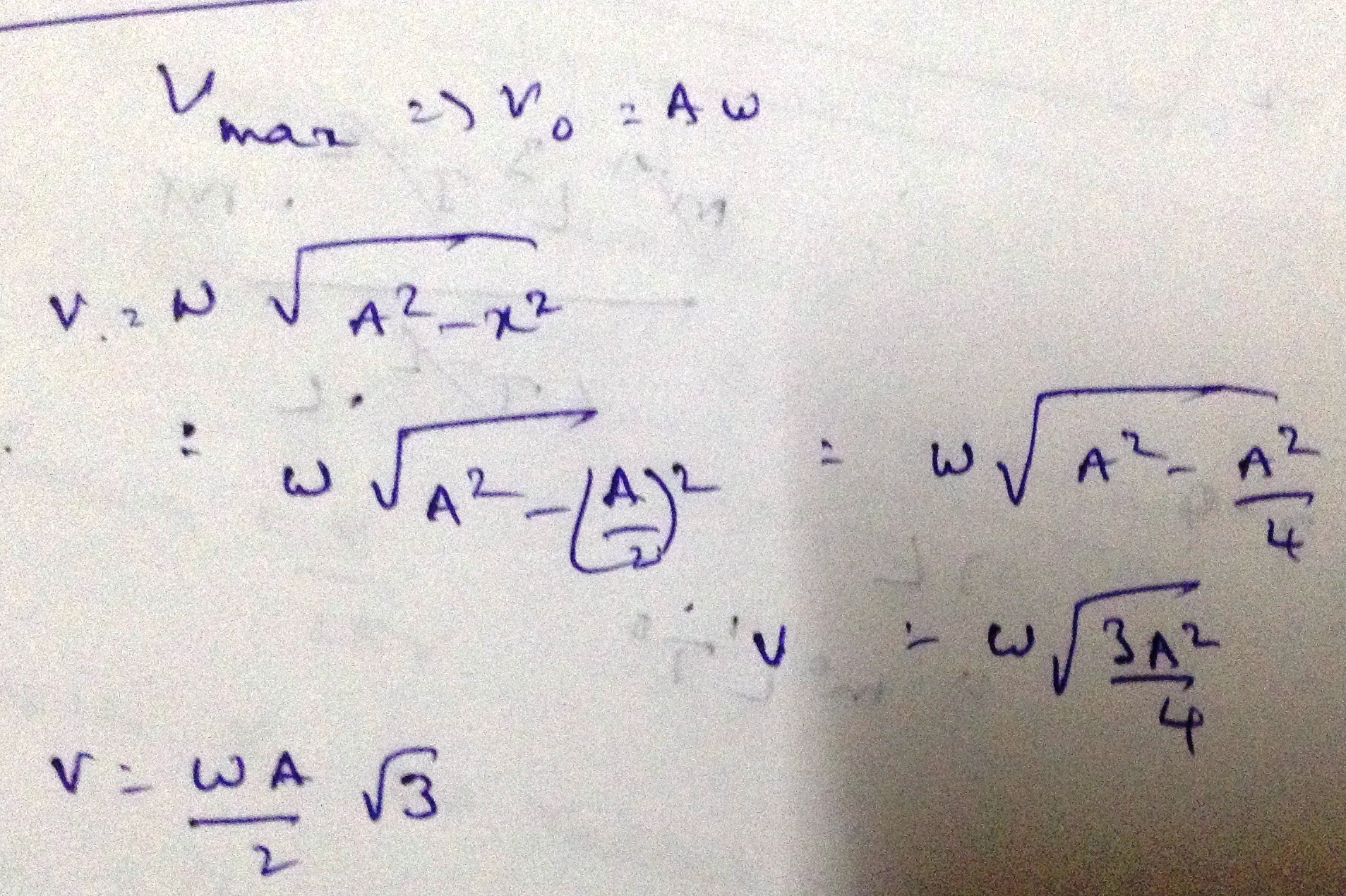Oscillations - Class 11 Medical Physics - Extra Questions
Two SHM's are represented by $$x_1 = a_1 \, sin (\omega t + \alpha_1)$$ and $$x_2 = a_2 sin (\omega t + \alpha_2)$$. Obtain the expression for the displacement, amplitude and initial phase of the resultant motion.
A particle is executing SHM with amplitude A and has maximum velocity $$ V_0 $$. Find its speed when it is located at distance of A/2 from mean position.
If the displacement $$x$$ of a particle of mass $$m$$ is directly proportional to time, net force acting on it is _____________.
A particle of mass $$2 kg $$ is acted upon by a force of $$F = (8 - 2x) N$$. It is released from rest at $$x = 6 m$$. Write the equation of motion of the particle.
The equation of simple harmonic progressive wave is given by $$Y=0.05\sin { \pi } \left[ 20t-\cfrac { x }{ 6 } \right] $$, where all quantities are in S.I units. Calculate the displacement of particle at $$5m$$ from origin and at the instance $$0.1$$ second.
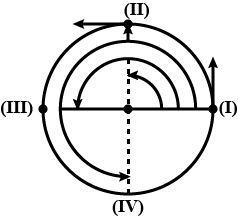
What will be the equation of displacement in the following different conditions?
A particle having mass 10 g oscillates according to the equation x = (2.0 cm) sin [(100 $$s^-$$$$^1$$ t + $$\pi$$/6]. Find.
(a) the amplitude, the time period and the force constant
(b) the position, the velocity and the acceleration at t = 0.
A string of length $$0.5m$$ carries a bob with a period $$2\pi s$$. Calculate the angle of inclination of string with vertical and tension in the string.
A body of mass $$0.1kg$$ is executing simple harmonic motion according to the equation
$$x=0.5\cos { \left( 100t+\cfrac { 3\pi }{ 4 } \right) } $$ metre. Find: (i) the frequency of oscillation, (ii) initial phase, (iii) maximum velocity, (iv) maximum acceleration, (v) total energy.
Can a motion be oscillatory but not simple harmonic?
A particle of mass 4 gm. lies in a potential field given by V=200$$x^{2}$$ + 150 ergs/gm. Deduce the frequency of vibration.
The periodic time of a linear harmonic oscillator is $$2\pi $$ seconds, with maximum displacement of $$1 cm$$, if the particle starts from extreme position, find displacement of the particle after $$\dfrac{\pi }{3}$$ seconds.
A particle is executing SHM given by X = A $$ sin (\pi t+\phi ) $$ . The intial displacement of particle is 1 cm and its initial velocity is $$ \pi cm / sec $$. Find the amplitude of motion and initial phase of the particle?
A body executing $$SHM$$ has its velocity $$16cm/sec$$ when passing through mean position. If it goes $$1\ cm$$ either side of mean position, then find its maximum period.
A particle moving with simple harmonic motion has speed $$3 cm /s$$ and $$4 cm /s$$ at displacement $$8 cm$$ and $$6 cm$$, respectively, from the equilibrium position. Find
(a) the period of oscillation, and
(b) the amplitude of oscillation.
The frequency of a particle performing SHM is 12 Hz. Its amplitude is 4 cm.Its initial extreme displacement is 2 cm toward positive extreme position. Its equation for displacement.
1 kg ice at -$${10^0}C$$ is mixed with 1 kg water at $${100^0}C$$.then find equilibrium temperature and mixture content.
A particle is executing SHM with amplitude A and has maximum velocity $$V_{0}$$. Its speed at displacement A/2 will be
Part of a simple harmonic motion is graphed in the figure, where y is the displacement from the mean position. The correct equation describing this S.H.M is :-
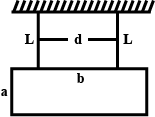
A rectangular plate of sides $$a$$ and $$b$$ is suspended from a ceiling by two parallel strings of length $$L$$ each. The separation between the strings is $$d$$. The plate is displaced slightly in its plane keeping the strings tight. Show that it will execute simple harmonic motion. Find the time period.
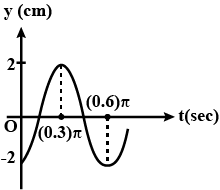
The displacement of a particle executing simple harmonic motion is given by equation y=0.3 sin 20$$\pi $$ (t+0.05) where time t is in second and displacement y is in metre. calculate the values of amplitude, time period initial phase and initial displacement of the particle .
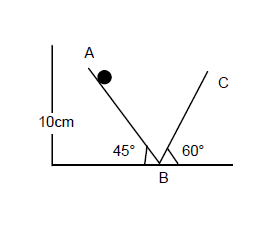
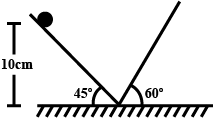
Find the time period of the motion of the particles shown in figure. Neglect the small effect of the bend near the bottom.
A spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
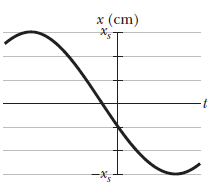
What is the phase constant for the harmonic oscillator with the position function $$x(t)$$ given in (above figure) if the position function has the form $$x=x_{m}\cos \left ( \omega t+\phi \right )$$? The vertical axis scale is set by $$x_{x}=6.0cm$$.
The position function $$x=\left ( 6.0m \right )\cos \left [ \left ( 3\pi rad/s \right )t+\pi /3 rad\right]$$ gives the simple harmonic motion of a body. At $$t= 2.0 s$$, what are the (a) displacement, (b) velocity, (c) acceleration and (d) phase of the motion? Also,what are the (e) frequency and (f) period of the motion?
Suppose that a simple pendulum consists of a small $$60.0g$$ bob at the end of a cord of negligible mass. If the angle $$\theta$$ between the cord and the vertical is given by $$\theta=\left ( 0.0800rad\right )\cos \left [ \left ( 4.43rad/s\right)t+\phi\right]$$, what are (a) the pendulums length and (b) its maximum kinetic energy?
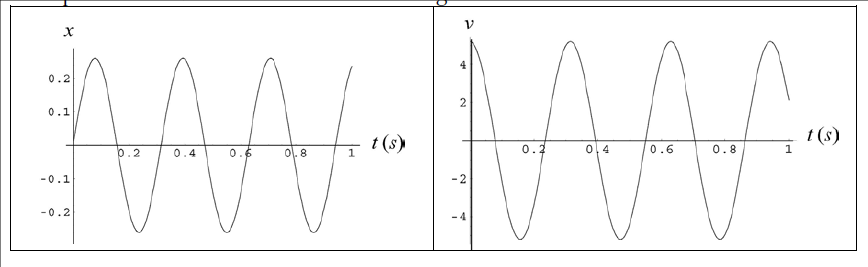
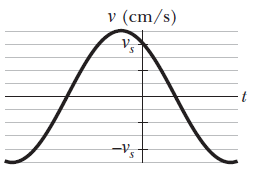
In above figure $$(a)$$ partial graph of the position function $$x(t)$$ for a simple harmonic oscillator with an angular frequency of $$1.20rad/s$$; and Fig. $$(b)$$ is a partial graph of the corresponding velocity function $$v(t)$$. The vertical axis scales are set by $$x_{s}=5.0cm$$ and $$v_{s}=5.0cm/s$$. What is the phase constant of the SHM if the position function $$x(t$$) is in the general form $$x=x_{m}\cos \left ( \omega t+\phi\right)$$?
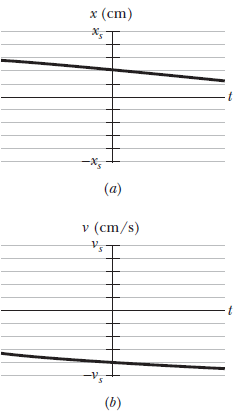
What is the phase constant for the harmonic oscillator with the velocity function $$v(t)$$ given in above figure, if the position function $$x(t)$$ has the form $$x=x_{m}\cos \left ( \omega t+\phi\right)$$? The vertical axis scale is set by $$v_{s}=4.0cm/s$$.
If the phase angle for a blockspring system in SHM is $$\pi/6rad$$ and the blocks position is given by $$x=x_{m}\cos\left ( \omega t+\phi\right)$$, what is the ratio of the kinetic energy to the potential energy at time $$t=0$$?
A performer seated on a trapeze is swinging back and forth with a period of $$8.85s$$. If she stands up, thus raising the center of mass of the $$trapeze+performer$$ system by $$35.0cm$$, what will be the new period of the system? Treat $$trapeze+performer$$ as a simple pendulum.
An oscillating blockspring system has a mechanical energy of $$1.00J$$, an amplitude of $$10.0cm$$, and a maximum speed of $$1.20m/s$$. Find (a) the spring constant, (b) the mass of the block and (c) the frequency of oscillation.
A $$2.00kg$$ block hangs from a spring. A $$300g$$ body hung below the block stretches the spring $$2.00cm$$ farther. (a) What is the spring constant? (b) If the $$300g$$ body is removed and the block is set into oscillation, find the period of the motion.
A $$55.0g$$ block oscillates in SHM on the end of a spring with $$k=1500 N/m$$ according to $$x=x_{m}\cos\left ( \omega t+\phi \right )$$. How long does the block take to move from position $$+0.800x_{m}$$ to (a) position $$+0.600x_{m}$$ and (b) position $$-0.800x_{m}$$?
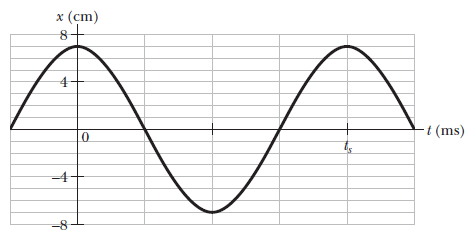
Above figure gives the position $$x(t)$$ of a block oscillating in SHM on the end of a spring ($$t_{s}=40.0ms$$). What are (a) the speed and (b) the magnitude of the radial acceleration of a particle in the corresponding uniform circular motion?
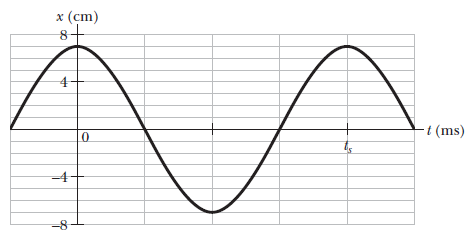
Above figure gives the position of a $$20g$$ block oscillating in SHM on the end of a spring. The horizontal axis scale is set by $$t_{s}=40.0ms$$. What are (a) the maximum kinetic energy of the block and (b) the number of times per second that maximum is reached? (Hint: Measuring a slope will probably not be very accurate. Find another approach).
A particle executes linear SHM with frequency $$0.25 Hz$$ about the point $$x=0$$. At $$t=0$$, it has displacement $$x=0.37cm$$ and zero velocity. For the motion, determine the (a) period, (b) angular frequency, (c) amplitude, (d) displacement $$x(t)$$, (e) velocity $$v(t)$$, (f) maximum speed, (g) magnitude of the maximum acceleration, (h) displacement at $$t=3.0s$$ and (i) speed at $$t=3.0s$$.
A $$3.0kg$$ particle is in simple harmonic motion in one dimension and moves according to the equation $$x=\left ( 5.0m \right )\cos \left [ \left ( \pi /3rad/s \right )t-\pi /4rad \right ]$$ with $$t$$ in seconds. (a) At what value of $$x$$ is the potential energy of the particle equal to half the total energy? (b) How long does the particle take to move to this position $$x$$ from the equilibrium position?
The tip of one prong of a tuning fork undergoes SHM of frequency $$1000Hz$$ and amplitude $$0.40mm$$. For this tip, what is the magnitude of the (a) maximum acceleration, (b) maximum velocity, (c) acceleration at tip displacement $$0.20mm$$ and (d) velocity at tip displacement $$0.20mm$$?
A block is in SHM on the end of a spring, with position given by $$x=x_{m}\cos \left ( \omega t+\phi \right )$$. If $$\phi=\pi/5rad$$, then at $$t=0$$ what percentage of the total mechanical energy is potential energy?
A $$1.2kg$$ block sliding on a horizontal frictionless surface is attached to a horizontal spring with $$k=480 N/m$$. Let $$x$$ be the displacement of the block from the position at which the spring is unstretched. At $$t=0$$ the block passes through $$x=0$$ with a speed of $$5.2 m/s$$ in the positive $$x$$ direction. What are the (a) frequency and (b) amplitude of the blocks motion? (c)Write an expression for $$x$$ as a function of time.
A $$2.0 kg$$ block executes SHM while attached to a horizontal spring of spring constant $$200 N/m$$. The maximum speed of the block as it slides on a horizontal frictionless surface is $$3.0m/s$$. What are (a) the amplitude of the blocks motion, (b) the magnitude of its maximum acceleration, and (c) the magnitude of its minimum acceleration? (d) How long does the block take to complete $$7.0$$ cycles of its motion?
What is the phase constant for SMH with $$a(t)$$ given in above figure, if the position function $$x(t)$$ has the form $$x=x_{m}\cos \left ( \omega t+\phi \right )$$ and as $$a_{s}=4.0m/s^{2}$$?
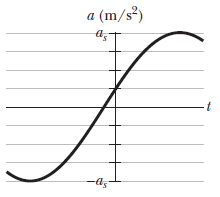
When a $$20N$$ can is hung from the bottom of a vertical spring, it causes the spring to stretch $$20cm$$. (a) What is the spring constant? (b) This spring is now placed horizontally on a frictionless table. One end of it is held fixed, and the other end is attached to a $$5.0N$$ can. The can is then moved (stretching the spring) and released from rest. What is the period of the resulting oscillation?
A plane eletromagnetic wave falls at right angles to the surface of a plane parallel plate of thickness $$l$$. The plate is made of non-magnetic substance whose permittivity decreases exponentially from a value $$\varepsilon_{1}$$ at the front surface down to a value $$\varepsilon_{2}$$ at the rear one. How long does it take a given wave phase to travel across this plate?
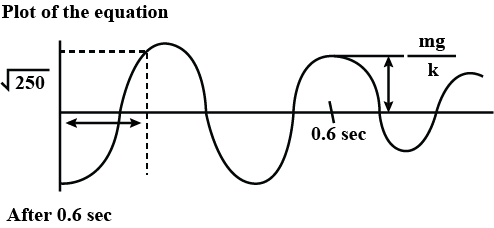
A block of mass m is suspended from the ceiling of a stationary elevator through a spring of spring constant k. Suddenly the cable breaks and the elevator starts falling freely. Show that the block now executes a simple harmonic motion of amplitude mg/k in the elevator.
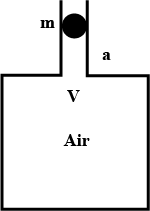
An air chamber having a volume V and a cross-sectional area of the neck is $$a$$ into which a ball of mass $$m$$ can move up and down without friction. Show that when the ball is pressed down a little and released, it executes $$SHM$$. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal.
A rigid rod of mass $$m$$ with a ball of mass $$M$$ attached to the free end is restrained to oscillate in a vertical plane. Find the natural frequency of oscillation.

Potential Energy(U) of a body of unit mass moving in a one-dimension conservative force field is given by $$U=(x^2-4x+3)$$. All units are in S.I.
(i) Find the equilibrium positions of the body.
(ii) Show that oscillations of the body about this equilibrium positions is simple harmonic motion & find its time period.
(iii) Find the amplitude of oscillations if speed of the body at equilibrium position is $$2\sqrt{6}$$ m/s.
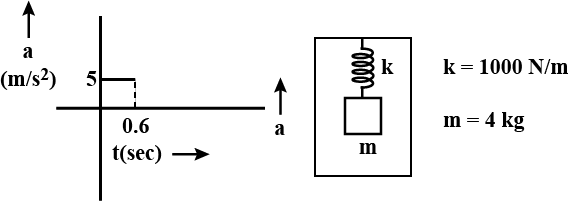
A spring block (force constant k=1000 N/m and mass m=4 kg) system is suspended from the ceiling of an elevaror such that block is initially at rest.The elevator begins to move upwards at t=0.Acceleration time graph of the elevator is shown in the figure. Draw the displacement x (from its initial position taking upwards as positive) vs time graph of the block with respect to the elevator starting from t=0 to t=1 sec.Take $$\pi^2=10$$.
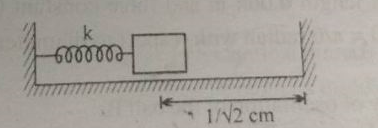
A block of mass $$0.9kg$$ attached to a spring of force constant $$k$$ is lying on a frictionless floor. The spring is compressed to $$\sqrt { 2 } cm$$ and the block is at a distance $$1/\sqrt { 2 } cm$$ from the wall as shown in the figure. When the block is released, it makes elastic collision with the wall and its period of motion is $$0.2sec$$. Find the approximate value of $$k$$.
A body is executing SHM under the action of force whose maximum magnitude is $$50N$$. Find the magnitude of force acting on the particle at the time when its energy is half kinetic and half potential.
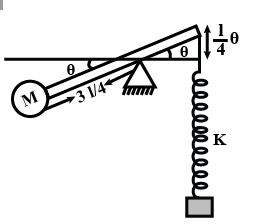
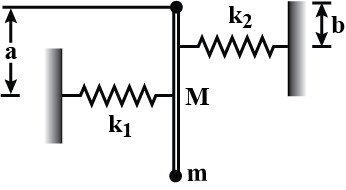
A rod of mass $$M$$ and length $$L$$ is hinged at its one end and carries a particle of mass $$m$$ at its lower end. A spring of force constant $${k}_{1}$$ is installed at distance $$a$$ from the hinge and another of force constant, $${k}_{2}$$ at a distance $$b$$ as shown in the figure. The whole arrangement rests on a smooth horizontal table top. Find the frequency of vibration.
A $$25kg$$ uniform solid sphere with a $$20cm$$ radius is suspended by a vertical wire such that the point of suspension is vertically above the centre of the sphere. A torque of $$0.10N-m$$ is required to rotate the sphere through an angle of $$1.0rad$$ and then the orientation is maintained. If the sphere is then released, its time period of the oscillation will be _____.
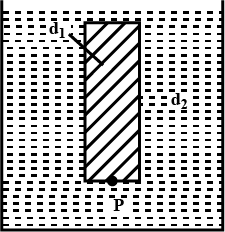
A thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density $$d_{1}$$ of the rod is smaller than the density $$d_{2}$$ of the liquid. The rod is displaced by a small angle $$\theta$$ from its equilibrium position and then released. Show that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters.
Earth revolves around sun in 365 days.Calculate its angular speed.
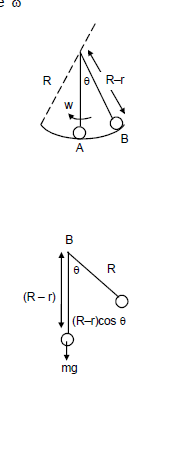
In the system shown in figure spring, pulley and strings are ideal and block is in equilibrium. Find period of small oscillations of block if it displaced and released.

An object of mass $$0.2kg$$ executes simple harmonic oscillation along x-axis with a frequency of $$( 25 \pi )$$ Hz. At the position $$x= 0.04$$, the object has Kinetic energy of $$0.5$$ J and potential energy $$0.4 J$$. The amplitude of oscillations is .............m.
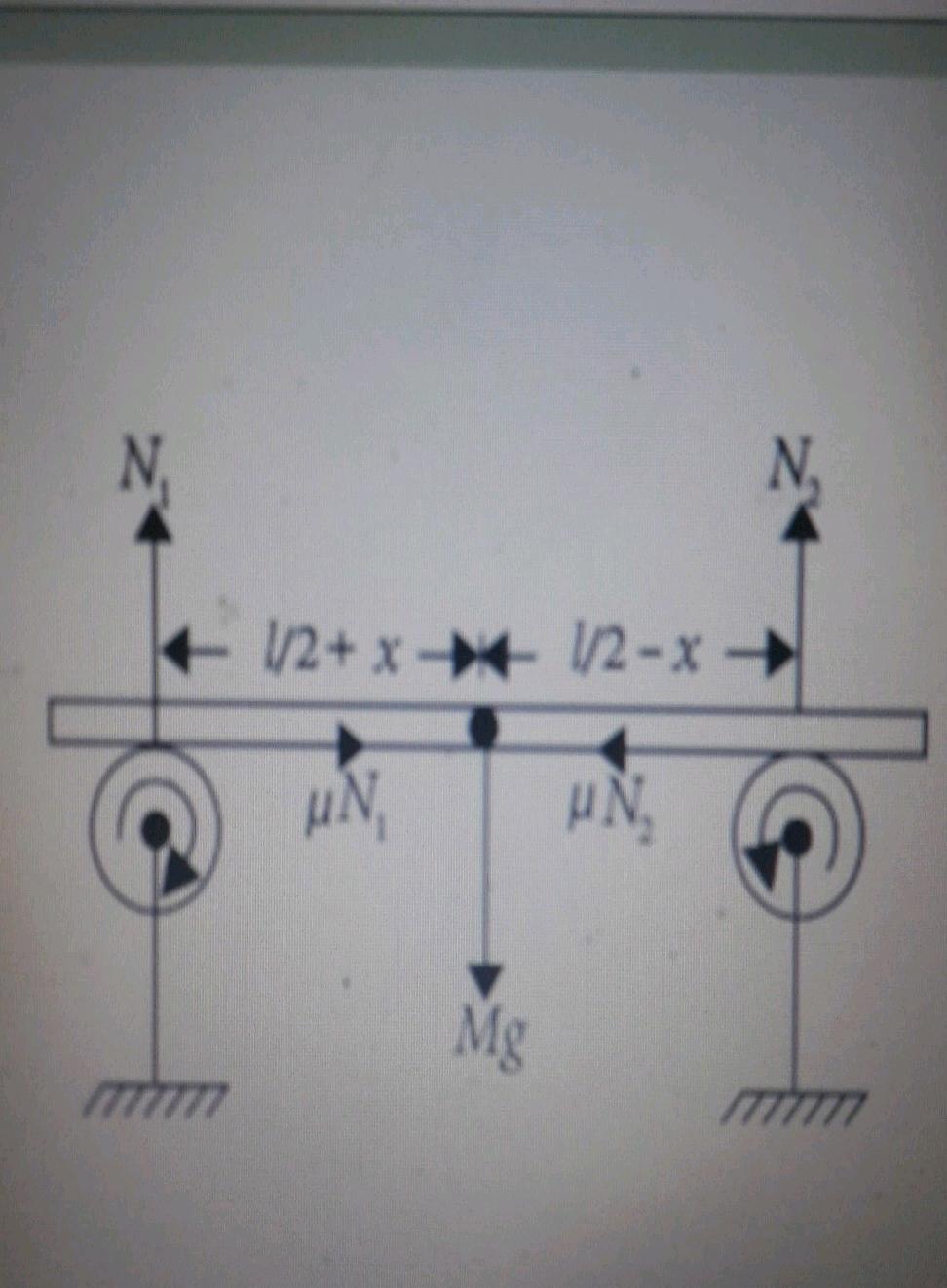
A uniform plate of mass M stays horizontally and symmetrically on two wheels rotating in opposite directions. The separation between the wheels is L. The friction coefficient between each wheel and the plate is $$\mu$$. Find the time period of oscillation of the plate if it is slightly displaced along its length and released.
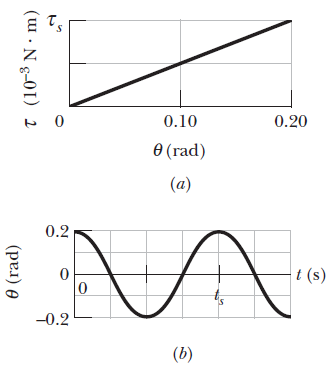
A torsion pendulum consists of a metal disk with a wire running through its center and soldered in place. The wire is mounted vertically on clamps and pulled taut. Above figure (a) gives the magnitude $$t$$ of the torque needed to rotate the disk about its center (and thus twist the wire) versus the rotation angle $$\theta$$. The vertical axis scale is set by $$\tau _{s}=4.0*10^{-3}N\cdot m$$. The disk is rotated to $$\theta=0.200rad$$ and then released. Above figure (b), shows the resulting oscillation in terms of angular position $$u$$ versus time $$t$$. The horizontal axis scale is set by $$t_{s}=0.40s$$. (a) What is the rotational inertia of the disk about its center? (b) What is the maximum angular speed $$d\theta /dt$$ of the disk? (Caution: Do not confuse the (constant) angular frequency of the SHM with the (varying) angular speed of the rotating disk, even though they usually have the same symbol $$\omega$$. Hint:The potential energy $$U$$ of a torsion pendulum is equal to $$\frac{1}{2}\kappa\theta ^{2}$$, analogous to $$U=\frac{1}{2}kx^{2}$$ for a spring).
A $$0.10 kg$$ block oscillates back and forth along a straight line on a frictionless horizontal surface. Its displacement from the origin is given by $$x=\left ( 10cm \right )\cos \left [ \left ( 10rad/s \right )t+\pi/2rad \right ]$$. (a) What is the oscillation frequency? (b) What is the maximum speed acquired by the block? (c) At what value of $$x$$ does this occur? (d) What is the magnitude of the maximum acceleration of the block? (e) At what value of $$x$$ does this occur? (f) What force, applied to the block by the spring, results in the given oscillation?
Write down the one-dimensional differential equation of a wave and examine which of the following are possible equations of the one-dimensional wave :
(i) y = 2 sinx cos ut
(ii) y = 5 sin 2x cos ut?
A simple pendulum performs S.H.M. of period $$ 4 $$ seconds . How much time after crossing the mean position, will the displacement of the bob be one third of its amplitude .
Class 11 Medical Physics Extra Questions
- Gravitation Extra Questions
- Kinetic Theory Extra Questions
- Laws Of Motion Extra Questions
- Mechanical Properties Of Fluids Extra Questions
- Mechanical Properties Of Solids Extra Questions
- Motion In A Plane Extra Questions
- Motion In A Straight Line Extra Questions
- Oscillations Extra Questions
- Systems Of Particles And Rotational Motion Extra Questions
- Thermal Properties Of Matter Extra Questions
- Units And Measurement Extra Questions
- Waves Extra Questions
- Work, Energy And Power Extra Questions