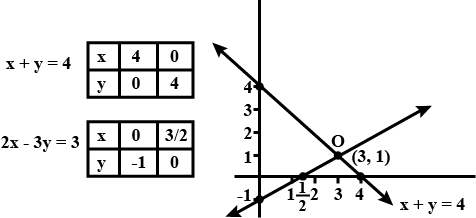
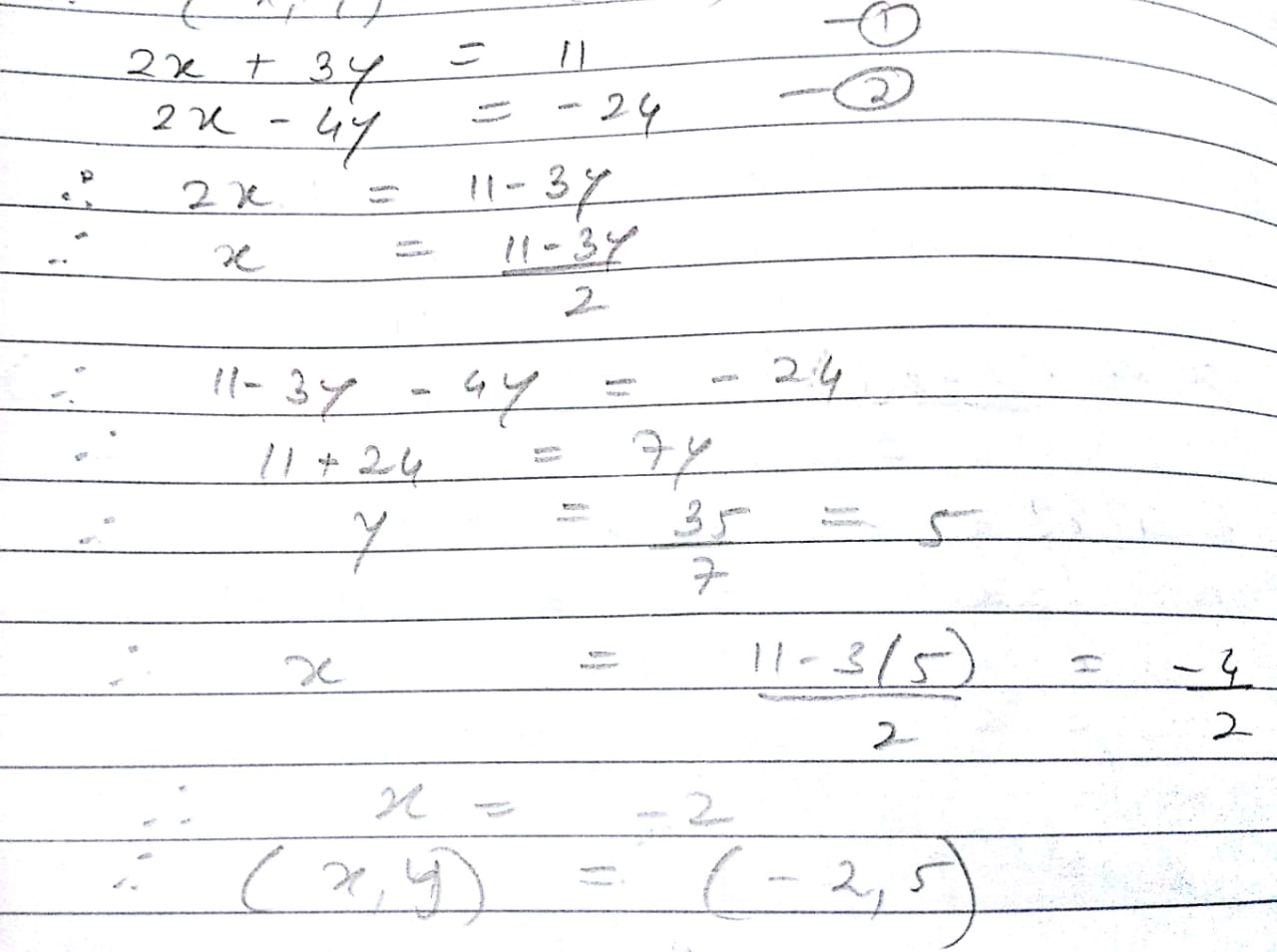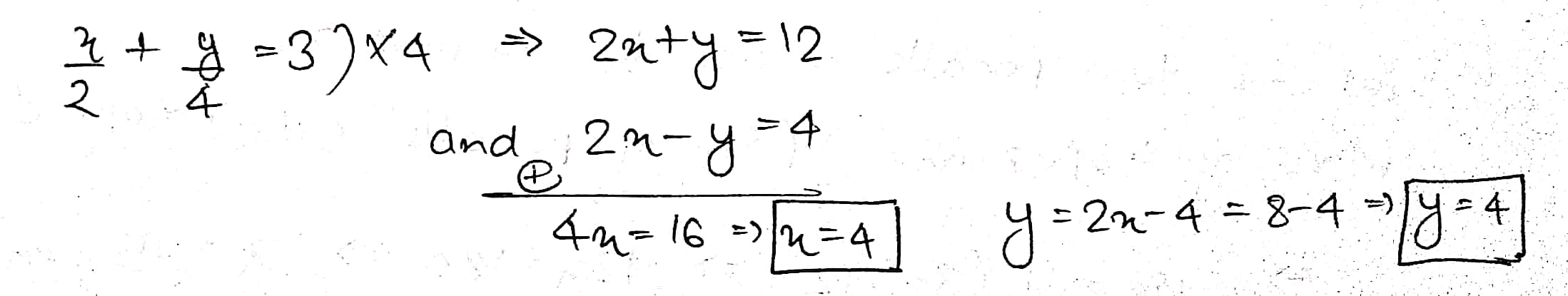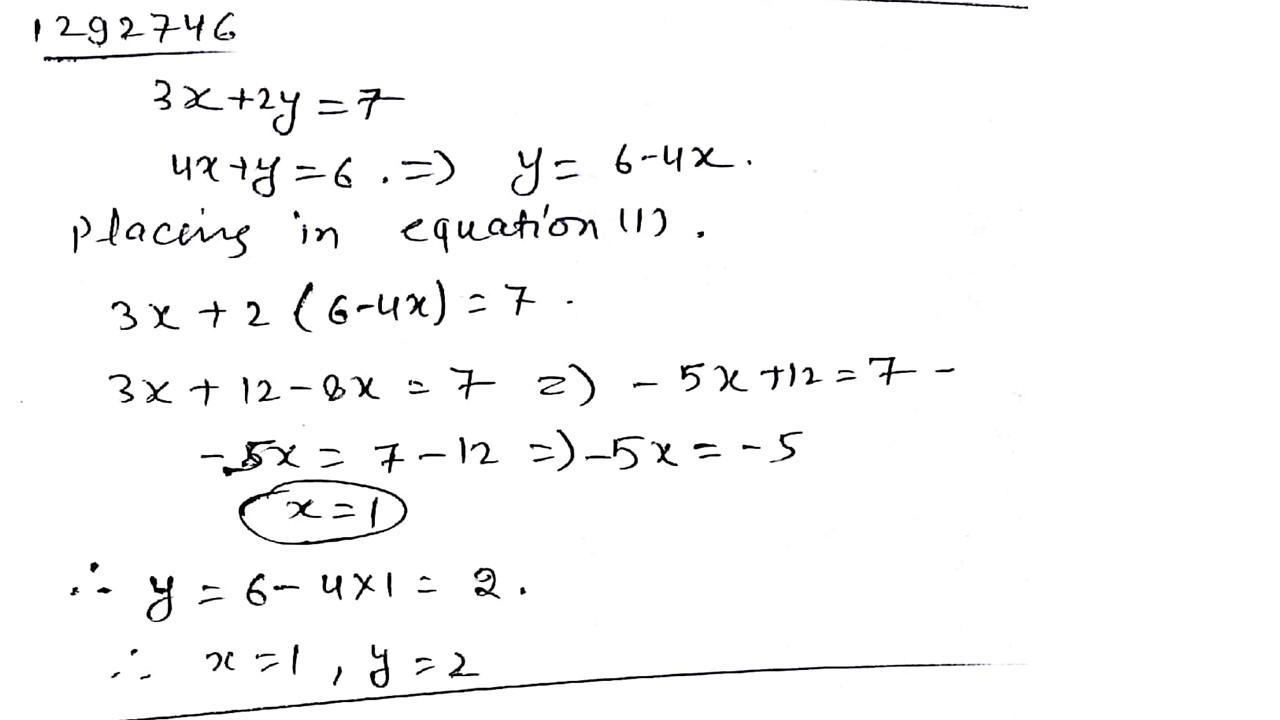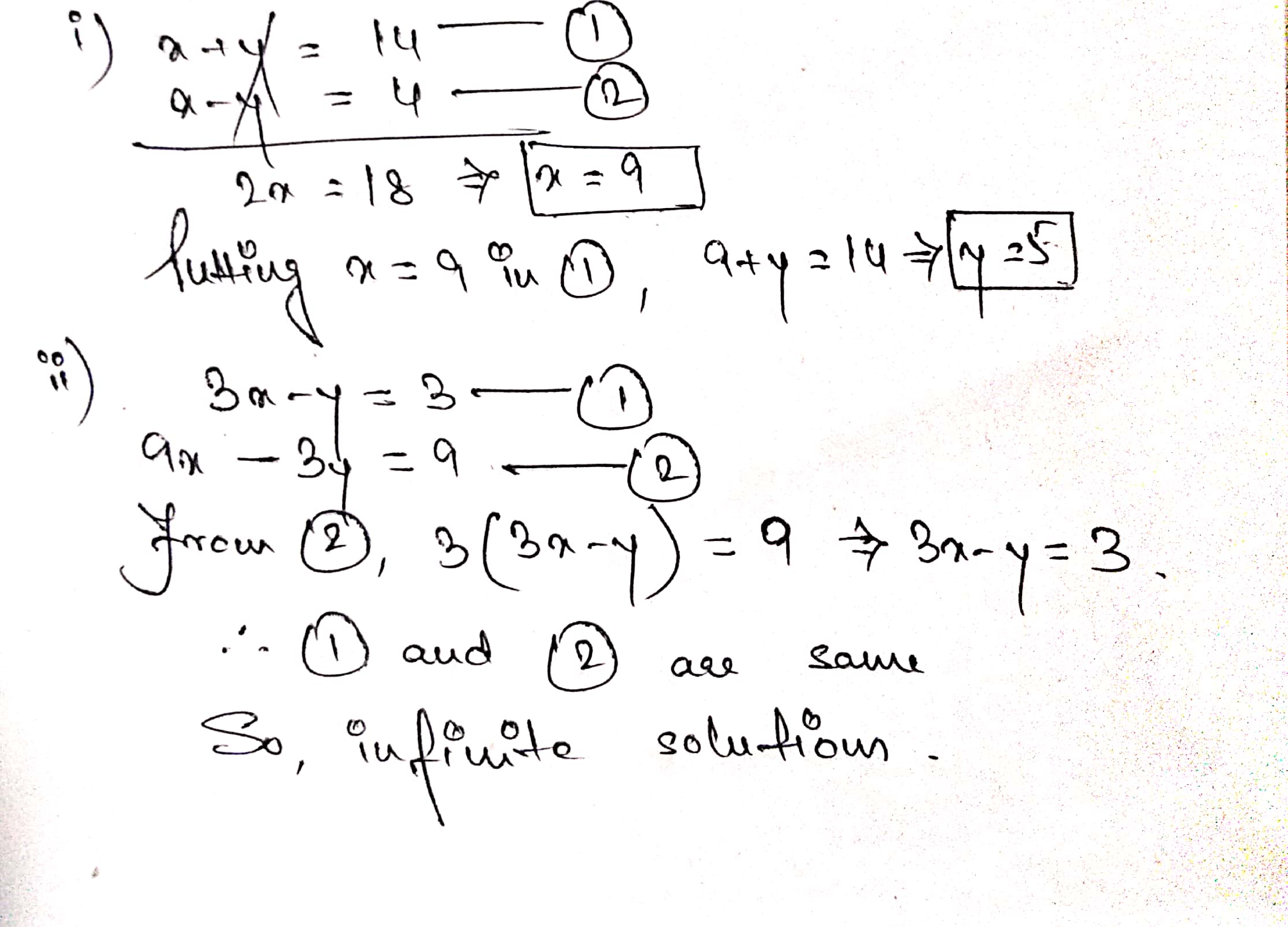Pair Of Linear Equations In Two Variables - Class 10 Maths - Extra Questions
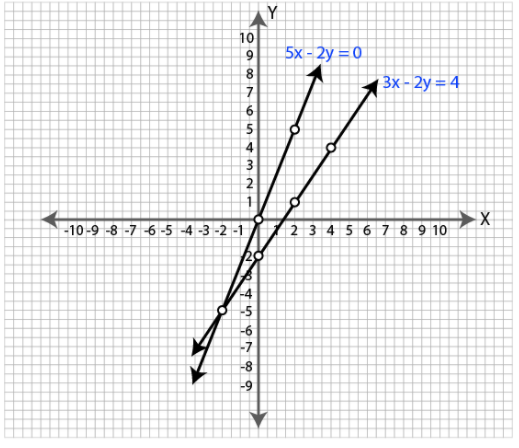
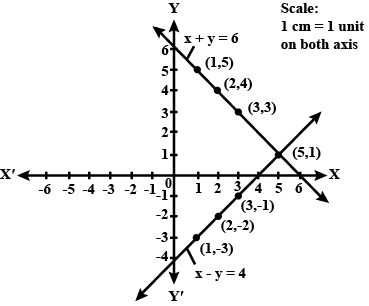
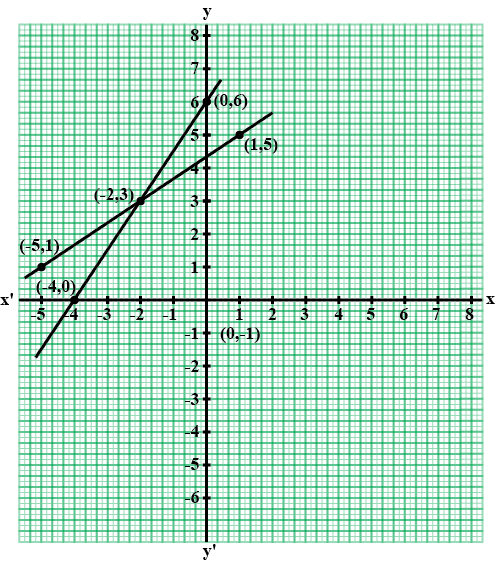
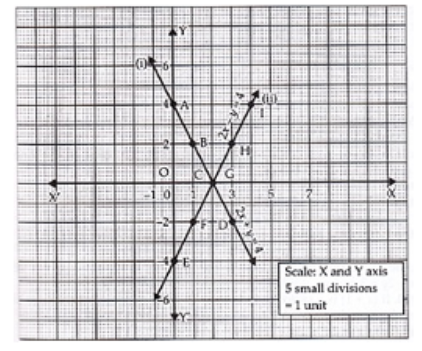
Solve the following equations graphically: $$3x-2y = 4$$, $$5x-2y = 0$$
$$3x-2y = 4$$ ..(i)
$$2y = 3x-4$$
$$y = (3x-4)/2$$
When $$x = 0,$$
$$y = (3×0-4)/2 = (0-4)/2 = -4/2 = -2$$
when $$x = 2,$$
$$y = (3×2-4)/2 = (6-4)/2 = 2/2 = 1$$
when $$x = 4,$$
$$y = (3×4-4)/2 = (12-4)/2 = 8/2 = 4$$
Plot the above points on graph. Join them.
$$5x-2y = 0$$ …(ii)
$$2y = 5x$$
$$y = 5x/2$$
When $$x = 0,$$
$$y = 0$$
When $$x = 2,$$
$$y = 5×2/2 = 5$$
When $$x = -2,$$
$$y = 5×-2/2 = -5$$
Plot the above points on graph. Join them.
It is clear from the graph that the two lines intersect at $$(-2,-5).$$
So the solution of the given equations are $$x = -2$$ and $$y = -5.$$
$$2y = 3x-4$$
$$y = (3x-4)/2$$
When $$x = 0,$$
$$y = (3×0-4)/2 = (0-4)/2 = -4/2 = -2$$
when $$x = 2,$$
$$y = (3×2-4)/2 = (6-4)/2 = 2/2 = 1$$
when $$x = 4,$$
$$y = (3×4-4)/2 = (12-4)/2 = 8/2 = 4$$
| $$x=$$ | $$0$$ | $$,2$$ | $$,4$$ |
| $$y=$$ | $$-2$$ | $$,1$$ | $$,4$$ |
$$5x-2y = 0$$ …(ii)
$$2y = 5x$$
$$y = 5x/2$$
When $$x = 0,$$
$$y = 0$$
When $$x = 2,$$
$$y = 5×2/2 = 5$$
When $$x = -2,$$
$$y = 5×-2/2 = -5$$
| $$x=$$ | $$0$$ | $$,2$$ | $$,-2$$ |
| $$y=$$ | $$0$$ | $$,5$$ | $$,-5$$ |
It is clear from the graph that the two lines intersect at $$(-2,-5).$$
So the solution of the given equations are $$x = -2$$ and $$y = -5.$$
Solve the following pairs of linear equations by substition method;
$$3x - y = 3$$
$$9x - 3y = 9$$
Solve the following pair of linear equations by substitution method:
$$x + y = 2m$$
$$mx - ny = m^2+n^2 $$
Solve the following pair of linear equations by substitution method:
$$\dfrac{x}{2} + y = 0.8$$
$$x + \dfrac{y}{2} = \dfrac{7}{10}$$
Solve the following pair of linear equations by substitution method:
$$\dfrac{x}{a} +\dfrac{y}{b} = 2 , a\neq 0,b \neq 0$$
$$ax - by = a^2 - b^2 $$
Solve graphically the following system of linear equations if it has unique solution :
$$3x + y = 2$$
$$6x + 2y = 1$$
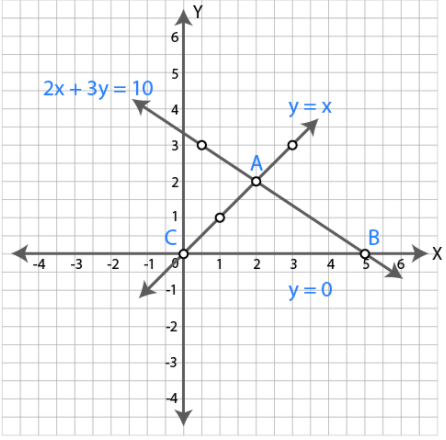
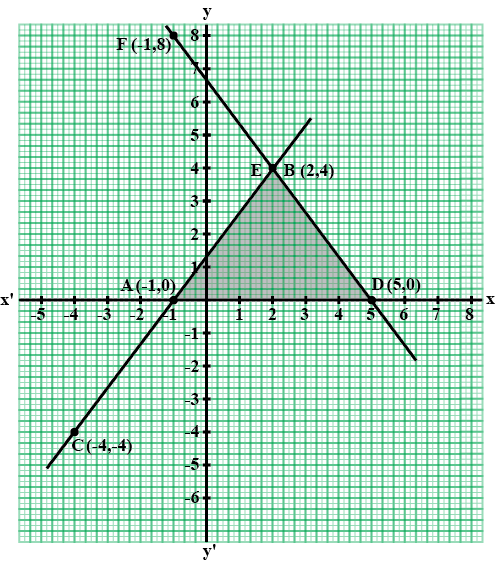
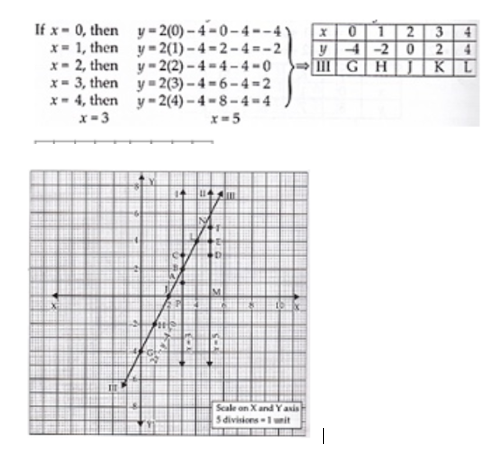
Find graphically the co-ordinates of the vertices of the triangle formed by the lines $$y = 0, y = x$$ and $$2x + 3y= 10$$. Hence find the area of the triangle formed by these lines.
$$y = 0 \quad ........(i)$$
The graph of $$y = 0$$ is the $$X$$ axis.
$$y = x \quad ........(ii)$$
When $$x = 1, y = 1.$$
When $$x = 2, y = 2.$$
When $$x = 3, y = 3.$$
Mark the above points on graph. Join them.
$$2x+3y = 10 \quad ....(iii)$$
$$3y = 10-2x$$
$$y = \dfrac{10-2x}{3}$$
When $$x = 0.5, y = \dfrac{(10-2×0.5)}{3} = \dfrac{10-1}{3} = \dfrac{9}{3} = 3$$
Mark the above points on graph. Join them.
From the graph, it is clear that the vertices of the triangle formed by the lines are $$A(2,2), B(5,0)$$ and $$C(0,0)$$.
Area of triangle formed by these lines $$=\dfrac{1}{2}\times base\times height$$
$$\Rightarrow \dfrac{1}{2}\times 5\times 2$$
$$\Rightarrow 5 $$ square units
Hence area of the triangle is $$5 $$ square units.
The graph of $$y = 0$$ is the $$X$$ axis.
$$y = x \quad ........(ii)$$
When $$x = 1, y = 1.$$
When $$x = 2, y = 2.$$
When $$x = 3, y = 3.$$
| $$x=$$ | $$1$$ | $$,2$$ | $$,3$$ |
| $$y=$$ | $$1$$ | $$,2$$ | $$,3$$ |
$$2x+3y = 10 \quad ....(iii)$$
$$3y = 10-2x$$
$$y = \dfrac{10-2x}{3}$$
When $$x = 0.5, y = \dfrac{(10-2×0.5)}{3} = \dfrac{10-1}{3} = \dfrac{9}{3} = 3$$
When $$x = 2, y = \dfrac{(10-2×2)}{3} = \dfrac{10-4}{3} = \dfrac{6}{3} = 2$$
When $$x = 5, y = \dfrac{10-2×5}{3} = \dfrac{10-10}{3} = 0$$
| $$x=$$ | $$0.5$$ | $$,2$$ | $$,5$$ |
| $$y=$$ | $$3$$ | $$,2$$ | $$,0$$ |
From the graph, it is clear that the vertices of the triangle formed by the lines are $$A(2,2), B(5,0)$$ and $$C(0,0)$$.
Area of triangle formed by these lines $$=\dfrac{1}{2}\times base\times height$$
$$\Rightarrow \dfrac{1}{2}\times 5\times 2$$
$$\Rightarrow 5 $$ square units
Hence area of the triangle is $$5 $$ square units.
Solve the following pair of linear equations by substitution method:
0.5x - 0.8y = 3.4
0.6x + 0.3y = 0.3
Solve the following pair of linear equations by substitution method:
$$S - t = 3$$
$$\dfrac{s}{3} + \dfrac{t}{2} = 6$$
Using the same axes of co-ordinates and the same unit, solve graphically.
$$x+y = 0, 3x 2y = 10$$
$$x+y = 0$$ ..(i)
$$y = -x$$
When $$x = -3,$$
$$y = 3$$
When $$x = -2,$$
$$y = 2$$
When $$x = -1,$$
$$y = 1$$
Mark the above points on graph. Join them.
$$3x-2y = 10$$ ..(ii)
$$3x= 2y+10$$
$$x = (2y+10)/3$$
When $$y = 1$$
$$x = (2×1+10)/3 = 12/3 = 4$$
When $$y = -2$$
$$x = (2×-2+10)/3 = 6/3 = 2$$
When $$y = 4$$
$$x = (2×4+10)/3 = 18/3 = 6$$
Mark the above points on graph. Join them.
It is clear from the graph that the two lines intersect at $$(2,-2).$$
So the solution of the given equations are $$x = 2$$ and $$y = -2$$.
$$y = -x$$
When $$x = -3,$$
$$y = 3$$
When $$x = -2,$$
$$y = 2$$
When $$x = -1,$$
$$y = 1$$
| $$x=$$ | $$-3$$ | $$,-2$$ | $$,-1$$ |
| $$y=$$ | $$3$$ | $$,2$$ | $$,1$$ |
$$3x-2y = 10$$ ..(ii)
$$3x= 2y+10$$
$$x = (2y+10)/3$$
When $$y = 1$$
$$x = (2×1+10)/3 = 12/3 = 4$$
When $$y = -2$$
$$x = (2×-2+10)/3 = 6/3 = 2$$
When $$y = 4$$
$$x = (2×4+10)/3 = 18/3 = 6$$
| $$x=$$ | $$4$$ | $$,2$$ | $$,6$$ |
| $$y=$$ | $$1$$ | $$,-2$$ | $$,4$$ |
It is clear from the graph that the two lines intersect at $$(2,-2).$$
So the solution of the given equations are $$x = 2$$ and $$y = -2$$.
Solve the following pair of linear equations by substitution method:
$$7x - 15y = 2$$
$$x + 2y = 3$$
Solve the following systems equations by eliminations method;
$$3x - 5y - 4 = 0...(i)$$
$$9x = 2y + 7....(ii)$$
Solve the following systems equations by eliminations method;
$$8x + 5y = 9$$
$$ 3x + 2y = 4$$
Solve the following systems equations by eliminations method;
$$0.4x + 1.5y = 6.5$$
$$ 0.3x - 0.2y = 0.9$$
Solve the following systems equations by eliminations method;
$$\sqrt{2}x - \sqrt{3}y = 0$$
$$ \sqrt{5}x + \sqrt{.2}y = 0$$
Solve the following systems equations by eliminations method;
$$2x + 3y = 8$$
$$4x + 6y =7 $$
Solve the following pair of linear equations by substitution method:
$$\dfrac{bx}{a} + \dfrac{ay}{b} = a^2 + b^2$$
$$x + y = 2ab $$
Solve graphically the following system of linear equations if is has unique solution:
$$2x - 6y + 10 = 0$$
$$3x - 9y + 15 =0$$
Solve the following systems equations by eliminations method;
$$3x + 4y - 10...(i)$$
$$2x - 2y = 2....(ii)$$
Solve the following systems equations by eliminations method;
$$2x + 3y = 46$$
$$ 3x + 5y = 74$$
Solve the following systems equations by eliminations method;
$$x + y = 5$$
$$2x - 3y = 4$$
The sum of two numbers is $$16$$ and the sum of their reciprocals is $$ 1 / 3 . $$ Find the numbers.
Solve the following equations by elimination method
$$\dfrac{1}{x} - \dfrac{1}{y} = 1$$
$$\dfrac{1}{x} + \dfrac{1}{y} = 7.x \neq 0.y \neq 0$$
Two positive numbers differ by 3 and their product isFind the numbers.
Solve the following equations bu elimination method:
$$99x + 101y = 499$$
$$101x + 99y = 501$$
Solve the following equations bu elimination method:
$$29x - 23y = 110$$
$$23x - 29y = 98$$
Solve the following systems of equations by elimination method:
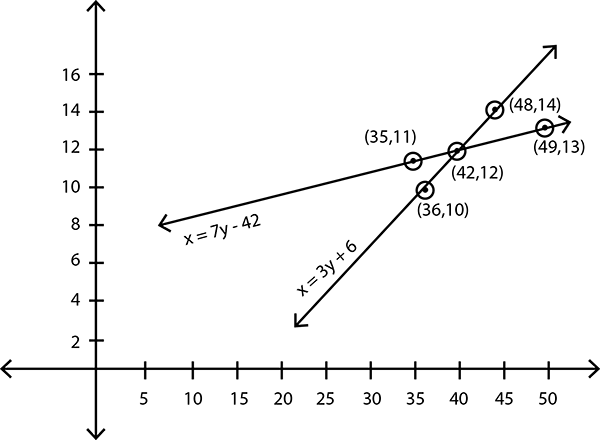
$$\dfrac{x}{6} + \dfrac{y}{15}= 4 , \dfrac{x}{3} - \dfrac{y}{12} =\dfrac{19}{4} $$
Solve the following system of equations by elimination method:
$$x + \dfrac{6}{y} = 6 ,3x - \dfrac{8}{y} = 5$$
Solve the following system of equations by elimination method:
$$2x + 5y = 1$$
$$2x + 3y = 3$$
Solve the following equations bu elimination method:
$$217x + 131y = 913$$
And $$131x + 217y = 827$$
Solve the following systems of equations by elimination method:
$$3x - \dfrac{8}{y} = 5$$$$ x - \dfrac{y}{3} = 3$$
Solve the following equations by elimination method
$$\dfrac{4}{x} + \dfrac{7}{y} = 11, \dfrac{3}{x} - \dfrac{5}{y} = -2\ \ (x = \neq 0.y \neq 0)$$
Two numbers differ by 2 and their product is $$ 360 . $$ Find the numbers.
Two numbers differ by 4 and their product is 192 . Find the numbers.
Solve the following equations by elimination method
$$x = y = 2xy$$ ,
$$x - y = 6xy$$
Solve the following equations by elimination method
$$5x + y = 19xy ,
7x - 2y = 8xy$$
Solve the following equations by elimination method
$$\dfrac{3a}{x} - \dfrac{2b}{y} + 5 = 0 , \dfrac{a}{x} - \dfrac{3b}{y} - 2 = 0(x = \neq 0.y \neq 0)$$
Solve the following equations by elimination method
$$x + y = 7xy$$ ,
$$2x - 3y = -xy$$
A number consisting of two digits is seven times the sum of its digits. When 27 is subtracted from the number, the digits are reversed. Find the number.
Solve the following equations by elimination method
$$\dfrac{2x + 5y}{xy} = 6 , \dfrac{4x - 5y}{xy} = -3(where x = \neq 0 and y \neq 0)$$
Solve the following equations by elimination method
$$\dfrac{2}{x} + \dfrac{3}{y} = 13$$
$$\dfrac{5}{x} - \dfrac{4}{y} = 2.x \neq 0.y \neq 0$$
The age of the father is 3 years more than 3 times the son's age. 3 years here, the age of the father will be 10 years more than twice the age of the son. Find their present ages.
For which value of a, the following system of linear equations has no solutions :
$$ax + 3y = a - 2, 12x + ay = a$$
Ten years hence, a man's age will be twice the age of his son. Ten years ago, the man was four times as old as his son. Find their present ages
Form the pairs of linear equations for the following problems and find their solutions by elimination method:
Aftab tells his daughter,"seven years ago, I was seven times as old as you were then, Also, three years from now I shall be three times as old as you will be.'Find their present ages.
The sum of the digits of a two-digit number is $$ 15 . $$ The number obtained by interchanging the digits exceeds the given number by $$ 9 . $$ Find the number.
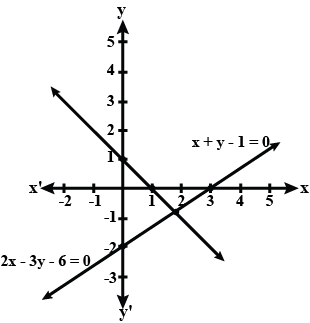
Check whether the following equations are consistent or inconsistent, solve them graphically.
$$5x - 3y = 11 $$ $$ -10x + 6 y = -22$$
$$5x - 3y = 11 ..... (i)$$
$$-10x + 6y = -22 ..... (ii)$$
From (i) and (ii)
$$\dfrac {a_{1}}{a_{2}} = \dfrac {5}{-10} = \dfrac {-1}{2}$$
$$\dfrac {b_{1}}{b_{2}} = \dfrac {-3}{6} = \dfrac{-1}{2}$$
$$\dfrac {c_{1}}{c_{2}} = \dfrac {11}{-22} = \dfrac {-1}{2}$$,
$$\therefore \dfrac {a_{1}}{a_{2}} = \dfrac {b_{1}}{b_{2}} = \dfrac {c_{1}}{c_{2}}$$
$$\Rightarrow$$ The linear equation are consistent and the lines are coincident
Hence they have infinitely many solutions .
Since, both lines (i) and (ii) are coincident, Hence represent the same line.
$$5x - 3y = 11 \Rightarrow y = \dfrac {5x - 11}{3} .... (\star)$$
(1) put $$x = 0$$ in $$(\star) \Rightarrow y = \dfrac {-11}{3}$$
(2) Put $$y = 0$$ in $$(\star) \Rightarrow 5x - 11 = 0\Rightarrow x = \dfrac {11}{5}$$
| $$x$$ | $$0$$ | $$\dfrac {11}{5}$$ |
| $$y$$ | $$\dfrac {-11}{3}$$ | $$0$$ |
The sum of two digit number and the number obtained by reversing the digit is 66 . If the digit of the number differ by 2 . Find the number . How many such numbers are there?
Form the pairs of linear equations for the following problems and find their solutions by elimination method:
Five years ago, Nuri was thrice as old as sonu. Ten years later, Nuri will be twice as old as sonu. How old are Nuri and Sonu?
Form the pairs of linear equations for the following problems and find their solutions by elimination method:
The difference between two numbers is 26 and one number is three times the other find them
Five years ago, A was thrice as old as B and ten years later, A shall be twice as old as B. What are the present ages of A and B?
Solve each of the following pairs of equation by reducing then to a pair of linear equations.
$$\dfrac{x+y}{xy}=2,\dfrac{x-y}{xy}=6$$
Check whether the following equations are consistent or inconsistent , solve them graphically.
2x -2y -2 = 0 and 4x - 4y -5 =0
2x -2y -2 = 0 and 4x - 4y -5 =0
$$ \dfrac{a_{1}}{a_{2}} = \dfrac{2}{4}=\dfrac{1}{2} ,\dfrac{b_{1}}{b_{2}}=\dfrac{-2}{-4}=\dfrac{1}{2} =\dfrac{c_{1}}{c_{2}}=\dfrac{-2}{-5}=\dfrac{2}{5} $$
$$ \therefore \dfrac{a_{1}}{a_{2}} = \dfrac{b_{1}}{b_{2}} \neq \dfrac{c_{1}}{c_{2}}$$
$$\therefore $$ the linear equation are consistent
$$\therefore $$ They have infinity solutions.
2x - 2y-2 = 0 4x - 4y -5 =0
x y (x ,y) x y (x,y)
0 -1 (0,-1) 2$$\frac{3}{4}$$
Solve each of the following pairs of equation by reducing then to a pair of linear equations.
$$\dfrac{1}{3x+y}+\dfrac{1}{3x-y}=\dfrac{3}{4},\dfrac{1}{2(3x+y)}-\dfrac{1}{2(3x-y)}=\dfrac{-1}{8}$$
Check whether the following equations are consistent or inconsistent , solve them graphically.
2x + y - 6 = 0 and 4x - 2y -4 = 0
2x + y - 6 = 0 and 4x - 2y -4 = 0
$$ \dfrac{a_{1}}{a_{2}} = \dfrac{2}{4}=\dfrac{1}{2} ,\dfrac{b_{1}}{b_{2}}=\dfrac{1}{-2} \dfrac{c_{1}}{c_{2}}=\dfrac{-6}{-4}=\dfrac{3}{2} $$
$$ \therefore \dfrac{a_{1}}{a_{2}} \neq \dfrac{b_{1}}{b_{2}}$$
$$\therefore $$ the linear equation are consistent
$$\therefore $$ They have infinity solutions.
2x + y = 6 4x - 2y = 4
x y (x ,y) x y (x,y)
3 0 (0,6) 0 2 (0,-2)
For solving each pair of equation, in this exercise, use the method of elimination by equating coefficients:
$$ \frac{x-y}{6}=2(4-x) $$
$$ 2x+y=3(x-4) $$
For solving each pair of equation, in this exercise, use the method of elimination by equating coefficients:
$$ \frac{1}{5}(x-2)=\frac{1}{4}(1-y) $$
$$ 26x+3y=-4 $$
For solving each pair of equation, in this exercise, use the method of elimination by equating coefficients:
$$ 3-(x-5)=4+2 $$
$$ 2(x+y)=4-3y $$
Solve each of the following pairs of equation by reducing then to a pair of linear equations.
$$\dfrac{10}{x+y}+\dfrac{2}{x-y}=4,\dfrac{15}{x+y}-\dfrac{5}{x-y}=-2$$
For solving each pair of equation, in this exercise, use the method of elimination by equating coefficients:
$$ \frac{5y}{2}-\frac{x}{3}=8 $$
$$ \frac{y}{2}+\frac{5x}{3}=12 $$
Check whether the following equations are consistent or inconsistent , solve them graphically.
$$ \dfrac{4}{3} x + 2y = 8 , 2x + 3y = 12$$
Solve the following simultaneous equation graphically.
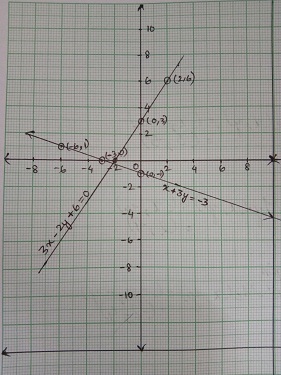
$$x - 3y = 1$$; $$3x - 2y + 4 =0$$
$$x - 3y = 1$$
$$y=\dfrac{x-1}{3}$$
$$|x=1,4,7|$$
$$|y=0,1,2|$$
$$3x - 2y + 4 = 0$$
$$y=\dfrac{3x+4}{2}$$
$$|x=0,2,4|$$
$$y=\dfrac{x-1}{3}$$
$$|x=1,4,7|$$
$$|y=0,1,2|$$
$$3x - 2y + 4 = 0$$
$$y=\dfrac{3x+4}{2}$$
$$|x=0,2,4|$$
$$|y=2,5,8|$$
The solution of the given equations is the point of intersection of the two lines i.e (-2, -1)
The solution of the given equations is the point of intersection of the two lines i.e (-2, -1)
The sum of digits of a two digit number is $$ 11 .$$If the digit at ten's place is increased by $$ 5 $$ and the digit at unit' place is decreased by $$ 5 $$ , the digits of the number are found to be reversed.Find the original number.
In the figure given above, ABCD is a parallelogram. Find the value of x and y.
Solve using the method of elimination by equating coefficients:
$$ 2x-3y-3=0 $$
$$ \dfrac{2x}{3}+4y+\dfrac{1}{2}=0 $$
$$ \dfrac{2x}{3}+4y+\dfrac{1}{2}=0 $$
From the pair of leaner equation in the following problems , and find their solution graphically .
5 pencils and 7 pens together cost Rs , 50 whereas 7 pencils and 5 pens together cost Rs . 46 .Find the cost of a pencils and on one pen .
Cost of each pencil be $$Rs 'X'$$
Cost of pen be $$Rs 'Y'$$
$$ 5x+ 7y = 50...........(i) $$
$$7x + 5y = 46 ...........(ii) $$
Equation (i)
Cost of pen be $$Rs 'Y'$$
$$ 5x+ 7y = 50...........(i) $$
$$7x + 5y = 46 ...........(ii) $$
Equation (i)
$$y=\dfrac{50-5x}{7}$$
$$x=3,0$$
$$y=5,7.143$$
Equation (ii)
$$y=\dfrac{46-7x}{5}$$
$$x=3,5$$
$$y=5,2.2$$
Point intersect $$(3,5)$$
$$\therefore x=3,y=5$$
Cost of each pencil be $$Rs 3$$
Cost of pen be $$Rs 5$$
Cost of pen be $$Rs 5$$
$$ A $$ and $$ B $$ both have some pencils . if $$ A $$ gives $$ 10 $$ pencils to $$ B $$ , then $$ B $$ will have twice as many as $$ A $$. And if $$ B $$ gives $$ 10 $$ pencils to $$ A $$, then they will have the same number of pencils . how many pencils does each have ?
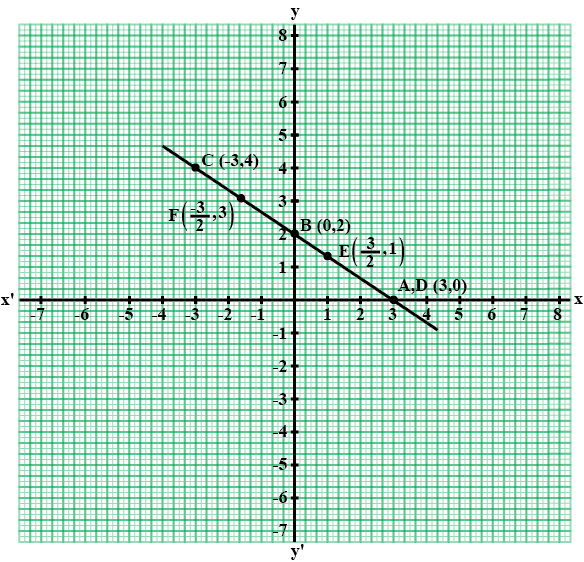
The graph of $$3x + 2y = 6$$ meets the $$x=axis$$ at point $$P$$ and the $$y-axis$$ at point $$Q$$. Use the graphical method to find the co-ordinates of points $$P$$ and $$Q$$.
by choosing a couple of values for $$x, -1, 0, 1$$
calculate the corresponding $$y$$ values.
$$x$$ $$-2$$ $$0$$ $$2$$
$$y$$ $$6$$ $$3$$ $$0$$
According to the graph, the line intersect $$x$$ axis at $$(2, 0)$$ and $$y$$ at $$(0, 3)$$.
The coordinates of $$P(x-axis)$$ and $$Q(y-axis)$$ are $$(2, 0)$$ and $$(0, 3)$$ respectively.
Solve:
$$ 11(x-5)+10(y-2)+54=0 $$
$$ 7(2x-1)+9(3y-1)=25 $$
Given the linear equation $$ 2x + 3 y - 8 = 0 $$ write linear equation in two variable such that the geometrical representation of the pair so formed is :
Intersecting lines
Solve the following pair of linear equation by the substituting method .
$$ 0 . 2x + 0 . 3y = 1.3 $$
$$ 0.4 x + 0.5y = 2.3 $$
Form the pair of linear equation for the following problems and find their solution by substituting method .
The taxi charges in a city consist of a fixed charge together with the charge for the distance covered . For distance of $$10 $$ the charge paid is Rs $$ 105 $$ and for a journey of $$15 $$ km the charge paid is Rs $$ 155 $$ . What are the fixed charges and the charge per km? How much does a person have to pay for travelling a distance of a $$ 25 $$ km ?
Solve the following pair of linear equation by the substituting method .
$$ \dfrac{3x}{2} - \dfrac{5y}{3} = -2 $$
$$ \dfrac{x}{3} + \dfrac{y}{2} = \dfrac{13}{2}$$
Form the pair of linear equation for the following problems and find their solution by substituting method .
The difference between two number is $$ 26 $$ and one number is three times the other. Find them.
Form the pair of linear equation for the following problems and find their solution by substituting method .
The larger of two supplementary angles axceeds the smaller by $$ 18 $$ degrees . Find them .
Solve the following pair of linear equation by the substituting method .
$$ s - t = 3 $$
$$ \dfrac{s}{3} + \dfrac{t}{2} = 6 $$
Solve the following pair of linear equation by the substituting method .
$$ 3x - y = 3 $$
$$ 9x - 3y = 9 $$
Solve the following pair of linear equation by the substituting method .
$$ x + y = 14 $$
$$ x - y = 14 $$
Form the pair of linear equation for the following problems and find their solution by substituting method .
The coach of a cricket them buys $$ 7 $$ bats and $$ 6 $$ balls for Rs $$ 3800 $$ . Later , she buys $$ 3$$ bats and $$ 5 $$ balls for Rs $$ 1750 $$ Find the cost of each bat and each ball.
Solve the following pair of linear equation by the substituting method .
$$ \sqrt{2x} + \sqrt{ 3y} = 0 $$
$$ \sqrt{3x} - \sqrt{8 y} = 0 $$
Form the pair of linear equation for the following problems and find their solution by substituting method .
A fraction becomes $$ \dfrac{9}{11} $$ if $$2 $$ is added to both the numerator and the denominator . If $$ 3 $$ is added to both the numerator and the denominator it becomes $$ \dfrac{5}{6} $$ .Find the fraction .
Write the number of solutions of the following pair of liner equations
Solve the following pair of linear equations graphically and write nature of solution.
$$2x - y = 4; x + y = -1$$
Given linear pair
$$2x - y = 4$$
$$2x - y - 4 = 0$$ ........(i)
$$x + y = -1$$
$$x + y + 1 = 0$$ .......(ii)
Comparing equation (i) and (ii) by linear pair
$$a_{1}x + b_{1}y + c_{1} = 0$$ and $$a_{2}x + b_{2}y + c_{2} = 0$$
$$a_{1} = 1, b_{1} = -1$$ and $$c_{1} = 4$$
$$a_{2} = 1, b_{2} = 1$$ and $$c_{1} = -1$$
$$\dfrac{a_1}{a_2} = \dfrac{2}{1}, \dfrac{b_1}{b_2} = \dfrac{-1}{1}$$
Thus $$\dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2}$$
Linear pair is consistent which all will have unique solutions.
Graphical Method:
By equation (i),
$$2x - y = 4$$
Putting $$x = 0, 2 \times 0 - y = 4$$
$$y = -4$$
Putting $$x = 1, 2 \times1 - y = 4$$
$$-y = 4 - 2=2$$
$$2x - y = 4$$
$$2x - y - 4 = 0$$ ........(i)
$$x + y = -1$$
$$x + y + 1 = 0$$ .......(ii)
Comparing equation (i) and (ii) by linear pair
$$a_{1}x + b_{1}y + c_{1} = 0$$ and $$a_{2}x + b_{2}y + c_{2} = 0$$
$$a_{1} = 1, b_{1} = -1$$ and $$c_{1} = 4$$
$$a_{2} = 1, b_{2} = 1$$ and $$c_{1} = -1$$
$$\dfrac{a_1}{a_2} = \dfrac{2}{1}, \dfrac{b_1}{b_2} = \dfrac{-1}{1}$$
Thus $$\dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2}$$
Linear pair is consistent which all will have unique solutions.
Graphical Method:
By equation (i),
$$2x - y = 4$$
Putting $$x = 0, 2 \times 0 - y = 4$$
$$y = -4$$
Putting $$x = 1, 2 \times1 - y = 4$$
$$-y = 4 - 2=2$$
$$y=-2$$
Putting $$x = 2, 2 \times 2 - y = 4$$
$$4 - y = 4$$
$$y = 0$$
Table $$: 1$$
$$x=0,1,2$$
Putting $$x = 2, 2 \times 2 - y = 4$$
$$4 - y = 4$$
$$y = 0$$
Table $$: 1$$
$$x=0,1,2$$
$$y=$$
By equation (ii),
$$x + y = -1$$
Putting $$x = 0. 0 + y = -1$$
$$y = -1$$
Putting $$x = 1, +1 + y = -1$$
$$y = -1 - 1$$
$$y = -2$$
Putting $$x = 2,$$
$$2 + y = -1$$
$$y = -3$$
Table $$: 2$$
$$x=0,1,2$$
By equation (ii),
$$x + y = -1$$
Putting $$x = 0. 0 + y = -1$$
$$y = -1$$
Putting $$x = 1, +1 + y = -1$$
$$y = -1 - 1$$
$$y = -2$$
Putting $$x = 2,$$
$$2 + y = -1$$
$$y = -3$$
Table $$: 2$$
$$x=0,1,2$$
$$y=-1,-2,-3$$
By plotting the points of Table and 2 we get two straight lines.
From above graph, it is clear that both the straight lines cut each other at point $$P(1, -2).$$
Thus, $$x = 1, y = -2$$ are required solution
By plotting the points of Table and 2 we get two straight lines.
From above graph, it is clear that both the straight lines cut each other at point $$P(1, -2).$$
Thus, $$x = 1, y = -2$$ are required solution
Solve the following pair of linear equations graphically and find the coordinates of the triangle so formed with the y-axis and the lines.
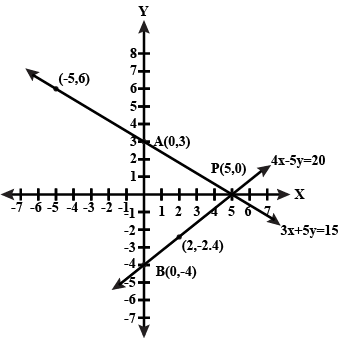
$$4x - 5y = 20,$$
$$3x + 5y = 15$$
Given, pair of linear equation
$$4x - 5y = 20$$ ..........(i)
and $$3x + 5y = 15$$ .........(ii)
From equation (i),
$$4x - 5y = 20$$
$$5y = 4x - 20$$
$$y = \dfrac{4x - 20}{5}$$
Putting $$x = 0,$$
$$y = \dfrac{4 \times 0 - 20}{5} = \dfrac{-20}{5}$$
$$y = -4$$
Putting $$x = 2, y = \dfrac{4 \times 2 - 20}{5} = \dfrac{8 - 20}{5} $$
$$y = \dfrac{-12}{5}$$
$$y = -2.4$$
Putting $$x = 5, y = \dfrac{4 \times 5 - 20}{5} = \dfrac{20 - 20}{5}$$
$$y = 0$$
Table : 1
$$x=0,\,\,\,2,\,\,\,5$$
$$4x - 5y = 20$$ ..........(i)
and $$3x + 5y = 15$$ .........(ii)
From equation (i),
$$4x - 5y = 20$$
$$5y = 4x - 20$$
$$y = \dfrac{4x - 20}{5}$$
Putting $$x = 0,$$
$$y = \dfrac{4 \times 0 - 20}{5} = \dfrac{-20}{5}$$
$$y = -4$$
Putting $$x = 2, y = \dfrac{4 \times 2 - 20}{5} = \dfrac{8 - 20}{5} $$
$$y = \dfrac{-12}{5}$$
$$y = -2.4$$
Putting $$x = 5, y = \dfrac{4 \times 5 - 20}{5} = \dfrac{20 - 20}{5}$$
$$y = 0$$
Table : 1
$$x=0,\,\,\,2,\,\,\,5$$
$$y=-4,-2.4,0$$
From equation (ii),.
$$3x + 5y = 15$$
$$5y = 15 - 3x$$
$$y = \dfrac{15 - 3x}{5}$$
Putting $$x = 0, y = \dfrac{15 - 3 \times 0}{5}$$
$$= \dfrac{15 - 0}{5}$$
$$y = 3$$
Putting $$x = 5, y = \dfrac{15 - 3 \times (5)}{5}$$
$$= \dfrac{15 - 15}{5}$$
$$y = 0$$
Putting $$x = -5, y = \dfrac{15 - 3 \times (-5)}{5}$$
$$= \dfrac{15 + 15}{5}$$
$$= 6$$
Table : 2
$$x=0,5,-5$$
From equation (ii),.
$$3x + 5y = 15$$
$$5y = 15 - 3x$$
$$y = \dfrac{15 - 3x}{5}$$
Putting $$x = 0, y = \dfrac{15 - 3 \times 0}{5}$$
$$= \dfrac{15 - 0}{5}$$
$$y = 3$$
Putting $$x = 5, y = \dfrac{15 - 3 \times (5)}{5}$$
$$= \dfrac{15 - 15}{5}$$
$$y = 0$$
Putting $$x = -5, y = \dfrac{15 - 3 \times (-5)}{5}$$
$$= \dfrac{15 + 15}{5}$$
$$= 6$$
Table : 2
$$x=0,5,-5$$
$$y=3,0,6$$
Plot the points obtained from Table (1) and (2) on graph paper. By joining these points two straight lines are obtained.
From the given graph it is clear that two lines intersect each other at point $$P(5, 0)$$
$$\therefore x = 5$$ and $$y = 0$$ are required solution.
$$(0, 3), (0, -4)$$ and $$(5, 0)$$ are co-ordinates of vertices of $$\Delta ABP$$ formed by two straight lines at y-axis.
Plot the points obtained from Table (1) and (2) on graph paper. By joining these points two straight lines are obtained.
From the given graph it is clear that two lines intersect each other at point $$P(5, 0)$$
$$\therefore x = 5$$ and $$y = 0$$ are required solution.
$$(0, 3), (0, -4)$$ and $$(5, 0)$$ are co-ordinates of vertices of $$\Delta ABP$$ formed by two straight lines at y-axis.
Solve the following pair of linear equations, graphically and find the coordinates of that points where lines represented by these cuts y-axis.
$$2x - 5y + 4 = 0; 2x + y - 8 = 0$$
Given pair of linear equations
$$2x - 5y + 4 = 0$$ ..........(i)
and $$2x + y - 8 = 0$$ ......(ii)
From equation (i),
$$2x - 5y + 4 = 0$$
$$2x = 5y - 4$$
$$x = \dfrac{5y - 4}{2}$$
Putting $$y = 0, x = \dfrac{5 \times 0 - 4}{2} = \dfrac{-4}{2} = -2$$
Putting $$y = 2, x = \dfrac{5 \times 2 - 4}{2} = \dfrac{6}{2} = 3$$
Putting $$y = -2, x = \dfrac{5 \times (-2) - 4}{2} = \dfrac{-14}{2} = -7$$
Table : 1
$$x=-2,3,7$$
$$2x - 5y + 4 = 0$$ ..........(i)
and $$2x + y - 8 = 0$$ ......(ii)
From equation (i),
$$2x - 5y + 4 = 0$$
$$2x = 5y - 4$$
$$x = \dfrac{5y - 4}{2}$$
Putting $$y = 0, x = \dfrac{5 \times 0 - 4}{2} = \dfrac{-4}{2} = -2$$
Putting $$y = 2, x = \dfrac{5 \times 2 - 4}{2} = \dfrac{6}{2} = 3$$
Putting $$y = -2, x = \dfrac{5 \times (-2) - 4}{2} = \dfrac{-14}{2} = -7$$
Table : 1
$$x=-2,3,7$$
$$y=0,2,-2$$
By equation (ii),
$$2x + y - 8 = 0$$
or $$y - 2 + 8 = 0$$
Putting $$x = 4, y = -2 \times 4 + 8$$
$$= -8 + 8 = 0$$
Putting $$x = 3, y = -2 \times 3 + 8$$
$$= -6 + 8$$
$$= 2$$
Putting $$x = 2, y = -2 \times 2 + 8$$
$$= -4 + 8$$
$$= 4$$
Table : 2
$$x=4,3,2$$
$$y=0,2,4$$
By equation (ii),
$$2x + y - 8 = 0$$
or $$y - 2 + 8 = 0$$
Putting $$x = 4, y = -2 \times 4 + 8$$
$$= -8 + 8 = 0$$
Putting $$x = 3, y = -2 \times 3 + 8$$
$$= -6 + 8$$
$$= 2$$
Putting $$x = 2, y = -2 \times 2 + 8$$
$$= -4 + 8$$
$$= 4$$
Table : 2
$$x=4,3,2$$
$$y=0,2,4$$
Plot the points from Table (1) and (2) on graph.
By joining these points two straight lines are obtained.
From given graph it is clear that two straight lines intersect each other at point $$P(3, 2).$$
$$\therefore$$ Its required solutions are $$x = 3$$ and $$y = 2.$$
and two straight lines cuts the y-axis at $$(0, 0.8)$$ and $$(0, 8).$$
By joining these points two straight lines are obtained.
From given graph it is clear that two straight lines intersect each other at point $$P(3, 2).$$
$$\therefore$$ Its required solutions are $$x = 3$$ and $$y = 2.$$
and two straight lines cuts the y-axis at $$(0, 0.8)$$ and $$(0, 8).$$
Solve the following pair of linear equations graphically and find the coordinates of that points where lines are represented by these cuts y-axis.
$$3x + 2 = 12; 5x - 2y = 4$$
Given pair of linear equations
$$3x + 2y = 12$$ .........(i)
and $$5x - 2y = 4$$ ...........(ii)
From equation (i),
$$3x + 2y = 12$$
$$2y = 12 - 3x$$
$$y = \dfrac{12 - 3x}{2}$$
Putting $$x = 0, y = \dfrac{12 - 3 \times 0}{2} = \dfrac{12}{2} = 6$$
$$3x + 2y = 12$$ .........(i)
and $$5x - 2y = 4$$ ...........(ii)
From equation (i),
$$3x + 2y = 12$$
$$2y = 12 - 3x$$
$$y = \dfrac{12 - 3x}{2}$$
Putting $$x = 0, y = \dfrac{12 - 3 \times 0}{2} = \dfrac{12}{2} = 6$$
Putting $$x = 2, y = \dfrac{12 - 3 \times 2}{2} = \dfrac{6}{2} = 3$$
Putting $$y = 4, y = \dfrac{12 - 3 \times 4}{2} = \dfrac{0}{2} = 0$$
Table : 1
$$x=0,2,4$$
Table : 1
$$x=0,2,4$$
$$y=6,3,0$$
From equation (ii),
$$5x - 2y = 4$$
$$2y = 5x - 4$$
$$y = \dfrac{5x - 4}{2}$$
Putting $$x = 2, y = \dfrac{5 \times 2 - 4}{2} = \dfrac{6}{2} = 3$$
$$5x - 2y = 4$$
$$2y = 5x - 4$$
$$y = \dfrac{5x - 4}{2}$$
Putting $$x = 2, y = \dfrac{5 \times 2 - 4}{2} = \dfrac{6}{2} = 3$$
Putting $$x = 0, y = \dfrac{5 \times 0 - 4}{2} = \dfrac{-4}{2} = -2$$
Putting $$x = 4, y = \dfrac{5 \times 4 - 4}{2} = \dfrac{16}{2} = 8$$
Table : 2
$$x=2,0,4$$
Table : 2
$$x=2,0,4$$
$$y=3,-2,8$$
Plot the points from Tables (1) and (2) on graph paper. By joining these points two straight lines are obtained.
From the above graph, it is clear that two straight lines intersect each other at point $$P(2, 3).$$
$$\therefore x = 2$$ and $$y = 3$$ are required solutions and two straight lines cut y-axis at $$(0, 6)$$ and $$(0, -2).$$
Plot the points from Tables (1) and (2) on graph paper. By joining these points two straight lines are obtained.
From the above graph, it is clear that two straight lines intersect each other at point $$P(2, 3).$$
$$\therefore x = 2$$ and $$y = 3$$ are required solutions and two straight lines cut y-axis at $$(0, 6)$$ and $$(0, -2).$$
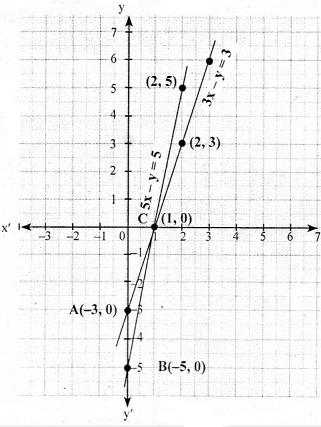
Draw the graphs of the equations 5x - y = 5 and 3x - y = 3 . Determine the coordinates of the vertices of the triangle formed by these lines and the y -axis .
vertices are A(-3,0),B(-5,0),C(1,0)
Roohl travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60km by bus and if she travels 100 km by bus , it takes 10 minutes longer . Find the speed of the train and the bus separately
Solve the following systems of simultaneous linear equations by the method of elimination by equating the coefficient.
$$\dfrac{x}{7} + \dfrac{y}{3} = 5$$
$$\dfrac{x}{2} - \dfrac{y}{9} = 6$$
Solve graphically:
$$3x - 4y = 1; -2x + \dfrac{8}{3}y = 5$$
From the given equation
$$3x - 4y = 1$$
$$\Rightarrow 4y = 3x - 1$$
$$\Rightarrow y = \dfrac{3x - 1}{4}$$
(Expressing y in terms of x) .......(i)
when $$x = 3, y = \dfrac{3 \times 3 - 1}{4} = \dfrac{8}{4} = 2$$
when $$x = 0, y = \dfrac{3 \times 0 - 1}{4} = -0.25$$
when $$x = -1, y = \dfrac{3 \times (-1) - 1}{4}$$
$$= \dfrac{-3 - 1}{4} = -1$$
Table for equation (i)
Similarly from equation
$$-2x + \dfrac{8}{3}y = 5$$
$$\Rightarrow -6x + 8y = 15$$
$$\Rightarrow 8y = 15 + 6x$$
$$\Rightarrow y = \dfrac{15 + 6x}{8}$$ ..........(i)
when $$x = 0, y = \dfrac{15 + 6 \times 0}{8} = \dfrac{15}{8} = 1.8$$
when $$x = -2.5, y =\dfrac{15+6\times(-2.5)}{8}$$
$$3x - 4y = 1$$
$$\Rightarrow 4y = 3x - 1$$
$$\Rightarrow y = \dfrac{3x - 1}{4}$$
(Expressing y in terms of x) .......(i)
when $$x = 3, y = \dfrac{3 \times 3 - 1}{4} = \dfrac{8}{4} = 2$$
when $$x = 0, y = \dfrac{3 \times 0 - 1}{4} = -0.25$$
when $$x = -1, y = \dfrac{3 \times (-1) - 1}{4}$$
$$= \dfrac{-3 - 1}{4} = -1$$
Table for equation (i)
| $$x=$$ | $$3,$$ | $$0,$$ | $$-1$$ |
| $$y=$$ | $$2,$$ | $$-0.25,$$ | $$-1$$ |
$$-2x + \dfrac{8}{3}y = 5$$
$$\Rightarrow -6x + 8y = 15$$
$$\Rightarrow 8y = 15 + 6x$$
$$\Rightarrow y = \dfrac{15 + 6x}{8}$$ ..........(i)
when $$x = 0, y = \dfrac{15 + 6 \times 0}{8} = \dfrac{15}{8} = 1.8$$
when $$x = -2.5, y =\dfrac{15+6\times(-2.5)}{8}$$
$$=\dfrac{15-15}{8}=0$$
$$\Rightarrow x = \dfrac{-15}{6}$$
$$\Rightarrow x = -2.5$$
Table for equation (ii)
Now plotting and joining the points from table (i) and (ii) on the same graph paper we find that these lines are parallel to each other it means no solution.
Hence, the system of equations has no solutions.
$$\Rightarrow x = \dfrac{-15}{6}$$
$$\Rightarrow x = -2.5$$
Table for equation (ii)
| $$x=$$ | $$0,$$ | $$-2$$.$$5$$ |
| $$y=$$ | $$1.8,$$ | $$0$$ |
Hence, the system of equations has no solutions.
Solve the following systems of simultaneous linear equations by the method of elimination by equating the coefficient.
$$2x + y = 13$$
$$5x - 3y = 16$$
Solve the following systems of simultaneous linear equations by the method of substitution.
$$8x + 5y = 9$$
$$3x + 2y = 4$$
Solve the following systems of simultaneous linear equations by the method of substitution.
$$3x + 2y = 11$$
$$2x + 3y = 4$$
Solve the following systems of simultaneous linear equations by the method of substitution.
$$4x - 5y = 39$$
$$2x - 7y = 51$$
Solve the following systems of simultaneous linear equations by the method of substitution.
$$x + 2y = -1$$
$$2x - 3y = 12$$
Solve the following systems of simultaneous linear equations by the method of elimination by equating the coefficient.
$$0.4x + 0.3y = 1.7$$
$$0.7x - 0.2y = 0.8$$
Solve the following systems of simultaneous linear equations by the method of substitution.
$$5x - 2y = 19$$
$$3x + y = 18$$
Solve the following systems of simultaneous linear equations by the method of elimination by equating the coefficient.
$$11x + 15y = -23$$
$$7x - 2y = 20$$
Solve the following systems of simultaneous linear equations by the method of elimination by equating the coefficient.
$$\dfrac{1}{2x} - \dfrac{1}{y} = -1$$
$$\dfrac{1}{x} + \dfrac{1}{2y} = 8$$
Solve the following systems of simultaneous linear equations by the method of elimination by equating the coefficient.
$$\dfrac{5}{x + y} - \dfrac{2}{x - y} = -1$$
$$\dfrac{15}{x + y} + \dfrac{7}{x - y} = 10$$
Solve the following systems of simultaneous linear equations by the method of elimination by equating the coefficient.
$$3x - 7y + 10 = 0$$
$$y - 2x = 3$$
Solve the following system of equations
$$2x + 3y = 9$$
$$3x + 4y = 5$$
Solve the following systems of simultaneous linear equations by the method of elimination by equating the coefficient.
$$x + 2y = \dfrac{3}{2}$$
$$2x + y = \dfrac{3}{2}$$
A two digit number is $$4$$ times its sum of digits and $$2$$ times the product of its digits. Find the number.
Solve the question :
Thilo and Toby buy some boats and trains from the toy shop.
The cost of one boat is b cents and the cost of one train is t cents.
(i) Toby buys $$3$$ boats and $$4$$ trains for $$ $5.70$$.
Complete this equation.
$$3b + 4t $$ = ..................
(ii) Thilo buys $$1$$ boat and $$2$$ trains for $$ $2.40$$.
Write this information as an equation.
................... = ......................
(iii) Solve your two equations to find the cost of a boat and the cost of a train.
You must show all your working.
The difference between two numbers is $$26$$ and the larger number exceeds thrice of the smaller number by $$4$$. Find the numbers.
Solve the following systems of simultaneous linear equations by the method of elimination by equating the coefficient.
$$8v - 3u = 5uv$$
$$6v - 5u = -2uv$$
Solve for 'u' and 'v', $$2(3u-v)=5uv$$; and $$2(u+3v)=5$$uv.
Determine the point on the graph of the linear equation $$2x+5y=19$$, whose ordinate is $$1\dfrac{1}{2}$$ times its abscissa.
Solve the following simultaneous equations
$$\dfrac {1}{2}x-y=\dfrac {5}{2};x+\dfrac {1}{3}y=\dfrac {8}{3}$$
Solve the following pairs of equations by reducing them to a pair of linear equations:
(i) $$\dfrac{1}{2x}+\dfrac{1}{3y}=2 ; \dfrac{1}{3x}+\dfrac{1}{2y}=\dfrac{13}{6}$$
(ii) $$\dfrac{2}{\sqrt{x}}+\dfrac{3}{\sqrt{y}}=2 ; \dfrac{4}{\sqrt{x}}-\dfrac{9}{\sqrt{y}}=-1$$
(iii) $$\dfrac{4}{x}+3y=14 ; \dfrac{3}{x}-4y=23$$
(iv) $$\dfrac{5}{x-1}+\dfrac{1}{y-2}=2 ; \dfrac{6}{x-1}-\dfrac{3}{y-2}=1$$
(v) $$\dfrac{7x-2y}{xy}=5 ; \dfrac{8x+7y}{xy}=15$$
(vi) $$6x + 3y = 6xy ; 2x + 4y = 5xy$$
(vii) $$\dfrac{10}{x+y}+\dfrac{2}{x-y}=4 ; \dfrac{15}{x+y}-\dfrac{5}{x-y}=-2$$
(viii) $$\dfrac{1}{3x+y}+\dfrac{1}{3x-y}=\dfrac{3}{4} ; \dfrac{1}{2(3x+y)}-\dfrac{1}{2(3x-y)}=\dfrac{-1}{8}$$
Mary told her daughter, Seven years ago, I was seven times as old as you were then. Also three years from now, I shall be three times as old as you will be, Find the present age of Mary and her daughter.
Solve:
$$\dfrac{2}{x}+\dfrac{2}{3y}=\dfrac{1}{16}$$: $$\dfrac{3}{x}+\dfrac{2}{y}=0$$
A two -digit number is obtained by either multiplying the sum of the digits by $$ 8 $$ and then subtracting $$ 5 $$ or by multiplying the difference of the digits by $$ 16 $$ and then adding $$ 3 $$ . find the number.
From the pair of linear equations in the following problems , and find their solutions ( if they exist ) by the elimination method :
If we add 1 to the numerator and subtract 1 from the denominator , a fraction reduces toIt becomes $$ \dfrac{1}{2}$$ if we only add 1 to the denominator . What is the fraction ?
From the pair of linear equations in the following problems , and find their solutions ( if they exist ) by the elimination method :
Five years ago , Nuri was thrice as old as Sonu . Ten years later , Nuri will be twice as old as sonu . How old are Nuri and Sonu ?
State whether True or False.There is no common point to the graph of the equation: $$y = 2x + 3$$ and $$y = -2x + 3$$.
Given equations:
On putting the value of $$x = 0$$ in both the equations, we get
$$y = 3$$ and $$y = 3$$.
So, at $$x = 0$$, both the equations will meet at $$y = 3$$ on the graph.
Hence, the given statement is false.
$$y = 2x + 3$$(green line)
and
$$y = -2x + 3$$(blue line)
On putting the value of $$x = 0$$ in both the equations, we get
$$y = 3$$ and $$y = 3$$.
So, at $$x = 0$$, both the equations will meet at $$y = 3$$ on the graph.
Hence, the given statement is false.
Find the value of $$x + y$$, if
$$12 x + 13 y = 29$$
and $$13x + 12y = 21$$
Verify if the following simultaneous equations are consistent or inconsistent.
I. $$2x+5y=17$$, $$5x+3y=14$$
II. $$2x+6y=7$$, $$6x+18y=10$$
If $$x + y = 5$$ and $$x = 3$$, then the value of $$y$$.
Find the value of $$k$$ for which the given simultaneous equations have infinitely many solutions: $$4x+y=7, 16x+ky=28$$.
Solve the following simultaneous equations using graphical method
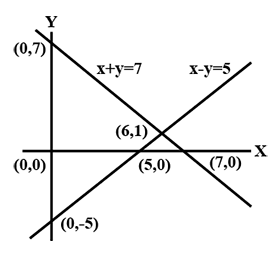
$$x + y = 7$$
$$x - y = 5$$
Clearly, the graphs cut at $$x=6$$ and $$y=1$$.
Therefore, solution is $$x=6$$ and $$y=1$$
Therefore, solution is $$x=6$$ and $$y=1$$
Solve the pair of equations by Elimination method.
$$2x + y - 5 = 0, \quad 3x - 2y - 4 = 0$$
Solve the following equations using graphical method.
$$x + y = 6$$
$$x - y = 4$$
Given: (1) $$x + y = 6$$
$$\therefore y = 6 -x$$
(2) $$x - y = 4$$
$$\therefore y = x - 4$$
$$\therefore y = 6 -x$$
| $$x$$ = | $$1$$ | $$2$$ | $$3$$ |
| $$y$$ = | $$5$$ | $$4$$ | $$3$$ |
$$(x, y)$$ | = $$(1, 5)$$ | $$(2, 4)$$ | $$(3, 3)$$ |
(2) $$x - y = 4$$
$$\therefore y = x - 4$$
| $$x$$ = | $$1$$ | $$2$$ | $$3$$ |
| $$y$$ = | $$-3$$ | $$-2$$ | $$-1$$ |
$$(x, y)$$ = | $$(1, -3)$$ | $$(2, -2)$$ | $$(3, -1)$$ |
From the graph, it can be seen clearly that $$(x,y) = (5,1)$$ is the solution to the pair of simultaneous equations
Solve the following system of equations.
$$7x - 2y = 1$$
$$3x + 4y = 15$$
Solve graphically the equations $$2x-y=1$$; $$x+2y=8$$
We find three points for each equation, by choosing three values of $$x$$ and computing the corresponding $$y$$ values. We'll put our results in tables.
Line 1: $$2x-y=1$$
$$y=2x-1$$
Substituting $$x=-1, 0, 1$$ in the above equation, we find
Line 2: $$x+2y=8$$
$$2y=-x+8 \Rightarrow y=-\dfrac{x}{2}+4$$
Substituting $$x=-2, 0, 2$$ in above equation, we get
We plot the points $$\left( -1,-3 \right) $$, $$\left( 0,-1 \right)$$ and $$ \left( 1,1 \right)$$ in a graph sheet and draw the line through them. Next, we plot the points $$ \left( -2,5 \right) $$, $$\left( 0,4 \right)$$ and $$ \left( 2,3 \right)$$ in the same graph sheet and draw the line through them. We find that the two graphs are intersecting at the point $$ \left( 2,3 \right) $$. Hence, the system of equations has only one solution (unique solution|) and the solution is $$x=2$$, $$y=3$$. Therefore the solution is $$\left( 2,3 \right) $$.
Line 1: $$2x-y=1$$
$$y=2x-1$$
Substituting $$x=-1, 0, 1$$ in the above equation, we find
| $$y=2x-1$$ |
| $$x$$ | $$-1$$ | $$0$$ | $$1$$ |
| $$2x$$ | $$-2$$ | $$0$$ | $$2$$ |
| $$y=2x-1$$ | $$-3$$ | $$-1$$ | $$1$$ |
$$2y=-x+8 \Rightarrow y=-\dfrac{x}{2}+4$$
Substituting $$x=-2, 0, 2$$ in above equation, we get
| $$y=-\dfrac{x}{2}+4$$ |
| $$x$$ | $$-2$$ | $$0$$ | $$2$$ |
| $$-\dfrac{x}{2}$$ | $$1$$ | $$0$$ | $$-1$$ |
| $$y=-\dfrac{x}{2}+4$$ | $$5$$ | $$4$$ | $$3$$ |
Solve the following systems of equations graphically:
$$3x+y+1=0$$
$$2x-3y+8=0$$
Given: equations of two lines: $$3x+y+1=0$$ and $$2x-3y+8 =0$$
(1) Intercept of line $$3x+y+1=0$$
at $$ x = 0 , y = -1 $$
at $$ y=0, x = \dfrac{-1}{3}$$
Now plot the first line on the graph using intercepts.
(2) Intercepts of the line $$2x-3y+8 = 0$$
at $$x=0, y=\dfrac{8}{3}$$
at $$y = 0, x = -4$$
Now plot the second line on the graph using intercepts.
Solve the following systems of equations graphically:
$$x+y=6$$
$$x-y=2$$
We can see that two lines intersect at a point $$x=4,y=2$$
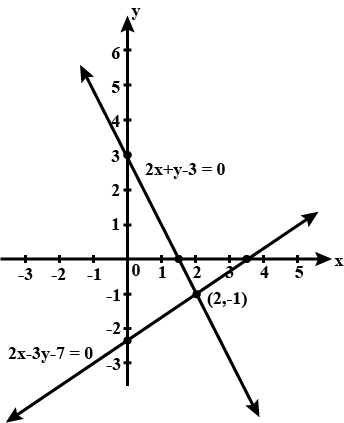
Solve the following systems of equations graphically:
$$2x+y-3=0$$
$$2x-3y-7=0$$
We can see that two lines intersect at a point $$x=2,y=-1$$
Solve the following systems of equations graphically:
$$x+y=4$$
$$2x-3y=3$$
We can see that two lines intersect at a point $$x=3,\,y=1$$
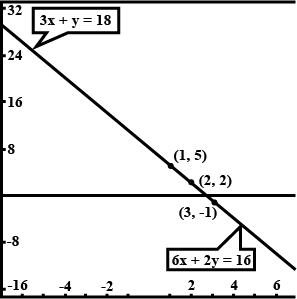
Show graphically that each one of the following systems of equations has infinitely many solutions:
$$x-2y+11=0$$
$$3x-6y+33=0$$
Both lines have same x-intercept and same y-intercept
x-intercept =-11
y-intercept =$$\dfrac {11}{2}$$
And both lines have same Slope
Slope =$$\dfrac {-1}{-2}=\dfrac {1}{2}$$
$$\Rightarrow $$both lines coincide and have infinite solutions
Show graphically that each one of the following systems of equations has infinitely many solutions:
$$3x+y=8$$
$$6x+2y=16$$
| x | 1 | 3 |
| y | 5 | -1 |
Both lines have same x-intercept and same y-intercept
x-intercept =$$\dfrac{8}{3}$$
y-intercept =6
And both lines have same Slope
Slope =$$\dfrac {-3}{1}=\dfrac {-6}{2}$$
$$\Rightarrow $$both lines coincide and therefore they have infinite intersection points
$$\therefore $$this system has infinite solutions
Find the value of a if the three equations are consistent
$$(a + 1)^3 x + (a + 2)^3 y = (a + 3)^3$$
$$(a + 1) x + (a + 2) y = a + 3$$
$$x + y = 1$$.
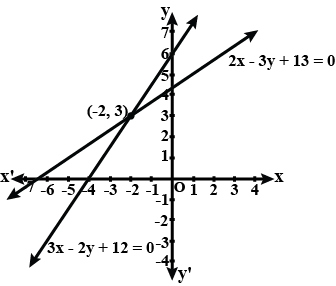
Solve the following systems of equations graphically:
$$2x-3y+13=0$$
$$3x-2y+12=0$$
We can see that two lines intersect at a point $$x=-2,\,y=3$$
Show graphically that each one of the following systems of equations has infinitely many solutions:
$$x-2y=5$$
$$3x-6y=15$$
Both lines coincide each other and has infinite solutions
Both lines same slopes, same x-intercept and same y-intercept
Solve the following systems of equations graphically:
$$2x+3y=4$$
$$x-y+3=0$$
We can see that two lines intersect at a point $$x=-1,\,y =2$$
Determine, by drawing graphs, whether the following system of linear equation has a unique solution or not:
$$2x-3y=6,\ x+y=1$$
We can see in the graph that two lines at a point $$\left (\dfrac {9}{5},\dfrac {-4}{5}\right) $$
$$\therefore $$ System of equations has a unique solution
For what value of $$k$$ the following system of equations will be inconsistent?
$$4x+6y=11$$
$$2x+ky=7$$
Find $$x-y$$ for the following system of linear equations,
$$2x-y-4=0$$ and $$x+y+1=0$$.
Solve each of the following pairs of equations by the elimination method.
$$8x+5y=9$$
$$3x+2y=4$$
Find the value of $$(x+2y)$$ satisfying the equations,
$$x+y=3$$ and $$3x-2y=4$$.
Solve for $$x$$ and $$y$$: $$47x+31y=63,\ 31x+47y=15$$
Solve:$$a= b + 2$$$$2a - b =7$$and hence find out $$2a+b$$.
Solve each of the following pairs of equations by the elimination method.
$$2x+3y=8$$
$$4x+6y=7$$
For each real value of $$c$$, the pair of equations $$x-2y=8;5x-10y=c$$ has a unique solution. Justify whether it is True or False.
Meena went to a bank to withdraw Rs.She asked the cashier to give her Rs. 50 and Rs. 100 notes only. Meena got 25 notes in all. Find how many notes of Rs. 50 and Rs. 100 she received ?
Solve: $$0.2p + 0.3q = 1.3$$
$$0.4p + 0.5q = 2.3$$
Solve the following pair of linear equations by the substitution method.
$$x + y = 14$$
$$x - y = 4$$
Solve :3x + 4y = 25, 5x - 6y = -9 by elimination method.
By the method of substitution, find the solution set of the pair of linear equations $$x+2y=5$$ and $$3.x+7y=17$$
solve:
$$4x + \frac{{x - y}}{8} = 17$$
$$2y + x - \frac{{5y + 2}}{3} = 2$$
Solve for $$x$$ and $$y$$:
$$11x + 15y + 23 = 0,7x - 2y - 20 = 0$$
Solve:$$x-y=0;2x-y=2$$.
Solve the equation by substitution method
$$2\,x\, + \,3\,y\, = \,9\,,\,\,3\,x\, + \,4\,y\, = \,5$$
Solve $$x-y+2=0$$
$$7x+9y=130$$
Solve the following pairs of linear equations :
$$2x + 3y = 2xy, \, 6x + 12y = 7 xy$$
Solve the following equations.
(i) $$10 - q = 6$$ (ii) $$2t - 5 = 3$$
The sum of two fraction is $$\dfrac{5}{8}$$. One fraction is greater by $$1$$ that the other fraction. What are the two fraction.
$$a+b=7$$ and $$a-b=3$$ find $$a$$ and $$b$$
Solve the following equation
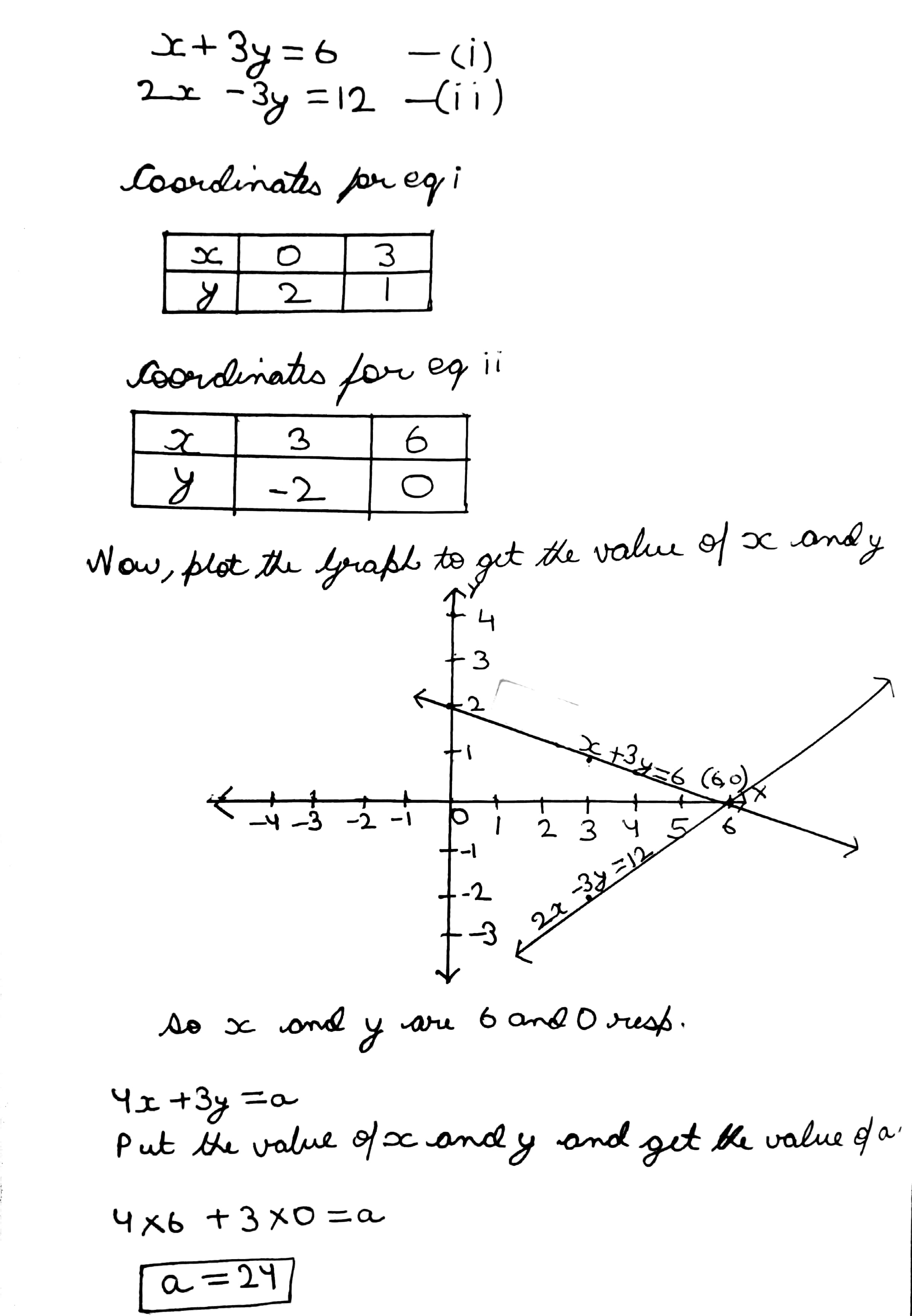
$$x+3y=6 \\ 2x-3y=12$$
Solve the following pair of linear equations :
$$\begin{gathered} px + qy = p - q \hfill \\ qx - py = p + q \hfill \\ \end{gathered} $$
Solve by elimination method
$$x+y=5$$
$$2x-3y=4$$
$$2x-3y=4$$
Solve : $$2x + 5y + 72 = 30$$
$$3x - 6y + 52 = 15$$
Solve $$3x+4y=10$$ and $$2x-2y=2$$ by substitution method.
$$2x + 3y = 8\\2x = 2 + 3y$$ Find the values of $$x$$ and $$y$$
Solve the following pair of equation by the elimination method.$$x+y=14,x-y=4$$
Solve the equation by substitution method $$2x + 3y = 9$$ , $$3x + 4y = 5$$
Solve by elimination method :
$$2x\ +\ 5y\ =\ 12$$
$$7x\ +\ 3y\ =\ 13$$
Solve each pair of equation by using the substitution method.
$$x+3y=-1$$
$$2x-3y=12$$
Solve the following pair of linear (simultaneous) equations by the method of elimination:
$$2x+3y=8$$
$$4x+6y=7$$
Solve for $$x$$ and $$y$$$$6 x - 9 y = 15$$
$$6 x - 8 y = 14$$
$$6 x - 8 y = 14$$
Solve the following system of equations by substitution method:
$$x+y=2 \\ x-y=2$$
Solve the following equations :
$$x+2y=2,\ 2x+3y=3$$
Solve the following system of equations by substitution method:$$2x+3y=11 \\ 2x-4y=-24$$
Given: Two linear equations in two variables.
$$ 2x+3y = 11 ...(1) $$
$$ 2x-4y = -24 ...(2)$$
Using eq.(1) we get,
$$ 2x = 11-3y $$
$$x = \dfrac{11-3y}{2} $$...........(3)
Putting this value of $$x$$ in (2) we get,
$$ 2\times \dfrac{(11-3y)}{2}-4y = -24 $$
$$ 11+24 = 7y $$
$$ \therefore y = \dfrac{35}{7} = 5 $$
Putting this value of $$y$$ in (3) we get,
$$ \therefore x = \dfrac{11-3(5)}{2} = \dfrac{-4}{2} $$
$$ \therefore x = -2 $$
$$ \therefore (x,y) = (-2,5) $$
Solve : $$px + qy = p - q$$
$$qx - py = p + q$$
Solve
$$2x+3y=8$$
$$2x=2+3y$$
The sum of two numbers is $$80$$ and the greater number exceed twice the smaller by $$11$$. Find the larger number.
Solve:$$3a+5b=26\\ a+5b=22$$
Solve by elimination method
$$3x+4y=-25$$;
$$2x-3y=6$$
If x=a , y=b is the solution of the pair of equations $$x-y=2$$ and $$x+y=4$$, find the values of a and b.
Solve the following pair of linear equations by the substitution method.
$$0.2x+0.3y=1.3 \\ 0.4x+0.5y=2.3$$
The number of solutions for $$2 x + 3 y = 10$$ and $$4x+6y=25$$ are
Solve:
$$50x + 24y = 1000$$
$$x + y = 100$$
Solve :
$$\dfrac{4}{x}+\dfrac{5}{y}=7;\ \dfrac{3}{x}+\dfrac{4}{y}=5$$
Solve the following pair of equations:
$$13x+11y=70, 11x+13y=74$$
$$\dfrac{x}{10}+\dfrac{y}{5}-1=0$$$$\dfrac{x}{8}+\dfrac{y}{6}=15$$
Solve By method elimination
Solve the following simultaneous equation by elimination method :
$$3x-4y=10;\quad 4x+3y=5$$.
Solve for $$x,y$$
$$4x-y=4;x-4y=16$$
Solve using the method of substitution
2x - 3y = 7 ; 5x + y = 9
Solve for $$x$$ and $$y$$ : $$\dfrac{x}{2}+\dfrac{y}{4}=3, 2x-y=4$$.
$$\dfrac{x}{2}+\dfrac{y}{4}=3)\times 4\Rightarrow 2x+y=12$$
$$2x-y=4$$
_______________
$$4x=16\Rightarrow x=4$$
$$y=2x-4=8-4$$
$$\Rightarrow y=4$$.
Solve the following simultaneous equation:
(a) $$x+y=4,x-y=6$$
Solve by elimination method: $$13x + 11y = 70, 11x + 13y = 74$$.
Solve $$8x + 3y = 14 ; 3x + y = 5$$ by using substitution method.
Solve the equations :
$$2x-y=2$$
$$4x-y=4$$
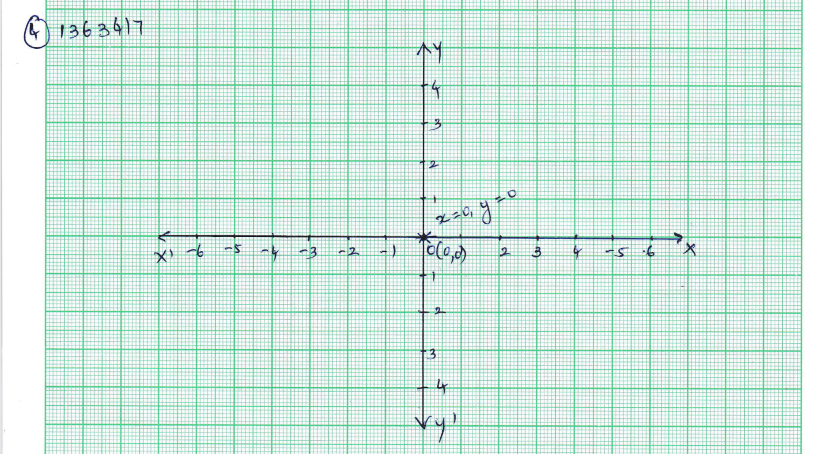
Draw the graph of the equation $$x=0,\,y=0$$
$$x=0$$ is the graph of $$y-$$axis
$$\therefore$$ the graph of $$x=0$$ is the line $$YO{Y}^{\prime}$$
$$y=0$$ is the graph of $$x-$$axis
$$\therefore$$ the graph of $$y=x=0$$ is the line $$XO{X}^{\prime}$$
Solve
$$x-2y=-1,2x-y=7$$
Solve :$$3x-2y=1$$$$2x+y=3$$
Solve $$x+y=14$$, $$x-y=4$$
Find the solution of $$x+2y=10$$ and $$2x+4y=8$$ graphically.
Given, $$x + 2y = 10 \quad $$
$$\Rightarrow x=10-2y$$
For $$y=3$$
$$x=10-2(3)=4$$
For $$y=4$$
$$x=10-2(4)=2$$
$$x=10-2(4)=2$$
| $$x$$ | $$4$$ | $$2$$ |
| $$y$$ | $$3$$ | $$4$$ |
For $$2x + 4y = 8 \quad$$
$$\Rightarrow x + 2y = 4$$
$$\Rightarrow x=4-2y$$
For $$y = 1$$
$$x=4-2(2)=2$$
For $$y = 3$$
$$x = 4-2(3)=-2$$
| $$x$$ | $$2$$ | $$-2$$ |
| $$y$$ | $$1$$ | $$3$$ |
The graph $$x + 2y = 10$$ cuts the $$x$$ and $$y$$-axis at $$\left( 10, 0 \right)$$ and $$\left( 0, 5 \right)$$ respectively, while the graph of $$2x + 4y = 8$$ cuts the $$x$$ and $$y$$-axis at $$\left( 4, 0 \right)$$ and $$\left( 0, 2 \right)$$ respectively.
Since the graph consists of a pair of parallel lines, the system of equations has no solution.
Solve :$$x+y=110$$, $$y=x+4$$.
Check whether the following equations are consistent or inconsistent , solve them graphically.
x - y = 8 , 3x - 3y = 16
x - y = 8 , 3x - 3y = 16
$$ \dfrac{a_{1}}{a_{2}} = \dfrac{1}{3} ,\dfrac{b_{1}}{b_{2}}=\dfrac{-1}{-3}= \dfrac{1}{3} \dfrac{c_{1}}{c_{2}}=\dfrac{8}{16}=\dfrac{1}{2} $$
$$ \therefore \dfrac{a_{1}}{a_{2}} = \dfrac{b_{1}}{b_{2}} \dfrac{c_{1}}{c_{2}} $$
$$\therefore $$ the linear equation are consistent
$$\therefore $$ They have infinity solutions.
x y = 8 x +3y = 16
x y (x ,y) x y (x,y)0
-8 (0,-8) 2 $$- \dfrac{10}{3}$$
Solve, graphically, the following pairs of equations:
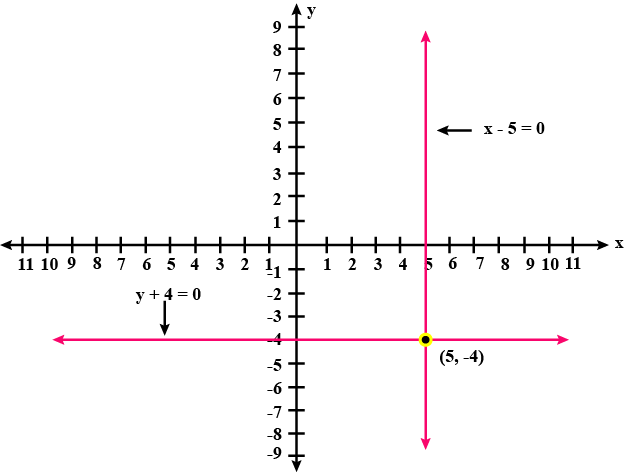
$$x - 5 = 0$$
$$y + 4 = 0$$.
$$x - 5 = 0\Rightarrow x = 5$$
$$y + 5 = 0\Rightarrow y = -4$$
Following is the graph of the two equations
$$x = 5$$ and $$y = -4$$.
$$y + 5 = 0\Rightarrow y = -4$$
Following is the graph of the two equations
$$x = 5$$ and $$y = -4$$.
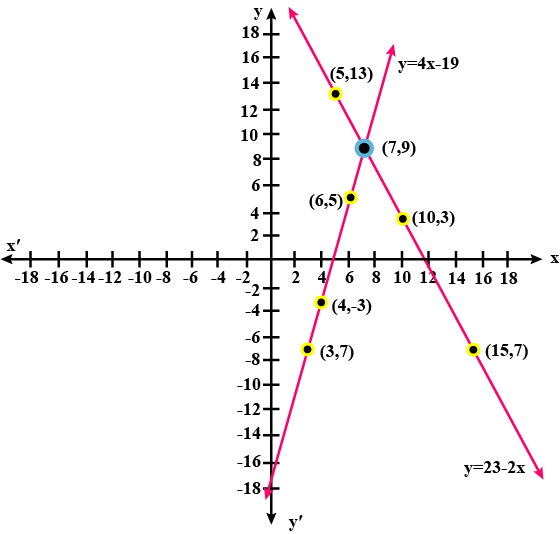
Solve, graphically, the following pairs of equations:
$$2x + y = 23$$
$$4x - y = 19$$.
$$2x + y = 23\Rightarrow y = 23 - 2x$$
The table for $$y = 23 - 2x$$ is
Also, we have
$$4x - y = 19$$
$$\Rightarrow y = 4x - 19$$
The table for $$y = 4x - 19$$ is
Intersecting point $$= (7, 9)$$.
The table for $$y = 23 - 2x$$ is
| $$x$$ | $$5$$ | $$10$$ | $$15$$ |
| $$y$$ | $$13$$ | $$3$$ | $$-7$$ |
$$4x - y = 19$$
$$\Rightarrow y = 4x - 19$$
The table for $$y = 4x - 19$$ is
| $$x$$ | $$3$$ | $$4$$ | $$6$$ |
| $$y$$ | $$-7$$ | $$-3$$ | $$5$$ |
Use the graphical method to find the value of $$k$$, if $$(k, -3)$$ lies on the straight line $$2x + 3y = 1$$.
$$2x + 3y = 1$$
$$\Rightarrow 3y = 1 - 2x$$
$$\Rightarrow y = \dfrac {1 - 2x}{3}$$
The table for $$2x + 3y = 1$$ is
Hence, from the graph, we can conclude that $$k = 5$$.
$$\Rightarrow 3y = 1 - 2x$$
$$\Rightarrow y = \dfrac {1 - 2x}{3}$$
The table for $$2x + 3y = 1$$ is
| $$x$$ | $$-1$$ | $$2$$ | $$5$$ |
| $$y$$ | $$1$$ | $$-1$$ | $$-3$$ |
Some people collected money to be donated in some orphanages. A part of the donation is fixed and the remaining depends on the number of children in the orphanage. If they donated Rs. $$9500$$, in the orphanage having $$50$$ children and Rs. $$13,250$$ with $$75$$ children, find the fixed part of the donation and the amount donated for each child.
What values do these people possess?
Use the graphical method to find the value of $$k$$, if $$(5, k - 2)$$ lies on the straight line $$x - 2y + 1 = 0$$.
$$x - 2y + 1 = 0$$
$$\Rightarrow 2y = x + 1$$
$$\Rightarrow y = \dfrac {x + 1}{2}$$
The table for $$x - 2y + 1 = 0$$ is
Hence, from the graph, we can conclude that,
$$k - 2 = 3$$
$$k = 5$$.
$$\Rightarrow 2y = x + 1$$
$$\Rightarrow y = \dfrac {x + 1}{2}$$
The table for $$x - 2y + 1 = 0$$ is
| $$x$$ | $$1$$ | $$3$$ | $$5$$ |
| $$y$$ | $$1$$ | $$2$$ | $$3$$ |
$$k - 2 = 3$$
$$k = 5$$.
The force exerted to pull a cart is directly proportional to the acceleration produced in the body. Express the statement as linear equation in two variables and draw the graph of the same by taking the constant mass equal to 6 kg. Read from the graph, the force required when the acceleration produced is (i) $$5$$ $$m/sec^{2}$$ , (ii) $$6$$ $$m/sec^{2}$$
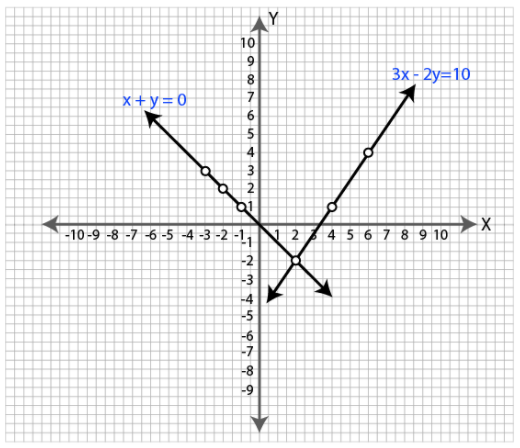
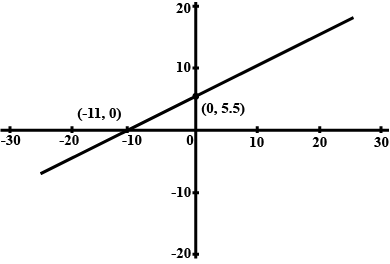
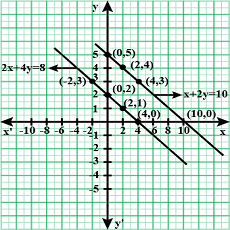
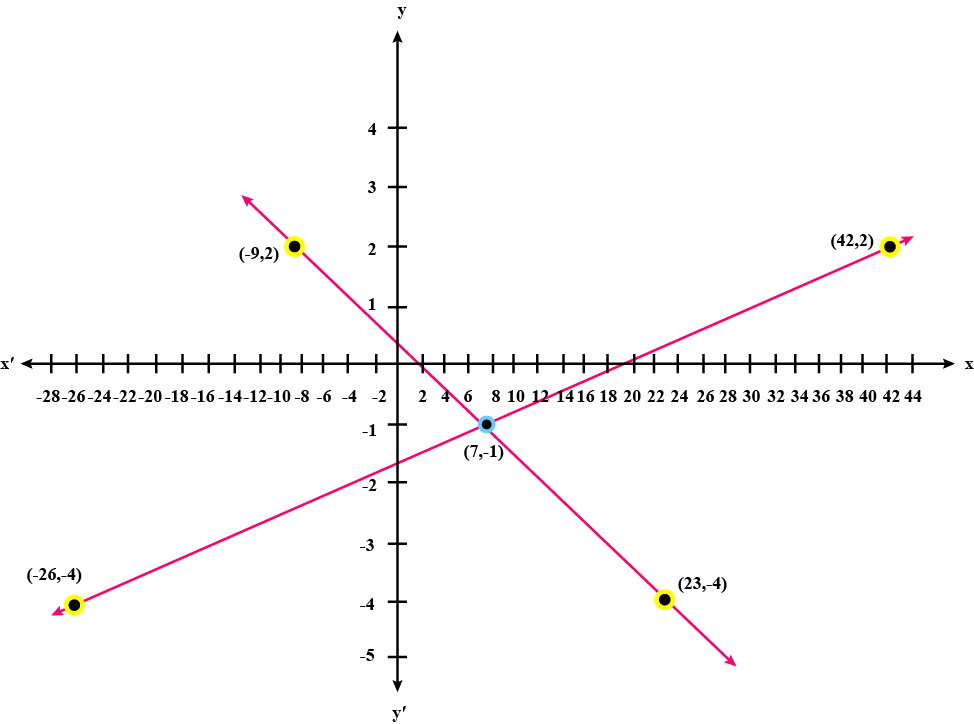
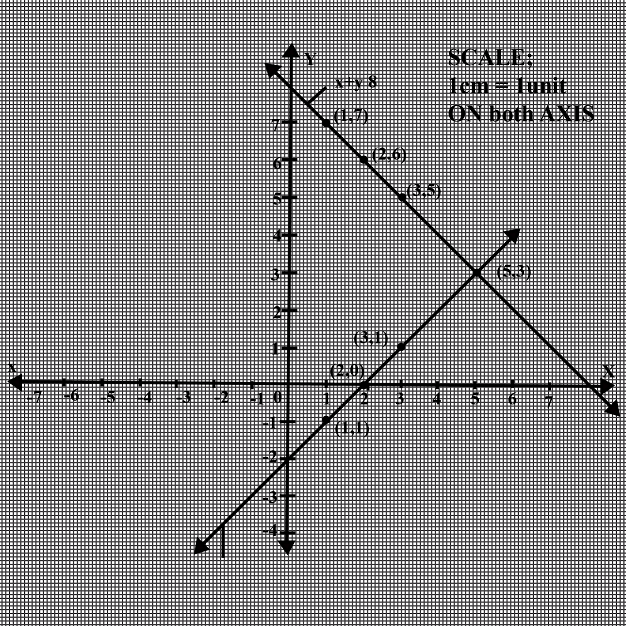
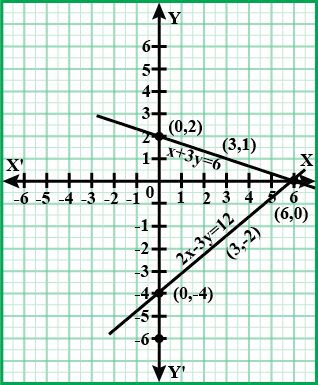
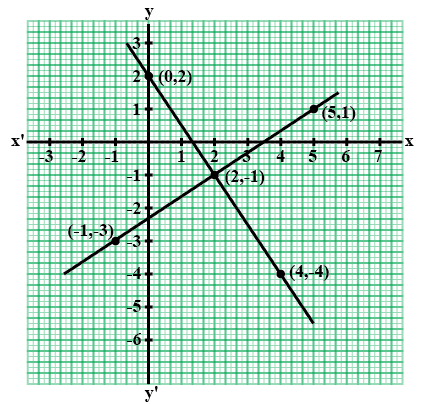
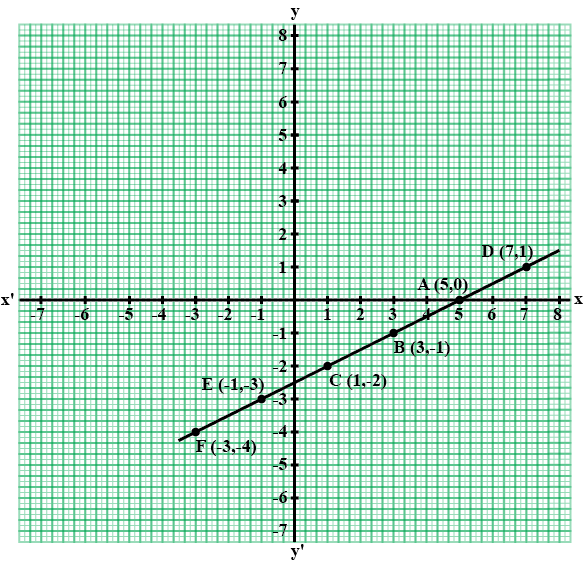
Using the same axes of co-ordinates and the same unit, solve graphically:
$$x + y = 0$$ and $$3x - 2y = 10$$.
(Take at least $$3$$ points for each line drawn).
$$x + y = 0$$
$$y = -x$$
The table of $$x + y = 0$$ is
$$3x - 2y = 10\Rightarrow x = \dfrac {10 + 2y}{3}$$
The table of $$3x - 2y = 10$$ is
Intersection point $$= (2, -2)$$
i.e., $$x = 2$$ and $$y = -2$$.
$$y = -x$$
The table of $$x + y = 0$$ is
| $$x$$ | $$5$$ | $$2$$ | $$-5$$ |
| $$y$$ | $$-5$$ | $$-2$$ | $$5$$ |
The table of $$3x - 2y = 10$$ is
| $$x$$ | $$4$$ | $$6$$ | $$2$$ |
| $$y$$ | $$1$$ | $$4$$ | $$-2$$ |
i.e., $$x = 2$$ and $$y = -2$$.
Use the graphical method to find the value of $$'x'$$ for which the expressions $$\dfrac {x + 2}{2}$$ and $$\dfrac {3}{4}x - 2$$ are equal.
$$y = \dfrac {3x + 2}{2}$$
The table for $$y = \dfrac {3x + 2}{2}$$ is
$$y = \dfrac {3}{4} x - 2$$
The table for $$y = \dfrac {3}{4}x - 2$$ is
$$x = -4$$.
The table for $$y = \dfrac {3x + 2}{2}$$ is
| $$x$$ | $$2$$ | $$4$$ | $$-2$$ |
| $$y$$ | $$4$$ | $$7$$ | $$-2$$ |
The table for $$y = \dfrac {3}{4}x - 2$$ is
| $$x$$ | $$4$$ | $$-4$$ | $$8$$ |
| $$y$$ | $$1$$ | $$-5$$ | $$4$$ |
Solve, graphically, the following pairs of equations:
$$\dfrac {x + 1}{4} = \dfrac {2}{3}(1 - 2y)$$
$$\dfrac {2 + 5y}{3} = \dfrac {x}{7} - 2$$.
$$\dfrac {x + 1}{4} = \dfrac {2}{3} (1 - 2y)$$
$$\Rightarrow \dfrac {x + 1}{4} = \dfrac {2}{3} - \dfrac {4y}{3}$$
$$\Rightarrow 12\times \dfrac {x + 1}{4} = 12\times \dfrac {2}{3} - 12\times \dfrac {4y}{3}$$
$$\Rightarrow 3(x + 1) = 8 - 16y$$
$$\Rightarrow 3x + 3 = 8 - 16y$$
$$\Rightarrow 3x + 3 - 8 = -16y$$
$$\Rightarrow 3x - 5 = -16y$$
$$\Rightarrow x = \dfrac {5 - 16y}{3}$$
The table for $$\dfrac {x + 1}{4} = \dfrac {2}{3} (1 - 2y)$$ is
Also, we have
$$\dfrac {2 + 5y}{3} = \dfrac {x}{7} - 2$$
$$\Rightarrow 21 \times \dfrac {2 + 5y}{3} = 21\times \dfrac {x}{7} - 21\times 2$$
$$\Rightarrow 7(2 + 5y) = 3x - 42$$
$$\Rightarrow 14 + 35y = 3x - 42$$
$$\Rightarrow 3x = 14 + 35y + 42$$
$$\Rightarrow 3x = 56 + 35y$$
$$\Rightarrow x = \dfrac {56 + 35y}{3}$$
The table for $$\dfrac {2 + 5y}{3} = \dfrac {x}{7} - 2$$ is
Intersection point = $$(7, -1)$$.
$$\Rightarrow \dfrac {x + 1}{4} = \dfrac {2}{3} - \dfrac {4y}{3}$$
$$\Rightarrow 12\times \dfrac {x + 1}{4} = 12\times \dfrac {2}{3} - 12\times \dfrac {4y}{3}$$
$$\Rightarrow 3(x + 1) = 8 - 16y$$
$$\Rightarrow 3x + 3 = 8 - 16y$$
$$\Rightarrow 3x + 3 - 8 = -16y$$
$$\Rightarrow 3x - 5 = -16y$$
$$\Rightarrow x = \dfrac {5 - 16y}{3}$$
The table for $$\dfrac {x + 1}{4} = \dfrac {2}{3} (1 - 2y)$$ is
| $$x$$ | $$7$$ | $$-9$$ | $$23$$ |
| $$y$$ | $$-1$$ | $$2$$ | $$-4$$ |
$$\dfrac {2 + 5y}{3} = \dfrac {x}{7} - 2$$
$$\Rightarrow 21 \times \dfrac {2 + 5y}{3} = 21\times \dfrac {x}{7} - 21\times 2$$
$$\Rightarrow 7(2 + 5y) = 3x - 42$$
$$\Rightarrow 14 + 35y = 3x - 42$$
$$\Rightarrow 3x = 14 + 35y + 42$$
$$\Rightarrow 3x = 56 + 35y$$
$$\Rightarrow x = \dfrac {56 + 35y}{3}$$
The table for $$\dfrac {2 + 5y}{3} = \dfrac {x}{7} - 2$$ is
| $$x$$ | $$7$$ | $$-28$$ | $$42$$ |
| $$y$$ | $$-1$$ | $$-4$$ | $$2$$ |
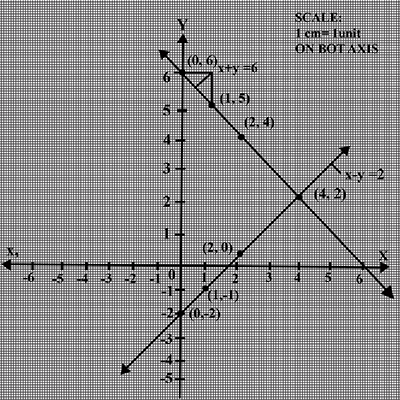
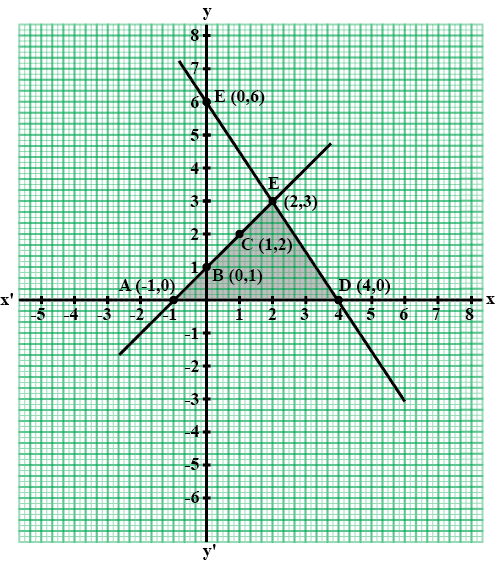
Draw the graph of the pair of equations 2x + y = 4 and 2x -y =Write the vertices of the triangle formed by these lines and the y-axis.
Clearly from the graph the vertices of formed triangle are $$(0,0), (0,4), (2,0)$$
By the graphical method, find whether the following pair of equations are consistent or not. If consistent, solve them.
$$x + y = 3$$ and $$3x + 3y = 9$$
| $$x$$ | 1 | 2 | 3 |
| $$y$$ | 2 | 1 | 0 |
| $$x$$ | 1 | 2 | 3 |
| $$y$$ | 2 | 1 | 0 |
$$x+y-3=0$$ .......eq1 and $$3x+3y-9=0$$ .........eq2
Here, $$\cfrac{a_1}{a_2}=\cfrac{1}{3},\cfrac{b_1}{b_2}=\cfrac{1}{3},\cfrac{c_1}{c_2}=\cfrac{3}{9}=\cfrac{1}{3}$$
$$\therefore \cfrac{a_1}{a_2}=\cfrac{b_1}{b_2}=\cfrac{c_1}{c_2}$$
Thus, the given pair of equation is consistent.
Solve the following pair of equations:$$x+y=3.3 \\ \cfrac{0.6}{3x-2y}=-1;\ 3x-2y \neq 0$$
Draw the graphs of $$x + 3y + 3 = 0$$ and $$3x - 2y + 6 = 0.$$ Plot only three points per line and mark the intersection point.
$$x+3y+3=0$$
$$\implies x=-3-3y$$
Let, $$y=0, $$ then $$x=-3-3(0)=-3$$
Similarly, when $$y=-1, x=0$$ and when $$y=1, x=-6$$
$$\therefore $$ the coordinates are $$(-3,0), (0,-1), (-6,1)$$
Now,
$$3x-2y+6=0$$
$$\implies 2y=3x+6$$
$$\implies y=\dfrac{3x+6}{2}$$
Let, $$x=0$$, $$y=3$$
Similarly, when $$x=-2, y=0, $$ and $$x=2, y=6$$
$$\therefore $$ the coordinates are $$(0,3),(-2,0),(2,6)$$
$$\therefore$$ the intersecting point is marked with the dark black dot
A purse contains only 25 paise and 10 paise coins. The total amount in the purse is Rs. 8.If the number of 25 paise coins is one-third the number of 10 paise coins, then the total number of coins in the purse is:
A train covers a certain distance at a uniform speed. If the train could have been $$10 km/hr$$ faster, it would have taken $$2$$ hours less than the scheduled time. And if the train were slower by $$10 km/hr$$, it would have taken $$3$$ hours more than the scheduled time. Find the distance covered by the train.
Find the number of solutions for $$2x-3y=5$$ and $$4x-6y=7$$ .
Solve the following system of equations
$$\displaystyle \frac{6}{x+y}=\frac{7}{x-y}+3,\frac{1}{2\left ( x+y \right )}=\frac{1}{3\left ( x-y \right )} $$ where $$\displaystyle x+y\neq 0\: \: and\: \: x-y\neq 0 $$
The owner of a milk store finds that, he can sell $$980$$ litres of milk each week at Rs $$14$$/litre and $$1220$$ litres of milk each week at Rs $$16$$/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs $$17$$/litre
A trust fund has $$Rs. 30,000$$ that must be invested in two different types of bonds. The first bond pays $$5$$% interest per year, and the second bond pays $$7$$% interest per year. Determine how to divide $$Rs. 30,000$$ among the two types of bonds. If the trust fund must obtain an annual total interest of
(a) $$Rs. 1800$$
(b) $$Rs. 2000$$
Father says to son "I am 9 times as old as you were when i was as old as you are". If the sum of their present ages is 50 years. What is the age of father ?
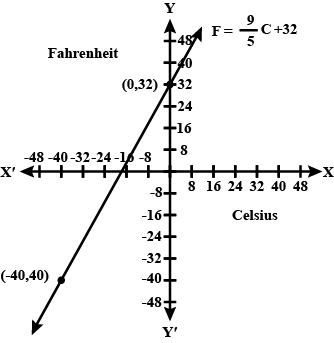
In countries like USA and Canada, temperature is measured in Fahrenheit, whereas in countries like India, it is measured in Celsius. Here is a linear equation that converts Fahrenheit to Celsius:
$$F=\left(\dfrac{9}{5}\right)C+32$$
(i) Draw the graph of the linear equation above using Celsius for $$x$$-axis and Fahrenheit for $$y$$-axis.
(ii) If the temperature is $$30^oC$$, what is the temperature in Fahrenheit?
(iii) If the temperature is $$95^oF$$, what is the temperature in Celsius?
(iv) If the temperature is $$0^oC$$, what is the temperature in Fahrenheit and if the temperature is $$0^oF$$, what is the temperature in Celsius?
(v) Is there a temperature which is numerically the same in both Fahrenheit and Celsius? If yes, find it.
(i) Since the equation between $$F$$ and $$C$$ is given, the graph can be drawn as shown above.
(ii) Given $$c=30$$, so $$F=\dfrac { 9 }{ 5 } \times 30+32=86 \ F$$.
(iii) Given $$F=95$$, so $$C=\dfrac { 5 }{ 9 } \times (F-32)=35 \ C$$.
(iv) Given $$C=0$$, so $$F=32$$ and if $$F=0$$, we get $$C=-\dfrac{160}9$$.
(v) Put $$F=C=x$$ in given equatin, we get $$\dfrac { 4x }{ 5 } =-32$$, from which we get $$x=-40$$
Yes, there is a temperature which is numerically the same in both fahrenheit and celsius, the numerical value is $$-40$$.
The cost of $$2\ kg$$ of apples and $$1\ kg$$ of grapes on a day was found to be $$Rs \ 160$$. After a month, the cost of $$4\ kg$$ of apples and $$2\ kg$$ of grapes is $$Rs\ 300$$. Represent the situation algebraically and geometrically.
| $$x$$ | $$65$$ | $$55$$ | $$45$$ | $$35$$ |
| $$ y$$ | $$20$$ | $$40$$ | $$60$$ | $$80$$ |
So the algebraic representation can be as follows:
$$2x + y = 160$$
$$4x + 2y = 300 \Rightarrow 2x +y = 150 $$
$$4x + 2y = 300 \Rightarrow 2x +y = 150 $$
The situation can be represented graphically by plotting these two equations.
$$2x + y = 160 \Rightarrow y = 160-2x$$
$$2x + y = 150 \Rightarrow y = 150-2x$$
| $$x$$ | $$70$$ | $$60$$ | $$50$$ | $$40$$ |
| $$y = 160-2x$$ | $$20$$ | $$40$$ | $$60$$ | $$80$$ |
| $$x$$ | $$65$$ | $$55$$ | $$45$$ | $$35$$ |
| $$y = 150-2x$$ | $$20$$ | $$40$$ | $$60$$ | $$80$$ |
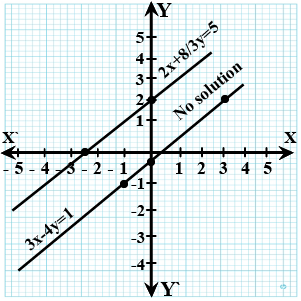
On comparing the ratios $$\dfrac{a_1}{a_2}, \dfrac{b_1}{b_2}$$ and $$\dfrac{c_1}{c_2}$$, find out whether the following pair of linear equations are consistent, or inconsistent.
(i) $$3x + 2y = 5 ; 2x -3y = 7$$
(ii) $$2x -3y = 8 ; 4x -6y = 9$$
(iii) $$\dfrac{3}{2}x+\dfrac{5}{3}y=7 ; 9x -10y = 14$$
(iv) $$5x -3y = 11 ; -10x + 6y = -22$$
(v) $$\dfrac{4}{3}x+2y=8 ; 2x + 3y = 12$$
Draw the graphs of the equations $$x- y + 1 = 0$$ and $$3x + 2y -12 = 0$$. Determine the coordinates of the vertices of the triangle formed by these lines and the $$x$$-axis, and shade the triangular region.
$$x-y+1=0$$
Plot $$(0, 1)$$ and $$(1, 2)$$ on graph and join them to get eqn (i)
Plot point $$(0, 6)$$ and $$(4, 0)$$ on graph and join them to get eqn (ii)
$$x-y=-1$$ ...(i)
$$3x+2y-12=0$$
$$3x+2y=12$$ ...(ii)
$$x-y=-1$$
$$y=1+x$$
| $$x$$ | $$0$$ | $$-1$$ |
| $$y$$ | $$1$$ | $$0$$ |
For $$3x+2y=12$$
$$\Rightarrow 2y=12-3x$$
$$\Rightarrow r=\dfrac{12-3x}{2}$$
| $$x$$ | $$ 0$$ | $$ 4$$ |
| $$y$$ | $$ 6$$ | $$ 0$$ |
$$\triangle ABC$$ is the required triangle with coordinates of $$A$$ as $$(2, 3), B(-1, 0)$$ and $$C(4, 0)$$.
Form the pair of linear equations in the following problems, and find their solutions graphically.
(i) $$10$$ students of Class X took part in a Mathematics quiz. If the number of girls is $$4$$ more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) $$5$$ pencils and $$7$$ pens together cost Rs $$50,$$ whereas $$7$$ pencils and $$5$$ pens together cost Rs $$46.$$ Find the cost of one pencil and that of one pen.
and number of girls $$= y.$$
According to the question,
$$x + y = 10$$
or, $$y = 10 - x $$ ………(i)
$$y = x + 4$$ ………..(ii)
or, $$y = 10 - x $$ ………(i)
$$y = x + 4$$ ………..(ii)
| $$x$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ |
| $$ y$$ | $$9$$ | $$8$$ | $$7$$ | $$6$$ |
| $$x$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ |
| $$y$$ | $$5$$ | $$6$$ | $$7$$ | $$8$$ |
(ii) Consider price of a pencil is $$x$$
and price of a pen is $$y.$$
According to the question,
$$5x + 7y = 50$$.....(i)
$$7x + 5y = 46$$ .….(ii)
$$7x + 5y = 46$$ .….(ii)
| $$x$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ |
| $$y$$ | $$7.8$$ | $$6.4$$ | $$5$$ | $$4.2$$ |
| $$x$$ | $$1$$ | $$2$$ | $$3$$ | $$4$$ |
| $$ y$$ | $$6.4$$ | $$5.7$$ | $$5$$ | $$ 4.2$$ |
Graphical solution :
Price of a pencil is Rs $$3$$
Price of a pen is Rs $$5.$$
Find the value of $$k$$, if $$x=2, y=1$$ is a solution of the equation $$2x+3y=k$$.
Which one of the following options is true, and why?
$$y=3x+5$$ has
(i) a unique solution,
(ii) only two solutions,
(iii) infinitely many solutions
Solve the following pair of linear equations by the substitution method.
(i) $$x + y = 14; x -y = 4$$
(ii) $$s -t = 3; \dfrac{s}{3}+\dfrac{t}{2}=6$$
(iii) $$3x -y = 3 ; 9x -3y = 9$$
(iv) $$0.2x + 0.3y = 1.3 ; 0.4x + 0.5y = 2.3$$
(v) $$\sqrt{2}x+\sqrt{3}y=0 ; \sqrt{3}x-\sqrt{8}y=0$$
(vi) $$\dfrac{3x}{2}-\dfrac{5y}{3}=-2 ; \dfrac{x}{3}+\dfrac{y}{2}=\dfrac{13}{6}$$
Aftab tells his daughter, "Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be." (Isnt this interesting?) Represent this situation algebraically and graphically.
Consider Aftab's age as $$x$$ and his daughter's age as $$y.$$
Then , seven years ago,
Aftab's age $$= x -7$$
His daughter's age $$=y-7$$
According to the question,
$$ x - 7 = 7 \left ( y-7 \right )$$
$$ x -7 = 7y - 49 $$
$$x-7y = -49 +7$$
$$x-7y = -49 +7$$
$$x-7y = - 42 $$ …(i)
After three years,
Aftab's age $$ = x +3$$
His daughter's age $$ = y+3$$
According to the question,
$$x + 3 = 3 \left(y + 3\right)$$
$$x + 3 = 3 y + 9$$
$$x -3 y = 9- 3$$
$$x -3 y =6 $$ …(ii)
Representing equation $$(i)$$ and $$(ii)$$ geometrically, we plot these equations by finding points on the lines representing these two equations
$$x-7y = - 42 \Longrightarrow x = 7y - 42$$
| $$x = 7y-42$$ | $$42$$ | $$35$$ | $$49$$ |
| $$y$$ | $$12$$ | $$11$$ | $$13$$ |
$$x - 3y = 6 \Longrightarrow x = 3y + 6$$
| $$x = 3y+6$$ | $$42$$ | $$36$$ | $$48$$ |
| $$y$$ | $$12$$ | $$10$$ | $$14$$ |
From the graph we can see that two lines will intersect at a point.
$$x-7y = - 42 $$
$$x -3 y =6 $$
On subtracting the two equations, we get
$$4y = 48$$
or $$y = 12$$
Substituting value of $$y$$ in (2),
$$x - 36 = 6$$
$$ \therefore x= 42 $$
Form the pair of linear equations in the following problems, and find their solutions(if they exist) by the elimination method :
(i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces toIt becomes $$\dfrac{1}{2}$$ if we only add 1 to the denominator. What is the fraction?
(ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
(iii) The sum of the digits of a two-digit number isAlso, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
(iv) Meena went to a bank to withdraw Rs.$$ 2000$$. She asked the cashier to give her Rs. $$50$$ and Rs. $$100$$ notes only. Meena got 25 notes in all. Find how many notes of Rs. $$50$$ and Rs. $$ 100$$ she received.
(v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid Rs. $$27$$ for a book kept for seven days, while Susy paid Rs. $$21$$ for the book she kept for five days. Find the fixed charge and the charge for each extra day.
(i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces toIt becomes $$\dfrac{1}{2}$$ if we only add 1 to the denominator. What is the fraction?
(ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
(iii) The sum of the digits of a two-digit number isAlso, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
(iv) Meena went to a bank to withdraw Rs.$$ 2000$$. She asked the cashier to give her Rs. $$50$$ and Rs. $$100$$ notes only. Meena got 25 notes in all. Find how many notes of Rs. $$50$$ and Rs. $$ 100$$ she received.
(v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid Rs. $$27$$ for a book kept for seven days, while Susy paid Rs. $$21$$ for the book she kept for five days. Find the fixed charge and the charge for each extra day.
Solve the following pair of linear equations:
$$(i) \;\quad px + qy = p- q ; \;qx -py = p + q$$
$$(ii) \quad ax + by = c ; \;bx + ay = 1 + c$$
Draw the graphs of the equations $$5x- y = 5$$ and $$3x -y = 3$$. Determine the co-ordinates of the vertices of the triangle formed by these lines and the y axis.
For the equation $$3x-y=3$$
$$y=3x-3$$
If $$x=0,\ y=-3$$
For $$x=1,\ y=0$$
For $$x=2,\ y=3$$
For the equation $$5x-y=5$$
$$y=3x-3$$
If $$x=0,\ y=-3$$
For $$x=1,\ y=0$$
For $$x=2,\ y=3$$
| $$x$$ | $$0$$ | $$1$$ | $$2$$ |
| $$y$$ | $$-3$$ | $$0$$ | $$3$$ |
$$\Rightarrow y=5x-5$$
If $$x=0,\ y=-5$$
For $$x=1,\ y=0$$
For $$x=2,\ y=5$$
For $$x=1,\ y=0$$
For $$x=2,\ y=5$$
| $$x$$ | $$0$$ | $$1$$ | $$2$$ |
| $$y$$ | $$-5$$ | $$0$$ | $$5$$ |
Plotting the equations on the graph, we get $$\Delta ACE $$ with $$A (1,0),\ C (0,-3),$$ and $$E (0,-5)$$
Solve the following pair of linear equations by the elimination method and the substitution method :
(i) $$x + y = 5$$ and $$2x -3y = 4$$
(ii) $$3x + 4y = 10$$ and $$2x -2y = 2$$
(iii) $$3x -5y -4 = 0$$ and $$9x = 2y + 7$$
(iv) $$\dfrac{x}{2}+\dfrac{2y}{3}=-1$$ and $$x-\dfrac{y}{3}=3$$
(ii) $$3x + 4y = 10$$ and $$2x -2y = 2$$
(iii) $$3x -5y -4 = 0$$ and $$9x = 2y + 7$$
(iv) $$\dfrac{x}{2}+\dfrac{2y}{3}=-1$$ and $$x-\dfrac{y}{3}=3$$
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method :
(i) A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for $$20$$ days she has to pay $$\text{Rs. } 1000$$ as hostel charges whereas a student B, who takes food for $$26$$ days, pays $$\text{Rs. } 1180$$ as hostel charges. Find the fixed charges and the cost of food per day.
(ii) A fraction becomes $$\dfrac{1}{3}$$ when $$1$$ is subtracted from the numerator and it becomes $$\dfrac14$$ when $$8$$ is added to its denominator. Find the fraction.
(i) A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for $$20$$ days she has to pay $$\text{Rs. } 1000$$ as hostel charges whereas a student B, who takes food for $$26$$ days, pays $$\text{Rs. } 1180$$ as hostel charges. Find the fixed charges and the cost of food per day.
(ii) A fraction becomes $$\dfrac{1}{3}$$ when $$1$$ is subtracted from the numerator and it becomes $$\dfrac14$$ when $$8$$ is added to its denominator. Find the fraction.
Solve $$2x + 3y = 11$$ and $$2x -4y = -24$$ and hence find the value of m for which $$y = mx + 3$$.
The students of a class are made to stand in rows. If 3 students are extra in a row, there would be 1 row less. If 3 students are less in a row, there would be 2 rows more. Find the number of students in the class.
One says, "Give me a hundred, friend! I shall then become twice as rich as you." The other replies, "If you give me ten, I shall be six times as rich as you." Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara II]
In a $$\triangle ABC; \angle C=3 \angle B=2(\angle A+\angle B)$$. Find the three angles.
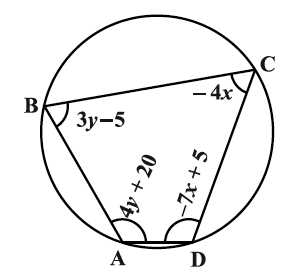
ABCD is a cyclic quadrilateral. Find the angles of the cyclic quadrilateral.
$$x+y+3z=600$$
$$ x+ y+z=400$$
In the system of equations above, what is the value of $$x + y$$ ?
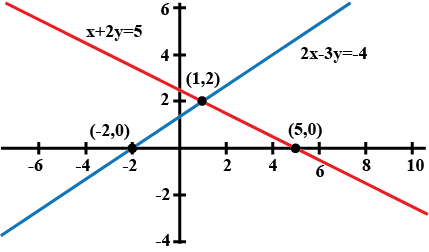
Solve the following system of equations graphically. Also find the points where the lines meet the $$X$$-axis.
$$\displaystyle x+2y=5$$
$$\displaystyle 2x-3y=-4$$
Given equations, $$x+2y=5$$ ...(1) and $$2x-3y=-4$$...(2)
From the graph it is clear that,point of intersection is $$(1,2)$$
Point of intersection of equation(1) with X-axis =$$(5,0)$$
Point of intersection of equation(2) with Y-axis=$$(-2,0)$$
Solve given pair of equations, by elimination method
$$3x-y=5, 5x-2y=4$$
Solve the following system of equations by the method of substitution:
$$3a - 2b = 12$$, $$4a - 5b = 16$$
Solve the following system of equations by the method of substitution:
$$5x + 4y - 4 = 0$$, $$x - 20 = 12y$$
Solve the following system of equations by the method of substitution:
$$3x - 4y = 10$$, $$4x + 3y = 5$$
Find the common solution:
$$5x+3y=28$$
$$7x-2y=2$$
Find the common solution:
$$2x+y=8$$
$$x-y=1$$
Solve the following system of equations by the method of substitution:
$$3x - 7y = 7$$, $$11x + 5y = 87$$
Solve the following system of equations by the method of substitution:
$$x + y = 10$$, $$x - y = 12$$
Solve the following system of equations by the method of substitution:
$$2p + 3q = -5$$, $$3p - 2q = 12$$
Use elimination method for solving the following equations:
$$2x + y = 0$$, $$3x - y = -5$$
Use elimination method for solving the following equations:
$$41x + 53y = 135$$, $$53x + 41y = 147$$
Solve the following system of equations by the method of substitution:
$$2x + 3y = 5$$, $$3x + 4y = 6$$
Solve the following system by elimination method:
$$5x - 4y = -14$$,$$3x + 2y = -4$$
Use elimination method for solving the following equations:
$$2x + y = 7$$, $$2x - 3y = 3$$
Use elimination method for solving the following equations:
$$100x + 200y = 700$$, $$200x + 100y = 800$$
Use elimination method for solving the following equations:
$$3x + y = 10$$, $$x - y = 2$$
Use elimination method for solving the following equations:
$$x - y = 7$$, $$3x + y = 10$$
Solve the following system of equations by the method of substitution:
$$7x + 5y = 10$$, $$3x + y = 2$$
Solve the equations $$x + y = 3$$ and $$3x - 2y = 4$$ using graph
We draw graphs of the equations $$x + y = 3$$ and $$3x - 2y = 4$$. Then locate their point of intersection.
Recall, that it is enough to know two points to draw a straight line. Consider $$x + y = 3$$. Taking $$x = 0$$, we get $$y = 3$$. Taking $$y = 0$$, we get $$x = 3$$. Thus $$(0, 3)$$ and $$(3, 0)$$ are on the straight line $$x + y = 3$$.
Take a graph paper. Fix your coordinate system $$x\Leftrightarrow y$$ axis on the graph paper. Locate $$A = (3, 0)$$ and $$B = (0, 3)$$ with respect to this coordinate system.
Join $$A$$ and $$B$$ and extend it to a straight line.
Consider the equation $$3x - 2y = 4$$. If we take $$x = 0$$, we obtain $$y = -2$$. Similarly, $$x = 4$$ gives $$y = 4$$. Thus $$C = (0, -2)$$ and $$D = (4, 4)$$ are points on the straight line $$3x - 2y = 4$$. Locate these points on the graph paper. Join them and extend to a straight line.
Now we have two straight line. They intersect at a point E. Looking at the graph, you see that $$E$$ has coordinates $$(2, 1)$$. Thus $$x = 2$$ and $$y = 1$$ is the solution. We may verify it: $$2 + 1 = 3$$ and $$3(2) - 2(1) = 6 - 2 = 4$$.
Recall, that it is enough to know two points to draw a straight line. Consider $$x + y = 3$$. Taking $$x = 0$$, we get $$y = 3$$. Taking $$y = 0$$, we get $$x = 3$$. Thus $$(0, 3)$$ and $$(3, 0)$$ are on the straight line $$x + y = 3$$.
Take a graph paper. Fix your coordinate system $$x\Leftrightarrow y$$ axis on the graph paper. Locate $$A = (3, 0)$$ and $$B = (0, 3)$$ with respect to this coordinate system.
Join $$A$$ and $$B$$ and extend it to a straight line.
Consider the equation $$3x - 2y = 4$$. If we take $$x = 0$$, we obtain $$y = -2$$. Similarly, $$x = 4$$ gives $$y = 4$$. Thus $$C = (0, -2)$$ and $$D = (4, 4)$$ are points on the straight line $$3x - 2y = 4$$. Locate these points on the graph paper. Join them and extend to a straight line.
Now we have two straight line. They intersect at a point E. Looking at the graph, you see that $$E$$ has coordinates $$(2, 1)$$. Thus $$x = 2$$ and $$y = 1$$ is the solution. We may verify it: $$2 + 1 = 3$$ and $$3(2) - 2(1) = 6 - 2 = 4$$.
Solve the following system by elimination method:
$$2x + 3y = 13$$, $$4x + y = 11$$
Solve the following simultaneous equations using graphical method.
$$x + y = 8$$
$$x - y = 2$$
$$x + y = 8$$
$$\therefore y = 8 - x$$
$$\therefore y = 8 - x$$
| $$x$$ | $$1$$ | $$2$$ | $$3$$ |
| $$y$$ | $$7$$ | $$6$$ | $$5$$ |
$$(x, y)$$ | $$(1, 7)$$ | $$(2, 6)$$ | $$(3, 5)$$ |
$$x - y = 2$$
$$\therefore y = x - 2$$
$$\therefore y = x - 2$$
| $$x$$ | $$1$$ | $$2$$ | $$3$$ |
| $$y$$ | $$-1$$ | $$0$$ | $$1$$ |
$$(x, y)$$ | $$(1, -1)$$ | $$(2, 0)$$ | $$(3, 1)$$ |
From the graph, we can clearly see that $$(x,y)=(5,3)$$ is the solution to the given pair of simultaneous equations.
If $$7x + 13y = 27$$ and $$13x + 7y = 33$$, find $$x + y$$
Solve the following system by evaluating proportional value of the variables:
$$3x + 2y = 4$$, $$2x - 3y = 7$$
Solve the following system by elimination method:
$$3x + 2y = 5$$, $$5x - 4y = 23$$
Solve the following simultaneous equations:
$$\dfrac {7}{2x + 1} + \dfrac {13}{y + 2} = 27, \dfrac {13}{2x + 1} + \dfrac {7}{y + 2} = 33$$
Solve the following simultaneous equations using graphical method
$$x + y = 6$$
$$x - y = 2$$
$$x + y = 6$$
$$\therefore y = 6 - x$$
$$\therefore y = 6 - x$$
| $$x$$ | $$0$$ | $$1$$ | $$2$$ |
| $$y$$ | $$6$$ | $$5$$ | $$4$$ |
$$(x, y)$$ | $$(0, 6)$$ | $$(1, 5)$$ | $$(2, 4)$$ |
$$x - y = 2$$
$$\therefore y = x - 2$$
$$\therefore y = x - 2$$
| $$x$$ | $$0$$ | $$1$$ | $$2$$ |
| $$y$$ | $$-2$$ | $$-1$$ | $$0$$ |
$$(x, y)$$ | $$(0, -2)$$ | $$(1, -1)$$ | $$(2, 0)$$ |
From the graph it is clear that $$(x,y) = (4,2)$$ is the solution of the given pair of equations.
Solve the simultaneous equations:
$$\dfrac {1}{x} + \dfrac {1}{y} = 12, \dfrac {3}{x} - \dfrac {2}{y} = 1$$
Find '$$x+y$$' for the following simultaneous equations : $$2x+3y=12$$ and $$3x+2y=13$$.
Solve the following simultaneous equations:
$$12x + 13y = 62$$;
$$13x + 12y = 63$$
Find '$$x+y$$' for the following simultaneous equations : $$4x+3y=8$$ and $$3x+4y=20$$.
Find '$$x+y$$' for the following simultaneous equations : $$x+2y=2$$ and $$2x+y=7$$.
Solve
$$\dfrac{33}{u + 2} + \dfrac{12}{v - 3} = 123$$
and $$\dfrac{12}{u + 2} + \dfrac{33}{v - 3} = 102$$
Solve the following simultaneous equations:
$$\cfrac { 10 }{ x+y } +\cfrac { 2 }{ x-y } =4$$;
$$\cfrac { 5 }{ x+y } -\cfrac { 5 }{ 3(x-y) } =\cfrac { -2 }{ 3 } $$
Find '$$m+n$$' for the following simultaneous equations : $$7m+3n=12$$ and $$3m+7n=8$$.
The cost of 2 exercise books and 3 pencils is Rs. 17 and the cost of 3 exercise books and 4 pencils is Rs.Formulate the problem algebrically and solve it graphically.
Let the cost of an exercise book be $$Rs. x$$
Let the cost of a pencil be $$Rs. y$$
$$2x+3y = 17$$ Blue line
$$3x+4y=24$$ Red line
Corresponding graph is shown in the attached figure. From the graph, it can be seen the solution is $$x=4,y=3$$.
Hence, the cost of exercise book is $$Rs. 4$$ and that of a pencil is $$Rs. 3$$.
Solve the following simultaneous equations using graphical method
$$4x = y - 5$$
$$y = 2x + 1$$
$$4x=y-5$$
$$y = 2x+1$$
Plotting both the equations on graph, as shown, $$(x,y) = (-2,-3)$$ is the solution of the given pair of equations.
| $$x$$ | $$0$$ | $$2$$ | $$-2$$ |
| $$y$$ | $$5$$ | $$13$$ | $$-3$$ |
| $$x$$ | $$0$$ | $$2$$ | $$-2$$ |
| $$y$$ | $$1$$ | $$5$$ | $$-3$$ |
Solve the following pair of equations by reducing them to a pair of linear equations
$$\cfrac { 5 }{ x-1 } +\cfrac { 1 }{ y-2 } =2$$ and $$\cfrac { 6 }{ x-1 } -\cfrac { 3 }{ y-2 } =1$$
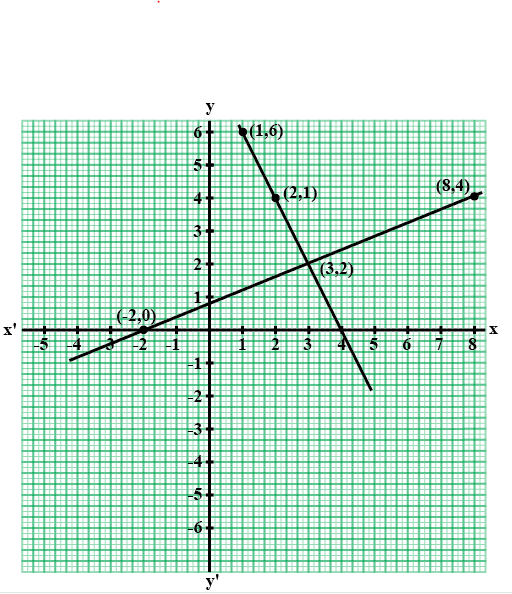
Solve the pair of linear equations graphically.
$$2x + y - 6 = 0$$
$$4x - 2y - 4 = 0$$
clearly, from graph
$$x=2,y=2$$ is solution. (intersection point)
$$x=2,y=2$$ is solution. (intersection point)
Draw a graph for the following pair of linear equations in two variables and find their solution from the graph.
$$2x+y=5$$
$$3x-2y=4$$
Clearly, from figure graph of both lines cut at $$x=2, y=1$$
Hence, solution is $$x=2,y=1$$
Hence, solution is $$x=2,y=1$$
Solve the equations
$$\dfrac{5}{x - 1} + \dfrac{1}{y - 2} = 2$$ and $$\dfrac{6}{x - 1} - \dfrac{3}{y - 2} = 1$$
Draw the graph of $$2x+3y=12$$.
First, we rewrite the equation $$2x+3y=12$$ in the form of $$y=mx+c$$.
$$2x+3y=12$$ implies $$y=-\dfrac{2}{3}x+4$$
Substituting $$x=-3, 0, 3$$ in the above equation, we find the values of $$y$$ as follows
Plot the points $$\left( -3,6 \right) ,\left( 0,4 \right)$$ and $$ \left( 3,2 \right) $$ and draw a line passing through these points. Now we get the required graph.
$$2x+3y=12$$ implies $$y=-\dfrac{2}{3}x+4$$
Substituting $$x=-3, 0, 3$$ in the above equation, we find the values of $$y$$ as follows
| $$y=-\dfrac{2}{3}x+4$$ |
| $$x$$ | $$-3$$ | $$0$$ | $$3$$ |
| $$-\dfrac{2}{3}x$$ | $$2$$ | $$0$$ | $$-2$$ |
| $$y=-\dfrac{2}{3}x+4$$ | $$6$$ | $$4$$ | $$2$$ |
Solve the following pair of linear equations by Substitution method
$$2x-3y=19$$ and $$3x-2y=21$$.
The coach of a cricket team buys one bat and $$2$$ balls for $$Rs. 300$$. Later he buys another $$2$$ bats and $$3$$ balls of the same kind for $$Rs. 525$$. Represent this situation algebraically and solve it by graphical method. Also, find out that how much money the coach will pay for the purchase of one bat and one ball.
Let cost of one bat be $$Rs.\ x$$
Let cost of one ball be $$Rs.\ y$$
$$x+2y = 300 ...........(i)$$ Blue line
$$2x+3y = 525 ...........(ii)$$ Red line
The graphs for the equation are shown in the attached plot.
From graph, solution is $$x =150, y=75$$
Hence, cost of one bat is $$Rs.\ 150$$ and cost of one ball is $$Rs.\ 75$$
Cost of one bat and one ball is $$Rs.\ 150+Rs.\ 75 = Rs.\ 225 $$
Solve the following equations graphically.
$$3x - y = 7$$,
$$2x + 3y = 1$$
Clearly, from figure both line intersect at $$x=2,y=-1$$
Therefore, solution is $$x=2,y=-1$$
Therefore, solution is $$x=2,y=-1$$
Solve by substitution method $$\dfrac{1}{x} + \dfrac{1}{y} = 4$$ and $$\dfrac{2}{x} + \dfrac{3}{y} = 7, x \neq 0, y \neq 0$$
Solve $$x + 3y = 16, 2x - y = 4$$ by using substitution method.
Solve by elimination method $$3x+4y=-45, 2x-3y=6$$.
Solve $$3x- 5y = -16, 2x+ 5y = 31$$
Prove that there is a value of $$c$$ for which the system-
$$cx + 2y = c - 2$$
$$8x + cy = c$$
has infinitely many solutions. Find this value.
Find the solution of given pair of linear equation by elimination method
$$3x + 4y = - 17$$ ...... (1)
$$5x + 2y = - 19$$ ....... (2)
Solve the following system of equations by elimination method:
$$3x+5y=20$$
$$6x-10y=-4$$
Solve the following system of equation by Substitution method.
$$x+y=7$$
$$3x-2y=11$$
Prove that there is a value of c for which the system $$cx+2y=c-2, 8x+cy=c$$ has infinitely many solutions. Find this value.
Solve the following system of equations of elimination by equating the coefficients method: $$3x-4y-11=0, 5x-7y+4=0$$.
Solve the following system of equations by elimination method.
$$3x - 4y - 11 = 0$$
$$5x - 7y + 4 = 0$$.
Solve the following system of equation by elimination method:
$$3x+2y=11,2x+3y=4$$
Solve the following systems of equations graphically:
$$x-2y=5$$
$$2x+3y=10$$
We can see that two lines intersect at the point $$x=5,y=0$$. So, the solution of the given system of equation is $$(5,0)$$.
Solve graphically the system of linear equations:
$$4x-3y+4=0$$
$$4x+3y-20=0$$
Find the area bounded by these lines and $$x$$-axis.
$$\dfrac { x }{ 7 } +\dfrac { y }{ \left( 4/3 \right) } =1\quad \longrightarrow \left( a \right) $$
$$\dfrac { x }{ 5 } +\dfrac { y }{ \left( 20/3 \right) } =1\quad \longrightarrow \left( b \right) $$
Intersection $$\rightarrow$$ $$x=2$$, $$y=3$$
Area $$=\dfrac { 1 }{ 2 } \times 6\times 3=9$$ sq. units.
Solve the following system of linear equations graphically:
$$4x-5y-20=0$$
$$3x+5y-15=0$$
Determine the vertices of the triangle formed by the lines representing the above equation and the $$y$$-axis.
Taking equation $$(1)$$
$$4x-5y-20=0$$
$$x$$ $$0$$ $$5$$
$$Y$$ $$-4$$ $$0$$
tAKING EQUATION $$(2)$$
$$3X+5Y-15=0$$
$$X$$ $$0$$ $$5$$
$$Y$$ $$3$$ $$0$$
$$\Rightarrow \ $$ Solution is given by the point where $$2$$ times intersect each others i.e $$(5,0)$$
$$\therefore \ x=5\ y=0$$ (required solution)
$$\Rightarrow $$ Vertices of triangle $$ABC=(0,3)(5,0)(0,-4)$$
Solve the following system of equations graphically:
$$2x-3y+6=0$$
$$2x+3y-18=0$$
$${\textbf{Hint: Draw both lines on graph and find point of intersection}}$$
$${\textbf{Step - 1: Finding table of value satisfying the given equation}}$$
$${\text{Given, }}{{\text{L}}_{\text{1}}} \equiv {\text{ 2x }}{\text{ - 3y + 6 = 0}}$$
$${\text{and }}{{\text{L}}_{\text{2}}}{\text{ }} \equiv {\text{ 2x + 3y - 18 = 0}}$$
$${\text{For }}{{\text{L}}_{\text{1}}}{\text{ }}\equiv 2x-3y+6=0$$
| $$x$$ | 0 | 3 |
| $$y=\dfrac{2x+6}{3}$$ | 2 | 4 |
$${\text{For }}{{\text{L}}_{\text{2}}}{\text{}}\equiv 2x+3y-18=0$$
| $$x$$ | 0 | 9 |
| $$y=\dfrac{-2x+18}{3}$$ | 6 | 0 |
$$\textbf{Step 2: Plot these points on XY-Plane and join them to get the graph of the given lines.}$$
$${\textbf{Step - 3: Finding intersection point}}$$
$${\text{From
the graph, we can clearly see that the two lines are intersecting at a point C(3,4)}}{\text{.}}$$
Solve the following systems of equations graphically:
$$x+y=3$$
$$2x+5y=12$$
We can see in the figure that two lines intersect at a point in 1st quadrant
$$\Rightarrow 2x+2 y=6$$
$$\Rightarrow 2x+5y=12$$
Subtract two equations ;
$$\Rightarrow 3y=6$$
$$\Rightarrow y=2$$
$$\Rightarrow x=3-y=3-2=1$$
$$\Rightarrow x=1,y=2$$
Draw the graphs of $$x-y+1=0$$ and $$3x+2y-12=0$$. Determine the coordinates of the vertices of the triangle formed by these lines and $$x$$-axis and shade the triangular area.
Given,
$$x-y+1=0$$....(1)
$$3x+2y-12=0$$....(2)
put $$x=0$$ in (1)
$$0-y+1=0\Rightarrow y=1$$
$$(0,1)$$.....(a)
put $$y=0$$ in (2)
$$3x+2(0)-12=0\rightarrow x=4$$
$$(4,0)$$.....(b)
put $$x=0$$ in (2)
$$3(0)+2y-12=0\rightarrow y=6$$
$$(0,6)$$......(c)
put $$y=0$$ in (1)
$$x-0+1=0\Rightarrow x=-1$$
$$(-1,0)$$...(d)
From figure, the vertices of triangle are $$(-1,0),(2,3),(4,0)$$
Solve the following system of linear equations graphically:
$$3x+y-11=0,\ x-y-1=0.$$
Shade the region bounded by these lines and $$y$$-axis. Also, find the area of the region bounded by the these lines and $$y$$-axis.
Given,
$$3x+y-11=0$$
$$\Rightarrow 3x+y=11$$........(1)
$$x-y-1=0$$
$$\Rightarrow y=x-1$$......(2)
substitute the value of "y" in (1), we get,
$$3x+(x-1)=11$$
$$\therefore x=3$$
$$\therefore y=2$$
$$(x,y)=(3,2)$$
area of triangle formed by vertices $$a(3,2),b(0,11),c(0,-1)$$
$$A=\dfrac{1}{2}\times BC\times AD$$
$$=\dfrac{1}{2}\times 12\times 3$$
$$=18sq. units$$
Represent the following pair of equations graphically and write the coordinates of points where the line intersects $$y$$-axis
$$x+3y=6$$
$$2x-3y=12$$
$$x+3y=6$$
plotting graph$$:$$
$$y\,$$ axis coordinates are (0,2) and (0,-4).
$$2x-3y=12$$
plotting graph$$:$$
$$x+3y=6$$
|
$$x$$ |
$$0$$ |
$$6$$ |
$$3$$ |
|
$$y$$ |
$$2$$ |
$$0$$ |
$$-1$$ |
$$2x-3y=12$$
|
$$x$$ |
$$0$$ |
$$6$$ |
$$9$$ |
|
$$y$$ |
$$-4$$ |
$$0$$ |
$$2$$ |
Show graphically that each one of the following systems of equations is in-consistent (i.e. has no solution):
$$3x-5y=20$$
$$6x-10y=-40$$
We can see that both the lines have same Slope=$$\dfrac {3}{5}$$
Constant of two lines is different
$$\Rightarrow $$lines are parallel
$$\therefore $$lines have no solution ie, they do not intersect and system of equations is in-consistent
Meena went to a bank to withdraw $$Rs\ 2000$$. She asked the cashier to give her $$Rs\ 50$$ and $$Rs\ 100$$ notes only. Meena got $$25$$ notes in all. Find how many notes $$Rs\ 50$$ and $$Rs\ 100$$ she received.
Solve graphically the following systems of linear equations. Also find the coordinates of the points where the lines meet axis of $$y$$.
$$x+2y-7=0$$,
$$2x-y-4=0$$
The lines$$:$$
plotting graph $$:$$ $$2x-y-4=0$$
The solution $$(3,2)$$
$$x+2y-7=0$$
$$2x-y-4=0$$
plotting graph $$:$$ $$x+2y-7=0$$
|
$$x$$ |
$$0$$ |
$$7$$ |
$$-1$$ |
|
$$y$$ |
$$\cfrac {7}{2}$$ |
$$0$$ |
$$4$$ |
|
$$x$$ |
$$0$$ |
$$2$$ |
$$3$$ |
|
$$y$$ |
$$-4$$ |
$$0$$ |
$$2$$ |
The point where they meet $$y$$-axis $$,$$ $$(0,\cfrac {7}{2})$$ and $$(0,-4)$$ $$.$$
$$12x + 10y = 13000$$
$$10x + 12y = 13400$$
Find $$x,y$$
Solve $$3 - \left( {x - 5} \right) = y + 2$$
$$2\left( {x + y} \right) = 4 - 3y$$
Solve the following system of equations by using the method of substitution,
$$3x-5y=-1$$ and $$x-y=-1$$.
Find $$x+y$$ for the following system of linear equations graphically,
$$x-y=1$$ and $$2x+y=8$$.
Given linear equation are $$x-y=1$$ and $$2x+y=8$$
let us find two points on the line $$x-y=1$$
$$x-y=1\Rightarrow x-1=y$$
For $$x=1\Rightarrow y=0$$
For $$x=2\Rightarrow y=1$$
Now we find two points on the line $$2x+y=8$$
$$2x+y=8\Rightarrow y=8-2x$$
For $$x=1\Rightarrow y=6$$
For $$x=2\Rightarrow y=4$$
Lets us plot those line on graph
So we see lines intersect at point $$(3,2)$$. Hence $$x=3, y=2$$
Hence $$(x+y)=(3+2)$$
$$=5$$
Solve: $$2x - 3y - 3 = 0$$
$$\dfrac{{2x}}{3} + 4y + \dfrac{1}{2} = 0$$
Solve the following system of equations graphically
$$x+3y=6$$
$$2x-3y=12$$
and hence find the value of a, if $$4x+3y=a$$.
Solve the following system of linear equations graphically. Also, find the coordinates of the points where the lines meet the $$y\ -$$ axis.
$$2x-y-5=0$$$$x-y-3=0$$
Given lines: $$2x-y-5=0$$ and $$x-y-3=0$$
The line $$2x-y-5=0$$ can be written as $$y=2x-5$$ $$...(1)$$
| $$x$$ | 0 | 1 | 3 |
| $$y$$ | -5 | -3 | 1 |
The line $$x-y-3=0$$ can be written as $$x=3+y$$ $$...(2)$$
| $$x$$ | 0 | 3 | 4 |
| $$y$$ | -3 | 0 | 1 |
Let us substitute $$x=3+y$$ in equation $$(1)$$
$$\Rightarrow 2(3+y)-y-5=0$$
$$\Rightarrow 6+2y-y-5=0$$
$$\Rightarrow y=-1$$
$$\therefore\ x=2$$
$$\therefore $$ The lines meet at the point $$(2,-1)$$
The coordinates where the lines meet $$y\ -$$ axis are $$(0,-3)$$ and $$(0,-5).$$
Solve graphically the following systems of linear equations. Also find the coordinates of the points where the lines meet axis of $$y$$.
$$2x+y-11=0$$,
$$x-y-1=0$$
$$2x+y-11=0$$
The solution is $$(4,3)$$
$$x-y-1=0$$
plotting graph $$:$$ $$2x+y-11=0$$
|
$$x$$ |
$$0$$ |
$$\cfrac {11}{2}$$ |
$$5$$ |
|
$$y$$ |
$$11$$ |
$$0$$ |
$$1$$ |
plotting graph$$:$$ $$x-y-1=0$$
|
$$x$$ |
$$0$$ |
$$1$$ |
$$2$$ |
|
$$y$$ |
$$-1$$ |
$$0$$ |
$$1$$ |
The points where the lines meet $$y$$-axis are$$:$$
$$(0,11)$$ and $$(0,-1)$$$$.$$
Determine, by drawing graphs, whether the following system of linear equation has a unique solution or not:
$$2y=4x-6,\ 2x=y+3$$
Given $$2y=4x-6$$
$$\implies 2x-y-3=0----(1)$$
$$2x=y+3\implies 2x-y-3=0-----(2)$$
So from graph there exists infinite number of solutions.
Solve the following system of equations:
$$8v=3u+5uv$$
$$6v-5u=-2uv$$.
Solve:$$3(2u+v)=7uv$$ and
$$3(u+3v)=11uv$$.
$$3(u+3v)=11uv$$.
Solve the following system of equations for $$x$$ and $$y$$,
$$\dfrac{a}{x}-\dfrac{b}{y}=0$$ and
$$\dfrac{ab^2}{x}+\dfrac{a^2b}{y}=a^2+b^2$$, where $$x, y$$$$\neq 0$$.
$$\dfrac{ab^2}{x}+\dfrac{a^2b}{y}=a^2+b^2$$, where $$x, y$$$$\neq 0$$.
Solve the following system of equations by using the method of elimination by equating the coefficients:
$$\dfrac{x}{10}+\dfrac{y}{5}+1=15$$ and $$\dfrac{x}{8}+\dfrac{y}{6}=15$$.
$$\dfrac{x}{10}+\dfrac{y}{5}+1=15$$ and $$\dfrac{x}{8}+\dfrac{y}{6}=15$$.
Solve the following systems of linear equations by using the method of elimination by equating the coefficients:
(i) $$3x+2y=11$$
(ii)$$2x+3y=4$$
Solve the following systems of equations by using the method of substitution,
$$2x+3y=9$$ and $$3x+4y=5$$.
Solve: $$\dfrac{1}{2(2x+3y)}+\dfrac{12}{7(3x-2y)}=\dfrac{1}{2}$$ and
$$\dfrac{7}{2x+3y}+\dfrac{4}{3x-2y}=2$$, where $$2x+3y\neq 0$$ and $$3x-2y\neq 0$$.
$$\dfrac{7}{2x+3y}+\dfrac{4}{3x-2y}=2$$, where $$2x+3y\neq 0$$ and $$3x-2y\neq 0$$.
For what value of k, will the following system of equations has infinitely many solutions?
$$2x+3y=4$$
$$(k+2)x+6y=3k+2$$
Solve $$\dfrac{2}{x}+\dfrac{2}{3y}=\dfrac{1}{6}$$ and $$\dfrac{3}{x}+\dfrac{2}{y}=0$$ and hence find 'a' for which, $$y=ax-4$$.
Solve the following system of equations,
$$\dfrac{1}{2x}-\dfrac{1}{y}=-1$$ and $$\dfrac{1}{x}+\dfrac{1}{2y}=8$$, where $$x\neq 0, y\neq 0$$.
$$\dfrac{1}{2x}-\dfrac{1}{y}=-1$$ and $$\dfrac{1}{x}+\dfrac{1}{2y}=8$$, where $$x\neq 0, y\neq 0$$.
Find solution of a pair of linear equations in two variables by elimination method$$2x+3y=0$$$$3x+4y=5$$
Find solution of a pair of linear equations in two variables by elimination method
Solve for $$x$$ and $$y$$ $$2x-3y=8$$$$5x$$$$-7y=19$$
Solve: $$\dfrac{20}{x+y}+\dfrac{3}{x-y}=7$$, $$\dfrac{8}{x-y}-\dfrac{15}{x+y}=5$$
Solve for $$'x'$$ and $$'y'$$ $$2x-3y=13,7x-2y=20$$
Solve:$$5x-4y+8=0$$
$$7x+6y-9=0$$
$$7x+6y-9=0$$
Solve graphically the system of linear equation: $$x+3y=6$$, $$2x-3y=12$$
$$x+3y=6\\ $$
|
X |
6 |
3 |
0 |
|
Y |
0 |
1 |
2 |
$$2x-3y=12$$
|
X |
0 |
6 |
3 |
|
Y |
-4 |
0 |
-2 |
Solve the following systems of linear equations by using the method of elimination by equating the coefficients:
$$8x+5y=9$$
$$3x+2y=4$$
If the pair of integers whose sum is zero but difference is $$12$$ are $$x\ and\ y $$. Then $$xy=-m$$.Find $$m$$
Solve the following systems of equations by using the method of substitution:
$$x+2y=-1$$
$$2x-3y=12$$
Find out whether the lines representing the following pairs of linear equation intersect at a point, are parallel or coincident: $$5x-4y+8=0$$ and $$7x+6y-9=0$$
It can take $$12$$ hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for four hours and the pipe of smaller diameter for $$9$$ hours, only half of the pool can be filled. How long would it take for each pipe to fill the pool separately?
Solve: $$3x+4y=25, \ 5x-6y=-9$$ by elimination method.
Solve: $$3x+2y=15$$ and $$10x-4y=2$$
Find the values of $$'a'$$ and $$'b'$$ for which the given pair of linear equations $$2x+3y=7;2ax+(a+b)=28$$ have infinite number of solutions.
For which value of $$k$$ will the following pair of linear equations have no solution?
$$3x+y=1$$ and $$(2k-1)x+(k-1)y=2k+1$$
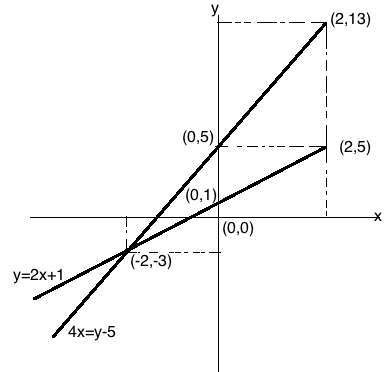
Solve graphically : $$y = 2x + 1 $$ and $$ x = 2y - 5$$
$$ x=2y-5$$
$$y=2x+1\\$$
| x | -3 | -1 | 1 |
| y | 1 | 2 | 3 |
$$y=2x+1\\$$
| x | 0 | 1 | -1 |
| y | 1 | 3 | -1 |
The graph has been plotted using the above points and the point of intersectio comes out to be $$(1,3)$$.
Solve:
$$4x+\dfrac {x-y}{8}=17$$
$$2y+x-\dfrac {5y+2}{3}=2$$
Solve the following pairs of equations by reducing them to a pair of linear equations:
$$\dfrac{1}{2x}+\dfrac{1}{3y}=2$$ , $$\dfrac{1}{3x}+\dfrac{1}{2y}=\dfrac{13}{6}$$
Write the condition for pair of linear Equation having Infinite number or solutions
$$a_{1}x + b_{1}y + c_{1} = 0$$ and $$a_{2}x + b_{2}y + c_{2} = 0$$.
By elimination method find the solution set of the given pair$$4x-3y=5$$ and $$7x-15y=-1$$
Solve graphically: $$2x-y-2=0$$, $$4x-y-4=0$$
Graph of the equation of given two lines intersect at $$(1,0)$$ hence, it is the solution of the given equations.
What is meant by consistent? What is meant by inconsistent?
Solve the pair of linear equations $$2x+3y=11$$ and $$2x-4y=-24$$.
Solve $$3x+2y=8$$
$$2x-3y=1$$
Solve for $$x$$ and $$y$$ if $$3(2x+y)=7xy $$ and $$3(x+3y)=11x$$.
Solve the equation by elimination method
$$ 11x + 15y + 23 = 0 $$, $$7x - 2y - 20 = 0$$
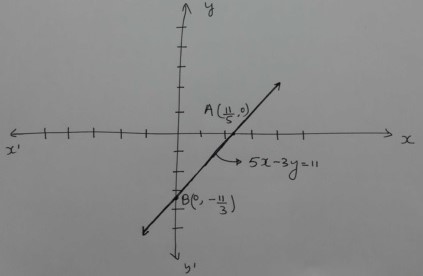
Find the value of x and y:$$5x-3y=11$$, $$10x+6y=-22$$
If $$-2x=4y+6$$ and $$2(2y+3)=3x-5$$, what is the solution $$(x,y)$$ to the system of equations above?
Draw the graph for each of the equation $$x + y = 6$$ and $$x - y = 2$$ on the same graph paper and find the coordinates of the point where the two straight lines intersect.
As we can see from the graph that the two given lines that there are $$x+y=6$$ and $$x-y=2$$ intersect at $$(4,2)$$
Solve :
$$\dfrac{5}{x + y} - \dfrac{2}{x - y} + 1 = 0 , \\ \, \dfrac{15}{x + y} + \dfrac{7}{x - y } -10 = 0 $$
Solve the following pairs of equations by reducing them to a pair of linear equations:
$$6x+3y=6xy$$$$2x+4y=5xy$$
Solve graphically: $$x+3y=6$$ and $$2x+3y=12$$.
REF.Image.
Let straight
A : x+3y = 6 &
B = 2x+3y = 12
For A
| x | 0 | 6 |
| y | 2 | 0 |
For B
| x | 0 | 6 |
| y | 4 | 0 |
We have a linear equation $$2x+3y-8=0$$. Write another linear equation in two variables x and y such that the geometrical representation of the pair so formed is intersecting lines.
Solve the following pairs of equations by reducing them to a pair of linear equations:
$$\dfrac{2}{\sqrt{x}}+\dfrac{2}{\sqrt{y}}=2$$ , $$\dfrac{4}{\sqrt{x}}-\dfrac{9}{\sqrt{y}}=-1$$
$$\frac{5}{x+y}-\frac{2}{x-y}=-1$$
$$\frac{15}{x+y}+\frac{7}{x-y}=10$$
Solve the following pairs of equations by reducing them to a pair of linear equations:
$$\dfrac{4}{x}+3y=14$$ , $$\dfrac{3}{x}-4y=23$$
Draw the graph of i) $$y = 2x + 5$$ , ii) $$y = 2x - 5$$, iii) $$y = 2x$$ and find the point of intersection on $$x$$-axis. Is the $$x$$-coordinates of these points also the zero of the polynomial ?
i)
$$y=2x+5$$
if $$x=0,y=5$$
if $$x=2,y=9$$
if $$y=5,x=0$$
if $$y=0,x=2.5$$
ii)
$$y=2x-5$$
if $$x=0,y=-5$$
if $$x=2,y=-1$$
if $$x=3,y=1$$
iii)
$$y=2x$$
if $$x=0,y=0$$
if $$x=1,y=2$$
if $$x=2,y=4$$
if $$x=3,y=6$$
Solve the following pair of linear equation by the substitution method.
$$0.2x+0.3y=1.3$$
$$0.4x+0.5y=2.3$$
I have a total of $$Rs.\ 300$$ in coins of denomination $$Rs.\ 1$$, $$Rs.\ 2$$, $$Rs.\ 5$$. The number of $$Rs.\ 2$$ coins is $$3$$ times the number of $$Rs.\ 5$$ coins. The total number of coins is $$160$$. How many coins of each denomination are with me?
Graphical seclusion: Solve : $$x+y=10$$
$$x+y= 8$$
$$x+y=10\\\therefore\>x=0,\>y\>=10\>hence\>point\>(0,10)\\and\>if\>x\>=10,\>y\>=0\>hence\>point\>(10,0)\\for\>x+y=8\\at\>x\>=0,\>y=8,\>so\>point\>(0,8)\\and\>x=8,\>y\>=0,\>so\>point\>(8,0)$$
As both line are parallel to each other and hence there are no solution to the given system of equations.
The present age of sahil's mother is three times the present age of sahil. After $$5$$ years their ages add to $$66$$ years find their present age.
Solve for x and y:$$\frac{3x}{2}-\frac{5y}{3}+2=0$$
$$\frac{x}{3}+\frac{y}{2}=2\frac{1}{6}$$
$$\frac{x}{3}+\frac{y}{2}=2\frac{1}{6}$$
Solve following equation by elimination method
$$3x+2y=11$$
$$2x+3y=4$$
There are some $$20$$ paise and some $$25$$ paise coins in a bag. The total number of coins is $$50$$ and the amount in the bag is $$Rs.\ 11.25$$. Find the number of coins of each value in the bag by method of elimination?
Solve the system of equations
$$2x + 5y = 1$$
$$3x + 2y = 7$$.
Solve the following pairs of linear equation:
$$\dfrac{2}{x}+\dfrac{2}{3y}=\dfrac{1}{6}$$
$$\dfrac{2}{x}-\dfrac{1}{y}= 1$$
Solve the following equation
$$3x-4y=1$$;
$$-2x+\dfrac{8}{3}y=5 $$
solve the following equation graphically.
$$x+2y=5$$ and $$3x-y=1$$
$$x+2y=5$$
$$3x-y=1$$
These lines intersect at the point $$P(1,2)$$ and therefore, the solution of given equations is $$x=1, y=2$$.
Find the solution of lines :$$\begin{array}{l}x + y = 4\\2x - 3y = 3\end{array}$$
$$x+y=4$$
$$2x-3y=3$$
$$x+y=4\,\,\,\,\Rightarrow 2x+2y=8 \Rightarrow 5y=\,5\Rightarrow y=1$$
$$2x-3y=3\Rightarrow 2x-3y=3\Rightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=3$$
From the figure it is clear that
Sol is $$x=3, y=1$$
Sol is $$x=3,y=1$$
$$\therefore \boxed{(x,y)=(3,1)}$$
Solve the following pair of linear equation graphically.
$$x + 3y = 6;2x - 3y = 12$$
$$x+3y=6......(1)$$
$$2x-3y=12....(2)$$
Solving $$(1)$$ [Ref image 1]
$$4+3y-6=0$$
When $$x=0$$
$$y=2$$
When $$y=0$$
$$x=6$$(Ref image (1)).
Solving $$(2)$$ [Ref. image 2]
When
$$x=0$$
$$y=-4$$
When
$$y=0$$
$$x=6$$
$$\therefore$$ They intersect at $$(6, 0)$$ [Ref. image 3]
Solve the following sets of simultaneous equations.
$$3x-5y=16; x-3y=8$$
If $$3x-2y=5$$ and $$3y-2x=3$$ then find the value of $$(x+y)$$.
If $$\dfrac{1}{x-y}=\dfrac{1}{2}$$ and $$\dfrac{1}{x+y}=\dfrac{1}{14}$$ then find the value of x.
Solve:
$$\dfrac{5}{x-1}+\dfrac{1}{y-1}=2,\dfrac{6}{x-1}-\dfrac{3}{y-1}=1$$
Solve the following sets of simultaneous equations.
$$x+y=4; 2x-5y=1$$
Solve the following sets of simultaneous equations.
$$2x+y=5; 3x-y=5$$
Solve the following pairs of liner equation by the method of substitution:
$$3x-y=0, x-y+6=0$$
For what value of $$K$$ will the following pair of linear equations have infinitely many solutions?
$$Kx+3y-(K-3)=0$$
$$12x+Ky-K=0$$
$$12x+Ky-K=0$$
Solve by elimination:
$$12x+15y=-18$$
$$18x-7y=-86$$
Solve by elimination
$$8x+13y=29$$
$$12x-7y=17$$
Solve the following sets of simultaneous equations.
$$2x+3y+4=0; x-5y=11$$
Solve : $$\dfrac{3x}{2} - \dfrac{5y }{3} = -2$$, $$\dfrac{x}{3} + \dfrac{y}{2} = \dfrac{13}{6}$$
Solve the following sets of simultaneous equations.
$$2x-7y=7; 3x+y=22$$
A passenger is allowed some free luggage by Rajdhani express. Two passengers have a total of $$105kg$$ luggage and they have to pay $$Rs. 18$$ and $$Rs. 12$$ as luggage charges respectively. If one passenger having the same $$kg$$ of luggage then he would have to pay $$Rs.36$$, find how much free luggage each passenger is allowed to carry.
Solve the following equations by graphical method $$2x+3y=0$$.
REF.Image
$$2x+3y=0$$ solve by graphical method
$$2x+3y=0$$
$$2x=-3y$$
$$x=-\dfrac{3y}{2}$$
when $$y=0, x=0$$
$$y=2, x=-3$$
Now
If $$y=-2, =x=3$$
Solve for $$x$$ and $$y$$$$3 x - 4 y = 26$$
$$6 x - 10 y = 40$$
$$6 x - 10 y = 40$$
The cost of some books is $$60$$. Cost of every book is the same. If the book sell decreases the cost of the book by $$1$$, one gets $$5$$ books more for the same amount. What is the cost of each book and how many books are purchased?
If $$\frac{{5 + 2\sqrt 3 }}{{7 + 4\sqrt 3 }} = $$$$a + b\sqrt 3 $$ , then find the value of a and b
A student bought some pens at $$Rs 8$$ each and some pencils at $$ Rs1.50$$ each. If total number of pens and pencils purchased is 16 and their total cost is $$Rs 50$$ , how many pens did he buy?
Solve the following pair of linear equations :
$$0.2x+0.3y=1.3$$
$$0.4x+0.5y=2.3$$
Solve
$$x+y=3$$
$$x-y=1$$
Solve the following equations.
$$3x-y=7; x+4y=11$$
Draw the graphs of the pair of linear equations in two variables $$x + 3 y = 6,2 x - y = 5$$. Find its solution set.
$$x + 3y = 6$$
$$+ (2x - y = 5)3$$
______________
$$7x = 21$$
______________
$$x = 3 \, ; \, y = 1$$
writing equation in intercept form
$$\dfrac{x}{6} + \dfrac{y}{2} = 1$$
$$\dfrac{x}{\dfrac{5}{2}} + \dfrac{y}{-5} = 1$$
Solve: $$x+2y=3,\,\,2x-y=5$$
What value of K, will the following pair of the linear equations have infinitely many solutions?
$$2x+3y-13=0 ; 6x-ky-39=0$$
Find the value of x and y
$$\dfrac{5}{{x - 1}} + \dfrac{1}{{y - 2}} = 2$$ and $$ \dfrac{6}{{x - 1}} - \dfrac{3}{{y - 2}} = 1$$
$$\dfrac{5}{{x - 1}} + \dfrac{1}{{y - 2}} = 2$$ and $$ \dfrac{6}{{x - 1}} - \dfrac{3}{{y - 2}} = 1$$
Solve the pair of linear equation $$: 2X-5Y-4=0, 4X-8Y=8.$$
Solve :$$x+5y=17\\2x+3y=13$$
Solve $$x+4y=24xy$$, $$x+2y=21xy$$.
Solve the following pair of an equation by elimination the coefficient method:
$$x+2y=11$$
$$2x-y=2$$
Solve the following pair of linear equation by substitution method:
$$3x + 2y - 7 = 0$$
$$4x + y - 6 = 0$$
$$3x+2y=7$$
$$4x+y=6\Rightarrow y=6-4x$$
placing in equation (1)
$$3x+2(6 - 4x)=7$$
$$3x+12-8x=7 \Rightarrow -5x+12=7$$
$$-5x=7-12\Rightarrow -5x=-5$$
x=1
$$ \therefore $$ y = 6 - 4$$ \times 1 = 2 $$
$$ \therefore $$ x = 1, y = 2
Find the equations of the lines for which $$\tan{\theta}=\dfrac{3}{4}$$, where $$\theta$$ is the angle of inclination of the line and $$y-$$ intercept is $$\dfrac{-5}{3}$$
Simplify:
$$0.2x + 0.3y = 1.3$$
$$0.4x + 0.5y = 2.3$$
Solve the following system of equation
$$2x +3y +8 = 0$$
$$4x + 5y + 14 = 0$$
Solve:
$$x+y=7;x-y=3$$
Solve :$$3x-2y=1$$$$2x+y=3$$
Solve:
$$x-y=5;3x+2y=25$$
Solve the following simultaneous equation graphically.
$$2x+3y=12;\ x-y=1$$
$$2x + 3y = 12$$
$$y=\dfrac{12-2x}{3}$$
Put $$x=0$$,
$$y=\dfrac{12}{3}$$
$$\Rightarrow y=4$$
Put $$x=6$$
$$\dfrac{0}{3}$$
$$\Rightarrow y=0$$
Draw the line joining the point $$(0,4)$$ and $$(6,0)$$ to get the graph of $$2x+3y=12$$
Consider,
$$x - y = 1$$
$$y=x-1$$
$$x - y = 1$$
$$y=x-1$$
Put $$x=0$$
$$\Rightarrow y=-1$$
Put $$x=1$$
$$\Rightarrow y=0$$
Draw the line joining the point $$(0,-1)$$ and $$(1,0)$$ to get the graph of $$x-y=1$$
From the graph it can be seen that point of intersection of two lines $$(3,2)$$
Hence required solution is $$(3,2)$$
Solve the following pairs of equations by reducing them to a pair of linear equations.
$$\dfrac{5}{x-1}-\dfrac{1}{y-2}=2$$ & $$\dfrac{6}{x-1}-\dfrac{3}{y-2}=1$$
Solve: $$3 x - 4 y = -7$$ ; $$5 x - 2 y = 0$$
Solve:$$\dfrac { x+1 }{ 2 } +\dfrac { y-1 }{ 3 } =8 $$
$$ \dfrac { x-1 }{ 3 } +\dfrac { y+1 }{ 2 } =9$$
$$ \dfrac { x-1 }{ 3 } +\dfrac { y+1 }{ 2 } =9$$
If $$12x +17y = 48$$ and $$17x +12y = 68$$, then find $$x-y$$.
Solve the following equation:
$$\cfrac{3x}{2} +\cfrac {2y}{3} = \cfrac{40}{3}$$ ; $$\cfrac {2x}{3} +\cfrac {3y}{2} = \cfrac{25}{3}$$
Solve the equations graphically . $$x+y=10$$
$$ y=x+4$$
$$ y=x+4$$
$$x+y=10$$
$$x+x+4=10$$ since $$y=x+4$$
$$2x=10-4=6$$
$$x=\dfrac{6}{2}=3$$
Put $$x=3$$ in $$y=x+4$$ we get $$y=3+4=7$$
$$\therefore \left(3,7\right)$$ is the point of intersection of the lines $$x+y=4$$ and $$y=x+4$$ as shown in the graph.
Solve the following simultaneous equation
$$\dfrac{{30}}{{x - y}} + \dfrac{{44}}{{x + y}} = 10\ ;\\ \dfrac{{40}}{{x - y}} + \dfrac{{55}}{{x + y}} = 13$$
Solve the simultaneously equations $$2y - x = 0, 10x+15y=105$$
Solve :$$10x+3y=75$$; $$6x-5y=11$$
Solve by the method of substitution $$x+y=5,$$ $$x-y=1$$
Solve the following pair of linear equations by the elimination method and the subsitution method:
$$3x-5y-4=0$$ and $$9x=2y+7$$
Solve each of the following system of equations graphically:
$$2x+3y=8$$,
$$x-2y+3=0$$
$$2x+3y=8$$....(1)
$$x-2y+3=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$2x+3y=8$$
$$2x=8-3y$$
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$x-2y+3=0$$
or $$x=2y-3$$
Graph:
Both the lines intersect each other at point $$(1, 2)$$.
So, $$x=1, y=2$$
$$x-2y+3=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$2x+3y=8$$
$$2x=8-3y$$
| $$x:$$ | $$4$$ | $$1$$ | $$-2$$ |
| $$y:$$ | $$0$$ | $$2$$ | $$4$$ |
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$x-2y+3=0$$
or $$x=2y-3$$
| $$x:$$ | $$-3$$ | $$-1$$ | $$1$$ |
| $$y:$$ | $$0$$ | $$1$$ | $$2$$ |
Graph:
Both the lines intersect each other at point $$(1, 2)$$.
So, $$x=1, y=2$$
Solve :
$$3x-2y=4$$$$2x+y=5$$
Solve for $$x$$ and $$y$$:
$$x-y=3,$$
$$\dfrac x3+\dfrac y2=6$$
Solve :$$s-t=3$$
$$\cfrac{s}{3}+\cfrac{t}{2}=6$$
Solve each of the following system of equations graphically:
$$2x+3y=2$$
$$x-2y=8$$
$$2x+3y=2$$......(1)
$$x-2y=8$$ ........(2)
Step 1: From equation (1), isolate $$x$$
$$2x=2-3y$$
or $$x=(2-3y)/2$$
Choose any values for $$y$$ and get corresponding value of $$x$$:
Plot above points on the graph and join them.
Step 2: From equation (2)
$$x-2y=8$$
or $$x=8+2y$$
Choose any values for $$y$$ and get corresponding value of $$x$$:
Plot above points on the graph and join them.
Step 3:
Graph:
Step 4: Both the lines intersect each other at point $$(4, -2)$$.
So, $$x=4, y=-2$$
$$x-2y=8$$ ........(2)
Step 1: From equation (1), isolate $$x$$
$$2x=2-3y$$
or $$x=(2-3y)/2$$
Choose any values for $$y$$ and get corresponding value of $$x$$:
| $$x:$$ | $$1$$ | $$-2$$ | $$4$$ |
| $$y:$$ | $$0$$ | $$2$$ | $$-2$$ |
Step 2: From equation (2)
$$x-2y=8$$
or $$x=8+2y$$
Choose any values for $$y$$ and get corresponding value of $$x$$:
| $$x:$$ | $$6$$ | $$4$$ | $$2$$ |
| $$y:$$ | $$-1$$ | $$-2$$ | $$-3$$ |
Step 3:
Graph:
Step 4: Both the lines intersect each other at point $$(4, -2)$$.
So, $$x=4, y=-2$$
Solve for $$x$$ and $$y$$:
$$x+y=3$$.
$$4x-3y=26$$.
Solve each of the following system of equations graphically:
$$3x+2y=4$$
$$2x-3y=7$$
$$3x+2y=4$$....(1)
$$2x-3y=7$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$3x+2y=4$$
or $$x=(4-2y)/3$$
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$2x-3y=7$$
$$x=(3y+7)/2$$
Graph:
Both the lines intersect each other at point $$(2, -1)$$.
So, $$x=2, y=-1$$
$$2x-3y=7$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$3x+2y=4$$
or $$x=(4-2y)/3$$
| $$x:$$ | $$0$$ | $$2$$ | $$4$$ |
| $$y:$$ | $$2$$ | $$-1$$ | $$-4$$ |
$$2x-3y=7$$
$$x=(3y+7)/2$$
| $$x:$$ | $$5$$ | $$2$$ | $$-1$$ |
| $$y:$$ | $$1$$ | $$-1$$ | $$-3$$ |
Graph:
Both the lines intersect each other at point $$(2, -1)$$.
So, $$x=2, y=-1$$
Solve the following pair of linear equations
(i) $$x+y=14$$
$$x-y=4$$
(ii) $$3x-y=3$$
$$9x-3y=9$$
Solve each of the following system of equations graphically:
$$2x-5y+4=0$$,
$$2x+y-8=0$$
$$2x-5y+4=0$$....(1)
$$2x+y-8=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$2x-5y+4=0$$
or $$2x=5y-4$$
$$x=(5y-4)/2$$
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$2x+y-8=0$$
or $$y=8-2x$$
Graph:
Both the lines intersect each other at point $$(3, 2)$$.
So, $$x=3, y=2$$
$$2x+y-8=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$2x-5y+4=0$$
or $$2x=5y-4$$
$$x=(5y-4)/2$$
| $$x:$$ | $$-2$$ | $$3$$ | $$8$$ |
| $$y:$$ | $$0$$ | $$2$$ | $$4$$ |
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$2x+y-8=0$$
or $$y=8-2x$$
| $$x:$$ | $$1$$ | $$2$$ | $$3$$ |
| $$y:$$ | $$6$$ | $$4$$ | $$2$$ |
Both the lines intersect each other at point $$(3, 2)$$.
So, $$x=3, y=2$$
Solve each of the following system of equations graphically:
$$x+2y+2=0$$
$$3x+2y-2=0$$
$$x+2y+2=0$$....(1)
$$3x+2y-2=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$x+2y+2=0$$
or $$x=-2y-2$$
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$3x+2y-2=0$$
or $$x=(2-2y)/3$$
Graph:
As expressed in above graph where red line=> $$x+2y+2=0$$ & blue line =>$$3x+2y-2=0$$
Both the lines intersect each other at point $$(2, -2)$$.
So, $$x=2, y=-2$$
$$3x+2y-2=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$x+2y+2=0$$
or $$x=-2y-2$$
| $$x:$$ | $$-2$$ | $$0$$ | $$2$$ |
| $$y:$$ | $$0$$ | $$-1$$ | $$-2$$ |
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$3x+2y-2=0$$
or $$x=(2-2y)/3$$
| $$x:$$ | $$0$$ | $$2$$ | $$-2$$ |
| $$y:$$ | $$1$$ | $$-2$$ | $$4$$ |
Graph:
As expressed in above graph where red line=> $$x+2y+2=0$$ & blue line =>$$3x+2y-2=0$$
Both the lines intersect each other at point $$(2, -2)$$.
So, $$x=2, y=-2$$
Solve each of the following system of equations graphically:
$$2x+3y+5=0$$
$$3x-2y-12=0$$
$$2x+3y+5=0$$....(1)
$$3x-2y-12=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$2x+3y+5=0$$
$$2x=-3y-5$$
$$x=(-3y-5)/2$$
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$3x-2y-12=0$$
or $$3x=2y+12$$
or $$x=(2y+12)/3$$
Graph:
Both the lines intersect each other at point $$(2, -3)$$.
So, $$x=2, y=-3$$
$$3x-2y-12=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$2x+3y+5=0$$
$$2x=-3y-5$$
$$x=(-3y-5)/2$$
| $$x:$$ | $$-4$$ | $$-1$$ | $$2$$ |
| $$y:$$ | $$1$$ | $$-1$$ | $$-3$$ |
$$3x-2y-12=0$$
or $$3x=2y+12$$
or $$x=(2y+12)/3$$
| $$x:$$ | $$4$$ | $$0$$ | $$2$$ |
| $$y:$$ | $$0$$ | $$-6$$ | $$-3$$ |
Graph:
Both the lines intersect each other at point $$(2, -3)$$.
So, $$x=2, y=-3$$
Solve for $$x$$ and $$y$$:
$$2x-\dfrac {3y}4=3$$,
$$5x=2y+7$$.
Solve each of the following system of equations graphically:
$$3x+2y=12$$
$$5x-2y=4$$
$$3x+2y=12$$....(1)
$$5x-2y=4$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$3x+2y=12$$
$$3x=12-2y$$
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$5x-2y=4$$
$$5x=4+2y$$
or $$x=(4+2y)/5$$
Graph:
Both the lines intersect each other at point $$(2, 3)$$.
So, $$x=2, y=3$$
$$5x-2y=4$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$3x+2y=12$$
$$3x=12-2y$$
| $$x:$$ | $$4$$ | $$2$$ | $$0$$ |
| $$y:$$ | $$0$$ | $$3$$ | $$6$$ |
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$5x-2y=4$$
$$5x=4+2y$$
or $$x=(4+2y)/5$$
| $$x:$$ | $$0$$ | $$2$$ | $$4$$ |
| $$y:$$ | $$-2$$ | $$3$$ | $$8$$ |
Both the lines intersect each other at point $$(2, 3)$$.
So, $$x=2, y=3$$
Solve for $$x$$ and $$y$$:
$$2x+5y=8/3$$,
$$3x-2y=5/6$$.
Solve each of the following system of equations graphically:
$$2x+3y-4=0$$
$$3x-y+5=0$$
$$2x+3y-4=0$$....(1)
$$3x-y+5=0$$......(2)
Isolate $$x$$ from equation (1) and find the values of $$x$$ and $$y$$.
$$2x+3y-4=0$$
or $$x=\dfrac{4-3y}{2}$$
So, $$x=-1, y=2$$ is the solution of the given system of equations.
$$3x-y+5=0$$......(2)
Isolate $$x$$ from equation (1) and find the values of $$x$$ and $$y$$.
$$2x+3y-4=0$$
or $$x=\dfrac{4-3y}{2}$$
Hence,
| $$x:$$ | $$2$$ | $$-1$$ | $$5$$ |
| $$y:$$ | $$0$$ | $$2$$ | $$-2$$ |
Now, plot the points $$(2,0),\ (-1,2)\ and\ (5,-2)$$ on the graph to get the straight line represented by the equation $$2x+3y-4=0$$.
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$3x-y+5=0$$
or $$y=5+3x$$
or $$y=5+3x$$
| $$x:$$ | $$0$$ | $$-1$$ | $$-2$$ |
| $$y:$$ | $$5$$ | $$2$$ | $$-1$$ |
Now, plot the points $$(0,5),\ (-1,2)\ and\ (-2,-1)$$ on the graph to get the straight line represented by the equation $$3x-y+5=0$$.
The graph of both the lines will be as shown in the figure given above.
We can see from the graph that, both the lines intersect each other at point $$(-1, 2)$$.
So, $$x=-1, y=2$$ is the solution of the given system of equations.
Hence, $$(-1,2)$$ is the required solution.
Solve for $$x$$ and $$y$$:
$$2x-3y=13$$
$$7x-2y=20$$.
Solve each of the following system of equations graphically:
$$3x+y+1=0$$
$$2x-3y+8=0$$
$$3x+y+1=0$$....(1)
$$2x-3y+8=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$3x+y+1=0$$
or $$y=-3x-1$$
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$2x-3y+8=0$$
$$x=(3y-8)/2$$
Graph:
Both the lines intersect each other at point $$(-1, 2)$$.
So, $$x=-1, y=2$$
$$2x-3y+8=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$3x+y+1=0$$
or $$y=-3x-1$$
| $$x:$$ | $$0$$ | $$-1$$ | $$-2$$ |
| $$y:$$ | $$-1$$ | $$2$$ | $$5$$ |
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$2x-3y+8=0$$
$$x=(3y-8)/2$$
| $$x:$$ | $$-4$$ | $$-1$$ | $$2$$ |
| $$y:$$ | $$0$$ | $$2$$ | $$4$$ |
Graph:
Both the lines intersect each other at point $$(-1, 2)$$.
So, $$x=-1, y=2$$
Solve each of the following system of equations graphically:
$$2x-3y+13=0$$
$$3x-2y+12=0$$
$$2x-3y+13=0$$....(1)
$$3x-2y+12=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$2x-3y+13=0$$
or $$2x=3y-13$$
or $$x=(3y-13)/2$$
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$3x-2y+12=0$$
or $$x=(2y-12)/3$$
Graph:
Both the lines intersect each other at point $$(-2, 3)$$.
So, $$x=-2, y=3$$
$$3x-2y+12=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$2x-3y+13=0$$
or $$2x=3y-13$$
or $$x=(3y-13)/2$$
| $$x:$$ | $$-5$$ | $$-2$$ | $$1$$ |
| $$y:$$ | $$1$$ | $$3$$ | $$5$$ |
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$3x-2y+12=0$$
or $$x=(2y-12)/3$$
| $$x:$$ | $$-4$$ | $$-2$$ | $$0$$ |
| $$y:$$ | $$0$$ | $$3$$ | $$6$$ |
Graph:
Both the lines intersect each other at point $$(-2, 3)$$.
So, $$x=-2, y=3$$
Solve for $$x$$ and $$y$$:
$$4x-3y=8$$
$$6x-y=29/3$$
Solve for $$x$$ and $$y$$:
$$7(y+3)-2(x+2)=14$$,
$$4(y-2)+3(x-3)=2$$.
Solve each of the following system of equations graphically and find the vertices and area of the triangle formed by these lines and the $$x-$$axis:
$$4x-3y+4=0,\ 4x+3y-20=0$$
$$4x-3y+4=0$$....(1)
$$4x+3y-20=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$4x-3y+4=0$$
$$\Rightarrow x=\dfrac{3y-4}{4}$$
Graph:
$$4x+3y-20=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$4x-3y+4=0$$
$$\Rightarrow x=\dfrac{3y-4}{4}$$
| $$x$$ | $$y$$ |
| $$-1$$ | $$0$$ |
| $$2$$ | $$4$$ |
| $$-4$$ | $$-4$$ |
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$4x+3y-20=0$$
$$\Rightarrow x=\dfrac{20-3y}{4}$$
$$4x+3y-20=0$$
$$\Rightarrow x=\dfrac{20-3y}{4}$$
| $$x$$ | $$y$$ |
| $$5$$ | $$0$$ |
| $$2$$ | $$4$$ |
| $$-1$$ | $$8$$ |
On plotting $$(-1,0),\ (2,4)\text{ and } (-4,-4)$$ on the $$xy-plane$$, we will get the graph of the linear equation $$4x-3y+4=0$$.
Similarly, on plotting $$(5,0),\ (2,4)\text{ and } (-1,8)$$ on the $$xy-plane$$, we will get the graph of the linear equation $$4x+3y-20=0$$.
The obtained graph is shown above.
We can see from the graph that both the lines intersect each other at point $$(2, 4)$$ and $$x-$$ axis at $$A(-1, 0)$$ and $$D(5, 0)$$.
We can see from the graph that both the lines intersect each other at point $$(2, 4)$$ and $$x-$$ axis at $$A(-1, 0)$$ and $$D(5, 0)$$.
Area of $$\triangle BAD$$:
Area of $$\triangle BAD=\dfrac{1}{2}\times base \times altitude$$
$$\Rightarrow \dfrac{1}{2} \times 6\times 4$$
$$\Rightarrow 12\ square\ units$$.
Area of $$\triangle BAD=\dfrac{1}{2}\times base \times altitude$$
$$\Rightarrow \dfrac{1}{2} \times 6\times 4$$
$$\Rightarrow 12\ square\ units$$.
Hence, the vertices of the triangle formed by the given lines and $$x-axis$$ are $$A(-1,0),\ B(2,4)\text { and }D(5,0)$$, and the area of the triangle is $$12\ square\ units$$.
Solve each of the following system of equations graphically and find the vertices and area of the triangle formed by these lines and the $$x-$$axis:
$$x-y+1=0,\ 3x+2y-12=0$$
$$x-y+1=0$$....(1)
$$3x+2y-12=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$x-y+1=0$$
or $$x=y-1$$
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$3x+2y-12=0$$
or $$x=(12-2y)/3$$
Graph:
Both the lines intersect each other at point $$E(2, 3)$$ and $$x-$$ axis at $$A(-1, 0)$$ and $$D(4, 0)$$
To find the area of triangle $$BAD$$:
Area of $$\triangle EAD=1/2(base \times altitude)$$
$$=1/2 \times 5\times 3$$
$$=7.5\ sq.units$$.
$$3x+2y-12=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$x-y+1=0$$
or $$x=y-1$$
| $$x$$ | $$y$$ |
| $$-1$$ | $$0$$ |
| $$0$$ | $$1$$ |
| $$1$$ | $$2$$ |
$$3x+2y-12=0$$
or $$x=(12-2y)/3$$
| $$x$$ | $$y$$ |
| $$4$$ | $$0$$ |
| $$2$$ | $$3$$ |
| $$0$$ | $$6$$ |
Both the lines intersect each other at point $$E(2, 3)$$ and $$x-$$ axis at $$A(-1, 0)$$ and $$D(4, 0)$$
To find the area of triangle $$BAD$$:
Area of $$\triangle EAD=1/2(base \times altitude)$$
$$=1/2 \times 5\times 3$$
$$=7.5\ sq.units$$.
Solve for $$x$$ and $$y$$:
$$\dfrac5x+6y=13\\\dfrac3x+4y=7\quad(x\neq 0)$$
Solve for $$x$$ and $$y$$:
$$0.3x+0.5y=0.5$$
$$0.5x+0.7y=0.74$$.
Solve for $$x$$ and $$y$$:
$$2x+3y+1=0$$,
$$(7-4x)/3=y$$
Solve for $$x$$ and $$y$$:
$$2x-\dfrac3y=9$$$$3x+\dfrac7y=2\quad(y\neq 0)$$
Show graphically that each of the following given system of equation has infinitely many solutions:
$$2x+3y=6,\ 4x+6y=12$$
$$2x+3y=6$$....(1)
$$4x+6y=12$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$2x+3y=6$$
or $$x=(6-3y)/2$$
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$4x+6y=12$$
or $$x=(12-6y)/4$$
Graph:
From the graph, we can see that, all the points lie on the same straight line.
Which shows that, system has infinite many solutions.
$$4x+6y=12$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$2x+3y=6$$
or $$x=(6-3y)/2$$
| $$x$$ | $$y$$ |
| $$3$$ | $$0$$ |
| $$0$$ | $$2$$ |
| $$-3$$ | $$4$$ |
$$4x+6y=12$$
or $$x=(12-6y)/4$$
| $$x$$ | $$y$$ |
| $$3$$ | $$0$$ |
| $$3/2$$ | $$1$$ |
| $$-3/2$$ | $$3$$ |
Graph:
From the graph, we can see that, all the points lie on the same straight line.
Which shows that, system has infinite many solutions.
Solve each of the following system of equations graphically and find the vertices and area of the triangle formed by these lines and the $$y$$-axis:
$$4x-y-4=0,\ 3x+2y-14=0$$
Given equations are
$$4x-y-4=0\quad...(1)$$
$$3x+2y-14=0\quad...(2)$$
Write $$y$$ in terms of $$x$$ for equation $$(1)$$.
$$4x-y-4=0$$
$$\Rightarrow y=(4x-4)$$
Substitute different values of $$x $$ in the above equation to get corresponding values of $$y$$
For $$x=1, \quad y=0$$
For $$x=0, \quad y=-4$$
For $$x=2, \quad y=4$$
Now plot the points $$A(1,0),\ B(0,-4)$$ and $$C(2,4)$$ in the graph paper and join $$A,\ B$$ and $$C$$ to get the graph of $$4x-y-4=0$$
Similarly, Write $$y$$ in terms of $$x$$ for equation $$(2)$$.
$$3x+2y-14=0$$
$$\Rightarrow y=\dfrac{(14-3x)}2$$
Substitute different values of $$x $$ in the above equation to get corresponding values of $$y$$
For $$x=0, \quad y=7$$
For $$x=2, \quad y=4$$
For $$x=4, \quad y=1$$
Now plot the points $$D(0,7),\ E(2,4)$$ and $$F(4,1)$$ in the graph paper and join $$D,\ E$$ and $$F$$ to get the graph of $$3x+2y-14=0$$
From the graph:
Both the lines intersect each other at point $$C(2, 4)$$ and $$y$$-axis at $$B(0, -4)$$ and $$D(0, 7)$$ respectively
$$\therefore$$ Area of $$\triangle BCD=\dfrac12(\text{base} \times \text{altitude})$$
$$=\dfrac12 \times 11\times 2\ \text{sq.units}$$
$$=11\ \text{sq.units}$$.
Solve each of the following system of equations graphically and find the vertices and area of the triangle formed by these lines and the $$x-$$axis:
$$x-2y+2=0,\ 2x+y-6=0$$
Line 1: $$x-2y+2=0$$....(1)
Line 2: $$2x+y-6=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$x-2y+2=0$$
or $$x=2y-2$$
Similarly, isolate $$y$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$2x+y-6=0$$
or $$y=6-2x$$
By Plotting the Graph we found that:
Both the lines intersect each other at point $$C(2, 2)$$ and $$y-$$ axis at $$A(-2, 0)$$ and $$F(3, 0)$$
Now, To find the area of triangle $$CAF$$:
Area of $$\triangle CAF=\dfrac{1}{2}(base \times altitude)$$
$$=\dfrac{1}{2} \times (3-(-2))\times (2-0)$$
$$=5\ sq.units$$.
Line 2: $$2x+y-6=0$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$x-2y+2=0$$
or $$x=2y-2$$
| At $$x=-2,0,2$$ | $$\Rightarrow y=0,1,2$$ respectively |
$$2x+y-6=0$$
or $$y=6-2x$$
| At $$x=0,2,3$$ | $$\Rightarrow y=6,2,0$$ respectively |
Both the lines intersect each other at point $$C(2, 2)$$ and $$y-$$ axis at $$A(-2, 0)$$ and $$F(3, 0)$$
Now, To find the area of triangle $$CAF$$:
Area of $$\triangle CAF=\dfrac{1}{2}(base \times altitude)$$
$$=\dfrac{1}{2} \times (3-(-2))\times (2-0)$$
$$=5\ sq.units$$.
Find two numbers such that the sum of twice the first and thrice the second is $$92$$, and four times the first exceeds seven times the second by $$2$$.
Find two numbers such that the sum of thrice the first and the second is $$142$$, and four times the first exceeds the second by $$138$$.
A lady has only $$25$$ paisa and $$50$$ paisa coins in her purse. If she has $$50$$ coins in all totalling $$Rs.\ 19.50$$, how many coins of each kind does she have?
The sum of a two digit number and the number obtained by receiving the order of its digits is $$121$$, and the two digits differ by $$3$$. Find the number.
Show that the following systems of equation has a unique solution and solve it:
$$x/2+y/2=9, x-2y=2$$
The sum of two numbers is $$80$$. The larger number exceeds four times the smaller one by $$5$$. Find the numbers.
Show graphically that each of the following given system of equation has infinitely many solutions:
$$2x+y=6,\ 6x+3y=18$$
$$2x+y=6$$....(1)
$$6x+3y=18$$......(2)
Isolate $$y$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$2x+y=6$$
or $$y=6-2x$$
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$6x+3y=18$$
or $$x=(18-3y)/6$$
Graph:
Both the lines coincide each other.
This system has infinitely many solutions.
$$6x+3y=18$$......(2)
Isolate $$y$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$2x+y=6$$
or $$y=6-2x$$
| $$x$$ | $$y$$ |
| $$0$$ | $$6$$ |
| $$2$$ | $$2$$ |
| $$4$$ | $$-2$$ |
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$6x+3y=18$$
or $$x=(18-3y)/6$$
| $$x$$ | $$y$$ |
| $$3$$ | $$0$$ |
| $$1$$ | $$4$$ |
| $$5$$ | $$-4$$ |
Both the lines coincide each other.
This system has infinitely many solutions.
Show graphically that the following given system of the equation has infinitely many solutions:
$$3x-y=5,\ 6x-2y=10$$
$$3x-y=5$$....(1)
$$6x-2y=10$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$3x-y=5$$
or $$y=3x-5$$
$$6x-2y=10$$......(2)
Isolate $$x$$ from equation (1) and find the value of $$x$$ and $$y$$.
$$3x-y=5$$
or $$y=3x-5$$
At,
Similarly, isolate $$x$$ from equation (2) and find the values of $$x$$ and $$y$$.
$$6x-2y=10$$
| $$x$$ | $$y$$ |
| $$0$$ | $$-5$$ |
| $$1$$ | $$-2$$ |
| $$3$$ | $$4$$ |
$$6x-2y=10$$
or $$y=(6x-10)/2$$
At,
| $$x$$ | $$y$$ |
| $$2$$ | $$1$$ |
| $$4$$ | $$7$$ |
| $$3$$ | $$4$$ |
Using the above points and plotting the Graph we get,
Both the lines coincide with each other that means that system has infinite many solutions.
Both the lines coincide with each other that means that system has infinite many solutions.
$$5$$ chairs and $$4$$ tables together cost $$Rs.\ 5600$$, while $$4$$ chairs and $$3$$ tables together cost $$Rs.\ 4340$$. Find the cost of a chair and that of a table.
Show graphically that each of the following given system of equation has infinitely many solutions:
$$x-2y=5,\ 3x-6y=15$$
Let,
$$x-2y=5$$....$$(1)$$$$3x-6y=12$$......$$(2)$$
Isolate $$x$$ from equation $$(1)$$ and find the value of $$x$$ and $$y$$.
$$x-2y=5$$
or $$x=5+2y$$
| $$x$$ | $$y$$ |
| $$5$$ | $$0$$ |
| $$3$$ | $$-1$$ |
| $$1$$ | $$-2$$ |
$$3x-6y=15$$
or $$x=(15+6y)/3$$
| $$x$$ | $$y$$ |
| $$7$$ | $$1$$ |
| $$-1$$ | $$-3$$ |
| $$-3$$ | $$-4$$ |
All the points lie on the same line.
Which shows that, lines coincide each other. Hence, the system has infinite many solutions.
$$\dfrac{4}{3}x+2y=8\ ;$$
$$2x+3y=12$$
From the pair of linear equations in this problem, and find its solution graphically:
10 students of class X took part in a Mathematics quiz If the girls is 4 more than the number of boys, find the number of boy and girls who took part in the quiz.
Let $$x$$ be the number of girls and $$y$$ be the number of boys.
According to the questions, we have
$$\quad x=y+4$$
$$\Rightarrow x-y=4\qquad...(i)$$
Substituting different values of $$x$$ in equation $$(i)$$ to get corresponding values of $$y$$, we get the following table :
| $$x$$ | $$0$$ | $$4$$ | $$7$$ |
| $$y$$ | $$-4$$ | $$0$$ | $$3$$ |
Plot the points $$(0,-4),(4,0),(7,3)$$ in the graph paper and join them to get the line represented by $$x-y=4$$
Again, the total number of students $$=10$$
$$\Rightarrow x+y=10\qquad...(ii)$$
Substituting different values of $$x$$ in equation $$(ii)$$ to get corresponding values of $$y$$, we get the following table :
| $$x$$ | $$0$$ | $$10$$ | $$7$$ |
| $$y$$ | $$10$$ | $$0$$ | $$3$$ |
Plot the points $$(0,10),(10,0),(7,3)$$ in the graph paper and join them to get the line represented by $$x+y=10$$
From the graph,
The two lines intersect at the point $$(7,3)\ \ \ \Rightarrow x=7\ ,\ y=3$$
Hence, the number of girls $$=7$$
And the number of boys $$=3$$
Solve the following pairs of equations by reducing them to a pair of linear equations:
(i) $$\dfrac{7x-2y}{xy}=5\ \ ;\ \ \dfrac{8x+7y}{xy}=15$$
(ii) $$\dfrac{1}{3x+y}+\dfrac{1}{3x-y}=\dfrac{3}{4}\ \ ;\ \ \dfrac{1}{2(3x+y)}-\dfrac{1}{2(3x-y)}=\dfrac{-1}{8}$$
The sum of two numbers is $$60$$ and their difference is $$30$$.
The number are ______ and _______.
$$5x-4y+8=0\\7x-6y-9=0$$
$$\dfrac{3}{2}x+\dfrac{5}{3}y=7\ ;$$
$$9x-10y=14$$
Is the following pair of linear equations consistent? Justify your answer.
$$2ax+by=a,\quad 4ax+2by-2a=0;\quad a,b \neq0$$
Solve the following pairs of linear equation by the elimination method and the substitution method:
(i) $$3x-5y-4=0$$ and $$9x=2y+7$$
(ii) $$\dfrac{x}{2}+\dfrac{2y}{3}=-1$$ and $$x-\dfrac{y}{3}=3$$
Find whether the following pair of linear equations has a unique solution. If yes, find the solution?
$$7x-4y=49 $$ and $$5x-6y=57$$
Show graphically that the given system of equations $$2x+4y=10$$ and $$3x+6y=12$$ has no solution.
Given equations are,
$$2x+4y=10$$ and $$3x+6y=12$$
Now, $$2x+4y=20$$
$$\Rightarrow 4x=10-2x \\\Rightarrow y=\dfrac{5-x}{2}$$
Thus, we have the following table
| $$x$$ | $$3$$ | $$1$$ | $$5$$ |
| $$y$$ | $$1$$ | $$2$$ | $$0$$ |
Plot the points $$A(1,2), B(3,1)$$ and $$C(5.0)$$ on the graph paper, Join $$A,B$$ and $$C$$ and extent it on both sides to obtain the equation $$2x+4y=10$$.
Again, $$3x+6y=12$$
$$\Rightarrow 6y=12-3x \\ \Rightarrow y=\dfrac{5-x}{2}$$
Thus, we have the following table
| $$x$$ | $$2$$ | $$0$$ | $$4$$ |
| $$y$$ | $$1$$ | $$2$$ | $$0$$ |
Plot the points $$D(2,1), E(0,2)$$ and $$F(4,0)$$ on the same graph paper. Join $$D,E$$ and $$F$$ and extend on both sides to obtain the graph of the equation $$3x+6y=12$$
We find that the lines represented by equation $$2x+4y=10$$ and $$3x+6y=12$$ are parallel.
So the two lines have no common point.
Hence, the given system of equations has no solution.
Solve the following pairs of linear equations :
$$ 4x +\dfrac {6}{y} =15, 6x - \dfrac {8}{y} = 14, y \neq 0 $$
For which values of $$ a $$ and $$ b $$ , will the following pair of linear equations has infinitely many solution $$ Rs $$
$$ x +2y = 1 $$
$$ (a-b)x + (a+b)y = a+b -2 $$
IF $$ 2x +y = 23 $$ and $$ 4x-y=19 $$ then find the values of $$ 5y -2x $$ and $$ (y/x)-2$$
Solve the following pairs of linear equations :
$$ \dfrac {1}{2x} -\dfrac {1}{y} = -1, \dfrac {1}{x} + \dfrac {1}{2y} = 8 , x,y \neq 0 $$
Solve the following pairs of linear equations :
$$ \frac {x}{3} + \dfrac {y}{4} = 4 , \dfrac {5x}{6}-\dfrac {y}{8} = 4 $$
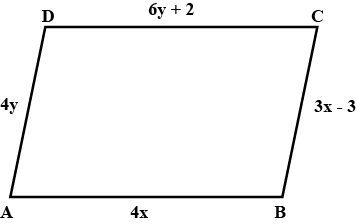
Find the values of $$ x $$ and $$ y $$ in the following rectangle :
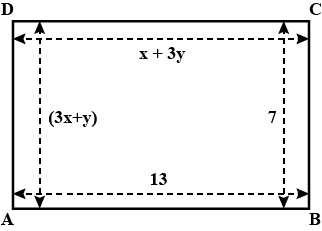
Solve the following pairs of linear equations :
$$ x + y = 3.3 , \dfrac {0.6}{ 3x -2y} = -1, 3x -2y = 0 $$
Two straight paths are represented by the equations $$ x-3y = 2 $$ and $$ -2x +6y = 5 $$ check whether the paths will cross each other or not.
Find the values of $$ p $$ in (i) to (iv) and $$ p \quad q $$ in (v) for the following pair of equations :
$$ 2x +3y = 7 $$ and $$ px -6y - 8 = 0 $$ if the pair of equations has infinitely many solutions.
For Which value(s) of $$ \lambda $$ do the pair of linear equations $$ \lambda x + y + = \lambda^2 $$ and $$ x + \lambda y = 1 $$ have
a unique solution $$ Rs $$
Two years ago salim was thrice as old is daughter and six years later he will be four years older than twice her age .how old are they now $$ rs $$.
By the graphical method, find the whether the following pair of equation are consistent or not . if consistent solve them.
$$ 3x +y +4 = 0 $$ and $$ 6x -2y +4 = 0$$
Given equation are
3x+y+4=0...(i)3x+y+4=0...(i)
Solve the following pairs of linear equations :
$$ \frac {2xy}{x+y} = \frac {3}{2}, \frac {xy}{2x-y} = \frac {-3}{10} , x+y \neq 0 ,2x-y \neq 0$$
The age of the father is twice the sum of the ages of his two children .after $$ 20 $$ years,his age will be equal to the sum of the ages of his children . find the age of the father.
Draw the graph of the pair of equations $$ 2x +y = 4 $$ and $$ 2x -y= 4 $$ write the vertices of the triangle formed by these lines and the y-axis .also find the area of this triangle.
$$ 2x +y = 4 ...(i) $$
$$ \Rightarrow y = 4 -2 x $$
If $$ x = 0 , y = 4 - 2( 0 ) = 4 -0 = 4 $$
$$ x = 1 , y = 4-2 (1) = 4 -2 = 2 $$
$$ x = 2, y = 4 -2(2) = 4 -4 = 0 $$
$$ x $$ $$ 0 $$ $$ 1 $$ $$ 2 $$ $$ 3 $$
$$ y $$ $$ 4 $$ $$ 2 $$ $$ 0 $$ $$ -2 $$
$$ (i) $$ $$ A $$ $$ B $$ $$ C $$ $$ -2 $$
$$2x -y= 4 ...(ii) $$
$$ \Rightarrow y = 2x - 4 $$
If $$ x = 0 , y = 2 (0 ) -4 = 0 -4 = -4 $$
$$ x = 1 , y = 2(1) -4 = 2 -4 = -2 $$
$$ x = 2, y =2(2) - 4 = 4-4 = 0 $$
$$ x $$ $$ 0 $$ $$ 1 $$ $$ 2 $$ $$ 3 $$ $$ 4 $$
$$ y $$ $$ - 4 $$ $$ -2 $$ $$ 0 $$ $$ 2 $$ $$ 4 $$
$$ (ii) $$ $$ E $$ $$ F $$ $$ G $$ $$ H $$ $$ I $$
triangle formed by the lines with y -axis $$ \Delta AEC $$ coordinates of vertices are $$ A(0,4), E(0 , -4) $$ and $$ C ( 2, 0 ) $$
Area of $$ \Delta AEC = \dfrac {1}{2} \quad Base \times Altitude $$
$$= \dfrac {1}{2} AE \times CO $$
$$ = \dfrac {1}{2} \times [ 4 -(-4)] \times ( 2- 0 ) $$
$$ = \dfrac {1}{2} \times 8 \times 2 = 8 $$
$$ \therefore $$ Area of $$ \Delta AEC = $$ Square units.
Find the solution of the pair of equations $$ \frac {x}{10}+ \frac {y}{5} -1 = 0 $$ and $$ \frac {x}{8} +\frac {y}{6} = 15 $$ hence find $$ \lambda $$if y =$$ \lambda x +5 $$
A shopkeeper given books on rent for reading .She takes a fixed charge for the first two days and an additional charge for each day thereafter. Latika paid $$ Rs 22 $$ for a book kept for six days, while anand paid $$ rs 16 $$ for the book kept for days . find the fixed charges and the charge for each extra day.
Solve the following pairs of linear equations :
$$ 43x +67 y = -24 , 67x +43y =24 $$
Graphically , solve the following pair of equations $$ 2x +y = 6 $$ and $$ 2x-y +2 = 0 $$ find the ratio of the areas of the two triangles formed by the lines representing these equations with equations with the $$ x-axis $$ and the lines with the $$ y -axis $$
Given equation is $$ 2x + y = 6 $$
$$ y = 6 -2x ....(i) $$
If $$ x = 0 , y = 6 - 2 (0) = 6 $$
$$ x = 1 , y = 6 -2 (1) = 6 -2 = 4 $$
$$ x = 2 , y = 6 -2(2) = 6-4 = 2 $$
$$ x $$ $$ 0 $$ $$ 1 $$ $$2 $$
$$ y $$ $$ 6 $$ $$ 4 $$ $$ 2 $$
$$ I $$ $$ A $$ $$ B $$ $$ C $$
given equation is $$ 2x - y + 2 = 0 $$
$$ \Rightarrow y = 2x +2 ....(ii) $$
IF $$ x = 0 , y = 2(0) = 0 +2 = 2 $$
$$ x = , y = 2(1) +2 = 2 +2 = 4 $$
$$ x = 2, y = 2(2) + 2 = 4 +2 = 6 $$
$$ X $$ $$ 0$$ $$ 1 $$ $$ 2 $$
$$ y $$ $$ 2 $$ $$ 4 $$ $$ 6 $$
$$ II $$ $$ D $$ $$ E $$ $$ F $$
The area of $$ \Delta BGH $$ formed by lines and x axis $$ = \dfrac {1}{2} GH \times BJ $$
$$ = \dfrac {1}{2} [ 3 -(-1) \times ( 4- 0) = \dfrac {1}{2} \times 4 \times 4 = 8 $$ sq units.
the area of $$ \Delta BAD $$ formed by lines and Y axis $$ = \dfrac {1}{2} AD \times KB $$
$$ = \dfrac {1}{2} [ ( 6 -2) \times ( 1-0 ) = \dfrac {1}{2} \times 4 \times 1 = 2 $$ sq units
$$ \therefore $$ ratio of areas of two $$ \Delta s \dfrac {Area \Delta BGH }{ Area \Delta BAD } = \dfrac {8}{2} = \dfrac {4}{1} = 4 : 1 $$
By the graphical method, find the whether the following pair of equation are consistent or not . if consistent solve them.
$$ x-2y = 6 $$ and$$ 3x -6y = 0 $$
Draw the graphs of the equations $$ x = 3, x = 5 $$ and $$ 2x -y-4 = 0 $$ also find area of the quadrilateral formed by the lines and the x-axis.
| x | 0 | 1 | 2 | 3 | 4 |
| y | -4 | -2 | 0 | 2 | 4 |
| III | G | H | J | K | L |
$$ x = 3 ....(i) $$
$$ x = 5 .....(ii) $$
$$ 2x - y - 4 = 0 $$
$$ \Rightarrow y = 2x - 4 $$
| $$ x $$ | $$ 3$$ | $$ 3$$ | $$3 $$ | $$ x $$ | $$ 5$$ | $$ 5 $$ | $$ 5$$ | |
| $$ y $$ | $$ 1$$ | $$ 2$$ | $$ 3 $$ | $$ y $$ | $$ 3 $$ | $$ 4 $$ | $$ 5 $$ | |
| $$ I $$ | $$ A $$ | $$ B $$ | $$ C $$ | $$ II $$ | $$ D $$ | $$ E $$ | $$F $$ |
Solve the following pair of linear equations by any suitable method:
$$ x+y=5 $$
$$ 2 x-3 y=5 $$
Solve the following simultaneous linear equation
$$x+y=5.5$$ and $$x-y=0.9$$
A motor boat can travel $$ 30 $$ km upstream and $$ 28 $$ km downstream in $$ 7 $$ hours , it can travel $$ 21 $$ km upstream and return in $$ 5 hours $$ find the speed of the boat in still water and the speed of the stream.
Solve the following simultaneous linear equation
$$x+y=7xy$$ and $$2x-3y+xy=0$$
Determine , algebraically , the vertices of the triangle formed by the lines $$ 3x -y =3 , 2x -3y = 2 $$ and $$ x +2y = 8 $$.
The cost of $$ 4 $$ pens and $$ 4 $$ pencil boxes is $$ Rs 100 $$ . Three times the cost of a pen is $$ Rs 15 $$ more than the cost of pencil box. from the pair of linear equations for the above situation. find the cost of a pen and a pencil box.
A railway half ticket costs half the full fare, but the reservation charges are the same on a half ticket as on a full ticket . one reserved first class ticket from the station $$ A $$ to $$ B $$ cost $$ rs 2530 $$ . Also On reserved first class ticket and one reserved first class half ticket from $$ A $$ to $$ B $$ cost $$ rs 3810 $$ . Find the full first class fare from station $$ A $$ to $$ B $$, and also the reservation charges for a ticket.
Akita travels $$ 14 $$ km to her home partly by rickshaw and partly by bus. she takes half an hour if she travels $$ 2$$ km by rickshaw and the remaining distance by bus . On the other hand , if she travels $$ 4$$ km by rickshaw and the remaining distance by bus, she takes $$ 9 $$ minutes longer. find the speed of the rickshaw and of the bus.
Determine , graphically , the vertices of the triangle formed by the lines $$ y = x, 3y = x, x +y = 8 $$.
Given equation are
$$ y = x ...(i) $$
$$ x = 3y ....(ii) $$
$$ x +y = 8 ....(iii) $$
$$ \Rightarrow y = 8 -x [ from (iii) ] $$
If $$ x = 0 , y = 8 -0 = 8 $$
$$ x = 1 , y = 8 -1 = 7 $$
$$ x 2 ,y = 8 -2 = 6 $$
$$ y = 8 -x $$
$$ III $$ $$ J $$ $$ K $$ $$ L $$ $$ M $$
$$ x $$ $$ 0 $$ $$ 1 $$ $$ 2 $$ $$ 8 $$
$$ y $$ $$ 8 $$ $$ 7 $$ $$ 6 $$ $$0 $$
$$ y = x $$
$$ I $$ $$ A $$ $$ B $$ $$ C $$ $$ D $$
$$ X $$ $$ 0$$ $$ 1$$ $$ 2 $$ $$ 3 $$
$$ y $$ $$ 0 $$ $$ 1 $$ $$ 2 $$ $$ 3 $$
$$ x = 3y $$
$$ II $$ $$ E $$ $$ F $$ $$ G $$ $$H $$
$$ x $$ $$0 $$ $$ 1 $$ $$ 2$$ $$ 3 $$
$$ y $$ $$ 0 $$ $$ 3 $$ $$ 6 $$ $$ 9 $$
Hence the vertices of $$ \Delta GNA$$ formed by $$ 3 $$ lines are $$ G ( 2, 6 ) , N( 4 , 4 ) $$ and $$ A ( 0 , 0) $$.
The cost of $$5$$ kg of sugar and $$7$$ kg of rice is Rs. $$153$$, and the cost of $$7$$ kg of sugar and $$5$$ kg of rice is Rs. $$147$$. Find the cost of $$6$$ kg of sugar and $$10$$ kg of rice.
The class IX students of a certain public school wanted to give a farewell party to the outgoing students of class X. They decided to purchase two kinds of sweets, one costing Rs. $$70$$ per kg and the other costing Rs. $$84$$ per kg. They estimated that $$36$$ kg of sweets were needed. If the total money spent on sweets was Rs. $$2800$$, find how much sweets of each kind they purchased.
The sum of two numbers is $$43$$. If the larger is doubled and the smaller is tripled, the difference is $$36$$. Find the two numbers.
$$2$$ men and $$5$$ women can do a piece of work in $$4$$ days, while one man and one woman can finish it in $$12$$ days. How long would it take for $$1$$ man to do the work?
There are $$38$$ coins in a collection of $$20$$ paise coins and $$25$$ paise coins. If the total value of the collection is Rs. $$8.50$$, how many of each are there?
Solve the following simultaneous linear equation
$$3x+2y=2xy$$
$$\dfrac{1}{x}+\dfrac{2}{y}=1\dfrac{1}{6}$$
Solve the following simultaneous linear equation
$$ax+by=a-b$$ and $$bx-ay=a+b$$
A shopkeeper sells a table at $$8\%$$ profit and a chair at $$10\%$$ discount, thereby getting Rs. $$1008$$. If he had sold the table at $$10\%$$ profit and chair at $$8\%$$ discount, he would have got Rs. $$20$$ more. Find the cost price of the table and the list price of the chair.
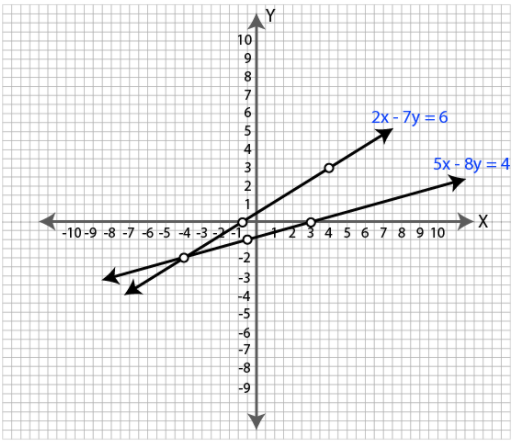
Solve the following pair of equations graphically. Plot at least $$3$$ points for each straight line $$2x -7y = 6, 5x -8y = -4.$$
$$2x-7y = 6$$ ….(i)
$$2x = 7y+6$$
$$x = (7y+6)/2$$
when $$y = 0$$
$$x = (7×0+6)/2 = 6/2 = 3$$
when $$y = -1$$
$$x = (7×-1+6)/2 = -1/2 = -0.5$$
when $$y = -2$$
$$x = (7×-2+6)/2 = -8/2 = -4$$
Mark the above points on graph. Join them.
$$5x-8y = -4$$ …(ii)
$$5x = 8y-4$$
$$x = (8y-4)/5$$
when $$y = 0$$
$$x = (8×0-4)/5 = -4/5 = 0.8$$
when $$y = 3$$
$$x = (8×3-4)/5 = (24-4)/5 = 20/5 = 4$$
when $$y = -2$$
$$x = (8×-2-4)/5 = (-16-4)/5 = -20/5 = -4$$
Mark the above points on graph. Join them.
It is clear from the graph that the two lines intersect at $$(-4,-2).$$
So the solution of the given equations are $$x = -4$$ and $$y = -2.$$
$$2x = 7y+6$$
$$x = (7y+6)/2$$
when $$y = 0$$
$$x = (7×0+6)/2 = 6/2 = 3$$
when $$y = -1$$
$$x = (7×-1+6)/2 = -1/2 = -0.5$$
when $$y = -2$$
$$x = (7×-2+6)/2 = -8/2 = -4$$
| $$x=$$ | $$3$$ | $$,-0.5$$ | $$,-4$$ |
| $$y=$$ | $$0$$ | $$,-1$$ | $$,-2$$ |
$$5x-8y = -4$$ …(ii)
$$5x = 8y-4$$
$$x = (8y-4)/5$$
when $$y = 0$$
$$x = (8×0-4)/5 = -4/5 = 0.8$$
when $$y = 3$$
$$x = (8×3-4)/5 = (24-4)/5 = 20/5 = 4$$
when $$y = -2$$
$$x = (8×-2-4)/5 = (-16-4)/5 = -20/5 = -4$$
| $$x=$$ | $$0.8$$ | $$,4$$ | $$,-4$$ |
| $$y=$$ | $$0$$ | $$,3$$ | $$,-2$$ |
It is clear from the graph that the two lines intersect at $$(-4,-2).$$
So the solution of the given equations are $$x = -4$$ and $$y = -2.$$
Class 10 Maths Extra Questions
- Areas Related To Cricles Extra Questions
- Arithmetic Progressions Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Introduction To Trigonometry Extra Questions
- Pair Of Linear Equations In Two Variables Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadratic Equations Extra Questions
- Real Numbers Extra Questions
- Some Applications Of Trigonometry Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions