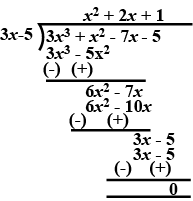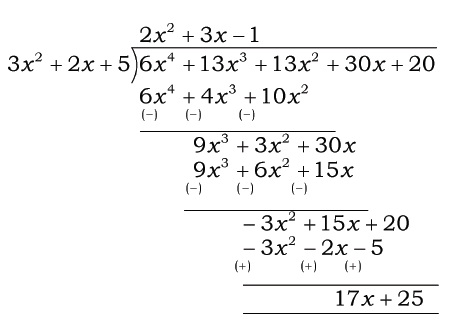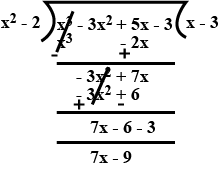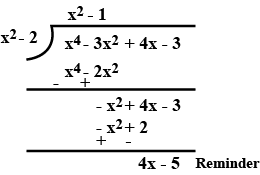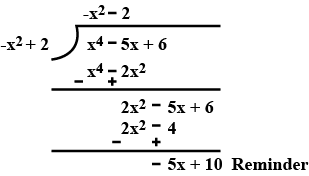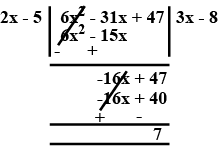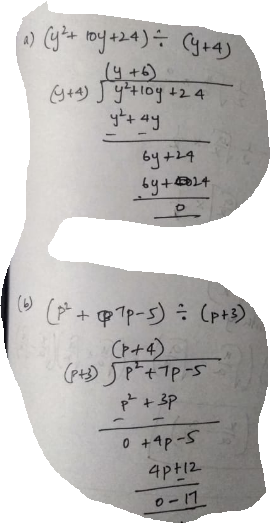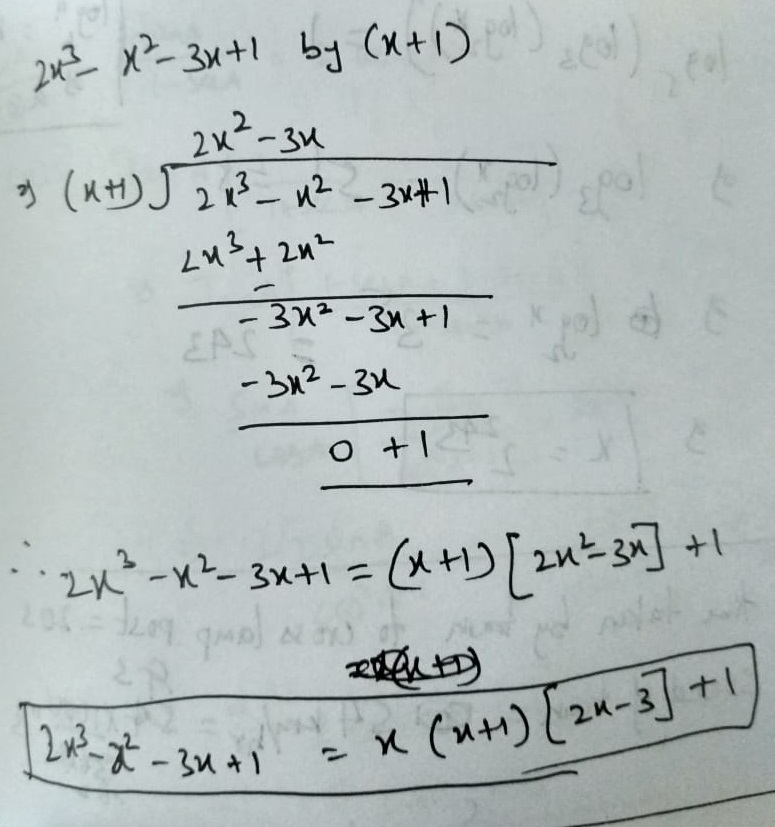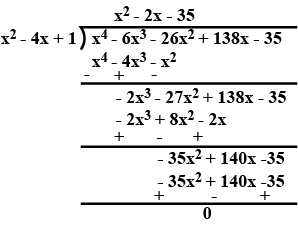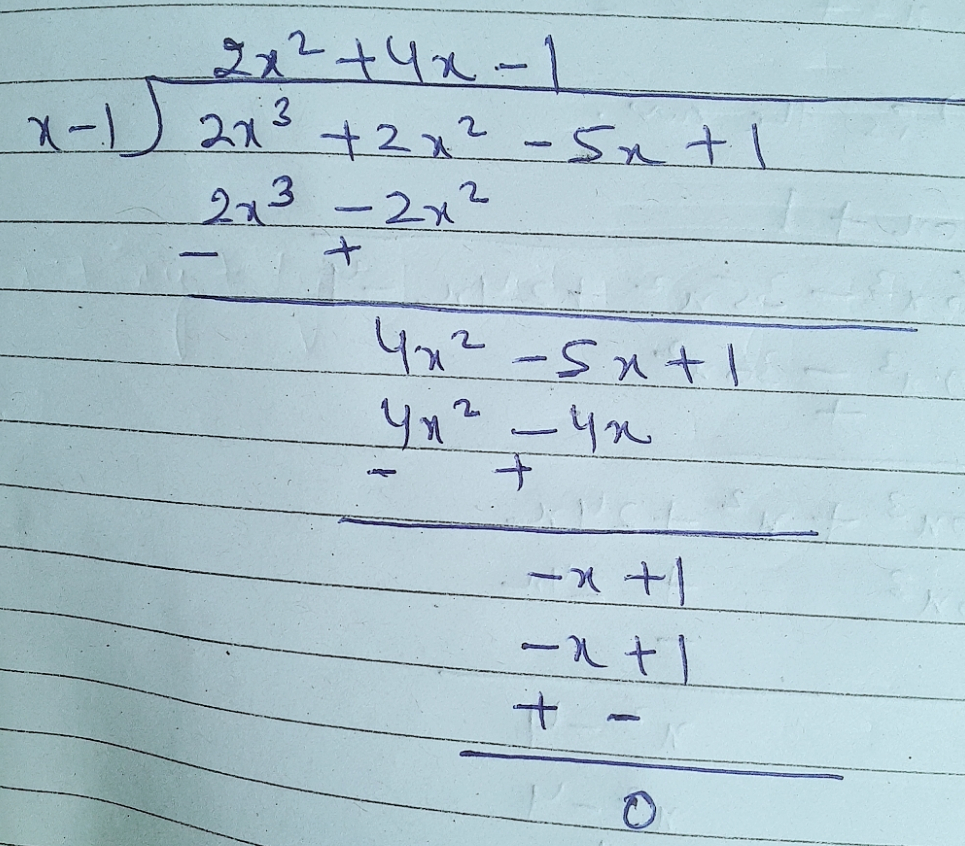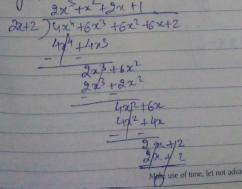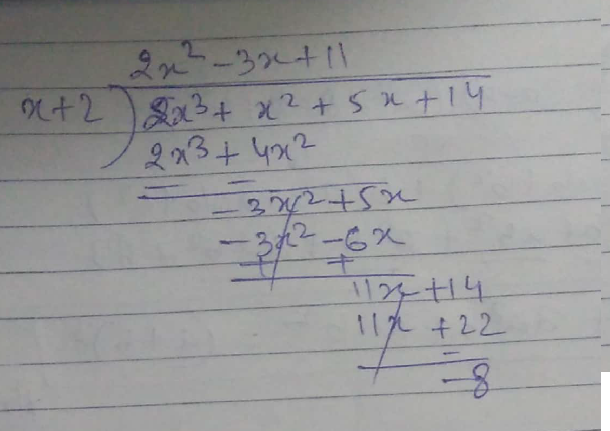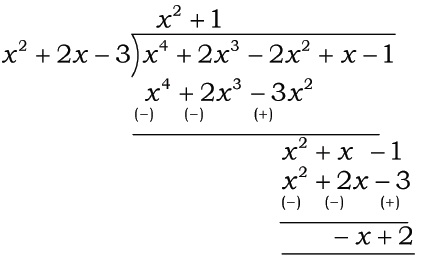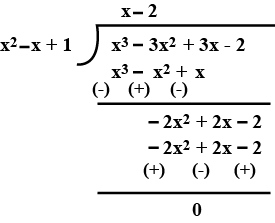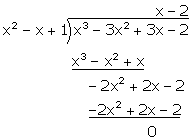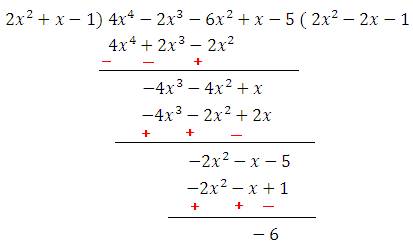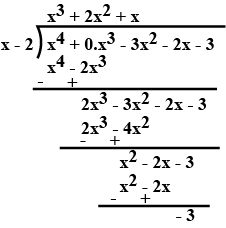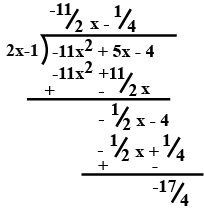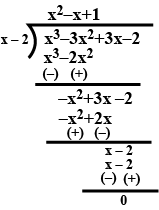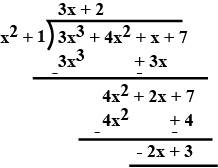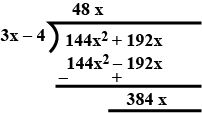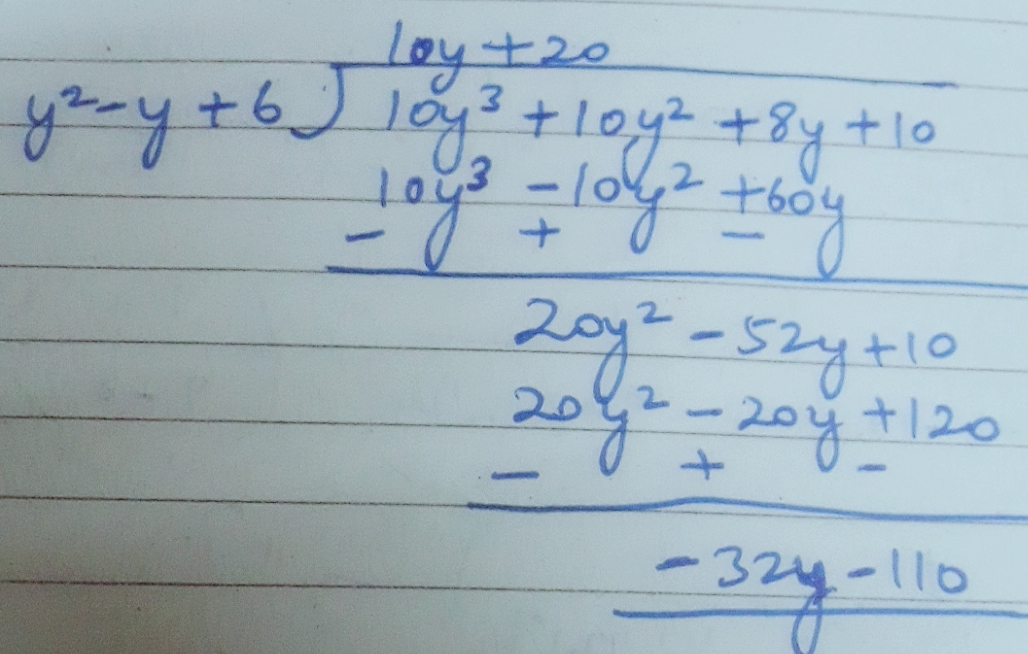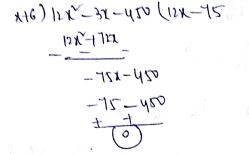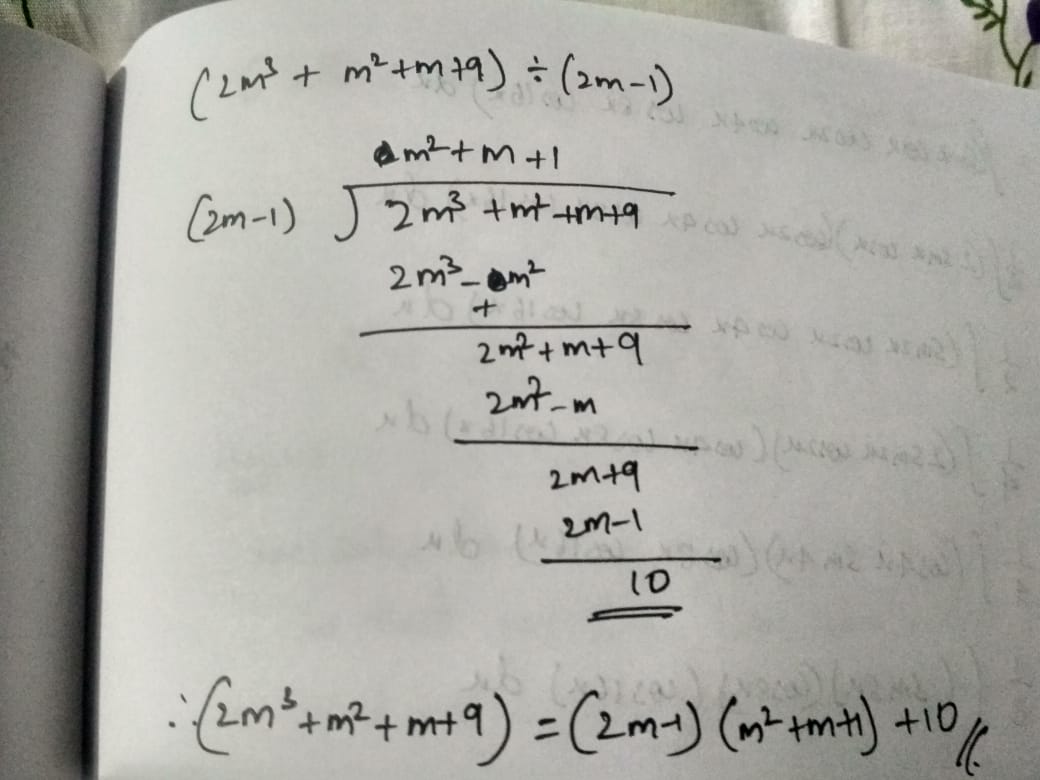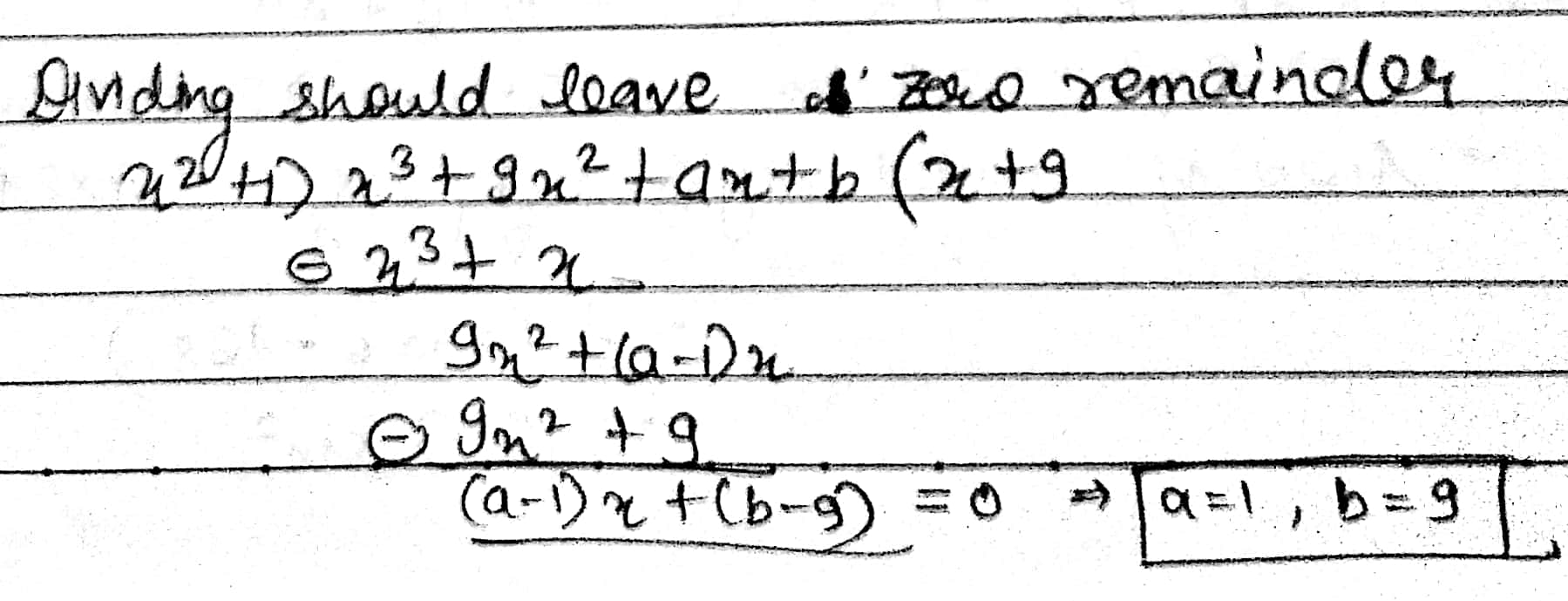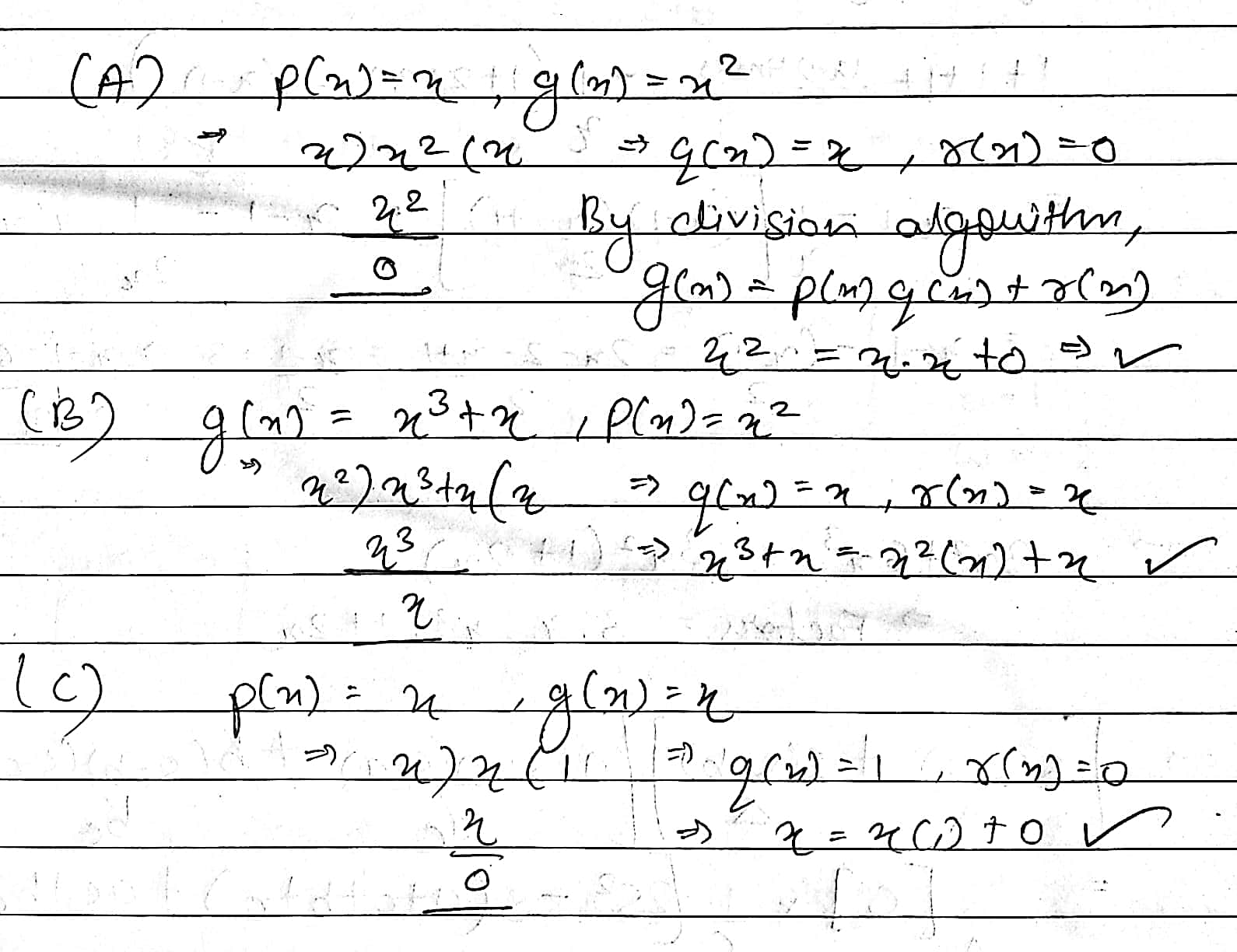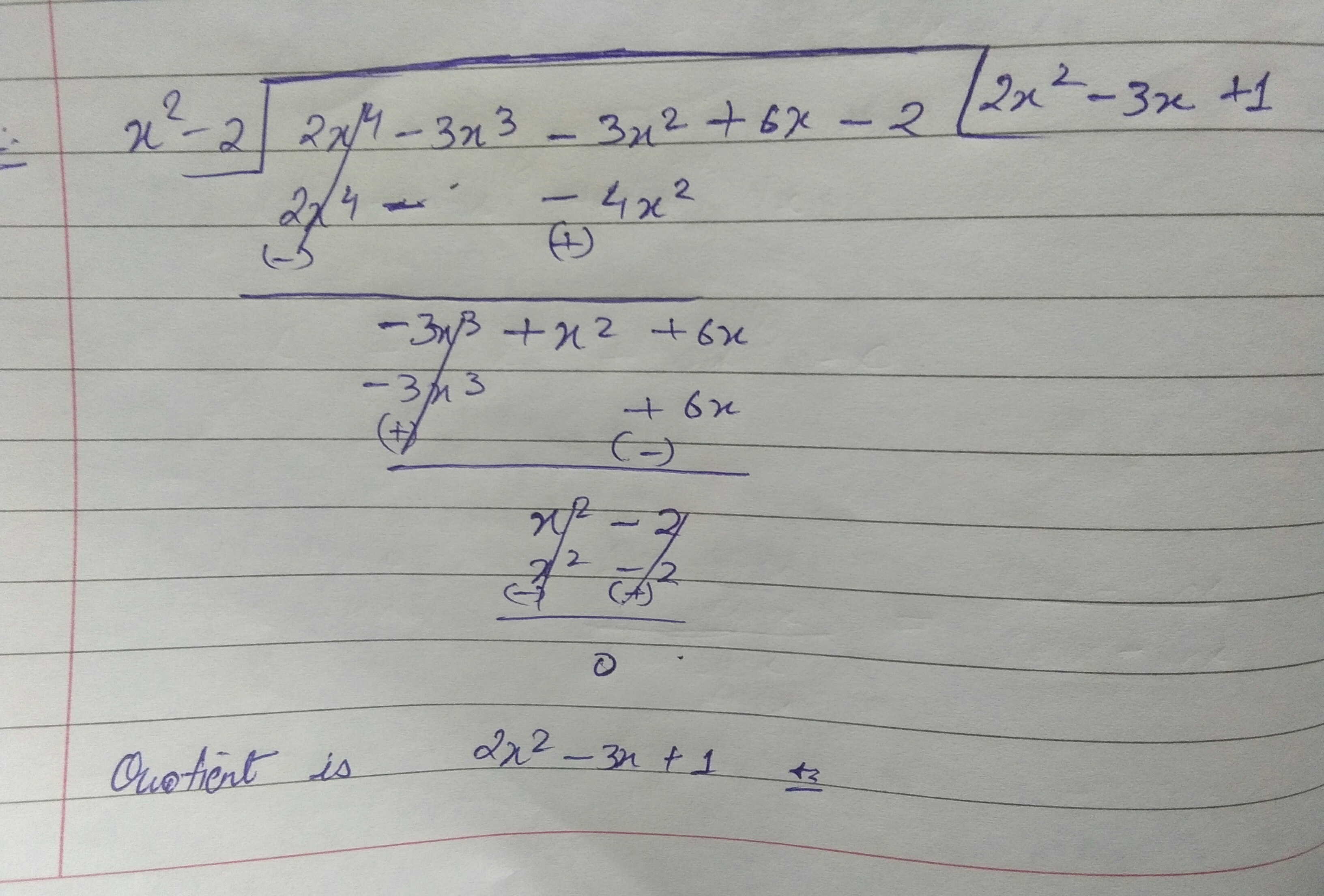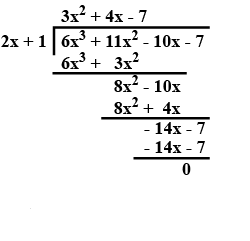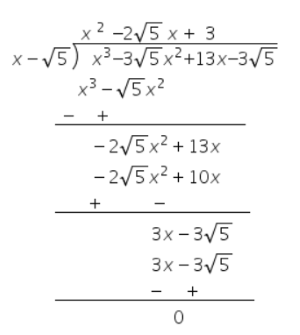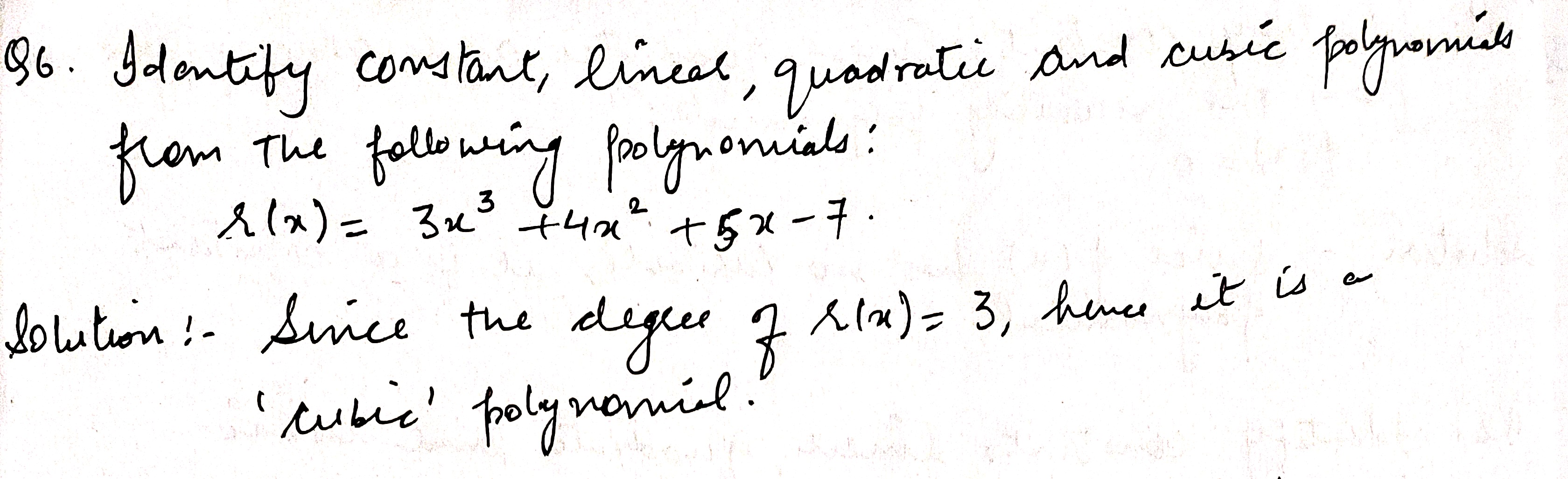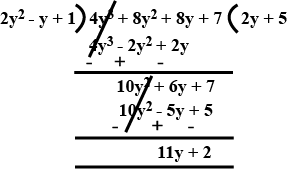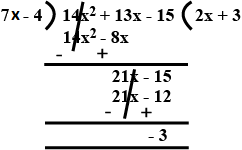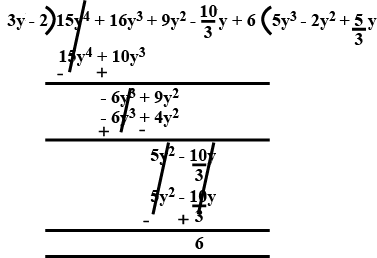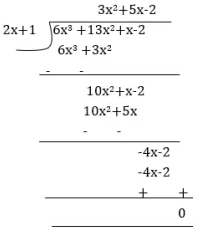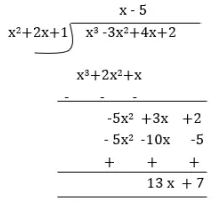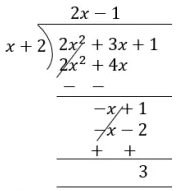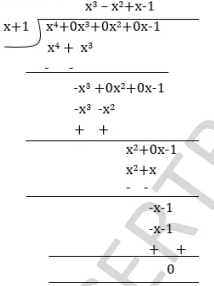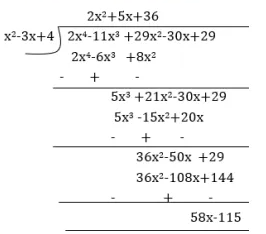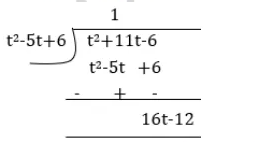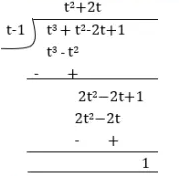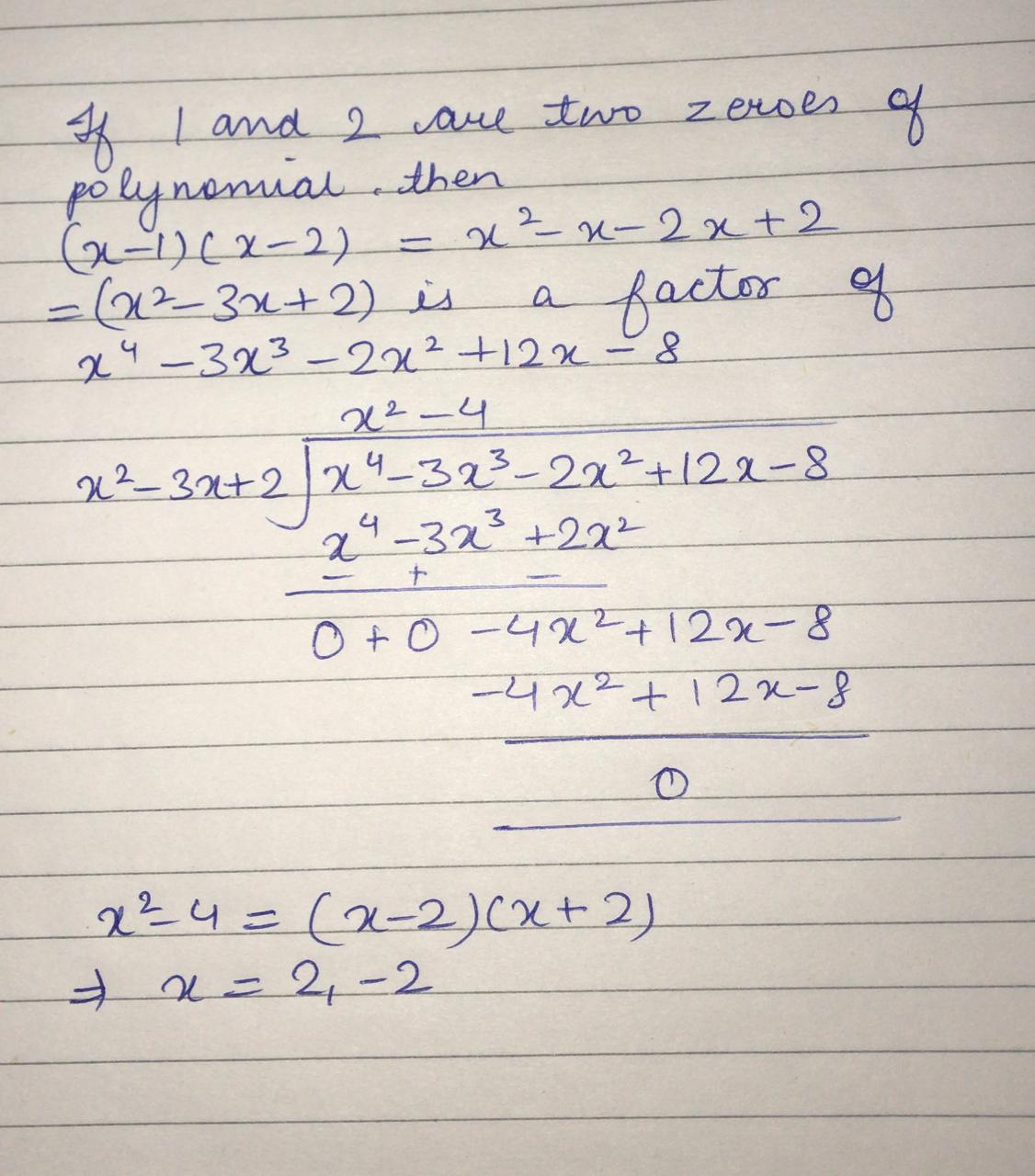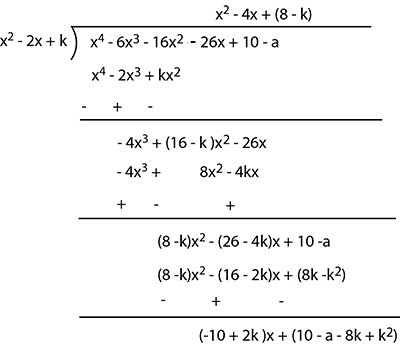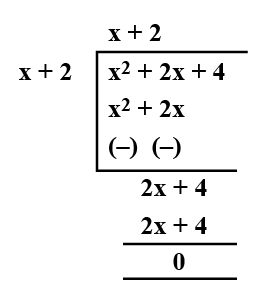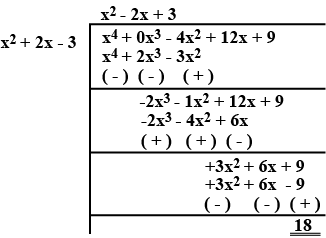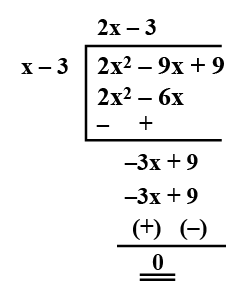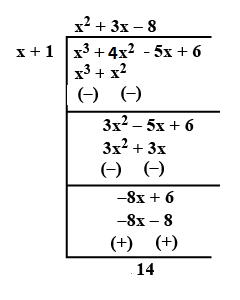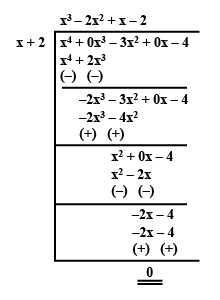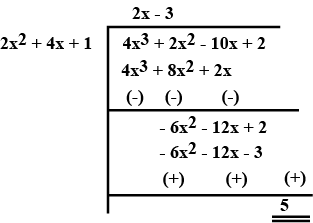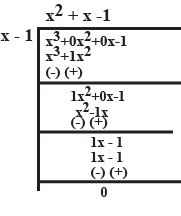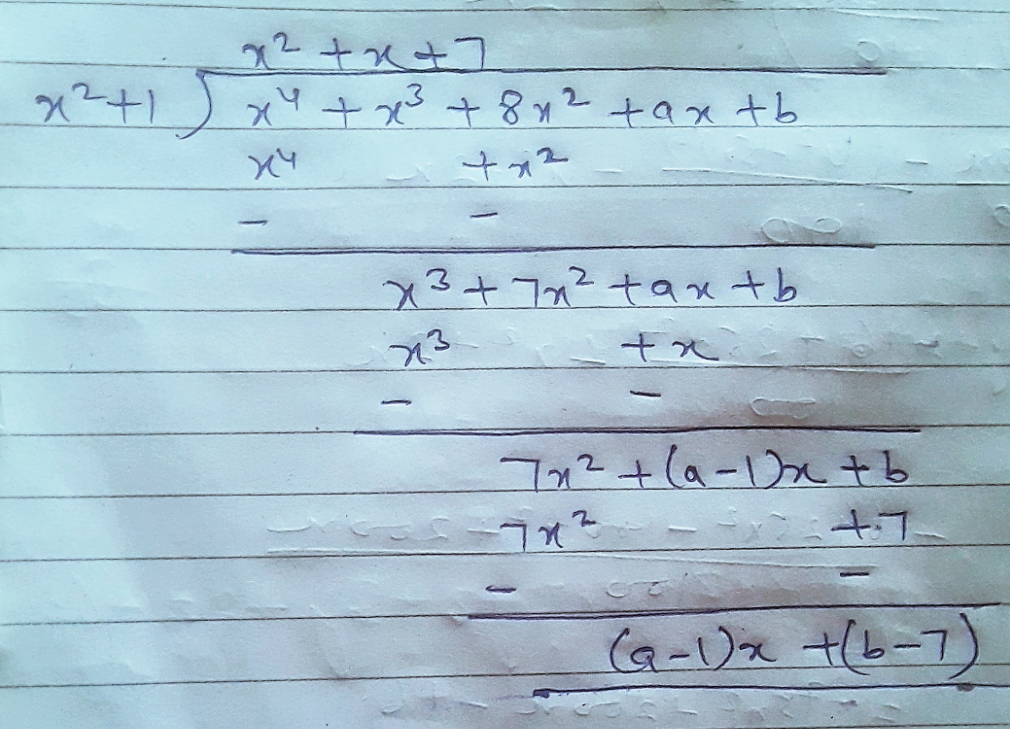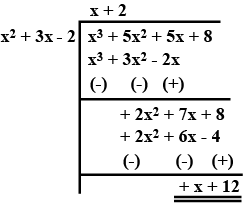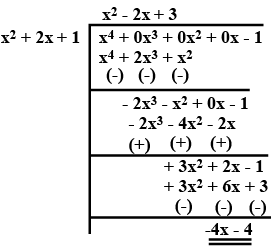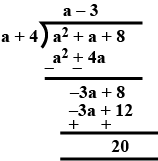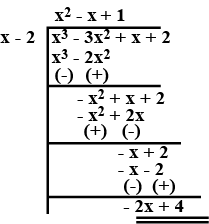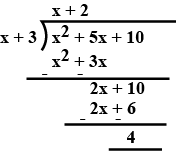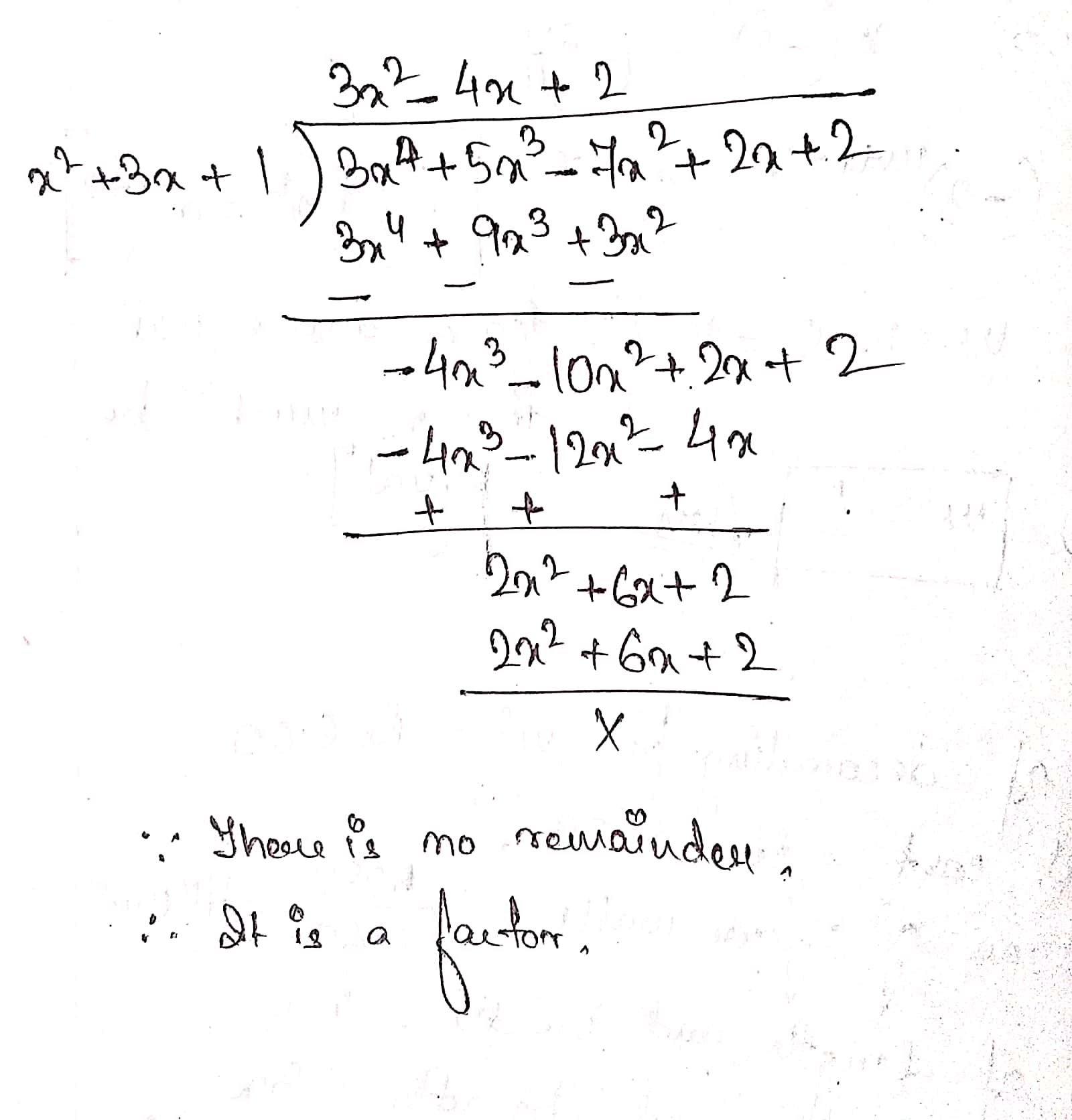Polynomials - Class 10 Maths - Extra Questions
Can $$(x^2 -1)$$ be the quotient on division of $$x^6 + 2x^3 + x- 1$$ by a polynomial in $$x$$ of degree 5?
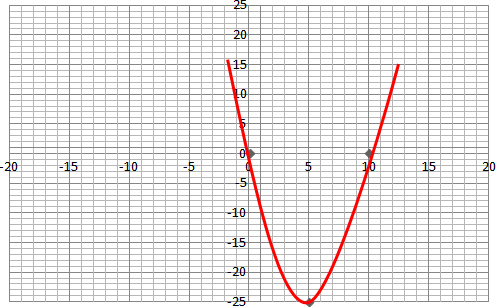
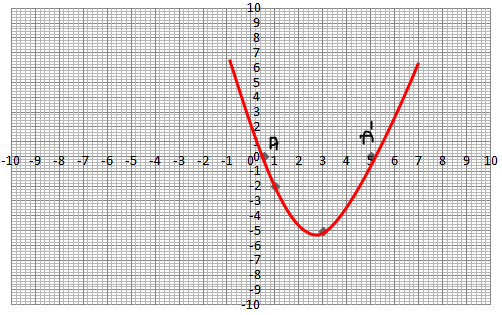
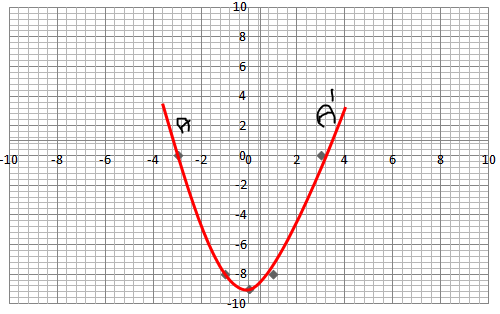
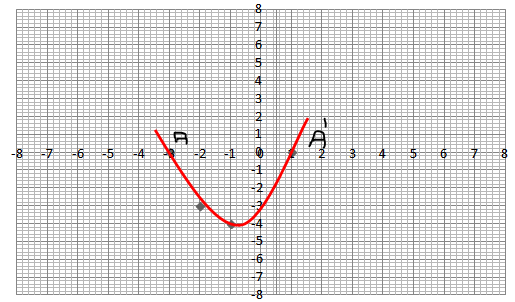
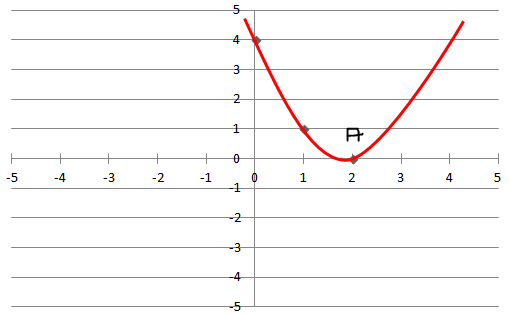
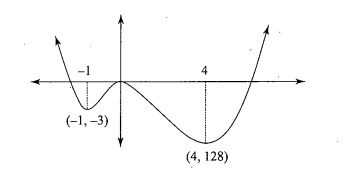
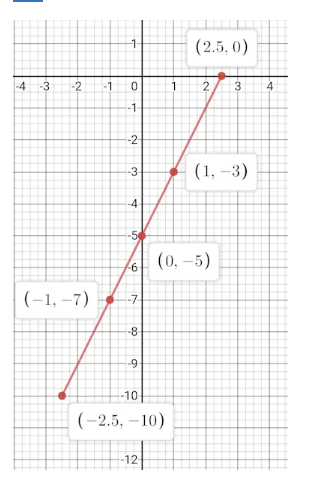
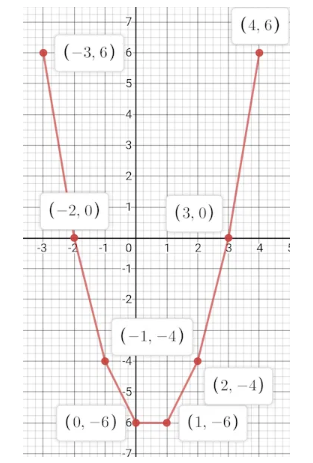
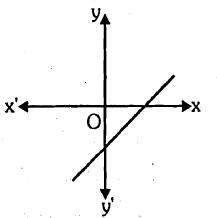
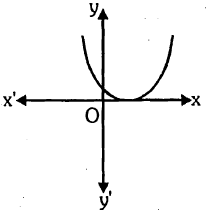
Look at the graphs given. It is the graph of $$y = p(x)$$, where p(x) is a polynomial. Find the number of zeros of $$p(x).$$
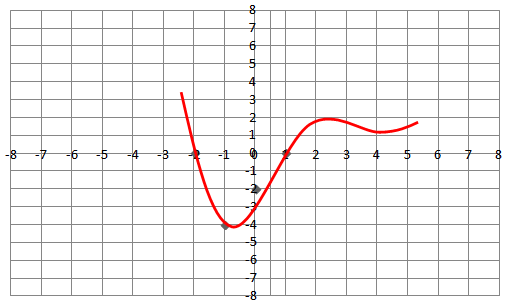
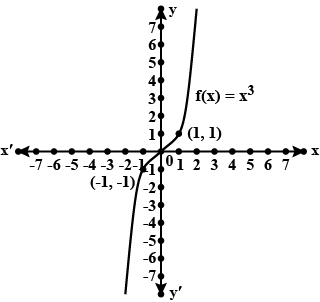
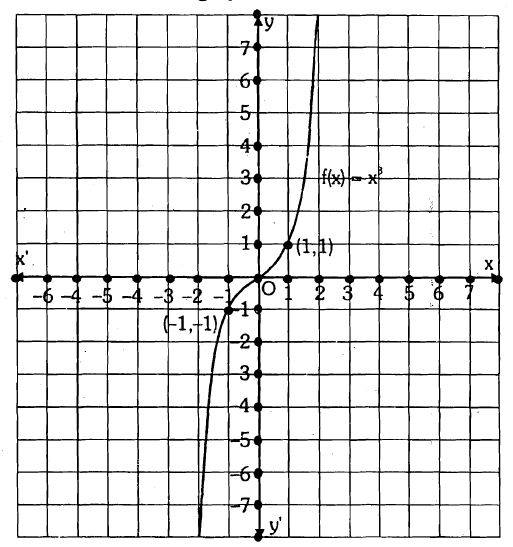
Let $$f(x)=x^3$$. The graph of the polynomial is shown in the figure. Find the number of zeros of polynomial f(x).
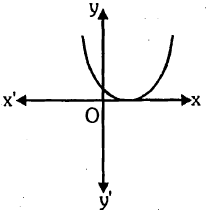
Look at the graph given. It is the graph of $$y = p(x)$$, where p(x) is a polynomial. Find the number of zeros of $$p(x).$$
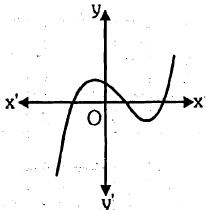
Look at the graph given. It is the graph of $$y = p(x)$$, where p(x) is a polynomial. Find the number of zeros of $$p(x)$$.
Look at the graph given. It is the graph of y = p(x), where p(x) is a polynomial. Find the number of zeros of p(x).
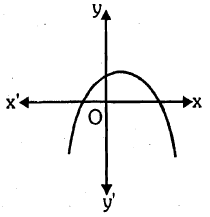
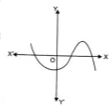
The graph of y = p(x) is given in fig below, for some polynomial p(x). Find the number of zeros of p(x).
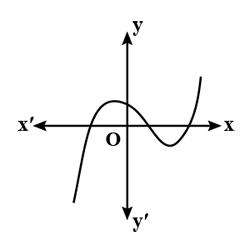
The graph of $$y = p(x)$$ is given in figure for some polynomial $$p(x)$$. The number of zeros of $$p(x)$$ are
Let $$f(x)=x^3$$
The graph of the polynomial is shown in fig.The co-ordinates of the points, at which the graph intersects the x-axis is (0,0)
If true then enter $$1$$ and if false then enter $$0$$
If true then enter $$1$$ and if false then enter $$0$$
The graph of $$y = p(x)$$ is given in the figure for some polynomial $$p(x)$$. The number of zeros of $$p(x)$$ is:
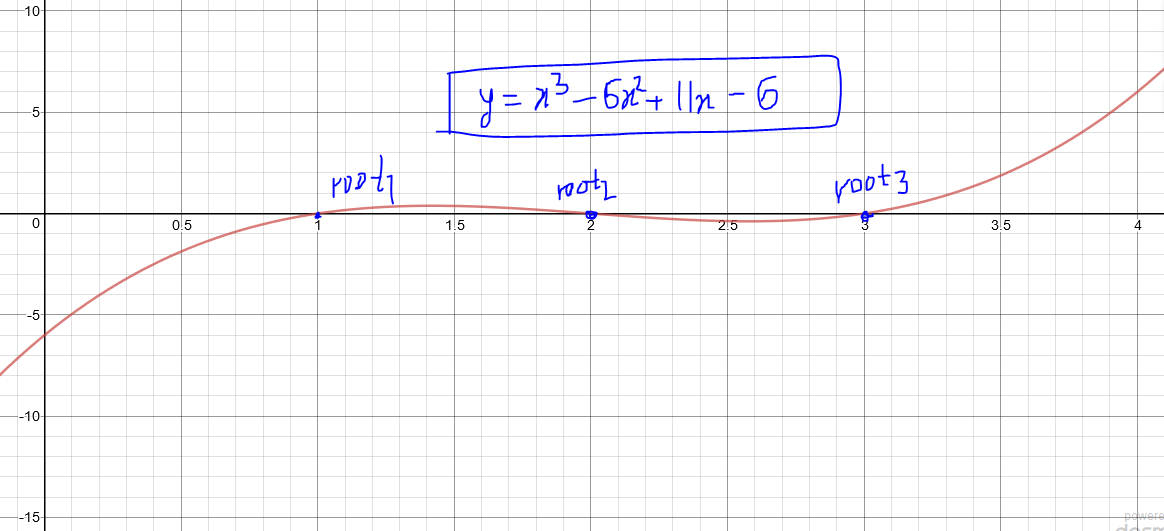
Construct a graph and represent the zeroes of the cubic polynomial for the equation: $$y=x^3-6x^2+11x-6$$
The zeroes of polynomial $$y={x^3-6x^2+11x-6}$$ are $$1,2,3$$
On dividing $$3x^{3} + x^{2} + 2x + 5$$ by a polynomial $$g(x)$$, the quotient and remainder are $$(3x - 5)$$ and $$(9x + 10)$$ respectively. Find $$g(x)$$
If we divide $$f(x)=3x^3 + x^2 +2x +5$$ by $$g(x)$$ we get $$q(x)=(3x-5)$$ as quotient and $$r(x)=(9x+10)$$ as remainder.
By using division algorithm,
$$f(x)=g(x)q(x)+r(x)$$
$$\implies 3x^3+x^2+2x+5=g(x)(3x-5)+(9x+10)$$
$$\implies g(x)=\dfrac{3x^3+x^2+2x+5-9x-10}{(3x-5)}$$
$$\implies g(x)=\dfrac{3x^3+x^2-7x-5}{(3x-5)}$$
Hence, $$g(x)=x^2+2x+1$$
A polynomial $$p(x)$$ is divided by $$(2x - 1)$$. The quotient and remainder obtained are $$(7x^{2} + x + 5)$$ and $$4$$ respectively. Find $$p(x)$$
What must be subtracted from $$6x^{4} + 13x^{3} + 13x^{2} + 30x + 20$$, so that the resulting polynomial is exactly divisible by $$3x^{2} + 2x + 5$$?
$$p(x) = g(x)\times q(x) + r(x)$$ [Division algorithm for polynomials]
$$\Rightarrow p(x) - r(x) = g(x) \times q(x)$$
It is clear the RHS of the above equation is divisible by $$g(x)$$. i.e., the divisor.
$$\therefore$$ LHS is also divisible by the divisor.
Therefore, if we subtract remainder $$r(x)$$ from dividend $$p(x)$$, then it will be exactly divisible by the divisor $$g(x)$$]
Let us divide, $$6x^{4} + 13x^{3} + 13x^{2} + 30x + 20$$ by $$3x^{2} + 2x + 5$$
we get, quotient $$q(x) = 2x^{2} + 3x - 1$$ remainder $$r(x) = 17x + 25$$
$$\therefore$$ If we subtract $$17x + 25$$ from $$6x^{4} + 13x^{3} + 13x^{2} + 30x + 20$$, it will be exactly divisible by $$(3x^{2} + 2x + 5)$$.
$$\Rightarrow p(x) - r(x) = g(x) \times q(x)$$
It is clear the RHS of the above equation is divisible by $$g(x)$$. i.e., the divisor.
$$\therefore$$ LHS is also divisible by the divisor.
Therefore, if we subtract remainder $$r(x)$$ from dividend $$p(x)$$, then it will be exactly divisible by the divisor $$g(x)$$]
Let us divide, $$6x^{4} + 13x^{3} + 13x^{2} + 30x + 20$$ by $$3x^{2} + 2x + 5$$
we get, quotient $$q(x) = 2x^{2} + 3x - 1$$ remainder $$r(x) = 17x + 25$$
$$\therefore$$ If we subtract $$17x + 25$$ from $$6x^{4} + 13x^{3} + 13x^{2} + 30x + 20$$, it will be exactly divisible by $$(3x^{2} + 2x + 5)$$.
Which type of polynomial, the given expression $$x^{3} + x + 4$$ is?
Based on degree, which type of polynomial, the given expression $$5x^{2} + x - 7$$ is?
Which type of polynomial, the given expression $$x - 1$$ is?
Which type of polynomial, the given expression $$3p$$ is?
Which type of polynomial, the given expression $$x - x^{3}$$ is?
Classify the following expression as linear, quadratic, or cubic polynomials.
$$\pi r^{2}$$
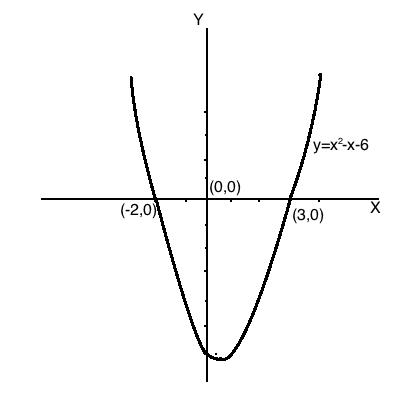
Draw the graph of $$y = x^2 - x - 6$$ and find zeroes. Justify the answer.
Clearly graph of $$y=x^2-x-6$$ cut the x-axis at $$x=-2,3$$.
$$\Rightarrow x=-2,3$$ are zeros of $$y=x^2-x-6$$.
Justification:
when $$x=-2;$$$$y=4+2-6=0$$
when $$x=3;$$$$y=9-3-6=0$$
$$\Rightarrow x=-2,3$$ are zeros of $$y=x^2-x-6$$.
Justification:
when $$x=-2;$$$$y=4+2-6=0$$
when $$x=3;$$$$y=9-3-6=0$$
Divide the polynomials $$p(x)$$ by the polynomials $$q(x)$$. Find the quotient and remainder. $$p\left( x \right) = {x^3} - 3{x^2} + 5x - 3,\,\,\,\,\,\,\,\,\,\,\, q\left( x \right) = {x^2} - 2$$
Consider the given polynomial.
$$p\left( x \right)={{x}^{3}}-3{{x}^{2}}+5x-3$$
$$q\left( x \right)={{x}^{2}}-2$$
Therefore, the working steps are shown in figure,
Hence, the quotient is $$(x-3)$$ and remainder is $$(7x-9)$$.
Classify the following as linear, quadratic and cubic polynomials
$$5{x}^{2}+x-7$$
Find a quadratic polynomial whose sum and product respectively of the zeros are as given. Also, find the zeros of these polynomials by
$$\dfrac{-8}{3},\dfrac{4}{3}$$
Classify the following as linear, quadratic and cubic polynomials
$$x-1$$
Classify the following as linear, quadratic and cubic polynomials
$${x}^{2}+x+4$$
What is meant by division algorithm give example?
Classify whether $$x-x^3$$ is linear, quadratic, or a cubic polynomial.
Divide the polynomial $$p(x)$$ by the polynomial $$g(x)$$ and find the quotient and remainder in each of the following.
$$p(x)=x^{4}-3x^{2}+4x-3\quad g(x)=x^{2}-2$$
Quotient $$=x^2-1$$
Reminder$$=4x-5$$
Find the remainder when $$x^4 + 5x^2 + 6 $$ is divided by $$x^2 + 1$$.
Divide $$(y^{3} - 3y^{2} + 5y - 1)$$ by $$(y - 1)$$ to find quotient and remainder.
Divide the polynomial $$p(x)$$ by the polynomial $$g(x)$$ and find the quotient and remainder in each of the following.
$$p(x)=x^{4}-5x+6\quad g(x)=2-x^{2}$$
Quotent$$=-x^2-2$$
Reminder$$=-5x+10$$
Divide $$6x^2-31x+47$$ by $$2x-5$$ and verify the division algorithm.
$$g(x) = 2x - 5$$
$$q(x) = 3x - 8 $$
and $$r = 7$$
$$\therefore$$ By division algorithm,
$$p(x) = g(x) \times q(x) + r$$
$$= (2x - 5) (3x - 8) + 7$$
$$= 6x^2 - 15x - 16x + 40 + 7$$
$$= 6x^2 - 31x + 47$$
$$ = p(x)$$
Hence division algorithm is verified.
Classify the following as linear, quadratic and cubic polynomials
$$3p$$
Divide and also verify the result $${x^2} + 3x + 2$$ by $$\left( {x + 2} \right)$$
Give an example of a quadratic binomial.
Divide and write the quotient and remainder.
(a) $$(y^2+10y+24) \div (y+4)$$
(b) $$(p^2+7p-5) \div (p+3)$$
(a) Quotient $$=(y+6)$$
Remainder $$=0$$
(b) Quotient $$=(p+4)$$
Remainder $$=-17$$
Divide and write the quotient and remainder.
$$(y^2+10y+24) \div (y+4)$$
(a) Quotient $$=(y+6)$$
Remainder $$=0$$
(b) Quotient $$=(p+4)$$
Remainder $$-17$$
(c) Quotient $$=(4{x}^{2}+18x+75)$$
Remainder $$=300$$
Divide:
$$2{x^3} - {x^2} - 3x + 1\,\,\,\ by\,\,\ (x + 1)$$
$$2{x^3} - {x^2} - 3x + 1\,\,\,\ by\,\,\ (x + 1)$$
Find the quotient and remainder.
(a) $$\dfrac{{{a^2} + 8a - 9}}{{a - 7}}$$
(b) $$\dfrac{{{x^2} + 6x - 11}}{{x - 3}}$$
(a) $$\dfrac{{{a^2} + 8a - 9}}{{a - 7}}$$
(b) $$\dfrac{{{x^2} + 6x - 11}}{{x - 3}}$$
(a) $$\dfrac{a^2+8a-9}{a-7}$$
$$(a+15)$$
___________
$$(a-7))a^2+8a-9$$
$$a^2-7a$$
____________
$$15a-9$$
$$15a-105$$
___________
$$96$$
$$\therefore$$ Quotient $$=(a+15)$$
remainder$$=96$$
(b) $$\dfrac{x^2+6x-11}{x-3}$$
$$(x+9)$$ ----Quotient
___________
$$x-3)x^2+6x-11$$
$$x^2-3x$$
____________
$$9x-11$$
$$9x-27$$
____________
$$16$$ --- remainder
Quotient$$=(x+9)$$
Remainder$$=16$$.
Fill in the blacks.
A polynomial of degree $$1$$ is called a _____ polynomial
Identify constant, linear, quadratic, cubic and quartic polynomial from the following.
$$-p$$.
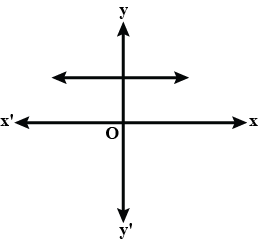
If the graph of a polynomial intersects the $$ x - asis $$ at only one point, can it be a quadratic polynomial ?
Examine, seeing the graph of the polynomial given below, whether they are a linear or quadratic polynomial or neither linear nor quadratic polynomial:
Classify the following as linear , quadratic and cubic polynomial :
$$ 1 + x $$
Classify the following as linear , quadratic and cubic polynomial :
3t
Classify the following as linear , quadratic and cubic polynomial :
$$ y + y^{2} + 4 $$
Classify the following polynomial as linear, quadratic and cubic polynomial .
$$a^{2}$$
Classify the following as linear , quadratic and cubic polynomial :
$$ r^{2}$$
Find the zeroes of the following polynomials by factorisation method and verify the relation between the zeroes and the coefficients of the polynomials:
$$3x^2 + 4x- 4$$.
Find the zeroes of the following polynomials by factorisation method and verify the relation between the zeroes and the coefficients of the polynomials:
$$4x^2 + 5 \sqrt{2}x -3$$
If one root of the equation $$x^{3}-13x^{2}+15x+189= 0$$ exceeds other by $$2$$ then find its smallest root.
If $$\alpha$$ and $$\beta$$ are the zeros of the polynomial $$x^2 -8x + k$$ such that $$\alpha^2+\beta^2=40$$, then the value of $$k$$ is
Prove that there do not exist natural numbers $$x$$ and $$y,$$ with $$x > 1,$$ such that $$\displaystyle \frac {x^7-1}{x-1}=y^5+1$$.
Verify that $$-5, \displaystyle \frac{1}{2}, \frac{3}{4}$$ are zeros of cubic polynomial $$8x^3 + 30x^2 -47x + 15$$. Also verify the relationship between the zeros and the coefficients.
$$3x^{2}+2x-1=0$$ is a equation of degree _____
Classify the following as linear, quadratic and cubic polynomials:
(i) $$x^2+x$$
(ii) $$x-x^3$$
(Iii) $$y+y^2+4$$
(iv) $$1+x$$
(v) $$3t$$
(vi) $$r^2$$
(vii) $$7x^3$$
The graphs of $$y = p(x)$$ are given in the figure, for some polynomials $$p(x)$$. Find the number of zeroes of $$p(x)$$, in each case.
Give the geometric representations of $$2x+9=0$$ as an equation
(i) in one variable
(ii) in two variable
(i) In one variable
Given equation is $$2x+9=0$$
$$\Rightarrow 2x=-9$$
$$\Rightarrow x=\dfrac{-9}{2}=-4.5$$
(ii) Given equation is $$2x+9=0$$
$$\Rightarrow 2x+0y+9=0$$
$$\Rightarrow 2x=-9$$
$$\Rightarrow x=\dfrac{-9}{2}=-4.5$$
It is line parallel to $$y$$-axis at a negative distance.
Two points lying it are the points $$A(-4.5, 0), B(-4.5, 2).$$
Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) $$x^2 - 2x - 8$$ (ii) $$4s^2 - 4s + 1$$ (iii) $$6x^2 - 3 - 7x$$
(iv) $$4u^2 + 8u$$ (v) $$t^2 - 15$$ (vi) $$3x^2 - x - 4$$
If two zeroes of the polynomial $$x^4- 6x^3 - 26x^2 + 138x -35$$ are $$2\pm \sqrt{3}$$, find the other zeroes.
Therefore, $$(x-2+ \sqrt{3})(x-2- \sqrt{3}) = x^2+4-4x-3$$
= $$x^2-4x+1$$ is a factor of the given polynomial.
Using division algorithm, we get
$$x^4 -6x^3 -26x^2 + 138x -35 = (x^2-4x+1)(x^2-2x-35)$$
So, $$(x^2-2x-35)$$ is also a factor of the given polynomial.
$$x^2-2x-35 = x^2-7x+5x-35$$
$$=x(x-7)+5(x-7)$$
$$ = (x - 7)(x + 5)$$
Hence, $$7$$ and $$-5 $$are the other zeros of this polynomial.
On dividing $$x^3- 3x^2 + x + 2$$ by a polynomial g(x), the quotient and remainder were $$( x-2 )$$ and $$(-2x + 4)$$, respectively. Find $$g(x).$$
Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
(i) $$t^2 - 3, 2t^4 + 3t^3-2t^2-9t -12$$
(ii) $$x^2+3x+1, 3x^4 + 5x^3 - 7x^2 + 2x + 2$$
(iii) $$x^3 - 3x + 1, x^5 - 4x^3 + x^2 + 3x + 1$$
Remainder is 0, hence $$t^2 -3$$ is a factor of $$2t^4 + 3t^3-2t^2-9t -12$$
(ii) $$x^2+3x+1, 3x^4 + 5x^3 - 7x^2 + 2x + 2$$
Remainder is 0, hence $$x^2 + 3x +1$$ is a factor of $$3x^4 + 5x^3 - 7x^2 + 2x + 2$$
Remainder is 0, hence $$x^2 + 3x +1$$ is a factor of $$3x^4 + 5x^3 - 7x^2 + 2x + 2$$
(iii) $$x^3 - 3x + 1, x^5 - 4x^3 + x^2 + 3x + 1$$
Remainder is 2, hence $$x^3-3x +1$$ is not a factor of $$x^5 - 4x^3 + x^2 + 3x + 1$$
Remainder is 2, hence $$x^3-3x +1$$ is not a factor of $$x^5 - 4x^3 + x^2 + 3x + 1$$
Give examples of polynomials $$p(x), g(x), q(x)$$ and $$r(x)$$, which satisfy the division algorithm and
(i) deg $$p(x) = $$deg $$q(x)$$ (ii) deg $$q(x) = $$deg $$r(x)$$ (iii) deg $$r(x) = 0$$
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
(i) $$2x^3+x^2-5x+2; \dfrac{1}{2}, 1, -2$$
(ii) $$x^3-4x^2+5x-2; 2, 1, 1$$
Divide the polynomial $$p(x)$$ by the polynomial $$g(x)$$ and find the quotient and remainder in each of the following:
(i) $$p(x) = x^3 -3x^2 + 5x -3,\ g(x) = x^2 -2$$
(ii) $$p(x) = x^4 -3x^2 + 4x + 5,\ g(x) = x^2 + 1 -x$$
(iii) $$p(x) = x^4 -5x + 6,\ g(x) = 2- x^2$$
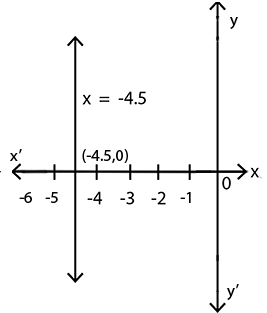
Sketch the graph and identify zeroes of a linear polynomial: $$\dfrac{x + 10}{4}$$.
Let $$y = \dfrac{x + 10}{4}$$
$$4y = 10 + x$$
$$y = \dfrac{10+x}{4}$$
From equation (1) assume the value of $$x$$ and $$y$$ to satisfy the equation to zero.
Plotting $$(0, 2.5), (-10, 0)$$ and joining them, we get another straight line.
The graph of $$4y - x = 10$$ intersect the x-axis at $$(-10, 0)$$. Hence the zero of given polynomial is $$(-10, 0)$$ as it intersects at $$x$$-axis at $$(-10, 0)$$.
$$4y = 10 + x$$
$$y = \dfrac{10+x}{4}$$
From equation (1) assume the value of $$x$$ and $$y$$ to satisfy the equation to zero.
Plotting $$(0, 2.5), (-10, 0)$$ and joining them, we get another straight line.
The graph of $$4y - x = 10$$ intersect the x-axis at $$(-10, 0)$$. Hence the zero of given polynomial is $$(-10, 0)$$ as it intersects at $$x$$-axis at $$(-10, 0)$$.
Construct a graph which represent the zeroes of the quadratic polynomial for an equation$$y=x^2-10x$$.
Factor of $$y=x^2-10x = x(x-10)=0$$ or $$x = 0, x = 10$$
Plotting $$(0, 0) (5, -25) (10, 0)$$ and joining them.
Here, the graph cuts $$x$$-axis at two distinct points $$A$$ and $$A'$$.
The $$x$$-coordinates of $$A(10, 0)$$ and $$A'(0, 0)$$ are the two zeroes of the quadratic polynomial $$y=x^2-10x$$.
Plotting $$(0, 0) (5, -25) (10, 0)$$ and joining them.
Here, the graph cuts $$x$$-axis at two distinct points $$A$$ and $$A'$$.
The $$x$$-coordinates of $$A(10, 0)$$ and $$A'(0, 0)$$ are the two zeroes of the quadratic polynomial $$y=x^2-10x$$.
Graphically represent the zeros of the given linear polynomial: $$y=x-12$$
It is known that if the curve of $$y=f(x)$$ cuts the $$x-$$ axis at point $$(p,0)$$ then $$p$$ is said to be the zero of $$y=f(x)$$.
Plotting $$(0, -12), (12, 0)$$ and joining them, we get ]graph of $$y=x-12$$.
The graph of $$x - y = 12$$ intersect the $$x$$-axis at $$(12, 0)$$. Hence the zero of $$x - 12$$ is $$12$$.
Graphically represent the zeroes of the quadratic polynomial for an equation $$y=2x^2-11x+5$$ in graph.
Factor of $$y=2x^2-11x+5 = (x-0.5)(x-5)$$
Plotting $$(0.5, 0) (1, -2) (3, -5) (5, 0)$$ and joining them.
Here, the graph cuts $$x$$-axis at two distinct points A and A'.
The x-coordinates of $$A(0.5, 0)$$ and $$A'(5, 0)$$ are the two zeroes of the quadratic polynomial $$y=2x^2-11x+5$$.
Plotting $$(0.5, 0) (1, -2) (3, -5) (5, 0)$$ and joining them.
Here, the graph cuts $$x$$-axis at two distinct points A and A'.
The x-coordinates of $$A(0.5, 0)$$ and $$A'(5, 0)$$ are the two zeroes of the quadratic polynomial $$y=2x^2-11x+5$$.
What are the zeroes of the quadratic polynomial from the graph?
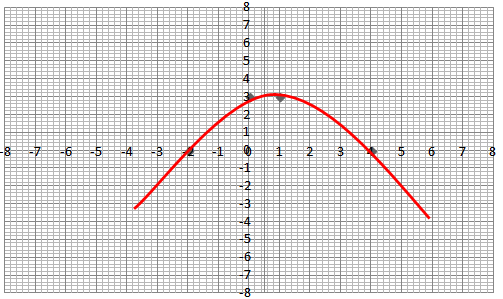
Find the zeroes of the quadratic polynomial from the graph.
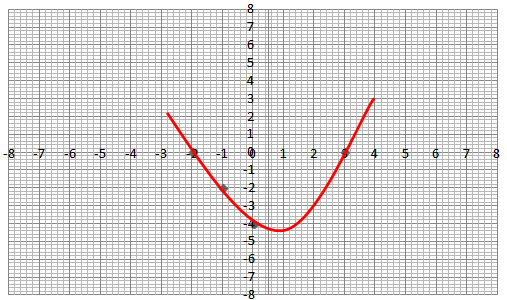
Represent the zeroes of the quadratic polynomial for an equation $$ y=x^2+x-9$$ in graph.
Factor of $$x^2+x-9 = (x-3)(x+3)$$
Plotting $$(-3, 0) (-1, -8) (0, -9) (1, -8) (3, 0)$$ and joining them.
Here, the graph cuts $$x$$-axis at two distinct points $$A$$ and $$A'$$.
The x-coordinates of $$A(-3, 0)$$ and $$A (3, 0)$$ are the two zeroes of the quadratic polynomial $$x^2+x-9$$.
Plotting $$(-3, 0) (-1, -8) (0, -9) (1, -8) (3, 0)$$ and joining them.
Here, the graph cuts $$x$$-axis at two distinct points $$A$$ and $$A'$$.
The x-coordinates of $$A(-3, 0)$$ and $$A (3, 0)$$ are the two zeroes of the quadratic polynomial $$x^2+x-9$$.
Sketch a graph and represent the zeroes of the quadratic polynomial for the equation $$y = x^2+2x-3$$.
Factor of $$x^2+2x-3 = (x+3)(x-1)$$
Plotting $$(-3, 0) (-2, -3) (-1, -4) (1, 0$$) and joining them.
Here, the graph cuts $$x$$-axis at two distinct points $$A$$ and $$A'$$.
The $$x$$-coordinates of $$A(-3, 0)$$ and $$A'(1, 0)$$ are the two zeroes of the quadratic polynomial $$y = x^2+2x-3$$.
Plotting $$(-3, 0) (-2, -3) (-1, -4) (1, 0$$) and joining them.
Here, the graph cuts $$x$$-axis at two distinct points $$A$$ and $$A'$$.
The $$x$$-coordinates of $$A(-3, 0)$$ and $$A'(1, 0)$$ are the two zeroes of the quadratic polynomial $$y = x^2+2x-3$$.
Graphically represent the zeroes of the cubic polynomial: $$y=x^3+4x^2+x-6$$
Factor of $$y=x^3+4x^2+x-6 = (x+2)(x-1)(x+3)$$
Plotting $$(1, 0), (-1, -4), (2, 0), (-3, 0)$$ and joining them.
Here $$1, -2, -3$$ are the zeroes of the cubic polynomial.
These co-ordinates are the $$x$$-coordinates of the three points where the graph of $$y=x^3+4x^2+x-6$$ intersects the $$x$$-axis.
Plotting $$(1, 0), (-1, -4), (2, 0), (-3, 0)$$ and joining them.
Here $$1, -2, -3$$ are the zeroes of the cubic polynomial.
These co-ordinates are the $$x$$-coordinates of the three points where the graph of $$y=x^3+4x^2+x-6$$ intersects the $$x$$-axis.
Using division algorithm, divide the polynomial $$2x^3+2x^2-5x+1$$ by $$(x-1)$$.
We divide the polynomial $$2x^3+2x^2-5x+1$$ by $$(x-1)$$ as shown in the above image:
Hence, the quotient is $$2x^2+4x-1$$ and the remainder is $$0$$.
Graphically represent the zeroes of the cubic polynomial: $$y=x^3-3x+2$$
Factor of $$x^3-3x+2 = (x-1)(x-1)(x+2)$$
Plotting $$(-2, 0), (-1, -4), (0, -2), (1, 0)$$ and joining them.
Here $$-1, -1, 2$$ are the zeroes of the cubic polynomial.
These co-ordinates are the $$x$$-coordinates of the three points where the graph of $$x^3-3x+2$$ intersects the $$x$$-axis.
Plotting $$(-2, 0), (-1, -4), (0, -2), (1, 0)$$ and joining them.
Here $$-1, -1, 2$$ are the zeroes of the cubic polynomial.
These co-ordinates are the $$x$$-coordinates of the three points where the graph of $$x^3-3x+2$$ intersects the $$x$$-axis.
$$y=x^3-3x^2-6x+8$$, Draw a graphical representation of the polynomial.
The zeroes of polynomial $$y={x^3-3x^2-6x+8}$$ are $$1,-2,4$$
Quadratic polynomial: $$y=x^2-4x+4$$, draw a graph and represent the zeroes of the polynomial.
Given quadratic polynomial is $$y=x^2-4x+4$$
To find the points on the graph, we will substitute few values of $$x$$ and find the values of $$y$$.
If $$x=0$$, then $$y=0^{2}-4\times0+4=0-0+4=4$$
If $$x=1$$, then $$y=1^{2}-4\times1+4=1-4+4=1$$
If $$x=2$$, then $$y=2^{2}-4\times2+4=4-8+4=0$$
So, the points are $$(0, 4), (1, 1), (2, 0)$$.
Plotting $$(0, 4), (1, 1), (2, 0)$$ and joining them.
Here, the graph cuts $$x$$-axis at one distinct point $$\text{A}$$.
The $$x$$-coordinates of $$\text{A} (2, 0)$$ is the one zeroes of the quadratic polynomial $$y=x^2-4x+4$$
Plotting $$(0, 4), (1, 1), (2, 0)$$ and joining them.
Here, the graph cuts $$x$$-axis at one distinct point $$\text{A}$$.
The $$x$$-coordinates of $$\text{A} (2, 0)$$ is the one zeroes of the quadratic polynomial $$y=x^2-4x+4$$
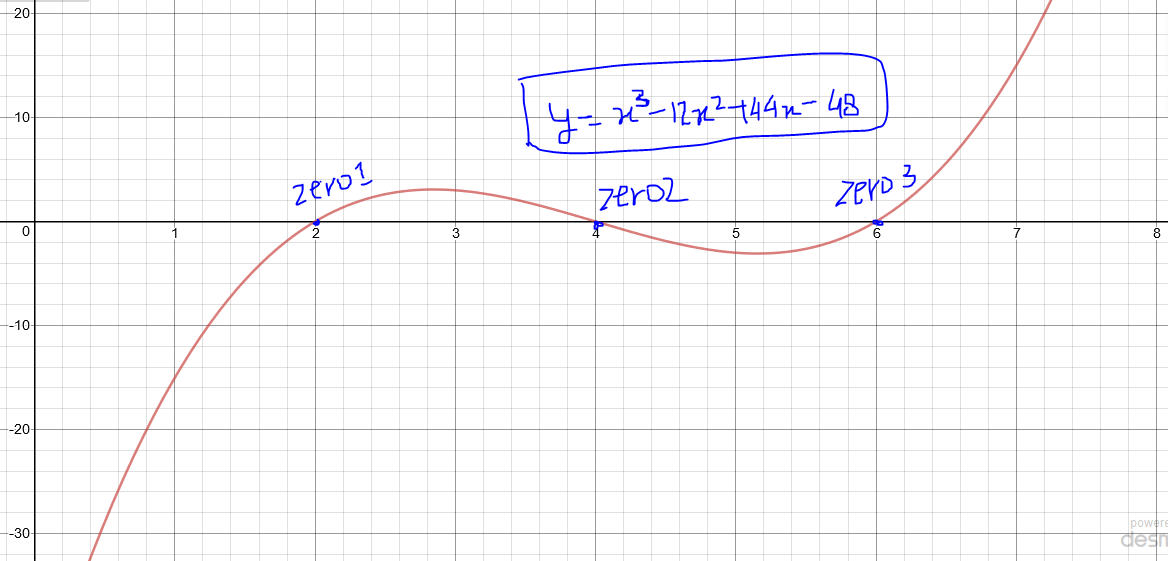
Sketch a graphical representation of the zeros of the given polynomial: $$y=x^3-12x^2+44x-48$$
The zeroes of polynomial $$y={x^3-12x^2+44x-48}$$ are $$2,4,6$$
Divide: $$2x^4+x^3+8x^2+14x+5$$ by $$(2x+1)$$ (use division algorithm method).
Use synthetic division to find the quotient Q and Remainder R when dividing
$$\dfrac12{x}^{3}-\dfrac13{x}^{2}-\dfrac32x+\dfrac13$$ by $$x-\dfrac12$$
Since the divisor $$=x-\dfrac{1}{2}$$
The zero of $$x-\dfrac{1}{2}=0$$
$$\Rightarrow x=\dfrac{1}{2}$$
$$\therefore$$ The quotient is $$: \dfrac{1}{2}x^2-\dfrac{1}{12}x -\dfrac{37}{24}$$
$$\Rightarrow$$ Remainder $$=\dfrac { \left( \dfrac { -21 }{ 48 } \right) }{ \left( x-\dfrac { 1 }{ 2 } \right) } .$$
Hence, solved.
Use synthetic division to find the quotient Q and Remainder R when dividing
$$7{x}^{5}-2{x}^{4}-5{x}^{3}+{x}^{2}-3x+5$$ by $$x-2$$
$$\Rightarrow Q=7x^4+12x^3+19x^2+39x+75$$
$$\Rightarrow R=155.$$
Hence, solved.
Use synthetic division to find the quotient Q and Remainder R when dividing
$$4{x}^{3}+{x}^{2}-2x+3$$ by $$x+2$$
$$\Rightarrow Q=4x^2-7x+12$$
$$\Rightarrow R=-21$$
Hence, solved.
$$\dfrac{3x^4+x^3+6x^2-16x-6}{3x+1}$$ = ? (Use division algorithm method).
Given $$f(x) =$$ $$4x^4+6x^3+6x^2+6x+2$$, $$g(x) =$$ $$2x+2$$. Divide $$\dfrac{f(x)}{g(x)}$$ (Use division algorithm method)
$$f\left( x \right) =4x^4+6x^3+6x^2+6x+2$$
$$g\left( x \right) =2x+2$$
$$\dfrac{f\left( x \right)}{g\left( x \right)}$$ using division algorithm method,
so, the quotient $$=2x^3+x^2+2x+1$$
Hence, the answer is $$2x^3+x^2+2x+1.$$
Find the quotient and remainder on dividing $$p(x) = x^{3} - 6x^{2} + 15x - 8$$ by $$g(x) = x - 2$$
Divide $$(5x + x^{2} + 14 + 2x^{3})$$ by $$(x + 2)$$
Quotient : $$2x^2-3x+11$$
Remainder : $$-8.$$
Hence, solve.
A polynomial $$p(x)$$ is divided by $$g(x)$$, the obtained quotient $$q(x)$$ and the remainder $$r(x)$$ are given in the table. Find $$p(x)$$ in each case.
| Sl. | $$p(x)$$ | $$g(x)$$ | $$q(x)$$ | $$r(x)$$ |
| i | ? | $$x - 2$$ | $$x^{2} - x + 1$$ | $$4$$ |
| ii | ? | $$x + 3$$ | $$2x^{2} + x + 5$$ | $$3x + 1$$ |
| iii | ? | $$2x + 1$$ | $$x^{3} + 3x^{2} - x + 1$$ | $$0$$ |
| iv | ? | $$x - 1$$ | $$x^{3} - x^{2} - x - 1$$ | $$2x - 4$$ |
| v | ? | $$x^{2} + 2x + 1$$ | $$x^{4} - 2x^{2} + 5x - 7$$ | $$4x + 12$$ |
What must be added to the polynomial $$p(x) = x^{4} + 2x^{3} - 2x^{2} + x - 1$$ so that the resulting polynomial is exactly divisible by $$x^{2} + 2x - 3$$
We know, $$p(x) = [g(x) \times q(x)] + r(x)$$
$$\therefore p(x) - r(x) = g(x) \times q(x)$$
$$\therefore p(x) + \left \{-r(x) \right \} = g(x) \times q(x)$$
It is clear that RHS is divisible by $$g(x)$$. $$\therefore LHS$$ is also divisible by $$g(x)$$
Thus, if we add $$-r(x)$$ to $$p(x)$$, then the resulting polynomial is divisible by $$g(x)$$.
Let us divide $$p(x)=x^4+2x^3-2x^2+x-1$$ by $$g(x)=x^2+2x-3$$ to find the remainder $$r(x)$$.
$$\therefore r(x) = -x + 2\Rightarrow \left \{-r(x)\right \} = x - 2$$
Hence, we should add $$(x - 2)$$ to $$p(x)=x^4+2x^3-2x^2+x-1$$ so that the resulting polynomial is exactly divisible by $$x^2+2x-3$$.
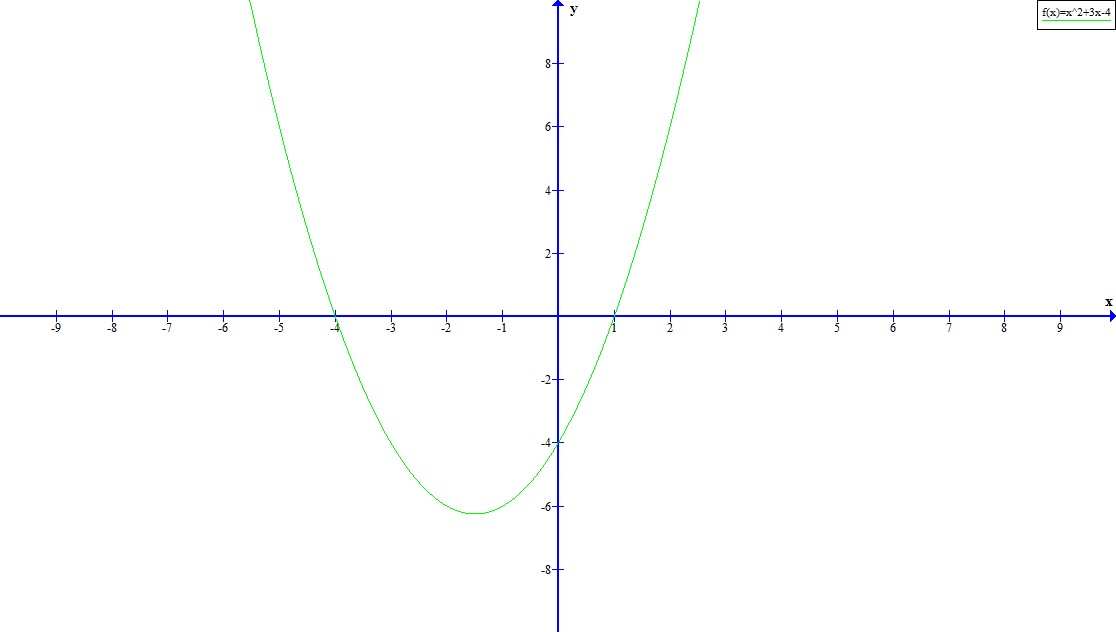
Draw the graph of $$p(x) = x^{2} + 3x - 4$$ and find zeroes.
Verify the zeroes of the polynomials
The graph of $$p(x)$$ is given above.
Clearly, from the graph $$x=-4,1$$ are zeros of $$p(x)$$.
Verification:-
$$p(-4)=(-4)^2+3\times-4-4=16-12-4=0$$
$$p(1)=(1)^2+3\times1-4=1+3-4=0$$
Clearly, from the graph $$x=-4,1$$ are zeros of $$p(x)$$.
Verification:-
$$p(-4)=(-4)^2+3\times-4-4=16-12-4=0$$
$$p(1)=(1)^2+3\times1-4=1+3-4=0$$
By which polynomial we should divide $$(4x^{4} - 5x^{3} - 39x^{2} - 46x - 2)$$ to get quotient as $$( x^{2} - 3x - 5 )$$ and remainder as $$( -5x + 8 )$$.
If $$\alpha, \beta, \gamma$$ are the zeroes of the cubic polynomial $$x^3 + 4x + 2$$, then find the value of
$$\dfrac{1}{\alpha + \beta} + \dfrac{1}{\beta + \gamma} + \dfrac{1}{\gamma + \alpha}$$
When a polynomial $$f(x)$$ is divided by $$(x - 1)$$, the remainder is $$5$$ and when it is divided by $$(x - 2)$$, the remainder is $$7$$. Find the remainder when it is divided by $$(x -1) (x - 2)$$.
Find $$k$$ so that $$x^2+2x+k$$ is a factor of $$2x^4+x^3-14x^2+5x+6$$. Also, find the zeroes of the two polynomials.
If $$9a+5B$$ is divisible by 14, then prove that $$5B+9a$$ is also divisible by $$14$$.
If $$x = \dfrac{2}{3}$$ and $$x = -3$$ are the roots of the equation $$ax^2 \, + \, 7x \, + \, b \, = \, 0,$$ find the value of $$a^2+ b^2$$.
Use division algorithm to show that any positive odd integer is of the form $$6q+1$$ or $$6q+3$$ or $$6q+5$$, where $$q$$ is some integer.
Check whether $${x^2} - x + 1\,$$ is a factor in $${x^3} - 3{x^2} + 3x - 2$$
Given polynomial is $$x^3-3x^2+3x-2$$.
To find out: Whether $$x^2-x+1 $$ is a factor of the given polynomial or not.
$$x^2-x+1 $$ will be a factor of $$x^3-3x^2+3x-2$$ when the remainder is zero.
Dividing $$x^3-3x^2+3x-2$$ by $$x^2-x+1 $$, as shown in the figure. We get:
Quotient as $$x-2$$.
and Remainder as $$0$$.
Since the remainder is $$0$$, $$x^2-x+1$$ is a factor of $$x^3-3x^2+3x-2$$.
Check $$x^2-x+1$$ is a factor of $$x^3-3x^2-3x-2$$
We divide $$x^3-3x^2-3x-2$$ by $$x^2-x+1$$ and if we get the remainder as $$0$$ then it means that $$x^2-x+1$$ is a factor of $$x^3-3x^2-3x-2$$.
From the above division, we have the quotient $$x-2$$ and the remainder is $$0$$.
Hence, $$x^2-x+1$$ is a factor of $$x^3-3x^2-3x-2$$.
How many zeros does cubic polynomial has?
Find the reminder when $$x^{3}+3x^{3}+3x+1$$ is divided by
a) $$5+2x$$
b) $$x-\dfrac{1}{2}$$
If $$\alpha $$ and $$\beta$$ are roots of given equation $$8x^2-8\sqrt2 x+ 4=0$$ and $$\alpha\beta=\dfrac{1}{m}$$, then find $$m$$.
Divide $$6x^2-x-15$$ by $$(2x+3)$$ and also verify the result.
What must be subtracted from $$4x^{4}-2x^{3}-6x^{2}+x-5$$ so that result is exactly divisible by $$2x^{2}+x-1$$?
We divide $$4x^4−2x^3−6x^2+x−5$$ by $$2x^2+x−1$$ as shown in the below image:
From the division, we observe that the quotient is $$2x^2-2x-1$$ and the remainder is $$-6$$.
Find the remainder when $$ 4x^3-3x^2+4x-2$$ divided by (i) $$x-1$$ (ii) $$x-2$$
Find the remainder when $${x}^{3} + {3x}^{2} + {3x} + 1$$ is divided by
$$X+1$$
Find the values of $$a$$ and $$b$$ so that the polynomial $$({x}^{3}-10{x}^{2}+ax+b)$$ is exactly divisible by $$(x-1)$$ as well as $$(x-2)$$
Find :
$$\dfrac{x^4-3x^2-2x-3}{(x-2)}$$
We divide $$x^4-3x^2-2x-3$$ by $$(x-2)$$ as shown in the above image:
From the division, we observe that the quotient is $$x^3+2x^2+x$$ and the remainder is $$-3$$.
Hence, the quotient is $$x^3+2x^2+x$$ and the remainder is $$-3$$.
Divide using the long division method and check the answer.
$$-11x+5x-4$$ by $$2x-1$$
We divide $$-11x^2+5x-4$$ by $$(2x-1)$$ as shown in the above image:
From the division, we observe that the quotient is $$-\dfrac {11}{2}x-\dfrac {1}{4}$$ and the remainder is $$-\dfrac {17}{4}$$.
We know that the division algorithm states that:
Dividend$$=$$Divisor$$\times$$Quotient$$+$$Remainder
We apply the division algorithm to check the answer as follows:
$$Dividend=Divisor\times Quotient+Remainder\\ -11x^{ 2 }+5x-4=\left[ (2x-1)\left( -\dfrac { 11 }{ 2 } x-\dfrac { 1 }{ 4 } \right) \right] -\dfrac { 17 }{ 4 } \\ -11x^{ 2 }+5x-4=-11x^{ 2 }-\dfrac { 1 }{ 2 } x+\dfrac { 11 }{ 2 } x+\dfrac { 1 }{ 4 } -\dfrac { 17 }{ 4 } \\ -11x^{ 2 }+5x-4=-11x^{ 2 }+\dfrac { 10 }{ 2 } x-\dfrac { 16 }{ 4 } \\ -11x^{ 2 }+5x-4=-11x^{ 2 }+5x-4\\ Hence\quad verified.$$
Find the remainder when $$y^3 +y^2-2y+1$$ is divided by $$(y-a).$$
On dividing polynomial $$x^3-3 x^2+x+2$$ by a polynomial $$g(x)$$, the quotient and remainder were $$x-2$$ and $$-2x+4$$, respectively. Find $$g(x)$$.
$$\text{Dividend} = \text{Divisor} \times \text{Quotient} + \text{Remainder} ..... \left( 1 \right)$$
According to the question,
$$\text{Dividend} = f{\left( x \right)} = {x}^{3} - 3{x}^{2} + x + 2$$
$$\text{Divisor} = g{\left( x \right)} = ?$$
$$\text{Quotient} = q{\left( x \right)} = x - 2$$
$$\text{Remainder} = r{\left( x \right)} = -2x + 4$$
Now, from $${eq}^{n} \left( 1 \right)$$, we have
$$f{\left( x \right)} = g{\left( x \right)} \times q{\left( x \right)} + r{\left( x \right)}$$
$${x}^{3} - 3{x}^{2} + x + 2 = g{\left( x \right)} \times \left( x - 2 \right) + \left( -2x + 4 \right)$$
$$\left( {x}^{3} - 3{x}^{2} + x + 2 \right) - \left( -2x + 4 \right) = g{\left( x \right)} \times \left( x - 2 \right)$$
$$\Rightarrow g{\left( x \right)} = \cfrac{\left( {x}^{3} - 3 {x}^{2} + 3x - 2 \right)}{\left( x - 2 \right)}$$
As from the attached image, we have
$$\left( {x}^{3} - 3 {x}^{2} + 3x - 2 \right) \div \left( x - 2 \right) = {x}^{2} - x + 1$$
$$\therefore g{\left( x \right)} = \cfrac{\left( {x}^{3} - 3 {x}^{2} + 3x - 2 \right)}{\left( x - 2 \right)} = \left( {x}^{2} - x + 1 \right)$$
Divide using the long division method and check the answer.
$$x^{2}-3x+2$$ by $$x-2$$
Divide using the long division method and check the answer.
$$3x^{2}+4x^{2}+x+7$$ by $$x^{2}+1$$
We divide $$3x^3+4x^2+x+7$$ by $$(x^2+1)$$ as shown in the above image:
From the division, we observe that the quotient is $$3x+4$$ and the remainder is $$-2x+3$$.
Now we will apply the division algorithm to check the answer as follows:
$$\begin{aligned}{}{\text{Dividend}} &= {\text{Divisor}} \times {\text{Quotient}} + {\text{Remainder}}\\3{x^3} + 4{x^2} + x + 7 &= \left[ {({x^2} + 1)\left( {3x + 4} \right)} \right] - 2x + 3\\ &= (3{x^3} + 4{x^2} + 3x + 4) - 2x + 3\\& = 3{x^3} + 4{x^2} + 3x - 2x + 4 + 3\\3{x^3} + 4{x^2} + x + 7 &= 3{x^3} + 4{x^2} + x + 7\quad\quad\quad\quad[\text{Which is true}]\end{aligned}$$
Hence verified
Solve:
$$\left( {{y^2} + 10y + 24} \right) \div \left( {y + 4} \right)$$
Divide $$2x^{2}+{3x}+{1}$$ by $$x+2$$ and find quotient and remainder.
We divide $$2x^2+3x+1$$ by $$(x+2)$$ as shown in the above image:
From the division, we observe that the quotient is $$2x-1$$ and the remainder is $$3$$.
Hence, the quotient is $$2x-1$$ and the remainder is $$3$$.
$$(2x^{4} + 3x^{3} + 4x - 2x^{2})\div (x + 3)$$.
Divide $$z^2+16z+64$$ by $$z+8$$.
Divide. Write the quotient and the remainder.
(a) $$(21{x}^{4}-14{x}^{2}+7x)\div 7{x}^{3}$$
(b) $$(6{x}^{5}-4{x}^{4}+8{x}^{3}+2{x}^{2})\div 2{x}^{2}$$
(c) $$(25{m}^{4}-15{m}^{3}+10m+8)\div 5{m}^{3}$$
$$16x(9x+12)$$ by $$(3x-4)$$
The given polynomial $$16x(9x+12)$$ can be rewritten as $$144x^2+192x$$.
We now divide $$144x^2+192x$$ by $$(3x-4)$$ as shown in the above image:
From the division, we observe that the quotient is $$48x$$ and the remainder is $$384x$$.
Hence, the quotient is $$48x$$ and the remainder is $$384x$$.
Rewrite the terms in proper order and then divide
$$12+10y^{3}+10y^{2}+8y-2$$ by $$y^{2}-y+6$$
The given polynomial $$12+10y^3+10y^2+8y-2$$ can be rewritten as $$10y^3+10y^2+8y+10$$.
We now divide $$10y^3+10y^2+8y+10$$ by $$(y^2-y+6)$$ as shown in the above image:
From the division, we observe that the quotient is $$10y+20$$ and the remainder is $$-32y-110$$.
Hence, the quotient is $$10y+20$$ and the remainder is $$-32y-110$$.
Divide $$10x^4+12x^3-62x^2+30x-3$$ by $$2x^2+7x-1$$.
Solve:
$$x+6-{3x-5-2(x-5)}=2x-9-{2x+5-3(x+1)}$$
Divide $$\left( { 12x }^{ 2 }-3x-450 \right) \div (x+6)$$.
$$\therefore \left( 12{ x }^{ 2 }-3x-450 \right) \div \left( x+6 \right) =12x-75$$
Solve :
$$\left( {2{m^3} + {m^2} + m + 9} \right) \div \left( {2m - 1} \right)$$
Given: $$(2m^3+m^2+m+9)\div (2m-1)$$
$$m^2+m+1$$
__________________
$$(2m-1))$$ $$ 2m^3+m^2+m+9$$
$$2m^3-m^2$$
__________________
$$2m^2+m+9$$
$$2m^2-m$$
_______________
$$2m+9$$
$$2m-1$$
____________
$$10$$
$$\therefore (2m^3+m^2+m+9)=(2m-1)(m^2+m+1)+10$$.
If $$ \alpha = 3 , \beta = 5 , \gamma = 2 ,$$ find the cubic polynomial
$$\alpha = 3 , \beta 5, \gamma =2$$
Cubic polynomial $$\Rightarrow (x-\alpha )(x-\beta )(x-\gamma )$$
$$\Rightarrow (x-3)(x-5)(x-2)=0$$
$$\Rightarrow (x^2-8x+15)(x-2)=0$$
$$\Rightarrow x^3 - 8x^2+15 x - 2x^2 +16 x-30 =0$$
$$\Rightarrow x^3 - 10x^2 +31 x - 30 =0$$
$$\therefore $$ Cubic polynomial is $$x^3 - 10x^2 +31 x-30=0$$
Find values of $$a$$ and $$b$$, if $$(x^2 + 1)$$ is a factor of the polynomial $$x^2+ x^3 +8x^2 + ax + b$$.
Using division algorithm, find the quotient and remainder on dividing.
$$8x^{4}+14x^{3}-2x^{2}+8x-12$$ by $$4x^{2}+3x-2$$
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
Check whether $$2{x}^{4}-3{x}^{3}-3{x}^{2}+6x-2$$ is divisible by $${x}^{2}-2$$
If $$a{x}^{n-1}+b{x}^{n-2}+c{x}^{n-3}$$ is a cubic polynomial where $$n\in N$$, then find the value of $$n$$
Divide $$(2x^{4}+3x^{3}+4x-2x^{2})\div (x+3)$$
$$x+3)2x^4+3x^3-2x^2+4x(2x^3-3x^2+7x-17$$
$$2x^4+6x^3$$
_______________
$$-3x^3-2x^2+4x$$
$$-3x^3-9x^2$$
_________________
$$7x^2+4x$$
$$7x^2+21x$$
__________________
$$-17x$$
$$-17x-51$$
___________________
$$51$$
For which value of a and b, the zeroes of $$q\left(x\right)=x^{3}+2x^{2}+a$$ are also the zeroes of the polynomial $$p\left(x\right)=x^{5}-x^{4}-4x^{3}+3x^{2}+3x+b$$ ?
$$\Rightarrow 3-a-4=0,3a+3=0,b-2a=0$$
$$\Rightarrow -a-1=0,3\left(a+1\right)=0,b=2a$$
$$\Rightarrow -a=1,a=-1,b=2a$$
$$\therefore a=-1$$,$$b=2a=2\times -1=-2$$
$$\therefore a=-1,b=-2$$
'
What is cubic polynomial ?
Divide the polynomial $${ 6x }^{ 3 }+{ 11x }^{ 2 }-10x-7$$ by the binomial $$2x + 1$$. Write the quotient and the remainder.
From the above division, we can conclude that,
The quotient is $$3x^2+4x-7$$ and the remainder is $$0.$$
Find all zeroes of the polynomial $$2x^3+x^2-6x-3$$ if two of its zeroes are $$-\sqrt{3}$$ & $$\sqrt{3}$$
The graph of a polynomial $$y=p(x)$$ is given below. By looking at the graph, find the number of zeroes of $$p(x)$$.
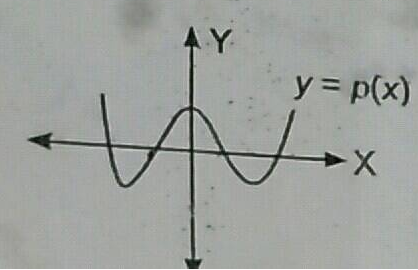
Given that $$x - \sqrt 5 $$ is a factor of the cubic polynomial $${x^3} - 3\sqrt 5 {x^2} + 13x - 3\sqrt 5 ,$$ Find all the zeros of the polynomial.
Given
polynomial is $$x^3-3\sqrt5x^2+13x-3\sqrt5$$
And $$(x-\sqrt5)$$ is a factor.
So, we use long division to find the other factor as shown in the image,
$$\therefore x^3-3\sqrt5x^2+13x-3\sqrt5=(x-\sqrt5)(x^2-2\sqrt5x+3)$$
Now using quadratic formula for $$x^2-2\sqrt5x+3$$ , We get
$$x=\sqrt5\pm\sqrt2$$
Hence the roots are $$\sqrt5,\ \sqrt5+\sqrt2$$ and $$ \sqrt5-\sqrt2$$
Find the zeroes of the given polynomial by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials
$${ 7y }^{ 2 }-\dfrac { 11 }{ 3 } y-\dfrac { 2 }{ 3 } $$
Given that the zeroes of the cubic polynomial $$f(x)=x^3-6x^2+3x+10$$ are of the form $$a,a+b,a+2b$$ for some real numbers $$a$$ and $$b$$, find the values of $$a$$ and $$b$$ as well as the zeros of the given polynomial.
Identify constant, linear, quadratic and cubic polynomials from the following polynomials:
$$r(x) = 3x^{3} + 4x^{2} + 5x - 7$$.
Find the zeros of the following polynomial by factorization method and verify the relations between the zeroes and the coefficient of the polynomials :
$$v^{ 2 }+4\sqrt { 3 } v-15$$
Obtain all the zeroes of the polynomial $$2x^4+x^3-14x^2-19x-6$$. If two zeroes are $$-2$$ and $$-1$$.
Identify constant, linear, quadratic and cubic polynomials from the following polynomials:
$$g(x) = 2x^{3} - 7x + 4$$.
What must be added to $$x^{3} - 3x^{2} - 12x + 19$$ so that the result is exactly divisibly by $$x^{2} + x - 6$$?
Find the cubic polynomial with the sum of zeroes, sum of the products of its zeroes taken two at a time and product of its zeroes as $$-4,\dfrac { 1 }{ 2 } ,\dfrac { -1 }{ 3 } $$
Find the zeros of the following polynomial by factorization method and verify the relations between the zeroes and the coefficient of the polynomials :
$${ 4x }^{ 2 }-3x-1$$
What must be added to $$3x^{3} + x^{2} - 22x + 9$$ so that the result is exactly divisible by $$3x^{2} + 7x - 6$$?
Divide each of the following and find the quotient and remainder:
$$30x^{4} + 11x^{3} - 82x^{2} - 12x + 48$$ by $$3x^{2} + 2x - 4$$.
Verify division algorithm i.e, $$Dividend = Divisor \times Quotient + Remainder$$, in each of the following. Also, write the quotient and remainder:
$$4y^{3} + 8y + 8y^{2} + 7$$ by $$2y^{2} - y + 1$$.
$$\dfrac{4y^3 + 8y + 8y^2 + 7}{2y^2 - y + 1} \Rightarrow \dfrac{4y^3 + 8y^2 + 8y + 7}{2y^2 - y + 1}$$
ref. image
$$Q = 2y + 5 , R = 11 y+ 2$$
Divided = (Divisor $$\times$$ Quotient ) + Remainder
$$= ((2y^2 - y + 1) \times (2y + 5)) + 11y + 2$$
$$= 4y^3 - 2y^2 + 2y + 10y^2 - 5y + 5 + 11y + 2$$
$$= 4y^3 + 8y^2 + 8y + 7$$
Divide each of the following and find the quotient and remainder:
$$9x^{4} - 4x^{2} + 4$$ by $$3x^{2} - 4x + 2$$.
Divide the polynomial $$f(x) = 3x^2 - x^3 - 3x + 5$$ by the polynomial $$g(x) = x - 1 - x^2 $$ and verify the division algorithm.
Given data :- Given Polynomial , $$f(x) = 3x^2 - x^3 - 3x + 5$$
$$g(x) = x - 1 - x^2$$
Solution :-
Ref. image
Now, to verify the division algorithm.
$$f(x) = g(x) . p(x) + r(x)$$
$$= (-x^2 + x - 1) (x - 2) + 3 ... (p(x) = (x - 2)$$ &
$$= -x^3 + 2x^2 + x^2 - 2x + 2 + 3 - x$$
$$= -x^3 + 3x^2 - 3x + 5$$
Hence its verified.
Divide the first polynomial by the second polynomial in each of the following. Also, write the quotient and remainder:
$$10x^{2} - 7x + 8, 5x - 3$$.
Write the quotient and remainder:
Divide $$14x^{2} + 13x - 15$$ by $$7x - 4$$
Quotient $$=2x+3$$
Remainder $$=-3$$
Verify divison algorithm for the polynomial $$ f(x) = 8 +20 x +x^2 - 6x^3 $$ by $$ g(x) = 2 +5x - 3x^2 $$
Divide the first polynomial by the second polynomial in each of the following. Also, write the quotient and remainder:
$$x^{4} - x^{3} + 5x, x - 1$$.
Verify division algorithm i.e, $$Dividend = Divisor \times Quotient + Remainder$$, in each of the following. Also, write the quotient and remainder:
$$15y^{4} - 16y^{3} + 9y^{2} - \dfrac {10}{3} y + 6$$ by $$3y - 2$$.
$$\dfrac{15y^4 - 16y^3 + 9y^2 - \dfrac{10}{3} y + 6}{3y - 2}$$
Ref. image
$$Q = 5y^3 - 2y^2 + \dfrac{5}{3} y, \, R= 6$$
Verification:
$$Divi$$ $$= (Divis \times Q) + R$$
$$= ((5y^3 - 2y^2 + \dfrac{5}{3} y) (3y - 2)) + 6$$
$$= 15y^4 - 6y^3 + 5y^2 - 10y^3 + 4y^2 + \dfrac{10}{3} y + 6$$
$$= 15 y^4 - 16 y^3 + 9y^2 - \dfrac{10}{3} y + 6$$
State division algorithm for polynomials.
Identify constant, linear, quadratic, cubic and quartic polynomial from the following.
$$6y$$.
Identify constant, linear, quadratic, cubic and quartic polynomial from the following.
$$-7+x$$.
Identify constant, linear, quadratic, cubic polynomial from the following.
$$-z^3$$.
What must be added to $$f(x) = 4x^4 + 2x^3 - 2x^2 + x - 1$$ so that the resulting polynomial is divisible by $$g(x) = x^2 + 2x - 3?$$
Identify constant, linear, quadratic, cubic and quartic polynimial from the following.
$$1+x+x^2$$.
Identify constant, linear, quadratic, cubic and quartic polynomial from the following.
$$-6x^2$$.
Identify constant, linear, quadratic, cubic polynomial from the following.
$$1-y-y^3$$.
The graphs of $$y=p(x)$$ for some polynomials (for question 1 to 4) are given below. Find the number of Zero in each case.
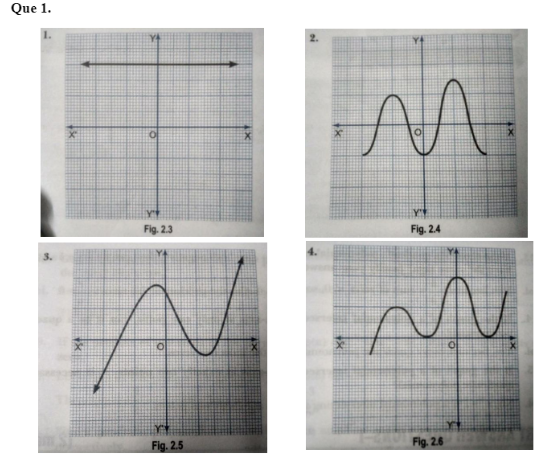
If $$\alpha , \beta , \gamma$$ be Zero of polynomial $$6x^3 +3x^2 -5x +1$$ then find the value of $$\alpha^{-1} , \beta^{-1} , \gamma^{-1}$$
Verify the division algorithm for the polynomials $$p(x)=2x^4-6x^3+2x^2-x+2$$ and $$g(x)=x+2$$.
Find the values of $$ a $$ for which all the roots of the equation $$ x^{4} $$ $$ -4 x^{3}-8 x^{2}+a=0 $$ are real
Given,
$$x^4-4x^3-8x^2+a=0$$
Let $$f(x)=x^{4}-4 x^{3}-8 x^{2}$$
$$ \Rightarrow f^{\prime}(x)=4 x^{3}-12 x^{2}-16 x=4 x\left(x^{2}-3 x-4\right)=4 x(x-4)(x+1) $$ Hence, graph of $$ y=f(x) $$
Now, graph of $$ y=f(x)+a $$ moves up or down depending on values of $$ a $$. It is clear that if equation $$ f(x)+a=0 $$ has four real roots,
then$$0 \leq a<3$$.
If the graph of a polynomial intersects the $$x-axis$$ at exactly two points,is it necessarily a quadratic polynomial?
State whether the following expression is polynomials or not? Justify your answer.
$$\dfrac{(x - 2)(x - 4)}{x}$$
State whether the following expression are polynomials or not? Justify your answer.
$$\dfrac{1}{x + 1}$$
State whether the following expression is polynomials or not? Justify your answer.
$$\dfrac{1}{5x^{-2}} + 5x + 7$$
State whether the following expression is polynomials or not? Justify your answer.
$$1 - \sqrt{5x}$$
State whether the following expression are polynomials or not? Justify your answer.
$$\dfrac{1}{2x}$$
State whether the following expression is polynomials or not? Justify your answer.
$$\sqrt {3}\ x^2 - 2x$$
Classify the following as a constant, linear quadratic and cubic polynomials:
$$5t - \sqrt{7}$$
Classify the following polynomial as polynomials in one variable, two variable etc.
$$x^2 + x + 1$$
Classify the following as a constant, linear quadratic and cubic polynomials:
$$2 - x^2 + x^3$$
Classify the following polynomial as polynomials in one variable, two variable etc.
$$x^2 - 2xy + y^2 + 1$$
Classify the following as a constant, linear quadratic and cubic polynomials:
$$4 - 5y^2$$
Classify the following as a constant, linear quadratic and cubic polynomials:
$$3x^3$$
Classify the following as a constant, linear quadratic and cubic polynomials:
$$1 + x + x^3$$
Classify the following as a constant, linear quadratic and cubic polynomials:
$$2 + x$$
Classify the following as a constant, linear quadratic and cubic polynomials:
$$y^3 - y$$
Classify the following as a constant into linear quadratic and cubic polynomials:
$$\sqrt{2}x - 1$$
Classify the following as a constant into linear, quadratic and cubic polynomials:
$$t^2$$
Which of the following is quadratic polynomial?
i) $$2-\dfrac{1}{3}x^2$$
ii) $$x+\dfrac{1}{\sqrt{x}}$$
iii)$$x+\dfrac{1}{x}$$
iv) $$x^2+3\sqrt{x^{+2}}$$
Which of the following is a quadratic polynomial?
$$2x^2+1$$
Fill in the blanks:
$$ax^n+bx+c$$ is a quadratic polynomial if n=........
Which of the following is a quadratic polynomial?
$$x^2+\dfrac{1}{\sqrt{x}}$$
Which of the following is a quadratic polynomial?
$$3\sqrt{x^2+1}+x$$
Which of the following is a polynomial?
$$\dfrac{\sqrt{3}}{2}+x^2$$
Fill in the blanks:
The value of the quadratic polynomial $$x^2-5x+4$$ for $$x=1$$ is..............
Fill in the blanks: $$x^2+x+3$$ is a ................. polynomial.
Which of the following is a quadratic polynomial?
$$\sqrt{x^2+1}+\dfrac{1}{\sqrt{x}}$$
Apply Division Algorithm to find the quotient $$q(x)$$ and remainder $$r(x)$$ on dividing $$p(x)$$ by $$g(x)$$ as given below:
$$p(x) = 6x^3 + 13x^2 + x - 2, g(x) = 2x + 1$$
$$p(x) = 6x^3 + 13x^2 + x - 2, g(x) = 2x + 1$$
Dividend $$= 6x^3 + 13x^2 + x - 2$$
Divisor $$= 2x + 1$$
Here, dividend and divisor both are in the standard form.
Now, on dividing $$p(x)$$ by $$g(x)$$ we get the following division process
Quotient $$= 3x^2 + 5x - 2$$
Remainder $$= 0$$
Dividend $$= 6x^3 + 13x^2 + x - 2$$
Divisor $$= 2x + 1$$
Here, dividend and divisor both are in the standard form.
Now, on dividing $$p(x)$$ by $$g(x)$$ we get the following division process
Quotient $$= 3x^2 + 5x - 2$$
Remainder $$= 0$$
Apply Division Algorithm to find the quotient $$q(x)$$ and remainder $$r(x)$$ on dividing $$p(x)$$ by $$g(x)$$ as given below:
$$p(x) = x^3 - 3x^2 + 4x + 2, g(x) = x^2+2x+1$$
$$p(x) = x^3 - 3x^2 + 4x + 2, g(x) $$$$= x^2+2x+1$$
Dividend $$= x^3 - 3x^2 + 4x + 2$$
Divisor $$= x^2+2x+1$$
Here, dividend and divisor both are in the standard form.
Now, on dividing $$p(x)$$ by $$g(x)$$ we get the following division process
Quotient $$= x - 5$$
Remainder $$= 13x + 7 $$
Dividend $$= x^3 - 3x^2 + 4x + 2$$
Divisor $$= x^2+2x+1$$
Here, dividend and divisor both are in the standard form.
Now, on dividing $$p(x)$$ by $$g(x)$$ we get the following division process
Quotient $$= x - 5$$
Remainder $$= 13x + 7 $$
Apply Division Algorithm to find the quotient $$q(x)$$ and remainder $$r(x)$$ on dividing $$p(x)$$ by $$g(x)$$ as given below:
$$p(x) = 2x^2 + 3x + 1, g(x) = x + 2$$
$$p(x) = 2x^2 + 3x + 1, g(x) = x + 2$$
Dividend $$= 2x^2 + 3x + 1$$
Divisor $$= x + 2$$
Apply the division algorithm we get,
$$q(x)= 2x - 1$$
$$r(x)= 3$$
Dividend $$= 2x^2 + 3x + 1$$
Divisor $$= x + 2$$
Apply the division algorithm we get,
$$q(x)= 2x - 1$$
$$r(x)= 3$$
Apply Division Algorithm to find the quotient $$q(x)$$ and remainder $$r(x)$$ on dividing $$p(x)$$ by $$g(x)$$ as given below:
$$p(x) = x^4 - 1, g(x) = x + 1$$
$$p(x) = x^4 - 1, g(x) = x + 1$$
Dividend $$= x^4 - 1$$
Divisor $$= x + 1$$
Here, dividend and divisor both are in the standard form.
Now, on dividing $$p(x)$$ by $$g(x)$$ we get the following division process
Quotient $$=x^3 - x^2 + x - 1$$;
Dividend $$= x^4 - 1$$
Divisor $$= x + 1$$
Here, dividend and divisor both are in the standard form.
Now, on dividing $$p(x)$$ by $$g(x)$$ we get the following division process
Quotient $$=x^3 - x^2 + x - 1$$;
Remainder $$= 0$$
Examine, seeing the graph of the polynomial given below, whether it is a linear or quadratic polynomial or neither linear nor quadratic polynomial:
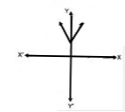
Applying the Division Algorithm, check whether the first polynomial is a factor of the second polynomial: $$x^2 - 3x + 4, 2x^4 - 11x^3 + 29x^2 - 30x + 29$$
Let us divide $$2x^4 - 11x^3 + 29x^2 - 30x + 29$$ by $$x^2 - 3x + 4$$
The division process is
Here, the remainder is $$58x - 115$$,
therefore, $$x^2 - 3x + 4$$ is not a factor of $$2x^4 - 11x^3 + 29x^2 - 30x + 29$$
The division process is
Here, the remainder is $$58x - 115$$,
therefore, $$x^2 - 3x + 4$$ is not a factor of $$2x^4 - 11x^3 + 29x^2 - 30x + 29$$
Apply Division Algorithm to find the quotient $$q(x)$$ and remainder $$r(x)$$ on dividing $$p(x)$$ by $$g(x)$$ as given below:
$$p(x) = x^3 - 3x^2 + 5x - 3, g(x) = x^2 - 2$$
$$p(x) = x^3 - 3x^2 + 5x - 3, g(x) = x^2 - 2$$
Dividend $$= x^3 - 3x^2 + 5x - 3$$
Divisor $$= x^2 - 2$$
Apply the division algorithm we get,
$$q(x)= x - 3$$
$$r(x)= 7x - 9$$
Dividend $$= x^3 - 3x^2 + 5x - 3$$
Divisor $$= x^2 - 2$$
Apply the division algorithm we get,
$$q(x)= x - 3$$
$$r(x)= 7x - 9$$
Examine, seeing the graph of the polynomial given below, whether it is a linear or quadratic polynomial or neither linear nor quadratic polynomial:
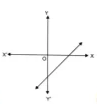
Applying the Division Algorithm, check whether the first polynomial is a factor of the second polynomial: $$x - 2, x^3 + 3x^2 - 12x + 4$$
Let us divide $$x^3 + 3x^2 - 12x + 4$$ by $$x - 2$$
The division process is
Here, the remainder is $$0$$,
therefore, $$x - 2$$ is a factor of $$x^3 + 3x^2 - 12x + 4$$
The division process is
Here, the remainder is $$0$$,
therefore, $$x - 2$$ is a factor of $$x^3 + 3x^2 - 12x + 4$$
Applying the Division Algorithm, check whether the first polynomial is a factor of the second polynomial: $$x^2 - 4x + 3, x^3 - x^3 - 3x^4 - x + 3$$
Let us divide $$x^3 + 3x^2 - x + 3$$ by $$x^2 - 4x + 3$$
The division process is
Here, the remainder is $$0$$,
therefore, $$x^2 - 4x + 3$$ is a factor of $$x^3 - 3x^2 - x + 3$$
The division process is
Here, the remainder is $$0$$,
therefore, $$x^2 - 4x + 3$$ is a factor of $$x^3 - 3x^2 - x + 3$$
Applying the Division Algorithm, check whether the first polynomial is a factor of the second polynomial: $$t^2 - 5t + 6, t^2 + 11t - 6$$
Let us divide $$t^2 + 11t - 6$$ by $$t^2 - 5t + 6$$
The division process is
Here, the remainder is $$16t - 12$$,
Therefore, $$t^2 - 5t + 6$$ is not a factor of $$t^2 + 11t - 6$$
The division process is
Here, the remainder is $$16t - 12$$,
Therefore, $$t^2 - 5t + 6$$ is not a factor of $$t^2 + 11t - 6$$
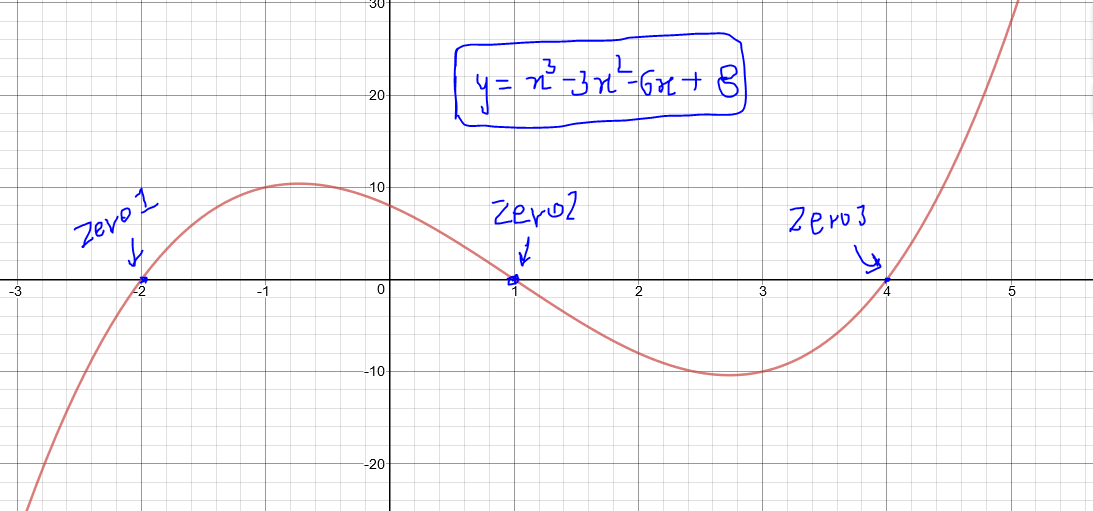
Verify that the numbers given alongside of the cubic polynomial are its zeroes. Also verify the relationship between the zeroes and the coefficients in each case:
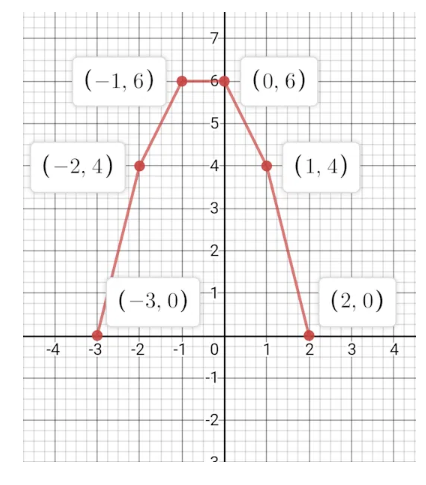
$$x^3 - 6x^2
+ 11x - 6; 1, 2, 3 $$
Find a cubic polynomial with the sum of its zeroes, sum of the products of its zeroes taken two at a time, and product of its zeroes as the numbers are: $$\dfrac{2}{5}, \dfrac{1}{10}, \dfrac{1}{2}$$
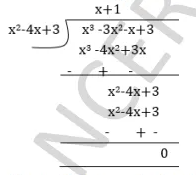
Applying the Division Algorithm, check whether the first polynomial is a factor of the second polynomial: $$t - 1, t^3 + t^2 - 2t + 1$$
Let us divide $$t^3 + t^2 - 2t + 1$$ by $$t - 1$$
The division process is
Here, the remainder is $$1$$,
therefore, $$t - 1$$ is not a factor of $$t^3 + t^2 - 2t + 1$$
The division process is
Here, the remainder is $$1$$,
therefore, $$t - 1$$ is not a factor of $$t^3 + t^2 - 2t + 1$$
Verify that, $$3, - 1, - \frac{1}{3}$$ are the zeroes of the cubic polynomial $$p(x) = 3x^2 - 5x^2 - 11x - 3$$ and then verify the relationship between the zeroes and the coefficients.
Use division algorithm to show that the square any positive integer is of the form or $$3p$$ or $$3p+1$$.
Verify that 1,-1 and + 3 are the zeroes of the cubic polynomial $$ x^{3} - 3x^{2}- x + 3 $$ and also verify the relationship between zeroes and the coefficient.
State which of the following statement are true and which are false ? Given reasons for your choice
$$ \dfrac{1}{x^{2}-5x + 6} $$ is a quadratic polynomial
Show that one and only one out of $$n,n+2$$ or $$n+4$$ is divided by $$3$$, where $$n$$ is any positive integer.
Use division algorithm to show that the cube of any positive integer is of the form $$9m,9m+1$$ or $$9m+8$$.
Draw the graphs of
$$6 - x - x^{2} $$
and find the zeroes in each case.
$$6 - x - x^{2} $$
When $$x=-3$$
$$y=6-(-3)-(-3)^2=6+3-9=0$$
When $$x=-2$$
$$y=6-(-2)-(-2)^2=6+2-4=4$$
When $$x=-1$$
$$y=6-(-1)-(-1)^2=6+1-1=6$$
When $$x=0$$
$$y=6-0-0^2=6$$
When $$x=1$$
$$y=6-1-1^2=4$$
When $$x=2$$
$$y=6-2-2^2=4-4=0$$
List of $$x$$ and $$y$$
$$x \,\,\,\,\ -3 \,\,\,\,\,\ -2\,\,\,\,\,\ -1 \,\,\,\,\,\ 0 \,\,\,\,\,\ 1 \,\,\,\,\,\,\,\ 2$$
$$y \,\,\,\,\,\,\,\,\,\, 0\,\,\,\,\,\,\,\,\,\,\,\,\,4\,\,\,\,\,\,\,\,\,\,\,\,6\,\,\,\,\,\,\,\ 6 \,\,\,\,\, 4 \,\,\,\,\,\,\,\,\ 0$$
$$(x, y)= (-3, 0), (-2, 4), ((-1, 6), (0,6), (1, 4), (2, 0).$$
$$\therefore $$ graph $$6 - x - x^{2} $$ cuts $$X -$$ axis at the points $$- 3$$ and $$-2$$
$$\therefore $$ The zeroes of quadratic polynomial are $$- 3$$ and $$2.$$
When $$x=-3$$
$$y=6-(-3)-(-3)^2=6+3-9=0$$
When $$x=-2$$
$$y=6-(-2)-(-2)^2=6+2-4=4$$
When $$x=-1$$
$$y=6-(-1)-(-1)^2=6+1-1=6$$
When $$x=0$$
$$y=6-0-0^2=6$$
When $$x=1$$
$$y=6-1-1^2=4$$
When $$x=2$$
$$y=6-2-2^2=4-4=0$$
List of $$x$$ and $$y$$
$$x \,\,\,\,\ -3 \,\,\,\,\,\ -2\,\,\,\,\,\ -1 \,\,\,\,\,\ 0 \,\,\,\,\,\ 1 \,\,\,\,\,\,\,\ 2$$
$$y \,\,\,\,\,\,\,\,\,\, 0\,\,\,\,\,\,\,\,\,\,\,\,\,4\,\,\,\,\,\,\,\,\,\,\,\,6\,\,\,\,\,\,\,\ 6 \,\,\,\,\, 4 \,\,\,\,\,\,\,\,\ 0$$
$$(x, y)= (-3, 0), (-2, 4), ((-1, 6), (0,6), (1, 4), (2, 0).$$
$$\therefore $$ graph $$6 - x - x^{2} $$ cuts $$X -$$ axis at the points $$- 3$$ and $$-2$$
$$\therefore $$ The zeroes of quadratic polynomial are $$- 3$$ and $$2.$$
Draw the graph of
$$2x$$ and find the point of intersection on X - axis. Is the zeroes of the polynomial?
Let $$y = 2x$$
When $$x=0$$
$$y=2\times 0=0$$
When $$x=-1$$
$$y=2\times-1=-2$$
When $$x=1$$
$$y=2\times1=2$$
List of $$x$$ and $$y$$
$$x \,\,\,\,\,\,\,\ 0 \,\,\,\,\,\,\ -1 \,\,\,\,\,\,\ 1 $$
$$y \,\,\,\,\,\,\,\, 0 \,\,\,\,\,\,\ -2 \,\,\,\,\,\,\ 2 $$
$$(x, y)= (0,0), (-1, -2), ((1, 2)$$
$$\therefore $$ The graph $$y = 2x$$ passes through the origin $$(0, 0)$$.
$$\therefore $$The zeroes of the polynomial is zero.
When $$x=0$$
$$y=2\times 0=0$$
When $$x=-1$$
$$y=2\times-1=-2$$
When $$x=1$$
$$y=2\times1=2$$
List of $$x$$ and $$y$$
$$x \,\,\,\,\,\,\,\ 0 \,\,\,\,\,\,\ -1 \,\,\,\,\,\,\ 1 $$
$$y \,\,\,\,\,\,\,\, 0 \,\,\,\,\,\,\ -2 \,\,\,\,\,\,\ 2 $$
$$(x, y)= (0,0), (-1, -2), ((1, 2)$$
$$\therefore $$ The graph $$y = 2x$$ passes through the origin $$(0, 0)$$.
$$\therefore $$The zeroes of the polynomial is zero.
Draw the graph of $$ 2x + 5$$ and find the point of intersection on X - axis. Is the zeroes of the polynomial?
Let $$y = 2x + 5$$
when $$x=0$$
$$y=2(0)+5=5$$
when $$x=-1$$
$$y=2(-1)+5=3$$
when $$x=1$$
$$y=2(1)+5=7$$
when $$x=2.5$$
$$y=2(2.5)+5=10$$
when $$x=-2.5$$
$$y=2(-2.5)+5=0$$
List of $$x$$ and $$y$$
$$x \,\,\,\,\,\,\,0\,\,\,\,\,\,\,-1\,\,\,\,\,\,\,\ 1\,\,\,\,\,\,\, 2.5 \,\,\,\,\,\,\,\,- 2.5$$
$$y \,\,\,\,\,\,\,5\,\,\,\,\,\,\,\,\,\,\,\,\ 3\,\,\,\,\,\,\,\,\,7\,\,\,\,\,\,\,10 \,\,\,\,\,\,\,\,\,\,\,\,\,\,0$$
$$(x,y)= (0, 0), (-1, 3), ((1, 7), (2,5, 10), (-2.5, 0)$$
$$\therefore $$ The graph $$y = 2 x + 5$$ cuts $$X -$$ axis at the point $$(-2.5, 0)$$
$$\therefore $$ the zeroes of the polynomial is $$- 2.5$$
when $$x=0$$
$$y=2(0)+5=5$$
when $$x=-1$$
$$y=2(-1)+5=3$$
when $$x=1$$
$$y=2(1)+5=7$$
when $$x=2.5$$
$$y=2(2.5)+5=10$$
when $$x=-2.5$$
$$y=2(-2.5)+5=0$$
List of $$x$$ and $$y$$
$$x \,\,\,\,\,\,\,0\,\,\,\,\,\,\,-1\,\,\,\,\,\,\,\ 1\,\,\,\,\,\,\, 2.5 \,\,\,\,\,\,\,\,- 2.5$$
$$y \,\,\,\,\,\,\,5\,\,\,\,\,\,\,\,\,\,\,\,\ 3\,\,\,\,\,\,\,\,\,7\,\,\,\,\,\,\,10 \,\,\,\,\,\,\,\,\,\,\,\,\,\,0$$
$$(x,y)= (0, 0), (-1, 3), ((1, 7), (2,5, 10), (-2.5, 0)$$
$$\therefore $$ The graph $$y = 2 x + 5$$ cuts $$X -$$ axis at the point $$(-2.5, 0)$$
$$\therefore $$ the zeroes of the polynomial is $$- 2.5$$
General form of a quadratic polynomial and cubic polynomial in variable x.
Draw the graph of $$2x - 5$$ and find the point of intersection on X - axis. Is the zeroes of the polynomial?
Let $$y = 2x - 5$$
When $$x=0$$
$$y=2\times 0-5=-5$$
When $$x=-1$$
$$y=2\times-1-5=-7$$
When $$x=1$$
$$y=2\times1-5=-3$$
When $$x=2.5$$
$$y=2\times2.5-5=0$$
When $$x=-2.5$$
$$y=2\times(-2.5)-5=-10$$
List of $$x$$ and $$y$$
$$x \,\,\,\,\,\,0\,\,\,\,\,\,\ -1\,\,\,\,\,\ 1,\,\,\,\,\ 2.5\,\,\,\,\,\,\,-2.5$$
$$y\,\,\,\,\,\,5 \,\,\,\,\,\,\,\,\ -7\,\,\,\ -3\,\,\,\,\,\,\ 0 \,\,\,\,\,\,\,\,-10$$
$$(x, y )= (0, -5), (-1, -7), ((1, -3), (2.5, 0), (-2.5, 0)$$
$$\therefore $$ The graph $$y = 2x - 5$$ cuts $$X - $$axis at he point $$(2.5, 0)$$
$$\therefore $$ The zeroes of the polynomial is $$2.5$$
When $$x=0$$
$$y=2\times 0-5=-5$$
When $$x=-1$$
$$y=2\times-1-5=-7$$
When $$x=1$$
$$y=2\times1-5=-3$$
When $$x=2.5$$
$$y=2\times2.5-5=0$$
When $$x=-2.5$$
$$y=2\times(-2.5)-5=-10$$
List of $$x$$ and $$y$$
$$x \,\,\,\,\,\,0\,\,\,\,\,\,\ -1\,\,\,\,\,\ 1,\,\,\,\,\ 2.5\,\,\,\,\,\,\,-2.5$$
$$y\,\,\,\,\,\,5 \,\,\,\,\,\,\,\,\ -7\,\,\,\ -3\,\,\,\,\,\,\ 0 \,\,\,\,\,\,\,\,-10$$
$$(x, y )= (0, -5), (-1, -7), ((1, -3), (2.5, 0), (-2.5, 0)$$
$$\therefore $$ The graph $$y = 2x - 5$$ cuts $$X - $$axis at he point $$(2.5, 0)$$
$$\therefore $$ The zeroes of the polynomial is $$2.5$$
Write three quadratic polynomial that gave 2 zeroes each.
Verify that the numbers given alongside that cubic polynomials below are its zeroes . Also verify the relationship between the zeroes and coefficient in each case.
$$ 2x^{3} + x^{2} - 5x + 2 ,\left ( \dfrac{1}{2},1 .-2 \right ) $$
Write one quadratic polynomial that has one zero.
Draw the graphs of
$$y = x^{2} - x - 6$$
and find the zeroes in each case.
$$y = x^{2} - x - 6$$
When $$x=-3$$
$$y=-3^2-(-3)-6=9+3-6=6$$
When $$x=-2$$
$$y=-2^2-(-2)-6=4-2-6=0$$
When $$x=-1$$
$$y=-1^2-(-1)-6=1+1-6=-4$$
When $$x=0$$
$$y=0^2-0-6=6$$
When $$x=1$$
$$y=1^2-1-6=-6$$
When $$x=2$$
$$y=2^2-2-6=4-8=-4$$
When $$x=3$$
$$y=3^2-3-6=9-9=0$$
List of $$x$$ and $$y$$
$$x \,\,\,\ -3\,\,\,\,\ -2 \,\,\,-1 \,\,\,\,\,\,\, 0 \,\,\,\,\,\,\,\,\,\,\,1 \,\,\,\,\,\ 2\,\,\,\,\, 3$$
$$y \,\,\,\,\,\,\,\,\,\,6 \,\,\,\,\,\,\,\,\,\,\,0\,\,\ -4 \,\,\ -6 \,\,\,\, -6\,\, -4 \,\,\, 0$$
$$(x, y)= (-3, 6), (-2, 0), ((-1, -4), (0, -6), (1, -6), (2, -4).(3,0)$$
$$\therefore $$The graph $$y = x^{2} - x - 6$$cuts $$X- $$axis at the points $$3$$ and $$- 2$$
$$\therefore $$ The zeroes of quadratic polynomial are $$-2$$ and $$3.$$
When $$x=-3$$
$$y=-3^2-(-3)-6=9+3-6=6$$
When $$x=-2$$
$$y=-2^2-(-2)-6=4-2-6=0$$
When $$x=-1$$
$$y=-1^2-(-1)-6=1+1-6=-4$$
When $$x=0$$
$$y=0^2-0-6=6$$
When $$x=1$$
$$y=1^2-1-6=-6$$
When $$x=2$$
$$y=2^2-2-6=4-8=-4$$
When $$x=3$$
$$y=3^2-3-6=9-9=0$$
List of $$x$$ and $$y$$
$$x \,\,\,\ -3\,\,\,\,\ -2 \,\,\,-1 \,\,\,\,\,\,\, 0 \,\,\,\,\,\,\,\,\,\,\,1 \,\,\,\,\,\ 2\,\,\,\,\, 3$$
$$y \,\,\,\,\,\,\,\,\,\,6 \,\,\,\,\,\,\,\,\,\,\,0\,\,\ -4 \,\,\ -6 \,\,\,\, -6\,\, -4 \,\,\, 0$$
$$(x, y)= (-3, 6), (-2, 0), ((-1, -4), (0, -6), (1, -6), (2, -4).(3,0)$$
$$\therefore $$The graph $$y = x^{2} - x - 6$$cuts $$X- $$axis at the points $$3$$ and $$- 2$$
$$\therefore $$ The zeroes of quadratic polynomial are $$-2$$ and $$3.$$
Use division algorithm to show that any odd positive integer is of the form $$6q+1$$ or $$6q+3$$ or $$6q+5$$, where $$q$$ is some integer.
If the zeroes of the polynomial $$ x^{3} - 3x^{2}+ x+1$$ are $$a - b , a, a + b $$, find $$a$$ and $$b.$$
How will you verify if a quadratic polynomial has only one zero?
If $$\alpha ,\beta ,\gamma $$ are the zeroes of the cubic polynomial $$x^{3} + 4x^{2} - 5x - 2$$, find the values of the exoressions given below:
$$ \alpha +\beta +\gamma , \alpha \beta + \beta \gamma + \gamma \alpha $$ and $$\alpha \beta \gamma $$.
Given examples of polynomials p (x) , g (x) , q (x) , q (x) and r (x) , Which satisfy the division algirithm and deg p ( x ) = deg (x)
If $$\alpha ,\beta ,\gamma $$ are the zeroes of the cubic polynomial $$4x^{3} + 8x^{2} - 6x - 2$$, find the values of the expressions given below:
$$\alpha +\beta + \gamma , \alpha \beta + \beta \gamma + \gamma \alpha $$ and $$\alpha \beta \gamma $$.
If $$\alpha ,\beta ,\gamma $$ are the zeroes of the cubic polynomials $$x^{3} + 5x^{2} + 4$$, find the values of the expressions given below: $$ \alpha +\beta +\gamma , \alpha \beta + \beta \gamma + \gamma \alpha $$ and $$\alpha \beta \gamma $$.
If $$\alpha ,\beta ,\gamma $$ are the zeroes of the cubic polynomial $$x^{3} + 3x^{2} - x - 2$$, find the values of the expressions given below:
$$ \alpha + \beta + \gamma , \alpha \beta + \beta \gamma + \gamma \alpha $$ and $$\alpha \beta \gamma $$.
Given examples of polynomials p (x) , g (x) , q (x) , q (x) and r (x) , Which satisfy the division algirithm and deg r (x ) = 0
Given examples of polynomials p (x) , g (x) , q (x) , q (x) and r (x) , Which satisfy the division algirithm anddeg q (x) = deg r (x)
Classify the following polynomial as linear, quadratic or cubic polynomial:
$$2x^{2} + 3x + 1 $$
Classify the following polynomial as linear, quadratic and cubic polynomial .
$$3r^{3}$$
Classify the following polynomial as linear, quadratic and cubic polynomial .
$$m^{3} + 7m^{2} + \dfrac{5}{2}m - \sqrt{7}$$
Classify the following polynomial as linear, quadratic and cubic polynomial .
$$\sqrt{2}y - \dfrac{1}{2}$$
Classify the following polynomial as linear, quadratic and cubic polynomial .
$$5p$$
Classify the following as linear , quadratic and cubic polynomial :
$$ x^{2} + x $$
Using division algorithm, find quotient and remainder dividing $$f(x)$$ by $$g(x)$$.
$$f(x)=x^3-3x^2+5x+3,g(x)=x^2-2$$
If $$a-b,a, a+b$$ are zero of polynomial $$x^3 -3x^2 +x+1$$, then find $$a$$ and $$b$$.
Classify the following as linear , quadratic and cubic polynomial :
$$ x - x^{3} $$
State whether the following expression is a polynomials in one variable or not ? State reasons for your answers.
$$y^{2} + 2\sqrt{3}$$
Classify the following as linear, quadratic or cubic polynomial:
$$ 7x^{3}$$
Using division algorithm, find quotient and remainder dividing $$f(x)$$ by $$g(x)$$.
$$f(x)=3x^3+x^2+2x+5,g(x)=1+2x+x^2$$
Using division algorithm, find quotient and remainder dividing $$f(x)$$ by $$g(x)$$.
$$f(x)=x^3-6x^2+11x-6,g(x)=x+2$$
Using division algorithm, find quotient and remainder dividing $$f(x)$$ by $$g(x)$$.
$$f(x)=9x^4-4x^2+4,g(x)=3x^2+x-1$$
Divide $$x^3 -3x^2 +3x-5$$ by $$x-1-x^2 $$ and test division algorithm.
State whether the following expression is a polynomials in one variable or not ? State reasons for your answers.
$$3x^{2} - 5x + 13$$
State whether the following expression is a polynomials in one variable or not ? State reasons for your answers.
$$2\sqrt{x} + \sqrt{3}x$$
State whether the following expression is a polynomials in one variable or not ? State reasons for your answers.
$$y + \dfrac{3}{y}$$
If $$1$$ and $$2$$ are two zeros of the polynomial $$x^4-3x^3-2x^2+12x-8$$, then the remaining of two zeros are _____.
If the polynomial $$x^2-2x+k$$ is a factor of $$x^4- 6x^3 + 16x^2 -26x + 10-a$$, then find the value of $$k$$ and $$a.$$
After dividing polynomial $$x^4- 6x^3 + 16x^2 -26x + 10 - x - a$$ by $$x^2-2x+k$$ we got remainder, $$(-10+2k)x+(10-a-8k+k^2).$$
Which will be equal to zero if,
$$-10 + 2k = 0\text{ and } 10-a-8k+k^2 = 0$$
For $$-10 + 2k = 0$$
$$\Rightarrow 2k = 10$$
$$\Rightarrow k = 5$$
For $$10-a-8k+k^2 = 0$$
$$\Rightarrow 10 - a - 8 \times 5+25 = 0$$
$$\Rightarrow -5 - a = 0$$
$$\Rightarrow a = -5$$
So, $$k = 5, a = -5$$
Divide $$p(x)$$ by $$g(x)$$ in the following case and verify division algorithm
$$p(x) = x^{2} + 4x + 4; g(x) = x + 2$$
The division of $$p(x)=x^2+4x+4$$ by $$g(x)=x+2$$ is as shown above:
Now we know that the division algorithm states that:
Dividend$$=($$Divisor$$\times$$quotient$$)+$$Remainder
Here, the dividend is $$x^2+4x+4$$, the divisor is $$x+2$$, the quotient is $$x+2$$ and the remainder is $$0$$, therefore,
$$x^{ 2 }+4x+4=[(x+2)(x+2)]+0\\ \Rightarrow x^{ 2 }+4x+4=[x(x+2)+2(x+2)]\\ \Rightarrow x^{ 2 }+4x+4=x^{ 2 }+2x+2x+4\\ \Rightarrow x^{ 2 }+4x+4=x^{ 2 }+4x+4$$
Hence, the division algorithm is verified.
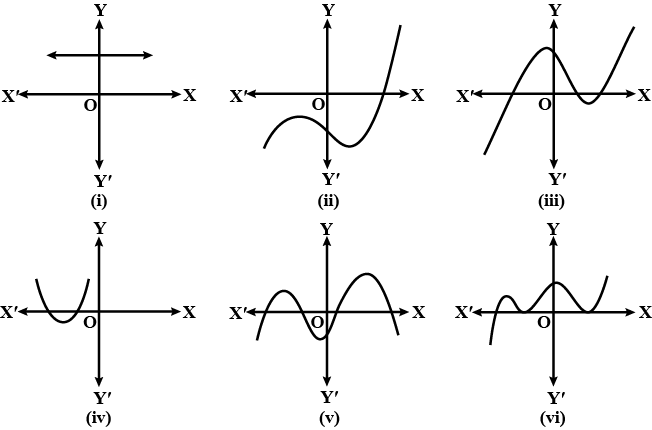
Give 4 different reasons why the graph cannot be the graph of the polynomial $$p$$ given by
$$p(x)={x}^{4}-{x}^{2}+1$$
Divide $$p(x)$$ by $$g(x)$$ in the following cases and verify division algorithm.
$$p(x) = x^{4} - 4x^{2} + 12x + 9; g(x) = x^{2} + 2x - 3$$
The division of $$p(x)=x^4-4x^2+12x+9$$ by $$g(x)=x^2+2x-3$$ is as shown above:
Now we know that the division algorithm states that:
Dividend$$=($$Divisor$$\times$$quotient$$)+$$Remainder
Here, the dividend is $$x^4-4x^2+12x+9$$, the divisor is $$x^2+2x-3$$, the quotient is $$x^2-2x+3$$ and the remainder is $$18$$, therefore,
$$x^{ 4 }-4x^{ 2 }+12x+9=[(x^{ 2 }+2x-3)(x^{ 2 }-2x+3)]+18\\ \Rightarrow x^{ 4 }-4x^{ 2 }+12x+9=[x^{ 2 }(x^{ 2 }-2x+3)+2x(x^{ 2 }-2x+3)-3(x^{ 2 }-2x+3)]+18\\ \Rightarrow x^{ 4 }-4x^{ 2 }+12x+9=(x^{ 4 }-2x^{ 3 }+3x^{ 2 }+2x^{ 3 }-4x^{ 2 }+6x-3x^{ 2 }+6x-9)+18\\ \Rightarrow x^{ 4 }-4x^{ 2 }+12x+9=x^{ 4 }-2x^{ 3 }+2x^{ 3 }+3x^{ 2 }-4x^{ 2 }-3x^{ 2 }+6x+6x-9+18\\ \Rightarrow x^{ 4 }-4x^{ 2 }+12x+9=x^{ 4 }-4x^{ 2 }+12x+9$$
Hence, the division algorithm is verified.
Divide $$p(x)$$ by $$g(x)$$ in the following case and verify division algorithm.
$$p(x) = 2x^{2} - 9x + 9; g(x) = x - 3$$
The division of $$p(x)=2x^2-9x+9$$ by $$g(x)=x-3$$ is as shown above:
Now we know that the division algorithm states that:
Dividend$$=($$Divisor$$\times$$quotient$$)+$$Remainder
Here, the dividend is $$2x^2-9x+9$$, the divisor is $$x-3$$, the quotient is $$2x-3$$ and the remainder is $$0$$, therefore,
$$2x^{ 2 }-9x+9=[(x-3)(2x-3)]+0\\ \Rightarrow 2x^{ 2 }-9x+9=[x(2x-3)-3(2x-3)]\\ \Rightarrow 2x^{ 2 }-9x+9=x^{ 2 }-3x-6x+9\\ \Rightarrow 2x^{ 2 }-9x+9=2x^{ 2 }-9x+9$$
Hence, the division algorithm is verified.
Let $$P(x)$$ be a cubic polynomial with zeroes $$\alpha,\beta,
\gamma$$ if $$\displaystyle \frac{P\left(\dfrac{1}{2}\right)+P\left(-\dfrac{1}{2}\right)}{P(0)}=100 $$find $$ \sqrt{\displaystyle \frac{1}{\alpha\beta}+\frac{1}{\beta\gamma}+\frac{1}{\gamma a}}$$.
Divide $$p(x)$$ by $$g(x)$$ in the following case and verify division algorithm.
$$p(x) = x^{3} + 4x^{2} - 5x + 6; g(x) = x + 1$$
The division of $$p(x)=x^3+4x^2-5x+6$$ by $$g(x)=x+1$$ is as shown above:
Now we know that the division algorithm states that:
Dividend$$=($$Divisor$$\times$$quotient$$)+$$Remainder
Here, the dividend is $$x^3+4x^2-5x+6$$, the divisor is $$x+1$$, the quotient is $$x^2+3x-8$$ and the remainder is $$14$$, therefore,
To check:
$$x^{ 3 }+4x^{ 2 }-5x+6=[(x+1)(x^{ 2 }+3x-8)]+14\\ \text{R.H.S}\Rightarrow [x(x^{ 2 }+3x-8)+1(x^{ 2 }+3x-8)]+14\\ =x^{ 3 }+3x^{ 2 }-8x+x^{ 2 }+3x-8+14\\ =x^{ 3 }+3x^{ 2 }+x^{ 2 }-8x+3x-8+14\\ =x^{ 3 }+4x^{ 2 }-5x+6=\text{L.H.S}$$
Hence, the division algorithm is verified.
Divide $$p(x)$$ by $$g(x)$$ in the following case and verify division algorithm.
$$p(x) = x^{4} - 3x^{2} - 4; g(x) = x + 2$$
The division of $$p(x)=x^4-3x^2-4$$ by $$g(x)=x+2$$ is as shown above:
Now we know that the division algorithm states that:
Dividend$$=($$Divisor$$\times$$quotient$$)+$$Remainder
Here, the dividend is $$x^4-3x^2-4$$, the divisor is $$x+2$$, the quotient is $$x^3-2x^2+x-2$$ and the remainder is $$0$$, therefore,
$$x^{ 4 }-3x^{ 2 }-4=[(x+2)(x^{ 3 }-2x^{ 2 }+x-2)]+0\\ \Rightarrow x^{ 4 }-3x^{ 2 }-4=[x(x^{ 3 }-2x^{ 2 }+x-2)+2(x^{ 3 }-2x^{ 2 }+x-2)]+0\\ \Rightarrow x^{ 4 }-3x^{ 2 }-4=x^{ 4 }-2x^{ 3 }+x^{ 2 }-2x+2x^{ 3 }-4x^{ 2 }+2x-4+0\\ \Rightarrow x^{ 4 }-3x^{ 2 }-4=x^{ 4 }-2x^{ 3 }+2x^{ 3 }+x^{ 2 }-4x^{ 2 }-2x+2x-4\\ \Rightarrow x^{ 4 }-3x^{ 2 }-4=x^{ 4 }-3x^{ 2 }-4$$
Hence, the division algorithm is verified.
Find the divisor $$g(x)$$, when the polynomial $$p(x) = 4x^{3} + 2x^{2} - 10x + 2$$ is divided by $$g(x)$$ and the quotient and remainder obtained are $$(2x^{2} + 4x + 1)$$ and $$5$$ respectively
We know that the division algorithm states that:
Dividend$$=($$Divisor$$\times$$quotient$$)+$$Remainder
Here it is given that the dividend is $$p(x)=4x^3+2x^2-10x+2$$, the divisor is $$g(x)$$, the quotient is $$2x^2+4x+1$$ and the remainder is $$5$$, therefore,
$$4x^{ 3 }+2x^{ 2 }-10x+2=[g(x)(2x^{ 2 }+4x+1)]+5\\ \Rightarrow g(x)=\cfrac { 4x^{ 3 }+2x^{ 2 }-10x+2 }{ 2x^{ 2 }+4x+1 }$$
The division is shown above.
Hence, from the above division, we get that the divisor is $$g(x)=2x-3$$
Divide $$p(x)$$ by $$g(x)$$ in the following case and verify division algorithm.
$$p(x) = x^{3} - 1; g(x) = x - 1$$
The division of $$p(x)=x^3-1$$ by $$g(x)=x-1$$ is as shown above:
Now we know that the division algorithm states that:
Dividend$$=($$Divisor$$\times$$quotient$$)+$$Remainder
Here, the dividend is $$x^3-1$$, the divisor is $$x-1$$, the quotient is $$x^2+x+1$$ and the remainder is $$0$$, therefore,
$$x^{ 3 }-1=[(x-1)(x^{ 2 }+x+1)]+0\\ \Rightarrow x^{ 3 }-1=[x(x^{ 2 }+x+1)-1(x^{ 2 }+x+1)]+0\\ \Rightarrow x^{ 3 }-1=x^{ 3 }+x^{ 2 }+x-x^{ 2 }-x-1+0\\ \Rightarrow x^{ 3 }-1=x^{ 3 }+x^{ 2 }-x^{ 2 }+x-x-1\\ \Rightarrow x^{ 3 }-1=x^{ 3 }-1$$
Hence, the division algorithm is verified.
Find the values of a and b so that $$x^4+x^3+8x^2+ax+b$$ is divisible by $$x^2+1$$.
Let us first divide the given polynomial $$x^4+x^3+8x^2+ax+b$$ by $$(x^2+1)$$ as shown in the above image:
From the division, we observe that the quotient is $$x^2+x+7$$ and the remainder is $$(a-1)x+(b-7)$$.
Since it is given that $$x^4+x^3+8x^2+ax+b$$ is exactly divisible by $$x^2+1$$, therefore, the remainder must be equal to $$0$$ that is:
$$(a-1)x+(b-7)=0\\ \Rightarrow (a-1)x+(b-7)=0\cdot x+0\\ \Rightarrow (a-1)=0,\quad (b-7)=0\quad \quad \quad \quad (By\quad comparing\quad coefficients)\\ \Rightarrow a=1,\quad b=7$$
Hence, $$a=1$$ and $$b=7$$.
What must be subtracted from $$(x^{3} + 5x^{2} + 5x + 8)$$ so that the resulting polynomial is exactly divisible by $$(x^{2} + 3x - 2)$$?
It is given that the dividend is $$p(x)=x^3+5x^2+5x+8$$, the divisor is $$g(x)=x^2+3x-2$$, therefore, the division is as shown above.
Therefore, from the division, we get that the remainder is $$x+12$$.
Hence, $$x+12$$ must be subtracted from $$x^3+5x^2+5x+8$$ so that the resulting polynomial is exactly divisible by $$x^2+3x-2$$.
What should be added to $$(x^{4} - 1)$$ so that it is exactly divisible by $$(x^{2} + 2x + 1)$$?
It is given that the dividend is $$p(x)=x^4-1$$, the divisor is $$g(x)=x^2+2x+1$$, therefore, the division is as shown above.
Therefore, from the division, we get that the remainder is $$r(x)=(-4x-4)$$ that is $$-r(x)=4x+4$$.
Hence, $$4x+4$$ should be added to $$x^4-1$$ so that the resulting polynomial is exactly divisible by $$x^2+2x+1$$.
The product of two polynomials is $$6x^{3} + 29x^{2} + 44x + 21$$ and one of the polynomials is $$3x + 7$$. Find the other polynomial.
Let $$A$$ be the other polynomial. It is given that one of the polynomial is $$3x+7$$ and the product of the polynomials is $$6x^3+29x^2+44x+21$$ that is:
$$(3x+7)\times A=6x^{ 3 }+29x^{ 2 }+44x+21\\ A=\dfrac { 6x^{ 3 }+29x^{ 2 }+44x+21 }{ 3x+7 }$$
We now divide $$6x^3+29x^2+44x+21$$ by $$(3x+7)$$ as shown below:
From the division, we observe that the quotient is $$2x^2+5x+3$$ and the remainder is $$0$$.
Hence, the other polynomial is $$2x^2+5x+3$$.
Rewrite the terms in proper order and then divide
$$a+a^{2}+8$$ by $$a+4$$
The given polynomial $$a+a^2+8$$ can be rewritten as $$a^2+a+8$$.
We now divide $$a^2+a+8$$ by $$(a+4)$$ as shown in the above image:
From the division, we observe that the quotient is $$a-3$$ and the remainder is $$20$$.
Hence, the quotient is $$a-3$$ and the remainder is $$20$$.
If polynomial $$p(x)$$ is divided by $$x^{2} + 3x + 5$$, the quotient polynomial and the remainder polynomials are $$2x^{2} + x + 1$$ and $$x = 3$$ respectively. Find $$P(x)$$.
On dividing the polynomial $$p(x) = x^{3} - 3x^{2} + x + 2$$ by a polynomial $$g(x)$$, the quotient and remainder were $$(x - 2)$$ and $$(-2x + 4)$$ respectively. Find $$g(x)$$
We know that the division algorithm states that:
Dividend$$=($$Divisor$$\times$$quotient$$)+$$Remainder
Here it is given that the dividend is $$p(x)=x^3-3x^2+x+2$$, the divisor is $$g(x)$$, the quotient is $$x-2$$ and the remainder is $$-2x+4$$, therefore,
$$x^{ 3 }-3x^{ 2 }+x+2=[g(x)(x-2)]+(-2x+4)\\ \Rightarrow g(x)=\cfrac { x^{ 3 }-3x^{ 2 }+x+2 }{ x-2 }$$
The division is shown above.
Hence, from the above division, we get that the divisor is $$g(x)=x^2-x+1$$
Divide using the long division method and check the answer.
$$6x^{2}+5x-4$$ by $$2x-1$$
Divide $$32x^{2}+200-160x$$ by $$\left(8x-20\right)$$
Divide using the long division method and check the answer.
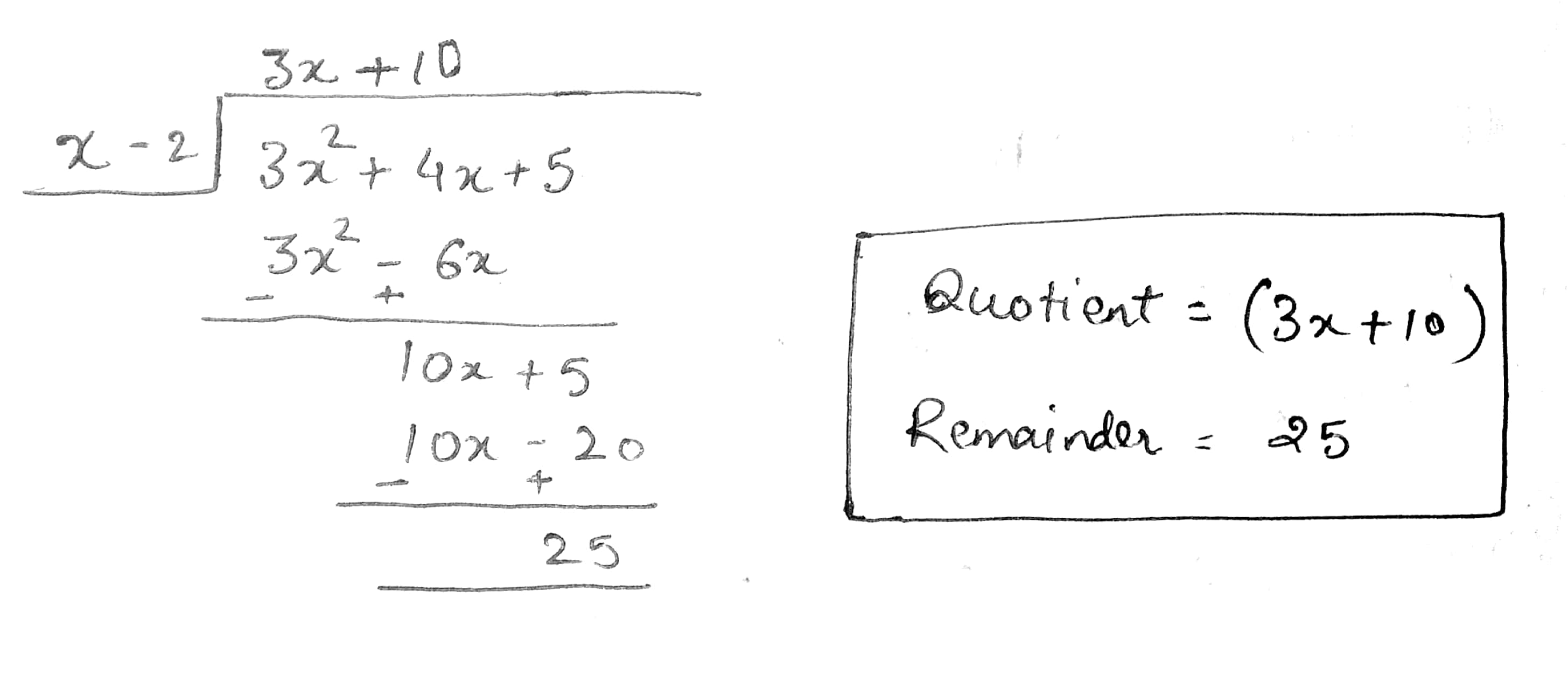
$$x^{2}+5x+10$$ by $$x+3$$
We divide $$x^2+5x+10$$ by $$(x+3)$$ as shown in the above image:
From the division, we observe that the quotient is $$x+2$$ and the remainder is $$4$$.
We know that the division algorithm states that:
Dividend$$=$$Divisor$$\times$$Quotient$$+$$Remainder
We apply the division algorithm to check the answer as follows:
$$Dividend=Divisor\times Quotient+Remainder\\ x^{ 2 }+5x+10=[(x+3)(x+2)]+4\\ x^{ 2 }+5x+10=(x^{ 2 }+2x+3x+6)+4\\ x^{ 2 }+5x+10=x^{ 2 }+5x+6+4\\ x^{ 2 }+5x+10=x^{ 2 }+5x+10\\ Hence\quad verified.$$
Divide the first polynomial by the second polynomial in each of the following. Also, write the quotient and remainder:
$$3x^{2} + 4x + 5, x - 2$$.
Check whether $${ x }^{ 2 }+3x+1$$ is a factor of
$$3{ x }^{ 4}+{ 5x }^{ 3 }-{ 7x }^{ 2 }+2x+2?$$
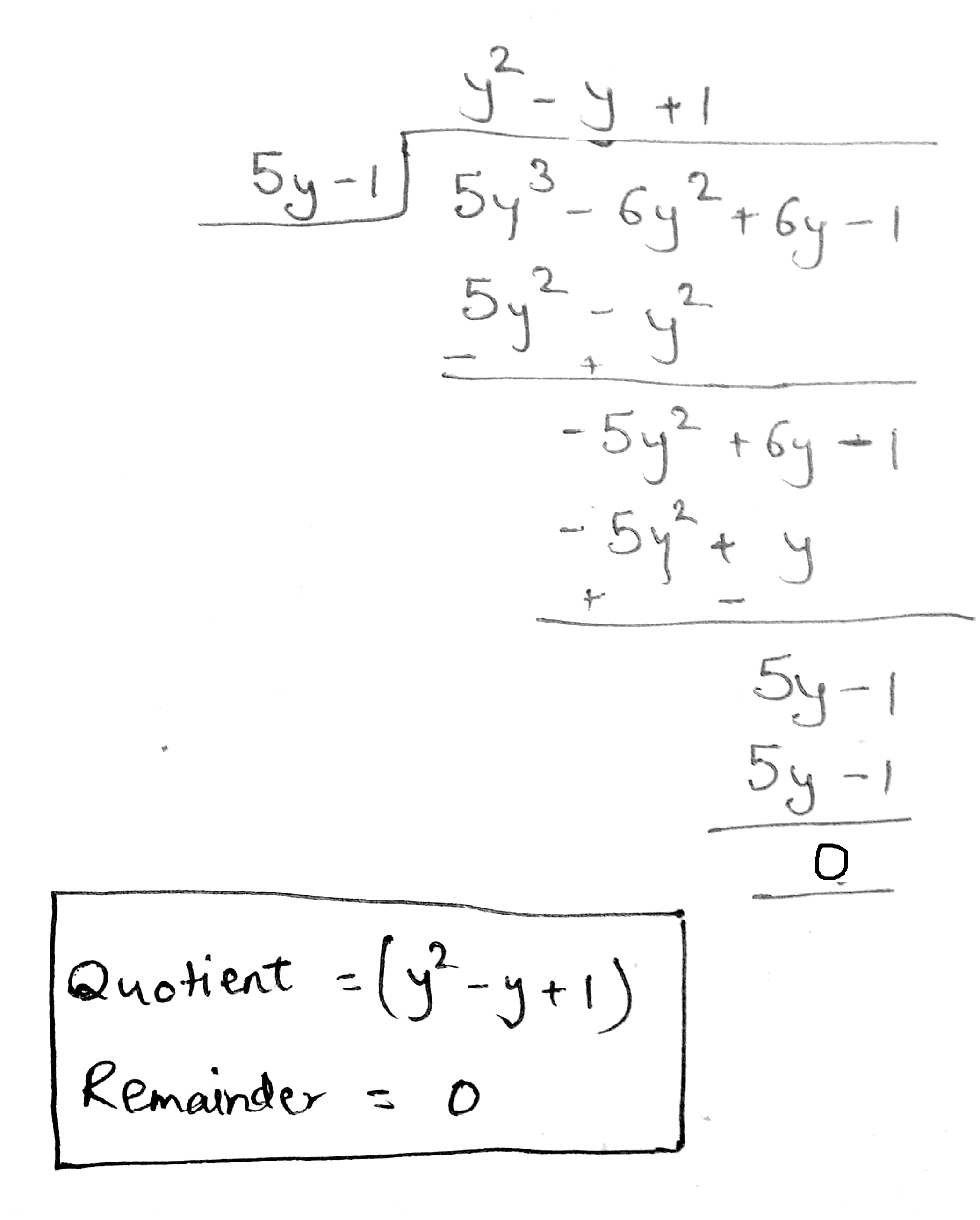
Divide the first polynomial by the second polynomial in each of the following. Also, write the quotient and remainder:
$$5y^{3} - 6y^{2} + 6y - 1, 5y - 1$$.
Class 10 Maths Extra Questions
- Areas Related To Cricles Extra Questions
- Arithmetic Progressions Extra Questions
- Circles Extra Questions
- Constructions Extra Questions
- Coordinate Geometry Extra Questions
- Introduction To Trigonometry Extra Questions
- Pair Of Linear Equations In Two Variables Extra Questions
- Polynomials Extra Questions
- Probability Extra Questions
- Quadratic Equations Extra Questions
- Real Numbers Extra Questions
- Some Applications Of Trigonometry Extra Questions
- Statistics Extra Questions
- Surface Areas And Volumes Extra Questions
- Triangles Extra Questions