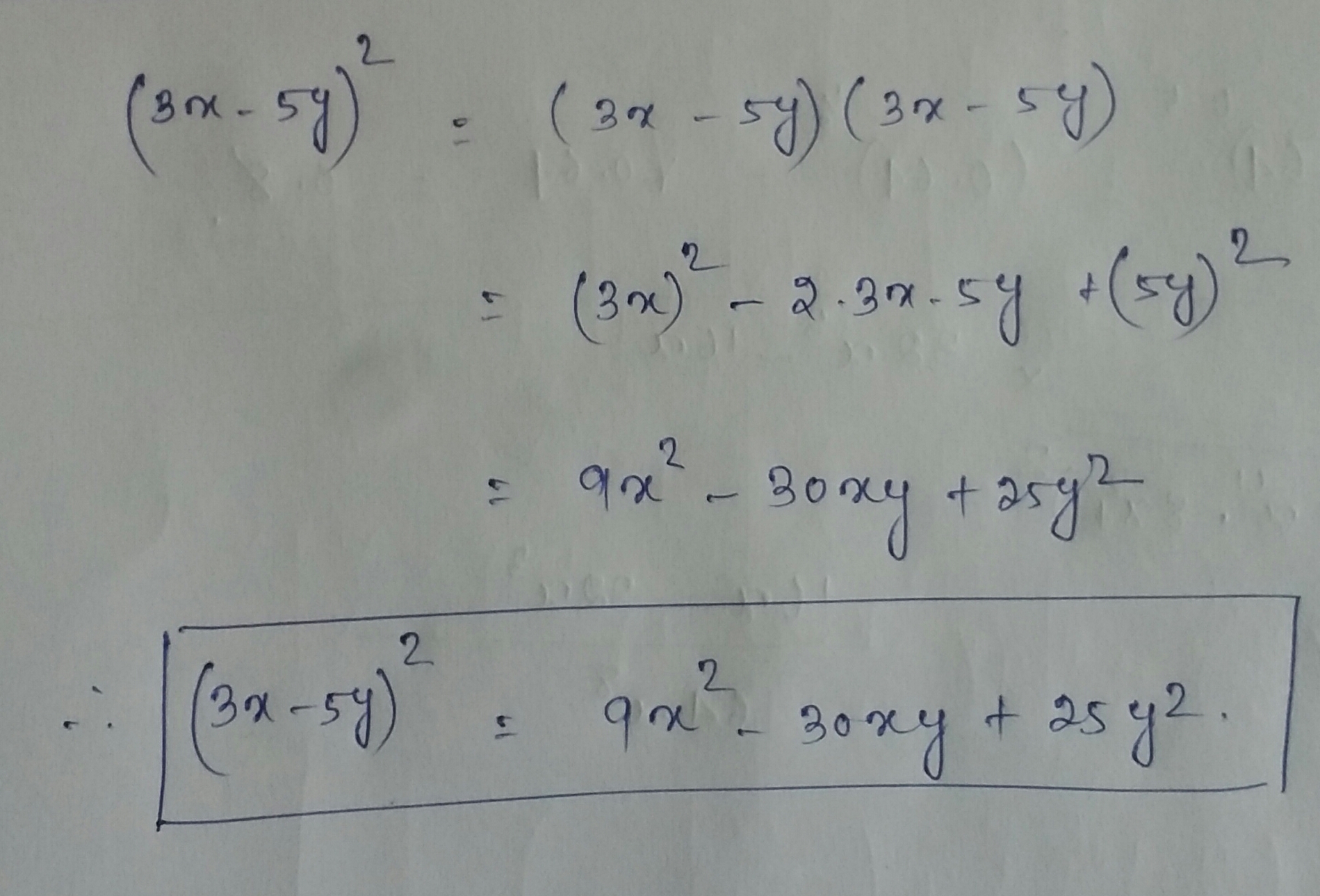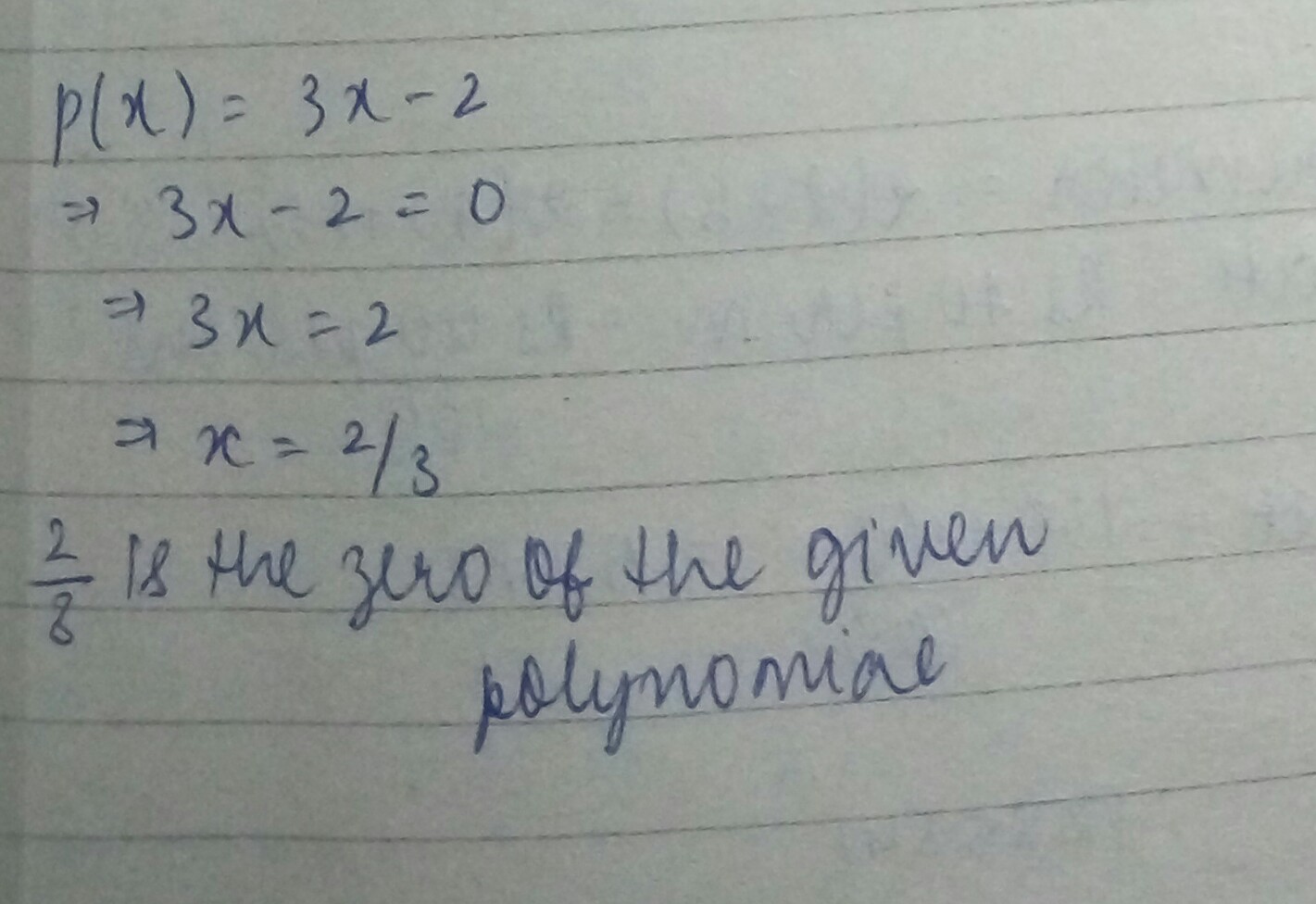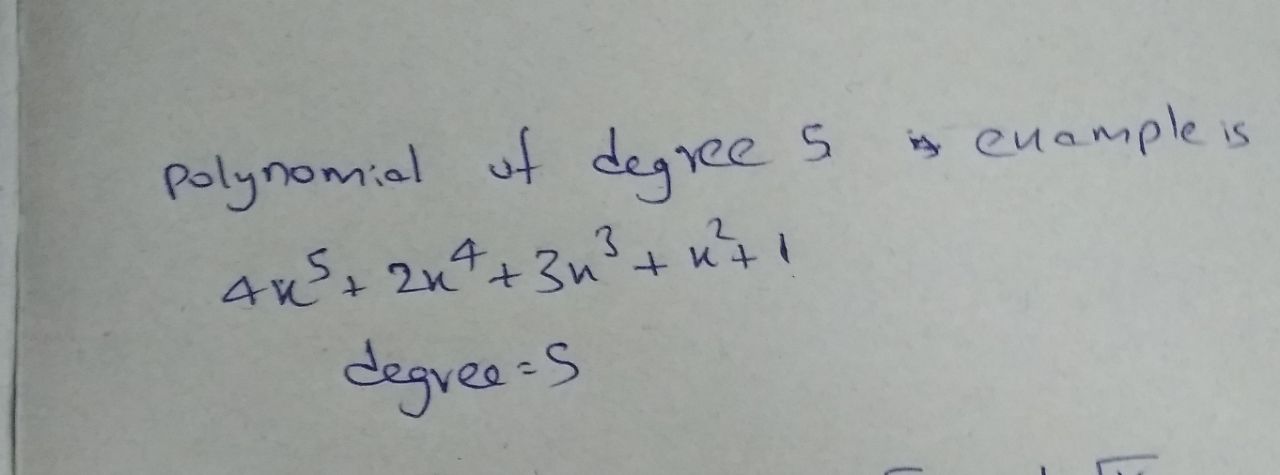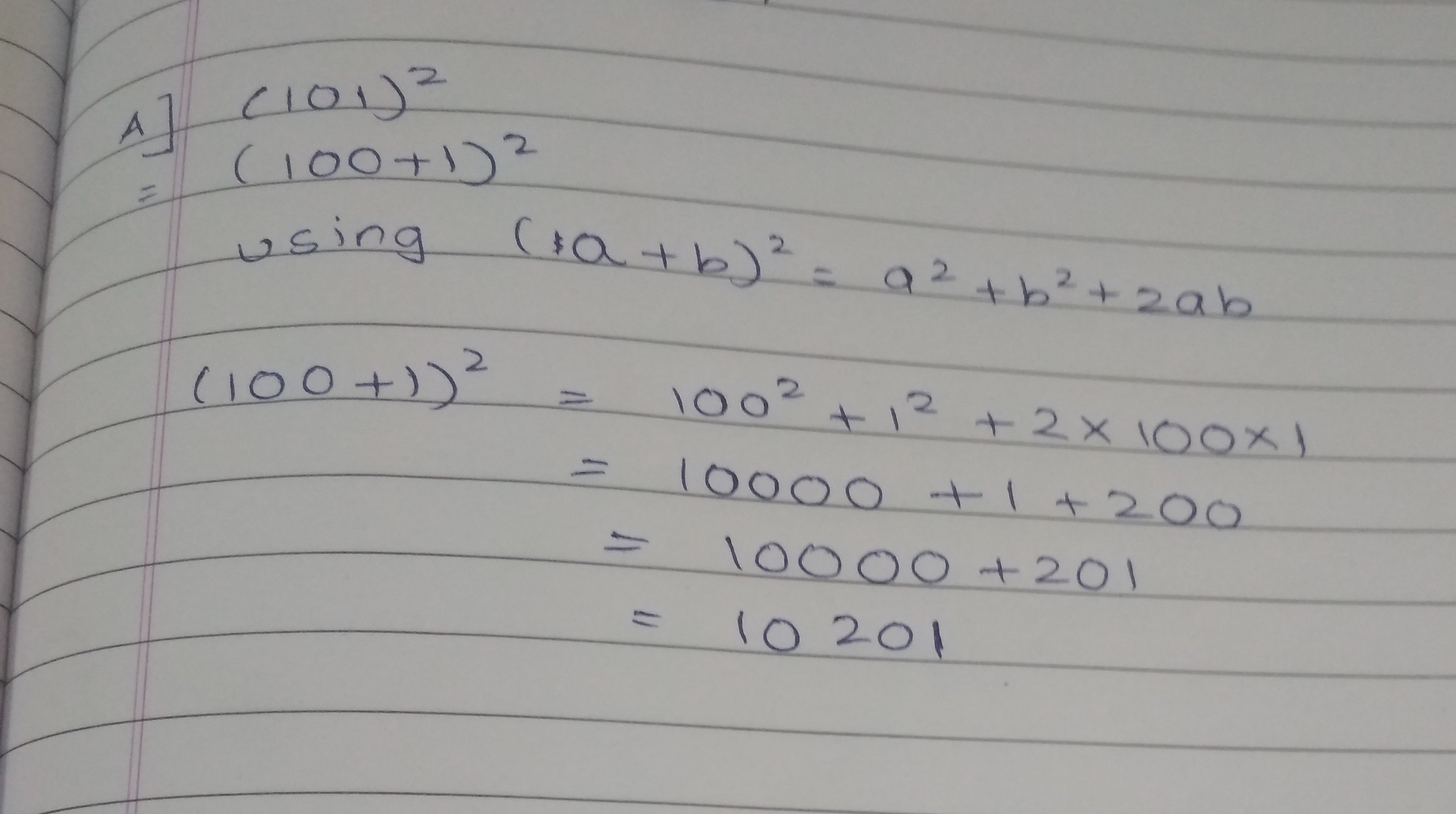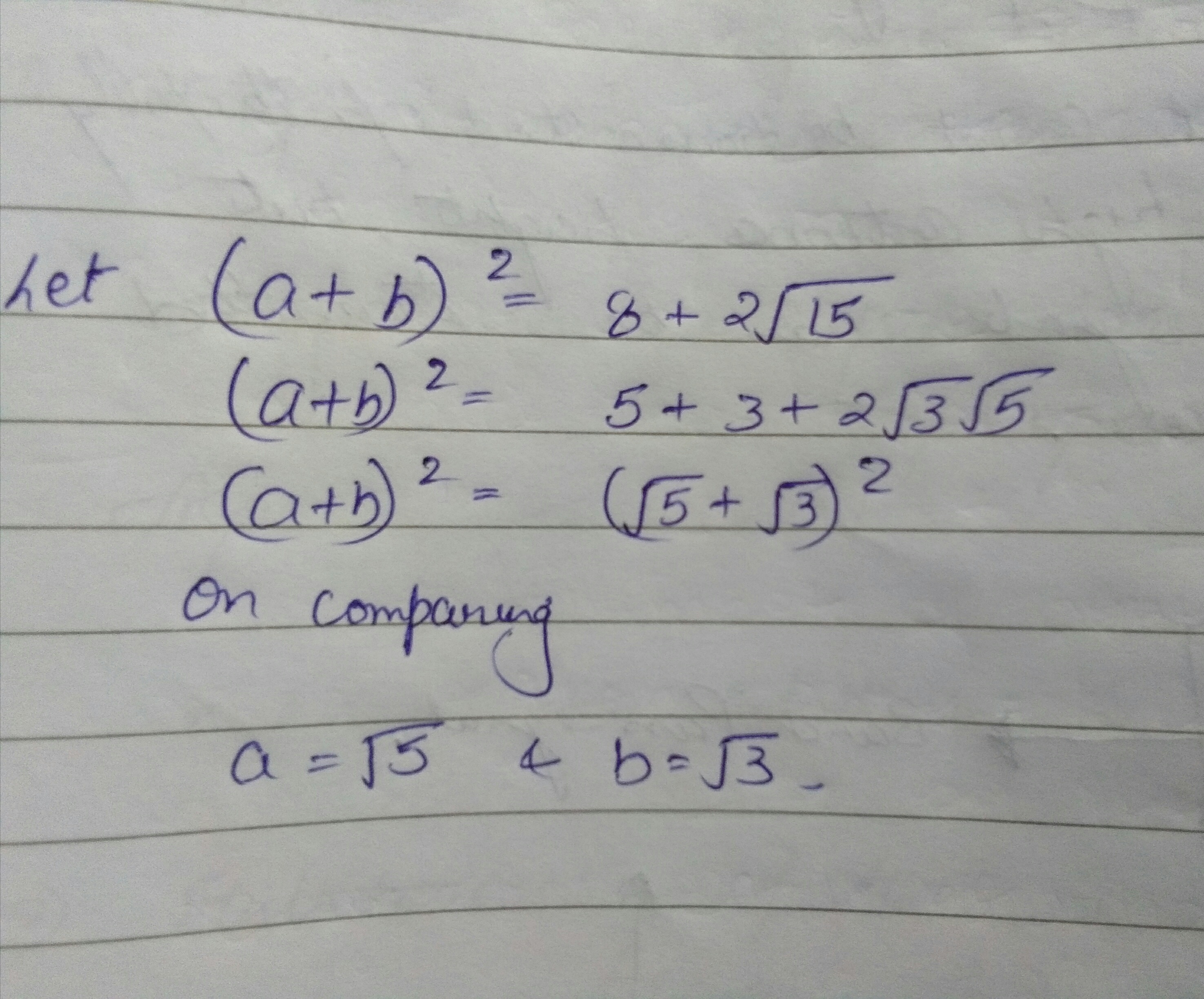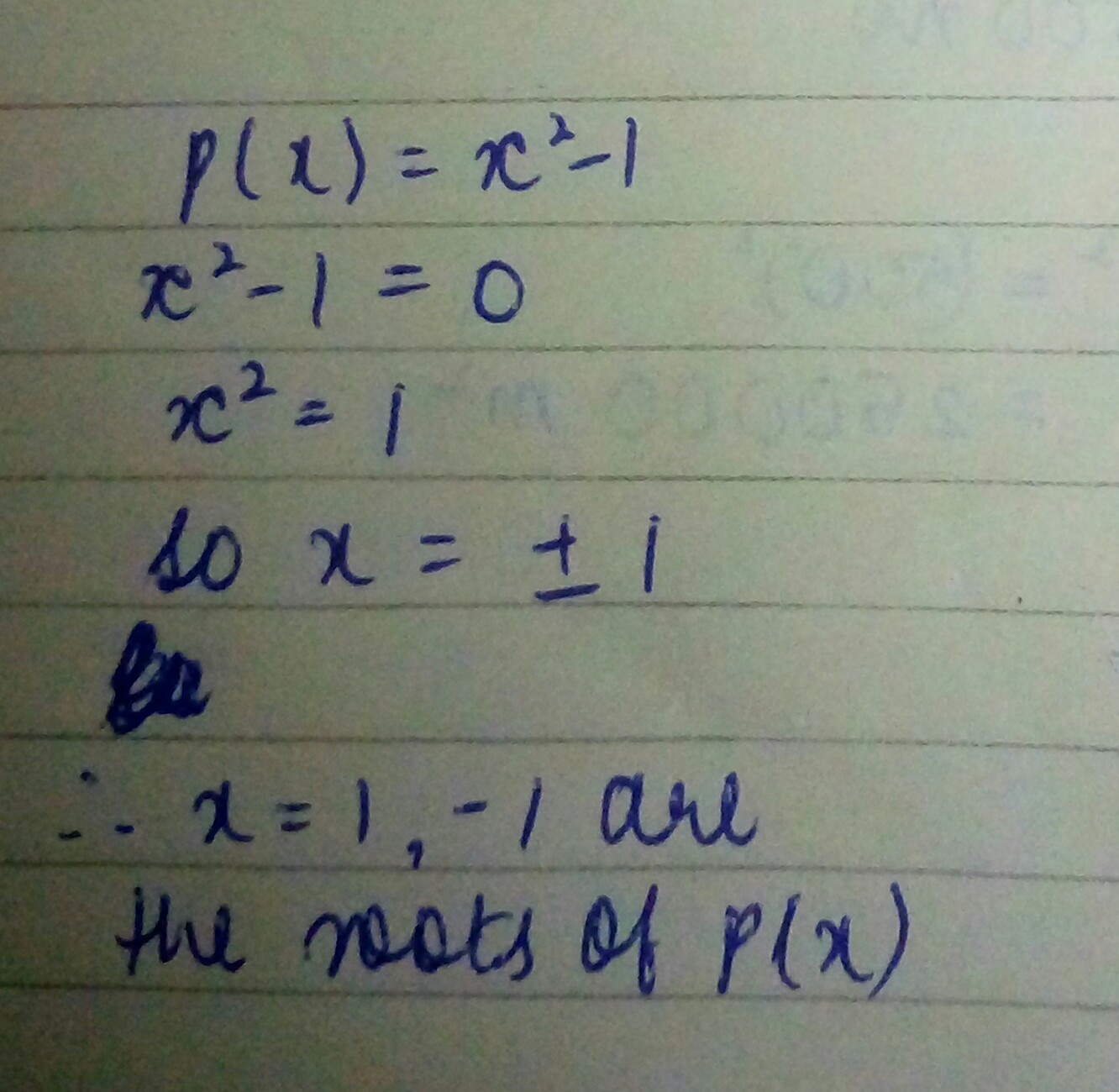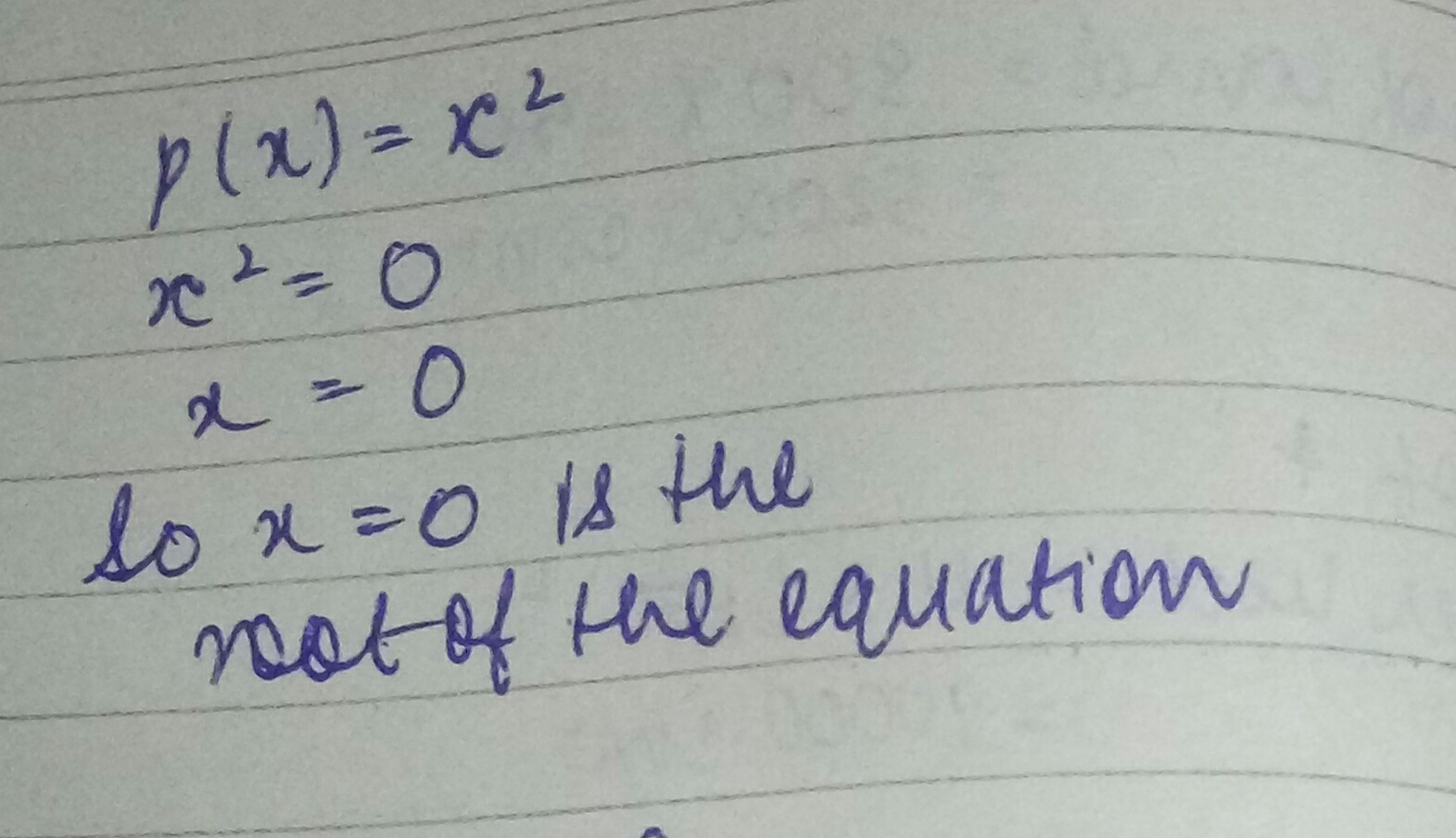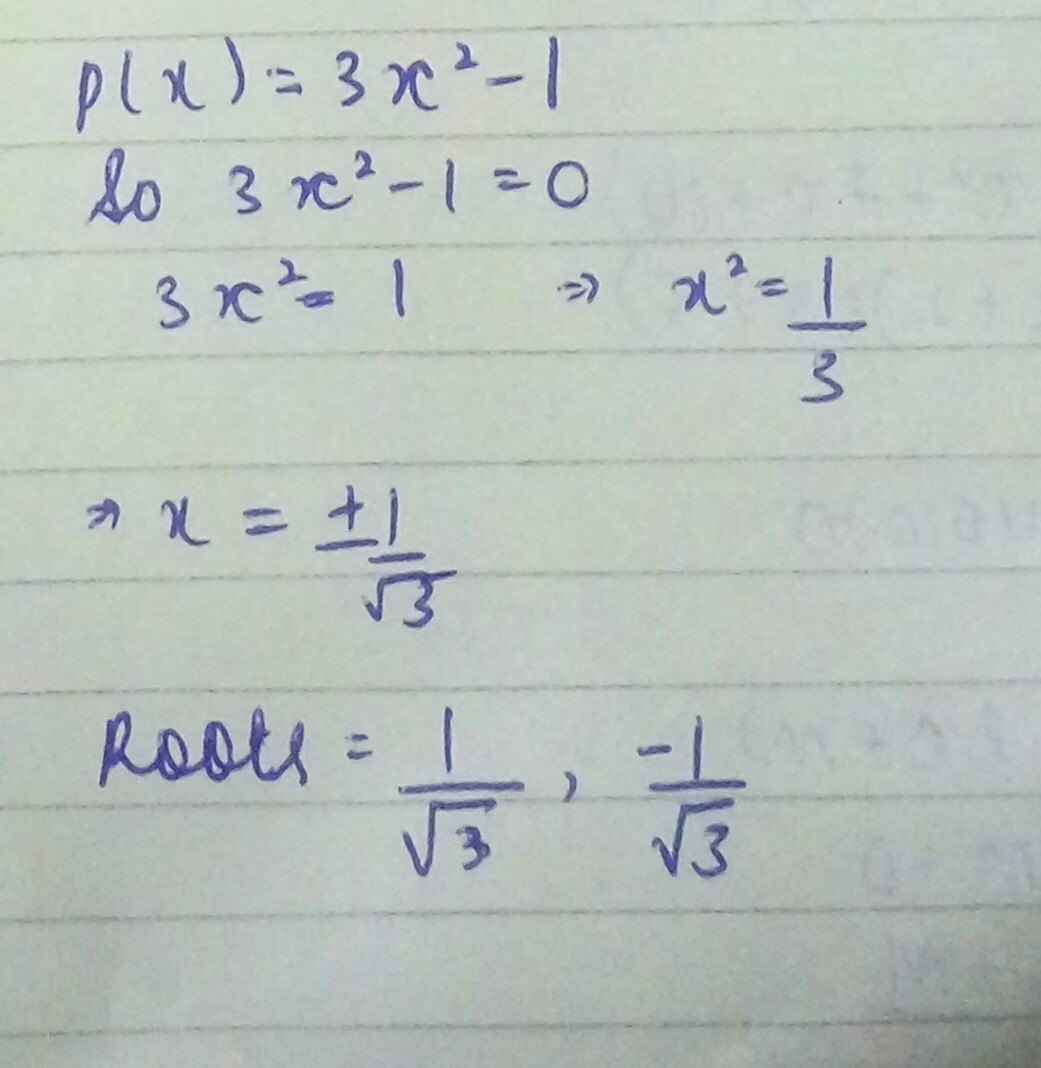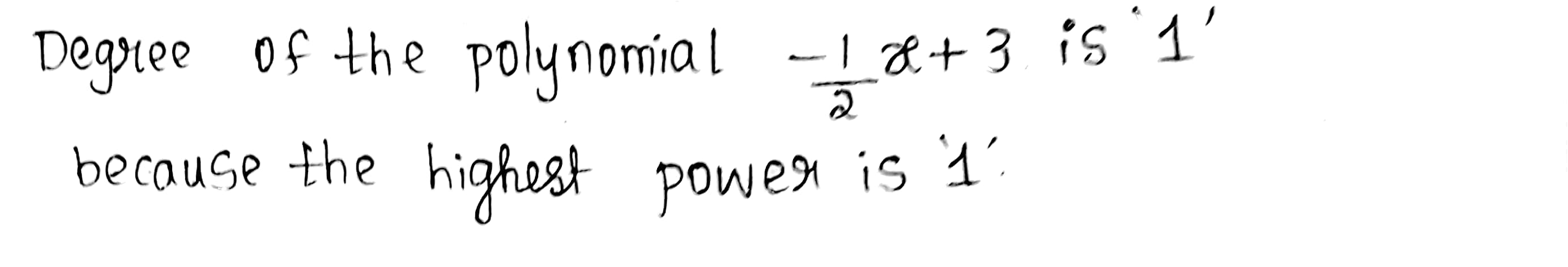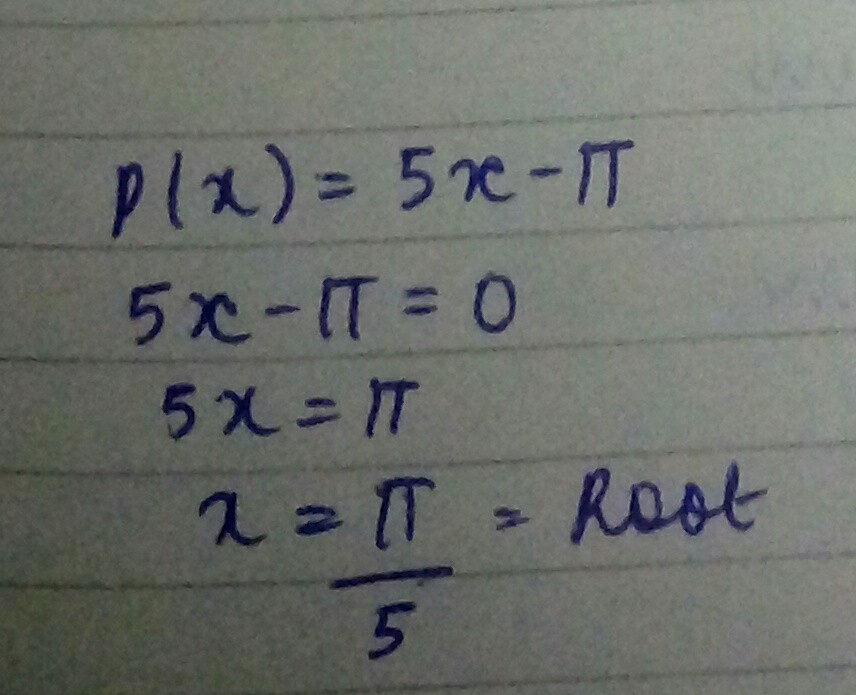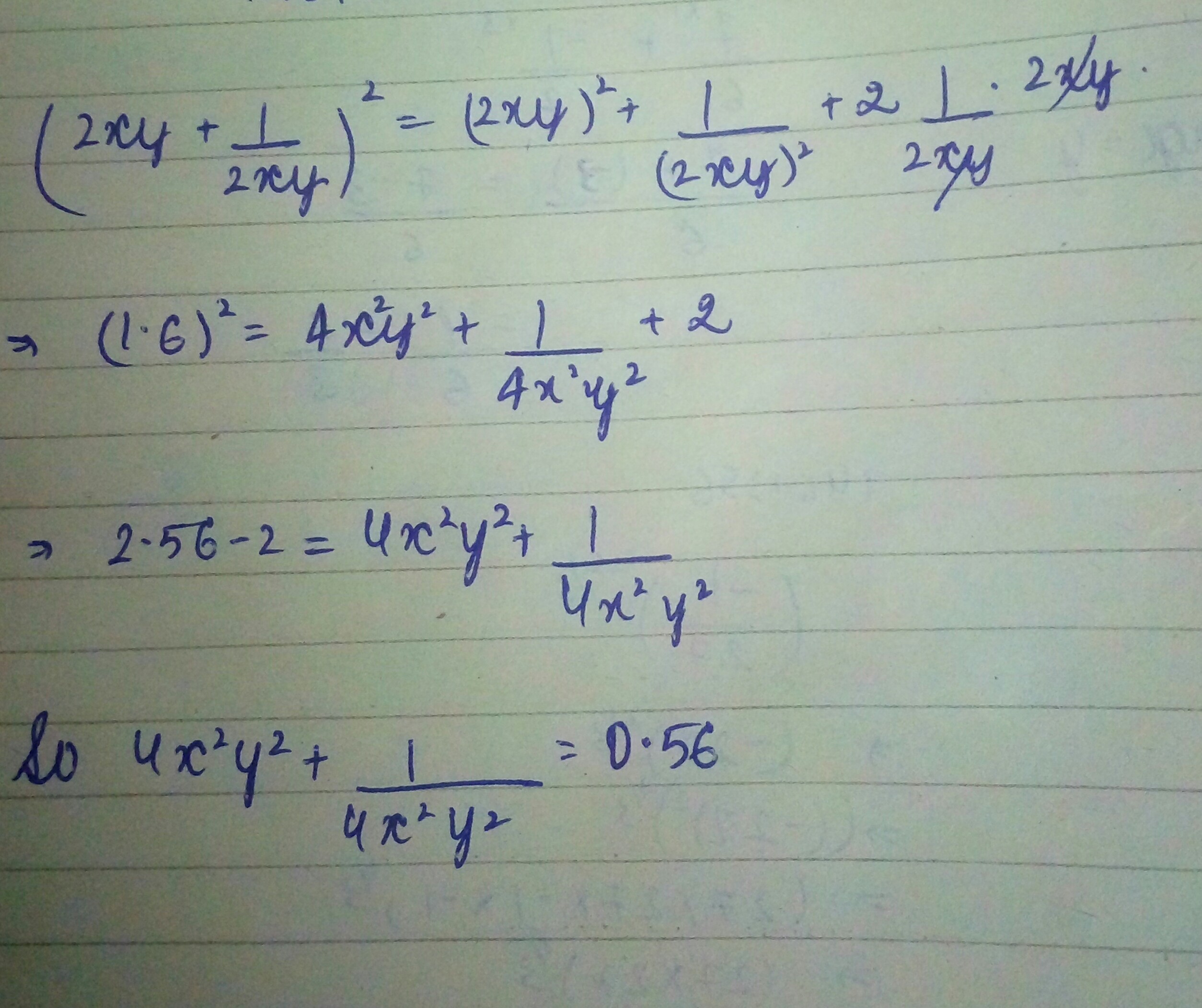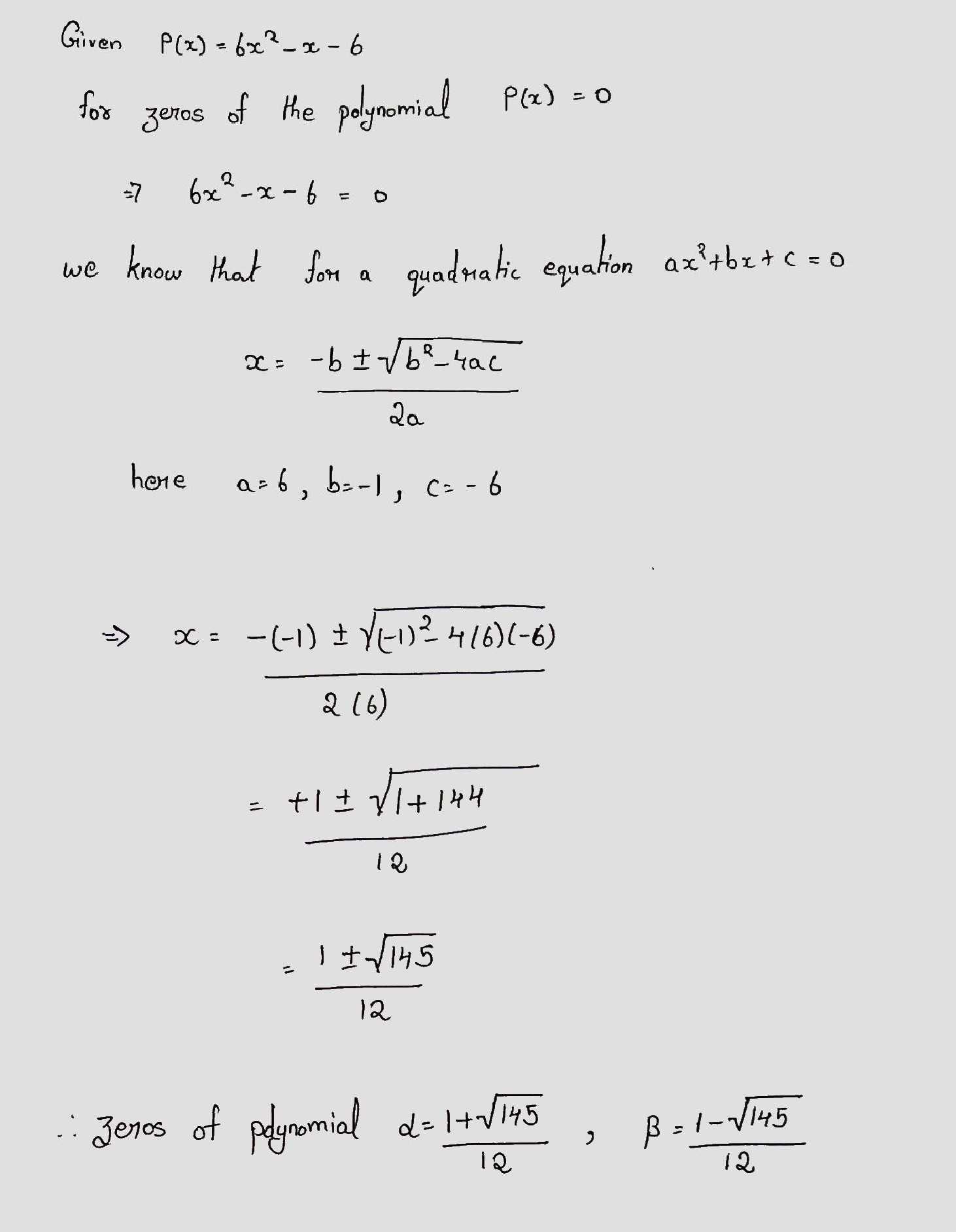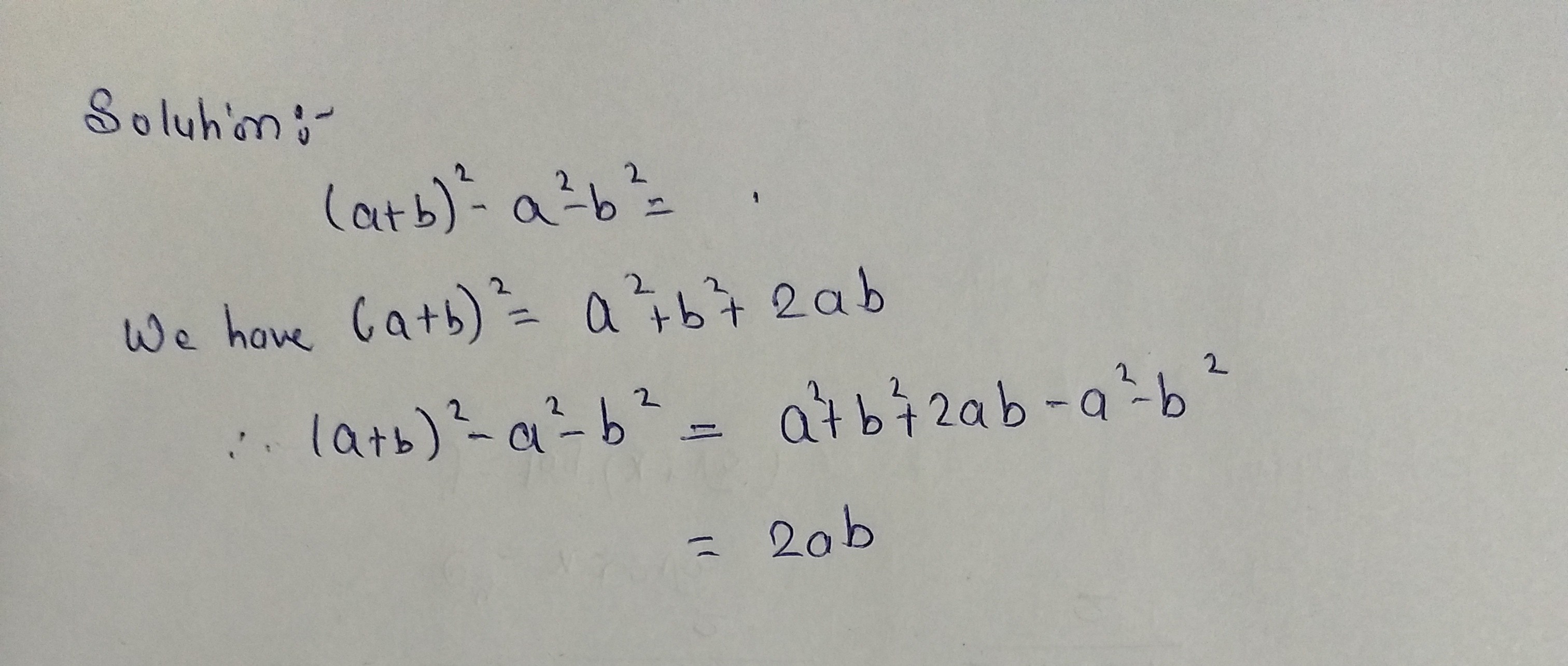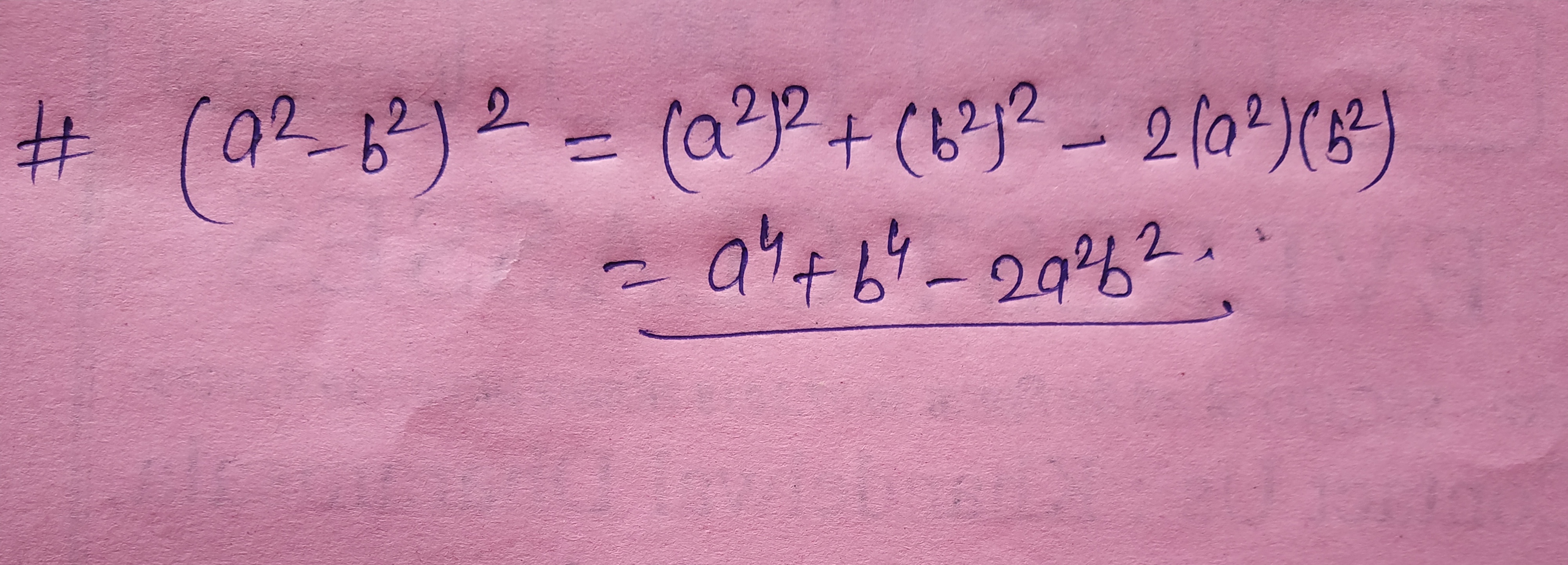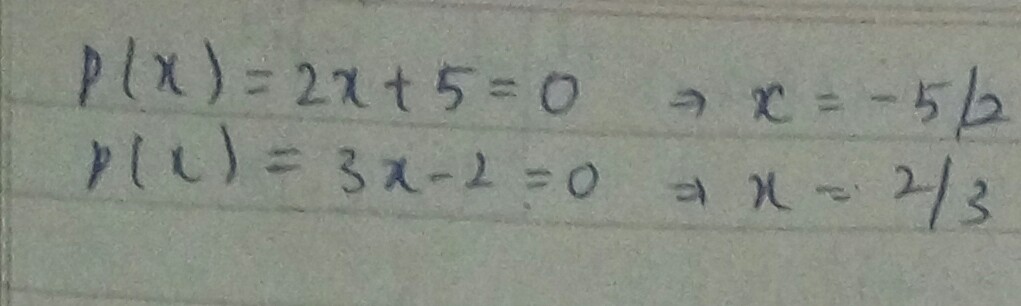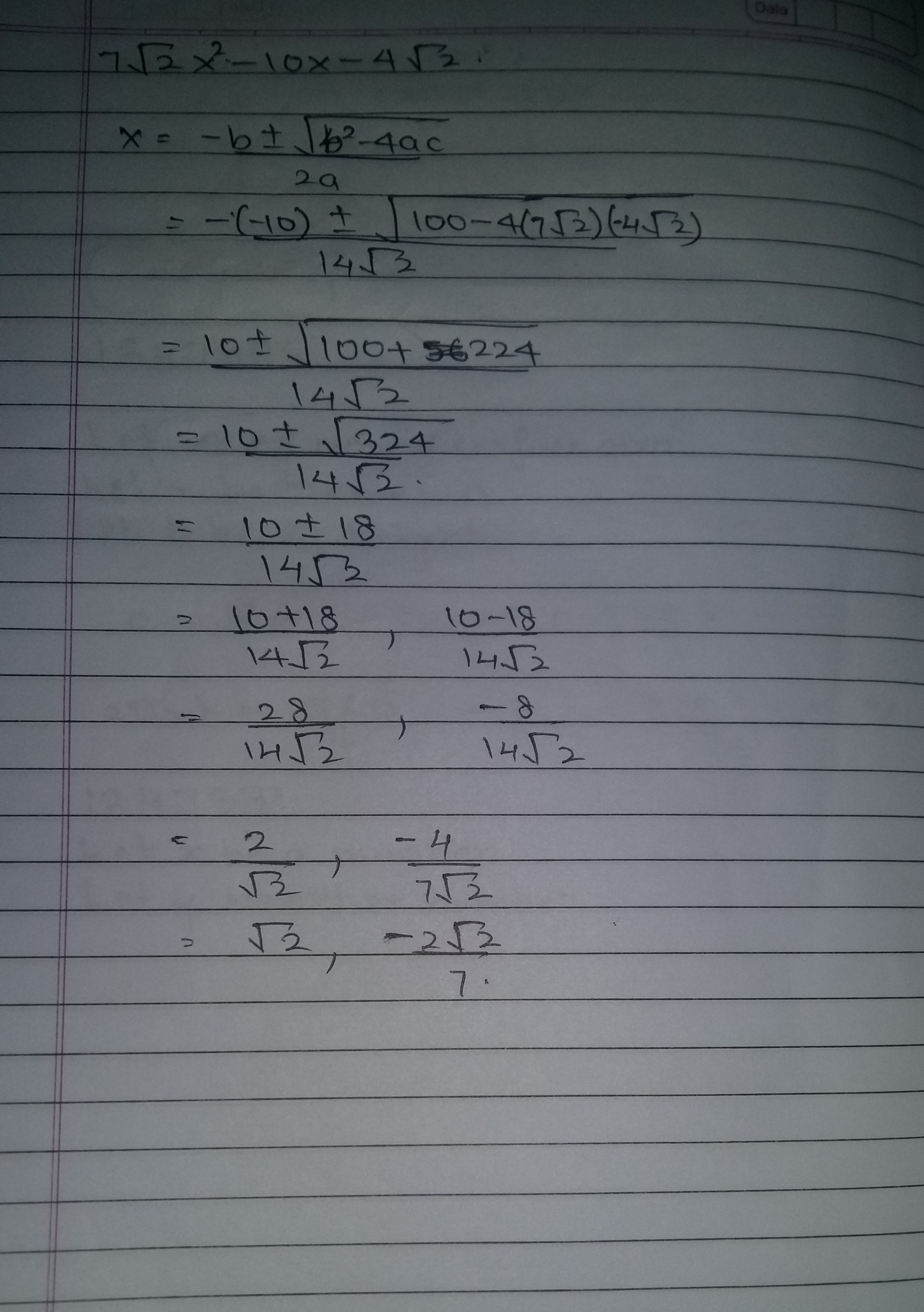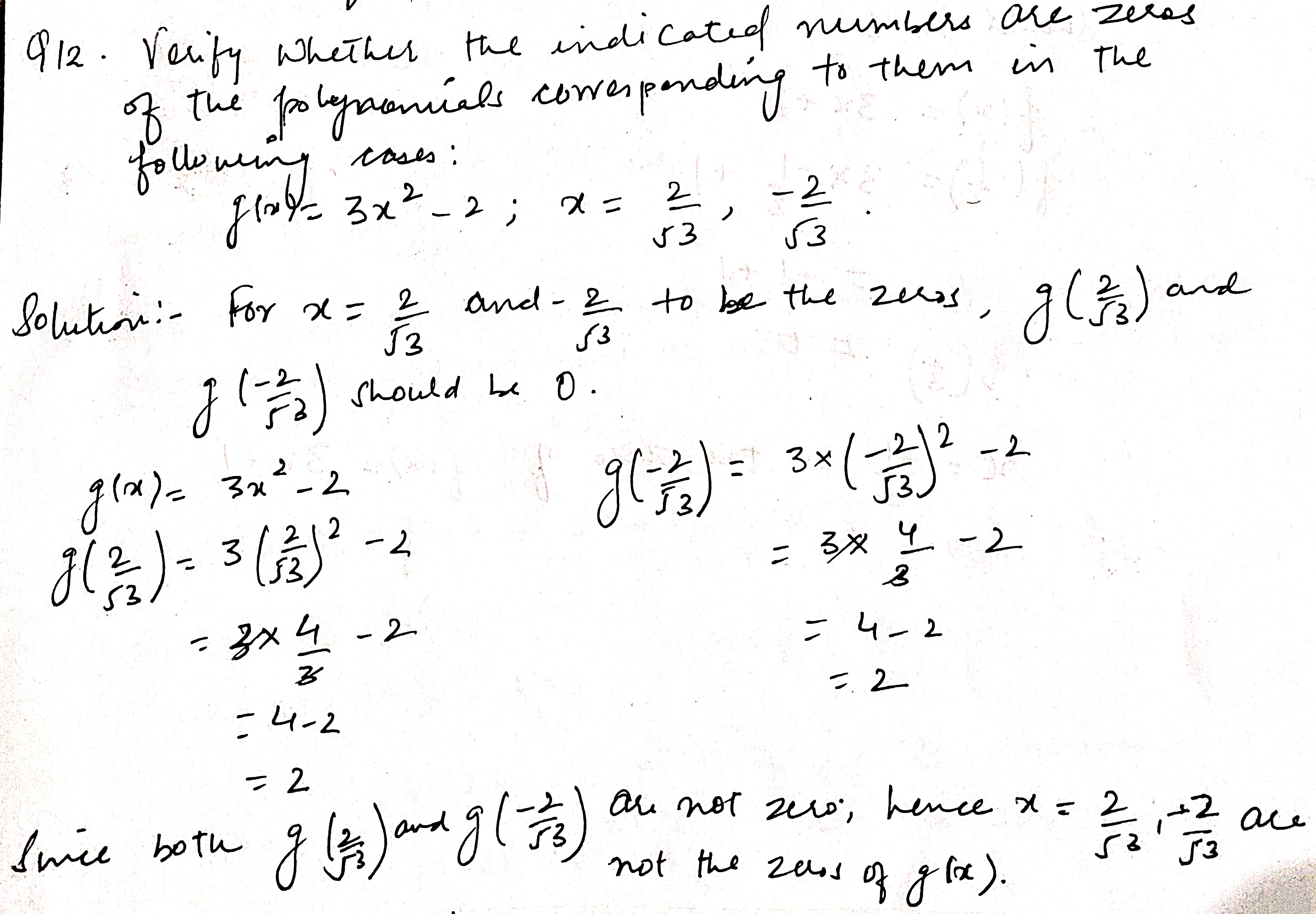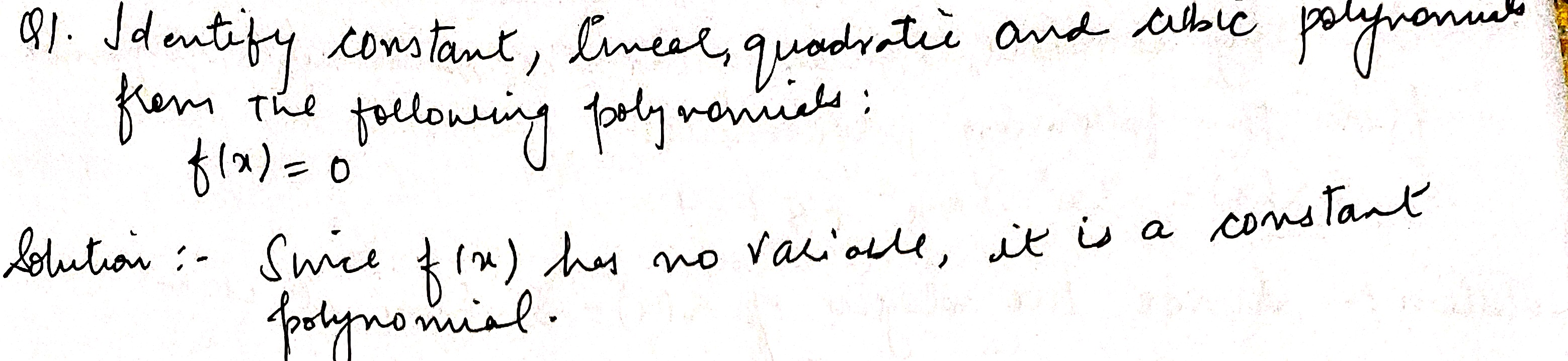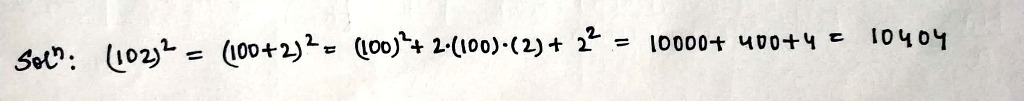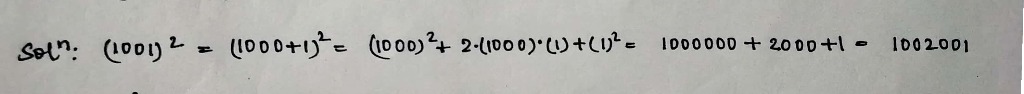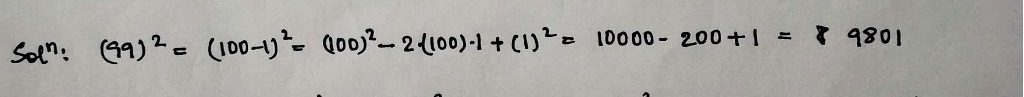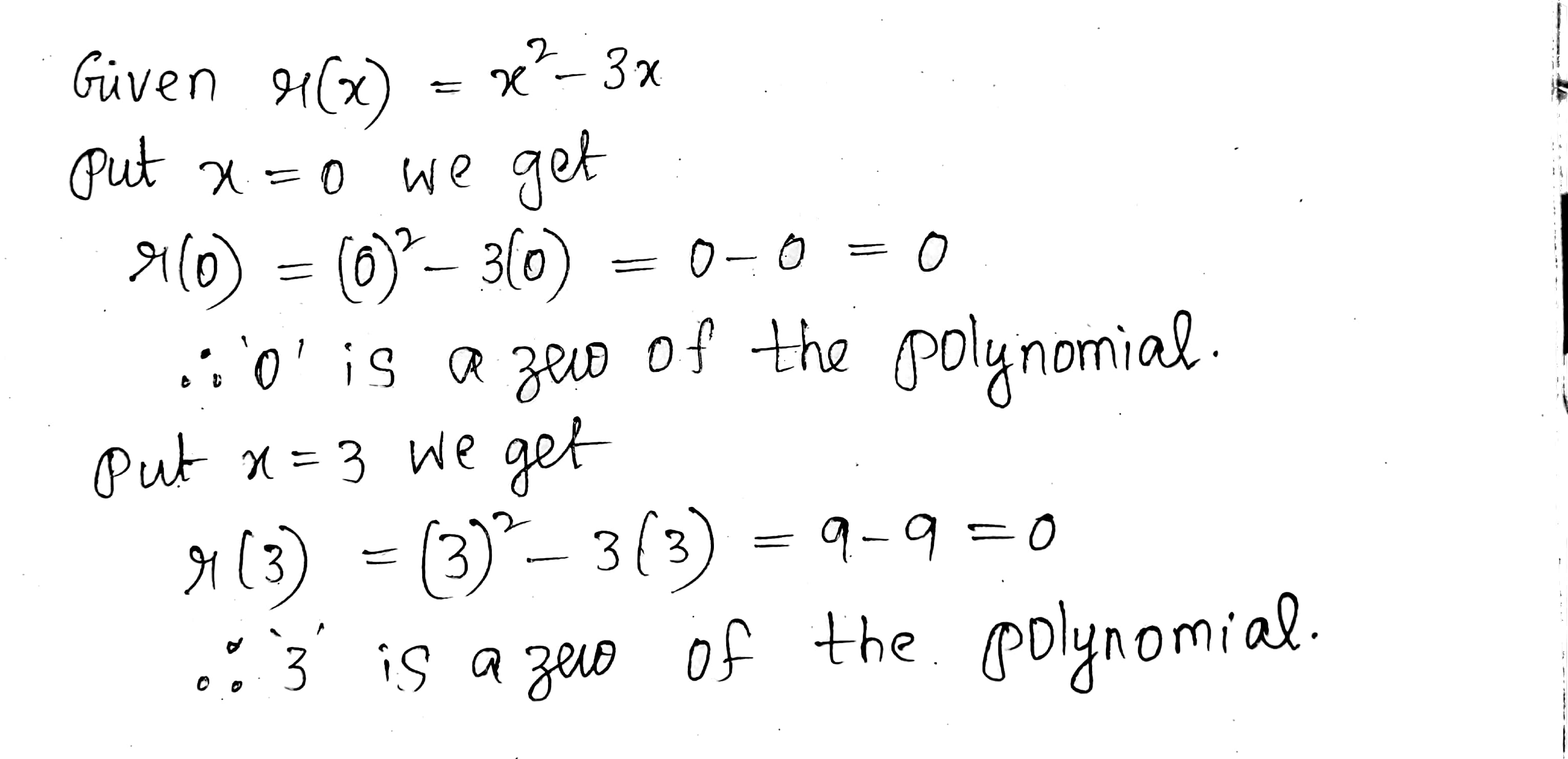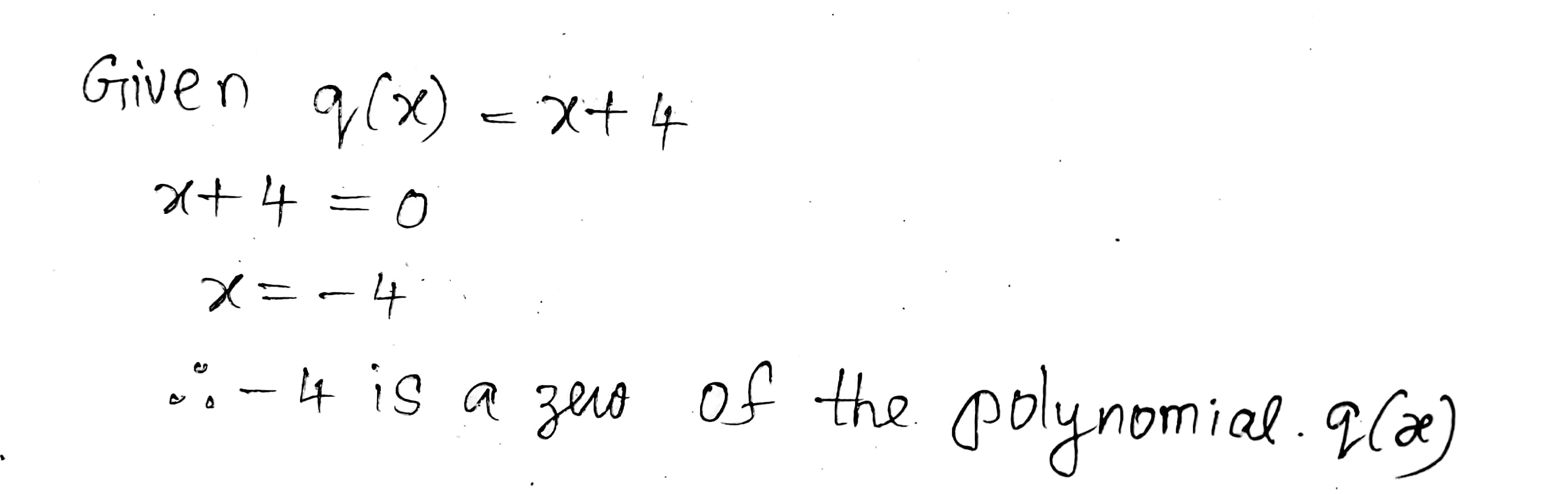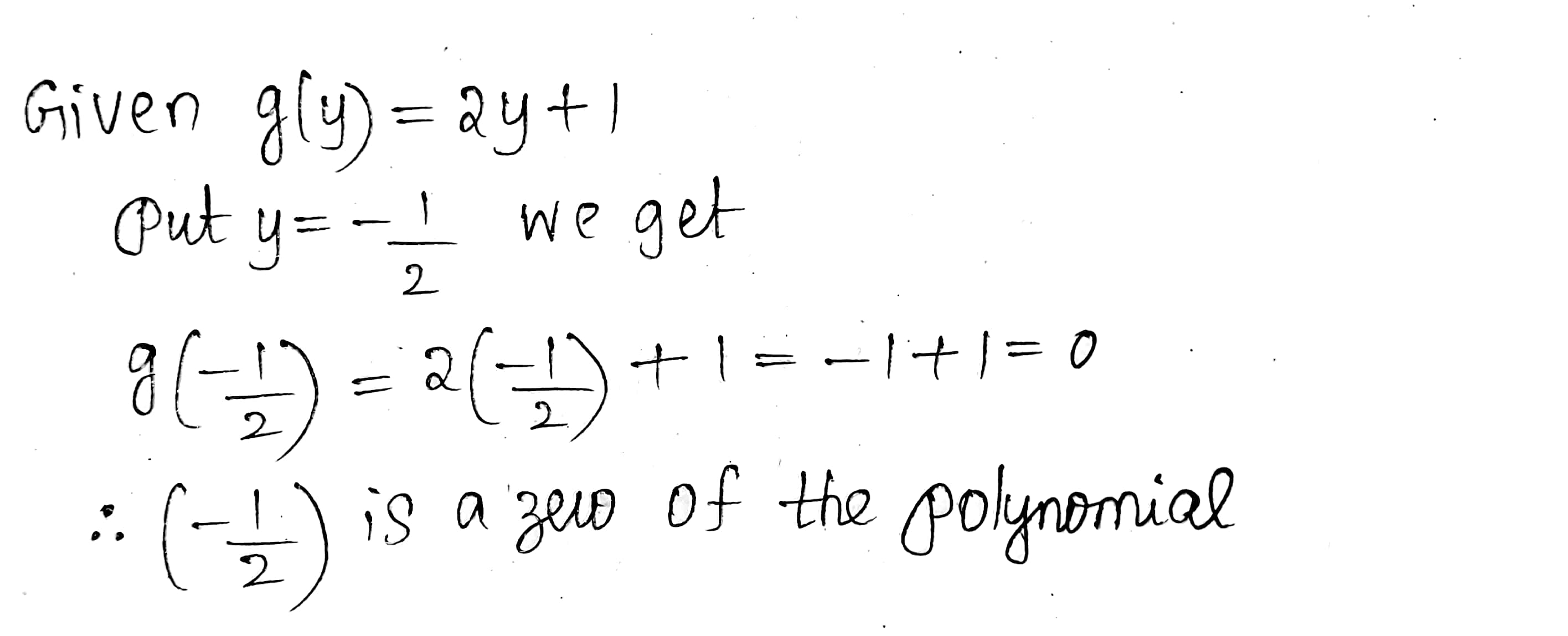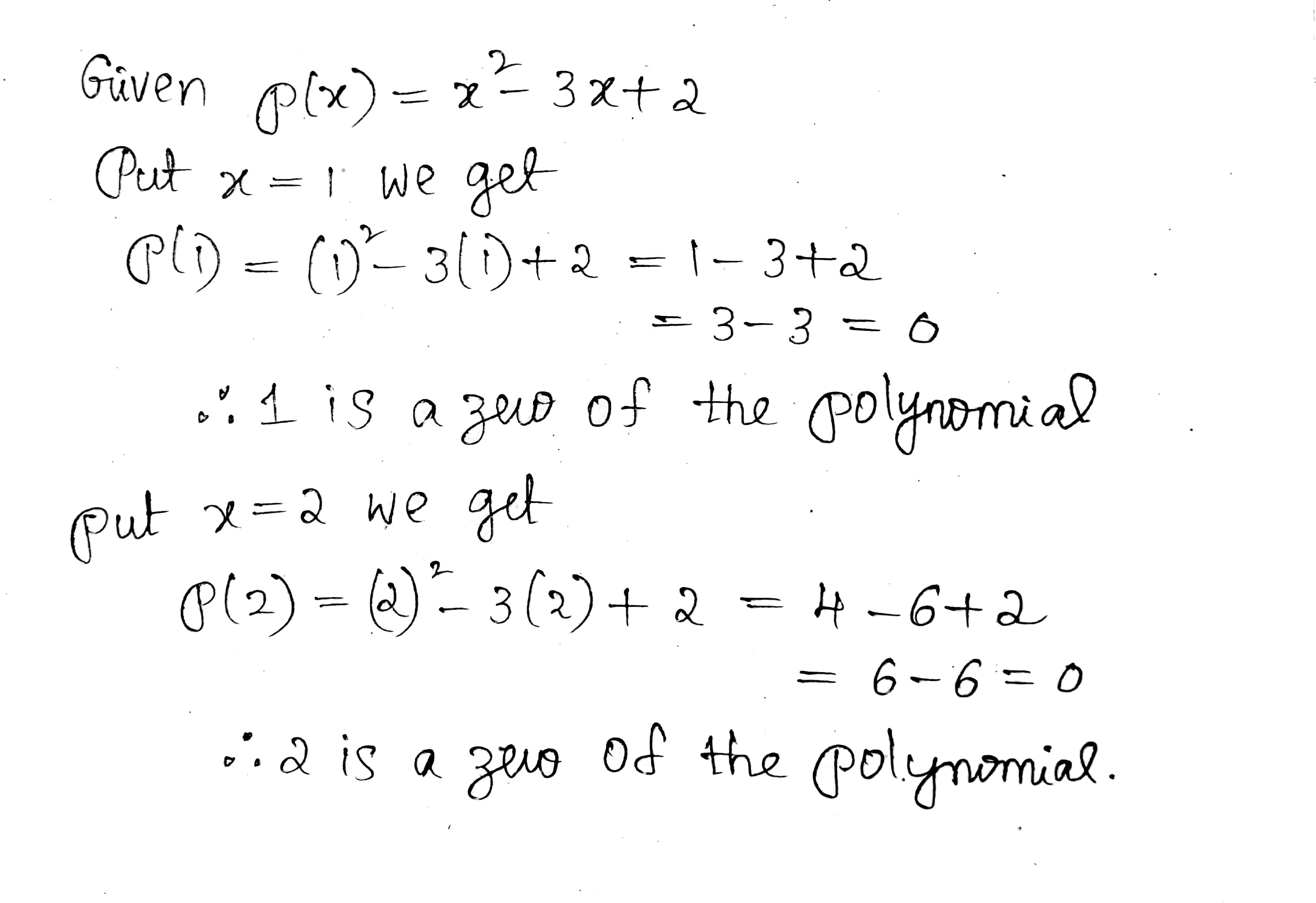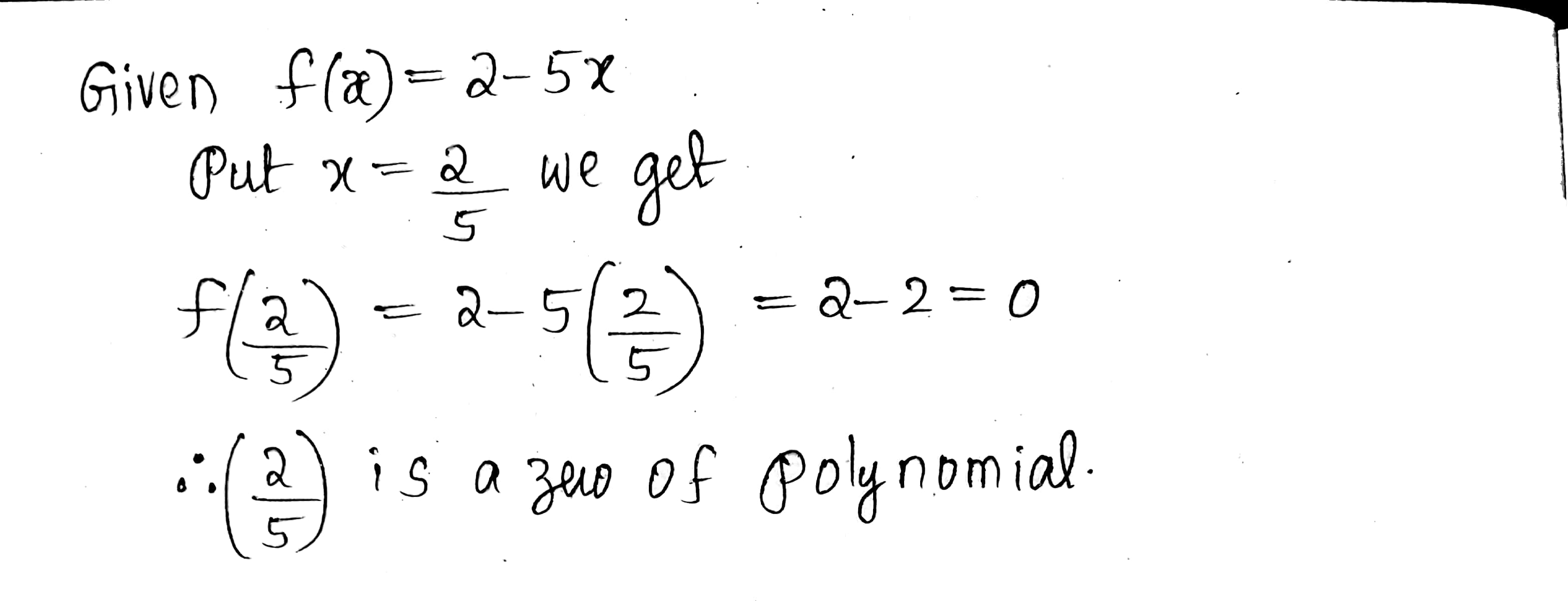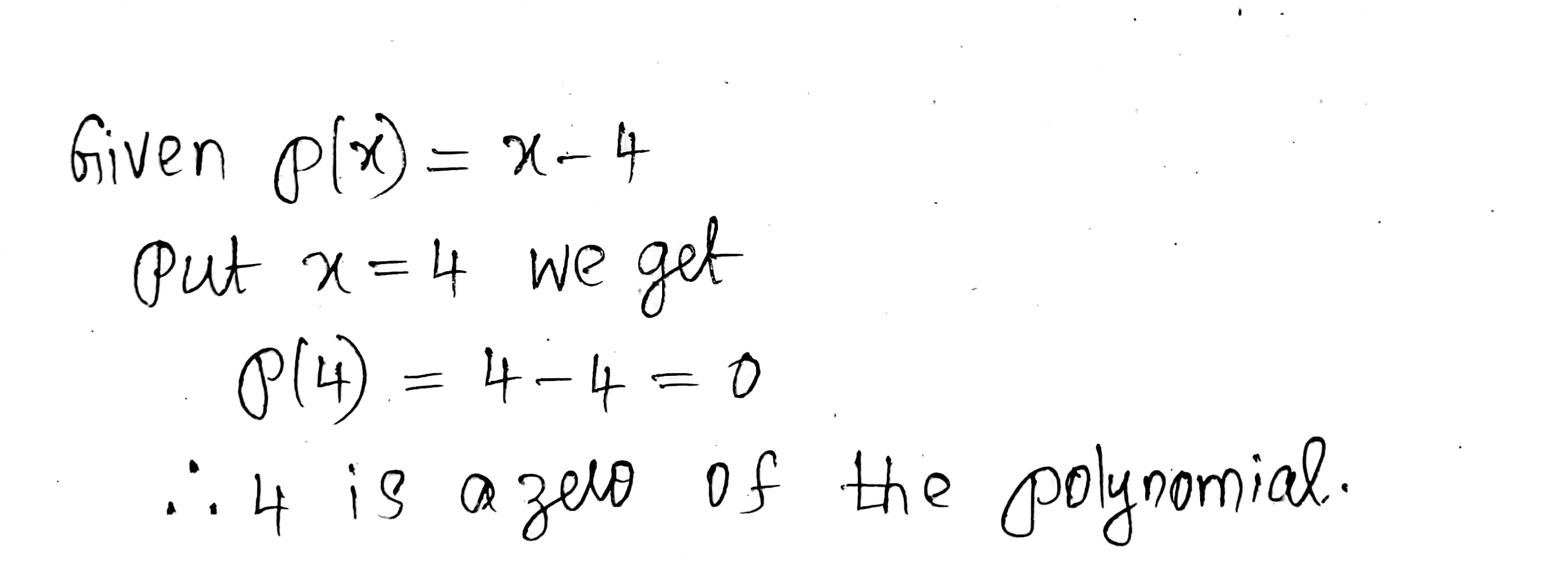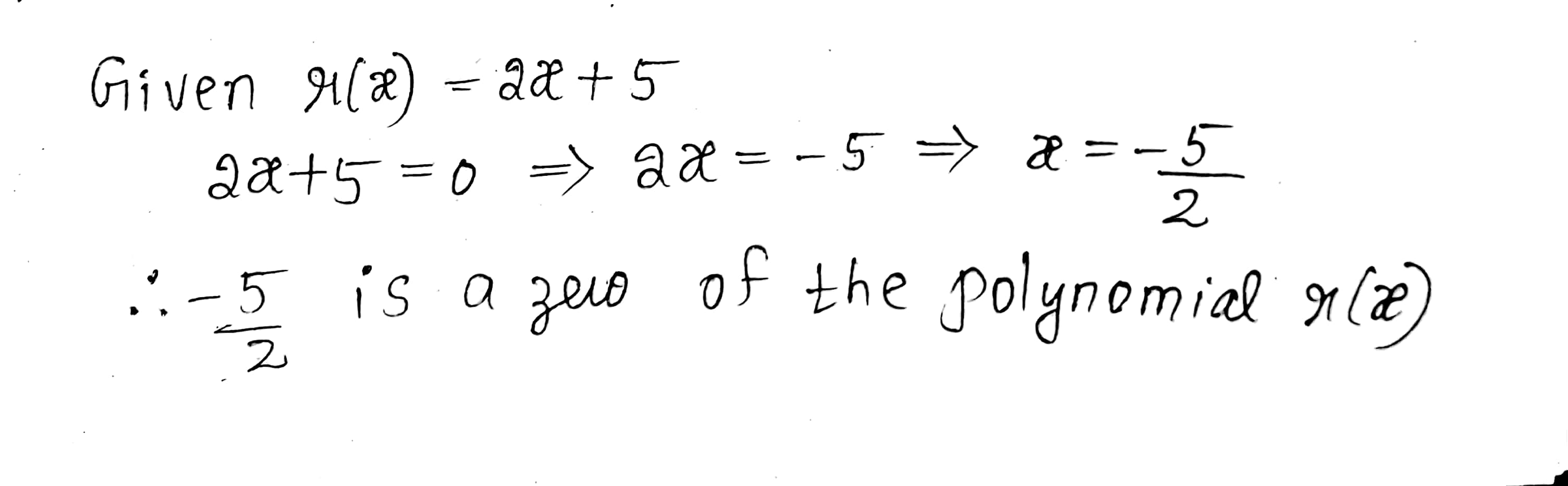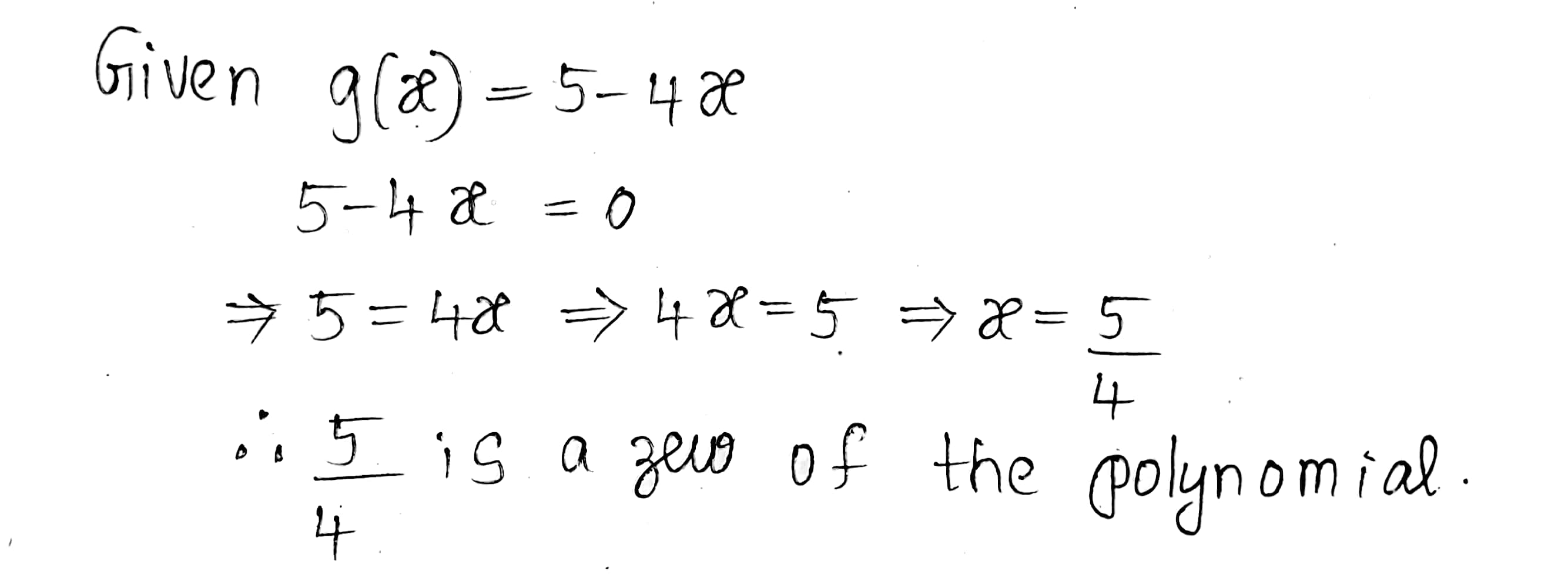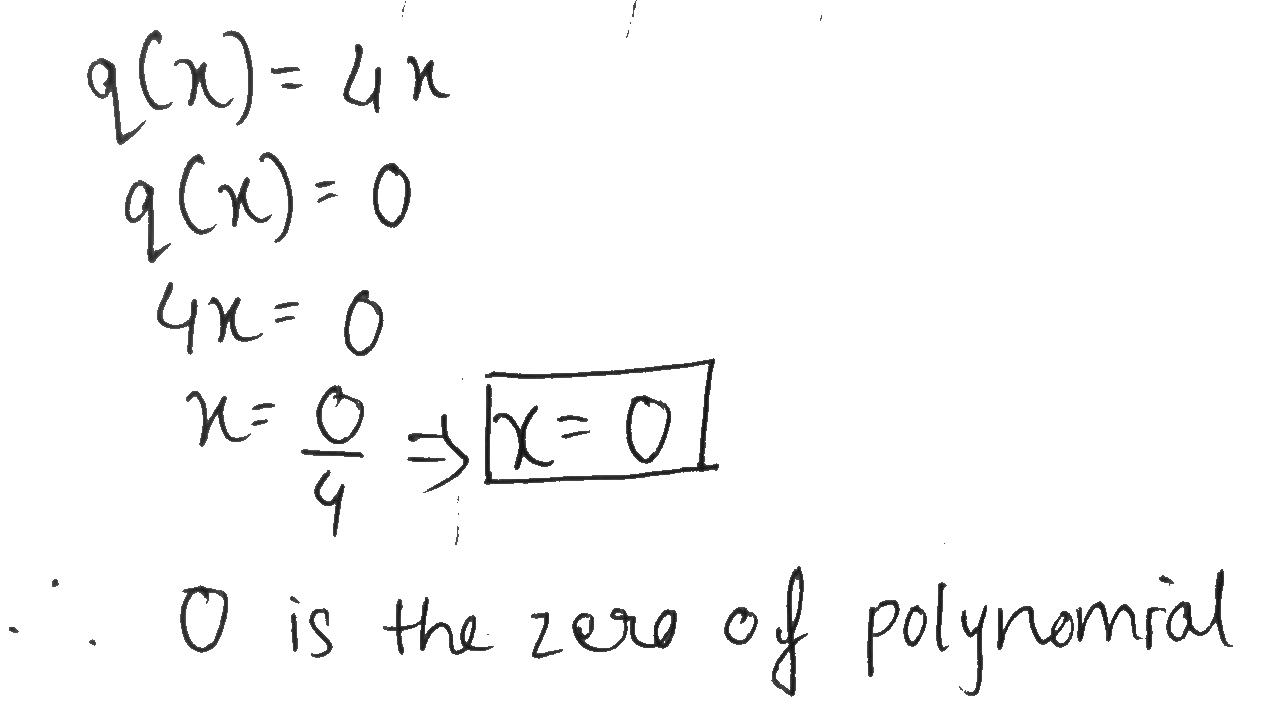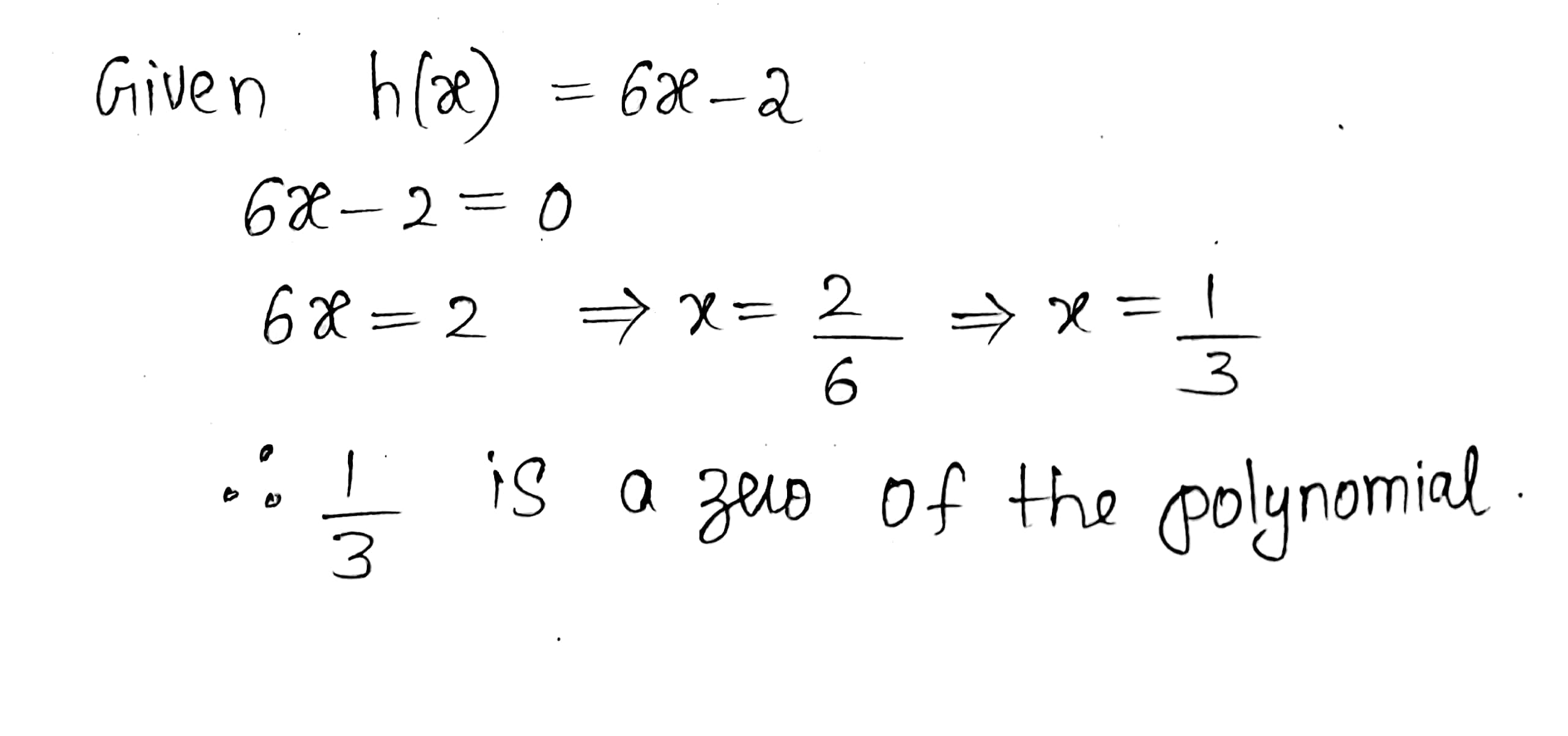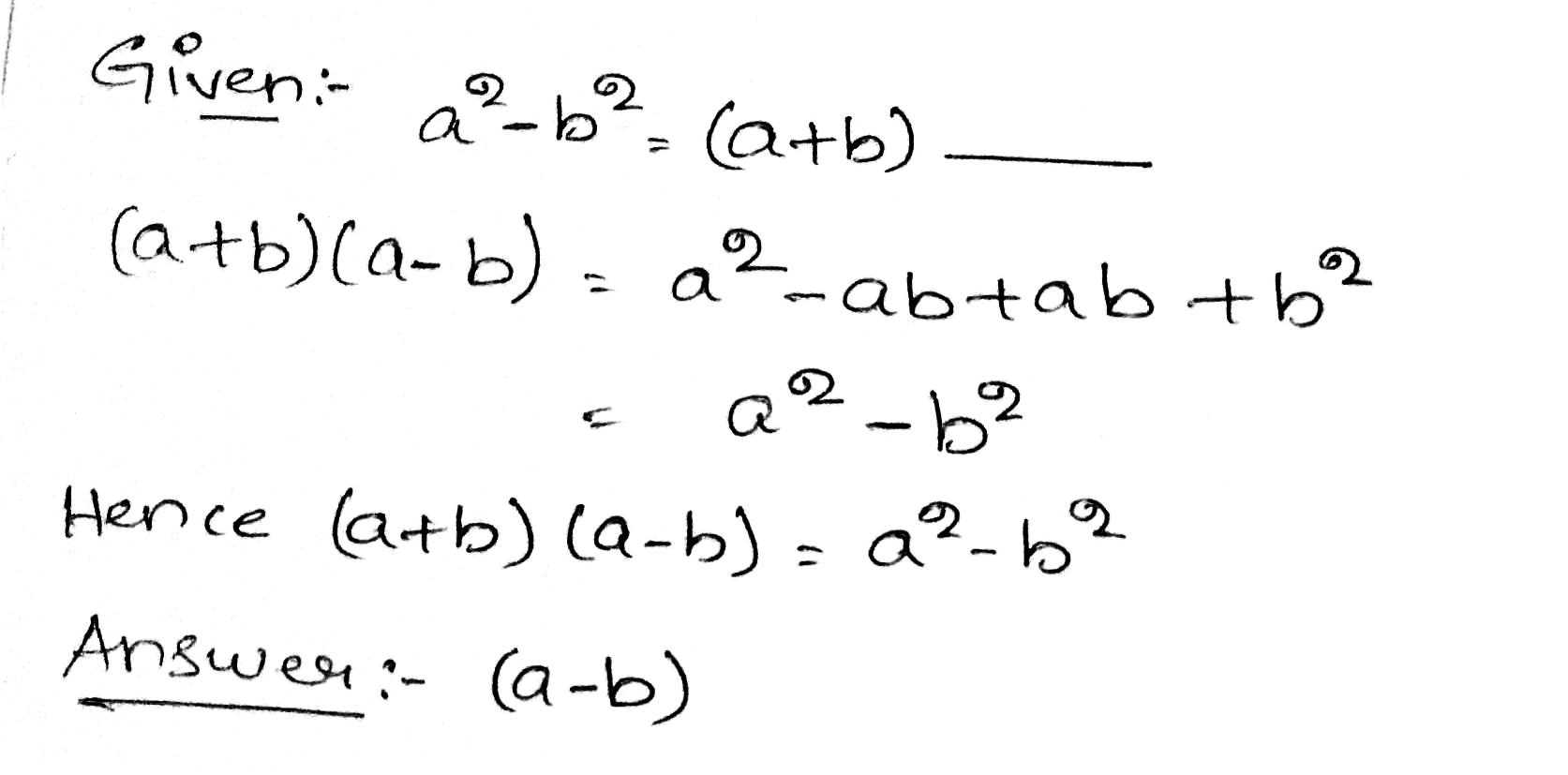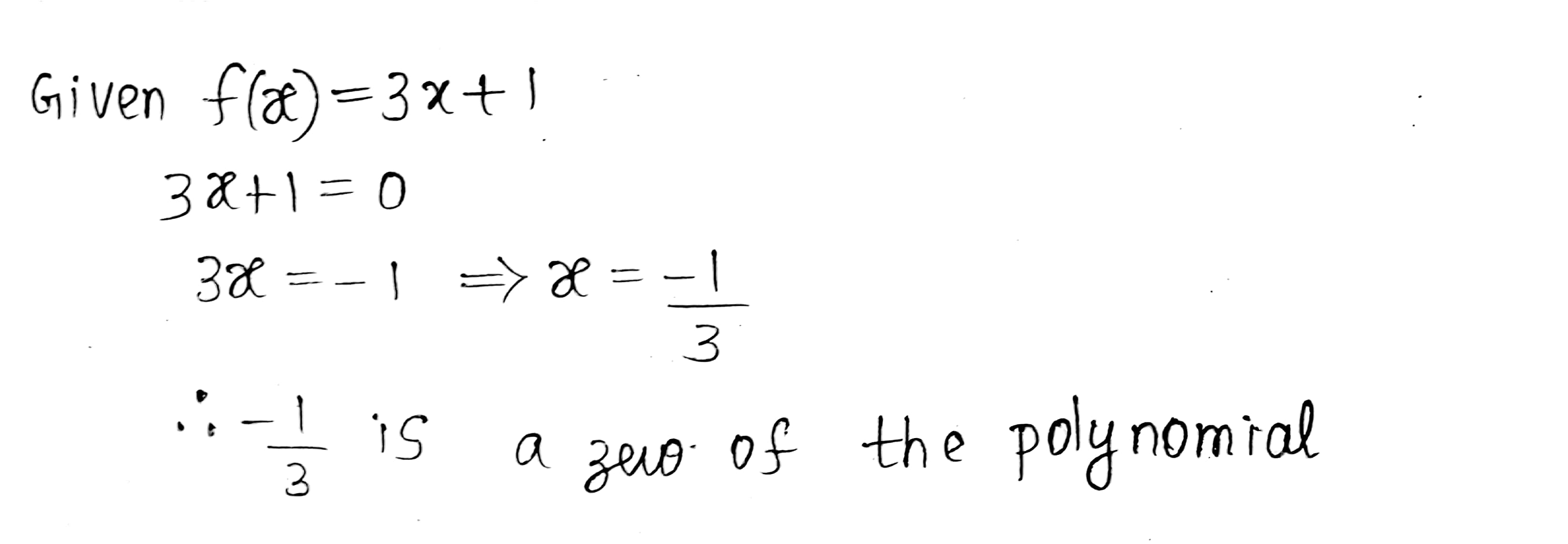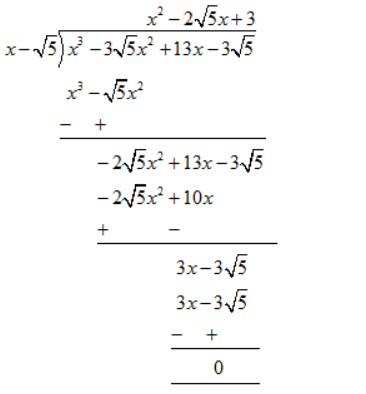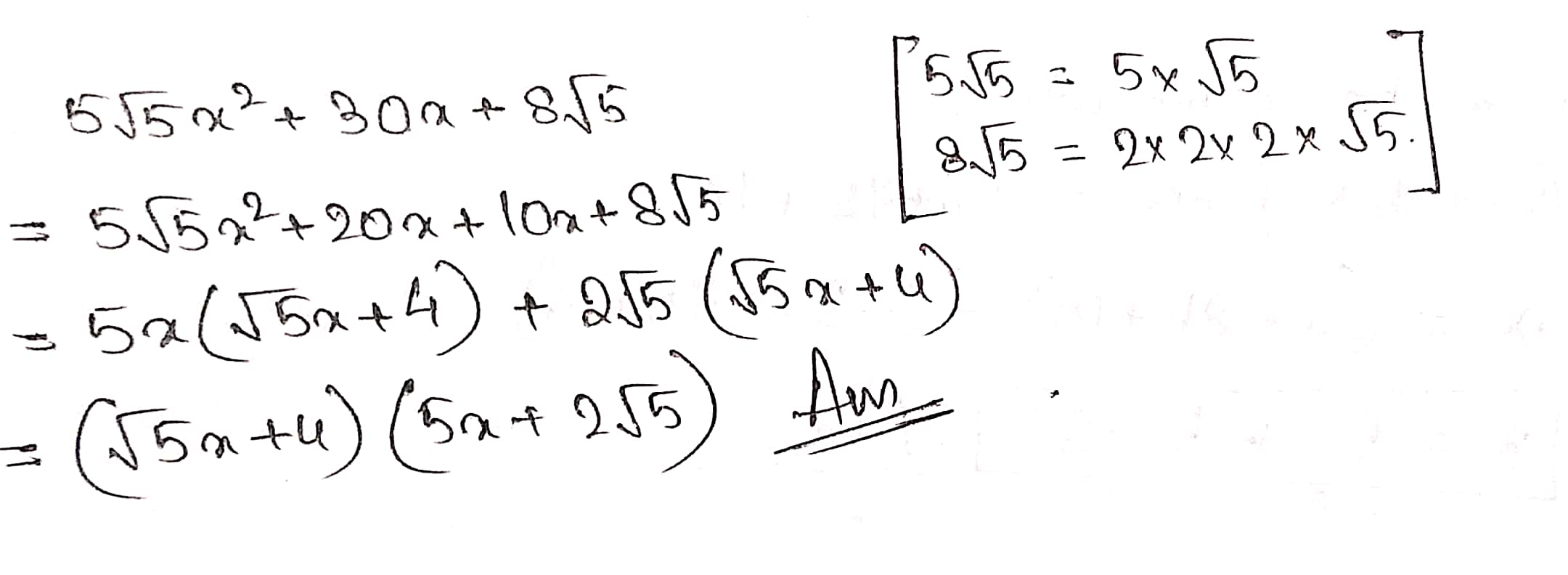Class 9 Maths - Polynomials

Write the degree of the polynomial given below:
$$ y- 6y^2 + 5y^8 $$

Degree of a polynomial is the highest degree of the degree of all its terms.

Degree of $$y = 1 $$
Degree of $$ - 6{y}^{2} = 2 $$
Degree of $$ 5{y}^{8} = 8 $$

Hence, degree of the polynomial $$ y - 6{y}^{2} + {y}^{8} $$ is $$ 8 $$.

Find the degree of the polynomial: $$7x^3+2x^2+x$$

$$7x^3+2x^2+x$$
The degree is the value of the greatest exponent of any expression (except the constant ) in the polynomial.
Here, term with greatest exponent $$= 7x^3$$

Exponent of this term $$=3$$
Thus, degree $$=3$$

Find the degree of the polynomial: $$5-x^2$$

$$5-x^2$$
The degree is the value of the greatest exponent of any expression (except the constant ) in the polynomial.
Here, term with greatest exponent $$= -x^2$$
exponent of this term $$=2$$
Thus, degree $$=2$$

Show that -1 is a zero of the polynomial $$2x^3-x^2+x+4$$.

Let the given polynomial be $$p(x)=2x^3-x^2+x+4$$.

We know that, $$x=a$$ is a zero of a polynomial, $$f(x)$$, if and only if $$f(a)=0$$.

Now, $$p(-1)=2(-1)^3-(-1)^2+(-1)+4$$

$$=-2-1-1+4$$

$$=0$$
Here, $$p(-1)=0$$

Hence, $$-1$$ is a zero of the polynomial $$2x^3-x^2+x+4$$.

Find the degree of the polynomial: $$3x^2-4x+2$$

Given polynomial is $$3x^2-4x+2$$
The degree is the value of the greatest exponent of any expression (except the constant ) in the polynomial.
Here, term with greatest exponent $$= 3x^2$$
exponent of this term $$=2$$
Thus, degree $$=2$$

Find the value of the polynomial $$p(x)=5x^2-3x+7$$ at $$x=1$$.

Given $$p(x)=5x^2-3x+7$$
At $$x=1$$
$$p(1)=5(1)^2-3(1)+7$$
$$=5-3+7$$
$$=9$$

Find the degree of the polynomial: $$1+2x+3x^2-11x^4$$

$$1+2x+3x^2-11x^4$$
The degree is the value of the greatest exponent of any expression (except the constant ) in the polynomial.
Here, term with greatest exponent $$= -11x^4$$
exponent of this term $$=4$$
Thus, degree $$=4$$

Find the degree of the polynomial: $$4-y^2$$

$$4-y^2$$
Term with the highest power of $$y=-y^2$$
heighest Exponent of y in the the given polynomial is $$=2$$
$$\therefore$$ Degree of this polynomial $$=2$$.

Evaluate
i)$$(38)^2-(37)^2$$
ii)$$(75)^2-(74)^2$$
iii)$$(141)^2-(140)^2$$

(i)
$$(38)^2-(37)^2$$
Using $$a^2-b^2=(a+b)(a-b)$$ we get,
$$=(38+37)(38-37)$$
$$=(75)(1)$$
$$=75$$
(ii)
$$(75)^2-(74)^2$$
Using $$a^2-b^2=(a+b)(a-b)$$ we get,
$$=(75+74)(75-74)$$
$$=(149)(1)$$
$$=149$$
(iii)
$$(141)^2-(140)^2$$
Using $$a^2-b^2=(a+b)(a-b)$$ we get,
$$=(141+140)(141-140)$$
$$=(281)(1)$$
$$=281$$

Show that $$1$$ is not a zero of the polynomial $$4x^4-3x^3+2x^2-5x+1$$.

Let $$p(x)=4x^4-3x^3+2x^2-5x+1$$
Now, $$p(1)=4(1)^4-3(1)^3+2(1)^2-5(1)+1=4-3+2-5+1=-1$$
Clearly, $$p(1)\ne0$$
Therefore, $$1$$ is not the zero of $$4x^4-3x^3+2x^2-5x+1$$.

Therefore, hence showed.

Show that: $$(4pq + 3q)^2 -(4pq -3q)^2 = 48pq^2$$

$$(4pq + 3q)^2 -(4pq -3q)^2 = 48pq^2$$
LHS$$=(4pq)^2+2(4pq)(3q)+(3q)^2 - [(4pq)^2-2(4pq)(3q)+(3q)^2]$$
$$=16p^{ 2 }q^{ 2 }+24pq^{ 2 }+9q^2-16p^2q^2+24pq^2-9q^2$$
$$=48pq^2$$
=RHS
LHS=RHS

Show that: $$(9p - 5q)^2 + 180pq = (9p + 5q)^2$$

$$(9p - 5q)^2 + 180pq = (9p + 5q)^2$$

LHS$$=(9p)^2-2(9p)(5q)+(5q)^2+180pq$$
$$= 81p^2 - 90pq + 25q^2 + 180pq$$
$$= 81p^2 + 90pq + 25q^2$$

RHS$$= (9p + 5q)^2$$
$$=(9p)^2+2(9p)(5q)+(5q)^2$$
$$= 81p^2 + 90pq + 25q^2$$

LHS=RHS

Use the identity $$(a + b)(a - b) = a^2 - b^2$$ to find the product of $$(x + 6)(x - 6)$$

Using the identity $$(a+b)(a-b)$$ = $$a^2-b^2$$
Hence $$(x+6)(x-6)$$= $$x^2-6^2$$
The answer is $${x^2-36}$$

What is the expansion of $$(4p - 3q)^2$$?

Here we use $$(a- b)^2 = a^2 - 2ab + b^2$$.
Taking $$a = 4p$$ and $$b = 3q$$,
we obtain $$(4p - 3q)^2 = (4p)^2 - 2(4p)(3q) + (3q)^2 = 16p^2 -24pq + 9q^2$$

Give one example each of a binomial of degree $$35$$ and of a monomial of degree $$100$$.

$$\textbf{Step -1: Writing a Binomial Expression of degree 35 }$$

$$\text{A binomial with degree 35}$$

$$\implies ax^{35}+bx^c, \text{where }0\leq c<35$$

$$\text{On taking any value of a and b}$$

$$\implies 3x^{35}-4$$

$$\textbf{Step -2: Writing a Monomial Expression}$$

$$\text{A monomial with degree 100}$$

$$\implies ax^{100}$$

$$\text{On taking any value of a}$$

$$\implies 5x^{100}$$

$$\textbf{Hence, required expressions are }\mathbf{3x^{35}-4,5x^{100} .}$$

Expand:$$(2t + 5)(2t - 5)$$

Given that: $$(2t+5)$$$$(2t-5)$$
$$=$$ $$2t(2t-5)-5(2t-5)$$
$$=$$ $$4t^2 -10t-10t+25$$

Hence $${4t^2 -20t+25}$$ is the correct answer

Use appropriate formula to compute $$185^2- 115^2$$

Using the identity: $$a^2-b^2$$ =$$(a-b)(a+b)$$
We can write $$(185)^2-(115)^2$$ =$$(185+115)(185-115)$$ using the above identity
$$\Rightarrow$$ $$(185 +115)(185 -115)=(300)(70)$$
Hence the answer is $${21000}$$

Use the identity $$(a + b)(a - b) = a^2 - b^2$$ to find the product of $$(3x + 5)(3x - 5)$$

Using identity $$(a+b)(a-b)$$ = $$a^2-b^2$$
Hence$$(3x+5)(3x-5)$$ = $$(3x)^2-5^2$$ $$= 9x^2 -25$$

The answer is $${9x^2-25}$$

Find a zero of the polynomial $$2x - 1$$

Given polynomial $$p(x)=2x-1$$

We know that p(x) is zero polynomial the value of $$p(x)=0$$

$$\therefore 2x-1=0$$

Add 1 both sides we get

$$3x-1+1=1$$

$$\Rightarrow 2x=1$$

Divided by 2 we get

$$x=\cfrac{1}{2}$$

So $$p(-\cfrac{1}{2})$$ is the zero polynomial $$2x-1$$

Find the degree of each of the polynomials given below
$$4 - y^{2}$$

We know that the degree is the value of the greatest exponent of expression (except the constant ) in the polynomial. To find the degree all that you have to do is find the largest exponent in the polynomial.

In polynomial $$4-y^{2}$$

The value of the largest exponent is 2 since the second term is largest exponent

Then degree is 2

Find the volume of the cuboid with dimensions $$(x-1), (x-2)$$ and $$(x-3)$$.

We have to find $$(x-1)(x-2)(x-3)$$. In the identity
$$(x+a)(x+b)(x+c)={x}^{3}+{x}^{2}(a+b+c)+x(ab+bc+ca)+abc$$
We take $$a=-1$$, $$b=-2$$ and $$c=-3$$.Hence
$$a+b+c=-6,ab+bc+ca=2+6+3=11,abc=-6$$
We obtain the volume as
$${ x }^{ 3 }-6{ x }^{ 2 }+11x-6$$

Write the degree of the following polynomial:
$$7 - x + 3x^{2}$$

In polynomial $$7-x+3x^{2}$$7x3+5x2+2x−6

The value of the largest exponent is 2 since the last term is square

Then degree is 2

Write the degree of the following polynomial:
$$7x^{3} + 5x^{2} + 2x - 6$$

We know that the degree is the value of the greatest exponent of expression (except the constant ) in the polynomial. To find the degree all that you have to do is, find the largest exponent in the polynomial.

In polynomial $$7x^{3}+5x^{2}+2x-6$$, the value of the largest exponent is $$3$$, since the first term is cube.

Then degree of the polynomial is $$3$$.

Find the degree of the polynomial given below:
$$x^{5} - x^{4} + 3$$

In polynomial $$x^{5}-x^{4}+3$$

The value of the largest exponent is $$5$$ since the first term is largest exponent

Then degree is $$5$$

Write the degree of the following polynomial:
$$5p - \sqrt {3}$$

We know that the degree is the value of the greatest exponent of expression (except the constant) in the polynomial.

To find the degree, all that you have to do is find the largest exponent in the polynomial.

In the polynomial $$5p-\sqrt{3}$$,

The value of the largest exponent is 1 since the first term is one.

Then degree is 1.

Find the degree of each of the polynomials given below
$$5t - \sqrt {3}$$

In polynomial $$5t-\sqrt{3}$$

The value of the largest exponent is 1 since the frist term is largest exponent

Then degree is 1

Find the degree of each of the polynomials given below
$$x^{2} + x - 5$$

In polynomial $$x^{2}+x-5$$

The value of the largest exponent is 2 since the first term is largest exponent

Then degree is 2

Verify whether the value of $$x$$ given in each case are the zeroes of the polynomial or not?
$$p(x) = ax + b; x = -\dfrac {b}{a}$$

Given polynomial $$p(x)=ax+b$$ and value $$x=-\cfrac{b}{a}$$

$$p(x)=ax+b$$

Replace x by $$-\cfrac{b}{a}$$ we get

$$p\left ( -\cfrac{b}{a} \right )=a\left ( -\cfrac{b}{a} \right )+b$$

$$\Rightarrow p \left (-\cfrac{b}{a} \right )=-b+b$$

$$\Rightarrow p\left ( \cfrac{b}{a} \right )=0$$

Then polynomial $$p(x)=ax+b$$ the value is zero when $$x=-\cfrac{b}{a}$$

So the polynomial $$p(x)=ax+b$$ the value is zero polynomial when $$x=-\cfrac{b}{a}$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?
$$p(x) = 5x - \pi; x = \dfrac {3}{2}$$

Given polynomial $$p(x)=5x-\pi$$ and value $$x=-\cfrac{3}{2}$$

$$p(x)=5x-\pi$$

Replace x by $$-\cfrac{3}{2}$$

$$p\left ( -\cfrac{3}{2} \right )=5\left ( -\cfrac{3}{2} \right )-\cfrac{22}{7}$$

$$\Rightarrow p\left ( -\cfrac{3}{2} \right )=-\cfrac{15}{2}-\cfrac{22}{7}$$

$$\Rightarrow p\left ( -\cfrac{3}{2} \right ) =\cfrac{-105-44}{14}$$

$$\Rightarrow p\left ( -\cfrac{3}{2} \right )=-10.64$$

So polynomial value with $$-\cfrac{3}{2}$$ not zero

So the polynomial is not zero polynomial for value $$x=-\cfrac{3}{2}$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?
$$p(x) = x^{2} - 1; x = \pm 1$$

Given polynomial $$p(x)=x^{2}-1$$ value $$x\pm 1$$

$$p(x)=x^{2}-1$$

Replace x by 1 we get

$$p(1)=(1)^{2}-1$$

$$p(1)=1-1$$

$$p(1)=0$$

Replace x by -1 we get

$$p(-1)=(-1)^{2}-1$$

$$p(-1)=1-1$$

$$p(-1)=0$$

So the value of polynomial is zero

Then polynomial $$p(x)=x^{2}-1$$ for value $$x\pm 1$$ is zero polynomial

Fill in the blanks:
Linear Polynomial Zero of the polynomial
$$x + a$$ $$-a$$
$$x - a$$ _
$$ax + b$$ _
$$ax - b$$ $$\dfrac {b}{a}$$

A polynomial is zero polynomial when $$p(x) =0$$

(1) $$x-a=0$$

Add $$a$$ both sides, we get

$$x-a+a=a$$ $$\Rightarrow x=a $$

So, answer is $$a$$.

(2) $$ax+b=0$$

Add $$-b$$ both sides, we get

$$ax+b-b=-b\Rightarrow ax=-b$$

Divide both sides by $$a$$, we get

$$x=-\dfrac{b}{a}$$

So, answer is $$-\dfrac{b}{a}$$.

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?
$$f(x) = 2x - 1, x = \dfrac {1}{2}, \dfrac {-1}{2}$$

Given polynomial $$2x-1$$ and value $$x=\cfrac{1}{2},-\cfrac{1}{2}$$

$$p(x)=2x-1$$

Replace x by $$\cfrac{1}{2}$$ we get

$$p\left ( \cfrac{1}{2} \right )=2\times \cfrac{1}{2}-1$$

$$\Rightarrow p\left ( \cfrac{1}{2} \right )=1-1=0$$

$$p(x)=2x-1$$

Replace x by $$-\cfrac{1}{2}$$

$$p\left ( -\cfrac{1}{2} \right )=2\times- \cfrac{1}{2}-1$$

$$\Rightarrow p\left (- \cfrac{1}{2} \right )=-1-1=-2$$

Then polynomial $$p(x)=2x-1$$ value zero for value $$x=\cfrac{1}{2}$$ and non zero value for $$x=-\cfrac{1}{2}$$

So polynomial $$p(x)=2x-1$$ value zero polynomial for value $$x=\cfrac{1}{2}$$ and not zero polynomial value for $$x=-\cfrac{1}{2}$$

Verify whether the value of $$x$$ given in each case are the zeroes of the polynomial or not?
$$p(x) = (x - 1)(x + 2); x = -1, -2$$

Given polynomial $$p(x)=(x-1)(x+2)$$

Replace x by -1 we get

$$p(-1)=(-1-1)(-1+2)$$

$$\Rightarrow p(-1)=-2\times 1$$

$$\Rightarrow p(1)=-2$$

Replace x by -2 we get

$$p(-2)=(-2-1)(-2+2)$$

$$\Rightarrow p(-2)=-3\times 0$$

$$\Rightarrow p(-2)=0$$

Then polynomial $$p(x)=(x-1)(x+2)$$ is zero polynomial for value for x=-2 and not zero polynomial for value x=-1

Verify whether the given value of $$x$$ is the zero of the polynomial or not?
$$p(x) = 2x + 1; x = -\dfrac {1}{2}$$

Given polynomial $$p(x)=2x+1$$ and value of $$x=-\cfrac{1}{2}$$

$$p(x)=2x+1$$

Replace $$x$$ by $$-\cfrac{1}{2}$$

$$p\left ( -\cfrac{1}{2} \right )=2\left (- \cfrac{1}{2} \right )+1$$

$$\Rightarrow p\left ( -\cfrac{1}{2} \right )=-1+1$$

$$\Rightarrow p\left (- \cfrac{1}{2} \right )=0$$

The value of polynomial $$p(x)$$ is zero for $$x=-\cfrac{1}{2}$$

Hence, the given value of $$x$$ is the zero of the given polynomial .

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?
$$f(x) = 3x^{2} - 1; x = -\dfrac {1}{\sqrt {3}}, \dfrac {2}{\sqrt {3}}$$

Given polynomial $$p(x)=3x^{2}-1$$ and value $$x=\left ( -\cfrac{1}{\sqrt{3}},\cfrac{2}{\sqrt{3}} \right )$$

$$p(x)=3x^{2}-1$$

Replace x by $$-\cfrac{1}{\sqrt{3}}$$

$$p\left ( -\cfrac{1}{\sqrt{3}} \right )=3\left ( -\cfrac{1}{\sqrt{3}} \right )^{2}-1$$

$$\Rightarrow p\left ( -\cfrac{1}{\sqrt{3}} \right )=1-1=0$$

Replace x by $$\cfrac{2}{\sqrt{3}}$$

$$p\left ( \cfrac{2}{\sqrt{3}} \right )=3\left ( \cfrac{2}{\sqrt{3}} \right )^{2}-1$$

$$\Rightarrow p\left ( \cfrac{2}{\sqrt{3}} \right )=4-1=3$$

Then polynomial $$p(x)=3x^{2}-1$$ is zero for value $$x=\left ( -\cfrac{1}{\sqrt{3}}\right )$$ and non zero value for $$x=\left ( \cfrac{2}{\sqrt{3}} \right )$$

So polynomial $$p(x)=3x^{2}-1$$ is zero polynomial for value $$x=\left ( -\cfrac{1}{\sqrt{3}}\right )$$ and not zero polynomial value for $$x=\left ( \cfrac{2}{\sqrt{3}} \right )$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?
$$p(y) = y^{2}; y = 0$$

Given polynomial $$p(y)=y^{2}$$

Replace y by 0 we get

$$p(0)=(0)^{2}$$

$$\Rightarrow p(0)=0$$

Then polynomial $$p(y)=y^{2}$$ is zero for value y=0

So polynomial $$p(y)=y^{2}$$ is zero polynomial for value y=0

Find the zero of the polynomial in each of the following cases.
$$f(x) = px, p\neq 0$$

Given polynomial $$f(x)=px$$

we know that for zero polynomial f(x)=0

$$px=0$$

$$\cfrac{px}{p}=\cfrac{0}{p}$$

$$\Rightarrow x=0$$ (because $$p\neq 0$$)

Then for value of x=0 the polynomial is zero polynomial

Find $${196}^{2}$$

$${196}^{2}={(200-4)}^{2}$$
$$={200}^{2}-2(200)(4)+{4}^{2}$$
$$=40000-1600+16$$
$$=38416$$

Find the zero of the polynomial in each of the following cases.
$$f(x) = x^{2}$$

Given polynomial $$f(x)=x^{2}$$

We know that a polynomial is zero polynomial when f(x)=0

$$\therefore x^{2}=0$$

$$\Rightarrow x=0$$

So value of x for zero polynomial is 0

Use suitable identities to find the product of :
$$(x - 5)(x - 5)$$

We know $$(x-5)(x-5)=(x-5)^2$$

Now using identity $$(x-y)^{2}=x^{2}-2xy+y^{2}$$

Here $$x=x$$ and $$y=5$$

$$(x-5)^{2}=(x)^{2}-2\times x\times 5+(5)^{2}$$

$$=x^{2}-10x+25$$

If $$2$$ is a zero of the polynomial $$p(x) = 2x^{2} - 3x + 7a$$, find the value of $$a$$

Given polynomial $$p(x)=2x^{2}-3x+7a$$ is zero polynomial if x is 2

Replace x by 2 we get

$$\therefore 2(2)^{2}-3(2)+7a=0$$

$$\Rightarrow 2\times 4-3\times 2+7a=0$$

$$\Rightarrow 8-6+7a=0$$

$$\Rightarrow 2+7a=0$$

Add -2 both sides we get

$$2+7a-2=0-2$$

$$\Rightarrow 7a=-2$$

Divided by 7 both side we get

$$a=-\cfrac{2}{7}$$

So $$a=-\cfrac{2}{7}$$

Find the zero of the polynomial in each of the following cases.
$$f(x) = 2x - 3$$

Given polynomial $$f(x)=2x-3$$

We know that a polynomial is zero polynomial when $$f(x)=0$$.

$$\therefore 2x-3=0$$

Adding $$3$$ both side we get:

$$2x-3+3=3$$

$$2x=3$$

Dividing by $$2$$ both sides, we get:

$$x=\cfrac{3}{2}$$

So value of $$x$$ for zero polynomial is $$\cfrac{3}{2}$$.

Find the zero of the polynomial in each of the following cases.
$$f(x) = px + q, p\neq 0, pq$$ are real numbers

Given polynomial $$f(x)=px+q$$

we know that for zero polynomial f(x)=0

$$px+q=0$$

$$px+q-q=-q$$

$$\Rightarrow px=-q$$

$$x=-\cfrac{q}{p}$$ (because $$p\neq 0$$,pq are real number )

Then for value of x is $$-\cfrac{q}{p}$$ the polynomial is zero polynomial

Find $$407\times 393$$

$$407\times 393=(400+7)(400-7)$$
$$={400}^{2}-{7}^{2}$$
$$=160000-49$$
$$=159951$$

If $$p(t) = t^3 - 1$$, find the values of $$p(1), p(-2).$$

Given: $$p(t)=t^3-1$$
$$p(1)=1^3-1$$

$$=1-1=0$$

$$p(-2)=(-2)^3-1$$

$$=-8-1=-9$$

Find out the degree of the polynomials and the leading coefficients of the polynomials given below:
$$x^{2} - 2x^{3} + 5x^{7} - \dfrac {8}{7}x^{3} - 70x - 8$$

$$x^2-2x^3+5x^7-\dfrac{8}{7}x^3-70x-8$$

Degree (highest power) of the polynomial $$=7$$

Leading coefficient i.e Coefficient of the term with highest degree $$=5$$

Find out the degree of the polynomials and the leading coefficients of the polynomials given below:
$$13x^{3} - x^{13} - 113$$

$$13x^3-x^{13}-113$$

Degree (highest power) of the polynomial $$=13$$

Leading Coefficient i.e coefficient of the term with highest degree$$=-1$$

Classify the following polynomials as monomials, binomials and trinomials:
$$3x^{2}, \,3x + 2, \,x^{2} - 4x + 2, \,x^{5} - 7, \,x^{2} + 3xy + y^{2}, \,s^{2} + 3st - 2t^{2}, \, xy + yz + zx, \,a^{2}b + b^{2}c, \,2l + 2m$$

Monomials: $$3x^{2}$$
Binomials: $$3x + 2, x^{5} - 7, a^{2}b + b^{2}c, 2l + 2m$$.
Trinomials: $$x^{2} - 4x + 2, x^{2} + 3xy + y^{2}, s^{2} + 3st - 2t^{2}$$

Find $$302\times 308$$

$$302\times 308=(300+2)(300+8)$$
$$={300}^{2}+(2+8)(300)+(2)(8)$$
$$=90000+(10\times 300)+16$$
$$=90000+3000+16=93016$$

The zero of the linear polynomial $$ax + b$$ is:

Zero of a polynomial is the value of $$x$$ when value of polynomial is equal to zero.

$$\Rightarrow ax+b=0\\ \Rightarrow x=-\dfrac ba$$

Find $$93\times 104$$

$$93\times 104=(100+(-7))(100+4)$$
$$93\times 104=(100-7)(100+4)$$
$$={100}^{2}+(-7+4)(100)+(-7)(4)$$
$$=10000+(-3)(100)+(-28)$$
$$=10000-300-28$$
$$=10000-328=9672$$

Write the degree of the following polynomial. $$12-x+4x^3$$

Let $$p(x) = 12-x+4x^{3}$$

The degree of a polynomial is the highest power of $$x$$ in its expression.

Constant (non-zero) polynomials, linear polynomials, quadratics, cubics and quartics are polynomials of degree 0, 1, 2 , 3 and 4 respectively.

Highest power of $$x$$ in $$p(x) $$ is $$=3$$

Hence, degree of $$p(x)$$ is $$=3$$

Evaluate the following by using the identity $$(a-b)^2=a^2+b^2-2ab$$ :
$$2.8^{2}$$

$$(a-b)^2=a^2+b^2-2ab$$

$$2.8^2=(3-.02)^2=3^2+0.2^-2\times0.2\times3=7.84$$

Write the degree of the following polynomial:
$$5y+\sqrt{2}$$

Let $$p(y) = 5y+\sqrt2$$

The degree of a polynomial is the highest power of $$y$$ in its expression.

Constant (non-zero) polynomials, linear polynomials, quadratics, cubics and quartics are polynomials of degree 0, 1, 2 , 3 and 4 respectively.

Highest power of $$y$$ in $$p(y) $$ is $$=1$$

Hence Degree $$=1$$

Evaluate the following by using the identities:
$$9.7\times 9.8$$.

Given that, $$9.7\times 9.8$$.

The given expression can be written as ,

$$9.7\times 9.8$$ $$=(10-0.2)(10-0.3)$$.

We know, $$(x+a)(x+b)=x^2+(a+b)x+ab$$.

Then, we get ,

$$9.7\times 9.8$$ $$=(10-0.2)(10-0.3)$$

$$=(10)^2+(-0.2-0.3)10+(-0.2)(-0.3)$$

$$=100+(-0.5)10+0.06$$

$$=100-5+0.06$$

$$=95+0.06$$

$$= 95.06$$.

Hence, the required answer is $$95.06$$.

Find out the following squares by using the identities:
$$(3x + 5)^{2}$$

We have the identity $$(a+b)^2=a^2+2ab+b^2$$

Here $$a=3x, b=5$$

By using this identity, we can solve further as

$$(3x+5)^2=(3x)^2+5^2+2\times 3x\times 5=9x^2+25+30x$$

This is the required answer.

Find out the degree of the polynomials and the leading coefficients of the polynomials given below:
$$-77 + 7x^{2} - x^{7}$$

$$-77+7x^2-x^7$$

Degree (highest power) of the polynomial $$=7$$

Leading Coefficient i.e coefficient of the term with highest degree $$=-1$$

Find out the following squares by using the identities:
$$(a - 5)^{2}$$

We know identity $$(x+y)^2=x^2+2xy+y^2$$

By using this identity we can solve further as

$$(a-5)^2=a^2+5^2-2\times 5\times a=a^2+25-10a$$

This is the required answer.

Find out the degree of the polynomials and the leading coefficients of the polynomials given below:
$$-181 + 0.8y - 8y^{2} + 115y^{3} + y^{8}$$

$$-180+0.8y-8y^2+115y^3+y^8$$

Degree (highest power) of the given polynomial $$=8$$

Leading coefficient i.e coefficient of the term with highest power $$=1$$

Write the degree of $$4-3x^2$$

If $$f(x) = a_{n}x^{n} + a_{n−1}x^{n−1} + ... + a_{2}x^{2} + a_1x + a_0 $$ is a polynomial.

Then the degree of a polynomial is the highest power of $$x$$ in the expression.

Given: $$p(x) = 4-3x^{2}$$

Highest power of $$x$$ in $$p(x) $$ $$=2$$

Hence, the degree of the given polynomial is $$2.$$

Find the zeros of the following polynomials.
$$p(x)=4x-1$$

A polynomial is a function of the form $$f(x) = a_{n}x^{n} + a_{n−1}x^{n−1} + ... + a_{2}x^{2} + a_1x + a_0 $$

where $$a_{n}, a_{n−1} , ... a_{2} ,a_1 , a_0 $$ . are contants

and $$n$$ is a natural number.

To find Zeroes :

$$p(x)=0$$

Given $$p(x)=4x-1$$

$$p(x)=4x-1 =0$$

$$\Rightarrow 4x-1 =0$$

$$\Rightarrow x=\dfrac14$$

Hence, $$x=\dfrac14$$ is Zero of polynomial $$p(x)$$

Find the root of $$x-3=0$$

The roots of $$x-3=0$$ or $$x=3$$
the roots are $$x=3$$

Classify the following polynomial based on their degree.
$$3x^2+2x+1$$

A polynomial is a function of the form $$f(x) = a_{n}x^{n} + a_{n−1}x^{n−1} + ... + a_{2}x^{2} + a_1x + a_0 $$

where $$a_{n}, a_{n−1} , ... a_{2} ,a_1 , a_0 $$ . are contants

and $$n$$ is a natural number.

Let $$p(x) = 3x^{2}+2x+1$$

The degree of a polynomial is the highest power of $$x$$ in its expression.

Constant (non-zero) polynomials, linear polynomials, quadratics, cubics and quartics are polynomials of degree 0, 1, 2 , 3 and 4 respectively.

Highest power of $$x$$ in $$p(x) $$ is $$=2$$

Thus, the degree of $$p(x)$$ is $$2$$.

Hence, it is a quadratic polynomial.

Classify the following polynomial based on their degrees:
$$2x$$

# A polynomial is a function of the form $$f(x) = a_{n}x^{n} + a_{n−1}x^{n−1} + ... + a_{2}x^{2} + a_1x + a_0 $$

where $$a_{n}, a_{n−1} , ... a_{2} ,a_1 , a_0 $$ . are contants

and $$n$$ is a natural number.

Let $$p(x) = 2x$$

The degree of a polynomial is the highest power of $$x$$ in its expression.

Highest power of $$x$$ in $$p(x) $$ is $$=1$$

Thus, the degree of $$p(x)$$ is $$1$$

Hence, $$p(x) = 2x $$ is a Linear polynomial.

Find the degree of given polynomial :$$4x^3-1$$

A polynomial is a function of the form $$f(x) = a_{n}x^{n} + a_{n−1}x^{n−1} + ... + a_{2}x^{2} + a_1x + a_0 $$ .

where $$a_{n}, a_{n−1} , ... a_{2} ,a_1 , a_0 $$ . are contants

and $$n$$ is a natural number.

Let $$p(x) = 4x^{3}-1$$

The degree of a polynomial is the highest power of $$x$$ in its expression.

Constant (non-zero) polynomials, linear polynomials, quadratics, cubics and quartics are polynomials of degree 0, 1, 2 , 3 and 4 respectively.

Highest power of $$x$$ in $$p(x) $$ is $$=3$$

Thus, the degree of $$p(x)$$ is $$3$$

$$p(x) = 4x^{3}-1$$ is a cubic polynomial.

Find the root of −9x=0

The give equation is $$-9x=0$$

Thus the root of $$-9x=0$$ is $$x=0$$.

The above root satisfies the equation (left-hand side $$=$$ right-hand side)

Classify the following polynomial based on their degrees:
$$y+3$$

A polynomial is a function of the form $$f(x) = a_{n}x^{n} + a_{n−1}x^{n−1} + ... + a_{2}x^{2} + a_1x + a_0 $$ .

where $$a_{n}, a_{n−1} , ... a_{2} ,a_1 , a_0 $$ . are contants

and $$n$$ is a natural number.

Let $$p(y) = y+3$$

The degree of a polynomial is the highest power of $$y$$ in its expression.

Now, highest power of $$y$$ in $$p(y) $$ is $$=1$$

Thus, the degree of $$p(y)$$ is $$1$$

Polynomial of degree $$1$$ is a linear polynomial respectively.

Hence, $$p(y) = y+3 $$ is a Linear polynomial.

Classify the following polynomial based on their degrees:
$$4x^3$$

A polynomial is a function of the form $$f(x) = a_{n}x^{n} + a_{n−1}x^{n−1} + ... + a_{2}x^{2} + a_1x + a_0 $$ .

where $$a_{n}, a_{n−1} , ... a_{2} ,a_1 , a_0 $$ . are contants

and $$n$$ is a natural number.

Let $$p(x) = 4x^{3}$$

The degree of a polynomial is the highest power of $$x$$ in its expression.

Highest power of $$x$$ in $$p(x) $$ is $$=3$$

Thus, the degree of $$p(x)$$ is $$3$$

Polynomial of degree $$3$$ is a cubic polynomial.

Hence, $$p(x) = 4x^{3}$$ is a Cubic polynomial.

Verify Whether the following are roots of the polynomial equations indicated against them.
$$x^2-5x+6=0; (x=2, 3)$$

putting values in equation $$x=2$$

$$2^2-5\times2+6=4-10+6=0$$

for $$x=3$$

$$3^2-5\times3+6=9-15+6=0$$

Thus the values of $$x=2,3$$ are the roots of the polynomial equation mentioned above.

Classify the following polynomial based on their degrees:
$$y^2-4$$

A polynomial is a function of the form $$f(x) = a_{n}x^{n} + a_{n−1}x^{n−1} + ... + a_{2}x^{2} + a_1x + a_0 $$ .

where $$a_{n}, a_{n−1} , ... a_{2} ,a_1 , a_0 $$ . are contants

and $$n$$ is a natural number.

Let $$p(y) = y^{2}-4$$

The degree of a polynomial is the highest power of $$y$$ in its expression.

The highest power of $$y$$ in $$p(y) $$ is $$=2$$

Thus, the degree of $$p(y)$$ is $$2$$

Quadratic polynomials is of degree $$2$$.

Hence, $$p(y) = y^{2}-4 $$ is a Quadratic polynomial.

Verify Whether the following are roots of the polynomial equations indicated against them.
$$x^2+4x+3=0; (x=-1, 2)$$

putting the $$x=-1$$

$$(-1)^2+4(-1)+3=0$$

Thus $$x=1$$ is a root of the polynomial

$$x=2$$

$$2^2+4\times 2+3=15$$

$$\therefore x=2$$ is not a root of the polynomial

Find the roots of the following polynomial equations.
$$x-6=0$$

Given that $$x-6=0 \rightarrow x=6$$
$$\therefore x=6$$ is a root of $$x-6=0$$

Classify the following polynomials based on their degree.
(i)$$ p(x)=3$$
(ii) $$p(y)=\frac{5}{2}y^2+1$$
(iii)$$p(x)=2x^3-x^2+4x+1$$
(iv)$$ p(x)=3x^2$$
(v)$$ p(x)=x+3$$
(vi) $$p(x)=-7$$
(vii) $$p(x)=x^3+1$$
(viii) $$p(x)=5x^2-3x+2$$
(ix)$$p(x)=4x$$
(x) $$p(x)=\dfrac {3}{2}$$
(xi) $$p(x)=\sqrt{3}x+1$$
(xii) $$p(y)=y^3+3y$$

$$p(x)=3, p(x)=-7, p(x)=\dfrac{3}{2}$$ are constant polynomials.

$$p(x)=x+3, p(x)=4x, p(x)=\sqrt{3}x+1$$ are linear polynomials, since the highest degree of the variable x is one.

$$p(x)=5x^2-3x+2, p(y)=\frac{5}{2}y^2+1, p(x)=3x^2$$ are quadratic polynomials, since the highest degree of the variable is two.

$$p(x)=2x^3-x^2+4x+1, p(x)=x^3+1, p(y)=y^3+3y$$ are cubic polynomials, since the highest degree of the variable is three.

Find the roots of the following polynomial equations.
$$2x+1=0$$

$$2x+1=0$$

$$\implies2x=-1$$
$$\implies x=\dfrac{-1}{2}$$

$$\therefore$$ Root is $$\dfrac{-1}{2}$$

What number should replace $$n$$ such that $$3(n+6)=(3\times 5)+(3\times 6)$$.

$$3(n+6)=(3\times5)+(3\times6)$$

$$3(n+6)=15+18$$

$$3(n+6)=33$$

$$n+6=11$$

$$n=11-6$$

$$n=5$$

$${(\dfrac {\sqrt {2}}{3}x+2\sqrt {5}y)}^{2} =$$

$$\left(\dfrac{\sqrt{2}}{3}x+2\sqrt{5}y\right)^2$$

We know, $$(a+b)^2=a^2+2ab+b^2$$

$$\Rightarrow$$ $$\left(\dfrac{\sqrt{2}}{3}x\right)^2+2\times \dfrac{\sqrt{2}}{3}x\times 2\sqrt{5}y+(2\sqrt{5}y)^2$$

$$\Rightarrow$$ $$\dfrac{2}{9}x^2+4\dfrac{\sqrt{2}\sqrt{5}}{3}xy+20y^2$$

$$\Rightarrow$$ $$\dfrac{2}{9}x^2+\dfrac{4\sqrt{10}}{3}xy+20y^2$$

Multiplying equation by 9 we get,

$$\Rightarrow$$ $$2x^2+12\sqrt{10}xy+180y^2$$

Determine the degree of the the polynomial.
$$(3x - 2)(2x^3 + 3x^2)$$

$$(3x - 2)(2x^3 + 3x^2)$$

$$=6x^4+9x^3-4x^3-6x^2$$

$$=6x^4+5x^3-6x^2$$

From the above it is clear that the given polynomial is of degree $$4$$.

Solve $$2{y}^{3}+{y}^{2}-2y-1$$

$$\begin{array}{l}2{y^3} + {y^2} - 2y - 1\\ = {y^2}\left( {2y + 1} \right) - 1\left( {2y + 1} \right)\\ = \left( {{y^2} - 1} \right)\left( {2y + 1} \right)\\ = \left( {y - 1} \right)\left( {y + 1} \right)\left( {2y + 1} \right)\end{array}$$

What is the value if a?
$$8=5+2a$$

$$8=5+2a$$

$$\Rightarrow 8-5=2a$$

$$\Rightarrow 3=2a$$

$$\Rightarrow 2a=3$$

$$\Rightarrow a=\dfrac{3}{2}$$

Determine by substitution, if $$7$$ is a root of $$3x - 5 = 16$$.

We substitute $$x=7$$ in LHS side

$$\Rightarrow 3(7)-15=16=RHS $$

$$\therefore $$ 7 is a root of $$3x-5=16$$

Write the degree of each of the following polynomials:
$$\left( i \right)\,\,5{x^3} + 4{x^2} + 7x$$
$$\left( {ii} \right)\,\,4 - {y^2}$$
$$\left( {iii} \right)\,\,5t - \sqrt 7 $$
$$\left( {iv} \right)\,\,3$$

(i) $$5{x^3} + 4{x^2} + 7x$$

Degree $$= 3$$ highest power

(ii) $$4 - {y^2}$$

Degree $$= 2$$

(iii) $$5t=\sqrt7$$ , degree $$=1$$

(iv) $$3$$ , degree $$=0$$

solve:-
$${\left( {a + b} \right)^2} = $$

$${\left(a+b\right)}^{2}=\left(a+b\right)\left(a+b\right)$$

$$=a\left(a+b\right)+b\left(a+b\right)$$

$$={a}^{2}+ab+ba+{b}^{2}$$

$$={a}^{2}+2ab+{b}^{2}$$

Verify that whether $$2$$ is a zero of the polynomial $$x^{3}+4x^{2}-3x-18$$.

Given polynomial: $$f(x)=x^3+4x^2-3x-18$$.

If $$x=2$$ is zero of polynomial, then $$f(2)=0$$.

Then,

$$f(2)=(2)^3+4(2)^2-3( 2)-18$$

$$f(2)=8+16-6-18$$

$$f(2)=24-24= 0$$.

Hence, $$2$$ is zero of the given polynomial.

Therefore, verified.

For $$\dfrac{x^3 + 2x + 1}{5} - \dfrac{7}{2} x^2 - x^6$$, write
i) the degree of the polynomial
ii) the coefficient of $$x^3$$
iii) the coefficient of $$x^6$$
iv) the constant term

The given polynomial is,

$$\dfrac{x^{3}+2x+1}{5}-\dfrac{7}{2}x^{2}-x^{6}$$

$$=\dfrac{1}{5}x^{3}+\dfrac{2}{5}x+\dfrac{1}{5}-\dfrac{7}{2}x^{2}-x^{6}$$

(1) Degree of the polynomial is the Highest degree of its terms, which is $$6$$ in this case (degree of $$x^{6}$$ )

(2) Coefficient of $$x^{3}$$ is $$\dfrac{1}{5}$$

(3) Coefficient of $$x^{6}$$ is $$-1$$

(4) The constant term in the polynomial is $$\dfrac{1}{5}$$

Find the zeroes of polynomial $$p\left( x \right) =6{ x }^{ 2 }-3$$

We have,

$$P\left( x \right)=6{{x}^{2}}-3$$

Zeros of polynomial is

$$ p\left( x \right)=0 $$

$$ 6{{x}^{2}}-3=0 $$

$$ 6{{x}^{2}}=3 $$

$$ {{x}^{2}}=\dfrac{3}{6} $$

$$ {{x}^{2}}=\dfrac{1}{2} $$

$$ x=\pm{\sqrt {\dfrac{1}{2}}} $$

Hence, this is the answer.

If $${(a + b)^2} = 4ab$$ then prove that $$a=b$$

$${\left( {a + b} \right)^2} = 4ab$$

$$ \Rightarrow {a^2} + {b^2} + 2ab = 4ab$$

$$ \Rightarrow {a^2} + {b^2} - 2ab = 0$$

$$ \Rightarrow {\left( {a - b} \right)^2} = 0$$

$$ \Rightarrow a = b$$

Solve $$(a+b)^3-a^3-b^3$$

Given $$(a+b)^3$$$$-a^3-b^3$$

$$=$$ $$(a^3+3a^2b+3ab^2+b^3)-a^3-b^3$$

$$=$$ $$a^3+3a^2b+3ab^2+b^3-a^3-b^3$$

$$=$$ $$3a^2b+3ab^2$$

$$=$$ $$3ab(a+b)$$

Use the identity and expand the following $${(2x+y)}^{2}$$

using ientity $$\rightarrow (a+b)^{2}=a^{2}+b^{2}+2ab$$

$$\therefore (2x+y)^{2}=(2x)^{2}+(y)^{2}+2(2x)(y)$$

$$=4x^{2}+y^{2}+4xy$$

If $${(a + b)^2} = 4ab$$, then prove that $$a=b$$.

$${\left( {a + b} \right)^2} = 4ab$$

$$ {a^2} + {b^2} + 2ab = 4ab$$

$$ {a^2} + {b^2} - 2ab = 0$$

$$ {\left( {a - b} \right)^2} = 0$$

$$ a = b$$

Hence, proved.

Solve:
$${\left( {4a + 36} \right)^2} - {\left( {4a - 36} \right)^2} + 48ab$$

We have,

$${{\left( 4a+36 \right)}^{2}}-{{\left( 4a-36 \right)}^{2}}+48ab$$

$$ ={{\left( 4a+36 \right)}^{2}}-{{\left( 4a-36 \right)}^{2}}+48ab $$

$$ ={{\left( 4a \right)}^{2}}+{{\left( 36 \right)}^{2}}+2\times 4a\times 36-\left[ {{\left( 4a \right)}^{2}}+{{\left( 36 \right)}^{2}}-2\times 4a\times 36 \right]+48ab $$

$$ ={{\left( 4a \right)}^{2}}+{{\left( 36 \right)}^{2}}+2\times 4a\times 36-{{\left( 4a \right)}^{2}}-{{\left( 36 \right)}^{2}}+2\times 4a\times 36+48ab $$

$$ =288a+288a+48ab $$

$$ =576a+48ab $$

$$ =48a\left( 12+b \right) $$

Hence, the answer is $$48a\left( 12+b \right)$$.

The zeroes of the polynomial $$2x+3$$ is:

To find the zeros, equate the given expression to zero,

$$2x+3=0$$

$$2x=-3$$

$$x=\dfrac {-3}{2}$$

$$(a^{2}-b^{2})^{2}=?$$

$${\textbf{Step-1: Use the standard identity }}$$$${\left( {{\textbf{a - b}}} \right)^{\textbf{2}}}{\textbf{ = }}{{\textbf{a}}^{\textbf{2}}}{\textbf{ - 2ab + }}{{\textbf{b}}^{\textbf{2}}}$$

$${\text{Using,}(\text{x - y})^2 = \text{x$^2$-2xy+y$^2$} \text{ where x = a$^2$ and y = b$^2$}}$$

$${\text{Given,}}$$ $${\left( {{{\text{a}}^{{{\text{2}}^{}}}}{\text{ - }}{{\text{b}}^{\text{2}}}} \right)^{\text{2}}}$$$$\text{ = }$$$${{\text{(}}{{\text{a}}^{\text{2}}}{\text{)}}^{\text{2}}}{\text{ - 2(}}{{\text{a}}^{\text{2}}}{\text{)(}}{{\text{b}}^{\text{2}}}{\text{) + (}}{{\text{b}}^{\text{2}}}{{\text{)}}^{\text{2}}}$$

$${\text{ = }}{{\text{a}}^{\text{4}}}{\text{ - 2}}{{\text{a}}^{\text{2}}}{{\text{b}}^{\text{2}}}{\text{ + }}{{\text{b}}^{\text{4}}}$$

$${\textbf{Thus,}}$$$$\boldsymbol{(a^2-b^2) }$$$${\textbf{ = }}{{\textbf{a}}^{\textbf{4}}}{\textbf{ - 2}}{{\textbf{a}}^{\textbf{2}}}{{\textbf{b}}^{\textbf{2}}}{\textbf{ + }}{{\textbf{b}}^{\textbf{4}}}$$

Solve: $$6xy - 4y + 6 - 9x$$

$$6xy-4y+6-9x$$

$$2y(3x-2)-3(3x-2)$$

$$(3x-2)(2y-3)$$

$$\therefore 6xy-4y+6-9x=(3x-2)(2y-3)$$

If $$a-b=5$$ and $$a^2+b^2=53$$, then find the value of $$ab$$.

Given that, $$a - b = 5$$ and $$a^2 + b^2 = 53$$

We know that $$ (a - b)^2 = a^2 + b^2 - 2ab $$

$$\implies (5)^2 = 53 - 2ab$$

$$\implies 25 = 53 - 2ab$$

$$\implies 2ab = 53 - 25$$

$$\implies 2ab = 28$$

$$\implies ab = \dfrac{28}{2}$$

$$\therefore ab = 14 $$ (Ans)

Evaluate
$$(5x+2y)^{2}+(5x-2y)^{2}$$

$$(5x+2y)^2+(5x-2y)^2$$

$$=25x^2+4y^2+20xy+25x^2+4y^2-20xy$$

$$=50x^2+8y^2$$

Solve :
$$4x^2 - 9y^2 $$=0

$$4x^{2}-9y^{2}=0$$

$$\Rightarrow (2x)^{2}-(3y)^{2}=0$$

$$\Rightarrow (2x+3y)(2x-3y)=0$$ $$a^{2}-b^{2}=(a+b)(a-b)$$

$$\Rightarrow (2x+3y) = 0$$ or $$(2x-3y) =0$$

$$\Rightarrow x=\dfrac{-3y}{2} or x = \dfrac{3y}{2}$$

If $$a = 6 - \sqrt 35$$. find the value of $$a^2 + \dfrac{1}{a^2}$$.

$${ a }={ 6 }-\sqrt { 35 } \\ { a }+\frac { 1 }{ a } ={ 6-\sqrt { 35 } }+\frac { { 6+\sqrt { 35 } } }{ (6-\sqrt { 35 } )(6+\sqrt { 35 } ) } \\ =({ 6-\sqrt { 35 } }+\quad { 6 }+\sqrt { 35 } )\\ =12\\ { ({ a }+\dfrac { 1 }{ a } ) }^{ 2 }={ { a }^{ 2 } }+{ \dfrac { 1 }{ { a }^{ 2 } } }+{ 2 }\\ \Rightarrow { { 12 }^{ 2 } }={ a }^{ 2 }+{ \dfrac { 1 }{ { a }^{ 2 } } }+2\\ \Rightarrow { { a }^{ 2 } }+{ \dfrac { 1 }{ { a }^{ 2 } } }={ 142 }$$

Simplify $${a^2} + {b^2} = ?$$

This is derived by the formula of

$${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab\,\,\,\,\And \,\,\,{{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\,\,$$

Then,

$$ {{a}^{2}}+{{b}^{2}}={{\left( a+b \right)}^{2}}-2ab $$

$$ {{a}^{2}}+{{b}^{2}}={{\left( a-b \right)}^{2}}-2ab\,\, $$

Hence, this is the answer.

Expand using identities:
$${\left( {3x - 5y} \right)^2}$$

$$ (3x-5y)^{2} = (3x-5y)(3x-5y) $$

$$ = (3x)^{2}-2.3x.5y+(5y)^{2} $$

$$ = 9x^{2}-30xy+25y^{2} $$

$$ \therefore (3x-5y)^{2}=9x^{2}-30xy+25y^{2} $$

1107375_1134411_ans_68c1a1d146ef4fd19a9f0d3092e68f3c.jpg

$$(a+b)^2=?$$

$${\textbf{Step -1: Simplify the equation to find the value}}{\textbf{.}}$$

$${\left( {a + b} \right)^2}$$

$$ = \left( {a + b} \right)\left( {a + b} \right)$$

$$ = a\left( {a + b} \right) + b\left( {a + b} \right)$$

$$ = {a^2} + ab + ab + {b^2}$$

$$ = {a^2} + 2ab + {b^2}$$

$${\textbf{Hence, the value of }}{\mathbf{\left( {a + b} \right)^2}}{\textbf{ is }}\mathbf{{a^2} + 2ab + {b^2}.}$$

Simplify $$(a^2-b^2)^2$$.

$$(a^{2}-b^{2})^{2}$$

=$${(a+b)(a-b)}^{2}$$

=$$(a+b)^{2}(a-b)^{2}$$.

Solve:
$${\left( {a + b} \right)^2} $$

$${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$$

Write the degree of the following polynomials.
(i) $$p + p^3 + p^7$$
(ii) $$a + a^3 - a^0$$
(iii) $$m + a^4m + a^5m^3 - m^2 - a^4m^7$$

We have,

(i) $$p + p^3 + p^7$$

We know that the maximum number of power of the expression is degree.

So, the degree of above expression $$=7$$

(ii) $$a + a^3 - a^0$$

The degree of above expression $$=3$$

(iii) $$m + a^4m + a^5m^3 - m^2 - a^4m^7$$

The degree of above expression $$=5$$

Hence, this is the answer.

Prove if $${\cot}\theta + \dfrac{1}{{{{\cot }}\theta }} = 2$$ then $${\cot ^2}\theta + \dfrac{1}{{{{\cot }^2}\theta }} = 2$$

$${ { ({ \cot { \theta } }+\dfrac { 1 }{ \cot { \theta } } }) }^{ 2 }=\cot ^{ 2 }{ \theta } +\dfrac { 1 }{ \cot ^{ 2 }{ \theta } } +{ 2 }\times { \cot { \theta } }\times \dfrac { 1 }{ \cot { \theta } }$$

$$ \\ \Rightarrow { 2 }^{ 2 }\quad =\quad \cot ^{ 2 }{ \theta } +\dfrac { 1 }{ \cot ^{ 2 }{ \theta } } +{ 2 }\\ \Rightarrow \cot ^{ 2 }{ \theta } +\dfrac { 1 }{ \cot ^{ 2 }{ \theta } } ={ 2 }$$

Write the numerical coefficients of the terms (other than constants) in each of the following algebraic expressions.
(a) $$5ab^2c$$
(b) $$3 - 4y^2$$
(c) $$-3xyz + 5x^2 - 6$$
(d) $$2(l + b + h)$$

We have,

(a) $$5ab^2c$$

The numerical coefficient of the term above algebra expression

$$=5$$

(b) $$3 - 4y^2$$

The numerical coefficient of the term above algebra expression

$$=-4$$

The numerical coefficient of the term above algebra expression

$$=-3$$ and $$5$$.

(d) $$2(l + b + h)$$

The numerical coefficient of the term above algebra expression

$$=2$$

Hence, this is the answer.

Find $$\left(3x+4y\right)^{2}$$

$$(3x + 4y)^2 $$

$$ = (3x)^2 + 2(3x)(4y) + (4y)^2$$

$$= 9x^2 + 24xy + 16y^2$$

$$[\because (a + b)^2 = a^2 = 2ab + b^2 ]$$

Check whether $$\left(-\dfrac{m}{l}\right)$$ is a zero of the polynomial $$p(x)=lx+m$$

$$p\left(-\dfrac{m}{l}\right)=l\left(-\dfrac{m}{l}\right)+m=-m+m=\boxed{0}$$
Therfore, $$\left(-\dfrac{m}{l}\right) \textbf{ is}$$ a zero of the polynomial.

The degree of $${x^3} - 3{x^2} + 1$$

The highest power of the variable $$x$$ in the given expression is $$3$$.

$$\implies $$ the degree is $$3$$

Solve: $$3x^2-2x+\dfrac 13=0$$

$$3x^2-2x+\dfrac{1}{3}=0$$

$$\Rightarrow 9x^2-6x+1=0$$

$$\Rightarrow (3x)^2-2(3x)(1)+(1)^2=0$$

$$\Rightarrow (3x-1)^2=0$$

$$x=\dfrac{1}{3},\dfrac{1}{3}$$

Find the degree of the given polynomials.
$$x^{o}$$

The degree is the value of the greatest exponent of any expression (except the constant ) in the polynomial.

$$x^0$$

Here the largest exponent of x is 0.

Therefore the degree of polynomial is 0.

Simplify $${\left( {2x + \dfrac{1}{{3y}}} \right)^2} - {\left( {2x - \dfrac{1}{{3y}}} \right)^2}$$

$$\left(2x+\dfrac{1}{3y}\right)^2-\left(2x-\dfrac{1}{3y}\right)^2$$

$$\left\{\therefore (a+b)^2=a^2+b^2+2ab, (a-b)^2=a^2+b^2-2ab\right\}$$.

$$\left[(2x)^2+\left(\dfrac{1}{3y}\right)^2+2\times 2x\times \dfrac{1}{3y}\right]-\left[(2x)^2+\left(\dfrac{1}{3y}\right)^2-2\times 2x\times \dfrac{1}{3y}\right]$$

$$\Rightarrow \dfrac{8x}{3y}$$

Solve : $$x^2+x-12$$

$$x^2+x-12=0$$

$$(x+4)(x-3)=0$$

$$x=3,-4$$

Solve: $$ (205)^2 - (195)^2 $$

$$(205)^2-(195)^2$$

$$=(205-195)(205+195)$$ ...... using $$A^2-B^2=(A-B)(A+B)$$

$$=10\times 400=4000$$

Find the zero of the polynomial in each of the following
$$p(x)=3x-2$$

$$p(x)=3x-2$$

$$\Rightarrow 3x-2=0$$

$$\Rightarrow 3x=2$$

$$\Rightarrow x=\dfrac{2}{3}$$

$$\dfrac{2}{3}$$ is the zero of the given polynomial.

1195837_1263989_ans_fb5bbfb7bfc44f31a5ba19256594ab69.jpg

Solve : $$(2xy+5y)^2$$

Given expression is $$(2xy+5y)^2$$

We know that, $$(a+b)^2=a^2+2ab+b^2$$

Hence, $$ (2xy+5y)^2=(2xy)^2+2(2xy)(5y)+(5y)^2$$

$$\Rightarrow 4x^2y^2+20xy^2+25y^2$$

Hence, $$(2xy+5y)^2=4x^2y^2+20xy^2+25y^2$$.

Solve
$$4u^2+8u=0$$

$$4u^2+8u=0$$

$$4u(u+2)=0$$

$$u=0,-2$$

Find the zero of the polynomial
$$p(x)=x-5$$

$$p(x)=x-5$$

$$\Rightarrow x-5=0$$

$$\Rightarrow x=5$$ is the zero of the polynomial.

Select a suitable identity and find the product of $$(m^{2}-n^{2})(m^{2}+n^{2})$$

Given: $$\left( {m}^{2} - {n}^{2} \right) \left( {m}^{2} + {n}^{2} \right)$$

Using identity: $$\left( a - b \right) \left( a + b \right) = {a}^{2} - {b}^{2}$$

Therefore, $$\left( {m}^{2} - {n}^{2} \right) \left( {m}^{2} + {n}^{2} \right)$$ $$= {\left( {m}^{2} \right)}^{2} - {\left( {n}^{2} \right)}^{2}$$

$$= {m}^{4} - {n}^{4}$$

Find the degree of the given polynomials.
$$2p-\sqrt{7}$$

The degree is the value of the greatest exponent of variable in any expression (except the constant ) in the polynomial.

Here largest exponent of p is 1.

Therefore, the degree of the polynomial is 1.

Write a polynomial of degree 5 using variable x.

Polynomial of degree 5 example is

$$ 4x^{5}+2x^{4}+3x^{3}+x^{2}+1$$

degree = 5

1210585_1305304_ans_91715bb7df1e4764aa5311424c3c7f9e.jpg

select a suitable identity and find the following products
$$(7d-9e)(7d-9e)$$

$$\left( 7d - 9e \right) \left( 7d - 9e \right)$$

$$= {\left( 7d - 9e \right)}^{2}$$

$$= {\left( 7d \right)}^{2} + {\left( 9e \right)}^{2} - 2 \left( 7d \right) \left( 9e \right) \quad \left[ \text{Using identity: } {\left( a - b \right)}^{2} = {a}^{2} + {b}^{2} -2ab \right]$$

$$= 49 {d}^{2} + 81 {e}^{2} - 126de$$

Evaluate the value of $$\left(101\right)^{2}$$by using suitable identity

$$(101)^2$$

$$=(100+1)^2$$

Using $$(a+b)^2=a^2+b^2+2ab$$

$$(100+1)^2=100^2+1^2+2\times 100\times 1$$

$$=10000+1+200$$

$$=10000+201$$

$$=10201$$.

1206427_1319898_ans_5a23e36b29cf4068ac2aa832ab326cf6.jpg

Find the degree of the given polynomials.
$$\sqrt{2}m^{10}-7$$

The degree is the value of the greatest exponent of any expression (except the constant ) in the polynomial .

Here largest exponent of m is 10.

Therefore, the degree of polynomial is 10.

Find the degree of the given polynomials.
$$x^{2}$$

The degree is the value of the greatest exponent of any expression (except the constant ) in the polynomial .

Here largest exponent of x is 2.

Therefore, the degree of polynomial is 2.

Find the degree of the given polynomials.
$$7y-y^{3}+y^{5}$$

The degree is the value of the greatest exponent of any expression (except the constant ) in the polynomial .

Here largest exponent is of $$y$$ which is 5.

Therefore, the degree of polynomial is $$5$$.

select a suitable identity and find the following products
$$(3k+4l)(3k+4l)$$

$$\left( 3k + 4l \right) \left( 3k + 4l \right)$$

$$= {\left( 3k + 4l \right)}^{2}$$

$$= {\left( 3k \right)}^{2} + {\left( 4l \right)}^{2} + 2 \left( 3k \right) \left( 4l \right) \quad \left[ \text{Using identity: } {\left( a + b \right)}^{2} = {a}^{2} + {b}^{2} + 2ab \right]$$

$$= 9 {k}^{2} + 16 {l}^{2} + 24 kl$$

select a suitable identity and find the following products
$$(2b-a)(2b+c)$$

$$\left( 2b - a \right) \left( 2b + c \right)$$

$$= 2b \cdot 2b - a \cdot 2b + c \cdot 2b - a \cdot c$$

$$= 4 {b}^{2} - 2ab + 2bc - ac$$

If $$P(x) = 5x^7-6x^5+7x-6$$ then degree of $$P(x)$$?

$$The\ degree\ of\ a\ polynomial\ is\ maximum\ power\ of\ variable$$

Degree of P(x) is 7.

Write the highest degree of $$2\dfrac{2}{3}{x}^{3}-5{x}^{2}+3x+2$$

The highest power of the polynomial is called degree of the polynomial.

Highest power is $$3$$

select a suitable identity and find the following products
$$(kl-mn)(kl+mn)$$

$$\left( kl - mn \right) \left( kl + mn \right)$$

Using identity: $$\left( a - b \right) \left( a + b \right) = {a}^{2} - {b}^{2}$$

Therefore,

$$\left( kl - mn \right) \left( kl + mn \right)$$

$$= {\left( kl \right)}^{2} - {\left( mn \right)}^{2}$$

$$= {k}^{2}{l}^{2} - {m}^{2}{n}^{2}$$

select a suitable identity and find the following products
$$(6x+5)(6x+6)$$

$$\left( 6x + 5 \right) \left( 6x + 6 \right)$$

$$= \left( 6x \right) \left( 6x \right) + 5 \left( 6x \right) + 6 \left( 6x \right) + 6 \cdot 5$$

$$= 36 {x}^{2} + 30x + 36x + 30$$

$$= 36 {x}^{2} + 66x + 30$$

Prove that :
$$(3x-2y)^{2}+24xy=(3x+2y)^{2}$$

To prove: $$(3x-2y)^{2}+24xy=(3x+2y)^{2}$$

On solving LHS we get

$$(3x-2y)^{2}+24xy$$

$$= (3x)^{2}+(2y)^{2}-2\times 3x\times 2y+24xy$$

$$=9x^{2}+4y^{2}-12xy+24xy$$

$$= 9x^{2}+4y^{2}+12xy$$

$$= (3x)^{2}+(2y)^{2}+2\times 3x\times 2y$$

$$= (3x+2y)^{2}$$

$$= RHS$$

Hence, proved.

Solve:
$$\dfrac{9x}{8}+1=10$$

$$\dfrac{9x}{8}=10-1$$

$$\Rightarrow 9x=9\times 8$$

$$\Rightarrow x=\dfrac{9\times 8}{9}$$

$$\therefore x=8$$

If $$8+2\sqrt{15}=(a+b)^{2}, $$ Find a and b.

Let$$(a+b)^{2}=8+2\sqrt{15}$$

$$(a+b)^{2}=5+3+2\sqrt{3}\sqrt{5}$$

$$(a+b)^{2}=(\sqrt{5}+\sqrt{3})^{2}$$

on comparing

$$a=\sqrt{5} $$ &$$b=\sqrt{3}$$

1206574_1359349_ans_10b114bdf95d4af7850d69622fcc2bfd.JPG

select a suitable identity and find the following products
$$(3t+9s)(3t-9s)$$

$$\left( 3t + 9s \right) \left( 3t - 9s \right)$$

Using identity: $$\left( a + b \right) \left( a - b \right) = {a}^{2} - {b}^{2}$$

Therefore,

$$\left( 3t + 9s \right) \left( 3t - 9s \right)$$

$$= {\left( 3t \right)}^{2} - {\left( 9s \right)}^{2}$$

$$= 9{t}^{2} - 81 {s}^{2}$$

Write the degree of $$x$$ in $$x^{3}-3.$$

In the polynomial $$x^{3}-3,$$ the highest power of the variable $$x$$ is $$3.$$ Hence, the degree of the polynomial is $$3.$$

Find the degree of the polynomial $${ x }^{ 5 }-{ x }^{ 4 }-x+5$$

We have,

$$x^5-x^4-x+5$$

Hence, the degree of the polynomial is $$5$$.

Solve: $$x+5=2x+3$$

given, $$x+5=2x+3$$

$$\Rightarrow\,x+5-2x-3=0$$

$$\Rightarrow\,-x+2=0$$

$$\Rightarrow\,-x=-2$$

$$\therefore\,x=2$$

Verify whether the following are zeroes of the polynomial, indicated against them.
$$p\left( x \right) ={ x }^{ 2 }-1,x=1,-1$$

$$p(x)=x^2-1$$

$$x^2-1=0$$

$$x^2=1$$

So $$x=\pm 1$$

$$\therefore x=1, -1$$ are the roots of $$p(x)$$.

1209782_1461045_ans_7dcaa5ea2e5b47d29ebf25e410f2f8a4.jpg

Verify whether the following are zeroes of the polynomial, indicated against them.
$$p\left( x \right) ={ x }^{ 2 },x=0$$

$$p(x)=x^2$$

$$x^2=0$$

$$x=0$$

So $$x=0$$ is the root of the equation.

1209781_1461050_ans_9816498a574f4a6080c4e991b770c18e.jpg

Find the zeros of the polynomial $${ 2x }^{ 2 }+{ 5x }^{ 2 }+2x.$$

$$2x^{2}+5x^{2}+2x=7x^{2}+2x$$

$$=x(7x+2)$$ $$7x+2=0, x=-\frac{2}{7}$$

$$\therefore $$ zeros of $$2x^{2}+5x^{2}+2x$$ are $$0,\frac{-2}{7}$$

Solve:$$8x-9=10$$

given, $$8x+9=10$$

$$\Rightarrow\,8x+9-9=10-9$$

$$\Rightarrow\,8x=1$$

$$\Rightarrow\,x=\dfrac{1}{8}$$

Find the zeroes of the polynomial:
$$3x^2-x-4$$.

Now,

$$3x^2-x-4$$

$$=3x^2-4x+3x-4=0$$

$$=x(3x-4)+1(3x-4)=0$$

$$=(3x-4)(x+1)=0$$.

So the zeroes of the polynomial are $$x=\dfrac{4}{3}$$ and $$x=-1$$.

Verify whether the following are zeroes of the polynomial, indicated against them.
$$p\left( x \right) =3{ x }^{ 2 }-1,x=-\dfrac { 1 }{ \sqrt { 3 } } ,\dfrac { 1 }{ \sqrt { 3 } } $$

$$p(x)=3x^2-1$$

So $$3x^2-1=0$$

$$3x^2=1$$

$$\Rightarrow x^2=\dfrac{1}{3}$$

$$\Rightarrow x=\pm \dfrac{1}{\sqrt{3}}$$

Roots $$=\dfrac{1}{\sqrt{3}}, \dfrac{-1}{\sqrt{3}}$$.

1209768_1461055_ans_abded9d9c4f24b17bde4a44b7e927b68.jpg

Verify whether the following are zeroes of the polynomial, indicated against them.
$$p\left( x \right) =3x+1,x=-\dfrac { 1 }{ 3 } $$

$$p(x)=3x+1$$

$$3x+1=0$$

$$3x=-1$$

$$x=\dfrac{-1}{3}$$

So $$x=\dfrac{-1}{3}$$ is the root of the equation.

Determine the degree of the following polynomial.
$$-\dfrac{1}{2}x+3$$.

1678623_1715887_ans_c1c526d60c1241c194b633cfebb82f86.jpg

Identify constant, linear, quadratic, cubic and quartic polynomial from the following.
$$-13$$.

$$-13$$ is a constant polynomial because it has a degree of $$0$$

Find the zero of the polynomial $$p(x)=x-5$$.

Given polynomial $$p(x)=x-5$$.

To get zeroes of the polynomial equate the polynomial to zero.

$$\implies p(x)=0$$

$$\implies x-5=0$$

$$\implies x=5$$.

Therefore, $$5$$ is the zero of polynomial $$p(x)=x-5$$.

$$p(x)=x^2+3x+4$$ Find $$p(3)$$

$$p(x)=x^2+3x+4\\p(3)=3^2+3(3)+4\\p(3)=9+9+4=22$$

Verify whether the following are zeroes of the polynomial, indicated against them.
$$p\left( x \right) =5x-\pi ,x=\dfrac { \pi }{ 5 } $$

$$p(x)=5x-\pi$$

$$5x-\pi =0$$

$$5x=\pi$$

$$x=\dfrac{\pi}{5}=$$Root.

1209764_1461060_ans_83b10a554dfa43948c1672b027bc28e1.jpg

Find $$4{ x }^{ 2 }{ y }^{ 2 }+\dfrac { 1 }{ 4{ x }^{ 2 }{ y }^{ 2 } } ,$$ if $$\left( 2xy+\dfrac { 1 }{ 2xy } \right) =1.6.$$

$$\left(2xy+\dfrac{1}{2xy}\right)^2=(2xy)^2+\dfrac{1}{(2xy)^2}+2\dfrac{1}{2xy}\cdot 2xy$$

$$\Rightarrow (1.6)^2=4x^2y^2+\dfrac{1}{4x^2y^2}+2$$

$$\Rightarrow 2.56-2=4x^2y^2+\dfrac{1}{4x^2y^2}$$

So $$4x^2y^2+\dfrac{1}{4x^2y^2}=0.56$$.

1209734_1461375_ans_5b990c81ce7c407b9543fe4a68147b5f.jpg

If $$x+\dfrac{1}{x}=4$$, find the value of
(i) $$x^{2}+\dfrac{1}{x^{2}}$$
(ii) $$x^{4}+\dfrac{1}{x^{4}}$$

$$\textbf{Step – 1: Find the required values. }$$

$$\text{Given, }x+\dfrac{1}{x}=4........(1)$$

$$\text{We know, }$$

$$\Rightarrow\left(x+\dfrac{1}{x}\right)^2=x^2+\dfrac{1}{x^2}+2$$

$$\Rightarrow\left(4\right)^2=x^2+\dfrac{1}{x^2}+2$$ $$\textbf{[From (1)]}$$

$$\Rightarrow 16=x^2+\dfrac{1}{x^2}+2$$

$$\Rightarrow x^2+\dfrac{1}{x^2}=16-2$$

$$\Rightarrow x^2+\dfrac{1}{x^2}=14........(2)$$

$$\textbf{Step – 2: Find value of the square of }\mathbf{ x^2+\dfrac{1}{x^2}}$$

$$\text{Again, }$$

$$\Rightarrow\left(x^2+\dfrac{1}{x^2}\right)^2=\left(x^2\right)^2+\dfrac{1}{\left(x^2\right)^2}+2$$

$$\Rightarrow 14^2=x^4+\dfrac{1}{x^4}+2$$ $$\textbf{[From (2)]}$$

$$\Rightarrow x^4+\dfrac{1}{x^4}=196-2=194$$

$$\textbf{Hence, the required values are (i) }\mathbf{x^2+\dfrac{1}{x^2}=14, }$$ $$\textbf{(ii) }\mathbf{x^4+\dfrac{1}{x^4}=194.}$$

Verify whether the following are zeroes of the polynomial, indicated against them:
$$p\left( x \right) =2x+1,x=\dfrac { 1 }{ 2 } $$.

Given, $$p(x)=2x+1$$.

We know, $$a$$ is a root of $$f(x)$$, only if $$f(a)=0$$.

Here,

$$p(x)=0$$

$$\implies$$ $$2x+1=0$$

$$\implies$$ $$2x=-1$$

$$\implies$$ $$x=\dfrac{-1}{2}$$, that is, $$x=\dfrac{1}{2}$$ is not the zero of the given polynomial.

To verify this, we find $$p(\dfrac{1}{2})$$.

If $$p(\dfrac{1}{2})=0$$, then $$x=\dfrac{1}{2}$$ is a zero of the given polynomial.

That is, $$p(\dfrac{1}{2})$$ $$=2(\dfrac{1}{2})+1=1+1=2\ne0$$.

Hence, proved that the given $$x$$ is not a zero of the given polynomial.

Expand :-$$(ax+by)^{2}$$

$$(ax+by)^2\\ Using \, \, (a+b)^2=a^2+2ab+b^2\\=(ax)^2+2(ax)(by)+(by)^2\\=a^2+x^2+2abxy+b^2y^2$$

Verify whether the following are zeroes of the polynomial, indicated against them.
$$p\left( x \right) =lx+m,x=-\dfrac { m }{ l } $$

Given, $$p(x)=lx+m$$.

We know, $$a$$ is a root of $$f(x)$$, only if $$f(a)=0$$.

Here,

$$p(x)=0$$

$$\implies$$ $$lx+m=0$$

$$\implies$$ $$lx=-m$$

$$\implies$$ $$x=\dfrac{-m}{l}$$, that is, $$x=-\dfrac{m}{l}$$ is the zero of the given polynomial.

To verify this, we find $$p(-\dfrac{m}{l})$$.

If $$p(-\dfrac{m}{l})=0$$, then$$x=-\dfrac{m}{l}$$ is a zero of the given polynomial.

That is, $$p(-\dfrac{m}{l})$$ $$=l(-\dfrac{m}{l})+m=-m+m=0$$.

Hence, proved that the given $$x$$ is a zero of the given polynomial.

Write the degree of each of the following polynomials:
$$3x - 15$$

The degree $$3x - 15$$ is $$1$$
$$3x$$ is the term which has the highest degree.

Write down the degree of following polynomials in x:$$1-x^2$$

The component of the term $$1-x^2=2$$
$$\therefore$$ the degree of polynomial $$1-x^2=2$$

Determine the degree of the following polynomial.
$$-8$$.

1678626_1715888_ans_46268f1dbd914ca0a28deb10b1ab559c.jpg

Write the degree of the following polynomials:
$$\dfrac{2}{5}x^3-7x^2-\dfrac{1}{2}x+3$$

Degree is 3, as it is the highest power of $$x$$

Write the degree of the polynomial $$ P(x)=2 x^{2}-x^{3}+5 $$.

The degree of the polynomial is the highest power in the exponent of its variable terms, therefore the degree of $$ P(x)=2 x^{2}-x^{3}+5 $$ is $$3$$.

Write the degree of the polynomial $$f(x)=x^2-3x^3+2$$.

The degree of polynomials in one variable is the highest power of the variable in the algebraic expression.

In the given polynomial :$$f(x)=x^2-3x^3+2$$

The degree of the equation is $$3$$ .i.e. the highest power of the variable in the equation.

For each of the following monomials , write its degree :
$$7y$$

The degree of $$7y$$ is $$1$$ .

The expression $$13+90$$ is a _____

$$\bullet$$ The expression $$13 + 90=103$$, which is a constant.
$$\textbf{Therefore, the expression 13 + 90 is a constant.}$$

Write the degree of each polynomial given below:
$$y-6y^2 +5y^8$$

$$y-6y^2 +5y^8$$

Degree $$=8$$ [$$\because$$ highest power of $$y$$ is $$8$$]

Write the degree of the polynomial for the following .
$$ ax^{7} + bx^{9} $$ (a,b are constant.)

The highest power of the variable in a polynomial of one variable is called the degree of the polynomial . Also, the highest sum of the powers of the variables in each term of the polynomial in more than one variable is the degree of the polynomial
The degree of the polynomial $$ ax^{7} + bx^{9} $$ is $$9$$

Write the degree of the given polynomial .
$$x^{0}$$

Write the degree of the given polynomial .
$$x^{2}$$

The highest power of the variable in a polynomial of one variable is called the degree of the polynomial . Therefore degree of the polynomial $$x^{2}$$ is $$2$$

Write the degree of each polynomial given below:
$$x\ y\ z-3$$

$$x\ y\ z-3$$

Degree $$=3$$ [$$\because$$ the variable is $$xyz=x^1y^1z^1$$. So, $$1+1+1=3$$]

Write the degree of each polynomial given below:
$$xy+yz^2 -zx^3$$

Degree $$=4$$ [$$\because$$ the highest power variable is $$zx^3=z^1x^3$$. So, $$1+3=4$$]

Write the degree of the following polynomial:
$$ 3 $$.

The highest power of the variable in a polynomial in one variable is called the degree of the polynomial.

Here, in the given polynomial is a constant polynomial $$ 3 $$, that is $$3=3x^0$$, the highest power of the variable $$x$$ is $$0$$.

$$\therefore$$ The degree of the given polynomial is $$0$$.

Write the degree of the polynomial for the following .
7

The highest power of the variable in polynomial in one variable is called the degree of the polynomial .
The degree of the polynomial $$7=7\times x^0=7x^0$$ is 0.

Write the degree of the given polynomial .$$\sqrt{5}$$

The highest power of the variable in a polynomial of variable is called the degree of the polynomial .
$$\sqrt{5} = \sqrt{5} \times x^0 \\= \sqrt{5}x^{0}$$
Hence the degree of the polynomial $$\sqrt{5}$$ is $$0$$

Write the degree of the following polynomial:
$$3 + 4t^{2}$$.

The highest power of the variable in a polynomial in one variable is called the degree of the polynomial.

Here, in the given polynomial $$3 + 4t^{2}$$, the highest power of the variable $$t$$ is $$2$$.

$$\therefore$$ The degree of the given polynomial is $$2$$.

Evaluate:
$$(3x-4y)(3x+4y)(9x^2+16y^2)$$ is equal to $$81x^4-256y^4$$.
If true then enter $$1$$ and if false then enter $$0$$.

Given, $$ (3x-4y)(3x+4y)(9x^2+16y^2) $$.

We know, $$(a+b)(a-b)$$ $$=(a^{2}-b^{2})$$.

Multiply by using direct method, we get,

$$ (3x-4y)(3x+4y)(9x^2+16y^2) $$ $$ = [(3x)^2-(4y)^2](9x^2+16y^2)$$
$$ = (9x^2-16y^2)(9x^2+16y^2)$$ $$ = (9x^2+16y^2)(9x^2-16y^2)$$.

Now, by using formula $$(a^{2}-b^{2})=(a+b)(a-b)$$, we get,

$$ = ((9x^2)^2-(16y^2)^2)$$
$$ = 81x^4-256y^4$$.

Hence, the statement is true.

Therefore, $$1$$ is the correct answer.

Evaluate:
$$(3-2x)(3+2x)(9+4x^2)$$ is equal to $$81-16x^4$$.
If true then enter $$1$$ and if false then enter $$0$$.

Given, $$ (3-2x)(3+2x)(9+4x^2) $$.

We know, $$(a+b)(a-b)$$ $$=(a^{2}-b^{2})$$.

Multiply by using direct method, we get,

$$ (3-2x)(3+2x)(9+4x^2) $$ $$ = [(3)^2-(2x)^2](9+4x^2)$$
$$ = (9-4x^2)(9+4x^2)$$ $$ = (9+4x^2)(9-4x^2)$$.

Now, by using formula $$(a^{2}-b^{2})=(a+b)(a-b)$$, we get,

$$ = ((9)^2-(4x^2)^2)$$
$$ = 81-16x^4$$.

Hence, the statement is true.

Therefore, $$1$$ is the correct answer.

Evaluate:
$$(a+b)(a-b)(a^2+b^2)$$ is $$a^4-b^4$$.
If true, then enter $$1$$ and if false, then enter $$0$$.

Given, $$ (a+b)(a-b)(a^{ 2 }+b^2) $$.

We know, $$(a+b)(a-b)$$ $$=(a^{2}-b^{2})$$.

Multiply by using direct method, we get,
$$ (a+b)(a-b)(a^{ 2 }+b^2) = [a^2-b^2](a^{ 2 }+b^2)$$
$$ = (a^{ 2 }+b^2)(a^{ 2 }-b^2)$$.

Now, by using formula $$(a^{2}-b^{2})=(a+b)(a-b)$$, we get,

$$ = ((a^{ 2 })^2-(b^2)^2)$$
$$ = a^{ 4 }-b^4$$.

Hence, the statement is true.

Therefore, $$1$$ is the correct answer.

Write the degree of each polynomial given below:
$$ x^2 - 6x^3 + 8 $$

Degree of a polynomial is the highest degree of the degree of all its terms.

Degree of $$ {x}^{2} = 2 $$
Degree of $$ - 6{x}^{3} = 3 $$
Degree of $$ 8 = 0 $$

Hence, degree of the polynomial $$ {x}^{2} - 6{x}^{3} + 8 $$ is $$ 3 $$.

Evaluate:
$$(2a-b)(2a+b)(4a^2+b^2)$$ is $$16a^4-b^4$$.
If true, then enter $$1$$ and if false, then enter $$0$$.

Given, $$ (2a-b)(2a+b)(4a^{ 2 }+b^2) $$.

We know, $$(a+b)(a-b)$$ $$=(a^{2}-b^{2})$$.

Multiply by using direct method, we get,
$$ (2a-b)(2a+b)(4a^{ 2 }+b^2) = [(2a)^2-b^2](4a^{ 2 }+b^2)$$
$$ = (4a^{ 2 }-b^2)(4a^{ 2 }+b^2)$$ $$ = (4a^{ 2 }+b^2)(4a^{ 2 }-b^2)$$.

Now, by using formula $$(a^{2}-b^{2})=(a+b)(a-b)$$, we get,

$$ = (((4a)^{ 2 })^2-(b^2)^2)$$
$$ = 16a^{ 4 }-b^4$$.

Hence, the statement is true.

Therefore, $$1$$ is the correct answer.

Evaluate using expansion of $$(a+b)^2$$ or $$(a-b)^2$$:
$$(45)^2$$

$$ {45}^{2} = {(40 + 5)}^{2} $$
It is the form of $$ {(a+b)}^{2} $$, where $$ a = 40, b = 5 $$
Applying the formula $$ { (a+b) }^{ 2 } = {a}^{2} + { b }^{ 2 } + 2ab $$
$$ {45}^{2} = {(40 + 5)}^{2} $$
$$= {40}^{2} + { 5 }^{ 2 } + 2\times 40 \times 5 $$
$$= 1600 + 25 + 400$$
$$ = 2025 $$

Evaluate using expansion of $$(a+b)^2$$ or $$(a-b)^2$$:
$$(20.7)^2$$ is 428.49
If true then enter $$1$$ and if false then enter $$0$$

By using formula $$(a+b)^{2}=a^{2}+2ab+b^{2}$$
$${ 20.7 }^{ 2 }=({ 20+0.7 })^{ 2 }$$
$${ 20.7 }^{ 2 }=({ 20 })^{ 2 }+{ 0.7 }^{ 2 }+2*0.7*20$$
$${ 20.7 }^{ 2 }=400+0.49+28$$
$${ 20.7 }^{ 2 }=428.49$$

If $$1$$ is the zero of $$f(x)=kx^2-3kx+3k-1$$ then the value(s) of $$k$$ is

$$f(x)=kx^2-3kx+3k-1$$
If $$1$$ is the zero of $$f(x)$$, then $$f(1)=0$$
Thus,
$$f(1)=0$$
$$=>k(1)^2-3k(1)+3(1)-1=0$$
$$=>k-3k+3-1=0$$
$$=>-2k+2=0$$
$$=>-2k=-2$$
$$=>k=1$$

State whether True or False: 0 for true, 1 for false
$$\displaystyle (2\sqrt{3}+3\sqrt{2})^{2} = 12+ 18 + 12\sqrt{6} = 30+ 12\sqrt{6}$$

Given $$(2{ \sqrt { 3 } +3\sqrt { 2 } ) }^{ 2 }$$
On squaring we get,
$$ 4\times 3+9\times 2+12\sqrt { 6 }$$
$$=30+12 \sqrt {6}$$

Evaluate the following by using identities:
$$(97)^2$$

$$(97)^2=(100-3)^2$$
Using identity,$$ (a-b)^2=a^2-2ab-b^2$$
$$=(100)^2-2\times 100\times 3+(3)^2$$
$$=10000-600+9=9409$$

If $$3$$ is the zero of $$f(x)=x^4-x^3-8x^2+kx+12$$ then the value of $$k$$ is equal to

$$f(x)=f(x)=x^4-x^3-8x^2+kx+12$$
If $$3$$ is the zero of $$f(x)$$,then,
$$f(3)=0$$
$$=3^4-3^3-8(3)^2+k(3)+12$$
$$=81-27-72+3k+12$$
$$=93-99+3k$$
$$=>3k=6$$
$$=>k=2$$

If $$g(x)=\cfrac{{x}^{3}-ax}{4}$$ and $$g(2)=\cfrac{1}{2}$$, what is the value of $$g(4)$$?

$$g(2)=\cfrac 12$$ and $$g(2) = \cfrac{{(2)}^{2}-a(2)}{4}$$
$$\Rightarrow 8-2a=2$$

$$\Rightarrow 2a=6$$

$$\Rightarrow a=3$$

$$\Rightarrow g(x)=\cfrac{{x}^{3}-3x}{4}$$

$$g(4)=\cfrac{{(4)}^{3}-3(4)}{4}=\cfrac{4({4}^{2}-3(1))}{4}=\cfrac{16-3}{1}=13$$

Find $$p(0), p(1)$$ and $$p(2)$$ for each of the following polynomials:
(i) $$p(y)=y^2-y+1$$
(ii) $$p(t)=2+t+2t^2-t^3$$
(iii) $$p(x)=x^3$$
(iv) $$p(x)=(x-1)(x+1)$$

(i) $$p(y)=y^{2}-y+1$$

$$p(0)=(0)^{2}-(0)+1=0+0+1=1$$

$$p(1)=(1)^{2}-(1)+1=1-1+1=1$$

$$p(2)=(2)^{2}-(2)+1=4-2+1=3$$

(ii) $$p(t)=2+t+2t^{2}-t^{3}$$

$$p(0)=2+(0)+2(0)^{2}-t^{3}=2+0+0-0=2$$

$$p(1)=2+(1)+2(2)^{2}-(1)^{3}=2+1+2-1=4$$

$$p(2)=2+(2)+2(2)^{2}-(2)^{3}=2+2+8-8=4$$

(iii) $$p(x)=x^{3}$$

$$p(0)=(0)^{3}=0$$

$$p(1)=(1)^{3}=1$$

$$p(2)=(2)^{3}=8$$

(iv) $$p(x)=(x-1)(x+1)$$

$$p(0)=(0-1)(0+1)=(-1)(1)=-1$$

$$p(1)=(1-1)(1+1)=(0)(2)=0$$

$$p(2)=(2-1)(2+1)=(1)(3)=3$$

Find the value of the polynomial $$5x-4x^2+3$$ at
(i) $$x=0$$
(ii) $$x=-1$$
(iii) $$x=2$$

Given polynomial $$5x-4x^{2}+3$$

(i) If $$x=0$$

Then $$5(0)-4(0)^{2}+3= 0-0+3= 3$$

(ii) If $$x=-1$$

Then $$5(-1)-4(-1)^{2}+3=- 5-4+3=-6 $$

(iii) If $$x=0$$

Then $$5(2)-4(2)^{2}+3=1 0-16+3=- 3$$

Find the zero of the polynomial in each of the following cases:
(i) $$p(x)=x+5$$
(ii) $$p(x)=x-5$$
(iii) $$p(x)=2x+5$$
(iv) $$p(x)=3x-2$$
(v) $$p(x)=3x$$
(vi) $$p(x)=ax, a\neq 0$$
(vii) $$p(x)=cx+d, c\neq 0, c, d$$ are real numbers.

To find zero of the polynomial, $$p(x)=0$$

$$(i)$$ If $$p(x)=x+5=0$$ $$ $$then $$x=-5$$, i.e. $$-5$$ is the zero.

$$(ii)$$ If $$p(x)=x-5=0$$ $$ $$then $$x=5$$, i.e. $$5$$ is the zero.

$$(iii)$$ If $$p(x)=2x+5= 0$$ then $$x=\dfrac{-5}{2}$$, i.e. $$\dfrac{-5}{2}$$ is the zero.

$$(iv)$$ If $$p(x)=3x-2= 0$$ then $$x=\dfrac{2}{3}$$, i.e. $$\dfrac{2}{3}$$ is the zero.

$$(v)$$ If $$p(x)=3x= 0$$ then $$x=0$$, i.e. $$0$$ is the zero.

$$(vi)$$ If $$p(x)= ax= 0$$ then $$x=0$$, i.e. $$0$$ is the zero.

$$(vii)$$ If $$p(x)=cx+d= 0$$ then $$x=\dfrac{-d}{c}$$, i.e. $$\dfrac{-d}{c}$$ is the zero.

Write the degree of each of the following polynomials:
(i) $$5x^3+4x^2+7x$$
(ii) $$4-y^2$$
(iii) $$5t-\sqrt 7$$
(iv) $$3$$

(i) The power of term is $$5x^{3}$$ and exponent is $$3$$. So degree is $$3$$.

(ii) The power of term is $$y^{2}$$ and exponent is $$2$$. So degree is $$2$$.

(iii) The power of term is $$5t$$ and exponent is $$1$$. So degree is $$1$$.

(iv) The only term here is $$3$$ which can be written as $$3x^{0}$$ and so exponent is $$0$$ or degree is $$0$$.

Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
(i) $$4x^2-3x+7$$
(ii) $$y^2+\sqrt 2$$
(iii) $$3\sqrt t+ t\sqrt 2$$
(iv) $$ y+\displaystyle\frac{2}{y}$$
(v) $$x^{10}+y^3+t^{50}$$

(i) In $$4x^{2}-3x+7$$. all the indies of $$x$$ are whole numbers. So, it is a polynomial in one variable $$x$$.

(ii) In $$y^{2}+\sqrt{2}$$ the index of $$y$$ is a whole number. So, it is a polynomial in one variable $$y$$.

(iii) In $$3\sqrt{t}+t\sqrt{2}=3t^{\frac{1}{2}}+\sqrt{2}\ t$$, here the exponent of first term is $$\dfrac{1}{2}$$, which is not whole number therefore is it not a polynomial.

(iv) In $$y+\dfrac{2}{y}=y+2y^{-1}$$, here the exponent of first term is $$-1$$, which is not whole number, therefore, is it not a polynomial.

(v) In $$x^{10}+y^{3}+t^{50}$$ is not a polynomial in one variable as three variable $$x,y$$ and $$t$$ occur in it.

Obtain all other zeroes of $$3x^4 +6x^3-2x^2-10x-5$$, if two of its zeroes are $$\sqrt{\dfrac{5}{3}}$$ and $$-\sqrt{\dfrac{5}{3}}$$.

Two zeroes are $$\sqrt{\dfrac{5}{3}}$$ and $$-\sqrt{\dfrac{5}{3}}$$

So we can write it as, x = $$\sqrt{\dfrac{5}{3}}$$ and x = $$-\sqrt{\dfrac{5}{3}}$$

we get $$x-\sqrt{\dfrac{5}{3}}=0$$ and $$x+\sqrt{\dfrac{5}{3}}=0$$

Multiply both the factors we get,
$$x^2-\dfrac{5}{3}=0$$

Multiply by $$3$$ we get
$$3x^2-5 = 0$$ is the factor of $$3x^4 +6x^3-2x^2-10x-5$$

Now divide, $$3x^4 +6x^3-2x^2-10x-5$$ by $$3x^2-5 = 0$$ we get,
Quotient is $$x^2+2x+1=0$$

Compare the equation with quadratic formula,
$$x^2 - (Sum \space\ of \space\ root)x + (Product \space\ of \space\ root) = 0$$

$$\Rightarrow$$Sum of root $$= 2$$

$$\Rightarrow$$Product of the root $$= 1$$

So, we get

$$\Rightarrow$$$$x^2+ x+x+1 = 0$$

$$\Rightarrow$$$$x(x + 1) + 1(x + 1) = 0$$

$$\Rightarrow$$$$x + 1 = 0, x + 1= 0$$

$$\Rightarrow$$$$x = -1, x = -1$$

So, our zeroes are $$-1, -1,$$ $$\sqrt{\dfrac{5}{3}}$$ and $$-\sqrt{\dfrac{5}{3}}$$

Use the identity $$(x+a)\;(x+b)=x^2+(a+b)x+ab$$ to find following products.
(i) $$(x+3)\;(x+7)$$
(ii) $$(4x+5)\;(4x+1)$$
(iii) $$(4x-5)\;(4x-1)$$
(iv) $$(4x+5)\;(4x-1)$$
(v) $$(2x+5y)\;(2x+3y)$$
(vi) $$(2a^2+9)\;(2a^2+5)$$
(vii) $$(xyz-4)\;(xyz-2)$$

(i) $$(x+3)(x+7)$$

$$=x^3+(3+7)x+(3)(7)$$

$$=x^2+10x+21$$

(ii) $$(4x)^2+(5+1)\;4x+(5)(1)$$
$$=16x^2+24x+5$$

(iii) $$(4x-5)(4x-1)$$

$$=(4x)^2+[(-5)+(-1)]4x+(-5)(-1)$$
$$=16x^2-24x+5$$

(iv) $$(4x)^2+[(5)+(-1)]4x+(5)(-1)$$
$$16x^2+16x-5$$

(v) $$(2x)^2+(5y+3y)(2x)+(5y)(3y)$$
$$=4x^2+16xy+15y^2$$

(vi) $$(2a^2)^2+(9+5)(2a^2)+(9) (5)$$
$$=4a^2+28a^2+45$$

(vii) $$(xyz)^2+[(-4)+(-2)](xyz)+(-4)(-2)$$
$$=x^2y^2z^2-6xyz+8$$

Simplify:
(i) $$(a^2-b^2)^2$$
(ii) $$(2x+5)^2-(2x-5)^2$$
(iii) $$(7m -8n)^2 + (7m + 8n)^2$$
(iv) $$(4m+5n)^2+ (4n+5m)^2$$
(v) $$(2.5p-1.5q)^2-(1.5p-2.5q)^2$$
(vi) $$(ab+bc)^2-2ab^2c$$
(vii) $$(m^2-n^2m)^2+2m^3n^2$$

i) $$(a^2-b^2)^2 =(a^2)^2 +(b^2)^2-2(a^2)(b^2)$$ $$\because [(a+b)^2$$$$=a^2+b^2+2ab]$$

$$=a^4+b^4-2a^2b^2$$

ii) $$(2x+5)^2 - (2x-5)^2$$

Let $$A=2x+5$$ and $$B=2x-5$$

$$\therefore (2x+5)^2 - (2x-5)^2 = A^2-B^2$$

$$=(A+B)(A-B)$$ $$[\because a^2-b^2=(a+b)(a-b)]$$

$$=[2x+5+(2x-5)][2x+5-(2x-5)]$$

$$=[2x+5+2x-5][2x+5-2x+5]$$

$$=(4x)(10)$$

$$=40x$$

iii) $$(7m-8n)^2 + (7m+8n)^2$$

$$=(7m)^2+(8n)^2-2(7m)(8n)+(7m)^2+(8n)^2+2(7m)(8n)$$

$$=49m^2+64n^2-112mn+49m^2+64n^2+112mn$$

$$=98m^2+128n^2$$

iv) $$(4m+5n)^2 + (5m+4n)^2$$

$$=(4m)^2+(5n)^2+2(4m)(5n)+(5m)^2+(4n)^2+2(5m)(4n)$$ $$[\because (a-b)^2=a^2-2ab+b^2]$$

$$=16m^2+25n^2+40mn+25m^2+16n^2+40mn$$

$$=41m^2+41n^2+80mn$$

v) $$(2.5p-1.5q)^2-(1.5p-2.5q)^2$$

$$=(2.5p)^2+(1.5q)^2-2(2.5p)(1.5q)-[(1.5p)^2+(2.5q)^2-2(1.5p)(2.5q)]$$

$$=6.25p^2+2.25q^2-7.5pq-2.25p^2-6.25q^2+7.5pq$$

$$=4p^2-4q^2$$

$$=4(p^2-q^2)$$

$$=4(p-q)(p+q)$$

vi) $$(ab+bc)^2-2ab^2c$$

$$=(ab)^2+(bc)^2+2(ab)(bc)-2ab^2c$$

$$=a^2b^2+b^2c^2+2ab^2c-2ab^2c$$

$$=b^2(a^2+c^2)$$

vii) $$(m^2-n^2m)^2+2m^3n^2$$

$$=(m^2)^2+(n^2m)^2-2(m^2)(n^2m)+2m^3n^2$$

$$=m^4+m^2n^4-2m^3n^2+2m^3n^2$$

$$=m^2(m^2-n^4)$$

Find and correct errors of the following mathematical expressions:
$$(z+5)^{2} = z^{2} +25 $$

The statement is incorrect.

Above expression can be expanded by using formula $$(a+b)^2=a^2+2ab+b^2$$
The correct statement is
$$ (z+5)^{2} = z^{2}+10z+25 $$

Find the square of the following numbers
(i) $$32 $$
(ii) $$35$$
(iii) $$86$$
(iv)$$ 93$$
(v) $$71$$
(vi) $$46$$

(i) $$ 32^{2} = (30+2) (30+2) $$

$$= 900 + 60 + 60 + 4 $$

$$= 1024 $$

(ii) $$ 35^{2} = (30+5) (30+5) $$

$$= 900+ 150 + 150 + 25 $$

$$= 1225 $$

(iii) $$ 86^{2} = (80+6) (80+6) $$

$$= 6400 + 480 + 480 + 36 $$

$$= 7396 $$

(iv) $$ 93^{2} = (90 + 3) (90 + 3) $$

$$= 8100 + 270 + 270 + 9 $$

$$= 8649 $$

(v)$$ 71^{2} = (70 + 1) (70 + 1)$$

$$ = 4900 + 140 + 1$$

$$= 5041 $$

(vi) $$ 46^{2} = (40+6) (40+6) $$

$$= 1600 + 480 + 36$$

$$ = 2080 + 36$$

$$ = 2116 $$.

Using $$a^2-b^2=(a+b)(a-b)$$, find
(i) $$51^2-49^2$$
(ii) $$1.02^2-0.98^2$$
(iii) $$153^2-147^2$$
(iv) $$12.1^2-7.9^2$$

We know that

$$a^2-b^2 = (a-b)(a+b)$$

(i) $$51^2-49^2 = (51-49)(51+49) $$

$$= 2\times100 $$

$$= 200$$

(ii) $$1.02^2 - 0.98^2 = (1.02-0.98)(1.02+0.98) $$

$$= 0.04\times2.00 $$

$$= 0.08$$

(iii) $$153^2 - 147^2 = (153-147)(153+147) $$

$$= 6\times300 $$

$$= 1800$$

(iv) $$12.1^2 - 7.9^2 = (12.1-7.9)(12.1+7.9) $$

$$= 4.2\times20 $$

$$= 84$$

Find and correct errors of the following mathematical expressions:ind and correct error
$$ (3x+2) ^{2} = 3x^{2} +6x+4 $$

The statement is incorrect.

LHS can be expanded by using formula, $$(a+b)^2=a^2+2ab+b^2$$

$$\therefore (3x+2)^2=(3x)^2+2(3x)(2)+2^2=9x^2+12x+4$$
Therefore the correct statement is
$$ (3x+2)^{2} = 9x^{2}+12x+4 $$

Find and correct errors of the following mathematical expressions:
$$ (y-3)^{2} = y^{2} -9 $$

The statement is incorrect.

It can be expanded by using formula $$(a-b)^2$$. But instead of this the formula used here is $$a^2-b^2$$ which is incorrect.
Therefore the correct statement is
$$ (y-3)^{2} = y^{2} -2\times y\times 3 +9 = y^{2}-6y +9 $$

If the zeroes of the polynomial $$x^3- 3x^2 + x + 1$$ are $$a- b,\ a,\ a + b$$ find $$a$$ and $$ b$$.

$$P(x)=$$ $$x^3- 3x^2 + x + 1$$

zeroes are $$a - b, a, a + b$$

Comparing the given polynomial with $$px^3 + qx^2+rx+t$$, we obtain

$$p = 1, q = -3, r = 1, t = 1$$

Sum of zeroes = $$a - b + a + a + b = \dfrac{-q}{p}=3a$$

$$\Longrightarrow \dfrac{-q}{p}=3a$$

$$\Longrightarrow \dfrac{-(-3)}{1}=3a$$

$$\Longrightarrow 3 = 3a$$

$$\Longrightarrow a=1$$

$$\Rightarrow$$Then the zeroes becomes, $$1 - b , 1, 1 + b$$

$$\Rightarrow$$Multiplication of zeroes $$= (1 - b) \times 1 \times (1 + b) = \dfrac{-t}{p}=1 -b^2$$

$$\Longrightarrow \dfrac{-1}{1}=1 -b^2$$

$$\Longrightarrow b^2 = 2$$

$$b = \pm \sqrt{2}$$

Therefore, $$a = 1$$ and $$b =$$ $$\pm \sqrt{2}$$

Find the degree of each of the following:
(i) $$3{ x }^{ 2 }+2x+1$$
(ii) $$x+1$$
(iii) $$2y+3-5{ y }^{ 3 }$$
(iv) $${ u }^{ 7 }-3{ u }^{ 3 }+2u$$
(v) $${ y }^{ 4 }+2{ y }^{ 3 }-3{ y }^{ 2 }+8$$

The degree is the value of the greatest exponent of any expression.

(i) 2 which is of $$3x^2$$

(i) 1 which is of $$x$$

(i) 3 which is of $$5y^3$$

(i) 7 which is of $$u^7$$

(v) 4 which is of $$y^4$$

Find the product: $$(a+3)(a+5)$$

Using the given formula: $$(x+a)(x+b)$$ = $$x^2+(a+b)x+ab$$

Taking $$x=a$$ $$a=3$$ $$b=5$$ substituing in the given formula we get: $$(a+3)(a+5)$$ = $$a^2+(3+5)a+ (3)(5)= $$ $$a^2+8a+15$$
Hence the correct answer is $${a^2+8a+15}$$

Find the product of $$(a-8)(a+2)$$

Using the formula: $$(x+p)(x+q)=x^2+(p+q)x+pq.$$

Taking $$x=a$$, $$p= -8$$, $$q=2$$ and substituting in the above formula we get,

$$(a-8)(a+2)=a^2+ \left[(-8)+2\right]a+(-8)(2)$$

$$=$$ $$a^2-6a-16$$

Hence the correct answer is $${a^2-6a-16}.$$

Compute $$54 \times 46$$

Here again, identities are useful.
We make use of $$(a+b)(a b) =a^2- b^2$$.
Taking $$a = 50$$ and $$b = 4$$, we see that
$$54 \times 46 = (50 + 4)(50 - 4) = (50)^2 - (4)^2 = 2500 - 16 = 2484$$.

Find the product:$$(3t+1)(3t+4)$$

Using the formula $$(x+a)(x+b)$$ =$$x^2+(a+b)x+ab$$
Taking $$x=3t$$ $$a=1$$ $$b=4$$ and substitutig in the above formula we get: $$(3t+1)(3t+4)$$ = $$(3t)^2 +(1+4)3t+(4)(1)$$ $$=$$ $$9t^2+(5)3t+4$$
Hence the answer is $${9t^2+15t+4}$$

Compute $$(4.9)^2$$.

We can use identities for this problem. Observe
$$(4.9)^2 = (5 - 0.1)^2 = 5^2 - 2(5)(0.1) + (0.1)^2 = 25 - 1 + 0.01 = 24.01$$.
We may verify this by directly computing $$(4.9)^2$$.

Find the product of $$(a-6)(a-2)$$

Using the formula $$(x+p)(x+q)$$ =$$x^2+(p+q)x+pq$$

Taking $$x=a$$, $$p= -6$$, $$b= -2$$ and substituting in the above formula we get:

$$(a-6)(a-2)$$ = $$a^2+[(-6)+(-2)]a+ (-6)(-2)$$ = $$a^2-8a-+12$$

Hence the correct answer is $${a^2-8a+12}$$

Expand:$$(xy+8)(xy-8)$$

Using: $$(x+a)(x+b)$$ =$$x^2+(a+b)x+ab$$
In this formula substituitng $$x=xy$$, $$a=8$$, $$b= -8$$
$$(xy+8)(xy-8)$$ = $$(xy)^2+ (8-8)xy+ (8)(-8)$$ $$=$$ $$(xy)^2+0-64$$

Hence $${(xy)^2-64}$$ is the correct answer

Expand:$$(2x+3y)(2x-3y)$$

The given expression $$(2x+3y)(2x-3y)$$ can be expanded as shown below:

$$(2x+3y)(2x-3y)\\ =[(2x\times 2x)+(2x\times -3y)+(3y\times 2x)+(3y\times -3y)]\\ ={ 4x }^{ 2 }-6xy+6xy-9y^{ 2 }\\ ={ 4x }^{ 2 }-9y^{ 2 }$$

Hence $$(2x+3y)(2x-3y)=4x^2-9y^2$$

Find $$(2x + 3y)^2$$.

We use the identity: $$(a + b)^2 = a^2 + 2ab + b^2$$.
Taking $$a = 2x$$ and $$b = 3y$$,
we get $$(2x + 3y)^2 = (2x)^2 + 2(2x)(3y) + (3y)^2 = 4x^2 + 12xy + 9y^2$$.

Using the identity $$(a + b)^2 = a^2 + 2ab + b^2$$, simplify $$(a+6)^2$$

As We Know from the question, substituting the values
we Get,
$$({ a+6 })^{ 2 }= (a )^{ 2 }+2\times a\times 6+ (6 )^{ 2 }$$
Final Solution - $$ { a }^{ 2 }+12a+36$$

Using the identity $$(a + b)^2 = a^2 + 2ab + b^2$$, simplify $$(2p+3q)^2$$

As given in the Question- $$(a + b)^2 = a^2 + 2ab + b^2$$
Using this Identity,

$$(2p+3q)^{ 2 }$$ =$$( 2p) ^{ 2 }+2( 2p\times 3q ) +( 3q ) ^{ 2 }$$
= $$4{ p }^{ 2 }+2(6pq)+9{ q }^{ 2 }$$
= $$4p^2+12pq+9q^2$$

Using the identity $$(a + b)^2 = a^2 + 2ab + b^2$$, simplify $$(x^2+5)^2$$

Using the identity $$\left( a+b \right) ^{ 2 }={ a }^{ 2 }+2ab+{ b }^{ 2 }$$
To simplify $$\left( { x }^{ 2 }+5 \right) ^{ 2 }$$ = $$(x ^ 2)^ 2 +2( { x }^{ 2 }\times 5) + (5) ^{ 2 }$$
= $$x^4+2(5x^2)+25$$
=$$x^4+10x^2+25$$

Is it possible to imitate the case of the identity $$(x+a)(x+b) = x^2+(a+b)x+ab$$, and get a similar expression for the product $$(x + a)(x + b)(x + c)$$?

As per given expansion, we can write $$(x+a)(x+b)=x^2+(a+b)x+ab$$

Further expression can be expanded as,

$$(x+a)(x+b)(x+c)=[x^2+(a+b)x+ab](x+c)=[x^2+(a+b)x+ab]x+[x^2+(a+b)x+ab]c$$

Further solving the equation we get the result,

$$(x+a)(x+b)(x+c)=x^3+(a+b+c)x^2+(ab+bc+ac)x+abc$$

Yes, it is possible to get the desired result. We got an cubic expression after aaplying the identity.

Using the identity $$(a + b)^2 = a^2 + 2ab + b^2$$, simplify $$(3x+2y)^2$$

Using the identity from question $$( a+b) ^{ 2 }={ a }^{ 2 }+2ab+{ b }^{ 2 }$$
$$( 3x+2y) ^{ 2 }= (3x) ^{ 2 }+2\times \left\lceil 3x\times 2y \right\rceil +{ \left( 2y \right) }^{ 2 }$$
$$( 3x+2y) ^{ 2 }$$= $$9x^2+2(6xy)+4y^2$$
solution = $${ 9x }^{ 2 }+12xy+4{ y }^{ 2 }$$

Evaluate:$$103\times 96$$

We can write $$103$$ as $$ 100+3$$ and $$96$$ as $$100-4$$

Using the identity: $$(x+a)(x+b)$$ = $$x^2+(a+b)x+ab$$
We get,

$$\Rightarrow$$ $$(100+3)(100-4)$$ = $$100^2+[(3)+(-4)]100+(3)(-4)$$
$$\Rightarrow$$ $$10000+(-1)100-12$$
$$\Rightarrow$$ $$10000-100-12$$
$$\Rightarrow$$ $$9888$$
The solution is $${9888}$$

Evaluate:$$102\times 106$$

Using the formula $$(x+a)(x+b)$$ = $$x^2+(a+b)x+ab$$

Writing $$102 = 100+2$$ and $$106= 100+6$$

Taking $$x = 100$$, $$a = 2$$, $$b=6$$ and substituing in the above formula we get: $$(100+2)(100+6)$$ = $$100^2+(2+6)100+(2)(6)$$ $$= 10000+800+12$$
Hence the answer is $${10812}$$

Evaluate: $$53\times 55$$

So Dividing $$53= 50+3$$ and $$55 =50+5$$
So we get, $$(50+3)(50+5)$$
Using formula $$(x+a)(x+b)$$ = $$x^2+(a+b)x+ab$$
= $$50^2+[(3+5)60]+(3)(5)$$
= $$2500+480+15$$
Solution:- $$2995$$

Evaluate $$(34)^2$$ by using the identity $$(a + b)^2 = a^2 + 2ab + b^2$$.

To find: Using $$(a + b)^2 = a^2 + 2ab + b^2$$ to evaluate $${ 34 }^{ 2 }$$
First we will write $$34$$ as $$(30+4)$$
$$\therefore$$ $$((30+4)^{2})$$ $$={30}^{2}+2\times 30\times 4 +{4}^{2}$$ = $$900+240+16$$
Hence the answer is $${ 1156 }$$

Evaluate: $$34\times 36$$

$$(x+a)(x+b)$$ = $$x^2+(a+b)x+ab$$

Substitute $$x=30,\ a=4$$ and $$b=6,$$

$$(30+4)(30+6)=30^2+(4+6)30+(4)(6)$$

$$34\times36=900+300+24$$

$$=1224$$

Hence, the given product is equal to $$ {1224}.$$

Evaluate $$(10.2)^2$$ by using the identity $$(a + b)^2 = a^2 + 2ab + b^2$$

Using $$(a + b)^2 = a^2 + 2ab + b^2$$
We can write $$(10.2)^2$$ =$$(10+0.2)^2$$ $$=$$ ($$10)^2+2(10)(0.2)+(0.2)^2$$ $$=$$ $$100+4+0.04$$
Hence the answer is $${104.04}$$

Using the identity $$(a - b)^2 = a^2 - 2ab + b^2$$ compute $$(p^2 - q^2)^2$$;

Using Identity $$(a-b)^2$$= $$a^2-2ab+b^2$$
We have: $$(p^2-q^2)^2$$
Therefore, $$(p^2-q^2)^2$$ = $$(p^2)^2-2(p^2)(q^2)+(q^2)^2$$ $$=$$ $$p^4-2p^2q^2+q^4$$
The answer is $${p^4-2p^2q^2+q^4}$$

Evaluate $$(49)^2$$ using the identity $$(a - b)^2 = a^2 - 2ab + b^2$$.

Using $$(a-b)^2$$= $$a^2-2ab+b^2$$ to calculate the value of $$(49)^2$$
We can write $$(49)^2$$ as $$(50-1)^2$$
$$(50 -1 )^2$$ $$= 50^2-2 \times 50 \times 1+1^2$$ $$=$$ $$2500-100+1$$
The answer is $${2401}$$

Using the identity $$(a - b)^2 = a^2 - 2ab + b^2$$ ,compute $$(5a - 4b)^2$$;

Using $$(a-b)^2 = a^2-2ab+b^2$$ ,
$$(5a-4b)^2= (5a)^2-2(5a \times 4b)+(4b)^2$$
$$= 25a^2-2(20ab)+16b^2$$
$$= 25a^2-40ab+16b^2$$

Evaluate $$(41)^2$$ by using the identity $$(a + b)^2 = a^2 + 2ab + b^2$$

Using $$(a+b)^2$$= $$a^2+2ab+b^2$$
Writing $$(41)^2$$ as $$(40+1)^2$$
$$=$$ $$40^2+2\times 40+1+1^2$$
$$=$$ $$1600+80+1$$
The solution is $${1681}$$

Evaluate $$(59)^2$$ using the identity $$(a - b)^2 = a^2 - 2ab + b^2$$

$$(59)^2 = (60 - 1)^2$$
$$(a - b)^2 = a^2 - 2ab + b^2$$ Here $$a = 60, b =1$$
$$(60 - 1)^2 = 60^2 - (2)(60)(1) + 12 = 3600 - 120 + 1$$
$$59^2 = 3481$$

Using the identity $$(a -b)^2 = a^2- 2ab + b^2$$ compute $$(x- 6)^2$$

Using the identity: $$(a-b)^2$$= $$a^2-2ab+b^2$$
We have $$(x-6)^2$$= $$x^2-2(x)(6)+6^2$$
The answer is $${x^2-12x+36}$$

Using the identity $$(a - b)^2 = a^2 - 2ab + b^2$$ compute $$(3x -5y)^2$$

Using $$(a-b)^2$$= $$a^2-2ab+b^2$$
To Compute $$(3x-5y)^2$$
$$(3x)^2-2(3x \times 5y)+(5y)^2$$
$$9x^2-2(15xy) + 25y^2$$
Solution - $$ 9x^2-30xy+25y^2$$

Evaluate $$(53)^2$$ by using the identity $$(a + b)^2 = a^2 + 2ab + b^2$$

Using $$(a+b)^2$$= $$a^2+2ab+b^2$$
We can write $$(53)\ as\ (50+3)^2$$
$$\Rightarrow $$ $$(50+3)^2$$= $$50^2+2\times 50 \times 3+3^2$$ $$=$$ $$2500+300+9$$
Hence the answer is $${2809}$$

Evaluate $$(9.8)^2$$ by using the identity $$(a - b)^2 = a^2 - 2ab + b^2$$.

Using the given identity $$(a−b)^2=a^2−2ab+b^2$$ to evaluate $$(9.8)^2$$
We can write $$(9.8)^2$$ = $$(10-0.2)^2$$
$$\therefore $$ $$(10-0.2)^2$$= $$10^2-2(10)(0.2)+0.2^2$$ $$=$$ $$100-4+0.04$$
Hence the answer is $${96.04}$$

Use the identity $$(a + b)(a - b) = a^2 - b^2$$ to find the products of $$(2a + 4b)(2a - 4b)$$

Using identity $$(a+b)(a-b)=$$ $$a^2-b^2$$
$$(2a+4b)(2a-4b)$$ $$=(2a)^2-(4b)^2$$

$$= 4a^2 - 16 b^2$$
The answer is $${4a^2-16b^2}$$

Evaluate $$55\times 45$$ using suitable identity.

Using Formula $$(x+a)(x+b)$$ = $$x^2+(a+b)x+ab$$
Writing $$55 \ as \ 50+5$$ and $$45 \ as\ 50-5$$
$$\Rightarrow$$ $$(50+5)(50-5)$$ = $$50^2+[5+(-5)]50+(5)(-5)$$
$$=$$ $$2500+(0)50-25$$
$$=$$ $$2475$$
The answer is $${2475}$$

Evaluate $$8.5 \times 9.5$$ using suitable standard identity.

As we know the standard identity $$(a+b)(a-b)$$ $$=a^2-b^2$$

Now, writing $$8.5$$ as $$(9-0.5)$$ and $$9.5$$ as $$(9+0.5)$$ we get,

$$\Rightarrow$$ $$(9+0.5)(9-0.5)$$ $$=9^2-(0.5)^2$$ $$=$$ $$81-0.25$$

Hence the answer is $$ {80.75}$$.

Find the product of $$(p+2)(p-2)(p^2+4)$$

We know that $$(a-b)(a+b)=a^2-b^2$$
So $$(p+2)(p-2)= p^2-(2)^2$$
$$(p+2)(p-2)= p^2-4$$
So $$(p^2-4)(p^2+4)$$
$$= (p^2)^2-(4)^2$$
$$= p^4-16$$

Evaluate $$(198)^2$$ using the identity $$(a - b)^2 = a^2 - 2ab + b^2$$

Using $$(a-b)^2$$= $$a^2-2ab+b^2$$

to evaluate $$(198)^2$$
Writing $$(198)^2$$ as $$(200-2)^2$$
$$\Rightarrow$$ $$(200-2)^2$$ = $$200^2-2 \times 200\times 2+2^2$$ $$= $$ $$40000-800+4$$
Hence the answer is $${39204}$$

Use the identity $$(a + b)(a - b) = a^2 - b^2$$ to find the product of $$(\dfrac{2x}{3} + 1)(\dfrac{2x}{3}- 1)$$

Using the given identity $$(a+b)(a-b)$$=$$a^2-b^2$$
So $$\left(\dfrac{2x}{3}+1\right)\left(\dfrac{2x}{3}−1\right)$$ = $$\left(\dfrac{2x}{3}\right)^2$$ - $$(1)^2$$$$=$$ $$\left(\dfrac{4x^2}{9}\right)$$ -$$(1)$$
The answer is $${\dfrac{4x^2}{9}-1}$$

Evaluate $$102\times 98$$ using suitable standard identity.

Using the identity $$(x+a)(x+b)$$ = $$x^2+(a+b)x+ab$$
Writing $$102$$ as $$100+2$$ and $$98$$ as $$100-2$$
Hence $$(100+2)(100-2)$$ = $$100^2+[2+(-2)]100+(2)(-2)$$
$$=$$ $$10000+(0)100-4$$
$$=$$ $$9996$$
The answer is $${9996}$$

Evaluate $$33\times 27$$ using suitable identity.

Using Formula $$(x+a)(x+b)$$ = $$x^2+(a+b)x+ab$$
Writing $$33\ as\ 30+3$$ and $$27\ as\ 30-3$$
$$\Rightarrow$$ $$(30+3)(30-3)$$ = $$30^2+[3+(-3)]30+(3)(-3)$$
$$=$$ $$900+[(0)30]-9$$
$$=$$ $$891$$
Hence the answer is $${891}$$

Find the product of $$(2a+3)(2a-3)(4a^2+9)$$

Using the formula $$(a+b)(a-b)$$ = $$a^2-b^2$$
$$(2a+3)(2a-3)=(2a)^2-(3)^2$$
$$=4a^2-9$$
$$\implies (4a^2-9)(4a^2+9)=(4a^2)^2-(9)^2$$
$$= {16a^4-81}$$

Find the product : $$(x-3)(x+3)(x^2+9)$$

As we know formula $$(a+b)(a-b)$$ = $$a^2-b^2$$
Similarly $$(a+b)(a+b)$$ = $$a^2+b^2$$
As given $$(x-3)(x+3)(x^2+9)$$
= $$(x+3)(x-3)(x+3)(x+3)$$
= $$(x+3)(x-3)$$ = $$(x-3)^2$$
= $$(x^2-9)(x^2+9)$$
Using the formula:- $$a^2-b^2$$
= $$(x^2)^2-(9)^2$$
= $$x^4-81$$

Find the product of $$(2x-y)(2x+y)(4x^2+y^2)$$

As we know the formula $$(a+b)(a+b)$$= $$a^2+b^2$$
Similarly $$(a-b)(a+b)$$=$$a^2-b^2$$
So $$(2x-y)(2x+y)$$ =$$(2x)^2-(y)^2$$
= $$4x^2-y^2$$
So = $$(4x^2-y^2)(4x^2-y^2)$$
= $$(4x^2)^2-(y^2)^2$$
= $$16x^4-y^4$$

Expand: $$(x-1)(x + 1)(x^2 +1)(x^4+1)$$

Consider $$(x-1)(x+1)(x^2+1)(x^4+1)$$

Now, $$(x-1)(x+1) = x^2-1^2$$ ............. $$\because (a+b)(a-b) = (a^2-b^2)$$
$$\implies (x-1)(x+1)(x^2+1)(x^4+1)=(x^2 - 1)(x^2+1)(x^4+1)$$

Taking $$a=x^2, b=1$$ in $$(a+b)(a-b) = (a^2-b^2)$$

$$\implies (x-1)(x+1)(x^2+1)(x^4+1)=((x^2)^2 - (1)^2)(x^4+1)$$

$$=(x^4 - 1)(x^4 + 1)$$
We have, $$(x^4-1)(x^4+1)$$= $$(x^4)^2-(1)^2$$ ....... [Again by the formula]

$$\implies (x-1)(x+1)(x^2+1)(x^4+1)=(x^8-1)$$
Hence, the answer is $${x^{8}-1}$$

Use appropriate formula to compute $$107\times 93$$

Using the identity $$(a+b)(a-b)$$=$$a^2-b^2$$
We can write: $$107=100+7$$ and $$93=100-7$$
after using formula we get: $$(100+7)(100-7)$$ = $$100^2-7^2$$ $$=10000-49$$ $$=$$ $$9951$$
Hence the answer is $${9951}$$

Use appropriate formula to compute $$1008\times 992$$

Using the identity $$(a+b)(a-b)$$= $$a^2-b^2$$
Writing $$1008$$ as $$1000+8$$ and $$992$$ as $$1000-8$$
$$\Rightarrow$$ $$(1008) \times (992)$$ = $$(1000+8)(1000-8)$$
$$\Rightarrow$$ $$(1000+8)(1000-8)$$ = $$1000^2-8^2$$ $$=$$ $$1000000-64$$ $$=$$ $$999936$$
Hence the answer is $${999936}$$

Expand: $$(2x-y)(2x + y)(4x^2 +y^2)$$

We need to expand $$(2x-y)(2x+y)(4x^2+y^2)$$

By using identity $$(a-b)(a+b)=(a^2-b^2)$$

Here $$a=2x, b=y$$

Thus $$(2x-y)(2x+y)=(4x^2-y^2)$$

Again using the same identity, here $$x=4x^2, b=y^2$$

Thus the value of $$(4x^2-y^2)(4x^2+y^2)$$ is $$(16x^4-y^4)$$.

Use appropriate formula to compute $$(103)^2$$

Using Formula of $$(a+b)^2=a^2+2ab+b^2$$
So, writing the given question as

$$(103)^2=(100+3)^2$$
Now using the formula we get :
$$(100+3)^2=100^2+2(100)(3)+3^2$$

$$=10000+600+9$$

$$=10609$$
The answer is $${10609}$$

Find the product of $$(\frac{1}{2}m-\frac{1}{3})(\frac{1}{2}m+\frac{1}{3})(\frac{1}{4}m^2+\frac{1}{9})$$

Using the formula $$(a+b)(a-b)$$ = $$a^2-b^2$$
So $$(\dfrac{1}{2}m-\dfrac{1}{3})(\dfrac{1}{2}m+\dfrac{1}{3})$$ = $$(\dfrac{1}{2}m)^2-(\dfrac{1}{3})^2$$
$$= $$ $$(\dfrac{1}{4}m^2-\dfrac{1}{9})$$
Now we have $$(\dfrac{1}{4}m^2-\dfrac{1}{9})$$$$(\dfrac{1}{4}m^2+\dfrac{1}{9})$$ $$=(\dfrac{1}{4}m^2)^2-(\dfrac{1}{9})^2$$
So $$=$$ $$\dfrac{1}{16}m^4 - \dfrac{1}{81}$$
The answer is $${\dfrac{1}{16}m^4 - \dfrac{1}{81}}$$

Simplify: $$(x + y)^2 + (x - y)^2$$;

Using the given identities

$$(x-y)^2$$ = $$x^2-2xy+y^2$$ ..... $$(eq 1)$$
and $$(x+y)^2$$ = $$x^2+2xy+y^2$$ .......$$(eq \ \ 2)$$
Using (eq 1) and (eq 2) to Simplify:-
$$(x+y)^2$$+$$(x-y)^2$$
$$=$$ $$x^2-2xy+y^2$$+ $$x^2+2xy+y^2$$
$$=$$ $$x^2+x^2+y^2+y^2$$
$$=$$ $$2x^2+2y^2$$

Further Simplifying we get: $$2(x+y)^2$$
Hence the answer is $${2(x+y)^2}$$

Find the product : $$(2x-3y)(2x+3y)(4x^2+9y^2)$$

As we know the formula $$(a+b)(a+b)$$= $$a^2+b^2$$
Similarly $$(a-b)(a+b)$$=$$a^2-b^2$$
So = $$(2x-3y)(2x+3y)$$ =$$(2x)^2-(3y)^2$$
= $$4x^2-9y^2$$ ... ($$eq1$$)
So = $$(4x^2-9y^2)(4x^2-9y^2)$$ .. using $$(eq1)$$
= $$(4x^2)^2-(9y^2)^2$$
= $$16x^4-81y^4$$

Use the appropriate formula to compute $$(96)^2$$.

Using the idenitity $$(a-b)^2=$$ $$a^2-2ab+b^2$$

We can write: $$(96)^2=$$ $$(100-4)^2$$

$$\Rightarrow$$ $$(100-4)^2$$$$=100^2-2(100)(4)+4^2$$

$$=10000-800+16$$ $$=9216$$

Hence the answer is $${9216}$$.

Express the given expression $$(x + 98)(x + 102)$$ as difference of two squares

$$\left( x+98 \right) \left( x+102 \right) $$

$$=\left\{ \left( x+100 \right) -2 \right\} \left\{ \left( x+100 \right) +2 \right\} $$

$$\Rightarrow$$ using $$\left( a-b \right) \left( a+b \right) =a^2-b^2$$

$$={ \left( x+100 \right) }^{ 2 }-2^2$$

Hence, the answer is $${ \left( x+100 \right) }^{ 2 }-2^2.$$

Find the degree of the following polynomial.
$$x^{3} + 17x - 21 - x^{2}$$

In the given polynomial $$x^3+17x-21-x^2$$, the exponents of the variable $$x$$ are $$3,2$$ and $$1$$.

We know that the highest exponent of the variable $$x$$ is the degree of the polynomial.

Hence, the degree of the polynomial $$x^3+17x-21-x^2$$ is $$3$$.

Simplify: $$(x + y)^2 \times (x - y)^2.$$

$${\textbf{Step - 1: Expaning the square of the terms}}.$$

$${\text{We have the expression }}{(x + y)^2} \times {(x - y)^2}.$$

$${\text{So first expanding }}{(x + y)^2}{\text{ we get,}}$$

$${\text{ }}{(x + y)^2} = {x^2} + 2xy + {y^2}$$

$${\text{Now expanding }}{(x - y)^2},{\text{we get}}$$

$${\text{ }}{(x + y)^2} = {x^2} - 2xy + {y^2}$$

$${\textbf{Step - 2: Evaluating }}{(x + y)^2} \times {(x - y)^2}.$$

$${\text{Substituting }}{(x + y)^2} = {x^2} + 2xy + {y^2}{\text{ and }}{(x - y)^2} = {x^2} - 2xy + {y^2},{\text{ we get}}$$

$${(x + y)^2} \times {(x - y)^2} = {\text{ (}}{x^2} + 2xy + {y^2}{\text{ )}} \times {\text{(}}{x^2} - 2xy + {y^2})$$

$${\text{now, we can group the terms as,}}$$

$${(x + y)^2} \times {(x - y)^2} = {\text{ ((}}{x^2} + {y^2}{\text{) }} + 2xy{\text{)}} \times {\text{((}}{x^2} + {y^2}) - 2xy)$$

$$ = {({x^2} + {y^2})^2} - {(2xy)^2}$$ $$\mathbf{[{\text{(as }}(a + b)(a - b) = {a^2} - {b^2})]}$$

$${\text{Again expanding (}}{x^2} + {y^2}{)^2},{\text{we can write}}$$

$${(x + y)^2} \times {(x - y)^2} = {\text{ (}}{x^2}{)^2} + {({y^2})^2} + 2{x^2}{y^2} - 4{x^2}{y^2}$$

$$\Rightarrow {(x + y)^2} \times {(x - y)^2} = {\text{ }}{x^4} + {y^4} - 2{x^2}{y^2}$$

$${\textbf{Hence, we get }}\mathbf{{(x + y)^2}} \mathbf{\times {(x - y)^2} = {\text{ }}{x^4} + {y^4} - 2{x^2}{y^2}.}$$

Find the product $$\left( 3+\sqrt { 2 } \right) \left( 3-\sqrt { 2 } \right) $$.

We use the relation $$\left( a+b \right) \left( a-b \right) ={ a }^{ 2 }-{ b }^{ 2 } $$.

Here $$a=3$$ and $$b=\sqrt{2}$$.

Thus $$\left( 3+\sqrt { 2 } \right) \left( 3-\sqrt { 2 } \right) ={ 3 }^{ 2 }-{ \left( \sqrt { 2 } \right) }^{ 2 }$$

$$=9-2$$

$$=7$$

Expand: $${ \left( \sqrt { 5 } +\sqrt { 2 } \right) }^{ 2 }$$.

We use the expansion $$( a+b) ^{ 2 }={ a }^{ 2 }+2ab+{ b }^{ 2 }$$.
Taking $$a=\sqrt{5}$$ and $$b=\sqrt{2}$$, we obtain
$${ \left( \sqrt { 5 } +\sqrt { 2 } \right) }^{ 2 }={ (\sqrt { 5 } ) }^{ 2 }+2\sqrt { 5 } \sqrt { 2 } +{ (\sqrt { 2 } ) }^{ 2 }=7+2\sqrt { 10 } $$

Find the degree of the following polynomial.
$$x^{3} + 2x^{2} - 5x - 6$$

In the given polynomial $$x^3+2x^2-5x-6$$, the exponents of the variable $$x$$ are $$3,2$$ and $$1$$.

We know that the highest exponent of the variable $$x$$ is the degree of the polynomial.

Hence, the degree of the polynomial $$x^3+2x^2-5x-6$$ is $$3$$.

Find the degree of the following polynomial.
$$x^{2} - 9x + 20$$

In the given polynomial $$x^2-9x+20$$, the exponents of the variable $$x$$ are $$2$$ and $$1$$.

We know that the highest exponent of the variable $$x$$ is the degree of the polynomial.

Hence, the degree of the polynomial $$x^2-9x+20$$ is $$2$$.

Find the degree of the following polynomial.
$$2x + 4 + 6x^{2}$$

In the given polynomial $$2x+4+6x^2$$, the exponents of the variable $$x$$ are $$2$$ and $$1$$.

We know that the highest exponent of the variable $$x$$ is the degree of the polynomial.

Hence, the degree of the polynomial $$2x+4+6x^2$$ is $$2$$.

Simplify: $${ \left( \sqrt { 2 } x-2y \right) }^{ 2 }$$.

Using the form $$\left( a-b \right) ^{ 2 }={ a }^{ 2 }-2ab+{ b }^{ 2 }$$,

we have to take $$a=\sqrt{2} x$$ and $$b=2y$$. Hence
$${ \left( \sqrt { 2 } x-2y \right) }^{ 2 }={ (\sqrt { 2 } x) }^{ 2 }-2(\sqrt { 2 } x)(2y)+{ (2y) }^{ 2 }=2{ x }^{ 2 }-4\sqrt { 2 } xy+4{ y }^{ 2 }$$

Simplify: $${ (3m+5n) }^{ 2 }-{ (2n) }^{ 2 }$$

We have: $${ \left( 3m+5n \right) }^{ 2 }-{ \left( 2n \right) }^{ 2 }$$

Using the identity: $$(x+y)^{ 2 }=x^{ 2 }+y^{ 2 }+2xy$$ for the above expression we get,

$${ \left( 3m+5n \right) }^{ 2 }-{ \left( 2n \right) }^{ 2 }=\left[ { \left( 3m \right) }^{ 2 }+\left( 5n \right) ^{ 2 }+\left( 2\times 3m\times 5n \right) \right] -4n^{ 2 }$$

$$=9m^{ 2 }+25n^{ 2 }+30mn-4n^{ 2 }=9m^{ 2 }+21n^{ 2 }+30mn$$

$$=3(3m^2+7n^2+10mn)$$

Hence, $${ \left( 3m+5n \right) }^{ 2 }-{ \left( 2n \right) }^{ 2 }=3(3m^{ 2 }+7n^{ 2 }+10mn)$$.

Find $${204}^{2}$$

$${204}^{2}={(200+4)}^{2}$$
$$={(200)}^{2}+2(200)(4)+{4}^{2}$$
$$=40000+1600+16$$
$$=41616$$

Verify whether $$2$$ and $$1$$ are zeroes of the polynomial $$x^{2} - 3x + 2$$.

Let $$p(x) = x^{2} - 3x + 2$$
Replace $$x$$ by $$2$$
$$p(2) = (2)^{2} - 3(2) + 2$$
$$= 4 - 6 + 2 = 0$$
Also replace $$x$$ by $$1$$
$$p(1) = (1)^{2} - 3(1) + 2$$
$$= 1 - 3 + 2$$
$$= 0$$
Hence, both $$2$$ and $$1$$ are zeroes of the polynomial $$x^{2} - 3x + 2$$.
It is a quadratic polynomial. Hence, a quadratic polynomial has two zeroes.

Use suitable identities for the following product :
$$(1 + x)(1 + x)$$

The value of $$(1+x)(1+x)$$ is $$(1+x)^2$$

We know suitable identities is $$(x+y)^{2}=x^{2}+2xy+y^{2}$$

Therefore, the value of $$ (1+x)^{2}$$ is

$$=(1)^{2}+2(1)(x)+x^{2}$$

$$=1+2x+x^{2}$$

$$=x^{2}+2x+1$$

The degree of monomial $$2$$ is?

The degree of the polynomial is the highest or the greatest degree of a variable in the polynomial. It indicates the highest exponential power in the polynomial (ignoring the coefficients).

Since, the given polynomial $$2$$ can be rewritten as $$2x^0$$ that is $$2=2x^0$$

Therefore, the exponential power of the term $$2$$ is $$0$$

Hence, the degree of the polynomial $$2$$ is $$0$$.

Use suitable identity to find the following product:
$$(x + 5)(x + 2)$$

We need to find value of $$(x+5)(x+2)$$

We know identity $$(x+a)(x+b)=x^{2}+(a+b)x+ab$$

Therefore,

$$(x+5)(x+2)$$

$$=x^{2}+(5+2)x+5\times 2$$

$$=x^{2}+7x+10$$

Hence, solved.

Find the degree of the following polynomial.
$$\sqrt {3}x^{3} + 19x + 14$$

In the given polynomial $$\sqrt { 3 } x^{ 3 }+19x+14$$, the exponents of the variable $$x$$ are $$3$$ and $$1$$.

We know that the highest exponent of the variable $$x$$ is the degree of the polynomial.

Hence, the degree of the polynomial $$\sqrt { 3 } x^{ 3 }+19x+14$$ is $$3$$.

Use suitable identities to find the product :
$$\left (x^{2} + \dfrac {1}{x^{2}}\right )\left (x^{2} -\dfrac {1}{x^{2}}\right )$$

We need to find value of $$\left ( x^{2}+\dfrac{1}{x^{2}} \right )\left ( x^{2}-\dfrac{1}{x^{2}} \right )$$

The suitable identities $$(x+y)(x-y)=x^{2}-y^{2}$$

Therefore, value of $$ \left ( x^{2}+\dfrac{1}{x^{2}} \right )\left ( x^{2}-\dfrac{1}{x^{2}} \right )$$ is

$$=\left ( (x^{2})^{2}-\dfrac{1}{(x^{2})^{2}} \right )$$

$$=x^{4}-\dfrac{1}{x^{4}}$$

Using the identity $$(x + a)(x + b) = x^{2} + (a + b)x + ab$$, find the values of the following:
$$55\times 56$$

Value of $$55\times 56,$$ using identity $$\left( x+a \right) \left( x+b \right) =x^2+\left( a+b \right) x+ab$$

$$\Rightarrow 55\times 56=\left( 50+5 \right) \times \left( 50+6 \right) ={ \left( 50 \right) }^{ 2 }+\left( 5+6 \right) \left( 50 \right) +\left( 5\times 6 \right) $$

$$=2500+\left( 11\times 50 \right) +30$$

$$=2500+550+30$$

$$=3080$$

Hence, the answer is $$3080.$$

If $$p(x) = x^{2} - 5x - 6$$; find the value of $$p(3)$$

Given, $$p(x)=x^2-5x-6$$
$$\Rightarrow p(3)=3^2-5\times3-6$$
$$\Rightarrow p(3)=9-15-6$$
$$\Rightarrow p(3)=-12$$

Find $${987}^{2}-{13}^{2}$$

$${987}^{2}-{13}^{2}=(987+13)(987-13)$$
$$=1000\times 974=974000$$

Evaluate the following by using the identities:
$$28\times 32$$

$$28\times 32$$

$$=\left( 30-2 \right) \left( 30+2 \right) $$

$$={ \left( 30 \right) }^{ 2 }-{ \left( 2 \right) }^{ 2 }$$

$$=900-4$$

$$=896.$$

Hence, the answer is $$896.$$

Evaluate the following by using the identities:
$$96\times 104$$

$$96\times 104$$

$$=\left( 100-4 \right) \left( 100+4 \right) $$

$$={ \left( 100 \right) }^{ 2 }-{ \left( 4 \right) }^{ 2 }$$

$$=10000-16$$

$$=9984.$$

Hence, the answer is $$9984.$$

Evaluate the following by using the identities:
$$(12.1)^{2} -(79)^{2}$$

12.1²– 7.9²= (12.1 + 7.9)(12.1 - 7.9)
= 20 x 4.2
= 84

Using the identity $$(x + a)(x + b) = x^{2} + (a + b)x + ab$$, find the value of $$95\times 103$$

Given: $$95 \times 103=(100-5)(100+3)$$

Using identity, $$\left( x+a \right) \left( x+a \right) =x^2+\left( a+b \right) x+ab$$

$$\Rightarrow \left( 100-5 \right) \left( 100+3\right) =\left( 100 \right) ^2+\left( -5+3 \right)100-5\times 3$$

$$=10000-200-15$$

$$=9785$$

Evaluate the following by using the identities:
$$81\times 79$$

$$81\times 79$$

$$=\left( 80+1 \right) \left( 80-1 \right) $$

$$={ \left( 80 \right) }^{ 2 }-{ \left( 1 \right) }^{ 2 }$$

$$=6400-1$$

$$=6399.$$

Hence, the answer is $$6399.$$

Evaluate the following by using the identities:
$$53\times 47$$

$$53\times 47$$

$$\left( 50+3 \right) \left( 50-3 \right) $$

$$\Rightarrow$$ Using $$\left( a+b \right) \left( a-b \right) =a^2-b^2$$

$$={ \left( 50 \right) }^{ 2 }-{ \left( 3 \right) }^{ 2 }$$

$$=2500-9$$

$$=2491.$$

Hence, the answer is $$2491.$$

Verify Whether the following are roots of the polynomial equations indicated against them.
$$x^3-2x^2-5x+6=0; (x=1, -2 \ and \ 3)$$

Polynomial $$=x^3-2x^2-5x+6$$

To verify whether the values of $$x$$ given are the roots of polynomial or not, we can substitute the values of $$x$$ in polynomial and find whether it evaluates to zero. If it does, then that value will be the zero for polynomial.

For, $$x=1 = \left( 1 \right) ^{ 3 }-2\left( 1 \right) ^{ 2 }-5\left( 1 \right) +6$$

$$=1-2-5+6$$

$$=0$$

For, $$x=-2 = \left( -2 \right) ^{ 3 }-2\left( -2 \right) ^{ 2 }-5\left( -2 \right) +6$$

$$=-8-8+10+6$$

$$=0$$

For, $$x=3 = \left( 3 \right) ^{ 3 }-2\left( 3 \right) ^{ 2 }-5\left( 3 \right) +6$$

$$=27-18-15+6$$

$$=0$$

So, all $$x=1,-2,3$$ are the zeroes of polynomial.

Hence, the answer verified.

Find the zeros of the following polynomial:
$$p(x)=2x -3$$

A polynomial is a function of the form $$f(x) = a_{n}x^{n} + a_{n−1}x^{n−1} + ... + a_{2}x^{2} + a_1x + a_0 $$

where $$a_{n}, a_{n−1} , ... a_{2} ,a_1 , a_0 $$ . are contants

and $$n$$ is a natural number.

To find Zeroes :

$$p(x)=0$$

Given that polynomial is

$$p(x)=2x-3$$

To find zero of given polynomial

$$p(x)=2x-3 =0$$

$$\Rightarrow 2x-3 =0$$

$$\Rightarrow x=\dfrac{3}{2}$$

$$x=\dfrac32$$ is the Zero of polynomial $$p(x)$$

Write the degree of the following polynomial:
5

We know that degree of a Polynomial is the highest or the greatest degree of a variable in the polynomial. It indicates the highest exponential power in the polynomial(ignoring the coefficients).

Any constant can be written with a variable with the exponential power of zero.

Here, we have constant term $$= 5$$.

Polynomial form $$P(x)= 5x^0$$

Hence, the degree of the polynomial $$6$$ is $$0$$.

Expand the following using identities
$$(2a + 3b)^2$$

$$(2a + 3b)^2 = (2a)^2 + 2 (2a)(3b) + (3b)^2$$

$$= 4a^2 + 12 ab + 9b^2$$

Find the zero of the following polynomial equation.
$$11x+1=0$$

$$11x+1=0$$

Zero of this polynomial can be found by evaluating the value of $$x.$$

$$\Rightarrow 11x=-1$$

$$\Rightarrow x=\dfrac{-1}{11}.$$

Hence, the answer is $$\dfrac{-1}{11}.$$

Verify Whether the following are roots of the polynomial equations indicated against them.
$$x^3-2x^2-x+2=0; (x=-1, 2 \ and \ 3)$$

$${ x }^{ 3 }-{ 2x }^{ 2 }-x+2$$

$$\Rightarrow$$ For $$x=-1$$

$$\Rightarrow { \left( -1 \right) }^{ 3 }-2{ \left( 1 \right) }^{ 2 }-\left( -1 \right) +2=-1-2+1+2=0$$

Hence, $$x=-1$$ is a zero of polynomial

Similarly, for $$x=2$$

$$\Rightarrow { \left( 2 \right) }^{ 3 }-2{ \left( 2 \right) }^{ 2 }-\left( 2 \right) +2=0$$

So, $$x=2$$ is also a zero.

For $$x=3$$

$$\Rightarrow { \left( 3 \right) }^{ 3 }-2{ \left( 3 \right) }^{ 2 }-\left( 3 \right) +2=27-18-3+2\neq 0$$

Hence, $$x=3$$ is not a zero.

Hence, verified.

Using the identity $$(x + a)(x + b) = x^{2} + (a + b)x + ab$$, find the values of the following:
$$501\times 505$$

Value of $$501\times 505,$$ using identity $$\left( x+a \right) \left( x+b \right) =x^2+\left( a+b \right) x+b^2$$

$$\Rightarrow 501\times 505=\left( 500+1 \right) \left( 500+5 \right) $$

$$={ \left( 500 \right) }^{ 2 }+\left( 1\times 5 \right) \left( 100 \right) +\left( 1\times 5 \right) $$

$$=250000+\left( 5\times 500 \right) +5$$

$$=250000+2500+5$$

$$=252505.$$

Hence, the answer is $$252505.$$

For polynomial $$P(x)=6x^3+29x^2+44x+21$$ find $$P(-2).$$

Given: $$P(x)=6x^3+29x^2+44x+21$$

Let $$x=-2$$ in $$P(x)$$

Then, $$P(-2)=6(-2)^{3}+29(-2)^{2}+44(-2)+21=6(-8)+29(4)+44(-2)+21=1$$

Hence, $$P(-2)=1$$.

Expand the following with suitable identity
$$(-4x+2yz)^2$$.

Since $$(a+b)^2=a^2+2ab+b^2$$

$$\therefore(-4x+2yz)^2=(-4x)^2+2(-4x)(2yz)+(2yz)^2$$

$$=16x^2-16xyz+4y^2z^2$$

Find the degree of each of the polynomials given below
(i) $$
x^5 - x^4 + 3
$$
(ii) $$
x^2 + x - 5
$$
(iii) $$5$$
(iv) $$
3x^6 + 6y^3 - 7
$$
(v) $$
4 - y^2
$$
(vi) $$
5t - \sqrt 3
$$

Degree of each polynomial,

$$i). x^5-x^4+3$$

Degree means the highest power of exponent in a polynomial.

$$\Rightarrow$$ So, Degree $$=5$$

$$ii). x^2+x-5$$

$$\Rightarrow$$ Degree $$=2$$

$$iii). 5$$

$$\Rightarrow$$ Degree $$=0$$

$$iv). 3x^6+6y^3-7$$

$$\Rightarrow$$ Degree $$=6$$

$$v). 4-y^2$$

$$\Rightarrow$$ Degree $$=2$$

$$vi). 5t-\sqrt{3}$$

$$\Rightarrow$$ Degree $$=1$$

Hence, solved.

Find the number of real zeros of the following polynomial $$p(x)=x^2-2x$$

To find the zeroes of the given polynomial $$p(x)=x^2-2x$$, let us factorize it by equating it to zero as shown below:

$$x^{ 2 }-2x=0\\ \Rightarrow x(x-2)=0\\ \Rightarrow x=0,\quad x-2=0\\ \Rightarrow x=0,\quad x=2$$

Therefore, the zeroes of the polynomial are $$0$$ and $$2$$ and they both are real numbers.

Hence, the number of real zeroes of the polynomial $$p(x)=x^2-2x$$ is $$2$$.

Find the value of a given polynomial at the indicated value of variables.
$$p(t) = 4t^{4} + 5t^{3} - t^{2} + 6$$ at $$t = 0$$

Given : $$p(t) = 4t^{4} + 5t^{3} - t^{2} + 6$$ at $$t = 0$$

$$p(0)=4\times0+5\times0-0+6$$

$$=6$$

Expand $$9{(x+a)}^{2}-4{x}^{2}$$

given $$9(x+a)^2-4x^2$$

$$\Rightarrow 9(x+a)^2-4x^2=9(x^2+a^2+2ax)-4x^2$$

$$\Rightarrow =9x^2-4x^2+9a^2+18ax=5x^2+9a^2+18ax$$

Determine the number of real and imaginary roots of the following polynomial $$a{x}^{2}+b{x}^{2}+cx+d=0$$

$$ax^2+bx^2+cx+d=0$$

$$(a+b)x^2+cx+d=0$$

to find the roots:

$$\dfrac {-b\pm \sqrt{b^2-4ac}}{ 2a}$$

Values of a,b and c from given equation are:

$$a=(a+b), b=c $$ and $$c=d$$

Substituting the values of a,b and c in the formula, we get,

$$\dfrac {-c\pm \sqrt{c^2-4(a+b)d}}{ 2(a+b)}$$

if $$\sqrt{b^2-4ac}> 0$$ we have 2 real roots

$$\dfrac {-c+\sqrt{b^2-4ac}} {2(a+b)}$$ and $$\dfrac {-c-\sqrt{b^2-4ac}} {2(a+b)}$$

if $$\sqrt{b^2-4ac}< 0$$ we have 2 imaginary roots

$$\dfrac {-c+i\sqrt{b^2-4ac}} {2(a+b)}$$ and $$\dfrac {-c-i\sqrt{b^2-4ac}} {2(a+b)}$$

Without actual calculations, find the value of the following expression:
$$28^{2} - 27^{2}$$.

Given, $$28^2-27^2$$.

We know, $$(a+b)(a-b)=a^2-b^2$$.

Then,

$$28^2-27^2=(28-27)(28+27)=1\times55=55$$.

Hence, $$55$$ is the required answer.

Find the value of a given polynomial at the indicated value of variables.
$$p(x) = 5x^{2} - 3x + 7$$ at $$x = 1$$.

$$p(1)=5\times1^2-3\times1+7$$

$$=12-3$$

$$=9$$

Find the value of a given polynomial at the indicated value of variables.
$$q(y) = 3y^{2} -4y\sqrt{11} +8\sqrt{11}$$ at $$y =2$$

Given : $$q(y) = 3y^{2} -4y\sqrt{11} +8\sqrt{11}$$

$$q(2)=3\times2^2-4\times2\sqrt{11}+8\sqrt{11}$$

$$=3\times4$$

$$=12$$

Simplify the following using idenitive $$(1025)^{2}-(975)^{2}$$

$$a^{2}-b^{2}=(a+b)(a-b)$$

$$(1025)^{2}-(975)^{2}=(1025+975)(1025-975)$$

$$=2000\times 50$$

$$=1,00,000$$

Find the zero of the polynomial in each of the following in each of the following cases:
$$p(x)=ax,a\neq0 $$

$$p\left( x \right) = ax$$

To find the zero of the polynomial,

$$p\left( x \right) = 0$$

$$ax = 0$$

$$x = 0$$

Evaluate the following using suitable identity :
(a) $${ \left( 10x-1 \right) }^{ 2 }$$

(b) $${ \left( x-8y \right) }^{ 2 }$$

(a) $${\left( {10x - 1} \right)^2} = {\left( {10x} \right)^2} + {\left( 1 \right)^2} - 2 \times 10x \times 1$$ (since $${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$$)

$$ = 100{x^2} - 20x + 1$$

(b) $${\left( {x - 8y} \right)^2} = {\left( x \right)^2} + {\left( {8y} \right)^2} - 2 \times x \times 8y$$ ($${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$$)

$$ = {x^2} - 16xy + 64{y^2}$$

Factorise:
$$25a^{2} - 9b^{2}$$

$$25a^2 - 9b^2 = (5a)^2 - (3b)^2$$

$$ =(5a-3b)(5a+3b)$$

Hence factorised

Formula:

$$x^2 - y^2 =(x-y)(x+y)$$

Evaluate the following:
$${ \left( 7x-2y \right) }^{ 2 }$$
$${ \left( 3x+7y \right) }^{ 2 }$$

(a) $${\left( {7x - 2y} \right)^2} = {\left( {7x} \right)^2} + {\left( {2y} \right)^2} - 2 \times 7x \times 2y$$ ($${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$$)

$$ = 49{x^2} - 28xy + 4{y^2}$$

(b) $${\left( {3x + 7y} \right)^2} = {\left( {3x} \right)^2} + {\left( {7y} \right)^2} + 2 \times 3x \times 7y$$ ($${\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab$$)

$$ = 9{x^2} + 42xy + 49{y^2}$$

Find the zero of the polynomial in each of the following in the following case:
$$p(x)=x+5$$

To find the zero of the given polynomial $$p(x)=x+5$$, equate it to $$0$$ as shown below:

$$p(x)=0\\ \Rightarrow x+5=0\\ \Rightarrow x=-5 $$

Hence, $$x=-5$$ is the zero of the given polynomial.

Find the zero of the polynomial in the following case:
$$p(x)=cx+d,c\neq d$$ are real numbers.

To find the zero of the given polynomial $$p(x)=cx+d$$, equate it to $$0$$ as shown below:

$$p(x)=0\\ \Rightarrow cx+d=0\\ \Rightarrow cx=-d\\ \Rightarrow x=-\dfrac { d }{ c }$$

Hence, $$x=-\dfrac { d }{ c }$$ is the zero of the given polynomial.

Verify whether the values of $$x$$ given in each case are the zeros of the polynomial or not?
$$p(x)=x^{2}-1;x=+1$$

$$p(x)=x^2-1$$

For zeroes of the equation, Let $$p(x)=0$$

Therefore, $$x^2-1=0$$

$$x^2=1$$

$$x=\pm 1$$ or $$x=1,-1$$

Hence roots are $$1,\;-1$$

So, $$+1$$ is one of the root of polynomial.

Hence verify.

Find the zero of the polynomial in each of the following in each of the following cases:
$$p(x)=x-5$$

$$p\left( x \right) = x - 5$$

To find the zero of the polynomial, put $$p\left( x \right) = 0$$.

$$x - 5 = 0$$

$$x = 5$$

5 is the zero of the given polynomial.

Find the value of k, if $$x=2$$ is a zero of $$p(x)=x^2+5x+2k$$.

Here , at $$x= 2 p(x)= p (2) =0$$

now, $$p (x) = x^{2}+ 5x+ 2k$$

now, let pet put $$x= 2$$.

we get,

$$p(2) = (2)^{2}+ 5 (2)+ 2k$$

$$\therefore 0 = 4+10+2k.$$

So, $$ \therefore 2k= -14$$

$$\therefore = -\dfrac{14}{2}.$$

$$\therefore k = -7$$

So, the value of $$k$$ is $$(-7)$$

$$p(x) = x^{2}+ 5x+ 2 (-7)$$

$$p (x)= x^{2}+ 5x- 14$$

Evaluate: $$\dfrac {198\times 198-{102}\times 102}{96}$$

Applying the identity $${a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right)$$ in $$\dfrac{{198 \times 198 - 102 \times 102}}{{96}}$$.

$$\dfrac{{198 \times 198 - 102 \times 102}}{{96}} = \dfrac{{\left( {198 + 102} \right)\left( {198 - 102} \right)}}{{96}}$$

$$ = \dfrac{{300 \times 96}}{{96}}$$

$$ = 300$$

Find the zero of the polynomial in each of the following cases :
$$p(x)=cx+d, c\neq 0, c, d$$ are real numbers.

Given $$p(x)=cx+d,c\neq0,c,d$$ are real numbers.

To find zero of a polynomial we put $$p(x)=0$$ and find $$x$$

$$\Rightarrow cx+d=0$$

$$\Rightarrow cx=-d$$

$$\Rightarrow x=-\dfrac{d}{c}$$

Therefore $$x=-\dfrac{d}{c}$$ is the zero of the given polynomial.

Find the square of : $$2a +b$$

$$\textbf{Step1 : Find the square of 2a+b.}$$

$$\text{We know that (a+b)}$$ $$^{2}$$$$= a^2+2ab+b^2$$

$${\text{(2a+b)}^2 = \text{(2a)}^2\text{+2(2a)(b)+(b)}^2}$$

$${\text{= 4a}^2\text{+4ab+b}^2}$$

$$\textbf{Hence the square of (2a+b) is}$$ $$\boldsymbol{\textbf{4a}^2\textbf{+4ab+b}^2.}$$

Evaluate $$(a+b)(a-b)+(b+c)(b-c)+(c+a)(c-a)$$.

We are given,

$$(a+b)(a-b)+(b+c)(b-c)+(c+a)(c-a)$$

$$=(a^2b^2)+(b^2-c^2)+(c^2-a^2)$$

$$=(a^2-a^2)+(b^2-b^2)+(c^2-c^2)$$

$$=0$$

So, $$\boxed {(a+b)(a-b)+(b+c)(b-c)+(c+z)(c-a)}$$

Find the number of zeroes of the quadratic $${x}^{2}+7x+10$$ and verify the relationship between the zeroes and the the co-efficients.

For zeroes

$${x^2} + 7x + 10=0$$

$$x^2+5x+2x+10=0$$

$$x(x+5)+2(x+5)=0$$

$$( x+5)(x+2)=0$$

$$x=-2,-5$$

$$\alpha =-2,\beta=-5$$

$$\alpha +\beta =-7$$

$$\alpha \beta=10$$

$$\dfrac{-b}{a}=\dfrac{-7}{1}=-7$$

$$\dfrac{c}{a}=\dfrac{10}{1}=10$$

$$\alpha +\beta=\dfrac{-b}{a}$$ and $$\alpha \beta=\dfrac{c}{a}$$

Hence proved

Find the roots of: $$x^{4}-26x^{2}+25=0$$

$$x^{4}-26x^{2}+25=0$$

$$x^{4}-x^{2}-25x^{2}+25=0$$

$$x=\pm 1,\pm 5$$

Simplify the following using the rules for identities :
(i) $$69^{2}-59^{2}$$
(ii) $$101^{2}-91^{2}$$
(iii) $$1002^{2}-998^{2}$$

As $$a^{2}-b^{2}=(a-b)(a+b)$$

i) $$(69)^{2}-(59)^{2}=(69-59)(69+59)=(10)(128)=1280$$

Hence the answer $$1280$$

ii) $$(101)^{2}-(91)^{2}=(101-91)(101+91)=(10)(192)=1920$$

Hence the answer $$1920$$

iii) $$(1002)^{2}-(998)^{2}=(1002-998)(1002+998)=(4)(2000)=8000$$

Hence the answer $$8000$$

Simplify : $$\left( 4+\sqrt { 3 } \right) \left( 4-\sqrt { 3 } \right) $$

$$(4+\sqrt 3)(4-\sqrt 3)$$

This is in the form of $$(a+b)(a-b)=a^2-b^2$$. Using this formula we get,

$$\Rightarrow (4+\sqrt 3)(4-\sqrt 3)=4^2-(\sqrt 3)^2$$

$$\Rightarrow (4+\sqrt 3)(4-\sqrt 3)=16-3=13$$

Therefore $$\Rightarrow (4+\sqrt 3)(4-\sqrt 3)=13$$

Find the zero of the polynomial
$$p\left( x \right) = 2{x^2} - 5x - 3$$

$$p\left( x \right) = 2{x^2} - 5x - 3$$
To find zero of polynomial $$p\left( x \right) = 0$$
$$\begin{array}{l}p\left( x \right) = 2{x^2} - 5x - 3\\p\left( x \right) = 0\\ \Rightarrow 2{x^2} - 5x - 3 = 0\\ \Rightarrow 2{x^2} - 6x + x - 3 = 0\\ \Rightarrow 2x\left( {x - 3} \right) + 1\left( {x - 3} \right) = 0\\ \Rightarrow \left( {2x + 1} \right)\left( {x - 3} \right) = 0\\x = \frac{{ - 1}}{2},3\end{array}$$

$$(9a-5b)^2+186ab=(9a+5b)^2$$.

We are given that,

$$ (9a-5b)^{2}+186ab = (9a+5b)^{2}$$

So,

$$ \therefore (9a-5b)^{2}-(9a+5b)^{2} = -186ab $$

now, $$ a^{2}-b^{2} = (a+b)(a-b)$$

$$ \therefore (9a-5b+9a+5b)(9a-5b-9a-5b) = -186 ab$$

$$ (18a)(-10b) = -186ab $$

$$ -180ab + 186ab = 0 $$

$$ 6ab = 0 $$

$$ \boxed{ab = 0 } $$

If $$2(a^2+b^2)=(a+b)^2$$, then show that $$a=b$$.

Acccording to question,

$$2( a^{2} + b^{2} )= (a+b)^{2} $$

$$ \Rightarrow 2 a^{2} +2 b^{2} = a^{2} + b^{2} +2ab$$

$$ \Rightarrow a^{2} + b^{2} -2ab=0$$

$$ \Rightarrow (a-b)^{2}=0$$

Therefore,

$$ \Rightarrow a=b$$

Using identity $$ (a+b)^2=(a^2+2ab+b^2)$$ Evaluate (i) $$(609)^2$$ (ii) $$(725)^2$$

(i) $$(609)^2=(600+9)^2=(600)^2+2\times600\times9+(9)^2=360000+10800+81=370881$$

(ii) $$(725)^2=(700+25)^2=(700)^2+2\times700\times25+(25)^2=490000+35000+625=525625$$

If $$3x - 2y = 5$$ and $$xy = 4$$ then find the value of $$9{x^2} + 4{y^2}$$

Given:-

$$3x-2y=5\quad\quad\quad\dots(i)$$

$$xy=4\quad\quad\quad\quad\quad\dots(ii)$$

By squaring equation $$(i),$$

$$\begin{aligned}{}{\left( {3x - 2y} \right)^2}& = {5^2}\\{\left( {3x} \right)^2} - 2\left( {3x} \right)\left( {2y} \right) + {\left( {2y} \right)^2}& = 25\\9{x^2} + 4{y^2} - 12xy &= 25\\9{x^2} + 4{y^2} &= 25 + 12xy\quad\quad\quad\quad\dots(iii)\end{aligned}$$

Now, by using equation $$(ii)$$ and $$(iii),$$

$$\begin{aligned}{}9{x^2} + 4{y^2}& = 25 + 12xy\\ &= 25 + 12\left( 4 \right)\\& = 25 + 48\\& = 73\end{aligned}$$

Find $$p$$ and $$q$$ such that $$(x+1)$$ and $$(x-1)$$ are factors of the polynomial $${x^4} + p{x^3} - 3{x^2} + qx + q$$.

Let

$$ A={ x }^{ 4 }+{ px }^{ 3 }-{ 3x }^{ 2 }+qx+x $$ with $$(x+1)$$ & $$(x-1)$$ are the 2 factors

$$\therefore \quad x=1\quad \& \quad x=-1\quad satisfies\quad A$$

Derivation of p

$$\quad \Rightarrow \quad (-1)^{ 4 }-p-3-q+q=0$$

$$\quad \Rightarrow \quad p=-2$$

Derivation of q

$$\quad \Rightarrow \quad 1+p-3+q+q=0\quad $$

$$\quad \Rightarrow \quad p+2q=2$$

$$\quad \Rightarrow \quad 2q=4$$

$$\quad \Rightarrow \quad q=2$$

$$Hence,(p,q)=(-2,2)$$

Find the zeroes of the polynomial $$p(x) = {x^3} - x$$.

The zeroes of the polynomial are the values of x when $$p(x)=0$$

$$\Rightarrow$$ $$x^3-x=0$$

$$\Rightarrow$$ $$x(x^2-1)=0$$

$$\Rightarrow$$ $$x(x-1)(x+1)=0$$

$$\Rightarrow$$ $$x=0,1,-1$$

Hence zeroes of $$p(x)$$ are $$0,1,-1$$.

find zeros of polynomial $$f(x) = -(x - 1)^3 (x + 1)^2$$.

$$\begin{array}{l}f\left( x \right) = 0\\ \implies- {\left( {x - 1} \right)^3}{\left( {x + 1} \right)^2} = 0\\ \implies {\left( {x - 1} \right)^3} = 0\, or\, {\left( {x + 1} \right)^2} = 0\end{array}$$

So,

$$x-1=0$$ or $$x+1=0$$

$$x=1$$ or $$x=-1$$

Solve the equation:
$$\dfrac{{{{\left( {2x + 1} \right)}^2} + {{\left( {2x - 1} \right)}^2}}}{{{{\left( {2x + 1} \right)}^2} - {{\left( {2x - 1} \right)}^2}}} = \dfrac{{17}}{8}$$

We have,

$$ \dfrac{{{\left( 2x+1 \right)}^{2}}+{{\left( 2x-1 \right)}^{2}}}{{{\left( 2x+1 \right)}^{2}}-{{\left( 2x-1 \right)}^{2}}}=\dfrac{17}{8} $$

$$ \Rightarrow \dfrac{4{{x}^{2}}+1+4x+4{{x}^{2}}+1-4x}{4{{x}^{2}}+1+4x-4{{x}^{2}}-1+4x}=\dfrac{17}{8} $$

$$ \Rightarrow \dfrac{8{{x}^{2}}+2}{8x}=\dfrac{17}{8} $$

$$ \Rightarrow \dfrac{8{{x}^{2}}+2}{x}=\dfrac{17}{1} $$

$$ \Rightarrow 8{{x}^{2}}+2=17x $$

$$ \Rightarrow 8{{x}^{2}}-17x+2=0 $$

$$ \Rightarrow 8{{x}^{2}}-\left( 16+1 \right)x+2=0 $$

$$ \Rightarrow 8{{x}^{2}}-16x-1x+2=0 $$

$$ \Rightarrow 8x\left( x-2 \right)-1\left( x-2 \right)=0 $$

$$ \Rightarrow \left( x-2 \right)\left( 8x-1 \right)=0 $$

$$ \Rightarrow x-2=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,8x-1=0 $$

$$ \Rightarrow x=2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x=\dfrac{1}{8} $$

Hence, this is the answer.

Using $$(x + a) (x + b) = x^2 + (a + b) x + ab$$ find $$105 \times 107$$

$$105\times 107$$

$$\Rightarrow (100+5)(100+7)$$ [is of the form $$(x+a)(x+b)$$]

$$\Rightarrow (100^2)+(7+5)(100)+7\times 5$$ $$[(x+a)(x+b)=x^2+(a+b)x+ab]$$

$$\Rightarrow 10000+1200+35$$

$$\Rightarrow 11235$$

$$\therefore 105\times 107=11235$$.

How many zeros does the polynomial $${ ax }^{ 3 }+{ bx }^{ 2 }+cx+d$$ have ?

Three zeroes as its a polynomial with degree 3.

Zero of the polynomial $$p(x)=2 - 5x$$ is

Consider the given polynomial.

$$p\left( x \right)=2-5x$$

Put $$p\left( x \right)=0$$

Therefore,

$$ 2-5x=0 $$

$$ 5x=2 $$

$$ x=\dfrac{2}{5} $$

Hence, the zero of the given polynomial is $$\dfrac{2}{5}$$.

The value of $$\left( x+3y \right) ^{ 2 }+\left( x-3y \right) ^{ 2 }$$ is

The given expression $$(x+3y)^2+(x-3y)^2$$ can be solved as shown below:

$$(x+3y)^{ 2 }+(x-3y)^{ 2 }\\ =[(x)^{ 2 }+(3y)^{ 2 }+(2\times x\times 3y)]+[(x)^{ 2 }+(3y)^{ 2 }-(2\times x\times 3y)]\\ (\because \quad (a+b)^{ 2 }=a^{ 2 }+b^{ 2 }+2ab,\quad (a-b)^{ 2 }=a^{ 2 }+b^{ 2 }-2ab)\\ =x^{ 2 }+9y^{ 2 }+6xy+x^{ 2 }+9y^{ 2 }-6xy\\ =(x^{ 2 }+x^{ 2 })+(9y^{ 2 }+9y^{ 2 })+(6xy-6xy)\quad \quad \quad \quad (Combining\quad like\quad terms)\\ =2x^{ 2 }+18y^{ 2 }\\ =2(x^{ 2 }+9y^{ 2 })$$

Hence, $$(x+3y)^{ 2 }+(x-3y)^{ 2 }=2(x^{ 2 }+9y^{ 2 })$$.

Using identity find the value of $$(4.7)^2$$.

$$(4.7)^2$$

$$\Rightarrow (4+0.7)^2$$

$$\Rightarrow(4)^2+(0.7)^2+2(0.7)(4)$$ $$((a+b)^2=a^2+b^2+2ab)$$

$$\Rightarrow 16+0.49+5.6$$

$$\Rightarrow 21.6+0.49$$

$$\Rightarrow \boxed{22.09}$$

If $$p(x)=3x^2-4x+7$$,find $$p(\dfrac{1}{2})$$ and $$p(-2)$$

Given,

The polynomial $$p\left( x \right) =3{ x }^{ 2 }-4x+7$$

For $$x=\dfrac { 1 }{ 2 } $$,

$$p\left( \dfrac { 1 }{ 2 } \right)=3{ \left( \dfrac { 1 }{ 2 } \right) }^{ 2 }-4\left( \dfrac { 1 }{ 2 } \right) +7$$

$$=\dfrac { 3 }{ 4 } -2+7$$

$$=\dfrac { 3-8+28 }{ 4 } $$

$$=\dfrac { 23 }{ 4 } $$

Again, for $$x=-2$$,

$$p\left( -2 \right) =3{ \left( -2 \right) }^{ 2 }-4\left( -2 \right) +7$$

$$=12+8+7$$

$$=27$$.

Find the a zero of the polynomial $$p(x) = 3x + 1 \ $$

Given $$p(x)=3x+1$$

zero of the polynomial is $$3x+1=0\implies x=-\dfrac 13$$

Using identity find the value of $$(7.2)^2$$

$$(7.2)^2$$

$$\Rightarrow (7+0.2)^2$$

$$\Rightarrow 7^2+(0.2)^2+2(0.2)(7)$$

$$\Rightarrow 49+0.04+(0.4)(7)$$

$$\Rightarrow 49.04+2.8$$

$$\Rightarrow 51.84$$.

$$A^2-B^2=(a+b)(a-b)$$.

$$A^2 - B^2 = (a+b)(a-b)$$

$$(A+B)(A-B) = (a+b)(a-b)$$

$$(a+b)^2$$ Solve it.

$$a^2 + 2ab + b^2$$

if $$x = (-1)$$ , then solve
$$p(x) = 5x - 4x^{2} + 3$$.

$$p(x)=5*-1-4*-1*-1+3$$

$$=-5-4+3$$

$$=-9+3$$

$$=-6$$

Simplify $${ \left( 1-z \right) }^{ 2 }-{ \left( 1+z \right) }^{ 2 }$$

Given equation $$(1-2)^2-(1+z)^2$$

Since, we know that $$(a-b)^2 =a^2+b^2-2ab---(1)$$

and $$(a+b)^2=a^2+b^2+2ab---(2)$$

So, using formulas we get

$$(1-z)^2=1^2+z^2-2.1.z\quad \left\{1\right\} ---(3)$$

$$(1+z)^2=1^2+z^2+2.1.z\quad \left\{2\right\} ---(4)$$

Subtract $$(4)$$ from $$(3)$$

i.e. $$(1-z)^2-(1+z)^2 =1+z^2-2z-1-z^2-2z$$

$$=-4z$$

Simplify : $$(x - y)^2 - 7(x^2 - y^2) + 12 (x + y)^2$$

$$(x - y)^2 - 7(x^2 - y^2) + 12 (x + y)^2$$

$$=x^2+y^2-2xy-7x^2+7y^2+12(x^2+y^2+2xy)$$

$$=-6x^2+8y^2-2xy+12x^2+12y^2+24xy$$

$$=6x^2+20y^2+22xy$$

Find k, if 3 is the zero of $$3{ x }^{ 2 }+\left( k-3 \right) x+9x=0$$ .

$$3$$ is the zero of $$3x^2+(k-3)x+9x=0$$

Therefore,

$$27+3k-9+27=0$$

$$3k+45=0$$

$$3k=-45$$

$$k=-15$$

Evaluate
$$(2-\dfrac{7}{2})^{2}+(3+\dfrac{5}{2})^{2}=r^{2}$$.

$$\left(2-\dfrac{7}{2}\right)^2+\left(3+\dfrac{5}{2}\right)^2=r^2$$

$$\left(\dfrac{4-7}{2}\right)^2+\left(\dfrac{6+5}{2}\right)^2=r^2$$

$$\left(\dfrac{-3}{2}\right)^2+\left(\dfrac{11}{2}\right)^2=r^2$$

$$\left(\dfrac{9}{4}\right)+\left(\dfrac{121}{4}\right)=r^2$$

$$\dfrac{9+121}{4}=r^2$$

$$\dfrac{130}{4}=r^2$$

$$\dfrac{65}{2}=r^2$$

$$r=\sqrt{\dfrac{65}{2}}$$

Simplify:
i) $${\left( {{a^2} - {b^2}} \right)^2}$$
ii) $${\left( {2x + 5} \right)^2} - {\left( {2x - 5} \right)^2}$$

$$(i)\ (a^2-b^2)^2 =(a^2)^2-2.a^2.b^2+(b^2)^2$$

$$\quad =a^4-2a^2b^2+b^4$$

$$(ii)\ (2x+5)^2-(2x-5)^2$$

$$\quad =(2x)^2+2\times2x\times5+5^2-\left\{(2x)^2-2\times2x\times5+(5)^2 \right\}$$

$$\quad =4\times2x\times5$$

$$\quad =40x$$

Find the zeros of the following quadratic polynomial :
$$p(x)=6x^{2}-x-6$$

1381175_1131643_ans_7afafeb885ca4c5fba58e67da5fe2d14.jpg

Solve:
$$ (x+4)^2 - (x-5)^2 = 9 $$

$$(x+4)^{2}-(x-5)^{2}=9$$

$$(x^{2}+16+8x)-(x^{2}+25-10x)=9$$

$$-9+18x=9$$

$$\Rightarrow 18x=18\Rightarrow x=1$$

The zeros of $$p(x)=2+x-x^2$$ are

Factorization.

$$P(x)=2+x-x^2$$

solve for $$P(x)=0$$ & get value of those $$x$$.

$$P(x)=2+2x-x-x^2$$

$$=2(1+x)-x(1+x)$$

$$=(2-x)(1+x)$$

$$P(x)=0\Rightarrow (2-x)=0$$ or $$(1+x)=0$$

$$\Rightarrow x=2, -1$$.

Find the zeroes of the polynomial $$f(x)=4{x}^{2}+8x$$ and verify the relationship between the zeroes and its coefficients.

Given polynomial can be written as $$4x^2+8x=4x(x+2)=0$$

Hence the roots are $$x=0,x=-2$$

The sum of roots are $$\dfrac{-b}{a}=-2$$

and the product of roots are $$\dfrac{c}{a}=0$$

Solve:
$${(a + b)^2} - {a^2} - {b^2}$$=?

Solution :-

$$\displaystyle (a+b)^{2}-a^{2}-b^{2} = $$

we have $$ \displaystyle(a+b)^{2} = a^{2}+b^{2}+2ab $$

$$\displaystyle \therefore (a+b)^{2}-a^{2}-b^{2} = a^{2}+b^{2}+2ab-a^{2}-b^{2} $$

$$ \displaystyle = 2ab $$

1106801_1176786_ans_8ae0bfc889a440388b725f4135923f68.jpg

Find the zeros of the quadratic polynomial $$\sqrt { 3 } x ^ { 2 } - 8 x + 4 \sqrt { 3 }$$.

$$\sqrt{3}x^2-8x+4\sqrt{3}=0$$

$$\sqrt{3}x^2-6x-2x+4\sqrt{3}=0$$

$$\sqrt{3}x(x-2\sqrt{3})-2(x-2\sqrt{3})=0$$

$$(x-2\sqrt{3})(\sqrt{3}x-2)=0$$

$$x=2\sqrt{3}$$ or $$\dfrac{2}{\sqrt{3}}$$

Show that $${ \left( 3x+7 \right) }^{ 2 }-84x={ \left( 3x-7 \right) }^{ 2 }$$

$$(3x+7)^2-84x=(3x-7)^2$$

$$\Rightarrow$$ $$L.H.S. =(3x+7)^2-84x$$

$$=(3x)^2+2(3x)(7)+(7)^2-84x$$

$$=9x^2+42x+49-84x$$

$$=9x^2-42x+49$$

$$=(3x-7)^2$$

$$\therefore$$ $$L.H.S=R.HS.$$

$$\therefore$$ $$(3x+7)^2-84x=(3x-7)^2$$ ---- [ Hence proved ]

Solve it:-
$${\left( {a + 2b} \right)^2} - {a^2}$$

Solve

$$(a+2b)^{2}-a^{2}$$

Apply formula $$(x+y)^{2}=x^{2}+y^{2}+2xy$$

$$=a^{2}+(2b)^{2}+2a(2b)-a^{2}$$

$$=a^{2}+4b^{2}+4ab-a^{2}$$

$$=4b^{2}+4ab$$

$$=4b(b+a)$$

$$4b(a+b)$$

Find the zeroes of the following polynomial:$$5\sqrt 5 {x^2} + 30x + 8\sqrt 5 $$

Consider the given expression,

$$ \Rightarrow 5\sqrt{5}{{x}^{2}}+30x+8\sqrt{5} $$

$$ \Rightarrow 5\sqrt{5}{{x}^{2}}+20x+10x+8\sqrt{5} $$

$$ \Rightarrow 5\sqrt{5}{{x}^{2}}+4.\sqrt{5}.\sqrt{5}x+2.\sqrt{5}\sqrt{5}x+8\sqrt{5} $$

$$ \Rightarrow \sqrt{5}x\left( x+4\sqrt{5} \right)+2.\sqrt{5}\left( x+4\sqrt{5} \right) $$

$$ \Rightarrow \left( x+4\sqrt{5} \right)\left( \sqrt{5}x+2\sqrt{5} \right) $$

When,

$$ \left( x+4\sqrt{5} \right)=0 $$

$$ x=-4\sqrt{5} $$

When,

$$ \left( \sqrt{5}x+2\sqrt{5} \right)=0 $$

$$ x=-2 $$

Hence, this is the answer.

Find the zero of the polynomial
$$2x-3$$

Zero of the polynomial implies value of x at which value of polynomial is 0.

Hence,

$$2x-3=0\\ \Rightarrow x=\dfrac { 3 }{ 2 } $$

Find the zeros of the quadratic polynomial:
$$x^2-5x+6$$.

Given the polynomial is $$x^2-5x+6=0$$

$$x^2-3x-2x+6=(x-2)(x-3)=0$$.

From this it is clear that the zeros of the quadratic polynomial is $$2,3$$.

Find the zeroes of the quadratic polynomial $$9x^2-5$$.

Given polynomial is $$9x^2-5$$

We know that, for a quadratic equation of the form $$ax^2+bx+c=0$$,

$$x = \dfrac{-b \pm \sqrt{b^{2}-4ac}}{2a}$$

Here, $$a=9,\ b=0,\ c=-5$$

$$\therefore \ x=\dfrac{\pm \sqrt{180}}{18}$$

$$\Rightarrow x= \dfrac{\pm 6\sqrt{5}}{18}$$

Hence, $$x= \dfrac{6\sqrt{5}}{18}$$ or $$x= \dfrac{-6\sqrt{5}}{18}$$

$$\Rightarrow x= \dfrac{\sqrt{5}}{3}$$ or $$x=\dfrac{-\sqrt{5}}{3}$$

Hence, $$x= \dfrac{\sqrt{5}}{3},\ x= \dfrac{-\sqrt{5}}{3}$$ is the solution of the given polynomial.

Simplify: $$\left( a ^ { 2 } - b ^ { 2 } \right) ^ { 2 }$$

# $$(a^{2}-b^{2})^{2}=(a^{2})^{2}+(b^{2})^{2}-2(a^{2})(b^{2})$$

$$=a^{4}+b^{4}-2a^{2}b^{2}$$

1105709_1181090_ans_580f793fbf474cc9bd34adfcb63d6277.jpg

$$\begin{array} { l } { \text { Evaluate using expansion of } ( a + b ) ^ { 2 } }or { ( a - b ) ^ { 2 } : } \end{array}$$
(i) $$( 208 ) ^ { 2 }$$ (ii) $$( 92 ) ^ { 2 }$$

(i)$$ (208)^{2} = (200+8)^{2} = 40000+3200+64....... [(a+b)^{2} = a^{2}+2ab+b^{2}]$$

$$ = 43264$$

(ii) $$ (92)^{2}=(100-8)^{2} = 10000-1600+64..... [(a-b)^{2}=a^{2}-2ab+b^{2}]$$

$$ = 8464$$

Find the zeros of the given polynomials
$$t^{2}-15$$

Let, $$P(t)= t^2 - 15 $$

$$ = (t)^2 - (\sqrt{15})^2 $$

$$ = (t + \sqrt{15})(t - \sqrt{15})$$

$$P(t)= 0 $$ when $$t = - \sqrt{15}$$ or $$t = \sqrt{15}$$

Hence, Zeros of the polynomial $$t^2 - 15$$ are $$-\sqrt{15}, \sqrt{15}$$

Solve: $$3{y}^{2}=15y$$

$$3y^2=15y$$

$$3y^2-15y=0$$

$$3y(y-15)=0$$

$$\therefore y=0, y=15$$

Solve:
$$2{y^3} - 3{y^2} + 1 = 0$$

1108496_1189486_ans_055e3731f9dd495b8536d88994d6eb08.jpeg

Find the zeroes of the quadratic polynomial $$6x^2-13x+6$$ and verify the relation between the zeroes and its coefficients?

Given, the polynomial

$${ 6x }^{ 2 }-13x+6=0\\ \Rightarrow { 6x }^{ 2 }-9x-4x+6=0\\ \Rightarrow 3x(2x-3)-2(3x-3)=0\\ \Rightarrow (2x-3)(3x-2)=0\\ \therefore 2x-3=0\\ \Rightarrow x=\dfrac { 3 }{ 2 } \\ 3x-2=0\\ \Rightarrow x=\dfrac { 2 }{ 3 } $$

Let, $$\alpha =\dfrac { 3 }{ 2 } ,\\ \beta =\dfrac { 2 }{ 3 } $$

From the polynomial we get, $$a=6,b=-13,c=6$$

$$\therefore$$ Relation between the zeroes and coefficients,

Sum of the zeroes=$$\dfrac { 3 }{ 2 } +\dfrac { 2 }{ 3 } =\dfrac { 13 }{ 6 } =-\dfrac { (-13) }{ 6 } =\dfrac { b }{ a } $$

and product of the zeroes=$$\dfrac { 3 }{ 2 } \times \dfrac { 2 }{ 3 } =\dfrac { 6 }{ 6 } =\dfrac { c }{ a } $$

Hence, the relation between the zeroes and the coefficients of the polynomial is verified.

If $$5x+\cfrac{1}{5x}=23$$ and $$5x-\cfrac{1}{5x}=17$$, find the value of $$25{x}^{2}-\cfrac{1}{25}{x}^{2}$$

$$25x^2-\dfrac{1}{25x^2}=(5x)^2-\left(\dfrac{1}{5x}\right)^2$$

We know $$a^2-b^2=(a-b)(a+b)$$

$$(5x)^2-\left(\dfrac{1}{5x}\right)^2=\left(5x-\dfrac{1}{5x}\right)\left(5x-\dfrac{1}{5x}\right)$$

$$=17\times23$$

$$=391$$

If one zero of the quadratic polynomial $${x^2} + 3x + k$$ is 2, then find the value of k.

Given polynomial $$x^2+3x+k=f(x)$$

Also, given that $$2$$ is one of the zeros of the polynomial.

$$\therefore \ f(2)=0$$

$$\Rightarrow 4+6+k=0$$

$$\Rightarrow \ k=-10$$

Hence, the value of $$k$$ is $$-10$$

Find: $$(5m+7n)^{2}$$

$$ (5m+7n)^{2} = (5m)^{2}+2(5m)(7n)+(7n)^{2}$$

$$ = 25m^{2}+70\, mn+49n^{2}$$

Show that:
$${(a+b)}^{2}-{(a-b)}^{2}=4ab$$

$$LHS=(a+b)^2-(a-b)^2$$

$$=a^2+b^2+2ab-(a^2+b^2-2ab)$$

$$=a^2+b^2+2ab-a^2-b^2+2ab$$

$$=4ab$$

$$=RHS$$

Find the zero of the polynomial
$$x^{2}-16$$

$${ x }^{ 2 }-16=0\\ \Rightarrow { x }^{ 2 }=16\\ \Rightarrow x=\sqrt { 16 } =+4\ or\ -4$$

Simplify $$( a + b ) ^ { 2 }$$

$$ (a+b)^{2} = (a+b)(a+b)$$

$$ = a^{2}+ab+ba+b^{2}$$

$$ = a^{2}+2ab+b^{2}$$

Solve the following equation;
$$x^{4}-10x^{2}+9=0$$

$$x^4-10x^2+9=0$$

$$x^4-9x^2-x^2+9=0$$

$$x^2(x^2-9)-1(x^2-9)=0$$

$$(x^2-9)(x^2-1)=0$$

Now, $$x^2-9=0\\x=\pm 3$$ or $$x^2-1=0\\x=\pm 1$$

So, $$x=-3,+3,-1,+1$$

Following polynomars write the degree of each.
$$1)$$. $$6x^{2}+x+1$$
$$2)$$. $$y^{9}-3y^{7}+\frac{3}{2}y^{2}+4$$
$$3) $$. $$2x+1$$
$$4)$$. $$5t-\sqrt{11}$$

$$Example - [4x{y^2} + 3x - 8]$$

Define:- An expression that can have constants (like $$4$$) variables (like $$x$$ or $$ y$$) and exponents (like the $$2$$ in $${y^2}$$), that can be combined using addition subtraction, multiplication and division, but:

$$ \bullet $$ no division by a variable

$$ \bullet $$ a variable's exponents can only be $$0,1,2,3,...$$ etc

$$ \bullet $$ it can not have an infinite number of terms.

So that the

$$A. 6{x^2} + x + 1$$ Degree $$ = 2$$

$$B. {y^9} - 3{y^7} + \frac{3}{2}{y^2} + 4$$ Degree $$ = 9$$

$$C. 2x + 1$$ Degree $$ = 1$$

$$D. 5t - \sqrt {11} $$ Degree $$ = 1$$

Prove: $${\left( {4x + 7y} \right)^2} - {\left( {4x - 7y} \right)^2} = 112xy$$

$$ (4x+7y)^{2}-(4x-7y)^{2}$$

we know $$(a+b)^{2}-(a-b)^{2} = 4ab$$

$$ \therefore (4x+7y)^{2}-(4x-7y)^{2} = 4.4x.7y$$

$$ = 112xy$$

Solve:
$$\left( {{p^2} - {q^2}} \right)\left( {{p^2} + {q^2}} \right) $$

$$(p^2-q^2)(p^2+q^2)$$

$$\Rightarrow$$ We know $$(a-b)(a+b)=a^2-b^2$$

$$\therefore (p^2-q^2)(p^2+q^2)$$

$$\Rightarrow p^4-q^4$$

Simplify:
$$\left( 3 m - \dfrac { 4 } { 5 } n \right) ^ { 2 }$$

$$(3m-(\dfrac{4}{5})n)^2\\=(3m)^2+((\dfrac{4n}{5}))^2-2\cdot(3m\cdot(\dfrac{4n}{5}))\\=9m^2+(\dfrac{16n^2}{25})-(\dfrac{24n}{5})$$

Solve:
$$2{x^2} + 5\sqrt 3 x + 6 = 0$$

$$2x^2+5\sqrt{3}x+6=0$$

$$\Rightarrow 2x^2+4\sqrt{3}x+\sqrt{3}x+6=0$$

$$\Rightarrow 2x(x+2\sqrt{3})+\sqrt{3}(x+2\sqrt{3})=0$$

$$\Rightarrow (x+2\sqrt{3})(2x+\sqrt{3})=0$$

$$\Rightarrow x=-2\sqrt{3}, -\dfrac{\sqrt{3}}{2}$$.

Decide whether $$x=2$$ is a zero of $${x}^{2}+4x-12=0$$.

$$x-a$$ divides a polynomial $$p(x'): ff......p(a)=0$$

$$\Rightarrow$$ Let $$P(x)=x^2+4x-12$$.

$$\Rightarrow P(2)=2^2+4\times 2-12$$

$$=4+8-12$$

$$=0$$

$$\Rightarrow x-2$$ divides $$x^2+4x-12$$.

Evaluate:
$$( a - 3 b ) ^ { 2 } - 4 ( a - 3 b ) - 21$$

$$(a-3b)^2-4(a-3b)-21\\Let\quad a-3b=x\\x^2-4x-21\\=x^2-7x+3x-21\\=x(x-7)+3(x-7)\\=(x-7)(x+3)\\=(a-3b-7)(a-3b+3)$$

$$(a^{2}-9)x=a^{3}+27$$

$$\left( { a }^{ 2 }-9 \right) x={ a }^{ 3 }+27$$

$$\left( a+3 \right) \left( a-3 \right) x=\left( a+3 \right) \left( { a }^{ 2 }-3a+9 \right) $$

$$\therefore x=\cfrac { { a }^{ 2 }-3a+9 }{ a-3 } $$

Simplify:
$$( a x + b y ) ^ { 2 } + ( b x - a y ) ^ { 2 }$$

$$(ax+by)^2+(bx-ay)^2$$

$$=a^2x^2+b^2y^2+2abxy+b^2x^2+a^2y^2-2abxy$$

$$=(a^2+b^2)x^2+(a^2+b^2)y^2$$

Solve:

$$\dfrac { 97 ^ { 2 } - 43^2 } { 97 - 43 }$$

$$\dfrac{97^{2}-43^{2}}{97-43}\Rightarrow \dfrac{(97-43)(97+43)}{(97-43)}$$

$$\Rightarrow 140$$

Factorize :$$2y^2+9y+10=0$$

$$2{ y }^{ 2 }+9y+10=0\\ \Rightarrow 2{ y }^{ 2 }+4y+5y+10=0\\ \Rightarrow 2y\left( y+2 \right) +5\left( y+2 \right) =0\\ \Rightarrow \left( y+2 \right) \left( 2y+5 \right) =0$$

$$y=-2$$ or $$y=\frac { -5 }{ 2 } $$

Find the roots of $$ 21x^2+2x+\dfrac{1}{21}=0$$ by factorization method.

$$21x^2+2x+\cfrac{1}{21}=0$$

$$\implies 21x^2+x+x+\cfrac{1}{21}=0$$

$$\implies(x+\cfrac{1}{21})(21x+1)=0$$

So, $$x=\pm\cfrac{1}{21}$$

Using $${a^2} - {b^2} = \left( {a + b} \right)\left( {a - b} \right),$$ find
1) $${51^2} - {49^2}$$
2) $${\left( {1.02} \right)^2} - {\left( {0.98} \right)^2}$$
3) $${153^2} - {147^2}$$
4) $${12.1^2} - {7.9^2}$$

$$a^2-b^2=(a+b)(a-b)$$ -Identity

$$1)$$ $$51^2-49^2=(51+49)(51-49)$$

$$=(100)\times (2)$$

$$=200$$

$$2)$$ $$(1.02)^2-(0.98)^2=(1.02+0.98)(1.02-0.98)$$

$$=(2)\times (0.04)$$

$$=0.08$$

$$3)$$ $$(153)^2-(147)^2=(153+147)(153-147)$$

$$=(300)\times (6)$$

$$=1800$$

$$4)$$ $$(12.1)^2-(7.9)^2=(12.1+7.9)(12.1-7.9)$$

$$=(20)\times (4.2)$$

$$=84$$.

Verify whether the following is zeros of the polynomial, indicated against them.
$$p(x)=x^{2},\ x=0$$

$$p(x)=x^2$$

Fpr $$x=0$$ $$,p(0)=0$$

So, $$x=0$$ is zero of $$p(x)$$.

Find the zero of the polynomial in each of the following
$$p(x)=3x$$

$$p(x)=3x$$

$$3x=0$$

$$x=0$$

$$0$$ is the zero of the polynomial.

Find the zeros of the given polynomials.
$$p(x)=(x+2)(x+3)$$

FOR ZEROS P(X) =0

X + 2 = 0 OR X + 3 = 0

X = -2 OR X = -3

Verify whether the following is zeros of the polynomial, indicated against them.
$$p(x)=(x+1)(x-2),\ x=-1,2$$

$$p(x)=(x+1)(x-2)$$

$$p(-1)=0$$

$$p(2)=0$$

Since $$p(x)=0$$ for $$x=-1,2$$

So, we can say that they are zeroes of $$p(x)$$

Show that:
$$(a - b)(a + b) + (b - c)(b + c) + (c - a)(c + a) = 0$$

$$(a-b)(a+b)+(b-c)(b+c)+(c-a)(c+a)$$

$$\Rightarrow (a^2-b^2)+(b^2-c^2)+(c^2-a^2)$$

$$=0$$

Solve the following quadratic equation by factorization and find its root :
$$ 6x^2-x-2=0 $$

$$6x^2-x-2=0$$

$$6x^2-4x+3x-2=0$$

$$2x(3x-2)+(3x-2)=0$$

$$(2x+1)(3x-2)=0$$

$$x=\dfrac{-1}{2}, \dfrac{2}{3}$$.

Verify whether the following is zeros of the polynomial, indicated against them.
$$p(x)=x^{2}-1,\ x=1,-1$$

$$p(x)=x^2-1$$

$$x=\pm1$$

$$p(1)=1^2-1=0$$

$$p(-1)=(-1)^2-1=0$$

Since $$p(x)=0$$ for $$x=\pm1$$

So, $$x=\pm 1$$ are zero of $$p(x)$$

Solve the following quadratic equation by factorization :
$$ 64x^2-9=0 $$

$$64x^2-9=0$$

$$\Rightarrow (8x-3)(8x+3)=0$$

$$\Rightarrow x=\dfrac{3}{8}, \dfrac{-3}{8}$$

Solve : $$x^2 - 6x + 8 $$

$$x^2-6x+8=0$$

$$\Rightarrow x^2-4x-2x+8=0$$

$$\Rightarrow x(x-4)-2(x-4)=0$$

$$\Rightarrow (x-4)(x-2)=0$$

$$\Rightarrow x=2,4$$

Solve: $$( 4 m + 5 n ) ^ { 2 } + ( 5 m + 4 n ) ^ { 2 }$$

$$(4m+5n)^2+(5m+4n)^2$$

$$=16m^2+40mn+25n^2+25m^2+40mn+16n^2$$

$$=41m^2+80mn+41n^2$$

division algorithm.
If one zero of the Polynomial $$x ^ { 2 } + 3 x + k$$ is $$2$$ find $$k.$$

$$f\left( x \right) ={ x }^{ 2 }+3x+k$$

has a zero at $$x=2$$

$$\Rightarrow f\left( 2 \right) =0$$ (remainder theorem)

$$\Rightarrow 4+6+k=0$$

$$\Rightarrow k=-12$$

Write the zero of the polynomial:
$$2x-3$$

1338055_1276746_ans_e2998e2f2e0e4080b3fc3c17a6668005.PNG

Simplify:
$$\left(2x-y\right)^{2}-18\left(3x-y\right)+72$$

$$(2x - y)^2 - 18 (3x - y) + 72$$

$$4x^2 + y^2 - 2(2x)y - 54 x + 18y + 72$$

$$4x^2 + y^2 - 4xy - 54x + 18y + 72$$

Find the value of the polynomial $$p\left(x\right)=5{x}^{2}-3x+7$$ at $$x=1$$

$$p\left(x\right)=5{x}^{2}-3x+7$$

Put, $$x=1$$

$$p\left(1\right)=5\times{1}^{2}-3\times1+7=5-3+7=2+7=9$$

Verify whether $$2$$ is a zero of the polynomial $$x^{3}+4x^{2}-3x-18$$ or not?

Let,

$$f(x)=x^3+4x^2-3x-18$$

If $$2$$ is a zero, then $$f(2)$$ must be equal to $$0.$$

So,

$$f(2)=2^3+4(2)^2-3(2)-18$$

$$=8+16-6-18$$

$$=24-24$$

$$=0$$

Hence, $$2$$ is a zero of the polynomial.

Find the zero of the polynomial
(i) $$2 x - 3$$
(ii) $$x ^ { 4 } - 16$$

1) $$2x-3=0$$

$$x=3/2$$ is the zero

2) $${ x }^{ 4 }-16=0$$

$$\left( { x }^{ 2 }+4 \right) \left( { x }^{ 2 }-4 \right) =0$$

$${ x }^{ 2 }=-4\quad \quad { x }^{ 2 }=4$$

$$x=2i,-2i$$ $$x=2,-2$$

$$\therefore$$ , Zeroes are $$2,-2,2i,-2i$$

Find the roots of equation $$x^2-3x-10=0 $$.

$$x^2-3x-10=0$$

$$\Rightarrow x^2-5x+2x-10=0$$

$$\Rightarrow (x-5)(x+2)=0$$

$$\Rightarrow x=5,-2$$

Zero of Polynomial $${\text{P}}\left( {\text{x}} \right)\;{\text{ = }}\;\;{{\text{x}}^{\text{2}}}\;{\text{ - }}\;{\text{5x}}\;{\text{ + }}\;{\text{6}}$$

We have,

$$P(x)=x^2-5x+6$$

To find the zeroes of this polynomial.

So, $$P(x)=0$$

$$x^2-5x+6=0$$

$$x^2-3x-2x+6=0$$

$$x(x-3)-2(x-3)=0$$

$$(x-2)(x-3)=0$$

$$x=2, 3$$

Hence, this is the answer.

What will be the number of real zeros of the polynomial $$x^{2}+1$$.

We have,

Given polynomial is

$${{x}^{2}}+1=0$$

So,

$${{x}^{2}}+0x+1=0$$

On comparing that,

$$A{{x}^{2}}+Bx+Cx=0$$

Now,

$$A=1,\,B=0,\,C=1$$

Using quadratic formula,

$$ x=\dfrac{-B\pm \sqrt{{{B}^{2}}-4AC}}{2A} $$

$$ x=\dfrac{-0\pm \sqrt{{{0}^{2}}-4\times 1\times 1}}{2\times 1} $$

$$ x=\dfrac{\sqrt{-4}}{2} $$

$$ x=\pm \dfrac{2i}{2} $$

$$ x=\pm i $$

It is complax number

So, it has no real roots.

Hence, this is the answer.

What should be added to $$x^2+6x$$ to get $$(x+3)^2$$

We know,

$$(x+3)^2 = x^2 + 9+ 6x$$

Therefore, $$'9'$$ should be added to $$(x^2 + 6x)$$, to get $$(x+3)^2$$.

Show that :
$$\dfrac{(4ab+3cd)^{2}-(4ab-3cd)^{2}}{48}=abcd$$

Given: $$\dfrac{(4ab + 3cd)^{2} - (4ab - 3cd)^{2}}{48}$$

Using the identity $$(a+b)^2=a^2+b^2+2ab$$ and $$(a-b)^2=a^2+b^2-2ab$$ we get,

$$ = \dfrac{16a^{2}b^{2}+9c^{2}d^2+ 24abcd - 16a^{2}b^{2} - 9c^{2}d^{2}+24abcd}{48}$$

$$ = \dfrac{48abcd}{48}$$

$$ = abcd$$

Hence, proved.

1209986_1299339_ans_34e048702c6b4b8d856aba13a56afd42.jpg

Find the zero of the polynomial in each of the following cases :
(i) $$p(x) = 2x+5$$
(ii) $$p(x) = 3x-2$$

1194414_1310009_ans_285d3ab129c343d8ba0850c7df65c2b7.jpg

If $$x+\dfrac{1}{x}=2$$ then find the value of $${ x }^{ 2 }+\dfrac { 1 }{ { x }^{ 2 } } $$.

Given,

$$x+\dfrac{1}{x}=2$$.

Now squaring both sides we get,

$$x^2+\dfrac{1}{x^2}+2=4$$

or, $$x^2+\dfrac{1}{x^2}=2$$.

Find the zeros of the following quadratic polynomials and verify the relationship between the zeros and the coefficients.
$$6x^{2}-3-7x$$

We have,

$$\begin{array}{l} 6{ x^{ 2 } }-7x-3=0 \\ 6{ x^{ 2 } }-9x+2x-3=0 \\ \left( { 3x+1 } \right) \left( { 2x-3 } \right) =0 \\ \therefore x=\dfrac { 3 }{ 2 } \, \, and\, x=\dfrac { { -1 } }{ 3 } \\ Hence,\, roots\, of\, eq{ u^{ n } }\, are\, \dfrac { 3 }{ 2 } and \dfrac { { -1 } }{ 3 } \\ { { Relation } }\, between\, roots\, of\, eq{ u^{ n } }\, \\ a{ x^{ 2 } }+bx+c=0 \\ Sum\, of\, roots=\dfrac { { -b } }{ a } \\ oduct\, of\, roots=\dfrac { c }{ a } \\ In\, above\, \, eq{ u^{ n } }\, \\ sum\, of\, roots:\dfrac { 3 }{ 2 } -\dfrac { 1 }{ 3 } =\dfrac { { -\left( { -7 } \right) } }{ 6 } =\dfrac { 7 }{ 6 } \\ product\, of\, \, roots\, :\, \dfrac { 3 }{ 2 } \times \dfrac { { -1 } }{ 3 } =\dfrac { { -1 } }{ 2 } \\ Hence,\, we\, verified\, \, the\, data. \end{array}$$

Use the identity $$(x+a)(x+b)=x^{2}+(a+b)x+ab$$ to find the following product.
$$(2a^{2}+9)(2a^{2}+5)$$

$$(2a^2 + 9) (2a^2 + 5)$$

$$= (2a^2)^2 + (9 + 5) ( 2a^2) + (9×5)$$

$$= 4a^4 + 28a^2 + 45$$

Find the value of :$$(987)^{2}-(13)^{2}$$

We know that,

$$a^2 - b^2 = ( a + b)(a - b)$$

Therefore,

$$987^2 - 13^2 = ( 987 + 13 ) ( 987 - 13 )$$

$$= 1000 \times 974$$

$$= 974000$$

Find zeros of polynomial $$p(x)=(x-2)^{2}-(x+2)^{2}$$

$$P(x) = {(x - 2)^2} - {(x - 2)^2}$$

This is in the form of $${a^2} - {b^2}$$

$$\begin{array}{l} P(x)=(x-2+x+2)(x-2-(x+2)) \\ P(x)=2x(x-2-x-2) \\ P(x)=2x(-4) \\ P(x)=0 \\ -8x=0 \\ x=0 \end{array}$$

Hence,

$$x=0$$ is the zero of the polynomial $$P(x)$$

Solve
$$(2a+3b)(2a-3b)(4a^{2}+9b^{2})=?$$

Using the identity $$(a+b)(a-b)=a^2-b^2$$, the given expression can be written as:

$$(2a+3b)(2a-3b)(4a^2+9b^2)$$$$=(4a^2-9b^2)(4a^2+9b^2)$$

$$=(4a^2)^2-(9b^2)^2$$

$$=16a^4-81b^4$$.

Find $$249\times 251$$ without actual multiplication.

$$249×251$$
$$(250-1)(250+1)$$
It is in the form of $$(a-b)(a+b)$$
$$\Rightarrow (250)^2 - (1)^2$$
$$\Rightarrow 62500-1$$
$$\Rightarrow 62499$$

$$62499$$ is the product of $$249×251$$.

Find the zero of the polynomial $$2 x ^ { 2 } - 9.$$

$${\textbf{Step-1:}}$$ $$\mathbf{{\alpha ,\beta}}$$ $${\textbf{be the roots of quadratic equation}}$$

$$\text{Let }\alpha ,\beta $$ $${\text{be the roots of quadratic equation}}$$ $${\text{2}}{{x}^{\text{2}}}{ + 0x - 9 = 0}$$

$${(\sqrt{2x})}^{2} - ({3})^{2} = 0$$

$$(\sqrt{2x} + 3)$$ $$(\sqrt{2x} - 3) = 0$$

$$\sqrt{2x} + 3 = 0$$ $${\text{or}}$$ $$\sqrt{2x} - 3 = 0$$

$$x = -$$ $${\dfrac{3}{\sqrt2}}$$ $${\text{or}}$$ $$x =$$ $${\dfrac{3}{\sqrt2}}$$

$$\textbf{Hence: The zeros of polynomial }\mathbf{2x^2 - 9 } \textbf{ is}$$ $$\mathbf{x = -}$$ $$\mathbf{\dfrac{3}{\sqrt2}}$$ $${\textbf{or}}$$ $$\mathbf{x =}$$ $$\mathbf{\dfrac{3}{\sqrt2}}.$$

Evaluate
$$(107)^{2}-(93)^{2}$$.

$$a^2-b^2=(a+b)(a-b)$$

$$ =(107-93)(107+93)$$

$$=14\times200=2800$$

Using identities, evaluate:
$$(1.02)^{2}-(0.98)^{2}$$

We have,

Let $$a=1.02$$ and $$b=0.98$$

$$\begin{array}{l} { a^{ 2 } }-{ b^{ 2 } }=\left( { a+b } \right) \left( { a-b } \right) \\ =\left( { 1.02+0.98 } \right) \left( { 1.02-0.98 } \right) \\ =2\left( { 0.04 } \right) \\ =0.08 \end{array}$$

Hence,

We get $$0.08$$

Simplify :
$$(2x+3y)^{2}$$

Given: $$ { \left( { 2x+3y } \right) ^{ 2 } } $$

We know that: $$ { { { \left( { a+b } \right) }^{ 2 } }={ a^{ 2 } }+2ab+{ b^{ 2 } } } $$

Therefore,

$$ { \left( { 2x+3y } \right) ^{ 2 } } $$ $$=(2x)^2+2\times (2x)\times (3y)+(3y)^2 $$

$$= 4{ x^{ 2 } }+12xy+9{ y^{ 2 } } $$

Prove $$L.H.S = R.H.S$$ : $$( A + B ) ^ { 2 } =A^2+B^2+2AB$$

We have

$$\begin{array}{l} L.H.S={ \left( { A+B } \right) ^{ 2 } } \\ =\left( { A+B } \right) \left( { A+B } \right) \\ =A\left( { A+B } \right) +B\left( { A+B } \right) \, \, \, \, \left[ { By\, simple\, multiplication } \right] \\ =A.A+AB+AB+B.B \\ ={ A^{ 2 } }+{ B^{ 2 } }+2AB \\ =R.H.S \\ Hence \\ L.H.S=R.H.S \\ poved. \end{array}$$

degree of polynomial
$$(2m^{3}+m^{2}+m+9)$$

1900730_1315121_ans_e5fe9e475c13483cbd5564334c87eb09.jpg

Solve the following equation by suitable identity:
$${a^2}{z^2} - {b^2} = 0$$

1213549_1311353_ans_45c30fab3feb4c49b1b6f48eb72ce65c.JPG

Solve the following:
$$(a+b)(a-b)(a^{2}+b^{2})(a^{4}+b^{4})$$

$$\begin{array}{l} \left( { a+b } \right) \left( { a-b } \right) \left( { { a^{ 2 } }+{ b^{ 2 } } } \right) \left( { { a^{ 4 } }+{ b^{ 4 } } } \right) \\ \Rightarrow \left( { { a^{ 2 } }-{ b^{ 2 } } } \right) \left( { { a^{ 2 } }+{ b^{ 2 } } } \right) \left( { { a^{ 4 } }+{ b^{ 4 } } } \right) \\ \Rightarrow \left( { { a^{ 4 } }-{ b^{ 4 } } } \right) \left( { { a^{ 4 } }+{ b^{ 4 } } } \right) \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \left[ { \left( { { a^{ 2 } }-{ b^{ 2 } } } \right) =\left( { a-b } \right) \left( { a+b } \right) } \right] \\ \left( { { a^{ 8 } }-{ b^{ 8 } } } \right) \end{array}$$

Simplify :
$$(8a-5b)^{2}$$

We will use $$\left( { a-b } \right) ^{ 2 } ={ a^{ 2 } }-2ab+{ b^{ 2 } } $$ to simplify the given expression.

$${\left( {8a - 5b} \right)^2} = {\left( {8a} \right)^2} - 2\left( {8a} \right)\left( {5b} \right) + {\left( {5b} \right)^2}$$

$$ = 64{a^2} - 80ab + 25{b^2}$$

Hence the given expression simplifies to $$ 64{a^2} - 40ab + 25{b^2}.$$

Find out the value of the polynomial, $$5x-4x^2+3$$ for $$x=0$$

Let,

$$P(x)=5x-4x^2+3$$

putting $$x=0$$

$$P(0)=5(0)-4(0)^2+3$$

$$=0-0+3$$

$$=3$$

If $$0$$ and $$1$$ are the zeros of the polynomial $$f(x)=2x^{3}-3x^{2}+ax+b$$, find the value of a and b

Given,

$$f(x)=2x^3-3x^2+ax+b$$

Roots $$x=0,1$$

$$f(0)=0\Rightarrow 2(0)^3-3(0)^2+a(0)+b=0\Rightarrow b=0$$

$$f(1)=0\Rightarrow 2(1)^3-3(1)^2+a(1)+0=0\Rightarrow -1+a=0\Rightarrow a=1$$

$$\therefore a=1,b=0$$

If the zeroes of the polynomial $${ x }^{ 3 }-{ 3x }^{ 2 }+x+1$$ are (a-b), a, (a+b), find a and b.

$$ x^{3} - 3x^{2}+x+1$$

Roots $$= (a - b), a, (a + b)$$

So $$a - b + a + a + b = $$ $$\dfrac{-(-3)}{1} \quad \quad [\alpha +\beta +\gamma = \dfrac{-b}{a}]$$

$$ \Rightarrow 3a = 3 \Rightarrow a =1$$

$$ (a-b) (a) (a+b) = \dfrac{-1}{1} \ \ \quad \quad \quad \quad [\alpha \beta \gamma = -\dfrac{d}{a}]$$

$$ \Rightarrow (1-b)(1+b) = -1$$

$$\Rightarrow b^{2}-1 = 1$$

$$ \Rightarrow b = \sqrt{2} = 1.414$$

so roots are $$=1-\sqrt2, 1, 1+\sqrt 2$$

Find what value of $$k,-4$$ is a zero of the polynomial $$x^{2}-x-(2k+2)$$?

Given polynomial-

$${x}^{2} - x - \left( 2k + 2 \right) = 0$$

Since $$-4$$ is a zero of the given polynomial.

Therefore,

$${\left( -4 \right)}^{2} - \left( -4 \right) - \left( 2k + 2 \right) = 0$$

$$16 + 4 - 2k - 2 = 0$$

$$18 - 2k = 0$$

$$k = \cfrac{18}{2} = 9$$

If $$\alpha$$ and $$\beta$$ are zeroes of the polynomial $$x ^ { 2 } - a ( x + 1 ) - b$$ such that $$( \alpha + 1 )( \beta + 1 ) = 0 ,$$ find the value of $$b .$$

Given polynomial is

$$x ^ { 2 } - a ( x + 1 ) - b=0$$

$$x^{2}-ax-a-b=0$$

$$x^{2}-ax-(a+b)=0$$

$$\alpha +\beta =a, \alpha \beta =-a-b$$.......... given

$$(\alpha +1)(\beta +1)= \alpha \beta +\alpha +\beta +1$$

$$=\alpha \beta +(\alpha +\beta )+1$$

$$=-a-b+a+1=0\Rightarrow b=1$$

Verify that $$1, -1,$$ and $$ -3$$ are the zeroes of the cubic polynomial, $$x^3+x^2- x - 3$$ and verify the relationship between zeroes and the coefficients.

Given polynomial is $$x^3+3x^2-x-3$$

Let zeros be $$\alpha =1$$, $$\beta =-1$$, $$\gamma =-3$$

a) $$\alpha^3+3\alpha^2-\alpha -3$$

$$1+3-1-3=0$$

$$\implies \alpha$$ is a zero

b) $$\beta^3+3\beta^2-\beta -3$$

$$-1+3+1-3=0$$

$$\implies \beta$$ is a zero

c) $$\gamma^3+3\gamma^2-\gamma-3$$

$$-27+27+3-3-=0$$

$$\implies \gamma$$ is a zero

We know that

$$1)~~ \alpha +\beta +\gamma =\dfrac{-b}{a}$$

LHS$$=1-1-3=-3$$

RHS$$=\dfrac{-3}{1}$$

$$=-3$$

$$\therefore$$ LHS=RHS

$$2) ~~\alpha\beta +\beta\alpha +\alpha\gamma =\dfrac{c}{a}$$

LHS$$=-1+3-3$$

$$=-1$$

RHS=$$-1$$

$$\therefore$$ LHS=RHS

$$3)~~ \alpha\beta\gamma =\dfrac{-d}{a}$$

LHS$$=1(-1)(-3)$$$$=3$$

RHS$$=-(\dfrac{-3}{1})$$$$=3$$

$$\therefore$$ LHS=RHS

Find the zeroes of a polynomial $$v ^ { 2 } + 4 \sqrt { 3 } v - 15.$$

We have,

$$ {v^2} - 4\sqrt 3 v - 15\\$$

$$ {v^2} + 5\sqrt 3 v - \sqrt 3 v - 15\\$$

$$ v\left( {v + 5\sqrt 3 } \right) - \sqrt 3 \left( {v + 5\sqrt 3 } \right)\\$$

$$\left( {v + 5\sqrt 3 } \right)\left( {v - \sqrt 3 } \right)=0\\$$

So,

$$v = \sqrt 3 \,\,and\,\, - 5\sqrt 3 \\$$

Hence, this is the answer.

Find $$k$$ if $$x=\dfrac{-3}{2}$$ is root of $${ 6x }^{ 2 }+kx+3=0$$

Given , $$6x^{2}+kx+3=0$$ _________ (1)

and $$x=-\frac{3}{2}$$

Substituting the value of x in (1), we get

$$6(-\frac{3}{2})^{2}+k(-\frac{3}{2})+3=0$$

$$\Rightarrow 6(\frac{9}{4})-k(\frac{3}{2})+3=0$$

$$\Rightarrow \frac{27}{2}-\frac{3k}{2}+3=0$$

$$\Rightarrow 27-3k+6=0$$

$$\Rightarrow 3k=33$$

$$\Rightarrow k=11$$

Find the zeros of the polynomial $$f(x)={ x }^{ 2 }-2$$ and verify the relationship between its zeros and coefficients.

We have,

$$f(x)=x^2-2$$

$$=x^2-(\sqrt{2})^2$$

$$=(x-\sqrt{2})(x+\sqrt{2})$$

The zeroes of$$f(x)$$ are given by $$f(x)=0$$

$$(x-\sqrt{2})(x+\sqrt{2})=0$$

$$(x-\sqrt{2})=0 $$ or$$,(x+\sqrt{2})=0$$

$$x=\sqrt{2}$$ or $$x=-\sqrt{2}$$

Thus ,the zeroes of $$f(x)$$ are $$ \alpha=\sqrt{2}$$ and $$\beta=-\sqrt{2}$$

Now,

Sum of the zeroes$$=\alpha+\beta=\sqrt{2}+(-\sqrt{2})$$

$$=0$$

and, $$-\left(\dfrac{coefficient \ of \ x}{coefficient \ of\ x^2} \right)=-(\dfrac{0}{1})=0$$

Therefore sum of the zeroes$$=- \left(\dfrac{coefficient \ of \ x}{coefficient \ of \ x^2} \right)$$

Product of the zeroes$$=\alpha\times{\beta}=\sqrt{2}\times{-\sqrt{2}}=-2$$

and,$$\dfrac{constant \ term}{coefficient \ of \ x^2}=\dfrac{-2}{1}=-2$$

Therefore, product of zeros $$=\dfrac{constant \ term}{coefficient \ of \ x^2}$$

Find the missing terms such that the given polynomial become a perfect square trinomial :
_________$$+4xy+4$$

We have find the missing terms such that

_________$$4xy+4$$

Becomes a perfect square

It can be written as ______$$+2(2x)y+2^2$$

Hence missing tower should be $$(xy)^2+2.2.x.y+2^2=(xy+2)^2$$

Find the zero of the polynomial $$5x-6$$

Consider, $$5x-6=0$$

$$\Rightarrow x=\dfrac{6}{5}$$

$$\therefore\,\dfrac{6}{5}$$ is the zero of the polynomial

The zeros of polynomial $$p(x)=x^2-3x+2$$ are

The zeros of polynomial $$p(x)=x^2-3x+2$$ can be given y $$p(x)=0$$

$$\implies x^2-3x+2=0\\x^2-2x-x+2=0\\x(x-2)-1(x-2)=0\\(x-1)(x-2)=0\\x=1,2$$

Find the zeroes of the polynomial $$g\left( x \right) =7\sqrt { 2 } { x }^{ 2 }-10x-4\sqrt { 2 } $$

$$7\sqrt{2}x^{2}-10x-4\sqrt{2}$$

$$x=\frac{-b+\sqrt{b^{2}-4ac}}{2a}$$

$$\frac{(-10)+\sqrt{100-4(7\sqrt{2})(-4\sqrt{2})}}{14\sqrt{2}}$$

$$\frac{10+\sqrt{100+224}}{14\sqrt{2}}$$

$$\frac{10+\sqrt{324}}{14\sqrt{2}}$$

$$\frac{10+18}{14\sqrt{2}}$$, $$\frac{10-18}{14\sqrt{2}}$$

$$\frac{28}{14\sqrt{2}}$$ ,$$\frac{-8}{14\sqrt{2}}$$

$$\frac{2}{\sqrt{2}}$$,$$\frac{-4}{7\sqrt{2}}$$

$$=\sqrt{2}$$ $$\frac{-2\sqrt{2}}{7}$$

1208410_1347071_ans_df4613a87194431bbe51500b61dd9770.jpg

Find zeros of $$5\sqrt {5}x^{2}+30x+8\sqrt {5}$$

$$5\sqrt{5}x^2+30x+8\sqrt{5}=0$$

$$x_{1,2}=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$$

$$x=\dfrac{-30+\sqrt{30^2-4\cdot 5\sqrt{5}8\sqrt{5}}}{2\cdot 5\sqrt{5}}=-\dfrac{2\sqrt{5}}{5}$$

$$x=\dfrac{-30-\sqrt{30^2-4\cdot 5\sqrt{5}8\sqrt{5}}}{2\cdot 5\sqrt{5}}=-\dfrac{4\sqrt{5}}{5}$$

$$x=-\dfrac{2\sqrt{5}}{5},x=-\dfrac{4\sqrt{5}}{5}$$

Find the polynomial whose zeros are $$\alpha=1/2$$ and $$\beta=1/2$$.

Given zeroes of the polynomial$$=\alpha=\dfrac{1}{2}$$ and $$\beta=\dfrac{1}{2}$$

Sum of the roots$$=\alpha+\beta=\dfrac{1}{2}+\dfrac{1}{2}=1$$

Product of the roots$$=\alpha\beta=\dfrac{1}{2}\times\dfrac{1}{2}=\dfrac{1}{4}$$

The polynomial is $${x}^{2}-\left(\alpha+\beta\right)x+\alpha\beta=0$$

$${x}^{2}-x+\dfrac{1}{4}$$

or $$4{x}^{2}-4x+1$$ is the required polynomial.

Find the zeros of the polynomial: $$6x^2-3-7x$$.

Now,

$$6x^2-3-7x=0$$

$$\Rightarrow 6x^2-7x-3=0$$

$$\Rightarrow 6x^2-9x+2x-3=0$$

$$\Rightarrow 3x(2x-3)+1(2x-3)=0$$

$$\Rightarrow (2x-3)(3x+1)=0$$.

So the zeroes of the polynomial are $$x=\dfrac{3}{2}$$ and $$x=-\dfrac{1}{3}$$ respectively.

Find the zeroes of the polynomial:
$$x^2-2x-8$$.

Splitting the middle term:

$$x^2-2x-8$$$$=x^2-4x+2x-8=0$$

$$=(x-4)(x+2)$$

Equating the above expression equal to $$0$$ to find the zeroes:

$$(x-4)(x+2)=0$$

$$x-4=0$$ or $$x+2=0$$

$$x=4$$ or $$x=-2$$

Thus, zeroes of the polynomial is $$4,-2$$.

If zero of the polynomial $$ax-10$$ is $$5$$, then find the value of $$a$$

zero of the polynomial $$ax-10$$ is $$5$$

$$\Rightarrow x=5$$

$$\Rightarrow 5a-10=0$$

$$\Rightarrow 5a=10$$

$$\therefore a=\dfrac{10}{5}=2$$

Solve:$$2{x}^{2}-8=0$$

$$2{x}^{2}-8=0$$

$$\Rightarrow\,2\left({x}^{2}-4\right)=0$$

$$\Rightarrow \left(x-2\right)\left(x+2\right)=0$$

$$\therefore\,x=2,-2$$

What is the degree of the polynomial $$p(x)=2x+\dfrac{3}{2} x^{3}-7$$.

Given the polynomial is $$p(x)=2x+\dfrac{3}{2} x^{3}-7$$.

Now the highest power of $$x$$ involved in the equation is $$3$$.

So it is a degree $$3$$ polynomial.

Make parts of like terms :
$${ 2x }^{ 2 },-3y,{ 6y }^{ 2 },-{ 3x }^{ 2 },-{ 4y }^{ 2 },8y$$

$$\left\{2{x}^{2},6{y}^{2},-3{x}^{2},-4{y}^{2}\right\}$$ based on degree

$$\left\{-3y,8y\right\}$$

Solve:
$${ x }^{ 2 }-30=70$$

$${x}^{2}-30=70$$

$$\Rightarrow {x}^{2}=70+30=100$$

$$\Rightarrow x=\pm\sqrt{100}=\pm 10$$

Verify whether the following are zeroes of the polynomial, indicated against them.
$$p\left( x \right) =\left( x+1 \right) \left( x-2 \right) ,x=-1,2$$

We know, if $$a$$ is a zero of $$p(x)$$, then $$p(a)=0$$.

Given, $$p(x)=(x+1)(x-2)$$.

Let $$x=-1$$:

Then $$p(-1)=((-1)+1)((-1)-2)=0\times(-3)=0$$.

That is, $$x=-1$$ is a zero of the given polynomial $$p(x)$$.

Now let $$x=2$$:

Then $$p(2)=((2)+1)((2)-2)=3\times0=0$$.

That is, $$x=2$$ is a zero of the given polynomial $$p(x)$$.

Hence, $$x=-1,2$$ are the zeros of the given polynomial.

Solve:$${x}^{2}-5=4$$

$${x}^{2}-5=4$$

$$\Rightarrow\,{x}^{2}-5-4=0$$

$$\Rightarrow\,{x}^{2}-9=0$$

$$\Rightarrow\,\left(x-3\right) \left(x+3\right)=0$$

$$\therefore\,x=3,-3$$

Write the degree of each of the following polynomials:
$${ x }^{ 5 }{ y }^{ 6 }-7{ x }^{ 3 }{ y }^{ 10 }+20{ x }^{ 5 }{ y }^{ 6 }{ z }^{ 5 }$$

The degree of a polynomial is the highest of the degrees of its monomials with non-zero coefficients.

Finding degrees for each term:

First term $${x}^{5}{y}^{6}=5+6=11$$

Second term $$(-7{x}^{3}{y}^{10})=3+10=13$$

Third term $$20{x}^{5}{y}^{6}{z}^{5}=5+6+5=16$$

It is observed that the highest power is $$16$$

$$\therefore $$ Degree of the polynomial$$=16$$

If equation $$\left({a}^{2}-4\right){x}^{2}+\left({a}^{2}-6a+8\right) x +\left({a}^{2}-3a+2\right)=0$$ has more than two roots then $$a$$ is

$$\left({a}^{2}-4\right){x}^{2}+\left({a}^{2}-6a+8\right)x+\left({a}^{2}-3a+2\right)=0$$

$$\left(a-2\right)\left(a+2\right){x}^{2}+\left({a}^{2}-4a-2a+8\right) x +\left({a}^{2}-2a-a+2\right)=0$$

$$\Rightarrow\left(a-2\right)\left(a+2\right){x}^{2}+\left(a-4\right)\left(a-2\right)x+\left(a-2\right)\left(a-1\right)=0$$ as it is an identity.

$$\Rightarrow \left(a-2\right)\left(a+2\right)=0\Rightarrow\,a=2,-2$$

$$\Rightarrow \left(a-4\right)\left(a-2\right)=0\Rightarrow\,a=4,2$$

$$\Rightarrow \left(a-2\right)\left(a-1\right)=0\Rightarrow\,a=2,1$$

So,$$\left\{2,-2\right\}\cap\left\{4,2\right\}\cap\left\{2,1\right\}=2$$

So $$a=2$$

Simplify $${\left(101\right)}^{2}$$ using suitable identity.

$${101}^{2}={\left(100+1\right)}^{2}$$ is of the form $${\left(a+b\right)}^{2}$$

where $$a=100,b=1$$

We know $${\left(a+b\right)}^{2}={a}^{2}+{b}^{2}+2ab$$

$$\therefore {\left(100+1\right)}^{2}={100}^{2}+{1}^{2}+2\times 100\times 1$$

$$=10000+1+200=10201$$

Using identities, find the value of $$72^2-18^2$$.

$$72^{2}-18^{2}$$

We know that

$$a^{2}-b^{2}=(a+b)(a-b)$$

$$a=72$$ $$b=18$$

$$72^{2}-18^{2}=(72+18)(72-18)$$

$$=90\times 54$$

$$=4860$$

Expand $${\left(99\right)}^{2}$$ using suitable identities.

$${\left(99\right)}^{2}={\left(100-1\right)}^{2}$$

$${\left(100-1\right)}^{2}$$ is of the form $${\left(a-b\right)}^{2}={a}^{2}+{b}^{2}-2ab$$ where $$a=100,b=1$$

$$\therefore {\left(100-1\right)}^{2}={100}^{2}+{1}^{2}-2\times 100\times 1$$

$$=10000+1-200=10000-199=9801$$

Expand. $$(5a+6b)^2$$

$$\textbf{Use the expansion:} \mathbf{(a+b)^2}$$

We have

$$(5a+6b)^2$$

$$=(5a)^2+2\times 5a\times 6b+(6b)^2$$ $$[\because (a+b)^2=a^2+2ab+b^2]$$

$$\mathbf{=25a^2+60ab+36b^2}$$

$$\textbf{Hence the solution is obtained}$$

Define zero or root of a polynomial.

Zero of a polynomial is that value of the variable in the polynomial, which when substituted in the polynomial gives the value of the polynomial as zero $$(0)$$.

For example, consider the polynomial $$p(x)=x+2$$.

Suppose, $$x=-2,2$$.

When $$x=-2$$,

$$p(-2)=(-2)+2=0$$.

That is, $$-2$$ is a zero of the polynomial $$p(x)=x+2$$.

Now, when $$x=2$$,

$$p(2)=(2)+2==4\ne0$$.

That is, $$2$$ is not a zero of the polynomial $$p(x)=x+2$$.

Verify the identity $${ \left( a+b \right) }^{ 2 }={ a }^{ 2 }+2ab+{ b }^{ 2 }$$ for $$a=2,b=4$$

taking $$a = 2, b = 4$$

$$(a+b)^{2}=(2+4)^{2}=6^{2}=36$$

$$a^{2}+b^{2}+2ab=2^{2}+4^{2}+2\times 2\times 4=4+16+16=36$$

$$\therefore (a+b)^{2}=a^{2}+b^{2}+2ab$$

Find the zeros of the following polynomial by factorization method and verify the relations between the zeroes and the coefficient of the polynomials :
$$y^{ 2 }+\dfrac { 3 }{ 2 } \sqrt { 5 } y-5$$

Let $$f(y) = y^2 + \dfrac{3}{2}\sqrt{5}y - 5$$

For zeroes of $$f(y), f(y) = 0$$

$$\Rightarrow y^2 + \dfrac{3}{2} \sqrt{5}y -5= 0$$

$$\Rightarrow 2y^2 + 3 . \sqrt{5}y-10 = 0$$

$$\Rightarrow 2y^2 + 4 \sqrt{5}y - 1 \sqrt{5}y - 10 =0$$

$$\Rightarrow 2y(y + 2\sqrt{5}) - \sqrt{5}[y + 2\sqrt{5}] = 0$$

$$\Rightarrow (y + 2 \sqrt{5}) (2y - \sqrt{5}) = 0$$

$$\Rightarrow y+2\sqrt{5}=0$$ or $$2y - \sqrt{5} = 0$$

$$\Rightarrow y = -2\sqrt{5}$$ or $$y = \dfrac{\sqrt{5}}{2}$$

verification:

$$\alpha = -2 \sqrt{5}, \beta = \dfrac{\sqrt{5}}{2}$$,

$$a = 1, b = \dfrac{3}{2}\sqrt{5}$$ and $$c = -5$$

$$\alpha +\beta = \dfrac{-b}{a}$$

$$\Rightarrow -2\sqrt{5} + \dfrac{\sqrt{5}}{2} = \dfrac{\dfrac{-3}{2}\sqrt{5}}{1}$$

$$\Rightarrow \dfrac{-4\sqrt{5} + \sqrt{5}}{2} = \dfrac{-3}{2} \sqrt{5}$$

$$\Rightarrow \dfrac{-3\sqrt{5}}{2} = \dfrac{-3}{2} \sqrt{5}$$

$$\Rightarrow LHS = RHS$$

Hence, verified.

$$\alpha . \beta - \dfrac{c}{a}$$

$$\Rightarrow (-2\sqrt{5}) \left(\dfrac{\sqrt{5}}{2}\right) = \dfrac{-5}{1}$$

$$\Rightarrow -5 = -5$$

$$\Rightarrow LHS = RHS$$

Hence, verified.

Verify whether $$-3$$ and $$2$$ are the zeroes of the polynomial $$x^{3} - x^{2} +x - 6$$.

We know, if $$a$$ is a zero of $$f(x)$$, then $$f(a)=0$$.

Given, $$f(x)=x^3-x^2+x-6$$.

Let $$x=-3$$:

Then $$f(-3)=(-3)^3-(-3)^2+(-3)-6=-27-9-3-6=-45\ne0$$.

That is, $$x=-3$$ is not a zero of the given polynomial $$f(x)$$.

Now let $$x=2$$:

Then $$f(2)=(2)^3-(2)^2+(2)-6=8-4+2-6=0$$.

That is, $$x=2$$ is a zero of the given polynomial $$f(x)$$.

Hence, $$x=2$$ is a zero of the given polynomial $$f(x)$$ but $$x=-3$$ is not.

Check whether $$-2,-5$$ are the zeros of the polynomial $$p(x)=x^2+7x+10$$

$$p(x)=x^2+7x+10\\p(-2)=4-14+10=0\\p(-5)=25-35+10=0$$

So, $$(-2)\&(-5)$$ are zeroes.

Find the zeroes of the polynomial : $$p(x)=(x-2)^{2}-(x+2)^{2}$$

Let $$P(x) = (x - 2)^2 - (x + 2)^2$$

As fining a zero of $$p(x)$$, is same as solving the equation $$p(x) = 0$$

So, $$p(x) = 0 \Rightarrow (x - 2)^2 - (x + 2)^2 = 0$$

$$\Rightarrow (x - 2 + x + 2) (x - 2 - x - 2) = 0$$

$$\Rightarrow 2x (-4) = 0 \Rightarrow -8x = 0 \Rightarrow x = 0$$

Hence, $$x = 0$$ is the only one zero of $$p(x)$$.

Verify whether the indicated numbers are zeroes of the polynomial corresponding to them in the following case:
$$f(x) = x^{2} - 1, x = 1, -1$$.

We know, if $$a$$ is a zero of $$p(x)$$, then $$p(a)=0$$.

Given, $$f(x)=x^2-1$$.

Let $$x=1$$:

Then $$f(1)=(1)^2-1=1-1=0$$.

That is, $$x=1$$ is a zero of the given polynomial $$f(x)$$.

Now let $$x=-1$$:

Then $$f(-1)=(-1)^2-1=1-1=0$$.

That is, $$x=-1$$ is a zero of the given polynomial $$f(x)$$.

Hence, verified that $$x=1,-1$$ are the zeroes of the given polynomial.

If $$p(x)=x^{2}-4x+3$$ , evaluate: $$p(2)-p(-1)+p(\frac{1}{2})$$

We have $$p(x) = x^2 - 4x + 3$$

$$\therefore p(2) - p(-1) + p \left(\dfrac{1}{2}\right) = (2^2 - 4 \times 2 + 3) - \{(-1)^2 - 4(-1) + 3\} + \left\{\left(\dfrac{1}{2}\right)^2 - 4 \times \dfrac{1}{2} + 3\right\}$$

$$= (4 - 8 +3) - (1 + 4 + 3) + \left(\dfrac{1}{4} - 2 + 3\right)$$

$$= -1 - 8 + \dfrac{5}{4}$$

$$= -9 + \dfrac{5}{4} = \dfrac{-36 + 5}{4} = \dfrac{-31}{4}$$

How many zeroes of polynomials are there for the polynomial $$p(x)=x^{3}-3x^{2}$$.

Given, the polynomial $$p(x)=x^3-3x^2$$.

Here, the highest power of the polynomial is $$3$$.

That is, the degree of the given polynomial is $$3$$.

We know, the number of zeroes a polynomial is equal to the degree of the polynomial.

Hence, the polynomial $$p(x)=x^3-3x^2$$ has $$3$$ zeroes.

Verify whether the indicated numbers are zeroes of the polynomial corresponding to them in the following case:
$$f(x) = 3x + 1, x = -\dfrac {1}{3}$$.

We know, if $$a$$ is a zero of $$p(x)$$, then $$p(a)=0$$.

Given, $$f(x)=3x+1$$.

Let $$x=-\dfrac{1}{3}$$:

Then $$f(-\dfrac{1}{3})$$$$=3(-\dfrac{1}{3})+1=-1+1=0$$.

That is, $$x=-\dfrac{1}{3}$$ is a zero of the given polynomial $$f(x)$$.

Hence, verified that $$x=-\dfrac{1}{3}$$ is the zero of the given polynomial.

Verify whether the indicated numbers are zeroes of the polynomial corresponding to them in the following case:
$$p(x) = x^{3} - 6x^{2} + 11x - 6, x = 1, 2, 3$$.

We know, if $$a$$ is a zero of $$p(x)$$, then $$p(a)=0$$.

Given, $$p(x)=x^3-6x^2+11x-6$$.

Let $$x=1$$:

Then,

$$p(1)=(1)^3-6(1)^2+11(1)-6\\=1-6+11-6\\=12-12\\=0$$.

That is, $$x=1$$ is a zero of the given polynomial $$p(x)$$.

Now let $$x=2$$:

Then,

$$p(2)=(2)^3-6(2)^2+11(2)-6\\=8-24+22-6\\=30-30\\=0$$.

That is, $$x=2$$ is a zero of the given polynomial $$p(x)$$.

Now let $$x=3$$:

Then,

$$p(3)=(3)^3-6(3)^2+11(3)-6\\=27-54+33-6\\=60-60\\=0$$.

That is, $$x=3$$ is a zero of the given polynomial $$p(x)$$.

Hence, it is verified that $$x=1,2,3$$ are the zeroes of the given polynomial.

The zero of polynomial $$p(x)=4x+5$$ is :

Given, $$f(x)=4x+5$$.

To find the zero of a polynomial, we use $$f(x)=0$$.

Then, $$4x+5=0$$

$$\implies$$ $$4x=-5$$

$$\implies$$ $$x=\dfrac{-5}{4}$$.

Hence, $$\dfrac{-5}{4}$$ is the zero of the polynomial $$4x+5$$.

Verify whether the indicated numbers are zeroes of the polynomial corresponding to them in the following case:
$$f(x) = 5x - \pi, x = \dfrac{4} {5}$$.

We know, if $$a$$ is a zero of $$p(x)$$, then $$p(a)=0$$.

Given, $$f(x)=5x-\pi$$.

Let $$x=\dfrac{4}{5}$$:

Then $$f(\dfrac{4}{5})$$ $$=5(\dfrac{4}{5})-\pi=4-\pi\ne0$$.

That is, $$x=\dfrac{4}{5}$$ is not a zero of the given polynomial $$f(x)$$.

Hence, verified that $$x=\dfrac{4}{5}$$ is not a zero of the given polynomial.

Verify whether the indicated numbers are zeros of the polynomials corresponding to them in the following cases:
$$g(x) = 3x^{2} - 2, x = \dfrac {2}{\sqrt {3}}, -\dfrac {2}{\sqrt {3}}$$.

1432970_1668821_ans_cdf450319748484282db95641f3a5a12.jpg

If $$(x^{2}+y^{2})(a^{2}+b^{2})=(ax+by)^{2}$$ prove that $$\dfrac{x}{a}=\dfrac{y}{b}$$

As we know that

$$(a+b)^2=a^2+b^2+2 a b,(a-b)^2=a^2+b^2-2 a b$$

Given $$(x^2+y^2)(a^2+b^2)=(a x+b y)^2$$

$$x^2(a^2+b^2)+y^2(a^2+b^2)=(a x)^2+(b y)^2+2(a x)(b y)$$

$$\implies a^2 x^2+b^2 x^2+a^2 y^2+b^2 y^2=a^2 x^2+b^2 y^2+2 a b x y $$

$$\implies b^2 x^2+a^2 y^2=2 a b x y$$

$$\implies (b x)^2+(a y)^2-2(b x)(a y)=0$$

$$\implies (b x-a y)^2=0$$

$$\implies b x=a y$$

$$\implies \dfrac{x}{a}=\dfrac{y}{b}$$

Identify constant, linear, quadratic and cubic polynomials from the following polynomials:
$$f(x) = 0$$.

1432915_1668715_ans_561dba52b13e4f4aad35deba2985a099.jpg

Verify whether the indicated numbers are zeroes of the polynomial corresponding to them in the following case:
$$f(x) = x^{2}, x = 0$$.

We know, if $$a$$ is a zero of $$p(x)$$, then $$p(a)=0$$.

Given, $$f(x)=x^2$$.

Let $$x=0$$:

Then $$f(0)=(0)^2=0$$.

That is, $$x=0$$ is a zero of the given polynomial $$f(x)$$.

Hence, verifies that $$x=0$$ is the zero of the given polynomial.

Write the degree of each of the following polynomials:
$$5x^{2} - 3x +2$$.

The degree is the value of the greatest exponent of any expression (except the constant) in the polynomial.

Given: $$5x^2 - 3x + 2$$ (is a polynomial in $$x$$)

The greatest exponent of $$x$$ in the expression is $$2$$

Write each of the following polynomials in the standard form. Also, write their degree:
$$x^{2} + 3 + 6x + 5x^{4}$$.

Standard form of the given polynomial is $$5x^4 + x^2 + 6x + 3$$

When we write a polynomial in standard form, the highest-degree term comes first and lowest-degree term as last.

degree is $$4$$

Write the degree of the following polynomial:
$$3x^{3} + 1$$.

The degree is the value of the greatest exponent of any expression (except the constant) in the polynomial.

Given: $$(3x^3 + 1)$$ (polynomial in $$x$$)

The greatest exponent of $$x$$ in the expression is $$3$$.

Therefore, the degree is $$3$$.

Write the degree of each of the following polynomials:
$$\dfrac {1}{2} y^{7} - 12y^{6} + 48 y^{5} - 10$$.

The degree is the value of the greatest exponent of any expression (except the constant) in the polynomial.

Given: $$\dfrac{1}{2}y^7-12y^6+48y^5-10$$ (is a polynomial in $$y$$)

The greatest exponent of $$y$$ in the expression is $$7$$.

Write the degree of the following polynomial:
$$2x^{3} + 5x^{2} - 7$$.

The given polynomial is $$2x^3+5x^2-7$$.

We know that, the degree of a polynomial is the greatest exponent value of the variable in the polynomial.

$$2x^3+5x^2-7$$ is a polynomial in $$x$$ and the greatest exponent of $$x$$ is $$3$$.

Hence, the degree of the given polynomial is $$3$$.

Using the formula for squaring a binomial, evaluate the following.
$$(102)^2$$.

1511587_1673126_ans_3e9c72305b8c4674b62f30137770f542.jpg

Write the degree of the following polynomial:
$$5$$

The degree is the value of the greatest exponent of any expression (except the constant) in the polynomial.

Given: $$5$$

Since the only constant term is there thus degree $$=0$$

Write the degree of each of the following polynomials:
$$2x + x^{2} - 8$$.

The degree is the value of the greatest exponent of any expression (except the constant) in the polynomial.

Given: $$2x+x^2-8$$ (is a polynomial in $$x$$)

The greatest exponent of $$x$$ in the expression is $$2$$

$$\therefore$$ Degree is $$2$$

Write the degree of each of the following polynomials:
$$20x^{3} + 12x^{2}y^{2} - 10y^{2} + 20$$.

The degree is the value of the greatest exponent of any expression (except the constant) in the polynomial.

Given: $$20x^3 + 12x^2y^2 - 10y^2 +20$$ (polynomial is $$x$$ and $$y$$)

The greatest powers of exponent combined are : $$4$$

$$\therefore $$ degree $$=4$$

State whether the following expression is polynomial or not. In case of a polynomial, write its degree.
$$t^2-\dfrac{2}{5}t+\sqrt{5}$$.

Given expression is $$t^2-\dfrac{2}{5}t+\sqrt{5}$$.

∵ All the exponents of $$t$$ are whole numbers and the highest exponent of $$t$$ is $$2.$$

It is a polynomial of degree $$2$$.

State whether the following expression is polynomial or not. In case of a polynomial, write its degree.
$$\dfrac{3}{5}x^2-\dfrac{7}{3}x+9$$.

Given expression is $$\dfrac{3}{5}x^2-\dfrac{7}{3}x+9$$.

∵ All the exponents of $$x$$ are whole numbers and the highest exponent of $$x$$ is $$2.$$

It is a polynomial of degree $$2$$.

State whether the following expression is polynomial or not. In case of a polynomial, write its degree.
$$x^4-x^{\tfrac{3}{2}}+x-3$$.

The power of $$x$$ in the given expression is not a whole number.

It is not a polynomial.

Using the formula for squaring a binomial evaluate the following.
$$(703)^2$$.

Now,

$$(703)^2$$

$$=(700+3)^2$$

$$=700^2+2\cdot 700\cdot 3+3^2$$

$$=490,000+4,200+9$$

$$=494,209$$.

Using the formula for squaring a binomial, evaluate the following.
$$(1001)^2$$.

1511591_1673128_ans_8f7afe88100f48f2a647849afcc090fb.jpg

Using the formula for squaring a binomial, evaluate the following.
$$(999)^2$$.

Now,

$$(999)^2$$

$$=(1000-1)^2$$

$$=(10^3)^2-2\cdot 1000\cdot 1+1$$

$$=10^6-2,000+1$$

$$=1000,000-2,000+1$$

$$=998,000+1$$

$$=998,001$$.

State whether the following expression is polynomial or not. In case of a polynomial, write its degree.
$$\sqrt[3]{2}x^2-8$$.

Given expression is $$\sqrt[3]{2}x^2-8$$.

∵ All the exponents of $$x$$ are whole numbers and the highest exponent of $$x$$ is $$2.$$

It is a polynomial of degree $$2$$

Using the formula for squaring a binomial, evaluate the following.
$$(99)^2$$.

1511590_1673127_ans_ee5ef747b76e4d7e9c39ae58fa8c8cac.jpg

Write the zeroes of the quadratic polynomial $$ f(x) = 6x^2 -3 $$

To find the zeros of the quadratic polynomial, put $$f(x) = 0$$.

$$ 6x^2 -3 = 0$$
$$ 3(2x^2 -1) = 0$$
$$ 2x^2 = 1$$
$$ x^2= \dfrac12 $$
$$ or \ x = \pm \dfrac{1 }{ \sqrt {2}} $$

zeros of the given polynomial are $$ \dfrac{1 }{ \sqrt {2}}$$ and $$-\dfrac1 { \surd {2} }$$

State whether the following expression is polynomial or not. In case of a polynomial, write its degree.
$$x^5+2x^3+x+\sqrt{3}$$.

Given expression is $$x^5+2x^3+x+\sqrt{3}$$.

$$\because\ $$ All the exponents of $$x$$ are whole numbers and the highest exponent of $$x$$ is $$5.$$, The given expression is a polynomial of degree $$5$$.

Hence, the given expression is a polynomial of degree $$5$$.

Verify that $$0$$ and $$3$$ are the zeros of the polynomial, $$r(x)=x^2-3x$$.

1681309_1715915_ans_8202bd5f8bcb45479024ad0e91335fec.jpg

Determine the degree of the following polynomial.
$$y^2(y-y^3)$$.

1678622_1715886_ans_e6521782f53e4b7e8c5be2f2cfe8cccd.jpg

Find the zero of the polynomial $$q(x)=x+4$$.

1681311_1715916_ans_9d6c9885d44842dea5725f0392bb464a.jpg

Verify that $$\dfrac{-1}{2}$$ is a zero of the polynomial, $$g(y)=2y+1$$.

1681304_1715912_ans_86371c44f51242479ed2f56a6abeaf1c.jpg

Verify that $$2$$ and $$-3$$ are the zeros of the polynomial, $$q(x)=x^2+x-6$$.

The given polynomial is

$$q(x)=x^2+x-6$$

Putting, $$x=2$$

$$q(2)=2^2+2-6$$

$$=4+2-6$$

$$=0$$

So, $$2$$ is a zero of the polynomial $$q(x)$$

Again, putting, $$x=-3$$

$$q(-3)=(-3)^2+(-3)-6$$

$$=9-3-6$$

$$=0$$

So, $$-3$$ is a zero of the polynomial $$q(x)$$

Hence, $$2$$ and $$-3$$ are the zeros of the polynomial $$q(x)$$.

Verify that $$1$$ and $$2$$ are the zeros of the polynomial, $$p(x)=x^2-3x+2$$.

1681305_1715913_ans_ecc6c51e859143db8be59473ac5f7f2f.jpg

Verify that $$\dfrac{2}{5}$$ is a zero of the polynomial, $$f(x)=2-5x$$.

1681300_1715911_ans_4e2ca87b1e874d38a562399babde1e16.jpg

Verify that $$4$$ is a zero of the polynomial, $$p(x)=x-4$$.

1681295_1715909_ans_767eef7de96b4616b770ceba736d2043.jpg

Find the zero of the polynomial $$r(x)=2x+5$$.

1681316_1715917_ans_03253f48fc7946dd98f1c7b6d7f9d7bd.jpg

State whether the following expression is polynomial or not. In case of a polynomial, write its degree.
$$2x^3+3x^2+\sqrt{x}-1$$.

The power of $$x$$ in the given expression is not a whole number.

It is not a polynomial.

Find the zeros of the polynomial $$f(x) = x^3 - 12x^2 +39x -28$$, if it is given that the zeros are in A.P.

If $$\alpha ,\beta ,\gamma $$ are in $$A.P$$., then
$$\beta - a = \gamma - \beta \Rightarrow 2\beta = \alpha + y$$ .............$$(i)$$
$$\alpha + \beta + \gamma = \frac{-b}{a} = \frac{-(-12)}{1}=12 \Rightarrow \alpha + \gamma = 12 - \beta $$ ...... $$(ii)$$
From (i) and (ii)
Putting the value of $$\beta$$ in $$(i)$$ we have
$$8=\alpha + \gamma $$ .............$$(iii)$$
$$\alpha \beta \gamma = -\frac{d}{\alpha } = \frac{-(-28)}{1}= 28$$
$$(\alpha \gamma ) 4 = 28 $$ or $$\alpha \gamma = 7$$ or $$= \frac{7}{\alpha }$$ ................ $$(iv)$$
Putting the value of $$\gamma = \frac{7}{\alpha }$$ in (iii) we get
$$8 = \alpha + \frac{7}{\alpha }$$ $$\Rightarrow$$ $$8a =\alpha ^2 + 7$$
$$\Rightarrow \alpha ^2 -8a + 7 = 0$$ $$\Rightarrow$$ $$\alpha ^2 - 7\alpha - 1\alpha + 7 = 0$$
$$\Rightarrow \alpha (\alpha - 7) - 1(\alpha -7)=0$$ $$\Rightarrow$$ $$\alpha ^2 - 7\alpha - 1\alpha + 7 = 0$$
$$\Rightarrow \alpha = 1$$ or $$\alpha = 7$$

Find the zero of the polynomial $$g(x)=5-4x$$.

1681321_1715919_ans_0bafc70ec36640bbbcbd5c0a79b79d8c.jpg

Find the zero of the polynomial $$q(x)=4x$$.

1677030_1715922_ans_63d016c5dffb477180afdd8928ef0e70.jpg

Find the zero of the polynomial $$h(x)=6x-2$$.

1681323_1715920_ans_4465e0c76c434733bba7f2be0f1da1a6.jpg

In each of the following, determine whether the given numbers are solutions of the given equation or not:
(i) $$x^{2}-3 \sqrt{3} x+6=0 \ ;\ x=\sqrt{3},-2 \sqrt{3}$$
(ii) $$x^{2}-\sqrt{2} x-4=0\ ;\ x=-\sqrt{2}, 2 \sqrt{2}$$

(i) $$p(x)=x^{2}-3 \sqrt{3} x+6=0\ ;\ x=\sqrt{3},-2 \sqrt{3}$$

Let us substitute the given values in the expression and check,

When, $$x=\sqrt{3}$$

$$p(\sqrt3)=(\sqrt{3})^{2}-3 \sqrt{3}(\sqrt{3})+6\\=3-9+6=-9+9=0$$

When, $$x=-2 \sqrt{3}$$

$$p(-2\sqrt3)=(-2 \sqrt{3})^{2}-3 \sqrt{3}(-2 \sqrt{3})+6\\=4(3)+18+6=12+18+6=36\not=0$$

$$\therefore \sqrt{3}$$ is a solution of the equation.

But $$-2 \sqrt{3}$$ is not a solution of the equation.

(ii) $$f(x)=x^{2}-\sqrt{2} x-4=0 \ \ ;\ x=-\sqrt{2}, 2 \sqrt{2}$$

Let us substitute the given values in the expression and check,

When, $$x=-\sqrt{2}$$

$$f(-\sqrt{2})=(-\sqrt{2})^{2}-\sqrt{2}(-\sqrt{2})-4\\=2+2-4=4-4=0$$

When, $$x=2 \sqrt{2}$$

$$f(2\sqrt2)=(2 \sqrt{2})^{2}-\sqrt{2}(2 \sqrt{2})-4\\=4(2)-4-4=8-8=0$$

$$\therefore 2 \sqrt{2}$$ and $$-\sqrt2$$ are the solution of the equation.

Find the zero of the polynomial $$p(x)=ax, a\neq 0$$.

Given polynomial, $$p(x)=ax$$

Putting, $$p(x)=0$$

$$\Rightarrow ax=0$$

$$\Rightarrow x=\dfrac{0}{a}$$

$$\Rightarrow x=0$$

Hence the zero of the polynomial is $$0$$

$$a^{2}-b^{2} = (a+b)$$ __________ .

1975363_1792721_ans_4a02af39252347ac95805a7c8ae990d6.jpg

Expand the following, using suitable identities: $$(xy + yz)^{2}$$

Using the identity $$(a+b)^{2}=a^{2}+b^{2}+2ab$$

We have, $$(xy + yz)^{2} =(xy)^2+(yz)^2+2(xy)(yz)$$

$$= x^{2}y^{2}+y^{2}z^{2}+2xy^{2}z$$

Find the zero of the polynomial $$f(x)=3x+1$$.

1681319_1715918_ans_51b779919db1463aaea3937c46bd50a4.jpg

Determine the degree of the following polynomials :
$$y^3 ( 1 - y^4)$$

$$y^3 (1 - y^4) = y^3 - y^7$$ since the highest power of y is $$7,$$ the degree of the polynomial is $$7.$$

Determine the degree of the following polynomials :
$$-10$$

$$-10$$ is a non-zero constant. A non-zero constant term is always regarded as having degree $$0.$$

State whether the following expression are polynomials or not? Justify your answer.
$$8$$

$$8$$ is a constant polynomial

Determine the degree of the following polynomials :
$$x^3 - 9x + 3x^5$$

Since the highest power of x is $$5,$$ the degree of the polynomial $$x^3 - 9x + 3x^5$$ is $$5.$$

Determine the degree of the following polynomials :
$$2x - 1$$

Since the highest power of $$x$$ is $$1$$, the degree of the polynomial $$2x - 1$$ is $$1.$$

Classify the following as a constant, linear quadratic and cubic polynomials:
$$3$$

We know that
(a) a polynomial in which exponent of the variable is zero is called a constant polynomial.
(b) a polynomial of degree $$1$$ is called a linear polynomial.
(c) A polynomial of degree $$2$$ is called a quadratic polynomial.
(d) A polynomial of degree $$3$$ is called a cubic polynomial.
Hence, given polynomial is a constant polynomial.

Expand the following, using suitable identities: $$(x^{2}y - xy^{2})^{2}$$

Using the identity $$(a-b)^{2}=a^{2}+b^{2}-2ab$$

We get, $$(x^{2}y-xy^{2})^{2}$$

$$ =(x^2y)^2+(xy^2)^2-2(x^2y)(xy^2)$$

$$= x^{4}y^{2}+x^{2}y^{4}-2x^{3}y^{3}$$

Find the zeros of the polynomial of the following:
$$g(x) = 3 - 6x$$

Solving the equation $$g(x) = 0,$$ we get its zeros.

$$3 - 6x = 0,$$ which gives us $$x = \dfrac{1}{2}$$

So, $$\dfrac{1}{2}$$ is a zero of the polynomial $$3 - 6x.$$

Find the zeros of the polynomial of the following:
$$h(y) = 2y$$

Solving the equation $$h(y) = 0,$$ we get its zeros.

$$2y = 0,$$ which gives us $$y = 0$$

So, $$0$$ is a zero of the polynomial $$2y.$$

Find the zeroes of the polynomial of the following:
$$p(x) = x - 4$$

Solving the equation $$p(x) = 0,$$ we get its zeros.

$$x - 4 = 0,$$ which give us $$x = 4$$

So, $$4$$ is a zero of the polynomial $$x - 4$$

Factorise the following:
$$9x^2 - 12x + 4$$

We have,

$$9x^2 - 12x + 4 \\= (3x)^2 - 2(3x)(2) + (2)^2$$

$$= (3x - 2)^2\qquad [\because a^2 - 2ab + b^2 = (a - b)^2]$$

$$= (3x - 2)(3x - 2)$$

Find the zeros of the polynomial of the following:
$$q(x) = 2x - 7$$

Solving the equation $$q(x) = 0,$$ we get its zeros.

$$2x - 7 = 0,$$ which gives us $$x = \dfrac{7}{2}$$

So, $$\dfrac{7}{2}$$ is a zero of the polynomial $$2x - 7.$$

Write down the degree of following polynomials in x: $$3-2x$$

(i) the exponent of the first term $$-2x=1$$
Therefore, the degree of the polynomial $$3-2x=1$$

The degree of the polynomial $$3x^2-2x^2+5$$ is........

Highest power of $$x$$ in the given expression is $$2$$ thus degree of the polynomial $$3x^2-2x^2+5$$ is $$2$$.

Find the zeroes of the polynomial $$ P(x)=x^{2}-3 $$

$$ P(x)=0 $$

$$ x^{2}-3=0 $$

$$ (x)^{2}-(\sqrt{3})^{2}=0 $$

$$ (x+\sqrt{3})(x-\sqrt{3})=0 $$

$$ x=\pm \sqrt{3} $$

The zeroes of the polynomial $$ P(x)=x^{2}-3 $$ are $$ x=\pm \sqrt{3} $$

$$ 6(x+3y)^3 + 8( x +2y)^2 $$

Write the degree of the polynomial:
$$\dfrac{2}{5}x^4 - \sqrt 3x^2 + 5x - 1$$

The given polynomial is $$\dfrac{2}{5}x^4 - \sqrt 3x^2 + 5x - 1$$

Degree of a polynomial is the highest power of the variable among all the terms.

Here, the highest power of the variable $$x$$ is in the first term, which is $$4$$.

Hence, the degree of the polynomial is $$4$$.

Write down the degree of following polynomials in x: $$x^2-6x^7+x^8$$

(i) the exponent of the first term $$x^2=2$$

(ii) the exponent of the second term $$-6x^7=7$$

(iii) the exponent of the third term $$x^8$$
Since, the greatest exponent is 8,
Therefore, the degree of the polynomial $$x^2-6x^7+x^8=8$$

$$ 2(x -2y)^2 -50y^2 $$

$$ 2(x -2y)^2 -50y^2 $$
Take out common in all terms,
$$ 2[ (x-2y)^2 - 25y^2 ] $$
$$ 2 [ (x-2y)^2 - (5y)^2 ] $$
We know that , $$ a^2 -b^2 = (a +b)(a-b) $$
$$ 2 [ (x -2y + 5y )( x -2y -5y) ] $$
$$ 2 [ ( x+ 3y )(x -7y) ]$$
$$ 2 [ (x +3y)(x -37y) ] $$

Write down the degree of following polynomials in x:-2

$$2$$ is a constant term. Therefore power of the variable is $$0$$
so, degree of polynomial is $$0$$

The degree of the polynomial $$3-5x^2+7x^3-x^4$$ is ........

The degree of the polynomial $$3-5x^2+7x^3-x^4$$ is 4.

Simplify the following:
$$\left(\dfrac{7a}{2} - \dfrac{5b}{2}\right)^2 - \left(\dfrac{5a}{2} - \dfrac{7b}{2}\right)^2$$

$$\left(\dfrac{7a}{2} - \dfrac{5b}{2}\right)^2 - \left(\dfrac{5a}{2} - \dfrac{7b}{2}\right)^2$$

$$=\Big[ \Big( \dfrac{7}{2}a \Big)^2 - 2 \times \dfrac{7}{2}a \times \dfrac{5}{2}b + \Big( \dfrac{5}{2} b \Big)^2 \Big] - \Big[ \Big( \dfrac{5}{2}a \Big)^2 - 2 \times \dfrac{5}{2}a \times \dfrac{7}{2}b + \Big( \dfrac{7}{2} b \Big)^2 \Big]$$

$$ = \Big[ \dfrac{49}{4}a^2 - \dfrac{35}{2} ab + \dfrac{25}{4} b^2 \Big] - \Big[\dfrac{25}{4}a^2 - \dfrac{35}{2}ab + \dfrac{49}{4} b^2 \Big]$$

$$ = \dfrac{49}{4}a^2 - \dfrac{25}{4}a^2 + \dfrac{25}{4}b^2 - \dfrac{49}{4}a^2$$

$$ = \dfrac{24}{4}a^2 + \dfrac{(-24)}{4}b^2$$

$$ = 6a^2 - 6b^2$$

$$ 108a^2 -3 (b+c)^2 $$

$$ 108a^2 -3 (b+c)^2 $$
Take out common in all terms,
$$ 3 [ 36a^2 - ( b-c)^2 ] $$
$$ 3 [ (6a)^2 - ( b-c)^2 ] $$
We know that $$ a^2 -b^2 = (a+b)(a-b) $$
$$ 3 [ ( 6a +b-c) ( 6a -b +c) ] $$

A real number $$\alpha$$ will called the zero of the quadratic polynomial $$ax^2+bx+c$$ if............. Is equal to zero.

$$a\alpha^2+b\, \alpha +c=0$$

$$\because $$ The zeroes of a polynomial are $$ \alpha$$

$$\therefore$$ to be zero$$, a\alpha^2+b\, \alpha +c=0$$

Fill in the blanks:
The degree of the polynomial $$2x^2+4x-x^3$$ is ............

The degree of the polynomial $$2x^2+4x-x^3$$ is 3

$$\because$$ The degree is the highest power of the term in the expression, so it is 3.

Which of the following is a polynomial?Find its degree and the zeroes.
$$2-\dfrac{1}{2}x^2$$

The highest power is 2,so the degree is also 2.

Equating the expression with 0,

$$2-\dfrac{1}{2}x^2=0$$

$$2=\dfrac{1}{2}x^2$$

$$x^2=4$$

$$x =\pm 2$$

Yes, the above expression is a polynomial, as it has no negative powers in any of the terms and its zeroes are 2 and -2.

Is -1 a zero of the quadratic polynomial $$x^2-2x-3$$?

Putting the value of -1,in the given polynomial,

$$(-1)^2-2(-1)-3$$

$$=1+2-3$$

$$=3-3$$

$$=0$$

$$\because$$ the values comes out to be 0.

$$\therefore$$ -1 is one of the zeroes of the given polynomial.

Is $$-2$$ a zero of the quadratic polynomial $$3x^2+x=10$$?

Putting the value of -2,in the given polynomial,
$$3(-2)^2+(-2)-10$$
$$=3(4)-2-10$$
$$=12-12$$
$$=0$$
$$\because$$ the values comes out to be 0.
$$\therefore$$ -2 is one of the zeroes and yes $$3x^2+x-10$$ is a quadratic polynomial.

$$ 32 -2 ( x -4)^2 $$

Given expression is $$ 32 -2 ( x -4)^2 $$

Taking out $$2$$ common from all terms, we get:
$$ 2[ 16 - (x -4)^2 ] $$
$$\Rightarrow 2 [ 4^2 -(x -4)^2 ] $$
we know that $$ a^2 -b^2 = (a+b)(a-b) $$

$$\Rightarrow 2 [ ( 4 + x -4)(4-x+4) ] $$

$$\Rightarrow 2 [ (x) (8-x) ] $$

$$\Rightarrow 2x ( 8 -x) $$

Hence, $$ 32 -2 ( x -4)^2 =2x ( 8 -x)$$

Which of the following is a polynomial?Find its degree and the zeroes.
$$x+\dfrac{1}{\sqrt{x}}$$

$$\because$$ the power of a term is in negative $$(-\dfrac{1}{2}).$$

$$\therefore$$ The above given expression is not a polynomial.

Find the zeroes of the given polynomials
$$P (x) = 3 x$$

$$P (x) = 3x$$ This is a linear polynomial .

It has only one zero.
Let $$P ( x) = 0$$
then,
$$3 x = 0$$
$$\Rightarrow x = \dfrac{0}{3}=0$$
$$\therefore $$ the zero of the given polynomial is zero.

Write the degree of each of the following polynomials :
$$ 1 - 100x^{20} $$

The degree of the polynomial is the greatest of sums of degree of two or more variables of the given polynomial
Therefore, the degree of the given polynomial $$ 1 - 100x^{20} $$ is $$20$$

Write the degree of each of the following polynomials :
$$ x^3 - x^8 + x^{10} $$

The degree of the polynomial is the greatest of sums of degree of two or more variables of the given polynomial
Therefore, the degree of the given polynomial $$ x^3 - x^8 + x^{10} $$ is $$10$$

Which of the following expressions is a polynomial? Find the degree and zeroes of the polynomial.i) $$\dfrac{x}{2}+\dfrac{2}{x}$$ ii) $$x^2+2x$$

In the above expressions, only the second one has a positive power,unlike others.

$$\therefore$$ It is the only polynomial.

Equating the expression with 0,

$$x^2+2x=0$$

$$x(x+2)=0$$

$$\therefore x=0$$ or $$ x+2-0$$

$$X=0 $$ or $$X=-2$$

The zeroes of the polynomial $$x^2+2x$$ are 2 and -2, having a degree of 2, being the highest power of the terms in the same expression.

Find the zeroes.
$$4-\dfrac{1}{4}x^2$$

In the above expressions,only the third one has the positive power unlike others.

$$\therefore$$ It is the only polynomial.

Equating the expression with 0,

$$4-\dfrac{1}{4}x^2=0$$

$$4=\dfrac{1}{4}x^2$$

$$x^2=16$$

$$\therefore x=\pm 4$$

The zeroes of the polynomial $$4-\dfrac{1}{4}x^2$$ are 4 and -4.

If P (x) = $$ = 5x^{7} - 6x^{5} + 7x - 6 $$ Find,
Degree of P (x)

The degree of a polynomial is maximum power of variable.
$$\therefore $$ Degree of $$P(x)=7$$

Write the degree of the following polynomial :
$$ 5x^2 - 7x + 2 $$

A polynomial's degree is the highest or the greatest power of a variable in a polynomial equation.
Therefore, the degree of the given polynomial $$ 5x^2 - 7x + 2 $$ is $$ 2$$.

Write the degree of each of the following polynomials :
$$ 4 + 4x - 4x^3 $$

The degree of the polynomial is the greatest of sums of degree of two or more variables of the given polynomial
Therefore, the degree of the given polynomial $$ 4 + 4x - 4x^3 $$ is $$3$$

Write the degree of each of the following polynomials :
$$ x + x^2 $$

The degree of the polynomial is the greatest of sums of degree of two or more variables of the given polynomial
Therefore, the degree of the given polynomial $$ x + x^2 $$ is $$2$$

State which of the following statement are true and which are false ? Given reasons for your choice
The degree of the polynomial .
$$ \sqrt{2} x^{2} - 3x + 1$$ is $$\sqrt{2} $$

False ,
because $$ \sqrt{2} $$ is coefficient of $$x$$ not degree.

Write the degree of the polynomial for the following expression.
$$ 5 + 3x^{4}$$

The highest power of the variable in polynomial having only one variable is called the degree of the polynomial .
Therefore, the degree of the polynomial $$ 5 + 3x^{4}$$ $$\Rightarrow$$ $$4. $$

State which of the following statement are true and which are false ? Given reasons for your choice
The degree of a polynomial is one more the number of term in it .

False ,
because degree of a polynomial is not related with number of terms.

Find the zeroes of the given polynomials
$$c^{4}-16$$

$$ P (x) = x ^{4}-16$$
Let ,
$$ P ( x ) = 0$$
$$ \Rightarrow x^{4} - 16 = 0 $$

$$\Rightarrow (x^{2})^{2}-4^2 = 0$$

$$\Rightarrow (x^{2}-4)(x^{2}+4) = 0$$
$$\Rightarrow ( x +2) (x - 2 ) ( x ^{2}+4) = 0$$

$$\Rightarrow x +2 = 0 , x - 2 = 0, x ^{2}+4=0$$
$$\Rightarrow x = -2 , x = 2 , x = \pm \sqrt{-4}$$
$$\therefore$$ The zeroes of the polynomial are
$$ -2, 2$$ and $$\pm \sqrt{-4}$$

Check whether $$3$$ and $$-2$$ are the zeroes of the polynomial $$P (x)$$ when
$$x^{2}- x-6 $$

Let,
$$ P (3) = 3^{2} - 3 -6 = 9 -9 = 0 $$
$$ P (-2) = (-2)^{2} - (-2) - 6 $$
$$= 4 + 2 - 6 = 0$$
$$ P (3) = 0$$ and $$P (-2)= 0$$
$$ \therefore 3$$ and $$-2$$ are the zeroes of the polynomials $$x^{2}- x-6 $$

Write three quadratic polynomials that have no real zeroes.

A quadratic polynomial $$ax^2+bx+c=0$$ has no solution when $$D=b^2-4ac<0$$

These quadratic polynomials have no zeroes

$$y = 2x^{2} - 4x + 5\Rightarrow D=(-4)^2-4(2)(5)=16-40=-24 \\y = 2x - 3x^{2} +2\Rightarrow D=(-3)^2-4(2)(2)=-7$$

$$y = x^{2} - 2x + 4\Rightarrow D=(-2)^2-4(1)(4)=-12$$

Check whether $$-2$$ and $$2$$ are the zeroes of the polynomials $$ x^{4}- 16 $$

Let $$ P (x) = x^{4} - 16 $$
$$P(-2) = (-2)^{4} - 16 = 16 - 16 = 0$$
$$P (2) = (2)^{4} - 16 = 16 - 16 = 0 $$
$$P (2) = 0$$ and $$P (-2) = 0 $$
$$\therefore $$ -2 and 2 are the zeroes of the polynomial $$x^{4} - 16 $$

Write the degree of the given polynomial:
$$ 2p - \sqrt{7}$$.

The highest power of the variable in a polynomial in one variable is called the degree of the polynomial.

Here, the highest power of $$p$$ is $$1$$.

$$\therefore$$The degree of the polynomial $$ 2p - \sqrt{7}$$ is $$1$$.

State which of the following statement are true and which are false ? Given reasons for your choice
The degree of a constant term is 0

True , for any constant term , degree is zero.

for example:-

(i) $$5=5x^0$$

(ii) $$-7=-7x^0$$

Write the degree of the given polynomial .
$$\sqrt{2}m^{10} - 7 $$

The highest power of the variable in a polynomial of one variable is called the degree of the polynomial. Also, the highest sum of the powers of the variables in each term of the polynomial in more than one variable is the degree of the polynomial.
The degree of the polynomial $$\sqrt{2}m^{10} - 7 $$ is $$10$$

Evaluate:
$$(4a+3b)^2-(4a-3b)^2+48ab$$

$$\left ( 4a + 3b \right )^{2} - \left ( 4a - 3b \right )^{2} + 48ab$$
Using,
$$(a-b)^2=(a^2-2ab+b^2) \,and\, (a+b)^2=(a^2+2ab+b^2)$$
$$=[( 4a)^2+2(4a)(3b)+(3b)^2]-[(4a)^2-2(4a)(3b)+(3b)^2]+48ab$$
$$=16a^2+24ab+9b^2-16a^2+24ab-9b^2+48ab$$
$$=96ab$$

Write the degree of the given polynomial:
$$7 y - y^{3} + y^{5}$$.

The highest power of the variable in a polynomial in one variable is called the degree of the polynomial.

Here, the highest power of $$y$$ is $$5$$.

$$\therefore$$The degree of the polynomial $$7 y - y^{3} + y^{5}$$ is $$5$$.

Write the degree of the polynomial $$3x^3 – x^4 + 5x + 3$$.

The highest power of the variable in a polynomial in one variable is called the degree of the polynomial.

Here, in the given polynomial,

$$3x^3 - x^4 + 5x + 3$$

$$ =- x^4 +3x^3+ 5x + 3$$.

Then, the highest power of the variable $$x$$ is $$4$$.

$$\therefore$$ The degree of the given polynomial is $$4$$.

Find the zero of the Polynomial , $$P(x) = a^2x,\,a \neq 0$$

$$P(x) = a^2x$$
$$a^2x = 0$$
$$x = \dfrac{0}{a^{2}}$$
$$x = 0$$

Verify whether the following are zeroes of the polynomial , induce against them.
$$ p (x) = 3x^{2} - 1 ; x = -\dfrac{1}{\sqrt{3}} , \dfrac{2}{\sqrt{3}} $$

$$ p (x) = 3x^{2} - 1 ; x = -\dfrac{1}{\sqrt{3}} , \dfrac{2}{\sqrt{3}} $$
$$ p \left ( - \dfrac{1}{\sqrt{3}} \right ) = 3 \left ( - \dfrac{1}{\sqrt{3}} \right )^{2} - 1 $$
$$ = 3 \left ( + \dfrac{1}{3} \right ) - 1 $$
$$ = 1 - 1 $$
$$p \left ( - \dfrac{1}{\sqrt{3}} \right ) = 0 $$

$$\therefore x=\dfrac{-1}{\sqrt{3}}$$ is zero of the polynomial

$$ p \left ( \dfrac{1}{\sqrt{3}} \right ) = 3 \left ( \dfrac{1}{\sqrt{3}} \right )^{2} - 1 $$
$$ = 3 \left ( \dfrac{1}{3} \right ) - 1 $$
$$ = 1 - 1 $$
$$p \left ( \dfrac{1}{\sqrt{3}} \right ) = 0 $$

$$\therefore x=\dfrac{1}{\sqrt{3}}$$ is zero of the polynomial

Verify whether the following are zeroes of the polynomial , induce against them.
$$ p (x) = 3x + 1 ; x = -\dfrac{1}{3} $$

$$ p (x) = 3x + 1 ; x = -\dfrac{1}{3} $$
$$ p \left ( - \dfrac{1}{3} \right ) = 3 \left ( -\dfrac{1}{3} \right ) + 1 $$
$$ = - 1 + 1 $$
$$ p \left ( -\dfrac{1}{3} \right ) = 0 $$

Here value of p (x) is zero

Hence its zero is $$-\dfrac{1}{3}$$

Verify whether the following are zeroes of the polynomial , induce against them.
$$ p (x) = x^{2} - 1 ; x = 1 , -1 $$

$$ p (x) = x^{2} - 1 ; x = 1 , -1 $$
$$ p (1) = (1)^{2} - 1 $$$$ = 1 - 1 $$
$$ p (1) = 0 $$
Here value of p (x) is zero
Hence its zero is $$1$$

$$ p (-1) = (-1)^{2} - 1 $$$$ = 1 - 1 $$
$$ p (-1) = 0 $$
Here value of p (x) is zero
Hence its zero is $$-1$$

Verify whether the following are zeroes of the polynomial , induce against them.
$$ p (x) =l x + m ; x = - \dfrac{m}{l} $$

$$ p (x) = i x + m ; x = - \dfrac{m}{l} $$
$$ p \left ( - \dfrac{m}{l} \right ) = l \left ( -\dfrac{m}{l} \right ) + m $$
$$ = - m + m $$
$$ = 0 $$

$$\therefore x=-\dfrac{m}{l}$$ is zero of the polynomial

Write the degree of the following polynomial:
$$ 5t - \sqrt{7} $$.

The highest power of the variable in a polynomial in one variable is called the degree of the polynomial.

Here, in the given polynomial $$ 5t - \sqrt{7} $$, the highest power of the variable $$t$$ is $$1$$.

$$\therefore$$ The degree of the given polynomial is $$1$$.

Verify whether the following are zeroes of the polynomial , induce against them.
$$ p (x) = x^{2} ; x = 0 $$

$$ p (x) = x^{2} ; x = 0 $$
$$ p (0) = (0)^{2} $$
$$ p (0) = 0 $$

$$\therefore x=0$$ is zero of the polynomial

Verify whether the following are zeroes of the polynomial , induce against them.
$$ p (x) = 5x - \pi ; x = \dfrac{4}{5} $$

$$ p (x) = 5x - \pi ; x = \dfrac{4}{5} $$
$$ p \left ( \dfrac{4}{5} \right ) = 5\left ( \dfrac{4}{5} \right ) - \pi $$
$$ p\left ( \dfrac{4}{5} \right ) = 4 - \pi $$

Here $$p(\dfrac{4}{5})\neq0$$

$$\therefore x=\dfrac{4}{5}$$ is not zero of the polynomial

Write the degree of the following polynomial:
$$ 4 - y^{2} $$.

The highest power of the variable in a polynomial is called the degree of the polynomial.

Here, in the given polynomial $$ 4 - y^{2} $$, the highest power of the variable $$y$$ is $$2$$.

$$\therefore$$ The degree of the given polynomial is $$2$$.

Verify whether the following are zeroes of the polynomial , induce against them.
$$ p (x) = (x + 1) (x - 2), x = -1 , 2 $$

$$ p (x) = (x + 1) (x - 2), x = -1 , 2 $$
$$ p (x) = x^{2} - 2x + x - 2 $$
$$ p (x) = x^{2} - x -2 $$

$$x = -1 $$
$$ p (-1) = (-1)^{2} - (-1) - 2 $$
$$ = 1 + 1 - 2 $$
$$ p (-1) = 0 $$

$$\therefore x=-1$$ is zero of the polynomial.

$$ p (x) = x^{2} - x -2 $$

$$x = 2 $$
$$ p (2) = (2)^{2} - (2) - 2 $$
$$ = 4 -4 $$
$$ p (2) = 0 $$

$$\therefore x=2$$ is zero of the polynomial.

Write the degree of the following polynomial:
$$ 5x^{3} + 4x^{2} + 7x $$ .

The highest power of the variable in a polynomial in one variable is called the degree of the polynomial.

Here, in the given polynomial $$ 5x^{3} + 4x^{2} + 7x $$, the highest power of the variable $$x$$ is $$3$$.

$$\therefore$$ The degree of the given polynomial is $$3$$.

If $$x - \sqrt{5}$$ is a factor of the cubic polynomial $$x^{3} - 3 \sqrt{5} x^{2} + 13x - 3 \sqrt{5} $$, then find all the zeroes of the polynomial.

Let $$f(x) = x^{3} - 3 \sqrt{5} x^{2} + 13x - 3 \sqrt{5} $$

Given, $$(x - \sqrt{5}) $$ is a factor $$f(x)$$,

Applying division algorithm, we have:

We know that , dividend = divisor $$ \times $$ quotient + remainder

2006559_1953199_ans_d9f26116cdea4c65b9828966e82d005b.png

Verify whether the following are zeroes of the polynomial , induce against them.
$$ p (x) = 2x + 1; x = \dfrac{1}{2} $$

$$ p (x) = 2x + 1; x = \dfrac{1}{2} $$
$$ p \left ( \dfrac{1}{2} \right ) = 2 \left ( \dfrac{1}{2} \right ) + 1 $$
$$ = 1 + 1 $$
$$ p \left ( \dfrac{1}{2} \right ) = 2 $$

$$\therefore x=\dfrac{1}{2}$$ is zeros of the polynomial

Find the zero of the polynomial in each of the following cases ;
$$ p (x) = 3x - 2 $$

$$ p (x) = 3x - 2 $$
If $$p(x) = 0$$ .

then,
$$p (x) = 3x - 2 = 0$$
$$3x = 2$$
$$ -\dfrac{2}{3} $$ is the zero of p(x)

Write the degree of the following polynomial:
$$5y - \sqrt{2}$$.

The highest power of the variable in a polynomial in one variable is called the degree of the polynomial.

Here, in the given polynomial $$5y - \sqrt{2}$$ , the highest power of the variable $$y$$ is $$1$$.

$$\therefore$$ The degree of the given polynomial is $$1$$.

State whether the following expression is a polynomials in one variable or not ? State reasons for your answers.
$$3$$

No given expression is not a polynomial in one variable.
$$3$$ is a constant polynomial.

Write the degree of the following polynomial:
$$12 - 3x + 2x^{2}$$.

The highest power of the variable in a polynomial in one variable is called the degree of the polynomial.

Here, in the given polynomial $$12 - 3x + 2x^{2}$$, the highest power of the variable $$x$$ is $$3$$.

$$\therefore$$ The degree of the given polynomial is $$3$$.

Write the degree of the polynomial:
$$9$$.

The highest power of the variable in a polynomial in one variable is called the degree of the polynomial.

Here, in the given polynomial is a constant polynomial $$ 9 $$, that is $$9=9x^0$$, the highest power of the variable $$x$$ is $$0$$.

$$\therefore$$ The degree of the given polynomial is $$0$$.

What is the zero of polynomial?

$$\textbf{Step 1: Apply the relevant property of polynomial.}$$

$$\text{The zero polynomial is represented as follows:}$$

$$\text{P(x) = 0}$$

$$\text{The zero of any polynomial is the value of x for which the value of the polynomial becomes zero.}$$

$$\text{For example, the zero of the polynomial p(x) = x - 1 is x = 1, since for }$$

$$\text{the value of x = 1, the value}$$$$\text{of the polynomial becomes 0.}$$

$$\textbf{Hence, answer.}$$

Find all the common zeroes of the polynomials : $$x^{3} + 5x^{2} - 9x - 45 $$ and $$x^{3} + 8x^{2} + 15x $$.

Let $$P(x) = x^{3} + 5x^{2} - 9x - 45$$ and $$Q(x) = x^{3} + 8x^{2} + 15x $$.

Let $$P(x) = x^{3} + 5x^{2} - 9x - 45 = x^{2} (x + 5) - 9(x + 5) $$

$$ = (x + 5) ( x^{2} - 9) $$

$$ = (x + 5) (x + 3) ( x - 3) $$

$$Q(x) = x^{3} + 8x^{2} + 15x = x (x^{2} + 8x + 15) $$

$$ = x(x + 5) (x + 3) $$

$$ \therefore $$ The common zeroes of the polynomials are $$(x + 5)$$ and $$(x + 3) $$.

Show that:
(i) $$(3x+7)^2-84x=(3x-7)^2$$

(ii) $$(9p-5q)^2+180pq = (9p+5q)^2$$

(iii) $$\left(\dfrac 43m-\dfrac 34n\right)^2 +2mn=\dfrac {16}{9}m^2+ \dfrac {9}{16}n^2$$

(iv) $$(4pq+3q)^2-(4pq-3q)^2=48pq^2$$

(v) $$(a-b)(a+b)+(b-c)(b+c)+(c-a)(c+a) = 0$$

We know that

$$(a\pm b)^2 = a^2 + b^2 \pm 2ab$$

and,

$$(a-b)(a+b) = a^2 - b^2$$

Now,

(i)

$$(3x+7)^2 - 84x$$

$$= (3x)^2 + 7^2 + 2(3x)(7) - 84x $$

$$= (3x)^2 + 7^2 - 42x $$
$$= (3x- 7)^2$$

(ii)

$$(9p-5q)^2 + 180pq$$

$$= (9p)^2 + (5q)^2 - 2(9p)(5q) + 180pq $$
$$= (9p)^2 + (5q)^2 - 90pq + 180pq$$

$$= (9p)^2 + (5q)^2 + 90pq $$

$$= (9p + 5q)^2$$

(iii)

$$\left(\dfrac43m- \dfrac34n\right)^2 + 2mn$$

$$=\left(\dfrac43m\right)^2 + \left(\dfrac34n\right)^2 - 2\left(\dfrac43m\right)\left(\dfrac34n\right) + 2mn$$

$$=\left(\dfrac43m\right)^2 + \left(\dfrac34n\right)^2 -2mn + 2mn$$

$$= \dfrac{16}9m^2 + \dfrac9{16}n^2$$

(iv)

$$(4pq+3q)^2 - (4pq - 3q)^2$$

$$=(4pq)^2 + (3q)^2 + 2(4pq)(3q) - \left((4pq)^2 +(3q)^2 - 2(4pq)(3q)\right)$$

$$=(4pq)^2 + (3q)^2 + 2(4pq)(3q) - (4pq)^2 -(3q)^2 + 2(4pq)(3q)$$

$$=24pq^2+24pq^2 $$

$$= 48pq^2$$

(v)

$$(a-b)(a+b) + (b-c)(b+c) + (c-a)(c+a)$$

$$= a^2- b^2 + b^2-c^2 + c^2 - a^2$$

$$ = 0$$

Find the following squares by using the identities.
(i) $$(b-7)^2$$

(ii) $$(xy+3z)^2$$

(iii) $$ (6x^2-5y)^2$$

(iv) $$\left(\dfrac 23 m + \dfrac 32n \right)^2$$

(v) $$(0.4p-0.5q)^2$$

(vi) $$(2xy+5y)^2$$

i) $$(b-7)^2$$

$$=b^2+7^2-2(b)(7) $$

$$=b^2+49-14b$$ $$\because [(a-b)^2$$$$=a^2+b^2-2ab]$$

ii) $$(xy+3z)^2$$

$$=(xy)^2+(3z)^2+2(xy)(3z) $$

$$=x^2y^2+9z^2+6xyz$$ $$\because [(a+b)^2$$$$=a^2+b^2+2ab]$$

iii) $$(6x-5y)^2$$

$$=(6x)^2+(5y)^2-2(6x)(5y) $$

$$=36x^2+25y^2-60xy$$ $$\because [(a-b)^2$$$$=a^2+b^2-2ab]$$

iv) $$\left(\dfrac 23m+\dfrac 32n\right)^2$$

$$=\left(\dfrac 23m\right)^2+\left(\dfrac 32n\right)^2+2\left(\dfrac 23m\right)\left(\dfrac 32n\right) $$

$$=\dfrac {4}{16}m^2+\dfrac 94n^2+2mn$$ $$\because [(a+b)^2$$$$=a^2+b^2+2ab]$$

v) $$(0.4p-0.5q)^2$$

$$=(0.4p)^2+(0.5q)^2-2(0.4p)(0.5q) $$

$$=0.16p^2+0.25q^2-4pq$$ $$\because [(a-b)^2$$$$=a^2+b^2-2ab]$$

vi) $$(2xy+5y)^2$$

$$=(2xy)^2+(5y)^2+2(2xy)(5y) $$

$$=4x^2y^2+25y^2+20xy^2$$ $$\because [(a+b)^2$$$$=a^2+b^2+2ab]$$

$$=y^2(4x^2+20x+25)$$

Verify whether the following are zeroes of the polynomial, indicated against them.
(i) $$p(x)=3x+1, x=-\displaystyle\frac{1}{3}$$
(ii) $$p(x)=5x-\pi, x=\displaystyle\frac{4}{5}$$
(iii) $$p(x)=x^2-1, x= 1, -1$$
(iv) $$p(x)=(x+1)(x-2), x=-1, 2$$
(v) $$p(x)=x^2, x= 0$$
(vi) $$p(x)=lx+m, x=-\displaystyle\frac{m}{l}$$
(vii) $$p(x)=3x^2-1, x=-\displaystyle\frac{1}{\sqrt 3},\frac{2}{\sqrt 3}$$
(viii) $$p(x)=2x+1, x=\displaystyle\frac{1}{2}$$

In order to verify the values are zeros of polynomial $$p(x)$$, we must replace the variable $$x$$ with the given values.

If $$p(x) = 0$$, then that given value is zero of polynomial $$p(x)$$.

(i) $$p(x) = 3x+1$$:

Put $$x=-\dfrac 13$$, we get,

$$p(x) = p(\dfrac{-1}{3}) =3\left(-\dfrac 13\right)+1 = -1+1 = 0$$.

So, $$x=-\dfrac 13$$ is the zero of the given polynomial $$p(x)$$.

(ii) $$p(x) = 5x-\pi$$:

Put $$x=\dfrac 45$$, we get,

$$p(x) = p(\dfrac45)=5\left(\dfrac 45\right)-\pi = 4-\pi \neq 0$$.

So, $$x=\dfrac 45$$ is not the zero of the given polynomial $$p(x)$$.

(iii) $$p(x) = x^2-1$$:

Put $$x=1$$, we get,

$$p(x) =p(1)= (1)^2-1 = 1-1 = 0$$.

So, $$x=1$$ is the zero of the given polynomial $$p(x)$$.

Now put $$x=-1$$, we get,

$$p(x) p(-1)= (-1)^2-1 = 1-1 = 0$$.

So, $$x=-1$$ is the zero of the given polynomial $$p(x)$$.

(iv) $$p(x) = (x+1)(x-2)$$:

Put $$x=-1$$, we get,

$$p(x) = (-1+1)(-1-2)= 0(-3) = 0$$.

So, $$x=-1$$ is the zero of the given polynomial $$p(x)$$.

Now put $$x=2$$, we get,

$$p(x) = (2+1)(2-2)= 3(0) = 0$$.

So, $$x=2$$ is the zero of the given polynomial $$p(x)$$.

(v) $$p(x) = x^2$$:

Put $$x=0$$, we get,

$$p(x)=p(0)=(0)^2=0$$.

So, $$x=0$$ is the zero of the given polynomial $$p(x)$$.

(vi) $$p(x) = lx+m$$:

Put $$x=-\dfrac ml$$, we get,

$$p(x) = p(-\dfrac ml)=l\left(-\dfrac ml\right)+m= -m+m = 0$$.

So, $$x=-\dfrac ml$$ is the zero of the given polynomial $$p(x)$$.

(vii) $$p(x) =3x^2-1$$:

Put $$x=-\dfrac {1}{\sqrt 3}$$, we get,

$$p(x)=p(-\dfrac{1}{\sqrt3}) = 3\left(-\dfrac {1}{\sqrt 3}\right)^2-1= \left(3 \times \dfrac 13\right)-1 =1-1= 0$$.

So, $$x=-\dfrac {1}{\sqrt3}$$ is the zero of the given polynomial $$p(x)$$.

Now put $$x=\dfrac {2}{\sqrt 3}$$, we get,

$$p(x) = p(\dfrac{2}{\sqrt3})=3\left(\dfrac {2}{\sqrt 3}\right)^2-1= \left(3 \times \dfrac 43\right)-1 = 4-1=3 \neq 0$$.

So, $$x=\dfrac {2}{\sqrt3}$$ is not the zero of the given polynomial $$p(x)$$.

(viii) $$p(x) =2x+1$$:

Put $$x=\dfrac 12$$, we get,

$$p(x) = p(\dfrac 12)=2\left(\dfrac 12\right)+1= 1+1 = 2 \neq 0$$.

So, $$x=\dfrac 12$$ is not the zero of the given polynomial $$p(x)$$.

Use a suitable identity to get each of the following products.
(i) $$(x+3)\;(x+3)$$

(ii) $$(2y+5)\;(2y+5)$$

(iii) $$(2a-7)\;(2a-7)$$

(iv) $$\begin{pmatrix}3a-\dfrac{1}{2}\end{pmatrix}\;\begin{pmatrix}3a-\dfrac{1}{2}\end{pmatrix}$$

(v) $$(1.1m-0.4)\;(1.1m+0.4)$$

(vi) $$(a^2+b^2)\;(-a^2+b^2)$$

(vii) $$(6x-7)\;(6x+7)$$

(viii) $$(-a+c)\;(-a+c)$$

(ix) $$\begin{pmatrix}\dfrac{x}{2}+\dfrac{3y}{4}\end{pmatrix}\;\begin{pmatrix}\dfrac{x}{2}+\dfrac{3y}{4}\end{pmatrix}$$

(x) $$(7a-9b)\;(7a-9b)$$

(i) $$(x+3)^2$$

$$=x^2+6x+9$$ $$\because [(a+b)^2$$$$=a^2+b^2+2ab]$$

(ii) $$(2y+5)^2$$
$$=4y^2+25+20y$$ $$\because [(a+b)^2$$$$=a^2+b^2+2ab]$$

(iii) $$(2a-7)^2$$

$$=4a^2-28a+49$$ $$\because [(a-b)^2$$$$=a^2+b^2-2ab]$$

(iv) $$3a^2-2(3a)\begin{pmatrix}\dfrac{1}{2}\end{pmatrix}+\begin{pmatrix}\dfrac{1}{2}\end{pmatrix}^2$$
$$=9a^2-3a+\dfrac{1}{4}$$ $$\because [(a-b)^2$$$$=a^2+b^2-2ab]$$

(v) $$(1.1m-0.4)(1.1m+0.4)$$

$$=1.21m^2-0.16$$ $$\because [(a^2-b^2)$$$$=(a+b)(a-b)]$$

(vi) $$(a^2+b^2)(-a^2+b^2)$$

$$=(b^2+a^2)(b^2-a^2)$$

$$=b^4-a^4$$ $$\because [(a^2-b^2)$$$$=(a+b)(a-b)]$$

(vii) $$(6x-7)(6x+7)$$

$$=(6x)^2-(7)^2$$
$$=36x^2-49$$ $$\because [(a^2-b^2)$$$$=(a+b)(a-b)]$$

(viii) $$(-a+c)(-a+c)$$

$$=(-a+c)^2$$
$$=a^2-2ac+c^2$$ $$\because [(a-b)^2$$$$=a^2+b^2-2ab]$$

(ix)$$\left (\dfrac x2+\dfrac {3y}{4}\right)\left (\dfrac x2+\dfrac {3y}{4}\right)$$

$$=\begin{pmatrix}\dfrac{x}{2}+\dfrac{3y}{4}\end{pmatrix}^2$$
$$=\begin{pmatrix}\dfrac{x}{2}\end{pmatrix}^2+2\begin{pmatrix}\dfrac{x}{2}\end{pmatrix}\begin{pmatrix}\dfrac{3y}{4}\end{pmatrix}+\begin{pmatrix}\dfrac{3y}{4}\end{pmatrix}^2$$
$$=\dfrac{x^2}{4}+\dfrac{3xy}{4}+\dfrac{9y^2}{16}$$ $$\because [(a+b)^2$$$$=a^2+b^2+2ab]$$

(x) $$(7a-9b)(7a-9b)$$

$$=(7a-9b)^2$$
$$=49a^2-126ab+81b^2$$ $$\because [(a-b)^2$$$$=a^2+b^2-2ab]$$

Simplify: $${ (2x-3y) }^{ 2 }+12xy$$

Using the identity: $$(x-y)^{ 2 }=x^{ 2 }+y^{ 2 }-2xy$$.

Given: $${ \left( 2x-3y \right) }^{ 2 }+12xy$$

We apply the above identity as follows:

$${ \left( 2x-3y \right) }^{ 2 }+12xy=\left[ { \left( 2x \right) }^{ 2 }+\left( 3y \right) ^{ 2 }-\left( 2\times 2x\times 3y \right) \right] +12xy $$

$$=4x^{ 2 }+9y^{ 2 }-12xy+12xy$$

$$=4x^{ 2 }+9y^{ 2 }$$

Hence, $${ \left( 2x-3y \right) }^{ 2 }+12xy=4x^{ 2 }+9y^{ 2 }$$.

prove that
$${(3x+7)}^{2}-{(3x-7)}^{2}= 84x$$

$${ \left( 3x+7 \right) }^{ 2 }-{ \left( 3x-7 \right) }^{ 2 }$$

$$\left( ^{ 2 }{ C }_{ 0 }{ \left( 3x \right) }^{ 2 }+^{ 2 }{ C }_{ 1 }\left( 3x \right) \left( 7 \right) +^{ 2 }{ C }_{ 2 }{ \left( 7 \right) }^{ 2 } \right) -\left( ^{ 2 }{ C }_{ 0 }{ \left( 3x \right) }^{ 2 }-^{ 2 }{ C }_{ 1 }\left( 3x \right) \left( 7 \right) +^{ 2 }{ C }_{ 2 }{ \left( 7 \right) }^{ 2 } \right) $$

$$\left( { \left( 3x \right) }^{ 2 }+2\left( 21x \right) +49 \right) -\left( 9{ x }^{ 2 }-42x+49 \right) $$

$$9{ x }^{ 2 }+42x+49-9{ x }^{ 2 }+42x-49$$$$=84x$$

Expand using binomial theorem $$(a+b)^{2}$$.

Apply binomial theorem to the term $${\left( {a + b} \right)^2}$$.

$${\left( {a + b} \right)^2} = {}^2{C_0}{a^2}{b^0} + {}^2{C_1}{a^1}{b^1} + {}^2{C_2}{a^0}{b^2}$$

$${\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}$$

Give the zeros of polynomial and list their multiplicities:
$$P(x)=(x+2)(x-1)$$

The zeroes of a polynomial function $$p(x)$$ are the x-values that yield $$0$$ as the function's value. That is, the zeros of the polynomial $$p(x)$$ are the roots, or solutions, to the equation $$p(x)=0$$. Zeros are also called the x-intercepts of the polynomial, or points where the graph of the polynomial touches the x-axis.

From the factor theorem, we know that when $$c$$ is a zero of the polynomial $$p(x)$$, then $$x-c$$ is a factor of $$p(x)$$. The multiplicity of the number of factors of $$x-c$$ in the linear factorisation of $$p(x)$$.

Hence, polynomial $$P(x)=(x+2)(x-1)$$ has the zero $$-2$$ with multiplicity $$1$$ and the zero $$1$$ with multiplicity $$1$$.

$$\left[ \dfrac { 1 }{ 2 } x-\left( -\dfrac { 2 }{ 5 } y \right) \right] \left[ \dfrac { 1 }{ 2 } x+\left( -\dfrac { 2 }{ 5 } y \right) \right]$$

$$\left( \cfrac { 1 }{ 2 } x+\cfrac { 2 }{ 5 } y \right) \left( \cfrac { 1 }{ 2 } x-\cfrac { 2 }{ 5 } y \right) $$

$$=\cfrac { 1 }{ 4 } { x }^{ 2 }-\cfrac { 4 }{ 25 } { y }^{ 2 }$$

Solve:
$$(a+b)(a-b)+(b+c)(b-c)+(c+a)(c-a)$$.

The given expression $$(a+b)(a−b)+(b+c)(b−c)+(c+a)(c−a)$$ can be solved as follows:

$$[(a+b)(a−b)]+[(b+c)(b−c)]+[(c+a)(c−a)]\\ =(a^{ 2 }-b^{ 2 })+(b^{ 2 }-c^{ 2 })+(c^{ 2 }-a^{ 2 })\quad \quad \quad \quad \quad (\because \quad x^{ 2 }-y^{ 2 }=(x-y)(x+y))\\ =a^{ 2 }-b^{ 2 }+b^{ 2 }-c^{ 2 }+c^{ 2 }-a^{ 2 }\\ =0$$

Hence, $$(a+b)(a−b)+(b+c)(b−c)+(c+a)(c−a)=0$$.

Expand $${ \left( a+5 \right) }^{ 2 }$$ using appropriate identity

Using, the identity $$(x+y)^{ 2 }=x^{ 2 }+y^{ 2 }+2xy$$.

Given, $$(a+5)^2$$ we apply the above identity as follows:

$$(a+5)^2=a^2+5^2+(2\times a\times 5)=a^2+25+10a$$

Hence, $$(a+5)^2=a^2+10a+25$$.

Find the zeros of the following quadratic polynomial:
$$p(x)=6x^{2}-7x-3$$

Let $$P\left(x\right)=6{x}^{2}-7x-3$$

Zero of polunominal is value of X where $$P\left(x\right)=0$$

Putting $$p\left(x\right)=0$$

$$6{x}^{2}-7x-3$$

We find roots using splitting the middle term method

$$6{x}^{2}-9x+2x-3=0$$

$$3x \left(2x-3\right) + 1\left(2x-3\right)=0$$

$$\left(3x+1\right)\left(2x-3\right)$$

So $$3x+1=0 \Rightarrow x=-\dfrac{1}{3}$$

& $$2x-3=0 \Rightarrow x=\dfrac{3}{2}$$

Prove that $$\left(\dfrac{4}{3}m-\dfrac{3}{4}n\right)^2+2mn=\dfrac{16}{9}m^2+\dfrac{9}{16}n^2$$.

Consider the LHS of the given equality as shown below:

$$\left( \dfrac { 4 }{ 3 } m-\dfrac { 3 }{ 4 } n \right) ^{ 2 }+2mn\\ =\left[ \left( \dfrac { 4 }{ 3 } m \right) ^{ 2 }+\left( \dfrac { 3 }{ 4 } n \right) ^{ 2 }-\left( 2\times \dfrac { 4 }{ 3 } m\times \dfrac { 3 }{ 4 } n \right) \right] +2mn\quad \quad \quad \quad (\because \quad (a-b)^{ 2 }=a^{ 2 }+b^{ 2 }-2ab)\\ =\dfrac { 16 }{ 9 } m^{ 2 }+\dfrac { 9 }{ 16 } n^{ 2 }-2mn+2mn\\ =\dfrac { 16 }{ 9 } m^{ 2 }+\dfrac { 9 }{ 16 } n^{ 2 }$$

Hence, $$\left( \dfrac { 4 }{ 3 } m-\dfrac { 3 }{ 4 } n \right) ^{ 2 }+2mn=\dfrac { 16 }{ 9 } m^{ 2 }+\dfrac { 9 }{ 16 } n^{ 2 }$$

If $$a=3,\ b=-3$$, find the value of
$$(a-2)^{2}+(b-2)^{2}$$

Let us substitute $$a=3$$ and $$b=-3$$ in the given expression $$(a−2)^2+(b−2)^2$$ as shown below:

$$(a−2)^{ 2 }+(b−2)^{ 2 }=(3−2)^{ 2 }+(-3−2)^{ 2 }=1^{ 2 }+(-5)^{ 2 }=1+25=26$$

Hence, $$(a−2)^2+(b−2)^2=26$$ if $$a=3$$ and $$b=-3$$.

Find the zeros of the following quadratic polynomial:
$$p(x)=4x^{2}+9x+5$$

In the given polynomial $$4x^2+9x+5$$,

The first term is $$4x^2$$ and its coefficient is $$4$$.

The middle term is $$9x$$ and its coefficient is $$9$$.

The last term is a constant term $$5$$.

Multiply the coefficient of the first term by the constant $$4\times 5=20$$.

We now find the factor of $$20$$ whose sum equals the coefficient of the middle term, which is $$9$$ and then factorize the polynomial $$4x^2+9x+5$$ and equate it to $$0$$ as shown below:

$$4x^{ 2 }+9x+5=0\\ \Rightarrow 4x^{ 2 }+4x+5x+5=0\\ \Rightarrow 4x(x+1)+5(x+1)=0\\ \Rightarrow (x+1)(4x+5)=0\\ \Rightarrow (x+1)=0,\quad (4x+5)=0\\ \Rightarrow x=-1,\quad 4x=-5\\ \Rightarrow x=-1,\quad x=-\dfrac { 5 }{ 4 }$$

Hence, the zeroes of the polynomial $$4x^2+9x+5$$ are $$-1,-\dfrac {5}{4}$$.

Find the value of the unknown variable from the given equation
$$3={ \left( y-3 \right) }^{ 2 }-{ \left( y+3 \right) }^{ 2 }$$

$$3=\left(y-3 \right)^{2}-\left(y+3 \right)^{2}$$

or, $$3= \left(y-3+y+3 \right) \ \left(y-3-y-3 \right)$$

or, $$2y \left(9 \right) =3$$

or, $$6y=1 \Rightarrow \boxed {y=1/6}$$ Ans.

Find the zeros of the following quadratic polynomials :
$$p(x)=x^{2}+4x-21$$

In the given polynomial $$x^2+4x-21$$,

The first term is $$x^2$$ and its coefficient is $$1$$.

The middle term is $$4x$$ and its coefficient is $$4$$.

The last term is a constant term $$-21$$.

Multiply the coefficient of the first term by the constant $$1\times -21=-21$$.

We now find the factor of $$-21$$ whose sum equals the coefficient of the middle term, which is $$4$$ and then factorize the polynomial $$x^2+4x-21$$ and equate it to $$0$$ as shown below:

$$x^{ 2 }+4x-21=0\\ \Rightarrow x^{ 2 }+7x-3x-21=0\\ \Rightarrow x(x+7)-3(x+7)=0\\ \Rightarrow (x-3)(x+7)=0\\ \Rightarrow (x-3)=0,\quad (x+7)=0\\ \Rightarrow x=3,\quad x=-7$$

Hence, the zeroes of the polynomial $$x^2+4x-21$$ are $$-7,3$$.

Prove the following result by using suitable identities.
$${ \left( x-y \right) }^{ 2 }+{ \left( y-z \right) }^{ 2 }+{ \left( z-x \right) }^{ 2 }=2\left( { x }^{ 2 }+{ y }^{ 2 }+{ z }^{ 2 }-xy-yz-zx \right) $$

$$LHS$$

$$=(x-y)^2+)(y-z)^2+(z-x)^2$$

$$=x^2-2xy+y^2+y^2-2yz+z^2+z^2-2zx+x^2$$

$$=2x^2+2y^2+2z^2-2xy-2yz-2zy$$

$$=2(x^2+y^2+z^2 -xy-yz-zx)=RHS$$ (Proved)

Find zeroes of the following polynomials and verify the relation between the zeroes
(a) $$6x^{2}_{} + 5x -1$$
(b) $$11x^{2}_{} -8x-3$$

The given polynomials are $$6x^2+5x-1$$ and $$11x^2-8x-3$$.

$$(a)$$ Let us first find the zeroes of the given polynomial $$6x^2+5x-1$$ by equating it to $$0$$ as shown below:

$$6x^{ 2 }+5x-1=0\\ \Rightarrow 6x^{ 2 }+6x-x-1=0\\ \Rightarrow 6x(x+1)-1(x+1)=0\\ \Rightarrow (6x-1)(x+1)=0\\ \Rightarrow (6x-1)=0,\quad (x+1)=0\\ \Rightarrow 6x=1,\quad x=-1\\ \Rightarrow x=\dfrac { 1 }{ 6 } ,\quad x=-1$$

Therefore, the zeroes are $$\dfrac { 1 }{ 6 }$$ and $$-1$$.

In the polynomial $$6x^2+5x-1$$, we have $$a=6,b=5$$ and $$-1$$. Now, consider

Sum of zeroes

$$\dfrac { 1 }{ 6 } +(-1)=\dfrac { 1 }{ 6 } -1=\dfrac { 1-6 }{ 6 } =-\dfrac { 5 }{ 6 } =-\dfrac { b }{ a }$$

Product of zeroes

$$\dfrac { 1 }{ 6 } \times (-1)=-\dfrac { 1 }{ 6 } =\dfrac { c }{ a }$$

Hence, the relation between the zeroes and coefficients is verified.

$$(b)$$ Let us first find the zeroes of the given polynomial $$11x^2-8x-3$$ by equating it to $$0$$ as shown below:

$$11x^{ 2 }-8x-3=0\\ \Rightarrow 11x^{ 2 }-11x+3x-3=0\\ \Rightarrow 11x(x-1)+3(x-1)=0\\ \Rightarrow (11x+3)(x-1)=0\\ \Rightarrow (11x+3)=0,\quad (x-1)=0\\ \Rightarrow 11x=-3,\quad x=1\\ \Rightarrow x=-\dfrac { 3 }{ 11 } ,\quad x=1$$

Therefore, the zeroes are $$-\dfrac { 3 }{ 11 }$$ and $$1$$.

In the polynomial $$11x^2-8x-3$$, we have $$a=11,b=-8$$ and $$-3$$. Now, consider

Sum of zeroes

$$-\dfrac { 3 }{ 11 } +1=\dfrac { -3+11 }{ 11 } =\dfrac { 8 }{ 11 } =-\dfrac { (-8) }{ 11 } =-\dfrac { b }{ a }$$

Product of zeroes

$$-\dfrac { 3 }{ 11 } \times 1=-\dfrac { 3 }{ 11 } =\dfrac { c }{ a } $$

Hence, the relation between the zeroes and coefficients is verified.

$$3$$ is a zero of $$P(x) = 3x^{3} - x^{2} - ax - 45$$.
Find $$a$$.

It is given that $$3$$ is a zero of the polynomial $$p(x)=3x^3-x^2-ax-45$$ which means that $$p(3)=0$$, so let us substitute $$x=3$$ in $$p(x)$$ to find the value of $$a$$ as shown below:

$$p(3)=3(3)^{ 3 }-(3)^{ 2 }-a(3)-45\\ \Rightarrow 0=(3\times 27)-9-3a-45\\ \Rightarrow 0=81-9-3a-45\\ \Rightarrow 0=81-54-3a\\ \Rightarrow 0=27-3a\\ \Rightarrow 3a=27\\ \Rightarrow a=\dfrac { 27 }{ 3 } \\ \Rightarrow a=9$$

hence, $$a=9$$.

$$(16a^4)^2-(b^4)^2$$.

\begin{array}{l} (16{ a^{ 4 } }-{ b^{ 4 } })\, (16{ a^{ 2 } }+{ b^{ 4 } }) \\ [{ (2a)^{ 4 } }-{ b^{ 4 } }]\, \, (16{ a^{ 4 } }+{ b^{ 4 } }) \\ [{ \{ { (2a)^{ 2 } }\} ^{ 2 } }-{ ({ b^{ 2 } })^{ 2 } }]\, (16{ a^{ 4 } }+{ b^{ 4 } }) \\ (2a-b)(2a+b)(4{ a^{ 2 } }+{ b^{ 2 } })(16{ a^{ 4 } }+{ b^{ 4 } }) \end{array}

Check whether $$-2$$ and $$2$$ are the zeros of the polynomial $${ x }^{ 4 }-16$$.

Let us substitute $$x=-2$$ in the given polynomial $$f(x)=x^4-16$$ as shown below:

$$f(-2)=(-2)^{ 4 }-16=16-16=0$$

Since $$f(-2)=0$$

$$ \therefore$$, $$-2$$ is the zero of the polynomial $$f(x)=x^4-16$$.

Now substitute $$x=2$$ as shown follows:

$$f(2)=(2)^{ 4 }-16=16-16=0$$

Since $$f(2)=0$$,

$$ \therefore$$, $$2$$ is the zero of the polynomial $$f(x)=x^4-16$$.

Hence, $$-2$$ and $$2$$ are the zeroes of the polynomial $$f(x)=x^4-16$$.

Find the zeros of the following quadratic polynomial:
$$p(x)=x^{2}-2x-8$$

Let $$p\left(x\right)= {x}^{2}-2x-8$$

Zero of polunominal is value of $$x$$ where P $$\left(x\right)=0$$

Putting $$p\left(x\right)=0$$

$${x}^{2}-2x-8=0$$

We find roots using splitting the middle e term method

] Here, we need two term where sum$$=-2$$ product $$=-8\times1=-8$$

$${x}^{2}-4x+2x-8=0$$

$$x\left(x-4\right)+2 \left(x-4\right)=0$$

$$\left(x+2\right)\left(x-4\right)$$

So $$x=-2,4$$

Therefore , $$\alpha=-2$$ & $$\beta=4$$ or zero of polunominal

Find the zeros, the sum and the product of zeros of $$p(x) = 4x^{2} + 12x + 5$$.

In the given polynomial $$4x^2+12x+5$$,

The first term is $$4x^2$$ and its coefficient is $$4$$.

The middle term is $$12x$$ and its coefficient is $$12$$.

The last term is a constant term $$5$$.

Multiply the coefficient of the first term by the constant $$4\times 5=20$$.

We now find the factor of $$20$$ whose sum equals the coefficient of the middle term, which is $$12$$ and then factorize the polynomial $$4x^2+12x+5$$ and equate it to $$0$$ as shown below:

$$4x^{ 2 }+12x+5=0\\ \Rightarrow 4x^{ 2 }+2x+10x+5=0\\ \Rightarrow 2x(2x+1)+5(2x+1)=0\\ \Rightarrow (2x+1)(2x+5)=0\\ \Rightarrow 2x=-1,\quad 2x=-5\\ \Rightarrow x=-\dfrac { 1 }{ 2 } ,\quad x=-\dfrac { 5 }{ 2 }$$

Therefore, the zeroes of the polynomial $$4x^2+12x+5$$ are $$-1,\dfrac {4}{3}$$.

Now, the sum and the product of the zeroes of the given quadratic polynomial is as follows:

$$-\dfrac { 1 }{ 2 } +\left( -\dfrac { 5 }{ 2 } \right) =-\dfrac { 1 }{ 2 } -\dfrac { 5 }{ 2 } =-\dfrac { 6 }{ 2 } =-3$$

$$\left( -\dfrac { 1 }{ 2 } \right) \times \left( -\dfrac { 5 }{ 2 } \right) =\dfrac { 1 }{ 2 } \times \dfrac { 5 }{ 2 } =\dfrac { 5 }{ 4 }$$

Hence, the sum of the zeroes is $$-3$$ and the product of the zeroes is $$\dfrac{5}{4}$$.

Obtain all zeroes of $$2x^4+7x^3-19x^2-14x+30$$, if two of its zeroes are $$\sqrt{2}$$ and $$-\sqrt{2}$$.

$$p\left( x \right) =2{ x^{ 4 } }+7{ x^{ 3 } }-19{ x^{ 2 } }-14x+30$$

Two of its zeroes are

$$\begin{array}{l} \sqrt { 2 } \, \, \& \, \, -\sqrt { 2 } \\ so,g\left( x \right) =\left( { x-\sqrt { 2 } } \right) \left( { x+\sqrt { 2 } } \right) \Rightarrow { x^{ 2 } }-2 \\ divisor={ x^{ 2 } }-2 \\ Quotient=2{ x^{ 2 } }+7x-15 \\ { { Re } }mainder=0 \\ q\left( x \right) =-2{ x^{ 2 } }+7x-15 \\ 2{ x^{ 2 } }+10x-3x-15=0 \\ 2x\left( { x+5 } \right) -3\left( { x+5 } \right) =0 \\ \left( { 2x-3 } \right) \left( { x+5 } \right) =0 \\ 2x-3=0 \\ 2x=3 \\ x=\frac { 3 }{ 2 } \\ x+5=0 \\ x=-5 \\ so,\, roots\, \, of\, \, equation\, \, is \\ \sqrt { 2 } ,\, -\sqrt { 2 } ,\frac { 3 }{ 2 } \, \, \& \, \, -5 \end{array}$$

Solve : $$5m^{2}-22m-15=0$$

$$5m^{2}-22m- 15=0$$

$$5m^{2}-25m+3m-15=0$$

$$5m(m-5)+3(m-5)=0$$

$$(m-5)(5m+3)=0$$

$$(m-5)=0, 5m+3=0$$

$$m=5, 5m=-3$$

$$m= -3/5$$

$$\therefore m=5, m=-3/5$$

Find the roots of
$$4{ u }^{ 2 }+8u=0$$

Let $$4u^2+8u=0$$

$$\Rightarrow 4u\left(u+2\right)=0$$

$$4u=0$$ or $$u+2=0$$

$$\Rightarrow u=0$$ or $$u=-2$$

Find the zeros, the sum of the zeros and the product of the zeros of the quadratic polynomial as follow:
$$p(x)=3x^{2}-x-4$$

In the given polynomial $$3x^2-x-4$$,

The first term is $$3x^2$$ and its coefficient is $$3$$.

The middle term is $$-x$$ and its coefficient is $$-1$$.

The last term is a constant term $$-4$$.

Multiply the coefficient of the first term by the constant $$3\times -4=-12$$.

We now find the factor of $$12$$ whose sum equals the coefficient of the middle term, which is $$-1$$ and then factorize the polynomial $$3x^2-x-4$$ and equate it to $$0$$ as shown below:

$$3x^{ 2 }-x-4=0\\ 3x^{ 2 }+3x-4x-4=0\\ 3x(x+1)-4(x+1)=0\\ (x+1)(3x-4)=0\\ (x+1)=0\quad or\quad (3x-4)=0\\ x=-1,\quad 3x=4\\ x=-1,\quad x=\dfrac { 4 }{ 3 }$$

Therefore, the zeroes of the polynomial $$3x^2-x-4$$ are $$-1,\dfrac {4}{3}$$.

Now, the sum and the product of the zeroes of the given quadratic polynomial is as follows:

Sum of Zeroes$$=-1+\dfrac { 4 }{ 3 } =\dfrac { -3+4 }{ 3 } =\dfrac { 1 }{ 3 } $$

Product of Zeroes$$=-1\times \dfrac { 4 }{ 3 } =-\dfrac { 4 }{ 3 } $$

Hence, the sum of the zeroes is $$\dfrac{1}{3}$$ and the product of the zeroes is $$-\dfrac{4}{3}$$.

Solve the following:
$$(3x+7)(3x-7)(9x^{2}+49)$$

$$\begin{array}{l} \left( { 3x+7 } \right) \left( { 3x-7 } \right) \left( { 9{ x^{ 2 } }+49 } \right) \\ \Rightarrow \left( { 9{ x^{ 2 } }-49 } \right) \left( { 9{ x^{ 2 } }+49 } \right) \, \, \left[ { { a^{ 2 } }-{ b^{ 2 } }=\left( { a-b } \right) \left( { a+b } \right) } \right] \\ \Rightarrow \left( { 81{ x^{ 4 } }-2401 } \right) \end{array}$$

Find the zeros and number of zeros of $$p(x) = x^{2} + 9x + 18$$.

The given polynomial is $$x^{ 2 }+9x+18=0$$

$$x^{ 2 }+9x+18=0\\ \Rightarrow x^{ 2 }+3x+6x+18=0\\ \Rightarrow x(x+3)+6(x+3)=0\\ \Rightarrow (x+3)(x+6)=0\\ \Rightarrow (x+3)=0,\quad (x+6)=0\\ \Rightarrow x=-3,\quad x=-6$$

Hence, the zeroes of the polynomial $$x^2+9x+18$$ are $$-3,-6$$ and therefore, the number of zeroes is two.

Find the zeroes of the quadratic polynomial
$$\sqrt{3}x^{2}-8x+4\sqrt{3}$$

$$\sqrt { 3 } { x }^{ 2 }-8x+4\sqrt { 3 } =0$$

$$\sqrt { 3 } { x }^{ 2 }-6x-2x+4\sqrt { 3 } =0$$

$$\sqrt { 3 } { x }\left( x-2\sqrt { 3 } \right) -2\left( x-2\sqrt { 3 } \right) =0$$

$$\left( \sqrt { 3 } x-2 \right) \left( x-2\sqrt { 3 } \right) =0$$

$$\sqrt { 3 } x-2=0;x-2\sqrt { 3 } =0$$

$$x=\cfrac { 2 }{ \sqrt { 3 } } ;x=2\sqrt { 3 } $$

$$\therefore $$Zeroes are $$\cfrac { 2 }{ \sqrt { 3 } } ,2\sqrt { 3 } $$

Find the zeroes of the following polynomial:
$$5\sqrt 5 {x^2} + 30x + 8\sqrt 5 $$

1293049_1353118_ans_ea3ce70be4f3445f86a6ebd238b66ef4.jpg

Solve the following:
$$(p+q)(p-q)(p^{2}+q^{2})(p^{4}+q^{4})(p^{8}+q^{8})$$

$$\begin{array}{l} \left( { p+q } \right) \left( { p-q } \right) \left( { { p^{ 2 } }+{ q^{ 2 } } } \right) \left( { { p^{ 4 } }+{ q^{ 4 } } } \right) \left( { { p^{ 8 } }+{ q^{ 8 } } } \right) \\ \Rightarrow \left( { { p^{ 2 } }-{ q^{ 2 } } } \right) \left( { { p^{ 2 } }+{ q^{ 2 } } } \right) \left( { { p^{ 4 } }+{ q^{ 4 } } } \right) \left( { { p^{ 8 } }+{ q^{ 8 } } } \right) \\ \Rightarrow \left( { { p^{ 4 } }-{ q^{ 4 } } } \right) \left( { { p^{ 4 } }+{ q^{ 4 } } } \right) \left( { { p^{ 8 } }+{ q^{ 8 } } } \right) \\ \Rightarrow \left( { { p^{ 8 } }-{ q^{ 8 } } } \right) \left( { { p^{ 8 } }+{ q^{ 8 } } } \right) \, \, \, \, \left[ { { a^{ 2 } }-{ b^{ 2 } }=\left( { a-b } \right) \left( { a+b } \right) } \right] \\ \left( { { p^{ 16 } }-{ q^{ 16 } } } \right) \, \, Ans. \end{array}$$

Solve the following:
$$\left(\dfrac {2}{3}x+7\right) \left(\dfrac {2}{3}x-7\right) \left(\dfrac {4x^{2}}{9}x+49\right)$$

$$\begin{array}{l} \left( { \dfrac { { 2x } }{ 3 } +7 } \right) \left( { \dfrac { { 2x } }{ 3 } -7 } \right) \left( { \dfrac { { 4{ x^{ 2 } } } }{ 9 } +49 } \right) \\ \Rightarrow \left( { \dfrac { { 4{ x^{ 2 } } } }{ 9 } -49 } \right) \left( { \dfrac { { 4{ x^{ 2 } } } }{ 9 } +49 } \right) \, \, \, \, \left[ { { a^{ 2 } }-{ b^{ 2 } }=\left( { a-b } \right) \left( { a+b } \right) } \right] \\ \Rightarrow \left( { \dfrac { { 16{ x^{ 4 } } } }{ { 81 } } -2401 } \right) \, \, Ans. \end{array}$$

Find the zero of the quadratic polynomial $$x^2-3$$, and verify the relationship between the zeros and coefficients.

Let $$p\left(x\right)={x}^{2}-3$$

Zero of the polynomial is the value of $$x$$ where $$p\left(x\right)=0$$

Put $$p\left(x\right)=0\Rightarrow {x}^{2}-3=0$$

$$\Rightarrow {x}^{2}-{\left(\sqrt{3}\right)}^{2}=0$$

So,$$x=\sqrt{3}\,,-\sqrt{3}$$

$$\therefore \alpha=\sqrt{3}$$ and $$\beta=-\sqrt{3}$$ are zeroes of the polynomial.

We can write $$p\left(x\right)={x}^{2}-3={x}^{2}+0-3$$ is of the form $$a{x}^{2}+bx+c$$ where $$a=1\,,b=0\,,c=-3$$

L.H.S$$=$$Sum of the zeroes$$=\alpha+\beta=\sqrt{3}-\sqrt{3}=0$$

and R.H.S$$=$$Sum of the zeroes$$=\dfrac{-b}{a}=\dfrac{-0}{1}=0$$

L.H.S$$=$$Product of the zeroes$$=\alpha\beta=\sqrt{3}\times -\sqrt{3}=-3$$

and R.H.S$$=$$product of the zeroes$$=\dfrac{c}{a}=\dfrac{-3}{1}=-3$$

Since L.H.S$$=$$R.H.S

Hence relationship between zeroes and coefficient is verified.

Linear Polynomial	Zero of the polynomial
$$x + a$$	$$-a$$
$$x - a$$	_____
$$ax + b$$	_____
$$ax - b$$	$$\dfrac {b}{a}$$

Polynomials - Class 9 Maths - Extra Questions

Write the degree of the polynomial given below:$$ y- 6y^2 + 5y^8 $$

Find the degree of the polynomial: $$7x^3+2x^2+x$$

Find the degree of the polynomial: $$5-x^2$$

Show that -1 is a zero of the polynomial $$2x^3-x^2+x+4$$.

Find the degree of the polynomial: $$3x^2-4x+2$$

Find the value of the polynomial $$p(x)=5x^2-3x+7$$ at $$x=1$$.

Find the degree of the polynomial: $$1+2x+3x^2-11x^4$$

Find the degree of the polynomial: $$4-y^2$$

Evaluatei)$$(38)^2-(37)^2$$ii)$$(75)^2-(74)^2$$iii)$$(141)^2-(140)^2$$

Show that $$1$$ is not a zero of the polynomial $$4x^4-3x^3+2x^2-5x+1$$.

Show that: $$(4pq + 3q)^2 -(4pq -3q)^2 = 48pq^2$$

Show that: $$(9p - 5q)^2 + 180pq = (9p + 5q)^2$$

Use the identity $$(a + b)(a - b) = a^2 - b^2$$ to find the product of $$(x + 6)(x - 6)$$

What is the expansion of $$(4p - 3q)^2$$?

Give one example each of a binomial of degree $$35$$ and of a monomial of degree $$100$$.

Expand:$$(2t + 5)(2t - 5)$$

Use appropriate formula to compute $$185^2- 115^2$$

Use the identity $$(a + b)(a - b) = a^2 - b^2$$ to find the product of $$(3x + 5)(3x - 5)$$

Find a zero of the polynomial $$2x - 1$$

Find the degree of each of the polynomials given below$$4 - y^{2}$$

Find the volume of the cuboid with dimensions $$(x-1), (x-2)$$ and $$(x-3)$$.

Write the degree of the following polynomial:$$7 - x + 3x^{2}$$

Write the degree of the following polynomial:$$7x^{3} + 5x^{2} + 2x - 6$$

Find the degree of the polynomial given below:$$x^{5} - x^{4} + 3$$

Write the degree of the following polynomial:$$5p - \sqrt {3}$$

Find the degree of each of the polynomials given below$$5t - \sqrt {3}$$

Find the degree of each of the polynomials given below$$x^{2} + x - 5$$

Verify whether the value of $$x$$ given in each case are the zeroes of the polynomial or not?$$p(x) = ax + b; x = -\dfrac {b}{a}$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?$$p(x) = 5x - \pi; x = \dfrac {3}{2}$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?$$p(x) = x^{2} - 1; x = \pm 1$$

Fill in the blanks:Linear PolynomialZero of the polynomial$$x + a$$$$-a$$$$x - a$$_____$$ax + b$$_____$$ax - b$$$$\dfrac {b}{a}$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?$$f(x) = 2x - 1, x = \dfrac {1}{2}, \dfrac {-1}{2}$$

Verify whether the value of $$x$$ given in each case are the zeroes of the polynomial or not?$$p(x) = (x - 1)(x + 2); x = -1, -2$$

Verify whether the given value of $$x$$ is the zero of the polynomial or not?$$p(x) = 2x + 1; x = -\dfrac {1}{2}$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?$$f(x) = 3x^{2} - 1; x = -\dfrac {1}{\sqrt {3}}, \dfrac {2}{\sqrt {3}}$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?$$p(y) = y^{2}; y = 0$$

Find the zero of the polynomial in each of the following cases.$$f(x) = px, p\neq 0$$

Find $${196}^{2}$$

Find the zero of the polynomial in each of the following cases.$$f(x) = x^{2}$$

Use suitable identities to find the product of : $$(x - 5)(x - 5)$$

If $$2$$ is a zero of the polynomial $$p(x) = 2x^{2} - 3x + 7a$$, find the value of $$a$$

Find the zero of the polynomial in each of the following cases.$$f(x) = 2x - 3$$

Find the zero of the polynomial in each of the following cases.$$f(x) = px + q, p\neq 0, pq$$ are real numbers

Find $$407\times 393$$

If $$p(t) = t^3 - 1$$, find the values of $$p(1), p(-2).$$

Find out the degree of the polynomials and the leading coefficients of the polynomials given below:$$x^{2} - 2x^{3} + 5x^{7} - \dfrac {8}{7}x^{3} - 70x - 8$$

Find out the degree of the polynomials and the leading coefficients of the polynomials given below:$$13x^{3} - x^{13} - 113$$

Classify the following polynomials as monomials, binomials and trinomials:$$3x^{2}, \,3x + 2, \,x^{2} - 4x + 2, \,x^{5} - 7, \,x^{2} + 3xy + y^{2}, \,s^{2} + 3st - 2t^{2}, \, xy + yz + zx, \,a^{2}b + b^{2}c, \,2l + 2m$$

Find $$302\times 308$$

The zero of the linear polynomial $$ax + b$$ is:

Find $$93\times 104$$

Write the degree of the following polynomial. $$12-x+4x^3$$

Evaluate the following by using the identity $$(a-b)^2=a^2+b^2-2ab$$ :$$2.8^{2}$$

Write the degree of the following polynomial: $$5y+\sqrt{2}$$

Evaluate the following by using the identities:$$9.7\times 9.8$$.

Find out the following squares by using the identities:$$(3x + 5)^{2}$$

Find out the degree of the polynomials and the leading coefficients of the polynomials given below:$$-77 + 7x^{2} - x^{7}$$

Find out the following squares by using the identities:$$(a - 5)^{2}$$

Find out the degree of the polynomials and the leading coefficients of the polynomials given below:$$-181 + 0.8y - 8y^{2} + 115y^{3} + y^{8}$$

Write the degree of $$4-3x^2$$

Find the zeros of the following polynomials.$$p(x)=4x-1$$

Find the root of $$x-3=0$$

Classify the following polynomial based on their degree.$$3x^2+2x+1$$

Classify the following polynomial based on their degrees: $$2x$$

Find the degree of given polynomial :$$4x^3-1$$

Find the root of −9x=0−9x=0

Classify the following polynomial based on their degrees:$$y+3$$

Classify the following polynomial based on their degrees:$$4x^3$$

Verify Whether the following are roots of the polynomial equations indicated against them.$$x^2-5x+6=0; (x=2, 3)$$

Classify the following polynomial based on their degrees:$$y^2-4$$

Verify Whether the following are roots of the polynomial equations indicated against them.$$x^2+4x+3=0; (x=-1, 2)$$

Find the roots of the following polynomial equations.$$x-6=0$$

Find the roots of the following polynomial equations.$$2x+1=0$$

What number should replace $$n$$ such that $$3(n+6)=(3\times 5)+(3\times 6)$$.

$${(\dfrac {\sqrt {2}}{3}x+2\sqrt {5}y)}^{2} =$$

Determine the degree of the the polynomial.$$(3x - 2)(2x^3 + 3x^2)$$

Solve $$2{y}^{3}+{y}^{2}-2y-1$$

What is the value if a?$$8=5+2a$$

Determine by substitution, if $$7$$ is a root of $$3x - 5 = 16$$.

Write the degree of the polynomial given below:
$$ y- 6y^2 + 5y^8 $$

Evaluate
i)$$(38)^2-(37)^2$$
ii)$$(75)^2-(74)^2$$
iii)$$(141)^2-(140)^2$$

Find the degree of each of the polynomials given below
$$4 - y^{2}$$

Write the degree of the following polynomial:
$$7 - x + 3x^{2}$$

Write the degree of the following polynomial:
$$7x^{3} + 5x^{2} + 2x - 6$$

Find the degree of the polynomial given below:
$$x^{5} - x^{4} + 3$$

Write the degree of the following polynomial:
$$5p - \sqrt {3}$$

Find the degree of each of the polynomials given below
$$5t - \sqrt {3}$$

Find the degree of each of the polynomials given below
$$x^{2} + x - 5$$

Verify whether the value of $$x$$ given in each case are the zeroes of the polynomial or not?
$$p(x) = ax + b; x = -\dfrac {b}{a}$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?
$$p(x) = 5x - \pi; x = \dfrac {3}{2}$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?
$$p(x) = x^{2} - 1; x = \pm 1$$

Fill in the blanks:
Linear Polynomial Zero of the polynomial
$$x + a$$ $$-a$$
$$x - a$$ _
$$ax + b$$ _
$$ax - b$$ $$\dfrac {b}{a}$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?
$$f(x) = 2x - 1, x = \dfrac {1}{2}, \dfrac {-1}{2}$$

Verify whether the value of $$x$$ given in each case are the zeroes of the polynomial or not?
$$p(x) = (x - 1)(x + 2); x = -1, -2$$

Verify whether the given value of $$x$$ is the zero of the polynomial or not?
$$p(x) = 2x + 1; x = -\dfrac {1}{2}$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?
$$f(x) = 3x^{2} - 1; x = -\dfrac {1}{\sqrt {3}}, \dfrac {2}{\sqrt {3}}$$

Verify whether the values of $$x$$ given in each case are the zeroes of the polynomial or not?
$$p(y) = y^{2}; y = 0$$

Find the zero of the polynomial in each of the following cases.
$$f(x) = px, p\neq 0$$

Find the zero of the polynomial in each of the following cases.
$$f(x) = x^{2}$$

Use suitable identities to find the product of :
$$(x - 5)(x - 5)$$

Find the zero of the polynomial in each of the following cases.
$$f(x) = 2x - 3$$

Find the zero of the polynomial in each of the following cases.
$$f(x) = px + q, p\neq 0, pq$$ are real numbers

Find out the degree of the polynomials and the leading coefficients of the polynomials given below:
$$x^{2} - 2x^{3} + 5x^{7} - \dfrac {8}{7}x^{3} - 70x - 8$$

Find out the degree of the polynomials and the leading coefficients of the polynomials given below:
$$13x^{3} - x^{13} - 113$$

Classify the following polynomials as monomials, binomials and trinomials:
$$3x^{2}, \,3x + 2, \,x^{2} - 4x + 2, \,x^{5} - 7, \,x^{2} + 3xy + y^{2}, \,s^{2} + 3st - 2t^{2}, \, xy + yz + zx, \,a^{2}b + b^{2}c, \,2l + 2m$$

Evaluate the following by using the identity $$(a-b)^2=a^2+b^2-2ab$$ :
$$2.8^{2}$$

Write the degree of the following polynomial:
$$5y+\sqrt{2}$$

Evaluate the following by using the identities:
$$9.7\times 9.8$$.

Find out the following squares by using the identities:
$$(3x + 5)^{2}$$

Find out the degree of the polynomials and the leading coefficients of the polynomials given below:
$$-77 + 7x^{2} - x^{7}$$

Find out the following squares by using the identities:
$$(a - 5)^{2}$$

Find out the degree of the polynomials and the leading coefficients of the polynomials given below:
$$-181 + 0.8y - 8y^{2} + 115y^{3} + y^{8}$$

Find the zeros of the following polynomials.
$$p(x)=4x-1$$

Classify the following polynomial based on their degree.
$$3x^2+2x+1$$

Classify the following polynomial based on their degrees:
$$2x$$

Find the root of −9x=0

Classify the following polynomial based on their degrees:
$$y+3$$

Classify the following polynomial based on their degrees:
$$4x^3$$

Verify Whether the following are roots of the polynomial equations indicated against them.
$$x^2-5x+6=0; (x=2, 3)$$

Classify the following polynomial based on their degrees:
$$y^2-4$$

Verify Whether the following are roots of the polynomial equations indicated against them.
$$x^2+4x+3=0; (x=-1, 2)$$

Find the roots of the following polynomial equations.
$$x-6=0$$

Find the roots of the following polynomial equations.
$$2x+1=0$$

Determine the degree of the the polynomial.
$$(3x - 2)(2x^3 + 3x^2)$$

What is the value if a?
$$8=5+2a$$

Write the degree of each of the following polynomials:
$$\left( i \right)\,\,5{x^3} + 4{x^2} + 7x$$
$$\left( {ii} \right)\,\,4 - {y^2}$$
$$\left( {iii} \right)\,\,5t - \sqrt 7 $$
$$\left( {iv} \right)\,\,3$$

solve:-
$${\left( {a + b} \right)^2} = $$

For $$\dfrac{x^3 + 2x + 1}{5} - \dfrac{7}{2} x^2 - x^6$$, write
i) the degree of the polynomial
ii) the coefficient of $$x^3$$
iii) the coefficient of $$x^6$$
iv) the constant term

Solve:
$${\left( {4a + 36} \right)^2} - {\left( {4a - 36} \right)^2} + 48ab$$

Evaluate
$$(5x+2y)^{2}+(5x-2y)^{2}$$

Solve :
$$4x^2 - 9y^2 $$=0

Expand using identities:
$${\left( {3x - 5y} \right)^2}$$

Solve:
$${\left( {a + b} \right)^2} $$

Write the degree of the following polynomials.
(i) $$p + p^3 + p^7$$
(ii) $$a + a^3 - a^0$$
(iii) $$m + a^4m + a^5m^3 - m^2 - a^4m^7$$

Write the numerical coefficients of the terms (other than constants) in each of the following algebraic expressions.
(a) $$5ab^2c$$
(b) $$3 - 4y^2$$
(c) $$-3xyz + 5x^2 - 6$$
(d) $$2(l + b + h)$$

Find the degree of the given polynomials.
$$x^{o}$$

Find the zero of the polynomial in each of the following
$$p(x)=3x-2$$

Solve
$$4u^2+8u=0$$

Find the zero of the polynomial
$$p(x)=x-5$$

Find the degree of the given polynomials.
$$2p-\sqrt{7}$$

select a suitable identity and find the following products
$$(7d-9e)(7d-9e)$$

Find the degree of the given polynomials.
$$\sqrt{2}m^{10}-7$$

Find the degree of the given polynomials.
$$x^{2}$$

Find the degree of the given polynomials.
$$7y-y^{3}+y^{5}$$

select a suitable identity and find the following products
$$(3k+4l)(3k+4l)$$

select a suitable identity and find the following products
$$(2b-a)(2b+c)$$

select a suitable identity and find the following products
$$(kl-mn)(kl+mn)$$

select a suitable identity and find the following products
$$(6x+5)(6x+6)$$

Prove that :
$$(3x-2y)^{2}+24xy=(3x+2y)^{2}$$

Solve:
$$\dfrac{9x}{8}+1=10$$

select a suitable identity and find the following products
$$(3t+9s)(3t-9s)$$

Verify whether the following are zeroes of the polynomial, indicated against them.
$$p\left( x \right) ={ x }^{ 2 }-1,x=1,-1$$

Verify whether the following are zeroes of the polynomial, indicated against them.
$$p\left( x \right) ={ x }^{ 2 },x=0$$

Find the zeroes of the polynomial:
$$3x^2-x-4$$.

Verify whether the following are zeroes of the polynomial, indicated against them.
$$p\left( x \right) =3{ x }^{ 2 }-1,x=-\dfrac { 1 }{ \sqrt { 3 } } ,\dfrac { 1 }{ \sqrt { 3 } } $$

Verify whether the following are zeroes of the polynomial, indicated against them.
$$p\left( x \right) =3x+1,x=-\dfrac { 1 }{ 3 } $$

Determine the degree of the following polynomial.
$$-\dfrac{1}{2}x+3$$.

Identify constant, linear, quadratic, cubic and quartic polynomial from the following.
$$-13$$.