Probability - Class 9 Maths - Extra Questions

Two coins are tossed once. Find the probability of getting:
(i) $$2$$ heads
(ii) at least $$1$$ tail.

Two coins are tossed. The sample set $$S$$ will be $$\{HH,HT,TH,TT\}$$
(i) Let $$A$$ be the event of getting two heads. Then event $$A$$ will contain the outcome $$\{HH\}$$
$$P(A) = \dfrac{n(A)}{n(S)} = \dfrac14$$

(ii) Let $$B$$ be the event of getting at least $$1$$ tail. Then, $$B$$ will contain the outcomes $$\{HT,TH,TT\}$$
$$P(B) = \dfrac{n(B)}{n(S)} = \dfrac34$$


A card is drawn at random from a well-shuffled pack of $$52$$ playing cards. Find the probability of the events that the card drawn is:
$$(a)$$ a king  $$(b)$$ a face card

Let $$S$$ be the sample space.
There are $$52$$ playing cards in a pack
$$\therefore$$ $$n(S)=52$$
Let $$A$$ be the event that the card drawn is a king
Total king in pack $$=4$$
$$\therefore$$ $$n(A)=4$$
$$\therefore$$ $$P(A)=\cfrac { n(A) }{ n(S) } =\cfrac{4}{52}=\cfrac{1}{13}$$
Let $$B$$ be the event that the card drawn is a face card
Total face card in a pack $$=12$$
$$\therefore$$ $$n(B)=12$$
$$\therefore$$ $$P(B)=\cfrac { n(B) }{ n(S) } =\cfrac { 12 }{ 52 } =\cfrac { 3 }{ 13 } $$


If two coin are tossed, then find the probability of the event that no head turns up.

Let $$S$$ be the sample
Two coins are tossed.
$$\therefore S = \{HH, HT, TH, TT\}$$
$$\therefore n(S) = 4$$
Let $$A$$ be the event of getting no head.
$$\therefore  A = {TT}$$
$$\therefore n(A) = 1$$
$$P(A) = \dfrac{n(A)}{n(S)} = \dfrac{1}{4}$$


A die has $$6$$ faces marked by the given numbers as shown below:
The die is thrown once. What is the probability of getting a positive integer?

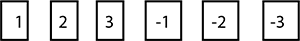
583682.png

No.of sample space $$n(S) = 6$$
a positive integer $$= \left \{1, 2, 3\right \}$$
No. of favourables $$n(E) = 3$$
$$\therefore P(E) = \dfrac{n(E)}{n(S)} = \dfrac36 = \dfrac12$$


If $$n(A) = 1$$ and $$n(S) =13$$, then find $$P(A)$$.


2159728_592990_ans_f558b5ae9ec9427ea55e31f091d1a6e1.jpg


If $$A$$ is required event and $$S$$ is the sample space, $$n\left(A\right)=3$$, $$n\left(S\right)=6$$, then find $$P\left(A\right)$$.

Given, $$n\left( A \right) =3$$
            $$n\left( S \right) =6$$
Thus,
$$P\left( A \right) =\dfrac { n\left( A \right)  }{ n\left( S \right)  } \\=\dfrac { 3 }{ 6 } \\=\dfrac { 1 }{ 2 } $$.


A die has $$6$$ faces marked by the given numbers as shown below:
The die is thrown once. What is the probability of getting the smallest integer?
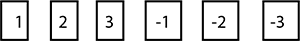
583685.png

No. of sample space $$n(S) = 6$$
Smallest integer $$= -3$$
Probability of smallest integer $$\dfrac {n(E)}{n(S)} = \dfrac {1}{6}$$.


If two coins are tossed, then find the probability of the event that at least one tail turns up.

Let $$S$$ be the sample. Two coins are tossed
$$S = \{HH, HT, TH, TT\}$$
$$\therefore n(S) = 4$$
Let $$A$$ be the event of getting atleast one tail
$$A = \{HT, TH, TT\}$$
$$\therefore n(A) = 3$$
$$P(A) = \dfrac{n (A)}{n (S)} = \dfrac{3}{4}$$


A die has $$6$$ faces marked by the given numbers as shown below:
The die is thrown once. What is the probability of getting an integer greater than $$-3$$?

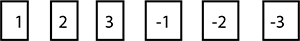
583684.png

No. of sample space $$n(S) = 6$$
an integer greater than $$-3 = \left \{1, 2, 3, -1, -2\right \}$$
No. of favourables $$n(E) = 5$$
Probability $$= \dfrac {n(E)}{n(S)} = \dfrac {5}{6}$$


Three coins are tossed simultaneously. Find the probability that at least two heads turn up.

Three coins are tossed simultaneously:
$$S = \left \{HHH, HHT, HTH, TTT, THT, TTH, HTT, THH\right \}$$
$$\therefore n(S) = 8$$
Let $$A$$ be an event that at least two heads turn up.
$$A = \left \{HHH, HHT, HTH, THH\right \}$$
$$\therefore n(A) = 4$$
$$\therefore P(A) = \dfrac {n(A)}{n(S)}$$
$$= \dfrac {4}{8}$$
$$= \dfrac {1}{2}$$.


A game of number has cards marked with $$11, 12, 13, .... 40$$. A card is drawn at random. Find the Probability that the number on the card drawn is a perfect square

Total number of all possible outcomes $$= 30$$.
Since required (favourable) outcomes are: $$16, 25$$ and $$36$$
$$\therefore$$ The number of favourable outcomes $$= 3$$.
$$\therefore P$$ (A perfect square) $$= \dfrac {3}{30} = \dfrac {1}{10}$$.


An unbiased cubical die whose faces are numbered $$1$$ to $$6$$ is rolled once. Find the probability of getting a square number on the top face.

Solution:
S$$=\left\{1,2,3,4,5,6\right\}$$
$$n(S)=6$$
Let $$A=$$ square number $$=\left\{1,4\right\}$$
$$n(A)=2$$
$$p(A)=\cfrac{n(A)}{n(S)}=\cfrac26=\cfrac13$$


Find the probability of getting a head when a coin is tossed once. Also find the probability of getting a tail.

Let $$S$$ be the sample space of tossing a coin
$$S=\{H,T\}$$
Probability of getting head $$=\displaystyle \cfrac {\text{no. of favorable outcomes}}{\text{no. of total outcomes}}=\dfrac 12$$
Probability of getting tail $$=\displaystyle \cfrac {\text{no. of favorable outcomes}}{\text{no. of total outcomes}}=\frac 12$$


A page is opened at random from a book containing $$90$$ pages. Then probability of a page number is a perfect square, is _____.

Number of perfect square from $$1$$ to $$90$$ are $$1,4,9,16,25,36,49,64,81$$.

Total cases $$=90$$

Favorable cases $$=9$$

Therefore, probability $$=\dfrac{9}{90}=\dfrac1{10}$$


There are $$500$$ wrist watches in a box. Out of these $$50$$ wrist watches are found defective. One watch is drawn randomly from the box. Find the probability that wrist watch chosen is a defective watch.

Total number of watches $$n(S) = 500$$
Number of defective watches $$n(A) = 50$$
$$P(A) = \dfrac {n(A)}{n(S)}$$
$$\Rightarrow P(A) = \dfrac {50}{500}$$
Probability of watch to be defective $$= \dfrac {1}{10}$$


A bag contains $$5$$ red and $$8$$ white balls. If a ball is drawn at random from the bag, what is the probability that it will be:
(i) White ball,   (ii) Not a white ball?

Total balls $$=5+8=13$$
(i) Probability of while ball $$=\dfrac8{13}$$
(ii) Probability of not a while ball $$=1-$$ probability of while ball $$=1-\dfrac8{13}=\dfrac5{13}$$


A box contains $$5$$ red marbles, $$8$$ white marbles and $$4$$ green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be
(i) red, (ii) white, (iii) not green?

Box has $$5$$ red, $$8$$ white, $$4$$ green marbles.
the probability that the marble taken out will be red is $$\dfrac { \text{no. of favourable outcomes} }{ \text{total no. of possible outcomes} } $$.
$$\Rightarrow \dfrac { 5 }{ 5+8+4 } =0.29$$
the probability that the marble taken out will be white is $$\dfrac { \text{no. of favourable outcomes} }{ \text{total no. of possible outcomes} } $$.
$$\Rightarrow \dfrac { 8 }{ 5+8+4 } =0.47$$
the probability that the marble taken out will be green is $$\dfrac { \text{no. of favourable outcomes} }{ \text{total no. of possible outcomes} } $$.
$$\Rightarrow \dfrac { 5+8 }{ 5+8+4 } =0.76$$


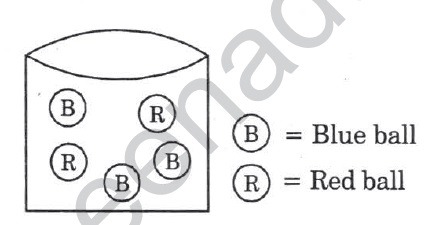
From the figure, the probability to get Blue colour ball is ___________.
608727.jpg

Box has $$2$$ red and $$3$$ blue marbles.
The probability that the marble taken out will be blue is $$\dfrac {\text{No. of favourable outcomes} }{\text{Total no. of possible outcomes }} $$
$$\Rightarrow \dfrac { 3 }{ 2+3 } =\dfrac 35=0.6$$


$$1500$$ families with $$2$$ children were selected randomly, and the following data were recorded:
 No. of girls in a family $$2$$$$1$$ $$0$$ 
 No. of families$$475$$ $$814$$ $$211$$ 
Compute the probability of a family, chosen at random, having
(i) $$2$$ girls
(ii) $$1$$ girl
(iii) No girl
Also check whether the sum of these probabilities is $$1$$.

(i) Number of families having $$2$$ girls $$= 475$$
Total families $$= 475+814+211=1500$$     
$$P (2$$ girls$$)\ = \dfrac{475}{\text{Total families}}$$

$$=\dfrac{475}{1500} = \dfrac{19}{60}$$

(ii) $$P (1$$ girl$$) = \dfrac{814}{1500} = \dfrac{407}{750}$$

(iii) $$P ($$No girl$$)\ = \dfrac{211}{1500}$$

Sum of all these probabilities 
$$= \dfrac{19}{60} + \dfrac{407}{750} + \dfrac{211}{1500}$$

$$= \dfrac{475+814+211}{1500}$$

$$= \dfrac{1500}{1500} = 1$$

Sum of these probabilities $$= 1$$


 OpinionNo. of students 
 like$$135$$ 
dislike $$65$$ 
To know the opinion of the students about the subject statistics, a survey of $$200$$ students was conducted. The data is recorded in the following table.
Find the probability that a student chosen at random
(i) likes statistics.
(ii) does not like statistics.

Total number of students $$= 135+65=200$$
(i) Number of students like statistics $$= 135$$
$$Probability= \dfrac{135}{200} = \dfrac{27}{40}$$

(ii) Number of students who don't like statistics $$= 65$$
$$Probability= \dfrac{65}{200} = \dfrac{13}{40}$$


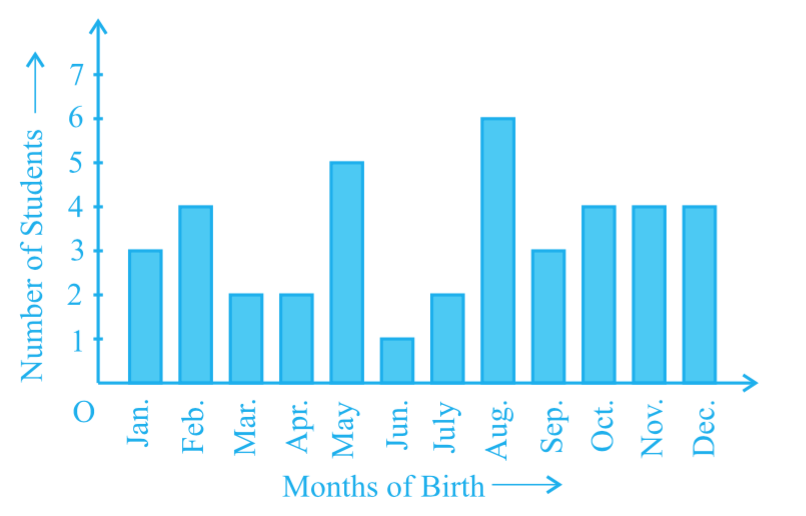
In a particular section of class IX, 40 students were asked about the month of their birth and following graph was prepared for data so obtained:
Find the probability that a student of the class was born in August.
464445.png

Number of students born in August $$= 6$$
Total number of students $$=3+4+2+2+5+1+2+6+3+4+4+4=40$$
Probability of students born in August 
$$= \dfrac{\text{Number of students born in August}}{\text{Total number of students}}$$

$$= \dfrac{6}{40} \\= \dfrac{3}{20}$$


 Vehicles per family $$\Rightarrow$$

Monthly income (Rs.) $$\Downarrow$$		0 1 2 Above 2 
 Less than 7,00010 160 25 0 
 7,000 - 10,0000 305 27 2 
10,000 - 13,000 1 535 29 1 
13,000 - 16,000 2 469 59 25 
16,000 or more 1 579 82 88 
An organisation selected $$2400$$ families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below:
Suppose a family is chosen. Find the probability that the family chosen is
(i) earning $$Rs. 10000 - 13000$$ per month and owning exactly $$2$$ vehicles.
(ii) earning $$Rs. 16000$$ or more per month and owning exactly $$1$$ vehicle.
(iii) earning less than $$Rs. 7000$$ per month and does not own any vehicle.
(iv) earning $$Rs. 13000 - 16000$$ per month and owning more than $$2$$ vehicles.
(v) owning not more than $$1$$ vehicle.

Number of families surveyed 
$$= 10+60+25+0+0+305+27+2+1+535+\\ \quad\quad\quad\quad29+1+2+469+55+25+579+82+88$$
$$= 2400$$

(i) Number of families earning Rs. $$10000 - 13000$$ per month and owning exactly $$2$$ vehicles $$= 29$$
$$P= \dfrac{29}{2400}$$

(ii) Number of families earning Rs. 16000 or more per month and owning exactly $$1$$ vehicle $$= 579$$
$$P= \dfrac{579}{2400}$$

(iii) Number of families earning less than Rs. $$7000$$ per month and does not own any vehicle $$=10$$
$$P= \dfrac{10}{2400} = \dfrac{1}{240}$$

(iv) Number of families earning Rs. $$13000 - 16000$$ per month and owning more than $$2$$ vehicles $$= 25$$
$$P= \dfrac{25}{2400} = \dfrac{1}{96}$$

(v) Number of families owning not more than $$1$$ vehicle 
$$= 10+160+0+305+1+535+2+469+1+579 = 2062$$

$$P= \dfrac{2062}{2400} = \dfrac{1031}{1200}$$



 MarksNumber of Students 
 $$0-20$$$$7$$ 
 $$20-30$$$$10$$ 
 $$30-40$$$$10$$ 
 $$40-50$$$$20$$ 
 $$50-60$$$$20$$ 
 $$60-70$$$$15$$ 
 $$70-$$ Above$$8$$ 
 Total$$90$$ 
A teacher wanted to analyze the performance of two sections of students in a mathematics test of 100 marks. Looking at their performance, she found that a few students got, under 20 marks and a few got 70 marks or above. So she decided to group them into intervals of varying sizes as follows: $$0-20, 20-..., 60-70, 70-100$$ Then she formed the following table.
(i) Find the probability that a student obtained less than $$20$$% in the mathematics test.
(ii) Find the probability that a student obtained marks $$60$$ or above.

Total students $$= 90$$

(i) Number of students getting less than $$20\%$$ marks in the test $$=7$$
$$P= \dfrac{7}{90}$$

(ii) Number of students obtaining marks $$60$$ or above $$= 15+8 = 23$$
$$P= \dfrac{23}{90}$$


Eleven bags of wheat flour, each marked $$5 kg$$, actually contained the following weights of flour (in kg):
$$4.97\ \ \ 5.05\ \ \  5.08 \ \ \  5.03\ \ \  5.00\ \ \  5.06\ \ \  5.08\ \ \   4.98\ \ \   5.04\ \ \  5.07\ \ \  5.00$$
Find the probability that any of these bags chosen at random contains more than $$5\ kg$$ of flour.

Total bags $$= 11$$
Number of bags containing more than $$5 kg$$ of flour $$= 7$$
Probability $$= \dfrac{7}{11}$$


A study was conducted to find out the concentration of sulphur dioxide in the air in parts per million (ppm) of a certain city. The data obtained for 30 days is as follows:
$$\begin{matrix} 0.03 & 0.08 & 0.08 & 0.09 & 0.04 & 0.17 \\ 0.16 & 0.05 & 0.02 & 0.06 & 0.18 & 0.20 \\ 0.11 & 0.08 & 0.12 & 0.13 & 0.22 & 0.07 \\ 0.08 & 0.01 & 0.10 & 0.06 & 0.09 & 0.18 \\ 0.11 & 0.07 & 0.05 & 0.07 & 0.01 & 0.04 \end{matrix}$$
Using this table, find the probability of the concentration of sulphur dioxide in the interval $$0.12 - 0.16$$ on any of these days.

 Concentration of
sulphur dioxide (in ppm)		 Frequency
 $$0.00 - 0.04$$$$4$$ 
$$0.04 - 0.08$$ $$9$$ 
$$0.08 - 0.12$$ $$9$$ 
$$0.12 - 0.16$$ $$2$$ 
$$0.16 - 0.20$$ $$4$$ 
$$0.20 - 0.24$$$$2$$ 
Total $$30$$ 

Number of days for which $$S{O}_{2}$$ concentration was in the interval of $$0.12-0.16 = 2$$
Total bags $$=30$$
P $$= \dfrac{2}{30} = \dfrac{1}{15}$$


The blood groups of 30 students of Class VIII are recorded as follows:
$$A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O,$$
$$A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O$$.
Use this table to determine the probability that a student of this class, selected at random, has blood group $$AB$$.

 Blood group No. of students
 A9 
B 6 
O 12 
AB 3 
Total 30 
Number of students having blood group $$AB=3$$
Total students $$=30$$
P $$= \dfrac{3}{30} = \dfrac{1}{10}$$


The distance (in km) of $$40$$ engineers from their residence to their place of work were found as follows:
$$\begin{matrix} 5 & 3 & 10 & 20 & 25 & 11 & 13 & 7 & 12 & 31 \\ 19 & 10 & 12 & 17 & 18 & 11 & 32 & 17 & 16 & 2 \\ 7 & 9 & 7 & 8 & 3 & 5 & 12 & 15 & 18 & 3 \\ 12 & 14 & 2 & 9 & 6 & 15 & 15 & 7 & 6 & 12 \end{matrix}$$
What is the empirical probability that an engineer lives:
(i) less than $$7\ km$$ from her place of work?
(ii) more than or equal to $$7\ km$$ from her place of work?
(iii) within $$\dfrac{1}{2}\ km$$ from her place of work?

 Distance (in km.) No. of engineers
 Less than $$7\ km.$$ $$9$$
 More than $$7\ km.$$ $$31$$
 Total$$40$$ 
Total number of engineers $$= 40$$
(i) Number of engineers living less than $$7 km$$ from their place of work $$=9$$
$$P= \dfrac{9}{40}$$
(ii) Number of engineers living more than or equal to $$7 km$$ from their place of work $$= 40-9 = 31$$
$$P= \dfrac{31}{40}$$
(iii) Number of engineers living within $$\dfrac{1}{2}km$$ from her place of work $$= 0$$
$$P= \dfrac{0}{40} = 0$$


There are three boys and two girls. A committee of two is to be formed. Find the probability of the following events:
Event $$A$$: The committee contains at least one boy.
Event $$B$$: The committee contains one boy and one girl

Committee of two is to be formed from $$3$$ boys and $$2$$ girls.
Let $$3$$ boys be $$B_{1}, B_{2}, B_{3}$$ and $$2$$ girls be $$G_{1}, G_{2}$$.
$$S = \left \{B_{1}B_{2}, B_{1}B_{3}, B_{2}B_{3}, G_{1}G_{2}, B_{1}G_{1}, B_{1}G_{2}, B_{2}G_{1}, B_{2}G_{2}, B_{3}G_{1}, B_{3}G_{2}\right \}$$
$$\therefore n(S) = 10$$
$$A$$ is the event that the committee contains atleast one boy.
$$\therefore A = \left \{B_{1}B_{2}, B_{1}B_{3}, B_{2}B_{3}, B_{1}G_{1}, B_{1}G_{2}, B_{2}G_{1}, B_{2}G_{2}, B_{3}G_{1}, B_{3}G_{2}\right \}$$
$$n(A) = 9$$
$$\therefore P(A) = \dfrac {n(A)}{n(S)} = \dfrac {9}{10}$$
and $$B$$ is the event that the committee contains one boy and one girl.
$$\therefore B = \left \{B_{1}G_{1}, B_{1}G_{2}, B_{2}G_{1}, B_{2}G_{2}, B_{3}G_{1}, B_{3}G_{2}\right \}$$
$$n(B) = 6$$
$$\therefore P(B) = \dfrac {n(B)}{n(S)} = \dfrac {6}{10} = \dfrac {3}{5}$$


If two coins are tossed, then find the probability of the event that at the most one tail turns up.

Let $$S$$ be sample space of experiment and $$A$$ be event that at the most one tail turns up.
Then,
$$S=\left\{HH,HT,TH,TT\right\}$$
$$A=\left\{HH,HT,TH\right\}$$
$$\text{Total number of cases}=4$$
$$\text{Total number of favorable cases}=3$$

$$\therefore \ \text{Required probability}=\dfrac{\text{No. of favorable cases}}{\text{Total no. of cases}}=\dfrac34$$


Two digits are formed from the digits $$0, 1, 2, 3, 4$$ where digits are not repeated. Find the probability of the events that the number so formed is an even number.

Let $$S$$ be sample space of number formed. Then,
$$S=\left\{10,12,13,14,20,21,23,24,30,31,32,34,40,41,42,43\right\}$$
$$n(S) =16$$
Let $$A$$ be event of Even number. then,
$$A=\left\{10,12,14,20,24,30,32,34,40,42,\right\}$$
$$\therefore, P(A)=\dfrac{10}{16}=\dfrac58$$


Two digits are formed from the digits $$0, 1, 2, 3, 4$$ where digits are not repeated. Find the probability of the events that the number so formed is a prime number.

Let $$S$$ be sample space of number formed. Then,
$$S=\left\{10,12,13,14,20,21,23,24,30,31,32,34,40,41,42,43\right\}$$
$$n(S) =16$$
Let $$A$$ be event of prime number. then,
$$A=\left\{13,23,31,41,43\right\}$$
$$\therefore, P(A)=\frac{5}{16}$$


Two digit numbers are formed from the digits $$0, 1, 2, 3, 4$$ where digits are not repeated. Find the probability of the events that
(1) the number formed is an even number.
(2) the number formed is prime number.

Two-digit numbers are formed from the digits $$0, 1, 2, 3, 4$$ without repeating the digits.
$$\therefore$$ Sample space $$S = \{10, 12, 13, 14, 20, 21, 23, 24, 31, 32, 34, 40, 41, 42, 43\}$$
$$\therefore n(S) = 16$$
(1) Let $$A$$ be the event of getting an even number.
$$A = \{10, 12, 14, 20, 24, 30, 32, 34, 40, 42\}$$
$$\therefore n (A) = 10$$
Probability, $$P (A) = \dfrac{n(A)}{n(S)} = \dfrac{10}{16} = \dfrac{5}{8}$$
(2) Let $$B$$ the event of getting a prime number.
$$B = \{13, 23, 31, 41, 43\}$$
$$\therefore n(B) = 5$$
Probability, $$P(B) = \dfrac{n(B)}{n(S)} = \dfrac{5}{16}$$


A bag contains $$5$$ white balls, $$6$$ red balls and $$9$$ green balls. A ball is drawn at random from the bag. Find the probability that the ball drawn is :
(i) a green ball.
(ii) a white or a red ball.
(iii) is neither a green ball nor a white ball.

$$\dfrac { White }{ 5 }$$               $$ \dfrac { Red }{ 6 }$$                $$ \dfrac { Green }{ 9 }$$
Total number of balls $$ =5+6+9$$
                                  $$ =20$$
(i) Probability $$=\dfrac { favourable\  cases }{ Total\  cases }$$
    P(Green) $$ =\dfrac { 9 }{ 20 }$$
(ii)  P(White or red) $$=\dfrac { 5+6 }{ 20 }$$
                               $$ =\dfrac { 11 }{ 20 }$$
(iii) P(neither green nor white) $$=$$ P(Red)
                                                $$=\dfrac { 6 }{ 20 }$$
                                                $$ =\dfrac { 3 }{ 10 } $$


A box contains $$20$$ cards marked with numbers $$1$$ to $$20$$. One card is drwan from the box at random. What is the probability of the following events:
$$(1)$$ That number on the card is a prime number,
$$(2)$$ The number on the card is a perfect square.

A box contains $$20$$ cards.

$$S=\left\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20\right\}$$

$$\therefore n(S)=20$$

$$(1)$$  Let $$A$$ be the event that the number is a prime number.

         $$A=\left\{2, 3, 5, 7, 11, 13, 17, 19\right\}$$
         $$\therefore n(A)=8$$
         $$\therefore P(A)=\displaystyle\frac{n(A)}{n(S)}=\frac{8}{20}=\frac{2}{5}$$.

$$(2)$$ Let $$B$$ be the event that the number is a perfect square.
            
            $$B=\left\{1, 4, 9, 16\right\}$$
           $$\therefore n(B)=4$$
           $$\therefore P(B)=\displaystyle\frac{n(B)}{n(S)}=\frac{4}{20}=\frac{1}{5}$$.


One card is drawn from well shuffled deck of 52 cards. Find the probability of getting:
(i) A king of red colour,
(ii) A face card,
(iii) The jack of hearts,
(iv) A red face card,
(v) A spade,
(vi) The queen of diamonds.

Given that, one card is drawn from a well shuffled deck of $$52$$ cards.
To find out: The probability of getting:
                (i) A king of red colour,
               (ii) A face card,
              (iii) The jack of hearts,
              (iv) A red face card,
               (v) A spade,
              (vi) The queen of diamonds.

We know that,
The probability of an event $$E, P(E)=\dfrac{\text{Number of favourable outcomes}}{\text{Total number of outcomes}}=\dfrac{n(E)}{n(S)}$$

Applying the concept of probability as shown above, let's calculate all the probabilities one by one.

$$(i)$$ Probability of getting a king of red colour:
We know that, there are $$26$$ red cards, $$13$$ each of hearts and diamonds. Hence, there will be $$1$$ king each in hearts and diamonds.
$$\therefore \ $$ Number of kings of red colour, $$n(E)=2$$
Also, total number of cards, $$n(S)=52$$

$$\therefore \ $$ Probability of getting a king of red colour $$=\dfrac{n(E)}{n(S)}=\dfrac{2}{52}$$
$$\Rightarrow \dfrac{1}{26}$$
Hence, the required probability is $$\dfrac{1}{26}$$.

$$(ii)$$ Probability of getting a face card:
We know that, each suit has $$3$$ face cards (Jack, Queen and King). Hence, there will be $$12$$ face cards in total.
$$\therefore \ $$ Number of face cards, $$n(E)=12$$
Also, total number of cards, $$n(S)=52$$

$$\therefore \ $$ Probability of getting a face card $$=\dfrac{n(E)}{n(S)}=\dfrac{12}{52}$$
$$\Rightarrow \dfrac{3}{13}$$
Hence, the required probability is $$\dfrac{3}{13}$$.

$$(iii)$$ Probability of getting the jack of hearts:
We know that, there is only one jack in hearts.
$$\therefore \ $$ Number of jack of hearts, $$n(E)=1$$
Also, total number of cards, $$n(S)=52$$

$$\therefore \ $$ Probability of getting the jack of hearts $$=\dfrac{n(E)}{n(S)}=\dfrac{1}{52}$$
Hence, the required probability is $$\dfrac{1}{52}$$.

$$(iv)$$ Probability of getting a red face card:
We know that, there are $$26$$ red cards, $$13$$ each of hearts and diamonds. Both hearts and diamonds have $$3$$ face cards each.
$$\therefore \ $$ Number of red face cards, $$n(E)=6$$
Also, total number of cards, $$n(S)=52$$

$$\therefore \ $$ Probability of getting a red face card $$=\dfrac{n(E)}{n(S)}=\dfrac{6}{52}$$
$$\Rightarrow \dfrac{3}{26}$$
Hence, the required probability is $$\dfrac{3}{26}$$.

$$(v)$$ Probability of getting a spade:
We know that, there are $$13$$ cards of spades.
$$\therefore \ $$ Number of spades, $$n(E)=13$$
Also, total number of cards, $$n(S)=52$$

$$\therefore \ $$ Probability of getting a spade $$=\dfrac{n(E)}{n(S)}=\dfrac{13}{52}$$
$$\Rightarrow \dfrac{1}{4}$$
Hence, the required probability is $$\dfrac{1}{4}$$.

$$(vi)$$ Probability of getting the queen of diamonds:
We know that, there are $$13$$ cards of diamonds. There is $$1$$ queen of diamonds.
$$\therefore \ $$ Number of queens in diamonds, $$n(E)=1$$
Also, total number of cards, $$n(S)=52$$

$$\therefore \ $$ Probability of getting the queen of diamonds $$=\dfrac{n(E)}{n(S)}=\dfrac{1}{52}$$
Hence, the required probability is $$\dfrac{1}{52}$$.


In a survey conducted among $$400$$ students of $$X$$ standard in Pune district, $$187$$ students offered to join Science faculty after $$X$$ standard and $$125$$ students offered to join Commerce faculty after $$X$$. If a student is selected at random from this group, find the probability that the student prefers Science or Commerce faculty.

Total number of students $$= 40$$
$$\therefore n(S) = 400$$
Let $$A$$ be the event of students joining science faculty.
$$n(A) = 187$$
$$\therefore P(A) = \dfrac {187}{400}$$
Let $$B$$ be the event of students joining commerce faculty.
$$n(B) = 125$$
$$\therefore P(B) = \dfrac {125}{400}$$
Probability that student prefers Science or Commerce faculty.
$$\therefore P(A\cup B) = P(A) + P(B)$$
$$= \dfrac {187}{400} + \dfrac {125}{400}$$
$$= \dfrac {312}{400} = \dfrac {39}{50}$$
Hence probability that student prefers Science or Commerce faculty is $$\dfrac {39}{50}$$.


A die is thrown, Find the probability of the following events:
(1) Getting prime numbers on the upper surface
(2) Getting a number which is less than $$7$$ on upper surface

A die is thrown 
$$(S)=\left\{ 1,2,3,4,5,6 \right\} $$
$$n(S)=6$$
(1) Let $$A$$ be in the event of getting a prime number
$$A=\left\{ 2,3,5 \right\} $$
$$n(A)=3$$
$$\therefore$$ $$P(A)=\cfrac{n(A)}{n(S)}$$
$$=\cfrac{3}{6}$$
$$=\cfrac{1}{2}$$
(2) Let $$B$$ be an event of getting a number less than $$7$$
$$B=\left\{ 1,2,3,4,5,6 \right\} $$
$$\therefore$$ $$n(B)=6$$
$$\therefore$$ $$P(B)=\cfrac{n(B)}{n(S)}$$
$$=\cfrac{6}{6}=1$$
$$\therefore$$ $$P(A)=\cfrac{1}{2},P(B)=1$$


Two dice are thrown simultaneously. Find the probability of getting
(a) same number on both faces and 
(b) both faces having multiples of five.

Given, two dice are thrown simultaneously.
Let $$S$$ denote the sample space i.e. the set of all possible outcomes.
$$\therefore$$ $$S=\{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),$$
            $$(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),$$$$(3,6),(4,1),(4,2),(4,3),(4,4),$$
            $$(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),$$
            $$(6,4),(6,5),(6,6)\}$$
No. of elements in $$S=n(S)=36$$
(a) Let $$A$$ be an event of getting same number on both faces.
     $$\therefore$$  $$A=\{(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)\}$$
     $$\therefore$$  $$n(A)=6$$
     We know that  $$P(A)=\dfrac {n(A)}{n(S)}$$
     $$\therefore$$  $$P(A)=\dfrac{6}{36}$$
     $$\therefore$$  $$P(A)=\dfrac{1}{6}$$
(b) Let $$B$$ be an event of getting both faces having multiples of five.
     $$\therefore$$  $$B=\{(5,5)\}$$
     $$\therefore$$  $$n(B)=1$$
     We know  $$P(B)=\dfrac{n(B)}{n(S)}$$
     $$\therefore$$  $$P(B)=\dfrac{1}{36}$$


Define empirical probability

It is the ratio of the no. of outcomes in which a specified event occurs to the total no. of trials,not in a therotical sample space.


A pair of dice is thrown. What is the probability of getting an even number on the first die or a total of $$8$$?

The total number of possible outcomes is $$36$$.
i.e., $$n(S)=36$$
Let $$A$$: Event of getting an even number on the first die 
For this condition, the first die can show $$1$$ out of $$3$$ even numbers and the second die can show any number among the $$6$$ possible outcomes.
$$n(A)=3\times6=18$$

$$B$$=Event of getting the sum as $$8$$
Possible outcomes are=$$\left\{(2,6),(6,2),(3,5),(5,3),(4,4)\right\}$$
$$n(B)=5$$

And, $$(A\cap B)=$$$$\left\{(2,6),(6,2),(4,4)\right\}$$
$$n(A\cap B)=3$$

$$\therefore$$ Required probability
$$=\cfrac{n(A\ or\  B)}{n(S)}$$ $$=\cfrac{n(A)+n(B)-n(A\cap B)}{n(S)}=\cfrac{20}{36}=\dfrac{5}{9}$$


Cards numbered from $$11$$ to $$60$$ are kept in a box. If a card is drawn at random from the box, find the probability that the number on the drawn card is
(i) an odd number  (ii) a perfect square number  (iii) divisible by $$5$$   (iv) a prime number less than $$20$$

Solution(i):

Let $$E$$ be the event of drawing a number from the cards numbered from $$11$$ to $$60$$

Odd numbers from $$11$$ to $$60 = 11,13,15,.....,89$$
No. of favorable outcomes$$ = 25$$
Total no. of possible outcomes $$= 50$$

We know that, Probability $$P(E)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$=\dfrac{25}{50}$$$$=\dfrac{1}{2}$$

Therefore, the probability of an odd number from the cards numbered $$11$$ to $$60$$$$=\dfrac{1}{2}$$

Solution(ii):

Let $$F$$ be the event of drawing a perfect square number from the cards numbered from $$11$$ to $$60$$

Perfect square numbers from $$11$$ to $$60 = 16,25,36,49$$
No. of favorable outcomes$$ = 4$$
Total no. of possible outcomes $$= 50$$

We know that, Probability $$P(F)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$=\dfrac{4}{50}$$$$=\dfrac{2}{25}$$

Therefore, the probability of drawing a perfect square number from the cards numbered from $$11$$ to $$60$$$$=\dfrac{2}{25}$$

Solution(iii):

Let $$G$$ be the event of drawing a number divisible by $$5$$ from the cards numbered from $$11$$ to $$60$$

Numbers divisible by $$5$$ from $$11$$ to $$60 = 15,20,25,30,35,40,45,50,55,60$$
No. of favorable outcomes$$ = 10$$
Total no. of possible outcomes $$= 50$$

We know that, Probability $$P(G)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$=\dfrac{10}{50}$$$$=\dfrac{1}{5}$$

Therefore, the probability of drawing a number divisible by $$5$$ from the cards numbered from $$11$$ to $$60$$$$=\dfrac{1}{5}$$

Solution(iv):

Let $$H$$ be the event of drawing a prime number less than $$20$$ from the cards numbered from $$11$$ to $$60$$

Prime numbers less than $$20$$ from $$11$$ to $$60 = 11,13,17,19$$
No. of favorable outcomes$$ = 4$$
Total no. of possible outcomes $$= 50$$

We know that, Probability $$P(H)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$=\dfrac{4}{50}$$$$=\dfrac{2}{25}$$

Therefore, the probability of drawing a prime number less than $$20$$ from the cards numbered from $$11$$ to $$60$$$$=\dfrac{2}{25}$$


When a die is thrown, find the probability of the event of getting
a) A prime number.
b) A number greater than $$6$$.

a) A prime number:

Prime numbers on a die are $$2,3$$ and $$5$$
Number of favourable outcomes$$=3$$
total number of outcomes$$=6$$

$$\therefore$$ Probability of getting a prime number $$=\dfrac{3}{6}$$
                                                                   $$=\dfrac{1}{2}$$

Hence, the probability of getting a prime number is $$\dfrac{1}{2}$$.

b) A number greater than $$6$$:

Numbers on a die greater than $$6$$ $$=None$$
Number of favourable outcomes$$=0$$
total number of outcomes$$=6$$

$$\therefore$$ Probability of getting a number greater than $$6$$ $$=\dfrac{0}{6}$$
                                                                                 $$=0$$

Hence, probability of getting a number greater than $$6$$ is $$0$$.


A bag contains cards numbered from $$1$$ to $$49$$. A card is drawn from the bag at random, after mixing the card thoroughly. Find the probability that the number on the drawn card is
(i) an odd number  (ii) a multiple of $$5$$   (iii) a perfect square  (iv) an even prime number

Solution(i):

Let $$E$$ be the event of drawing an odd-numbered card from the cards numbered $$1$$ to $$49$$

Odd numbers from $$1$$ to $$49 = 1,3,5,.....,49$$
No. of favorable outcomes$$ = 25$$
Total no. of possible outcomes $$= 49$$

We know that, Probability $$P(E)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$=\dfrac{25}{49}$$

Therefore, the probability of an odd number card from the cards numbered $$1$$ to $$49$$$$=\dfrac{25}{49}$$

Solution(ii):

Let $$G$$ be the event of drawing a number - multiple of $$5$$ from the cards numbered from $$1$$ to $$49$$

Multiples of $$5$$ from $$1$$ to $$49 = 5,10,15,20,25,30,35,40,45$$
No. of favorable outcomes$$ = 9$$
Total no. of possible outcomes $$= 49$$

We know that, Probability $$P(G)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$=\dfrac{9}{49}$$

Therefore, the probability of drawing a multiple of $$5$$ from the cards numbered from $$1$$ to $$49$$$$=\dfrac{9}{49}$$

Solution(iii):

Let $$F$$ be the event of drawing a perfect square number from the cards numbered from $$1$$ to $$49$$

Perfect square numbers from $$1$$ to $$49 = 1,4,9,16,25,36,49$$
No. of favorable outcomes$$ = 7$$
Total no. of possible outcomes $$= 49$$

We know that, Probability $$P(F)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$=\dfrac{7}{49}$$$$=\dfrac{1}{7}$$

Therefore, the probability of drawing a perfect square number from the cards numbered from $$1$$ to $$49$$$$=\dfrac{1}{7}$$

Solution(iv):

Let $$H$$ be the event of drawing an even prime number from the cards numbered $$1$$ to $$49$$

Even prime number from $$1$$ to $$49 = 2$$ $$( 2$$ is the only even prime number $$)$$
No. of favorable outcomes$$ = 1$$
Total no. of possible outcomes $$= 49$$

We know that, Probability $$P(H)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$=\dfrac{1}{49}$$

Therefore, the probability of drawing an even prime number from the cards numbered $$1$$ to $$49$$$$=\dfrac{1}{49}$$


In a bag there are $$44$$ identical cards with figure of circle or square on them. There are $$24$$ circles, of which $$9$$ are blue and rest are green and $$20$$ squares of which $$11$$ are blue and rest are green. One card is drawn from the bag at random. Find the probability that it has the figure of (i) square  (ii) green colour  (iii) blue circle and  (iv) green square

No. of cards in the bag $$=44$$
No. of cards with circles $$=24$$
No. of cards with blue circles $$=9$$
No. of cards with green circles $$=24-9=15$$
No. of cards with squares $$=20$$
No. of cards with blue squares $$=11$$
No. of cards with green squares $$=9$$

Solution(i):
Let $$E$$ be the event of drawing a square card from the bag

We know that, Probability $$P(E)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$= \dfrac{20}{44}$$$$= \dfrac{5}{11}$$

Therefore, the Probability that the square card is drawn $$= \dfrac{5}{11}$$

Solution(ii):
Let $$E$$ be the event of drawing a green card from the bag

No. of green cards $$= 15+9=24$$

We know that, Probability $$P(E)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$= \dfrac{24}{44}$$$$= \dfrac{6}{11}$$

Therefore, the Probability that the green card is drawn $$= \dfrac{6}{11}$$

Solution(iii):
Let $$E$$ be the event of drawing a blue circle from the bag

We know that, Probability $$P(E)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$= \dfrac{9}{44}$$

Therefore, the Probability that the blue circle is drawn $$= \dfrac{9}{44}$$

Solution(iii):
Let $$E$$ be the event of drawing a green square from the bag

We know that, Probability $$P(E)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$= \dfrac{9}{44}$$

Therefore, the Probability that the green square is drawn $$= \dfrac{9}{44}$$


A bag contains tickets numbered $$11,12,13,..... 30$$. A ticket is taken out from the bag at random. Find the probability that the number on the drawn ticket (i) is a multiple of $$7$$ (ii) is greater than $$15$$ and a multiple of $$5$$.

Solution(i):

Let $$E$$ be event of getting a multiple of $$7$$ from the numbers $$11$$ to $$30$$

Multiples of $$7$$ from $$11$$ to $$30 = 14, 21, 28 $$
No. of favorable outcomes$$ = 3$$
Total no. of possible outcomes $$= 20$$
We know that, Probability $$P(E)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$ = \dfrac{3}{20}$$

Therefore, the probability that a number selected from the numbers $$11, 12,13,....,30$$ is a multiple of $$7$$  $$=\dfrac{3}{20}$$


Solution(i):

Let $$E$$ be event of getting a no. greater than $$15$$ and a multiple of $$5$$ from the numbers $$11$$ to $$30$$

Nos. greater than $$15$$ and multiple of $$5$$ from the numbers $$11$$ to $$ 30 \ (= 20, 25, 30) $$
No. of favorable outcomes$$ = 3$$
Total no. of possible outcomes $$= 20$$
We know that, Probability $$P(E)$$ $$= \dfrac{\text{(No.of favorable outcomes)}}{\text{(Total no.of possible outcomes)}}$$$$ = \dfrac{3}{20}$$

Therefore, the probability that a number selected from the numbers $$11, 12,13,....,30$$ is greater than $$15$$ and multiple of $$5$$ is $$\dfrac{3}{20}$$



Two different dice are tossed together. Find the probability:
(i) of getting a doublet
(ii) of getting a sum $$10$$, of the number on the two dice.

When two dice are tossed together,
Total possible outcomes  $$=6^2=36$$.

$$(i)\quad P(doublet)\ :$$
The favorable outcomes $$=\left\{(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)\right\}$$
Number of favorable outcomes  $$=6$$
$$\therefore$$  Probability of getting a doublet  $$=P(doublet)=\dfrac{6}{36}=\dfrac{1}{6}.$$

$$(ii)\quad P(sum=10)\ :$$
The favourable outcomes  $$=\left\{(4,6),(5,5),(6,4)\right\}$$
Number of favorable outcomes  $$=3$$
$$\therefore$$  Probability of getting a sum 10  $$=P(sum=10)=\dfrac{3}{36}=\dfrac{1}{12}.$$


An die is tossed twice. Find the probability of getting $$4,5$$ or $$6$$ on the toss and $$1,2,3$$ or $$4$$ on the second toss.

Total possible outcomes $$6$$

Favourable outcomes for first event $$4,5,6$$

Probability of first event $$\dfrac 36=\dfrac 12$$

Favourable outcomes for second event $$1,2,3,4$$

Probability of first event $$\dfrac 46=\dfrac 23$$

The events are independant 

So Required proabability is $$\dfrac 12\times \dfrac 23=\dfrac 13$$


A pair of die is thrown. Find the probability of getting the sum $$8$$ or more if $$4$$ appears on the second die. 

Second die always shows $$=4$$ 

So the favourable outcome for First die is $$4,5,6$$

The No. of possible outcomes is $$6$$ 

Probabity $$=\dfrac{3}{6}=\dfrac 12$$


A die is thrown 100 times and outcomes are noted as given below:
Outcome:123456
Frequency:21914231815
If a die is thrown at random, find the probability of getting a/an. 5




Given,

Total number of trials = 100

Number of times “5” comes up = 18

Probability of getting 3 = $$\dfrac{Frequency\: \:  of\: \:  getting\: \:  5}{Total\: \: numbers\: \: of\: \: trails}$$

= $$\dfrac{18}{100}$$

= $$0.18$$

So, If a die is thrown at random, probability of getting 5 is 0.18.


The percentage of marks obtained by a student in the monthly tests are given below :
Test$$I$$$$II$$$$III$$$$IV$$$$V$$
Percentage marks obtained $$69$$$$71$$$$73$$$$69$$$$74$$
Find the probability that a student gets more than $$70\%$$ marks.

Total no. of unit tests $$= 5$$
Number of tests in which the student scored more than $$70 \%$$ marks $$= 3$$
Therefore,
Probability that a student gets more than $$70 \%$$ marks $$= \cfrac{\text{No. of tests in which the student scored more than } 70 \% \text{ marks}}{\text{Total no. of tests}} \\ = \cfrac{3}{5} = 0.6$$



A die is thrown. Find the probability of getting an odd number.

Total number of outcomes $$6$$

No .of favourable outcomes $$3(1,3,5)$$

Probability $$=\dfrac36=\dfrac 12$$


A die is thrown, then find the probability of getting an odd number.

Total number of outcomes $$=6$$

No .of favourable outcomes $$=(1,3,5) \implies n=3$$

Probability $$=\dfrac36=\dfrac 12$$


A card is drawn at random from a pack of $$52$$ cards. Find the probability that the card drawn is a jack, a queen or a king.

We have,

Total card$$=52$$

And

The card drawn is a jack, a queen or a king$$=12$$

Then,

Probability $$=\dfrac{12}{52}=\dfrac{3}{13}$$

Hence, this is the answer.


A die is thrown. Find the probability of getting a prime number.

Total number of outcomes $$=6$$

No .of favourable outcomes $$(2,3,5)  \implies n=3.$$

Probability $$=\dfrac36=\dfrac 12$$


Check whether $$\dfrac {7}{6}$$ can be an empirical probability or not. Give reasons. 

Empirical probability cannot be greater then 1.

In an empirical probability the no. of favorable outcomes is always smaller then the total number of outcomes.

But, $$\dfrac 76=1.16$$

Here the probability is greater than $$1$$.

Hence, $$\dfrac 76$$ cannot be an empirical probability.


A coin is tossed 1000 times with the following frequencies:
Head: 445, Tail: 555
When a coin is tossed at random, what is the probability of getting a tail?

Given,
Total number of times a coin is tossed $$= 1000$$

Number of times a head comes up $$= 445$$

Probability of getting a head = $$\dfrac{Number\: \:  of \: \: tails}{Total\: \: number \: \: of \: \: tosses \, of \, coins}$$ 

$$=\dfrac{555}{1000}$$

$$=0.555$$

So, When a coin is tossed at random, probability of getting a tail is 0.555.


A box contains two pair of socks of two colors (black and white). I have picked out a white sock. I pick out one more with my eyes closed. What is the probability that I will make a pair?

We know that,
$$P(E)=\dfrac{n(E)}{n(S)}$$

where, $$P(E)$$ is the probability of an event $$E$$ 
$$n(E)$$ is the number of favorable outcomes and 
$$n(S)$$ is the total number of otcomes.

Let $$E$$ be the event of me drawing out a pair.
While closing the eye, one can draw either of the socks.

Here, $$n(E)=1$$ , as only one white sock is there
and $$n(S)=3$$, as only 3 socks are remaining in the box.

$$\therefore P(E)=\dfrac13$$


Two dice are thrown simultaneously. Find the probability of getting sum more than $$7$$


2173786_1285366_ans_5d356791bad24aefaebd198cc22d6bc9.jpg


Class 9 Maths Extra Questions