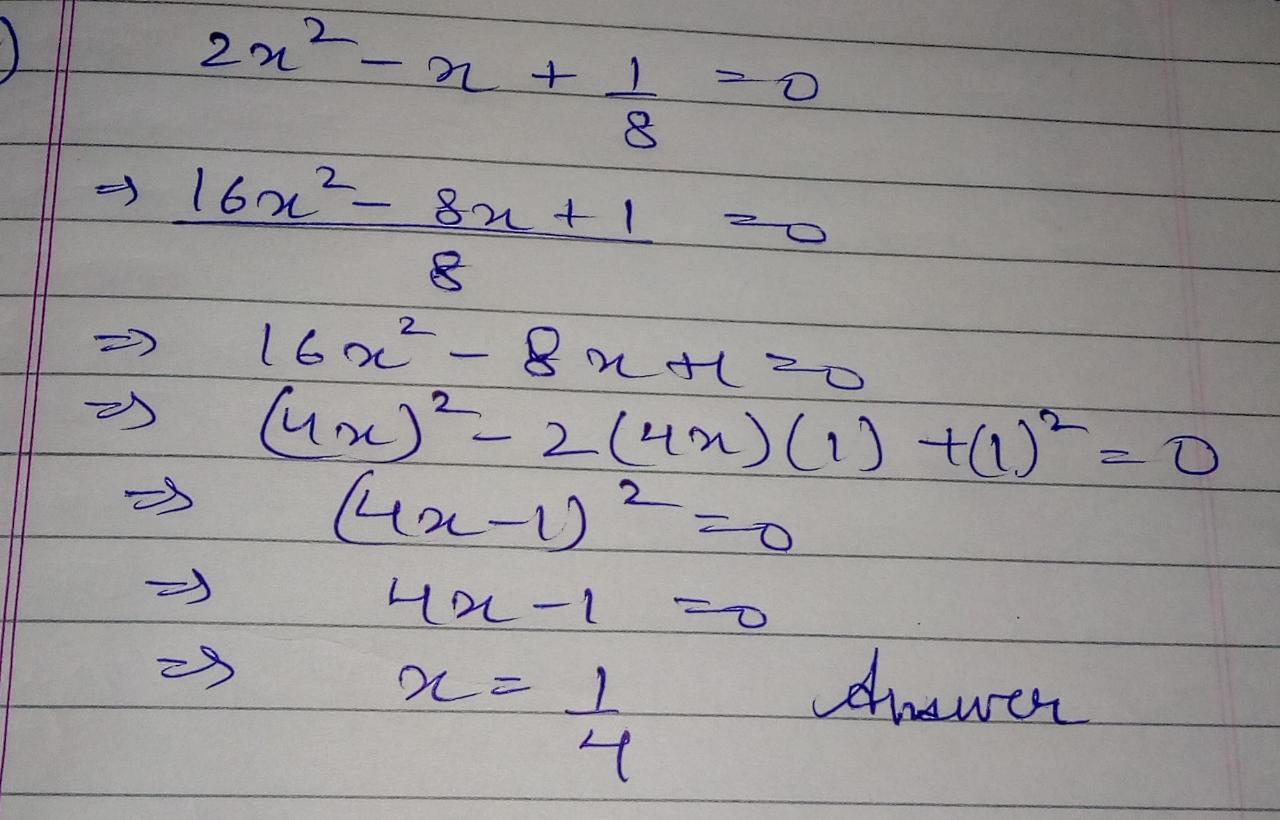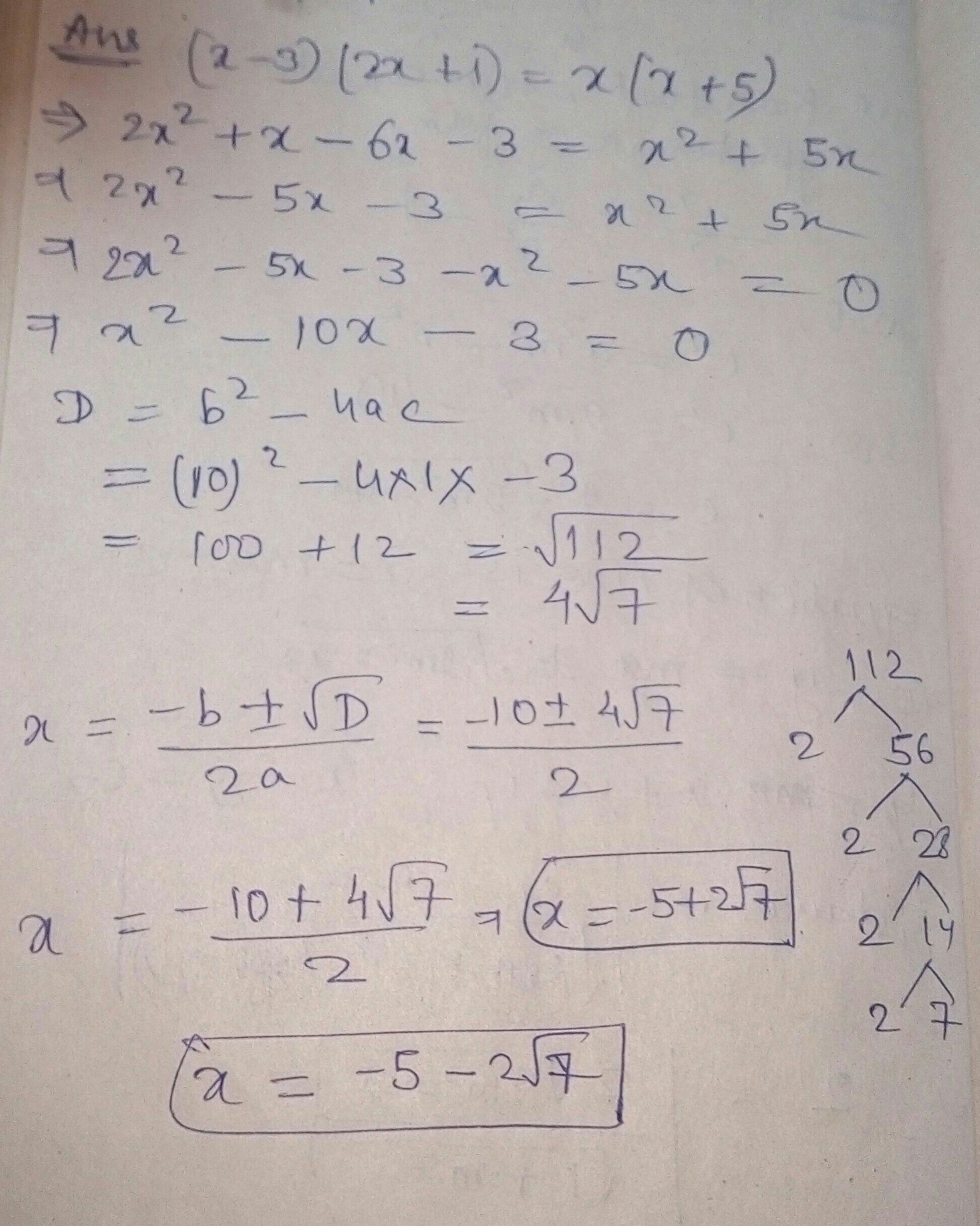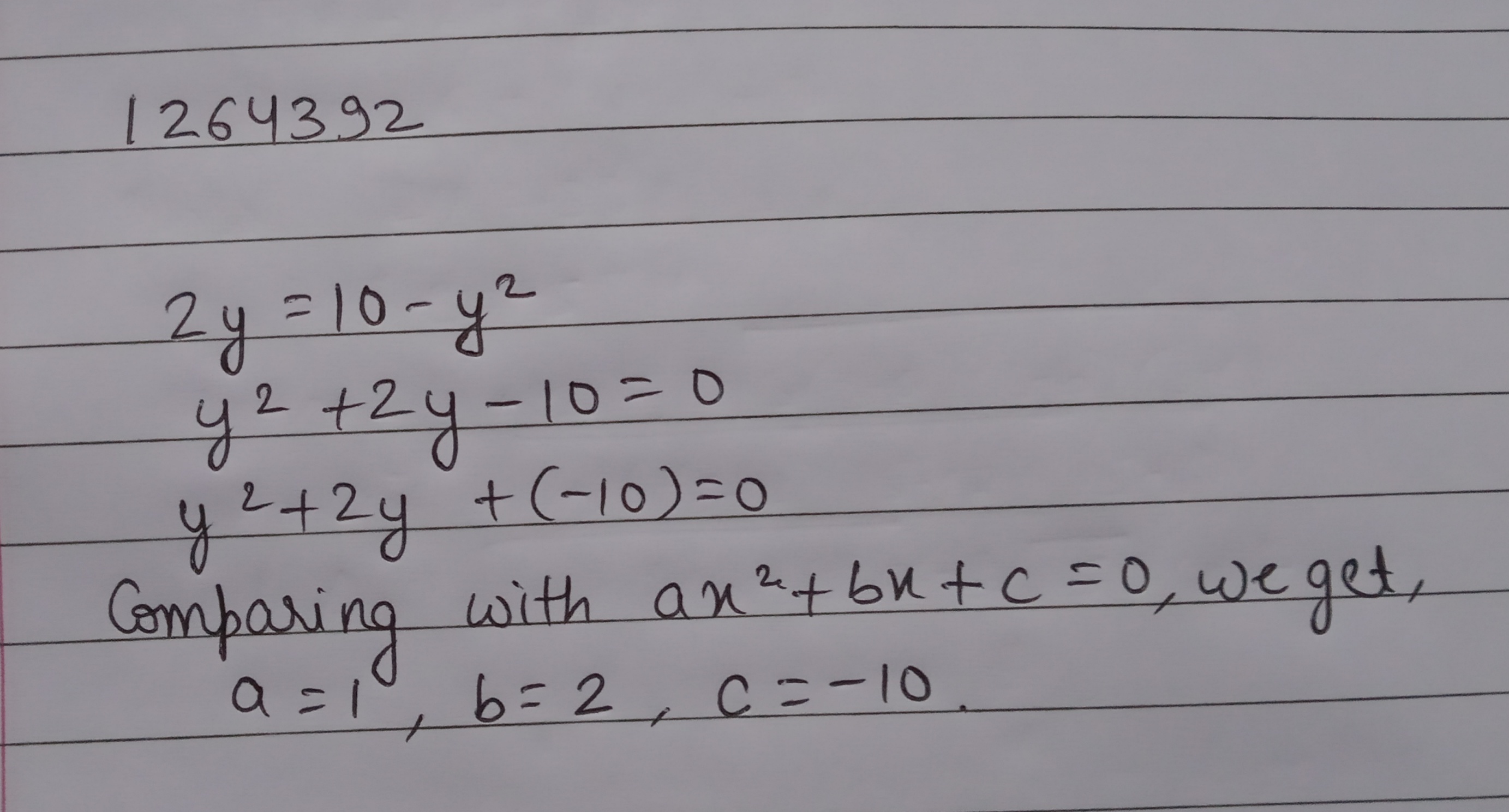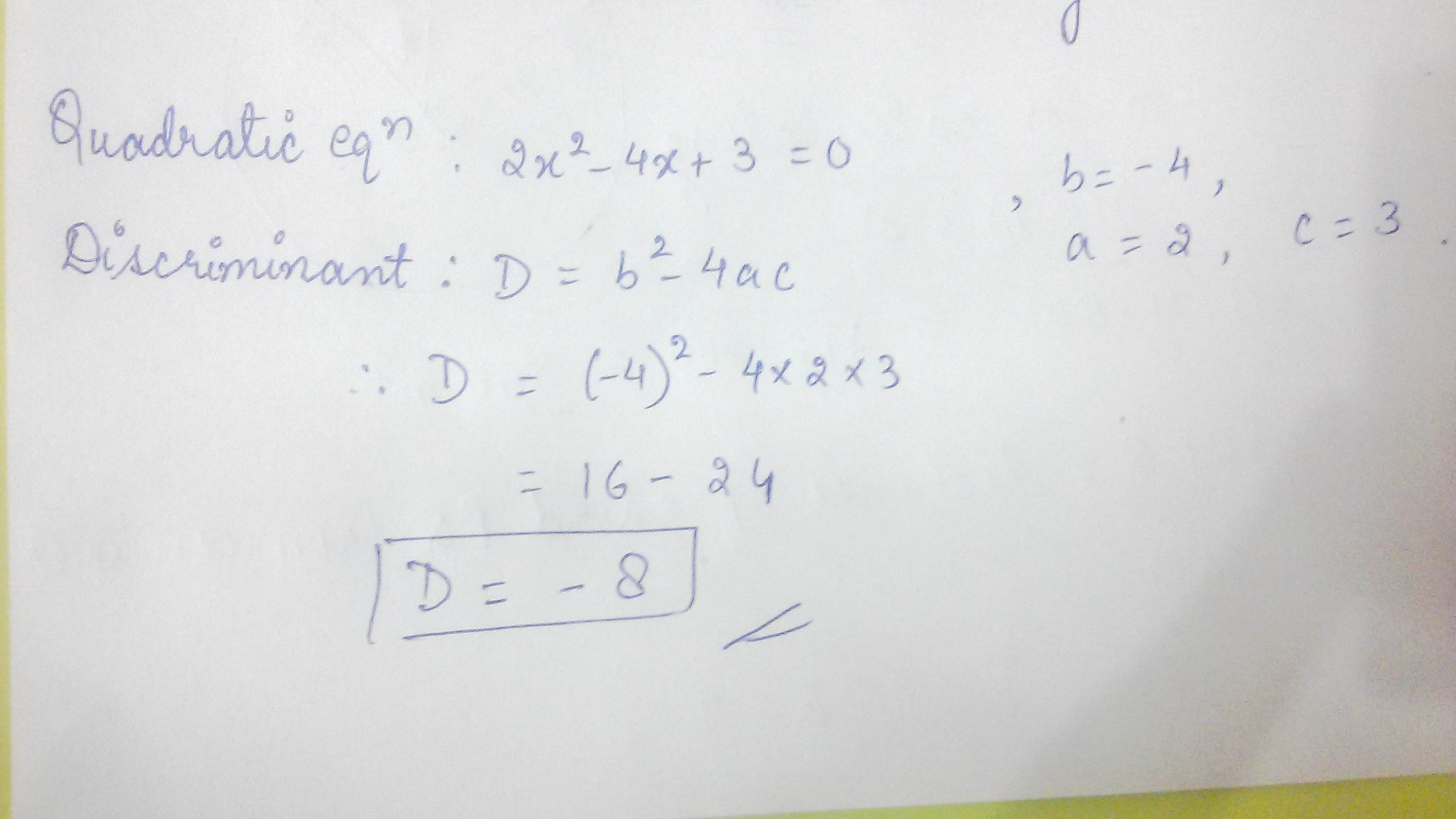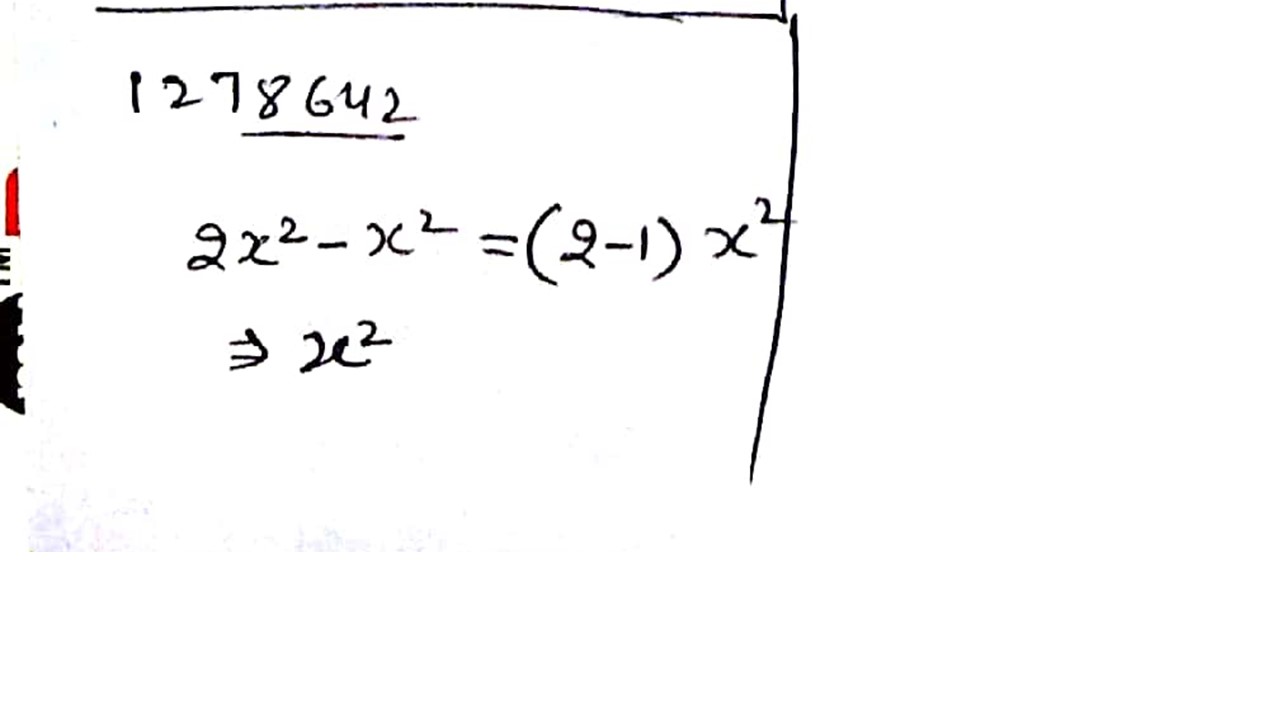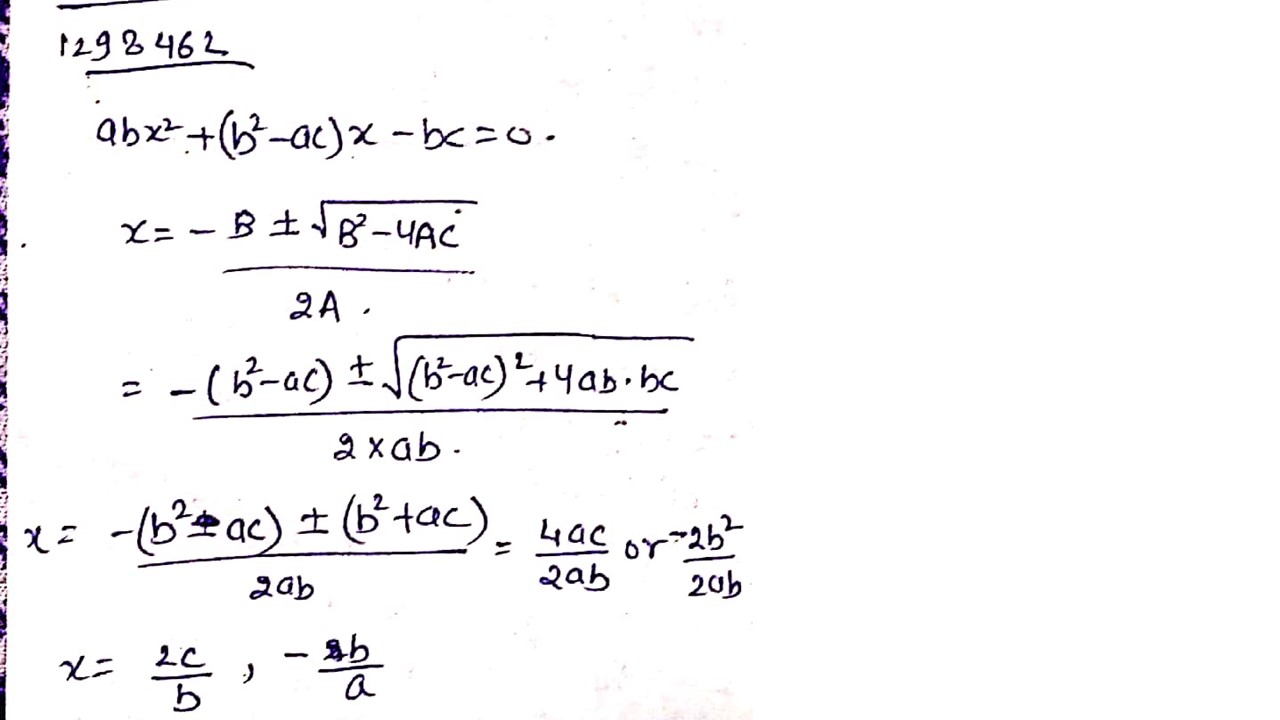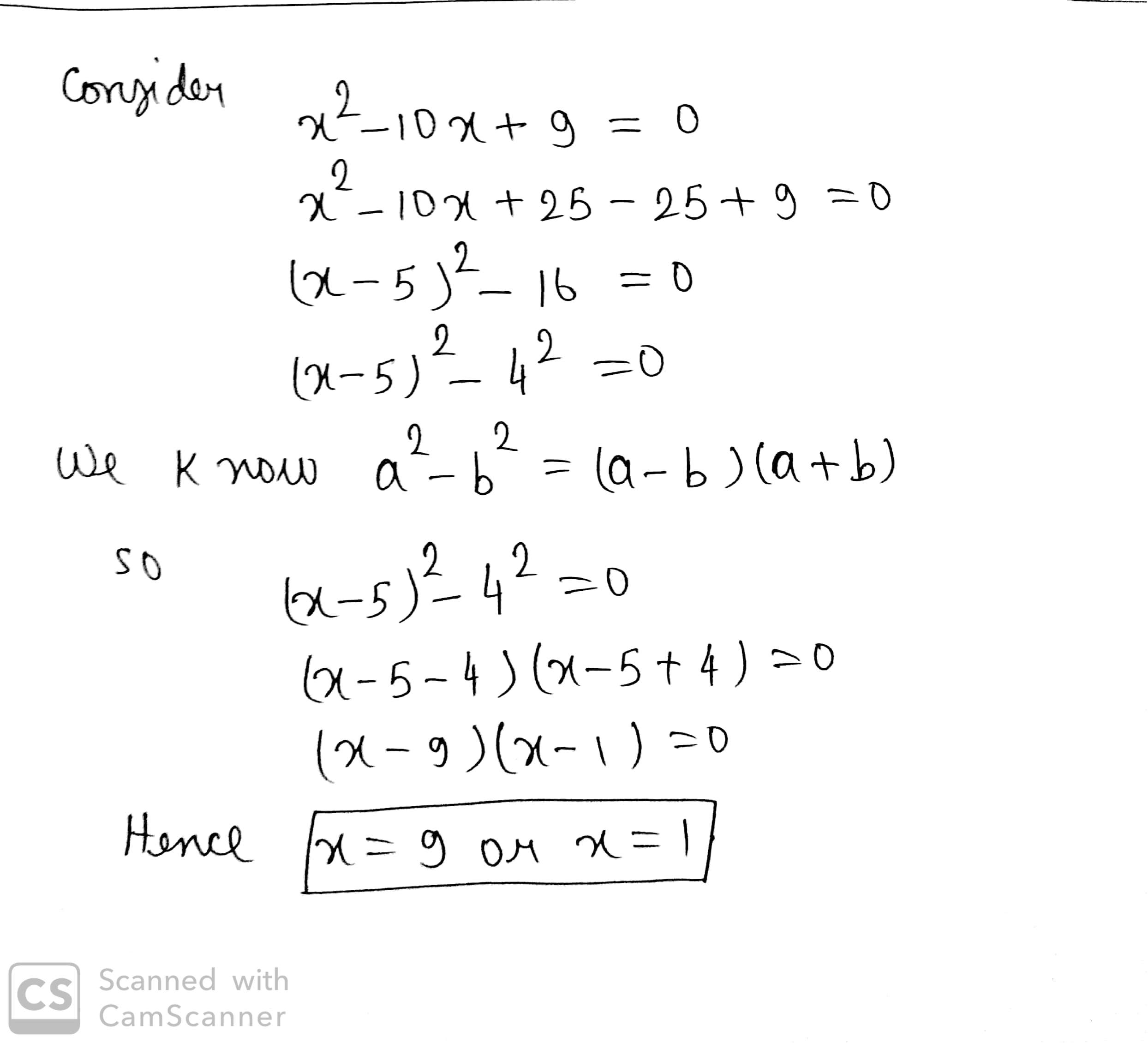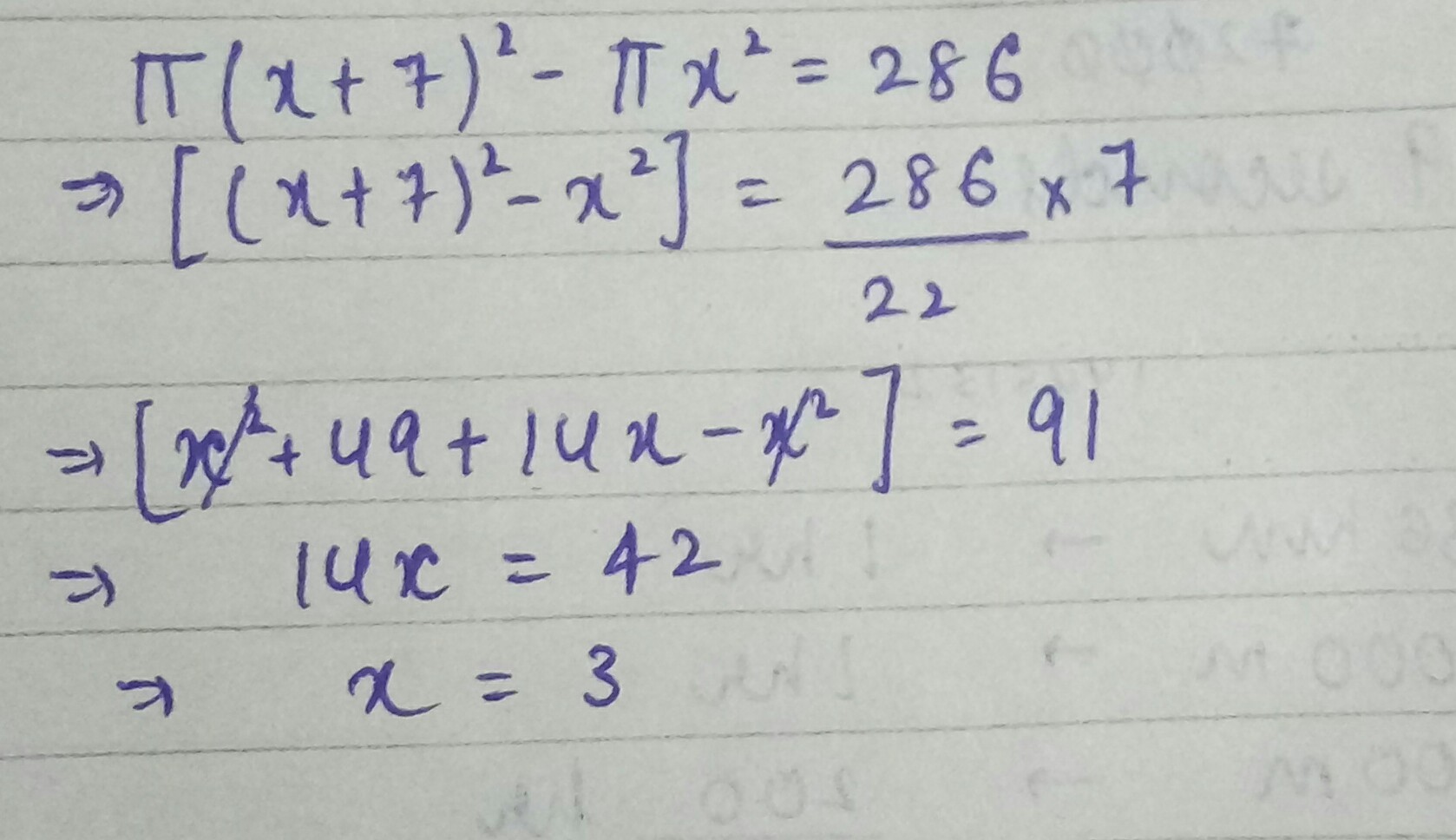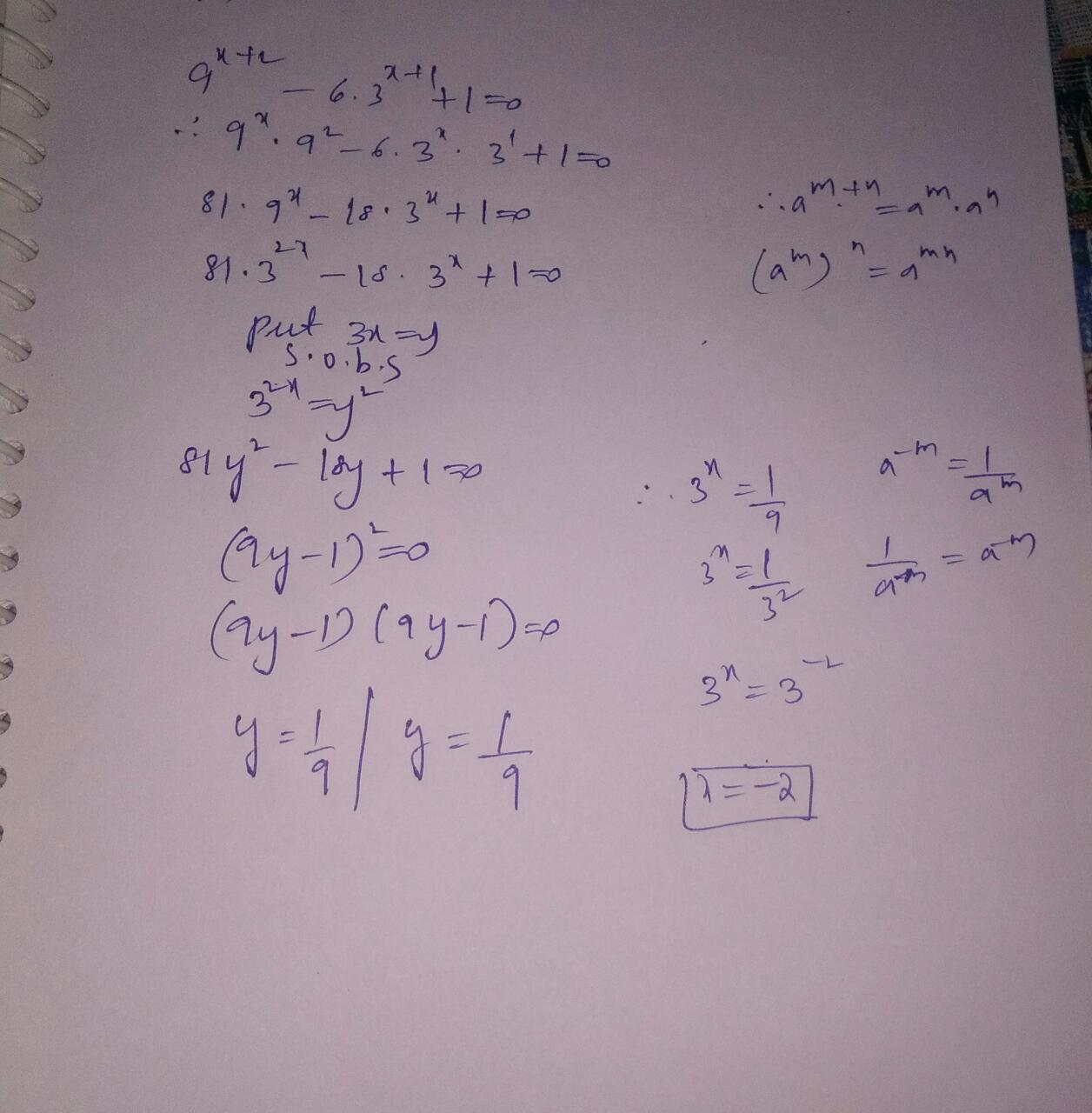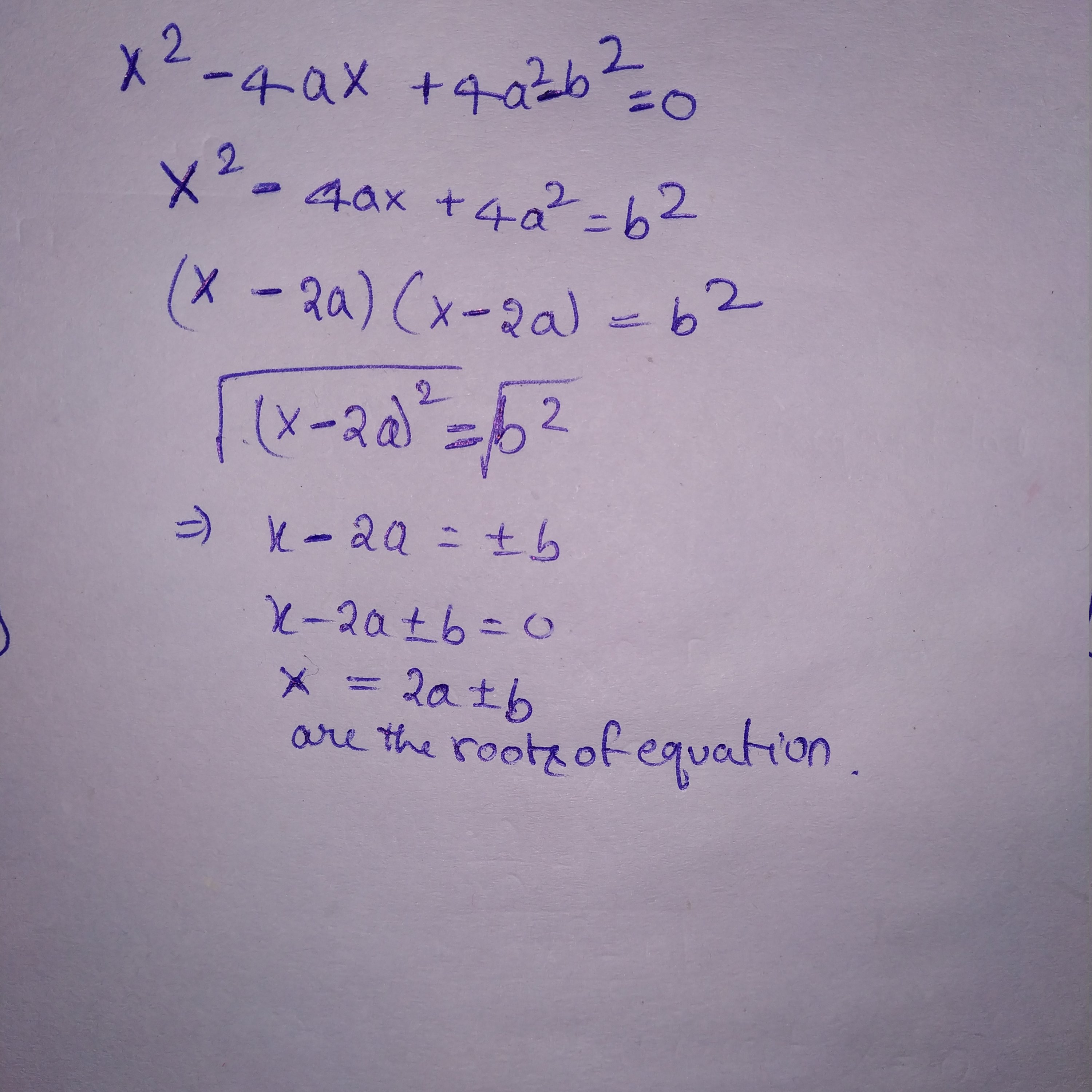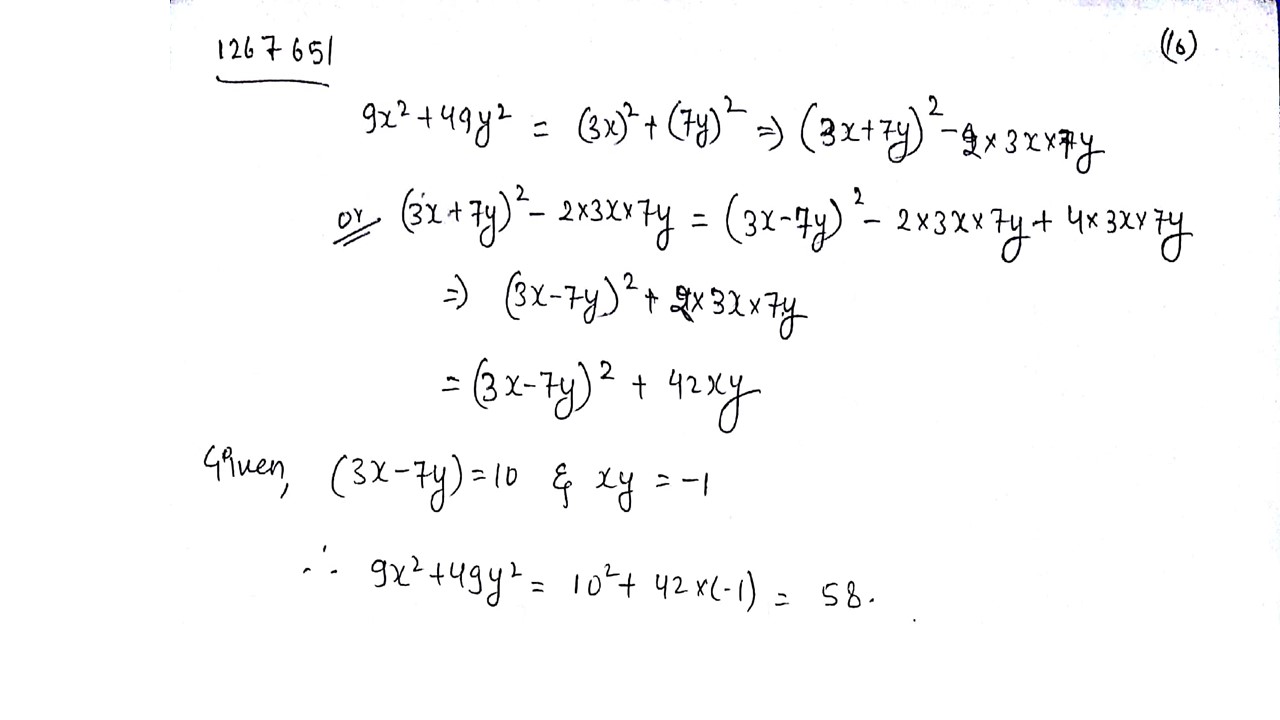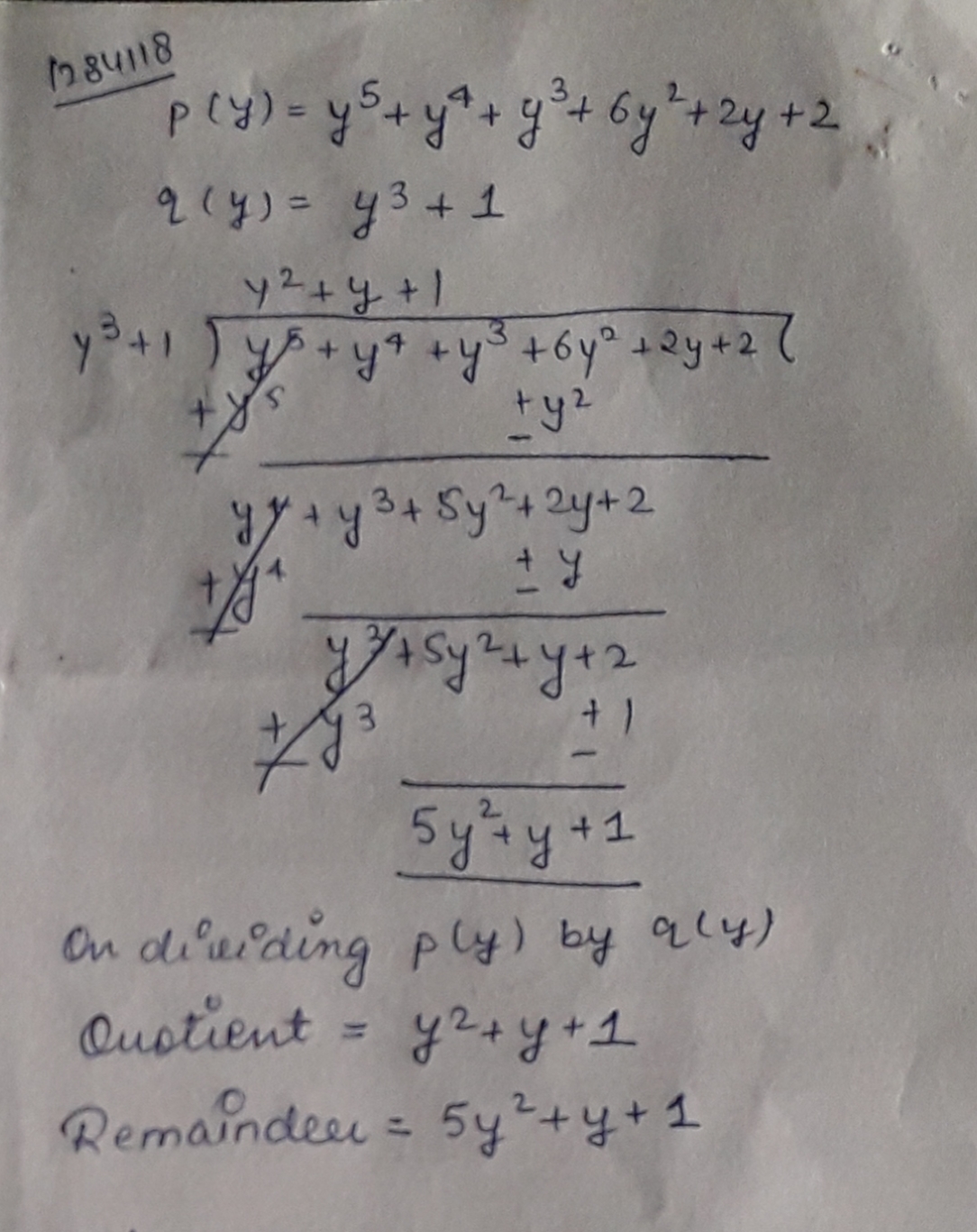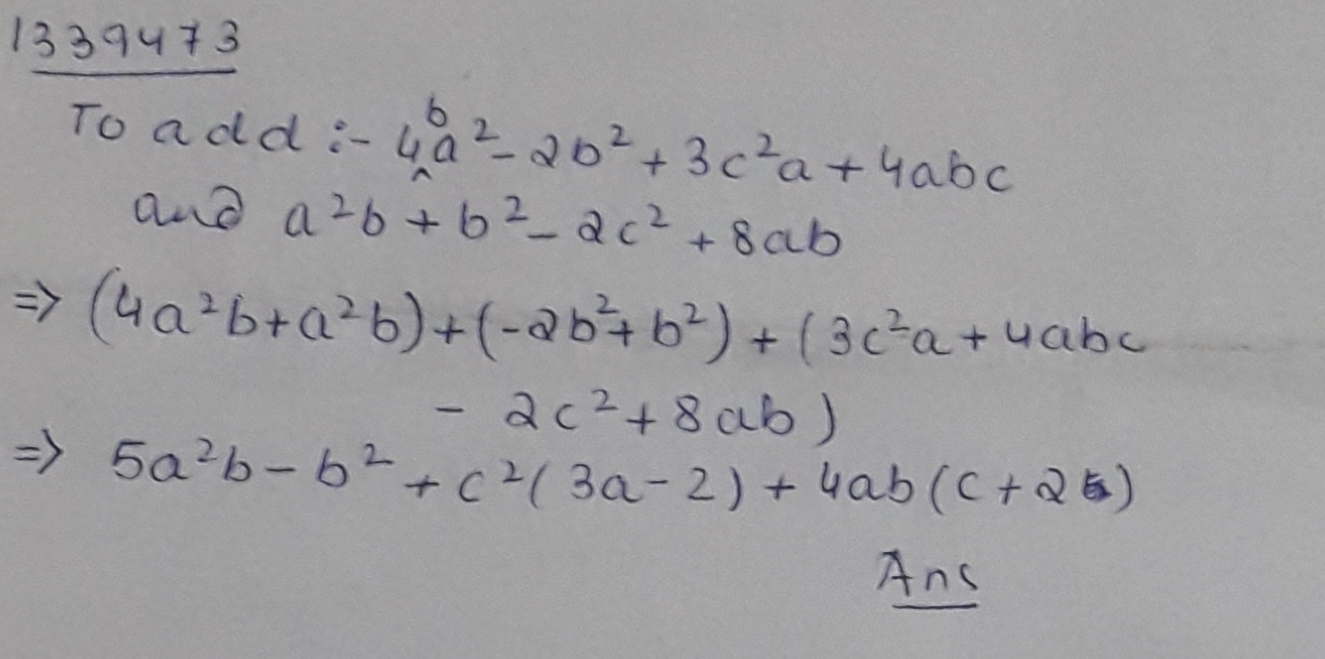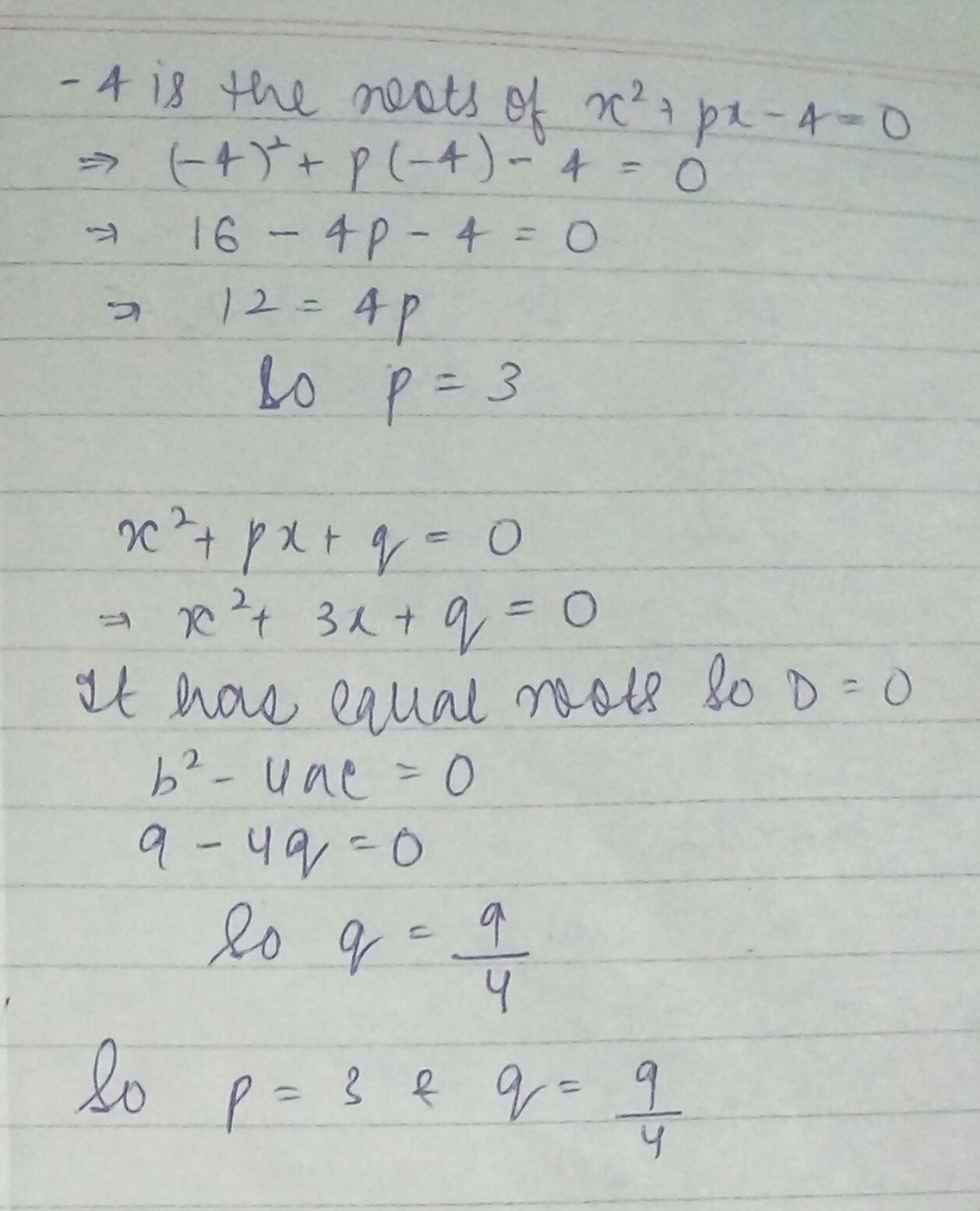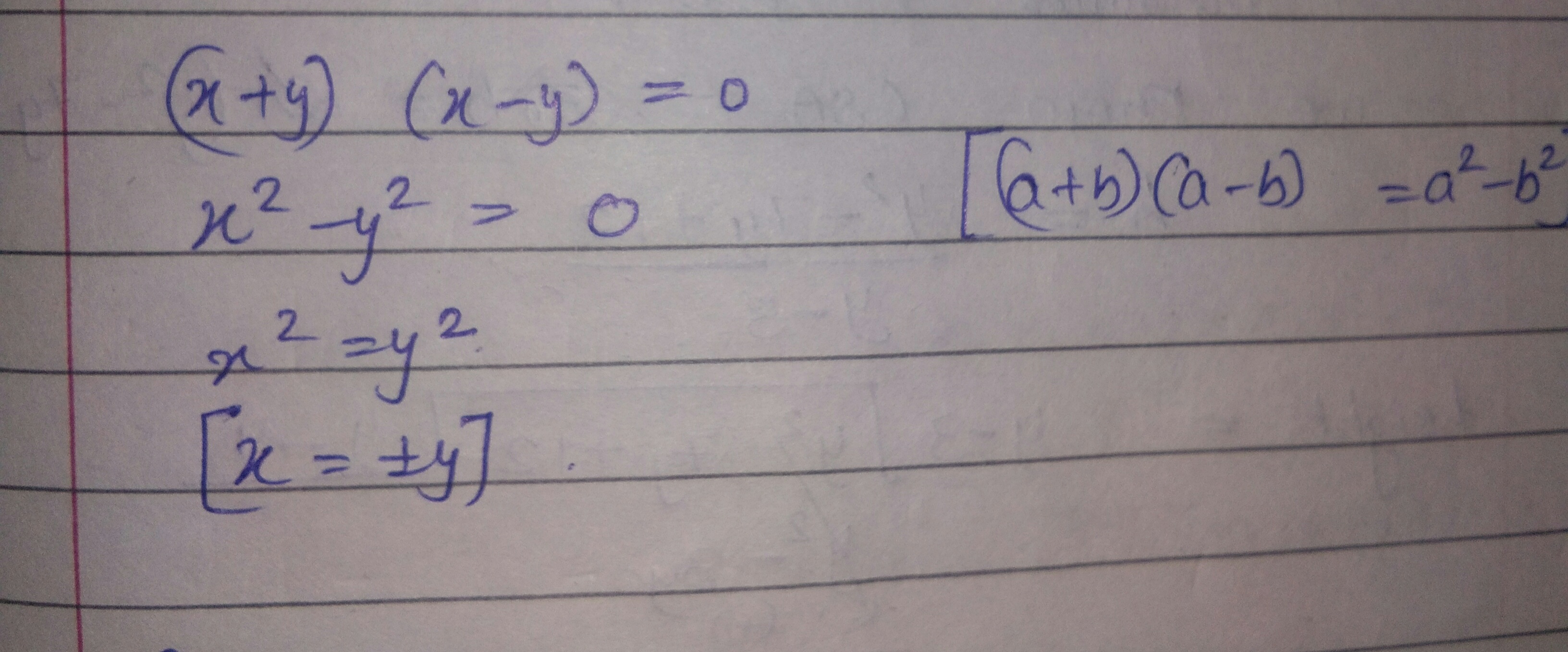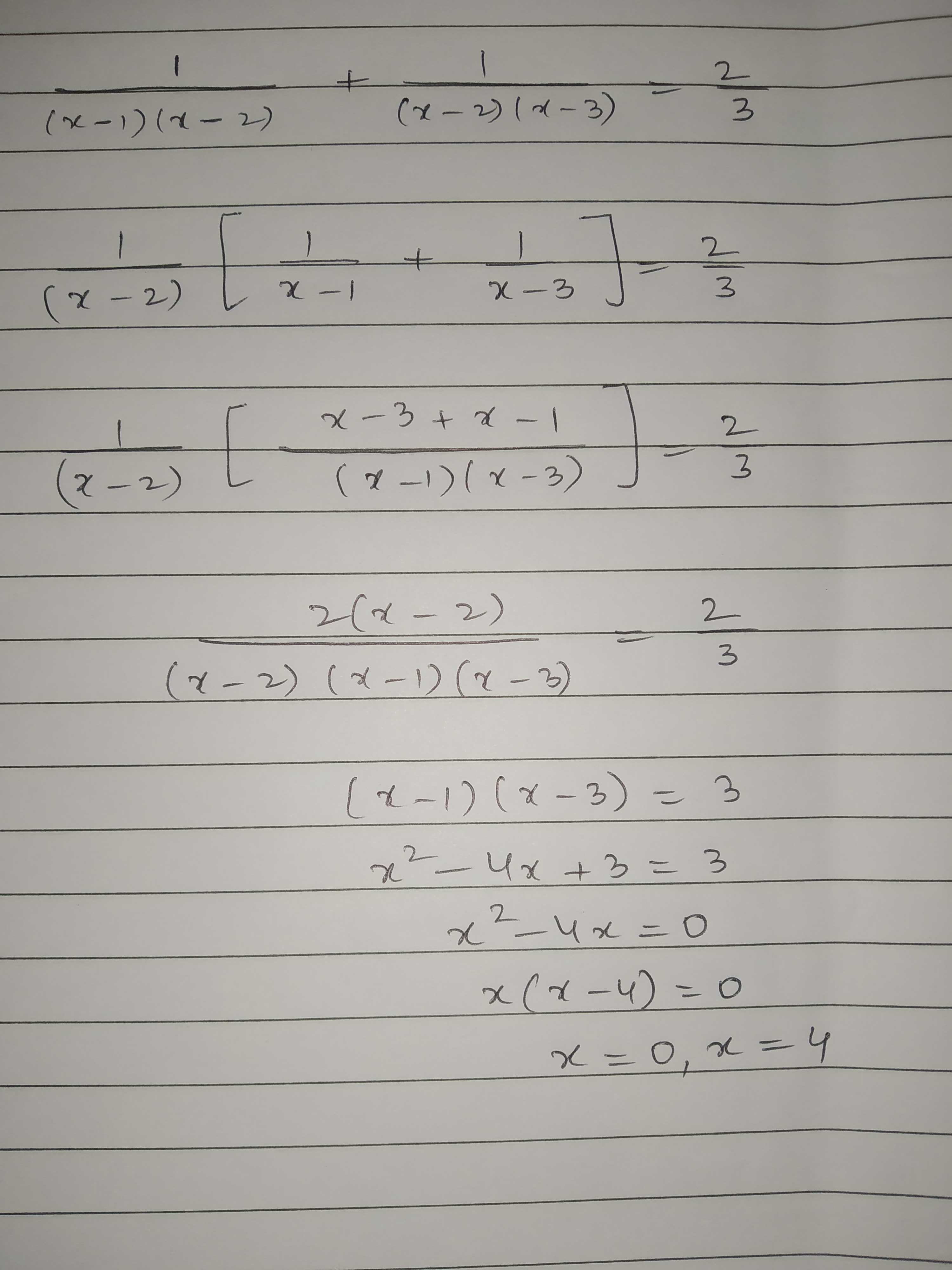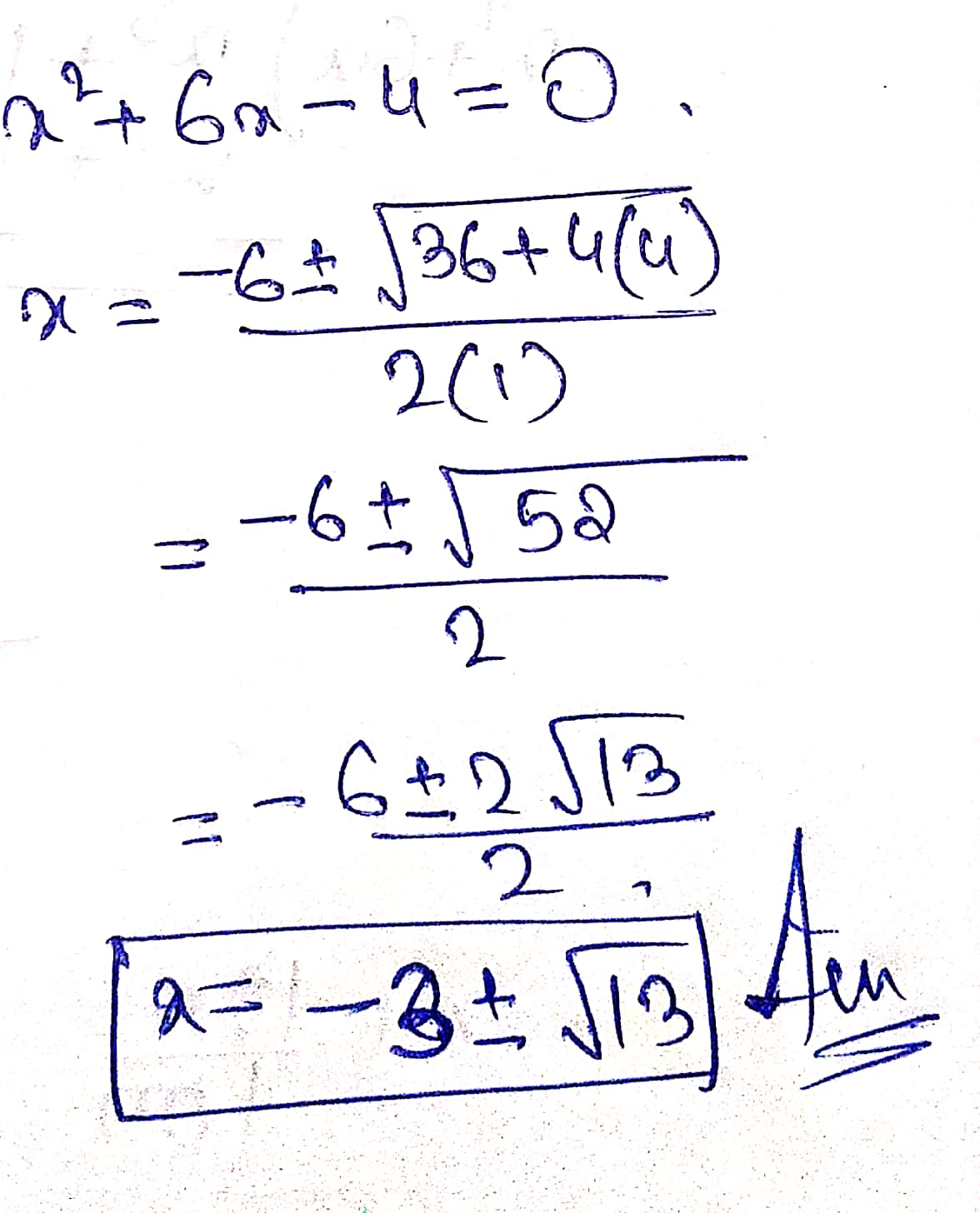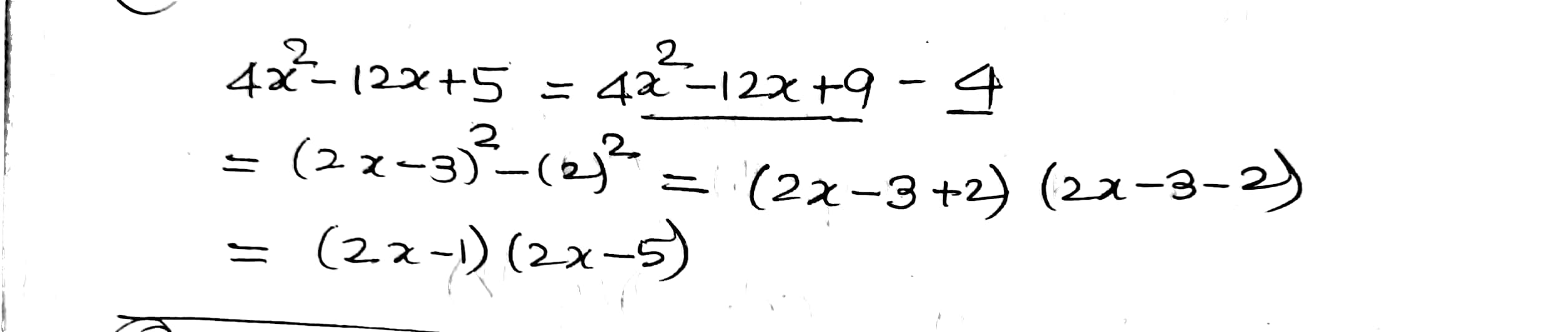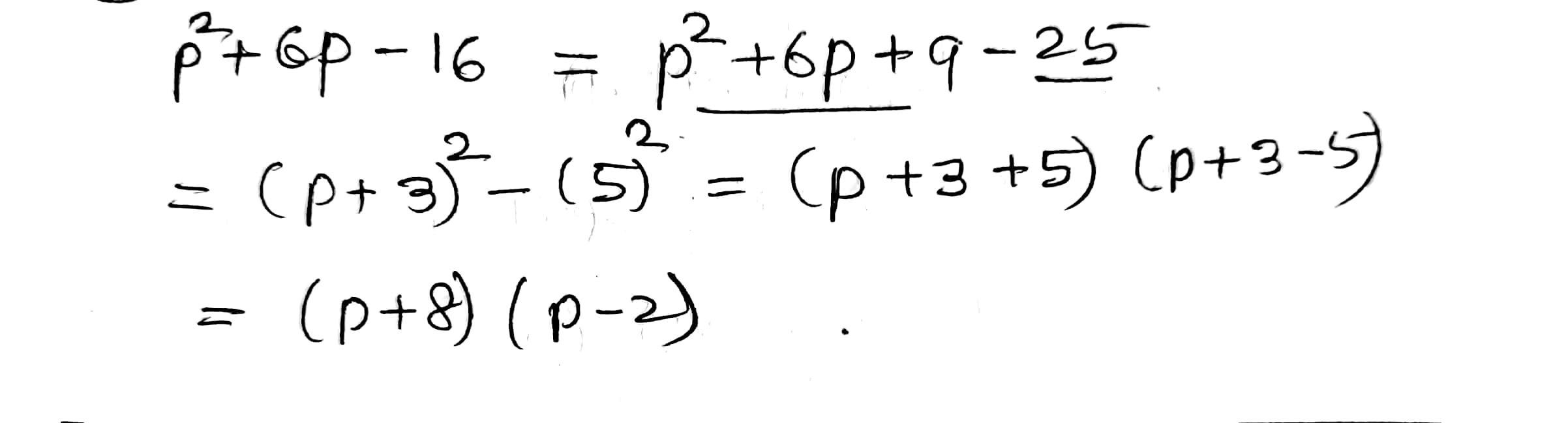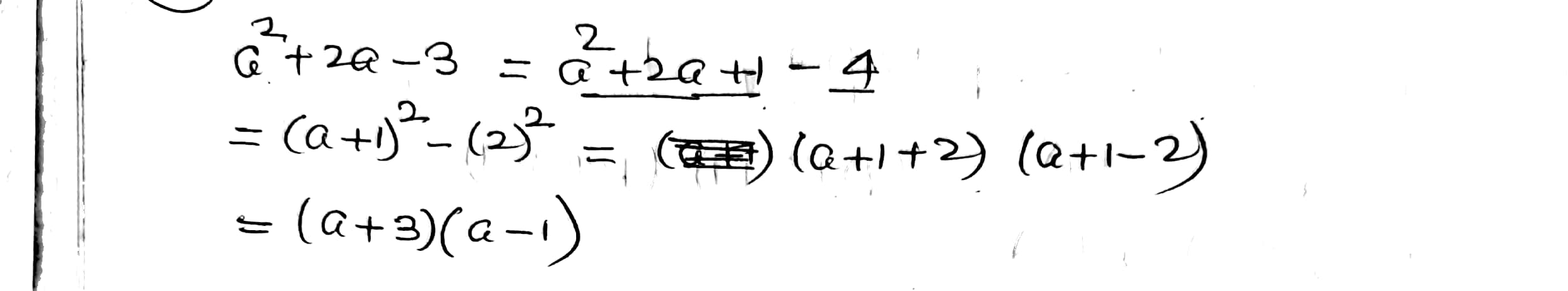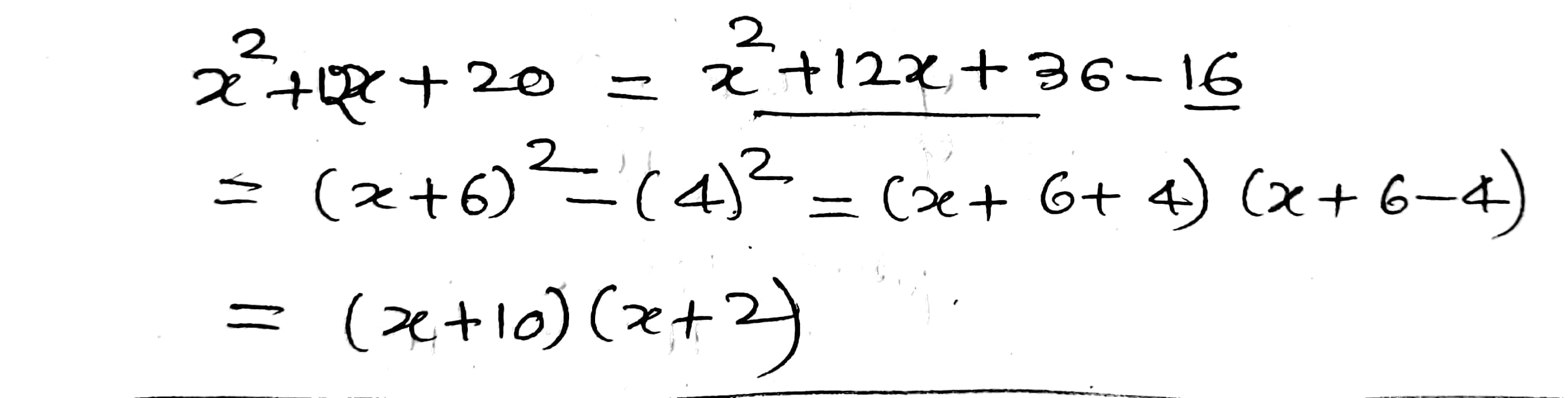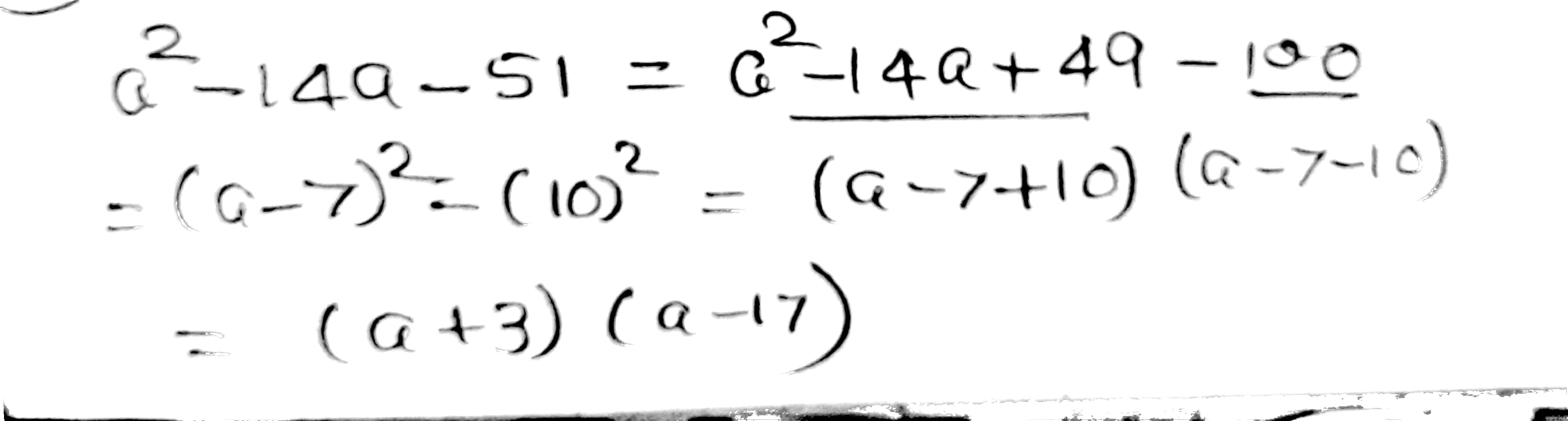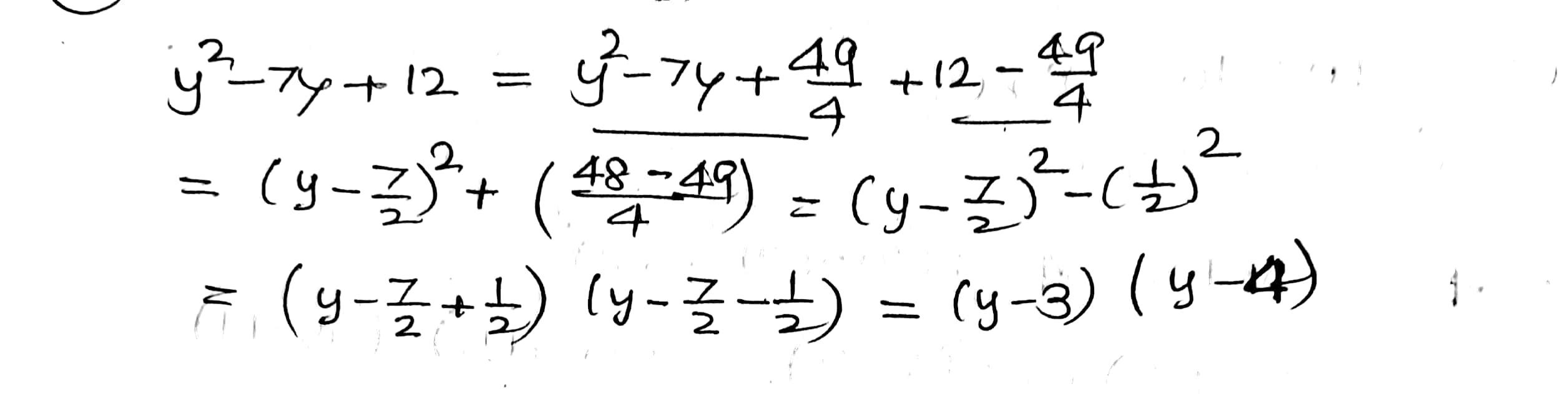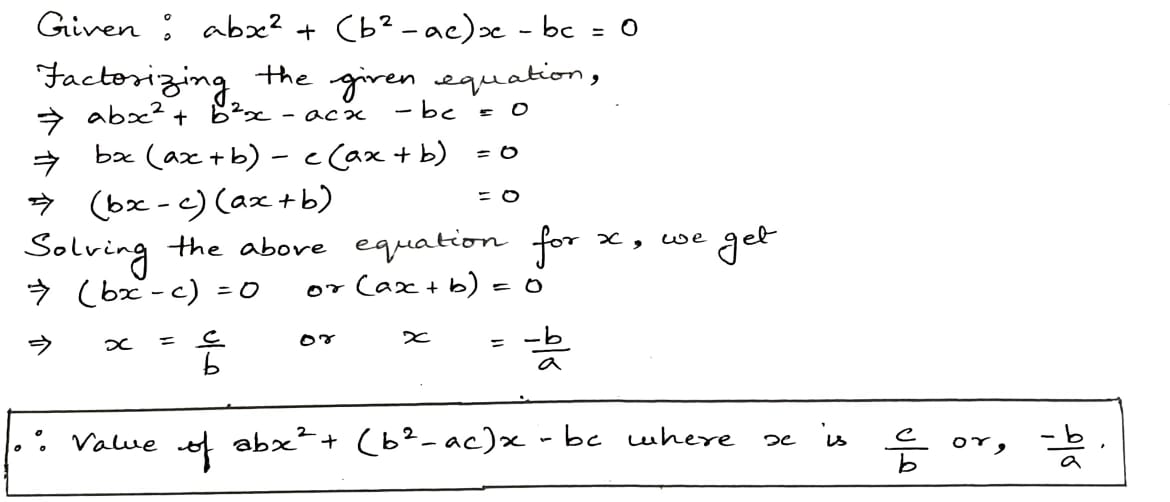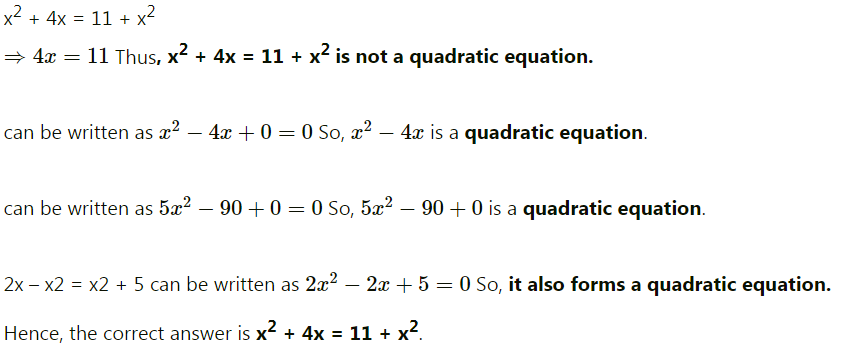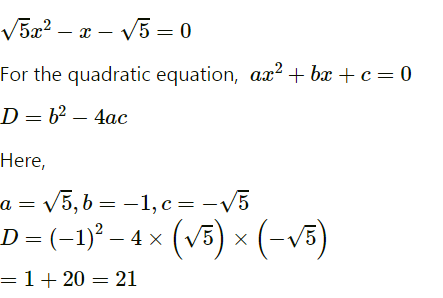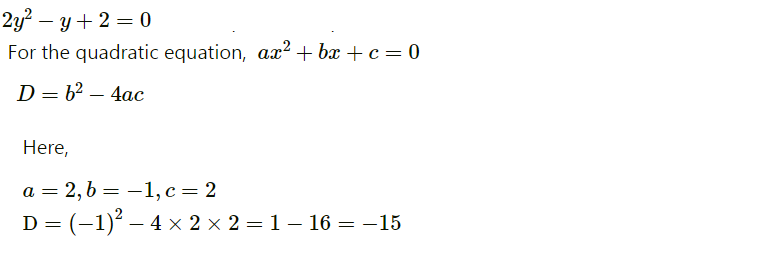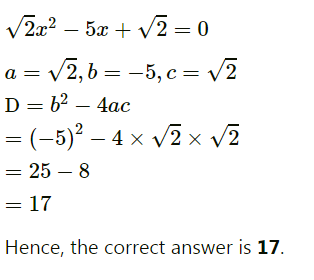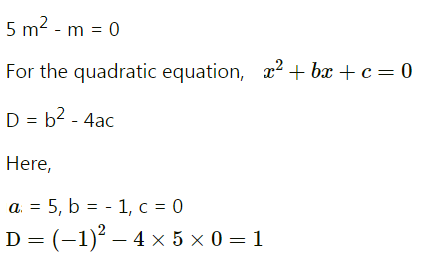Class 10 Maths - Quadratic Equations

If the roots of the equation $(b-c)x^{2}+(c-2)x+(a-b)=0$ are equal, then prove that $2b=a+c$

Given

$(b-c)x^{2}+(c-2)x+(a-b)=0$

For roots to be equal

$D=0$

$\Rightarrow (c-a)^{2}-(b-c)(a-b)=0$

$\Rightarrow c^{2}+a^{2}+4b^{2}-2ac-4ab+4ac-4bc=0$

$\Rightarrow (c+a-2b)^{2}=0$

$[\because (a+b+c)^2=a^2+b^2+c^2+2(ab+bc+ca)]$

$\Rightarrow c+a-2b=0$

$c+a=2b$

Hence Proved.

Is the given equation quadratic? Enter 1 for True and 0 for False.
$n\,-\, 3\, =\, 4n^{2}$

The equation,

$n-3 = 4n^2$ has the highest power as 2.

Thus, it is a quadratic equation.

Solve: $\displaystyle 25x^{2}-30x+9=0$

$\displaystyle 25x^{2}-30x+9=0$

$\displaystyle \Rightarrow (5x)^{2}-2(5x)\times 3+(3)^{2}=0$

$\Rightarrow \displaystyle (5x-3)^{2}=0$

This gives

$\displaystyle x=\frac{3}{5},\frac{3}{5}$ or simply

$\displaystyle x=\frac{3}{5}$ as the required solution.

Solve the equation :
$\displaystyle { 27x }^{ 2 }-10x+1=0$

The given quadratic equation is

$\displaystyle { 27x }^{ 2 }-10x+1=0$
On comparing this equation with

$\displaystyle { ax }^{ 2 }+bx+c=0$ ,
we obtain

$\displaystyle a=27,b=-10,$ and

$c=1$
Therefore, the discriminant of the given equation is

$\displaystyle D={ b }^{ 2 }-4ac={ \left( -10 \right) }^{ 2 }-4\times 27\times 1=100-108=-8$
Therefore, the required solutions are

$\displaystyle \frac { -b\pm \sqrt { D } }{ 2a } =\frac { -\left( -10 \right) \pm \sqrt { -8 } }{ 2\times 27 } =\frac { 10\pm 2\sqrt { 2 }i }{ 54 }$

$\displaystyle =\frac { 5\pm \sqrt { 2 } i }{ 27 } =\frac { 5 }{ 27 } \pm \frac { \sqrt { 2 } }{ 27 } i$

Solve the equation : $\displaystyle { x }^{ 2 }-2x+\frac { 3 }{ 2 } =0$

This given equation can also be written as

$\displaystyle { 2x }^{ 2 }-4x+3=0$
On comparing this equation with

$\displaystyle { ax }^{ 2 }+bx+c=0$ ,
we obtain

$\displaystyle a=2,b=-4,$ and

$c=3$
Therefore, the discriminant of the given equation is,

$\displaystyle D={ b }^{ 2 }-4ac={ \left( -4 \right) }^{ 2 }-4\times 2\times 3=16-24=-8$
Therefore, the required solutions are

$\displaystyle \frac { -b\pm \sqrt { D } }{ 2a } =\frac { -\left( -4 \right) \pm \sqrt { -8 } }{ 2\times 2 } =\frac { 4\pm 2\sqrt { 2i } }{ 4 }$

$\displaystyle =\frac { 2\pm \sqrt { 2 } i }{ 2 } =1\pm \frac { 1}{ \sqrt{2} } i$

Solve the equation $\displaystyle \sqrt { 2 } { x }^{ 2 }+x+\sqrt { 2 } =0$

The given quadratic equation is

$\displaystyle \sqrt { 2 } { x }^{ 2 }+x+\sqrt { 2 } =0$
On comparing the given equation with

$\displaystyle { ax }^{ 2 }+bx+c=0$ ,
we obtain

$\displaystyle a=\sqrt { 2 } ,b=1,$ and

$c=\sqrt { 2 }$
Therefore, the discriminant of the given equation is

$\displaystyle D={ b }^{ 2 }-4ac=1^{ 2 }-4\times \sqrt { 2 } \times \sqrt { 2 } =1-8=-7$
Therefore, the required solutions are

$\displaystyle \frac { -b\pm \sqrt { D } }{ 2a } =\frac { -\left( 1 \right) \pm \sqrt { -7 } }{ 2\times \sqrt { 2 } } =\frac { -1\pm \sqrt { 7 }i }{ 2\sqrt { 2 } }$

Solve the equation $\displaystyle { 21x }^{ 2 }-28x+10=0$

The given quadratic equation is,

$\displaystyle { 21x }^{ 2 }-28x+10=0$
On comparing this equation with

$\displaystyle { ax }^{ 2 }+bx+c=0$ ,
we obtain

$\displaystyle a=21,b=-28,$ and

$c=10$
Therefore, the discriminant of the given equation is

$\displaystyle D={ b }^{ 2 }-4ac={ \left( -28 \right) }^{ 2 }-4\times 21\times 10=784-840=-56$
Therefore, the required solutions are

$\displaystyle \frac { -b\pm \sqrt { D } }{ 2a } =\frac { -\left( -28 \right) \pm \sqrt { -56 } }{ 2\times 21 } =\frac { 28\pm \sqrt { 56 }i }{ 42 }$

$\displaystyle =\frac { 28\pm 2\sqrt { 14 } i }{ 42 } =\frac { 28 }{ 42 } \pm \frac { 2\sqrt { 14 } }{ 42 } i=\frac { 2 }{ 3 } \pm \frac { \sqrt { 14 } }{ 21 } i$

Solve the equation $\displaystyle { x }^{ 2 }+\frac { x }{ \sqrt { 2 } } +1=0$

The given quadratic equation is

$\displaystyle { x }^{ 2 }+\frac { x }{ \sqrt { 2 } } +1=0$
This equation can also be written as

$\displaystyle \sqrt { 2 } { x }^{ 2 }+x+\sqrt { 2 } =0$
On comparing the given equation with

$\displaystyle { ax }^{ 2 }+bx+c=0$ ,
we obtain

$\displaystyle a=\sqrt { 2 } ,b=1,$ and

$c=\sqrt { 2 }$

$\displaystyle \therefore$ discriminant

$D \displaystyle ={ b }^{ 2 }-4ac={ 1 }^{ 2 }-4\sqrt { 2 } \times \sqrt { 2 } =1-8=-7$
Therefore, the required solutions are

$\displaystyle \frac { -b\pm \sqrt { D } }{ 2a } =\frac { -1\pm \sqrt { -7 } }{ 2\sqrt { 2 } } =\frac { -1\pm \sqrt { 7i } }{ 2\sqrt { 2 } }$

Solve the equation $\displaystyle { x }^{ 2 }+3x+5=0$ for $x$ .

The given quadratic equation is

$\displaystyle { x }^{ 2 }+3x+5=0$

On comparing the given equation with

$\displaystyle { ax }^{ 2 }+bx+c=0$ ,
we obtain

$\displaystyle a=1,b=3,$ and

$c=5$

Therefore, the discriminant of the given equation is

$\displaystyle D={ b }^{ 2 }-4ac={ 3 }^{ 2 }-4\times 1\times 5=9-20=-11$

Therefore, the required solutions are

$\displaystyle x=\frac { -b\pm \sqrt { D } }{ 2a } =\frac { -3\pm \sqrt { -11 } }{ 2\times 1 } =\frac { -3\pm \sqrt { 11 }\ i }{ 2 }$

Solve the equation $\displaystyle { 2x }^{ 2 }+x+1=0$

The given quadratic equation is

$\displaystyle { 2x }^{ 2 }+x+1=0$
On comparing the given equation with

$\displaystyle { ax }^{ 2 }+bx+c=0$ ,
we obtain

$\displaystyle a=2,b=1$ and

$c=1$
Therefore, the discriminant of the given equation is

$\displaystyle D={ b }^{ 2 }-4ac={ 1 }^{ 2 }-4\times 2\times 1=1-8=-7$
Therefore, the required solutions are

$\displaystyle \frac { -b\pm \sqrt { D } }{ 2a } =\frac { -1\pm \sqrt { -7 } }{ 2\times 2 } =\frac { -1\pm \sqrt { 7 } i }{ 4 }$

Check whether $2x + x^2 + 1 = 0$ a quadratic equations.

Given that:

$2x + x^2 + 1 = 0$
Arrange the terms in descending order of their powers.

$\Rightarrow x^2 + 2x + 1 = 0$
It is in the standard form

$ax^2 + bx + c = 0$

$\therefore$ The given equation is a quadratic equation.

Solve the quadratic equation $3{x}^{2}+5x+2=0$ using formula method.

Given,

$3{x}^{2}+5x+2=0$
On comparing this equation with

$a{ x }^{ 2 }+bx+c=0$ , we get

$a=3,b=5$ and

$c=2$
Now,

${ b }^{ 2 }-4ac={ (5) }^{ 2 }-4\times 3\times 2$

$=25=24$

$=1$

$x=\cfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a\quad }$

$==\cfrac { -5\pm \sqrt { 1 } }{ 2\times 3 }$

$=\cfrac { -5\pm 1 }{ 6 }$

$x=\cfrac { -5+1 }{ 6 }$

$x=\cfrac { -5-1 }{ 6 }$

$\therefore$

$\cfrac{-2}{3}$ and

$-1$ are the roots of the given quadratic equation.

Solve the following quadratic equation by completing square method
$x^2 + 11x + 24 = 0$

Given equation:

$x^2+11x+24=0$

Adding

$\left(\dfrac{11}{2}\right)^2$ on both side, we get

$x^2+11x+\dfrac{121}{4} + 24=\dfrac{121}4$

$\Rightarrow \left(x+\cfrac{11}2\right)^2 = \cfrac{121}4 - 24 = \dfrac{25}4$

$\Rightarrow x+\cfrac{11}2 = \pm\dfrac{5}2$

$\Rightarrow x = \pm\dfrac{5}2 - \cfrac{11}2$

$\Rightarrow x = -8$ or

$x =-3$

$6x^3 + x^2 = 2$ is a quadratic equations

Given thet:

$6x^3 + x^2 = 2$
By rearranging the terms, we get

$6x^3 + x^2 - 2 = 0$
The highest degree of the variable is 3.

$\therefore$ The given equation is not a quadratic equation.

Solve the quadratic equation $2{x}^{2}+5x+3=0$ using formula method.

Given,

$2{x}^{2}+5x+3=0$
On comparing it with

$a{ x }^{ 2 }+bx+c=0$ where

$a=2,b=5$ and

$c=3$

$\therefore$

${ b }^{ 2 }-4ac={ (5) }^{ 2 }-4\times 2\times 3$

$25-24=1$

$x=\cfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a\quad }$

$=\cfrac { -5\pm \sqrt { { (5) }^{ 2 }-4\times 2\times 3 } }{ 2\times 2 } \quad \quad =\cfrac { -5\pm \sqrt { 25-24 } }{ 4 } =\cfrac { -5\pm 1 }{ 4 }$

$x=\cfrac { -5-1 }{ 4 }$

$x=\cfrac { -5+1 }{ 4 }$

$x=\cfrac{-4}{4}$ and

$x=\cfrac{-6}{4}$

Decide whether $\cfrac{3}{y}-4=y$ is a quadratic equation or not.

$\cfrac{3}{y}-4=y$

$\therefore$

$3-4y={y}^{2}$

$\therefore$

${y}^{2}+4y-3=0$
comparing with

$a{y}^{2}+by+c=0$
Here,

$a=1,b=4,c=-3$

$\therefore$ It is a quadratic equation.

Solve the equation $3y^{2} + 8y + 5 = 0$ by using formula method

$3y^{2} + 8y + 5 = 0$
This equation comparing with

$ay^{2} + by + c = 0$ , we get

$a = 3, b = 8, c = 5$

$\therefore y = \dfrac {-b\pm \sqrt {b^{2} - 4ac}}{2a}$

$\Rightarrow y = \dfrac {-8 \pm \sqrt {64 - 4 \times 3\times 5}}{2\times 3}$

$\Rightarrow y = \dfrac {-8\pm \sqrt {64 - 60}}{6}$

$\Rightarrow y = \dfrac {-8\pm 2}{6}$
Taking

$'+'$ sign, we get

$therefore y = \dfrac {-8 + 2}{6} = \dfrac {-6}{6} = -1$
Taking

$'-'$ sign, we get

$\therefore y = \dfrac {-8 - 2}{6}$

$= \dfrac {-10}{6}$

$= \dfrac {-5}{3}$

$\therefore y = -1$
or

$y = -\dfrac {5}{3}$

Solve the following quadratic equation by using formula method
$3y^2 + 7y + 4 = 0$

The given quadratic equation is

$3y^2 + 7y + 4 = 0$
Comparing this with

$ax^2 + bx + c = 0$
Here,

$a = 3, b = 7, c = 4$

$\therefore y = \dfrac{-b \pm \sqrt{b^2} - 4ac}{2a}$

$= \dfrac{-7 \pm \sqrt{(7^2) - 4 \times 3 \times 4}}{2(3)}$

$= \dfrac{-7 \pm \sqrt{49 - 48}}{6} = \dfrac{-7 \pm \sqrt 1}{6} = \dfrac{-7 \pm 1}{6}$

$\therefore y = \dfrac{-7 + 1}{6}$ or

$y = \dfrac{-7 - 1}{6}$

$\therefore y = \dfrac{-6}{6}$ or

$y = - \dfrac{8}{6}$

$\therefore y = - 1$ or

$y - \dfrac{4}{3}$

If $a = 1, b = 8$ and $c = 15$ , then find the value of $b^2-4ac =$

Given,

$a = 1, b = 8$ and

$c = 15$
then,

$b^2 - 4ac = (8)^2 - 4 \times 1 \times 15$

$= 64 - 60 = 4$

Solve the following quadratic equation using the formula method:
$4{x}^{2}+7x+2=0$

$4{x}^{2}+7x+2=0$
Comparing with the

$a{ x }^{ 2 }+bx+c=0$

$a=4,b=7,c=2$

$\quad x=\cfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a\quad }$

$=\cfrac { -7\pm \sqrt { { (7) }^{ 2 }4\times 4\times 2 } }{ 2\times 4 }$

$=\cfrac { -7\pm \sqrt { 49-32 } }{ 8 }$

$=\cfrac { -7\pm \sqrt { 17 } }{ 8 }$

$\therefore$

$x=\cfrac { -7+\sqrt { 17 } }{ 8 }$ and

$x=\cfrac { -7-\sqrt { 17 } }{ 8 }$

Solve the following quadratic equation by using the formula method: $m^{2} - 3m - 10 = 0$

$m^{2} - 3m - 10 = 0$
Comparing with

$ax^{2} + bx + c = 0$

$a = 1, b = -3, c = -10$

$m = \dfrac {-b\pm \sqrt {b^{2} - 4ac}}{2a}$

$= \dfrac {3\pm \sqrt {(-3)^{2} - 4(1) (-10)}}{2\times 1}$

$= \dfrac {3\pm \sqrt {9 + 40}}{2} = \dfrac {3\pm \sqrt {49}}{2} = \dfrac {3\pm 7}{2}$

$\therefore m = \dfrac {3 + 7}{2}$ and

$\dfrac {3 - 7}{2}$

$\therefore m = \dfrac {10}{2}$ and

$\dfrac {-4}{2}$

$\therefore m = 5$ and

$-2$ .

The discriminant of the quadratic equation $px^{2} + qx + r = 0$ is ________

We know that,

$D=\sqrt{{b}^{2}-4ac}$ for a quadratic equation of the form

$ax^2+bx+c=0$

Here,

$a=p,\quad b=q$ and

$c=r$

So,

$D=\sqrt{{(q)^{2}-4pr}}$

or,

$D=\sqrt{{q}^{2}-4pr}$

Solve $x^2 + 6x - 7 = 0$ by the method of completing the square

Solution:

Completing the square method:

$x^2+6x=7$

Adding

$\left[\cfrac12\times \text{coefficient of}\, x\right]^2$ both sides we get,

$x^2+6x+\left[\cfrac12\times6\right]^2=7+\left[\cfrac12\times6\right]^2$

or,

$x^2+6x+3^2=7+3^2$

or,

$(x+3)^2=16$

or,

$x+3=\sqrt{16}$

or,

$x+3=\pm4$

or,

$x=4-3$ or

$x=-4-3$

or,

$x=1$ or

$x=-7$

Write the discriminant of the equation $ax^2 + bx + c = 0$ .

Solution:

Discriminant

$D=b^2-4ac$

Decide whether $m^{2} + m + 2 = 4m$ is a quadratic equation

$m^{2} + m + 2 = 4m$

$m^{2} + m - 4m + 2 = 0$

$m^{2} - 3m + 2 = 0$

$\therefore$ It is a quadratic equation it is in the form of

$ax^{2} + bx + c = 0$

$\therefore$ The given equation is a quadratic equation.

Solve the quadratic equation $2x^{2} + x - 4 = 0$ by completing the square

The given quadratic equation is

$2x^2+x-4=0$

$\Rightarrow x^2+\cfrac x2-2=0$

$\Rightarrow x^2+\cfrac x2=2$

On adding both sides

$\cfrac1{16}$ we get

$x^2+\cfrac x2+\cfrac1{16}=2+\cfrac1{16}$

$\Rightarrow \left(x+\cfrac14\right)^2=\cfrac{33}{16}$

$\Rightarrow x+\cfrac14=\pm\cfrac{\sqrt{33}}{4}$

$\Rightarrow x=\pm\cfrac{\sqrt{33}}{4}-\cfrac14$

$\Rightarrow x=\cfrac{-1-\sqrt{33}}{4},\cfrac{-1+\sqrt{33}}{4}$

Solve the quadratic equation $x^{2} - 4x + 2 = 0$ by formula method.

$x^{2} - 4x + 2 = 0$

$a = 1, b = -4, c = 2$

$x = \dfrac {-b \pm \sqrt {b^{2} - 4ac}}{2a}$

$x = \dfrac {-(-4) \pm \sqrt {(-4)^{2} - 4(1)(2)}}{2(1)}$

$x = \dfrac {4\pm \sqrt {16 - 8}}{2}$

$x = \dfrac {4\pm \sqrt {8}}{2}$

$x = \dfrac {4\pm 2\sqrt {2}}{2}$

$= \dfrac {2(2\pm \sqrt {2})}{2}$

$x =2\pm \sqrt {2}$ .

If $x=\cfrac { \sqrt { 3 } -\sqrt { 2 } }{ \sqrt { 3 } +\sqrt { 2 } } ,y=\cfrac { \sqrt { 3 } +\sqrt { 2 } }{ \sqrt { 3 } -\sqrt { 2 } }$ , find the value of $3{ x }^{ 2 }-5xy+3{ y }^{ 2 }$

We have $x = \dfrac{\sqrt{3} - \sqrt{2}}{\sqrt{3}+\sqrt{2}} = \dfrac{\sqrt{3} - \sqrt{2}}{\sqrt{3}+\sqrt{2}} \times \dfrac{\sqrt{3} - \sqrt{2}}{\sqrt{3}- \sqrt{2}} = 5 – 2\sqrt{6}$

and

$y = \dfrac{\sqrt{3} + \sqrt{2}}{\sqrt{3}-\sqrt{2}} = \dfrac{\sqrt{3} + \sqrt{2}}{\sqrt{3}-\sqrt{2}} \times \dfrac{\sqrt{3} + \sqrt{2}}{\sqrt{3}+ \sqrt{2}} = 5 + 2\sqrt{6}$

Thus

$x^2 = (5 – 2\sqrt{6})^2 = 49 – 4\sqrt{6}$ ,

$y^2 = (5 – 2\sqrt{6})^2 = 49 + 4\sqrt{6}$ and

$xy = 1$

Therefore,

$3x^2 – 5xy + 3 y^2 = 3 \times (49 – 4\sqrt{6}) – 5 + 3 \times (49 + 4\sqrt{6}) = 289$

Solve the equation by using the formula:
${m}^{2}-2m=2$

Given the equation

${m}^{2}-2m=2$

${m}^{2}-2m-2=0$

Here,

$a=1$

$b=-2$

$c=-2$

$x=\cfrac { -b \pm \sqrt { { b }^{ 2 }-4ac } }{ 2a }$

$m=\cfrac { -(-2)\pm \sqrt { { (-2) }^{ 2 }-4\times 1\times (-2) } }{ 2\times 1 }$

$=\cfrac { 2\pm \sqrt { 4+8 } }{ 2 } \\=\cfrac { 2\pm \sqrt { 12 } }{ 2 }$

$=\cfrac { 2\pm \sqrt { 4\times 3 } }{ 2 } \\= { 1\pm \sqrt { 3 } }$

Thus,

$m=1\pm \sqrt { 3 }$

The formula of discriminant of quadratic equation $ax^{2} + bx + c = 0$ is $D =$ ______.

The formula of the discriminant of the given quadratic equation is given by

$D = b^{2} - 4ac$ .

Find the value of $k$ for which the given equations has real and equal roots:
(i) $(k - 12)x^{2} + 2(k - 12)x + 2 = 0$
(ii) $k^{2}x^{2} - 2(k - 1)x + 4 = 0$ .

Quadratic equations have real and equal roots if discriminant is zero.

$\Rightarrow D=0$

$(i)$

$(2(k-12))^2-4(2)(k-12)=0\Rightarrow (k-12)^2-2(k-12)=0$

$(k-12)(k-12-2)=0\Rightarrow (k-12)(k-14)=0$

$k=12,k=14$

$(ii)$

$(-2(k-1))^2-4(4)(k^2)=0\Rightarrow (k-1)^2-4k^2=0$

$3k^2+2k-1=0\Rightarrow (3k-1)(k+1)=0$

$k=\dfrac{1}{3},k=-1$

Solve the equation $a^2x^2-3abx+2b^2=0$ by completing the square.

There is nothing to prove if a = 0. For

$a \neq 0$ , we have

$a^2x^2-3abx+2b^2=0$

$\rightarrow x^2-\cfrac{3b}{a}x+\cfrac{2b^2}{a^2}=0$

$\rightarrow x^2-2 \left ( \cfrac{3b}{2a} \right )x=\cfrac{-2b^2}{a^2}$

$\rightarrow x^2-2 \left ( \cfrac{3b}{2a} \right )x+\cfrac{9b^2}{4a^2}-\cfrac{2b^2}{a^2}$

$\rightarrow \left ( x-\cfrac{3b} {2a}\right )^2=\cfrac{9b^2-8b^2}{4a^2} \rightarrow \left ( x-\cfrac{3b}{2a} \right )^2=\cfrac{b^2}{4a^2}$

$\rightarrow x-\cfrac{3b}{2a}=\pm \cfrac{b}{2a} \rightarrow x=\cfrac{3b \pm b}{2a}$

Therefore, the solution set is

$\left \{ \cfrac{b}{a}, \cfrac{2b}{a} \right \}$ .

An equation whose maximum degree of variable is two is called ............... equation.

The correct answer is quadratic.

Check whether the given equation is a quadratic equation or not:
$x(x + 1) + 8 = (x + 2)(x - 2)$

$x\left( x+1 \right) -8=\left( x+2 \right) \left( x-2 \right)$

$\Rightarrow { x }^{ 2 }+x+8={ x }^{ 2 }-4$

$\Rightarrow x=-12$ (Not a quadratic equation)

Find the roots of the following quadratic equation (if they exist) by the method of completing the square.
$x^2 \, - \, 4ax \, + \, 4a^2 \, - \, b^2 \, = \, 0$

$x^{2}-4ax+4a^{2}-b^{2}=0$

Completing the square :

$\Rightarrow x^{2}-2(2a)x+(2a)^{2}=b^{2}$

$\Rightarrow (x-2a)^{2}=b^{2}$

$\Rightarrow x=\pm b+2a$

$\Rightarrow x=2a+b$ or

$x=2a-b$

Show that the roots of the equation $x^2 - 2x + 3 = 0$ are imaginary.

For equation

$ax^{2}+bx+c=0$

Roots are given as

$= \dfrac{-b \pm \sqrt{b^{2}-4ac}}{2a}$

Now let us compare

$ax^{2}+bx+c=0$ with

$x^{2}-2x+3=0$ to find the values of

$a,b,c$

After it we can directly put

$a,b,c$ into the formula to find the roots

By comparing

$a=1,b=-2,c=3$

So roots

$= \dfrac{-(-2) \pm \sqrt{(-2)^{2}-4(1)(3)}}{2\times1}$

$= \dfrac{2 \pm \sqrt{4-12}}{2}$

$= \dfrac{2 \pm \sqrt{-8}}{2}$

$= 1 \pm i\sqrt{2}$

Hence the roots of the equation

$x^2 - 2x+3=0$ are imaginary

Simplify $\cfrac { \left( { x }^{ 2 }+1 \right) \left( { x }^{ 2 }+2 \right) }{ \left( { x }^{ 2 }+3 \right) \left( { x }^{ 2 }+4 \right) } =$

$\dfrac{\left(x^2+1\right)\left(x^2+2\right)}{\left(x^2+3\right)\left(x^2+4\right)}$

$=\dfrac{x^2x^2+x^2\cdot \:2+1\cdot \:x^2+1\cdot \:2}{x^2x^2+x^2\cdot \:4+3x^2+3\cdot \:4}$

$=\dfrac{x^2x^2+2x^2+1\cdot \:x^2+1\cdot \:2}{x^2x^2+4x^2+3x^2+3\cdot \:4}$

$=\dfrac{x^4+3x^2+2}{x^4+7x^2+12}$

$=1+\dfrac{-4x^2-10}{x^4+7x^2+12}$

Find the root of the following quadratic equation (if they exist) by the method of completing the square.
$\sqrt{3}x^2 \, + \, 10x \, + \, 7\sqrt{3} \, = \, 0$

Consider the given equation.

$\sqrt{3}{{x}^{2}}+10x+7\sqrt{3}=0$

${{x}^{2}}+\dfrac{10}{3}x+7=0$

${{x}^{2}}+2\times \dfrac{1}{2}\times \dfrac{10}{\sqrt{3}}x+7=0$

${{x}^{2}}+2\times \dfrac{5}{\sqrt{3}}\times x+{{\left( \dfrac{5}{\sqrt{3}} \right)}^{2}}-{{\left( \dfrac{5}{\sqrt{3}} \right)}^{2}}+7=0$

${{\left( x+\dfrac{5}{\sqrt{3}} \right)}^{2}}=\dfrac{25-21}{3}$

${{\left( x+\dfrac{5}{\sqrt{3}} \right)}^{2}}=\dfrac{4}{3}$

$x+\dfrac{5}{\sqrt{3}}=\pm \dfrac{2}{\sqrt{3}}$

$x=-\sqrt{3},-\dfrac{7}{\sqrt{3}}$

Hence, this is the solution of the given equation by completing the squares.

Write standard form of quadratic equation and find the roots of the equations $3x^2+5\sqrt{2}+2=0$ using general formula.

The polynomial of degree 2 is called quadratic polynomial and

$ax^{2}+bx+c=0$ where

$a\neq{0}$ is standard form of quadratic equation.

Given:

$P(x)=3x^{2}+5\sqrt{2}x+2$

Here

$a=3$

$b=5\sqrt{2}$

$c=2$

$x=\dfrac{-b\pm\sqrt{b^{2}-4ac}}{2a}$

$x=\dfrac{-5\sqrt{2}\pm\sqrt{50-4\times 3\times 2}}{2\times 3}$

$x=\dfrac{-5\sqrt{2}\pm\sqrt{26}}{6}$

So,

$x=\dfrac{-5\sqrt{2}+\sqrt{26}}{6}$ ,

$x=\dfrac{-5\sqrt{2}-\sqrt{26}}{6}$

Write the discriminant of the given quadratic equation
${ x }^{ 2 }+px+2q=0\quad$

The given equation is

${ x }^{ 2 }+px+2q=0\quad$

Here,

$a=1,b=p,c=2q$

$\therefore D={ b }^{ 2 }-4ac$

$={ (p) }^{ 2 }-4\times 1\times 2q$

$={ (p) }^{ 2 }-8q$

Solve $4ab=2(a^2-b^2)\sqrt-1$

$4ab = 2(a^2-b^2)\sqrt{-1}$

$4ab = 2(a^2-b^2)i$

$4ab=2ia^2+2ib^2$

$2ab=ia^2-ib^2$

Find the roots of the following quadratic equation, $2x^2+x-4=0$

$\displaystyle{2{ x }^{ 2 }+x+4=0\\ x=\frac { -1\pm \sqrt { 1-4(2)(4) } }{ 2(2) } \\ x=\frac { -1\pm \sqrt { -15 } }{ 4 } \\ x=\frac { -1\pm \sqrt { 15 } i }{ 4 } }$

Solve the following quadratic equations by the method of perfect the square.
$3x^2-5x+2=0$

$3{ x }^{ 2 }-5x+2=0\\ { x }^{ 2 }-\dfrac { 5 }{ 3 } x+\dfrac { 2 }{ 3 } =0\\ { x }^{ 2 }-\dfrac { 5 }{ 3 } x+\dfrac { 25 }{ 36 } -\dfrac { 25 }{ 36 } +\dfrac { 2 }{ 3 } =0\\ { \left( x-\dfrac { 5 }{ 3 } \right) }^{ 2 }-\dfrac { 1 }{ 36 } =0\\ { \left( x-\dfrac { 5 }{ 3 } \right) }^{ 2 }=\dfrac { 1 }{ 36 } \\ \left( x-\dfrac { 5 }{ 3 } \right) =\pm \dfrac { 1 }{ 6 } \\ x=\dfrac { 5 }{ 3 } \pm \dfrac { 1 }{ 6 } \\ x=\dfrac { 11 }{ 6 } ,\dfrac { 9 }{ 6 }$

If $\alpha$ and $\beta$ are the zeros of $x^{2}+x-2$ then find value of $\dfrac{1}{\alpha}-\dfrac{1}{\beta}$

$\displaystyle{a{ x }^{ 2 }+bx+c=0\\ \alpha +\beta =-\frac { b }{ a } \\ \alpha \beta =\frac { c }{ a } \\ \frac { 1 }{ \alpha } +\frac { 1 }{ \beta } =\frac { \alpha +\beta }{ \alpha \beta } =-\frac { b }{ c } }$

Solve the following quadratic equations by the method of perfect the square.
$5x^2-6x-2=0$

$5{ x }^{ 2 }-6x-2\\ { x }^{ 2 }-\dfrac { 6 }{ 5 } x-\dfrac { 2 }{ 5 } =0\\ { x }^{ 2 }-\dfrac { 6 }{ 5 } x+\dfrac { 36 }{ 100 } -\dfrac { 36 }{ 100 } -\dfrac { 2 }{ 5 } =0\\ { \left( x-\dfrac { 6 }{ 5 } \right) }^{ 2 }=\dfrac { 76 }{ 100 } \\ x-\dfrac { 6 }{ 5 } =\pm \dfrac { \sqrt { 76 } }{ 10 } \\ x=\dfrac { 6 }{ 5 } \pm \dfrac { \sqrt { 76 } }{ 10 }$

Solve the following quadratic equations by the method of perfect the square.
$2x^2+x+4=0$

$2{ x }^{ 2 }+x+4=0\\ { x }^{ 2 }+\dfrac { x }{ 2 } +2=0\\ { x }^{ 2 }+\dfrac { x }{ 2 } +\dfrac { 1 }{ 16 } -\dfrac { 1 }{ 16 } +2=0\\ { \left( x+\dfrac { 1 }{ 4 } \right) }^{ 2 }+\dfrac { 31 }{ 16 } =0\\ { \left( x+\dfrac { 1 }{ 4 } \right) }=\pm \dfrac { \sqrt { 31 } i }{ 4 } \\ x=-\dfrac { 1 }{ 4 } \pm \dfrac { \sqrt { 31 } i }{ 4 }$

$x^{2}+3\left| x \right| +2=0$ Find the value of $x$ .

when

$x < 0 | x| = -x$

$x^2 - 3x + 2 = 0$

$x^2 - 2x -x +2 = 0$

$x(x -2) -1 (x- 2) =0$

$(x-2) (x-1) = 0$

$x = 2, 1$

when

$x > 0\quad |x| =x$

$x^2 +3x+2=0$

$x^2 + 2x + x+2 =0$

$x(x+2) 1 (x+2) =0$

$(x+2) (x+1) = 0$

$x= -2 , -1$

Find a quadratic equation with real co-efficient whose one root is $3-2i$ .

As we seek a quadratic equation with real co-efficient whose one root is

$3-2i$ then the other root is

$3+2i$ .

Then the quadratic equation is

$x^2-\{(3+2i)+(3-2i)\}x+(3+2i)(3-2i)=0$

or,

$x^2-6x+13=0$ .

Solve the following quadratic equations by the method of perfect the square.
$4x^2+3x+5=0$

$4{ x }^{ 2 }+3x+5=0\\ { x }^{ 2 }+\dfrac { 3 }{ 4 } x+\dfrac { 5 }{ 4 } =0\\ { x }^{ 2 }+\dfrac { 3 }{ 4 } x+\dfrac { 9 }{ 16 } -\dfrac { 9 }{ 16 } +\dfrac { 5 }{ 4 } =0\\ { \left( x+\dfrac { 3 }{ 4 } \right) }^{ 2 }=-\dfrac { 11 }{ 16 } \\ \left( x+\dfrac { 3 }{ 4 } \right) =\pm \dfrac { \sqrt { 11 } i }{ 4 } \\ x=-\dfrac { 3 }{ 4 } \pm \dfrac { \sqrt { 11 } i }{ 4 } \\$

Solve
${ x }^{ 2 }+5x-2=0$

$a{ x }^{ 2 }+bx+c=0$

$x=\cfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a }$

${ x }^{ 2 }+5x-2=0$

$x=\cfrac { -5\pm \sqrt { 25-4\times 1\times (-2) } }{ 2\times 1 }$

$=\cfrac { -5\pm \sqrt { 33 } }{ 2 }$

${ x }_{ 1 }=\cfrac { -5-\sqrt { 33 } }{ 2 } ;{ x }_{ 2 }=\cfrac { -5+\sqrt { 22 } }{ 2 }$

Solve ${x}^{2}-3x+12=5$

$\dfrac{dy}{dx}=1+x+y+xy$

$\dfrac{dy}{dx}=y(x+1)+(x+1)$

$\dfrac{dy}{dx}=(x+1)(y+1)$

$\dfrac{dy}{y+1}=(x+1)dx$

Now, integrating both sides,

$\int\dfrac{dy}{dx}=\int(x+1)dx$

$\Rightarrow$

$ln(y+1)=\dfrac{x^2}{2}+x+c$

Now, taking exponential both sides,

$\Rightarrow$

$y+1=e^{\dfrac{x^2}{2}+x+c}$

$\therefore$

$y=e^{\dfrac{x^2}{2}+x+c}-1$

${x^2} - 3x + 12 = 5$

$\Rightarrow {x^2} - 3x + 12 = 0$

$\Rightarrow x = \dfrac{{3 \pm \sqrt {{{\left( { - 3} \right)}^2} - 4 \times 1 \times 7} }}{2}$

$\Rightarrow x = \dfrac{{3 \pm \sqrt {9 - 28} }}{2}$

$\Rightarrow x = \dfrac{{3 \pm \sqrt { - 19} }}{2}$

$\Rightarrow x = \dfrac{{3 \pm \sqrt {19} i}}{2}$

Factorise : $2\sqrt{2}x^2 + 9x + 5 \sqrt{2}=0$

$2\sqrt{2}x^{2}+9x+5\sqrt{2}=0$

$2\sqrt{2}x^{2}+4x+5x+5\sqrt{2}=0$

$2\sqrt{2}x(x+\sqrt{2})+5(x+\sqrt{2})=0$

$(2\sqrt{2}x+5)(x+\sqrt{2})=0$

$(2\sqrt{2}x+5)=0$ or

$(x+\sqrt{2})=0$

$x=-\frac{5}{2\sqrt{2}}=-\frac{5}{4}\sqrt{2}$ or

$x=-\sqrt{2}$

Check whether the following is quadratic equation.
$(x+1)^2=2(x-3)$

$(x+1)^2=2(x-3)$

$\Rightarrow$

$x^2+2x+1=2x-6$

$\Rightarrow$

$x^2+2x+1-2x+6=0$

$\Rightarrow$

$x^2+7=0$

$\Rightarrow$ A quadratic equation is an equation of the second degree, meaning it contains at least one term that is squared

$\Rightarrow$ Comparing given equation

$x^2+7=0$ with standard form of quadratic equation

$ax^2+bx+c=0.$

$\Rightarrow$ We get,

$a=1,\,b=0,\,c=7$

$\therefore$ The given equation is quadratic equation.

The equation $x^2 + 2(m-1)x + (x + 5) = 0$ has real and equal roots. Find the value of $m$ .

Given the equation

$x^2 + 2(m-1)x + (x + 5) = 0$ or,

$x^2+(2m-1)x+5=0$ ......(1) has real and equal roots.

Then the discreminant

$=0$

or,

$(2m-1)^2-4.5.1=0$

or,

$4m^2-4m-19=0$

or,

$m=\dfrac{4\pm\sqrt{4^2+4.4.19}}{2.4}$

or,

$m=\dfrac{4\pm4\sqrt{1+19}}{2.4}$

or,

$m=\dfrac{1\pm\sqrt{20}}{2.4}$

or,

$m=\dfrac{1\pm2\sqrt{5}}{2}$ .

The quadratic equation $ax^2 + bx + c = 0$ , ( $a\ne 0$ ) has atmost _____ roots.

We are given a quadratic equation then it can have atmost

$2$ roots. The roots may be real or imaginary or equal or distinct.

So the quadratic equation

$ax^2 + bx + c = 0$ , (

$a\ne 0$ ) has atmost

$2$ roots

$2\sqrt{5}{x}^{2}-3x-\sqrt{5}=0$ Find $x$ .

$\begin{array}{l} 2\sqrt { 5 } { x^{ 2 } }-3x-\sqrt { 5 } =0 \\ \Rightarrow 2\sqrt { 5 } { x^{ 2 } }+2x-5x\sqrt { 5 } =0 \\ \Rightarrow 2x\left( { \sqrt { 5 } x+1 } \right) -\sqrt { 5 } \left( { \sqrt { 5 } x+1 } \right) \\ \Rightarrow \left( { \sqrt { 5 } x+1 } \right) \left( { 2x-\sqrt { 5 } } \right) =0 \\ \Rightarrow \sqrt { 5 } x+1=0\, \, or\, \, 2x-\sqrt { 5 } =10 \\ \Rightarrow x=\dfrac { { -1 } }{ { \sqrt { 5 } } } \, \, \, or\, \, x=\dfrac { { \sqrt { 5 } } }{ 2 } \end{array}$

Find the values of a : $7{a^2} + 7a - 20=0$

$7a^2+7a-20=0$

$x_{1,\:2}=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$a=\dfrac{-7\pm \sqrt{7^2-4\cdot \:7\left(-20\right)}}{2\cdot \:7}$

$=\dfrac{-7\pm \sqrt{49+560}}{14}$

$=\dfrac{-7\pm \sqrt{609}}{14}$

Find the co-ordinates points where the graph of polynomial ${x^2} + x + 12$ intersects the x-axis.

Let ,

$y={{x}^{2}}+x+12=0$

It cut x-axis then, at x-axis $y=0$

${{x}^{2}}+x+12=0$

$x = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x = \dfrac{-(1) \pm \sqrt{(1)^2-4*1*12}}{2*1}$

$x = \dfrac{-1 \pm \sqrt{-47}}{2}$

Hence required coordinates.

$\left( x,y \right)=\left(\dfrac{-1+\sqrt{-47}}{2},\ 0\right)$

$\left( x,y \right)=\left(\dfrac{-1-\sqrt{-47}}{2},\ 0\right)$

Check whether the following is quadratic equation.
$x^2+3x+1=(x-2)^2$

Given,

$x^2+3x+1=(x-2)^2$

or,

$x^2+3x+1=x^2-4x+4$

or,

$7x-3=0$ .

This is a linear equation which not a quadratic equation.

Solve the following quadratic equation by completing the square method.
$x^2+2\ x-5=0$

$x^2+2x-5=0$

$x^2+2x+1-1-5=0$

$(x+1)^2=6$

$x=-1\pm\sqrt(6)$

Find the nature of the roots of the following quadratic equations. If roots are real, find them.
$5x^{2}-3x+2=0$

$\Rightarrow 5x^{2}-3x+2=0$

discriminant

$= b^{2}-4ac.$

$\Rightarrow (-3)^{2}-4(5)(2)=9-40$

$=-31$ ( negative )

$\therefore$ Roots are lmaginary

Check whether the following is quadratic equation.
$(x+2)^3=2x(x^2-1)$

$(x+2)^3=2x(x^2-1)$

$x^3+8+6x^2+12x=2x^3-2x$

Equation has degree 3.

It is a cubic equation, not a quadratic equation.

Check whether the following is quadratic equation.
$x^2-2x=(-2)(3-x)$

$x^2-2x=(-2)(3-x)$

$\Rightarrow$

$x^2-2x=-6+6x$

$\Rightarrow$

$x^2-2x-6x+6=0$

$\Rightarrow$

$x^2-8x+6=0$

$\Rightarrow$ A quadratic equation is an equation of the second degree, meaning it contains at least one term that is squared.

$\Rightarrow$ Comparing given equation

$x^2-8x+6=0$ with standard form of quadratic equation

$ax^2+bx+c=0.$

$\Rightarrow$ We get,

$a=1,\,b=-8,\,c=6$

$\therefore$ Given equation is quadratic equation.

Check whether the following in quadratic equation.
$(x-3)(2x+1)=x(x=5)$

$(x-3)(2x+1)=x(x-5)$

$\Rightarrow$

$2x^2+x-6x-3=x^2-5x$

$\Rightarrow$

$2x^2+x-6x-3-x^2+5x=0$

$\Rightarrow$

$x^2-3=0$

$\Rightarrow$ A quadratic equation is an equation of the second degree, meaning it contains at least one term that is squared

$\Rightarrow$ Comparing given equation with standard form of quadratic equation

$ax^2+bx+c=0.$

$\Rightarrow$ We get,

$a=1,\,b=0,\,c=3$

$\therefore$ Given equation is quadratic equation

Check whether the following is quadratic equation.
$(x-2)(x+1)=(x-1)(x+3)$

$(x-2)(x+1)=(x-1)(x+3)$

$x^2-x-2=x^2+2x-3$

this is not a quadratic equation as term of

$x^2$ vanishes.

Solve the quadratic equation : $4x^2-4ax+(a^2-b^2)=0$

$4x^2 - 4ax + (a^2-b^2) = 0$

$\implies 4x^2 - 4ax + a^2 = b^2$

$\implies (2x-a)^2 = b^2$

$\implies 2x-a = \pm b$

$\implies 2x = a \pm b$

$\implies Roots\ of\ given\ quadratic\ equation\ are:$

$x_1 = \dfrac{a+b}{2},\ x_2 = \dfrac{a-b}{2}$

Solve each of the following equation by using the method of completing the square:
$\dfrac {2}{x^{2}}-\dfrac {5}{x}+2=0$

Given,

$\dfrac{2}{x^2}-\dfrac{5}{x}+2=0$

$2-5x+2x^2=0$

$2x^2-5x+2=0$

$2x^2-4x-x+2=0$

$2x(x-2)-1(x-2)=0$

$(x-2)(2x-1)=0$

$\therefore x=2,\dfrac{1}{2}$

$(x + 2)(x + 3) + (x - 3)(x - 2) - 2x(x + 1) = 0$

Given that,

$(x+2)(x+3)+(x-3)(x-2)-2x(x+1)=0$

$\Rightarrow {{x}^{2}}+2x+3x+6+{{x}^{2}}-3x-2x+6-2{{x}^{2}}-2x=0$

$\Rightarrow 2{{x}^{2}}-2{{x}^{2}}+5x-5x-2x+12=0$

$\Rightarrow -2x+12=0$

$\Rightarrow -2x=-12$

$\Rightarrow x=6$

Solve each of the following equation by using the method of completing the square:
$8x^{2}+14x-1=0$ ?

Given,

$8x^2+14x-1=0$

$x^2+\left ( \dfrac{14}{8} \right )x-1=0$

$x^2+\left ( \dfrac{7}{4} \right )x-1=0$

add and subtract

$\left ( \dfrac{7}{8} \right )^2$

$x^2+\left ( \dfrac{7}{4} \right )x-1+\left ( \dfrac{7}{8} \right )^2-\left ( \dfrac{7}{8} \right )^2=0$

$x^2+\left ( \dfrac{7}{4} \right )x+\left ( \dfrac{7}{8} \right )^2-1-\left ( \dfrac{7}{8} \right )^2=0$

$\left ( x+ \dfrac{7}{8}\right )^2=1+\dfrac{49}{64}=\dfrac{113}{64}$

$x+ \dfrac{7}{8}=\pm\dfrac{\sqrt{113}}{8}$

$\therefore x=\pm\dfrac{\sqrt{113}}{8}-\dfrac{7}{8}$

Factorise:
${x}^{2}-x-12$

$=x^{2}-x-12$

$=x^{2}-4x+3x-12$

$=x(x-4)+3(x-4)$

$=(x+3)(x-4)$

Solve each of the following equation by using the method of completing the square:
$5x^{2}+6x-2=0$ ?

Given,

$5x^2+6x-2=0$

$x^2+\dfrac{6}{5}x-\dfrac{2}{5}=0$

add and subtract

$\left ( \dfrac{3}{5} \right )^2$ , we get

$x^2+\dfrac{6}{5}x-\dfrac{2}{5}+\left ( \dfrac{3}{5} \right )^2-\left ( \dfrac{3}{5} \right )^2=0$

$x^2+\dfrac{6}{5}x+\left ( \dfrac{3}{5} \right )^2-\dfrac{2}{5}-\left ( \dfrac{3}{5} \right )^2=0$

$\left ( x+ \dfrac{3}{5}\right )^2-\dfrac{2}{5}- \dfrac{9}{25}=0$

$\left ( x+ \dfrac{3}{5}\right )^2=\dfrac{2}{5}+ \dfrac{9}{25}=\dfrac{19}{25}$

$\therefore x+ \dfrac{3}{5}=\pm\dfrac{19}{25}$

$\Rightarrow x=\pm\dfrac{19}{25}-\dfrac{3}{5}$

$\therefore x=\dfrac{19}{25}-\dfrac{3}{5}=\dfrac{4}{25}$

$\therefore x=-\dfrac{19}{25}-\dfrac{3}{5}=-\dfrac{34}{25}$

Solve the quadratic equation : $4x^2+4bx-(a^2-b^2)=0$

$4x^2 + 4bx - (a^2-b^2) = 0$

$\implies 4x^2 + 4bx + b^2 = a^2$

$\implies (2x+b)^2 = a^2$

$\implies 2x+b = \pm a$

$\implies 2x = b \pm a$

$\implies Roots\ of\ given\ quadratic\ equation\ are:$

$x_1 = \dfrac{a+b}{2},\ x_2 = \dfrac{b-a}{2}$

Solve each of the following equation by using the method of completing the square:
$3x^{2}-2x-1=0$

Given,

$3x^2-2x-1=0$

$3x^2-3x+x-1=0$

$3x(x-1)+1(x-1)=0$

$(x-1)(3x+1)=0$

$\therefore x=1,-\dfrac{1}{3}$

Find the roots of given equation $2y^{2}-y-1=0$

We have,

$2{{y}^{2}}-y-1=0$

$2{{y}^{2}}-2y+y-1=0$

$2y\left( y-1 \right)+1\left( y-1 \right)=0$

$\left( y-1 \right)\left( 2y+1 \right)=0$

$\Rightarrow y=1,-\dfrac{1}{2}$

Hence, this is the answer.

Solve $\sqrt 5 {x^2} + x + \sqrt 5 = 0$ .

Given that quadetric equation is $\sqrt{5}x^2+x+\sqrt{5}=0$

[If given qudratics equation as $ax^2+bx+c=0$ , then $x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$ ]

Then we compare given quadratic equation with standrad form, we get $a=\sqrt5, b=1, c=\sqrt5$ , then

$x=\dfrac{-1\pm\sqrt{1-\left(4\times\sqrt{5}\times\sqrt{5}\right)}}{2\sqrt{5}}$

$x=\dfrac{-1\pm\sqrt{-19}}{2\sqrt5}$

$x=\dfrac{-1+\sqrt{19}i}{2\sqrt5}$ and $x=\dfrac{-1-\sqrt{19}i}{2\sqrt5}$

Find the roots of the equations by the method of completing the square.
$x^{2}+7x-6=0$

$x^2+7x-6=0$

$\Rightarrow$ Here,

$a=1,\,b=7,\,c=-6$

$\Rightarrow$

$x^2+7x=6$

Now,

$\left(\dfrac{b}{2}\right)^2=\left(\dfrac{7}{2}\right)^2=\dfrac{49}{4}$

Adding,

$\dfrac{49}{4}$ on both sides,

$\Rightarrow$

$x^2+7x+\dfrac{49}{4}=6+\dfrac{49}{4}$

$\Rightarrow$

$\left(x+\dfrac{7}{2}\right)^2=\dfrac{73}{4}$

$\Rightarrow$

$x+\dfrac{7}{2}=\pm\dfrac{\sqrt{73}}{2}$

$\Rightarrow$

$x+\dfrac{7}{2}=\dfrac{\sqrt{73}}{2}$ and

$x+\dfrac{7}{2}=-\dfrac{\sqrt{73}}{2}$

$\Rightarrow$

$x=\dfrac{\sqrt{73}}{2}-\dfrac{7}{2}$ and

$x=-\dfrac{\sqrt{73}}{2}-\dfrac{7}{2}$

Solve each of the following equation by using the method of completing the square:
$x^{2}-(\sqrt {2}+1)x+\sqrt {2}=0$

Given,

$x^2-(\sqrt{2}+1)x+\sqrt{2}=0$

$x^2-x-\sqrt{2}x+\sqrt{2}=0$

$x(x-1)-\sqrt{2}(x-1)=0$

$(x-1)(x-\sqrt{2})=0$

$\therefore x=1,\sqrt 2$

Solve each of the following equation by using the method of completing the square:
$\sqrt {2}x^{2}-3x-2\sqrt {2}=0$

Given,

$\sqrt{2}x^2-3x-2\sqrt{2}=0$

$\sqrt{2}x^2-4x+x-2\sqrt{2}=0$

$\sqrt{2}x(x-2\sqrt{2})+1(x-2\sqrt{2})=0$

$(x-2\sqrt{2})(\sqrt{2}x+1)=0$

$\therefore x=2\sqrt{2},-\dfrac{1}{\sqrt{2}}$

Solve $2x^2-5x+3=0$ .

$x^2-\cfrac{5x}{2}+\cfrac{3}{2} = 0$

$x^2-\cfrac{10x}{4} + \cfrac{25}{16} - \cfrac{25}{16} + \cfrac{3}{2} = 0$

$(x-\cfrac{5}{2})^2 = \cfrac{1}{16}$

$(x-\cfrac{5}{2}) = \pm \cfrac{1}{4}$

$x = \cfrac{11}{4}$ or

$\cfrac{9}{4}$

Solve:
$2x^2+x+4=0$ .

$2{ x }^{ 2 }+x+4=0\\ x=\cfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a }$

here ,

$b=1 , a=2 ,c=4$

$x=\cfrac { -1\pm \sqrt { 1-32 } }{ 4 } =\cfrac { -1\pm \sqrt { -31 } }{ 4 } \\ x=\cfrac { -1\pm i\sqrt { 31 } }{ 4 } \quad ,i=\sqrt { -1 }$

Solve ${x^2} - 4x + 1 = 0$ by completing square method.

$\\x^2-4x+1=0$

$\\(x-2)^2-4+1=0$

$\\(x-2)^2=3$

$\\(x-2)=+\sqrt3\>or\>-\sqrt3$

$\\x=2+\sqrt3\>or\>x=2-\sqrt3$

Write the equation by the method of completing the square.
$x^{2}+7x-6=0$

$x^2+7x-6=0$

Here,

$a=1,\,b=7,\,c=-6$

$\Rightarrow$

$x^2+7x=6$

Now,

$\left(\dfrac{b}{2}\right)^2=\left(\dfrac{7}{2}\right)^2=\dfrac{49}{4}$

Adding

$\dfrac{49}{4}$ on both sides of equation

$\Rightarrow$

$x^2+7x+\dfrac{49}{4}=6+\dfrac{49}{4}$

$\Rightarrow$

$\left(x+\dfrac{7}{2}\right)^2=\dfrac{24+49}{4}$

$\Rightarrow$

$\left(x+\dfrac{7}{2}\right)^2=\dfrac{73}{4}$

$\Rightarrow$

$x+\dfrac{7}{2}=\pm\dfrac{\sqrt{73}}{2}$

$\Rightarrow$

$x=\dfrac{\sqrt{73}-7}{2}$ and

$x=-\dfrac{\sqrt{73}-7}{2}$

Find the roots of the equations by the method of completing the square.
$x^{2}-10x+9=0$

$x^2-10x+9=0$

$\Rightarrow$ Here,

$a=1,\,b=-10,\,c=9$

$\Rightarrow$

$x^2-10x=-9$

Now,

$\left(\dfrac{b}{2}\right)^2=\left(\dfrac{10}{2}\right)^2=25$

Adding

$25$ on both sides,

$\Rightarrow$

$x^2-10x+25=-9+25$

$\Rightarrow$

$(x-5)^2=16$

$\Rightarrow$

$x-5=\pm4$

$\Rightarrow$

$x-5=4$ and

$x-5=-4$

$\therefore$

$x=9$ and

$x=1$

Find the factor of the polynomial given below.
$12x^{2}+16x+77$

Factor of polynomial -

$12x^{2}+16x+77$

$(\sqrt{12}x)^{2}+16x+77$

$(\sqrt{12}x)^{2}+16x+77+\left(\dfrac{4}{\sqrt{3}}\right)^{2}-\left(\dfrac{4}{\sqrt{3}}\right)^{2}$

$(\sqrt{12}x)^{2}+16x+\left(\dfrac{4}{\sqrt{3}}\right)^{2}+77-\left(\dfrac{4}{\sqrt{3}}\right)^{2}$

$=\left(\sqrt{12}x+\dfrac{4}{\sqrt{3}}\right)^{2}+77-\dfrac{16}{3}$

$=\left(\sqrt{12}x+\dfrac{4}{\sqrt{3}}\right)^{2}+\dfrac{215}{3}$

$=2\sqrt{12}b=16$

$\displaystyle b=\frac{8}{\sqrt{12}}=\frac{4}{\sqrt{3}}$

Solve the quadratic equation.
$8 x ^ { 2 } - 22 x - 21 = 0$

Given,

$8x^2-22x-21=0$

$8x^2-28x+6x-21=0$

$4x(2x-7)+3(2x-7)=0$

$(2x-7)(4x+3)=0$

$\therefore x=-\dfrac{3}{4},\dfrac{7}{2}$

solve:
$\dfrac{20\pm \sqrt{400-4(5)(18)}}{2(5)}$ =?

$\dfrac{20\pm \sqrt{400-4(5)(18)}}{2(5)}$

$=\dfrac{20\pm \sqrt{400-360}}{10}$

$=\dfrac{20\pm \sqrt{40}}{10}$

$=\dfrac{20\pm 2\sqrt{10}}{10}$

$=2\pm\dfrac{\sqrt {10}}{5}$

Find the values of $'k'$ $2x^{2}+kx+3=0$ so that they have two equal roots ?

Given equation has equal roots,

So, its Discriminant,

$D=0$

$D=k^2-4(2)(3)=0$

$\implies k^2=24$

$\implies k=_-^+\sqrt{24}$

Evaluate
$6x+29=\dfrac{5}{x}$

$6x+29=\dfrac{5}{x}$

$x(6x+29)=5$

$6x^2+29x-5$

By Shridharacharya

$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$

$x=\dfrac{-29\pm\sqrt{29^2-4\times6\times(-5)}}{2\times6}$

$x=\dfrac{-29\pm31}{12}$

$x=\dfrac{-29+31}{12}$

$x=\dfrac{2}{12}$

$x=\dfrac{1}{6}$

$x=\dfrac{-29-31}{12}$

$x=\dfrac{-60}{12}$

$x=-5$

Therefore,

$x=\dfrac{1}{6} \ or\ -5$

$(2x-1) (x-3) = (x+5)(x-1)$
Solve the above equations

$(2x-1)(x-3)=(x+5)(x-1)$

$\Rightarrow 2x^{2}-6x-x+3=x^{2}-x+5x-5$

$\Rightarrow x^{2}-11x+8=0$

$\Rightarrow x=\dfrac{-(11)\pm \sqrt{(-11)^{2}-4(1)(8)}}{2(1)}$

$x=\dfrac{11\pm \sqrt{81}}{2}$

Solve using formula.
$5x^{2} + 13x + 8 = 0$ .

$5x^2+13x+8=0$

$a=5,b=13,c=8$

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\dfrac{-13\pm \sqrt{13^2-4\cdot 5\cdot 8}}{2\cdot 5}$

$=\dfrac{-13\pm3}{10}$

$x=-1,-\dfrac{8}{5}$

Find the roots of the equation $2x^2 - x + \dfrac {1}{8} = 0$

Roots are

$\dfrac{1}{4} , \dfrac{1}{4}$
1085818_1142927_ans_35d84b2ced7c46ae82345a63229793e5.jpeg

Solve the quadratic equation $(x-2)^{2}+1=17$

According to question,

$(x-1)^2+1=17$

$(x-1)^2=16$

$(x-1)^2=4^2$

$x-1=4$ &

$x-1=-4$

$x=5$ &

$x=-3$

Solve using formula.
$5m^{2} - 4m - 2 = 0$ .

$5m^2-4m-2=0$

$a=5,b=-4,c=-2$

$m=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$m=\dfrac{-\left(-4\right)\pm\sqrt{\left(-4\right)^2-4\cdot 5\left(-2\right)}}{2\cdot 5}$

$=\dfrac{4\pm\sqrt{56}}{10}$

$m=\dfrac{2\pm\sqrt{14}}{5}$

Solve using formula.
$x^{2} - 3x - 2 = 0$ .

$x^{2}-3x-2 = 0$

$a=1,b=-3,c=-2$

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\dfrac{-\left(-3\right)\pm\sqrt{\left(-3\right)^2-4\cdot 1\left(-2\right)}}{2\cdot 1}$

$x=\dfrac{3\pm\sqrt{17}}{2}$

Solve using the Quadratic formula.
$3m^{2} + 2m - 7 = 0$ .

The quadratic formula for the standard Quadratic equation of the form :

$ax^2+bx+c=0$ is :

$x={\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}}$

Now Comparing the given equation

$3m^{2} + 2m - 7 = 0$ to the standard form we get:

$a=3$ ,

$b=2$ and

$c=-7$

Substituting value of a,b and c in the quadratic formula we get:

$x={\dfrac{-2\pm \sqrt{2^2-4\times 3 \times (-7)}}{2\times3}}$

$\Rightarrow x={\dfrac{-2\pm \sqrt{88}}{6}}$

$\Rightarrow x={\dfrac{2\times(-1\pm\sqrt{22})}{2\times3}}$

$\therefore$

$x={\dfrac{(-1+\sqrt{22})}{2}}$ or

$x={\dfrac{(-1-\sqrt{22})}{2}}$

Is $x=-2$ a solution of the equation ${ x }^{ 2 }-2x+8=0$ ?

Let,

$p(x)=x^2-2x+8$

$\implies p(-2)=(-2)^2-(-2)2+8$

$\implies p(-2)=16$

Hence it is not the solution of given eq.

Find the roots of $ax^2 + bx + c = 0 (a \neq 0)$ by the method of completing the square.

$ax^2+bx+c=0$

$\Rightarrow ax^2+bx+\left(\dfrac{b}{2\sqrt{a}}\right)^2-\left(\dfrac{b}{2\sqrt{a}}\right)^2+c=0$

$\Rightarrow \left(\sqrt{a}x+\dfrac{b}{2\sqrt{a}}\right)^2-\dfrac{b^2}{4a}+c=0$

$\Rightarrow \left(\sqrt{a}+\dfrac{b}{2\sqrt{a}}\right)^2-\left(\sqrt{\dfrac{b^2-ac}{4a}}\right)^2=0$

$\Rightarrow \left(\sqrt{a}x+\dfrac{b}{2\sqrt{a}}+\sqrt{\dfrac{b^2-4ac}{4a}}\right)\left(\sqrt{a}x+\dfrac{b}{2\sqrt{a}}-\sqrt{\dfrac{b^2-4ac}{2a}}\right)=0$

$\sqrt{a}x+\dfrac{b}{2\sqrt{a}}+\sqrt{\dfrac{b^2-4ac}{4a}}=0$ ,

$\sqrt{a}x+\dfrac{b}{2\sqrt{a}}-\sqrt{\dfrac{b^2-4ac}{2a}}=0$

$x=\dfrac{-b+\sqrt{b^2-4ac}}{2\sqrt{a}\cdot\sqrt{a}}, x=\dfrac{-b-\sqrt{b^2-4ac}}{2\sqrt{a}\cdot \sqrt{a}}$

$\therefore x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$ .

How can solve by completing square method $x^2 - 5x + 5 = 0$

$x^{2}-5x+5=0$

$x^{2}-5x=-5$

(1) Divide the equation by the coefficient of

$x^{2}$

$x^{2}-\cfrac{5}{1}x=-\cfrac{5}{1}$

(2) Add the square of half the coefficient of

$x$ , both sides

$x^{2}-5x+\left ( \cfrac{5}{2} \right )^{2}=-5+\left ( \cfrac{5}{2} \right )^{2}$

$\left ( x-\cfrac{5}{2} \right )^{2}=-5+\cfrac{25}{4}=\cfrac{5}{4}$

$\Rightarrow x-\cfrac{5}{2}=\pm \sqrt{\cfrac{5}{4}}=\pm \cfrac{\sqrt{5}}{2}$

$x=\cfrac{5}{2}\pm \cfrac{\sqrt{5}}{2}$

Solve $(x^{2}-2x+1)^{n+1}=1$

1183200_1154060_ans_85b11f5540ea4645903a2bfb1257ace2.jpg

$5x( x+2) = 3$

$5x \left( x + 2 \right) = 3$

$5x \left( x \right) + 5x \left( 2 \right) = 3$

$5 {x}^{2} + 10x = 3$

$5 {x}^{2} + 10x - 3 = 0$

Here,

$a = 5, b = 10, c = -3$

Now, by quadratic formula, we have

$x = \cfrac{-10 \pm \sqrt{{\left( 10 \right)}^{2} - \left( 4 \times \left( 5 \right) \times \left( -3 \right) \right)}}{2 \times 5}$

$\Rightarrow x = \cfrac{-10 \pm \sqrt{100 + 60}}{10}$

$\Rightarrow x = \cfrac{-10 \pm 4 \sqrt{10}}{10}$

$\Rightarrow x = \cfrac{-5 \pm 2 \sqrt{10}}{5}$

Hence for the given expression,

$x = \cfrac{-5 \pm 2 \sqrt{10}}{5}$ .

The sum of a natural number and its positive square root is $132$ . Find the number.

suppose requires natural number

$=x$

sum of natural number and its square root

$=x+\sqrt x$

putting

$\begin{array}{l} \sqrt { x } =y \\ x={ y^{ 2 } } \end{array}$

$\begin{array}{l} { y^{ 2 } }+y=132 \\ { y^{ 2 } }+12y-11y-132=0 \\ y\left( { y+12 } \right) -11\left( { y+12 } \right) =0 \\ \left( { y+12 } \right) \left( { y-11 } \right) \\ y=11 \\ \sqrt { x } =11 \\ x={ \left( { 11 } \right) ^{ 2 } } \\ x=121 \end{array}$

The sum of a natural number and its square is $156$ . Find the number.

Suppose the natural number

$=x$

its square

${x^2}$

$\begin{array}{l} x+{ x^{ 2 } }=156 \\ { x^{ 2 } }+x-156=0 \\ { x^{ 2 } }+13x-12x-156=0 \\ x\left( { x+13 } \right) -12\left( { x+13 } \right) =0 \\ \left( { x+13 } \right) \left( { x-12 } \right) \\ x=12 \\ x=-13 \end{array}$

$x=$ 12

Solve:
${ x }^{ 2 }+8x+16= ?$

$x^2+8x+16=0$

Here,

$a=1,\,b=8,\,c=16$

$\Rightarrow$

$x^2+8x=-16$

Now,

$\left(\dfrac{b}{2}\right)^2=\left(\dfrac{8}{2}\right)^2=16$

Adding

$16$ on both sides we get,

$\Rightarrow$

$x^2+8x+16=-16+16$

$\Rightarrow$

$(x+4)^2=0$

$\Rightarrow$

$(x+4)(x+4)=0$

$\therefore$

$x=-4,\,-4$

For $p=99$ then find the value of $p^3+3p^2+3p$

We have,

$p=99$

Since,

$\Rightarrow {{p}^{3}}+3{{p}^{2}}+3p+1-1$

$\Rightarrow {{\left( p+1 \right)}^{3}}-1$

$\Rightarrow {{\left( 99+1 \right)}^{3}}-1$

$\Rightarrow {{\left( 100 \right)}^{3}}-1$

$\Rightarrow 1000000-1$

$\Rightarrow 999999$

Hence, this is the answer.

Find the roots of the equation $5x^{2}-6x-2=0$ .

$\Rightarrow$ The given quadratic equation is

$5x^2-6x-2=0$ , comparing it with

$ax^2+bx+c=0$

$\Rightarrow$ We get,

$a=5,\,b=-6,\,c=-2$

$\Rightarrow$

$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$

$=\dfrac{-(-6)\pm\sqrt{(-6)^2-4(5)(-2)}}{2(5)}$

$=\dfrac{6\pm\sqrt{36+40}}{10}$

$=\dfrac{6\pm\sqrt{76}}{10}$

$=\dfrac{6\pm2\sqrt{19}}{10}$

$=\dfrac{3\pm\sqrt{19}}{5}$

$x=\dfrac{3+\sqrt{19}}{5}$ and

$x=\dfrac{3-\sqrt{19}}{5}$

simplify :
$\left( {x - 3} \right)\left( {2x + 1} \right) = x\left( {x + 5} \right)$

1125400_1201300_ans_ed0c37a0c7a54fcd967ffdd73aa512cc.JPG

Find the value of k for which the following equations has equal roots. $x^{2}+4kx+(k^{2}-k+2)=0.$

$x^2+4kx+(k^2-k+2)=0$

For equal roots

$D=0$

$D=b^2-4ac$

$D=(4k)^2-4(k^2-k+2)=0$

$\implies 3k^2+k-2=0$

$\implies 3k(k+1)-2(k+1)=0$

$\implies k=-1,k=2/3$

For

$k=-1,\quad x^2-4x+4=0$

$\implies (x-2)^2=0\implies x=\pm 2$

For

$k=2/3, \quad x^2+(8/3)x+(16/9)=0$

Solve ${{x}^{2}}-12x+36=0$

Consider given equation,

${{x}^{2}}-12x+36=0$

${{x}^{2}}-6x-6x+36=0$

$x\left( x-6 \right)-6\left( x-6 \right)=0$

$\left( x-6 \right)\left( x-6 \right)=0$

Hence, $x=6,6$

Hence, this is the answer.

Factorise $8x ^{2}-34x +30=0$

$8x^2-34x+30=8x^2-24x-10x+30=8x(x-3)-10(x-3)=(x-3)(8x-10)$

Find factors of $x ^ { 4 } + 2 x ^ { 3 } - 7 x ^ { 2 } - 8 x + 12$

$f(x)={X}^{4}+2{x}^{3}-7{x}^{2}-8x+12$

$A+x=0$

$f(x)=0$ By hit and trial

so,

$(n-1)$ is its factor

$f(x)=(x-1)({x}^{3}+3{x}^{2}-4x-12)$

$=(x-1)(x-2)({x}^{2}+5x+6)$

$f(x)=(x-1)(x-2)(x+5)(x+7)$

$x^{2}-5x+4$ =

Given,

$x^2-5x+4=0$

$x^2-x-4x+4=0$

$x(x-1)-4(x-1)=0$

$(x-1)(x-4)=0$

$\therefore x=1,4$

Solve:
$9x^2-3x-2=0$

Using the quadratic formula:-

$x = \dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a} = \dfrac{3\pm \sqrt{9+72}}{18}$

$x = \dfrac{3\pm 9}{18}$

so,

$x = \dfrac{3+9}{18} = \dfrac{12}{18} = \dfrac{2}{3}$ or

$x = \dfrac{3-9}{18} = \dfrac{-6}{18} = \dfrac{-1}{3}$

Find the roots of the quadratic equation $x - \dfrac{1}{x} = 3$ .

Given equation is

$x-\cfrac{1}{x}=3$

Solving the equation further, we get:

$\Rightarrow x^2-3x-1=0\quad ......(i)$

We know that, for a quadratic equation of the form

$ax^2+bx+c=0$ ,

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

For

$(i)$ , we have

$a=1,\ b=-3\text{ and }c=-1$

$\therefore \ x=\cfrac{3\pm\sqrt{(-3)^2-4(1)(-1)}}{2(1)}$

$\Rightarrow x=\cfrac{3\pm\sqrt{13}}2{}$

Hence,

$x=\cfrac{3+\sqrt{13}}2{}$

$,\cfrac{3-\sqrt{13}}2{}$

Find the roots of $5x^2+13x+8=0$ by using quadratic formula.

$\Rightarrow$ The given quadratic equation is

$5x^2+13x+8=0$ , comparing it with

$ax^2+bx+c=0$

$\Rightarrow$ We get,

$a=5,\,b=13,\,c=8$

$\Rightarrow$

$x=\dfrac{-b\pm\sqrt{b^-4ac}}{2a}$

$=\dfrac{-13\pm\sqrt{(13)^2-4(5)(8)}}{2(5)}$

$=\dfrac{-13\pm\sqrt{169-160}}{10}$

$=\dfrac{-13\pm\sqrt{9}}{10}$

$=\dfrac{-13\pm3}{10}$

$\Rightarrow$

$x=\dfrac{-13+3}{10}$ and

$x=\dfrac{-13-3}{10}$

$\therefore$

$x=-1$ and

$x=\dfrac{-8}{5}$

If $(x^{2}-2x+1)$ =0 then the value of x is

${{x}^{2}}-2x+1=0$

$\Rightarrow {{\left( x-1 \right)}^{2}}=0$

$\Rightarrow (x-1)(x-1)=0$

$x=1$

What is the formula to solve general form of quadratic equation and what is its discriminant value.

Quadratic equation :

$ax^2 + bx + c = 0$

Discriminant ,

$D = b^2 - 4 ac$

Now,

$x = \dfrac{-b \pm \sqrt{D}}{2a}$

Write the following quadratic equation in the form of $ax^2 + bx + c$ , then write the values of a,b,c:
$2y=10-y^2$

1338766_1264392_ans_68e0d21f62124ca69a5932ddb5a46226.jpg

Find the roots of the following quadratic equation (if they exist ) by the method of completing the square.
$4x^{2}+4\sqrt {3}x+3=0$

Given,

$4x^{2}+4\sqrt{3}x+3=0$

The standard quadratic equation is

$ax^2+bx+c=0$

$D=b^2-4ac= 48-4(4)(3)=0$

Therefore, the roots exist and are real and equal.

Equation can be rewritten as

$4x^{2}+2\sqrt{3}x+2\sqrt{3}x+3=0$

$2x(2x+\sqrt{3})+\sqrt{3}(2x+\sqrt{3})=0$

$(2x+\sqrt{3})^{2}=0$

$\Rightarrow x=-\dfrac{\sqrt{3}}{2}$

Solve: $4x^2-2(a^2+b^2)x+a^2b^2=0$

$4x^2-2a^2x+2b^2x+a^2b^2=0$

$2x(2x-a^2)-b^2(2x-a^2)=0$

$(2x-a^2)(2x-b^2)=0$

$2x-b^2=0 \ \ \ \ \ \ \ 2x-a^2=0$

$x=\dfrac{b^2}{2}\ \ \ \ x=\dfrac{a^2}{2}$

Find the discrimination of the quadratic equation $2x^{2}-4x+3=0$

1125118_1224185_ans_0f08ab9071a24413855afc022d73e796.jpg

Solve:
$\sqrt { 2 } x ^ { 2 } + 7 x + 5 \sqrt { 2 } = 0$

Given,

$\sqrt{2}x^2+7x+5\sqrt{2}=0$

$\sqrt{2}x^2+2x+5x+5\sqrt{2}=0$

$\sqrt{2}x(x+\sqrt{2})+5(x+\sqrt{2})=0$

$(x+\sqrt{2})(\sqrt{2}x+5)=0$

$x=-\sqrt{2},x=-\dfrac{5}{\sqrt{2}}$

What must be subtracted from $3a^{2}-6ab-3b^{2}-1$ to get $4a^{2}-7ab-4b^{2}$ .

Let x be subtracted.

Then,

$(3a^2-6ab-3b^2-1)-x=4a^2-7ab-4b^2$

$\Rightarrow 3a^2-6ab-3b^2-1-4a^2+7ab+4b^2=x$

$\Rightarrow 3a^2-4a^2-6ab+7ab-3b^2+4b^2-1=x$

$\Rightarrow \therefore x=ab-a^2+b^2-1$ .

1155507_1282335_ans_71e9ea8551e146d48567abc055b0dfce.jpg

Solve: $2x^2 - x^2 =$ ?

$2x^{2}-x^{2}=(2-1)x^{2}$

$\Rightarrow x^{2}$

1117415_1278642_ans_977358429e0345ffb9e4678c886c92e1.JPG

Solve using quadratic formula,
$3x^{2}+2(3+2a)\ x+8a=0$

$3x^2+2\left(3+2a\right)x+8a=0$

$3x^2+\left(6+4a\right)x+8a=0$

$x=\dfrac{-\left(6+4a\right)\pm\sqrt{\left(6+4a\right)^2-4\cdot 3\cdot 8a}}{2\cdot 3}$

$x=-2,-\dfrac{4a}{3}$

Equation $y = x ^ { 2 } + 7 x - 5$ can be written in the form $y = ( x + a ) ^ { 2 } +$ $b$ . Find the value of $a$ and $b$ .

Given:

$x^{2} + 7x - 5$

$= x^{2} +2.\left ( \dfrac{7}{2} \right )x + \left ( \dfrac{7}{2} \right )^{2} -\left ( \dfrac{7}{2} \right )^{2}-5$

$= \left(x + \dfrac{7}{2} \right)^{2} - \left(\dfrac{49}{4} + 5 \right)$

$=\left (x + \dfrac{7}{2} \right)^{2} - \displaystyle \left(\dfrac{49 + 20}{4} \right)$

$=\left (x + \dfrac{7}{2} \right)^{2} - \left(\dfrac{69}{4} \right)$

$= (x + a)^{2} + b$

$\therefore a = 7/2$ and

$b = -69/4.$

Solve for $x$ :
$x ^ { 2 } + 21 x - 100=0$

$x^2+21x-100=0$

$x^2-4x+25x-100=0$

$x(x-4)+25(x-4)=0$

$(x-4)(x+25)=0$

$\therefore x=-25,4$

Solve :
$\sqrt {2x+\sqrt {2x+4}}=4$

$\sqrt{2x+\sqrt{2x+4}}=4$

squaring on both sides

$2x+\sqrt{2x+4}=16$

$\sqrt{2x+4}=16-2x$

squaring on both sides

$2x+4=256-64x+4x^2$

$4x^2-66x+252=0$

$x=\dfrac{-\left(-66\right)\pm\sqrt{\left(-66\right)^2-4\cdot 4\cdot 252}}{2\cdot 4}$

$x=\dfrac{21}{2},6$

Check whether the following is Quadratic equations:
${\left( {x + 1} \right)^2} = 2\left( {x - 3} \right)$

${\left(x+1\right)}^{2}=2\left(x−3\right)$

$\Rightarrow {x}^{2}+2x+1-2x+6=0$

$\Rightarrow {x}^{2}+7=0$ is a quadratic equation where degree of

$x$ is

$2$

Solve:
$2x^{2}+5x+3=$ ?

$2x^2+5x+3=0$

$2x^2+2x+3x+3=0$

$2x(x+1)+3(x+1)=0$

$(x+1)(2x+3)=0$

$x=-1,-\dfrac{3}{2}$

Solve :
$\sqrt {2x+9}+x=13$

$\sqrt{2x+9}+x=13$

$\sqrt{2x+9}=13-x$

squaring on both sides, we get

$2x+9=169-26x+x^2$

$x^2-28x+160=0$

$x=\dfrac{-\left(-28\right)\pm \sqrt{\left(-28\right)^2-4\cdot 1\cdot 160}}{2\cdot 1}$

$x=8,20$

Solve:
$\sqrt {3x^{2}-2}+1=2x$

$\sqrt{3x^2-2}+1=2x$

$\sqrt{3x^2-2}=2x-1$

Squaring on both sides

$\Rightarrow 3x^2-2=4x^2-4x+1$

$\Rightarrow x^2-4x+3=0$

$\Rightarrow x^2-x-3x+3=0$

$\Rightarrow x(x-1)-3(x-1)=0$

$\Rightarrow (x-1)(x-3)=0$

$\therefore x=1,3$

Solve the following by using the method of completing square.
$3y^{2}-7y-20=0$

According to question,

$\begin{array}{l} \Rightarrow 3\left[ { { y^{ 2 } }-\dfrac { 7 }{ 3 } y+\dfrac { { 49 } }{ { 36 } } -\dfrac { { 49 } }{ { 36 } } } \right] -20=0 \\ \Rightarrow 3{ \left( { y-\dfrac { 7 }{ 6 } } \right) ^{ 2 } }-\dfrac { { 49 } }{ { 12 } } -20=0 \\ =20+\dfrac { { 49 } }{ { 12 } } \\ \Rightarrow { \left( { y-\dfrac { 7 }{ 6 } } \right) ^{ 2 } }=\dfrac { { 289 } }{ { 36 } } \\ hence,we\, \, get \\ \Rightarrow y=\dfrac { { -10 } }{ 6 } =\dfrac { { -5 } }{ 3 } \\ \Rightarrow y=\dfrac { { 24 } }{ 6 } =4 \end{array}$

Solve the following by using the method of completing square.
$6x^{2}-11x+3=0$

We have,

$\begin{array}{l} 6{ x^{ 2 } }-11x+3=0 \\ \Rightarrow 6\left[ { { x^{ 2 } }-\dfrac { { 11 } }{ 6 } x+{ { \left( { \dfrac { { 11 } }{ { 12 } } } \right) }^{ 2 } }-{ { \left( { \dfrac { { 11 } }{ { 12 } } } \right) }^{ 2 } } } \right] +3=0 \\ \Rightarrow 6{ \left( { x-\dfrac { { 11 } }{ { 12 } } } \right) ^{ 2 } }-6\times \dfrac { { 121 } }{ { 144 } } +3=0 \\ \Rightarrow 6{ \left( { x-\dfrac { { 11 } }{ { 12 } } } \right) ^{ 2 } }=\dfrac { { 121 } }{ { 24 } } -3 \\ \Rightarrow 6{ \left( { x-\dfrac { { 11 } }{ { 12 } } } \right) ^{ 2 } }=\dfrac { { 49 } }{ { 24 } } \\ \Rightarrow { \left( { x-\dfrac { { 11 } }{ { 12 } } } \right) ^{ 2 } }=\dfrac { { 49 } }{ { 144 } } \\ \Rightarrow x-\dfrac { { 11 } }{ { 12 } } =\pm \dfrac { 7 }{ { 12 } } \\ \therefore x=\dfrac { 3 }{ 2 } \, \, or\, \, x=\dfrac { 1 }{ 3 } \end{array}$

Write constant term
$7x^2-11$

Constant term of

$7x^2-11$ is

$-11$

Obtain the roots of the following quadratic equation by using the general formula the solution:
$3x^{2}-2x+2=0$

We have the given equation

$3{x^2} - 2x + 2 = 0$

Here,

$a=3$

$b=-2$

$c=-2$

The formula for the roots of quadratic equation is

$\dfrac{{ - b \pm {{\left( {{b^2} - 4ac} \right)}^{\dfrac{1}{2}}}}}{{2a}}$

now,

First root

${x_1} = {\dfrac{{ - \left( { - 2} \right) + \left[ {{{\left( { - 2} \right)}^2} - 4 \times 3 \times \left( { - 2} \right)} \right]}}{{2 \times 3}}^{\dfrac{1}{2}}}$

$= \dfrac{{1 + \sqrt 7 }}{3}$

And, second roots

${x_2} = {\dfrac{{ - \left( { - 2} \right) - \left[ {{{\left( { - 2} \right)}^2} - 4 \times 3 \times \left( { - 2} \right)} \right]}}{{2 \times 3}}^{\dfrac{1}{2}}}$

$= \dfrac{{1 - \sqrt 7 }}{3}$

Hence,

$\dfrac{{1 + \sqrt 7 }}{3},\,\dfrac{{1 - \sqrt 7 }}{3}$ are the roots of given quadratic equation.

Solve for x: $4x^{2}+14x+6$

$4{x^2} + 14x + 6$

$= 4{x^2} + 12x + 2x + 6$

$= 4x\left( {x + 3} \right) + 2\left( {x + 3} \right)$

$= \left( {4x + 2} \right)\left( {x + 3} \right)$

$= x = \dfrac{{ - 1}}{2},\,x = 3$

Solve the following by using the method of completing square.
$5x^{2}-4x-10=0$

Given,

$\begin{array}{l} 5{ x^{ 2 } }-4x-10=0 \\ \Rightarrow 5\left[ { { x^{ 2 } }-\dfrac { 4 }{ 5 } x+{ { \left( { \dfrac { 2 }{ 5 } } \right) }^{ 2 } }-{ { \left( { \dfrac { 2 }{ 5 } } \right) }^{ 2 } } } \right] -10=0 \\ \Rightarrow 5{ \left( { x-\dfrac { 2 }{ 5 } } \right) ^{ 2 } }-\dfrac { 4 }{ 5 } -10=0 \\ \Rightarrow { \left( { x-\dfrac { 2 }{ 5 } } \right) ^{ 2 } }=\dfrac { { 54 } }{ { 25 } } \\ x-\dfrac { 2 }{ 5 } =\pm \dfrac { { \sqrt { 54 } } }{ { 25 } } \\ x=\dfrac { { 2-\sqrt { 54 } } }{ 5 } \, \, \, or\, \, \dfrac { { 2+\sqrt { 54 } } }{ 5 } \end{array}$

Solve the following.
$ab{x^2} + ({b^2} - ac)x - bc = 0$

$abx^{2} + (b^{2}-ac) x-bc=0.$

$x = \frac{-B \pm \sqrt{B^{2}-4AC}}{2A}$

$= \frac{-(b^{2}-ac) \pm \sqrt{(b^{2}-ac)^{2} + 4ab.bc}}{2 \times ab}$

$x = \frac{-(b^{2}- ac) \pm (b^{2} + ac)}{2ab} = \frac{4ac}{2ab} or \frac{-2b^{2}}{2ab}$

$x = \frac{2c}{b} , \frac{-2b}{a}$

1212359_1298462_ans_8ba11ae03d0049659885c6354d9230f2.JPG

Solve : $x^{2}-8x+15=0$ by completing a square method.

Given equation

${x^2} - 8x + 15 = 0$

Let

$16$ add and subtraction in the given equation.

${x^2} - 8x + 16 - 16 + 15 = 0$

$\left( {{x^2} - 8x + 16} \right) - 1 = 0$

${\left( {x - 4} \right)^2} - 1 = 0$

$\begin{matrix} { \left( { x-4 } \right) ^{ 2 } }=1 \\ x-4=\sqrt { 1 } \\ x-4=1 \\ x=1+4=5 \\ \end{matrix}$ ]

Therefore,

$x=5,3$

Write constant term
$3y^2+5y-7$

Constant term of

$3y^2+5y-7$ is

$-7$

Solve.
$\dfrac{{{x^2}}}{9} - \dfrac{2}{3}x + 1 = 0$

Given,

$\dfrac{x^2}{9}-\dfrac{2}{3}x+1=0$

$x^2-6x+9=0$

$(x-3)(x-3)=0$

$x=3$

Find the value of $x$ : $x ^ { 2 } + 2 x - 7$

Given,

$x^2+2x-7=0$

$a=1,b=2,c=-7$

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\dfrac{-2\pm \sqrt{2^2-4(1)(-7)}}{2(1)}$

$=\dfrac{-2 \pm 4\sqrt{2}}{2}$

$=-1\pm 2\sqrt{2}$

solve.
$21{x^2} - 8x - 4 = 0$

Given quadratic equation

$21x^{2} -8x -4 = 0$

$\displaystyle x= \frac{-b\pm \sqrt{b^{2}-4ac}}{2a}\\\;\; = \frac{-(8)\pm \sqrt{64-4\times 21\times (-4)}}{2\times 21}$

$\displaystyle \;\;= \frac{8\pm \sqrt{64+936}}{42} = \frac{8\pm 20}{42} = \frac{28}{42};\frac{-12}{42}$

$\displaystyle \therefore x = \frac{2}{3}, \frac{-2}{7}$

Solve : $3x^{2}-4x+\dfrac{20}{3}=0$

Given,

$3x^2-4x+\dfrac{20}{3}=0$

$\Rightarrow 9x^2-12x+20=0$

$a=9,b=-12,c=20$

$x=\dfrac {-b \pm \sqrt{b^2-4ac}}{2a}$

$=\dfrac {12 \pm \sqrt{(-12)^2-4(9)(20)}}{2(9)}$

$=\dfrac{2}{3}\pm i\dfrac{4}{3}$

Solve:
$f(x)=x^{2}-11x+28$

Given that,

$f\left( x \right) = {x^2} - 11x + 28$

${x^2} - 11x + 28 = 0$

$x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$

$= \dfrac{{ - \left( { - 11} \right) \pm \sqrt {{{\left( { - 11} \right)}^2} - 4.1.28} }}{{2.1}}$

$= \dfrac{{11 \pm \sqrt {121 - 112} }}{2}$

$= \dfrac{{11 \pm \sqrt 9 }}{2}$

$= \dfrac{{11 + 3}}{2}, = \dfrac{{11 - 3}}{2}$

$x=7,4$

Since ,

We get

$x=7,4$

Simplify $\frac{a}{{x - a}} + \frac{b}{{x - b}} = \frac{{2c}}{{x - c}}$

$\frac{a}{x-a} + \frac{b}{x-b} = \frac{2c}{x-c}$

$\Rightarrow \frac{a(x-b)+b(x-a)}{(x-a)(x-b)} = \frac{2c}{(x-c)}$

$\Rightarrow (ax-ab+xb-ab)(x-c) = 2c (x^{2}-ax-bx+ab)$

$\Rightarrow [(a+b)x-2ab](x-c) = 2cx^{2}-2acx-2bcx+2abx.$

1213352_1305776_ans_79d7a88d0f76488885500eaf5d2f5348.JPG

Obtain the roots of the following quadratic equation by using the general formula the solution:
$\sqrt {3}\ x^{2}+10x-8\sqrt {3}=0$

Formula:

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

Given,

$\sqrt{3}x^2+10x-8\sqrt{3}=0$

$x=\dfrac{-10\pm\sqrt{10^2-4\sqrt{3}\left(-8\sqrt{3}\right)}}{2\sqrt{3}}$

$=\dfrac{-10\pm \sqrt{196}}{2\sqrt{3}}$

$=\dfrac{-10\pm 14}{2\sqrt{3}}$

$x=\dfrac{2\sqrt{3}}{3},-4\sqrt{3}$

Is $\sqrt{2}x^{2} +7x+5\sqrt{2}=0$ quadratic equation. If yes then give reason.

Yes, because its degree is

$2$

Solve :
$3x^{2}-6x+3=0$

$3x^{2}-6x+3=0$

$x^{2}-2x+1=0$

$x^{2}-x-x+1=0$

$x(x-1)-1(x-1)=0$

$(x-1)(x-1)=0$

$x=1,1$

Solve: $9m^{2}-10m+1$

$9{m}^{2}-10m+1=0$

$\Rightarrow 9{m}^{2}-9m-m+1=0$

$\Rightarrow 9m\left(m-1\right)-1\left(m-1\right)=0$

$\Rightarrow \left(9m-1\right)\left(m-1\right)=0$

$\therefore m=\dfrac{1}{9},1$

Solve the following quadratic equation ${ x }^{ 2 }+4x-5=0$ by completing the square method.

Given quadratic equation is

$x^{2}+4x-5=0$

$\implies (x+2)^{2}-4-5=0$

$\implies(x+2)^{2}-9=0$

$\implies(x+2)^{2}-3^{2}=0$

$\implies(x+5)(x-1)=0$

$\implies x=1,-5$

Find the discriminant of quadratic equation $x^{2}-4x+1=0$ .

Discriminant

$=\Delta={b}^{2}-4ac$ where

$a=1,b=-4,c=1$

$\Delta={\left(-4\right)}^{2}-4\times 1\times 1$

$=16-4=12$

Solve : ${ x }^{ 2 }-8x+15=0$ by completing a square method.

$x^2-8{x}+15=0$

$x^2-2(x)(4)+15=0$

$\implies x^2-2(x)(4)+16-1=0$

$\implies x^2-2(x)(4)+4^2=1$

$\implies (x-4)^2=1^2\implies x-4=\pm 1\implies x=4\pm 1\implies x=5,3$

Factorize :
$y^{2}-10y+25$

given,

$y^{2}-10y+25$

$=y^{2}-5y-5y+25$

$=y(y-5)-5(y-5)$

$=(y-5)(y-5)$

$=(y-5)^{2}$

By using the formula, find the roots of the following quadratic equation, $\left(x +7\right)\left(x + 3\right) = 5\left(x+4\right) \left(x +2\right) + 17x$

We have,

$\left(x+7\right)\left(x+3\right)=5\left(x+4\right)\left(x+2\right)+17x$

$x^2+10x+21=5x^2+47x+40$

$-4x^2-37x-19=0$

$4x^2+37x+19=0$

$a=4,b=37,c=19$

Since,

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\dfrac{-\left(37\right)\pm \sqrt{\left(37\right)^2-4\left(4\right)\left(19\right)}}{2\left(4\right)}$

$=\dfrac{37\pm \sqrt{\left(37\right)^2-304}}{8}$

$\therefore x=\dfrac{37\pm \sqrt{1065}}{8}$

Hence, this is the answer.

Find the value of k for which the quadratic equation $(k+4)x^{2}+(k+1)x+1=0$ has equal roots.

Discriminant,

$D=b^{2}-4ac$

$D=(k+1)^{2}-4(k+4)$

$D=k^{2}-2k-15$

$D=(k-5)(k+3)$

If the roots of the given equation are real and equal, then,

$D=0$

$(k-5)(k+3)=0$

$k=5,-3$

Solve $x^{2}-5x-36=0$ .

Given,

$x^{2}-5x-36=0$

$\implies x^{2}-9x+4x-36=0$

$\implies x(x-9)+4(x-9)=0$

$\implies (x-9)(x+4)=0$

$\implies x=9,-4$

Given reason whether the following is an equation or not:
$(x-2)^2=x^2-4x+4$ .

Given,

$\dfrac{dy}{dx}=\dfrac{2x}{1+x^2}-\dfrac{(-2x)}{1-x^2}$ .

This is not an equation as it is an identity.

If $a^{2}+\dfrac {1}{a^{2}}=23$ , find the value of $\left(a+\dfrac {1}{a}\right)$

Given,

$a^{2}+\dfrac {1}{a^{2}}=23$

or,

$\left(a+\dfrac{1}{a}\right)^2-2.a.\dfrac{1}{a}=23$

or,

$\left(a+\dfrac{1}{a}\right)^2=23+2$

or,

$\left(a+\dfrac{1}{a}\right)^2=25$

or,

$\left(a+\dfrac{1}{a}\right)=\pm 5.$

Solve for $x:$
$x^2-5x+6=0$ .

Given the quadratic equation is,

$x^2-5x+6=0$

Splitting the middle term, we get:

$x^2-3x-2x+6=0$

$(x-3)(x-2)=0$

$x=3,2$

$\frac{x-a}{x-b}+\frac{x-b}{x-a}=$

$\dfrac{x-a}{x-b}+\dfrac{x-b}{x-a}\\\dfrac{(x-a)^2+(x-b)^2}{(x-a)(x-b)}\\\dfrac{x^2-2ax-a^2+x^2-2bx-b^2}{x^2-(a+b)x+ab}\\\dfrac{2x^2-2(a+b)x-(a^2+b^2)}{x^2-(a+b)x+ab}$

Solve :
$x^{2}+10x+25=0$

$x^{2}+10x+25=0$

$x^{2}+5x+5x+25=0$

$x(x+5)+5(x+5)=0$

$(x+5)(x+5)=0$

$x=-5,-5$

Solve :
$x^{2}+4x+4=0$

$$x^{2}+4x+4=0$4

$x^{2}+2x+2x+4=0$

$x(x+2)+2(x+2)=0$

$(x+2)(x+2)=0$

$x=-2,-2$

Solve
$x^2+$ $4x$ $-8$ = 0

Given

$x^2+4{x}-8=0$

$\implies x^2+2(x)(2)+2^{2}-2^2-8=0$

$\implies (x+2)^2-4-8=0$

$\implies (x+2)^2=12\implies x+2=\pm 2\sqrt{3}\implies x=-2\pm 2\sqrt{3}$

Find $\displaystyle x^2 + 5x$ at $x=3$

$x^2+5x$ at

$x=3$

$\implies 3^3+5(3)\\9+15\\24$

For what value of $k$ does the quadratic equation $(k-5)x^{2}+2(k-5)x+2=0$ have equal roots?

Quadratic equation

$ax^2 + bx+c = 0$ has equal roots if

$b^2 - 4ac = 0$

$\Rightarrow [2(k-5)]^2 - 4 (2)(k-5) = 0$

$\Rightarrow 4(k-5)[k-5-2]=0$

$\Rightarrow k=5$ or

$k=7$

Check whether the following are Quadratic equations
${ x }^{ 2 }+3x+1={ \left( x-2 \right) }^{ 2 }$

${x}^{2}+3x+1={\left(x-2\right)}^{2}$

${x}^{2}+3x+1={x}^{2}-4x+4$

$\Rightarrow {x}^{2}+3x+1-{x}^{2}+4x-4=0$

$\Rightarrow 7x-3=0$ has its highest power

$1$

Hence it is not a quadratic equation.

Check whether the following is a quadratic equation or not.
$(x+1)^2=2(x-3)$

Given the equation is

$(x+1)^2=2(x-3)$

or,

$x^2+2x+1=2x-6$

or,

$x^2+7=0$ .

This is of the form

$ax^2+bx+c=0$ with

$a\ne 0$ .

So this is a quadratic equation.

Write the discriminant of the following equation :
$x^{2}-4x+2=0$

Consider the quadratic equation

$x^{2}-4x+2=0$ in the form

$ax^2+bx+c$

Here,

$a=1, b=-4, c=2$

Discriminant of the quadratic equation

$D=b^{2}-4ac$

$=(-4)^2-8$

$=8$

If $x^{2}+\dfrac {1}{x^{2}}=51$ , find the value of $\left(x-\dfrac {1}{x}\right)$

Given,

$x^{2}+\dfrac {1}{x^{2}}=51$

or,

$\left(x-\dfrac{1}{x}\right)^2+2.x.\dfrac{1}{x}=51$

or,

$\left(x-\dfrac{1}{x}\right)^2=51-2$

or,

$\left(x-\dfrac{1}{x}\right)^2=49$

or,

$\left(x-\dfrac{1}{x}\right)=\pm 7.$

If m = 2, find the value of $m^2-m+1$

$m^2-m+1\\2^2-2+1\\4-2+1\\2+1\\3$

Solve:
$x^2=9$

$x^2=9\\x=\sqrt9\\x=\pm3$

Solve:
$x^2+2xy \cot2 \alpha -y^2=0$

Now,

$x^2+2xy \cot2 \alpha -y^2=0$

or,

$x^2+2xy\cot \alpha-y^2(\cos ec^2 \alpha-\cot^2 \alpha)=0$ [ Since

$\cos ec^2 \alpha-\cot^2 \alpha=1$ ]

or,

$(x+y\cot \alpha)^2=(y\cos ec\alpha)^2$

or,

$(x+y\cot \alpha)=\pm y\cos ec\alpha$

or,

$x=y(-\cot \alpha\pm \cos ec\alpha)$

Solve :
$x^{2}-8x+16=0$

$x^{2}-8x+16=0$

$(x-4)^{2}=0$

$x=4$

Solve: ${x}^{2}-4x+1+3=0$

$\Rightarrow {x}^{2}-4x+4=0$

$\Rightarrow {x}^{2}-2\times x\times 2+{2}^{2}=0$

$\Rightarrow {\left(x-2\right)}^{2}=0$

$\therefore x=2$

If $\alpha$ and $\dfrac{1}{\alpha }$ are zeroes of $4x^{2}-17x+k-4$ , find value of k.

Given

$\alpha,\dfrac{1}{\alpha}$ are the zeroes of

$4 x^2-17 x+k-4$

As we know that

Product of zeroes of quadratic polynomial

$a x^2 +b x+c$ is

$\dfrac{c}{a}$

Here

$c=k-4,a=4$

$\implies \alpha\times \dfrac{1}{\alpha}=\dfrac{k-4}{4}$

$\implies 1=\dfrac{k-4}{4}$

$\implies k-4=4$

$\implies k=4+4$

$\implies k=8$

Factorise the polynomial by the method of completing the square.
$p^2+6p -16$

$p^{2}+6p-16=0$

$p^{2}+6p=16$

thrid term =

$(\dfrac{1}{2}\times$ coefficient of

$p)^{2}$

$=(\dfrac{1}{2}\times 6)^{2}=9$

Adding

$9$ on both sides

$p^{2}+6p+9=16+9$

$(p+3)^{2}=25$

Taking square root,

$p+3=\sqrt{25}$

$p+3=+5$ OR

$p+3=-5$

$p=2$ OR

$p=-8$

Thus ,

$p^{2}+6p-16=(p-2)(p+8)$

Write the coefficient of $m^{2}$ in $-4m^{2}+3m-7$

$-4 {m}^{2} + 3m - 7$

Here,

Coefficient of

${m}^{2} = -4$

Find the roots of the quadratics equation $3{ x }^{ 2 }-4\sqrt { 3 }x +4=0$ .

$3x^2-4\sqrt{3}x+4=0$

$3x^2-2\sqrt{3}x-2\sqrt{3}x+4=0$

$\sqrt{3}(\sqrt{3}x-2)-2(\sqrt{3}x-2)=0$

$(\sqrt{3}x-2)(\sqrt{3}x-2)=0$

$(\sqrt{3}x-2)^2=0$

$x=\dfrac{2}{\sqrt{3}}$

Roots

$=\dfrac{2}{\sqrt{3}}, \dfrac{2}{\sqrt{3}}$ .

Solve the given equation by the method of completing the squares:
$x^{2}+12x-45=0$

Given

$x^2+12 x-45=0$

$\implies x^2+2(x)(6)=45$

$\implies x^2+2(x)(6)+6^2=45+6^2$

$\implies (x+6)^2=45+36$

$\implies (x+6)^2=81$

$\implies (x+6)^2=9^2$

$\implies x+6=\pm 9$

$\implies x=-6\pm 9$

$\implies x=-6+9,-6-9$

$\implies x=3,-15$

Find the roots of the following quadratic equation, if they exist, by the method of completing the square:
$2{x}^{2}+x-4=0$

We have

$2{x}^{2}+x-4=0$
On dividing both sides by

$2$ we have

${ x }^{ 2 }+\cfrac{x}{2}-2=0$

$\Rightarrow$

${ x }^{ 2 }+\cfrac{1}{2}x+{ \left( \cfrac { 1 }{ 4 } \right) }^{ 2 }-2=0$

$[b=\cfrac{1}{2}$ (coefficeint of

$x$ )

$=\cfrac{1}{2}\times \cfrac{1}{2}=\cfrac{1}{4}]$

${ \left( x+\cfrac { 1 }{ 4 } \right) }^{ 2 }-\cfrac{1}{16}-2=0$

$\Rightarrow$

${ \left( x+\cfrac { 1 }{ 4 } \right) }^{ 2 }=\cfrac{1}{16}+2=\cfrac{1+32}{16}=\cfrac{33}{16}> 0$
Roots exist

$\therefore$

${ \left( x+\cfrac { 1 }{ 4 } \right) }^{ }=\pm \sqrt{\cfrac{33}{16}}$

$\Rightarrow$

$x+\cfrac{1}{4}=\pm \cfrac{\sqrt{33}}{4}$

$\Rightarrow$

$x+\cfrac{1}{4}=\cfrac{\sqrt{33}}{4}$ or

$x+\cfrac{1}{4}=-\cfrac{\sqrt{33}}{4}$

$\therefore$

$x-\cfrac{1}{4}=+\cfrac{\sqrt{33}}{4}$ or

$x=-\cfrac{1}{4}=-\cfrac{\sqrt{33}}{4}$

$\Rightarrow$

$x=\cfrac{\sqrt{33}-1}{4}$ or

$x=\cfrac{-(\sqrt{33}+1)}{4}$
Hence the roots of given equation are

$\cfrac{\sqrt{33}-1}{4}$ and

$\cfrac{-(\sqrt{33}+1)}{4}$

Evaluate: $\dfrac { 1 }{ \sqrt{ { x }^{ 2 }+2x+9 } }=1$

$\dfrac{1}{\sqrt{{x}^{2}+2x+9}}=1$

$\Rightarrow \sqrt{{x}^{2}+2x+9}=1$

$\Rightarrow {x}^{2}+2x+9-1=0$

$\Rightarrow {x}^{2}+2x+8=0$

$\Rightarrow {x}^{2}+2\times 1\times x+1-1+8=0$

$\Rightarrow {\left(x+1\right)}^{2}+7=0$

$\Rightarrow {\left(x+1\right)}^{2}=-7$

$\Rightarrow x+1=\pm\sqrt{-7}$

$\therefore x=-1\pm i\sqrt{7}$

Find the discriminant of the quadratic equation $4\sqrt{2}{x}^{2}+8x+2\sqrt{2}=0$

$D={ b }^{ 2 }-4ac={(8)}^{2}-4(4\sqrt{2})(2\sqrt{2})=64-64=0$

Factorise $x ^ { 2 } - 10 x + 9 = 0$ using completing square method.

1502769_1482157_ans_8c63feeffe4f43f09fbe69ef89372a4b.jpg

$\Pi \left( x+7 \right) ^{ 2 }-\Pi { x }^{ 2 }=286$

$\pi (x+7)^2-\pi x^2=286$

$\Rightarrow [(x+7)^2-x^2]=\dfrac{286}{22}\times 7$

$\Rightarrow [x^2+49+14x-x^2]=91$

$\Rightarrow 14x=42$

$\Rightarrow x=3$ .

1199890_1445153_ans_baca3a2fd21940fda8e7ee294bd16930.jpg

Find which of the following equations are quadratic:
$x^{2}+5 x-5=(x-3)^{2}$

$x^{2}+5 x-5=(x-3)^{2}$

$\Rightarrow x^{2}+5 x-5=x^{2}-6 x+9$

$\Rightarrow 11x-14=0 ;$
which is not of the general form

$\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}=0$
And it's a linear equation.
Thus, the given equation is not a quadratic equation.

Find which of the following equations are quadratic:
$7 x^{3}-2 x^{2}+10=(2 x-5)^{2}$

$7 x^{3}-2 x^{2}+10=(2 x-5)^{2}$

$\Rightarrow 7 x^{3}-2 x^{2}+10=4 x^{2}-20 x+25$

$\Rightarrow 7 x^{3}-6 x^{2}+20 x-15=0 ;$
which is not of the general form ax

$^{2}+b x+c=0$ .
And it's a cubic equation.
Thus, the given equation is not a quadratic equation.

Find which of the following equations are quadratic:
$5 x^{2}-8 x=-3(7-2 x)$

$\quad 5 x^{2}-8 x=-3(7-2 x)$

$\Rightarrow 5 x^{2}-8 x=6 x-21$

$\Rightarrow 5 x^{2}-14 x+21=0 ;$
which is of the general form

$a x^{2}+b x+c=0$
Thus, the given equation is a quadratic equation.

Find which of the following equations are quadratic:
$(\mathbf{x}-\mathbf{1})^{2}+(\mathbf{x}+\mathbf{2})^{2}+3(\mathbf{x}+\mathbf{1})=0$

$(x-1)^{2}+(x+2)^{2}+3(x+1)=0$

$\Rightarrow x^{2}-2 x+1+x^{2}+4 x+4+3 x+3=0$

$\Rightarrow 2 \mathrm{x}^{2}+5 \mathrm{x}+8=0 ;$
which is of the general form

$\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}=0$
Thus, the given equation is a quadratic equation.

$a(2a-b) -b^2$

$a(2a-b)-b^2$
Above term can written as,

$2a^2-ab-b^2$
Take out common in all terms we get,

$2a(a-b)+b(a-b)$

$(a-b)(2a+b)$

Find whether the following equations are quadratic or not:
$(3 x-1)^{2}=5(x+8)$

${\textbf{Step -1: Simplify the given equation.}}$

${\text{Consider,}}$

${\left( {3x - 1} \right)^2} = 5\left( {x + 8} \right)$

$\Rightarrow {\left( {3x} \right)^2} - 2\left( {3x} \right)\left( 1 \right) + {\left( 1 \right)^2} = 5x + 40$ $\left( {{\textbf{Using formula: }}{{\left(\mathbf{ {a + b}} \right)}^\mathbf2} = \mathbf{{a^2} + 2ab + {b^2}}} \right)$

$\Rightarrow 9{x^2} - 6x + 1 = 5x + 40$

$\Rightarrow 9{x^2} - 6x - 5x - 40 + 1 = 0$

$\Rightarrow 9{x^2} - 11x - 39 = 0$ $\ldots \left( 1 \right)$

${\textbf{Step -2: Compare equation }}\left(\mathbf 1 \right)$ ${\textbf{with standard form of quadratic equation.}}$

${\text{A quadratic equation is an equation of the form }}$ $a{x^2} + bx + c = 0$

${\text{Where}}$ $a,b,c$ ${\text{are knowns numbers}}$ ${\text{and}}$ $a \ne 0$ ${\text{and}}$ $x$ ${\text{is unknown variable}}{\text{.}}$

${\text{Here, }}$ ${\left( {3x - 1} \right)^2} = 5\left( {x + 8} \right)$ ${\text{can be written as}}$ $9{x^2} - 11x - 39 = 0.$

${\text{Which is a quadratic equation}}{\text{.}}$

${\textbf{ Hence, }}$ $\mathbf{{\left( {3x - 1} \right)^2} = 5\left( {x + 8} \right)}$ ${\textbf{is a quadratic equation.}}$

Find the roots of the following quadratic equation, if they exist, by the method of completing the square:
$4{x}^{2}+4\sqrt{3x}+3=0$

We have

$4{x}^{2}+4\sqrt{3x}+3=0$
On dividing both sides by

$4$ we have

${x}^{2}+\sqrt { 3x } +\cfrac{3}{4}=0$

$\Rightarrow$

${x}^{2}+\sqrt { 3x } +{ \left( \cfrac { \sqrt { 3 } }{ 2 } \right) }^{ 2 }-{ \left( \cfrac { \sqrt { 3 } }{ 2 } \right) }^{ 2 }+\cfrac{3}{4}=0$

$\Rightarrow$

${ \left( x+\cfrac { \sqrt { 3 } }{ 2 } \right) }^{ 2 }-\cfrac{3}{4}+\cfrac{3}{4}=0\Rightarrow { \left( x+\cfrac { \sqrt { 3 } }{ 2 } \right) }^{ 2 }=0$ ....(i)
Roots exist

$\therefore$ (i)

$\Rightarrow$

$x=-\cfrac { \sqrt { 3 } }{ 2 } ,-\cfrac { \sqrt { 3 } }{ 2 }$
Hence the roots of given equation are

$-\cfrac { \sqrt { 3 } }{ 2 }$ and

$-\cfrac { \sqrt { 3 } }{ 2 }$

Find which of the following equations are quadratic:
$(x-4)(3 x+1)=(3 x-1)(x+2)$

$\quad(x-4)(3 x+1)=(3 x-1)(x+2)$

$\Rightarrow 3 x^{2}+x-12 x-4=3 x^{2}+6 x-x-2$

$\Rightarrow 16 \mathrm{x}+2=0 ;$
which is not of the general form

$\mathrm{ax}^{2}+\mathrm{bx}+\mathrm{c}=0 .$
And it's a linear equation.
Thus, the given equation is not a quadratic equation.

If the roots of the equation $(a^{2}+b^{2})x^{2}-2(ac+bd)x+(c^{2}+d^{2})=0$ are equal, then prove that $\dfrac{a}{b}=\dfrac{c}{d}$ .

Given

$(a^{2}+b^{2})x^{2}-2(ac+bd)x+(c^{2}+d^{2})=0$

roots are equal

$D=b^{2}-4ac=0$

$\Rightarrow \left [ -2(ac+bd) \right ]^{2}-4(a^{2}+b^{2})(c^{2}+d^{2})=0$

$\Rightarrow 4(ac+bd)^{2}=4(a^{2}+b^{2})(c^{2}+d^{2})$

$\Rightarrow a^{2}c^{2}+b^{2}d^{2}+2abcd =a^{2}c^{2}+a^{2}d^{2}+b^{2}c^{2}+b^{2}d^{2}$

$\Rightarrow a^{2}d^{2}+b^{2}c^{2}-2abcd=0$

$\Rightarrow (ad-bc)^{2}=0$

$\Rightarrow ad=bc$

$\Rightarrow \dfrac{a}{b}=\dfrac{c}{d}$

Hence Proved.

If $P\left( x \right) ={ ax }^{ 2 }+bx+c$ and $Q\left( x \right) =-{ ax }^{ 2 }+bx+c$ , where $ac\neq 0$ , then show that $P\left( x \right) Q\left( x \right)$ =0 has at least two real roots.

$P\left( x \right) .Q\left( x \right) =\left( a{ x }^{ 2 }+bx+c \right) \left( -a{ x }^{ 2 }+bx+c \right)$
Now,

${ D }_{ 1 }={ b }^{ 2 }-4ac$ and

${ D }_{ 2 }={ b }^{ 2 }+4ac$
Clearly,

${ D }_{ 1 }+{ D }_{ 2 }=2{ b }^{ 2 }\ge 0$
Therefore at least one of

${ D }_{ 1 }$ and

${ D }_{ 2 }$ is (+ve).
Hence, at least two real roots.
Hence statement is true

If the equation ${ ax }^{ 2 }+2bx+c=0$ has real roots, $a,b,c$ being real numbers and if $m$ and $n$ are real number such that ${ m }^{ 2 }>n>0$ then show that the equation ${ ax }^{ 2 }+2mbx+nc=0$ has real roots.

Given roots of the equation

${ ax }^{ 2 }+2bx+c=0$ are real.

$\therefore { \left( 2b \right) }^{ 2 }-4ac\ge 0$

$\therefore { b }^{ 2 }-ac\ge 0$ .............(1)

Discriminant of

${ ax }^{ 2 }+2mbx+nc=0$ is

$D={ \left( 2mb \right) }^{ 2 }-4anc$

$D=4{ m }^{ 2 }{ b }^{ 2 }-4anc$ .............(2)

From (1)

${ b }^{ 2 }\ge ac$ ........(3)
and given

${ m }^{ 2 }>n$ .......(4)
So, from (3) and (4),

${ \therefore b }^{ 2 }{ m }^{ 2 }\ge anc$

$\Rightarrow 4{ m }^{ 2 }{ b }^{ 2 }-4anc\ge 0$

$\Rightarrow D\ge 0$ {from (2)}
Hence roots of equation

${ ax }^{ 2 }+2mbx+nc=0$ are real.

Is the given equation quadratic? Enter 1 for True and 0 for False.
$x^{2} +\, 4x\, =\, 11$

The equation,

$x^2 + 4x = 11$ has the highest power as 2.

Thus, it is a quadratic equation.

Find the value of discriminant for the following equation.
$x^{2}\, -\, 3x\, +\, 2\, =\, 0$

The value of discriminant of

$x^2 - 3x +2 =0$ is

$D = b^2 - 4ac$

$a=1, b=-3, c=2$

$\therefore D = (-3)^2 - 4\times1\times2$

$= 9 - 8$

$=1$

$\sqrt3x^{2}\, +\, 2\sqrt2x\, -\, 2\sqrt3\, =\, 0$

Given equation is :

$\sqrt 3 x^2+ 2 \sqrt2 x- 2\sqrt3=0$

Discriminant =

$b^2 - 4ac$

$a=\sqrt3. b=2 \sqrt2, c=-2 \sqrt3$

$\therefore D= (2\sqrt{2})^2 - 4(\sqrt{3})(-2\sqrt{3})$

$= 8 + 24$

$= 32$

If $z^{2}\, +\, 4z\, -\, 7\, =\, 0$ , then $z\, =\, -\, 2\, \pm\, \sqrt{11}$ .
If true then enter $1$ and if false then enter $0$

Given equation is

$z^2 + 4z -7 = 0$

$\therefore z^2 + 4z = 7$

On using completing the square method

Term to be added and subtracted

$=$

$\left(\dfrac 12 \times \mbox{coefficient of z}\right)^2$

$=$

$\left(\dfrac 12 \times 4\right)^2 = 4$

Adding

$4$ on both sides, we get

$z^2 + 4z + 4 = 4+7$

$\therefore (z+2)^2 = 11$

$\therefore (z + 2)$ = +

$\sqrt {11}$

$\therefore z= \sqrt {11} - 2$ OR

$z= -\sqrt {11} - 2$

Is the following equation quadratic? Enter 1 for True and 0 for False.
$m\, -\, \displaystyle \frac{5}{m}\, =\, 4m\, +\, 5$

The equation,

$m - \dfrac{5}{m} = 4m + 5$

can be framed as,

$m^2 - 5 = 4m^2 + 5m$

$3m^2 + 5m + 5 = 0$

The highest power of the equation is 2. hence, it is a quadratic equation.

Find the value of discriminant for the following equation.
$x^{2}\, -\, 6x\, +\, 7\, =\, 0$

The value of discriminant of

$x^2 - 6x + 7 =0$ is

$D = b^2 - 4ac$

$a=1, b=-6, c=7$

$\therefore D = (6)^2 - 4\times7\times1$

$= 36 - 28$

$= 8$

Discuss the nature of the roots of the equation $\displaystyle 4x^{2}-2x+1=0$

Discriminant

$\displaystyle =\left ( -2 \right )^{2}-4\left ( 4 \right )\left ( 1 \right )=4-16=-12< 0$
Since the discriminant is negative, the roots are imaginary.

Solve the equation $\displaystyle { x }^{ 2 }-x+2=0$

The given quadratic equation is

$\displaystyle { x }^{ 2 }-x+2=0$
On comparing the given equation with

$\displaystyle { ax }^{ 2 }+bx+c=0$ ,
we obtain

$\displaystyle a=1,b=-1,$ and

$c=2$

Therefore, the discriminant of the given equation is

$\displaystyle D={ b }^{ 2 }-4ac$

$=\left( -1 \right) ^{ 2 }-4\times 1\times 2$

$=1-8$

$=-7$

Therefore, the required solutions are

$\displaystyle \frac { -b\pm \sqrt { D } }{ 2a }$

$=\dfrac { -\left( -1 \right) \pm \sqrt { -7 } }{ 2\times 1 }$

$=\dfrac { 1\pm \sqrt { 7 }i }{ 2 }$

Roots of the quadratic equation $\displaystyle 3x^{2}-2\sqrt{15}x-2=0$ are
$\dfrac{\sqrt{15}\pm \sqrt{21}}{3}$ . If true answer is 1,else 0

We have

$\displaystyle 3x^{2}-2\sqrt{15}x-2=0$

$\displaystyle \Rightarrow x^{2}-2\frac{\sqrt{15}}{3}x-\frac{2}{3}=0$
[Dividing both sides by the coefficient of

$\displaystyle x^{2}$ ]

$\displaystyle \Rightarrow x^{2}-2\frac{\sqrt{15}}{3}x+\left ( \frac{\sqrt{15}}{3} \right )^{2}-\left ( \frac{\sqrt{15}}{3} \right )^{2}-\frac{2}{3}=0$
[Adding and subtracting the square of half the coefficient of x]

$\displaystyle \Rightarrow \left ( x-\frac{\sqrt{15}}{3} \right )^{2}-\frac{15}{9}+\frac{2}{3}=0$

$\displaystyle \Rightarrow \left ( x-\frac{\sqrt{15}}{3} \right )^{2}-\left ( \frac{15+6}{9} \right )=0$

$\displaystyle \Rightarrow \left ( x-\frac{\sqrt{15}}{3} \right )^{2}-\frac{21}{9}=0$

$\displaystyle \Rightarrow x-\frac{\sqrt{15}}{3}=\pm \frac{\sqrt{21}}{3}$
[Taking the square roots on both sides]

$\displaystyle \Rightarrow x=\frac{\sqrt{15}}{3}\pm \frac{\sqrt{21}}{3}=\frac{\sqrt{15}\pm \sqrt{21}}{3}$
Hence the requires solutions are

$\displaystyle x=\frac{\sqrt{15}+\sqrt{21}}{3}\: and\: x=\frac{\sqrt{15}-\sqrt{21}}{3}$

Solve the equation : $\displaystyle { 3x }^{ 2 }-4x+\frac { 20 }{ 3 } =0$

This given equation can also be written as

$\displaystyle { 9x }^{ 2 }-12x+20=0$
On comparing this equation with

$\displaystyle { ax }^{ 2 }+bx+c=0$ ,
we obtain

$\displaystyle a=9,b=-12$ and

$c=20$
Therefore, the discriminant of the given euation is

$\displaystyle D={ b }^{ 2 }-4ac={ \left( -12 \right) }^{ 2 }-4\times 9\times 20=144-720=-576$
Therefore, the required solutions are

$\displaystyle \frac { -b\pm \sqrt { D } }{ 2a } =\frac { -\left( -12 \right) \pm \sqrt { -576 } }{ 2\times 9 } =\frac { 12\pm \sqrt { 576 }i }{ 18 }$

$\displaystyle =\frac { 12\pm 24i }{ 18 } =\frac { 6\left( 2\pm 4i \right) }{ 18 } =\frac { 2\pm 4i }{ 3 } =\frac { 2 }{ 3 } \pm \frac { 4 }{ 3 } i$

Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
(i) $\displaystyle 2{ x }^{ 2 }-7x+3=0$
(ii) $\displaystyle 2{ x }^{ 2 }+x-4=0$
(iii) $\displaystyle 4{ x }^{ 2 }+4\sqrt { 3x } +3=0$
(iv) $2x^{2}+x+4=0$

$2{ x }^{ 2 }-7x+3=0\\ \Rightarrow{ x }^{ 2 }-\dfrac{ 7x }{ 2 }+\dfrac 32=0\\ \Rightarrow{ x }^{ 2 }-\dfrac {7x}{2} + \dfrac 32+ \dfrac { 49 }{ 16 }=\dfrac { 49 }{ 16 }\\ \Rightarrow { x }^{ 2 }-\dfrac {7x}{2} +\dfrac { 49 }{ 16 }=\dfrac { 49 }{ 16 }-\dfrac 32\\ \Rightarrow { \left(x-\dfrac 74\right) }^{ 2 }=\dfrac {25}{16}\\ \Rightarrow { \left(x-\dfrac 74\right) }=\pm \dfrac 54\\ \Rightarrow x=\dfrac 74+\dfrac 54 \quad \text{and} \quad x=\dfrac 74-\dfrac 54\\ \Rightarrow x=3,\dfrac 12$

ii)

$2{ x }^{ 2 }+x-4=0\\ \Rightarrow { x }^{ 2 }+\dfrac x2-{ 2 }=0\\ \Rightarrow { x }^{ 2 }+\dfrac x2+\dfrac {1}{16}=2+\dfrac {1}{16}\\ \Rightarrow { \left(x+\dfrac 14\right) }^{ 2 }=\dfrac {33}{16}\\ \Rightarrow x+\dfrac 14=\pm \dfrac {\sqrt { 33 } }{ 4 }\\ \Rightarrow x=\dfrac {\sqrt {33} -1}{4}, \dfrac {-\sqrt { 33 } -1}{ 4 }$

iii)

$4{ x }^{ 2 }+4\sqrt { 3 } x+3=0\\ \Rightarrow { x }^{ 2 }+\sqrt { 3 } x+\dfrac 34=0\\ \Rightarrow { x }^{ 2 }+\sqrt { 3 } x+\dfrac 34=-\dfrac 34+\dfrac 34\\ \Rightarrow { \left(x+\dfrac {\sqrt 3}{2}\right) }^{ 2 }=0\\ \Rightarrow x+\dfrac {\sqrt 3}{2}=0\\ \Rightarrow x=-\dfrac {\sqrt 3}{2}$

iv)

$2x^2+x+4=0$

$\Rightarrow x^2+\dfrac {x}{2}+2=0\\ \Rightarrow x^2+\dfrac {x}{2}+2=0\\ \Rightarrow x^2+\dfrac {x}{2}+\dfrac 14=\dfrac 14-2\\ \Rightarrow \left(x+\dfrac 12\right)^2=-\dfrac 74\\ \Rightarrow x=-\dfrac 12\pm \dfrac {\sqrt 7i}{2}$

Check whether the following are quadratic equations :
(i) $\displaystyle { \left( x+1 \right) }^{ 2 }=2\left( x-3 \right)$
(ii) $\displaystyle { x }^{ 2 }-2x=\left( -2 \right) \left( 3-x \right)$
(iii) $\displaystyle \left( x-2 \right) \left( x+1 \right) =\left( x-1 \right) \left( x+3 \right)$
(iv) $\displaystyle \left( x-3 \right) \left( 2x+1 \right) =x\left( x+5 \right)$
(v) $\displaystyle \left( 2x-1 \right) \left( x-3 \right) =\left( x+5 \right) \left( x-1 \right)$
(vi) $\displaystyle { x }^{ 2 }+3x+1={ \left( x-2 \right) }^{ 2 }$
(vii) $\displaystyle { \left( x+2 \right) }^{ 3 }=2x\left( { x }^{ 2 }-1 \right)$
(viii) $\displaystyle { x }^{ 3 }-4{ x }^{ 2 }-x+1={ \left( x-2 \right) }^{ 3 }$

${ (x+1) }^{ 2 }=2(x-3)$

${ x }^{ 2 }+2x+1=2x-6$

${ x }^{ 2 }+7=0\ \ \ \rightarrow$ Quadratic

ii)

${ x }^{ 2 }-2x=-2(3-x)$

${ x }^{ 2 }-2x=-6+2x$

${ x }^{ 2 }+4x+6=0\ \ \ \rightarrow$ Quadratic

iii)

$(x-2)(x+1)=(x-1)(x+3)$

${ x }^{ 2 }-x-2={ x }^{ 2 }+2x-3$

$3x=1\ \ \ \rightarrow$ Non Quadratic

iv)

$(x-3)(2x+1)=(x)(x+5)$

${ 2x }^{ 2 }-5x-3={ x }^{ 2 }+5x$

${ x }^{ 2 }+10x-3=0\ \ \ \rightarrow$ Quadratic

$(x-3)(2x-1)=(x-1)(x+5)$

${ 2x }^{ 2 }-7x+3={ x }^{ 2 }+4x-5$

${ x }^{ 2 }-11x+8=0\ \ \ \rightarrow$ Quadratic

vi)

${ x }^{ 2 }+3x+1={ (x-2) }^{ 2 }$

${ x }^{ 2 }+3x+1={ x }^{ 2 }-4x+4$

$7x=3\ \ \ \rightarrow$ Non Quadratic

vii)

${ (x+2) }^{ 3 }=2x({ x }^{ 2 }-1)$

${ x }^{ 3 }+8+6x(x+2)=2{ x }^{ 3 }-2x$

${ x }^{ 3 }+8+6{ x }^{ 2 }+12x=2{ x }^{ 3 }-2x$

${ -x }^{ 3 }+6{ x }^{ 2 }+14x+8=0\ \ \ \rightarrow$ Non Quadratic

viii)

$x^3-4x^2−x+1$

$=x^3+3x^2(−2)+3x(−2)^2+(−2)^3$

$x^3−4x^2−x+1=x^3−6x^2+12x−8$

$x^3−4x^2−x+1−x^3+6x^2−12x+8=0$

$2x^2−13x+9=0\ \ \ \rightarrow$ Non Quadratic

Find the roots of the following equations:
$\displaystyle \dfrac { 1 }{ x+4 } -\dfrac { 1 }{ x-7 } =\dfrac { 11 }{ 30 } ,x\neq -4,7$

$x-\dfrac{ 1 }{ x }=3$

$\Rightarrow { x }^{ 2 }-3x-1=0$

$\Rightarrow x=\dfrac{ -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a }$

$\Rightarrow a=1,b=-3,c=-1$

$\Rightarrow x=\dfrac{ 3\pm \sqrt { 9+4 } }{ 2 }$

$\Rightarrow x=\dfrac{ 3\pm \sqrt { 13 } }{ 2 }$

ii)

$\dfrac{ 1 }{ (x+4) }-\dfrac{ 1 }{ (x-7) }=\dfrac{ 11}{30 }$

$\Rightarrow \dfrac{ (x-7-x-4) }{ (x+4)(x-7) }=\dfrac{ 11}{30 }$

$\Rightarrow \dfrac{-11}{{ (x+4)(x-7) }}=\dfrac{ 11}{30 }$

$\Rightarrow -30={ x }^{ 2 }-3x-28$

$\Rightarrow { x }^{ 2 }-3x+2=0$

$\Rightarrow { x }^{ 2 }-2x-x+2=0$

$\Rightarrow x(x-2)-1(x-2)=0$

$\Rightarrow (x-2)(x-1)=0$

$\Rightarrow x=1,2$

Find the value of $\sqrt {a + \sqrt {a + \sqrt {a + ...... \infty}}}$

$\textbf{Step-1: Let}$ $x=\sqrt{a+\sqrt{a+\sqrt{a+...........\infty }}}$

$\text{On squaring both sides we get,}$

${{x}^{2}}=a+\sqrt{a+\sqrt{a+\sqrt{a+............\infty }}}$

$\Rightarrow {{x}^{2}}=a+x$

$\Rightarrow {{x}^{2}}-x-a=0$

$\textbf{Step-2: Solving the quadratic equation}$

$\Rightarrow x=\dfrac{1\pm \sqrt{1+4a}}{2}$ $\mathbf{[\because x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}]}$

$\textbf{ Therefore, the value of}$ $\mathbf{\sqrt{a+\sqrt{a+\sqrt{a+...........\infty }}}}$ $\textbf{ is }$ $\mathbf{{=\dfrac{1\pm \sqrt{1+4a}}{2}}}$

$4x^2 - 20x + 9 = 0$ .

The given quadratic equation is

$4x^2-20x+9=0$ .

Add and subtract

$25$ in the equation

$4x^2-20x+9=0$ to make a perfect square as shown below:

$4x^{ 2 }-20x+9=0\\ \Rightarrow 4x^{ 2 }-20x+25-25+9=0\\ \Rightarrow (2x)^{ 2 }-(2\times 2x\times 5)+5^{ 2 }+(-25+9)=0\\ \Rightarrow (2x-5)^{ 2 }-16=0\\ \Rightarrow (2x-5)^{ 2 }=16\\ \Rightarrow 2x-5=±4\\ \Rightarrow 2x-5=-4,\quad 2x-5=4\\ \Rightarrow 2x=1,\quad 2x=9\\ \Rightarrow x=\dfrac { 1 }{ 2 } ,\quad x=\dfrac { 9 }{ 2 }$

Hence,

$x=\dfrac { 1 }{ 2 }$ or

$x=\dfrac { 9 }{ 2 }$ .

Solve the quadratic equation $x^2 + 6x - 7 = 0$ by completing the square.

Given:

$x^2 + 6x - 7 = 0$

Now by using the identity

$(a+b)^2=a^2+2ab+b^2$

Let us now compare the given equation to the identity and we see that,

$a=x$

and

$2 \times a \times b = 6x$

$\Rightarrow2 \times x \times b = 6x (\because a = x)$

$\therefore b = \dfrac{6x}{2x}$

$\Rightarrow b = 3$

$\Rightarrow b^2=9$

Hence we can now complete the square for the above quadratic equation by adding

$9$ to both the sides

$x^2 + 6x - 7+9 = 0+9$

$\Rightarrow x^2 + 6x +9 = 9+7$ ...{By transposing

$7$ to R.H.S}

$\Rightarrow x^2 + 6x + 9 = 16$

This can be written as

$(x + 3)^2 = (4)^2$

$\therefore x + 3 = \pm 4$ ....{Taking square root on both sides}

Now if,

$x + 3 = 4$

$\Rightarrow x = 4 - 3$

$\Rightarrow x = 1$

or,

$x +3 = - 4$

$\Rightarrow x = - 4-3$

$\Rightarrow x=-7$

$\therefore$

$x= 1$ or

$- 7$ are the roots of

$x^2 + 6x - 7 = 0$

Check whether $3x - 10 = 0$ is a quadratic equation or not?

We know that the general form of quadratic equation is

$ax^2+bx+c=0$ .

The given equation is

$3x-10=0$ in which the variable

$x$ has degree

$1$ and therefore it is not of the form

$ax^2+bx+c=0$ .

Hence, the equation

$3x-10=0$ is not a quadratic equation, it is a linear equation.

Check whether $x^2 - y^2 = 0$ is a quadratic equation.

We know that the general form of quadratic equation is

$ax^2+bx+c=0$ .

The given equation is

$x^2-y^2=0$ in which there are two variables

$x$ and

$y$ and therefore it is not of the form

$ax^2+bx+c=0$ .

Hence, the equation

$x^2-y^2=0$ is not a quadratic equation.

Check whether $x^2 - \dfrac{29}{4} x + 5= 0$ is a quadratic equation

We know that the general form of quadratic equation is

$ax^2+bx+c=0$ .

The given equation is

$x^{ 2 }-\cfrac { 29 }{ 4 } x+5=0$ which is of the form

$ax^2+bx+c=0$ .

Hence, the equation

$x^{ 2 }-\cfrac { 29 }{ 4 } x+5=0$ is a quadratic equation.

$x(x+1) + 8 = (x+ 2) (x-2)$ is a quadratic equation.

Given that:

$x(x+1) + 8 = (x+ 2) (x-2)$
By simplifying we get

$x^2 + x + 8 = x^2 - 4 \\ x^2 - x^2 + x + 8 + 4 = 0 \\ x + 12 = 0$
It is not of the form

$ax^2 + bx + c = 0$
The variable x is only in the first degree.

$\therefore$ It is not a quadratic equation.

Solve $3x^2 - 5x + 2 = 0$ by completing the square method.

Given

$3x^2 - 5x + 2 = 0$

Here, the coefficient of

$x^2$ is 3 and it is not a perfect square.

$\therefore$ Multiply the equation throughout by 3.

$\Rightarrow (3x^2 - 5x + 2 = 0) \times 3 \therefore 9x^2 - 15x + 6 = 0$

Now, half of the coefficient of x is

$\dfrac{5}{2}. \therefore b = \dfrac{5}{2}$ and

$b^2 = \left ( \dfrac{5}{2} \right )^2$

So,

$9x^2 - 15x + \left ( \dfrac{5}{2} \right )^2 - \left ( \dfrac{5}{2} \right )^2 + 6 = 0, (3x)^2 - 15x + \left ( \dfrac{5}{2} \right )^2 = \left (\dfrac{5}{2} \right )^2 - 6$

$\left ( 3x - \dfrac{5}{2} \right )^2 = \dfrac{25}{4} - 6 = \dfrac{1}{4}$
(Taking square root on both the sides)

$\therefore 3x - \dfrac{5}{2} = \pm \dfrac{1}{2}$

$\therefore 3x - \dfrac{5}{2} = \pm \dfrac{1}{2}$ or

$3x - \dfrac{5}{2} = - \dfrac{1}{2}$

$3x = \dfrac{1}{2} + \dfrac{5}{2}$

$3x = \dfrac{5}{2} - \dfrac{1}{2}$

$3x = \dfrac{6}{2} = 3$

$3x = \dfrac{4}{2} = 2$

$\therefore x = 1$

$x = \dfrac{2}{3}$

Check whether $x^3 - 10x + 74 = 0$ is a quadratic equation.

We know that the general form of quadratic equation is

$ax^2+bx+c=0$ .

The given equation is

$x^3-10x+74=0$ in which the variable

$x$ has highest degree

$3$ and therefore it is not of the form

$ax^2+bx+c=0$ .

Hence, the equation

$x^3-10x+74=0$ is not a quadratic equation.

$\left( x + \dfrac{3}{4} x \right ) (x - 8 ) + 10 = 0$ is a quadratic equations

Given that:

$\left( x + \dfrac{3}{4} x \right ) (x - 8 ) + 10 = 0$
By simplifying we get:

$x^2 - 8x + \dfrac{3}{4} x^2 - \dfrac{24}{4} x + 10 = 0$

$4x^2 - 32x + 3x^2 - 24 x + 40 = 0$

$7x^2 - 56 x + 40 =0$ . It is of the form

$ax^2 + bx + c = 0$

$\therefore$ It is a quadratic equation.

Check whether $5 - 6x = \dfrac{2}{5} x^2$ is a quadratic equation.

We know that the general form of quadratic equation is

$ax^2+bx+c=0$ .

The given equation is

$5-6x=\frac { 2 }{ 5 } x^2$ which can be rewritten as

$\frac { 2 }{ 5 } x^2+6x-5=0$ and therefore it is of the form

$ax^2+bx+c=0$ .

Hence, the equation

$5-6x=\frac { 2 }{ 5 } x^2$ is a quadratic equation.

$2x^2 + 5x - 3 = 0$

The given quadratic equation is

$2x^2+5x-3=0$ . Multiply the equation by

$2$ then we get

$4x^2+10x-6=0$ .

Add and subtract

$\frac { 25 }{ 4 }$ in the equation

$4x^2+10x-6=0$ to make a perfect square as shown below:

$2x^{ 2 }+5x-3=0\\ \Rightarrow 2x^{ 2 }+5x+\frac { 25 }{ 4 } -\frac { 25 }{ 4 } -3=0\\ \Rightarrow (2x)^{ 2 }+\left( 2\times 2x\times \frac { 5 }{ 2 } \right) +\left( \frac { 5 }{ 2 } \right) ^{ 2 }+\left( -\frac { 25 }{ 4 } -3 \right) =0\\ \Rightarrow \left( 2x+\frac { 5 }{ 2 } \right) ^{ 2 }-\frac { 49 }{ 4 } =0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (∵(a+b)^{ 2 }=a^{ 2 }+b^{ 2 }+2ab)\\ \Rightarrow \left( 2x+\frac { 5 }{ 2 } \right) ^{ 2 }=\frac { 49 }{ 4 } \\ \Rightarrow 2x+\frac { 5 }{ 2 } =±\sqrt { \frac { 49 }{ 4 } } \\ \Rightarrow 2x+\frac { 5 }{ 2 } =±\frac { 7 }{ 2 } \\ \Rightarrow 2x+\frac { 5 }{ 2 } =-\frac { 7 }{ 2 } ,\quad 2x+\frac { 5 }{ 2 } =\frac { 7 }{ 2 } \\ \Rightarrow 2x=-\frac { 7 }{ 2 } -\frac { 5 }{ 2 } ,\quad 2x=\frac { 7 }{ 2 } -\frac { 5 }{ 2 } \\ \Rightarrow 2x=-\frac { 12 }{ 2 } ,\quad 2x=\frac { 2 }{ 2 } \\ \Rightarrow 2x=-6,\quad 2x=1\\ \Rightarrow x=-\frac { 6 }{ 2 } ,\quad x=\frac { 1 }{ 2 } \\ \Rightarrow x=-3,\quad x=\frac { 1 }{ 2 }$

Hence,

$x=\frac { 1 }{ 2 }$ or

$x=-3$ .

Solve the following equation and calculate the answer correct to two decimal places.
$x^2-5x-10=0$ .

Given:

$x^2-5x-10=0$

On comparing the given equation with

$ax^2+bx+c=0$ , we get:

$a=1, b=-5$ and

$c=-10$

For

$ax^2+bx+c=0$ , we know that,

$x=\displaystyle\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$ [Quadratic formula]

$\therefore \ x=\cfrac{5\pm \sqrt{(-5)^2-4\times 1\times (-10)}}{2\times 1}=\dfrac{5\pm \sqrt{65}}{2}$

$\Rightarrow \displaystyle\cfrac{5\pm 8.06}{2}$

$\Rightarrow \displaystyle\cfrac{5+8.06}{2}, \cfrac{5-8.06}{2}$

$\Rightarrow \displaystyle\cfrac{13.06}{2}, -\cfrac{3.06}{2}$

Hence,

$x=6.53, \text{ or }x=-1.53$ .

$x^2 - 3x + 1 = 0$

The given quadratic equation is

$x^2-3x+1=0$ .

Add and subtract

$\frac { 9 }{ 4 }$ in the equation

$x^2-3x+1=0$ to make a perfect square as shown below:

$x^{ 2 }-3x+1=0\\ \Rightarrow x^{ 2 }-3x+\dfrac { 9 }{ 4 } -\dfrac { 9 }{ 4 } +1=0\\ \Rightarrow (x)^{ 2 }-\left( 2\times x\times \frac { 3 }{ 2 } \right) +\left( \dfrac { 3 }{ 2 } \right) ^{ 2 }+\left( -\dfrac { 9 }{ 4 } +1 \right) =0\\ \Rightarrow \left( x-\dfrac { 3 }{ 2 } \right) ^{ 2 }-\dfrac { 5 }{ 4 } =0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (∵(a-b)^{ 2 }=a^{ 2 }+b^{ 2 }-2ab)\\ \Rightarrow \left( x-\dfrac { 3 }{ 2 } \right) ^{ 2 }=\dfrac { 5 }{ 4 } \\ \Rightarrow x-\dfrac { 3 }{ 2 } =±\sqrt { \dfrac { 5 }{ 4 } } \\ \Rightarrow x-\frac { 3 }{ 2 } =±\dfrac { \sqrt { 5 } }{ 2 } \\ \Rightarrow x-\dfrac { 3 }{ 2 } =-\dfrac { \sqrt { 5 } }{ 2 } ,\quad x-\dfrac { 3 }{ 2 } =\dfrac { \sqrt { 5 } }{ 2 } \\ \Rightarrow x=-\dfrac { \sqrt { 5 } }{ 2 } +\dfrac { 3 }{ 2 } ,\quad x=\dfrac { \sqrt { 5 } }{ 2 } +\dfrac { 3 }{ 2 } \\ \Rightarrow x=\dfrac { 3-\sqrt { 5 } }{ 2 } ,\quad x=\dfrac { 3+\sqrt { 5 } }{ 2 }$

Hence,

$x=\dfrac { 3-\sqrt { 5 } }{ 2 }$ or

$x=\dfrac { 3+\sqrt { 5 } }{ 2 }$ .

$x^2 + 16 x - 9 = 0$

The given quadratic equation is

$x^2+16x-9=0$ .

Add and subtract

$64$ in the equation

$x^2+16x-9=0$ to make a perfect square as shown below:

$x^{ 2 }+16x-9=0\\ \Rightarrow x^{ 2 }+16x+64-64-9=0\\ \Rightarrow (x)^{ 2 }+\left( 2\times x\times 8 \right) +8^{ 2 }+\left( -64-9 \right) =0\\ \Rightarrow \left( x+8 \right) ^{ 2 }-73=0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (∵(a+b)^{ 2 }=a^{ 2 }+b^{ 2 }+2ab)\\ \Rightarrow \left( x+8 \right) ^{ 2 }=73\\ \Rightarrow x+8=±\sqrt { 73 } \\ \Rightarrow x+8=-\sqrt { 73 } ,\quad x+8=\sqrt { 73 } \\ \Rightarrow x=-\left( \sqrt { 73 } +8 \right) ,\quad x=\sqrt { 73 } -8$

Hence,

$x=-\left( \sqrt { 73 } +8 \right)$ or

$x=\sqrt { 73 } -8$ .

Solve for $x$ using the quadratic formula. Write your answer correct to two significant figures. $(x - 1)^{2} - 3x + 4 = 0$

Given:

$(x - 1)^{2} - 3x + 4 = 0$

$\Rightarrow x^{2} + 1 - 2x - 3x + 4 = 0$

$\Rightarrow x^{2} - 5x + 5 = 0$
Comparing

$x^{2} - 5x + 5 = 0$ with

$ax^{2} + bx + c = 0$ , we get

$a = 1, b = -5, c = 5$ .

$\therefore x = \cfrac {-b\pm \sqrt {b^{2} - 4ac}}{2a}$

$x = \cfrac {(-5) \pm \sqrt {(-5)^{2} - 4(1)(5)}}{2\times 1}$

$= \cfrac {5\pm \sqrt {25 - 20}}{2} = \dfrac {5\pm \sqrt {5}}{2}$

$= \cfrac {5\pm 2.236}{2} = \dfrac {5 + 2.236}{2}$ and

$\dfrac {5-2.236}{2}$

$= \cfrac {7.236}{2}$ and

$\dfrac {2.764}{2}$

$= 3.62$ and

$1.38$

Solve the quadratic equation $x^{2} - 3(x + 3) = 0$ ; Given your answer correct to two significant figures.

Given:

$x^{2} - 3 (x + 3) = 0$

$x^{2} - 3x - 9 = 0$

Comparing

$x^{2} - 3x - 9$ with

$ax^{2} + bx + c = 0$ , we get

$a = 1, b = -3, c = -9$

We know,

$x = \cfrac {-b\pm \sqrt {b^{2} - 4ac}}{2a}$

$= \cfrac {-(-3) \pm \sqrt {(-3)^{2} - 4\times 1\times (-9)}}{2\times 1}$ $

$= \cfrac {3\pm \sqrt {9 + 36}}{2} = \cfrac {3\pm \sqrt {45}}{2}$

$= \cfrac {3\pm 3\sqrt {5}}{2} = \cfrac {3\pm 3\times 2.236}{2}$

$x = \cfrac {3\pm 6.708}{2}$

$x = \cfrac {3 + 6.708}{2}$ and

$\cfrac {3-6.708}{2}$

$x = 4.85$ and

$-1.85$

$4x^2 + x - 5 = 0$

The given quadratic equation is

$4x^2+x-5=0$ .

Add and subtract

$\frac { 1 }{ 16 }$ in the equation

$4x^2+x-5=0$ to make a perfect square as shown below:

$4x^{ 2 }+x-5=0\\ \Rightarrow 4x^{ 2 }+x+\frac { 1 }{ 16 } -\frac { 1 }{ 16 } -5=0\\ \Rightarrow (2x)^{ 2 }+\left( 2\times 2x\times \frac { 1 }{ 4 } \right) +\left( \frac { 1 }{ 4 } \right) ^{ 2 }+\left( -\frac { 1 }{ 16 } -5 \right) =0\\ \Rightarrow \left( 2x+\frac { 1 }{ 4 } \right) ^{ 2 }-\frac { 81 }{ 16 } =0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (∵(a+b)^{ 2 }=a^{ 2 }+b^{ 2 }+2ab)\\ \Rightarrow \left( 2x+\frac { 1 }{ 4 } \right) ^{ 2 }=\frac { 81 }{ 16 } \\ \Rightarrow 2x+\frac { 1 }{ 4 } =±\sqrt { \frac { 81 }{ 16 } } \\ \Rightarrow 2x+\frac { 1 }{ 4 } =±\frac { 9 }{ 4 } \\ \Rightarrow 2x+\frac { 1 }{ 4 } =-\frac { 9 }{ 4 } ,\quad 2x+\frac { 1 }{ 4 } =\frac { 9 }{ 4 } \\ \Rightarrow 2x=-\frac { 9 }{ 4 } -\frac { 1 }{ 4 } ,\quad 2x=\frac { 9 }{ 4 } -\frac { 1 }{ 4 } \\ \Rightarrow 2x=-\frac { 10 }{ 4 } ,\quad 2x=\frac { 8 }{ 4 } \\ \Rightarrow 2x=-\frac { 5 }{ 2 } ,\quad 2x=2\\ \Rightarrow x=-\frac { 5 }{ 2\times 2 } ,\quad x=\frac { 2 }{ 2 } \\ \Rightarrow x=-\frac { 5 }{ 4 } ,\quad x=1$

Hence,

$x=-\frac { 5 }{ 4 }$ or

$x=1$ .

Solve the following equation and give your answer correct to 3 significant figures
$5x^2-3x-4=0$

$5x^2-3x-4=0$

$\Rightarrow x=\cfrac{3\pm\sqrt{9+80}}{10}$

$\Rightarrow x=\cfrac{3-\sqrt{89}}{10},\cfrac{3+\sqrt{89}}{10}$

$\Rightarrow x=-0.643,12.434$

Solve the quadratic equation $2{ x }^{ 2 }+5x+2=0$

The given quadratic equation is

$2{ x }^{ 2 }+5x+2=0$

On comparing with

$a{ x }^{ 2 }+bx+c=0$
We get,

$a=2,b=5,c=2$

$D= { b }^{ 2 }-4ac$

$={ (5) }^{ 2 }-4\times 2\times 2$

$=25-16$

$=9$

$x=\cfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a\quad }$

$=\cfrac { -5\pm \sqrt { 9 } }{ 2\times 2 } \quad =\cfrac { -5\pm 3 }{ 4 }$

$\quad x=\cfrac { -5+3 }{ 4 }$ or

$\quad x=\cfrac { -5-3 }{ 4 }$

$\implies x=-\cfrac { 1 }{ 2 }$ or

$x=-2$

$\therefore$

$-\cfrac{1}{2}$ and

$-2$ are the roots of given quadratic equation.

Solve the quadratic equation $2{x}^{2}+3x+1=0$ using formula method.

Given

$2{x}^{2}+3x+1=0$
On comparing this equation with

$a{x}^{2}+bx+c=0$ , where

$a=2,b=3,c=1$

$\therefore$

${ b }^{ 2 }-4ac={ (5) }^{ 2 }-4\times 2\times 1$

$=9-8$

$=1$

$x=\cfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a\quad }$

$=\cfrac { -3\pm \sqrt { 1 } }{ 2\times 2 }$

$x=\cfrac { -3+1 }{ 4 }$ or

$x=\cfrac { -3-1 }{ 4 }$

$x=\cfrac{-2}{4}$ or

$x=\cfrac{-4}{4}$

$x=\cfrac{-1}{2}$ or

$x=-1$

Solve the following quadratic equation by completing square method
$x^2 + 11 x + 30 =0$

$x^2 + 11x + 30 = 0$

$\therefore x^2 + 11x = - 30$ ..........

$(i)$

Third term

$= \left(\dfrac{1}{2} \text{coefficient of}\, x\right)^2$

$= \left ( \dfrac{1}{2} \times 11 \right)^2$

$= \dfrac{121}{4}$

Adding

$\dfrac{121}{4}$ to both sides of equation (i), we get

$x^2 + 11x + \dfrac{121}{4} = - 30 + \dfrac{121}{4}$

$\therefore \left (x + \dfrac{11}{2} \right )^2 = \dfrac{1}{4}$

$\therefore \left (x + \dfrac{11}{2} \right )^2 = \left ( \dfrac{1}{2} \right )^2$

Taking square roots on both sides.

$x + \dfrac{11}{2}= \pm \dfrac{1}{2}$

$x = -\dfrac{11}{2} \pm \dfrac{1}{2}$

$x = - \dfrac{11}{2} + \dfrac{1}{2} = \dfrac{-10}{2} = -5$

$x = \dfrac{-11}{2} - \dfrac{1}{2} = \dfrac{-12}{2} = - 6$

Hence

$- 5$ and

$- 6$ are the roots of the given quadratic equation

Solve the following quadratic equation using formula method $3x^2+7x+4=0$ .

$3x^2 +7x+4 = 0$

Comparing this with the general form of quadratic equation

$ax^2+bx+c=0$ , we get

$a = 3, b = 7, c = 4$

By formula method,

$x = \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$\Rightarrow x=\cfrac{-7\pm\sqrt{7^2-4\times4\times3}}{2\times3}$

$\Rightarrow x=\cfrac{-7\pm\sqrt{49-48}}{6}$

$\Rightarrow x=\cfrac{-7\pm1}{6}$

$\Rightarrow x=-1,\cfrac{-4}{3}$

Solve the following quadratic equation by completing square method
$x^2 + 10 x + 24 = 0$

$x^2 + 10 x + 24 =x$

$\therefore x^2 + 10 = -24$ .......

$(i)$

Third term

$= \left(\dfrac{1}{2} \text{coefficient of}\, x\right)^2$

$= \left ( \dfrac{1}{2} \times 10 \right )^2$

$= 25$

Adding 25 to both sides of equation (1), we get

$x^2 + 10 x + 25 = - 24 + 25$

$\therefore (x + 5)^2 = (1)^2$

Taking square roots on both sides

$x + 5 = \pm 1$

$x = - 5 \pm 1$

$x = - 5 + 1 = - 4$

$x = - 5 - 1 = - 6$

Hence

$-4$ and

$-6$ are the roots of the given quadratic equation.

Solve the following quadratic equation by completing the square method:
${m}^{2}-3m-1=0$

${m}^{2}-3m-1=0$

${m}^{2}-3m=1$

$\rightarrow$ (1)
Third term

$={(\cfrac{1}{2}coeeficient\quad of\quad m)}^{2}$

${(\cfrac{1}{2}\times (-3))}^{2}={(\cfrac{-3}{2})}^{2}=\cfrac{9}{4}$
Adding

$\cfrac{9}{4}$ to both sides of equation (1), we get

${m}^{2}-3m+\cfrac{9}{4}=1+\cfrac{9}{4}$

$\therefore$

${m}^{2}-3m+\cfrac{9}{4}=\cfrac{4+9}{4}$

$\therefore$

${(m-\cfrac{3}{2})}^{2}=\cfrac{13}{4}$
Taking square roots on both sides

$\therefore$

$m-\cfrac{3}{2}=\pm \cfrac{\sqrt{13}}{2}$

$\therefore$

$m=\cfrac{3}{2}+\cfrac{\sqrt{13}}{2}$ or

$m=\cfrac{3}{2}-\cfrac{\sqrt{13}}{2}$

$m=\cfrac{3+\sqrt{13}}{2},\cfrac{3-\sqrt{13}}{2}$ are the roots of the given quadratic equation.

Solve the following quadratic equation using formula method:
$6x^{2} - 7x - 1 = 0$

Given,

$6x^{2} - 7x - 1 = 0$

Comparing with

$ax^{2} + bx + c = 0$ , we get

$a = 6, b = -7$ and

$c = -1$

Now,

$x = \dfrac {-b\pm \sqrt {b^{2} - 4ac}}{2a}$

$= \dfrac {-(-7) \pm \sqrt {(-7)^{2} - 4(6) (-1)}}{2\times 6}$

$= \dfrac {7\pm \sqrt {49 + 24}}{12}$

$= \dfrac {7\pm \sqrt {73}}{12}$

$\therefore$ Solution set

$= \left \{\dfrac {7 + \sqrt {73}}{12}, \dfrac {7 - \sqrt {73}}{12}\right \}$

Solve the following quadratic equation by completing square method
$x^2 + 10 x + 21 = 0$

we have,

$x^2 + 10 x + 21 = 0$

$\therefore x^2 + 10 x = - 21$ .......

$(i)$

Third term

$= \left ( \dfrac{1}{2} \text{coefficient of} x \right )^2$

$= \left( \dfrac{1}{2} \times 10 \right )^2$

$= 25$

Adding

$25$ to both sides of equation

$(i)$ , we get

$\therefore x^2 + 10 x + 25 = - 21 + 25$

$\therefore (x + 5)^2 = 4$

$\therefore (x + 5)^2 = (2)^2$

Taking square roots on both sides

$x + 5 = \pm 2$

$x = - 5 \pm 2$

$x = -5 + 2 = - 3$ or

$x = -5 - 2 = - 7$

Hence

$-3$ and

$-7$ are the roots of the given quadratic equation

Solve the following quadratic equation by using quadratic formula method: $x^{2} + 4x + 1 = 0$

The given quadratic equation is

$x^{2} + 4x + 1 = 0$

Here,

$a = 1, b = 4, c = 1$

$x = \dfrac {-b\pm \sqrt {b^{2} - 4ac}}{2a}$

$= \dfrac {-4\pm \sqrt {16-4\times1\times 1}}{2}$

$= \dfrac {-4\pm 2\sqrt {3}}{2}$

$= \dfrac {-4 + 2\sqrt {3}}{2}$ or

$\dfrac {-4 - 2\sqrt {3}}{2}$

$= \dfrac {-2(2 - \sqrt {3})}{2}$ or

$\dfrac {-2(2 + \sqrt {3})}{2}$

$= -1(2 - \sqrt {3})$ or

$-1 (2 + \sqrt {3})$

$Roots = (- 2 + \sqrt {3}, -2 - \sqrt {3})$

Solve the following quadratic equation by completing square method
$5y^2 - 4y - 1 = 0$

$5y^2 - 4y - 1 = 0$

$\Rightarrow y^2 - \dfrac{4}{5} y - \dfrac{1}{5} = 0$

$\Rightarrow y^2 - \dfrac{4}{5} y + \dfrac{4}{25} - \dfrac{1}{5} - \dfrac{4}{25} = 0$

$\Rightarrow \left ( y - \dfrac{2}{5} \right )^2 - \dfrac{9}{25} = 0$

$\Rightarrow \left ( y - \dfrac{2}{5} \right )^2 - \left ( \dfrac{3}{5} \right )^2 = 0$

$\Rightarrow \left( y - \dfrac{2}{5} - \dfrac{3}{5} \right ) \left (y - \dfrac{2}{5} + \dfrac{3}{5} \right ) = 0$

$\Rightarrow (y - 1) \left ( y + \dfrac{1}{5} \right ) = 0$

$\therefore y - 1 = 0 \Rightarrow y = 1$

and

$y + \dfrac{1}{5} = 0 \Rightarrow y = - \dfrac{1}{5}$

Solve the following quadratic equation by the formula method : $3{x}^{2}+7x+2=0$ .

Given equation is

$3{ x }^{ 2 }+7x+2=0$
Comparing with

$a{ x }^{ 2 }+bx+c=0$ , we get

$a=3$ ,

$b=7$ ,

$c=2$
Then,

${ b }^{ 2 }-4ac={ \left( 7 \right) }^{ 2 }-4\times 3\times 2$

$=49-24=25$

$x=\dfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a }$

$x=\dfrac { -7\pm \sqrt { 25 } }{ 2\times 3 }$

$x=\dfrac { -7\pm 5 }{ 6 }$

$x=\dfrac { -7+5 }{ 6 }$ and

$x=\dfrac { -7-5 }{ 6 }$

$x=\dfrac { -2 }{ 6 }$ and

$x=\dfrac { -12 }{ 6 }$
Hence,

$x=\dfrac { -1 }{ 3 }$ and

$x=-2$ are the roots of the given quadratic equation.

Compare quadratic equation ${x}^{2}+3x-1=0$ with the general form $a{x}^{2}+bx+c=0$ and write the value of ' $a$ ' and ' $b$ '.

Here,

$a=1$ and

$b=3$

Find the roots of equation $2x^2 - x - 4 = 0$ by the method of completing the square.

Method of completing the square,

Given equation is

$2x^{2}-x-4=0$

The coefficient of

$x^{2}$ is

$2$ , make it

$1$ by dividing by

$2$ on both the sides.

i.e.

$x^{2}-\dfrac x2-2=0$

Transpose the constant term to the right.

$x^{2}-\dfrac x2=2$

Add the square of half the coefficient of

$x$ on both sides.

$x^{2}-\dfrac x2+\dfrac1{16}=2+\dfrac1{16}$

$\left(x-\dfrac 14\right)^{2}=\dfrac{33}{16}$

The equation is of the form

$a^{2}=b$

which implies

$a=\pm\sqrt b$

Therefore,

$x-\dfrac14=\pm\dfrac{\sqrt{33}}4$

So,

$x=\dfrac14+\dfrac{\sqrt{33}}4$ or

$x=\dfrac14-\dfrac{\sqrt{33}}4$

State whether the given equation is quadratic or not. Give reason.
$\displaystyle\frac{5}{4}m^2-7=0$ .

Here variable term is

$m$

$\dfrac{5}{4}$

$m^{2}$

$-7$

$=0$

$5 m^{2}$

$-28=0$

It is a quadratic equation because power of variable is 2.

Solve the quadratic equation for x :
$4{ x }^{ 2 }-4{ a }^{ 2 }x+\left( { a }^{ 4 }-{ b }^{ 4 } \right) =0$

it is in the form of

$a{ x }^{ 2 }+bx+c$

the solution is

$x=\dfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a }$

here

$a=4,b=-4{a}^{2},c=(a^4-b^4)$

$\Rightarrow x=\dfrac { -4{ a }^{ 2 }\pm \sqrt { { (-4{ a }^{ 2 }) }^{ 2 }-4(4)({ a }^{ 4 }-{ b }^{ 4 }) } }{ 2(4) } \\ \\ \Rightarrow x=\dfrac { -4{ a }^{ 2 }\pm \sqrt { +16{ b }^{ 4 } } }{ 8 } \\ \Rightarrow x=\dfrac { -4{ a }^{ 2 }\pm 4{ b }^{ 2 } }{ 8 }$

therefore

$\Rightarrow x=\dfrac { -{ a }^{ 2 }\pm { b }^{ 2 } }{ 2 }$

Let $a, b, c$ be the sides of a triangle. No two of them are equal and $\lambda \epsilon R$ . If the roots of the equation $x^{2} + 2(a + b + c)x + 3\lambda (ab + bc + ca) = 0$ are real then.

As roots are real

$\therefore D\geq0$

$\Rightarrow 4(a+b+c)^2 −4(3\lambda)(ab+bc+ca)≥0$

$(a^2+b^2+c^2)+(2-3\lambda)(ab+bc+ca)\geq 0$

$\Rightarrow λ\leq \dfrac{(a^2+b^2+c^2)}{3(ab+bc+ca)}+\dfrac{2}{3}$ ......

$(1)$

Since in a triangle

$|b-a|<c \Rightarrow a^2 +b^2 −2ab<c^2$

$|b-c|<a \Rightarrow b^2+c^2−2cb<a^2$

$|c-a|<b\Rightarrow c^2+a^2−2ca<b^2$

Add all three inequalities, we get

$\dfrac{(a^2+b^2+c^2)}{(ab+bc+ca)}<2$

So, equation

$(1)$ becomes,

$\Rightarrow \lambda<\dfrac{4}{3}$

Solve the equation $4x^2-5x-3=0$ .

Given that,

$4x^2-5x-3=0$

We know that, for a quadratic equation of the form

$ax^2+bx+c=0$ ,

$x=\displaystyle\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

Here,

$a=4,\ b=-5\text{ and }c=-3$

$\therefore \ x=\displaystyle\frac{5\pm\sqrt{(5)^2-4(4)(-3)}}{2(4)}$

$\Rightarrow x=\dfrac{5\pm \sqrt{73}}{8}$

$\therefore \ x=\dfrac{5-\sqrt{73}}{8}$ or

$x=\dfrac{5+\sqrt{73}}{8}$

Number of solutions of the equations $|2x^2 + x -1| = |x^2+ 4x + 1|$

$2x^2+x-1>0$ for

$x\in (-\infty, -1)\cup (1/2, \infty)$

and

$x^2+4x+1> 0$ for

$x\in (-\infty, -(2+\sqrt3))\cup ((-2+\sqrt3), \infty))$

Case 1:

$-\infty <x<-(2+\sqrt3)$ , then

$2x^2+x-1=x^2+4x+1\implies x^2-3x-2=0$

$x=\dfrac{3\pm\sqrt{17}}{2}$ , do not satisfy the condition for case 1.

Case 2:

$-(2+\sqrt3)<x <-1$

$2x^2+x-1=-(x^2+4x+1)\implies 3x^2+5x=0$

$x=0,\, -5/2$ , do not satisfy the condition for case 2.

Case 3:

$-1<x< -2+\sqrt3$

$-(2x^2+x-1)=-(x^2+4x+1)\implies x^2-3x-2=0$

$x=\dfrac{3-\sqrt{17}}{2}$ , satisfies the condition for case 3.

Case 4:

$-2+\sqrt3<x< 1/2$

$-(2x^2+x-1)=x^2+4x+1\implies 3x^2+5x=0$

$x=0$ , satisfies the condition for case 4.

Case 5 :

$x>1/2$

$2x^2+x-1=x^2+4x+1\implies x^2-3x-2=0$

$x=\dfrac{3+\sqrt{17}}{2}$ , satisfies the condition for case 5.

$3$ solutions are possible for

$x$ .

Find the value of $p$ in the equation $2{ x }^{ 2 }+3x-p=0$ if the roots are real and equal.

Given quadratic equation

$2{ x }^{ 2 }+3x-p=0......(i)$
where

$a=2,b=3,c=-p$
If the roots of the equation are equal then the descriminant

$D=0$

$\Rightarrow$

$\sqrt { { b }^{ 2 }-4ac }=0$

$\Rightarrow$

${3}^{2}-4\times 2\times (-p)=0$

$\Rightarrow$

$9+8p=0$

$\Rightarrow$

$8p=-9$

$\Rightarrow$

$p=-\cfrac{9}{8}$

Solve the equation $3x-\displaystyle\frac{3}{x}=-8$ by formula method.

$\displaystyle 3x-\frac{3}{x}=-8$

$\Rightarrow 3x^2+8x-3=0$
On comparing the equation by

$ax^2+bx+c=0$
Here

$a=3, b=8, c=-3$

$x=\displaystyle\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\displaystyle\frac{-8\pm \sqrt{(8)^2-4\times 3\times (-3)}}{2\times 3}$

$x=\displaystyle\frac{-8\pm \sqrt{64+36}}{6}$

$x=\displaystyle\frac{-8\pm 10}{6}$

On considering positive sign,

$x=\displaystyle\frac{-8+10}{6} \Rightarrow x=\frac{1}{3}$

On considering negative sign,

$x=\displaystyle\frac{-8-10}{6} \Rightarrow x=-3$ .

Hence,

$x=\cfrac 13$ or

$x=-3$ .

Solve the quadratic equation $5x^2-6x-2=0$ by completing the square.

Given quadratic equation is

$5x^2-6x-2=0$ .

$\rightarrow x^2-\dfrac{6}{5}x-\dfrac{2}{5}=0$ (Divide on both sides by 5)

$\rightarrow x^2-2\left ( \dfrac{3}{5} \right )x+\dfrac{9}{25}=\dfrac{9}{25}+\dfrac{2}{5}$ (add

$\left ( \dfrac{3}{5} \right )^2=\dfrac{9}{25}$ on both sides)

$\rightarrow \left ( x-\dfrac{3}{5} \right )^2=\dfrac{19}{25}$

$\rightarrow x-\dfrac{3}{5}=\pm \sqrt{\dfrac{19}{25}}$ (take square root on both sides)

Thus, we have

$x=\dfrac{3}{5}\pm \dfrac{\sqrt{19}}{5}=\dfrac{3\pm \sqrt{19}}{5}$ .

Hence, the solution set is

$\left \{\dfrac{3+\sqrt{19}}{5}, \dfrac{3-\sqrt{19}}{5} \right \}$ .

Solve the following quadratic equation by formula method-
$3x^{2} + 8x - 3 = 0$

$3x^{2} + 8x - 3 = 0$
On comparing with general quadratic equation :

$ax^{2} + bx + c = 0$
We get

$a = 3, b = 8, c = -3$
Formula

$x = \cfrac {-b \pm \sqrt {b^{2} - 4ac}}{2}$

$x = \cfrac {-8 \pm \sqrt {8^{2} - 4.3.(-3)}}{2.3}$

$x = \cfrac {-8\pm \sqrt {64 + 36}}{6}$

$x = \cfrac {-8 \pm \sqrt {100}}{6}$

$x = \cfrac {-8\pm 10}{6}$
On taking positive sign

$x = \cfrac {-8 + 10}{6}$

$x = \cfrac {2}{6} = \dfrac {1}{3}$
On taking negative sign

$x = \cfrac {-8 - 10}{6}$

$x = \cfrac {-18}{6} = -3$
Thus, the solution of the equations are

$x = \cfrac {1}{3}, x = -3$ .

Write standard form of quadratic equation and find the roots of the equation $3x^2 + 5 \sqrt 2 x + 2 = 0$ using general formula.

The standard form of a quadratic equation is

$ax^2 + bx + c = 0, a \neq 0$ .
(That is, when the terms of the quadratic equation are written in descending order of their degrees, then we get the standard form of the equation.)
For the equation

$3x^2 + 5 \sqrt 2 x + 2 = 0$ , we get

$a = 3, b = 5 \sqrt 2, c = 2$
Using the general form, we get

$D = b^2 - 4ac = (5 \sqrt 2)^2 - 4(3)(2) = 26.$
Here,

$D > 0,$ so the equation has real and distinct roots.
Let the roots be

$\alpha$ and

$\beta$ .
So,

$\alpha = \dfrac{- a + \sqrt D}{2a}$ and

$\beta = \dfrac{- b - \sqrt D}{2a}$

$\alpha = \dfrac{-5 \sqrt 2 + \sqrt{26}}{2(3)}$ and

$\beta = \dfrac{-5 \sqrt 2 - \sqrt{26}}{2(3)}$

$\alpha = \dfrac{-5 \sqrt 2 + \sqrt{26}}{6}$ and

$\beta = \dfrac{-5 \sqrt 2 - \sqrt{26}}{6}$

$\therefore$ Roots of the given equation are

$\dfrac{-5 \sqrt 2 + \sqrt{26}}{6}$ and

$\dfrac{-5 \sqrt 2 - \sqrt{26}}{6}$ .

Find the value of discriminant $(\Delta)$ for the quadratic equation: $x^2+3x+1=0$ .

Discriminant of

$ax^2+bx+c=0$ is given by

$\Delta=b^2-4ac$

Here

$a=1, b=3, c=1$

$\therefore \Delta =3^2-4\cdot 1\cdot 1=9-4=5$

Solve the following equation:
$2{ x }^{ 2 }-13x+15=0$

Given equation is

$2{ x }^{ 2 }-13x+15=0$
Here

$a=2,b=-13,c=15$
Formula:

$x=\cfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a }$

$\quad x=\cfrac { -(-13)\pm \sqrt { { (-13) }^{ 2 }-4\times 2\times 15 } }{ 2\times 2 }$

$\Rightarrow x=\cfrac { 13\pm \sqrt { 169-120 } }{ 4 }$

$\Rightarrow x=\cfrac { 13\pm \sqrt { 49 } }{ 4 }$

$\Rightarrow x=\cfrac { 13\pm 7 }{ 4 }$
Taking

$+$ ve sign

$x=\cfrac { 13+7 }{ 4 } =\cfrac { 20 }{ 4 } =5$
Taking

$-$ ve sign

$x=\cfrac { 13-7 }{ 4 } =\cfrac { 6 }{ 4 } =\cfrac { 3 }{ 2 }$
Hence, the required solutions are

$x=5,\cfrac{3}{2}$

Find the smallest solution in positive integers of ${ x }^{ 2 }=41{ y }^{ 2 }-1$ .

We can write

$\sqrt { 41 } =6+\sqrt { 41 } -6$

$=6+\cfrac { 5 }{ \sqrt { 41 } +6 }$

$\cfrac { \sqrt { 41 } +6 }{ 5 } =2+\cfrac { \sqrt { 41 } -4 }{ 5 }$

$=2+\cfrac { 5 }{ \sqrt { 41 } +4 }$

$\cfrac { \sqrt { 41 } +4 }{ 5 } =2+\cfrac { \sqrt { 41 } -6 }{ 5 } =2+\cfrac { 1 }{ \sqrt { 41 } +6 }$

Therefore,

$\sqrt { 41 } =6+\cfrac { 1 }{ 2+ } \cfrac { 1 }{ 2+ } \cfrac { 1 }{ 12+ } ....$

Here penultimate is

$\cfrac { 32 }{ 5 }$ , and since the no. of quotients in the period is odd,

$x=32,y=5$ is a solution.

Penultimate convergent

$=6+\cfrac { 1 }{ 2+\cfrac { 1 }{ 2 } }$

$=6+\cfrac { 2 }{ 5 } =\cfrac { 32 }{ 5 }$

Find the general solution in positive integers of ${ x }^{ 2 }-17{ y }^{ 2 }=-1$ .

Given equation is

$x^2-17y^2=-1$ .

$\sqrt { 17 } =4+\cfrac { 1 }{ 8+ } \cfrac { 1 }{ 8+ } ....$

$\therefore x=4,y=1$ is a solution.

(

$\because$ Penultimate convergent is

$\cfrac { 4 }{ 1 } ,\because$ RHS

$=-1$ )

Thus,

$\left( x+y\sqrt { 17 } \right) \left( x-y\sqrt { 17 } \right) ={ \left( 4+\sqrt { 17 } \right) }^{ n }{ \left( 4-\sqrt { 17 } \right) }^{ n }$

$n$

$\epsilon$ odd positive integer

Thus

$2x={ \left( 4+\sqrt { 17 } \right) }^{ n }+{ \left( 4-\sqrt { 17 } \right) }^{ n }$

$\Rightarrow 2\sqrt { 17 } y={ \left( 4+\sqrt { 17 } \right) }^{ n }-{ \left( 4-\sqrt { 17 } \right) }^{ n }$

Find a general formula to express two positive integers which are such that the result obtained by adding their product to the sum of their squares is a perfect square.

Let x,y be integers; then;-

${ x }^{ 2 }+xy+{ y }^{ 2 }=$ perfect square

$={ z }^{ 2 }$

$x\left( x+y \right) ={ x }^{ 2 }-{ y }^{ 2 }$

Putting,

$mx=n(z+y),n(x+y)=m(z-y)$

Then,

$\cfrac { x }{ 2mn+{ n }^{ 2 } } =\cfrac { y }{ { m }^{ 2 }-{ n }^{ 2 } } =\cfrac { z }{ { m }^{ 2 }+mn+{ n }^{ 2 } }$

Find the general solution in positive integers of ${ x }^{ 2 }-5{ y }^{ 2 }=1$ .

Given equation is

$x^2-5y^2=1$ .

$\sqrt { 5 } =2+\cfrac { 1 }{ 4+ } \cfrac { 1 }{ 4+ } ....$

Penultimate convergent

$=2+\cfrac { 1 }{ 4 } =\cfrac { 9 }{ 4 }$

$x=9,y=4$ is a solution.

${ x }^{ 2 }+5{ y }^{ 2 }={ \left( { 9 }^{ 2 }-5.{ ,4 }^{ 2 } \right) }^{ n }={ \left( 9+4\sqrt { 5 } \right) }^{ n }{ \left( 9-4\sqrt { 5 } \right) }^{ n }$

Therefore,

$2x={ \left( 9+4\sqrt { 5 } \right) }^{ n }+{ \left( 9-4\sqrt { 5 } \right) }^{ n }$

$\Rightarrow 2\sqrt { 5 } y={ \left( 9+4\sqrt { 5 } \right) }^{ n }-{ \left( 9-4\sqrt { 5 } \right) }^{ n }$

If the product of all solution of the equation $\dfrac{(2009)x}{2010}=(2009)^{\log_x(2010)}$ can be expressed in the lowest form as $\dfrac{m}{n}$ then the value of $(m+n)$ is

$\cfrac { 2009 }{ 2010 } x={ \left( 2009 \right) }^{ \log _{ x }{ \left( 2010 \right) } }$

Taking

$\text{log}$ to the base

$10$ on both sides,

$\log { \left( \cfrac { 2009 }{ 2010 } \right) } +\log { x } =\log _{ x }{ \left( 2010 \right) } \log { \left( 2009 \right) }$

$-\left[ \log { 2010 } -\log { 2009 } \right] +\log { x } =\cfrac { \log { 2010 } }{ \log { x } } \log { 2009 }$

${ \left( \log { x } \right) }^{ 2 }-\left[ \log { 2010 } -\log { 2009 } \right] \log { x } -\log { 2010 } \log { 2009 } =0$

The obtained equation is an quadratic equation in

$\text{log} x$

$\log { x } =\cfrac { \log { 2010 } -\log { 2009 } \pm \sqrt { { \left( \log { 2010 } -\log { 2009 } \right) }^{ 2 }+4\left( \log { 2010 } \log { 2009 } \right) } }{ 2 }$

$\log { x } =\cfrac { \log { 2010 } -\log { 2009 } \pm \sqrt { { \left( \log { 2010 } +\log { 2009 } \right) }^{ 2 } } }{ 2 }$

$\log { x } =\cfrac { \log { 2010 } -\log { 2009 } \pm \left( \log { 2010 } +\log { 2009 } \right) }{ 2 }$

$\log { x } =\log { 2010 } ,\log { x } =-\log { 2009 }$

Simplifying further,

$\Rightarrow x=2010,\\\log { x } =\log { { \left( 2009 \right) }^{ -1 } }$

$\Rightarrow x={ \left( 2009 \right) }^{ -1 }$

$\text{Products of roots} =\cfrac { m }{ n } \\=\cfrac { 2010 }{ 2009 }$

$m+n=2010+2009$

$=4019$

Show that the roots of the equation
$(x - a)(x - b)(x - c) - f^{2}(x - a) - g^{2}(x - b) - h^{2}(x - c) + 2fgh = 0$ are all real.

From the given equation, we have

$(x - a)\left \{(x - b)(x - c) - f^{2}\right \} - \left \{g^{2}(x - b) - h^{2}(x - c) - 2fgh\right \} = 0$
Let

$p, q$ be the roots of the quadratic

$(x - b)(x - c) - f^{2} = 0$ ,
and suppose

$p$ to be not less than

$q$ .

By solving the quadratic formula, we have

$2x = b + c\pm \sqrt {(b - c)^{2} + 4f^{2}} .... (1)$ ;
Now the value of the surd is greater than

$b\sim c$ , so that

$p$ is greater than

$b$ or

$c$ , and

$q$ is less than

$b$ or

$c$ .
In the given equation substitute for

$x$ successively the values

$+\infty, p, q, -\infty$ ;
The results are respectively

$+\infty, -(g\sqrt {p - b} - h\sqrt {p - c})^{2}, + (g\sqrt {b - q} - h\sqrt {c - q})^{2}, -\infty$ ,
Since

$(p - b)(p - c) = f^{2} = (b - q)(c - q)$ .
Thus, the given equation has three real roots, one greater than

$p$ , one between

$p$ and

$q$ , and one less than

$q$ .
If

$p = q$ , then from

$(1)$ we have

$(b - c)^{2} + 4f^{2} = 0$ and therefore

$b = c, f = 0$ .
In this case the given equation becomes

$(x - b)\left \{(x - a)(x - b) - g^{2} - h^{2}\right \} = 0$ ;
thus the roots are all real.
If

$p$ is a root of the given equation, the above investigation fails; for it only shows that there is one root between

$q$ and

$+\infty$ , namely

$p$ . But as before, there is a second real root less than

$q$ ; hence the third root must also be real. Similarly if

$q$ is a root of the given equation we can show that all the roots are real.

Solve $x^2+7x=7$ and give your answer correct to two decimal places.

Given equation is

$x^2+7x=7$

$\Rightarrow x^2+7x-7=0$

Using the quadratic formula, we get:

$x=\dfrac{-7\pm\sqrt{49+28}}{2\times1}$

$\Rightarrow x = \dfrac{-7\pm\sqrt{77}}{2} = 0.89,-7.89$

Thus, there are two values of

$x$ i.e

$0.89$ and

$-7.89$ (correct up to two decimal places)

Solve the following equation:
$\displaystyle\, \left ( \left ( \sqrt[5]{27} \right )^{x/4 - \sqrt{x/3}} \right )^{x/4 + \sqrt{x/3}} = \sqrt{27}$

$\bigg((\sqrt[5]{27})^{x/4-\sqrt{x/3}}\bigg)^{x/4+\sqrt{x/3}}=\sqrt{27}$

$(\sqrt[5]{27})^{(x/4)^{2}-x/3}=27^{1/2}$

$(x/4)^{2}-x/3=5/2\implies 3{x^{2}}-16{x}-120=0\implies x=\dfrac{16\pm\sqrt{256+1440}}{6}=\dfrac{8\pm\sqrt{424}}{3}$

Check if the equation $x \, + \, \dfrac{1}{x} \, = \, x^2 , \, x \, \neq \, 0$ is quadratic.

$x+\dfrac { 1 }{ x } ={ x }^{ 2 }$ ,

$x\neq 0$

$\Rightarrow \dfrac { { x }^{ 2 }+1 }{ x } ={ x }^{ 2 }$

$\Rightarrow { x }^{ 3 }-{ x }^{ 2 }-1=0 \longrightarrow \left( a \right)$

Cubic format

$\rightarrow { Ax }^{ 3 }+{ Bx }^{ 2 }+Cx+D=0$

In eq.

$(a)$ ,

$C=0$ , which satisfy it's cubic equation not a quadratic equation

Solve the following equations.
$\displaystyle log \, (5 \, - \, x) \, + \, log \,(3 \, - \, x) \, = \, 1.$

$\log(5-x)+\log(3-x)=1$

Here,

$x<3$

$\implies \log(x^2-8x+15)=1$

$\implies x^2-8x+15=10$

$\implies x^2-8x+5=0$

$\implies x=\dfrac{8\pm\sqrt{44}}{2}=4\pm\sqrt{11}$

Hence,

$x=4-\sqrt{11}$

Find the roots of the quadratic equation (if they exist) by the method of completing the square.

$2x^2 + x + 4 = 0$

$2x^2+x+4=0$ can be written as

$x^2+\dfrac{x}{2}+2=0$

$\Rightarrow x^2+\dfrac{x}{2}=-2$

Add the coefficient of

$\left( \dfrac{x}{2}\right )^2$ to both sides

$x^2+\dfrac{x}{2}+\left(\dfrac{1}{4}\right)^2=-2+\left(\dfrac{1}{4}\right)^2$

$\left(x+\dfrac{1}{4}\right)^2=-2+\dfrac{1}{16}$

$\left(x+\dfrac{1}{4}\right)^2=\dfrac{-32+1}{16}$

$\left(x+\dfrac{1}{4}\right)^2=\dfrac{-31}{16}$

$x+\dfrac{1}{4}=\sqrt{-\dfrac{31}{16}}$

Since root cannot be negative

Therefore, no real roots exist.

Discriminant of the following quadratic equation is :
$2x^2$ - 5x + 3 = 0

$\Rightarrow$ The given quadratic equation is

$2x^2-5x+3=0$ , comparing it with

$ax^2+bx+c=0$

$\Rightarrow$ We get,

$a=2,\,b=-5$ and

$c=3$

$\Rightarrow$

$D=b^2-4ac$

$=(-5)^2-4(2)(3)$

$=25-24$

$=1$

$\therefore$ Discriminant of given quadratic equation is

$1$ .

Discriminant of the following quadratic equation is zero for k equal to:
$x^2$ - 2x + k = 0, k $\epsilon$ R

$\Rightarrow$ Given quadratic quation is

$x^2-2x+k=0$ , comparing it with

$ax^2+bx+c=0$

$\Rightarrow$ We get,

$a=1,\,b=-2$ and

$c=k$

$\Rightarrow$ It is given that discriminant is equal to

$0$ .

$\therefore$

$b^2-4ac=0$

$\Rightarrow$

$(-2)^2-4(1)(k)=0$

$\Rightarrow$

$4-4k=0$

$\Rightarrow$

$4k=4$

$\therefore$

$k=1$

Verify the equation $(x+1)^2=2(x-3)$ is a quadratic equation

$\left(x+1\right)^{2}=2\left(x-3\right)$

${x}^{2}+2x+1=2x-6$

${x}^{2}+7=0$

A polynomial equation of degree

$2$ is a quadratic equation.

Discriminant of the following quadratic equation is :
$\sqrt{3}x^2 \, + \, 2\sqrt{2}x \, - \, 2\sqrt{3} \, = \, 0$

$\Rightarrow$ The given quadratic equation is

$\sqrt{3}x^2+2\sqrt{2}x-2\sqrt{3}=0$ , comparing it with

$ax^2+bx+c=0$

$\Rightarrow$ We get,

$a=\sqrt{3},\,b=2\sqrt{3},\,c=-2\sqrt{3}$

$\Rightarrow$

$D=b^2-4ac$

$=(2\sqrt{2})^2-4(\sqrt{3})(-2\sqrt{3})$

$=8+24$

$=32$

$\therefore$ Discriminant of the give quadratic equation is

$32$ .

Two pipes running together can fill a tank in $11\dfrac{1}{9}$ minutes. If one pipe takes $5$ minutes more than the other to fill the tank , find the product of the time in which each pipe would fill the tank .

Two pipes together fill tank in

$11\cfrac{1}{9}$ min.

Let the time taken by one pipe to fill them separately be

$x$ min.

Time taken by another pipe to fill tank separately is

$x+5$ min.

$\Rightarrow \cfrac{(x)(x+5)}{x+x+5}=\cfrac{100}{9}$

$\Rightarrow9(x^{2}+5x)=200x+500$

$\Rightarrow 9x^{2}-155x-500=0$

$x=\cfrac{155\pm205}{2(9)}$

$\Rightarrow x=\cfrac{360}{2(9)}$

$\Rightarrow x=20$ - Equation 1

$\Rightarrow x+5=25$ -Equation 2

Product of times taken by them both separately=

$(x)(x+5)=500$

Negative of Discriminant of the following quadratic equation is :
$x^2$ - x + 1 = 0

$\textbf{Given expression is , }$

$x^2-x+1=0$ ,

$\textbf{ Step : 1 comparing the above equation with }$

$ax^2+bx+c=0$ .

$\Rightarrow$ We get,

$a=1,\,b=-1,\,c=1$

$\textbf{ Step : 2 Finding the Discriminant}$

$D=b^2-4ac$

$=(-1)^2-4(1)(1)$

$=1-4$

$=-3$

$\therefore$ Discriminant

$=-3$

$\Rightarrow$

$\textbf{Negative of discriminant}$

$=-(-3)=3$

Discriminant of the following quadratic equation is :
$x^2 -2x - 4 = 0$

$\Rightarrow$ The given quadratic equation is

$x^2-2x-4=0$ , comparing it with

$ax^2+bx+c=0$

$\Rightarrow$ We get,

$a=1,\,b=-2$ and

$c=-4$

$\Rightarrow$

$D=b^2-4ac$

$=(-2)^2-4(1)(-4)$

$=4+16$

$=20$

$\therefore$ Discriminant of the given quadratic equation is

$20$ .

Solve $2x^2+x-6$ by completing square method

$2x^{2}+x-6$

Completing the square,

$\Rightarrow x^{2}+\cfrac{x}{2}-3=0$

$\Rightarrow x^{2}+\cfrac{x}{2}+\cfrac{1}{16}-\cfrac{1}{16}-3=0$

$\Rightarrow(x+\cfrac{1}{4})^{2}-\cfrac{49}{16}=0$

$\Rightarrow (x+\cfrac{1}{4}-\cfrac{7}{4})(x+\cfrac{1}{4}+\cfrac{7}{4})=0$

$\Rightarrow (x-\cfrac{3}{2})(x+2)=0$

$\Rightarrow x=\cfrac{3}{2},-2$

Find the Discriminant of the equation :
$(x - 1)(2x - 1) = 0$

$\textbf{Step 1: Simplying given equation into standard quadratic equation}$

$\text{Given : }(x-1)(2x-1)=0$

$\Rightarrow$

$x(2x-1)-1(2x-1)=0$

$\Rightarrow$

$2x^2-x-2x+1=0$

$\Rightarrow$

$2x^2-3x+1=0$

$\textbf{Step 2: Finding the discriminant of the given equation}$

$\text{Comparing given quadratic equation with standard quadratic equation } {ax^2+bx+c=0}$

$\text{We get,}$

$a=2,\,b=-3,\,c=1$

$D =b^2-4ac$

$=(-3)^2-4(2)(1)$

$=9-8$

$=1$

$\boldsymbol{\therefore}$

$\textbf{Discriminant of given quadratic equation is 1}$

If the roots of the equation $(b - c)x^2 + (c - a)x + (a - b) = 0$ are equal, then prove that $2b = a + c$ .

D = 0

$\Rightarrow$

$(c \, - \, a)^2$ - 4 (b - c) (a - b) = 0

$\Rightarrow$

$c^2 \, + \, a^2 \, + \, 4b^2$ - 2ac - 4ab + 4ac - 4bc = 0

$\Rightarrow$

$(c \, + \, a \, - \, 2ab)^2 \, = \, \Rightarrow \, c \, + \, a \, - \, 2b \, = \, 0$

ALITER

Clearly, x = 1 satisfies the given equation. Since it has equal roots.

So, both roots are equal to 1.

$\therefore$ Product of the roots = 1.

$\Rightarrow \, \dfrac{a \, - \, b}{b \, - \, c} \, = \, 1 \, \Rightarrow \, a \, - \, b \, = \, b \, - \, c \, \Rightarrow \, 2b \, = \, a \, + \, c$

$(7 \, - \, 4 \sqrt 3)^{x^2 \, - 4x \, + \, 3} \, + \, (7 \, + \, 4 \sqrt 3)^{x^2 \, - 4x \, + \, 3} \, = \, 14$

$(7 - 4\sqrt{3}) (7 + 4\sqrt{3}) = 7^2-(4\sqrt{3})^2$

$=49 - 48 = 1$

$\implies 7+4\sqrt3=\dfrac{1}{7-4\sqrt3}$

From the given equation, we can observed:

$(7 - 4\sqrt{3})^{x^2-4x+3} +(7 + 4\sqrt{3})^{x^2-4x+3} = 14$

$(7-4\sqrt3)+(7+4\sqrt3)=7+7\dots 1$

On comparing the above equations, we get that:

$x^2-4x+3=1$ or

$x^2-4x+3=-1$

$x^2 + 4x + 2 = 0$ or

$x^2 - 4x + 4 = 0$

$\therefore \, x \, = \, -2 \, \pm \, \sqrt{2}$ or

$x = 2,2$

(a) Prove that the roots of
$(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=0$
are always real and they will be equal if and only if $a=b=c$ .
(b) Examine the nature of the roots of the quadratic ${ \left( b-x \right) }^{ 2 }-4(a-x)(c-x)=0$ where a,b,c are real.
(c) Discuss the nature of the roots of the equation ${ x }^{ 2 }+2(3\lambda +5)x+2(9{ \lambda }^{ 2 }+25)=0$

(a) The given equation is

$3{ x }^{ 2 }-2x(a+b+c)+(ab+bc+ca)=0$
Roots Equal.

$\Rightarrow { B }^{ 2 }-4AC=0$
or

$4{ \left( a+b+c \right) }^{ 2 }-12(ab+bc+ca)=0$
or

$({ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 }+2\sum { ab } -3\sum { ab } )=0$
or

$({ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 }-ab-bc-ca=0$
or

$\frac { 1 }{ 2 } [2{ a }^{ 2 }+2{ b }^{ 2 }+2{ c }^{ 2 }-2ab-2bc-2ca]=0$
or

$\Delta =\frac { 1 }{ 2 } [{ \left( a-b \right) }^{ 2 }+{ \left( b-c \right) }^{ 2 }+{ \left( c-a \right) }^{ 2 }]=0$
Clearly

$\Delta \ge 0$

$\therefore$ Roots are real
They will be equal if

$\Delta =0$ . Hence

$a-b=0, b-c=0, c-a=0$ or

$a=b=c$ .
Converse : If

$a=b=c$ then the given equation reduces to

$3{ \left( x-a \right) }^{ 2 }=0$ which clearly has equal roots.
(b) The given equation can be written as

$3{ x }^{ 2 }-[4(a+c)-2b]x-({ b }^{ 2 }-4ac)=0$

$\Delta ={ \left[ 4(a+c)-2b \right] }^{ 2 }+12({ b }^{ 2 }-4ac)$

$={ 4\left[ 2(a+c)-b \right] }^{ 2 }+({ 3b }^{ 2 }-12ac)$

$=4[4({ a }^{ 2 }+{ c }^{ 2 }+2ac)+{ b }^{ 2 }-4b(a+c)+3{ b }^{ 2 }-12ac]$

$=16[{ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 }-ab-bc-ca]$ .........(1)

$=8[{ \left( a-b \right) }^{ 2 }+{ \left( b-c \right) }^{ 2 }+{ \left( c-a \right) }^{ 2 }]=+ive$

$\therefore$ Roots are real.
Note : we can also use the inequality

${ a }^{ 2 }+{ b }^{ 2 }+{ c }^{ 2 }>ab+bc+ca$ in (1)
as

${ a }^{ 2 }+{ b }^{ 2 }>2ab,{ b }^{ 2 }+{ c }^{ 2 }>2bc,{ c }^{ 2 }+{ a }^{ 2 }>2ca$ .
(c)

$D=-4{ \left( 3\lambda -5 \right) }^{ 2 }$ If

$\lambda \neq \frac { 5 }{ 3 }$ their D is always

$-ive$ and hence roots are complex. But if

$\lambda =\frac { 5 }{ 3 }$ their

$D=0$ and is that case the root will be equal.

Using the Completing Square Method convert the following quadratic equation in the form of $(x+p)^2=q$ and then find out its roots.
$5x^2-6x-2=0$

$5{ x }^{ 2 }-6x-2=0$

$\Rightarrow (\sqrt { 5 } x-\dfrac { 3 }{ \sqrt { 5 } } )^{ 2 }=2+\dfrac { 9 }{ 5 }$

$\Rightarrow (\sqrt { 5 } x-\dfrac { 3 }{ \sqrt { 5 } } )^{ 2 }=\dfrac { 19 }{ 5 }$

$\Rightarrow \sqrt { 5 } x-\dfrac { 3 }{ \sqrt { 5 } } =\pm \dfrac { \sqrt { 19 } }{ \sqrt { 5 } }$

$\Rightarrow x=\dfrac { \pm \sqrt { 19 } +3 }{ 5 }$

$\therefore x=\dfrac { 3\pm \sqrt { 19 } }{ 5 }$

If the roots of the equation
$({ c }^{ 2 }-ab){ x }^{ 2 }-2({ a }^{ 2 }-bc)x+({ b }^{ 2 }-ac)=0$
be equal, prove that either $a=0$
or ${ a }^{ 3 }+{ b }^{ 3 }+{ c }^{ 3 }+=3abc$ .

$({ c }^{ 2 }-ab){ x }^{ 2 }-2({ a }^{ 2 }-bc)x+({ b }^{ 2 }-ac)=0$
If the roots be equal, then

${ B }^{ 2 }-4AC=0$

$\therefore$

$4{ \left( { a }^{ 2 }-bc \right) }^{ 2 }-4({ c }^{ 2 }-ab)({ b }^{ 2 }-ac)=0$
or

$[{ a }^{ 4 }-2{ a }^{ 2 }bc+{ b }^{ 2 }{ c }^{ 2 }]-[{ b }^{ 2 }{ c }^{ 2 }-a{ b }^{ 3 }-a{ c }^{ 3 }+{ a }^{ 2 }bc]=0$
or

$a[{ a }^{ 3 }+{ b }^{ 3 }+{ c }^{ 3 }+-3abc]=0$

$\therefore$ Either

$a-0$ or

${ a }^{ 3 }+{ b }^{ 3 }+{ c }^{ 3 }-3abc=0$ .

${x^2} - (\sqrt 2 + 1)x + \sqrt 2 = 0$

${ x }^{ 2 }-(\sqrt { 2 } +1)x+\sqrt { 2 } =0\\ { x }^{ 2 }-\sqrt { 2 } x-x+\sqrt { 2 } =0\\ (x-\sqrt { 2 } )(x-1)=0\\ \therefore x=1,\quad \sqrt { 2 }$

Solve the following equations :
$\sqrt{3x+1}$ $-$ $\sqrt{x-1}$ = $2$

$\Longrightarrow \sqrt { 3x+1 } -\sqrt { x-1 } =2 \\ \Longrightarrow \sqrt { 3x+1 } =2+\sqrt { x-1 } \\ \Longrightarrow { \left( \sqrt { 3x+1 } \right) }^{ 2 }={ \left( 2+\sqrt { x-1 } \right) }^{ 2 } \\ \Longrightarrow 3x+1=4+{ \left( \sqrt { x-1 } \right) }^{ 2 }+2\left( 2 \right) \left( \sqrt { x-1 } \right) \\ \Longrightarrow 3x+1=4+x-1+4\sqrt { x-1 } \\ \Longrightarrow 3x+1-4-x+1=4\sqrt { x-1 } \\ \Longrightarrow 2x-2=4\sqrt { x-1 } \\ \Longrightarrow { \left( 2x-2 \right) }^{ 2 }={ 4 }^{ 2 }\left( x-1 \right) \\ \Longrightarrow 4{ x }^{ 2 }+4-8x=16\left( x-1 \right) \\ \Longrightarrow 4{ x }^{ 2 }+4-8x=16x-16 \\ \Longrightarrow 4{ x }^{ 2 }-8x-16x=-4-16 \\ \Longrightarrow 4{ x }^{ 2 }-24x=-20 \\ \Longrightarrow 4{ x }^{ 2 }-24x+20=0 \\ \Longrightarrow { x }^{ 2 }-6x+5=0 \\ \Longrightarrow { x }^{ 2 }-5x-x+5=0\\ \Longrightarrow x\left( x-5 \right) -1\left( x-5 \right) =0 \\ \Longrightarrow \left( x-5 \right) \left( x-1 \right) =0 \\ \Longrightarrow x=1\quad or\quad x=5$

$4x^2+4\sqrt{3}x+3=0$

$4{ x }^{ 2 }-4\sqrt { 3 } x+3=0$

$\Rightarrow (2x+\sqrt { 3 } )^{ 2 }=0$

$\Rightarrow 2x+\sqrt { 3 } =0$

$\Rightarrow x=-\dfrac { \sqrt { 3 } }{ 2 }$

Write the zeroes of the polynomial :
$x^2+2x+1$

$x^{2}+2x+1=0$

$\left(x+1\right)^{2}=0$

$\therefore$ Zeros are

$-1,-1$

If $\alpha, \beta$ are the roots of $x^2 \, + \, ax \, + \, b \, = \, 0$ . Then prove that $\dfrac{\alpha }{\beta }$ is a root of the equation $bx^2 \, +\, (2b \, - \,a^2) \, x \, + \, b \,= \, 0$ .

Given

$\alpha,\beta$ are roots of the equation

$x^2+ax+b=0$ ,

Then,

$\alpha \, + \, \beta \, = \, -a, \, \alpha\beta \, = \, b$ .......(1).

Now, we to prove

$\dfrac{\alpha}{\beta}$ to be the root of the equation

$bx^2+(2b-a^2)x+b=0$ , we have to prove that

$b\left(\dfrac{\alpha}{\beta} \right )^2 \, +(2b \, - \, a^2) \dfrac{\alpha}{\beta} \, + \, b \, = \, 0$
or

$b(\alpha^2 \, + \, \beta^2) \, + \, (2b \, - \, a^2) \alpha\beta \, = \, 0$
Now,

$b(\alpha^2 \, + \, \beta^2) \, + \, (2b \, - \, a^2) \alpha\beta$

$=b\{(\alpha \, + \, \beta)^2-2\alpha.\beta\} \, + \, (2b \, - \, a^2) \alpha\beta$

$=b\{(a)^2-2b\} \, + \, (2b \, - \, a^2) b$ [Using (1)]

$=b(a^{2}-2b)\, - \, (a^{2}-2b)b$

$=0$

Solve the equation $2{ x }^{ 2 }-5x+3=0$ by the method of completing square.

We have,

$2{ x }^{ 2 }-5x+3=0$

$\Rightarrow { x }^{ 2 }-\cfrac { 5 }{ 2 } x+\cfrac { 3 }{ 2 } =0$ (Dividing throughough by

$2$ )

$\Rightarrow { x }^{ 2 }-\cfrac { 5 }{ 2 } x=-\cfrac { 3 }{ 2 }$ (Shifting the constant term on RHS)

$\Rightarrow { x }^{ 2 }-2\left( \cfrac { 5 }{ 4 } \right) x+{ \left( \cfrac { 5 }{ 4 } \right) }^{ 2 }={ \left( \cfrac { 5 }{ 4 } \right) }^{ 2 }-\cfrac { 3 }{ 2 }$ (Adding

${ \left( \quad \cfrac { 1 }{ 2 } \quad Coeff.\quad of\quad x \right) }^{ 2 }$ onboth sides)

$\Rightarrow { \left( x-\cfrac { 5 }{ 4 } \right) }^{ 2 }=\cfrac { 25 }{ 16 } -\cfrac { 3 }{ 2 } \quad \Rightarrow { \left( x-\cfrac { 5 }{ 4 } \right) }^{ 2 }=\cfrac { 1 }{ 16 } \quad \Rightarrow x-\cfrac { 5 }{ 4 } =\pm \cfrac { 1 }{ 4 } \Rightarrow x=\cfrac { 5 }{ 4 } \pm \cfrac { 1 }{ 4 }$

$\Rightarrow x=\cfrac { 5 }{ 4 } +\cfrac { 1 }{ 4 } =\cfrac { 6 }{ 4 } \quad or\quad x=\cfrac { 5 }{ 4 } -\cfrac { 1 }{ 4 } =\cfrac { 4 }{ 4 } \Rightarrow x=\cfrac { 3 }{ 2 } \quad or\quad x=1\quad$

Here the roots of the equation are

$\cfrac{3}{2}$ and

$1$

$x+\cfrac { 3 }{ x } ={ x }^{ 2 }$

$\Rightarrow \cfrac { { x }^{ 2 }+3 }{ x } ={ x }^{ 2 }\Rightarrow { x }^{ 2 }+3{ x }^{ 3 }\Rightarrow { x }^{ 3 }-{ x }^{ 2 }-3=0\quad \quad \quad$
Clearly,

${ x }^{ 3 }-{ x }^{ 2 }-3$ being a polynomial of degree

$3$ , is not a quadratic polynomial.

So, the given equation is not a quadratic equation.

${ x }^{ 2 }-6x+4=0$

Let

$p(x)={ x }^{ 2 }-6x+4=0$

$x^2-6x+4=0$

$\Rightarrow$ A quadratic equation is an equation of the second degree, meaning it contains at least one term that is squared.

$\Rightarrow$ Comparing equation

$x^2-6x+4=0$ with standard form of quadratic equation

$ax^2+bx+c=0$ .

$\Rightarrow$ We get,

$a=1,\,b=-6,\,c=4$

$\therefore$ The equation

$x^2-6x+4=0$ is quadratic equation.

Find the roots of the given equation $4{ x }^{ 2 }+4bx-\left( { a }^{ 2 }-{ b }^{ 2 } \right) =0$ by the method of completing the square.

$\textbf{Given expression}$

$4{ x }^{ 2 }+4bx-\left( { a }^{ 2 }-{ b }^{ 2 } \right) =0$

$\Rightarrow { x }^{ 2 }+bx-\cfrac { { a }^{ 2 }-{ b }^{ 2 } }{ 4 } =0$

$\textbf{Step : 1 Converting the quadratic equation into a perfect square form}$

$\Rightarrow { x }^{ 2 }+2\left( \cfrac { b }{ 2 } \right) x+{ \left( \cfrac { b }{ 2 } \right) }^{ 2 } - \dfrac{a^2}{4} = 0$

$\Rightarrow { \left( x+\cfrac { b }{ 2 } \right) }^{ 2 }=\cfrac { { a }^{ 2 } }{ 4 }$ ,

$\boldsymbol{[\because (a+b)^2 = a^2 + b^2 +2ab]}$

$\Rightarrow x+\cfrac { b }{ 2 } =\pm \cfrac { a }{ 2 }$

$\Rightarrow x=\cfrac { -b }{ 2 } \pm \cfrac { a }{ 2 }$

$\Rightarrow x=\cfrac { -b-a }{ 2 } ,\cfrac { -b+a }{ 2 }$

Hence, the roots are

$-\left (\cfrac{a+b}{2} \right )$ and

$\left (\cfrac{a-b}{2} \right )$

Solve the quadratic equation $9{ x }^{ 2 }-15x+6=0\quad$ by the method of completing the square.

We have

$9{ x }^{ 2 }-15x+6=0\quad$

$\Rightarrow { x }^{ 2 }-\cfrac { 15 }{ 9 } x+\cfrac { 6 }{ 9 } =0$ (Dividing throughout by

$9$ )

$\Rightarrow { x }^{ 2 }-\cfrac { 5 }{ 3 } x+\cfrac { 2 }{ 3 } =0\Rightarrow { x }^{ 2 }-\cfrac { 5 }{ 3 } x=-\cfrac { 2 }{ 3 }$ (Shifting the constant term on RHS)

$\Rightarrow { x }^{ 2 }-2\left( \cfrac { 5 }{ 6 } \right) x+{ \left( \cfrac { 5 }{ 6 } \right) }^{ 2 }={ \left( \cfrac { 5 }{ 6 } \right) }^{ 2 }-\cfrac { 2 }{ 3 }$ (Adding square of half of coefficient of

$x$ on both sides)

$\Rightarrow { \left( x-\cfrac { 5 }{ 6 } \right) }^{ 2 }=\cfrac { 25 }{ 36 } -\cfrac { 2 }{ 3 } \Rightarrow { \left( x-\cfrac { 5 }{ 6 } \right) }^{ 2 }=\cfrac { 1 }{ 36 } \Rightarrow x-\cfrac { 5 }{ 6 } =\pm \cfrac { 1 }{ 6 }$ (Taking square root on both sides)

$\Rightarrow x=\cfrac { 5 }{ 6 } +\cfrac { 1 }{ 6 } =1\quad or\quad x=\cfrac { 5 }{ 6 } -\cfrac { 1 }{ 6 } =\cfrac { 2 }{ 3 } \Rightarrow x=1\quad or\quad x=\dfrac23$

Hence the roots of the equation are

$1$ and

$\dfrac23$

By using the method of completing the square, show that the equation $4{ x }^{ 2 }+3x+5=0$ has no real roots.

We have

$4{ x }^{ 2 }+3x+5=0$

$\Rightarrow { x }^{ 2 }+\cfrac { 3 }{ 4 } x+\cfrac { 5 }{ 4 } =0\quad \quad \\\Rightarrow { x }^{ 2 }+2\left( \cfrac { 3 }{ 8 } x \right) x=-\cfrac { 5 }{ 4 } \\\Rightarrow { x }^{ 2 }+2\left( \cfrac { 3 }{ 8 } x \right) +{ \left( \cfrac { 3 }{ 8 } \right) }^{ 2 }={ \left( \cfrac { 3 }{ 8 } \right) }^{ 2 }-\cfrac { 5 }{ 4 } \\\Rightarrow { \left( x+\cfrac { 3 }{ 8 } \right) }^{ 2 }=-\cfrac { 71 }{ 64 }$
Clearly, RHS is negative. But

${ \left( x+\cfrac { 3 }{ 8 } \right) }^{ 2 }$ cannot be negative for any real value of

$x$ . Hence, the given equation has no real roots.

Find the roots of the equation $5{ x }^{ 2 }-6x-2=0,$ by the method of completing the square.

We have

$5{ x }^{ 2 }-6x-2=0$

$\Rightarrow { x }^{ 2 }-\cfrac { 6 }{ 5 } x-\cfrac { 2 }{ 5 } =0$ (Dividing throughout by

$5$ )

$\Rightarrow { x }^{ 2 }-\cfrac { 6 }{ 5 } x=\cfrac { 2 }{ 5 } \Rightarrow { x }^{ 2 }-2\left( \cfrac { 3 }{ 5 } \right) x+{ \left( \cfrac { 3 }{ 5 } \right) }^{ 2 }=\cfrac { 2 }{ 5 } +{ \left( \cfrac { 3 }{ 5 } \right) }^{ 2 }\Rightarrow { \left( x-\cfrac { 3 }{ 5 } \right) }^{ 2 }=\cfrac { 19 }{ 25 }$

$\Rightarrow x-\cfrac { 3 }{ 5 } =\pm \cfrac { \sqrt { 19 } }{ 5 } \Rightarrow x=\cfrac { 3 }{ 5 } \pm \cfrac { \sqrt { 19 } }{ 5 } =\cfrac { 3\pm \sqrt { 19 } }{ 5 } \Rightarrow x=\cfrac { 3+\sqrt { 19 } }{ 5 } \quad or\quad x=\cfrac { 3-\sqrt { 19 } }{ 5 }$

Hence, the roots of the given equation are

$\cfrac { 3+\sqrt { 19 } }{ 5 }$ and

$\cfrac { 3-\sqrt { 19 } }{ 5 }$

Solve:
$4x^2+4\sqrt{3}x+3=0$ .

$4x^2+4\sqrt 3x+3=0$

$a=4, b=4\sqrt 3, c=3$

$D=b^2-4ac=(4\sqrt 3)^2-4\times 4\times 3$

$=48-48$

$=0$

$\therefore$ Equal roots

$x=\dfrac{-b\pm \sqrt D}{2a}=\dfrac{-4\sqrt 3\pm 0}{2\times 4}$

$x=\dfrac{-4\sqrt 3}{8}$

$\boxed{x=\dfrac{-\sqrt 3}{2}}$

Find the value of $'K'$ if $Q.E$
$(2k+1){x}^{2}+2(k+3)x+(k+5)=0$ has equal roots

We have the given equation

$\left( {2k + 1} \right){x^2} + 2\left( {k + 3} \right)x + \left( {k + 5} \right) = 0$

using the formula of

${b^2} - 4ac = 0$ we get

${[2\left( {k + 3} \right)x]^2} - 4 \times \left( {2k + 1} \right)\left( {k + 5} \right) = 0$ [On putting the value of

$a,b\,and \,\,c$ from the above given equation]

$4\left( {k + 3} \right){x^2} - \left( {2k + 1} \right)\left( {k + 5} \right) = 0$

${k^2} + 9 + 6k - \left( {2{k^2} + 10k + k + 5} \right) = 0$

${k^2} + 9 + 6k - 2{k^2} - 11k - 5 = 0$

$- {k^2} - 5k + 4 = 0$

${k^2} + 5k - 4 = 0$ [multiply both side by the sign

$-ve$ ]

Now again use the formula of

${b^2} - 4ac = 0$ we get

$k = \dfrac{{ - 5 \pm \sqrt {{5^2} + 4 \times 1 \times 4} }}{{2 \times 1}}$

$= \dfrac{{ - 5 \pm \sqrt {25 + 16} }}{2}$

$= \dfrac{{ - 5 \pm \sqrt {41} }}{2}$

Which is the required answer

$x=\sqrt {6+\sqrt {6}+\sqrt {6}...}$

$x=\sqrt{6+\sqrt{6+\sqrt{6+......}}}$

squaring on both sides

$x^{2}=6+\sqrt{6+\sqrt{6+\sqrt{6+....}}}=6+x\implies x^{2}-x-6=0\implies x=3,-2$

Check whether the following is quadratic equation.
$(2x-1)(x-3)=(x+5)(x-1)$

Sol :- Given

$(2x-1)(x-3) = (x+5)(x-1)$

also given, to check whether the given Equation is

in a quadratic form

So, let us now Expand the given Equation we get,

$(2x-1)(x-3) = (x+5)(x-1)$

$\Rightarrow 2x^{2}-6x-x+3 = x^{2}-x+5x-5$

by further simplification we get,

$\Rightarrow 2x^{2}-7x+3 = x^{2}+4x-5$

$\Rightarrow 2x^{2}-x^{2}-7x-4x+3+5 = 0$

$\Rightarrow x^{2}-11x+8 = 0 \rightarrow eq (1)$

Here eq (1) represent a quadratic from of

$ax^{2}+bx+c = 0$

where,

$a = 1, b = -11, c = 8$

So the given

$(2x-1)(x-3) = (x+5)(x-1)$ is a

quadratic Equation.

1155480_1070340_ans_dbaa4c7fe15e454fad8de1c7161cd0a0.jpg

Is the mathematical statement $(a+4)(a+2)=a^{2}+8$ correct? given the reasons to support your answer.

The given mathematical statement is $\left( {a + 4} \right)\left( {a + 2} \right) = {a^2} + 8$ .

Simplifying the LHS of $\left( {a + 4} \right)\left( {a + 2} \right) = {a^2} + 8$

$\left( {a + 4} \right)\left( {a + 2} \right) = {a^2} + 2a + 4a + 8$

$= {a^2} + 6a + 8$

$\ne {\rm{RHS}}$

Therefore, the given mathematical statement is not correct.

An equation is condition on a _________

An equation is condition on a

$\underline{Variable}$ .

For what value of $'k',\ (k^2 - 4)x^2 + 2x - 9=0$ can not be quadratic equation?

The given equation,

$(k^2 - 4)x^2 + 2x -9=0$ will not be a quadratic one, if the co-efficient of

$x^2$ is

$0$ .

Then we will have,

$k^2-4=0$

or,

$k^2=4$

or,

$k=\pm 2$ .

So for

$k=\pm 2$ the given equation will not be a quadratic equation.

Solve ${x^2} - 15x + 54$

$x^2$

$-$

$15x$

$+$

$54$ can be written as:

$x^2$

$-$

$6x$

$-$

$9x$

$+$

$54$

$x(x-6)$

$-$

$9(x-6)$

$(x-6) (x-9)$

$x= 6, 9$

Find the value of $\sqrt{6+\sqrt{6+\sqrt{6+......to \infty}}}$

$\sqrt{6+\sqrt{6+\sqrt{6+.....+\infty}}}$

Let,

$x=\sqrt{6+\sqrt{6+\sqrt{6+.....+\infty}}}$

$\therefore x=\sqrt{6+x}$

$\implies x^2=6+x$

$\implies x^2-x-6=0$

$\implies x^2-3x+2x-6=0$

$\implies x(x-3)+2(x-3)=0$

$\implies (x+2)(x-3)=0$

So,

$x=-2$ ,

$x=3$

$\Rightarrow x=3$

If $x=3+i$ then prove that $x^2-6x+13=0$ .

Given,

$x=3+2i$

or,

$x-3=2i$

Now squaring both sides we get,

$(x-3)^2=-4$

or,

$x^2-6x+9=-4$

or,

$x^2-6x+13=0$ .

Solve the following
Find the roots of quadratic equation $2x^{2}-4x+3=0$ by completing the square find the roots of quadratic equation by using the formula

$2{ x }^{ 2 }-4x+3=0$

Roots are

$\cfrac { 4\pm \sqrt { 16-4\left( 3 \right) \left( 2 \right) } }{ 2{ x }^{ 2 } }$

$=\cfrac { 4\pm \sqrt { 16-24 } }{ 4 } =\cfrac { 4\pm \sqrt { -8 } }{ 4 }$

$=\cfrac { 4\pm 2\sqrt { 2 } i }{ 4 }$

$=\cfrac { 2\pm \sqrt { 2 } i }{ 2 }$

Roots are

$\cfrac { 2+\sqrt { 2 } i }{ 2 } ,\cfrac { 2-\sqrt { 2 } i }{ 2 }$

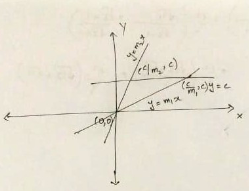
Show that the area of the triangle formed by the lines $y = m_1\ x, y = m_2\ x \ and \ y = c$ is equal to $\dfrac{c^2}{4} (\sqrt{33} + \sqrt{11}),$ where $m_1, m_2$ are the roots of the equation $x^2 + (\sqrt {3} + 2)x + \sqrt {3} - 1 = 0$ .

coordinates of

$\triangle$ are

$(x, y) = (o, o) , (x_2, y_2) = \left(\dfrac{c}{m_1}, c\right), (x_3, y_3) = \left(\dfrac{c}{m_2}, c\right)$

Area of

$\triangle = \dfrac{1}{2} \left|det\begin{vmatrix} x_1 &x_2&x_3 \\ y_1&y_2&y_3\\ 1&1&1\end{vmatrix}\right|$

$=\dfrac{1}{2}\left|det\begin{vmatrix}0&\dfrac{c}{m_1}&\dfrac{c}{m_2} \\0 & c&c\\ 1&1&1\end{vmatrix}\right|= \dfrac{c^2}{2} \left(\dfrac{1}{m_1} - \dfrac{1}{m_2}\right) = \dfrac{c^2}{2}\left(\dfrac{m_2-m_1}{m_1m_2}\right)$

$m_1, m_2$ are the roots of

$x^2 + (\sqrt{3}+ 2)x + (\sqrt{3}-1) = 0$

$\therefore m_1 + m_2 = \dfrac{-(\sqrt{3} + 2)}{1}$

$\left(\because \alpha + \beta = -\dfrac{b}{a}\right)$

$m_1m_2 = \dfrac{\sqrt{3} - 1}{1}$

$\left(\because \alpha \beta = \dfrac{c}{a}\right)$

$(m_2-m_1)^2 = (m_2+m_1)^2 - 4m_1m_2$

$=(-(\sqrt{3} + 2))^2 - 4 (\sqrt{3} - 1) = 3 + 4 + 4\sqrt{3} - 4 \sqrt{3} - 4 \sqrt{3} + 4 = 11$

$m_{2}-m_{1}=\sqrt{11}$

$\therefore$ Area of

$\triangle = \dfrac{e^2}{2} \left(\dfrac{\sqrt{11}}{\sqrt{3} - 1}\right) = \dfrac{c^2}{2} \left(\dfrac{\sqrt{11}}{\sqrt{3} - 1} \times \dfrac{\sqrt{3}+1}{\sqrt{3}+1}\right)$

$= \dfrac{c^2}{2} \left( \dfrac{\sqrt{33} + \sqrt{11}}{2}\right) = \dfrac{c^2}{4}(\sqrt{33} + \sqrt{11})$

1431950_1029787_ans_d00dd8acd0e34244a6fc762afc553f42.png

Solve the equation: $11{x^2} - 21x - 92 = 0$

$11x^2-21x-92=0$

$x_{1,\:2}=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\dfrac{-\left(-21\right)+\sqrt{\left(-21\right)^2-4\cdot \:11\left(-92\right)}}{2\cdot \:11}:\quad 4$

$x=\dfrac{-\left(-21\right)-\sqrt{\left(-21\right)^2-4\cdot \:11\left(-92\right)}}{2\cdot \:11}:\quad -\dfrac{23}{11}$

$x=4,\:x=-\dfrac{23}{11}$

Solve for x : $\sqrt 2 {x^2} + 7x + 5\sqrt 2 = 0$

$\sqrt{2}x^2+7x+5\sqrt{2}=0$

$\alpha=\cfrac{-7+\sqrt{49-4(\sqrt{2})(5\sqrt{2})}}{2\sqrt{2}}$

$\implies \alpha=\cfrac{-7+3}{2\sqrt{2}}$

$\implies \alpha=\cfrac{-2}{\sqrt{2}}$

$\implies \alpha=-\sqrt{2}$

$\beta=\cfrac{-7-\sqrt{49-4(\sqrt{2})(5\sqrt{2})}}{2\sqrt{2}}$

$\implies \beta=\cfrac{-7-3}{2\sqrt{2}}$

$\implies \beta=\cfrac{-5}{\sqrt{2}}$

$\implies \beta=\cfrac{-5\sqrt{2}}{2}$

Solve:
$abx^2+(b^2-ac)x-bc=0$

The given quadratic equation is

$abx^2+(b^2-ac)x-bc=0$ , on comparing it with

$Ax^2+Bx+C=0.$ We get,

$A=ab,\,B=(b^2-ac),\,C=bc$

Now, by using the quadratic formula,

$x=\dfrac{-B\pm\sqrt{B^2-4AC}}{2A}$

$=\dfrac{-(b^2-ac)\pm\sqrt{(b^2-ac)^2-4(ab)(-bc)}}{2(ab)}$

$=\dfrac{-b^2+ac\pm\sqrt{b^4-2b^2ac+a^2c^2+4b^2ac}}{2ab}$

$=\dfrac{-b^2+ac\pm\sqrt{b^4+2b^2ac+a^2c^2}}{2ab}$

$=\dfrac{-b^2+ac\pm\sqrt{(b^2+ac)^2}}{2ab}$

$=\dfrac{-b^2+ac\pm(b^2+ac)}{2ab}$

$x=\dfrac{-b^2+ac+b^2+ac}{2ab}$ or

$x=\dfrac{-b^2+ac-b^2-ac}{2ab}$

$x=\dfrac{2ac}{2ab}$ or

$x=\dfrac{-2b^2}{2ab}$

$\therefore$

$x=\dfrac{c}{b}$ or

$x=-\dfrac{b}{a}$

Find the value of $k$ if $x=4;y=-2$ is a solution of the equation $5x+4y=k$

Given that,

$x=4,\ y=-2$ is a solution of the equation

$5x+4y=k$

To find out: The value of

$k$ .

On substituting the values of

$x$ and

$y$ in the equation, the LHS and RHS should be equal.

$\therefore\ 5(4)+4(-2)=k$

$\Rightarrow 20-8=k$

$\therefore \ k=12$

Hence, if

$x=4,\ y=-2$ is a solution of the equation

$5x+4y=k$ , then the value of

$k$ is

$12$ .

Solve:
$(4x+2)\sqrt{x^2+x+1}$

$\left(4x+2\right)\sqrt{x^2+x+1}$

$=4x\sqrt{x^2+x+1}+2\sqrt{x^2+x+1}$

$=2\sqrt{x^2+x+1}\left(2x+1\right)$

$=2(2x+1)\sqrt{x^2+x+1}$

Solve the following equations
$16x - \dfrac{{10}}{x} = 27$

$\dfrac{1}{x} - \dfrac{1}{{x - 2}} = 3,\,x \ne 0,2$

$x - \dfrac{2}{x} = 3,\,x \ne 0$

$16x-\dfrac{10}{x}=27$

$16x^2-10=27x$

$16x^2-27x-10=0$

$16x^2-32x+5x-10=0$

$16x(x-2)+5(x-2)=0$

$x=\dfrac{-5}{16}, +2$

$\dfrac{1}{x}-\dfrac{1}{x-2}=3$

$\Rightarrow \dfrac{x-2-x}{x^2-2x}=3$

$-2=3x-6x$

$3x^2-6x+2=0$

Roots

$=\dfrac{6\pm \sqrt{3.6-4\times 2\times}}{2\times 3}$

$=\dfrac{6\pm \sqrt{12}}{6}$

$x-\dfrac{2}{x}=3$

$x^2-2=3x$

$\Rightarrow x^2-2x-x-2=0$

Roots

$=\dfrac{3\pm \sqrt{9-4\times 1\times (-2)}}{2\times 1}$

$=\dfrac{3\pm\sqrt{17}}{2}$ .

The roots of the quadratic equation
${x^2} - .2ax + {a^2} + {b^2} - {c^2} = 0$ are where a,b,c $\in \,R:$

${x}^{2}-2ax+{a}^{2}={c}^{2}-{b}^{2}$

$\Rightarrow\,{\left(x-a\right)}^{2}={c}^{2}-{b}^{2}$

$\Rightarrow\,x-a=\pm\sqrt{{c}^{2}-{b}^{2}}$

$\Rightarrow\,x=a\pm\sqrt{{c}^{2}-{b}^{2}}$

$\therefore\,x=\left\{a+\sqrt{{c}^{2}-{b}^{2}},a-\sqrt{{c}^{2}-{b}^{2}}\right\}$

Multiply:
$\left( {\frac{1}{3}{x^2} - \frac{1}{2}x + 5} \right)\,by\,\left( {\frac{1}{2}{x^2} - \frac{1}{3}x + 1} \right)$

$(\dfrac{1}{3} x^2 -\dfrac{1}{2} x+5)*(\dfrac{1}{2} x^2 -\dfrac{1}{3} x+1)$

$= \dfrac{1}{6} x^4- \dfrac{1}{9} x^3+\dfrac{1}{3}x^2-\dfrac{1}{4} x^3+\dfrac{1}{6} x^2-\dfrac{1}{2}x +\dfrac{5}{2}x^2-\dfrac{5}{3}x+5$

$= \dfrac{1}{6}x^4-\dfrac{13}{36} x^3+\dfrac{2+1+15}{6} x^2 -\dfrac{13}{6} x +5$

$= \dfrac{1}{6} x^4 -\dfrac{13}{36} x^3 + 3x^2 -\dfrac{13}{6} x+5$

$yx^{2}-12x+k$ is a perfect square find the numerical nature of $k$

Considering the equation to be:

$4x^2-12x+k$

$(a-b)^2=a^2-2ab+b^2$

$4x^2-12x+k=a^2-2ab+b^2$

$a=2x$

$-2ab=-12x$

$\Rightarrow ab=6x$

$\Rightarrow (2x)b=6x \Rightarrow b=3$

$\therefore k=3$

Find the value of a and b.
$\frac{{7 + \sqrt 5 }}{{7 - \sqrt 5 }} - \frac{{7 - \sqrt 5 }}{{7 + \sqrt 5 }} = a + \frac{7}{{11}}\sqrt 5 b$
Hence factorise the polynomial : $24{x^2} - (a + 41)x + (b + 11)$

The value of

$\dfrac{7+\sqrt5}{7-\sqrt5}-\dfrac{7-\sqrt5}{7+\sqrt5}=\dfrac{(7+\sqrt5)^2-(7-\sqrt5)^2}{7^2-(\sqrt5)^2}=\dfrac{7}{11}\sqrt5$

Hence a=0 and b=1, substitute the same in the polynomial

$24x^2-41x+12$

$24x^2-32x-9x+12$

$8x(3x-4)-3(3x-4)$

$\Rightarrow (8x-3)(3x-4)$

Find the roots of the equation:

$x - \dfrac{1}{x} =3,x \ne 0$

$\begin{array}{l}x - \dfrac{1}{x} = 3\\\dfrac{{{x^2} - 1}}{x} = 3\,\\{x^2} - 1 = 3x\\{x^2} - 3x - 1 = 0\\x = \dfrac{{3 \pm \sqrt {{3^2} - \left( 9 \right)\left( { - 1} \right)} }}{2}\\x = \dfrac{{3 \pm \sqrt {13} }}{2}\end{array}$

Solve $2 \cos^{2} \theta-\sqrt{3} \sin \theta +1=0$

Consider the given equation,

$2{{\cos }^{2}}\theta -\sqrt{3}\sin \theta +1=0$

$2\left( 1-{{\sin }^{2}}\theta \right)-\sqrt{3}\sin \theta +1=0$ $[\because \cos ^2 \theta=1-\sin^2 \theta]$

$2-2{{\sin }^{2}}\theta -\sqrt{3}\sin \theta +1=0$

$2{{\sin }^{2}}\theta +\sqrt{3}\sin \theta -3=0$

$\sin \theta =\dfrac{-\sqrt{3}\pm \sqrt{3-4\times 2\times -3}}{2\times 2}$ (use quadratic formula)

$\sin \theta =\dfrac{-\sqrt{3}\pm \sqrt{3+24}}{2\times 2}$

$\sin \theta =\dfrac{-\sqrt{3}\pm 3\sqrt{3}}{4}$

$\therefore \sin \theta =\dfrac{\sqrt{3}}{2},-\sqrt{3}$

If $\frac{{{x^2} + 1}}{x} = 2\frac{1}{2}$ , find the value of:
$x - \frac{1}{x}$

Given,

$\dfrac{x^2+1}{x}=2\cdot \dfrac{1}{2}$

$\dfrac{x^2+1}{x}=\dfrac{5}{2}$

$2x^2+2=5x$

$2x^2-5x+2=0$

$(x-2)(2x-1)=0$

$x=2,\dfrac{1}{2}$

(i)

$x-\dfrac{1}{x}$

$=2-\dfrac{1}{2}$

$=\dfrac{3}{2}$

(ii)

$x-\dfrac{1}{x}$

$=\dfrac{1}{2}-2$

$=-\dfrac{3}{2}$

Check whether the following is quadratic equation.
$x^3-4x^2-x+1=(x-2)^3$

$x^{3}-4x^{2}-x+1 = (x-2)^{3}...(A)$

for a equation to be quadratic it is

similar to

$ax^{2}+bx+c = 0 ...(1)$

where

$a, b, c$ are integers

Now, from eq. (A)

$x^{3}-4x^{2}-x+1 = (x-2)^{3}$

$x^{3}-4x^{2}-x+1 = x^{3}-8-6x+12x^{2}$

$16x^{2}-5x-9 = 0 ...(2)$

On comparing eq (2) & (1)

we observe that eq (1) & (2) are

similar

Hence eq

$(A)$ represent t a quadratic equation.

Solve the following quadratic equation by completing the square method.
$m^2-5m=-3$

$m^2-5m+3=0$

$\Rightarrow m^2-5m+\dfrac{25}{4}-\dfrac{25}{4}+3=0$

$\Rightarrow (m-\dfrac{5}{2})^2=\dfrac{13}{4}$

$\Rightarrow m=+\dfrac{5}{2}\pm\sqrt{\dfrac{13}{4}}$

on simplifying,

$\Rightarrow m=+\dfrac{5}{2}+\dfrac{\sqrt{13}}{2}$ or

$m=+\dfrac{5}{2}-\dfrac{\sqrt{13}}{2}$

Solve the following quadratic equation by completing the square method.
$5x^2=4x+7$

$5x^2=4x+7$

$5x^2-4x=7$

$x^2-\dfrac{4}{5}x=\dfrac{7}{5}$

$x^2-\dfrac{4}{5}x+\dfrac{4}{25}=\dfrac{7}{5}+\dfrac{4}{25}$

$x^2-2\left ( \dfrac{2}{5} \right )x+\left ( \dfrac{2}{5} \right )^2=\dfrac{39}{25}$

$\left ( x-\dfrac{2}{5} \right )^2=\dfrac{39}{25}$

$x-\dfrac{2}{5} =\pm \sqrt{\dfrac{39}{25}}$

$x=\dfrac{2}{5}\pm \dfrac{\sqrt{39}}{5}$

$\therefore x=\dfrac{2\pm \sqrt{39}}{5}$

Solve the following quadratic equation by completing the square method.
$9y^2-12y+2=0$

$9y^2-12y+2=0$

$9y^2-12y+4-4+2=0$

$(3y-2)^2=2$

$3y=2\pm\sqrt2$

$y=\dfrac{2\pm\sqrt2}{3}$

on siyplifying,

$y=\dfrac{2+\sqrt2}{3}$ and

$y=\dfrac{2-\sqrt2}{3}$

If $p,q,r \in R$ and the quadratic equation $p{x^2} + qx + r = 0$ has no real root, then

Given that,

$p{{x}^{2}}+qx+r=0$ $p,q,r$ $\in R$

We know that if a quadratic equation has no real root then,

$D<0$

${{B}^{2}}-4AC=0$

$\Rightarrow {{q}^{2}}-4pr<0$

$\Rightarrow {{q}^{2}}<4pr$

$\left(\frac{1}{4}a-\frac{1}{2}b+1\right)^2$

$((\frac{a}{4})-(\frac{b}{2})+1)^2\\=(\frac{a}{4})^2+(\frac{-b}{2})^2+1^2+2\times(\frac{a}{4})(\frac{-b}{2})+2(\frac{-b}{2})\times1+2\times1\times(\frac{a}{4})\\=(\frac{a^2}{16})+(\frac{b^2}{4})+1-(\frac{ab}{2})-b+(\frac{a}{2})$

Solve the following quadratic equation by completing the square method.
$x^2+x-20=0$

$x^2+x-20=0$

$x^2+x+\dfrac{1}{4}-\dfrac{1}{4}-20=0$

$(x+\dfrac{1}{2})^2=\dfrac{81}{4}$

$x+\dfrac{1}{2}=\pm\sqrt{\dfrac{81}{4}}$

$x=-\dfrac{1}{2}\pm\sqrt{\dfrac{81}{4}}$

$x=-\dfrac{1}{2}\pm\dfrac{9}{2}$

on simplifying,

$x=4,-5$

Write one quadratic polynomial that has one zero?

Quadratic polynomial having only one zero, is like

$(x-1)^{2}$

$f(x)\Rightarrow x^{2}-2x+1$

Only one i.e., at

$x=1$

Note:- We can take any polynomial

$(x-2)^{2},(x-5)^{2}$ .....

Solve : $5x - 4x^2 + 3$

We know that the solution of the quadratic equation

$ax^2+bx+c=0$ is given by

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$5x-4x^2+3=0$

$\implies 4x^2-5x-3=0$

$\implies x=\dfrac{-(-5)\pm\sqrt{(-5)^2-4(4)(-3)}}{2(4)}$

$\implies x=\dfrac{5\pm\sqrt{25+48}}{8}$

$\implies x=\dfrac{5\pm\sqrt{73}}{8}$

Find quadratic equation such that its roots are square of sum of the roots and square of difference of the roots of equation
$2{x}^{2}+2(p+q)x+{p}^{2}+{q}^{2}=0$

Let the roots of the required equation be $M$ and $N$

let the roots of the equation $2x²+2(p+q)x+p²+q²=0$ be $a$ and $b$

$\Rightarrow a + b = -(p+q)$

$\Rightarrow ab = \dfrac{(p^2 + q^2)}{ 2}$

$\Rightarrow (a+b)^2 = (p+q)^2$

$\Rightarrow (a-b)^2 = (a+b)^2 - 4ab$

$\Rightarrow (a-b)^2 = -(p - q)^2$

we wanted the values of square of sum of the roots and square of difference of the roots

Now $\Rightarrow M = (a+b)^2 = (p+q)^2$ and

$\Rightarrow N = (a-b)^2 = -(p - q)^2$

$\Rightarrow M + N = 4pq$

$\Rightarrow MN = (p+q)^2 [-(p - q)^2]$

$\Rightarrow MN= -(p^2 - q^2)^2$

hence the required equation is

$\Rightarrow x^2 - (4pq)x - (p^2 - q^2)^2 = 0$

Find the roots of the following equation:
$27- 125a^2- 135 a+ 225a^2$

Given: $27-125a^2-135a+225a^2$

$\Rightarrow 100a^2-135a+27=0$

Here, $a=100, b = -135, c=27$

$a =\dfrac{-(b)\pm \sqrt{(b)^2-4\times a\times c}}{2\times a}$

Using quadratic formula to find roots we get,

$a =\dfrac{-(-135)\pm \sqrt{(-135)^2-4\times 100\times 27}}{2\times 100}$

$=\dfrac{135\pm \sqrt{18225-10800}}{200}$

$= \dfrac{135\pm \sqrt{7425}}{200}$

$=\dfrac{135\pm 5\sqrt{297}}{200}$

$=\dfrac{27\pm \sqrt{297}}{40}$

Find the roots of the equation $5{x}^{2}-6x-2$ by completing the square method

Given quadratic equation,

$5x^2-6x-2=0$

Adjusting first term as square we get :

$(\sqrt{5})^2$

Adjusting second terms as

$-2ab$ we get :

$-2(\sqrt{5}x)\left ( \dfrac{3}{\sqrt{5}} \right )$

Hence adding and subtracting

$\left ( \dfrac{3}{\sqrt{5}} \right )^{2}$ to make the equation of the form perfect square.

Then the equation becomes :

$(\sqrt{5}x)^{2}-2(\sqrt{5}x)\left ( \dfrac{3}{\sqrt{5}} \right )+\left ( \dfrac{3}{\sqrt{5}} \right )^{2}-2-\dfrac{9}{5}=0$

$\Rightarrow \left ( x\sqrt{5}-\dfrac{3}{\sqrt{5}} \right )^{2}=\dfrac{19}{5}$

$\Rightarrow x\sqrt{5}-\dfrac{3}{\sqrt{5}}=\pm \dfrac{\sqrt{19}}{\sqrt{5}}$

$\Rightarrow x\sqrt{5}=\dfrac{3\pm \sqrt{19}}{\sqrt{5}}$

$\Rightarrow x=\dfrac{3\pm \sqrt{19}}{5}$

What constant number must be added or subtracted to $4x^{2}+12x+8=0$ to solve it by method of completing the square?

Consider the given equation,

$4{{x}^{2}}+12x+8=0$

${{x}^{2}}+3x+2=0$ ..... (1)

Add and subtract ${{\left( \dfrac{3}{2} \right)}^{2}}$ in equation (1), we get

${{x}^{2}}+3x+2+{{\left( \dfrac{3}{2} \right)}^{2}}-{{\left( \dfrac{3}{2} \right)}^{2}}=0$

${{\left( x+\dfrac{3}{2} \right)}^{2}}+2-\dfrac{9}{4}=0$

${{\left( x+\dfrac{3}{2} \right)}^{2}}-\dfrac{1}{4}=0$

Hence, need to add $\dfrac{1}{4}$ so that ${{x}^{2}}+3x+2=0$ become a perfect square.

The set of values of 'c' for which the equation ${x^2} - 4x - c - \sqrt {8{x^2} - 32x - 8c} = 0$ has exactly two distinct real solution is $(a, b)$ then find the value of $(b - a)$ .

$x^2-4x-c-\sqrt 8\sqrt {x^2 -4x-c}=0$

$\sqrt {x^2-4x-c} (\sqrt {x^2 -4x-c} -\sqrt 8)=0$

$x^2-4x-c=0\quad$ &

$\quad x^2-4x-c=8$

$D=b^2-4ac\quad \quad D=b^2-4ac$

$D=16+4c\quad \quad D=16+4c+32$

$16+4c > 0\quad \quad 48+4c > 0$

$c > -4\quad \quad \quad c > -12$

$c > -4$ then

$4$ solution

$-12 < c < -4$ then two distinct solutions

$(a, b)=(-12, -4)$

$\therefore b-a=-4+12=8$

Solve each of the following equation by using the method of completing the square:
$4x^{2}+4\sqrt {3}x+3=0$ ?

$4{ x }^{ 2 }+4\sqrt { 3x } +3=0$

Dividing by

$4$

${ x }^{ 2 }+\sqrt { 3x } +\dfrac { 3 }{ 4 } =0$

${ x }^{ 2 }+\sqrt { 3x } =-\dfrac { 3 }{ 4 }$

Third term

$={ \left( \frac { 1 }{ 2 } \times \sqrt { 3 } \right) }^{ 2 }=\dfrac { 3 }{ 4 }$

adding

$\dfrac { 3 }{ 4 }$ on both sides

${ x }^{ 2 }+\sqrt { 3x } +\dfrac { 3 }{ 4 } =-\dfrac { 3 }{ 4 } +\dfrac { 3 }{ 4 }$

${ x }^{ 2 }+\sqrt { 3x } +\dfrac { 3 }{ 4 } =0$

$x+\sqrt { \dfrac { 3 }{ 2 } } =0$ or

$x=-\sqrt { \dfrac { 3 }{ 2 } }$

By using the method of completing the square show that ${4x}^{2}+3x+5=0$ has no real roots.

${ x }^{ 2 }+3x+5=0$

${ x }^{ 2 }+\frac { 3 }{ 4 } x+\frac { 5 }{ 4 } =0$

${ x }^{ 2 }+\frac { 3 }{ 4 } x+{ \left( \frac { 3 }{ 8 } \right) }^{ 2 }=\frac { -5 }{ 4 } +\frac { 9 }{ 64 }$

${ \left( x+\frac { 3 }{ 8 } \right) }^{ 2 }=\frac { -71 }{ 64 }$

$x+\frac { 3 }{ 8 } =\sqrt { \frac { -71 }{ 64 } }$

$Hence\quad QE\quad has\quad no\quad real\quad roots.$

Solve the following equation by using the method of completing the square:
$x^{2}-4x+1=0$

The difference of squares identity can be written:

${ A }^{ 2 }−{ B }^{ 2 }=(A−B)(A+B)$

We can complete the square and use this with as follows:

${ x }^{ 2 }−4x+10=0$

${ x }^{ 2 }−4x+4−30=0$

$(x−2)2−(\sqrt { 3 } )20=0$

$((x−2)−\sqrt { 3 } )((x−2)+\sqrt { 3 } )=0$

$(x−2−\sqrt { 3 } )(x−2+\sqrt { 3 } )=0$

$Hence:x=2±\sqrt { 3 }$

Solve the quadratic equation : $4x^2-4a^2x+(a^4-b^4)=0$

$4x^2 - 4a^{2}x + (a^4-b^4) = 0$

$\implies 4x^2 - 4a^{2}x + a^4 = b^4$

$\implies (2x-a^2)^2 = b^4$

$\implies 2x-a^2 = \pm b^2$

$\implies 2x = a^2 \pm b^2$

$\implies Roots\ of\ given\ quadratic\ equation\ are:$

$x_1 = \dfrac{a^2+b^2}{2},\ x_2 = \dfrac{a^2-b^2}{2}$

Solve the following equation by using the method of completing the square:
$x^{2}-6x+3=0$

The given equation is

$x^2-6x+3=0$

Now,

$x^2-6x+3=0$

$\Rightarrow x^2-6x=-3$

$\Rightarrow x^2-2\times x\times 3+3^2=-3+3^2$ [adding

$3^2$ on both side]

$\Rightarrow(x-3)^2=6$ [Using algebraic identity :

$a^2-2ab+b^2=(a-b)^2$ ]

$\Rightarrow x-3=\pm \sqrt 6$

$\Rightarrow x=3\pm \sqrt 6$

Hence, the solution is

$x=(3+\sqrt 6)$ or

$(3-\sqrt 6)$

$v_1+v_2=4$ and $v^2_1+v^2_2=16$ . Find value of $v_1$ and $v_2$ .

$v_1+v_2=4$

$v_1=4-v_2$

substitute

$v_1=4-v_2$ in the second equation.

${v_1}^2+{v_2}^2=16$

${4-v_2}^2+{v_2}^2=16$

$16+{v_2}^2-8v_2+{v_2}^2=16$

${v_2}^2-8v_2+{v_2}^2=0$

$2{v_2}^2-8v_2=0$

${v_2}^2-4v_2=0$

$v_2(v_2-4)=0$

$v_2-4=0$

$v_2=4$

now, substitute

$v_2=4$ in first equation.

$v_1+4=4$

$v_1=0$

so,

$v_1=0$ and

$v_2=4$ or

$v_1=4$ and

$v_2=0$

Solve the equation ${3x}^{2}- 5x + 2 = 0$ by the method of completing the square

Solution:

$3x^² -5x +2 =0$

Now divide the $x^²$ coefficient throughout,

$\Rightarrow x^2-\dfrac{5x}{3}+\dfrac{2}{3}$

Divide the coefficient of x by 2 and square it. Now add and subtract it in the LHS.

$\Rightarrow x^2-\dfrac{5x}{3}+\dfrac{2}{3}+\dfrac{25}{36}-\dfrac{25}{36}=0$

$\Rightarrow x^2-\dfrac{5x}{3}+\dfrac{25}{36}=\dfrac{1}{36}$

$\Rightarrow \dfrac{x-5}{6}=\pm \dfrac{1}{6}$

$\therefore \dfrac{x-5}{6}=\dfrac{1}{6}\quad or \quad\dfrac{x-5}{6}=\dfrac{-1}{6}$

$\Rightarrow x=1\ or\ x=\dfrac{2}{3}$

Find the root of the following quadratic equation (if they exist) by the method of completing the square.
$2x^2-7x+3=0$ .

$2x^2 - 7x + 3 = 0$

$\Rightarrow 2\left(x^2 - \dfrac{7}{2}x \right) + 3 = 0$

$\Rightarrow 2 \left(x^2 - 2 \cdot \dfrac{7}{4}x + \dfrac{49}{16}\right) - \dfrac{49}{8} + 3 = 0$

$\Rightarrow 2 \left(x - \dfrac{7}{4}\right)^2 - \dfrac{25}{8} = 0$

$\Rightarrow \left(x - \dfrac{7}{4}\right)^2 = \dfrac{25}{16}$

$\Rightarrow x - \dfrac{7}{4} = \pm \dfrac{5}{4}$

$\Rightarrow x = 3$ or

$\dfrac{1}{4}$

$\therefore$ The roots are

$3$ and

$\dfrac{1}{2}$ .

Solve each of the following equation by using the method of completing the square:
$7x^{2}+3x-4=0$

$7x^2+3x-4=0$

$\Rightarrow$

$x^2+\dfrac{3}{7}x-\dfrac{4}{7}=0$

Here.

$a=1,b=\dfrac{3}{7},\,c=-\dfrac{4}{7}$

$\Rightarrow$

$x^2+\dfrac{3}{7}x=\dfrac{4}{7}$

Now,

$\left(\dfrac{b}{2}\right)^2=\left(\dfrac{3}{7\times 2}\right)^2=\dfrac{9}{196}$

Adding

$\dfrac{9}{196}$ , on both sides of equation,

$\Rightarrow$

$x^2+\dfrac{3}{7}x+\dfrac{9}{196}=\dfrac{4}{7}+\dfrac{9}{196}$

$\Rightarrow$

$\left(x+\dfrac{3}{14}\right)^2=\dfrac{112+9}{196}$

$\Rightarrow$

$\left(x+\dfrac{3}{14}\right)^2=\dfrac{121}{196}$

Taking square roots on both sides,

$\Rightarrow$

$x+\dfrac{3}{14}=\pm\dfrac{11}{14}$

$\Rightarrow$

$x=\dfrac{11}{14}-\dfrac{3}{14}$ and

$x=-\dfrac{11}{14}-\dfrac{3}{14}$

$\therefore$

$x=\dfrac{4}{7}$ and

$x=-1$

Solve each of the following equation by using the method of completing the square:
$4x^{2}+4bx-(a^{2}-b^{2})=0$

Dividing the entire equation by 4

${ x }^{ 2 }+bx-\frac { (a²-b²) }{ 4 } =0$

Adding and Subtracting the equation by

${\dfrac{b}{4}}^{2}$

$x²+bx+{ \left( \dfrac { b }{ 2 } \right) }^{ 2 }={ \left( \dfrac { b }{ 2 } \right) }^{ 2 }+\dfrac { (a²-b²) }{ 4 }$

$x²+bx+{ \left( \dfrac { b }{ 2 } \right) }^{ 2 }$ this quadratic equation can be written as perfect square as

${ \left( \dfrac { x+b }{ 2 } \right) }^{ 2 }$

${ \left( \dfrac { x+b }{ 2 } \right) }^{ 2 }={\dfrac{b}{4}^2}+{\dfrac{a}{4}^2}-\dfrac { b² }{ 4 }$

${ \left( \dfrac { x+b }{ 2 } \right) }^{ 2 }=\dfrac { a² }{ 4 }$

$\dfrac { x+b }{ 2 } =±\dfrac { a }{ 2 }$

$x=\dfrac { (a-b) }{ 2 }$

$x=\dfrac { (-a-b) }{ 2 }$

The roots are

$\dfrac { a-b }{ 2 }$ and

$\dfrac { -a-b }{ 2 }$

Find the root of the following quadratic equation (if they exist) by the method of completing the square.
$4x^2+4\sqrt{3}x+3=0$ .

1156585_1112820_ans_5204339902934ae89f7ccfb8c900a520.jpg

Solve the equations by completing the square
$x^{2}+7x-6=0$

${x}^{2}+7x-6=0 \Rightarrow {x}^{2}+2.\dfrac{7}{2}x+{\left(\dfrac{7}{2}\right)}^{2}-6-\dfrac{49}{4}=0.$

${\left(x+\dfrac{7}{2}\right)}^{2}-\dfrac{73}{4}=0.$

${\left(x+\dfrac{7}{2}\right)}^{2}-{\left(\dfrac{\sqrt{73}}{2}\right)}^{2}=0 \Rightarrow \left(x+\dfrac{7+\sqrt{73}}{2}\right) \left(x+\dfrac{7-\sqrt{73}}{2}\right)=0$

$\therefore \boxed{x=-\left(\dfrac{7+\sqrt{73}}{2}\right)}$ or,

$\boxed{x=-\left(\dfrac{7-\sqrt{73}}{2}\right)}$

If $6x-x^2=1$ , then the value of $\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)$ is?

Given:

$6x-{x}^{2}=1$

$6x=1+{x}^{2}$

$6x-2x=1+{x}^{2}-2x$ {subtracting

$2x$ on each side}

$4=\cfrac{{x}^{2}-2x+1}{x}$

$\cfrac{{(x-1)}^{2}}{x}=4$

$\cfrac{x-1}{\sqrt{x}}=\pm 2$

$\sqrt{x}-\cfrac{1}{\sqrt{x}}=\pm 2$

Find the roots of the following quadratic equation, if they exist, by the method completing the square:
$2x^2-7x + 3=0$

1315106_1122986_ans_e33ab01daf61437eae99c3173adeda18.jpg

If the roots of the given equation $(a-b)x^2+(b-c)x+(c-a)=0$ are equal, prove that $b+c=2a$ .

Given

$(a-b)x^2+(b-c)x+(c-a)=0$

Therefore,

$D=(b-c)^2-4(a-b)(c-a)$

For real and equal roots,

$D=0$ .

Now,

$(b-c)^2-4(a-b)(c-a)=0$

$4a^2+b^2+c^2-4ab+2bc-4ac=0$

$[\because (x+y+z)^2=x^2+y^2+z^2+2(xy+yz+xz)]$

$(-2a+b+c)^2=0$

$-2a+b+c=0$

$b+c=2a$

Solve the following Quadratic equation:
$x^{2} + 6x - (a^{2} + 2a - 8) = 0$ .

Formula for roots of quadratic

expression

$ax^{2}+bx+c = 0$ is

$= \dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

So for

$x^{2}+6x-(a^{2}+2a-8)$ is

$= \dfrac{-6\pm \sqrt{36+4(a^{2}+2a-8)}}{2}$

$= \dfrac{-6}{2}\pm \sqrt{9-8+a^{2}+2a}$

$= \dfrac{-6}{2}\pm \sqrt{(a+1)^{2}}$

$= -3\pm (a+1)$

If $a-b=1$ and $ab=12$ , find the value of $(a^2+b^2)$ .

Given that,

$a - b = 1$ and

$ab = 12$

$a^2 + b^2 = (a - b)^2 + 2ab$

$= (1)^2 + 2(12)$

$= 1 + 24$

$= 25$

Find the discriminant of the quadratic equation $32 \sqrt { 3 } x ^ { 2 } + 21 x - \sqrt { 3 } = 0$ .

Given,

$32\sqrt{3}x^2+21x-\sqrt{3}=0$

$a=32\sqrt{3},b=21,c=-\sqrt{3}$

discriminant

$D=b^2-4ac$

$=(21)^2-4(32\sqrt{3})(-\sqrt{3})$

$=441+384$

$\therefore D=825$

$\sqrt { { 3x }^{ 2 }-7x-30 } -\sqrt { { 2x }^{ 2 }-7x-5 } =x-5$

$\sqrt{3{x}^{2}-7x-30}-\sqrt{2{x}^{2}-7x-5}=x-5$

$\sqrt{3{x}^{2}-7x-30}=x-5+\sqrt{2{x}^{2}-7x-5}$

${\sqrt{3{x}^{2}-7x-30}}^{2}={x-5+\sqrt{2{x}^{2}-7x-5}}^{2}$ by squaring both sides

$\Rightarrow 3{x}^{2}-7x-30={\left(x-5\right)}^{2}+2{x}^{2}-7x-5+2\left(x-5\right)\sqrt{\left(2{x}^{2}-7x-5\right)}$

$\Rightarrow 3{x}^{2}-7x-30={x}^{2}-10x+25+2{x}^{2}-7x-5+2\left(x-5\right)\sqrt{\left(2{x}^{2}-7x-5\right)}$

$\Rightarrow 3{x}^{2}-7x-30=3{x}^{2}-17x+20+2\left(x-5\right)\sqrt{\left(2{x}^{2}-7x-5\right)}$

$\Rightarrow -7x+17x-30-20=2\left(x-5\right)\sqrt{\left(2{x}^{2}-7x-5\right)}$

$\Rightarrow 10x-50=2\left(x-5\right)\sqrt{\left(2{x}^{2}-7x-5\right)}$

$\Rightarrow 10\left(x-5\right)=2\left(x-5\right)\sqrt{\left(2{x}^{2}-7x-5\right)}$

$\Rightarrow 5=\sqrt{\left(2{x}^{2}-7x-5\right)}$

$\Rightarrow 25=2{x}^{2}-7x-5$ by squaring on both sides

$\Rightarrow 2{x}^{2}-7x-5-25=0$

$\Rightarrow 2{x}^{2}-7x-30=0$

$\Rightarrow \left(2x+5\right)\left(x-6\right)=0$ on factorising

$\therefore x=\dfrac{-5}{2},6$

For

$x=\dfrac{-5}{2}$ the

$\sqrt{3{x}^{2}-7x-30}-\sqrt{2{x}^{2}-7x-5}=x-5$ equation becomes

$\sqrt{3{\left(\dfrac{-5}{2}\right)}^{2}-7\times \dfrac{-5}{2}-30}-\sqrt{2{\left(\dfrac{-5}{2}\right)}^{2}-7\times \dfrac{-5}{2}-5}=\dfrac{-5}{2}-5$

$=\sqrt{\dfrac{75}{4}+\dfrac{35}{2}-30}-\sqrt{2\times \dfrac{25}{4}+\dfrac{35}{2}-5}$

$=\sqrt{\dfrac{145-120}{4}}-\sqrt{\dfrac{40}{2}}$

$=\sqrt{\dfrac{25}{4}}-\sqrt{20}=\dfrac{5}{2}-4\sqrt{5}\neq$ RHS

$\because x-5=\dfrac{-5}{2}-5=\dfrac{-15}{2}$

Hence

$x=\dfrac{-5}{2}$ is not a solution

For

$x=6$ the

$\sqrt{3{x}^{2}-7x-30}-\sqrt{2{x}^{2}-7x-5}=x-5$ equation becomes

$\sqrt{3{\left(6\right)}^{2}-7\times 6-30}-\sqrt{2{\left(6\right)}^{2}-7\times 6-5}=6-5$

$=\sqrt{108-72}-\sqrt{72-47}=1$

$=\sqrt{36}-\sqrt{25}=6-5=1$

Thus,

$x=6$ is the only solution for the above equation

Find the roots of $4x^{2}+3x+5=0$ by the method of completing the square.

Given equation

$4x^2+3x+5=0$

Dividing by 4

$\dfrac{4x^2}{4}+\dfrac{3x}{4}+\dfrac{5}{4}=0$

$x^2+\dfrac{3x}{4}+\dfrac{5}{4}=0$

We know that

$(a+b)^2=a^2+2ab+b^2$

Here

$a=x$

$2ab=\dfrac{3x}{4}$

$2b=\dfrac{3}{4}$

$b=\dfrac{3}{8}$

Adding and subtracting

$\left(\dfrac{3}{8}\right)^2$

$x^2+\dfrac{3x}{4}+\dfrac{5}{4}+\left(\dfrac{3}{8}\right)^2-\left(\dfrac{3}{8}\right)^2=0$

$\left(x+\dfrac{3}{8}\right)^2+\dfrac{5}{4}-\left(\dfrac{3}{8}\right)^2=0$

$\left(x+\dfrac{3}{8}\right)^2=\dfrac{9}{64}-\dfrac{5}{4}$

$\left(x+\dfrac{3}{8}\right)^2=\dfrac{9-80}{64}$

$\left(x+\dfrac{3}{8}\right)^2=\dfrac{-71}{64}$

Since square of any number cannot be negative

So, answer does not exist.

Solve ${x}+{\dfrac {1}{x}}=25{\dfrac {1}{25}}$

$x+\dfrac{1}{x}=25\dfrac{1}{25}$

$\dfrac{x^2+1}{x}=\dfrac{626}{25}$

$25x^2+25=626x$

$25x^2-626x+25=0$

using Shridharacharya rule

$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$

$x=\dfrac{626\pm\sqrt{626^2-4\times25\times25}}{2\times25}$

$x=\dfrac{626\pm624}{50}$

$x=\dfrac{626+624}{50}=25$

$x=\dfrac{626-624}{50}=\dfrac{1}{25}$

Therefore

$x=25\ or\ \dfrac{1}{25}$

Find the roots of the equations by the method of completing the square.
$5x^{2}-6x-2=0$

$5x^2-6x-2=0$

$\Rightarrow$

$x^2-\dfrac{6}{5}x-\dfrac{2}{5}=0$

Here,

$a=1,\,b=\dfrac{6}{5},\,c=\dfrac{2}{5}$

$\Rightarrow$

$x^2-\dfrac{6}{5}x=\dfrac{2}{5}$

Now,

$\left(\dfrac{b}{2}\right)^2=\left(\dfrac{6}{5\times 2}\right)^2=\dfrac{36}{100}$

Adding

$\dfrac{36}{100}$ on both sides,

$\Rightarrow$

$x^2-\dfrac{6}{5}x+\dfrac{36}{100}=\dfrac{2}{5}+\dfrac{36}{100}$

$\Rightarrow$

$\left(x-\dfrac{6}{10}\right)^2=\dfrac{40+36}{100}$

$\Rightarrow$

$\left(x-\dfrac{6}{10}\right)^2=\dfrac{76}{100}$

$\Rightarrow$

$\left(x-\dfrac{6}{10}\right)=\pm\dfrac{2\sqrt{19}}{10}$

$\Rightarrow$

$x=\dfrac{2\sqrt{19}}{10}+\dfrac{6}{10}$ and

$x=-\dfrac{2\sqrt{19}}{10}+\dfrac{6}{10}$

$\Rightarrow$

$x=\dfrac{2(\sqrt{19}+3)}{10}$ and

$x=-\dfrac{2(\sqrt{19}-3)}{10}$

$\Rightarrow$

$x=\dfrac{\sqrt{19}+3}{5}$ and

$x=\dfrac{-\sqrt{19}+3}{5}$

The equation $4\sin ^{ 2 }{ x } -2\left( \sqrt { 3 } +1 \right) \sin { x } +\sqrt { 3 } =0$ has -

$4\sin^2 x-2(\sqrt{3}+1)\sin x+\sqrt{3}=0$

Let

$\sin x=y$

$4y^2-2(\sqrt{3}+1)y+\sqrt{3}=0$

Solving the quadratic equation,

$y=\cfrac{2(\sqrt{3}+1)\pm \sqrt{4(\sqrt{3}+1)^2 -16\sqrt{3}}}8$

First solution,

$y=\cfrac{2(\sqrt{3}+1)\\+\sqrt{4(\sqrt{3}+1)^2 -16\sqrt{3}}}8$

Second solution,

$y=\cfrac{2(\sqrt{3}+1)\\- \sqrt{4(\sqrt{3}+1)^2 -16\sqrt{3}}}8$

Solving it further for the first solution,

$y=\cfrac{2(\sqrt{3}+1)\\+\sqrt{16+8\sqrt{3}-16\sqrt{3}}}8$

$y=\cfrac{2(\sqrt{3}+1)\\+\sqrt{16-8\sqrt{3}}}8$

$y=\cfrac{2(\sqrt{3}+1)\\+\sqrt{4\left ( \sqrt{3}-1 \right )^2 }}8$

$y=\cfrac{2(\sqrt{3}+1)\\+2(\sqrt{3}-1)}8$

$y=\cfrac{4\sqrt{3}}{8}$

$y=\cfrac{\sqrt{3}}{2}$

Solving it further for the second solution,

$y=\cfrac{2(\sqrt{3}+1)\\-\sqrt{16+8\sqrt{3}-16\sqrt{3}}}8$

$y=\cfrac{2(\sqrt{3}+1)\\-\sqrt{16-8\sqrt{3}}}8$

$y=\cfrac{2(\sqrt{3}+1)\\-\sqrt{4\left ( \sqrt{3}-1 \right )^2 }}8$

$y=\cfrac{2(\sqrt{3}+1)\\-2(\sqrt{3}-1)}8$

$y=\cfrac{4}{8}$

$y=\cfrac{1}{2}$

Now,

$sinx=\cfrac{\sqrt{3}}{2}$ and

$sinx=\cfrac{1}{2}$

$x=60^0$ and

$x=30^0$

Find the roots of the quadratic equation $\sqrt{2x^{2}+1}$

$\sqrt{2x^2+1}=0$

$2x^2+1=0$

$x^2=-\dfrac{1}{2}$

$x=\pm \dfrac{i}{\sqrt{2}}$

Solve using formula.
$x^{2} + 6x + 5 = 0$ .

$x^2+6x+5=0$

Solution of

$ax^2+bx+c$ are

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\Rightarrow$ Here,

$x=\dfrac{-6\pm \sqrt{36-20}}{2}=\dfrac{-6\pm \sqrt{16}}{2}=\dfrac{-6\pm 4}{2}$

$\Rightarrow x=-5$ or

$x=-1$

Solve the equation: $2{ \left( x-3 \right) }^{ 2 }+3(x-2)(2x-3)=8(x+4)(x-4)-1$

According to question,

$2(x-3)^2+3(x-2)(2x-3)=8(x+4)(x-4)-1$

$\Rightarrow 2(x^2-6x+9)+3(2x^2-7x+6)=8(x^2-16)-1$

$\Rightarrow 2x^2-12x+18+6x^2-21x+18=8x^2-128-1$

$\Rightarrow 165=33x$

$\Rightarrow x=\dfrac{165}{33}$

$\Rightarrow x=5$

prove that ${a^3}{\left( {b - c} \right)^3} + {b^3}{\left( {c - a} \right)^3} + {c^3}{\left( {a - b} \right)^3} =$ ${{a}^{3}}\left( c-b \right)+{{b}^{3}}\left( a-c \right)+{{c}^{3}}\left( b-a \right)$

We have,

$a{{\left( b-c \right)}^{3}}+b{{\left( c-a \right)}^{3}}+c{{\left( a-b \right)}^{3}}$

$\Rightarrow a\left( {{b}^{3}}-{{c}^{3}}-3bc\left( b-c \right) \right)+b\left( {{c}^{3}}-{{a}^{3}}-3ac\left( c-a \right) \right)+c\left( {{a}^{3}}-{{b}^{3}}-3ab\left( a-b \right) \right)$

$\Rightarrow a\left( {{b}^{3}}-{{c}^{3}}-3{{b}^{2}}c+3b{{c}^{2}} \right)+b\left( {{c}^{3}}-{{a}^{3}}-3a{{c}^{2}}+3{{a}^{2}}c \right)+c\left( {{a}^{3}}-{{b}^{3}}-3{{a}^{2}}b+3a{{b}^{2}} \right)$

$\Rightarrow a{{b}^{3}}-a{{c}^{3}}-3a{{b}^{2}}c+3ab{{c}^{2}}+b{{c}^{3}}-b{{a}^{3}}-3ab{{c}^{2}}+3{{a}^{2}}bc+c{{a}^{3}}-c{{b}^{3}}-3{{a}^{2}}bc+3a{{b}^{2}}c$

$\Rightarrow a{{b}^{3}}-a{{c}^{3}}+b{{c}^{3}}-b{{a}^{3}}+c{{a}^{3}}-c{{b}^{3}}$

$\Rightarrow {{a}^{3}}\left( c-b \right)+{{b}^{3}}\left( a-c \right)+{{c}^{3}}\left( b-a \right)$

Hence proved.

Solve $8{x^2} - 10x - 3=0$ .

Given quadratic equation is

$8x^{2}+10x-3=0$

We know that, for a quadratic equation of the form

$ax^2+bx+c=0$ ,

$x = \dfrac{-b \pm \sqrt{b^{2}-4ac}}{2a}$

Here,

$a=8,\ b=-10\ and\ c=-3$

$\therefore \ x = \dfrac{-(-10)\pm \sqrt{(10)^{2}+4\times 8\times 3}}{2\times 8}$

$= \dfrac{10\pm \sqrt{100+96}}{16}$

$\Rightarrow x = \dfrac{10\pm 14}{16}$

$\Rightarrow x = \dfrac{10+14}{16} = \dfrac{24}{16}$

$\therefore \ x= \dfrac{3}{2}$

and

$x = \dfrac{10-14}{16} = \dfrac{-4}{16}$

$\therefore \ x = \dfrac{-1}{4}$

Hence, the solution of the given quadratic equation is

$x=\dfrac32$ or

$x=\dfrac{-1}{4}$ .

Solve using formula.
$y^{2} + \dfrac {1}{3}y = 2$ .

$y^2+\dfrac{1}{3}y=2$

$3y^2+y-6=0$

$a=3,b=1,c=-6$

$y=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$y=\dfrac{-1+\sqrt{1^2-4\cdot 3\left(-6\right)}}{2\cdot 3}$

$=\dfrac{-1\pm\sqrt{73}}{6}$

Solve the following equation $y^{2}-2y=5$ which number should be added in given equation therefore, equation becomes complete square.

${y}^{2} - 2y = 5$

$\Rightarrow {y}^{2} - 2y - 5 = 0$

$\Rightarrow {\left( y - \cfrac{2}{2} \right)}^{2} - \cfrac{{\left( 2 \right)}^{2}}{4} - 5 = 0$

$\Rightarrow {\left( y - 1 \right)}^{2} - 6 = 0$

From the above expression, we can say that

$6$ should be added in given equation

$\left( {y}^{2} - 2y = 5 \right)$ so that the equation becomes complete square.

Hence the correct answer is

$6$ .

Solve:
$x^2-4x-5$

$x^2=4x-5$

By moving the constant to the right side

$x^2-4x=5$

Adding

$4$ on both sides to create a perfect square trinomial to find the solution.

$x^2-4x+4=5+4$

$(x-2)^2=9\quad as (x^2+2^2-2*2x)=({x-2})^2$

$x-2=\sqrt {9}$

Taking the postive value

$=3$

$x=3+2$

$x=5$

Solve the given problem and find value of x :-
$\dfrac{1}{x} + \dfrac{1}{{x - 2}} = 3 ; x \ne 0,2$

given,

$\dfrac {1} {x}$

$+$

$\dfrac {1} {x-2}$

$=$

$3$

$Multiplying$

$both$

$sides$

$by$

$x(x-2),$

$x-2$

$+$

$x$

$=$

$3x(x-2)$

$2x - 2$

$=$

$3x^2$

$-$

$6x$

$3x^2 - 8x + 2$

$=$

$0$

$Multiplying$

$the$

$equation$

$throughout$

$by$

$3,$

$9x^2 - 24x + 6$

$=$

$0$

$(3x)^2 - 2 \times (3x) \times 4 + 6$

$=$

$0$

$(3x)^2 - 2 \times (3x) \times 4 + 4^2 - 4^2 + 6$

$=$

$0$

$(3x - 4)^2 - 16 + 6$

$=$

$0$

$(3x - 4)^2 - 10$

$=$

$0$

$(3x - 4)^2$

$=$

$10$

$3x - 4$

$=$

$\sqrt {10}$

$or$

$3x - 4$

$=$

$-\sqrt {10}$

$Therefore,$

$x = \dfrac {\sqrt {10} +4} {3}$

$OR$

$x = \dfrac {-\sqrt {10} +4} {3}$

Check whether the equation $5{x^2} - 6x - 2 = 0$ has real roots and if it has, find them by the method of completing the square. Also verify that roots obtained satisfy the given equation.

$5x^{2}-6x-2 = 0$

$D = b^{2}-4ac = 36-4(5)(-2) = 76$

$x = \frac{-b\pm \sqrt{D}}{2a} = \frac{-(-6)\pm \sqrt{76}}{10} = \frac{6\pm \sqrt{76}}{10} = \frac{3\pm \sqrt{19}}{5}$

$5x^{2}-6x-2 = 5(\frac{3+\sqrt{19}}{5})^{2}-6(\frac{3+\sqrt{19}}{5})-2$

$= \frac{9+19+6\sqrt{19}}{5}-\frac{(18+6\sqrt{19})}{5}-2$

$= 2-2 = 0$

similarly

$(\frac{3-\sqrt{19}}{5})$ also can be checked

Solve: $c^2-3c-10= 0$

${ c }^{ 2 }-3c-10=0\\ \Rightarrow { c }^{ 2 }-2.\dfrac { 3 }{ 2 } .c+{ \left( \dfrac { 3 }{ 2 } \right) }^{ 2 }-{ \left( \dfrac { 3 }{ 2 } \right) }^{ 2 }-10=0\\ \Rightarrow { \left( c-\dfrac { 3 }{ 2 } \right) }^{ 2 }=\dfrac { 49 }{ 4 } \\ \Rightarrow c-\dfrac { 3 }{ 2 } =\pm \sqrt { \dfrac { 49 }{ 4 } } \\ \Rightarrow c=\left( \dfrac { 3 }{ 2 } +\dfrac { 7 }{ 2 } \right) \quad and\quad \left( \dfrac { 3 }{ 2 } -\dfrac { 7 }{ 2 } \right) \\ \Rightarrow c=5\quad and\quad -2$

Solve the given equation and find the value of $x$ -
${x^2} + 2ab = (2a + b)x$

Consider the following question.

${{x}^{2}}+2ab=(2a+b)x$

$\text{Subtract}\,\left( 2a+b \right)x\,\text{from}\,\text{both}\,\text{sides}$

${{x}^{2}}+2ab-\left( 2a+b \right)x=\left( 2a+b \right)x-\left( 2a+b \right)x$

${{x}^{2}}-\left( 2a+b \right)x+2ab=0$

${{x}_{1,\,2}}=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$

${{x}_{1,\,2}}=\dfrac{-\left( -2a-b \right)\pm \sqrt{{{\left( -2a-b \right)}^{2}}-4\cdot \times 1\times \,2ab}}{2\times 1}$

$\text{x=2a,}\,\,\,\text{x=b}$

Hence, this is the required answer.

Solve for x :-
$\sqrt 3 {x^2} - 2\sqrt 2 x - 2\sqrt 3 = 0$

$\sqrt {3} x^2$

$-$

$2\sqrt {2} x$

$-$

$2\sqrt {3}$

$=$

$0$

$Multiplying$

$the$

$equation$

$throughout$

$by$

$\sqrt {3},$

$3x^2$

$-$

$2 \times \sqrt {3} \times \sqrt {2} \times x$

$-$

$6$

$=$

$0$

$(\sqrt {3} x)^2$

$-$

$2 \times \sqrt {3}x \times \sqrt {2}$

$+$

$(\sqrt {2})^2$

$-$

$(\sqrt {2})^2$

$-$

$6$

$=$

$0$

$(\sqrt {3}x - \sqrt {2})^2$

$-$

$2$

$-$

$6$

$=$

$0$

$(\sqrt {3}x - \sqrt {2})^2$

$=$

$8$

$(\sqrt {3}x - \sqrt {2})$

$=$

$8$

$Or,$

$(\sqrt {3}x - \sqrt {2})$

$=$

$-8$

$Therefore,$

$x$

$=$

$\dfrac {(8 + \sqrt {2})} {\sqrt {3}}$

$Or,$

$x$

$=$

$\dfrac {(-8 + \sqrt {2})} {\sqrt {3}}$

If the of $3{x^2} + 2x + a = 0$ is double the discriminant of ${x^2} - 4x + 2 = 0$ then find $'a'$ .

Given,

The discriminant of

$3x^{2}+2x+a=0$ is double the discriminant of

$x^{2}-4x+2=0$

We know that the discriminant of a quadratic equation

$ax^{2}+bx+c=0$ is given by:

$b^{2}-4ac$

Hence,

$(2)^2-4\times3\times a=2\times((-4)^2-4\times1\times 2)$

$4-12a=2\times(16-8)$

$4-12a=16$

$12a=4-16$

$12a=-12$

$a=-1$

If $\alpha$ and $\beta$ are the roots of the equation $3{x^2} - 6x + 4 = 0$ , fid the value of
${\alpha}^2$ + ${\beta}^2$ .

Given Equation:

$3x^2-6x+4=0$
We know that,

$If \,\,ax^2+bx+c=0$ is a quadratic equation then root are

$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$

Substituting the values of

$a, b$ and

$c$

$x=\dfrac{-6\pm\sqrt{36-48}}{6}$

$\Rightarrow \alpha=\dfrac{-6+\sqrt12 i}{6}\, \& \beta=\dfrac{-6-\sqrt12 i}{6}$

$\Rightarrow \alpha=\dfrac{-3+\sqrt3 i}{3}\, \& \beta=\dfrac{-3-\sqrt3 i}{3}$

Finding

$\alpha^2+\beta^2$

$= \left (\dfrac{-3+\sqrt3 i}{3}\right)^2+\left (\dfrac{-3-\sqrt3 i}{3} \right)^2$

$= \dfrac{9-6\sqrt3 i-3}{9}+\dfrac{9+6\sqrt3 i-3}{9}$

$=\dfrac{12}{9}$ =

$\dfrac{4}{3}$

$\therefore$ The value of

$\alpha^2+\beta^2$ =

$\dfrac{4}{3}$

If $x=-2$ is the root of equation $3{x^2} + 7x + p = 0$ find the value of show that the root of equation ${x^2} + K\left( {4x + K - 1} \right) + p = 0$ are equal.

Given

$x=-2$ is root of equation

$3x^{2}+7x+p=0$

$\therefore x=-2$ satisfies the given equation

$3(-2)^{2}+7 (-2)+P=0$

$12+ (-14)+P=0$

$P=2$

The given equation becomes

$3x^{2}+7x+2=0$

$3x^{2}+6x+x+2=0$

$3x(x+2)+1(x+2)=0$

$(3x+1)(x+2)=0$

$x= \dfrac{-1}{3}$ or

$x=-2$

Now,

$x^{2}+K (4x+k-1)+ P=0$

roots are equal

$\therefore D=0 D= b^{2}-4ac$

$x^{2}+4xk+k^{2}-k+2=0$

$a=1 \ b=4k\ C= k^{2}- k+2=0$

$(4k)^{2}-4(k^{2}-k+2)=0$

$16k^{2}-4k^{2}+4k-8=0$

$12k^{2}+4k-8=0$

$12k^{2}+12k-8k-8=0$

$2k (k+1)-8 (k+1)= 0$

$k =\dfrac{8}{12}=\dfrac{2}{3} k=-1$ .

Find the roots of the equation $\begin{array} { l } { \frac { 1 } { x + 1 } + \frac { 2 } { x + 2 } } \\ { = \frac { 4 } { x + 4 } } \end{array}$

$\dfrac{1}{x+1}+\dfrac{2}{x+2}=\dfrac{4}{x+4}$

$\left(x+2\right)\left(x+4\right)+2\left(x+1\right)\left(x+4\right)=4\left(x+1\right)\left(x+2\right)$

$x^2+6x+8+2(x^2+5x+4)=4(x^2+3x+2)$

$x^2+6x+8+2x^2+10x+8=4x^2+12x+8$

$3x^2+16x+16=4x^2+12x+8$

$4x+8=x^2$

$-x^2+4x+8=0$

$x_{1,\:2}=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\dfrac{-4+\sqrt{4^2-4\left(-1\right)8}}{2\left(-1\right)}:\quad -2\left(\sqrt{3}-1\right)$

$x=\dfrac{-4-\sqrt{4^2-4\left(-1\right)8}}{2\left(-1\right)}:\quad 2\left(1+\sqrt{3}\right)$

$x=-2\left(\sqrt{3}-1\right),\:x=2\left(1+\sqrt{3}\right)$

If roots of quadratic equation $(b-c){x}^{2}+(c-a)x+(a-b)=0$ are real and equal then prove that $2b=a+c$ .

If roots of a quadratic equation are equal, then discriminant of the quadratic equation is 0

$D=b^2-4ac=0$

$(b-c)x^2+(c-a)x+(a-b)=0$

Comparing with

$ax^2+bx+c=0$

Here,

$a=(b-c),\ b=(c-a)\ and \ c=(a-b)$

So,

$\Rightarrow (c-a)^2-4(b-c)(a-b)=0$

$\Rightarrow c^2+a^2-2ac-4(ab-b^2-ac+bc)=0$

$\Rightarrow c^2+a^2-2ac-4ab+4b^2+4ac-4bc=0$

$\Rightarrow c^2+a^2+2ac+4b^2-4ab-4bc=0$

$\Rightarrow (c+a)^2+4b^2-4b(a+c)=0$

$\Rightarrow (c+a)^2+(2b)^2-2(c+a)(2b)=0$

$\Rightarrow[(c+a)-(2b)]^2=0$

$\Rightarrow c+a-2b=0$

$\Rightarrow 2b=c+a$

Solve $7{x}^{2}-30x-25=0$ by completing square method

$7x^2-30x-25=0$

$x^2-\dfrac {30x}{7}-\dfrac {25}{7}=0$

$\Rightarrow x^2-2\times x\times \dfrac {15}{7}x+\dfrac {225}{49}-\dfrac {25}{7}-\dfrac {225}{49}=0$

$\Rightarrow \left(x-\dfrac {15}{7}\right)^2=\dfrac {225}{49}+\dfrac {25}{7}$

$\Rightarrow \left(x-\dfrac {15}{7}\right)^2=\dfrac {225+175}{49}$

$\Rightarrow \left(x-\dfrac {15}{7}\right)^2=\dfrac {400}{49}$

$\therefore x-\dfrac {15}{7}=\dfrac {20}{7}$ or

$x-\dfrac{15}{7}=\dfrac{-20}{7}$

$x = \dfrac{37}{5}$ or

$x = \dfrac{-5}{7}$

$x=5, \dfrac{-5}{7}$

Solve: $4+y-14y^2=0$

Given,

$4+y-14y^2=0$

$\Rightarrow \dfrac{2}{7}+\dfrac{y}{14}-y^2=0$

$\left ( y+\dfrac{1}{2} \right )\left ( y-\dfrac{4}{7} \right )=0$

$\therefore y=-\dfrac{1}{2},\dfrac{4}{7}$

$\sqrt{x^{2}+1}$

Consider the given equation,

$\sqrt{{{x}^{2}}+1}=0$

${{x}^{2}}+1=0$

${{x}^{2}}=-1$

$x=\sqrt{-1}$

$x=i$

Hence, this is the answer.

Solve: $f(x)=\{(x-2)\}^2$

Consider the given equation,

$f\left( x \right)={{\left( x-2 \right)}^{2}}$

$={{x}^{2}}+{{2}^{2}}-2\times x\times 2$

$={{x}^{2}}+4-4x$

$f\left( x \right)={{x}^{2}}-4x+4$

Hence, this is the answer. .

Solve:
$x^2-3x-4= 0$

Given,

${ x }^{ 2 }-3x-4=0\\ { x }^{ 2 }-3x-4+4=4\\ { x }^{ 2 }-3x=4$

To make a trinomial square on the left side of the equation, We have to find a value that is equal to the square of half of

$b$ , the coefficient of

$x$ .

So,

${ (\dfrac { b }{ 2 } })^{ 2 }={ (-\dfrac { 3 }{ 2 } ) }^{ 2 }$

Adding the term to both sides of the equation,

${ x }^{ 2 }-3x+{ (-\dfrac { 3 }{ 2 } ) }^{ 2 }=4+{ (-\dfrac { 3 }{ 2 } ) }^{ 2 }\\ { x }^{ 2 }-3x+\dfrac { 9 }{ 4 } =\dfrac { 25 }{ 4 } \\ { x }^{ 2 }+2\cdot x\cdot (-\dfrac { 3 }{ 2 } )+{ (-\dfrac { 3 }{ 2 } ) }^{ 2 }=\dfrac { 25 }{ 4 } \\ { (x-\dfrac { 3 }{ 2 } ) }^{ 2 }=\dfrac { 25 }{ 4 }$

Taking square root of both sides we get,

$\sqrt { { (x-\dfrac { 3 }{ 2 } ) }^{ 2 } } =\pm \sqrt { \dfrac { 25 }{ 4 } } \\ x-\dfrac { 3 }{ 2 } =\pm \dfrac { 5 }{ 2 }$

$x-\dfrac { 3 }{ 2 } =\dfrac { 5 }{ 2 } \\ x=\dfrac { 5 }{ 2 } +\dfrac { 3 }{ 2 } =4$

$x-\dfrac { 3 }{ 2 } =-\dfrac { 5 }{ 2 } \\ \\ x=-\dfrac { 5 }{ 2 } +\dfrac { 3 }{ 2 } =-1$

Hence, the solution is

$x=4,-1.$

$\frac{1}{x(x^{4}-1)}$

Given that,

$\Rightarrow \dfrac{1}{x\left( {{x}^{4}}-1 \right)}$

$\Rightarrow \dfrac{1}{{{x}^{5}}-x}$

Hence, this is the answer.

$\sqrt{2}x^{2}+2x+5x+5\sqrt{2}=0$

Given equation

$\sqrt 2{x}^{2}+2x+5x+5\sqrt 2=0$

$\Rightarrow$

$\sqrt 2{x}^{2}+7x+5\sqrt 2=0$

Here

$a=\sqrt 2,b=7,c=5\sqrt 2$

Roots

$=\cfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a } =\cfrac { -7\sqrt { 49-4\left( \sqrt { 2 } \right) \left( 5\sqrt { 2 } \right) } }{ 2\left( \sqrt { 2 } \right) } =\cfrac { -71\sqrt { 49-40 } }{ 2\sqrt { 2 } }$

$=\cfrac { -7\pm 3 }{ 2\sqrt { 2 } }$

$=\cfrac { -7+3 }{ 2\sqrt { 2 } } \quad or\quad \cfrac { -7-3 }{ 2\sqrt { 2 } }$

$=\cfrac { -4 }{ 2\sqrt { 2 } } =-\sqrt { 2 } \quad or\quad \cfrac { -10 }{ 2\sqrt { 2 } }$

$=-\cfrac { 5 }{ \sqrt { 2 } }$

Solve the Quadratic Equation: ${b}^{2}-kb+ak$

$\rightarrow b^{2}-kb+ak=0$

Quadratic in b

From Sri Dharacharya

formula,

$b=\dfrac{k\pm \sqrt{k^{2}-4(ak)}}{2}$

are solutions of this

equation.

Solve :
${x^2} + x - 2664 = 0$

$\begin{array}{l} { x^{ 2 } }+x-2664=0 \\ \dfrac { { 4{ { \left( { x+\dfrac { 1 }{ 2 } } \right) }^{ 2 } } } }{ { 10657 } } =1 \\ { \left( { x+\dfrac { 1 }{ 2 } } \right) ^{ 2 } }-\dfrac { { 10657 } }{ 4 } =0 \\ Hence,\, the\, solution\, is\, x=-\dfrac { 1 }{ 2 } -\dfrac { { \sqrt { 10657 } } }{ 2 } ,x=\dfrac { { \sqrt { 10657 } } }{ 2 } -\dfrac { 1 }{ 2 } \end{array}$

Solve for $y$ :
$5 y ^ { 2 } + 5 y - 10 = 0$

$5y^2+5y-10=0$

$y=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$y=\dfrac{-5 \pm \sqrt{25-4(5)(-10)}}{2(5)}$

$y=\dfrac{-5\pm \sqrt{225}}{10}=\dfrac{-5\pm 15}{10}$

$y=-2$ or

$1$ .

Find the value of x, if $4{ x }^{ 2 }-5x+20=0$

$x = \dfrac { - ( - 5 ) \pm \sqrt { ( - 5 ) ^ { 2 } - 4.4 .20 } } { 2.4 }$

$\begin{array} { l } { = \dfrac { .5 \pm \sqrt { 25 - 320 } } { 8 } } \\ { = \dfrac { 5 \pm \sqrt { - 295 } } { 8 } } \\ { = \dfrac { 5 \pm \sqrt { 295 } i } { 8 } } \end{array}$

Find $x$ :
$x^{2}+\left(\dfrac{a}{a+b}+\dfrac{a+b}{a}\right)x+1=0$

$x^{2}+(\dfrac{a}{a+b}+\dfrac{a+b}{a})x+1 = 0$

$\Rightarrow x^{2}+\dfrac{a}{a+b}x+\dfrac{a+b}{a}x+(\dfrac{a}{a+b})(\dfrac{a+b}{a}) = 0$

$\Rightarrow x(x+\dfrac{a}{a+b})+(\dfrac{a+b}{a})(x+\dfrac{a}{a+b}) = 0$

$\Rightarrow (x+\dfrac{a}{a+b}) (x+\dfrac{a+b}{a}) = 0$

$\Rightarrow x\in \left \{ -\dfrac{a}{a+b}, -\dfrac{a+b}{a} \right \}$

Check whether $(x+3)^3=x^3-8$ is a quadratic equation?.

We have,

${\left( {x + 3} \right)^3} = {x^3} - 8$

${x^3} + {\left( 3 \right)^3} + 3 \times {x^2} \times 3 + 3 \times x \times {3^2} = {x^3} - 8$

${x^3} + 27 + 9{x^2} + 27x = {x^3} - 8$

$9{x^2} + 27x + 27 + 8 = 0$

$9{x^2} + 27x + 35 = 0$

Yes, it is a quadratic equation.

Solve for $x : 9x^2-6ax+(a^2-b^2)=0.$

Given

$9x^2-6ax+a^2-b^2=0$

$\Rightarrow 9x^2-6ax+(a-b)(a+b)=0$

$\Rightarrow 9x^2-3x(a-b)-3x(a+b)+(a-b)(a+b)=0$

$\Rightarrow 3x[3x-(a-b)]-(a+b)[3x-(a-b)]=0$

$\Rightarrow[3x-(a-b)][3x-(a+b)]=0$

$3x-(a-b)=0$

$3x=a-b$

$x=\dfrac{a-b}{3}$

$3x-(a+b)=0$

$3x=(a+b)$

$x=\dfrac{a+b}{3}$

$\therefore x=\dfrac{(a-b)}{3}$ or

$x=\dfrac{(a+b)}{3}$

Solve: $\displaystyle {{98} \over {121}}{x^2} = {1 \over 2}$

$\dfrac{98}{121}x^2=\dfrac{1}{2}$

$\Rightarrow x^2=\dfrac{121}{98\times 2}\Rightarrow \dfrac{121}{196}$

$\Rightarrow x=\pm \dfrac{11}{14}$

Evaluate
$x^{2}-(\sqrt{2}+1)x+\sqrt{2}=0$

${ x }^{ 2 }-\left( \sqrt { 2 } +1 \right) x+\sqrt { 2 } =0$

$\Rightarrow { x }^{ 2 }-\sqrt { 2 } x-x+\sqrt { 2 } =0$

$\Rightarrow x\left( x-\sqrt { 2 } \right) -1\left( x-\sqrt { 2 } \right) =0$

$\Rightarrow \left( x-\sqrt { 2 } \right) \left( x-1 \right) =0$

$\Rightarrow x=\sqrt { 2 }$ or

$x=1$

Solve:
${x}^{2}-5x+7=0$

$x^{2}-5x+7 = 0$

$\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}.$

where

a = 1, b = -5, c = 7

$\dfrac{-(-5)\pm \sqrt{(-5)^{2}-4(1)(7)}}{2(1)}$

$\dfrac{5\pm \sqrt{25-28}}{2}$

$\dfrac{5\pm \sqrt{-3}}{2} = \dfrac{5\pm i\sqrt{3}}{2}$

Using the quadratic formula, solve the equation $9x^{2}+7x-2=0$ .

$9x^{2}+7x-2=0$

$\Rightarrow x=\cfrac { -7\pm \sqrt { 49+72 } }{ 18 } =\cfrac { -7\pm \sqrt { 121 } }{ 18 }$

$=\cfrac { -7\pm 11 }{ 18 } =\cfrac { 4 }{ 18 } ,\cfrac { -18 }{ 18 }$

$=\cfrac { 2 }{ 9 } ,-1$

$\therefore x=\cfrac { 2 }{ 9 } ,-1$

Solve the equation by the method of completing the squares:
$x^{2}+12x-45=0$

$x^2+12x-45=0$

$\Rightarrow x^2+12x+36-45-36=0$

$x^2+12x+36=81$

$\left( x+6\right)^2=81$

$\left( x+6\right) =\pm \sqrt{81}$

$x=-6\pm 9$

$x=-6+9,x=-6-9$

$\Rightarrow x=3,x=-15.$

Hence, the answer is

$3,-15.$

Solve:
$3 x ^ { 2 } + 2 \sqrt { 5 } x - 5 = 0$

$3x^2+2\sqrt{5}x-5=0$

Roots=

$\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$=\dfrac{-2\sqrt 5\pm \sqrt{20-4\times 3\times (-5)}}{2\times 3}$

$=\dfrac{-2\sqrt{5}\pm \sqrt{80}}{6}=\dfrac{-2\sqrt{5}\pm 4\sqrt{5}}{6}$

So Roots

$=-\sqrt{5}$ &

$\dfrac{\sqrt{5}}{3}$

Find the roots of the equation $16x^2-27x-10 = 0$ .

$16x^{2}-27x-10=0$

Compare the given equation with

$ax^2+bx+c=0$ we get,

$a=16, b=-27, c=-10$

The roots can be found using the formula

$x=\cfrac{-b\pm\sqrt{b^{2}-4ac}}{2a}$

$\therefore x =\cfrac{27\pm \sqrt{(27)^{2}-4\times 16\times (-10)}}{2\times 16}$

$=\cfrac{27\pm{\sqrt {1369}}}{32}\\=\cfrac{27\pm 37}{32}\\=\cfrac{64}{32},\cfrac{-10}{32}$

$\therefore$ The roots are

$\cfrac{-5}{16}$ and

$2$ .

Find the roots of $x^{2}-4x-8=0$ by the method of completing square.

${ x }^{ 2 }-4x-8=0$

$\Rightarrow { x }^{ 2 }-4x+4-12=0$

$\Rightarrow { \left( x-2 \right) }^{ 2 }-{ \left( \sqrt { 12 } \right) }^{ 2 }=0$

$\Rightarrow \left( x-2+\sqrt { 12 } \right) \left( x-2-\sqrt { 12 } \right) =0$

$\therefore x=2-\sqrt { 12 } ;x=2+\sqrt { 12 }$

$\dfrac{1}{2(1-x)}\left[\dfrac{\sqrt{1-x}}{\sqrt{1+x}}+\dfrac{\sqrt{1+x}}{\sqrt{1-x}}\right]$ .

$\cfrac{1}{2(1-x)}[\cfrac{\sqrt{1-x}}{\sqrt{1+x}}+\cfrac{\sqrt{1+x}}{\sqrt{1-x}}]$

$=\cfrac{1}{2(1-x)}[\cfrac{(\sqrt{1-x})^2+(\sqrt{1+x})^2}{\sqrt{1+x}\sqrt{1-x}}]$

$=\cfrac{1}{(1-x)\sqrt{1-x^2}}$

Find the value of discriminant of $x^2 + 7x - 1 = 0$

Given equation is

$x^2 + 7x - 1 = 0$

here

$a=1,b=7$ and

$c=-1$

Discriminant

$\Delta={b}^{2}-4ac$

$\Rightarrow \Delta={7}^{2}-4\times 1\times -1$

$=49+4$

$=53$

$\therefore \Delta>0$

Find the root of the following quadratic equation (if they exist) by the method of completing the square.
$\sqrt {2}x^{2}-3x-2\sqrt {2}=0$

$\sqrt{2}x^{2}-3x-2\sqrt{2}=0$

$x^{2}-\frac{3}{\sqrt{2}}x -2=0$

$x^{2}-\frac{2.3}{2\sqrt{2}}x +\frac{9}{8}= 2+\frac{9}{8}$

$(x-\frac{3}{2\sqrt{2}})^{2}=\frac{25}{8}$

$x-\frac{3}{2\sqrt{2}}=\pm \frac{5}{2\sqrt{2}}$

$x=\frac{8}{2\sqrt{2}}$ or

$\frac{1}{\sqrt{2}}$

1167411_1250836_ans_876673c225fe46e5991acbacff7cd031.jpg

solve for x, ${9}^{x+2} - 6.{3}^{x+1} + 1=0$

1116601_1256160_ans_65e1e68cadb94134be53565405cfbb92.jpeg

Find the roots of the following quadratic equations (if they exist ) by the method of completing the square.
$x^{2}-4ax+4a^{2}-b^{2}=0$

$X^{2}-4aX+4a^{2}-b^{2}=0$

$X^{2}-4aX+4a^{2}=b^{2}$

$(X-2a)(X-2a)=b^{2}$

$\sqrt{(X-2a)^{2}}=\sqrt{b^{2}}$

$\Rightarrow X-2a=\pm b$

$X-2a\pm b=0$

$X=2a\pm b$

are the roots of equation.

1167408_1250858_ans_cd994c0d84634b97948ab75e4ff7ca85.jpg

If $3x - 7y = 10$ and $xy = -1$ then value of $9x^2 + 49y^2$ is?

$9x^2+49y^2=(3x)^2+(7y)^2$

$\Rightarrow (3x+7y)^2-2\times 3x\times 7y$

$(3x+7y)^2-2\times 3x\times 7y=(3x-7y)^2-2\times 3x\times 7y+4\times 3x\times 7y$

$\Rightarrow (3x-7y)^2+2\times 3x\times 7y$

$=(3x-7y)^2+42xy$

Given,

$(3x-7y)=10$ &

$xy=-1$

$\therefore 9x^2+49y^2=10^2+42\times (-1)=58$ .

1117120_1267651_ans_1f1a809dcf084b62a874684134047ba2.JPG

Find the zeros of polynomial $6x^{2}-3-7x$ .

$6x^2-7x-3=0$

$6x^2-9x+2x-3=0$

$3x(2x-3)+1(2x-3)=0$

$(2x-3)(3x+1)=0$

$x=\dfrac{3}{2},-\dfrac{1}{3}$

If $\displaystyle \frac {1}{a+b+x} = \frac{1}{a}+ \frac {1}{b}+ \frac {1}{x}$ , what is $x =$ ?

1352000_1268925_ans_85a8f3fc00b14bcfaac587b07ec7f168.PNG

Solve:
$x^2-2x-8$

$x^2-2x-8=0$

$x^2-4x+2x-8=0$

$x(x-4)+2(x-4)=0$

$(x+2)(x-4)=0$

$x=-2,4$

Find the roots of the following equation $4x^2+4bx-(a^2-b^2)=0$ by the method of completing the square.

we have,

$4x^2+4bx-(a^2-b^2)=0$

Taking

$4$ common, we get:

$x^2+bx-\left(\dfrac{a^2-b^2}{4}\right)=0$

Rewriting

$bx$ as

$2\times \dfrac{b}{2}x$ ,

$x^2+2\left(\dfrac{b}{2}\right)x=\dfrac{a^2-b^2}{4}$

Adding

$\left(\dfrac{b}{2}\right)^2$ on both sides,

$x^2+2\left(\dfrac{b}{2}\right)x+\left(\dfrac{b}{2}\right)^2=\dfrac{a^2-b^2}{4}+\left(\dfrac{b}{2}\right)^2$

Using the identity

$(a+b)^2=a^2+2ab+b^2$ , the equation can be written as:

$\left(x+\dfrac{b}{2}\right)^2=\dfrac{a^2}{4}$

Now, taking square root on both sides,

$x+\dfrac{b}{2}=\pm \dfrac{a}{2}$

$\Rightarrow x=\dfrac{-b}{2}\pm \dfrac{a}{2}\Rightarrow x=\dfrac{-b-a}{2}, \dfrac{-b+a}{2}$ .

Hence, the roots are

$\left(\dfrac{-a-b}{2}\right)$ and

$\left(\dfrac{a-b}{2}\right)$ .

Find the roots of the following quadratic equations, if they exist, by the method of completing the square :
(i) $2 x ^ { 2 } - 7 x + 3 = 0$ (ii) $2 x ^ { 2 } + x - 4 = 0$
(iii) $4 x ^ { 2 } + 4 \sqrt { 3 } x + 3 = 0$ (iv) $2 x ^ { 2 } + x + 4 = 0$

$a).$

$2x^2-7x+3=0$

$\Rightarrow x^2-\dfrac{7}{2}x=-\dfrac{3}{2}$

Adding

$\left( \dfrac{7}{4}\right)^2$ on both sides

$\Rightarrow x^2-\dfrac{7}{2}x+\left( \dfrac{7}{4}\right)^2=\dfrac{-3}{2}+\left( \dfrac{7}{4}\right)^2$

$\Rightarrow \left( x-\dfrac{7}{4}\right)^2=\dfrac{-3}{2}+\dfrac{49}{16}$

$\Rightarrow \left( x-\dfrac{7}{4}\right)^2=\dfrac{25}{16}$

$\Rightarrow \left( x-\dfrac{7}{4}\right)^2=\left( \dfrac{5}{4}\right)^2$

Taking square root on both sides

$\Rightarrow \left( x-\dfrac{7}{4}\right)=\pm\dfrac{5}{4}$

$\Rightarrow x-\dfrac{7}{4}=\dfrac{5}{4},$

$x-\dfrac{7}{4}=\dfrac{-5}{4}$

$x=\dfrac{5}{4}+\dfrac{7}{4}$

$x=\dfrac{-5}{4}+\dfrac{7}{4}$

$x=3$

$x=\dfrac{1}{2}$

$b).$

$2x^2+x-4=0$

$x^2+\dfrac{x}{2}=2$

Adding

$\left( \dfrac{1}{4}\right)^2$ on both sides

$\Rightarrow x^2+\dfrac{x}{2}+\left( \dfrac{1}{4}\right)^2=2+\left( \dfrac{1}{4}\right)^2$

$\left( x+\dfrac{1}{4}\right)^2=2+\dfrac{1}{16}$

$\left( x+\dfrac{1}{4}\right)^2=\dfrac{33}{16}$

Taking square root on both sides

$\Rightarrow x+\dfrac{1}{4}=\pm \dfrac{\sqrt{33}}{4}$

$\Rightarrow x=\pm \dfrac{\sqrt{33}}{4}-\dfrac{1}{4},$

$x=\dfrac{-\sqrt{33}}{4}-\dfrac{1}{4}$

$\Rightarrow x=\pm \dfrac{\sqrt{33-1}}{4},$

$x=\dfrac{-\sqrt{33-1}}{4}$

$c).$

$4x^2+4\sqrt{32}+3=0$

$\Rightarrow x^2+\sqrt{3}x+\dfrac{3}{4}=0$

$x^2+\sqrt{3}x=\dfrac{-3}{4}$

Adding

$\left( \dfrac{\sqrt{3}}{2}\right)62$ on both sides

$\Rightarrow x^2+\sqrt{3}x+\left( \dfrac{\sqrt{3}}{2}\right)^2=\dfrac{-3}{4}+\left(\dfrac{\sqrt{3}}{2}\right)^2$

$\Rightarrow \left( x+\dfrac{\sqrt{3}}{2}\right)^2=\dfrac{-3}{4}+\dfrac{3}{4}$

$\Rightarrow \left( x+\dfrac{\sqrt{3}}{2}\right)^2=0$

$x=\dfrac{-\sqrt{3}}{2},\dfrac{-\sqrt{3}}{2}$

same roots.

$d).$

$2x^2+x+4=0$

$\Rightarrow x^2+\dfrac{x}{2}+2=0$

$x^2+\dfrac{x}{2}=-2$

Adding

$\left( \dfrac{1}{4}\right)^2$ on both sides

$\Rightarrow x^2+\dfrac{x}{2}+\left( \dfrac{1}{4}\right)^2=-2+\left( \dfrac{1}{4}\right)62$

$\Rightarrow \left( x+\dfrac{1}{4}\right)^2=-2+\dfrac{1}{16}$

$\Rightarrow \left( x+\dfrac{1}{4}\right)^2=-\dfrac{-31}{16}$

Hence, solved.

Find the roots
$\sqrt 2 {x^2} - 3x + 2\sqrt 2 = 0$

$\sqrt{2}x^2-3x+2\sqrt{2}=0$

$x=\dfrac{3\pm\sqrt{9-4\times \sqrt{2}\times 2\sqrt{2}}}{2\times \sqrt{2}}$

$x=\dfrac{3\pm \sqrt{7}i}{2\sqrt{2}}$ .

Find the roots of fraction $\frac { x }{ (x+3)(x-4) } =1$

$\begin{array}{l} We\, have \\ x=\left( { x+3 } \right) \left( { x-4 } \right) \\ \Rightarrow x={ x^{ 2 } }+3x-4x-12 \\ \Rightarrow { x^{ 2 } }-2x-12=0 \\ u\sin g\, formula \\ x=\dfrac { { -b\pm \sqrt { { b^{ 2 } }-4ac } } }{ { 2a } } \\ x=\dfrac { { 2\pm \sqrt { 4+48 } } }{ 2 } \\ =\dfrac { { 2\pm 2\sqrt { 13 } } }{ 2 } \\ =1\pm \sqrt { 13 } \\ Hence, \\ Roots\, of\, quadratic\, are\, 1+\sqrt { 13 } \, \, and\, 1-\sqrt { 13 } . \end{array}$

Divide $p(y)$ by $q(y)$
$P(y)=y^{5}+y^{4}+y^{3}+y6{2}+2y+2$ and $q(y)=y^{3}+1$

1180205_1284118_ans_68df8ac0d5264373a096b9623d398713.jpg

Find the roots.
$2{x^2} + {x} - 4 = 0$

$2x^2+x-4=0$

On comparing with standard quadratic equation

$ax^2+bx+c=0$ , we get:

$a=2$

$b=1$

$c=-4$

Using the quadratic formula:

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

Substituting the values:

$x=\dfrac{-1\pm\sqrt{1+4\times 2\times 4}}{4}$

$=\dfrac{-1\pm\sqrt{33}}{4}$

$x=\dfrac{-1+\sqrt{33}}{4}$ ,

$\dfrac{-1-\sqrt{33}}{4}$ .

If $x = \sin t$ and $y = \sin p t ,$ prove that: $\left( 1 - x ^ { 2 } \right) y _ { 2 } - x y _ { 1 } + p ^ { 2 } y = 0$

$x=\sin t\rightarrow \dfrac{dx}{dt}=\cos t$

$y=\sin pt \rightarrow \dfrac{dy}{dt}= p \cos pt$

$\dfrac{dy}{dx}=\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=\dfrac{p \cos pt}{\cos t}$

$y_1=\dfrac{p \cos pt}{\cos t}$

$y_1\cos t =p\cos pt$

squaring on both sides

$y_1^2\cos ^2t=p^2\cos ^2pt$

$y_1^2(1-\sin ^2t)=p^2(1-\sin ^2pt)$

$y_1^2(1-x^2)=p^2(1-y^2)$

differentiating on both sides

$2y_1y_2(1-x^2)-2xy_1^2=p^2(-2yy_1)$

$y_2(1-x^2)-xy_1=-p^2y$

$y_2(1-x^2)-xy_1+p^2y=0$

Solve the equation $a ^ { 2 } x ^ { 2 } - 3 a b x + 2 b ^ { 2 } = 0$ by the method of completing the square.

$a^2x^2-3abx+2b^2=0$

$(ax)^2-2(ax)\left(\dfrac{3b}{2}\right)+2b^2+\left(\dfrac{3b}{2}\right)^2=\left(\dfrac{3b}{2}\right)^2$

$(ax)^2-2(ax)\left(\dfrac{3b}{2}\right)+\left(\dfrac{3b}{2}\right)^2=\dfrac{9b^2}{4}-2b^2$

$\left[ax-\dfrac{3b}{2}\right]^2=\dfrac{9b^2-8b^2}{4}$

$\left(ax-\dfrac{3b}{2}\right)=\pm\sqrt{\dfrac{b^2}{4}}=\pm\dfrac{b}{2}$

$ax=\dfrac{3b}{2}+\dfrac{b}{2}$ ;

$ax=\dfrac{3b}{2}-\dfrac{b}{2}$

$ax=\dfrac{4b}{2}$ ;

$ax=\dfrac{2b}{2}$

$ax=2b$ ;

$ax=b$

$x=\dfrac{2b}{a}$ ;

$x=\dfrac{b}{a}$ .

Solve:
$x^2-135x+3500=0$

Now,

$x^2-135x+3500=0$

or,

$x^2-100x-35x+3500=0$

or,

$(x-100)(x-35)=0$

or,

$x=100,35$ .

Find the minimum value of $\cos^{2}\theta+$ $\sec^{2}\theta$

Let

$f\left( \theta \right) =y=\cos ^{ 2 }{ \theta } +\sec ^{ 2 }{ \theta } =\cfrac { \cos ^{ 4 }{ \theta } +1 }{ \cos ^{ 2 }{ \theta } }$

For

$\cfrac { max }{ { min }_{ 1 } }$

$\cfrac { dy }{ dx } =0$

$\cfrac { dy }{ dx } =\cfrac { -\cos ^{ 2 }{ \theta } \left( 4\cos ^{ 3 }{ \theta } \right) \sin { \theta } +2\cos { \theta } \sin { \theta } \left( \cos ^{ 4 }{ \theta } +1 \right) }{ { \left( \cos ^{ 4 }{ \theta } +1 \right) }^{ 2 } } =0$

So,

$2\cos { \theta } \sin { \theta } \left[ 1+\cos ^{ 4 }{ \theta } -2\cos ^{ 4 }{ \theta } \right] =0$

$2\cos ^{ 4 }{ \theta } \sin { \theta } \left( 1-\cos ^{ 4 }{ \theta } \right) =0$

$\sin { \theta } =0,\cos { \theta } =0$

So,

$\cos { \theta } =\pm 1$

So,

$\theta =n\pi ,\theta =\left( 2n+1 \right) \cfrac { \pi }{ 2 } ,\theta =n\pi$

$f\left( n\pi \right) =\cfrac { 1+1 }{ 1 } =2$

$f\left( \left( 2n+1 \right) \cfrac { \pi }{ 2 } \right) =\cfrac { 0+1 }{ 0 } =\infty$

So, minima arrives at

$\theta =n\pi$

Thus, minimum value

$=2$

Obtain the roots of the following quadratic equation by using the general formula the solution:
$p^{2}x^{2}+(p^{2}-q^{2})\ x-q^{2}=0$

Formula:

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

Given,

$p^2x^2+\left(p^2-q^2\right)x-q^2=0$

$x=\dfrac{-\left(p^2-q^2\right)\pm \sqrt{\left(p^2-q^2\right)^2-4p^2\left(-q^2\right)}}{2p^2}$

$=\dfrac{-\left(p^2-q^2\right)\pm (p^2+q^2)}{2p^2}$

$x=\dfrac{q^2}{p^2},-1$

Add :- $4{a}^{2}b-2{b}^{2}+3{c}^{2}a+4abc5$ and ${a}^{2}b+{b}^{2}-2{c}^{2}+8ab$

To add :-

$4a^{2}b - 2b^{2}+3c^{2}a+4abc$

and

$a^{2}b+b^{2}-2c^{2}+8ab$

$\Rightarrow (4a^{2}b+a^{2}b) + (-2b^{2}+b^{2}) + (3c^{2}a+4abc - 2c^{2}+8ab)$

$\Rightarrow 5a^{2}b-b^{2}+c^{2}(3a-2) + 4ab(c+2)$

1178346_1339473_ans_2dcfe5c7296242fc8dfb1dcadba09270.jpg

If $-4$ is a root of the equation $x^{2}+px-4=0$ and the equation $x^{2}+px+q=0$ has equal root, find the values of $p$ and $q$ .

$-4$ is the root of

$x^{2}+px-4=0$

$\Rightarrow (-4)^{2}+p(-4)-4=0$

$\Rightarrow 16-4p-4=0$

$\Rightarrow 12=4p$

$p =3$

$x^{2}+px-q=0$

$\Rightarrow x^{2}+3x+q=0$

It has equal roots so

$D=0$

$b^{2}-4ae=0$

$9-4q=0$

$q =\dfrac{9}{4}$

$p=3$ &

$q=\dfrac{9}{4}$ .

1215260_1353592_ans_d8340fec1aaf43d1a833251ad3499b89.jpg

Find the root of the following quadratic equation, if they exist , by the method of completing the square:
$2x^{2}-7x+3=0$

$\begin{array}{l} Assuming \, \, x=a\, \, \, and\, \, \dfrac { 7 }{ 4 } =b,\, \, \, the\, \, L.H.S\, \, of\, \, equation\, \, is\, \, made\, \, in\, \, the\, \, form\, \, \, of\, \, { \left( { a-b } \right) ^{ 2 } } \\ \Rightarrow { \left( { x-\dfrac { 7 }{ 4 } } \right) ^{ 2 } }=\dfrac { { 49 } }{ { 16 } } -\dfrac { 3 }{ 2 } \\ \Rightarrow { \left( { x-\dfrac { 7 }{ 4 } } \right) ^{ 2 } }=\dfrac { { 49-24 } }{ { 16 } } \\ \Rightarrow { \left( { x-\dfrac { 7 }{ 4 } } \right) ^{ 2 } }=\dfrac { { 25 } }{ { 16 } } \\ case\, \, 1: \\ \Rightarrow x-\dfrac { 7 }{ 4 } =\dfrac { 5 }{ 4 } \\ \Rightarrow x=\dfrac { 7 }{ 4 } +\dfrac { 5 }{ 4 } =\dfrac { { 12 } }{ 4 } =3 \\ case\, 2: \\ \Rightarrow x-\dfrac { 7 }{ 4 } =-\dfrac { 5 }{ 4 } \\ \Rightarrow x=\dfrac { 7 }{ 4 } +\frac { { -5 } }{ 4 } =\dfrac { 2 }{ 4 } =\dfrac { 1 }{ 2 } \\ Hence,\, x=3\, \, and\, \, x=\dfrac { 1 }{ 2 } \end{array}$

Convert to quadratic equation
$16x-\dfrac{10}{x}=27$ .

We have,

$16x - \dfrac{{10}}{x} = 27$

$16{x^2} - 10 = 27x$

Then,

We get equation

$16{x^2} - 27x - 10 = 0$

Write the following equation in the form $ax^{2}+bx+c=0$ .
$x(x+2)=3$

$x(x+2)=3\Rightarrow x^{2}+2x=3\Rightarrow x^{2}+2x-3=3-3$

$\Rightarrow x^{2}+2x-3=0$ Here a = 1, b = 2, c = -3

1188315_1344302_ans_631a76c731934abbb74148aada3a6f42.jpg

Solve the following for $x$ :
$\dfrac {1}{2a+b+2x}=\dfrac {1}{2a}+\dfrac {1}{b}+\dfrac {1}{2x}$

$\dfrac{1}{2a+b+2x}=\dfrac{1}{2a}+\dfrac{1}{b}+\frac{1}{2x}$

$\dfrac{1}{2a+b+2x}+\dfrac{1}{2x}=\dfrac{2a+b}{2ab}$

$\dfrac{2x+2a+b+2x}{2x.(2a+b+2x)}=\dfrac{2a+b}{2ab}$

$\dfrac{2a+b+4x}{2ax+bx+2x^{2}}=\dfrac{2a+b}{ab}$

$2a^{2}b+ab^{2}+4abx=4a^{2}+2abx+4ax^{2}+2abx+b^{2}x+2bx^{2}$

$2a^{2}b+ab^{2}=x^{2}(4a+2b)+x(4a^{2}+b^{2})$

$x=\pm\left [\dfrac{-(4a^{2}+b^{2})+\sqrt{(4a^{2}+b^{2})^{2}}+4(4a+2b)(2a^{2}b+ab^{2})}{2(4a+2b)} \right]$

Find the product of the rational expressions $\dfrac{3x^{2}+8x-3}{2x^{2}-x-6}$ and $\dfrac{x^{2}-4}{x+3}$ .

$\dfrac{3x^{2}+8x-3}{2x^{2}-x-6} \times\dfrac{x^{2}-4}{x+3}$

$=\dfrac{(x+3)(3x-1)}{(2x+3)(x-2)} \times \dfrac{(x-2)(x+2)}{(x+3)}$

$=\dfrac{(3x-1)(x+2)}{2x+3}$

$=\dfrac{3x^{2}+5x-2}{2x+3}$

(x+y) (x-y) =0

(x+y) (x-y) = 0

$x^{2}-y^{2}=0$

$[(a+b)(a-b)=a^{2}-b^{2}]$

$x^{2}=y^{2}$

$[x= \pm y]$

1194637_1375714_ans_9f09f398175b4f65a3977477b9f5101d.JPG

What is a Quadratic Equation ?

${\textbf{Step -1: Definition of quadratic equation}}{\textbf{.}}$

${\text{A quadratic is a type of problem that deals with a variable multiploed by itself,}}$

${\text{an operation known as squaring}}{\text{.}}$

${\textbf{Step -2: Identification and examples of quadratic equation}}{\textbf{.}}$

${\text{The standard form of quadratic equation is }}a{x^2} + bx + c,{\text{ where }}a,b,c{\text{ represent}}$

${\text{known numbers, where }}a \ne {\text{0}}{\text{. If }}a = 0,{\text{ then the equation is linear,}}$

${\text{not quadratic as there is no }}a{x^2}{\text{ term}}{\text{.}}$

${\text{The quadratic formula for the roots of the general quadratic equation is,}}$

$x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$

${\text{Examples,}}$

$y = 3x - 1{\text{ }}\left[ {{\text{Linear equation as }}a = 0} \right]$

$y = 2{x^2} + 7x + 10{\text{ }}\left[ {{\text{Quadratic equation as }}a \ne 0} \right]$

${\textbf{}}{\textbf{Hence, quadratic equation is of form }}\mathbf{a{x^2} + bx + c}{\textbf{ with a degree of}}\mathbf{2}{\textbf{.}}$

Which constant should be added and subtracted to solve the quadratic equation $5x^{2}-\sqrt{2x}+3=0$ by the method of completing the square?

$5x^{2}-\sqrt{2}+3=0$

$(\sqrt{5}x)^{2}-\sqrt{2}x+3+(\sqrt{\frac{2}{20}})^{2}-(\frac{\sqrt{2}}{\sqrt{20}})^{2}=0$

$(\sqrt{5}x-\sqrt{\frac{1}{10}})^{2}+3-\frac{1}{10}=0$

Hence for making it square the construct

$\frac{1}{10}$ should be added and subtracted

1183756_1359138_ans_852ca2e900654e08a5cf95354597d0cf.JPG

Factorise:
$4x^{4}-12x^{2}+9$

$4{x}^{4}-12{x}^{2}+9$

$={\left(2{x}^{2}\right)}^{2}+9-12{x}^{2}$

$={\left(2{x}^{2}-3\right)}^{2}$

$x^2=\dfrac{3}{2}$

$x=\pm\dfrac{\sqrt 3}{\sqrt 2}$

Find the value of $2{a}^{2}-3{b}^{2}+4{c}^{2}-5{d}^{2}$ when $a=3,\,b=0,c=2$ and $d=1$

By substituting the value of

$a=3,\,b=0,c=2$ and

$d=1$ in

$2{a}^{2}-3{b}^{2}+4{c}^{2}-5{d}^{2}$ we get

$2{a}^{2}-3{b}^{2}+4{c}^{2}-5{d}^{2}$

$=2{\left(3\right)}^{2}-3{\left(0\right)}^{2}+4{\left(2\right)}^{2}-5{\left(1\right)}^{2}$

$=2\times 9-3\times 0+4\times 4-5\times 1$

$=18-0+16-5$

$=34-5=29$

Find the value of $k$ if the quadratic equation $3x^{2}-k\sqrt {3}x+4=0$ equal roots.

Given:Roots are equal

$\Rightarrow$ Discriminant

$=0$

$\Rightarrow {b}^{2}-4ac=0$ where

$a=3,b=-k\sqrt{3}, c=4$

$\Rightarrow {\left(-k\sqrt{3}\right)}^{2}-4\times 3\times 4=0$

$\Rightarrow 3\left({k}^{2}-16\right)=0$

$\Rightarrow {k}^{2}-16=0$

$\therefore k=4,-4$

Prove that the equation $x^{2}(a^{2}+b^{2})+2x(ac+bd)+(c^{2}+d^{2})=0$ has no real root, if $ad \neq bc$ .

Discriminant,

$D=4(ac+bd)^{2}-4(a^{2}+b^{2})(c^{2}+d^{2})$

$D=4[(ac+bd)^{2}-(a^{2}+b^{2})(c^{2}+d^{2})]$

$D=4[a^{2}c^{2}+b^{2}d^{2}+2acbd-a^{2}c^{2}-a^{2}d^{2}-b^{2}c^{2}-b^{2}d^{2}]$

$D=4[2acbd-a^{2}d^{2}-b^{2}c^{2}]$

$D=-4[a^{2}d^{2}+b^{2}c^{2}-2adbc]$

$D=-4(ad-bc)^{2}$

We have,

$ad \neq bc$

Therefore,

$ad-bc \neq 0$

$(ad-bc)^{2} > 0$

$-4(ad-bc)^{2} < 0$

$D < 0$

Hence, the given equation has no real roots.

Find the roots of the following equation $4x^{2}+4bx-(a^{2}-b^{2})=0$ by the method of completing the square.

$4x^{2}+4bx-(a^{2}-b^{2})=0$

$x^{2}+bx-(\dfrac{a^{2}-b^{2}}{4})=0$

$x^{2}+2(\dfrac{b}{2})x=\dfrac{a^{2}-b^{2}}{4}$

$x^{2}+2(\dfrac{b}{2})x+(\dfrac{b}{2})^{2}=\dfrac{a^{2}-b^{2}}{4}+(\dfrac{b}{2})^{2}$

$(x+\dfrac{b}{2})^{2}=\dfrac{a^{2}}{4}$

$x+\dfrac{b}{2}=\pm \dfrac{a}{2}$

$x=-\dfrac{b}{2} \pm \dfrac{a}{2}$

Verify:
$(a+b)^2-(a-b)^2=4ab$ , for $a=4,b=3$ .

For

$a=4,b=3$ .

Now,

$a+b=7$ ......(1) and

$a-b=4-3=1$ .....(2).

Now, (1)

$^2+$ (2)

$^2$ we get,

$(a+b)^2-(a-b)^2$

$=7^2-1^2$

$=49-1$

$=48$ ......(3).

Now,

$4ab$

$=4\times 3\times 4$

$=48$ .....(4).

From (3) and (4) it is varified.

Solve: ${ 150x }^{ 2 }-750x-8=0$

$150{x}^{2}-750x-8=0$

$\Rightarrow 2\left(125{x}^{2}-375x-4\right)=0$

$\Rightarrow 125{x}^{2}-375x-4=0$

$\Rightarrow {x}^{2}-\dfrac{375}{125}x-\dfrac{4}{125}=0$

$\Rightarrow {x}^{2}-3x-\dfrac{4}{125}=0$

$\Rightarrow {x}^{2}-2x\times\dfrac{3}{2}+\dfrac{{3}^{2}}{{2}^{2}}-\dfrac{{3}^{2}}{{2}^{2}}-\dfrac{4}{125}=0$

$\Rightarrow {\left(x-\dfrac{3}{2}\right)}^{2}=\dfrac{9}{4}+\dfrac{4}{125}$

$\Rightarrow {\left(x-\dfrac{3}{2}\right)}^{2}=\dfrac{1125+16}{500}=\dfrac{1141‬}{500}$

$\Rightarrow x-\dfrac{3}{2}=\pm\sqrt{\dfrac{1141‬}{500}}$

$\therefore x=\dfrac{3}{2}\pm\dfrac{1}{10}\sqrt{\dfrac{1141‬}{5}}$

Find the roots of the quadratic equation $2{x}^{2}+9x+10=0$

Given,

$2{x}^{2}+9x+10=0$

$2{x}^{2}+4x+5x+10=0$

$2x\left(x+2\right)+5\left(x+5\right)=0$

$\left(x+2\right)\left(2x+5\right)=0$

$x=-2,\,\dfrac{-5}{2}$

Solve
$2x^{2}-6x+3=0$

$2{x}^{2}-6x+3=0$

$\Rightarrow 2\left({x}^{2}-3x+\dfrac{3}{2}\right)=0$

$\Rightarrow {x}^{2}-3x+\dfrac{3}{2}=0$

$\Rightarrow {x}^{2}-2\times \dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{9}{4}+\dfrac{3}{2}=0$

$\Rightarrow {\left(x-\dfrac{3}{2}\right)}^{2}=\dfrac{9}{4}-\dfrac{3}{2}$

$\Rightarrow {\left(x-\dfrac{3}{2}\right)}^{2}=\dfrac{9-6}{4}$

$\Rightarrow {\left(x-\dfrac{3}{2}\right)}^{2}=\dfrac{3}{4}$

$\Rightarrow x-\dfrac{3}{2}=\pm\dfrac{\sqrt{3}}{2}$

$\therefore x=\dfrac{3\pm\sqrt{3}}{2}$

Express $\sqrt{3}y=2x$ in standard form

Given,

$\sqrt{3}y=2x$

Squaring both sides, we get

$3{y}^{2}=4{x}^{2}$

$3{y}^{2}-4{x}^{2}=0$ is the standard form.

Solve $2 x ^ { 3 } y - 14 y ^ { 2 } x - 12 x ^ { 2 } y - 4 x ^ { 2 } y - 2 x y ^ { 2 }$

Consider the given expression.

$\Rightarrow 2x^3y-14y^2x-12x^2y-4x^2y-2xy^2$

$\Rightarrow 2x^3y-16x^2y-16xy^2$

$\Rightarrow 2xy(x^2-16x-16y)$

Hence, this is the answer.

If the discriminant of equation $6x^{2}+bx+2=0$ is $1$ then find the value of $'b'$ .

Discriminant

$\Delta={b}^{2}-4ac$

Given:Discriminant

$=1$

$\Rightarrow {b}^{2}-4ac=1$ where

$a=6,b=b,c=2$

$\Rightarrow {b}^{2}-4\times 6\times 2=1$

$\Rightarrow {b}^{2}-48=1$

$\Rightarrow {b}^{2}=1+48=49$

$\therefore b=\pm 7$

Solve:
$2x^2-x+\dfrac{1}{8}=0$ .

Now,

$2x^2-x+\dfrac{1}{8}=0$

$\Rightarrow \dfrac{1}{8}(16x^2-8x+1)=0$

$\Rightarrow \dfrac{1}{8}(4x-1)^2=0$

$\Rightarrow (4x-1)^2=0$

$\Rightarrow x=\dfrac{1}{4}$ .

Solve the following equation:
$4 ( y - 5 ) = 16$

$4(y-5)=16$

$\Rightarrow$

$(y-5)=\dfrac{16}{4}$

$\Rightarrow$

$y-5=4$

$\Rightarrow$

$y=5+4$

$\therefore y=9$

Find the values of $'k'$ for which $x^{2}-2x+k=0$ has real roots.

Given : The equation has real roots.

Discriminant

$\Delta={b}^{2}-4ac> 0$ where

$a=1,b=-2,c=k$

$\Rightarrow {\left(-2\right)}^{2}-4\times 1\times k>0$

$\Rightarrow 4-4k> 0$

$\Rightarrow 4\left(1-k\right)> 0$

$\Rightarrow k-1< 0$

$\Rightarrow k <1$

$\therefore k\in\left(-\infty,1\right)$

The value of $x$ if $x+\dfrac 1x=2$

$x+\dfrac 1x=2\\ x^2+1=2x\\x^2-2x+1=0\\(x-1)^2=0\\x=1$

Check whether the equation $6 x^{2}-7 x+2=0$ has real roots. If it has, find them by method of completing square.

$6x^2-7x+2$

Condition for real roots

$b^2>4ac\\(-7)^2>4(6)(2)\\49>48$

$6x^2-7x+2=0\\x^2-\dfrac 76 x+\dfrac 13=0\\x^2-\dfrac 76x=-\dfrac 13\\x^2-2(1)\dfrac 7{12}x +\left(\dfrac7{12}\right)^2=\dfrac {-1}3+\left(\dfrac7{12}\right)^2\\\left(x-\dfrac{7}{12}\right)^2=\dfrac 1{144}\\x-\dfrac 7{12}=\pm \dfrac 1{12}\\x=\dfrac 23,\dfrac 12$

If the quadratic equation $x^{ 2 }-4x+k=0$ has equal roots , then find the value of k,

${x}^{2}-4x+k=0$ is of the form

$a{x}^{2}+bx+c=0$ where

$a=1\,\,b=-4\,\,c=k$

Roots are equal

$\Rightarrow$ Discriminant

$=0$

$\Rightarrow {b}^{2}-4ac=0$

$\Rightarrow {\left(-4\right)}^{2}-4\times 1\times k=0$

$\Rightarrow 16-4k=0$

$\Rightarrow -4k=-16$

$\therefore k=\dfrac{16}{4}=4$

Check whether the following are Quadratic equations
${ \left( x+2 \right) }^{ 3 }=2x\left( { x }^{ 2 }-1 \right)$

${\left(x+2\right)}^{3}=2x\left({x}^{2}-1\right)$

$\Rightarrow {x}^{3}+8+6x\left(x+2\right)=2{x}^{3}-2x$

$\Rightarrow {x}^{3}+8+6{x}^{2}+12x-2{x}^{3}+2x=0$

$\Rightarrow -{x}^{3}+4{x}^{2}+14x+8=0$ has its highest power

$3$

Hence it is not a quadratic equation.

Find the roots of the equation $5x^{2}-6x-2=0$ by the method of completing the square.

We have,

$5x^{2}-6x-2=0$

$x^{2}-\dfrac{6}{5}x-\dfrac{2}{5}=0$

$x^{2}-\dfrac{6}{5}x=\dfrac{2}{5}$

$x^{2}-2(\dfrac{3}{5})x+(\dfrac{3}{5})^{2}=\dfrac{2}{5}+(\dfrac{3}{5})^{2}$

$(x-\dfrac{3}{5})^{2}=\dfrac{19}{25}$

$x-\dfrac{3}{5}=\pm \dfrac{\sqrt{19}}{5}$

$x=\dfrac{3}{5} \pm \dfrac{\sqrt{19}}{5}$

Find the value of $k$ for which the quadratic equation $x(x-k)+5=0$ will have two real and equal roots.

Given the quadratic equation is

$x(x-k)+5=0$

or,

$x^2-kx+5=0$ .

If the quadratic equation has two real and equal roots then we have the discriminant will be

$0$ .

Then,

$(-k)^2-4\times 5\times 1=0$

or,

$k^2=20$

or,

$k=\pm \sqrt{20}$

or,

$k=\pm 2\sqrt{5}$ .

Check whether the following is a quadratic equation:
${ x }^{ 3 }-{ 4x }^{ 2 }-x+1={ \left( x-2 \right) }^{ 3 }$

${x}^{3}-4{x}^{2}-x+1={\left(x-2\right)}^{3}$

$\Rightarrow {x}^{3}-4{x}^{2}-x+1={x}^{3}-8-6x\left(x-2\right)$

$\Rightarrow -4{x}^{2}-x+1=-8-6{x}^{2}+12x$

$\Rightarrow -4{x}^{2}-x+1+8+6{x}^{2}-12x=0$

$\Rightarrow 2{x}^{2}-13x+9=0$

The above-obtained equation has its highest power

$2$ hence, it is a quadratic equation.

If $4x^{ 2 }-4x+k=0$ find $x$

$4{x}^{2}-4x+k=0$

$\Rightarrow {\left(2x\right)}^{2}-2\times 2x+1-1-k=0$

$\Rightarrow {\left(2x-1\right)}^{2}=k+1$

$\Rightarrow 2x=1\pm\sqrt{k+1}$

$\therefore x=\dfrac{1\pm\sqrt{k+1}}{2}$

If $\tan \theta +\dfrac {1}{\tan \theta}=2$ , prove $\tan^{2} \theta +\dfrac {1}{\tan^{2}\theta}=2$

Given

$\tan \theta+\dfrac{1}{\tan \theta}=2$

squaring on both sides

$\bigg(\tan \theta+\dfrac{1}{\tan \theta}\bigg)^2=4$

$\implies \tan^{2}\theta+\dfrac{1}{\tan^2 \theta}+2(\tan \theta)\bigg(\dfrac{1}{\tan \theta}\bigg)=4$

$\implies \tan^{2}\theta+\dfrac{1}{\tan^2 \theta}+2=4$

$\implies \tan^{2}\theta+\dfrac{1}{\tan^2 \theta}=2$

Show that
$\left( 4x-9 \right) ^{ 2 }+144x=\left( 4x+9 \right) ^{ 2 }$

L.H.S

$={\left(4x-9\right)}^{2}+144x$

$=16{x}^{2}+81-36x+144x$ ..........

$\because (a-b)^2= a^2-2ab+b^2$

$=16{x}^{2}+81+108x$

$={\left(4x\right)}^{2}+2\times 4x\times 9+81$

$={\left(4x+9\right)}^{2}$ ...........

$\because (a+b)^2= a^2+2ab+b^2$

$=$ R.H.S

Hence proved.

Find the quadratic equation, if $x=\sqrt{5+\sqrt{5+\sqrt{5+...\infty }}}$ and x is a natural number.

Given

$x=\sqrt{5+\sqrt{5+\sqrt{5+...\infty }}}$

Squaring on both sides

$x^2=5+\sqrt{5+\sqrt{5+\sqrt{5+...\infty }}}$

$\implies x^2=5+x$

$\implies x^2-x-5=0$

The quadratic equation is

$x^2-x-5=0$

Solve :
$\dfrac { { x }^{ 2 } }{ \left( { x }^{ 2 }+2 \right) \left( { 2x }^{ 2 }+1 \right) } =1$

$\dfrac{{x}^{2}}{\left({x}^{2}+2\right)\left(2{x}^{2}+1\right)}=1$

$\Rightarrow {x}^{2}=\left({x}^{2}+2\right)\left(2{x}^{2}+1\right)$

$\Rightarrow {x}^{2}=2{x}^{4}+{x}^{2}+4{x}^{2}+2$

$\Rightarrow 2{x}^{4}+4{x}^{2}+2=0$

$\Rightarrow 2\left({x}^{4}+2{x}^{2}+1\right)=0$ is of the form

${a}^{2}+2ab+{b}^{2}={\left(a+b\right)}^{2}$

$\Rightarrow {\left({x}^{2}+1\right)}^{2}=0$

$\Rightarrow {x}^{2}+1=0$

$\Rightarrow {x}^{2}=-1$

$\therefore x=\pm\sqrt{-1}=\pm i$

Solve for x : $\frac{1}{(x-1)(x-2)}+\frac{1}{(x-2)(x-3)}=\frac{2}{3},x\neq 1,2,3,$

1311787_1609018_ans_c4f544556d6a4de89471aca665b55f41.jpg

Solve the following quadratic equation for $x:$
$x^{2}-4ax-b^{2}+4a^{2}=0$

$x^2-4 a x-b^2+4 a^2=0$

$\Rightarrow x^2-4 a x+4 a^2=b^2$

$\Rightarrow (x)^2-2(x)(2 a)+(2 a)^2=b^2$

$\Rightarrow (x-2 a)^2=b^2$

$\Rightarrow x-2 a=\pm b$

$\Rightarrow x=2 a\pm b$

$\Rightarrow x=2 a+b,2 a-b$

Solve
$\dfrac {m}{n}x^ {2}+\dfrac {n}{m}=1-2x$

$\cfrac{m}{n} {x}^{2} + \cfrac{n}{m} = 1 - 2x$

$\Rightarrow {m}^{2} {x}^{2} + {n}^{2} = mn - 2mn x$

$\Rightarrow {m}^{2} {x}^{2} + 2mnx + {n}^{2} - mn = 0$

Here,

$a = {m}^{2}, \; b = 2mn, \; c = {n}^{2} - mn$

By using the quadratic formula, we have

$x = \cfrac{-b \pm \sqrt{{b}^{2} - 4ac}}{2a}$

$\Rightarrow x = \cfrac{-2mn \pm \sqrt{{\left( 2mn \right)}^{2} - 4 {m}^{2} \left( {n}^{2} - mn \right)}}{2 {m}^{2}}$

$\Rightarrow x = \cfrac{-2mn \pm \sqrt{4 {m}^{2}{n}^{2} - 4 {m}^{2}{n}^{2} + 4{m}^{3}n}}{2{m}^{2}}$

$\Rightarrow x = \cfrac{-2mn \pm 2m \sqrt{mn}}{2 {m}^{2}}$

$\Rightarrow x = \cfrac{-n \pm \sqrt{mn}}{m}$

Solve by completing square method:
${ x }^{ 2 }+8x+5$

$x^{2}+8x+5=0$

Third term =

$(\dfrac{1}{2}\times$ coefficient of

$x)^{2}=\left(\dfrac{1}{2}\times 8\right)^{2}=16$

Adding on both sides.

$x^{2}+8x+16+5=16$

$x^{2}+2\cdot4\cdot x+16=16-5$

$(x+4)^{2}=11$

Taking square root ,

$x+4=\pm \sqrt{11}$

$\therefore x=\sqrt{11}-4$ or

$x=-\sqrt{11}-4$

If $x^2-3x+3=0$ , then find the roots of the equation.

On comparing given quadratic equation with

$ax^2+bx+c=0$ we get,

$a=1,\;b=-3$ and

$c=3$

Now, by using quadratic formula,

$\begin{aligned}{}x& = \frac{{ - \left( { - 3} \right) \pm \sqrt {{{\left( { - 3} \right)}^2} - 4\left( 1 \right)\left( 3 \right)} }}{{2\left( 1 \right)}}\\ &= \frac{{3 \pm \sqrt {9 - 12} }}{2}\\ &= \frac{{3 \pm \sqrt { - 3} }}{2}\end{aligned}$

From the above expression, we can say that no real roots for the given quadratic equation exist.

Find the discriminant of $2{ x }^{ 2 }+10x+21=0.$

$2x^2+10x+21=0$

Comparing

$ax^2+bx+c=0$

$\therefore a=2, b=10, c=21$

For

$\Delta$

$\Delta =b^2-4ac$

$=10^2-4\times 2\times 21$

$=100-168$

$=-68$ .

Solve:
$x^2-2xy+y^2-2^2$

given,

${x}^{2} - 2xy + {y}^{2} - {2}^{2}$

$= {\left( x - y \right)}^{2} - {2}^{2} \quad \left( \because {\left( a - b \right)}^{2} = {a}^{2} - 2ab + {b}^{2} \right)$

$= \left( x - y - 2 \right) \left( x - y + 2 \right) \quad \left( \because {a}^{2} - {b}^{2} = \left( a - b \right) \left( a + b \right) \right)$

Hence

${x}^{2} - 2xy + {y}^{2} - {2}^{2} = \left( x - y - 2 \right) \left( x - y + 2 \right)$

Simplify the following expressions:
${(x+y+z)}^{2}+{ \left( x+\cfrac { y }{ 2 } +\cfrac { z }{ 3 } \right) }^{ 2 }-{ \left( \cfrac{x}{2}+\cfrac { y }{ 3 } +\cfrac { z }{ 4 } \right) }^{ 2 }$

Formula,

$(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca$

Given,

$(x+y+z)^2+\left ( x+\dfrac{y}{2}+\dfrac{z}{3} \right )^2-\left ( \dfrac{x}{2}+\dfrac {y}{3}+\dfrac{z}{4} \right )$

$=2xy+2xz+x^2+y^2+2yz+z^2+xy+\dfrac{2xz+yz}{3}+x^2+\dfrac{y^2}{4}+\dfrac{z^2}{9}-\dfrac{xy}{3}-\dfrac{xz+x^2}{4}-\dfrac{y^2}{9}-\dfrac{yz}{6}-\dfrac{z^2}{16}$

$=\dfrac{252x^2+384xy+348xz+164y^2+151z^2+312yz}{144}$

Classify the following polynomial as linear, quadratic, cubic and biquadratic polynomial:
$2x + x^{2}$ .

The degree of

$2x+x^2$ is

$2$ , so it is a 'quadratic polynomial'.

Classify the following polynomial as linear, quadratic, cubic and biquadratic polynomial:
$x + x^{2} - 4$ .

Step 1: Find the degree of the polynomial

$\text{ Let}$

$f(x)=x+x^2-4$

Since the degree of the polynomial is 2, hence given polynomial is a quadratic polynomial

Simplify the following products:
$(2{x}^{4}-4{x}^{2}+1)(2{x}^{4}-4{x}^{2}-1)$

$4{x}^{8}-16{x}^{6}+16{x}^{4}-1$

$(2{x}^{4}-4{x}^{2}+1)(2{x}^{4}-4{x}^{2}-1)$

$[(2{x}^{4}-4{x}^{2})+1][(2{x}^{4}-4{x}^{2})-1]$

$={(2{x}^{4}-4{x}^{2})}^{2}-{1}^{2}$

$=4{x}^{8}+16{x}^{4}-2\times 2{x}^{4}\times 4{x}^{2}-1$

$=4{x}^{8}+16{x}^{4}-16{x}^{6}-1$

Find the roots $x^{2}+6x-4=0$

1319445_1586964_ans_f370e5fbb7114e0da7b426a3f17a0886.jpg

Factorize the following quadratic polynomial by using the method of completing the square.
$4x^2-12x+5$ .

1590623_1673880_ans_c694a3cea8c4492eaef51ef48bba9c27.jpg

Solve the following equations by using the method of completing the square:
$8x^2-14x-15=0$

$8x^2 -14x-15=0$

$16x^2 -28x-30=0$

(multiplying both sides by

$2$ )

Adding

$(7/2)^2$ on both the sides

$(4x)^2 -2.4x.\dfrac{7}{2} +\left (\dfrac {7}{2}\right)^2=30+\left (\dfrac {7}{2}\right)^2$

$\left (4x-\dfrac {7}{2}\right)^2 =30+\dfrac {49}{4}=\dfrac {169}{4}=\left (\dfrac {13}{2}\right)^2$

$4x-7/2=13/2$ or

$4x-7/2 =-13/2$

$x=5/2$ or

$x=-3/4$

Solve the following equations by using the method of completing the square:
$3x^2-x-2=0$

$3x^2-x-2=0$

$9x^2-3x-6=0$
(multiplying both sides by

$3$ )

$9x^2-3x=6$

Adding

$(1/2)^2$ on both sides.

$(3x)^2-2.3x.\dfrac {1}{2} +\left (\dfrac {1}{2}\right)^2 =+\left (\dfrac {1}{2}\right)^2$

$\left (3x-\dfrac {1}{2}\right)^2=6+\dfrac {1}{4}=\dfrac {25}{4}=\left (\dfrac {5}{2}\right)^2$

$3x-1/2=5/2$ or

$3x-1/2=-5/2$

$x=1$ or

$x=-2/3$

Solve the following equations by using the method of completing the square:
$x^2+8x-2=0$

$x^2+8x-2=0$

$x^2+8x=2$

$x^2 -2. x.4+42=2+42$

(adding

$2^2$ on both sides)

$(x+4)^2=18$

Using algebraic identity :

$a^2-2b +b^2 =(a-b)^2$

$x+4=\pm \sqrt 2$

$x=-4 \pm 3 \sqrt 2$

$x=(-4+3\sqrt 2)$ or

$(-4 -3 \sqrt 2)$

Factorize the following quadratic polynomial by using the method of completing the square.
$p^2+6p-16$ .

1590503_1673871_ans_8206dccc26af41a38c22a64a3d5e50df.jpg

Factorize the following quadratic polynomial by using the method of completing the square.
$a^2+2a-3$ .

1590621_1673878_ans_ed6808dc17a3461b8bd29041ee0b1751.jpg

Factorize the following quadratic polynomial.
$x^2+12x+20$ .

1590505_1673873_ans_cd636c4ab3804c9382bfc14f73eb4d21.jpg

Factorize the following quadratic polynomial by using the method of completing the square.
$a^2-14a-51$ .

1590507_1673876_ans_b007da8b0a1740918acf2ceab5f92b8c.jpg

Factorize the following quadratic polynomial by using the method of completing the square.
$y^2-7y+12$ .

1590626_1673882_ans_16ebc601aa44415ca512224fb678d513.jpg

Check whether the following is quadratic equation in $x$ ?
$\sqrt{2}x^{2}+7x+5\sqrt{2}=0$

Given,

$\sqrt{2}x^{2}+7x+5\sqrt{2}=0$

Highest Degree

$2$

And it is of the form

$ax^2+bx+c=0$

Therefore it is a quadratic equation.

Find the discriminant of each of the following equations:
$2x^2-7x+6=0$

$2x^2-7x+6=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

Here,

$a=2, b=-7$ and

$c=6$

Determinant formula:

$D=b^2-4ac$

$(-7)^2-4\times 2 \times 6$

$D=1$

Check whether the following is quadratic equation in $x$ ?
$1/3x^{2}+1/5x-2=0$

Given,

$1/3x^{2}+1/5x-2=0$

Above equation can be simplify as

$5x^{2}+3x-2=0$

Highest Degree

$2$

And it is of the form

$ax^2+bx+c=0$

Therefore it is a quadratic equation.

What is the highest degree of the quadratic equation in $x$ ?
$2x^{2}+5/2 x-\surd{3}=0$

$2x^{2}+5/2 x-\sqrt{3}=0$

Highest Degree

$=2$

Find the discriminant of each of the following equation:
$\surd 3 x^2 +2\surd 2 x-2\surd 3=0$

$\sqrt 3 x^2+2\sqrt 2 x-2\sqrt 3=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

Here,

$a=\sqrt 3, b=2\sqrt 2, c=-2\sqrt 3$

Discriminant formula:

$D=b^2-4ac$

$=(2\sqrt 2)^2-4(\sqrt 3)(-2\sqrt 3)$

$\implies D=32$

Find the discriminant of each of the following equations:
$3x^2 -2x+8=0$

$3x^2-2x+8=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

Here,

$a=3, b=-2, c=8$

Determinant formula:

$D=b^2-4ac$

$=(-2)^2-4.3.8$

$=4-96$

$D=-92$

Solve the following equation by using the method of completing the square:
$2/x^2-5/x+2=0$

$2/x^2- 5/x+2=0$

$\dfrac {2-5x+2x^2}{x^2}=0$

$2x^2-5x+2=0$

$4x^2-10x=-4$ (multiplying both sides by

$2$ )

Adding

$(5/2)^2$ on both the sides

$(2x)^2-2.2x.\dfrac {5}{2}+\left (\dfrac {5}{2}\right)^2=-4+\left (\dfrac {5}{2}\right)^2$

$(2x)^ -2.2x. \dfrac {5}{2}+\left (\dfrac {5}{2}\right)^2=-4+\left (\dfrac {5}{2}\right)^2$

$2x-5/2=3/2$ or

$2x-5/2 =-3/2$

$x=2$ or

$x=1/2$

Solve the following equation by using the method of completing the square:
$5x^2-6x-2=0$

$5x^2-6x-2=0$

$25x^2-30x-10=0$
(multiplying both sides by

$5$ )

$25^2-30x=10$

Adding

$(3)^2$ on both the sides

$(5x)^2-2.5x.3+(3)^2=10+(3)^2$

$(5x-2)^2=10+9=19$

$5x-2=\surd {19}$ or

$5x-3=-\surd {19}$

$x=(3+\surd {19})/5$ or

$x=(3-\surd {19})/5$

Find the discriminant of each of the following equation:
$2x^2-5\sqrt 2x+4=0$

$2x^2-5\sqrt 2 x+4=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

Here,

$a=2, b=-5\sqrt 2, c=4$

Determinant formula:

$D=b^2-4ac$

$=(-5\sqrt 2)^2-4\times2\times4$

$=50-32$

$D=18$

What is the degree of the quadratic equation in $x$ ?
$x^{2}-x+3=0$

$x^{2}-x+3=0$

Highest Degree

$=2$

Find the roots of each of the following equation, if they exist, by applying the quadratic formula:
$16x^2 -24x-1=0$

$16x^2-24x-1=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

$a=16, b=-24, c=-1$

Finding discriminant:

$D=b^2-4ac$

$=(-24)^2-4(16)(-1)$

$=576+64$

$=640>0$

Roots of equation are real:

$x=\dfrac{-b \pm \sqrt D}{2a}$

$x=\dfrac{-(-24) \pm \sqrt{64\cdot 10}}{2\cdot 16}$

$=\dfrac{-(-24) \pm 8\sqrt{ 10}}{2\cdot 16}$

$=\dfrac{3\pm \sqrt{10}}{4}$ (Taking 8 common)

Roots are:

$x=\dfrac{3+\sqrt{10}}{4}$ or

$x=\dfrac{3-\sqrt {10}}{4}$

Find the roots of each of the following equations, if they exist, by applying the quadratic formula:
$2x^2 +x-4=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

$a=2, b=1, c=-4$

Find Discriminant:

$D=b^2-4ac$

$=(1)^2-4.2.-4$

$=1+32$

$=33>0$

Roots of equation are real.

$x=\dfrac{-b \pm \sqrt D}{2a}$

$=\dfrac{-1\pm \sqrt {33}}{4}$

Roots are:

$x=\dfrac{(-1+\sqrt{33})}{4}$

and

$x=\dfrac{(-1-\sqrt{33})}{4}$

Check whether the following is quadratic equation in $x$ ?
$x-6/x=3$

Given,

$x-6/x=3$

Simply as

$x^{2}-3x-6=0$

Degree

$2$

And it is of the form

$ax^2+bx+c=0$

Therefore it is a quadratic equation.

Find the discriminant of each of the following equation:
$(x-1)(2x-1)=0$

$(x-1)(2x-1)=0$

$2x^2-3x+1=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

Here,

$a=2, b=-3, c=-1$

Discriminant formula:

$D=b^2-4ac$

$=(-3)^2-4\times 2\times 1$

$D=1$

Find the roots of equation, if they exist, by applying the quadratic formula:
$25x^2 +30x+7=0$

$25x^2+30x+7=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

$a=25, b=30, c=7$

Find Discriminant:

$D=b^2-4ac$

$=(30)^2-4.25.7$

$=900-700$

$=200>0$

Roots of equation are real.

$x=\dfrac{-b \pm \sqrt D}{2a}$

$x=\dfrac{-30\pm \sqrt{200}}{2\times 25}$

$=\dfrac{-30\pm 10\sqrt 2}{50}$

$=\dfrac{-3\pm \sqrt 2}{5}$

Roots of the equation are:

$x=\dfrac{-3+\sqrt 2}{5}$

$x=\dfrac{-3-\sqrt 2}{5}$

Find the roots of each of the following equation, if they exist, by applying the quadratic formula:
$x^2- 6x+4=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

$a=1, b=-6, c=4$

Find discriminant:

$D=b^2-4ac$

$=(-6)^2-4.1.4$

$=36-16$

$D=20>0$
Roots of equation are real.

Find the roots:

$x=\dfrac{-b\pm \sqrt D}{2a}$

$=\dfrac{-(-6)\pm \sqrt{20}}{2\times 1}=\dfrac{6\pm 2\sqrt 5}{2}$

$=3\pm \sqrt 5$

$x=3+\sqrt 5$ and

$x=3-\sqrt 5$

Find the roots of each of the following equations, if they exist, by applying the quadratic formula:
$x^2 -4x-1=0$

$x^2-4x-1=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

Here,

$a=1, b=-4, c=-1$

Find discriminant:

$D=b^2-4ac$

$=(-4)^2-4\times 1\times -1$

$D=20>0$

$x=\dfrac{-b \pm \sqrt D}{2a}$

$x=\dfrac{-(-4))\pm \sqrt{20}}{2\times 1}$

$=\dfrac{4\pm 2\sqrt 5}{2}$

$x=2\pm \sqrt 5$

Therefore,

$x=2+\sqrt 5$ and

$x=2-\sqrt 5$

By using the method of completing the square, show that the equation $2x^2+x+4=0$ has no real roots:

$3x^2+x+4=0$

$4x^2+2x+8=0$

(multiplying both sides by

$2$ )

$4a^2+2x=-8$

Adding

$(1/1)^2$ both sides

$\left(2x+\dfrac {1}{2}\right)^2=-8+\dfrac {1}{4}=-\dfrac {31}{4}< 0$

But

$(2x+1/2)^2$ cannot be negative for any real value of

$x$

Then given equation has no real roots.

Solve the following equation by using the method of completing the square:
$\sqrt 3 x^2 +10x+7\sqrt 3 =0$

$\surd 3 x^2+10x-7\sqrt 3 =0$

Dividing each side by

$\surd 3$

$x^2+\dfrac {10}{\sqrt 3}x+7=0$

$(x)^2+2\times x\times \dfrac {5}{\sqrt 3}=-7$

Adding

$\left(\dfrac {5}{\sqrt 3}\right)^2$ to both sides.

$(x)^2 +2\times x\times \dfrac {5}{\sqrt 3}+\left(\dfrac {5}{\sqrt 3}\right)^2 =-7+\left(\dfrac {5}{\sqrt 3}\right)^2$

$\left(x+\dfrac {5}{\sqrt 3}\right)^2 =-7+\dfrac {25}{3}$

$=\dfrac {-21+25}{3}=\dfrac {4}{3}=\left(\pm \dfrac {2}{\sqrt 3}\right)^2$

$x+\dfrac {5}{\sqrt 3}=\pm \dfrac {2}{\sqrt 3}$

$x=\dfrac {-5}{\sqrt 3}\pm \dfrac {2}{\sqrt 3}$

$x=-\sqrt 3$ or

$\dfrac {-7}{\sqrt 3}$

Find the discriminant of each of the following equation:
$1-x=2x^2$

$1-x=2x^2$

$2x^2+x-1=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

Here,

$a=2, b=1, c=-1$

Discriminant formula :

$D=b^2-4ac$

$=(1)^2-4\times 2\times -1$

$D=9$

Find the roots of the following equation, by applying the quadratic formula:
$2x^2 -2\sqrt2 x+1=0$

Given equation is,

$2x^2-2\sqrt 2x+1=0$

Comparing given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

$a=2, b=-2\sqrt 2$ and

$c=1$

Discriminant,

$D=b^2-4ac$

$=(-2\sqrt 2)^2-4.2.1$

$=8-8$

$=0$

So, the equation has equal roots.

$x=\dfrac{-b \pm \sqrt D}{2a}$

$=\dfrac{2\sqrt 2 \pm 0}{4}$

$=\dfrac{\sqrt 2\pm0}{2}$

$=\dfrac{1\pm0}{\sqrt 2}$

Hence, the roots are

$\dfrac{1}{\sqrt 2}$ and

$\dfrac{1}{\sqrt 2}$ .

Check whether the following is quadratic equation in $x$ ?
$x+2/x=x^{2}$

Given,

$x+2/x=x^{2}$

Simplify above equation

$x^{3}-x^{2}=0$

Degree

$3$

And it is not of the form

$ax^2+bx+c=0$

Therefore it is not a quadratic equation.

Find the roots of each of the following equation, if they exist, by applying the quadratic formula:
$\surd 3 x^2 +10x-8\surd 3=0$

$\sqrt 3 x^2+10x-8\sqrt 3=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

$a=\sqrt 3, b=10, c=-8\sqrt 3$

Find Discriminant:

$D=b^2-4ac$

$=(10)^2-4.\sqrt 3.-8\sqrt 3$

$=100+96$

$=196>0$

Roots of the equation are real.

Find roots:

$x=\dfrac{-b \pm \sqrt D}{2a}$

$=\dfrac{-10 \pm \sqrt{196}}{2\times \sqrt 3}=\dfrac{-10\pm 14}{2\sqrt 3}$

Roots are:

$x=2/\sqrt 3/3$ and

$x=-4/ \sqrt 3$

Find the roots of each of the following equations, if they exist, by applying the quadratic formula:
$3x^2 -2\surd 6 x+2=0$

$3x^2-2\sqrt 6x+2=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

Thus here,

$a=3, b=-2\sqrt 6, c=2$

Find Discriminant:

$D=b^2-4ac$

$=(-2\sqrt 6)^2-4\times 3\times 2$

$=24-24$

$=0$

Roots of equation are equal.

Find roots:

$x=\dfrac{-b \pm \sqrt D}{2a}$

$=\dfrac{-(-2\sqrt 6) \pm \sqrt{0}}{2\times 3}$

$=\dfrac{2\sqrt 6}{6}$

Roots are:

$x=\dfrac{\sqrt 2}{\sqrt 3}$

Find the roots of each of the following equation, if they exist, by applying the quadratic formula:
$\surd 2 x^2 +7x+5\surd 2=0$

$\sqrt 2x^2+7x+5\sqrt 2=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

$a=\sqrt 2, b=7, c=5\sqrt 2$

Find Discriminant:

$D=b^2-4ac$

$=(7)^2-4.\sqrt 2. 5\sqrt 2$

$=49-40$

$=9>0$

Roots of equation are real.

Find roots:

$x=\dfrac{-b \pm \sqrt D}{2a}$

$=\dfrac{-7\pm \sqrt 9 }{2\times \sqrt 2}=\dfrac{-7\pm 3}{2\sqrt 2}$

Roots are

$x=-\sqrt 2$ and

$x=-5\sqrt 2$

Find the roots of each of the following equations, if they exist, by applying the quadratic formula:
$2\surd 3 x^2 -5x+\surd 3=0$

$2\sqrt 3x^2-5x+\sqrt 3=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

$a=2\sqrt 3, b=-5, c=\sqrt 3$

Find Discriminant:

$D=b^2-4ac$

$=(-5)^2-4.2\sqrt 3.\sqrt 3$

$=25-24$

$=1>0$

Roots if equation are real.

Find roots:

$x=\dfrac{-b \pm \sqrt D}{2a}$

$=\dfrac{-(-5) \pm \sqrt 1}{2\times 2\sqrt 3}=\dfrac{5\pm 1}{4\sqrt 3}$

Roots are:

$x=\sqrt 3/2$ and

$x=1/ \sqrt 3$

Find the roots of the following equation if they exist by applying the quadratic formula:
$15x^2-28=x$

$15x^2-x-28=0$

Compare the given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

$a=15, b=-1, c=-28$

Discriminant:

$D=b^2-4ac$

$=(-1)^2-4\times15\times(-28)$

$=1+1680$

$D=1681>0$

The roots of the equation are real.

$x=\dfrac{-b \pm \sqrt D}{2a}$

$=\dfrac{-(-1)\pm \sqrt {1681}}{2\times 15}=\dfrac{1\pm 41}{30}$

$x=7/5$ and

$x=-4/3$

Find the roots of each of the following equation, if they exist, by applying the quadratic formula:
$2x^2 +6\surd 3 x-60=0$

$2x^2+6\sqrt 3x-60=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

$a=2, b=6\sqrt 3, c=-60$

Find Discriminant:

$D=b^2-4ac$

$=(6\sqrt 3)^2-4.2.-60$

$=108+480$

$=588>0$

Roots of equation are real.

Find roots:

$x=\dfrac{-b \pm \sqrt D}{2a}$

$=\dfrac{-6\sqrt 3 \pm \sqrt{196 \times 3}}{2\times 2}$

$=\dfrac{-3\sqrt 3\pm 7\sqrt{3}}{2}$

Roots are :

$x=2\sqrt 3$ and

$x=-5 \sqrt 3$

Find the roots of the following equation, if they exist, by applying the quadratic formula:
$4\sqrt 3\ x^2 +5x-2\sqrt 3 =0$

$4\sqrt 3x^2+5x-2\sqrt 3=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

$a=4\sqrt 3, b=5, c=-2\sqrt 3$

Find Discriminant:

$D=b^2-4ac$

$=(5)^2-4\times 4\sqrt 3\times(-2\sqrt 3)$

$=25+96$

$=121>0$

The roots of the equation are real.

Finding roots:

$x=\dfrac{-b \pm \sqrt D}{2a}$

$=\dfrac{-5 \pm \sqrt {121}}{2\times 4\sqrt 3}=\dfrac{-5\pm 11}{8\sqrt 3}$

Roots are:

$x=\dfrac{6}{8\sqrt3}$ and

$x=\dfrac{-2}{ \sqrt 3}$

Find the roots of each of the following equations, if they exist, by applying the quadratic formula:
$\surd 3\ x^2 -2\surd 2 x- 2\surd 3=0$

$3x^2-2\sqrt 2x-2\sqrt 3=0$

Compare given equation with the general form of quadratic equation, which is

$ax^2+bx+c=0$

$a=\sqrt 3, b=-2\sqrt 2, c=-2\sqrt 3$

Find Discriminant:

$D=b^2-4ac$

$=(-2\sqrt 2)^2-4.\sqrt 3.-2\sqrt 3$

$=8+24$

$=32>0$

Roots of equation are real.

Find roots:

$x=\dfrac{-b \pm \sqrt D}{2a}$

$=\dfrac{2\sqrt 2 \pm 4\sqrt 2}{2\sqrt 3}$

$x=\sqrt 6$ and

$x=- \sqrt 2/ \sqrt 3$

Solve by using quadratic formula
(i)
(ii) $25 x^{2}+30 x+7=0$

(i) Given

$256 x^{2}-32 x+1=0$

Comparing with

$ax^2+bx+c=0$ form, we get

$a=256, b=-32, c=1$

By using the quadratic formula,

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$

$\Rightarrow x=\dfrac{32 \pm \sqrt{(-32)^{2}-4(256)(1)}}{2\times 256}$

$\Rightarrow x=\dfrac{32 \pm \sqrt{1024-1024}}{2\times256}$

$\Rightarrow x=\dfrac{32\pm}{2 \times 256}$

$\Rightarrow x=\dfrac{32}{512}=\dfrac 1{16}$

(ii) Given

$25 x^{2}+30 x+7=0$

Comparing with

$ax^2+bx+c=0$ form, we get

$a=25, b=30, c=7$

By using the quadratic formula,

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$

$\Rightarrow x=\dfrac{-30 \pm \sqrt{(30)^{2}-4(25)(7)}}{2 \times 25}$

$\Rightarrow x=\dfrac{-30\pm \sqrt{200}}{50}$

$\Rightarrow x=\dfrac{-30 \pm 10 \sqrt{2}}{50}$

$\Rightarrow x=\dfrac{-3\pm\sqrt{2}}{5}$

$\Rightarrow x=\dfrac{-3+\sqrt{2}}{5}$ or

$x=\dfrac{-3-\sqrt{2}}{5}$

Is the following equation a quadratic equation in $x$ ?
$(x+2)^{3}=x^{3}-8$

$(x+2)^{3}=x^{3}-8$

$x^{3}+8+6x^{2}+12x=x^{3}-8$

$-6x^{2}+12x+16=0$

Degree

$=2$

It is a quadratic equation

Solve by using quadratic formula
(i) $2 x^{2}-7 x+6=0$
(ii) $2 x^{2}-6 x+3=0$

(i)

$2 x^{2}-7 x+6=0$

Comparing with

$ax^2+bx+c=0$ form, we get

$a=2, b=-7, c=6$

So, by using the quadratic formula

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$

$\Rightarrow x=\dfrac{7 \pm \sqrt{(-7)^{2}-4(2)(6)}}{2 (2)}$

$\Rightarrow x=\dfrac{7 \pm \sqrt{49-48}}{4}$

$\Rightarrow x=\dfrac{7 \pm 1}{4}$

$\Rightarrow x=\dfrac{7+1}{4}$ and

$x=\dfrac{7 - 1}{4}$

$\Rightarrow x=\dfrac{8}{4}$ and

$x=\dfrac{6}{4}$

$\Rightarrow x=2$ and

$x=\dfrac32$

(ii)

$2 x^{2}-6 x+3=0$

Comparing with

$ax^2+bx+c=0$ form, we get

$a=2, b=-6, c=3$

So, by using the quadratic formula

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$

$\Rightarrow x=\dfrac{6 \pm \sqrt{(-6)^{2}-4(2)(3)}}{2 (2)}$

$\Rightarrow x=\dfrac{6 \pm \sqrt{36-24}}{4}$

$\Rightarrow x=\dfrac{6\pm \sqrt{12}}{4}$

$\Rightarrow x=\dfrac{6\pm 2\sqrt{3}}{4}$

$\Rightarrow x=\dfrac{3\pm \sqrt{3}}{2}$

$\Rightarrow x=\dfrac{3+ \sqrt{3}}{2}$ and

$x=\dfrac{3- \sqrt{3}}{2}$

Solve by using quadratic formula
(i) $x^{2}+7 x-7=0$
(ii) $(2 x+3)(3 x-2)+2=0$

(i)

$x^{2}+7 x-7=0$

Comparing with

$ax^2+bx+c=0$ form, we get

$a=1, b=7 c=-7$

So, by using the quadratic formula

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$

$\Rightarrow x=\dfrac{-7 \pm \sqrt{(7)^{2}-4(1)(-7)}}{2 (1)}$

$\Rightarrow x=\dfrac{-7 \pm \sqrt{49+28}}{2}$

$\Rightarrow x=\dfrac{-7 \pm \sqrt{77}}{2}$

$\Rightarrow x=\dfrac{-7+\sqrt{77}}2$ and

$x=\dfrac{-7-\sqrt{77}}2$

(ii)

$2 x^{2}-6 x+3=0$

$\Rightarrow 2x(3x-2)+3(3x-2)=0$

$\Rightarrow 6x^2-4x+9x-6=0$

$\Rightarrow 6 x^{2}+5 x-4=0$

Comparing with

$ax^2+bx+c=0$ form, we get

$a=6, b=5, c=-4$

So, by using the quadratic formula

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$

$\Rightarrow x=\dfrac{-5 \pm \sqrt{(5)^{2}-4(6)(-4)}}{2 (6)}$

$\Rightarrow x=\dfrac{-5 \pm \sqrt{25+96}}{12}$

$\Rightarrow x=\dfrac{-5\pm \sqrt{121}}{12}$

$\Rightarrow x=\dfrac{-5\pm 11}{12}$

$\Rightarrow x=\dfrac{-5+11}{12}$ and

$x=\dfrac{-5-11}{12}$

$\Rightarrow x=\dfrac{6}{12}$ and

$x=\dfrac{-16}{12}$

$\Rightarrow x=\dfrac12$ and

$x=-\dfrac{4}{3}$

Check whether the following equation is quadratic equation in $x$ or not?
$x^{2}-1/x^{2}=5$

$x^{2}-1/x^{2}=5$

Simplify above equation

$x^{4}-1=5x^{2}$

$x^{4}-5x^{2}-1=0$

Degree

$4$

Not a quadratic equation

$(x+1/x)^{2}=2(x+1/x)+3$

$(x^{4}+2x^{2}+1)/(x^{2}=(2x^{2}+2)/x+3$

$(x^{4}+2x^{2}+1)x=x^{2}(2x^{2}+2)+3$

Not a quadratic equation

Is the following equation a quadratic equation in $x$ ?
$(2x+3)(3x+2)=6(x-1)(x-2)$

$(2x+3)(3x+2)=6(x-1)(x-2)$

Simplify above equation

$6x^{2}+4x+9x+6=6x^{2}-12x-6x+12$

$31x-6=0$

Degree

$1$

Not a quadratic equation

Solve by using formula
(i) $2 \mathbf{x}^{2}+\sqrt{5} \mathbf{x}-5=0$
(ii) $\sqrt{3 x^{2}+10 x-8 \sqrt{3}=0}$

(i)

$2 x^{2}+\sqrt{5} x-5=0$

Let us consider,

$a=2, b=\sqrt{5}, c=-5$

So, by using the formula

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$

So let,

$b^{2}-4 a c=D$

$x=\dfrac{-b \pm \sqrt{D}}{2 a}$

$D=b^{2}-4 a c$

$=(\sqrt{5})^{2}-4(2)(-5)$

$=5+40$

$=45$

$\mathrm{So,}$

$x=[-(\sqrt{5}) \pm \sqrt{45}] / 2(2)$

$=[-\sqrt{5} \pm 3 \sqrt{5})] / 4$

$=[-\sqrt{5}+3 \sqrt{5})] / 4$ or

$[-\sqrt{5}-3 \sqrt{5}] / 4$

$=2 \sqrt{5 / 4}$ or

$-4 \sqrt{5 / 4}$

$=\sqrt{5 / 2}$ or

$-\sqrt{5}$

$\therefore$ Value of

$x=\sqrt{5} / 2,-\sqrt{5}$

(ii)

$\sqrt{3 x^{2}+10 x-8 \sqrt{3}=0}$

Let us consider,

$a=\sqrt{3}, b=10, c=-8 \sqrt{3}$

So, by using the formula,

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$

So let,

$b^{2}-4 a c=D$

$x=\dfrac{-b \pm \sqrt{D}}{2 a}$

$D=b^{2}-4 a c$

$\begin{array}{l}=(10)^{2}-4(\sqrt{3})(-8 \sqrt{3}) \\=100+96 \\=196\end{array}$

So,

$\begin{aligned}&\begin{aligned}\mathrm{x} &=[-(10) \pm \sqrt{196}] / 2(\sqrt{3}) \\&=[-10 \pm 14] / 2(\sqrt{3}) \\&=[-10+14)] / 2 \sqrt{3} \text { or }[-10-14)] / 2 \sqrt{3} \\&=4 / 2 \sqrt{3} \text { or }-24 / 2 \sqrt{3}\end{aligned}\\&\therefore \text { Value of } x=4 / 2 \sqrt{3},-24 / 2 \sqrt{3}\end{aligned}$

If the equation $2 x^{2}+4 x y+7 y^{2}-12 x-2 y+t=0$ where 't' is a parameter has exactly one real solution of the form $(x, y)$ , then find the value of $(x+y)$ .

Given,

$2 x^{2}+4 x(y-3)+7 y^{2}-2 y+t=0$

$D=0$ (for one solution)

$\Rightarrow 16(y-3)^{2}-8\left(7 y^{2}-2 y+t\right)=0$

$\Rightarrow 2(y-3)^{2}-\left(7 y^{2}-2 y+t\right)=0$

$\Rightarrow 2\left(y^{2}-6 y+9\right)-\left(7 y^{2}-2 y+t\right)=0$

$\Rightarrow-5 y^{2}-10 y+18-t=0$

$\Rightarrow 5 y^{2}+10 y+t-18=0$

Again

$D=0 \quad$ (for one solution)

$\Rightarrow 100-20(t-18)=0$

$\Rightarrow 5-t+18=0$

$\Rightarrow t=23$

for

$t=23 ; 5 y^{2}+10 y+5=0$

$(y+1)^{2}=0 \Rightarrow y=-1$

for

$y=-1 ; 2 x^{2}-16 x+32=0$

$x^{2}-8 x+16=0$

$x=4 \quad \Rightarrow \quad x+y=3$

Solve by using formula
(i) $\mathbf{a}\left(\mathbf{x}^{2}+\mathbf{1}\right)=\left(\mathbf{a}^{2}+\mathbf{1}\right) \mathbf{x}, \mathbf{a} \neq \mathbf{0}$
(ii) $4 x^{2}-4 a x+\left(a^{2}-b^{2}\right)=0$

(i) a

$\left(x^{2}+1\right)=\left(a^{2}+1\right) x, a \neq 0$
Let us simplify the expression,

$a x^{2}+a-a^{2} x+x=0$

$a x^{2}-\left(a^{2}+1\right) x+a=0$
Let us consider,

$a=a, b=-\left(a^{2}+1\right), c=a$
So, by using the formula,

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
So let,

$b^{2}-4 a c=D$

$x=\dfrac{-b \pm \sqrt{D}}{2 a}$

$\begin{aligned}D &=b^{2}-4 a c \\&=\left(-\left(a^{2}+1\right)\right)^{2}-4(a)(a) \\&=a^{4}+2 a^{2}+1-4 a^{2} \\&=a^{4}-2 a^{2}+1 \\&=\left(a^{2}-1\right)^{2} \\\text { So } & \\x &=\left[-\left(-\left(a^{2}+1\right)\right) \pm \sqrt{\left.\left(a^{2}-1\right)^{2}\right] / 2(a)}\right]\end{aligned}$

$=\left[\left(a^{2}+1\right) \pm\left(a^{2}-1\right)\right] / 2 a$

$=\left[\left(a^{2}+1\right)+\left(a^{2}-1\right)\right] / 2 a \operatorname{or}\left[\left(a^{2}+1\right)-\left(a^{2}-1\right)\right] / 2 a$

$=\left[a^{2}+1+a^{2}-1\right] / 2 a$ or

$\left[a^{2}+1-a^{2}+1\right] / 2 a$

$=2 a^{2} / 2 a$ or

$2 / 2 a$

$=\mathrm{a}$ or

$1 / \mathrm{a}$

$\therefore$ Value of

$\mathrm{x}=\mathrm{a}, 1 / \mathrm{a}$

(ii)

$4 x^{2}-4 a x+\left(a^{2}-b^{2}\right)=0$
Let us consider,

$a=4, b=-4 a, c=\left(a^{2}-b^{2}\right)$
So, by using the formula,

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
So let,

$b^{2}-4 a c=D$

$x=\dfrac{-b \pm \sqrt{D}}{2 a}$

$\begin{aligned} D &=b^{2}-4 a c \\ &=(-4 a)^{2}-4(4)\left(a^{2}-b^{2}\right) \\ &=16 a^{2}-16\left(a^{2}-b^{2}\right) \\ &=16 a^{2}-16 a^{2}+16 b^{2} \\ &=16 b^{2} \\ \mathrm{So} & \\ x &=[-(-4 a) \pm \sqrt{16 b^{2}}] / 2(4) \\ &=[4 a \pm 4 b] / 8 \\ &=4[a \pm b] / 8 \\ &=[a \pm b] / 2 \\ &=[a+b] / 2 \text { or }[a-b] / 2 \end{aligned}$

$\therefore$ Value of

$\mathrm{x}=[\mathrm{a}+\mathrm{b}] / 2,[\mathrm{a}-\mathrm{b}] / 2$

Solve the following equations by using the quadratic formula and give your answer correct to 2 decimal places:
(i) $4 x^{2}-5 x-3=0$
(ii) $2 x-\dfrac 1x=1$

$(i)$

$4 x^{2}-5 x-3=0$

We know that, for a quadratic equation of the form

$ax^2+bx+c=0$ ,

$x = \dfrac{-b \pm \sqrt{b^{2}-4ac}}{2a}$

Here,

$a=4, b=-5, c=-3$

Hence,

$x=\dfrac{-(-5)\pm\sqrt{(-5)^{2}-4(4)(-3)}}{2(4)}$

$x=\dfrac{-(-5)\pm\sqrt{25+48}}{2(4)}$

$x=\dfrac{-(-5) \pm \sqrt{73}}{ 2(4)}$

$=\dfrac{5 \pm 8.54}{ 8}$

$=\dfrac{5+8.54}{8}$ or

$\dfrac{5-8.54}{8}$

$=\dfrac{13.54}{8}$ or

$\dfrac{-3.54}{8}$

$=1.6925$ or

$-0.4425$

$\therefore\ x=1.69$ or

$-0.44$

$(ii)$

$2 x-\dfrac1 x=7$

On taking the

$LCM$ , we get:

$2 x^{2}-1=7 x$

$2 x^{2}-7 x-1=0$

We know that, for a quadratic equation of the form

$ax^2+bx+c=0$ ,

$x = \dfrac{-b \pm \sqrt{b^{2}-4ac}}{2a}$

Here,

$a=2, b=-7, c=-1$

Hence,

$x=\dfrac{-(-7)\pm\sqrt{(-7)^{2}-4(2)(-1)}}{2(2)}$

$x=\dfrac{-(-7)\pm\sqrt{49+8}}{2(2)}$

$x=\dfrac{-(-7) \pm \sqrt{57}}{ 2(2)}$

$=\dfrac{7 \pm 7.55}{ 4}$

$=\dfrac{7+7.55}{4}$ or

$\dfrac{7-7.55}{4}$

$=\dfrac{14.55}{4}$ or

$\dfrac{-0.55}{4}$

$=3.6375$ or

$-0.1375$

$\therefore\ x=3.64$ or

$-0.14$

Solve by using formula
$(\mathbf{i}) \mathbf{x}-\mathbf{1} / \mathbf{x}=\mathbf{3}, \mathbf{x} \neq \mathbf{0}$
(ii) $1 / x+1 /(x-2)=3, x \neq 0,2$

(i)

$x-1 / x=3, x \neq 0$
Let us simplify the given expression,
By taking LCM

$x^{2}-1=3 x$

$x^{2}-3 x-1=0$
Let us consider,

$a=1, b=-3, c=-1$
So, by using the formula,

$\begin{array}{l}x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \\\text { So let, } b^{2}-4 a c=D \\x=\dfrac{-b \pm \sqrt{D}}{2 a} \\D=b^{2}-4 a c \\=(-3)^{2}-4(1)(-1) \\=9+4 \\=13\end{array}\\$

$\mathrm{So,}$

$\begin{aligned}x &=[-(-3) \pm \sqrt{13}] / 2(1) \\&=[3 \pm \sqrt{13}] / 2 \\&=[3+\sqrt{13}] / 2 \text { or }[3-\sqrt{13}] / 2\end{aligned}\\$

$\therefore$ Value of

$x=[3+\sqrt{13}] / 2$ or

$[3-\sqrt{13}] / 2$

(ii)

$1 / x+1 /(x-2)=3, x \neq 0,2$
Let us simplify the given expression, By taking LCM

$[(x-2)+x] /[x(x-2)]=3$

$[x-2+x] /\left[x^{2}-2 x\right]=3$

$2 x-2=3\left(x^{2}-2 x\right)$

$2 x-2=3 x^{2}-6 x$

$3 x^{2}-6 x-2 x+2=0$

$3 x^{2}-8 x+2$
Let us consider,

$a=3, b=-8, c=2$
So, by using the formula,

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$
So let,

$b^{2}-4 a c=D$

$x=\dfrac{-b \pm \sqrt{D}}{2 a}$

$\begin{aligned}D &=b^{2}-4 a c \\&=(-8)^{2}-4(3)(2) \\&=64-24 \\&=40\end{aligned}$

$\begin{aligned}&\begin{aligned}\mathrm{x} &=[-(-8) \pm \sqrt{4} 0] / 2(3) \\&=[8 \pm 2 \sqrt{10}] / 6 \\&=2[4 \pm \sqrt{10}] / 6 \\&=[4 \pm \sqrt{10}] / 3 \\&=[4+\sqrt{10}] / 3 \text { or }[4-\sqrt{10}] / 3\end{aligned}\\&\therefore \text { Value of } \mathrm{x}=[4+\sqrt{10}] / 3 \text { or }[4-\sqrt{10}] / 3\end{aligned}$

Find the value of the discriminant of the quadratic equation $2 x^{2}-4 x+3=0$ .

$\textbf{Step 1 : Find value of discriminant using relevant formula}$

$\text{The standard quadratic equation is}$

$ax^2+bx+c=0$

$\text{Discriminant (D)}$

$=b^{2}-4 a c$

$\text{In the given equation}$

$2 x^{2}-4 x+3=0$ .

$a=2 , b=-4 , c=3$

$d=(-4)^{2}-(4 \times 2 \times 3)$

$d=16-24$

$d=-8$

$\textbf{Hence, the value of the discriminant is -8}$

Using quadratic formula, solve the following equation for $x:ab{x}^{2}+({b}^{2}-ac)x-bc=0$

1975267_1785348_ans_e6a3efc633634a008bb2d53a751b1e68.jpg

Solve by using formula
$(i) \dfrac{x-2}{x+2}+\dfrac{x+2}{x-2}=4$

$(i i) \dfrac{x+1}{x+3}=\dfrac{3 x+2}{2 x+3}$

$(i) \dfrac{x-2}{x+2}+\dfrac{x+2}{x-2}=4$
By taking LCM,

$\dfrac{(x-2)^{2}+(x+2)^{2}}{(x+2)(x-2)}=4$

$\dfrac{x^{2}-4 x+4+x^{2}+4 x+4}{x^{2}-4}=4$
By simplifying the equation, we get

$\begin{array}{l}2 x^{2}+8=4 x^{2}-16 \\2 x^{2}+8-4 x^{2}+16=0 \\-2 x^{2}+24=0 \\x^{2}-12=0\end{array}\\$
Let us consider,

$a=1, b=0, c=-12\\$
So, by using the formula,

$\begin{array}{l}x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \\\text { So let, } b^{2}-4 a c=D \\x=\dfrac{-b \pm \sqrt{D}}{2 a} \\D=b^{2}-4 a c \\=(0)^{2}-4(1)(-12) \\=0+48 \\=48\end{array}\\$
So,

$\begin{aligned}x &=[-(0) \pm \sqrt{48}] / 2(1) \\&=[\pm \sqrt{48}] / 2 \\&=[\pm \sqrt{(} 16 \times 3)] / 2 \\&=\pm 4 \sqrt{3} / 2 \\&=\pm 2 \sqrt{3} \\&=2 \sqrt{3} \text { or }-2 \sqrt{3}\end{aligned}\\$

$\therefore$ Value of

$x=2 \sqrt{3},-2 \sqrt{3}$

$(i i) \dfrac{x+1}{x+3}=\dfrac{3 x+2}{2 x+3}$
Let us cross multiply,
we get

$(x+1)(2 x+3)=(x+3)(3 x+2)$
Now by simplifying
we get

$2 x^{2}+3 x+2 x+3=3 x^{2}+9 x+2 x+6$

$2 x^{2}+5 x+3-3 x^{2}-11 x-6=0$

$-x^{2}-6 x-3=0$

$x^{2}+6 x+3=0$
Let us consider

$a=1, b=6, c=3$
So, by using the formula,

$\begin{array}{l}x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \\\text { So let, } b^{2}-4 a c=D \\x=\dfrac{-b \pm \sqrt{D}}{2 a} \\\begin{aligned}D &=b^{2}-4 a c \\&=(6)^{2}-4(1)(3) \\&=36-12 \\&=24\end{aligned}\end{array}$
So,

$\begin{aligned}&\begin{aligned}x &=[-(6) \pm \sqrt{24}] / 2(1) \\&=[-6 \pm \sqrt{(4 \times 6)]} / 2\\&=[-6 \pm 2 \sqrt{6}] / 2 \\&=-3 \pm \sqrt{6} \\&=-3+\sqrt{6} \text { or }-3-\sqrt{6}\end{aligned}\\&\therefore \text { Value of } x=-3+\sqrt{6},-3-\sqrt{6}\end{aligned}$

Solve by using formula
$\dfrac{1}{x-2}+\dfrac{1}{x-3}+\dfrac{1}{x-4}=0$

Let us simplify the expression,

$\dfrac{1}{x-2}+\dfrac{1}{x-3}+\dfrac{1}{x-4}=0$

$\dfrac{1}{x-2}+\dfrac{1}{x-3}=-\dfrac{1}{x-4}$
By takingLCM

$\dfrac{(x-3)+(x-2)}{(x-2)(x-3)}=-\dfrac{1}{x-4}$

$\dfrac{2 x-5}{x^{2}-5 x+6}=-\dfrac{1}{x-4}$
By cross multiplying,

$(2 x-5)(x-4)=-\left(x^{2}-5 x+6\right)$

$2 x^{2}-8 x-5 x+20=-x^{2}+5 x-6$

$2 x^{2}-8 x-5 x+20+x^{2}-5 x+6=0$

$3 x^{2}-18 x+26=0$
Let us consider

$a=3, b=-18, c=26$
So, by using the formula,

$\begin{array}{l}x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \\\text { So let, } b^{2}-4 a c=D \\x=\dfrac{-b \pm \sqrt{D}}{2 a} \\\begin{aligned}D &=b^{2}-4 a c \\&=(-18)^{2}-4(3)(26) \\&=324-312 \\&=12\end{aligned}\end{array}$
So,

$\begin{aligned}\mathrm{x} &=[-(-18) \pm \sqrt{12}] / 2(3) \\&=[18 \pm \sqrt{12}] / 6 \\&=[18+\sqrt{12}] / 6 \text { or }[18-\sqrt{12}] / 6 \\\therefore & \text { Value of } \mathrm{x}=[18+\sqrt{12}] / 6 \text { or }[18-\sqrt{12}] / 6\end{aligned}$

Solve the equation $5 x^{2}-3 x-4=0$ and give your answer correct to 3 significant figures:

${\textbf{Step -1: Writing the formula and its corresponding elements for the given equation}}$

${\text{If the quadratic equation is a}}{{\text{x}}^{\text{2}}}{\text{ + bx + c = 0, then the roots of the equation are given by}}$

$\Rightarrow {\text{ x = }}\dfrac{{{\text{ - b }} \pm {\text{ }}\sqrt {{{\text{b}}^{\text{2}}}{\text{ - 4ac}}} }}{{{\text{2a}}}}$

${\text{For the equation given in the question, a = 5, b = - 3 and c = - 4}}$

${\textbf{Step -2: Finding the roots of the equation}}$

${\text{Given, 5}}{{\text{x}}^{\text{2}}}{\text{ - 3x - 4 = 0}}$

$\Rightarrow {\text{ x = }}\dfrac{{{\text{ - b }} \pm {\text{ }}\sqrt {{{\text{b}}^{\text{2}}}{\text{ - 4ac}}} }}{{{\text{2a}}}}$

$\Rightarrow {\text{ x = }}\dfrac{{{\text{ - ( - 3) }} \pm {\text{ }}\sqrt {{{{\text{( - 3)}}}^{\text{2}}}{\text{ - 4(5)( - 4)}}} }}{{{\text{2(5)}}}}$

$\Rightarrow {\text{ x = }}\dfrac{{{\text{3 }} \pm {\text{ }}\sqrt {{\text{9 + 80}}} }}{{{\text{10}}}}$

$\Rightarrow {\text{ x = }}\dfrac{{{\text{3 }} \pm {\text{ }}\sqrt {{\text{89}}} }}{{{\text{10}}}}$

$\Rightarrow {\text{ x = }}\dfrac{{{\text{3 }} \pm {\text{ 9}}{\text{.434}}}}{{{\text{10}}}}$

$\Rightarrow {\text{ x = 1}}{\text{.243 or x = - 0}}{\text{.643}}$

${\textbf{Final Answer: On solving the given equation, we get x = 1}}{\textbf{.243 or - 0}}{\textbf{.643}}$

$2x^2 +13xy - 24y^2$

$2x^2+16xy-3xy-24y^2$
Take out common in all terms we get,

$2x(x+8y)-3y(x+8y)$

$(x+8y)(2x-3y)$

Solve the equation $x^2-12x+27=0$ by using formula.

We have a formula for solving quadratic equation

$ax^2+bx+c=0$ is

$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$

$x^2-12x+27=0$

here,

$a=1, b=-12,c=27$

$x=\dfrac{(12)\pm\sqrt{(12)^2-4\times 1\times 27}}{2\times 1}$

$=\dfrac{12\pm \sqrt{144-108}}{2}$

$=\dfrac{12\pm \sqrt{36}}{2}$

$=\dfrac{12\pm6}{2}$

$x=\dfrac{12+6}{2}$ or

$\dfrac{12-6}{2}$

$x=18/2$ or

$x=6/2$

$x=9$ , or

$x=3$

$5x^2 +17xy - 12y^2$

$5x^2+20xy-3xy-12y^2$
Take out common in all terms we get,

$5x(x+4y)-3y(x+4y)$

$(x+4y)(5x-3y)$

$x^4 +9x^2y^2 + 81y^4$

$x^4 +9x^2y^2 + 81y^4$
Above terms can be written as,

$x^4+18x^2y^2+81y^4-9x^2y^2$

$((x^2)^2+(2 \times x^2 \times 9y^2)+(9y^2)^2)-9x^2y^2$
We know that,

$(a+b)^2=a^2+2ab+b^2$

$(x^2+9y^2)^2-(3xy)^2$

$(x^2+9y^2+3xy)(x^2+9y^2-3xy)$

$9x^2 + 12x +4 -16 y^2$

$9x^2 + 12x +4 -16 y^2$
Above terms can be written as,

$(3x)^2+( 2 \times 3x \times 2)+2^2-16y^2$
Then,

$(3x+2)^2+(4y)^2$

$(3x+2+4y)(3x+2-4y)$

$x^2 -6xy -7y^2$

$x^2-7xy+xy-7y^2$
Take out common in all terms we get,

$x(x-7y)+y(x-7y)$

$(x-7y)(x+y)$

Solve $2 x^{2}-5 x+3=0$ by using formula.

The standard quadratic equation is

$ax^2+bx+c=0$

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$

$\text { Where } a=2 ; b=-5 ; c=3$

$x=\dfrac{-(-5) \pm \sqrt{(-5)^{2}-4(2)(3)}}{2(2)}$

$x=\dfrac{5 \pm \sqrt{25-24}}{4}$

$x=\dfrac{5 \pm \sqrt{1}}{4}$

$x_{1}=\dfrac{5+1}{4} ; x_{2}=\dfrac{5-1}{4}$

$x_{1}=1.5 ; \quad x_{2}=1$

Find the zeros of the polynomial $p(x)=x^2-15x+50$

We have a formula for solving quadratic equation

$ax^2+bx+c=0$ is

$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$

Here,

$a=1,b=-15,c=50$

$x=\dfrac{15\pm\sqrt{15^2-4(1)(50)}}{2(1)}$

$x=\dfrac{15\pm\sqrt{225-200}}{2}$

$x=\dfrac{15\pm5}{2}$

$x=10,5$

$21x^2 - 59 xy + 40 y^2$

$21x^2 - 59 xy + 40 y^2$
By multiplying the first and last term we get,

$21 \times 40=840$
Then,

$(-35) \times (-24)=840$
So,

$21x^2-35xy-24xy+40y^2$

$7x(3x-5y)-8y(3x-5y)$

$(3x-5y)(7x-8y)$

$6x^2 -5xy -6y^2$

$6x^2-9xy+4xy-6y^2$
Take out common in all terms we get,

$3x(2x-3y)+2y(2x-3y)$

$(2x-3y)(3x+2y)$

Check whether the following are quadratic equations:
$x(x+1)+8=(x+2)(x-2)$

Given,

$x(x+1)+8=(x+2)(x-2)$

$\Rightarrow x^2+x+8=x^2-2^2$

$\Rightarrow x^2+x+8-x^2+4=0$

$\Rightarrow x+12=0$

$\because$ The highest power of x in the equation is 1;

$\therefore$ It is not a quadratic equation.

Check whether the following is a quadratic equation or not:
$(x+2)^3=x^3-4$

Given equation is

$(x+2)^3=x^3-4$ .

Applying the algebraic property,

$(a+b)^3=a^3+3ab^2+3ba^2+b^3$ to solve the given equation further.

$\Rightarrow x^3+6x^2+12x+2^3=x^3-4$

$\Rightarrow x^3+6x^2+12x+2^3-x^3+4=0$

$\Rightarrow 6x^2+12x+12=0$

Here, the highest power of

$x$ in the equation is

$2$ .

Hence, it is a quadratic equation.

Check whether the following are quadratic equations:
$x^2-\dfrac{1}{x^2}=8$

Given,

$x^2-\dfrac{1}{x^2}=8$

$\Rightarrow x^4-1=8x^2$

$\Rightarrow x^4-8x^2-1=0$

$\because$ The highest power of x in the equation is 4;

$\therefore$ It is not a quadratic equation.

Check whether the following are quadratic equations:
$2x^2-3\sqrt{x}+5=0$

Given,

$2x^2-3\sqrt{x}+5=0$

$\Rightarrow 2x^2+5=3\sqrt{x}$

$\Rightarrow (2x^2+5)^2=(3\sqrt{x})^2$

$\Rightarrow 4x^4+20x^2+25=9x$

$\Rightarrow 4x^2+20x^2-9x+25=0$

$\because$ The highest power of x in the equation is 4;

$\therefore$ It is not a quadratic equation.

Check whether the following are quadratic equations:
$(x+1)(x-1)=(x+2)(x+3)$

Given,

$(x+1)(x-1)=(x+2)(x+3)$

$\Rightarrow x^2-1^2=x^2+5x+6$

$\Rightarrow x^2-1^2-x^2-5x-6=0$

$\Rightarrow -5x-7=0$

$\because$ The highest power of x in the equation is 1;

$\therefore$ It is not a quadratic equation.

Check whether the following are quadratic equations:
$(x-1)^2=(x+1)^2$

Given,

$(x-1)^2=(x+1)^2$

$\Rightarrow x^2-2x+1^2=x^2+2x+1^2$

$\Rightarrow x^2-2x+1-x^2-2x-1=0$

$\Rightarrow -4x=0$

$\because$ The highest power of x in the equation is 1;

$\therefore$ It is not a quadratic equation.

Check whether the following are quadratic equations:
$x-\dfrac{1}{x}=8$

Given,

$x-\dfrac{1}{x}=8$

$\Rightarrow x^2-1=8x$

$\Rightarrow x^2-8x-1=0$

$\because$ The highest power of x in the equation is 2;

$\therefore$ It is a quadratic equation.

Check whether the following are quadratic equations:
$x^2+\dfrac{1}{x}=5$

1960945_1814149_ans_b492ab4653794fd78a1f1bb710aff4e4.JPG

Check whether the following are quadratic equations:
$x(2x+3)=x^2+1$

Given,

$x(2x+3)=x^2+1$

$\Rightarrow 2x^2+3x=x^2+1$

$\Rightarrow 2x^2+3x-x^2-1=0$

$\Rightarrow x^2+3x-1=0$

$\because$ The highest power of x in the equation is 2;

$\therefore$ It is a quadratic equation.

Find the roots of the following quadratic equations,if they exist by the method of completing the square: $5x^2-6x-2=0$

$5x^2-6x-2=0$

Dividing by 5

$x^2-\dfrac{6x}{5}-\dfrac{2}{5}=0$

We know

$(a-b)^2=a^2-2ab=b^2$

Here,a=x and

$-2ab=-\dfrac{6x}{3}$

$-2xb=-\dfrac{6x}{5}(\because a=x)$

$-2b=-\dfrac{6}{5}$

$b=-\dfrac{6}{5 \times (-2)}$

$b=\dfrac{3}{5}$

$\therefore$ Equation becomes

$x^2-\dfrac{6x}{5}-\dfrac{2}{5}=0$

Add and subtract

$(\dfrac{3}{5})^2$

$x^2-\dfrac{6x}{5}-\dfrac{2}{5}+(\dfrac{3}{5})^2-(\dfrac{3}{5})^2=0$

$x^2-\dfrac{6x}{5}+(\dfrac{3}{5})^2-\dfrac{2}{5}-(\dfrac{3}{5})^2=0$

$(x-\dfrac{3}{5})^2=(\dfrac{3}{5})^2+\dfrac{2}{5}$

$(x-\dfrac{3}{5})^2=\dfrac{9}{25}+\dfrac{2}{5}$

$(x-\dfrac{3}{5})^2=\dfrac{9+2(5)}{25}$

$(x-\dfrac{3}5{})^2=\dfrac{9+10}{25}$

$(x-\dfrac{3}{5})^2=\dfrac{19}{25}$

$(x-\dfrac{3}{5})^2=\dfrac{(\sqrt{19})^2}{(5)^2}$

Cancelling squares both sides

$(x-\dfrac{3}{5})=\pm \dfrac{\sqrt{19}}{5}$

Solving

$(x-\dfrac{3}{5})=\dfrac{\sqrt{19}}{5}\ \ \ \ \ \ \ \ \ \ (x-\dfrac{3}{5})=-\dfrac{\sqrt{19}}{5}$

$x=\dfrac{\sqrt{19}}{5}+\dfrac{3}{5}\ \ \ \ \ \ \ \ \ \ \ \ x=\dfrac{-\sqrt{19}}{5}+\dfrac{3}{5}$

$x=\dfrac{\sqrt{19}+3}{5} \ \ \ \ \ \ \ \ \ \ \ \ \ x=\dfrac{-\sqrt{19}+3}{5}$

So,

$x=\dfrac{\sqrt{19}+3}{5}$ and

$x=\dfrac{-\sqrt{19}+3}{5}$ are the roots of the equation.

Solve the following equations by the method of completion of a square $5x^2-24x-5=0$

Divide both sides of the given quadratic equation by

$5,$

$\dfrac{5x^2}5-\dfrac{24x}{5}-\dfrac{5}{5}=0$

$\Rightarrow x^2-\dfrac{24x}{5}-1=0$

$\Rightarrow x^2-2\times x\times\dfrac{12}{5}-1=0$

Add and subtract the square of coefficient of

$2x,$

$\Rightarrow {x^2} - 2 \times x \times \dfrac{{12}}{5} + {\left( {\dfrac{{12}}{5}} \right)^2} - {\left( {\dfrac{{12}}{5}} \right)^2} - 1 = 0$

$\Rightarrow {\left( {x - \dfrac{{12}}{5}} \right)^2} = \dfrac{{144}}{{25}} + 1$

$\Rightarrow {\left( {x - \dfrac{{12}}{5}} \right)^2} = \dfrac{{169}}{{25}}$

$\Rightarrow {\left( {x - \dfrac{{12}}{5}} \right)^2} = {\left( {\dfrac{{13}}{5}} \right)^2}$

Now, take square root on both sides of the above-obtained equation,

$\Rightarrow x - \dfrac{{12}}{5} = \pm \dfrac{{13}}{5}$

$\Rightarrow x = \dfrac{{12 \pm 13}}{5}$

$\Rightarrow x = \dfrac{{12 + 13}}{5},\dfrac{{12 - 13}}{5}$

$\Rightarrow x = 5, - \dfrac{1}{5}$

Find the roots of the following quadratic equations,if they exist by the method of completing the square: $x^2-9x+18=0$

$x^2-9x+18$

Add the coefficient of

$(\dfrac{9}{2})^2=-18+(\dfrac{9}{2})^2$

$(x-\dfrac{9}{2})^2=-18+\dfrac{81}{4}$

$(x-\dfrac{9}{2})^2=\dfrac{-72+81}{4}$

$(x-\dfrac{9}{2})^2=\dfrac{9}{4}$

$x-\dfrac{9}{2}=\dfrac{\sqrt{9}}{\sqrt{4}}$

$x-\dfrac{9}{2}=\dfrac{\pm 3}{2}$

$x=-\dfrac{3}{2}+\dfrac{9}{2}\ \ \ \ x=\dfrac{3}{2}+\dfrac{9}{2}$

$x=\dfrac{6}{2}=3\ \ \ \ x=\dfrac{12}{2}=6$

Solve the following equations by the method of completion of a square $15x^2+53x+42=0$

Divide by 5

$x^2+\dfrac{53x}{15}=-\dfrac{42}{15}$

Add the square of coefficient of

$2x$ to both sides

$x^2+\dfrac{53x}{15}+(\dfrac{53}{30})^2=-\dfrac{42}{15}+(\dfrac{53}{30})^2$

$(x+\dfrac{53}{30})^2=-\dfrac{42}{15}+\dfrac{2809}{900}$

$(x+\dfrac{53}{30})^2=\dfrac{-2500+2809}{900}$

$x=\dfrac{53}{30}=\dfrac{\sqrt{289}}{\sqrt{900}}$

$x=\dfrac{17}{30}-\dfrac{53}{30}\ \ \ \ \ \ \ x=-\dfrac{17}{30}-\dfrac{53}{30}$

$x=-\dfrac{6}{5}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x=-\dfrac{7}{3}$

Solve the following equations by the method of completion of a square $7x^2-13x-2=0$

Divide by 7

$x^2-\dfrac{13x}{7}=\dfrac{2}{7}$

Add the square of coefficient of

$2x$ to both sides

$x^2-\dfrac{13x}{7}+(\dfrac{13}{14})^2=\dfrac{2}{7}+(\dfrac{13}{14})^2$

$(x-\dfrac{13}{14})^2=\dfrac{2}{7}+\dfrac{169}{196}$

$(x-\dfrac{13}{14})^2=\dfrac{56+169}{196}$

$(x-\dfrac{13}{14})^2=\dfrac{225}{196}$

$x-\dfrac{13}{14}=\dfrac{15}{14}$

$x=\dfrac{15+13}{14}\ \ \ \ \ \ \ x=\dfrac{-15+13}{14}$

$x=\dfrac{28}{14}=2\ \ \ \ \ \ \ x=-\dfrac{2}{14}=-\dfrac{1}{7}$

Find the roots of the following quadratic equations,if they exist by the method of completing the square: $x^2-6x+4=0$

$x^2-6x+4=0$

Add the coefficient of

$(\dfrac{x}{2})^2$ to both sides

$x^2-6x+(3)^2=-4+(3)^2$

$(x-3)^2=-4+9$

$x-3=\sqrt{5}$

$x=\pm \sqrt{5}+3$

Find the roots of the following quadratic equations,if they exist by the method of completing the square: $\sqrt{5}x^2+9x+4\sqrt{5}=0$

Divide by

$\sqrt{5}$

$x^2+\dfrac{9x}{\sqrt{5}}=-4$

Add the coefficient of

$(\dfrac{x}{2})^2$ to both sides

$x^2+\dfrac{9x}{\sqrt{5}}+(\dfrac{9}{2\sqrt{5}})^2$

$(x+\dfrac{9}{2\sqrt{5}})^2=-4+\dfrac{81}{20}$

$(x+\dfrac{9}{2\sqrt{5}})^2=\dfrac{-80+81}{20}$

$x+\dfrac{9}{2\sqrt{5}}=\dfrac{\sqrt{1}}{20}$

$x=\dfrac{1}{2\sqrt{5}}-\dfrac{9}{2\sqrt{5}}=\dfrac{-1}{2\sqrt{5}}-\dfrac{9}{2\sqrt{5}}$

$x=-\dfrac{8}{2\sqrt{5}}=-\dfrac{4}{\sqrt{5}}\ \ \ \ \ x=-\dfrac{10}{2\sqrt{5}}=-\dfrac{5}{\sqrt{5}}$

$x=-\dfrac{5}{\sqrt{5}}\times \dfrac{\sqrt{5}}{\sqrt{5}}=-\dfrac{5\sqrt{5}}{5}=-\sqrt{5}$

Find the roots of the following quadratic equations,if they exist by the method of completing the square: $2x^2+\sqrt{15}x+\sqrt{2}=0$

Divide by 2

$x^2+\dfrac{\sqrt{15}}{2}x=-\dfrac{\sqrt{2}}{2}$

Add the coefficient of

$(\dfrac{x}{2})^2$ to both sides.

$x^2+\dfrac{\sqrt{15}}{2}x+(\dfrac{\sqrt{15}}{4})^2=-\dfrac{\sqrt{2}}{2}+(\dfrac{\sqrt{15}}{4})^2$

$(x+\dfrac{\sqrt{15}}{4})^2=-\dfrac{\sqrt{2}}{2}+\dfrac{15}{16}$

$(x+\dfrac{\sqrt{15}}{4})^2=\dfrac{-8\sqrt{2}+15}{16}$

Since root cannot be negative

Therefore,it has no real roots.

Find the roots of the following quadratic equations,if they exist by the method of completing the square: $2x^2-5x+3=0$

$2x^2-5x+3=0$

Dividing by 2

$x^2-\dfrac{5x}{2}+\dfrac{3}{2}=0$

$x^2-\dfrac{5x}{2}=-\dfrac{3}{2}$

Add a coefficient of

$(\dfrac{x}{2})^2$ to both sides

$x^2-\dfrac{5x}{2}+(\dfrac{5}{4})^2=-\dfrac{3}{2}+(\dfrac{5}{4})^2$

$(x-\dfrac{5}{4})^2=-\dfrac{3}{2}+\dfrac{25}{16}$

$(x-\dfrac{5}{4})^2=\dfrac{-24+25}{16}$

$(x-\dfrac{5}{4})^2=\dfrac{1}{16}$

$x-\dfrac{5}{4}=\sqrt{\dfrac{1}{16}}$

$x=\dfrac{1}{4}+\dfrac{5}{4}\ \ \ \ \ x=-\dfrac{1}{4}+\dfrac{5}{4}$

$x=\dfrac{6}{4}=\dfrac{3}{2}\ \ \ \ \ x=\dfrac{4}{4}=1$

Find the roots of the following quadratic equations,if they exist by the method of completing the square: $x^2+x+3=0$

$x^2+x=-3$

Add the square of coefficient of

$2x$ to both sides

$x^2+x+(\dfrac{1}{2})^2=-3+(\dfrac{1}{2})^2$

$(x+\dfrac{1}{2})^2=-3+\dfrac{1}{4}$

$(x+\dfrac{1}{2})^2=\dfrac{-12+1}{4}$

$(x+\dfrac{1}{2})^2=\dfrac{-11}{4}$

$x+\dfrac{1}{2}=\sqrt{-\dfrac{11}{4}}$

Since root cannot be negative.

Therefore, it has no real roots.

Find the roots of the following quadratic equations,if they exist by the method of completing the square: $9x^2-15x+6=0$

Dividing by 9

$x^2-\dfrac{15x}{9}+\dfrac{6}{9}=0$

$x^2-\dfrac{15x}{9}=-\dfrac{2}{3}$

Add a coefficient of

$(\dfrac{x}{2})^2$ to both sides

$x^2-\dfrac{15x}{9}+(\dfrac{15}{18})^2=-\dfrac{2}{3}+(\dfrac{15}{18})^2$

$(x=\dfrac{15}{18})^2=-\dfrac{2}{3}+\dfrac{25}{36}$

$(x-\dfrac{15}{18})^2=\dfrac{25-24}{36}$

$(x-\dfrac{15}{18})^2=\dfrac{1}{36}$

$x-\dfrac{15}{18}=\pm\dfrac{\sqrt{1}}{\sqrt{36}}$

$x=\dfrac{1}{6}+\dfrac{5}{6}\ \ \ \ \ x=-\dfrac{1}{6}+\dfrac{5}{6}$

$x=\dfrac{6}{6}=1\ \ \ \ \ x=\dfrac{4}{6}=\dfrac{2}{3}$

Write the discriminate of each of the following quadratic equation: $x^2+4x+3=0$

$d=b^2-4ac$

$d=(4)^2-4(1)(3)$

$d=16-12$

$d=4$

Write the discriminate of each of the following quadratic equation: 4x^2+5x+7=0$$

$d=b^2-4ac$

$d=(5)^2-4(4)(7)$

$d=25-112$

$d=-87$

Solve the following equations by the method of completion of a square $7x^2+2x-5=0$

Divide by 7

$x^2+\dfrac{2x}{7}=\dfrac{5}{7}$

Add the square of coefficient of

$2x$ to both sides

$x^2+\dfrac{2x}{7}+(\dfrac{2}{14})^2=\dfrac{5}{7}+(\dfrac{2}{14})^2$

$(x+\dfrac{2}{14})^2=\dfrac{5}{7}+\dfrac{4}{196}$

$(x+\dfrac{2}{14})^2=\dfrac{140+4}{196}$

$(x+\dfrac{2}{14})^2=\dfrac{144}{196}$

$x+\dfrac{2}{14}=\dfrac{\sqrt{144}}{\sqrt{196}}$

$x+\dfrac{2}{14}=\dfrac{12}{14}$

$x=\dfrac{12-2}{14}\ \ \ \ \ \ \ \ \ x=\dfrac{-12-2}{14}$

$x=\dfrac{10}{14}=\dfrac{5}{7}\ \ \ \ \ \ \ \ \ \ x=-\dfrac{14}{14}=-1$

Write the discriminate of each of the following quadratic equation: $2x^2+4x+5=0$

$d=b^2-4ac$

$d=(4)^2-4(2)(5)$

$d=16-40$

$d=-24$

Write the discriminate of each of the following quadratic equation: $3x^2+5x+6=0$

$d=b^2-4ac$

$d=(5)^2-4(3)(6)$

$d=25-72$

$d=-47$

Solve the following quadratic equation by completing the square method.
$x^{2}+x-20=0$

$\begin{array}{l}x^{2}+x-20=0 \\x^{2}+2 \times x \times \dfrac{1}{2}+\left(\dfrac{1}{2}\right)^{2}=20+\left(\dfrac{1}{2}\right)^{2} \\\left(x+\dfrac{1}{2}\right)^{2}=20+\dfrac{1}{4} \\\left(x+\dfrac{1}{2}\right)^{2}=\dfrac{80+1}{4} \\\left(x+\dfrac{1}{2}\right)^{2}=\dfrac{81}{4} \\\left(x+\dfrac{1}{2}\right)=\pm \sqrt{\dfrac{81}{4}} \\\left(x+\dfrac{1}{2}\right)=\pm \dfrac{9}{2} \\x=-\dfrac{1}{2} \pm \dfrac{9}{2} \\x=\left(-\dfrac{1}{2}+\dfrac{9}{2}\right) \text { or } x=\left(-\dfrac{1}{2}-\dfrac{9}{2}\right) \\x=\dfrac{8}{2} \text { or } x=-\dfrac{10}{2} \\x=4 \text { or } x=-5\end{array}$

Decide whether the following equation is a quadratic equation or not.
$y^{2}+\dfrac{1}{y}=2$

Known:

Highest power/degree of a quadratic equation is

$2$

Given:

$y^{2}+\dfrac{1}{y}=2$

$\Rightarrow y^{3}+1=2 y$
Only one variable

$y.$
Maximum index/power

$=3$
So, it is not a quadratic equation.

Write any two quadratic equation

Quadratic equations in the form of

$ax^2+bx +c=0$

$\therefore$ Two quadratic equations are

$x^{2}+10 x-200=0$ and

$x^{2}+5 x-6=0$

One of the roots of equation $5{m}^{2}+2 {m}+{k}=0$ is $\dfrac{-7}{5}$ Complete the following activity to find the value of ' $k$ '.

$\dfrac{-7}{5}$ is a root of the quadratic equation

$5{m}^{2}+2{m}+{k}=0$

$\therefore$ Put

${m}=\dfrac{-7}{5}$ in the equation.

$5 \times (\dfrac{-7}{5})^{2}+2 \times \dfrac{-7}{5}+k=0$

$\dfrac{49}{5}+(\dfrac{-14}{5})+k=0$

$7+k=0$

$k=-7$

Solve the following quadratic equation by completing the square method.
$x^{2}+2 x-5=0$

$\begin{array}{l}x^{2}+2 x-5=0 \\\Rightarrow x^{2}+2 x+\left(1\right)^{2}-\left(1\right)^{2}-5=0 \\\Rightarrow\left(x^{2}+2 x+1\right)-1-5=0 \\\Rightarrow(x+1)^{2}-6=0 \\\Rightarrow(x+1)^{2}=6 \\\Rightarrow(x+1)^{2}=(\sqrt{6})^{2} \\\Rightarrow x+1=\sqrt{6} \text { or } x+1=-\sqrt{6} \\\Rightarrow x=\sqrt{6}-1 \text { or } x=-\sqrt{6}-1\end{array}$

Find the value of discriminant.
$2y^{2} - 5y + 10 = 0$

$2y^{2} - 5y + 10 = 0$
Comparing the given equation with

$ax^{2} + bx + c = 0$

$a = 2, b = -5$ and

$c = 10$

So, the discriminant

$b^{2} - 4ac = \left(-5 \right)^{2} - 4 \times 2 \times 10 = 25 - 80 = - 55$

Find the value of discriminant.
$x^{2} + 7x - 1 = 0$

$x^{2} + 7x - 1 = 0$
Comparing the given equation with

$ax^{2} + bx + c = 0$

$a = 1, b = 7$ and

$c = -1$
So, the discriminant

$b^{2} - 4ac = \left(7 \right)^{2} - 4 \times 1 \times \left(-1 \right) = 49 + 4 = 53$

Solve the following quadratic equation by completing the square method.
$9 y^{2}-12 y+2=0$

$\begin{array}{l}9 y^{2}-12 y+2=0 \\\Rightarrow y^{2}-\dfrac{12}{9} y+\dfrac{2}{9}=0 \\\Rightarrow y^{2}-\dfrac{4}{3} y+\dfrac{2}{9}=0 \\\Rightarrow y^{2}-\dfrac{4}{3} y+\left(\dfrac{4/3}{2}\right)^{2}-\left(\dfrac{4/3}{2}\right)^{2}+\dfrac{2}{9}=0 \\\Rightarrow y^{2}-\dfrac{4}{3} y+\left(\dfrac{2}{3}\right)^{2}-\left(\dfrac{2}{3}\right)^{2}+\dfrac{2}{9}=0 \\\Rightarrow\left[y^{2}-\dfrac{4}{3} y+\left(\dfrac{4}{9}\right)\right]-\left(\dfrac{4}{9}\right)+\dfrac{2}{9}=0 \\\Rightarrow\left(y-\dfrac{2}{3}\right)^{2}-\dfrac{2}{9}=0 \\\Rightarrow\left(y-\dfrac{2}{3}\right)^{2}=\dfrac{2}{9} \\\Rightarrow\left(y-\dfrac{2}{3}\right)^{2}=\left(\dfrac{\sqrt{2}}{3}\right)^{2} \\\Rightarrow y-\dfrac{2}{3}=\dfrac{\sqrt{2}}{3} \text { or } y-\dfrac{2}{3}=-\dfrac{\sqrt{2}}{3} \\\Rightarrow y=\dfrac{\sqrt{2}}{3}+\dfrac{2}{3} \text { or } y=-\dfrac{\sqrt{2}}{3}+\dfrac{2}{3} \\\Rightarrow y=\dfrac{\sqrt{2}+2}{3} \text { or } y=\dfrac{-\sqrt{2}+2}{3}\end{array}$

Solve the following quadratic equation by completing the square method.
$2 y^{2}+9 y+10=0$

$\begin{array}{l}2 y^{2}+9 y+10=0 \\\Rightarrow y^{2}+\dfrac{9}{2} y+5=0 \\\Rightarrow y^{2}+\dfrac{9}{2} y+\left(\dfrac{\dfrac{9}{2}}{2}\right)^{2}-\left(\dfrac{\dfrac{9}{2}}{2}\right)^{2}+5=0 \\\Rightarrow\left[y^{2}+\dfrac{9}{2} y+\left(\dfrac{9}{4}\right)^{2}\right]-\left(\dfrac{9}{4}\right)^{2}+5=0 \\\Rightarrow\left(y+\dfrac{9}{4}\right)^{2}=\dfrac{81}{16}-5 \\\Rightarrow\left(y+\dfrac{9}{4}\right)^{2}=\dfrac{1}{16} \\\Rightarrow\left(y+\dfrac{9}{4}\right)^{2}=\left(\dfrac{1}{4}\right)^{2} \\\Rightarrow y+\dfrac{9}{4}=\dfrac{1}{4} \text { or } y+\dfrac{9}{4}=-\dfrac{1}{4} \\\Rightarrow y=\dfrac{1}{4}-\dfrac{9}{4}=\dfrac{-8}{4}=-2 \text { or } y=-\dfrac{1}{4}-\dfrac{9}{4}=\dfrac{-10}{4}=-\dfrac{5}{2} \\\Rightarrow y=-2,-\dfrac{5}{2}\end{array}$

Solve the following quadratic equation by completing the square method.
$5 x^{2}=4 x+7$

$\begin{array}{l}5 x^{2}=4 x+7 \\\Rightarrow 5 x^{2}-4 x-7=0 \\\Rightarrow x^{2}-\dfrac{4}{5} x-\dfrac{7}{5}=0 \\\Rightarrow x^{2}-\dfrac{4}{5} x+\left(\dfrac{4/5}{2}\right)^{2}-\left(\dfrac{4/5}{2}\right)^{2}-\dfrac{7}{5}=0 \\\Rightarrow\left[x^{2}-\dfrac{4}{5} x+\left(\dfrac{2}{5}\right)^{2}\right]-\left(\dfrac{2}{5}\right)^{2}-\dfrac{7}{5}=0 \\\Rightarrow\left(x-\dfrac{2}{5}\right)^{2}=\dfrac{7}{5}+\dfrac{4}{25}=\dfrac{35+4}{25}=\dfrac{39}{25} \\\Rightarrow\left(x-\dfrac{2}{5}\right)^{2}=\dfrac{39}{25} \\\Rightarrow\left(x-\dfrac{2}{5}\right)^{2}=\left(\dfrac{\sqrt{39}}{5}\right)^{2} \\\Rightarrow x-\dfrac{2}{5}=\dfrac{\sqrt{39}}{5} \text { or } x-\dfrac{2}{5}=-\dfrac{\sqrt{39}}{5} \\\Rightarrow x=\dfrac{2+\sqrt{39}}{5} \text { or } x=\dfrac{2-\sqrt{39}}{5}\end{array}$

Solve the following quadratic equation by completing the square method.
$m^{2}-5 m=-3$

$\begin{array}{l}m^{2}-5 m=-3 \\\Rightarrow m^{2}-5 m+\left(\dfrac{-5}{2}\right)^{2}-\left(\dfrac{-5}{2}\right)^{2}=-3 \\\Rightarrow\left(m^{2}-5 m+\dfrac{25}{4}\right)-\dfrac{25}{4}=-3 \\\Rightarrow\left(m-\dfrac{5}{2}\right)^{2}=-3+\dfrac{25}{4} \\\Rightarrow\left(m-\dfrac{5}{2}\right)^{2}=\dfrac{13}{4} \\\Rightarrow\left(m-\dfrac{5}{2}\right)^{2}=\left(\dfrac{\sqrt{13}}{2}\right)^{2} \\\Rightarrow m-\dfrac{5}{2}=\dfrac{\sqrt{13}}{2} \text { or } m-\dfrac{5}{2}=-\dfrac{\sqrt{13}}{2} \\\Rightarrow m=\dfrac{\sqrt{13}}{2}+\dfrac{5}{2} \text { or } m=\dfrac{\sqrt{13}}{2}+\dfrac{5}{2} \\\Rightarrow m=\dfrac{\sqrt{13}+5}{2} \text { or } m=\dfrac{5-\sqrt{13}}{2}\end{array}$

Find the value of discriminant.
$\sqrt{2}x^{2} + 4x + 2 \sqrt{2} = 0$

$\sqrt{2}x^{2} + 4x + 2 \sqrt{2} = 0$
Comparing the given equation with

$ax^{2} + bx + c = 0$

$a = \sqrt{2}, b = 4$ and

$c = 2 \sqrt{2}$

So, the discriminant

$b^{2} - 4ac = \left(4\right)^{2} - 4 \times \sqrt{2} \times 2 \sqrt{2} = 16 - 16 = 0$

Solve using formula.
$5 m^{2}-4 m-2=0$

$5 m^{2}-4 m-2=0$

On comparing with the equation

$a x^{2}+b x+c=0$

$a=5, b=-4 \,\,a n d\,\, c=-2$

Now,

$b^{2}-4 a c=(-4)^{2}-4 \times 5 \times(-2)=16+40=56$

$x=\dfrac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}$

$x=\dfrac{-4 \pm \sqrt{56}}{2 \times 5}=\dfrac{-4 \pm \sqrt{56}}{10}$

$\Rightarrow x=\dfrac{-4+\sqrt{56}}{10}$ or

$x=\dfrac{-4-\sqrt{56}}{10}$

$\Rightarrow x=\dfrac{-2+\sqrt{14}}{5}$ or

$\dfrac{-2-\sqrt{14}}{5}$

Choose the correct answer for the following question.
Out of the following equations which one is not quadratic equation?
$x^{2} + 4x = 11 + x^{2}$
$x^{2} = 4x$
$5x^{2} = 90 + 5$
$2x - x^{2} = x^{2}$

A general form of quadratic equation is

$ax^2+bx +c=0$
1815232_1851009_ans_709729b021a74e68bb24e33032fda656.PNG

is the following equation quadratic?
$x^{2} + 2x + 11 = 0$

1809846_1851037_ans_3fb6548948bb47c79d7ef27ab137b34f.PNG

Find the value of discriminant of the following equation.
$\sqrt{5}x^{2} - x - \sqrt{5} = 0$

1809863_1851049_ans_9cfb3f3341b14c0ab0ddc71065e6778b.PNG

Find the value of discriminant of the following equation.
$2y^{2} - y + 2 = 0$

1810136_1851045_ans_21a04335b803463fb0c893cb4bd1545f.PNG

Write the formula to find the roots of Quadratic equation $ap^2 + bp + c = 0$ .

$ap^2 + bp + c = 0$ .

roots of Quadratic equation

$P=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

Choose the correct answer for the following question.
For $\sqrt{2}x^{2} - 5x + \sqrt{2} = 0$ find the value of the discriminant.
-5
17
$\sqrt{2}$
$2\sqrt{2} - 5$

1815240_1851021_ans_ffb9fff143a34a3daedc78f2887c3168.PNG

Is the following equation quadratic?
$\left(x + 2 \right)^{2} = 2x^{2}$

A quadratic equation in the form of

$ax^2+bx +c=0$

Find the value of discriminant of the following equation.
$5m^{2} - m = 0$

1809858_1851047_ans_4bc5830d918141a3b50bd7ff604a9777.PNG

Test, whether the following equation is quadratic equation.
$x(x+1)+8=(x+2)(x-2)$

Given equation

$x(x+1)+8=(x+2)(x-2)$
L.H.S.

$x(x+1)+8=x^2+x+8$
R.H.S

$(x+2)(x-2)=x^2-4$
[ formula

$(a+b)(a-b)=a^2 b^2$ ]
L.H.S.=R.H.S

$x^2+x+8=x^2-4$
By alternation,

$\Rightarrow x^2+x+8-x^2+4=0$

$\Rightarrow x+12=0$
Thus, this is not a equation of power

$2$

$\therefore$ Given equation is not a quadratic equation

is the following equation quadratic?
$x^{2} - 2x + 5 = x^{2}$

A quadratic equation in the form of

$ax^2+bx +c=0$

Solve the following equations by the method of completing square.
$5x^2-6x-2=0$

Given quadratic equation

$5x^2-6x-2=0$

$\Rightarrow x^2 -\dfrac {6}{5}x-\dfrac {2}{5}=0$

$\Rightarrow x^2-\dfrac {6}{5}x=\dfrac {2}{5}$
For completing square, adding

$\left[\dfrac{1}{2}\times \dfrac{6}{5}\right]^2$ on both sides,

$\Rightarrow x^2 -2\left(\dfrac {6}{10}\right)x+\left(\dfrac {6}{10}\right)^2 =\dfrac {2}{5}+\left(\dfrac {6}{10}\right)^2$
$$\Rightarrow \left(x-\dfrac {6}{10}\right)^2=\dfrac {2}{5}
+\dfrac {36}{100}$$

$\Rightarrow \left(x-\dfrac {6}{10}\right)^2 =\dfrac {40+36}{100}$

$\Rightarrow \left(x-\dfrac {6}{10}\right)^2 =\dfrac {76}{100}$
Taking square root,

$\Rightarrow x-\dfrac {6}{10}=\sqrt {\dfrac {76}{100}}$
or $$x-\dfrac {3}{5}
=\pm \sqrt {\dfrac {19}{25}}$$

$\Rightarrow x-\dfrac {3}{5}=\pm \dfrac {\sqrt {19}}{5}$
Taking +ve sign

$\Rightarrow x-\dfrac {3}{5}=\dfrac {\sqrt {19}}{5}$

$\Rightarrow x=\dfrac {\sqrt {19}}{5}+\dfrac {3}{5}$

$\Rightarrow x=\dfrac {\sqrt {19}+3}{5}$ or

$\dfrac {3+\sqrt {19}}{5}$
Taking -ve sign

$\Rightarrow x-\dfrac {3}{5}=-\dfrac {\sqrt{19}}{5}$

$\Rightarrow x=\dfrac {3}{5}-\dfrac {\sqrt {19}}{5}$

$\Rightarrow x=\dfrac {3-\sqrt {19}}{5}$
Hence, solution of given equation are

$x=\dfrac {3+\sqrt {19}}{5}, \dfrac {3-\sqrt {19}}{5}$

Solve the following equations by the method of completing square.
$3x^2-5x+2=0$

Given quadratic equation

$3x^2-5x+2=0$

$\Rightarrow x^2 -\dfrac {5}{3}x+\dfrac {2}{3}=0$

$\Rightarrow x^2-\dfrac {5}{3}x=-\dfrac {2}{3}$
For completing square, adding square of half the coefficients of

$x$ on both sides,

$\Rightarrow (x)^2-2\left(\dfrac {5}{6}\right) x+\left(\dfrac {5}{6}\right)^2 =\dfrac {2}{3}+\left(\dfrac {5}{6}\right)^2$

$\Rightarrow \left(x-\dfrac {5}{6}\right)^2 =\dfrac {25}{36}-\dfrac {2}{3}$

$\Rightarrow \left(x-\dfrac {5}{6}\right)^2 =\dfrac {25-24}{36}$

$\Rightarrow \left(x-\dfrac {5}{6}\right)^2 =\dfrac {1}{36}$
Taking square root,

$\Rightarrow x-\dfrac {5}{6}=\pm \sqrt {\dfrac {1}{6}}$

$\Rightarrow x-\dfrac {5}{6}=\pm \dfrac {1}{6}$
Taking

$+$ ve sign

$x-\dfrac {5}{6}=\dfrac {1}{6}$

$x=\dfrac {1}{6}+\dfrac {5}{6}=1$
Taking -ve sign

$x-\dfrac {5}{6}=-\dfrac {1}{6}$

$x=-\dfrac {1}{6}+\dfrac {5}{6}\Rightarrow \dfrac {4}{6} \Rightarrow \dfrac {2}{3}$
Hence, solution of given equation are

$x=1, \dfrac {2}{3}$

Solve the following equations by the method of completing square.
$4x^2+3x+5=0$

Given quadratic equation

$4x^2+3x+5=0$

$\Rightarrow x^2+\dfrac {3}{4}x+\dfrac {5}{4}=0$

$\Rightarrow x^2+\dfrac {3}{4}x=-\dfrac {5}{4}$
Adding square of half of coefficient of

$x$ i.e.,

$\left(\dfrac {3}{8}\right)^2$ on both sides.

$\Rightarrow x^2+\dfrac {3}{4}x+\left(\dfrac {3}{8}\right)x+\left(\dfrac {3}{8}\right)^2 =\dfrac {-5}{4}+\dfrac {9}{64}$

$\Rightarrow \left(x+\dfrac {3}{8}\right)^2$

$=\dfrac {-80+9}{64}$

$=\dfrac {-71}{64}$

$\Rightarrow \left(x+\dfrac {3}{8}\right)^2 =\dfrac {-71}{64}$

$\because RHS$ is negative

$\therefore$ Roots will not be real.

Solve the following equations by the method of completing square.
$2x^2+x-4=0$

Given quadratic equation

$2x^2 +x-4=0$

$\Rightarrow x^2 +\dfrac{1}{2}x-2=0$ [Dividing each term by

$2$ ]

$\Rightarrow x^2 +\dfrac{1}{2}x=2$
Adding square of half of the coefficient of

$x$

$\left(\dfrac{1}{4}\right)^2$ on both sides,

$\Rightarrow x^2 +\dfrac{1}{2}x+\left(\dfrac{1}{4}\right)^2=2+\left(\dfrac{1}{4}\right)^2$

$\Rightarrow x^2+2\times x\times \dfrac 14+\left(\dfrac{1}{4}\right)^2 =2+\dfrac {1}{16}$

$\Rightarrow \left(x+\dfrac{1}{4}\right)^2=2+\dfrac {1}{16}$

$\Rightarrow \left(x+\dfrac{1}{4}\right)^2=\dfrac {32+1}{16}$

$\Rightarrow \left(x+\dfrac{1}{4}\right)^2=\dfrac {33}{16}$

$\Rightarrow \left(x+\dfrac{1}{4}\right)^2=\pm \sqrt {\dfrac {33}{16}}=\pm \dfrac {\sqrt {33}}{\sqrt{16}}$

$\Rightarrow \left(x+\dfrac{1}{4}\right) =\pm \dfrac {\sqrt {33}}{4}$
Taking +ve sign

$x+\dfrac14 =\dfrac {\sqrt {33}}{4}$

$\Rightarrow x=\dfrac {\sqrt {33}}{4}-\dfrac 14$

$\therefore x=\dfrac {\sqrt {33}-1}{4}$
Taking -ve sign

$x+\dfrac 14 =\dfrac {-\sqrt {33}}{4}$

$\Rightarrow x=-\dfrac {\sqrt {33}}{4}-\dfrac 14$

$\therefore x=\dfrac {-\sqrt {33}-1}{4}$
Hence, root of given equation are

$\dfrac {-1+\sqrt {33}}{4}$ and

$\dfrac {-1-\sqrt {33}}{4}$

Solve the following equations by the method of completing square.
$4x^2+4bx-(a^2 -b^2)=0$

Given quadratic equation is

$4x^2+4bx-(a^2 -b^2)=0$

$\Rightarrow x^2 +bx-\left(\dfrac {a^2 -b^2}{4}\right)=0$

$\Rightarrow x^2 +bx=\left(\dfrac {a^2 -b^2}{4}\right)$
Adding square of half of the coefficient of

$x$
i.e.,

$\left(\dfrac {b}{2}\right)^2$ on both sides,

$\Rightarrow x^2 +bx+\left(\dfrac {b}{4}\right)^2=\left(\dfrac {a^2 -b^2}{4}\right)+\left(\dfrac {b}{2}\right)$

$\Rightarrow x^2 +2\left(\dfrac {b}{2}\right)x+\left(\dfrac {b}{2}\right)^2 =\dfrac {a^2}{4}-\dfrac {b^2}{4}+\dfrac {b^2}{4}$

$\Rightarrow \left(x+\dfrac {b}{2}\right)^2 =\dfrac {a^2}{4}$
Taking square root of both sides,

$\Rightarrow x+\dfrac {b}{4} =\pm \sqrt {\dfrac {a^2}{4}}$

$\Rightarrow x+\dfrac {b}{4}=\pm \dfrac {a}{2}$

$\Rightarrow x=\pm \dfrac {a}{2}-\dfrac {b}{2}$
Taking +ve sign

$x=\dfrac {a}{2}-\dfrac {b}{2}=\dfrac {a-b}{2}$
Taking -ve sign

$x=\dfrac {-a}{2}-\dfrac {b}{2}=-\left(\dfrac {a+b}{2}\right)$
Hence

$x=\dfrac {a-b}{2}$ and

$x=-\left(\dfrac {a+b}{2}\right)$ are solution of given equation.

Solve the following equations by the method of completing square.
$2x^2+x+4=0$

Given quadratic equation

$2x^2 +x+4=0$

$\Rightarrow x^2 +\dfrac {1}{2}x+2=0$ [Dividing each term by

$2$ ]

$\Rightarrow x^2 +\dfrac {1}{2}x+2=0$

$\Rightarrow x^2 +\dfrac {1}{2}x=-2$

$\Rightarrow (x)^2+2\times x\times \dfrac {1}{4}+\left(\dfrac {1}{4}\right)^2 =-2+\left(\dfrac {1}{4}\right)^2\quad \left[adding \ \left(\dfrac {1}{4}\right)^2 \ both\ sides \right]$

$\Rightarrow \left(x+\dfrac {1}{4}\right)^2 =-2+\dfrac {1}{16}$

$\Rightarrow \left(x+\dfrac {1}{4}\right)^2 =\dfrac {-32+1}{16}$

$\Rightarrow \left(x+\dfrac {1}{4}\right)^2 =\dfrac {-31}{16}$
Taking square root on both sides

$\Rightarrow x+\dfrac {1}{4}=\pm \sqrt {\dfrac {-31}{16}}$

$\Rightarrow x=-\dfrac {1}{4}\pm \dfrac {\sqrt {-31}}{4}$
which is an imaginary number.
Hence, roots of given equation are not real.

Solve the following equations by the method of completing square.
$4x^2+4\sqrt 3 x+3=0$

Given quadratic equation

$4x^2 +4\sqrt 3 x+3=0$

$\Rightarrow 4x^2+4\sqrt 3=-3$

$\Rightarrow x^2 +\dfrac {4\sqrt 3}{4}x=-\dfrac {3}{4}$

$\Rightarrow x^2 +\sqrt 3 x=-\dfrac {3}{4}$

$\Rightarrow x^2 +\sqrt 3 x+\left(\dfrac {\sqrt 3}{2}\right)^2 =-\dfrac {3}{4}+\left(\dfrac {\sqrt 3}{2}\right)^2$
[Adding square of half of the coefficients of

$x$ ]
$$\Rightarrow x^2+2\times 2\times x\times \dfrac {\sqrt 3}{2}+\left(\dfrac {\sqrt 3}{2}\right)^2 =-\dfrac 34
+\left(\dfrac {\sqrt 3}{2}\right)^2$$

$\Rightarrow \left(x+\dfrac {\sqrt 3}{2}\right)^2=-\dfrac 34 +\dfrac 34$

$\Rightarrow \left(x+\dfrac {\sqrt 3}{2}\right)^2=0$

$\Rightarrow \left(x+\dfrac {\sqrt 3}{2}\right) \left(x+\dfrac {\sqrt 3}{2}\right) =0$
i.e.,

$x+\dfrac {\sqrt 3}{2}=0$

$\Rightarrow x=-\dfrac {\sqrt 3}{2}$
or

$x+\dfrac {\sqrt 3}{2}=0$

$\Rightarrow x=-\dfrac {\sqrt 3}{2}$
Hence roots of given equation

$-\dfrac {\sqrt 3}{2}$ and

$-\dfrac {\sqrt 3}{2}$

Solve for $x$ ;
$x^2 -4ax-b^2+4a^2 +4a^2=0$ .

Given quadratic equation

$x^2 -4ax-b^2+4a^2=0$
Comparing it by quadratic standard equation

$Ax^2+Bx +C=0$

$A=1, B=-4a$ and

$C=-(b^2-4a^2)$ By Shridhar Acharya formula

$x=\dfrac {-B \pm \sqrt {B^2 -4AC}}{2A}$

$=\dfrac {-(-4a)\pm \sqrt {(-4a)^2 -4\times 1\times -(b^2 -4a^2)}}{2\times 1}$

$\dfrac {4a\pm \sqrt {16a^2 +4b^2-16a^2}}{2}$

$\dfrac {4a\pm \sqrt {4b^2}}{2}=\dfrac {4a\pm 2b}{2}=2a \pm b$
Hence

$x=2a +b$ and

$x=2x-b$ .

Test, whether the following equation is quadratic equation.
$x+\dfrac 1x+x^2, x\neq 0$

Given equation

$x+\dfrac 1x+x^2, x\neq 0$
Taking L.C.M.

$\dfrac {x^2+1+x^3}{x}=0$

$\Rightarrow x^3+x^2+1=0$
Thus, this is not a quadratic equation

Solve for $x$ the quadratic equation $x^2-4x-8=0$
Give your answer correct to three significant figures.

Given quadratic equation is

$x^2-4x-8=0$

We have a formula for solving quadratic equation

$ax^2+bx+c=0$ is

$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$

By using quadratic formula, we have

$x=\dfrac{-(-4)\pm\sqrt{(-4)^2-4(1)(-8)}}{2(1)}=\dfrac{4\pm\sqrt{16+32}}{2}$

$=\dfrac{4\pm \sqrt{48}}{2}=\dfrac{4\pm 4\sqrt{3}}{2}=2\pm 2\sqrt{3}$

$=2(1\pm\sqrt{3})=2(1\pm 1.73205)=2(2.73205)$ or

$2(-0.73205)$

$=5.46410$ or

$-1.4641$

$=5.46$ or

$-1.46$

Find the value of $k$ for which the quadratic equation $kx(x - 2) + 6 = 0$ has two equal roots.

Given equation

$kx^{2} - 2kx + 6 = 0$

For two equal roots

$D = 0$

$\Rightarrow\ b^{2} - 4ac = 0$

$\Rightarrow\ 4k^{2} - 4k \times 6 = 0$

$\Rightarrow\ 4k^{2} = 24k\ \Rightarrow\ 4k^{2} = 24k = 0$

$\Rightarrow\ 4k (k - 6) = 0$

$\Rightarrow\ k = 6$

[

$k \neq 0$ , as if

$k = 0$ then the given equation

$r$ is not a valid equation ]

Using completing the square method, show that the equation $x^{2} - 8x + 18 = 0$ has no solution.

$x^{2} - 8x + 18 = 0$

$\Rightarrow\ x^{2} - 8x + 16 - 16 + 18 = 0$

$\Rightarrow\ (x - 4)^{2} + 2 = 0$

$\Rightarrow\ (x - 4)^{2} = -2$

But square of a number can't be negative.

Hence the equation has no solution.

Solve the following equations.
$3x^{2} + 7x - 5 = 0$
Show all your working and give your answer correct to $2$ decimal places.

On comapring given quadratic equation with

$ax^2+bx+c=0$ we get,

$a=2,\;b=7$ and

$c=-5$

Now by using quadratic formula,

$\begin{aligned}{}x &= \frac{{ - 7 \pm \sqrt {{7^2} - 4 \times 3 \times - 5} }}{{2 \times 3}}\\ &= \frac{{ - 7 \pm \sqrt {49 + 60} }}{6}\\& = \frac{{ - 7 \pm \sqrt {109} }}{6}\\x &= \frac{{ - 7 + \sqrt {109} }}{6}\text{ and }x = \frac{{ - 7 - \sqrt {109} }}{6}\\x &= 0.57\text{ and }x = - 2.91\end{aligned}$

So, the solutions of the given quadratic equation are

$0.57$ and

$-2.91.$

Examine the nature of the roots of the quadratic $\displaystyle \left ( b-x \right )^{2}-4\left ( a-x \right )\left ( c-x \right )=0$ where a, b, c are real.

The given equation can be written as

$\displaystyle 3x^{2}-\left [ 4\left ( a+c \right )-2b \right ]x\left ( b^{2}-4ac \right )=0$

$\displaystyle \Delta =\left [ 4\left ( a+c \right )-2b \right ]^{2}+12\left ( b^{2}-4ac \right )$

$\displaystyle =4\left [ 2\left ( a+c \right )-b \right ]^{2}+\left ( 3b^{2}-12ac \right )$

$\displaystyle =4\left [ 2\left ( a^{2}+c^{2} \right )+2ac +b^{2}-4b\left ( a+c \right )+3b^{2}-12ac\right ]$

$\displaystyle =16\left [ a^{2}+b^{2}+c^{2}-ab-bc-ca \right ]$

$\displaystyle =8\left [ \left ( a-b \right )^{2}+\left ( b-c \right ) ^{2}+\left ( c-a \right )^{2}\right ]=+ive$

$\displaystyle \therefore$ Roots are real.

Find the number of real solutions of the quadratic equation ${x}^{2}+2=x+5$ .

Given:

$x^2+2=x+5$

$x^2+2-x-5=0$

$x^2-x-3=0$

Now we find the roots of above quadratic equation as shown below:

$x=\dfrac { -b\pm \sqrt { { b }^{ 2 }-4ac } }{ 2a }$

Here,

$a=1, b=-1, c=-3$

$=\dfrac { -(-1)\pm \sqrt { { (-1) }^{ 2 }-4(1)(-3) } }{ 2(1) } \\$

$=\dfrac { 1\pm \sqrt { 1+12 } }{ 2 } \\$

$=\dfrac { 1\pm \sqrt { 13 } }{ 2 }$

Therefore,

$x=\dfrac { 1\pm \sqrt { 13 } }{ 2 }$

Hence, the quadratic equation has

$2$ real solutions

Find the number of real solution to the rational equation
$\dfrac {2}{(x+1)}-\dfrac {1}{(x-2)}=-1$ find value of $x^2$

Solve the given equation as follows:

$\dfrac {2}{(x+1)}-\dfrac {1}{(x-2)}=-1$

$\Rightarrow 2(x-2)-(x+1)=-[(x+1)(x-2)]$

$\Rightarrow 2x-4-x-1=-[x^2-x-2]$

$\Rightarrow x-5=-x^2+x+2$

$\Rightarrow x^2-7=0$

$\Rightarrow x^2=7$

$\Rightarrow x=\pm \sqrt { 7 }$

Check whether $x^2 - x = 0$ is a quadratic equation.

We know that the general form of quadratic equation is

$ax^2+bx+c=0$ .

The given equation is

$x^2-x=0$ which can be rewritten as

$x^2-x+0=0$ and therefore it is of the form

$ax^2+bx+c=0$ .

Hence, the equation

$x^2-x=0$ is a quadratic equation.

Find the values (s) of $k$ so that the quadratic equation $3x^2 - 2kx + 12 = 0$ has equal roots.

The given quadratic equation is

$3x^2 - 2kx + 12 = 0$
On comparing it with the general quadratic equation

$ax^2 + b x + c = 0$ , we obtain

$a = 3, b = -2k$ and

$c = 12$
Discriminant,

$'D'$ of the given quadratic equation is given by

$D = b^2 - 4ac$

$= (-2k)^2 - 4 \times 3 \times 12$

$= 4k^2 - 144$
For equal roots of the given quadratic equations, Discriminant will be equal to 0.
i.e.,

$D=0$

$\Rightarrow 4k^2-144=0$

$\Rightarrow 4(k^2-36)=0$

$\Rightarrow k^2=36$

$\Rightarrow k=\pm 6$
Therefore, the values of k for which the quadratic equation

$3x^2 - 2kx + 12 = 0$ will have equal roots are

$6$ and

$-6.$

Check whether $\sqrt 3 x = \dfrac{22}{13}$ is a quadratic equation.

We know that the general form of quadratic equation is

$ax^2+bx+c=0$ .

The given equation is

$\sqrt { 3 } x=\frac { 22 }{ 13 }$ in which the variable

$x$ has degree

$1$ and therefore it is not of the form

$ax^2+bx+c=0$ .

Hence, the equation

$\sqrt { 3 } x=\frac { 22 }{ 13 }$ is not a quadratic equation. The given equation is a linear equation.

Check whether $x^2 + \dfrac{1}{2} x = 0$ is a quadratic equation.

We know that the general form of quadratic equation is

$ax^2+bx+c=0$ .

The given equation is

$x^{ 2 }+\frac { 1 }{ 2 } x=0$ which can be rewritten as

$x^{ 2 }+\frac { 1 }{ 2 } x+0=0$ and therefore it is of the form

$ax^2+bx+c=0$ .

Hence, the equation

$x^{ 2 }+\frac { 1 }{ 2 } x=0$ is a quadratic equation.

Check whether $\sqrt{2}x^2+3x =0$ is a quadratic equation.

We know that the general form of quadratic equation is

$ax^2+bx+c=0$ .

The given equation is

$\sqrt { 2 } x^{ 2 }+3x=0$ which can be rewritten as

$\sqrt { 2 } x^{ 2 }+3x+0=0$ and therefore it is of the form

$ax^2+bx+c=0$ .

Hence, the equation

$\sqrt { 2 } x^{ 2 }+3x=0$ is a quadratic equation.

Check whether $x^2 = 8$ is a quadratic equation.

We know that the general form of quadratic equation is

$ax^2+bx+c=0$ .

The given equation is

$x^2=8$ which can be rewritten as

$x^2-0x-8=0$ and therefore it is of the form

$ax^2+bx+c=0$ .

Hence, the equation

$x^2=8$ is a quadratic equation.

Solve $x + 2 + y + 3 + \sqrt {(x + 2)(y + 3)} = 39$ .
$(x + 2)^{2} + (y + 3)^{2} + (x + 2)(y + 3) = 741$ .

$x+2+y+3+\sqrt { \left( x+2 \right) \left( y+3 \right) } =39$

${ \left( x+2 \right) }^{ 2 }+{ \left( y+3 \right) }^{ 2 }+\left( x+2 \right) \left( y+3 \right) =741$
Let

$x+2=p,y+3=q.$

$p+q+\sqrt { pq } =39\longrightarrow I$

${ p }^{ 2 }+{ q }^{ 2 }+pq=741\longrightarrow II$

$\Longrightarrow p+q-39=-\sqrt { pq }$

Squaring on both sides:-

$\Longrightarrow { p }^{ 2 }+{ q }^{ 2 }+1521+2pq-78p-78q=pq$

$\Longrightarrow { p }^{ 2 }+{ q }^{ 2 }+pq=78p+78q-1521\longrightarrow III$

Subtracting

$II$ from

$III$

$78p+78q-1521-741=0$

$78p+78q-2262=0$

$p+q=29\longrightarrow IV$

From

$I$

$\sqrt { pq } =10$

$pq=100\longrightarrow V$

$p-q=\sqrt { { \left( p+q \right) }^{ 2 }-4pq }$

$=\sqrt { 841-400 }$

$=\sqrt { 441 } =21\longrightarrow VI$

Adding

$IV$ and

$VI$

$2p=50$

$p=25,q=4$

$x+2=25,y+3=4$

$\boxed { x=23,y=1 }$

$t^2 + 3t = 7$

The given quadratic equation is

$t^2+3t=7$ which can be rewritten as

$t^2+3t-7=0$ .

Add and subtract

$\frac { 9 }{ 4 }$ in the equation

$t^2+3t-7=0$ to make a perfect square as shown below:

$t^{ 2 }-3t-7=0\\ \Rightarrow t^{ 2 }-3t+\frac { 9 }{ 4 } -\frac { 9 }{ 4 } -7=0\\ \Rightarrow (t)^{ 2 }+\left( 2\times t\times \frac { 3 }{ 2 } \right) +\left( \frac { 3 }{ 2 } \right) ^{ 2 }+\left( -\frac { 9 }{ 4 } -7 \right) =0\\ \Rightarrow \left( t+\frac { 3 }{ 2 } \right) ^{ 2 }-\frac { 37 }{ 4 } =0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (∵(a+b)^{ 2 }=a^{ 2 }+b^{ 2 }+2ab)\\ \Rightarrow \left( t+\frac { 3 }{ 2 } \right) ^{ 2 }=\frac { 37 }{ 4 } \\ \Rightarrow t+\frac { 3 }{ 2 } =±\sqrt { \frac { 37 }{ 4 } } \\ \Rightarrow t+\frac { 3 }{ 2 } =±\frac { \sqrt { 37 } }{ 2 } \\ \Rightarrow t+\frac { 3 }{ 2 } =-\frac { \sqrt { 37 } }{ 2 } ,\quad t+\frac { 3 }{ 2 } =\frac { \sqrt { 37 } }{ 2 } \\ \Rightarrow t=-\frac { \sqrt { 37 } }{ 2 } -\frac { 3 }{ 2 } ,\quad t=\frac { \sqrt { 37 } }{ 2 } -\frac { 3 }{ 2 } \\ \Rightarrow t=-\left( \frac { \sqrt { 37 } +3 }{ 2 } \right) ,\quad t=\frac { \sqrt { 37 } -3 }{ 2 }$

Hence,

$t=-\left( \frac { \sqrt { 37 } +3 }{ 2 } \right)$ or

$t=\frac { \sqrt { 37 } -3 }{ 2 }$ .

If the difference between the roots of ${ x }^{ 2 }+2px+q=0$ be same as that between the roots of ${ x }^{ 2 }+2qx+p=0$ $\left( p\neq q \right)$ , then $p+q$ is equal to

Let

$\alpha$ and

$\beta$ are the roots of the equation

${ x }^{ 2 }+2px+q=0$ and

$\alpha '$ and

$\beta '$ be the roots of the equation

${ x }^{ 2 }+2qx+p=0$ .

$\alpha -\beta ={ \alpha }{ ' }-{ \beta }{ ' }\quad\quad\quad\dots[Given]$

$\Rightarrow\sqrt { { \left( \alpha +\beta \right) }^{ 2 }-4\alpha \beta } =\sqrt { { \left( \alpha '+\beta ' \right) }^{ 2 }-4{ \alpha }{ ' }\beta { ' } }$

$\Rightarrow\sqrt { { \left( -2p \right) }^{ 2 }-4q } =\sqrt { { \left( -2q \right) }^{ 2 }-4p }$

$\Rightarrow4{ p }^{ 2 }-4{ q }^{ 2 }=4{ q }-4{ p }$

$\Rightarrow{ p }^{ 2 }-{ q }^{ 2 }=q-p$

$\Rightarrow\left( p-q \right) \left( p+q \right) =-\left( p-q \right)$

$\Rightarrow p+q=-1$

Hence, value of

$p+q$ is equal to

$-1$ .

Solve each of the following equation by using the method of completing the square:
$x^{2}-8x-2=0$ ?

We will use the difference of squares identity ,which can be written

$a^2-b^2=(a-b)(a+b)$ with

$a=(x+4)$ and

$b=\sqrt{14}$ as follows:

$0=x^2+8x+2=(x+4)^2-16+2$

$=(x+4)2−(\sqrt { 14 } )2$

$=((x+4)−\sqrt { 14 } )((x+4)+\sqrt { 14 } )$

$=(x+4−\sqrt { 14 } )((x+4+\sqrt { 14 } )$

Hence:

$x=−4±\sqrt { 14 }$

$x=\sqrt { 14−4 }$ OR

$x=−\sqrt { 14−4 }$

$x=−0.258$ OR

$x=−7.742$

Solve the equation by completing the square method:
$x^{2}-10x+9=0$

$x^{2}-10x+9=0$

or,

$x^{2}-2\times x\times5+25+9-25=0$

or,

$(x-5)^{2}-(4)^{2}=0$

or,

$(x-5+4)(x-5-4)=0$

or,

$(x-1)(x-9)=0$

either,

$\boxed{x=1}$ or,

$\boxed{x=9}$

Hence, the solution is

$x=1,9$

Solve the following equation by using the general formula , if the equation has a solution R :
ii) $x + {1 \over x} = 3,x \ne 0$ iii) $3{x^2} + 2\sqrt {5x} - 5 = 0$
iv) $\sqrt 3 {x^2} - 2x + \sqrt 3 = 0$
v) ${1 \over {x + 1}} + {2 \over {x + 2}} = {4 \over {x + 4}}{\rm{ ;x}} \ne {\rm{1, - 2, - 4}}$
vi) $\sqrt 2 {x^2} + 7x + 5\sqrt {2 = 0}$

$\cfrac{1}{x}-\cfrac{1}{x-3}$

$\Rightarrow x-3-x=3x^{2}-9x$

$\Rightarrow 3x^{2}-9x+3=0$

$\Rightarrow x=\cfrac{9\pm\sqrt{81-36}}{2(3)}$

$\Rightarrow x=\cfrac{9+\sqrt45}{6}, \cfrac{4-\sqrt45}{6}$

ii)

$x^{2}-3x+1=0$

$x=\cfrac{3\pm \sqrt{9-4}}{2}$

$x=\cfrac{3+\sqrt5}{2},\cfrac{3-\sqrt5}{2}$

iii)

$3x^{2}+2\sqrt5x-5=0$

$x=\cfrac{2\sqrt5\pm\sqrt{20+60}}{2(3)}$

$x=\sqrt5,\cfrac{-5\sqrt5}{3}$

iv)

$\sqrt3x^{2}+2\sqrt5x-5=0$

$D\equiv 4-3(4)<0$ No

$x\notin R$

$(x+2)(x+4)+2(x+1)(x+4)=4(x+1)(x+2)$

$\Rightarrow x^{2}-4x-8=0$

$x=\cfrac{4\pm\sqrt{16+32}}{2}$

$x=2+8\sqrt3, 2-8\sqrt3$

vi)

$\sqrt2x^{2}+7x+5\sqrt2=0$

$x=\cfrac{-7\pm\sqrt{49-40}}{2\sqrt2}$

$x=-\sqrt2, \cfrac{-5}{\sqrt2}$

Solve each of the following equation by using the method of completing the square:
$2x^{2}+5x-3=0$ ?

We will use the difference of squares identity, which can be written:

${ a }^{ 2 }−{ b }^{ 2 }=(a−b)(a+b)$ First,

to reduce the amount of arithmetic involving fractions, first multiply through by

${ 2 }^{ 3 }=8$ toget:

$0={ 16x }^{ 2 }+40x−24$

$={ 4x }^{ 2 }+2(5)(4x)−24$

$={ (4x+5) }^{ 2 }−25−24$

$={ (4x+5) }^{ 2 }−{ 7 }^{ 2 }$

$=((4x+5)−7)((4x+5)+7)$

$=(4x−2)(4x+12)$

$=(2(2x−1)2(2x+6))$

$=4(2x−1)(2x+6)$ Hence

$x=\dfrac{1}{2}$ or

$x=−3$

Solve each of the following equation by using the method of completing the square:
$3x^{2}+x-2=0$ ?

$3x^{ 2 }−2x=2$ Divide both sides by

$3x^{ 2 }−\dfrac { 2x }{ 3 } =\dfrac { 2 }{ 3 }$

$x^ 2−\dfrac { 2x }{ 3 } +\dfrac { 1 }{ 9 } =\dfrac { 2 }{ 3 } +\dfrac { 1 }{ 9 } =\dfrac { 7 }{ 9 }$

$(x−\dfrac { 1 }{ 3 } )^{ 2 }=\dfrac { 7 }{ 9 }$

$x−\dfrac { 1 }{ 3 } =±\sqrt { \dfrac { 7 }{ 9 } }$

$x=\dfrac { 1 }{ 3 } ±\sqrt { \dfrac { 7 }{ 9 } }$

Solve the equations by completing the square
$x^{2}-5x+5=0$

${x}^{2}-5x+5=0$

Or,

${x}^{2}-2.\dfrac{5}{2}x+{\left(\dfrac{5}{2}\right)}^{2}-{\left(\dfrac{5}{2}\right)}^{2}+5=0$

$,\left(x-\dfrac{5}{2}\right)^{2}+5-\dfrac{25}{4}=0$

Or,

$\left(x-\dfrac{5}{2}\right)^{2}-{\left(\dfrac{\sqrt{5}}{2}\right)}^{2}=0$

Or,

$\left(x-\dfrac{5}{2}+\dfrac{\sqrt{5}}{2}\right) \left(x-\dfrac{5}{2}-\dfrac{\sqrt{5}}{2}\right)=0$

$\therefore \boxed{x=\dfrac{5-\sqrt{5}}{2}}$ or

$\boxed{x=\dfrac{5+\sqrt{5}}{2}}$

$x^{2} - (2b - 1)x + (b^{2} - b - 20) = 0$ .

${ x }^{ 2 }-\left( 2b-1 \right) x+{ b }^{ 2 }-b-20=0$

The roots are:

$x=\cfrac { \left( 2b-1 \right) \pm \sqrt { { \left( 2b-1 \right) }^{ 2 }-4\times \left( { b }^{ 2 }-b-20 \right) } }{ 2 } \\ =\cfrac { \left( 2b-1 \right) \pm \sqrt { 4{ b }^{ 2 }+1-4b-4{ b }^{ 2 }+4b+80 } }{ 2 } \\ =\cfrac { \left( 2b-1 \right) \pm \sqrt { 81 } }{ 2 } \\ =\cfrac { \left( 2b-1 \right) \pm 9 }{ 2 }$

$\therefore x=\cfrac { 2b-1+9 }{ 2 } =b+4\\ or,\quad x=\cfrac { 2b-1-9 }{ 2 } =b-5$

If $x^2-(5m-2)x+4m^2 +10m+25=0$ were to be a perfect square then find the value of $m$ ?

$x^2-(5m-2)x+4m^2 +10m+25=0$ is a perfect square

$\Rightarrow D=0$

$D={b}^{2}-4ac$

${\left(5m-2\right)}^{2}-4\left(4{m}^{2}+10m+25\right)=0$

$25{m}^{2}+4-20m-16{m}^{2}-40m-100=0$

$\Rightarrow 9{m}^{2}-60m-96=0$

$\Rightarrow 3{m}^{2}-20m-32=0$

$m=\dfrac{20\pm\sqrt{400+384}}{6}=\dfrac{20\pm 28}{5}$

$\therefore m=8,\dfrac{-4}{3}$

Find the value of $k$ for which the quadratic equation $(k-2)x^ {2}+(2k-3)x+(5k-6)=0$ has equal roots.

Given the equation has equal roots

$\Rightarrow$ Discriminant

$= D ={b}^{2}-4ac=0$

$\Rightarrow {\left(2k-3\right)}^{2}-4\times \left(k-2\right)\left(5k-6\right)=0$

$\Rightarrow 4{k}^{2}+9-12k-4\left(5{k}^{2}-6k-10k+12\right)=0$

$\Rightarrow 4{k}^{2}+9-12k-4\left(5{k}^{2}-16k+12\right)=0$

$\Rightarrow 4{k}^{2}+9-12k-20{k}^{2}+64k-48=0$

$\Rightarrow -16{k}^{2}+52k-39=0$

$\Rightarrow 16{k}^{2}-52k+39=0$

Now solving the Quadratic equation by completing the square method we get:

$\Rightarrow {\left(4k\right)}^{2}-2\times 4k\times \dfrac{13}{2}+\dfrac{169}{4} -\dfrac{169}{4} +39=0$

$\Rightarrow {\left(4k-\dfrac{13}{2}\right)}^{2}=\dfrac{169}{4}-39$

$\Rightarrow {\left(4k-\dfrac{13}{2}\right)}^{2}=\dfrac{169-156}{4}$

$\Rightarrow {\left(4k-\dfrac{13}{2}\right)}^{2}=\dfrac{13}{4}$

$\Rightarrow 4k-\dfrac{13}{2}=\pm\dfrac{\sqrt{13}}{2}$

$\Rightarrow 4k=\dfrac{13\pm\sqrt{13}}{2}$

$\therefore k=\dfrac{13\pm\sqrt{13}}{8}$

Thus the value of

$k$ can be

$\dfrac{13+\sqrt{13}}{8}$ or

$\dfrac{13-\sqrt{13}}{8}$

Solve the following equation $x^2+\dfrac{x}{\sqrt{2}}+1=0$ .

${ x^{ 2 } }+\frac { x }{ { \sqrt { 2 } } } +1=0 \\ Discriminant\, \, \left( D \right) ={ b^{ 2 } }-4ac \\ \Rightarrow { \left( { \frac { 1 }{ { \sqrt { 2 } } } } \right) ^{ 2 } }-4\times 1\times 1 \\ \Rightarrow \frac { 1 }{ 2 } -4=\frac { { -3 } }{ 2 } \\ Roots=\frac { { -\frac { 1 }{ { \sqrt { 2 } } } \pm \sqrt { \frac { { -3 } }{ 2 } } } }{ { 2\times 1 } } \\ Roots=\left( { \frac { { \frac { { -1 } }{ { \sqrt { 2 } } } \pm \sqrt { \frac { 3 }{ 2 } } i } }{ 2 } } \right) \\ Roots=\left( { \frac { { \sqrt { \frac { 3 }{ 2 } } i-\frac { 1 }{ { \sqrt { 2 } } } } }{ 2 } } \right) \, \, \, \, \, and\, \, \, -\left( { \frac { { \sqrt { \frac { 3 }{ 2 } } i+\frac { 1 }{ { \sqrt { 2 } } } } }{ 2 } } \right) \,$

Determine whether the values given against the quadratic equation are the roots of the quadratic equation or not:
$2{m^2} - 5m = 0,m = 2,\dfrac{5}{2}$

$f(m)=2m^{2}-5m$

The roots of the above equation are

$2m^{2}-5m=0$

$\Rightarrow m(2m-5)=0$

$\Rightarrow m=0$ or

$m=\cfrac{5}{2}$

So,

$m=\cfrac{5}{2}$ is a root whereas

$m=2$ is not a root.

Check whether the following equation is quadratic equation in $x$ or not?
$x^{2}-3x-\sqrt{x}+4=0$

1669810_1714149_ans_2fe45d1fa26a4e7d8bd57a94f103d8ef.jpg

Expand : $( 3 x + 2 ) ^ { 2 }$

Hint: Use the formula of $(a+b)^2=a^2+b^2+2ab$

Step 1: Expand $(3x+2)^2$

We know,

$(a+b)^2=a^2+b^2+2ab$

Hence,

$(3x+2)^2=(3x)^2+2^2+2\times3x\times2$

$\Rightarrow(3x+2)^2=9x^2+4+12x$

Therefore, expanding $(3x+2)^2$ , we get $9x^2+4+12x$

Quadratic Equations - Class 10 Maths - Extra Questions

If the roots of the equation (b−c)x2+(c−2)x+(a−b)=0(b-c)x^{2}+(c-2)x+(a-b)=0 are equal, then prove that 2b=a+c2b=a+c

Is the given equation quadratic? Enter 1 for True and 0 for False.n\,-\, 3\, =\, 4n^{2}n\,-\, 3\, =\, 4n^{2}

Solve: \displaystyle 25x^{2}-30x+9=0\displaystyle 25x^{2}-30x+9=0

Solve the equation :\displaystyle { 27x }^{ 2 }-10x+1=0\displaystyle { 27x }^{ 2 }-10x+1=0

Solve the equation : \displaystyle { x }^{ 2 }-2x+\frac { 3 }{ 2 } =0\displaystyle { x }^{ 2 }-2x+\frac { 3 }{ 2 } =0

Solve the equation \displaystyle \sqrt { 2 } { x }^{ 2 }+x+\sqrt { 2 } =0\displaystyle \sqrt { 2 } { x }^{ 2 }+x+\sqrt { 2 } =0

Solve the equation \displaystyle { 21x }^{ 2 }-28x+10=0\displaystyle { 21x }^{ 2 }-28x+10=0

Solve the equation \displaystyle { x }^{ 2 }+\frac { x }{ \sqrt { 2 } } +1=0\displaystyle { x }^{ 2 }+\frac { x }{ \sqrt { 2 } } +1=0

Solve the equation \displaystyle { x }^{ 2 }+3x+5=0\displaystyle { x }^{ 2 }+3x+5=0 for xx.

Solve the equation \displaystyle { 2x }^{ 2 }+x+1=0\displaystyle { 2x }^{ 2 }+x+1=0

Check whether 2x + x^2 + 1 = 02x + x^2 + 1 = 0 a quadratic equations.

Solve the quadratic equation 3{x}^{2}+5x+2=03{x}^{2}+5x+2=0 using formula method.

Solve the following quadratic equation by completing square methodx^2 + 11x + 24 = 0x^2 + 11x + 24 = 0

Check whether 6x^3 + x^2 = 26x^3 + x^2 = 2 is a quadratic equations

Solve the quadratic equation 2{x}^{2}+5x+3=02{x}^{2}+5x+3=0 using formula method.

Decide whether \cfrac{3}{y}-4=y\cfrac{3}{y}-4=y is a quadratic equation or not.

Solve the equation 3y^{2} + 8y + 5 = 03y^{2} + 8y + 5 = 0 by using formula method

Solve the following quadratic equation by using formula method3y^2 + 7y + 4 = 03y^2 + 7y + 4 = 0

If a = 1, b = 8a = 1, b = 8 and c = 15c = 15, then find the value of b^2-4ac =b^2-4ac =

Solve the following quadratic equation using the formula method:4{x}^{2}+7x+2=04{x}^{2}+7x+2=0

Solve the following quadratic equation by using the formula method: m^{2} - 3m - 10 = 0m^{2} - 3m - 10 = 0

The discriminant of the quadratic equation px^{2} + qx + r = 0px^{2} + qx + r = 0 is ________

Solve x^2 + 6x - 7 = 0x^2 + 6x - 7 = 0 by the method of completing the square

Write the discriminant of the equation ax^2 + bx + c = 0ax^2 + bx + c = 0.

Decide whether m^{2} + m + 2 = 4mm^{2} + m + 2 = 4m is a quadratic equation

Solve the quadratic equation 2x^{2} + x - 4 = 02x^{2} + x - 4 = 0 by completing the square

Solve the quadratic equation x^{2} - 4x + 2 = 0x^{2} - 4x + 2 = 0 by formula method.

Solve the equation by using the formula:{m}^{2}-2m=2{m}^{2}-2m=2

The formula of discriminant of quadratic equation ax^{2} + bx + c = 0ax^{2} + bx + c = 0 is D =D = ______.

Find the value of kk for which the given equations has real and equal roots:(i) (k - 12)x^{2} + 2(k - 12)x + 2 = 0(k - 12)x^{2} + 2(k - 12)x + 2 = 0(ii) k^{2}x^{2} - 2(k - 1)x + 4 = 0k^{2}x^{2} - 2(k - 1)x + 4 = 0.

Solve the equation a^2x^2-3abx+2b^2=0a^2x^2-3abx+2b^2=0 by completing the square.

An equation whose maximum degree of variable is two is called ............... equation.

Check whether the given equation is a quadratic equation or not:x(x + 1) + 8 = (x + 2)(x - 2)x(x + 1) + 8 = (x + 2)(x - 2)

Find the roots of the following quadratic equation (if they exist) by the method of completing the square.x^2 \, - \, 4ax \, + \, 4a^2 \, - \, b^2 \, = \, 0x^2 \, - \, 4ax \, + \, 4a^2 \, - \, b^2 \, = \, 0

Show that the roots of the equation x^2 - 2x + 3 = 0x^2 - 2x + 3 = 0 are imaginary.

Simplify \cfrac { \left( { x }^{ 2 }+1 \right) \left( { x }^{ 2 }+2 \right) }{ \left( { x }^{ 2 }+3 \right) \left( { x }^{ 2 }+4 \right) } =\cfrac { \left( { x }^{ 2 }+1 \right) \left( { x }^{ 2 }+2 \right) }{ \left( { x }^{ 2 }+3 \right) \left( { x }^{ 2 }+4 \right) } =

Find the root of the following quadratic equation (if they exist) by the method of completing the square.\sqrt{3}x^2 \, + \, 10x \, + \, 7\sqrt{3} \, = \, 0\sqrt{3}x^2 \, + \, 10x \, + \, 7\sqrt{3} \, = \, 0

Write standard form of quadratic equation and find the roots of the equations 3x^2+5\sqrt{2}+2=03x^2+5\sqrt{2}+2=0 using general formula.

Write the discriminant of the given quadratic equation{ x }^{ 2 }+px+2q=0\quad { x }^{ 2 }+px+2q=0\quad

Solve 4ab=2(a^2-b^2)\sqrt-14ab=2(a^2-b^2)\sqrt-1

Find the roots of the following quadratic equation, 2x^2+x-4=02x^2+x-4=0

Solve the following quadratic equations by the method of perfect the square.3x^2-5x+2=03x^2-5x+2=0

If \alpha\alpha and \beta\beta are the zeros of x^{2}+x-2x^{2}+x-2 then find value of \dfrac{1}{\alpha}-\dfrac{1}{\beta}\dfrac{1}{\alpha}-\dfrac{1}{\beta}

Solve the following quadratic equations by the method of perfect the square.5x^2-6x-2=05x^2-6x-2=0

Solve the following quadratic equations by the method of perfect the square.2x^2+x+4=02x^2+x+4=0

x^{2}+3\left| x \right| +2=0x^{2}+3\left| x \right| +2=0 Find the value of xx.

Find a quadratic equation with real co-efficient whose one root is 3-2i3-2i.

Solve the following quadratic equations by the method of perfect the square.4x^2+3x+5=04x^2+3x+5=0

Solve{ x }^{ 2 }+5x-2=0{ x }^{ 2 }+5x-2=0

Solve {x}^{2}-3x+12=5{x}^{2}-3x+12=5

Factorise : 2\sqrt{2}x^2 + 9x + 5 \sqrt{2}=02\sqrt{2}x^2 + 9x + 5 \sqrt{2}=0

Check whether the following is quadratic equation.(x+1)^2=2(x-3)(x+1)^2=2(x-3)

The equation x^2 + 2(m-1)x + (x + 5) = 0x^2 + 2(m-1)x + (x + 5) = 0 has real and equal roots. Find the value of mm.

The quadratic equation ax^2 + bx + c = 0ax^2 + bx + c = 0, (a\ne 0a\ne 0) has atmost _____ roots.

2\sqrt{5}{x}^{2}-3x-\sqrt{5}=02\sqrt{5}{x}^{2}-3x-\sqrt{5}=0 Find xx.

Find the values of a : 7{a^2} + 7a - 20=07{a^2} + 7a - 20=0

Find the co-ordinates points where the graph of polynomial {x^2} + x + 12{x^2} + x + 12 intersects the x-axis.

Check whether the following is quadratic equation.x^2+3x+1=(x-2)^2x^2+3x+1=(x-2)^2

Solve the following quadratic equation by completing the square method.x^2+2\ x-5=0x^2+2\ x-5=0

Find the nature of the roots of the following quadratic equations. If roots are real, find them.5x^{2}-3x+2=05x^{2}-3x+2=0

Check whether the following is quadratic equation.(x+2)^3=2x(x^2-1)(x+2)^3=2x(x^2-1)

Check whether the following is quadratic equation.x^2-2x=(-2)(3-x)x^2-2x=(-2)(3-x)

Check whether the following in quadratic equation.(x-3)(2x+1)=x(x=5)(x-3)(2x+1)=x(x=5)

Check whether the following is quadratic equation.(x-2)(x+1)=(x-1)(x+3)(x-2)(x+1)=(x-1)(x+3)

Solve the quadratic equation : 4x^2-4ax+(a^2-b^2)=04x^2-4ax+(a^2-b^2)=0

Solve each of the following equation by using the method of completing the square:\dfrac {2}{x^{2}}-\dfrac {5}{x}+2=0\dfrac {2}{x^{2}}-\dfrac {5}{x}+2=0

(x + 2)(x + 3) + (x - 3)(x - 2) - 2x(x + 1) = 0(x + 2)(x + 3) + (x - 3)(x - 2) - 2x(x + 1) = 0

Solve each of the following equation by using the method of completing the square:8x^{2}+14x-1=08x^{2}+14x-1=0 ?

Factorise:{x}^{2}-x-12{x}^{2}-x-12

Solve each of the following equation by using the method of completing the square:5x^{2}+6x-2=05x^{2}+6x-2=0 ?

Solve the quadratic equation :4x^2+4bx-(a^2-b^2)=04x^2+4bx-(a^2-b^2)=0

Solve each of the following equation by using the method of completing the square:3x^{2}-2x-1=03x^{2}-2x-1=0

Find the roots of given equation 2y^{2}-y-1=02y^{2}-y-1=0

Solve \sqrt 5 {x^2} + x + \sqrt 5 = 0\sqrt 5 {x^2} + x + \sqrt 5 = 0.

Find the roots of the equations by the method of completing the square.x^{2}+7x-6=0x^{2}+7x-6=0

Solve each of the following equation by using the method of completing the square:x^{2}-(\sqrt {2}+1)x+\sqrt {2}=0x^{2}-(\sqrt {2}+1)x+\sqrt {2}=0

Solve each of the following equation by using the method of completing the square:\sqrt {2}x^{2}-3x-2\sqrt {2}=0\sqrt {2}x^{2}-3x-2\sqrt {2}=0

Solve 2x^2-5x+3=02x^2-5x+3=0.

Solve:2x^2+x+4=02x^2+x+4=0.

If the roots of the equation $(b-c)x^{2}+(c-2)x+(a-b)=0$ are equal, then prove that $2b=a+c$

Is the given equation quadratic? Enter 1 for True and 0 for False.
$n\,-\, 3\, =\, 4n^{2}$

Solve: $\displaystyle 25x^{2}-30x+9=0$

Solve the equation :
$\displaystyle { 27x }^{ 2 }-10x+1=0$

Solve the equation : $\displaystyle { x }^{ 2 }-2x+\frac { 3 }{ 2 } =0$

Solve the equation $\displaystyle \sqrt { 2 } { x }^{ 2 }+x+\sqrt { 2 } =0$

Solve the equation $\displaystyle { 21x }^{ 2 }-28x+10=0$

Solve the equation $\displaystyle { x }^{ 2 }+\frac { x }{ \sqrt { 2 } } +1=0$

Solve the equation $\displaystyle { x }^{ 2 }+3x+5=0$ for $x$ .

Solve the equation $\displaystyle { 2x }^{ 2 }+x+1=0$

Check whether $2x + x^2 + 1 = 0$ a quadratic equations.

Solve the quadratic equation $3{x}^{2}+5x+2=0$ using formula method.

Solve the following quadratic equation by completing square method
$x^2 + 11x + 24 = 0$

$6x^3 + x^2 = 2$ is a quadratic equations

Solve the quadratic equation $2{x}^{2}+5x+3=0$ using formula method.

Decide whether $\cfrac{3}{y}-4=y$ is a quadratic equation or not.

Solve the equation $3y^{2} + 8y + 5 = 0$ by using formula method

Solve the following quadratic equation by using formula method
$3y^2 + 7y + 4 = 0$

If $a = 1, b = 8$ and $c = 15$ , then find the value of $b^2-4ac =$

Solve the following quadratic equation using the formula method:
$4{x}^{2}+7x+2=0$

Solve the following quadratic equation by using the formula method: $m^{2} - 3m - 10 = 0$

The discriminant of the quadratic equation $px^{2} + qx + r = 0$ is ________

Solve $x^2 + 6x - 7 = 0$ by the method of completing the square

Write the discriminant of the equation $ax^2 + bx + c = 0$ .

Decide whether $m^{2} + m + 2 = 4m$ is a quadratic equation

Solve the quadratic equation $2x^{2} + x - 4 = 0$ by completing the square

Solve the quadratic equation $x^{2} - 4x + 2 = 0$ by formula method.

Solve the equation by using the formula:
${m}^{2}-2m=2$

The formula of discriminant of quadratic equation $ax^{2} + bx + c = 0$ is $D =$ ______.

Find the value of $k$ for which the given equations has real and equal roots:
(i) $(k - 12)x^{2} + 2(k - 12)x + 2 = 0$
(ii) $k^{2}x^{2} - 2(k - 1)x + 4 = 0$ .

Solve the equation $a^2x^2-3abx+2b^2=0$ by completing the square.

Check whether the given equation is a quadratic equation or not:
$x(x + 1) + 8 = (x + 2)(x - 2)$

Find the roots of the following quadratic equation (if they exist) by the method of completing the square.
$x^2 \, - \, 4ax \, + \, 4a^2 \, - \, b^2 \, = \, 0$

Show that the roots of the equation $x^2 - 2x + 3 = 0$ are imaginary.

Simplify $\cfrac { \left( { x }^{ 2 }+1 \right) \left( { x }^{ 2 }+2 \right) }{ \left( { x }^{ 2 }+3 \right) \left( { x }^{ 2 }+4 \right) } =$

Find the root of the following quadratic equation (if they exist) by the method of completing the square.
$\sqrt{3}x^2 \, + \, 10x \, + \, 7\sqrt{3} \, = \, 0$

Write standard form of quadratic equation and find the roots of the equations $3x^2+5\sqrt{2}+2=0$ using general formula.

Write the discriminant of the given quadratic equation
${ x }^{ 2 }+px+2q=0\quad$

Solve $4ab=2(a^2-b^2)\sqrt-1$

Find the roots of the following quadratic equation, $2x^2+x-4=0$

Solve the following quadratic equations by the method of perfect the square.
$3x^2-5x+2=0$

If $\alpha$ and $\beta$ are the zeros of $x^{2}+x-2$ then find value of $\dfrac{1}{\alpha}-\dfrac{1}{\beta}$

Solve the following quadratic equations by the method of perfect the square.
$5x^2-6x-2=0$

Solve the following quadratic equations by the method of perfect the square.
$2x^2+x+4=0$

$x^{2}+3\left| x \right| +2=0$ Find the value of $x$ .

Find a quadratic equation with real co-efficient whose one root is $3-2i$ .

Solve the following quadratic equations by the method of perfect the square.
$4x^2+3x+5=0$

Solve
${ x }^{ 2 }+5x-2=0$

Solve ${x}^{2}-3x+12=5$

Factorise : $2\sqrt{2}x^2 + 9x + 5 \sqrt{2}=0$

Check whether the following is quadratic equation.
$(x+1)^2=2(x-3)$

The equation $x^2 + 2(m-1)x + (x + 5) = 0$ has real and equal roots. Find the value of $m$ .

The quadratic equation $ax^2 + bx + c = 0$ , ( $a\ne 0$ ) has atmost _____ roots.

$2\sqrt{5}{x}^{2}-3x-\sqrt{5}=0$ Find $x$ .

Find the values of a : $7{a^2} + 7a - 20=0$

Find the co-ordinates points where the graph of polynomial ${x^2} + x + 12$ intersects the x-axis.

Check whether the following is quadratic equation.
$x^2+3x+1=(x-2)^2$

Solve the following quadratic equation by completing the square method.
$x^2+2\ x-5=0$

Find the nature of the roots of the following quadratic equations. If roots are real, find them.
$5x^{2}-3x+2=0$

Check whether the following is quadratic equation.
$(x+2)^3=2x(x^2-1)$

Check whether the following is quadratic equation.
$x^2-2x=(-2)(3-x)$

Check whether the following in quadratic equation.
$(x-3)(2x+1)=x(x=5)$

Check whether the following is quadratic equation.
$(x-2)(x+1)=(x-1)(x+3)$

Solve the quadratic equation : $4x^2-4ax+(a^2-b^2)=0$

Solve each of the following equation by using the method of completing the square:
$\dfrac {2}{x^{2}}-\dfrac {5}{x}+2=0$

$(x + 2)(x + 3) + (x - 3)(x - 2) - 2x(x + 1) = 0$

Solve each of the following equation by using the method of completing the square:
$8x^{2}+14x-1=0$ ?

Factorise:
${x}^{2}-x-12$

Solve each of the following equation by using the method of completing the square:
$5x^{2}+6x-2=0$ ?

Solve the quadratic equation : $4x^2+4bx-(a^2-b^2)=0$

Solve each of the following equation by using the method of completing the square:
$3x^{2}-2x-1=0$

Find the roots of given equation $2y^{2}-y-1=0$

Solve $\sqrt 5 {x^2} + x + \sqrt 5 = 0$ .

Find the roots of the equations by the method of completing the square.
$x^{2}+7x-6=0$

Solve each of the following equation by using the method of completing the square:
$x^{2}-(\sqrt {2}+1)x+\sqrt {2}=0$

Solve each of the following equation by using the method of completing the square:
$\sqrt {2}x^{2}-3x-2\sqrt {2}=0$

Solve $2x^2-5x+3=0$ .

Solve:
$2x^2+x+4=0$ .

Solve ${x^2} - 4x + 1 = 0$ by completing square method.

Write the equation by the method of completing the square.
$x^{2}+7x-6=0$